16 资产波动率模型特征

金融数据中最关心的除了资产价格、收益率，就是资产波动率。资产波动率度量某项资产的风险，有多种定义。本章：

理解波动率特点；
学习ARCH、GARCH等波动率模型；
学习如何对波动率建模，如何应用波动率模型。

波动率是期权定价和资产分配的关键因素。波动率对计算风险管理中的VaR（风险值）有重要作用。一些波动率指数已经成为金融工具，如CBOE(Chicargo Board of Option Exchange)比值的VIX波动率指数已经从2004-03-26开始成为期货产品。

波动率的数学模型已经提出多种，本章包括：

(R. F. Engle 1982) 的ARCH模型（自回归条件异方差模型）
(Bollerslev 1986) 的GARCH模型（广义自回归条件异方差模型）
(Nelson 1991) 的EGARCH模型（指数GARCH模型）
Glosten等(1993)和Zakoian(1994)提出的TGARCH（门限GARCH模型）
Engle和Ng(1993)以及Duan(1995)提出的NGARCH模型（非对称GARCH）
Melino和Turnbull(1990)、Taylor(1994)、Harvey等(1994)以及Jacquier等(1994) 分别提出的随机波动率(Stochastic Volatility, SV)模型

16.1 波动率的特征

这是原书(Tsay 2013)§4.1内容。

波动率(volatility)指的是资产价格的波动强弱程度，类似于概率论中随机变量标准差的概念。波动率不能直接观测，可以从资产收益率中看出波动率的一些特征。

存在波动率聚集(volatility clustering)
波动率随时间连续变化，一般不出现波动率的跳跃式变动
波动率一般在固定的范围内变化，意味着动态的波动率是平稳的
在资产价格大幅上扬和大幅下跌两种情形下，波动率的反映不同，大幅下跌时波动率一般也更大，这种现象称为杠杆效应（leverage effect）

这些性质对波动率模型的提出、改进有重要意义，许多新的波动率模型都是诊断原有模型不能反映上面的某型特征而提出的。例如， EGARCH模型和TGARCH模型可以反映出波动率在价格上扬和下跌时的不对称性。

不同的波动率计算方法使用不同的数据源。例如，对IBM股票有如下三种数据源：

每个交易日的日收益率；
伴随IBM股票的期权数据
盘中交易和报价的分笔数据；

分别可以计算如下三种不同的波动率：

作为日收益率的条件标准差（或条件方差），建模计算。本章的模型是针对这种波动率定义。
隐含波动率：根据期权的理论公式如BS公式，从股票价格和期权价格数据反解出模型中的波动率，这样的得到的波动率称为隐含波动率。隐含波动率倾向于比用日收益率建模得到的波动率数值要大。 CBOE的VIX指数就是隐含波动率。
实际波动率：利用一天内所有的收益率数据，如每5分钟的收益率，估计一天收益率的方差（波动率平方）。已实现波动率（realized volatility, RV）是这样的波动率。

类似于利率，度量波动率的时间区间一般也取为一年，波动率一般是年化波动率。如果有了日波动率，可以将其乘以\(\sqrt{252}\)转换成年化的波动率。

16.2 波动率模型的结构

这是原书(Tsay 2013)§4.2内容。

波动率是收益率的条件标准差。设\(r_t\)是某种资产在时刻\(t\)的基于某时间单位（如天、月、年）的对数收益率，一般认为\(\{ r_t \}\)序列是前后不相关的，或者是低阶相关的，表现为其ACF基本都在零上下的界限内波动，或者仅前一两个略超出界限。但是，\(\{ r_t \}\)序列一般也不是前后独立的。

以Intel公司股票从1973-1到2009-12的月度对数收益率为例，有444个观测值。读入数据：

d.intel <- read_table(
  "m-intcsp7309.txt",
  col_types=cols(
    .default=col_double(),
    date=col_date("%Y%m%d")
  ))

前20行数据：

knitr::kable(d.intel[1:20,])

date	intc	sp
1973-01-31	0.010050	-0.017111
1973-02-28	-0.139303	-0.037490
1973-03-30	0.069364	-0.001433
1973-04-30	0.086486	-0.040800
1973-05-31	-0.104478	-0.018884
1973-06-29	0.133333	-0.006575
1973-07-31	0.625000	0.037982
1973-08-31	0.117647	-0.036685
1973-09-28	0.234818	0.040096
1973-10-31	0.144262	-0.001291
1973-11-30	-0.240688	-0.113861
1973-12-31	0.188679	0.016569
1974-01-31	0.139683	-0.010046
1974-02-28	0.155989	-0.003624
1974-03-29	-0.163855	-0.023280
1974-04-30	0.162824	-0.039051
1974-05-31	0.148699	-0.033551
1974-06-28	-0.148867	-0.014665
1974-07-31	-0.448669	-0.077791
1974-08-30	-0.151724	-0.090279

将其转换成对数收益率后保存成xts类型，并将日期类型改为yearmon，生成一个ts类型副本:

xts.intel <- xts(
  log(1 + d.intel[["intc"]]), d.intel[["date"]]
)
tclass(xts.intel) <- "yearmon"
ts.intel <- ts(c(coredata(xts.intel)), start=c(1973,1), frequency=12)

作Intel对数收益率的时间序列图：

plot(ts.intel, ylab="log return", 
     main="Intel Stock Price Monthly Log Return")

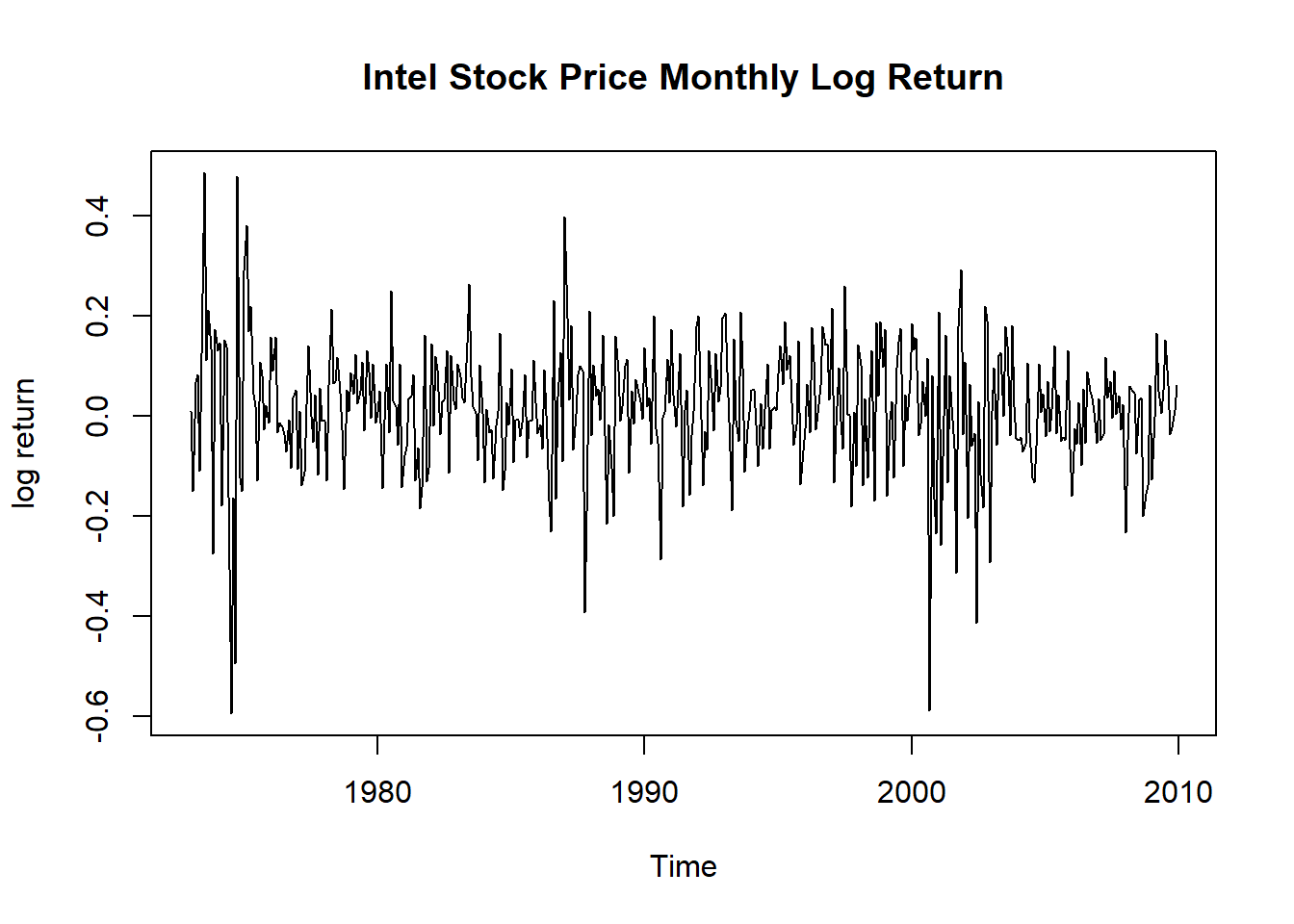
图16.1: Intel对数收益率时间序列

作对数收益率序列的ACF图：

forecast::Acf(ts.intel, main="ACF of log return")

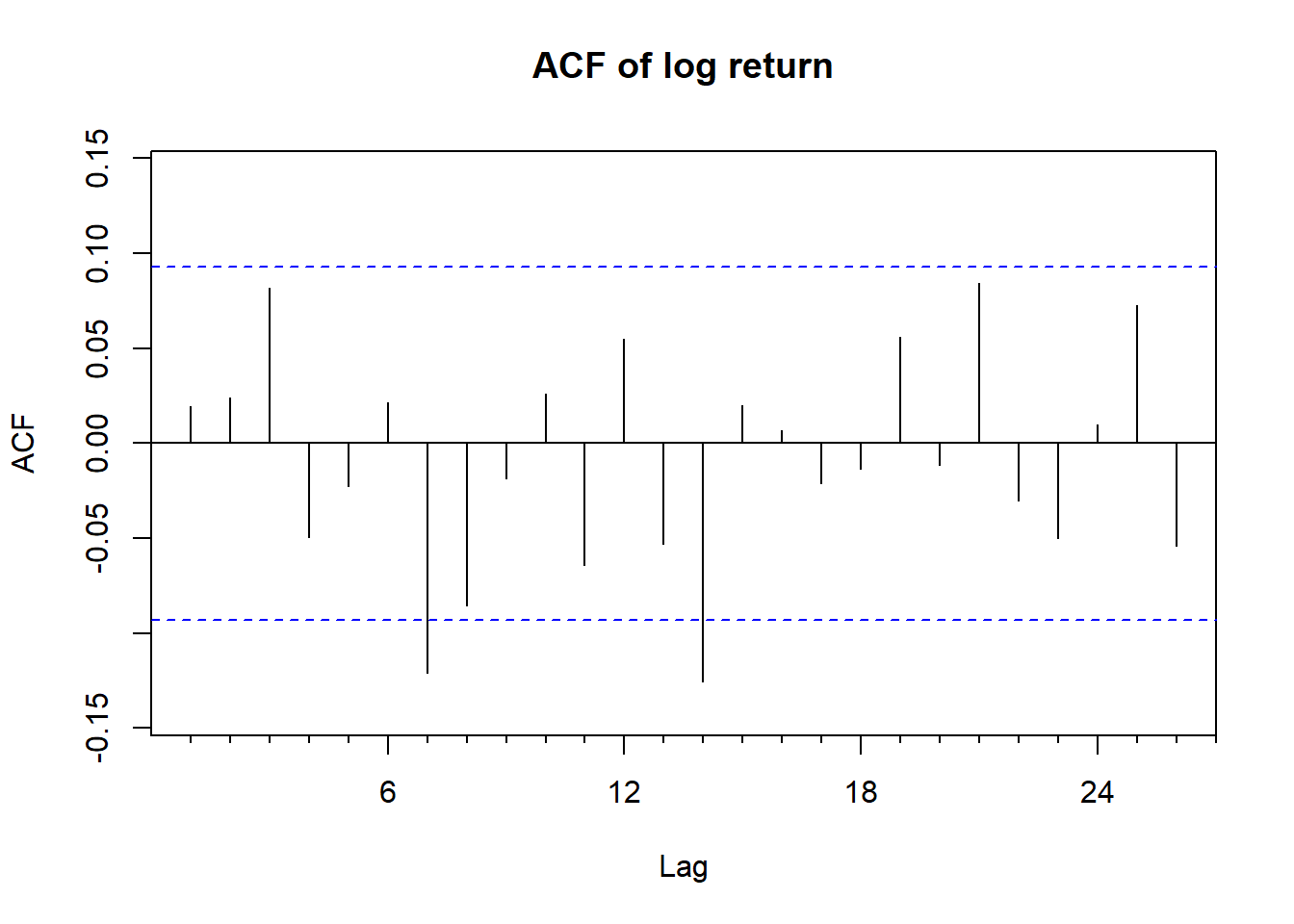
图16.2: Intel对数收益率的ACF估计

从\(\{ r_t \}\)的ACF图来看，除了滞后7和滞后14两个点略微出界，其它的自相关都在零水平线的界限内，可以认为基本是白噪声（这里的白噪声特指零均值、不相关的弱平稳时间序列）。

作Ljung-Box白噪声检验：

Box.test(ts.intel, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  ts.intel
## X-squared = 18.676, df = 12, p-value = 0.09665

在0.05水平下通过了白噪声检验。

可以检验\(\{ r_t \}\)序列的均值是否等于零：

t.test(as.vector(ts.intel))

## 
##  One Sample t-test
## 
## data:  as.vector(ts.intel)
## t = 2.3788, df = 443, p-value = 0.01779
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  0.00249032 0.02616428
## sample estimates:
## mean of x 
## 0.0143273

p值小于0.05，可认为平均收益率显著大于0。

考虑\(\{ | r_t | \}\)序列。作其ACF：

forecast::Acf(abs(ts.intel), 
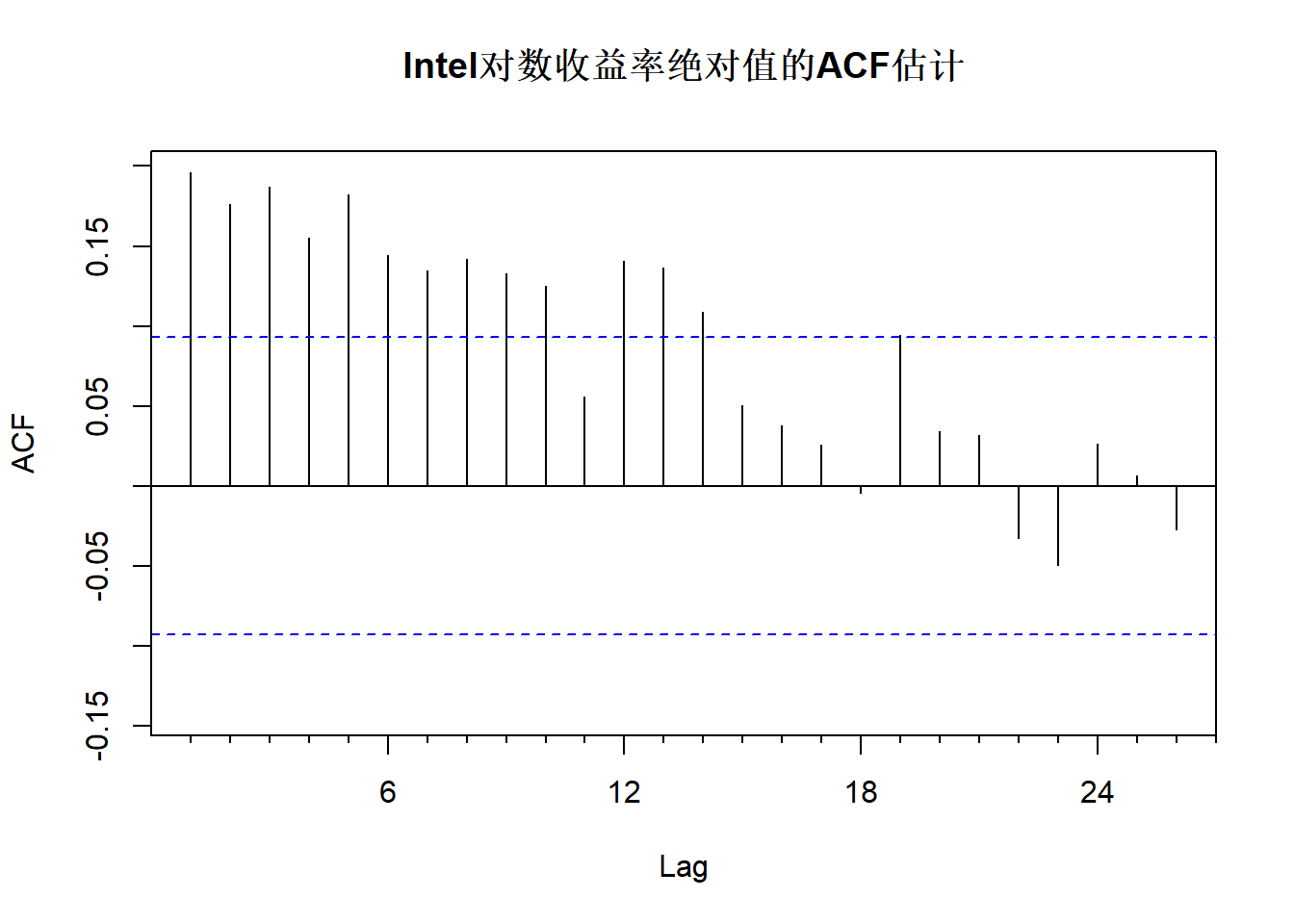
  main="Intel对数收益率绝对值的ACF估计")

图16.3: Intel对数收益率绝对值的ACF估计

可以看出，多个自相关值超出了界限。作Ljung-Box白噪声检验：

Box.test(abs(ts.intel), lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  abs(ts.intel)
## X-squared = 124.91, df = 12, p-value < 2.2e-16

结果显著地拒绝了白噪声零假设。这说明\(\{ r_t \}\)表现为平稳、不相关，但并不前后独立。

作\(\{ r_t^2 \}\)的ACF:

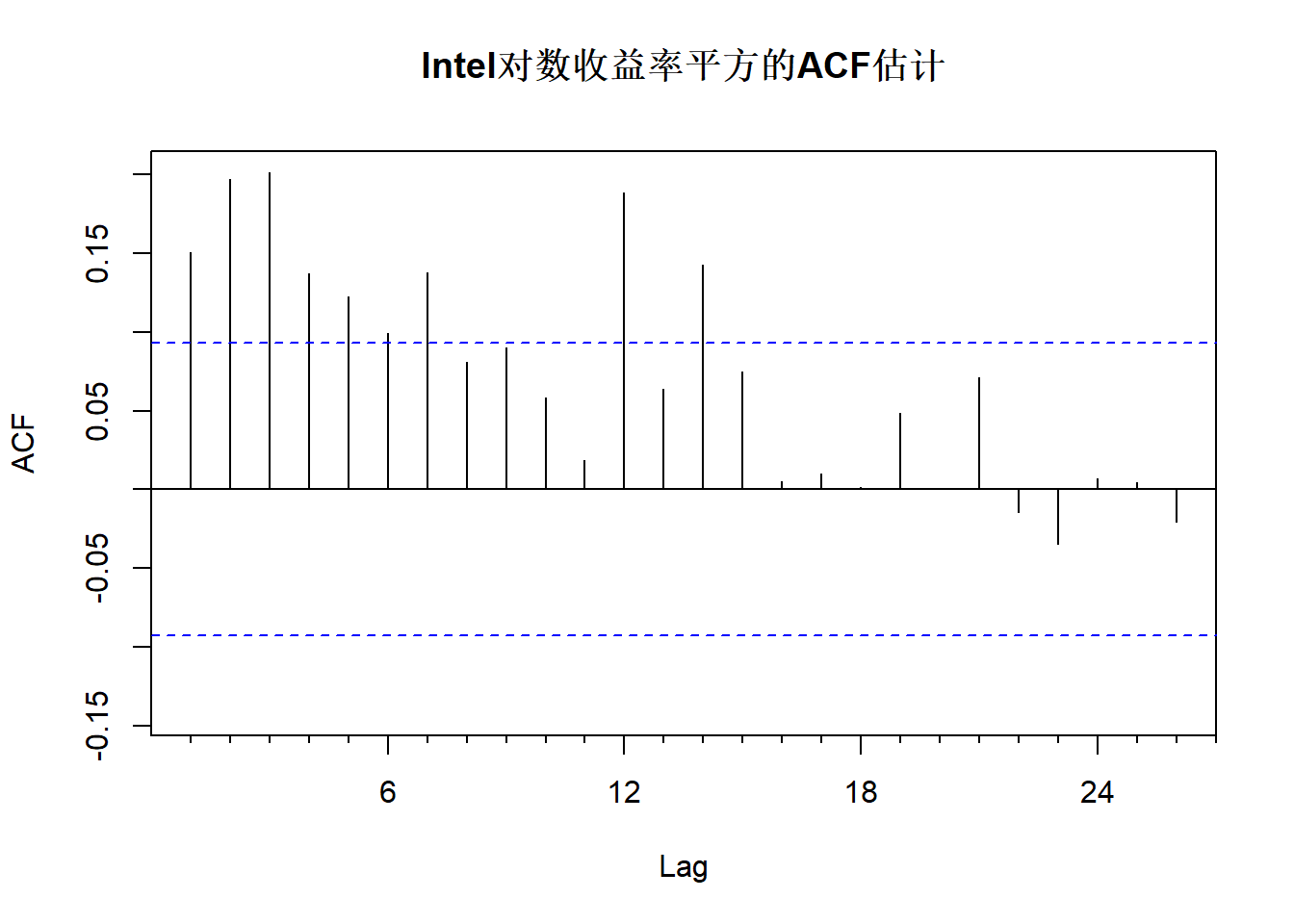
forecast::Acf(ts.intel^2, main="Intel对数收益率平方的ACF估计")

图16.4: Intel对数收益率平方的ACF估计

对\(\{ r_t^2 \}\)序列作Ljung-Box白噪声检验：

Box.test(ts.intel^2, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  ts.intel^2
## X-squared = 98.783, df = 12, p-value = 9.992e-16

\(\{ r_t^2 \}\)的ACF估计和白噪声检验都说明它存在相关性，这说明\(\{ r_t \}\)不是独立序列。

一元波动率模型就是试图刻画收益率这种本身不相关或低阶自相关，但是不独立的性质。用\(F_{t-1}\)表示截止到\(t-1\)时刻的收益率信息，尤其是包括这些收益率的线性组合，考察\(r_t\)在\(F_{t-1}\)条件下的条件均值和条件方差：

\[\begin{align} \mu_t = E(r_t | F_{t-1}), \quad \sigma_t^2 = \text{Var}(r_t | F_{t-1}) = E[(r_t - \mu_t)^2 | F_{t-1}] \tag{16.1} \end{align}\]

通过分析实例的经验可知， (16.1)中\(\{r_t \}\)通常比较简单，如平稳ARMA(\(p,q\))序列。例如，对Intel股票价格对数收益率序列\(\{r_t \}\)，可设\(r_t = \mu_t + a_t\), 其中\(\mu_t = \mu\)为常数， \(a_t\)为不相关的白噪声列。

对一般的对数收益率\(\{r_t \}\)，设其服从ARMA(\(p,q\))模型： \[ r_t = \phi_0 + \sum_{j=1}^p \phi_j r_{t-j} + a_t + \sum_{j=1}^q \theta_j a_{t-j} \] 其中\(\{a_t \}\)为不相关的白噪声列（注意第6章的ARMA定义中要求独立同分布，这里放宽要求）。于是 \[\begin{align} \mu_t = E(r_t | F_{t-1}) = \phi_0 + \sum_{j=1}^p \phi_j r_{t-j} + \sum_{j=1}^q \theta_j a_{t-j} = r_t - a_t \tag{16.2} \end{align}\] 这里我们对白噪声列假定\(a_t = r_t - E(r_t | F_{t-1})\)，称这样的白噪声列\(\{a_t \}\)为平稳列\(\{ r_t \}\)的新息列(innovation)或扰动列。 \(r_t\)可分解为 \[ r_t = \mu_t + a_t . \]

如果可以获得其他的解释变量（外生变量），可以建立模型\(r_t = \mu_t + a_t\)，其中 \[\begin{align} \mu_t = \phi_0 + \sum_{i=1}^k \beta_i x_{i, t-1} + \sum_{j=1}^p \phi_j y_{t-j} + \sum_{j=1}^q \theta_j a_{t-j} \tag{16.3} \end{align}\] 其中\(x_{i,t-1}\)是第\(i\)个解释变量在\(t-1\)时刻的值， \(y_{t-j}\)是剔除解释变量影响后的\(r_{t-j}\)的值。 (16.3)是第10章模型的一个应用。

\(\mu_t\)服从的ARMA(\(p,q\))的阶与数据的采样频率有关，股票指数的日频数据往往有较小的前后相关性，月度数据则可能没有任何显著的前后相关。

模型(16.3)中的自变量比较灵活，例如，可以取日期星期一哑变量为自变量，考察所谓的周末效应。在资产定价模型(Capital Asset Pricing Model, CAPM)中， \(r_t\)的的方程可以写成 \[ r_t = \phi_0 + \beta r_{m,t} + a_t \] 其中\(r_{m,t}\)是市场收益率，一般用综合指数收益率代替。

综合(16.2)和(16.3)，都有 \[\begin{align} \sigma_t^2 = \text{Var}(r_t | F_{t-1}) = \text{Var}(a_t | F_{t-1}) = E(a_t^2 | F_{t-1}) . \end{align}\] 这里的\(\sigma_t\)就是波动率，是收益率的条件标准差。如果假设模型中的白噪声\(\{ a_t \}\)是独立序列，则\(\sigma_t^2 \equiv \sigma^2\)，波动率就没有建模的可能。这里假定\(\{a_t \}\)是零均值不相关平稳列，满足\(E (a_t | F_{t-1}) = 0\)，但不是独立序列。

本章的问题就是对\(\sigma_t^2\)建模，这种模型叫做条件异方差模型。条件异方差模型分为两类：

用确定函数来刻画\(\sigma_t^2\)的变化，ARCH和GARCH模型属于这一类；
用随机方程描述\(\sigma_t^2\)的变化，随机波动率(SV)模型属于这一类。

(16.2)和(16.3)中的\(\mu_t\) 的模型称为\(r_t\)的均值方程， \(\sigma_t^2\)的模型称为\(r_t\)的波动率方程。条件异方差模型就是在原来对\(r_t\)的均值\(\mu_t\)建模的基础上，再增加一个描述资产收益率的条件方差随时间变化的模型。这可以更精确刻画给定\(r_1, r_2, \dots, r_t\)后\(r_{t+1}\)所服从的条件分布。

16.3 波动率模型的建立

这是原书(Tsay 2013)§4.3内容。

对资产收益率序列建立波动率模型需要如下四个步骤：

通过检验序列的自相关性建立均值的方程，必要时还可以引入适当的解释变量；
对均值方程的残差作白噪声检验，通过后，对残差检验ARCH效应；
如果ARCH效应检验结果显著，则指定一个波动率模型，对均值方程和波动率方程进行联合估计；
对得到的模型进行验证，需要时做改进。

关于均值方程，资产收益率一般没有自相关（注意，这并不是独立）或者仅有弱的自相关。如果样本均值显著不等于零，需要从数据中减去样本均值，这称为中心化。对某些日收益率或更高频的序列可能需要建立简单的AR模型。某些情况下可以加入额外的解释变量或者与日期有关的解释变量，比如反映周末的哑变量，反映一月份的哑变量，等等。例如，在Intel股票月对数收益率的均值方程建模时，其均值方程为一个常数。

16.4 ARCH效应的检验

这是原书(Tsay 2013)§4.4内容。

为了检验ARCH效应，先建立均值模型，拟合\(\mu_t\)，计算残差\(a_t = r_t - \mu_t\)。用残差序列的平方\(\{ a_t^2 \}\)作ARCH效应检验。

有两种检验方法。一种是对\(\{ a_t^2 \}\)作Ljung-Box白噪声检验，检验不显著时没有ARCH效应，检验显著时有ARCH效应。

另一种检验方法是(R. F. Engle 1982)提出的。考虑如下的最小二乘问题： \[ a_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2 + e_t, \ t=m+1, \dots, T \] 其中\(T\)为样本量，\(m\)是适当的AR阶数， \(e_t\)为回归残差。零假设为 \[ H_0: \ \alpha_1 = \dots = \alpha_m = 0 \] 拒绝\(H_0\)时有ARCH效应。这称为Engle的拉格朗日乘子法检验。

用普通最小二乘方法估计上述回归问题并计算残差\(\hat e_t\)。令 \[ \text{SSR}_0 = \sum_{t=m+1}^T (a_t^2 - \bar\omega)^2 \] 其中\(\bar\omega = \frac{1}{T} \sum_{t=1}^T a_t^2\)是\(\{a_t^2\}\)的样本均值。令 \[ \text{SSR}_1 = \sum_{t=m+1}^T \hat e_t^2 \] 令 \[ F = \frac{(\text{SSR}_0 - \text{SSR}_1)/m}{\text{SSR}_1/(T-2m-1)} \] 则在\(H_0\)成立时\(F\)近似服从\(F(m, T-2m-1)\)。当\(T\)很大时\(F\)的分母渐近一个常数， \(mF\)近似服从\(\chi^2(m)\)，用\(\chi^2(m)\)分布计算\(F\)的右侧p值进行检验。

执行Engle的ARCH效应检验的函数定义如下：

"archTest" <- function(x, m=10){
  # Perform Lagrange Multiplier Test for ARCH effect of a time series
  # x: time series, residual of mean equation
  # m: selected AR order

  y <- (x - mean(x))^2
  T <- length(x)
  atsq <- y[(m+1):T]
  xmat <- matrix(0, T-m, m)
  for (j in 1:m){
    xmat[,j] <- y[(m+1-j):(T-j)]
  }
  lmres <- lm(atsq ~ xmat)
  summary(lmres)
}

16.4.1 Intel公司股票月对数收益率ARCH效应的检验

下面对Intel公司股票月对数收益率序列检验ARCH效应。因为\(r_t\)的均值方程仅有常数项，令\(a_t = r_t - \bar r\)。先对\(\{ a_t^2 \}\)作Ljung-Box白噪声检验：

Box.test((ts.intel - mean(ts.intel))^2, 
         lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  (ts.intel - mean(ts.intel))^2
## X-squared = 92.939, df = 12, p-value = 1.332e-14

结果高度显著，说明有ARCH效应。

用Engle的拉格朗日乘子法检验ARCH效应：

archTest(ts.intel - mean(ts.intel), m=12)

## 
## Call:
## lm(formula = atsq ~ xmat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.07440 -0.01153 -0.00658  0.00395  0.35255 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.005977   0.002249   2.658 0.008162 ** 
## xmat1        0.093817   0.048147   1.949 0.052013 .  
## xmat2        0.153085   0.048102   3.183 0.001569 ** 
## xmat3        0.146087   0.048614   3.005 0.002815 ** 
## xmat4        0.023539   0.049126   0.479 0.632075    
## xmat5        0.007347   0.049107   0.150 0.881139    
## xmat6        0.010342   0.047027   0.220 0.826050    
## xmat7        0.057183   0.047027   1.216 0.224681    
## xmat8        0.014320   0.047079   0.304 0.761149    
## xmat9        0.007157   0.046968   0.152 0.878965    
## xmat10      -0.019742   0.046566  -0.424 0.671810    
## xmat11      -0.057537   0.046041  -1.250 0.212116    
## xmat12       0.161945   0.045965   3.523 0.000473 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.03365 on 419 degrees of freedom
## Multiple R-squared:  0.1248, Adjusted R-squared:  0.0997 
## F-statistic: 4.978 on 12 and 419 DF,  p-value: 9.742e-08

检验的p值为\(9.7\times 10^{-8}\)，高度显著，说明有ARCH效应。

注意程序中Box.test()输入的是\(a_t^2\)， archTest()输入的是\(a_t\)，没有平方。

16.4.2 美元对欧元汇率日对数收益率ARCH效应的检验

其它金融时间序列也存在ARCH效应。考虑美元对欧元汇率日对数收益率，从1999-01-04到2010-08-20。

读入数据:

d.useu <- read_table(
  "d-useu9910.txt", 
  col_types=cols(.default=col_double())
)
str(d.useu)

## spec_tbl_df [2,930 x 4] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ year: num [1:2930] 1999 1999 1999 1999 1999 ...
##  $ mon : num [1:2930] 1 1 1 1 1 1 1 1 1 1 ...
##  $ day : num [1:2930] 4 5 6 7 8 11 12 13 14 15 ...
##  $ rate: num [1:2930] 1.18 1.18 1.16 1.17 1.16 ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   .default = col_double(),
##   ..   year = col_double(),
##   ..   mon = col_double(),
##   ..   day = col_double(),
##   ..   rate = col_double()
##   .. )

共2930个观测。保存成xts，计算对数收益率：

xts.useu <- with(d.useu, xts(rate, make_date(year, mon, day)))
xts.useu.lnrtn <- diff(log(xts.useu))[-1,]
eu <- c(coredata(xts.useu.lnrtn))

对数收益率的时间序列图：

plot(xts.useu.lnrtn, main="", 
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years",
     format.labels="%Y")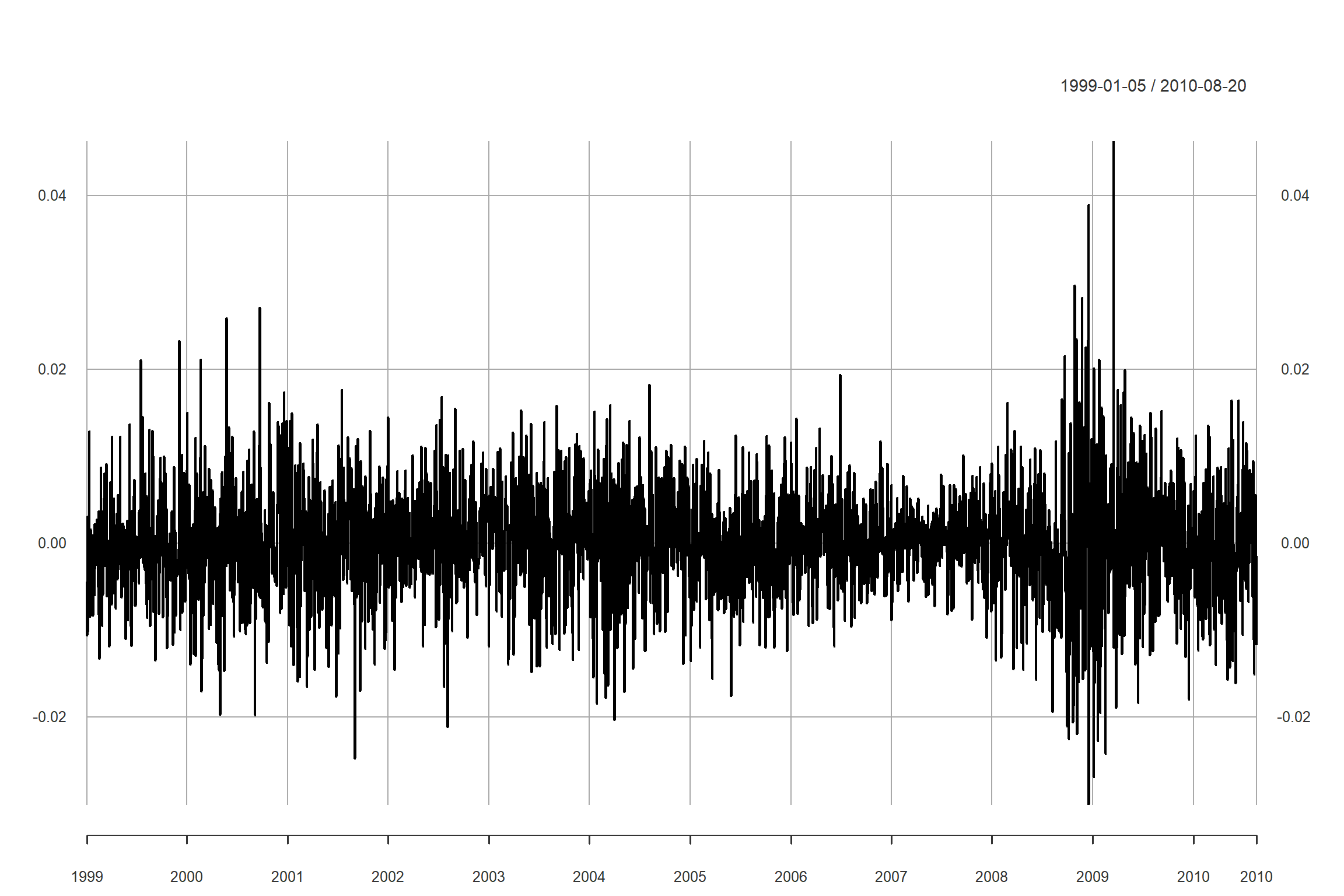

图16.5: 美元对欧元汇率日对数收益率

此序列有波动率聚集现象，在2008年下半年和2009年上半年有较高的波动率。

作ACF图：

forecast::Acf(eu, main="")

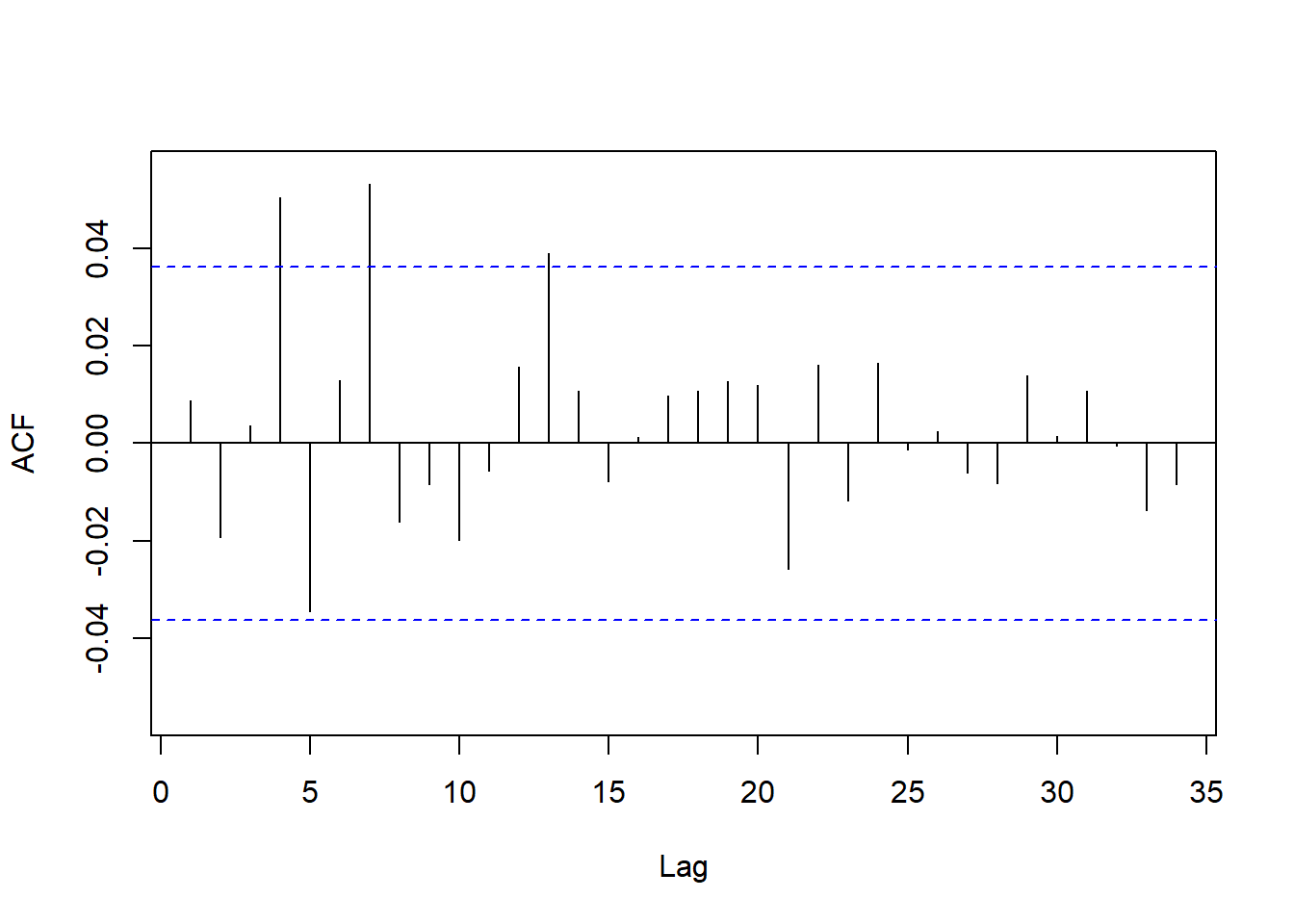
图16.6: 美元对欧元汇率日对数收益率的ACF

基本符合白噪声的ACF表现。

作Ljung-Box白噪声检验：

Box.test(eu, lag=20, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  eu
## X-squared = 30.585, df = 20, p-value = 0.06091

在0.05水平下可以承认对数收益率为白噪声列。

检验对数收益率均值是否等于零：

t.test(eu)

## 
##  One Sample t-test
## 
## data:  eu
## t = 0.20217, df = 2928, p-value = 0.8398
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -0.0002122342  0.0002610303
## sample estimates:
##    mean of x 
## 2.439805e-05

结果说明对数收益率均值为零。所以\(r_t\)的均值方程为\(r_t = a_t\)（\(\mu_t=0\)）。

对\(r_t^2\)作ACF图：

forecast::Acf(eu^2, main="")

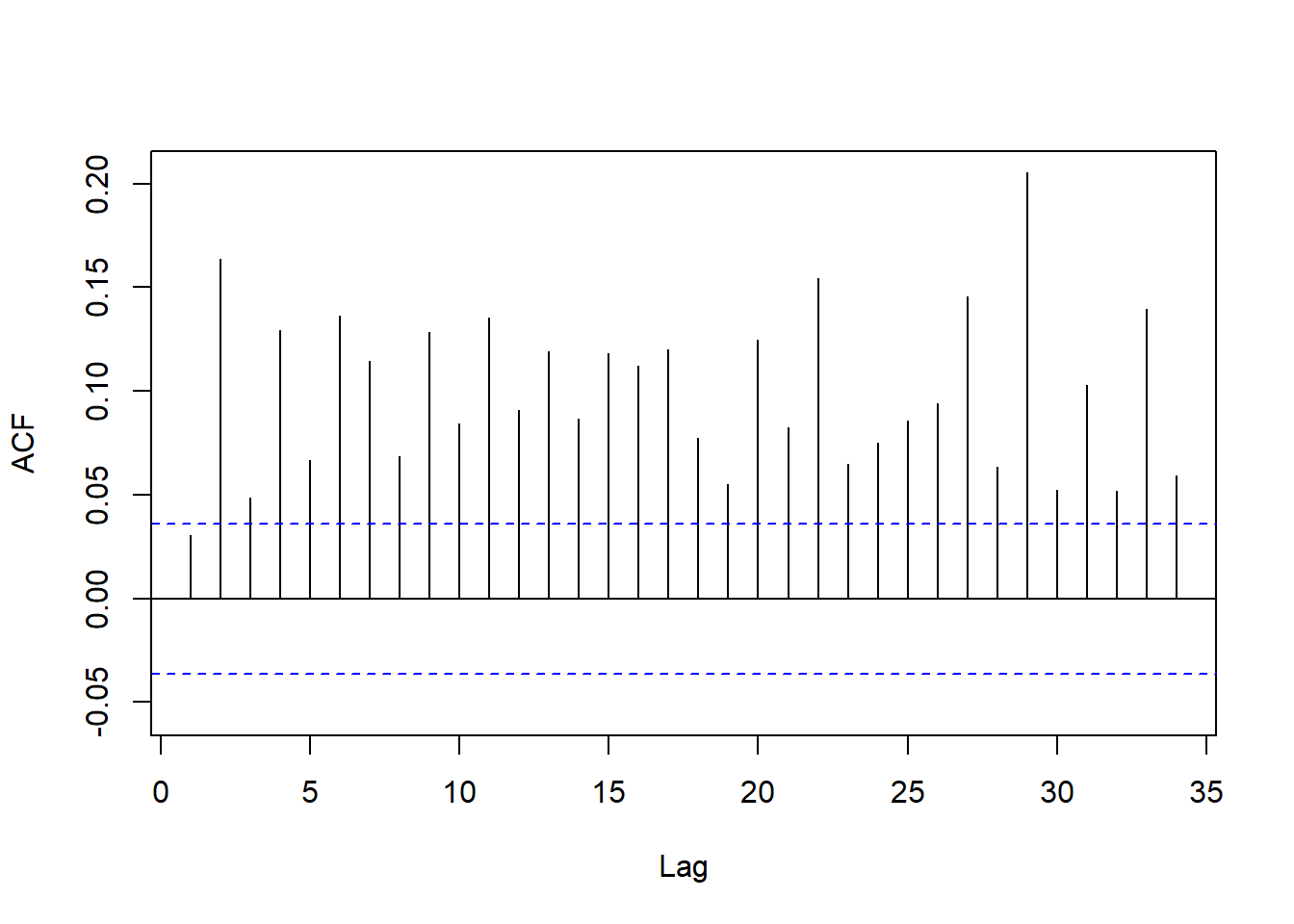
图16.7: 美元对欧元汇率日对数收益率平方的ACF

此ACF明显非白噪声，且不像是低阶MA。

对\(r_t^2\)作PACF图：

pacf(eu^2, main="")

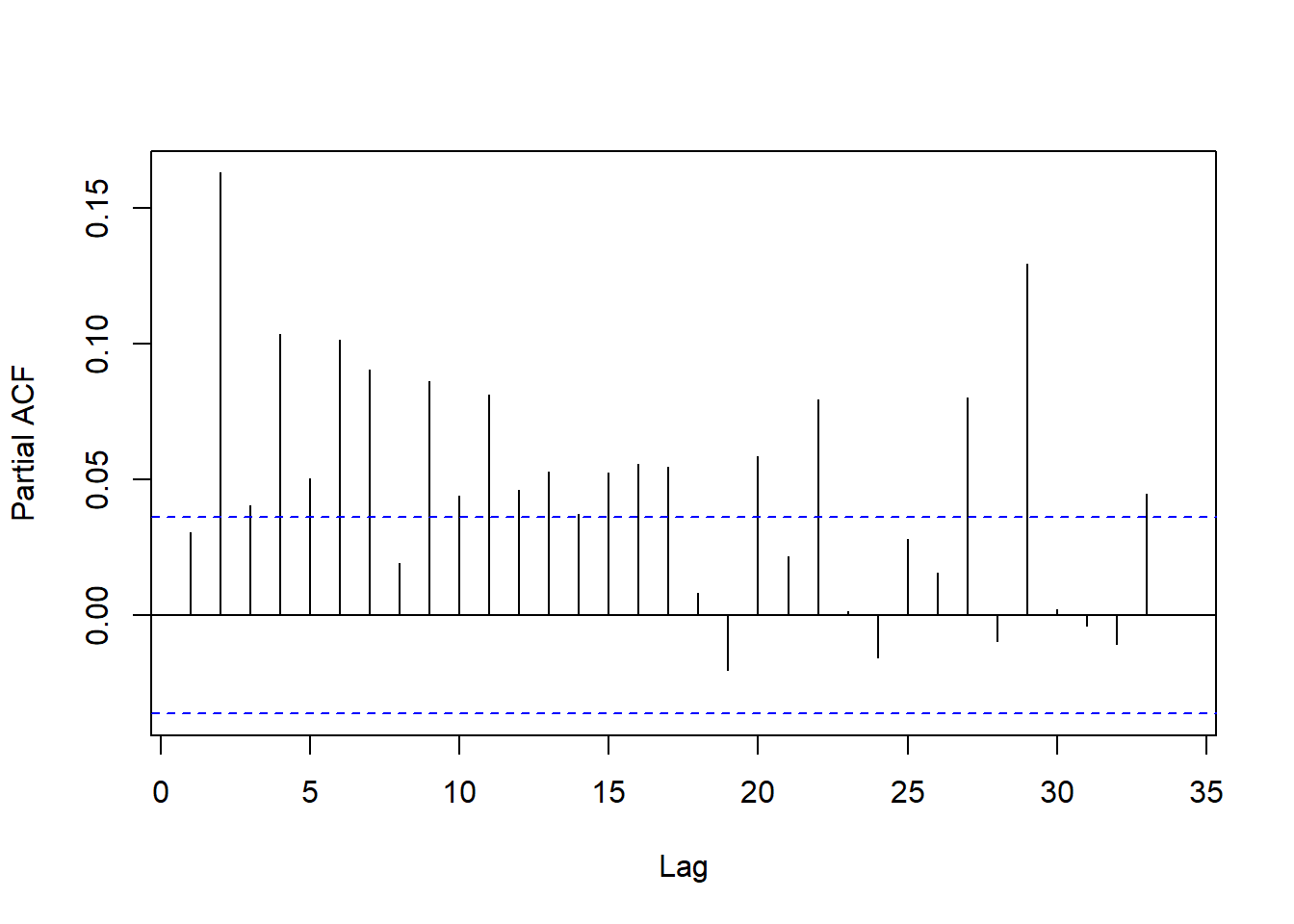
图16.8: 美元对欧元汇率日对数收益率平方的PACF

此PACF表现不像是低阶的AR。

对\(r_t^2\)作Ljung-Box白噪声检验：

Box.test(eu^2, lag=20, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  eu^2
## X-squared = 661.45, df = 20, p-value < 2.2e-16

检验结果拒绝白噪声假设，说明汇率的日对数收益率有ARCH效应。

对\(r_t^2\)序列作Engle的拉格朗日乘子法检验：

archTest(eu, m=20)

## 
## Call:
## lm(formula = atsq ~ xmat)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -3.229e-04 -3.369e-05 -1.949e-05  9.360e-06  2.100e-03 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.281e-05  2.535e-06   5.054 4.60e-07 ***
## xmat1       -3.022e-02  1.858e-02  -1.626 0.103966    
## xmat2        9.441e-02  1.859e-02   5.080 4.02e-07 ***
## xmat3       -1.226e-02  1.867e-02  -0.657 0.511513    
## xmat4        5.309e-02  1.864e-02   2.848 0.004428 ** 
## xmat5        2.668e-03  1.864e-02   0.143 0.886202    
## xmat6        7.200e-02  1.862e-02   3.868 0.000112 ***
## xmat7        5.625e-02  1.866e-02   3.015 0.002594 ** 
## xmat8       -1.599e-03  1.869e-02  -0.086 0.931828    
## xmat9        6.060e-02  1.867e-02   3.245 0.001188 ** 
## xmat10       2.794e-02  1.867e-02   1.497 0.134592    
## xmat11       6.413e-02  1.867e-02   3.435 0.000602 ***
## xmat12       4.020e-02  1.867e-02   2.153 0.031439 *  
## xmat13       4.375e-02  1.869e-02   2.341 0.019299 *  
## xmat14       2.900e-02  1.867e-02   1.553 0.120458    
## xmat15       4.927e-02  1.863e-02   2.645 0.008222 ** 
## xmat16       5.349e-02  1.865e-02   2.868 0.004163 ** 
## xmat17       5.702e-02  1.865e-02   3.058 0.002251 ** 
## xmat18       1.873e-03  1.868e-02   0.100 0.920136    
## xmat19      -1.836e-02  1.859e-02  -0.987 0.323583    
## xmat20       5.844e-02  1.859e-02   3.144 0.001683 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.483e-05 on 2888 degrees of freedom
## Multiple R-squared:  0.09265,    Adjusted R-squared:  0.08636 
## F-statistic: 14.74 on 20 and 2888 DF,  p-value: < 2.2e-16

结果说明有显著的ARCH效应。

B 参考文献

Bollerslev, T. 1986. “Generalized Autoregressive Conditional Heterskedastici.” Journal of Econom. 31: 307–27.

Engle, R. F. 1982. “Autoregressive Conditional Heteroscedasticity with Estmates of the Varinance of United Kingdom Inflation.” Econometrica 50: 987–1007.

Nelson, D. B. 1991. “Conditional Heteroskedasticity in Asset Returns: A New Approach.” Econometrica 59: 347–70.

———. 2013. 金融数据分析导论：基于R语言. 机械工业出版社.