6 ARMA模型
6.1 ARMA模型的概念
AR模型有偏自相关函数截尾性质； MA模型有相关函数截尾性质。 有些因果线性时间序列有与AR和MA类似的表现， 但是不能在低阶实现偏自相关函数截尾或者相关函数截尾。
ARMA模型结合了AR和MA模型， 在对数据拟合优度相近的情况下往往可以得到更简单的模型， 而且不要求偏自相关函数截尾也不要求相关函数截尾。
ARMA(1,1)模型为 \[ X_t = \phi_0 + \phi_1 X_{t-1} + \varepsilon_t + \theta_1 \varepsilon_{t-1} , \] 或 \[ X_t - \phi_1 X_{t-1} = \phi_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1} , \] 其中\(|\phi_1|<1\), \(|\theta_1|<1\), \(-\phi_1 \neq \theta_1\)。 \(\{\varepsilon_t \}\)是独立同分布零均值白噪声列, \(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立。
一般的ARMA(\(p,q\))类似。
AR(\(p\))可以看成ARMA(\(p\), 0), MA(\(q\))可以看成是ARMA(0, \(q\))。
在ARMA(1,1)的系数条件中， \(|\phi_1|<1\)是平稳解条件， \(|\theta_1|<1\)是可逆性条件， \(-\phi_1 \neq \theta_1\)是为了模型不至于退化： 模型也可以写成 \[ (1 - \phi_1 B) X_t = \phi_0 + (1 + \theta_1 B) \varepsilon_t . \] 如果不加这个条件，两边的滞后算子的多项式就可以消去。
6.2 ARMA模型的性质
形式地， \[\begin{aligned} \frac{1}{1 - \phi_1 z} =& \sum_{j=0}^\infty \phi_1^j z^j, \\ \frac{1}{1 - \phi_1 B} =& \sum_{j=0}^\infty \phi_1^j B^j, \\ \frac{1 + \theta_1 z}{1 - \phi_1 z} =& 1 + (\phi_1 + \theta_1) \sum_{j=1}^\infty \phi_1^{j-1} z^j, \\ \frac{1 + \theta_1 B}{1 - \phi_1 B} =& 1 + (\phi_1 + \theta_1) \sum_{j=1}^\infty \phi_1^{j-1} B^j, \end{aligned}\] 于是
\[\begin{align} X_t =& \frac{1}{1 - \phi_1 B} \left\{ \phi_0 + (1 + \theta_1 B) \varepsilon_t \right\} \nonumber\\ =& \frac{\phi_0}{1 - \phi_1} + \frac{1 + \theta_1 B}{1 - \phi_1 B}\varepsilon_t \nonumber\\ =& \frac{\phi_0}{1 - \phi_1} + \varepsilon_t + (\phi_1 + \theta_1) \sum_{j=1}^\infty \phi_1^{j-1} \varepsilon_{t-j} . \tag{6.1} \end{align}\]
这是因果型线性时间序列，是弱平稳的，满足上述ARMA(1,1)模型方程。 \[\begin{aligned} E X_t =& \frac{\phi_0}{1 - \phi_1}, \\ \text{Var}(X_t) =& \sigma^2 \left( 1 + (\phi_1+\theta_1)^2 \sum_{j=1}^\infty (\phi_1^2)^{j-1} \right) = \sigma^2 \frac{1 + \theta_1^2 + 2\phi_1 \theta_1}{1 - \phi_1^2} . \end{aligned}\]
由方差的表达式可知\(|\phi_1|<1\)是平稳性的必要条件。
求自协方差函数和自相关函数。 因为协方差与均值无关， 而\(\phi_0\)只影响到均值， 所以求协方差与自相关函数时可以假定\(\phi_0=0\)。 对
\[\begin{align} X_t - \phi_1 X_{t-1} = \varepsilon_t + \theta_1 \varepsilon_{t-1} , \tag{6.2} \end{align}\]
在(6.2)两边乘以\(X_{t-1}\)并取期望得 \[ \gamma_1 - \phi_1 \gamma_0 = \theta_1 E(\varepsilon_{t-1} X_{t-1}) . \] 由(*)可知\(E(\varepsilon_t X_t) = \sigma^2\), 所以\(E(\varepsilon_{t-1} X_{t-1}) = \sigma^2\) \[ \gamma_1 - \phi_1 \gamma_0 = \sigma^2 \theta_1, \] \[ \gamma_1 = \sigma^2 \frac{(\phi_1 + \theta_1)(1 + \theta_1\phi_1)}{1 - \phi_1^2} . \]
在(6.2)两边乘以\(X_{t-k}\)(\(k\geq 2\))并取期望，得 \[ \gamma_k - \phi_1 \gamma_{k-1} = 0, \quad \gamma_k = \phi_1 \gamma_{k-1} = \phi_1^{k-1} \gamma_1 . \] 所以ARMA(1,1)的自相关函数为 \[ \rho_k = \begin{cases} \dfrac{(\phi_1 + \theta_1)(1 + \phi_1 \theta_1) }{1 + 2\phi_1 \theta_1 + \theta_1^2}, & k=1, \\ \phi_1 \rho_{k-1} = \phi_1^{k-1} \rho_1, & k \geq 2 . \end{cases} \]
所以ARMA(1,1)的ACF与AR(1)的ACF很相似， 但是从\(k=2\)处才开始负指数衰减。 与AR类似， 自相关函数不能有限步截尾。
ARMA(1,1)的偏自相关函数与MA(1)的偏自相关函数类似， 但负指数衰减从\(k=2\)开始， 也不能在有限步截尾。
总之， ARMA(1,1)的平稳性条件与AR(1)相同， 自相关函数与偏自相关函数均不能有限步截尾 (设\(\phi_1\neq 0\), \(\theta_1 \neq 0\))。
6.3 一般ARMA模型
一般ARMA模型为 \[ X_t = \phi_0 + \phi_1 X_{t-1} + \dots + \phi_p X_{t-p} + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q} . \] 其中\(\{ \varepsilon \}\)为独立同分布零均值白噪声列， \(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立。 \(1 - \phi_1 z - \dots - \phi_p z^p\)称为特征多项式， 特征多项式的根都在单位园外，这是平稳性条件。 一般要求\(1 + \theta_1 z + \dots + \theta_q z^q\)的根也都在单位圆外， 这个条件称为可逆性条件。 两个多项式没有公共根， 否则同一模型可能会有不同的表示。
平稳解的均值为 \[ EX_t = \frac{\phi_0}{1 - \phi_1 - \dots - \phi_p} . \]
6.4 ARMA模型辨识
可以逐个从低阶模型尝试， \(p+q\)越小越好， 找到AIC最小的选择， 用精确最大似然或者条件最大似然方法估计参数。 对残差进行白噪声检验以验证模型是否充分。
R的forecast包提供了一个auto.arima()函数，
可以自动进行模型选择。
TSA包提供了一个armasubsets()函数用于模型选择。
Tsay和Tiao(1984)提出了一个对ARMA定阶的辅助工具EACF， 其结果可以用与\((p,q)\)有关的二维表格表示， 结果包含由字母“O”组成的三角形， 锐角顶点在\((p,q)\)位置。如
\[ \begin{array}{*9c} & \text{MA} \\ \text{AR} & 0 & 1 & 2 & 3 & 4 &5 & 6 & 7 \\ \hline 0 & X & X & X & X & X & X & X & X \\ 1 & X & O & O & O & O & O & O & O \\ 2 & * & X & O & O & O & O & O & O \\ 3 & * & * & X & O & O & O & O & O \\ 4 & * & * & * & X & O & O & O & O \\ 5 & * & * & * & * & X & O & O & O \end{array} \]
例6.1 考虑3M公司股票从1946年2月到2008年12月的月对数收益率， 共有755个观测。
d <- read_table(
"m-3m4608.txt",
col_types=cols(.default=col_double(),
date=col_date(format="%Y%m%d")))
mmm <- xts(log(1 + d[["rtn"]]), d$date)
rm(d)
tclass(mmm) <- "yearmon"
ts.3m <- ts(coredata(mmm), start=c(1946,2), frequency=12)
head(ts.3m)## Series 1
## [1,] -0.081125460
## [2,] 0.018421282
## [3,] -0.105360516
## [4,] 0.190518702
## [5,] 0.005114897
## [6,] 0.073743834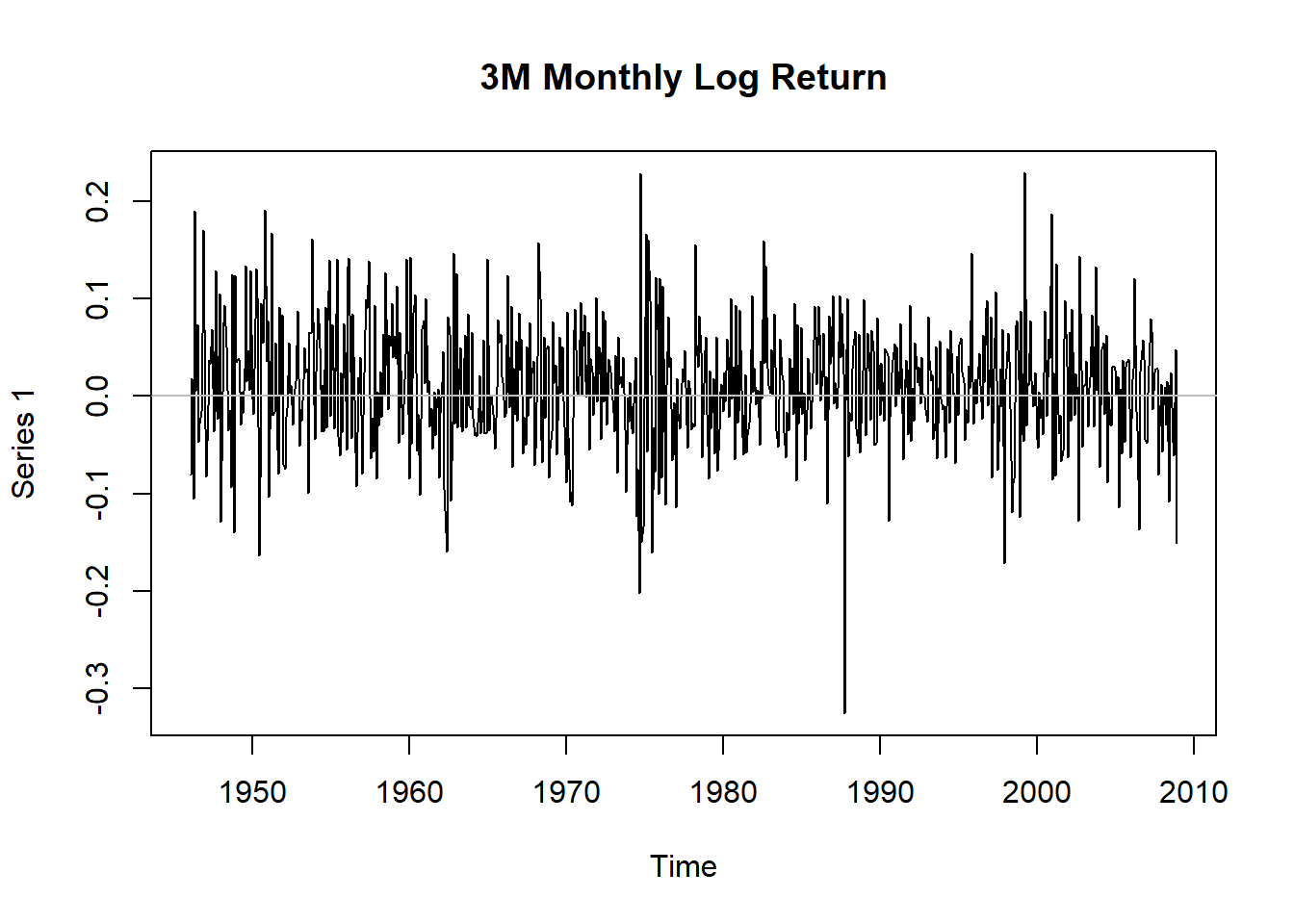
图6.1: 3M公司月对数收益率
ACF图形：
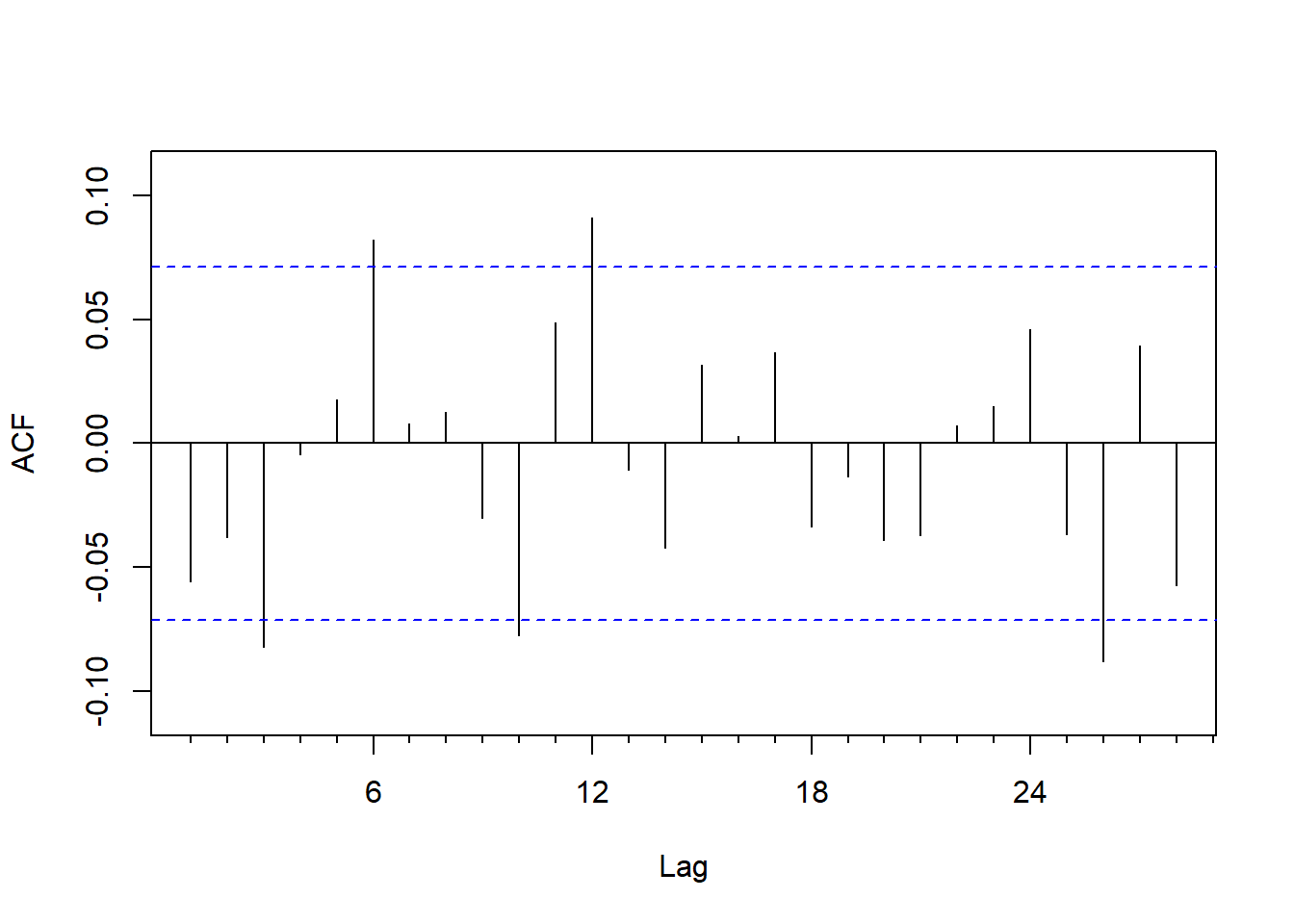
图6.2: 3M公司月对数收益率的ACF
ACF很接近于白噪声。
PACF图形：
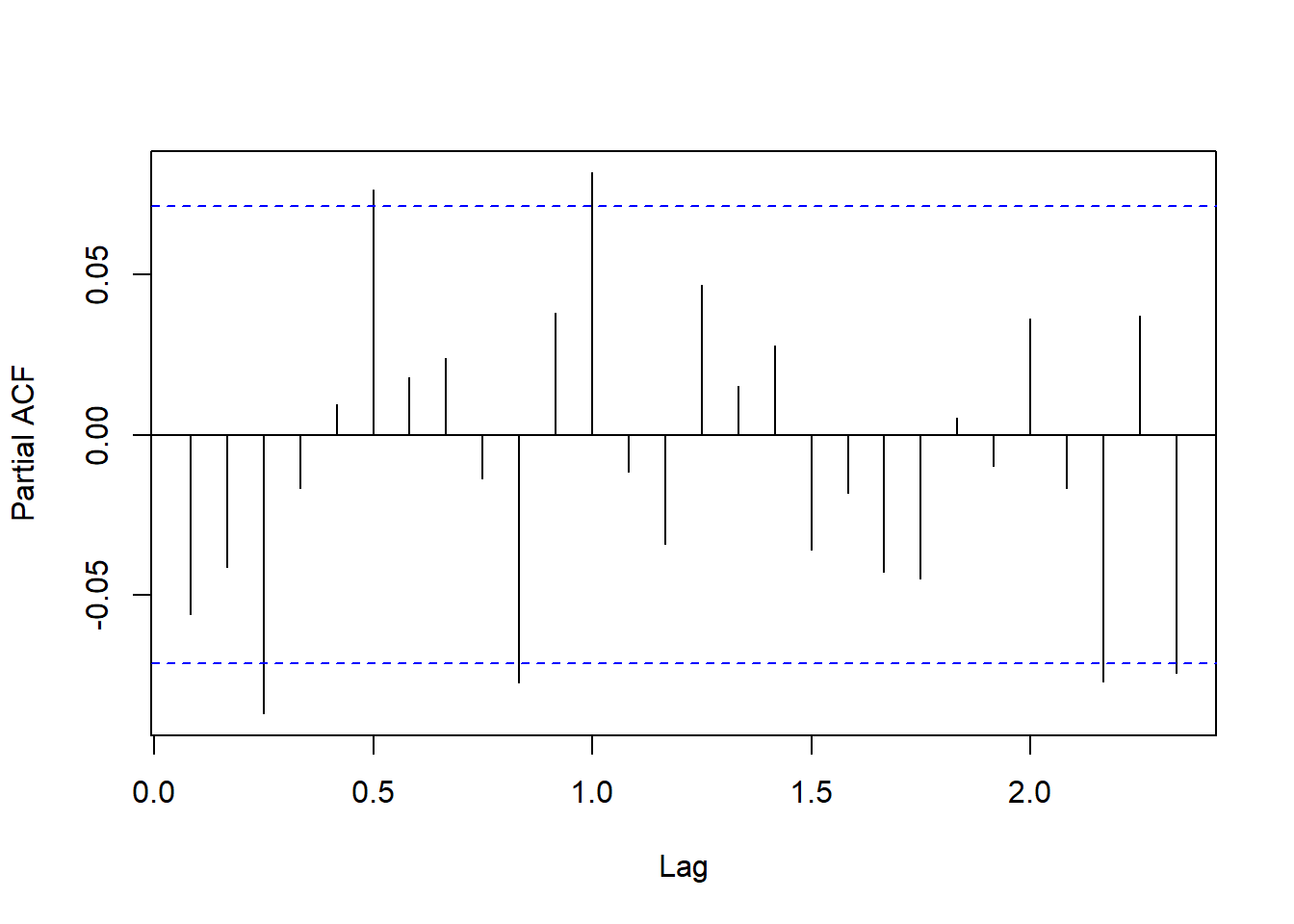
图6.3: 3M公司月对数收益率的PACF
PACF也比较接近于白噪声但是有比较多的超出界限的值， 尽管超出量不大。
用TSA包提供的eacf()函数辨识模型：
## AR/MA
## 0 1 2 3 4 5 6 7 8 9 10 11 12
## 0 o o x o o x o o o x o x o
## 1 x o x o o x o o o o o x o
## 2 x x x o o x o o o o o o o
## 3 x x x o o o o o o o o o o
## 4 x o x o o o o o o o o o o
## 5 x x x o x o o o o o o o o
## 6 x x x x x o o o o o o o o从上面的结果不易选择ARMA阶。 函数的默认检验系数非零的检验水平是0.05水平。 如果用0.01水平， 则选择\(p=q=0\)。
TSA包还提供了armasubsets()函数用来选择ARMA模型阶，
办法是用长阶自回归获得新息\(\varepsilon_t\)的估计，
然后用普通最小二乘估计ARMA系数，
用回归的自变量选择方法进行模型选择。
如：
选项nar和nma分别是AR部分和MA部分最多考虑的阶数，
图形中方格的每一行是一种回归子集选择，
默认采用BIC比较不同模型，
可以用scale选项选择其它比较准则，
结果第一行对应于BIC最优的模型，
从结果看，
是仅有截距项和\(\theta_{12}\)的模型。
用forecasts包的auto.arima()函数定阶：
## Series: ts.3m
## ARIMA(3,0,1)(1,0,1)[12] with non-zero mean
##
## Coefficients:
## ar1 ar2 ar3 ma1 sar1 sma1 mean
## 0.0453 -0.0285 -0.0837 -0.1124 0.5319 -0.4435 0.0103
## s.e. 0.3146 0.0417 0.0387 0.3147 0.2885 0.3049 0.0023
##
## sigma^2 = 0.003998: log likelihood = 1016.63
## AIC=-2017.25 AICc=-2017.06 BIC=-1980.24auto.arima()函数选择了一个季节ARMA模型。
参数max.p, max.q, max.P, max.Q分别指定要考虑的模型各个最大阶数。
使用stats::arima()估计模型：
##
## Call:
## arima(x = ts.3m, order = c(3, 0, 1), seasonal = list(order = c(1, 0, 1), period = 12))
##
## Coefficients:
## ar1 ar2 ar3 ma1 sar1 sma1 intercept
## 0.0453 -0.0285 -0.0837 -0.1124 0.5319 -0.4435 0.0103
## s.e. 0.3146 0.0417 0.0387 0.3147 0.2885 0.3049 0.0023
##
## sigma^2 estimated as 0.003961: log likelihood = 1016.63, aic = -2017.25stats::arima()是使用状态空间模型卡尔曼滤波来进行精确最大似然估计的。
状态空间模型能够自然地处理缺失值问题，
所以我们测试有缺失时的情况：
##
## Call:
## arima(x = ts.3m.miss, order = c(3, 0, 1), seasonal = list(order = c(1, 0, 1),
## period = 12))
##
## Coefficients:
## ar1 ar2 ar3 ma1 sar1 sma1 intercept
## 0.1638 -0.0369 -0.0977 -0.2174 0.7152 -0.6368 0.0107
## s.e. 0.2187 0.0400 0.0407 0.2176 0.2258 0.2481 0.0024
##
## sigma^2 estimated as 0.003841: log likelihood = 960.01, aic = -1904.026.5 ARMA模型预测
ARMA(\(p,q\))的预测与AR和MA的预测都有关系。 对AR部分仍是递推地向前预测， 对MA部分， 需要估计新息\(\varepsilon_t\)的值。
超前一步预测： \[ \hat x_h(1) = \phi_0 + \sum_{j=1}^p \phi_j x_{h+1-j} + \sum_{j=1}^q \theta_j \hat\varepsilon_{h+1-j} . \] 其中\(\hat\varepsilon_i = E(\varepsilon_i | X_1, \dots, X_h)\)。
对超前\(k\)步预测有 \[ \hat x_h(k) = \phi_0 + \sum_{j=1}^p \phi_j \hat x_{h+k-j} + \sum_{j=1}^q \theta_j \hat\varepsilon_{h+k-j} . \] 其中\(h+k-j \leq h\)时\(\hat x_{h+k-j} = x_{h+k-j}\), \(h+k-j>h\)时\(\hat\varepsilon_{h+k-j}=0\)。 预测误差为\(e_h(k) = x_{h+k} - \hat x_{h+k}\)。
6.6 ARMA模型的三种表示
设ARMA(\(p,q\))模型的系数满足平稳性条件与可逆性条件。
第一种表示： \[ (1 - \phi_1 B - \dots - \phi_p B^p) X_t = \phi_0 + (1 + \theta_1 B + \dots + \theta_q B^q) \varepsilon_t . \]
6.6.1 ARMA模型的MA表示
用滞后算子的性质， 令\(P(z) = 1 - \sum_{j=1}^p \phi_p z^j\), \(Q(z) = 1 + \sum_{j=1}^q \theta_q z^j\)， 则 \[ \Psi(z) = \frac{Q(z)}{P(z)} = \sum_{j=0}^\infty \psi_j z^j, \] 其中\(\{ \psi_j \}\)绝对可和（实际上，\(j\to\infty\)时\(c_j\)以负指数速度衰减）。 所以 \[ X_t = \mu + \Psi(B) \varepsilon_t = \mu + \sum_{j=0}^\infty \psi_j \varepsilon_{t-j}, \ t \in \mathbb Z . \] 这称为ARMA模型的MA表示或者Wold表示。 \(\mu=EX_t = \phi_0/P(1) = \phi_0 / (1 - \phi_1 - \dots - \phi_p)\)。 \(\psi_0=1\)。 系数\(\{ \psi_j, j=0,1,\dots \}\)称为ARMA模型的脉冲响应函数或者Wold系数。 \(\psi_j\)是脉冲响应函数的意义是， 如果\(\epsilon_t=1\)， 它将给\(X_{t+j}\)施加一个\(\psi_j\)的增量影响。
\(\psi_j\)随\(j\to+\infty\)以负指数速度衰减， 这样的性质是合理的， 即一个时刻发生的事情的影响应该随历史向前推进而迅速降低。
MA表示对估计多步预测的均方误差有影响。 理论上
\[\begin{align} E(X_{h+k} | \mathscr F_h) = \mu + \sum_{i=0}^\infty \psi_{i+k} \varepsilon_{h-i} . \tag{6.3} \end{align}\]
其中\(\mathscr F_h\)是包含\(\{ X_s, s \leq t \}\)的最小\(\sigma\)代数， 表示到时刻\(h\)为止的观测信息， \(E(\varepsilon_{h+k} | \mathscr F_h)=0\), \(k \geq 1\)。 于是理论的预测误差为 \[ e_h(k)= X_{h+k} - E(X_{h+k} | \mathscr F_h) = \sum_{j=0}^{k-1} \psi_j \varepsilon_{h+k-j} . \] 均方误差为 \[ \text{Var}(e_h(k)) = \sigma^2 \sum_{j=0}^{k-1} \psi_j^2 . \]
因为\(\{ \psi_j \}\)绝对可和， 所以(6.3)中的级数当\(k\to\infty\)时趋于0， 于是长期预测值趋于\(\mu\)， 这称为均值反转。 当\(k\to\infty\)是多步预测的均方误差趋于 \(\sigma^2 \sum_{j=0}^{\infty} \psi_j^2 = \text{Var}(X_t)\)， 即用均值作为预测的均方误差。
6.6.2 ARMA模型的AR表示
当平稳性与可逆性条件都成立时， 令 \[ \pi(z) = \frac{P(z)}{Q(z)}, \] 则 \[ \pi(z) = \sum_{j=0}^\infty \pi_j z^j, \] \(\{ \pi_j \}\)绝对可和， 当\(j\to\infty\)时\(\pi_j\)以负指数速度收敛到0。 \(\pi_0=1\)。 于是ARMA模型有如下的AR表示
\[ \pi(B) X_t = \frac{\phi_0}{Q(1)} + \varepsilon_t . \] 或 \[ X_t = \tilde\phi_0 - \pi_1 X_{t-1} - \pi_2 X_{t-2} - \dots + \varepsilon_t . \] 其中\(\tilde\phi_0 = \phi_0/Q(1) = \phi_0 / (1 + \theta_1 + \dots + \theta_q)\)。 这称为ARMA的AR表示或者长阶自回归形式。 这说明平稳可逆ARMA序列可以用自回归模型近似表示。 \(\pi_j\)称为ARMA模型的\(\pi\)权重。
6.7 附录
文献和历史：
- EVGENIJ EVGENIEVICH SLUTZKY和GEORGE UDNY YULE在19世纪初提出了MA模型和AR模型。
- HERMAN WOLD(1938), A Study in the Analysis of Stationary Time Series, Almquist and Wicksell, Stockholm. 博士论文。 完善了线性时间序列模型。
- GEORGE E.P. BOX and GWILYM M. JENKINS(1970), Time Series Analysis: Forecasting and Control, Holden Day, San Francisco et al.; 2nd enlarged edition 1976. 本书给出了应用线性时间序列模型的理论与方法。
- 下面的文献提出， 一元时间序列模型短期预测常常优于大量经济变量的联立方程的预测： CLIVE W.J. GRANGER and PAUL NEWBOLD(1975), Economic Forecasting: The Atheist’s Viewpoint, in: G.A. RENTON (ed.), Modelling the Economy, Heinemann, London pp. 131 – 148.