30 局部水平模型
状态空间模型是时间序列分析领域中一类强大、灵活、多样的模型, 配合卡尔曼滤波技术,可以涵盖ARIMA模型、许多非平稳的、带有外生变量的模型, 比前面所述的线性时间序列模型更为灵活。 R扩展包statespacer实现了许多基于线性高斯状态空间模型的模型, 并且可以自定义模型。
参考:
作为入门, 先介绍一个局部水平模型。 这个模型很简单, 所以可以用来演示状态空间模型的表示和估计。
30.1 模型
设\(\{ y_t, t=1,2,\dots,T\}\)为时间序列, 满足如下模型 \[\begin{align} y_t =& \mu_t + e_t, \ \{e_t\} \sim \text{iid N}(0, \sigma_e^2), \ t=1,2,\dots,n, \tag{30.1}\\ \mu_{t+1} =& \mu_t + \eta_t, \ \{\eta_t\} \sim \text{iid N}(0, \sigma_{\eta}^2), \tag{30.2} \end{align}\] 其中\(\{e_t\}\)与\(\{\eta_t\}\)相互独立, 初始值\(\mu_1\)为给定值或者是服从正态分布的随机变量, 且与\(\{e_t, \eta_t, t>0\}\)相互独立。 称\(\{\mu_t\}\)为\(\{y_t\}\)的水平, 模型中\(\{y_t\}\)可观测而\(\{\mu_t\}\)不可观测。
方程(30.1)-(30.2)是线性高斯状态空间模型的一个特例。 \(\{\mu_t\}\)代表系统在\(t\)时刻所处的状态, 不可观测,方程(30.2)称为状态方程, 描述了系统的内在演变规律; \(\{y_t\}\)代表系统在\(t\)时刻的观测值或输出值, (30.1)称为观测方程, \(\{e_t\}\)是观测误差, 仅影响到\(t\)时刻, 是一个瞬态的误差或噪声。
这个模型称为局部水平模型, 也是“结构时间序列模型”的一个特例。
对于实际数据, 需要估计其中的参数\(\sigma_e^2\)和\(\sigma_\eta^2\)。 设\(\alpha_1 \sim \text{N}(a_1, P_1)\), 易见\(\boldsymbol y = (y_1, \dots, y_T)^T\)服从多元正态分布\(\text{N}(\boldsymbol\alpha, \Omega)\), 其中\(\boldsymbol\alpha\)和\(\Omega\)是\(\sigma_e^2\)和\(\sigma_\eta^2\)的函数。 可以写出其似然函数 \[ (2\pi)^{-T/2} |\Omega|^{-1/2} \exp(-\frac{1}{2} (\boldsymbol y - \boldsymbol\alpha)^T \Omega^{-1} (\boldsymbol y - \boldsymbol\alpha)) . \] 当\(T\)较大时计算似然函数涉及到\(T \times T\)矩阵\(\Omega\)的求逆, 计算量较大而且容易发生数值不稳定。 利用这一章讲的Kalman滤波算法可以将普通方阵的求逆问题, 转换成对角阵的求逆问题, 简化了似然函数计算而且数值稳定性得到保障。
如果参数\(\sigma_e^2\)和\(\sigma_\eta^2\)已知, 在给定\(\boldsymbol y\)后可以进行预测, 或者对局部水平\(\mu_t\)进行推断。
例30.1 考虑Alcoa股票日现实波动率数据, 时间期间为2003-01-02到2004-05-07, 共340个观测。 日现实波动率是用交易日内每隔10分钟的对数收益率的平方和计算的。
da <- read_table("aa-3rv.txt",
col_names = FALSE,
show_col_types = FALSE)
ts.alcoa <- ts(log(da[[2]]))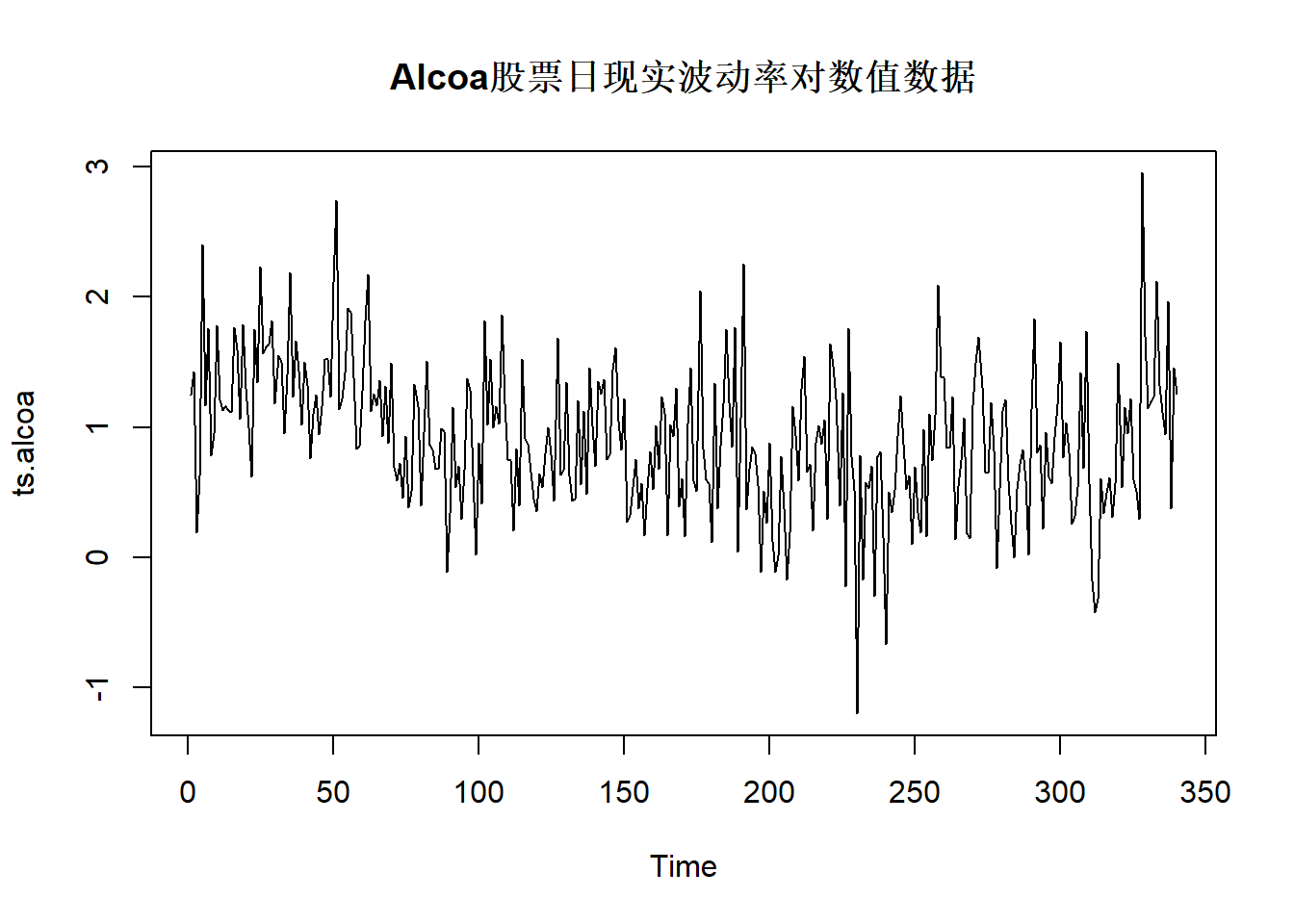
可以用局部水平模型获得\(\{\mu_t\}\), 作为去噪声的波动率估计。
30.2 局部水平模型与ARIMA模型的关系
注意到 \[ y_t - y_{t-1} = \eta_{t-1} + e_t - e_{t-1}, \] 记\(\xi_t = \eta_{t-1} + e_t - e_{t-1}\), 易见\(\xi_t\)的自相关函数在1以后截尾, 所以\(\xi_t\)服从一个MA(1)模型。 由多元正态分布的性质可知存在\(\{a_t \} \sim \text{N}(0, \sigma_a^2)\)和\(|\theta|\leq 1\)使得 \[ y_t - y_{t-1} = a_t + \theta a_{t-1}, \] 从而\(y_t\)服从一个高斯的ARIMA(0,1,1)模型。
由 \[\begin{aligned} \text{Var}(\xi_t) =& 2 \sigma_e^2 + \sigma_{\eta}^2 = \sigma_a^2 (1 + \theta^2), \\ \text{Cov}(\xi_t, \xi_{t-1}) =& -\sigma_e^2 = \theta \sigma_a^2, \end{aligned}\] 可以求解出\(\theta\)且使得\(-1 < \theta < 0\): \[\begin{aligned} \theta = \frac{b + \sqrt{b^2 + 4}}{2}, \text{ 其中 } b = -2 - \frac{\sigma_{\eta}^2}{\sigma_e^2} < -2 . \end{aligned}\]
反过来,如果\(y_t\)服从一个ARIMA(0,1,1)模型且\(\theta\)为负值, 则可以将其写成(30.1)-(30.2)的形式。 如果\(\theta\)为正值, 可以写成\(\sigma_e=0\)的形式。
例30.2 对Alcoa股票日现实波动率对数值数据用ARIMA建模。
##
## Call:
## arima(x = ts.alcoa, order = c(0, 1, 1))
##
## Coefficients:
## ma1
## -0.8582
## s.e. 0.0397
##
## sigma^2 estimated as 0.2688: log likelihood = -258.98, aic = 521.95得到的ARIMA(0,1,1)模型为: \[\begin{aligned} (1-B) y_t = (1 - 0.8582 B) a_t, \ a_t \sim \text{WN}(0, 0.2688) . \end{aligned}\]
通过\(\sigma_e^2\), \(\sigma_{\eta}^2\)与\(\theta\), \(\sigma_a^2\)的关系, 可以解出 \[ \sigma_e^2 = -\theta \sigma_a^2 = 0.2307, \quad \sigma_{\eta}^2 = \sigma_a^2(1 + \theta^2) - 2\sigma_e^2 =0.0054 \]
可见噪声严重超过了信号的扰动。
下面用R的statespacer扩展包估计局部水平模型。
library(statespacer)
ssr1 <- statespacer(
y = cbind(as.vector(ts.alcoa)),
local_level_ind = TRUE,
initial = rep(0.5*log(var(ts.alcoa)), 2),
verbose = TRUE)## Starting the optimisation procedure at: 2024-05-21 15:26:28## initial value 1.022439
## iter 10 value 0.765458
## iter 20 value 0.764395
## final value 0.764395
## converged## Finished the optimisation procedure at: 2024-05-21 15:26:28## Time difference of 0.0222549438476562 secs上面的程序中输入数据需要是矩阵形式,
每列为一个时间序列分量,
一元时间序列也需要输入为仅有一列的矩阵。
选项local_level_ind = TRUE表示有局部水平成分。
initial给出超参数初值选取,
为了保证\(\sigma_e^2\)和\(\sigma_{\eta}^2\)估计为正数,
模型中使用了其对数值作为参数,
所以初值取了对数。
查看估计的\(\sigma_e^2\)和\(\sigma_{\eta}^2\):
## sigmasqr_e sigmasqr_level
## 0.230623632 0.005404681与从ARIMA模型换算的结果基本相同。
statespacer利用了(Durbin and Koopman 2012)的模型和记号,
\(H\)表示观测方程误差项方差阵,
\(Q\)表示系统方程误差项方差阵。
设statespacer()的输出为ssr,
这是一个列表,
其中ssr$system_matrices$H$H是观测方程的方差阵估计,
这里即\(\sigma_e^2\),
但保存成\(1 \times 1\)矩阵;
ssr$system_matrices$Q是与系统方程方差阵有关的输出,
而局部水平的状态方程对应的误差项的方差阵则为ssr$system_matrices$Q$level,
这里就是\(\sigma_{\eta}^2\),
保存成\(1 \times 1\)矩阵。
30.3 滤波、平滑和预报
对状态空间模型如(30.1)-(30.2), 输入数据\(\{y_t, t=1,2,\dots, n \}\), 如果认为模型中参数(这里是\(\sigma_e^2\)和\(\sigma_\eta^2\))已知, 经常讨论如下的统计推断问题:
- 滤波:计算给定\(\{y_1, \dots, y_t \}\)时\(\mu_t\)的条件分布;
- 平滑:计算给定\(\{y_1, \dots, y_n \}\)时\(\{\mu_1, \mu_2, \dots, \mu_n \}\)的条件分布;
- 预报:计算给定\(\{y_1, \dots, y_t \}\)时\(\mu_{t+h}\)或\(y_{t+h}\)(\(h>0\))的条件分布。
设\(\mu_1 \sim \text{N}(a_1, P_1)\), 且与扰动序列独立。 由正态分布的性质, 状态空间模型(30.1)-(30.2)是高斯过程, 其条件分布仍为高斯分布, 只要给出条件期望和条件方差(联合分布还需要条件协方差)。 条件期望为最小均方误差估计, 也是最小方差线性无偏估计。
当参数已知, 记\(y_{1:t} = (y_1, \dots, y_t)\), 易见:
- 滤波需要计算\(E(\mu_t | y_{1:t})\)和\(\text{Var}(\mu_t | y_{1:t})\);
- 平滑需要计算\(E(\mu_t | y_{1:n})\)和\(\text{Var}(\mu_t | y_{1:n})\), 对于联合分布还需要计算\(\text{Cov}(\mu_t, \mu_s | y_{1:n})\);
- 预报需要计算\(E(\mu_{t+h} | y_{1:t})\)和\(\text{Var}(\mu_{t+h} | y_{1:t})\), 或\(E(y_{t+h} | y_{1:t})\)和\(\text{Var}(y_{t+h} | y_{1:t})\)。
\(\mu_t\)在\(y_{1:s}\)下的条件分布完全由条件期望和条件方差决定。 记\(\mu_{t|s} = E(\mu_t | y_{1:s})\), 记\(\Sigma_{t|s} = \text{Var}(\mu_t | y_{1:s})\)。 记\(y_{t|s} = E(y_t | y_{1:s})\)。 特别地, 记\(a_t = E(\mu_t | y_{1:t-1})\), \(P_t = \text{Var}(\mu_t | y_{1:t-1})\)。 由高斯分布性质, 条件方差都是非随机的。
记 \[ v_t = y_t - E(y_t | y_{1:t-1}), \] 这是对\(y_t\)做最优一步预报时的误差, 显然\(E v_t = 0\), 令 \[ F_t = E v_t^2 = \text{Var}(v_t), \] 由多元正态分布性质, \(v_t\)与\(y_{1:t-1}\)独立, 所以也有 \[\begin{aligned} F_t =& \text{Var}(v_t) = E(v_t^2) = E(v_t^2 | y_{1:t-1}) \\ =& E[ (y_t - E(y_t | y_{1:t-1}))^2 | y_{1:t-1}] \\ =& \text{Var}(y_t | y_{1:t-1}) . \end{aligned}\]
于是由观测方程可得 \[\begin{align} y_{t|t-1} =& E(y_t | y_{1:t-1}) = E(\mu_t + e_t | y_{1:t-1}) = \mu_{t|t-1} = a_t, \\ v_t =& y_t - y_{t|t-1} = y_t - a_t, \tag{30.3} \\ F_t =& \text{Var}(y_t - y_{t|t-1} | y_{1:t-1}) = \text{Var}(\mu_t + e_t - \mu_{t|t-1} | y_{1:t-1}) \\ =& \text{Var}(\mu_t - \mu_{t|t-1} | y_{1:t-1}) + \text{Var}(e_t | y_{1:t-1}) \\ =& \Sigma_{t|t-1} + \sigma_e^2 = P_{t} + \sigma_e^2 . \tag{30.4} \end{align}\]
由多元正态分布性质可知预报误差\(v_t\)与\(y_{1:s}\)(\(s<t\))独立, 所以 \[ \text{Cov}(v_t, y_s) = 0, \ t > s . \] 从而\(\{v_t, t=1,2, \dots, n \}\)相互独立。 由多元正态性质, \[ \sigma(y_1, \dots, y_{t-1}, y_t ) = \sigma(y_{1:t-1}, v_t ) . \] 其中\(\sigma(\cdot)\)表示由其中的随机变量所生成的最小\(\sigma\)代数。
对随机向量\(\boldsymbol X, \boldsymbol Y\), 记\(\boldsymbol\mu_{\boldsymbol X} = E \boldsymbol X\), \(\Sigma_{\boldsymbol X \boldsymbol X} = \text{Var}(\boldsymbol X)\), \(\Sigma_{\boldsymbol X \boldsymbol Y} = \text{Cov}(\boldsymbol X, \boldsymbol Y)\)。 从多元正态分布性质有如下定理(Tsay 2010) P.562:
定理30.1 设随机向量\(\boldsymbol X\), \(\boldsymbol Y\), \(\boldsymbol Z\)的联合分布为多元正态分布, \(\Sigma_{XX}\)和\(\Sigma_{ZZ}\)非退化, \(\Sigma_{\boldsymbol X \boldsymbol Z} = \boldsymbol 0\)。 则有如下性质: \[\begin{aligned} (1)\ & E(\boldsymbol Y | \boldsymbol X) = \boldsymbol\mu_Y + \Sigma_{\boldsymbol Y \boldsymbol X} \Sigma_{\boldsymbol X \boldsymbol X}^{-1} (\boldsymbol X - \boldsymbol\mu_{\boldsymbol X}) ; \\ (2)\ & \text{Var}(\boldsymbol Y | \boldsymbol X) = \Sigma_{\boldsymbol Y \boldsymbol Y} - \Sigma_{\boldsymbol Y \boldsymbol X} \Sigma_{\boldsymbol X \boldsymbol X}^{-1} \Sigma_{\boldsymbol X \boldsymbol Y} ; \\ (3)\ & E(\boldsymbol Y | \boldsymbol X, \boldsymbol Z) = E(\boldsymbol Y | \boldsymbol X) + E(\boldsymbol Y - \boldsymbol\mu_{\boldsymbol Y} | \boldsymbol Z) \\ & \qquad\qquad\quad = E(\boldsymbol Y | \boldsymbol X) + \Sigma_{\boldsymbol Y \boldsymbol Z} \Sigma_{\boldsymbol Z \boldsymbol Z}^{-1} (\boldsymbol Z - \boldsymbol\mu_{\boldsymbol Z}); \\ (4)\ & \text{Var}(\boldsymbol Y | \boldsymbol X, \boldsymbol Z) = \text{Var}(\boldsymbol Y | \boldsymbol X) - \Sigma_{\boldsymbol Y \boldsymbol Z} \Sigma_{\boldsymbol Z \boldsymbol Z}^{-1} \Sigma_{\boldsymbol Z \boldsymbol Y} \\ & \qquad\qquad\quad\ \ = \Sigma_{\boldsymbol Y \boldsymbol Y} - \Sigma_{\boldsymbol Y \boldsymbol X} \Sigma_{\boldsymbol X \boldsymbol X}^{-1} \Sigma_{\boldsymbol X \boldsymbol Y} - \Sigma_{\boldsymbol Y \boldsymbol Z} \Sigma_{\boldsymbol Z \boldsymbol Z}^{-1} \Sigma_{\boldsymbol Z \boldsymbol Y} . \end{aligned}\] 另外, \(\boldsymbol Y - E(\boldsymbol Y | \boldsymbol X)\)与\(\boldsymbol X\)独立,所以 \[ \text{Var}(\boldsymbol Y | \boldsymbol X) = E \left[ (\boldsymbol Y - E(\boldsymbol Y | \boldsymbol X))^2 | \boldsymbol X \right] = E \left[ (\boldsymbol Y - E(\boldsymbol Y | \boldsymbol X))^2 \right], \] 等于\(\boldsymbol X\)对\(\boldsymbol Y\)的最优估计的均方误差。
推论30.1 设\((X, Y)\)服从二元正态分布, \(X \sim \text{N}(\mu_X, \sigma_X^2)\), \(Y \sim \text{N}(\mu_Y, \sigma_Y^2)\), \(\text{corr}(X, Y) = \rho\)。 则\(Y | X=x\)服从正态分布 \[ N\left( \mu_Y + \rho\frac{\sigma_Y}{\sigma_X} (x - \mu_X), \quad (1-\rho^2) \sigma_Y^2 \right), \] 令 \[ Z = Y - E(Y | X) = Y - \mu_Y - \rho\frac{\sigma_Y}{\sigma_X} (X - \mu_X), \] 则\(Z\)与\(X\)相互独立, 且 \[ Z \sim \text{N}(0, \ (1-\rho^2) \sigma_Y^2 ) . \]
30.4 卡尔曼滤波
卡尔曼滤波是一种递推算法, 对\(t=1,2,\dots\), 基于\(\mu_t | y_{1:t-1}\)的条件分布\(N(a_t, P_t)\)和新得到的观测值\(y_t\), 求\(\mu_t | y_{1:t}\)条件分布, 这等于\(\mu_t | (y_{1:t-1}, v_t)\)条件分布, 只要求条件高斯分布的期望和方差。
由前一节, \(\mu_t | y_{1:t-1} \sim \text{N}(a_t, P_t)\), \(v_t \sim \text{N}(0, F_t)\)与\(y_{1:t-1}\)独立。 注意\(\{e_t \}\)与\(\{\eta_t\}\)独立所以\(\{e_t\}\)与\(\{\mu_t \}\)独立, 利用定理30.1, 条件期望为 \[\begin{aligned} & \mu_{t|t} = E(\mu_t | y_{1:t}) \\ =& E(\mu_t | y_{1:t-1}, v_t) \\ =& E(\mu_t | y_{1:t-1}) + E(\mu_t - E\mu_t | v_t) \\ =& a_t + \frac{\text{Cov}(\mu_t - E\mu_t, v_t)}{\text{Var}(v_t)} v_t \\ =& a_t + \frac{\text{Cov}(\mu_t, v_t)}{F_t} v_t . \end{aligned}\] 其中 \[\begin{aligned} & \text{Cov}(\mu_t, v_t) \\ =& E(\mu_t v_t) \quad(\text{注意} Ev_t = 0) \\ =& E[\mu_t (y_t - a_t)] \\ =& E[\mu_t (\mu_t + e_t - a_t)] \\ =& E[\mu_t (\mu_t - a_t)] + E[\mu_t e_t] \\ =& E[\mu_t (\mu_t - a_t)] + 0 \\ =& E \left\{ E \left[ (\mu_t - a_t)^2 | y_{1:t-1} \right] \right\} \\ =& E \{ P_t \} = P_t . \end{aligned}\] 于是 \[ E(\mu_t | y_{1:t-1}, v_t) = a_t + \frac{P_t}{F_t} v_t, \] 记 \[\begin{align} K_t = \frac{P_t}{F_t} = \frac{P_t}{P_t + \sigma_e^2} , \tag{30.5} \end{align}\] 称\(K_t\)为卡尔曼增益。 可以将条件期望写成 \[ E(\mu_t | y_{1:t-1}, v_t) = a_t + K_t v_t , \] 这个公式将\(y_1, \dots, y_{t-1}, y_t\)对\(\mu_t\)的最优预报(滤波)公式分解为两部分, 第一部分是\(y_1, \dots, y_{t-1}\)对\(\mu_t\)的最优预报, 第二部分是\(y_t\)新增的信息\(v_t\)对\(\mu_t\)的最优预报, \(v_t\)的系数为卡尔曼增益\(K_t\), 最优预报是线性的。
再来求条件方差\(\text{Var}(\mu_t | y_{1:t-1}, v_t)\)。 由定理30.1, \[\begin{aligned} & \Sigma_{t|t} = \text{Var}(\mu_t | y_{1:t}) \\ =& \text{Var}(\mu_t | y_{1:t-1}, v_t) \\ =& \text{Var}(\mu_t | y_{1:t-1}) - \frac{[\text{Cov}(\mu_t, v_t)]^2}{\text{Var}(v_t)} \\ =& P_t - \frac{P_t^2}{F_t} = P_t (1 - \frac{P_t}{F_t}) \\ =& P_t (1 - K_t ) . \end{aligned}\] 记 \[\begin{align} L_t = 1 - K_t = \frac{\sigma_e^2}{P_t + \sigma_e^2}, \tag{30.6} \end{align}\] 则有 \[ \Sigma_{t|t} = P_t L_t . \]
因此,滤波公式为: \[\begin{align} \mu_{t|t} =& a_t + K_t v_t, \tag{30.7} \\ \Sigma_{t|t} =& P_t (1 - K_t), \tag{30.8} \\ K_t =& \frac{P_t}{F_t} . \end{align}\]
有了\(\mu_t | y_{1:t}\)分布后, 可以给出一步预测的条件分布\(\mu_{t+1} | y_{1:t}\), 这也只需要计算条件期望和条件方差: \[\begin{align} a_{t+1} =& \mu_{t+1|t} = E(\mu_{t+1} | y_{1:t}) = E(\mu_{t} + \eta_t | y_{1:t}) \\ =& \mu_{t|t} + 0 = \mu_{t|t} , \tag{30.9} \\ P_{t+1} =& \Sigma_{t+1|t} = \text{Var}(\mu_{t+1} | y_{1:t}) = \text{Var}(\mu_{t} | y_{1:t}) + \text{Var}(\eta_t | y_{1:t}) \\ =& \Sigma_{t|t} + \sigma_{\eta}^2 . \tag{30.10} \end{align}\]
在上式推导中要注意\(\eta_t\)是\(\mu_{t+1}\)所对应的状态方程的误差项, \(\eta_t\)与\(y_{1:t}\)和\(\mu_1, \dots, \mu_t\)独立。
(30.7)–(30.10)构成了卡尔曼滤波的一轮操作。 在下一轮中, 输入了新的观测\(y_{t+1}\)后, 计算\(\mu_{t+1} | y_{1:t+1}\)的均值\(\mu_{t+1 | t+1}\)和方差\(\Sigma_{t+1 | t+1}\), 再计算\(\mu_{t+2} | Y_{t+1}\)的均值\(a_{t+2}\)和方差\(P_{t+2}\),……。
各个关键变量的含义汇总:
- \(y_{1:t} = \{y_1, y_2, \dots, y_t\}\)。
- \(a_t = E(\mu_t | y_{1:t-1})\), \(P_t = \text{Var}(\mu_t | y_{1:t-1})\), \(\mu_t\)一步预报分布为 \(\mu_t | y_{1:t-1} \sim \text{N}(a_t, P_t)\)。
- \(\mu_{t|t} = E(\mu_t | y_{1:t})\), \(\Sigma_{t|t} = \text{Var}(\mu_t | y_{1:t})\), \(\mu_t\)的滤波分布为 \(\mu_t | y_{1:t} \sim \text{N}(\mu_{t|t}, \Sigma_{t|t})\)。
- \(v_t = y_t - E(y_t | y_{1:t-1})\)是\(y_t\)的一步预报误差, \(F_t = E(v_t^2) = \text{Var}(y_t | y_{1:t-1})\), \(v_t \sim \text{N}(0, F_t)\)与\(y_{1:t-1}\)独立。
- \(K_t = \frac{P_t}{F_t}\)称为Kalman增益, 是用\(y_{1:t-1}, v_t\)对\(\mu_t\)作最优线性预测时\(v_t\)的系数。
- \(y_t\)的一步预报分布为\(y_t | y_{1:t-1} \sim \text{N}(a_t, F_t)\)。
设初始状态\(\mu_1\)服从\(\text{N}(\mu_{1|0}, \Sigma_{1|0}) = \text{N}(a_1, P_1)\), 将(30.7)-(30.8) 代入到(30.9)-(30.10)中, 得卡尔曼滤波过程如下: \[\begin{equation} \left\{ \begin{aligned} v_t =& y_t - a_t, \\ F_t =& P_t + \sigma_e^2, \\ K_t =& P_t / F_t, \\ a_{t+1} =& \mu_{t+1|t} = a_t + K_t v_t, \\ P_{t+1} =& \Sigma_{t+1|t} = P_t (1 - K_t) + \sigma_{\eta}^2, \ t=1,2,\dots, n. \end{aligned} \right. \tag{30.11} \end{equation}\]
算法中初始分布参数\(a_1 = \mu_{1|0}\)和\(P_1 = \Sigma_{1|0}\)的选取有很大影响, 后面将专门说明。
(30.11)的卡尔曼滤波算法在给定参数 \(\sigma_e^2\)和\(\sigma_{\eta}^2\)和初始分布参数\(a_1, P_1\)后可以迭代计算\((y_1, y_2, \dots, y_n)\)的联合密度, 因此可以用来进行最大似然估计, 见30.11。
如果不假定模型中的\(\mu_t, y_t\)都服从多元正态分布, 将滤波问题看成是将\(y_{1:t}\)看成已知量, 用\(y_{1:t}\)对\(\mu_t\)做最优线性无偏估计(Minimum Variance Linear Unbiased Estimate, MVLUE,也称为BLUE或BLUP)的问题, 结果将得到完全相同的公式。 所以卡尔曼滤波可以看成是递推的最优线性无偏估计算法。
如果将模型中的\(\mu_t\)看成是随机参数, 将\(y_t\)看成是观测值, 从先验分布\(\mu_t | y_{1:t-1}\)到后验分布\(\mu_t | (y_{1:t-1}, y_t)\)的计算公式也和卡尔曼滤波公式完全相同。 参见(Durbin and Koopman 2012)第2.2节。
例30.3 对前面Alcoa现实波动率对数值数据, 利用估计的模型参数进行卡尔曼滤波计算。
将原始序列与滤波结果(\(\mu_{t|t}\),图中绿色线), 一步预测结果(\(y_{t|t-1} = a_t\),图中红色线)同时显示:
plot(ts.alcoa, ylim=c(-2, 4))
lines(as.vector(time(ts.alcoa)),
ssr1$filtered$level, col="green")
lines(as.vector(time(ts.alcoa)),
ssr1$predicted$yfit, col="red")
legend("topleft", lty=1, col=c("black", "green", "red"),
legend=c("Obs", "Filtered", "Predicted 1 step"))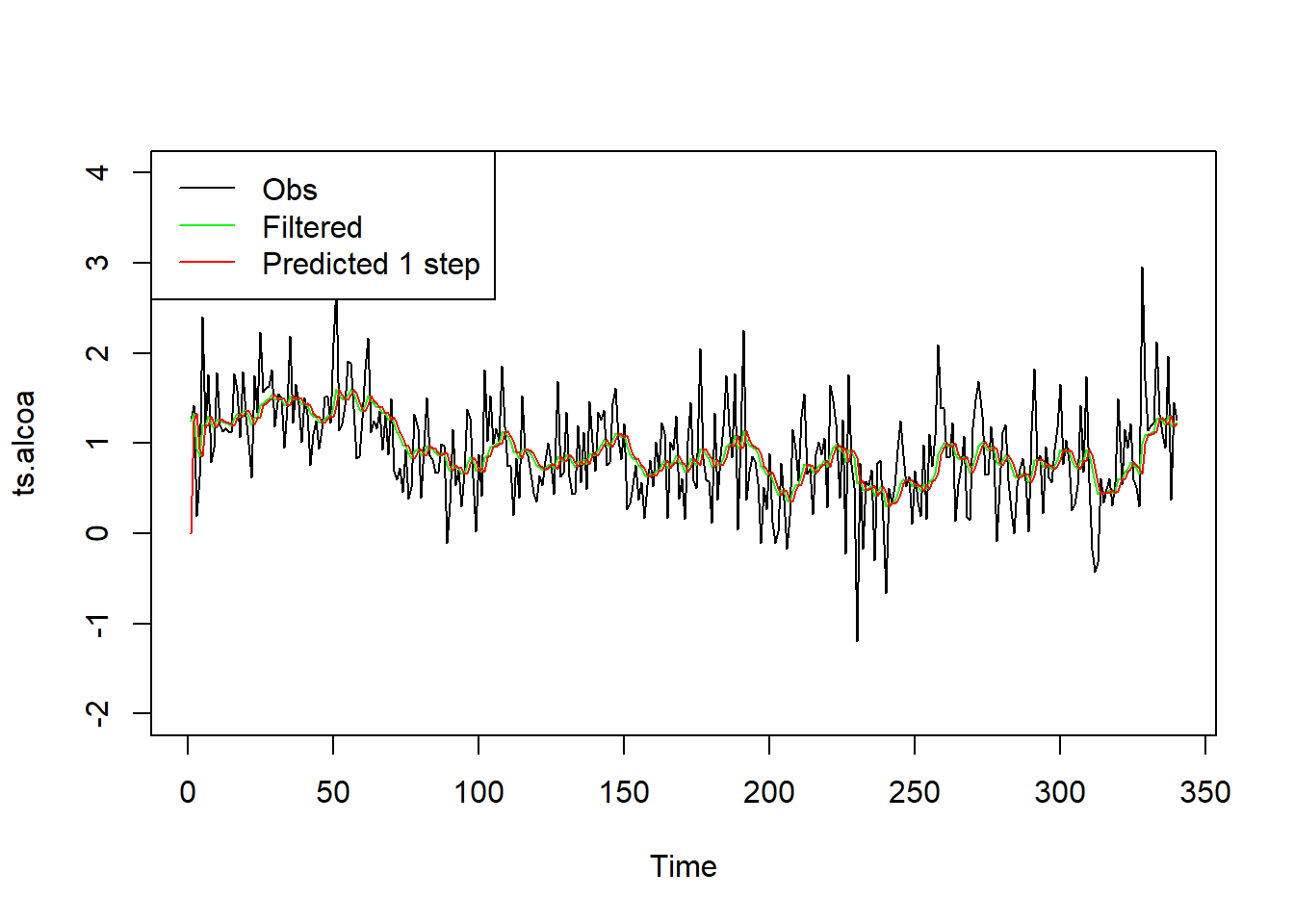
滤波值和一步预测值的序列都比较光滑。
程序中,
拟合结果的$filtered成分保存滤波结果,
$filtered$level为\(\{\mu_t \}\)的滤波结果\(\{\mu_{t|t}\}\);
拟合结果的$predicted成分保存一步预报结果,
$predicted$yfit保存对\(y_t\)的一步预报\(\{y_{t|t-1} \}\)。
$filtered中还有$filtered$a表示状态的滤波,
这里即\(\{ \mu_{t|t} \}\),
$filtered$P表示滤波方差,即\(\{ \Sigma_{t|t} \}\),
是一个\(1 \times 1 \times n\)数组,
\(n\)为时间序列观测长度。
$predicted中还有$predicted$v,即\(\{ v_t \}\),
$predicted$Fmat即\(\{ F_t \}\),
$predicted$a即\(\{ a_t \}\),
$predicted$P即\(\{ P_t \}\)。
一步预测误差(\(v_t\))的图形:
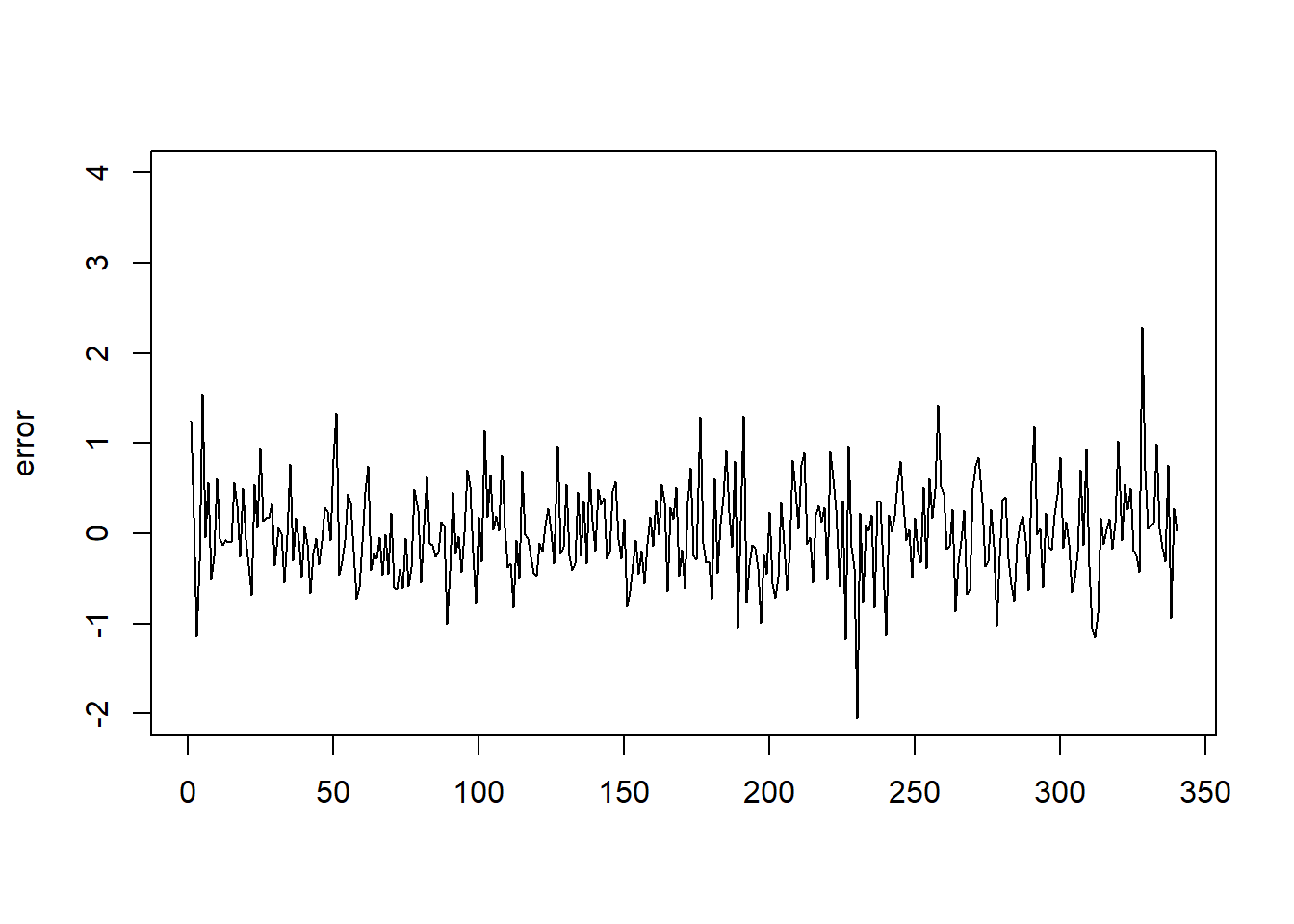
一步预测误差较大, 这可能是因为用高频数据计算波动率, 本身就有较大的观测噪声。
滤波的水平\(\mu_t\)及其95%置信区间的图形:
plot(ts.alcoa, ylim=c(-2, 4))
lines(as.vector(time(ts.alcoa)),
ssr1$filtered$level, col="red")
lines(as.vector(time(ts.alcoa)),
ssr1$filtered$level + 1.96*sqrt(ssr1$filtered$P[1,1,]),
col="green", lty=3)
lines(as.vector(time(ts.alcoa)),
ssr1$filtered$level - 1.96*sqrt(ssr1$filtered$P[1,1,]),
col="green", lty=3)
legend("topleft", lty=c(1,1,3), col=c("black", "red", "green"),
legend=c("Obs", "Filtered", "95% CI of level"))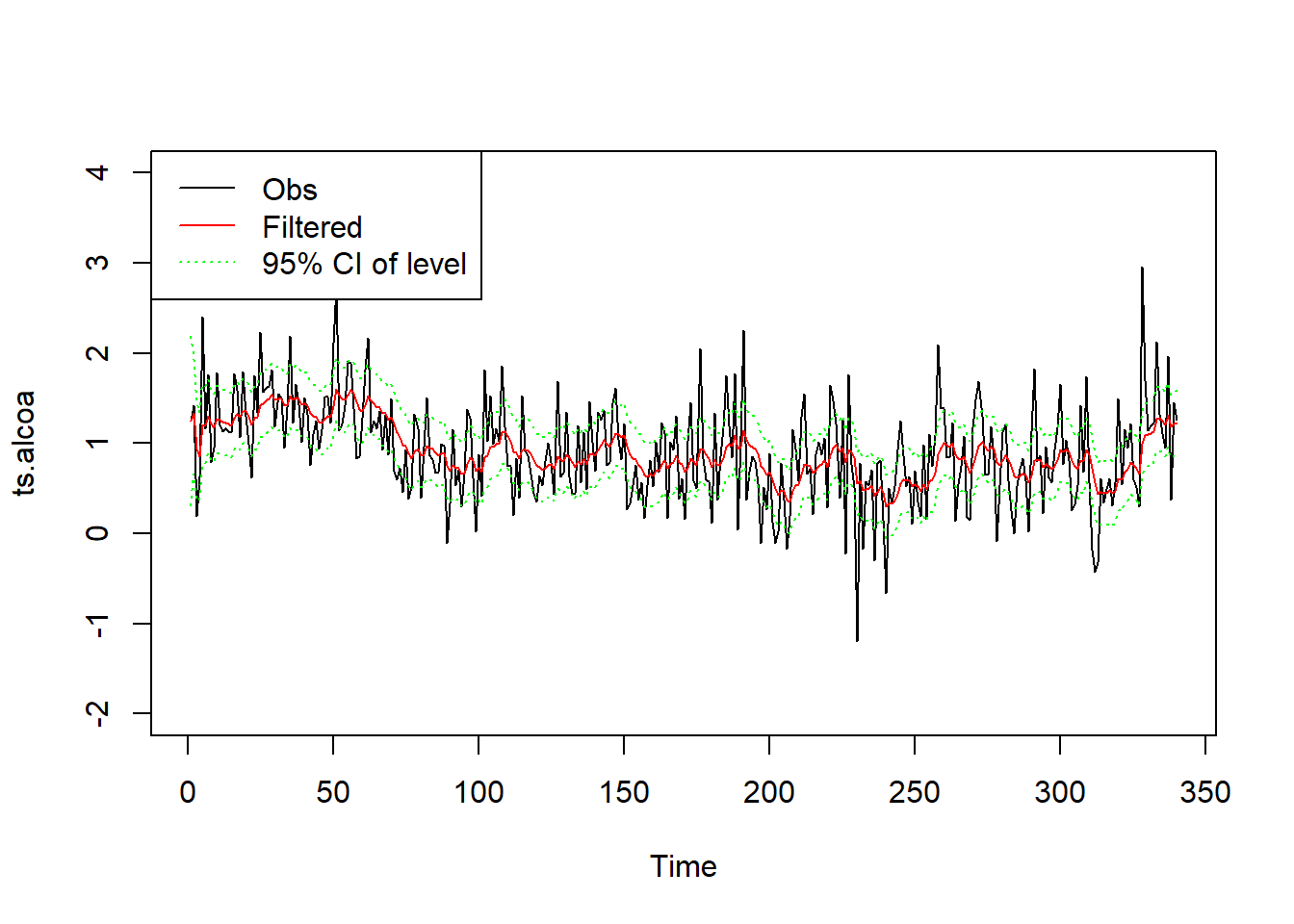
30.5 一步预报误差
一步预报误差序列\(\{v_t \}\)在滤波算法和参数估计中起到重要作用。 从初值\(\mu_1\)的分布\(N(a_1, P_1)\)出发, 可以递推计算\(\{v_t, t=1,2,\dots,n \}\), \(v_t\)是\(y_1, y_2, \dots, y_t\)的线性组合, 如: \[\begin{aligned} v_1 =& y_1 - a_1, \\ v_2 =& y_2 - a_2 = y_2 - a_1 - K_1(y_1 - a_1), \\ v_3 =& y_3 - a_3 = y_3 - a_1 - K_2(y_2 - a_1) - K_1 (1 - K_2)(y_1 - a_1), \\ & \cdots\cdots \end{aligned}\]
将从\(y\)到\(v\)的这些线性变换写成矩阵形式, 令\(Y_n = (y_1, \dots, y_n)^T\), \(\boldsymbol v = (v_1, \dots, v_n)^T\), \(\boldsymbol 1_T\)表示元素都等于1的\(n\)维列向量, 则 \[\begin{align} \boldsymbol v = \boldsymbol K (Y_n - a_1 \boldsymbol 1_n), \tag{30.12} \end{align}\] 其中 \[ K = \begin{pmatrix} 1 & 0 & 0 & \cdots & 0 \\ k_{21} & 1 & 0 & \cdots & 0 \\ k_{31} & k_{32} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ k_{n1} & k_{n2} & k_{n3} & \cdots & 1 \end{pmatrix} , \] 而\(k_{i,i-1} = -K_{i-1}\), \(i=2,3,\dots,n\); 对\(i=3,4,\dots,T\)和\(j=1,2,\dots,i-2\),有 \(k_{ij} = -(1 - K_{i-1})(1 - K_{i-2}) \dots (1 - K_{j+1}) K_j\)。
从卡尔曼滤波的公式可以看出, 卡尔曼增益\(K_t, t=1,2,\dots,n\)并不依赖于观测值\(\{y_t\}\), 只依赖于参数\(\sigma_{\eta}^2\), \(\sigma_e^2\)以及初始分布方差\(P_1\), 是非随机的。
\(\{v_t \}\)是相互独立的随机变量序列。 事实上, \((y_1, y_2 \dots, y_n)\)的联合密度函数为 \[ p_y(y_1, y_2, \dots, y_n) = p_y(y_1) \prod_{t=2}^n p_y(y_t | Y_{t-1}), \] 从(30.12)看出, 从\((y_1, y_2 \dots, y_n)\)到\((v_1, v_2 \dots, v_n)\)的变换的雅科比行列式绝对值等于1。 由多元的连续型随机向量变换的密度公式可知 \[\begin{aligned} & p_v(v_1, v_2, \dots, v_n) = p_y(y_1, y_2, \dots, y_n) = p_y(y_1) \prod_{t=2}^n p_y(y_t | Y_{t-1}) \\ =& p_v(v_1) \prod_{t=2}^n p_v(v_t) = \prod_{t=1}^n p_v(v_t), \end{aligned}\] 其中\(p_y(y_1)\)表示\(y_1\)的分布密度, \(p_v(v_1)\)表示\(v_1\)的分布密度, 因为\(y_1 = \mu_1 + e_1 \sim \text{N}(a_1, P_1 + \sigma_e^2)\), 而\(v_1 = y_1 - y_{1|0} = y_1 - \mu_{1|0} \sim \text{N}(0, P_1 + \sigma_e^2)\), 所以 \[ p_y(y_1) = \Phi'(\frac{y_1 - a_1}{\sqrt{P_1 + \sigma_e^2}}) = \Phi'(\frac{v_1}{\sqrt{P_1 + \sigma_e^2}}) = p_v(v_1), \] 对\(t \geq 2\), \(y_t | Y_{t-1} \sim \text{N}(a_t, F_t)\), \(v_t = y_t - y_{t|t-1} \sim \text{N}(0, F_t)\), \(F_t = P_t + \sigma_e^2\), 所以 \[ p_y(y_t | Y_{t-1}) = \Phi'(\frac{y_t - a_t}{\sqrt{F_t}}) = \Phi'(\frac{v_t}{\sqrt{F_t}}) = p_v(v_t) , \] 其中\(\Phi(\cdot)\)表示标准正态分布函数。
从上述的\((v_1, v_2, \dots, v_n)\)的联合密度可知各个分量相互独立, 均值为0, \(v_t\)的方差为\(F_t = P_t + \sigma_e^2\)。
从另一个角度看, \(\boldsymbol v\)是对\(Y_n\)的正交化, 类似于Gram-Schimdt正交化方法, \((v_1, \dots, v_t)\)与\((y_1, \dots, y_t)\)可以互相线性表示。 记\(\text{Var}(Y_n) = \Omega\), 由(30.11)可知 \[\begin{aligned} \text{Var}(\boldsymbol v) =& \text{diag}(F_1, F_2, \dots, F_n) = K \Omega K^T, \\ \Omega =& K^{-1}\,\text{diag}(F_1, F_2, \dots, F_n)\, (K^{-1})^T, \end{aligned}\] 其中\(K^{-1}\)为下三角矩阵且对角线元素都等于1, 这构成了对\(\boldsymbol y\)的方差阵\(\Omega\)的Cholesky分解。
30.6 状态的一步预报误差
令 \[\begin{align} \zeta_t = \mu_t - \mu_{t|t-1} = \mu_t - E(\mu_t | y_{1:t-1}), \tag{30.13} \end{align}\] 则 \[ \text{Var}(\zeta_t | y_{1:t-1}) = E \zeta_t^2 = \text{Var}(\zeta_t) = P_t, \] 由卡尔曼滤波公式得 \[ v_t = y_t - \mu_{t|t-1} = \mu_t + e_t - \mu_{t|t-1} = \zeta_t + e_t, \] 下一个时间点 \[\begin{aligned} \zeta_{t+1} =& \mu_{t+1} - \mu_{t+1|t} \\ =& \mu_t + \eta_t - (\mu_{t|t-1} + K_t v_t) \\ =& \mu_t - \mu_{t|t-1} + \eta_t - K_t (\zeta_t + e_t) \\ =& \zeta_t + \eta_t - K_t(\zeta_t + e_t) \\ =& (1 - K_t) \zeta_t + \eta_t - K_t e_t \\ =& L_t \zeta_t + \eta_t - K_t e_t, \end{aligned}\] 于是有 \[\begin{align} v_t =& \zeta_t + e_t, \tag{30.14}\\ \zeta_{t+1} =& L_t \zeta_t + \eta_t - K_t e_t, \ t=1,2,\dots, T . \tag{30.15} \end{align}\] 这构成了以\(\{v_t \}\)为观测, \(\{ \zeta_t \}\)为状态的系数时变的线性高斯状态空间模型。
30.7 状态平滑
模型的滤波, 是利用已有观测\(\{ y_1, \dots, y_t \}\)估计\(\mu_t\) 得\(\mu_t | y_{1:t}\)。 在获得所有的观测\(\{ y_1, \dots, y_n \}\)后, 可以利用所有的观测来估计\(\mu_t\), 得到\(\mu_t | Y_n\)的分布, 这个问题称为平滑问题。
注意:
- 所有的联合分布都是正态的, 所以记\(\mu_t| y_{1:n} \sim \text{N}(\mu_{t|n}, \Sigma_{t|n}) = \text{N}(\hat\mu_t, V_t)\), 称\(\hat\mu_t\)为平滑状态(smoothed state), 称\(V_t\)为平滑状态方差。
- \(\{ v_1, v_2, \dots, v_t \}\)相互独立, 可以与\(\{ y_1, y_2, \dots, y_t \}\)互相线性表示。 \(E v_t = 0\), \(\text{Var}(v_t) = F_t\)。
显然 \[ \sigma(y_1, \dots, y_{t-1}, y_t, \dots, y_n) = \sigma(y_1, \dots, y_{t-1}, v_t, \dots, v_n) . \] 条件分布\(\mu_t | y_{1:n}\), 等于条件分布\(\mu_t | y_{1:t-1}, v_t, \dots, v_n\)。 条件分布为高斯分布, 只要求条件期望和条件方差。
注意\(v_t, \dots, v_n\)与\(y_{1:t-1}\)独立, 由定理30.1, 条件期望为 \[\begin{aligned} & \hat\mu_t = E(\mu_t | y_{1:n}) = E(\mu_t | y_{1:t-1}, v_t, \dots, v_n) \\ =& E(\mu_t | y_{1:t-1}) + E(\mu_t - E\mu_t | v_t, \dots, v_n) \\ =& a_t + \text{Cov}(\mu_t, (v_t, \dots, v_n)) \text{Var}^{-1}((v_t, \dots, v_n)) (v_t, \dots, v_n)^T \\ =& a_t + (\text{Cov}(\mu_t, v_t), \text{Cov}(\mu_t, v_{t-1}), \dots, \text{Cov}(\mu_t, v_n))) \\ & \qquad\text{diag}(F_t^{-1}, F_{t+1}^{-1}, \dots, F_n^{-1}) (v_t, \dots, v_n)^T \\ =& a_t + \sum_{j=t}^n \frac{\text{Cov}(\mu_t, v_j)}{F_j} v_j . \end{aligned}\] 只要求\(\text{Cov}(\mu_t, v_j)\), \(j=t,t+1,\dots,n\)。
对\(j \geq t\),注意到\(\zeta_j, e_j, \eta_j, v_j\)都与\(y_{1:t-1}\)独立, \(e_j\)与\(\zeta_j\)独立, 有 \[\begin{aligned} & \text{Cov}(\mu_t, v_j) = E[(\mu_t v_j)] \\ =& E \{ E(\mu_t v_j | y_{1:t-1}) \} \\ =& E\{ E[(\mu_t - \mu_{t|t-1}) v_j | y_{1:t-1}] \} \\ =& E\{ E[\zeta_t v_j | y_{1:t-1}] \} = E[\zeta_t v_j], \end{aligned}\] 对\(j=t, t+1, \dots, n\)计算\(E[\zeta_t v_j]\): \[\begin{aligned} E(\zeta_t v_t) =& E[\zeta_t (\zeta_t + e_t)] = E(\zeta_t^2) + 0 = P_t, \\ E(\zeta_t v_{t+1}) =& E[\zeta_t (\zeta_{t+1} + e_{t+1})] = E[\zeta_t \zeta_{t+1}] + 0 \\ =& E[\zeta_t (L_t \zeta_t + \eta_t - K_t e_t)] = E[L_t \zeta_t^2] + 0 + 0 \\ =& P_t L_t, \\ E(\zeta_t v_{t+2}) =& E[\zeta_t (\zeta_{t+2} + e_{t+2})] = \dots = P_t L_t L_{t+1}, \\ \vdots \\ E(\zeta_t v_{n}) =& P_t \prod_{j=t}^{n-1} L_j . \end{aligned}\]
从而,\(\hat\mu_t = \mu_{t|n}\)公式为 \[\begin{aligned} \hat\mu_t =& \mu_{t|n} = a_t + P_t \frac{v_t}{F_t} + P_t L_t \frac{v_{t+1}}{F_{t+1}} + P_t L_t L_{t+1} \frac{v_{t+2}}{F_{t+2}} \\ & + \dots + P_t L_t L_{t+1} \dots L_{n-1} \frac{v_{n}}{F_{n}} \\ \equiv& a_t + P_t r_{t-1}, \end{aligned}\] 其中 \[\begin{align} r_{t-1} =& \frac{v_t}{F_t} + L_t \frac{v_{t+1}}{F_{t+1}} + L_t L_{t+1} \frac{v_{t+2}}{F_{t+2}} + \dots + L_t L_{t+1} \dots L_{n-1} \frac{v_{n}}{F_{n}}, \tag{30.16} \end{align}\] 是新息\((v_t, v_{t+1}, \dots, v_n)\)的线性函数, 满足如下递推公式: \[\begin{aligned} r_{t-1} =& \frac{v_t}{F_t} + L_t \left( \frac{v_{t+1}}{F_{t+1}} + L_{t+1} \frac{v_{t+2}}{F_{t+2}} + \dots + L_{t+1} \dots L_{n-1} \frac{v_{n}}{F_{n}} \right) \\ =& \frac{v_t}{F_t} + L_t r_t, \end{aligned}\] 令\(r_n = 0\), 有反向递推算法 \[\begin{aligned} r_{t-1} = \frac{v_t}{F_t} + L_t r_t, \ t=n, n-1, \dots, 2, 1 . \end{aligned}\]
所以, 为了求得\(\hat\mu_t = \mu_{t|n}\), 需要先进行卡尔曼滤波求出\(a_t\), \(P_t\), \(v_t\), \(F_t\), \(K_t\), \(L_t\), 然后令\(r_n = 0\),用反向递推计算: \[\begin{align} r_{t-1} =& \frac{v_t}{F_t} + L_t r_t, \\ \hat\mu_t =& \mu_{t|n} = a_t + P_t r_{t-1}, \ t=n, n-1, \dots, 2, 1 . \tag{30.17} \end{align}\]
因为\(r_{t}\)是\(v_{t+1}, \dots, v_n\)的线性组合, 由\(v_1, \dots, v_n\)的独立性可知\(r_t, r_{t+1}, \dots, r_n\)与\(v_1, v_2, \dots, v_t\)相互独立,\(r_t\)与\(y_{1:t}\)相互独立。
30.7.1 状态平滑方差计算
记\(v_{t:n} = (v_t, v_{t+1}, \dots, v_n)^T\), 则\(y_{1:t-1}\)和\(v_{t:n}\)独立, 由定理30.1, \[\begin{aligned} V_t =& \Sigma_{t|n} = \text{Var}(\mu_t | y_{1:n}) = \text{Var}(\mu_t | y_{1:t-1}, v_t, \dots, v_n) \\ =& \text{Var}(\mu_t | y_{1:t-1}, v_{t:n}) \\ =& \text{Var}(\mu_t | y_{1:t-1}) - [\text{Cov}(\mu_t, v_{t:n} )]^T [\text{Var}(v_{t:n} )]^{-1} [\text{Cov}(\mu_t, v_{t:n} )] \\ =& P_t - \sum_{j=t}^{n} \frac{[\text{Cov}(\mu_t, v_j)]^2}{F_j}, \end{aligned}\] 其中\(\text{Cov}(\mu_t, v_j) = E(\zeta_t v_j)\)已经在前面给出公式。 所以 \[\begin{aligned} V_t =& \Sigma_{t|n} \\ =& P_t - P_t^2 \frac{1}{F_t} - P_t^2 L_t^2 \frac{1}{F_{t+1}} - \dots - P_t^2 (\prod_{j=t}^{n-1} L_j^2) \frac{1}{F_{n}} \\ =& P_t - P_t^2 N_{t-1}, \end{aligned}\] 其中 \[\begin{align} N_{t-1} =& \frac{1}{F_t} + L_t^2 \frac{1}{F_{t+1}} + L_t^2 L_{t+1}^2 \frac{1}{F_{t+2}} + \dots + (\prod_{j=t}^{n-1} L_j^2) \frac{1}{F_{n}} \tag{30.18} \\ =& \frac{1}{F_t} + L_t^2 N_t . \end{align}\]
取\(N_n=0\), \(N_{t-1}\)是\(t-1\)之后的一步预报误差方差倒数的加权和, 并且由\(r_{t-1}\)中各个\(v_t\)的独立性恰好有 \[\begin{aligned} \text{Var}(r_{t-1}) =& \frac{1}{F_t} + L_t^2 \frac{1}{F_{t+1}} + L_t^2 L_{t+1}^2 \frac{1}{F_{t+2}} + \dots + (\prod_{j=t}^{n-1} L_j^2) \frac{1}{F_{n}} \\ =& N_{t-1} . \end{aligned}\]
取\(N_n=0\), 状态平滑方差\(V_t = \Sigma_{t|n}\)可以反向递推计算如下: \[\begin{align} N_{t-1} =& \frac{1}{F_t} + L_t^2 N_t, \tag{30.19}\\ V_t =& \Sigma_{t|n} = P_t - P_t^2 N_{t-1}, \ t = n, n-1, \dots, 2, 1 . \tag{30.20} \end{align}\]
例30.4 Alcoa股票日现实波动率对数值数据的平滑。
Alcoa股票日现实波动率对数值数据以及平滑结果图形:
plot(ts.alcoa, ylim=c(-2, 4))
lines(as.vector(time(ts.alcoa)),
ssr1$smoothed$level, col="red")
lines(as.vector(time(ts.alcoa)),
ssr1$smoothed$level + 1.96*sqrt(ssr1$smoothed$V[1,1,]),
col="green", lty=3)
lines(as.vector(time(ts.alcoa)),
ssr1$smoothed$level - 1.96*sqrt(ssr1$smoothed$V[1,1,]),
col="green", lty=3)
legend("topleft", lty=c(1,1,3), col=c("black", "red", "green"),
legend=c("Obs", "Smoothed", "95% CI of level"))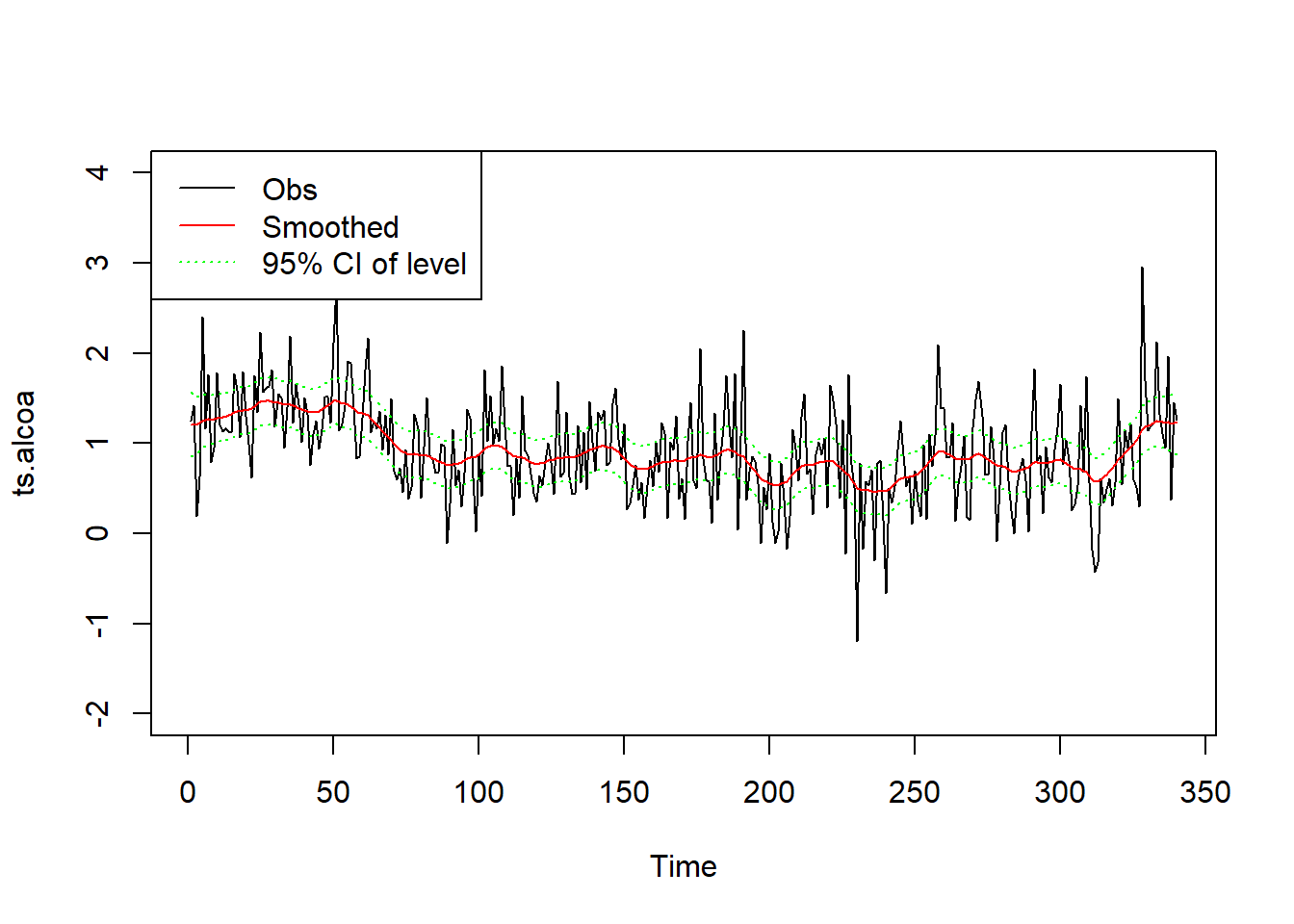
模型结果中smoothed成分保存平滑结果,
smoothed$level保存局部水平\(\mu_t\)的平滑结果,
smoothed$V保存平滑方差估计,
这里是\(1 \times 1 \times n\)数组。
实际上,
R的基本的stats包提供了StructTS()函数,
可以直接拟合包括局部水平模型的结构时间序列模型,
如:
##
## Call:
## StructTS(x = ts.alcoa, type = "level")
##
## Variances:
## level epsilon
## 0.005403 0.230652plot(ts.alcoa, ylim=c(-2, 4),
main="Alcoa smoothed with StructTS")
lines(tsSmooth(sts.al), col="green")
legend("topleft", lty=c(1,1),
col=c("black", "green"),
legend=c("Obs", "Smoothed"))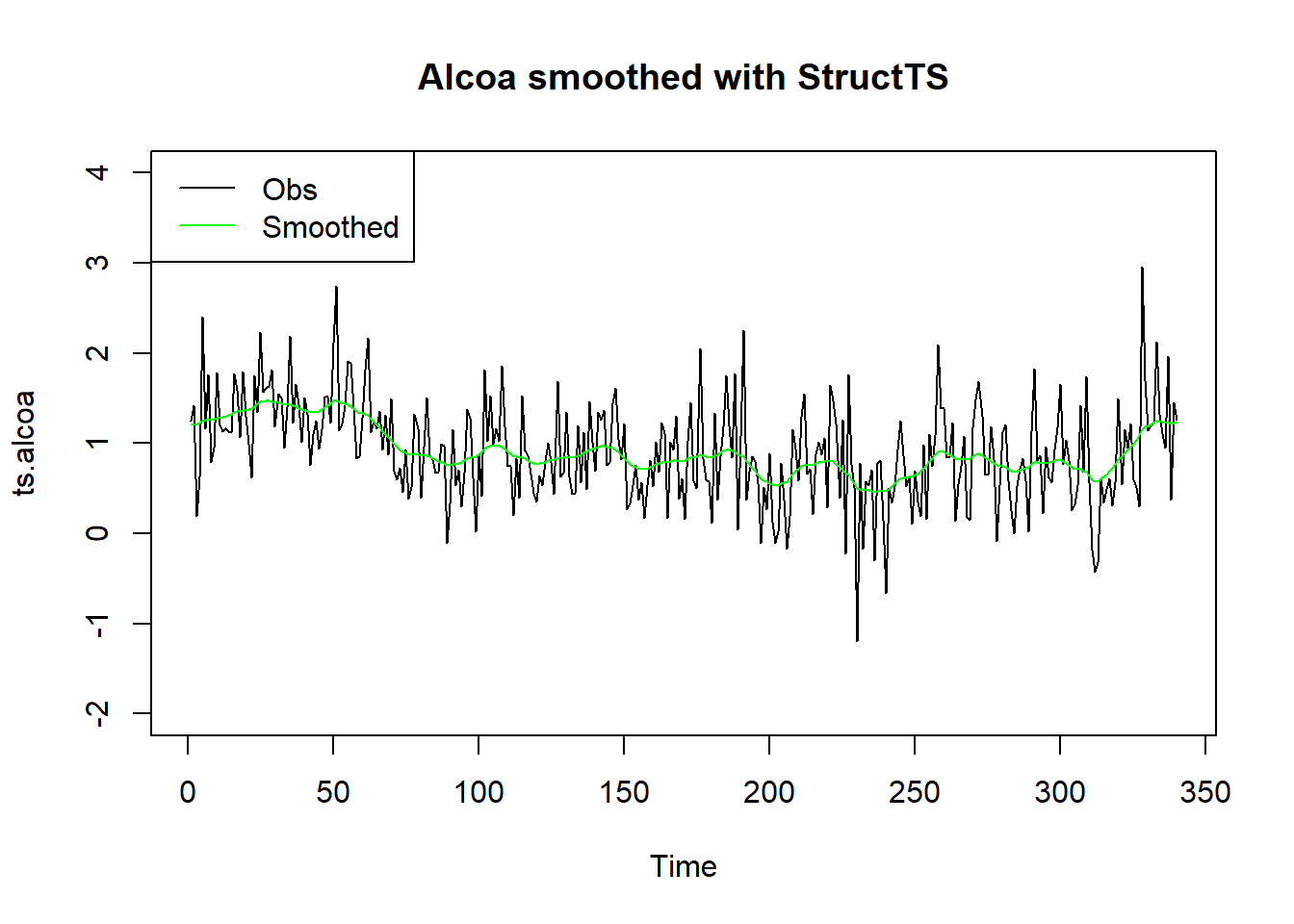
对StructTS()的结果,
用tsSmooth()可以提取平滑结果,
用fitted()可以提取滤波结果。
可以用predict()或者forecast::forecast()进行预报。
30.8 扰动的平滑
有了所有观测值\(\{y_1, y_2, \dots, y_n \}\)以后, 不仅可以利用这些信息估计状态\(\mu_t\), 得到平滑状态和平滑方差, 还可以估计\(e_t\)和\(\eta_t\)的条件分布, 这个问题称为扰动的平滑。
估计\(e_t\)和\(\eta_t\)在\(Y_n\)下的条件期望和条件方差, 可以用来进行模型诊断, 查找状态的突变点(对局部水平模型相当于水平的跳跃点或变点), 查找观测误差的异常值。
记 \[\begin{aligned} \hat e_t = E(e_t | y_{1:n}), \quad \hat\eta_t = E(\eta_t | y_{1:n}), \ t=1,2,\dots, n . \end{aligned}\]
因为\(e_t = y_t - \mu_t\), 在\(y_{1:n}\)条件下\(y_t\)已知, 所以 \[ e_t | y_{1:n} \sim \text{N} (y_t - \mu_{t|n}, \Sigma_{t|n}) = \text{N}(y_t - \hat\mu_t, V_t). \]
对\(\eta_t\), 易见 \[ \hat\eta_t = E(\mu_{t+1} | y_{1:n}) - E(\mu_{t} | y_{1:n}) = \mu_{t+1|n} - \mu_{t|n} = \hat\mu_{t+1} - \hat\mu_t, \] 但\(\eta_t | y_{1:n}\)的条件方差公式需要用到平滑的协方差, 下面给出另一种计算条件方差的算法。
30.8.1 观测方程扰动的递推平滑公式
从计算效率出发, 为了获得\(e_t\)和\(\eta_t\)在\(y_{1:n}\)下的条件分布, 直接从\(r_t\)和\(N_t\)计算更简单。 关于\(e_t | y_{1:n}\)的公式为 \[\begin{aligned} E(e_t | y_{1:n}) =& \sigma_e^2 \left(F_t^{-1} v_t - K_t r_t \right), \\ \text{Var}(e_t | y_{1:n}) =& \sigma_e^2 - \sigma_e^4\left( \frac{1}{F_t} + K_t^2 N_t \right) ,\\ &\quad t=n, n-1, \dots, 2, 1 . \end{aligned}\]
证明: 由于\(F_t = P_t + \sigma_e^2\), \(K_t = \frac{P_t}{F_t}\), \(L_t = 1 - K_t = \frac{\sigma_e^2}{F_t}\), 有 \[\begin{aligned} E(e_t | y_{1:n}) =& E(y_t - \mu_t | y_{1:n}) = y_t - \mu_{t|n} \\ =& y_t - a_t - P_t r_{t-1} \\ =& v_t - P_t \left[ \frac{v_t}{F_t} + L_t r_t \right] \\ =& \left(1 - \frac{P_t}{F_t} \right) v_t - P_t L_t r_t \\ =& \frac{\sigma_e^2}{F_t} v_t - P_t \frac{\sigma_e^2}{F_t} r_t \\ =& \sigma_e^2 \left( \frac{v_t}{F_t} - K_t r_t \right) . \end{aligned}\]
记 \[ u_t = \frac{v_t}{F_t} - K_t r_t = \sigma_e^{-2} E(e_t | y_{1:n}), \] 称\(u_t\)为平滑误差(smoothing error)。
为了求\(\text{Var}(e_t | y_{1:n})\), 注意在联合正态分布下条件分布的方差是非随机的, 由公式\(\text{Var(Y)} = E[\text{Var}(Y|X)] + \text{Var}[E(Y|X)]\), 以及\(v_t\)与\(r_t\)独立, \(\text{Var}(r_t) = N_t\),可得 \[\begin{aligned} \text{Var}(e_t | y_{1:n}) =& E[\text{Var}(e_t | y_{1:n})] = \text{Var}(e_t) - \text{Var}[E(e_t | y_{1:n})] \\ =& \sigma_e^2 - \sigma_e^4\left( \frac{1}{F_t} + K_t^2 N_t \right) . \end{aligned}\]
30.8.2 状态方程扰动的递推平滑公式
对\(\eta_t | y_{1:n}\)有 \[\begin{aligned} \hat\eta_t =& E(\eta_t | y_{1:n}) = \sigma_{\eta}^2 r_t, \\ \text{Var}(\eta_t | y_{1:n}) =& \sigma_{\eta}^2 - \sigma_{\eta}^4 N_t, \ t=n, n-1, \dots, 2, 1 . \end{aligned}\]
\(r_t\)与\(\hat\eta_t\)的关系也说明了\(r_t\)和\(N_t\)的一个解释, \(r_t\)是平滑的状态扰动项\(\hat\eta_t\)的常数倍, 注意\(\text{Var}(r_t)=N_t\), 于是\(\text{Var}(\hat\eta_t) = \sigma_{\eta}^4 N_t\), 所以\(r_t\)的无条件方差\(N_t\)是平滑的状态扰动无条件方差\(\text{Var}(\hat\eta_t)\)的常数倍。
证明: \[\begin{aligned} E(\eta_t | y_{1:n}) =& E(\mu_{t+1} - \mu_t | y_{1:n}) = \mu_{t+1|n} - \mu_{t|n} \\ =& a_{t+1} + P_{t+1} r_t - a_t - P_t r_{t-1} \\ =& (a_{t+1} - a_t) + \left( P_t \frac{\sigma_e^2}{F_t} + \sigma_{\eta}^2 \right) r_t - P_t \left( \frac{v_t}{F_t} + \frac{\sigma_e^2}{F_t} r_t \right) \\ =& K_t v_t + (K_t \sigma_e^2 + \sigma_{\eta}^2) r_t - K_t v_t - \sigma_e^2 K_t r_t \\ =& \sigma_{\eta}^2 r_t . \end{aligned}\] 而 \[\begin{aligned} \text{Var}(\eta_t | y_{1:n}) =& E[ \text{Var}(\eta_t | y_{1:n}) ] \\ =& \text{Var}(\eta_t) - \text{Var}[E(\eta_t | y_{1:n})] \\ =& \sigma_{\eta}^2 - \sigma_{\eta}^4 N_t . \end{aligned}\]
30.9 缺失值处理和预测
一般的时间序列模型都很难处理出现在时间区间内部的缺失值。 状态空间模型的一大优势就是可以比较容易的允许观测有缺失值。 在局部水平模型中, 设\(\{y_t\}_{t=\ell+1}^{\ell+h}\)缺失。 状态空间模型可以用多种方法解决缺失值问题, 这里使用不改变时间步数和模型形式的方法。
对\(t \in \{ \ell+1, \dots, \ell+h \}\), 有 \[ \mu_t = \mu_{t-1} + \eta_{t-1} = \dots = \mu_{\ell+1} + \sum_{j=\ell+1}^{t-1} \eta_j, \] 这里约定求和下标下限大于下标上限时和为0。 于是 \[\begin{aligned} E(\mu_t | Y_{t-1}) =& E(\mu_t | Y_{\ell}) = a_{\ell+1}, \\ \text{Var}(\mu_t | Y_{t-1}) =& \text{Var}(\mu_t | Y_{\ell}) = P_{\ell+1} + (t-\ell-1) \sigma_{\eta}^2 , \end{aligned}\] 于是有递推式 \[\begin{align} a_t =& \mu_{t|t-1} = \mu_{t-1|t-2} = a_{t-1}, \tag{30.21} \\ P_t =& \Sigma_{t|t-1} = P_{t-1} + \sigma_{\eta}^2, \ t=\ell+2, \dots, \ell+h . \tag{30.22} \end{align}\]
所以,局部水平模型有缺失值时仍可使用(30.11)进行滤波计算, 但是对缺失的\(y_t\), 应该相应地取\(v_t=0\), \(K_t=0\)。 这也符合常识, 因为观测缺失时就没有新息\(v_t\)的信息, 也没有卡尔曼增益\(K_t\)。
实际上, 在已知\(y_1, y_2, \dots, y_n\)后对\(y_{n+1}, \dots, y_{n+h}\)进行预测时, 最优线性无偏估计得到的预测公式, 与设\(y_{n+1}, \dots, y_{n+h}\)为缺失值, 令\(v_{n+1} = \dots = v_{n+h} = K_{n+1} = \dots = K_{n+h} = 0\)后进行滤波计算的计算公式完全相同。 所以预测问题可以看成有缺失值时的滤波问题的特例。 这时 \[\begin{aligned} E(y_{n+j} | y_{1:n}) =& E(\mu_{n+j} | y_{1:n}) = a_{n+1}, \\ \text{Var}(y_{n+j} | y_{1:n}) =& \text{Var}(\mu_{n+j} | y_{1:n}) + \sigma_e^2 = P_n + (j-1) \sigma_{\eta}^2 + \sigma_e^2 . \end{aligned}\]
30.10 初值分布参数选取
卡尔曼滤波计算需要假定已知\(\mu_1 \sim \text{N}(a_1, P_1)\)。 实际中\(a_1\)和\(P_1\)是未知的。 利用滤波公式得 \[\begin{aligned} v_1 =& y_1 - a_1, \quad F_1 = P_1 + \sigma_e^2, \\ a_2 =& a_1 + \frac{P_1}{F_1} v_1 = a_1 + \frac{P_1}{F_1} (y_1 - a_1) \\ \to& y_1 \quad(P_1 \to \infty), \\ P_2 =& P_1 \left(1 - \frac{P_1}{P_1 + \sigma_e^2} \right) + \sigma_{\eta}^2 \\ =& \frac{P_1}{P_1 + \sigma_e^2} \sigma_e^2 + \sigma_{\eta}^2 \\ \to& \sigma_e^2 + \sigma_{\eta}^2 \quad(P_1 \to \infty), \end{aligned}\] 因此\(P_1 \to \infty\)时相当于认为\(y_1\)是非随机的确定值, 而\(\mu_1 \sim \text{N}(y_1, \sigma_e^2)\)。 这种初始化方法称为扩散(diffuse)初始化或者扩散先验。 扩散先验相当于对初始状态分布没有任何知识。
对于取扩散先验时的平滑问题, \(t=n, n-1, \dots, 2\)的反向递推仍完全原样进行。 对\(t=1\), 利用\(L_1 = 1 - K_1 = F_1^{-1} \sigma_e^2\), \(F_1 = P_1 + \sigma_e^2\),得 \[\begin{aligned} \hat\mu_1 =& \mu_{1|n} = a_1 + P_1 r_0 \\ =& a_1 + P_1 \left[ \frac{1}{P_1 + \sigma_e^2} v_1 + \left(1 - \frac{P_1}{P_1 + \sigma_e^2} \right) r_1 \right] \\ =& a_1 + \frac{P_1}{P_1 + \sigma_e^2}(v_1 + \sigma_e^2 r_1) \\ \to& a_1 + v_1 + \sigma_e^2 r_1 = y_1 + \sigma_e^2 r_1 \quad(P_1 \to \infty), \\ V_1 =& \Sigma_{1|n} = P_1 - P_1^2 \left[ \frac{1}{P_1 + \sigma_e^2} + \left(1 - \frac{P_1}{P_1 + \sigma_e^2} \right)^2 N_1 \right] \\ =& P_1 \left(1 - \frac{P_1}{P_1 + \sigma_e^2} \right) - \left(1 - \frac{P_1}{P_1 + \sigma_e^2} \right)^2 P_1^2 N_1 \\ =& \left(\frac{P_1}{P_1 + \sigma_e^2} \right) \sigma_e^2 - \left(\frac{P_1}{P_1 + \sigma_e^2} \right)^2 \sigma_e^4 N_1 \\ \to& \sigma_e^2 - \sigma_e^4 N_1 \quad(P_1 \to \infty) . \end{aligned}\]
另一种想法是将\(\mu_1\)也作为一个未知参数, 并且仅根据\(y_1\)一个样本点估计\(\mu_1\)。 因为\(y_1 | \mu_1 \sim \text{N}(\mu_1, \sigma_e^2)\), 所以\(\mu_1\)的估计为\(y_1\), 估计方差为\(\sigma_e^2\), 即从\(\mu_1 | y_1 \sim \text{N}(y_1, \sigma_e^2)\)向前滤波。 这与先验\(P_1 \to \infty\)公式相同。
30.11 模型参数估计
30.11.1 初始分布已知情形
滤波和平滑算法都是假定模型参数\(\sigma_e^2\)和\(\sigma_{\eta}^2\)已知的。 为了估计参数可以使用最大似然估计法, 计算似然函数时可以利用滤波算法进行计算。
\((y_1, y_2, \dots, y_n)\)的似然函数为 \[\begin{aligned} & p_y(y_1, y_2, \dots, y_n | \sigma_e^2, \sigma_{\eta}^2) \\ =& p_y(y_1 | \sigma_e^2, \sigma_{\eta}^2) \prod_{t=2}^n p_y(y_t | Y_{t-1}, \sigma_e^2, \sigma_{\eta}^2) \\ =& p_v(v_1 | \sigma_e^2, \sigma_{\eta}^2) \prod_{t=2}^T p_v(v_t | \sigma_e^2, \sigma_{\eta}^2), \end{aligned}\] 其中\(y_1 \sim \text{N}(a_1, P_1)\), \(v_t \sim \text{N}(0, F_t)\), 设\(a_1, P_1\)已知, 可得对数似然函数为 \[\begin{aligned} \ln L(\sigma_e^2, \sigma_{\eta}^2) = -\frac{n}{2} \ln(2\pi) - \frac{1}{2} \sum_{t=1}^n \left( \ln F_t + \frac{v_t^2}{F_t} \right) . \end{aligned}\] 给定初始值\(a_1, P_1\)以及一组参数值\(\sigma_e^2, \sigma_{\eta}^2\) 就可以用卡尔曼滤波算法计算出\(v_t, F_t\)从而得到对数似然函数值。 用数值优化算法可以求得似然函数关于\(\sigma_e^2\)和\(\sigma_\eta^2\)的最大值点。
具体计算可以用R的statespacer扩展包, KFAS, bssm扩展包等, 还有许多其它软件也可以进行状态空间模型建模。
30.11.2 发散先验情形
若\(P_1 \to \infty\), 则\(F_1 \to \infty\), 但\(F_2\)有限。 所以对数似然函数中\(t=1\)的项会与\(P_1\)有关为\(\log F_1 + v_1^2/F_1\), 这一项会趋于无穷。 所以可以将对数似然函数替换成 \[\begin{aligned} \log L_d =& \lim_{P_1 \to \infty} (\log L + \frac{1}{2} \log P_1) \\ =& -\frac{n}{2} \ln(2\pi) - \frac{1}{2} \sum_{t=2}^n \left( \ln F_t + \frac{v_t^2}{F_t} \right) . \end{aligned}\]
这相当于从对数似然函数中去掉了\(t=1\)的项。 给定\(P_1\), \(\log L_d\)与\(\log L\)最大值点相同, 所以当\(P_1\)取为很大的值时, 获得的是发散先验条件下最大似然估计近似值。
30.12 滤波的极限状态
如果\(t \to \infty\)时\(P_t\)存在极限\(\bar P\), 则\(F_t \to \bar P + \sigma_e^2\), \(K_t \to \frac{\bar P}{\bar P + \sigma_e^2}\), \(t\)充分大时滤波算法中的\(K_t\), \(P_t\), \(L_t\)都可以取为常数值, 且 \[ a_{t+1} = a_t + \bar K v_t . \]
为了检查是否有极限状态, 令\(P_{t+1} = P_t = \bar P\), 由\(P_{t+1}\)的递推式有 \[ \bar P = \bar P \left(1 - \frac{\bar P}{\bar P + \sigma_e^2} \right) + \sigma_\eta^2 . \] 记\(q = \sigma_\eta^2 / \sigma_e^2\), \(x = \bar P / \sigma_e^2\), 则\(x\)的方程为 \[ x^2 - qx + q = 0, \] 解为 \[ x = (q + \sqrt{q^2 + 4q})/2 . \] 所以\(P_t\)的极限存在。
30.13 模型诊断
30.14 附录:局部水平模型建模的R程序
这里直接利用本章给出的算法编制局部水平模型建模的R语言程序。
30.14.1 用卡尔曼滤波计算似然函数
# 设状态初值分布参数$a_1$, $P_1$已知,
# 观测误差方差$\sigma_e^2$和状态方程误差方差$\sigma_\eta^2$已知,
# 进行滤波,并计算对数似然函数值。
kfll_winit <- function(
y, # 观测值序列
a1, # 状态初始分布均值
P1, # 状态初始分布方差
var_err_obs, # 观测误差方差$\sigma_e^2$
var_err_sys # 状态方程误差方差$\sigma_\eta^2$
) {
n <- length(y)
# 对y进行归一化以免y取值过大、过小使得算法中的阈值不合适
y0 <- y
my <- mean(y, na.rm=TRUE)
sigy <- sd(y, na.rm=TRUE)
y <- (y - my)/sigy
# 预先分配一步预报分布的存储空间
v <- numeric(n)
F <- numeric(n)
K <- numeric(n)
a <- numeric(n+1); a[1] <- a1
P <- numeric(n+1); P[1] <- P1
# 向前进行Kalman滤波
for(t in seq(n)){
v[t] = y[t] - a[t]
F[t] = P[t] + var_err_obs
K[t] = P[t]/F[t]
a[t+1] = a[t] + K[t]*v[t]
P[t+1] = P[t]*(1-K[t]) + var_err_sys
}
# 计算对数似然函数
logL <- ( -0.5*n*log(2*pi)
- 0.5*sum(log(F)) - 0.5*sum(v^2 / F) )
list(logLik=logL, mean_y=my, sigma_y=sigy)
}30.14.2 参数最大似然估计(发散先验初始化)
# 计算最大似然估计的程序
# 设初始化用发散先验,$a_1=0$
# 注意滤波程序内对输入观测值进行了归一化,
# 所以两个方差参数在恢复时需要乘以y的方差
mle_ll <- function(y){
a1 <- 0
P1 <- 1E6
# 负对数似然函数值
# 参数为$\log(\sigma_e^2)$, $\log(\sigma_eta^2)$
negLL <- function(wpars){
pars <- exp(wpars)
var_err_obs <- pars[1]
var_err_sys <- pars[2]
-kfll_winit(y, a1, P1, var_err_obs, var_err_sys)$logLik
}
# 需要两个方差的初值
wpars <- log(rep(var(y), 2))
res <- nlm(negLL, wpars)
pars <- exp(res$estimate)
var_err_obs <- pars[1] * var(y, na.rm=TRUE)
var_err_sys <- pars[2] * var(y, na.rm=TRUE)
logL <- -res$minimum
list(var_err_obs=var_err_obs,
var_err_sys=var_err_sys,
logLik=logL)
}用波动率对数值数据测试:
## $var_err_obs
## [1] 0.2306524
##
## $var_err_sys
## [1] 0.005403459
##
## $logLik
## [1] -461.4858结果与statespacer结果相同。
30.14.3 平滑程序(发散先验初始化)
# 设状态初值分布参数$a_1$, $P_1$已知,
# 观测误差方差$\sigma_e^2$和状态方程误差方差$\sigma_\eta^2$已知,
# 进行滤波和平滑,输出平滑分布参数。
smll_winit <- function(
y, # 观测值序列
a1, # 状态初始分布均值
P1, # 状态初始分布方差
var_err_obs, # 观测误差方差$\sigma_e^2$
var_err_sys # 状态方程误差方差$\sigma_\eta^2$
) {
n <- length(y)
# 预先分配向前滤波存储空间
v <- numeric(n)
F <- numeric(n)
K <- numeric(n)
a <- numeric(n+1); a[1] <- a1
P <- numeric(n+1); P[1] <- P1
# 向前进行Kalman滤波
for(t in seq(n)){
v[t] = y[t] - a[t]
F[t] = P[t] + var_err_obs
K[t] = P[t]/F[t]
a[t+1] = a[t] + K[t]*v[t]
P[t+1] = P[t]*(1-K[t]) + var_err_sys
}
# 计算对数似然函数
logL <- ( -0.5*n*log(2*pi)
- 0.5*sum(log(F)) - 0.5*sum(v^2 / F) )
# 预先分配平滑存储空间
r <- numeric(n+1); r[n+1] <- 0
N <- numeric(n+1); N[n+1] <- 0
L <- 1-K
for(t in n:1){
r[t] <- v[t] / F[t] + L[t]*r[t+1]
N[t] <- 1/F[t] + L[t]^2*N[t+1]
}
mu_sm <- a[1:n] + P[1:n]*r[1:n]
var_sm <- P[1:n] -P[1:n]^2 * N[1:n]
list(logLik=logL, mean_sm_mu=mu_sm, var_sm_mu=var_sm)
}用Alcoa数据测试:
res2 <- smll_winit(
as.vector(ts.alcoa), a1=as.vector(ts.alcoa)[1], P1=1E6,
var_err_obs=res1$var_err_obs,
var_err_sys=res1$var_err_sys)结果与statespacer结果相同。