11 指数平滑和时间序列分解

10.1中介绍了时间序列分解方法和相关的程序模板。 本章更详细地介绍分解的不同成分以及相关的统计模型——结构时间序列(ETS)模型， 基于结构时间序列模型可以进行统计推断， 比如计算预测区间， 基于AIC等指标进行模型比较。

这一章的内容来自(Tsay 2013)和(R. J. Hyndman and Athanasopoulos 2021)的第8章。

11.1 简单指数平滑

指数平滑最早是来自一种简单的预测方法： 用历史数据的线性组合预测下一时间点的值， 线性组合系数随距离变远而按负指数（几何级数）衰减， 不考虑季节性， 也不考虑趋势变化： \[ \hat x_h(1) \approx w x_h + w^2 x_{h-1} + \dots = \sum_{j=1}^\infty w^j x_{h+1-j}. \] 其中\(0<w<1\)， \(w\)越小， 距离远的历史观测对预测的贡献越小。

因为是加权平均， 所以所有加权的和应该等于零， 注意到 \[ \sum_{j=1}^\infty w^j = \frac{w}{1-w}, \] 所以第\(j\)个权重应为 \[ \frac{w^j}{\frac{w}{1-w}} = (1-w) w^{j-1}, \ j=1,2,\dots \] 于是 \[\begin{equation} \hat x_h(1) = (1-w)(x_h + w x_{h-1} + w^2 x_{h-2} + \dots) = (1-w) \sum_{j=0}^\infty w^j x_{h-j}. \tag{11.1} \end{equation}\] 这种预测方法叫做指数平滑方法(exponential smoothing method)， 在早期应用中权重\(w\)是凭经验选取的。

简单指数平滑， 相当于只用一个变化的水平值\(\ell_t\)拟合数据\(y_t\)， \[\begin{equation} \ell_t = \alpha y_t + (1 - \alpha) \ell_{t-1}, \tag{11.2} \end{equation}\] 公式的含义是\(t\)时刻水平用当前观测值和上一个水平加权平均估计， \(\alpha\)越大，越强调最新的观测的作用， 历史值的影响越小。 基于\(y_1, \dots, y_t\)对\(y_{t+h}\)的预测为 \[\begin{equation} \hat y_{t+h|t} = \ell_t , \ h=1,2,\dots \tag{11.3} \end{equation}\] 递推可得 \[\begin{equation} \ell_t \approx \sum_{j=0}^\infty \alpha (1-\alpha)^j y_{t-j} . \tag{11.4} \end{equation}\] 相当于(11.1)中\(w = 1-\alpha\)。 如果仅递推到\(t=0\)时刻， 则(11.4)变成 \[\begin{equation} \ell_t = \sum_{j=0}^{t-1} \alpha (1-\alpha)^j y_{t-j} + (1-\alpha)^t \ell_0 . \tag{11.5} \end{equation}\]

(11.3)超前\(h\)步的预测不论\(h\)取值都给出相同的预测值， 这是ARIMA(0,1,1)模型预测的特征。

经研究， ARIMA(0,1,1)的\(\hat x_h(1)\)的公式恰好具有(11.1)的形式。 考虑如下的ARIMA(0,1,1)模型： \[\begin{equation} (1-B) X_t = (1 - \theta B) \varepsilon_t. \tag{11.6} \end{equation}\] 在(11.6)两边除以\(1 - \theta B\)，由于 \[ \frac{1}{1 - \theta z} = \sum_{j=0}^\infty \theta^j z^j. \] 所以模型可以化为 \[\begin{aligned} & (1 - B) \sum_{j=0}^\infty \theta^j X_{t-j} = \varepsilon_t, \\ & \sum_{j=0}^\infty \theta^j X_{t-j} - \sum_{j=0}^\infty \theta^j X_{t-j-1} = \varepsilon_t, \\ & X_t + \sum_{j=1}^\infty \theta^j X_{t-j} - \sum_{j=1}^\infty \theta^{j-1} X_{t-j} = \varepsilon_t, \\ & X_t - (1-\theta) \sum_{j=1}^\infty \theta^{j-1} X_{t-j} = \varepsilon_t, \\ & X_t - (1-\theta) \sum_{j=0}^\infty \theta^j X_{t-1-j} = \varepsilon_t. \end{aligned}\] 以\(t=h+1\)代入得 \[ X_{h+1} = (1-\theta) \sum_{j=0}^\infty \theta^j X_{h-j} + \varepsilon_{h+1}. \] 于是 \[ \hat x_h(1) = E(X_{h+1} | \mathscr F_h) = (1-\theta) \sum_{j=0}^\infty \theta^j X_{h-j}. \] 这就是\(w=\theta\)的指数平滑预测公式。

因为指数平滑预测与ARIMA(0,1,1)预测的等价性， 可以用ARIMA建模方法估计权重\(w\)。 注意arima()函数估计的MA系数是\(1 + \theta_1 z + \dots + \theta_q z^q\)形式的系数， 而(11.6)中用了\(1 - \theta B\)形式。 也可以用ARIMA模型的充分性检验来判断指数平滑预测是否有意义。

另一种估计权重的方法是计算残差和残差平方和， 用最小二乘方法估计权重： \[ \min \sum e_t^2 = \min \sum (y_t - \ell_{t-1})^2, \] 其中\(\ell_t\)按(11.2)递推计算， 初值\(\ell_0\)可以简单取为\(y_1\)或者也当成参数进行最小二乘估计。

例11.1 考虑CBOE的波动率指数（VIX）2004-01-02到2011-11-21的日收盘价的对数序列， 用指数平滑方法作一步预测。 共1988个观测。

解答： 读入数据，从中计算日收盘价对数值序列：

da <- read_table("d-vix0411.txt", col_types=cols(.default = col_double()))
xts.vix <- xts(da[,-(1:3)], make_date(da$year, da$mon, da$day))
str(xts.vix)
## An xts object on 2004-01-02 / 2011-11-21 containing: 
##   Data:    double [1988, 4]
##   Columns: Open, High, Low, Close
##   Index:   Date [1988] (TZ: "UTC")
vix <- log(xts.vix[,"Close"])
delta.vix <- diff(vix)[-1]

作日对数收盘价的时间序列图：

plot(vix, type="l", main="VIX Daily Log Close",
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="auto")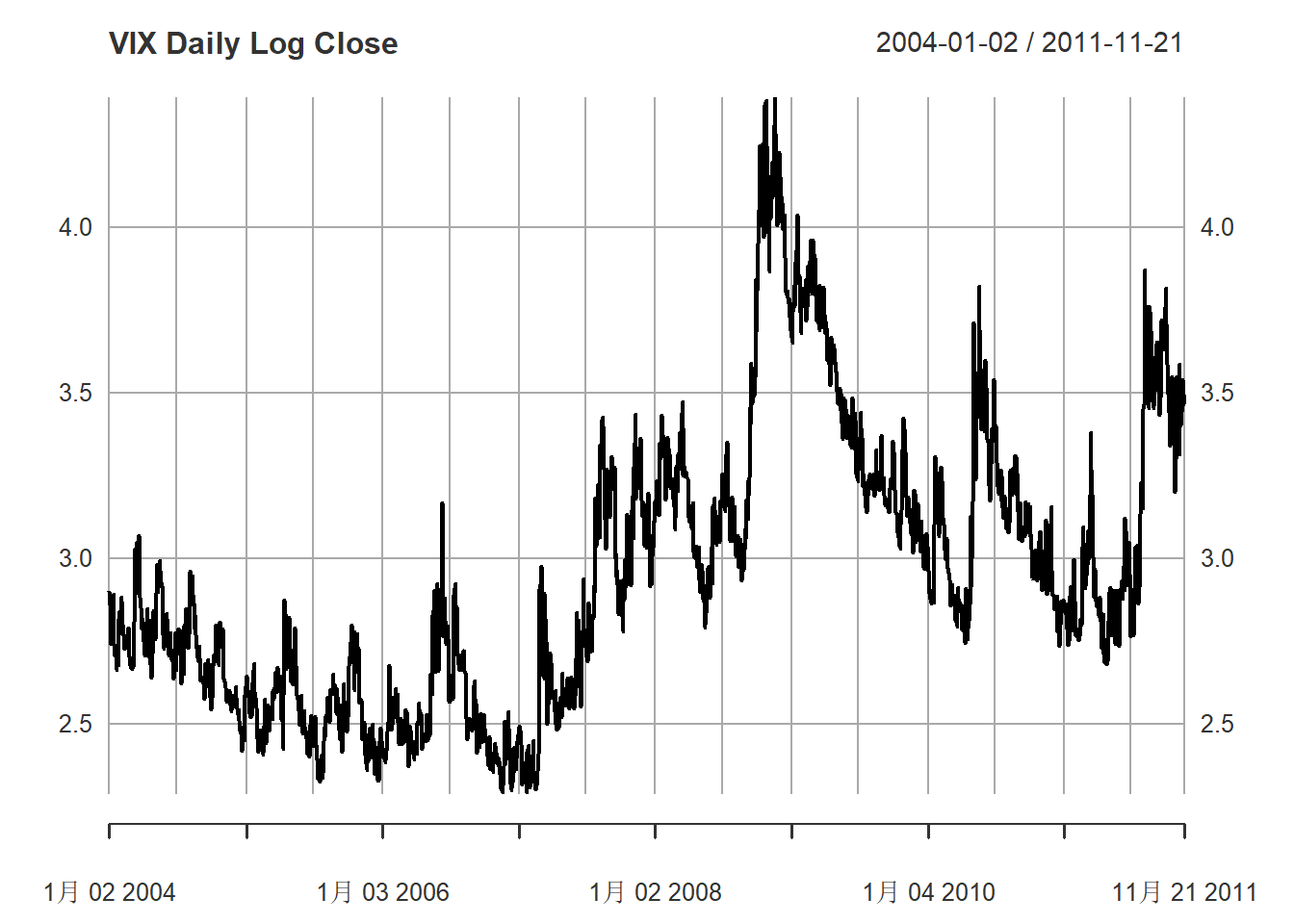
VIX日对数收盘价

图11.1: VIX日对数收盘价

明显不平稳且没有固定趋势。

作日对数收益率的时间序列图：

plot(delta.vix, type="l", main="VIX Daily Log Return",
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="auto")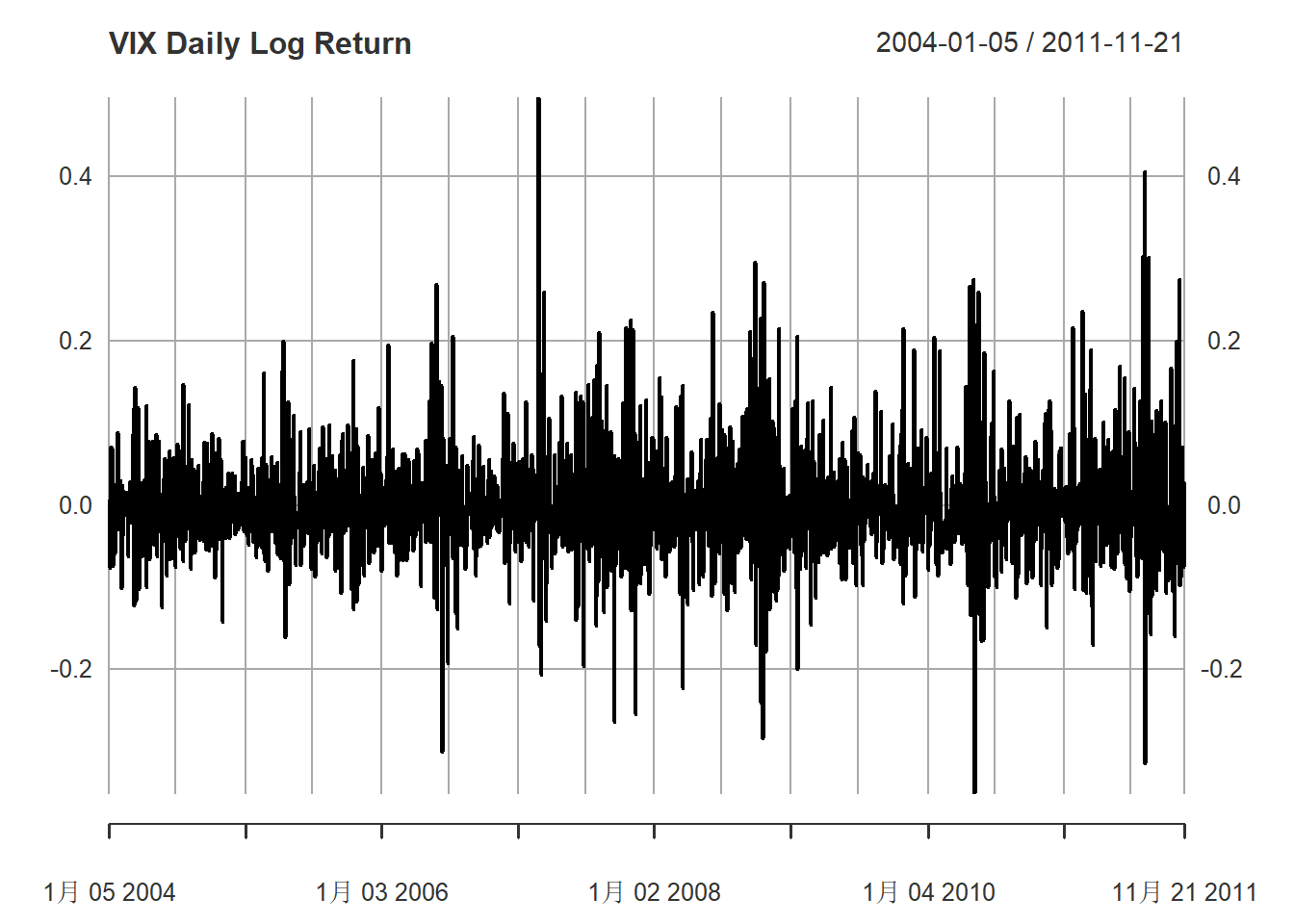
VIX日对数收益率

图11.2: VIX日对数收益率

日对数收益率的ACF:

forecast::Acf(c(coredata(delta.vix)), main="")
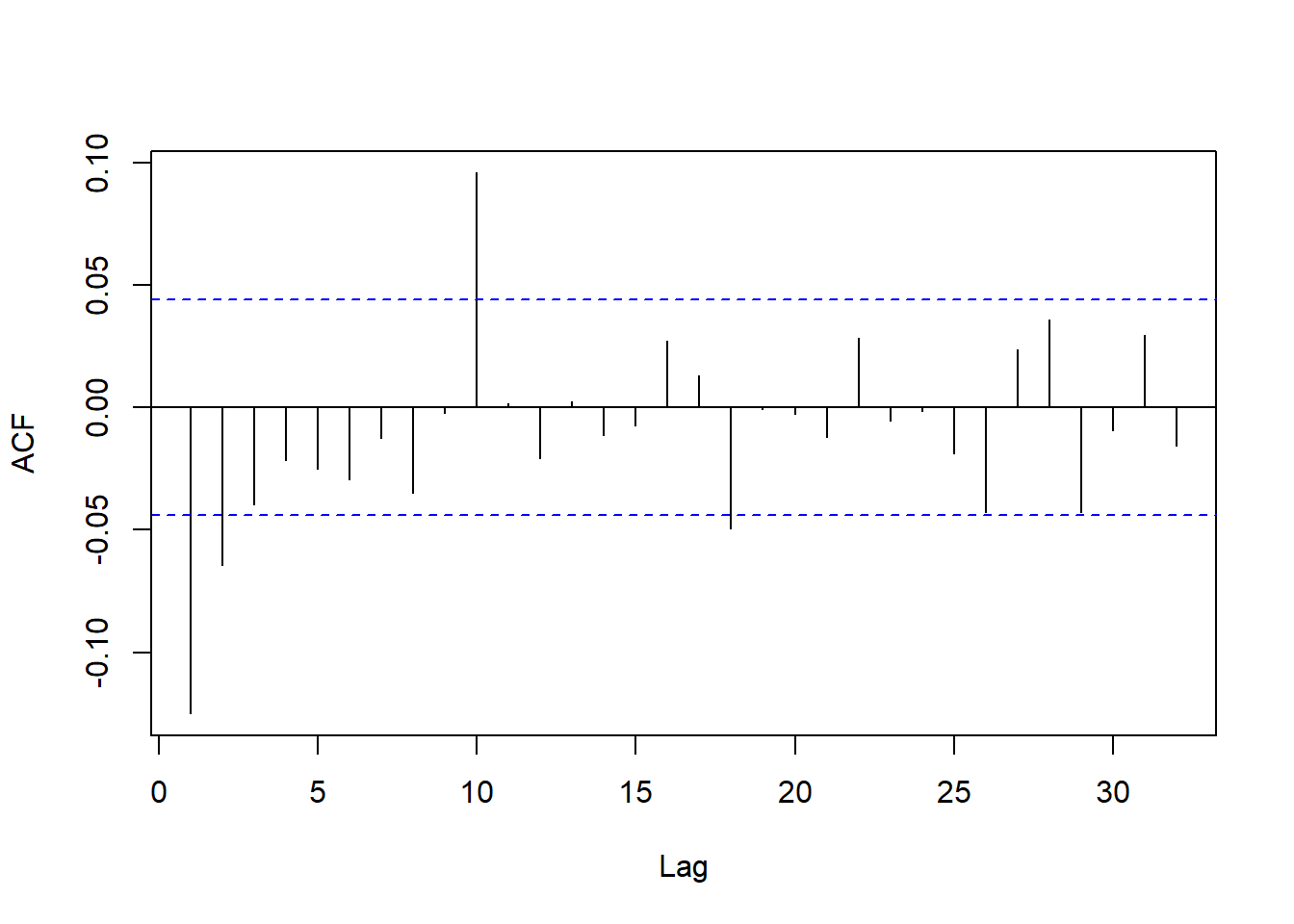
VIX日对数收益率的ACF

图11.3: VIX日对数收益率的ACF

虽然在滞后10的位置ACF也超界， 但是在低阶就只有滞后1明显超界， 所以对数收盘价用ARIMA(0,1,1)还是合理的。 ARIMA建模：

resm <- forecast::Arima(c(coredata(vix)), order=c(0,1,1)); resm
## Series: c(coredata(vix)) 
## ARIMA(0,1,1) 
## 
## Coefficients:
##           ma1
##       -0.1500
## s.e.   0.0244
## 
## sigma^2 = 0.004563:  log likelihood = 2535.71
## AIC=-5067.42   AICc=-5067.41   BIC=-5056.23

建立的模型为 \[ X_t = X_{t-1} + \varepsilon_t - 0.1500 \varepsilon_{t-1}. \] 其中\(\hat\sigma^2 = 0.004561\)。 \(\theta = 0.1500\)。

检验残差是否白噪声：

Box.test(resm$residuals, lag=10, fitdf=1)
## 
##  Box-Pierce test
## 
## data:  resm$residuals
## X-squared = 47, df = 9, p-value = 3.925e-07

白噪声检验很显著， 说明模型有所不足。 从差分序列的\(\hat\rho_{10}\)很大可以预见这个问题。

另行试验ARIMA(0,1,10):

resm2 <- forecast::Arima(c(coredata(vix)), order=c(0,1,10)); resm2
## Series: c(coredata(vix)) 
## ARIMA(0,1,10) 
## 
## Coefficients:
##           ma1      ma2      ma3      ma4      ma5      ma6      ma7      ma8
##       -0.1493  -0.0716  -0.0484  -0.0258  -0.0303  -0.0401  -0.0131  -0.0181
## s.e.   0.0223   0.0226   0.0228   0.0225   0.0226   0.0236   0.0231   0.0219
##          ma9    ma10
##       0.0092  0.0966
## s.e.  0.0245  0.0230
## 
## sigma^2 = 0.004475:  log likelihood = 2559.57
## AIC=-5097.13   AICc=-5097   BIC=-5035.59
Box.test(resm2$residuals, lag=20, fitdf=10)
## 
##  Box-Pierce test
## 
## data:  resm2$residuals
## X-squared = 9.5782, df = 10, p-value = 0.4782

这个模型的白噪声检验通过，而且AIC也更好。

注意我们用了8年的数据， 教材(Tsay 2013)用的数据是2008-05-01到2010-04-19为两年数据。 两年数据可能ARIMA(0,1,1)就足够。

也可以使用fabletools包， 简单指数平滑是ETS模型的特例， 可以用model()函数建模估计。 为了图形的辨识度我们只使用较晚的数据。

library(tsibble)
library(fable)
library(fabletools)
vix_tsib <- tibble(
    date = zoo::index(vix), 
    log_vix = coredata(vix)) |>
  filter(date >= ymd("2011-01-01")) |>
  mutate(iday = row_number()) |>
  as_tsibble(index = iday)
vix_ses <- vix_tsib |>
  model(ETS(
    log_vix ~ error("A") + trend("N") 
    + season("N") ))

ETS()函数用结构时间序列模型建模， 模型中水平\(\ell_t\)总是存在的， error("A")表示加性的随机误差项， trend("N")表示水平的增速项（见11.2）不存在， season("N")表示季节项不存在。

显示模型参数：

vix_ses |>
  tidy() |>
  knitr::kable()
.model term estimate
ETS(log_vix ~ error(“A”) + trend(“N”) + season(“N”)) alpha 0.8724598
ETS(log_vix ~ error(“A”) + trend(“N”) + season(“N”)) l[0] 2.8665077

这表明估计的\(\alpha=0.87\)，\(\ell_0 = 2.87\)。

拟合与预测图形：

vix_fore <- vix_ses |>
  forecast(h = 5)
vix_fore |>
  autoplot(vix_tsib) +
  geom_line(data = augment(vix_ses),
    aes(y = .fitted),
    color="red", alpha = 0.3)

可以看出指数平滑给出的拟合值总是比原始值变化慢了一步。

分解结果图形：

vix_ses |>
  components() |>
  autoplot()
## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).

三个图分别是原始数据、水平估计、拟合残差(remainder，或称随机误差项)。 每个图左侧的竖直阴影条长度代表该图形的纵轴放大倍数， 放大倍数越大， 该时间序列的实际取值范围越窄。

○○○○○

11.2 加入斜率项

11.2.1 传统的斜率项模型

可以在(11.2)-(11.3)基础上增加一个线性的斜率项\(b_t\)，变成： \[\begin{equation} \begin{aligned} \ell_t =& \alpha y_t + (1 - \alpha) (\ell_{t-1} + b_{t-1}), \\ b_t =& \beta (\ell_t - \ell_{t-1}) + (1 - \beta) b_{t-1} , \\ \hat y_{t+h|t} =& \ell_t + h b_t, \ h=1,2,\dots \end{aligned} \tag{11.7} \end{equation}\]

这里， \(\ell_t\)仍是水平值， \(t\)时刻的水平值用当前观测值\(y_t\)和用水平与水平变化量计算的对\(t\)时刻水平的一个预测值\(\ell_{t-1} + b_{t-1}\)作加权平均计算。 \(b_t\)表示水平值的一个比较稳定的增长速率， 称为斜率， \(b_t\)本身也用对\(b_t\)的一个估计\(\ell_t - \ell_{t-1}\)和上一个值\(b_{t-1}\)加权平均计算。 预测时，要在当前水平基础上加上水平值的斜率乘以预测步数， 所以预测值关于步数\(h\)是一个线性函数， 不是简单指数平滑那样的一条水平线。

可以看出这个模型对应于二阶差分平稳的模型， 一阶差分不能使得这样的\(\{y_t\}\)变得平稳。

例11.2 tsibbledata包的global_economy中有各国GDP， 对中国的人均GDP用带斜率项的指数平滑模型建模预测。

解答： 数据整理和时间序列图：

data(global_economy, package="tsibbledata")
gdppc_tsib <- global_economy |>
  filter(Country == "China") |>
  mutate(GDP_per_capita = GDP / Population) |>
  select(Year, GDP_per_capita) 
gdppc_tsib |>
  autoplot(GDP_per_capita) +
  labs(y = "USD", title = "中国年人均GDP")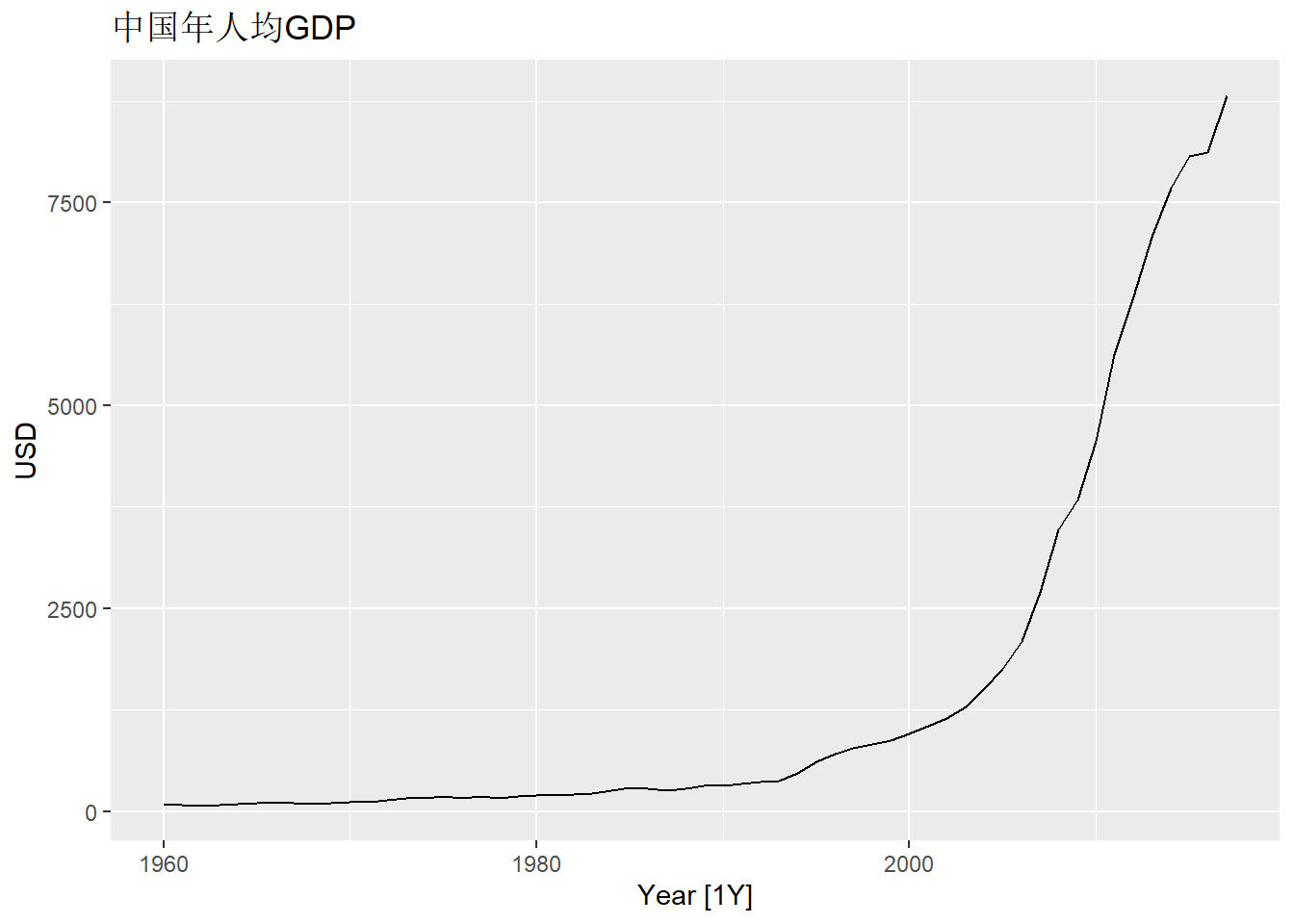

用fabletools的model()函数配合ETS()建模估计：

gdppc_fit <- gdppc_tsib |>
  model(AAN = ETS(GDP_per_capita ~
    error("A") + trend("A") + season("N")))
gdppc_fore <- gdppc_fit |>
  forecast(h = 5)

ETS()中的trend("A")表示模型中有加性的水平增速项\(b_t\)。 水平项是始终存在的。

查看gddpc_fit内部存储变量可以知道\(\alpha = 1.00\)， \(\beta = 0.557\)， 说明水平主要依赖于当前值， 斜率项的更新也很快，不够稳定。

拟合与预测结果作图：

gdppc_fore |>
  autoplot(gdppc_tsib) +
  geom_line(data = augment(gdppc_fit),
    aes(y = .fitted),
    color="red", alpha = 0.3)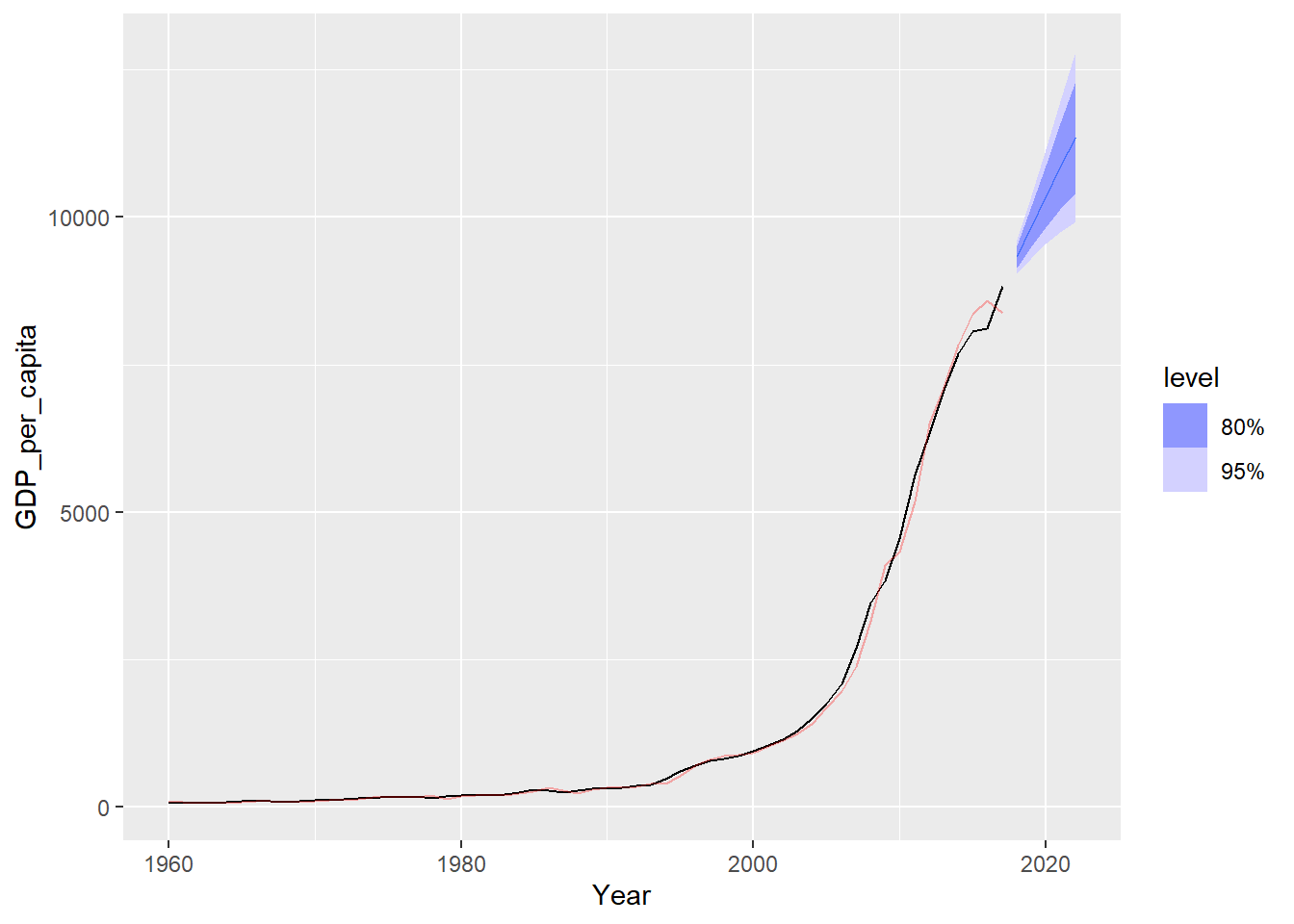

分解结果作图：

gdppc_fit |>
  components() |>
  autoplot()
## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).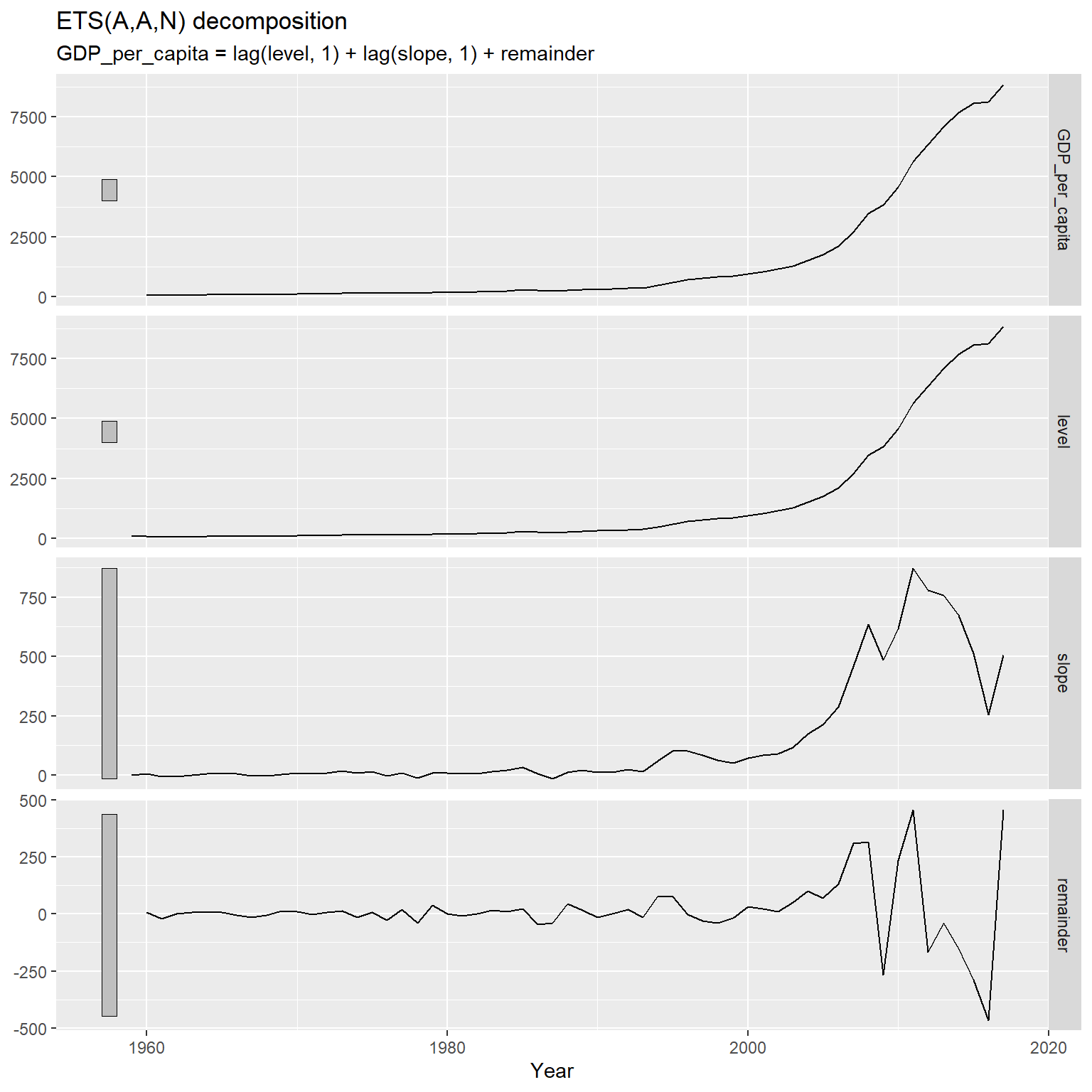

注意分解结果每个图形左侧的竖直阴影条， 此条越长， 代表这个图的纵轴范围越小， 纵轴方向的放大倍数越大。 原始值和水平值在同一个取值区间， 而斜率项和随机误差(remainder)都很小。

实际上， 由于中国人均GDP变化曲线非线性非常强， 加入斜率项的模型也并不够合适。 作对数变换可能更好。

○○○○○○

11.2.2 带衰减的斜率项模型

上述加入斜率项的模型在预测时总是按相同增速增长， 在实际应用中常常会高估。 Gardner & McKenzie (1985)提出了在预测时斜率项按负指数速度衰减的模型。 该模型仅修改了预测公式， 在预测公式中增加了一个衰减参数\(\phi\)，变成：

\[\begin{equation} \begin{aligned} \ell_t =& \alpha y_t + (1 - \alpha) (\ell_{t-1} + b_{t-1}), \\ b_t =& \beta (\ell_t - \ell_{t-1}) + (1 - \beta) b_{t-1} , \\ \hat y_{t+h|t} =& \ell_t + (\phi + \phi^2 + \dots + \phi^h) b_t, \ h=1,2,\dots \end{aligned} \tag{11.8} \end{equation}\] 预测公式中的\(h b_t = (1 + 1 + \dots + 1) b_t\)变成了\(h\)越大衰减越多的\((\phi + \phi^2 + \dots + \phi^h) b_t\)。

例11.3 仍考虑中国的人均GDP， 用带斜率项的指数平滑模型以及带斜率项衰减的模型建模预测。

解答：

因为人均GDP的时间序列曲线非线性非常严重， 我们仅用2001年以后的数据建模预测。

gdppc_fit2 <- gdppc_tsib |>
  filter(Year >= 2001) |>
  model(AAN = ETS(GDP_per_capita ~
    error("A") + trend("A") + season("N")),
    AANd = ETS(GDP_per_capita ~
    error("A") + trend("Ad", phi = 0.9) 
    + season("N")))
gdppc_fore2 <- gdppc_fit2 |>
  forecast(h = 5)

预测图形（不画水平值拟合线）：

gdppc_fore2 |>
  autoplot(gdppc_tsib |> filter(Year >= 2001), 
    level=NULL) +
  labs("中国人均GDP用两种斜率模型预测")

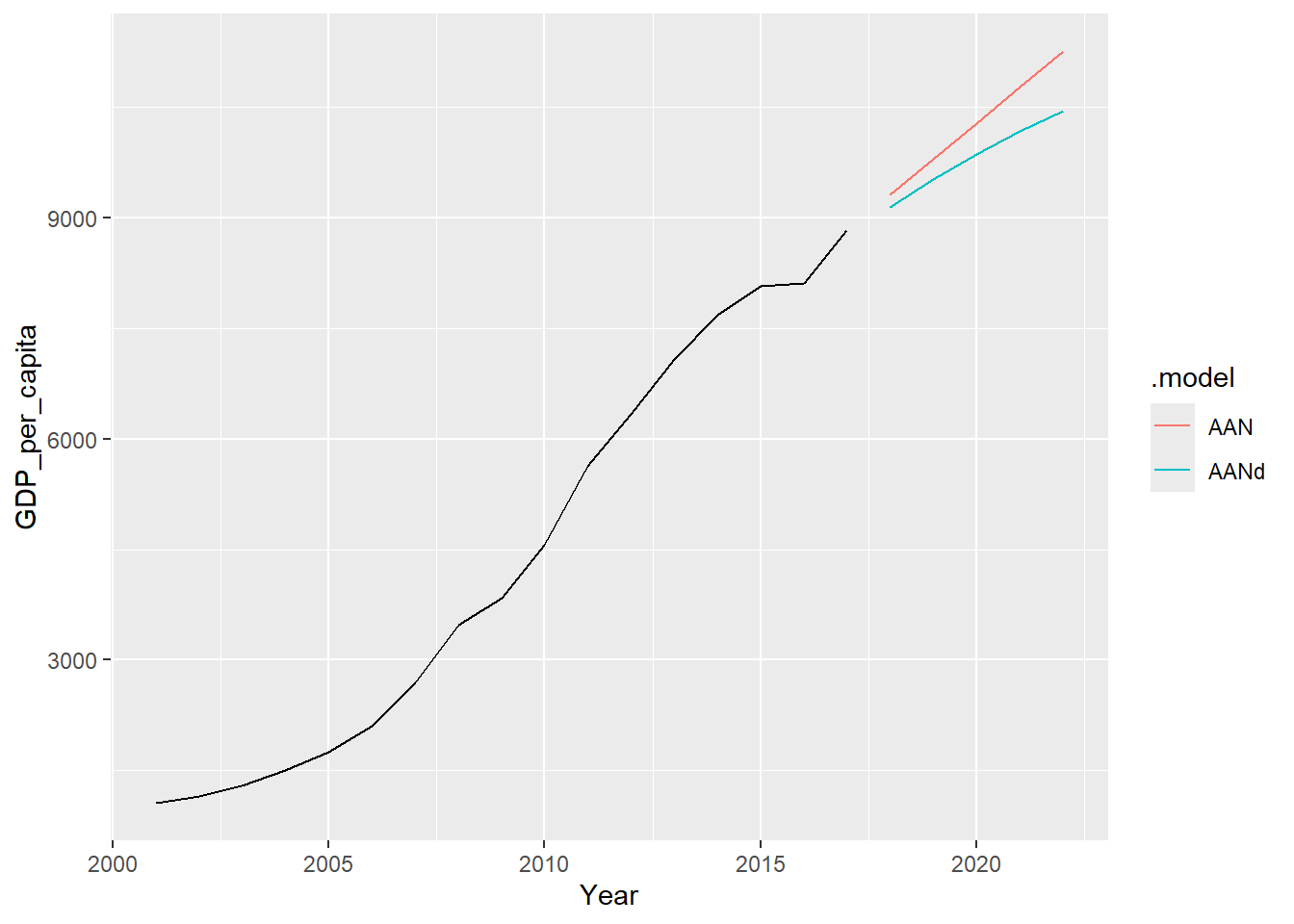
这里红色线是斜率项不衰减的， 浅蓝色线是斜率项衰减的。 可以看出带衰减的预测是一条下降的曲线， 不带衰减的预测是一条直线。

基于例11.2的讨论， 我们将因变量作对数变换， 仍考虑两种预测：

gdppc_fit3 <- gdppc_tsib |>
  filter(Year >= 2001) |>
  model(log_AAN = ETS(log(GDP_per_capita) ~
    error("A") + trend("A") + season("N")),
    log_AANd = ETS(log(GDP_per_capita) ~
    error("A") + trend("Ad", phi = 0.9) 
    + season("N")))
gdppc_fore3 <- gdppc_fit3 |>
  forecast(h = 5)

预测图形：

gdppc_fore3 |>
  autoplot(gdppc_tsib |> filter(Year >= 2001), 
    level=NULL) +
  labs("中国人均GDP对数变换用两种斜率模型预测") +
  scale_y_log10()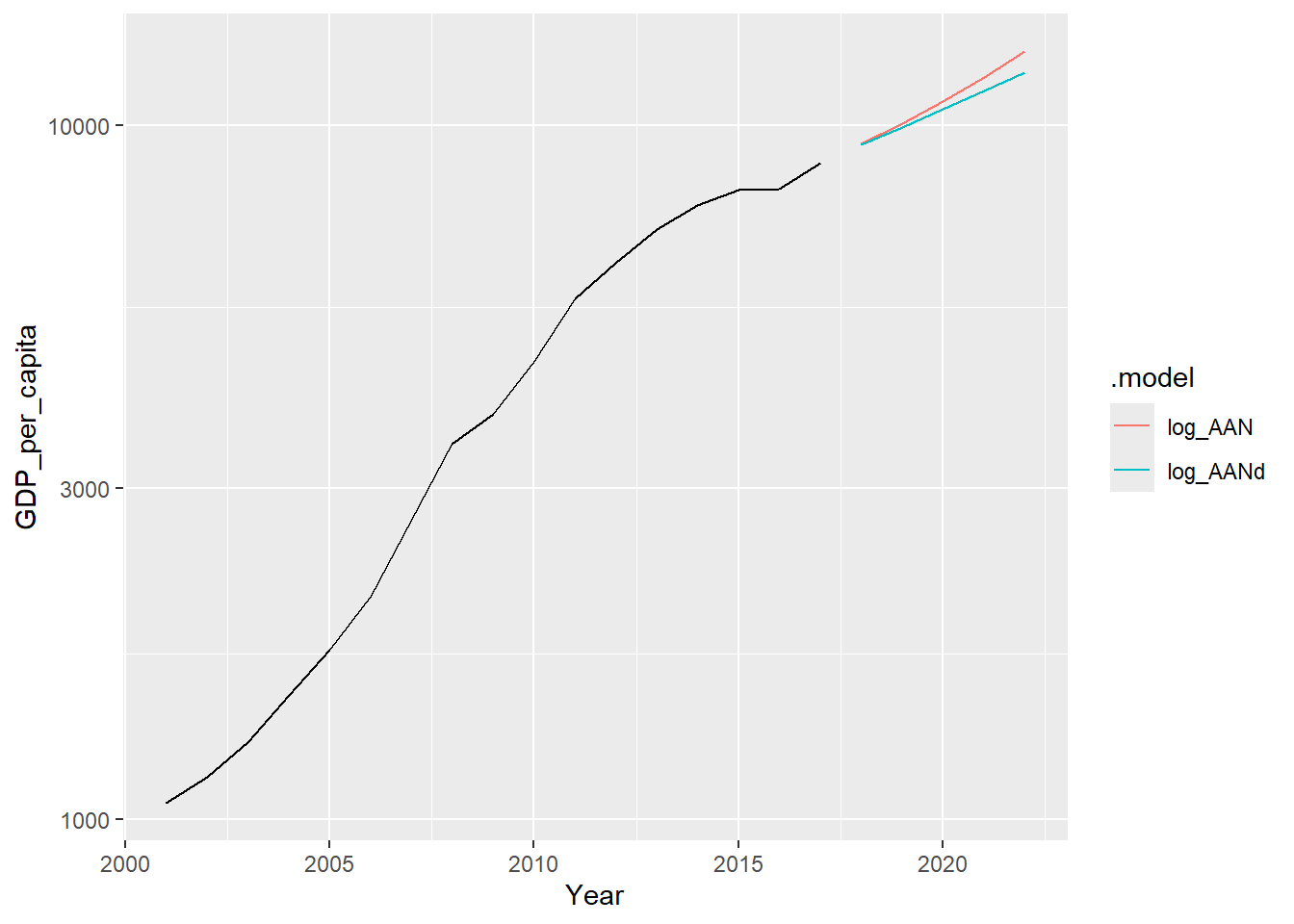

要注意模型中的因变量是做了对数变换的， 而上图纵轴使用对数刻度， 但刻度值为原始尺度。

○○○○○○

例11.4 基本R中的WWWusage变量是某地一个逐分钟上网用户数的时间序列数据， 共100分钟。 用不同的指数平滑模型建模预测， 比较预测精度。

解答： 10.3.8中讲了预测精度概念和计算程序。 先将ts类型时间序列转换为tsibble类型并作图：

wwwu_tsib <- WWWusage |>
  as_tsibble()
wwwu_tsib |>
  autoplot(value) +
  labs(y = "Number of users", x = "Minute",
    title = "Internet users per minute")

用三种不同指数平滑方法建模， 用stretch_tsibble()函数建立每次向前滚动一步的多个训练数据集， 进行滚动向前一步预测， 然后计算一步预测的精度指标：

wwwu_tsib |>
  stretch_tsibble(.init = 10) |>
  model(
    SES = ETS(value 
      ~ error("A") + trend("N") + season("N")),
    Holt = ETS(value 
      ~ error("A") + trend("A") + season("N")),
    Damped = ETS(value
    ~ error("A") + trend("Ad") + season("N")) ) |>
  forecast(h = 1) |>
  accuracy(wwwu_tsib) |>
  knitr::kable()
## Warning: The future dataset is incomplete, incomplete out-of-sample data will be treated as missing. 
## 1 observation is missing at 101
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
Damped Test 0.2878487 3.686810 2.999724 0.3468877 2.264128 0.6628854 0.6356913 0.3359403
Holt Test 0.0610064 3.874378 3.174028 0.2442952 2.382212 0.7014035 0.6680322 0.2962490
SES Test 1.4573097 6.049937 4.813149 0.9035711 3.548391 1.0636199 1.0431489 0.8029695

其中SES是简单指数平滑（仅含水平项）， Holt是带有斜率项的指数平滑， Damped是带有衰减斜率项的指数平滑。 从滚动一步预测的MAE和RMSE来看都是带有衰减斜率项的指数平滑最优。

程序结果中的警告来自于基于时刻1到100的训练数据作向前一步预测时， 响应的因变量真值未知所以无法对此步计算预测误差。

选用所有数据拟合带衰减斜率项的指数平滑模型， 查看估计的模型参数：

wwwu_fit <- wwwu_tsib |>
  model(Damped = ETS(
    value ~ error("A") + trend("Ad") + season("N") ))
wwwu_fit |>
  tidy() |>
  knitr::kable()
.model term estimate
Damped alpha 0.9999000
Damped beta 0.9966439
Damped phi 0.8149580
Damped l[0] 90.3517674
Damped b[0] -0.0172823

\(\alpha\)和\(\beta\)的估计值都接近于1， 所以水平主要由当前值决定， 斜率也主要由水平的变化决定，与过往斜率关系不大。 斜率在预测中的衰减系数\(\phi = 0.81\)。 分解图形：

wwwu_fit |>
  components() |>
  autoplot()
## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).

从每个图右侧的竖直阴影条可以看出斜率项和误差项作用不大。

拟合与预测图形：

wwwu_fore <- wwwu_fit |>
  forecast(h = 10)
wwwu_fore |>
  autoplot(wwwu_tsib) +
  labs(y = "Number of users", x = "Minute",
    title = "Internet users per minute")

由于预测中的斜率项作用是指数衰减的， 所以预测曲线随着\(h\)增大趋于水平线。

○○○○○○

11.3 加入季节成分

指数平滑方法可以增加季节项\(s_t\)， 称为Holt-Winters方法。 水平项、季节项、误差项可以相加， 也可以相乘， 如果季节项的振幅基本不变， 就适合加性模型； 如果季节项振幅越来越大， 就适合乘性模型。

11.3.1 加性Holt-Winters模型

Holt-Winters的加性模型用加权平均公式表示如下： \[\begin{equation} \begin{aligned} \ell_t =& \alpha (y_t - s_{t-m}) + (1 - \alpha) (\ell_{t-1} + b_{t-1}), \\ b_t =& \beta (\ell_t - \ell_{t-1}) + (1 - \beta) b_{t-1} , \\ s_t =& \gamma (y_t - \ell_{t-1} - b_{t-1}) + (1 - \gamma) s_{t-m}, \\ \hat y_{t+h|t} =& \ell_t + h b_t + s_{t - m + h_m^+} , \ h=1,2,\dots \end{aligned} \tag{11.9} \end{equation}\] 其中\(m\)是季节频率，如月度数据为12， 季度数据为4。 \(t - m + h_m^+\)是\(t, t-1, \dots, t-m+1\)中与\(t-m+h\)同月（季度）的值。

模型中的水平是将调整后的当前观测值与预测的水平作加权平均， 调整当前观测值的做法是扣除季节性估计， 仅剩下水平和误差部分， 预测的水平是上一步水平加上斜率项（增速）。 模型中的斜率项仍是估计的斜率项与上一斜率项的加权平均。 模型中的季节项是调整后的当前观测值与预测的季节项的加权平均， 观测值的调整是从观测值中扣除水平的预测值， 仅剩下季节部分和误差部分； 预测的季节项用已有的同月（季度）的季节项估计。 在预测\(y_{t+h}\)是， 取预测的水平加上预测的季节项， 预测的季节项是已有数据中最后一年与\(t+h\)同月（季度）的季节项。

11.3.2 乘性Holt-Winters模型

Holt-Winters的乘性模型为 \[\begin{equation} \begin{aligned} \ell_t =& \alpha \frac{y_t}{s_{t-m}} + (1 - \alpha) (\ell_{t-1} + b_{t-1}), \\ b_t =& \beta (\ell_t - \ell_{t-1}) + (1 - \beta) b_{t-1} , \\ s_t =& \gamma \frac{y_t}{\ell_{t-1} + b_{t-1}} + (1 - \gamma) s_{t-m}, \\ \hat y_{t+h|t} =& (\ell_t + h b_t) \times s_{t - m + h_m^+} , \ h=1,2,\dots \end{aligned} \tag{11.10} \end{equation}\]

这里假定斜率项的作用仍是加性的， 但水平与季节、误差项都是相乘的关系。

例11.5 对航空乘客数据用加性和乘性Holt-Winters方法建模。

解答： 数据准备

ap_tsib <- AirPassengers |>
  as_tsibble()
ap_tsib |>
  autoplot(value) +
  labs(title = "航空乘客数月度数据")

Holt-Winters方法建模：

ap_fit <- ap_tsib |>
  model(
    additive = ETS(
      value ~ error("A") + trend("A") + season("A")  ),
    multiplicative = ETS(
      value ~ error("M") + trend("A") + season("M") ) )

其中的trend("A")是表示水平的估计是用\(l_{t-1} + b_{t-1}\)， 用了加法。

向前预测1年， 作预测图形：

ap_fore <- ap_fit |>
  forecast(h = "1 years")
ap_fore |>
  autoplot(ap_tsib) +
  labs(x = "Year", 
    title = "航空乘客数用加性与程序Holt-Winters方法预测")

加性模型分解成分图形：

ap_fit |>
  components() |>
  filter(.model == "additive") |>
  autoplot() +
  labs(title = "加性模型的分解")
## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_line()`).

加性模型估计的季节项不够合理， 使得季节项被归并到了残差中。

乘性模型的分解图形：

ap_fit |>
  components() |>
  filter(.model == "multiplicative") |>
  autoplot()+
  labs(title = "乘性模型的分解")
## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_line()`).

对本例而言， 可以看出乘性模型的分解和预测合理， 加性模型的分解和预测不合理。

○○○○○○

11.3.3 斜率项带有衰减的Holt-Winters模型

在预测时， 关于斜率项进行衰减， 比如加性模型的公式为 \[\begin{equation} \begin{aligned} \ell_t =& \alpha (y_t - s_{t-m}) + (1 - \alpha) (\ell_{t-1} + \phi b_{t-1}), \\ b_t =& \beta (\ell_t - \ell_{t-1}) + (1 - \beta) \phi b_{t-1} , \\ s_t =& \gamma (y_t - \ell_{t-1} - \phi b_{t-1}) + (1 - \gamma) s_{t-m}, \\ \hat y_{t+h|t} =& \ell_t + h b_t + s_{t - m + h_m^+} , \ h=1,2,\dots \end{aligned} \tag{11.11} \end{equation}\] 这称为带有衰减的Holt-Winters方法。 加性模型与乘性模型都可以这样修改， 在model()的ETS()中写成trend("Ad")。

下面的例子对日数据以每周为一个周期建模。

例11.6 tsibble包的pedestrian数据集包含了墨尔本的4个探头每小时记录的行人个数。 选取其中的Southern Cross Station站点， 汇总为日数据， 选取2016年7月份数据， 然后用带衰减的Holt-Winters方法建模， 查看预测效果。

解答： 数据整理

ped_tsib <- pedestrian |>
  filter(Date >= "2016-07-01",
    Sensor == "Southern Cross Station") |>
  index_by(Date) |>
  summarise(Count = sum(Count)/1000)

注意上述程序中Date是日期型， 这里直接与字符型"2016-07-01"比较是利用了R的转换规则， 会自动将日期型转换为同样的字符型进行比较。

查看7月份的时间序列曲线：

ped_tsib |>
  filter(Date <= "2016-07-31") |>
  autoplot() +
  labs(y = "人数(千人)", 
    title = "Southern Cross Station站点日行人数")
## Plot variable not specified, automatically selected `.vars = Count`

图形中呈现出与星期几有关的模式。 利用7月份数据建模，以一星期为一个周期：

ped_fit <- ped_tsib |>
  filter(Date <= "2016-07-31") |>
  model(
    hw = ETS(Count ~ 
      error("M") + trend("Ad") + season("M")) ) 
ped_fore <- ped_fit |>
  forecast(h = "2 weeks") 
ped_fore |>
  autoplot(ped_tsib |> filter(Date <= "2016-08-14")) +
  labs(title = "日行人数预测",
    y="人数(千人)")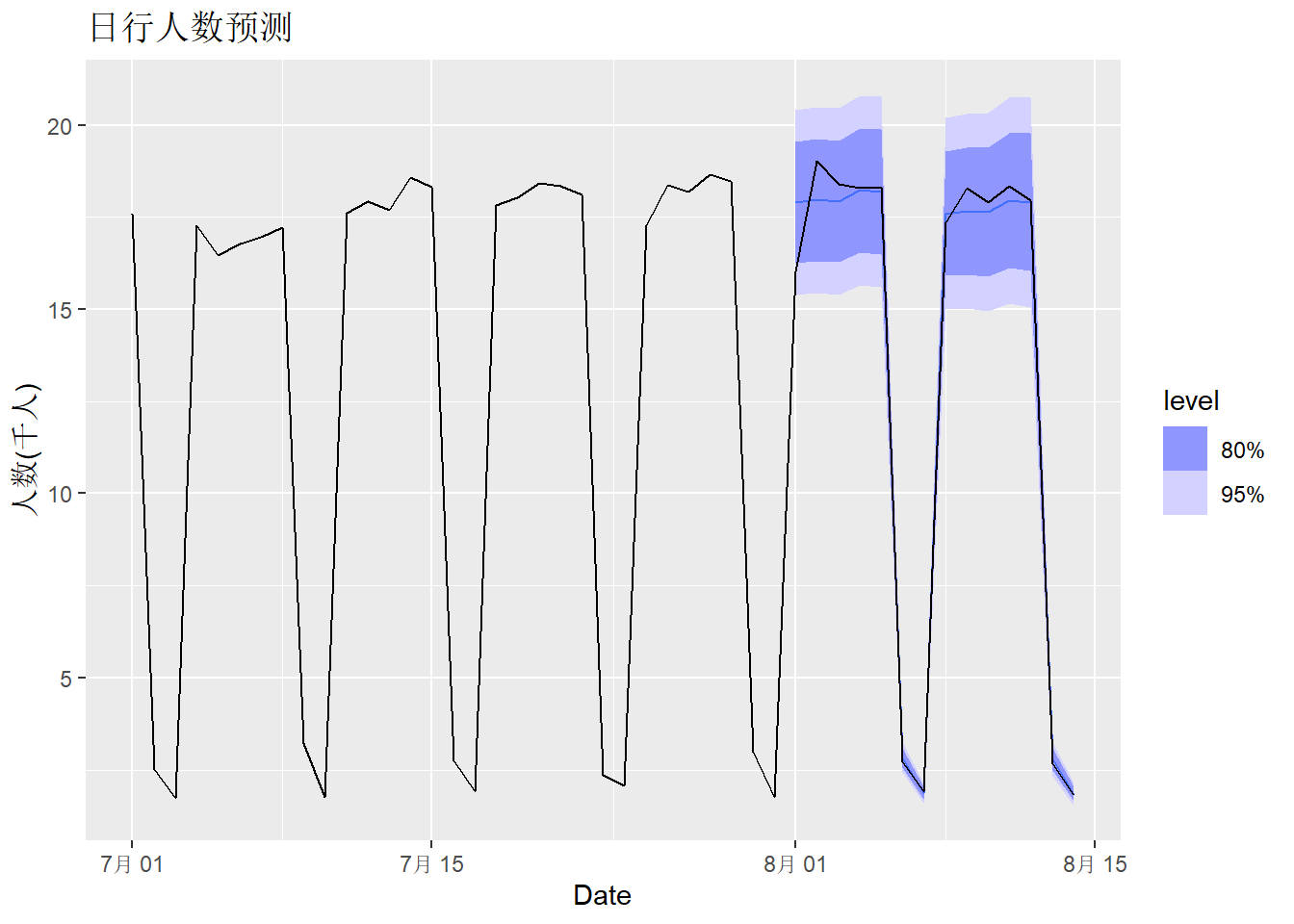

选用了带衰减的Holt-Winters乘性模型， 预测与真实值比较接近。

○○○○○○

11.4 fable包的指数平滑方法介绍

fable包提供了一个ETS函数， 这是Holt-Winters指数平滑方法用统计模型建模的一个完整体系的调用界面， 配合fabletools的model(), forecast(), autoplot()等函数可以进行Holt-Winters类型的时间序列分解建模和预测。

本节先介绍ETS函数支持的各个模型， 然后讨论其背后的统计理论。 前面几节给出的公式如(11.9)可以用来估计平滑参数， 计算预测值， 但无法计算预测区间， 无法进行假设检验、模型比较等统计推断。 本节将介绍如何使用统计模型实现ETS的功能。

11.4.1 专用记号

ETS()函数的第一个自变量是R公式对象， 公式左侧是因变量， 右侧用trend(), season(), error()规定不同的组合方式。

trend()用不同输入参数区分\(\ell_{t-1}\)与\(b_{t-1}\)的组合方式， "N"表示没有斜率项仅有水平项， "A"表示水平与斜率项之间是相加的， "Ad"表示水平与衰减的斜率项相加。

season()用来规定季节项加入模型中的方式， 输入参数"N"表示没有季节项， 输入"A"表示水平与季节项相加， 输入"M"表示水平与季节项相乘。

这样，trend()有"N", "A", "Ad"三种选择， season()有"N", "A", "M"三种选择， 两两搭配有九种不同模型。

以这些缩写表示不同的模型， 常见模型如下：

  • (N, N)表示没有斜率项也没有季节项， 这正是原始的简单指数平滑方法；
  • (A, N)是加入了斜率项、没有季节项的模型；
  • (Ad, N)是加入了衰减的斜率项、没有季节项的模型；
  • (A, A)是加性Holt-Winters方法， 水平项、斜率项、季节项都有；
  • (A, M)是乘性Holt-Winters方法， 水平项、斜率项、季节项都有；
  • (Ad, M)是衰减的乘性Holt-Winters方法。

11.4.2 ETS的状态空间模型表示

我们用状态空间模型(见30)表示指数平滑类方法。 状态空间模型定义了若干变量作为系统在时刻\(t\)的状态， 有一个“状态方程”规定从时刻\(t\)到时刻\(t+1\)的变化方式， 有一个“观测方程”规定在\(t\)时刻如何从状态变量获得观测值\(y_t\)。

对指数平滑方法在用状态空间模型表示时， 误差项可以是加性的也可以是乘性的， 两种误差项产生的预测区间不同。 ETS()函数中error()区分这两种误差项， error("A")表示加性， error("M")表示乘性。

参考：

  • Hyndman, R. J., Koehler, A. B., Ord, J. K., & Snyder, R. D. (2008). Forecasting with exponential smoothing: The state space approach. Springer-Verlag.

11.4.2.1 ETS(A,N,N)：加性误差项的简单指数平滑

这就是11.1中的简单指数平滑。 用这个简单方法来演示如何将指数平滑的递推和预测公式转换成状态空间模型表示。

简单指数平滑的递推和一步预测公式分别为： \[\begin{equation} \begin{aligned} \ell_t =& \alpha y_t + (1 - \alpha) \ell_{t-1} , \\ \hat y_{t+1|t} =& \ell_t + b_t . \end{aligned} \tag{11.12} \end{equation}\]

从\(\ell_t\)的递推公式变换可得 \[\begin{aligned} \ell_t =& \alpha y_t + (1 - \alpha) \ell_{t-1} \\ =& \ell_{t-1} + \alpha (y_t - \ell_{t-1}), \end{aligned}\] 其中\(\ell_{t-1} = \hat y_{t|t-1}\)， 所以记\(\varepsilon_t = y_t - \ell_{t-1}\)， 这是对\(y_t\)作一步预测的预测误差， 有 \[\begin{equation} \ell_t = \ell_{t-1} + \alpha \varepsilon_t . \tag{11.13} \end{equation}\]

\(\{y_t \}\)是实际观测值序列， 而\(\ell_t\)是一个潜在的不可观测序列， 代表当前取值水平， 是观测序列的一种平滑结果。 称\(\ell_t\)为状态变量， 称(11.13)是“状态方程”， 状态方程表示状态变量如何演变。 (11.13)代表了上一步的状态变量\(\ell_{t-1}\)在获得新的观测值\(y_t\)后如何修正为新的\(\ell_t\)， 当\(y_t\)对应的预测误差\(\varepsilon_t\)为正误差时， 说明水平偏低了， 所以将上一个水平加上用\(\alpha\)乘子衰减后的误差大小， 将水平向上调整； 反之则向下调整。 \(\alpha\)取值越接近于1， 调整越距离， 结果估计出的水平曲线越不光滑。

由\(\hat y_{t|t-1} = \ell_{t-1}\)和\(\varepsilon_t = y_t - \hat y_{t|t-1}\)得到 \[ y_t = \ell_{t-1} + \varepsilon_t, \] 这称为观测方程。 将状态方程与观测方程写在一起， 统称为状态空间模型： \[\begin{aligned} \ell_t =& \ell_{t-1} + \alpha \varepsilon_t , \\ y_t =& \ell_{t-1} + \varepsilon_t . \end{aligned}\]

这是一个“新息”状态空间模型， 这里的定语“新息”是指状态方程和观测方程共享了误差项\(\{\varepsilon_t \}\)， 而普通的状态空间模型这两个方程一般使用相互独立的误差项。

通常设\(\{\varepsilon_t \}\)独立同\(\text{N}(0, \sigma^2)\)分布， \(\alpha\)和\(\sigma^2\)是此模型的两个未知参数。

11.4.2.2 ETS(M,N,N)：乘性误差项的简单指数平滑

乘性误差项将误差表示为以预测值为分母的相对预测误差： \[ \varepsilon_t = \frac{y_t - \hat y_{t|t-1}}{\hat y_{t|t-1}} . \] 其中\(\hat y_{t|t-1} = \ell_{t-1}\)， 于是有 \[ y_t = \ell_{t-1} + \ell_{t-1} \times \varepsilon_t = \ell_{t-1}(1 + \varepsilon_t) . \] 若记\(e_t = y_t - \hat y_{t|t-1}\)， 则 \[ e_t = \ell_{t-1} \times \varepsilon_t . \] 所以一步预测误差是水平的预测乘以模型误差项。 把\(\ell_t\)的变化误差仍用\(e_t\)乘以一个衰减系数\(\alpha\)表示， 即\(\ell_t = \ell_{t-1} + \alpha e_t\)， 就变成了 \[ \ell_t = \ell_{t-1} + \alpha \ell_{t-1} \varepsilon_t = \ell_{t-1} (1 + \alpha \varepsilon_t) . \] 状态空间模型为 \[\begin{aligned} \ell_t =& \ell_{t-1} (1 + \alpha \varepsilon_t) , \\ y_t =& \ell_{t-1} (1 + \varepsilon_t) . \end{aligned}\] 这个模型不再是线性高斯状态空间模型， 处理起来比线性高斯情形要复杂得多。

11.4.2.3 ETS(A,A,N)：加性误差项和加性斜率项的的Holt方法

设一步预报误差为 \[ \varepsilon_t = y_t - (\ell_{t-1} + b_{t-1}) . \] 状态空间模型形式为 \[\begin{aligned} \ell_t =& \ell_{t-1} + b_{t-1} + \alpha \varepsilon_t, \\ b_t =& b_{t-1} + \beta \varepsilon_t, \\ y_t =& \ell_{t-1} + b_{t-1} + \varepsilon_t . \end{aligned}\] 仍写成了新息状态空间模型形式， 即状态方程与观测方程共享新息的形式。

11.4.2.4 ETS(M,A,N)：乘性误差项和加性斜率项的的Holt方法

仍用\(\ell_{t-1} + b_{t-1}\)预测\(y_t\)，但定义新息为 \[ \varepsilon_t = \frac{y_t - (\ell_{t-1} + b_{t-1})}{\ell_{t-1} + b_{t-1}} . \] 这是乘性的误差。 状态空间模型形式为 \[\begin{aligned} \ell_t =& \ell_{t-1}(1 + \alpha \varepsilon_t), \\ b_t =& b_{t-1} + \beta (\ell_{t-1} + b_{t-1}) \varepsilon_t, \\ y_t =& (\ell_{t-1} + b_{t-1})(1 + \varepsilon_t) . \end{aligned}\]

其它的各种Holt-Winters方法都可以写成新息状态空间模型形式。

11.4.3 ETS模型估计与模型选择

将Holt-Winters方法表达成新息状态空间模型形式后， 因为假定了新息\(\{\varepsilon_t \}\)独立同\(\text{N}(0, \sigma^2)\)分布， 所以有了观测数据\(y_1, y_2, \dots, y_T\)后可以写出似然函数， 对参数进行最大似然估计。 fable包算法中将平滑参数\(\alpha\), \(\beta\), \(\gamma\)等， 以及初值\(\ell_0, b_0, s_0, s_{-1}\dots, s_{-m+1}\)等作为未知参数进行估计。 这些未知参数需要满足一定约束，如\(0 < \alpha < 1\)。

如果都是加性模型， 则点估计结果与最小二乘法得到的结果相同。 如果有乘性成分， 则结果与最小二乘法结果不同。

为了进行模型选择， 可以定义AIC、BIC等准则， AIC为 \[ \text{AIC} = -2 \log L + 2k, \] 其中\(L\)是似然函数的最大值， \(k\)是要最大化的参数（包括初值）的个数。

修正(corrected)的AIC定义为 \[ \text{AIC}_{c} = \text{AIC} + \frac{2k(k-1)}{T-k+1} . \] 修正的AIC在小样本情况下可以一定程度上修正AIC定阶的高估问题。

BIC定义为

\[ \text{BIC} = \text{AIC} + k[\log(T) - 2] . \]

如果ETS()函数中的error(), trend(), season()任意组合， 有三种情况会导致数值计算失败， 这三个组合是ETS(A, N, M), ETS(A, A, M), ETS(A, Ad, M)。 一般不使用这三个模型。

当\(y_t\)仅取正值时， 乘性误差的模型可能是有用的； 如果\(y_t\)有正有负， 最大似然估计也可能失败， 这时建议仅使用加性模型。

例11.7 tsibble包的tourism数据集包含了澳大利亚从1998年到2016年的旅行人数的季度数据。 对其中的度假旅游人数用ETS建模预测。

解答： 数据整理

holi_tsib <- tourism |>
  filter(Purpose == "Holiday") |>
  summarise(Trips = sum(Trips)/1000)
holi_tsib |>
  autoplot(Trips) +
  labs(title = "澳大利亚旅游人数",
    y = "人数(千人)")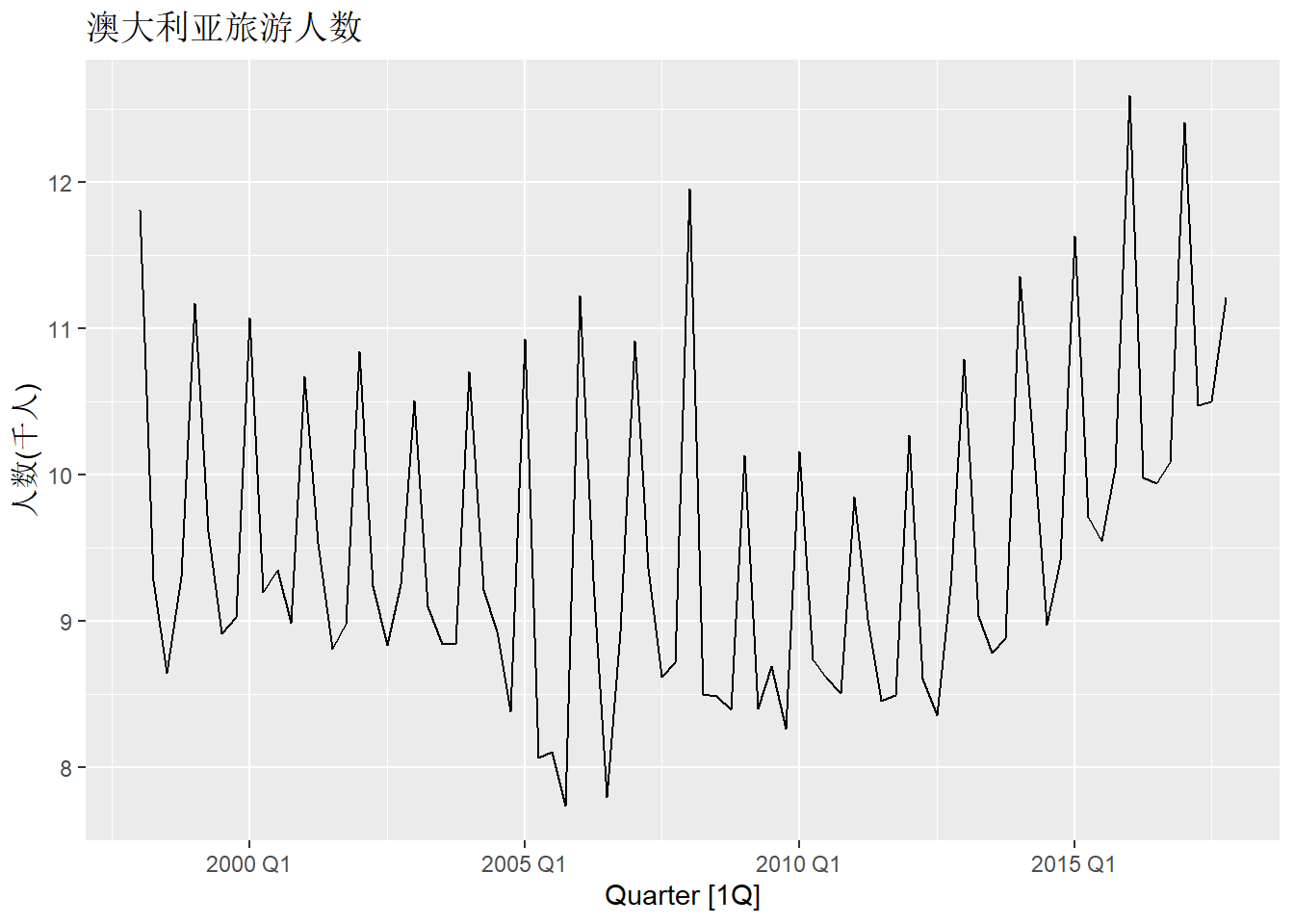

数据明显呈现出季节项， 而且不同年份有明显变化。 用ETS()函数自动选择模型类型， 用report()报告参数估计值和AIC等模型选择指标：

holi_fit <- holi_tsib |>
  model(ETS(Trips))
report(holi_fit)
## Series: Trips 
## Model: ETS(M,N,A) 
##   Smoothing parameters:
##     alpha = 0.3484054 
##     gamma = 0.0001000018 
## 
##   Initial states:
##      l[0]       s[0]      s[-1]      s[-2]    s[-3]
##  9.727072 -0.5376106 -0.6884343 -0.2933663 1.519411
## 
##   sigma^2:  0.0022
## 
##      AIC     AICc      BIC 
## 226.2289 227.7845 242.9031

结果选择的模型是乘性误差项， 没有斜率项， 加性季节项。

模型公式可以写成 \[\begin{aligned} \ell_t =& \ell_{t-1} + \alpha (\ell_{t-1} + s_{t-m}) \varepsilon_t, \\ s_t =& s_{t-m} + \gamma (\ell_{t-1} + s_{t-m}) \varepsilon_t, \\ y_t =& (\ell_{t-1} + s_{t-m})(1 + \varepsilon_t) . \end{aligned}\] 估计结果为\(\hat\alpha = 0.35\), \(\hat\gamma = 0.00010\)， 结果中还有初值\(\ell_0, s_0, s_{-1}, \dots, s_{-3}\)的估计值。 \(\hat\gamma\)很小， 说明季节项的逐年变化不大。

分解的各个成分作图：

holi_fit |>
  components() |>
  autoplot()
## Warning: Removed 4 rows containing missing values or values outside the scale range
## (`geom_line()`).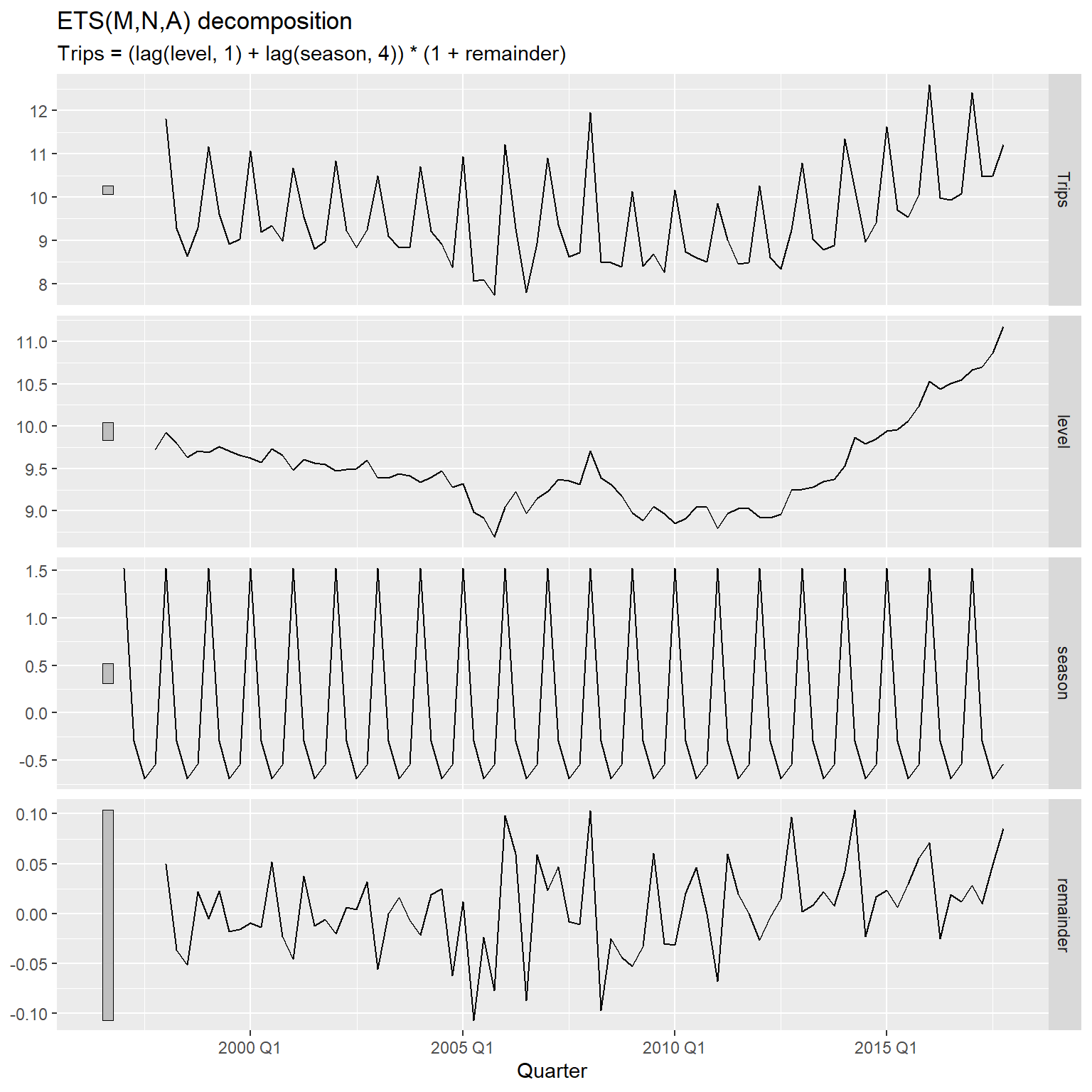

可以看出季节成分基本不变。 每个图左侧的竖直阴影条长度代表了该图纵轴放大倍数， 放大倍数越大， 对应的分解成分取值范围越小， 方差越小。 误差项(remainder)部分的阴影条很长， 说明残差方差很小， 但这是乘性的误差项， 不等于拟合残差， 而是一个相对误差， 所以所以拟合残差的大小从图中不好判断。

可以用augment()函数对拟合结果计算拟合值、拟合残差和新息残差， 在ETS()中新息残差就是前述的\(\{\varepsilon_t \}\)。 作图：

holi_fit |>
  augment() |>
  autoplot(.innov)

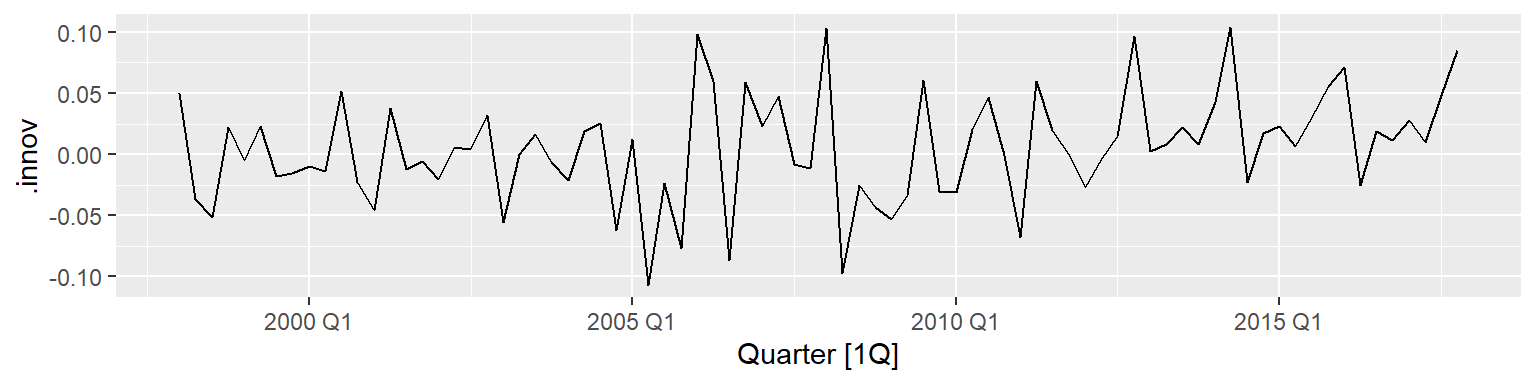
可见remainder与.innov相同。

.resid作图，这是拟合残差，即\(y_t - \hat y_{t|t-1}\)：

holi_fit |>
  augment() |>
  autoplot(.resid)

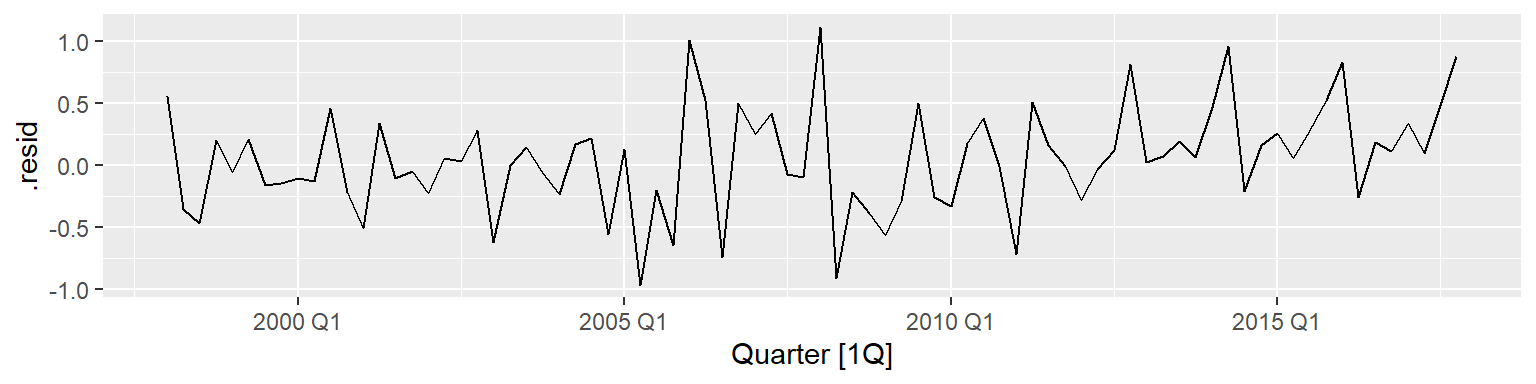
11.4.4 ETS模型预测

11.4.4.1 点预测

在估计了ETS模型参数后， 为了计算点预测\(\hat y_{T+h}\)， 只要按照模型取\(\varepsilon_{T+h} \equiv 0\)向前递推即可。

比如， 对ETS(M, A, N)， 按照状态空间模型， \[ y_{T+1} = (\ell_T + b_T)(1 + \varepsilon_{T+1}), \] 令\(\varepsilon_{T+1} = 0\), 得\(\hat y_{T+1|T} = \ell_T + b_T\)。

继续递推， \[\begin{aligned} y_{T+2} =& (\ell_{T+1} + b_{T+1})(1 + \varepsilon_{T+2}) \\ =& \ell_{T+1} + b_{T+1} \\ =& (\ell_T + b_T) (1 + \alpha \varepsilon_{T+1}) + b_T + \beta (\ell_T + b_T) \varepsilon_{T+1}) \\ =& \ell_T + 2 b_T . \end{aligned}\] 这与加性误差项时的预测公式相同。

ETS这样计算的点预测在加性模型时为预测分布的均值， 但有乘性季节项时不是。

fable包的forecast()函数从model()和ETS()拟合的结果中计算预测值。 这个函数总是计算预测分布的均值， 所以有乘性项时计算的预测值可能与传统Holt-Winters方法计算的预测值不同。

例如，澳大利亚度假旅游人数预测：

holi_fit |>
  forecast(h = 8) |>
  autoplot(holi_tsib) +
  labs(title = "澳大利亚度假旅游人数ETS预测",
    y = "人数(千人)")

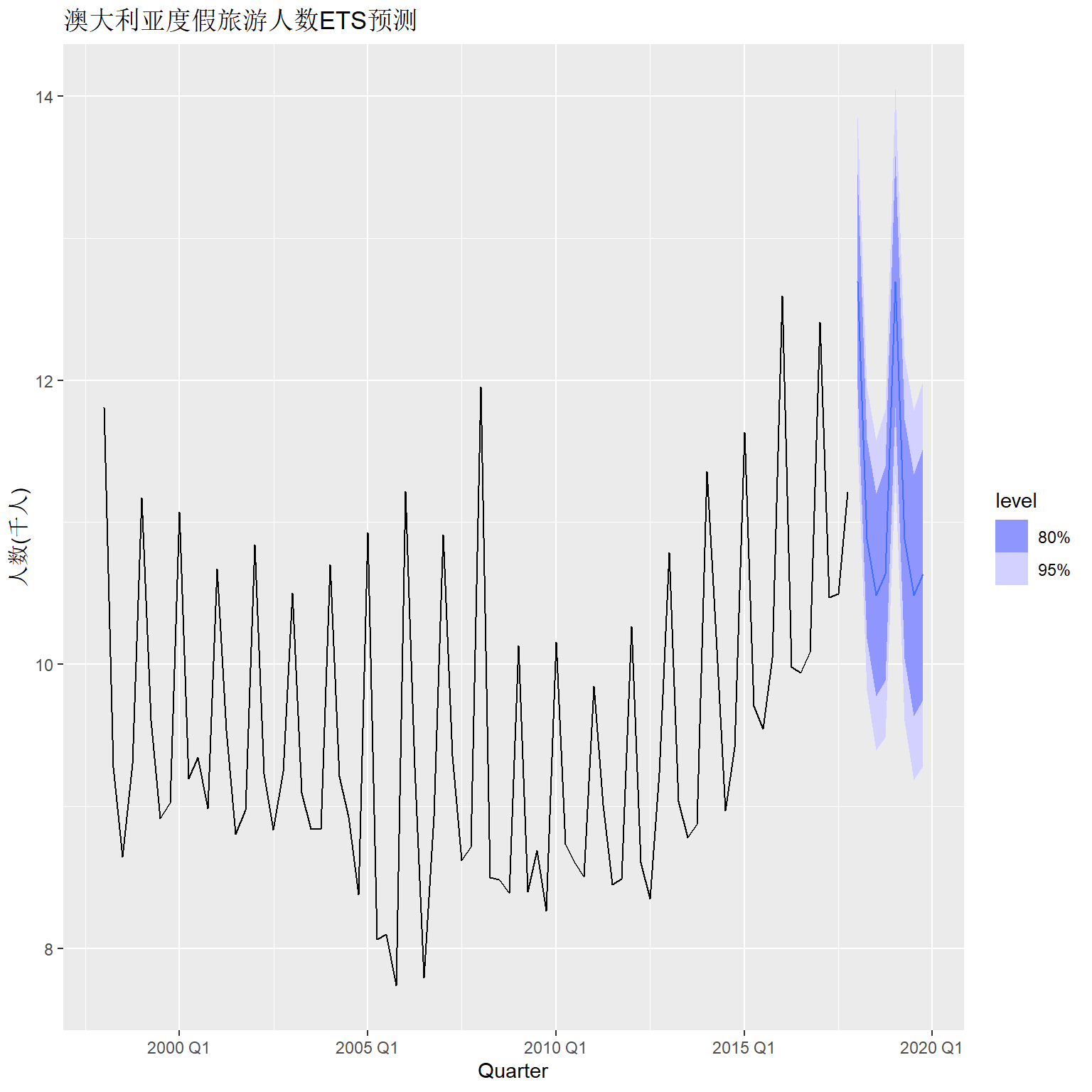
11.4.4.2 预测区间

有了统计模型后， 基于\(y_1, \dots, y_T\)可以计算\(y_{T+h}\)的预测分布； 只要取预测分布的\(\alpha/2\)和\(1 - \alpha/2\)就可以获得预测区间的下限和上限。

如果因变量没有做对数变换等非线性变换， 则ETS计算的预测区间形式一般是 \[ \hat y_{T+h|T} \pm \lambda \sigma_h, \] 其中\(\lambda\)由置信度决定， \(\sigma_h^2\)是向前\(h\)步预测分布的方差， 其公式比较复杂。 部分计算公式见(R. J. Hyndman and Athanasopoulos 2021)节8.7。 对简单指数平滑有\(\sigma_h^2 = \sigma^2 (1 + \alpha^2(h-1))\)。

11.5 计数数据的Croston方法

本节内容来自(R. J. Hyndman and Athanasopoulos 2021)节13.2。

时间序列数据如果是计数数据， 而且数值比较小， 可以取零， 这样的数据用ETS、ARIMA等模型都不容易得到好的预测。 Croston(1972)提出了一种简单的指数平滑方法。 对取非负整数值的\(\{y_t \}\)， 记\(\{q_i \}\)为\(\{y_t \}\)中第\(i\)个非零值， 记\(\{a_i \}\)为\(q_{i-1}\)和\(q_i\)之间的零值的个数， 对这两个序列分别用简单指数平滑拟合并预测。 这个模型原来用来对销售、进货等问题建模， 所以\(q_i\)称为“需求”， \(a_i\)称为“到来间隔”。

取两个平滑参数\(\alpha_q \in (0,1)\), \(\alpha_a \in (0,1)\)， 平滑公式为 \[\begin{aligned} \hat q_{i+1 | i} =& (1 - \alpha_q) \hat q_{i | i-1} + \alpha_q q_i, \\ \hat a_{i+1 | i} =& (1 - \alpha_a) \hat a_{i | i-1} + \alpha_a a_i . \end{aligned}\] 设\(t=1,2,\dots,T\)中最后一个非零值为\(q_j\)， 则对\(y_{T+h}\)的预测为 \[ \hat y_{T+h} = \hat q_{j+1} / \hat a_{j+1} , h=1,2,\dots \]

fable包的CROSTON()函数实现了这种方法， 并可以估计平滑参数\(\alpha_q\)和\(\alpha_a\)的值。

例11.8 考虑tsibbledata中PBS数据， 其中包含了澳大利亚各种药物用量的月度数据， 对其中免疫血清和免疫球蛋白产品进行预测。

解答： 提取数据

h02_tsib <- PBS |>
  filter(ATC2 == "J06") |>
  summarise(Scripts = sum(Scripts))

共有204个月的数据， 时间截止2008年6月。

作图：

h02_tsib |>
  autoplot(Scripts) +
  labs(title = "免疫血清和免疫球蛋白产品销量",
    y = "")

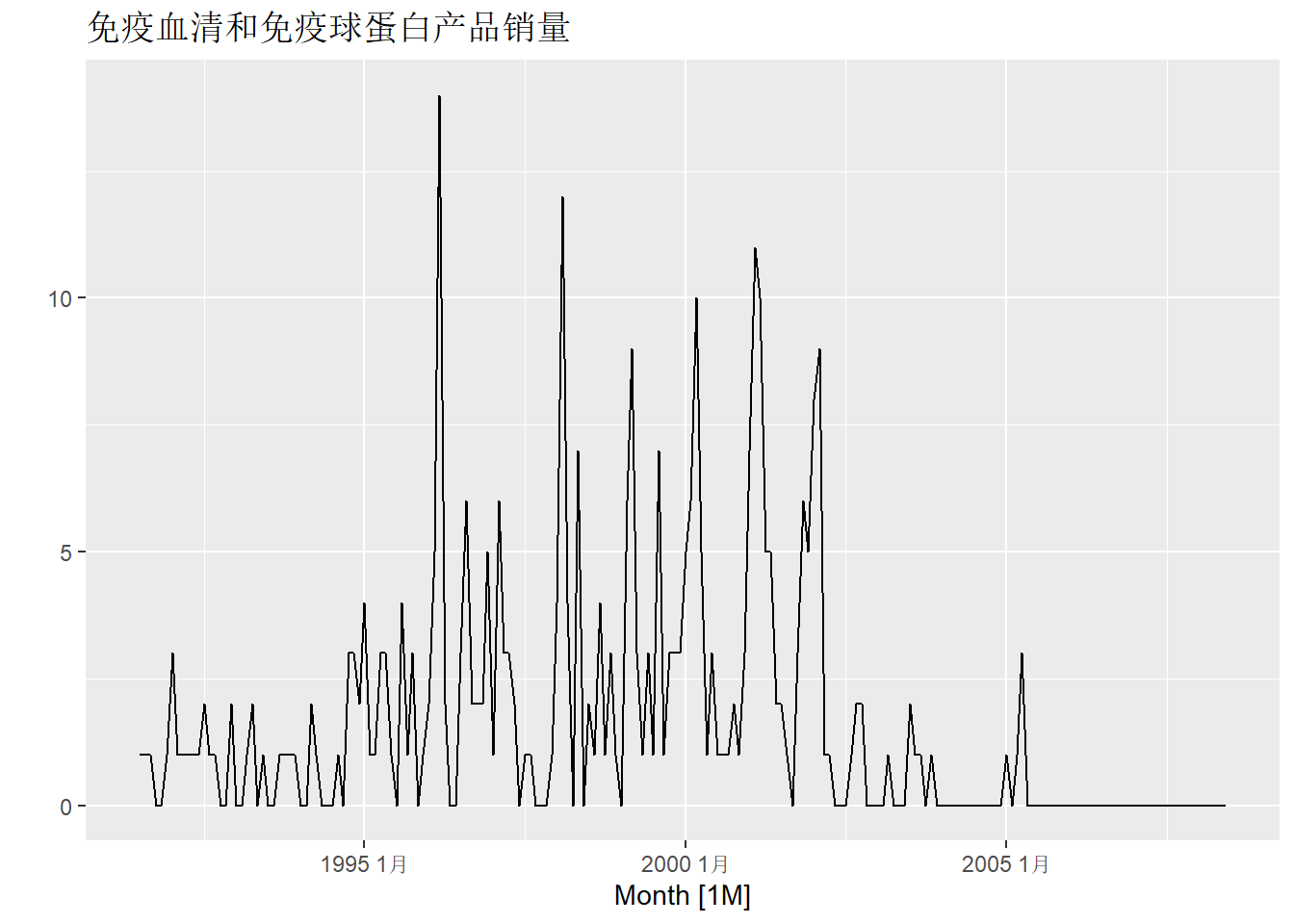
取值为非负整数值， 对取值作频率统计：

h02_tsib |>
  count(Scripts) |>
  knitr::kable()
Scripts n
0 90
1 49
2 18
3 19
4 5
5 7
6 5
7 3
8 1
9 2
10 2
11 1
12 1
14 1

取值中有许多0， 所以0是很重要的情况， 需要与非零区分开， 用Croston方法建模。

h02_fit <- h02_tsib |>
  model(CROSTON(Scripts))

预测：

h02_fore <- h02_fit |>
  forecast(h = 6) 
h02_fore |>
  knitr::kable()
.model Month Scripts .mean
CROSTON(Scripts) 2008 7月 0.9735062 0.9735062
CROSTON(Scripts) 2008 8月 0.9735062 0.9735062
CROSTON(Scripts) 2008 9月 0.9735062 0.9735062
CROSTON(Scripts) 2008 10月 0.9735062 0.9735062
CROSTON(Scripts) 2008 11月 0.9735062 0.9735062
CROSTON(Scripts) 2008 12月 0.9735062 0.9735062

B 参考文献

Hyndman, R. J., and G Athanasopoulos. 2021. Forecasting: Principles and Practice. 3rd edition. OTexts: Melbourne, Australia. http://OTexts.com/fpp3.
———. 2013. 金融数据分析导论：基于R语言. 机械工业出版社.