22 随机波动率模型
本章内容来自自(Tsay 2013)§4.13和§4.14内容。
22.1 随机波动率模型
前面的波动率方程中\(\sigma_t^2 = \text{Var}(a_t | F_{t-1})\)都是被\(\sigma_{t-1}, \dots\)和 \(a_{t-1}, \dots\)完全决定。 另一种方法是假定\(\sigma_t^2\)的模型本身有新息, 这样的模型称为随机波动率(Stochastic Volatility, SV)模型。 模型写成 \[\begin{aligned} a_t = \sigma_t \varepsilon_t, \quad (1 - \alpha_1 B - \dots - \alpha_m B^m) \ln \sigma_t^2 = \alpha_0 + v_t . \end{aligned}\] 其中\(\sigma_t^2\)取对数是为了取消系数必须为非负的限制。 \(\{ \varepsilon_t \}\)独立同标准正态分布, \(\{ v_t \}\)独立同N(\(0, \sigma_v^2\))分布, \(\{ \varepsilon_t \}\)和\(\{ v_t \}\)相互独立。 \(\alpha_i\)为常数, 特征多项式\(1 - \alpha_1 z - \dots - \alpha_m z^m\)根都在单位圆外。 记\(\xi_t = \ln\sigma_t^2\), 则\(\{ \xi_t \}\)是一个严平稳AR(\(m\))序列。
加入\(v_t\)新息后, 收益率\(r_t\)的一个新息\(a_t\)就包含了\(\varepsilon_t\)和\(v_t\)两个新息, 这增加了模型的自由度, 但是使得从\(r_t\)数据估计模型参数变得更加困难, 需要使用Kalman滤波或者随机模拟方法计算拟似然估计。
当\(m=1\)时,有 \[\begin{aligned} \ln\sigma_t^2 \sim& \text{N}\left( \frac{\alpha_0}{1-\alpha_1}, \frac{\sigma_v^2}{1 - \alpha_1^2} \right) = \text{N}(\mu_h, \sigma_h^2) , \\ E a_t^2 =& \exp\left( \mu_h + \frac12 \sigma_h^2 \right) , \\ E a_t^4 =& 3 \exp\left( 2 \mu_h^2 + 2 \sigma_h^2 \right) , \\ \rho(a_t^2, a_{t-i}^2) =& \frac{e^{\sigma_h^2 \alpha_1^i} - 1}{3 e^{\sigma_h^2} - 1} . \end{aligned}\]
SV模型经常在拟合上有所改善, 但是波动率的样本外预测时好时坏。
22.2 长记忆随机波动率模型
对资产收益率的实证分析发现, 收益率本身没有长记忆性, 但是其平方序列或者绝对值序列的ACF往往衰减很慢。 前面GARCH类模型的建模中\(\sigma_{t-1}^2\)的系数很接近于1, 也提示有长记忆。
下面对1962年到2003年标普500指数和IBM股票的日对数收益率序列的绝对值作ACF, 可以看到长记忆现象存在。
da <- read_table(
"d-ibmvwewsp5-6203.txt",
col_types=cols(
.default=col_double(),
date=col_date(format="%Y%m%d")))
xts.ibm <- xts(log(1 + da[,-1]), da[["date"]])
ibm <- coredata(xts.ibm)[,"ibm"]
sp5 <- coredata(xts.ibm)[,"sp5"]标普500指数日对数收益率绝对值的ACF:
np <- 200; nt <- length(sp5)
tmpa <- acf(abs(sp5), lag.max=np, main="", plot=FALSE)
plot(seq(np), tmpa$acf[2:(np+1)], type="h",
xlab="Lag", ylab="acf", ylim=c(-0.05, 0.3))
abline(h=c(2,-2)/sqrt(nt), lty=2, col="blue")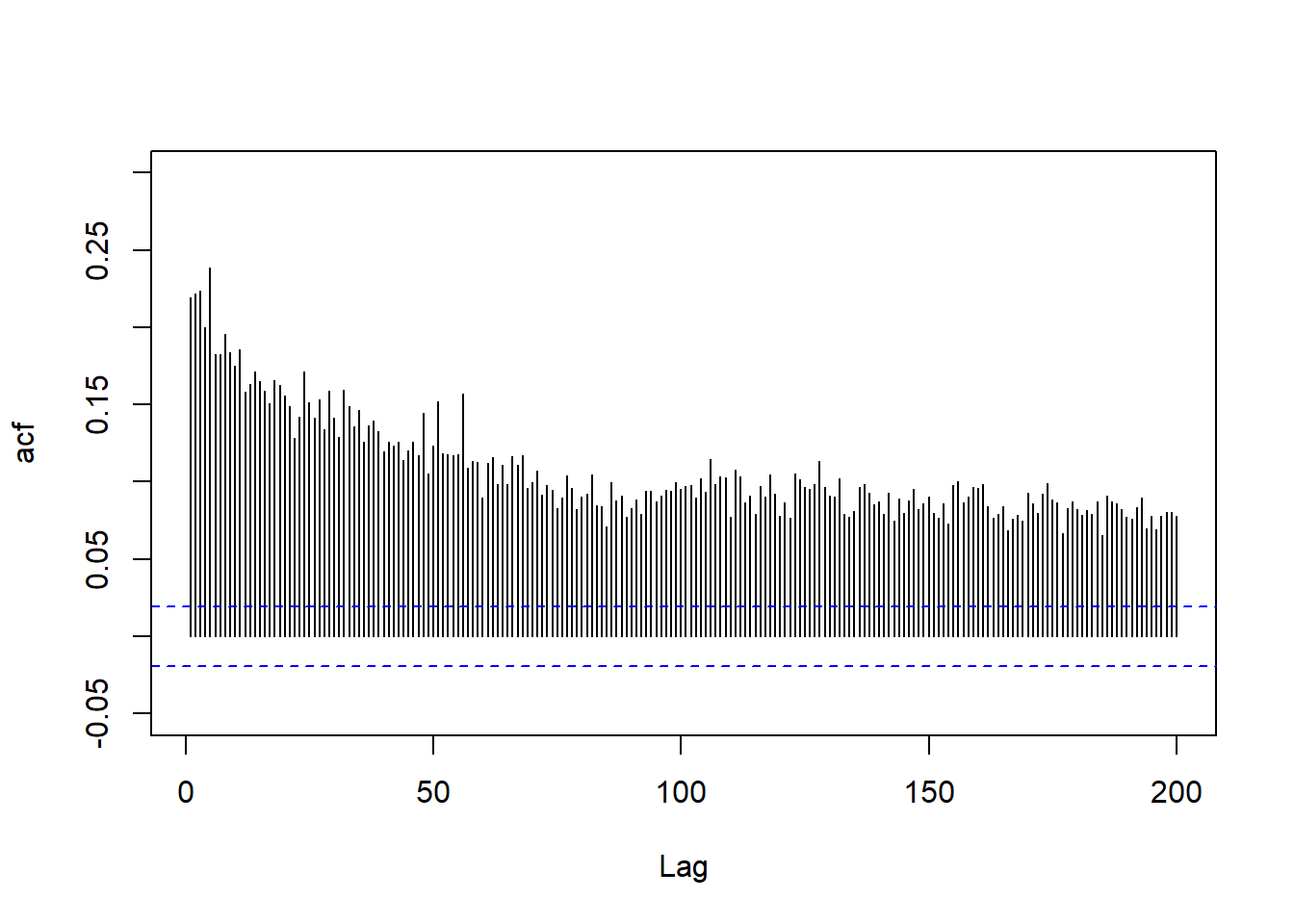
图22.1: 标普500指数日对数收益率绝对值的ACF
IBM股票日对数收益率绝对值的ACF:
np <- 200; nt <- length(sp5)
tmpa <- acf(abs(ibm), lag.max=np, main="", plot=FALSE)
plot(seq(np), tmpa$acf[2:(np+1)], type="h",
xlab="Lag", ylab="acf", ylim=c(-0.05, 0.3))
abline(h=c(2,-2)/sqrt(nt), lty=2, col="blue")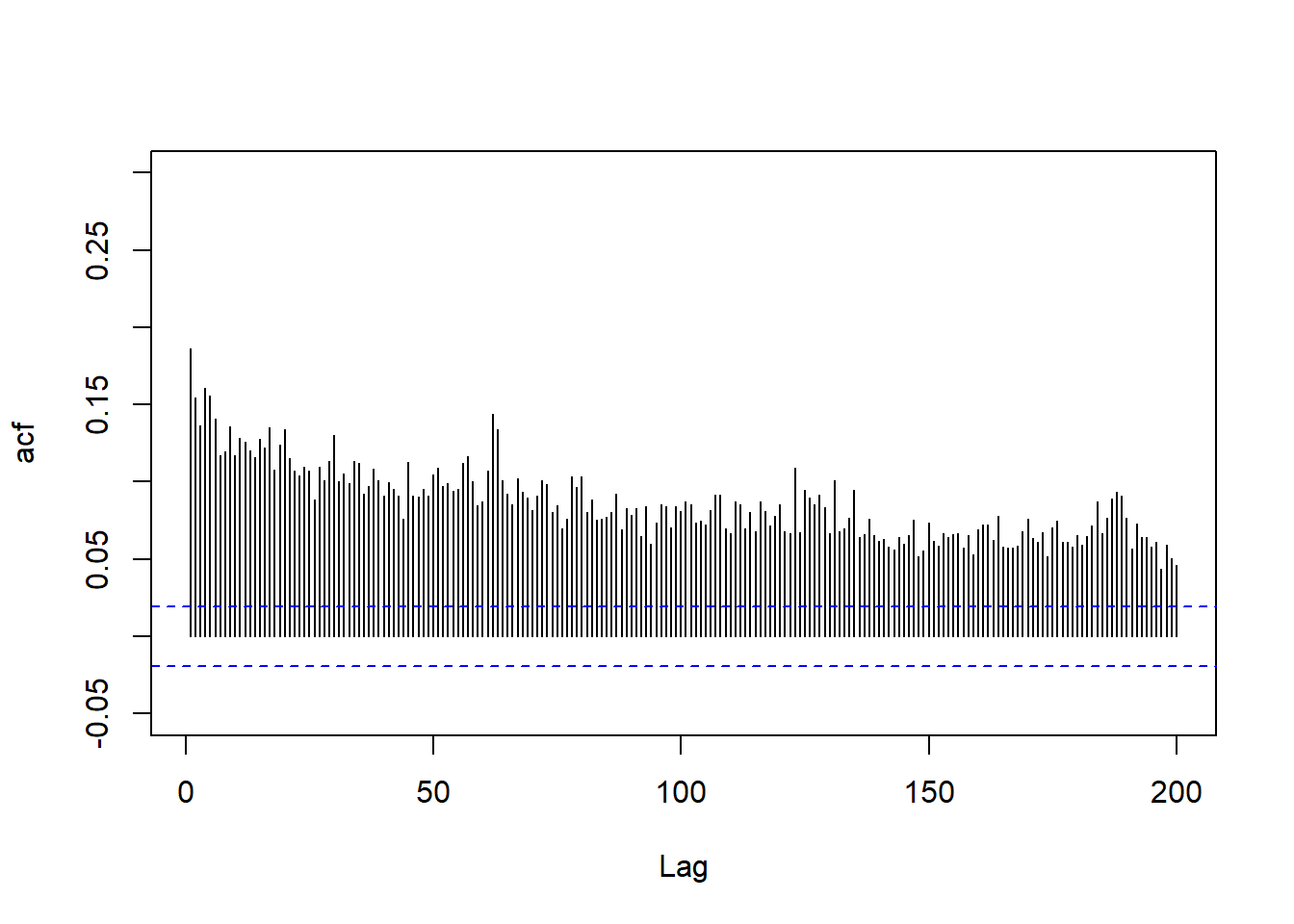
图22.2: IBM股票日对数收益率绝对值的ACF
简单的长记忆随机波动率(LMSV)模型可以写成 \[\begin{aligned} a_t = \sigma_t \varepsilon_t, \quad \sigma_t = \sigma e^{\frac12 u_t}, \quad (1 - B)^d u_t = \eta_t . \end{aligned}\] 其中\(\sigma>0\), \(\{\varepsilon_t \}\)和\(\{\eta_t\}\)是两个相互独立的独立同分布高斯白噪声列, \(\varepsilon_t \sim \text{N}(0,1)\), \(\eta_t \sim \text{N}(0, \sigma_\eta^2)\), \(0<d<0.5\)。 长记忆来源于分数差分\((1-B)^d\), 这使得\(u_t\)的ACF以负幂速度衰减而非负指数速度衰减。
对LMSV有 \[\begin{aligned} \ln a_t^2 =& \ln(\sigma_t^2 \varepsilon_t^2) = \ln \sigma^2 + u_t + \ln\varepsilon_t^2 \\ =& (\ln \sigma^2 + E \ln\varepsilon_t^2) + u_t + (\ln\varepsilon_t^2 - E \ln\varepsilon_t^2) \\ =& \mu + u_t + e_t . \end{aligned}\] 其中\(u_t\)是一个长记忆的平稳高斯时间序列, \(e_t\)是一个非高斯的独立同分布白噪声列。
LMSV估计比较复杂, 分数参数\(d\)可以用拟最大似然估计法或者回归方法估计。 标普500指数成份股日收益率平方的对数序列的\(d\)估计的中位数是0.38。 同一行业的股票的长记忆成分往往相同。