3 线性时间序列模型
3.1 介绍
课程采用蔡瑞胸（Ruey S. Tsay）的《金融数据分析导论：基于R语言》(Tsay 2013) （An Introduction to Analysis of Financial Data with R）作为主要教材之一。 “线性时间序列模型”这一部分是教材的第二章和第三章的授课笔记， 本章讲授时间序列的线性模型，包括：
- 一些基本概念
- AR, MA, ARMA模型
- 单位根过程
- 指数平滑
- 季节模型
- 回归模型中误差项有序列相关的处理
- 长记忆的分数阶差分模型
- 模型比较
- 实例分析
3.1.1 例子：苹果公司2007年到2017年股票日收盘价
chartSeries(
AAPL, type="line", TA=NULL,
subset="2003/2017",
major.ticks="years", minor.ticks=FALSE,
theme="white", name="Apple"
)
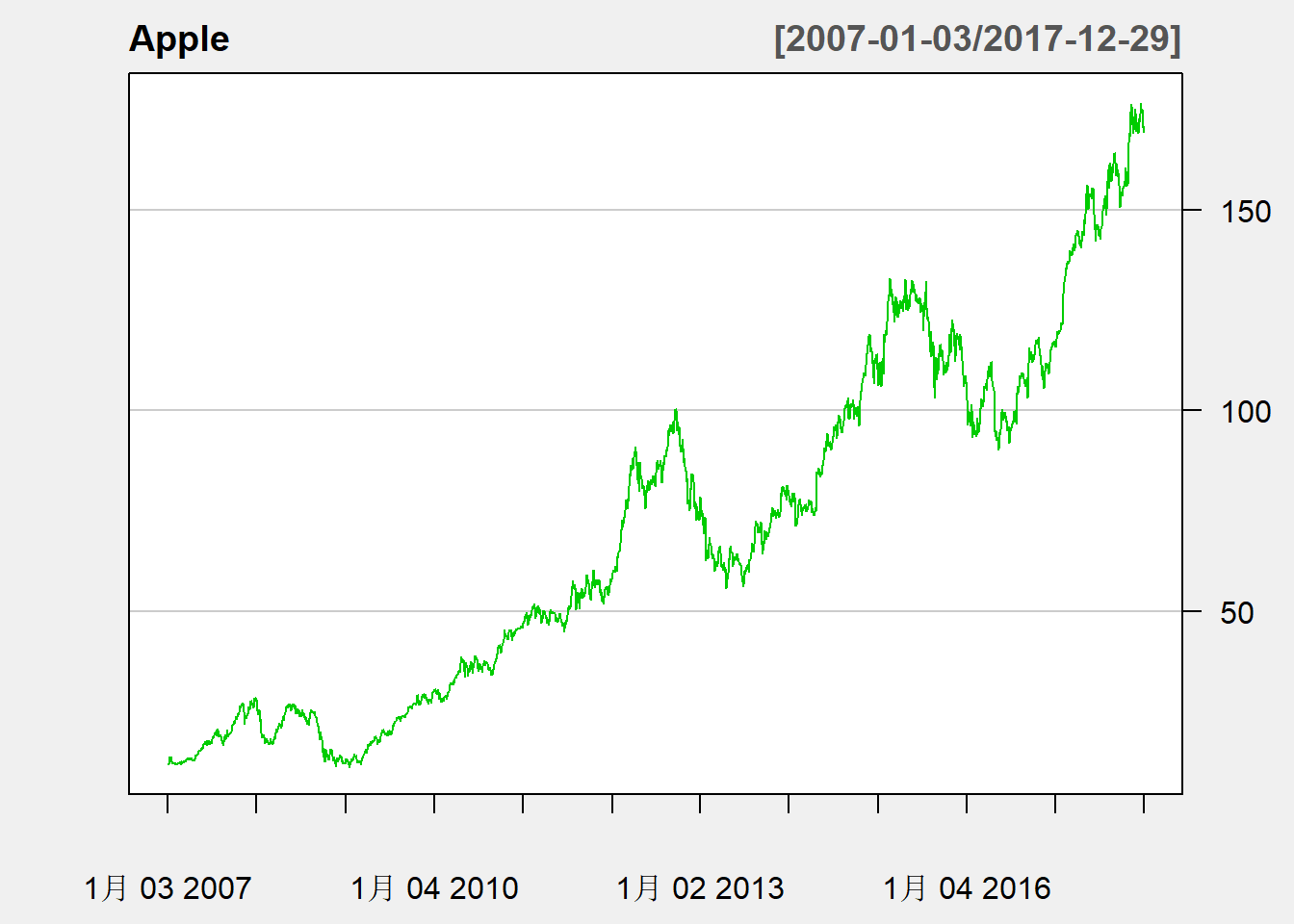
图3.1: 苹果公司股票日收盘价
股价序列呈现缓慢的、非单调的上升趋势， 局部又有短暂的波动。
3.1.2 例子：可口可乐公司盈利季度数据
可口可乐公司每季度发布的每股盈利数据。 读入：
da <- read_table(
"q-ko-earns8309.txt",
col_types=cols(
.default = col_double(),
pends = col_date("%Y%m%d"),
anntime = col_date("%Y%m%d")
) )
ko.Rqtr <- xts(da[["value"]], da[["pends"]])时间序列图：
chartSeries(
ko.Rqtr, type="line", TA=NULL,
major.ticks="years", minor.ticks=FALSE,
theme="white", name="Coca Kola Quarterly Return"
)
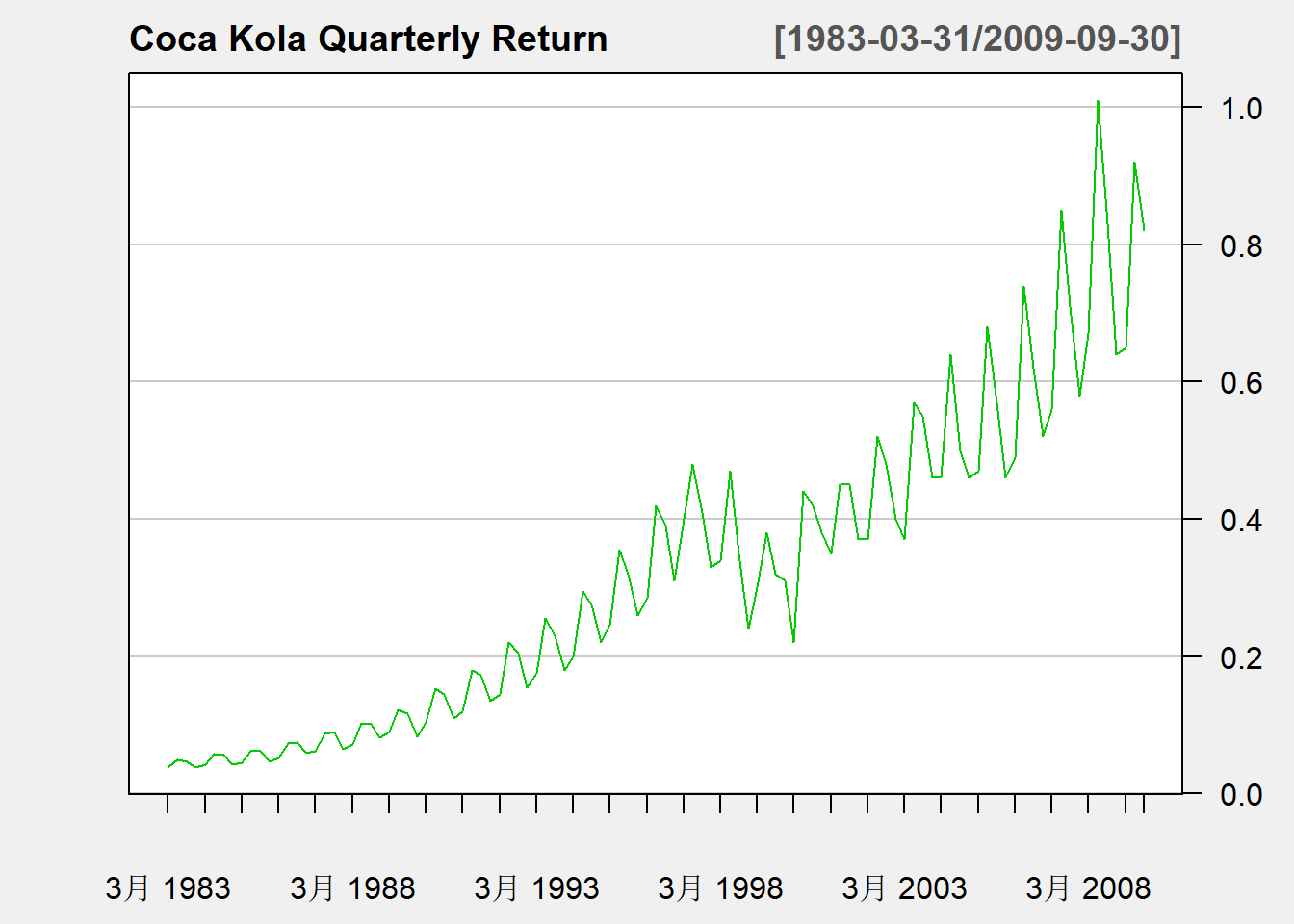
图3.2: 可口可乐季度盈利
序列仍体现出缓慢的、非单调的上升趋势，又有明显的每年的周期变化（称为季节性）， 还有短期的波动。
下面用基本R的plot()作图并用不同颜色标出不同季节。
tmp.x <- year(index(ko.Rqtr)) + (quarter(index(ko.Rqtr))-1)/4
tmp.y <- c(coredata(ko.Rqtr))
plot(tmp.x, tmp.y, type="l", col="gray",
xlab="year", ylab="Return")
cpal <- c("green", "red", "yellow", "black")
points(tmp.x, tmp.y, pch=16,
col=cpal[quarter(index(ko.Rqtr))])
legend("topleft", pch=16, col=cpal,
legend=c("Spring", "Summer", "Autumn", "Winter"))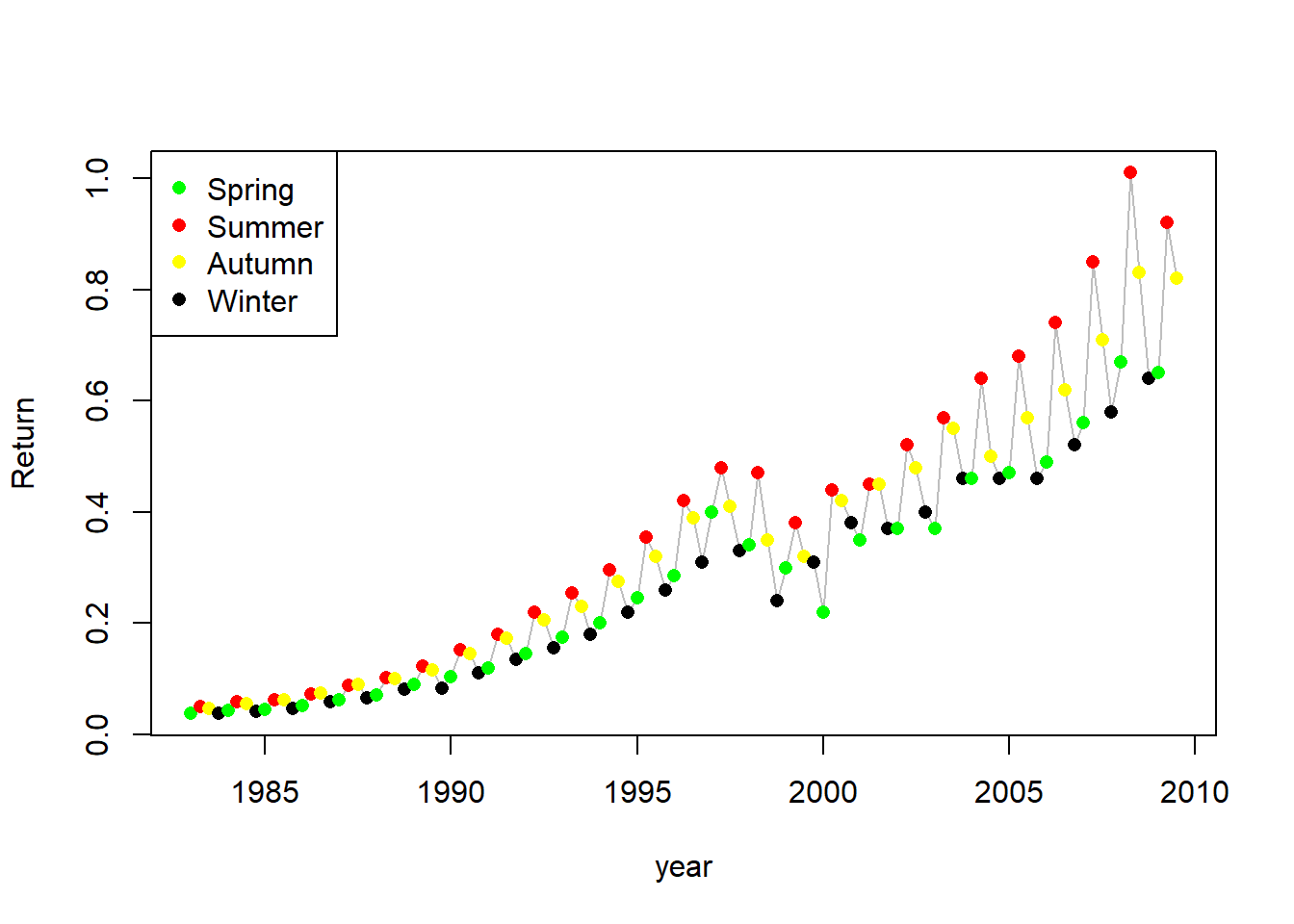
用ggplot2包绘图：
da_b <- da %>%
mutate(time = as.yearqtr(pends),
qtr = factor(quarter(pends),
levels = 1:4,
labels=c("Spring", "Summer", "Autumn", "Winter")))
ggplot(data = da_b, mapping = aes(
x = time, y = value)) +
geom_point(mapping=aes(color=qtr)) +
geom_line()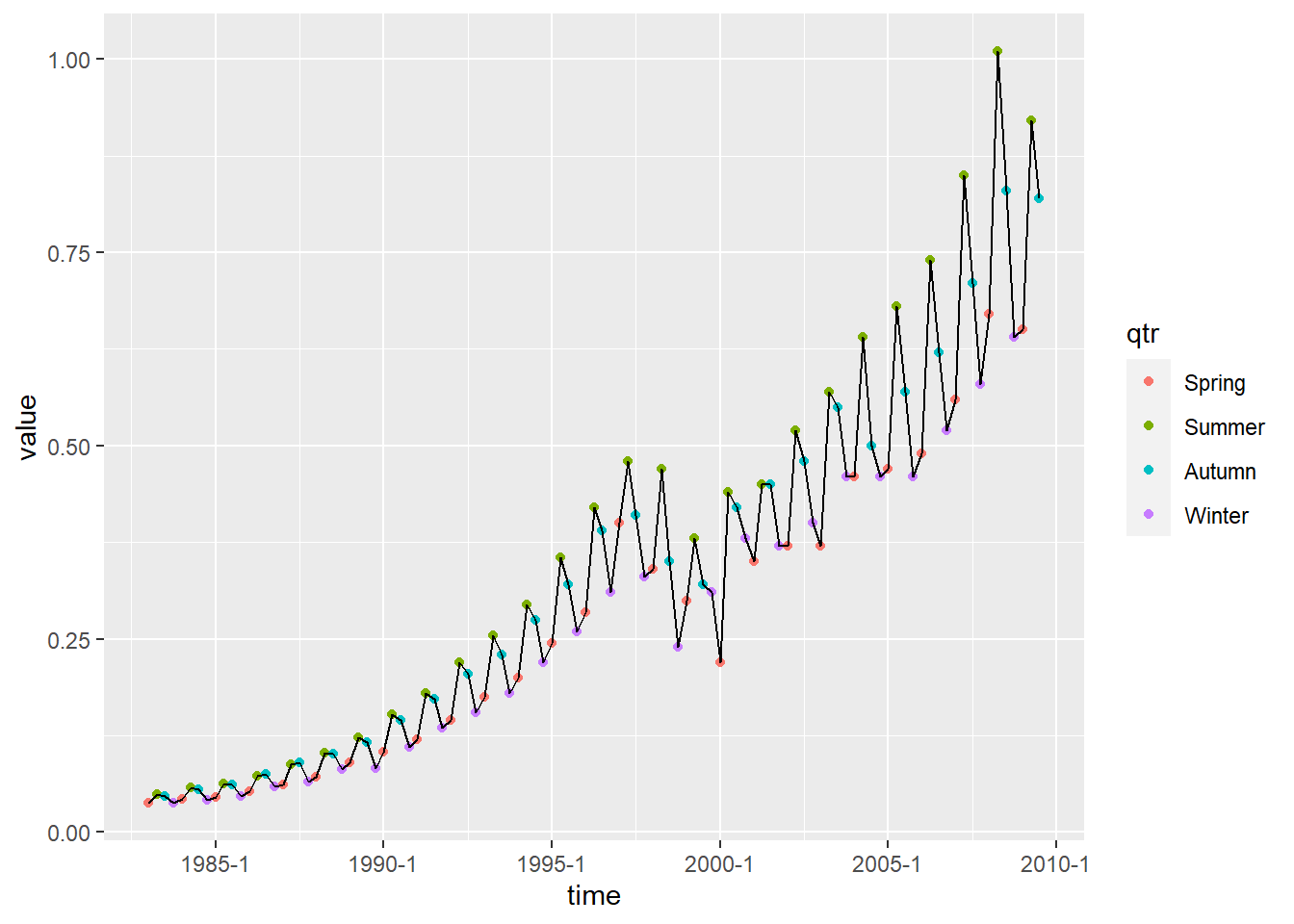
现在可以看出，每年一般冬季和春季最低， 夏季最高，秋季介于夏季和冬季之间。
3.1.3 例子：标普500指数月对数收益率
d <- read_table(
"m-ibmsp-2611.txt",
col_types=cols(.default=col_double(),
date=col_date(format="%Y%m%d")))
sp.rmon <- xts(log(1 + d[["sp"]]), d[["date"]])chartSeries(
sp.rmon, type="line", TA=NULL,
major.ticks="auto", minor.ticks=FALSE,
theme="white", name="S&P 500 Monthly Returns"
)
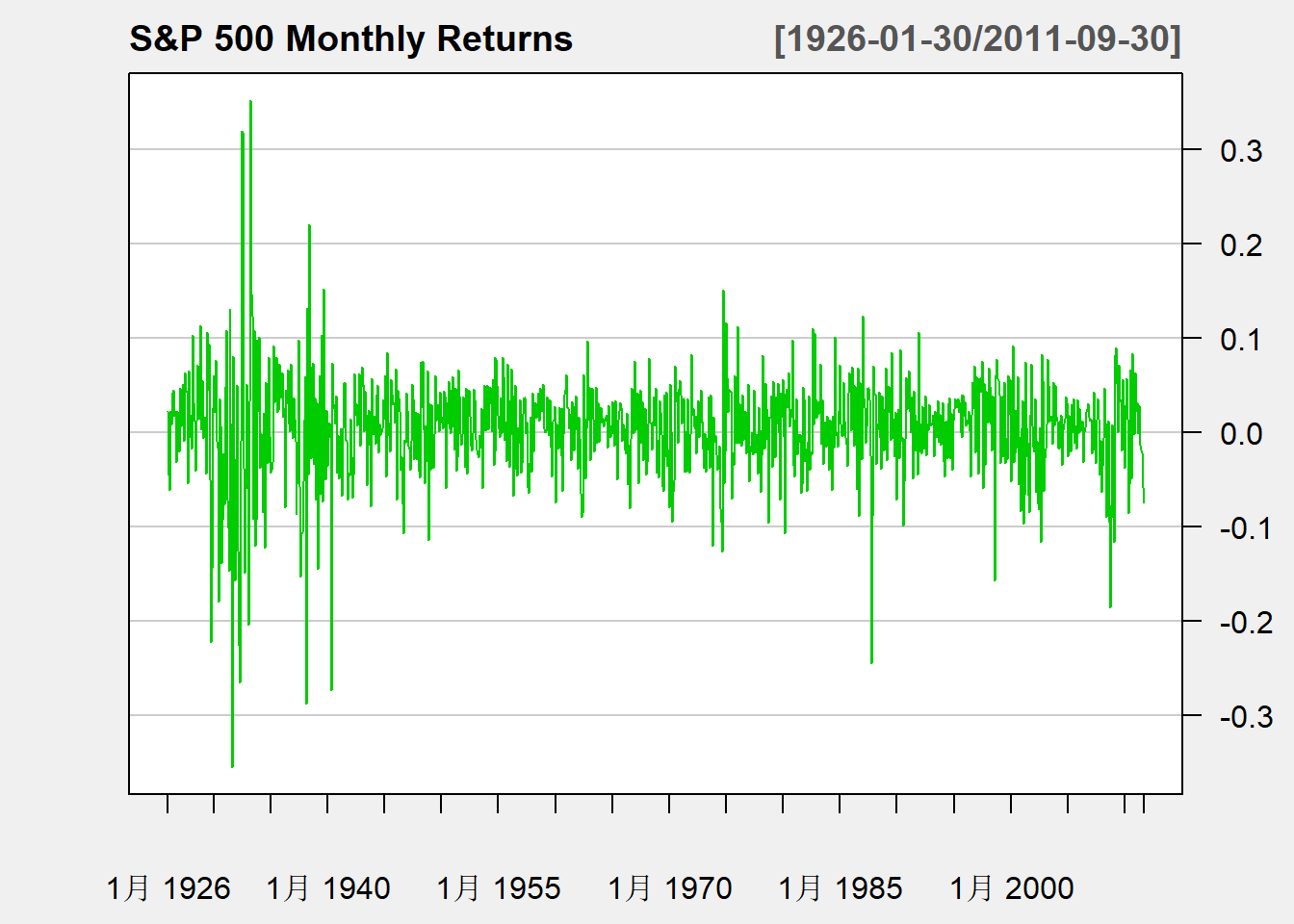
图3.3: 标普500月收益率
收益率在0上下波动，除了个别时候基本在某个波动范围之内。
3.1.4 例子：美国国债3月期和6月期周利率
## Warning: `read_table2()` was deprecated in readr 2.0.0.
## Please use `read_table()` instead.x1 <- xts(d[["rate"]], make_date(d[["year"]], d[["mon"]], d[["day"]]))
d <- read_table2(
"w-tb6ms.txt",
col_types=cols(.default=col_double()))## Warning: `read_table2()` was deprecated in readr 2.0.0.
## Please use `read_table()` instead.x2 <- xts(d[["rate"]], make_date(d[["year"]], d[["mon"]], d[["day"]]))
tb36ms <- merge(x1, x2)
names(tb36ms) <- c("tb3ms", "tb6ms")
rm(d, x1, x2)用xts包的plot()函数作图：
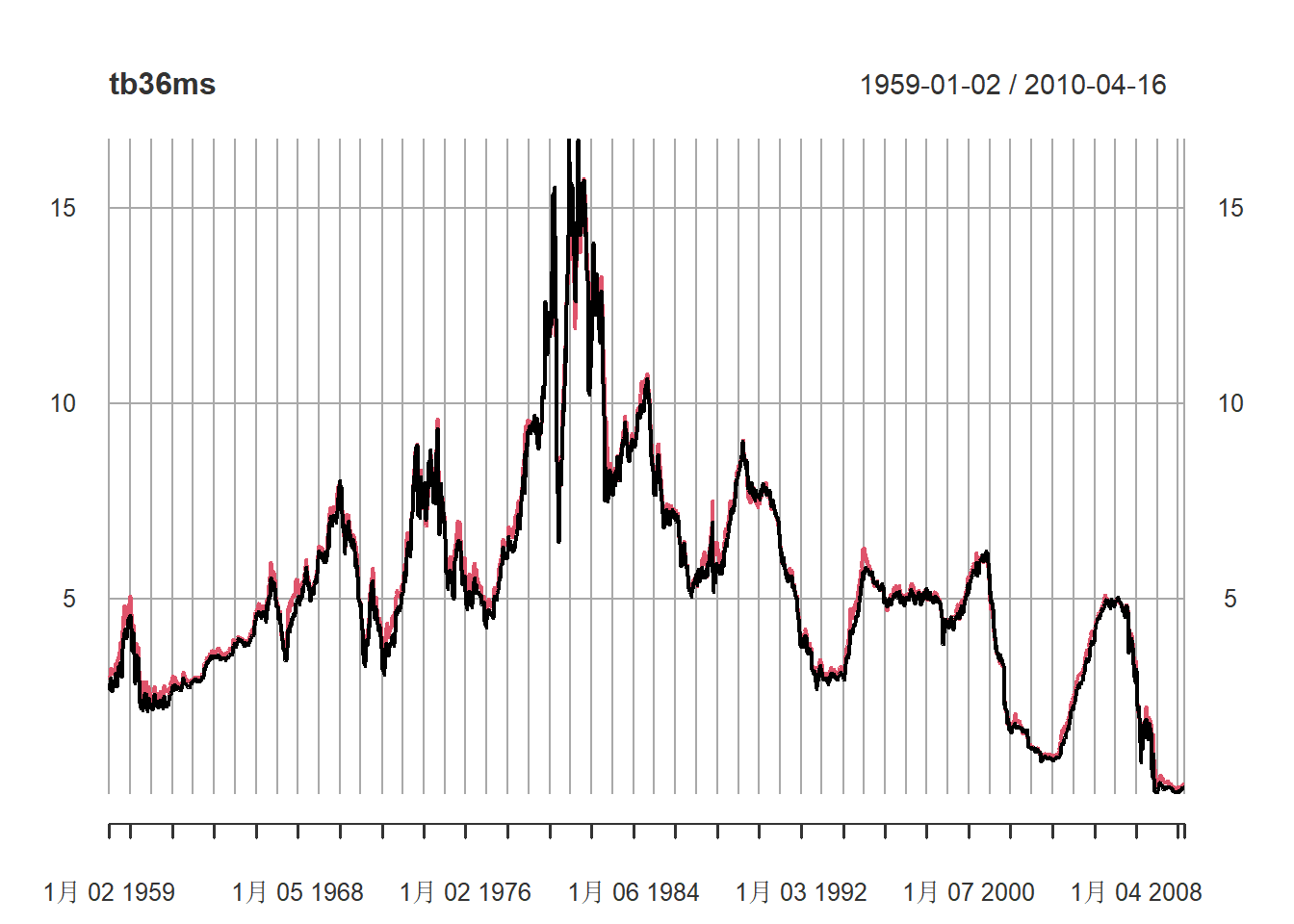
图3.4: 美国3月期和6月期国债周利率
聚焦到2004年的数据：
红色是6月期国债利率， 黑色是3月期国债。 一般6月期高， 但是有些时期3月期超过了6月期，如1980年：
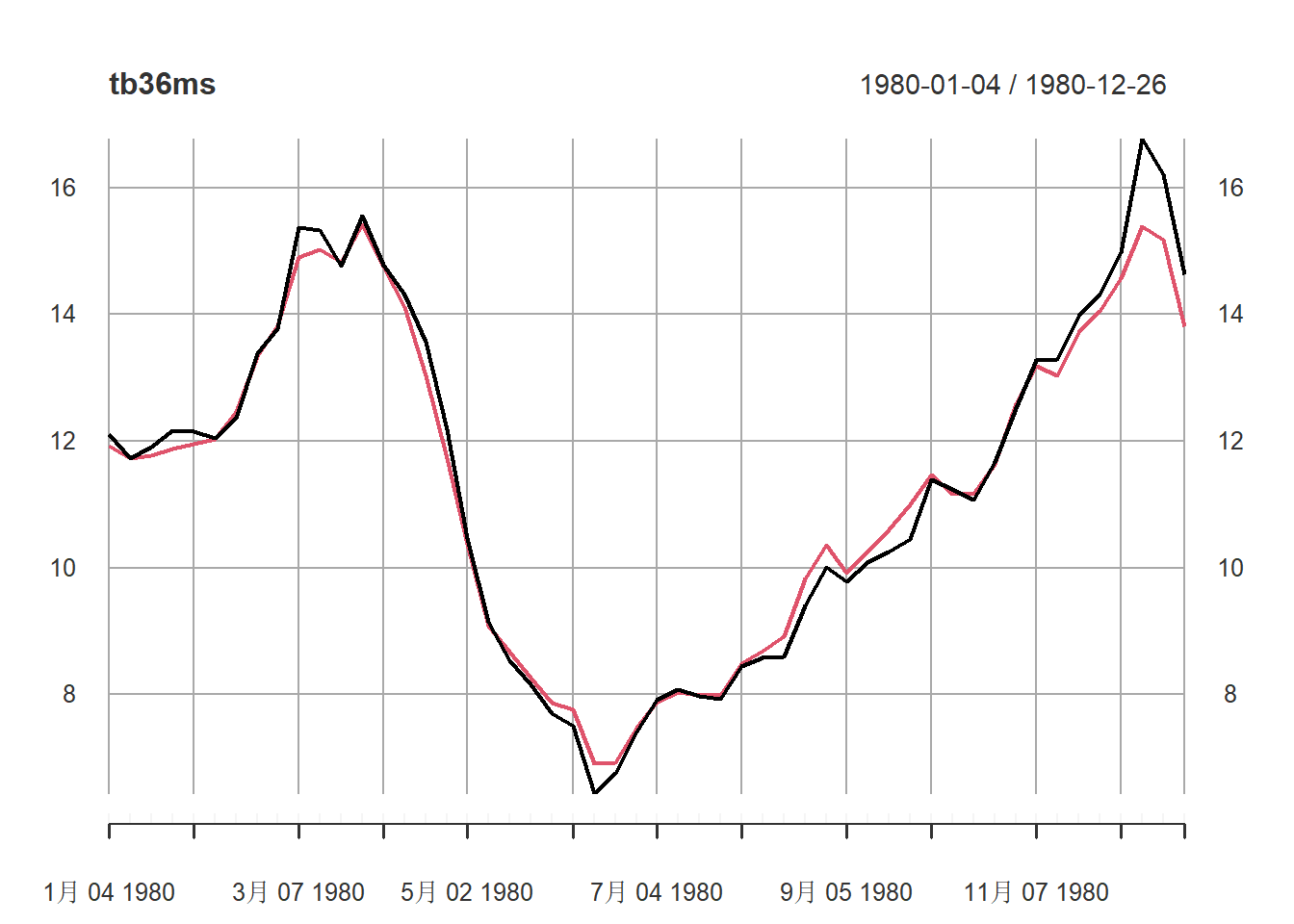
3.2 平稳性
如图3.3那样的收益率数据基本呈现出在一个水平线（一般是0）上下波动， 且波动范围基本不变。 这样的表现是时间序列“弱平稳序列”的表现。 由弱平稳性， 可以对未来的标普500收益率预测如下： 均值在0左右，上下幅度在\(\pm 0.2\)之间。
弱平稳需要一阶矩和二阶矩有限。 记\(Ex_t = \mu\)不变， \(\gamma_0 = \text{Var}(x_t) = E(x_t - \mu)^2\)不变。 某些分布是没有有限的二阶矩的，比如柯西分布， 这样的分布就不适用传统的线性时间序列理论。
稍后给出弱平稳的理论定义。
如图3.2这样的价格序列则呈现出水平的上下起伏， 如果分成几段平均的话， 各段的平均值差距较大。 这体现出非平稳的特性。
时间序列：设有随机变量序列 \(\{ x_t, t=\dots, -2, -1, 0, 1, 2, \dots \}\)， 称其为一个时间序列。其中\(x_t\)是一个随机变量， 也可以写成大写的\(X_t\)。 时间序列\(\{ X_t \}\)严格来说是一个二元的函数 \(X(t, \omega)\), \(t \in \mathbb Z\)(\(\mathbb Z\)表示所有整数组成的集合)， \(\omega \in \Omega\)， \(\Omega\)表示在一定的条件下所有可能的试验结果的集合。 经济和金融中的时间序列我们只能观察到其中某一个\(\omega_0 \in \Omega\)对应的结果， 称为一条“轨道”。 而针对随机变量的许多理论性质都是在\(\omega \in \Omega\)上讨论的， 比如\(E X_t = \int X_t(\omega) P(d\omega)\)是\(X_t(\omega)\)对\(\omega\in \Omega\)的平均。
为了能够用一条轨道的观测样本得到所有\(\omega\in\Omega\)的性质， 需要时间序列满足“遍历性”。
时间序列的样本： 设\(\{x_t, t=1,2,\dots, T \}\)是时间序列中的一段。 仍将\(x_t\)看成随机变量，也可以写成大写的\(X_t\)。 如果有了具体数值， 那么样本就是一条轨道中的一段。
自协方差函数： 时间序列\(\{ X_t \}\)中两个随机变量的协方差 \(\text{Cov}(X_s, X_t)\)叫做自协方差。 如果\(\text{Cov}(X_s, X_t) = \gamma_{|t-s|}\)仅依赖于\(t-s\)， 则称 \[ \gamma_k = \text{Cov}(X_{t-k}, X_t), k=0,1,2,\dots \] 为时间序列\(\{X_t \}\)的自协方差函数。 因为\(\text{Cov}(X_s, X_t) = \text{Cov}(X_t, X_s)\)， 所以\(\gamma_{-k} = \gamma_k\)。 易见\(\gamma_0 = \text{Var}(X_t)\)。
由Cauchy-Schwartz不等式， \[ |\gamma_k | = \left| E[ (X_{t-k} - \mu) (X_t - \mu)] \right| \leq \left( E(X_{t-k} - \mu)^2 \; E(X_t - \mu)^2 \right)^{1/2} = \gamma_0 \]
弱平稳序列(宽平稳序列，weakly stationary time series): 如果时间序列\(\{ X_t \}\)存在有限的二阶矩且满足：
(1) \(EX_t = \mu\)与\(t\)无关；
(2) \(\text{Var}(X_t) = \gamma_0\)与\(t\)无关;
(3) \(\gamma_k = \text{Cov}(X_{t-k}, X_t)\), \(k=1,2,\dots\)与\(t\)无关，
则称\(\{ X_t \}\)为弱平稳序列。
适当条件下可以用时间序列的样本估计自协方差函数， 这是用一条轨道的信息推断所有实验结果\(\Omega\)， 估计公式为 \[ \hat\gamma_k = \frac{1}{T} \sum_{t=k+1}^T (x_{t-k} - \bar x)(x_t - \bar x), k=0,1,\dots, T-1 \] 称\(\hat\gamma_k\)为样本自协方差。 注意这里用了\(1/T\)而不是\(1/(T-k)\)， 用\(1/(T-k)\)在获得无偏性的同时会造成一些理论上的困难。
3.3 相关系数和自相关函数
3.3.1 相关系数
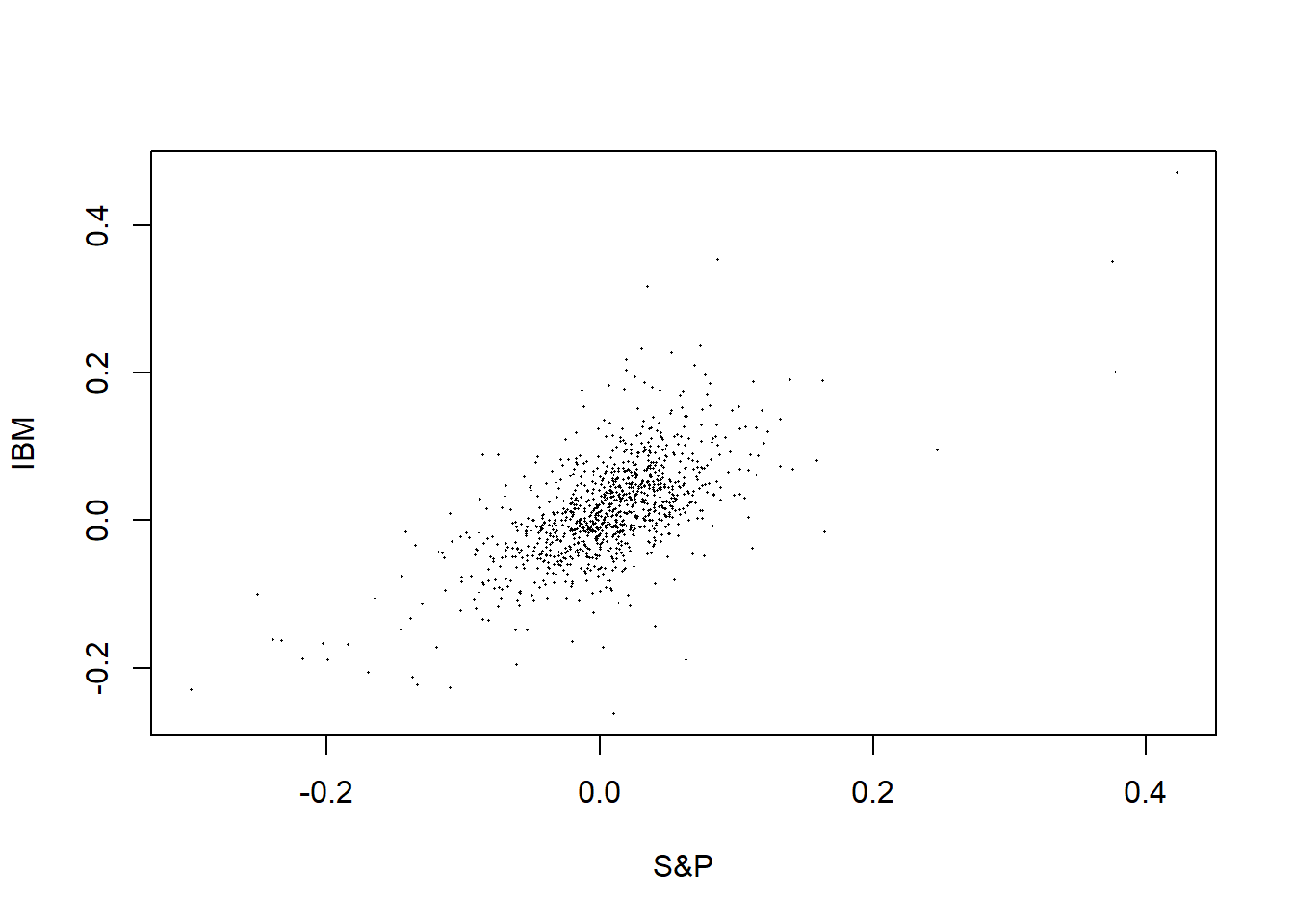
图3.5: IBM对标普500月度简单收益率
图3.5是IBM股票月度简单收益率对标普500收益率的散点图。 从图中看出， 两者有明显的正向相关关系。
两个随机变量\(X\)和\(Y\)的相关系数定义为 \[ \rho(X,Y) = \rho_{xy} = \frac{\text{Cov}(X,Y)}{\sqrt{\text{Var}(X) \text{Var}(Y)}} = \frac{E[(X-\mu_x)(Y-\mu_y)]}{\sqrt{E(X-\mu_x)^2 E(Y-\mu_y)^2}} \]
如果有\((X,Y)\)的独立同分布样本\((x_t, y_t)\)， \(t=1,2,\dots,T\)， 可估计相关系数为 \[ \hat\rho_{xy} = \frac{\sum_{t=1}^T (x_t - \bar x)(y_t - \bar y)} {\sqrt{\sum_{t=1}^T (x_t - \bar x)^2 \sum_{t=1}^T (y_t - \bar y)^2}} \]
对于不独立的样本， 比如时间序列样本， 也可以计算相关系数， 其估计合理性需要一些模型假设。
对于联合分布非正态的情况， 有时相关系数不能很好地反映\(X\)和\(Y\)的正向或者负向的相关。 斯皮尔曼（Spearman）相关系数是计算\(X\)的样本的秩（名次）与\(Y\)的样本的秩之间的相关系数， 也称为Spearman rank correlation。
另一种常用的非参数相关系数是肯德尔tau(Kendall’s \(\tau\))系数， 反映了一致数对和非一致数对之间的差别。 对随机向量\((X, Y)\)， 设\((X_1, Y_1)\), \((X_2, Y_2)\)相互独立且联合分布与\((X,Y)\)联合分布相同， 定义\(X\)和\(Y\)的肯德尔tau系数为 \[ \tau = P\left[ (X_1 - X_2)(Y_1 - Y_2) > 0 \right] - P\left[ (X_1 - X_2)(Y_1 - Y_2) < 0 \right] \] 即两个观测的分量次序一致的概率减去分量次序相反的概率。 一致的概率越大，说明两个的正向相关性越强。
对IBM收益率与标普收益率数据计算这三种相关系数：
## [1] 0.6395979## [1] 0.6065789## [1] 0.43280663.3.2 自相关函数与白噪声
设\(\{X_t \}\)为弱平稳序列， \(\{ \gamma_k \}\)为自协方差函数。 则 \[ \rho(X_{t-k}, X_t) = \frac{\text{Cov}(X_{t-k}, X_t)}{\sqrt{\text{Var}(X_{t-k})\text{Var}(X_{t})}} = \frac{\gamma_k}{\sqrt{\gamma_0 \gamma_0}} = \frac{\gamma_k}{\gamma_0}, \ k=0,1,\dots, \ \forall t \] 记\(\rho_k = \gamma_k / \gamma_0\)， 这是\(X_{t-k}\)与\(X_t\)的相关系数且与\(t\)无关， 称\(\{ \rho_k, k=0,1,\dots \}\)为时间序列\(\{ X_t \}\)的自相关函数 （Autocorrelation function, ACF）。 \(\rho_0=1\)。
如果弱平稳序列\(\{ X_t \}\)满足\(\rho_k=0\), \(k=1,2,\dots\)， 称\(\{ X_t \}\)为白噪声序列。 如果随机变量序列\(\{ X_t \}\)独立且期望和方差不随时间而变， 则\(\{ X_t \}\)是白噪声序列， 称为独立白噪声。 如果独立白噪声还是同分布的， 称为独立同分布白噪声。
适当条件下\(\rho_k\)可以从时间序列样本估计为 \[ \hat\rho_k = \frac{\hat\gamma_k}{\hat\gamma_0},\ k=0,1,\dots \] \(\hat\rho_0=1\)。 称\(\hat\rho_k, k=1,2,\dots\)为样本自相关函数。
如果时间序列严平稳遍历， 则\(\hat\rho_k\)是\(\rho_k\)的强相合估计。
若\(\{ X_t \}\)为有二阶矩的独立同分布随机变量列， 则 \(\hat\rho_k\)(\(k>0\))渐近服从\(\text{N}(0, \frac{1}{T})\)。
如果\(\{\varepsilon_t \}\)是零均值独立同分布白噪声， \(q\)为非负整数， \(\{ \psi_j, j=0,1,\dots, q \}\)是数列，\(\psi_0=1\)， \[ X_t = \mu + \sum_{j=0}^q \psi_j \varepsilon_{t-j}, \ t \in \mathbb Z, \] 则从\(\{ X_t, t=1,\dots,T \}\)计算的ACF满足: 当\(k > q\)时， \(\sqrt{T}\hat\rho_k\)渐近服从\(\text{N}(0, 1 + 2 \sum_{j=0}^q \rho_j^2)\), 这称为Bartlett公式。 参见 (何书元 2003) P.131 §4.2的例2.1。 原始文献： MAURICE STEVENSON BARTLETT, On the Theoretical Specification and Sampling Properties of Auto-Correlated Time Series, Journal of the Royal Statistical Society (Supplement) 8 (1946), pp. 24-41.
在基本R软件中，
acf(x)可以估计时间序列x的自相关函数并对其前面若干项画图。
例3.1 例：CRSP的第10分位组合的月对数收益率， 1967-1到2009-12。 第10分位组合是NYSE、AMEX、NASDAQ市值最小的10%股票组成的投资组合， 每年都重新调整。
- CRSP是Center for Research in Security Prices, 位于Chicago Booth。
- NYSE(The New York Stock Exchange, 纽约证券交易所),
- AMEX(American Stock Exchange, 美国证券交易所，在纽约华尔街附近)，
- NASDAQ(National Association of Securities Dealers Automated Quotations，纳斯达克，位于纽约)。
d <- read_table2(
"m-dec12910.txt", col_types=cols(
.default=col_double(),
date=col_date(format="%Y%m%d")))## Warning: `read_table2()` was deprecated in readr 2.0.0.
## ℹ Please use `read_table()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.dec <- xts(as.matrix(d[,-1]), d$date)
tclass(dec) <- "yearmon"
d10 <- ts(coredata(dec)[,"dec10"], start=c(1967,1), frequency=12)
plot(d10, main="CRSP Lower 10% Mothly Returns")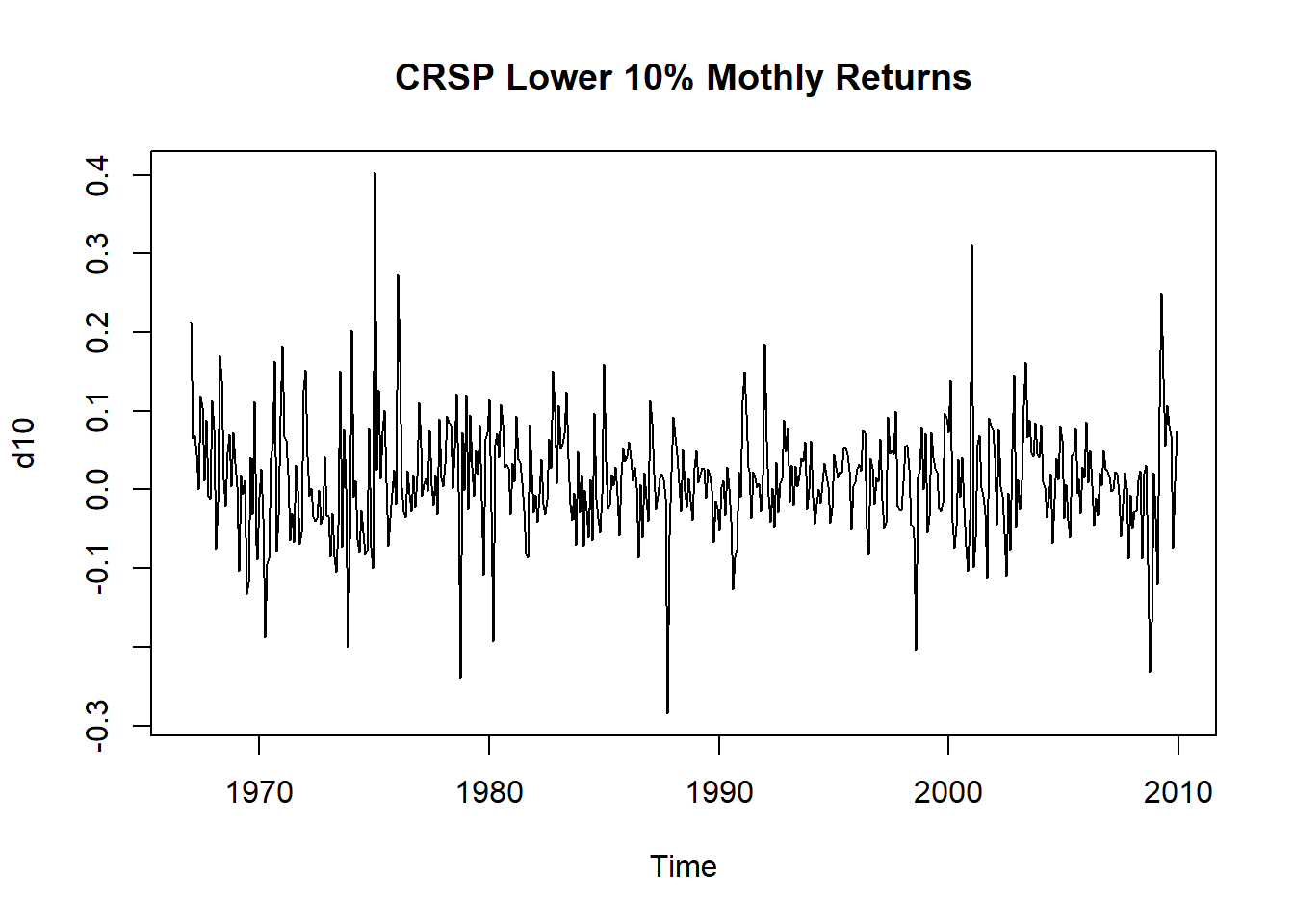
图3.6: CRSP第10分位组合月对数收益率
用acf()作时间序列的自相关函数图：
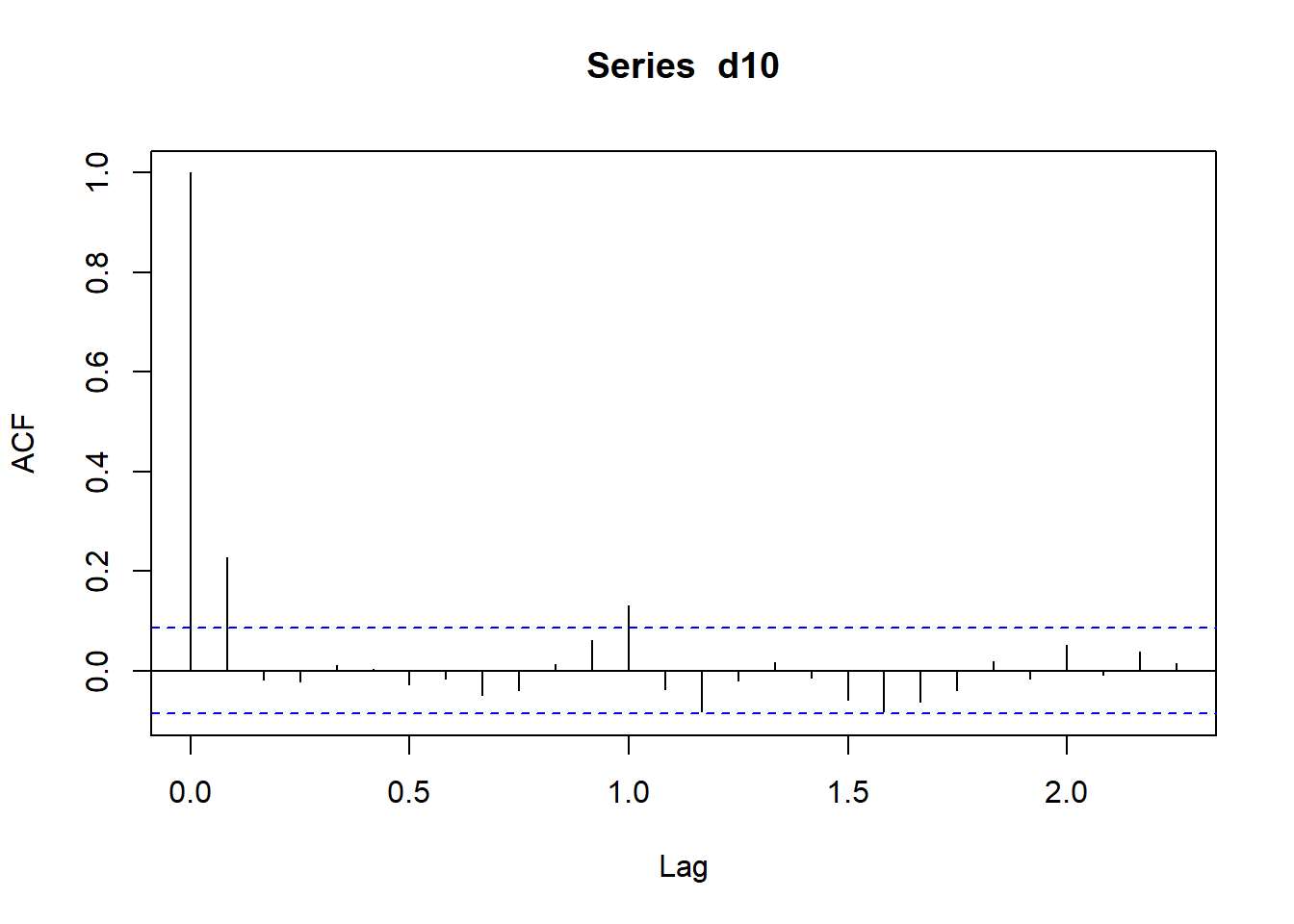
图3.7: CRSP第10分位组合月对数收益率的ACF
acf()的返回值是一个列表，其中lag相当于\(k\)，
acf相当于\(\hat\rho_k\)。
用plot=FALSE取消默认的图形输出。
ACF图中横轴上下两条水平下是在独立同分布白噪声假设下的加减两倍标准差， 即\(\pm \frac{2}{\sqrt{T}}\)。 如果独立同分布白噪声假设成立， 每个\(\hat\rho_k\)有95%以上的概率落入这两条线之间。
ACF图\(k=0\)处总对应\(\hat\rho_0=1\)。
上图的\(\hat\rho_1\)和\(\hat\rho_{12}\)都超出了界限 （因为是月度数目，横轴的单位是\(1/12\)为一个时间点）。 从此图可以认为此投资组合的收益率不是白噪声。
标准库stats的acf()作自相关函数图总是有\(\rho_0 = 1\)，
这在其它系数很小时会使得其它系数显得很难分辨，
另外，当时间序列是月度或季度数据时，
横坐标是以年为单位。
所以，forecast包提供了一个类似功能的Acf()函数，如：
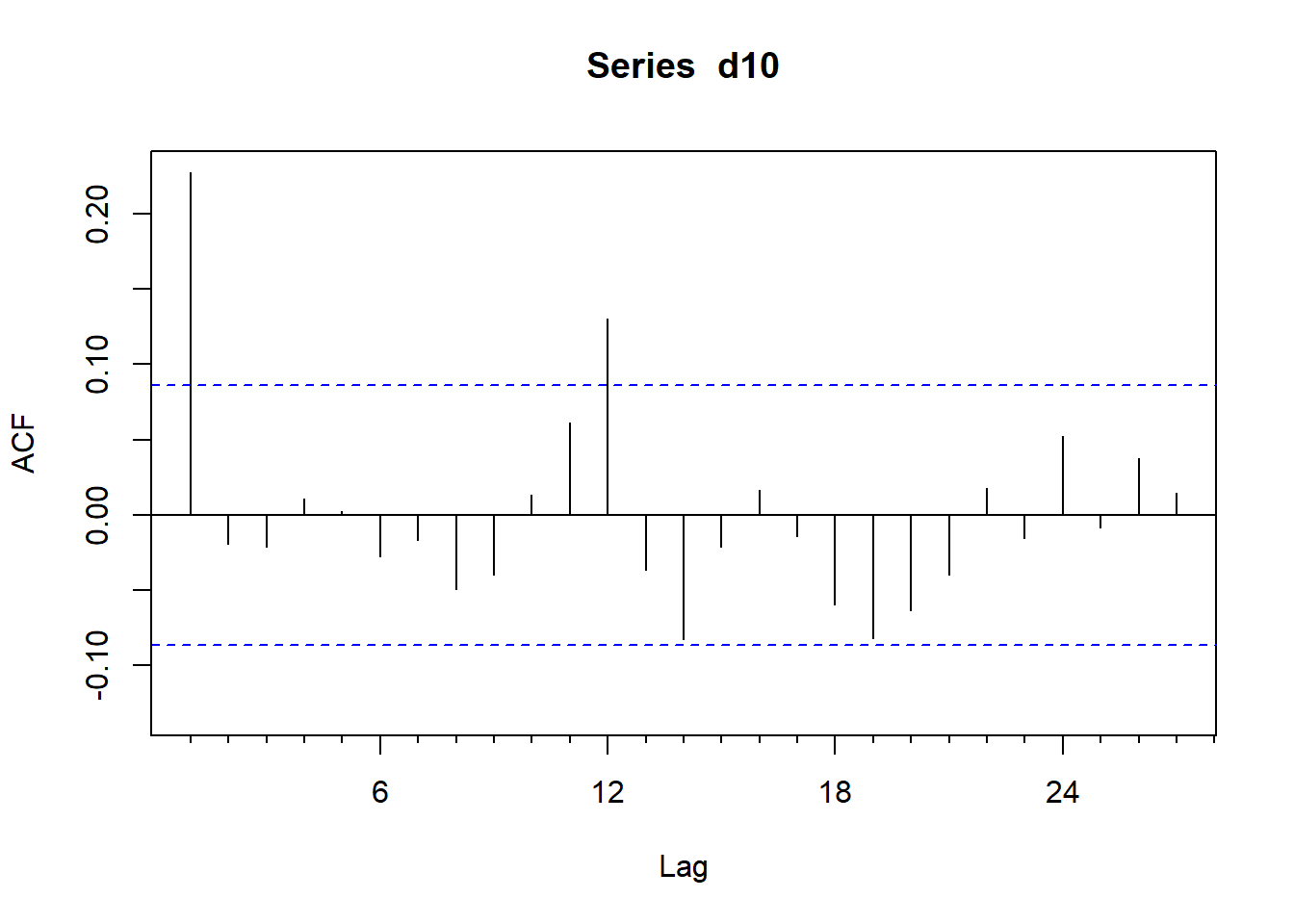
图3.8: CRSP第10分位组合月对数收益率的ACF
TSA包的acf()函数也不做滞后0的点，如：
## Registered S3 methods overwritten by 'TSA':
## method from
## fitted.Arima forecast
## plot.Arima forecast
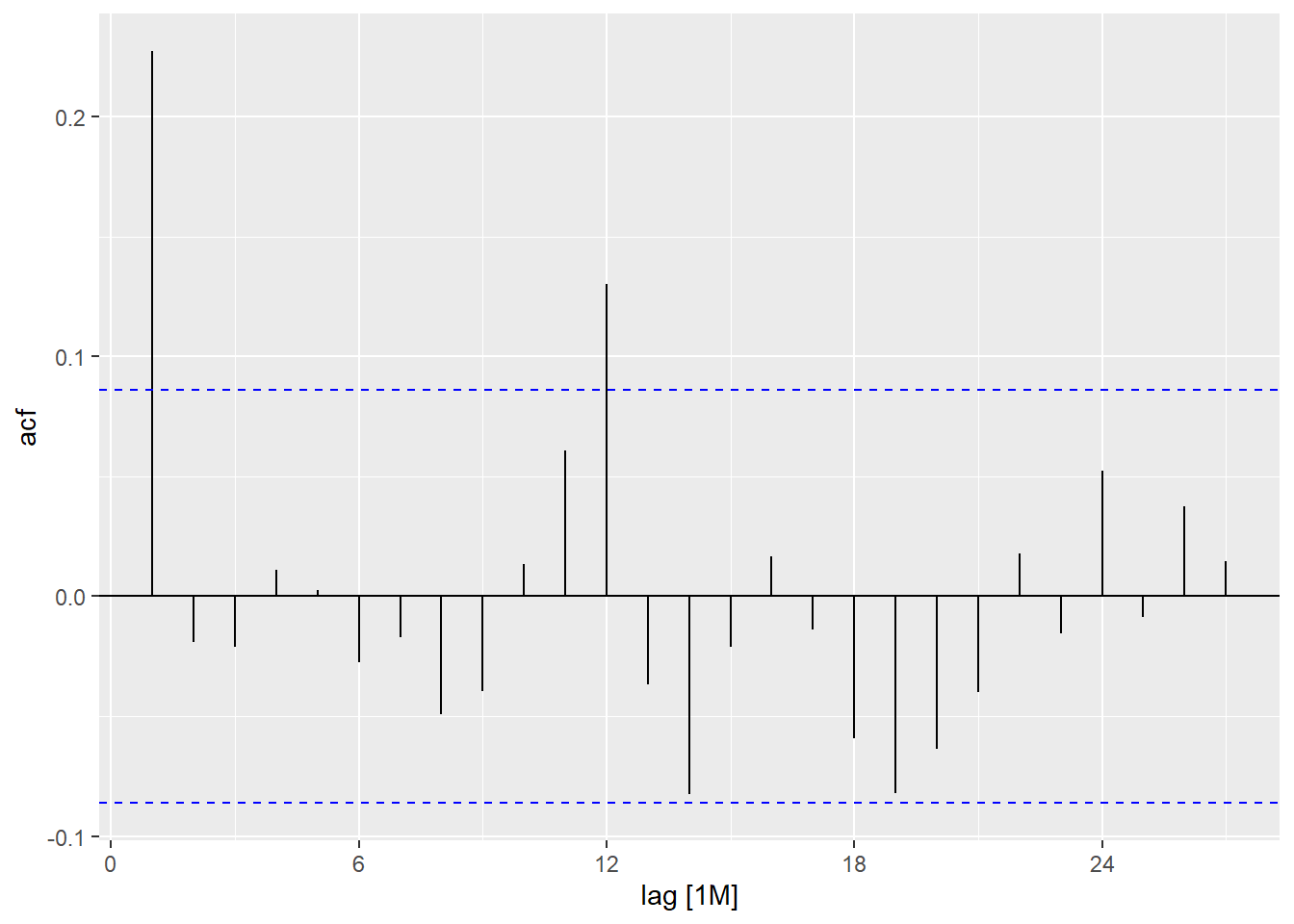
图3.9: CRSP第10分位组合月对数收益率的ACF
○○○○○
3.3.3 用单个自相关系数作白噪声检验
如果\(\{ X_ t \}\)是独立同分布白噪声， 则\(\hat\rho_k\)(\(k\geq 1\))近似\(\text{N}(0, 1/T)\)。 若\(H_0\)是序列为白噪声， 取统计量
\[ t = \sqrt{T} \hat\rho_k \]
如果\(|t| > \text{qnorm}(1-\alpha/2)\)， 则拒绝白噪声零假设。 实际中常取\(\alpha=0.05\), \(\text{qnorm}(1-\alpha/2) \approx 2\)， 当\(\hat\rho_1\)超出\(\pm 2 /\sqrt{T}\)则拒绝\(H_0\)， 有多个\(\hat\rho_k\)超出\(\pm 2/\sqrt{T}\)也可拒绝\(H_0\)， 有一个\(t\)统计量值很大（比如超出\(\pm 3\)）也可拒绝\(H_0\)。
在判断\(\{ X_t \}\)是否\(X_t = \mu + \sum_{j=0}^q \psi_j \varepsilon_{t-j}\) 这样的模型时， 根据Bartlet公式， 可取 \[ t = \frac{\hat\rho_k}{\sqrt{\frac{1}{T} \left( 1 + 2\sum_{j=1}^{k-1} \hat\rho_j^2 \right)}},\ k>q \]
当\(t\)超出\(\text{qnorm}(1-\alpha/2)\)时拒绝这样的模型。
例3.2 这是例3.1 的继续。 有研究者认为小市值股票倾向于在每年的一月份有正的收益率。
为此，用\(H_0: \rho_{12} = 0\)对\(H_a: \rho_{12} \neq 0\)的检验来验证。 如果一月份有取正值的倾向， 则相隔12个月的值会有正相关。
计算\(\hat\rho_{12}\)的值：
## [1] 0.130411计算\(t\)统计量的值，检验p值：
## [1] 2.962369## [1] 0.003052812\(p\)值小于0.05, 拒绝了\(H_0: \rho_{12}=0\)， 这个检验的结果支持一月份效应的存在性。
○○○○○
3.3.4 Ljung-Box白噪声检验
为了检验时间序列样本是否来自白噪声序列， 可以检验\(\rho_k=0, k=1,2,\dots\)的零假设。 前面检验单个\(\rho_k\)的做法如果针对多个进行检验就有多重检验的第一类错误增大的问题。
Box和Pierce(G. Box and Pierce 1970)提出了混成统计量(Portmanteau statistic) \[ Q_*(m) = T \sum_{j=1}^m \hat\rho_j^2 \]
用来检验
\[ H_0: \rho_1 = \dots = \rho_m = 0 \longleftrightarrow H_a: \text{不全为零} \]
在\(\{X_t \}\)是独立白噪声序列条件下， \(Q_*(m)\)近似服从\(\chi^2(m)\)分布。 给定检验水平\(\alpha\)， 当\(Q_*(m) > \text{qchisq}(1-\alpha, m)\)时拒绝\(H_0\)， 否定白噪声假设。 如果检验的序列是线性时间序列估计的残差序列， 则卡方自由度应改为\(m\)减去估计的系数个数。
Ljung和Box(Ljung and Box 1978)对此检验方法进行了改进。 统计量改为
\[ Q(m) = T(T+2) \sum_{j=1}^m \frac{\hat\rho_j^2}{T-j} \] 在独立同分布白噪声假设下仍近似服从\(\chi^2(m)\)分布。 当\(Q(m) > \text{qchisq}(1-\alpha, m)\)时拒绝\(H_0\)， 否定白噪声假设。 这个检验称为Ljung-Box白噪声检验。 如果检验的序列是线性时间序列估计的残差序列， 则卡方自由度应改为\(m\)减去估计的系数个数。 比如， 对ARMA(\(p,q\))模型建模的残差作白噪声检验， 卡方自由度应改为\(m - (p+q)\)。
在R软件中，
Box.test(x, type="Ljung-Box")执行Ljung-Box白噪声检验。
Box.test(x, type="Box-Pierce")执行Box-Pierce混成检验。
用fitdf=指定要减去的自由度个数。
R的portes包提供了多种一元和多元白噪声检验功能。
例3.3 检验IBM股票月收益率是否白噪声。
考虑IBM股票从1926-01到2011-09的月度收益率数据， 简单收益率和对数收益率分别考虑。
读入数据：
d <- read_table(
"m-ibmsp-2611.txt", col_types=cols(
.default=col_double(),
date=col_date(format="%Y%m%d")))
ibm <- ts(d[["ibm"]], start=c(1926,1), frequency=12)读入的是简单收益率的月度数据。 作ACF图：
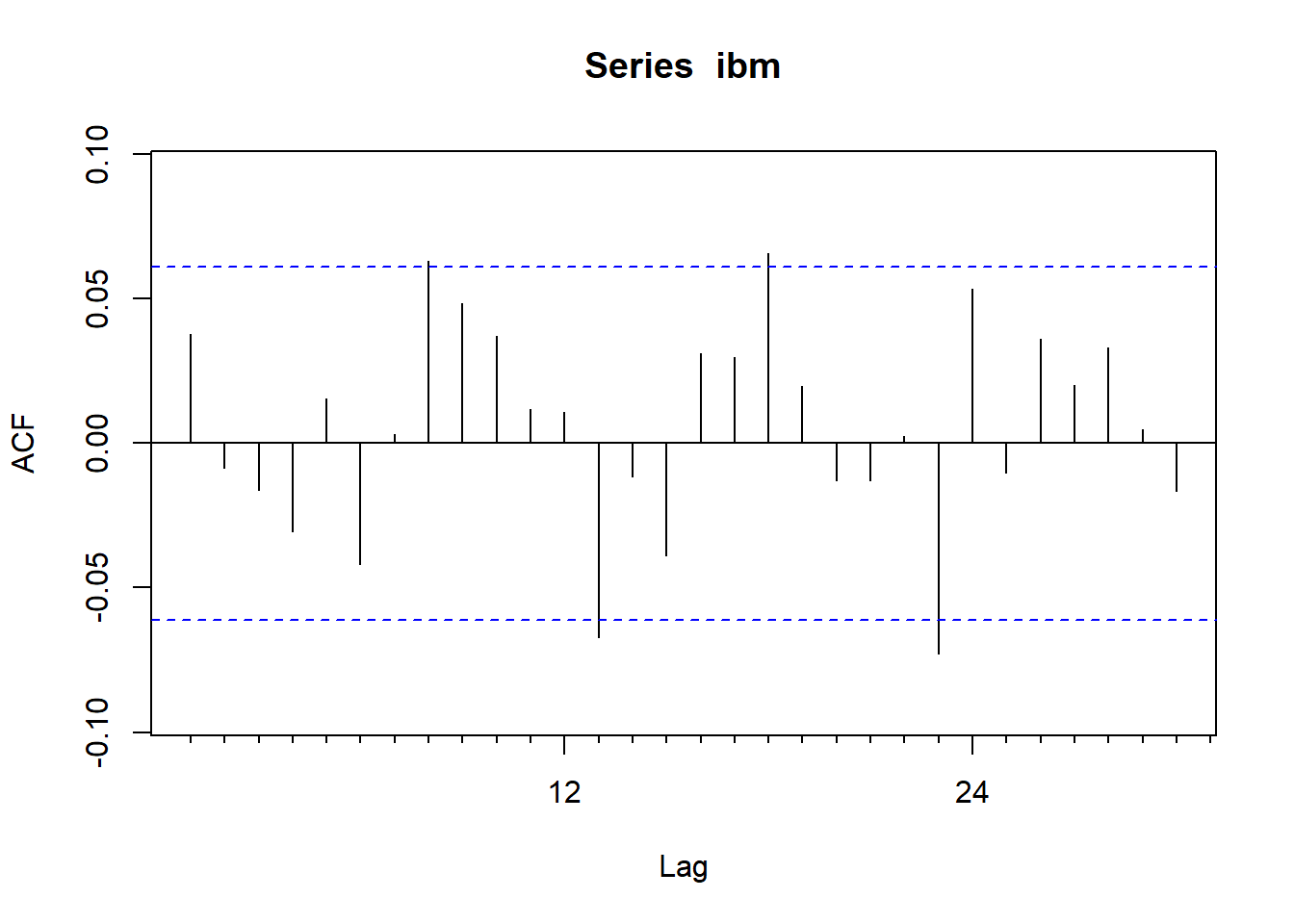
从ACF来看月度简单收益率是白噪声。
作Ljung-Box白噪声检验， 分别取\(m=12\)和\(m=24\)：
##
## Box-Ljung test
##
## data: ibm
## X-squared = 13.098, df = 12, p-value = 0.362##
## Box-Ljung test
##
## data: ibm
## X-squared = 35.384, df = 24, p-value = 0.0629在0.05水平下均不拒绝零假设， 支持IBM月度简单收益率是白噪声的零假设。
从简单收益率计算对数收益率， 并进行LB白噪声检验：
##
## Box-Ljung test
##
## data: log(1 + ibm)
## X-squared = 12.814, df = 12, p-value = 0.3827##
## Box-Ljung test
##
## data: log(1 + ibm)
## X-squared = 34.506, df = 24, p-value = 0.07607在0.05水平下不拒绝零假设。
○○○○○
Box-Pierce检验和Ljung-Box检验受到\(m\)取值的影响， 建议采用\(m \approx \ln T\)， 且序列为季度、月度这样的周期序列时， \(m\)应取为周期的整数倍。
此组合的收益率序列的ACF:
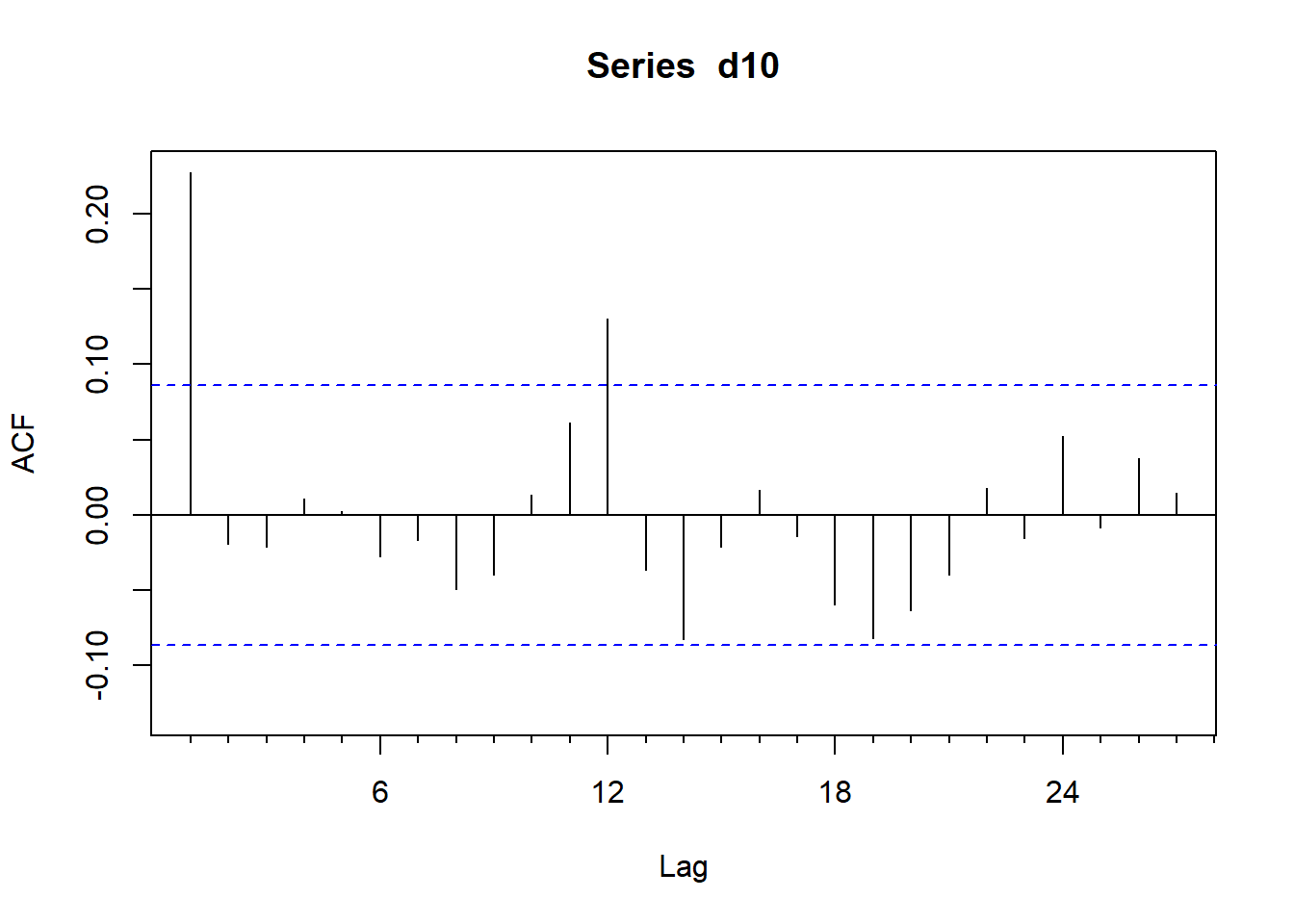
针对\(m=12\)和\(m=24\)作Ljung-Box白噪声检验：
##
## Box-Ljung test
##
## data: d10
## X-squared = 41.06, df = 12, p-value = 4.789e-05##
## Box-Ljung test
##
## data: d10
## X-squared = 56.246, df = 24, p-value = 0.0002122在0.05水平下均拒绝零假设， 认为CRSP最低10分位的投资组合的月度简单收益率不是白噪声。
○○○○○
有效市场假设认为收益率是不可预测的， 也就不会有非零的自相关。 但是，股价的决定方式和指数收益率的计算方式等可能会导致在观测到的收益率序列中有自相关性。 高频金融数据中很常见自相关性。
常见的白噪声检验还有TREVOR S. BREUSCH (1978) 和LESLIE G. GODFREY (1978)提出的拉格朗日乘子法检验（LM检验）。 零假设为白噪声， 对立假设为AR、MA或者ARMA。 参见：
- TREVOR S. BREUSCH(1978), Testing for Autocorrelation in Dynamic Linear Models, Australian Economic Papers 17, pp. 334 – 355
- LESLIE G. GODFREY(1978), Testing Against General Autoregressive and Moving Average Error Models When Regressors Include Lagged Dependent Variables, Econometrica 46 , S. 1293 – 1302
3.4 线性时间序列
设\(\{ X_t \}\)是独立同分布的二阶矩有限的随机变量， 称\(\{ X_t \}\)为独立同分布白噪声(white noise)。 最常用的白噪声一般假设均值为零。 如果\(\{ X_t \}\)独立同\(\text{N}(0, \sigma^2)\)分布， 称\(\{ X_t \}\)为高斯(Gaussian)白噪声或正态白噪声。
白噪声序列的自相关函数为零（\(\rho_0=1\)除外）。
实际应用中如果样本自相关函数近似为零 （ACF图中都位于控制线之内或基本不超出控制线）， 则可认为该序列是白噪声的样本。
R的Box.test()函数提供了Box-Pierce检验和Ljung-Box检验功能。
R的portes包提供了多种一元和多元白噪声检验功能。
如：IBM月度收益率可以认为是白噪声（见例3.3）； CRSP最低10分位投资组合月度收益率不是白噪声（见例3.4）。
设\(\{ \varepsilon_t \}\)是零均值独立同分布白噪声， \(\text{Var}(\varepsilon_t)=\sigma^2\), 数列\(\{ \psi_j \}\)满足\(\sum_j \psi_j^2 < \infty\)， \(\psi_0=1\), 令 \[\begin{align} X_t = \mu + \sum_{j=0}^\infty \psi_j \varepsilon_{t-j}, t \in \mathbb Z \tag{3.1} \end{align}\] 则称\(\{ X_t \}\)是（因果）线性时间序列， \(\varepsilon_t\)代表了在时刻\(t\)增加的变动信息， 称为新息(innovation)或者扰动(shock)。 因果线性时间序列满足新息\(\varepsilon_{t+j}\)(\(j\geq 1\))与历史的\(X_t, X_{t-1}\)独立。 而且， \(\{ X_{t-1}, X_{t-2}, \dots \}\)与 \(\{ \varepsilon_{t-1}, \varepsilon_{t-2}, \dots\}\)可以互相线性地表示。
这个定义可以放宽到\(\{ \varepsilon_t \}\)是宽平稳的不相关列（宽白噪声）的情形。 这时，称(3.1)为\(\{X_t \}\)的Wold分解， 称\(\{ X_t \}\)为纯非决定性序列。 参见:
- 何书元(2003), 应用时间序列分析. 北京大学出版社. 第5章。
- HERMAN WOLD(1938), A Study in the Analysis of Stationary Time Series, Almquist and Wicksell, Stockholm .(博士论文)
许多弱平稳时间序列是线性时间序列， 后面讲到的AR模型、MA模型、ARMA模型都属于线性时间序列。 另外的许多弱平稳时间序列可以被线性时间序列近似。 非平稳的时间序列不是线性时间序列。
\(\{\psi_j \}\)称为模型的\(\psi\)权重。 易见 \[ E X_t = \mu, \quad \text{Var}(X_t) = \sigma^2 \sum_{j=0}^\infty \psi_j^2, \] 自协方差函数为 \[ \begin{aligned} \gamma_{k} =& \text{Cov}(X_t, X_{t-k}) = E \left[ \left( \sum_{i=0}^\infty \psi_i \varepsilon_{t-i} \right) \left( \sum_{i=0}^\infty \psi_i \varepsilon_{t-i-l} \right)\right] \\ =& E \left( \sum_{i,j=0}^\infty \psi_i \psi_j \varepsilon_{t-i} \varepsilon_{t-j-k} \right) = \sigma^2 \sum_{i,j=0}^\infty \psi_i \psi_j \delta_{i-j-k} \\ =& \sigma^2 \sum_{j=0}^\infty \psi_j \psi_{j+k} \end{aligned} \] 其中\(\delta_k\)当\(k=0\)时为1， 当\(k\neq 0\)时为0。
自相关函数为 \[ \rho_k = \frac{\gamma_k}{\gamma_0} = \frac{\sum_{j=0}^\infty \psi_j \psi_{j+k}}{1 + \sum_{j=1}^\infty \psi_j^2}, \ k \geq 0 \]
线性时间序列模型满足\(\psi_j \to 0\), \(j \to \infty\)， 所以历史上的扰动的影响会逐渐消失。 另外\(\rho_k \to 0\), \(k \to \infty\)， 所以相距较远的观测之间的相关性很小。
不是所有的弱平稳时间序列都有这样的性质。 非平稳序列更是不需要满足这些性质。
3.5 附录：补充知识
3.5.1 严平稳
对时间序列\(\{ X_t, t \in \mathbb Z \}\)， 如果对任意的\(t \in \mathbb Z\)和正整数\(n\), \(k\)， \((X_t, \dots, X_{t+n-1})\)总是与 \((X_{t+k}, \dots, X_{t+n-1+k})\)同分布， 则称\(\{ X_t \}\)为严平稳时间序列。
如果严平稳时间序列\(\{X_t \}\)有二阶矩， 则它也是宽平稳的。
如果宽平稳时间序列\(\{X_t \}\)的任意有限维分布都服从广义正态分布， 则\(\{X_t \}\)也是严平稳的。
如果\(\{ \varepsilon_t \}\)为独立同分布零均值白噪声， 方差为\(\sigma^2\)， \(\{ \psi_j \}\)绝对可和或者平方可和， 则线性时间序列 \[ X_t = \mu + \sum_{j=0}^\infty \psi_j \varepsilon_{t-j}, t \in \mathbb Z \] 同时宽平稳和严平稳的时间序列。
3.5.2 严平稳遍历性
时间序列建模， 是从理论上无穷长度的随机变量序列\(\{ X_t(\omega), t=\dots, -1, 0, 1, \dots , \omega \in \Omega \}\) 中获得一段观测值， 称为一条轨道， 如\(\{X_1(\omega_0), X_2(\omega_0), \dots, X_T(\omega_0) \}\)， 其中\(\omega_0\)是概率空间\(\Omega\)中的一个结果点。 虽然\(T\)可以越来越大， 但是我们还是仅仅观测到结果空间中的一个点， 希望据此推断所有\(\omega \in \Omega\)的性质。 这需要序列\(\{ X_t \}\)具有遍历性。
许多序列没有遍历性。 例如， \(X_t \equiv \xi\)， 其中\(\xi\)为U(0,1)随机变量， 则每条轨道是一个常数， 但不同轨道的常数值不同， 从一条轨道无法推断所有结果。 有如，设随机变量\(U\)服从\(\text{U}(0, 2\pi)\)， \(A>0\), \(f \in (0, 2\pi)\)为常数，则时间序列 \[ X_t = A \cos(f t + U), \ t \in \mathbb Z \] 是宽平稳时间序列， 但其每条轨道是一条正弦曲线上的离散点， 不同轨道的相位不同， 从一条轨道无法推断所有轨道的分布情况。
如果从时间序列的一条轨道就可以推断出它的所有有限维分布， 就称其为严平稳遍历的。 这里不给出遍历性的严格定义， 仅给出一些严平稳遍历的充分条件。 可以证明， 宽平稳的正态时间序列是严平稳遍历的， 上述由零均值独立同分布白噪声产生的线性序列是严平稳遍历的。
严平稳遍历的性质：
定理: 如果\(\{ X_t \}\)是严平稳遍历序列， 则
(1) 强大数律: 如果\(E|X_1|<\infty\)则 \[ \lim_{T\to\infty} \frac{1}{T} \sum_{t=1}^T X_t = E X_1, \ \text{a.s.} \]
(2) 对任意函数\(\phi(x_1, x_2, \dots, x_m)\)， \(Y_t = \phi(X_t, X_{t-1}, \dots, X_{t+m-1})\)也是严平稳遍历序列。