4 自回归模型

4.1 自回归模型的概念

如果\(\rho_1 \neq 0\)， 则\(X_t\)与\(X_{t-1}\)相关， 可以用\(X_{t-1}\)预测\(X_t\)。 最简单的预测为线性组合， 如下模型：

\[\begin{align} X_t = \phi_0 + \phi_1 X_{t-1} + \varepsilon_t \tag{4.1} \end{align}\] 称为一阶自回归模型(Autoregression model)，记作AR(1)模型。 其中\(\{ \varepsilon_t \}\)是零均值独立同分布白噪声序列， 方差为\(\sigma^2\)， 并设\(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立。 系数\(|\phi_1|<1\)。 更一般的定义中仅要求\(\{ \varepsilon_t \}\)是零均值白噪声， 不要求独立同分布。

这个模型与一元线性回归模型\(Y_i = \phi_0 + \phi_1 x_i + \varepsilon_i\)在某些方面类似， 比如， \(\varepsilon_t\)都是起到误差或者扰动的作用。 但是， 在自回归模型中，自变量\(X_{t-1}\)在时刻\(t-1\)时作为因变量， 所以自回归模型中因变量和自变量不是两个变量而是同一个变量的不同时刻。 回归模型的理论结果不能直接应用到自回归模型当中。

AR(1)模型也是马尔可夫(Markov)过程： \(X_t\)在\(X_{t-1}, X_{t-2}, \dots\)条件下的条件分布， 只与\(X_{t-1}\)有关。 已知\(X_{t-1}\)后， 用\(X_{t-1}, X_{t-2}, \dots\)去预测\(X_t\)， 与仅用\(X_{t-1}\)去预测的效果相同。 这种性质称为马氏性。

条件期望和条件方差： \[ E(X_t | X_{t-1}) = \phi_0 + \phi_1 X_{t-1}, \quad \text{Var}(X_t | X_{t-1}) = \sigma^2 \] 即在\(X_{t-1}=x_{t-1}\)已知后， \(X_t\)条件的条件分布是期望为\(\phi_0 + \phi_1 x_{t-1}\), 方差为\(\sigma^2\)的分布。 可以证明 \[ \text{Var}(X_t) = \frac{\sigma^2}{1 - \phi_1^2} \] 因为\(|\phi_1|<1\)， 所以\(X_t\)在\(X_{t-1}=x_{t-1}\)已知条件下的条件方差小于其无条件方差， 也就是说用\(X_{t-1}\)的信息去预测\(X_t\)， 可以使得\(X_t\)的波动减小， 能够达到预测的效果。

AR(1)模型的推广是AR(\(p\))模型： \[\begin{align} X_t = \phi_0 + \phi_1 X_{t-1} + \dots + \phi_p X_{t-p} + \varepsilon_t \tag{4.2} \end{align}\]

其中\(\{ \varepsilon_t \}\)是零均值独立同分布白噪声序列，方差为\(\sigma^2\)， 且\(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立。 系数\(\phi_1, \dots, \phi_p\)需要满足如下条件：方程 \[ 1 - \phi_1 z - \dots - \phi_p z^p = 0 \] 的所有复根\(z_*\)都满足\(|z_*|>1\)， 上述方程的左边的多项式称为AR(p)模型的特征多项式， 特征多项式的所有复根称为特征根， 对系数的条件称为“特征根都在单位圆外”。 在有的教材中将特征多项式的根的倒数定义为特征根， 在(Tsay 2013)中就是以倒数为特征根。 对AR(1)就是要求\(|\phi_1|<1\)。

更一般的定义中仅要求\(\{ \varepsilon_t \}\)是零均值白噪声， 不要求独立同分布。

4.2 滞后算子

设\(\{ \xi_t, t \in \mathbb Z \}\)为弱平稳时间序列或者常数列， 定义如下的滞后算子\(B\): \[ B \xi_t = \xi_{t-1}, \quad B^j \xi_t = \xi_{t-j}, \ j \in \mathbb Z \]

考虑复变函数\(P(z) = \sum_{j=0}^\infty a_j z^j\)， 其中\(\{ a_j \}\)为实数列， 设\(\sum_{j=0}^\infty |a_j| < \infty\)（称为系数绝对可和）， 有限阶多项式为\(P(z)\)的特例。 定义 \[ P(B) \xi_t = \sum_{j=0}^\infty a_j \xi_{t-j} . \] \(P(B)\)也称为一个（常系数时齐）线性滤波器， \(P(B)\xi_t\)是\(\{ \xi_t \}\)序列的一个滑动平均变换。

设\(Q(z) = \sum_{j=0}^\infty b_j z^j\)，\(\{ b_j \}\)为实数列，绝对可和， 则\(C(z) = P(z) Q(z) = \sum_{j=0}^\infty c_j z^j\)， 其中 \[ c_j = \sum_{i=0}^{j} a_i b_{j-i}, \ j=0,1,\dots \] 且\(\{ c_j \}\)绝对可和， 称数列\(\{ c_j \}\)是数列\(\{ a_j \}\)和数列\(\{ b_j \}\)的离散卷积。 对任意弱平稳列或者常数列\(\{ \xi_t \}\)均有 \[ P(B) Q(B) \xi_t = Q(B) P(B) \xi_t = C(B) \xi_t, \ t \in \mathbb Z \]

若\(\xi_t \equiv \xi\)与\(t\)无关， 则\(B^j \xi = \xi\)。 比如， \(B^j 1 = 1\)， \(P(B) 1 = P(1)\)。

令\(D(z)=\frac{P(z)}{Q(z)}\)， 若\(Q(z) \neq 0\)对任意满足\(|z| \leq 1\)的复数\(z\)均成立， 则\(D(z) = \sum_{j=0}^\infty d_j z^j\), \(\{ d_j \}\)绝对可和，且 \[ P(B) \xi_t = Q(B) D(B) \xi_t = D(B) Q(B) \xi_t, \ t \in \mathbb Z \]

4.3 AR(1)模型的性质

研究AR模型的性质， 可以在对实际数据选择适当模型时， 知道那些情况下使用AR模型， 使用何种AR模型是合适的。

对理论证明感兴趣的同学请参见(何书元 2003)的论述。

AR(1)模型(4.1)要求\(|\phi_1|<1\)， 这是(4.1)中的\(\{ X_t \}\)有弱平稳解的充分必要条件。

充分性： 当\(|\phi_1|<1\)且\(\phi_0=0\)时， 因为 \[ \frac{1}{1 - \phi_1 z} = \sum_{j=0}^\infty \phi_1^j z^j, \quad \frac{1}{1 - \phi_1 B} = \sum_{j=0}^\infty \phi_1^j B^j \] 取 \[ X_t^* = \sum_{j=0}^\infty \phi_1^j \varepsilon_{t-j} \] 右侧的随机变量级数均方收敛且a.s.收敛。 将上式代入\(X_t = \phi_1 X_{t-1} + \varepsilon_t\)， 直接验证或者利用滞后算子性质可以证明\(X_t^*\)满足方程。 所以\(\phi_0 = 0\), \(|\phi_1|<1\)时AR(1)模型有\(X_t^*\)这样的因果线性时间序列形式的弱平稳解。 对于一般的\(\phi_0\)，因为平稳要求\(EX_t = EX_{t-1}=\mu\)所以要求 \(\mu = \phi_0 + \phi_1 \mu\)即\(\mu = \frac{\phi_0}{1 - \phi_1}\)， 令 \[ X_t^* = \mu + \sum_{j=0}^\infty \phi_1^j \varepsilon_{t-j} \] 可以验证其满足AR(1)模型， 是因果线性时间序列形式的弱平稳解。

必要性证明： 如果模型有弱平稳解\(X_t\)， 因为要求\(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立， 在模型两边求方差得 \[ \begin{aligned} & \text{Var}(X_t) = \text{Var}(\phi_0 + \phi_1 X_{t-1} + \varepsilon_t) = \phi_1^2 \text{Var}(X_{t-1}) + \sigma^2, \\ & \sigma_X^2 = \phi_1^2 \sigma_X^2 + \sigma^2, \\ & \sigma_X^2 = \frac{\sigma^2}{1 - \phi_1^2} \end{aligned} \] 因为\(\sigma_X^2>0\)所以\(1-\phi_1^2>0\), \(|\phi_1|<1\)。

上述证明过程也证明了

\[ \mu=EX_t = \frac{\phi_0}{1 - \phi_1}, \quad \sigma_X = \text{Var}(X_t) = \frac{\sigma^2}{1 - \phi_1^2} . \]

注：可以证明， \(\phi_1 = 1\)时， 一定没有弱平稳列满足方程\(X_t = \phi_0 + \phi_1 X_{t-1} + \varepsilon_t\)。 当\(|\phi_1| > 1\)时， 取 \[ X_t = \mu -\sum_{j=1}^\infty \phi_1^{-j} \varepsilon_{t+j}, \ t \in \mathbb Z \] 则\(\{X_t \}\)是满足\(X_t = \phi_0 + \phi_1 X_{t-1} + \varepsilon_t\)的弱平稳时间序列， 但\(\varepsilon_t\)不再与\(X_{t-1}, X_{t-2}, \dots\)相互独立。

由\(\mu=\phi_0/(1-\phi_1)\)得\(\phi_0 = (1-\phi_1)\mu\)， AR(1)模型可以写成 \[ X_t = (1-\phi_1)\mu + \phi_1 X_{t-1} + \varepsilon_t \] 即\(t\)时刻的值， 是历史均值与\(t-1\)时刻值的加权平均， 加上一个与历史值相互独立的扰动。

当\(\phi_1=0\)时，AR(1)模型就退化成白噪声， 所以AR(1)模型通常都认为\(\phi_1 \neq 0\)。 \(|\phi_1|\)越接近于1， 说明前后的相关性越强。

4.4 AR(1)模型的自相关函数

AR(1)模型的平稳解满足\(\epsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立。 将模型写成

\[\begin{align} X_t - \mu = \phi_1 (X_{t-1} - \mu) + \varepsilon_t \tag{4.3} \end{align}\]

在(4.3)两边乘以\(\varepsilon_t\)后取期望，有 \[ E[\varepsilon_t(X_t - \mu)] = \phi_1 E[\varepsilon_t(X_{t-1} - \mu)] + \sigma^2 = \sigma^2 \]

在(4.3)两边乘以\(X_t-\mu\)后取期望，有 \[ \gamma_0 = \phi_1 \gamma_1 + \sigma^2 \]

在(4.3)两边乘以\(X_{t-j}-\mu\)后取期望，有 \[ \gamma_j = \phi_1 \gamma_{j-1}, \ j=1,2,\dots \] 即有 \[\begin{align} \gamma_0 =& \sigma_X^2 = \frac{\sigma^2}{1 - \phi_1^2} = \phi_1 \gamma_1 + \sigma^2 \\ \gamma_j =& \phi_1 \gamma_{j-1}, \ j=1,2,\dots \end{align}\]

于是ACF为 \[ \rho_j = \frac{\gamma_j}{\gamma_0} = \phi_1^j, \ j=1,2,\dots \]

当\(0<\phi_1 < 1\)时， ACF为正的单调下降序列， 以负指数速度（几何级数）下降。 当\(-1 < \phi_1 < 0\)时， ACF为负正交替的序列， 绝对值以负指数速度下降。

例：\(\phi_1=0.8\)的ACF图形：

tmp.x <- 0:15
tmp.y <- 0.8^tmp.x
plot(tmp.x, tmp.y, type="h", xlab="lag", ylab="ACF",
     ylim=c(-1, 1))
abline(h=0)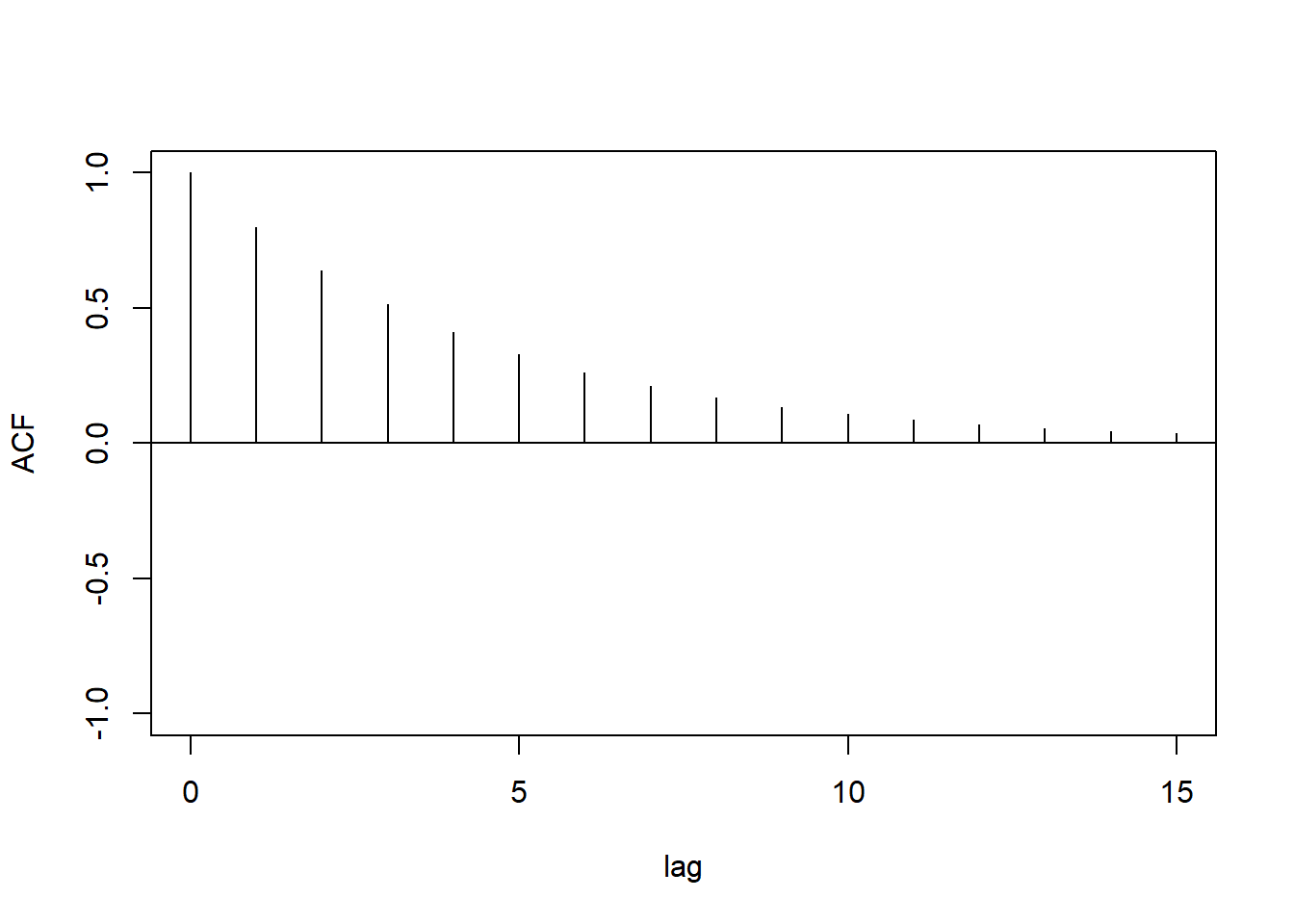

例：\(\phi_1=-0.8\)的ACF图形：

tmp.x <- 0:15
tmp.y <- (-0.8)^tmp.x
plot(tmp.x, tmp.y, type="h", xlab="lag", ylab="ACF",
     ylim=c(-1, 1))
abline(h=0)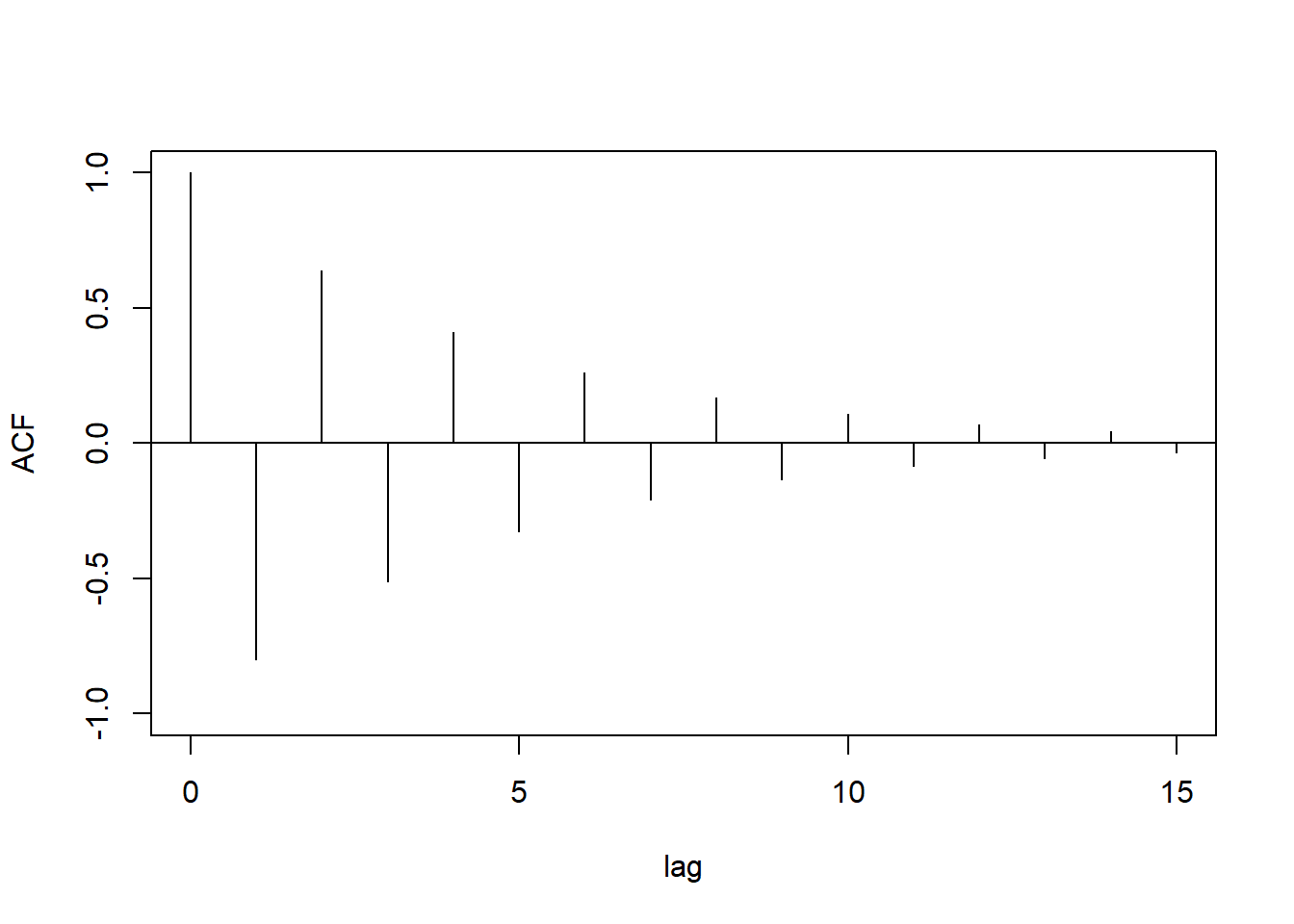

4.5 AR(2)模型的性质

AR(2)模型为 \[\begin{align} X_t = \phi_0 + \phi_1 X_{t-1} + \phi_2 X_{t-2} + \varepsilon_t \tag{4.4} \end{align}\] 其中\(\{\varepsilon_t \}\)为独立同分布的零均值白噪声, \(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立。 系数满足特征方程的根都在单位圆外要求。 特征方程为

\[\begin{align} 1 - \phi_1 z - \phi_2 z^2 = 0 \tag{4.5} \end{align}\]

这个模型有因果线性时间序列形式的弱平稳解。 对(4.4)两边取期望得\(\mu=EX_t\)的方程 \[ \mu = \phi_0 + \phi_1 \mu + \phi_2 \mu \] 所以 \[ \mu = \frac{\phi_0}{1 - \phi_1 - \phi_2} \]

将(4.4)中的\(X_t\)减去\(\mu\)， 方程变成

\[\begin{align} X_t - \mu = \phi_1 (X_{t-1}-\mu) + \phi_2 (X_{t-2}-\mu) + \varepsilon_t \tag{4.6} \end{align}\]

在(4.6)两边乘以\(X_{t-j}-\mu\)， 并利用\(\varepsilon_t\)与\(X_{t-1}, X_{t-2}, \dots\)独立的性质，可得 \[ \gamma_j = \phi_1 \gamma_{j-1} + \phi_2 \gamma_{j-2}, \ j=1, 2, \dots \] 两边除以\(\gamma_0\)得

\[\begin{align} \rho_j = \phi_1 \rho_{j-1} + \phi_2 \rho_{j-2}, \ j=1,2,\dots \tag{4.7} \end{align}\]

这种形式的递推称为齐次线性差分方程。 (4.7)可以用滞后算子写成

\[\begin{align} (1 - \phi_1 B - \phi_2 B^2) \rho_j = 0, \ j=1,2,\dots \tag{4.8} \end{align}\]

可以看出， 递推中用到的\(1 - \phi_1 B - \phi_2 B^2\) 就是将特征多项式中的\(z\)替换成了滞后算子\(B\)， 这样递推得到的\(\rho_j\)的性质自然就是由特征多项式决定的。

(4.7)的递推需要初值\(\rho_0\)和\(\rho_1\)。 \(\rho_0=1\)，而 \[ \rho_1 = \phi_1 \rho_0 + \phi_2 \rho_1, \quad \rho_1 = \frac{\phi_1}{1 - \phi_2} \] 这样就可以给定\(\phi_1, \phi_2\)后递推计算出\(\rho_j, j=1,2,3,\dots\)。 特征根都在单位圆外的条件可以保证\(\lim_{j\to\infty} \rho_j = 0\) （参见(何书元 2003)§2.1），且衰减速度为负指数速度。 \(\lim_{j\to\infty} \rho_j = 0\)也是弱平稳列的必要条件。

特征多项式\(1 - \phi_1 z - \phi_2 z^2=0\)的根的判别式为 \(\Delta = \phi_1^2 + 4 \phi_2\)， 当\(\phi_2 \geq -4 \phi_1^2\)时为实根， 当\(\phi_2 < -4 \phi_1^2\)时为复根。 两个特征根都在单位圆外的充分必要条件是 \[ |\phi_1| < 2, \ |\phi_2| < 1, \ \phi_2 < 1 \pm \phi_1 \]

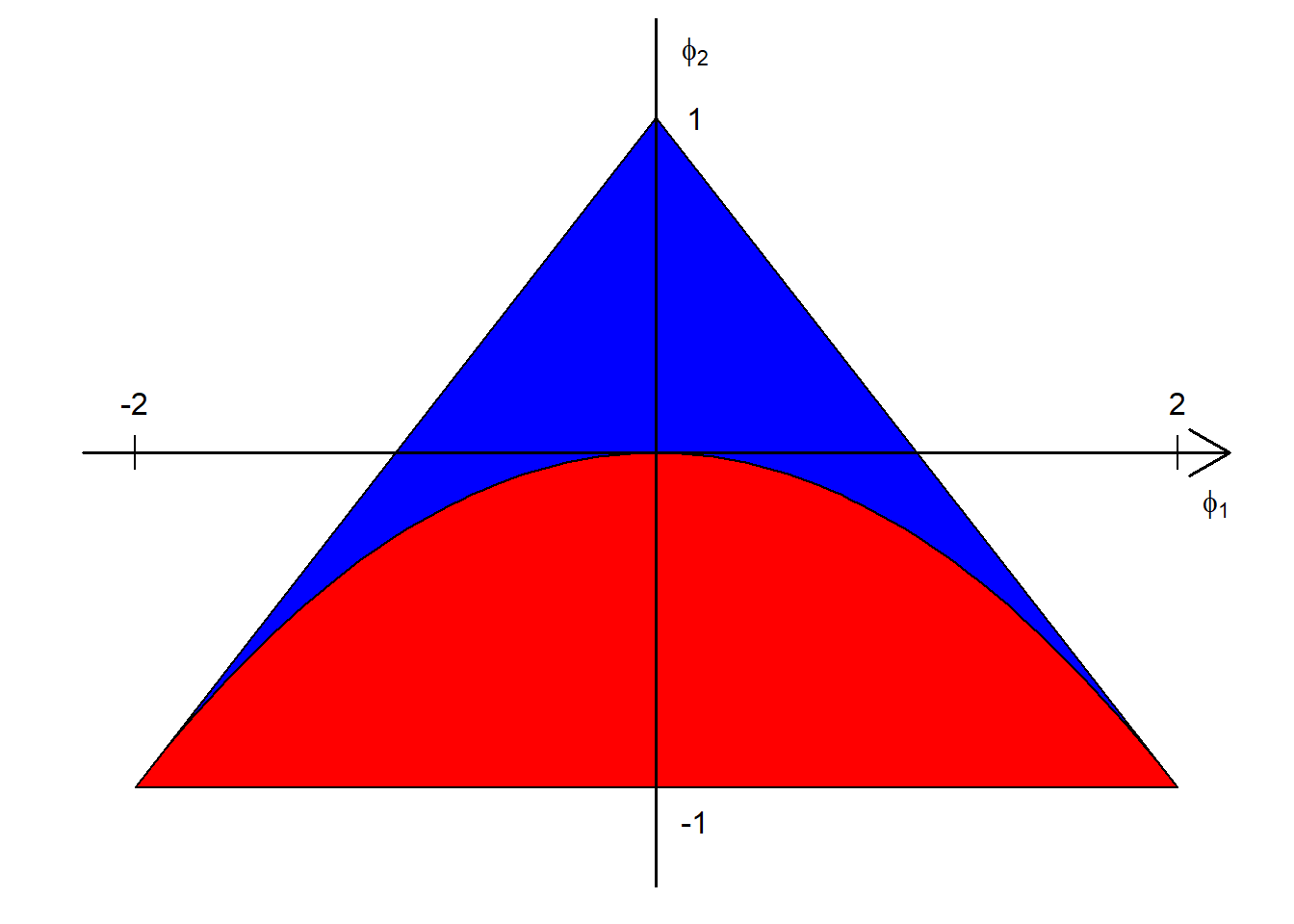
AR(2)的平稳区域

图4.1: AR(2)的平稳区域

图4.1的三角形阴影部分代表了\((\phi_1, \phi_2)\)使得模型有平稳解的区域， 不包含三角形边界； 蓝色区域以及蓝色和红色边界线为两个实特征根的区域， 红色区域为两个共轭复根的区域。

有两个实根时，两个根为 \[ z_1, z_2 = \frac{\phi_1 \pm \sqrt{\phi_1^2 + 4\phi_2}}{-2\phi_2} \]

这两个根的绝对值都大于1。 付过两个根都是正的，则\(\rho_j\)为正，呈现出负指数速度单调衰减。 如果两个根正负不同，则绝对值仍以负指数速度衰减但是不单调， 当负根绝对值更小时会正负交替衰减。

有共轭复根时，两个根为 \[ z_1, z_2 = \frac{\phi_1}{-2\phi_2} \pm i \frac{\sqrt{|\phi_1^2 + 4\phi_2}|}{-2\phi_2} \] 复根的模为 \[ |z_i| = \frac{1}{\sqrt{-\phi_2}} \] 辐角为 \[ \omega = \cos^{-1} \frac{\phi_1}{2\sqrt{-\phi_2}} \] 反过来有 \[ \phi_2 = -\frac{1}{|z_1|^2}, \ \phi_2 = \frac{2}{|z_1|} \cos\omega \]

\(\omega\)这个辐角对应的周期为 \[ P = \frac{2\pi}{\omega} = \frac{2\pi}{\cos^{-1} \frac{\phi_1}{2\sqrt{-\phi_2}}} \] 这样的AR(2)模型会体现出随机地平均以周期\(P\)的波动； \(\rho_j\)序列呈现出以周期\(P\)震荡的幅度负指数衰减的变化。

下面对不同的\(\phi_1, \phi_2\)取值画出ACF的典型图形。

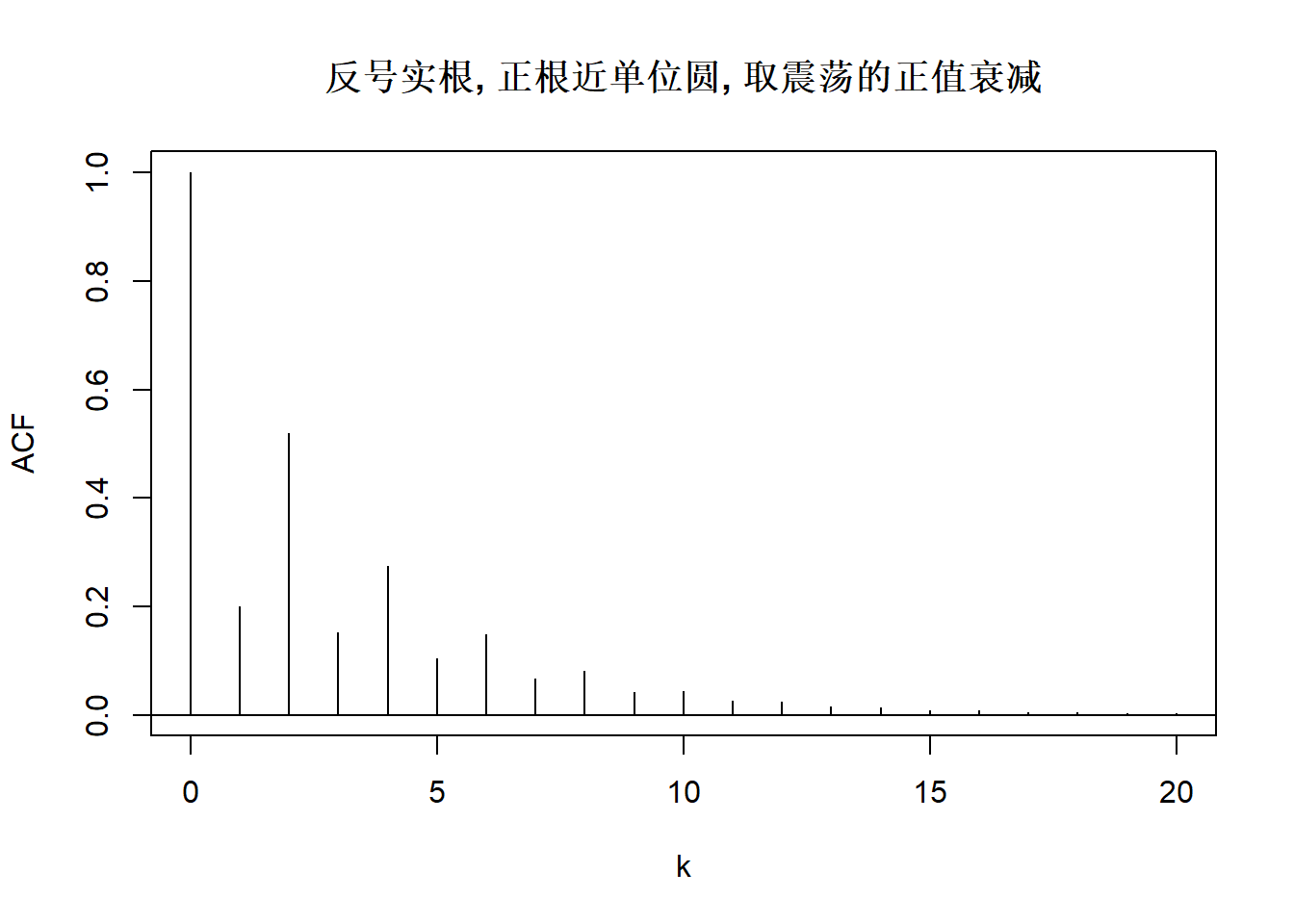
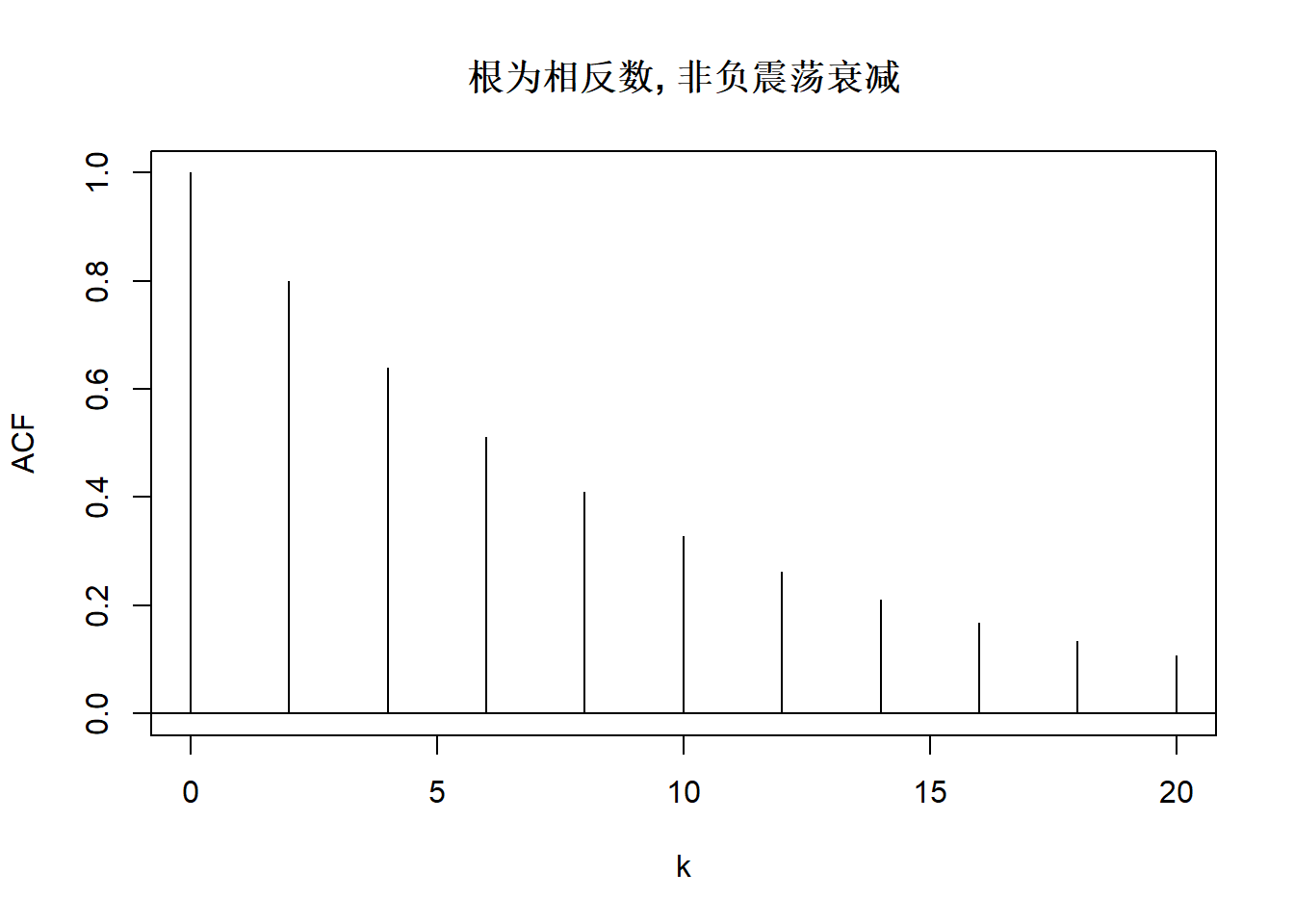
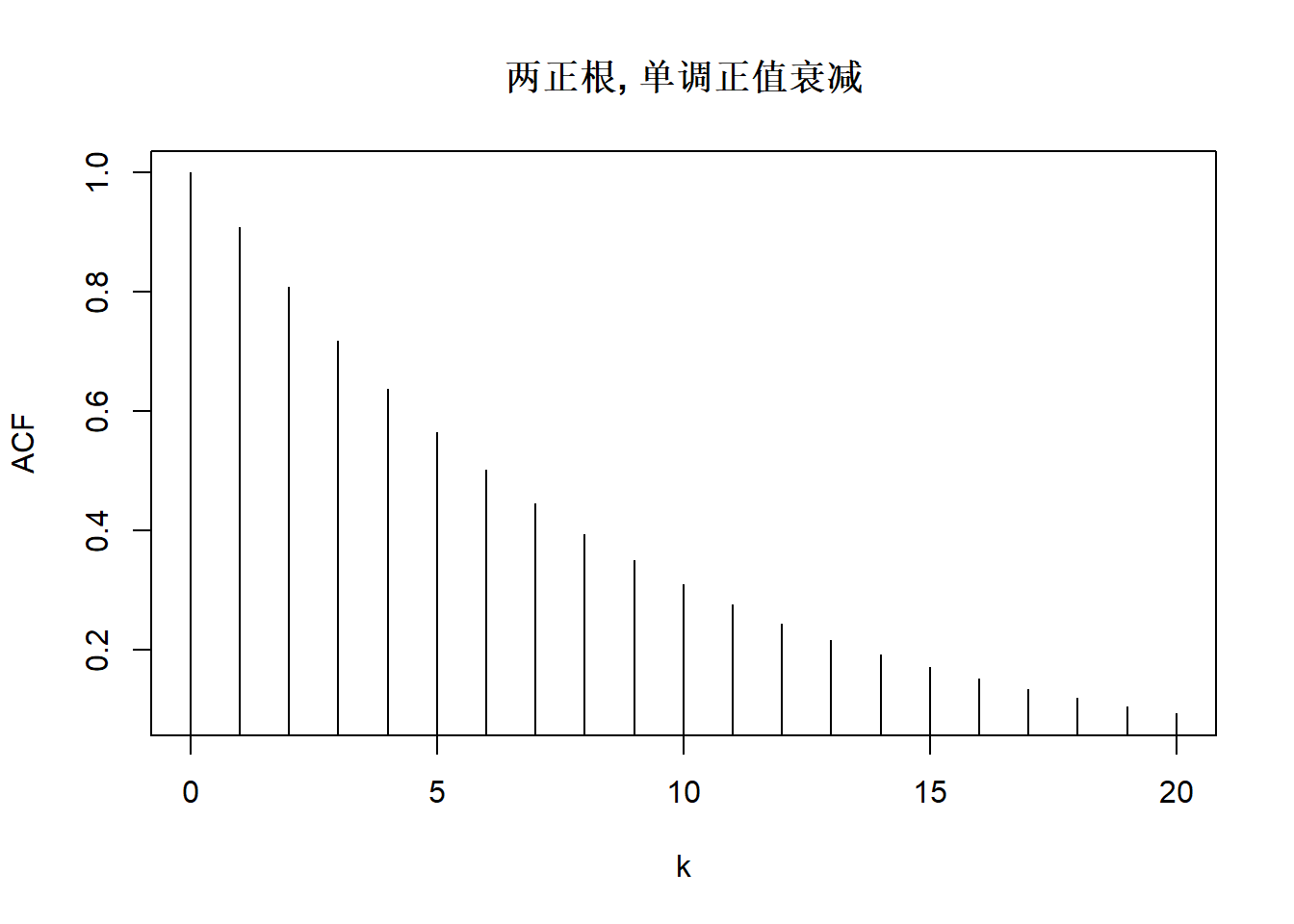
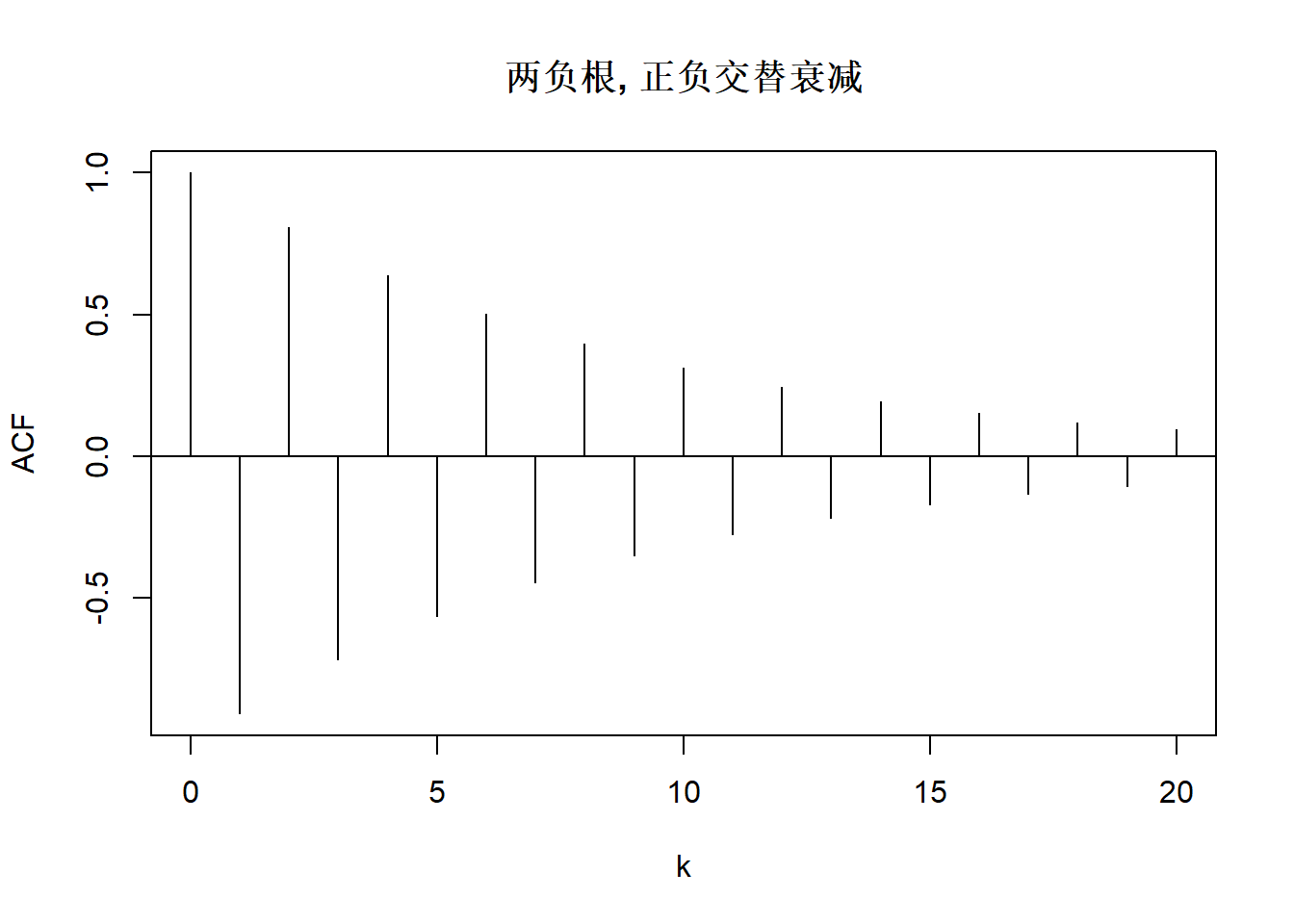
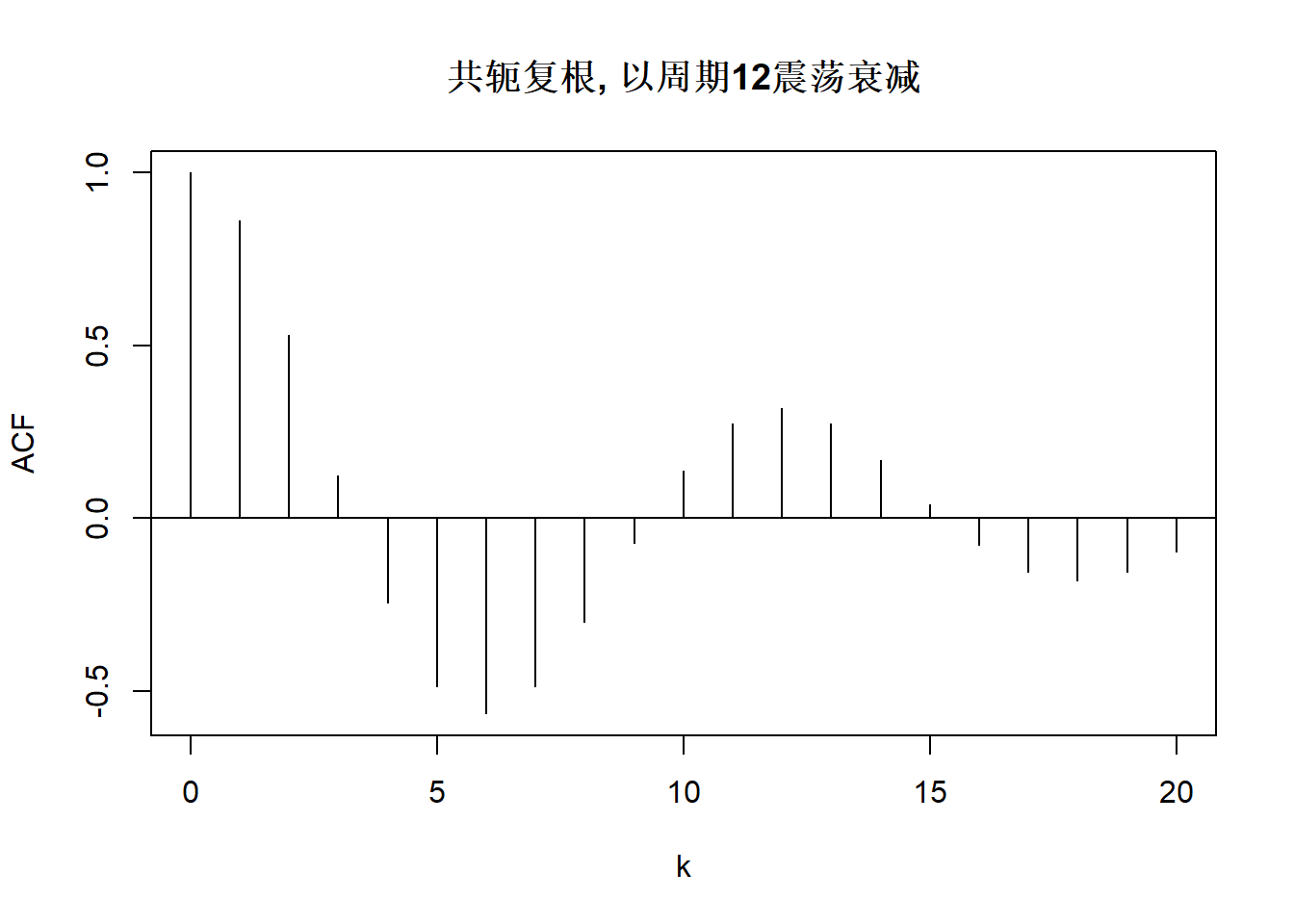
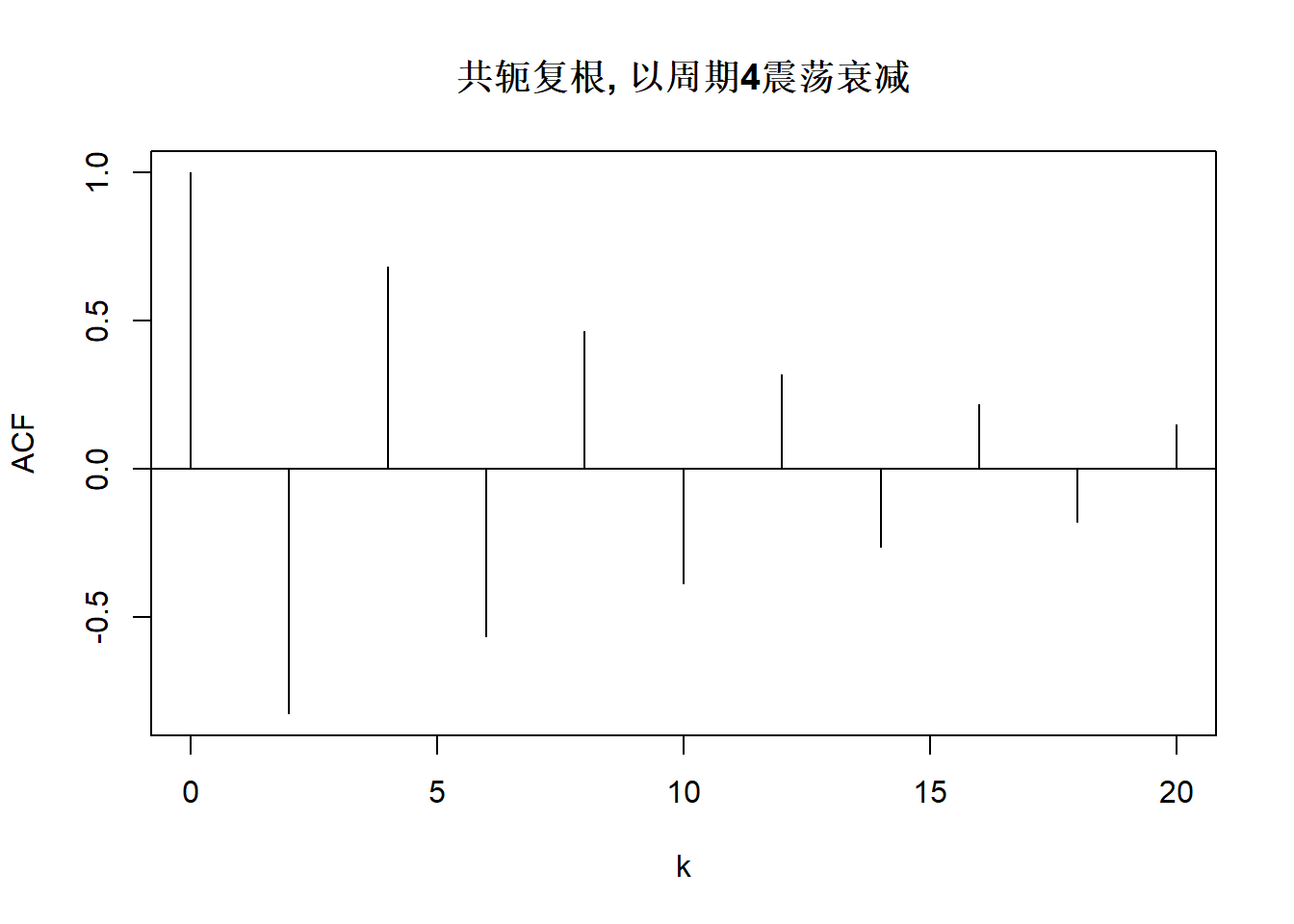
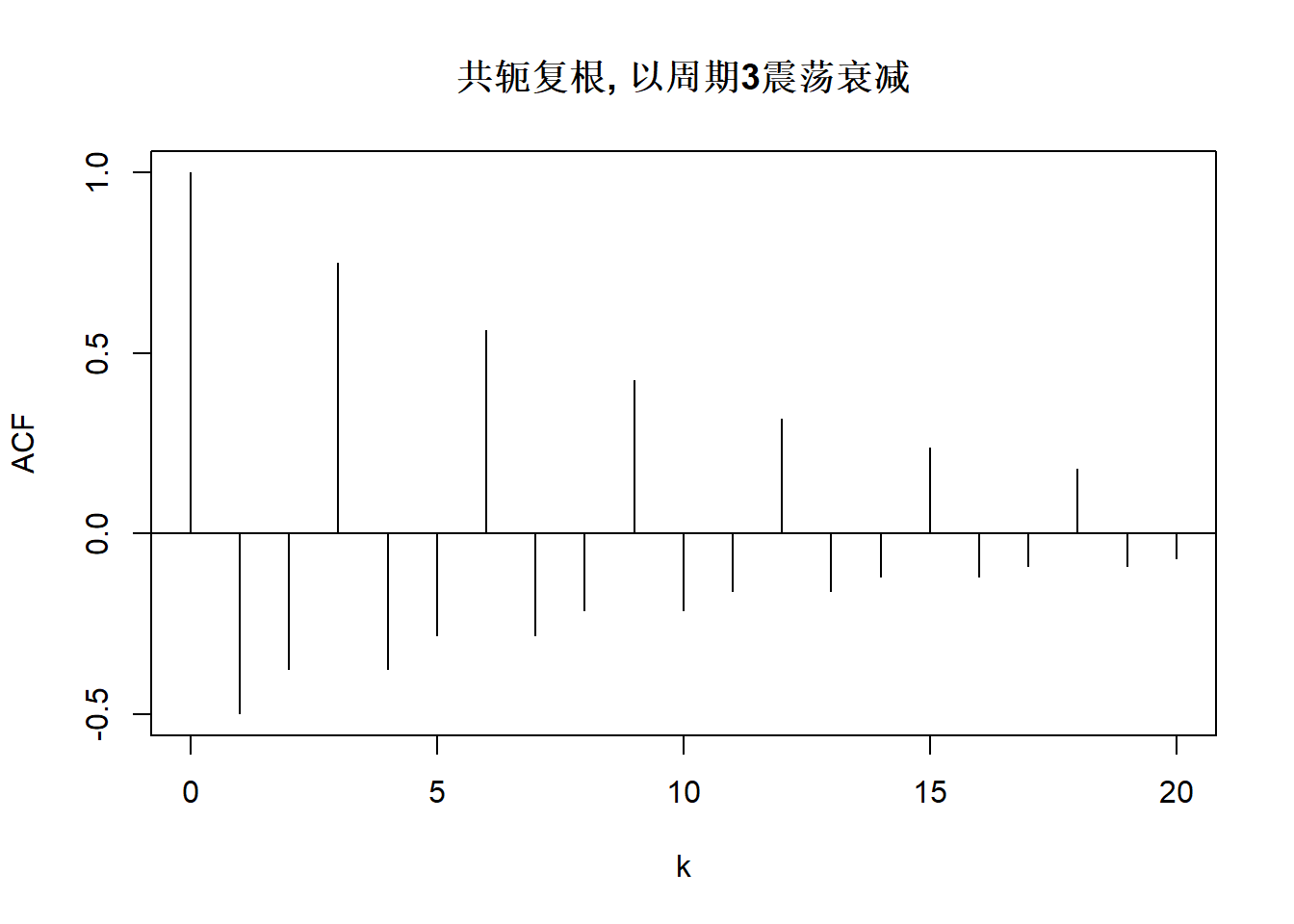
上图中的模型AR(2)分别为：

\[ \begin{aligned} X_t =& 0.1 X_{t-1} + 0.5 X_{t-2} + \varepsilon_t \\ X_t =& -0.1 X_{t-1} + 0.5 X_{t-2} + \varepsilon_t \\ X_t =& 0.8 X_{t-1} + \varepsilon_t \\ X_t =& X_{t-1} - 0.1 X_{t-2} + \varepsilon_t \\ X_t =& -X_{t-1} - 0.1 X_{t-2} + \varepsilon_t \\ X_t =& \left(\frac{2}{1.1}\cos\frac{\pi}{6}\right) X_{t-1} - \frac{1}{1.1^2} X_{t-2} + \varepsilon_t \\ X_t =& \left(\frac{2}{1.1}\cos\frac{\pi}{2}\right) X_{t-1} - \frac{1}{1.1^2} X_{t-2} + \varepsilon_t \\ X_t =& \left(\frac{2}{1.1}\cos\frac{2\pi}{3}\right) X_{t-1} - \frac{1}{1.1^2} X_{t-2} + \varepsilon_t \\ \end{aligned} \]

例4.1 考虑美国的国民生产总值(GNP)经过季节调整后的季度增长率。 时间是1947年第二季度到2010年第一季度，总计252个观测值。

读入数据并计算对数增长率：

da <- read_table("q-gnp4710.txt", col_types=cols(.default = col_double()))
gnp <- ts(da[["VALUE"]], start=c(1947, 1), frequency=4)

这个序列从1947年第一季度到2010年第一季度共253个观测。

GNP的对数值的图形：

plot(log(gnp), xlab="year", ylab="log(GNP)")

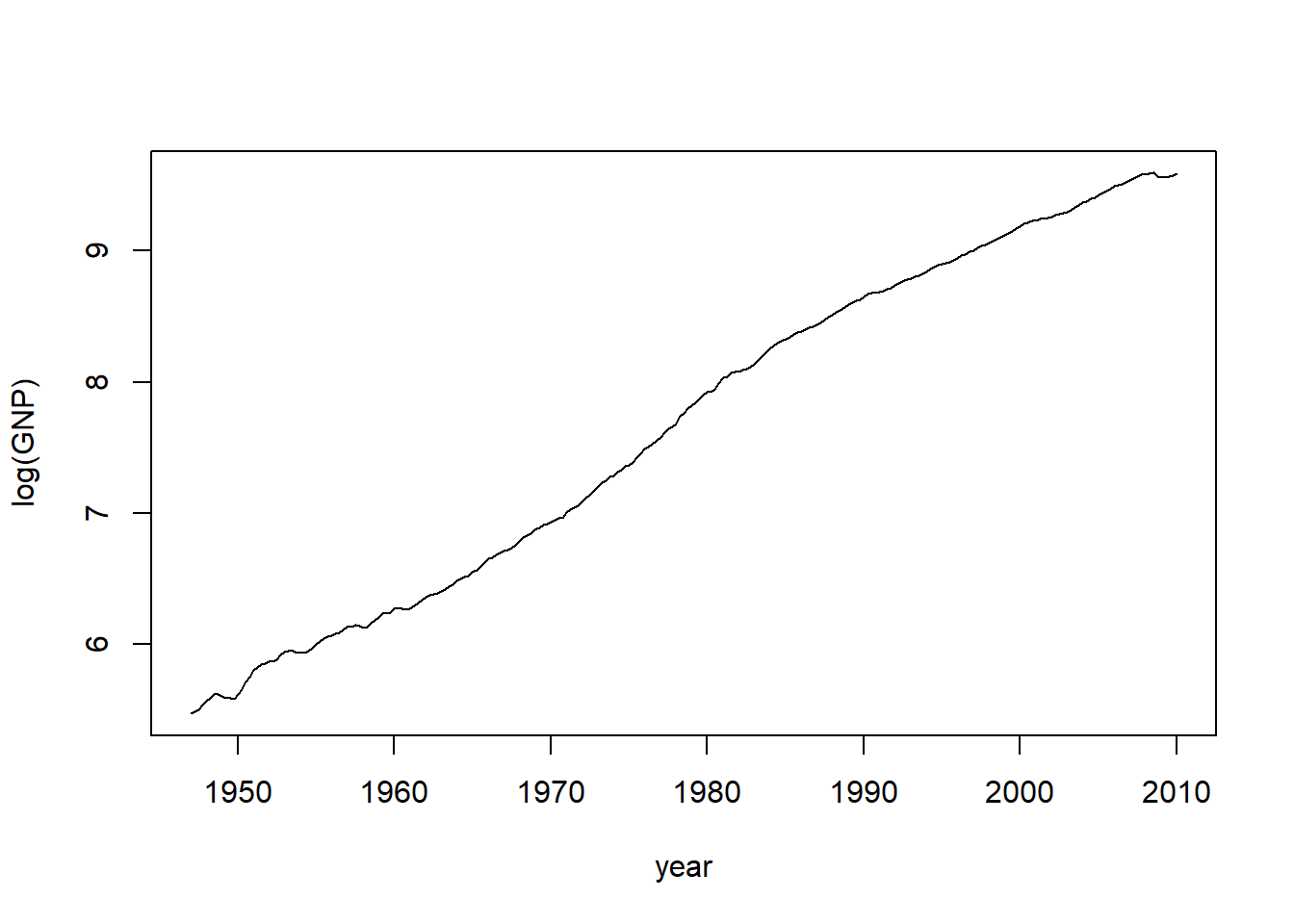
以上的GNP是经过季节调整的，所以看不出季节性。

计算GNP的对数值的差分作为对数增长率，并作图：

rate <- diff(log(gnp))
plot(rate, xlab="Year", ylab="Growth")
abline(h=0, col="gray")

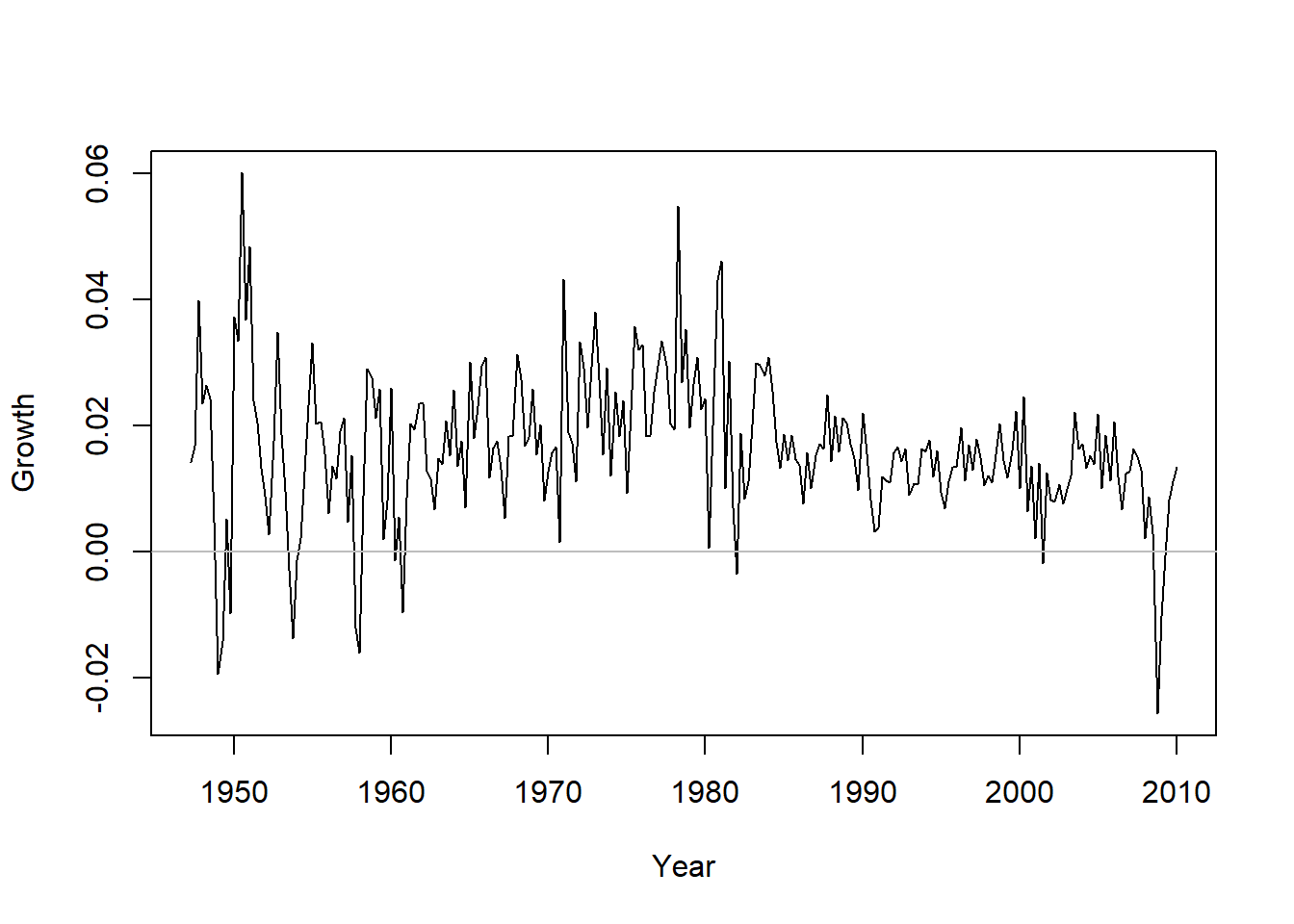
增长率的ACF估计：

forecast::Acf(rate, xlab="Years", main="")

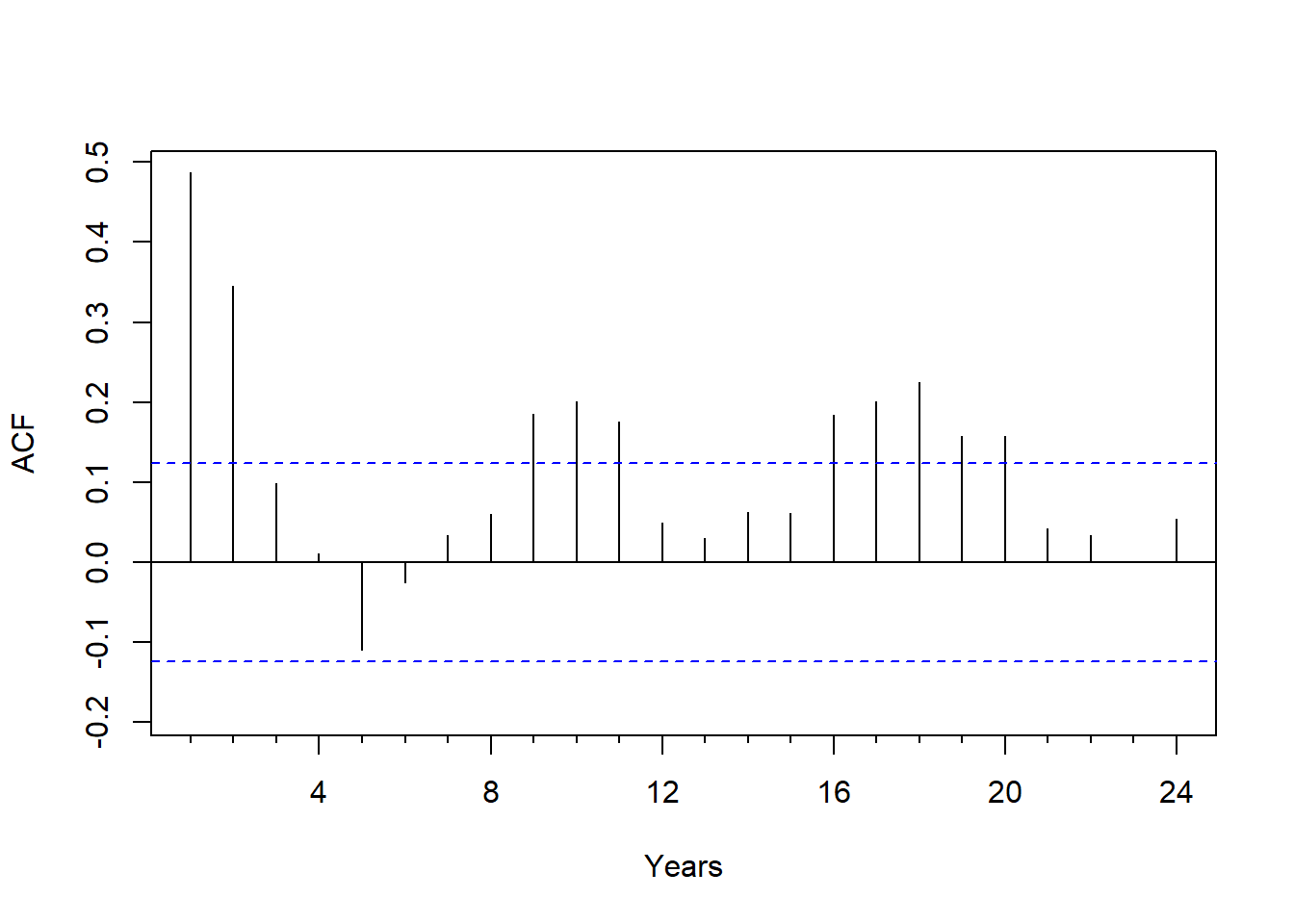
这个图形呈现出一定周期的震荡衰减， 可尝试AR建模。

拟合的模型为 \[ (1 - 0.438B - 0.206B^2 + 0.156 B^3)(X_t - 0.016) = \varepsilon_t, \ \sigma^2=\text{Var}(\epsilon_t) = 9.55\times 10^{-5} \]

R函数polyroot(x)可以求出多项式的所有复根， x是多项式按升幂排列的系数。

roots <- polyroot(c(1, -0.438, -0.206, 0.156)); roots
## [1]  1.614790+0.866168i -1.909068+0.000000i  1.614790-0.866168i
abs(roots)
## [1] 1.832429 1.909068 1.832429

有一个实根\(-1.9091\)和一对共轭复根\(1.6148\pm 0.8662 i\), 复根的模为\(1.8324\)， 复根对应的周期为

2*pi/Arg(roots[1])
## [1] 12.7619

12.8个季度，约为3年。这是美国GNP的随机周期， 也是ACF震荡的周期。

时间序列的周期研究是很常用的工具。

○○○○○

4.6 AR(\(p\))模型的性质

对于一般的AR(p)模型， 其ACF的性质以及序列的随机周期， 也由其特征根决定。 ACF可以是单调衰减、震荡衰减、正负交替衰减、呈周期震荡衰减。 在有复特征根根或者有接近\(-1\)的特征根时时间序列呈现出一定的随机周期变化。

由平稳性得 \[ \mu = \frac{\phi_0}{1 - \phi_1 - \dots - \phi_p} \]

自相关函数(ACF)满足如下的递推（差分方程） \[ (1 - \phi_1 B - \dots - \phi_p B^p) \rho_j = 0, \ j=1,2,\dots \]

AR(\(p\))模型的平稳解是线性时间序列。

4.7 偏自相关函数

实际数据用AR模型建模时，阶数\(p\)是未知的， 确定\(p\)的问题称为定阶。 一般常用偏自相关函数和AIC准则。

设\(X_1, \dots, X_n, Y\)为随机变量， \[ L(Y|X_1, \dots, X_n) = \mathop{\text{argmin}}_{\hat Y = b_0 + b_1 X_1 + \dots + b_n X_n} E(Y - \hat Y)^2 \] 称为用\(X_1, \dots, X_n\)对\(Y\)的最优线性预测。 \(Y - L(Y|X_1, \dots, X_n)\)与\(Z - L(Z|X_1,\dots, X_n)\) 的相关系数称为\(Y\)和\(Z\)在扣除\(X_1, \dots, X_n\)影响后的偏相关系数。

对平稳线性时间序列， 对\(n=1,2,\dots\)， 有 \[ L(X_t|X_{t-1}, \dots, X_{t-n}) = \phi_{n0} + \phi_{n1} X_{t-1} + \dots + \phi_{nn} X_{t-n} \] 其中\(\phi_{nj}, j=0,1,\dots,n\)与\(t\)无关。 称\(\phi_{nn}\)为时间序列\(\{X_t \}\)的偏自相关系数， \(\{ \phi_{nn} \}\)序列称为时间序列\(\{X_t \}\)的偏自相关函数(PACF)。

\(\phi_{nn}\)实际是\(X_t\)与\(X_{t-n}\)在扣除\(X_{t-2}, \dots, X_{t-n+1}\)的影响后的偏相关系数。 \(\phi_{11}\)就是\(\rho_1\)。

\(\phi_{nn}\)用样本进行估计， 得到的估计值\(\hat\phi_{nn}, n=1,2,\dots\)称为样本偏自相关函数。 在R软件中用pacf(x)估计并作图。

如果\(\{ X_t \}\)服从如下AR(\(p\))模型：

\[ X_t = \phi_0 + \phi_1 X_{t-1} + \dots + \phi_p X_{t-p} + \varepsilon_t, \ \phi_p \neq 0 \] 这意味着用\(X_{t-1}, X_{t-2},\dots\)的线性组合预测\(X_t\)时， 只需要用到\(X_{t-1}, \dots, X_{t-p}\)， 增加\(X_{t-p-1}, X_{t-p-2},\dots\)不能改进预测。 这意味着\(\phi_{kk}=0\), \(k>p\)。 这种性质叫做AR模型的偏自相关函数截尾性。

AR(p)序列的样本偏自相关函数\(\hat\phi_{kk}\)满足如下性质：

  • \(T\to\infty\)时\(\hat\phi_{pp} \to \phi_p \neq 0\)。
  • 对\(k>p\), \(\hat\phi_{kk} \to 0\)(\(T\to\infty\))。
  • 对\(k>p\)，\(\hat\phi_{kk}\)渐近方差为\(\frac{1}{T}\)。

这样，可以用类似对ACF的白噪声检验那样给PACF图画出\(\pm\frac{2}{\sqrt{T}}\)的上下界限， 以此判断PACF在哪里截尾。

例4.2 考虑CRSP价值加权指数月度收益率， 时间从1926-1到2008-12。

d <- read_table(
  "m-ibm3dx2608.txt",
  col_types=cols(.default=col_double(),
                 date=col_date(format="%Y%m%d")))
ibmind <- xts(as.matrix(d[,-1]), d$date)
tclass(ibmind) <- "yearmon"
vw <- ts(coredata(ibmind)[,"vwrtn"], start=c(1926,1), frequency=12)
head(ibmind)
##             ibmrtn     vwrtn     ewrtn     sprtn
## 1月 1926 -0.010381  0.000724  0.023174  0.022472
## 2月 1926 -0.024476 -0.033374 -0.053510 -0.043956
## 3月 1926 -0.115591 -0.064341 -0.096824 -0.059113
## 4月 1926  0.089783  0.038358  0.032946  0.022688
## 5月 1926  0.036932  0.012172  0.001035  0.007679
## 6月 1926  0.068493  0.056888  0.050487  0.043184
plot(vw, main="CRSP Value Weighted Index Monthly Return")
abline(h=0, col="gray")
CRSP价值加权指数月收益率

图4.2: CRSP价值加权指数月收益率 

forecast::Acf(vw, main="")
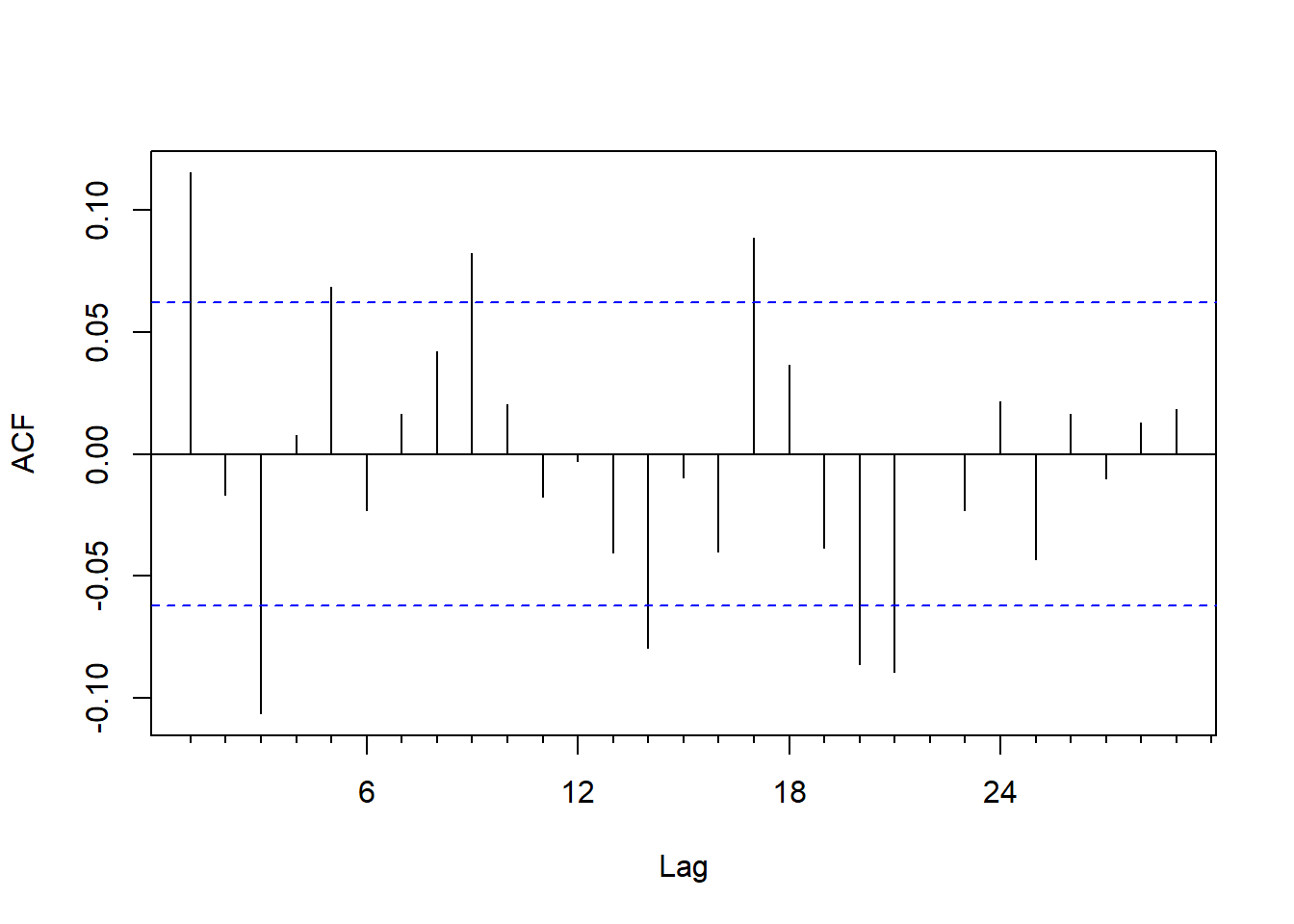
CRSP价值加权指数月收益率的ACF

图4.3: CRSP价值加权指数月收益率的ACF

ACF到\(k=21\)还没有截尾。 PACF图:

pacf(vw, main="")
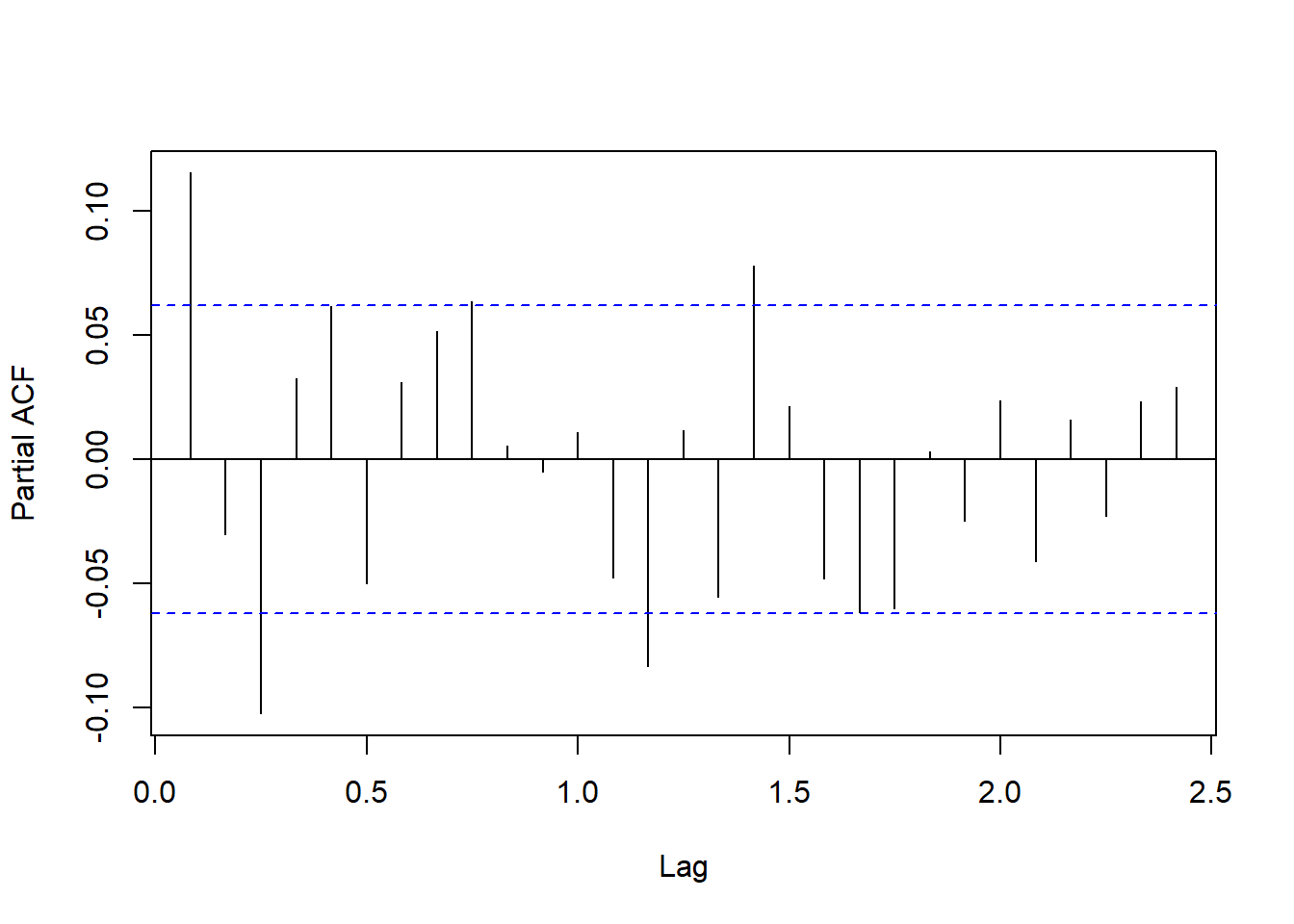
CRSP价值加权指数月度收益率的PACF

图4.4: CRSP价值加权指数月度收益率的PACF

两倍的渐近标准差为:

2/sqrt(length(vw))
## [1] 0.06337243

PACF值的列表：

tmp <- pacf(vw, main="", plot=FALSE, lag.max=12)
cbind(k=round(tmp$lag*12), pacf=round(tmp$acf, 4))
##        k    pacf
##  [1,]  1  0.1154
##  [2,]  2 -0.0304
##  [3,]  3 -0.1025
##  [4,]  4  0.0326
##  [5,]  5  0.0618
##  [6,]  6 -0.0502
##  [7,]  7  0.0312
##  [8,]  8  0.0517
##  [9,]  9  0.0635
## [10,] 10  0.0053
## [11,] 11 -0.0052
## [12,] 12  0.0109

如果仅看前12个PACF， 取\(p=3\)应该可以， 但是实际上PACF在\(k=17\)仍未截尾。

例4.3 考虑例4.1中的美国经过季节调整后的GNP季度对数增长率数据。

forecast::Acf(rate, xlab="Years", main="")

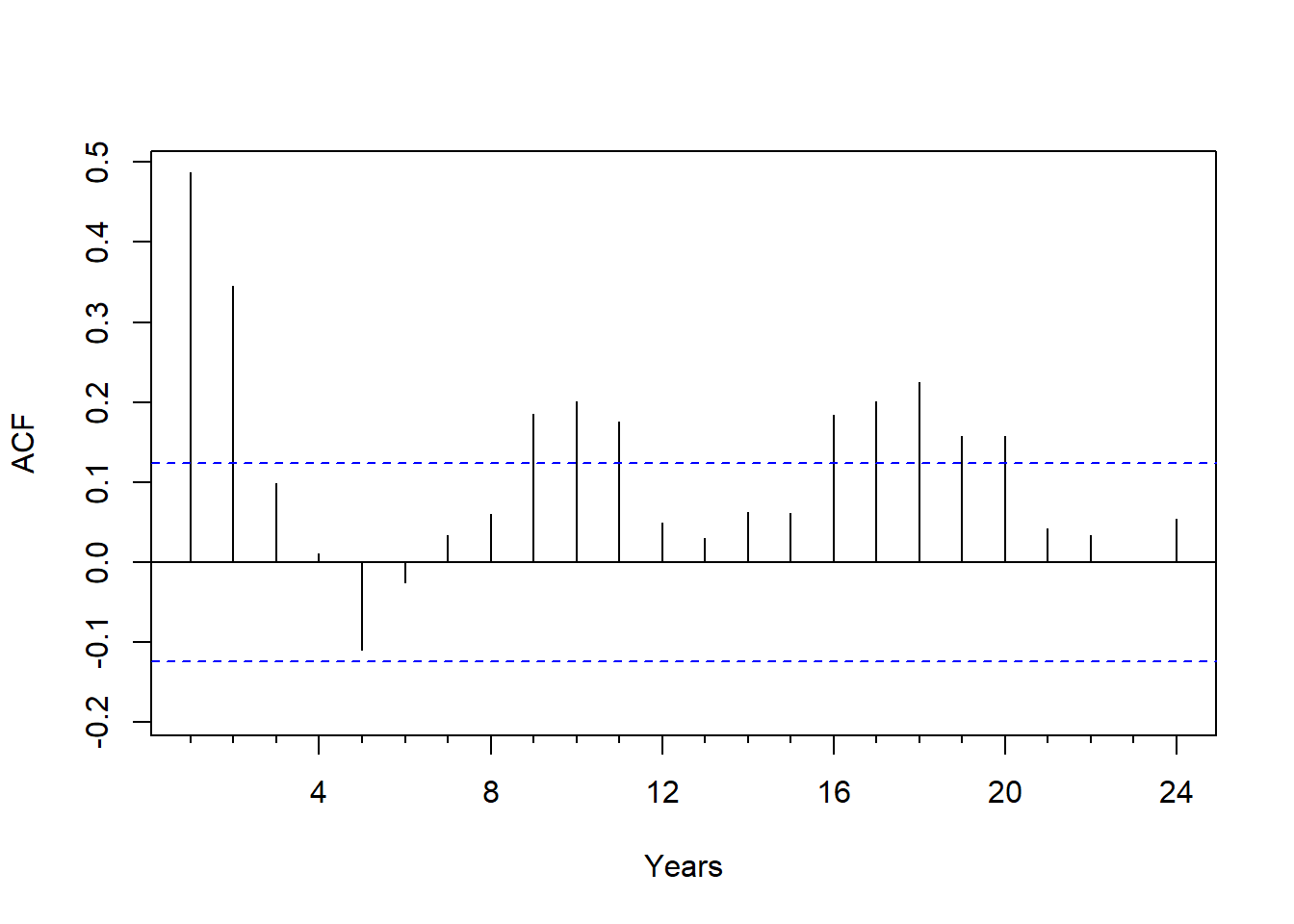
ACF明显不截尾。

pacf(rate, xlab="Years", main="")

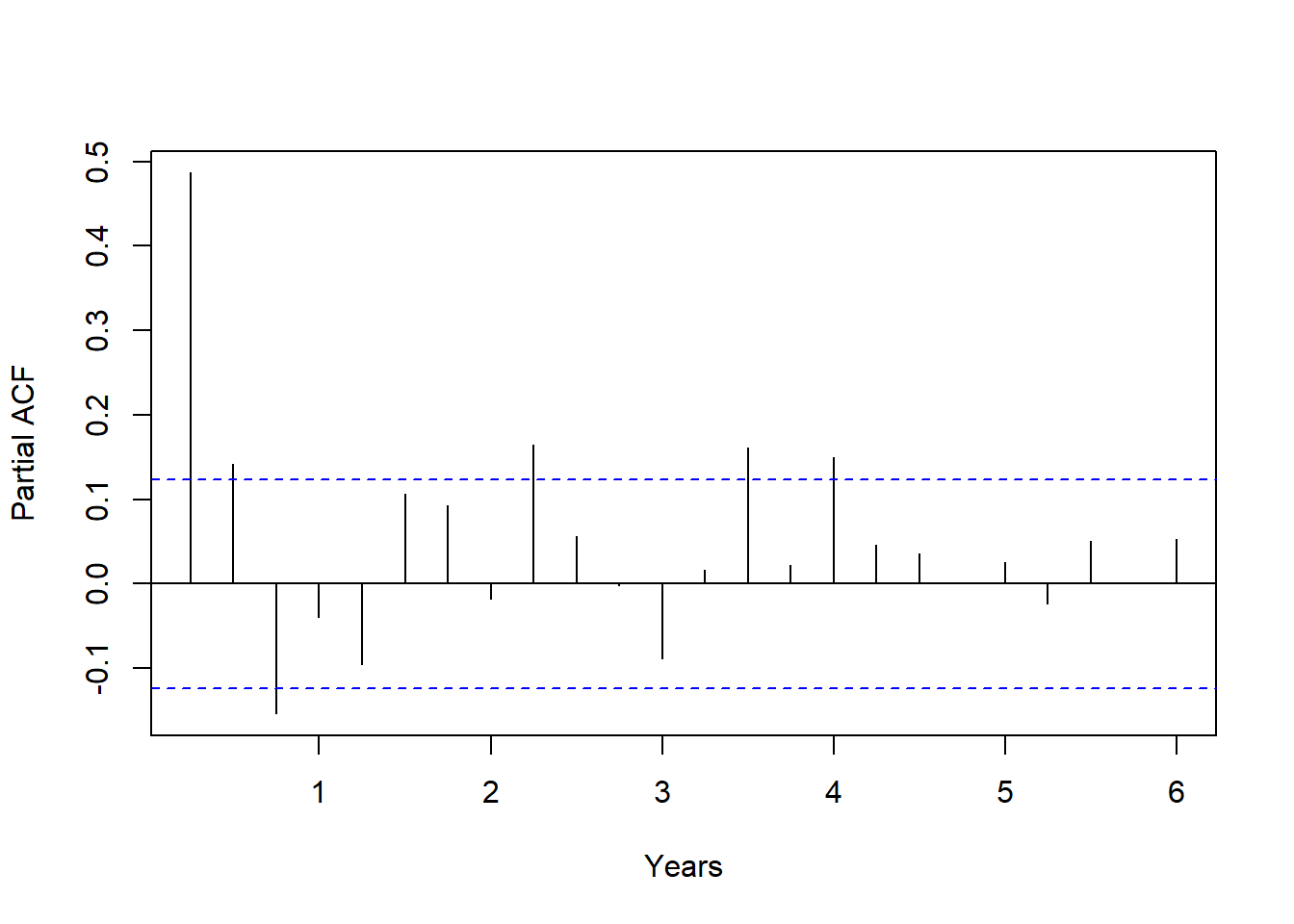
PACF虽然在\(k=3, 9, 14, 16\)等位置超出界限， 但是超出不多， 可考虑用AR(3)建模。

4.8 信息准则

信息准则是统计建模中常用的模型比较工具， 其基本思想是模型拟合数据的拟合优度与模型简单化的折衷。

AIC准则（Akaike’s Information Criterion）： \[ \text{AIC} = -\frac{2}{T}\ln(\text{似然函数值}) + \frac{2}{T} (\text{参数个数}) \] 其中似然函数值是在参数最大似然估计处的似然函数值。 当模型为高斯AR(p)，即\(\{\epsilon_t\}\)是独立同\(\text{N}(0,\sigma^2)\)序列时的AR(\(p\))模型时， AIC公式为 \[ \text{AIC}(k) = \ln \tilde\sigma_k^2 + \frac{2k}{T} \] 其中\(k\)是模型的阶， \(\tilde\sigma_k^2\)是阶为\(k\)的条件下\(\varepsilon_t\)的方差的最大似然估计。 \(\ln \tilde\sigma_k^2\)代表了模型对数据的拟合优劣， 此值越大拟合越差； \(\frac{2k}{T}\)是对模型复杂程度的惩罚， 此值越大， 模型越复杂， 稳定性越差， 对未来的情况的适应性也越差。 在某个范围内取\(k\)使得AIC(\(k\))最小， 就达成了拟合优度与模型简单程度的折衷。

另一个常用的信息准则是BIC准则(Bayesian Information Criterion)， 高斯AR模型为： \[ \text{BIC}(k) = \ln \tilde\sigma_k^2 + \frac{k \ln T}{T} \] BIC倾向于取比AIC更低阶的模型。

可以取\(k=0,1,\dots,P_0\)计算AIC或BIC， 取最小值点的\(k\)。 \(P_0\)可取为\(10 \log_{10} T\)。

参考：

  • HIROTUGU AKAIKE, Fitting Autoregressive Models for Prediction, Annals of the Institute of Statistical Mathematics AC-19 (1974), pp. 364 – 385
  • GIDEON SCHWARZ, Estimating the Dimensions of a Model, Annals of Statistics 6(1978), pp. 461 – 464

例4.4 考虑例4.1中的美国经过季节调整后的GNP季度对数增长率数据的AR建模定阶。

基本R软件stats包中的ar()函数可以对时间序列样本进行AR建模， 默认采用AIC准则定阶。 用选项aic=FALSE, order.max=p可以指定\(p\)阶模型。

gnprate <- diff(log(gnp))
resm <- ar(gnprate, method="mle"); resm
## 
## Call:
## ar(x = gnprate, method = "mle")
## 
## Coefficients:
##       1        2        3        4        5        6        7        8  
##  0.4318   0.1985  -0.1180   0.0189  -0.1607   0.0900   0.0615  -0.0814  
##       9  
##  0.1940  
## 
## Order selected 9  sigma^2 estimated as  8.918e-05

产生了一个9阶的模型。 作其AIC的图形：

plot(as.numeric(names(resm$aic)), resm$aic, type="h",
     xlab="k", ylab="AIC")
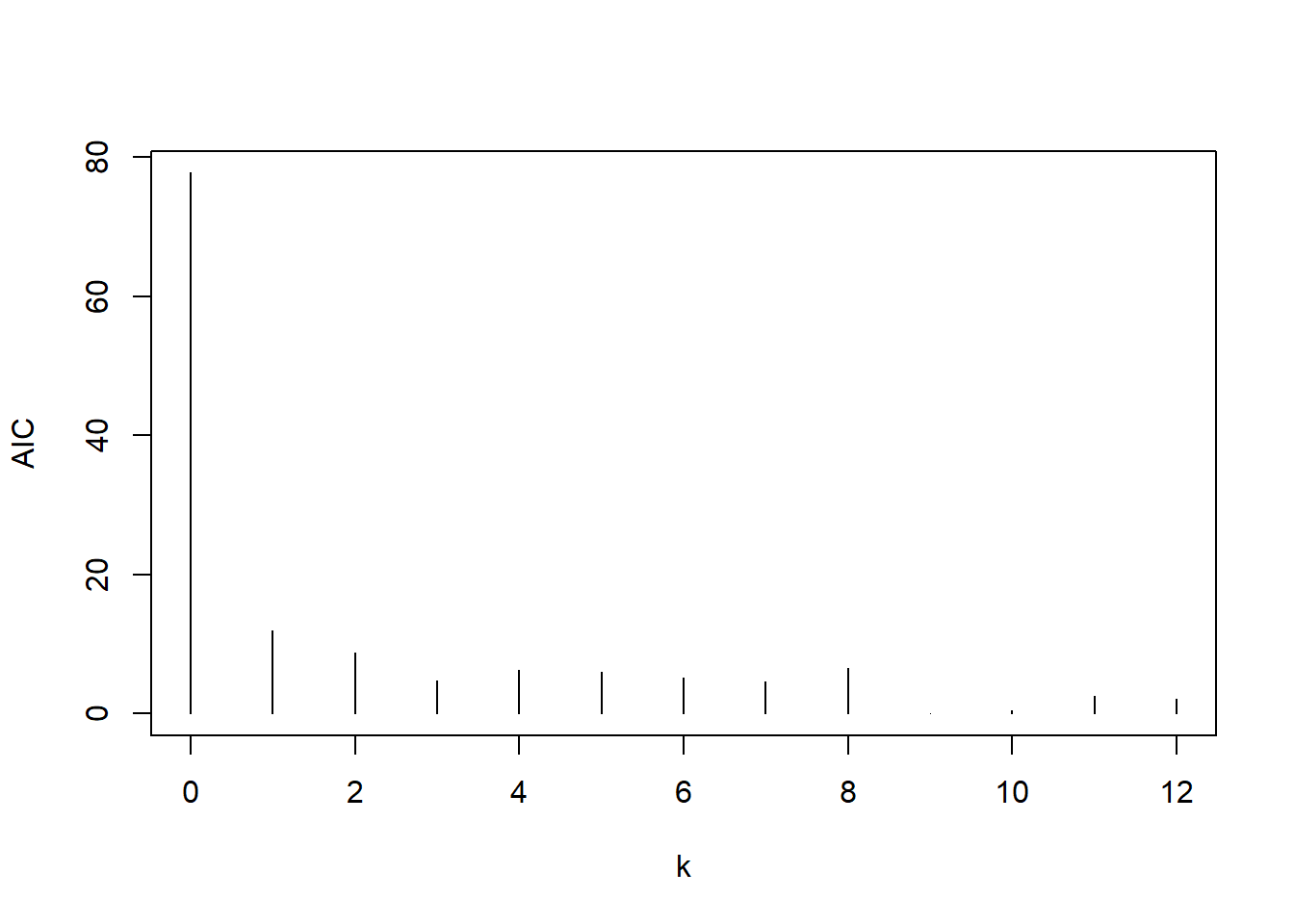
GNP对数增长率用AR建模的AIC

图4.5: GNP对数增长率用AR建模的AIC

从AIC图形可以看出，如果取较低的阶， 3阶也是可以的。

虽然ar()函数没有提供BIC的值， 但是因为\(\text{BIC}(k) - \text{AIC}(k) = \frac{k(\ln T - 2)}{T}\), 可以自己计算：

tmp.T <- length(gnprate)
tmp.bic <- resm$aic + as.numeric(names(resm$aic)) * (log(tmp.T) - 2)/tmp.T
plot(as.numeric(names(resm$aic)), tmp.bic, type="h",
     xlab="k", ylab="BIC")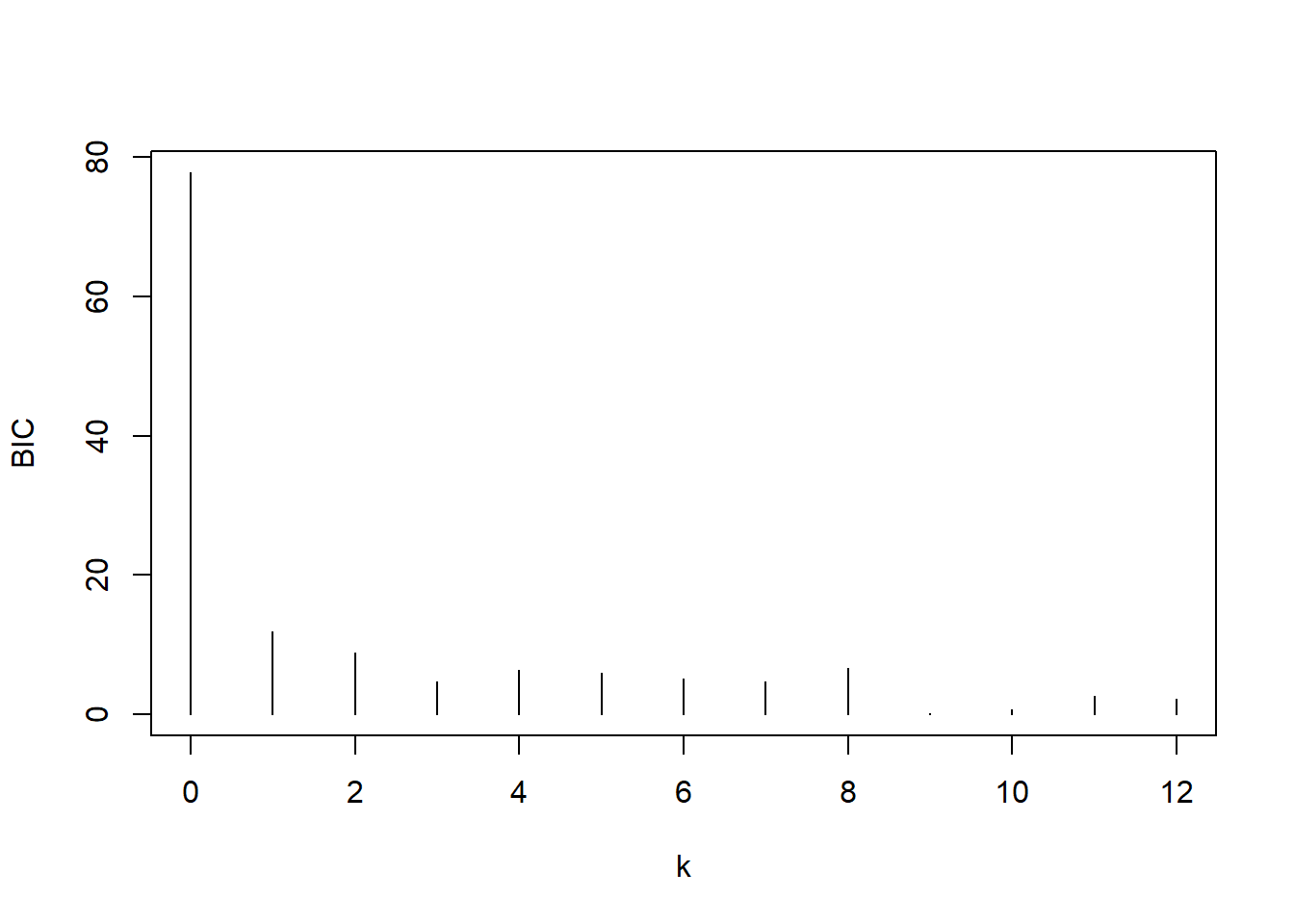
GNP对数增长率用AR建模的BIC

图4.6: GNP对数增长率用AR建模的BIC

BIC也建议\(p=9\)。

4.9 AR模型参数估计方法

AR模型有多种估计方法， 比如， 用普通线性回归的最小二乘法估计， 假设正态分布用最大似然估计， Yule-Walker递推计算， Burg递推计算，等等。

在stats::ar()函数中， method="ols"为最小二乘估计， 设\(\phi_i\)的估计为\(\hat\phi_i\)， 则拟合值为 \[ \hat x_t = \hat\phi_0 + \hat\phi_1 x_{t-1} + \dots + \hat\phi_p x_{t-p}, \ t=p+1, \dots, T \] 残差为 \[ e_t = x_t - \hat x_t, \ t=p+1, \dots, T \] 相应的新息方差\(\sigma^2=\text{Var}(\varepsilon_t)\)的估计为 \[ \hat\sigma^2 = \frac{1}{T-2p-1}\sum_{t=p+1}^T e_t^2 \]

如果使用高斯条件最大似然估计（认为\(x_1, \dots, x_p\)固定）， 则\(\hat\phi_i\)估计不变， 但是新息方差得估计变成了 \[ \tilde\sigma^2 = \frac{1}{T-p} \sum_{t=p+1}^T e_t^2 = \frac{T-2p-1}{T-p} \sum_{t=p+1}^T e_t^2 \]

例4.5 对例4.5的CRSP价值加权指数月度收益率用AR(3)建模。

先用AIC定阶：

resm <- ar(vw, method="mle"); resm
## 
## Call:
## ar(x = vw, method = "mle")
## 
## Coefficients:
##       1        2        3        4        5        6        7        8  
##  0.1167  -0.0112  -0.1126   0.0217   0.0735  -0.0452   0.0254   0.0462  
##       9  
##  0.0660  
## 
## Order selected 9  sigma^2 estimated as  0.002831

用AIC定阶为9阶。AIC数值：

round(resm$aic, 2)
##     0     1     2     3     4     5     6     7     8     9    10    11    12 
## 22.33 10.99 12.07  3.35  4.37  2.46  1.96  3.04  2.24  0.00  1.97  3.94  5.81

从AIC数值看出，选较低阶时\(p=3\)是一个可以接受的选择。 使用arima()函数估计，这个函数的输出比较容易解释。

mean.vw <- mean(vw); mean.vw
## [1] 0.00890439
resm2 <- arima(vw, order=c(3,0,0))
resm2
## 
## Call:
## arima(x = vw, order = c(3, 0, 0))
## 
## Coefficients:
##          ar1      ar2      ar3  intercept
##       0.1158  -0.0187  -0.1042     0.0089
## s.e.  0.0315   0.0317   0.0317     0.0017
## 
## sigma^2 estimated as 0.002875:  log likelihood = 1500.86,  aic = -2991.73

结果中的intercept实际是均值\(\mu\)的估计， \(\hat\mu = 0.0089\)。 \(\hat\sigma=0.054\)。 模型为: \[ (X_t - 0.0089) = 0.1158 (X_{t-1} - 0.0089) - 0.0187 (X_{t-2} - 0.0089) - 0.1042 (X_{t-3} - 0.0089) \]

结果还给出了系数的标准误差。 以\(\hat\theta \pm 2 SE(\hat\theta)\)作为简单的近似95%置信区间， 结果标准误差说明\(\mu, \rho_1, \rho_3\)是显著不等于0的， 而\(\rho_2\)不显著。

\(\hat\mu = 0.008904\)， 这是CRSP价值加权指数的平均月度简单收益率。 折合成年收益率，再换算到1926-2008年共83年的总简单收益率：

(1 + mean.vw)^12 - 1
## [1] 0.1122442
((1 + mean.vw)^12)^83 - 1
## [1] 6832.002

按平均月度简单增长率0.8904%计算， 得到年度简单增长率为11.22%； 83年可增长6832倍。

按实际数据83年的实际增长计算83年的总简单增长率， 然后折合到一年的复利：

prod(1 + vw) - 1
## [1] 1591.953
prod(1 + vw)^(1/83) - 1
## [1] 0.09290084

实际的复利年均增长率为9.29%，而不是11.22%; 实际的83年的简单增长率是1592倍， 而不是6832倍。

用\(\hat\mu\)计算的结果与用真实数据计算的结果的83年增长率有这么大差距， 是因为\(\hat\mu>0\)， 按\(\hat\mu\)计算总是在按几何级数增长； 但是按\(\prod (1 + x_t)\)计算则有时增长有时下降， 所以实际的总增长率要低得多。

R的forecast包提供了一个auto.arima()函数， 可以自动进行模型选择。

tseries包的arma()函数可以用条件极小二乘方法估计ARMA模型参数， 使用了optim()函数来求极值。结果可以用summary()显示。 tseries::arma()的结果还支持print(), plot(), coef(), vcov(), residuals(), fitted()等信息提取函数。

○○○○○

4.10 AR模型检验

拟合AR模型后， 如果模型是能够准确表示数据的规律的， 则拟合的残差应该近似为白噪声， 应该能通过白噪声检验。 因为残差是从模型估计计算得到的， 自由度有损失， 在Box.test()中用fitdf=\(p\)指定自由度减少个数。

例4.6 例如，对例4.5 的CRSP价值加权指数月简单收益率的AR(3)模型的残差进行白噪声检验：

resm2 <- arima(vw, order=c(3,0,0))
Box.test(resm2$residuals, lag=12, type="Ljung", fitdf=3)
## 
##  Box-Ljung test
## 
## data:  resm2$residuals
## X-squared = 16.352, df = 9, p-value = 0.05988

结果在0.05水平下不显著，说明模型拟合是充分的。

从例4.5的估计结果看出\(\phi_2\)不限制。 在arima()函数中可以用fixed=指定某些系数固定为给定值， NA表示不规定。这样做的一个潜在问题是得到的模型可能不符合平稳性条件。

resm3 <- arima(vw, order=c(3,0,0), fixed=c(NA, 0, NA, NA)); resm3
## Warning in arima(vw, order = c(3, 0, 0), fixed = c(NA, 0, NA, NA)): some AR
## parameters were fixed: setting transform.pars = FALSE
## 
## Call:
## arima(x = vw, order = c(3, 0, 0), fixed = c(NA, 0, NA, NA))
## 
## Coefficients:
##          ar1  ar2      ar3  intercept
##       0.1136    0  -0.1063     0.0089
## s.e.  0.0313    0   0.0315     0.0017
## 
## sigma^2 estimated as 0.002876:  log likelihood = 1500.69,  aic = -2993.38

检验稳定性：

abs(polyroot(c(1, -coef(resm3)[1:3])))
## [1] 2.031585 2.279433 2.031585

三个根都在单位圆外，符合平稳性条件。

对固定\(\phi_2 = 0\)后的模型进行残差的白噪声检验：

Box.test(resm3$residuals, lag=12, type="Ljung", fitdf=2)
## 
##  Box-Ljung test
## 
## data:  resm3$residuals
## X-squared = 16.828, df = 10, p-value = 0.07827

不否认残差为白噪声。 提取残差也可以用residuals(resm3)。

也可以用forecast::checkresiduals()函数进行模型诊断：

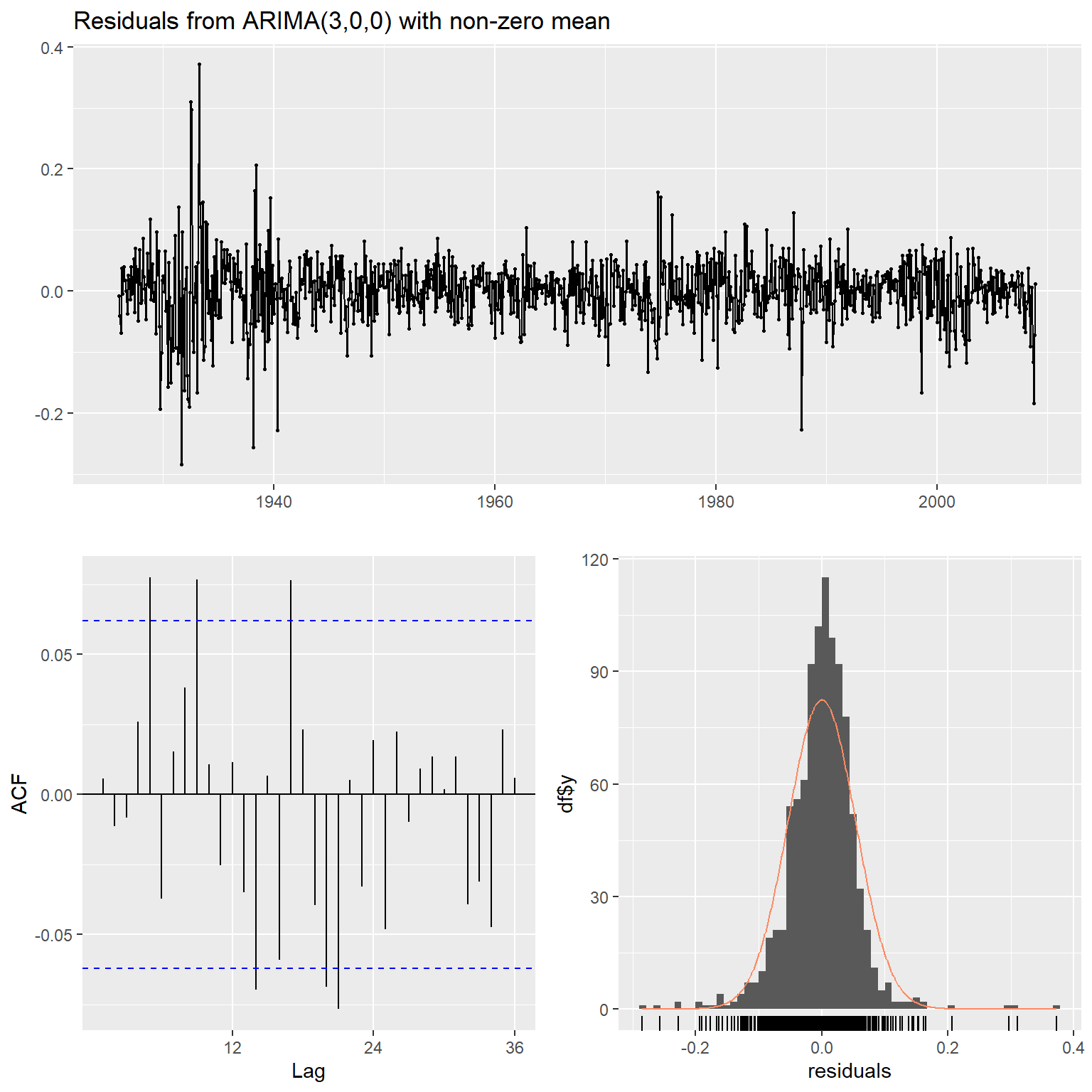
forecast::checkresiduals(resm3, lag=12, df=10)

## 
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(3,0,0) with non-zero mean
## Q* = 16.828, df = 9, p-value = 0.05148
## 
## Model df: 3.   Total lags used: 12

结果图形中包括残差， 残差的ACF图，残差的直方图和正态密度拟合。 函数结果还包括残差的Ljung-Box白噪声检验， 用lag选项指定Ljung-Box检验使用的平方和项数， 即要检验几个自相关系数等于零， 用df选项指定零假设成立时卡方统计量的自由度参数。 注意resm3中AR和MA部分的系数仅有2个， 所以自由度等于\(12-2=10\)。

stats包的tsdiag()函数也可以对模型残差进行诊断， 包括标准化残差图、残差的ACF图、残差的Ljung-Box白噪声检验p值， 包括使用不同平方和项数的检验p值， 但是可能没有进行自由度调整。 程序如：

tsdiag(resm3)

○○○○○

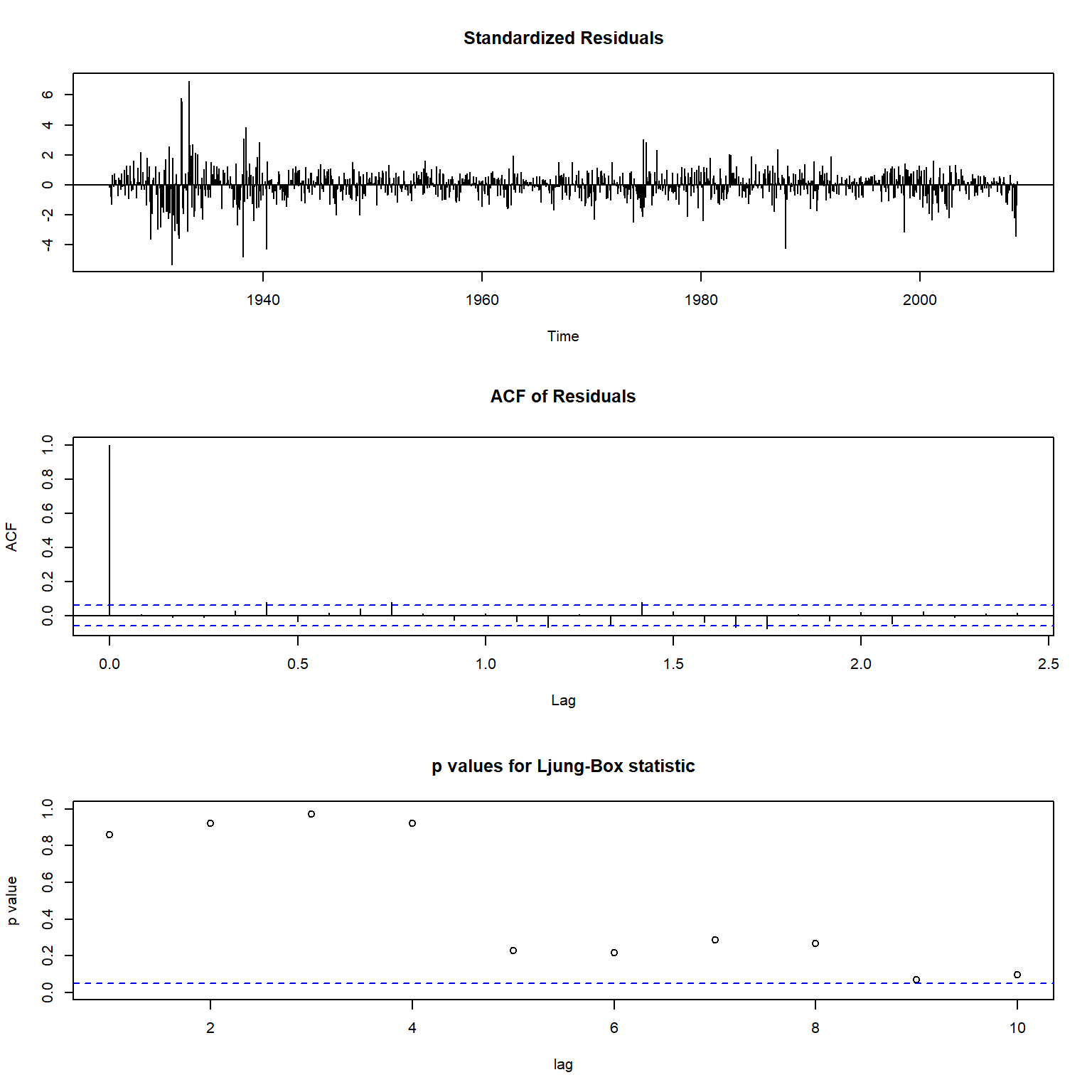
4.11 AR模型拟合优度指标

类似于线性回归模型的拟合优度判断， 在线性时间序列建模中，也可以定义如下的拟合优度\(R^2\)统计量

\[ R^2 = 1 - \frac{残差平方和}{序列的总离差平方和} \] 比如，拟合了AR(\(p\))模型后，可以计算\(R^2\)为 \[ R^2 = 1 - \frac{\sum_{t=p+1}^T e_t^2}{\sum_{t=p+1}^T (x_t - \bar x)^2} \] 其中\(\bar x = \frac{1}{T-p} \sum_{t=p+1}^T x_t\)。 \(0 \leq R^2 \leq 1\)。 \(R^2\)越大， 说明模型对数据拟合越好， 残差越小。 这样的指标仅对线性时间序列有意义。 如果是非平稳的单位根过程， 拟合AR模型的\(R^2\)会趋于1。

只要数据不变，\(R^2\)随阶数\(p\)的增加而增大。 根据统计学中的精简性原则（称为Ocam’s razor原则）， 应尽可能选择简单模型。 所以提出调整的\(R^2\)指标(adjusted \(R^2\))，定义为 \[ R_{\text{Adj}}^2 = 1 - \frac{\hat\sigma^2}{\hat\sigma_x^2} \] 其中\(\hat\sigma^2\)是新息方差\(\sigma^2\)的估计， \(\hat\sigma_x^2\)是\(X_t\)的样本方差。 仍有\(0 \leq R_{\text{Adj}}^2 \leq 1\)， 但\(R_{\text{Adj}}^2\)对阶数\(p\)的增加有惩罚。

4.12 用估计的AR模型进行预测

前面定义的\(L(Y|X_1, \dots, X_n)\)是最佳线性预测。 还可以定义\(\hat Y\)为\(X_1, \dots, X_n\)的任意函数， 使得\(E(Y - \hat Y)^2\)最小， 称为最佳预测（最优预测）。 最佳预测等于条件期望\(E(Y|X_1, \dots, X_n)\)。

对AR(\(p\))模型（新息为独立同分布白噪声）， 最佳预测与最佳线性预测相同。

在时刻\(h\)，用截止到\(h\)为止的信息预测\(x_{h+\ell}\)， 得到的最佳预测记为\(\hat x_h(\ell)\)。

4.12.1 超前一步预测

对\(\ell=1\)，因为 \[ X_{h+1} = \phi_0 + \phi_1 X_{h} + \dots + \phi_p X_{h+1-p} + \varepsilon_{h+1} \] 以及\(E(\varepsilon_{h+1}|X_1, \dots, X_h)=0\)， 有（设\(h \geq p\)） \[ \hat x_h(1) = E(X_{h+1} | X_1,\dots, X_h) = \phi_0 + \phi_1 X_{h} + \dots + \phi_p X_{h+1-p} . \] 一步预测误差为 \[ e_h(1) = x_{h+1} - \hat x_h(1) = \varepsilon_{h+1}, \ E|e_h(1)|^2 = \text{Var}(e_h(1)) = \sigma^2 . \] 可见模型中的新息方差\(\sigma^2\)也是超前一步预测的均方误差。

如果\(\varepsilon_t\)服从正态分布且\(\sigma\)已知， 则\(X_{h+1}\)的超前一步预测的95%预测区间为 \(\hat x_h(1) \pm 1.96 \sigma\)。

对于时间序列数据， 真实的系数\(\phi_i\)是未知的， 只能得到估计量\(\hat\phi_i\)， 当\(T\)充分大时可以在预测公式中用\(\hat\phi_i\)代替\(\phi_i\)进行预测。 这样得到的预测区间是不够准确的， 更好做法是用MCMC，参见(Tsay 2010)第12章。

4.12.2 超前二步预测

要计算\(\hat x_h(2)\)，注意到 \[ X_{h+2} = \phi_0 + \phi_1 X_{h+1} + \dots + \phi_p X_{h+2-p} + \varepsilon_{h+2} \] 所以 \[ \begin{aligned} \hat x_h(2) =& E(x_{h+2} | x_1, \dots, x_h) = \phi_0 + \phi_1 E(x_{h+1} | x_1, \dots, x_h) + \phi_2 x_h + \dots + \phi_p x_{h+2-p} \\ =& \phi_0 + \phi_1 \hat x_h(1) + \phi_2 x_h + \dots + \phi_p x_{h+2-p} . \end{aligned} \] 预测误差为 \[ e_h(2) = x_{h+2} - \hat x_h(2) = \phi_1 e_h(1) + \varepsilon_{h+2} . \] 预测均方误差为 \[ E[e_h(2)]^2 = \text{Var}(e_h(2)) = \sigma^2(1 + \phi_1^2) . \] 这里用到了\(\varepsilon_{h+2}\)与\(e_h(1) = x_{h+1} - \hat x_h(1) = \varepsilon_{h+1}\)独立。 显然超前两步预测均方误差大于等于超前一步均方误差， 这对一般情况都是合理的， 预测得越远， 我们现有知识的作用就越小。

4.12.3 超前多步预测

一般地有 \[ \hat x_h(\ell) = \phi_0 + \sum_{j=1}^p \phi_j \hat x_h(\ell-j) \] 其中 \[ \hat x_h(i) =\begin{cases} x_{h+i}, & \text{当} i \leq 0 \\ \hat x_h(i), & \text{当} i > 0 \end{cases} \] 为了计算\(\hat x_h(\ell)\)， 只要递推计算\(\hat x_h(1), \dots, \hat x_h(\ell-1)\)， 就可以按上面的公式得到\(\hat x_h(\ell)\)。 超前\(\ell\)步的预测误差为 \[ e_h(\ell) = x_{h+\ell} - \hat x_h(\ell) \]

对平稳AR(\(p\))模型， 当超前步数\(\ell\to+\infty\)时， \(\hat x_h(\ell) \to \mu\)。 这种性质称为均值回转(mean reversion)。

对AR(1)模型的零均值平稳解\(\{ x_t \}\)， 可以看出 \[ \hat x_h(\ell) = \phi_1^\ell x_h \] 这也是与极限\(0\)之间的差距， 而\(|\phi_1|^\ell\)则代表了趋向于极限的速度， 当\(|\phi_1|^\ell=\frac12\)时趋向于极限0就可以认为极限过程已经到了一半， 这个\(\ell=\ln(0.5)/\ln|\phi_1|\)称为均值回转的半衰期。 半衰期越短， 多步预报的作用越差。

例4.7 例如，对例4.5 的CRSP价值加权指数月简单收益率的AR(3)模型的残差进行多步预测。 用前82年的984个观测预测最后一年的12个观测。

resm4 <- arima(vw[1:984], order=c(3,0,0))
pred4 <- predict(resm4, n.ahead=12, se.fit=TRUE)
cbind(Observed=round(c(vw[985:996]), 4), 
      Predict=round(c(pred4$pred), 4), 
      SE=round(c(pred4$se), 3))
##       Observed Predict    SE
##  [1,]  -0.0623  0.0075 0.053
##  [2,]  -0.0220  0.0160 0.054
##  [3,]  -0.0105  0.0117 0.054
##  [4,]   0.0511  0.0098 0.054
##  [5,]   0.0238  0.0088 0.054
##  [6,]  -0.0786  0.0092 0.054
##  [7,]  -0.0132  0.0094 0.054
##  [8,]   0.0110  0.0096 0.054
##  [9,]  -0.0981  0.0095 0.054
## [10,]  -0.1847  0.0095 0.054
## [11,]  -0.0852  0.0095 0.054
## [12,]   0.0215  0.0095 0.054

对预测结果的作图。 这个预测是知道真实值的。

plot(window(vw, start=c(2007, 1), end=c(2008,12)),
     ylab="", type="b", ylim=c(-0.2, 0.2), lwd=2)
lines(ts(c(pred4$pred), start=c(2008,1), frequency = 12), 
      col="red", lwd=1, lty=2, type="b", pch=2)
lines(ts(c(pred4$pred) - 2*c(pred4$se), start=c(2008,1), frequency = 12), 
      col="green", lwd=1, lty=3, type="l")
lines(ts(c(pred4$pred) + 2*c(pred4$se), start=c(2008,1), frequency = 12), 
      col="green", lwd=1, lty=3, type="l")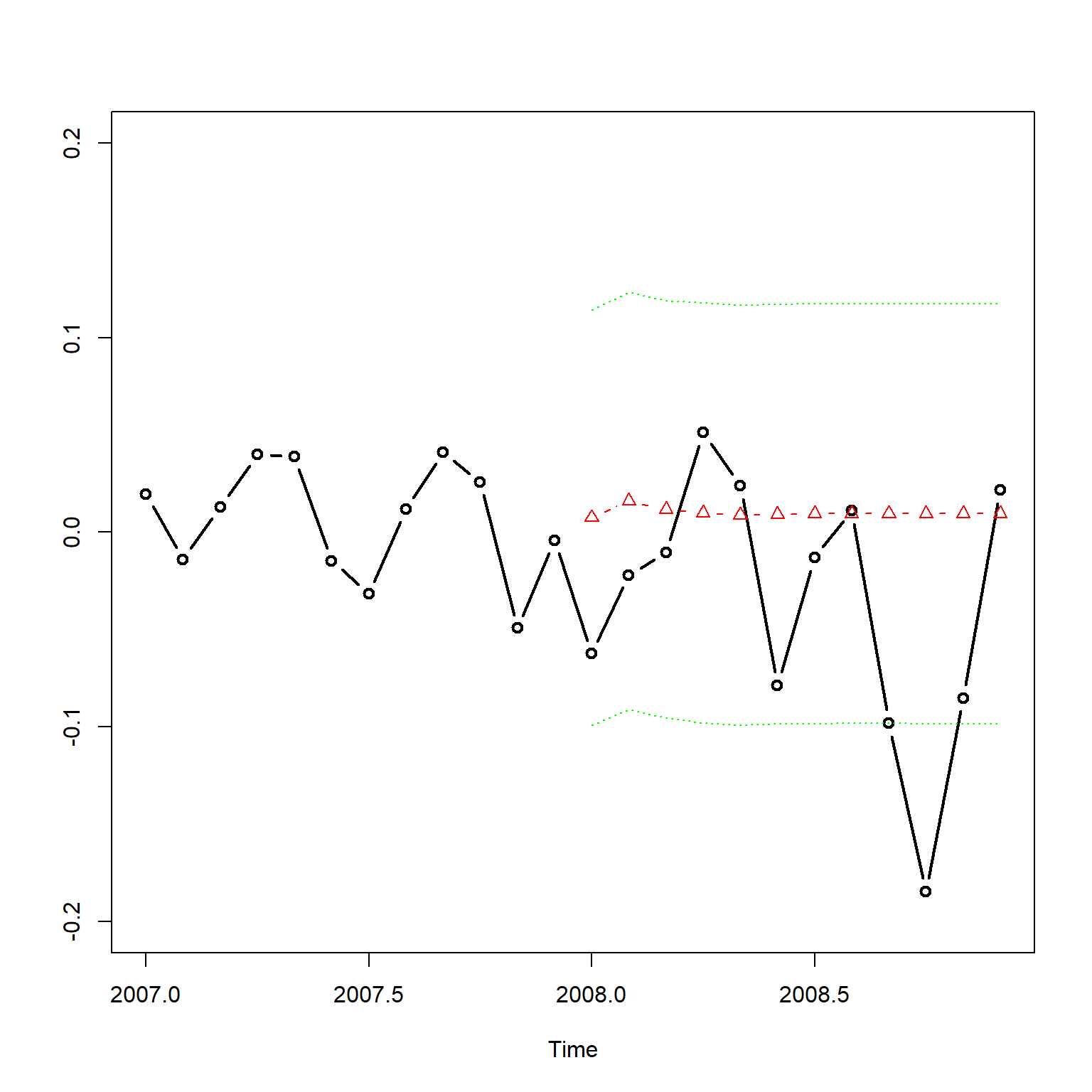
CRSP价值加权简单月收益率AR(3)模型12步预测

图4.7: CRSP价值加权简单月收益率AR(3)模型12步预测 

#foreplot(pred=pred4, rt=vw, orig=984, start=(83-2)*12+1, p=0.95)

图中黑色线是真实值， 红色点是多步预测值， 绿色线是95%预测界限。 可以看出多步预测基本是按均值预测。

用forecast包计算超前多步预报：

fc <- forecast::forecast(resm4, h=12)
fc
##     Point Forecast       Lo 80      Hi 80       Lo 95     Hi 95
## 985    0.007455686 -0.06083694 0.07574831 -0.09698887 0.1119002
## 986    0.015952488 -0.05270459 0.08460957 -0.08904946 0.1209544
## 987    0.011701663 -0.05695841 0.08036174 -0.09330486 0.1167082
## 988    0.009806653 -0.05927763 0.07889093 -0.09584863 0.1154619
## 989    0.008770886 -0.06033071 0.07787249 -0.09691089 0.1144527
## 990    0.009164644 -0.05993698 0.07826627 -0.09651718 0.1148465
## 991    0.009432520 -0.05967458 0.07853962 -0.09625768 0.1151227
## 992    0.009565095 -0.05954249 0.07867268 -0.09612583 0.1152560
## 993    0.009530555 -0.05957703 0.07863814 -0.09616037 0.1152215
## 994    0.009495151 -0.05961250 0.07860281 -0.09619589 0.1151862
## 995    0.009477748 -0.05962992 0.07858541 -0.09621331 0.1151688
## 996    0.009480420 -0.05962725 0.07858808 -0.09621063 0.1151715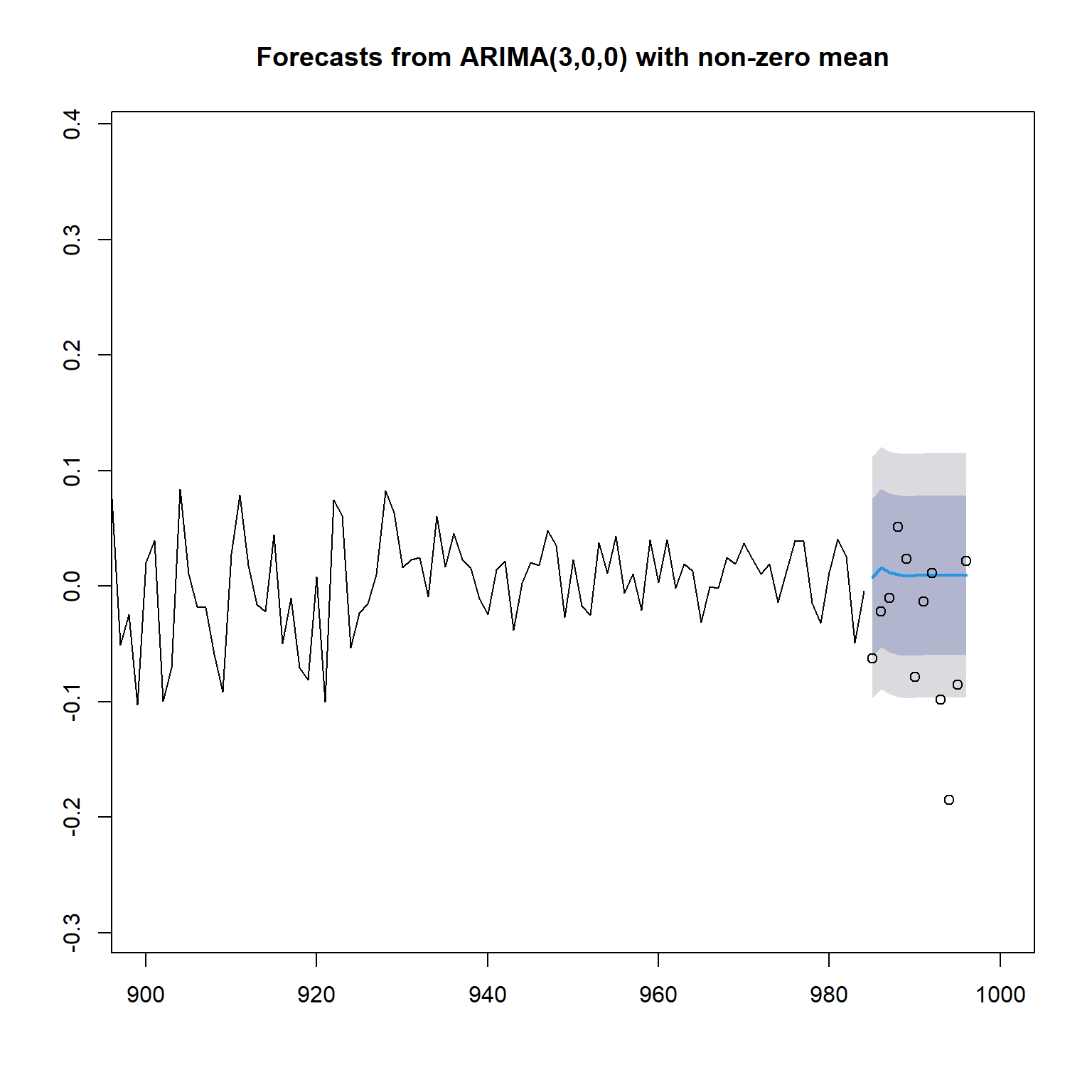
plot(fc, xlim=c(900, 1000))
points(985:996, vw[985:996])

○○○○○

B 参考文献

Tsay, Ruey S. 2010. Analysis of Financial Time Series. 3rd Ed. John Wiley & Sons, Inc.
———. 2013. 金融数据分析导论：基于R语言. 机械工业出版社.
何书元. 2003. 应用时间序列分析. 北京大学出版社.