10 时间序列预测

用时间序列的数学模型进行预测，是经济学、金融学、气象学等自然科学、社会科学中比较可靠的预测方法。对时间序列建模后进行预测，实际上假定了未来的变量变化规律是保持和建模时相同的，所以时间序列方法一般只能进行短期预测而不适合用于长期预测。

常见的预测形式包括点预测和区间预测。设\(y_1, \dots, y_T\)为时间序列观测数据，建模后对给出\(\hat y_{T+h}\)作为\(y_{T+h}\)的预测值（\(h=1,2,\dots\)）称为点预测，如果用\([l_{T+h}, u_{T+h}]\)区间作为\(y_{T+h}\)的预测，并且声称置信度为\(1-\alpha\)，则这个区间是\(y_{T+h}\)的预测区间。实际上，最好能够给出\(y_{T+h} | y_1, \dots, y_{T}\)条件分布的一个估计，这样可以作出更多的推断。

本章讲述用(R. J. Hyndman and Athanasopoulos 2021)一书讲的方法进行预测，使用R扩展包fpp3、tsibble、fable、fabletools、feasts。

10.1 时间序列分解方法

经济和金融中的时间序列常常可以分解为趋势项、季节项、经济周期项、随机项。其中季节项主要存在于月度和季度数据，有固定的周期；经济周期项代表经济运行的不同阶段的影响，没有固定的周期。在时间序列中一般将趋势项与经济周期项合并，统称为趋势项。

季节项最常见的是月度数据和季度数据对应的周期12和周期4情形，但有可能出现多个季节成分，比如每小时记录的数据，可能既有按日的周期，又有近似按月的的周期，以及近似按年的周期。

将时间序列分解成不同成分，可以更好地理解其变化规律，可以去除季节性影响，分别预报各个成分后综合可以预报时间序列。

时间序列分解可以是加性模型：

\[ y_t = T_t + S_t + R_t, \] 其中\(T_t, S_t, R_t\)分别为趋势项、季节项、随机项。这样的模型中\(y_t\)随时间变化时季节性震荡幅度变化不大。

分解可以是乘性模型： \[ y_t = T_t \times S_t \times R_t, \] 这样的模型中\(y_t\)随时间变化时季节性震荡幅度一般会越来越大。程序模型可以取对数变成加性模型： \[ \log y_t = \log T_t + \log S_t + \log R_t, \] 但这样的非线性变换会增加预测时的困难。

fabletools、fable包提供了若干种时间序列分解建模计算方法，涉及到的函数有model(), ETS(), STL()，classical_decomposition()等。 R软件中其它的时间序列分解方法有：

stats包的HoltWinters()函数提供11所述的指数平滑方法。
forecast包的ets()函数能自动选择合适的指数平滑方法并进行预报。
stats包的StructTS()使用最大似然估计方法估计供11所述的分解，仅支持加性模型。
stats包的stl()用局部多项式拟合方法进行分解。
stats包的decompose()用简单的滑动平均方法估计分解成分。

10.1.1 时间序列变换

时间序列中的变化，有一部分是可以解释的，为此可以预先对数据进行变换，将这部分变化先排除掉。

一部分影响来自日历。比如，商店的月销售额，明显受到当月天数的影响。所以，将数据变换为每天（或者每个营业天）的销售额，就可以排除不同月份天数不同的影响。

另一种影响是要考察的总体大小的变化。比如，要研究某城市每年购房交易数，这可能受到人口数量变化的影响，可以将其变换为人均的购房交易数。

经济、金融数据还会受到通货膨胀影响。房屋均价的上涨，一部分原因是通货膨胀，所以可以将价格按照某年为基准扣除通货膨胀影响计算。

可以对时间序列进行某些数学变换，使其分布更接近于正态分布，或限制其取值范围，比如取对数，计算平方根，线性变换到\([0,1]\)范围内，等等。 Box-Cox变换是一种常用的变换，通常用来将非正态分布的数据变得更接近于正态分布。此变换有一个参数\(\lambda\)，变换公式为 \[ w_t = \begin{cases} \ln y_t, & \lambda = 0, \\ \lambda^{-1}[\text{sign}(y_t) |y_t|^{\lambda} - 1], & \lambda \neq 0 . \end{cases} \]

fabletools包的features()函数指定feature = guerrero可以求合适的\(\lambda\)值，函数box_cox()执行Box-Cox变换。

如：

library(tsibble)
library(fabletools)
library(feasts)

ap_tsib <- as_tsibble(AirPassengers) |>
  mutate(
    ap = value,
    log_ap = log(value)  ) |>
  select(-value)
lam <- ap_tsib |>
  features(ap, features = guerrero) |>
  pull(lambda_guerrero)
ap_tsib |>
  autoplot(box_cox(ap, lam)) +
  labs(y = "", x="",
    title = paste("Air Passengers Box-Cox Trans lambda =", 
      round(lam, 2)))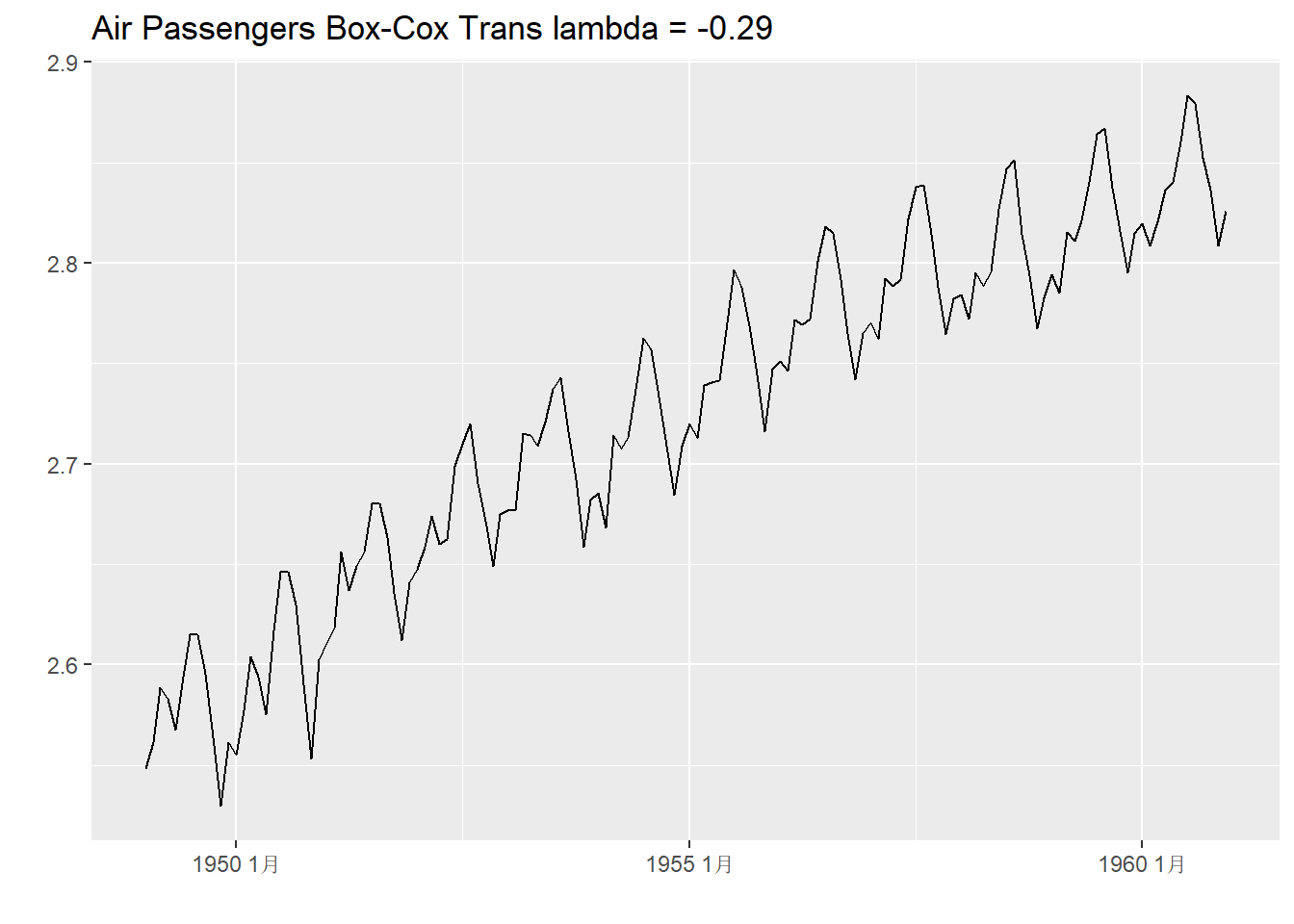

还有一些变换可以用来满足时间序列取值范围约束条件。比如，某些数据必须取正值，预测或者拟合为负值是完全不合理的，可以令\(z_t = \log y_t\)，对\(z_t\)建模就不会使得\(y_t\)的拟合、预测出现零或者负值。

如果要求\(y_t\)取值落在\((a,b)\)区间内，可以令 \[ z_t = \log \frac{x-a}{b-x}, \] 则\(z_t\)不再有限制，反变换得到\(y_t\)值会满足区间约束条件。这个变换没有内置函数，所以fabletools提供了new_transformation()函数用来自定义变换和逆变换，定义好了以后就可以用在model()函数中。比如，限制区间为\((300, 400)\)，则定义变换和逆变换为：

scaled_logit <- function(
    x, lower = 0, upper = 1) {
  log((x - lower) / (upper - x))
}
inv_scaled_logit <- function(
    x, lower = 0, upper = 1) {
  lower + 
    (upper - lower) * exp(x) / (1 + exp(x))
}
my_scaled_logit <- new_transformation(
  scaled_logit, inv_scaled_logit)
example_tsib |>
  model(
    ETS(my_scaled_logit(
      y, lower = 300, upper = 400)) )

在预测时fable包会考虑到这些非线性变换的影响进行偏差修正，而预测区间则只要简单地将区间上下限进行逆变换即可。

10.1.2 简单的滤波方法分解

最简单的一种分解方法是使用滑动平均估计趋势项，去掉趋势后(对加性模型用减法，对乘性模型用除法)同月份(设数据为月度数据)平均估计季节项，然后用原始序列减去（或除去）这两部分的结果估计随机项。这种方法得到的季节项是不变的模式。计算滑动平均时，可以用stats::filter()函数，也可以用slider::slide_dbl()函数。

设输入序列为\(\{y_t \}\)，滑动平均部分的一个简单做法是 \[ T_t = \sum_{j=-6}^{6} b_j y_{t-j}, \] 其中\(b_{-6} = b_{6} = \frac{1}{24}\)，其余\(b_j = \frac{1}{12}\)。对加性模型计算\(y_t - T_t\)，然后将\(y_t - T_t\)中属于1月份的数据平均，作为季节项1月份的估计，其它月份以此类推。最后用\(y_t\)减去趋势、季节项作为随机项。

fabletools包的model()与feasts包的classical_decomposition()配合可以进行这种分解。

比如，航空乘客数进行对数变换用这种方法分解：

library(tsibble)
library(feasts)
library(fabletools)

ap_tsib |>
  model(classical_decomposition(
    log_ap, type = "additive") ) |>
  components() |>
  autoplot() +
  labs(title = "航空乘客数对数值分解")

## Warning: Removed 6 rows containing missing values or values outside the scale range
## (`geom_line()`).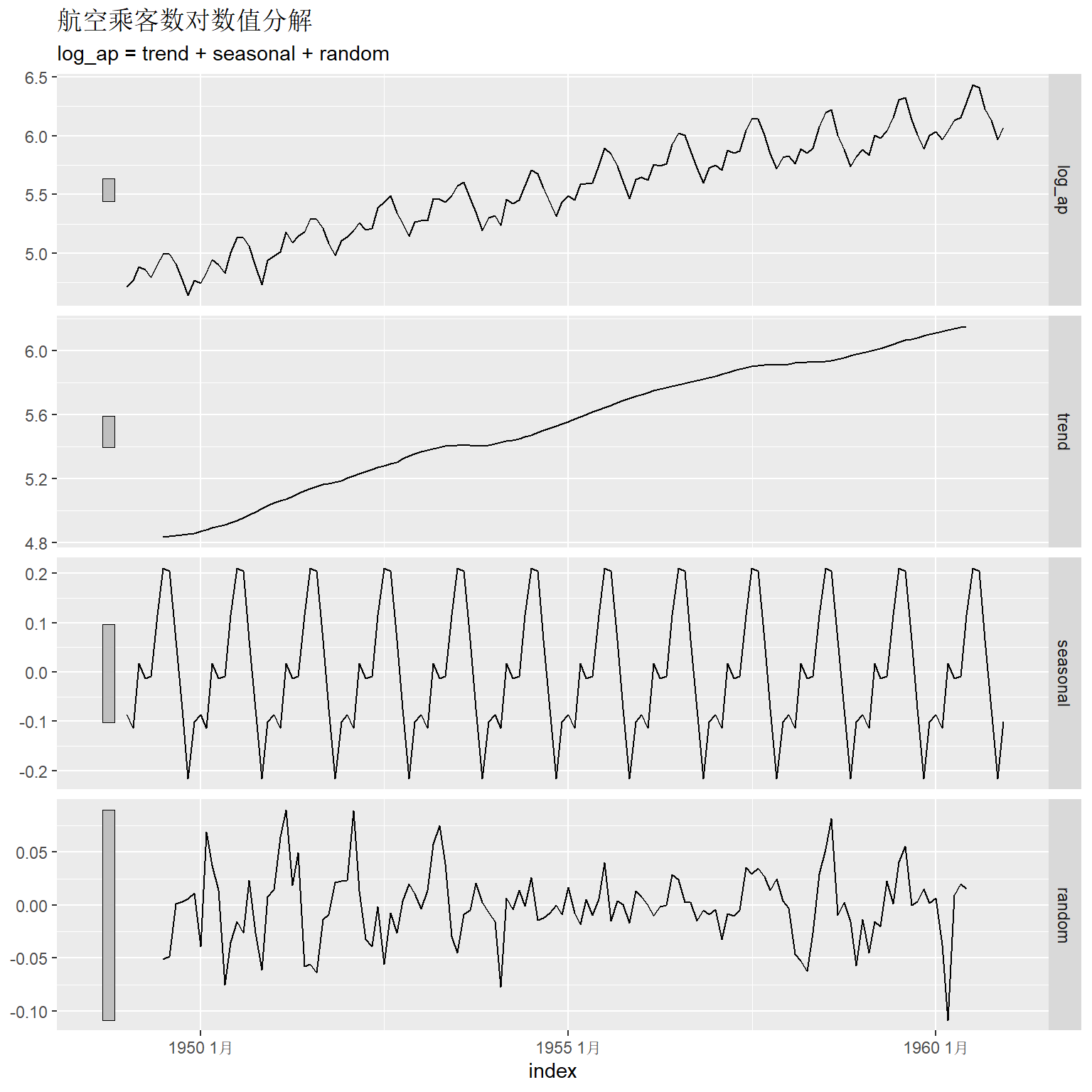

图中各部分依次是原始数据、趋势、季节项、随机项。图中左侧的条形用来比较不同坐标系中y轴范围大小，这些条形在坐标系中按y坐标计算的高度是相同的，但y轴范围越大，这些条形就越短。所以这些条形长度代表了纵轴的放大倍数。

因为用了对称的滑动平均估计趋势项，所以开头和结尾的6项无法估计。这种方法得到的季节项是完全重复的。趋势估计有可能过于平滑，对于某些局部的变化估计结果不够稳健。

不做对数变换，用乘性的移动平均进行分解：

ap_tsib |>
  model(classical_decomposition(
    log_ap, type = "multiplicative") ) |>
  components() |>
  autoplot() +
  labs(title = "航空乘客数乘性分解")

## Warning: Removed 6 rows containing missing values or values outside the scale range
## (`geom_line()`).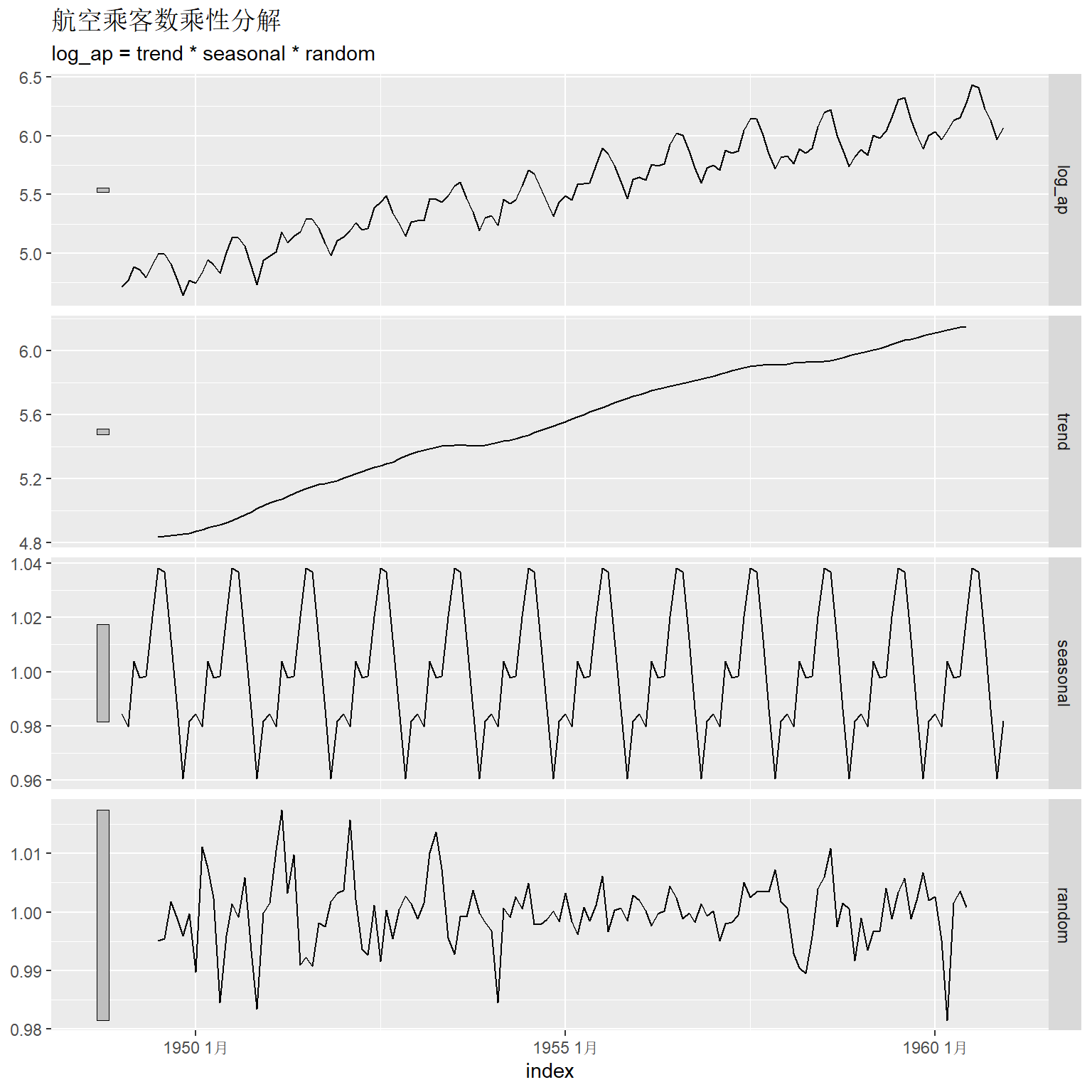

乘性的分解在用滑动平均估计了趋势项后，用除法去掉趋势，然后再对同月的数据平均得到季节项，用原始数据除以这两项的结果作为随机项。

这种简单的分解方法的优缺点如下：

计算简单；
因为用了对称的滑动平均（滤波），所以首尾的6个点（对月度数据而言）无法得到分解值，这也使得利用这种方法预测比较困难。
季节项在不同年份是严格重复的，不支持随时间而变化的季节项。
如果数据中有某些突变点，比如经济危机影响，此分解方法不能很好响应这些变化。

10.1.3 用X11和SEATS季节调整方法分解

各国的官方统计机构往往需要对经济数据进行季节调整和预测。 X11和SEATS是美国、澳大利亚等国官方统计用于对月度、季度数据进行季节调整的算法。 X11主要使用反复滤波，而SEATS则建立ARIMA模型并提取其中的分解成分。这些算法经过多年研究改进，已经比较成熟可靠。

下面的程序利用了R的seasonal包进行计算。 seasonal扩展包调用X13软件功能（包括X11方法和SEATS方法）进行计算。 seasonalview扩展包提供了更方便的交互界面。 seasonal只是X13软件的一个界面，所以如何使用还需要参考X13软件的原始手册，比较容易的用法是像下面的程序那样利用fabletools扩展包的model()函数调用。可以在http://www.seasonal.website/网站测试使用seasonal包的功能。 seasonal包提供了genhol()函数用来支持用户自定义的节假日数据，所以在自己输入节假日的前提下也可以用于中国数据。

library(seasonal)

ap_tsib |>
  model(x11 = X_13ARIMA_SEATS(ap ~ x11())) |>
  components() -> x11_ap
autoplot(x11_ap) + 
  labs(title = "航空乘客数X11分解")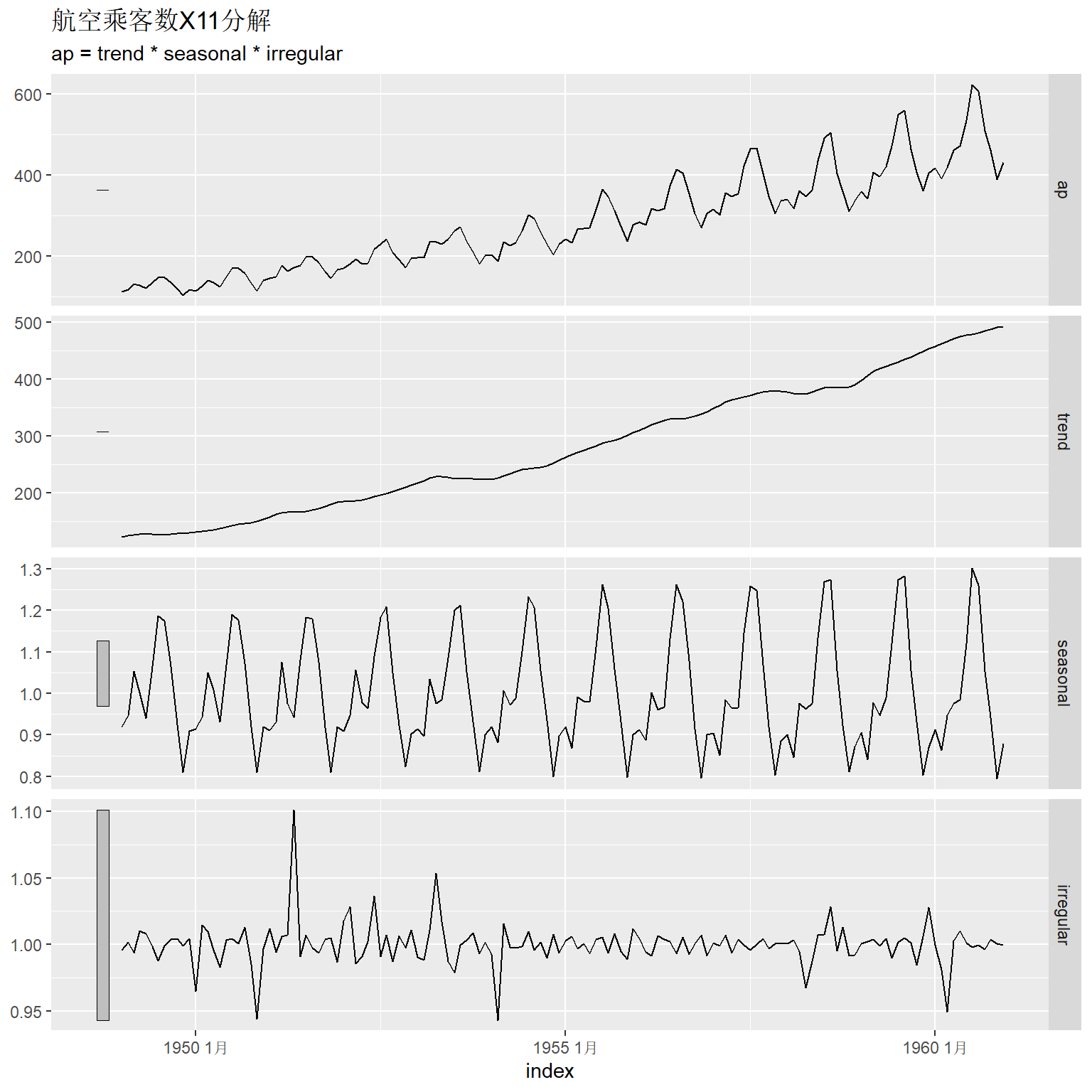

对季节调整作图：

x11_ap |>
  ggplot(aes(x = index)) +
  geom_line(aes(y = ap, colour = "Data")) +
  geom_line(aes(y = season_adjust,
    colour = "Seasonally Adjusted")) +
  geom_line(aes(y = trend, colour = "Trend")) +
  labs(y = "乘客数 (千人)", x = "",
    title = "航空乘客数")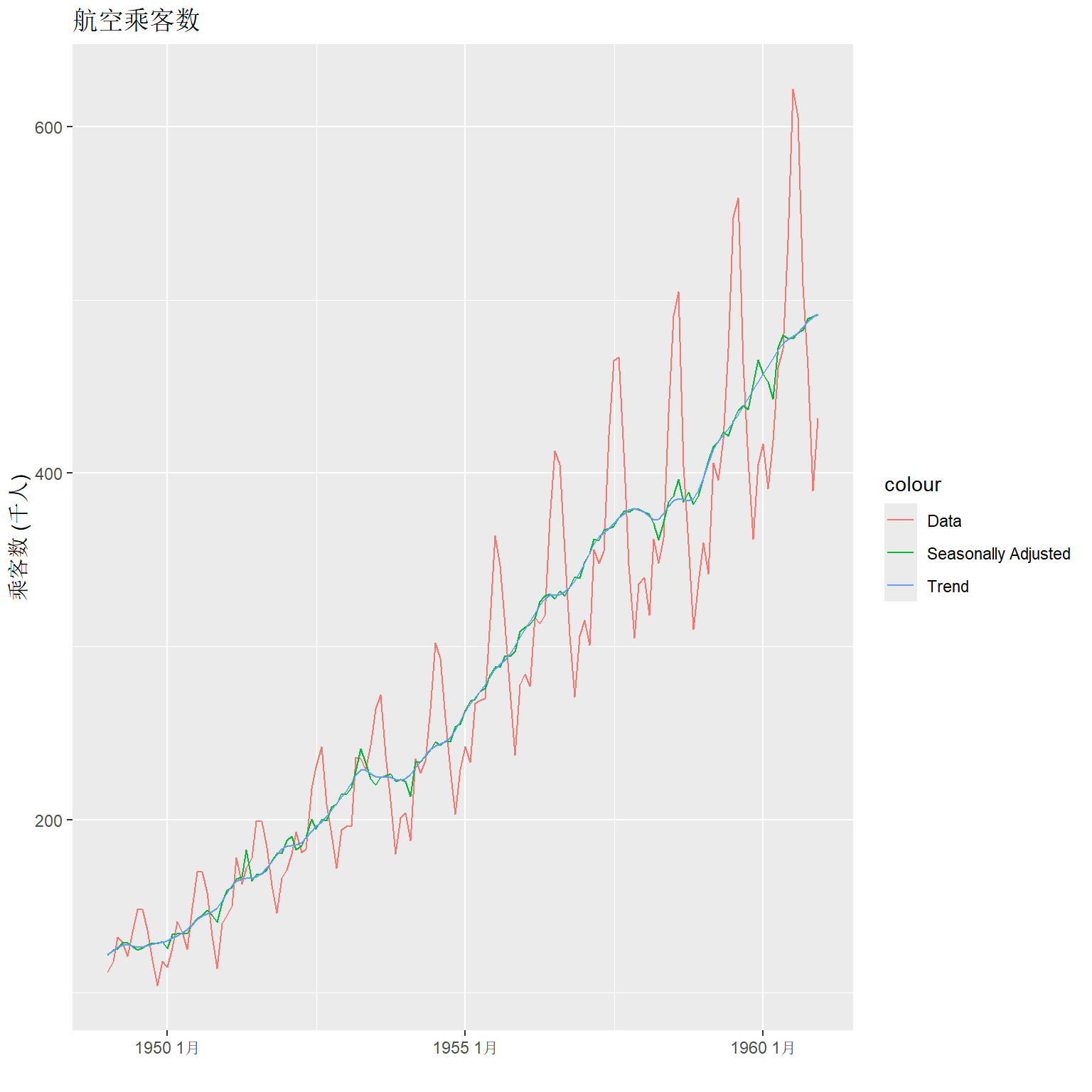

X11得到的季节项是缓慢变化的，分月作图：

x11_ap |>
  gg_subseries(seasonal)

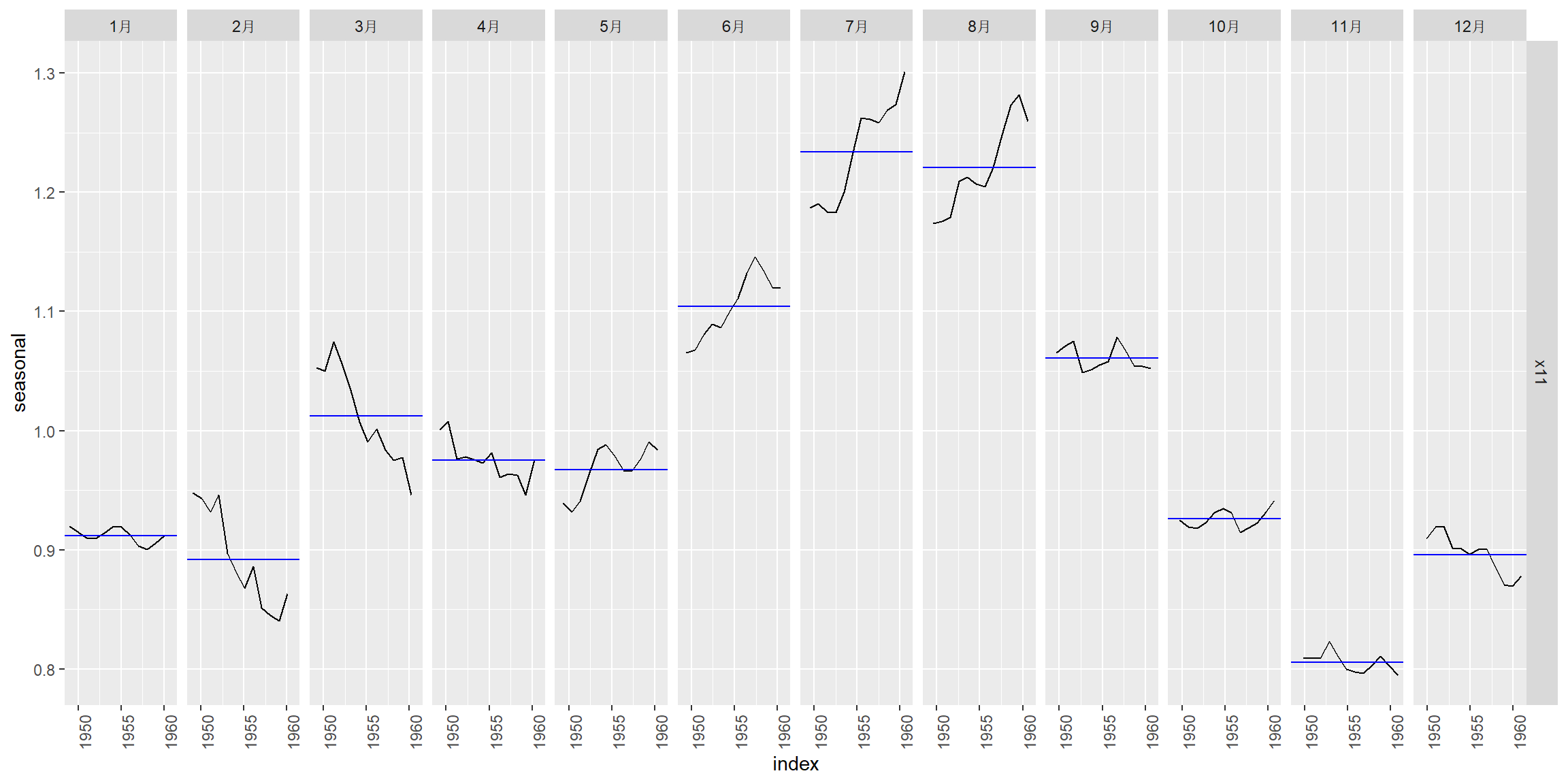
SEATS是另外一套季节调整算法，由西班牙统计机构开发。

ap_tsib |>
  model(seats = X_13ARIMA_SEATS(ap ~ seats())) |>
  components() -> seats_ap
autoplot(seats_ap) +
  labs(title = "航空乘客数用SEATS分解")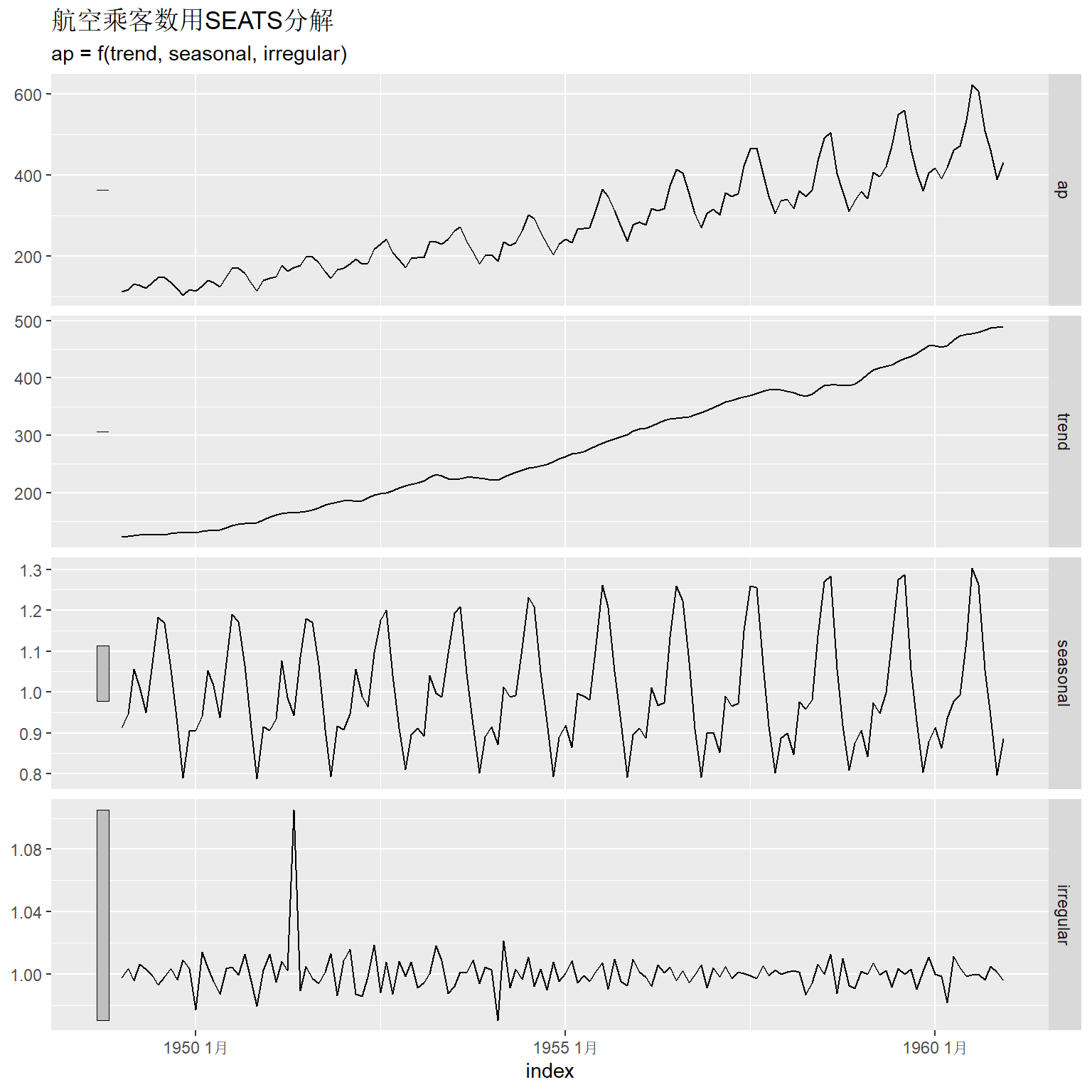

10.1.4 用STL方法

STL方法用loess，即局部多项式平滑方法进行分解。 STL能够处理多种季节频率，季节项可以随时间缓慢变化，趋势项的光滑程度可以用参数调节，可以进行稳健的分解。但是，STL不提供工作日和节假日调整，仅能进行加性的分解。

feasts包的STL()与fabletools包的model()配合可以提供STL分解。

ap_tsib |>
  model(stl = STL(ap)) -> ap_stl

components(ap_stl)中包含了原始数据和分解结果，如：

head(components(ap_stl))

## # A dable: 6 x 7 [1M]
## # Key:     .model [1]
## # :        ap = trend + season_year + remainder
##   .model    index    ap trend season_year remainder season_adjust
##   <chr>     <mth> <dbl> <dbl>       <dbl>     <dbl>         <dbl>
## 1 stl    1949 1月   112  123.      -17.0      5.83           129.
## 2 stl    1949 2月   118  124.      -17.2     11.5            135.
## 3 stl    1949 3月   132  124.        7.52     0.174          124.
## 4 stl    1949 4月   129  125.       -1.15     5.27           130.
## 5 stl    1949 5月   121  126.       -3.78    -0.822          125.
## 6 stl    1949 6月   135  126.       18.9    -10.2            116.

分解结果中包含趋势、季节项、随机项，还包含季节调整结果。

可以用autoplot()对分解结果作图：

components(ap_stl) |>
  autoplot()

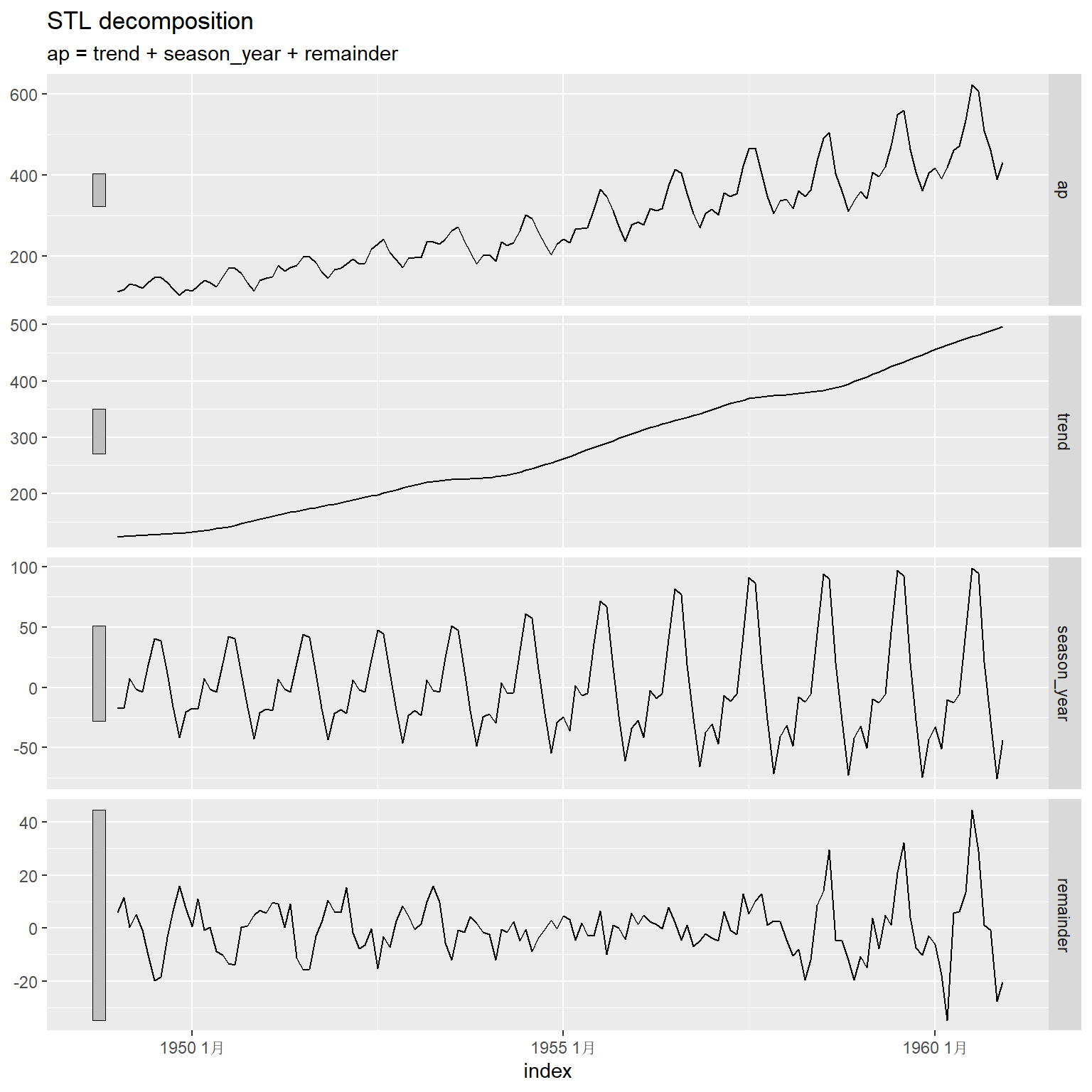
这是加性模型，所以季节项的振幅随时间增加而变大。

原始数据与季节调整数据的叠加图形：

components(ap_stl) |>
  as_tsibble() |>
  autoplot(ap, colour = "gray") +
  geom_line(aes(y=season_adjust), colour = "#0072B2") +
  labs(y = "乘客数 (千人)",
    title = "航空乘客季节调整")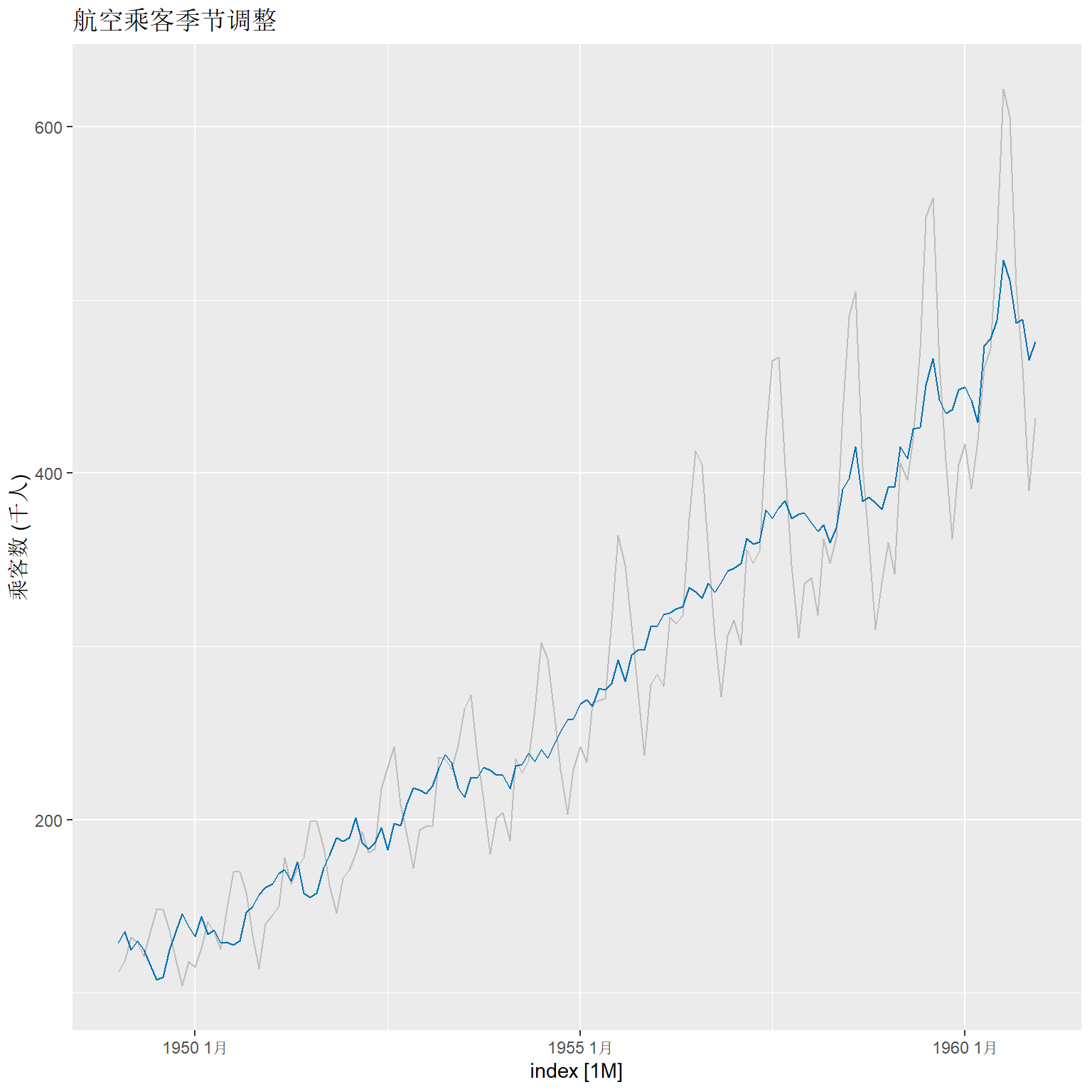

因为使用了加性模型而非乘性模型，所以季节调整的效果不佳。

STL()函数可以指定趋势、季节项的选项，可以要求进行稳健拟合（减少突变点的影响），如：

ap_tsib |>
  model(stl = STL(
    ap ~ trend(window = 7) +
      season(window = "periodic"),
    robust = TRUE)) |>
  components() |>
  autoplot()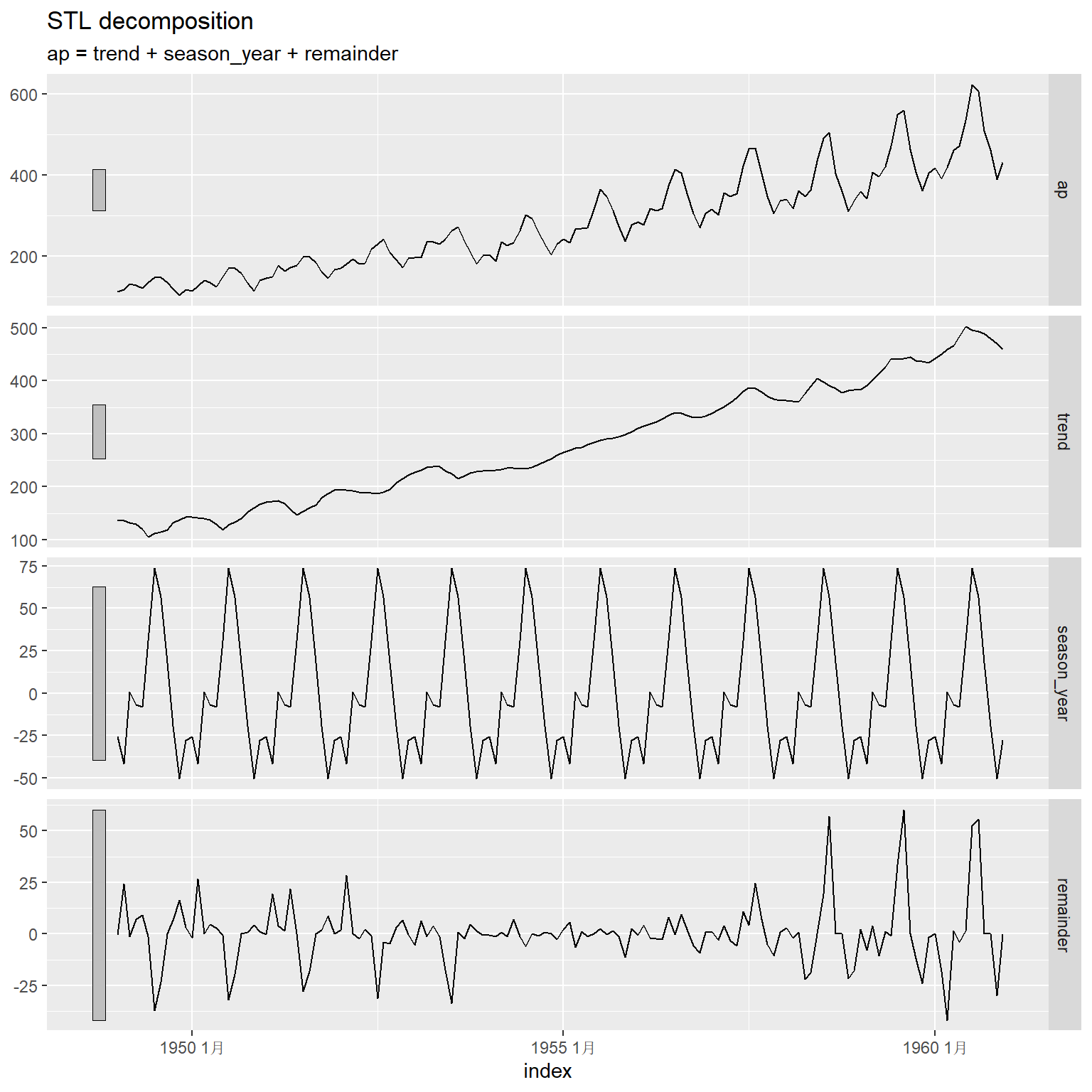

其中trend()的window选项的大小影响趋势项的光滑程度，取值越大得到的趋势项越光滑，必须取奇数值。 season()的window选项如果取为"periodic"则各年的季节项完全重复，取为奇数值，代表估计季节项时使用的年数，结果得到渐变的季节项，取值越小变化越快。

如果指定了robust = TRUE，则数据中的异常值会被归结到残差项（随机误差项）中，趋势和季节部分的估计不受影响。

对航空乘客数据，其季节性是震荡越来越大的，上面程序中自动选择参数的做法（model(stl = STL(ap))）正确地提取了振幅越来越大的季节项，指定季节项完全重复的做法（season(window = "periodic")）则不能适应季节性的变化，使得季节性变换被混入到了残差中。 fable包支持对因变量作变换，并在拟合、预测时自动调整回原始变量尺度，如：

ap_tsib |>
  model(STL(
    log(ap) ~ trend(window = 7) +
      season(window = "periodic"),
    robust = TRUE)) |>
  components() |>
  autoplot()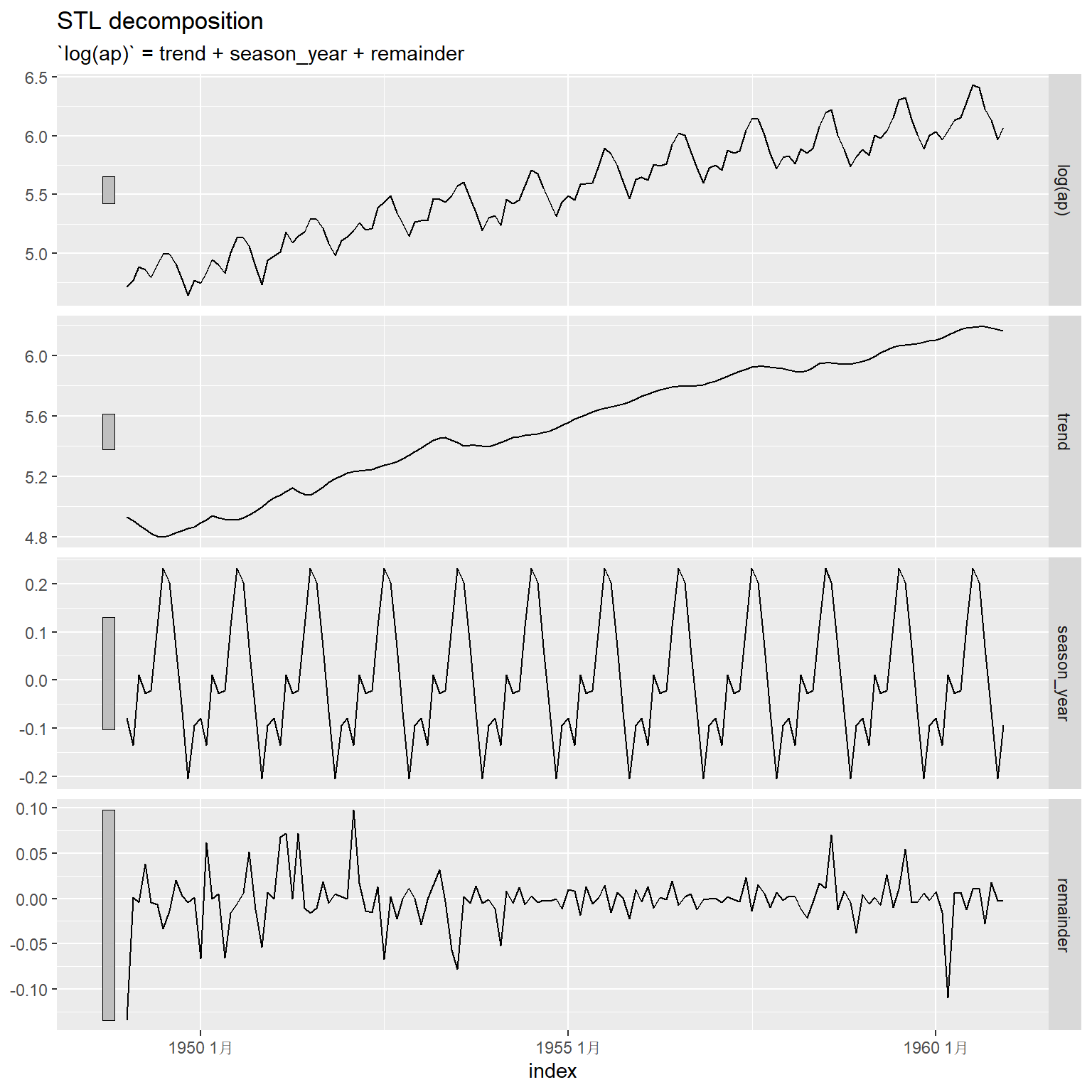

以上分解图形都是在对数变换基础上显示的。在拟合和预测时fable包都会转换到原始变量尺度。

10.2 时间序列特征提取

feasts扩展包可以从时间序列计算各种特征量和统计量。

10.2.1 一些基本统计量的计算

一些非时间序列的常见统计量比如样本均值、样本标准差等，可以用features()函数提取，也可以直接用tidyverse系统的summarise()、across()函数计算，但一定要注意到tsibble时间序列类型中key变量会自动作为分组汇总用的分组变量。

例如， tsibble扩展包中的tourism数据集包含了澳大利亚旅行人数的数据集，为季度数据，包含分类变量Region、State和Purpose，这三个变量都作为tsibble类型的key变量，旅行人次数以千人为单位保存在变量Trips中。

如果用features()函数提取基本统计量，结果将自动按三个key变量分组，每组分别沿时间轴计算平均值、标准差等统计量，如：

data(tourism, package="tsibble")
tourism |>
  features(
    Trips,
    list(
      mean = mean, 
      std = sd ))

## # A tibble: 304 × 5
##    Region         State              Purpose    mean   std
##    <chr>          <chr>              <chr>     <dbl> <dbl>
##  1 Adelaide       South Australia    Business 156.   35.6 
##  2 Adelaide       South Australia    Holiday  157.   27.1 
##  3 Adelaide       South Australia    Other     56.6  17.3 
##  4 Adelaide       South Australia    Visiting 205.   32.5 
##  5 Adelaide Hills South Australia    Business   2.66  4.30
##  6 Adelaide Hills South Australia    Holiday   10.5   6.37
##  7 Adelaide Hills South Australia    Other      1.40  1.65
##  8 Adelaide Hills South Australia    Visiting  14.2  10.7 
##  9 Alice Springs  Northern Territory Business  14.6   7.20
## 10 Alice Springs  Northern Territory Holiday   31.9  18.1 
## # ℹ 294 more rows

如果用基本的tidyverse方法计算统计量，结果与上面类似，也会自动按三个key变量分组，即使人为用group_by()指定分组变量也是一样：

tourism |>
  group_by(Purpose) |>
  summarise(across(
    Trips,
    list(
      mean = mean, 
      std = sd
    ) ))

## # A tsibble: 320 x 4 [1Q]
## # Key:       Purpose [4]
##    Purpose  Quarter Trips_mean Trips_std
##    <chr>      <qtr>      <dbl>     <dbl>
##  1 Business 1998 Q1       47.4      80.7
##  2 Business 1998 Q2       49.0      81.0
##  3 Business 1998 Q3       57.3     102. 
##  4 Business 1998 Q4       49.9      91.1
##  5 Business 1999 Q1       43.9      73.8
##  6 Business 1999 Q2       62.0     123. 
##  7 Business 1999 Q3       55.1      96.3
##  8 Business 1999 Q4       48.7      95.7
##  9 Business 2000 Q1       46.9      89.5
## 10 Business 2000 Q2       52.9     105. 
## # ℹ 310 more rows

为了仅按某一个变量分组，可以将tsibble转换为tibble再计算，如：

as_tibble(tourism) |>
  group_by(Purpose) |>
  summarise(across(
    Trips,
    list(
      mean = mean, 
      std = sd
    ) ))

## # A tibble: 4 × 3
##   Purpose  Trips_mean Trips_std
##   <chr>         <dbl>     <dbl>
## 1 Business       53.0      97.3
## 2 Holiday       126.      145. 
## 3 Other          12.6      23.4
## 4 Visiting       92.5     135.

10.2.2 自相关函数计算

前面的章节已经提到过，可以用ACF()提取自相关函数，然后用autoplot()绘图。如：

ap_tsib |>
  ACF(ap, lag_max=36) |>
  autoplot()

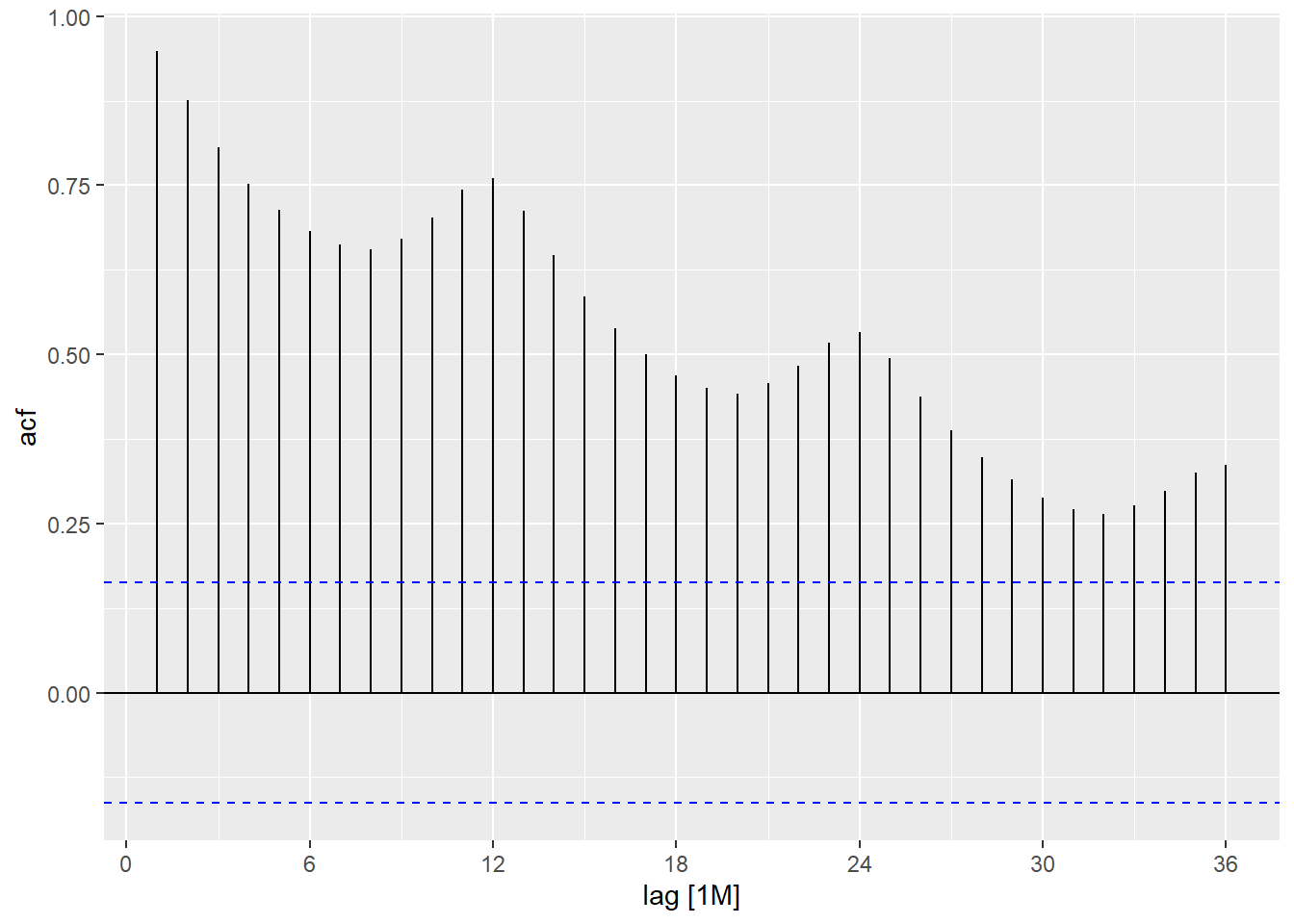
在features()函数中选feat_acf特征可以输出预先定义的若干个与自相关函数有关的量，包括滞后1处的ACF、前10个ACF平方和，一阶差分后的这两个统计量，二阶差分后的这两个统计量，对季节性数据还输出滞后在周期处的ACF值。如：

ap_tsib |>
  features(ap, feat_acf)

## # A tibble: 1 × 7
##    acf1 acf10 diff1_acf1 diff1_acf10 diff2_acf1 diff2_acf10 season_acf1
##   <dbl> <dbl>      <dbl>       <dbl>      <dbl>       <dbl>       <dbl>
## 1 0.948  5.67      0.303       0.409     -0.191       0.251       0.760

10.2.3 STL分解特征

feasts包通过比较趋势项、季节项、随机项的方差，定义了趋势强度和季节性强度指标，都取值于0和1之间。设分解为\(y_t = T_t + S_t + R_t\)，定义趋势的强度为 \[ F_T = \max\left(0, 1 - \frac{\text{Var}(R_t)}{\text{Var}(T_t + R_t)} \right). \] 定义季节项的强度为 \[ F_S = \max\left(0, 1 - \frac{\text{Var}(R_t)}{\text{Var}(S_t + R_t)} \right). \]

如：

ap_tsib |>
  features(ap, feat_stl) |>
  pivot_longer(everything(),
    names_to="Strength",
    values_to="Value")

## # A tibble: 9 × 2
##   Strength                  Value
##   <chr>                     <dbl>
## 1 trend_strength            0.991
## 2 seasonal_strength_year    0.941
## 3 seasonal_peak_year        7    
## 4 seasonal_trough_year     11    
## 5 spikiness                 3.03 
## 6 linearity              1325.   
## 7 curvature               131.   
## 8 stl_e_acf1                0.509
## 9 stl_e_acf10               0.930

与随机项相比，趋势项和季节项都很强。 feat_stl还输出了其它一些特征，比如季节项达到最高的季节、最低的季节，随机项中尖锐变化的程度，趋势项与线性函数的接近程度，趋势项弯曲程度，随机项的一阶自相关系数，随机项的前10个自相关系数平方和。

10.2.4 主成分特征

可以用prcomp()函数计算主成分分析输出主成分得分作为特征，加scale = TRUE表示消除各个时间序列分量的量纲影响，实际是在算法中使用相关系数矩阵而不是协方差阵来计算分解。

10.2.5 其它特征

10.1.1给出了用Guerrero方法估计变换参数然后进行变换的例子，用到了features()函数。 10.1.4中用features()函数提取与趋势、季节项有关的一些概括统计量。

feasts包仅提供了几十种特征的计算，但是用户自己可以编写自定义函数，输入一个一元时间序列，输出一个包含若干特征的向量。

feasts提供的其它特征有：

coef_hurst: 与长记忆有关的Hurst指数。
feat_spectral: 时间序列的Shannon谱熵，取0到1之间的值。谱熵越接近于0，序列越容易预测，谱熵越接近于1，序列越难预测。
box_pierce: 白噪声检验的Box-Pierce检验统计量和检验p值。
ljung_box: 白噪声检验的Ljung-Box检验统计量和检验p值。
feat_pacf: 与偏相关系数函数有关的特征。
unitroot_kpss: Kwiatkowski-Phillips-Schmidt-Shin (KPSS)单位根检验统计量和检验p值。
unitroot_pp Phillips-Perron 单位根检验统计量和检验p值。
unitroot_ndiffs: 基于KPSS检验计算需要多少阶差分才能使得序列平稳。
unitroot_nsdiffs: 计算需要多少阶季节差分才能使得序列平稳。
var_tiled_mean: 将序列依次分成小段，每一段计算平均值，然后计算这些平均值的方差，用来考察平稳性。有时称为稳定性（stability）特征。
var_tiled_var: 将序列依次分成小段，每一段计算方差，然后计算这些方差的方差，用来考察平稳性。有时称为lumpiness特征。
shift_level_max：在滑动窗口上计算均值并求接连两个均值跳跃最大值。可以发现水平变点。
shift_level_index: 返回上述跳跃位置。
shift_var_max: 在滑动窗口上计算方差并求接连两个方差跳跃最大值。可以发现波动率变点。
shift_var_index: 返回上述跳跃位置。
shift_kl_max：使用滑动窗口，计算连续两个窗口之间分布的KL散度，求其最大值。这可以发现分布变点。
shift_kl_index：返回上述变点位置。
n_crossing_points: 计算序列曲线穿过中位数的次数。
longest_flat_spot: 计算基本保持不变的时间段的个数。
stat_arch_lm: 计算Engle的LM方法的ARCH检验。
guerrero: 如前所述，计算Box-Cox变换所需的最优参数。

可以用feature_set(pkg="feasts")指定输出所有能计算的特征，如：

ap_tsib |>
  features(ap, feature_set(pkg="feasts")) |>
  pivot_longer(
    everything(),
    names_to = "feature",
    values_to = "value")

## # A tibble: 48 × 2
##    feature                   value
##    <chr>                     <dbl>
##  1 trend_strength            0.991
##  2 seasonal_strength_year    0.941
##  3 seasonal_peak_year        7    
##  4 seasonal_trough_year     11    
##  5 spikiness                 3.03 
##  6 linearity              1325.   
##  7 curvature               131.   
##  8 stl_e_acf1                0.509
##  9 stl_e_acf10               0.930
## 10 acf1                      0.948
## # ℹ 38 more rows

10.3 预测方法软件工具

R中提供了许多时间序列建模工具，典型的有forecast扩展包的Arima()和auto.arima()等函数， stats包的ets()函数， statespacer等支持状态空间模型的扩展包，等等。

这里主要介绍fpp3, feasts, fable, fabletools等扩展包提供的时间序列建模工具，包括简单预测方法、模型是否充分拟合的验证、计算预测区间、预测精度指标等内容。这些扩展包的优点是使用了tidyverse系统的“整洁数据”和“整洁建模”理念，使得相应R程序比较典雅、易读、易学。

10.3.1 一般流程

要介绍的这套工具基于整洁数据和整洁建模思想，所以需要将数据预先整理成tsibble时间序列类型。 tsibble是基于tibble数据框的时间序列类型，为了进行整理可以使用tidyverse扩展包体系的各种功能，参见李东风的R软件教程和(Wickham and Grolemund 2022)“R for Data Science”第二版。

整理好数据后，先用各种数据可视化（作图）方法查看时间序列的各种特征，判断可能需要做的变换，以及可行的模型。然后，指定一个或几个模型进行建模，用数据估计模型参数，然后对模型效果进行评估，这是仍可用可视化方法判断模型效果。如果模型效果不够好，就继续改进。模型不再改进后就可以利用模型进行预测。

为了说明上述流程，用tsibbledata扩展包中的global_economy数据进行说明。这已经是tsibble类型数据，以键变量(key variable)Country分组，每个国家是单独一组，有多个时间序列分量，其中一个分量是GDP。

因为GDP是国家的国内生产总值，受到国家大小影响，所以在数据准备阶段将其除以人口数变成人均GDP:

data(global_economy, package="tsibbledata")
gdppc <- global_economy |>
  mutate(GDP_per_capita = GDP / Population)

显示中国的逐年人均GDP时间序列曲线：

gdppc |>
  filter(Country == "China") |>
  autoplot(GDP_per_capita) +
  labs(y = "USD", title = "中国年人均GDP")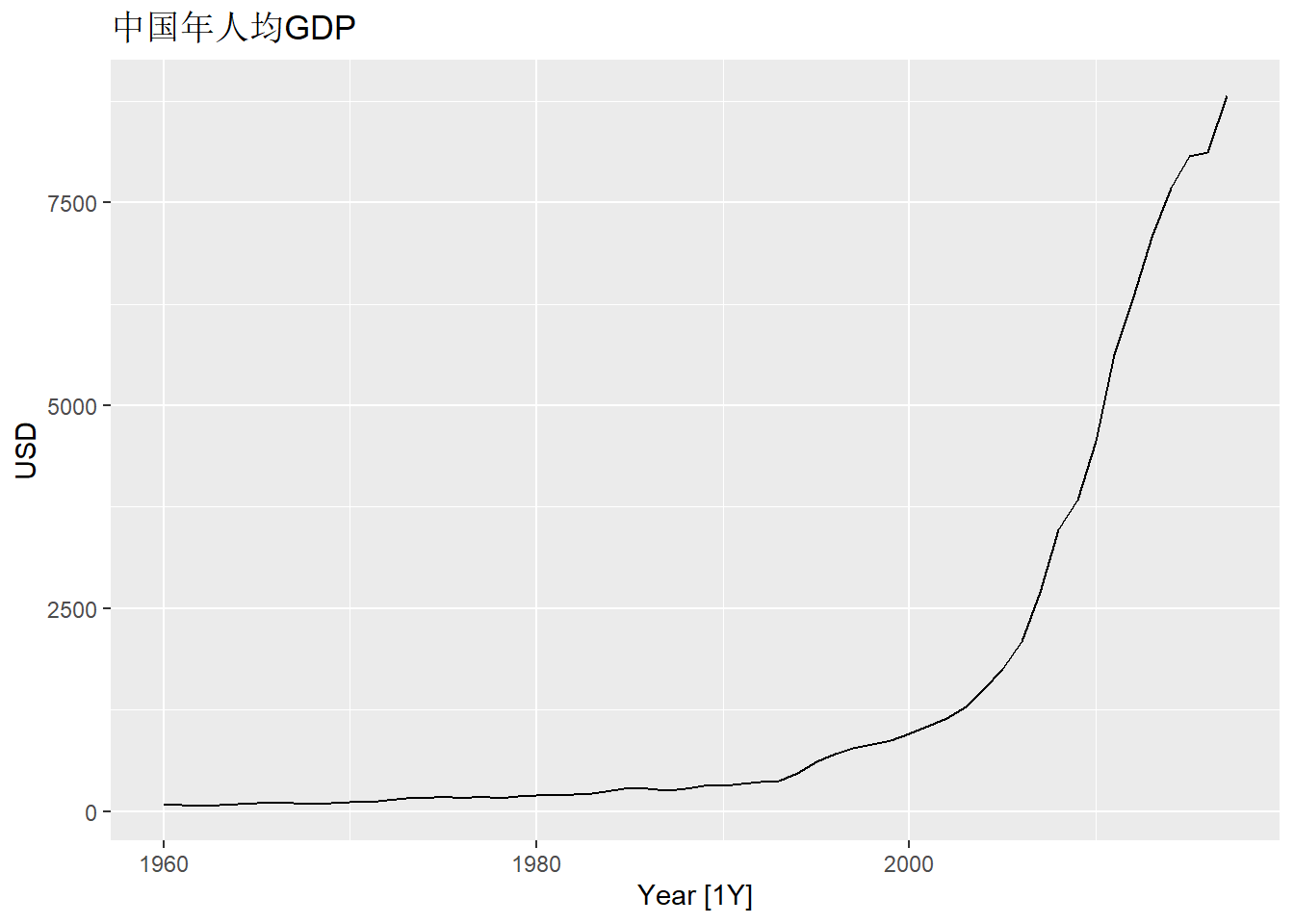

改为用对数纵坐标轴：

gdppc |>
  filter(Country == "China") |>
  autoplot(GDP_per_capita) +
  scale_y_log10() +
  labs(y = "USD", title = "中国年人均GDP")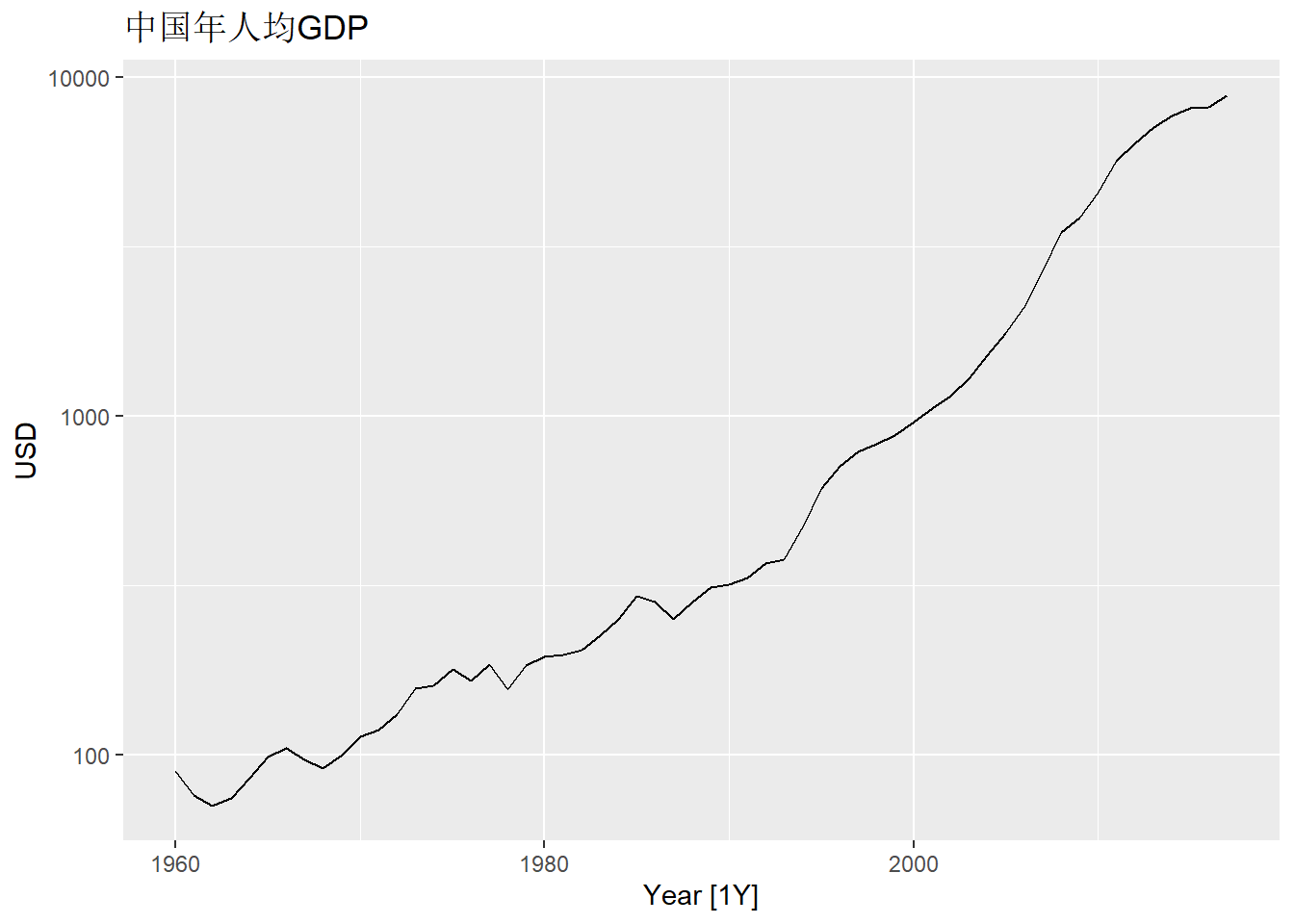

可以尝试将时间序列的对数值建立关于时间线性增长的模型，利用fable扩展包的TSLM()函数设置为TSLM(log10(GDP_per_capita ) ~ trend())。实际建模估计用fabletools的model()函数，如：

loglin_mod <-
  gdppc |>
  filter(Country == "China") |>
  model(loglin_mod 
    = TSLM(log10(GDP_per_capita ) ~ trend()))
loglin_mod

## # A mable: 1 x 2
## # Key:     Country [1]
##   Country loglin_mod
##   <fct>      <model>
## 1 China       <TSLM>

关于如何验证模型拟合优度，计算预测精度，参见后面的小节。

为了获得预测值，使用fabletools扩展包提供的forecast()函数。如：

loglin_mod |>
  forecast(h = "3 years")

## # A fable: 3 x 5 [1Y]
## # Key:     Country, .model [1]
##   Country .model      Year   GDP_per_capita .mean
##   <fct>   <chr>      <dbl>           <dist> <dbl>
## 1 China   loglin_mod  2018 t(N(3.8, 0.028)) 6338.
## 2 China   loglin_mod  2019 t(N(3.8, 0.028)) 6901.
## 3 China   loglin_mod  2020 t(N(3.8, 0.028)) 7515.

以上结果是fabletools产生的一个预测结果表格，简称为fable。参数h =用来指定向前预测多少期。结果中.model指定所用模型，以因变量GDP_per_capita名为列名的结果列是预测分布，其中t()表示因变量有变换， N(3.8, 0.028)是因变量对数值的预测分布。 .mean列是因变量（非对数值）的点预测值。

预测结果可以用autoplot()作图，图中出了画出点预测值以外，还用阴影画出置信度\(80\%\)和置信度\(95\%\)的预测区间。如：

loglin_mod |>
  forecast(h = "3 years") |>
  autoplot(gdppc) +
  scale_y_log10() +
  labs(y = "USD", title = "中国人均GDP对数线性模型预测")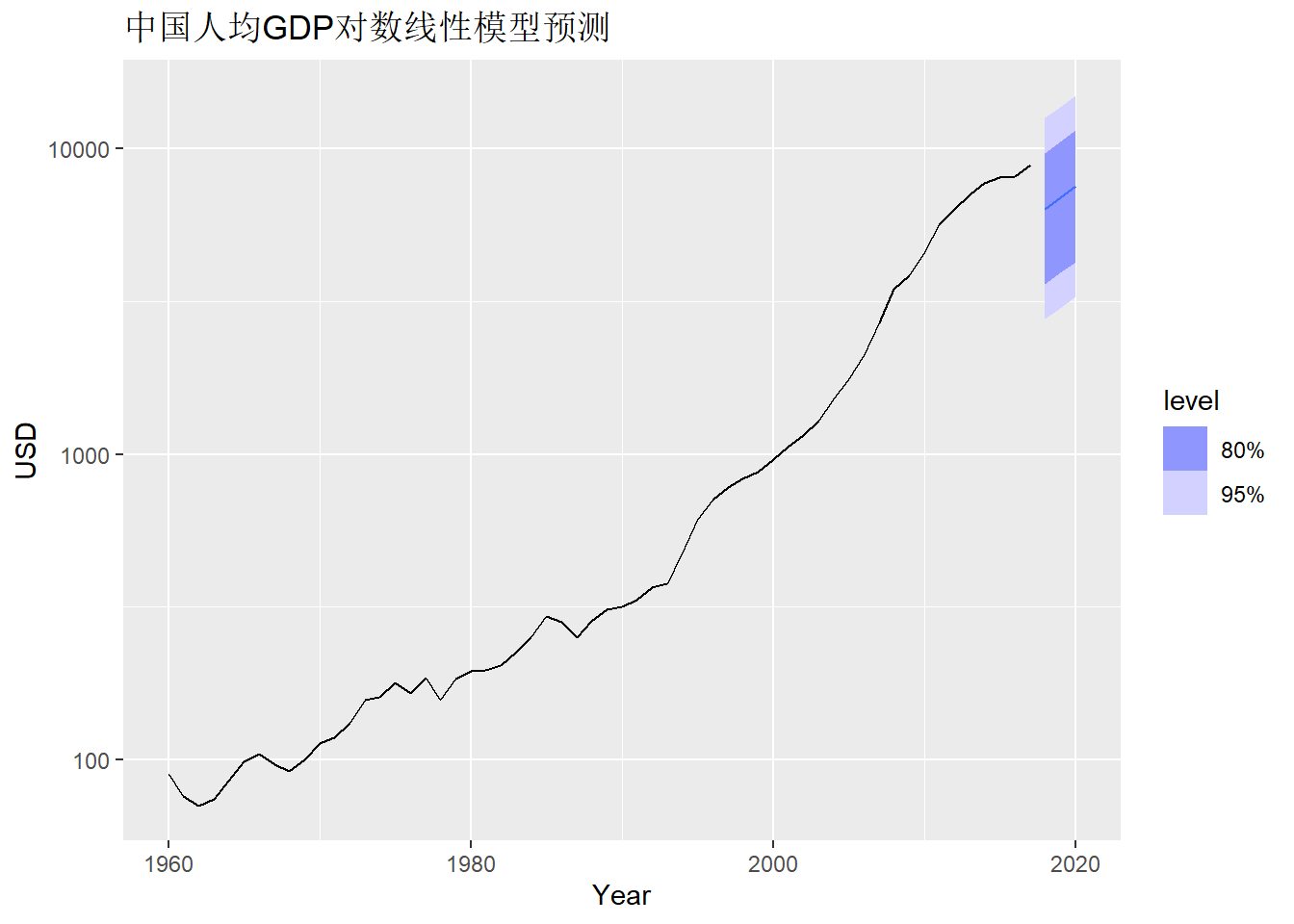

可以看出预测明显有一个断层，是不合理的。线性模型是一个全局模型，没有考虑到应该尽可能多利用时间最靠近的观测值进行预测，所以预测结果不够好。如果使用ARIMA模型，则会主要使用最时间最靠近的观测值计算预测值。

10.3.2 最简单的一些预测方法

如果要比较模型的预测效果，首先可以考虑一些最简单朴素的预测方法，将这些方法作为基准，如果某种预测模型的结果不如这些简单朴素方法，则模型没有意义。

这些最简单方法包括：

用训练样本的平均值作为未来值的预测，适用于平稳的序列；
用最后一个观测值作为预测值，称为简单平移预测，适用于随机游动模型；
用已知数据中同季度的值作为未来值的预测，适用于季节性影响特别大的序列，称为季节平移预测；
从训练样本中计算一个平均增速，然后对未来值从最后一个已知值按平均增速线性增长进行预测。

fabletools扩展包提供了预测功能，其中也包含这些最简单的预测函数。

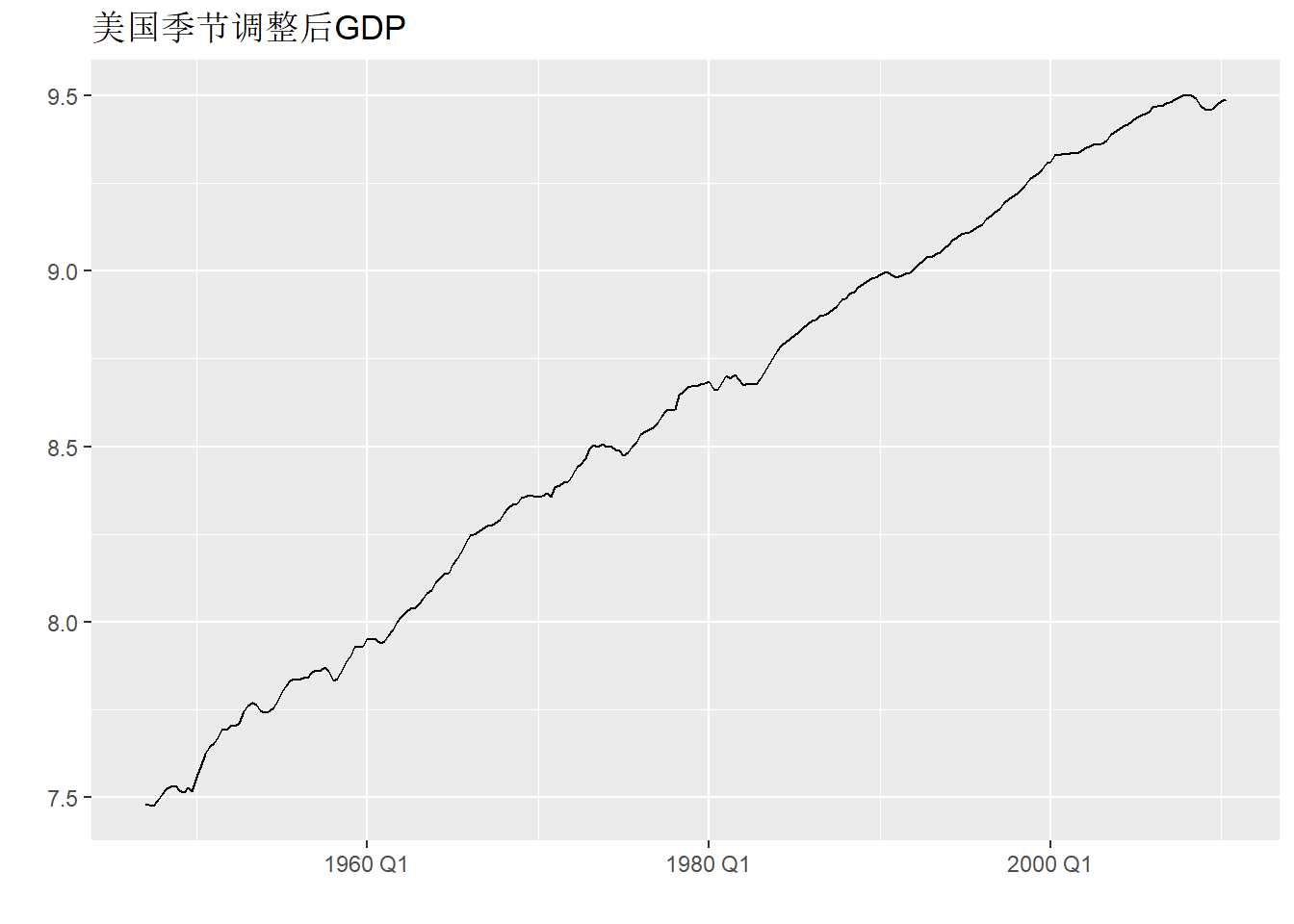
例10.1 以美国GDP季度数据为例。数据是从1947年第一季度到2010年第二季度的美国GDP季节调整后序列，以2005年GDP为基础进行了通胀调整，单位为2005年的十亿美元。

读入数据，计算GDP的对数值和对数增长率：

library(tsibble)
library(fabletools)
library(fable)

da <- read_table("q-gdpc96.txt")

## 
## ── Column specification ────────────────────────────────────────────────────────
## cols(
##   Year = col_double(),
##   Mon = col_character(),
##   Day = col_character(),
##   gdp = col_double()
## )

gdp <- ts(log(da[["gdp"]]), start=c(1947,1), frequency=4)
dgdp <- diff(gdp)
gdp_tsib <- as_tsibble(gdp)

时间序列图：

gdp_tsib |>
  autoplot(value) +
  labs(y="", x="",
    title="美国季节调整后GDP")

取1947-2008年的数据，用均值预报：

gdp_tsib |>
  filter_index("1947 Q1" ~ "2008 Q4") |>
  select(value) |>
  model(NAIVE(value)) -> fit_gdp_nai_1
fit_gdp_nai_1 |>
  forecast(h = 6) -> pred_gdp_nai_1
pred_gdp_nai_1 |> knitr::kable()

.model	index	value	.mean
NAIVE(value)	2009 Q1	N(9.5, 0.00016)	9.472217
NAIVE(value)	2009 Q2	N(9.5, 0.00033)	9.472217
NAIVE(value)	2009 Q3	N(9.5, 0.00049)	9.472217
NAIVE(value)	2009 Q4	N(9.5, 0.00065)	9.472217
NAIVE(value)	2010 Q1	N(9.5, 0.00082)	9.472217
NAIVE(value)	2010 Q2	N(9.5, 0.00098)	9.472217

程序中的value是保存在tsibble时间序列对象中的时间序列分量的默认变量名， filter_index()按时间选择时间序列子集，格式是用~连接开始时间字符串和结尾时间字符串，缺省值用小数点代替。以上预测是用最后一个观测平移作为后续所有超前步的预测值。

作预测图形：

pred_gdp_nai_1 |>
  autoplot(gdp_tsib |> filter_index("2000 Q1" ~ .)) +
  labs(y="", x="",
    title="美国季节调整后GDP对数值用平移方法预测")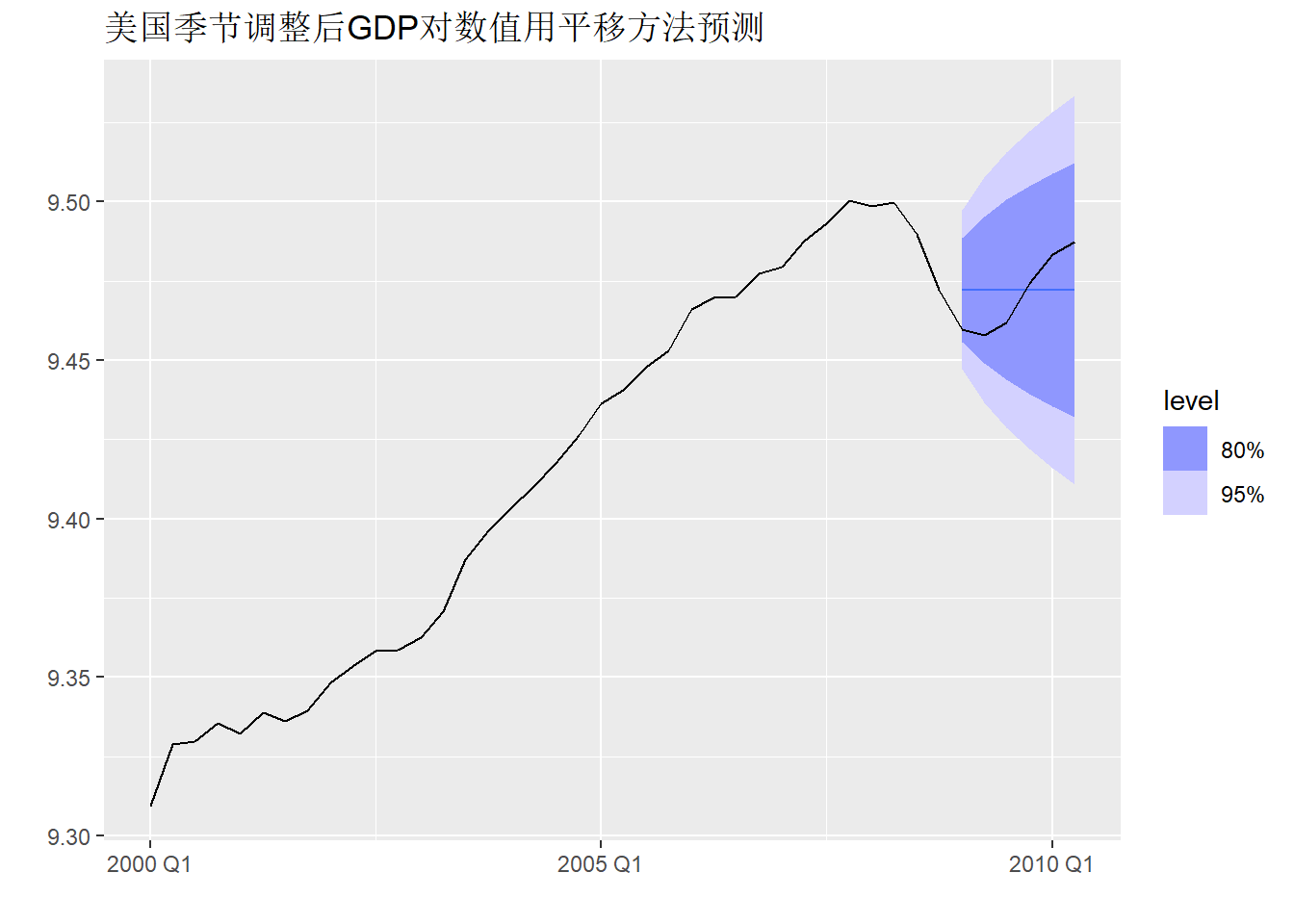

四种简单预报方法为(设要预报的时间序列分量的变量名为value)：

MEAN(value)是用平均值预报；
NAIVE(value)是用最后一个观测值预报;
SNAIVE(value ~ lag("year"))是用最后一个同季节值预报；
RW(value ~ drift())是用带漂移的随机游动模型预报，即估计一个平均增速从最后一个观测值按平均增速线性增长预报。

同时用多个方法预测的例子：

gdp_tsib |>
  filter_index("1947 Q1" ~ "2008 Q4") |>
  select(value) |>
  model(
    pred_mean = MEAN(value),
    pred_naive = NAIVE(value),
    pred_drift = RW(value ~ drift())) |>
  forecast(h = 2) |>
  knitr::kable()

.model	index	value	.mean
pred_mean	2009 Q1	N(8.6, 0.36)	8.563740
pred_mean	2009 Q2	N(8.6, 0.36)	8.563740
pred_naive	2009 Q1	N(9.5, 0.00016)	9.472217
pred_naive	2009 Q2	N(9.5, 0.00033)	9.472217
pred_drift	2009 Q1	N(9.5, 9.9e-05)	9.480283
pred_drift	2009 Q2	N(9.5, 2e-04)	9.488349

实际上，预测原始的未作对数变换的GDP也是可以的，但应该输入包含原始GDP的tsibble数据，并将建模步写成类似于model(NAIVE(log(value)))这样。

10.3.3 拟合值和残差

设时间序列观测数据为\(y_1, y_2, \dots, y_T\)，用这些数据估计了一个模型，然后用模型计算了\(y_t\)的估计值，记为\(\hat y_t\)，称为\(y_t\)的拟合值(fitted value)。注意拟合值\(\hat y_t\)利用了整个时间段的信息，而不仅仅是截止到\(t-1\)时刻的信息，所以拟合值不是真正的预测值，可以用\(\hat y_t\)与\(y_t\)的接近程度考察模型描述现有数据的准确程度，但不能完全依赖拟合值来评估预测的精度。

\(e_t = y_t - \hat y_t\)称为模型的残差(residual)。残差越小，说明模型对当前数据描述越好，一般来说预报效果也越好，但存在“过度拟合”危险，所以不能拿残差小作为预测好的根据。

因为时间序列建模时常常作一些变换，如对数变换，有时在变换后的尺度上计算残差更有意义，这样的残差在fabletools中称为新息残差(innovation residuals)，但实际上还是一种拟合残差，理论时间序列分析中对新息深刻的定义。

对model()输出的结果，可以用augment()提取拟合值、残差：

fit_gdp_nai_1 |>
  augment() |>
  slice_tail(n=4) |>
  knitr::kable()

.model	index	value	.fitted	.resid	.innov
NAIVE(value)	2008 Q1	9.498461	9.500281	-0.0018210	-0.0018210
NAIVE(value)	2008 Q2	9.499949	9.498461	0.0014886	0.0014886
NAIVE(value)	2008 Q3	9.489751	9.499949	-0.0101977	-0.0101977
NAIVE(value)	2008 Q4	9.472217	9.489751	-0.0175341	-0.0175341

其中.fitted是模型的拟合值， .resid是拟合残差，而.innov是变换尺度上残差（新息残差），本例没有在模型中指定变换，所以.innov与.resid相同，如果模型中有变换则这两者不相同。

10.3.4 模型的残差诊断

可以用新息残差（如果有变换，这是变换后数据的拟合残差）判断模型拟合是否有明显缺陷，称为模型的残差诊断。残差应该近似为白噪声，而且均值应该等于0。有明显缺陷就必须进行修正；即使没有这样的明显缺陷，也可能有其它的改进方案。

对预测\(y_t\)本身而言，残差最好具有方差不变性，即不能某一时间段方差大，另一段方差小。残差最好近似服从正态分布。如果这两个要求不满足，有可能可以改进模型，但不一定总能有办法改进。

考虑10.3.2中关于美国季节调整后GDP对数值时间序列的平移预测方法的残差诊断。

fit_gdp_nai_1 |>
  augment() |>
  mutate(mean_innov = mean(.innov, na.rm=TRUE)) |>
  autoplot(.innov) +
  geom_hline(aes(yintercept=mean_innov), color="red") +
  labs(title = "拟合残差图")

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).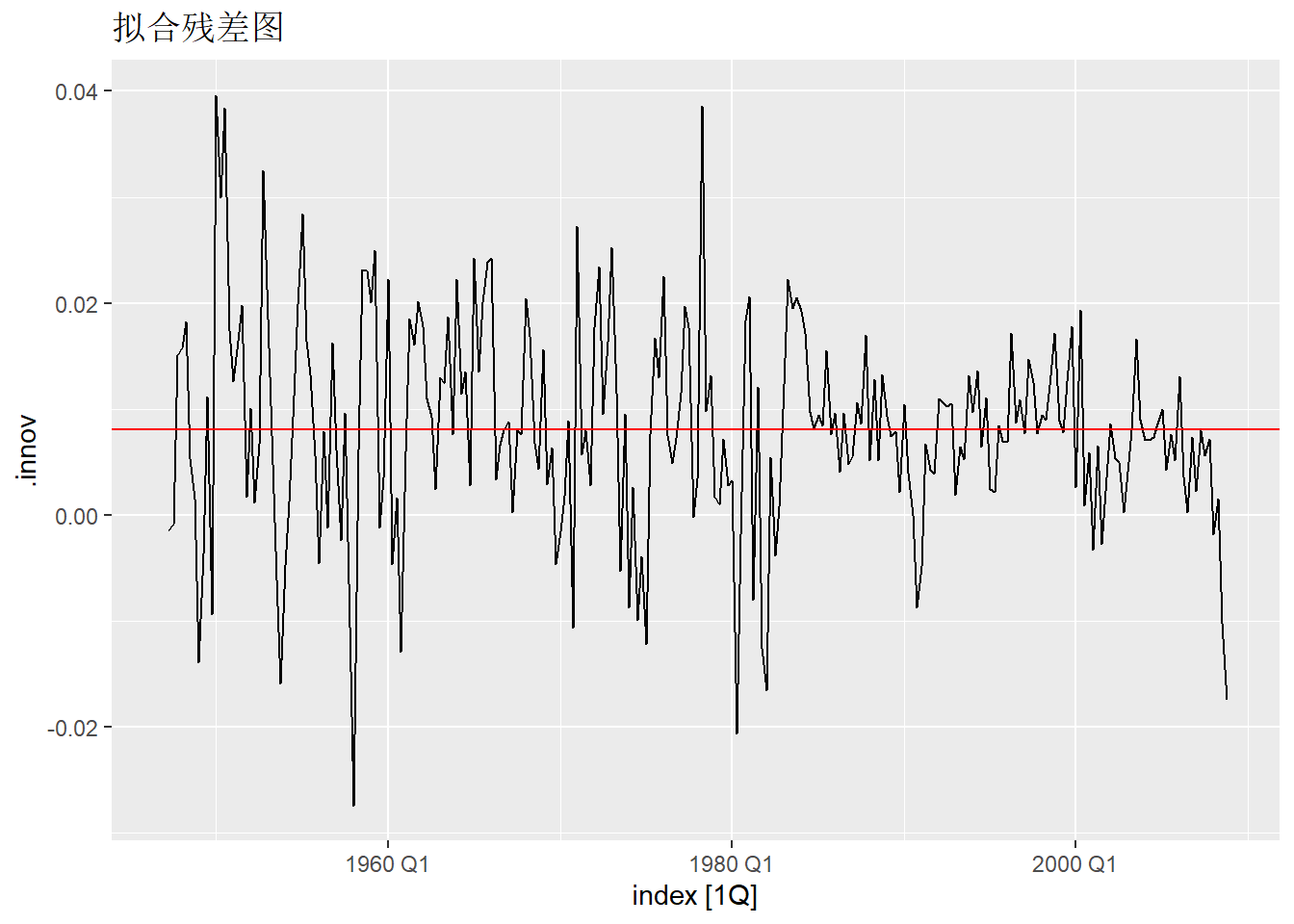

上面是残差的时间序列图，横线为残差的均值，可见均值不等于0。

作残差的ACF图，考察是否有残余的相关性：

fit_gdp_nai_1 |>
  augment() |>
  ACF(.innov) |>
  autoplot() +
  labs(title="残差的ACF")

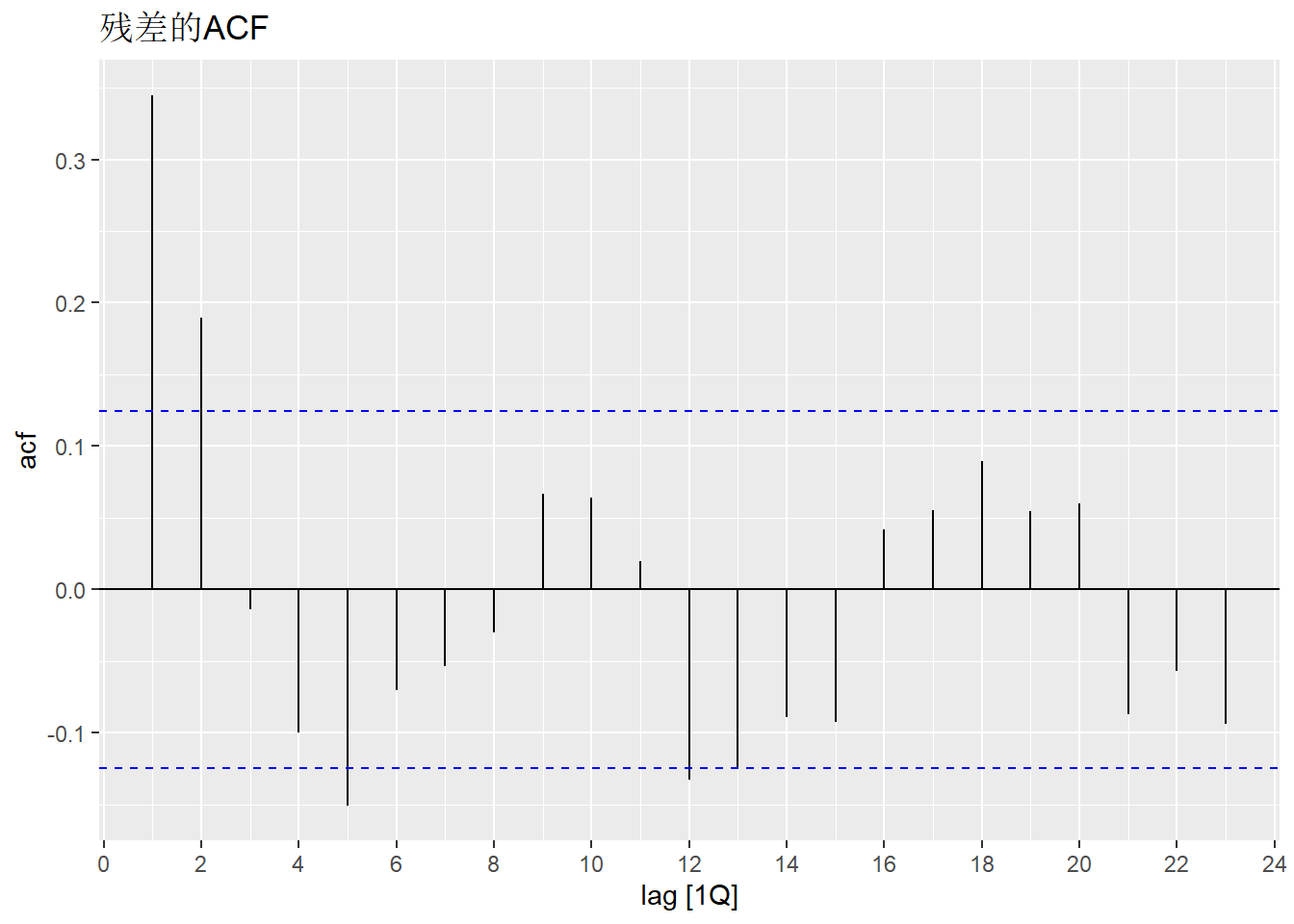
可以看出残差不符合白噪声的表现。

作残差直方图，考察分布是否正态：

fit_gdp_nai_1 |>
  augment() |>
  ggplot(aes(x = .innov)) +
  geom_histogram() +
  labs(title="残差直方图")

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

## Warning: Removed 1 row containing non-finite outside the scale range
## (`stat_bin()`).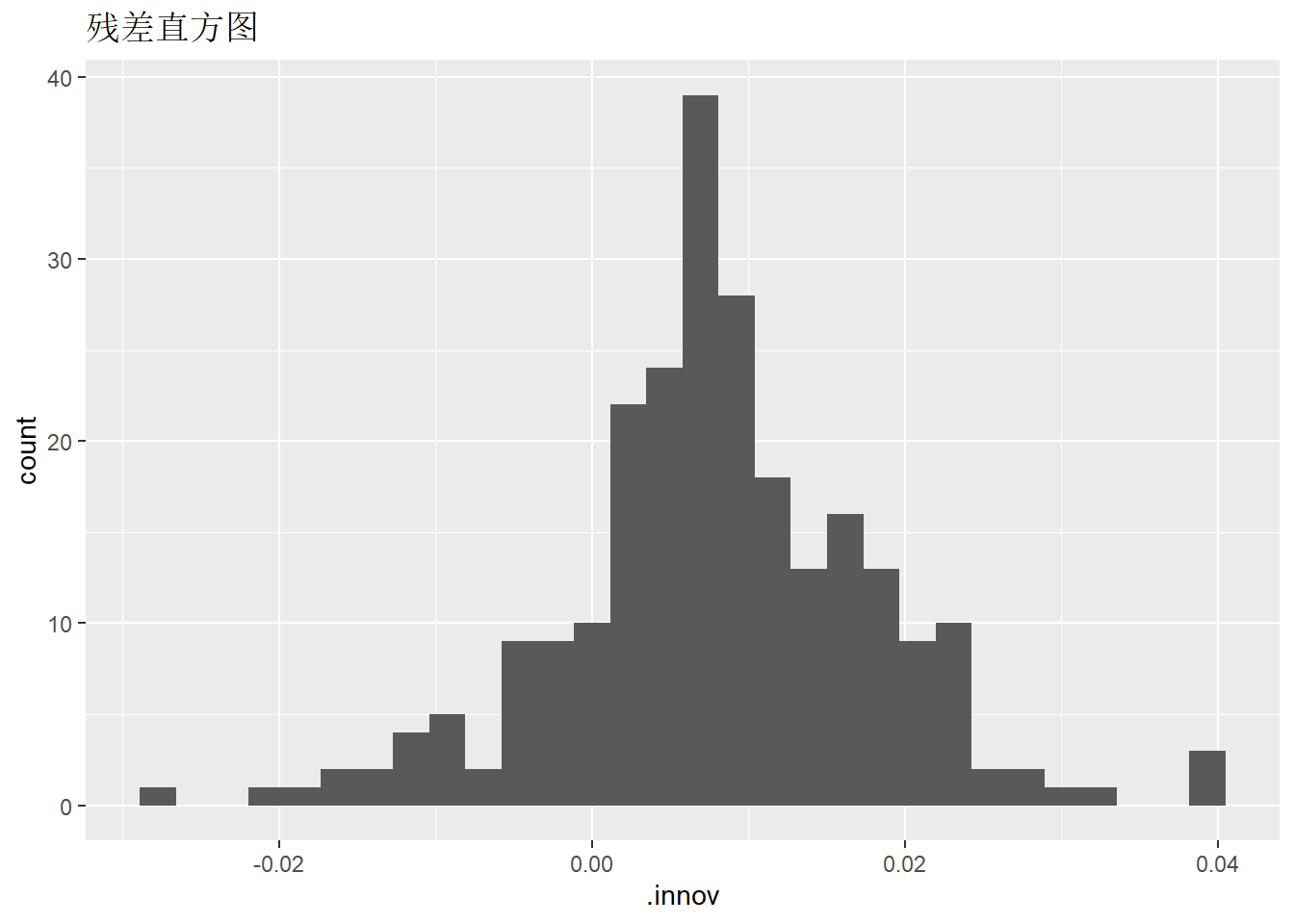

从直方图可以看出分布有重尾性，有正态分布有区别。

可以对建模结果（没有用augment()计算之前）用gg_tsresiduals()函数作残差图、残差ACF图和残差的直方图：

fit_gdp_nai_1 |>
  gg_tsresiduals() +
  labs(title="残差诊断")

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_point()`).

## Warning: Removed 1 row containing non-finite outside the scale range
## (`stat_bin()`).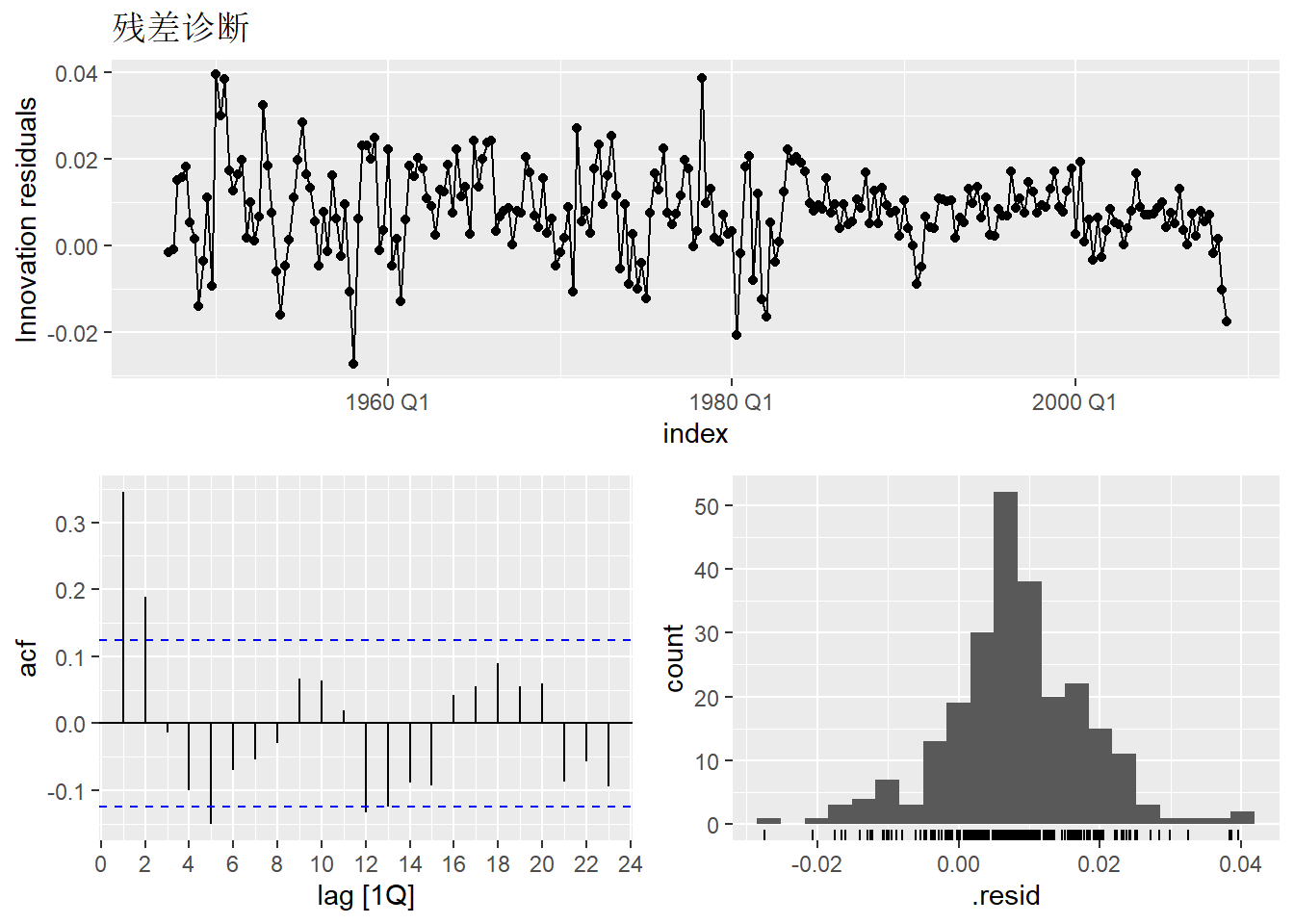

为了考察残差是否近似白噪声，还可以作白噪声检验。 Box-Pierce白噪声检验：

fit_gdp_nai_1 |>
  augment() |>
  features(.innov, box_pierce, lag = 8)

## # A tibble: 1 × 3
##   .model       bp_stat    bp_pvalue
##   <chr>          <dbl>        <dbl>
## 1 NAIVE(value)    48.5 0.0000000786

从结果p值看应拒绝是白噪声的零假设。

Ljung-Box白噪声检验：

fit_gdp_nai_1 |>
  augment() |>
  features(.innov, ljung_box, lag = 8)

## # A tibble: 1 × 3
##   .model       lb_stat    lb_pvalue
##   <chr>          <dbl>        <dbl>
## 1 NAIVE(value)    49.3 0.0000000551

从GDP对数值时间序列图形看，带漂移的随机游动可能更合适。用漂移随机游动模型建模的残差诊断：

gdp_tsib |>
  filter_index("1947 Q1" ~ "2008 Q4") |>
  select(value) |>
  model(RW(value ~ drift())) |>
  augment() |>
  features(.innov, ljung_box, lag = 8)

## # A tibble: 1 × 3
##   .model              lb_stat    lb_pvalue
##   <chr>                 <dbl>        <dbl>
## 1 RW(value ~ drift())    49.3 0.0000000551

此模型的残差仍不符合白噪声要求。

10.3.5 用条件分布预测以及预测区间

从10.3.2可以看出，我们可以有许多预测方法，有些方法很简单，也有一些理论上比较复杂。用这些方法预测\(y_{t+h}\)，都可以给出一个预测值\(\hat y_{t+h}\)。而预测结果的用户仅靠一个预测值，不能了解这个预测的误差大小，也无法判断哪一种预测方法更可信。所以，每种预测最好能够提供一个预测区间，与某个置信度联系，预测区间越大，说明误差越大；同样宽度的置信区间置信度越低，误差也越大。预测区间可以通过预测值的标准误差来计算，也可以用bootstrap方法计算。

更进一步，如果能够对\(y_{T+h}\)在给定\(y_1, y_2, \dots, y_T\)的条件下的条件分布给出一个估计，称为预测分布，就可以对未来情况作出更精细的判断。如果模型的预测分布是正态分布，就只要估计均值和方差两个参数。

10.3.5.1 预测区间计算

如果预测分布是正态分布，模型估计了预测分布的均值\(\hat y_{T+h}\)和方差\(\hat\sigma^2_h\)，则\(1 - \alpha\)预测区间为 \[\begin{equation} \hat y_{T+h} \pm z_{1 - \frac{\alpha}{2}} \hat\sigma_{h} . \tag{10.1} \end{equation}\] 其中\(z_{1 - \frac{\alpha}{2}}\)是标准正态分布双侧\(\alpha\)分位数。当\(1 - \alpha = 0.95\)时， \(z_{1 - \frac{\alpha}{2}} = 1.96 \approx 2.0\)，所以常用的一个\(95\%\)置信度的预测区间简单公式为 \[ \hat y_{T+h} \pm 2 \hat\sigma_{h} . \]

10.3.5.2 标准差估计和预测

如果数据\(y_1, y_2, \dots, y_T\)的模型平稳，或者是经过变换以后平稳的，则模型的拟合残差方差估计为 \[\begin{equation} \hat\sigma^2 = \frac{1}{T-K-p} \sum e_t^2, \tag{10.2} \end{equation}\] 其中\(e_t\)是拟合残差， \(p\)是模型中未知参数个数， \(T-K\)是能计算的残差的个数。

预测分布如果假设为正态分布，对超前一步预测(\(h=1\))， (10.1)中的\(\hat\sigma_{h}\)常常用(10.2)计算。对于ARMA模型， (10.2)给出了新息方差的估计，所以理论上是一步预测误差方差的合理估计。当超前步数\(h > 1\)时，通常预测分布的方差会增大，参见4.12。某些模型可以理论上给出\(\hat\sigma_h\)的计算公式，但未考虑从随机样本中估计得到的模型参数的随机性的影响，所以从理论得到的\(\hat\sigma_h\)会略微偏低。

fable扩展包对10.3.2中讲的四种简单预测方法，在假定预测残差不相关前提下，计算了每种方法对应的\(\hat\sigma_h\)。这个不相关假定显然在很多情况下是不成立的。所以，尽管许多软件在作预测时能够给出预测区间，用户也不要盲目相信其准确性，这些预测区间都是需要一定的模型假定才成立的。

fable包在用forecast()函数预测后，结果包括一个预测分布和一个点预测值；为了计算预测区间，可以对预测结果使用hilo()函数提取预测区间，缺省情况下会输出\(80\%\)和\(95\%\)预测区间，可以用level参数指定置信度。比如，用简单平移方法对美国季节调整后GDP对数值预测后，提取预测区间：

pred_gdp_nai_1 |>
  hilo() |>
  knitr::kable()

.model	index	value	.mean	80%	95%
NAIVE(value)	2009 Q1	N(9.5, 0.00016)	9.472217	[9.455821, 9.488613]80	[9.447141, 9.497293]95
NAIVE(value)	2009 Q2	N(9.5, 0.00033)	9.472217	[9.449029, 9.495405]80	[9.436755, 9.507680]95
NAIVE(value)	2009 Q3	N(9.5, 0.00049)	9.472217	[9.443818, 9.500616]80	[9.428784, 9.515650]95
NAIVE(value)	2009 Q4	N(9.5, 0.00065)	9.472217	[9.439425, 9.505010]80	[9.422065, 9.522369]95
NAIVE(value)	2010 Q1	N(9.5, 0.00082)	9.472217	[9.435554, 9.508880]80	[9.416146, 9.528289]95
NAIVE(value)	2010 Q2	N(9.5, 0.00098)	9.472217	[9.432055, 9.512380]80	[9.410794, 9.533640]95

在将forecast()的预测结果输入给autoplot()作图时，将自动用阴影部分作\(80\%\)和\(95\%\)预测区间。可以用level参数控制需要的置信度。

10.3.5.3 Bootstrap预测区间

前面的预测区间计算假定了预测分布是正态分布，也没有考虑到从随机样本中估计的模型参数的随机误差的影响。

首先放松预测分布是正态分布的假定，但假定模型的预测残差独立同分布。这样，计算出拟合残差\(e_1, e_2, \dots, e_T\)后，从这些残差中任意随机抽样，仍近似服从残差服从的分布。于是，可以利用从残差中随机抽样的方法用模型产生向前的多条路径，利用路径的平均值可以产生点预测，利用路径的分位数可以产生预测区间。这种方法在模型非正态时可以得到更准确的点预测值和预测区间，比如，如果模型中对数据做了对数变换，从变换后的数据进行预测然后直接进行反变换会有一定偏差，利用bootstrap来作，因为在计算预测值和预测区间时是基于未变换的尺度，所以能够修正偏差。

以AR(1)模型\(X_t = \phi X_{t-1} + \varepsilon_t\)为例，设从\(X_1, \dots, X_T\)估计了参数\(\hat\phi\)和\(\hat\sigma^2\)，计算了拟合残差\(e_t = X_t - \hat\phi X_{t-1}\)，\(t=2,\dots,T\)。为了预测\(X_{T+1}\)，从\(\{e_t \}\)随机有放回抽取\(e^{(b)}_{T+1}\), 令\(X_{T+1}^{(b)} = \hat\phi X_{T+1} + e^{(b)}_{T+1}\)，对\(b=1,\dots,B\)重复这个步骤\(B\)次，得到\(X_{T+1}^{(b)}\)，\(b=1,\dots,B\)，作为\(X_{T+1}\)的预测分布的随机样本，用这些随机样本的平均值作为点预测值，用这些随即样本的\(\frac{\alpha}{2}\)和\(1 - \frac{\alpha}{2}\)分位数作为\(1-\alpha\)预测区间的下界和上界。

以上做法仍没有考虑拟合的模型中参数估计带来的随机误差。另一种更精细的做法是，对残差随机抽样生成新的残差序列，利用新的残差序列和估计的模型生成许多组新的模拟观测数据，从每一组模拟观测数据重新估计模型参数，利用新估计的模型参数和原始观测序列进行预测，从多组预测中计算平均值作为点预测，计算分位数作为预测区间。

fable的bootstrap预测没有生成新的模拟观测数据，而只是模拟生成了未来时间的多条路径，生成这些路径时模型参数保持原始参数。

例如，美国季节调整后GDP对数值的预测：

fit_gdp_nai_1 |>
  forecast(h = 6, 
    bootstrap = TRUE,
    times = 10000) -> predbt_gdp_nai_1
predbt_gdp_nai_1 |>
  hilo() |>
  knitr::kable(digits=4)

.model	index	value	.mean	80%	95%
NAIVE(value)	2009 Q1	sample[10000]	9.4723	[9.460289, 9.484176]80	[9.451245, 9.492550]95
NAIVE(value)	2009 Q2	sample[10000]	9.4723	[9.454902, 9.489390]80	[9.443953, 9.500855]95
NAIVE(value)	2009 Q3	sample[10000]	9.4723	[9.450412, 9.493708]80	[9.438103, 9.506320]95
NAIVE(value)	2009 Q4	sample[10000]	9.4723	[9.447271, 9.496915]80	[9.432177, 9.511667]95
NAIVE(value)	2010 Q1	sample[10000]	9.4723	[9.444273, 9.500100]80	[9.427975, 9.515662]95
NAIVE(value)	2010 Q2	sample[10000]	9.4723	[9.442079, 9.503095]80	[9.424770, 9.518911]95

predbt_gdp_nai_1 |>
  autoplot(gdp_tsib |> filter_index("2000 Q1" ~ .)) +
  labs(title = "美国季节调整后GDP对数值平移法bootstrap预测")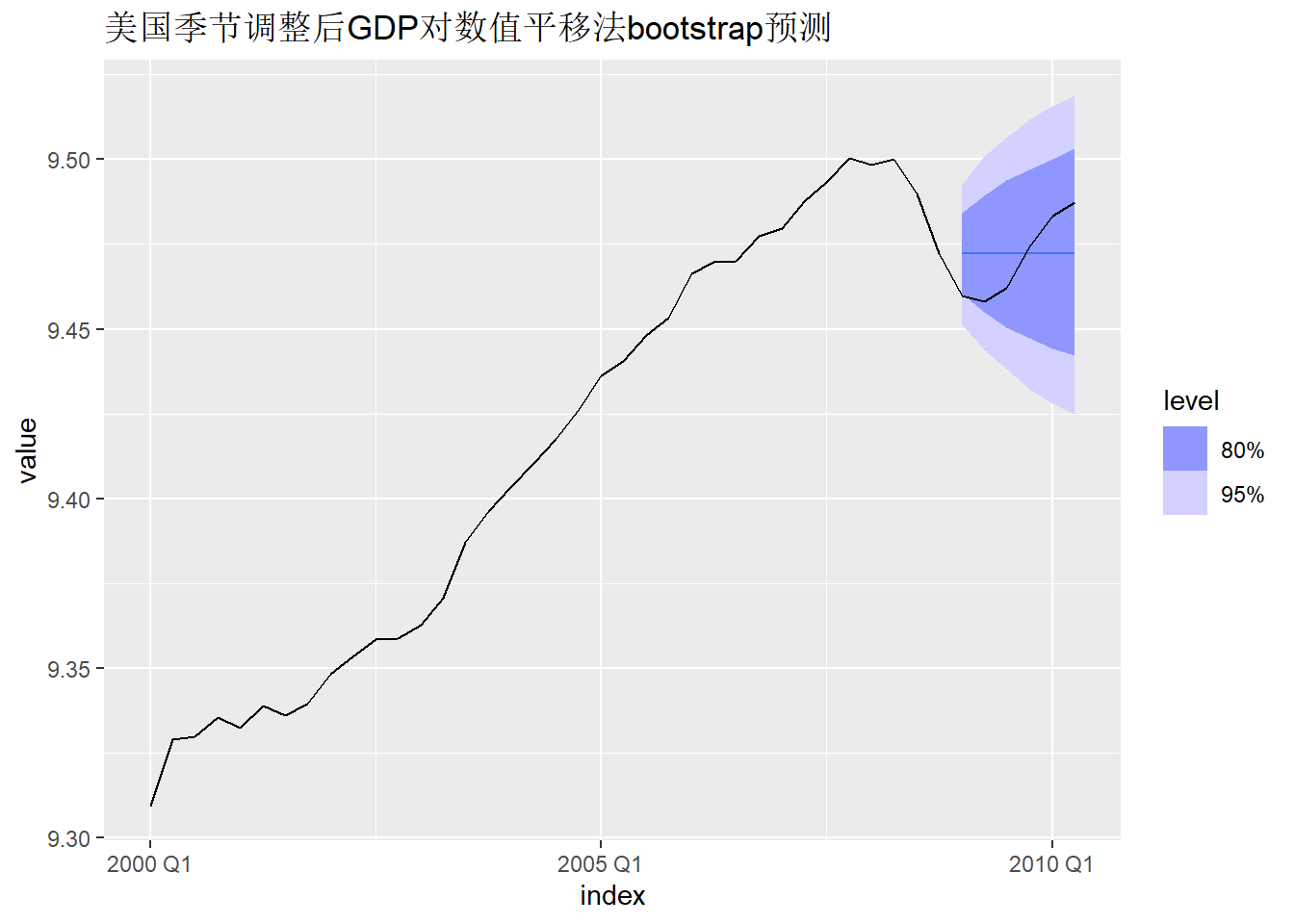

参数times控制生成的预测路径的多少。

10.3.6 建模时的变换

当时间序列\(\{y_t\}\)非高斯时间序列时，有可能需要作变换\(g(\cdot)\)，如对数变换，Box-Cox变换，对变换后的序列\(\{x_t = g(y_t) \}\)建模预测，得到预测\(\hat x_{t+h}\)后，再反变换得到\(\hat y_{t+h} = g^{-1}(\hat x_{t+h})\)。因为变换是非线性的，所以可能带来偏差。如果\(X \sim \text{N}(\mu, \sigma^2)\)， \(Y = e^X\)，则 \[ E(Y) = e^{\mu + \frac{1}{2} \sigma^2}, \quad \text{Var}(Y) = e^{2\mu + \sigma^2}(e^{\sigma^2} - 1) . \] 所以当变换后的模型假设为高斯过程时，反变换公式应该使用 \[ \hat y_{T+1} = e^{\hat x_{T+1} + \frac{1}{2} \hat\sigma^2}, \] 其中\(x_{T+1}\)和\(\hat\sigma^2\)是\(x_{T+1}\)的预测分布的均值和方差。 fabletools的forecast()函数自动进行这样的调整。

预测区间的计算不受变换影响，不需要偏差调整。只要在\(\{x_t\}\)尺度上计算了预测区间，再将两个区间端点反变换就得到了\(\{y_t \}\)尺度上的预测区间，置信度保持不变。

如果用fabletools的forecast()函数预报时使用了bootstrap方法，则可以从\(\{x_t \}\)生成bootstrap预测样本，经过反变换得到\(y_{t+h}\)的bootstrap预测样本，这样得到的\(\{y_t \}\)尺度的预测值均值已经是合理定义的。

10.3.7 基于时间序列分解的预测方法

若用时间序列分解方法\(y_t = T_t + S_t + R_t\)进行建模，为了预测\(y_{T+h}\)，只要用与\(T+h\)同月份（或季度）的已有\(\hat S_t\)的值预测\(S_{T+h}\)，记为\(\hat S_{T+h}\)；然后基于季节调整序列 \[ \hat A_t = \hat T_t + \hat R_t, \ t=1,2,\dots,T, \] 预测\(\hat A_{T+h}\)，用\(\hat S_{t+h} + \hat A_{T+h}\)预测\(y_{T+h}\)。

用\(\{\hat A_t \}\)预测\(A_{T+h}\)时，可以用各种不涉及季节性的时间序列模型，如10.3.2中的漂移随机游动， 11.1中的指数平滑方法，不带季节项的ARIMA模型，等等。

如果建立的是乘性模型\(y_t = T_t S_t R_t\)，则仍用最后可用值估计\(\hat S_{T+h}\)，从\(\hat A_t = T_t R_t\), \(t=1,2,\dots,T\)建模预测得到\(\hat A_{T+h}\), 用\(\hat S_{T+h} \hat A_{T+h}\)预测\(y_{T+h}\)。

fabletools包的decomposition_model()函数可以直接将建模和预测方法设定合成在一步中。

下面用时间序列分解方法预测航空乘客数据。

ap_tsib |>
  model(dec = decomposition_model(
    STL(log_ap ~ trend(window=7)),
    RW(season_adjust ~ drift())  )) -> stl_ap
stl_ap |>
  forecast(h = 12) |>
  autoplot(ap_tsib ) +
  labs(y="", title = "航空乘客数对数值STL预测")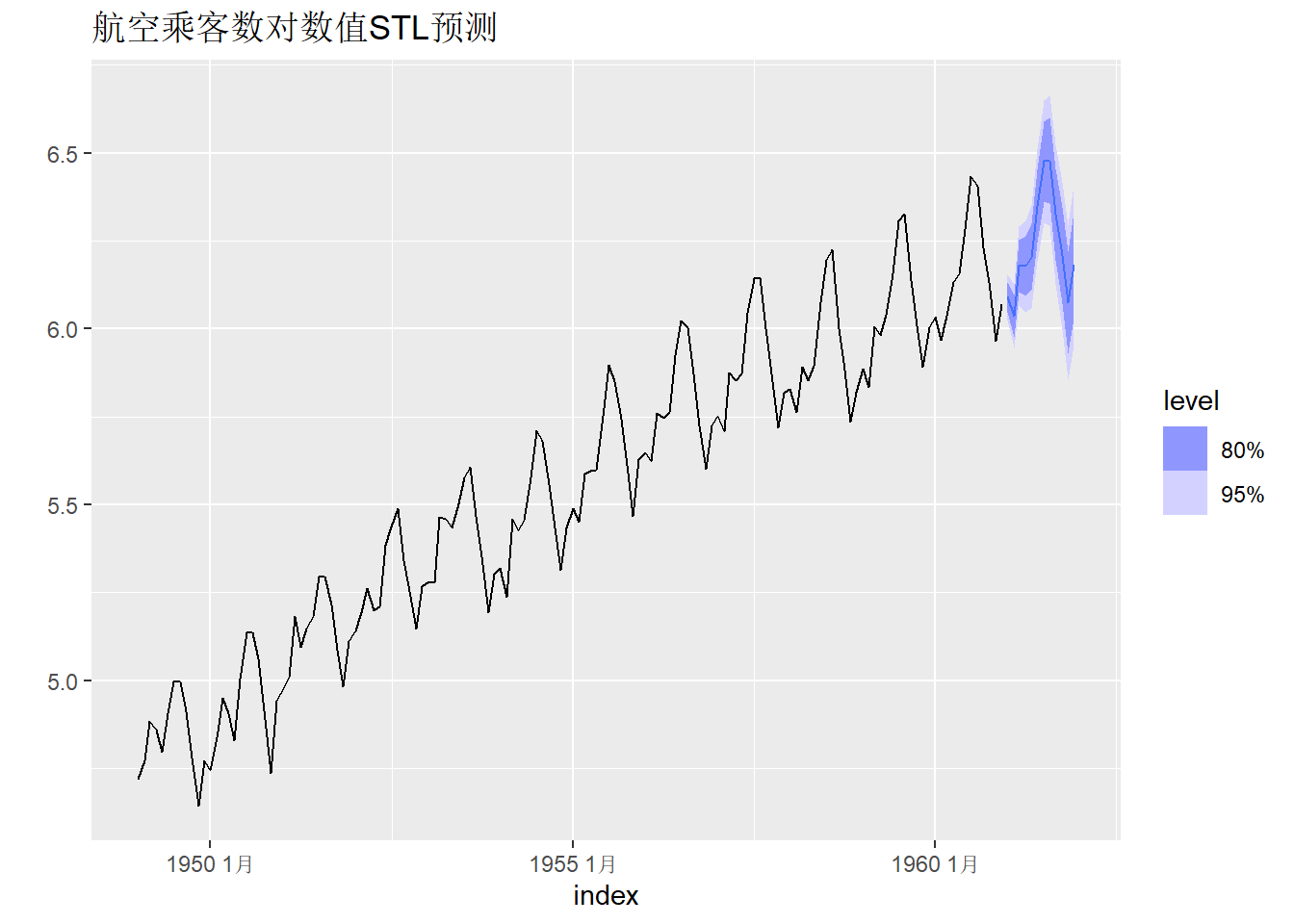

模型残差诊断：

stl_ap |>
  gg_tsresiduals()

## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_line()`).

## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_point()`).

## Warning: Removed 12 rows containing non-finite outside the scale range
## (`stat_bin()`).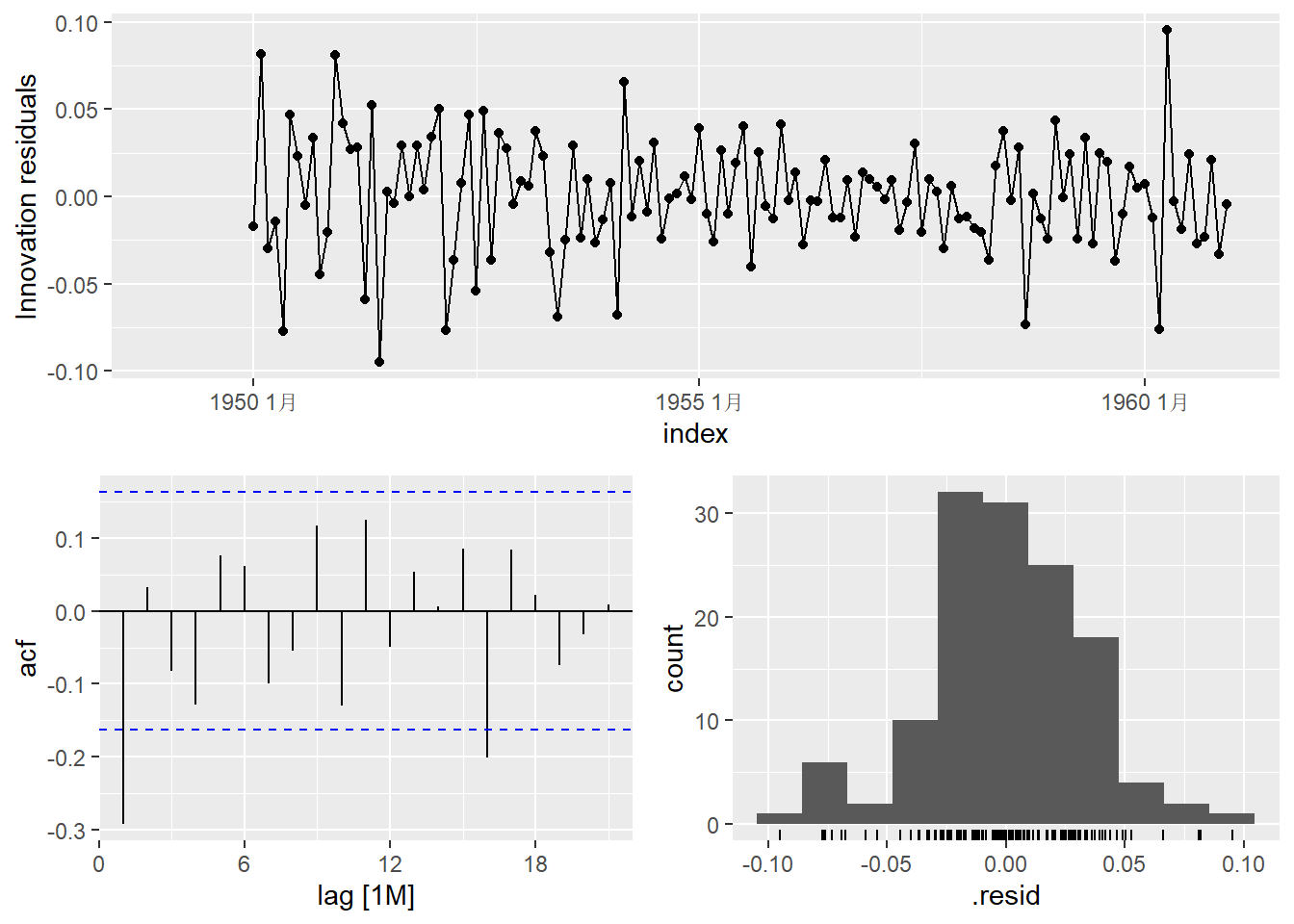

从残差诊断的ACF图看模型拟合有待改进。

10.3.8 预测精度评估

10.3.8.1 精度指标定义

前面说过，拟合残差的大小不能完全反映模型预测误差的大小，因为在计算拟合残差时，用到了从所有观测值\(y_1, y_2, \dots, y_T\)估计得到的模型参数，所以拟合残差不完全是预测误差。

为此，应该将\(y_1, y_2, \dots, y_T\)分为前后两段， \(y_1, y_2, \dots, y_n\)(\(n < T\))用来拟合模型，计算拟合残差，以及基于拟合残差的一些模型优度指标，称这一段数据为“训练数据”；然后，基于估计得到的模型，对\(y_{n+1}, y_{n+2}, \dots, y_T\)进行预测，称这一段数据为“测试数据”，记\(h = T-n\)，即\(T = n+h\)。

如果作多步预报，应该基于训练数据\(y_1, y_2, \dots, y_n\)建模，利用得到的模型和观测数据\(y_1, y_2, \dots, y_n\)，向前作1步，2步，……，\(h\)步预报，得到预测值\(\hat y_{n+1}, \hat y_{n+2}, \dots, \hat y_{n+h}\)。

令 \[ e_{n+j} = y_{n+j} - \hat y_{n+j}, \ j=1,2,\dots, h, \] 称这些\(\{ e_{n+j} \}\)为预测误差，这些预测误差的大小比拟合误差更准确地反映了用模型作预报时的误差大小。

设各个误差为\(e_{n+1}, \dots, e_{n+h}\)，则可以计算平均绝对误差 \[ \text{MAE} = \frac{1}{h} \sum_{j=1}^h |e_{n+j}|, \] 计算根均方误差 \[ \text{RMSE} = \sqrt{\frac{1}{h} \sum_{j=1}^h |e_{n+j}|^2} . \]

注意对于超前多步预测误差，超前步数越多，实际上误差也应该越大，以上的等权求和的计算公式并不能反映这一事实。

MAE和RMSE与原始数据量纲相同。可以计算相对误差，是无量纲的误差指标： \[ \text{MAPE} = \frac{1}{h} \sum_{j=1}^h \left| \frac{e_{n+j}}{y_{n+j}} \right| . \]

但是，MAPE当\(y_{n+j}\)接近于0时会被放大。有人提出了其它的消除量纲的方法，将\(e_{n+j}\)除以拟合模型时得到的某个误差度量。例如，设时间序列季节周期为\(m\)（无季节性时取\(m=1\)），令 \[ q_{n+j} = \frac{e_{n+j}}{ \frac{1}{n-m} \sum_{t=m+1}^n |y_{t} - y_{t-m}|}, \] 上式的分母是利用简单地平移预测方法预测时在训练数据尾部估计的拟合误差。利用\(\{q_{n+j} \}\)，可以计算去量纲化的平均绝对误差 \[ \text{MASE} = \frac{1}{h} \sum_{j=1}^h |q_{n+j}|, \]

若令 \[ \tilde q_{n+j}^2 = \frac{e_{n+j}^2}{ \frac{1}{n-m} \sum_{t=m+1}^n |y_{t} - y_{t-m}|^2}, \] 则可以计算去量纲化的根均方误差 \[ \text{RMSSE} = \sqrt{\frac{1}{h} \sum_{j=1}^h \tilde q_{n+j}^2} . \]

10.3.8.2 多步预报精度评估例子

fabletools提供了一个accuracy()函数，可以直接基于多步预报计算各种精度指标。

例如，10.3.1中的中国GDP预测。

gdppc |>
  filter(Country == "China") |>
  select(GDP_per_capita) |>
  filter(Year >= 1991) -> chn_gdp
chn_gdp |>
  filter(Year <= 2010) -> chn_train
chn_train |>
  model(loglin_mod 
    = TSLM(log10(GDP_per_capita ) 
           ~ trend())) -> chn_fit
chn_fit |>
  forecast(h=7) -> chn_pred
chn_pred

## # A fable: 7 x 4 [1Y]
## # Key:     .model [1]
##   .model      Year    GDP_per_capita .mean
##   <chr>      <dbl>            <dist> <dbl>
## 1 loglin_mod  2011 t(N(3.6, 0.0033)) 4434.
## 2 loglin_mod  2012 t(N(3.7, 0.0034)) 5059.
## 3 loglin_mod  2013 t(N(3.8, 0.0035)) 5772.
## 4 loglin_mod  2014 t(N(3.8, 0.0036)) 6586.
## 5 loglin_mod  2015 t(N(3.9, 0.0037)) 7514.
## 6 loglin_mod  2016 t(N(3.9, 0.0038)) 8574.
## 7 loglin_mod  2017   t(N(4, 0.0039)) 9783.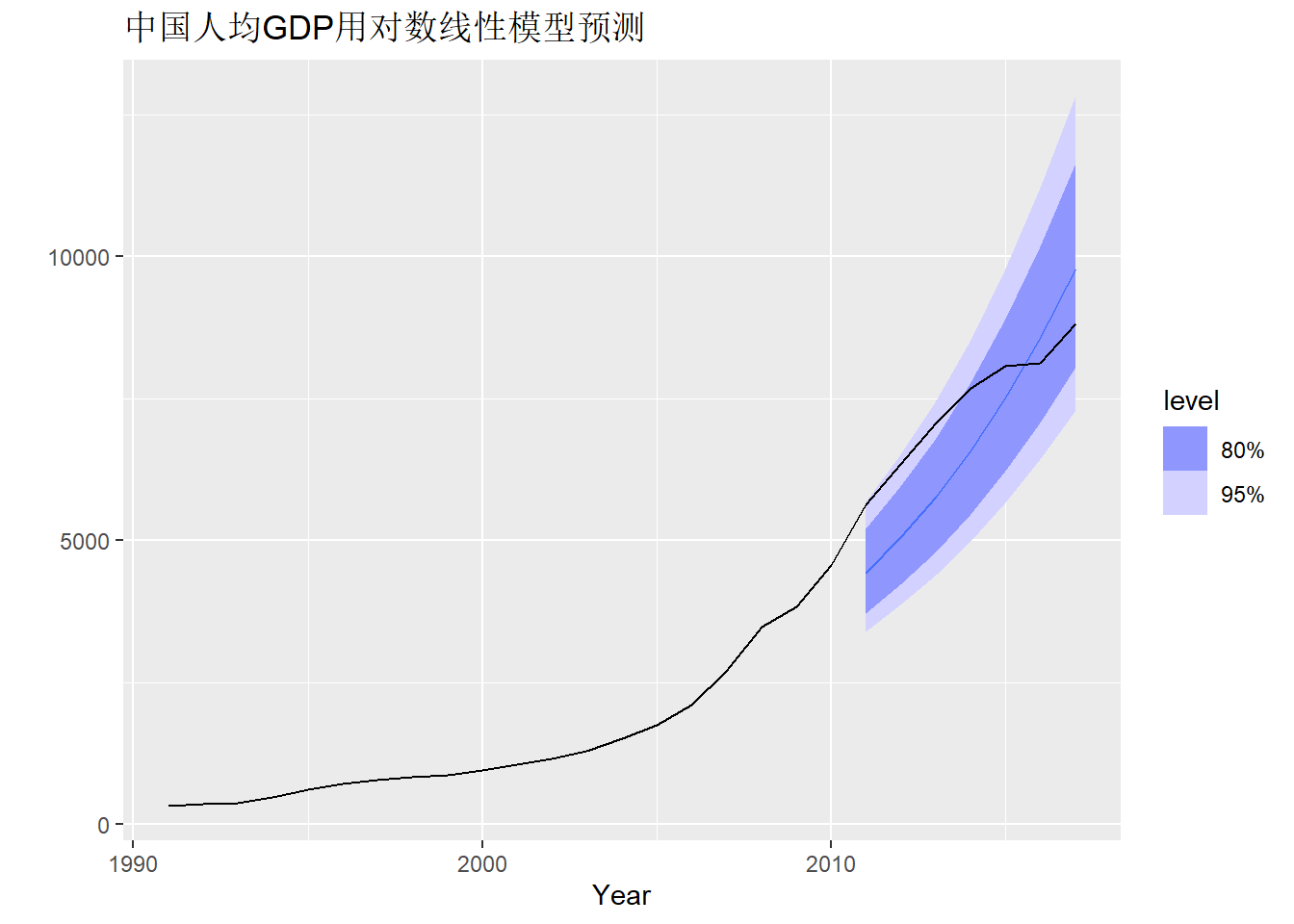

chn_pred |>
  autoplot(chn_gdp) +
  labs(y="", title="中国人均GDP用对数线性模型预测")

计算多步预报的精度指标：

accuracy(chn_pred, chn_gdp) |>
  pivot_longer(c(-.model, -.type),
    names_to = "指标", values_to = "值")

## # A tibble: 8 × 4
##   .model     .type 指标        值
##   <chr>      <chr> <chr>    <dbl>
## 1 loglin_mod Test  ME     575.   
## 2 loglin_mod Test  RMSE  1029.   
## 3 loglin_mod Test  MAE    978.   
## 4 loglin_mod Test  MPE      9.23 
## 5 loglin_mod Test  MAPE    13.9  
## 6 loglin_mod Test  MASE     4.40 
## 7 loglin_mod Test  RMSSE    3.22 
## 8 loglin_mod Test  ACF1     0.573

其中MAPE单位是\(1\%\)。

10.3.8.3 滚动向前一步预报精度评估

为了比较不同的模型，比较常用的比较方法是比较其单步预测误差大小。但是，如果仅计算一个单步预测值，就不能用计算平均值的方法得到比较精确的误差指标。为了得到多个单步预测值，需要使用滚动向前一步预报的做法。

这种做法是，从\(y_1, \dots, y_n\)估计模型后，固定模型的结构不变，但是在预测\(y_{n+j}\)时，要利用\(y_1, \dots, y_{n+j-1}\)重新估计模型参数，然后利用新估计的模型预测\(y_{n+j}\)，对\(j=1,2,\dots,h\)分别预报一次，得到\(\hat y_{n+1}, \hat y_{n+2}, \dots, \hat y_{n+h}\)，并计算\(e_{n+j} = y_{n+j} - \hat y_{n+j}\)。称这种做法为滚动建模的超前一步预报。随后可以基于\(e_{n+1}, e_{n+2}, \dots, e_{n+h}\)计算各种预测精度指标，这样计算的预测精度指标比用向前多步预测误差计算的预测精度指标更合理。

要计算滚动向前一步预测的预测精度指标， fabletools没有直接提供相应的功能。需要使用tsibble包stretch_tsibble()函数制作成用键变量区分的多个时间序列分量，每个分量比上一个分量增加一个时间点的观测值，这样就可以获得多个建模训练数据，训练数据每次增加一个时间点，仅进行向前一步预报。

下面用中国GDP年数据的预测举例。 chn_gdp是一个tsibble类型时间序列，其中包含了1991年到2017年的一共27年的数据，我们以1991年到2010年为滚动超前一步预测的起点。保持1991年到2010年的20个数据不进行预测，但是从2011年起都进行一步预测，可以滚动地得到7个一步预测误差。为此，用stretch_tsibble()函数建立一个额外的tsibble键值.id，将所有数据分为7类:

第一类包含1991年到2010年，用来确定一个模型结构，然后估计模型，预测2011年；
第二类包括1991年到2011年，用已经确定的模型结构，基于1991年到2011年数据重新估计模型参数，然后预测2012年；
…………;
第七类包括1991年到2016年，用已经确定的模型结构，基于1991年到2016年数据重新估计模型参数，然后预测2017年。

对每一类的数据建模然后作一步预测，配合原始数据就可以计算出7个一步预报误差。基于这些一步预报误差计算MAE, RMSE, MAPE等预测精度指标。

用stretch_tsibble()增加这样的键值：

chn_gdp |>
  stretch_tsibble(
    .init = 20, .step = 1 ) |>
  filter(.id < max(.id)) -> chn_gdp_cv

其中的.init用来指定第一个类的观测个数， .step是两类之间的时间差距，最后一步的filter是为了去掉1991年到2017年的那一组，那一组如果不去掉就会去预测2018年， 2018年的真实值不在我们使用的数据集中。

fabletools的建模函数和预测函数可以对tsibble中用键变量分组的每一个时间序列分量分别建模和预测：

chn_gdp_cv |>
  model(loglin_mod 
    = TSLM(log10(GDP_per_capita ) 
           ~ trend())) |>
  forecast(h=1) -> chn_roll_pred
chn_roll_pred |> knitr::kable()

.id	.model	Year	GDP_per_capita	.mean
1	loglin_mod	2011	t(N(3.6, 0.0033))	4434.447
2	loglin_mod	2012	t(N(3.7, 0.0037))	5308.416
3	loglin_mod	2013	t(N(3.8, 0.0038))	6286.418
4	loglin_mod	2014	t(N(3.9, 0.0037))	7371.461
5	loglin_mod	2015	t(N(3.9, 0.0036))	8534.665
6	loglin_mod	2016	t(N(4, 0.0034))	9729.699
7	loglin_mod	2017	t(N(4, 0.0035))	10884.910

下面只要将键变量.id删除，就可以与原始数据配合计算滚动一步预测精度指标了：

chn_roll_pred |>
  select(-.id) |>
  accuracy(chn_gdp) |>
  pivot_longer(c(-.model, -.type),
    names_to = "指标", values_to = "值") |>
  knitr::kable()

.model	.type	指标	值
loglin_mod	Test	ME	-114.7985653
loglin_mod	Test	RMSE	1211.4601535
loglin_mod	Test	MAE	1066.8585441
loglin_mod	Test	MPE	0.5467410
loglin_mod	Test	MAPE	14.5314150
loglin_mod	Test	MASE	3.4263919
loglin_mod	Test	RMSSE	2.8096363
loglin_mod	Test	ACF1	0.6102374

本例的一步预报的结果还不如多步预报的结果。这可能是因为我们用了全局性的线性模型（对数变换后），这个模型并不会考虑预测时应该使得最新获得的数据在预测中起到更重要作用。如果使用ARIMA模型，滚动一步预报的结果应该会比多步预报结果更好一些。

滚动一步预报也可以修改为滚动多步预报。下面进行滚动超前1步和超前2步预测，分别评估1步和2步的预测精度。

按训练集长度生成6个组：

chn_gdp |>
  stretch_tsibble(
    .init = 20, .step = 1 ) |>
  filter(.id <= max(.id)-2) -> chn_gdp_cv2

对每个组，作超前1步和超前2步预测：

chn_gdp_cv2 |>
  model(loglin_mod 
    = TSLM(log10(GDP_per_capita ) 
           ~ trend())) |>
  forecast(h=2) -> chn_roll_pred2
chn_roll_pred2 |> knitr::kable()

.id	.model	Year	GDP_per_capita	.mean
1	loglin_mod	2011	t(N(3.6, 0.0033))	4434.447
1	loglin_mod	2012	t(N(3.7, 0.0034))	5059.280
2	loglin_mod	2012	t(N(3.7, 0.0037))	5308.416
2	loglin_mod	2013	t(N(3.8, 0.0038))	6075.966
3	loglin_mod	2013	t(N(3.8, 0.0038))	6286.418
3	loglin_mod	2014	t(N(3.9, 0.0039))	7211.248
4	loglin_mod	2014	t(N(3.9, 0.0037))	7371.461
4	loglin_mod	2015	t(N(3.9, 0.0038))	8467.559
5	loglin_mod	2015	t(N(3.9, 0.0036))	8534.665
5	loglin_mod	2016	t(N(4, 0.0036))	9808.514
6	loglin_mod	2016	t(N(4, 0.0034))	9729.699
6	loglin_mod	2017	t(N(4, 0.0035))	11176.862

以上输出的预测数据集中缺少区分预测步数的变量，加入此变量：

chn_roll_pred2 |>
  group_by(.model, .id) |>
  mutate(h = row_number()) |>
  ungroup() |>
  as_fable(response = "GDP_per_capita", 
    distribution = GDP_per_capita) -> chn_roll_pred2b
chn_roll_pred2b |>
  select(-.id) |>
  accuracy(chn_gdp, by = c(".model", "h")) |>
  select(h, MAE, RMSE, MAPE) |>
  pivot_longer(c(-h),
    names_to = "指标", values_to = "值") |>
  arrange(`指标`, h)

## # A tibble: 6 × 3
##       h 指标      值
##   <int> <chr>  <dbl>
## 1     1 MAE    902. 
## 2     2 MAE   1199. 
## 3     1 MAPE    13.1
## 4     2 MAPE    15.5
## 5     1 RMSE  1003. 
## 6     2 RMSE  1379.

10.3.8.4 简化滚动向前一步预报精度评估

前面的滚动向前一步预报方法在每一步都需要重新估计模型参数。另一种较简单的做法是直接将数据划分为前\(n\)个为训练集，从训练集估计模型；数据的后\(h = T-n\)个作为测试集，在预测\(y_{n+j}\)时，保持估计的模型参数不变，但利用\(y_1, \dots, y_{n+j-1}\)预测\(y_{n+j}\)。 fable包的refit()函数可以在测试集上执行这样的一步预测。如：

chn_gdp |>
  filter(Year > 2010) -> chn_test
chn_fit |>
  refit(chn_test) |>
  accuracy() |>
  select(RMSE, MAE, MAPE)

## # A tibble: 1 × 3
##    RMSE   MAE  MAPE
##   <dbl> <dbl> <dbl>
## 1 1051.  990.  14.2

10.3.9 预测分布精度评估

预测分布的评估比较困难。

10.3.9.1 分位数分数

设对\(y_t\)的预测分布已知，对\(0 < p < 1\)，记\(f_{p,t}\)为此预测分布的\(p\)分位数。定义分位数分数 \[ Q_{p,t} = \begin{cases} 2 (1-p) (f_{p,t} - y_t), & \text{若} y_t < f_{p,t}, \\ 2 p (y_t - f_{p,t}), & \text{若} y_t \geq f_{p,t} . \end{cases} \] 这个分数类似于绝对误差，分数值越小说明预测分布越准确。当\(p=0.5\)时这恰好就等于\(y_t - f_{0.5,t}\)。若\(p=0.9\)，则\(y_t\)应该比较大可能性在\(f_{p,t}\)下方，比较小可能性在\(f_{p,t}\)上方，所以这时\(|y_t - f_{p,t}|\)乘的因子是\(2 p = 1.8 > 1\)，对于\(y \geq f_{p,t}\)的情况添加比较大的惩罚，而\(y < f_{p,t}\)的情况产生比较小的分数值。

在accuracy函数中可以添加计算分位数分数的选项，例如：

chn_pred |>
  filter(Year == 2011) |>
  accuracy(chn_gdp, list(qs=quantile_score), probs=0.10)

## # A tibble: 1 × 3
##   .model     .type    qs
##   <chr>      <chr> <dbl>
## 1 loglin_mod Test   384.

10.3.9.2 Winkler分数

Winkler分数用于评估预测区间的精度。设预测区间的置信度为\(1-\alpha\)，预测区间为\((l_{\alpha,t}, u_{\alpha,t})\)， Winkler分数定义为预测区间长度加上真值落入区间外部时的惩罚项： \[ W_{\alpha,t} = \begin{cases} (u_{\alpha,t} - l_{\alpha,t}) + \frac{2}{\alpha}(l_{\alpha,t} - y_t), & \text{若} y_t < l_{\alpha,t}, \\ u_{\alpha,t} - l_{\alpha,t}, & \text{若} l_{\alpha,t} \leq y_t \leq u_{\alpha,t}, \\ (u_{\alpha,t} - l_{\alpha,t}) + \frac{2}{\alpha}(y_t - u_{\alpha,t}), & \text{若} y_t > u_{\alpha,t} . \end{cases} \]

如果预测区间是利用预测分布的\(\alpha/2\)和\(1 - \alpha/2\)分位数构造的，则 \[ W_{\alpha,t} = (Q_{\alpha/2,t} + Q_{1 - \alpha/2,t}) / \alpha . \]

例如：

chn_pred |>
  filter(Year == 2011) |>
  accuracy(chn_gdp, list(qs=winkler_score), level = 80)

## # A tibble: 1 × 3
##   .model     .type    qs
##   <chr>      <chr> <dbl>
## 1 loglin_mod Test  5786.

10.3.9.3 连续秩概率分数

前面两种分数或者针对特定的预测分布分位数精度，或者针对某个给定置信度的预测区间精度。还需要针对预测分布整体定义一种精度指标。可以将针对所有概率\(p\)的分位数分数进行平均，得到连续秩概率分数(CRPS)。

下面计算中国GDP预测的7个超前步的CRPS分数的平均值：

chn_pred |>
  accuracy(chn_gdp, list(qs=CRPS))

## # A tibble: 1 × 3
##   .model     .type    qs
##   <chr>      <chr> <dbl>
## 1 loglin_mod Test   672.

10.3.9.4 无量纲的精度指标

以上三种分数都是与原始数据同量纲的，如果要对多个不同时间序列建模并比较预测分布的精度，就需要无量纲的精度指标。在点预测时，可以将精度指标除以某种基准预测方法的精度指标。另一种做法是利用技巧分数，技巧分数既可以用在点预测的精度比较中，也可以用在预测分布的精度比较中。

技巧分数方法是计算要研究的精度指标与某种简单预测方法的精度指标之间的相对误差大小。 fabletools的skill_score()指标默认与简单平移预报方法比较，但如果数据有季节性，则默认与季节平移预报方法比较。如果要计算模型\(M\)相对于简单平移方法的CRPS指标的技巧分数，计算公式为 \[ \frac{\text{CRPS}_{\text{Naive}} - \text{CRPS}_{M}}{ \text{CRPS}_{\text{Naive}}}, \] 其中\(\text{CRPS}_{M}\)和\(\text{CRPS}_{\text{Naive}}\)分别是模型\(M\)和简单平移预测方法在测试集上的CRPS分数的平均值。这个公式计算模型\(M\)的CRPS分数相对于简单平移预测方法的CRPS的改善比例。

下面的例子计算中国GDP的超前1到7年的预测的CRPS分数的技巧分数的平均值：

chn_pred |>
  accuracy(chn_gdp, list(skill = 
    skill_score(CRPS)))

## # A tibble: 1 × 3
##   .model     .type skill
##   <chr>      <chr> <dbl>
## 1 loglin_mod Test  0.730

这说明对数线性模型比简单平移预测模型的预测分布精度有较大改善。

上面的程序计算了CRPS的技巧分数，也可以计算MAE, RMSE等针对点预测精度指标的技巧分数。技巧分数需要比较大的测试集，否则精度指标的变化会比较大。

10.4 德尔菲方法

德尔菲法(Delphi)是由兰德公司的奥拉夫·赫尔默和诺曼·达尔基于20世纪50年代发明的一种由专家组进行决策的一种决策方法，也可以用于预测。这属于主观预测方法。主观预测方法主要适用于没有历史数据可以用来建立统计模型的情况，也可以用来改进统计模型预测。主观预测要尽量做到系统化、尽可能获得详细的信息依据、详细记录过程和理由、预测者不能对预测目标有主观偏向。

用德尔菲法作预测的执行流程为：

指定一个有经验的召集人，由召集人负责整个的预测流程。
针对要解决的问题召集一组相关专家，一般为5到20人，专家应来自相关的不同研究领域，专家应匿名参加以免决策受到专家权威性干扰；
将准确定义的预测问题分发给每一位专家；
收集每一位专家的判断和判断依据，整理成概略资料；
将整理的概略资料发给每一位专家，专家参考这些概略资料修改自己的预测。这样的过程可以重复二到三次，直到达成一定的共识。
整合专家意见产生最终预测。应该对所有专家的预测采取相同权重，但也要注意异常值的过大影响。

10.5 用回归模型预报

尽管我们在13中列出了当自变量、因变量为时间序列时使用普通回归方法的理论缺陷，但如果仅考虑预测的话，线性和非线性回归方法在时间序列数据建模预报中也常常有很好的效果。

这一节参考(R. J. Hyndman and Athanasopoulos 2021)一书讲如何用fabletools等扩展包建立回归模型、诊断、预测。

10.5.1 线性回归模型

考虑一元线性回归模型 \[ y_t = \beta_0 + \beta_1 x_t + e_t, \ t = 1,2,\dots,n . \] 在回归模型中，假定\(x_1, \dots, x_n\)为非随机数值， \(\{e_t \}\)独立同分布，零均值，方差为\(\sigma^2\)。实际应用中， \(\{x_t \}\)和\(\{y_t \}\)常常都是时间序列。这时，需要\(\{e_t \}\)为白噪声， \(\{x_t \}\)和\(\{y_t \}\)平稳，没有单位根； \(\{e_t \}\)与\(\{x_t \}\)独立。

一元线性回归模型可以自然地推广为多元线性回归模型，如 \[ y_t = \beta_0 + \beta_1 x_{t1} + \beta_2 x_{t2} + \dots + \beta_p x_{tp}+ e_t, \ t = 1,2,\dots,n . \]

线性回归模型用最小二乘方法估计： \[ \min \sum_{t=1}^n \left[ y_t - \left( \beta_0 + \beta_1 x_{t1} + \beta_2 x_{t2} + \dots + \beta_p x_{tp}\right) \right] . \] 这个问题归结为一个线性方程组求解，有高效、稳定的算法。设估计得到的参数值为\(\hat\beta_0, \hat\beta_1, \dots, \hat\beta_p\), \(\{e_t \}\)的方差\(\sigma^2\)的估计为\(\hat\sigma^2\)。

得到模型估计后，可以计算\(y_t\)的拟合值为 \[ \hat y_t = \hat\beta_0 + \hat\beta_1 x_{t1} + \dots + \hat\beta_p x_{tp} , \ t=1,2,\dots, n . \] 可以计算拟合残差 \[ r_t = y_t - \hat y_t, \ t=1,2,\dots, n . \]

评估线性回归模型表达的关系强弱常用复相关系数平方 \[ R^2 = 1 - \frac{\sum r_t^2}{\sum (y_t - \bar y)^2} . \] 这是\(\{y_t \}\)与\(\{ \hat y_t \}\)的相关系数平方，取值于0到1之间，取值越大表面模型预测能力越强，但增加自变量个数必然增大\(R^2\)值，所以有过度拟合危险。

10.5.2 模型估计

金融数学中一个典型的回归模型是CAPM模型，一种表达方法是如下回归模型： \[ r_t = \alpha + \beta m_t + e_t . \] 其中\(r_t\)是个股超额收益率， \(m_t\)是市场超额收益率。假设\(\{e_t \}\)独立同分布下可以用普通回归方法估计这样的模型。

在基本R中可以用lm()函数计算线性回归模型，对回归结果用pred()函数作预测。

利用fabletools扩展包，可以在model()函数中TSLM()函数建立线性回归模型。

例10.2 文件m-ibmsp-2611.csv中包含IBM股票和标普500的月度收益率数据。用建立回归模型用标普收益率预报IBM收益率。

解答：首先将数据读入为tsibble格式。

library(tidyverse)
da <- read_csv("m-ibmsp-2611.csv",
   col_types=cols(
    .default=col_double(),
    date=col_date(format="%Y%m%d")))
da |>
  mutate(date = yearmonth(date)) |>
  as_tsibble(index="date") -> ibmsp_tsib

数据从1926年1月到2011年9月，收益率分别保存在ibm和sp变量中。

作散点图：

ibmsp_tsib |>
  ggplot(aes(x = sp, y = ibm)) +
  geom_point(size = 1, alpha = 0.2) +
  labs(title = "IBM收益率对标普收益率")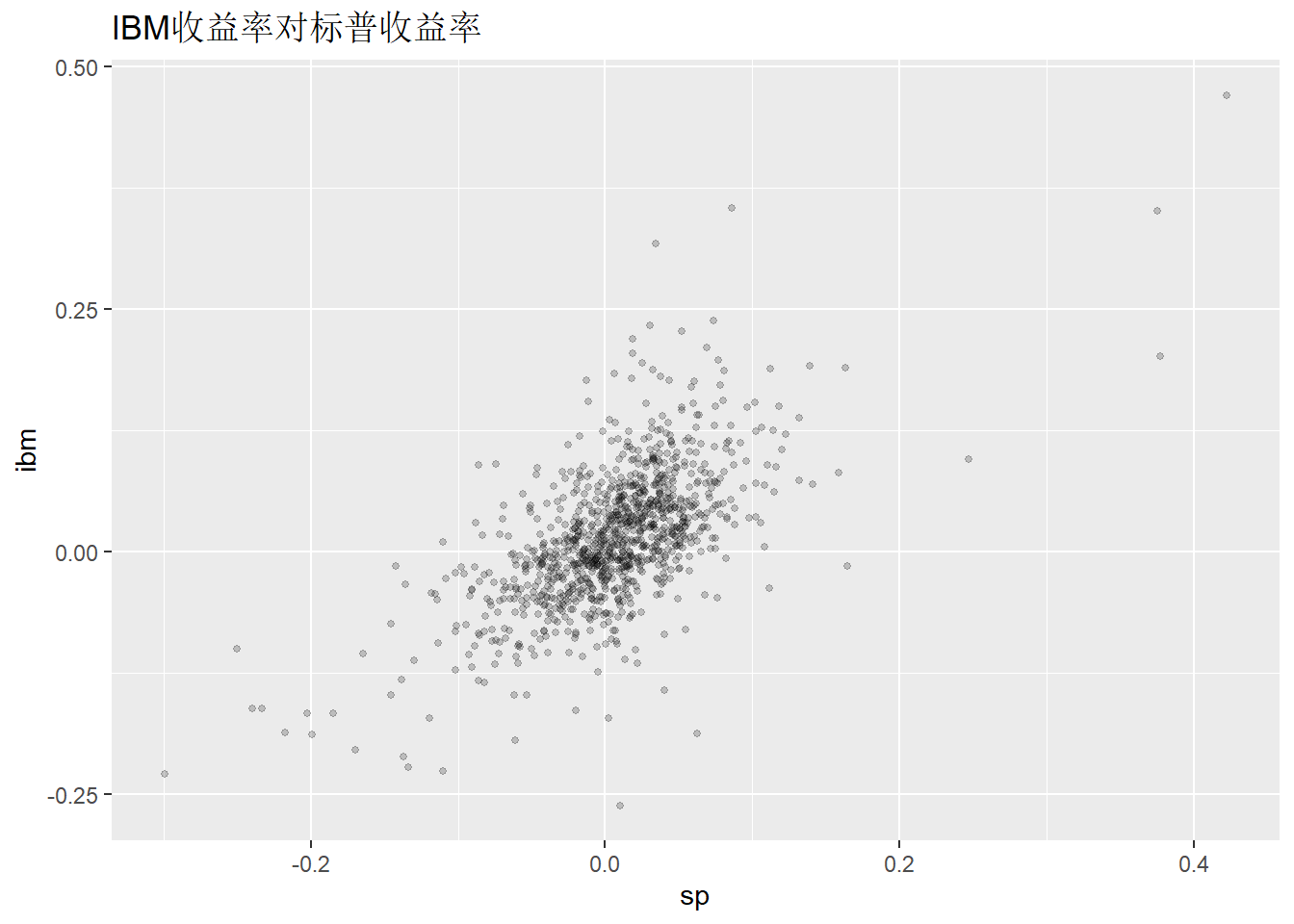

用model()和TSLM()建模，用report()显示结果：

ibmsp_tsib |>
  model(TSLM(ibm ~ sp)) -> ibmsp_fit
ibmsp_fit |> 
  report()

## Series: ibm 
## Model: TSLM 
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.279155 -0.032137 -0.002261  0.030647  0.280313 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.008974   0.001706   5.259 1.76e-07 ***
## sp          0.818776   0.030707  26.664  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.05443 on 1027 degrees of freedom
## Multiple R-squared: 0.4091,  Adjusted R-squared: 0.4085
## F-statistic:   711 on 1 and 1027 DF, p-value: < 2.22e-16

熟悉R软件的读者可以看出，这就是lm()和summary()的结果。同样的结果也可以用如下程序得到：

ibmsp_tsib |>
  lm(ibm ~ sp, data = _) |>
  summary()

按CAPM模型写法，估计的回归模型可以写成 \[ r_t = 0.008974 + 0.818776 m_t + e_t, \ e_t \sim (0, 0.05443^2) . \]

可以用augment()函数计算拟合值、拟合残差等：

ibmsp_fit |>
  augment() |>
  tail() |>
  knitr::kable()

.model	date	ibm	.fitted	.resid	.innov
TSLM(ibm ~ sp)	2011 4月	0.046054	0.0323048	0.0137492	0.0137492
TSLM(ibm ~ sp)	2011 5月	-0.005276	-0.0020805	-0.0031955	-0.0031955
TSLM(ibm ~ sp)	2011 6月	0.015509	-0.0059754	0.0214844	0.0214844
TSLM(ibm ~ sp)	2011 7月	0.060041	-0.0086086	0.0686496	0.0686496
TSLM(ibm ~ sp)	2011 8月	-0.050536	-0.0375253	-0.0130107	-0.0130107
TSLM(ibm ~ sp)	2011 9月	0.017218	-0.0497832	0.0670012	0.0670012

结果中的.innov仍是在对因变量做了变换的模型中，输出变换后的模型的残差， .resid总是针对原始数据的拟合残差。这里模型没有对因变量作变换所以.innov和.resid相同。

作因变量值对拟合值的散点图：

ibmsp_fit |>
  augment() |>
  ggplot(aes(x = .fitted, y = ibm)) +
  geom_point(size = 1, alpha = 0.3) +
  geom_abline(intercept = 0, slope = 1,
    color = "red") +
  labs("用标普预测IBM的因变量对拟合值散点图")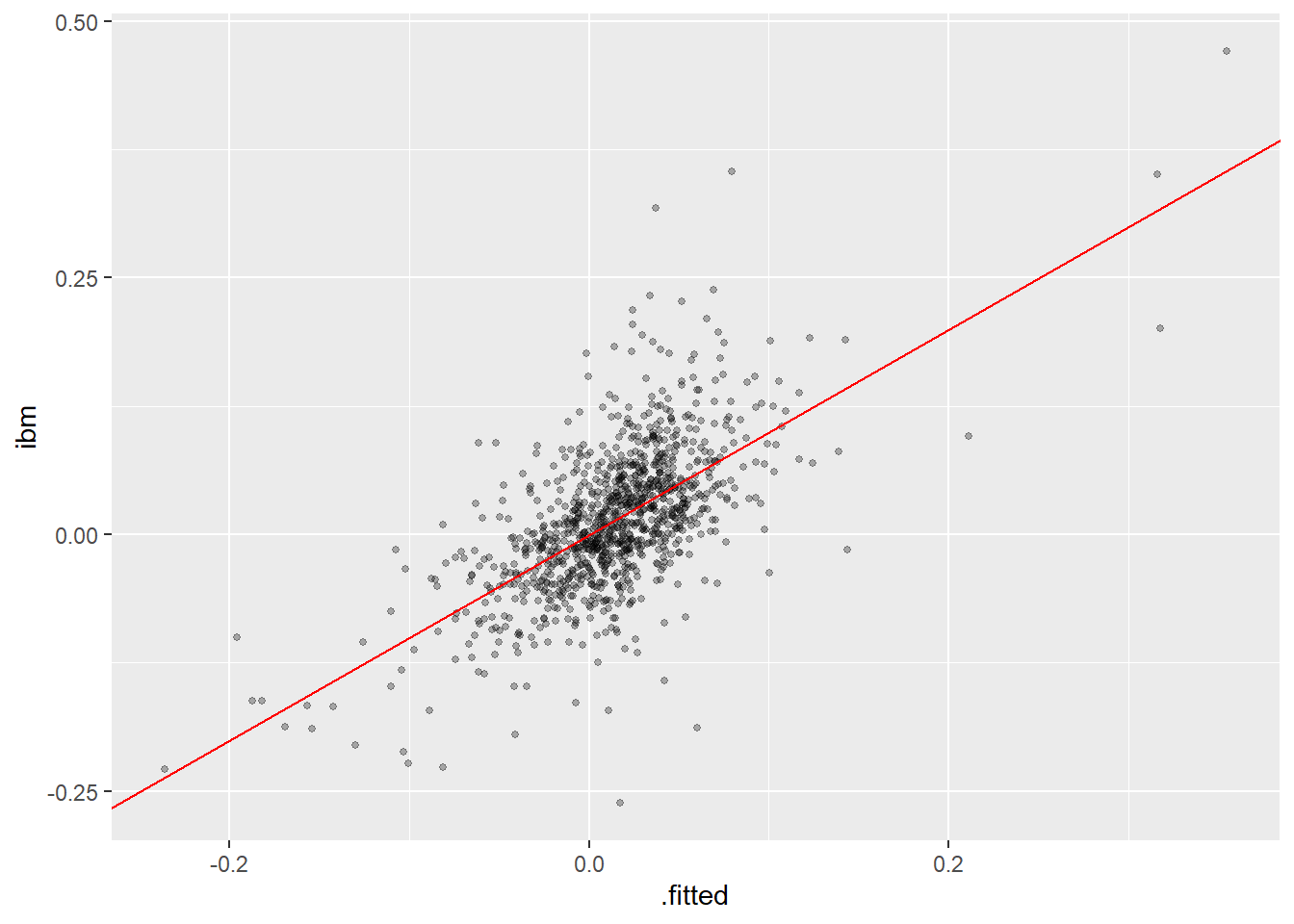

○○○○○○

例10.3 fpp3包的us_change数据是美国若干经济季度指标的变化率或变化量。这些变量包括个人消费支出、个人可支配收入、生产率、储蓄率、失业率，时间跨度为1970年到2016年。之所以使用变化率或变化量是为了使得时间序列不含单位根。建立用其它变量预测个人消费支出的线性回归模型。

解答：模型估计：

us_change |>
  model(tslm = TSLM(
    Consumption ~ Income + Production
    + Unemployment + Savings)) -> usch_fit
usch_fit |> report()

## Series: Consumption 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.90555 -0.15821 -0.03608  0.13618  1.15471 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.253105   0.034470   7.343 5.71e-12 ***
## Income        0.740583   0.040115  18.461  < 2e-16 ***
## Production    0.047173   0.023142   2.038   0.0429 *  
## Unemployment -0.174685   0.095511  -1.829   0.0689 .  
## Savings      -0.052890   0.002924 -18.088  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3102 on 193 degrees of freedom
## Multiple R-squared: 0.7683,  Adjusted R-squared: 0.7635
## F-statistic:   160 on 4 and 193 DF, p-value: < 2.22e-16

10.5.3 模型评估

10.5.3.1 残差的自相关性诊断分析

针对时间序列的回归模型，必须检验其随机误差项独立的假定。可以作拟合残差的ACF图。 gg_tsresiduals()函数作残差诊断，会作残差的时间序列图、ACF图和直方图。例如：

ibmsp_fit |>
  gg_tsresiduals() +
  labs(title = "IBM收益率对标普收益率回归的残差诊断")

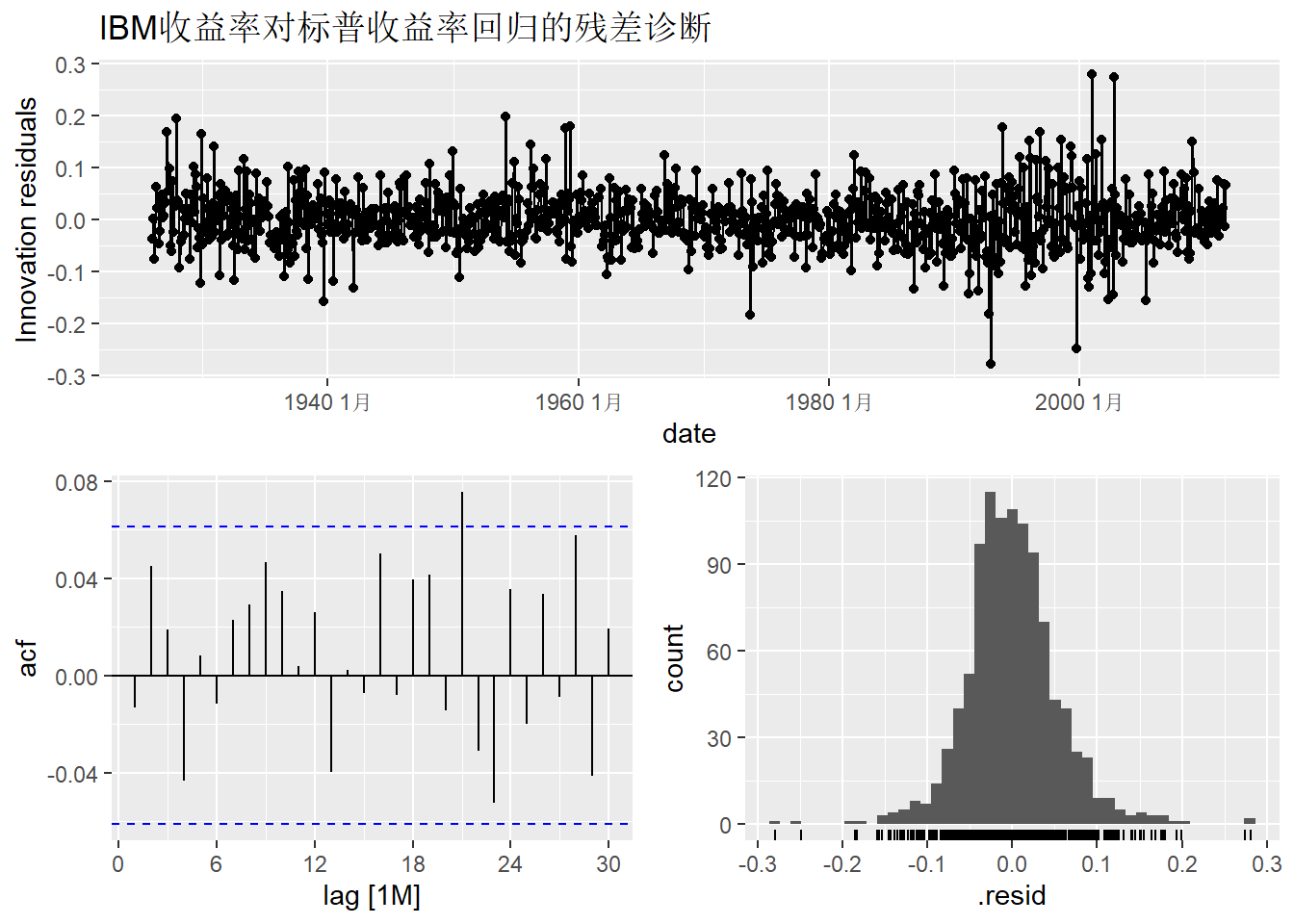
从残差的ACF可以看出残差基本是白噪声。

可以对残差作Ljung-Box白噪声检验：

ibmsp_fit |>
  augment() |>
  features(.innov, ljung_box, lag=10)

## # A tibble: 1 × 3
##   .model         lb_stat lb_pvalue
##   <chr>            <dbl>     <dbl>
## 1 TSLM(ibm ~ sp)    9.72     0.465

从p值看符合白噪声的表现。

10.5.3.2 残差对自变量的散点图

作残差\(r_t\)对自变量\(x_t\)的散点图，可以发现模型缺陷。比如，如果残差对自变量的图形呈现某种曲线模式，就说明线性模型不足以充分刻画因变量和自变量之间的关系。

程序如：

ibmsp_fit |>
  augment() |>
  left_join(ibmsp_tsib, by = "date") |>
  ggplot(aes(x = sp, y = .resid)) +
  geom_point(size=1, alpha=0.3) +
  labs(y = "残差", x = "标普")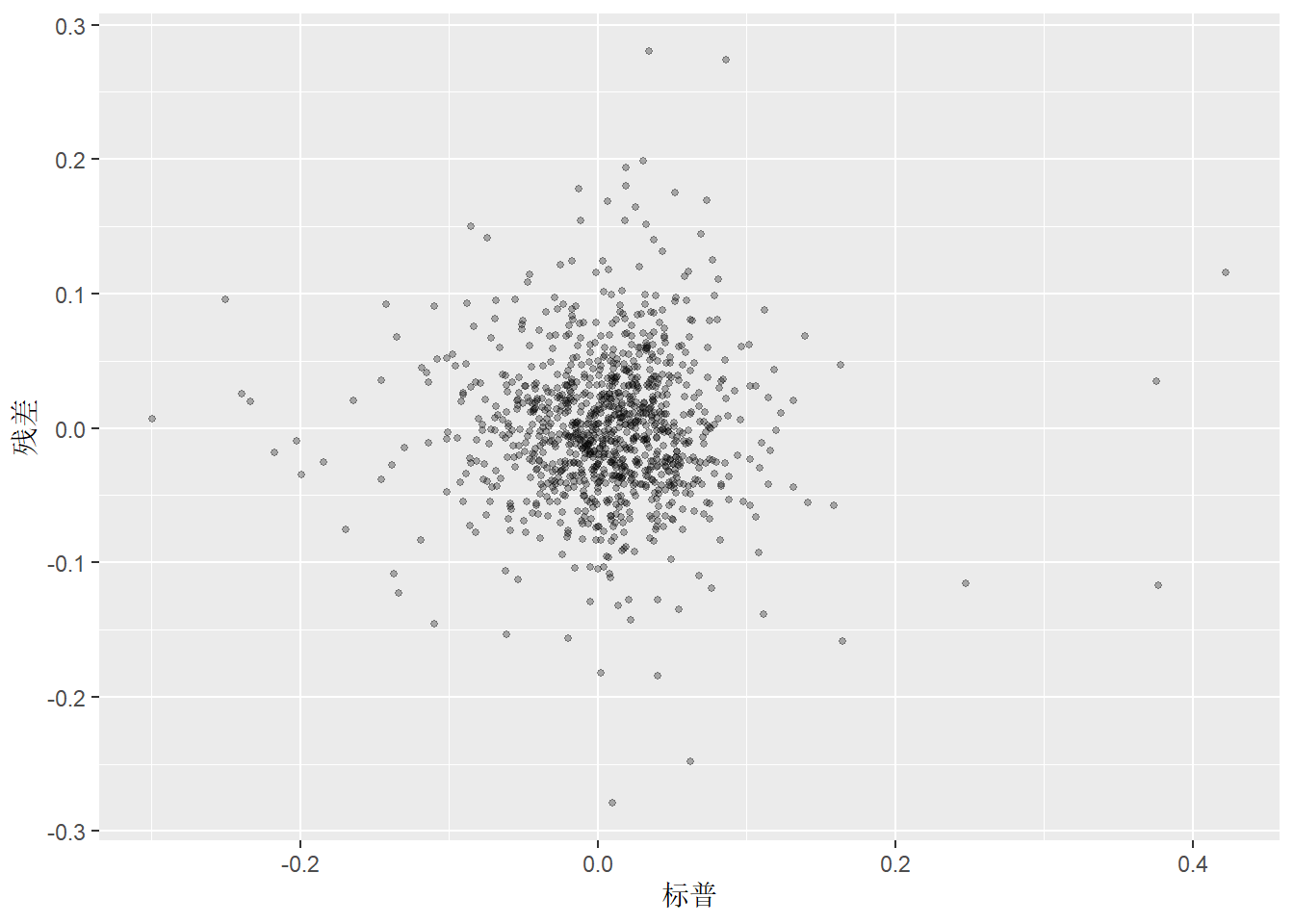

以上图形没有体现出模型的缺陷。

如果有多个自变量，可以针对每个自变量作残差对自变量的散点图。

10.5.3.3 残差对拟合值的散点图

为了考察残差的异常表现，可以只作残差对拟合值的散点图。这可以发现异方差等异常情况。

程序如：

ibmsp_fit |>
  augment() |>
  ggplot(aes(x = .fitted, y = .resid)) +
  geom_point(size=1, alpha=0.3) +
  labs(y = "残差", x = "拟合值")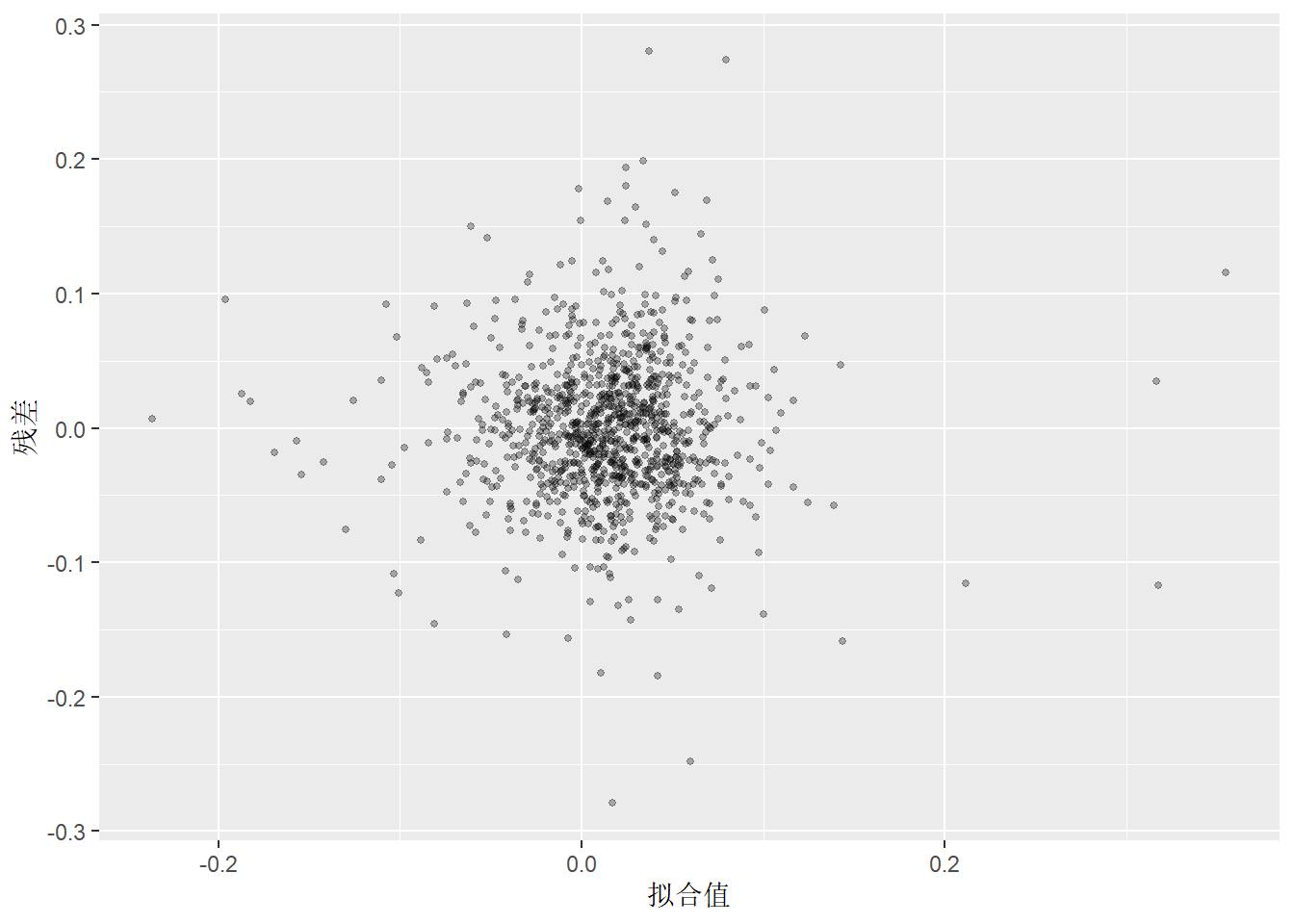

以上图形没有表现出模型有缺陷。

10.5.3.4 异常值和强影响点

线性回归使用最小二乘准则，这个准则对因变量和自变量当中的离群值比较敏感，回归结果受到这样的点的影响比较大。

针对基本的lm()函数的结果， R提供了plot()函数，可以作残差对拟合值散点图，残差正态QQ图，刻度对位置散点图，残差对杠杆图。其中残差对杠杆图可以用来发现因变量离群值和自变量强影响点。参见https://www.math.pku.edu.cn/teachers/lidf/docs/Rbook/html/_Rbook/stat-reg.html#stat-base-reg-regsimp-diag。

10.5.3.5 虚假回归

如果回归的随机误差项\(\{e_t \}\)中包含单位根，回归结果是完全错误的，根本没有相合估计；如果\(\{e_t \}\)是相关的平稳列而不是白噪声列，则回归结果中的标准误差、假设检验、预测区间也是错误的。详见27.1。

10.5.4 常见时间序列回归模型

10.5.4.1 确定性趋势模型

对于比较稳定的时间序列趋势，可以用线性或者二次曲线模型，如： \[ y_t = \beta_0 + \beta_1 t + e_t, \] 或 \[ y_t = \beta_0 + \beta_1 t + \beta_2 t^2 + e_t. \]

在TSLM()中可以用trend()表示线性回归形式的趋势。

10.5.4.2 哑变量

许多影响因变量因素可以表达为回归哑变量形式，即取0和1的自变量或自变量组合。

R的lm()函数会自动将分类变量转换为哑变量编码。 TSLM()基于lm()，所以也能自动处理回归自变量中的分类变量。

下面给出一些典型的哑变量应用。

比如，某项政策在\(t_0\)后开始执行，则可以令\(x_t\)在\(t_0\)后取1，之前取0，将\(x_t\)加入到自变量集合中。

为了纳入某个节假日比如春节对因变量的影响，可以定义\(x_t\)使其在该节假日期间取1，其余时间取0，将\(x_t\)加入到自变量集合中。

为了克服某个异常值的影响，一种做法是剔除此值或用邻近值或平均值代替，另一种做法可以是在这个异常值所在处增加一个代表这个时间点的哑变量。

为了考虑12个不同月份的影响，可以定义11个哑变量区分这12个月份，将哑变量集合加入到自变量集合中。星期几的效应也可以用哑变量处理。在TSLM()函数中可以用season()指定表示季节性的哑变量。关于哑变量编码可参见https://www.math.pku.edu.cn/teachers/lidf/docs/Rbook/html/_Rbook/stat-base-reg-fdm.html#stat-base-reg-fdm-designm。

季节性还可以用三角级数表示，比如针对周数据的季节性回归，可以表达为 \[ y_t = \beta_0 + \sum_{j=1}^{m/2} \beta_j \cos(\frac{2\pi j}{12} t) + \sum_{j=1}^{m/2-1} \beta_{m/2+j} \sin(\frac{2\pi j}{12} t) + e_t . \] 其中\(m=52\)。其中的高频项可以忽略使得模型简化，在TSLM()中可以用fourie(K=?)表示，比如周数据减少到4个余弦项和3个正弦项，可以写成fourie(K=4)。

10.5.5 变量选择

如果仅考虑\(R^2\)指标，模型中的自变量个数越多，则\(R^2\)值越大，但是在模型中加入与因变量无关的自变量会使得模型不稳定，增大参数估计误差，对新数据的预测能力变差。所以多元回归模型需要进行自变量选择。

简单地一次性将所有的回归系数不显著的自变量都剔除掉是不可取的，因为自变量之间的相关性可能造成两个自变量都加入模型时都不显著，但单个加入模型时都是显著的。用“逐步回归”方法选择自变量集合是可取的做法。

fabletools包提供了glance()函数，可以从模型拟合结果查看一些模型优度指标如AIC等，如：

ibmsp_fit |>
  glance() |>
  select(adj_r_squared, CV, AIC, AICc, BIC) |>
  knitr::kable()

adj_r_squared	CV	AIC	AICc	BIC
0.40851	0.0029713	-5986.592	-5986.569	-5971.783

这些指标可以用来比较不同的自变量子集。

adj_r_squared为修正\(R^2\)，这个指标克服了\(R^2\)指标在增加自变量时一定会增加的缺点，在增加无用自变量时有可能会降低。

CV是每次留出一个观测值用其它观测建模预测留出的观测值得出的残差均方误差，比简单的残差均方误差更合理，也可以有简单公式计算。

AIC、AICc、BIC是对拟合优度和参数个数进行折衷的指标。

建议一般情况下使用AICc指标，样本量特别大时使用BIC指标。

基本R提供了step()函数进行逐步回归，提供了add1()和drop1()函数选择自变量添加或者剔除。

10.5.6 回归模型预测

10.5.6.1 预测时自变量值是否可得

在用回归模型预测时，基于时间点\(1,2,\dots,T\)的数据，要预测\(y_{T+1}, \dots, y_{T+h}\)。设模型为\(y_t = \beta_0 + \beta_1 x_t + e_t\)，为了预测，就需要\(x_{T+1}, \dots, x_{T+h}\)的数据。一般都是假设在时间点\(T\)的时候\(x_{T+1}, \dots, x_{T+h}\)的数据是可以获得的。

比如，如果模型中仅包含了确定性趋势、用哑变量表示的季节性和节假日调整，则在任何时刻自变量值都是已知的。如果自变量本身就是滞后值，比如\(x_t\)代表\(t-1\)时刻的某经济指标，则在超前一步预测时\(x_{T+1}\)是已知的。

但是，许多情况下，在时间点\(T\)的时候\(x_{T+1}, \dots, x_{T+h}\)的数据也是未知的。这就需要设法去预测\(x_{T+1}, \dots, x_{T+h}\)，显然，用\(x\)的预测值代入回归模型去预测\(y_{T+1}, \dots, y_{T+h}\)，预测精度会受到\(x\)的预测精度的影响。

10.5.6.2 情景预测

有时用回归模型预测不是基于自变量真实值去预测，而是假想自变量达到什么值时，因变量的响应。在金融领域这称为压力测试。

例10.4 计算考虑美国个人消费支出数据。基于现有数据(截止2019年第二季度)，假想随后4个季度保持失业率不变，可支配收入增长率和储蓄率增长分别取\(1\%\)和\(0.5\%\)的支出预测，以及取\(-1\%\)和\(-0.5\%\)的情况。

解答： fabletools包提供了scenarioss()函数用来构建预测自变量的变化数据。

usch_fit <-
  us_change |>
  model(
    lm = TSLM(Consumption 
      ~ Income + Savings + Unemployment)  )
future_scenarios <- scenarios(
  Increase = new_data(us_change, 4) |>
    mutate(Income=1, Savings=0.5, Unemployment=0),
  Decrease = new_data(us_change, 4) |>
    mutate(Income=-1, Savings=-0.5, Unemployment=0),
  names_to = "Scenario")

函数new_data(.data, n)根据输入数据集的格式生成新数据集，适合用来产生回归预测用的新自变量数据。对时间序列可以自动按时间间隔延长时间。 scenarios()将多个新数据合并成一个大数据集但是保存代表情景的分类变量。

对新数据进行预测，如果需要外生变量，在forecast()中需要用new_data选项输入要用到的外生变量值的数据集。

预测，图示：

usch_fore <- forecast(
  usch_fit, new_data = future_scenarios)

us_change |>
  autoplot(Consumption) +
  autolayer(usch_fore) +
  labs(title = "US consumption", y = "% change")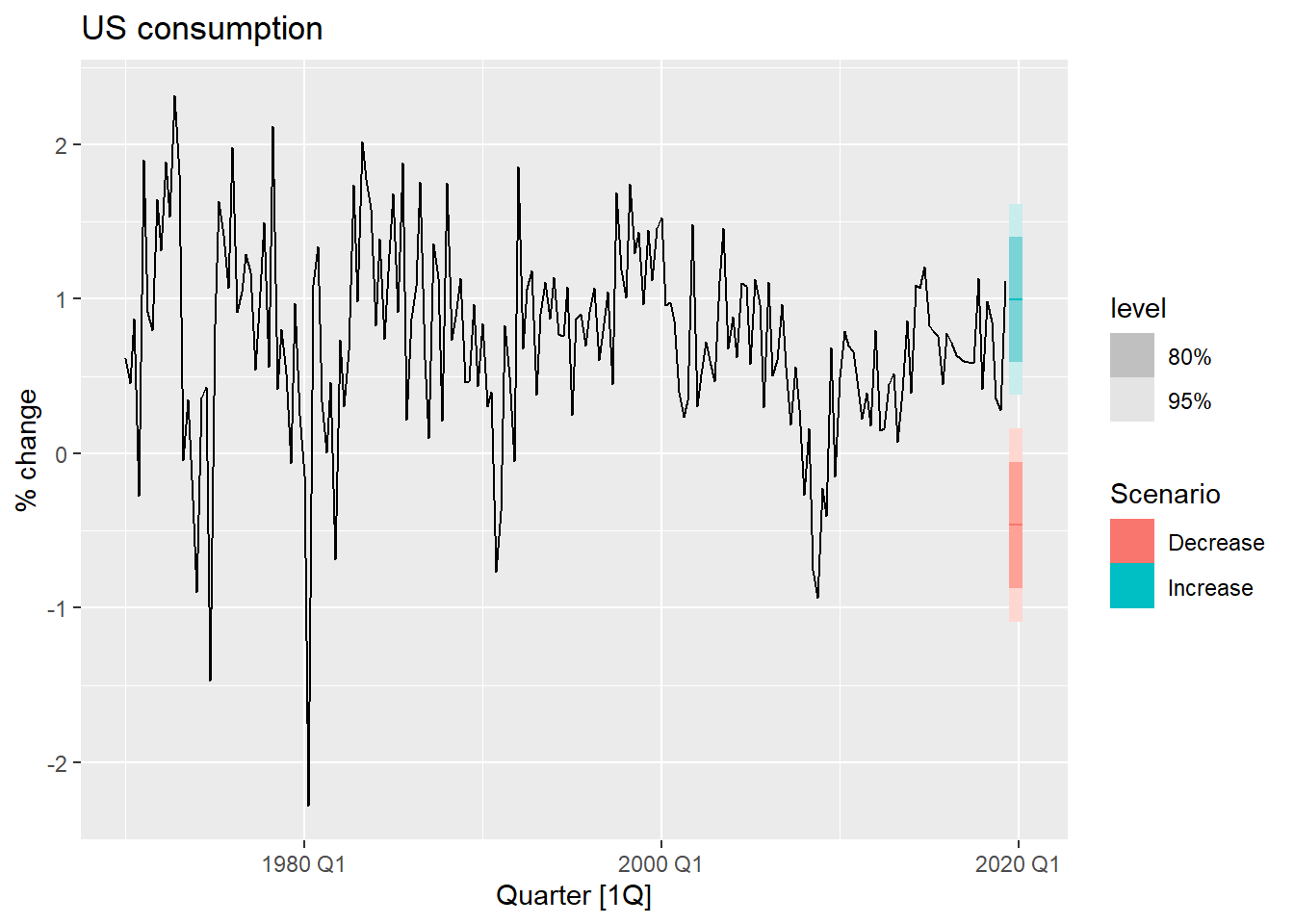

结果用浅蓝色表示了收入和储蓄增加时的预测区间，用红色表示了减少时的预测区间。

○○○○○○

例10.5 仍考虑美国个人消费支出数据，仅使用可支配收入预测个人消费支出。基于现有数据(截止2019年第二季度)，考虑收入保持为均值的情形，和收入保持为以往最大值的倾向，进行预测。

解答：

usch_fit2 <- us_change |>
  model(TSLM(Consumption ~ Income))
new_cons <- scenarios(
  "Average increase" = new_data(us_change, 4) |>
    mutate(Income = mean(us_change$Income)),
  "Extreme increase" = new_data(us_change, 4) |>
    mutate(Income = 12),
  names_to = "Scenario" )
usch_fore2 <- forecast(usch_fit2, new_cons)
us_change |>
  autoplot(Consumption) +
  autolayer(usch_fore2) +
  labs(title = "US consumption", y = "% change")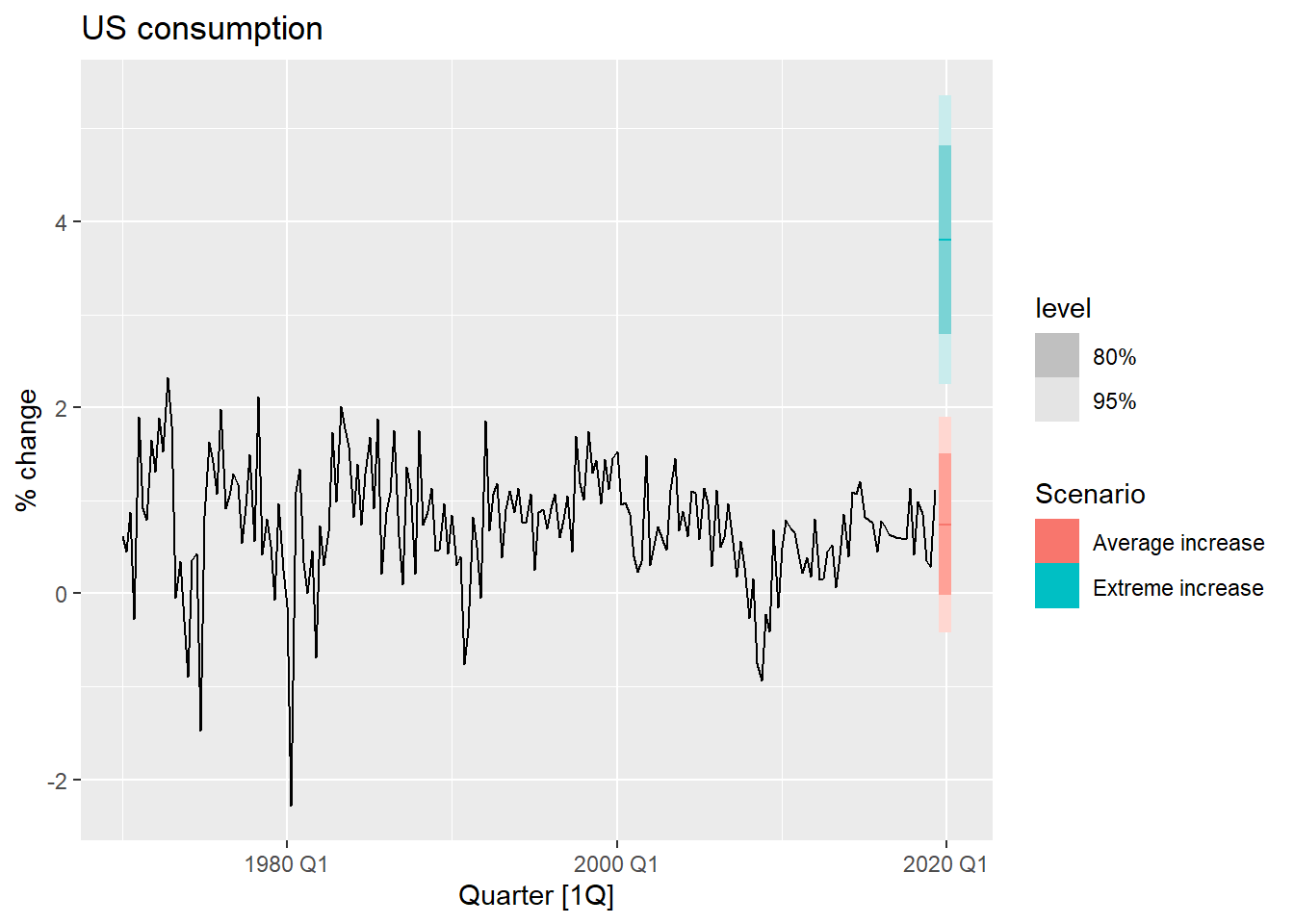

10.5.7 非线性回归模型

一般的非线性回归模型可以写成 \[ y_t = f(x_{t1}, \dots, x_{tp}) + e_t, \ t=1,2,\dots,T. \]

比较简单的非线性回归模型是将因变量和/或自变量作非线性变换，关于变换后的变量的模型仍是线性模型，但因变量与自变量已经是非线性关系。

比如，若\(y = A e^{b x}\)，则\(\ln y = \ln A + b x\)， \(y\)和\(x\)的关系是非线性的，但\(\ln y\)和\(x\)的关系是线性的。

更一般的非线性模型，可以考虑增加自变量的高次项和交叉项（乘积项），可以考虑自变量的分段线性函数，自变量的样条函数。样条函数是一种光滑的分段三次多项式函数。

例10.6 fpp3包中的boston_marathon是波士顿每年不同马拉松项目的冠军成绩。对其中男子比赛的数据用回归模型建模预测。

解答：数据：

mara_tsib <- boston_marathon |>
  filter(
    Year >= 1924,
    Event == "Men's open division") |>
  mutate(Minutes = as.numeric(Time)/60)
mara_tsib |>
  autoplot(Minutes) +
  labs("波士顿男子马拉松冠军成绩")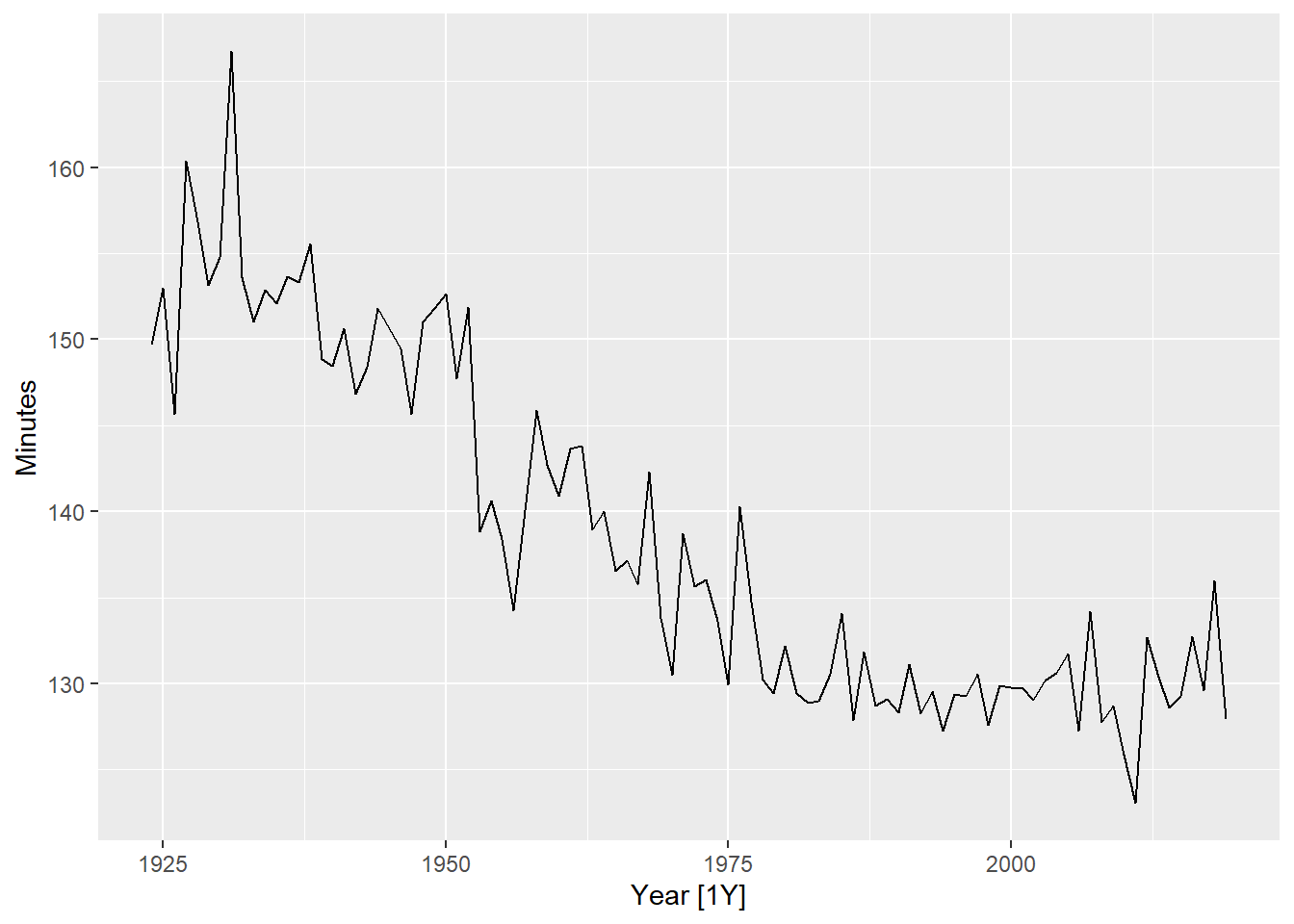

可以用关于时间的确定性趋势回归建模，但看起来存在非线性。先用线性回归建模：

mara_lm <- mara_tsib |>
  model(lm = TSLM(Minutes ~ trend()))
mara_tsib |>
  autoplot(Minutes) +
  geom_line(
    data = fitted(mara_lm),
    aes(y = .fitted),
    color = "red") +
  labs(title="波士顿男子马拉松成绩线性回归模型")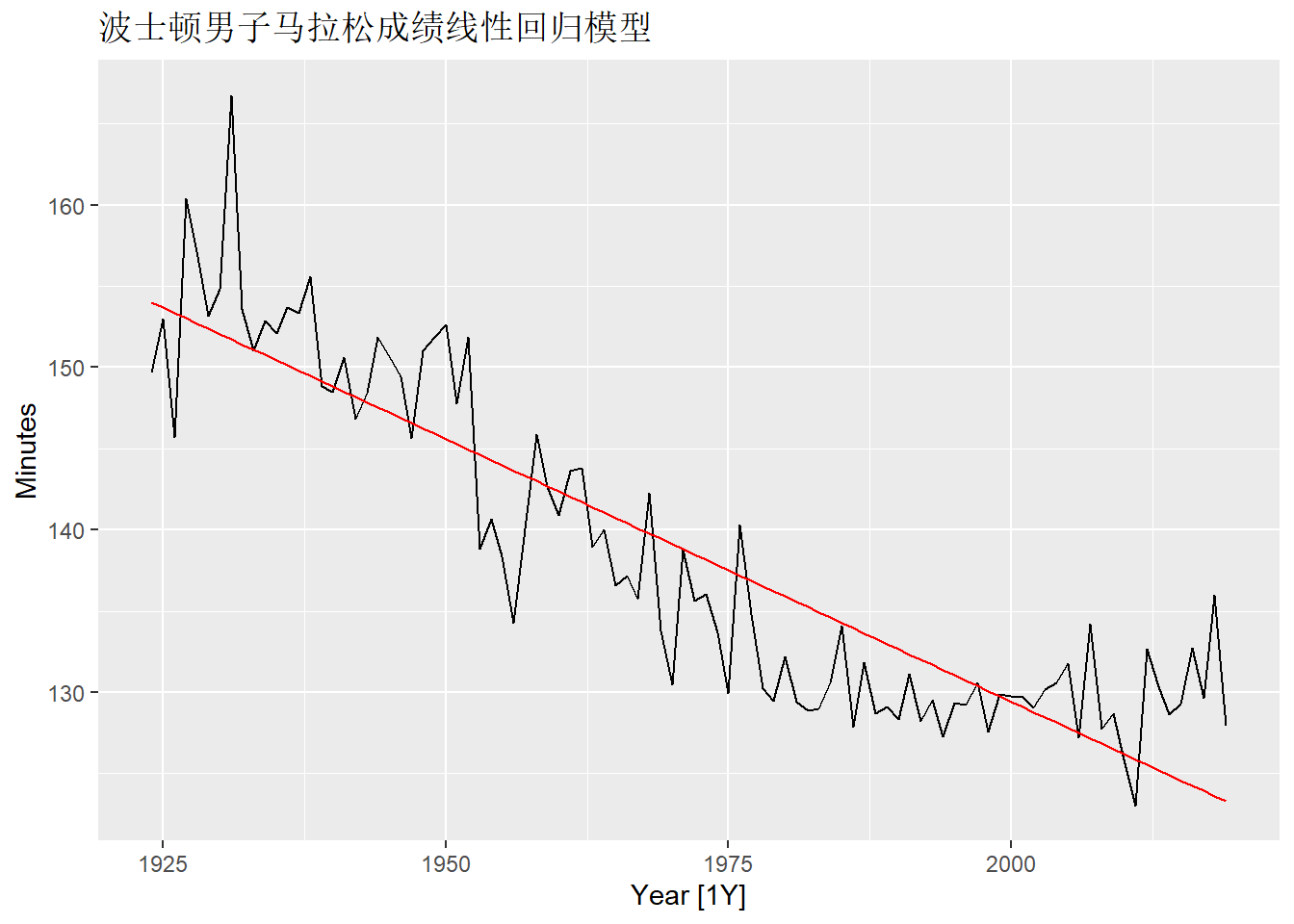

从如下的残差时间序列图可以看出有非线性存在：

mara_lm |> 
  augment() |>
  autoplot(.resid) +
  labs(title="波士顿男子马拉松成绩线性回归模型残差")

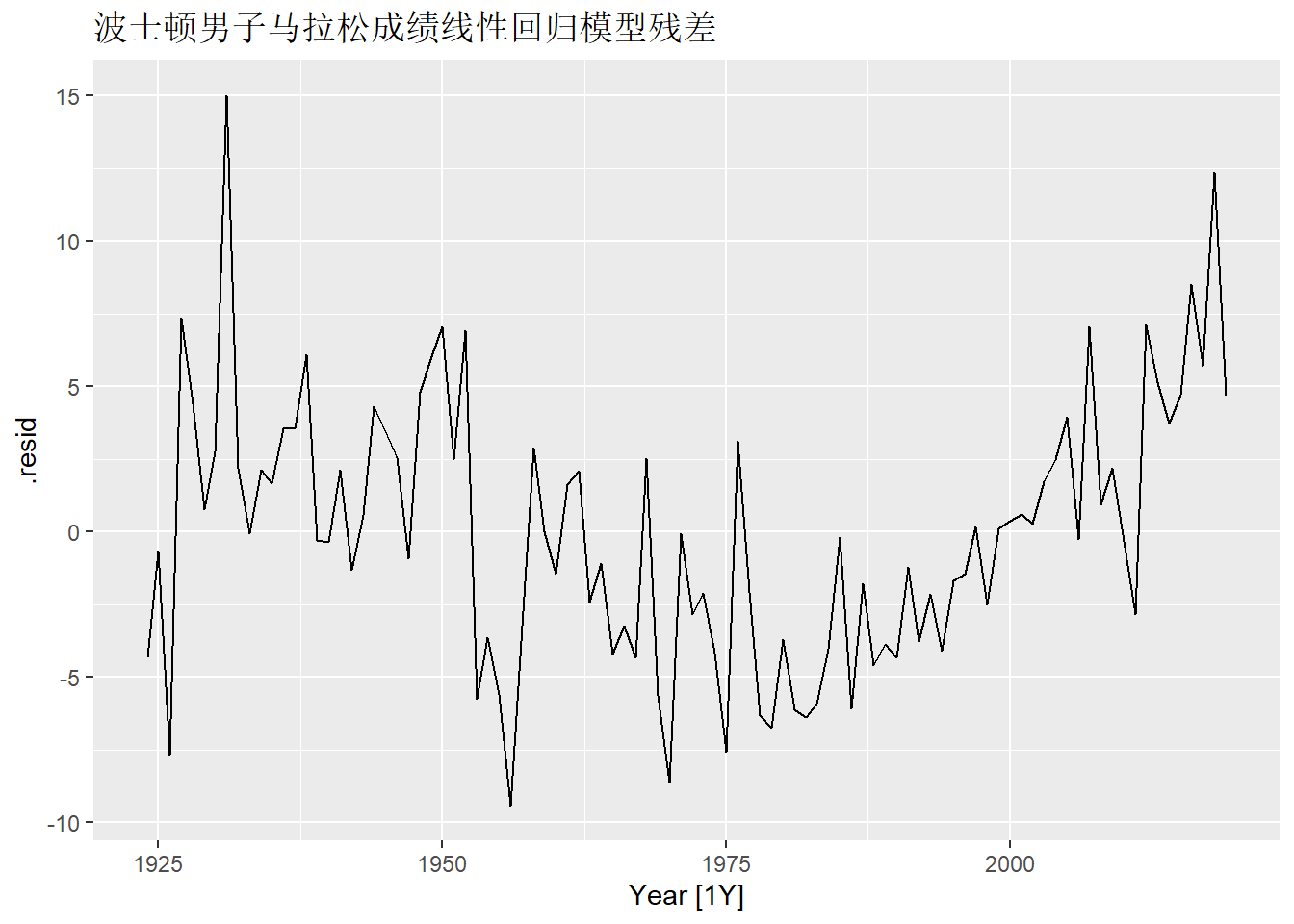
尝试对因变量作对数变换，或使用分段线性趋势，模型变成：

mara_fits <- mara_tsib |>
  model(
    linear = TSLM(Minutes ~ trend()),
    exponential = TSLM(log(Minutes) ~ trend()),
    piecewise_linear = TSLM(
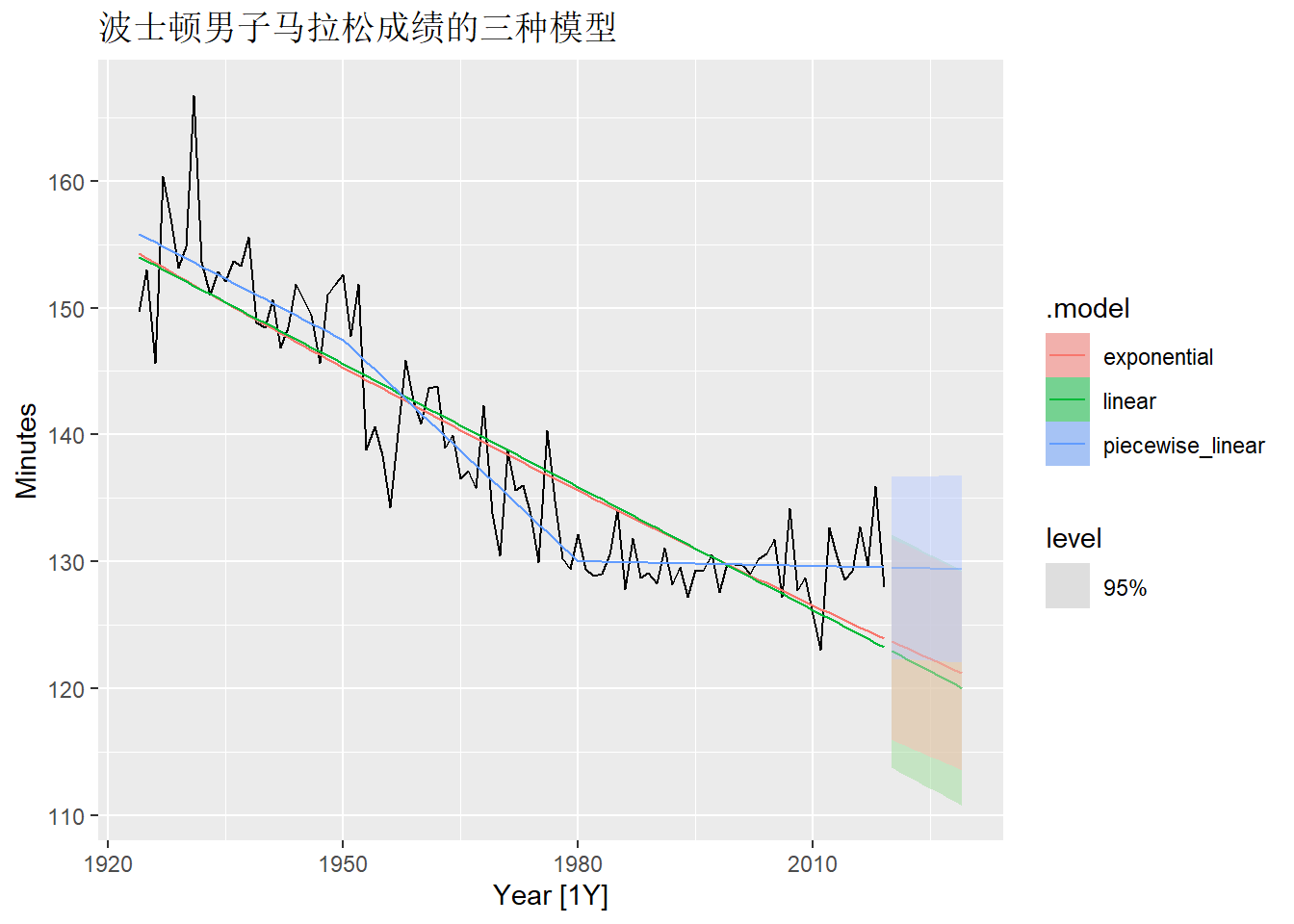
      Minutes ~ trend(knots = c(1950, 1980))))

trends()中的knots参数指定分段线性函数的分界点。

计算向前10期的预测值：

mara_fore <- mara_fits |>
  forecast(h = 10)

三种不同模型的拟合与预测图形：

mara_tsib |>
  autoplot(Minutes) +
  geom_line(data = fitted(mara_fits),
    aes(y = .fitted, color = .model)) +
  autolayer(mara_fore, alpha = 0.5, level = 95) +
  labs(y = "Minutes", 
    title = "波士顿男子马拉松成绩的三种模型")

10.5.8 模型解释

回归模型是建立在变量之间的相关性之上的模型，而相关性与因果性有本质区别。仅从预测角度看，变量之间即使没有因果性，仅有相关性，预测结果仍然是可用的。

如果两个自变量之间有强相关性，这会使得两个自变量的因变量的影响的分配难以评估，但不影响预测。

如果自变量之间存在强线性相关性，称为多重共线性，这可能会使得模型参数估计误差增大，会影响预测，尤其是区间预测。

当回归模型用于新数据的预测时，模型仅适用于自变量与建模时的自变量差别不大时，如果变化很大，模型不一定适用。

B 参考文献

Hyndman, R. J., and G Athanasopoulos. 2021. Forecasting: Principles and Practice. 3rd edition. OTexts: Melbourne, Australia. http://OTexts.com/fpp3.

Wickham, Hadley, and Garrett Grolemund. 2022. R for Data Science. 2nd ed. O’Reilly. https://r4ds.hadley.nz/.