22 波动率模型的应用

22.1 GARCH波动率期限结构

下面研究GARCH模型导致的波动率期限结构， 比如， 日对数收益率的波动率与月对数收益率的波动率的关系。 以时间\(t\)为基础， 距离\(t\)时刻\(h\)期（比如\(h\)个交易日）的对数收益率为 \[\begin{aligned} r_{t,h} = \sum_{i=1}^h r_{t+i} \end{aligned}\] 于是 \[ E(r_{t,h} | F_t) = \sum_{i=1}^h E( r_{t+i} | F_t ) \] \(h\)期的条件方差，即波动率平方为 \[\begin{aligned} \text{Var}(r_{t,h} | F_t) = \sum_{i=1}^h \text{Var}(r_{t+i} | F_t) + \sum_{1 \leq i < j \leq h} \text{Cov}(r_{t+i}, r_{t+j} | F_t) \end{aligned}\] 实证分析和有效市场理论都认为协方差接近零，所以可假定 \[\begin{aligned} \text{Var}(r_{t,h} | F_t) = \sum_{i=1}^h \text{Var}(r_{t+i} | F_t) \end{aligned}\] 对于GARCH模型，这就是 \[\begin{aligned} \sigma_{t,h}^2 = \text{Var}(r_{t,h} | F_t) = \sum_{\ell=1}^h \sigma_t^2(\ell) \end{aligned}\] 其中\(\sigma_{t,h}^2\)表示以\(h\)期为单位的基于时刻\(t\)计算的条件方差， 即\(h\)期的对数收益率的波动率平方， \(\sigma_t^2(\ell)\)是基于时刻\(t\)的单期对数收益率的波动率的超前\(\ell\)步预测。

考虑GARCH(1,1)模型的超前\(\ell\)步预测问题。模型为： \[\begin{align} \sigma_t^2 =& \alpha_0 + \alpha_1 a_{t-1}^2 + \beta_1 \sigma_{t-1}^2 \tag{22.1} \end{align}\] 其中\(\alpha_0>0\), \(\alpha_1, \beta_1 \in [0, 1)\), \(\alpha_1 + \beta_1 < 1\)。 已证明 \[ \text{Var}(a_t) = \sigma^2 = \frac{\alpha_0}{1 - \alpha_1 - \beta_1} \] 可以将(22.1)改写成 \[\begin{align} (\sigma_t^2 - \sigma^2) = \alpha_1 (a_{t-1}^2 - \sigma^2) + \beta_1 (\sigma_{t-1}^2 - \sigma^2) \tag{22.2} \end{align}\] 这个式子可以看成是\(a_t^2\)的一步预测\(E(a_t^2|F_{t-1})\)与长期预测\(\sigma^2\)的偏离的模型。

波动率的基于\(F_t\)的超前一步预测为 \[ \sigma_t^2(1) = \alpha_0 + \alpha_1 a_{t}^2 + \beta_1 \sigma_{t}^2 \] 超前\(\ell\)步预测为 \[\begin{aligned} \sigma_t^2(\ell) = \alpha_0 + (\alpha_1 + \beta_1) \sigma_t^2(\ell - 1), \ \ell=2,3,\dots \end{aligned}\] 以\(\sigma^2 = \alpha_0/(1-\alpha_1 - \beta_1)\)代入上式可变成 \[\begin{aligned} \sigma_t^2(\ell) - \sigma^2 =& (\alpha_1 + \beta_1) [\sigma_t^2(\ell-1) - \sigma^2] \\ =& (\alpha_1 + \beta_1)^{\ell-1} [\sigma_t^2(1) - \sigma^2] \end{aligned}\]

当\(\alpha_1 + \beta_1<1\)时令\(\ell \to \infty\)， 有\(\sigma_t^2(\ell) \to \sigma^2\)， 即波动率平方的长期预测是均值回转的。 均值回转的速度可以用半衰期 \[ \ell_m = \ln 0.5 / \ln (\alpha_1 + \beta_1) \] 度量。

对CAT、CSCO和GE三支股票日对数收益率建模发现， \(\alpha_1 + \beta_1\)很接近于1（分别是\(0.9776\), \(0.9770\), \(0.9991\)）， 使得波动率持续性很强， 半衰期分别为31、30、770。

有了上面的多期预测公式， GARCH模型就可以用来从单期对数收益率波动率换算多期对数收益率波动率。

多期波动率一定大于单期波动率， 为了不同期限的波动率可比， 可将其标准化为年化波动率， 公式为 \[\begin{aligned} \sigma_{t,h,a} = \sqrt{\frac{252}{h}} \sigma_{t,h} \end{aligned}\] 其中\(\sigma_{t,h}\)是基于时刻\(t\)预测的\(h\)期波动率， 是从第\(t\)期到第\(t+h\)期的多期对数收益率的条件方差； \(\sigma_{t,h,a}\)是此多期波动率年化的结果。

下面写一个从GARCH(1,1)模型估计计算\(h\)期波动率， 并将其年化的函数。 输入为GARCH(1,1)模型估计结果， \(a_t\)序列，\(h\)是一到多个多期数值， 输出一个年化多期波动率的矩阵， 其中第\(t\)行代表从时间\(t\)对\(t+h\)时刻的多期波动率预测， 注意：输出的不同\(h\)在同一时刻\(t\)代表的不是该时刻的某个收益率的年化波动率， 而是用前一期(相隔\(h\)日)的波动率对其进行的预测值。

volatility_interval <- function(modres, at, h=1){
  vola <- volatility(modres)
  at <- at - mean(at)
  co <- coef(modres)
  omega <- co["omega"]
  alpha1 <- co["alpha1"]
  beta1 <- co["beta1"]
  ab <- alpha1 + beta1
  nt <- length(vola)
  predi <- numeric(nt)
  resm <- matrix(0.0, nrow=nt, ncol=length(h))
  hmax <- max(h)
  for(j in seq(along=h)){
    hj <- h[j]
    predi[] <- 
      omega + alpha1*at^2 + beta1*vola^2
    resm[,j] <- predi
    if(hj > 1){
      for(jj in 2:hj){
        predi <- omega + ab * predi
        resm[,j] <- resm[,j] + predi
      }
    }
    resm[,j] <- sqrt(252/hj*resm[,j])
  }
  
  resm
}

22.1.1 CAT股票日对数收益率的波动率期限结构

作为例子， 考虑CAT(卡特彼勒)股票日对数收益率的期限结构， 时间从2001-01-02到2010-12-31。 以百分之一单位表示。

d.cat <- read_table(
  "d-c2c-0110.txt", 
  col_types=cols(.default=col_double())
)
d.sp500 <- read_table(
  "d-sp500-0110.txt", 
  col_names = FALSE,
  col_types=cols(.default=col_double())
)
time.cat <- seq(2001, 2010, length.out=nrow(d.cat))
rtn.cat <- log(1 + d.cat[["CAT"]])*100
rtn.csco <- log(1 + d.cat[["CSCO"]])*100
rtn.sp500 <- d.sp500[[1]]*100

CAT股票日对数收益率时间序列图形：

plot(time.cat, rtn.cat, 
  type="l", xlab="Year", ylab="ln(return)")

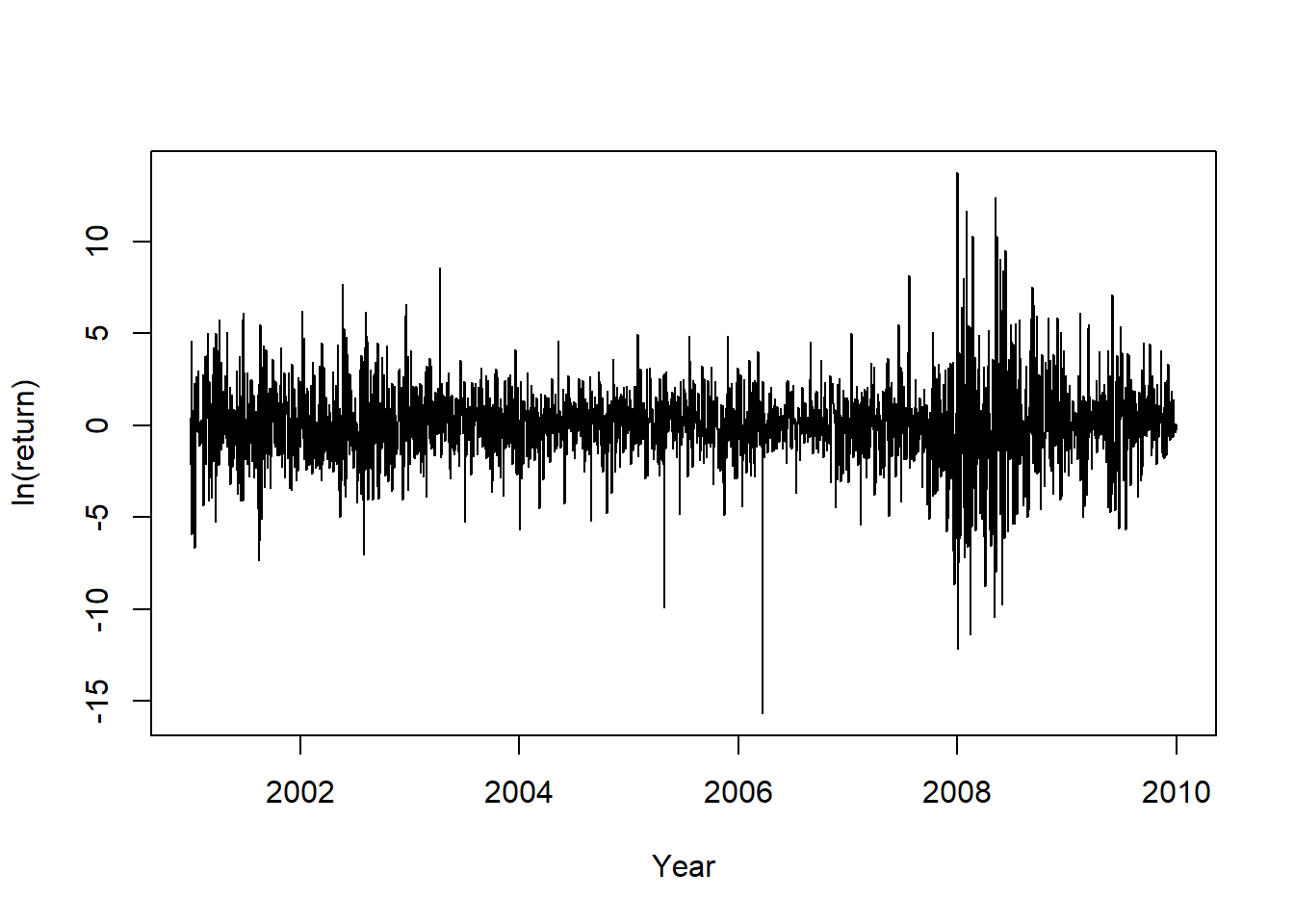
图22.1: CAT股票日对数收益率

CAT股票日对数收益率时间序列ACF：

forecast::Acf(rtn.cat, lag.max = 30, main="")

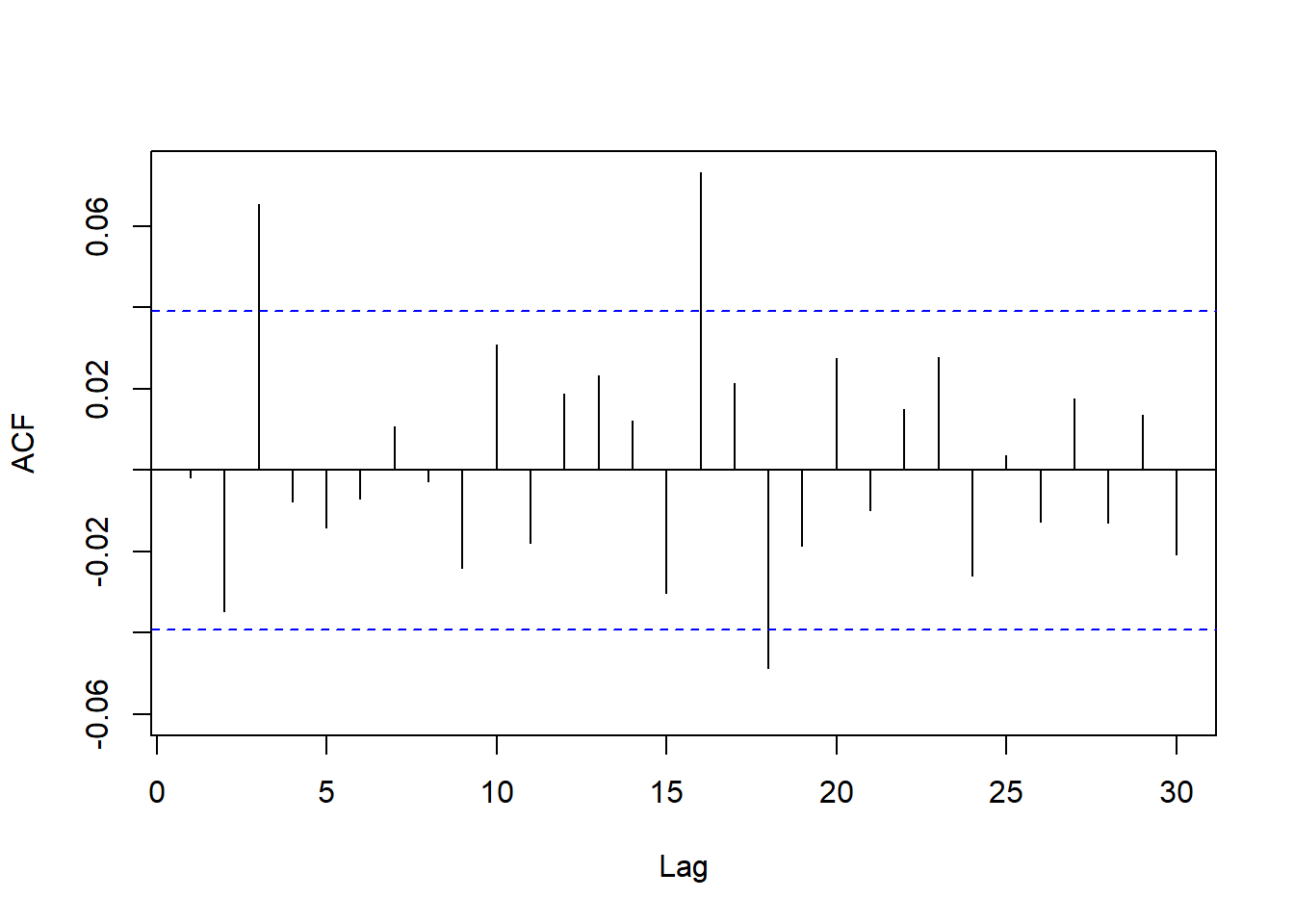
图22.2: CAT股票日对数收益率ACF

建立GARCH(1,1)模型：

library(fGarch)
mod1.cat <- garchFit(~ 1 + garch(1,1), data=rtn.cat, trace=FALSE)
summary(mod1.cat)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.cat, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aab9ff53a0>
##  [data = rtn.cat]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.103702  0.095669  0.053109  0.924455  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu       0.10370     0.03713    2.793  0.00522 ** 
## omega    0.09567     0.03385    2.826  0.00471 ** 
## alpha1   0.05311     0.01134    4.682 2.84e-06 ***
## beta1    0.92446     0.01787   51.739  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -5297.634    normalized:  -2.106415 
## 
## Description:
##  Fri Apr 21 08:03:50 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value  
##  Jarque-Bera Test   R    Chi^2  2397.079  0        
##  Shapiro-Wilk Test  R    W      0.9720346 0        
##  Ljung-Box Test     R    Q(10)  11.99378  0.2854729
##  Ljung-Box Test     R    Q(15)  16.40952  0.355369 
##  Ljung-Box Test     R    Q(20)  21.94146  0.3436959
##  Ljung-Box Test     R^2  Q(10)  1.323393  0.9993882
##  Ljung-Box Test     R^2  Q(15)  3.737861  0.9984771
##  Ljung-Box Test     R^2  Q(20)  4.956939  0.9997407
##  LM Arch Test       R    TR^2   2.67451   0.9974382
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 4.216011 4.225283 4.216006 4.219376

模型基本充分。

plot(time.cat, volatility(mod1.cat), type="l", 
     main="CAT股票日对数收益率波动率GARCH(1,1)估计", 
     xlab="年")

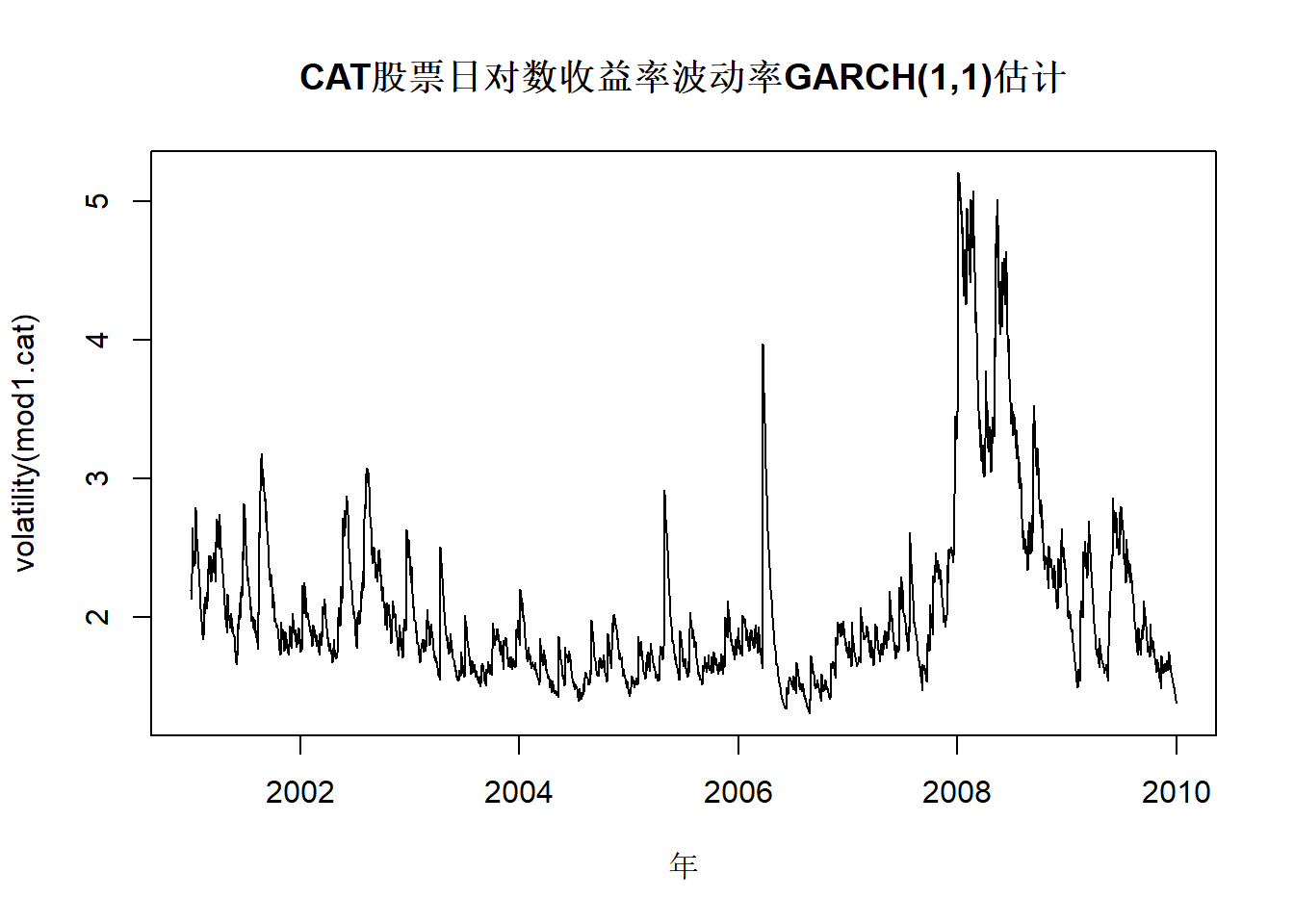
图22.3: CAT股票日对数收益率波动率

日波动率分布的盒形图：

boxplot(volatility(mod1.cat), ylab="日波动率", xlab="")

图22.4: CAT股票日对数收益率波动率盒形图

利用GARCH(1,1)模型结果计算1日、5日、20日年化波动率并作图：

volay.cat <- volatility_interval(
  mod1.cat, at=rtn.cat, h=c(1,5,20)
)

matplot(
  time.cat, volay.cat, type="l", 
  col=c("black", "green", "blue"),
  main="CAT股票日对数收益率1、5、20日年化波动率GARCH(1,1)估计", 
  xlab="年")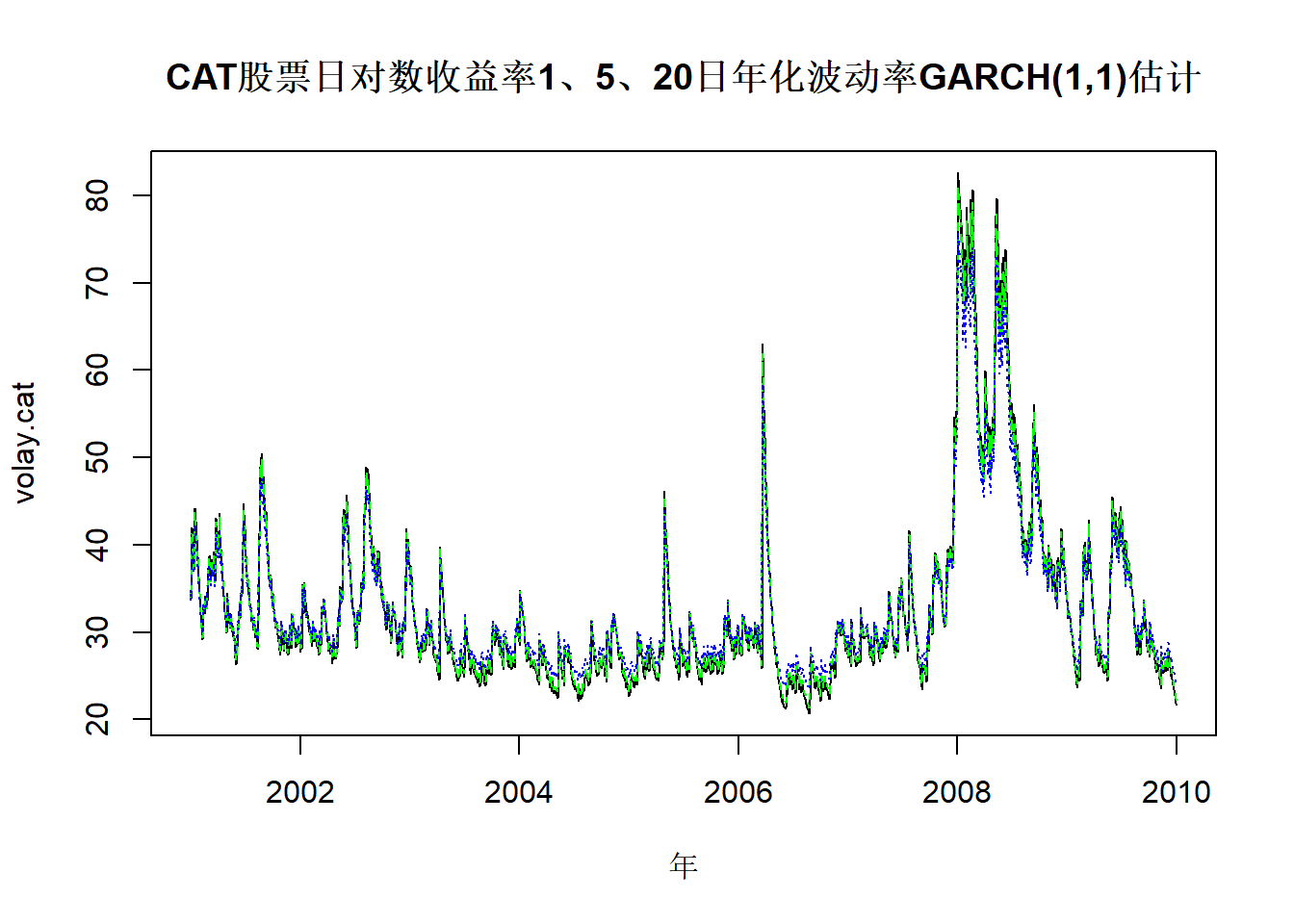

图22.5: CAT股票日对数收益率1、5、20日年化波动率

matplot(
  time.cat[2011:2515], volay.cat[2011:2515,], type="l", 
  col=c("black", "green", "blue"),
  main="CAT股票日对数收益率1、5、20日年化波动率GARCH(1,1)估计", 
  xlab="年")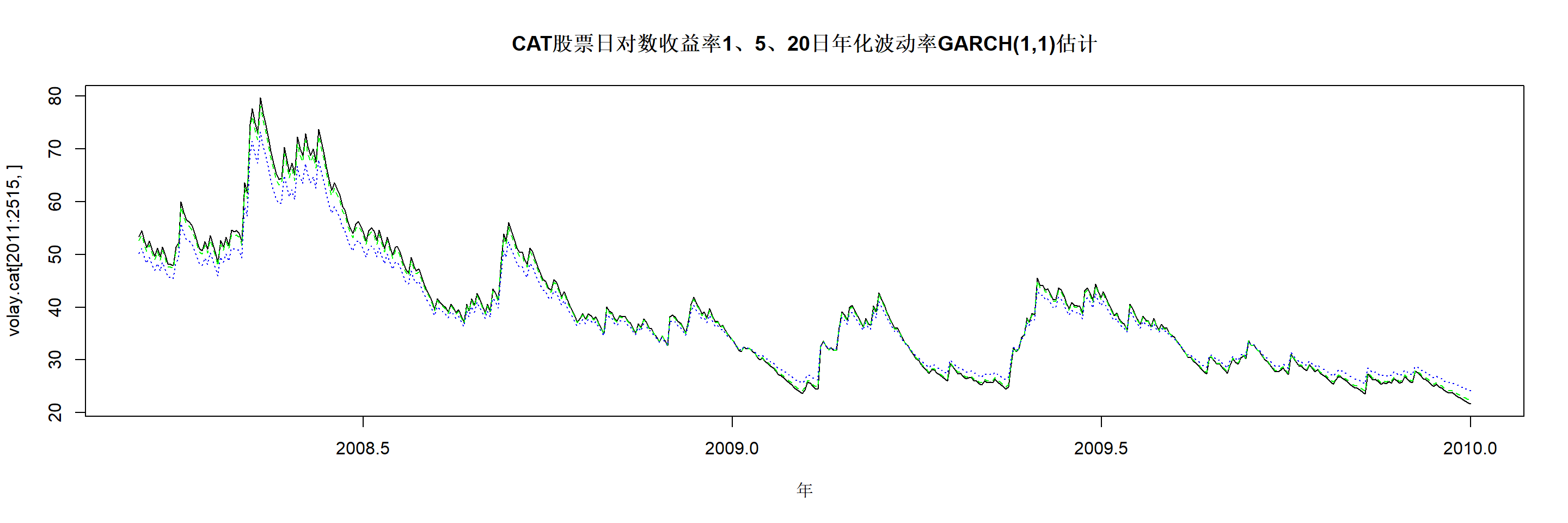

图22.6: CAT股票日对数收益率1、5、20日年化波动率2008-2009

在局部波动率较高时， 20日波动率低于单日波动率， 可能是因为在预测20日波动率时发生了均值回转。

22.1.2 欧元对美元汇率日对数收益率的波动率期限结构

作为例子， 考虑从1999年1月4日到2010年8月20日的欧元对美元汇率的日对数收益率序列。 以百分之一为单位。

d.useu <- read_table(
  "d-useu9910.txt", 
  col_types=cols(.default=col_double())
)
xts.useu <- with(d.useu, xts(rate, make_date(year, mon, day)))
xts.useu.lnrtn <- diff(log(xts.useu))[-1,]*100
eu <- c(coredata(xts.useu.lnrtn))

日对数收益率图形（单位百分之一）：

plot(xts.useu.lnrtn,
     main="欧元汇率日对数收益率", 
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years")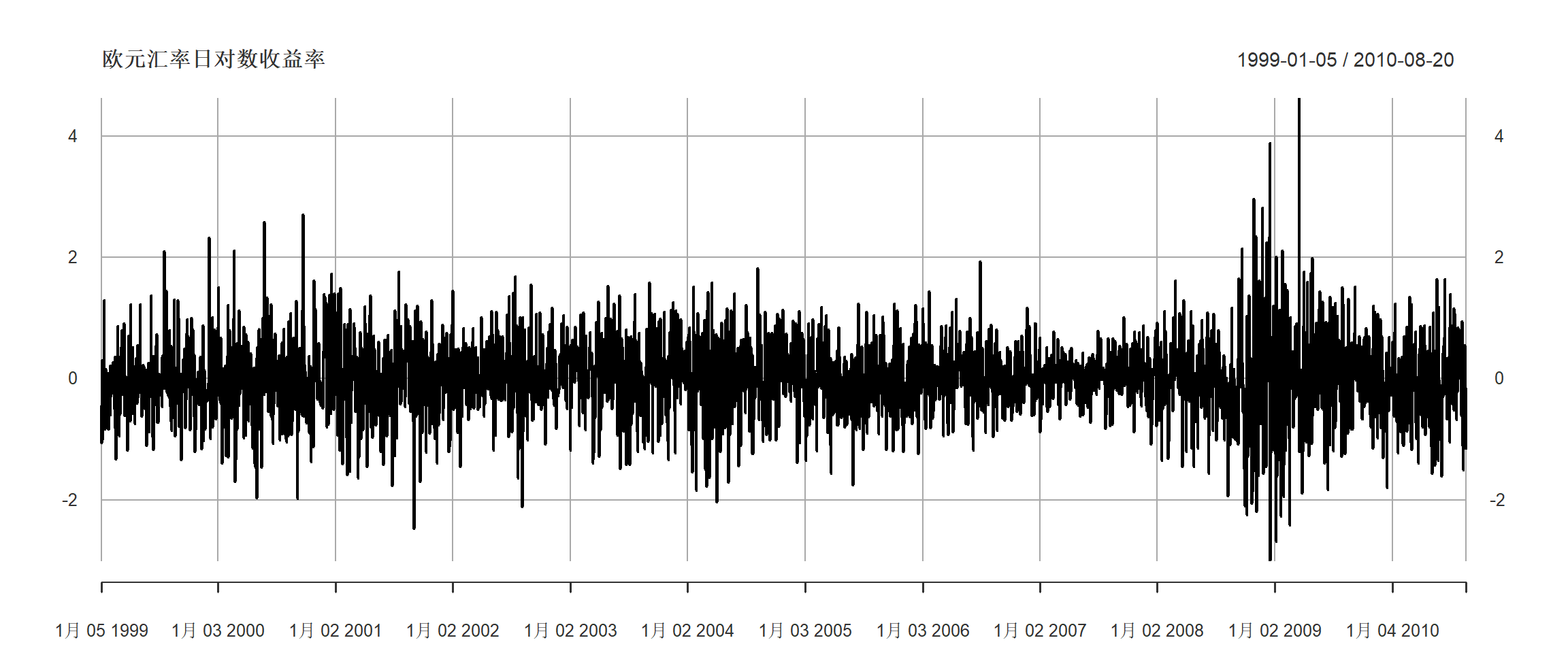

图22.7: 欧元对美元汇率日对数收益率

日对数收益率分布盒形图：

boxplot(eu, ylab="日对数收益率", xlab="")

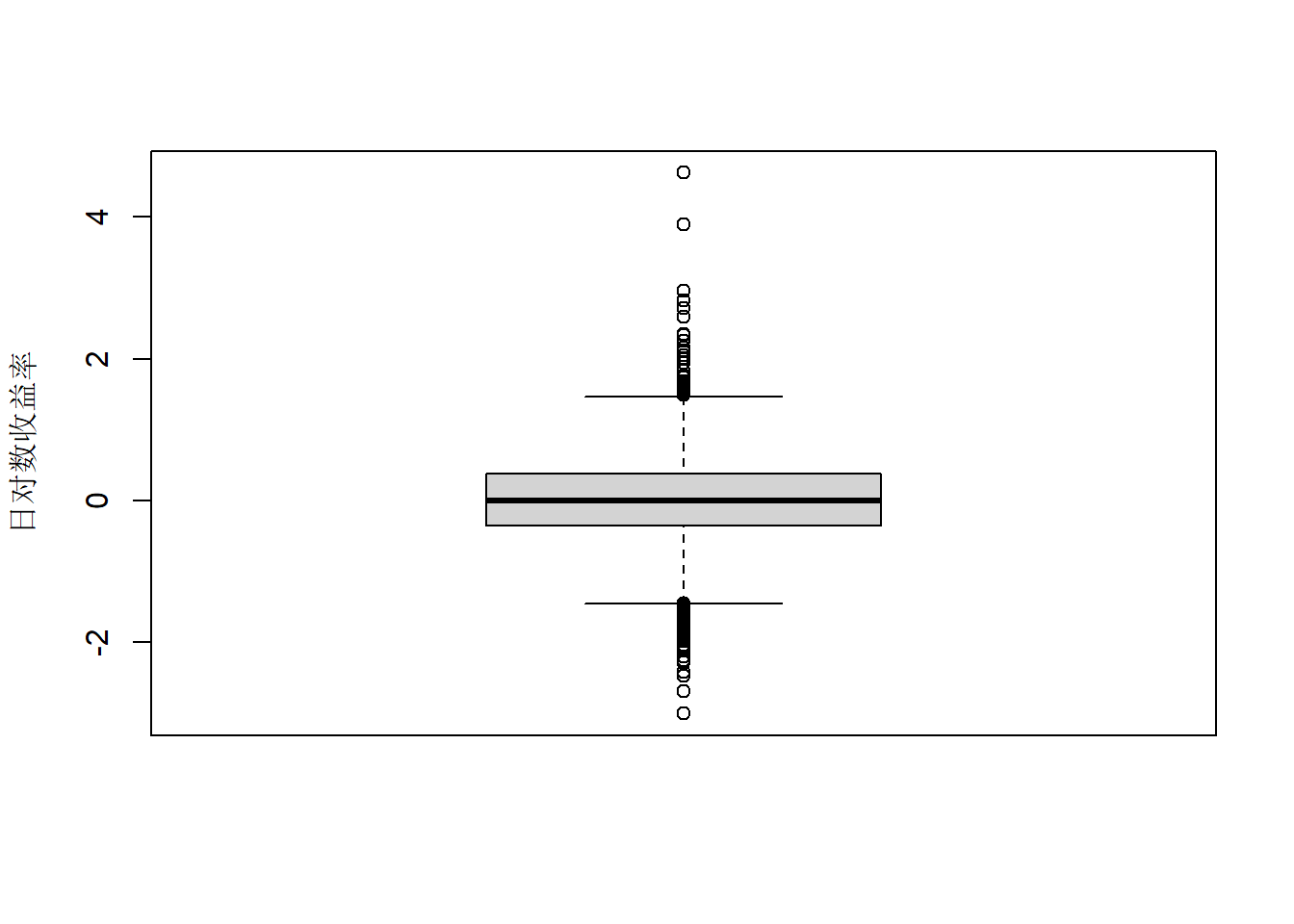
图22.8: 欧元对美元汇率日对数收益率分布盒形图

日对数收益率比较集中在\(\pm 2\%\)之间。

建立均值方程为常数、条件正态分布的GARCH(1,1)模型：

mod1 <- garchFit(~ 1 + garch(1,1), data=eu, trace=FALSE)
summary(mod1)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = eu, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aab0a49a80>
##  [data = eu]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##        mu      omega     alpha1      beta1  
## 0.0148834  0.0011236  0.0292729  0.9685221  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu     0.0148834   0.0106235    1.401   0.1612    
## omega  0.0011236   0.0005602    2.006   0.0449 *  
## alpha1 0.0292729   0.0037996    7.704 1.31e-14 ***
## beta1  0.9685221   0.0038946  248.685  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -2733.418    normalized:  -0.9332256 
## 
## Description:
##  Fri Apr 21 08:03:52 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  54.69227  1.329603e-12
##  Shapiro-Wilk Test  R    W      0.9954108 7.170686e-08
##  Ljung-Box Test     R    Q(10)  13.33532  0.205523    
##  Ljung-Box Test     R    Q(15)  20.08275  0.1687813   
##  Ljung-Box Test     R    Q(20)  22.64627  0.3064951   
##  Ljung-Box Test     R^2  Q(10)  13.31502  0.2065881   
##  Ljung-Box Test     R^2  Q(15)  17.40896  0.29501     
##  Ljung-Box Test     R^2  Q(20)  28.78138  0.09215406  
##  LM Arch Test       R    TR^2   14.96898  0.2431374   
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 1.869182 1.877352 1.869179 1.872125

模型检验基本通过。

日对数收益率波动率的图形：

plot(xts(volatility(mod1), index(xts.useu.lnrtn)),
     main="欧元汇率日对数收益率波动率GARCH(1,1)估计", 
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years")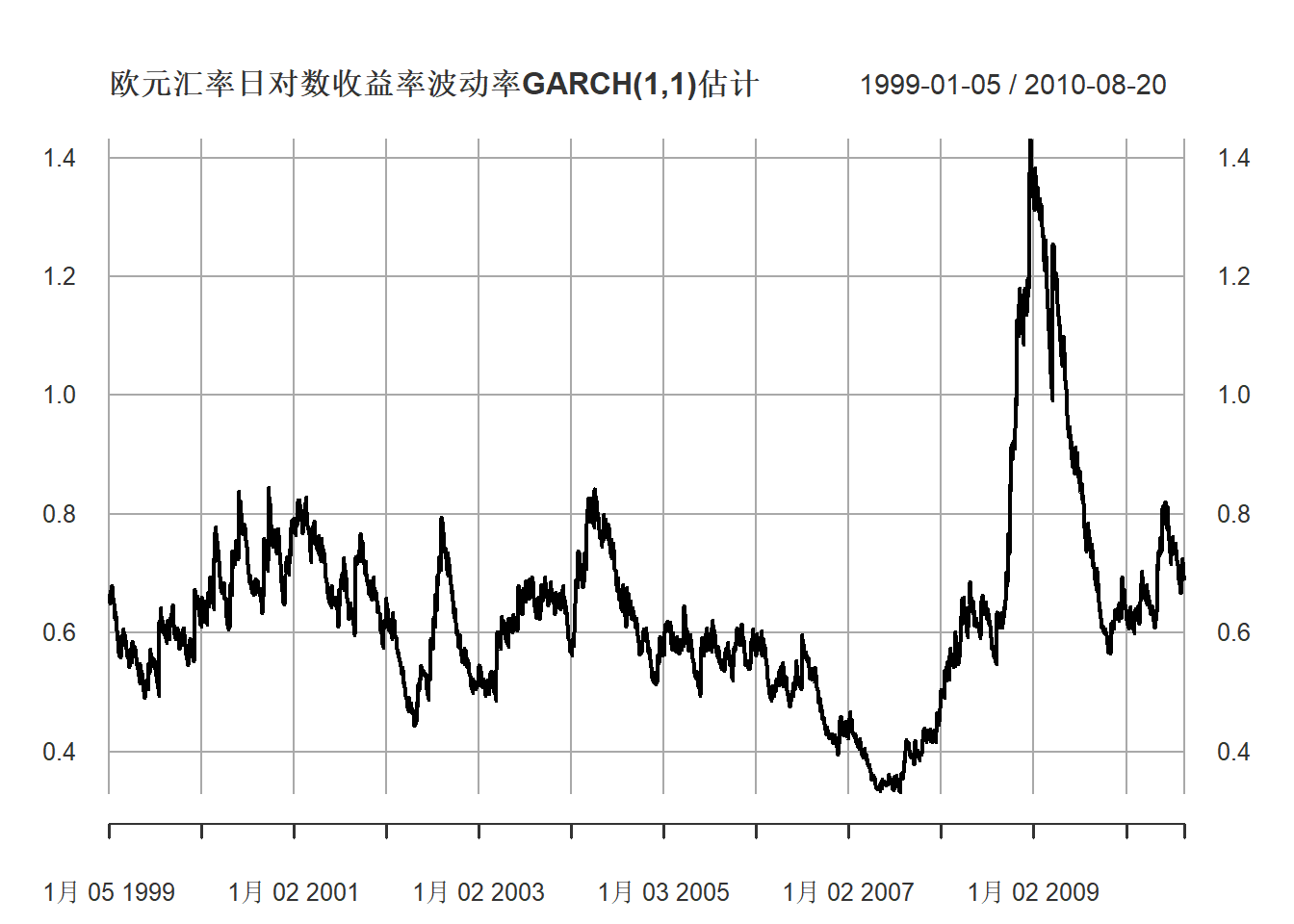

图22.9: 欧元汇率日对数收益率波动率

日波动率分布的盒形图：

boxplot(volatility(mod1), ylab="日波动率", xlab="")

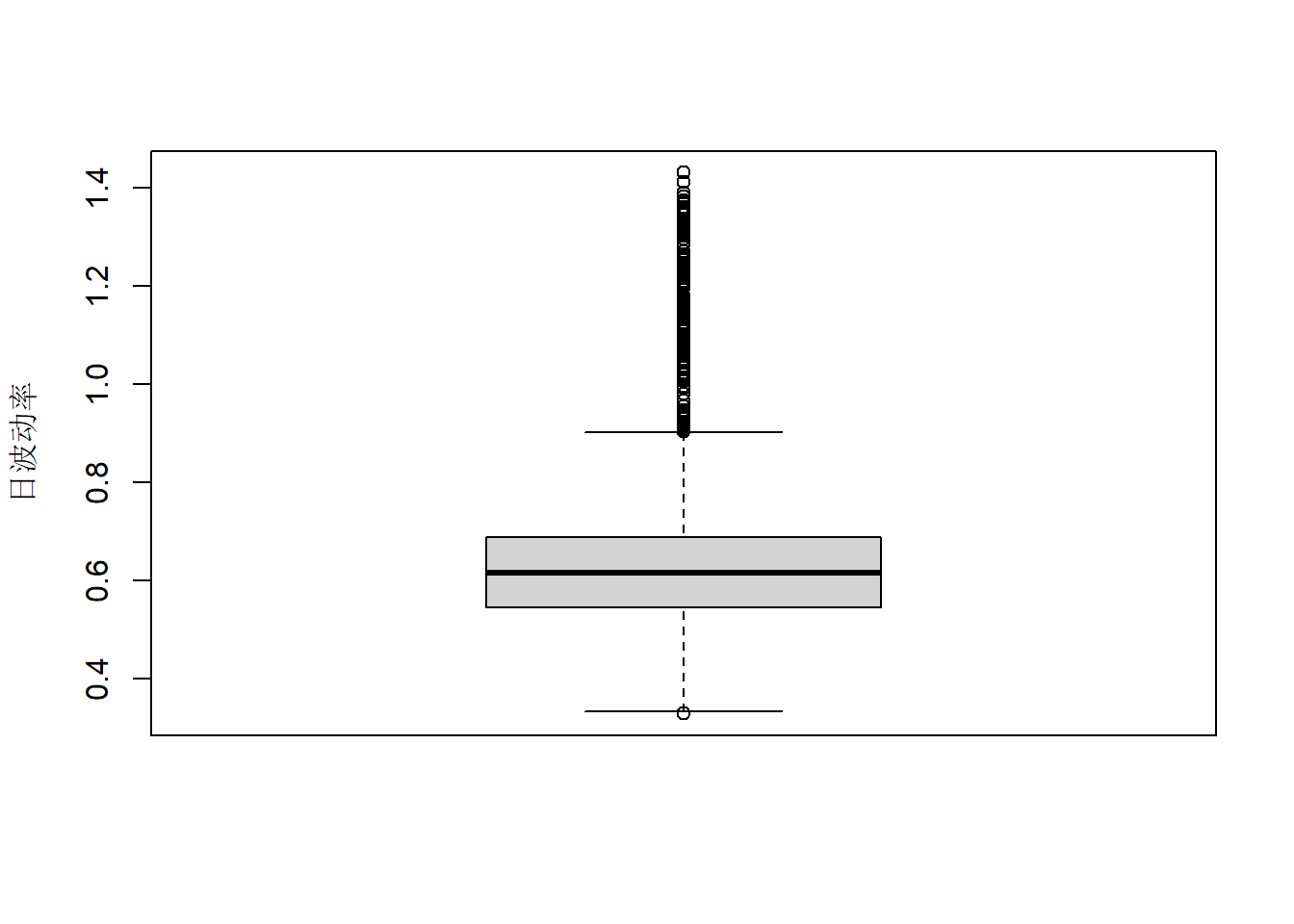
图22.10: 欧元汇率日对数收益率波动率

波动率中位数为\(0.6\%\)左右， 主要集中在\(0.4\%\)到\(1.0\%\)之间。

利用GARCH(1,1)模型结果计算1日、5日、20日年化波动率并作图：

volay.eu <- volatility_interval(
  mod1, at=eu, h=c(1,5,20)
)

plot(xts(volay.eu, index(xts.useu.lnrtn)),
     col=c("black", "green", "blue"),
     main="欧元汇率1、5、20日年化波动率GARCH(1,1)估计", 
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years")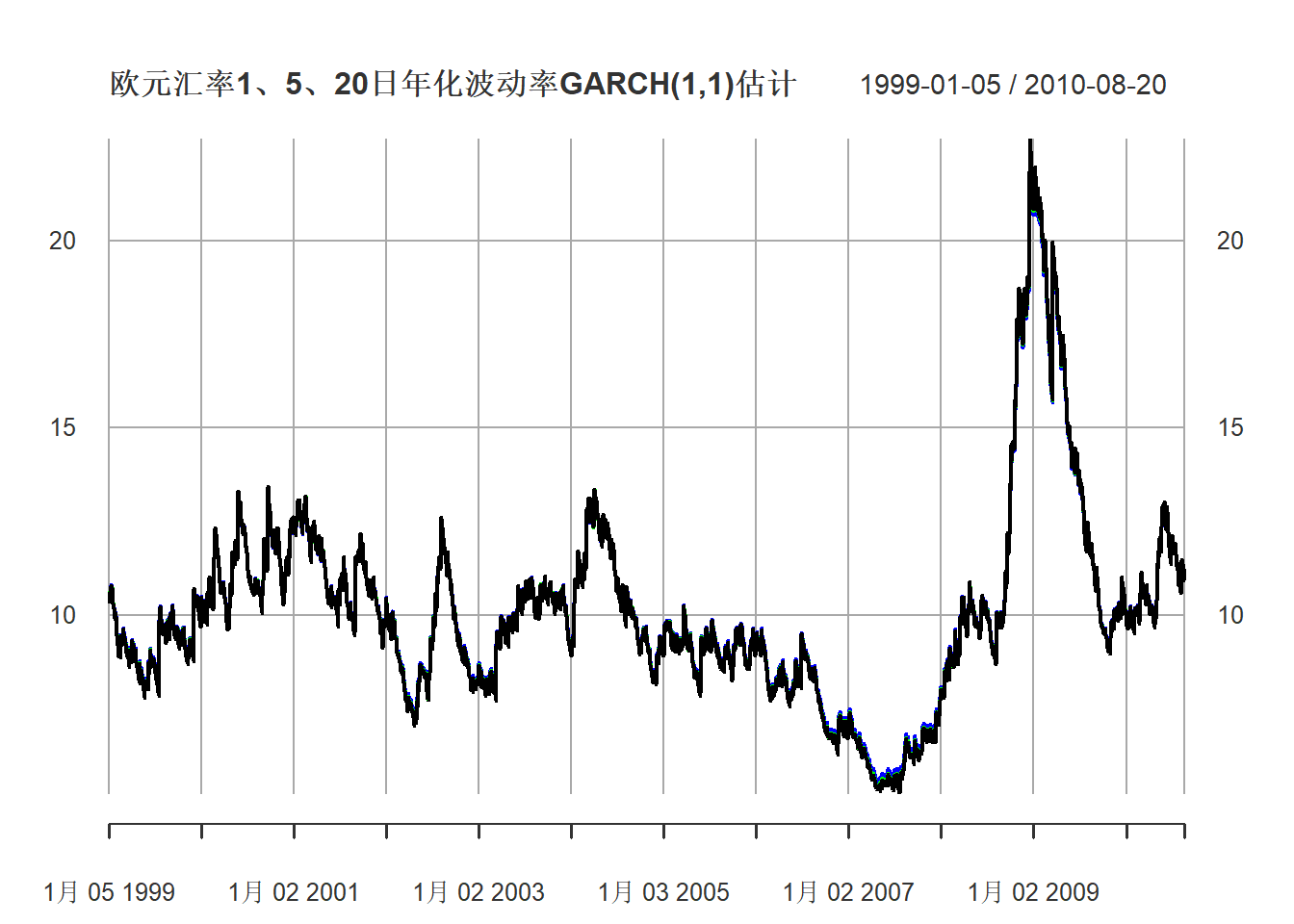

图22.11: 欧元汇率1、5、20日年化波动率

plot(xts(volay.eu, index(xts.useu.lnrtn)),
     subset="2010",
     col=c("black", "green", "blue"),
     main="欧元汇率1、5、20日年化波动率GARCH(1,1)估计", 
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years")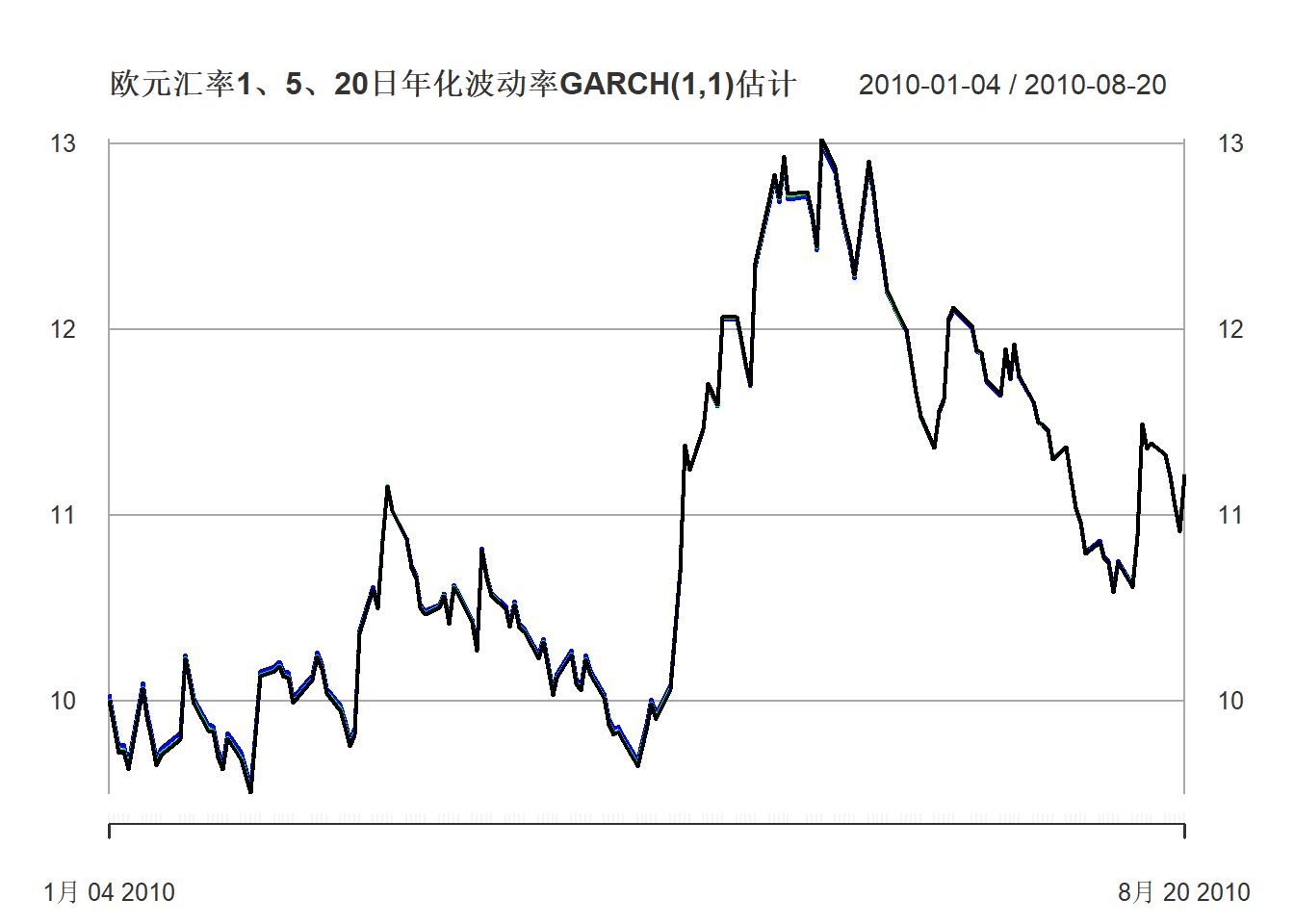

图22.12: 欧元汇率1、5、20日年化波动率预测2010年

黑色是日波动率，绿色是5日波动率，蓝色是20日波动率。 不同期的年化波动率差距不大。

22.2 期权定价和对冲

波动率的一个重要应用是对金融衍生产品定价， 如著名的Black-Scholes期权定价公式， 其中设波动率为常数。

有多位学者研究了在期权定价中使用GARCH模型表示出变化的波动率， 基于GARCH模型进行期权定价。

单只股票的标准期权定价中假设股票价格服从如下的几何布朗运动： \[\begin{aligned} \frac{dP_t}{P_t} = r dt + \sigma d W_t \end{aligned}\] 其中\(r\)是无风险利率， \(\sigma\)是波动率， \(W_t\)是标准维纳(Wiener)过程（连续时随机过程）。 根据伊藤(Ito)引理， 股票的对数价格\(\ln P_t\)服从如下随机微分方程 \[\begin{aligned} d \ln P_t = \left(r - \frac12 \sigma^2 \right) dt + \sigma d W_t \end{aligned}\]

实践中假定\(r\)和\(\sigma\)为已知， 随机性来自\(W_t\)。 离散化形式为 \[\begin{align} P_t = P_{t-1} \exp\left\{ r - \frac12 \sigma^2 + \sigma \varepsilon_t \right\} \tag{22.3} \end{align}\] 其中\(\{ \varepsilon_t \}\)独立同标准正态分布。

设当前时刻为0， 当前股价为\(P_0\)， 期权的执行价格为\(K\)， 到期时间为\(T\)， 通过产生一个独立同标准正态分布的\(\{ \varepsilon_1, \dots, \varepsilon_T \}\)， 用式(22.3)可以模拟一条价格轨道（实现）， 重复模拟\(N\)次得到\(N\)条价格轨道 \(\{ P_t^{(i)}, t=1,\dots, T, \ i=1,\dots, N \}\)。 可以用\(P_T^{(i)}\)的样本平均值估计最终价格的期望\(E P_T\)。

利用模拟的\(N\)条轨道， 可以计算欧式看涨期权价格为 \[\begin{aligned} C(P_0) =& e^{-r T} E \left[ \max(P_T - K, \ 0) \right] \\ \approx& \frac{1}{N} e^{-r T} \sum_{i=1}^N \max \left(P_T^{(i)} - K, \ 0 \right) \end{aligned}\]

亚式看涨期权使用其轨道的平均值， 公式为 \[\begin{aligned} C(P_0) \approx& \frac{1}{N} e^{-r T} \sum_{i=1}^N \max \left( \frac{1}{T} \sum_{t=1}^T P_t^{(i)} - K, \ 0 \right) \end{aligned}\]

以上的模拟使用了常数波动率。 对于GARCH(1,1)模型， 在模拟价格轨道时可以同时计算变化的波动率\(\sigma_t\)， 这时波动率方程中的\(\varepsilon_t\) 就是式(22.3)中的\(\varepsilon_t\)。 为了模拟一条轨道， 可对\(t=1,2,\dots, T\)递推计算 \[\begin{aligned} \sigma_t^2 =& \alpha_0 + \alpha_1 \sigma_{t-1}^2 \varepsilon_{t-1}^2 + \beta_1 \sigma_{t-1}^2 \\ P_t =& P_{t-1} \exp\left\{ r - \frac12 \sigma_t^2 + \sigma_t \varepsilon_t \right\} \end{aligned}\] 初值\(\sigma_0^2\)可取为模型的无条件方差\(\alpha_0 / (1 - \alpha_1 - \beta_1)\)。 \(\{ \varepsilon_t, t=0,1,\dots,T \}\)用独立同标准正态分布随机数模拟。

利用差分近似， 还可以计算相应的GARCH期权的\(\delta\)值和\(\gamma\)值，如 \[\begin{aligned} \delta =& \frac{1}{2\Delta} \left\{ C(P_0 + \Delta) - C(P_0 - \Delta) \right\} \\ \gamma =& \frac{1}{\Delta^2} \left\{ C(P_0 + \Delta) - 2 C(P_0) + C(P_0 - \Delta) \right\} \end{aligned}\]

由于\(C(P_0)\)是随机模拟得到的， 所以其计算存在不稳定性。

上述定价公式是根据完美对冲得到的， 在随机波动率的假设下不可能实现。 但(Duan 1995)证明存在如下局部的风险中心价格关系： \[\begin{aligned} r_t =& r - \frac12 \sigma_t^2 + \lambda \sigma + \sigma_t \varepsilon_t \\ \sigma_t^2 =& \alpha_0 + \alpha_1 \sigma_{t-1}^2 ( \varepsilon_{t-1} - \theta)^2 + \beta_1 \sigma_{t-1}^2 \end{aligned}\] 在期权定价中可以用这样的NGARCH(1,1)模型模拟价格轨道。

22.3 随时间变化的协方差和贝塔值

22.3.1 随时间变化的协方差

GARCH模型的另一个应用是对多元资产收益率估计随时间变化的协方差。 设有两个资产收益率序列\(x_t\)和\(y_t\)， 因为 \[\begin{aligned} \text{Var}(x_t + y_t) =& \text{Var}(x_t) + \text{Var}(y_t) + 2 \text{Cov}(x_t, y_t) \\ \text{Var}(x_t - y_t) =& \text{Var}(x_t) + \text{Var}(y_t) - 2 \text{Cov}(x_t, y_t) \end{aligned}\] 所以 \[\begin{aligned} \text{Cov}(x_t, y_t) = \frac14 \left[ \text{Var}(x_t + y_t) - \text{Var}(x_t - y_t) \right] \end{aligned}\]

这样，如果\(\text{Var}(x_t + y_t)\)和\(\text{Var}(x_t - y_t)\)是变化的， 则\(\text{Cov}(x_t, y_t)\)也是变化的。

设\(\sigma_{x+y,t}\), \(\sigma_{x-y,t}\), \(\sigma_{x,t}\), \(\sigma_{y,t}\) 分别为 \(x_t + y_t\), \(x_t - y_t\), \(x_t\)和\(y_t\)的波动率， 则\(x_t\)和\(y_t\)之间变化的相关系数为 \[\begin{aligned} \rho_{t,0} = \frac{\sigma_{x+y,t}^2 - \sigma_{x-y,t}^2}{4 \sigma_{x,t} \sigma_{y,t}} \end{aligned}\]

22.3.2 CAT与CSCO随时间变化的协方差

以CAT股票和CSCO股票日对数收益率为例， 时间是2010-01-02到2010-12-31。 分别记\(x_t\)和\(y_t\)为CAT和\(CSCO\)股票日对数收益率序列， 逐个地对\(x_t + y_t\), \(x_t - y_t\), \(x_t\), \(y_t\)建立GARCH(1,1)模型：

library(fGarch, quietly = TRUE)
mod1.cov <- garchFit(~ 1 + garch(1,1), data=rtn.cat + rtn.csco, trace=FALSE)
summary(mod1.cov)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.cat + rtn.csco, 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aaba1e8770>
##  [data = rtn.cat + rtn.csco]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.142970  0.218821  0.070019  0.915827  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu       0.14297     0.06456    2.215  0.02679 *  
## omega    0.21882     0.07328    2.986  0.00283 ** 
## alpha1   0.07002     0.01464    4.782 1.74e-06 ***
## beta1    0.91583     0.01782   51.404  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -6830.321    normalized:  -2.715833 
## 
## Description:
##  Fri Apr 21 08:03:53 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value  
##  Jarque-Bera Test   R    Chi^2  596.8548  0        
##  Shapiro-Wilk Test  R    W      0.9828596 0        
##  Ljung-Box Test     R    Q(10)  10.25333  0.4185564
##  Ljung-Box Test     R    Q(15)  19.2436   0.2029067
##  Ljung-Box Test     R    Q(20)  21.87413  0.3473793
##  Ljung-Box Test     R^2  Q(10)  6.559944  0.7662327
##  Ljung-Box Test     R^2  Q(15)  9.018078  0.8765703
##  Ljung-Box Test     R^2  Q(20)  11.85996  0.9208116
##  LM Arch Test       R    TR^2   9.634916  0.6479546
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 5.434848 5.444120 5.434842 5.438213

mod2.cov <- garchFit(~ 1 + garch(1,1), data=rtn.cat - rtn.csco, trace=FALSE)
summary(mod2.cov)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.cat - rtn.csco, 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aab13267d8>
##  [data = rtn.cat - rtn.csco]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.083118  0.055334  0.017893  0.972639  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.083118    0.046294    1.795   0.0726 .  
## omega   0.055334    0.011895    4.652 3.29e-06 ***
## alpha1  0.017893    0.002860    6.257 3.93e-10 ***
## beta1   0.972639    0.004222  230.358  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -5835.676    normalized:  -2.320348 
## 
## Description:
##  Fri Apr 21 08:03:54 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value  
##  Jarque-Bera Test   R    Chi^2  11268.67  0        
##  Shapiro-Wilk Test  R    W      0.9233503 0        
##  Ljung-Box Test     R    Q(10)  8.862267  0.5452231
##  Ljung-Box Test     R    Q(15)  15.47437  0.4178174
##  Ljung-Box Test     R    Q(20)  17.3576   0.6296459
##  Ljung-Box Test     R^2  Q(10)  1.871285  0.9972348
##  Ljung-Box Test     R^2  Q(15)  4.504232  0.9955568
##  Ljung-Box Test     R^2  Q(20)  5.879926  0.9990502
##  LM Arch Test       R    TR^2   3.000405  0.9955412
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 4.643877 4.653150 4.643872 4.647242

mod3.cov <- garchFit(~ 1 + garch(1,1), data=rtn.cat, trace=FALSE)
summary(mod3.cov)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.cat, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aabc332668>
##  [data = rtn.cat]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.103702  0.095669  0.053109  0.924455  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu       0.10370     0.03713    2.793  0.00522 ** 
## omega    0.09567     0.03385    2.826  0.00471 ** 
## alpha1   0.05311     0.01134    4.682 2.84e-06 ***
## beta1    0.92446     0.01787   51.739  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -5297.634    normalized:  -2.106415 
## 
## Description:
##  Fri Apr 21 08:03:55 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value  
##  Jarque-Bera Test   R    Chi^2  2397.079  0        
##  Shapiro-Wilk Test  R    W      0.9720346 0        
##  Ljung-Box Test     R    Q(10)  11.99378  0.2854729
##  Ljung-Box Test     R    Q(15)  16.40952  0.355369 
##  Ljung-Box Test     R    Q(20)  21.94146  0.3436959
##  Ljung-Box Test     R^2  Q(10)  1.323393  0.9993882
##  Ljung-Box Test     R^2  Q(15)  3.737861  0.9984771
##  Ljung-Box Test     R^2  Q(20)  4.956939  0.9997407
##  LM Arch Test       R    TR^2   2.67451   0.9974382
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 4.216011 4.225283 4.216006 4.219376

mod4.cov <- garchFit(~ 1 + garch(1,1), data=rtn.csco, trace=FALSE)
summary(mod4.cov)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.csco, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aabb223aa8>
##  [data = rtn.csco]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.032238  0.155836  0.082301  0.894726  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu       0.03224     0.04067    0.793    0.428    
## omega    0.15584     0.03941    3.954 7.69e-05 ***
## alpha1   0.08230     0.01784    4.612 3.98e-06 ***
## beta1    0.89473     0.02142   41.767  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -5714.663    normalized:  -2.272232 
## 
## Description:
##  Fri Apr 21 08:03:55 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value  
##  Jarque-Bera Test   R    Chi^2  10943.05  0        
##  Shapiro-Wilk Test  R    W      0.9417187 0        
##  Ljung-Box Test     R    Q(10)  9.690217  0.468079 
##  Ljung-Box Test     R    Q(15)  20.61778  0.1494922
##  Ljung-Box Test     R    Q(20)  22.97434  0.2900564
##  Ljung-Box Test     R^2  Q(10)  1.949596  0.9967121
##  Ljung-Box Test     R^2  Q(15)  2.781043  0.9997496
##  Ljung-Box Test     R^2  Q(20)  4.16767   0.9999349
##  LM Arch Test       R    TR^2   2.935696  0.9959812
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 4.547644 4.556917 4.547639 4.551010

变化的协方差\(\text{Cov}(x_t, y_t)\)和变化的相关系数\(\rho_{t,0}\)的估计：

vcov.cat <- 1/4*(volatility(mod1.cov)^2 - volatility(mod2.cov)^2)
vrho.cat <- vcov.cat / volatility(mod3.cov) / volatility(mod4.cov)

变化的相关系数的时间序列图：

plot(time.cat, vrho.cat, type="l", xlab="年", ylab="相关系数")

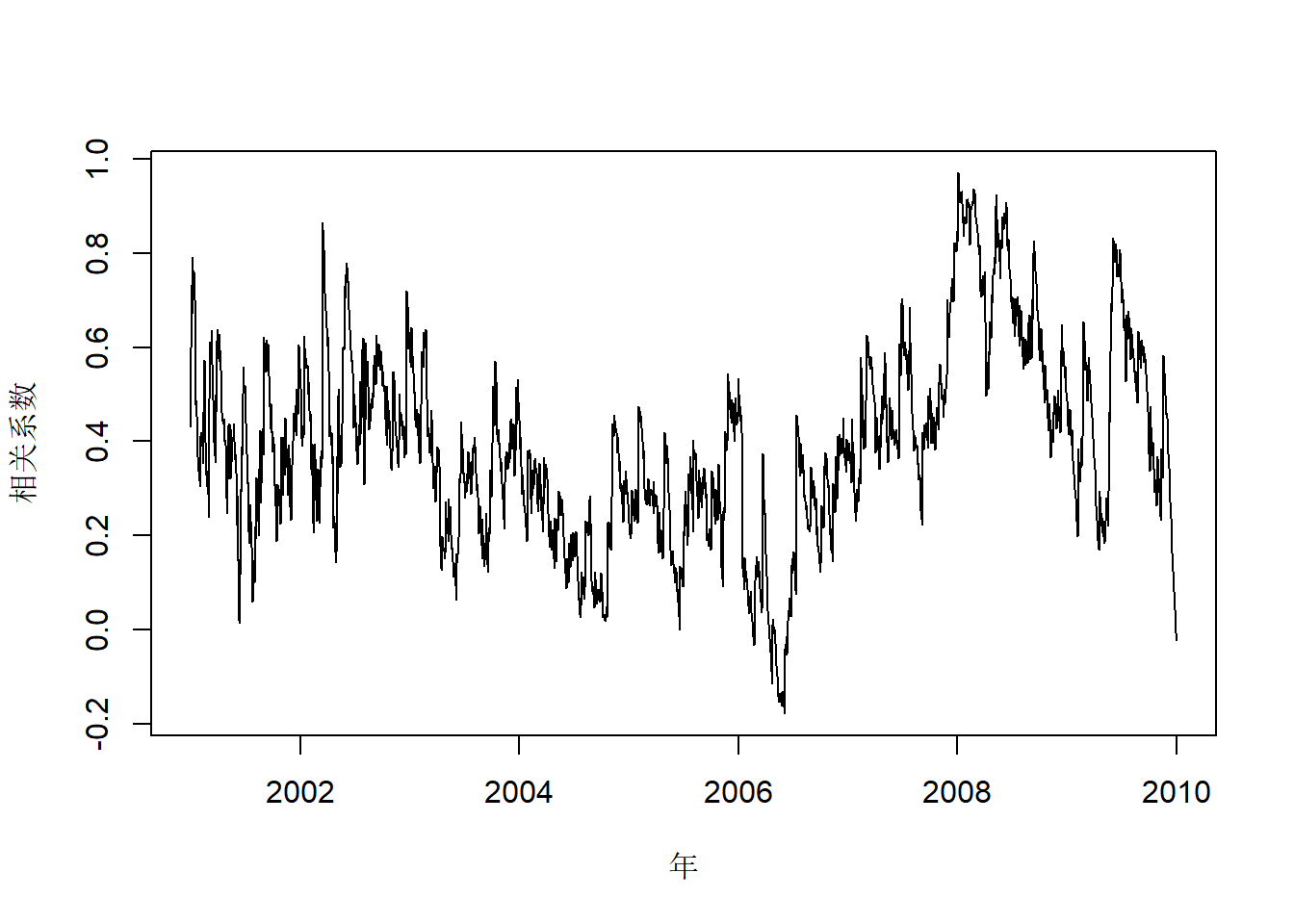
22.3.3 随时间变化的贝塔值

贝塔值的定义来自资产定价模型(CAPM): \[\begin{align} r_t =& \alpha + \beta r_{m,t} + e_t, \ t=1,2,\dots,T \tag{22.4} \end{align}\] 其中\(r_t\)是所研究的资产的收益率， \(r_{m,t}\)是市场的收益率（如综合股指的收益率）。 这里没有使用超额收益率。

这个一元线性回归模型提供了估计下列因子的方法：

• 股票对市场风险的敏感性的因子\(\beta\);
• 股票相对于市场的错误定价\(\alpha\);
• 特定股票回报\(e_t\)。

特定股票回报一般不重要， 在资产组合中这一部分经过线性组合后会接近于0。

\(\beta\)提供了股票相对于市场如何变化的测量， 如果\(\beta\)不显著地区别于零， 则股票变化与市场变化无关； 如果\(\beta\)显著地大于1， 则股票对市场变化的反应特别强烈， 这样的股票被认为是高风险的。 \(\beta<1\)的股票是低风险的。

\(\alpha\)是\(r_{m,t}=0\)时研究的股票的平均收益率， 在实践中，如果可能， 尽可能选取\(\alpha\)为正数、\(\beta\)较小的资产。

对(22.4)的CAPM模型， \(\beta\)的理论值为 \[\begin{aligned} \beta = \frac{\text{Cov}(r_t, r_{m,t})}{\text{Var}(r_{m,t})} \end{aligned}\]

\(\beta\)的定义依赖于市场指数\(r_{m,t}\)的选择。

一般相信\(\beta\)值是随时间而变的， 可以用前面估计变化的协方差的方法估计变化的贝塔值。 \(\text{Cov}(r_t, r_{m,t})\)可以通过\(\text{Var}(r_t + r_{m,t})\) 和\(\text{Var}(r_t - r_{m,t})\)估计。

22.3.4 CAT股票日对数收益率随时间变化的贝塔值

作为示例， 考虑CAT股票的日对数收益率\(r_t\)， 采用标普500指数的日对数收益率作为市场收益率\(r_{m,t}\)， 时间从2001-01-02到2010-12-31。

用CAPM模型计算不随时间变化的贝塔值：

lm1.cat <- lm(rtn.cat ~ rtn.sp500)
summary(lm1.cat)

## 
## Call:
## lm(formula = rtn.cat ~ rtn.sp500)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -15.8901  -0.7715  -0.0025   0.8066   9.9412 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.06688    0.03041   2.199   0.0279 *  
## rtn.sp500    1.14580    0.02209  51.870   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.525 on 2513 degrees of freedom
## Multiple R-squared:  0.5171, Adjusted R-squared:  0.5169 
## F-statistic:  2690 on 1 and 2513 DF,  p-value: < 2.2e-16

估计的CAPM模型为 \[\begin{aligned} r_t = 0.0669 + 1.146 r_{t,m} + e_t \end{aligned}\] \(e_t\)的标准差估计为\(1.525\)， 回归复相关系数平方为\(0.52\)。 贝塔值估计为\(\hat\beta=1.146\)。 贝塔值的近似\(95\%\)置信区间可以用估计值加减两倍标准误差计算， 为\((1.10, 1.19)\)位于1的右侧， 所以可以认为贝塔值显著地超过1。

估计变化的贝塔值：

mod1.beta <- garchFit(~ 1 + garch(1,1), data=rtn.cat + rtn.sp500, trace=FALSE)
summary(mod1.beta)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.cat + rtn.sp500, 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aaba64b250>
##  [data = rtn.cat + rtn.sp500]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.139285  0.140215  0.065339  0.919071  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.139285    0.050645    2.750 0.005956 ** 
## omega   0.140215    0.039482    3.551 0.000383 ***
## alpha1  0.065339    0.009868    6.621 3.56e-11 ***
## beta1   0.919071    0.012540   73.292  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -6187.054    normalized:  -2.460061 
## 
## Description:
##  Fri Apr 21 08:03:55 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  539.8153  0           
##  Shapiro-Wilk Test  R    W      0.9854249 2.198538e-15
##  Ljung-Box Test     R    Q(10)  8.709001  0.5599252   
##  Ljung-Box Test     R    Q(15)  15.89029  0.3893801   
##  Ljung-Box Test     R    Q(20)  22.16946  0.3313865   
##  Ljung-Box Test     R^2  Q(10)  8.114921  0.6176126   
##  Ljung-Box Test     R^2  Q(15)  10.04766  0.8167316   
##  Ljung-Box Test     R^2  Q(20)  10.86368  0.9496814   
##  LM Arch Test       R    TR^2   9.232218  0.6829784   
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 4.923303 4.932576 4.923298 4.926669

mod2.beta <- garchFit(~ 1 + garch(1,1), data=rtn.cat - rtn.sp500, trace=FALSE)
summary(mod2.beta)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.cat - rtn.sp500, 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aabc3a6fc0>
##  [data = rtn.cat - rtn.sp500]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.085274  0.035620  0.024234  0.960046  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.085274    0.028513    2.991 0.002784 ** 
## omega   0.035620    0.010593    3.363 0.000772 ***
## alpha1  0.024234    0.005045    4.804 1.56e-06 ***
## beta1   0.960046    0.008561  112.147  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -4554.109    normalized:  -1.810779 
## 
## Description:
##  Fri Apr 21 08:03:56 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value   
##  Jarque-Bera Test   R    Chi^2  11837.86  0         
##  Shapiro-Wilk Test  R    W      0.9329647 0         
##  Ljung-Box Test     R    Q(10)  21.67769  0.01683345
##  Ljung-Box Test     R    Q(15)  22.98638  0.08442948
##  Ljung-Box Test     R    Q(20)  27.82026  0.1137229 
##  Ljung-Box Test     R^2  Q(10)  1.764148  0.997849  
##  Ljung-Box Test     R^2  Q(15)  7.502387  0.9421823 
##  Ljung-Box Test     R^2  Q(20)  8.406546  0.9888179 
##  LM Arch Test       R    TR^2   6.229631  0.9040666 
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 3.624739 3.634011 3.624734 3.628104

mod3.beta <- garchFit(~ 1 + garch(1,1), data=rtn.sp500, trace=FALSE)
summary(mod3.beta)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = rtn.sp500, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000001aabc28c948>
##  [data = rtn.sp500]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1     beta1  
## 0.019327  0.012328  0.078912  0.912590  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.019327    0.017617    1.097    0.273    
## omega   0.012328    0.003061    4.028 5.63e-05 ***
## alpha1  0.078912    0.009468    8.335  < 2e-16 ***
## beta1   0.912590    0.009848   92.669  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -3723.516    normalized:  -1.480523 
## 
## Description:
##  Fri Apr 21 08:03:57 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  199.5819  0           
##  Shapiro-Wilk Test  R    W      0.989017  5.502816e-13
##  Ljung-Box Test     R    Q(10)  15.57277  0.1125331   
##  Ljung-Box Test     R    Q(15)  24.90961  0.05117063  
##  Ljung-Box Test     R    Q(20)  28.50665  0.09793796  
##  Ljung-Box Test     R^2  Q(10)  22.30558  0.01362135  
##  Ljung-Box Test     R^2  Q(15)  24.01634  0.06481646  
##  Ljung-Box Test     R^2  Q(20)  24.89998  0.2052845   
##  LM Arch Test       R    TR^2   26.01127  0.01069455  
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 2.964227 2.973500 2.964222 2.967593

betat.cat <- 1/4*(volatility(mod1.beta)^2 - volatility(mod2.beta)^2) / volatility(mod3.beta)^2

作变化的\(\beta\)的时间序列图：

plot(time.cat, betat.cat, 
  type="l", xlab="年", ylab="贝塔值")

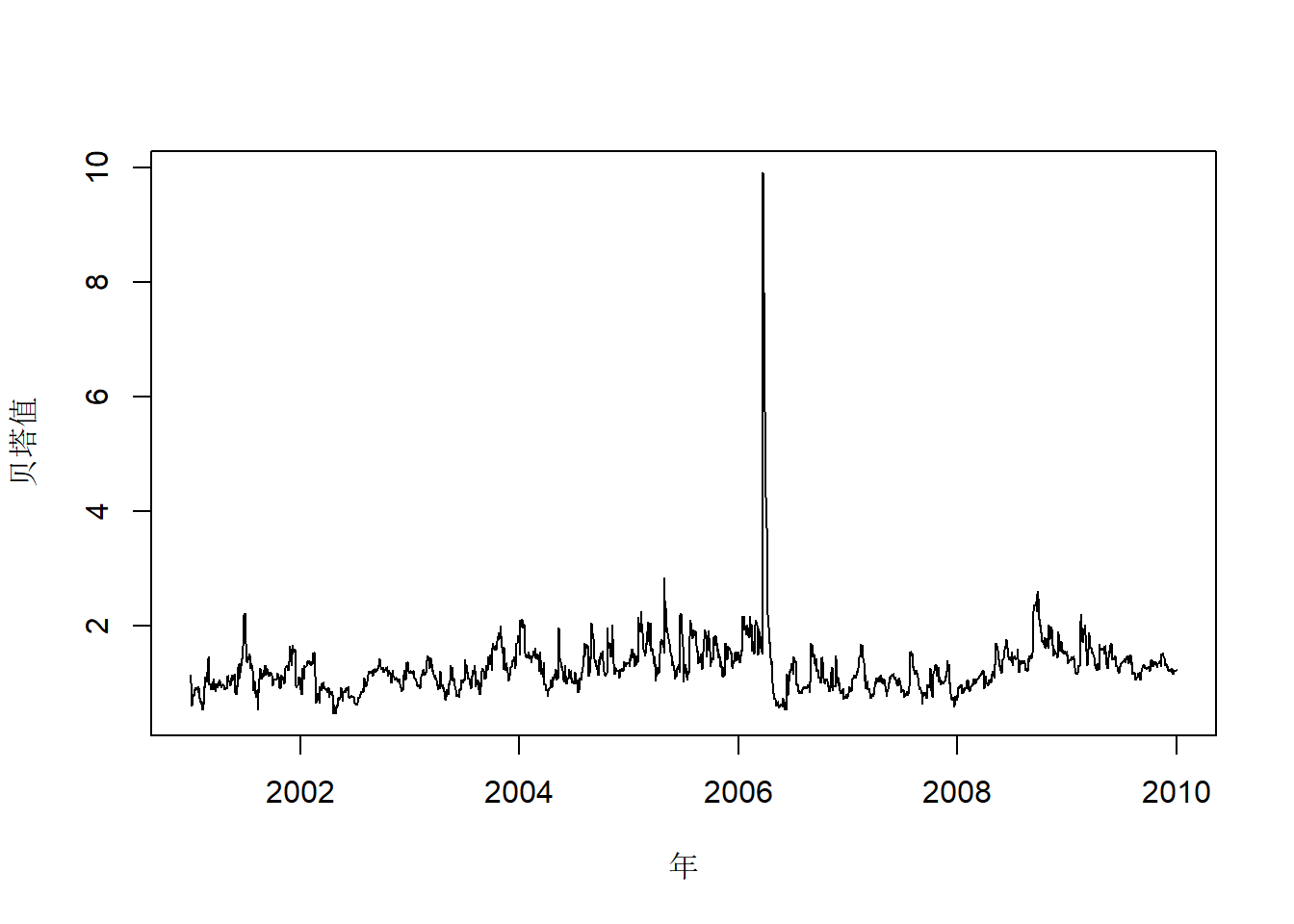
图22.13: CAT股票日对数收益率变化的贝塔值

这些贝塔值有一个明显的异常值， 检查数据发现CAT股票在2006-10-20有一个\(14.52\%\)跌幅。 去掉这个大的值以后作图：

plot(time.cat, betat.cat, 
  type="l", ylim=c(0.4, 3), 
  xlab="年", ylab="贝塔值")
abline(h=mean(betat.cat[betat.cat<4.0]), lty=3)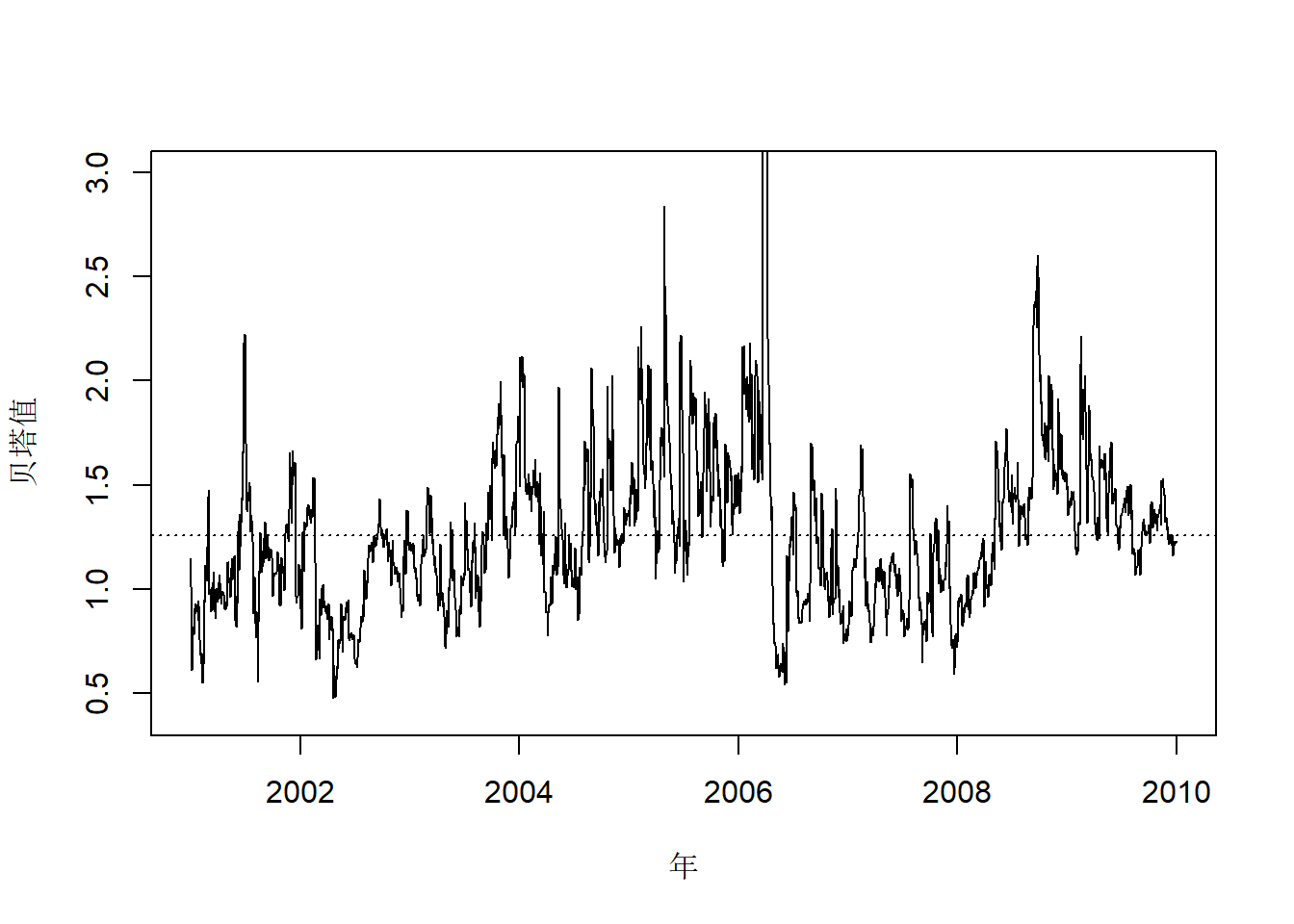

图22.14: CAT股票日对数收益率变化的贝塔值

这个序列看起来是平稳的，但不是不相关列。 如何检验这样一个序列是否均值为常数？ 建议：可以将其前后分成若干段，如4段， 然后引入表示分段的哑变量， 建立带有哑变量自变量的ARMA模型， 检验哑变量是否显著。

22.4 最小方差投资组合

GARCH模型的另外一个应用是在计算最小方差投资组合的过程当中， 计算随时间变化的协方差。

考虑(Markovitz 1959)提出的投资组合中的均值——方差分析， 这里集中考虑最小方差组合。 假设组合中有\(k\)个风险资产， 用组合的波动率（条件标准差）作为风险度量。 设这\(k\)个资产在\(t\)时刻的收益率为\(\boldsymbol r_t = (r_{1t}, \dots, r_{kt})^T\)， 设\(\text{Var}(\boldsymbol r_t) = V_t\)。 设\(t\)时刻组合的权重为\(\boldsymbol w_t = (w_{1t}, \dots, w_{kt})^T\)， 权重是投资组合中每项资产所占的百分比。 组合收益率为\(\boldsymbol w_t^T \boldsymbol r_t\)， 组合收益率的方差为\(\boldsymbol w_t^T V_t \boldsymbol w_t\)。

最小方差投资组合是选\(\boldsymbol w_t\)为如下约束优化问题的解： \[\begin{aligned} & \min_{\boldsymbol w_t} \boldsymbol w_t^T V_t \boldsymbol w_t , \ \text{s.t.}\\ & \boldsymbol 1^T \boldsymbol w_t = 1 \end{aligned}\] 其中\(\boldsymbol 1\)表示元素全是1的列向量， \(\boldsymbol 1^T \boldsymbol w_t = \sum_{i=1}^k w_{it}\)。

如果允许权重取负数， 即可以卖空资产， 上述优化问题的解是 \[\begin{aligned} \boldsymbol w_t = \frac{V_t^{-1} \boldsymbol 1} {\boldsymbol 1^T \boldsymbol V_t^{-1} \boldsymbol 1} \end{aligned}\] 其中分子是协方差阵\(V_t\)的逆矩阵\(V_t^{-1}\)的行和组成的向量， 分母是标量， 使得结果的元素和等于1。

事实上， 定义拉格朗日乘子函数 \[\begin{aligned} f(\boldsymbol w, \lambda) = \boldsymbol w^T V \boldsymbol w - \lambda (\boldsymbol 1^T \boldsymbol w - 1) \end{aligned}\] 令 \[\begin{aligned} \frac{\partial f}{\partial \boldsymbol w} =& 2 V \boldsymbol w - \lambda \boldsymbol 1 = 0 \\ \frac{\partial f}{\partial \lambda} =& -(\boldsymbol 1^T \boldsymbol w - 1) = 0 \end{aligned}\] 可得 \[ \boldsymbol w = \frac{\lambda}{2} V^{-1} \boldsymbol 1 \] 代入\(\boldsymbol 1^T \boldsymbol w - 1\)即可得 \[\begin{aligned} \boldsymbol w = \frac{V^{-1} \boldsymbol 1}{\boldsymbol 1^T V^{-1} \boldsymbol 1} \end{aligned}\]

优化问题的最小值， 即最小方差投资组合的方差，为 \[\begin{aligned} \boldsymbol w^T V \boldsymbol w = \frac{1}{\boldsymbol 1^T V^{-1} \boldsymbol 1} \end{aligned}\]

22.4.1 分段更新权重的最小方差投资组合

在实践中， 权重依赖于用来估计\(V_t\)的样本。 即使使用不随时间变化的权重， 也可以将时间分段， 每段时间采用一个固定权重。

下面将作者放在多个文件中2001年到2010的99只股票的日简单收益率数据， 统一地转换为一个多元xts时间序列对象：

library(tidyverse, quietly = TRUE)
fpath <- "../refs/IAFD/ch5/ch5data"
da <- read_table2(
  paste(fpath, "d-abt-0110.txt", sep="/"),
  col_types=cols(.default=col_double(),
                 date=col_date(format="%Y%m%d")))
date.0110 <- da$date
files.0110 <- c(
  "d-a2a-0110.txt", "d-b2b-0110.txt", "d-c2c-0110.txt", 
  "d-d2e-0110.txt", "d-f2g-0110.txt", "d-h2j-0110.txt", 
  "d-k2m-0110.txt", "d-n2p-0110.txt", "d-q2t-0110.txt", "d-u2x-0110.txt"
)
da.d0110 <- tibble(date=date.0110)
for(fn in files.0110){
  cat("===== Reading", fn, "\n")
  da <- read_table2(
    paste(fpath, fn, sep="/"), 
    col_types=cols(.default=col_double()))
  da.d0110 <- cbind(da.d0110, da)
}
xts.d0110 <- xts(da.d0110[,-1], da.d0110$date)
head(xts.d0110)
save(xts.d0110, file="xts-d0110.RData")

其中原始文件d-f2g-0110.txt有一些格式错误， 进行了编辑修改。读入的数据保存成了R的RData格式。

载入读取的2001-2010各个股票的日简单收益率数据：

load("xts-d0110.RData")

作为示例，仅考虑5只股票： 波音(BA)、卡特彼勒(CAT)、IBM、微软(MSFT)、宝洁(PG)。 将2001-2010的2515个交易日，分成三段： 1:756(2001-01-02到2004-01-07)， 757:1512(2004-01-08到2007-01-09), 1513:2515(2007-01-10到2010-12-31)。

对每一段计算日对数收益率最小方差投资组合的权重， 并计算其波动率的函数：

## x为多元xts类型的日对数收益率序列，
## 结果返回投资组合权重，
## 各成分股的波动率和组合波动率
portfolio.const <- function(x){
  xm <- coredata(x)
  k <- ncol(xm)
  vmat <- var(xm)
  w <- solve(vmat, rep(1.0, k))
  var.port <- 1 / sum(w)
  w <- w * var.port
  
  vola <- c(apply(xm, 2, sd, na.rm=TRUE), Portfolio=sqrt(var.port))
  
  list(weight=w, volatility=vola)
}

计算每一段的结果。将简单收益率转换成了对数收益率。

stocks5 <- c("BA", "CAT", "IBM", "MSFT", "PG")
per <- rbind(c(1,756), c(757,1512), c(1513,2515))
tab.5w <- tibble(
  "资产"=c("波音", "卡特彼勒", "IBM", "微软", "宝洁"),
  "交易日1--756"=0.0, "交易日757--1512"=0.0, "交易日1513--2515"=0.0
)
tab.5v <- tibble(
  "资产"=c("波音", "卡特彼勒", "IBM", "微软", "宝洁", "最小方差投资组合"),
  "交易日1--756"=0.0, "交易日757--1512"=0.0, "交易日1513--2515"=0.0
)
for(j in 1:3){
  res.5s <- portfolio.const(log(1 + xts.d0110[per[j,1]:per[j,2], stocks5]))
  tab.5w[,j+1] <- res.5s$weight*100
  tab.5v[,j+1] <- res.5s$volatility*100
}

三个阶段各个股票的权重(单位为百分之一)：

knitr::kable(tab.5w, digits=2)

资产	交易日1–756	交易日757–1512	交易日1513–2515
波音	6.73	9.09	2.05
卡特彼勒	14.43	3.77	-8.05
IBM	11.14	28.99	34.34
微软	4.45	15.79	0.42
宝洁	63.24	42.35	71.24

三个阶段各个股票的收益率的波动率和最小方差投资组合的收益率的波动率：

knitr::kable(tab.5v, digits=2)

资产	交易日1–756	交易日757–1512	交易日1513–2515
波音	2.37	1.35	2.27
卡特彼勒	2.08	1.64	2.61
IBM	2.22	0.99	1.67
微软	2.45	1.11	2.17
宝洁	1.41	0.89	1.38
最小方差投资组合	1.22	0.70	1.30

可以看出投资组合收益率的波动率低于各个成份股的波动率。 注意教材P.204表5-2中ABT应改为“波音”。

22.4.2 逐点更新权重的最小方差投资组合

上述每一段时间采用固定权重的最小方差投资组合是无法实际应用的， 因为每一段在计算权重时， 要使用本段所有样本来估计协方差阵， 但是投资操作需要预先确定权重。

可以选择比较短的时间段， 用上一时间段估计的协方差阵估计权重， 将估计的权重应用在下一阶段的投资中。

更进一步， 可以进行超前一步的协方差阵预测， 并解出最小方差投资组合权重，用于下一步的投资。 进行超前一步协方差阵预测时， 用现有的观测数据建立GARCH模型估计条件方差和条件协方差， 作为下一步的协方差阵的估计。

这样的方法的缺点是， 得到的协方差阵可能不正定。

作者的函数GMVP()输入一个对数收益率多元时间序列， 指定一个起点\(h\)， 基于时间\(1:h\)的数据建立多个GARCH模型估计第\(h\)步的协方差阵\(\hat V_{h}\)， 用\(\hat V_h\)当作\(h+1\)时刻的协方差阵解出\(h+1\)时刻的最小方差投资组合权重， 计算该组合的对数收益率； 然后基于时间\(1:(h+1)\)的数据重新建模求解\(h+2\)时刻的权重， 如此递推直到数据末尾。 程序如下：

"GMVP" <- function(rtn, start=500){
  ## compute the weights and variance of global minimum variance portfolio.
  ## The time period is from (start) to end of the data.
  ## uses cov(x,y) = [var(x+y)-var(x-y)]/4.

  library(fGarch, quietly = TRUE)
  rtn=as.matrix(rtn)
  
  T=dim(rtn)[1]
  k=dim(rtn)[2]
  wgt = NULL
  mVar=NULL
  VAR = NULL
  ONE=matrix(1,k,1)
  prtn=NULL
  Det=NULL
  for (t in start:T){
    # estimate variances and covariances at time "t".
    COV=matrix(0,k,k)
    for (i in 1:k){
      m1=garchFit(~1+garch(1,1), data=rtn[1:t,i], trace=FALSE)
      COV[i,i]=volatility(m1)[t]^2
      if(i < k){
        for (j in (i+1):k){
          x=rtn[1:t,i]+rtn[1:t,j]
          y=rtn[1:t,i]-rtn[1:t,j]
          m2=garchFit(~1+garch(1,1),data=x,trace=F)
          m3=garchFit(~1+garch(1,1),data=y,trace=F)
          v2=volatility(m2)[t]
          v3=volatility(m3)[t]
          COV[j,i]=(v2^2-v3^2)/4
          COV[i,j]=COV[j,i]
          # end of j-loop
        }
        # end of (if-statement)
      }
      # end of i-loop
    }
    Det=c(Det,det(COV))
    VAR=rbind(VAR,diag(COV))
    Psi=solve(COV, ONE)
    W=sum(Psi)
    Psi=Psi/W
    wgt=cbind(wgt,Psi)
    mVar=c(mVar,1/W)
    if(t < T){
      prtn=c(prtn,sum(rtn[t+1,]*Psi))
    }
    
  }
  
  list(weights=wgt, minVariance=mVar, variances=VAR, returns=prtn, det=Det)
}

函数结果为一个列表， weights是基于\(1:h\)时刻直到基于\(1:T\)时刻估计的投资权重， 但\(t\)时刻解出的权重用于\(t+1\)时刻的投资； minVariance是\((h+1):(T+1)\)时刻对应的最小方差投资组合的最小方差， variances是\(h:T\)时刻的各个个股的条件方差估计， returns是\((h+1):T\)时刻的最小方差投资组合日对数收益率。

这个函数需要对\(t=h,h+1,\dots,T\)每一步建立多个GARCH模型， 程序运行速度较慢， 可以考虑采用并行计算加快速度。

用上述办法对ABT、IBM和WMT(沃尔玛)进行逐步最小方差投资组合计算， 数据从2001-01-02到2010-12-31共2515个交易日， 从\(h=2011\)位置开始，该时间为2008-12-31, 资产组合投资从2009-01-02到2010-12-31日共504个投资。

res.3p <- GMVP(log(1 + coredata(
  xts.d0110[,c("ABT", "IBM", "WMT")])), start=2011)
save(res.3p, file="garchapp-port-abt-ibm-wmt.RData")

GMVP()的结果res.3p为一个列表， 除了returns之外都有对应于2011:2515的505个结果， 而returns则保存了对应于时刻2012:2515的504个最小方差投资组合的日对数收益率。

投资组合权重的取值范围：

range(res.3p$`weights`)

## [1] -0.5880472  1.0954013

最后的504天的投资组合的平均日对数收益率：

mean(res.3p$returns)

## [1] 0.0001088877

最后504天每个个股的平均日对数收益率：

T1 <- 2012; T2 <- 2515
colMeans(log(1 + coredata(
  xts.d0110[T1:T2,c("ABT", "IBM", "WMT")])))

##           ABT           IBM           WMT 
## -8.356484e-05  1.180094e-03  1.122753e-05

从投资组合的平均收益来看表现并不够好。

最后504天投资组合的日对数收益率的样本标准差：

sd(res.3p$returns)

## [1] 0.01026185

最后504天三个个股的日对数收益率的样本标准差：

T1 <- 2012; T2 <- 2515
apply(log(1 + coredata(
  xts.d0110[T1:T2,c("ABT", "IBM", "WMT")])), 2, sd)

##        ABT        IBM        WMT 
## 0.01315420 0.01460831 0.01171992

投资组合的对数收益率的样本标准差低于每个个股的样本标准差。

个股的条件方差的分布：

summary(res.3p$variances)

##        V1                  V2                  V3           
##  Min.   :7.438e-05   Min.   :6.389e-05   Min.   :5.303e-05  
##  1st Qu.:1.007e-04   1st Qu.:1.068e-04   1st Qu.:8.496e-05  
##  Median :1.377e-04   Median :1.579e-04   Median :1.055e-04  
##  Mean   :1.994e-04   Mean   :2.382e-04   Mean   :1.674e-04  
##  3rd Qu.:2.360e-04   3rd Qu.:2.767e-04   3rd Qu.:1.609e-04  
##  Max.   :7.029e-04   Max.   :1.369e-03   Max.   :6.714e-04

最小方差投资组合的方差的分布：

summary(res.3p$minVariance)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 3.194e-05 4.859e-05 6.913e-05 9.866e-05 1.072e-04 3.486e-04

可以看出最小方差投资组合的条件方差要低。用并列盒形图比较：

var.3p <- as.data.frame(res.3p$variances)
names(var.3p) <- c("ABT", "IBM", "WMT")
var.3p[["MinVarPortf"]] <- res.3p$minVariance
boxplot(var.3p, main="三个个股与最小方差投资组合的日对数收益率条件方差分布")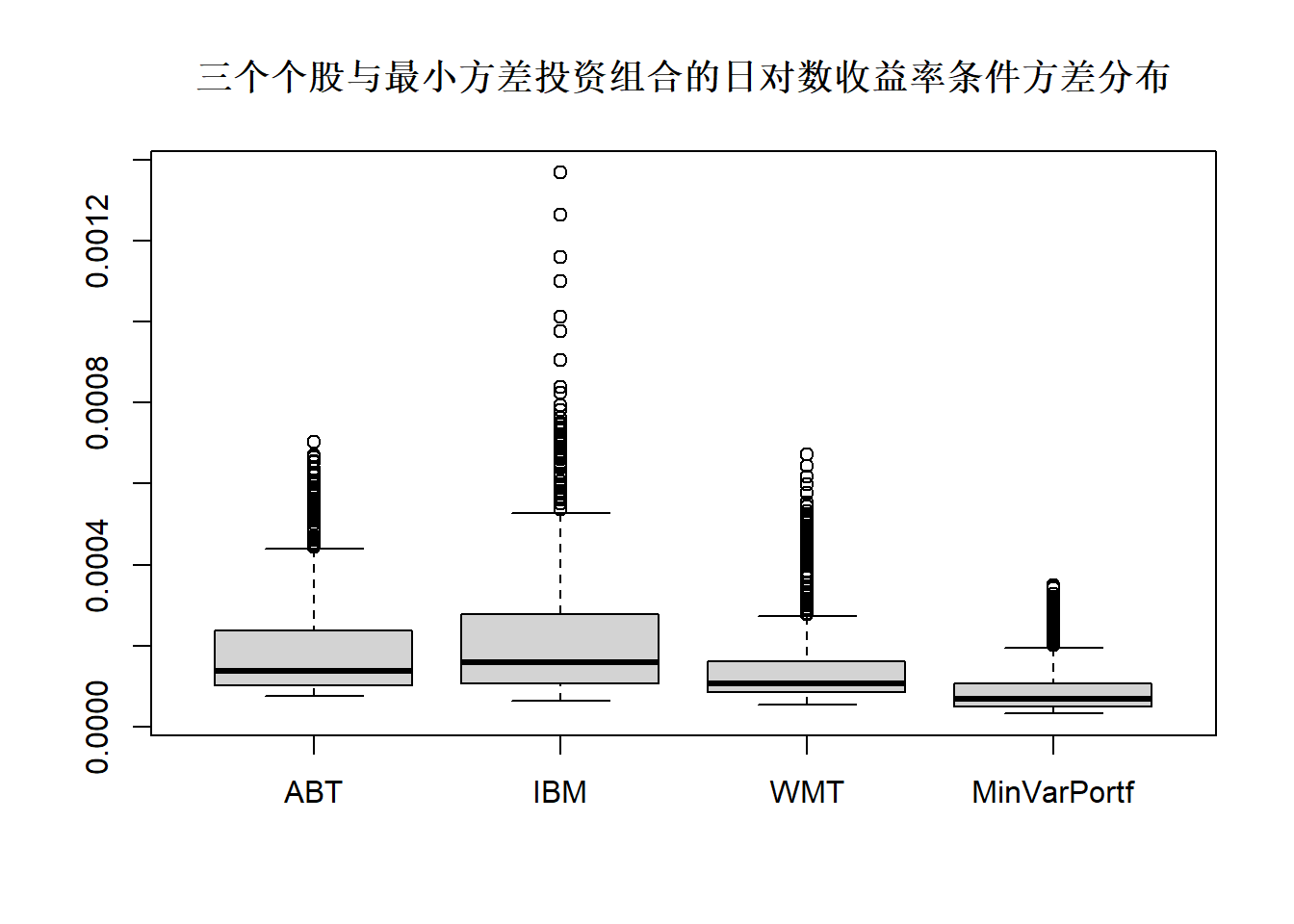

图22.15: 三个个股与最小方差投资组合的日对数收益率条件方差分布

最后的20个交易日的个股波动率与最小方差投资组合波动率的列表(单位：\(\%\))：

T2 <- length(index(xts.d0110))
T3 <- length(res.3p$minVariance)
vola.3p20 <- as.data.frame(matrix(0.0, 20, 4))
vola.3p20[,1:3] <- sqrt(res.3p$variances[(T3-19):T3,])*100
vola.3p20[,4] <- sqrt(res.3p$minVariance[(T3-19):T3])*100
names(vola.3p20) <- c("ABT", "IBM", "WMT", "MinVarPort")
vola.3p20 <- cbind("Date"=index(xts.d0110)[(T2-19):T2], vola.3p20)
knitr::kable(vola.3p20, digits=2)

Date	ABT	IBM	WMT	MinVarPort
2010-12-03	0.98	1.25	0.81	0.71
2010-12-06	0.97	1.19	0.80	0.70
2010-12-07	0.98	1.15	0.79	0.70
2010-12-08	0.96	1.12	0.81	0.69
2010-12-09	0.95	1.10	0.80	0.68
2010-12-10	0.95	1.07	0.79	0.66
2010-12-13	0.96	1.03	0.78	0.65
2010-12-14	0.95	1.00	0.77	0.64
2010-12-15	0.96	1.02	0.76	0.65
2010-12-16	0.95	1.01	0.76	0.64
2010-12-17	0.95	0.98	0.76	0.64
2010-12-20	0.94	0.95	0.76	0.63
2010-12-21	0.92	0.92	0.78	0.64
2010-12-22	0.92	0.93	0.77	0.63
2010-12-23	0.91	0.90	0.77	0.62
2010-12-27	0.89	0.87	0.77	0.61
2010-12-28	0.90	0.85	0.76	0.60
2010-12-29	0.89	0.83	0.75	0.59
2010-12-30	0.87	0.82	0.75	0.59
2010-12-31	0.86	0.80	0.74	0.58

22.5 预测

联合使用均值方程和波动率方程建模可以更好地描述数据特征， 也可以得到更合理的预测区间。

以石油价格的建模和预测为例。 2008年夏和2011年春的石油价格上涨对世界经济有很大的影响。 预测原油价格有重大意义， 但是石油价格收很多因素和外部扰动的影响， 不容易分析。

这里利用1997-01-03到2010-09-24的美国原油价格的周数据， 共717个观测值。 数据是以估计的进口数量（Freight on board，FOB）为权重的加权离岸价格的周数据， 用美元/桶表示。数据可以从 US Energy Information Administration网站下载。

载入数据：

# 输入文件用了空格和制表符分隔，read_table目前不支持。
d.oil <- read.table(
  "w-petroprice.txt", header=TRUE) |> 
  as_tibble()
xts.oil <- xts(
  d.oil[,4:5], make_date(
    d.oil[["Year"]], d.oil[["Mon"]], d.oil[["Day"]])
)
poil <- d.oil[["US"]]
doil <- diff(poil)

价格的时间序列图：

plot(xts.oil[,"US"], type="l", 
     main="美国石油价格周数据",
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years",
     col="red")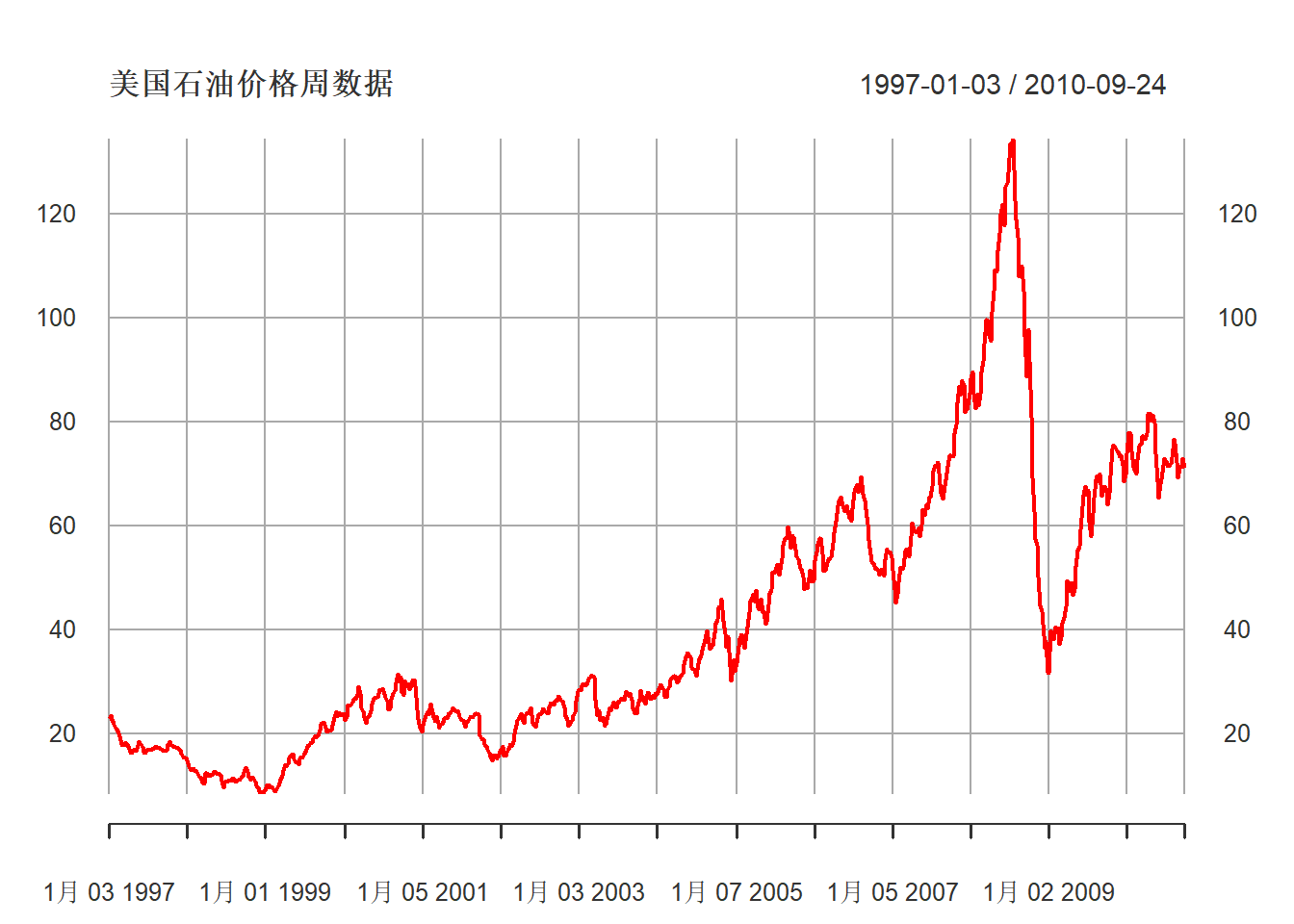

图22.16: 美国石油价格周数据

可以看出价格序列非平稳， 存在明显的趋势， 在2008年夏季有明显的峰值。

价格差分数据：

plot(diff(xts.oil[,"US"]), type="l", 
     main="美国石油价格周数据的变化量",
     major.ticks="years", minor.ticks=NULL, 
     grid.ticks.on="years",
     col="red")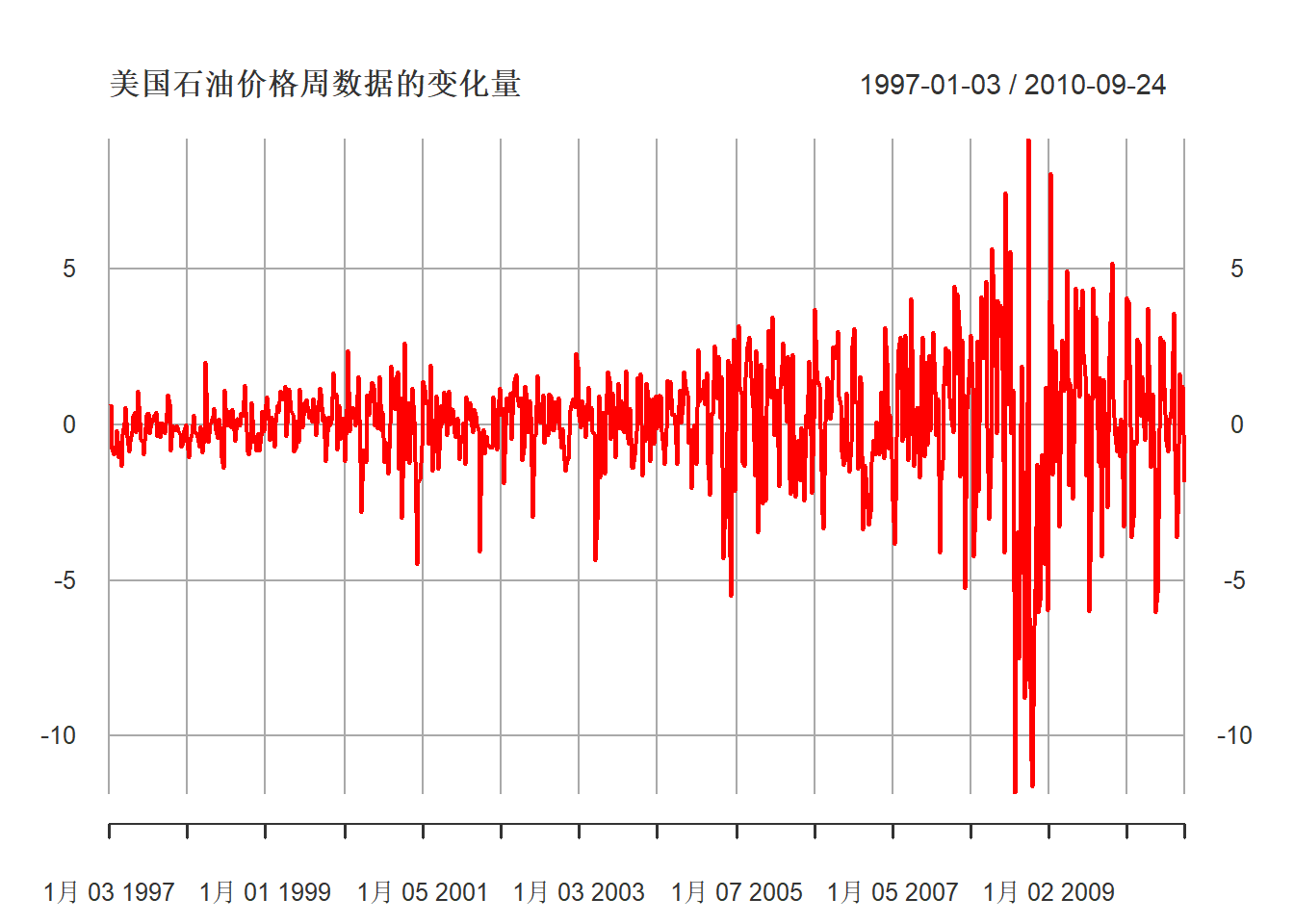

图22.17: 美国石油价格周数据差分

可以看出差分的均值基本是平稳的， 但存在波动率聚集， 用一般的ARMA模型无法解释这样的波动率聚集现象。

ARMA-GARCH模型用ARMA模型建立均值方程， 用GARCH模型描述波动率， 可以更好地解释上面的差分序列这样的具有波动率聚集的数据， 也能改善预测。

记\(C_t\)为价格差分序列， 对其建立平稳ARMA模型。 ACF图：

forecast::Acf(doil, lag.max = 30, main="")

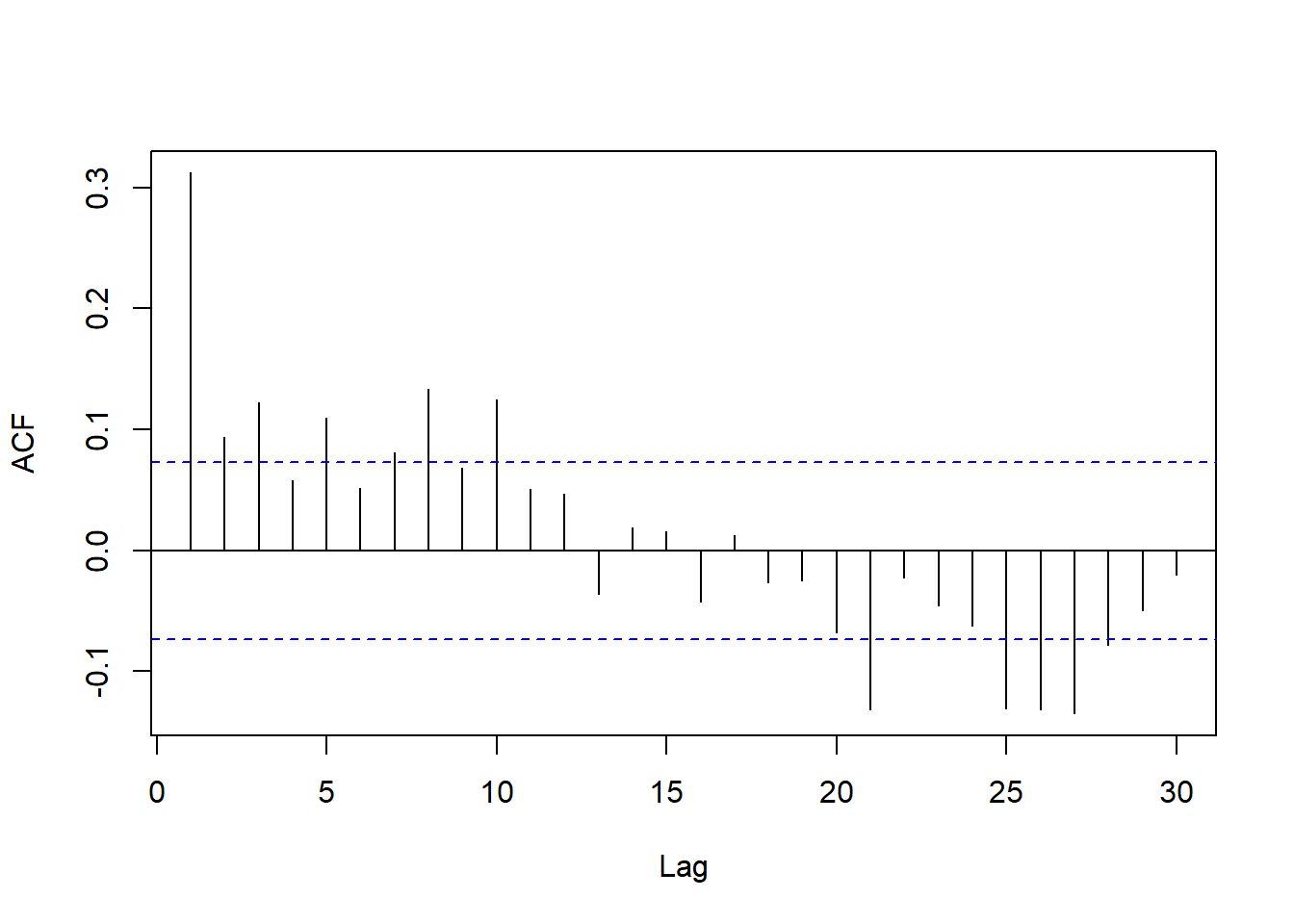
图22.18: 美国石油价格周数据差分的ACF

PACF图：

pacf(doil, lag.max = 30, main="")

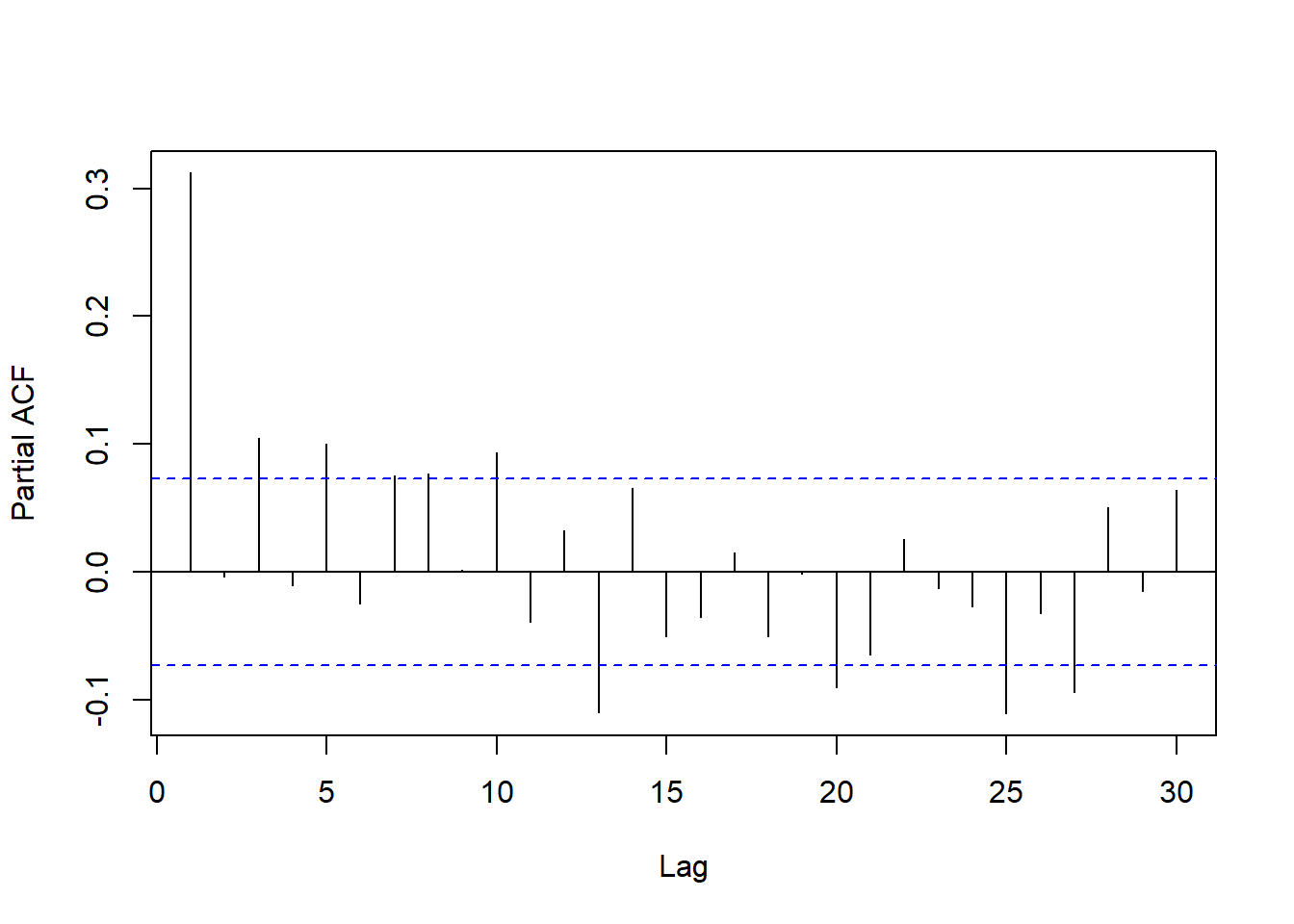
图22.19: 美国石油价格周数据差分的PACF

ACF和PACF中可以看出没有单位根， 相关性都不强， 但是PACF中滞后5、10、20、25处显著， 考虑用周期5的季节成分； 除此之外PACF只有滞后1、3显著， 可考虑AR(3)。 周期成分的PACF值也比较小， 考虑低阶的周期成分， 用ARMA\((3,0)(2,0)_5\)。

建模：

mod.oil1 <- arima(
  doil, order=c(3,0,0),
  seasonal=list(order=c(2,0,0), period=5)
)
mod.oil1

## 
## Call:
## arima(x = doil, order = c(3, 0, 0), seasonal = list(order = c(2, 0, 0), period = 5))
## 
## Coefficients:
##          ar1      ar2     ar3    sar1    sar2  intercept
##       0.3187  -0.0690  0.1071  0.0814  0.1177     0.0644
## s.e.  0.0372   0.0397  0.0375  0.0377  0.0376     0.1377
## 
## sigma^2 estimated as 3.632:  log likelihood = -1477.91,  aic = 2969.82

其中的均值(intercept)不显著， 去掉均值：

mod.oil2 <- arima(
  doil, order=c(3,0,0),
  seasonal=list(order=c(2,0,0), period=5),
  include.mean=FALSE
)
mod.oil2

## 
## Call:
## arima(x = doil, order = c(3, 0, 0), seasonal = list(order = c(2, 0, 0), period = 5), 
##     include.mean = FALSE)
## 
## Coefficients:
##          ar1      ar2     ar3    sar1    sar2
##       0.3191  -0.0689  0.1075  0.0817  0.1181
## s.e.  0.0372   0.0397  0.0375  0.0377  0.0376
## 
## sigma^2 estimated as 3.634:  log likelihood = -1478.02,  aic = 2968.04

系数只有AR2不显著，但也可以保留，模型为 \[\begin{aligned} & (1 - 0.32 B + 0.07 B^2 - 0.11 B^3)(1 - 0.08 B^5 - 0.13 B^{10}) C_t = \varepsilon_t, \\ & \text{Var}(\varepsilon_t) = 3.634 \end{aligned}\]

模型诊断：

tsdiag(mod.oil2)

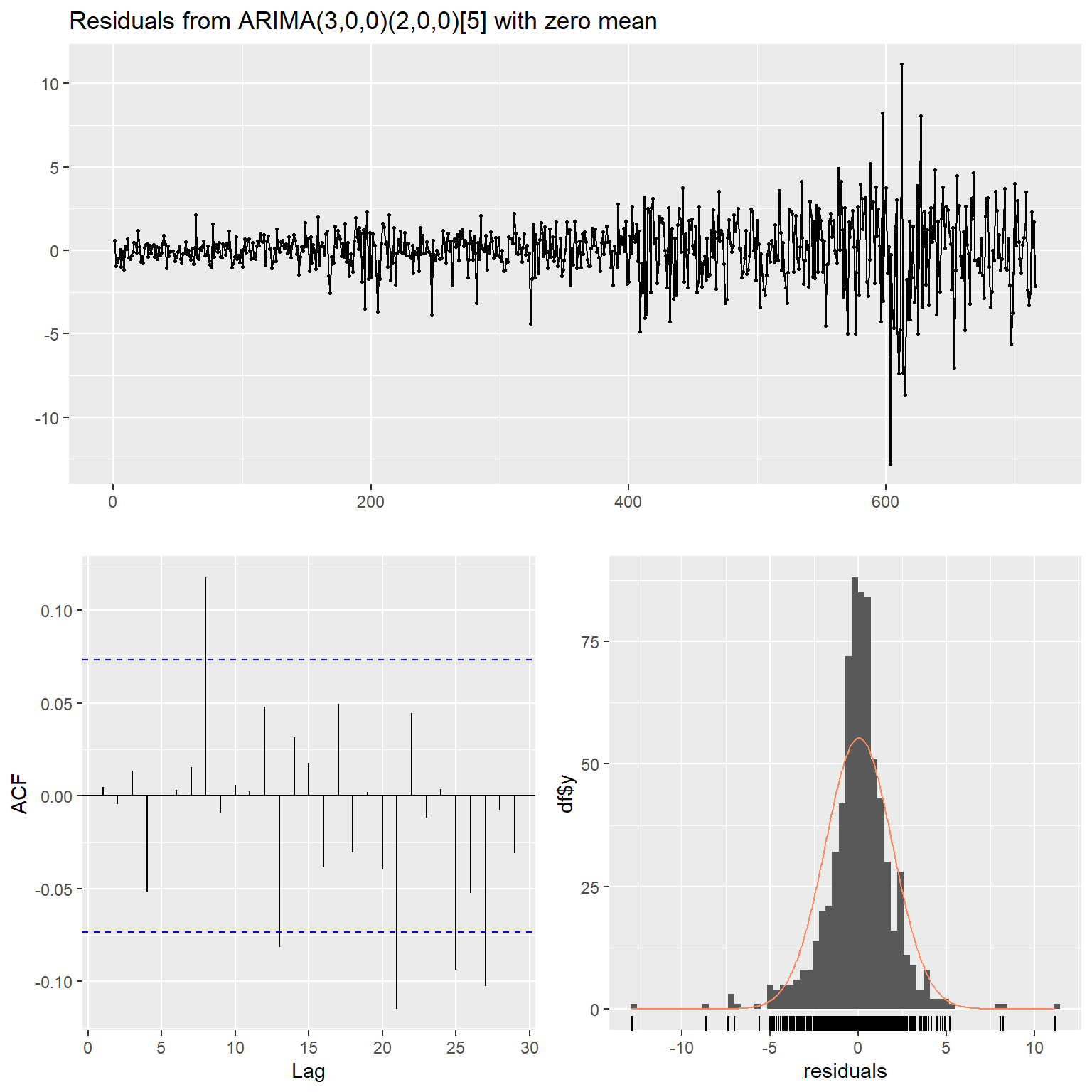
图22.20: 石油价格模型诊断

从模型诊断来看， 残差存在波动率聚集， 白噪声检验都是通过的。

因为EGARCH模型的程序不支持季节性的ARMA， 所以先建立一个纯季节模型， 对残差再进一步建模。

mod.oil3 <- arima(
  doil, order=c(0,0,0),
  seasonal=list(order=c(2,0,0), period=5),
  include.mean=FALSE
)
mod.oil3

## 
## Call:
## arima(x = doil, order = c(0, 0, 0), seasonal = list(order = c(2, 0, 0), period = 5), 
##     include.mean = FALSE)
## 
## Coefficients:
##         sar1    sar2
##       0.0983  0.1152
## s.e.  0.0371  0.0372
## 
## sigma^2 estimated as 4.057:  log likelihood = -1517.42,  aic = 3040.84

模型为 \[\begin{aligned} (1 - 0.0983 B^5 - 0.1152 B^{10}) C_t = C^*_t, \ t=11,12,\dots, 716 \end{aligned}\]

用三种不同的方法计算上述纯季节模型的残差：

ad1.oil <- residuals(mod.oil3) # 与输入序列等长
ad2.oil <- doil[11:716] - 0.0983*doil[6:711] - 0.1152*doil[1:706]
ad3.oil <- stats::filter(
  doil, c(1, rep(0,4), -0.0983, rep(0,4), -0.1152),
  method="convolution", side=1)
max(abs(ad1.oil[11:716] - ad2.oil))

## [1] 0.0004208447

max(abs(ad1.oil[11:716] - ad3.oil[11:716]))

## [1] 0.0004208447

adoil <- ad1.oil[11:716]

去掉季节项后的序列记为\(C^*_t\)， 其ACF和PACF为:

forecast::Acf(adoil, lag.max=30, main="")

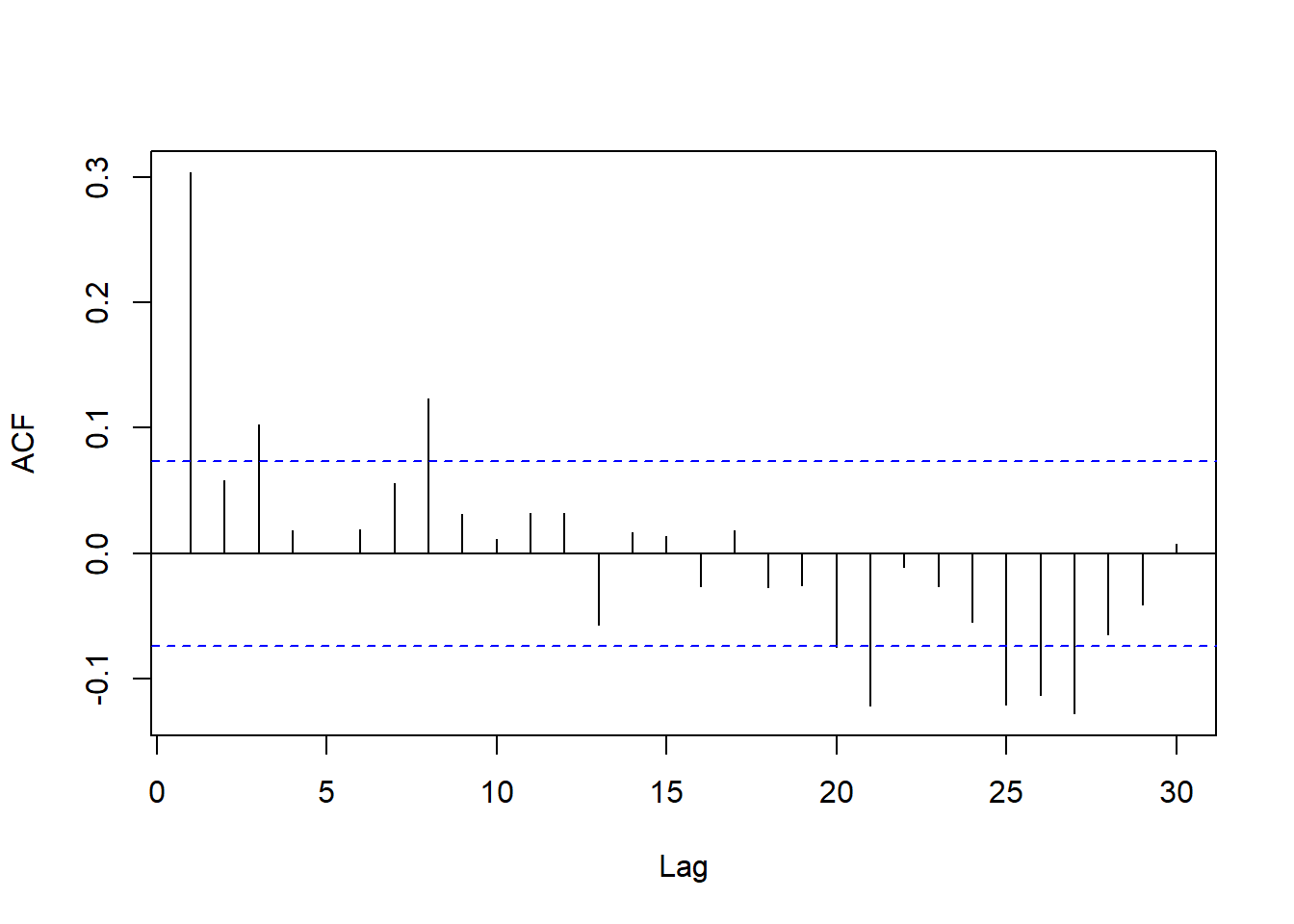
图22.21: 去掉季节项后的ACF

pacf(adoil, lag.max=30, main="")

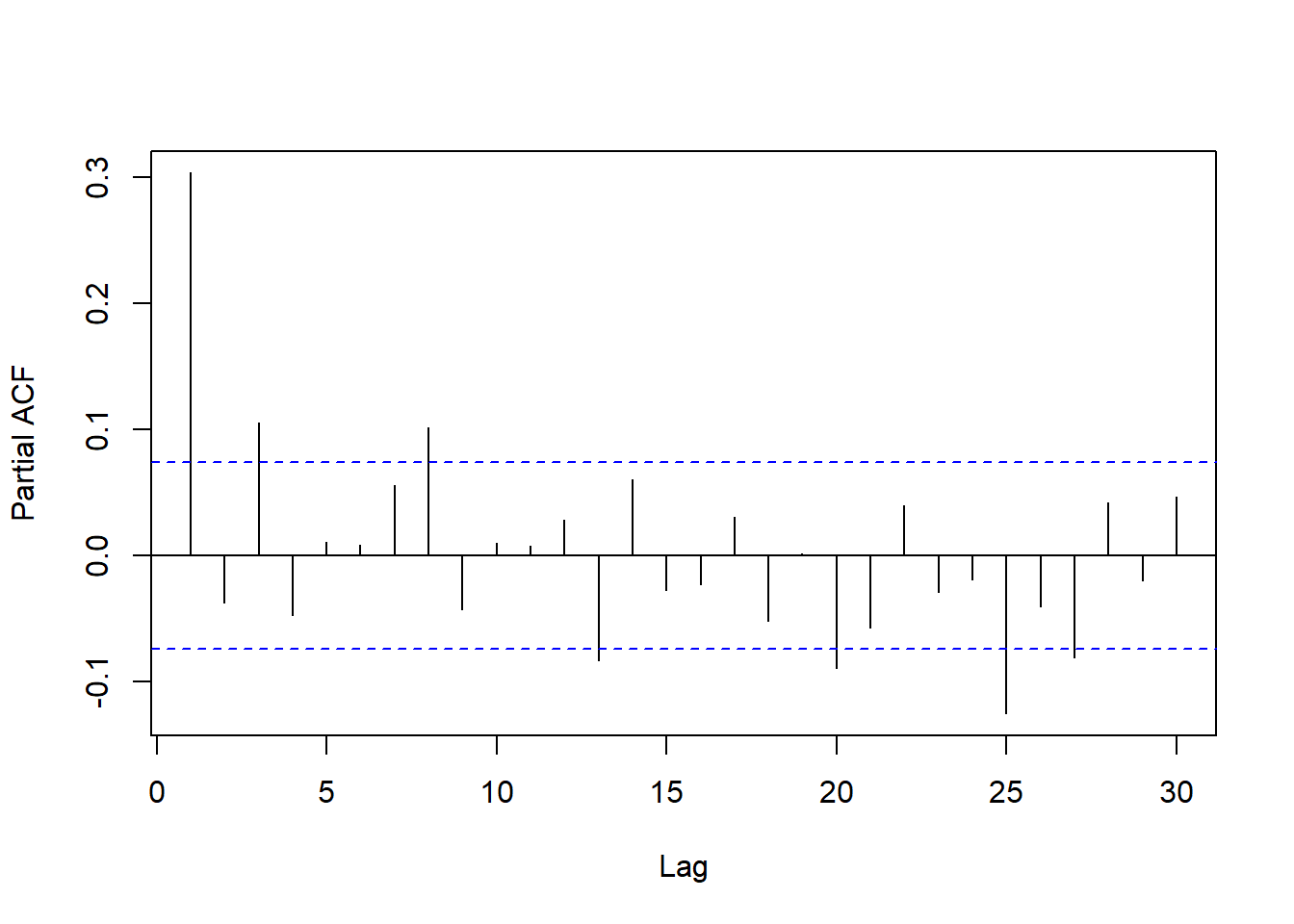
图22.22: 去掉季节项后的PACF

滞后5、10、15已经不显著， 虽然滞后20和25显著但在较高的滞后阶。

对\(C^*_t\)建立ARMA(3,0)结合GARCH(1,1)的模型。

oil.mod4 <- garchFit(
  ~ arma(3,0) + garch(1,1),
  data=adoil,
  include.mean=FALSE, trace=FALSE
)
summary(oil.mod4)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~arma(3, 0) + garch(1, 1), data = adoil, include.mean = FALSE, 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ arma(3, 0) + garch(1, 1)
## <environment: 0x000001aab3ae1b10>
##  [data = adoil]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       ar1        ar2        ar3      omega     alpha1      beta1  
##  0.323494  -0.092111   0.040486   0.016751   0.090404   0.910225  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## ar1     0.323494    0.040310    8.025 1.11e-15 ***
## ar2    -0.092111    0.041690   -2.209   0.0271 *  
## ar3     0.040486    0.040117    1.009   0.3129    
## omega   0.016751    0.008171    2.050   0.0403 *  
## alpha1  0.090404    0.015674    5.768 8.04e-09 ***
## beta1   0.910225    0.014837   61.349  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -1262.73    normalized:  -1.78857 
## 
## Description:
##  Fri Apr 21 08:03:59 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  174.5855  0           
##  Shapiro-Wilk Test  R    W      0.9767892 3.798343e-09
##  Ljung-Box Test     R    Q(10)  15.30529  0.1213217   
##  Ljung-Box Test     R    Q(15)  20.05642  0.1697791   
##  Ljung-Box Test     R    Q(20)  22.75188  0.3011415   
##  Ljung-Box Test     R^2  Q(10)  3.155885  0.9775137   
##  Ljung-Box Test     R^2  Q(15)  8.029569  0.9225918   
##  Ljung-Box Test     R^2  Q(20)  9.65231   0.9740473   
##  LM Arch Test       R    TR^2   3.59896   0.9896355   
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 3.594137 3.632887 3.593994 3.609110

估计的模型可以写成： \[\begin{aligned} C^*_t =& 0.323 C^*_{t-1} - 0.092 C^*_{t-2} + 0.040 C^*_{t-3} + a_t \\ a_t =& \sigma_t \varepsilon_t, \ \epsilon_t \text{ iid N}(0,1) \\ \sigma_t^2 =& 0.01675 + 0.0904 a_{t-1}^2 + 0.9102 \sigma_{t-1}^2 \end{aligned}\] 其中除了AR3系数以外都显著。 残差白噪声检验都通过了。

plot(oil.mod4, which=3)

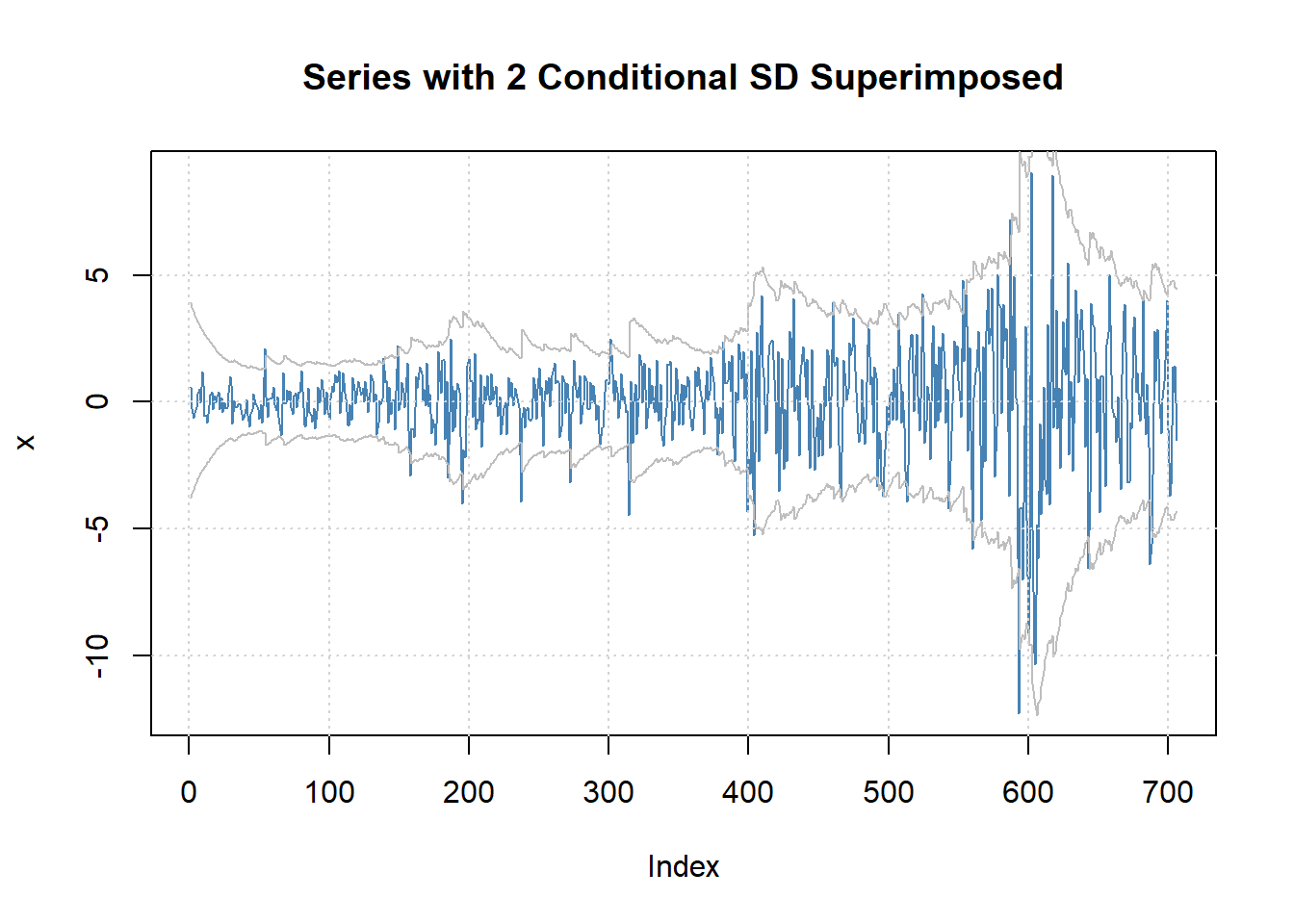
图22.23: 去除季节项后的序列及两倍波动率

plot(oil.mod4, which=13)

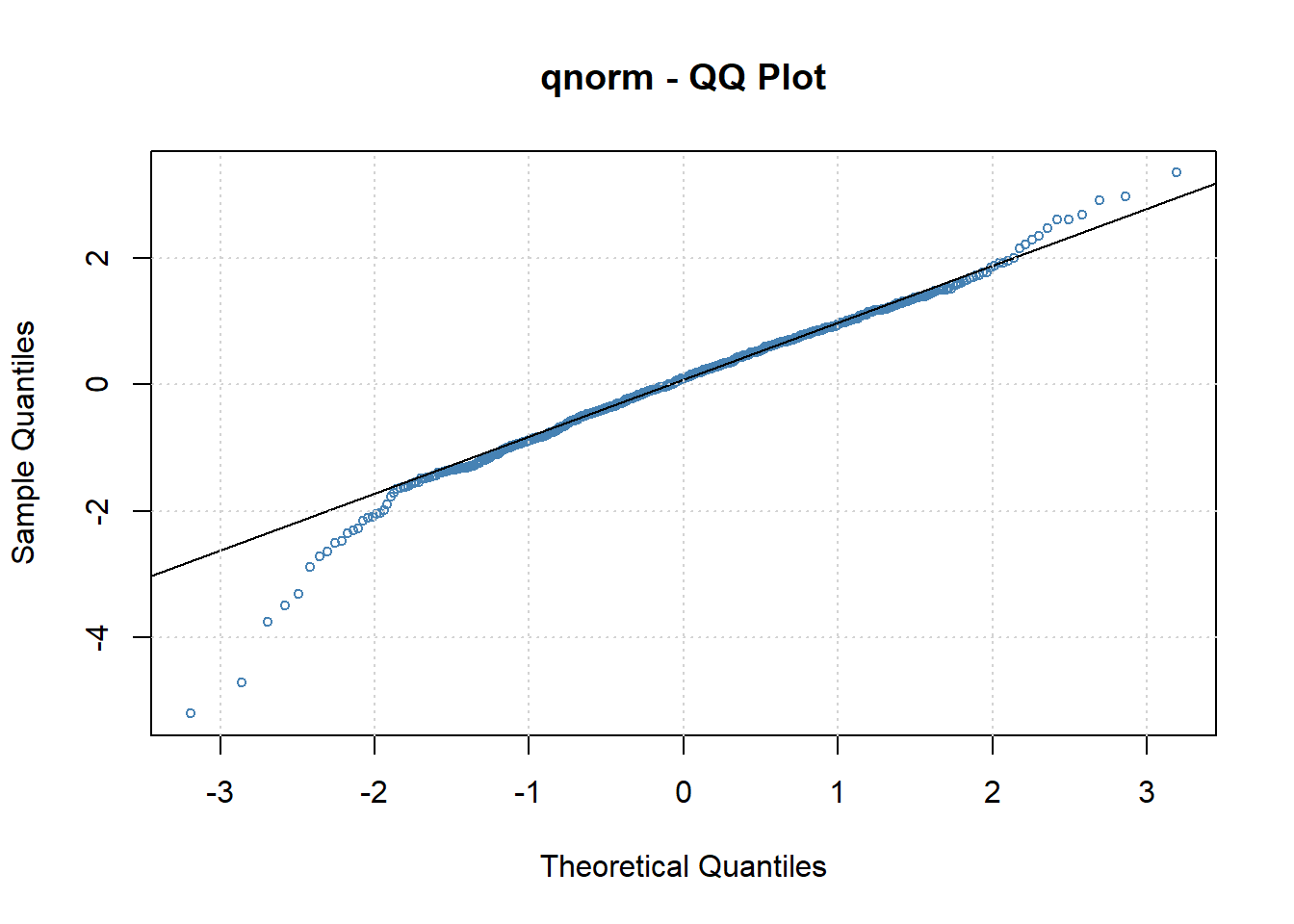
图22.24: 去除季节项后的ARMA-GARCH标准化残差QQ图

标准化残差比正态分布厚尾。

为了处理残差的厚尾性， 采用标准化t分布的GARCH模型。

oil.mod5 <- garchFit(
  ~ arma(3,0) + garch(1,1),
  cond.dist="std",
  data=adoil,
  include.mean=FALSE, trace=FALSE
)
summary(oil.mod5)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~arma(3, 0) + garch(1, 1), data = adoil, cond.dist = "std", 
##     include.mean = FALSE, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ arma(3, 0) + garch(1, 1)
## <environment: 0x000001aab876c4b0>
##  [data = adoil]
## 
## Conditional Distribution:
##  std 
## 
## Coefficient(s):
##       ar1        ar2        ar3      omega     alpha1      beta1      shape  
##  0.325396  -0.065110   0.056019   0.011176   0.119701   0.891778   6.761292  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## ar1     0.325396    0.038778    8.391  < 2e-16 ***
## ar2    -0.065110    0.040791   -1.596    0.110    
## ar3     0.056019    0.039464    1.420    0.156    
## omega   0.011176    0.008849    1.263    0.207    
## alpha1  0.119701    0.023879    5.013 5.36e-07 ***
## beta1   0.891778    0.019161   46.541  < 2e-16 ***
## shape   6.761292    1.582183    4.273 1.93e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -1245.39    normalized:  -1.764009 
## 
## Description:
##  Fri Apr 21 08:04:00 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value    
##  Jarque-Bera Test   R    Chi^2  278.6969  0          
##  Shapiro-Wilk Test  R    W      0.9715166 1.72838e-10
##  Ljung-Box Test     R    Q(10)  14.96489  0.1333472  
##  Ljung-Box Test     R    Q(15)  20.36323  0.158437   
##  Ljung-Box Test     R    Q(20)  22.95429  0.2910445  
##  Ljung-Box Test     R^2  Q(10)  4.517928  0.9209735  
##  Ljung-Box Test     R^2  Q(15)  8.788443  0.8883167  
##  Ljung-Box Test     R^2  Q(20)  10.55469  0.9569638  
##  LM Arch Test       R    TR^2   6.019291  0.9151065  
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 3.547847 3.593056 3.547653 3.565316

估计的模型可以写成： \[\begin{aligned} C^*_t =& 0.325 C^*_{t-1} - 0.065 C^*_{t-2} + 0.056 C^*_{t-3} + a_t \\ a_t =& \sigma_t \varepsilon_t, \ \epsilon_t \text{ iid }t^*(6.76) \\ \sigma_t^2 =& 0.0112 + 0.1197 a_{t-1}^2 + 0.8918 \sigma_{t-1}^2 \end{aligned}\] 系数中AR2, AR3不显著， \(\alpha_0 = 0.0112\)不显著。 白噪声检验都通过了。

作标准化残差相对于标准化t分布的QQ图：

plot(oil.mod5, which=13)

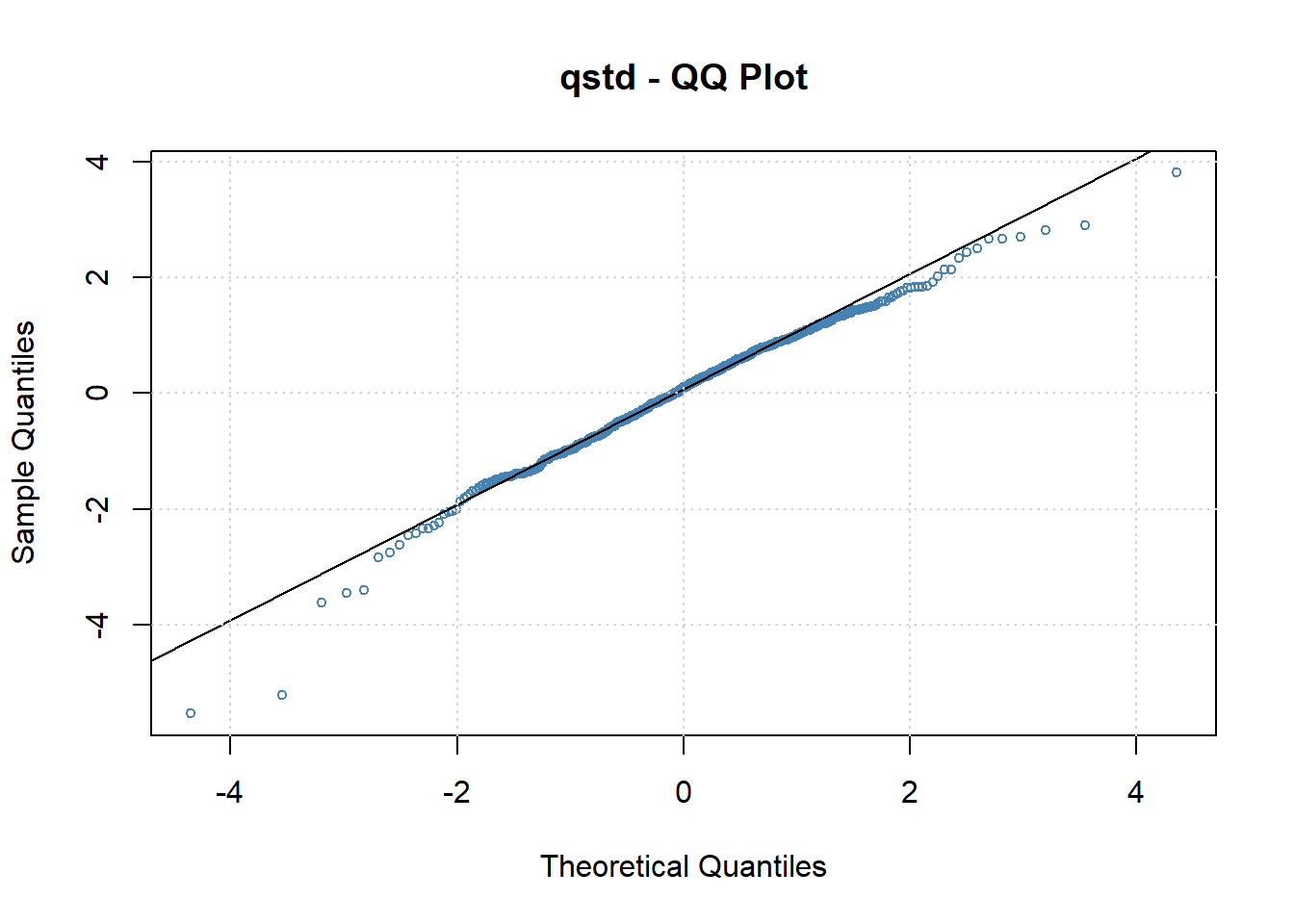
图22.25: 去除季节项后的t分布ARMA-GARCH标准化残差QQ图

这时厚尾性不太明显，但出现了左偏。

于是，改用有偏的标准化t分布作为GARCH模型的条件分布：

oil.mod6 <- garchFit(
  ~ arma(1,0) + garch(1,1),
  cond.dist="sstd",
  data=adoil,
  include.mean=FALSE, trace=FALSE
)
summary(oil.mod6)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~arma(1, 0) + garch(1, 1), data = adoil, cond.dist = "sstd", 
##     include.mean = FALSE, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ arma(1, 0) + garch(1, 1)
## <environment: 0x000001aab98264a8>
##  [data = adoil]
## 
## Conditional Distribution:
##  sstd 
## 
## Coefficient(s):
##      ar1     omega    alpha1     beta1      skew     shape  
## 0.294919  0.011334  0.121624  0.892569  0.861831  6.470838  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## ar1     0.294919    0.036755    8.024 1.11e-15 ***
## omega   0.011334    0.009021    1.256    0.209    
## alpha1  0.121624    0.024040    5.059 4.21e-07 ***
## beta1   0.892569    0.018457   48.359  < 2e-16 ***
## skew    0.861831    0.047753   18.048  < 2e-16 ***
## shape   6.470838    1.532285    4.223 2.41e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -1243.852    normalized:  -1.76183 
## 
## Description:
##  Fri Apr 21 08:04:00 2023 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  268.3856  0           
##  Shapiro-Wilk Test  R    W      0.9721041 2.393857e-10
##  Ljung-Box Test     R    Q(10)  17.27448  0.06850684  
##  Ljung-Box Test     R    Q(15)  22.22733  0.1019802   
##  Ljung-Box Test     R    Q(20)  24.927    0.204238    
##  Ljung-Box Test     R^2  Q(10)  4.370554  0.9290864   
##  Ljung-Box Test     R^2  Q(15)  8.949599  0.880138    
##  Ljung-Box Test     R^2  Q(20)  10.7288   0.9529546   
##  LM Arch Test       R    TR^2   5.740867  0.9285771   
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 3.540657 3.579407 3.540514 3.555630

估计的模型可以写成： \[\begin{align} C^*_t =& 0.295 C^*_{t-1} + a_t \\ a_t =& \sigma_t \varepsilon_t, \ \epsilon_t \text{ iid }t^*(6.76, 0.862) \\ \sigma_t^2 =& 0.0113 + 0.1216 a_{t-1}^2 + 0.8926 \sigma_{t-1}^2 \tag{22.5} \end{align}\] 其中参数\(0.8618<1\)表示左偏， 且其近似95%置信区间为\((0.766, 0.957)\)不包含1， 所以可以认为其显著地偏离1。

标准化残差相对有有偏的标准化t分布的QQ图：

plot(oil.mod6, which=13)

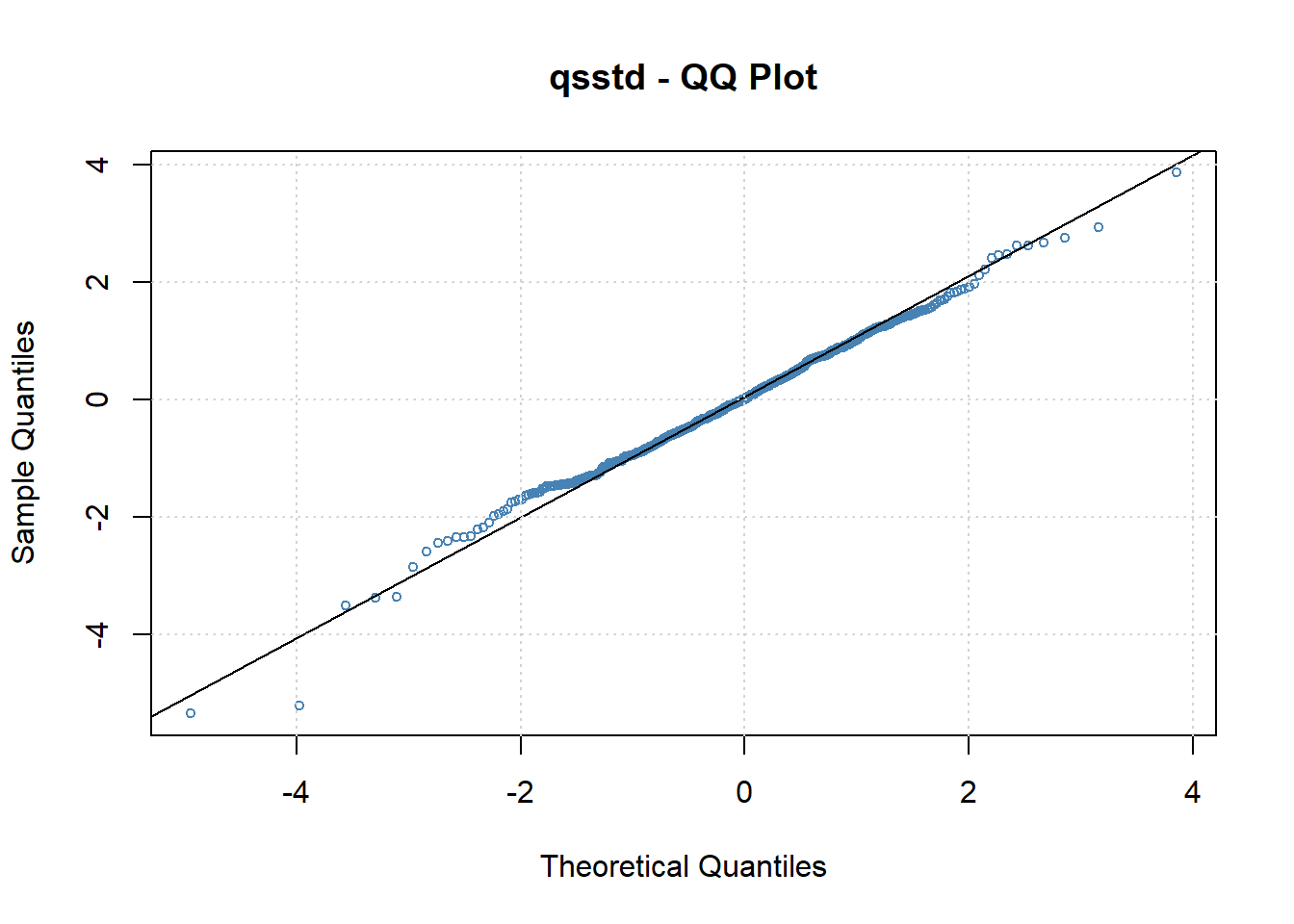
图22.26: 去除季节项后的有偏t分布ARMA-GARCH标准化残差QQ图

这个图形说明有偏t分布拟合数据很好。 模型残差的白噪声检验也都通过了。

模型的标准化残差的时间序列图：

plot(oil.mod6, which=9)

图22.27: 去除季节项后的有偏t分布ARMA-GARCH标准化残差

\(C^*_t\)序列叠加了两倍波动率的图形：

plot(oil.mod6, which=3)

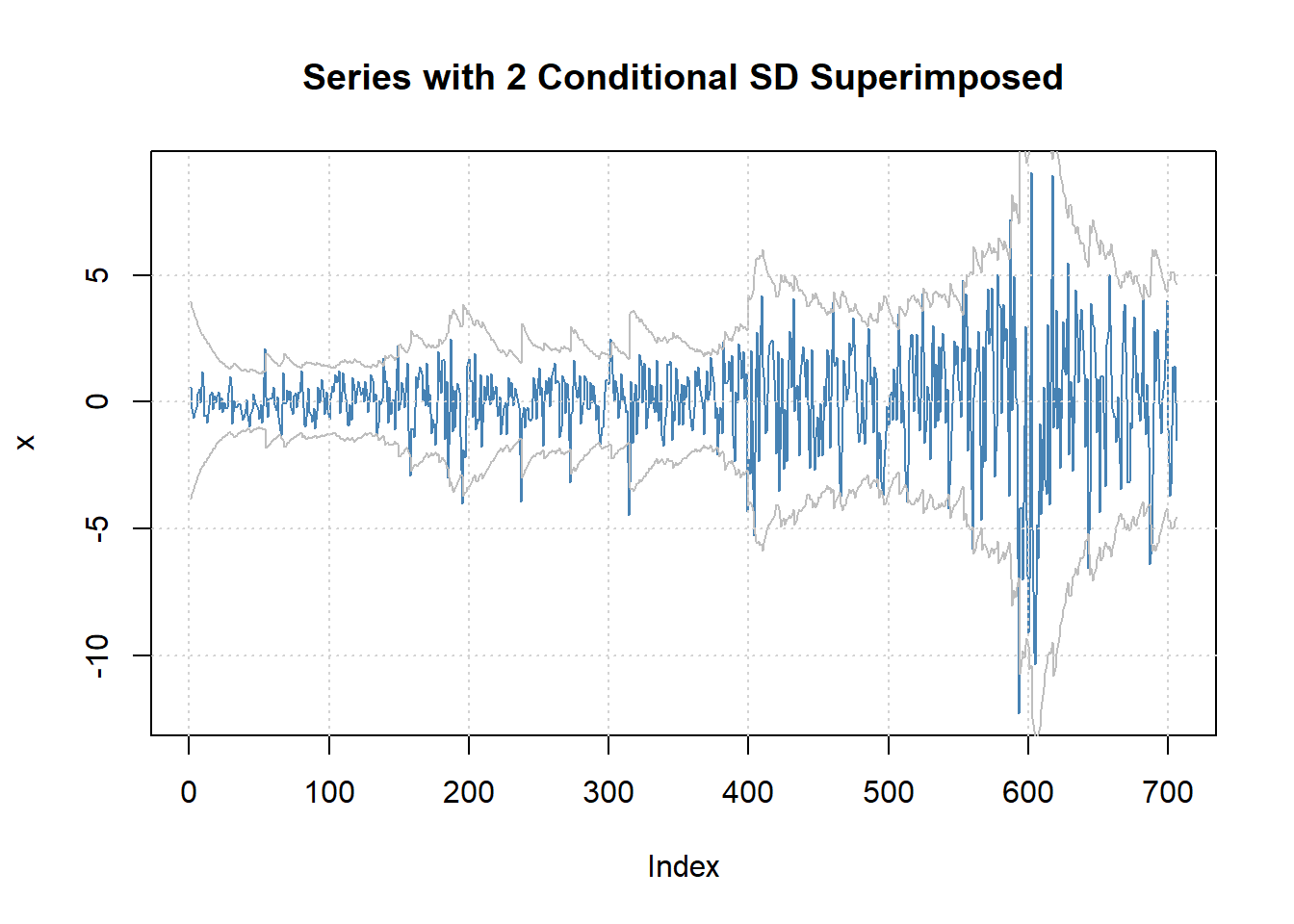
图22.28: 去除季节项后的序列及有偏t分布ARMA-GARCH两倍波动率

从样本内比较来看， 最后得到的去除季节项后的AR(1)-GARCH(1,1)用有偏t分布的模型 (22.5)效果最好。

对于样本外比较， 可以用季节调整后的\(C_t^*\)作为标准进行回测比较。 \(C_t^*\)共有706个观测， 从点\(t=650\)开始对最后的56个观测逐个地进行超前一步和超前两步预报。 采用如下的模型：

• AR(3)模型;
• 条件分布为有偏t分布的AR(1)–GARCH(1,1)模型。

AR(3)的超前一步和超前两步预测均方误差分别为2.368和2.558， AR-GARCH模型的结果为2.270和2.436， 均值的预测也有所改善。 当然， AR-GARCH的预测区间也更精确。

B 参考文献

Duan, J. 1995. “The GARCH Option Pricing Model.” Mathematical Finance 5: 13–32.

Markovitz, H. 1959. Portfolio Selection: Efficient Diversification of Investments. John Wiley & Sons, New York.