2 金融数据及其特征
课程采用蔡瑞胸(Ruey S. Tsay)的《金融数据分析导论:基于R语言》(Tsay 2013) (An Introduction to Analysis of Financial Data with R)作为主要教材之一。 这是第一章金融数据及其特征的授课笔记。
参考:
- (Tsay 2013)
- (Tsay 2010)
- (Tsay 2014)
- (吴喜之 and 刘苗 2018)
- (何书元 2003)
- (Lutkepohl and Kratzig 2004)
- (Cryer and Chan 2008)
- (Christoffersen 2003)
2.1 资产收益率
设\(P_t\)为某资产在\(t\)时刻的价格或净值, \(t\)按照某种时间单位(如年)计数。
2.1.1 简单收益率
这里假定计算收益率的时间单位保持不变。 常用年为单位。
单期简单毛收益率: \[ 1 + R_t = \frac{P_t}{P_{t-1}} \]
单期简单净收益率,简单收益率: \[ R_t = \frac{P_t}{P_{t-1}} - 1 = \frac{P_t - P_{t-1}}{P_{t-1}} \]
\(k\)期简单毛收益率: \[ 1 + R_t[k] = \frac{P_t}{P_{t-k}} = \prod_{j=0}^{k-1} (1 + R_{t-j}) . \]
\(k\)期净收益率: \[ R_t[k] = \frac{P_t}{P_{t-k}} - 1 = \frac{P_t - P_{t-k}}{P_{t-k}} \]
例2.1 (名义利率) 在实际中, 收益率(利率)一般按年为单位, 但是计息区间长度可以不等于一年。
设在银行借款金额为\(P\), 银行标称年利率为\(R\)(称为名义年利率), 但以半年计息一次的复利方式计算利息, 一年后偿还本金和利息。 如何计算本息?
解答:
年利率是名义利率, 因为每半年计息一次, 所以半年期的利率是\(R/2\), 即时间单位为半年时,简单收益率是\(R/2\), 这是金融行业计算利率的常见做法, 即利率按年标注, 但是不一定每一年计息一次, 如果每年计息\(n\)次, 则\(1/n\)年的简单收益率为\(R/n\)。
对于本例, 半年后本息合计为\(P(1+\frac{R}{2})\), 随后利息合并进入本金, 后半年的本息合计为\(P(1+\frac{R}{2})^2\), 所以一年后需要偿还的本息为\(P(1+\frac{R}{2})^2\)。
这里,称\(R\)为名义利率(nominal interest rate)。 因为每年计息两次且为复利, 所以定义实际利率(或译为有效利率,effective interest rate)\(R'\)为\(R'\)使得 \[ P(1 + R') = \text{在一年后未偿还的本息和} \] \(R'\)是以一年为时间单位的简单收益率。 在本例中实际年利率为 \[ R' = (1 + \frac{R}{2})^2 - 1 = 1 + R + \frac{1}{4} R^2 - 1 > R . \]
如果名义利率为\(R\),分\(n\)期计息,则实际利率\(R'\)为 \[ R' = (1 + \frac{R}{n})^n - 1 . \]
名义利率和实际利率的关系的深入讨论参见2.1.2。
○○○○○○
例2.2 (民间借贷) 民间借款经常用“几分利”的说法, 比如2分利, 这一般是指月利息, 单位是\(1\%\), 所以二分利是月名义利率\(2\%\), 相当于年利率\(24\%\)。 注意这里并不使用复利计算。
如果是年利率, 则一分一般是指\(10\%\), \(24\%\)的年利率称为“2分4厘”。
早一些的时候, 法律规定年利率\(24\%\)以下受到法律保护, \(36\%\)以上部分违法, \(24\%\)到\(36\%\)之间的部分承认债权但是法律不保护; 但最高人民法院2020年8月20日的规定是超过LPR(一年期贷款市场报价利率) 4倍的部分就属于法律不保护的。 比如,2025年6月20日一年期LPR为\(3.00\%\), 则超出\(12\%\)的利率部分就是法律不保护的。
如果指定了还款期限, 逾期时就可能约定从到期日时将本金和利息同时作为新的本金, 就是“驴打滚”借贷。
○○○○○○
例2.3 (九出十三归) 这是高利贷的一个典型范例。 古代的当铺以物品为抵押放出贷款, 但是号称放贷10元, 仅给9元贷款, 在放款时就已经收走了1元利息; 贷款期3个月, 每月利息1元, 到期需要还10元本金和3元利息(实际是9元本金和4元利息), 所以3个月的利率(简单收益率)是 \[ \frac{13 - 9}{9} = \frac{4}{9} = 44.4\%, \] 折合年利率为 \[ (1 + 4/9)^4 - 1 = 335\% . \]
当然, 这是远远超出我国当前法律规定允许的利率。
○○○○○
例2.4 苹果公司2011-12-02到2011-12-09的每日股票收盘价:
d.apple <- tibble(
date=c(ymd("2011-12-02"),
ymd("2011-12-05") + days(0:4)),
price=c(389.70, 393.01, 390.95, 389.09, 390.66, 393.62)
)
knitr::kable(d.apple)| date | price |
|---|---|
| 2011-12-02 | 389.70 |
| 2011-12-05 | 393.01 |
| 2011-12-06 | 390.95 |
| 2011-12-07 | 389.09 |
| 2011-12-08 | 390.66 |
| 2011-12-09 | 393.62 |
计算单期简单收益率的函数:
计算简单收益率(时间单位是交易日,无交易的日期忽略), 精确到百分数的小数点后2位:
| date | price | SR1 |
|---|---|---|
| 2011-12-02 | 389.70 | NA |
| 2011-12-05 | 393.01 | 0.85 |
| 2011-12-06 | 390.95 | -0.52 |
| 2011-12-07 | 389.09 | -0.48 |
| 2011-12-08 | 390.66 | 0.40 |
| 2011-12-09 | 393.62 | 0.76 |
从2011-12-02到2011-12-09是周五到周五, 这一周时间的多期简单收益率为:
## price
## 1 0.01005902即1.01%。
○○○○○
设某资产持有\(k\)年, 按复利计算的(平均)年化收益率为 \[ \left\{ \prod_{j=1}^{k} (1 + R_{t-j}) \right\}^{1/k} - 1 = \exp \left\{ \frac{1}{k}\sum_{j=1}^{k} \ln (1 + R_{t-j}) \right\} - 1 \] 当各\(R_{t-j}\)都很小时, 可近似\(\ln(1+x) \approx x\), \(e^x \approx 1 + x\), \(k\)期的平均年化复利近似为 \[ \frac{1}{k}\sum_{j=1}^{k} R_{t-j} \] 但是当单期利率较大时此公式误差较大。 如果使用连续复利收益率则不存在误差。
2.1.2 连续复利收益率
设某资产的的初始值为\(C\), 名义上的年利率为\(r\), 但是在一年内分成\(m\)次付息, 理论上每次付息\(C \frac{r}{m}\), 最终的资产净值应为\(C + C \frac{r}{m} \times m = C(1 + r)\); 但是,因为提前付息, 所以提前支付的利息也进入账户增值, 从第二次付息开始,支付的利息就超过了\(C \frac{r}{m}\), 使得一年后的净值要高于\(C (1 + r)\)。 一年后的净值为 \[ C \left(1 + \frac{r}{m} \right)^m \] 当\(m\to\infty\)时, 由极限\(\lim_{x\to +\infty} (1 + \frac{1}{x})^x = e\), 可知 \[ \lim_{m\to\infty} C \left(1 + \frac{r}{m} \right)^m = \lim_{m\to\infty} C \left[\left(1 + \frac{r}{m} \right)^{\frac{m}{r}} \right]^r = C e^r . \] 这时\(r\)称为连续复利, 它也对应某个时间单位(一般是年), \(R=e^r - 1\)是连续复利\(r\)对应的实际利率, \(r\)与\(R\)的关系为 \[ R = e^r - 1, \quad r = \ln (1 + R) \]
例2.5 取年连续复利\(r=0.10\), \(m=1,2,3,12,52,365, \infty\), 初始资产1元,多次付息并计入账户, 列出一年后净值。
解答:
m <- c(1, 2, 3, 12, 52, 365)
mlab <- c(paste(m), "Inf")
y <- c((1 + 0.10/m)^m, exp(0.10))
knitr::kable(tibble(`付息次数`=mlab, `年末净值`=y))| 付息次数 | 年末净值 |
|---|---|
| 1 | 1.100000 |
| 2 | 1.102500 |
| 3 | 1.103370 |
| 12 | 1.104713 |
| 52 | 1.105065 |
| 365 | 1.105156 |
| Inf | 1.105171 |
所以按连续复利计算, 连续复利的年利率10%, 等价于实际年利率为10.52%。
○○○○○○
按年连续复利的利率为\(r\), 初始资产价格为\(P_{t-n}\), 则\(n\)年后的资产净值为 \[ P_{t} = P_{t-n} e^{nr} \] 其中\(n\)可以是整数也可以不是整数。
当\(n=1\)时, \[ r_t = \ln\frac{P_t}{P_{t-1}} = \ln P_t - \ln P_{t-1} = \ln (1 + R_t) \] 其中\(R_t\)是一年期的简单收益率, \(r_t\)称为连续复合收益率或对数收益率, 这就是上面的连续复利, 但时间单位可以是任何时间单位。
当收益率较小时,有 \[ r_t = \log (1 + R_t) \approx R_t, \quad R_t = e^{r_t} - 1 \approx r_t, \] 两者很接近。
对多期连续复合收益率, \[ r_t[k] = \ln P_t - \ln P_{t-k} = \ln(1 + R_t[k]) = \ln \prod_{j=0}^{k-1} (1 + R_{t-j}) = \sum_{j=0}^{k-1} r_{t-j} \] 所以连续复利比简单复利的公式简单, 用加法代替了乘法。
例2.6 (加倍法则) 如果将资金投入一个以每年计息一次, 复利利率为\(R\)的账户中, 多少年后资金变成原来的两倍?
解答:
设初始资金为\(P\),即求\(n\)使得 \[ P (1 + R)^n \geq 2P \] 求解得 \[ n \geq \frac{\ln 2}{\ln (1+R)} = \frac{0.6931}{R} \cdot \frac{R}{\ln (1+R)} . \] 当\(R = 0.08\)时, \(\frac{R}{\ln (1+R)} = 1.039\), \(\ln 2 \cdot \frac{R}{\ln (1+R)} = 0.7205\), 所以对比较一般的R有 \[ n \geq \frac{0.72}{R} . \] 这个公式称为72算法。 比如, \(R = 0.14\)时, 按此算法需要18年, 精确公式为\(17.67\)年。 当\(r=0.18\), 按此算法需要\(4\)年, 精确公式为\(4.19\)年。
○○○○○
例2.7 给定一个价格序列,计算对数收益率序列的函数如下:
苹果公司股票的日对数收益率:
| date | price | SR1 | LR1 |
|---|---|---|---|
| 2011-12-02 | 389.70 | NA | NA |
| 2011-12-05 | 393.01 | 0.85 | 0.85 |
| 2011-12-06 | 390.95 | -0.52 | -0.53 |
| 2011-12-07 | 389.09 | -0.48 | -0.48 |
| 2011-12-08 | 390.66 | 0.40 | 0.40 |
| 2011-12-09 | 393.62 | 0.76 | 0.75 |
○○○○○○
2.1.3 现值分析
假设可以以每期计息一次的方式, 以每期\(R\)的名义利率借款和贷款。 这时, 第\(i\)期的期末支付\(v\)元的当前价值是多少?
应为\(P\)使得 \[ P(1+R)^i = v \] 即\(P = v(1+R)^{-i}\)。 \((1+R)^{-1}\)称为贴现因子, 即毛利率的倒数。 如果到期值为1, 则现值为 \[ \frac{1}{1+R} = 1 - \frac{R}{1+R}, \] 其中的\(d = \frac{R}{1+R}\)称为贴现率。
计算现值可以用于比较不同的现金流, 也可用于计算实际利率。
设在今后的\(n\)年, 每年年末分别收到\(x_1, x_2, \dots, x_n\)元。 名义年利率为\(R\)。 这个现金流的现值为 \[ x_1 (1+R)^{-1} + x_2 (1+R)^{-2} + \dots + x_n (1 + R)^{-n} = \sum_{i=1}^n x_i (1 + R)^{-i} . \]
2.1.3.1 贷款还款分析
设一个人抵押贷款金额为\(L\), 需要在今后\(n\)个月的的每月月末偿还等额\(A\)。 贷款的月名义利率是\(R\),每月计息一次(复利)。
- 已知\(L, n, R\),则\(A\)的值是多少?
- 在第\(j\)月的月末已经完成支付后,还剩下多少贷款的本金? 这一问题对于提前还款十分重要。
- 在第\(j\)月的支付中,多少是利息的支付, 多少是本金的支付?
解答1: 为了求得\(A\),只要按利率\(R\)计算各次支付的现值等于\(L\), 即 \[ L = \sum_{i=1}^n A (1 + R)^{-i} \] 记\(\beta=\frac{1}{1+R}\), 则 \[ L = A \sum_{i=1}^n \beta^i = A \beta \frac{1 - \beta^n}{1 - \beta} \] 于是 \[ A = L \frac{R}{1 - (1+R)^{-n}} \]
例如,设\(L=100\)万元, \(n=120\)个月(10年), \(R=0.006\), 则:
## [1] 1.171419## [1] 40.57025## [1] 0.03464018每月需要还款\(1.17\)万元,总共还利息40万元。 因为中间也还了一部分本金, 所以将分期偿还的这些本息看成是在10年末尾一起偿还的, 年利率只有3.5%; 但是,因为提前偿还了部分本息, 所以持有贷款的期间实际借款没有100万元那么多, 年利率就不止3.5%。 实际年利率是7.2%左右。
解答2:设在第\(i\)月的月末偿还\(A\)后还剩的本金为\(B_i\),\(i=0,1,\dots,n\), 则\(B_0=L\), \(B_n=0\)。 考虑\(\{ B_j \}\)之间的关系, 如果在第\(j\)月的月末偿还后还有\(B_j\)债务, 则在第\(j+1\)的月末还有\((1+R) B_j\)债务, 偿还\(A\)后还有\(B_{j+1}\)债务,即 \[ B_{j+1} = (1 + R) B_j - A, \ j=0,1,\dots,n-1 \] 记\(\alpha = 1 + R\),递推有 \[\begin{aligned} B_1 =& \alpha L - A \\ B_2 =& \alpha B_1 - A = \alpha^2 L - (1 + \alpha) A \\ B_3 =& \alpha B_2 - A = \alpha^3 L - (1 + \alpha + \alpha^2) A \end{aligned}\] 一般地,对\(j=1,2,\dots, n\)有 \[ B_j = \alpha^j L - A(1 + \alpha + \dots + \alpha^{j-1}) = L \alpha^j \frac{\alpha^{n-j} - 1}{\alpha^n - 1} \]
解答3: 设\(I_j\)和\(P_j\)分别表示在第\(j\)月的月末支付的利息和本金的扣除额, \(I_j + P_j = A\)。 第\(j-1\)个月的月末偿还后还剩\(B_{j-1}\)债务, 在第\(j\)个月需要偿还的利息为\(I_j = R B_{j-1}\), 于是 \[ I_j = L (\alpha - 1) \alpha^{j-1} \frac{\alpha^{n-j+1} - 1}{\alpha^n - 1} . \] 而 \[ P_j = A - I_j = L (\alpha - 1)\frac{\alpha^{j-1}}{\alpha^n - 1} . \] 可以看出本金的偿还额越到后期越多, 而还款前期主要支付的是利息。
例如,设\(L=100\)万元, \(n=120\)个月(10年), \(R=0.006\), 则:
loan_demo <- function(L = 100, n = 120, R = 0.006){
A <- L * R / (1 - (1 + R)^(-n))
alpha <- 1 + R
jvec <- 1:n
Bvec <- L * alpha^jvec * (alpha^(n - jvec) - 1) / (alpha^n - 1)
Ivec <- L * (alpha - 1) * (alpha^(n - jvec + 1) - 1) / (alpha^n - 1)
Pvec <- A - Ivec
data.frame(
"月份" = jvec,
"还款" = A,
"还本" = Pvec,
"利息" = Ivec,
"剩余" = Bvec
)
}
tmp.d <- loan_demo()
knitr::kable(tmp.d[seq(12, 120, by=12),], digits=2, row.names=FALSE)| 月份 | 还款 | 还本 | 利息 | 剩余 |
|---|---|---|---|---|
| 12 | 1.17 | 0.65 | 0.53 | 92.91 |
| 24 | 1.17 | 0.72 | 0.45 | 85.30 |
| 36 | 1.17 | 0.79 | 0.38 | 77.11 |
| 48 | 1.17 | 0.86 | 0.31 | 68.32 |
| 60 | 1.17 | 0.92 | 0.25 | 58.88 |
| 72 | 1.17 | 0.98 | 0.19 | 48.73 |
| 84 | 1.17 | 1.03 | 0.14 | 37.83 |
| 96 | 1.17 | 1.08 | 0.09 | 26.11 |
| 108 | 1.17 | 1.13 | 0.05 | 13.52 |
| 120 | 1.17 | 1.17 | 0.00 | 0.00 |
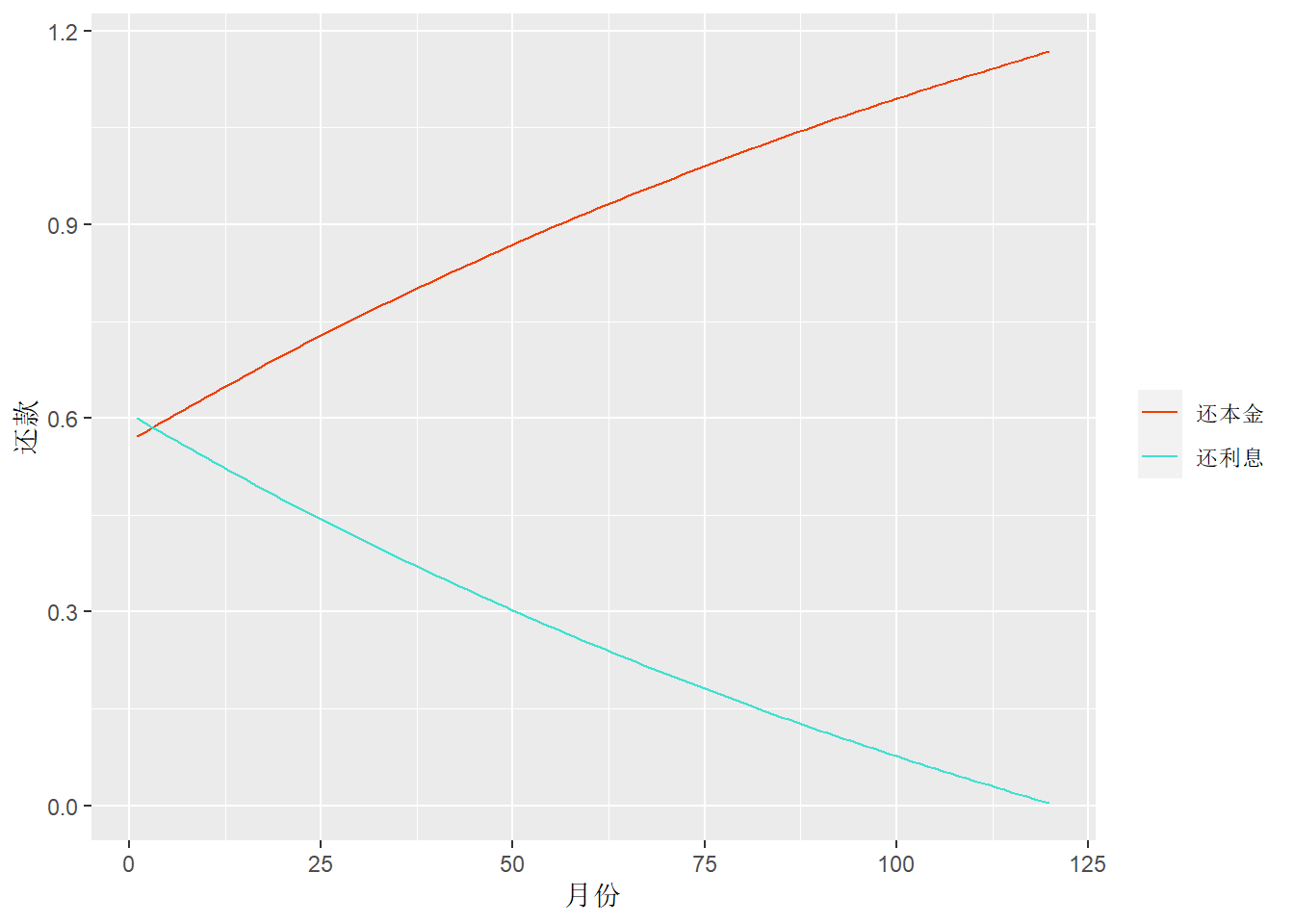
从计算例子看出, 这种等额还款, 前期还款中还利息的比例较高, 对贷款者不太有利。
○○○○○
2.1.3.2 回报率
考虑一项投资, 初始支出为\(a\), 随后每期分别得到回报\(b_1, b_2, \dots, b_n\), \(b_i \geq 0\), \(b_n>0\)。 定义该投资每期的回报率\(R\)为下述利率的值: \(R\)使得在该利率下现金流序列的复利现值等于零,即 \[ -a + \sum_{i=1}^n b_i (1 + R)^{-i} = 0 . \]
定义函数 \[ P(R) = -a + \sum_{i=1}^n b_i (1 + R)^{-i}, \ R \in [-1, \infty) \] 易见\(P(R)\)为严格单调减的连续函数, \(\lim_{R \to -1} = +\infty\), \(\lim_{R \to \infty} = -a\), 所以存在唯一的\(R_*\)使得\(P(R_*)=0\), \(R_*\)就是回报率。
由于\(P(0) = \sum b_i - a\), 所以\(\sum b_i > a\)时\(R_* > 0\), 否则\(R_* \leq 0\)。
当投资的每期回报率为\(R_*\)时, 通常称这个投资有每期\(100R_*\%\)的回报率。
求解\(P(R)=0\)的方程可以用二分法等数值方法。
如果现金流\(b_1, b_2, \dots, b_n\)表示贷出\(a\)元后每期的偿还额, 则\(R_*\)是贷款人的每期回报率, 也是借款人的实际每期利率。
如果现金流不满足\(b_i \geq 0\)的条件, 则函数\(P(R)\)不再是单调函数, \(P(R)=0\)不一定有唯一解, 即使有唯一解也不能确定解左边和右边的回报性质。
例2.8 投资100元, 分5年的回报分别为 \(20, 22, 25, 30, 40\)元。 求回报率。
解答:
R函数uniroot()可以用来求解一元连续函数的单个根。
x <- c(20, 22, 25, 30, 40)
fleft <- function(R) -100 + sum(x / (1+R)^(1:5))
uniroot(fleft, c(-0.99, 10.0), extendInt="downX")## $root
## [1] 0.1016542
##
## $f.root
## [1] -0.001301806
##
## $iter
## [1] 12
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05程序中uniroot()的第二个自变量是根可能存在的区间,
选项“extendInt="downX"”说明在初始区间两个端点函数值同号时,
允许按照减函数向外扩大搜索区间。
结果为\(R=10.16\%\)。
○○○○○○
例2.9 设某民间借贷10000元,借期1年, 采用“三分利”, 指月利率\(3\%\), 需要每月付息,不计复利, 到期偿还本金与最后一个月的利息。 大约相当于年利率\(36\%\), 用现值分析方法计算实际年利率。
解答:
这相当于初始投资10000万元, 然后每个月获得300元回报, 共11个月,最后一个月获得10300回报。 设实际年利率(回报率)为\(R\), 记\(a = 10000\), \(b_i = 300\), \(i=1,2,\dots, 11\), \(b_{12} = 10300\), 要解方程 \[ -a + \sum_{k=1}^{12} b_i (1 + R)^{-k} = 0 . \] 用R程序计算:
x <- c(rep(300, 11), 10300)
fleft <- function(R) -10000 + sum(x / (1+R)^(1:12))
uniroot(fleft, c(-0.99, 10.0),
extendInt="downX", check.conv=TRUE, tol=1E-6)## $root
## [1] 0.03000002
##
## $f.root
## [1] -0.001691696
##
## $iter
## [1] 12
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 5e-07求得的实际月利率(回报率)为\(3.00\%\), 折合年回报率\((1 + 0.0300)^{12} - 1 = 42.6\%\)。
○○○○○○
2.1.4 资产组合收益率
设有\(N\)项资产, 在\(t-1\)时刻组合净值为 \[ A_{p,t-1} = \sum_{j=1}^N A_{i,t-1} = A_{p,t-1} \sum_{j=1}^N w_i \] 其中\(w_i = A_{i,t-1}/A_{p,t-1}\)是第\(i\)项资产的权重。 于是 \[\begin{aligned} A_{p,t} =& \sum_{j=1}^N A_{i,t-1} (1 + R_{i,t}) = A_{p,t-1} \sum_{j=1}^n w_i (1 + R_{i,t}) \\ =& A_{p,t-1}\left( 1 + \sum_{j=1}^n w_i R_{i,t} \right) \end{aligned}\] 所以资产组合的简单收益率为 \[ R_{p,t} = \sum_{j=1}^n w_i R_{i,t} \] 注意其中\(w_i\)是第\(t-1\)时刻的权重。 如果继续计算\(R_{p,t+1}\), 权重应该使用\(t\)时刻的权重。 当然,如果资产比例变化不大, 使用不变的\(\{ w_i \}\)近似也是可以的。
对于对数收益率没有如此简单的公式。 当收益很小时近似有 \[ r_{p,t} \approx \sum_{j=1}^n w_i r_{i,t} \]
2.1.5 红利支付与收益率
对价格\(P_{t-1}\)的某资产, 如果在\(t-1\)到\(t\)之间每单位还支付\(D_t\)红利, 则到\(t\)时刻时, 收益为\(P_t - P_{t-1} + D_t\), 所以这时收益率应计算为 \[ R_t = \frac{P_t - P_{t-1} + D_t}{P_{t-1}}, \quad r_t = \ln(P_t + D_t) - \ln P_{t-1} \]
2.1.6 超额收益率
\[ Z_t = R_t - R_{0t}, \quad z_t = r_t - r_{0t} \] 其中\(R_{0t}\)和\(r_{0t}\)是某项参考资产的收益率, 如美国短期国债收益率。
超额收益率被认为是如下的套利投资组合的盈利: 对该资产持有多头头寸, 对参照资产持有空头头寸, 且初始净投资额为零。
多头金融头寸是指持有某资产。 空头头寸是指从持有某资产的投资者手里借入某资产, 然后卖出这些不属于自己的资产, 在随后的规定日期卖空者有义务通过买入相同数额的该资产偿还借出者, 不能偿还现金, 当规定日期时该资产价格下跌时空头持有者可以获利。 如果空头持有期间目标资产支付现金红利, 空头持有者有义务支付红利给借出者。
2.1.7 关系小结
简单收益率\(R_t\)与连续复合收益率(对数收益率)\(r_t\)的关系为 \[ r_t = \ln(1 + R_t), \quad R_t = e^{r_t} - 1 \]
简单的\(k\)期收益率为 \[ R_t[k] = (1 + R_t)(1 + R_{t-1}) \dots (1 + R_{t-k+1}) - 1 \]
\(k\)期对数收益率为 \[ r_t[k] = r_t + r_{t-1} + \dots + r_{t-k+1} \]
如果连续复合年利率固定为\(r\), 初始资产为\(C\), \(n\)年后资产为\(A\),则 \[ A = C e^{rn}, \quad C = A e^{-rn} \]
例2.10 若某项资产月对数收益率为4.46%, 则简单收益率为
## [1] 0.04560953即4.56%。 如果某项资产在一个季度的月对数收益率为 4.46%, -7.34%, 10.77%, 则该季度的对数收益率为
## [1] 0.0789即7.89%。
例2.11 IBM股票从2001-1-2到2010-12-31的日简单收益率和对数收益率分析。
解答:
d.ibm <- read_table(
"d-ibm-0110.txt",
col_types=cols(date=col_date(format="%Y%m%d"),
return=col_double()))
with(d.ibm, plot(
date, return, type="l",
xlab="Date", ylab=expression(R[t])))
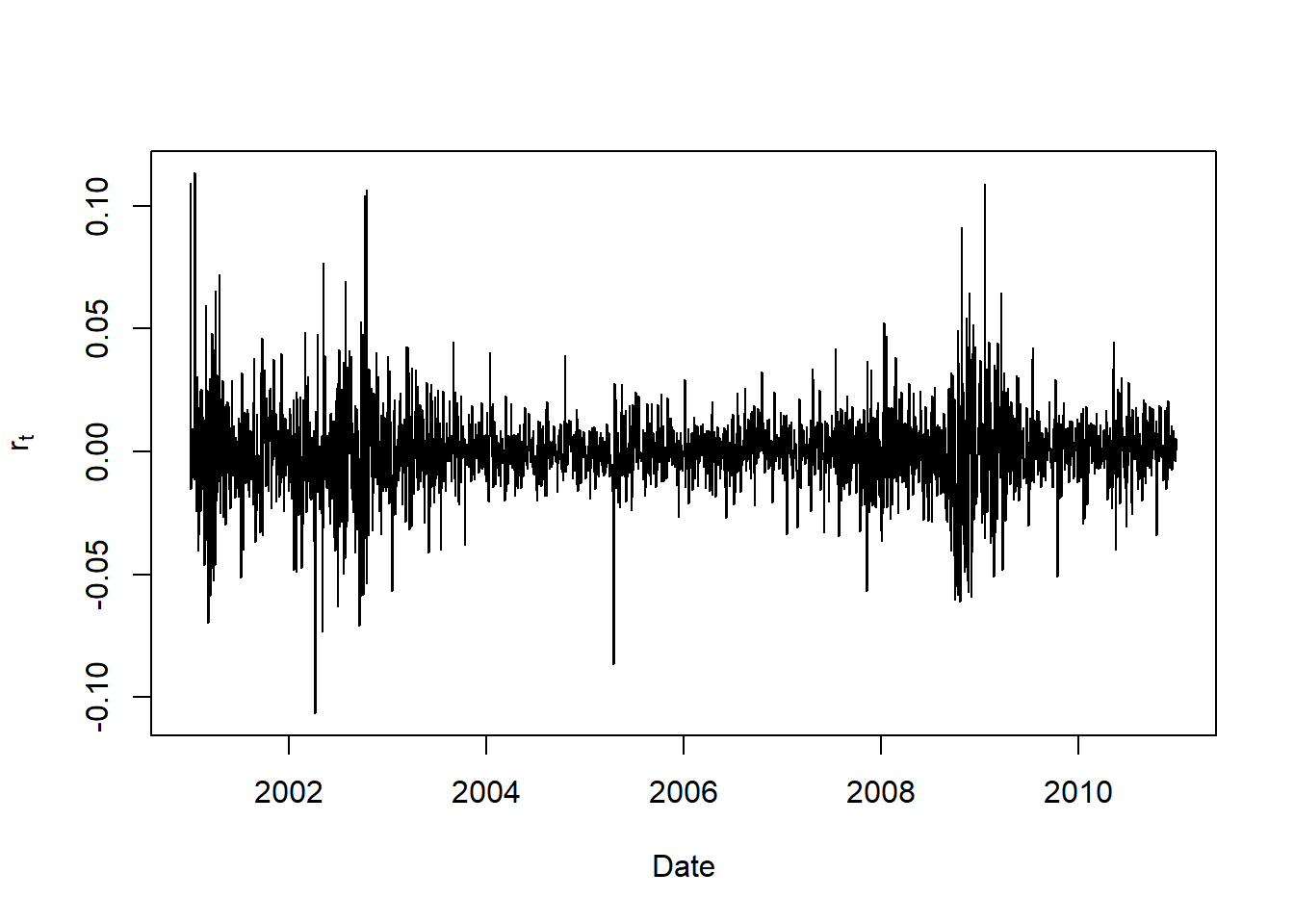
共有2515个观测。 简单收益率与对数收益率的相关系数:
## [1] 0.9997069为0.9997。 当收益率绝对值较小时简单收益率与对数收益率近似相等。
上面将IBM股票数据读成了tibble数据框。 也可以转换成xts类型时间序列,如
z.ibm <- xts(as.matrix(d.ibm[,-1]), d.ibm[["date"]])
quantmod::chartSeries(
z.ibm, type="line", theme="white",
xlab="Date", name="IBM Simple Return")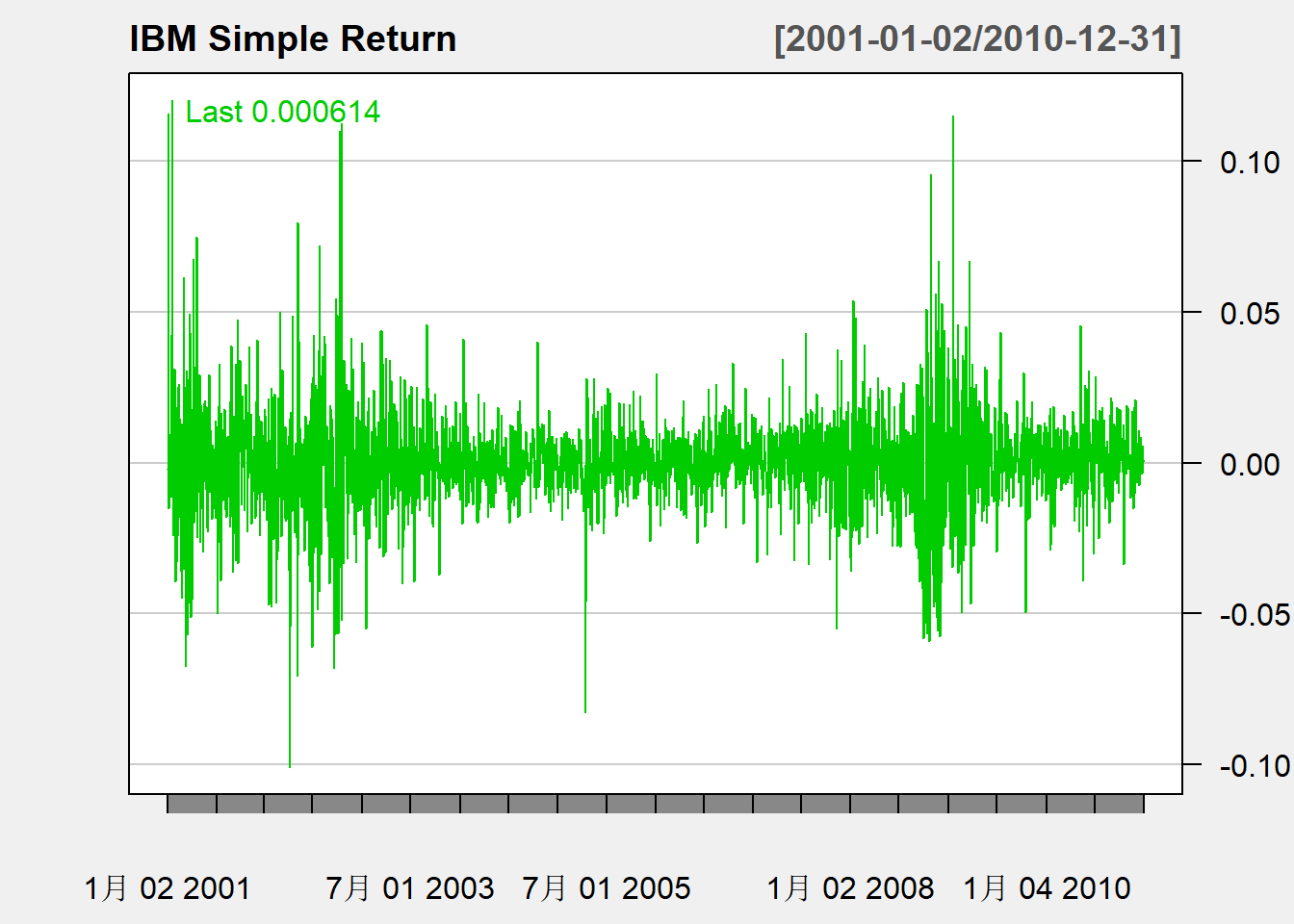
○○○○○○
2.2 债券收益和价格
2.2.1 债券类型
投资者以市场价格买入债券, 在到期日收回票面价格的现金。 买入价格低于票面价格。 有些债券还在持有期间定期派发利息, 利息按照票面利率(coupon payment)和面额计算, 比如, 面值为100元, 票面利率为6%, 如果每半年派发一次利息, 则每次派息\(100\times 0.06/2=3\)元。 有些债券不在中间派息,这样的债券称为零息债券。
2.2.2 当期收益率
当期收益率仅计算每年的表面收益, 不考虑资金的时间成本。 \[ \text{当期收益率} = \frac{\text{每年派息额}}{\text{买入价格}} \times 100\% \] 比如, 票面价格100元, 买入价格90元, 票面利率为每年5%, 则持有一年的表面的年收益率为 \[ (100 \times 0.05)/90 = 5.56\% \] 这没有考虑到期时票面价格与买入价格差值造成的收益。
2.2.3 到期收益率
对于零息债券, 持有期间没有任何利息收入。 如果购入价格为\(P\), 面值为\(F\), 持有\(k\)年到期,则收益率为 \[ \left(\frac{F}{P} \right)^{1/k} - 1 \] 这称为到期收益率(Yield To Maturity, YTM)。
如果持有期间有派息, 则到期收益率的计算很复杂, 方法是求\(y\), 令投资者在购入时的价格\(P\)等于持有期间、包括到期时的所有现金收入按照利率\(y\)贴水到购入时刻的现值。 设面额为\(F\), 售价为\(P\),共派息\(k\)次, 到期收益率为待定的\(y\),\(y\)对应的时间区间为两次派息之间的时间区间, 各次派息额为\(C_1, C_2, \dots, C_k\),则方程为 \[ P = \frac{C_1}{1+y} + \frac{C_2}{(1+y)^2} + \dots + \frac{C_k}{(1+y)^k} + \frac{F}{(1+y)^k} \] 当每年派一次息时\(y\)就是年化的到期收益率。
如果票面利率(名义年利率)为\(\alpha\), 持有\(n\)年, 每年派息\(m\)次,\(k=nm\), 每次派息\(F \alpha/m\), 设按\(1/m\)年计算的到期收益率为\(y\), 则方程为 \[ \begin{aligned} P =& F\frac{\alpha}{m}\left[ \frac{1}{1+y} + \frac{1}{(1+y)^2} + \dots + \frac{1}{(1+y)^k} \right] + \frac{F}{(1+y)^k} \\ =& \frac{F\alpha}{my}\left[ 1 - \frac{1}{(1+y)^k} \right] + \frac{F}{(1+y)^k} \end{aligned} \]
例2.12 设某债券面值为100元, 售价为\(P\), 持有时间为\(n=3\)年, 每年发息\(m=2\)次, 票面利率为\(\alpha=0.05\), 分析其到期收益率。
解答: 一共有\(k=nm=6\)次发息, 每次发息\(100 \times 0.05/m=2.5\)元。 设到期收益率按半年期利率计算为\(y\), 则售价与到期收益率\(y\)(半年期)之间的关系为 \[ \begin{aligned} P =& \frac{F\alpha}{my}\left[ 1 - \frac{1}{(1+y)^k} \right] + \frac{F}{(1+y)^k} \\ =& \frac{2.5}{y}\left[1 - (1+y)^{-6} \right] + 100(1 + y)^{-6} \end{aligned} \] 作\(P\)对\(y\)的曲线图如下:
f <- function(y) 2.5/y*(1 - (1+y)^-6) + 100*(1+y)^-6
curve(f(x), 0.028, 0.052, xlab="半年期到期收益率", ylab="售价")
abline(v=c(0.030, 0.035, 0.040, 0.045, 0.050), col="gray")
pr <- c(97.29, 94.67, 92.14, 89.68, 87.31)
abline(h=pr, col="gray")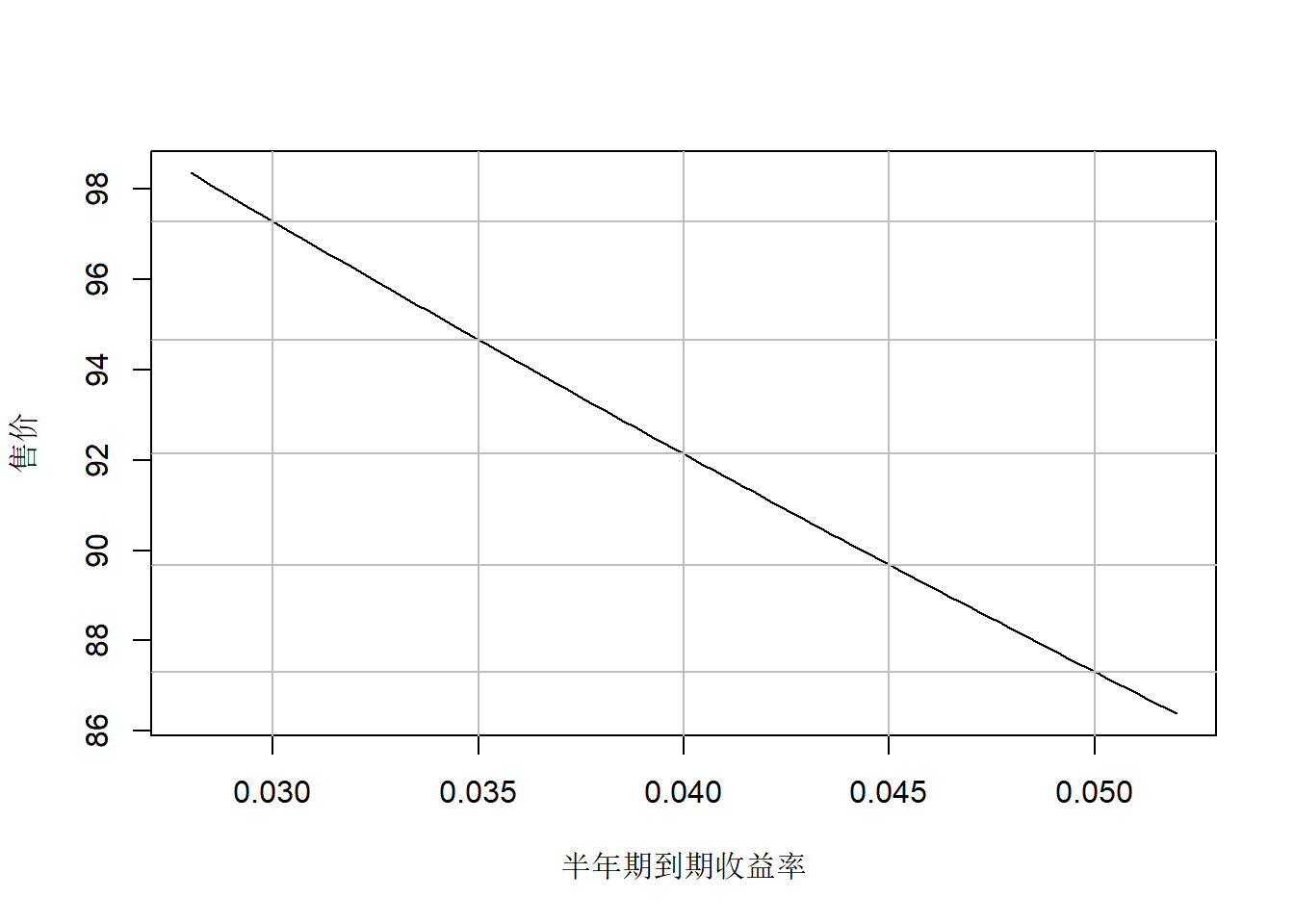
图中画出了半年期到期利率为3%, 3.5%, 4%, 4.5%, 5%时的售价。 如果半年期到期利率为3%, 售价为97.29元。 半年期到期利率3%转换为年化到期利率, 结果为 \[ (1 + 0.03)^2 - 1 = 0.0609 \] 教材P.6上的到期利率是按半年期利率计算的名义值, 实际年化利率应为\((1+y)^m - 1\)。
债券的售价\(P\)是到期收益率\(y\)的严格单调减函数\(P=g(y)\), 在已知\(F\), \(n\), \(m\), \(\alpha\),\(P\)的条件下用二分法或牛顿法求解\(g(y)=P\)可以求出\(y\)的精确值。 比如,用牛顿法求解到期收益率。 设要解的方程为\(f(x)=0\),(\(f(x) = g(x) - P\)) 牛顿法从某个\(x_0\)出发, 用如下公式迭代: \[ x_{t+1} = x_t - f(x_t)/f'(x_t) \] 其中\(f'(x_t)\)可以用数值微分方法估计为 \[ f'(x_t) \approx \frac{f(x_t + \delta) - f(x_t - \delta)}{2\delta}, \] 其中\(\delta=10^{-6}\)。 初值\(x_0\)取为 \[ x_0 = \frac{\alpha}{m} + \left(\frac{F}{P} \right)^{1/k} - 1 \]
ytm.newton <- function(
P=97.29, F=100, alpha=0.05, n=3, m=2){
k <- n*m
f <- function(y){
F*alpha/(m*y)*(1 - (1+y)^(-k)) + F*(1+y)^(-k) - P
}
x0 <- alpha/m + (F/P)^(1/k) - 1
eps <- 1E-6 # 方程左边绝对值小于此值时迭代结束
delta <- 1E-6 # 数值微分的步长
max.iter <- 100
iter <- 0
repeat{
iter <- iter + 1
dfx <- (f(x0 + delta) - f(x0 - delta))/(2*delta)
x0 <- x0 - f(x0)/dfx
cat(iter, x0, f(x0), "\n")
if(iter >= max.iter || abs(f(x0))<eps) break
}
x0 # 结果是1/m年的到期收益率
}
ytm.newton(P=97.29, F=100, alpha=0.05, n=3, m=2)## 1 0.03000207 0.0003023458
## 2 0.03000264 5.709069e-10## [1] 0.03000264仅迭代了两次就求得了精度有四位有效数字的结果。 注意, 牛顿法求根需要比较准确的初值, 如果初值取得太远, 牛顿法可能不收敛。
○○○○○○
2.2.4 美国政府债券
2.2.4.1 短期国债
Treasury Bills, T-Bills.
持有时间在1年及一年以下, 零息债券,购入时以低于面值购入。 常用期限:
- 28天(4周,一个月)
- 91天(13周,三个月)
- 182天(26周,半年)
- 364天(52周,一年)
其年化利率采用如下的简便公式计算: \[ \text{折现收益率(\%)} = \frac{F-P}{F} \times \frac{360}{\text{到期持有天数}} \times 100(\%) \]
更合理的到期收益率公式应为 \[ 到期收益率(\%) = \left[ \left( \frac{F}{P} \right)^{\frac{365.25}{\text{到期持有天数}}} - 1 \right] \times 100(\%) \]
设\(F=100\), \(P=95\), 到期持有天数在28到364之间变化时两种不同算法的变化曲线如下:
F <- 100
P <- 95
curve((F-P)/F*360/x*100, 28, 364, col="red",
xlab="Days", ylab="YTM")
curve(((F/P)^(365.25/x)-1)*100, 28, 364,
add=TRUE, lty=2, col="green")
legend("topright", lty=c(1,2), col=c("red", "green"),
legend=c("Standard", "Exact"))
两条曲线有较大差距, 这实际上是因为短期债券的售价太低导致利率过高引起的, 在正常利率范围内两者应该差距不大。
设年化利率规定在5%, 面值\(F=100\), 按标准公式计算的售价为 \[ P = F\left( 1 - R \frac{\text{天数}}{360} \right) = 100 \left( 1 - 0.05 \frac{\text{天数}}{360} \right) \]
按标准公式计算的折现率为5%, 计算相应的精确到期收益率:
days <- c(28, 91, 182, 364)
prices <- 100*(1 - 0.05*days/360)
rates <- ((100/prices)^(365.25/days)-1)*100
rbind(days, standard=5, exact=round(rates,2))## [,1] [,2] [,3] [,4]
## days 28.00 91.00 182.00 364.00
## standard 5.00 5.00 5.00 5.00
## exact 5.21 5.24 5.27 5.34精确利率要高。 在标准公式中计算利率用了\((F-P)/F\), 理论上应该用\((F-P)/P\), 所以标准公式低估了利率。 因为短期国债并不能很容易地自动转存, 所以低估是有一定合理性的。
2.2.4.2 中期国债
Treasury Notes, T Notes.
在1年到10年内到期, 每6个月支付一次利息,面值1000元。 在二级市场上以面值的特殊百分数报价, 百分数的小数部分\(1/32\)为单位, 比如报价95:08, 即报价\(1000 \times 95\frac{8}{32} \div 100 = 952.5\)。 10年期美国国债是报价频率最高、安全性最高的国债。
2.2.4.3 长期国债
Treasury Bonds, T-Bonds.
30年期的国债, 每6个月付息一次。
R扩展包quantmod包含了金融数据建模的功能, 比如可以从雅虎、谷歌财经等公开数据源下载多个经济和金融事件序列数据。
## TNX.Open TNX.High TNX.Low TNX.Close TNX.Volume TNX.Adjusted
## 2007-01-03 4.658 4.692 4.636 4.664 0 4.664
## 2007-01-04 4.656 4.662 4.602 4.618 0 4.618
## 2007-01-05 4.587 4.700 4.583 4.646 0 4.646
## 2007-01-08 4.668 4.678 4.654 4.660 0 4.660
## 2007-01-09 4.660 4.670 4.644 4.656 0 4.656
## 2007-01-10 4.666 4.700 4.660 4.682 0 4.682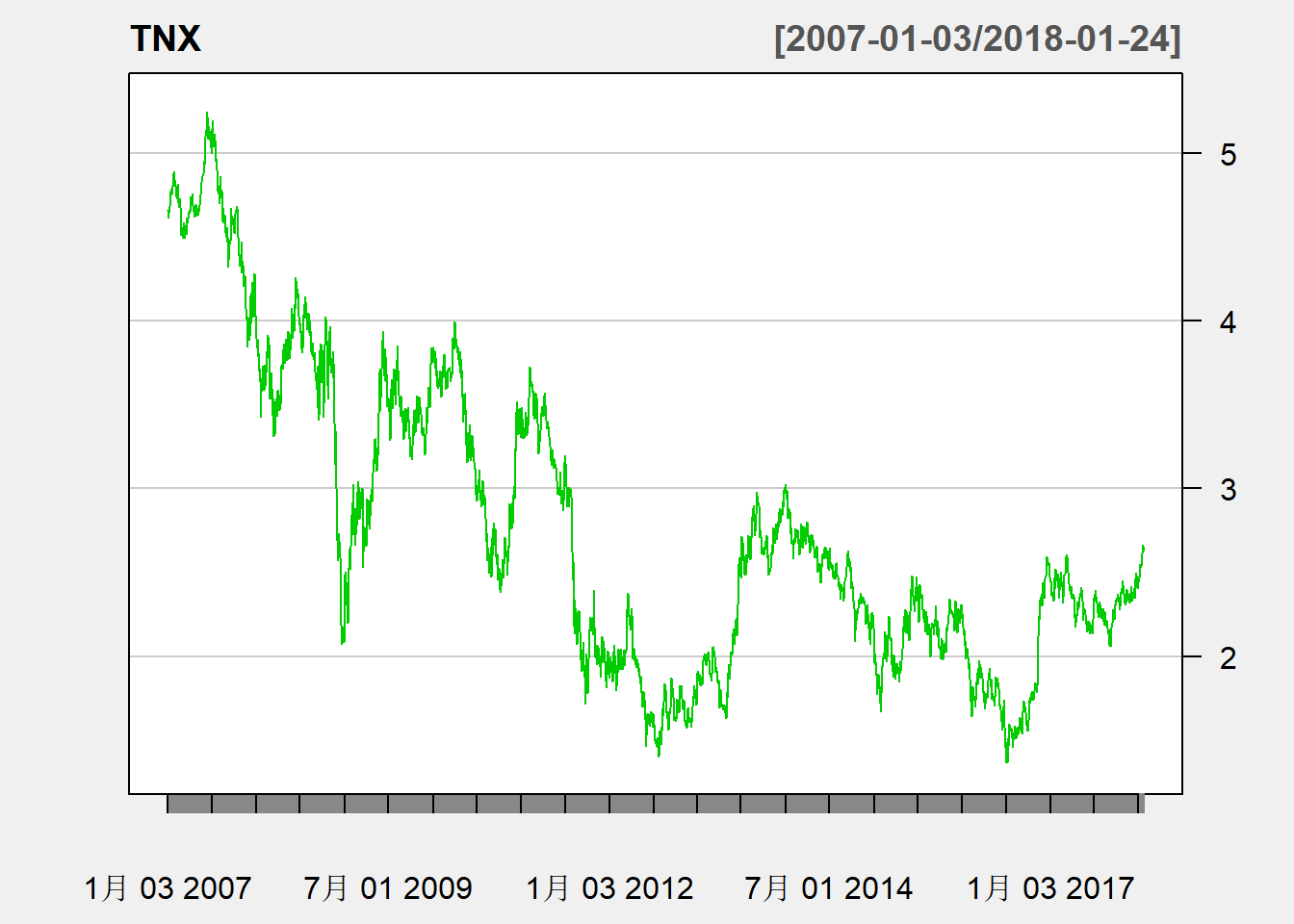
2.3 隐含波动率
- 股票期权(stock option)
- 看涨期权(call option)
- 看跌期权(put option)
- 执行价格(strike price):在未来规定的期间有权利以执行价格买入或者卖出一定数量的股票。
- 到期日(time to maturity)
- 欧式期权:只有在到期日才能行权
- 美式期权:在到期日及之前都可以行权
- CBOE, 美国芝加哥期权交易所
- 行权时根据给持有人的现金流的正、负、零分为 价内期权(in-the-money), 价外期权(out-of-the-money),平价期权(at-the-money)。 当然,只有价内期权会实际行权。
期权价格影响因素:
- 执行价格
- 无风险利率
- 当前股价
- 股票的波动率
Black-Scholes模型: 在假设股票价格服从几何布朗运动的条件下, 给出了期权价格的解析解, 其中包含不可观测的波动率。 波动率(volatility)是股票价格的条件标准差。 可以从股价、期权价格以及BS模型求解出波动率, 这样得到的波动率称为隐含波动率(implied volatility)。
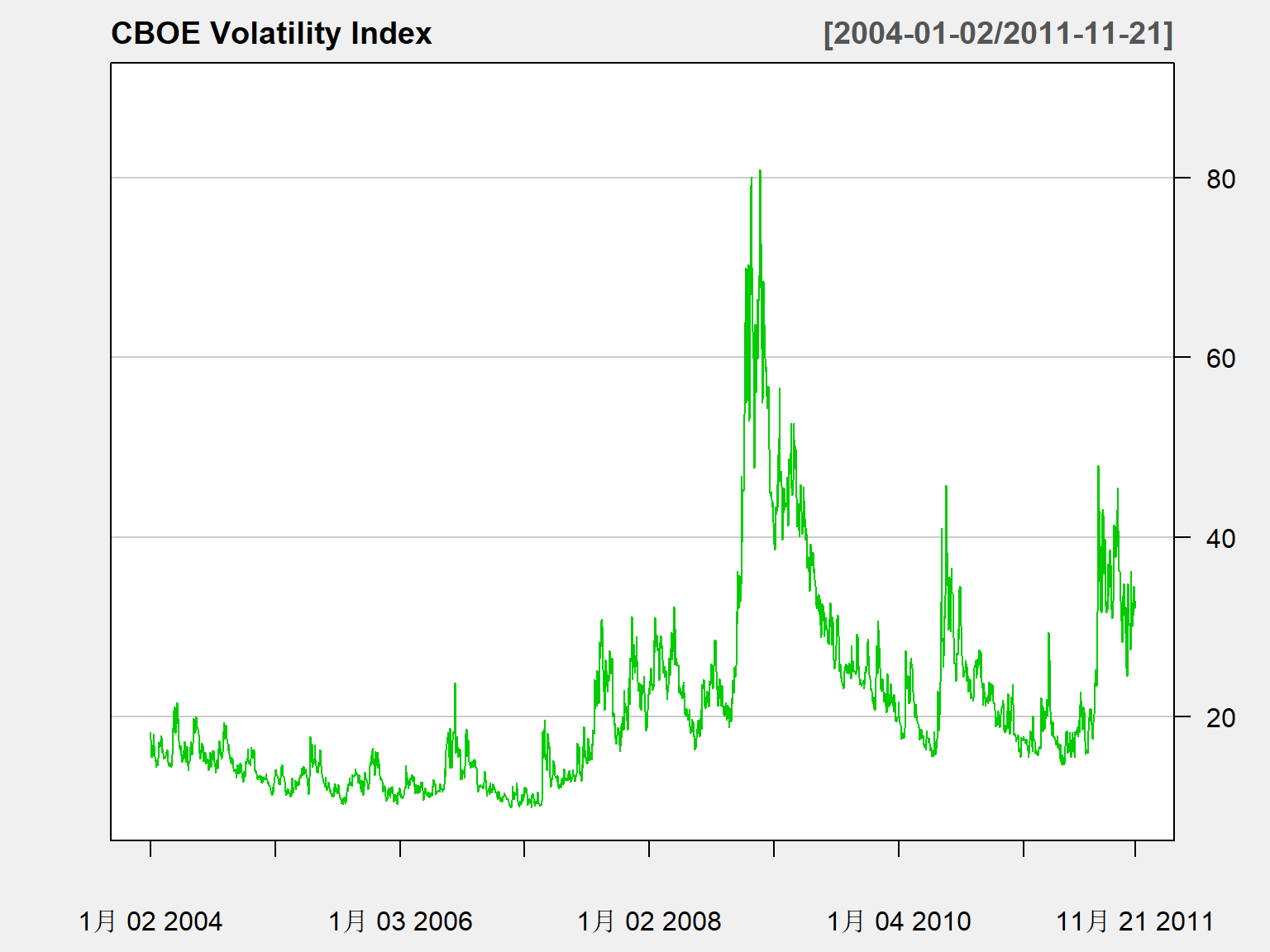
VIX: CBOE的波动率指数, 1993年提出,2003年修订。
蔡教授提供的文本文件d-vix0411.txt中,
前面几列用空格分隔,
后面几列用制表符分隔,
这使得程序读入这样的文件很困难,
同学一定不要制造这样的文件。
为了可以读取,
将所有行用readr::read_file()读入,
用字符串函数gsub()将所有制表符替换成空格,
然后再从修改后的字符串读取:
tmp.s <- read_file("d-vix0411.txt")
tmp.s <- gsub("\t", " ", tmp.s, fixed=TRUE)
d.vix <- read_table(tmp.s,
col_types=cols(.default = col_double()))
rm(tmp.s)
vix <- xts(d.vix[4:7],
make_date(d.vix[["year"]], d.vix[["mon"]], d.vix[["day"]]))
chartSeries(
vix, type="line", TA=NULL,
major.ticks="years", minor.ticks=FALSE,
theme="white", name="CBOE Volatility Index"
)
2.4 收益率分布特性的探索性分析
2.4.1 苹果公司股票日数据
苹果公司日数据下载:
library(quantmod)
AAPL <- getSymbols("AAPL", src="yahoo", auto.assign=FALSE)
logret.AAPL <- diff(log(AAPL$AAPL.Adjusted))*100 # 对数收益率计算对数收益率:
对数收益率时间序列2007-2017的曲线图:
chartSeries(
logret.AAPL, type="l", TA=NULL,
subset="2007/2017",
name="Apple Log Returns",
theme="white", major.ticks="years", minor.ticks=FALSE)
仅2017年的对数收益率曲线图:
chartSeries(
logret.AAPL, type="l", TA=NULL,
subset="2017/2017",
name="Apple Log Returns",
theme="white", major.ticks="months", minor.ticks=FALSE)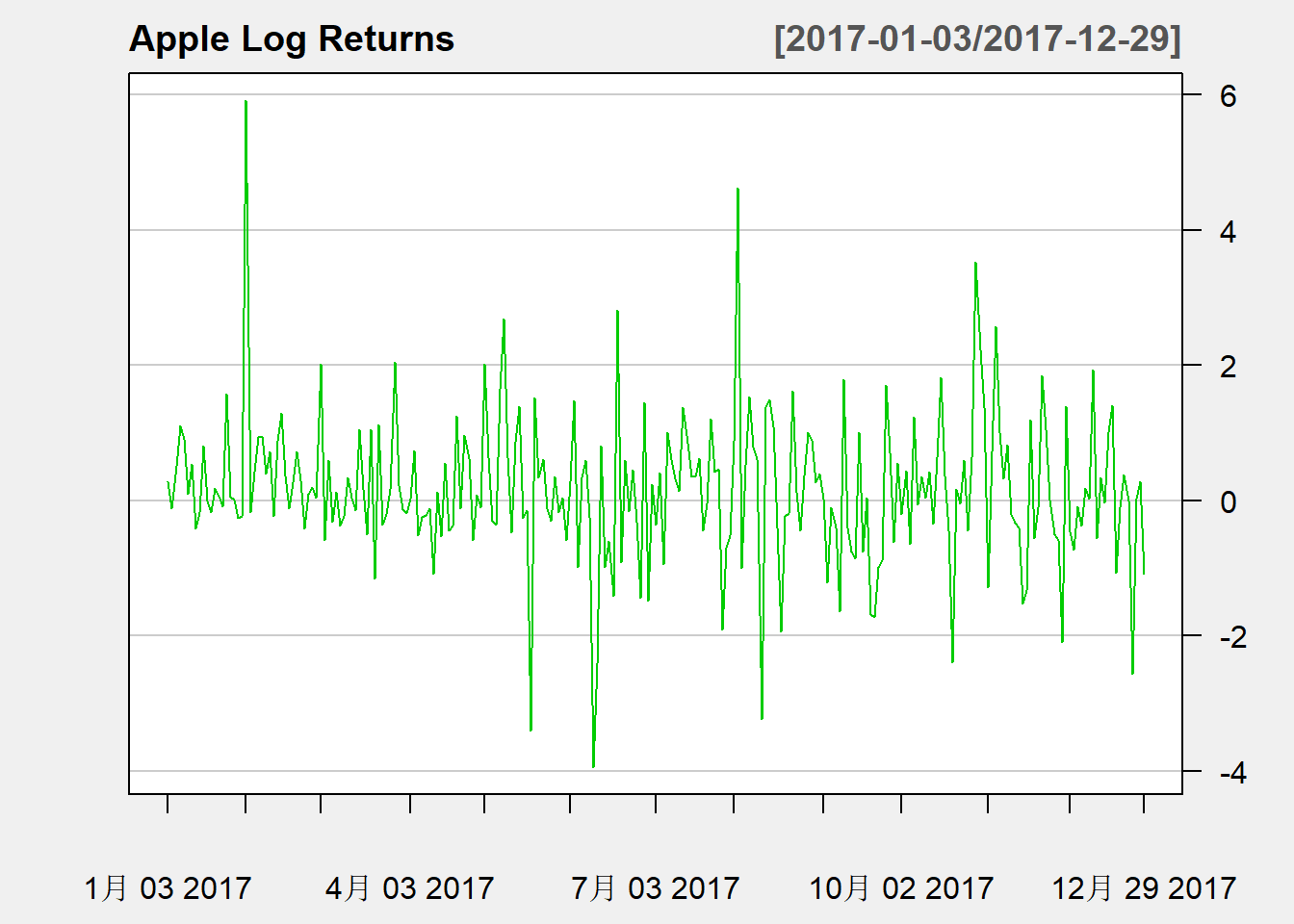
对数收益率的直方图:
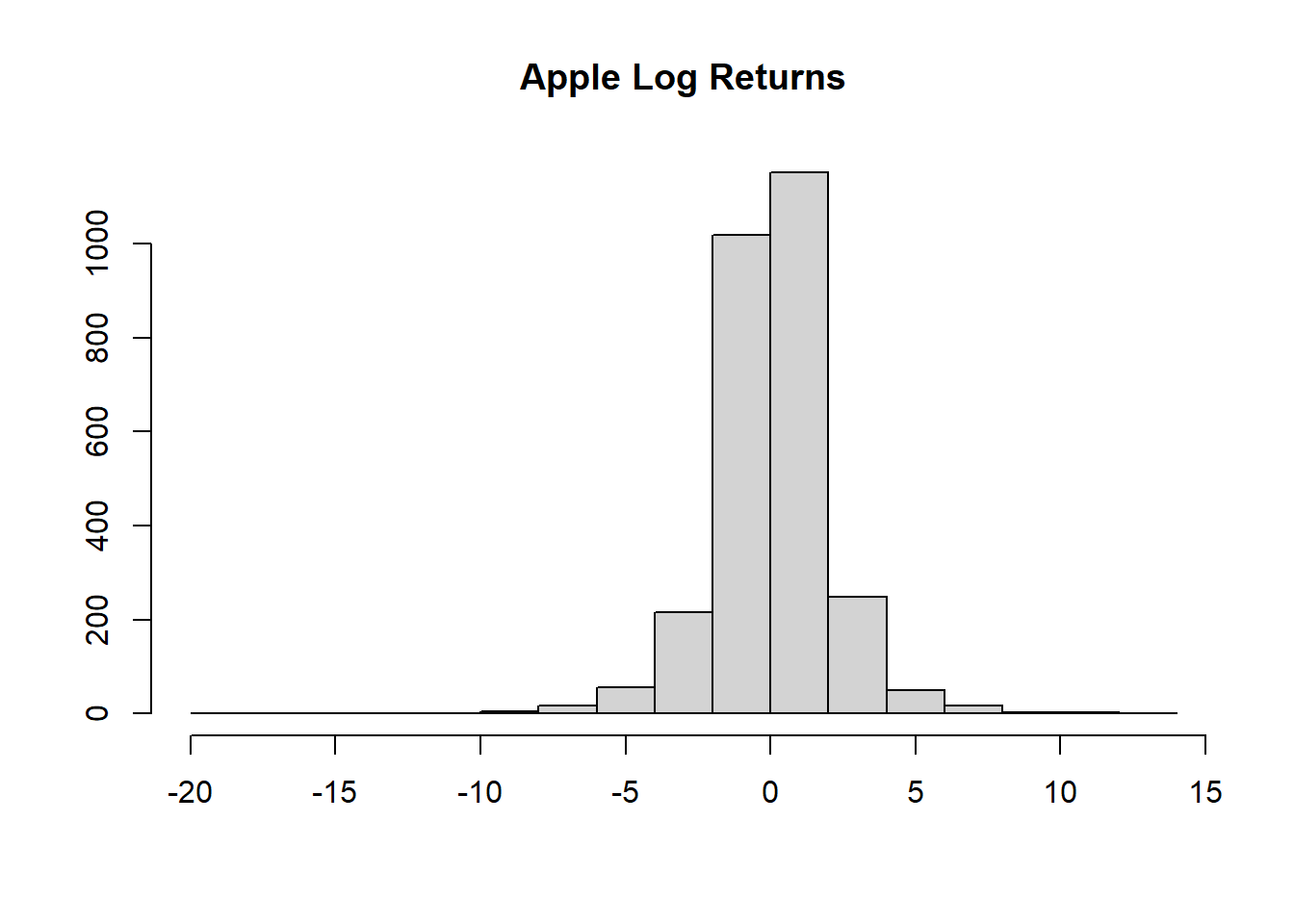
对数收益率的正态QQ图:
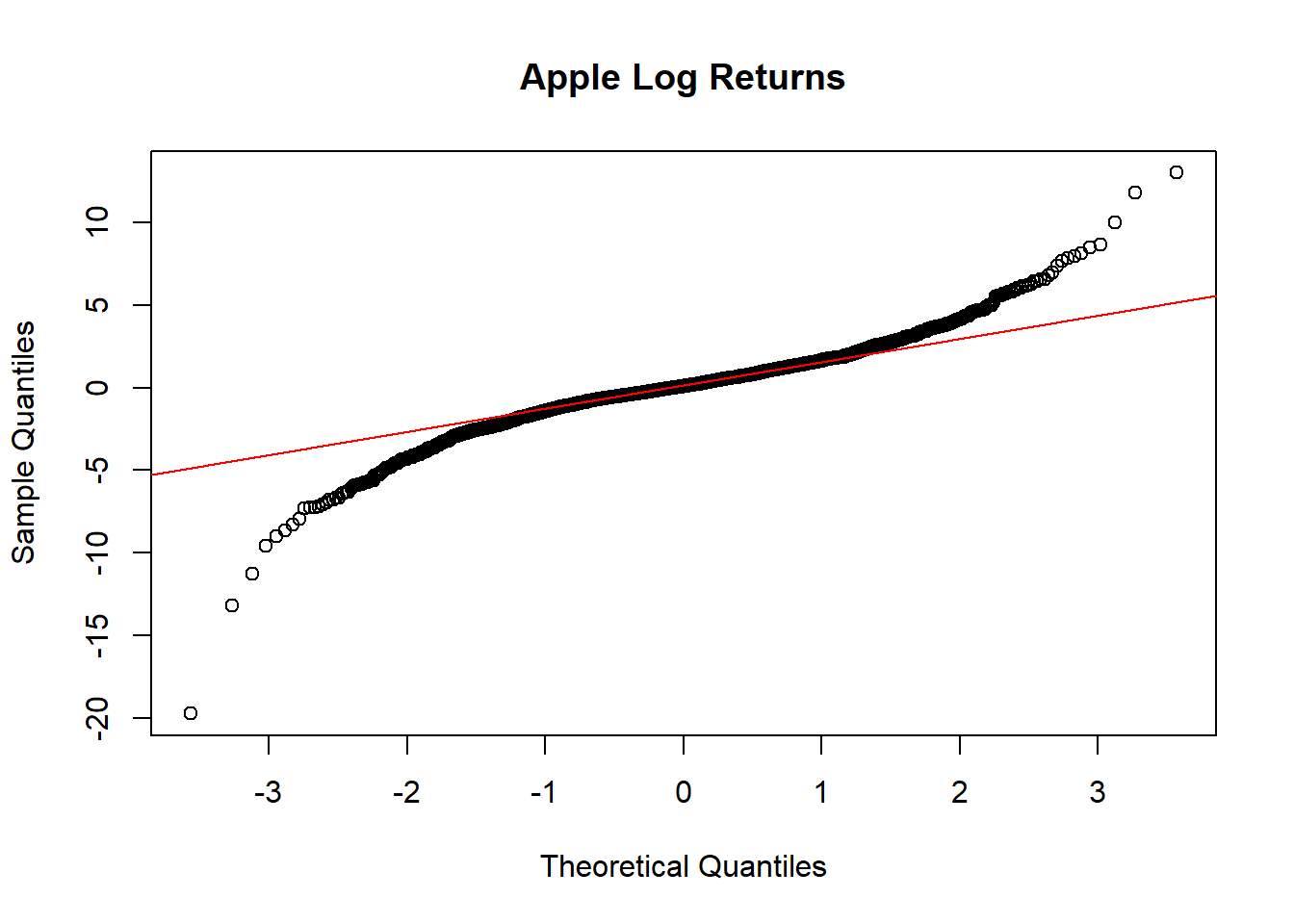
从时间序列曲线图、直方图、正态QQ图都可以看出股票对数收益率有厚尾现象。
2.4.2 美国十年期国债日数据
美国十年期国债日对数收益率下载和计算:
对数收益率时间序列2007-2017的曲线图:
chartSeries(
logret.TNX, type="l", TA=NULL,
subset="2007/2017",
name="US 10 Years T Notes Log Return",
theme="white", major.ticks="years", minor.ticks=FALSE)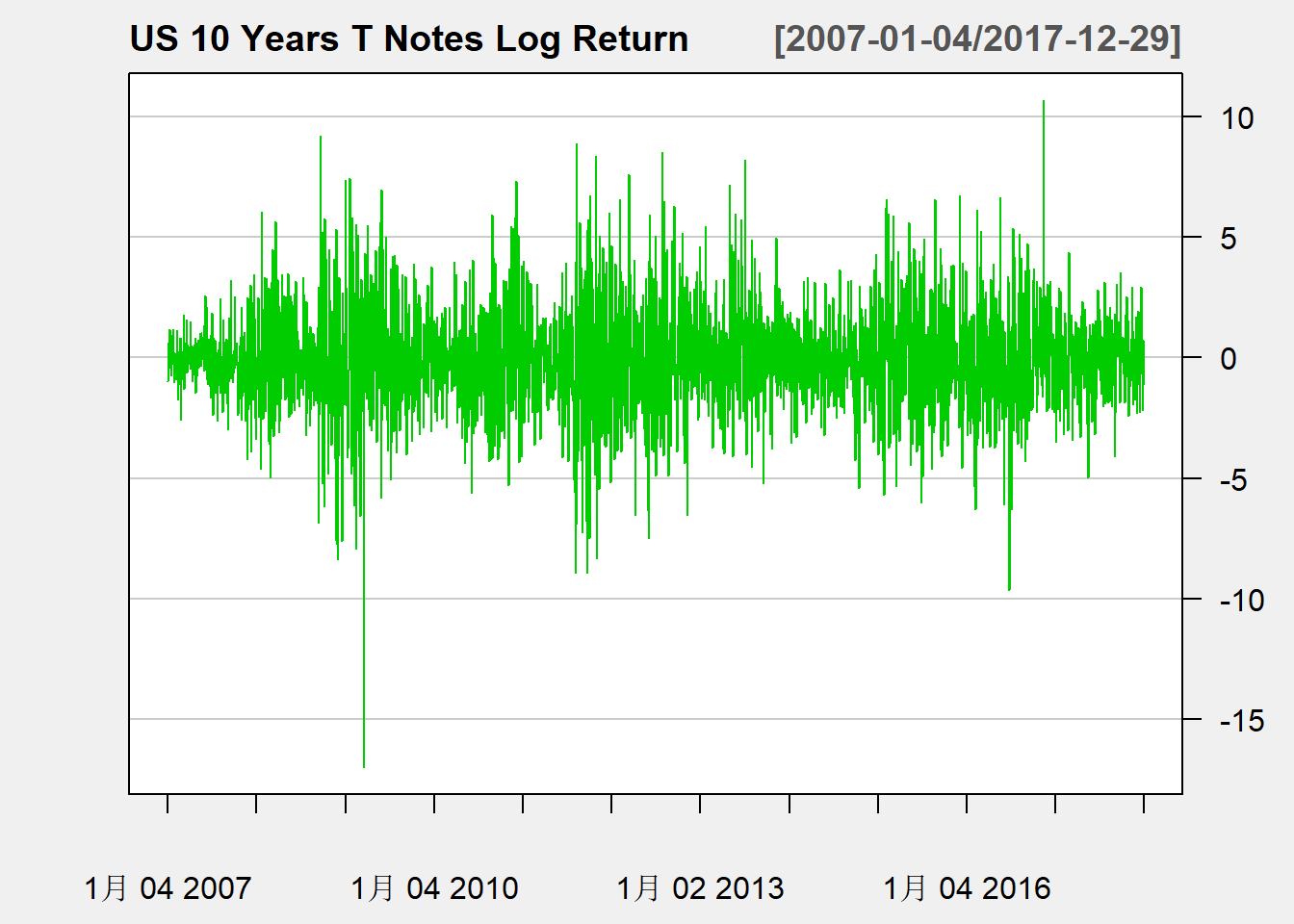
对数收益率的直方图:

对数收益率的正态QQ图:
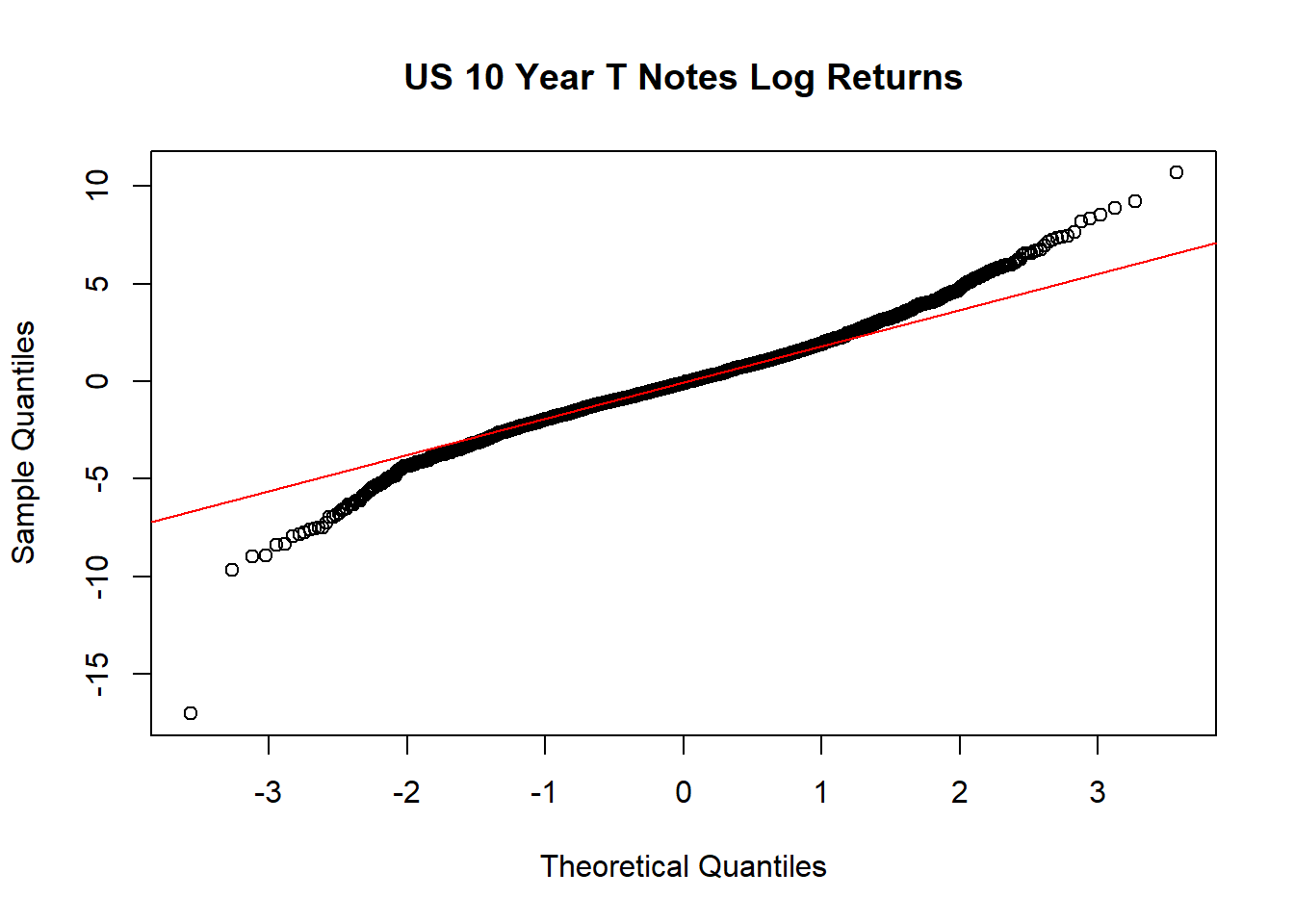
从时间序列曲线图、直方图、正态QQ图都可以看出股票对数收益率有厚尾现象。 比苹果股票收益率的厚尾性弱一些。
2.4.3 欧元对美元汇率日数据
下载欧元对美元汇率的日数据,一元时间序列:
汇率价格的曲线图:
chartSeries(
DEXUSEU, type="l", TA=NULL,
subset="2007/2017",
name="Euro to USD Price",
theme="white", major.ticks="years",
minor.ticks=FALSE)
对数收益率时间序列2007-2017的曲线图:
chartSeries(
logret.DEXUSEU, type="l", TA=NULL,
subset="2007/2017",
name="Euro to USD Log Returns",
theme="white", major.ticks="years", minor.ticks=FALSE)
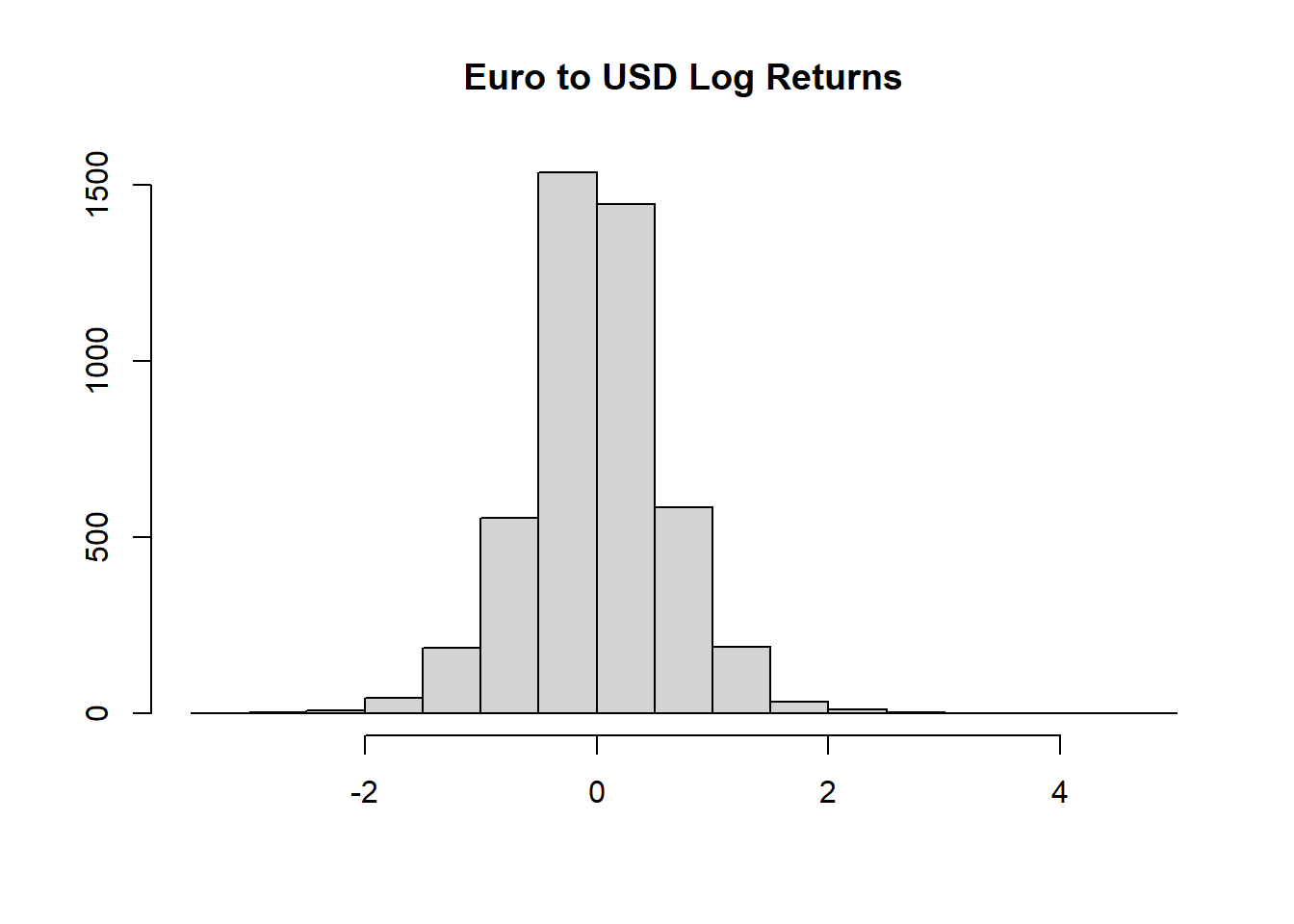
对数收益率的直方图:
对数收益率的正态QQ图:
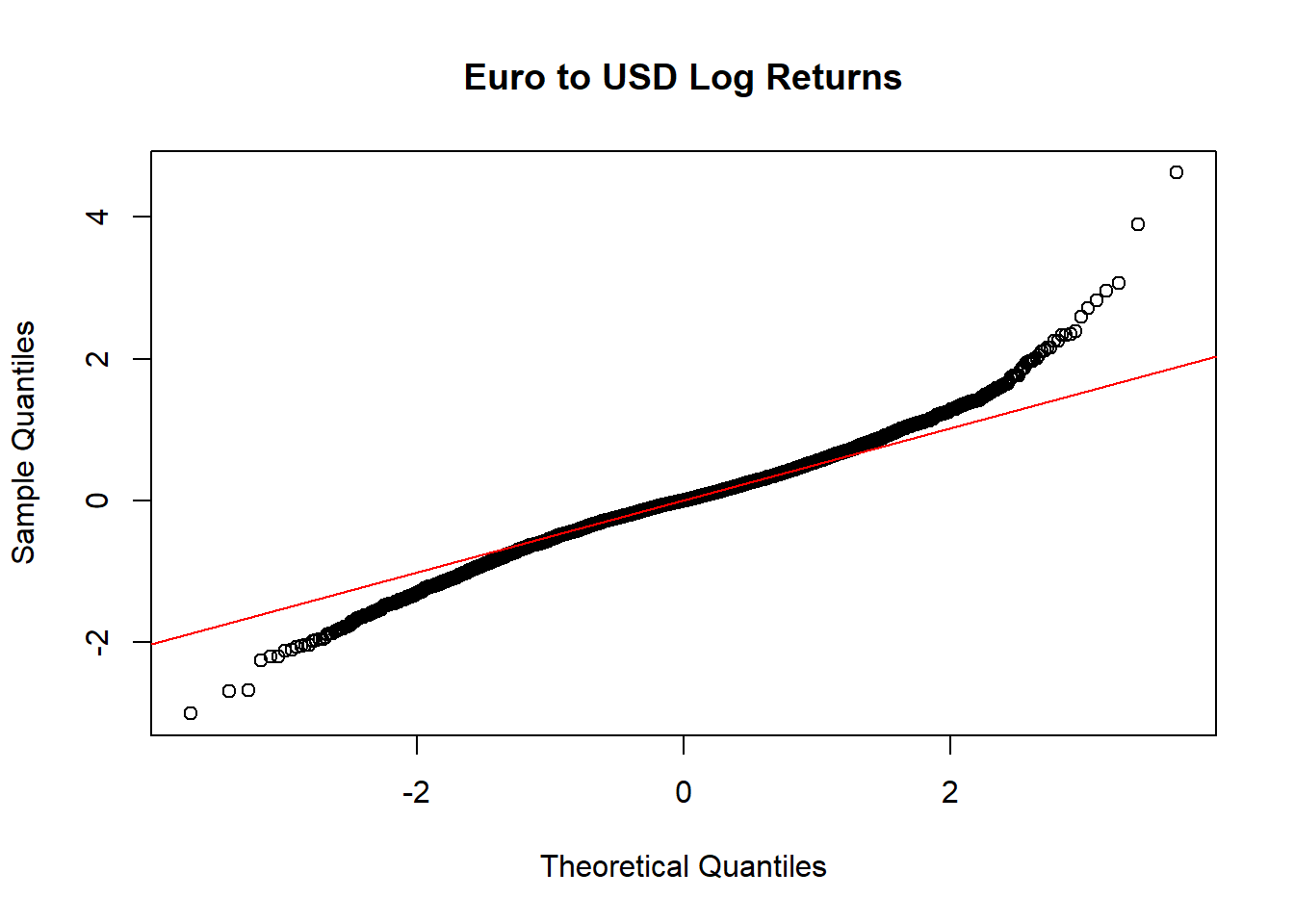
也呈现出厚尾性, 且右尾比左尾长。
2.5 收益率的分布特性
设\(i\)资产在时刻\(t\)的对数收益率为\(r_{it}\), 简单收益率为\(R_{it}\), 超额收益率为\(z_{it}\), \(i=1,\dots, N\), \(t=1,2,\dots, T\)。
2.5.1 统计分布复习
\(\mathbb R^k\)表示元素是有\(k\)个实数值分量的向量组成欧式空间。 \(\boldsymbol x \in \mathbb R^k\)表示其中一个点(向量)。
2.5.1.1 联合分布和边缘分布
随机向量的概念。
\[ F_{\boldsymbol X, \boldsymbol Y}(\boldsymbol x, \boldsymbol y | \boldsymbol\theta) = P_{\boldsymbol\theta}(\boldsymbol X \leq \boldsymbol x, \boldsymbol Y \leq \boldsymbol y) \] 表示随机变量\(\boldsymbol X\)和\(\boldsymbol Y\)的参数为\(\theta\)的联合分布函数, \(\boldsymbol x \in \mathbb R^{p}\), \(\boldsymbol y \in \mathbb R^{q}\)。
若\((\boldsymbol X, \boldsymbol Y)\)有联合密度函数 \(f_{\boldsymbol X, \boldsymbol Y}(\boldsymbol x, \boldsymbol y)\), 则 \[ F_{\boldsymbol X, \boldsymbol Y}(\boldsymbol x, \boldsymbol y) =\int_{-\infty}^{\boldsymbol x} \int_{-\infty}^{\boldsymbol y} f_{\boldsymbol X, \boldsymbol Y}(\boldsymbol x, \boldsymbol y) \,d\boldsymbol x\,d\boldsymbol y \]
已知联合分布, \(\boldsymbol X\)的边缘分布为 \[ F_{\boldsymbol X}(\boldsymbol x | \boldsymbol\theta) = F_{\boldsymbol X, \boldsymbol Y}(\boldsymbol x, \infty, \dots, \infty | \boldsymbol\theta) \]
一元随机变量\(X\)的分布函数(累积分布函数,cumulative distribution function, CDF) \[ F_X(x | \boldsymbol\theta) = P_{\boldsymbol\theta}(X \leq x) \] 其中\(\boldsymbol\theta\)是分布参数。 分布函数单调不减右连续, \(\lim_{x\to-\infty} F(x) = 0\), \(\lim_{x\to\infty} F(x) = 1\)。
2.5.1.2 分位数
如果\(X\)的一元分布函数\(F(x)\)严格单调递增且连续, 则\(\forall p \in (0,1)\), 存在唯一的\(x_p\)使得\(F(x_p)=p\), \(x_p\)称为随机变量\(X\)或者分布\(F(x)\)的\(p\)分位数, 也记作\(F^{-1}(p)\)。 一般地,令 \[ x_p = \inf \{ x | F_X(x) \geq p \}, \ \forall p \in (0, 1) \] 这样定义的\(x_p\)存在唯一。也记作\(F^{-1}(p)\)。
\(p\)分位数的另一定义是\(x_*\)满足 \[ P(X \leq x_*) \geq p, \ P(X \geq x_*) \geq 1-p \] 这样定义的分位数必存在但不一定唯一。
2.5.1.3 条件分布
在\(Y\leq y\)条件下\(X\)的条件分布为 \[ F(x | Y \leq y, \theta) = \frac{P(X\leq x, Y\leq y | \theta)}{P(Y \leq y | \theta)} = \frac{F(x, y | \theta)}{F_{Y}(y | \theta)} \]
有联合密度\(f(x,y|\theta)\)时, \(Y=y\)条件下\(X\)有条件密度 \[ f(x | y, \theta) = \frac{f(x, y |\theta)}{f_Y(y | \theta)}, \quad f(x, y | \theta) = f_Y(y) f(x | y, \theta) \] \(Y=y\)条件下可以计算条件概率 \[ P(X \leq x | Y=y, \theta) = \int_{-\infty}^x f(x|y,\theta) \,dx \] 条件期望 \[ E_{\theta}(X | Y=y) = \int x f(x|y, \theta) \,dx = g(y), \quad E_{\theta}(X | Y) = g(Y) \] 条件方差为 \[ \text{Var}(X | Y, \theta) = E_{\theta}\left( [X - E(X|Y)]^2 | Y \right) \]
2.5.1.4 矩
期望: \[ E X = \int x f(x) \,dx \] 经常记为\(\mu\)。
方差 \[ \text{Var}(X) = E (X - EX)^2 \] 经常记为\(\sigma^2\)。 \(\sigma\)称为标准差(standard deviation)。 对于资产收益率, 方差和标准差是度量其不确定性的指标, 可用于资产风险管理和度量。
随机变量\(X\)的\(k\)阶原点矩 \[ m_k' = E (X^k) \] 期望是一阶原点矩。
\(k\)阶中心矩 \[ m_k = E [(X - EX)^k] \] 方差是二阶中心矩。
随机变量分布中一元正态分布完全由其期望和方差决定, 其它分布可能需要更多矩。
偏度(Skewness): 令\(Y = \frac{X - EX}{\sqrt{\text{Var}(X)}}\), 称为\(X\)的标准化, \(Y\)的三阶矩称为\(X\)的偏度, 可以用来度量分布的对称性, 负偏度称为左偏, 反映左尾偏长的情况; 正偏度称为右偏, 反映右尾偏长的情况。
峰度(Kurtosis): 将\(X\)标准化为\(Y\), \(Y\)的四阶矩减去3称为\(X\)的超额峰度或峰度, 正态分布的超额分布等于0。 峰度大的分布有重尾或厚尾现象, 其分布密度在\(\pm\infty\)处趋于零速度较慢, 其样本具有较多的异常值(离群值,outliers)。
2.5.1.5 矩的估计和检验
样本均值 \[ \bar x = \hat\mu = \frac{1}{T} \sum_{t=1}^T x_t \] 样本方差 \[ S^2 = \hat\sigma^2 = \frac{1}{T-1} \sum_{t=1}^T (x_t - \bar x)^2 \]
样本偏度 \[ \hat{\text{Skew}} = \frac{1}{T-1} \sum_{t=1}^T \left(\frac{x_t - \bar x}{S} \right)^3 \]
样本超额峰度 \[ \hat{\text{Kurt}} = \frac{1}{T-1} \sum_{t=1}^T \left(\frac{x_t - \bar x}{S} \right)^4 - 3 \]
R软件中扩展包fBasics中的basicStats()函数可以计算各种基本的统计量。
收益率数据在大多数情况下表现得与独立同分布观测很接近,
所以尽管我们不能确保其独立同分布,
在实际统计分析时仍使用在独立同分布假设下的各种方法。
为检验\(H_0: \mu=0\), 可以用统计量 \[ Z = \frac{\bar x}{S/\sqrt{T}} \] 在\(H_0\)成立且\(T\)充分大时\(Z\)近似服从标准正态分布, 利用这样的分布计算检验的\(p\)值。 在R软件中
可以进行\(H_0:\mu=0\)的检验。
若观测为独立的正态分布样本, 则\(T\)充分大时样本偏度渐近服从\(\text{N}(0, 6/T)\)分布, 样本超额峰度渐近服从\(\text{N}(0, 24/T)\)分布, 据此可以计算检验\(H_0:\text{偏度}=0\)和\(H_0:\text{超额峰度}=0\)的\(p\)值。
Jarque和Bera(1987)提出了Jarque-Bera检验, 零假设是总体服从正态分布, 设观测为独立同分布样本, 统计量为 \[ \text{JB} = \frac{\hat{\text{Skew}}^2}{6/T} + \frac{[\hat{\text{Kurt}} - 3]^2}{24/T} \] 在零假设下JB统计量渐近服从\(\chi^2(2)\)分布。 计算右侧\(p\)值。 在R软件中
可以执行正态性JB检验。
tseries::jarque.bera.test()也可以执行Jarque-Bera检验。
JB检验的原始文献: CARLOS M. JARQUE and ANIL K. BERA(1980), Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals, Economics Letters 6, pp. 255-259.
2.5.2 收益率分布研究例子
作为示例, 对苹果公司股票日收盘价的收益率数据进行简单分析。
取2011-2017数据子集,计算收盘价的对数收益率:
基本统计量:
## x
## nobs 1760.000000
## NAs 0.000000
## Minimum -0.131885
## Maximum 0.085022
## 1. Quartile -0.006914
## 3. Quartile 0.009411
## Mean 0.000789
## Median 0.000574
## Sum 1.388711
## SE Mean 0.000377
## LCL Mean 0.000050
## UCL Mean 0.001528
## Variance 0.000250
## Stdev 0.015812
## Skewness -0.323171
## Kurtosis 5.486581这里的Kurtosis是超额峰度。 有左偏,重尾。
直方图:
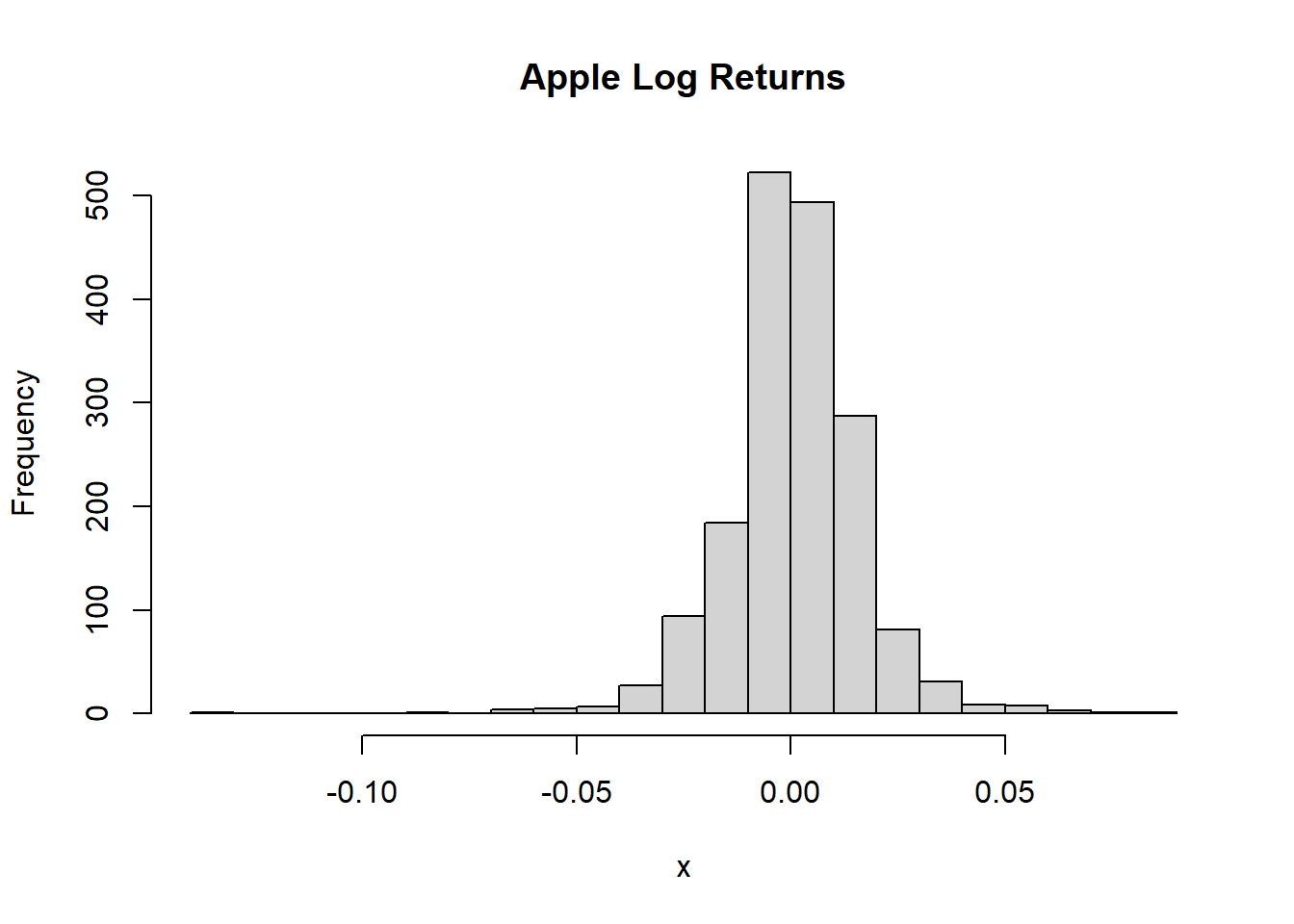
作核密度估计图并叠加正态密度估计:
tmp.1 <- density(x, na.rm=TRUE)
tmp.x <- seq(min(x, na.rm=TRUE), max(x, na.rm=TRUE),
length.out=100)
tmp.y <- dnorm(tmp.x, mean(x, na.rm=TRUE),
sd(x, na.rm=TRUE))
tmp.ra <- range(c(tmp.1$y, tmp.y), na.rm=TRUE)
plot(tmp.1, main="Apple Log Return",
ylim=tmp.ra)
lines(tmp.x, tmp.y, lwd=2, col="red")
legend("topleft", lwd=c(1,2),
col=c("black", "red"),
legend=c("Kernel density Est.",
"Parametric normal density est."))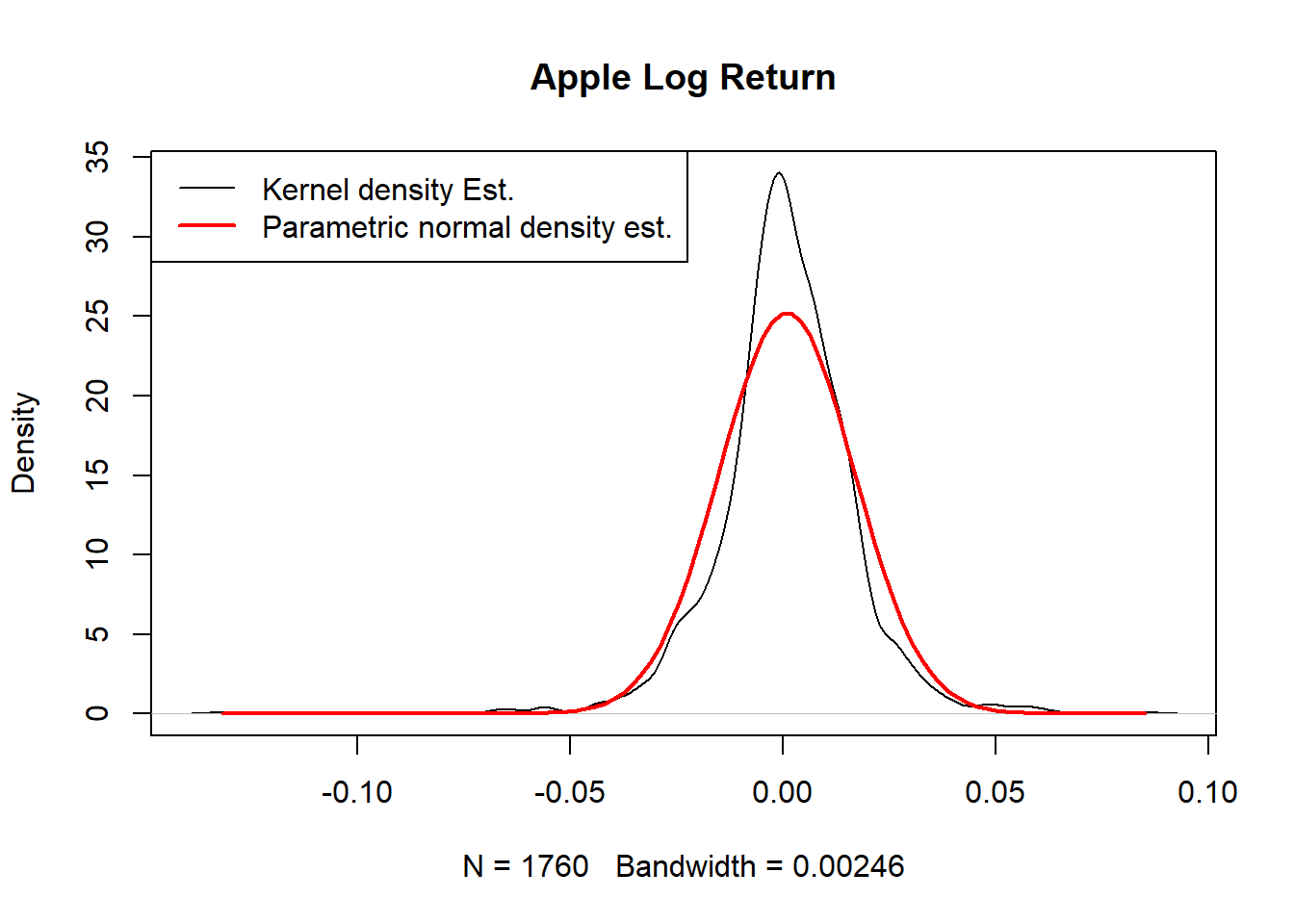
比正态密度明显重尾, 且左尾比右尾长。
均值为零的检验:
##
## One Sample t-test
##
## data: x
## t = 2.0935, df = 1759, p-value = 0.03644
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.0000498348 0.0015282461
## sample estimates:
## mean of x
## 0.0007890405检验\(p\)值为0.036,在0.05水平下显著, 可认为均值不为零,显著地大于零。
单独计算偏度,及其标准化:
## [1] -0.323171## [1] -5.534942标准化值的绝对值超过1.96, 在0.05水平下拒绝偏度等于零的假设。
单独计算超额峰度,及其标准化:
## [1] 5.486581## [1] 46.98427标准化值的绝对值超过1.96, 在0.05水平下拒绝峰度等于零的假设。
正态性JB检验:
##
## Title:
## Jarque - Bera Normalality Test
##
## Test Results:
## STATISTIC:
## X-squared: 2245.9834
## P VALUE:
## Asymptotic p Value: < 2.2e-16
##
## Description:
## Tue May 21 15:19:55 2024 by user: Lenovop值为小于万分之一的值, 在0.05水平下显著。
R的feasts扩展包提供了计算各种统计量的功能,
要求输入tsibble类型的时间序列数据。
例如,
m-bnd.txt中包含了各个期限的美国债券指数的月简单收益率数据,
从1942年1月值1999年12月,
读入为tsibble类型:
##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## `30yrs` = col_double(),
## `20yrs` = col_double(),
## `10yrs` = col_double(),
## `5yrs` = col_double(),
## `1yr` = col_double()
## )## # A tsibble: 6 x 3 [1M]
## # Key: key [1]
## index key value
## <mth> <chr> <dbl>
## 1 1942 1月 30yrs 0.00695
## 2 1942 2月 30yrs 0.00114
## 3 1942 3月 30yrs 0.00919
## 4 1942 4月 30yrs -0.00293
## 5 1942 5月 30yrs 0.00752
## 6 1942 6月 30yrs 0.00029计算指定的统计量:
| key | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|---|
| 10yrs | -0.06672 | -0.0058650 | 0.002485 | 0.004484727 | 0.0129075 | 0.09999 |
| 1yr | -0.01721 | 0.0010500 | 0.003410 | 0.004431494 | 0.0063925 | 0.05606 |
| 20yrs | -0.08406 | -0.0071600 | 0.002340 | 0.004527414 | 0.0148375 | 0.15235 |
| 30yrs | -0.07729 | -0.0081125 | 0.002230 | 0.004347586 | 0.0154850 | 0.13314 |
| 5yrs | -0.05802 | -0.0011325 | 0.002300 | 0.004594612 | 0.0094700 | 0.10612 |
其中的summary()可以替换成返回单个统计量的函数,
或者自定义的返回多个统计量的函数。
feasts包可以计算大量的与时间序列特征有关的统计量, 如:
2.6 金融数据的图形
- 时间序列曲线图
- K线图
- 叠加均线等
- 直方图,核密度估计,参数密度估计
- QQ图
- ACF和PACF等
2.6.1 时间序列曲线图实例
用quantmod::chartSeries()作图,
优点是支持曲线图、K线图、交易量同步显示、增加均线等分析。
缺点是可定制性受限。
苹果公司2017年日收盘价的时间序列图:
chartSeries(
AAPL, type="line",
subset="2017", TA=NULL,
theme="white", name="Apple Stock Price",
major.ticks="months", minor.ticks=FALSE)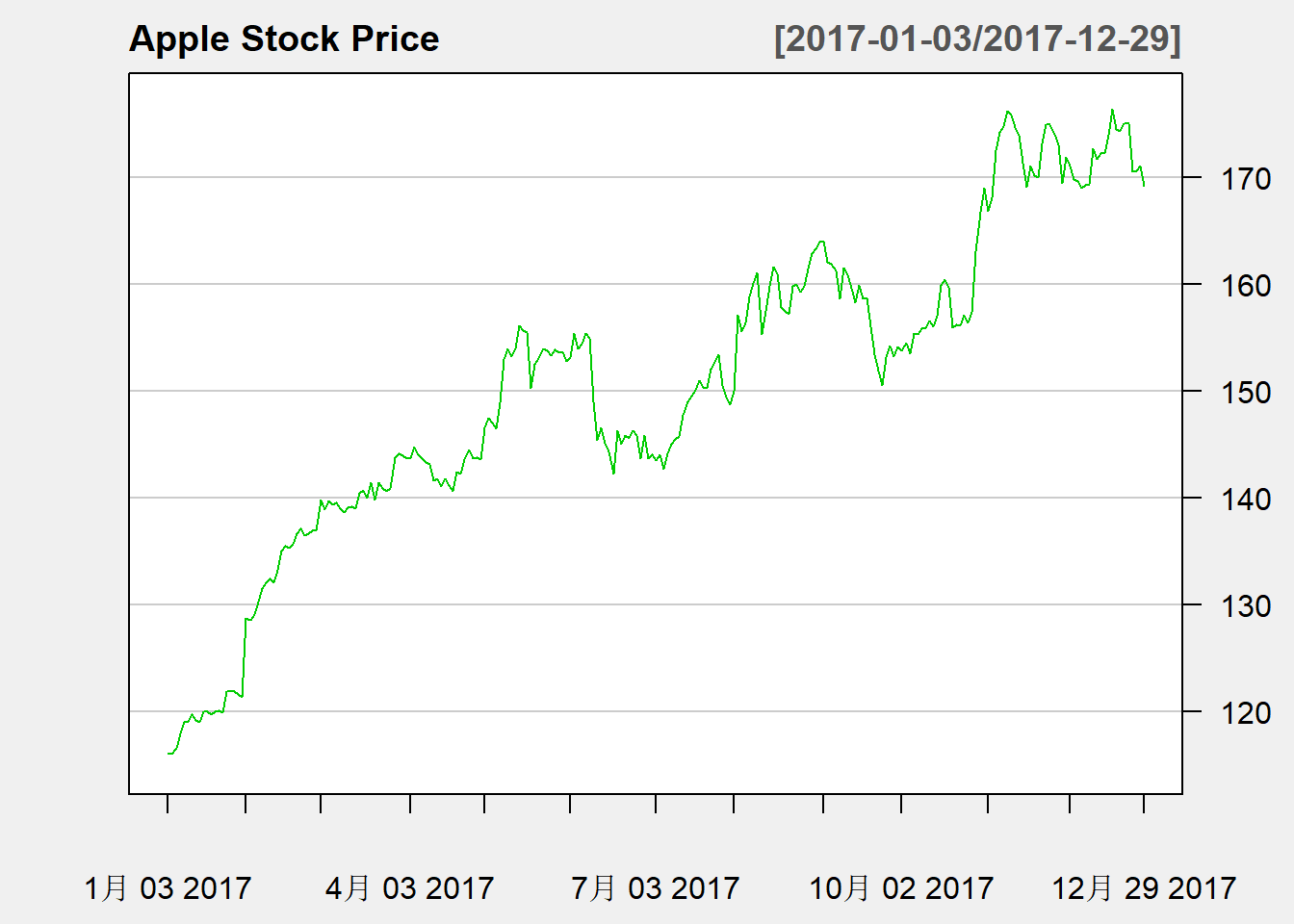
带有7日均线的曲线图:
chartSeries(
AAPL, type="line",
subset="2017", TA="addSMA(7)",
theme="white", name="Apple Stock Price",
major.ticks="months", minor.ticks=FALSE)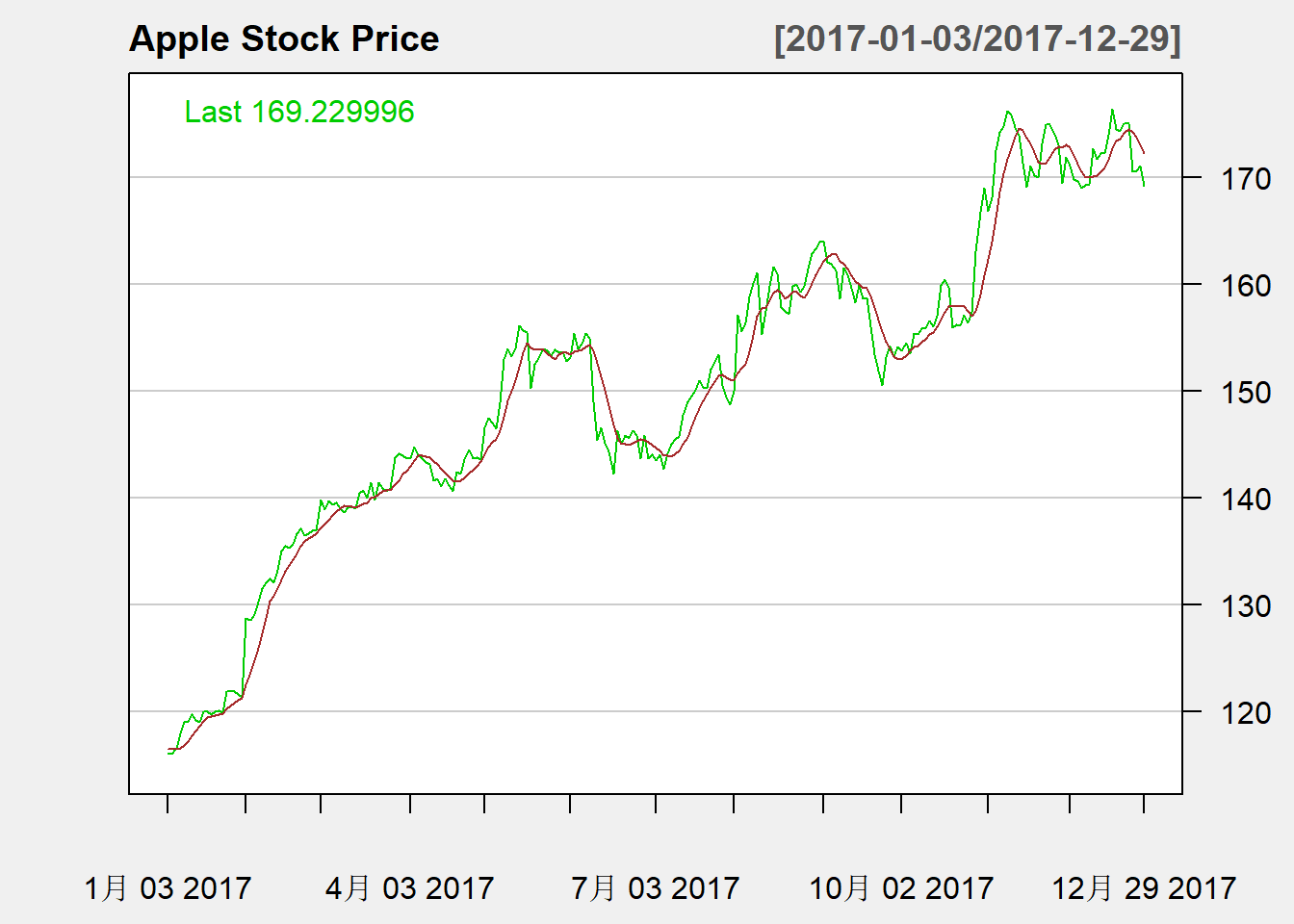
用TA="..."选项可以添加技术曲线。
详见quantmod::TA()的文档。
用ggplot2包的作图功能则可以进行较多的控制, 比如对时间坐标轴的精细控制。 如:
library(ggplot2)
p <- ggplot(data = tibble(
time=index(AAPL),
price=coredata(AAPL)[,"AAPL.Close",drop=TRUE]),
mapping = aes(x=time, y=price))
p + geom_line()
修改时间轴,每5年标数值,每年画竖线:
p + geom_line() +
scale_x_date(
name = "year",
date_breaks = "5 years",
date_labels = "%Y",
date_minor_breaks = "1 year",
expand = c(0, 0)) 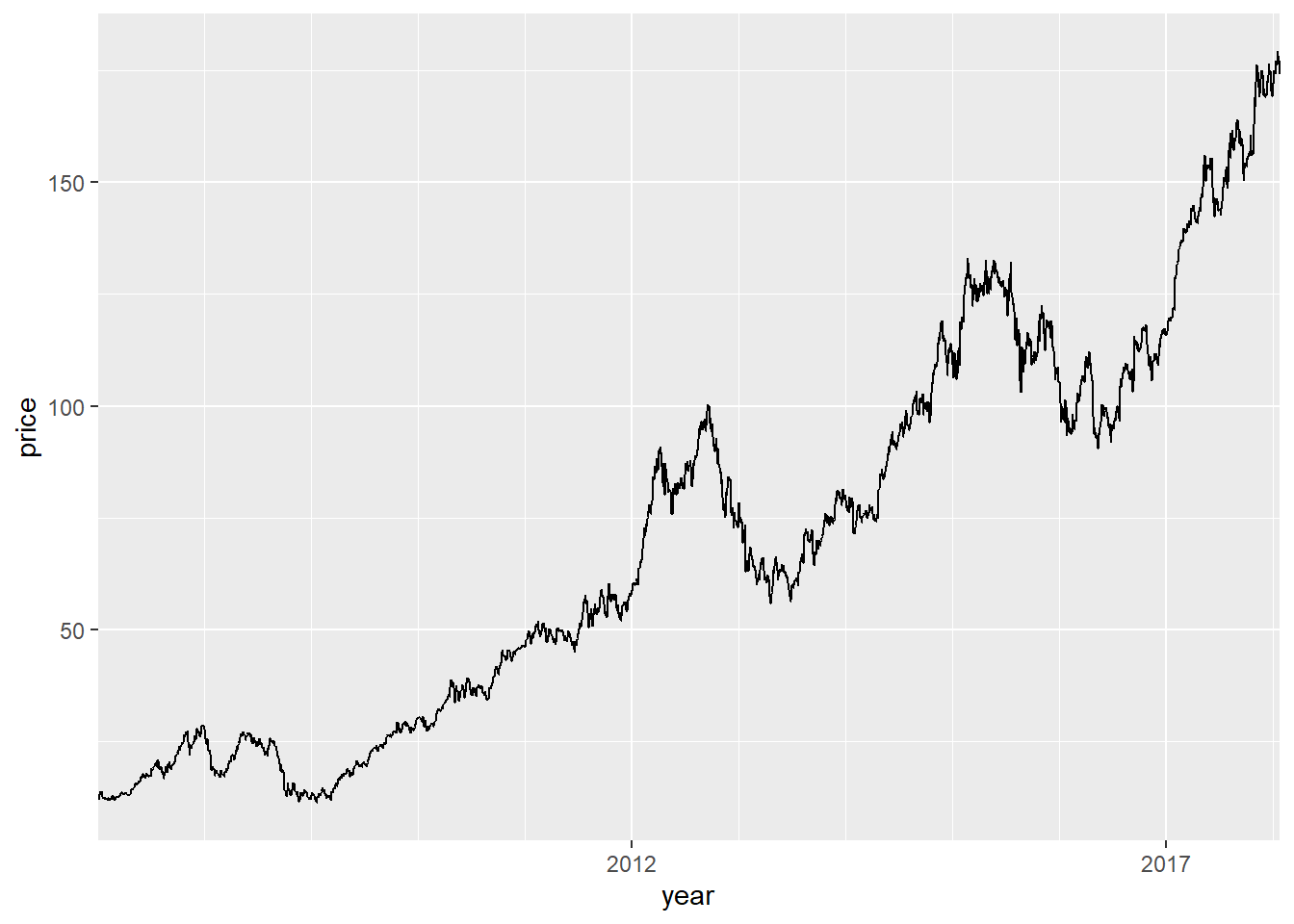
选项date_labels是日期刻度的一种格式规定, 比如”%Y”是四位数的年份,“%Y-%m”是年月格式,等等。
也可以人为指定年份:
p + geom_line() +
scale_x_date(
name = "year",
breaks = lubridate::make_date(c(2008, 2010, 2012, 2014, 2016)),
date_labels = "%Y",
date_minor_breaks = "1 year",
expand = c(0, 0)) 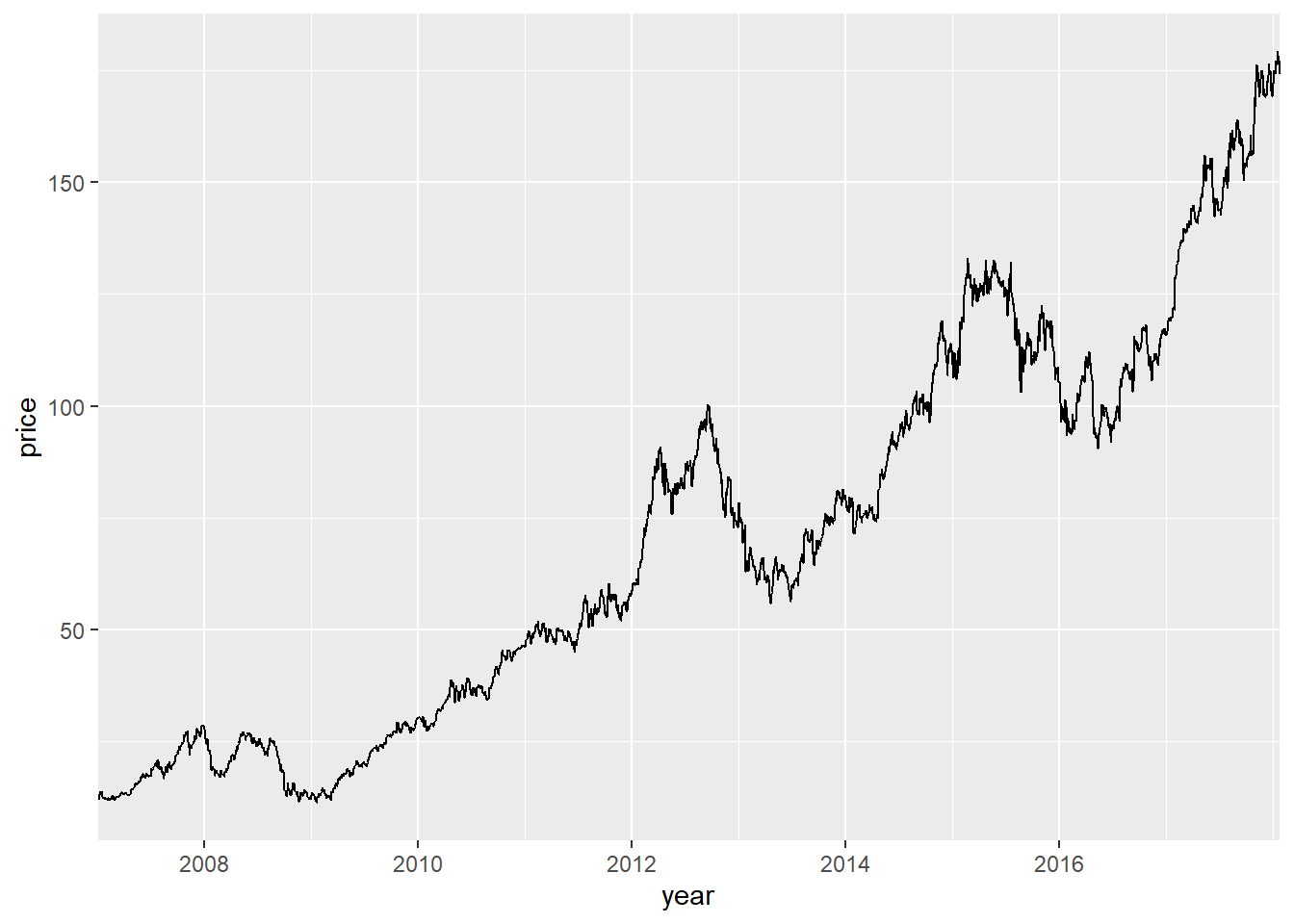
可以要求日期旋转45度显示:
p + geom_line() +
scale_x_date(
name = "year",
date_labels = "%Y-%m-%d",
expand = c(0, 0)) +
theme(
axis.text.x = element_text(
angle = 45, vjust = 1, hjust = 1) )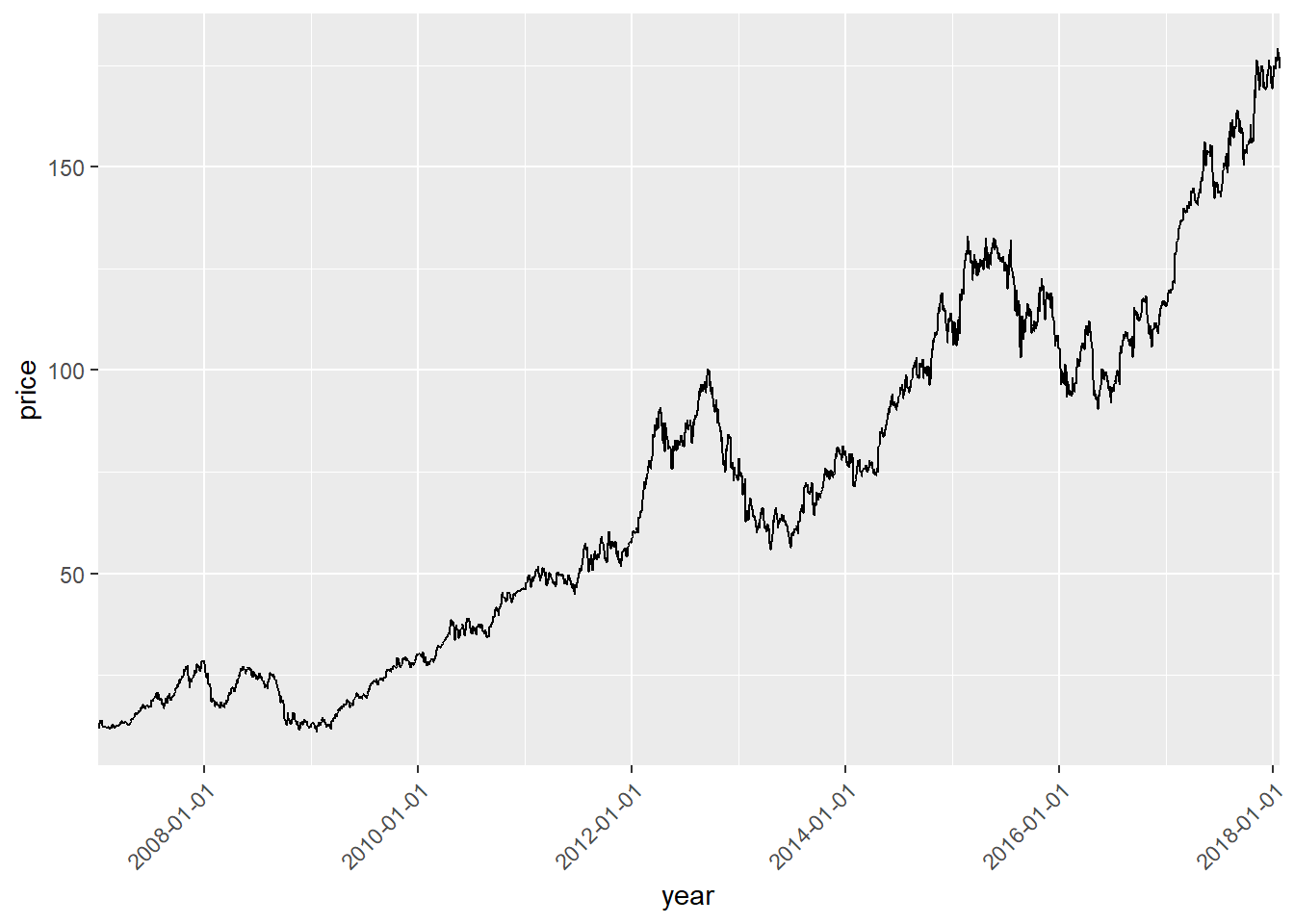
2.6.2 K线图实例
用quantmod::chartSeries()作图。
苹果公司2017年日收盘价的K线图,带有成交量:
chartSeries(
AAPL,
subset="2017",
theme="white", name="Apple Stock Price",
major.ticks="months", minor.ticks=FALSE)
当时间点比较多时,K线图画成了“火柴”形状,每一个K线单元用窄线画出。
仅画最后一个月:
chartSeries(
AAPL,
subset="2017-12",
theme="white", name="Apple Stock Price",
major.ticks="auto", minor.ticks=FALSE)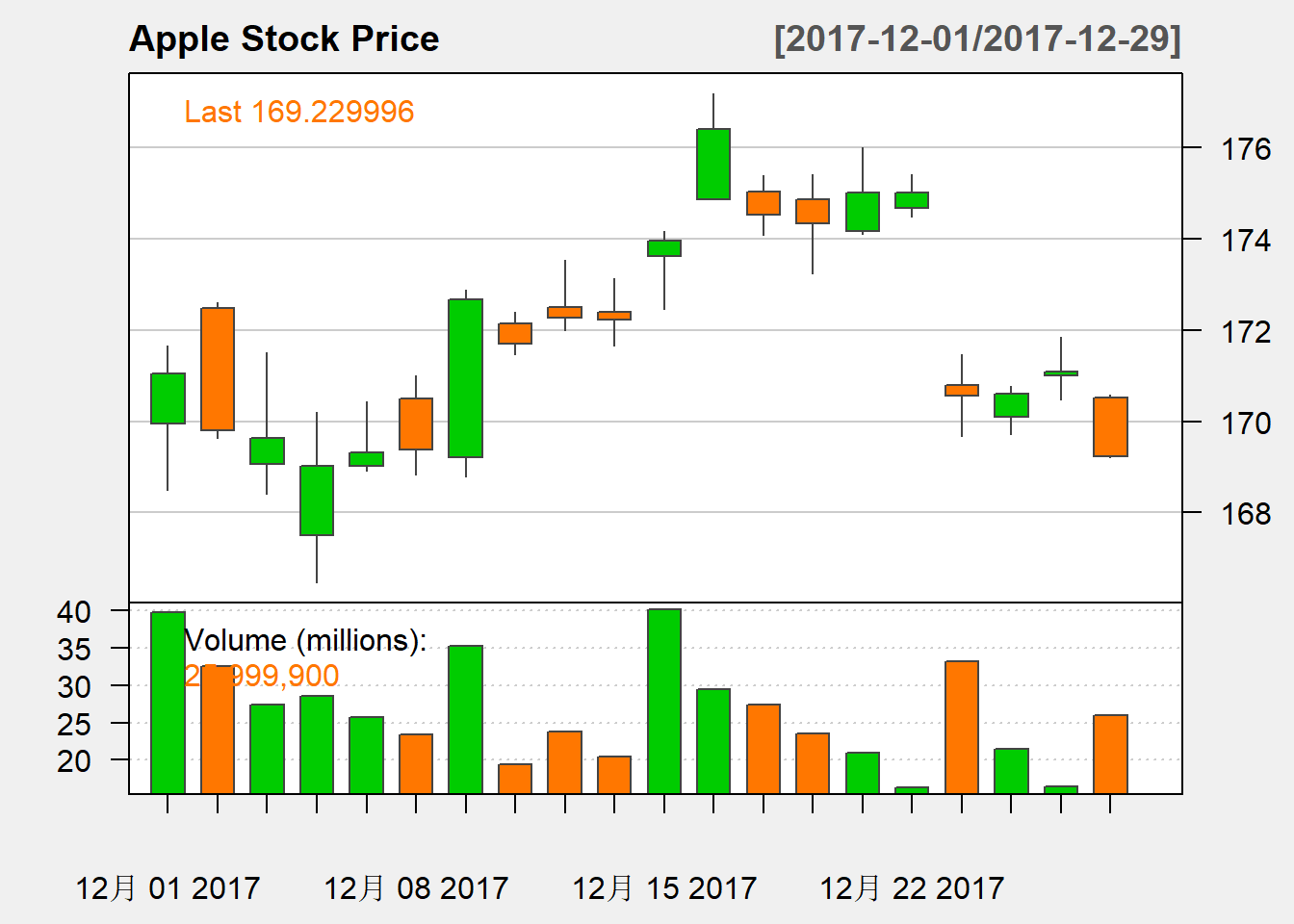
可见时间点比较少时,每个K线单元画成条形。
在K线图中, 条形两端纵坐标为开盘价和收盘价, 低开高收时为阳线, 高开低收时为阴线; 用单色显示时, 阳线显示成空心条形, 阴线显示成实心条形; 用红色和绿色显示时, 国内的习惯是红色阳线,绿色阴线, 而西方的习惯是绿色阳线,红色阴线。 如果最低、最高价不等于开盘价和收盘价, 则向下画短线或者向上画短线。 这样,每个K线单元都表示了OHLC四个值。
子集还可以指定成"from/to"的格式。
2.6.3 密度估计
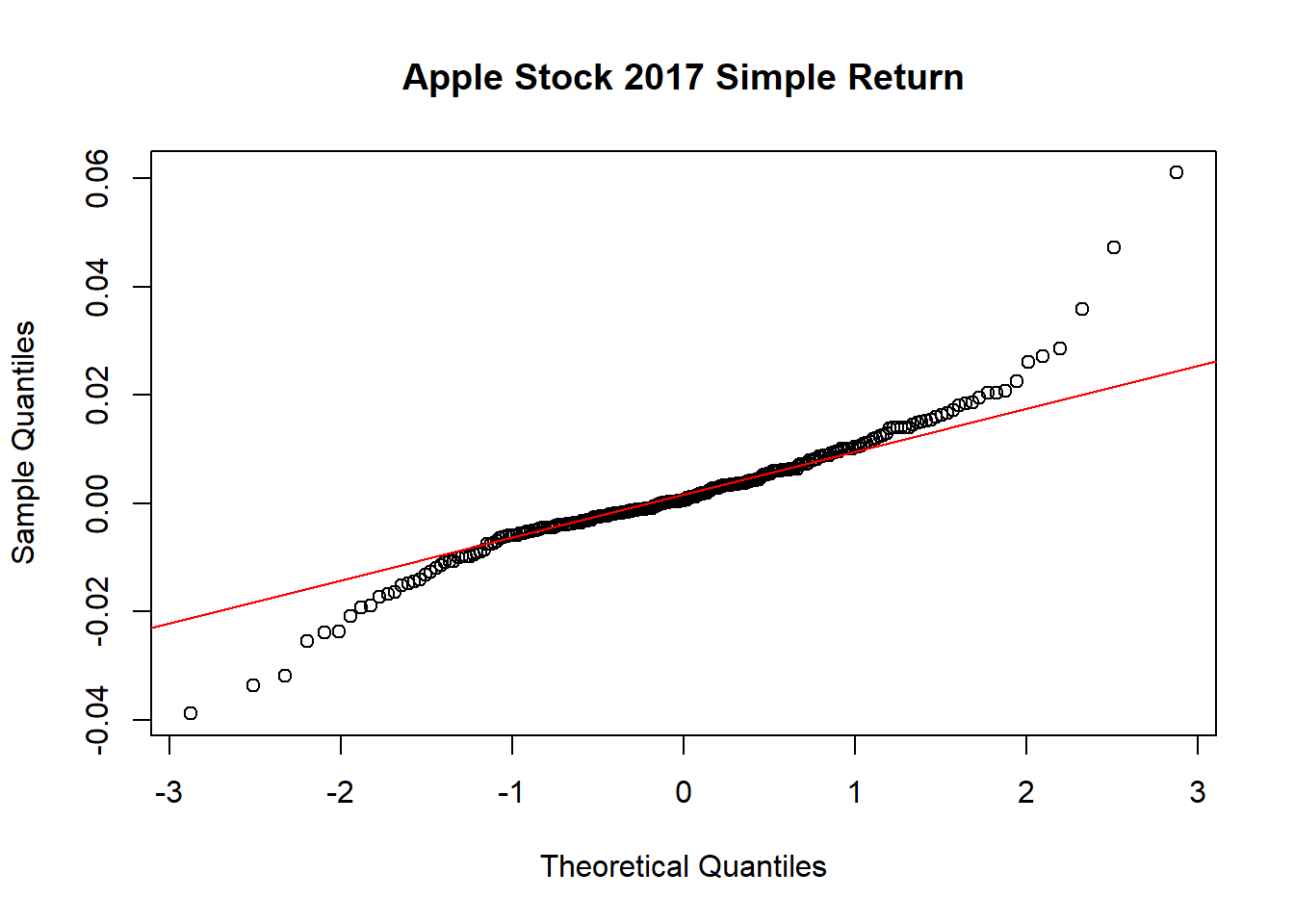
苹果公司2017年简单收益率的直方图:
x <- simple.return(AAPL["2017","AAPL.Adjusted"])
hist(x, main="Apple Stock 2017 Simple Return", xlab="")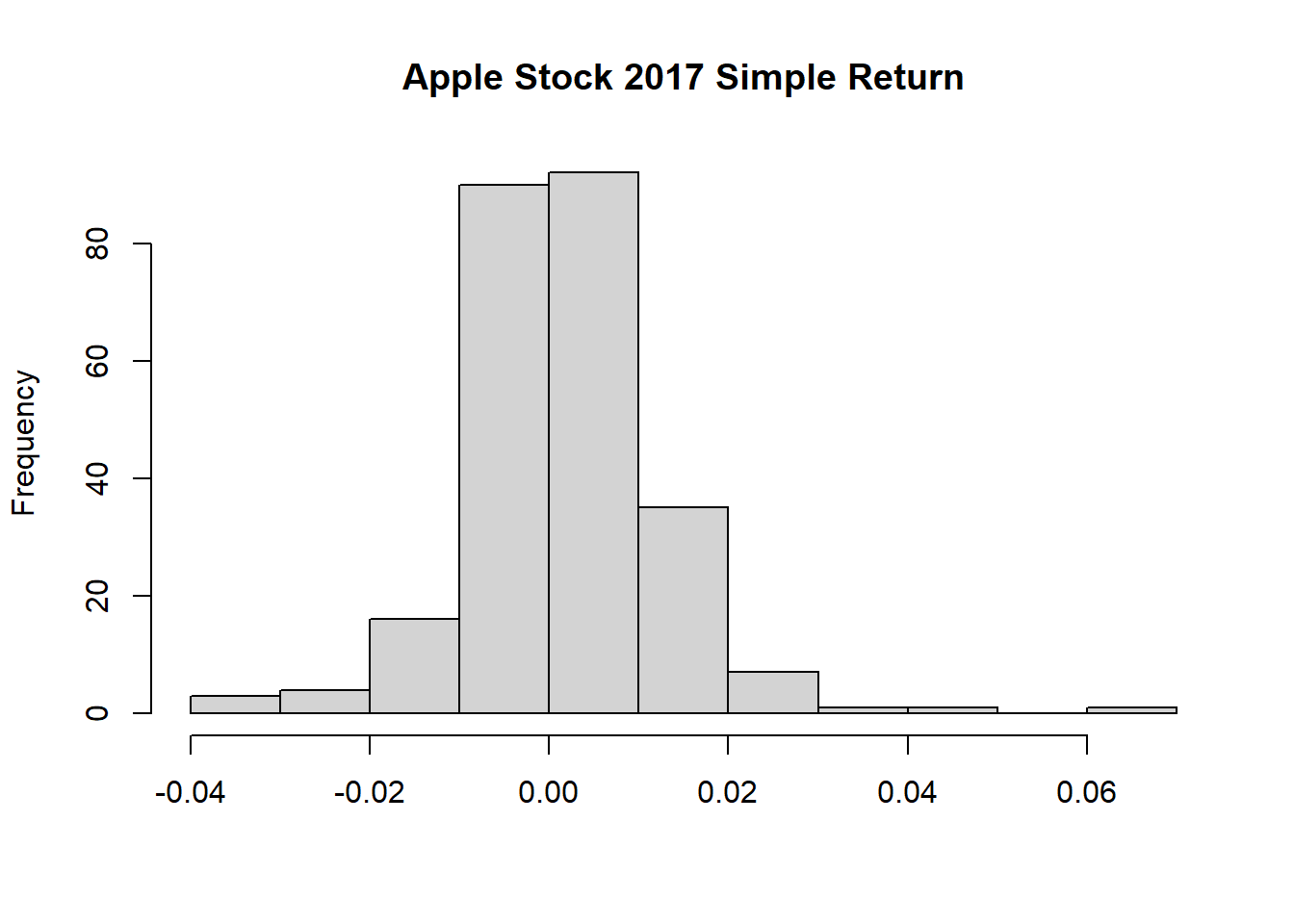
作核密度估计图并叠加正态密度估计(重复前面例子):
tmp.1 <- density(x, na.rm=TRUE)
tmp.x <- seq(min(x, na.rm=TRUE), max(x, na.rm=TRUE),
length.out=100)
tmp.y <- dnorm(tmp.x, mean(x, na.rm=TRUE),
sd(x, na.rm=TRUE))
tmp.ra <- range(c(tmp.1$y, tmp.y), na.rm=TRUE)
plot(tmp.1, main="Apple Stock 2017 Simple Return",
ylim=tmp.ra)
lines(tmp.x, tmp.y, lwd=2, col="red")
legend("topright", lwd=c(1,2),
col=c("black", "red"),
legend=c("Kernel density Est.",
"Parametric normal density est."))
2.6.5 散点图与回归直线
读入IBM和S&P的月度收益率数据,从1926-01到2011-09, 并转换为xts格式,时间下标改为yearmon格式:
d <- read_table(
"m-ibmsp-2611.txt",
col_types=cols(.default=col_double(),
date=col_date(format="%Y%m%d")))
ibmsp <- xts(as.matrix(d[,2:3]), d$date)
tclass(ibmsp) <- "yearmon"
head(ibmsp)## ibm sp
## 1月 1926 -0.010381 0.022472
## 2月 1926 -0.024476 -0.043956
## 3月 1926 -0.115591 -0.059113
## 4月 1926 0.089783 0.022688
## 5月 1926 0.036932 0.007679
## 6月 1926 0.068493 0.043184序列图:
chartSeries(
ibmsp[,"ibm"], type="lines",
theme="white", name="IBM returns",
major.ticks="years", minor.ticsk=FALSE)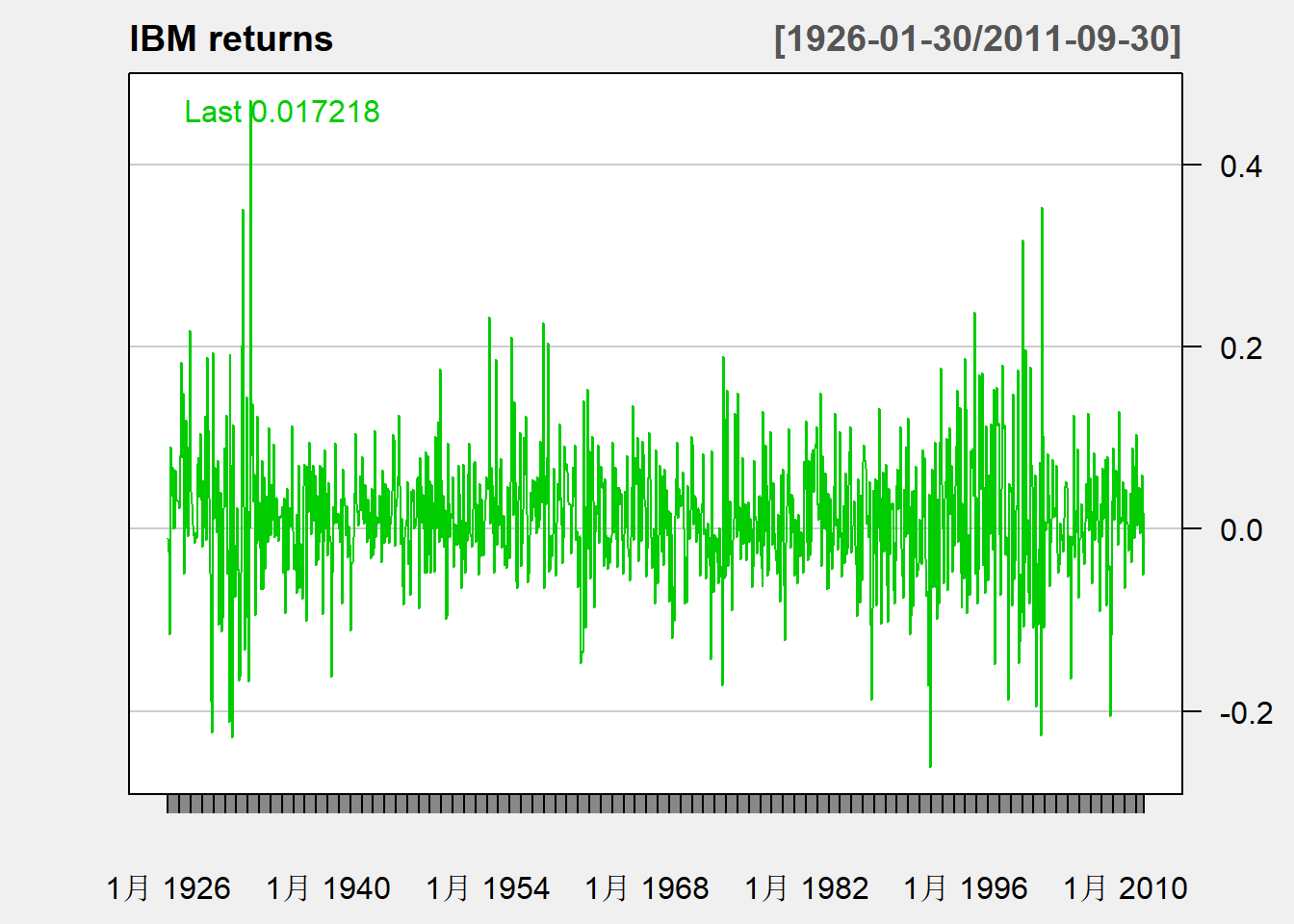
chartSeries(
ibmsp[,"sp"], type="lines",
theme="white", name="S&P returns",
major.ticks="years", minor.ticsk=FALSE)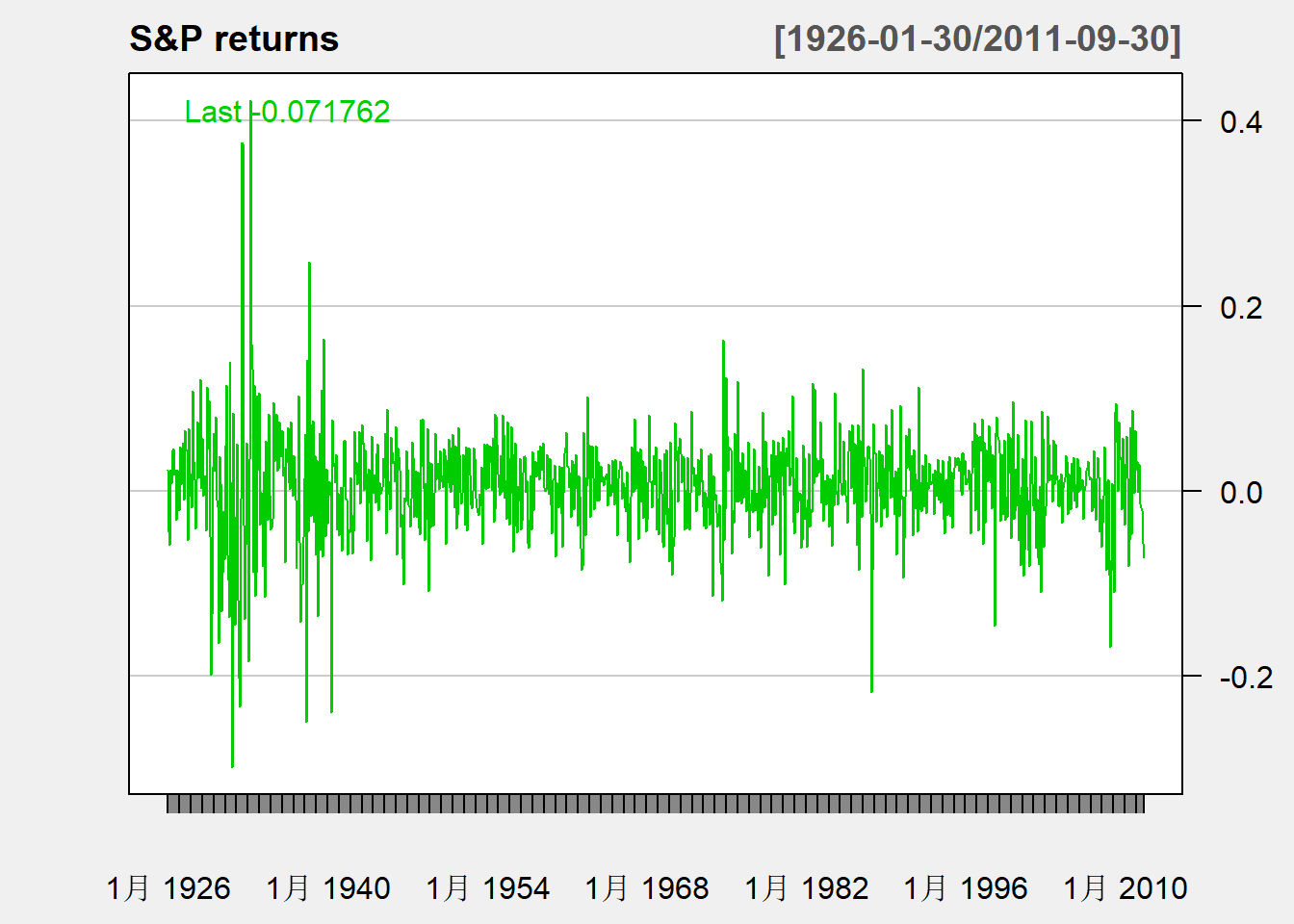
IBM收益率对标准普尔指数收益率的散点图:
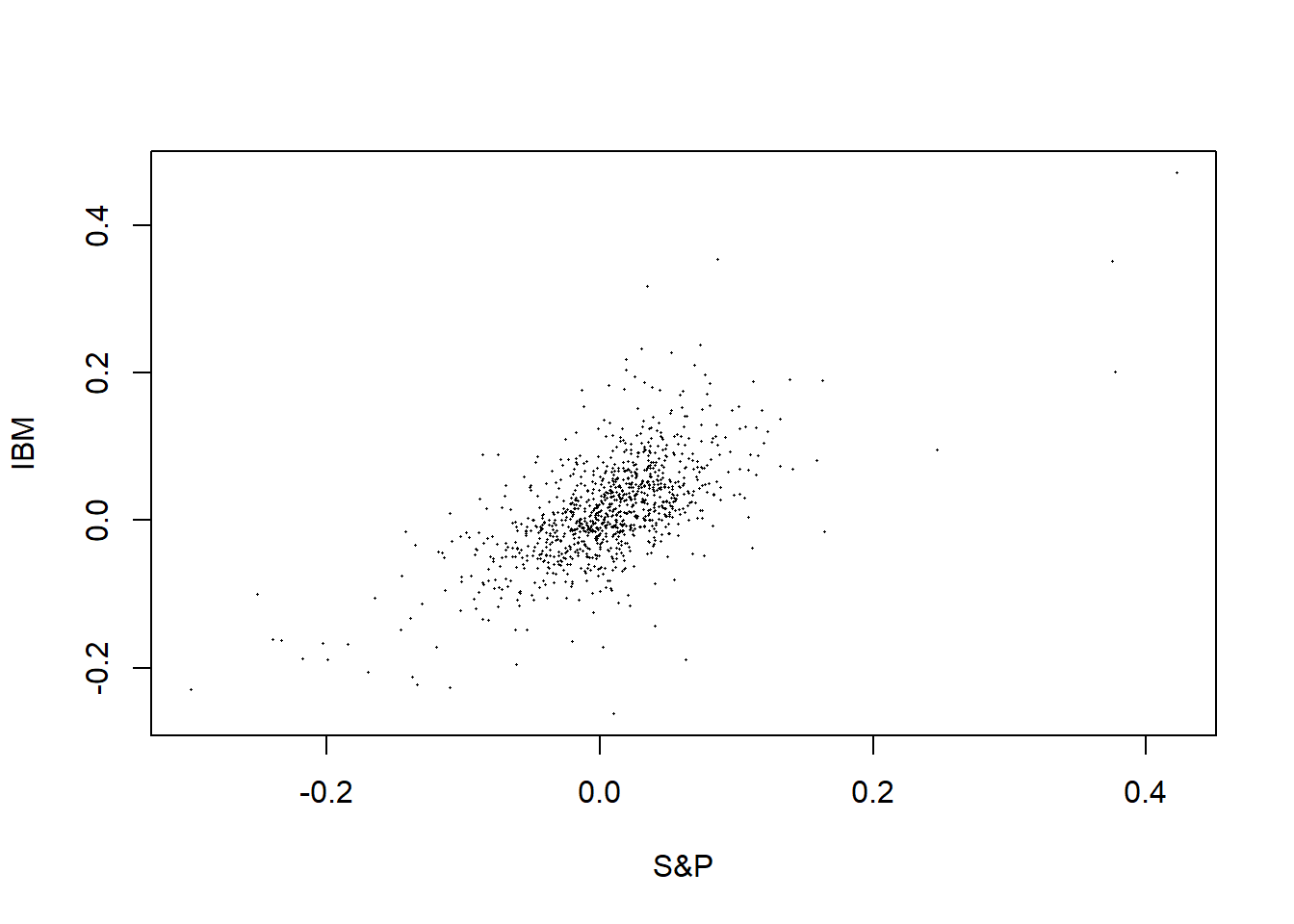
计算相关系数:
##
## Pearson's product-moment correlation
##
## data: d[, "sp"] and d[, "ibm"]
## t = 26.664, df = 1027, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.6020164 0.6743519
## sample estimates:
## cor
## 0.6395979相关系数为0.64,显著不等于零。
作线性回归并在散点图上叠加回归直线:
d <- as.data.frame(coredata(ibmsp))
plot(d[["sp"]], d[["ibm"]], pch=16, cex=0.2,
xlab="S&P", ylab="IBM")
lm1 <- lm(ibm ~ sp, data=d)
print(summary(lm1))##
## Call:
## lm(formula = ibm ~ sp, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.279155 -0.032137 -0.002261 0.030647 0.280313
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.008974 0.001706 5.259 1.76e-07 ***
## sp 0.818776 0.030707 26.664 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.05443 on 1027 degrees of freedom
## Multiple R-squared: 0.4091, Adjusted R-squared: 0.4085
## F-statistic: 711 on 1 and 1027 DF, p-value: < 2.2e-16
回归方程为 \[ \text{IBM} = 0.008474 + 0.818776 \text{S$\&$P} \]
一般地, \[ r_t = \alpha + \beta m_t + \varepsilon_t \] 其中\(r_t\)是某资产的收益率, \(m_t\)是市场的收益率, \(\alpha\)表示相对于市场收益的超额收益率。 这样的模型称为市场模型(market model)。
2.7 金融数据常用分布
2.7.1 正态分布
早期研究中假设简单收益率\(\{ R_t, t=1,2,\dots, T \}\)独立同分布, 服从正态分布。 但是存在不一致的问题:
- 简单收益率一定大于等于\(-100\%\),正态分布没有这样的限制;
- 多期毛收益率是单期毛收益率的乘积,不再服从正态分布;
- 收益率大多是厚尾分布,而正态分布超额峰度等于零。
2.7.2 对数正态分布
另一种假设是, 对数收益率\(r_t\)独立同分布, 同正态\(N(\mu, \sigma^2)\)分布。 这时, 简单收益率\(R_t = \exp(r_t) - 1\)服从对数正态分布,
\[\begin{align} E R_t =& \exp\left( \mu + \frac12 \sigma^2 \right) - 1, \nonumber \\ \text{Var}(R_t) =& \exp(2\mu + \sigma^2) \left(e^{\sigma^2} - 1 \right) \tag{2.1} \end{align}\]
反之,如果\(R_t\)服从对数正态分布, \(m_1 = E R_t\), \(m_2 = \text{Var}(R_t)\), 则\(r_t = \ln(1 + R_t)\)服从正态分布,且
\[\begin{align} E r_t =& \ln \left[ \frac{m_1 + 1}{\sqrt{1 + \frac{m_2}{(1 + m_1)^2}}} \right] \nonumber \\ \text{Var}(r_t) =& \ln\left[ 1 + \frac{m_2}{(1 + m_1)^2} \right] \tag{2.2} \end{align}\]
如果\(r_t\)是正态分布, 多期的对数收益率\(r_t[k]\)也是正态分布, 于是多期简单收益率\(R_t[k]\)也是对数正态分布。 \(R_t = e^{r_t} - 1 \geq -1\)总成立。 这样的假定一致性比较好。 但是, 有些股票的简单收益率的分布表现与对数正态分布不符, 对数收益率分布表现与正态分布不符。 对数收益率一般也有厚尾性。
2.7.3 稳态分布
稳态分布(stable distribution,或译为稳定分布)是正态分布的推广。 正态分布的一个重要特性是独立同分布的正态随机变量之和仍服从正态分布, 这符合连续复合收益率(对数收益率)\(r_t\)的分布要求。 稳态分布则是满足这样的性质的分布, 独立同稳态分布的随机变量之和仍服从稳态分布。 非正态的稳态分布可以实现厚尾性。 正态分布是稳态分布的特例。 关于稳态分布可参考(武东 and 汤银才 2007)。
除了正态分布以外, 其它的稳态分布都没有二阶矩, 但仍可以有位置参数、刻度参数, 和两个形状参数\(\alpha\)、\(\beta\)。 \(\alpha \in (0, 2]\)是稳定分布的特征参数, 与分布尾部厚薄有关, 正态分布对应于\(\alpha=2\); \(\beta\)刻画分布左偏和右偏的程度。 独立同稳态分布的随机变量和仍服从稳态分布, 且\(\alpha\)、\(\beta\)参数不变。
柯西(Cauchy)分布就是稳态分布,标准柯西分布密度为 \[ p(x) = \frac{1}{\pi(1 + x^2)}, \ x \in (-\infty, \infty) \] 分布密度对称,数学期望和方差都不存在。
2.7.4 混合正态分布
设\(\delta\)为正值随机变量, 比如服从Gamma分布, 设对数收益率在给定\(\delta\)条件下服从条件正态分布 \(\text{N}(\mu, \delta^{-1})\), 称\(r_t\)的边缘分布为尺度混合的正态分布。
若\(f_1(x)\)表示\(\text{N}(\mu, \sigma_1^2)\)的密度, \(f_2(x)\)表示\(\text{N}(\mu, \sigma_2^2)\)的密度, \(0 < \alpha < 1\),若对数收益率\(r_t\)密度为 \[ f(x) = \alpha f_1(x) + (1 - \alpha) f_2(x) \] 则称\(r_t\)服从混合正态分布。
例如,\(\mu=0\), \(\sigma_1=1\), \(\sigma_2=10\), \(\alpha=0.7\):
curve(dnorm(x, 0, 1), -5, 5,
ylab="", lwd=1, col="green",
main="Mixed Normal Distribution Density")
curve(0.7*dnorm(x, 0, 1) + 0.3*dnorm(x, 0, 10), -5, 5, add=TRUE,
lwd=2, col="red")
curve(dcauchy(x), -5, 5, add=TRUE, col="cyan")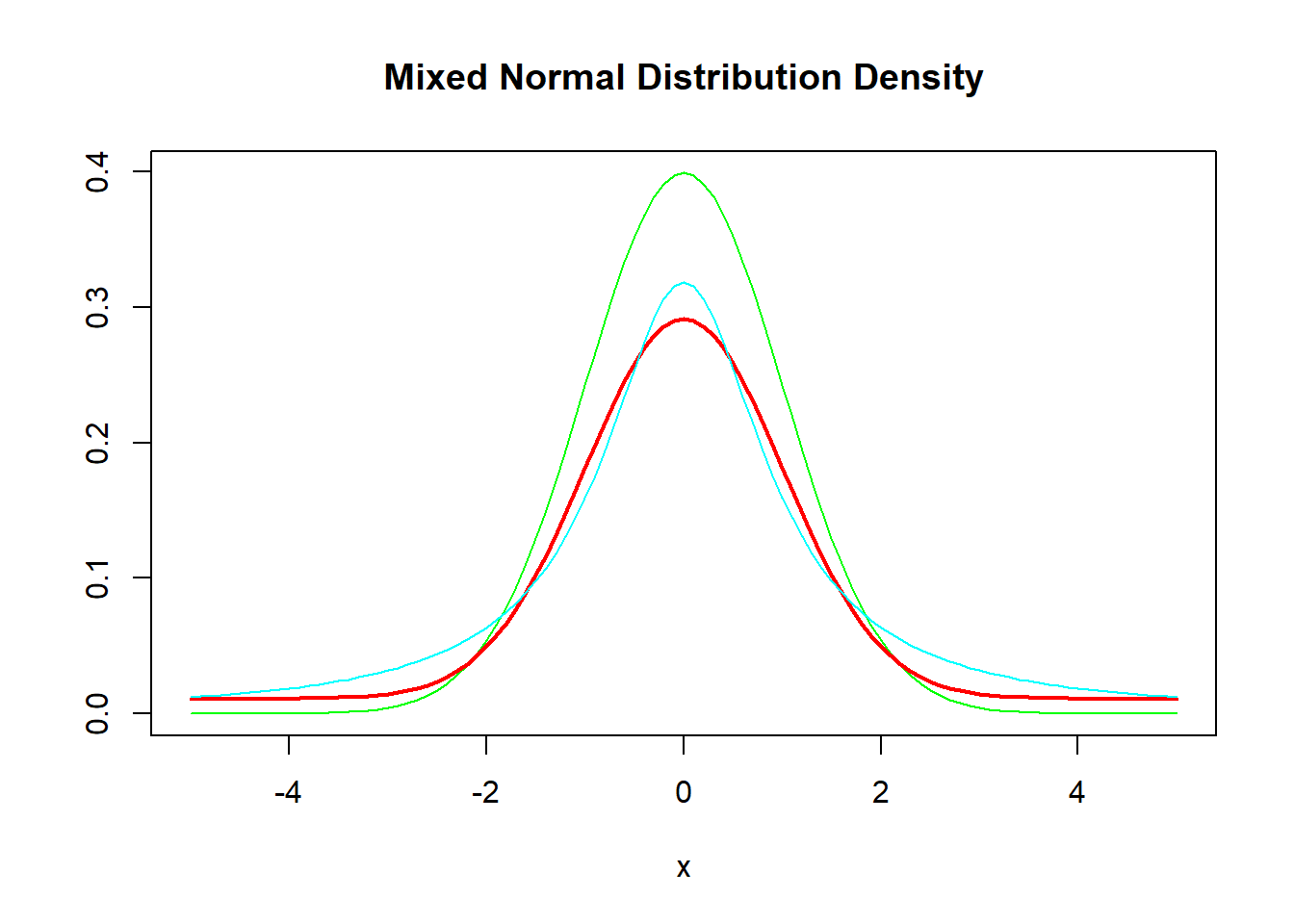
其中红色粗线为混合正态密度,绿色细线是标准正态密度。 从密度函数图形可以看出明显的重尾。 浅蓝色为标准柯西分布,重尾更为明显。
2.7.5 多元收益率的分布
金融中不关心一般的多元分布, 主要关心在\(r_{t-1}, \dots, r_1\)条件下\(r_t\)的条件分布, 尤其是条件期望和条件方差。
设随机向量\(\boldsymbol X = (X_1, \dots X_p)^T\), 期望和协方差矩阵为 \[ E \boldsymbol X = \boldsymbol\mu = [E X_1, \dots, E X_p]^T, \quad \text{Var}(\boldsymbol X) = \Sigma = E\left[ (\boldsymbol X - \boldsymbol\mu) (\boldsymbol X - \boldsymbol\mu)^T \right] \] \(\text{Var}(\boldsymbol X)\)是\(p \times p\)方阵, 主对角线位置是各个分量的方差, \((i,j)\)位置是\(X_i\)与\(X_j\)的协方差\(\text{Cov}(X_i, X_j)\)。
设\(\boldsymbol x_t\), \(t=1,2,\dots, T\)为多元观测, 则适当条件下(如独立同分布样本)可以估计多元分布的期望和方差: \[ \hat{\boldsymbol\mu} = \frac{1}{T} \sum_{t=1}^T \boldsymbol x_t, \quad \hat{\boldsymbol\Sigma} = \frac{1}{T-1} \sum_{t=1}^T (\boldsymbol x_t - \hat{\boldsymbol\mu}) (\boldsymbol x_t - \hat{\boldsymbol\mu})^T \] 这实际上就是一元的均值估计, 一元的方差估计, 和二元的协方差估计。
例如, 从1926-01到2011-09的IBM和S&P的月度收益率构成多元数据, 估计其均值:
## ibm sp
## 0.013818251 0.005916719计算协方差阵和相关系数阵:
## ibm sp
## ibm 0.005008351 0.002502326
## sp 0.002502326 0.003056181## ibm sp
## ibm 1.0000000 0.6395979
## sp 0.6395979 1.0000000psych包的mardia()函数进行推广的正态性偏度、峰度检验,
并作广义QQ图:

## Call: psych::mardia(x = x)
##
## Mardia tests of multivariate skew and kurtosis
## Use describe(x) the to get univariate tests
## n.obs = 1029 num.vars = 2
## b1p = 0.27 skew = 46.8 with probability <= 1.7e-09
## small sample skew = 47.03 with probability <= 1.5e-09
## b2p = 21 kurtosis = 52.12 with probability <= 0mvnormtest包的msharpiro.test()可以执行多元的Shapiro-Wilk正态检验。
零假设是服从多元正态分布。
##
## Shapiro-Wilk normality test
##
## data: Z
## W = 0.92228, p-value < 2.2e-16这些检验都显著地拒绝了正态性的零假设。
还可以模拟生成期望和协方差阵相同的多元正态随机样本数据,
观察真实样本与模拟正态样本散点图的差别。
mnormt包的rmnorm()函数生成独立的多元正态随机样本。
原始样本的散点图:
plot(x[["sp"]], x[["ibm"]], pch=16, cex=0.2,
xlim=c(-0.3, 0.5), ylim=c(-0.3, 0.5),
main="Sample Data",
xlab="S&P", ylab="IBM")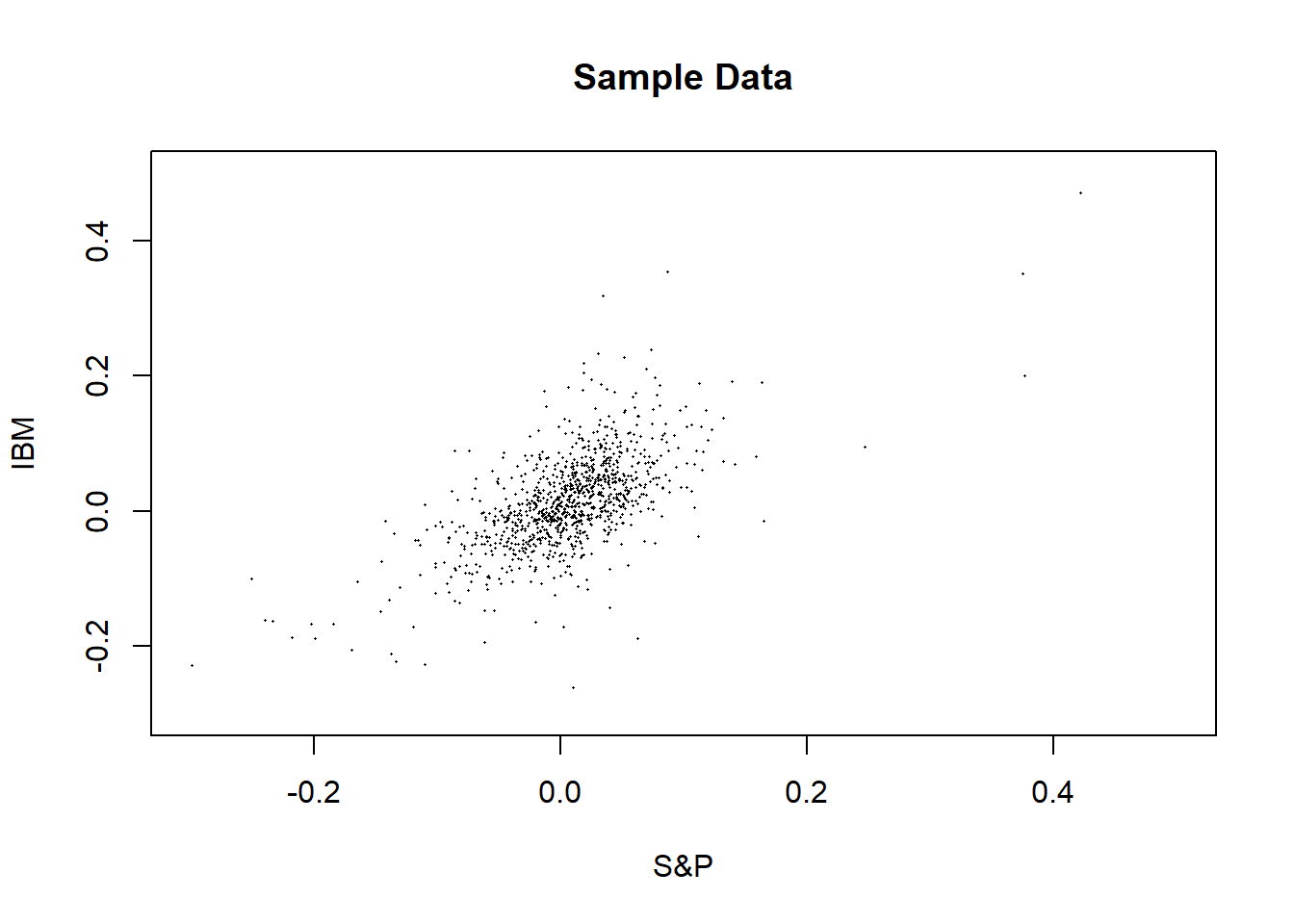
生成一、二阶矩相同的正态分布样本,作散点图:
y <- mnormt::rmnorm(nrow(x), mean=colMeans(x), varcov=var(x))
plot(y[,2], y[,1], pch=16, cex=0.2, col="green",
xlim=c(-0.3, 0.5), ylim=c(-0.3, 0.5),
main="Simulated Multivariate Normal",
xlab="S&P", ylab="IBM")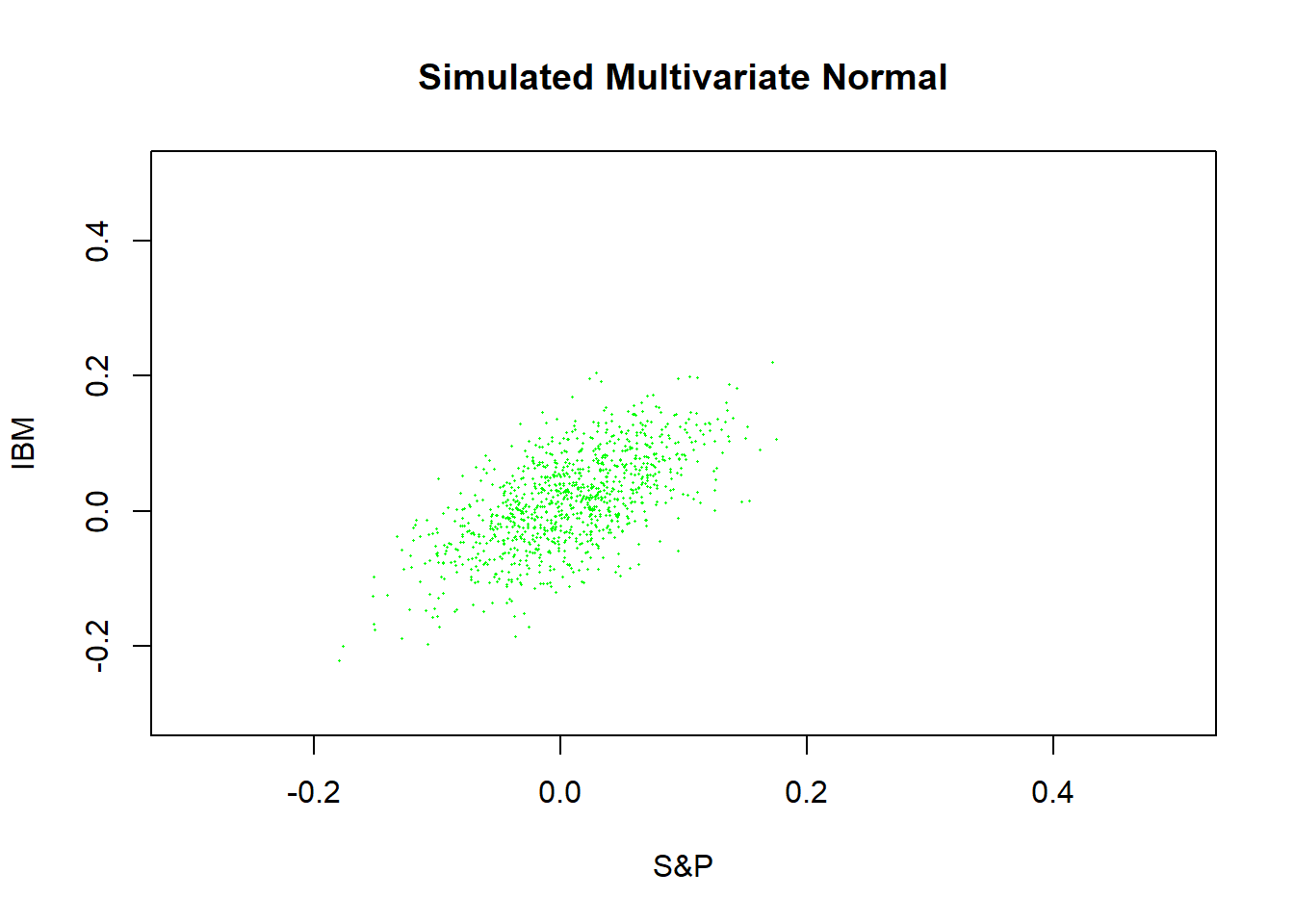
模拟数据分布集中得多。 注意两个图形比较时, 应采用相同的坐标范围。