13 带时间序列误差的回归模型
本章内容参考了(R. J. Hyndman and Athanasopoulos 2021)第十章。
13.1 模型
在统计学的数据分析中, 线性回归分析是最常用的分析工具之一。 线性回归以一元线性回归为例,模型如下
\[\begin{align} Y_t =& \beta_0 + \beta_1 X_t + e_t, \ t=1,2,\dots,T \tag{13.1} \end{align}\]
其中自变量\(\{ X_t \}\)为常数列, \(\beta_0, \beta_1\)为未知的系数, \(\{ e_t \}\)为零均值独立同分布随机误差序列, 方差为\(\sigma_e^2\), 因变量\(\{ Y_t \}\)为随机变量列。 参数\(\beta_0, \beta_1, \sigma_e^2\)可以用最小二乘法估计, 估计量无偏, 适当条件下系数的估计相合, 服从渐近正态分布。 为了对估计结果做假设检验或者用模型结果做预测, 一般还假设\(\{ e_t \}\)为零均值独立同正态分布序列。
在金融研究中, \(\{ X_t \}\)和\(\{ Y_t \}\)一般都是时间序列, 而且\(\{ e_t \}\)也是时间序列,有序列相关性。 这时, 最小二乘估计不是最有效的估计甚至于可能不相合, 基于\(\{ e_t \}\)独立同正态分布所做的标准误差估计、假设检验和预测都不再成立。 参见27.1。
(Cochrane and Orcutt 1949)的文章指出, 当\(\{ e_t \}\)彼此正相关时, 回归系数的标准误差估计偏低, 使得相应的t和F检验统计量的绝对值偏大。 (Durbin and Watson 1950)和(Durbin and Watson 1951)给出了一阶自相关的检验。 Durbin-Watson序列自相关检验使用检验统计量 \[ \text{DW} = \frac{\sum_{t=2}^T(\hat e_t - \hat e_{t-1})^2}{\sum_{t=1}^T \hat e_t^2} \approx 2(1 - \hat\rho_1) \] 其中\(\hat e_t\)是回归残差, 当无序列相关时DW统计量接近于2。 此统计量只用到一阶自相关。
当\(\{ e_t \}\)是平稳可逆ARMA序列时,
如果\(\{x_t\}\)为非随机序列,
或者\(\{x_t \}\)与\(\{y_t \}\)都平稳,
可以将线性回归模型与平稳可逆ARMA序列同时估计,
可以得到需要标准误差估计、假设检验和预测。
R的arima()函数提供了一个xreg=用来引入回归自变量。
fable包可以在model()函数的公式右侧引入回归自变量。
如果不关心\(\{ e_t \}\)的具体模型, 而只关心对回归系数的SE的正确估计以及假设检验的正确性, 可以仅假设\(\{ e_t \}\)的协方差结构而不考虑\(\{ e_t \}\)的建模。 这样的方法在混合线性模型中使用。
考虑如下的一个模型作为例子。 因变量\(y\)与自变量\(x_1, \dots, x_k\)构成线性回归, 回归误差表示为一个ARIMA(1,1,1): \[\begin{equation} \begin{aligned} y_t =& \beta_0 + \beta_1 x_{t1} + \dots + \beta_k x_{tk} + \xi_t, \\ (1 - \phi_1 B)(1 - B) \xi_t =& (1 + \theta_1 B) \varepsilon_t . \end{aligned} \tag{13.2} \end{equation}\] 其中\(\{\varepsilon_t \}\)为白噪声列。
13.2 模型估计
对(13.2)这样的回归误差含有单位根的模型, 用最小二乘法去估计回归系数会失效, 结果不相合。 为了能够估计模型参数, 需要通过差分去掉单位根。 在(13.2)中记\(\eta_t = (1-B) \xi_t\), 则\(\{\eta_t \}\)是平稳的ARMA序列, 在(13.2)的回归方程两边都取差分, 得到 \[ (1-B) y_t = \beta_1 (1-B) x_{t1} + \dots + \beta_k (1-B)x_{tk} + \eta_t . \] 如果\((1-B)y_t\)和所有\((1-B)x_{tj}\)都不再含有单位根, 模型就可以估计了。
有一个例外就是当\(y_t\)和\(x_t\)协整时, 存在\(y_t\)与\(x_t\)有单位根, 但回归误差仍然平稳, 且回归参数估计相合的情况, 参见27。
除非协整关系存在, 只要因变量和自变量时间序列有单位根, 回归模型两边就需要同时进行差分, 直到没有单位根。 否则模型无法估计。
fable包在指定了回归误差的ARIMA模型有单位根时会自动对因变量和自变量进行相应的差分变换,
所以不需要人为地将因变量和自变量差分;
但是stats::arima()和forecast::Arima()函数不支持规定回归误差项有单位根,
只能人为地将因变量和自变量差分,
见13.9。
13.3 用fable包建立误差项相关的回归模型
用fable包可以建立ARIMA模型,
格式为model(ARIMA(y ~ pdq(p,d,q)))。
其中\(y\)为因变量。
如果有自变量\(x\)(称为外生自变量)能够影响因变量\(y\),
则模型设定程序为model(ARIMA(y ~ x + pdq(p,d,q)))。
例如,
设(13.2)中\(k=1\)(仅有一个外生自变量),
则模型设定可以写成
model(ARIMA(y ~ x + pdq(1,1,1)))。
在估计时会自动将回归方程两边进行差分使得误差项不再有单位根。
这样的差分会使得回归截距项\(\beta_0\)消失,
为了令差分后的回归截距项存在,
可以写成model(ARIMA(y ~ 1 + x + pdq(1,1,1))),
这就类似于有漂移的单位根过程增加了外生自变量。
也可以直接写model(ARIMA(y ~ x)),
不写模型的具体阶数,
这时会自动确定是否需要差分以及模型的阶数。
是否需要差分是直接计算回归模型的最小二乘估计,
得到回归残差,
对回归残差作KPSS单位根检验来判断的。
如果需要差分,
则回归模型方程两边都进行差分然后作参数的最大似然估计。
在预测时,
将自动转换回到原始变量的尺度进行预测。
例13.1 考虑美国国债一年期与三年期利率, 数据为周数据, 从1962-01-05到2009-10-04, 共2467个观测。 记一年期利率序列为\(\{ x_{1t} \}\), 三年期利率序列为\(\{ x_{3t} \}\)。 以三年期利率为因变量, 以一年期序列为自变量, 建立回归模型。
先读入数据:
da1 <- read_table(
"w-gs1yr.txt",
col_types=cols(.default=col_double())) |>
mutate(date = make_date(year, mon, day)) |>
dplyr::rename(x1 = rate) |>
select(date, x1)
da2 <- read_table(
"w-gs3yr.txt",
col_types=cols(.default=col_double())) |>
mutate(date = make_date(year, mon, day)) |>
dplyr::rename(x3 = rate) |>
select(date, x3)
tb_tsib <- inner_join(da1, da2, by="date",
unmatched="error") |>
as_tsibble(index = "date")数据已经自动识别为周数据。
两个利率序列的时间序列图:
tb_tsib |>
pivot_longer(c(x1, x3),
names_to = "Series", values_to = "value") |>
ggplot(aes(x = date, y = value)) +
geom_line() +
facet_grid(Series ~ .) +
labs(title = "US Federal Bonds 1 Year and 3 Years")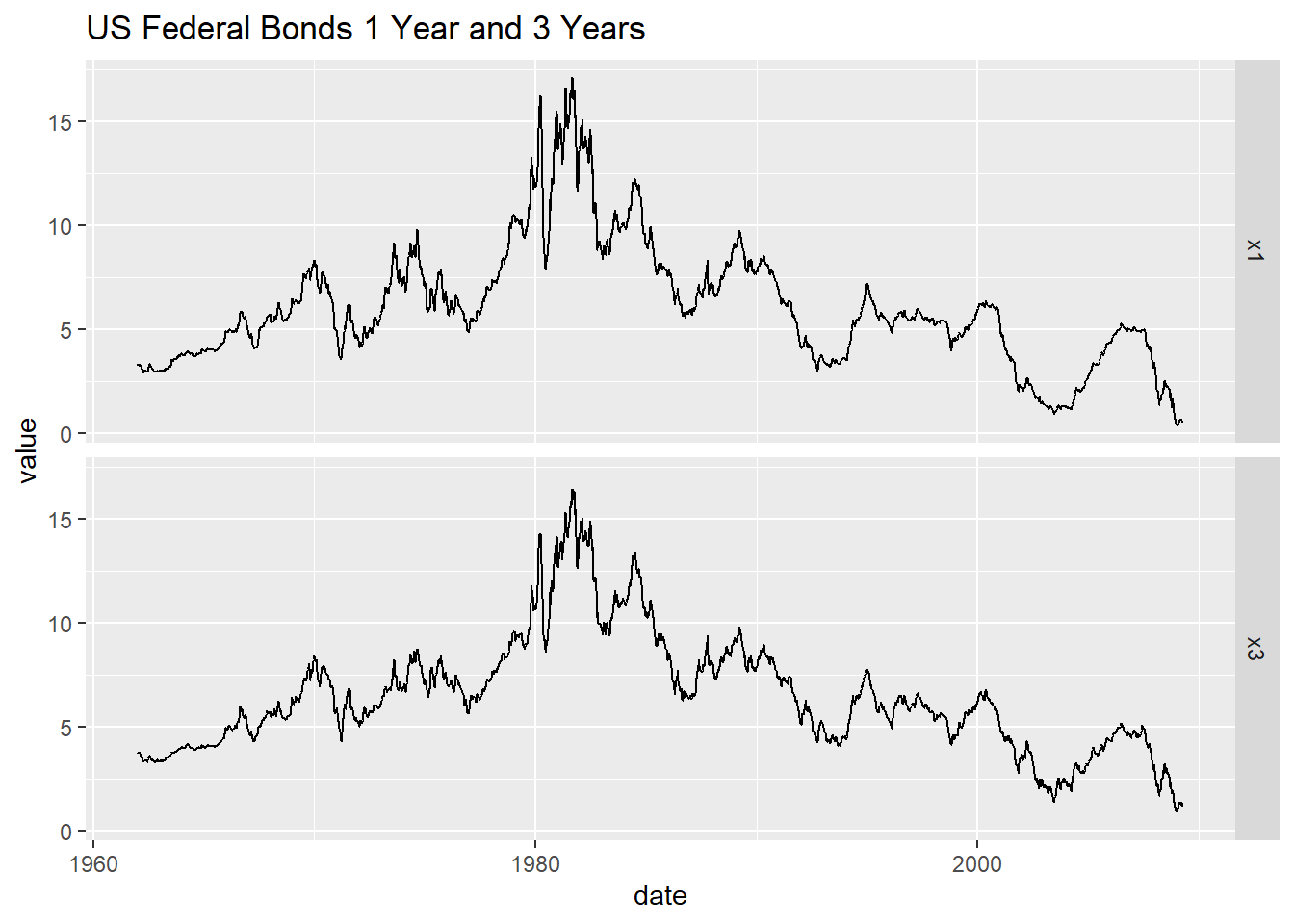
图13.1: 美国一年期与三年期国债利率周数据
tb_tsib |>
filter(year(date) > max(year(date)) - 3) |>
pivot_longer(c(x1, x3),
names_to = "Series", values_to = "value") |>
ggplot(aes(x = date, y = value)) +
geom_line() +
facet_grid(Series ~ .) +
labs(title = "US Federal Bonds 1 Year and 3 Years")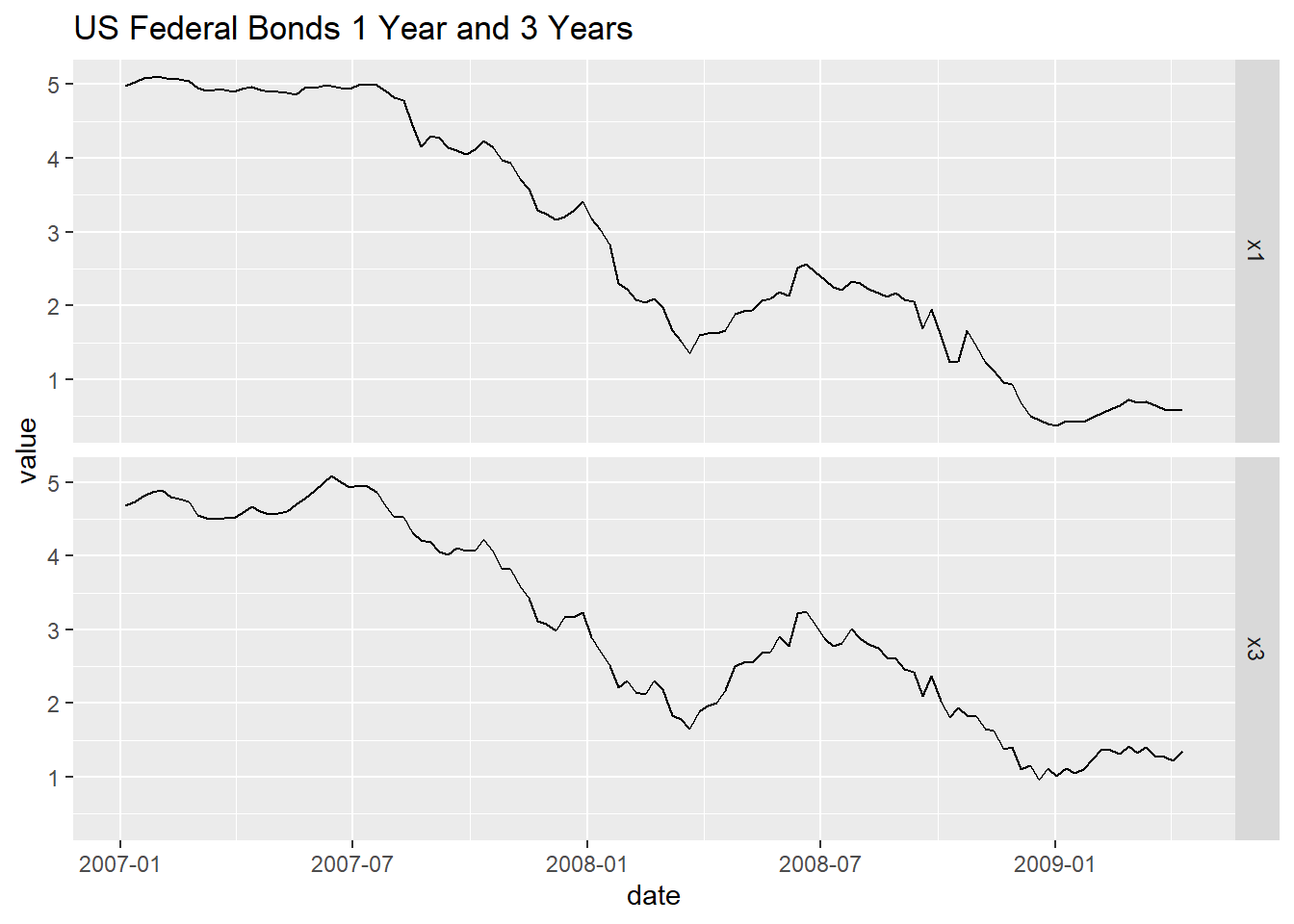
图13.2: 美国一年期与三年期国债利率周数据
这些数据作为时间序列呈现出不平稳的表现。 对一年期利率作ACF估计:
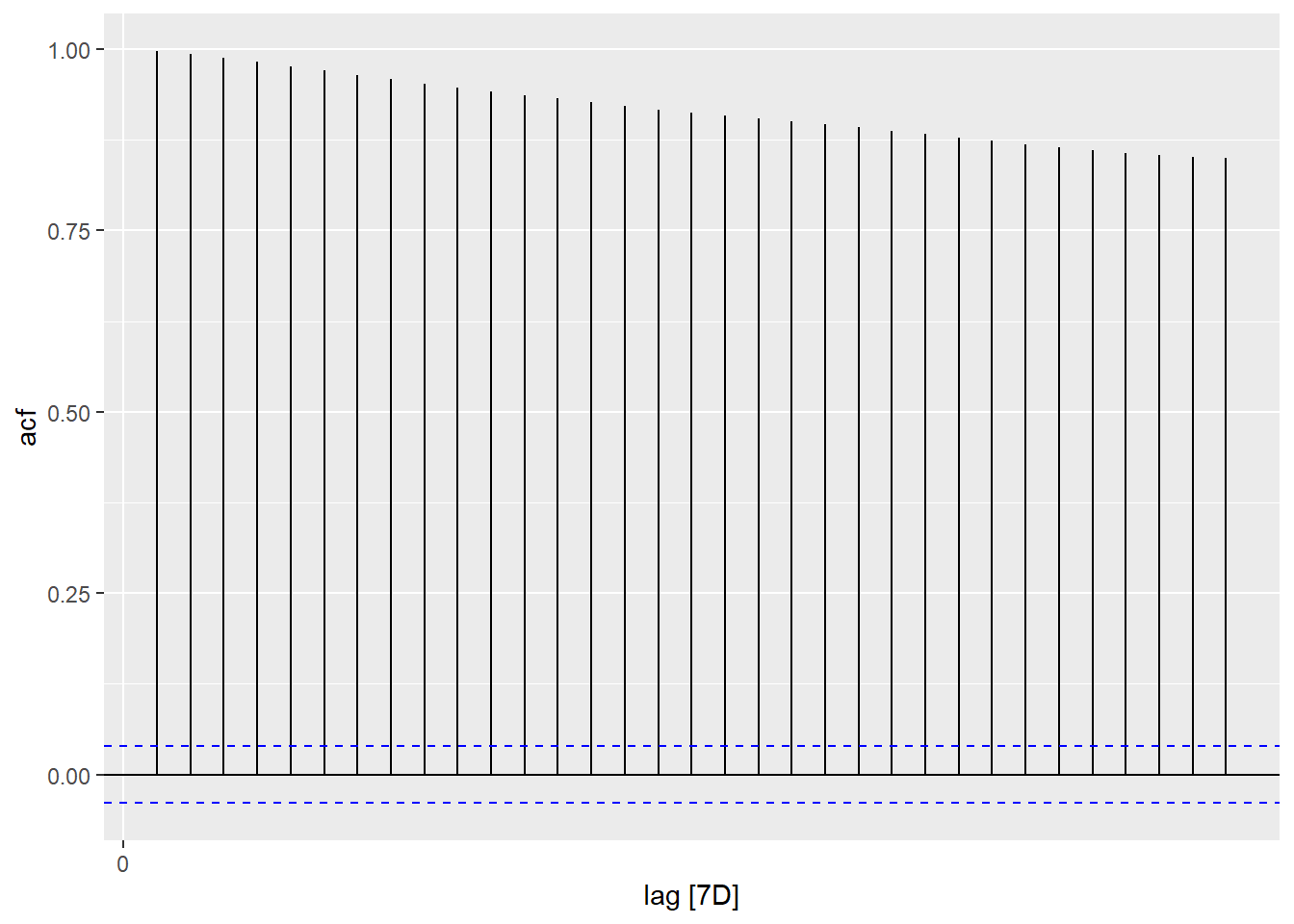
图13.3: 一年期利率ACF
这样的ACF是有缓慢变化趋势的典型表现。
对一年期利率序列作单位根检验:
## # A tibble: 1 × 2
## kpss_stat kpss_pvalue
## <dbl> <dbl>
## 1 6.05 0.01KPSS单位根检验的零假设是平稳, 以上结果在0.05水平下拒绝零假设, 所以认为一年期利率有单位根。
如果以\(x_{t3}\)为因变量, 以\(x_{t1}\)为自变量作线性回归: \[ x_{t3} = \beta_0 + \beta_1 x_{t1} + e_t, \] 就会遇到\(\{ e_t \}\)序列相关的问题, 甚至于\(\{ e_t \}\)可能有单位根造成方差线性增长, 有异方差问题, 估计结果可能不相合。
先用散点图考察两个序列的关系:
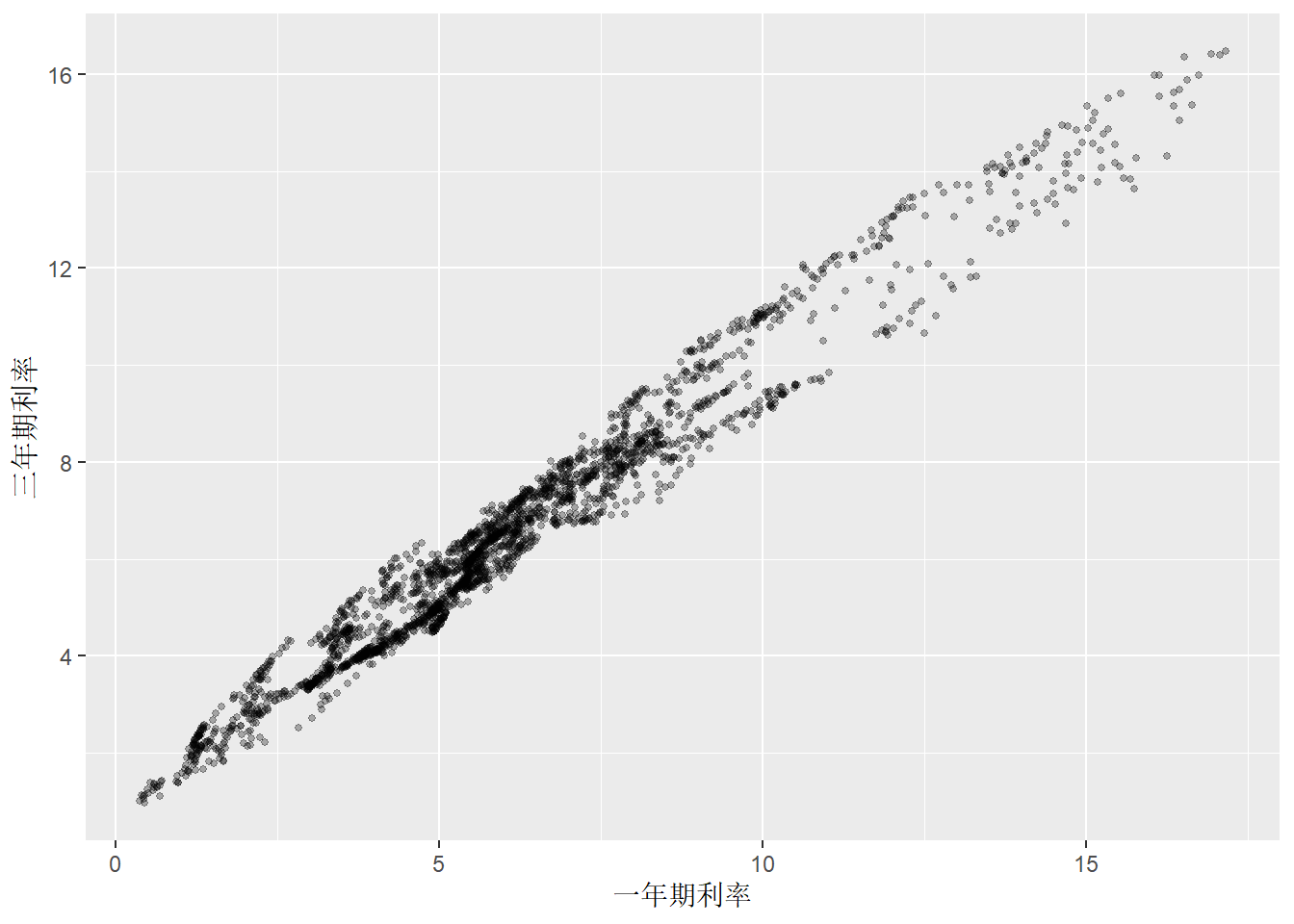
图13.4: 美国一年期与三年期国债利率周数据散点图
散点图显示同期的一年期利率和三年期利率高度相关。 尝试拟合线性回归模型(注意按前面的讨论这样做是错误的):
## Series: x3
## Model: TSLM
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.82319 -0.37691 -0.01462 0.38661 1.35679
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.83214 0.02417 34.43 <2e-16 ***
## x1 0.92955 0.00357 260.40 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5228 on 2465 degrees of freedom
## Multiple R-squared: 0.9649, Adjusted R-squared: 0.9649
## F-statistic: 6.781e+04 on 1 and 2465 DF, p-value: < 2.22e-16注意:不懂统计的人会盲目相信统计软件给出的如此专业的输出结果。 \(R^2 = 0.9649\)是一个十分令人欣喜的回归结果。 但是, 只有学习了相应的统计模型的有关知识并且知道模型的局限, 才能正确地运用统计模型。 上面的系数估计、\(\sigma_e^2\)估计、SE估计、\(t\)检验等等都是基于随机误差项独立同分布假定的。 如果假定不成立,\(\sigma_e^2\)的估计会严重低估, SE估计不相合,检验不准确。 在经济和金融数据分析中一定要对回归模型结果进行诊断分析, 最常用的是残差分析, 其中一项是残差序列相关性的检验。
传统的残差序列相关性检验有Durbin-Watson检验, 在时间序列分析软件的支持下, 我们可以做ACF图, 进行Ljung-Box白噪声检验。
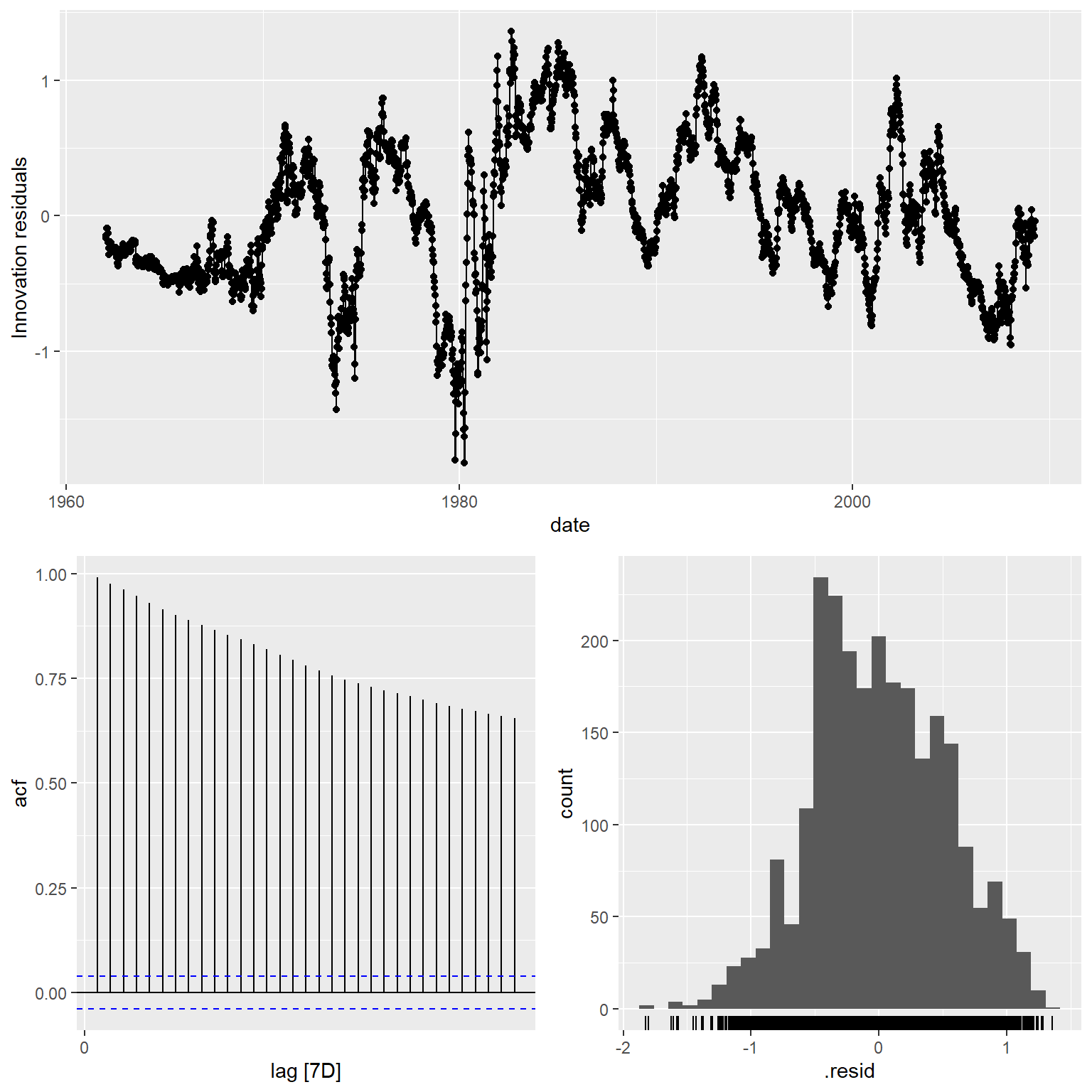
图13.5: 三年期对一年期利率回归残差诊断
残差的ACF表明结果仍有很强的自相关,甚至于可能有单位根。 对残差序列作KPSS单位根检验:
## # A tibble: 1 × 3
## .model kpss_stat kpss_pvalue
## <chr> <dbl> <dbl>
## 1 TSLM(x3 ~ x1) 2.35 0.01结果显著,认为回归残差不平稳, 有单位根, 直接估计回归模型是错误做法。
如果回归模型\(y_t = \beta_0 + \beta_1 x_t + e_t\) 中\(y_t\)和\(x_t\)都是单位根过程而\(e_t\)是线性时间序列, 则称\(\{ y_t \}\)与\(\{ x_t \}\)序列存在协整关系(cointegrated)。 在目前的数据中, 因为利率序列有单位根, 残差序列也有单位根, 不符合协整条件。
fable包支持自动判断回归误差项是否需要差分, 以及回归误差模型自动定阶。 自动建模:
## Series: x3
## Model: LM w/ ARIMA(4,1,2) errors
##
## Coefficients:
## ar1 ar2 ar3 ar4 ma1 ma2 x1
## 0.4507 -1.0140 0.1918 0.0060 -0.2694 0.9436 0.7956
## s.e. 0.0251 0.0368 0.0225 0.0222 0.0150 0.0317 0.0075
##
## sigma^2 estimated as 0.004531: log likelihood=3158.61
## AIC=-6301.21 AICc=-6301.15 BIC=-6254.73建立的模型可以写成:
\[
(1 - B) x_{t3} = 0.7956 (1 - B) x_{t1}
+ \eta_t,
\quad \eta_t \sim \text{ARMA}(4, 2) .
\]
结果中的sigma^2估计是ARMA(4,2)模型的新息(白噪声)的方差估计。
可以用residual()函数提取回归残差和ARMA模型的残差,
如:
bind_rows(
`回归残差` = residuals(
tb_regm2, type="regression") |>
as_tibble(),
`新息` = residuals(
tb_regm2, type="innovation") |>
as_tibble(),
.id = "type") |>
ggplot(aes(x = date, y = .resid)) +
geom_line() +
facet_grid(type ~ .)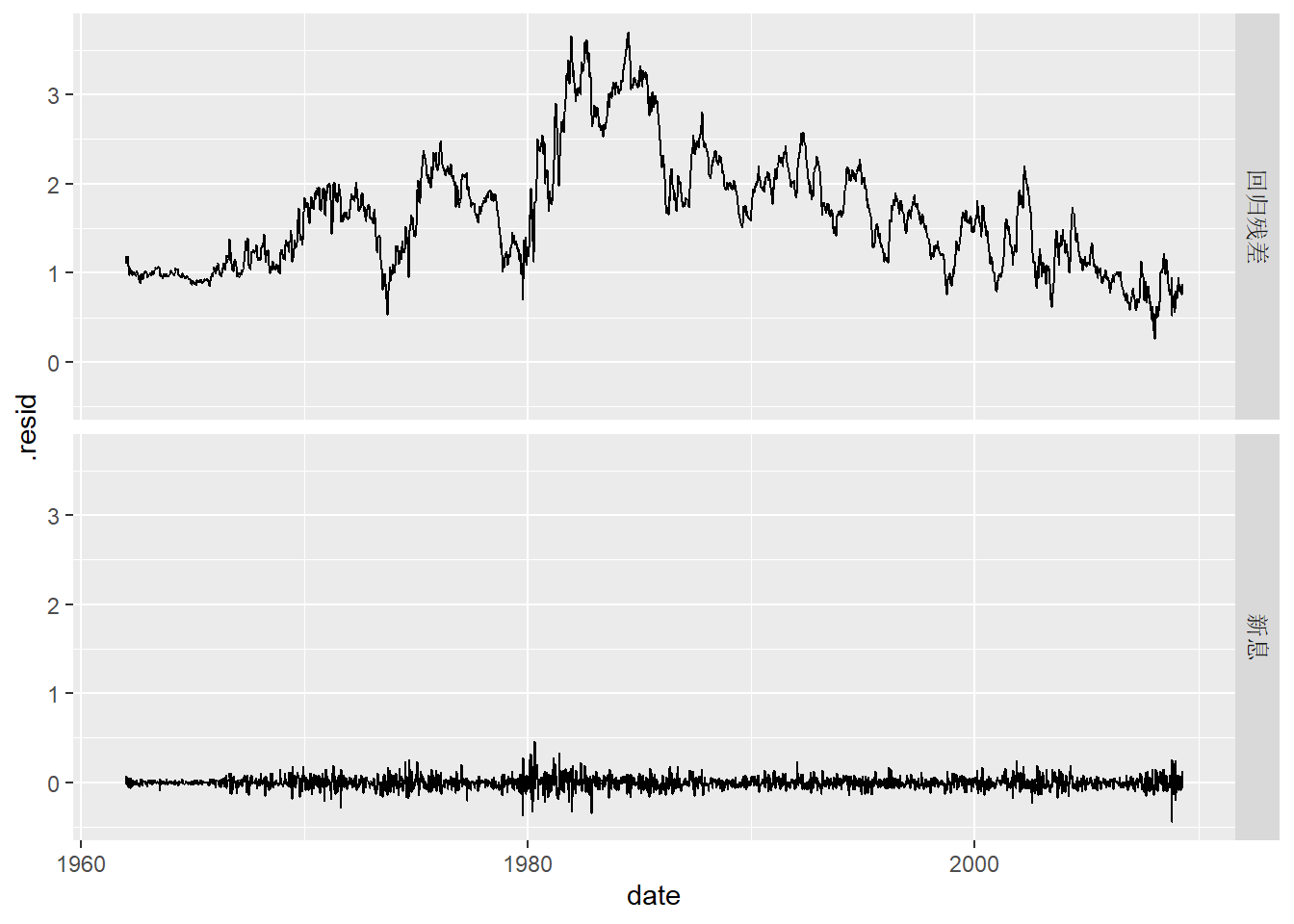
图13.6: 回归残差与新息
回归残差是在未差分的尺度上计算的, 所以残差较大。
回归的实际估计是针对差分后的因变量和自变量进行的, 我们做x1和x3的差分序列的散点图:
tb_tsib |>
mutate(
x1d = difference(x1),
x3d = difference(x3) ) |>
ggplot(aes(x = x1d, y = x3d)) +
geom_point(size = 1, alpha = 0.3) +
labs(x = "一年期利率差分", y = "三年期利率差分")## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_point()`).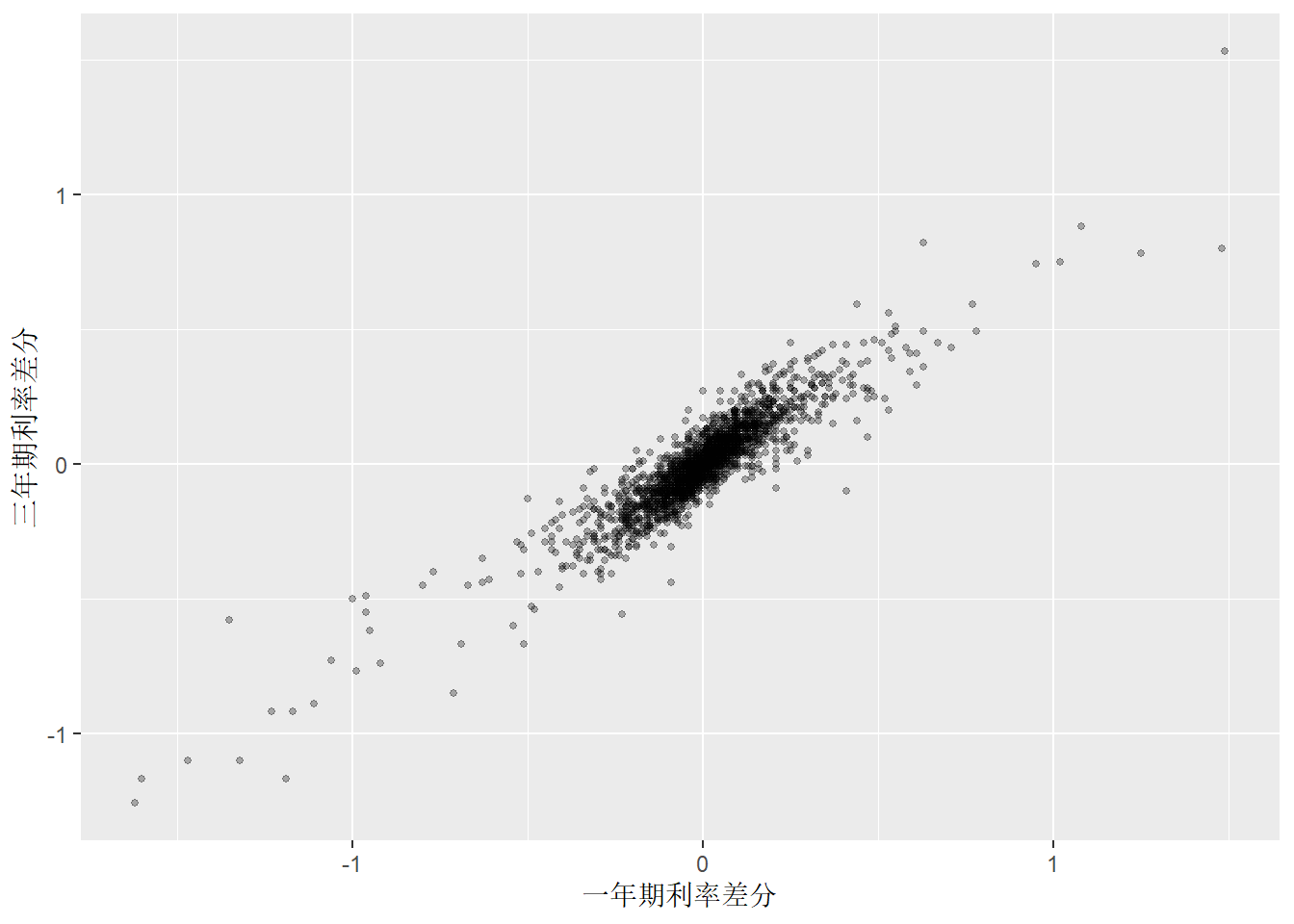
图13.7: 差分序列之间的散点图
差分序列之间仍表现出较强线性关系。
模型残差诊断:
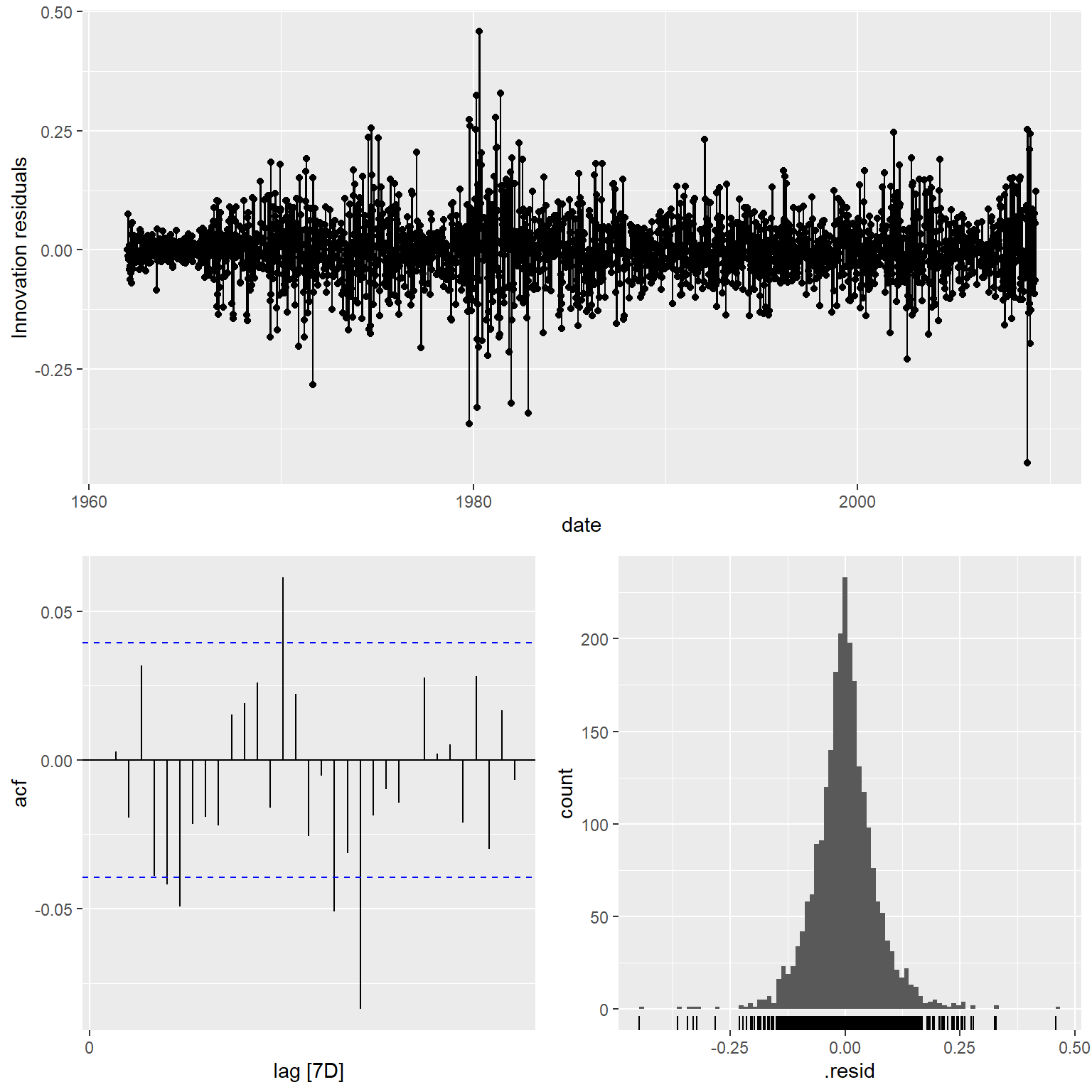
图13.8: 误差序列相关的回归模型新息诊断
新息的白噪声检验:
## # A tibble: 1 × 3
## .model lb_stat lb_pvalue
## <chr> <dbl> <dbl>
## 1 ARIMA(x3 ~ x1) 22.3 0.000462结果显著, 说明模型拟合不够好。 ARMA模型的残差(新息)的ACF也仍有几处超出界限, 这就属于不能完美拟合的情况。 残差的直方图也体现出重尾性。
关于残差分布的调整, 有可能加入一个关于条件方差的模型(如GARCH模型)会改善模拟。
13.4 预测
在使用误差序列相关的回归模型预测\(y_{T+h}\)时, 需要提供相应的自变量\(x_{T+h}\)的值。 有些自变量值是预先知道的, 比如某些节日效应的示性函数值; 未知的自变量值可以单独建模预测, 或者假定取某些值后预测因变量值, 作为一种假想情景的预测。
对前面的国债例子, 要预测随后的4周的三年期国债收益率, 假定一年期国债保持最后一个已知值不变:
tb_newd <- new_data(tb_tsib, 8) |>
mutate(x1 = tail(tb_tsib$x1, 1))
tb_fore <-
tb_regm2 |>
forecast(tb_regm2, new_data = tb_newd)## Warning: Input forecast horizon `h` will be ignored as `new_data` has been
## provided.tb_fore |>
autoplot(tb_tsib |> filter(year(date) >= 2008)) +
labs(title = "假定一年期利率维持最后一个值的预测",
y = "三年期利率")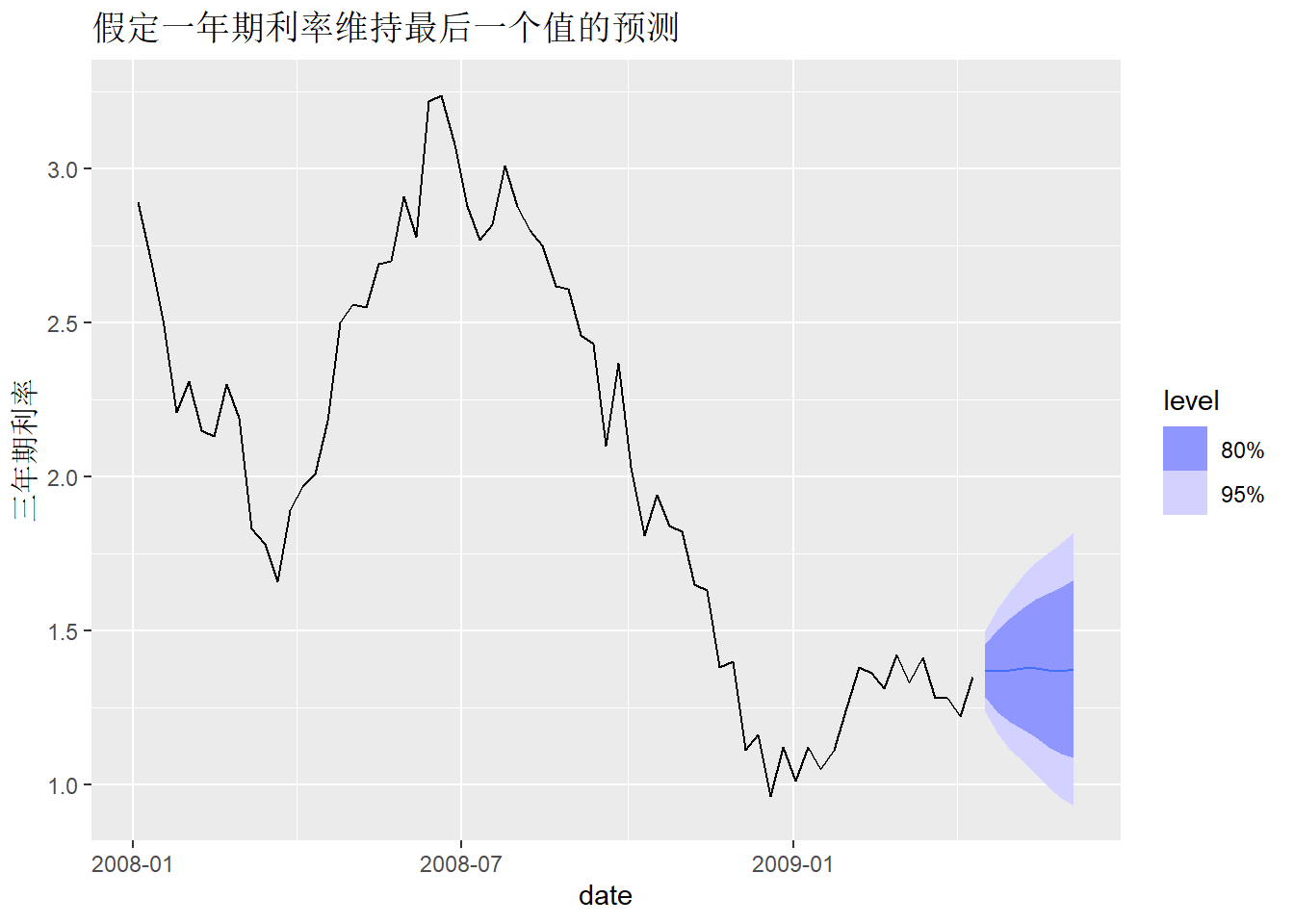
13.5 使用滞后自变量
回归模型在预测时需要知道自变量在未来时刻的值。 如果使用\(x_{t-h}\)作为\(y_t\)的自变量, 则在预测\(y_{T+1}, \dots, y_{T+h}\)时要用到的自变量为\(x_{T-(h-1)}\), \(x_{T-(h-2)}\), \(\ldots\), \(x_T\), 是已知值。
另外, 许多自变量对因变量的影响是逐渐起作用的, 而不是马上起作用, 这时就可以用\(x_{t-1}\)到\(x_{t-k}\)(或者其中的子集)作为自变量取估计\(y_t\)。
fable包在ARIMA()函数中可以用lag(x, k)加入\(x_{t-k}\)作为\(y_t\)的自变量。
例13.2 fpp3包的insurance数据包含了某保险公司为了提高业务量作广告的月度数据,
TVadverts是广告费用,
Quotes是业务量,
用滞后模型考察广告费用的影响。
解答: 数据整理与作图:
分别建立不同滞后的模型:
ad_fits <- ad_tsib |>
mutate(Quotes = c(NA, NA, NA, Quotes[4:40])) |>
model(
lag0 = ARIMA(Quotes ~ pdq(d = 0)
+ TVadverts),
lag1 = ARIMA(Quotes ~ pdq(d = 0)
+ lag(TVadverts)),
lag1a = ARIMA(Quotes ~ pdq(d = 0)
+ TVadverts + lag(TVadverts)),
lag2 = ARIMA(Quotes ~ pdq(d = 0)
+ lag(TVadverts, 2)),
lag2a = ARIMA(Quotes ~ pdq(d = 0)
+ TVadverts + lag(TVadverts)
+ lag(TVadverts, 2)),
lag3 = ARIMA(Quotes ~ pdq(d = 0)
+ lag(TVadverts, 3)),
lag3a = ARIMA(Quotes ~ pdq(d = 0)
+ TVadverts + lag(TVadverts)
+ lag(TVadverts, 2) + lag(TVadverts, 3)) )上面的程序中的mutate()是为了将自变量的前几个值变得不可用,
使得不同模型能够利用的数据长度完全相同。
如果不这样做我们用准则取比较不同模型就是不可比的。
查看AICc比较:
| .model | AICc |
|---|---|
| lag0 | 68.32890 |
| lag1 | 148.05768 |
| lag1a | 59.85279 |
| lag2 | 151.37122 |
| lag2a | 62.57799 |
| lag3 | 150.88193 |
| lag3a | 64.95977 |
从AICc判断, 这些模型中以\(x_t, x_{t-1}\)为自变量的模型最优。 如果不允许使用\(x_t\), 仅允许使用一个滞后值, 则使用\(x_{t-1}\)的模型最优。 这说明了广告效应存在滞后一个月的影响。
重新拟合选择的最优模型:
ad_fitb <- ad_tsib |>
model(ARIMA(Quotes ~ pdq(d = 0)
+ TVadverts + lag(TVadverts)))
ad_fitb |>
report()## Series: Quotes
## Model: LM w/ ARIMA(1,0,2) errors
##
## Coefficients:
## ar1 ma1 ma2 TVadverts lag(TVadverts) intercept
## 0.5123 0.9169 0.4591 1.2527 0.1464 2.1554
## s.e. 0.1849 0.2051 0.1895 0.0588 0.0531 0.8595
##
## sigma^2 estimated as 0.2166: log likelihood=-23.94
## AIC=61.88 AICc=65.38 BIC=73.7模型可以表示为 \[\begin{aligned} y_t =& 2.1554 + 1.2527 x_t + 0.1464 x_{t-1} + \eta_t, \\ \eta_t =& 0.5123 \eta_{t-1} + \varepsilon_t + 0.9169 \varepsilon_{t-1} + 0.4591 \varepsilon_{t-2}, \\ \eta_t \sim& \text{WN}(0, 0.2166) . \end{aligned}\]
为了向前预测, 需要知道自变量值。 假定广告费用在后续20个月维持在8个单位, 则随后20个月的预测为:
ad_newd <- new_data(ad_tsib, 20) |>
mutate(TVadverts = 8)
ad_fitb |>
forecast(new_data = ad_newd) |>
autoplot(ad_tsib) +
labs(title = "滞后一阶的预测")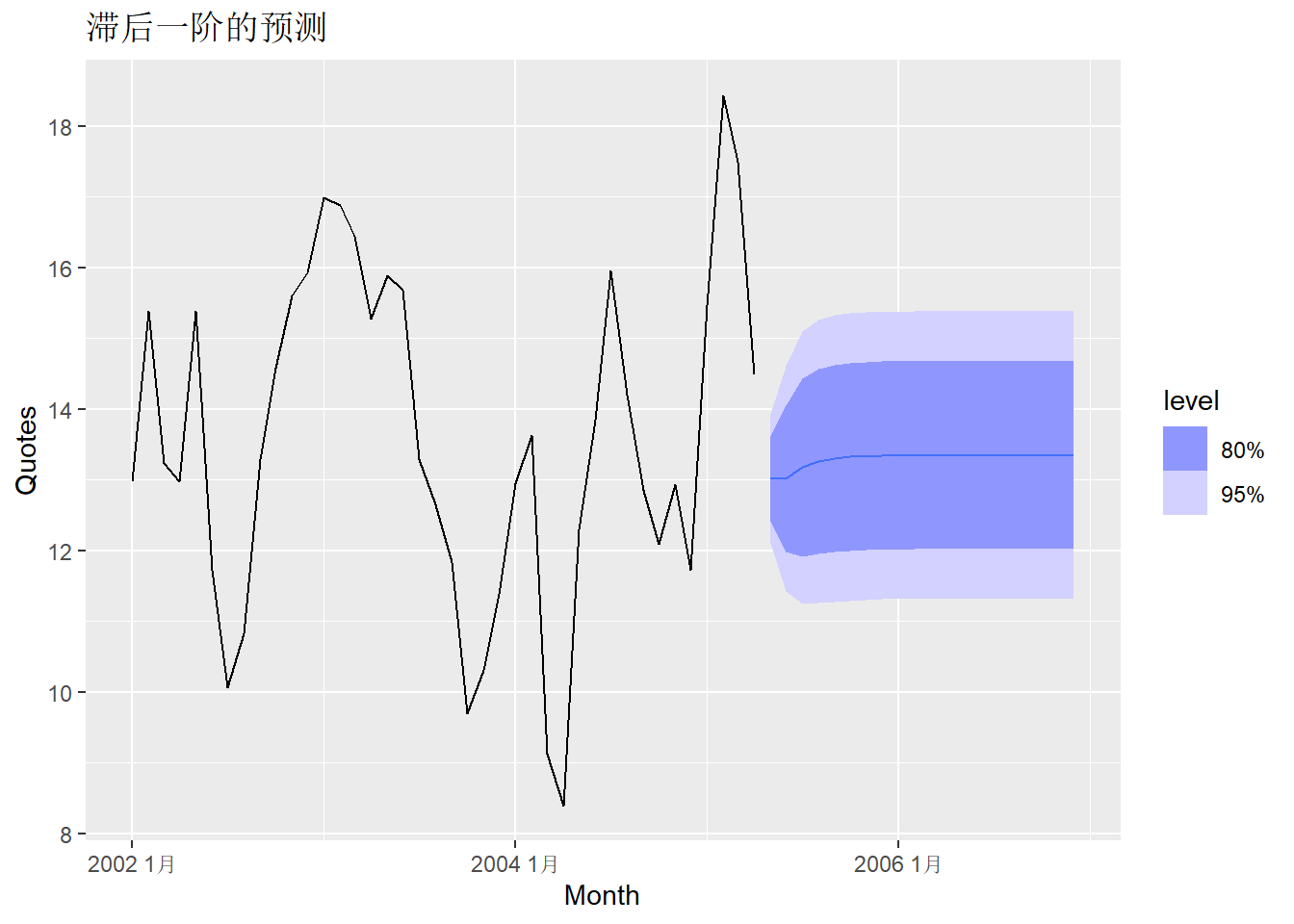
13.6 特殊的回归自变量
有一些特殊的自变量可以用作回归自变量,
比如ARIMA(y ~ trend())可以以\(t\)为自变量建立误差项相关的回归模型。
其它常用的回归自变量是表示节假日的哑变量,
表示政策变化的示性变量等。
fable包的ETS和ARIMA都不支持很大的周期, 典型的周期是12个月,4个季度, 52个星期,24个小时,等等。 ETS限制周期\(m \leq 24\)。 ARIMA模型的周期\(m\)一般限制在200以下。
较长或者非标准的周期可以借助三角级数回归实现, 以不同频率的余弦、正弦函数为自变量进行回归并允许误差项相关, 就可以实现对长周期的建模。 这样做的好处包括:
- 允许任意的固定周期;
- 允许同时有两种或更多周期;
- 可以通过舍弃三角级数中的高频部分令拟合序列更光滑;
- 近期相关性可以用ARMA模型表达。
缺点是不允许周期值随时间变化。
fable包在ARIMA()函数中用fourier(K=?)指定这样的三角级数回归,
周期从tsibble信息中获取。
也可以用period=?指定周期。
例13.3 tsibbledata包的aus_retail数据包含澳大利亚各州各行业月度销售额时间序列。
用其中的餐饮业月度数据为例建立用三角级数表达周期回归模型;
实际上月度数据不必要这样做,
这里的做法也适用于其它周期。
解答: 数据整理
cafe_tsib <- aus_retail |>
filter(
Industry == "Cafes, restaurants and takeaway food services",
year(Month) %in% 2004:2018 ) |>
summarise(Turnover = sum(Turnover))
cafe_tsib |>
autoplot(Turnover) +
labs("澳大利亚餐饮业月度营业额")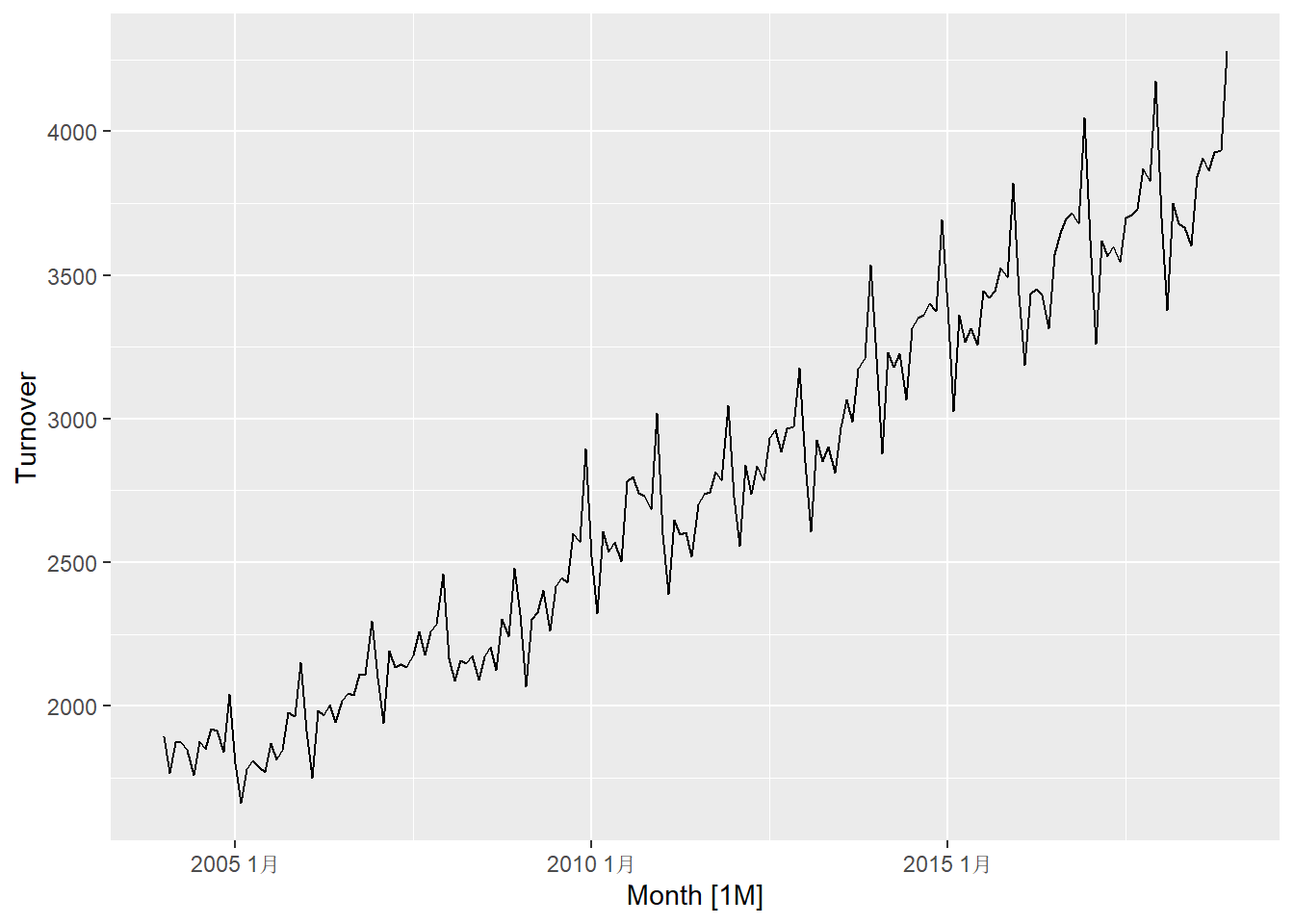
数据呈现趋势、周期性、放大的振幅, 需要进行指数变换。
下面用线性函数拟合对数变换后的趋势, 用三角级数项数来拟合周期性, 用\(K\)值控制周期项的光滑程度, 项数越少越光滑。
cafe_fits <- cafe_tsib |>
model(
`K = 1` = ARIMA(log(Turnover)
~ trend() + fourier(K=1) + pdq(0,0,0)),
`K = 2` = ARIMA(log(Turnover)
~ trend() + fourier(K=2) + pdq(0,0,0)),
`K = 3` = ARIMA(log(Turnover)
~ trend() + fourier(K=3) + pdq(0,0,0)),
`K = 4` = ARIMA(log(Turnover)
~ trend() + fourier(K=4) + pdq(0,0,0)),
`K = 5` = ARIMA(log(Turnover)
~ trend() + fourier(K=5) + pdq(0,0,0)),
`K = 6` = ARIMA(log(Turnover)
~ trend() + fourier(K=6) + pdq(0,0,0)) )这样的自变量是固定的, 在任何时刻其值都已知, 所以预测不需要人为输入自变量值:
cafe_fits |>
forecast(h = "2 years") |>
autoplot(cafe_tsib, level = 95) +
facet_wrap(vars(.model), ncol = 2) +
guides(colour = "none", fill = "none", level = "none") +
geom_label(
aes(x = yearmonth("2007 Jan"), y = 4250,
label = paste0("AICc = ", format(AICc))),
data = glance(cafe_fits) ) +
labs(title = "澳大利亚餐饮业营业额三角级数回归")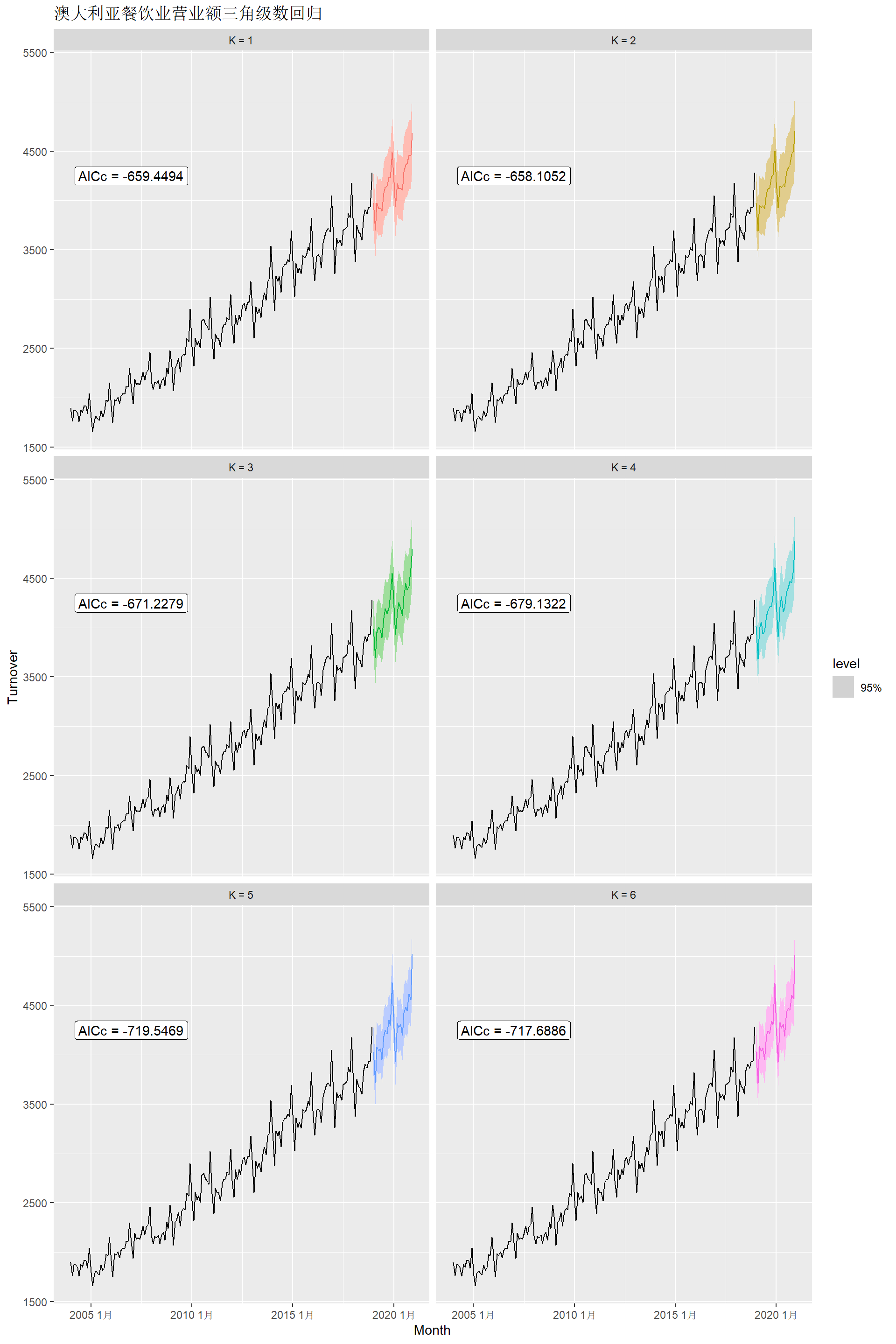
从AICc指标来看\(K=5\)最优。
13.7 复杂周期性的建模
13.7.1 问题介绍
本节内容来自本章内容来自(R. J. Hyndman and Athanasopoulos 2021)节12.1。
月度数据和季度数据是最常见的具有季节性的数据,
其处理比较简单,
可以用ETS()函数的season()来指定,
周期是已经在tsibble中固定下来的;
也可以用ARIMA()规定季节差分、季节AR、季节MA。
其它采样频率的数据可能有非标准的周期, 可能有多个周期。 比如, 周数据的一个周期是一年, 但一年中的周数不是整数, 而是\(365.25/7 \approx 52.18\)。 如果数据是每小时的, 则序列较长的情况下, 会有24小时周期代表每一天, 会有\(365.25 \times 24\)周期代表每一年。 更高频的数据也会有类似的周期性。
这里用一个高频数据举例说明。
fpp3包中有一个bank_calls数据,
是每5分钟记录的某银行客服收到呼叫次数数据,
客服在工作日工作时间从7:00到21:05,
共169个5分钟时间段,
所以一天的周期是169。
因为非工作日不工作,
所以还会有一周的周期,
这是以\(169 \times 5 = 845\)为周期。
数据持续时间从2003-03-03到2003-10-24,
共164个工作日。
下面作时间序列图,
为了时间轴标准正确,
用fill_gaps()函数将中间缺失的周末同等时间用显式的缺失值填补。
library(fpp3)
bank_calls |>
fill_gaps() |>
autoplot(Calls) +
labs(y = "接听电话个数",
title = "银行客服每五分钟接听数")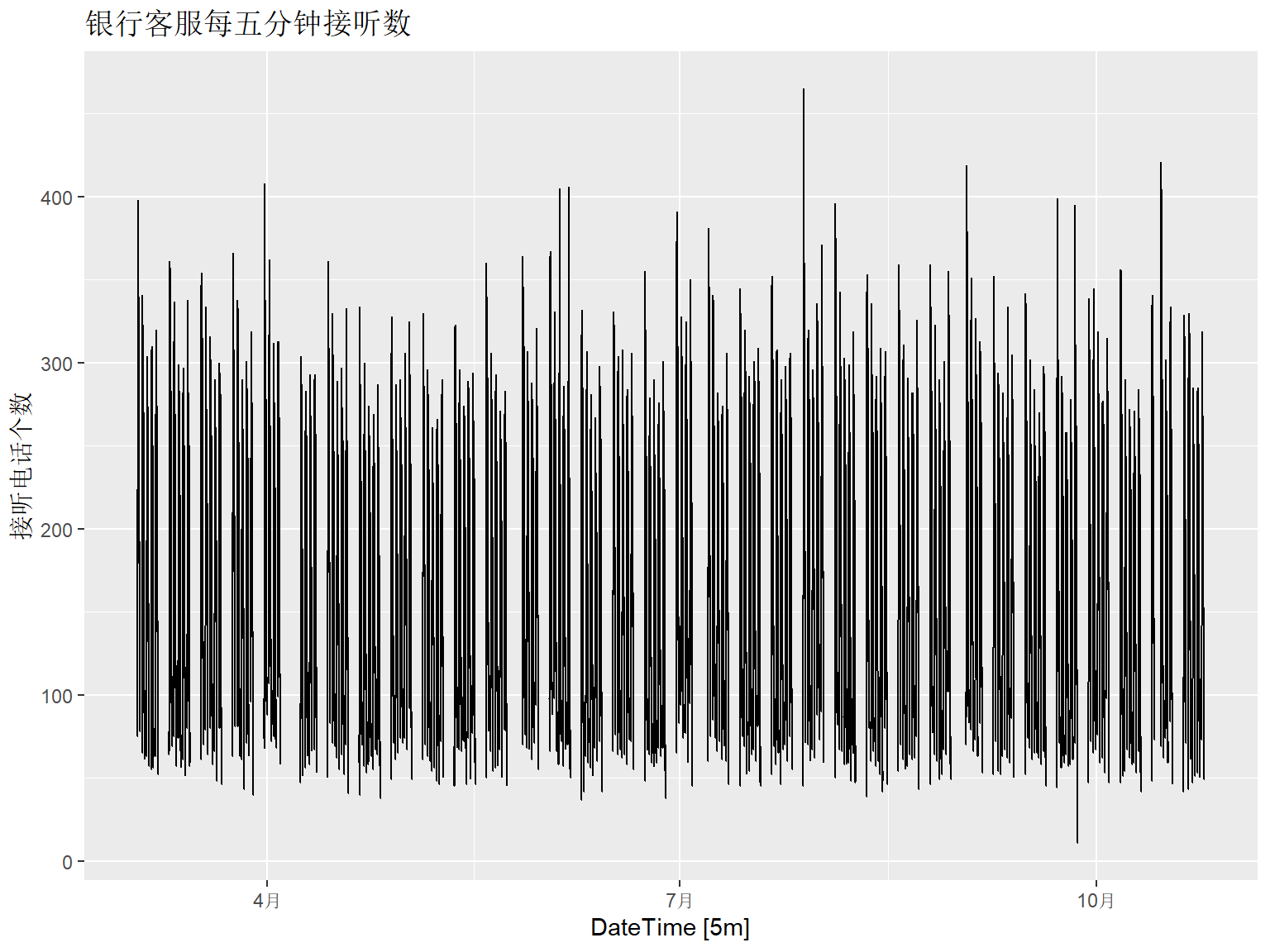
下面截取数据中最后4周作图:
bank_calls |>
slice_tail(n = 4*5*169) |>
fill_gaps() |>
autoplot(Calls) +
labs(y = "接听电话个数",
title = "银行客服每五分钟接听数最后四周")
13.7.2 用STL解决多周期
fable包的STL()函数允许有多个,
每个单独指定自己的周期。
因为客服电话呼叫数据有周末缺失值, 这些缺失值的时间是规则的, 所以可以将周末时间当作不存在(金融数据建模也都是这样做的), 这就需要对tsibble数据定义新的时间索引变量。
建立包含169和\(5 \times 169\)两种周期的STL分解模型:
calls_fit1 <- calls_tsib |>
model(
STL(sqrt(Calls) ~ season(period = 169)
+ season(period = 5*169)) ) 对分解成分作图:
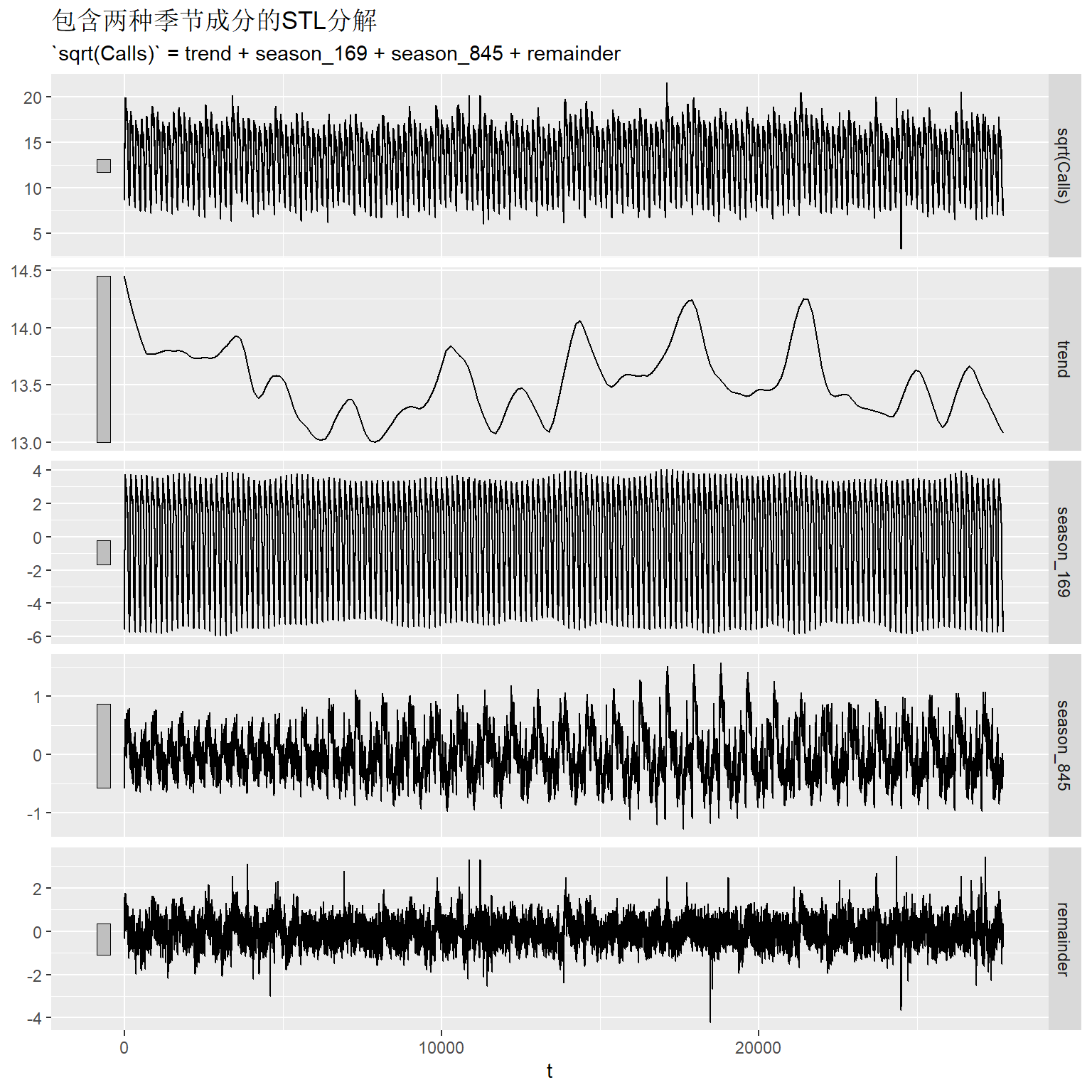
从图形左侧竖直阴影条长短看, 趋势部分在分解中占比较小, 以天为周期的季节性占比较大, 以周伟周期的季节项占比相对较小, 残差也比较大。
以上分解图形的一个缺点是横轴不是真实的时间而是以每5分钟为单位的观测序号。
为了作预测,
需要将STL与ETS结合使用;
fabletools::decomposition_model()输入两个模型,
第一个模型用来分解,
然后第二个模型利用第一个模型的分解结果作预测。
calls_decomp_spec <- decomposition_model(
STL(sqrt(Calls)
~ season(period = 169)
+ season(period = 5*169),
robust = TRUE),
ETS(season_adjust ~ season("N")) )以上程序构成了组合分解方法的设定,
其中的ETS部分指定了去掉了STL规定的季节性后剩余的季节调整后序列的ETS建模方法,
即不用ETS的周期项分解,其它水平、斜率项进行自动模型选择。
下面用这样的组合模型进行预测, 预测一周:
为了对预测结果作图, 希望时间轴使用真实的时间刻度而非观测序号。
calls_fore_ta <- bank_calls |>
# 向前7天的全部时间,包括下班时间
new_data(n = 7 * 24 * 60 / 5) |>
mutate(time = format(DateTime, format = "%H:%M:%S")) |>
filter( # 去掉下班时间和周末时间
time %in% format(
bank_calls$DateTime, format = "%H:%M:%S"),
wday(DateTime, week_start = 1) <= 5 ) |>
# 产生与建模时用的观测序号兼容的序号
mutate(t = row_number() + max(calls_tsib$t)) |>
# 按观测序号连接预测数据集与日期时间数据集
left_join(calls_fore, by = "t") |>
as_fable(response = "Calls", distribution = Calls)预测作图,已知数据仅显示最后三周(只有14个工作日):
calls_fore_ta |>
fill_gaps() |>
autoplot(bank_calls |>
slice_tail(n = 14*169) |>
fill_gaps()) +
labs(title = "两种周期的分解预测")## Warning: Removed 100 rows containing missing values or values outside the scale range
## (`geom_line()`).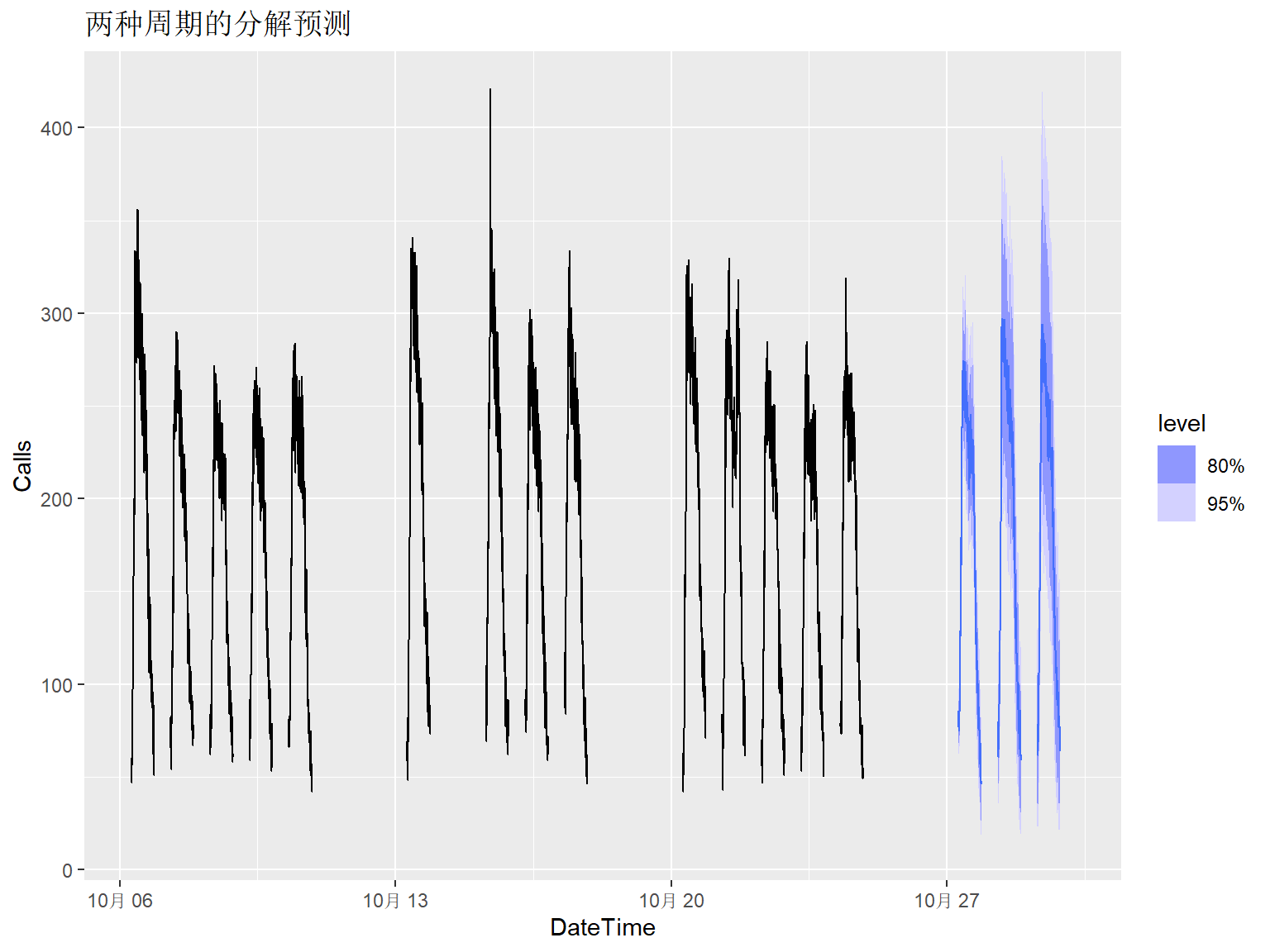
13.7.3 用三角级数回归解决多周期
对于周期非整数以及多个周期的情况, 都可以用三角级数项作为回归自变量解决。
比如,
客服电话呼叫数据,
可以用
\[
\cos(\frac{2\pi k t}{169}),
\ \sin(\frac{2\pi k t}{169}),
\ \cos(\frac{2\pi k t}{845}),
\ \sin(\frac{2\pi k t}{845}),
\]
作为回归自变量,
其中\(k=1,2,\dots\)。
在model()中fourier(period=?, K=?)可以产生产生这样的自变量。
下面用带有相关误差项的回归对客服电话呼叫数据建模。 如果用AICc等指标选择三角级数项数经常会高估, 所以人为选择每日的周期用\(K=10\), 每周的周期用\(K=5\)项。
calls_fit2 <- calls_tsib |>
model(
dhr = ARIMA(sqrt(Calls)
~ pdq(d = 0) + PDQ(0,0,0)
+ fourier(period=169, K=5)
+ fourier(period=5*169, K=2) ) )程序中的参数\(K\)如果取得太大会使得估计失败。
向前一周预测:
为了作预测图时时间轴正确显示日期, 用横向合并方法添加时间:
calls_fore2_ta <- bank_calls |>
new_data(n = 7 * 24 * 60 / 5) |>
mutate(time = format(
DateTime, format = "%H:%M:%S")) |>
filter(
time %in% format(
bank_calls$DateTime, format = "%H:%M:%S"),
wday(DateTime, week_start = 1) <= 5 ) |>
mutate(t = row_number() + max(calls_tsib$t)) |>
left_join(calls_fore2, by = "t") |>
as_fable(response = "Calls", distribution = Calls)
calls_fore2_ta |>
fill_gaps() |>
autoplot(bank_calls |>
tail(14*169) |>
fill_gaps()) +
labs(title = "用两种频率的三角级数回归建模预测")## Warning: Removed 100 rows containing missing values or values outside the scale range
## (`geom_line()`).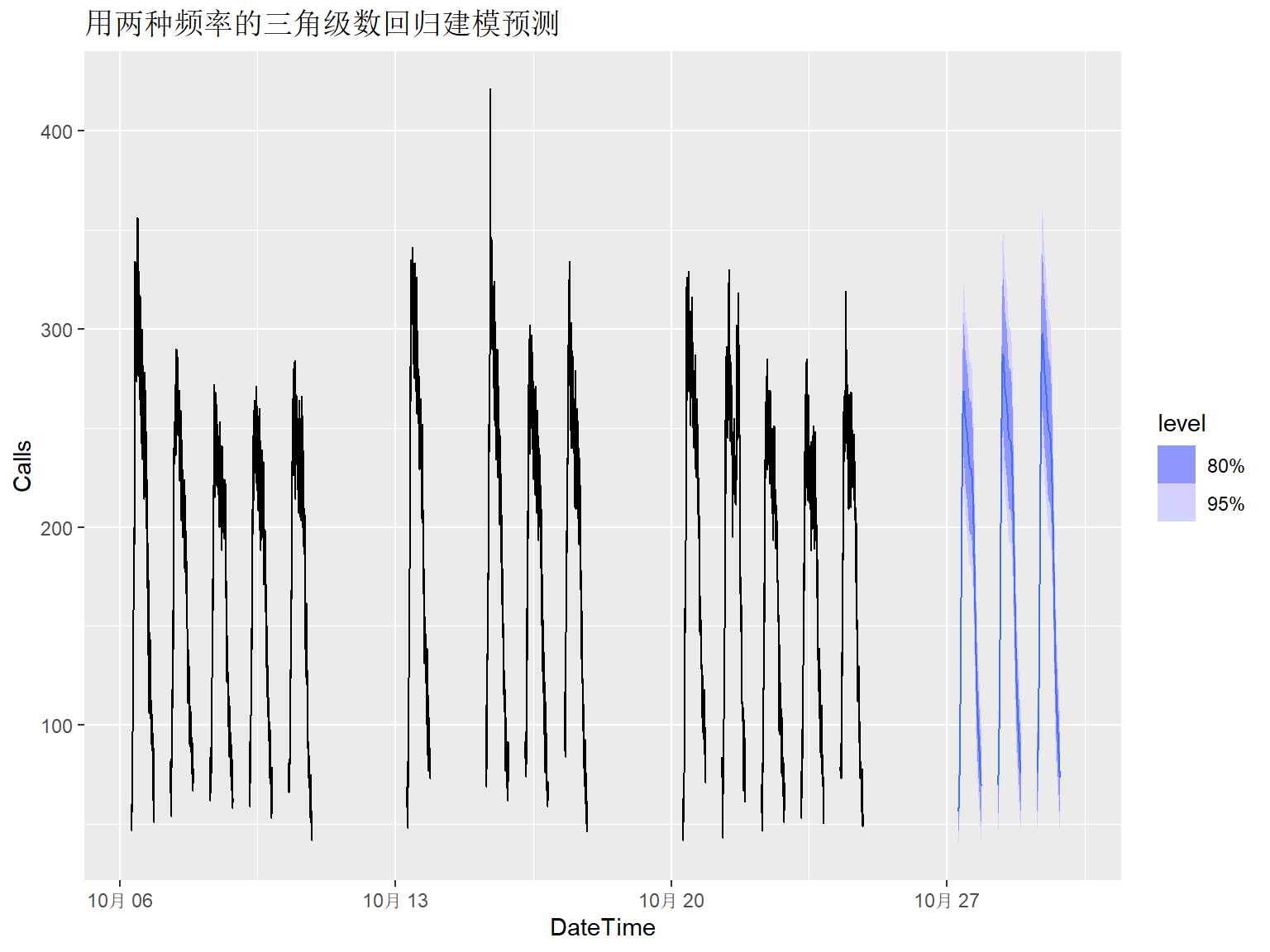
13.7.4 电力需求量问题建模
tsibbledata包的vic_elec是澳大利亚维多利亚州2012到2014年每半小时电力需求数据,
Demand是电力需求(单位:MWh),
Temperature是气温(单位:摄氏度)。
变量Time是日期时间,
变量Holiday表示是否节假日。
作图:
vic_elec |>
pivot_longer(
Demand:Temperature,
names_to = "Series") |>
ggplot(aes(x = Time, y = value)) +
geom_line() +
facet_grid(
rows = vars(Series),
scales = "free_y") +
labs(y = "")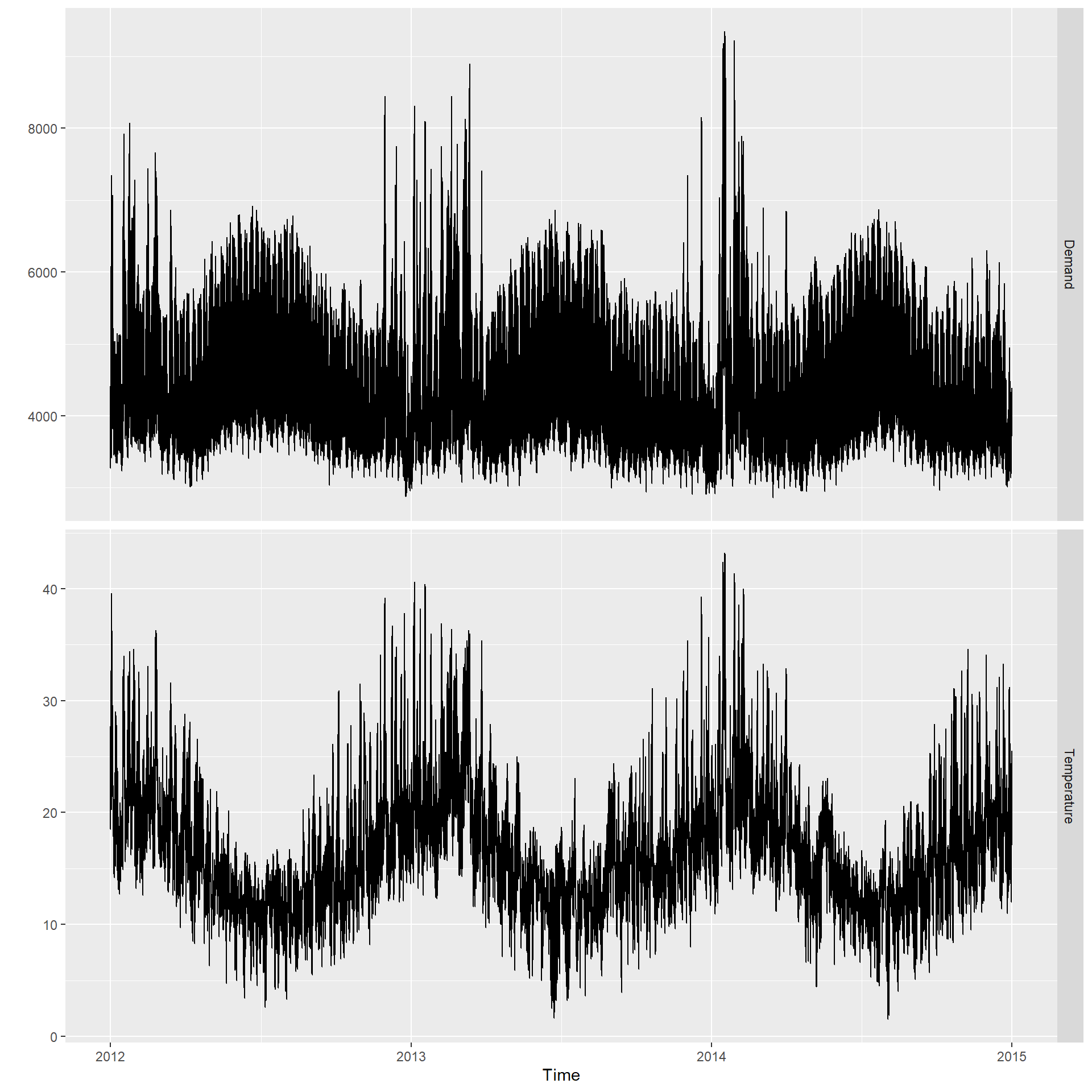
选取2014年10月绘图:
vic_elec |>
filter(year(Time)==2014, month(Time)==10 ) |>
pivot_longer(
Demand:Temperature,
names_to = "Series") |>
ggplot(aes(x = Time, y = value)) +
geom_line() +
facet_grid(
rows = vars(Series),
scales = "free_y") +
labs(y = "")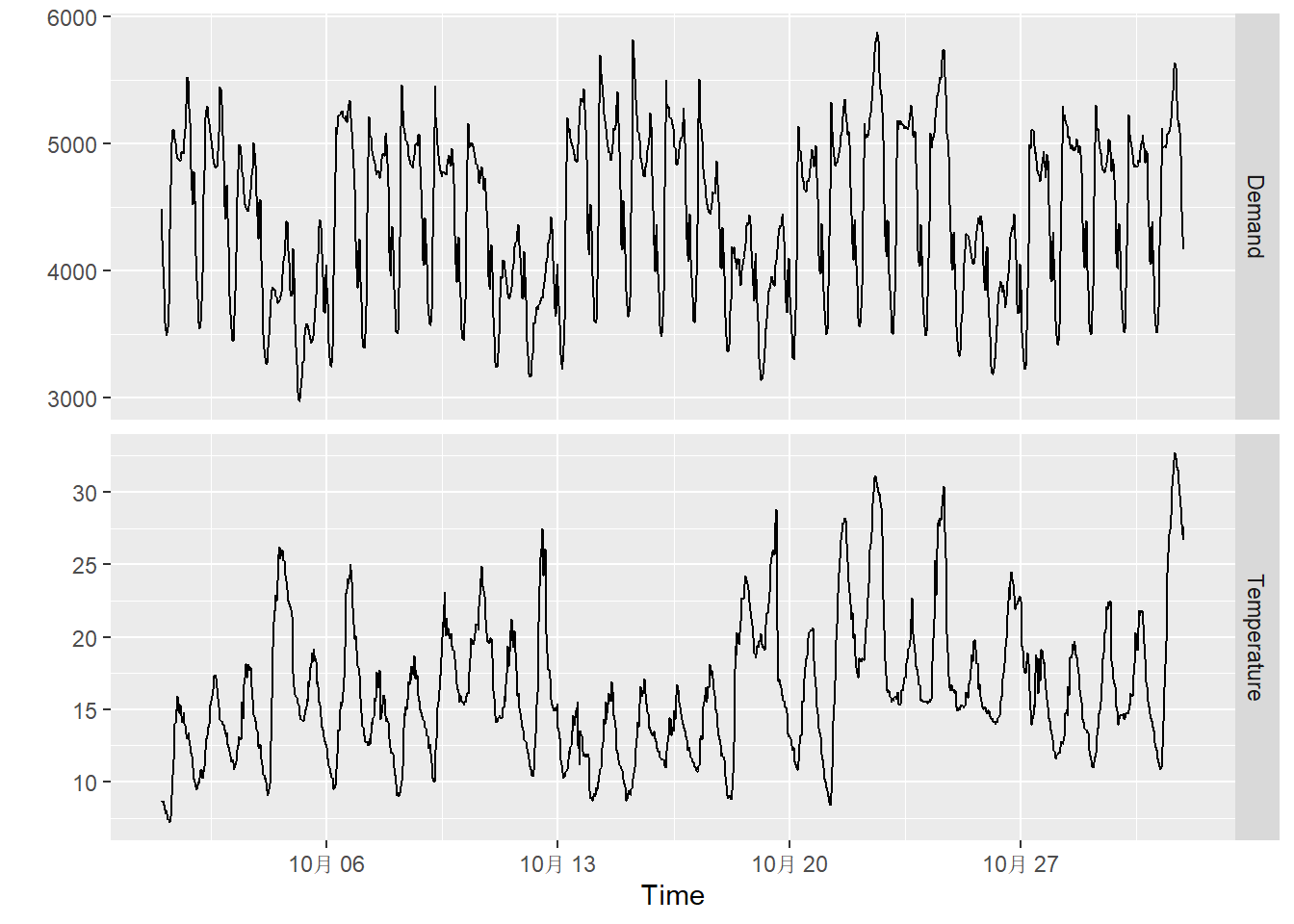
从上图中可以看出以天为周期的变化。 很可能有按周的变化, 我们用颜色表示:
vic_elec |>
filter(year(Time)==2014, month(Time)==10 ) |>
mutate(wday =
wday(Time, week_start = 1) <= 5 ) |>
pivot_longer(
Demand:Temperature,
names_to = "Series") |>
ggplot(aes(x = Time, y = value, color=wday, group=1)) +
geom_line() +
facet_grid(
rows = vars(Series),
scales = "free_y") +
labs(y = "")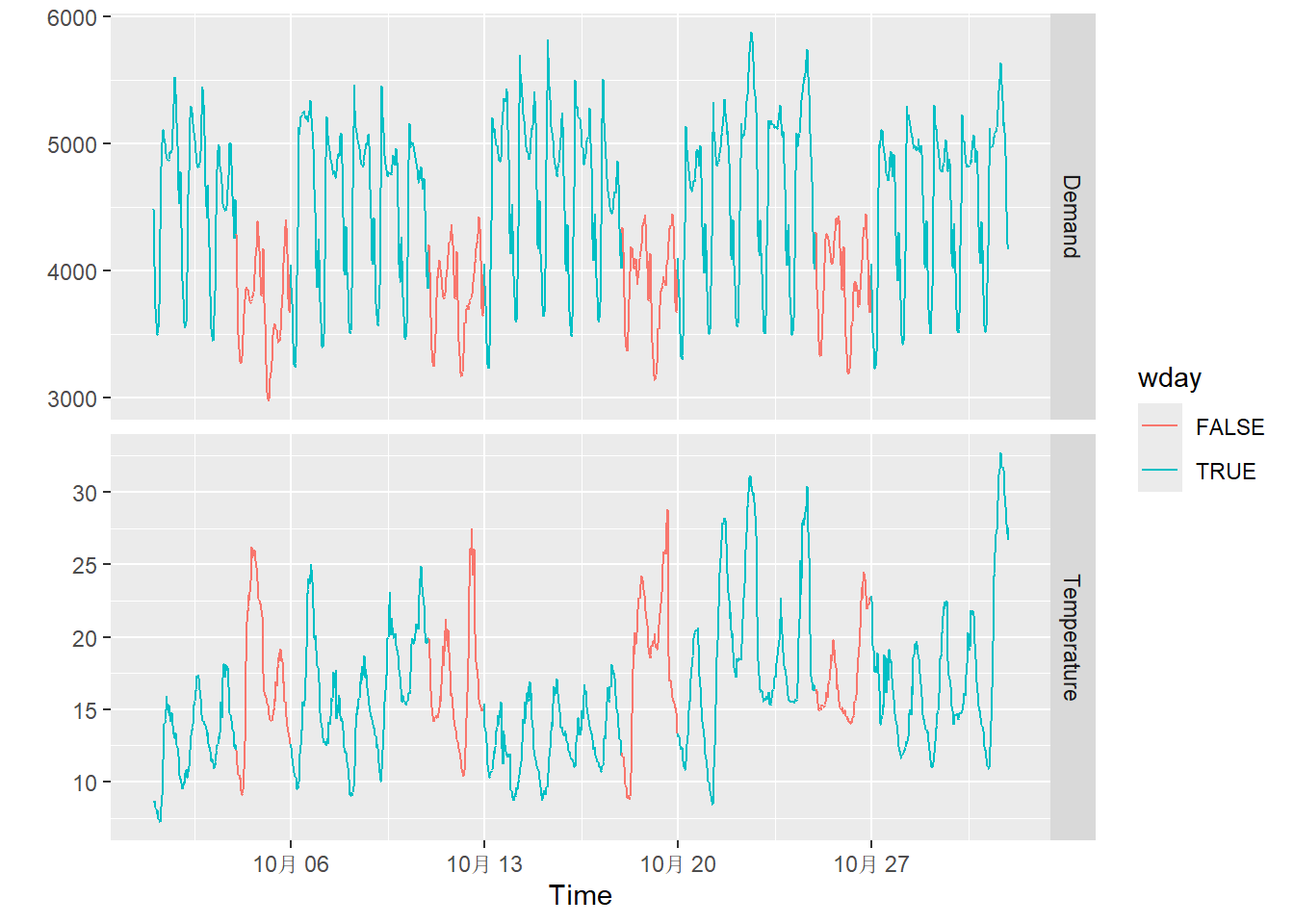
可能还有按年的周期。 我们汇总到日数据绘图查看。
vic_elec_day <- vic_elec |>
index_by(Date) |>
summarise(Demand = sum(Demand),
Temperature = max(Temperature),
Holiday = any(Holiday))vic_elec_day |>
pivot_longer(
Demand:Temperature,
names_to = "Series") |>
mutate(year = year(Date)) |>
ggplot(aes(x = Date, y = value,
color = as.factor(year))) +
geom_line() +
facet_grid(
rows = vars(Series),
scales = "free_y") +
labs(y = "")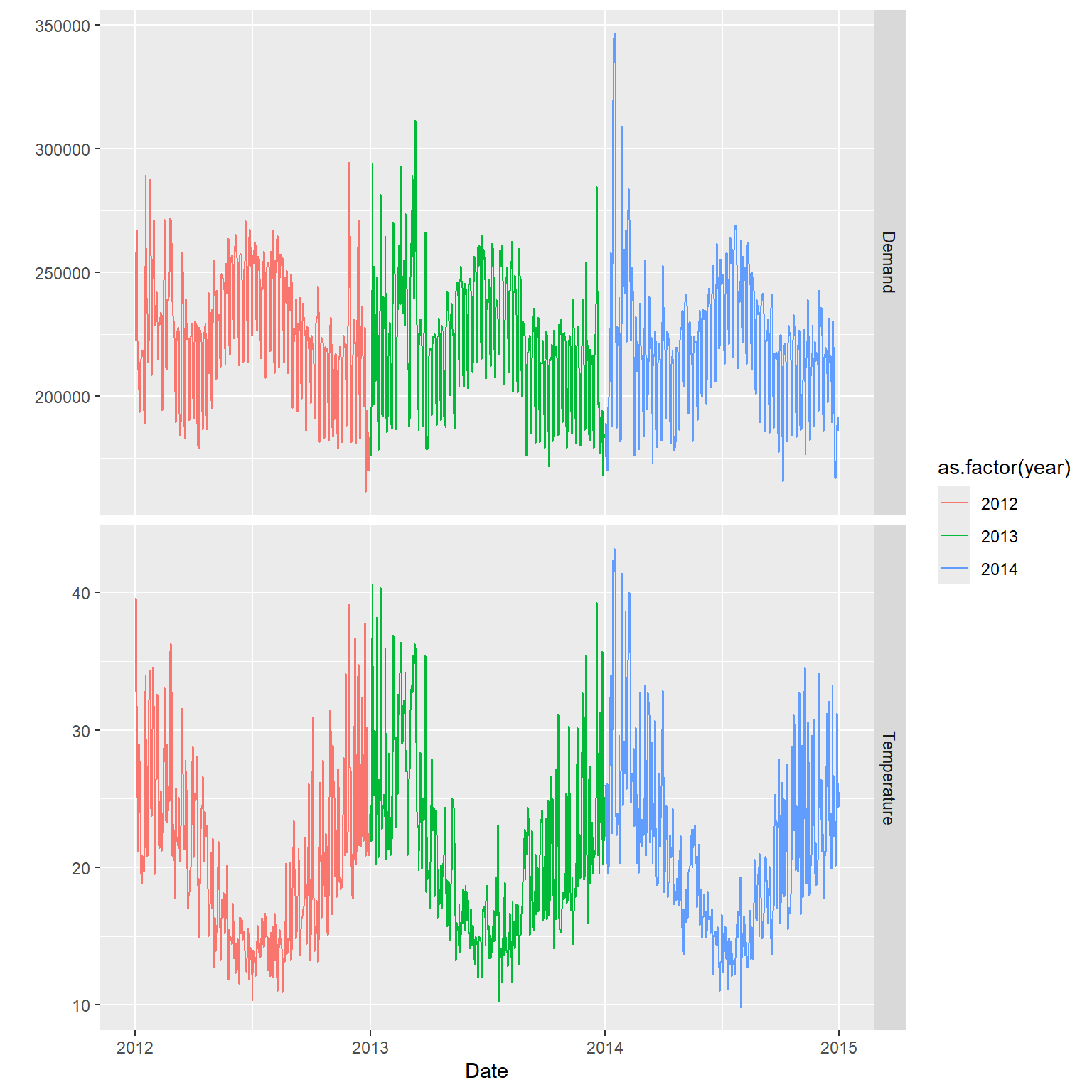
考察用电量和温度的关系, 用颜色区分是否节假日:
vic_elec_day |>
mutate(
working = !Holiday &
wday(Date, week_start = 1) <= 5) |>
ggplot(aes(y = Demand, x = Temperature,
color = working) ) +
geom_point(size=1, alpha=0.5) +
labs(x = "日最高气温", y = "用电量")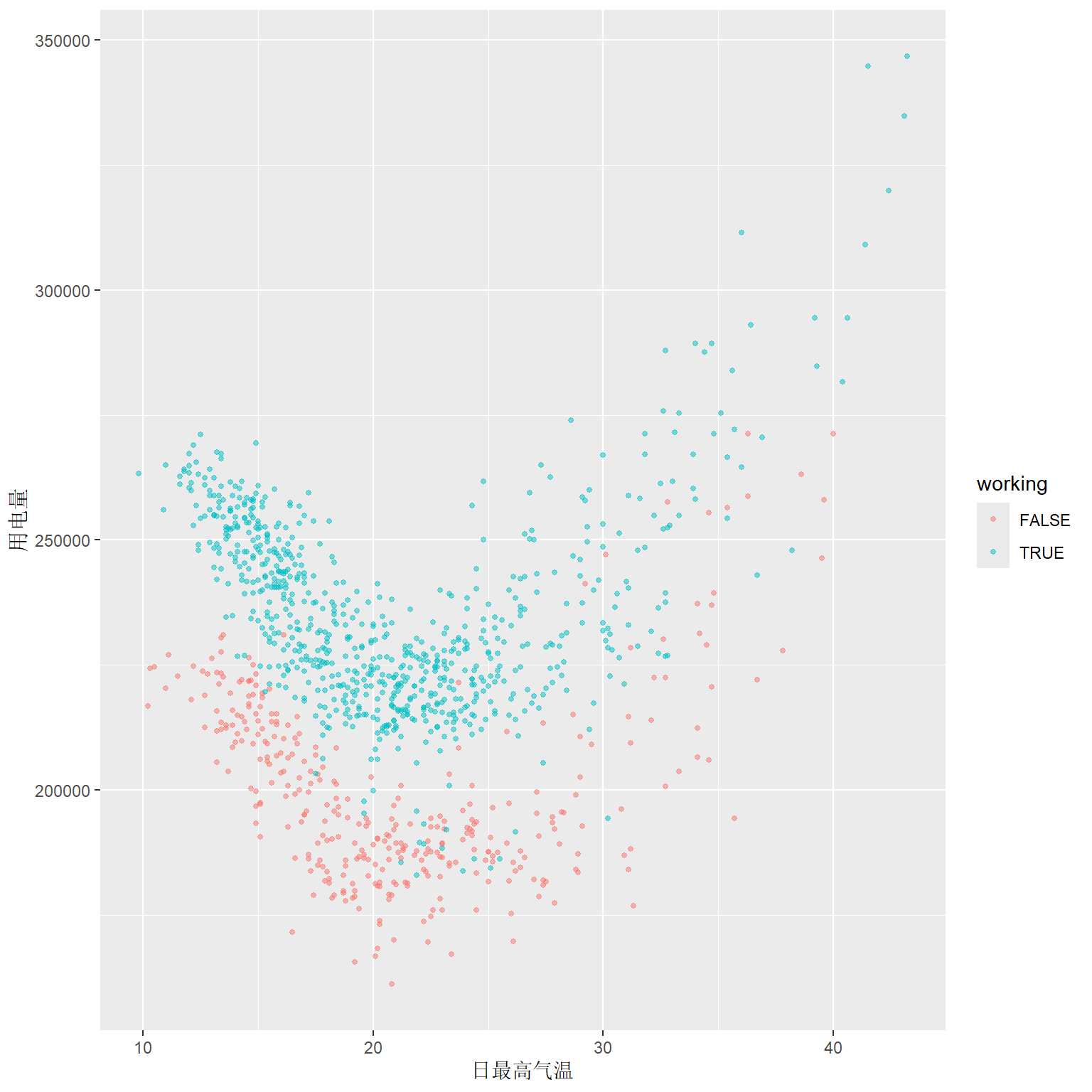
显然用电量与气温是非线性关系, 可以用分段线性函数来估计。
elec_tsib <- vic_elec |>
mutate(
wday = wday(Date, week_start = 1),
Working_Day = !Holiday & wday <= 5,
Cooling = pmax(Temperature, 18) )用Cooling变量将温度分成两段,
关于温度拟合一个分成两段的分段线性回归。
用Working_Day调整节假日效应。
用三角级数表示日、周、年三种周期效应。
elec_fit <- elec_tsib |>
model(ARIMA(
Demand ~ PDQ(0,0,0) + pdq(d = 0)
+ Temperature + Cooling + Working_Day
+ fourier(period = "day", K = 10)
+ fourier(period = "week", K = 5)
+ fourier(period = "year", K = 3) ))## Series: Demand
## Model: LM w/ ARIMA(1,0,5) errors
##
## Coefficients:
## ar1 ma1 ma2 ma3 ma4 ma5 Temperature Cooling
## 0.9258 0.6653 0.3209 0.3094 0.2354 0.0114 -9.0508 19.6214
## s.e. 0.0021 0.0051 0.0064 0.0067 0.0059 0.0047 0.8467 1.1121
## Working_DayTRUE fourier(period = "day", K = 10)C1_48
## 0.4319 235.2615
## s.e. 3.4542 7.9034
## fourier(period = "day", K = 10)S1_48
## 708.8534
## s.e. 8.0946
## fourier(period = "day", K = 10)C2_48
## 221.4974
## s.e. 4.2039
## fourier(period = "day", K = 10)S2_48
## -243.5861
## s.e. 4.2171
## fourier(period = "day", K = 10)C3_48
## 57.2103
## s.e. 2.6534
## fourier(period = "day", K = 10)S3_48
## -141.3368
## s.e. 2.6530
## fourier(period = "day", K = 10)C4_48
## -107.8348
## s.e. 1.8000
## fourier(period = "day", K = 10)S4_48
## 26.4643
## s.e. 1.7993
## fourier(period = "day", K = 10)C5_48
## 5.2271
## s.e. 1.2553
## fourier(period = "day", K = 10)S5_48
## -12.9059
## s.e. 1.2554
## fourier(period = "day", K = 10)C6_48
## -12.6297
## s.e. 0.8852
## fourier(period = "day", K = 10)S6_48
## 23.7667
## s.e. 0.8852
## fourier(period = "day", K = 10)C7_48
## 33.5311
## s.e. 0.6325
## fourier(period = "day", K = 10)S7_48
## -8.3898
## s.e. 0.6326
## fourier(period = "day", K = 10)C8_48
## -23.8163
## s.e. 0.4713
## fourier(period = "day", K = 10)S8_48
## 0.6284
## s.e. 0.4714
## fourier(period = "day", K = 10)C9_48
## 21.0150
## s.e. 0.3846
## fourier(period = "day", K = 10)S9_48
## -8.8583
## s.e. 0.3846
## fourier(period = "day", K = 10)C10_48
## -28.7275
## s.e. 0.3498
## fourier(period = "day", K = 10)S10_48
## 2.8307
## s.e. 0.3498
## fourier(period = "week", K = 5)C1_336
## 289.7959
## s.e. 15.3879
## fourier(period = "week", K = 5)S1_336
## -253.5877
## s.e. 15.3983
## fourier(period = "week", K = 5)C2_336
## -13.5512
## s.e. 14.2006
## fourier(period = "week", K = 5)S2_336
## 225.2604
## s.e. 14.2294
## fourier(period = "week", K = 5)C3_336
## -21.0677
## s.e. 12.7400
## fourier(period = "week", K = 5)S3_336
## -53.8642
## s.e. 12.7291
## fourier(period = "week", K = 5)C4_336
## -38.7898
## s.e. 11.2802
## fourier(period = "week", K = 5)S4_336
## 45.2539
## s.e. 11.2807
## fourier(period = "week", K = 5)C5_336
## 53.3979
## s.e. 9.9709
## fourier(period = "week", K = 5)S5_336
## -103.9556
## s.e. 9.9738
## fourier(period = "year", K = 3)C1_17532
## -188.0065
## s.e. 16.0330
## fourier(period = "year", K = 3)S1_17532
## 71.3175
## s.e. 15.8282
## fourier(period = "year", K = 3)C2_17532
## 174.5148
## s.e. 15.8036
## fourier(period = "year", K = 3)S2_17532
## 158.439
## s.e. 15.795
## fourier(period = "year", K = 3)C3_17532
## -88.7035
## s.e. 15.7845
## fourier(period = "year", K = 3)S3_17532 intercept
## 59.5526 4429.1793
## s.e. 15.7907 18.2769
##
## sigma^2 estimated as 5593: log likelihood=-301608.7
## AIC=603311.4 AICc=603311.5 BIC=603728.3预测需要未来的气温, 如果作短期预测可以从气象预报部门获得第二日的气温, 这里使用情景预测方法, 假设随后两周气温完全重复数据中最后两周:
elec_newd <- new_data(elec_tsib, 2*48) |>
mutate(
Temperature = tail(
elec_tsib$Temperature, 2 * 48),
Date = lubridate::as_date(Time),
wday = wday(Date, week_start = 1),
Working_Day = Date != "2015-01-01" &
wday <= 5,
Cooling = pmax(Temperature, 18) )
elec_fit |>
forecast(new_data = elec_newd) |>
autoplot(elec_tsib |> tail(10*48)) +
labs(title = "用电量预测")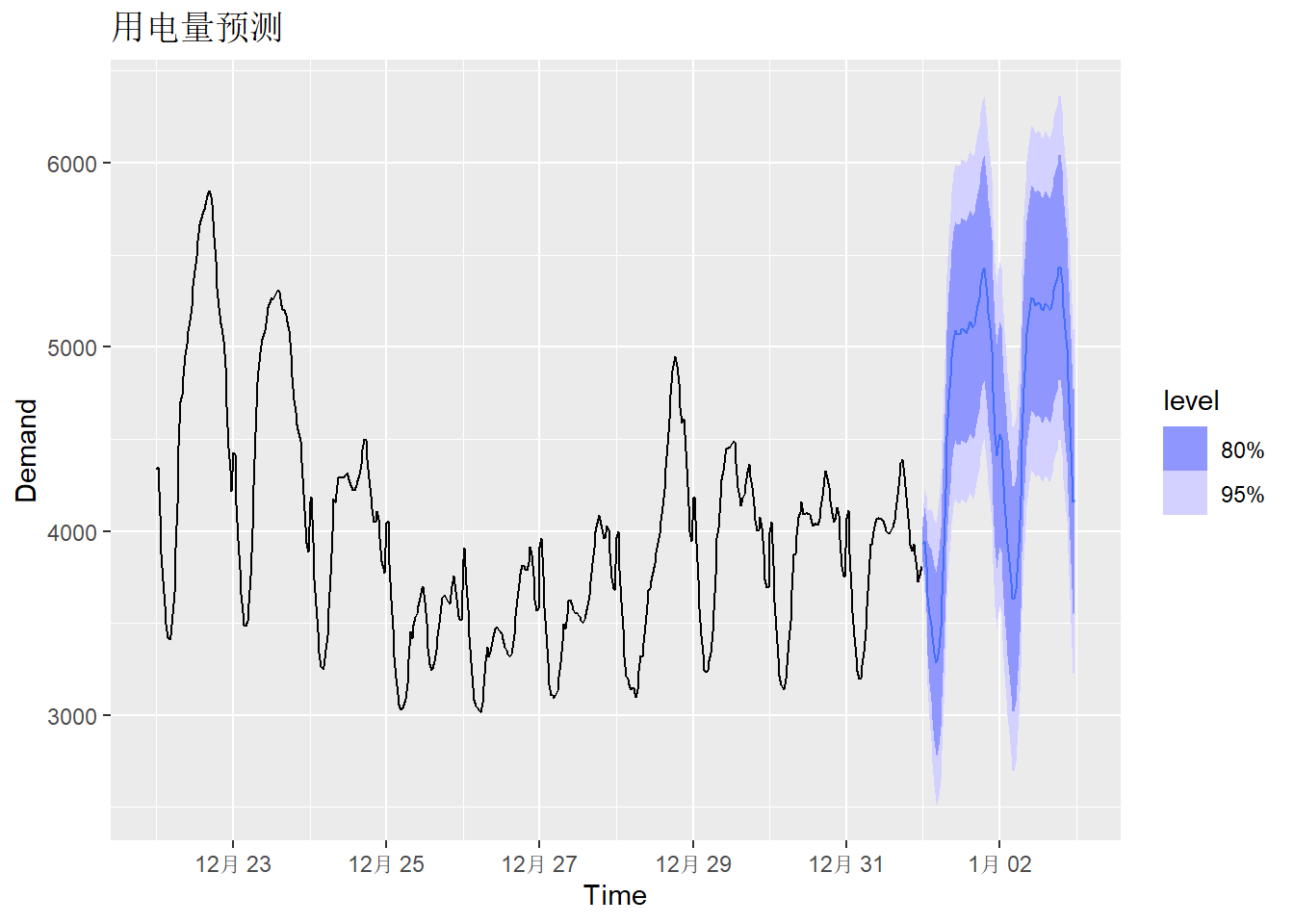
查看模型残差:
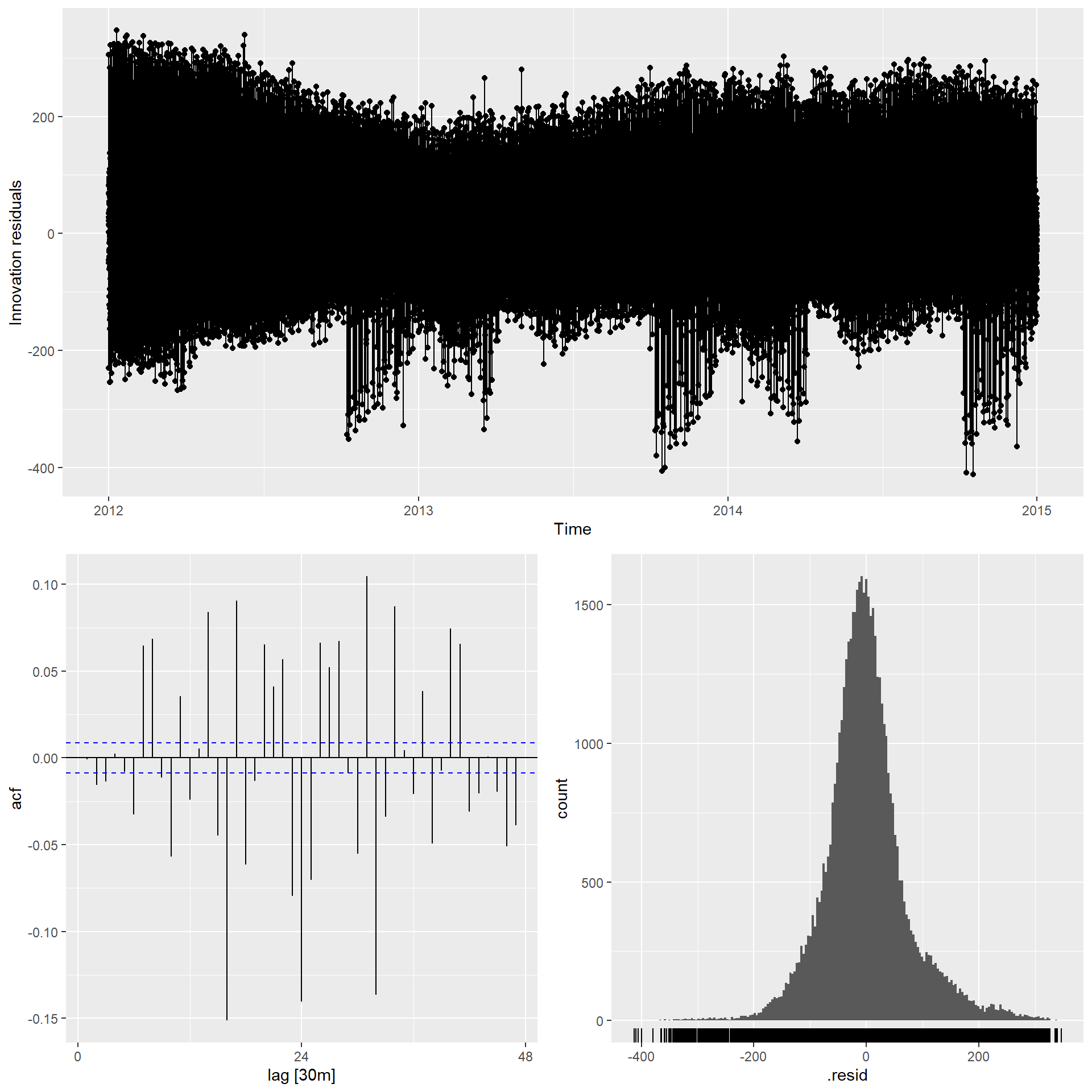
从模型残差看拟合并不够好, 残差的白噪声表现不好, 拟合误差有方差聚集性。
13.8 Prophet模型
Prophet模型是Facebook开发的用来对日数据建模预测的模型, 模型为 \[ y_t = g(t) + s(t) + h(t) + \varepsilon_t, \] \(g(t)\)表示趋势, 用分段线性函数建模, 节点自动选取; \(s(t)\)表示多个季节成分, 用三角级数回归表示; \(h(t)\)表示节假日效应, 使用简单的哑变量表示。 \(\varepsilon_t\)是白噪声,表示随机误差。 参考:
- Taylor, S. J., & Letham, B. (2018). Forecasting at scale. The American Statistician, 72(1), 37–45. https://doi.org/10.1080/00031305.2017.1380080
fable.prophet包实现了Prophet模型。
下面对前面的澳大利亚维多利亚州用电量问题, 使用Prophet模型建模预测。
## Warning: package 'fable.prophet' was built under R version 4.4.3## Loading required package: Rcppelec_fit2 <- elec_tsib |>
model(prophet(
Demand ~ Temperature + Cooling + Working_Day
+ season(period = "day", order = 10)
+ season(period = "week", order = 5)
+ season(period = "year", order = 3)) )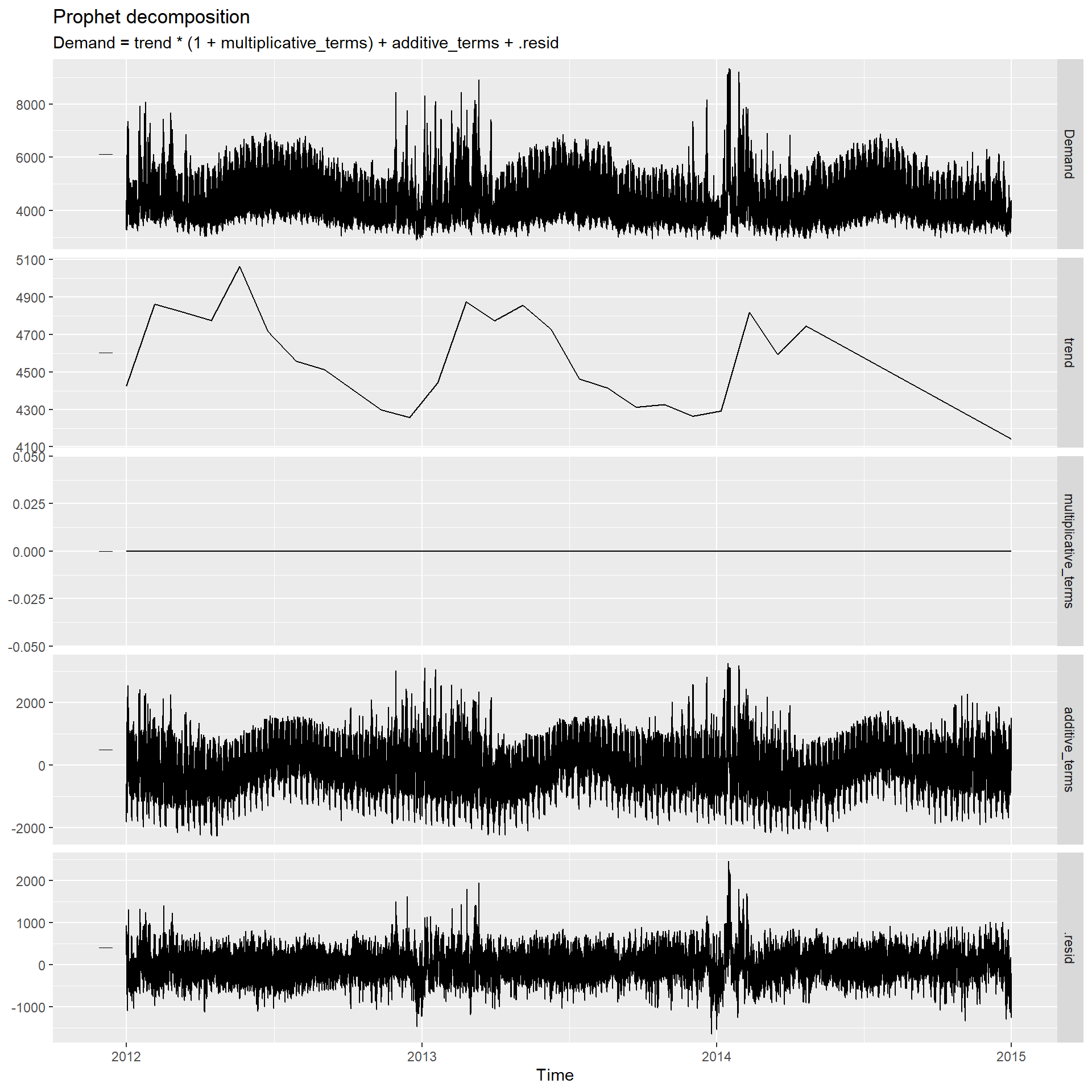
prophet()默认使用分段线性函数作为趋势模型,
且分段节点自动生成,
对本例来说其生成的趋势用作预测并不合适。
残差诊断:
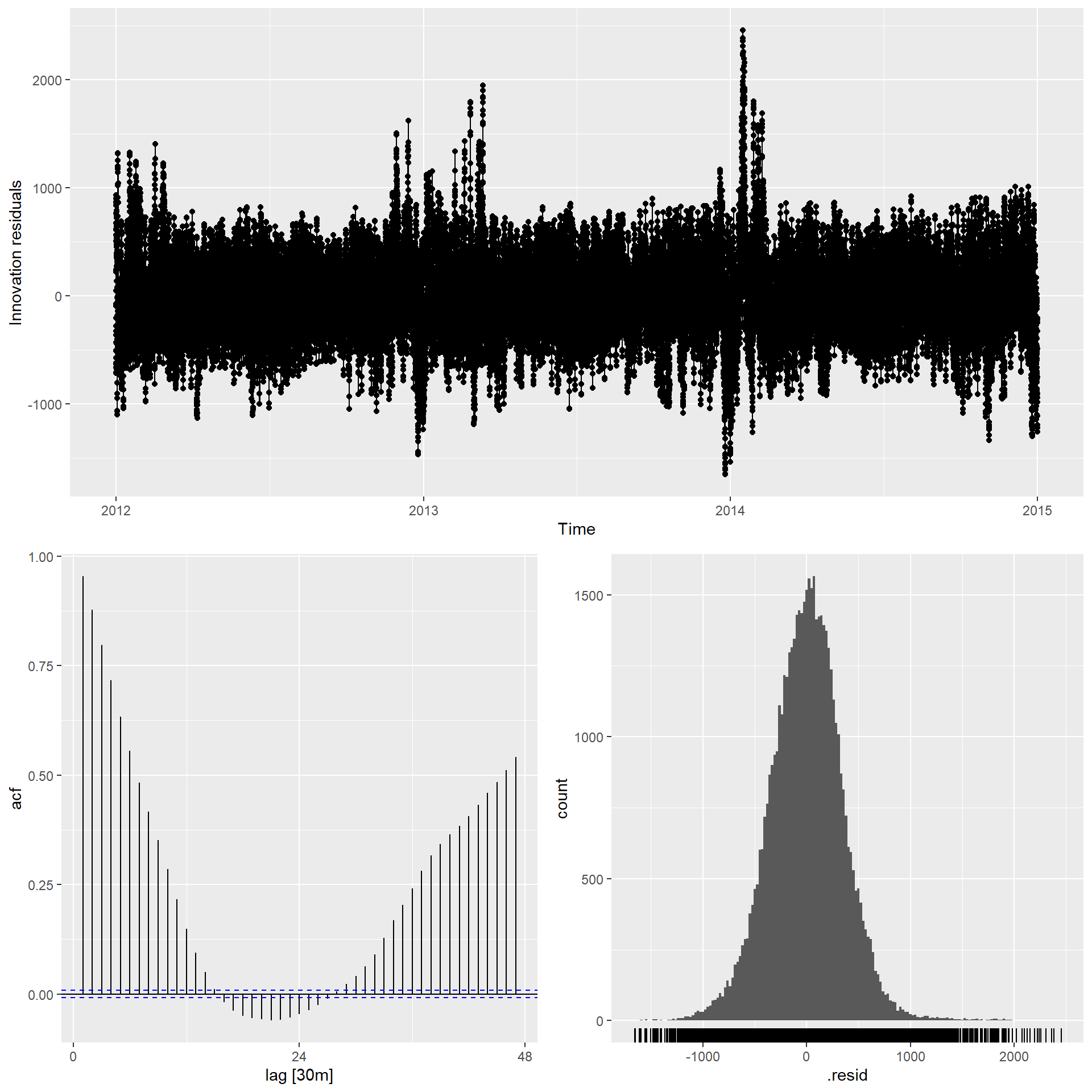
从残差ACF看拟合不够好, 怀疑是使用的三角级数回归引入了虚假的相关性。
预测:
elec_fore2 <- elec_fit2 |>
forecast(new_data = elec_newd)
elec_fore2 |>
autoplot(elec_tsib |> tail(10*48)) +
labs(x = "Date", y = "Demand(KWh)",
title = "用Prophet模型预测电力需求")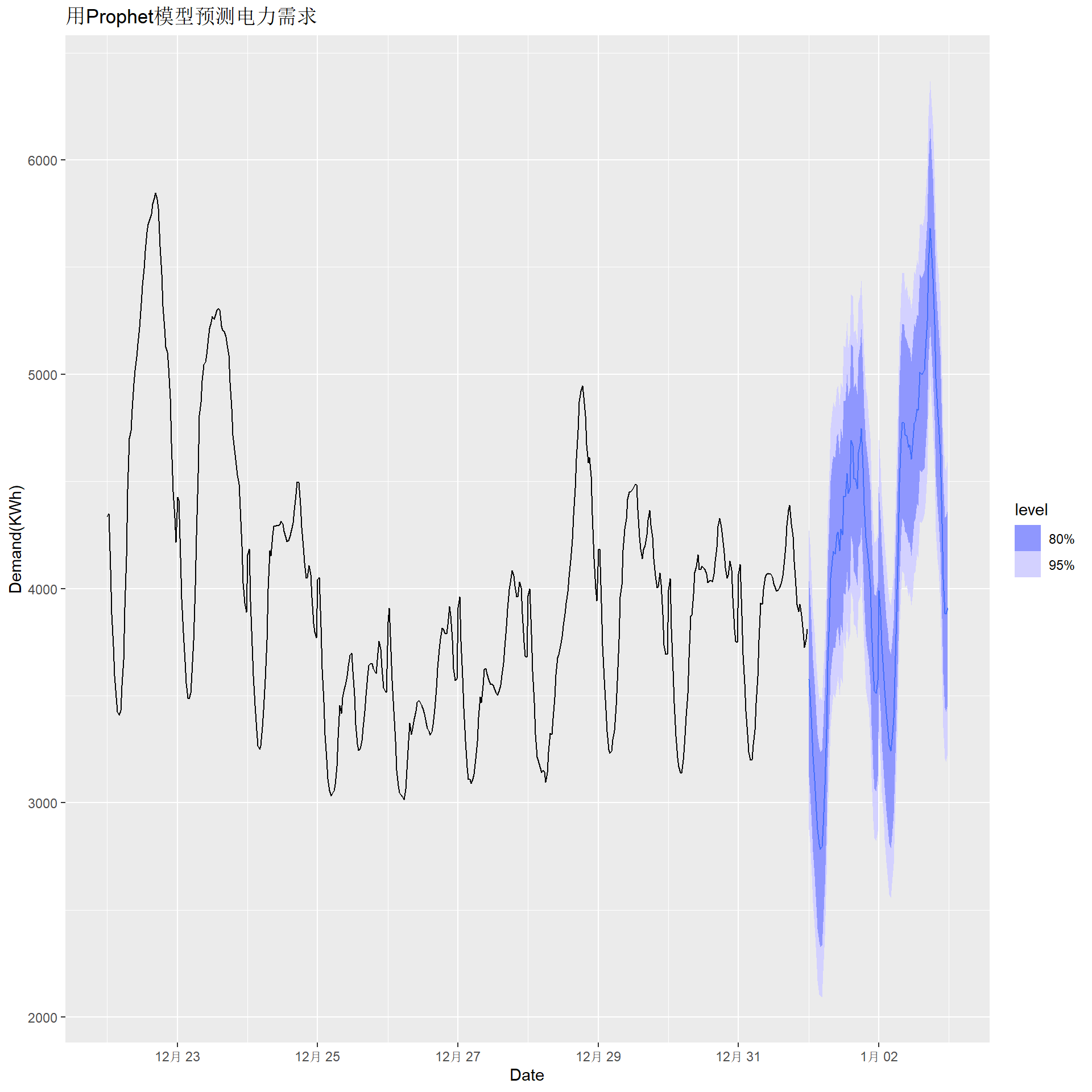
Prophet模型主要针对日数据或更高频率数据, 其计算速度更快, 但误差项仅考虑白噪声, 趋势使用分段线性函数, 其预测一般并不比带有回归自变量的ARIMA模型、ETS模型更好。
13.9 附录:arima函数说明
13.9.1 函数功能介绍
R中的stats::arima()函数和forecast包的Arima()函数功能类似,
forecast::Arima()比stats::arima()有所改进,
这两个函数的功能包括:
- 支持平稳可逆ARMA建模,
这时可以用
include.mean=TRUE设定有均值参数。 - 支持ARIMA建模,
如果差分阶大于零,
则
stats::arima()不允许include.mean=TRUE, 即单位根过程不允许带有漂移; 而forecast::Arima()允许使用include.mean=TRUE, 这时模型中的常数项代表漂移项。 - 支持带有季节项的ARIMA建模。
季节差分阶大于零时
stats::arima()不允许include.mean=TRUE, 而forecast::Arima()不受限制。 - 支持以平稳ARMA序列为误差项的回归建模。
平稳可逆ARMA模型, 表示为ARIMA\((p,0,q)(P,0,Q)_s\), 模型公式为: \[\begin{align} & (1 - \phi_1 B - \phi_2 B^2 - \dots - \phi_p B^p) (1 - \Phi_1 B^s - \Phi_2 B^{2s} - \dots - \Phi_P B^{P s}) (Y_t - \mu) \\ =& (1 + \theta_1 B + \theta_2 B^2 + \dots + \theta_q B^q) (1 + \Theta_1 B^s + \Theta_2 B^{2s} + \dots + \Theta_P B^{Q s}) \varepsilon_t, \tag{13.3} \end{align}\] 其中\(s\)是周期,\(\mu\)是\(\{Y_t\}\)的期望值。
13.9.2 没有外生自变量和单位根时
对于ARIMA\((p,d,q)(P,D,Q)_s\)模型\(\{Z_t \}\),
则令\(Y_t = (1-B)^d (1-B^s)^D Z_t\),
若include.mean=FALSE,
则\(\{Y_t\}\)服从(13.3)中\(\mu=0\)时的模型;
若使用forecast::Arima()建模且设置include.mean=TRUE,
\(\{Y_t\}\)服从(13.3)中\(\mu \neq 0\)时的模型。
13.9.3 有外生自变量但没有单位根时
如果ARIMA\((p,0,q)(P,0,Q)_s\)模型\(\{Z_t\}\)有xreg选项,
设输入的自变量或自变量矩阵(每列是一个自变量)的各个观测\(\boldsymbol x_t\)(标量或行向量),
则模型为
\[\begin{align}
Z_t = \beta_0 + \boldsymbol x_t \boldsymbol \beta + Y_t,
\tag{13.4}
\end{align}\]
\(Y_t\)服从(13.3)中\(\mu=0\)时的模型。
我们用模拟数据来进行这种带有外生自变量的情形的验证计算。
模型为
\[\begin{aligned}
y_t =& 100 + 2 x_t + e_t, \\
e_t =& 0.3 e_{t-1} + \varepsilon_t + 0.7 \varepsilon_{t-1} .
\end{aligned}\]
sima <- function(){
# 样本量
n <- 500
# 自变量
x <- runif(n, 10, 20)
# 作为误差项的ARMA
y <- arima.sim(model=list(ar=0.3, ma=0.7), n=n)
# 回归参数
a <- 100; b <- 2
# 输出的因变量
z <- a + b*x + y
cat("Z的样本均值 =", mean(z), "\n")
# 估计:
res <- forecast::Arima(z, order=c(1,0,1), xreg=x)
print(res)
}
set.seed(101)
sima()## Z的样本均值 = 129.9459
## Series: z
## Regression with ARIMA(1,0,1) errors
##
## Coefficients:
## ar1 ma1 intercept xreg
## 0.2927 0.7127 99.8338 1.9994
## s.e. 0.0511 0.0375 0.1643 0.0086
##
## sigma^2 = 0.8812: log likelihood = -676.45
## AIC=1362.89 AICc=1363.01 BIC=1383.96上述结果中intercept是(13.4)中回归截距项\(\beta_0\)的估计而不再是\(Z_t\)的均值\(\mu\)的估计。
xreg项是回归自变量对应的系数的估计。
13.9.4 有外生自变量和单位根时
如果包含回归自变量\(\{X_t\}\)时因变量\(\{Z_t\}\)有单位根,
这时最好先将两者都预先差分后再建模,
arima()函数不会自动建立关于差分之后的自变量和因变量的回归模型,
应使用模型
\[\begin{align}
\Delta Z_t =& a + b \Delta X_t + Y_t,
\tag{13.5}
\end{align}\]
其中\(\{Y_t\}\)服从平稳的ARMA模型,
\(\Delta Z_t\)和\(\Delta X_t\)预先计算。
如果不做差分,
则(13.5)对应的是
\[
Z_t - Z_0 = a t + b(X_t - X_0) + \sum_{s=1}^t Y_s,
\]
其中\(\sum_{s=1}^t Y_s\)服从有一阶单位根的ARIMA模型。
arima()函数和Arima()函数不能支持这样的模型,
所以必须按照(13.5)来估计。
下面用随机模拟验证, 设真实模型为(13.5), 其中\(a=100\), \(b=2\), \(Y_t\)服从ARMA(1,1)模型, AR系数为\(0.3\), MA系数为\(0.7\)。 模拟验证如下:
simb <- function(){
# 样本量
n <- 500
# 自变量
dx <- runif(n, 10, 20)
x <- cumsum(dx)
# 作为误差项的ARMA
dy <- arima.sim(model=list(
ar=0.3, ma=0.7), n=n)
# 回归参数
a <- 100; b <- 2
# 输出的因变量
dz <- a + b*dx + dy
z <- cumsum(dz)
# 估计,不预先差分:
res <- arima(z, order=c(1,1,1), xreg=x)
cat("不预先差分的arima()函数错误结果:\n")
print(res)
res2 <- forecast::Arima(
z, order=c(1,1,1), xreg=x,
include.mean=TRUE)
cat("\n\n不预先差分的forecast::Arima()函数错误结果:\n")
print(res2)
#估计,预先差分:
res3 <- forecast::Arima(
dz, order=c(1,0,1), xreg=dx)
cat("\n\n预先差分的正确结果:\n")
print(res3)
}
set.seed(101)
simb()## 不预先差分的arima()函数错误结果:
##
## Call:
## arima(x = z, order = c(1, 1, 1), xreg = x)
##
## Coefficients:
## ar1 ma1 x
## 0.9999 0.4827 1.9977
## s.e. 0.0002 0.0605 0.0094
##
## sigma^2 estimated as 1.29: log likelihood = -776.24, aic = 1560.49
##
##
## 不预先差分的forecast::Arima()函数错误结果:
## Series: z
## Regression with ARIMA(1,1,1) errors
##
## Coefficients:
## ar1 ma1 xreg
## 0.9999 0.4827 1.9977
## s.e. 0.0002 0.0605 0.0094
##
## sigma^2 = 1.298: log likelihood = -776.24
## AIC=1560.49 AICc=1560.57 BIC=1577.34
##
##
## 预先差分的正确结果:
## Series: dz
## Regression with ARIMA(1,0,1) errors
##
## Coefficients:
## ar1 ma1 intercept xreg
## 0.2927 0.7127 99.8338 1.9994
## s.e. 0.0511 0.0375 0.1643 0.0086
##
## sigma^2 = 0.8812: log likelihood = -676.45
## AIC=1362.89 AICc=1363.01 BIC=1383.96预先差分的缺点是predict()函数给出的预测也是关于\(\Delta Z_t\)的,
需要人为使用\(Z_{t+1} = Z_t + \Delta Z_t\)进行转换。
如果\(Z_t\)和\(X_t\)包含单位根,
而误差项\(Y_t\)为平稳的ARMA,
这时
\[
Z_t = \beta_0 + \beta X_t + Y_t,
\]
称\(Z_t\)和\(X_t\)有协整关系,
forecast::Arima函数能正确给出估计,
模拟验证如下:
simc <- function(){
# 样本量
n <- 500
# 自变量
dx <- runif(n, 10, 20)
x <- cumsum(dx)
# 作为误差项的ARMA
dy <- arima.sim(model=list(
ar=0.3, ma=0.7), n=n)
# 回归参数
a <- 100; b <- 2
# 输出的因变量
z <- a + b*x + dy
# 估计,不预先差分:
res <- forecast::Arima(
z, order=c(1,0,1), xreg=x)
cat("协整情况下的估计:\n")
print(res)
}
set.seed(101)
simc()## 协整情况下的估计:
## Series: z
## Regression with ARIMA(1,0,1) errors
##
## Coefficients:
## ar1 ma1 intercept xreg
## 0.2926 0.7128 99.7804 2e+00
## s.e. 0.0511 0.0374 0.2026 1e-04
##
## sigma^2 = 0.8811: log likelihood = -676.42
## AIC=1362.83 AICc=1362.95 BIC=1383.9如果\(X_t\)与\(Z_t\)都有单位根且误差项也有单位根, 这样的模型没有合理的定义, 应使用预先差分的做法。
总之,
在forecast::Arima()函数中用xreg=引入回归自变量(外生变量)时,
除非确定协整,
否则不要指定差分或者季节差分,
需要时应预先计算差分。
forecast包的auto.arima()函数可以自动定阶。