17 ARCH模型

这是原书(Tsay 2013)§4.5内容。

17.1 新息和条件方差

设$\{r_t \}$为对数收益率序列， 严平稳遍历， 令$F_t = \sigma(\{ r_s: s \leq t\})$， 令 $$\begin{aligned} \mu_t =& E(r_t | F_{t-1}), \\ a_t =& r_t - E(r_t | F_{t-1}) = r_t - \mu_t, \end{aligned}$$ 称$\{a_t \}$为$\{r_t \}$的新息序列。 显然 $$E(a_t | F_{t-1}) = 0, \ E(a_t) = 0 .$$ 考虑$\text{Var}(r_t | F_{t-1})$。 $$\begin{aligned} & \text{Var}(r_t | F_{t-1}) = E\{[r_t - E(r_t | F_{t-1})]^2 | F_{t-1} \} \\ =& E(a_t^2 | F_{t-1}) = \text{Var}(a_t | F_{t-1}) . \end{aligned}$$

设$r_t$在$F_{t-1}$下的条件密度为$p(r_t | F_{t-1})$， 这个条件密度可以用条件期望$\mu_t$和条件方差$\text{Var}(r_t | F_{t-1}) = E(a_t^2 | F_{t-1})$这两个数字特征描述。 均值可以用ARMA模型建模； 需要建立条件方差的模型。

17.2 ARCH模型公式

(R. F. Engle 1982) 提出了ARCH模型（自回归条件异方差模型）， 这是对将波动率定义为条件标准差， 第一次提出的波动率的理论模型。 基本思想是：

1. 资产收益率的扰动序列$a_t = r_t - E(r_t | F_{t-1})$是前后不相关的， 但是前后不独立。
2. $a_t$的不独立性， 描述为$\text{Var}(r_t | F_{t-1}) = \text{Var}(a_t | F_{t-1})$ 可以用$a_t^2$的滞后值的线性组合表示。

其中$F_t = \sigma(\{r_t, r_{t-1}, \ldots\})$。

定义17.1 设$\{ \varepsilon_t \}$是零均值单位方差的独立同分布白噪声， $\alpha_0 > 0$, $\alpha_i \geq 0$, $i=1,2,\dots,m$， 且$\alpha_1 + \dots + \alpha_m < 1$； $\{a_t \}$为时间序列， $\varepsilon_t$与$\{ a_s: s < t \}$相互独立， 满足 $$\begin{align} \begin{aligned} a_t =& \sigma_t \varepsilon_t , \\ \sigma_t^2 =& \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2 . \end{aligned} \tag{17.1} \end{align}$$ 则称(17.1)为ARCH($m$)模型； 若严平稳白噪声列$\{a_t \}$满足如上模型， 则称$\{a_t \}$为ARCH($m$)序列。

在(17.1)的波动率方程的右侧， 仅出现了截止到$t-1$时刻的 $a_{t-1}, \dots, a_{t-m}$的确定性函数而没有新增的随机扰动， 所以称ARCH模型为确定性的波动率模型， 这意味着$\sigma_t^2$关于$\sigma(\{a_s: s \leq t\})$可测， 即在$t-1$时刻可以确定条件方差$\sigma_t^2$的值。

$\varepsilon_t$的分布常取为标准正态分布， 标准化的t分布， 广义误差分布(Generalized Error Distribution)， 有些情况下还取为有偏的分布。

设$\{a_t \}$是$\{r_t\}$的新息列且满足ARCH(1)模型， 如果$\varepsilon_t \sim \text{N}(0,1)$， 则 $$r_t | F_{t-1} \sim \text{N}(\mu_t, \sigma_t^2) = \text{N}(\mu_t, \alpha_0 + \alpha_1 a_{t-1}^2) .$$ 所以在ARCH模型中$\varepsilon_t$的分布称为“条件分布”， 即在$F_{t-1}$条件下$r_t$的条件分布的类型。

因为系数$\alpha_j$都是非负数， 所以历史值$a_{t-j}^2$较大意味着$a_t$的条件方差较大， 于是在ARCH模型框架下， 大的扰动后面倾向于会出现较大的扰动。 这里“倾向于”不是指一定会出现大的扰动， 因为$a_{t-j}^2$较大使得条件方差$\sigma_t^2$较大， 而方差大只能说出现较大的$a_t$的概率变大， 而不是一定会出现大的扰动$a_t$。 这种现象能够解释资产收益率的波动率聚集现象。

设$\{a_t \}$是定义17.1中的ARCH($m$)序列， 设$\{F_t \}$是单调增的σ代数流， 且$a_t$关于$F_t$可测， 还假设$\varepsilon_t$与$F_{t-1}$独立。 这时 $$\begin{aligned} & E(a_t | F_{t-1}) = E(\sigma_t \varepsilon_t | F_{t-1}) \\ =& \sigma_t E(\varepsilon_t | F_{t-1}) = \sigma_t E(\varepsilon_t) \\ =& 0 . \\ & E(a_t) = 0 . \\ & E(a_t^2 | F_{t-1}) = E(\sigma_t^2 \varepsilon_t^2 | F_{t-1}) \\ =& \sigma_t^2 E(\varepsilon_t^2 | F_{t-1}) = \sigma_t^2 E(\varepsilon_t^2) \\ =& \sigma_t^2 \end{aligned}$$ 因为$\{a_t \}$是严平稳白噪声， 所以$E(a_t^2) = E(\sigma_t^2) = \sigma^2$为常数值。 求解 $$\sigma^2 = \alpha_0 + \alpha_1 \sigma^2 + \dots + \alpha_m \sigma^2,$$ 可得 $$\sigma^2 = E(a_t^2) = \text{Var}(a_t) = \frac{\alpha_0}{1 - \alpha_1 - \dots - \alpha_m} .$$

注意： 有些作者用$h_t = \sigma_t^2$作为条件方差的记号， 这时扰动$a_t = \varepsilon_t \sqrt{h_t}$。

定理17.1 存在严平稳遍历零均值白噪声列$\{a_t \}$满足定义17.1， 且如果严平稳列$\{e_t \}$也满足定义17.1， 则在a.s.意义下$a_t^2$与$e_t^2$相等。

参见(何书元 2023) P.276定理8.3.2。

17.3 ARCH模型的性质

以最简单的ARCH(1)为例讨论模型的性质。 模型为 $$\begin{align} a_t = \sigma_t \varepsilon_t, \ \sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 . \tag{17.2} \end{align}$$ 其中$\alpha_0>0$, $0 < \alpha_1 < 1$。 $\{\varepsilon_t \}$为独立同分布零均值单位方差的白噪声列， $\varepsilon_t$与$\{a_s: s < t \}$独立。 $\alpha_1>0$是因为如果等于零就不能算ARCH(1)， $\alpha_1<1$是为了$a_t$方差有限。

17.3.1 用作新息

令$F_t = \sigma(\{r_t, r_{t-1}, \dots\})$， $$a_t = r_t - E(r_t | F_{t-1}),$$ $\{ a_t \}$是$\{r_t \}$的新息序列。 已经证明$E(a_t | F_{t-1}) = E(a_t) = 0$。

用ARCH(1)对$\{a_t \}$建模， 则$\{a_t \}$是零均值严平稳遍历白噪声列， 有 $$\text{Var}(a_t) = E(a_t^2) = E(\sigma_t^2) = \frac{\alpha_0}{1 - \alpha_1} .$$ 而 $$\text{Var}(r_t | F_{t-1}) = E(a_t^2 | F_{t-1}) = \sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 .$$ 这给出了$r_t$的条件方差的模型。

17.3.2 对应的AR模型

所谓的ARCH效应， 在数据上就是$\{r_t \}$本身表现为白噪声， 但是$\{ r_t^2 \}$具有明显的相关性。 以(17.2)为例， 可以证明$a_t^2$服从一个AR(1)模型。

令 $$v_t = a_t^2 - \sigma_t^2 .$$ 则 $$\begin{align} a_t^2 =& \sigma_t^2 + (a_t^2 - \sigma_t^2) = \sigma_t^2 + v_t \\ =& \alpha_0 + \alpha_1 a_{t-1}^2 + v_t . \tag{17.3} \end{align}$$ 因为$0 < \alpha_1 < 1$， 如果$\{ v_t \}$是白噪声列， 则上式为关于$\{a_t^2 \}$的一个AR(1)模型。 下面证明适当条件下$\{ v_t \}$是白噪声列。

由于 $$v_t = a_t^2 - \sigma_t^2 = a_t^2 - E(a_t^2 | F_{t-1}),$$ 所以$\{ v_t \}$是鞅差序列， 是不相关列， 且$E(v_t) \equiv 0$。 考虑$\text{Var}(v_t)$。

$$\begin{aligned} \text{Var}(v_t) =& E(v_t^2) = E[(a_t^2 - \sigma_t^2)^2] \\ =& E[(\sigma_t^2 \epsilon_t^2 - \sigma_t^2)^2] \\ =& E[\sigma_t^4 (\epsilon_t^2 - 1)^2] \\ =& E \{ E[\sigma_t^4 (\epsilon_t^2 - 1)^2 | F_{t-1}] \} \\ =& E \{ \sigma_t^4 E[(\epsilon_t^2 - 1)^2 | F_{t-1}] \} \\ =& E \{ \sigma_t^4 E[(\epsilon_t^2 - 1)^2] \} \\ =& E[(\epsilon_t^2 - 1)^2] E(\sigma_t^4) . \end{aligned}$$ 记$c_1 = E[(\epsilon_t^2 - 1)^2]$， 则 $$\text{Var}(v_t) = c_1 E(\sigma_t^4) .$$ 来求$E(\sigma_t^4)$， 先考虑 $$\begin{aligned} E(a_t^4) =& E(\varepsilon_t^4 \sigma_t^4) = E[E(\varepsilon_t^4 \sigma_t^4 | F_{t-1})] \\ =& E[\sigma_t^4 E(\varepsilon_t^4 | F_{t-1})] = E[\sigma_t^4 E(\varepsilon_t^4)] \\ =& E(\varepsilon_t^4) E(\sigma_t^4) . \end{aligned}$$ 记$c_2 = E(\varepsilon_t^4)$， 则$E(\sigma_t^4) = c_2^{-1} E(a_t^4)$。 而 $$\begin{aligned} E(a_t^4) =& c_2 E(\sigma_t^4) \\ =& c_2 E[(\alpha_0 + \alpha_1 a_{t-1}^2)^2] \\ =& c_2 \alpha_0 + 2 c_2 \alpha_0 \alpha_1 E(a_{t-1}^2) + c_2 \alpha_1^2 E(a_{t-1}^4) \\ =& c_2 \alpha_0 + \frac{2 c_2 \alpha_0^2 \alpha_1}{1 - \alpha_1} + c_2 \alpha_1^2 E(a_{t-1}^4) . \end{aligned}$$ 这构成了$E(a_t^4)$的递推式。 设$E(a_t^4) < \infty$， 因为$\{a_t \}$严平稳遍历， 所以$E(a_t^4) = E(a_{t-1}^4)$， 可解得 $$\begin{align} E(a_t^4) = \frac{c_2 \alpha_0 + \frac{2 c_2 \alpha_0^2 \alpha_1}{1 - \alpha_1}}{ 1 - c_2 \alpha_1^2}, \ t=0,1,2,\dots. \tag{17.4} \end{align}$$ 只要参数$\alpha_0$, $\alpha_1$，$c_1, c_2$使得上式为正数值， 则$E(a_t^4)$存在且等于上面的常数值， 从而$\text{Var}(v_t)$为常数， 从而$\{v_t \}$是零均值白噪声列。 于是$\{a_t^2 \}$服从一个AR(1)模型。

17.3.3 高阶矩

前面关于$\{a_t^2\}$的AR模型的讨论用到了高阶矩。 有些应用也需要利用$a_t$的高阶矩， 例如， 为了研究$a_t$是否厚尾分布， 需要计算峰度， 峰度依赖于四阶矩。

高阶矩的存在要求(17.1)中的$\varepsilon_t$与$\{ \alpha_j \}$满足一定的约束性条件。 若(17.1)中的$\varepsilon_t$服从标准正态分布， 则其有任意阶矩， 这时条件四阶矩 $$\begin{aligned} E(a_t^4 | F_{t-1}) =& E(\sigma_t^4 \varepsilon_t^4 | F_{t-1}) = \sigma_t^4 E(\varepsilon_t^4 | F_{t-1})\\ =& 3 \sigma_t^4 = 3(\alpha_0 + \alpha_1 a_{t-1}^2)^2 , \end{aligned}$$ 从而无条件的四阶矩为 $$\begin{aligned} E(a_t^4) =& E[ E(a_t^4|F_{t-1})] = 3 E [ (\alpha_0 + \alpha_1 a_{t-1}^2)^2 ] \\ =& 3 \left[ \alpha_0^2 + 2\alpha_0 \alpha_1 E(a_{t-1}^2) + \alpha_1^2 E(a_{t-1}^4) \right] . \end{aligned}$$ 这构成了$E(a_t^4)$的递推式， 令$Ea_t^4 = Ea_{t-1}^4$，于是 $$(1 - 3 \alpha_1^2) Ea_t^4 = 3\left( \alpha_0 + 2\alpha_0 \alpha_1 \frac{\alpha_0}{1 - \alpha_1} \right) ,$$ 这要求$1 - 3\alpha_1^2>0$，即$0<\alpha_1 < \frac{\sqrt{3}}{3}$。 这时 $$Ea_t^4 = \frac{3\alpha_0^2(1+\alpha_1)}{(1-\alpha_1)(1-3\alpha_1^2)} .$$ 只要$E(a_0^4)$满足上式， 则上式对$t \geq 0$都成立。 由此可以计算$a_t$的峰度为 $$\frac{Ea_t^4}{[\text{Var}(a_t)]^2} = 3 \frac{1-\alpha_1^2}{1 - 3\alpha_1^2} > 3 .$$ $a_t$的超额峰度为 $$\frac{Ea_t^4}{[\text{Var}(a_t^2)]^2} - 3 = \frac{6\alpha_1^2}{1 - 3\alpha_1^2} > 0 .$$

这说明$\{a_t \}$序列是厚尾（重尾）分布， 其样本比均值和方差相同的正态序列有更多的离群值（outliers）。 这与实证分析中对资产收益率的分布观察结果一致。

17.3.4 一般ARCH模型的性质

对一般的ARCH($m$)模型， 其性质与ARCH(1)类似，但公式更复杂。

模型可推广为二次型表示， 见(Tsay 2010)第3章。

17.4 ARCH模型的优缺点

优点：

1. 可以产生波动率聚集；
2. 扰动$a_t$具有厚尾分布。

缺点：

1. 因为假定$a_{t-j}$通过$a_{t-j}^2$影响波动率$\sigma_t$， 所以正的扰动和负的扰动对波动率影响相同， 但是实际的资产收益率中正负扰动对波动率影响不同， 较大的负扰动比正扰动引起的波动更大。
2. ARCH模型对模型参数有较严格的约束条件， 即使是ARCH(1)， 为了能计算峰度，也需要$\alpha_1 \in (0, \frac{\sqrt{3}}{3})$， 高阶的ARCH($m$)的约束条件更为复杂。 这对带高斯新息的ARCH模型通过超额峰度表达厚尾性是一个限制。
3. 只能描述条件方差的变化， 但是不能解释变化的原因。
4. 由模型做的波动率预测会偏高。
5. 可能需要较大的$m$。

17.5 ARCH模型的建模步骤

17.5.1 定阶

在ARCH效应检验显著后， 可以通过考察$\{ a_t^2 \}$序列的PACF来对ARCH模型定阶。 下面解释理由。

首先， 模型为 $$\sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2$$ 因为$E(a_t^2 | F_{t-1}) = \sigma_t^2$， 所以认为近似有 $$a_t^2 \approx \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2$$ 这样可以用$\{ a_t^2 \}$序列的PACF的截尾性来估计ARCH阶$m$。

另一方面， 令$\eta_t = a_t^2 - \sigma_t^2$， 可以证明$\{\eta_t \}$为零均值不相关白噪声列， 则$a_t^2$有模型 $$a_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2 + \eta_t$$ 这是$\{a_t^2\}$的AR($m$)模型， 但不要求$\{\eta_t \}$独立同分布。 从这个模型用最小二乘法估计$\{ \alpha_j \}$是相合估计， 但不是有效（方差最小）估计。 因此从$\{a_t^2\}$的PACF估计$m$是合理的。

作为例子， 考虑§16.4.2的美元对欧元汇率日对数收益率问题， 画出对数收益率平方序列的PACF:

d.useu <- read_table(
  "d-useu9910.txt", 
  col_types=cols(.default=col_double())
)
xts.useu <- with(d.useu, 
  xts(rate, make_date(year, mon, day)))
xts.useu.lnrtn <- diff(log(xts.useu))[-1,]
eu <- c(coredata(xts.useu.lnrtn))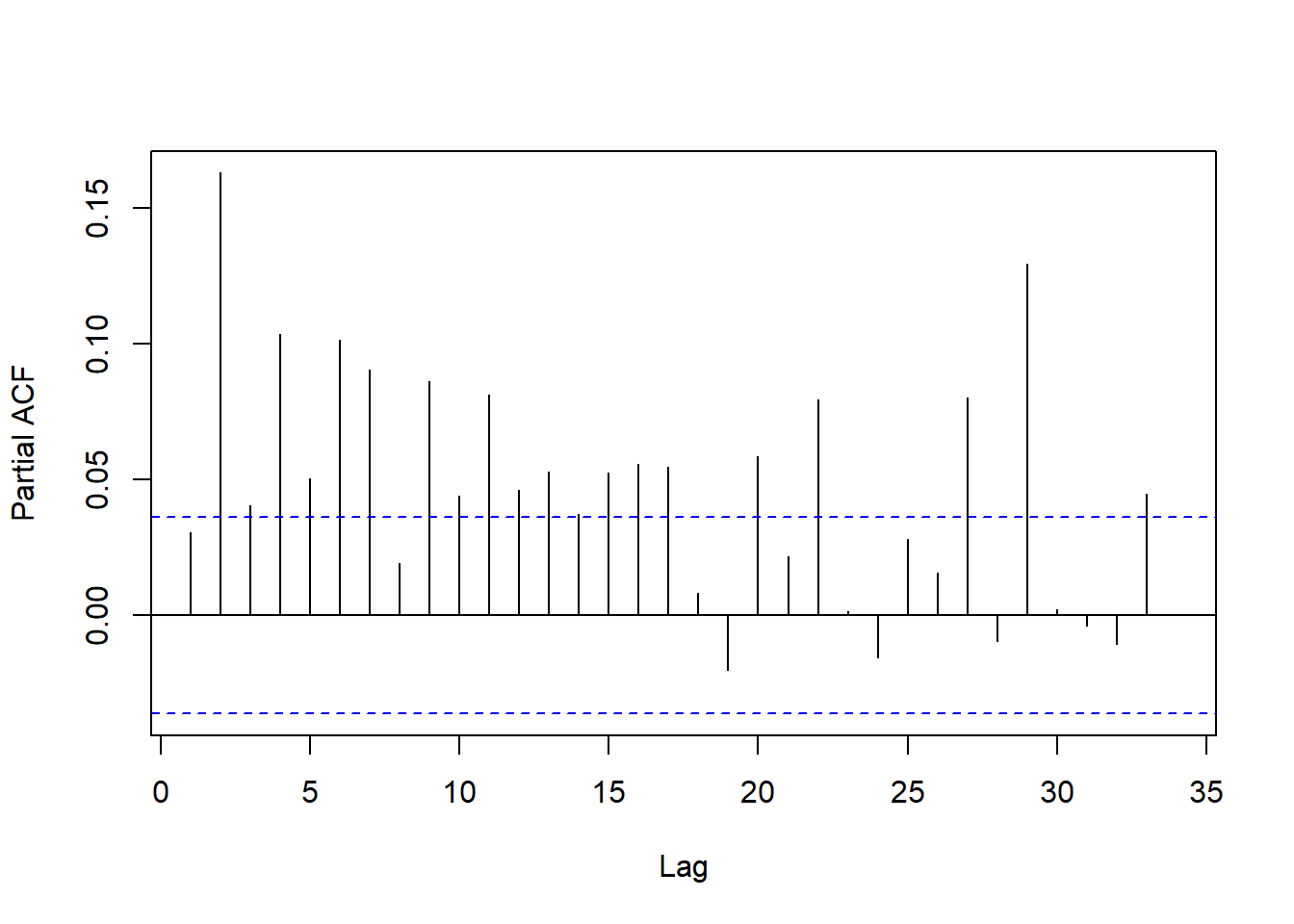

pacf(eu^2, main="")

图17.1: 美元对欧元日对数收益率平方的PACF

结果提示需要用高阶（如$m=29$）的ARCH模型， 从AR模型建模经验， 有可能采用类似ARMA格式的模型会减少参数使用。 GARCH模型可以进行这种改进。

17.5.2 模型估计

对ARCH($m$)模型，考虑最大似然估计或条件最大似然估计。 扰动$a_t = \varepsilon_t \sigma_t$, $\sigma^2_t = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2$， 记模型参数$\boldsymbol\alpha = (\alpha_0, \alpha_1, \dots, \alpha_m)^T$。 模型的似然函数与假定的$\varepsilon_t$的分布有关， 存在多种似然函数形式。

似然函数即$a_1, \dots, a_T$的联合密度为 $$\begin{aligned} & f(a_1, \dots, a_T | \boldsymbol\alpha) \\ =& f(a_T | F_{T-1}, \boldsymbol\alpha) f(a_{T-1} | F_{T-2}, \boldsymbol\alpha) \dots f(a_{m+1} | F_m, \boldsymbol\alpha) f(a_1, \dots, a_m | \boldsymbol\alpha) . \end{aligned}$$ 其中$f(a_t | F_{t-1}, \boldsymbol\alpha)$表示给定$t-1$时刻已知值条件下$a_t$的条件密度。

17.5.2.1 正态假设

当假定$\varepsilon_t$为独立同标准正态分布分布随机变量列时， 在已知$a_1, \dots, a_{t-1}$条件下， $$\sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2$$ 看成已知数， $a_t = \varepsilon_t \sigma_t$的条件分布为$\text{N}(0, \sigma_t^2)$， 于是似然函数为 $$f(a_1, \dots, a_T | \boldsymbol\alpha) = \prod_{t=m+1}^T \frac{1}{\sqrt{2\pi} \sigma_t} \exp\left(-\frac12 \frac{a_t^2}{\sigma_t^2} \right) f(a_1, \dots, a_m | \boldsymbol\alpha)$$ 其中$f(a_1,\dots, a_m|\boldsymbol\alpha)$形式比较复杂， 常常从似然函数中去掉此项， 变成条件似然函数， 当$T$较大时去掉此项的影响很小。 条件似然函数为 $$f(a_{m+1}, \dots, a_T | \boldsymbol\alpha) = \prod_{t=m+1}^T \frac{1}{\sqrt{2\pi} \sigma_t} \exp\left(-\frac12 \frac{a_t^2}{\sigma_t^2} \right)$$ 条件对数似然函数为 $$\begin{align} \ell(a_{m+1}, \dots, a_T | \boldsymbol\alpha) = -\frac12 \sum_{t=m+1}^T \left[ \ln\sigma_t^2 + \frac{a_t^2}{\sigma_t^2} \right] + \text{常数项} \tag{17.5} \end{align}$$ 其中$\sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2$是$\boldsymbol\alpha$的函数， 给定一组$\boldsymbol\alpha$， 就可以计算$\sigma_t^2$, $t=m+1, \dots, T$， 从而计算似然函数值。 最大化条件对数似然函数得到的估计称为正态假设下的条件最大似然估计。

17.5.2.2 t分布假设

因为收益率分布厚尾， 有些应用中假设$\{a_t \}$的方差模型中的$\varepsilon_t$服从标准化t分布， 自由度为$v$。 设$\xi$为服从t($v$)分布的随机变量， 则$v>2$时$E\xi=0$, $\text{Var}(\xi)=v/(v-2)$, 令$\eta=\frac{\xi}{\sqrt{v/(v-2)}}$， 称$\eta$的分布为标准化t($v$)分布， 设$\varepsilon_t$分布为标准化t($v$)分布，其分布密度为

$$\begin{align} f(\varepsilon_t | v) =& \frac{\Gamma\left( \frac{v+1}{2}\right)} {\Gamma\left( \frac{v}{2} \right) \sqrt{(v-2)\pi}} \left( 1 + \frac{\varepsilon_t^2}{v-2} \right)^{-\frac{v+1}{2}}, \tag{17.6}\\ & \ \varepsilon_t \in (-\infty, \infty), \quad (v>2) . \nonumber \end{align}$$

这时，由$a_t = \varepsilon_t \sigma_t$， 其中$\sigma_t^2 = \text{Var}(a_t | F_{t-1})$， 得条件似然函数 $$\begin{align} & f(a_{m+1}, \dots, a_T | \boldsymbol\alpha, a_1, \dots, a_m) \\ =& \left[ \frac{\Gamma\left( \frac{v+1}{2}\right)} {\Gamma\left( \frac{v}{2} \right) \sqrt{(v-2)\pi}} \right]^{T-m} \prod_{t=m+1}^T \frac{1}{\sigma_t} \left( 1 + \frac{\varepsilon_t^2}{(v-2)\sigma_t^2} \right)^{-\frac{v+1}{2}} . \tag{17.7} \end{align}$$

可以先验地取定自由度$v$的值， 在(17.7)中关于$\boldsymbol\alpha$求最大值； 也可以将$v$和$\boldsymbol\alpha$一起在(17.7)中求最大值。 这样得到的参数估计称为在t分布下得条件最大似然估计。

先验地设定自由度$v$时， 通常取$v$在3到6之间。 （条件）对数似然函数为 $$\begin{align} & \ell(a_{m+1}, \dots, a_T | \boldsymbol\alpha, a_1, \dots, a_m) \\ =& -\sum_{t=m+1}^T \left\{ \frac{v+1}{2}\ln \left( 1 + \frac{a_t^2}{(v-2)\sigma_t^2} \right) + \frac12 \ln\sigma_t^2 \right\} + \text{常数项} . \tag{17.8} \end{align}$$ 其中$\sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \dots + \alpha_m a_{t-m}^2$依赖于$\boldsymbol\alpha=(\alpha_0, \alpha_1, \dots, \alpha_m)^T$。

将自由度$v$也看作未知参数时， （条件）对数似然函数为 $$\begin{align} &\ell(a_{m+1}, \dots, a_T | v, \boldsymbol\alpha, a_1, \dots, a_m)\\ =& (T-m)\left[ \ln\Gamma\left(\frac{v+1}{2}\right) -\ln\Gamma\left(\frac{v}{2}\right) -\frac12 \ln((v-2)\pi) \right] \\ & + \ell(a_{m+1}, \dots, a_T | \boldsymbol\alpha, a_1, \dots, a_m) . \tag{17.9} \end{align}$$ 其中最后一项就是(17.8)的值。

17.5.2.3 有偏t分布假设

资产收益率分布除了厚尾之外还常常有偏。 可以修改t分布使其变成标准化的有偏的单峰密度。 有多种方法可以做这种修改， 这里使用(Fernandez and Steel 1998)的做法。 该方法可以在任何连续单峰且关于0对称的一元分布中引入有偏性。 将t($v$)分布进行有偏化后密度为

$$g(\varepsilon|v, \xi) =\begin{cases} \frac{2c_2}{\xi + \frac{1}{\xi}} f(\xi (c_2 \varepsilon_t + c_1) \,|\, v), & \varepsilon_t < -\frac{c_1}{c_2} ,\\ \frac{2c_2}{\xi + \frac{1}{\xi}} f((c_2 \varepsilon_t + c_1)/\xi \,|\, v), & \varepsilon_t \geq -\frac{c_1}{c_2} . \end{cases}$$ 其中$f(\cdot|v)$是(17.6)定义的标准化t($v$)分布密度， 参数$v$是自由度， 可以控制厚尾程度； 参数$\xi^2$是密度在峰值右边的面积与在峰度左边的面积之比， 代表了有偏的程度， 当$\xi=1$时还是标准化t($v$)分布， 当$\xi>1$时右偏， 当$\xi<1$时左偏， $$\begin{aligned} c_1 =& \frac{\Gamma\left( \frac{v-1}{2}\right) \sqrt{v-2}} {\sqrt{\pi} \Gamma\left( \frac{v}{2}\right)} \left(\xi - \frac{1}{\xi} \right) , \\ c_2^2 =& \xi^2 - \frac{1}{\xi^2} - 1 - c_1^2 . \end{aligned}$$

对标准化$t$分布，取$v=5,10,30$，作密度图：

dtstd <- function(x, df)
  sqrt(df/(df-2)) * dt(x*sqrt(df/(df-2)), df)

curve(dtstd(x, 5), -3, 3, lwd=1, lty=1, col="black",
      xlab="x", ylab="密度")
curve(dtstd(x, 10), -3, 3, lwd=1, lty=2, col="red", add=TRUE)
curve(dtstd(x, 30), -3, 3, lwd=1, lty=3, col="blue", add=TRUE)
legend("topleft", lty=c(1,2,3), col=c("black", "red", "blue"),
       legend=c(expression(v==5), expression(v==10), expression(v==30)))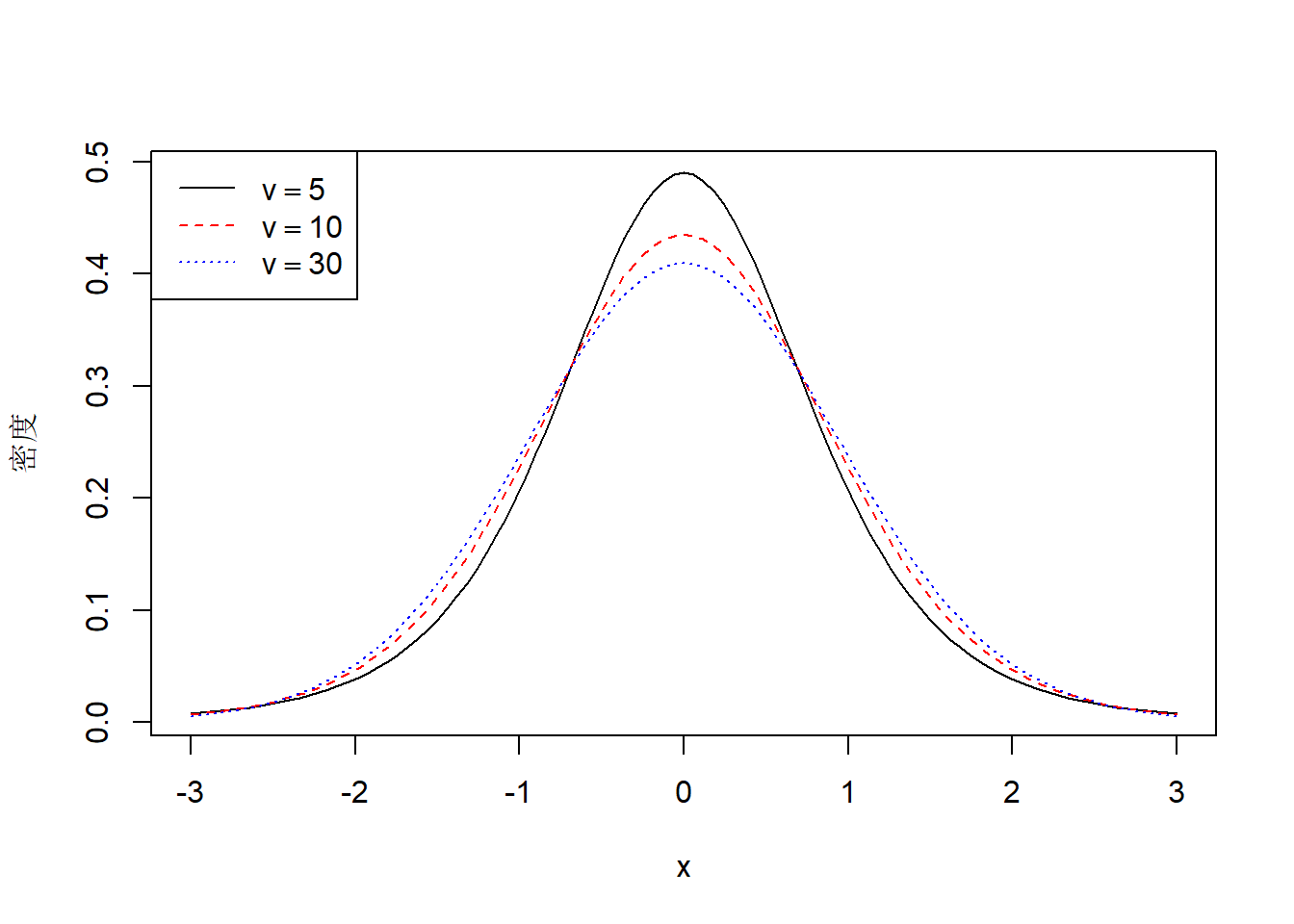

图17.2: 标准化t分布密度图

对有偏的$t$分布，取$v=5$，$\xi=0.75, 1, 1.5$, 作密度图：

dtskew <- function(x, df, xi){
  y <- numeric(length(x))
  par1 <- gamma((df-1)/2)*sqrt(df-2)/sqrt(pi)/gamma(df/2)*(xi - 1/xi)
  par2 <- sqrt(xi^2 + 1/xi^2 - 1 - par1^2)
  c1 <- 2*par2/(xi + 1/xi)
  sele <- x < -par1/par2
  y[sele] <- c1 * dtstd(xi*(par2*x[sele] + par1), df)
  y[!sele] <- c1 * dtstd((par2*x[!sele] + par1)/xi, df)
  
  y
}

curve(dtskew(x, 5, 1.0), -3, 3, ylim=c(0, 0.6),
      lwd=1, lty=1, col="black",
      xlab="x", ylab="密度")
curve(dtskew(x, 5, 0.75), -3, 3, lwd=1, lty=2, col="red", add=TRUE)
curve(dtskew(x, 5, 1.5), -3, 3, lwd=1, lty=3, col="blue", add=TRUE)
legend("topleft", lty=c(1,2,3), col=c("black", "red", "blue"),
       legend=c(expression(xi==1), expression(xi==0.75), expression(xi==1.5)))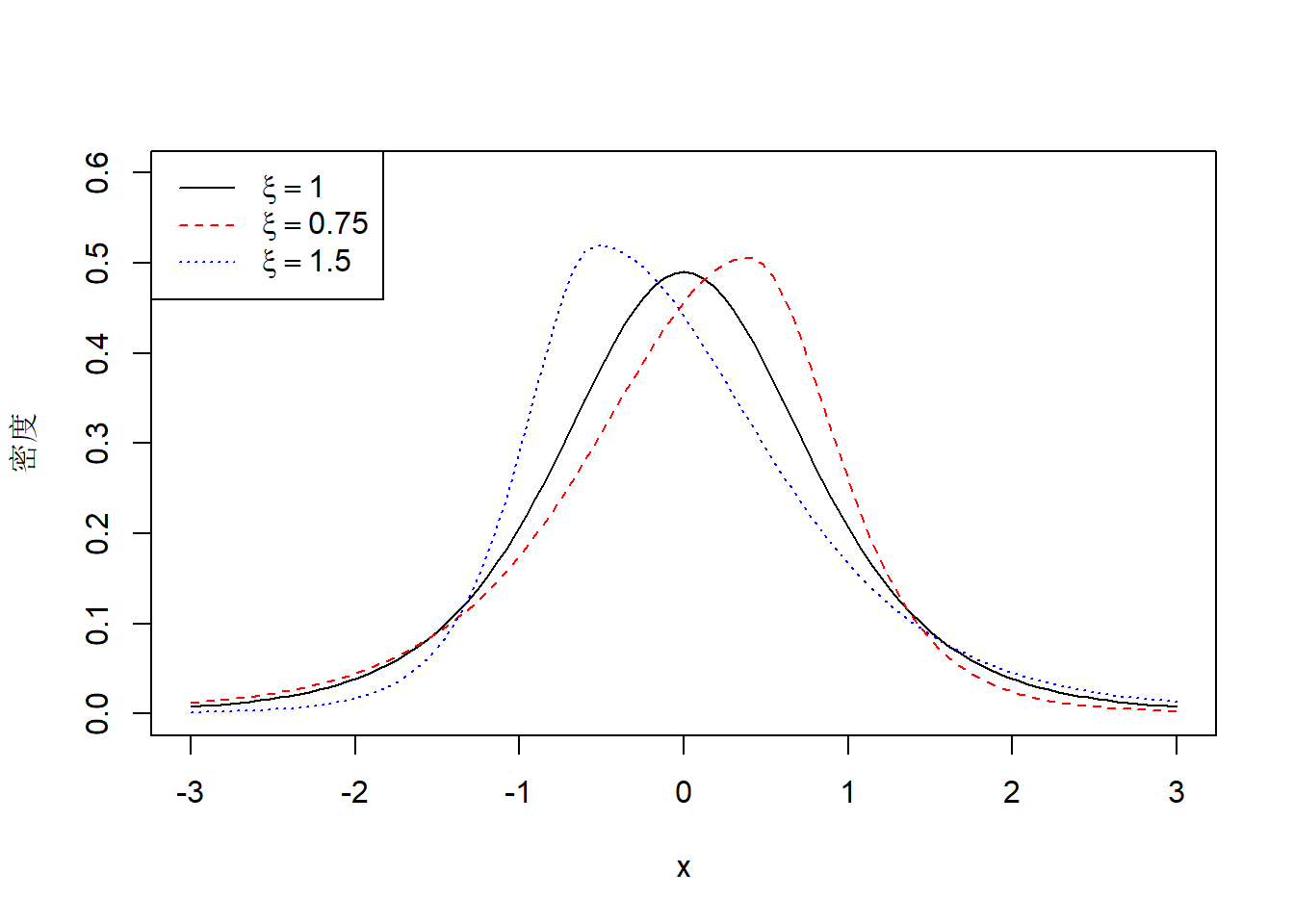

图17.3: 有偏t分布密度图

17.5.2.4 广义误差分布假设

$\varepsilon_t$的另一种可取分布是广义误差分布(GED)，密度为 $$f(x|v) = \frac{v}{\lambda 2^{1 + \frac{1}{v}} \Gamma(\frac{1}{v})} e^{-\frac12 \left| \frac{x}{\lambda} \right|^v}, \ x \in (-\infty, \infty) \ (0<v\leq \infty) .$$ 其中$v=2$时即标准正态分布， $0<v<2$时为厚尾分布。 $$\lambda=\left[ 2^{-\frac{2}{v}} \frac{\Gamma(\frac{1}{v})}{\Gamma(\frac{3}{v})} \right]^{\frac12} .$$

17.5.3 模型验证

对一个建立好的ARCH模型， 可计算标准化残差 $$\tilde a_t = \frac{a_t}{\sigma_t} ,$$ 其中$a_t$是均值方程的残差， $\sigma_t$是波动率方程拟合的值。 $\{\tilde a_t \}$应表现为零均值、单位标准差的独立同分布序列。

对$\{\tilde a_t \}$作Ljung-Box白噪声检验， 可以考察均值方程的充分性。 对$\{\tilde a_t^2 \}$作Ljung-Box白噪声检验， 可以考察波动率方程的充分性。 $\{\tilde a_t \}$的偏度、峰度、QQ图可以用来与$\varepsilon_t$的假定分布比较， 以检验模型假定的正确性。

R的fGarch扩展包可以估计ARCH模型， 并提供了多种诊断图。 rugarch包也可以估计和作图。

17.5.4 预测

ARCH模型的预测类似AR模型的预测。 从预测原点$h$出发， 对$\sigma_t^2$序列作超前一步预测， 即预测$\sigma_{h+1}^2$， 有 $$\sigma_h^2(1) = \sigma_{h+1}^2 = \alpha_0 + \alpha_1 a_{h}^2 + \dots + \alpha_m a_{h+1-m}^2 .$$

要做超前2步预测时，因为$a_{h+1}$未知， 有 $E(a_{h+1}^2 | F_{h}) = \sigma_h^2(1)$, 所以 $$\sigma_h^2(2) = \alpha_0 + \alpha_1 \sigma_h^2(1) + \alpha_2 a_{h}^2 + \dots + \alpha_m a_{h+2-m}^2 .$$

一般地， $\sigma_h^2(\ell)$可以滚动计算， $$\sigma_h^2(\ell) =\alpha_0 + \sum_{j=1}^m \alpha_j \sigma_h^2(\ell-j) .$$ 其中$l-j \leq 0$时$\sigma_h^2(\ell-j) = a_{m+\ell-j}^2$。

17.6 ARCH模型建模实例

两个实例，Intel公司股票月对数收益率序列的波动率建模， 美元对欧元的汇率的日对数收益率的波动率建模。

17.6.1 Intel公司股票ARCH建模实例

继续使用1973年到2009年Intel公司股票的月对数收益率。 ARCH效应检验一节进行了ARCH效应检验， 证明有ARCH效应。

数据读入：

d.intel <- read_table(
  "m-intcsp7309.txt",
  col_types=cols(
    .default=col_double(),
    date=col_date("%Y%m%d")
  ))
xts.intel <- xts(
  log(1 + d.intel[["intc"]]), d.intel[["date"]]
)
tclass(xts.intel) <- "yearmon"
ts.intel <- ts(c(coredata(xts.intel)), 
  start=c(1973,1), frequency=12)
at <- ts.intel - mean(ts.intel)

序列的均值模型是常数均值。 减去均值之后的残差的平方的ACF:

forecast::Acf(at^2, lag.max=36, main="")

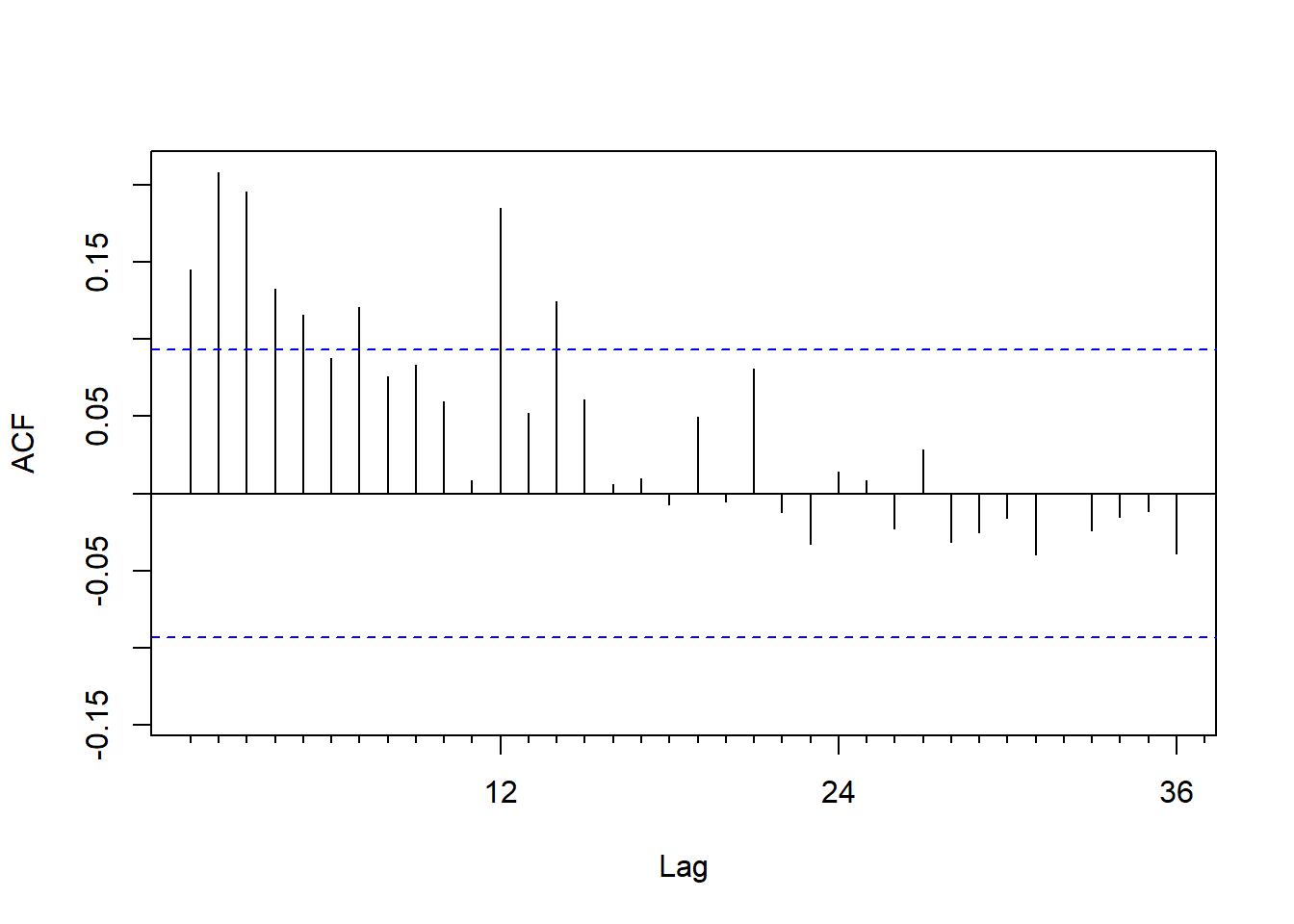
图17.4: Intel股票建模中心化的残差平方的ACF

在频率12处较高，另外在滞后1、2、3上较突出。

残差的平方的PACF:

pacf(at^2, lag.max=36, main="")

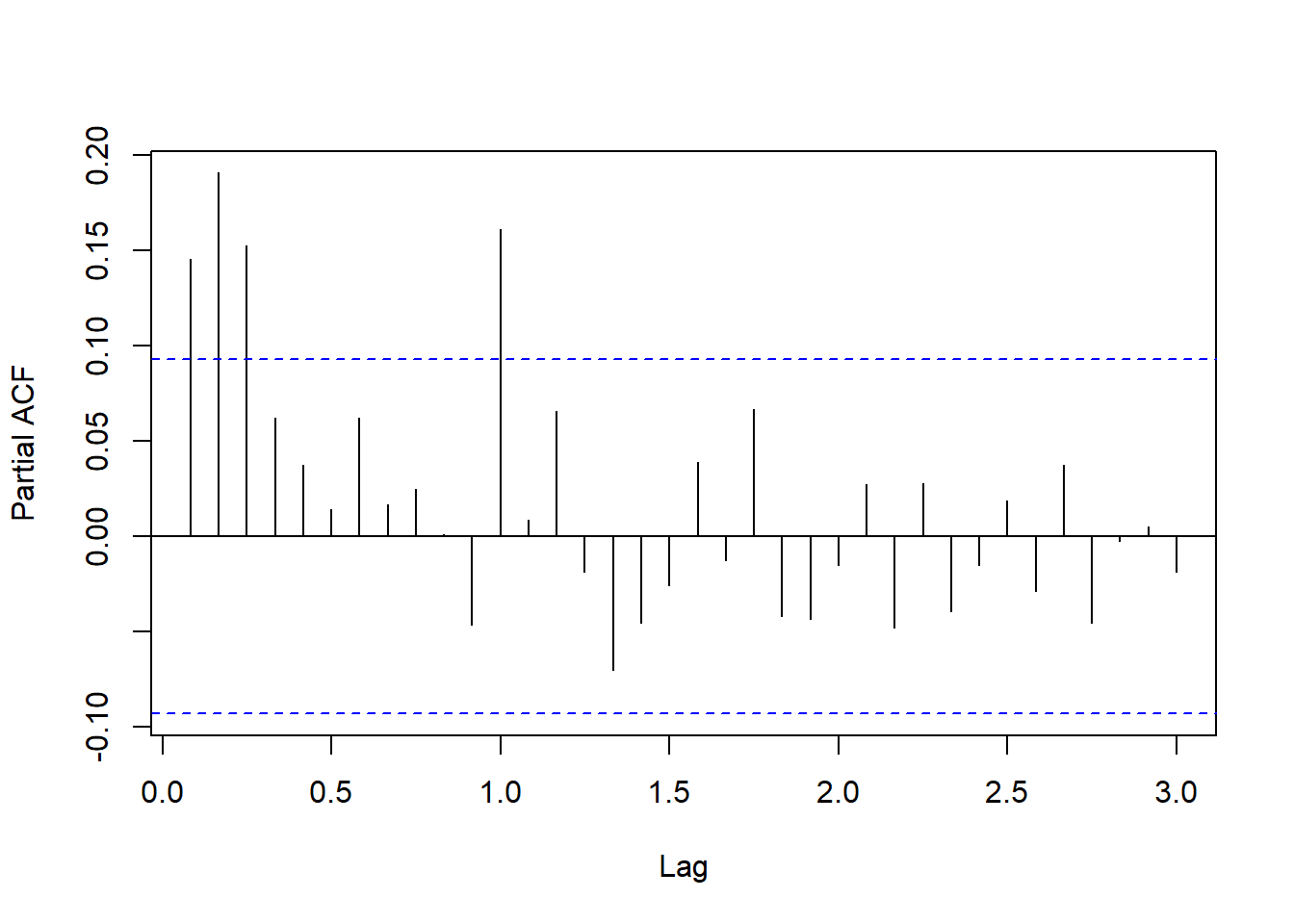
图17.5: Intel股票建模中心化的残差平方的PACF

残差平方的PACF在滞后12处较高， 另外在滞后1到3较高。 可考虑建立ARCH(3)作为波动率方程。

设$r_t$为收益率， 拟建立如下的均值方程和波动率方程：

$$\begin{aligned} r_t =& \mu + a_t, \quad a_t = \varepsilon_t \sigma_t, \\ \sigma_t^2 =& \alpha_0 + \alpha_1 a_{t-1}^2 + \alpha_2 a_{t-2}^2 + \alpha_3 a_{t-3}^2 . \end{aligned}$$

使用fGarch包的garchFit()函数建立ARCH模型。

library(fGarch)

## NOTE: Packages 'fBasics', 'timeDate', and 'timeSeries' are no longer
## attached to the search() path when 'fGarch' is attached.
## 
## If needed attach them yourself in your R script by e.g.,
##         require("timeSeries")

## 
## Attaching package: 'fGarch'

## The following object is masked from 'package:TTR':
## 
##     volatility

mod1 <- garchFit(
  ~ 1 + garch(3,0), 
  data=as.vector(ts.intel), 
  trace=FALSE)
summary(mod1)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(3, 0), data = as.vector(ts.intel), 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(3, 0)
## <environment: 0x00000164065beee8>
##  [data = as.vector(ts.intel)]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1    alpha2    alpha3  
## 0.012567  0.010421  0.232889  0.075069  0.051994  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.012567    0.005515    2.279   0.0227 *  
## omega   0.010421    0.001238    8.418   <2e-16 ***
## alpha1  0.232889    0.111541    2.088   0.0368 *  
## alpha2  0.075069    0.047305    1.587   0.1125    
## alpha3  0.051994    0.045139    1.152   0.2494    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  303.9607    normalized:  0.6845963 
## 
## Description:
##  Tue May 21 15:24:55 2024 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value    
##  Jarque-Bera Test   R    Chi^2  203.3622  0          
##  Shapiro-Wilk Test  R    W      0.9635971 4.89862e-09
##  Ljung-Box Test     R    Q(10)  9.260779  0.5075465  
##  Ljung-Box Test     R    Q(15)  19.36748  0.1975619  
##  Ljung-Box Test     R    Q(20)  20.46983  0.4289059  
##  Ljung-Box Test     R^2  Q(10)  7.322124  0.6947246  
##  Ljung-Box Test     R^2  Q(15)  27.41529  0.0255293  
##  Ljung-Box Test     R^2  Q(20)  28.1511   0.1058705  
##  LM Arch Test       R    TR^2   25.23346  0.01375453 
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -1.346670 -1.300546 -1.346920 -1.328481

程序中1 + garch(3,0)中garch(3,0)表示$\sigma_t^2$的ARCH(3)模型， 1表示均值方程是一个常数。 输出结果中mu为均值方程的均值， omega为$\alpha_0$， alpha1为$\alpha_1$。 所以得到的均值方程和波动率方程为：

$$\begin{aligned} r_t =& 0.0126 + a_t, \quad a_t = \varepsilon_t \sigma_t, \quad \varepsilon_t \ \text{i.i.d} \text{N}(0,1) , \\ \sigma_t^2 =& 0.0104 + 0.02329 a_{t-1}^2 + 0.0751 a_{t-2}^2 + 0.0520 a_{t-3}^2 . \end{aligned}$$

因为结果中$\alpha_2$和$\alpha_3$的估计值是不显著的， 可拟合ARCH(1)模型为波动率方程：

mod2 <- garchFit( ~ 1 + garch(1,0), 
  data=c(ts.intel), trace=FALSE)
summary(mod2)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 0), data = c(ts.intel), trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 0)
## <environment: 0x00000164002e34c0>
##  [data = c(ts.intel)]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##       mu     omega    alpha1  
## 0.013130  0.011046  0.374976  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.013130    0.005318    2.469  0.01355 *  
## omega   0.011046    0.001196    9.238  < 2e-16 ***
## alpha1  0.374976    0.112620    3.330  0.00087 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  299.9247    normalized:  0.675506 
## 
## Description:
##  Tue May 21 15:24:55 2024 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  144.3782  0           
##  Shapiro-Wilk Test  R    W      0.9678175 2.670339e-08
##  Ljung-Box Test     R    Q(10)  12.12247  0.2769434   
##  Ljung-Box Test     R    Q(15)  22.30704  0.1000021   
##  Ljung-Box Test     R    Q(20)  24.33411  0.228102    
##  Ljung-Box Test     R^2  Q(10)  16.57804  0.08423799  
##  Ljung-Box Test     R^2  Q(15)  37.44344  0.001089753 
##  Ljung-Box Test     R^2  Q(20)  38.8139   0.007031666 
##  LM Arch Test       R    TR^2   27.32894  0.006926884 
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -1.337499 -1.309824 -1.337589 -1.326585

这个模型的AIC为$-1.3375$， 比上一个模型的$-1.3467$要差一些。

输出中给出了标准化残差$\tilde a_t$的Ljung-Box白噪声检验结果， 滞后10的p值为0.2769, 承认白噪声； $\tilde a_t^2$的滞后10的Ljung-Box白噪声检验结果p值为0.08, 在0.05水平下也可以承认白噪声。

Jarque-Bera检验是正态分布的偏度峰度检验， Shapiro-Wilk检验是正态性检验， 零假设为$\varepsilon_t$服从正态分布， 这两个检验的结果表明标准化残差不服从正态分布。

模型方程：

$$\begin{align} r_t =& 0.0131 + a_t, \quad a_t = \varepsilon_t \sigma_t, \quad \varepsilon_t \ \text{i.i.d} \text{N}(0,1) \\ \sigma_t^2 =& 0.0110 + 0.3750 a_{t-1}^2 \tag{17.10} \end{align}$$

但是， 两个不同模型给出了不同的均值方程。 这说明均值方程和波动率方程的参数是同时估计的， 不是先估计均值方程然后利用均值方程的残差估计波动率方程。

为了进行模型验证， 可计算标准化残差 $$\tilde a_t = \frac{a_t}{\sigma_t} , t=m+1, m+2, \dots, T,$$ 其中$\sigma_t$从估计的ARCH模型中递推地计算。 $\{ \tilde a_t \}$应表现得像是独立同分布零均值白噪声列。

计算标准化残差$\{\tilde a_t\}$：

resi <- residuals(mod2, standardize=TRUE)

fGarch包的plot函数可以对建模结果绘制多种诊断图形，包括：

1. 输入序列的时间序列图；
2. 估计的波动率（条件标准差）折线图；
3. 输入序列图，与正负2倍波动率叠加；
4. 输入的ACF图；
5. 输入的平方（即$r_t^2$）的ACF图；
6. 互相关系数图（文档无说明）；
7. 拟合残差图；
8. 多个波动率图（文档无说明）；
9. 标准化残差图；
10. 标准化残差的ACF图；
11. 标准化残差平方的ACF图；
12. $r_t^2$和$r_t$的互相关系数函数图；
13. 标准化残差相对于$\varepsilon_t$理论分布（条件分布）的QQ图。

标准化残差的时序图：

plot(mod2, which=9)

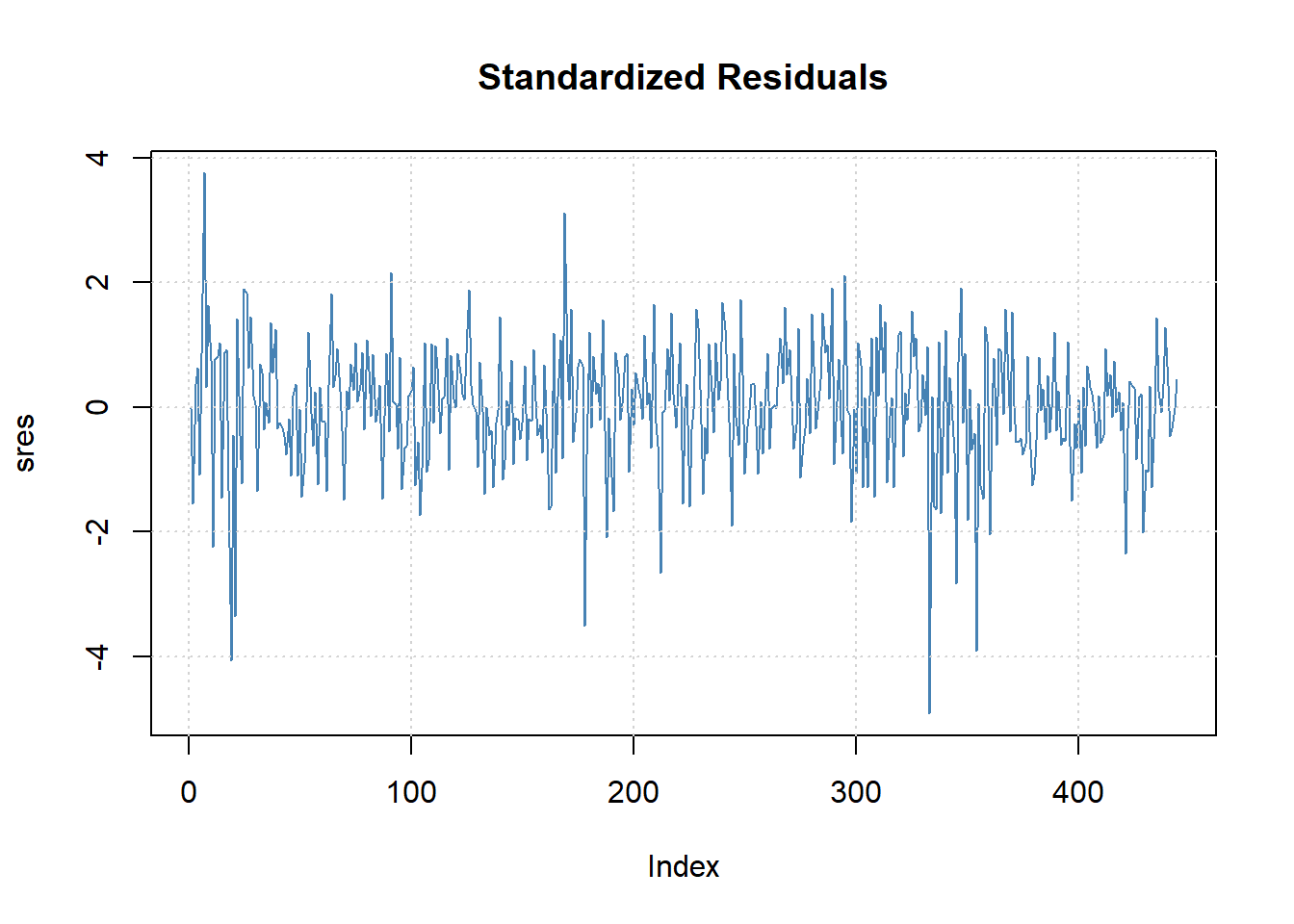
图17.6: Intel股票建模标准化残差

标准化残差$\{\tilde a_t\}$的ACF:

plot(mod2, which=10)

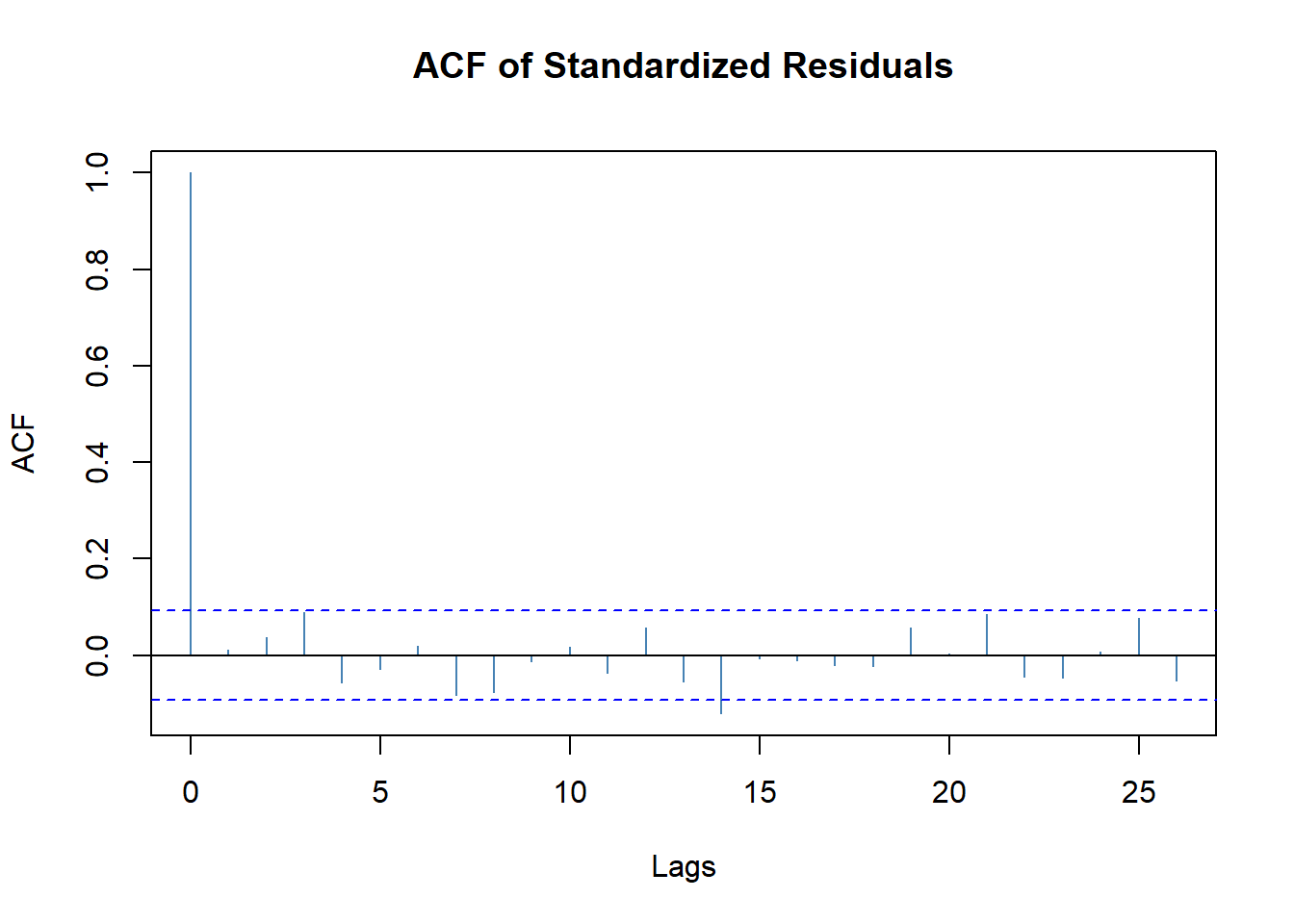
图17.7: Intel股票建模标准化残差的ACF

$\{\tilde a_t^2\}$的ACF:

plot(mod2, which=11)

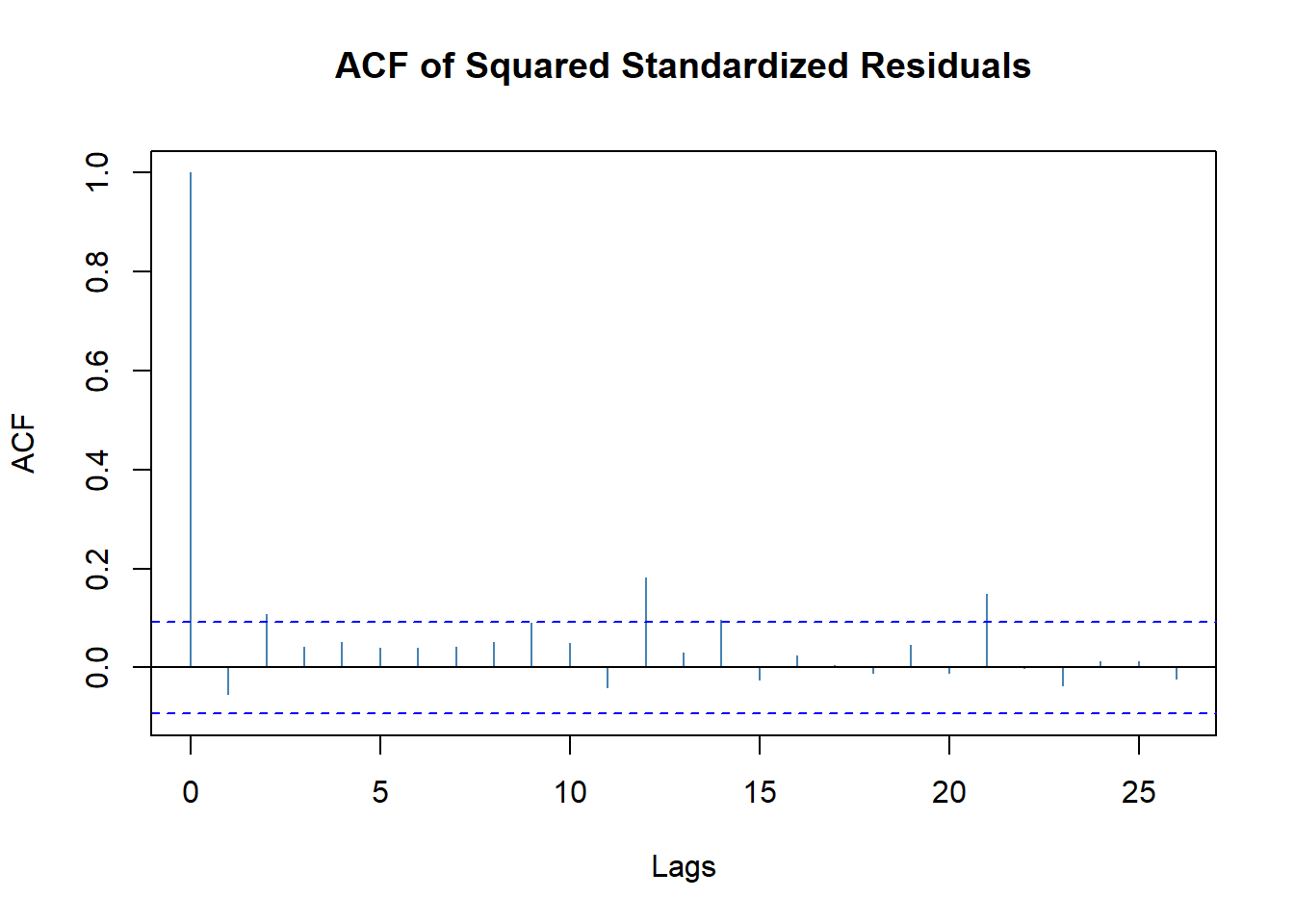
图17.8: Intel股票建模标准化残差平方的ACF

除了在滞后11、滞后21还略高以外已经没有了低阶的波动率相关。

$\{\tilde a_t^2\}$的PACF:

pacf(resi^2, lag.max=36, main="")

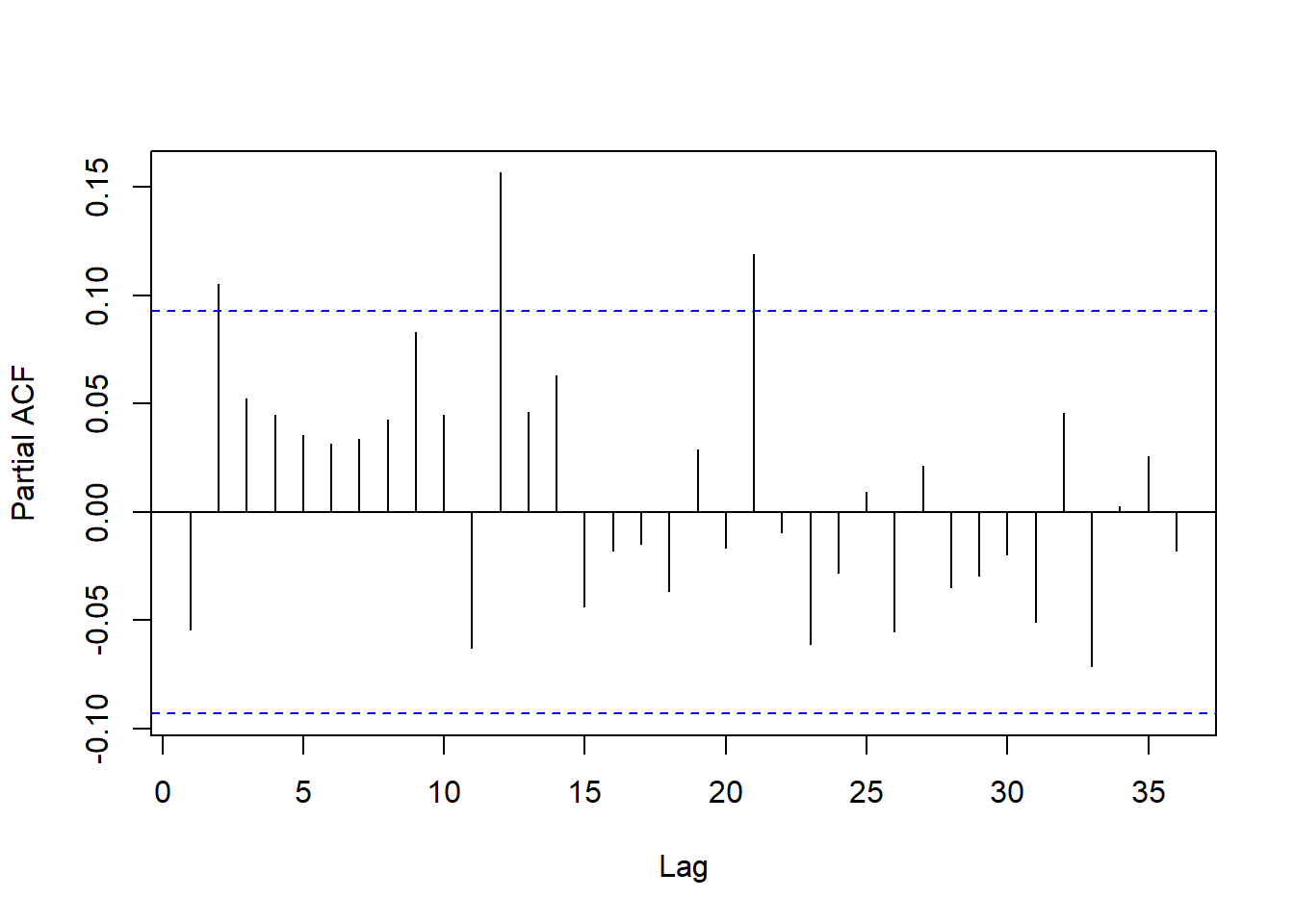
图17.9: Intel股票建模标准化残差平方的PACF

仅在高阶的滞后11、滞后21还较高。 作为低阶模型， ARCH(1)作为波动率方程已经比较适合。

标准化残差相对于标准正态分布的QQ图：

plot(mod2, which=13)

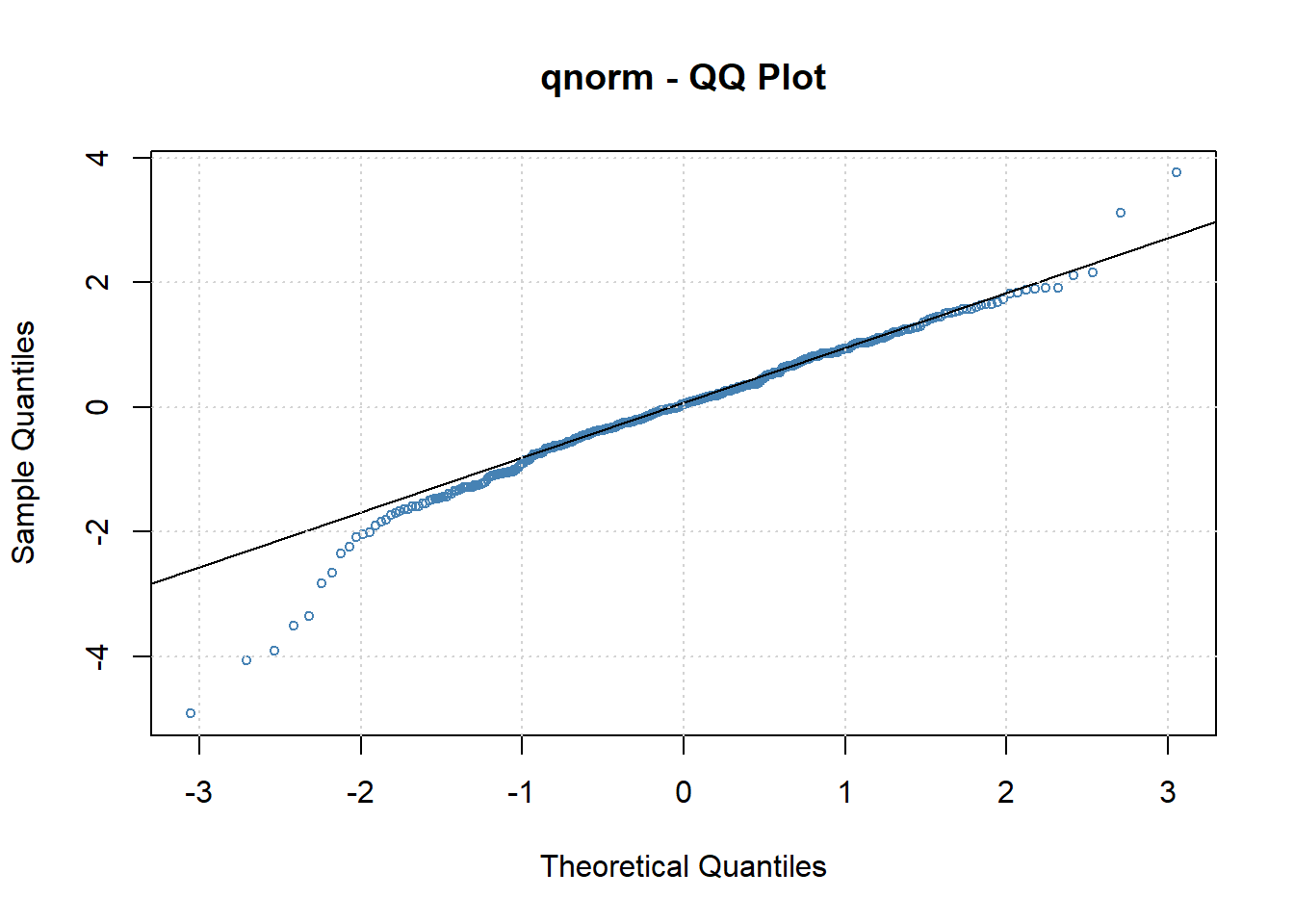
图17.10: Intel股票标准化残差正态QQ图

这个图形说明标准化残差相对于正态分布有重尾。 正态分布作为条件分布不够合适。

显示拟合的条件标准差序列（波动率序列）：

plot(mod2, which=2)

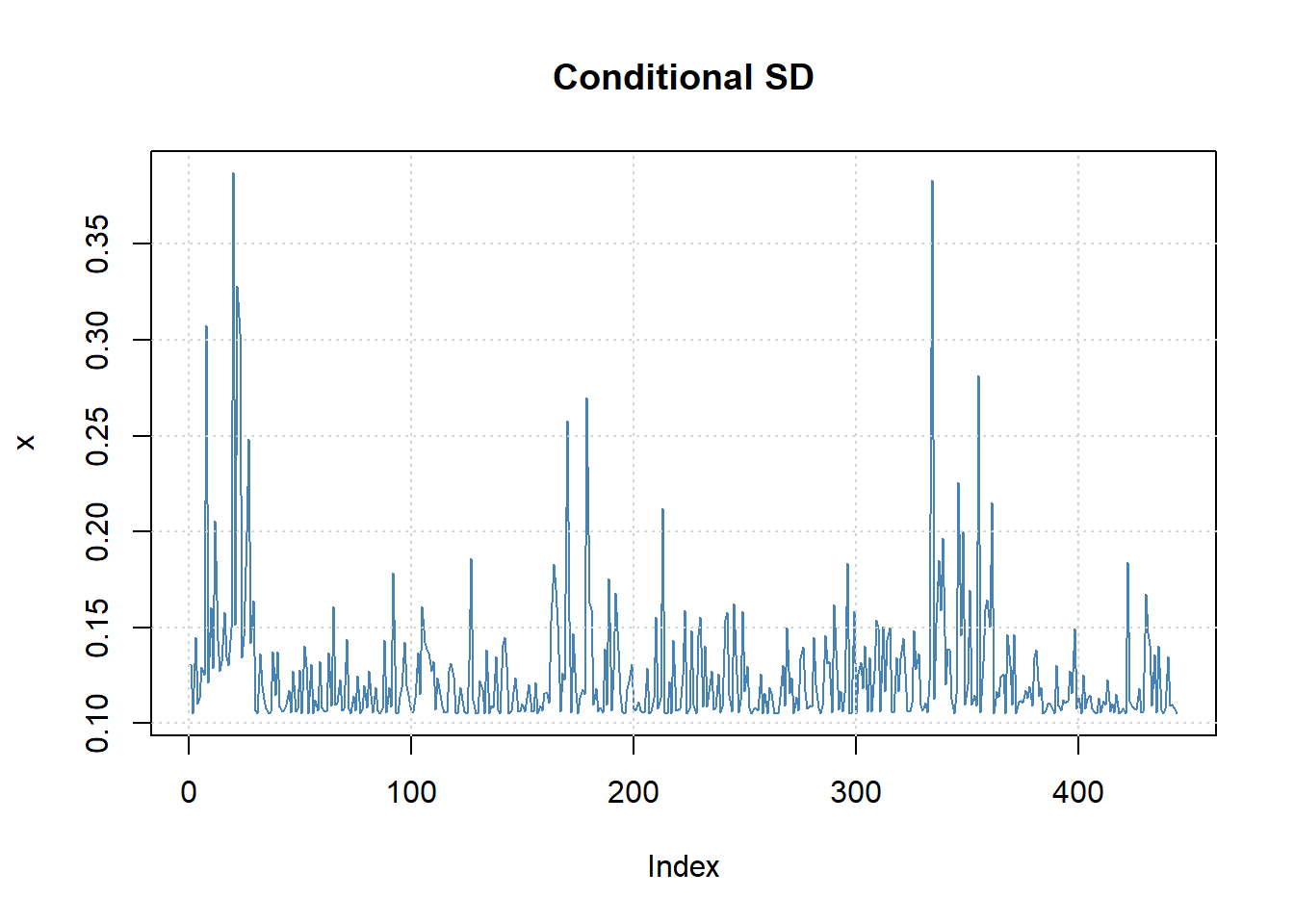
图17.11: Intel股票建模波动率

获得拟合的波动率用volatility()函数：

mod2v <- volatility(mod2)
head(mod2v)

## [1] 0.1306624 0.1051189 0.1450052 0.1101684 0.1134644 0.1294741

获得拟合的均值用fitted()函数。 按理说这个模型的均值方程应该是常数$0.0131$， 这里fitted()返回的是原始的$r_t$序列。

mod2f <- fitted(mod2)
head(mod2f)

##            1            2            3            4            5            6 
##  0.009999835 -0.150012753  0.067064079  0.082948635 -0.110348491  0.125162849

用predict()函数作超前若干步的预测，如：

mod2p <- predict(mod2, n.ahead=12)
mod2p

##    meanForecast meanError standardDeviation
## 1    0.01313002 0.1090512         0.1090512
## 2    0.01313002 0.1245214         0.1245214
## 3    0.01313002 0.1298481         0.1298481
## 4    0.01313002 0.1317900         0.1317900
## 5    0.01313002 0.1325108         0.1325108
## 6    0.01313002 0.1327801         0.1327801
## 7    0.01313002 0.1328809         0.1328809
## 8    0.01313002 0.1329187         0.1329187
## 9    0.01313002 0.1329329         0.1329329
## 10   0.01313002 0.1329382         0.1329382
## 11   0.01313002 0.1329402         0.1329402
## 12   0.01313002 0.1329410         0.1329410

预测包括均值的预测（显然是用$\mu$预测的）、 均值预测的标准误差、 波动率的预测（是用$a_t$的值滚动计算的）。 波动率长期预测接近于ARCH模型的无条件标准差。

模型(17.10)的一些特点：

第一， Intel股票月对数收益率是$1.31\%$， 年对数收益率是$15.72\%$， 这是很了不起的。

直接计算收益率均值：

mean(ts.intel)

## [1] 0.0143273

第二， $\alpha_1^2 = 0.3750^2 = 0.14 < 1/3$， 说明$a_t$序列有无条件四阶矩。

第三， $r_t$的无条件标准差为 $$\sqrt{0.0110 / (1 - 0.3750)} = 0.1327$$

直接从原始数据计算：

sd(ts.intel)

## [1] 0.1269101

结果相近但不相同。

第四， 模型可以用来估计和预测Intel股票收益率的月波动率。

17.6.2 Intel股票问题改用t分布

在fGarch的garchFit()函数中加选项cond.dist="std"。

mod3 <- garchFit(~ 1 + garch(1,0), data=ts.intel, 
  cond.dist="std", trace=FALSE)
summary(mod3)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 0), data = ts.intel, cond.dist = "std", 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 0)
## <environment: 0x0000016474f90a68>
##  [data = ts.intel]
## 
## Conditional Distribution:
##  std 
## 
## Coefficient(s):
##       mu     omega    alpha1     shape  
## 0.017202  0.011816  0.277476  5.970256  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu      0.017202    0.005195    3.311 0.000929 ***
## omega   0.011816    0.001560    7.574 3.62e-14 ***
## alpha1  0.277476    0.107183    2.589 0.009631 ** 
## shape   5.970256    1.529521    3.903 9.49e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  315.0899    normalized:  0.709662 
## 
## Description:
##  Tue May 21 15:24:57 2024 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  157.78    0           
##  Shapiro-Wilk Test  R    W      0.9663975 1.48822e-08 
##  Ljung-Box Test     R    Q(10)  12.8594   0.2316394   
##  Ljung-Box Test     R    Q(15)  23.40633  0.07588549  
##  Ljung-Box Test     R    Q(20)  25.374    0.1874954   
##  Ljung-Box Test     R^2  Q(10)  19.96094  0.02962426  
##  Ljung-Box Test     R^2  Q(15)  42.55552  0.0001845072
##  Ljung-Box Test     R^2  Q(20)  44.06742  0.001473957 
##  LM Arch Test       R    TR^2   29.76073  0.003033495 
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -1.401306 -1.364407 -1.401466 -1.386755

因为已经采用条件t分布， 所以结果中的JB检验和SW检验没有意义。

模型为 $$\begin{align} r_t =& 0.0172 + a_t, \quad a_t = \varepsilon_t \sigma_t, \quad \varepsilon_t \ \text{i.i.d} t^*(5.97) \\ \sigma_t^2 =& 0.0118 + 0.2775 a_{t-1}^2 \tag{17.11} \end{align}$$ 其中$t^*$表示标准化t分布。

$a_t$的无条件标准差按模型估计为 $\sqrt{0.0118/(1 - 0.2775)}= 0.1278$， 正态时为$0.1327$， 原始数据直接估计为$0.1269$。 标准化残差$\tilde a_t$的滞后10的Ljung-Box白噪声检验p值为0.23， 可承认白噪声； 标准化残差平方$\tilde a_t^2$的滞后10的Ljung-Box白噪声检验p值为0.03， 仍有一定的残余波动率相关性。

作标准化残差相对于标准化t分布的QQ图：

plot(mod3, which=13)

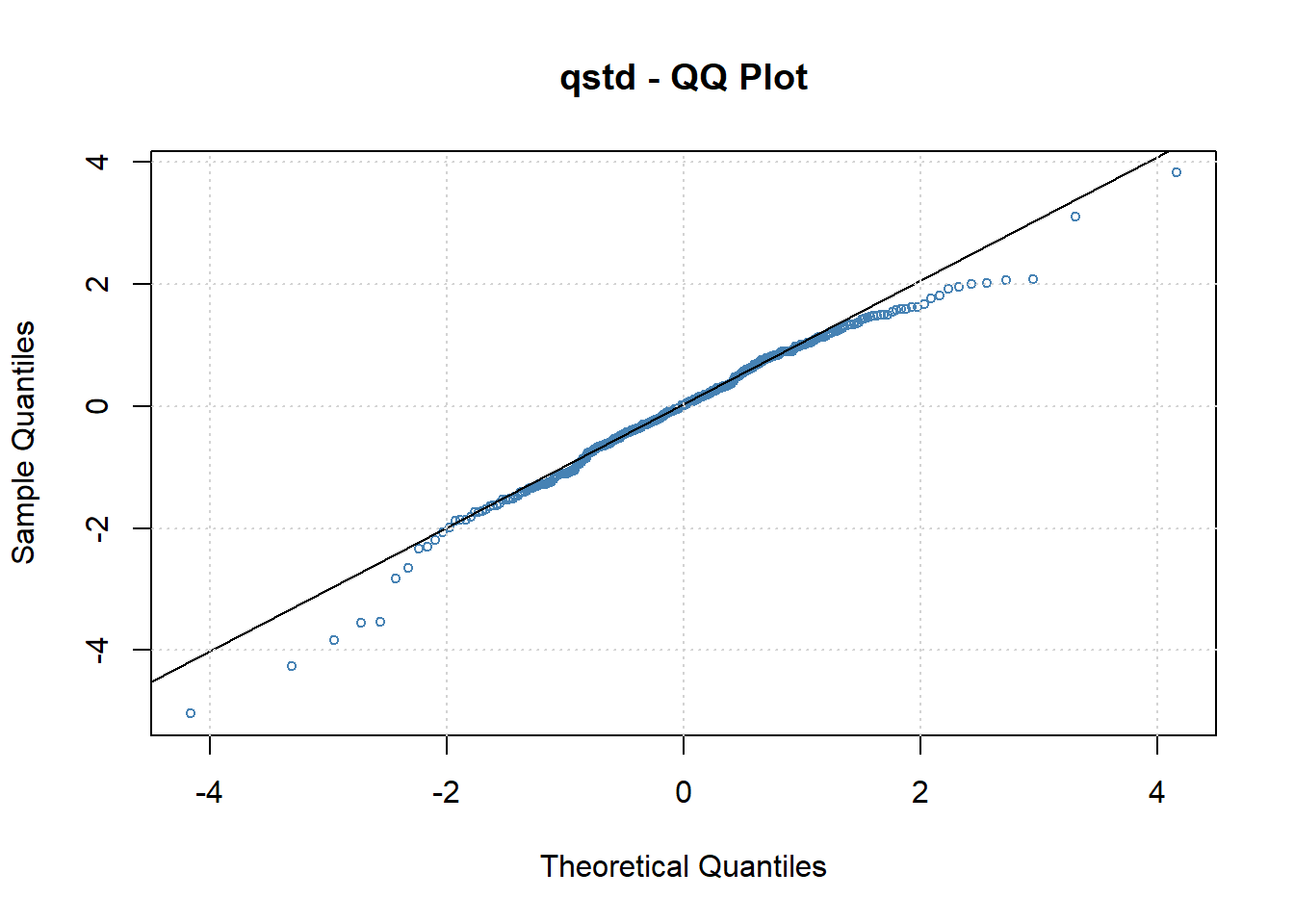
可见这个分布比正态分布更符合， 但仍存在左偏， 有可能需要使用有偏t分布。

改用t分布以后， $\alpha_1$估计值从原来正态时的$0.3750$降低到了$0.2775$， 说明厚尾的$\varepsilon_t$分布降低了ARCH效应。 本问题采用正态分布和t分布的结果差别不大。 后面将指出， Intel月对数收益率的波动率方程更合适的模型是GARCH(1,1)。

fGarch包的garchFit()函数支持多种条件分布， 默认为正态分布， 用cond.dist=指定分布：

• "norm": 正态；
• "snorm": 有偏正态;
• "ged": 广义误差分布；
• "sged": 有偏广义误差分布;
• "std": t分布;
• "sstd": 有偏t分布；
• "snig"
• "QMLE"：拟最大似然估计，仍假设正态但是采用稳健标准误差估计；

17.6.3 欧元汇率ARCH建模实例

考虑1999-01-04到2010-08-20的欧元对美元汇率的日对数收益率。 见§16.4.2。 均值方程为$r_t = a_t$， 并显示数据有ARCH效应。 该序列是纯条件异方差模型的典型例子。

d.useu <- read_table(
  "d-useu9910.txt", 
  col_types=cols(.default=col_double())
)
xts.useu <- with(d.useu, 
  xts(rate, make_date(year, mon, day)))
xts.useu.lnrtn <- diff(log(xts.useu))[-1,]
eu <- c(coredata(xts.useu.lnrtn))

$a_t^2$的ACF:

forecast::Acf(eu^2, lag.max=36, main="")

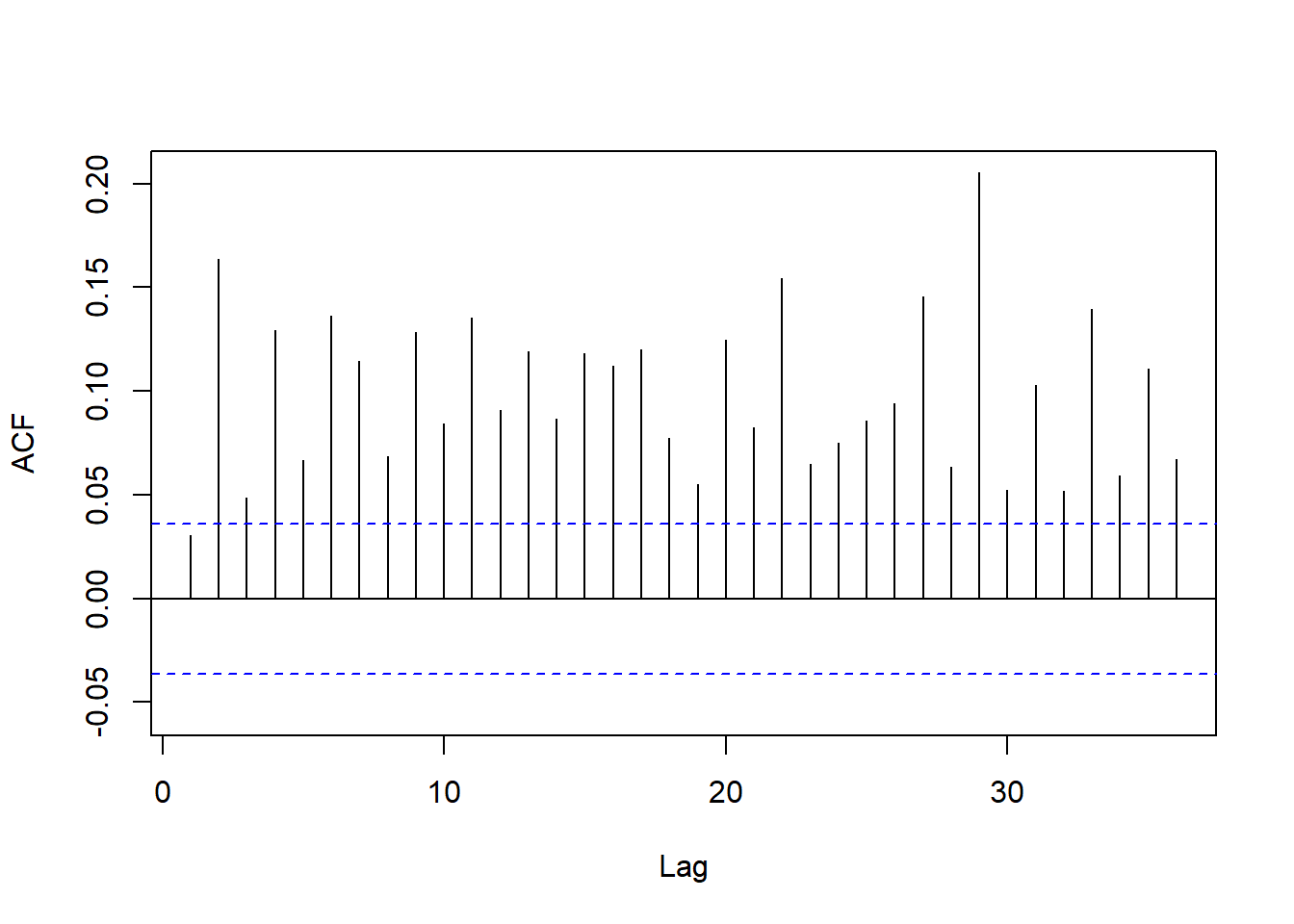
图17.12: 欧元汇率平方的ACF

呈现出低的较长期的相关。

$a_t^2$的PACF:

pacf(eu^2, lag.max=36, main="")

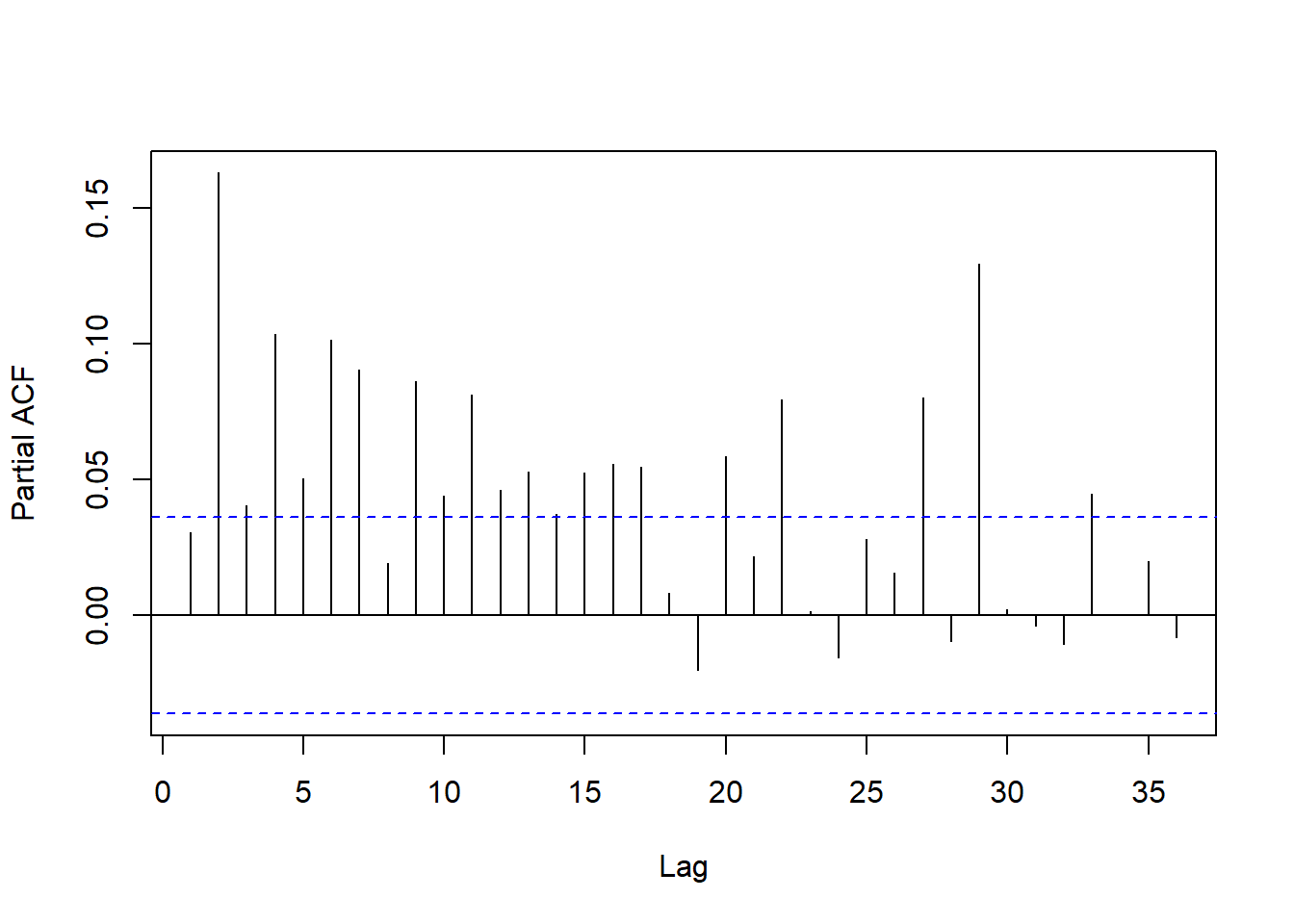
图17.13: 欧元汇率平方的PACF

在低阶到滞后11可以， 但是高阶仍有较大的值。 考虑建立ARCH(11)模型。 采用条件高斯似然函数：

mod4 <- garchFit(~ 1 + garch(11,0), data=eu, trace=FALSE)
summary(mod4)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(11, 0), data = eu, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(11, 0)
## <environment: 0x00000164023d4770>
##  [data = eu]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##         mu       omega      alpha1      alpha2      alpha3      alpha4  
## 1.2646e-04  1.8902e-05  1.6608e-02  4.4563e-02  2.7210e-02  8.0370e-02  
##     alpha5      alpha6      alpha7      alpha8      alpha9     alpha10  
## 5.0112e-02  9.2192e-02  7.5283e-02  6.9536e-02  3.3466e-02  2.7824e-02  
##    alpha11  
## 3.8774e-02  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##          Estimate  Std. Error  t value Pr(>|t|)    
## mu      1.265e-04   1.110e-04    1.140 0.254412    
## omega   1.890e-05   1.727e-06   10.944  < 2e-16 ***
## alpha1  1.661e-02   1.575e-02    1.055 0.291563    
## alpha2  4.456e-02   2.085e-02    2.137 0.032592 *  
## alpha3  2.721e-02   1.700e-02    1.601 0.109370    
## alpha4  8.037e-02   2.362e-02    3.402 0.000669 ***
## alpha5  5.011e-02   2.127e-02    2.355 0.018499 *  
## alpha6  9.219e-02   2.274e-02    4.053 5.05e-05 ***
## alpha7  7.528e-02   2.406e-02    3.129 0.001755 ** 
## alpha8  6.954e-02   2.455e-02    2.832 0.004622 ** 
## alpha9  3.347e-02   2.022e-02    1.655 0.097835 .  
## alpha10 2.782e-02   1.820e-02    1.528 0.126400    
## alpha11 3.877e-02   1.906e-02    2.035 0.041890 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  10698.47    normalized:  3.652603 
## 
## Description:
##  Tue May 21 15:25:08 2024 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  360.8056  0           
##  Shapiro-Wilk Test  R    W      0.9891734 3.893905e-14
##  Ljung-Box Test     R    Q(10)  15.77628  0.1062181   
##  Ljung-Box Test     R    Q(15)  21.50103  0.1215706   
##  Ljung-Box Test     R    Q(20)  24.77444  0.2101971   
##  Ljung-Box Test     R^2  Q(10)  4.801169  0.9040581   
##  Ljung-Box Test     R^2  Q(15)  16.73082  0.3352091   
##  Ljung-Box Test     R^2  Q(20)  27.5606   0.1202158   
##  LM Arch Test       R    TR^2   11.96808  0.4482465   
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -7.296329 -7.269777 -7.296368 -7.286766

通过对标准化残差$\tilde a_t$和$\tilde a_t^2$的Ljung-Box白噪声检验来看， 模型是充分的。 但是，Jarque-Bera检验是正态分布的偏度峰度检验， Shapiro-Wilk检验是正态性检验， 这两个检验表明标准化残差不服从正态分布。

模型为 $$\begin{aligned} r_t =& 0.0013 + \sigma_t \varepsilon_t, \ \varepsilon_t \ \text{i.i.d.} \text{N}(0,1) \\ \sigma_t^2 =& 1.89\times 10^{-5} + 0.0166 a_{t-1}^2 + \dots + 0.03877 a_{t-11}^2 \end{aligned}$$

下一节会指出， 改用GARCH模型可以得到更精简的模型。

17.7 补充推导

17.7.1 新息性质

设$\{r_t \}$为二阶矩过程， 令 $$\begin{aligned} F_t =& \sigma(\{r_t, r_{t-1}, \dots \}), \\ a_t =& r_t - E(r_t | F_{t-1}) . \end{aligned}$$ 则$\{a_t \}$为二阶矩过程。

$$\begin{aligned} E(a_t | F_{t-1}) =& E(r_t | F_{t-1}) - E[E(r_t | F_{t-1}) | F_{t-1}] \\ =& 0 . \end{aligned}$$ 称满足上式的序列$\{ a_t \}$为关于$\{F_t\}$的鞅差序列。

对鞅差序列， 有 $$\begin{aligned} E[a_t] =& E[E(a_t | F_{t-1})] = 0. \end{aligned}$$ 对$t > s$有 $$\begin{aligned} E[a_t | F_s] =& E[E(a_t | F_{t-1}) | F_s] \\ =& E[0 | F_s] = 0 . \end{aligned}$$ 于是 $$\begin{aligned} &\text{Cov}(a_t, a_s) = E(a_t a_s) \\ =& E[E(a_t a_s | F_s)] = E[a_s E(a_t | F_s)] = 0. \end{aligned}$$ 所以二阶矩有限的鞅差序列是不相关列。 如果$\text{Var}(a_t)$恒定， 则$\{a_t \}$是白噪声列。

17.7.2 白噪声性质

当$\{a_t \}$服从ARCH(1)模型时， 设时间$t$从0开始， 令 $$\begin{aligned} F_t = \sigma(\{r_0, \varepsilon_0, \dots, r_t, \varepsilon_t\}), \end{aligned}$$ 其中$\{ \varepsilon_t \}$ iid $(0,1)$， 且$\varepsilon_t$与$r_0, \dots, r_{t-1}$独立， 即$\varepsilon_t$与$F_{t-1}$独立。 设 $$\sigma_0^2 = \frac{\alpha_0}{1 - \alpha_1} .$$

这时，$\{a_t, F_t, t \geq 0 \}$仍为鞅差序列。

注意 $$\begin{aligned} a_0^2 =& \sigma_0^2 \varepsilon_0^2 \in F_0 , \\ \sigma_1^2 =& \alpha_0 + \alpha_1 a_0^2 \in F_0 , \\ a_1^2 =& \sigma_0^2 \varepsilon_1^2 \in F_1 , \\ \sigma_2^2 =& \alpha_0 + \alpha_1 a_1^2 \in F_1 , \end{aligned}$$ 归纳可知 $$a_t \in F_t, \quad \sigma_t \in F_{t-1} .$$

已知$\{a_t \}$是零均值不相关列。 来计算$\text{Var}(a_t)$。 $$\begin{aligned} & \text{Var}(a_t) = E(a_t^2) = E(\sigma_t^2 \varepsilon_t^2) \\ =& E \{ E(\sigma_t^2 \varepsilon_t^2 | F_{t-1}) \} = E \{ \sigma_t^2 E( \varepsilon_t^2 | F_{t-1}) \} \\ =& E \{ \sigma_t^2 E( \varepsilon_t^2 ) \} = E(\sigma_t^2) . \end{aligned}$$ 注意 $$\begin{aligned} E(\sigma_t^2) =& \alpha_0 + \alpha_1 E(a_{t-1}^2) \\ =& \alpha_0 + \alpha_1 E(\sigma_{t-1}^2), \end{aligned}$$ 为了$E(\sigma_t^2)$不依赖于$t$， 必须且只需 $$E(\sigma_t^2) = \frac{\alpha_0}{1 - \alpha_1},$$ 这只要取$\sigma_0^2$等于此值即可。 这时， $$\text{Var}(a_t) = E(\sigma_t^2) = \frac{\alpha_0}{1 - \alpha_1}, \ t=0,1,2,\dots .$$ 也可以取$\sigma_0^2$为期望等于此值的随机变量且与$F_t$独立（$\forall t \geq 0$）。

所以， 适当条件下ARCH(1)中的$\{a_t \}$是零均值白噪声列。 此结论可以推广到ARCH($p$)模型。

B 参考文献

Engle, R. F. 1982. “Autoregressive Conditional Heteroscedasticity with Estmates of the Varinance of United Kingdom Inflation.” Econometrica 50: 987–1007.

Fernandez, Carmen, and Mark F. J. Steel. 1998. “On Bayesian Modeling of Fat Tails and Skewness.” Journal of the American Statistical Association 93 (441): 359–71.

Tsay, Ruey S. 2010. Analysis of Financial Time Series. 3rd Ed. John Wiley & Sons, Inc.

———. 2013. 金融数据分析导论：基于R语言. 机械工业出版社.

———. 2023. 应用时间序列分析. 2nd ed. 北京大学出版社.