26 向量自回归模型
26.1 VAR(1)模型
多个资产收益率的联合模型中最常用的是向量自回归 (Vector Autoregression, VAR)模型。 称\(k\)元时间序列\(\boldsymbol r_t\)服从一个一阶向量自回归模型, 即VAR(1),若有 \[\begin{align} \boldsymbol r_t = \boldsymbol\phi_0 + \boldsymbol\Phi \boldsymbol r_{t-1} + \boldsymbol a_t \tag{26.1} \end{align}\] 其中\(\boldsymbol\phi_0\)是\(k\)维常数向量, \(\boldsymbol\Phi\)是\(k\)阶常数方阵, \(\{\boldsymbol a_t\}\)是序列不相关的弱平稳列, \(E\boldsymbol a_t = \boldsymbol 0\), \(\text{Var}(\boldsymbol a_t) = \boldsymbol\Sigma>0\)(对称正定矩阵)。
文献中经常假定\(\{ \boldsymbol a_t \}\)服从多元正态分布 \(N_k(\boldsymbol 0, \boldsymbol\Sigma)\), 则这时\(\boldsymbol a_t\)是独立同分布随机向量序列。
记\(\boldsymbol a_t = (a_{1t}, \dots, a_{kt})^T\), \(\boldsymbol\phi_0 = (\phi_{10}, \dots, \phi_{k0})^T\), \(\boldsymbol\Phi=(\phi_{ij})_{k\times k}\)。
26.2 模型结构和格兰杰因果性
考虑\(k=2\)的情形。 模型变成 \[\begin{align} \begin{cases} r_{1t} = \phi_{10} + \phi_{11} r_{1,t-1} + \phi_{12} r_{2,t-1} + a_{1t} \\ r_{2t} = \phi_{20} + \phi_{21} r_{1,t-1} + \phi_{22} r_{2,t-1} + a_{2t} \end{cases} \tag{26.2} \end{align}\]
如果\(\phi_{12} = \phi_{21} = 0\), 则\(r_{1t}\)和\(r_{2t}\)两个序列是分离的: \[\begin{aligned} r_{1t} =& \phi_{10} + \phi_{11} r_{1,t-1} + a_{1t} \\ r_{2t} =& \phi_{20} + \phi_{22} r_{2,t-1} + a_{2t} \end{aligned}\] 这时两个序列分别服从单独的一元AR(1)模型; 如果\(a_{1t}\)和\(a_{2t}\)不相关, 则\(\{ r_{1t} \}\)序列与\(\{ r_{2s} \}\)序列不相关。 称这样的分离的序列为非耦合的。
如果\(\phi_{12} \neq 0\), \(\phi_{21} \neq 0\), 这时两个序列之间有相互反馈关系。
如果\(\phi_{12}=0\), \(\phi_{21} \neq 0\), 模型变成 \[\begin{align} \begin{cases} r_{1t} = \phi_{10} + \phi_{11} r_{1,t-1} + a_{1t} \\ r_{2t} = \phi_{20} + \phi_{21} r_{1,t-1} + \phi_{22} r_{2,t-1} + a_{2t} \end{cases} \tag{26.3} \end{align}\] 这时\(r_{1t}\)不受到\(r_{2t}\)的过去值的影响, 但\(r_{2t}\)受到\(r_{1,t-1}\)的过去值的影响。 可以将\(r_{1t}\)作为输入变量, \(r_{2t}\)作为输出变量。
在统计学文献中, 如果\(a_{1t}\)和\(a_{2t}\)也不相关, 称式(26.3)的\(r_{1t}\)和\(r_{2t}\) 之间有传递函数(transfer function)关系。 传递函数模型是VARMA的一种特殊形式, 在控制工程中非常有用, 可以通过调整\(r_{1t}\)的值来影响\(r_{2t}\)。 在计量经济学文献中, 此模型意味着两个序列之间存在格兰杰因果关系, \(r_{1t}\)的过去值影响\(r_{2t}\), 但\(r_{2t}\)的过去值不影响\(r_{1t}\)。
(C. W. J. Granger 1969)提出了因果关系的概念, 适用于解释VAR模型的结果。 考虑一个二元序列\(\boldsymbol r_t=(r_{1t}, r_{2t})^T\) 的超前\(l\)步预测问题。 可以分别用VAR模型和每个分量的一元模型来进行预测。 如果\(r_{2t}\)的二元预测比它的一元预测更准确, 则称\(r_{1t}\)是\(r_{2t}\)的格兰格原因, 这是因为\(r_{1t}\)的信息提高了\(r_{2t}\)的预测精度。 这里预测精度用预测的均方误差来度量。 当然,\(r_{2t}\)也可以同时是\(r_{1t}\)的格兰格原因。
令\(F_t\)表示截止到时刻\(t\)的可用信息, 即\(F_t\)包含\(\{ \boldsymbol r_t, \boldsymbol r_{t-1}, \boldsymbol r_{t-2}, \dots\}\)。 令\(F_{-i,t}\)表示\(F_t\)中去掉第\(i\)个分量的信息的集合。 考虑(26.2)的二元VAR(1)模型。 \(F_t\)包含\(\{ r_{1t}, r_{2t}, r_{1,t-1}, r_{2,t-1}, \dots\}\), \(F_{-1,t}\)包含\(\{ r_{2t}, r_{2,t-1}, \dots\}\)。 考虑基于\(F_t\)的超前\(l\)步预测, 其预测误差为 \[ \boldsymbol e_t(l) = (e_{1t}(l), e_{2t}(l))^T= \boldsymbol r_{t+l} - E(\boldsymbol r_{t+l} | F_t) \] 其中对\(r_{2,t+l}\)的预测误差为 \[ e_{2t}(l) = r_{2,t+l} - E(r_{2,t+l} | F_t) \] 考虑基于\(F_{-1,t}\)对\(r_{2,t+l}\)的预测, 其预测误差为 \[ \tilde e_{2t}(l) = r_{2,t+l} - E(r_{2,t+l} | F_{-1,t}) = r_{2,t+l} - E(r_{2,t+l} | r_{2,t}, r_{2,t-1}, \dots) \] 如果 \[ E e_{2t}^2(l) = \text{Var}(r_{2,t+l} | F_t) < E \tilde e_{2t}^2(l) = \text{Var}(r_{2,t+l} | F_{-1,t}) \] 即使用截止到\(t\)时刻为止的全部信息预测\(r_{2,t+l}\), 均方误差比不利用第一个分量序列的均方误差小, 则称\(r_{1t}\)是\(r_{2t}\)的格兰格原因。
回到二元VAR(1)模型(26.2), 如果\(\phi_{12}=0\)而\(\phi_{21} \neq 0\), 则\(r_{2,t+1}\)依赖于\(r_{1,t}\), 预测\(r_{2,t+1}\)时需要利用\(r_{1t}\)的信息, 序列\(r_{1t}\)是序列\(r_{2t}\)的格兰格原因; \(r_{1,t+1}\)不依赖于\(r_{2,t}\), 预测\(r_{1,t+1}\)就不需要用到\(r_{2t}\), 所以序列\(r_{2t}\)不是序列\(r_{1t}\)的格兰格原因。
事实上,对(26.3), 不妨设\(\{\boldsymbol a_t\}\)是独立的多元弱平稳列, 这时 \(E(\boldsymbol a_{t+1} | F_t) = \boldsymbol 0\), \(E(a_{2,t+1} | F_{-1,t}) = 0\), \(\text{Var}(a_{2,t+1} | F_t) = \text{Var}(a_{2,t+1} | F_{-1,t}) = \sigma_{22}\), 又 \[\begin{aligned} E(r_{2,t+1} | F_t) =& \phi_{20} + \phi_{21} r_{1,t} + \phi_{22} r_{2,t} \\ \text{Var}(r_{2,t+1} | F_t) =& E[(r_{2,t+1} - E(r_{2,t+1} | F_t))^2 | F_t] \\ =& E(a_{2,t+1}^2 | F_t) = \sigma_{22} \end{aligned}\] 而 \[\begin{aligned} E(r_{2,t+1} | F_{-1,t}) =& \phi_{20} + \phi_{21} E(r_{1,t} | F_{-1,t}) + \phi_{22} r_{2,t} \\ \text{Var}(r_{2,t+1} | F_{-1,t}) =& E[(r_{2,t+1} - E(r_{2,t+1} | F_{-1,t}))^2 | F_{-1,t}] \\ =& E[ \left\{ \phi_{21} (r_{1,t} - E(r_{1,t} | F_{-1,t})) + a_{2,t+1} \right\}^2 | F_{-1,t}] \\ =& \phi_{21}^2 \text{Var}(r_{1,t} | F_{-1,t}) + \sigma_{22} > \sigma_{22} \end{aligned}\] 即\(r_{1t}\)是\(r_{2t}\)的格兰格原因。
另一方面, \[\begin{aligned} E(r_{1,t+1} | F_t) =& \phi_{10} + \phi_{11} r_{1,t} \\ \text{Var}(r_{1,t+1} | F_t) =& E[(r_{1,t+1} - E(r_{1,t+1} | F_t))^2 | F_t] \\ =& E(a_{1,t+1}^2 | F_t) = \text{Var}(a_{1,t+1}) = \sigma_{11} \\ E(r_{1,t+1} | F_{-2,t}) =& \phi_{10} + \phi_{11} r_{1,t} \\ \text{Var}(r_{1,t+1} | F_{-2,t}) =& E[(r_{1,t+1} - E(r_{1,t+1} | F_{-2,t}))^2 | F_{-2,t}] \\ =& E(a_{1,t+1}^2 | F_{-2,t}) = \text{Var}(a_{1,t+1}) = \sigma_{11} \end{aligned}\] 所以\(r_{2t}\)不是\(r_{1t}\)的格兰格原因。
如果\(\phi_{21} = 0\)而\(\phi_{12} \neq 0\), 则序列\(r_{2t}\)是序列\(r_{1t}\)的格兰格原因, 而序列\(r_{1t}\)不是序列\(r_{2t}\)的格兰格原因。
如果新息\(\boldsymbol a_t = (a_{1t}, a_{2t})^T\)的协方差阵\(\Sigma\)不是对角阵, 则\(r_{1t}\)和\(r_{2t}\)之间存在同步相关性, 这时两个序列存在即期(同期,瞬时)格兰格因果关系, 这种即期因果关系是双向的。
注意, 这样定义的格兰格因果性依赖于VAR(1)模型(26.1)这样的模型形式(称为简化形式), 如果改变模型的形式(比如改为下面的结构形式), 可能就不会在\(\phi_{12}\)和\(\phi_{21}\)这样的简单数值上反映出格兰格因果性。
更多分量的VAR(1)可以有更灵活的格兰格因果关系。 比如三元的模型, 如果\(\boldsymbol\Phi\)是下三角阵: \[ \left( \begin{matrix} \phi_{11} \\ \phi_{21} & \phi_{22} \\ \phi_{31} & \phi_{32} & \phi_{33} \end{matrix} \right) \] 则:
- \(r_{2t}\)和\(r_{3t}\)都不是\(r_{1t}\)的格兰格原因;
- \(r_{1t}\)是\(r_{2t}\)的格兰格原因, 但\(r_{3t}\)不是\(r_{2t}\)的格兰格原因;
- \(r_{1t}\)和\(r_{2t}\)都是\(r_{3t}\)的格兰格原因。
如果\(\boldsymbol\Phi\)有其他稀疏形式, 关系可能多种多样。
26.3 VAR的简化形式和结构形式
式(26.1)的系数矩阵\(\boldsymbol\Phi\) 度量了\(\boldsymbol r_t\)的动态相依性, \(r_{1t}\)与\(r_{2t}\)之间的同步相依性可以通过 \(\boldsymbol a_t\)的协方差阵\(\boldsymbol\Sigma\)的非对角元素 \(\sigma_{12}\)来反映。 如果\(\sigma_{12} = 0\), 则两个分量\(r_{1t}\)和\(r_{2t}\)之间没有同步线性关系。 在计量经济文献中式(26.1)中的VAR(1) 模型称为简化形式(reduced form)的模型, 因为该模型没有清楚地表现出分量序列之间的同步线性相依性。
可以利用矩阵变换对(26.1)进行变换, 得到显式地表现同步关系的模型。 对\(\boldsymbol\Sigma>0\)(正定), 存在Cholesky分解 \(\boldsymbol\Sigma = \boldsymbol L \boldsymbol G \boldsymbol L^T\), 其中\(\boldsymbol G\)是对角线元素都为正数的\(k\)阶对角方阵, \(\boldsymbol L\)为对角线元素都等于1的下三角阵, 定义 \[\begin{aligned} \boldsymbol b_t = \boldsymbol L^{-1} \boldsymbol a_t = (b_{1t}, \dots, b_{kt})^T \end{aligned}\] 则 \[\begin{aligned} E \boldsymbol b_t =& 0 \\ \text{Var}(\boldsymbol b_t) =& \boldsymbol L^{-1} \text{Var}(\boldsymbol a_t) L^{-T} = \boldsymbol G \end{aligned}\] 其中\(\boldsymbol L^{-T} = (\boldsymbol L^T)^{-1} = (\boldsymbol L^{-1})^T\)。 上式表明\(\boldsymbol b_t\)的各分量不相关。 将式(26.1)两边同时左乘\(\boldsymbol L^{-1}\), 得 \[\begin{align} \boldsymbol L^{-1} \boldsymbol r_t =& \boldsymbol L^{-1} \boldsymbol\phi_0 + \boldsymbol L^{-1} \boldsymbol\Phi \boldsymbol r_{t-1} + \boldsymbol L^{-1} \boldsymbol a_t \\ =& \boldsymbol\phi_0^* + \boldsymbol\Phi^* \boldsymbol r_{t-1} + \boldsymbol b_t \tag{26.4} \end{align}\]
记\(\boldsymbol\phi_0^* = (\phi_{10}^*, \dots, \phi_{k0}^*)^T\), \(\boldsymbol\Phi^* = (\phi_{ij}^*)_{k\times k}\), 设\(\boldsymbol L^{-1}\)的最后一行为 \((w_{k1}, \dots, w_{k,k-1}, 1)\), 则模型(26.4)的最后一个方程(第\(k\)个方程)为 \[\begin{align} r_{kt} + \sum_{i=1}^{k-1} w_{ki} r_{it} = \phi_{k0}^* + \sum_{i=1}^k \phi_{ki}^* r_{i,t-1} + b_{kt} \tag{26.5} \end{align}\]
对\(i<k\), 因为\(b_{kt}\)与\(b_{ki}\)不相关, 所以式(26.5)明确表示了 \(r_{kt}\)对\(r_{it}\)的同步依赖性。 在计量经济文献中式(26.5)称为\(r_{kt}\) 的一个结构方程(structural form)。
对\(\boldsymbol r_t\)的任何其它分量\(r_{jt}\)(\(j<k\)), 可以对VAR模型各个方程的次序进行重排, 比如, 将第\(j\)个方程与第\(k\)个方程对换位置, 再用前面的方法得到关于\(r_{jt}\)的结构方程。 因此, 式(26.1)的简化形式等价于式(26.5)的结构形式。
在时间序列分析中通常使用简化形式,因为
- 简化形式更容易估计;
- 在预测时,同步形式无法使用。
例2.1
为了说明从简化形式到结构方程的变换, 考虑如下的二元VAR(1)模型: \[\begin{aligned} \left(\begin{array}{c} r_{1t} \\ r_{2t} \end{array}\right) =& \left(\begin{array}{c} 0.2 \\ 0.4 \end{array}\right) + \left(\begin{array}{cc} 0.2 & 0.3 \\ -0.6 & 1.1 \end{array}\right) \left(\begin{array}{c} r_{1,t-1} \\ r_{2,t-1} \end{array}\right) + \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) \\ \text{Var}(\boldsymbol a_t) =& \boldsymbol\Sigma = \left(\begin{array}{cc} 2 & 1 \\ 1 & 1 \end{array}\right) \end{aligned}\] 对\(\boldsymbol\Sigma\)作Cholesky分解得 \(\boldsymbol\Sigma = L G L^T\), 其中 \[\begin{aligned} \boldsymbol G = \left(\begin{array}{cc} 2 & 0 \\ 0 & 0.5 \end{array}\right) \quad \boldsymbol L^{-1} = \left(\begin{array}{cc} 1 & 0 \\ -0.5 & 1 \end{array}\right) \end{aligned}\]
在简化形式的VAR(1)模型两边同时左乘\(\boldsymbol L^{-1}\), 得 \[\begin{aligned} \left(\begin{array}{cc} 1 & 0 \\ -0.5 & 1 \end{array}\right) \left(\begin{array}{c} r_{1t} \\ r_{2t} \end{array}\right) =& \left(\begin{array}{c} 0.2 \\ 0.3 \end{array}\right) + \left(\begin{array}{cc} 0.2 & 0.3 \\ -0.7 & 0.95 \end{array}\right) \left(\begin{array}{c} r_{1,t-1} \\ r_{2,t-1} \end{array}\right) + \left(\begin{array}{c} b_{1t} \\ b_{2t} \end{array}\right) \\ \text{Var}(\boldsymbol b_t) =& \boldsymbol G = \left(\begin{array}{cc} 2 & 0 \\ 0 & 0.5 \end{array}\right) \end{aligned}\] 其中第二个方程为 \[\begin{aligned} r_{2t} = 0.3 + 0.5 r_{1t} - 0.7 r_{1,t-1} + 0.95 r_{2,t-1} + b_{2t} \end{aligned}\] 此方程明确表现了\(r_{2t}\)对\(r_{1t}\)的同步依赖(系数\(+0.5\)), 方程中也有\(r_{2t}\)对\(r_{1,t-1}\)的交叉依赖, 对\(r_{2,t-1}\)的自身依赖。
为了给出\(r_{1t}\)的结构方程, 将简化形式的两个方程对换位置, 得(注意\(\boldsymbol\Phi\)需要行互换、列互换) \[\begin{aligned} \left(\begin{array}{c} r_{2t} \\ r_{1t} \end{array}\right) =& \left(\begin{array}{c} 0.4 \\ 0.2 \end{array}\right) + \left(\begin{array}{cc} 1.1 & -0.6 \\ 0.3 & 0.2 \end{array}\right) \left(\begin{array}{c} r_{2,t-1} \\ r_{1,t-1} \end{array}\right) + \left(\begin{array}{c} a_{2t} \\ a_{1t} \end{array}\right) \\ \boldsymbol\Sigma =& \left(\begin{array}{cc} 1 & 1 \\ 1 & 2 \end{array}\right) \end{aligned}\] 此\(\boldsymbol\Sigma\)的Cholesky分解有 \[\begin{aligned} \boldsymbol G = \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) \quad \boldsymbol L^{-1} = \left(\begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array}\right) \end{aligned}\] 在调换次序的VAR(1)模型的两边同时左乘\(\boldsymbol L^{-1}\),得 \[\begin{aligned} \left(\begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array}\right) \left(\begin{array}{c} r_{2t} \\ r_{1t} \end{array}\right) =& \left(\begin{array}{c} 0.4 \\ -0.2 \end{array}\right) + \left(\begin{array}{cc} 1.1 & -0.6 \\ -0.8 & 0.8 \end{array}\right) \left(\begin{array}{c} r_{2,t-1} \\ r_{1,t-1} \end{array}\right) + \left(\begin{array}{c} c_{1t} \\ c_{2t} \end{array}\right) \\ \text{Var}(\boldsymbol c_t) =& \boldsymbol G = \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) \end{aligned}\] 其中第二个方程为 \[\begin{aligned} r_{1t} = -0.2 + 1.0 r_{2t} - 0.8 r_{2,t-1} + 0.8 r_{1,t-1} + c_{2t} \end{aligned}\] 这个方程明确地表现了\(r_{1t}\)对\(r_{2t}\)的同步线性依赖。
○○○○○
利用R计算\(LGL^T\)分解的\(L^{-1}\)和\(G\)的程序:
ldl.decomp <- function(A){
R <- chol(A)
D <- diag(diag(R))
Linv <- solve(t(solve(D, R)))
G <- D^2
list(Linv=Linv, G=G)
}例如
## [,1] [,2]
## [1,] 2 1
## [2,] 1 1## $Linv
## [,1] [,2]
## [1,] 1.0 0
## [2,] -0.5 1
##
## $G
## [,1] [,2]
## [1,] 2 0.0
## [2,] 0 0.5## [,1] [,2]
## [1,] 1 1
## [2,] 1 2## $Linv
## [,1] [,2]
## [1,] 1 0
## [2,] -1 1
##
## $G
## [,1] [,2]
## [1,] 1 0
## [2,] 0 126.4 VAR(1)模型的平稳性条件和矩
设(26.1)式中的VAR(1)模型的\(\boldsymbol r_t\)是弱平稳的, 在方程两边取期望得 \[\begin{aligned} E \boldsymbol r_t = \boldsymbol\phi_0 + \boldsymbol\Phi E \boldsymbol r_{t-1} \end{aligned}\] 由\(E\boldsymbol r_t = E\boldsymbol r_{t-1}\) 得\(\boldsymbol I - \boldsymbol\Phi\)满秩(也叫做非奇异)时 \[\begin{aligned} \boldsymbol\mu = E \boldsymbol r_t = (\boldsymbol I - \boldsymbol\Phi)^{-1} \boldsymbol\phi_0 \end{aligned}\] 在式(26.1)中代入 \(\boldsymbol\phi_0 = (\boldsymbol I - \boldsymbol\Phi) \boldsymbol\mu\), 则模型(26.1)可以写成 \[\begin{aligned} \boldsymbol r_t - \boldsymbol \mu = \boldsymbol\Phi (\boldsymbol r_{t-1} - \boldsymbol\mu) + \boldsymbol a_t \end{aligned}\] 记中心化的\(\boldsymbol r_t\)为\(\tilde{\boldsymbol r}_t = \boldsymbol r_t - \boldsymbol\mu\), 则VAR(1)模型(26.1)变成 \[\begin{align} \tilde{\boldsymbol r}_t = \boldsymbol \Phi \tilde{\boldsymbol r}_{t-1} + \boldsymbol a_t \tag{26.6} \end{align}\]
将(26.6)递归得 \[\begin{align} \tilde{\boldsymbol r}_t = \boldsymbol a_t + \boldsymbol\Phi \boldsymbol a_{t-1} + \boldsymbol\Phi^2 \boldsymbol a_{t-2} + \dots = \sum_{j=0}^\infty \boldsymbol\Phi^j \boldsymbol a_{t-j} \tag{26.7} \end{align}\] 其中\(\boldsymbol\Phi^0=I_k\)。 这相当于一元时间序列的Wold表示。
由(26.7)可以推出:
- 因为\(\{ \boldsymbol a_t \}\)序列不相关, 所以\(\text{Cov}(\boldsymbol a_t, \boldsymbol r_{t-l})=0\)(\(l>0\)时)。 因此可以将\(\boldsymbol a_t\)称为序列\(\{\boldsymbol r_t\}\)在\(t\) 时刻的一个扰动或者新息(innovation)。 一般定义新息为\(\boldsymbol a_t = \boldsymbol r_t - E(\boldsymbol r_t | F_{t-1})\) 或\(\boldsymbol a_t = \boldsymbol r_t - L(\boldsymbol r_t | H_{t-1})\), \(L(\cdot | \cdot)\)表示均方误差最小线性预测, \(H_{t-1}\)表示由\(\{ \boldsymbol r_{t-1}, \boldsymbol r_{t-2}, \dots \}\)张成的Hilbert空间。 平稳的VAR(1)中\(a_{it}\)是用 \(\boldsymbol r_{t-1}, \boldsymbol r_{t-2}, \dots\)对\(r_{it}\)作最优线性预测的预测误差。
- 在(26.7)两边同时右乘\(\boldsymbol a_t^T\)后取期望, 得\(\text{Cov}(\boldsymbol r_t, \boldsymbol a_t)=\Sigma\)。
- 对VAR(1)模型(26.1)导出的Wold表示(26.7), \(\boldsymbol r_t\)按系数矩阵\(\boldsymbol\Phi^j\)依赖于过去的新息\(\boldsymbol a_{t-j}\)。 为了使得(26.7)收敛, 需要\(j\to\infty\)时\(\boldsymbol\Phi^j \to \boldsymbol 0\), 这当且仅当\(\boldsymbol\Phi\)的所有特征值的模都小于1。 如果存在模大于或等于1的特征值, 则\(j\to\infty\)时\(\boldsymbol\Phi^j\)发散或者不收敛到\(\boldsymbol 0\)矩阵。 仿照一元情形的特征多项式的讨论, 因为特征值的模小于1当且仅当 \(|\lambda \boldsymbol I - \boldsymbol\Phi|\)的根的模都小于1, 而\(|\lambda \boldsymbol I - \boldsymbol\Phi| = |\lambda|^k \; |\boldsymbol I - \boldsymbol\Phi \lambda^{-1}|\), 记\(z = \lambda^{-1}\), 称关于\(z\)的多项式\(|P(z)| = |\boldsymbol I - \boldsymbol\Phi z|\)为模型的(逆序)特征多项式, 则式(26.7)收敛的充分必要条件是特征多项式\(|P(z)|\)的根都在单位圆外。 这个条件称为VAR(1)模型的平稳性条件。 当且仅当平稳性条件成立时, 模型(26.1)存在满足 \(\boldsymbol a_t\)与\(\boldsymbol r_{t-1}, \boldsymbol r_{t-2}, \dots\)不相关条件的平稳解。
- 利用推移算子和特征多项式可以将模型(26.1)写成 \(P(B) \boldsymbol r_t = \boldsymbol\phi_0 + \boldsymbol a_t\)。
- 利用Wold表示(26.7)式还可得
\[\begin{aligned} \text{Var}(\boldsymbol r_t) = \boldsymbol\Sigma + \boldsymbol\Phi \boldsymbol\Sigma \boldsymbol\Phi^T + \boldsymbol\Phi^2 \boldsymbol\Sigma (\boldsymbol\Phi^2)^T + \dots = \sum_{j=0}^\infty \boldsymbol\Phi^j \boldsymbol\Sigma (\boldsymbol\Phi^j)^T \end{aligned}\]
考虑VAR(1)模型的互协方差阵和互相关阵。 将式(26.6)两边乘以\(\tilde{\boldsymbol r}_{t-l}^T\)后取期望, 得互协方差阵 \[\begin{align} \boldsymbol\Gamma_l =& E(\tilde{\boldsymbol r}_t \tilde{\boldsymbol r}_{t-l}^T) = \text{Cov}(\boldsymbol r_t, \boldsymbol r_{t-l}) \\ =& \boldsymbol\Phi E(\tilde{\boldsymbol r}_{t-1} \tilde{\boldsymbol r}_{t-l}^T) + E(\boldsymbol a_t \tilde{\boldsymbol r}_{t-l}) \\ =& \boldsymbol \Phi \boldsymbol \Gamma_{l-1}, \quad (l>0) \tag{26.8} \end{align}\] 这个结果是一元时间序列AR(1)模型性质的推广。
通过递推可得 \[\begin{aligned} \boldsymbol\Gamma_l = \boldsymbol\Phi^l \boldsymbol\Gamma_0, \quad l>0 \end{aligned}\] 其中\(\boldsymbol\Gamma_0 = \text{Var}(\boldsymbol r_t)\)。
设\(\boldsymbol D\)为\(\boldsymbol\Gamma_0\)的对角阵, 则VAR(1)模型的互相关阵为 \[\begin{aligned} \boldsymbol\rho_l =& \boldsymbol D^{-\frac12} \boldsymbol\Gamma_l \boldsymbol D^{-\frac12} = \boldsymbol D^{-\frac12} \boldsymbol\Phi \boldsymbol\Gamma_{l-1} \boldsymbol D^{-\frac12} \\ =& \boldsymbol D^{-\frac12} \boldsymbol\Phi \boldsymbol D^{\frac12} \boldsymbol D^{-\frac12} \boldsymbol\Gamma_{l-1} \boldsymbol D^{-\frac12} \\ =& \boldsymbol D^{-\frac12} \boldsymbol\Phi \boldsymbol D^{\frac12} \boldsymbol\rho_{l-1} = \boldsymbol\Upsilon \boldsymbol\rho_{l-1} \end{aligned}\] 其中\(\boldsymbol\Upsilon = \boldsymbol D^{-\frac12} \boldsymbol\Phi \boldsymbol D^{\frac12}\) (\(\boldsymbol\Upsilon\)读作Upsilon)。 递推得 \[\begin{aligned} \boldsymbol\rho_l = \boldsymbol\Upsilon^l \boldsymbol\rho_0, \quad l=1,2,\dots \end{aligned}\]
例2.2
考虑二元VAR(1)模型 \[\begin{aligned} \left(\begin{array}{c} r_{1t} \\ r_{2t} \end{array}\right) = & \left(\begin{array}{c} 5 \\ 3 \end{array}\right) + \left(\begin{array}{cc} 0.2 & 0.3 \\ -0.6 & 1.1 \end{array}\right) \left(\begin{array}{c} r_{1,t-1} \\ r_{2,t-1} \end{array}\right) + \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) \\ \boldsymbol\Sigma =& \left(\begin{array}{cc} 1 & 0.8 \\ 0.8 & 2 \end{array}\right) \end{aligned}\]
计算\(\boldsymbol\Phi\)的特征值的绝对值:
## [1] 0.8 0.5特征值的绝对值都小于1。 模型是平稳的。
注意\(\phi_{22}=1.1>1\), 但不影响平稳性。 多元弱平稳一定也是一元弱平稳的。
26.5 VAR(1)模型的边缘模型
对VAR(1)模型(26.1)的如上的Wold表示, 同时也将\(\boldsymbol r_t\)的每个分量, 表示成了一元的无穷阶MA,但其中的新息是多元的。 利用这种思想,将分量的一元模型可以写成一元ARMA模型。
设矩阵\(\boldsymbol A\)是可逆方阵, 令\(\boldsymbol C=(c_{ij})\), 其中\(c_{ij}\)是\(\boldsymbol A\)删除第\(i\)行和第\(j\)列后的子矩阵的行列式乘以\((-1)^{i+j}\), \(c_{ij}\)称为\(\boldsymbol A\)的\((i,j)\)元素的代数余子式, \(\boldsymbol C^T\)称为\(\boldsymbol A\)的伴随矩阵, 记为\(\text{adj}(\boldsymbol A)\), 有 \[\begin{aligned} \boldsymbol A^{-1} = \frac{1}{|\boldsymbol A|} \text{adj}(A), \quad \boldsymbol A \cdot \text{adj}(\boldsymbol A) = \text{adj}(A) \cdot \boldsymbol A = |\boldsymbol A| \cdot \boldsymbol I \end{aligned}\]
VAR(1)的Wold表示相当于 \[\begin{aligned} \boldsymbol r_t = (\boldsymbol I - \boldsymbol\Phi B)^{-1} \cdot (\boldsymbol\phi_0 + \boldsymbol a_t) \end{aligned}\] 利用伴随矩阵可得 \[\begin{aligned} |\boldsymbol I - \boldsymbol\Phi B| \boldsymbol r_t = \text{adj}(\boldsymbol I - \boldsymbol\Phi B) \cdot (\boldsymbol\phi_0 + \boldsymbol a_t) \end{aligned}\] 其中\(|\boldsymbol I - \boldsymbol\Phi z|\)是\(z\)的\(k\)阶多项式; \(\text{adj}(\boldsymbol I - \boldsymbol\Phi z)\)的每个元素是\(z\)的\(k-1\)阶多项式。 这样,分量\(r_{it}\)服从一个ARMA(\(k,q\))模型, 模型中的MA部分涉及到多元的新息, 但是可以设法转换成一元的新息。
例2.3
考虑例2.2中的模型。 \[\begin{aligned} \left(\begin{array}{c} r_{1t} \\ r_{2t} \end{array}\right) = & \left(\begin{array}{c} 5 \\ 3 \end{array}\right) + \left(\begin{array}{cc} 0.2 & 0.3 \\ -0.6 & 1.1 \end{array}\right) \left(\begin{array}{c} r_{1,t-1} \\ r_{2,t-1} \end{array}\right) + \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) \\ \boldsymbol\Sigma =& \left(\begin{array}{cc} 1 & 0.8 \\ 0.8 & 2 \end{array}\right) \end{aligned}\]
这时 \[\begin{aligned} \boldsymbol\Phi =& \left(\begin{array}{cc} 0.2 & 0.3 \\ -0.6 & 1.1 \end{array}\right) \\ \boldsymbol I - \boldsymbol\Phi z =& \left(\begin{array}{cc} 1 - 0.2 z & -0.3z \\ 0.6 z & 1 - 1.1 z \end{array}\right) \\ \text{adj}(\boldsymbol I - \boldsymbol\Phi z) =& \left(\begin{array}{cc} 1 - 1.1 z & 0.3z \\ -0.6 z & 1 - 0.2 z \end{array}\right) \\ | \boldsymbol I - \boldsymbol\Phi z | =& 1 - 1.3 z + 0.4 z^2 \end{aligned}\] 于是 \[\begin{aligned} & (1 - 1.3 B + 0.4 B^2) \left(\begin{array}{c} r_{1t} \\ r_{2t} \end{array}\right) \\ =& \left(\begin{array}{cc} 1 - 1.1 & 0.3 \\ -0.6 & 1 - 0.2 \end{array}\right) \left(\begin{array}{c} 5 \\ 3 \end{array}\right) + \left(\begin{array}{cc} 1 - 1.1 B & 0.3 B \\ -0.6 B & 1 - 0.2 B \end{array}\right) \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) \end{aligned}\] 所以分量\(r_{1t}\)的一元模型为 \[\begin{aligned} r_{1t} - 1.3 r_{1,t-1} + 0.4 r_{1,t-2} = 5.4 + a_{1t} + 0.3 a_{2,t-1} - 1.1 a_{1,t-1} \end{aligned}\] 令\(\eta_t=a_{1t} + 0.3 a_{2,t-1} - 1.1 a_{1,t-1}\), 易见\(\{ \eta_t \}\)是弱平稳列, 且其ACF在\(q=1\)之后截尾(即\(\rho_\eta(j)=0, j>1\))。 所以\(\{\eta_t \}\)是MA(1)序列, 从而分量\(r_{1t}\)服从一个一元的ARMA(2,1)模型。
一般地, \(k\)元的VAR(1)模型的分量服从一元的ARMA(\(k,k-1\))模型。 由于方程左右可能有公共根, 所以模型阶数可能会降低。
26.6 VAR(p)模型
称\(k\)元时间序列\(\boldsymbol r_t\)服从一个VAR(\(p\))模型, 如果 \[\begin{align} \boldsymbol r_t = \boldsymbol\phi_0 + \boldsymbol\Phi_1 \boldsymbol r_{t-1} + \dots + \boldsymbol\Phi_p \boldsymbol r_{t-p} + \boldsymbol a_t \tag{26.9} \end{align}\] 其中\(\boldsymbol\phi_0\)和\(\{ \boldsymbol a_t \}\)同VAR(1)的规定, \(\boldsymbol\Phi_{\ell}\)是\(k\)阶方阵(\(\ell=1,2,\dots,p\)), 其\((i,j)\)元素记为\(\phi_{ij}(\ell)\)。 利用向后推移算子(滞后算子)\(B\)可以将模型写成 \[\begin{aligned} (\boldsymbol I - \boldsymbol\Phi_1 B - \dots - \boldsymbol\Phi_p B^p) \boldsymbol r_t = \boldsymbol\phi_0 + \boldsymbol a_t \end{aligned}\] 记 \[\begin{align} P(z) = \boldsymbol I - \boldsymbol\Phi_1 z - \dots - \boldsymbol\Phi_p z^p \tag{26.10} \end{align}\] 这是一个从复数\(z\)到\(k\)阶方阵\(P(z)\)的变换, \(P(z)\)的每个元素是关于\(z\)的阶数不超过\(p\)的多项式。 称一元多项式函数\(\text{det}(P(z))\)(或记为\(|P(z)|\))为模型的(逆序)特征多项式。
利用矩阵推移函数\(P(B)\)可以将模型简记为 \[\begin{aligned} P(B) \boldsymbol r_t = \boldsymbol\phi_0 + \boldsymbol a_t \end{aligned}\]
如果\(\boldsymbol r_t\)弱平稳, 则在下式的逆矩阵存在的条件下 \[\begin{aligned} \boldsymbol\mu =& E \boldsymbol r_t = (\boldsymbol I - \boldsymbol\Phi_1 - \dots - \boldsymbol\Phi_p)^{-1} \boldsymbol\phi_0 = (P(1))^{-1} \boldsymbol\phi_0 \end{aligned}\] 中心化\(\boldsymbol r_t\)得\(\tilde{\boldsymbol r}_t = \boldsymbol r_t - \boldsymbol\mu\), 这时模型(26.9)变成 \[\begin{align} \tilde{\boldsymbol r}_t = \boldsymbol\Phi_1 \tilde{\boldsymbol r}_{t-1} + \dots + \boldsymbol\Phi_p \tilde{\boldsymbol r}_{t-p} + \boldsymbol a_t \tag{26.11} \end{align}\]
称VAR(\(p\))满足平稳性条件, 如果特征多项式\(\text{det}(P(z))\)的根都在单位圆外。 当VAR(\(p\))满足平稳性条件时, 有如下的Wold表示的平稳解: \[\begin{aligned} \boldsymbol r_t = \boldsymbol\mu + \sum_{j=0}^\infty \boldsymbol\Psi_j \boldsymbol a_{t-j}, \end{aligned}\] 其中\(j\to\infty\)时\(\boldsymbol\Psi_j\)的元素以负指数速度趋于0, \(\boldsymbol\Psi_j\)有如下的递推公式: \[\begin{aligned} \boldsymbol\Psi_0 =& \boldsymbol I, \\ \boldsymbol\Psi_j =& \sum_{s=0}^p \boldsymbol\Phi_s \boldsymbol\Psi_{j-s} , \end{aligned}\] 对\(s<0\)记\(\boldsymbol\Psi_s = \boldsymbol 0\)。
由上述Wold表示可知, 对平稳解\(\boldsymbol r_t\)有
- \(\text{Cov}(\boldsymbol r_t, \boldsymbol a_t) = \Sigma = \text{Var}(\boldsymbol a_t)\);
- \(\text{Cov}(\boldsymbol r_{t-l}, \boldsymbol a_t) = \boldsymbol 0\)(\(l>0\))。
互协方差阵满足如下递推关系 \[\begin{aligned} \boldsymbol\Gamma_l = \boldsymbol\Phi_1 \boldsymbol\Gamma_{l-1} + \dots + \boldsymbol\Phi_p \boldsymbol\Gamma_{l-p}, \ l>0 \end{aligned}\] 这个性质称为VAR(\(p\))的矩方程, 是一元AR(\(p\))模型的Yule-Walker方程的多元形式。 用CCM表示为 \[\begin{aligned} \boldsymbol\rho_l = \boldsymbol\Upsilon_1 \boldsymbol\rho_{l-1} + \dots + \boldsymbol\Upsilon_p \boldsymbol\rho_{l-p}, \ l>0 \end{aligned}\] 其中\(\boldsymbol\Upsilon_j = \boldsymbol D^{-\frac12} \boldsymbol\Phi_j \boldsymbol D^{\frac12}\), \(\boldsymbol D\)是\(\boldsymbol\Sigma\)的对角阵。
事实上,VAR(\(p\))模型可以改写成一个VAR(1)模型, 然后可以用VAR(1)模型的结果去研究VAR(\(p\))模型的性质。 令 \[\begin{aligned} \boldsymbol x_t=& \left(\begin{array}{c} \tilde{\boldsymbol r}_{t} \\ \tilde{\boldsymbol r}_{t-1} \\ \vdots \\ \tilde{\boldsymbol r}_{t-p+1} \\ \end{array}\right) \quad \boldsymbol b_t = \left(\begin{array}{c} \boldsymbol a_t \\ \boldsymbol 0_{k\times 1} \\ \vdots \\ \boldsymbol 0_{k\times 1} \\ \end{array}\right) \\ \text{Var}(\boldsymbol b_t) =& \left(\begin{array}{cc} \boldsymbol\Sigma & \boldsymbol 0_{k \times k(p-1)} \\ \boldsymbol 0_{k(p-1) \times k} & \boldsymbol 0_{k(p-1) \times k(p-1)} \end{array}\right) \\ \boldsymbol\Phi^* =& \left(\begin{array}{ccccc} \boldsymbol\Phi_{1} & \boldsymbol\Phi_{2} & \cdots & \boldsymbol\Phi_{p-1} & \boldsymbol\Phi_{p}\\ \boldsymbol I & \boldsymbol 0 & \cdots & \boldsymbol 0 & \boldsymbol 0 \\ \boldsymbol 0 & \boldsymbol I & \cdots & \boldsymbol 0 & \boldsymbol 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \boldsymbol 0 & \boldsymbol 0 & \cdots & \boldsymbol I & \boldsymbol 0 \end{array}\right) \end{aligned}\] 则 \[\begin{align} \boldsymbol x_t = \boldsymbol\Phi^* \boldsymbol x_{t-1} + \boldsymbol b_t \tag{26.12} \end{align}\] 是关于\(kp\)元时间序列\(\boldsymbol x_t\)的VAR(1)模型。
\(\boldsymbol r_t\)弱平稳当且仅当\(\boldsymbol x_t\)弱平稳, 其充分必要条件是\(\boldsymbol\Phi^*\)的所有特征值模小于1, 计算可知这相当于要求用行列式表示的\(z\)的多项式\(|P(z)|\)的根都在单位圆外, \(P(z)\)定义见(26.10)。 但是, 因为计算\(\text{det}(\boldsymbol I - \boldsymbol\Phi_1 z - \dots - \boldsymbol\Phi_p z^p)\)这种用行列式表示的多项式的根还需要求多项式的各个系数, 而求\(\boldsymbol\Phi^*\)的所有特征值或模最大的特征值则有比较成熟的数值方法, 所以为了判断一个VAR(\(p\))模型是否满足平稳性条件, 可以生成\(\boldsymbol\Phi^*\)并判断其模最大的特征值是否模小于1。
如果\(\text{det}(P(1)) = 0\), 或\(\boldsymbol\Phi^*\)有等于1的特征值, 即有单位根, 则\(\boldsymbol r_t\)的各个分量中至少有一个是单位根过程, 各个分量之间还有可能存在协整关系, 可以用VECM(向量误差修正模型)建模, 参见27。
对VAR(\(p\))模型, 系数矩阵\(\boldsymbol\Phi_l = (\phi_{ij}(l))_{k \times k}\)的值也表现了 \(\boldsymbol r_t\)各个分量之间的先导、滞后关系。 比如\(k=2\)时, 如果所有\(\phi_{12}(l)=0\), 但存在\(l>0\)使得\(\phi_{21}(l) \neq 0\), 则\(r_{1t}\)不依赖于\(r_{2t}\)的过去值, \(r_{2t}\)依赖于\(r_{1t}\)的过去值。 \(r_{1t}\)是\(r_{2t}\)的格兰杰原因, \(r_{2t}\)不是\(r_{1t}\)的格兰杰原因。
26.7 估计和定阶
VAR模型建模也基本遵循定阶、模型估计和模型检验这样的反复尝试过程。 一元的PACF可以推广到多元情形用以辅助定阶。
考虑如下的阶数递进的VAR模型: \[\begin{align} \boldsymbol r_t =& \boldsymbol\phi_0 + \boldsymbol\Phi_1 \boldsymbol r_{t-1} + \boldsymbol a_t \\ \boldsymbol r_t =& \boldsymbol\phi_0 + \boldsymbol\Phi_1 \boldsymbol r_{t-1} + \boldsymbol\Phi_2 \boldsymbol r_{t-2} + \boldsymbol a_t \\ & \vdots \\ \boldsymbol r_t =& \boldsymbol\phi_0 + \boldsymbol\Phi_1 \boldsymbol r_{t-1} + \dots + \boldsymbol\Phi_p \boldsymbol r_{t-p} + \boldsymbol a_t \tag{26.13} \end{align}\] 模型参数可以对每个方程分别用OLS(最小二乘)方法估计, 在多元统计分析文献中称为多元线性估计, 参见(Johnson and Wichern 1998)。
对于(26.13)的第\(i\)个方程, 令\(\hat{\boldsymbol\Phi}_j^{(i)}\)是\(\boldsymbol\Phi_j\)的最小二乘估计, \(\hat{\boldsymbol\phi}_0^{(i)}\)是\(\boldsymbol\phi_0\)的的最小二乘估计。 残差为 \[\begin{aligned} \hat{\boldsymbol a}_t^{(i)} =& \boldsymbol r_t - \hat{\boldsymbol\Phi}_1^{(i)} \boldsymbol r_{t-1} - \dots - \hat{\boldsymbol\Phi}_i^{(i)} \boldsymbol r_{t-i} \end{aligned}\] 当\(i=0\)时定义\(\hat{\boldsymbol a}_t^{(0)} = \boldsymbol r_t - \bar{\boldsymbol r}\), 其中\(\bar{\boldsymbol r}\)是\(\boldsymbol r_t\)的样本均值。
残差的方差阵估计为 \[\begin{aligned} \hat{\boldsymbol\Sigma}_i =& \frac{1}{T - (k+1)i - 1} \sum_{t=i+1}^T \hat{\boldsymbol a}_t^{(i)} [\hat{\boldsymbol a}_t^{(i)}]^T \end{aligned}\] (参见(Tsay 2014) 节2.5.1 P.34。)
为了定阶, 可以对\(l=1,2,\dots\)逐一地检验 \(H_0: \boldsymbol\Phi_l = \boldsymbol 0 \leftrightarrow H_a: \boldsymbol\Phi_l \neq \boldsymbol 0\)。
对\(l=1\),要检验 \(H_0: \boldsymbol\Phi_1 = \boldsymbol 0 \leftrightarrow H_a: \boldsymbol\Phi_1 \neq \boldsymbol 0\), 使用检验统计量 \[\begin{aligned} M(1) =& - (T - k - \frac52) \ln \frac{|\hat{\boldsymbol\Sigma}_1|}{|\hat{\boldsymbol\Sigma}_0|} \end{aligned}\] 在一些正则性条件下当\(H_0\)成立时\(M(1)\)渐近服从\(\chi^2(k^2)\)分布,参见(Tiao and Box 1981)。 计算右侧p值。
一般地, 可以通过(26.13)的第\(l-1\)个方程和第\(l\)个方程检验 \(H_0: \boldsymbol\Phi_l = \boldsymbol 0 \leftrightarrow H_a: \boldsymbol\Phi_l \neq \boldsymbol 0\)。 取检验统计量 \[\begin{aligned} M(l) = -(T - l - kl - \frac32) \ln \frac{|\hat{\boldsymbol\Sigma}_l|}{|\hat{\boldsymbol\Sigma}_{l-1}|} \end{aligned}\] 在\(H_0\)下\(M(l)\)渐近服从\(\chi^2(k^2)\)分布, 计算右侧p值。
另一种定阶方法是利用AIC或其它类似的信息准则。 设\(\{ \boldsymbol a_t \}\)是独立同多元正态分布的多元白噪声, 可以用最大似然(ML)方法估计模型, 对于VAR模型, 最小二乘估计\(\hat{\boldsymbol\phi}_0\)和\(\hat{\boldsymbol\Phi}_j\) 与条件最大似然估计等价, 但误差项方差阵\(\boldsymbol\Sigma\)的ML估计为 \[\begin{aligned} \tilde{\boldsymbol\Sigma}_i =& \frac{1}{T} \sum_{t=i+1}^T \hat{\boldsymbol a}_t^{(i)} [\hat{\boldsymbol a}_t^{(i)}]^T \end{aligned}\]
VAR(\(i\))模型在正态假定下的AIC值定义为 \[\begin{aligned} \text{AIC}(i) =& \ln|\tilde{\boldsymbol\Sigma}_i| + \frac{2 k^2 i}{T} \end{aligned}\] 取最终的阶\(p\)使得 \(\text{AIC}(p) = \min_{0 \leq i \leq p_0} \text{AIC}(i)\), 其中\(p_0\)是预先规定的可取的最大阶数。
类似的信息准则还有 \[\begin{aligned} \text{BIC}(i) =& \ln|\tilde{\boldsymbol\Sigma}_i| + \frac{k^2 i \ln T}{T} \\ \text{HQ}(i) =& \ln|\tilde{\boldsymbol\Sigma}_i| + \frac{k^2 i \ln\ln T}{T} \end{aligned}\] HQ准则是Hannan和Quinn(1979)提出的。
这些准则的选择结果不受量纲的影响, 对数据乘以常数\(\lambda\), 结果会使得\(\ln |\tilde{\Sigma}_i|\)固定地增加\(\ln (\lambda^{2k})\)。
26.7.1 英、加、美GDP的VAR建模
考虑英国、加拿大、美国GDP的季度增长率, 时间从1980年第二季度到2011年第二季度。 数据经过季节调整, 来自圣路易斯联邦储备银行的数据库。 GDP是以本国货币百亿为单位, 增长率表示为GDP的对数的差分。
读入数据,计算对数增长率:
##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## year = col_double(),
## mon = col_double(),
## uk = col_double(),
## ca = col_double(),
## us = col_double()
## )ts.gdp3 <- ts(as.matrix(da[,c("uk", "ca", "us")]),
start=c(1980,1), frequency=4)
ts.gdp3r <- diff(log(ts.gdp3))*100三个国家的季度GDP对数增长率的时间序列图:
plot(as.xts(ts.gdp3r), type="l",
multi.panel=TRUE, theme="white",
main="英国、加拿大、美国GDP的季度增长率(%)",
major.ticks="years",
grid.ticks.on = "years")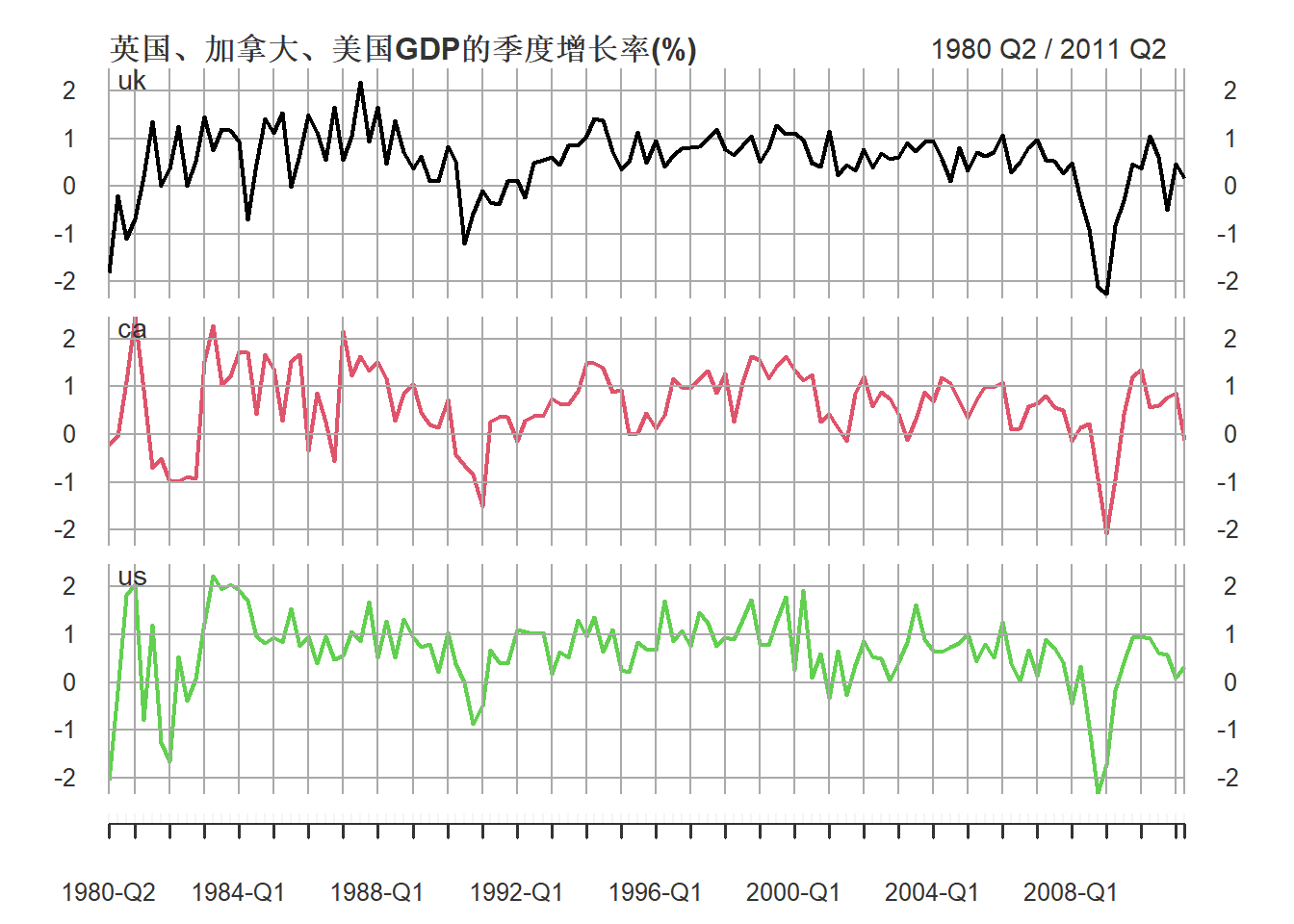
图26.1: 英国、加拿大、美国GDP的季度增长率
利用MTS包的VAR()函数估计VAR(1)模型:
## Constant term:
## Estimates: 0.1713324 0.1182869 0.2785892
## Std.Error: 0.06790162 0.07193106 0.07877173
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.434 0.189 0.0373
## [2,] 0.185 0.245 0.3917
## [3,] 0.322 0.182 0.1674
## standard error
## [,1] [,2] [,3]
## [1,] 0.0811 0.0827 0.0872
## [2,] 0.0859 0.0877 0.0923
## [3,] 0.0940 0.0960 0.1011
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.28933472 0.01965508 0.06619853
## [2,] 0.01965508 0.32469319 0.16862723
## [3,] 0.06619853 0.16862723 0.38938665
##
## det(SSE) = 0.02721916
## AIC = -3.459834
## BIC = -3.256196
## HQ = -3.377107估计VAR(2)模型:
## Constant term:
## Estimates: 0.1258163 0.1231581 0.2895581
## Std.Error: 0.07266338 0.07382941 0.0816888
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.393 0.103 0.0521
## [2,] 0.351 0.338 0.4691
## [3,] 0.491 0.240 0.2356
## standard error
## [,1] [,2] [,3]
## [1,] 0.0934 0.0984 0.0911
## [2,] 0.0949 0.1000 0.0926
## [3,] 0.1050 0.1106 0.1024
## AR( 2 )-matrix
## [,1] [,2] [,3]
## [1,] 0.0566 0.106 0.01889
## [2,] -0.1914 -0.175 -0.00868
## [3,] -0.3120 -0.131 0.08531
## standard error
## [,1] [,2] [,3]
## [1,] 0.0924 0.0876 0.0938
## [2,] 0.0939 0.0890 0.0953
## [3,] 0.1038 0.0984 0.1055
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.28244420 0.02654091 0.07435286
## [2,] 0.02654091 0.29158166 0.13948786
## [3,] 0.07435286 0.13948786 0.35696571
##
## det(SSE) = 0.02258974
## AIC = -3.502259
## BIC = -3.094982
## HQ = -3.336804VAR(1)的AIC为\(-3.46\),VAR(2)的AIC为\(-3.50\), VAR(2)占优。 设\(\boldsymbol r_t\)的三个分量分别是英国、加拿大、美国的GDP对数增长率(单位为百分之一), 得到的模型VAR(2)模型可以写成 \[\begin{aligned} \boldsymbol r_t =& \left(\begin{array}{c} 0.13 \\ 0.12 \\ 0.29 \end{array}\right) + \left(\begin{array}{rrr} 0.39 & 0.10 & 0.05 \\ 0.35 & 0.34 & 0.47 \\ 0.49 & 0.24 & 0.24 \end{array}\right) \boldsymbol r_{t-1} \\ &+ \left(\begin{array}{rrr} 0.06 & 0.11 & 0.02 \\ -0.19 & -0.18 & -0.01 \\ -0.31 & -0.13 & 0.09 \end{array}\right) \boldsymbol r_{t-2} + \boldsymbol a_t \\ \text{Var}(\boldsymbol a_t) =& \left(\begin{array}{rrr} 0.28 & 0.03 & 0.07 \\ 0.03 & 0.29 & 0.14 \\ 0.07 & 0.14 & 0.36 \end{array}\right) \end{aligned}\] 结果中也包括系数的标准误差,可以看出有些系数是不显著的。 比如,三个序列的次序为英国、加拿大、美国, \(\phi_{12}(l)\), \(\phi_{13}(l)\)(\(l=1,2\))都不显著, 说明英国的GDP季度增长率不受加拿大和美国的过去值的影响, 或者粗略地说, 加拿大和美国的GDP季度增长率不是英国的GDP季度增长率的格兰格原因。 更严格的分析应该进行假设检验。
利用MTS包的VARorder函数可以计算VAR定阶的\(M(i)\)统计量检验和各种信息准则:
## selected order: aic = 2
## selected order: bic = 1
## selected order: hq = 1
## Summary table:
## p AIC BIC HQ M(p) p-value
## [1,] 0 -30.9560 -30.9560 -30.9560 0.0000 0.0000
## [2,] 1 -31.8830 -31.6794 -31.8003 115.1329 0.0000
## [3,] 2 -31.9643 -31.5570 -31.7988 23.5389 0.0051
## [4,] 3 -31.9236 -31.3127 -31.6754 10.4864 0.3126
## [5,] 4 -31.8971 -31.0826 -31.5662 11.5767 0.2382
## [6,] 5 -31.7818 -30.7636 -31.3682 2.7406 0.9737
## [7,] 6 -31.7112 -30.4893 -31.2148 6.7822 0.6598
## [8,] 7 -31.6180 -30.1925 -31.0389 4.5469 0.8719
## [9,] 8 -31.7570 -30.1279 -31.0952 24.4833 0.0036
## [10,] 9 -31.6897 -29.8569 -30.9451 6.4007 0.6992
## [11,] 10 -31.5994 -29.5630 -30.7721 4.3226 0.8889
## [12,] 11 -31.6036 -29.3636 -30.6936 11.4922 0.2435
## [13,] 12 -31.6183 -29.1746 -30.6255 11.8168 0.2238
## [14,] 13 -31.6718 -29.0245 -30.5964 14.1266 0.1179从AIC比较来看,应该取\(p=2\)。 从检验来看, 从\(i=3\)阶开始\(\boldsymbol\Phi_i\)就不显著了, 但\(\boldsymbol\Phi_1\)和\(\boldsymbol\Phi_2\)显著, 所以应该取\(p=2\)阶。
○○○○○
还可以用vars包的VAR()函数估计。
估计VAR(1):
##
## VAR Estimation Results:
## =========================
## Endogenous variables: uk, ca, us
## Deterministic variables: const
## Sample size: 124
## Log Likelihood: -304.407
## Roots of the characteristic polynomial:
## 0.7091 0.08735 0.05004
## Call:
## vars::VAR(y = da1, p = 1)
##
##
## Estimation results for equation uk:
## ===================================
## uk = uk.l1 + ca.l1 + us.l1 + const
##
## Estimate Std. Error t value Pr(>|t|)
## uk.l1 0.43435 0.08106 5.358 4.12e-07 ***
## ca.l1 0.18888 0.08275 2.282 0.0242 *
## us.l1 0.03727 0.08716 0.428 0.6697
## const 0.17133 0.06790 2.523 0.0129 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.5468 on 120 degrees of freedom
## Multiple R-Squared: 0.3687, Adjusted R-squared: 0.3529
## F-statistic: 23.36 on 3 and 120 DF, p-value: 5.596e-12
##
##
## Estimation results for equation ca:
## ===================================
## ca = uk.l1 + ca.l1 + us.l1 + const
##
## Estimate Std. Error t value Pr(>|t|)
## uk.l1 0.18499 0.08587 2.154 0.0332 *
## ca.l1 0.24475 0.08766 2.792 0.0061 **
## us.l1 0.39166 0.09233 4.242 4.38e-05 ***
## const 0.11829 0.07193 1.644 0.1027
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.5792 on 120 degrees of freedom
## Multiple R-Squared: 0.4685, Adjusted R-squared: 0.4552
## F-statistic: 35.26 on 3 and 120 DF, p-value: < 2.2e-16
##
##
## Estimation results for equation us:
## ===================================
## us = uk.l1 + ca.l1 + us.l1 + const
##
## Estimate Std. Error t value Pr(>|t|)
## uk.l1 0.32153 0.09404 3.419 0.000859 ***
## ca.l1 0.18196 0.09600 1.895 0.060438 .
## us.l1 0.16740 0.10111 1.656 0.100410
## const 0.27859 0.07877 3.537 0.000577 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.6343 on 120 degrees of freedom
## Multiple R-Squared: 0.3044, Adjusted R-squared: 0.287
## F-statistic: 17.5 on 3 and 120 DF, p-value: 1.725e-09
##
##
##
## Covariance matrix of residuals:
## uk ca us
## uk 0.29898 0.02031 0.06841
## ca 0.02031 0.33552 0.17425
## us 0.06841 0.17425 0.40237
##
## Correlation matrix of residuals:
## uk ca us
## uk 1.00000 0.06413 0.1972
## ca 0.06413 1.00000 0.4742
## us 0.19722 0.47424 1.0000与MTS::VAR()的输出格式不同,
vars::VAR()对每个分量单独输出其方程,
好处是用我们熟悉的格式显示估计值、标准误差、检验统计量和p值。
得到的模型与MTS::VAR()结果相同,
白噪声方差估计略有差别。
用AIC自动选择阶,指定ic="AIC"和lag.max=5:
##
## VAR Estimation Results:
## =========================
## Endogenous variables: uk, ca, us
## Deterministic variables: const
## Sample size: 121
## Log Likelihood: -252.647
## Roots of the characteristic polynomial:
## 0.785 0.7516 0.7516 0.7336 0.7336 0.6144 0.6144 0.5679 0.5679 0.5165 0.5122 0.5122
## Call:
## vars::VAR(y = da1, lag.max = 5, ic = "AIC")
##
##
## Estimation results for equation uk:
## ===================================
## uk = uk.l1 + ca.l1 + us.l1 + uk.l2 + ca.l2 + us.l2 + uk.l3 + ca.l3 + us.l3 + uk.l4 + ca.l4 + us.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## uk.l1 0.515685 0.095298 5.411 3.8e-07 ***
## ca.l1 0.071863 0.094459 0.761 0.44844
## us.l1 0.063904 0.088668 0.721 0.47264
## uk.l2 -0.050370 0.101228 -0.498 0.61979
## ca.l2 0.160043 0.098620 1.623 0.10754
## us.l2 -0.001984 0.095495 -0.021 0.98346
## uk.l3 0.052363 0.102949 0.509 0.61205
## ca.l3 -0.278830 0.098341 -2.835 0.00547 **
## us.l3 0.141145 0.093728 1.506 0.13501
## uk.l4 0.040130 0.091050 0.441 0.66028
## ca.l4 0.261731 0.086947 3.010 0.00325 **
## us.l4 -0.246485 0.088234 -2.794 0.00617 **
## const 0.147957 0.074786 1.978 0.05043 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.5013 on 108 degrees of freedom
## Multiple R-Squared: 0.478, Adjusted R-squared: 0.42
## F-statistic: 8.242 on 12 and 108 DF, p-value: 7.84e-11
##
##
## Estimation results for equation ca:
## ===================================
## ca = uk.l1 + ca.l1 + us.l1 + uk.l2 + ca.l2 + us.l2 + uk.l3 + ca.l3 + us.l3 + uk.l4 + ca.l4 + us.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## uk.l1 0.37782 0.10199 3.705 0.000336 ***
## ca.l1 0.31603 0.10109 3.126 0.002276 **
## us.l1 0.40963 0.09489 4.317 3.52e-05 ***
## uk.l2 -0.17399 0.10834 -1.606 0.111193
## ca.l2 -0.25407 0.10554 -2.407 0.017771 *
## us.l2 0.06295 0.10220 0.616 0.539247
## uk.l3 0.09615 0.11018 0.873 0.384757
## ca.l3 0.12035 0.10525 1.143 0.255362
## us.l3 0.01366 0.10031 0.136 0.891925
## uk.l4 0.07470 0.09744 0.767 0.445006
## ca.l4 -0.09031 0.09305 -0.971 0.333959
## us.l4 -0.09781 0.09443 -1.036 0.302622
## const 0.07757 0.08004 0.969 0.334593
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.5365 on 108 degrees of freedom
## Multiple R-Squared: 0.5661, Adjusted R-squared: 0.5179
## F-statistic: 11.74 on 12 and 108 DF, p-value: 8.189e-15
##
##
## Estimation results for equation us:
## ===================================
## us = uk.l1 + ca.l1 + us.l1 + uk.l2 + ca.l2 + us.l2 + uk.l3 + ca.l3 + us.l3 + uk.l4 + ca.l4 + us.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## uk.l1 0.51905 0.10938 4.745 6.41e-06 ***
## ca.l1 0.17304 0.10841 1.596 0.1134
## us.l1 0.15039 0.10177 1.478 0.1424
## uk.l2 -0.21784 0.11618 -1.875 0.0635 .
## ca.l2 -0.15931 0.11319 -1.407 0.1622
## us.l2 0.22561 0.10960 2.058 0.0420 *
## uk.l3 0.04783 0.11816 0.405 0.6864
## ca.l3 -0.07856 0.11287 -0.696 0.4879
## us.l3 0.07384 0.10758 0.686 0.4939
## uk.l4 0.15409 0.10450 1.475 0.1433
## ca.l4 -0.15182 0.09979 -1.521 0.1311
## us.l4 -0.05350 0.10127 -0.528 0.5984
## const 0.23868 0.08584 2.781 0.0064 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.5754 on 108 degrees of freedom
## Multiple R-Squared: 0.4531, Adjusted R-squared: 0.3923
## F-statistic: 7.457 on 12 and 108 DF, p-value: 7.522e-10
##
##
##
## Covariance matrix of residuals:
## uk ca us
## uk 0.25130 0.04912 0.1001
## ca 0.04912 0.28783 0.1084
## us 0.10009 0.10840 0.3310
##
## Correlation matrix of residuals:
## uk ca us
## uk 1.0000 0.1826 0.3470
## ca 0.1826 1.0000 0.3512
## us 0.3470 0.3512 1.0000结果选择了4阶模型,
与MTS::VARorder()结果不同。
vars包的SVAR()函数可以用来估计VAR的结构形式,
但其定义不同于我们教材的定义。
○○○○○
26.8 模型检验
可以计算模型残差,
对残差进行多元白噪声检验(多元混成检验)。
残差的多元混成检验因为使用了估计的参数,
所以统计量的自由度会减少\(k^2 p\),
这是系数矩阵\(\boldsymbol\Phi_j\), \(j=1,2,\dots,p\)中的参数个数。
如果系数矩阵中某些参数固定为0,
应按无约束的参数个数计算要扣除的自由度。
在MTS包的mq()函数中用adj=指定需要减少的自由度。
例3.2 对例3.1的三个国家的GDP季度增速建模, VAR(2)模型的残差的多元混成检验程序如下:
## Ljung-Box Statistics:
## m Q(m) df p-value
## [1,] 1.000 0.816 -9.000 1.00
## [2,] 2.000 3.978 0.000 1.00
## [3,] 3.000 16.665 9.000 0.05
## [4,] 4.000 35.122 18.000 0.01
## [5,] 5.000 38.189 27.000 0.07
## [6,] 6.000 41.239 36.000 0.25
## [7,] 7.000 47.621 45.000 0.37
## [8,] 8.000 61.677 54.000 0.22
## [9,] 9.000 67.366 63.000 0.33
## [10,] 10.000 76.930 72.000 0.32
## [11,] 11.000 81.567 81.000 0.46
## [12,] 12.000 93.112 90.000 0.39
## [13,] 13.000 105.327 99.000 0.31
## [14,] 14.000 116.279 108.000 0.28
## [15,] 15.000 128.974 117.000 0.21
## [16,] 16.000 134.704 126.000 0.28
## [17,] 17.000 138.552 135.000 0.40
## [18,] 18.000 146.256 144.000 0.43
## [19,] 19.000 162.418 153.000 0.29
## [20,] 20.000 171.948 162.000 0.28
## [21,] 21.000 174.913 171.000 0.40
## [22,] 22.000 182.056 180.000 0.44
## [23,] 23.000 190.276 189.000 0.46
## [24,] 24.000 202.141 198.000 0.41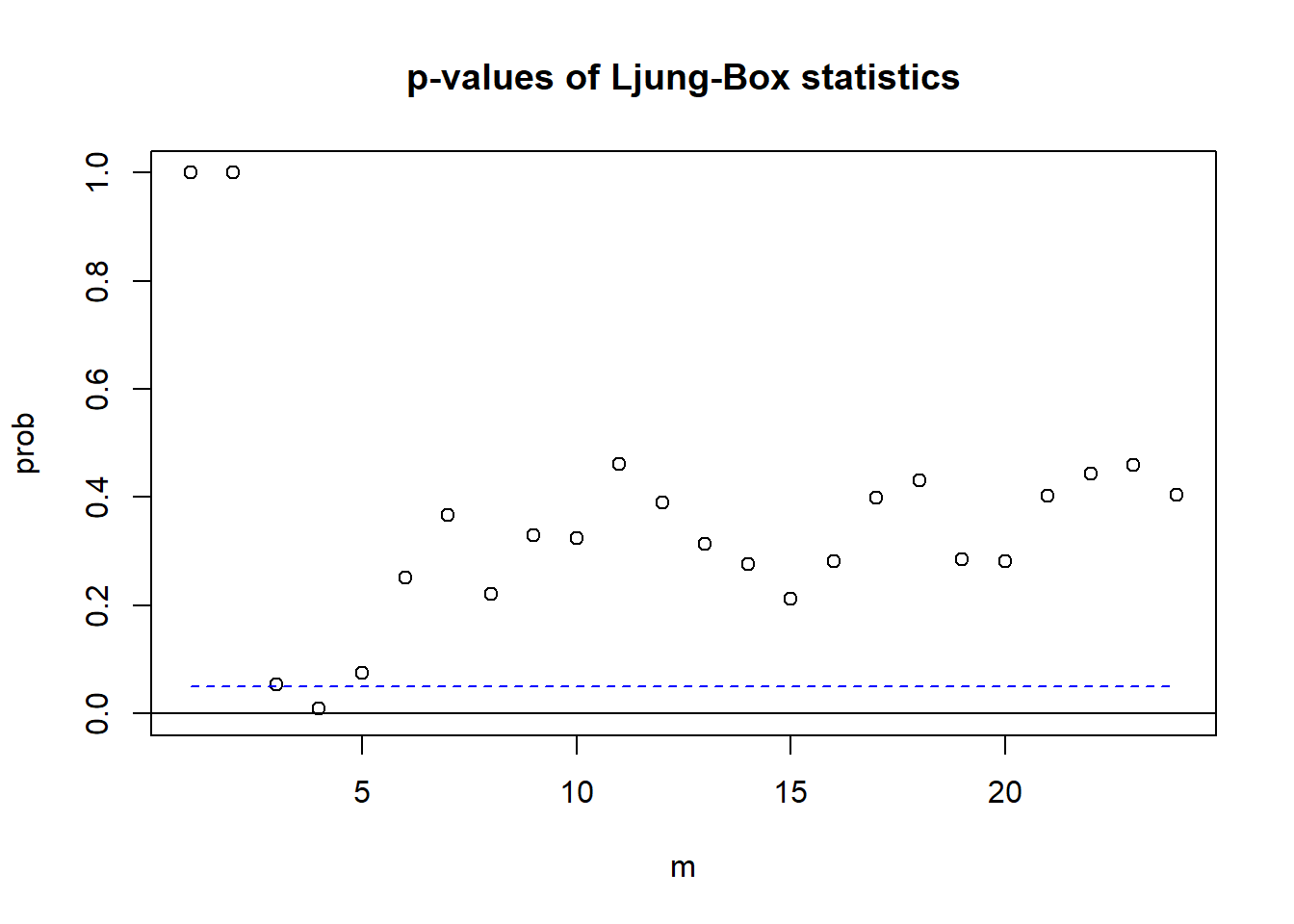
检验结果只有在滞后4显著, 基本可以认为模型是充分的。
对残差还可以进行异方差等检验。
26.9 模型简化
当VAR中分量个数\(k\)较大时, 模型有许多参数, 系数矩阵中参数个数为\(k^2 p\)个。 如果没有先验知识要求参数非零, 可以将不显著的参数约束为零再估计。
模型简化没有公认的最优做法。
一种办法是计算参数估计值与标准误差的比值,
称为t比值,
将t比值绝对值小于1.645(相当于0.10检验水平)或者小于1.96(相当于0.05检验水平)的系数设置为零。
MTS包的refVAR()函数输入无约束的VAR建模结果,
以及thres=1.645或thres=1.96这样的t比值界限,
生成设置部分系数为零的约束估计结果,
得到精简的模型。
可以通过AIC比较完全模型和约束模型。
例3.3 对三个国家的GDP对数增长率的VAR(2)模型进行化简。
## ================ Full model:## Constant term:
## Estimates: 0.1258163 0.1231581 0.2895581
## Std.Error: 0.07266338 0.07382941 0.0816888
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.393 0.103 0.0521
## [2,] 0.351 0.338 0.4691
## [3,] 0.491 0.240 0.2356
## standard error
## [,1] [,2] [,3]
## [1,] 0.0934 0.0984 0.0911
## [2,] 0.0949 0.1000 0.0926
## [3,] 0.1050 0.1106 0.1024
## AR( 2 )-matrix
## [,1] [,2] [,3]
## [1,] 0.0566 0.106 0.01889
## [2,] -0.1914 -0.175 -0.00868
## [3,] -0.3120 -0.131 0.08531
## standard error
## [,1] [,2] [,3]
## [1,] 0.0924 0.0876 0.0938
## [2,] 0.0939 0.0890 0.0953
## [3,] 0.1038 0.0984 0.1055
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.28244420 0.02654091 0.07435286
## [2,] 0.02654091 0.29158166 0.13948786
## [3,] 0.07435286 0.13948786 0.35696571
##
## det(SSE) = 0.02258974
## AIC = -3.502259
## BIC = -3.094982
## HQ = -3.336804##
##
## ================ Restricted model:## Constant term:
## Estimates: 0.1628247 0 0.2827525
## Std.Error: 0.06814101 0 0.07972864
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.467 0.207 0.000
## [2,] 0.334 0.270 0.496
## [3,] 0.468 0.225 0.232
## standard error
## [,1] [,2] [,3]
## [1,] 0.0790 0.0686 0.0000
## [2,] 0.0921 0.0875 0.0913
## [3,] 0.1027 0.0963 0.1023
## AR( 2 )-matrix
## [,1] [,2] [,3]
## [1,] 0.000 0 0
## [2,] -0.197 0 0
## [3,] -0.301 0 0
## standard error
## [,1] [,2] [,3]
## [1,] 0.0000 0 0
## [2,] 0.0921 0 0
## [3,] 0.1008 0 0
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.29003669 0.01803456 0.07055856
## [2,] 0.01803456 0.30802503 0.14598345
## [3,] 0.07055856 0.14598345 0.36268779
##
## det(SSE) = 0.02494104
## AIC = -3.531241
## BIC = -3.304976
## HQ = -3.439321无约束的VAR(2)的AIC值为\(-3.50\), 约束9个参数为零的VAR(2)的AIC值为\(-3.53\), 所以约束模型较优。 约束模型为 \[\begin{aligned} \boldsymbol r_t =& \left(\begin{array}{c} 0.16 \\ 0 \\ 0.29 \end{array}\right) + \left(\begin{array}{rrr} 0.47 & 0.21 & 0 \\ 0.33 & 0.27 & 0.50 \\ 0.47 & 0.23 & 0.23 \end{array}\right) \boldsymbol r_{t-1} \\ &+ \left(\begin{array}{rrr} 0 & 0 & 0 \\ -0.20 & 0 & 0 \\ -0.30 & 0 & 0 \end{array}\right) \boldsymbol r_{t-2} + \boldsymbol a_t \\ \text{Var}(\boldsymbol a_t) =& \left(\begin{array}{rrr} 0.29 & 0.02 & 0.07 \\ 0.02 & 0.31 & 0.15 \\ 0.07 & 0.15 & 0.36 \end{array}\right) \end{aligned}\]
对这个简化的模型的检验,
可以提取残差后用MTS::mq()函数检验,
这时自由度缩减个数由原来的\(3^2 \times 2=18\)个,
减少到\(18-8 = 10\)个,
因为模型中约束了8个系数矩阵元素等于零。
MTS包还提供了一个MTSdiag()函数,
输入模型结果和adj=自由度缩减个数,
作残差的CCM估计表、图和残差的多元混成检验:
## [1] "Covariance matrix:"
## uk ca us
## uk 0.2924 0.0182 0.0711
## ca 0.0182 0.3084 0.1472
## us 0.0711 0.1472 0.3657
## CCM at lag: 0
## [,1] [,2] [,3]
## [1,] 1.0000 0.0605 0.218
## [2,] 0.0605 1.0000 0.438
## [3,] 0.2175 0.4382 1.000
## Simplified matrix:
## CCM at lag: 1
## . . .
## . . .
## . . .
## CCM at lag: 2
## . . .
## . . .
## . . .
## CCM at lag: 3
## . . .
## . . .
## . . .
## CCM at lag: 4
## . . -
## . . .
## . . .
## CCM at lag: 5
## . . .
## . . .
## . . .
## CCM at lag: 6
## . . .
## . . .
## . . .
## CCM at lag: 7
## . . .
## . . .
## . . .
## CCM at lag: 8
## . . .
## . . .
## . . .
## CCM at lag: 9
## . . .
## . . .
## . . .
## CCM at lag: 10
## . . .
## . . .
## . . .
## CCM at lag: 11
## . . .
## . . .
## . . .
## CCM at lag: 12
## . . .
## . . .
## . . .
## CCM at lag: 13
## . - .
## . . .
## . . .
## CCM at lag: 14
## . - .
## . . .
## . . .
## CCM at lag: 15
## . + .
## . . .
## . . .
## CCM at lag: 16
## . . .
## . . .
## . . .
## CCM at lag: 17
## . . .
## . . .
## . . .
## CCM at lag: 18
## . . .
## . . .
## . . .
## CCM at lag: 19
## . . .
## . . +
## . . .
## CCM at lag: 20
## . . .
## . . .
## . . .
## CCM at lag: 21
## . . .
## . . .
## . . .
## CCM at lag: 22
## . . .
## . . .
## . . .
## CCM at lag: 23
## . . .
## . . .
## . . .
## CCM at lag: 24
## . . .
## . . .
## . . .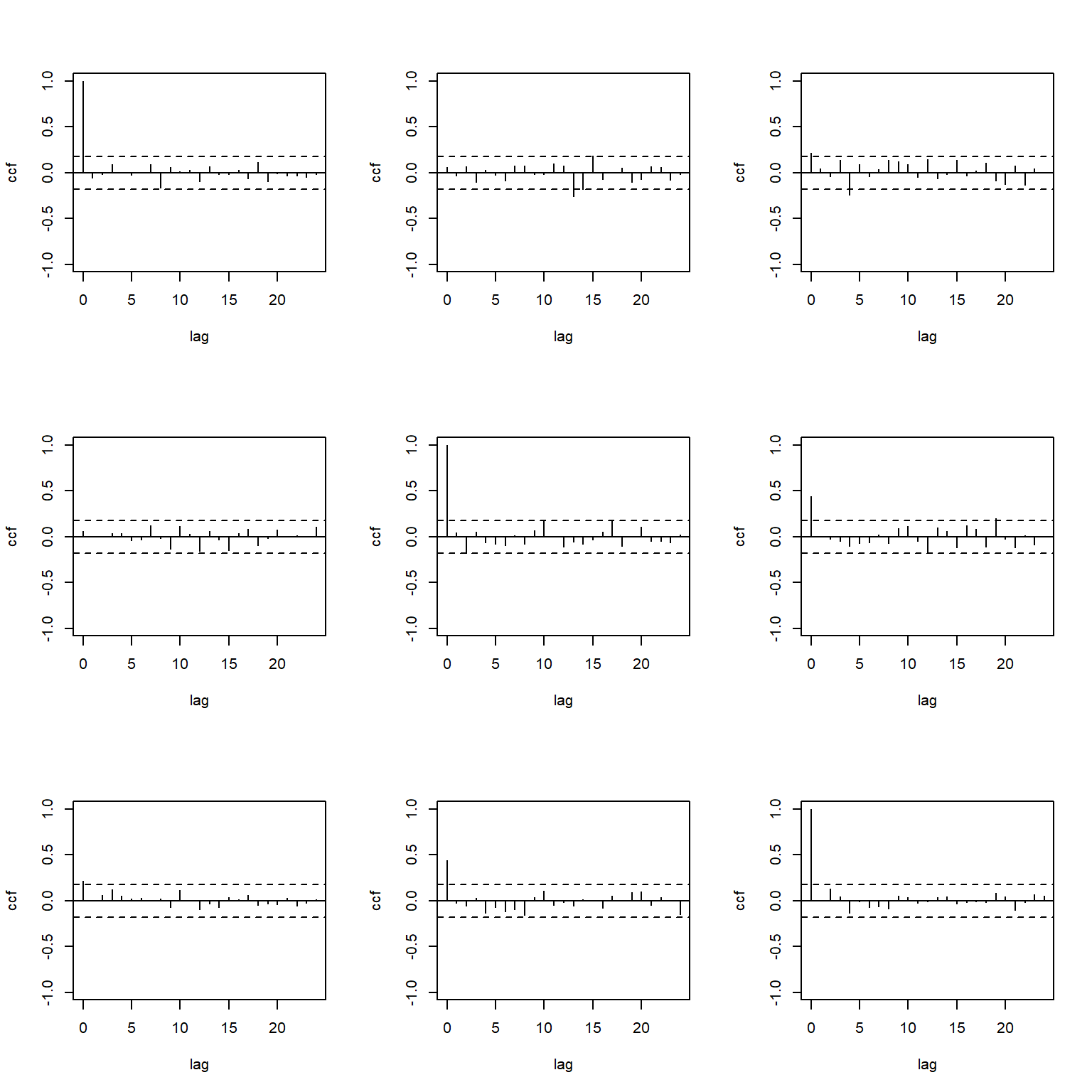
## Hit Enter for p-value plot of individual ccm: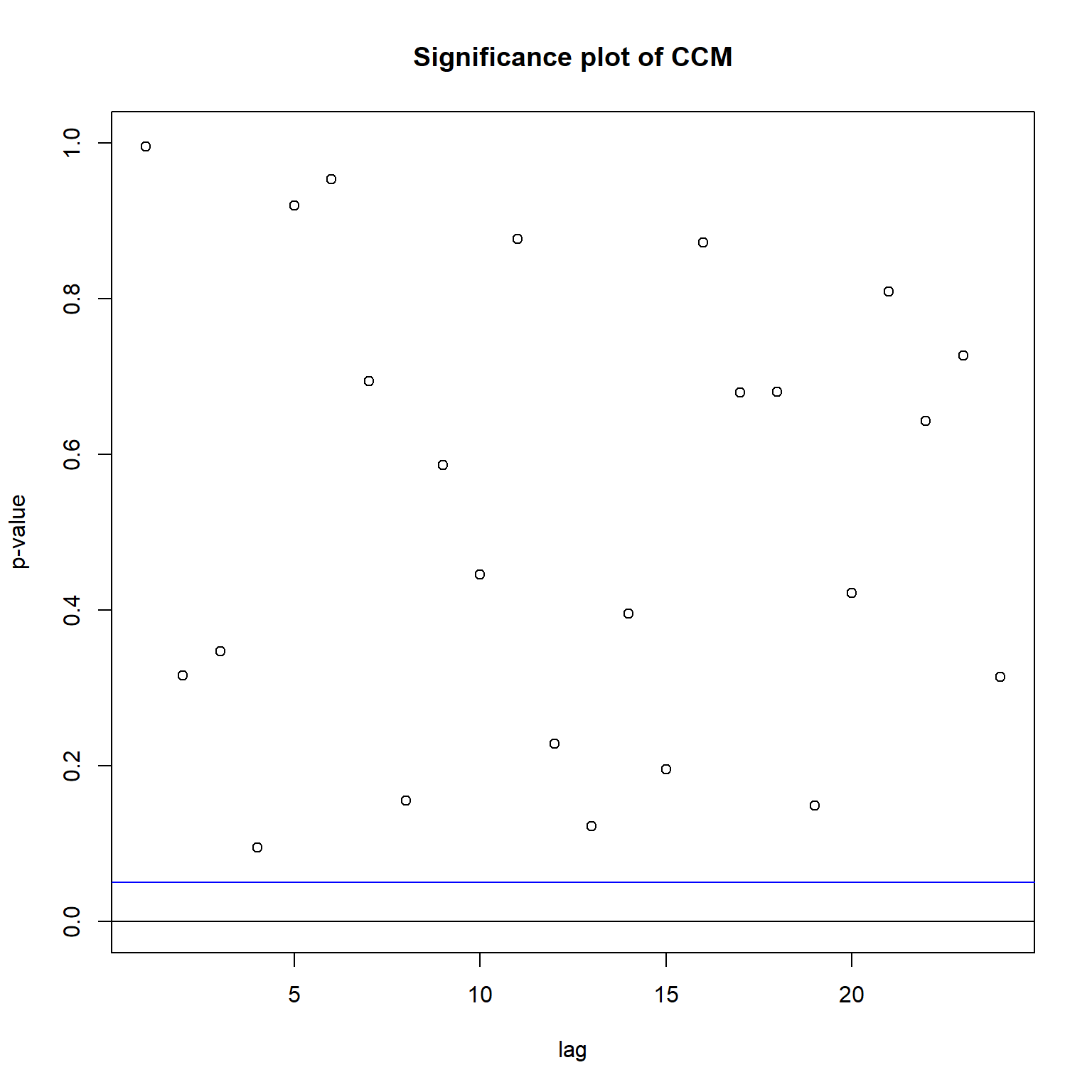
## Hit Enter to compute MQ-statistics:
##
## Ljung-Box Statistics:
## m Q(m) df p-value
## [1,] 1.00 1.78 -1.00 1.00
## [2,] 2.00 12.41 8.00 1.00
## [3,] 3.00 22.60 17.00 0.16
## [4,] 4.00 37.71 26.00 0.06
## [5,] 5.00 41.65 35.00 0.20
## [6,] 6.00 44.95 44.00 0.43
## [7,] 7.00 51.50 53.00 0.53
## [8,] 8.00 64.87 62.00 0.38
## [9,] 9.00 72.50 71.00 0.43
## [10,] 10.00 81.58 80.00 0.43
## [11,] 11.00 86.12 89.00 0.57
## [12,] 12.00 98.08 98.00 0.48
## [13,] 13.00 112.31 107.00 0.34
## [14,] 14.00 121.89 116.00 0.34
## [15,] 15.00 134.58 125.00 0.26
## [16,] 16.00 139.16 134.00 0.36
## [17,] 17.00 145.85 143.00 0.42
## [18,] 18.00 152.56 152.00 0.47
## [19,] 19.00 165.91 161.00 0.38
## [20,] 20.00 175.22 170.00 0.38
## [21,] 21.00 180.56 179.00 0.45
## [22,] 22.00 187.40 188.00 0.50
## [23,] 23.00 193.78 197.00 0.55
## [24,] 24.00 204.65 206.00 0.51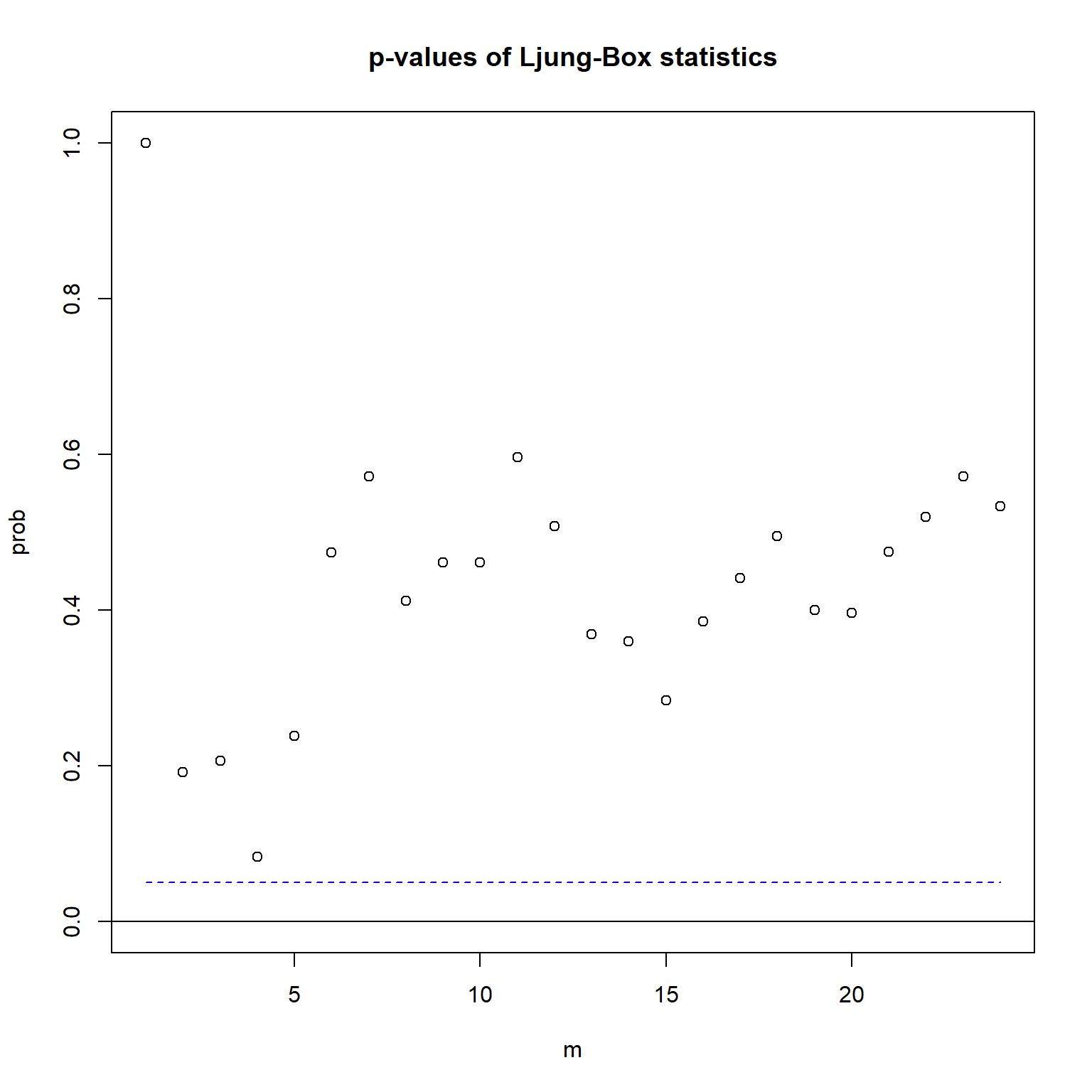
## Hit Enter to obtain residual plots: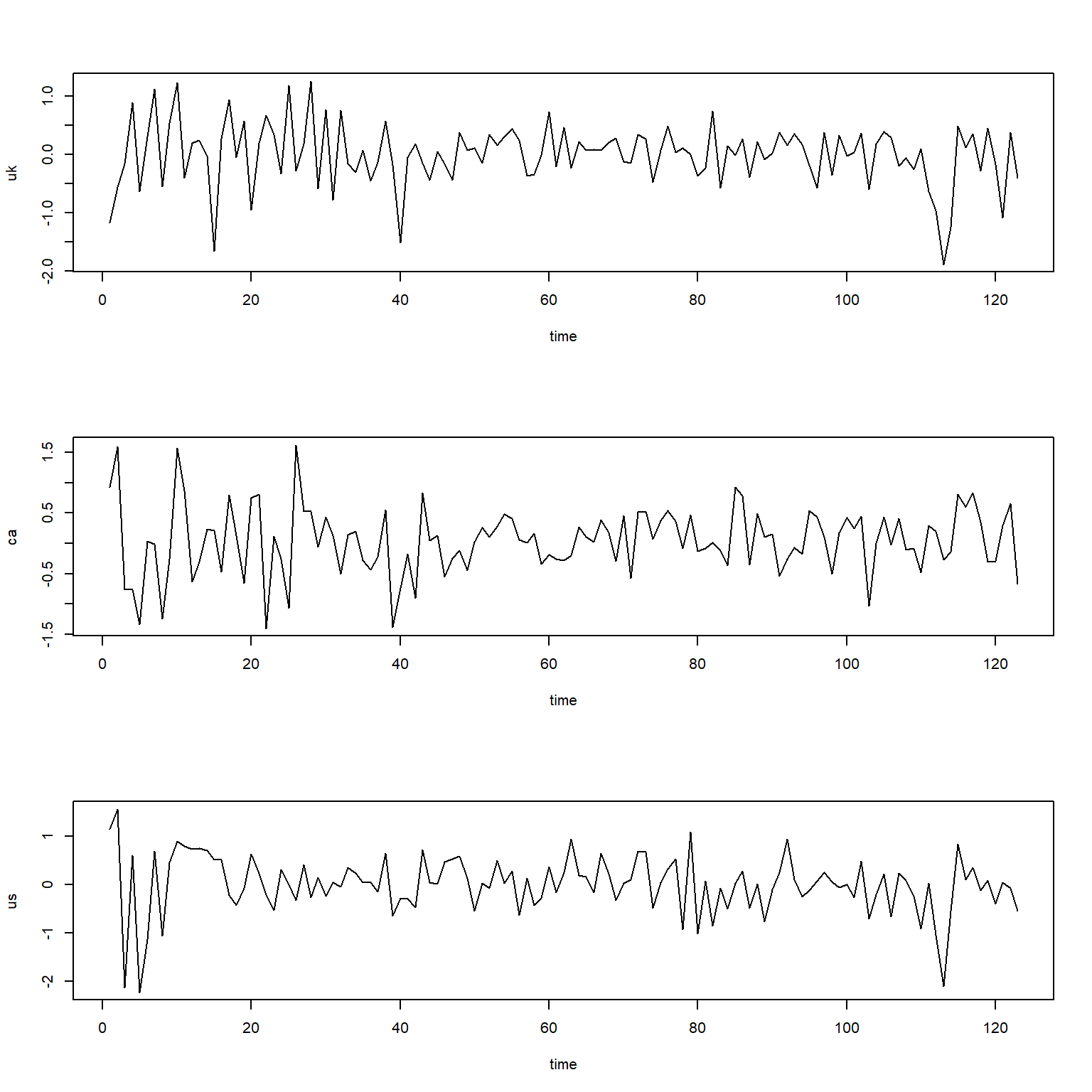
从残差的CCM和多元混成检验结果来看, 约束的模型是充分的。
注:蔡教授的多元金融时间序列专著中, 残差混成检验时调整的自由度是\(k^2 p\)还是\(k^2 p + k\), 没有讲得很清楚。 在§2.7.2(P.52)说明要调整的自由度是\(k^2 p\), 但是在§2.7.3(P.57)的例子中, 调整后的自由度为\(9m-12\), 这里扣除的12个自由度加上约束的9个零参数, 是21个参数,包括了\(\boldsymbol\phi_0\)部分。
从简化模型可以得到三国的GDP季度对数增长率服从如下的模型: \[\begin{aligned} \text{英国:}& r_{1t} = 0.16 + 0.47 r_{1,t-1} + 0.21 r_{2,t-1} + a_{1t} \\ \text{加拿大:}& r_{2t} = 0.33 r_{1,t-1} + 0.27 r_{2,t-1} + 0.50 r_{3,t-1} -0.20 r_{1,t-2} + a_{2t} \\ \text{美国:}& r_{3t} = 0.28 + 0.47 r_{1,t-1} + 0.23 r_{2,t-1} + 0.23 r_{3,t-1} -0.30 r_{1,t-2} + a_{3t} \end{aligned}\]
残差的相关阵为: \[\begin{aligned} \hat{\boldsymbol\rho}_0 =& \left(\begin{array}{rrr} 1.00 & 0.06 & 0.22 \\ 0.06 & 1.00 & 0.44 \\ 0.22 & 0.44 & 1.00 \end{array}\right) \end{aligned}\]
残差的相关阵计算程序:
## [,1] [,2] [,3]
## [1,] 1.00000000 0.06054285 0.2175489
## [2,] 0.06054285 1.00000000 0.4382489
## [3,] 0.21754885 0.43824891 1.000000026.10 基于VAR模型的格兰杰因果性检验
如果模型可以简化为某些代表格兰杰因果性的系数等于零, 则可以据此进行格兰杰因果性的检验。 在二元的VAR(1)模型中, 如果约束\(\phi_{12}(1)=0\)后的模型与无约束模型没有显著差异, 则\(r_{2t}\)不是\(r_{1t}\)的格兰杰原因。 \(p\)阶以及\(k\)元的情形类似。
为了比较无约束与约束的模型, 使用对数似然比检验, 得到的统计量在约束参数等于零的零假设下渐近服从卡方分布。
MTS包中GrangerTest()函数执行格兰杰因果性检验,
默认第一个分量为单向的格兰杰原因,
零假设表示预测第一分量时不需要利用其它分量的历史值。
可以用locInput=序号指定哪一个或者哪几个分量作为被预报的分量。
用基于VAR的方法检验格兰杰因果性,
局限是各分量也必须平稳,
不支持协整模型。
例3.4
检验美国的GDP季度增长率是不是英国和加拿大的增长率的单向格兰杰原因。
library(MTS, quietly = TRUE, warn.conflicts=FALSE)
Z <- coredata(as.xts(ts.gdp3r))
GrangerTest(Z, p=2, locInput=3)## Number of targeted zero parameters: 4
## Chi-square test for Granger Causality and p-value: 27.2262 1.789152e-05美国是第3个分量, 零假设为 \[ H_0: \phi_{31}(1) = \phi_{32}(1) = \phi_{31}(2) = \phi_{32}(2) = 0, \] 即预报\(x_{3t}\)时不需要用到\(x_{1,t-1}\), \(x_{2,t-1}\), \(x_{1,t-2}\), \(x_{2,t-2}\)。 结果p值小于0.05, 拒绝\(H_0\), 说明英国和加拿大是美国的格兰杰原因, 从而美国的GDP季度增长率不是英国和加拿大的增长率的单向格兰杰原因。
对加拿大进行检验:
## Number of targeted zero parameters: 4
## Chi-square test for Granger Causality and p-value: 48.83871 6.309173e-10检验结果显著, 所以美国和英国是加拿大的格兰杰原因, 从而加拿大不是美国、英国的单向格兰格原因。
对英国进行检验:
## Number of targeted zero parameters: 4
## Chi-square test for Granger Causality and p-value: 8.948851 0.06239076
## Constant term:
## Estimates: 0.2104448 0.1231581 0.2895581
## Std.Error: 0.06685632 0.07382941 0.0816888
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.473 0.000 0.000
## [2,] 0.351 0.338 0.469
## [3,] 0.491 0.240 0.236
## standard error
## [,1] [,2] [,3]
## [1,] 0.0899 0.000 0.0000
## [2,] 0.0949 0.100 0.0926
## [3,] 0.1050 0.111 0.1024
## AR( 2 )-matrix
## [,1] [,2] [,3]
## [1,] 0.151 0.000 0.00000
## [2,] -0.191 -0.175 -0.00868
## [3,] -0.312 -0.131 0.08531
## standard error
## [,1] [,2] [,3]
## [1,] 0.0859 0.0000 0.0000
## [2,] 0.0939 0.0890 0.0953
## [3,] 0.1038 0.0984 0.1055
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.30423344 0.02654091 0.07435286
## [2,] 0.02654091 0.29158166 0.13948786
## [3,] 0.07435286 0.13948786 0.35696571
##
## det(SSE) = 0.02443371
## AIC = -3.487791
## BIC = -3.17102
## HQ = -3.359104结果不显著,说明预测英国时不需要用到加拿大和美国的历史值, 结合前两个检验, 就说明了英国是加拿大和美国的单向格兰杰原因。 第三个检验结果中还给出了约束系数等于零的模型估计结果, 其中等于0的系数恰好是用加拿大、美国的历史值预测英国当前值的系数。
26.11 预测
若VAR(\(p\))模型已知, 满足平稳性条件, 设\(\{ \boldsymbol a_t \}\)是独立的弱平稳时间序列。 用\(F_t\)表示截止到\(t\)时刻为止的\(\boldsymbol r_s, s \leq t\)所包含的信息, 则\(E(\boldsymbol a_t | F_{t-1}) = 0\)。 基于\(t\)时刻的信息进行超前\(l\)步预测, 预测为 \[\begin{aligned} \boldsymbol r_t(l) =& E(\boldsymbol r_{t+l} | F_t) \end{aligned}\]
当\(l=1\)时 \[\begin{aligned} \boldsymbol r_t(1) = \boldsymbol\phi_0 + \boldsymbol\Phi_1 \boldsymbol r_{t} + \dots + \boldsymbol\Phi_p \boldsymbol r_{t+1-p} \end{aligned}\] 当\(l=2\)时 \[\begin{aligned} \boldsymbol r_t(2) =& E(\boldsymbol r_{t+2} | F_t) \\ =& \boldsymbol\phi_0 + \boldsymbol\Phi_1 E(\boldsymbol r_{t+1} | F_t) + \boldsymbol\Phi_2 \boldsymbol r_{t} + \dots + \boldsymbol\Phi_p \boldsymbol r_{t+2-p} \end{aligned}\]
若记 \[\begin{aligned} \boldsymbol r_t(l) = \begin{cases} E(\boldsymbol r_{t+l} | F_t), & l > 0 \\ \boldsymbol r_{t+l}, & l \leq 0 \end{cases} \end{aligned}\] 则超前\(l\)步预报可以写成 \[\begin{aligned} \boldsymbol r_t(l) =& E(r_{t+l} | F_t) = \boldsymbol\phi_0 + \sum_{j=1}^p \boldsymbol\Phi_j \boldsymbol r_t(l-j) \end{aligned}\] 可见超前多步预测可以递推地计算。
对于满足平稳性条件的VAR(\(p\))模型, 可以证明 \[\begin{aligned} \lim_{l\to\infty} \boldsymbol r_t(l) = \boldsymbol\mu = E \boldsymbol r_t \end{aligned}\] 即VAR(\(p\))的预测具有均值回归性。 均值回归速度由特征多项式\(|P(z)|\)的最接近单位圆的根的模与1的接近程度决定, 根越接近单位圆,均值回归越慢。
\(l\)步超前预测误差为 \[\begin{aligned} \boldsymbol e_t(l) = \boldsymbol r_{t+l} - \boldsymbol r_t(l) = \boldsymbol r_{t+l} - E(\boldsymbol r_{t+l} | F_t) \end{aligned}\]
为了研究预测误差方差阵, 最好利用VAR的无穷阶MA表示。
类似一元情形, VAR(\(p\))模型可以写成一个无穷阶MA形式 \[\begin{align} \boldsymbol r_t = \boldsymbol\mu + \sum_{l=0}^\infty \boldsymbol\Psi_l \boldsymbol a_{t-l} \tag{26.14} \end{align}\] 其中\(\boldsymbol\Psi_0=I\), \(\boldsymbol\mu = [P(1)]^{-1}\)(假定\([P(1)]^{-1}\)存在), 系数矩阵\(\boldsymbol\Psi_l\)可以通过下式使得方程两边\(z\)的同次项相等求解: \[\begin{aligned} (\boldsymbol I - \boldsymbol\Phi_1 z - \dots - \boldsymbol\Phi_p z^p) (\boldsymbol I + \boldsymbol\Psi_1 z + \boldsymbol\Psi z^2 + \dots) = \boldsymbol I \end{aligned}\]
易见 \[\begin{aligned} \boldsymbol e_t(l) = \boldsymbol a_{t+l} + \boldsymbol\Psi_1 a_{t+l-1} + \dots + \boldsymbol\Psi_{l-1} a_{t+1} \end{aligned}\] 从而 \[\begin{aligned} \text{Var}(\boldsymbol e_t(1)) =& \boldsymbol\Sigma \\ \text{Var}(\boldsymbol e_t(l)) =& \boldsymbol\Sigma + \sum_{j=1}^{l-1} \boldsymbol\Psi_j \boldsymbol\Sigma \boldsymbol\Psi_j^T \\ =& \text{Var}(\boldsymbol e_t(l-1)) + \boldsymbol\Psi_{l-1} \boldsymbol\Sigma \boldsymbol\Psi_{l-1}^T, \ l=2,3,\dots \end{aligned}\]
当\(l\to\infty\)时 \[\begin{aligned} \text{Var}(\boldsymbol e_t(l)) \to \sum_{j=0}^\infty \boldsymbol\Psi_j \boldsymbol\Sigma \boldsymbol\Psi_j^T = \text{Var}(\boldsymbol r_t) \end{aligned}\] 这一点与均值回归性质吻合。
如果模型是从数据中估计得到的, 则点预测仍利用相同的公式, 将估计参数代入即可: \[\begin{aligned} \boldsymbol r_t(1) =& \hat{\boldsymbol\phi}_0 + \hat{\boldsymbol\Phi}_1 \boldsymbol r_{t} + \dots + \hat{\boldsymbol\Phi}_p \boldsymbol r_{t+1-p} \\ \boldsymbol r_t(l) =& \hat{\boldsymbol\phi}_0 + \hat{\boldsymbol\Phi}_1 \boldsymbol r_t(l-1) + \dots + \hat{\boldsymbol\Phi}_p \boldsymbol r_t(l-p) \\ \end{aligned}\]
预测误差的估计还要考虑到参数估计带来的误差, 比较复杂,参见(Tsay 2014) §2.9.2。
MTS包的VARpred()函数可以从VAR的建模结果计算点预测值,
不考虑参数估计误差的预测标准误差(Standard errors of predictions),
考虑参数估计误差的预测标准误差(Root mean squared errors of predictions)。
例3.5
例3.1中建立的三个国家的GDP增速的VAR(2)模型是基于1980年第二季度到2011年第二季度的数据, 用建立的模型进行超前1到8步预测。 第一个预测对应2011年第三季度, 最后一个预测对应2013年第二季度。
## orig 125
## Forecasts at origin: 125
## uk ca us
## [1,] 0.3129 0.05166 0.1660
## [2,] 0.2647 0.31687 0.4889
## [3,] 0.3143 0.48231 0.5205
## [4,] 0.3839 0.53053 0.5998
## [5,] 0.4412 0.56978 0.6297
## [6,] 0.4799 0.59478 0.6530
## [7,] 0.5068 0.60967 0.6630
## [8,] 0.5247 0.61689 0.6688
## Standard Errors of predictions:
## [,1] [,2] [,3]
## [1,] 0.5315 0.5400 0.5975
## [2,] 0.5804 0.7165 0.7077
## [3,] 0.6202 0.7672 0.7345
## [4,] 0.6484 0.7785 0.7442
## [5,] 0.6629 0.7824 0.7475
## [6,] 0.6692 0.7838 0.7484
## [7,] 0.6719 0.7842 0.7486
## [8,] 0.6729 0.7843 0.7487
## Root mean square errors of predictions:
## [,1] [,2] [,3]
## [1,] 0.5461 0.5549 0.6140
## [2,] 0.6001 0.7799 0.7499
## [3,] 0.6365 0.7879 0.7456
## [4,] 0.6601 0.7832 0.7484
## [5,] 0.6689 0.7841 0.7488
## [6,] 0.6719 0.7844 0.7488
## [7,] 0.6730 0.7844 0.7487
## [8,] 0.6734 0.7844 0.7487多步预测会趋近到序列均值,计算序列均值:
## uk ca us
## 0.5223092 0.6153672 0.6473996可以看出在超前8步时的点预测值很接近于序列的均值。
不管是不考虑参数估计误差的标准误差(Standard errors of predictions) 还是考虑参数估计误差的标准误差(Root mean squared errors of predictions), 超前\(l\)步预报当\(l\to\infty\)时都应该趋于序列的标准差。 计算序列的样本标准差:
## uk ca us
## 0.7086442 0.7851955 0.7872912输出中的标准误差或者根均方误差可以用来计算预测区间。 比如, 计算美国GDP季度对数增长率超前2步预测区间, 即2011年第四季度的预测区间, 在95%置信度下可计算为 \(0.4889 \pm 1.96 \times 0.7077\)或 \(0.4889 \pm 1.96 \times 0.7499\), 后一个区间用到的标准误差包含了参数估计误差带来的额外误差估计。
26.12 脉冲响应函数
回忆一元ARMA模型的Wold表示:
\[ X_t = \sum_{j=0}^\infty \psi_j \varepsilon_{t-j}, \] 其中\(\{ \varepsilon_t \}\)是白噪声列, 称为\(\{X_t \}\)的新息, 当\(\{ \varepsilon_t \}\)为独立白噪声时有 \[ \varepsilon_t = X_t - E(X_t | X_{t-1}, X_{t-2}, \dots) . \] \(\{ \psi_j \}\)称为\(\{X_t \}\)的Wold系数, 又称为\(\{X_t \}\)的脉冲响应函数(IRF, impulse response function), 这里函数自变量为滞后\(j\)。 易见 \[ \frac{\partial X_t}{\partial \varepsilon_{t-j}} = \psi_j, \] 所以\(\psi_j\)代表了过去的输入项\(\varepsilon_{t-j}\)的一个单位的变化对\(j\)期后的\(X_t\)的影响大小。 “脉冲响应”这个名词是假想取输入\(\{\varepsilon_t \}\)为\(\varepsilon_0=1\), 其它的\(\varepsilon_t = 0\)时, 输入序列是一个脉冲, 这个脉冲在\(t>=0\)时刻的输出为\(X_t = \psi_t\), 所以\(\{\psi_j, j=0,1,2,\dots \}\)序列是脉冲输入对应的输出。
前面给出了VAR模型的无穷阶MA表示(26.14): \[\begin{aligned} \boldsymbol r_t = \boldsymbol\mu + \sum_{l=0}^\infty \boldsymbol\Psi_l \boldsymbol a_{t-l} \end{aligned}\] \(\boldsymbol\Psi_l\)是过去的信息对\(\boldsymbol r_t\)的影响的系数, 称\(\boldsymbol\Psi_l\)的元素为时间序列\(\boldsymbol r_t\)的脉冲响应函数的系数。 等价地, \(\boldsymbol\Psi_l\)的元素也是\(\boldsymbol a_t\)对未来的\(\boldsymbol r_{t+l}\)的线性影响的系数。
以\(k=2\)的序列\(\boldsymbol r_t = (r_{1t}, r_{2t})^T\)为例, 记\(\boldsymbol\Psi_l = (\psi_{ij}(l))_{k \times k}\), 考虑\(r_{1t}\)的一个变化对\(r_{2,t+j}\)的影响。 为此,设\(\boldsymbol\mu=\boldsymbol 0\), 设\(\boldsymbol a_t = \boldsymbol 0\)(\(t \leq 0\)时), 设\(\boldsymbol a_0 = (1, 0)^T\), \(\boldsymbol a_t = \boldsymbol 0\)(\(t \neq 0\)时), 这样来考虑\(a_{1,0}\)的变化引起的后续变化, 也可以认为是\(r_{1,0}\)的一个变化引起的后续变化。 这时 \[\begin{aligned} \boldsymbol r_0 =& \boldsymbol a_0 = \left(\begin{array}{c} 1 \\ 0 \end{array}\right) \\ \boldsymbol r_1 =& \boldsymbol\Psi_1 \boldsymbol a_0 = \left(\begin{array}{c} \psi_{11}(1) \\ \psi_{21}(1) \end{array}\right) \\ \boldsymbol r_2 =& \boldsymbol\Psi_2 \boldsymbol a_0 = \left(\begin{array}{c} \psi_{11}(2) \\ \psi_{21}(2) \end{array}\right) \\ & \vdots \end{aligned}\] 所以\(\Psi_l\)的\((i,j)\)元可以看成是\(r_{jt}\)的一个变动对\(r_{i,t+l}\)造成的影响。
记 \[ \underline{\boldsymbol\Psi}_n = \sum_{l=0}^n \boldsymbol\Psi_{l} \] \(\underline{\boldsymbol\Psi}_n\)表示对\(\boldsymbol r_t\)的单位冲击的累积响应, 称\(\underline{\boldsymbol\Psi}_n\)的元素为第\(n\)个短期乘数, 全部的响应的累积值 \[ \underline{\boldsymbol\Psi}_\infty = \sum_{l=0}^\infty \boldsymbol\Psi_{l} \] 称为总乘数或长期效应。
可以作\(\psi_{ij}(l)\)沿\(l=0,1,2,\dots\)变化的折线图, 称为脉冲响应函数图; 以及\(\sum_{l=0}^n \psi_{ij}(l)\)沿\(n=0,1,2,\dots\)变化的折线图, 称为累积响应函数图。
例3.6
对例3.2中建立的简化的VAR(2)模型作脉冲响应函数图和累积响应图。 三个分量两两的图形共\(3 \times 3 \times 2\)幅。

## Press return to continue
在脉冲响应的9幅图中, 右上角的图是\(\psi_{13}(l)\)的图形, 代表美国(分量3)的数据的一个冲击对英国(分量1)的延迟的影响。
○○○○○
这样的脉冲响应有一些问题。 由于新息\(\boldsymbol a_t\)存在分量间的同步相关性, 改变\(a_{1t}\)的值不可能不同时影响到\(a_{2t}\)的值。 所以原始的脉冲响应\(\boldsymbol\Psi_l\)不够实际。 用数学解释, 改变\(a_{1t}\)后对\(\boldsymbol r_{t+l}\)的影响, 可以看成是求 \(\frac{\partial \boldsymbol r_{t+l}}{\partial a_{1t}}\), 利用无穷阶MA表示(26.14), 因为\(\{ \boldsymbol a_t \}\)序列不相关, 所以(以\(k=2\)为例) \[\begin{aligned} \frac{\partial \boldsymbol r_{t+l}}{\partial a_{1t}} =& \boldsymbol\Psi_l \frac{\partial \boldsymbol a_{t}}{\partial a_{1t}} = \boldsymbol\Psi_l \left(\begin{array}{c} 1 \\ \frac{\partial a_{2t}}{\partial a_{1t}} \end{array}\right) \end{aligned}\] 其中\(a_{2t}\)不是\(a_{1t}\)的函数, 其关系可以用线性回归 \[\begin{aligned} a_{2t} = \frac{\sigma_{21}}{\sigma_{11}} a_{1t} + e \end{aligned}\] 表示, 因此\(\frac{\partial a_{2t}}{\partial a_{1t}}\)可估计为\(\frac{\sigma_{21}}{\sigma_{11}}\), 有 \[\begin{aligned} \frac{\partial \boldsymbol r_{t+l}}{\partial a_{1t}} =& \boldsymbol\Psi_l \left(\begin{array}{c} 1 \\ \frac{\sigma_{21}}{\sigma_{11}} \end{array}\right) \end{aligned}\] 所以\(a_{1t}\)对\(\boldsymbol r_{t+l}\)的影响不仅涉及\(\boldsymbol\Psi_l\)的第一列元素的影响, 还涉及\(\Sigma\)的第一列元素的影响以及\(\boldsymbol\Psi_l\)的第二列元素的影响。
可以利用Cholesky分解使得新息正交化(分量间不相关)。 对\(\boldsymbol a_t\)的方差阵\(\boldsymbol\Sigma\)有Cholesky分解 \(\boldsymbol\Sigma = \boldsymbol L \boldsymbol L^T\), 其中\(\boldsymbol L\)是对角线元素都为正数的下三角阵。 定义正交化的新息\(\boldsymbol b_t = L^{-1} \boldsymbol a_t\), 则\(\text{Var}(\boldsymbol b_t)=\boldsymbol I\)是单位阵, 从而\(\boldsymbol b_t\)各分量不相关。 令\(\boldsymbol\Psi_l^* = \boldsymbol\Psi_l L = (\psi_{ij}^*(l))_{k \times k}\), (26.14)可以用正交化的新息\(\boldsymbol b_t\)表示为 \[\begin{aligned} \boldsymbol r_t =& \boldsymbol\mu + \sum_{l=0}^\infty \boldsymbol\Psi_l L \cdot L^{-1} \boldsymbol a_{t-l} \\ =& \boldsymbol\mu + \sum_{l=0}^\infty \boldsymbol\Psi_l^* \boldsymbol b_{t-l} \end{aligned}\] 因为\(\boldsymbol b_t\)的分量不相关, 可得 \[ \frac{\partial r_{i,t+l}}{\partial b_{jt}} = \psi_{ij}^*(l) \] \(\psi_{ij}^*(l)\)是\(b_{jt}\)对未来的观测\(r_{i,t+l}\)的影响, 称系数矩阵\(\boldsymbol\Psi_l^*\)为 \(\boldsymbol r_t\)的带正交新息\(\boldsymbol b_t\)的脉冲响应系数, 称沿\(l=0,1,2,\dots\)变化的\(\psi_{ij}^*(l)\)为\(\boldsymbol r_t\) 的带正交新息\(\boldsymbol b_t\)的脉冲响应函数。
正交化以后, \(\psi_{ij}^*(0)\)是\(L^{-1}\)的第\((i,j)\)元素, 可以表示\(r_{jt}\)的一个冲击对\(r_{it}\)的即期影响。
这样的三角分解的缺点是结果依赖于\(\boldsymbol r_t\)的分量次序, 对脉冲函数的理解与\(\boldsymbol r_t\)的分量次序有关。 特别地, \(a_{1t} = \sqrt{\sigma_{11}} b_{1t}\), \(a_{1t}\)仅做了方差标准化。
例3.7
对例3.2中建立的简化的VAR(2)模型作正交化的脉冲响应函数图和累积响应图。
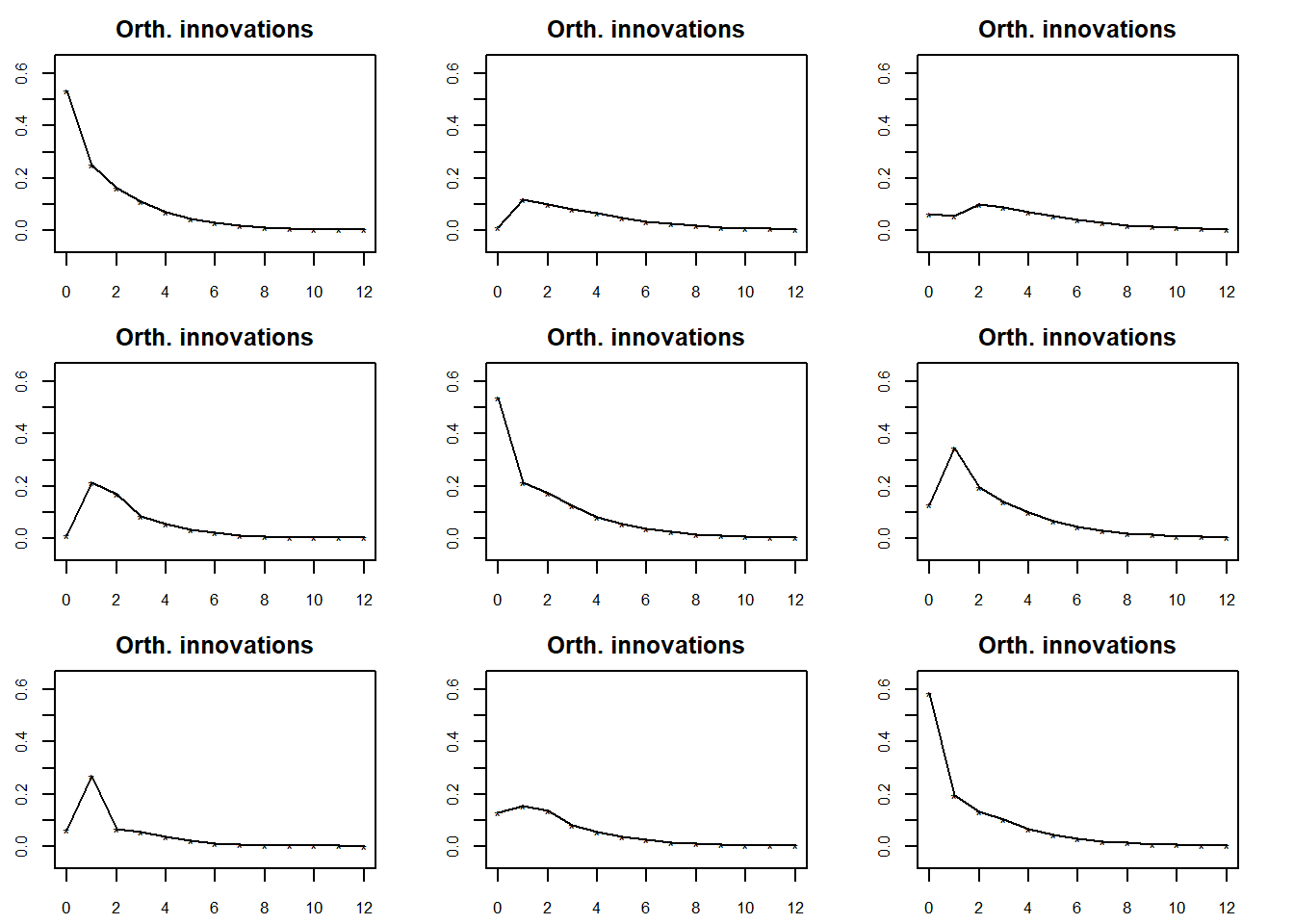
## Press return to continue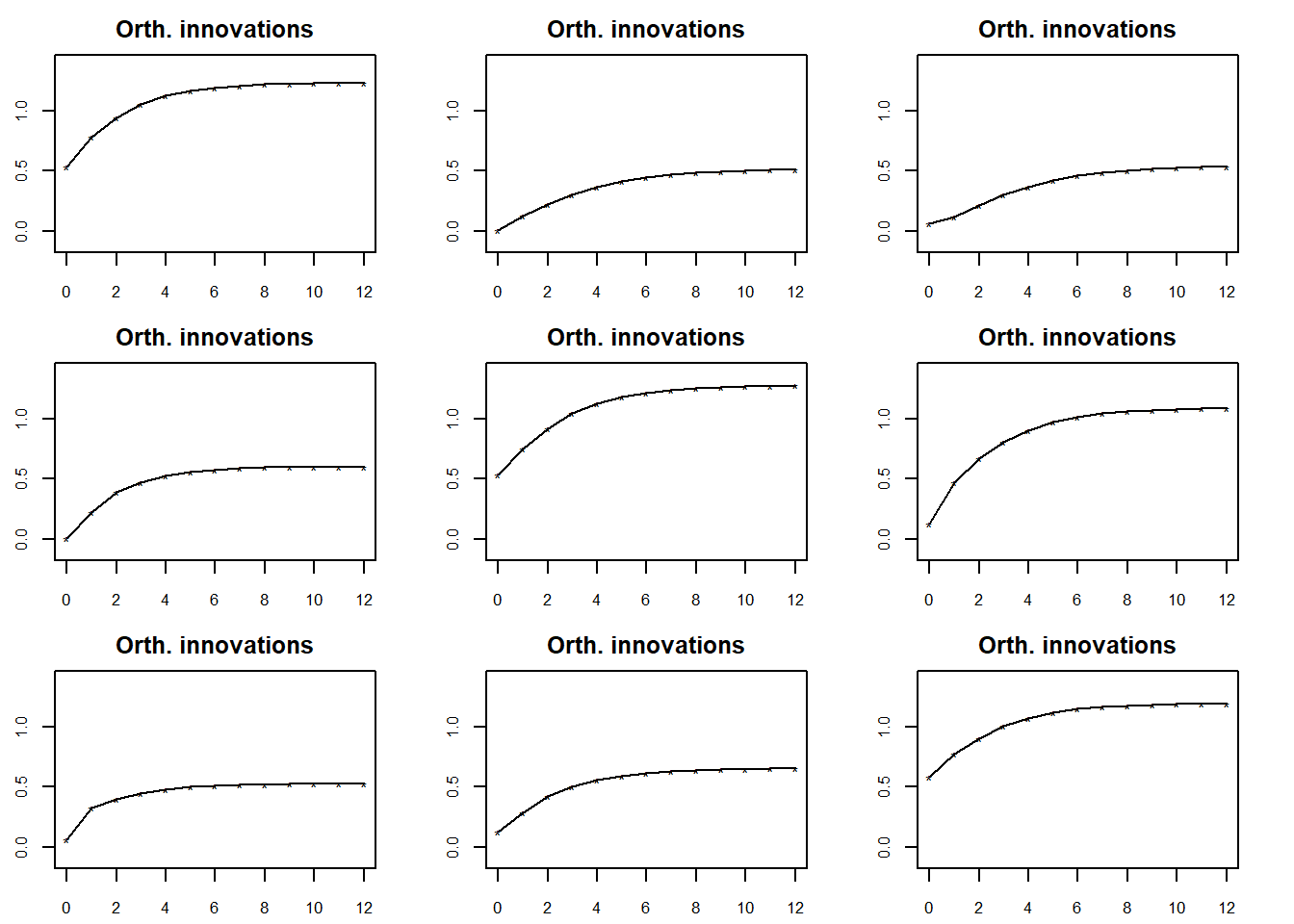
这三个分量的新息的即期相关不大, 所以正交化的脉冲响应与原始的表现相近。
○○○○○
26.13 GrangerTest()函数
MTS::GrangerTest()函数的用法文档不够明确。
我们模拟一个如下的VAR(1)模型:
\[
\boldsymbol r_t
= \begin{pmatrix}
100 \\ 200 \\ 300
\end{pmatrix}
+ \begin{pmatrix}
0.8 & 0 & 0 \\
0.2 & 0.4 & 0 \\
0.2 & 0.2 & 0.3
\end{pmatrix}
\boldsymbol r_{t-1}
+ \boldsymbol \varepsilon_t,
\]
其中
\[
\boldsymbol \varepsilon_t \sim \text{N}\left(
\boldsymbol 0, \text{diag}(1,2,3)\right) .
\]
这时,
\(r_{2t}\)和\(r_{3t}\)不是\(r_{1t}\)的格兰杰原因;
\(r_{3t}\)不是\(r_{2t}\)的格兰杰原因。
但是,
GrangerTest()仅能指定一个分量,
检验是否其它分量都不是此分量的格兰杰原因。
library(mvtnorm)
library(MTS)
# 模拟一个一般的VAR(1)的函数
sim_VAR1 <- function(
n=100, # 样本量
phi_mat = matrix(0, 2, 2), # 系数矩阵
Q = matrix(1, 2, 2), # 误差方差阵
mu_vec = c(0,0)) { # 均值向量
m <- nrow(phi_mat) # 维数
preheat <- 100 # 为避免初值影响
nn <- preheat + n
x <- matrix(0, nn, m)
eps <- rmvnorm(nn, sigma = Q)
for(tt in 2:nn){
x[tt,] <- phi_mat %*% x[tt-1,] + eps[tt,]
}
return(x[(preheat+1):nn,])
}
# 模拟前述的3维的VAR(1),系数矩阵下三角
sim11 <- function(n=500){
phi_mat <- matrix(c(
0.8, 0, 0,
0.2, 0.4, 0,
0.2, 0.2, 0.3 ),
ncol=3, nrow=3,
byrow=TRUE)
Q <- diag(c(1,2,3))
mu_vec <- c(100, 200, 300)
sim_VAR1(n=n, phi_mat=phi_mat, Q=Q, mu_vec=mu_vec)
}
# 执行模拟
set.seed(101)
Z <- sim11(500)
cat("\n\n========= 模型拟合结果:\n")##
##
## ========= 模型拟合结果:## Constant term:
## Estimates: -0.05060994 -0.04315222 0.02430918
## Std.Error: 0.04523537 0.06626087 0.07976303
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.796 0.0239 0.0109
## [2,] 0.250 0.3976 -0.0392
## [3,] 0.191 0.1954 0.3244
## standard error
## [,1] [,2] [,3]
## [1,] 0.0283 0.0273 0.0236
## [2,] 0.0415 0.0401 0.0346
## [3,] 0.0499 0.0482 0.0416
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.9827963 -0.10931049 0.10707160
## [2,] -0.1093105 2.10873290 -0.01167435
## [3,] 0.1070716 -0.01167435 3.05569891
##
## det(SSE) = 6.272251
## AIC = 1.872135
## BIC = 1.947998
## HQ = 1.901904##
##
## ========= locInput=1## Number of targeted zero parameters: 2
## Chi-square test for Granger Causality and p-value: 1.062548 0.5878557
## Constant term:
## Estimates: -0.05315053 -0.04315222 0.02430918
## Std.Error: 0.04508747 0.06626087 0.07976303
## AR coefficient matrix
## AR( 1 )-matrix
## [,1] [,2] [,3]
## [1,] 0.805 0.000 0.0000
## [2,] 0.250 0.398 -0.0392
## [3,] 0.191 0.195 0.3244
## standard error
## [,1] [,2] [,3]
## [1,] 0.0266 0.0000 0.0000
## [2,] 0.0415 0.0401 0.0346
## [3,] 0.0499 0.0482 0.0416
##
## Residuals cov-mtx:
## [,1] [,2] [,3]
## [1,] 0.9849060 -0.10931049 0.10707160
## [2,] -0.1093105 2.10873290 -0.01167435
## [3,] 0.1070716 -0.01167435 3.05569891
##
## det(SSE) = 6.285844
## AIC = 1.8663
## BIC = 1.925305
## HQ = 1.889453##
##
## ========= locInput=2## Number of targeted zero parameters: 2
## Chi-square test for Granger Causality and p-value: 36.4841 1.195577e-08##
##
## ========= locInput=3## Number of targeted zero parameters: 2
## Chi-square test for Granger Causality and p-value: 38.98995 3.415379e-09说明:在GrangerTest()中,
用locInput=输入一个分量序号,
检验零假设:其它所有分量都不是此分量的格兰杰原因。
不能进行其它的格兰杰原因的检验。
26.14 用fable包的VAR()函数
本例来自(R. J. Hyndman and Athanasopoulos 2021)节12.3。
fpp3包的us_change包含了美国个人消费支出、个人可支配收入的变化率。
用fable包的VAR()函数建模。
## Warning: package 'fpp3' was built under R version 4.4.3## Registered S3 method overwritten by 'tsibble':
## method from
## as_tibble.grouped_df dplyr## ── Attaching packages ──────────────────────────────────────────── fpp3 1.0.1 ──## ✔ tsibble 1.1.5 ✔ feasts 0.4.1
## ✔ tsibbledata 0.4.1 ✔ fable 0.4.1## Warning: package 'tsibbledata' was built under R version 4.4.3## Warning: package 'feasts' was built under R version 4.4.3## Warning: package 'fabletools' was built under R version 4.4.3## Warning: package 'fable' was built under R version 4.4.3## ── Conflicts ───────────────────────────────────────────────── fpp3_conflicts ──
## ✖ lubridate::date() masks base::date()
## ✖ dplyr::filter() masks stats::filter()
## ✖ xts::first() masks dplyr::first()
## ✖ tsibble::index() masks zoo::index()
## ✖ tsibble::intersect() masks base::intersect()
## ✖ tsibble::interval() masks lubridate::interval()
## ✖ dplyr::lag() masks stats::lag()
## ✖ xts::last() masks dplyr::last()
## ✖ tsibble::setdiff() masks base::setdiff()
## ✖ tsibble::union() masks base::union()
## ✖ fable::VAR() masks MTS::VAR()usc_fit <- us_change |>
model(
aicc = fable::VAR(vars(Consumption, Income)),
bic = fable::VAR(vars(Consumption, Income),
ic = "bic") )
usc_fit## # A mable: 1 x 2
## aicc bic
## <model> <model>
## 1 <VAR(5) w/ mean> <VAR(1) w/ mean>AICc准则选择了5阶模型, BIC准则选择了1阶模型。
## # A tibble: 2 × 6
## .model sigma2 log_lik AIC AICc BIC
## <chr> <list> <dbl> <dbl> <dbl> <dbl>
## 1 aicc <dbl [2 × 2]> -373. 798. 806. 883.
## 2 bic <dbl [2 × 2]> -408. 836. 837. 869.BIC选择的模型的残差诊断:
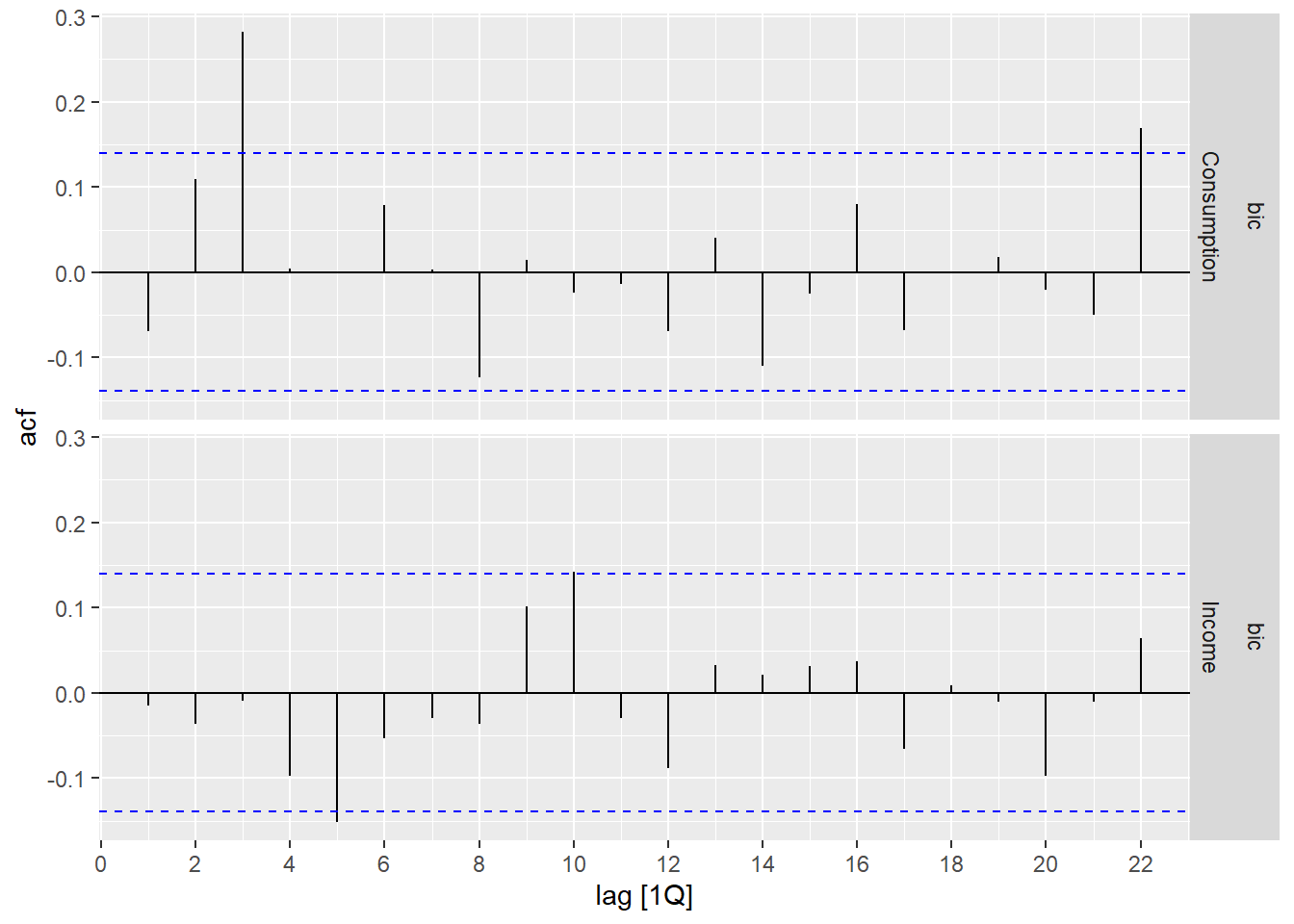
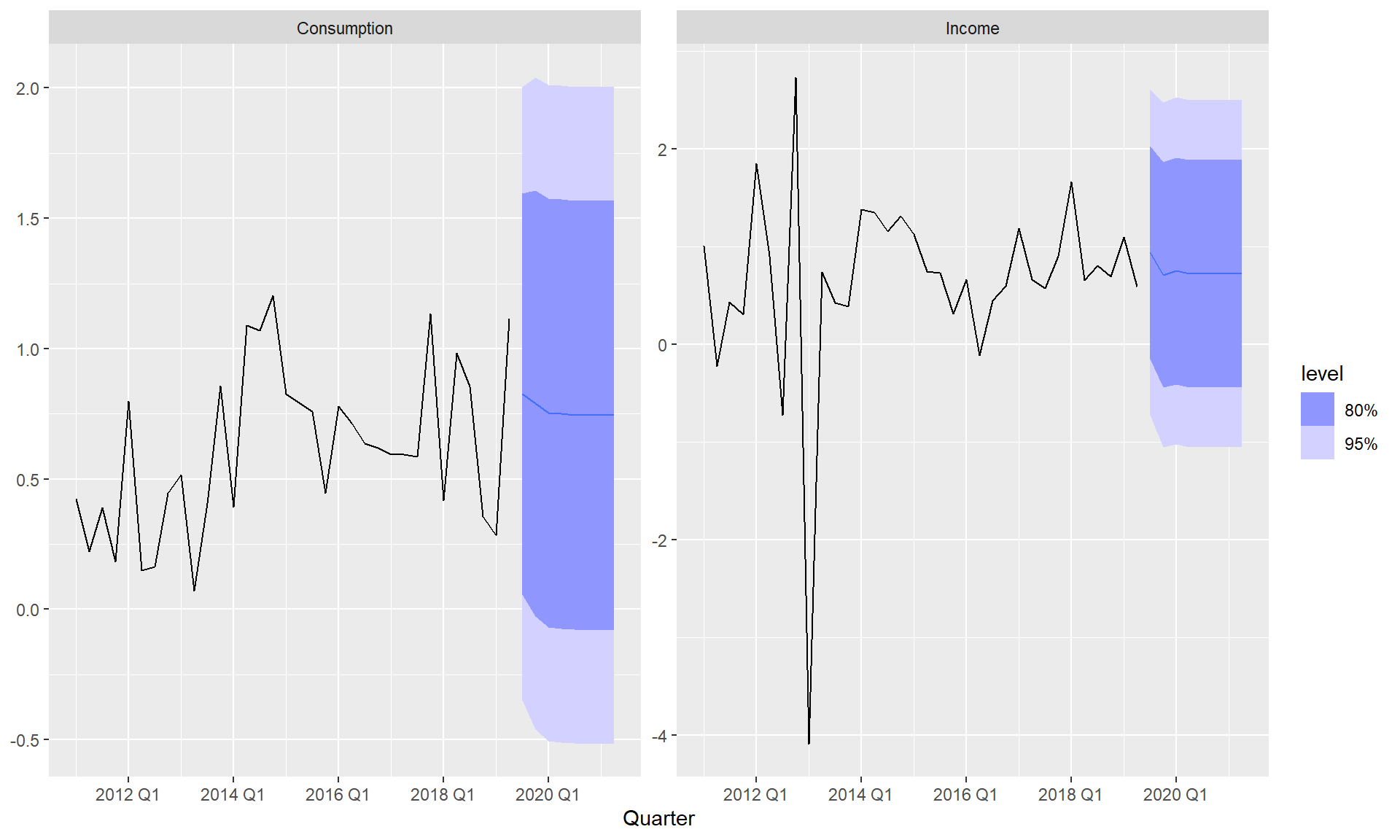
其中Consumption的残差在滞后3有较大突起。
用VAR(1)模型预测: