23 多元时间序列基本概念

经济的全球一体化和信息传播的发展使得各国的金融市场相互关联， 一个市场的价格变动可以很快地扩散到另一个市场。 持有多个资产的投资者也希望了解多个资产的收益率之间的关系。 这些问题属于多元时间序列分析的范畴。

多元时间序列包含多个一元时间序列作为分量， 各个一元时间序列的采样时间点相同， 所以数据可以用矩阵形式表示， 每行为一个时间点， 每列为一个一元时间序列。 在R中可以保存为矩阵、数据框、ts或者xts时间序列对象。 设\(\boldsymbol r_t = (r_{1t}, \dots, r_{kt})^T\) 表示\(k\)个资产在时刻\(t\)的对数收益率。

一元时间序列的某些方法可以推广到多元情形， 但是有些问题需要注意。 某些情况下需要提出新的模型和方法。

23.1 弱平稳与互相关矩阵

23.1.1 弱平稳列

考虑一个\(k\)元时间序列 \(\boldsymbol r_t = (r_{1t}, \dots, r_{kt})^T\)。 称\(\boldsymbol r_t\)是弱平稳的，如果 \[\begin{aligned} \begin{cases} E \boldsymbol r_t = \boldsymbol\mu \text{ 与}t\text{无关} \\ \text{Var}(\boldsymbol r_t) = \Gamma_0 \text{ 与}t\text{无关} \\ \text{Cov}(\boldsymbol r_t, \boldsymbol r_{t-l}) = \Gamma_l, \ l=0,1,2,\dots \text{ 与}t\text{无关} \end{cases} \end{aligned}\]

23.1.2 互相关阵

对\(k\)元弱平稳列\(\boldsymbol r_t\)， \(\Gamma_0 = \text{Var}(\boldsymbol r_t)\)是\(\boldsymbol r_t\)协方差阵， 是一个对称半正定\(k\)阶方阵， 记\(\Gamma_0 = (\Gamma_{ij}(0))_{k\times k}\)， 则\(\Gamma_{ii}(0)\)是分量\(r_{it}\)的方差， \(\Gamma_{ij}(0)\)是分量\(r_{it}\)与分量\(r_{jt}\)的协方差。

为了将协方差阵变成相关阵， 记 \[\begin{aligned} D = \text{diag}(\sqrt{\Gamma_{11}(0)}, \dots, \sqrt{\Gamma_{kk}(0)}) \end{aligned}\] 令 \[\begin{aligned} \boldsymbol\rho_0 = (\rho_{ij}(0))_{k\times k} = D^{-1} \Gamma_0 D^{-1} \end{aligned}\] 则\(\boldsymbol\rho_0\)是随机向量\(\boldsymbol r_t\)的相关阵， 称为多元时间序列\(\{ \boldsymbol r_t \}\)的同步的或者滞后为0的互相关阵。 其元素 \[\begin{aligned} \rho_{ij}(0) = \text{corr}(r_{it}, r_{jt}) = \frac{\text{Cov}(r_{it}, r_{jt})}{\sqrt{\text{Var}(r_{it}) \text{Var}(r_{jt})}} = \frac{\Gamma_{ij}(0)}{\sqrt{\Gamma_{ii}(0) \Gamma_{jj}(0)}} \end{aligned}\] \(\boldsymbol\rho_0\)是一个对角线元素全为1的对称半正定阵， 且\(|\rho_{ij}(0)| \leq 1\)， \(\rho_{ij}(0) = \rho_{ji}(0)\)。 称\(\rho_{ij}(0)\)为共点或同步相关系数， 因为它是两个分量在同一时刻\(t\)的相关系数。

多元时间序列分析中一个重要概念是引导与滞后关系。 为此， 用互相关阵来衡量时间序列之间的线性关系的强度。 \(k\)元弱平稳列\(\boldsymbol r_t\)的滞后\(l\)的互协方差阵定义为 \[\begin{aligned} \Gamma_l = (\Gamma_{ij}(l))_{k \times k} = E[ (\boldsymbol r_t - \boldsymbol\mu) (\boldsymbol r_{t-l} - \boldsymbol\mu)^T ] \end{aligned}\] 这是一元时间序列的自协方差函数\(\gamma_l\)的推广。 \(\Gamma_l\)仅依赖于滞后\(l\)而与时刻\(t\)无关。

\(k\)元弱平稳列\(\boldsymbol r_t\)的滞后\(l\)的互相关阵 (Cross Correlation Matrix, CCM)定义为 \[\begin{aligned} \boldsymbol\rho_l = (\rho_{ij}(l))_{k\times k} = D^{-1} \Gamma_l D^{-1} \end{aligned}\] 其中 \[\begin{aligned} \rho_{ij}(l) = \text{corr}(r_{it}, r_{j, t-l}) = \frac{\Gamma_{ij}(l)}{\sqrt{\Gamma_{ii}(0) \Gamma_{jj}(0)}} \end{aligned}\] 是\(r_{it}\)和\(r_{j,t-l}\)的相关系数。 注意\(\text{Var}(r_{j,t-l}) = \Gamma_{jj}(0)\)。

对\(l>0\)，如果\(\rho_{ij}(l) \neq 0\)， 可称先观测到的分量\(r_{j,t-l}\)对滞后的\(r_{i,t}\)有先导作用。 而\(\rho_{ji}(l)\)代表的是\(r_{i,t-l}\)对\(r_{j,t}\)的先导作用。 一般\(\rho_{ij}(l) \neq \rho_{ji}(l)\)， 所以\(l \neq 0\)时\(\boldsymbol\rho_l\)一般不是对称阵， \(\Gamma_l\)一般也不对称。

不同于一元时间序列的自协方差满足\(\gamma_l = \gamma_{-l}\)， 对\(k\)元时间序列有 \[\begin{aligned} \Gamma_{ij}(l) =& \text{Cov}(r_{it}, r_{j,t-l}) = \text{Cov}(r_{j,t-l}, r_{i,t}) = \text{Cov}(r_{j,t}, r_{i,t+l}) \\ =& \text{Cov}(r_{j,t}, r_{i,t-(-l)}) = \Gamma_{ji}(-l) \end{aligned}\] 即 \[\begin{aligned} \Gamma_{-l} = \Gamma_l^T \end{aligned}\]

对互相关阵\(\boldsymbol\rho_l\)也有 \[\begin{aligned} \boldsymbol\rho_{-l} = \boldsymbol\rho_l^T \end{aligned}\] 所以只需要考虑\(\boldsymbol\rho_l, l \geq 0\)。

23.1.3 时间序列之间的线性相依性的分类

多元弱平稳列的互相关阵\(\{ \boldsymbol\rho_l, l=0,1,\dots \}\) 包含如下方面的信息：

• 对角线元素\(\{ r_{ii}(l), l=0,1,\dots\}\)是一元时间序列 \(r_{it}\)的自相关函数(ACF);
• \(\rho_{ij}(0)\)是两个分量\(r_{it}\)与\(r_{jt}\)的同步线性关系；
• 对\(l>0\)，\(\rho_{ij}(l)\)表示\(r_{it}\)对另一分量的过去值\(r_{j,t-l}\) 的线性依赖。

如果对\(\forall l>0\)， 都有\(\rho_{ij}(l)=0\), 则\(r_{it}\)与过去的\(r_{j,t-l}\)都不相关。

两个分量\(r_{it}\)和\(r_{js}\)的线性相依关系可以分类为如下情况：

• 若\(\forall l \geq 0\)， \(\rho_{ij}(l)=\rho_{ji}(l)=0\)， 则两个分量\(r_{it}\)和\(r_{js}\)不相关(对任意\(s,t\)）。
• 若\(\rho_{ij}(0) \neq 0\)， 则两个分量\(r_{it}\)和\(r_{jt}\)具有同步相关。
• 若\(\forall l > 0\), \(\rho_{ij}(l)=\rho_{ji}(l)=0\)， 则两个分量\(r_{it}\)和\(r_{js}\)没有引导与滞后的关系但是可能有同步相关。 称这两个序列是分离的。
• 如果\(\forall l > 0\)， \(\rho_{ij}(l) = 0\)， 但存在\(v>0\)使得\(\rho_{ji}(v) \neq 0\)， 则\(r_{it}\)不依赖于过去的\(r_{j,t-l}\)， 但是\(r_{jt}\)依赖于过去的\(r_{i,t-v}\)， 这时从\(r_{i}(t)\)到\(r_j(s)\)有一个单向的引导（领先）关系。
• 如果存在\(l > 0\)和\(v>0\)使得 \(\rho_{ij}(l) \neq 0\), \(\rho_{ji}(v) \neq 0\), 则\(r_{it}\)和\(r_{js}\)之间存在相互的反馈关系， 互为引导和滞后。

23.2 样本互相关阵

类似于一元时间序列的自协方差函数估计\(\hat\gamma_l\)， 将互协方差阵\(\Gamma_l\)估计为 \[\begin{aligned} \hat\Gamma_l = \frac{1}{T} \sum_{t=l+1}^T (\boldsymbol r_t - \bar{\boldsymbol r}) (\boldsymbol r_{t-l} - \bar{\boldsymbol r})^T \end{aligned}\] 令\(\hat D\)为\(\hat\Gamma_0\)的对角线元素的平方根组成的对角阵， 估计互相关阵\(\boldsymbol\rho_l\)为 \[\begin{aligned} \hat{\boldsymbol\rho}_l = \hat D^{-1} \hat\Gamma_l \hat D^{-1} \end{aligned}\]

对二维时间序列\((x_t, y_t)\), \(t=1,2,\dots, T\)， R的ccf(x, y, type="covariance")可以计算互协方差函数并作图: \[ \hat\gamma_{xy}(l) = \frac{1}{T} \sum_{t=l+1}^T (x_t - \bar x)(y_{t-l} - \bar y), \ l=\ldots, -2, -1, 0, 1, 2, 3, \ldots, \] 用ccf(x, y)可以计算互相关系数函数并作图： \[ \hat\rho_{xy}(l) = \frac{\hat\gamma_{xy}(l)}{\sqrt{\hat\gamma_{xx}(0) \hat\gamma_{yy}(0)}}, \ l=\ldots, -2, -1, 0, 1, 2, 3, \ldots. \] 对\(l > 0\)，\(\hat\rho_{xy}(l)\)表示\(y\)对\(x\)的领先影响； 对\(l < 0\)，\(\hat\rho_{xy}(l)\)表示\(x\)对\(y\)的领先影响。

如果\(\boldsymbol r_t\)是白噪声列， 即\(\boldsymbol\rho_l\)对\(l>0\)都是零矩阵， 则在\(\Gamma_0\)正定的条件下，有 \[ \text{Var}(\hat\rho_{ij}(l)) \approx \frac{1}{T}, \ l > 0 \]

因为\(\hat{\boldsymbol\rho}_l\)的元素有\(i, j, l\)三个下标， 所以比较难以快速地辨识一个多元时间序列的CCM的特点。

为此， (Tiao and Box 1981)提出了一种显示简略的互相关阵的方法， 对样本相关阵\(\hat{\boldsymbol\rho}_l\)， 显示如下的符号矩阵\(\boldsymbol s_l\)： \[\begin{aligned} s_{ij}(l) = \begin{cases} + & \text{当} \hat\rho_{ij}(l) > \frac{2}{\sqrt{T}} \\ - & \text{当} \hat\rho_{ij}(l) < -\frac{2}{\sqrt{T}} \\ \cdot & \text{当} |\hat\rho_{ij}(l)| \leq \frac{2}{\sqrt{T}} \\ \end{cases} \end{aligned}\] 显示为\(+\)或\(-\)号的互相关系数在0.05渐近水平下显著不等于零。

23.2.1 例1.1：IBM和标普

多元时间序列的一些计算使用蔡瑞胸(R.S. Tsay)教授的MTS扩展包。

考虑IBM股票与标普500指数从1926年1月到2008年12月的月对数收益率， 共996个观测。单位为百分之一。

da1 <- read_table(
  "m-ibm3dx2608.txt",
  col_types=cols(.default=col_double(),
  date=col_date(format="%Y%m%d")))
ts.mibm <- ts(100*log(1 + da1[["ibmrtn"]]), 
              start=c(1926,1), frequency=12)
ts.msp5 <- ts(100*log(1 + da1[["sprtn"]]), 
              start=c(1926,1), frequency=12)

IBM的月对数收益率时间序列图：

plot(ts.mibm, xlab="Year", ylab="log(IBM Return)")

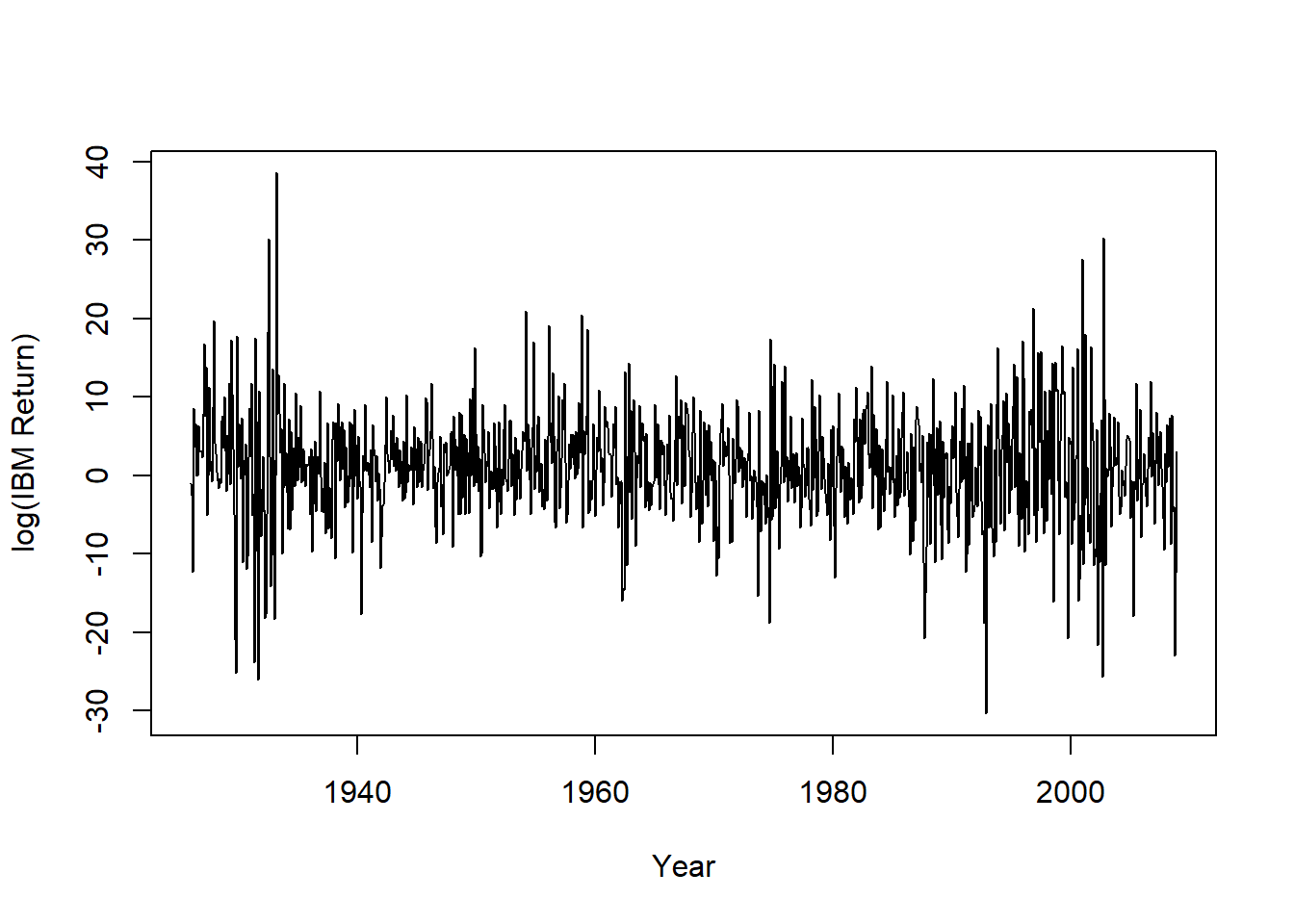
图23.1: IBM股票月对数收益率

标普500的月对数收益率时间序列图：

plot(ts.msp5, xlab="Year", ylab="log(SP500 Return)")

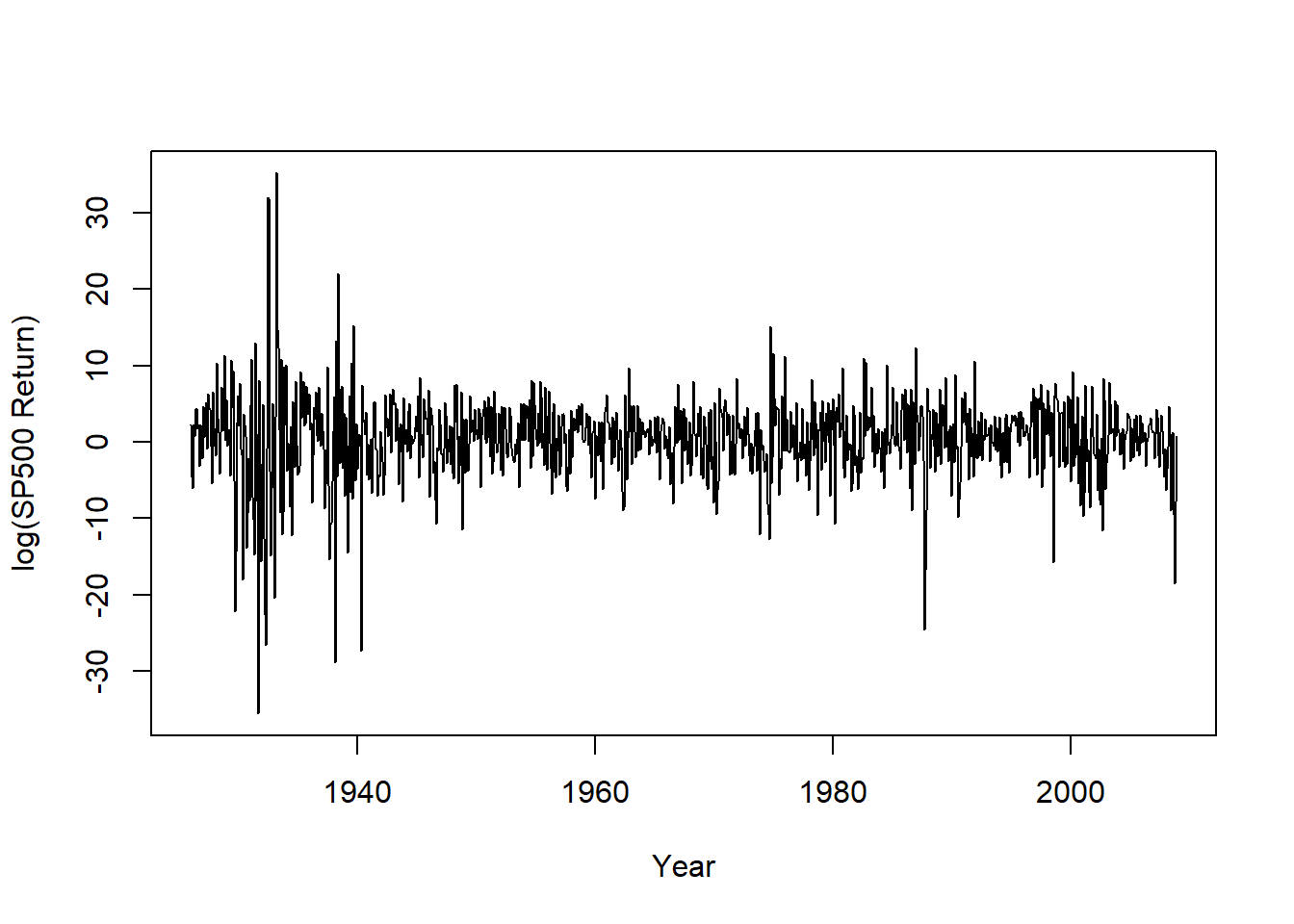
图23.2: 标普500指数月对数收益率

两个序列同时刻的散点图：

plot(as.vector(ts.msp5), as.vector(ts.mibm), 
     xlab="标普500[t]", ylab="IBM[t]")

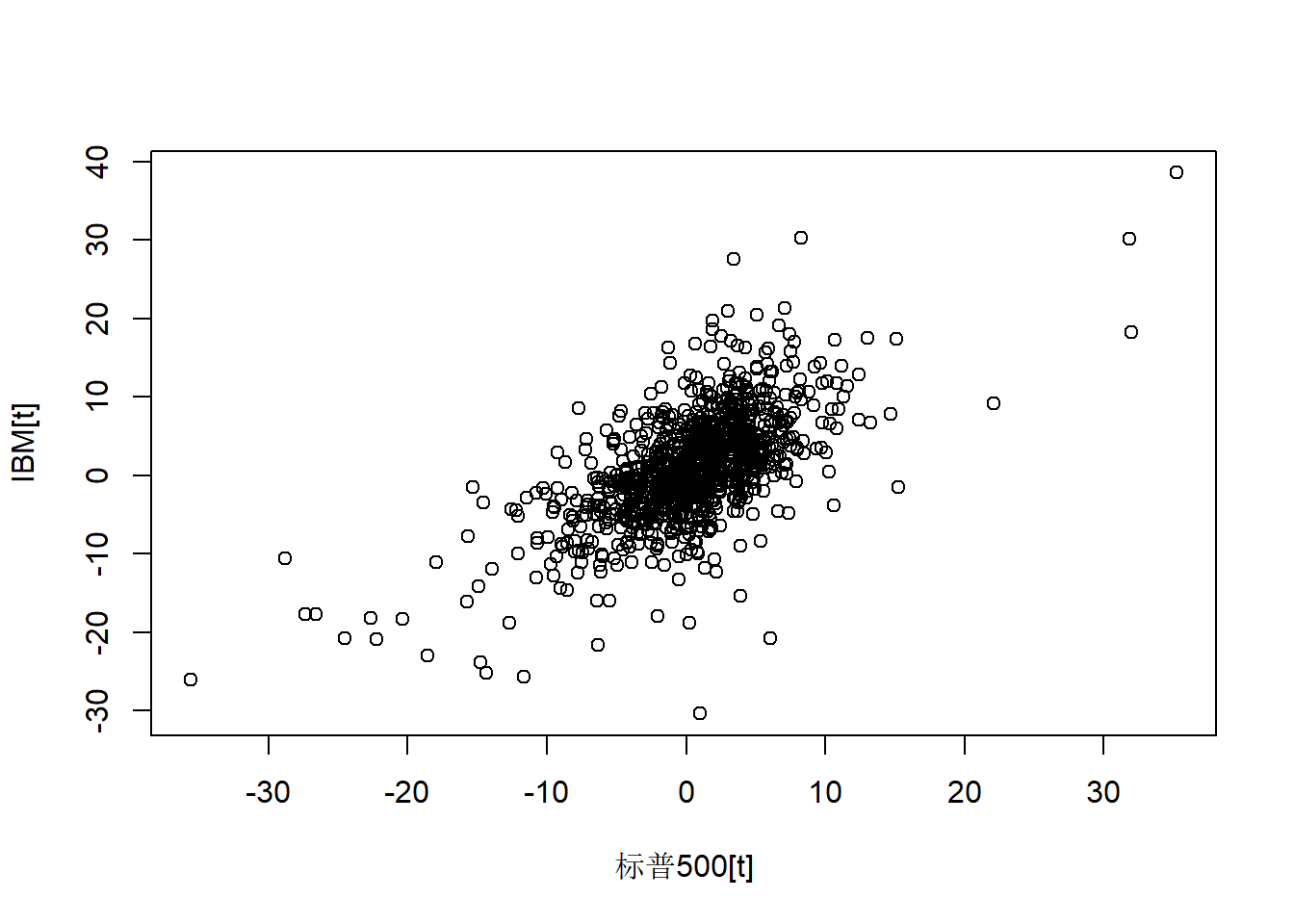
图23.3: IBM股票和标普500同时刻的月对数收益率

同时刻具有明显的正相关，样本相关系数：

cor.test(as.vector(ts.msp5), as.vector(ts.mibm))

## 
##  Pearson's product-moment correlation
## 
## data:  as.vector(ts.msp5) and as.vector(ts.mibm)
## t = 26.625, df = 994, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6074247 0.6800598
## sample estimates:
##       cor 
## 0.6451977

同时刻的相关系数为0.65，显著。

IBM对领先一个月的标普500：

plot(as.vector(ts.msp5)[-length(ts.mibm)], 
     as.vector(ts.mibm)[-1], 
     xlab="标普500[t-1]", ylab="IBM[t]")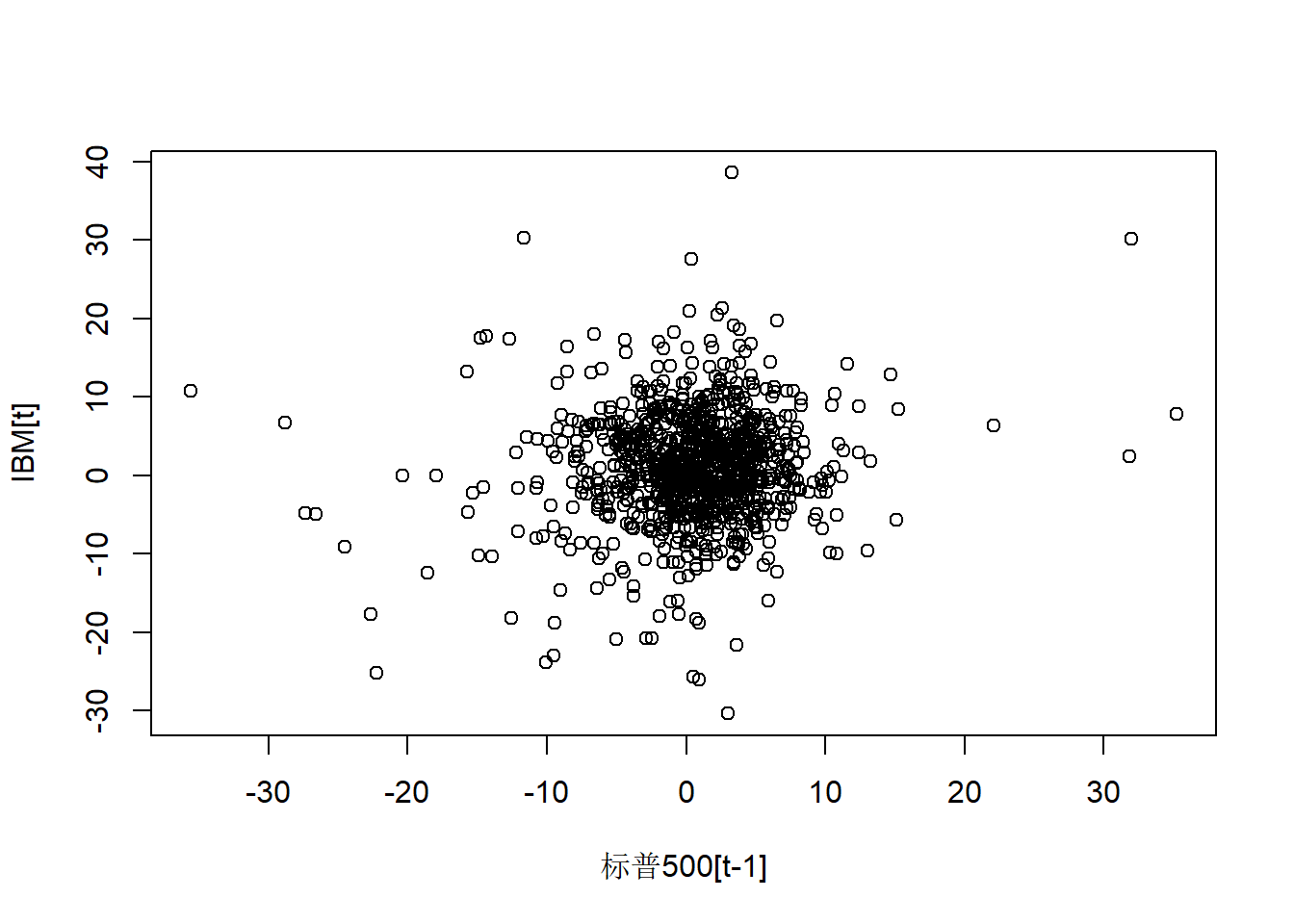

图23.4: IBM股票对滞后一步的标普500的月对数收益率

cor.test(as.vector(ts.msp5)[-length(ts.mibm)], 
         as.vector(ts.mibm)[-1])

## 
##  Pearson's product-moment correlation
## 
## data:  as.vector(ts.msp5)[-length(ts.mibm)] and as.vector(ts.mibm)[-1]
## t = 3.093, df = 993, p-value = 0.002037
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.03575303 0.15886892
## sample estimates:
##        cor 
## 0.09768469

相关系数很小，但显著不为零。

标普500对领先一个月的IBM：

plot(as.vector(ts.mibm)[-length(ts.mibm)], 
     as.vector(ts.msp5)[-1], 
     xlab="IBM[t-1]", ylab="标普500[t]")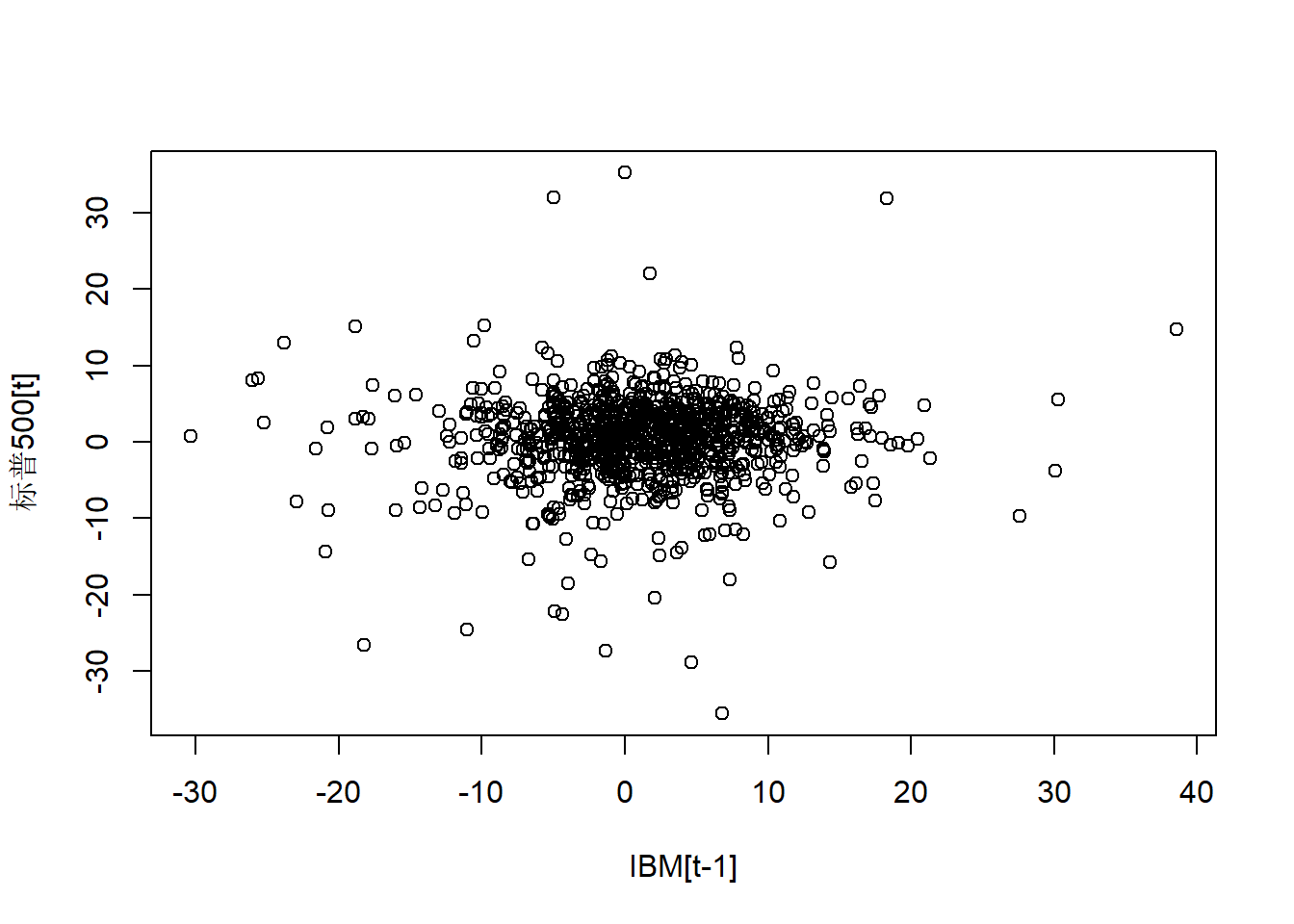

图23.5: 标普500对滞后一步的IBM股票的月对数收益率

cor.test(as.vector(ts.mibm)[-length(ts.mibm)], 
         as.vector(ts.msp5)[-1])

## 
##  Pearson's product-moment correlation
## 
## data:  as.vector(ts.mibm)[-length(ts.mibm)] and as.vector(ts.msp5)[-1]
## t = 1.1803, df = 993, p-value = 0.2382
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.02477745  0.09934653
## sample estimates:
##       cor 
## 0.0374289

相关系数很小，与零无显著差异。

用MTS包的MTSplot()函数绘制时间序列图：

MTS::MTSplot(cbind(ts.mibm, ts.msp5))

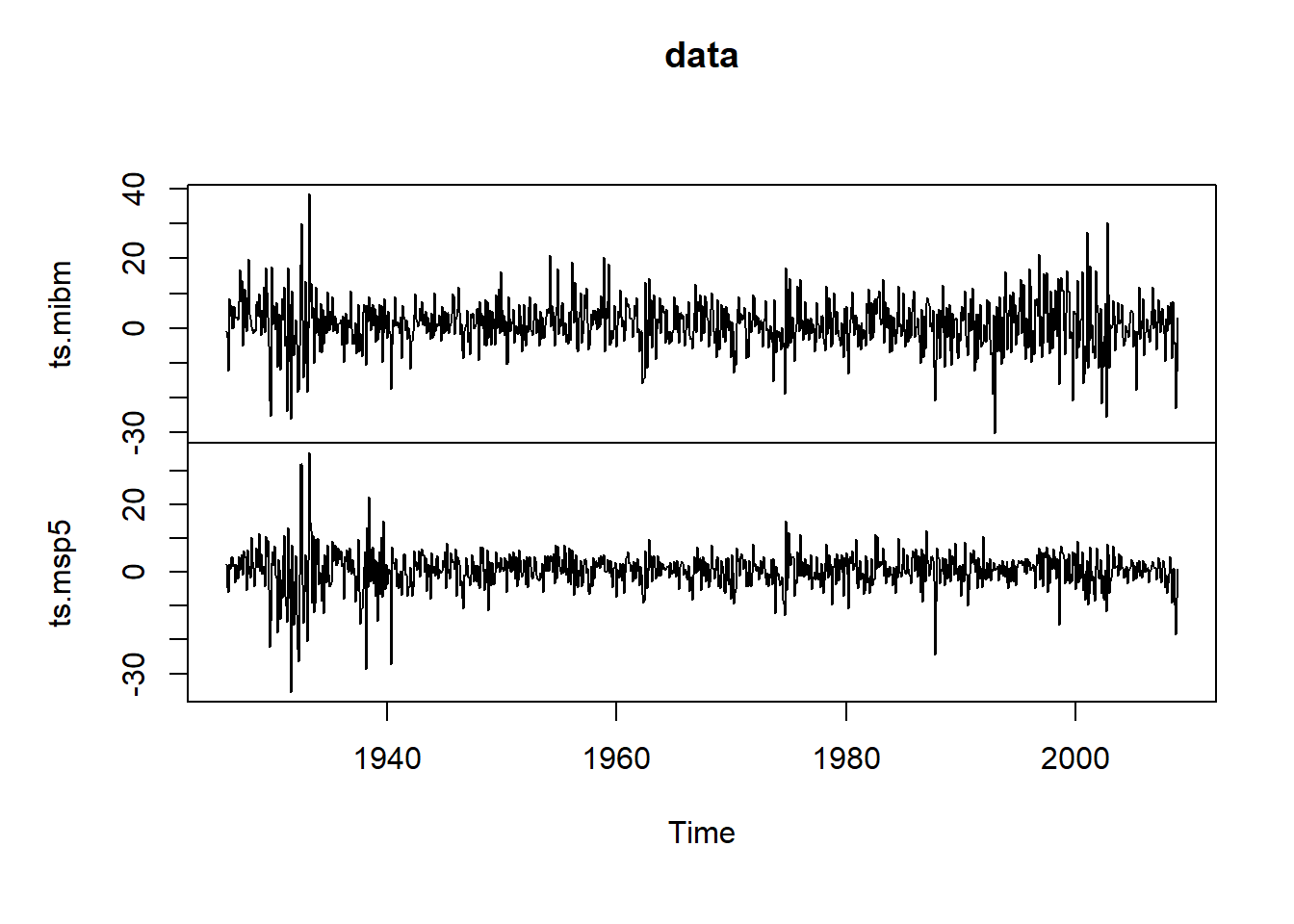
图23.6: IBM和标普500的对数收益率

计算两个序列的单样本简单样本统计量：

fBasics::basicStats(cbind(ts.mibm, ts.msp5))

##                 ts.mibm    ts.msp5
## nobs         996.000000 996.000000
## NAs            0.000000   0.000000
## Minimum      -30.368274 -35.585100
## Maximum       38.566232  35.222044
## 1. Quartile   -2.800141  -2.032465
## 3. Quartile    5.039744   3.546559
## Mean           1.089135   0.430068
## Median         1.095871   0.897907
## Sum         1084.778282 428.348045
## SE Mean        0.222860   0.175458
## LCL Mean       0.651806   0.085759
## UCL Mean       1.526464   0.774378
## Variance      49.467724  30.662294
## Stdev          7.033329   5.537354
## Skewness      -0.067766  -0.521287
## Kurtosis       2.621657   7.926907

从超额峰度(Kurtosis)来看两个序列有重尾分布， 而标普的重尾分布更明显。

用MTS包的ccm()函数显示简约的互相关阵序列和图形。 R.S Tsay教授的MTS包的ccm()函数的源代码见后面， 略作修改。

ccm(cbind(ts.mibm, ts.msp5), level=TRUE)

## [1] "Covariance matrix:"
##         ts.mibm ts.msp5
## ts.mibm    49.5    25.1
## ts.msp5    25.1    30.7
## CCM at lag:  0 
##       [,1]  [,2]
## [1,] 1.000 0.645
## [2,] 0.645 1.000
## Simplified matrix: 
## CCM at lag:  1 
## . + 
## . + 
## Correlations: 
##        [,1]   [,2]
## [1,] 0.0443 0.0976
## [2,] 0.0374 0.0836
## CCM at lag:  2 
## . - 
## . . 
## Correlations: 
##         [,1]    [,2]
## [1,] 0.00071 -0.0779
## [2,] 0.01505 -0.0178
## CCM at lag:  3 
## . . 
## . - 
## Correlations: 
##         [,1]    [,2]
## [1,] -0.0139 -0.0581
## [2,] -0.0524 -0.0951
## CCM at lag:  4 
## . . 
## . . 
## Correlations: 
##         [,1]    [,2]
## [1,] -0.0282 -0.0312
## [2,]  0.0384  0.0269
## CCM at lag:  5 
## . + 
## . + 
## Correlations: 
##         [,1]   [,2]
## [1,] 0.02370 0.0812
## [2,] 0.00452 0.0890
## CCM at lag:  6 
## . . 
## . . 
## Correlations: 
##         [,1]    [,2]
## [1,] -0.0397 -0.0166
## [2,] -0.0390 -0.0154
## CCM at lag:  7 
## . . 
## . . 
## Correlations: 
##         [,1]    [,2]
## [1,] 0.00822 -0.0109
## [2,] 0.01813  0.0266
## CCM at lag:  8 
## . . 
## + . 
## Correlations: 
##        [,1]   [,2]
## [1,] 0.0634 0.0301
## [2,] 0.0717 0.0480
## CCM at lag:  9 
## . . 
## . + 
## Correlations: 
##        [,1]   [,2]
## [1,] 0.0515 0.0331
## [2,] 0.0482 0.0749
## CCM at lag:  10 
## . . 
## . . 
## Correlations: 
##        [,1]   [,2]
## [1,] 0.0383 0.0256
## [2,] 0.0166 0.0133
## CCM at lag:  11 
## . . 
## . . 
## Correlations: 
##        [,1]     [,2]
## [1,] 0.0207  0.00321
## [2,] 0.0237 -0.00659
## CCM at lag:  12 
## . . 
## . . 
## Correlations: 
##        [,1]    [,2]
## [1,] 0.0122 -0.0118
## [2,] 0.0225  0.0203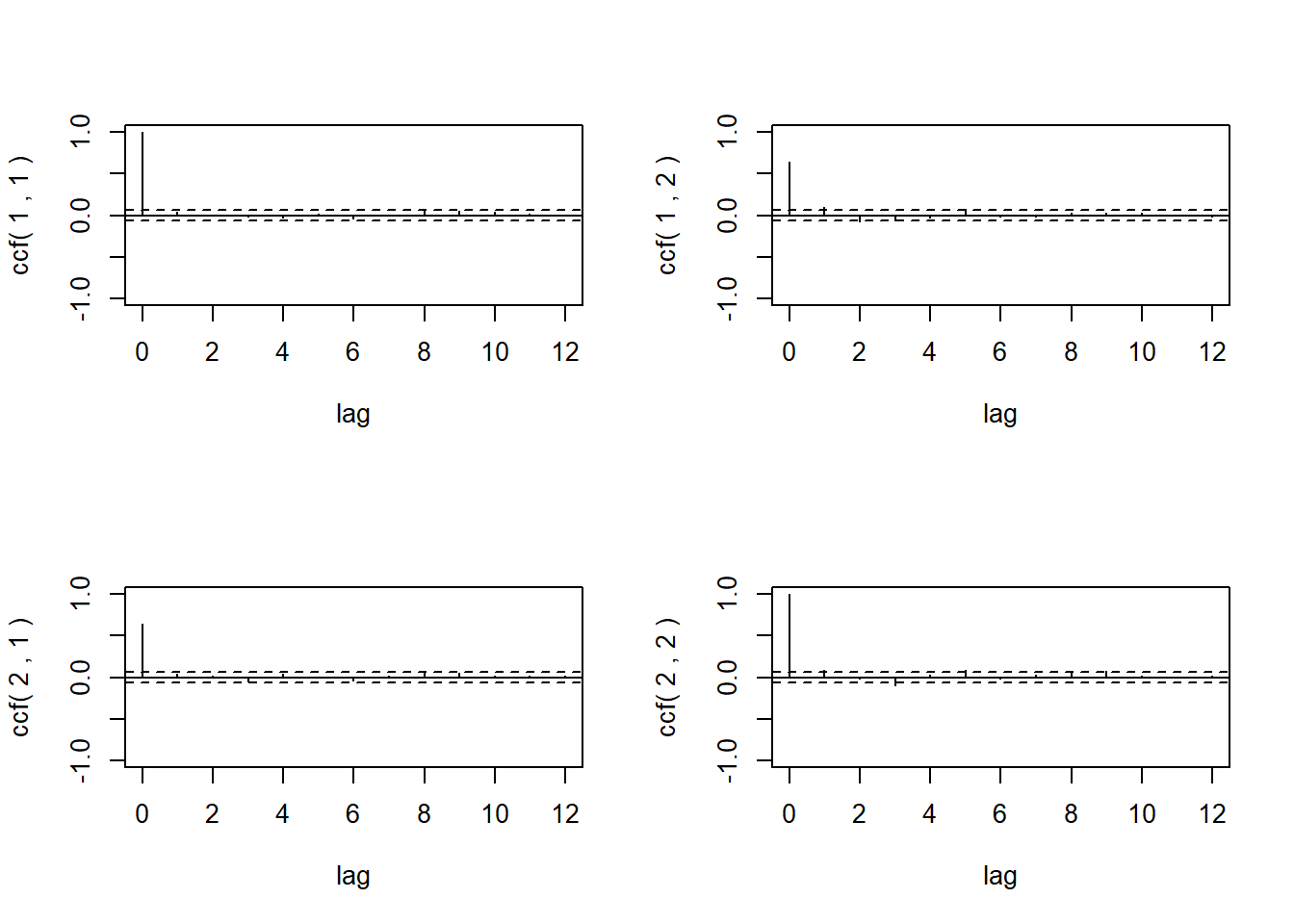

图23.7: IBM和标普500的对数收益率的CCM

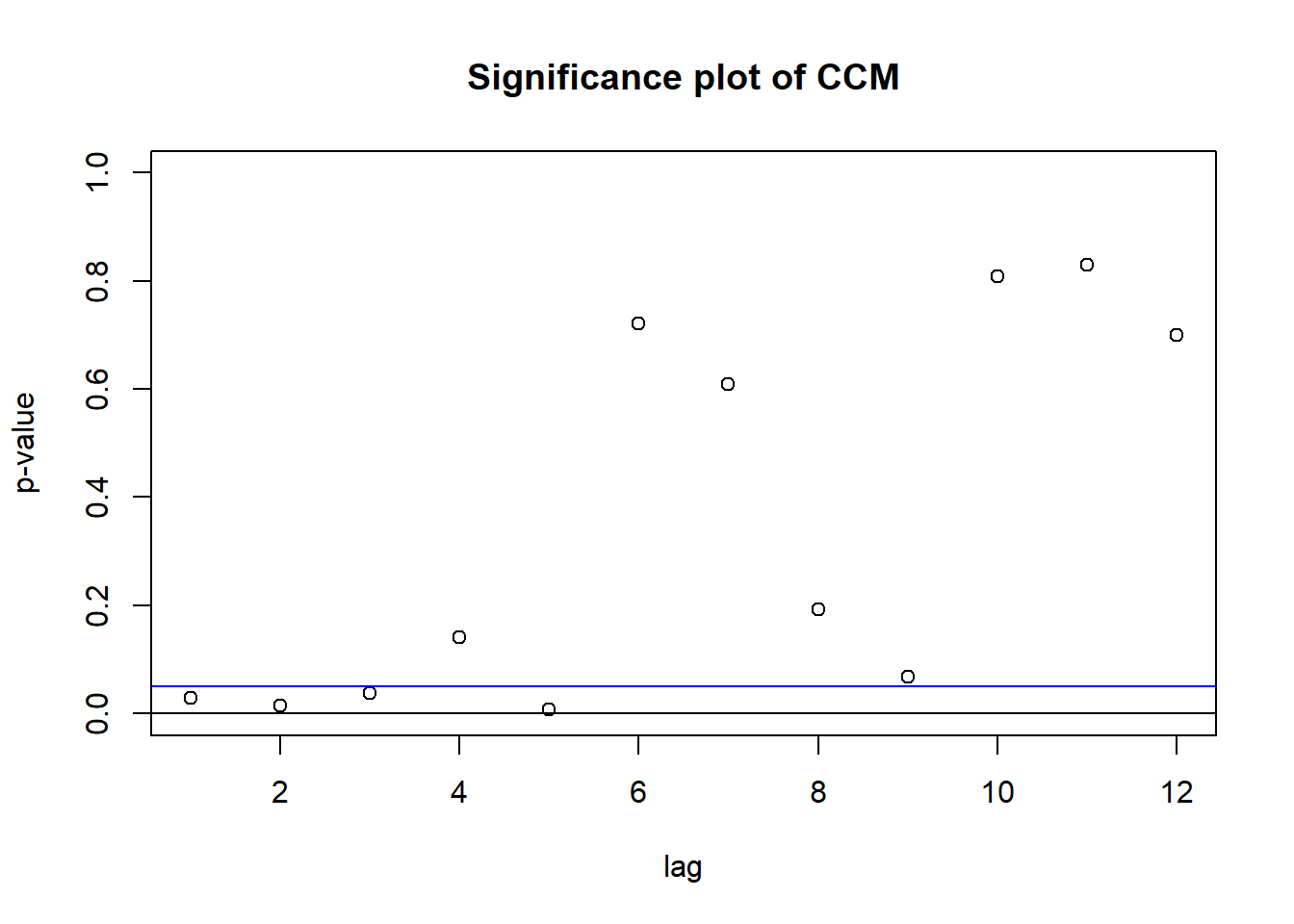
图23.8: IBM和标普500的对数收益率的CCM

记IBM对数收益率为\(r_{1t}\)， 记标普500对数收益率为\(r_{2t}\)， 记\(\boldsymbol r_t = (r_{1t}, r_{2t})^T\)， 则CCM为 \[\begin{aligned} \rho_l =& \left(\begin{array}{cc} \rho_{11}(l) & \rho_{12}(l) \\ \rho_{21}(l) & \rho_{22}(l) \end{array}\right) \\ =& \left(\begin{array}{cc} \text{corr}(x_{1t}, x_{1,t-l}) & \text{corr}(x_{1t}, x_{2,t-l}) \\ \text{corr}(x_{2t}, x_{1,t-l}) & \text{corr}(x_{2t}, x_{2,t-l}) \end{array}\right) \end{aligned}\]

结果中给出了\(\boldsymbol r_t\)的协方差阵估计，即\(\hat\Gamma_0\)； 给出了\(\boldsymbol r_t\)的相关阵估计，即\(\hat{\boldsymbol\rho}_0\)； 随后给出了\(l=1,2,\dots\)的CCM(即\(\hat{\boldsymbol\rho}_l\))的简化表示。 两个序列的同步的相关性较强， 相关系数为0.645； IBM对数收益率的序列自相关（矩阵的左上角元素）都不显著； 标普对数收益率的序列自相关（矩阵的右下角元素）在滞后1,3,5,9等位置显著； IBM受标普过去值的影响（矩阵的右上角元素）在滞后1,2,5位置显著； 标普受IBM过去值的影响（矩阵的左下角元素）都不显著。 这符合一般的常识。

在上面的四幅小图中， 左上图是IBM对数收益率的ACF， 右下图是标普500对数收益率的ACF； 右上图是\(\rho_{12}(l) = \text{corr}(x_{1t}, x_{2,t-l})\), \(l=0,1,2,\dots\)的图形， 即\(t\)时刻IBM对数收益率与滞后的\(t-l\)时刻的标普对数收益率之间的相关系数图， 因为时间的单向性可以看成是标普对IBM股票的领先作用。 左下图是标普对数收益率与滞后的IBM收益率的相关系数图， 可以看成是IBM股票对标普的领先作用。 虽然文本显示的\(\hat{\boldsymbol\rho}_l\)矩阵有正负号， 但是从图形来看除了同步情形以外自相关和互相关都比较弱, 同步时的互相关是显著的(注意右上图和左下图两个突出值都是\(\ell=0\)处的表示同步相关的值，等于0.645)。 标普对IBM有很弱的领先作用， 而IBM对标普没有领先作用。

最后的大图是检验每个\(\boldsymbol\rho_l\)为零矩阵的检验p值随\(l\)变化的图形。 结果表明\(l=1,2,3,5\)时显著不等于零矩阵， 其它各滞后值时不显著。

23.2.2 例1.2：美国国债

考虑各个期限的美国债券指数的月简单收益率， 包括30年、20年、10年、5年和1年期限， 数据来自CRSP数据库， 从1942年1月值1999年12月，共696个观测值。 读入数据后转换为对数收益率， 单位为百分之一。

da2 <- read_table(
  "m-bnd.txt",
  col_types=cols(.default=col_double()))
ts.mbnd <- ts(log(1 + da2)*100, start=c(1942,1), frequency=12)

序列的基本统计：

summary(ts.mbnd)

##      30yrs             20yrs             10yrs              5yrs        
##  Min.   :-8.0440   Min.   :-8.7804   Min.   :-6.9050   Min.   :-5.9771  
##  1st Qu.:-0.8146   1st Qu.:-0.7186   1st Qu.:-0.5882   1st Qu.:-0.1133  
##  Median : 0.2228   Median : 0.2337   Median : 0.2482   Median : 0.2297  
##  Mean   : 0.4024   Mean   : 0.4229   Mean   : 0.4284   Mean   : 0.4489  
##  3rd Qu.: 1.5366   3rd Qu.: 1.4728   3rd Qu.: 1.2825   3rd Qu.: 0.9425  
##  Max.   :12.4993   Max.   :14.1803   Max.   : 9.5301   Max.   :10.0858  
##       1yr         
##  Min.   :-1.7360  
##  1st Qu.: 0.1049  
##  Median : 0.3404  
##  Mean   : 0.4408  
##  3rd Qu.: 0.6372  
##  Max.   : 5.4545

5个序列的时间序列图：

#plot(ts.mbnd, plot.type="multiple", nc=1, yax.flip=TRUE, ylim=c(-10, 15))
plot(as.xts(ts.mbnd), type="l", multi.panel=TRUE, theme="white",
     main="美国国债月对数收益率（%）",
     major.ticks="years",
     grid.ticks.on = "auto")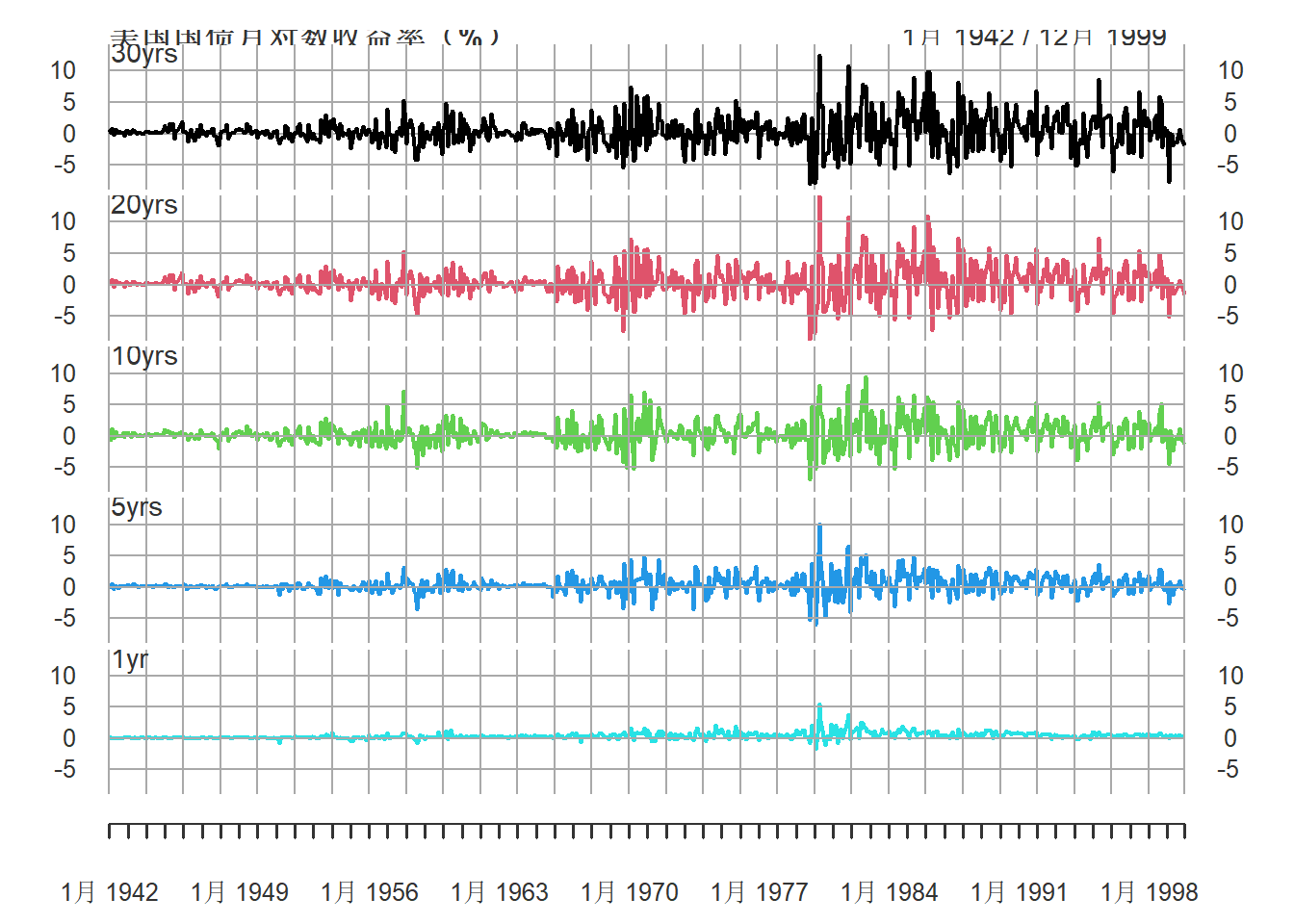

图23.9: 美国国债月对数收益率（%）

可以看出长期国债的收益率波动较大， 短期国债收益率波动较小。

样本均值：

colMeans(ts.mbnd)

##     30yrs     20yrs     10yrs      5yrs       1yr 
## 0.4024412 0.4228871 0.4283688 0.4488915 0.4407712

折合年利率在5%左右。

样本标准差：

apply(ts.mbnd, 2, sd)

##     30yrs     20yrs     10yrs      5yrs       1yr 
## 2.5014721 2.3970918 1.9521371 1.3783452 0.5282478

标准差折合成年标准差（波动率）为8.7%到1.8%之间(月标准差乘以\(\sqrt{12}\))。

同步相关阵：

round(cor(ts.mbnd), 2)

##       30yrs 20yrs 10yrs 5yrs  1yr
## 30yrs  1.00  0.98  0.92 0.85 0.63
## 20yrs  0.98  1.00  0.91 0.86 0.64
## 10yrs  0.92  0.91  1.00 0.90 0.67
## 5yrs   0.85  0.86  0.90 1.00 0.81
## 1yr    0.63  0.64  0.67 0.81 1.00

用ggcorrplot作相关系数矩阵图：

ggcorrplot::ggcorrplot(cor(ts.mbnd),
  hc.order=TRUE, lab=TRUE)

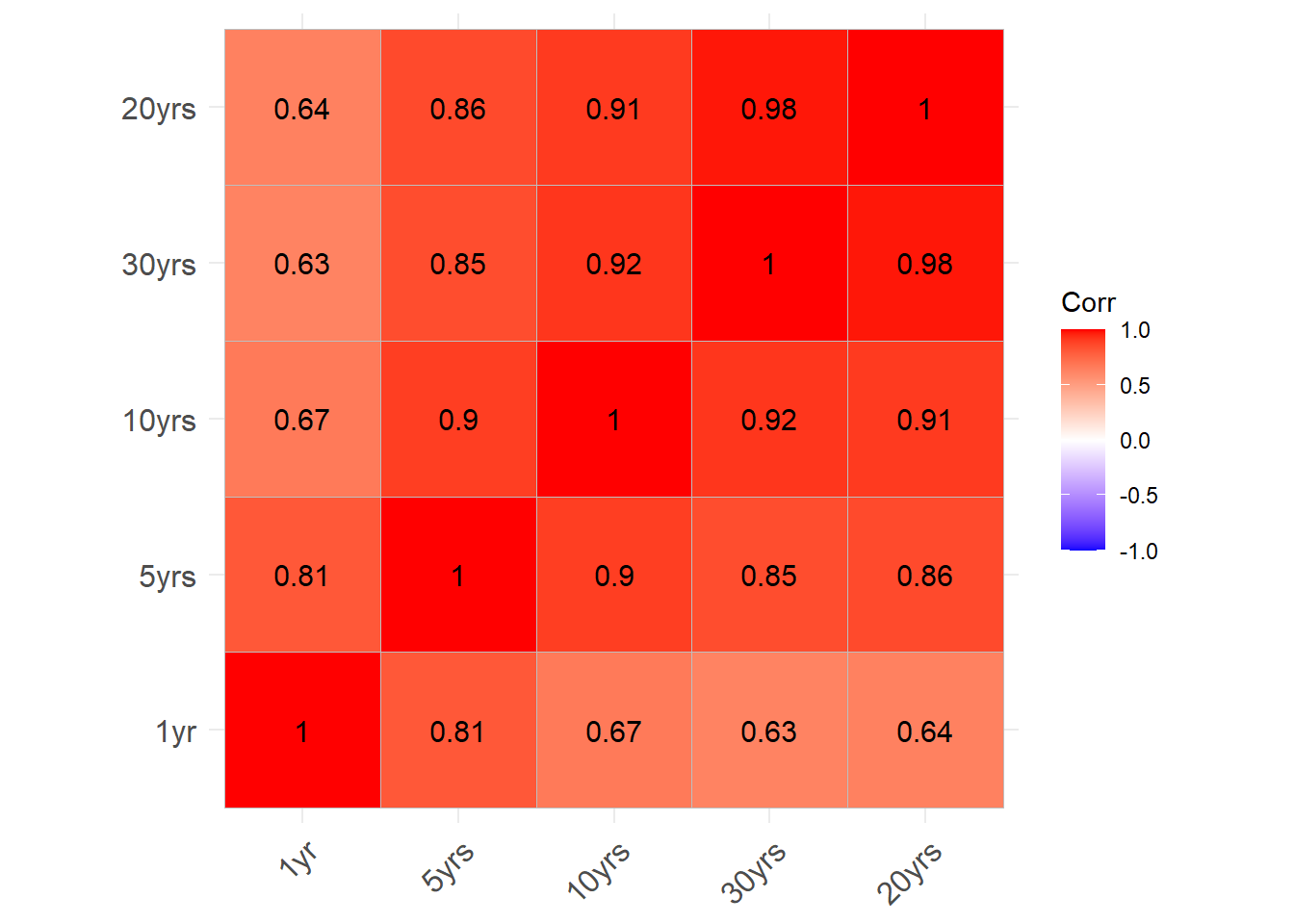
可以看出相关性都很强， 而且长期国债之间的相关比短期国债之间的相关要高。

作CCM统计表和图形：

ccm(ts.mbnd)

## [1] "Covariance matrix:"
##       30yrs 20yrs 10yrs  5yrs   1yr
## 30yrs  6.26 5.860 4.476 2.928 0.830
## 20yrs  5.86 5.746 4.279 2.830 0.806
## 10yrs  4.48 4.279 3.811 2.411 0.694
## 5yrs   2.93 2.830 2.411 1.900 0.592
## 1yr    0.83 0.806 0.694 0.592 0.279
## CCM at lag:  0 
##       [,1]  [,2]  [,3]  [,4]  [,5]
## [1,] 1.000 0.977 0.917 0.849 0.628
## [2,] 0.977 1.000 0.914 0.857 0.637
## [3,] 0.917 0.914 1.000 0.896 0.673
## [4,] 0.849 0.857 0.896 1.000 0.813
## [5,] 0.628 0.637 0.673 0.813 1.000
## Simplified matrix: 
## CCM at lag:  1 
## + + + + + 
## + . + + + 
## + . + + + 
## + + + + + 
## + + + + + 
## CCM at lag:  2 
## . . . . . 
## . . . . . 
## . . . . . 
## . . . . . 
## . . . . + 
## CCM at lag:  3 
## . - . . . 
## - - . . . 
## . . . . . 
## . - . . . 
## . . . . + 
## CCM at lag:  4 
## . + . . . 
## . . . . . 
## . . . . . 
## . . . . . 
## . . . . + 
## CCM at lag:  5 
## . . . + + 
## . . . + + 
## . . . . + 
## . . . . + 
## . . . + + 
## CCM at lag:  6 
## . . . . . 
## . . . . . 
## . . . . + 
## . . . . + 
## . . . . + 
## CCM at lag:  7 
## . . . . . 
## . . . . . 
## . . . . . 
## . . . . . 
## . . . . + 
## CCM at lag:  8 
## . . . . + 
## . . . . + 
## . . . . + 
## . . . . + 
## . . . + + 
## CCM at lag:  9 
## . . . . . 
## . . . . . 
## . . . . + 
## . . . . + 
## . . . . + 
## CCM at lag:  10 
## . . . . . 
## . . . . + 
## . . . . + 
## . . . . + 
## . . + + + 
## CCM at lag:  11 
## + + + + + 
## + + + + + 
## + + + + + 
## + + + + + 
## . . + + + 
## CCM at lag:  12 
## . . . . . 
## . . . . . 
## . . . . . 
## . . . . + 
## . . . . +

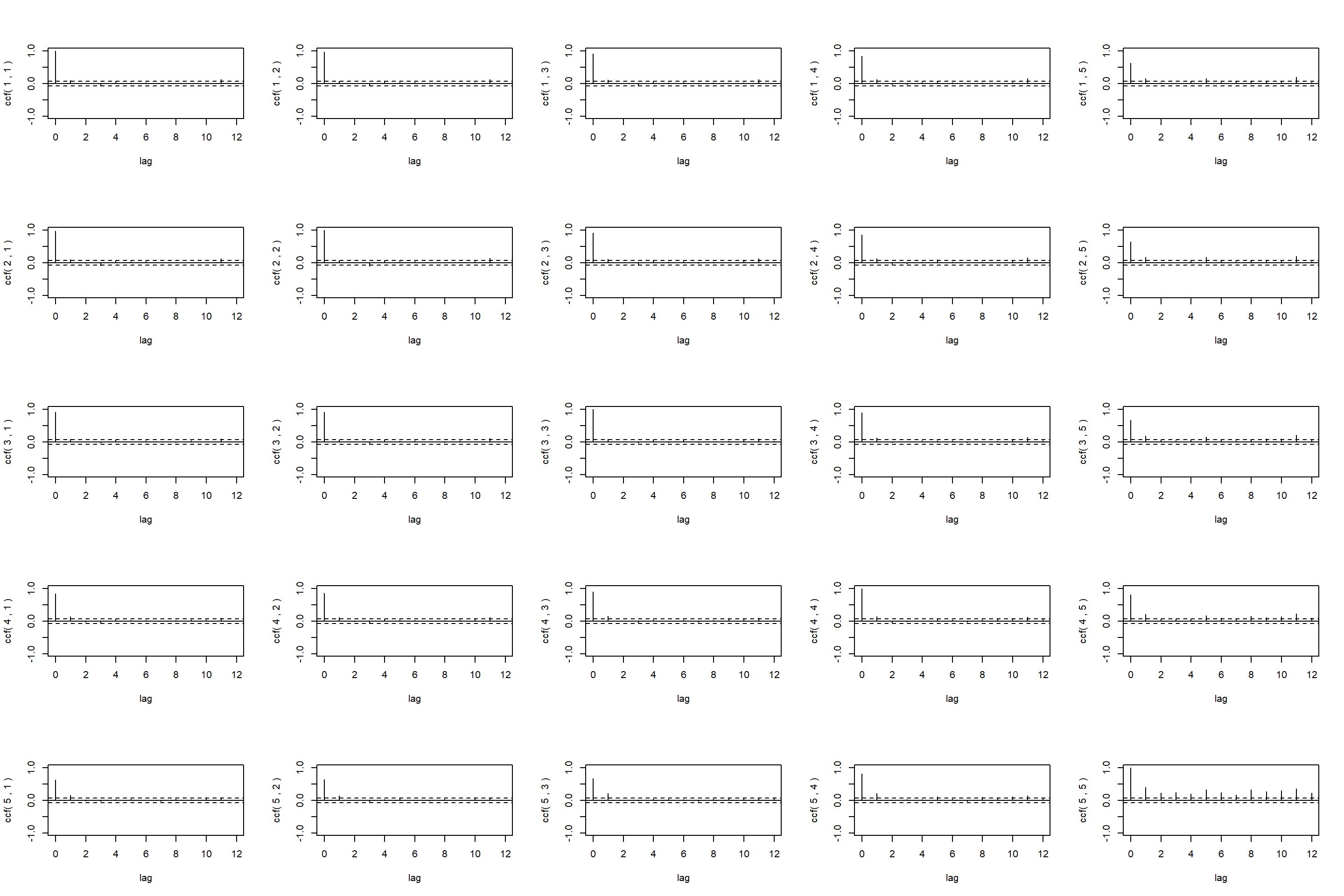
图23.10: 各期国债CCM图

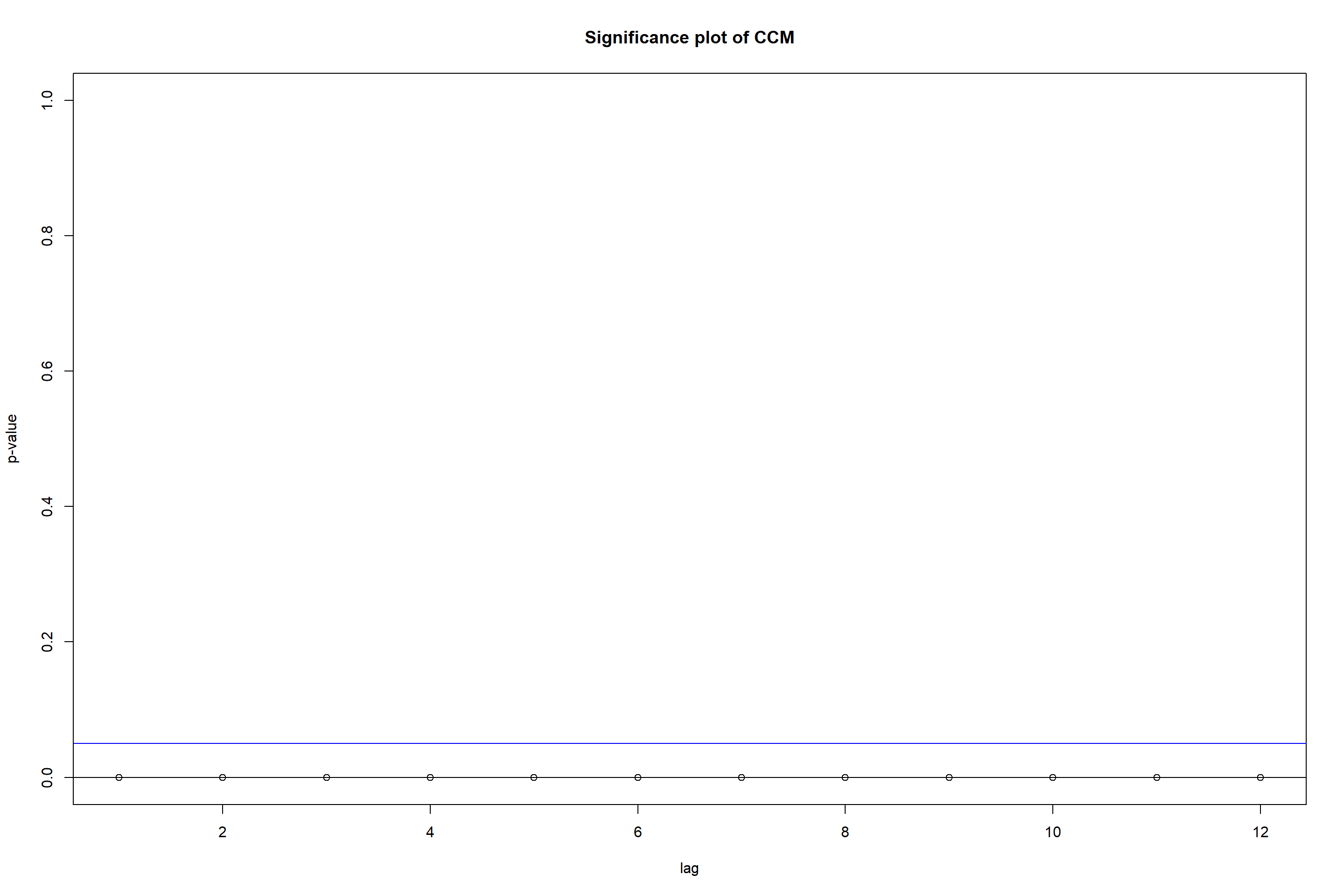
图23.11: 各期国债CCM图

从CCM简化矩阵输出看， 在滞后1时普遍有相互的反馈关系。 在滞后5时一年期国债对各期限都有领先作用。 最后一个p值的图是对每一个\(H_0: \Gamma_l = 0\)的检验p值， 横坐标是滞后\(l\)。

23.3 多元混成检验

Hosking(1980,1981), Li和McLeod(1981) 已经把一元的Ljung-Box白噪声检验推广到了多元的情形。 对一个多元序列，检验零假设 \[\begin{aligned} H_0: \boldsymbol\rho_1 = \dots = \boldsymbol\rho_m = \boldsymbol 0 \end{aligned}\] 对立假设是不全为零矩阵。 这可以检验多元时间序列\(\boldsymbol r_t\)为宽白噪声的零假设， 即\(\boldsymbol r_t\)为弱平稳列且无序列自相关， 可以有同步的分量间相关。

使用检验统计量 \[\begin{aligned} Q_k(m) = T^2 \sum_{l=1}^m \frac{1}{T-l} \text{tr}( \hat\Gamma_l^T \hat\Gamma_0^{-1} \hat\Gamma_l \hat\Gamma_0^{-1}) \end{aligned}\] 其中\(k\)是分量个数， \(T\)是样本序列长度， tr表示求矩阵的迹（对角线元素之和）。 在若\(\Gamma_l=\boldsymbol 0\), \(\forall l > 0\)， 且\(\boldsymbol r_t\)服从多元正态分布， 即\(\boldsymbol r_t\)为独立同多元正态分布， 则\(Q_k(m)\)渐近地服从\(\chi^2(k^2 m)\)分布， 计算右侧p值进行检验。 事实上， 这时\(\hat\Gamma_l\), \(l=1,\dots,m\)渐近服从零均值的相互独立的多元正态分布。

利用Kronecker积记号\(\otimes\)可以将\(Q_k(m)\)用样本互相关阵\(\hat{\boldsymbol\rho}_l\)表示： \[\begin{aligned} Q_k(m) = T^2 \sum_{l=1}^m \frac{1}{T-l} \boldsymbol b_l^T (\hat{\boldsymbol\rho}_0^{-1} \otimes \hat{\boldsymbol\rho}_0^{-1}) \boldsymbol b_l \end{aligned}\] 其中\(\boldsymbol b_l = \text{vec}(\hat{\boldsymbol\rho}_l^T)\), vec表示矩阵按列拉直运算。

对IBM和标普数据， 用MTS::mq()计算多元混成检验：

MTS::mq(cbind(ts.mibm, ts.msp5), lag=12)

## Ljung-Box Statistics:  
##         m       Q(m)     df    p-value
##  [1,]   1.0      10.9     4.0     0.03
##  [2,]   2.0      23.3     8.0     0.00
##  [3,]   3.0      33.5    12.0     0.00
##  [4,]   4.0      40.4    16.0     0.00
##  [5,]   5.0      54.2    20.0     0.00
##  [6,]   6.0      56.3    24.0     0.00
##  [7,]   7.0      59.0    28.0     0.00
##  [8,]   8.0      65.1    32.0     0.00
##  [9,]   9.0      73.8    36.0     0.00
## [10,]  10.0      75.5    40.0     0.00
## [11,]  11.0      77.0    44.0     0.00
## [12,]  12.0      79.2    48.0     0.00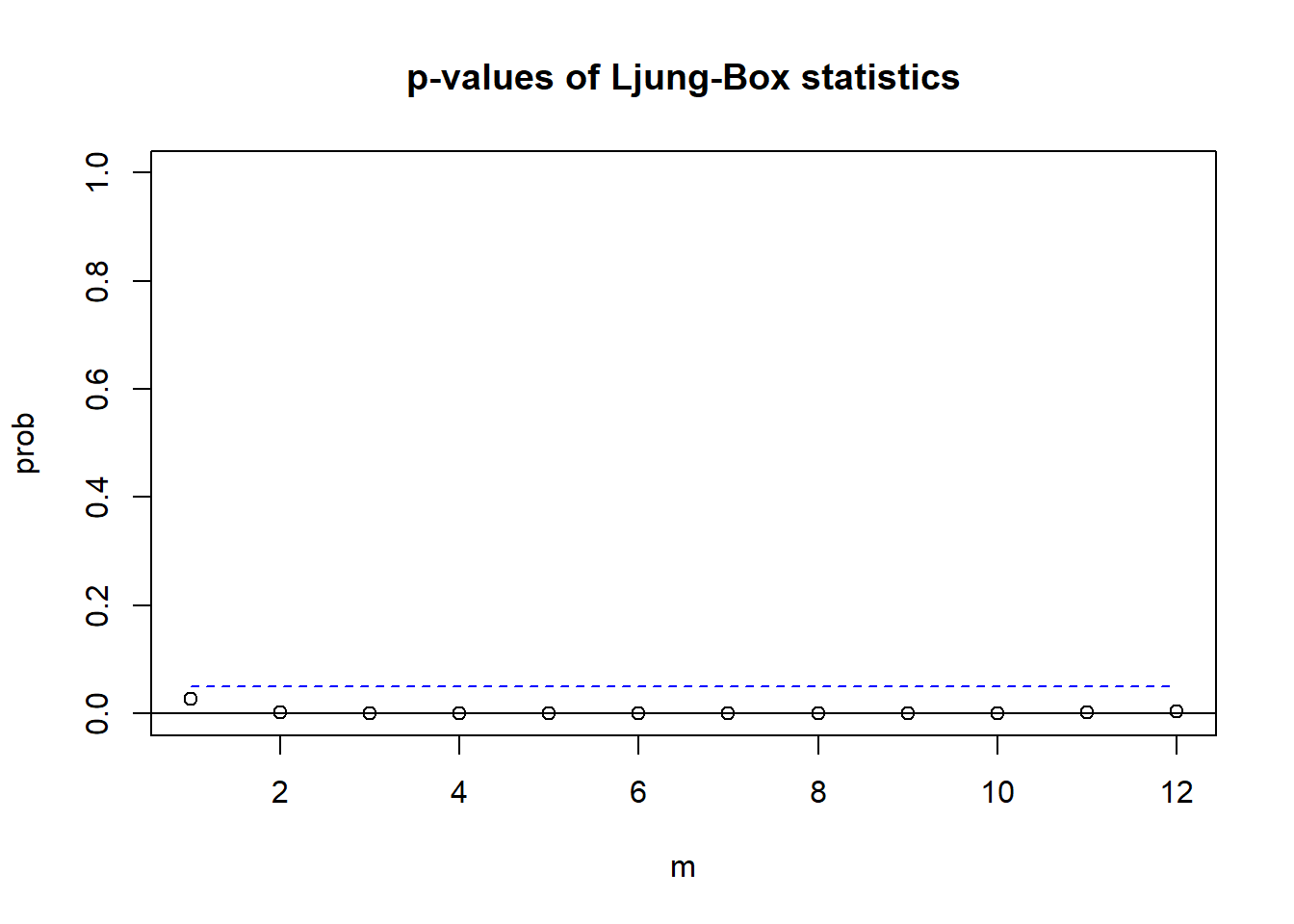

上面的程序对\(m=1,2,\dots, 12\)分别计算了检验， 并做了p值随\(m\)变化的图形。 在0.05水平下都是显著的。

对国债数据做多元混成检验：

MTS::mq(ts.mbnd, lag=12)

## Ljung-Box Statistics:  
##         m       Q(m)     df    p-value
##  [1,]     1       279      25        0
##  [2,]     2       454      50        0
##  [3,]     3       712      75        0
##  [4,]     4       861     100        0
##  [5,]     5      1076     125        0
##  [6,]     6      1268     150        0
##  [7,]     7      1412     175        0
##  [8,]     8      1623     200        0
##  [9,]     9      1835     225        0
## [10,]    10      2009     250        0
## [11,]    11      2213     275        0
## [12,]    12      2366     300        0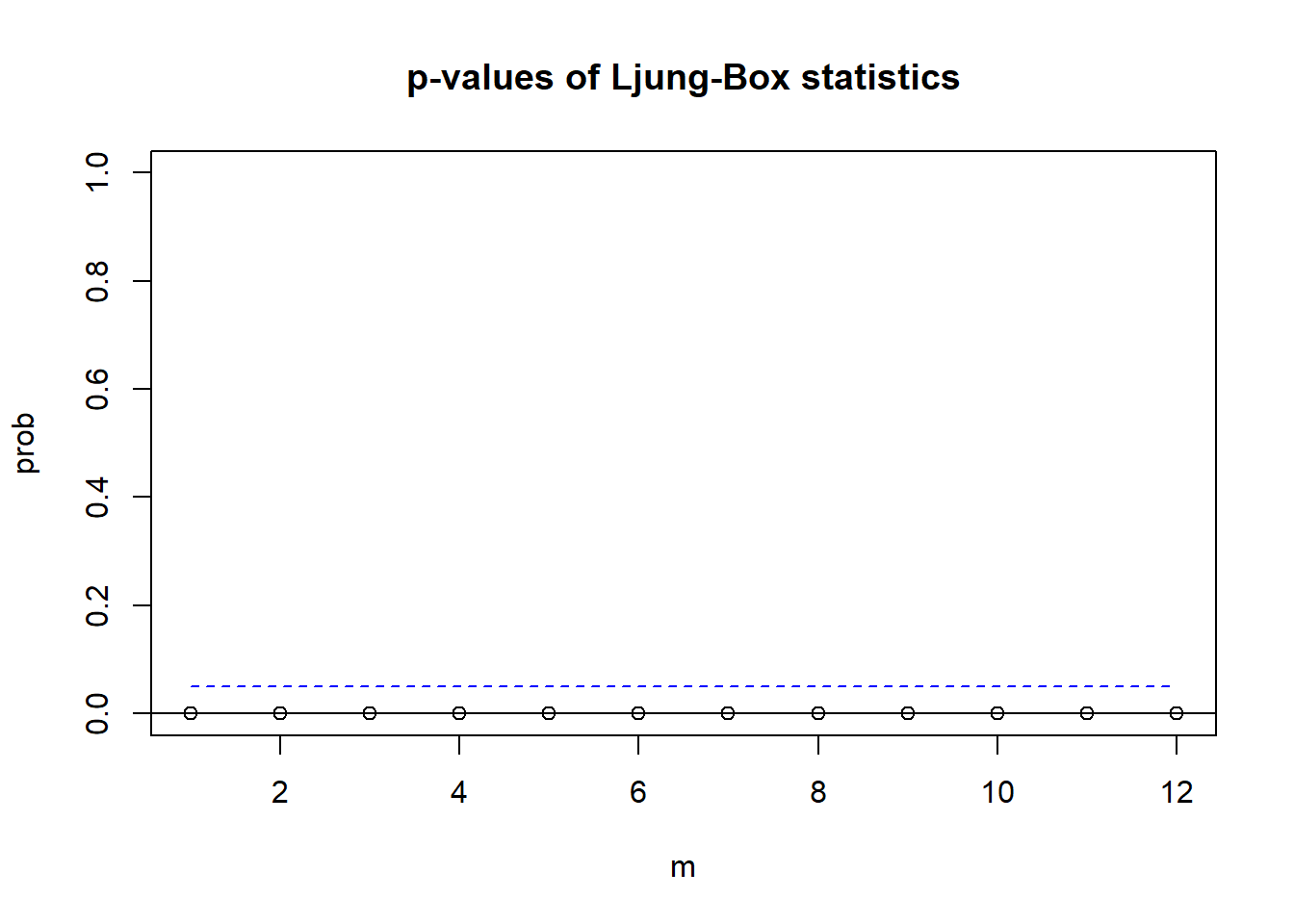

结果都是显著的。

\(Q_k(m)\)统计量是对\(\boldsymbol r_t\)的前\(m\)个互相关阵的一个联合检验， 如果结果显著， 就应该建立多元的均值模型描述序列分量之间的领先–滞后关系。 最常用的是向量自回归(VAR)模型。

23.4 附录：用到的源程序代码和数据

23.4.1 CCM计算和绘图的函数

"ccm" <- function(x, lags=12, level=FALSE, output=TRUE){
  # Compute and plot the cross-correlation matrices.
  # lags: number of lags used.
  # level: logical unit for printing.
  #
  if(!is.matrix(x)) x = as.matrix(x)
  nT=dim(x)[1]; k=dim(x)[2]
  if(output){
    opar <- par(mfcol=c(k,k))
    on.exit(par(opar))
  }
  if(lags < 1)lags=1
  
  # remove the sample means
  y = scale(x,center=TRUE,scale=FALSE)
  
  V1 = cov(y)
  if(output){
    print("Covariance matrix:")
    print(V1,digits=3)
  }
  
  se = sqrt(diag(V1))
  SD = diag(1/se)
  S0 = SD %*% V1 %*% SD
  ## S0 used later
  ksq = k*k
  wk = matrix(0, ksq, lags+1)
  wk[,1] = c(S0)
  j=0
  if(output){
    cat("CCM at lag: ",j,"\n")
    print(S0, digits=3)
    cat("Simplified matrix:","\n")
  }
  
  y = y %*% SD
  crit = 2.0/sqrt(nT)
  
  for (j in 1:lags){
    y1 = y[1:(nT-j),]
    y2 = y[(j+1):nT,]
    Sj = t(y2) %*% y1 / nT
    Smtx = matrix(".", k, k)
    for (ii in 1:k){
      for (jj in 1:k){
        if(Sj[ii,jj] > crit) Smtx[ii,jj] = "+"
        if(Sj[ii,jj] < -crit) Smtx[ii,jj] = "-"
      }
    }
    if(output){
      cat("CCM at lag: ", j, "\n")
      for (ii in 1:k){
        cat(Smtx[ii,],"\n")
      }
      if(level){
        cat("Correlations:","\n")
        print(Sj,digits=3)
      } 
    } ## end of if-(output) statement
    wk[, j+1] = c(Sj)
  }

  if(output){
    iik <- rep(1:k, k)
    jjk <- rep(1:k, each=k)
    tdx=c(0,1:lags)
    jcnt=0
    if(k > 10){
      print("Skip the plots due to high dimension!")
    } else {
      for (j in 1:ksq){
        plot(tdx, wk[j,], type='h', 
             xlab='lag', 
             ylab=paste('ccf(', iik[j], ",", jjk[j], ")"),
             ylim=c(-1,1))
        abline(h=c(0))
        crit=2/sqrt(nT)
        abline(h=c(crit),lty=2)
        abline(h=c(-crit),lty=2)
        jcnt=jcnt+1
      }
    }
    ## end of if-(output) statement
  }
  
  ## The following p-value plot was added on May 16, 2012 by Ruey Tsay.
  ### Obtain a p-value plot of ccm matrix
  r0i=solve(S0)
  R0=kronecker(r0i,r0i)
  pv=rep(0,lags)
  for (i in 1:lags){
    tmp=matrix(wk[,(i+1)],ksq,1)
    tmp1=R0%*%tmp
    ci=crossprod(tmp,tmp1)*nT*nT/(nT-i)
    pv[i]=1-pchisq(ci,ksq)
  }
  if(output){
    par(opar)
    plot(pv,xlab='lag',ylab='p-value',ylim=c(0,1))
    abline(h=c(0))
    abline(h=c(0.05),col="blue")
    title(main="Significance plot of CCM")
  }
  ccm <- list(ccm=wk,pvalue=pv)
}

B 参考文献

Tiao, G. C., and G. E. P. Box. 1981. “Modeling Multiple Time Series with Applications.” Journal of the Americal Statistical Association 76: 802–16.