25 协整分析与向量误差修正模型

25.1 虚假回归问题

线性回归分析是统计学的最常用的模型之一， 但是， 如果回归的自变量和因变量都是时间序列， 回归就不满足回归分析的基本假定： 模型误差项独立同分布。

比如，一元线性回归模型 \[ y_t = a + b x_t + e_t, \ t=1,2,\dots,n, \] 需要假定\(e_1, e_2, \dots, e_t\)不相关， 零均值，方差同为\(\sigma^2\)， \(x_1, x_2, \dots, x_n\)非随机， 这时最小二乘估计是无偏估计。

当\(\lim_{n\to\infty}\frac{1}{n}\sum_{t=1}^n x_t\)极限存在， \(\frac{1}{n}\sum_{t=1}^n (x_t - \bar x)^2\)有正极限时估计相合， 见定理25.1。

如果\(e_t\)，\(x_t\)，\(y_t\)之中有时间序列， 则回归可能不相合， 或者估计相合但是回归结果中的标准误差估计和假设检验有错误。 下面用一些例子说明。

例25.1 考虑一个标准的回归模型。

设\(e_t \text{ iid N}(0, 50^2)\)， \(x_t = t\), \[ y_t = 2 x_t + e_t, \ t=1,2,\dots,n . \]

这时回归是正常的，用模拟说明：

set.seed(101)
n <- 500
spureg01 <- function(n=500){
  x <- seq(n)
  eps <- rnorm(n)*50
  y <- 2 * x + eps
  lmr <- lm(y ~ x)
  summary(lmr) |> print()
  plot(x, y)
  abline(lmr, col="red")
  
  invisible(list(x=x, y=y))
}
spureg01(n)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -153.870  -33.591   -0.772   32.220  134.560 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.74231    4.32775   0.172    0.864    
## x            1.98451    0.01497 132.572   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 48.31 on 498 degrees of freedom
## Multiple R-squared:  0.9724, Adjusted R-squared:  0.9724 
## F-statistic: 1.758e+04 on 1 and 498 DF,  p-value: < 2.2e-16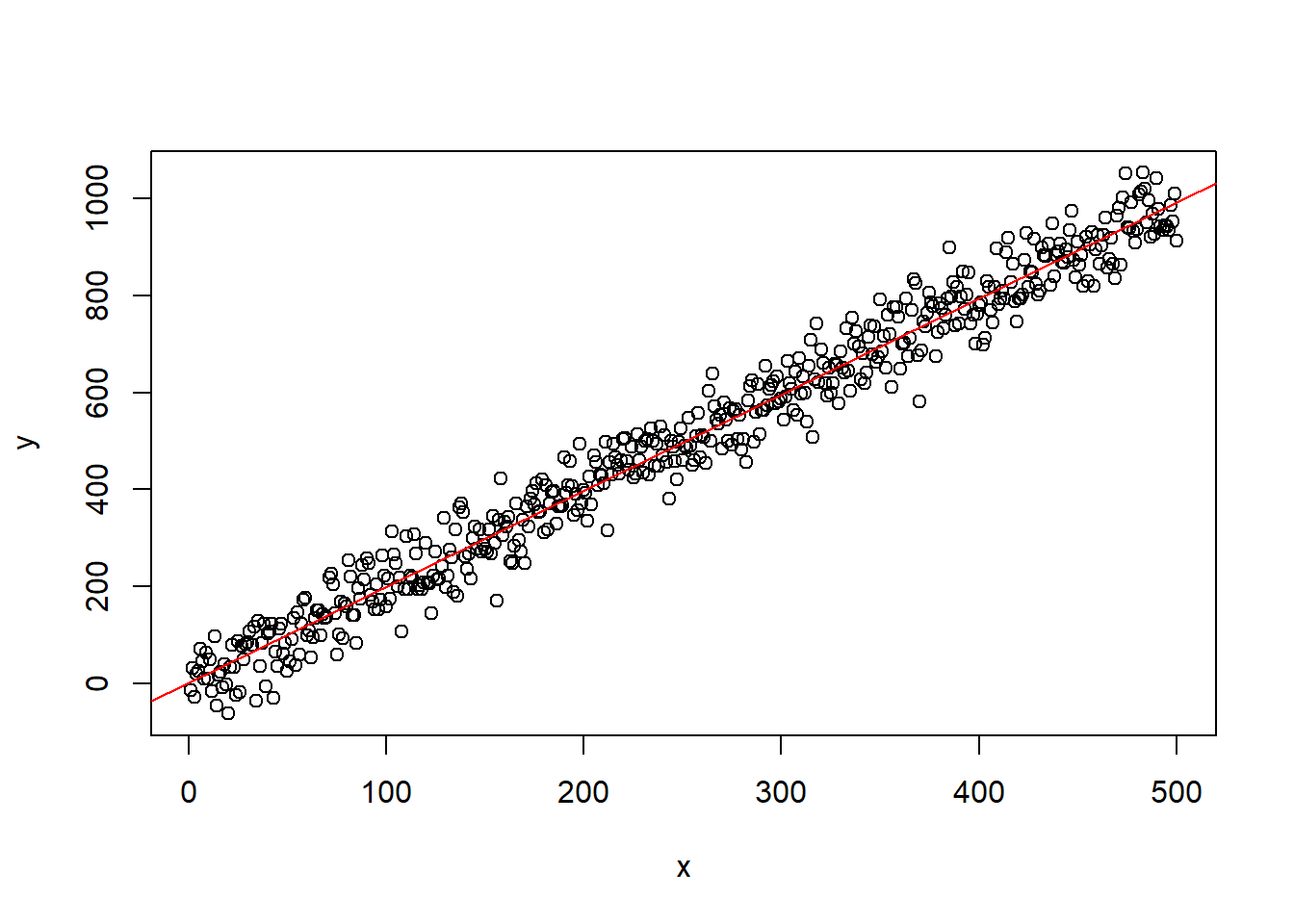

○○○○○

例25.2 考虑回归误差项为AR(1)序列的情形。

设\(x_t = t\), \(\varepsilon_t \text{ iid N} (0, 36^2)\), \[\begin{aligned} e_t =& 0.7 e_{t-1} + \varepsilon_t, \\ y_t =& 2 x_t + e_t, \ t=1,2,\dots,n . \end{aligned}\]

这时回归参数估计相合，无偏， 但是估计的标准误差和假设检验结果是错误的：

set.seed(101)
spureg02 <- function(n=500){
  x <- seq(n)
  eps <- arima.sim(
    model=list(ar=c(0.7)), n=n)*36
  y <- 2 * x + eps
  lmr <- lm(y ~ x)
  summary(lmr) |> print()
  plot(x, y)
  abline(lmr, col="red")
  
  invisible(list(x=x, y=y))
}
sim2 <- spureg02(n)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -137.413  -34.282    0.096   35.279  130.342 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.64699    4.36336  -0.148    0.882    
## x            1.96993    0.01509 130.524   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 48.71 on 498 degrees of freedom
## Multiple R-squared:  0.9716, Adjusted R-squared:  0.9715 
## F-statistic: 1.704e+04 on 1 and 498 DF,  p-value: < 2.2e-16

应该用同时估计回归与ARMA误差项的方法：

arima(sim2$y, order=c(1,0,0), xreg = sim2$x)

## 
## Call:
## arima(x = sim2$y, order = c(1, 0, 0), xreg = sim2$x)
## 
## Coefficients:
##          ar1  intercept  sim2$x
##       0.7018    -1.4932  1.9723
## s.e.  0.0317    10.2735  0.0355
## 
## sigma^2 estimated as 1197:  log likelihood = -2481.72,  aic = 4971.44

直接用普通回归估计的\(\hat b\)的标准误差为\(0.015\)， 考虑到误差项序列自相关后的标准误差估计为\(0.036\)。 有正的序列自相关时， 用普通回归方法估计的斜率项的标准误差容易偏小， 使得检验结果更倾向于显著。

○○○○○

例25.3 考虑回归误差项为I(1)序列的情形。

设\(x_t = t\), \(\varepsilon_t \text{ iid N}(0, 8^2)\), \[\begin{aligned} e_t =& e_{t-1} + \varepsilon_t, \\ y_t =& 2 x_t + e_t, \ t=1,2,\dots,n . \end{aligned}\]

这时回归参数估计不相合， 但是用普通的回归方法估计， 结果会有较大的\(R^2\)和系数显著性：

set.seed(101)
spureg03 <- function(n=500){
  x <- seq(n)
  eps <- cumsum(rnorm(n))*8
  y <- 2 * x + eps
  lmr <- lm(y ~ x)
  summary(lmr) |> print()
  plot(x, y)
  abline(lmr, col="red")
  
  invisible(list(x=x, y=y))
}
spureg03(n)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -101.312  -21.701    0.489   21.568   92.563 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.78482    3.31790   0.538    0.591    
## x            1.69680    0.01148 147.853   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 37.04 on 498 degrees of freedom
## Multiple R-squared:  0.9777, Adjusted R-squared:  0.9777 
## F-statistic: 2.186e+04 on 1 and 498 DF,  p-value: < 2.2e-16

\(R^2\)的值很大， 从估计的\(\hat b\)和\(\text{SE}(\hat b)\)看出， \(\hat b\)的估计显著地偏低。 这说明估计已经不满足相合性。

○○○○○

例25.4 如果\(x_t\)和\(y_t\)都是I(1)序列但是独立， 回归结果也可能很显著。

spureg04 <- function(){
  set.seed(110)
  n <- 500
  x <- cumsum(rnorm(n))
  y <- cumsum(rnorm(n))*2
  lmr <- lm(y ~ x)
  summary(lmr) |> print()
  plot(x, y)
  abline(lmr, col="red")
  
  invisible(list(x=x, y=y, lmr=lmr))
}
sim4 <- spureg04()

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -29.1795  -8.6775   0.0375   8.8982  25.6600 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.49701    0.81992   3.045  0.00245 ** 
## x            0.46871    0.02554  18.350  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.51 on 498 degrees of freedom
## Multiple R-squared:  0.4034, Adjusted R-squared:  0.4022 
## F-statistic: 336.7 on 1 and 498 DF,  p-value: < 2.2e-16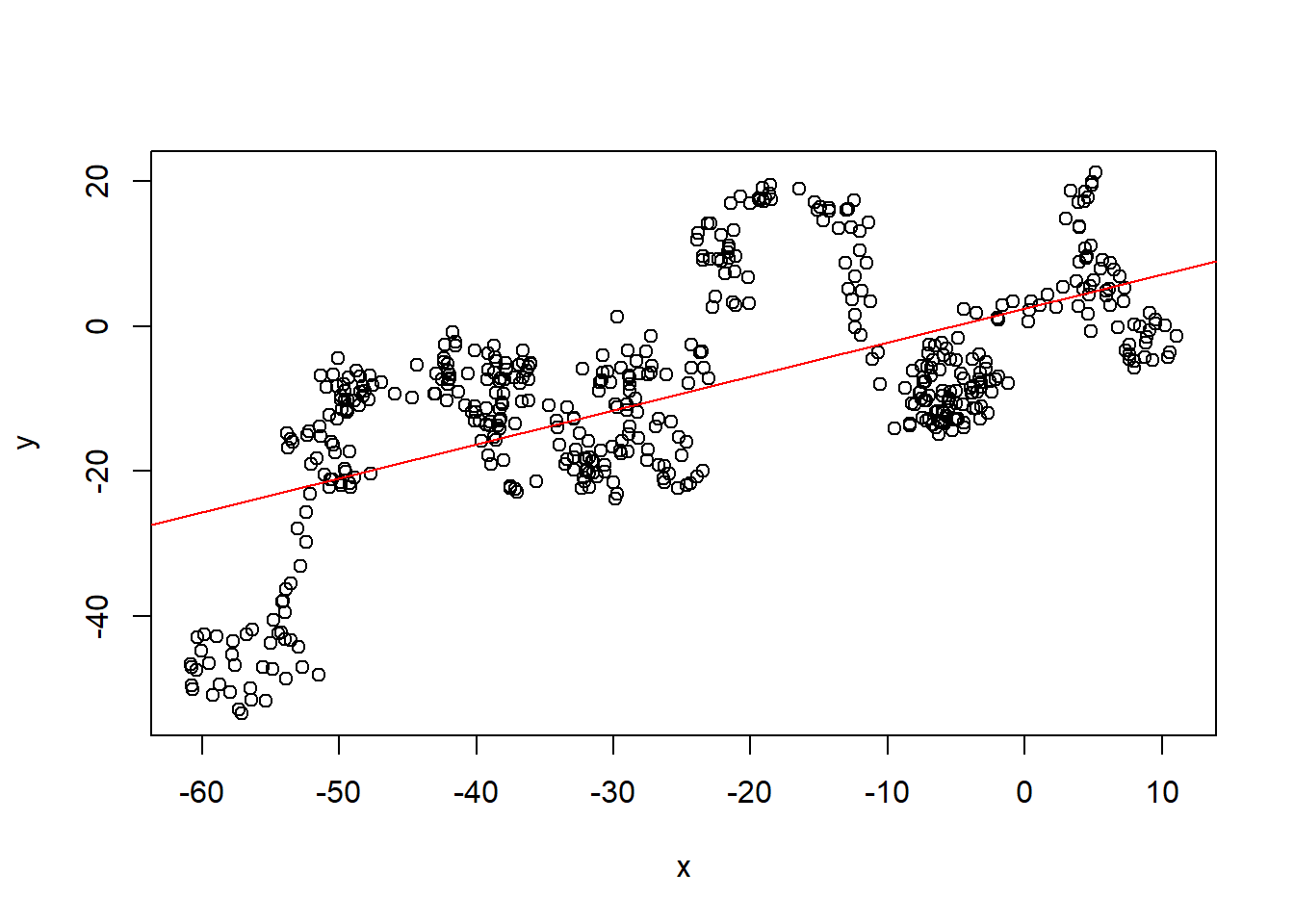

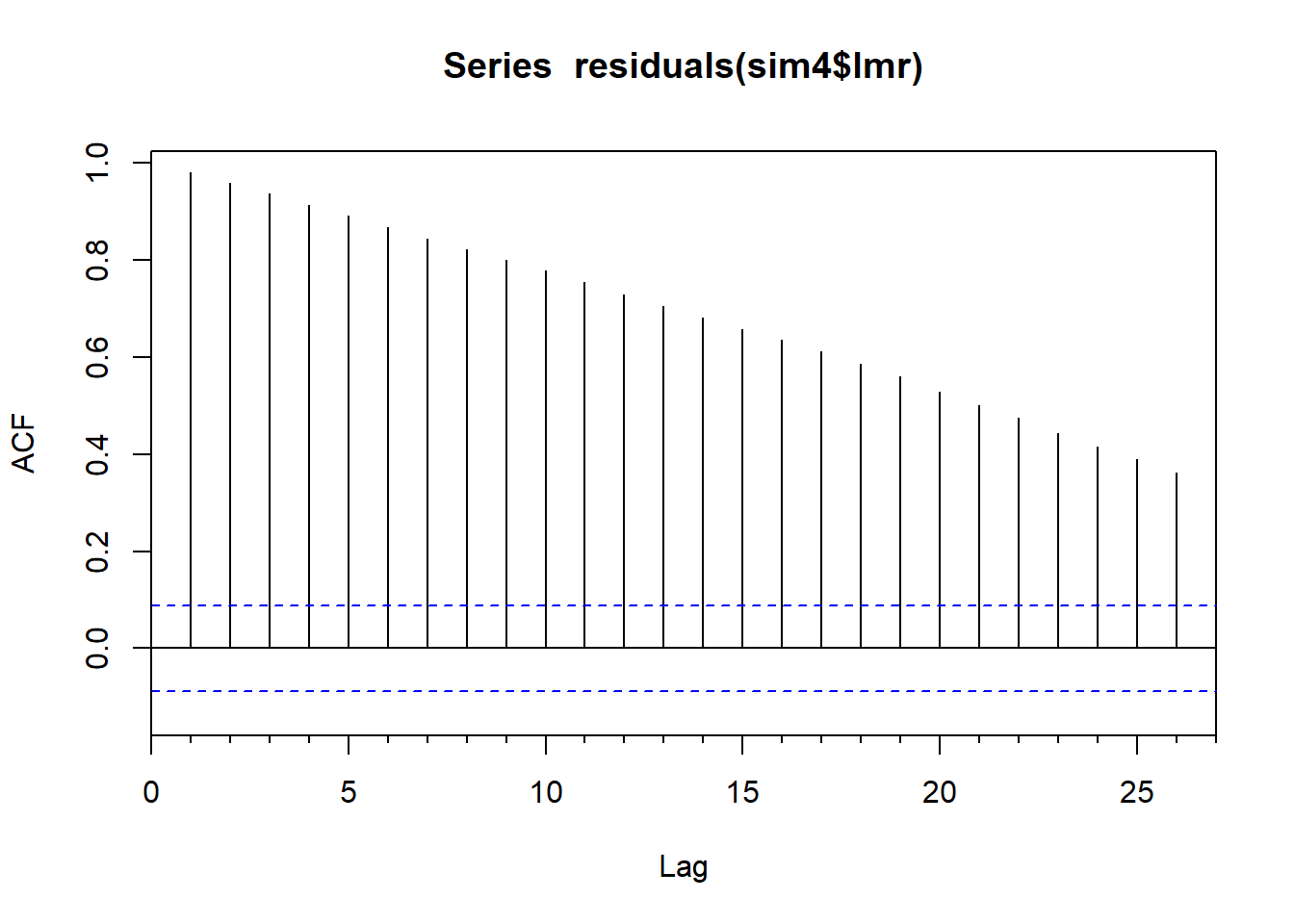
检验回归残差的序列相关性和单位根：

forecast::Acf(residuals(sim4$lmr))

fUnitRoots::adfTest(residuals(sim4$lmr), lags=1, type="c")

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -1.3595
##   P VALUE:
##     0.5525 
## 
## Description:
##  Wed May 10 07:54:08 2023 by user: Lenovo

结果显示回归残差有单位根。

这样的回归称为虚假回归。 两者不应该有线性关系的。

○○○○○

例25.5 如果\(x_t\)和\(y_t\)都是某个I(1)序列的线性变换， 则回归结果是有一定意义的， 称这两个序列有“协整关系”。

设 \(\varepsilon_t \text{ iid N}(0, 1)\), \(\xi_t \text{ iid N}(0, 2^2)\), \(\eta_t \text{ iid N}(0, 2^2)\), \[\begin{aligned} z_t =& z_{t-1} + \varepsilon_t, \\ x_t =& z_t + \xi_t, \\ y_t =& 2 z_t + \eta_t, \ t=1,2,\dots,n . \end{aligned}\]

set.seed(101)
spureg05 <- function(n=500){
  z <- cumsum(rnorm(n))
  x <- z + rnorm(n)*2
  y <- 2*z + rnorm(n)*2
  lmr <- lm(y ~ x)
  summary(lmr) |> print()
  plot(x, y)
  abline(lmr, col="red")
  
  invisible(list(x=x, y=y, lmr=lmr))
}
sim5 <- spureg05(n)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.2598  -2.6583   0.1401   2.6900  11.8576 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -1.0736     0.3024   -3.55 0.000421 ***
## x             1.8743     0.0256   73.23  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.181 on 498 degrees of freedom
## Multiple R-squared:  0.915,  Adjusted R-squared:  0.9149 
## F-statistic:  5362 on 1 and 498 DF,  p-value: < 2.2e-16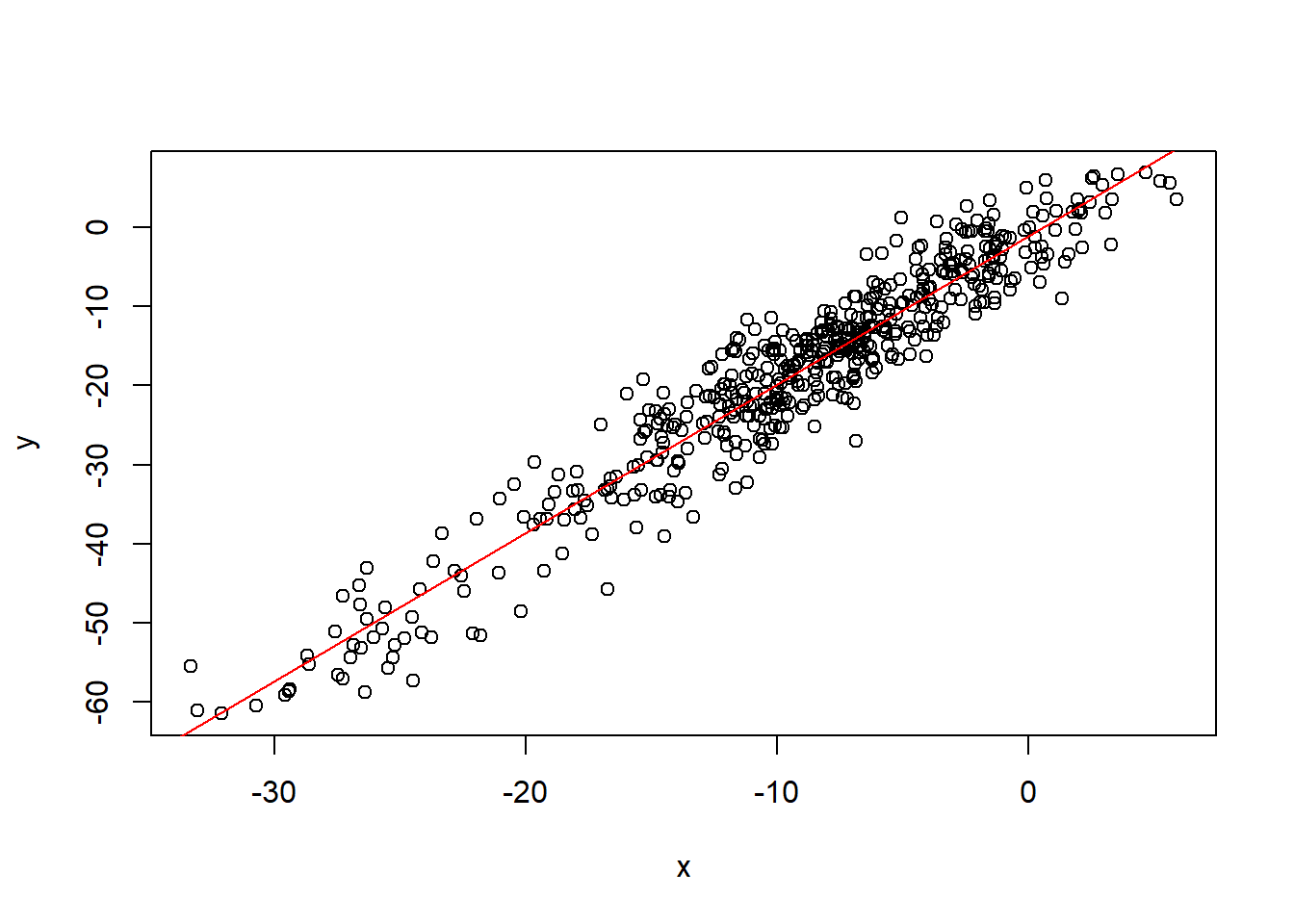

这个回归估计的标准误差仍不可信， 但是回归残差已经基本平稳：

forecast::Acf(residuals(sim5$lmr))

fUnitRoots::adfTest(residuals(sim5$lmr), lags=1, type="c")

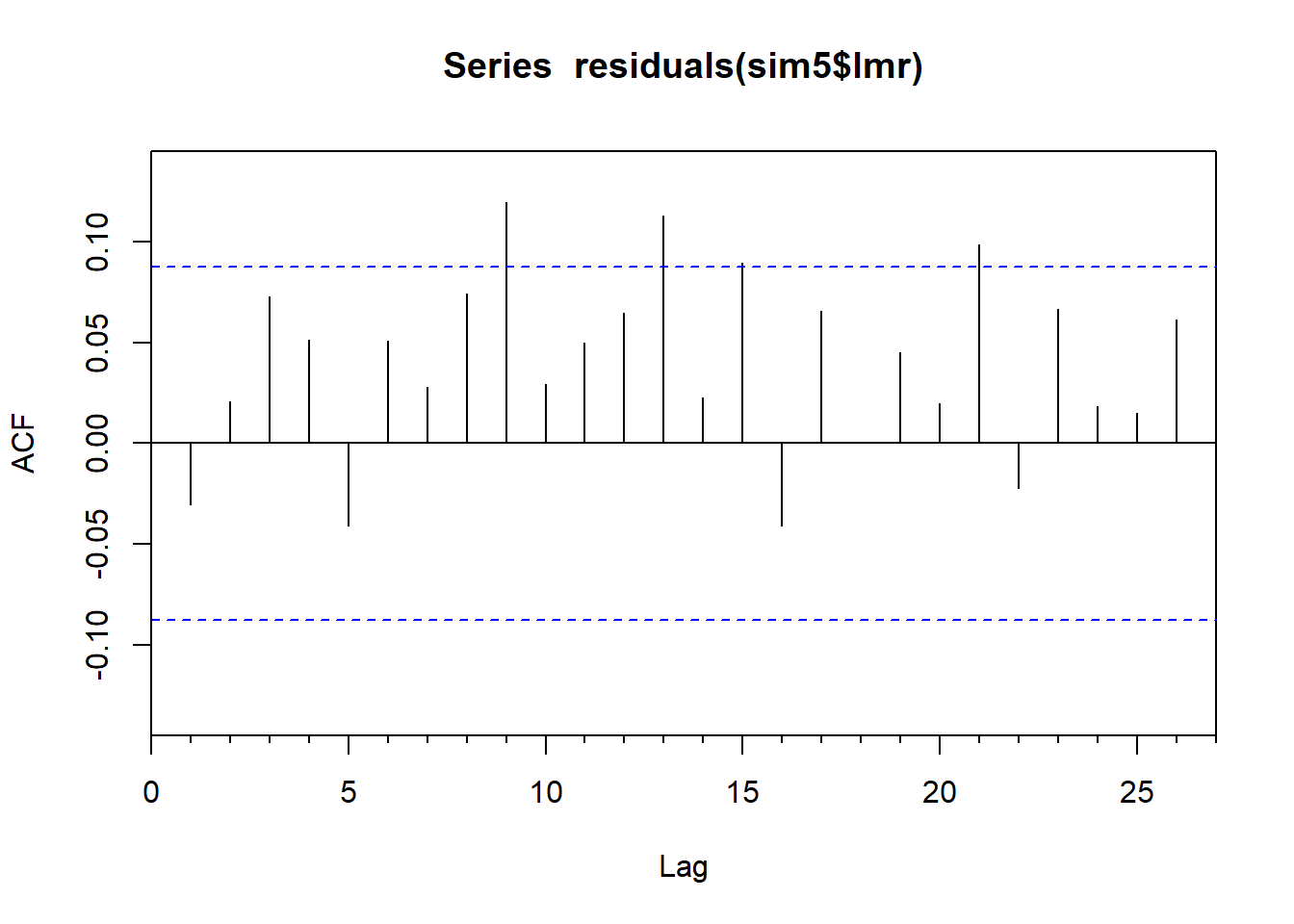
## Warning in fUnitRoots::adfTest(residuals(sim5$lmr), lags = 1, type = "c"):
## p-value smaller than printed p-value

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -15.6707
##   P VALUE:
##     0.01 
## 
## Description:
##  Tue May  9 16:33:10 2023 by user: Lenovo

结果显示回归残差没有单位根。

○○○○○

25.2 协整分析概念

对于二元时间序列\(\boldsymbol x_{t} = (x_{1t}, x_{2t})^T\)， 如果\(x_{1t}\)和\(x_{2t}\)都是一元单位根过程， 但存在非零线性组合\(\boldsymbol\beta = (\beta_1, \beta_2)\)使得 \(z_t = \beta_1 x_{1t} + \beta_2 x_{2t}\)弱平稳， 则称两个分量\(x_{1t}\)和\(x_{2t}\)存在协整关系（cointegration）， \((\beta_1, \beta_2)^T\)称为\(\boldsymbol x_t\)的协整向量。 多个分量的多元时间序列可以类似地定义协整关系， 多元时可以有多个协整向量。

25.3 Engle和Granger两阶段法

考虑两个分量的多元时间序列\(\boldsymbol r_t\)。 为了检验协整性， 首先要用一元的单位根检验（如ADF检验）确认两个分量都是单位根过程， 并且差分之后就没有单位根，这样的单位根过程称为“单整”的， 或I(1)序列。

其次，将\(x_{1t}\)当作因变量，\(x_{2t}\)当作自变量， 作一元线性回归，得到残差\(e_t\)序列， 和回归系数\(\beta_1\)，方程为 \[ x_{1t} = \beta_0 + \beta_1 x_{2t} + e_t \] 根据(R. R. Engle and Granger 1987)的研究， 回归在协整关系成立时参数估计相合， 但是系数的估计非正态， 所以用线性最小二乘估计得到的点估计可用， 但是结果中的t检验和F检验结果无效。

为了验证协整关系是否成立， 只要对\(e_t\)序列进行一元的单位根检验， 但是因为\(e_t\)是回归残差， 其自由度有变化， 所以统计量p值的计算需要进行调整， (Phillips and Ouliaris 1990)给出了利用回归残差进行协整检验的方法， 称为Phillips-Ouliaris协整检验。 如果经检验\(e_t\)不存在单位根， 则称两个分量是协整的。

这样的检验方法称为Engle和Granger两阶段法， 利用(Phillips and Ouliaris 1990)方法计算这个检验称为Phillips-Ouliaris协整检验。 但是，这里的两阶段， 其实第二阶段指的是在多元情况下需要找出所有的协整向量， 这需要利用向量误差修正模型(VECM)。

R扩展包tseries中po.test()可以执行基于EG两阶段法步骤的Phillips-Ouliaris协整检验， 零假设是非协整， 对立假设是存在协整关系。 参见(Phillips and Ouliaris 1990)。

R扩展包urca也提供了Phillips-Ouliaris协整检验。

例4.1

考虑(Pfaff 2008)中的一个例子， 数据为urca包的Raotbl3， 为英国经济的三个季度数据， 从1966年第4季度到1991年第2季度， 都经过季节调整并取了自然对数。 lc是消费，li是收入，lw是财富。

library(urca, quietly = TRUE)
data(Raotbl3)
ts.Raotbl3 <- ts(Raotbl3[,1:3], start=c(1966,4), frequency=4)

数据见附录。

三个序列的时间序列图：

library(quantmod, quietly = TRUE)
plot(as.xts(ts.Raotbl3), type="l", 
     multi.panel=FALSE, theme="white",
     main="英国消费、收入、财富季度数据",
     major.ticks="years",
     grid.ticks.on = "years")

图25.1: 英国消费、收入、财富季度数据

黑色为消费，红色为收入，绿色为财富。

作ADF单位根检验：

fUnitRoots::adfTest(Raotbl3$lc, lags=1, type="ct")

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -1.378
##   P VALUE:
##     0.8341 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

fUnitRoots::adfTest(Raotbl3$li, lags=1, type="ct")

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -2.0159
##   P VALUE:
##     0.57 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

fUnitRoots::adfTest(Raotbl3$lw, lags=1, type="ct")

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -1.0153
##   P VALUE:
##     0.9318 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

结果都不显著， 说明每个都有单位根。 检验其差分：

fUnitRoots::adfTest(diff(Raotbl3$lc), lags=1, type="c")

## Warning in fUnitRoots::adfTest(diff(Raotbl3$lc), lags = 1, type = "c"): p-value
## smaller than printed p-value

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -6.311
##   P VALUE:
##     0.01 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

fUnitRoots::adfTest(diff(Raotbl3$li), lags=1, type="c")

## Warning in fUnitRoots::adfTest(diff(Raotbl3$li), lags = 1, type = "c"): p-value
## smaller than printed p-value

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -7.0434
##   P VALUE:
##     0.01 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

fUnitRoots::adfTest(diff(Raotbl3$lw), lags=1, type="c")

## Warning in fUnitRoots::adfTest(diff(Raotbl3$lw), lags = 1, type = "c"): p-value
## smaller than printed p-value

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -5.9831
##   P VALUE:
##     0.01 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

结果都显著， 说明差分后没有单位根， 三个序列都是一阶差分平稳的（I(1)序列）。

urca包的ur.df()函数可以检验差分的阶数， 并可以对非随机趋势的类型选取进行检验。

来检验消费lc与收入li是否存在协整关系。 将lc对li作一元回归：

eglm1 <- lm(lc ~ li, data=Raotbl3); summary(eglm1)

## 
## Call:
## lm(formula = lc ~ li, data = Raotbl3)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.065949 -0.016067  0.001839  0.017844  0.057295 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.18007    0.14399  -1.251    0.214    
## li           1.00731    0.01322  76.203   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.02379 on 97 degrees of freedom
## Multiple R-squared:  0.9836, Adjusted R-squared:  0.9834 
## F-statistic:  5807 on 1 and 97 DF,  p-value: < 2.2e-16

结果中的检验不可信， 如果存在协整，因为回归模型是 \[ \text{lc} = -0.18 + 1.01 \text{li} + e_t \] 所以 \[ \text{lc} - 1.01 \text{li} = -0.18 + e_t \] 即\((\text{lc}, \text{li})^T\)的协整向量为\((1, -1.01)\)。

不考虑自由度调整问题，直接作ADF检验， 但其p值是不准确的，需要使用修改过的临界值。

fUnitRoots::adfTest(residuals(eglm1), lags=1, type="c")

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -2.6351
##   P VALUE:
##     0.09127 
## 
## Description:
##  Tue Feb 22 12:01:45 2022 by user: Lenovo

(Phillips and Ouliaris 1990)给出了利用回归残差进行协整检验的方法， 包含两种方法， 方差比方法和多元迹统计量方法。 R扩展包urca的ca.po()可以用来计算Phillips-Ouliaris检验。 选项demean="constant"指定有确定性常数趋势， demean="trend"指定有确定性线性趋势， 缺省为demean="none"，没有确定性趋势（无漂移）。 选项type="Pu"指定使用方差比方法， 选项type="Pz"指定使用多元迹方法， 多元迹方法对哪个分量作为回归因变量不敏感。

检验消费与收入的协整：

library(urca, quietly = TRUE)
summary(ca.po(Raotbl3[-(1:2),c("lc", "li")], type="Pz", demean="constant"))

## 
## ######################################## 
## # Phillips and Ouliaris Unit Root Test # 
## ######################################## 
## 
## Test of type Pz 
## detrending of series with constant only 
## 
## Response lc :
## 
## Call:
## lm(formula = lc ~ zr)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.047772 -0.007401  0.001410  0.008169  0.048541 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.01183    0.08952   0.132    0.895    
## zrlc         1.01799    0.05960  17.080   <2e-16 ***
## zrli        -0.01831    0.06074  -0.302    0.764    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01393 on 93 degrees of freedom
## Multiple R-squared:  0.9941, Adjusted R-squared:  0.994 
## F-statistic:  7844 on 2 and 93 DF,  p-value: < 2.2e-16
## 
## 
## Response li :
## 
## Call:
## lm(formula = li ~ zr)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.036705 -0.011532 -0.000549  0.008860  0.053870 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.09644    0.10642   0.906    0.367    
## zrlc         0.33183    0.07085   4.683  9.6e-06 ***
## zrli         0.66298    0.07220   9.182  1.1e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01656 on 93 degrees of freedom
## Multiple R-squared:  0.9914, Adjusted R-squared:  0.9912 
## F-statistic:  5334 on 2 and 93 DF,  p-value: < 2.2e-16
## 
## 
## 
## Value of test-statistic is: 39.7042 
## 
## Critical values of Pz are:
##                   10pct    5pct    1pct
## critical values 47.5877 55.2202 71.9273

零假设是没有存在协整关系， 0.05水平的右侧临界值为55.2， 统计量值为39.7， 没有超过临界值， 不拒绝零假设， 认为消费与收入不存在协整关系。 这也可能是PO方法的检验功效不足的问题。

Phillips Ouliaris协整检验在多元时不能用来确定多个独立的协整向量， 这需要利用VECM模型。

R扩展包urca提供了多种协整检验， 除了Phillips-Ouliaris协整检验， 还可以进行Johansen的迹和最大特征值检验。

R扩展包tsDyn提供了Johansen的协整检验， 并可以用AIC或BIC进行秩滞后值选择。

R扩展包CommonTrend可以从协整系统中提取共同的趋势， 并绘图。

R扩展包cointReg提供了协整的回归参数估计、推断功能。

R扩展包vars提供了VAR、VECM、结构VAR(SVAR)等模型的估计、检验， 因果性检验和协整检验的功能。

这里主要讨论从VAR模型的角度定义协整。

25.4 VARMA模型

仿照一元的ARMA模型， VAR模型可以推广成VARMA模型， 形如 \[\begin{align} P(B) \boldsymbol r_t = Q(B) \boldsymbol a_t \tag{25.1} \end{align}\] 其中 \[\begin{aligned} P(z) =& \boldsymbol I - \boldsymbol\Phi_1 z - \dots - \boldsymbol\Phi_p z^p \\ Q(z) =& \boldsymbol I + \boldsymbol\Theta_1 z + \dots + \boldsymbol\Theta_q z^q \end{aligned}\] 是两个矩阵值的多项式， 假设\(P(z)\)和\(Q(z)\)没有左公因子， 否则可以消去公因子化简。

VARMA存在同一个模型能够表示为不同参数形式的问题， 所以尽可能使用VAR，避免使用VARMA。

如果需要模拟VARMA或者VAR模型数据， 在R中有扩展包dse的ARMA()用来指定VARMA的系数， 函数simulate()根据输入的系数生成模拟数据。 如

library(dse, quietly = TRUE)
#自回归部分系数矩阵
Apoly <- array(c(
  1,-0.5,0,
  0,-0.4,-0.25,
  0,-0.1,0,
  1,-0.5,0),
  c(3,2,2))
Apoly[2,,]
#滑动平均部分系数矩阵，此处有变换
B <- matrix(c(3,0,0,2),ncol=2)*0.01
#生成模型
var2 <- ARMA(A=Apoly, B=B)
print(var2)
#模拟数据
varsim <- simulate(
  var2, sampleT=250, 
  noise=list(w=matrix(rnorm(500),nrow=250,ncol=2)),
  rng=list(seed=c(123456)))
vardat <- matrix(varsim$output, nrow=250, ncol=2)

25.4.1 VARMA模型协整关系

这里将VAR和VARMA模型略推广， 不要求模型一定满足平稳性条件。 如果不然， 因为多元弱平稳其分量一定也是一元弱平稳的， 就不能容许分量存在单位根。

考虑如下的二元VARMA(1,1)模型的例子。 \[\begin{align} & \left(\begin{array}{c} x_{1t} \\ x_{2t} \end{array}\right) - \left(\begin{array}{cc} 0.5 & -1.0 \\ -0.25 & 0.5 \end{array}\right) \left(\begin{array}{c} x_{1,t-1} \\ x_{2,t-1} \end{array}\right) \\ =& \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) + \left(\begin{array}{cc} 0.2 & -0.4 \\ -0.1 & 0.2 \end{array}\right) \left(\begin{array}{c} a_{1,t-1} \\ a_{2,t-1} \end{array}\right) \tag{25.2} \end{align}\] 其中的扰动\(\boldsymbol a_t\)的协方差阵\(\Sigma\)为正定阵。

这个模型不是弱平稳的， 因为\(|P(z)| = 1 - z\)有一个单位根。

将模型改写为 \[\begin{aligned} \left(\begin{array}{cc} 1 - 0.5B & B \\ 0.25B & 1 - 0.5B \end{array}\right) \left(\begin{array}{c} x_{1t} \\ x_{2t} \end{array}\right) = \left(\begin{array}{cc} 1 - 0.2B & 0.4B \\ 0.1B & 1 - 0.2B \end{array}\right) \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) \end{aligned}\] 利用伴随矩阵， 因为\(\boldsymbol A \cdot \text{adj}(\boldsymbol A) = |\boldsymbol A| \boldsymbol I\)， 模型两边都左乘\(P(B)\)的伴随矩阵 \[\begin{aligned} \left(\begin{array}{cc} 1 - 0.5B & -B \\ -0.25B & 1 - 0.5B \end{array}\right) \end{aligned}\] 而\(|P(B)| = 1 - B\)， 模型转化成 \[\begin{aligned} \left(\begin{array}{cc} 1-B & 0 \\ 0 & 1-B \end{array}\right) \left(\begin{array}{c} x_{1t} \\ x_{2t} \end{array}\right) = \left(\begin{array}{cc} 1-0.7B & -0.6B \\ -0.15B & 1-0.7B \end{array}\right) \left(\begin{array}{c} a_{1t} \\ a_{2t} \end{array}\right) \end{aligned}\] 即 \[\begin{aligned} x_{1t} - x_{1,t-1} =& a_{1t} - 0.7 a_{1,t-1} - 0.6 a_{2,t-1} \\ x_{2t} - x_{2,t-1} =& a_{2t} - 0.7 a_{2,t-1} - 0.15 a_{1,t-1} \end{aligned}\] 这两个模型左边是一阶差分， 右边是MA(1)序列， 所以\(x_{1t}\)和\(x_{2t}\)都是一元单位根过程。 这两个分量并不独立， 因为模型右边包含共同的扰动成分。

设法对两个分量进行线性变换， 使得单位根只出现在一个分量中。 令 \[\begin{aligned} \boldsymbol L =& \left(\begin{array}{cc} 1.0 & -2.0 \\ 0.5 & 1.0 \end{array}\right) \\ \boldsymbol y_t =& \left(\begin{array}{c} y_{1t} \\ y_{2t} \end{array}\right) = L \left(\begin{array}{c} x_{1t} \\ x_{2t} \end{array}\right) \\ \boldsymbol b_t =& L \boldsymbol a_t \end{aligned}\] 原来的\(\boldsymbol x_t\)模型可以写成 \[\begin{aligned} \boldsymbol x_t = \boldsymbol\Phi \boldsymbol x_{t-1} + \boldsymbol a_t + \boldsymbol\Theta \boldsymbol a_{t-1} \end{aligned}\] 两边左乘\(\boldsymbol L\)得到关于\(\boldsymbol y_t\)的模型： \[\begin{aligned} \boldsymbol y_t =& \boldsymbol L \boldsymbol x_t \\ =& \boldsymbol L \boldsymbol\Phi \boldsymbol x_{t-1} + \boldsymbol L \boldsymbol a_t + \boldsymbol L \boldsymbol\Theta \boldsymbol a_{t-1} \\ =& \boldsymbol L \boldsymbol\Phi \boldsymbol L^{-1} \boldsymbol y_{t-1} + \boldsymbol b_t + \boldsymbol L \boldsymbol\Theta \boldsymbol L^{-1} \boldsymbol b_{t-1} \end{aligned}\] 计算其中的系数矩阵，得到\(\boldsymbol x_t\)线性变换得到的\(\boldsymbol y_t\)序列的模型为 \[\begin{aligned} & \left(\begin{array}{c} y_{1t} \\ y_{2t} \end{array}\right) - \left(\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right) \left(\begin{array}{c} y_{1,t-1} \\ y_{2,t-1} \end{array}\right) \\ =& \left(\begin{array}{c} b_{1t} \\ b_{2t} \end{array}\right) + \left(\begin{array}{cc} -0.4 & 0 \\ 0 & 0 \end{array}\right) \left(\begin{array}{c} b_{1,t-1} \\ b_{2,t-1} \end{array}\right) \end{aligned}\] 即 \[\begin{aligned} y_{1t} - y_{1,t-1} =& b_{1t} - 0.4 b_{1,t-1} \\ y_{2t} =& b_{2t} \end{aligned}\] 其中 \[\begin{aligned} y_{1t} =& x_{1t} - 2 x_{2t} \\ y_{2t} =& 0.5 x_{1t} + x_{2t} \end{aligned}\] \(y_{1t}\)仍是一元单位根过程， 但\(y_{2t}\)已经是弱平稳列， 所以\(x_{1t}\)和\(x_{2t}\)之间存在协整关系。

一般地， 对于\(k\)元时间序列\(\boldsymbol x_t\)建立了VAR或者VARMA模型后， 如果分量都是一元单位根过程， 但AR部分的特征多项式\(|P(z)|\)的根1的重数小于\(k\)， 分量间就存在协整关系。 如果特征多项式的根1的重数为\(h<k\)， 称\(k-h\)为协整因子个数， 这是能找到的线性组合后平稳的线性独立的线性组合系数的个数。 这种线性组合称为协整向量。 在上面的例子中因为\(y_{2t}\)平稳所以\((0.5, 1)^T\)是一个协整向量。

25.5 误差修正模型与协整

25.5.1 误差修正模型

因为在协整系统中， 单位根非平稳分量的个数多于单位根的个数 （通过线性组合可以使得单位根非平稳的分量减少）， 所以如果对每个单位根非平稳分量计算差分， 虽然使得分量都平稳了， 但是会造成过度差分， 使得部分分量的ARMA模型的MA部分有单位根， 这样的模型平稳但不可逆， 不可逆的模型在估计和预测上比较困难。

(R. R. Engle and Granger 1987)讨论了协整系统的误差修正表示， 称为向量误差修正模型(VECM, vector error correction model)。

以(25.2)的协整系统为例。 令\(\Delta \boldsymbol x_t = \boldsymbol x_t - \boldsymbol x_{t-1}\)， 模型可以化为 \[\begin{aligned} \Delta\boldsymbol x_t =& \boldsymbol x_t - \boldsymbol x_{t-1} = \left(\begin{array}{c} \Delta x_{1t} \\ \Delta x_{2t} \end{array}\right) \\ =& \left(\begin{array}{cc} -0.5 & -1 \\ -0.25 & -0.5 \end{array}\right) \boldsymbol x_{t-1} + \boldsymbol a_t + \left(\begin{array}{cc} -0.2 & 0.4 \\ 0.1 & -0.2 \end{array}\right) \boldsymbol a_{t-1} \\ =& \left(\begin{array}{c} -1 \\ -0.5 \end{array}\right) \left(\begin{array}{cc} 0.5 & 1.0 \end{array}\right) \boldsymbol x_{t-1} + \boldsymbol a_t + \left(\begin{array}{cc} -0.2 & 0.4 \\ 0.1 & -0.2 \end{array}\right) \boldsymbol a_{t-1} \end{aligned}\] 注意到\(y_{2t} = (0.5, 1) \boldsymbol x_{t-1}\)是平稳的， 所以上式两边都是平稳的， MA部分没有出现单位根，不引入不可逆性。 上式描述了平稳序列。 这样的表示称为VECM。

此表示可以推广到一般的VARMA模型。 对(25.1)的VARMA模型， 如果其中有\(m\)个协整因子，\(m<k\)， 单位根的个数大于\(m\)， 必存在如下的误差修正形式(VECM): \[\begin{aligned} \Delta\boldsymbol x_t =& \boldsymbol\alpha \boldsymbol\beta^T \boldsymbol x_{t-1} + \sum_{j=1}^{p-1} \boldsymbol\Phi_j^* \Delta \boldsymbol x_{t-j} + \boldsymbol a_t + \sum_{j=1}^q \boldsymbol\Theta_j \boldsymbol a_{t-j} \end{aligned}\] 其中\(\boldsymbol\alpha\)和\(\boldsymbol\beta\)都是\(k\times m\)列满秩矩阵， MA部分没有单位根， \(m\)维时间序列\(\boldsymbol y_t = \boldsymbol\beta^T \boldsymbol x_t\)是平稳列（没有单位根）， \(\boldsymbol\beta\)的每一列都是\(\boldsymbol x_t\)的一个协整系数。 \(\boldsymbol\Phi_j^*\)和\(\boldsymbol\alpha\), \(\boldsymbol\beta\)都依赖于原来的AR部分的系数矩阵 \(\boldsymbol\Phi_j\)，关系为： \[\begin{aligned} \boldsymbol\Phi_j^* =& -\sum_{i=j+1}^p \boldsymbol\Phi_i, \ j=1,2,\dots, p-1\\ \boldsymbol\alpha \boldsymbol\beta^T =& \boldsymbol\Phi_p + \dots + \boldsymbol\Phi_1 - \boldsymbol I = -P(1) \end{aligned}\] 可以对\(-P(1)\)作奇异值分解得到\(\boldsymbol\alpha\)和\(\boldsymbol\beta\)， \(\boldsymbol\alpha\)和\(\boldsymbol\beta\)并不唯一。 当模型参数从样本估计时， 不会有严格的单位根， 也不能通过矩阵秩得到\(-P(1) = \boldsymbol\alpha \boldsymbol\beta^T\)这样的分解， 需要进行检验。

25.5.2 VAR模型的误差修正形式

为简单起见仅考虑VAR模型（不要求平稳性条件）。 VAR模型的估计与解释都更容易。

考虑\(\boldsymbol x_t\)的如下的带有非随机线性趋势项的\(k\)维VAR(\(p\))模型 \[\begin{align} \boldsymbol x_t =& \boldsymbol\mu_t + \boldsymbol\Phi_1 \boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_p \boldsymbol x_{t-p} + \boldsymbol a_t \tag{25.3} \end{align}\] 其中\(\boldsymbol a_t \sim \text{N}_k(\boldsymbol 0, \boldsymbol\Sigma)\)， \(\boldsymbol\mu_t = \boldsymbol\mu_0 + \boldsymbol\mu_1 t\)。

记 \[\begin{aligned} P(z) = \boldsymbol I - \boldsymbol\Phi_1 z - \dots - \boldsymbol\Phi_p z^p \end{aligned}\] 当用行列式\(|P(z)|\)表示\(z\)的多项式的所有根都在复平面的单位圆外时\(\{\boldsymbol x_t \}\) 是弱平稳的（简称平稳的）， 在讨论单位根和协整问题时记弱平稳列为I(0)序列。

为简单起见， 设\(\boldsymbol x_t\)的所有分量至多需要一次差分就可以变平稳， 即至多为I(1)序列。 这就是说， 如果分量\(x_{it}\)不平稳， \(\Delta x_{it} = x_{it} - x_{i,t-1}\)就一定是平稳的。 这也是实际的大部分序列都能满足的。

上面的VAR(\(p\))模型有如下的误差修正形式（VECM） \[\begin{align} \Delta \boldsymbol x_t =& \boldsymbol\mu_t + \boldsymbol\Pi \boldsymbol x_{t-1} + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \tag{25.4} \end{align}\] 其中 \[\begin{aligned} \boldsymbol\Phi_j^* =& -\sum_{i=j+1}^p \boldsymbol\Phi_i, \ j=1,2,\dots,p-1 \\ \boldsymbol\Pi =& \boldsymbol\alpha \boldsymbol\beta^T = -P(1) \end{aligned}\] \(\boldsymbol\alpha\)和\(\boldsymbol\beta\)是满秩的\(k \times m\)矩阵， \(m\)是协整向量个数。 容易看出\(\boldsymbol\Phi_j\)可以从VECM的参数中递推地反解为 \[\begin{aligned} \boldsymbol\Phi_1 =& \boldsymbol I + \boldsymbol\Pi + \boldsymbol\Phi_1^* \\ \boldsymbol\Phi_j =& \boldsymbol\Phi_j^* - \boldsymbol\Phi_{j-1}^*, \ j=2,\dots,p, \ \boldsymbol\Phi_p^*=\boldsymbol 0 \end{aligned}\]

因为假定每个分量至多\(I(1)\) 所以VECM式(25.4)中的\(\{ \Delta\boldsymbol x_t \}\)序列是I(0)序列。

如果\(\boldsymbol x_t\)有单位根， 则\(|P(1)|=0\)， 从而\(\boldsymbol\Pi = -P(1)\)不满秩。 根据\(\boldsymbol\Pi\)的秩， 将(25.4)的VECM分为如下三种情况：

情况1： \(\text{rank}(\boldsymbol\Pi)=0\)。 这时\(\boldsymbol\Pi=\boldsymbol 0\)， \(\boldsymbol x_t\)有\(k\)个单位根， 不存在协整关系， \(\boldsymbol x_t\)不是协整的， (25.4)的VECM变成了如下的关于\(\Delta\boldsymbol x_{t}\)的VAR(\(p-1\))模型 \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\mu_t + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \end{aligned}\] 只要关于差分序列建模即可。

情况2： \(\text{rank}(\boldsymbol\Pi)=k\)满秩。 这时\(|P(1)| \neq 0\)， 没有单位根， \(\boldsymbol x_t\)本身是平稳列， 只要直接关于\(\boldsymbol x_t\)建立平稳的VAR模型即可。

情况3： \(0 < m=\text{rank}(\boldsymbol\Pi)<k\)， 这时\(\boldsymbol x_t\)存在协整关系。 下面主要考虑情况3。

\(\boldsymbol\Pi\)可以分解为 \[ \boldsymbol\Pi_{k\times k} = \boldsymbol\alpha \boldsymbol\beta^T \] 其中\(\boldsymbol\alpha\)和\(\boldsymbol\beta\)都是\(k\times m\)的列满秩矩阵， \(\boldsymbol\beta\)的每一列都是\(\boldsymbol x_t\)的一个协整向量， \(m\)元时间序列\(\boldsymbol \omega_t = \boldsymbol\beta^T \boldsymbol x_t\)是I(0)序列。 \(\boldsymbol\alpha\)称为载荷矩阵(loadings matrix)。 \(\boldsymbol x_t\)有\(k-m\)个单位根， 这些单位根给出了\(\boldsymbol x_t\)的\(k-m\)个共同趋势， 相当于自由变化的趋势； 而\(m\)个协整分量\(\boldsymbol \omega_t\)， 则可以看成是\(\boldsymbol x_t\)的\(k\)个分量的\(m\)个线性约束， 或长期线性依赖关系。 本身就是I(0)的分量可以计入这\(m\)个当中。 (25.4)的VECM可以写成 \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\mu_t + \boldsymbol\alpha \boldsymbol\beta^T \boldsymbol x_{t-1} + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \end{aligned}\]

记\(m = \text{rank}(\boldsymbol\Pi)\)。 在\(0<m<k\)时， 得到这\(k-m\)个公共趋势的方法是先计算\(\boldsymbol\alpha\) 的正交补矩阵\(\boldsymbol\alpha_{\perp}\)， \(\boldsymbol\alpha_{\perp}\)是\(k \times (k-m)\)矩阵， \((\boldsymbol\alpha, \boldsymbol\alpha_{\perp})\)为满秩\(k\)阶方阵， 且\(\boldsymbol\alpha_{\perp}^T \boldsymbol\alpha = \boldsymbol 0\)。 令\(\boldsymbol y_t = \boldsymbol\alpha_{\perp}^T \boldsymbol x_t\), 则\(\boldsymbol y_t\)是\(m-k\)元的I(1)序列， \(\boldsymbol y_t\)不再有协整关系， 在(25.4)的VECM两边同时左乘\(\boldsymbol\alpha_{\perp}^T\)可以去掉 \(\boldsymbol\Pi \boldsymbol x_{t-1}\)项， 变成了 \[\begin{aligned} \Delta \boldsymbol y_t =& \boldsymbol\alpha_{\perp}^T \boldsymbol\mu_t + \boldsymbol\alpha_{\perp}^T \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\alpha_{\perp}^T \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol\alpha_{\perp}^T \boldsymbol a_t \end{aligned}\] 将\(\Delta \boldsymbol y_t\)表示成了右侧的\(k-m\)元平稳列的形式。

容易看出\(\boldsymbol\Pi=\boldsymbol\alpha \boldsymbol\beta^T\)的分解是不唯一的， 对任意\(m\)阶正交阵\(\boldsymbol\Omega\)， 都有 \[ \boldsymbol\alpha \boldsymbol\beta^T = \boldsymbol\alpha \boldsymbol\Omega \boldsymbol\Omega^T \boldsymbol\beta^T = (\boldsymbol\alpha \boldsymbol\Omega) (\boldsymbol\beta \boldsymbol\Omega)^T = \boldsymbol\alpha_* \boldsymbol\beta_*^T \] 其中\(\boldsymbol\alpha_*\)和\(\boldsymbol\beta_*\)也都是\(k \times m\)列满秩矩阵。 为此增加约束条件， 要求 \[\begin{aligned} \boldsymbol\beta = \left(\begin{array}{c} \boldsymbol I_m \\ \boldsymbol\beta_1 \end{array}\right) \end{aligned}\] \(\boldsymbol\beta_1\)为\((k-m) \times m\)矩阵。 将\(\boldsymbol x_t\)分解为 \[\begin{aligned} \boldsymbol x_t = \left(\begin{array}{c} \boldsymbol u_t \\ \boldsymbol v_t \end{array}\right) \end{aligned}\] \(\boldsymbol u_t\)为\(m\)元， \(\boldsymbol v_t\)为\(k-m\)元， 则 \(\boldsymbol\beta^T \boldsymbol x_t = \boldsymbol u_t + \boldsymbol\beta_1 \boldsymbol v_t\)。 实际中这可能需要将\(\boldsymbol x_t\)的各分量重新排序使得有单位根的分量（至少有\(m\)个）都排在前面， 将没有单位根的分量都排在后面。

为了使得\(\boldsymbol\omega_t = \boldsymbol\beta^T \boldsymbol x_t\)平稳， 还需要其它的参数条件， 就像没有协整的I(0)的VAR(1)需要平稳性条件那样。 比如， 考虑有一个协整向量的二元VAR(1)模型， 这里\(k=2\)， \(m=1\)， 两个分量都为单位根过程， VECM为 \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\mu_t + \left(\begin{array}{c} \alpha_1 \\ \alpha_2 \end{array}\right) \left(\begin{array}{cc} 1 & \beta_1 \end{array}\right) \boldsymbol x_{t-1} + \boldsymbol a_t \end{aligned}\] 两边同时左乘\(\boldsymbol\beta^T\)， 注意\(\omega_t = \boldsymbol\beta^T \boldsymbol x_t\) 则\(\Delta\omega_t = \boldsymbol\beta^T \Delta\boldsymbol x_t\)，所以 \[\begin{aligned} \Delta\omega_t =& \boldsymbol\beta^T \boldsymbol\mu_t + (\alpha_1 + \alpha_2 \beta_1) \omega_{t-1} + \boldsymbol\beta^T \boldsymbol a_t \end{aligned}\] 记\(b_t = \boldsymbol\beta^T \boldsymbol a_t\)， 则\(\{ b_t \}\)为白噪声列， 将方程左边的\(\omega_{t-1}\)移项到右边，得 \[\begin{aligned} \omega_t =& \boldsymbol\beta^T \boldsymbol\mu_t + (1 + \alpha_1 + \alpha_2 \beta_1) \omega_{t-1} + b_t \end{aligned}\] 为使得模型平稳需要\(\boldsymbol\alpha\)和\(\boldsymbol\beta\)满足 \[ | 1 + \alpha_1 + \alpha_2 \beta_1 | < 1 . \]

因为协整的条件是\(0<\text{rank}(\boldsymbol\Pi)<k\)， 所以从数据中估计得到VECM模型后对协整的检验就是对\(\text{rank}(\boldsymbol\Pi)\)的检验。 (Johansen 1988), (Johansen 1995), Reinsel和Ahn(1992)正是这样进行协整检验的。

25.5.3 关于VECM中的非随机趋势

为了基于VECM模型进行协整检验， 需要规定\(\boldsymbol\mu_t\)的形式， \(\boldsymbol\mu_t\)的形式会影响到检验统计量的极限分布。

设\(\boldsymbol x_t\)的所有分量都为I(1)序列。 文献中已有的\(\boldsymbol\mu_t\)的形式包括：

（1） \(\boldsymbol\mu_t = \boldsymbol 0\)。 这时\(\boldsymbol x_t\)的分量为不带漂移的I(1)过程， 平稳序列\(\boldsymbol\omega_t = \boldsymbol\beta^T \boldsymbol x_t\) 均值为零。

（2） \(\boldsymbol\mu_t = \boldsymbol\mu_0 = \boldsymbol\alpha \boldsymbol c_0\)， 即\(\boldsymbol\mu_t\)是有特殊形式的非零常数。 VECM变成 \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\alpha(\boldsymbol\beta^T \boldsymbol x_{t-1} + \boldsymbol c_0) + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \end{aligned}\] 这时\(\boldsymbol x_t\)的分量是不带漂移的I(1)过程， 但是平稳列\(\boldsymbol\omega_t\)的均值为非零的\(-\boldsymbol c_0\)。

（3） \(\boldsymbol\mu_t = \boldsymbol\mu_0 \neq \boldsymbol 0\)， 即\(\boldsymbol\mu_t\)是不带特殊结构的非零常数。 这时\(\boldsymbol x_t\)的分量是带有漂移项\(\boldsymbol\mu_0\)的I(1)序列， 且\(\boldsymbol\omega_t\)非零均值。

（4） \(\boldsymbol\mu_t = \boldsymbol\mu_0 + \boldsymbol\alpha \boldsymbol c_1 t\)， 即\(\boldsymbol\mu_t\)是线性项\(t\)的系数有特殊结构的线性函数， VECM变成 \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\mu_0 + \boldsymbol\alpha(\boldsymbol\beta^T \boldsymbol x_{t-1} + \boldsymbol c_1 t) + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \end{aligned}\] 这时\(\boldsymbol x_t\)的分量是带有漂移项\(\boldsymbol\mu_0\)的I(1)过程， 且\(\boldsymbol\omega_t\)有非随机的\(\boldsymbol c_1 t\)线性趋势项。

（5） \(\boldsymbol\mu_t = \boldsymbol\mu_0 + \boldsymbol\mu_1 t\)， \(\boldsymbol\mu_0\), \(\boldsymbol\mu_1\)非零。 这是没有约束的线性趋势。 这时\(\boldsymbol x_t\)的分量都是带有二次时间趋势的I(1)过程， \(\boldsymbol\omega_t\)是线性趋势项加平稳列。

最后一种情况不常见； 第一种情况在经济序列中也不常见。 第三种情况在许多对数价格序列中常见。

25.5.4 VECM的最大似然估计

设\(\boldsymbol x_t\)有观测数据 \(\{\boldsymbol x_t, t=1,2,\dots,T \}\)。 记\(\boldsymbol\mu_t = \boldsymbol\mu \boldsymbol d_t\)， 其中\(\boldsymbol d_t = (1, t)^T\)。 设\(\boldsymbol\Pi\)的秩为\(m\)， \(0<m<k\)。 VECM为 \[\begin{align} \Delta \boldsymbol x_t =& \boldsymbol\mu \boldsymbol d_t + \boldsymbol\alpha \boldsymbol\beta^T \boldsymbol x_{t-1} + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \tag{25.5} \end{align}\]

为了求各个参数的最大似然估计， 首先求解如下的多对多的线性回归问题 \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\gamma_0 \boldsymbol d_t + \boldsymbol\Omega_1 \Delta \boldsymbol x_{t-1} + \dots + \boldsymbol\Omega_{p-1} \Delta \boldsymbol x_{t-p+1} + \boldsymbol u_t \\ \boldsymbol x_{t-1} =& \boldsymbol\gamma_1 \boldsymbol d_t + \boldsymbol\Xi_1 \Delta \boldsymbol x_{t-1} + \dots + \boldsymbol\Xi_{p-1} \Delta \boldsymbol x_{t-p+1} + \boldsymbol v_t \end{aligned}\]

令\(\hat{\boldsymbol u}_t\)和\(\hat{\boldsymbol v}_t\)为最小二乘估计的残差， 定义如下的样本协方差阵 \[\begin{aligned} \boldsymbol S_{00} =& \frac{1}{T-p} \sum_{t=p+1}^T \hat{\boldsymbol u}_t \hat{\boldsymbol u}_t^T, \\ \boldsymbol S_{01} =& \frac{1}{T-p} \sum_{t=p+1}^T \hat{\boldsymbol u}_t \hat{\boldsymbol v}_t^T, \quad \boldsymbol S_{10} = \boldsymbol S_{01}^T,\\ \boldsymbol S_{11} =& \frac{1}{T-p} \sum_{t=p+1}^T \hat{\boldsymbol v}_t \hat{\boldsymbol v}_t^T \end{aligned}\]

然后，计算矩阵 \(\boldsymbol S_{10} \boldsymbol S_{00}^{-1} \boldsymbol S_{01}\)关于\(\boldsymbol S_{11}\)的广义特征值和特征向量， 即求\(\lambda\)和\(\boldsymbol\xi\)使得 \[ \boldsymbol S_{10} \boldsymbol S_{00}^{-1} \boldsymbol S_{01} \boldsymbol\xi = \lambda \boldsymbol S_{11} \boldsymbol\xi \] 设\(k\)个特征值、特征向量为\((\hat\lambda_i, \boldsymbol e_i)\)， 其中\(\hat\lambda_1 > \hat\lambda_2 > \dots > \hat\lambda_k\)， 记\(\boldsymbol e = (\boldsymbol e_1, \boldsymbol e_2, \dots, \boldsymbol e_k)\)， 标准化使得 \(\boldsymbol e^T \boldsymbol S_{11} \boldsymbol e = \boldsymbol I_k\)。

协整向量组成的矩阵\(\boldsymbol\beta\)的未标准化的最大似然估计为 \(\hat{\boldsymbol\beta} = (\boldsymbol e_1, \dots, \boldsymbol e_m)\)。 由此可以得到\(\boldsymbol\beta\)的满足可辨识条件和标准化条件的MLE， 将得到的估计记为\(\hat{\boldsymbol\beta}_c\)， 其中下标\(c\)表示需要满足一定的限制条件。

其它参数的MLE可以从下式用最小二乘方法得到： \[\begin{aligned} \Delta \boldsymbol x_t =& \boldsymbol\mu \boldsymbol d_t + \boldsymbol\alpha \hat{\boldsymbol\beta}_c \boldsymbol x_{t-1} + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t \end{aligned}\]

基于\(m\)个协整向量的似然函数的最大值满足 \[\begin{aligned} L_{\text{max}}^{-2/T} \propto |\boldsymbol S_{00}| \prod_{i=1}^m (1 - \hat\lambda_i) \end{aligned}\] 在计算关于\(\text{rank}(\boldsymbol\Pi)=m\)的似然比统计量时需要用到这个似然函数最大值。

\(\boldsymbol\alpha\)和\(\boldsymbol\beta\)的正交补可以用如下公式计算： \[\begin{aligned} \hat{\boldsymbol\alpha}_{\perp} =& \boldsymbol S_{00}^{-1} \boldsymbol S_{11} (\boldsymbol e_{m+1}, \dots, \boldsymbol e_{k}) \\ \hat{\boldsymbol\beta}_{\perp} =& \boldsymbol S_{11} (\boldsymbol e_{m+1}, \dots, \boldsymbol e_{k}) \end{aligned}\]

25.5.5 基于VECM最大似然估计的Johansen协整检验

在给定了\(\boldsymbol\mu_t\)形式后， 基于VECM的最大似然估计对\(\text{rank}(\boldsymbol\Pi)\)进行系列的似然比检验。 记\(H(m)\)表示零假设\(\text{rank}(\boldsymbol\Pi)=m\)， 在序贯地进行检验时可以看成是\(\text{rank}(\boldsymbol\Pi) \leq m\)， 有 \[ H(0) \subset H(1) \subset \dots \subset H(k) \]

将(25.5)变成 \[\begin{align} \Delta \boldsymbol x_t =& \boldsymbol\mu \boldsymbol d_t + \boldsymbol\Pi \boldsymbol x_{t-1} \\ & + \boldsymbol\Phi_1^* \Delta\boldsymbol x_{t-1} + \dots + \boldsymbol\Phi_{p-1}^* \Delta\boldsymbol x_{t-p+1} + \boldsymbol a_t, \\ & t=p+1, \dots, T \tag{25.6} \end{align}\] 目标是检验\(\boldsymbol\Pi\)的秩， 这等于\(\boldsymbol\Pi\)的非零奇异值的个数， 如果能得到\(\boldsymbol\Pi\)的相合估计就可以估计\(\text{rank}(\boldsymbol\Pi)\)。 从(25.6)可以看出， \(\boldsymbol\Pi\)是排除了\(\boldsymbol\mu_t\)和\(\Delta\boldsymbol x_{t-i}\), \(i=1,\dots,p-1\)的线性影响后， \(\Delta\boldsymbol x_t\)对\(\boldsymbol x_{t-1}\)的多对多的线性回归系数。 从上面的MLE步骤可知， 调整后的\(\Delta\boldsymbol x_t\)和\(\boldsymbol x_{t-1}\) 分别为\(\hat{\boldsymbol u}_t\)和\(\hat{\boldsymbol v}_t\)， 所以 \[ \hat{\boldsymbol u}_t = \boldsymbol\Pi \hat{\boldsymbol v}_t + \boldsymbol a_t \] 在正态性假定下， 可以根据\(\hat{\boldsymbol u}_t\)与\(\hat{\boldsymbol v}_t\) 的典型相关分析的方法估计\(\text{rank}(\boldsymbol\Pi)\)， \(\hat\lambda_i\)是\(\hat{\boldsymbol u}_t\)与\(\hat{\boldsymbol v}_t\) 的典型相关系数平方。

Johansen提出了两种检验方法。 首先， 考虑假设 \[\begin{aligned} H_0: \text{rank}(\boldsymbol\Pi) = m \longleftrightarrow H_a: \text{rank}(\boldsymbol\Pi) > m \end{aligned}\] (Johansen 1988)提出如下的似然比统计量： \[\begin{aligned} \text{LR}_{\text{tr}}(m) = -(T-p) \sum_{i=m+1}^k \ln(1 - \hat\lambda_i) \end{aligned}\] 如果\(\text{rank}(\boldsymbol\Pi) \leq m\)， 则\(i>m\)时\(\hat\lambda_i\)应该很小， 因此\(\text{LR}_{\text{tr}}(m)\)也应该很小， 当统计量值超过一个右侧临界值时拒绝零假设。 这个检验称为Johansen迹协整检验。 因为单位根的存在， 似然比统计量在零假设下的渐近分布不再服从卡方分布， 其临界值需要用模拟方法。 从\(H(0)\)开始到\(H(1)\)序贯地进行检验， 在第一次被接受时， 令被接受的\(H(m)\)的\(m\)为选定的秩。

(Johansen 1988)提出的另一种似然比检验方法针对如下假设 \[\begin{aligned} H_0: \text{rank}(\boldsymbol\Pi) = m \longleftrightarrow H_a: \text{rank}(\boldsymbol\Pi) = m+1 \end{aligned}\] 取最大特征值统计量 \[\begin{aligned} \text{LR}_{\text{max}}(m) = -(T-p) \ln(1 - \hat\lambda_{m+1}) \end{aligned}\] 当统计量值超过一个右侧临界值时拒绝零假设。 临界值也需要通过模拟获得。 从\(H(0)\)开始到\(H(1)\)序贯地进行检验， 在第一次被接受时， 令被接受的\(H(m)\)的\(m\)为选定的秩。

25.5.6 VECM预测

估计的VECM模型可以用于预测。 首先可以从模型得到\(\Delta\boldsymbol x_t\)序列的预测值， 然后可以从\(\Delta\boldsymbol x_t\)反解得到\(\boldsymbol x_t\)的预测值。 VECM预测与VAR预测的区别在于VECM允许有单位根和协整关系， VAR预测不允许有单位根。

25.5.7 Johansen方法进行协整检验的例子

R扩展包urca的ca.jo()函数可以进行计算Johansen的两种检验。 参见(Pfaff 2008)。

例4.2 考虑urca包的UKpppuip数据， 此数据用来检验英国经济的PPP和UIP假设。 季度数据，从1971年第1季度到1987年第2季度。 分量p1是英国批发价格指数， p2是外贸加权批发价格指数， e12是英镑实际汇率， i1是三月期国债利率， i2是三月期欧元利率， dpoil0是即期国际油价， dpoil1是上期国际油价。

载入数据：

library(urca, quietly = TRUE)
data(UKpppuip)
ts.UKpppuip <- ts(UKpppuip, start=c(1971,1), frequency=4)

数据表见附录。

时间序列图：

library(quantmod, quietly = TRUE)
plot(as.xts(ts.UKpppuip), type="l", 
     multi.panel=TRUE, theme="white",
     main="英国PPP-UIP数据",
     major.ticks="years",
     grid.ticks.on = "years")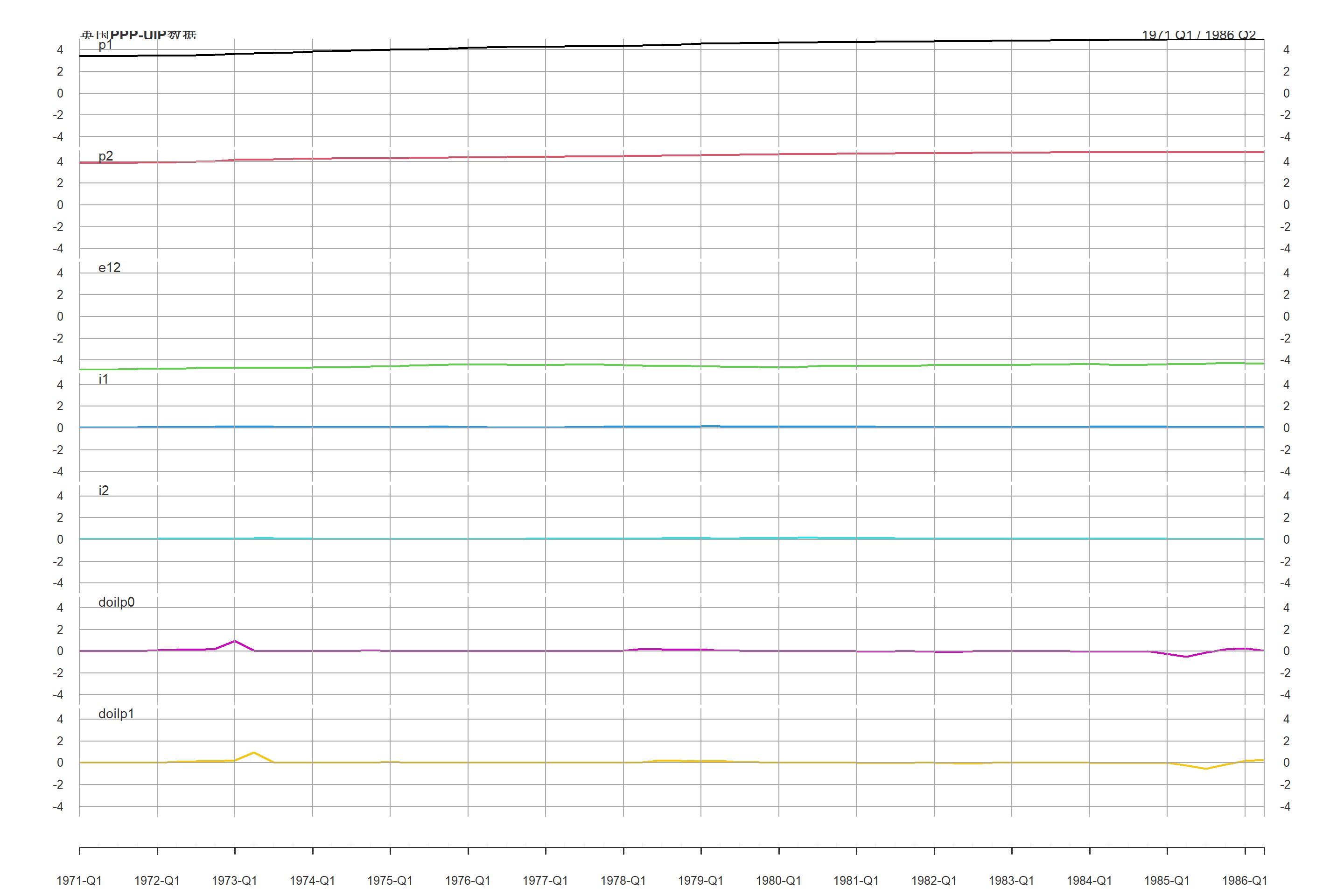

图25.2: 英国PPP-UIP数据

下面对p1, p2, e12, i1, i2执行Johansen的两种协整检验。 ADF结果表明部分序列有单位根。 以油价作为外生变量。 选项type="trace"使用\(\text{LR}_{\text{tr}}\)统计量， 选项type="eigen"使用\(\text{LR}_{\text{max}}\)统计量。 选项ecdet指定要考虑的非随机趋势， "none"表示没有非随机趋势， "constant"表示常数趋势， "trend"表示线性趋势。 选项K表示VAR模型的阶。 选项season=4表示有与季度数据相关联的哑变量存在， 用dumvar=输入保存了哑变量(外生变量)的数据框， 其行数必须与用来检验的输入数据行数相同。

dat1 <- UKpppuip[,c("p1", "p2", "e12", "i1", "i2")]
dat2 <- UKpppuip[,c("doilp0", "doilp1")]
summary(ca.jo(
  dat1, type="trace", K=2, season=4, dumvar=dat2))

## 
## ###################### 
## # Johansen-Procedure # 
## ###################### 
## 
## Test type: trace statistic , with linear trend 
## 
## Eigenvalues (lambda):
## [1] 0.40672818 0.28538240 0.25415335 0.10230406 0.08287097
## 
## Values of teststatistic and critical values of test:
## 
##           test 10pct  5pct  1pct
## r <= 4 |  5.19  6.50  8.18 11.65
## r <= 3 | 11.67 15.66 17.95 23.52
## r <= 2 | 29.26 28.71 31.52 37.22
## r <= 1 | 49.42 45.23 48.28 55.43
## r = 0  | 80.75 66.49 70.60 78.87
## 
## Eigenvectors, normalised to first column:
## (These are the cointegration relations)
## 
##             p1.l2      p2.l2    e12.l2      i1.l2      i2.l2
## p1.l2   1.0000000   1.000000  1.000000  1.0000000  1.0000000
## p2.l2  -0.9086265  -1.143047 -1.272628 -2.4001444 -1.4528820
## e12.l2 -0.9321133  -3.363042  1.113631  1.1221619 -0.4805235
## i1.l2  -3.3746393  35.243576  2.746828 -0.4088865  2.2775510
## i2.l2  -1.8906210 -32.917370 -2.835714  2.9863624  0.7628011
## 
## Weights W:
## (This is the loading matrix)
## 
##             p1.l2         p2.l2       e12.l2        i1.l2       i2.l2
## p1.d  -0.06816507  0.0011795779 -0.002790218  0.001373599 -0.01333013
## p2.d  -0.01773477  0.0001220008 -0.014159241  0.013178503  0.00755575
## e12.d  0.10065321 -0.0001432122 -0.055628059 -0.035400025 -0.04707585
## i1.d   0.03434737 -0.0041631581 -0.010363374  0.012309982 -0.02394672
## i2.d   0.05766426  0.0082830953  0.004821036  0.026984801 -0.01006765

summary(ca.jo(
  dat1, type="eigen", K=2, season=4, dumvar=dat2))

## 
## ###################### 
## # Johansen-Procedure # 
## ###################### 
## 
## Test type: maximal eigenvalue statistic (lambda max) , with linear trend 
## 
## Eigenvalues (lambda):
## [1] 0.40672818 0.28538240 0.25415335 0.10230406 0.08287097
## 
## Values of teststatistic and critical values of test:
## 
##           test 10pct  5pct  1pct
## r <= 4 |  5.19  6.50  8.18 11.65
## r <= 3 |  6.48 12.91 14.90 19.19
## r <= 2 | 17.59 18.90 21.07 25.75
## r <= 1 | 20.16 24.78 27.14 32.14
## r = 0  | 31.33 30.84 33.32 38.78
## 
## Eigenvectors, normalised to first column:
## (These are the cointegration relations)
## 
##             p1.l2      p2.l2    e12.l2      i1.l2      i2.l2
## p1.l2   1.0000000   1.000000  1.000000  1.0000000  1.0000000
## p2.l2  -0.9086265  -1.143047 -1.272628 -2.4001444 -1.4528820
## e12.l2 -0.9321133  -3.363042  1.113631  1.1221619 -0.4805235
## i1.l2  -3.3746393  35.243576  2.746828 -0.4088865  2.2775510
## i2.l2  -1.8906210 -32.917370 -2.835714  2.9863624  0.7628011
## 
## Weights W:
## (This is the loading matrix)
## 
##             p1.l2         p2.l2       e12.l2        i1.l2       i2.l2
## p1.d  -0.06816507  0.0011795779 -0.002790218  0.001373599 -0.01333013
## p2.d  -0.01773477  0.0001220008 -0.014159241  0.013178503  0.00755575
## e12.d  0.10065321 -0.0001432122 -0.055628059 -0.035400025 -0.04707585
## i1.d   0.03434737 -0.0041631581 -0.010363374  0.012309982 -0.02394672
## i2.d   0.05766426  0.0082830953  0.004821036  0.026984801 -0.01006765

Johansen检验是序贯进行的。 从迹方法的检验结果看出， 在0.05水平下， \(H_0: r=0\)（这里\(r\)就是前面的\(m\)，\(\boldsymbol\Pi\)的秩） 统计量为80.75，右侧临界值是70.60，拒绝零假设， 至少有一个协整关系； \(H_0: r=1\)的检验统计量为49.42， 右侧临界值为48.28， 拒绝零假设，认为至少有两个协整关系； \(H_0: r=2\)的检验统计量为29.26, 右侧临界值为31.52， 不拒绝零假设， 认为恰好有两个协整关系。 如果使用最大特征值方法， 检验结论则有所不同。

结果中包含了所有的协整变量， 前两个协整变量为 \[\begin{aligned} \left(\begin{array}{c|rr} \text{p1} & 1 & 1 \\ \text{p2} & -0.91 & -1.14 \\ \text{e12} & -0.93 & -3.36 \\ \text{i1} & -3.37 & 35.24 \\ \text{i2} & -1.89 & 32.91 \end{array}\right) \end{aligned}\]

人为地计算两个协整变量， 检验其平稳性：

dat1 <- UKpppuip[,c("p1", "p2", "e12", "i1", "i2")]
f <- function(){
  x1 <- as.matrix(dat1) %*% c(1, -0.91, -0.93, -3.37, -1.89)
  x2 <- as.matrix(dat1) %*% c(1, -1.14, -3.36, -35.24, -32.91)
  print(fUnitRoots::adfTest(x1, lags=1, type="c"))
  print(fUnitRoots::adfTest(x2, lags=1, type="c"))
  invisible()
}
f()

## Warning in if (class(x) == "timeSeries") x = series(x): 条件的长度大于一，因此只
## 能用其第一元素

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -2.5995
##   P VALUE:
##     0.0994 
## 
## Description:
##  Tue Feb 22 12:01:46 2022 by user: Lenovo

## Warning in if (class(x) == "timeSeries") x = series(x): 条件的长度大于一，因此只
## 能用其第一元素

## 
## Title:
##  Augmented Dickey-Fuller Test
## 
## Test Results:
##   PARAMETER:
##     Lag Order: 1
##   STATISTIC:
##     Dickey-Fuller: -3.0532
##   P VALUE:
##     0.03853 
## 
## Description:
##  Tue Feb 22 12:01:46 2022 by user: Lenovo

在0.05水平下， 第一个协整向量有单位根， 第二个协整向量没有单位根。 但是，因为估计这些权重消耗了自由度， 所以ADF检验的p值是不可用的。

25.6 附录A：线性模型估计相合性

考虑线性回归模型 \[ y_i = \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} + e_i, \ i=1,2,\dots \] 其中\(Ee_i=0\), \(\text{Var}(e_i) = \sigma^2\)， \(e_1, e_2, \dots\)为不相关列。 对\(n\)组观测值，写成线性模型 \[ \boldsymbol Y_n = X_n \boldsymbol\beta + \boldsymbol E_n, \] 其中\(\boldsymbol Y_n = (y_1, \dots, y_n)^T\), \(\boldsymbol E_n = (e_1, \dots, e_n)^T\), \(\boldsymbol\beta_n = (\beta_1, \dots, \beta_p)^T\), \(X_n\)为\(n \times p\)矩阵， 第\((i,j)\)元素为\(x_{ij}\)。 如果\(X_n\)列满秩， 最小二乘估计为 \[ \hat{\boldsymbol\beta}_n = (X_n^T X_n)^{-1} X_n^T Y_n . \]

定理25.1 (最小二乘估计的弱相合性) 记\(S_n = X_n^T X_n\), 设\(n\)充分大时\(X_n\)列满秩， 则\(\hat{\boldsymbol\beta}_n\)是\(\boldsymbol\beta\)的弱相合估计， 当且仅当\(\lim_{n\to\infty} S_n^{-1} = \boldsymbol 0\)。

充分性是\(E \hat{\boldsymbol\beta}_n = \boldsymbol\beta\) 以及\(\text{Var}(\hat{\boldsymbol\beta}_n) = \sigma^2 S_n^{-1}\)的推论。 事实上， \[\begin{aligned} E \| \hat{\boldsymbol\beta}_n - \boldsymbol\beta \|^2 =& \sigma^2 \text{tr}(S_n^{-1}) \to 0, \ n \to \infty . \end{aligned}\]

必要性的证明见陈希孺《数理统计引论》节5.6。

定理25.2 (最小二乘估计的强相合性) 若\(e_1, e_2, \dots\) 独立同N(0, \(\sigma^2\))分布， \(\lim_{n\to\infty} S_n^{-1} \to \boldsymbol 0\)， 则\(\hat{\boldsymbol\beta}_n\)是\(\boldsymbol\beta\)的强相合估计。

25.7 附录B：用到的数据

25.7.1 英国消费研究数据

knitr::kable(Raotbl3)

	lc	li	lw	dd682	dd792	dd883
1966.4	10.4831	10.5821	12.9481	NA	NA	NA
1967.1	10.4893	10.5800	12.9895	0	0	0
1967.2	10.5022	10.5990	13.0115	0	0	0
1967.3	10.5240	10.6262	13.0411	0	0	0
1967.4	10.5329	10.6145	13.0357	0	0	0
1968.1	10.5586	10.6307	13.0518	0	0	0
1968.2	10.5190	10.6316	13.0839	1	0	0
1968.3	10.5381	10.6132	13.1120	-1	0	0
1968.4	10.5422	10.6141	13.1183	0	0	0
1969.1	10.5361	10.6263	13.1144	0	0	0
1969.2	10.5462	10.6366	13.1009	0	0	0
1969.3	10.5459	10.6313	13.0882	0	0	0
1969.4	10.5552	10.6324	13.0402	0	0	0
1970.1	10.5548	10.6361	13.0391	0	0	0
1970.2	10.5710	10.6795	13.0417	0	0	0
1970.3	10.5861	10.6813	13.0261	0	0	0
1970.4	10.5864	10.6801	13.0032	0	0	0
1971.1	10.5802	10.6533	13.0364	0	0	0
1971.2	10.6006	10.6839	13.0461	0	0	0
1971.3	10.6168	10.6889	13.0850	0	0	0
1971.4	10.6275	10.7025	13.1107	0	0	0
1972.1	10.6414	10.7212	13.1241	0	0	0
1972.2	10.6629	10.7818	13.1605	0	0	0
1972.3	10.6758	10.7641	13.1748	0	0	0
1972.4	10.6881	10.7841	13.1612	0	0	0
1973.1	10.7240	10.8045	13.1050	0	0	0
1973.2	10.7143	10.8230	13.1082	0	0	0
1973.3	10.7222	10.8319	13.1059	0	0	0
1973.4	10.7156	10.8380	13.0140	0	0	0
1974.1	10.6964	10.8097	12.9301	0	0	0
1974.2	10.6990	10.7928	12.8427	0	0	0
1974.3	10.7081	10.8310	12.7710	0	0	0
1974.4	10.7142	10.8328	12.7281	0	0	0
1975.1	10.7078	10.8527	12.7692	0	0	0
1975.2	10.7073	10.8089	12.7492	0	0	0
1975.3	10.6954	10.8202	12.7664	0	0	0
1975.4	10.6910	10.8069	12.7554	0	0	0
1976.1	10.6967	10.8196	12.7605	0	0	0
1976.2	10.7015	10.8046	12.7471	0	0	0
1976.3	10.7083	10.8372	12.7238	0	0	0
1976.4	10.7127	10.8123	12.7156	0	0	0
1977.1	10.6922	10.7842	12.7555	0	0	0
1977.2	10.6874	10.7713	12.7517	0	0	0
1977.3	10.6989	10.7904	12.8018	0	0	0
1977.4	10.7224	10.8369	12.8388	0	0	0
1978.1	10.7452	10.8333	12.8438	0	0	0
1978.2	10.7462	10.8635	12.8540	0	0	0
1978.3	10.7663	10.8884	12.8618	0	0	0
1978.4	10.7633	10.8924	12.8491	0	0	0
1979.1	10.7737	10.9017	12.9232	0	0	0
1979.2	10.8282	10.9108	12.9022	0	1	0
1979.3	10.7872	10.9166	12.8737	0	-1	0
1979.4	10.8015	10.9673	12.8467	0	0	0
1980.1	10.8139	10.9324	12.8647	0	0	0
1980.2	10.7909	10.9344	12.8885	0	0	0
1980.3	10.8029	10.9506	12.9183	0	0	0
1980.4	10.7868	10.9465	12.9277	0	0	0
1981.1	10.7979	10.9488	12.9505	0	0	0
1981.2	10.8007	10.9294	12.9615	0	0	0
1981.3	10.8008	10.9248	12.9147	0	0	0
1981.4	10.7991	10.9326	12.9527	0	0	0
1982.1	10.7956	10.9202	12.9641	0	0	0
1982.2	10.8005	10.9373	12.9780	0	0	0
1982.3	10.8160	10.9269	13.0299	0	0	0
1982.4	10.8260	10.9315	13.0604	0	0	0
1983.1	10.8405	10.9399	13.1031	0	0	0
1983.2	10.8482	10.9599	13.1577	0	0	0
1983.3	10.8633	10.9563	13.1504	0	0	0
1983.4	10.8633	10.9637	13.1805	0	0	0
1984.1	10.8615	10.9703	13.2245	0	0	0
1984.2	10.8732	10.9778	13.1852	0	0	0
1984.3	10.8649	10.9801	13.2298	0	0	0
1984.4	10.8793	10.9942	13.2849	0	0	0
1985.1	10.8909	10.9840	13.2999	0	0	0
1985.2	10.8938	11.0120	13.2904	0	0	0
1985.3	10.9116	11.0120	13.3140	0	0	0
1985.4	10.9202	11.0237	13.3606	0	0	0
1986.1	10.9409	11.0300	13.4574	0	0	0
1986.2	10.9663	11.0624	13.4655	0	0	0
1986.3	10.9700	11.0556	13.4371	0	0	0
1986.4	10.9808	11.0644	13.5020	0	0	0
1987.1	10.9878	11.0618	13.5914	0	0	0
1987.2	11.0048	11.0839	13.6804	0	0	0
1987.3	11.0272	11.0944	13.7131	0	0	0
1987.4	11.0420	11.1095	13.5633	0	0	0
1988.1	11.0701	11.1116	13.5814	0	0	0
1988.2	11.0751	11.1413	13.6171	0	0	0
1988.3	11.0964	11.1507	13.6201	0	0	1
1988.4	11.1069	11.1680	13.6460	0	0	1
1989.1	11.1123	11.1713	13.6731	0	0	1
1989.2	11.1231	11.2032	13.6884	0	0	1
1989.3	11.1223	11.2009	13.7211	0	0	1
1989.4	11.1303	11.2064	13.7686	0	0	1
1990.1	11.1307	11.2160	13.6833	0	0	1
1990.2	11.1389	11.2147	13.7130	0	0	1
1990.3	11.1325	11.2286	13.6225	0	0	1
1990.4	11.1261	11.2352	13.6957	0	0	1
1991.1	11.1232	11.2189	13.7723	0	0	1
1991.2	11.1220	11.2276	13.7424	0	0	1

25.7.2 英国PPP研究数据

knitr::kable(UKpppuip)

p1	p2	e12	i1	i2	doilp0	doilp1
3.399837	3.846749	-4.899593	0.0470744	0.0505981	0.0000000	0.0000000
3.412952	3.856261	-4.894152	0.0467882	0.0485997	0.0066867	0.0000000
3.430709	3.864228	-4.832260	0.0598714	0.0554347	0.0000000	0.0066867
3.452861	3.881285	-4.803663	0.0725067	0.0580802	0.0022137	0.0000000
3.465303	3.913175	-4.785582	0.0789036	0.0762200	0.1020269	0.0022137
3.469929	3.953242	-4.785582	0.0714831	0.0829615	0.1327823	0.1020269
3.503215	3.997386	-4.723762	0.1065198	0.1058904	0.1395371	0.1327823
3.542607	4.020950	-4.712609	0.1152019	0.0948555	0.2369103	0.1395371
3.615693	4.130217	-4.719131	0.1160927	0.0877361	0.9655383	0.2369103
3.683799	4.172550	-4.733877	0.1101092	0.1165378	0.0434339	0.9655383
3.722781	4.207048	-4.730211	0.1084956	0.1242510	0.0195273	0.0434339
3.772879	4.236469	-4.713544	0.1066996	0.0977617	0.0553805	0.0195273
3.835640	4.253006	-4.694693	0.0960372	0.0698991	0.0063868	0.0553805
3.885598	4.270279	-4.662791	0.0917584	0.0633503	0.0000000	0.0063868
3.920515	4.271766	-4.619633	0.1017440	0.0719485	0.0000000	0.0000000
3.956147	4.285636	-4.594710	0.1072388	0.0637257	0.0957119	0.0000000
3.998746	4.295829	-4.583076	0.0859024	0.0538251	0.0000000	0.0957119
4.036117	4.320907	-4.497610	0.1038193	0.0587405	0.0000000	0.0000000
4.076345	4.340277	-4.471787	0.1108256	0.0558131	0.0000000	0.0000000
4.125455	4.358491	-4.397771	0.1354046	0.0509782	0.0000000	0.0000000
4.185891	4.362472	-4.431758	0.1035489	0.0511683	0.0491579	0.0000000
4.234323	4.374696	-4.429279	0.0732505	0.0560022	0.0000000	0.0491579
4.263965	4.389198	-4.431758	0.0624113	0.0628809	0.0492205	0.0000000
4.277778	4.401695	-4.453790	0.0565694	0.0685928	0.0000000	0.0492205
4.283250	4.419375	-4.480076	0.0580802	0.0720416	0.0000000	0.0000000
4.302169	4.441176	-4.420557	0.0809346	0.0748291	0.0000000	0.0000000
4.321394	4.454597	-4.429279	0.0884686	0.0859942	0.0000000	0.0000000
4.340256	4.468155	-4.429279	0.1084956	0.1100196	0.0000000	0.0000000
4.370716	4.488001	-4.451366	0.1158256	0.1004786	0.0616222	0.0000000
4.415330	4.505689	-4.505689	0.1166268	0.1013826	0.2077878	0.0616222
4.469429	4.518725	-4.553932	0.1294481	0.1144887	0.1832892	0.2077878
4.502292	4.541496	-4.522783	0.1459169	0.1374985	0.1562188	0.1832892
4.561852	4.575517	-4.572380	0.1541793	0.1579435	0.1885763	0.1562188
4.597851	4.597449	-4.588381	0.1539221	0.1057105	0.0565460	0.1885763
4.623419	4.616333	-4.611395	0.1399358	0.1140427	0.0466827	0.0565460
4.637637	4.629624	-4.646949	0.1301507	0.1578581	0.0270653	0.0466827
4.652340	4.648700	-4.662791	0.1157365	0.1521200	0.0636834	0.0270653
4.671239	4.666700	-4.622706	0.1121673	0.1610128	-0.0059685	0.0636834
4.684259	4.686902	-4.546235	0.1337439	0.1692363	-0.0072731	-0.0059685
4.700753	4.703789	-4.536252	0.1434941	0.1292723	0.0028523	-0.0072731
4.725350	4.718869	-4.552836	0.1280413	0.1400228	-0.0130594	0.0028523
4.740313	4.726432	-4.542918	0.1225716	0.1396750	-0.0345760	-0.0130594
4.750136	4.739622	-4.556120	0.1016537	0.1135072	-0.0029917	-0.0345760
4.759607	4.753597	-4.530662	0.0930349	0.0926703	0.0092772	-0.0029917
4.774913	4.759102	-4.428038	0.1039996	0.0888347	-0.0472742	0.0092772
4.792479	4.769929	-4.474163	0.0933993	0.0898407	-0.0911132	-0.0472742
4.803201	4.779922	-4.481255	0.0902976	0.0952193	0.0000000	-0.0911132
4.814620	4.789541	-4.461028	0.0865446	0.0938546	0.0000000	0.0000000
4.830711	4.801698	-4.442835	0.0855353	0.0963097	0.0000000	0.0000000
4.846546	4.811211	-4.419304	0.0847087	0.1080469	0.0000000	0.0000000
4.856707	4.817162	-4.396546	0.0979431	0.1120779	-0.0106300	0.0000000
4.869840	4.824625	-4.358630	0.0929437	0.0935814	-0.0107661	-0.0106300
4.892602	4.832971	-4.317755	0.1129715	0.0856271	-0.0145228	-0.0107661
4.908972	4.839915	-4.407938	0.1172496	0.0798273	-0.0110659	-0.0145228
4.919251	4.836898	-4.447697	0.1106465	0.0772388	-0.0300873	-0.0110659
4.927254	4.840464	-4.419322	0.1079571	0.0776090	0.0263713	-0.0300873
4.941642	4.836249	-4.359270	0.1115414	0.0747363	-0.2428249	0.0263713
4.950885	4.830666	-4.371976	0.0957646	0.0677521	-0.5284302	-0.2428249
4.958640	4.834564	-4.314818	0.0924880	0.0604364	-0.1409825	-0.5284302
4.966335	4.832189	-4.262680	0.1013826	0.0590233	0.1617462	-0.1409825
4.982236	4.840834	-4.286891	0.0993927	0.0616594	0.2504379	0.1617462
4.994506	4.841025	-4.326646	0.0874613	0.0676586	0.0653404	0.2504379

B 参考文献

Engle, R. R., and C. W. J. Granger. 1987. “Cointegration and Error Correction Representation, Estimation and Testing.” Econometrica 55: 251–76.

Johansen, S. 1988. “Analysis of Cointegration Vectors.” Journal of Economic Dynamics and Control 12: 231–54.

———. 1995. Likelihood Based Inference in Cointegrated Vector Error Correction Models. Oxford University Press, Oxford, UK.

Pfaff, Bernhard. 2008. Analysis of Integrated and Cointegrated Time Series with r. 2nd ed. Springer.

Phillips, P. C. B., and S. Ouliaris. 1990. “Asymptotic Properties of Residual Based Tests for Cointegration.” Econometrica 58: 165–93.