7 单位根过程
前面的AR、MA、ARMA主要应用于简单收益率和对数收益率。 对于价格序列, 一般其水平是缓慢变化的, 包括缓慢的增长趋势与一定的周期波动。 这样的序列不满足弱平稳的条件, 是非平稳时间序列。
典型的非平稳时间序列模型是单位根(unit root)非平稳时间序列。
7.1 随机游动
考虑\(\{ p_t \}\)的模型
\[\begin{align} p_t = p_{t-1} + \varepsilon_t, \ t=1,2,\dots \tag{7.1} \end{align}\]
其中\(\{ \varepsilon_t \}\)是零均值独立同分布白噪声列。 称\(\{ p_t \}\)是一个随机游动(random walk)。
如果\(p_t\)是股票的对数价格, \(p_0\)是初始上市(initial public offering)的对数价格(即IPO对数价格)。 若\(\varepsilon_t\)的分布关于0对称, 则给定\(p_{t-1}\)的条件下预测\(p_t\), 上升与下降的概率均为\(\frac12\),无法预测升降。
(7.1)表面上看起来像是AR(1)模型, 但是\(\phi_1 = 1\)不满足AR(1)的平稳性条件,而且
\[\begin{align} p_t = p_0 + \sum_{j=0}^{t-1} \varepsilon_{t-j} . \tag{7.2} \end{align}\]
于是 \[ E(p_t | p_0) = p_0, \quad \text{Var}(p_t | p_0) = \sigma^2 t . \] 所以\(\{ p_t \}\)非平稳。 从(7.2), 每个\(\varepsilon_{t-j}\)对\(p_t\)的影响的权重都等于1, 而对于AR(1)模型, \(\varepsilon_{t-j}\)对\(p_t\)的影响的权重等于\(|\phi_1|^j\), 随距离\(j\)的增大按负指数速度衰减。 称(7.2)中的\(\varepsilon_{t-j}\)对\(p_t\)是永久影响的。
随机游动的水平不可预测, 多步预测没有均值反转性质。易见 \[ \hat p_h(1) = E(p_{h} + \varepsilon_{h+1} | \mathscr F_{h}) = p_{h} , \] 其中\(\mathscr F_t\)代表截止到时刻\(t\)位置的所有观测信息, 定义是由\(p_t, p_{t-1}, \dots\)生成的\(\sigma\)代数。
又 \[ \hat p_h(2) = E(p_h + \varepsilon_{h+1} + \varepsilon_{h+2} | \mathscr F_{h}) = p_h . \] 可见\(\hat p_h(k)=p_h\), \(k=1,2,\dots\)。 所以随机游动只能用最后一个观测的水平不经衰减地预测, 没有均值反转。 而AR的预测则是均值与最近一个或几个观测的加权平均, 超前多步预测有均值反转。
\(\hat p_h(k)\)的预测均方误差为 \[ E(e_h(k))^2 = E(p_{h+k} - \hat p_h(k))^2 = E(\sum_{j=1}^k \varepsilon_{h+j})^2 = k \sigma^2 \to \infty \ (k\to\infty) . \] 这也说明了此模型不可预测。
从(7.2)也有\(\text{Var}(p_t | p_0) \to \infty\)(\(t\to\infty\))。 这意味着对数价格可以取到接近正负无穷值, 对于个股有合理性, 但是对于综合股指取负无穷则不太合理。
单位根过程的ACF估计是不相合的, 对单位根过程的样本作ACF图, 其衰减速度很慢很慢。
设\(p_0=0\), 单位根过程\(\{p_t\}\)有如下特点:
- \(p_t\)期望值等于0;
- \(p_t\)方差等于\(\sigma^2 t\),随\(t\)线性增长,趋于无穷;
- 历史的扰动(新息)的影响不衰减;
- 预测只能用最后一个观测值作为预测, 预测均方误差趋于无穷。
- 样本ACF表现为基本不衰减,近似等于1。
7.2 带漂移的随机游动
上面的随机游动模型的金融意义一般\(p_t\)是对数价格, 则\(\varepsilon_t\)是零均值的对数收益率。 实际的对数收益率常常是非零的,正数居多。 所以,模型可以推广为
\[ p_t = \mu + p_{t-1} + \varepsilon_t, \ t=1,2,\dots \] 其中\(\{ \varepsilon_t \}\)仍为零均值独立同分布白噪声列。 常数\(\mu\)并不代表均值, 而是对数价格\(p_t\)的增长速度,称为模型的漂移(drift)。 设初始价格为\(p_0\),则 \[\begin{aligned} p_1 =& p_0 + \mu + \varepsilon_1 \\ p_2 =& p_0 + 2\mu + \varepsilon_1 + \varepsilon_2 \\ & \cdots\cdots \\ p_t =& p_0 + t\mu + \varepsilon_1 + \dots + \varepsilon_t . \end{aligned}\] 于是 \[ E(p_t | p_0) = p_0 + \mu t, \quad \text{Var}(p_t | p_0) = \sigma^2 t . \] 所以带漂移的随机游动与不带漂移的随机游动相比, 其条件方差不变, 但是条件均值多了一个随\(t\)线性增长(若\(\mu>0\))的\(\mu t\)项。
这时,实际的序列的图形将沿着\(y = p_0 + \mu t\)这条直线附近变化。 如果\(\mu=0\),则图形也有缓慢的水平变化但是没有这样的固定趋势。
带漂移的随机游动\(p_t\), 可以分解为两部分: \[ p_t = (p_0 + \mu t) + p_t^*. \] 其中\(p_t^* = \sum_{j=1}^t \varepsilon_t\)是从0出发的不带漂移的随机游动, \(p_0 + \mu t\)是一个非随机的线性趋势。
例7.1 考虑例6.1中3M公司股票从1946年2月到2008年12月的月对数收益率, 共有755个观测。从中恢复对数价格。
d <- read_table(
"m-3m4608.txt",
col_types=cols(.default=col_double(),
date=col_date(format="%Y%m%d")))
mmm <- xts(log(1 + d[["rtn"]]), d$date)
rm(d)
tclass(mmm) <- "yearmon"
ts.3m <- ts(coredata(mmm), start=c(1946,2), frequency=12)
ts.3mlogp <- ts(cumsum(c(ts.3m)), start=c(1946,2), frequency=12)
c(mean=mean(ts.3m), sd=sd(ts.3m))## mean sd
## 0.01029941 0.06371910对数收益率的白噪声检验:
##
## Box-Ljung test
##
## data: ts.3m
## X-squared = 27.688, df = 12, p-value = 0.006143白噪声检验不能通过。暂时忽略这个问题。
上面恢复的对数价格假设开始日期前一月,即1946年1月的对数价格为0。 设对数收益率为均值非零的白噪声列, 则\(p_t\)模型为
\[ p_t = p_{t-1} + 0.01030 + \varepsilon_t, \] 其中\(\sigma_{\varepsilon}=0.06372\)。 分解成两部分即 \[ p_t = 0.01030 t + p_t^*, \] \(\{ p_t^* \}\)是随机游动,扰动(新息)的标准差为0.06372。
\(\{ p_t \}\)的ACF图形如下:
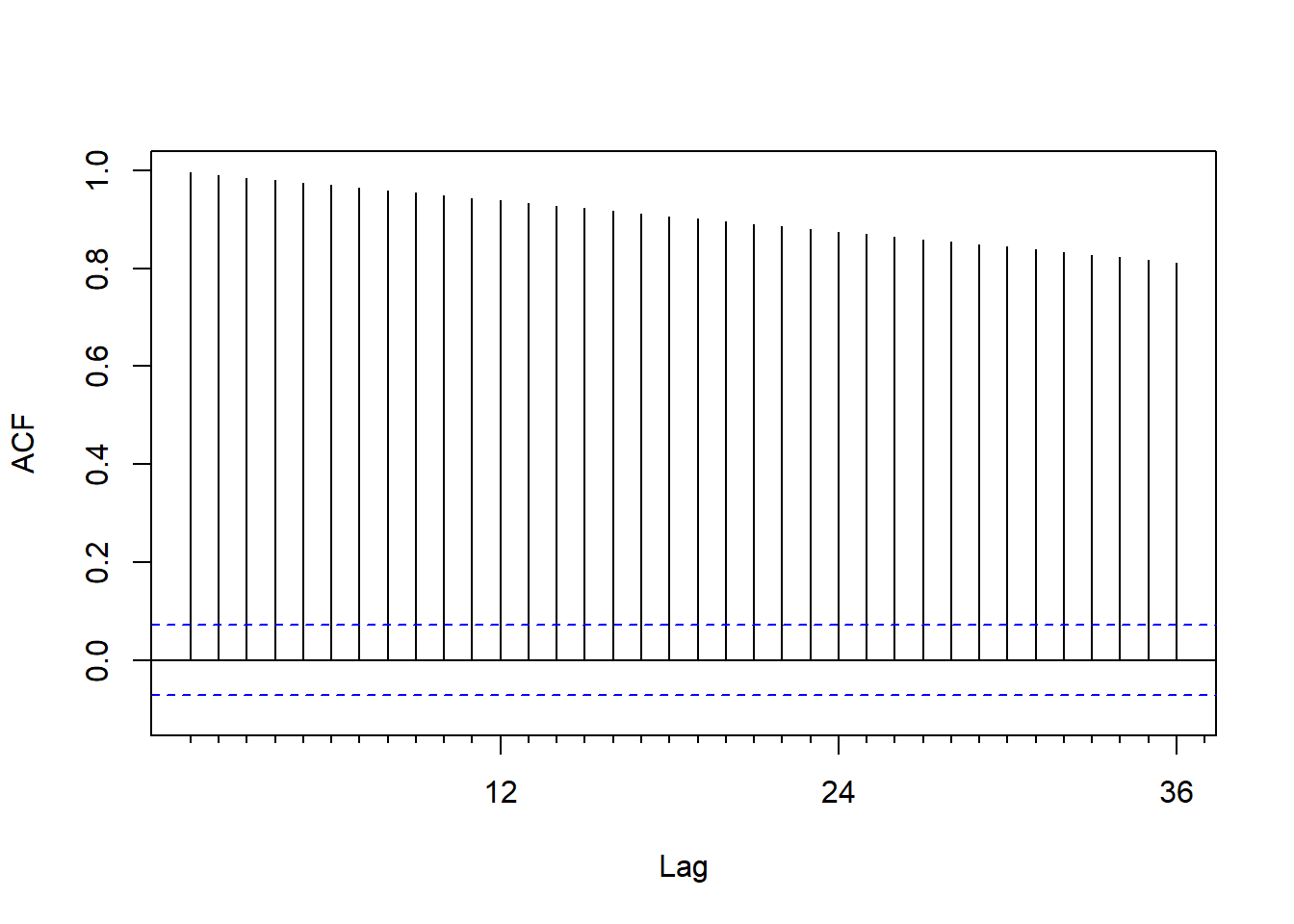
图7.1: 3M股票对数价格的ACF
下面做出\(p_t, p_t^*, 0.0130t\)这三个序列的图形:
plot(c(time(ts.3mlogp)), c(ts.3mlogp), ylim=c(-1, 8.2), type="l",
xlab="Year", ylab="ln(Price)")
tmp.x <- seq(length(ts.3mlogp))
tmp.y <- 0.01030*tmp.x
tmp.y2 <- c(ts.3mlogp) - tmp.y
tmp.y <- ts(tmp.y, start=c(1946,2), frequency=12)
lines(c(time(tmp.y)), c(tmp.y), col="red", lwd=2, lty=3)
lines(c(time(tmp.y)), c(tmp.y2), col="green")
legend("topleft", lty=c(1,3,1), col=c("black", "red", "green"),
legend=c("log(P)", "Linear Trend", "Random Walk"))
abline(h=0, col="gray", lty=3)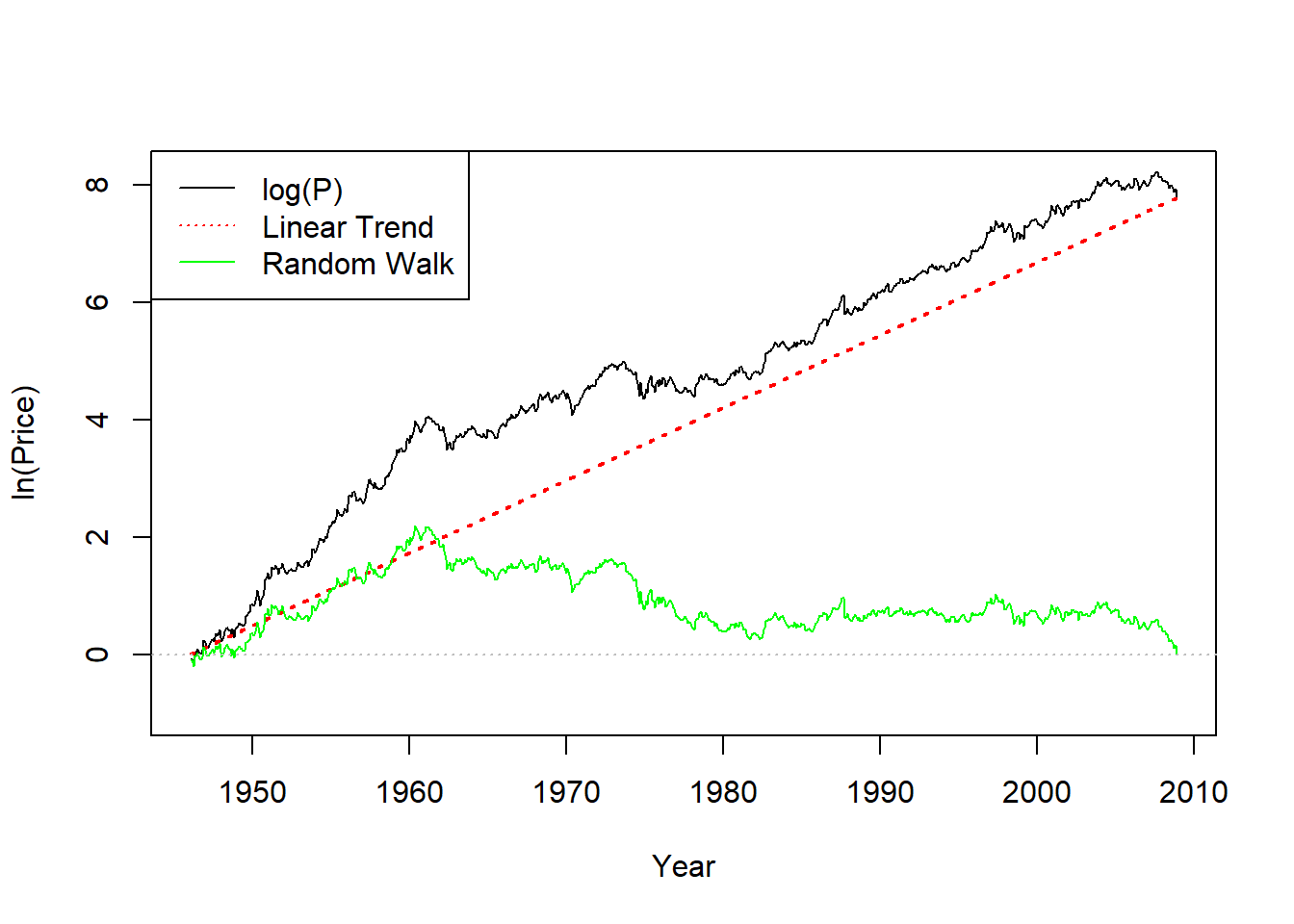
图7.2: 3M股票对数价格带漂移随机游动
7.3 固定趋势模型
设\(\{ X_t \}\)为弱平稳时间序列 令 \[ Y_t = a + b t + X_t. \] 则\(EY_t = (a + \mu_x) + bt\), \(\text{Var}(Y_t) = \text{Var}(X_t) = \sigma_x^2\), 均值非常数所以\(\{ Y_t \}\)非平稳。 但是, 减去一个固定趋势\(a + bt\)后\(\{ Y_t \}\)就变成了平稳列, 这样的\(\{ Y_t \}\)与随机游动或者带漂移的随机游动有着本质的区别。
随机游动\(p_t = p_{t+1} + \varepsilon_t\)与固定趋势加扰动 \(Y_t = a + bt + X_t\)都能呈现出缓慢的趋势变化。 区别在于:
- 随机游动的方差是线性增长的, 固定趋势的观测值方差不变;
- 随机游动的扰动的影响是永久的, 固定趋势的扰动的影响仅在一个时刻(如果扰动\(X_t\)是白噪声) 或者很短时间(如果是扰动\(X_t\)是线性时间序列);
- 随机游动的趋势没有固定方向, 固定趋势的变化形状是固定的;
- 固定趋势模型\(Y_t\)减去一个固定的回归函数\(Y = a + bt\)就可以变成平稳列, 随机游动减去任意的非随机函数都不能变平稳, 可以用差分运算变成平稳。
在AR和ARMA模型中, 常数项\(\phi_0\)与平稳均值有关。 但是在带漂移的随机游动模型中, 常数项\(\mu\)是每一步的平均增量,是固定线性趋势的斜率。 所以时间序列模型中的常数项可能会依模型的不同而具有迥然不同的含义。
7.4 ARIMA模型
将带漂移的随机游动模型中的白噪声替换成一个ARMA平稳列, 其主要的性质仍能保留。即 \[ Y_t = Y_{t-1} + \mu + X_t . \] 其中\(\{ X_t \}\)是零均值平稳可逆ARMA(\(p,q\))平稳列。 这时有 \[ Y_t = Y_0 + \mu t + \sum_{j=1}^t X_j . \] 于是 \[ E(Y_t|Y_0) = Y_0 + \mu t, \quad \text{Var}(Y_t | Y_0) = \text{随}t\text{增大而趋于}\infty . \] 当\(\mu=0\)时, \(\{ Y_t \}\)的均值固定。 \(Y_t\)的条件方差为\(t\)的线性函数。 \(X_{t-j}\)对\(Y_t\)的影响不衰减, 是永久有影响的。 这些表现与带漂移的随机游动基本相同。
称\(\{ Y_t \}\)服从ARIMA(\(p,1,q\))模型, 是非平稳的。 \(\{Y_t\}\)不能通过减去任何的非随机趋势变成平稳。 但是, 差分运算 \[ \Delta Y_t = (1-B)Y_t = Y_t - Y_{t-1} = \mu + X_t \] 将ARIMA(\(p,1,q\))序列\(\{Y_t\}\)转化成平稳可逆的ARMA(\(p,q\))序列。
设零均值平稳可逆ARMA(\(p,q\))序列\(\{X_t \}\)的模型为 \[ P(B) X_t = Q(B) \varepsilon_t , \] 其中\(\{ \varepsilon_t \}\)为零均值独立同分布白噪声列, \(P(z)=1 - \phi_1 z - \dots - \phi_p z^p\), \(Q(z)= 1 + \theta_1 z + \dots + \theta_q z^q\)。 因为\((1-B)Y_t = \mu + X_t\), 所以 \[ P(B) (1-B)Y_t = P(B)(\mu + X_t) = P(1)\mu + P(B) X_t = P(1)\mu + Q(B)\varepsilon_t . \] 记\(\tilde P(z) = P(z) (1-z)\), \(\phi_0 = P(1)\mu\),则\(Y_t\)的模型可以写成 \[ \tilde P(B) Y_t = \phi_0 + Q(B) \varepsilon_t . \] 这个模型形式上与一个ARMA(\(p+1,q\))模型相同, 但是其\(p+1\)个特征根中有一个等于1, 其余特征根才在单位圆外。
对ARIMA模型建模, 只要计算\(Y_t\)的差分, 然后对差分建立ARMA模型即可。
有些序列需要二阶差分才能平稳,二阶差分即 \[\begin{aligned} \Delta^2 Y_t =& (1-B)^2 Y_t = (1-B)(Y_t - Y_{t-1}) \\ =& (Y_t - Y_{t-1}) - (Y_{t-1} - Y_{t-2}) \\ =& Y_t - 2 Y_{t-1} + Y_{t-2} . \end{aligned}\]
如果\(\xi_t = a + bt\), 则 \[ (1-B) \xi_t = b . \] 即差分还可以消除线性趋势。
如果 \(\xi_t = a + bt + ct^2\), 则 \[ (1-B)^2 \xi_t = 2c . \] 即二阶差分可以消除二次多项式趋势。
在R中用diff(x)计算一阶差分,
结果从原来的第二个时间点给出;
用diff(x, differences=2)计算二阶差分,
结果从原来的第三个时间点给出。
如果\(Y_t\)本身已经是弱平稳列, 则不应对\(Y_t\)进行差分。 如果\(Y_t\)是非随机的线性趋势加平稳列, 虽然差分能将其变成平稳列, 但是也不应该使用差分来做而是应该用回归来做, 用差分来做会在ARMA模型的MA部分引入不必要的单位根, 使得ARMA模型不可逆。
7.5 单位根检验
单位根非平稳列是金融中最常用的非平稳模型, 单位根非平稳列不能使用平稳列的模型来建模。 所以, 要建模的序列应该进行“单位根检验”。 但是, 在金融建模实践中要注意, 不平稳的时间序列并不是只有单位根过程这样一种类型, 要根据图形、分段统计等方法综合判断时间序列是否平稳。
对不带漂移的单位根过程, 考虑如下的基础模型:
\[\begin{align} p_t = \phi_1 p_{t-1} + \varepsilon_t . \tag{7.3} \end{align}\]
其中\(\{\varepsilon_t\}\)是零均值独立同分布白噪声列。 \(|\phi_1| \leq 1\)。 考虑如下零假设与对立假设: \[ H_0: \phi_1 = 1 \longleftrightarrow H_a: \phi_1 < 1 . \] 这样的检验问题称为单位根检验问题。 基础模型也可以是带有常数项的:
\[\begin{align} p_t = \phi_0 + \phi_1 p_{t-1} + \varepsilon_t . \tag{7.4} \end{align}\]
对模型(7.3)作最小二乘估计 \[ \hat\phi_1 = \frac{\sum_{t=1}^T p_{t-1}p_t}{\sum_{t=1}^T p_t^2}, \quad \hat\sigma^2 = \frac{1}{T-1} \sum_{t=1}^T (p_t - \hat\phi_1 p_{t-1})^2 . \] 其中\(p_0=0\), \(T\)为样本量。取检验统计量 \[ \text{DF} = \frac{\hat\phi_1 - 1}{\text{SE}(\hat\phi_1)} = \frac{\sum_{t=1}^T p_{t-1} e_t }{\hat\sigma \sqrt{\sum_{t=1}^T p_{t-1}^2}} . \] 当\(T\)充分大时在\(H_0\)下有渐近分布, 当DF统计量足够小的时候拒绝\(H_0\)。 \(p\)值一般通过随机模拟计算。 这个检验称为Dicky-Fuller检验。
在使用(7.4)作为基础模型时, 如果实际上\(\phi_0=0\), 则DF统计量也有非标准的渐近分布, 可以用随机模拟方法计算p值。 如果实际上\(\phi_0\neq 0\), 则DF统计量渐近正态分布,但是需要很大的样本量。
许多经济和金融序列并不能仅用随机游动来描述, 可能需要用ARIMA。 因为ARMA模型可以看成长阶自回归, 所以检验是否ARIMA模型, 可以用\(q=0\)的ARIMA作为基础模型。 对序列\(\{ x_t \}\)为了检验其是否有单位根, 考虑如下的基础模型:
\[\begin{align} X_t = c_t + \beta X_{t-1} + \sum_{j=1}^{p-1} \phi_j \Delta X_{t-j} + e_t . \tag{7.5} \end{align}\]
当\(\beta=1\)时, 就是\(\Delta X_t\)的AR(\(p-1\))模型; 当\(\beta<1\)时, 是\(X_t\)的AR(\(p\))模型。 \(c_t\)是非随机的趋势部分, 可以取0,或常数,或\(a + bt\)这样的非随机线性趋势。 检验假设 \[ H_0: \beta = 1 \longleftrightarrow H_a: \beta < 1 . \] 如果拒绝\(H_0\), 就说明没有单位根。 使用统计量 \[ \text{ADF} = \frac{\hat\beta - 1}{\text{SE}(\hat\beta)} . \] 当ADF统计量足够小的时候拒绝\(H_0\)。
基础模型(7.5)也可以改写成 \[\begin{align} \Delta X_t = c_t + \beta_c X_{t-1} + \sum_{j=1}^k \phi_j \Delta X_{t-j} + e_t, \tag{7.6} \end{align}\] 其中\(\beta_c = \beta-1\),\(k=p-1\), 检验 \[ H_0: \beta_c = 0 \longleftrightarrow H_a: \beta_c < 0 , \] 这个检验称为ADF检验(Augmented Dicky-Fuller Test)。
fUnitRoots包的adfTest()函数可以执行单位根ADF检验。
其中的lags参数指定(7.6)中的差分后AR阶数\(k\)。
type参数对应((7.6))中的\(c_t\),
选项为:
nc: \(c_t = 0\);c: \(c_t = c\);ct: \(c_t = a + bt\)。
urca包的ur.df()函数,
tseries包的adf.test()函数也可以执行单位根ADF检验。
注意,单位根DF检验和ADF检验都是在拒绝\(H_0\)(显著)时否认有单位根(结论是平稳), 不显著时承认有单位根(结论是非平稳)。
例7.2 考虑美国的国民生产总值(GNP)经过季节调整后的对数值。 时间是1947年第一季度到2010年第一季度,总计253个观测值。
读入数据并计算季节调整后的GNP的对数值, 以及对数值的一阶差分:
da <- read_table("q-gnp4710.txt", col_types=cols(
.default = col_double()))
gnp <- ts(log(da[["VALUE"]]),
start=c(1947, 1), frequency=4)
dgnp <- diff(gnp)
rm(da)GNP的对数值的图形:
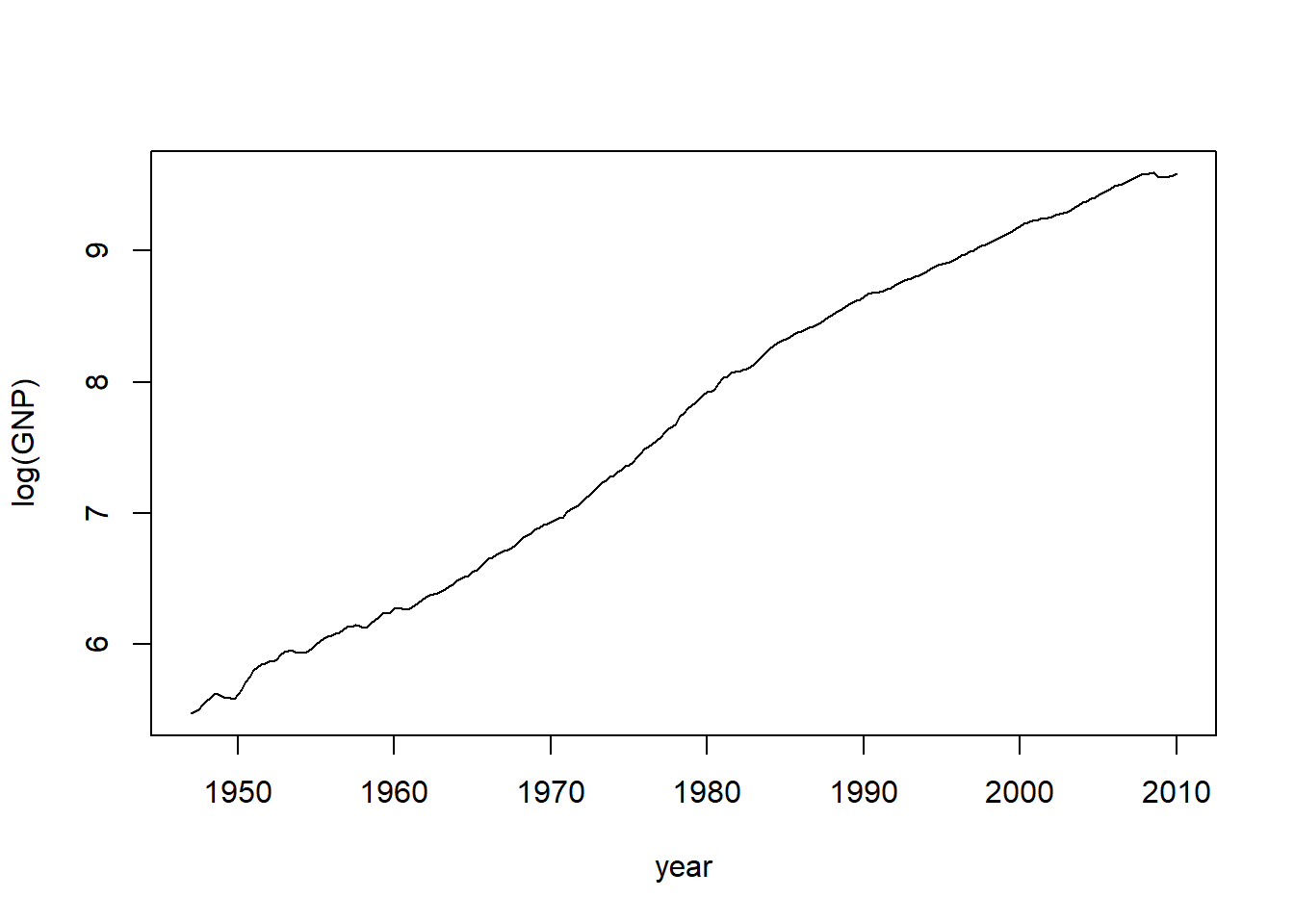
图7.3: 美国经季节调整的GNP对数值
对数GNP明显地不平稳。其ACF图形如下:
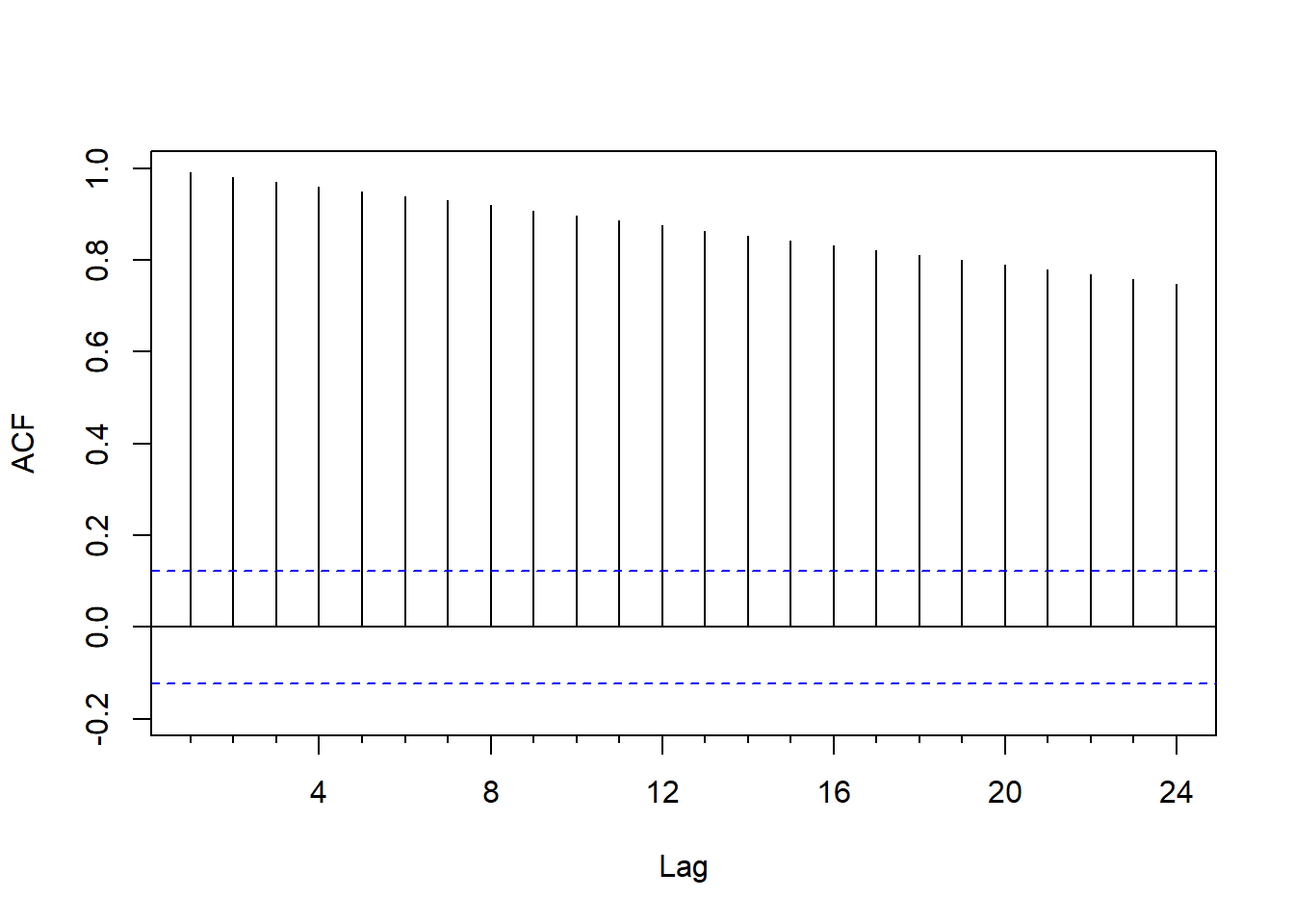
图7.4: 美国经季节调整的GNP对数值的ACF
对数GNP差分的时间序列图:
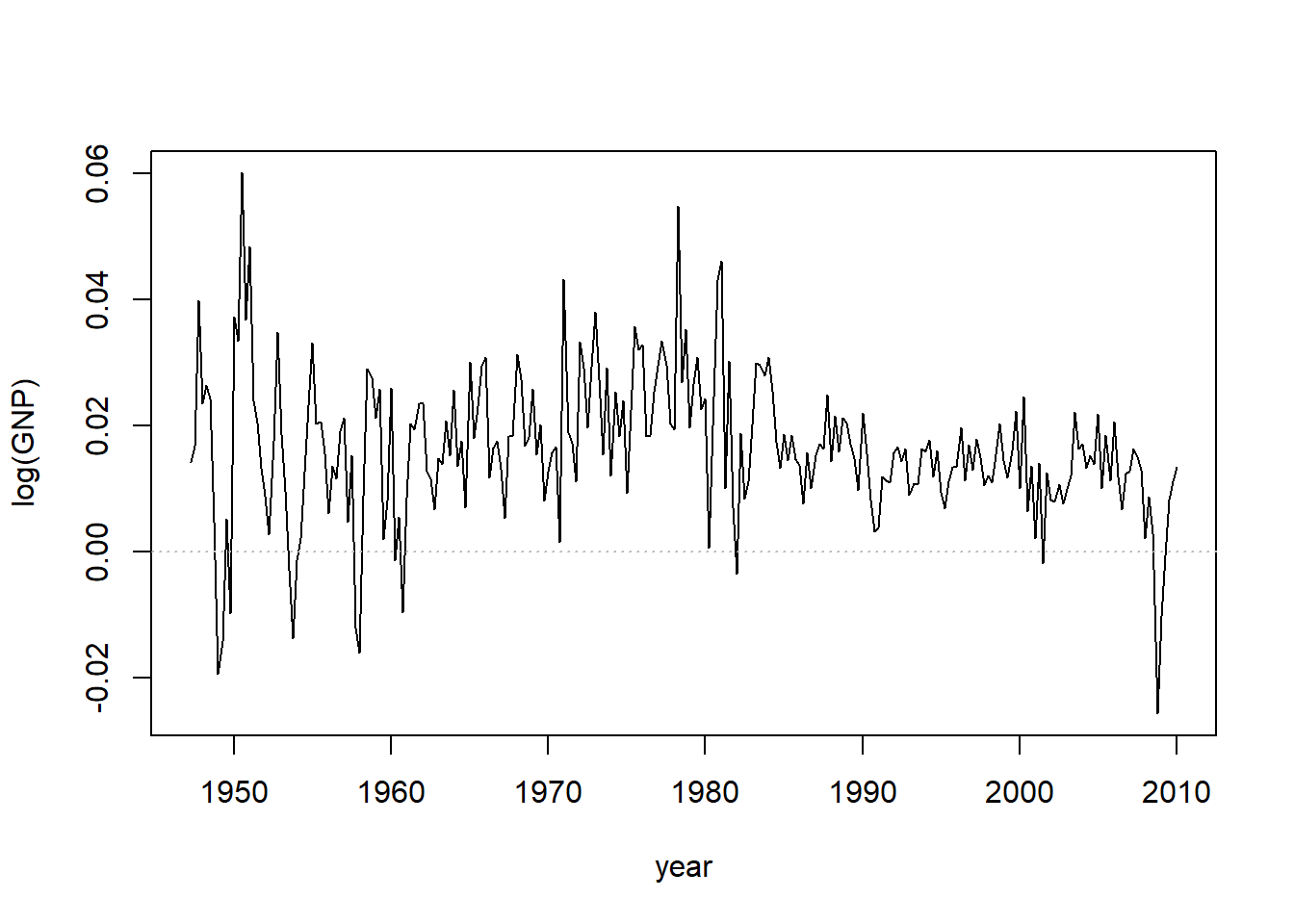
图7.5: 美国经季节调整的对数GNP差分
对数GNP差分的ACF:
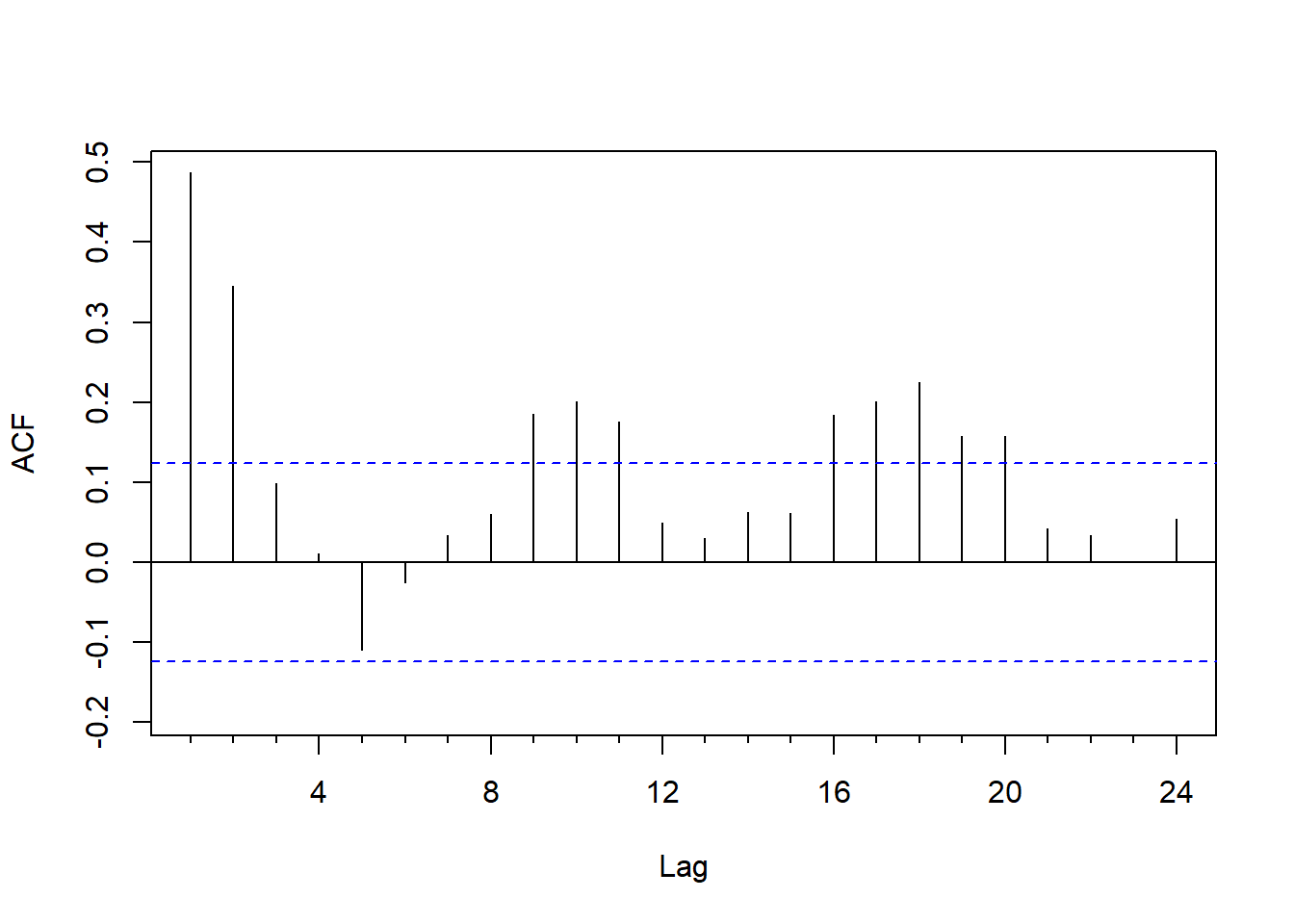
图7.6: 美国经季节调整的对数GNP差分的ACF
对数GNP差分的PACF:
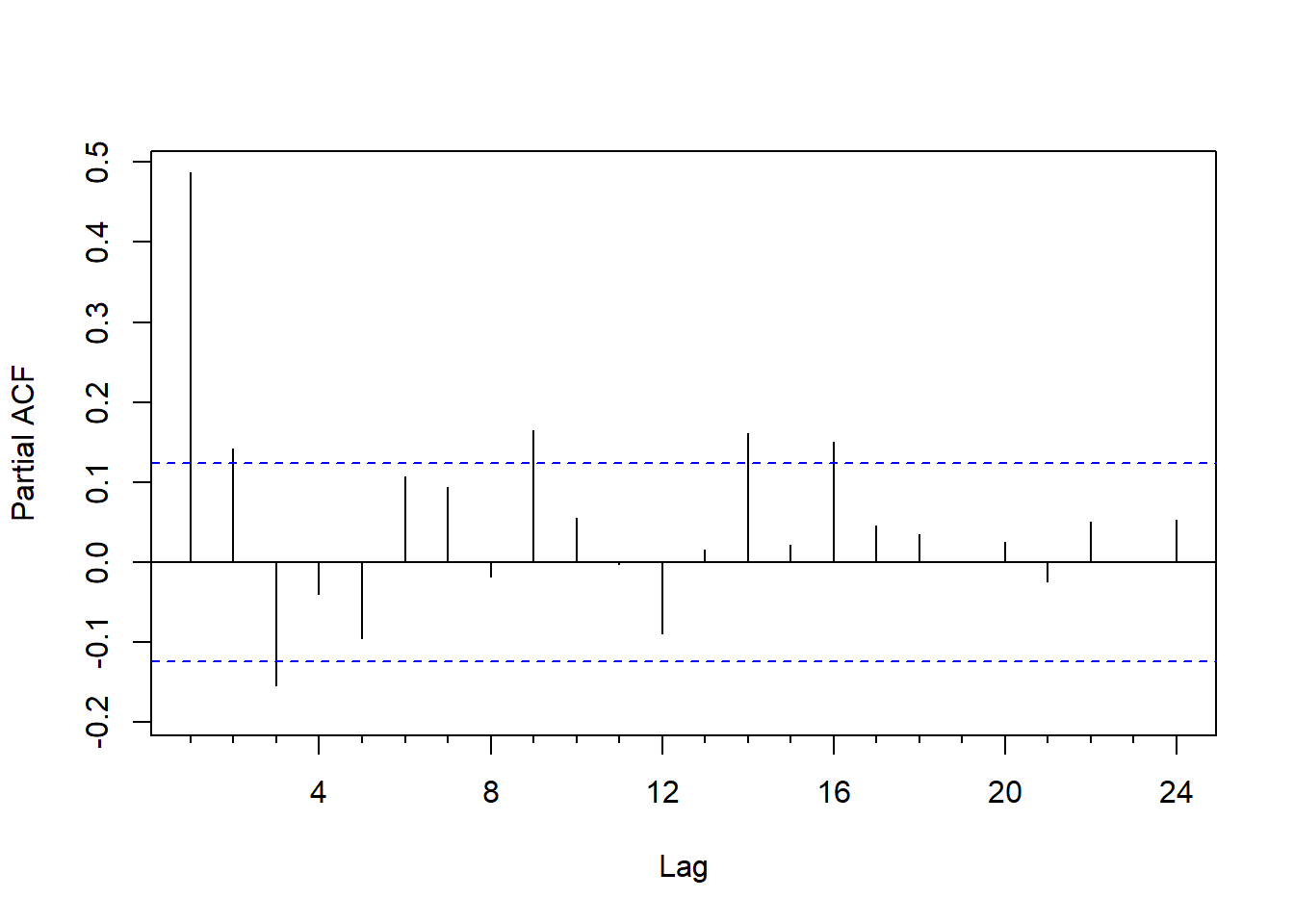
图7.7: 美国经季节调整的对数GNP差分的PACF
如果用AR(\(p\))为对数GNP差分序列建模, PACF图提示用\(p=16\)。 用AIC定阶:
##
## Call:
## ar(x = dgnp, method = "mle")
##
## Coefficients:
## 1 2 3 4 5 6 7 8
## 0.4318 0.1985 -0.1180 0.0189 -0.1607 0.0900 0.0615 -0.0814
## 9
## 0.1940
##
## Order selected 9 sigma^2 estimated as 8.918e-05差分序列用AIC取AR为9阶。
ADF的基础模型需要一个AR阶数,
这是差分序列的AR阶数,
取\(p=9\)。
用fUnitRoots::adfTest()对GNP的对数值进行ADF单位根检验:
##
## Title:
## Augmented Dickey-Fuller Test
##
## Test Results:
## PARAMETER:
## Lag Order: 9
## STATISTIC:
## Dickey-Fuller: -1.8467
## P VALUE:
## 0.3691
##
## Description:
## Tue May 21 15:20:27 2024 by user: Lenovo结果\(p\)值较大,说明不能拒绝零假设, 即对数GNP序列有单位根。
GNP对数序列的图形也像是有非随机线性增长趋势的情况。 为此,仍使用ADF检验,但是允许有非随机常数项和线性项:
## Warning in fUnitRoots::adfTest(gnp, lags = 9, type = "ct"): p-value greater
## than printed p-value##
## Title:
## Augmented Dickey-Fuller Test
##
## Test Results:
## PARAMETER:
## Lag Order: 9
## STATISTIC:
## Dickey-Fuller: -0.0094
## P VALUE:
## 0.99
##
## Description:
## Tue May 21 15:20:27 2024 by user: Lenovo结果仍是承认零假设, 认为有单位根存在。
尝试人为地拟合非随机线性增长趋势, 检验残差是否有单位根:
tmp.t <- c(time(gnp))
tmp.y <- residuals( lm(c(gnp) ~ tmp.t) )
fUnitRoots::adfTest(tmp.y, type="nc")##
## Title:
## Augmented Dickey-Fuller Test
##
## Test Results:
## PARAMETER:
## Lag Order: 1
## STATISTIC:
## Dickey-Fuller: -0.0763
## P VALUE:
## 0.592
##
## Description:
## Tue May 21 15:20:27 2024 by user: Lenovo结果说明用回归去掉非随机的线性增长趋势后仍有单位根存在。
使用urca包的ur.df()执行单位根ADF检验,基础模型带有常数漂移项:
##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.033589 -0.004595 0.000503 0.003911 0.035557
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0135157 0.0045219 2.989 0.00310 **
## z.lag.1 -0.0009040 0.0004895 -1.847 0.06606 .
## z.diff.lag1 0.3903745 0.0641690 6.084 4.81e-09 ***
## z.diff.lag2 0.2057039 0.0681595 3.018 0.00283 **
## z.diff.lag3 -0.1111342 0.0693754 -1.602 0.11053
## z.diff.lag4 0.0263875 0.0692327 0.381 0.70345
## z.diff.lag5 -0.1399063 0.0684739 -2.043 0.04216 *
## z.diff.lag6 0.0857675 0.0704276 1.218 0.22453
## z.diff.lag7 0.0520310 0.0696968 0.747 0.45610
## z.diff.lag8 -0.0879122 0.0685969 -1.282 0.20127
## z.diff.lag9 0.1816295 0.0639332 2.841 0.00490 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.009396 on 232 degrees of freedom
## Multiple R-squared: 0.3142, Adjusted R-squared: 0.2847
## F-statistic: 10.63 on 10 and 232 DF, p-value: 8.56e-15
##
##
## Value of test-statistic is: -1.8467 6.7291
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.44 -2.87 -2.57
## phi1 6.47 4.61 3.79可以将统计量的第一个(\(-1.8467\))与tau2统计量的5pct临界值(\(-2.87\))比较, 没有小于临界值, 所以可以接受零假设, 认为有单位根。 这个检验是左侧否定域。
urca::ur.df()的type参数也对应于(7.6)中的\(c_t\),
选项为:
"none": \(c_t = 0\);"drift": \(c_t = c\);"trend": \(c_t = a + bt\)。
使用tseries包的adf.test()执行单位根ADF检验,
对应于(7.6)中的\(c_t = a+bt\)。
参数\(k\)为(7.6)中的\(k\)。
## Warning in tseries::adf.test(gnp, k = 9): p-value greater than printed p-value##
## Augmented Dickey-Fuller Test
##
## data: gnp
## Dickey-Fuller = -0.0093764, Lag order = 9, p-value = 0.99
## alternative hypothesis: stationaryforecast包提供了一个ndiffs()函数,
可以用检验的方法估计需要多少次差分变成平稳,
如:
## [1] 1即需要进行一阶差分, 然后平稳。
○○○○○
例7.3 考虑标普500指数从1950-01-03到2008-04-11的OHLC数据日数据。 共14662个观测。
读入数据,从中计算日收盘价对数值序列及其一阶差分:
da <- read_table("d-sp55008.txt", col_types=cols(.default = col_double()))
xts.sp5d <- xts(da[,-(1:3)], make_date(da$year, da$mon, da$day))
str(xts.sp5d)## An 'xts' object on 1950-01-03/2008-04-11 containing:
## Data: num [1:14662, 1:6] 16.7 16.9 16.9 17 17.1 ...
## - attr(*, "dimnames")=List of 2
## ..$ : NULL
## ..$ : chr [1:6] "open" "high" "low" "close" ...
## Indexed by objects of class: [Date] TZ: UTC
## xts Attributes:
## NULL作日对数收盘价的时间序列图:
plot(sp5d, type="l", main="S&P 500 Daily Log Close",
major.ticks="years", minor.ticks=NULL,
grid.ticks.on="auto")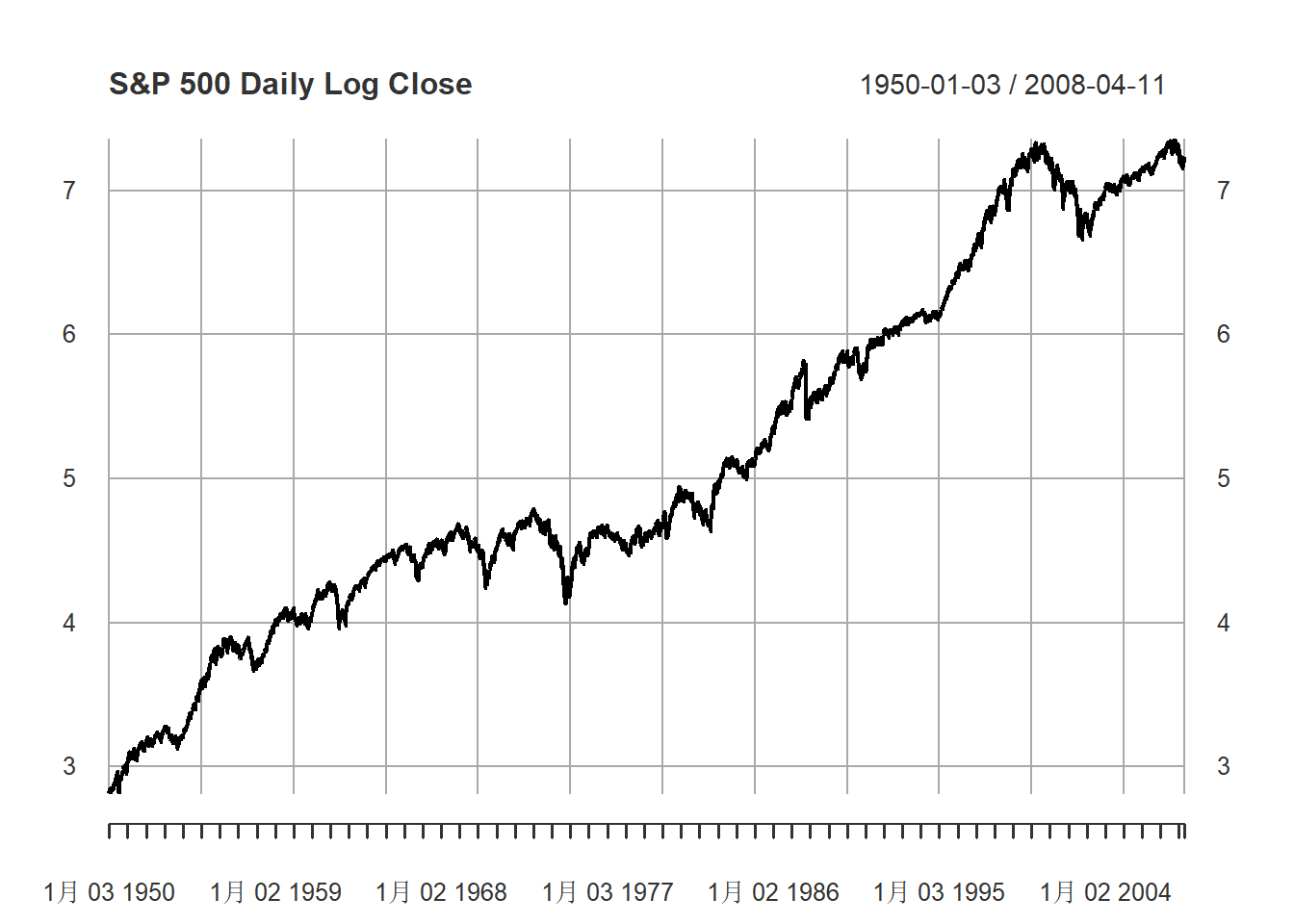
图7.8: S&P 500日对数收盘价
明显非平稳。一阶差分的时间序列图:
plot(diff(sp5d), type="l", main="S&P 500 Daily Log Return",
major.ticks="years", minor.ticks=NULL,
grid.ticks.on="auto")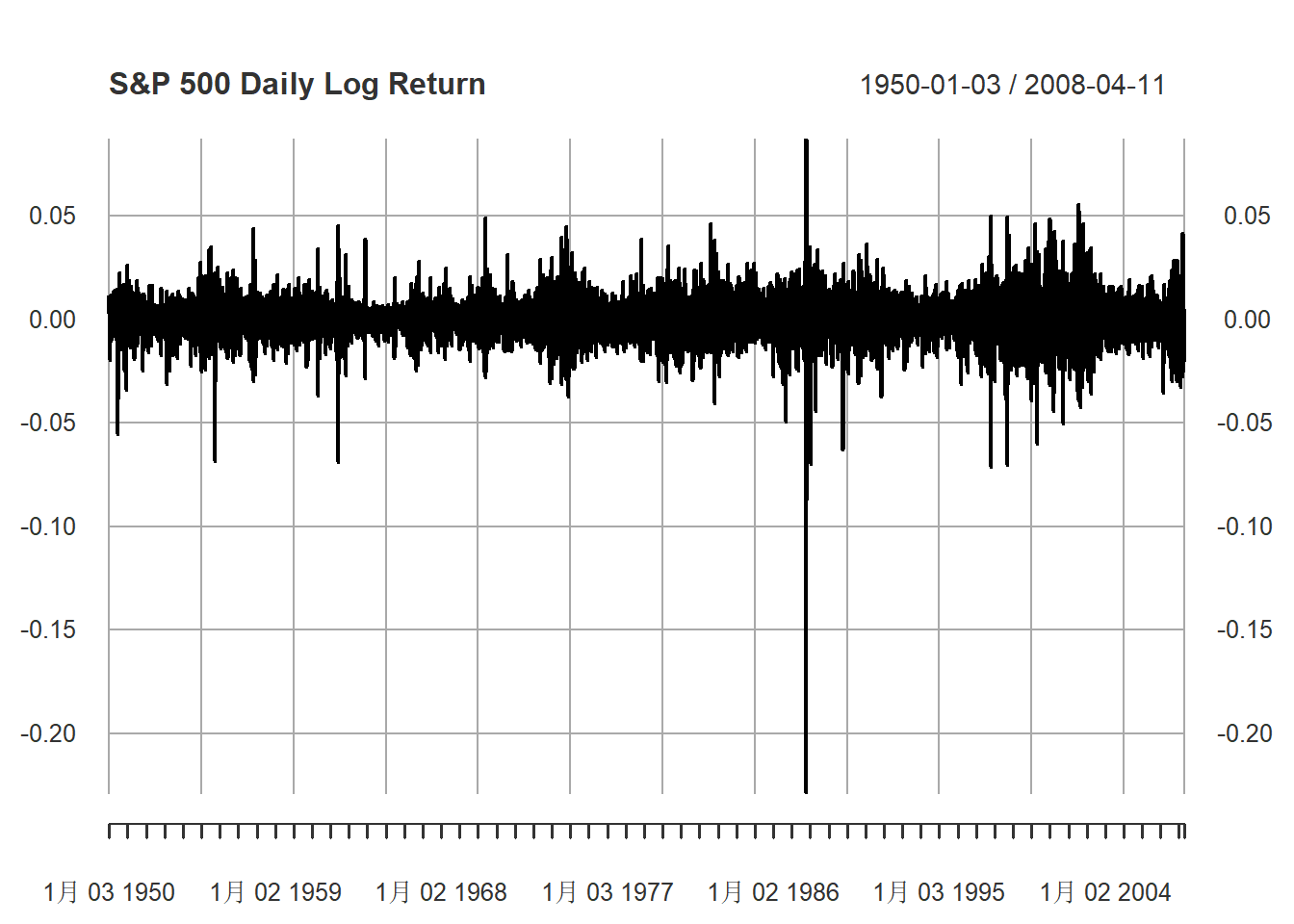
图7.9: S&P 500日对数收益率
一阶差分的PACF:
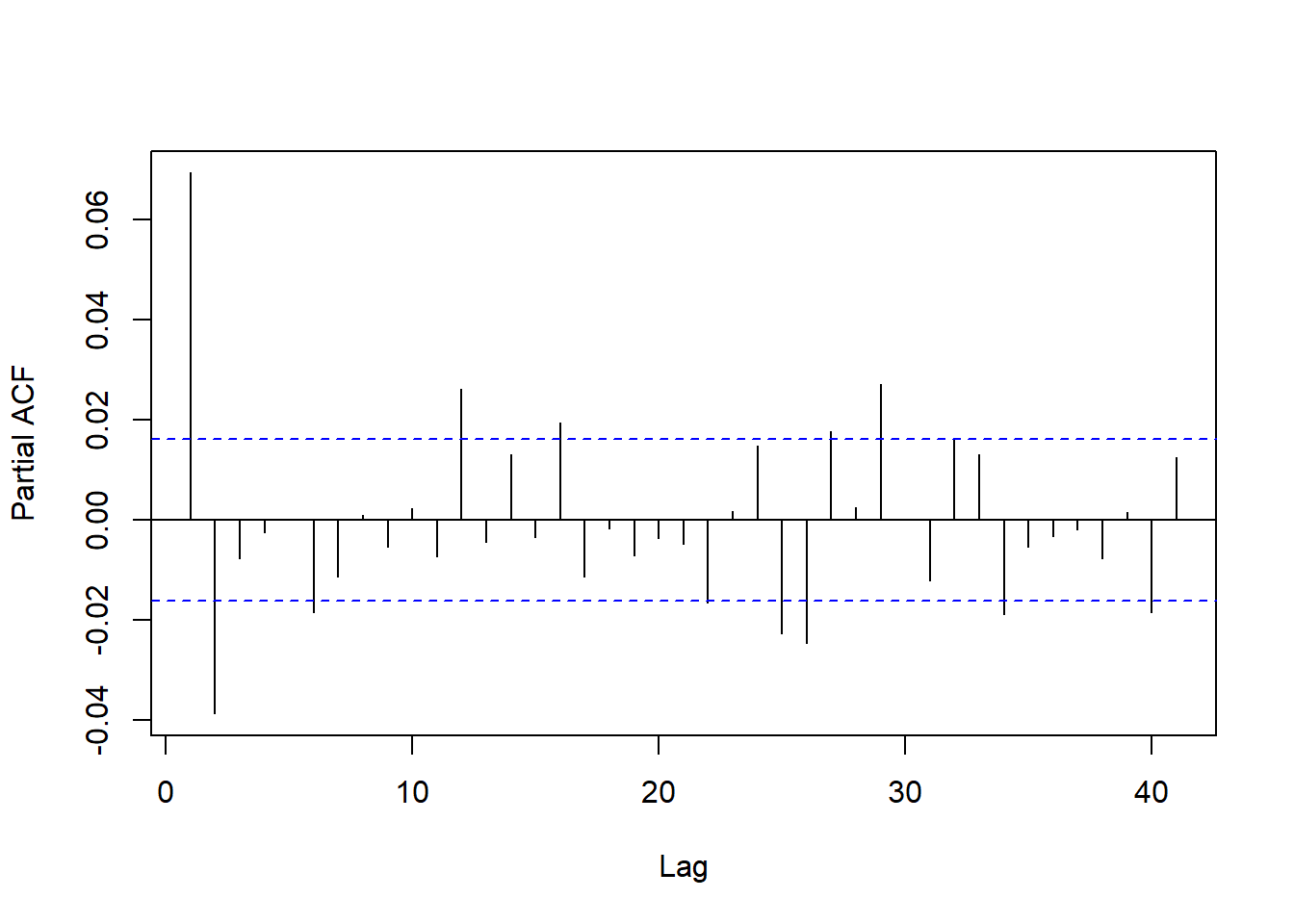
图7.10: S&P 500日对数收益率的PACF
用AIC对日对数收益率定阶:
##
## Call:
## ar(x = delta.sp5d, method = "mle")
##
## Coefficients:
## 1 2
## 0.0721 -0.0387
##
## Order selected 2 sigma^2 estimated as 8.068e-05AIC定阶\(p=2\)。按\(p=2\)对标普500日对数收盘价作ADF白噪声检验:
##
## Title:
## Augmented Dickey-Fuller Test
##
## Test Results:
## PARAMETER:
## Lag Order: 2
## STATISTIC:
## Dickey-Fuller: -2.0179
## P VALUE:
## 0.5708
##
## Description:
## Tue May 21 15:20:29 2024 by user: Lenovo检验不显著,说明存在单位根。 如果对日对数收益率(即对数收盘价序列的差分)进行ADF检验, 则显著,说明一阶差分后使得序列变得平稳:
## Warning in fUnitRoots::adfTest(delta.sp5d, lags = 2, type = "ct"): p-value
## smaller than printed p-value##
## Title:
## Augmented Dickey-Fuller Test
##
## Test Results:
## PARAMETER:
## Lag Order: 2
## STATISTIC:
## Dickey-Fuller: -70.5501
## P VALUE:
## 0.01
##
## Description:
## Tue May 21 15:20:29 2024 by user: Lenovo○○○○○