19 改进的GARCH模型

本章讲GARCH模型的一些有针对性的改进。来自(Tsay 2013)§4.9-4.11内容。

19.1 EGARCH模型

19.1.1 模型

(Nelson 1991)提出的指数GARCH(EGARCH)模型允许正负资产收益率对波动率有不对称的影响。考虑如下变换 \[\begin{align} g(\varepsilon_t) = \alpha\varepsilon_t + \gamma\left[ |\varepsilon_t| - E|\varepsilon_t| \right] , \tag{19.1} \end{align}\] 其中\(\alpha\)和\(\gamma\)是实常数。 \(\{\varepsilon_t \}\)和\(\{ |\varepsilon_t| - E|\varepsilon_t| \}\)都分别是零均值独立同分布白噪声，分布为连续分布。易见\(Eg(\varepsilon_t)=0\)。

\(g(\varepsilon_t)\)关于正的\(\varepsilon_t\)和负的\(\varepsilon_t\)结果不同，对于绝对值相等但符号相反的\(\varepsilon_t\)，设\(\alpha < 0\)，则负的\(\varepsilon_t\)对应的\(g(\varepsilon_t)\)更大，而正的\(\varepsilon_t\)对应的\(g(\varepsilon_t)\)更小。

当\(\varepsilon_t \sim \text{N}(0,1)\)时\(E|\varepsilon_t| = \sqrt{\frac{2}{\pi}}\)。对式(17.6)中的标准t分布，有 \[ E|\varepsilon_t| = \frac{2 \sqrt{v-2} \Gamma(\frac{v+1}{2})}{ (v-1)\Gamma(\frac{v}{2}) \sqrt{\pi}} . \]

EGARCH(\(m,s\))模型可以用滞后算子的形式写成

\[\begin{align} a_t = \sigma_t \varepsilon_t, \quad \ln\sigma_t^2 = \alpha_0' + \frac{1 + \alpha_2 B + \dots + \alpha_m B^{m-1}}{ 1 - \beta_1 B - \dots - \beta_s B^s} g(\varepsilon_{t-1}) \tag{19.2} \end{align}\] \(\alpha_0'\)为常数，其中\(B\)是滞后算子，多项式\(1 + \alpha_2 z + \dots + \alpha_m z^{m-1}\)和 \(1 - \beta_1 z - \dots - \beta_m z^m\)的根都在单位圆外且两个多项式没有公因子。

注意这里的模型阶相当于GARCH(\(m,s\))。 EGARCH(\(1,1,\))模型为 \[ \ln\sigma_t^2 = \alpha_0 + \alpha \varepsilon_{t-1} + \gamma[|\varepsilon_{t-1}| - E|\varepsilon_{t-1}|] + \beta \ln\sigma_{t-1}^2 . \]

记\(\xi_t = \ln\sigma_t^2\)，则(19.2)给出的\(\xi_t\)为一个平稳线性ARMA\((s, m-1)\)序列，以零均值独立同分布白噪声\(g(\varepsilon_{t-1})\)为新息；但是， \(\ln\sigma_t^2\)通过\(\varepsilon_{t-j} = a_{t-j} / \sigma_{t-j}\)对\(\{ a_t \}\)序列依赖。原始的GARCH模型的\(\sigma_t^2\)的方程是直接依赖于\(a_{t-j}^2\)的，\(\pm a_{t-j}\)对\(\sigma_t^2\)影响相同。

易见\(E\ln\sigma_t^2 = \alpha_0'\)。

EGARCH(\(m,s\))模型展开后可以写成

\[\begin{align} a_t =& \sigma_t \varepsilon_t, \\ \ln\sigma_t^2 =& \alpha_0 + \sum_{j=1}^m \left[\alpha_j \varepsilon_{t-j} + \gamma_j(|\varepsilon_{t-j}| - E |\varepsilon_{t-j}|) \right] + \sum_{i=1}^s \beta_i \ln \sigma_{t-i}^2 . \tag{19.3} \end{align}\]

在(19.3)中， \(\alpha_j\)代表了对数收益率的正负扰动对波动率的不同影响，如果\(\alpha_j=0\)，则正负扰动对波动率影响就相同了。

EGARCH与GARCH模型的区别还有：

使用条件方差的对数建模，因为对数值可正可负，这就取消了GARCH模型对系数必须非负的限制。
\(g(\varepsilon_{t-j})=g(a_{t-j}/\sigma_{t-j})\)的使用使得波动率对\(a_{t-j}\)的依赖关系与\(a_{t-j}\)的正负号有关，可以用来描述正负收益率对波动率的不同的影响，即杠杆效应。

19.1.2 EGARCH(1,1)模型

以最简单的EGARCH(1,1)为例来讨论。模型为

\[\begin{align} a_t =& \sigma_t \varepsilon_t, \\ \ln \sigma_t^2 =& \alpha_0 + \left[ \alpha_1 \varepsilon_{t-1} + \gamma_1 (|\varepsilon_{t-1}| - E|\varepsilon_{t-1}|) \right] + \beta_1 \ln\sigma_{t-1}^2 . \tag{19.4} \end{align}\]

其中\(\varepsilon_t\) iid N(0,1), 这个模型的阶类似GARCH(1,1)，模型实际上是关于\(\ln \sigma_t^2\)的一个AR(1)模型。

与一个GARCH(1,1)模型对比： \[\begin{aligned} \sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + \beta_1 \sigma_{t-1}^2 \end{aligned}\] 所以EGARCH模型用\(\ln\sigma_t^2\)替换了\(\sigma_t^2\)，用\(g(\varepsilon_{t-1})\)替换了\(\alpha_1 a_{t-1}^2\)，用\(\ln\sigma_{t-1}^2\)替换了\(\sigma_{t-1}^2\)。注意\(g(\varepsilon_{t-1}) = g(a_{t-1} / \sigma_{t-1})\)。

(19.4)中，设\(\alpha_1 < 0\)， \(\varepsilon_{t-1} \geq 0\)时， \(\ln\sigma_t^2\)变小， \(\varepsilon_{t-1} < 0\)时， \(\ln\sigma_t^2\)变大，对于相同的\(|a_{t-1}|\), 负值比正值产生更大的\(\ln\sigma_t^2\)。

波动率方程可以写成 \[\begin{aligned} \sigma_t^2 =\sigma_{t-1}^{2\beta_1} e^{\alpha_0''} \cdot \begin{cases} \exp\left[ (\gamma_1 + \alpha_1) \frac{|a_{t-1}|}{\sigma_{t-1}} \right], & a_{t-1} \geq 0 \\ \exp\left[ (\gamma_1 - \alpha_1) \frac{|a_{t-1}|}{\sigma_{t-1}} \right], & a_{t-1} < 0 \end{cases} \end{aligned}\] 其中\(\alpha_0'' = \alpha_0 - \gamma_1 E|\varepsilon_{t-1}|\)。

系数\(\gamma_1 + \alpha_1\)和\(\gamma_1 - \alpha_1\)表明当\(\alpha_1\neq 0\) 时模型对正的和负的\(a_{t-1}\)的响应是非对称的，由于一般负的扰动造成的波动更大，所以\(\alpha_1\)应该是负的才比较符合实际数据。

19.1.3 实例1：CRSP价值加权指数超额收益率

例子来自(Nelson 1991)的文章。考虑CRSP价值加权指数的超额收益率日数据，从1962年7月到1987年12月，共6408个观测值，超额收益率是价值加权指数的收益率减去国债的月收益率，假定一个月每天的国债收益率相等。

用\(r_t\)表示超额收益率，所用的模型为

\[\begin{aligned} r_t =& \phi_0 + \phi_1 r_{t-1} + c\sigma_{t}^2 + a_t, \quad a_t = \sigma_t \varepsilon_t,\\ \ln\sigma_t^2 =& \alpha_0 + \ln(1 + \omega N_t) + \frac{1 + \beta B}{1 - \alpha_1 B - \alpha_2 B^2} g(\varepsilon_{t-1}), \\ g(\varepsilon_{t-1}) =& \theta \varepsilon_{t-1} + \gamma (|\varepsilon_{t-1}| - E|\varepsilon_{t-1}|) . \end{aligned}\] 均值方程是带有回归自变量的AR(1)模型，回归自变量是波动率平方，这个回归自变量代表了风险溢价， \(c\)是风险溢价参数。波动率方程中的回归自变量\(N_t\)是第\(t-1\)交易日到第\(t\)交易日之间没有交易的天数，这一项解释了放假休市若干天以后增加的波动。 \(\varepsilon_t\)使用广义误差分布(GED), 波动率方程是是EGARCH(2,2)模型。这里所用的符号与19.1.1有所不同。 \(\theta\)代表了杠杆效应。

(Nelson 1991)论文中参数估计值与标准误差列表如下：

\[ \begin{array}{crr} \text{参数} & \text{估计值} & \text{标准误差} \\ \hline \alpha_0 & -10.06 & 0.346 \\ \omega & 0.183 & 0.028 \\ \gamma & 0.156 & 0.023 \\ \alpha_1 & 1.929 & 0.015 \\ \alpha_2 & -0.929 & 0.015 \\ \beta & -0.978 & 0.006 \\ \theta & -0.118 & 0.009 \\ \phi_0 & 3.5 \times 10^{-4} & 9.9\times 10^{-5} \\ \phi_1 & 0.205 & 0.012 \\ c & -3.361 & 2.026 \\ v & 1.576 & 0.032 \end{array} \]

估计中只有风险溢价参数\(c\)是不显著，其它参数，包括代表了不对称性的\(\theta\)，都是显著的， \(\theta\)估计为负，这表明模型的波动率收到负的扰动影响更大。

19.1.4 实例2：IBM股票月对数收益率

考虑IBM股票月对数收益率建模，从1967年1月到2009年12月， 561个观测值。建立EGARCH(1,1)模型，使用(19.4)的模型形式，模型为 \[\begin{aligned} r_t =& \mu + a_t, \\ a_t =& \sigma_t \varepsilon_t, \\ \ln \sigma_t^2 =& \alpha_0 + \left[ \alpha_1 \varepsilon_{t-1} + \gamma_1 (|\varepsilon_{t-1}| - E|\varepsilon_{t-1}|) \right] + \beta_1 \ln\sigma_{t-1}^2 . \end{aligned}\]

读入数据：

da <- read_table(
  "m-ibmsp6709.txt",
  col_types=cols(
    .default=col_double(),
    date=col_date(format="%Y%m%d")))
xts.ibm <- xts(log(1 + da[["ibm"]]), da[["date"]])
tclass(xts.ibm) <- "yearmon"
ts.ibm <- ts(log(1 + da[["ibm"]]), 
  start=c(1967,1), frequency=12)

对数收益率的时间序列图：

plot(xts.ibm, 
  format.labels="%Y",
  xlab="Year", ylab="Log return")

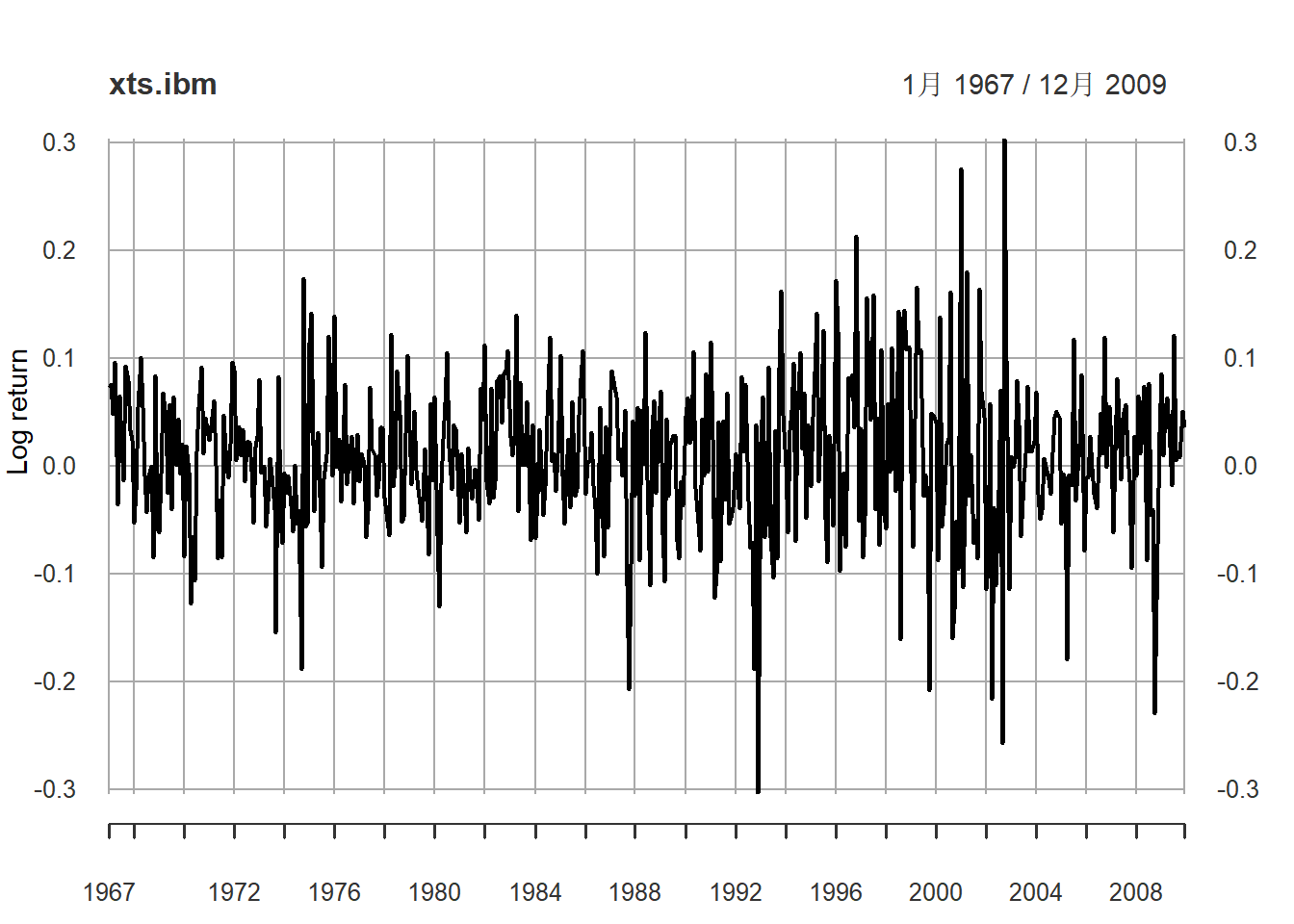
图19.1: IBM股票月对数收益率

ACF图：

forecast::Acf(xts.ibm, lag.max = 36, main="")

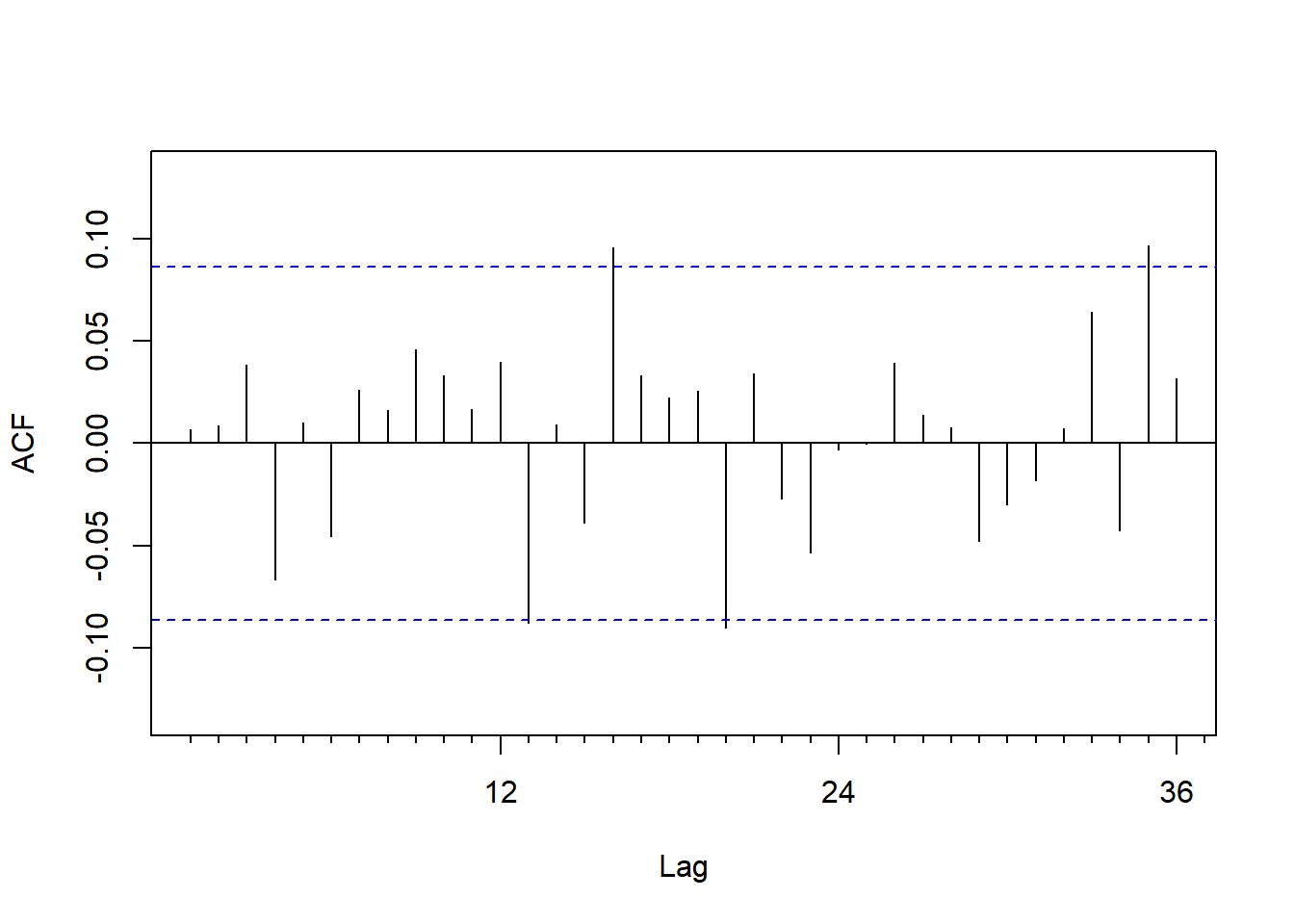
图19.2: IBM股票月对数收益率ACF

从对数收益率的ACF来看基本是白噪声。作Ljung-Box白噪声检验：

Box.test(xts.ibm, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  xts.ibm
## X-squared = 7.4042, df = 12, p-value = 0.8298

基本可以认为是（宽）白噪声。

\(a_t^2\)的ACF：

forecast::Acf(xts.ibm^2, lag.max = 36, main="")

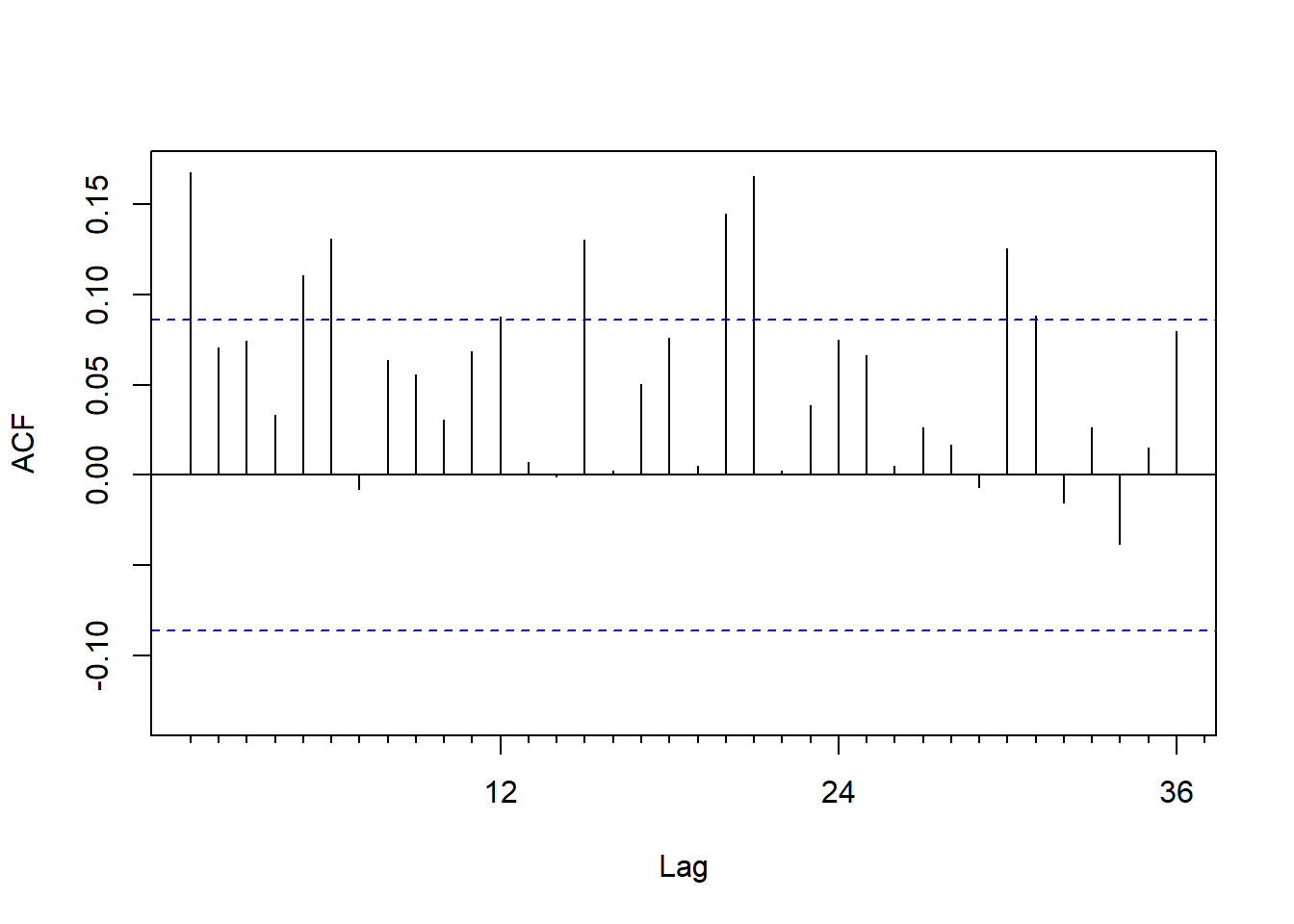
图19.3: IBM股票月对数收益率平方ACF

这表明有轻微的ARCH效应。

用rugarch扩展包可以估计EGARCH模型，程序如：

library(rugarch)

## Loading required package: parallel

## 
## Attaching package: 'rugarch'

## The following object is masked from 'package:purrr':
## 
##     reduce

## The following object is masked from 'package:stats':
## 
##     sigma

spec1 <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE  ),
  variance.model = list(
    model = "eGARCH", # exponential GARCH model
    garchOrder = c(1,1) ) )
mod1ru <- ugarchfit(spec = spec1, data = xts.ibm)
show(mod1ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : eGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.006649    0.002963   2.2442 0.024820
## omega  -0.423208    0.223673  -1.8921 0.058480
## alpha1 -0.094813    0.039373  -2.4081 0.016037
## beta1   0.920485    0.041729  22.0586 0.000000
## gamma1  0.218711    0.060802   3.5971 0.000322
## 
## Robust Standard Errors:
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.006649    0.003073   2.1635 0.030502
## omega  -0.423208    0.308230  -1.3730 0.169743
## alpha1 -0.094813    0.051835  -1.8291 0.067382
## beta1   0.920485    0.057270  16.0728 0.000000
## gamma1  0.218711    0.061770   3.5407 0.000399
## 
## LogLikelihood : 651.634 
## 
## Information Criteria
## ------------------------------------
##                     
## Akaike       -2.5063
## Bayes        -2.4652
## Shibata      -2.5065
## Hannan-Quinn -2.4902
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                      1.237  0.2661
## Lag[2*(p+q)+(p+q)-1][2]     1.344  0.3989
## Lag[4*(p+q)+(p+q)-1][5]     1.867  0.6501
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                   0.009633  0.9218
## Lag[2*(p+q)+(p+q)-1][5]  1.087446  0.8396
## Lag[4*(p+q)+(p+q)-1][9]  2.511467  0.8360
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]   0.09128 0.500 2.000  0.7626
## ARCH Lag[5]   1.10479 1.440 1.667  0.7021
## ARCH Lag[7]   2.20197 2.315 1.543  0.6746
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.1719
## Individual Statistics:              
## mu     0.21948
## omega  0.61756
## alpha1 0.15868
## beta1  0.61824
## gamma1 0.06386
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.28 1.47 1.88
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value   prob sig
## Sign Bias           0.1014 0.9192    
## Negative Sign Bias  0.2560 0.7980    
## Positive Sign Bias  0.1888 0.8503    
## Joint Effect        0.3726 0.9458    
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     13.07       0.8350
## 2    30     22.26       0.8094
## 3    40     28.03       0.9040
## 4    50     42.53       0.7314
## 
## 
## Elapsed time : 0.0812149

估计的模型可以写成：

\[\begin{aligned} r_t =& 0.0066 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \varepsilon_t \text{ iid N}(0,1) \\ \ln\sigma_t^2 =& -0.4232 - 0.0948 \varepsilon_{t-1} + 0.2187(|\varepsilon_{t-1}| - E|\varepsilon_{t-1}|) + 0.9205 \ln\sigma_{t-1}^2 . \end{aligned}\] 这种模型是关于\(\{ \ln\sigma_t^2 \}\)的一个AR(1)模型。输出中参数alpha1代表了正负收益率对波动率不对称影响的杠杆效应，在0.05水平下这一项显著，说明杠杆效存在。

取\(\varepsilon_{t-1}=\pm 2\)时，不同正负号的\(\varepsilon_{t-1}\)引起的\(\sigma_t^2\)的变化比值为 \[ e^{4 \times 0.0948} = 1.46, \] 所以这时幅度相等的负的扰动比正的扰动额外增加46%的波动率平方。幅度越大，额外增加的波动率也越大。

计算标准化残差\(\tilde a_t = a_t/\sigma_t\)和波动率\(\sigma_t\)：

stdresi <- residuals(mod1ru, standardize=TRUE)
vol <- sigma(mod1ru)

标准化残差图：

plot(stdresi, format.labels="%Y",
  xlab="Year", ylab="", 
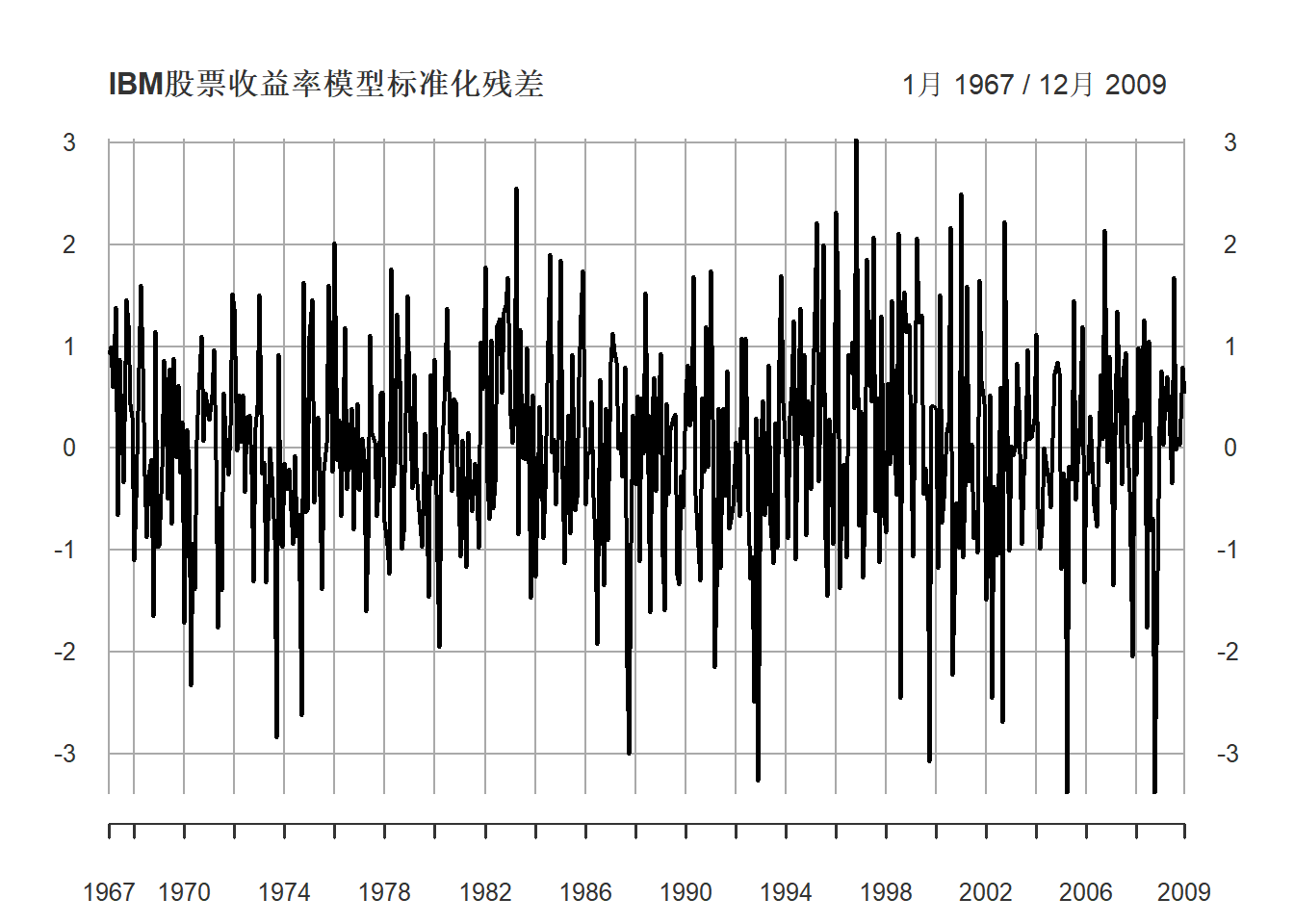
  main="IBM股票收益率模型标准化残差")

图19.4: IBM股票收益率模型标准化残差

估计的波动率：

plot(vol, format.labels="%Y",
  xlab="Year", ylab="", 
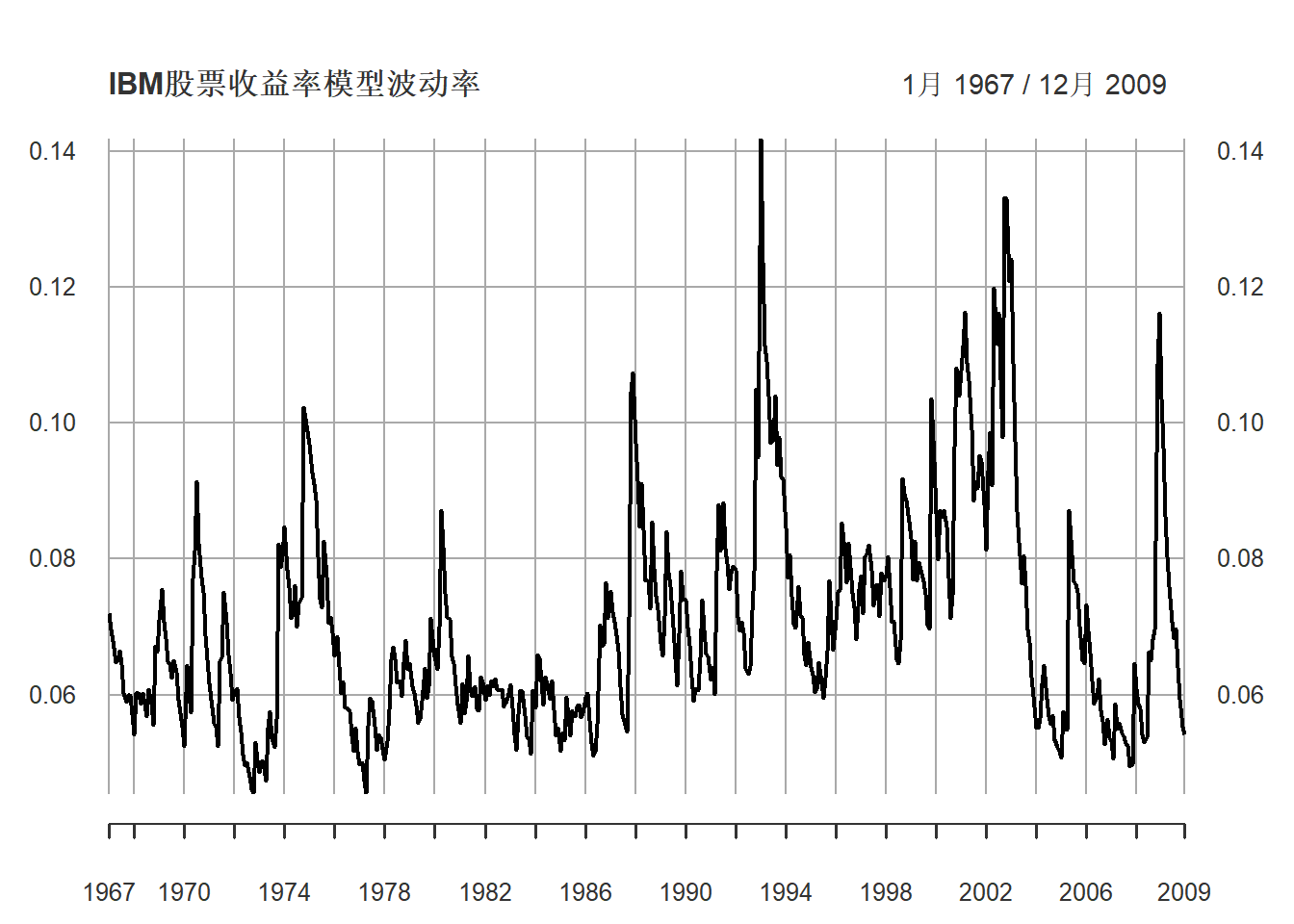
  main="IBM股票收益率模型波动率")

图19.5: IBM股票收益率模型波动率

标准化残差的ACF:

forecast::Acf(stdresi, lag.max = 36, main="")

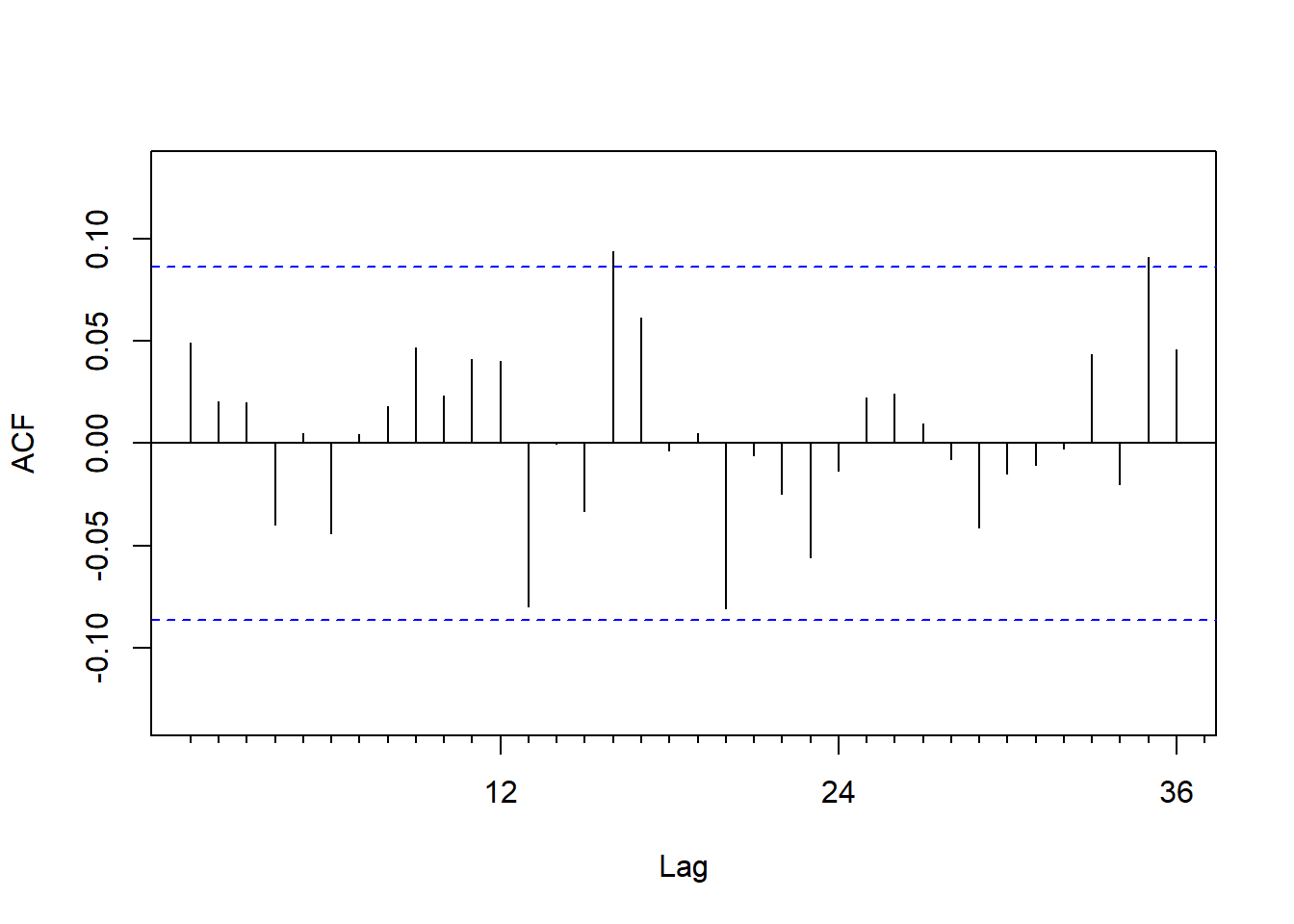
图19.6: IBM股票收益率模型标准化残差ACF

## 或：
## plot(mod1ru, which=10)

标准化残差的Ljung-Box白噪声检验：

Box.test(stdresi, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  stdresi
## X-squared = 6.894, df = 12, p-value = 0.8645

标准化残差平方的ACF:

forecast::Acf(stdresi^2, lag.max = 36, main="")

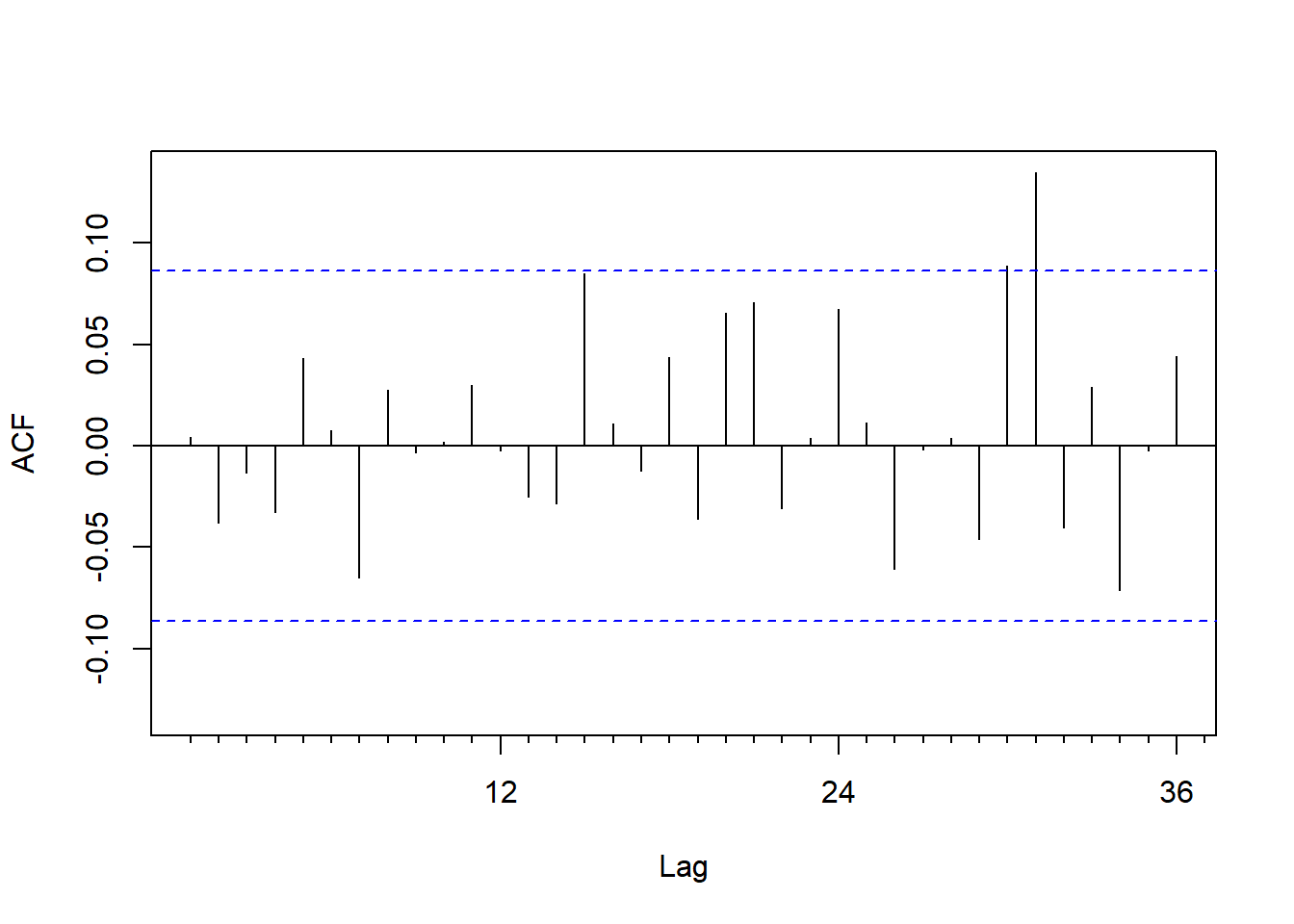
图19.7: IBM股票收益率模型标准化残差平方的ACF

## 或：
## plot(mod1ru, which=11)

标准化残差平方的Ljung-Box白噪声检验：

Box.test(stdresi^2, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  stdresi^2
## X-squared = 5.537, df = 12, p-value = 0.9376

从以上残差诊断看模型比较充分。从ugarchfit()的结果看，标准化残差及其残差的白噪声检验通过，分布的拟合优度检验通过，模型参数稳定性检验通过，杠杆效应的检验通过。

19.1.5 预测

以EGARCH(1,1)为例说明EGARCH模型的超前多步预测。设模型参数已知， \(\varepsilon_t\)服从标准正态分布。模型为（见(19.4)、(19.1)） \[\begin{aligned} \ln\sigma_t^2 =& \alpha_0 + \beta_1 \ln\sigma_{t-1}^2 + \alpha_1 \varepsilon_{t-1} + \gamma_1(|\varepsilon_{t-1}| - E|\varepsilon_{t-1}| ) . \end{aligned}\] 其中\(E|\varepsilon_{t-1}| = \sqrt{\frac{2}{\pi}}\)。记 \[ g(x) = \alpha_1 x + \gamma_1(|x| - \sqrt{\frac{2}{\pi}}), \] 则模型可以写成 \[ \ln\sigma_t^2 = \alpha_0 + \beta_1 \ln\sigma_{t-1}^2 + g(\varepsilon_{t-1}), \] 将模型写成指数形式为 \[\begin{aligned} \sigma_t^2 = e^{\alpha_0} \sigma_{t-1}^{2\beta_1} e^{g(\varepsilon_{t-1})} . \end{aligned}\]

以\(h\)为预测原点，超前一步预测是对\(\sigma_{h+1}^2\)的预测，而 \[\begin{aligned} \sigma_{h+1}^2 = e^{\alpha_0} \sigma_{h}^{2\beta_1} e^{g(\varepsilon_{h})} \in F_h , \end{aligned}\] 所以超前一步预测为 \[\begin{align} \hat\sigma_h^2(1) = E(\sigma_{h+1}^2 | F_h) = \sigma_{h+1}^2 . \tag{19.5} \end{align}\]

对\(t=h+2\)， \[\begin{aligned} \sigma_{h+2}^2 = e^{\alpha_0} \sigma_{h+1}^{2\beta_1} e^{g(\varepsilon_{h+1})} , \end{aligned}\] 注意到\(\sigma_{h+1}^2 \in F_h\)，\(\varepsilon_{h+1}\)与\(F_h\)独立，所以有 \[\begin{aligned} \hat\sigma_h^2(2) =& E(\sigma_{h+2}^2 | F_h) = e^{\alpha_0} \sigma_{h+1}^{2\beta_1} E[e^{g(\varepsilon_{h+1})} | F_h] \\ =& e^{\alpha_0} \sigma_{h+1}^{2\beta_1} E[e^{g(\varepsilon_{h+1})}] . \end{aligned}\]

只需要计算\(E[e^{g(\varepsilon_{h+1})}]\)。设\(\varepsilon \sim \text{N}(0,1)\)，则 \[\begin{aligned} E e^{g(\varepsilon)} =& \int_{-\infty}^\infty \exp\left\{ \alpha_1 u + \gamma_1 |u| - \gamma_1 \sqrt{\frac{2}{\pi}} \right\} \varphi(u) \,du \\ =& e^{- \gamma_1 \sqrt{\frac{2}{\pi}}} \left\{ \int_0^\infty \frac{1}{\sqrt{2\pi}} \exp\left[ -\frac12 u^2 + (\alpha_1 + \gamma_1)u \right] \,du \right. \\ & \left. + \int_{-\infty}^0 \frac{1}{\sqrt{2\pi}} \exp\left[ -\frac12 u^2 + (\alpha_1 - \gamma_1)u \right] \,du \right\} \end{aligned}\] 其中 \[\begin{aligned} -\frac12 u^2 + (\alpha_1 \pm \gamma_1)u =& -\frac12 [ u - (\alpha_1 \pm \gamma_1)]^2 + \frac12 (\alpha_1 \pm \gamma_1)^2 , \end{aligned}\] 所以 \[\begin{aligned} E e^{g(\varepsilon)} =& e^{- \gamma_1 \sqrt{\frac{2}{\pi}}} \left\{ e^{\frac12 (\alpha_1 + \gamma_1)^2} \int_0^\infty \frac{1}{\sqrt{2\pi}} \exp\left[ -\frac12 (u - (\alpha_1 + \gamma_1))^2 \right] \,du \right. \\ & \left. + e^{\frac12 (\alpha_1 - \gamma_1)^2} \int_{-\infty}^0 \frac{1}{\sqrt{2\pi}} \exp\left[ -\frac12 (u - (\alpha_1 - \gamma_1))^2 \right] \,du \right\} \\ =& e^{- \gamma_1 \sqrt{\frac{2}{\pi}}} \left\{ e^{\frac12 (\alpha_1 + \gamma_1)^2} \int_{-(\alpha_1 + \gamma_1)}^\infty \varphi(v) \,dv + e^{\frac12 (\alpha_1 - \gamma_1)^2} \int_{-\infty}^{-(\alpha_1 - \gamma_1)} \varphi(v) \,dv \right\} \\ =& e^{- \gamma_1 \sqrt{\frac{2}{\pi}}} \left\{ e^{\frac12 (\alpha_1 + \gamma_1)^2} [ 1 - \Phi(-(\alpha_1 + \gamma_1))] + e^{\frac12 (\alpha_1 - \gamma_1)^2} \Phi(-(\alpha_1 - \gamma_1)) \right\} \\ =& e^{- \gamma_1 \sqrt{\frac{2}{\pi}}} \left\{ e^{\frac12 (\gamma_1 + \alpha_1)^2} \Phi(\gamma_1 + \alpha_1) + e^{\frac12 (\gamma_1 - \alpha_1)^2} \Phi(\gamma_1 - \alpha_1) \right\} . \end{aligned}\] 其中\(\varphi(\cdot)\)和\(\Phi(\cdot)\)是标准正态分布的密度和分布函数。

于是，超前二步预测为 \[\begin{align} \hat\sigma_h^2(2) =& e^{\alpha_0} E e^{g(\varepsilon)} [\hat\sigma_h^2(1)]^{\beta_1} . \tag{19.6} \end{align}\]

超前三步： \[\begin{aligned} \sigma_{h+3}^2 = e^{\alpha_0} (\sigma_{h+2}^{2})^{\beta_1} e^{g(\varepsilon_{h+2})}, \end{aligned}\] 注意到\(F_h \subset F_{h+1}\), \(\sigma_{h+2}^2 \in F_{h+1}\), \(\varepsilon_{h+2}\)与\(F_{h+1}\)独立，可得 \[\begin{align} \hat\sigma_h^2(3) =& e^{\alpha_0} E \left\{ (\sigma_{h+2}^2)^{\beta_1} e^{g(\varepsilon_{h+2})} | F_h \right\} \\ =& e^{\alpha_0} E \left\{ E\left[ (\sigma_{h+2}^2)^{\beta_1} e^{g(\varepsilon_{h+2})} | F_{h+1} \right] | F_h \right\} \\ =& e^{\alpha_0} E \left\{ (\sigma_{h+2}^2)^{\beta_1} E\left[ e^{g(\varepsilon_{h+2})} | F_{h+1} \right] | F_h \right\} \\ =& e^{\alpha_0} E[e^{g(\varepsilon)}] E \left\{ (\sigma_{h+2}^2)^{\beta_1} | F_h \right\} \\ =& e^{\alpha_0} E[e^{g(\varepsilon)}] E \left\{ e^{\alpha_0 \beta_1} (\sigma_{h+1}^2)^{\beta_1^2} e^{\beta_1 g(\varepsilon_{h+1})} | F_h \right\} \\ =& e^{\alpha_0(1 + \beta_1)} E[e^{g(\varepsilon)}] E[e^{\beta_1 g(\varepsilon)}] (\hat\sigma_{h}^2(1))^{\beta_1^2} . \tag{19.7} \end{align}\]

对\(\hat\sigma^2_h(j)\)可类似计算。

19.2 GJR-GARCH模型

GJR-GARCH模型是另一个能够反映杠杆效应的波动率模型，参见(Glosten, Jagannathan, and Runkle 1993)和(Zakoian 1994)。或称为TGARCH。 GJR-GARCH(\(m,s\))模型的形式为 \[\begin{align} \sigma_t^2 = \alpha_0 + \sum_{i=1}^m (\alpha_i + \gamma_i N_{t-i}) a_{t-i}^2 + \sum_{j=1}^s \beta_j \sigma_{t-j}^2 \tag{19.8} \end{align}\] 其中\(N_{t-i}\)是表示\(a_{t-i}<0\)的示性函数，即 \[\begin{aligned} N_{t-i} = \begin{cases} 1, & a_{t-i} < 0 \\ 0, & a_{t-i} \geq 0 \end{cases} \end{aligned}\] \(\alpha_i, \gamma_i, \beta_j\)是非负参数，满足与GARCH模型类似的参数条件。

正的\(a_{t-i}\)对\(\sigma_t^2\)的影响为\(\alpha_i a_{t-i}^2\)，负的\(a_{t-i}\)对\(\sigma_t^2\)的影响为\((\alpha_i + \gamma_i) a_{t-i}^2\)，当\(\gamma_i>0\)时负的\(a_{t-i}\)影响较大。

模型用0作为\(a_{t-i}\)的门限，还可以用其它实数值作为门限。关于门限模型参见(Tsay 2010)第4章。

作为例子，考虑从1999年1月4日到2010年8月20日的欧元对美元汇率的日对数收益率序列。

读入数据：

d.useu <- read_table(
  "d-useu9910.txt", 
  col_types=cols(.default=col_double())
)
xts.useu <- with(d.useu, 
  xts(rate, make_date(year, mon, day)))
xts.useu.lnrtn <- diff(log(xts.useu))[-1,]*100

用rugarch包建模：

library(rugarch)
spec2 <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE  ),
  variance.model = list(
    model = "gjrGARCH", # GJR-GARCH or TGARCH model
    garchOrder = c(1,1) ) )
mod2ru <- ugarchfit(spec = spec2, data = xts.useu.lnrtn)
show(mod2ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : gjrGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.012262    0.010726   1.1432 0.252951
## omega   0.001274    0.000554   2.3013 0.021373
## alpha1  0.022402    0.004277   5.2373 0.000000
## beta1   0.968711    0.001779 544.4570 0.000000
## gamma1  0.012435    0.007027   1.7696 0.076789
## 
## Robust Standard Errors:
##         Estimate  Std. Error   t value Pr(>|t|)
## mu      0.012262    0.011704    1.0476 0.294800
## omega   0.001274    0.000620    2.0535 0.040021
## alpha1  0.022402    0.004777    4.6891 0.000003
## beta1   0.968711    0.000795 1219.2085 0.000000
## gamma1  0.012435    0.008047    1.5454 0.122258
## 
## LogLikelihood : -2731.85 
## 
## Information Criteria
## ------------------------------------
##                    
## Akaike       1.8688
## Bayes        1.8790
## Shibata      1.8688
## Hannan-Quinn 1.8725
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.2619  0.6088
## Lag[2*(p+q)+(p+q)-1][2]    0.3038  0.7936
## Lag[4*(p+q)+(p+q)-1][5]    3.3494  0.3469
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                      4.935 0.02632
## Lag[2*(p+q)+(p+q)-1][5]     7.136 0.04806
## Lag[4*(p+q)+(p+q)-1][9]     9.101 0.07748
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]     2.979 0.500 2.000 0.08435
## ARCH Lag[5]     3.239 1.440 1.667 0.25696
## ARCH Lag[7]     4.681 2.315 1.543 0.25882
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.4726
## Individual Statistics:              
## mu     0.20009
## omega  0.20231
## alpha1 0.06618
## beta1  0.08927
## gamma1 0.08316
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.28 1.47 1.88
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value     prob sig
## Sign Bias            1.663 0.096368   *
## Negative Sign Bias   2.386 0.017101  **
## Positive Sign Bias   1.740 0.082025   *
## Joint Effect        12.898 0.004863 ***
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     59.51    4.628e-06
## 2    30     70.40    2.676e-05
## 3    40     69.44    1.928e-03
## 4    50     81.46    2.454e-03
## 
## 
## Elapsed time : 0.19853

估计的模型为 \[\begin{aligned} r_t =& 0.0123 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \varepsilon_t \text{ i.i.d. N}(0,1) \\ \sigma_t^2 =& 0.0013 + (0.0224 + 0.0124 N_{t-1}) a_{t-1}^2 + 0.9687 \sigma_{t-1}^2, \end{aligned}\] 模型结果中mu不显著，在0.05水平下gamma1也不显著，说明杠杆效应不显著。模型标准化残差的白噪声检验通过，但标准化残差平方的白噪声检验没有通过，所以模型效果不够好。模型参数稳定性检验没有通过。拟合优度检验没有通过。

拟合的波动率\(\sigma_t\)序列图形(单位是百分之一)：

plot(sigma(mod2ru), 
  format.labels="%Y",
  main="欧元汇率日对数收益率波动率TGARCH估计(%)", 
  major.ticks="years", minor.ticks=NULL, 
  grid.ticks.on="years")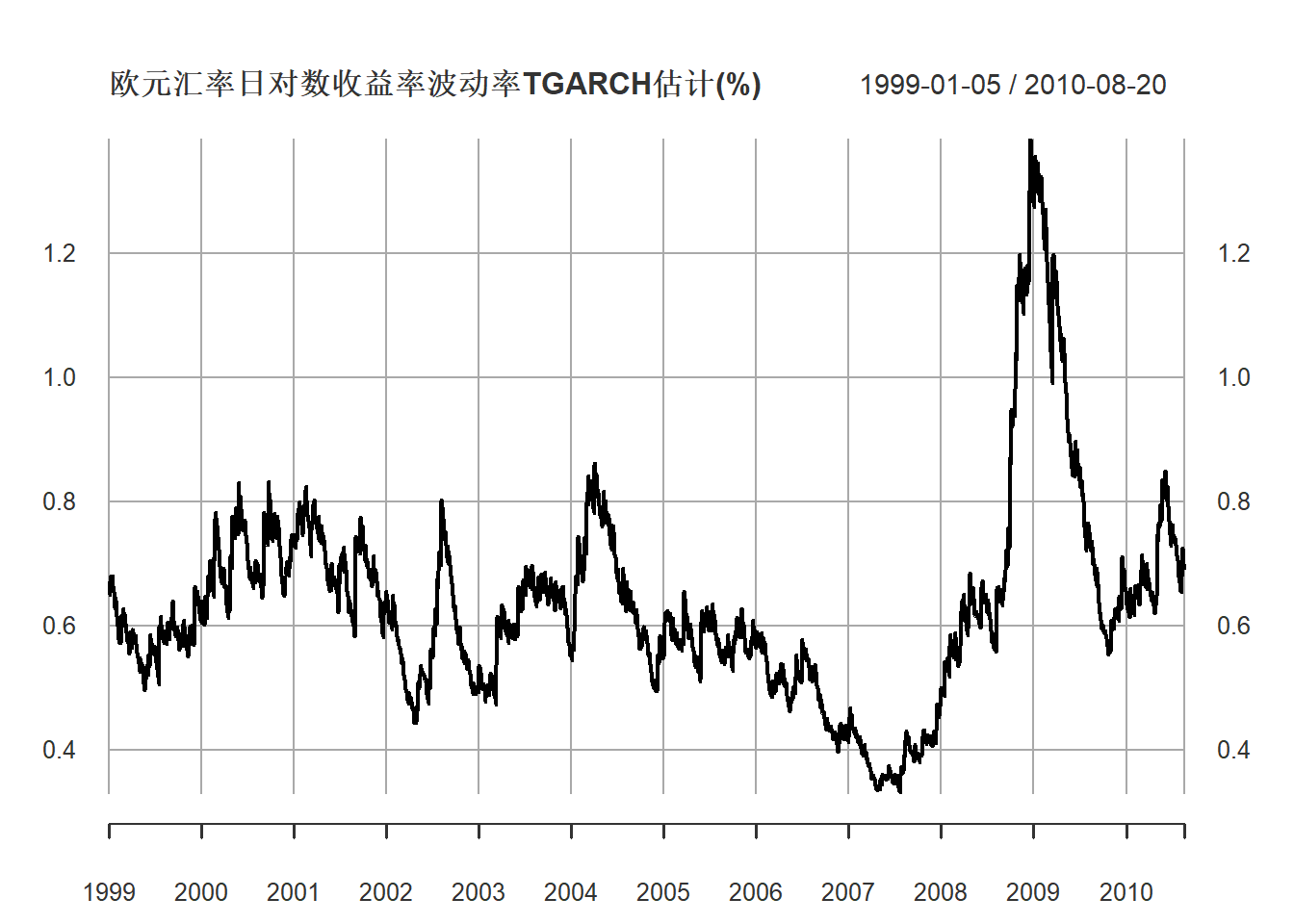

图19.8: 欧元汇率日对数收益率波动率TGARCH估计

波动率的最高值出现在2008年末、2009年初，次贷危机爆发时期。

为了进行模型诊断，计算标准化残差：

stdresi2 <- residuals(mod2ru, standardize=TRUE)

标准化残差的ACF:

forecast::Acf(stdresi2, lag.max=36, main="")

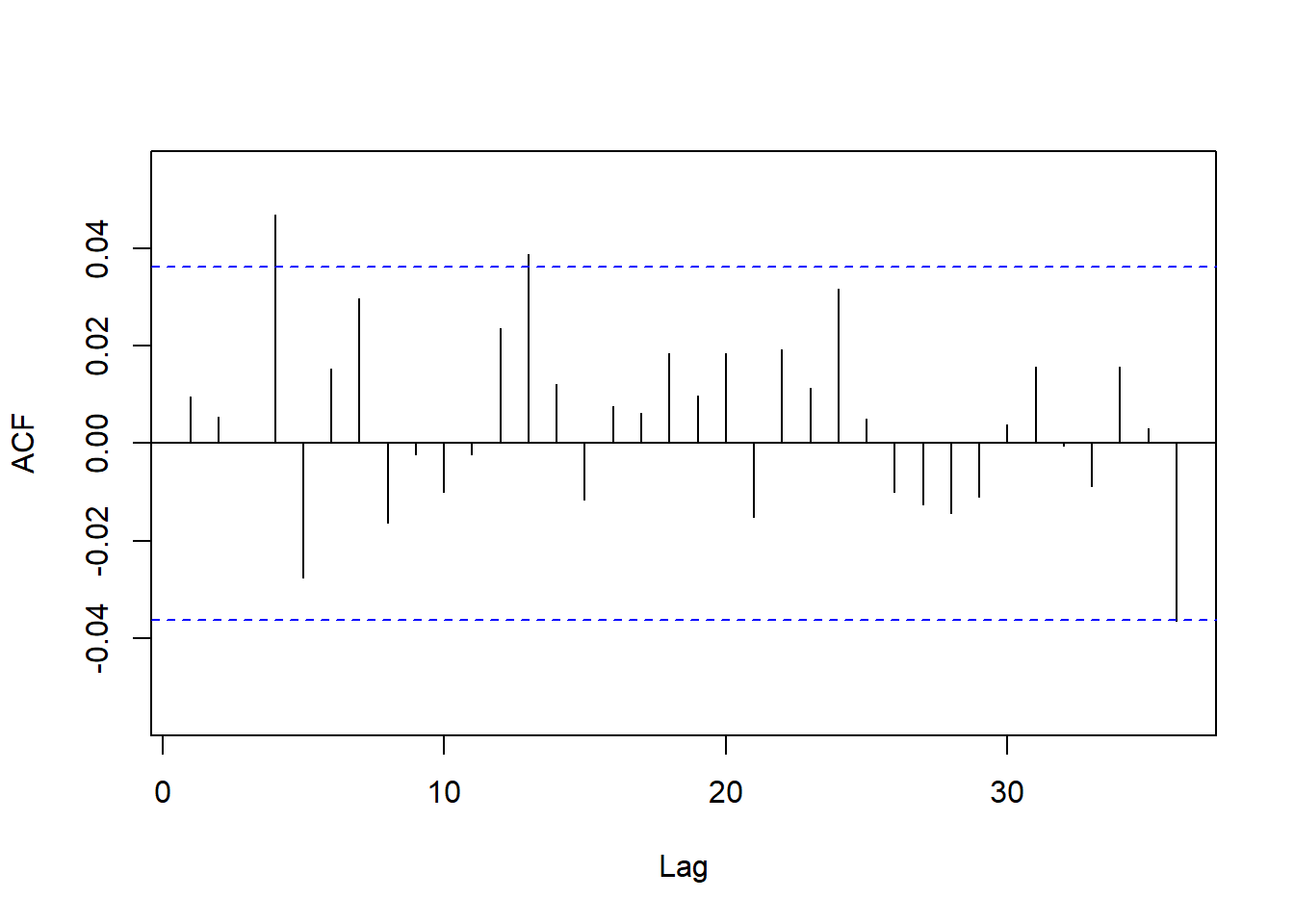
图19.9: 欧元汇率日对数收益率TGARCH标准化残差ACF

## 或：
## plot(mod2ru, which=10)

标准化残差平方的ACF:

forecast::Acf(stdresi2^2, lag.max=36, main="")

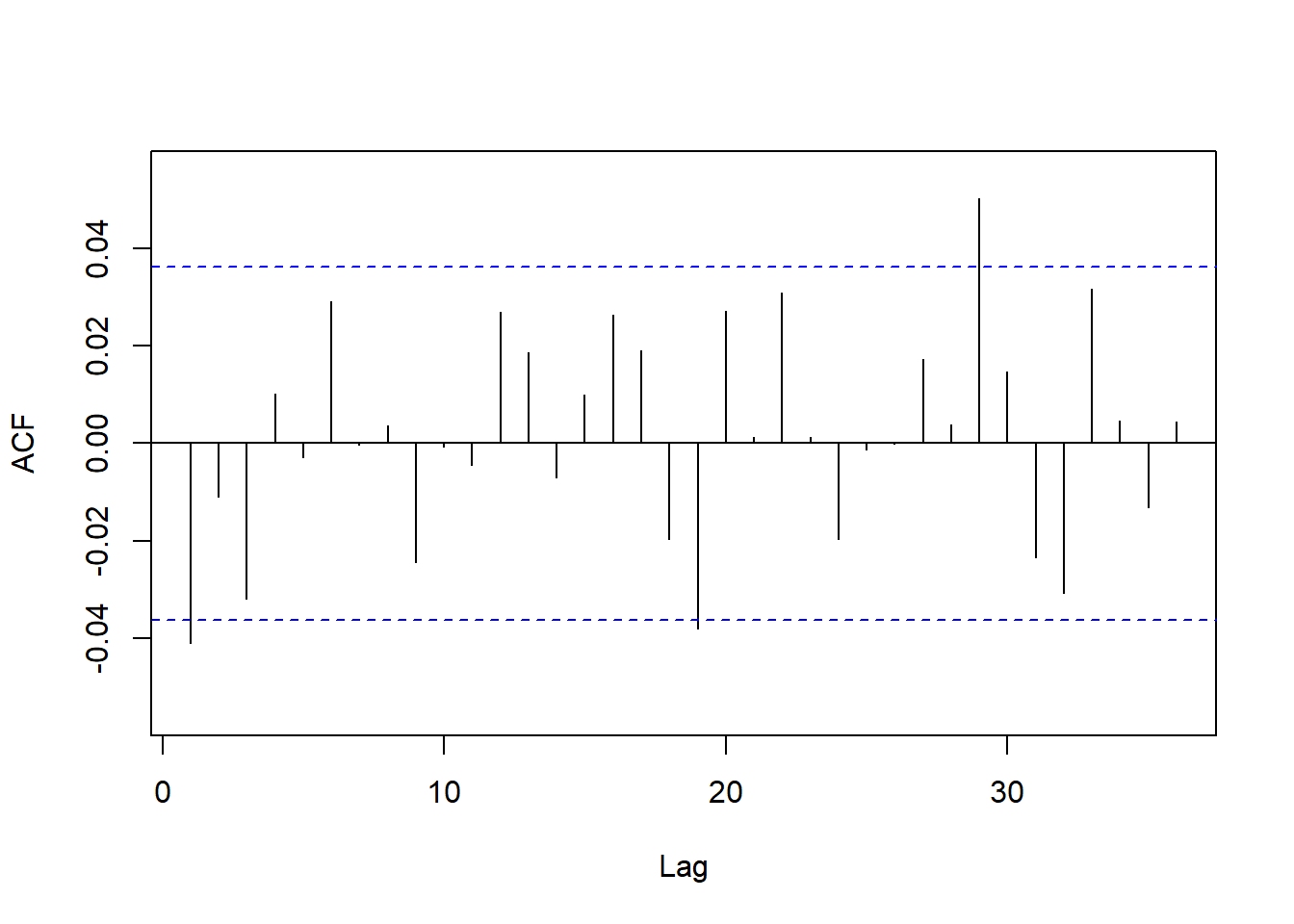
图19.10: 欧元汇率日对数收益率TGARCH标准化残差平方ACF

## 或：
## plot(mod2ru, which=11)

标准化残差的Ljung-Box白噪声检验：

Box.test(stdresi2, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  stdresi2
## X-squared = 15.029, df = 12, p-value = 0.2399

标准化残差平方的Ljung-Box白噪声检验：

Box.test(stdresi2^2, lag=12, type="Ljung")

## 
##  Box-Ljung test
## 
## data:  stdresi2^2
## X-squared = 15.094, df = 12, p-value = 0.2363

这些残差诊断的结果说明拟合的模型是基本符合的。

作标准化残差的盒形图：

boxplot(c(coredata(stdresi2)), 
  main="", xlab="标准化残差")

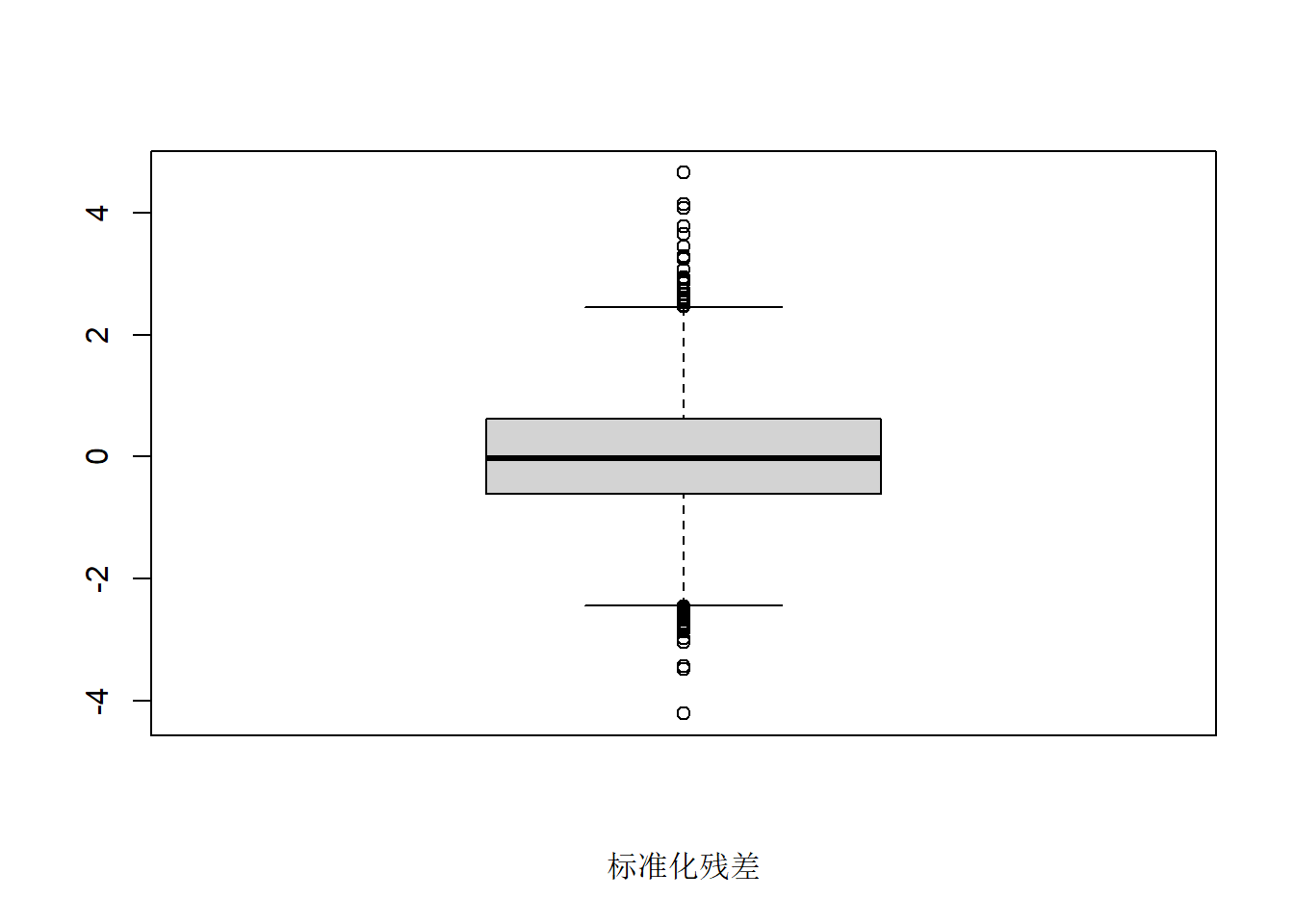
图19.11: 欧元汇率日对数收益率TGARCH标准化残差盒形图

标准化残差的正态QQ图：

plot(mod2ru, which=9)

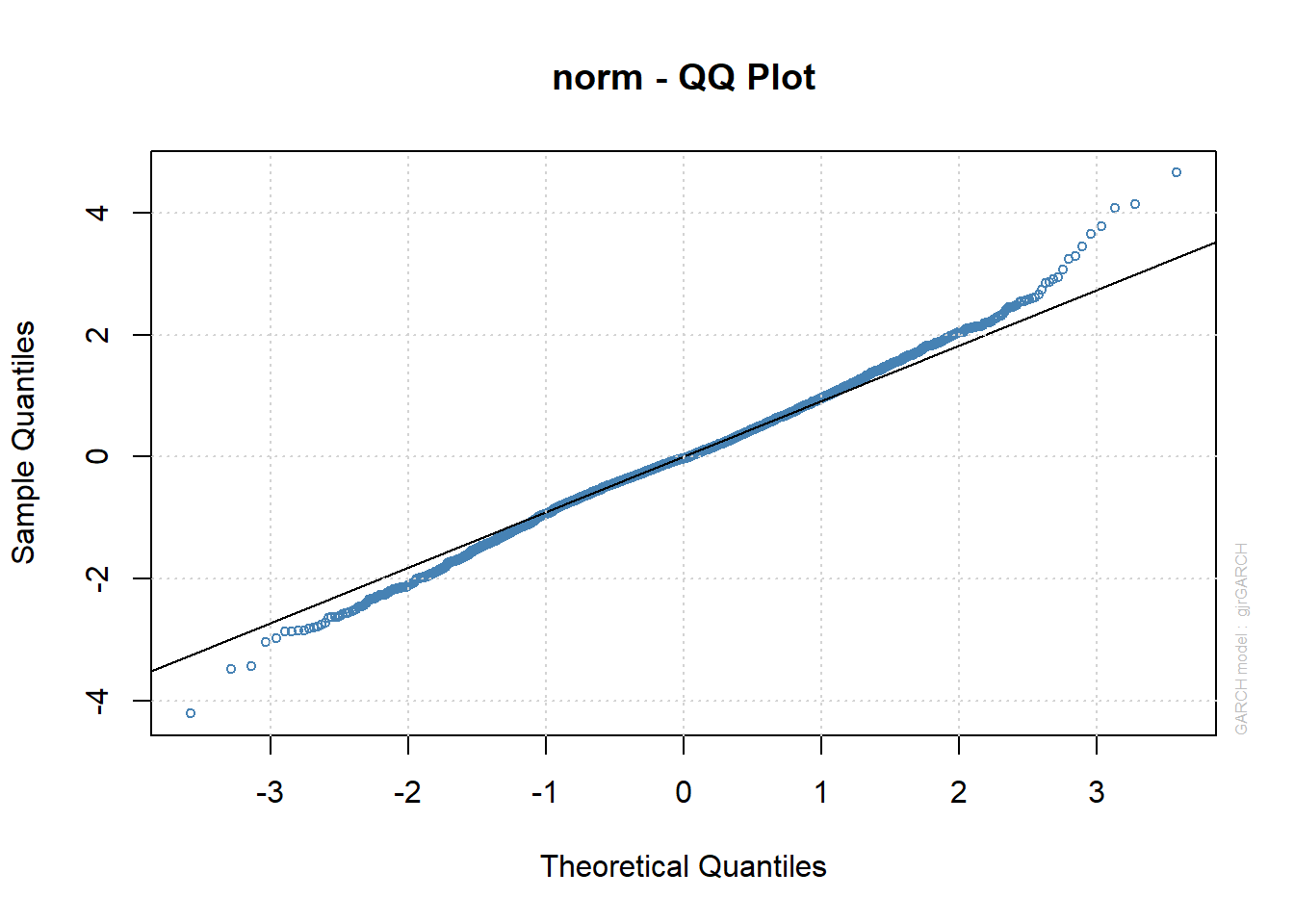
图19.12: 欧元汇率日对数收益率TGARCH标准化残差正态QQ图

从标准化残差的盒形图看有厚尾现象。

可以将GJR-GARCH得到的波动率与标准GARCH得到的波动率进行比较：

library(fGarch, quietly = TRUE)

## NOTE: Packages 'fBasics', 'timeDate', and 'timeSeries' are no longer
## attached to the search() path when 'fGarch' is attached.
## 
## If needed attach them yourself in your R script by e.g.,
##         require("timeSeries")

## 
## Attaching package: 'fGarch'

## The following object is masked from 'package:TTR':
## 
##     volatility

mod2sg <- garchFit( ~ 1 + garch(1,1), 
  data=xts.useu.lnrtn, trace=FALSE)

将两个波动率作图，黑色为GARCH结果，红色虚线为GJR-GARCH结果：

plot(cbind(volatility(mod2sg), sigma(mod2ru)), 
  main="欧元汇率日对数收益率波动率GARCH和NGARCH估计", 
  lty=c(1,2), 
  col=c("black", "red"),
  format.labels="%Y",
  major.ticks="years", minor.ticks=NULL, 
  grid.ticks.on="years")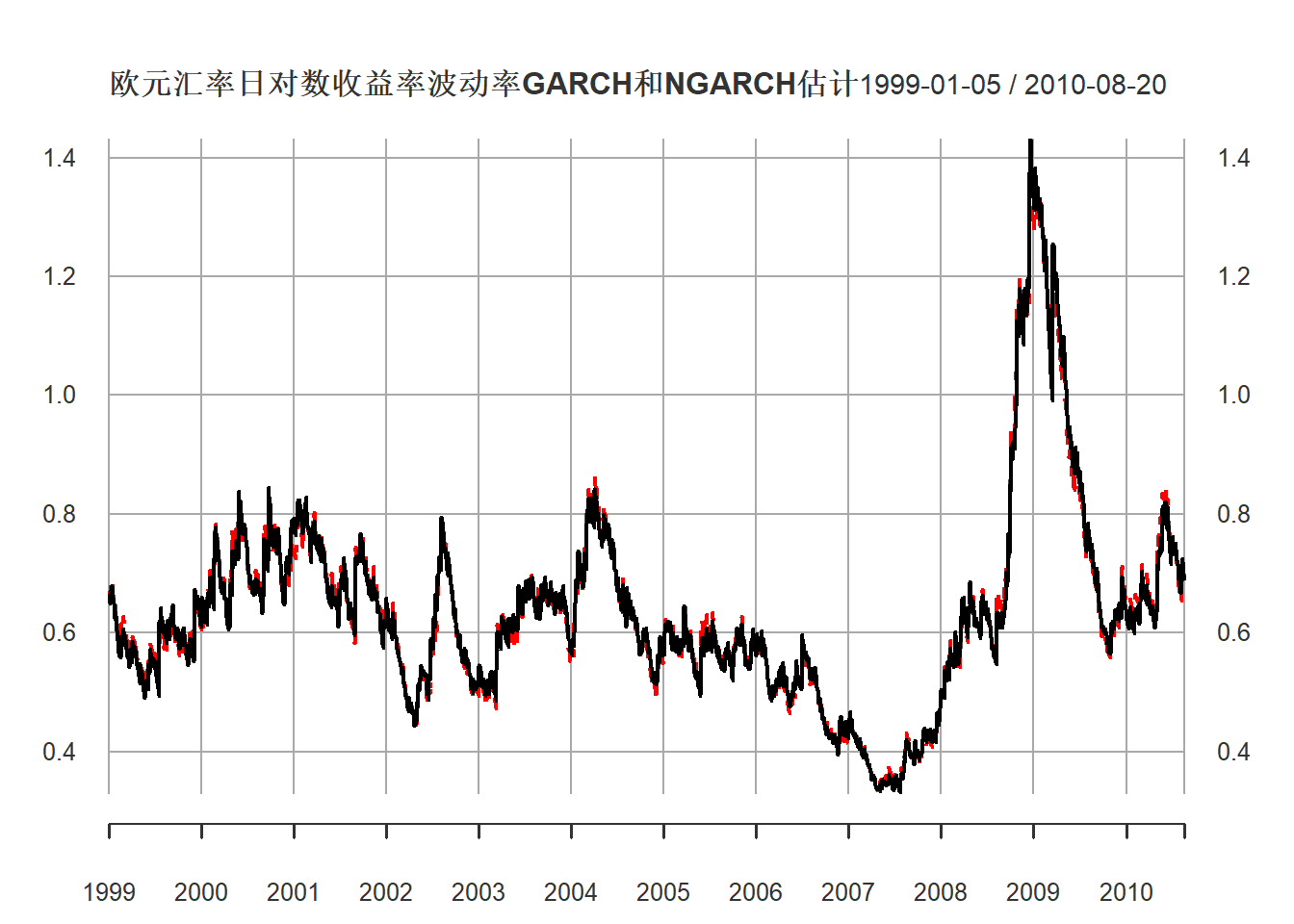

图19.13: 欧元汇率GARCH和NGARCH估计的波动率

放大显示其中2008年以后：

plot(cbind(volatility(mod2sg), sigma(mod2ru)), 
  subset="2008/",
  main="欧元汇率日对数收益率波动率GARCH和NGARCH估计", 
  lty=c(1,2), 
  col=c("black", "red"),
  format.labels="%Y",
  major.ticks="years", minor.ticks=NULL, 
  grid.ticks.on="years")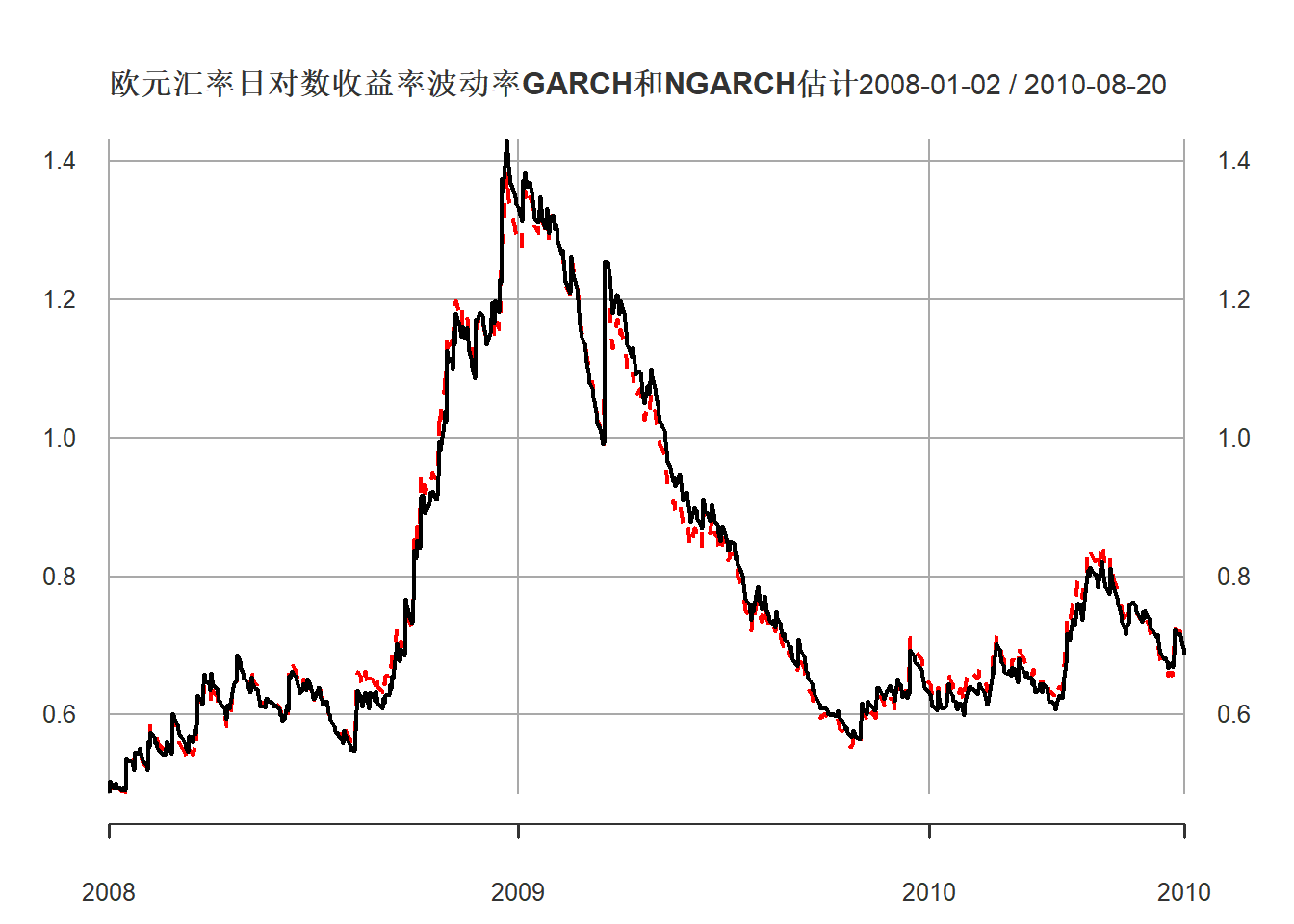

图19.14: 欧元汇率GARCH和NGARCH估计的波动率

19.3 APARCH模型

(Ding, Granger, and Engle 1993)提出了非对称幂(asymmetric power) ARCH模型(APARCH模型)，模型形式为 \[\begin{align} r_t =& \mu_t + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \varepsilon_t \sim D(0,1) \\ \sigma_t^\delta =& \omega + \sum_{i=1}^m \alpha_i (|a_{t-i}| - \gamma_i a_{t-i})^\delta + \sum_{j=1}^s \beta_j \sigma_{t-j}^\delta \tag{19.9} \end{align}\] 其中\(\mu_t\)是条件均值， \(D(0,1)\)表示某个零均值单位方差分布， \(\delta\)为正实数，系数\(\omega, \alpha_i, \gamma_i, \beta_j\)满足某些正则性条件使得波动率为正。

最常用的是最简单的APARCH(1,1)模型。这个模型中包含了许多其它模型。

当\(\delta=2\)且\(\gamma_j = 0\)时即普通的GARCH模型。

当\(\delta=2\)时即TGARCH模型（形式略有不同）。

当\(\delta=1\)时波动率方程直接使用波动率\(\sigma_{t}\)和新息\(a_t\)而非其平方。

APARCH中的幂变换旨在提高拟合程度，但幂次\(\delta\)没有很好解释。

R的fGarch::garchFit()函数中可以使用aparch(m,s)作为模型设定。作为例子，拟合欧元对美元汇率数据：

library(fGarch, quietly = TRUE)
modres3 <- garchFit( ~ 1 + aparch(1,1), 
  data=xts.useu.lnrtn, trace=FALSE)
summary(modres3)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + aparch(1, 1), data = xts.useu.lnrtn, 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + aparch(1, 1)
## <environment: 0x000002d778b3d3d8>
##  [data = xts.useu.lnrtn]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##        mu      omega     alpha1     gamma1      beta1      delta  
## 0.0127647  0.0015919  0.0313680  0.1135334  0.9689155  1.6743075  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu     0.0127647   0.0107626    1.186   0.2356    
## omega  0.0015919   0.0007226    2.203   0.0276 *  
## alpha1 0.0313680   0.0053350    5.880 4.11e-09 ***
## gamma1 0.1135334   0.0711911    1.595   0.1108    
## beta1  0.9689155   0.0038405  252.292  < 2e-16 ***
## delta  1.6743075   0.4057124    4.127 3.68e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -2731.172    normalized:  -0.9324587 
## 
## Description:
##  Tue May 21 15:25:28 2024 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  50.20526  1.253331e-11
##  Shapiro-Wilk Test  R    W      0.9956711 1.608388e-07
##  Ljung-Box Test     R    Q(10)  13.37689  0.2033562   
##  Ljung-Box Test     R    Q(15)  20.19634  0.1645295   
##  Ljung-Box Test     R    Q(20)  22.84736  0.2963514   
##  Ljung-Box Test     R^2  Q(10)  13.15611  0.2150739   
##  Ljung-Box Test     R^2  Q(15)  16.58008  0.34458     
##  Ljung-Box Test     R^2  Q(20)  27.44887  0.1231012   
##  LM Arch Test       R    TR^2   14.35739  0.2784708   
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 1.869014 1.881269 1.869006 1.873428

拟合的白噪声检验说明模型是充分的，但是\(\delta\)的估计为1.67, 标准误差为0.41，其95%置信区间为\((0.85, 2.49)\)包含2，所以与\(\delta=2\)没有显著差异，可以用TGARCH模型。 \(\gamma_1\)在0.05水平下不显著，可以不需要反映杠杆效应的模型。

拟合的APARCH模型为： \[\begin{aligned} r_t =& 0.0128 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \varepsilon_t \sim \text{N}(0,1) \\ \sigma_t^{1.67} =& 0.0016 + 0.0313 (|a_{t-1}| - 0.1135 a_{t-1})^{1.67} + 0.9689 \sigma_{t-1}^{1.67} \end{aligned}\]

固定\(\delta=2\)估计APARCH(1,1)模型：

modres4 <- garchFit( ~ 1 + aparch(1,1), 
  data=xts.useu.lnrtn, delta=2, 
  include.delta=FALSE, trace=FALSE)
summary(modres4)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + aparch(1, 1), data = xts.useu.lnrtn, 
##     delta = 2, include.delta = FALSE, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + aparch(1, 1)
## <environment: 0x000002d77de83080>
##  [data = xts.useu.lnrtn]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##        mu      omega     alpha1     gamma1      beta1  
## 0.0122646  0.0012745  0.0282723  0.1100242  0.9687115  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu     0.0122646   0.0107289    1.143   0.2530    
## omega  0.0012745   0.0005752    2.216   0.0267 *  
## alpha1 0.0282723   0.0038637    7.317 2.53e-13 ***
## gamma1 0.1100242   0.0649051    1.695   0.0900 .  
## beta1  0.9687115   0.0039421  245.735  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  -2731.85    normalized:  -0.9326902 
## 
## Description:
##  Tue May 21 15:25:29 2024 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  49.97677  1.405021e-11
##  Shapiro-Wilk Test  R    W      0.9956803 1.655881e-07
##  Ljung-Box Test     R    Q(10)  13.38285  0.2030469   
##  Ljung-Box Test     R    Q(15)  20.29833  0.1607845   
##  Ljung-Box Test     R    Q(20)  22.87265  0.2950907   
##  Ljung-Box Test     R^2  Q(10)  12.89586  0.2295531   
##  Ljung-Box Test     R^2  Q(15)  16.55288  0.3462876   
##  Ljung-Box Test     R^2  Q(20)  27.24036  0.128636    
##  LM Arch Test       R    TR^2   14.29661  0.2821695   
## 
## Information Criterion Statistics:
##      AIC      BIC      SIC     HQIC 
## 1.868795 1.879007 1.868789 1.872472

拟合的固定\(\delta=2\)的APARCH模型为： \[\begin{aligned} r_t =& 0.0123 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \varepsilon_t \sim \text{N}(0,1) \\ \sigma_t^2 =& 0.00127 + 0.0283 (|a_{t-1}| - 0.1100 a_{t-1})^2 + 0.9687 \sigma_{t-1}^2 \end{aligned}\] 其中的波动率方程可以借助\(N_{t-1}\)为\(a_{t-1}<0\)的示性函数写成 \[ \sigma_t^2 = 0.00127 + (0.0224 + 0.0125 N_{t-1}) a_{t-1}^2 + 0.9687 \sigma_{t-1}^2 . \]

与直接估计TGARCH(1,1)的结果对比： \[\begin{aligned} r_t =& 0.0123 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \varepsilon_t \text{ i.i.d. N}(0,1) \\ \sigma_t^2 =& 0.0013 + (0.0224 + 0.0124 N_{t-1}) a_{t-1}^2 + 0.9687 \sigma_{t-1}^2 . \end{aligned}\] 两个估计结果基本相同。

也可以用rugarch包估计APARCH模型：

library(rugarch)
spec3 <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE  ),
  variance.model = list(
    model = "apARCH", # APARCH model
    garchOrder = c(1,1) ) )
mod3ru <- ugarchfit(spec = spec3, 
  data = xts.useu.lnrtn)
show(mod3ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : apARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error   t value Pr(>|t|)
## mu      0.012516    0.010740    1.1654 0.243858
## omega   0.001683    0.000595    2.8299 0.004656
## alpha1  0.031692    0.000877   36.1495 0.000000
## beta1   0.969388    0.000679 1427.5230 0.000000
## gamma1  0.121817    0.072545    1.6792 0.093115
## delta   1.580101    0.129609   12.1913 0.000000
## 
## Robust Standard Errors:
##         Estimate  Std. Error   t value Pr(>|t|)
## mu      0.012516    0.011800    1.0607 0.288841
## omega   0.001683    0.000772    2.1804 0.029229
## alpha1  0.031692    0.002833   11.1859 0.000000
## beta1   0.969388    0.000680 1425.6414 0.000000
## gamma1  0.121817    0.084847    1.4357 0.151084
## delta   1.580101    0.082927   19.0542 0.000000
## 
## LogLikelihood : -2731.113 
## 
## Information Criteria
## ------------------------------------
##                    
## Akaike       1.8690
## Bayes        1.8812
## Shibata      1.8690
## Hannan-Quinn 1.8734
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.2823  0.5952
## Lag[2*(p+q)+(p+q)-1][2]    0.3207  0.7843
## Lag[4*(p+q)+(p+q)-1][5]    3.3970  0.3393
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                      5.165 0.02304
## Lag[2*(p+q)+(p+q)-1][5]     7.349 0.04264
## Lag[4*(p+q)+(p+q)-1][9]     9.341 0.06909
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]     2.896 0.500 2.000 0.08882
## ARCH Lag[5]     3.238 1.440 1.667 0.25703
## ARCH Lag[7]     4.723 2.315 1.543 0.25404
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.5207
## Individual Statistics:              
## mu     0.18789
## omega  0.18056
## alpha1 0.07682
## beta1  0.09516
## gamma1 0.38035
## delta  0.08651
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.49 1.68 2.12
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value     prob sig
## Sign Bias            1.641 0.100814    
## Negative Sign Bias   2.398 0.016537  **
## Positive Sign Bias   1.771 0.076666   *
## Joint Effect        12.991 0.004657 ***
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     62.92    1.323e-06
## 2    30     71.22    2.064e-05
## 3    40     73.65    6.628e-04
## 4    50     79.79    3.561e-03
## 
## 
## Elapsed time : 0.5444798

与fGarch包的估计结果不完全相同，参数值比较接近。

B 参考文献

Ding, Z., C. W. J. Granger, and R. F. Engle. 1993. “A Long Memory Property of Stock Returns and a New Model.” Journal of Empirical Finance 1: 83–106.

Glosten, L. R., R. Jagannathan, and D. E. Runkle. 1993. “On the Relation Between the Expected Value and the Volatility of Nominal Excess Return on Stocks.” J. Finance 48: 1779–1801.

Nelson, D. B. 1991. “Conditional Heteroskedasticity in Asset Returns: A New Approach.” Econometrica 59: 347–70.

Tsay, Ruey S. 2010. Analysis of Financial Time Series. 3rd Ed. John Wiley & Sons, Inc.

———. 2013. 金融数据分析导论：基于R语言. 机械工业出版社.

Zakoian, J. M. 1994. “Threshold Heteroscedastic Models.” J Econ Dyn Control 18: 931–55.