14 其它建模预测问题
在实际金融事件序列数据的建模中, 注意不存在所谓“正确的模型”, 只能是从多个比较适合的模型中选择最合适的一个, 或者将比较适合的多个模型的预测结果进行平均。
为了比较模型, 有样本内比较和样本外比较两种方法。
fable、fabletools、feasts等扩展包提供了更方便的编程工具,请参见10.3.8。
本章第3、4节的内容使用了比较初等的R编程实现, 做法比较麻烦, 所以这里仅保留作为资料。
14.1 模型平均
研究发现, 如果对同一数据建立多种模型, 然后分别预测后计算预测的平均值, 结果一般会优于单个的模型, 或者与最优模型预测相近。 也可以作加权平均, 权重选择如贝叶斯模型后验概率,等等。 参考:
- Wang, X., Hyndman, R. J., Li, F., & Kang, Y. (2023).
Forecast combinations: An over 50-year review.
International J Forecasting, 39(4), 1518–1547.
https://doi.org/10.1016/j.ijforecast.2022.11.005
fable包支持将所得的模型用简单语法平均。 下面举例说明。
tsibbledata包的aus_retail数据包含了澳大利亚各州各行业零售销售额月度数据,
时间区间为1982年4月到2018年12月。
选取其中与外卖有关的行业数据,
用模型平均方法预测。
数据整理:
library(fpp3)
tkw_tsib <- aus_retail |>
dplyr::filter(stringr::str_detect(
Industry, "Takeaway")) |>
summarise(Turnover = sum(Turnover))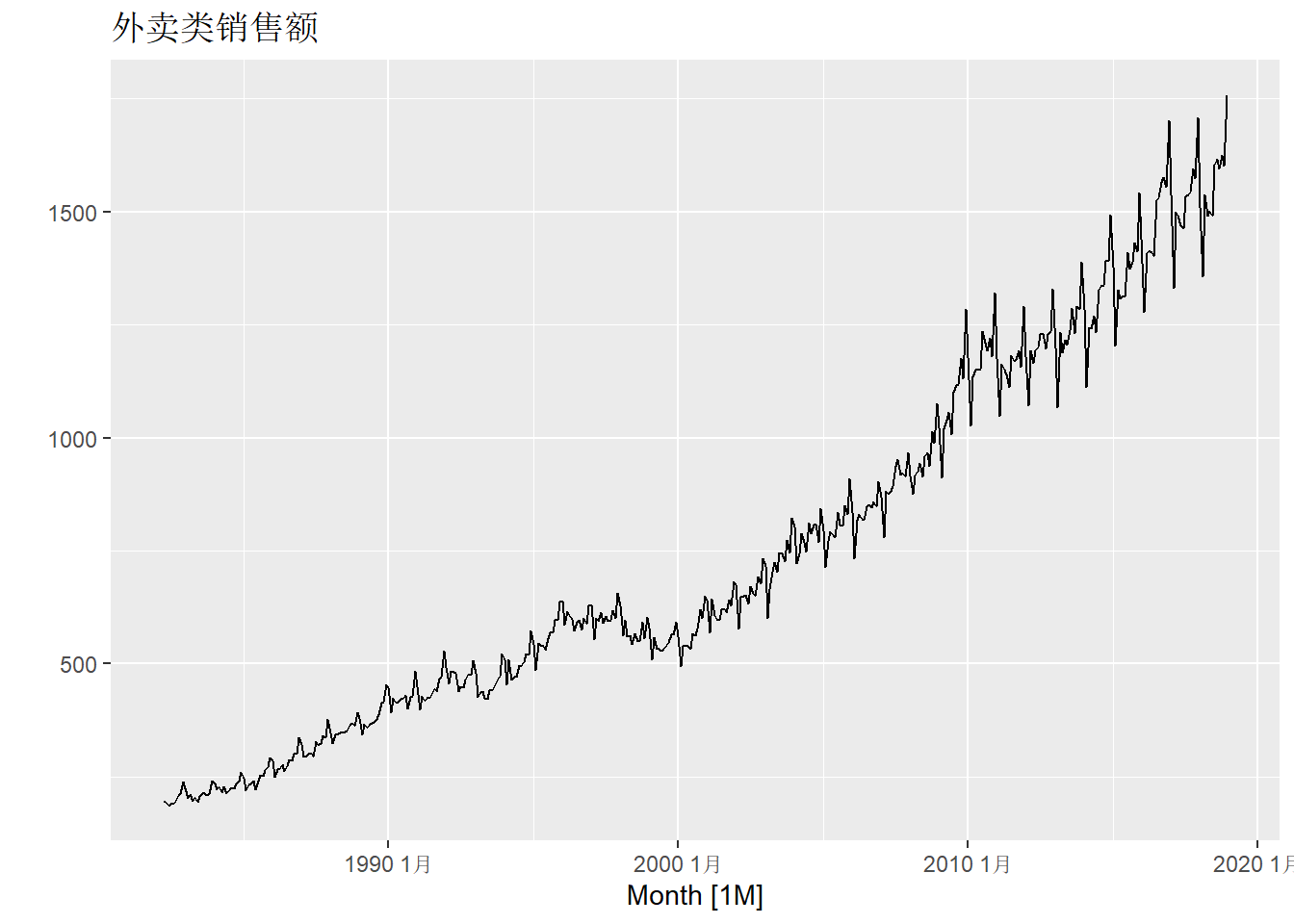
数据有震荡增强倾向, 可用对数变换调整。
留出最后5年作为测试集, 前面都作为训练集:
建立三个模型, 并规定三个模型平均产生的模型:
tkw_STLF <- decomposition_model(
STL(log(Turnover) ~ season(window = Inf)),
ETS(season_adjust ~ season("N")) )
tkw_fits <- tkw_train |>
model(
ets = ETS(Turnover),
stlf = tkw_STLF,
arima = ARIMA(log(Turnover)) ) |>
mutate(combination = (ets + stlf + arima) / 3)向前多步预测:
tkw_fore |>
autoplot(tkw_tsib |>
dplyr::filter(year(Month) > 2008),
level = NULL) +
labs(y = "$ billion",
title = "澳大利亚外卖销售额")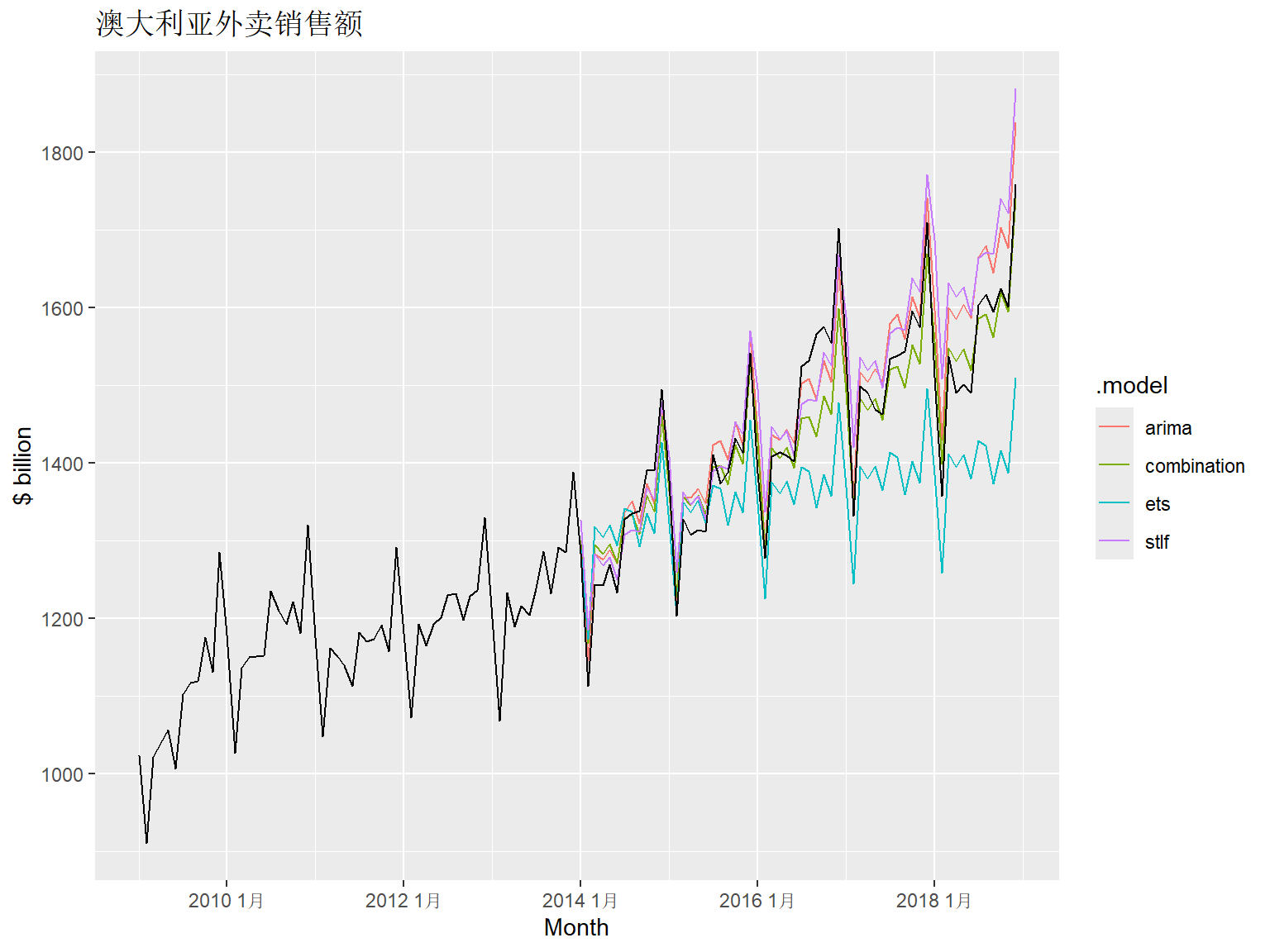
多步预测精度比较:
| .model | .type | ME | RMSE | MAE | MPE | MAPE | MASE | RMSSE | ACF1 |
|---|---|---|---|---|---|---|---|---|---|
| combination | Test | 8.091173 | 41.02526 | 31.84306 | 0.400687 | 2.189963 | 0.7764753 | 0.7899340 | 0.7468771 |
| arima | Test | -25.380983 | 46.24214 | 38.92141 | -1.766452 | 2.654548 | 0.9490768 | 0.8903842 | 0.7860515 |
| stlf | Test | -36.887892 | 64.08230 | 51.74028 | -2.545729 | 3.541498 | 1.2616577 | 1.2338932 | 0.7751640 |
| ets | Test | 86.542393 | 122.05610 | 100.83909 | 5.514241 | 6.664271 | 2.4589048 | 2.3501684 | 0.8795092 |
对这个例子而言, 模型平均的多步预测精度按RMSE和MAE评估都是最优的。
14.2 缺失值处理
时间序列中间如果有观测值缺失,
有可能使得算法无法进行,
或者对附近的拟合造成坏的影响。
fable包的ETS()和STL()遇到缺失值会出错,
无法估计模型;
而其中的ARIMA建模、回归、带有自相关误差的回归则都可以正常进行估计。
简单平移、同季节平移等方法也不受缺失值影响。
缺失值是否会对模型拟合造成坏的影响, 主要取决于缺失原因是否会影响序列表现。 如果缺失原因仅仅是记录人或仪器偶然出错, 何时缺失是完全随机的, 这一般对模型拟合不造成影响。 但是, 如果缺失是有特殊原因的, 比如由于节假日停业使得商店营业额缺失, 则恢复上班的第一天营业额可能会有一个跃升, 这样的缺失就会对模型拟合有影响, 可以用哑变量表示节假日以及节假日后恢复营业。
有时我们遇到了非常大的观测值, 正常情况下都不会出现, 去掉这样的观测值并不会对模型正常运行造成影响, 也会把这样的已知观测值变成缺失值看待。
如果我们使用的建模方法不允许有缺失值, 可以考虑两种方法。 一种方法是仅使用缺失值后面的观测子序列, 如果这样的子序列足够长则是合理的做法。 另一种做法是用一种允许有缺失值的模型预先建模并进行拟合, 用拟合值代替缺失值。
下面举例说明。
tsibble数据框的tourism包含了澳大利亚各州、地区、不同意图的出行人次数的季度数据。
选择其中Adelaide Hills地区出行意图为Visiting的出行人次数序列:
library(fpp3)
vis_tsib <- tourism |>
dplyr::filter(
Region == "Adelaide Hills",
Purpose == "Visiting") |>
select(Quarter, Trips)
vis_tsib |>
autoplot(Trips) +
labs(title = "澳大利亚Adelaide Hills访问人次数",
y = "人次数")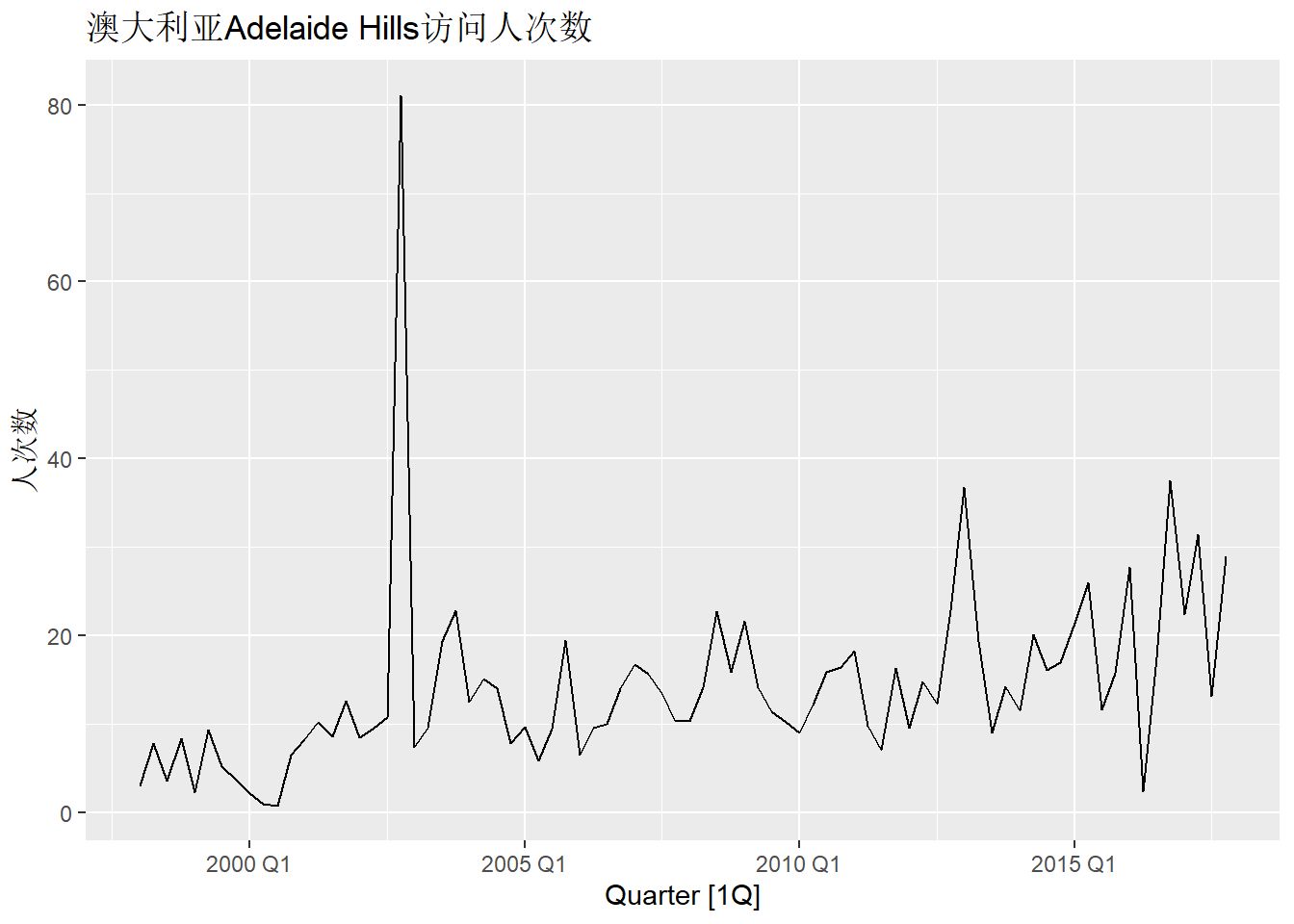
其中的2002第4季度数据是一个异常值, 将其转换为缺失值不会影响模型正常运动:
vis_miss_tsib <- vis_tsib |>
mutate(Trips = if_else(
Quarter %in% as.yearqtr("2002 Q4"), NA_real_, Trips))但是,
某些模型如STL不支持对含有缺失值的序列建模。
所以,
可以先建立一个ARIMA模型,
用interpolate()函数进行缺失值差别,
即用模型进行拟合:
这样, 缺失值就被ARIMA模型的拟合值补全了。
14.3 样本内比较
这一节内容过时,仅保留作为资料。 10.3.4讲了用残差诊断方法判断模型对数据拟合是否足够充分; 12.2.3讲了用AIC等信息准则指标在考虑到避免过度拟合问题情况下比较不同的模型。
如果建模目的是获得描述数据内在运动规律的参数模型, 可以用样本内比较, 利用全部数据建模, 并比较不同模型的某个优良性指标, 如AIC、BIC、新息方差等。 这些指标越小就认为模型越合适。
例14.1 考虑CRSP最高10分位资产组合的月简单收益率的不同模型, 从1970年1月到2008年12月共39年,468个观测。
读入数据:
da <- read_table(
"m-deciles08.txt",
col_types=cols(.default = col_double(),
date=col_date("%Y%m%d")))
xts.dec10 <- xts(da[["CAP1RET"]], ymd(da[["date"]]))
dec10 <- ts(da[["CAP1RET"]], start=c(1970, 1), frequency=12)首先拟合ARIMA\((1,0,1)(1,0,1)_{12}\):
##
## Call:
## arima(x = dec10, order = c(1, 0, 1), seasonal = list(order = c(1, 0, 1), period = 12))
##
## Coefficients:
## ar1 ma1 sar1 sma1 intercept
## -0.0639 0.2508 0.9882 -0.9142 0.0117
## s.e. 0.2205 0.2130 0.0092 0.0332 0.0125
##
## sigma^2 estimated as 0.004704: log likelihood = 584.69, aic = -1157.39其次,以是否一月份为哑变量, 做一个哑变量回归模型, 回归残差不继续建模:
##
## Call:
## lm(formula = c(dec10) ~ jan)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.30861 -0.03475 -0.00176 0.03254 0.40671
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.002864 0.003333 0.859 0.391
## jan 0.125251 0.011546 10.848 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.06904 on 466 degrees of freedom
## Multiple R-squared: 0.2016, Adjusted R-squared: 0.1999
## F-statistic: 117.7 on 1 and 466 DF, p-value: < 2.2e-16最后, 用带时间序列误差的回归, 回归自变量是一月份效应哑变量:
jan <- as.numeric(c(cycle(dec10))==1)
resm2 <- arima(
dec10, xreg=jan, seasonal=list(order=c(1,0,1), period=12))
resm2##
## Call:
## arima(x = dec10, seasonal = list(order = c(1, 0, 1), period = 12), xreg = jan)
##
## Coefficients:
## sar1 sma1 intercept jan
## -0.0920 0.2192 0.0027 0.1248
## s.e. 0.3585 0.3502 0.0037 0.0127
##
## sigma^2 estimated as 0.004671: log likelihood = 591.56, aic = -1173.12三个模型的\(\sigma_{\varepsilon}\)估计分别为:
## [1] 0.06858571## [1] 0.06904## [1] 0.06834471差距很小, 第一个模型和第三个模型的差距更小。 从描述数据规律的角度三个模型都可接受。
14.4 样本外比较
这一章内容已过时, 仅保留作为资料。 模型的样本外比较是指用模型向前预测, 计算向前预测的预测精度指标, 参见10.3.8。
如果建模的主要目的是预测, 则应以预测误差小为比较的原则。 这时,应该用前面的数据作为建模样本, 后面的样本不参加建模, 用模型对后面的样本进行预测并评估预测精度。 这种模型比较的方法叫做回测检验(backtesting)。
以超前一步预测问题为例。 设有\(t=1,2,\dots,T\)的样本, 取\(h\)使得\(h\)和\(T-h\)都比较大。 回测检验步骤如下:
对每个\(t=h, h+1, \dots, T-1\)重复如下操作: 用\(x_1, \dots, x_t\)作为样本建立模型, 用建立的模型预测\(x_{t+1}\), 计算超前一步预测误差\(e_t(1)\)。
计算预测误差的均方平方根(RMSE) \[ \text{RMSE} = \sqrt{\frac{1}{T-h} \sum_{t=h}^{T-1} [e_t(1)]^2} \]
比较不同模型的RMSE,以最小的一个为最优。
在建模时一般不对每一步都重新定阶。
其它的比较指标还有MAE(平均绝对误差) \[ \text{MAE} = \frac{1}{T-h} \sum_{t=h}^{T-1} |e_t(1)| \] 以及偏差 \[ \text{Bias} = \frac{1}{T-h} \sum_{t=h}^{T-1} e_t(1) \] 考虑美国季节调整后GDP序列。 进行对数变换:
##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## Year = col_double(),
## Mon = col_character(),
## Day = col_character(),
## gdp = col_double()
## )对数GDP的时间序列图:
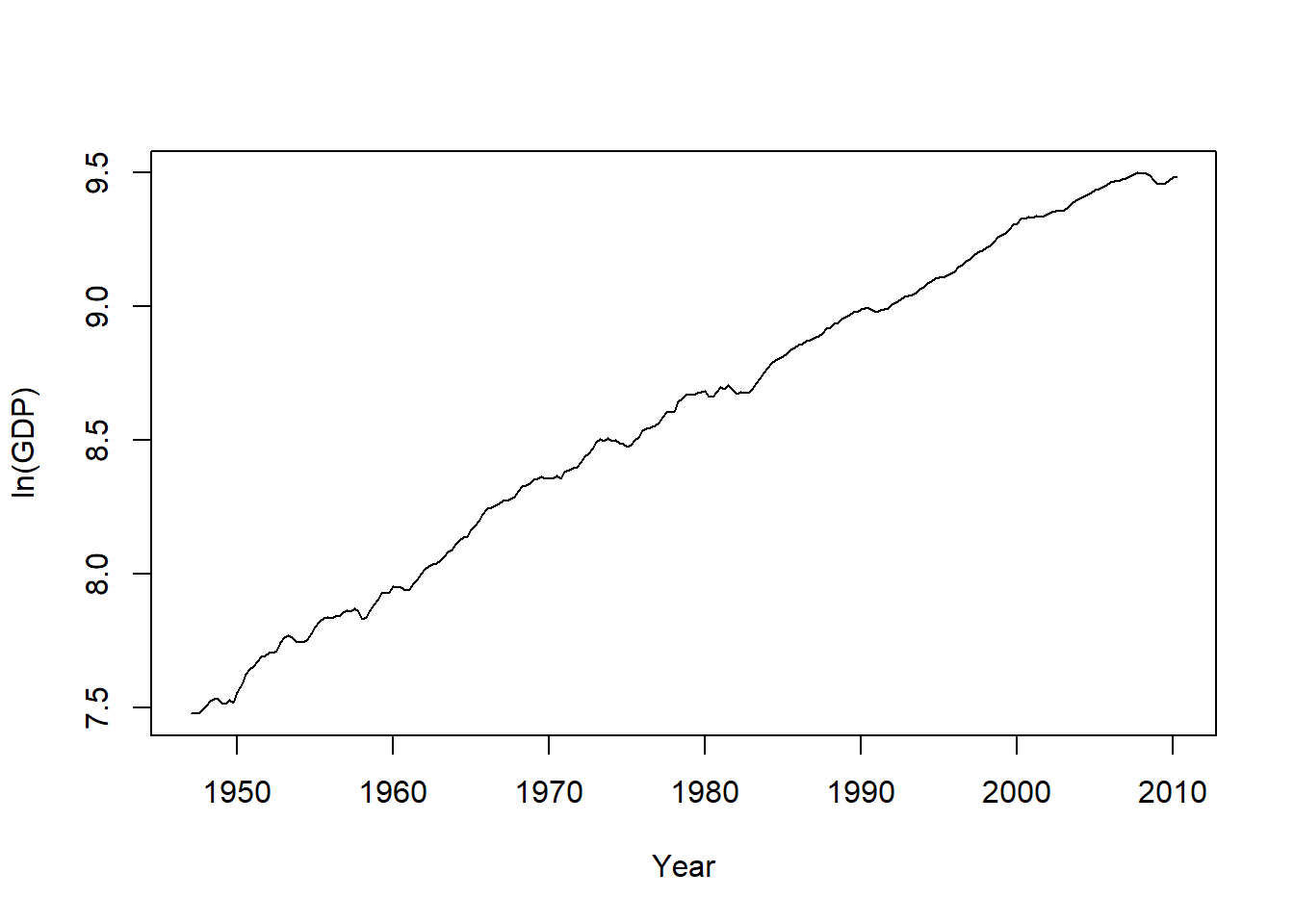
图14.1: 对数GDP的时间序列
这个序列明显地有趋势。 作其差分序列(对数增长率)的时间序列图:
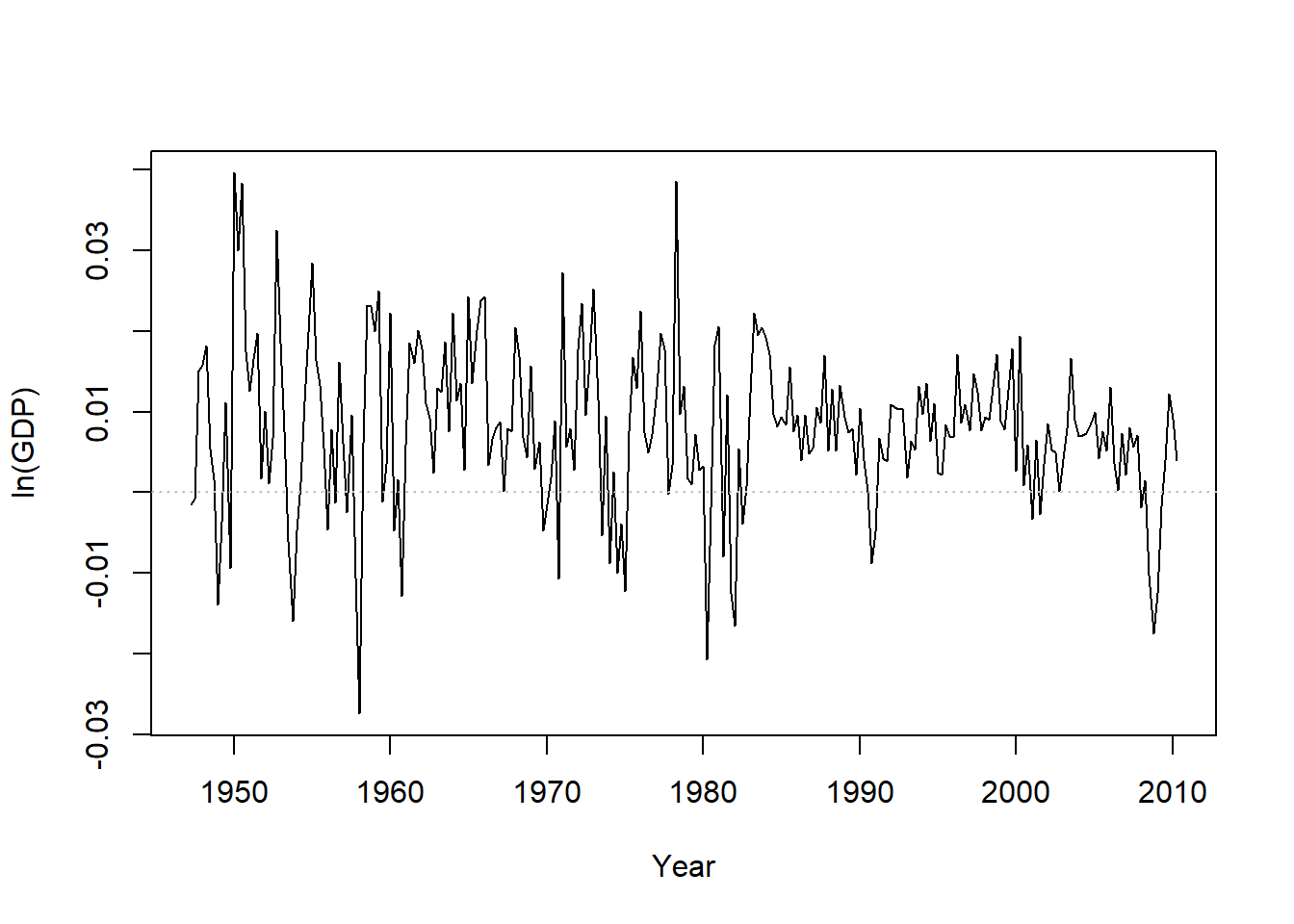
图14.2: GDP对数增长率的时间序列
这个图形没有明显趋势, 但是也不是白噪声的典型图形。
作对数增长率的ACF:
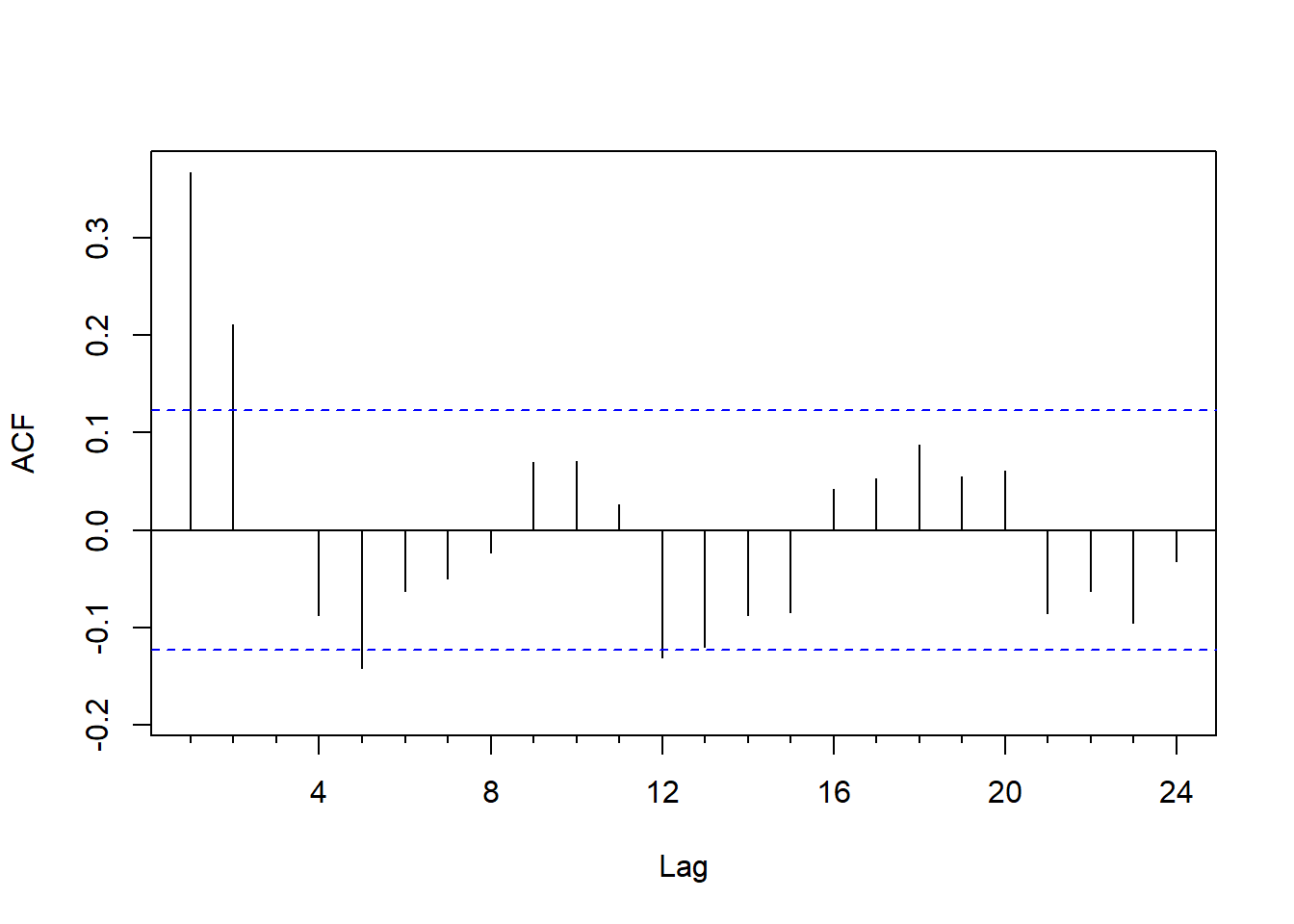
图14.3: GDP对数增长率的ACF
可考虑MA(2)模型。
作对数增长率的PACF:
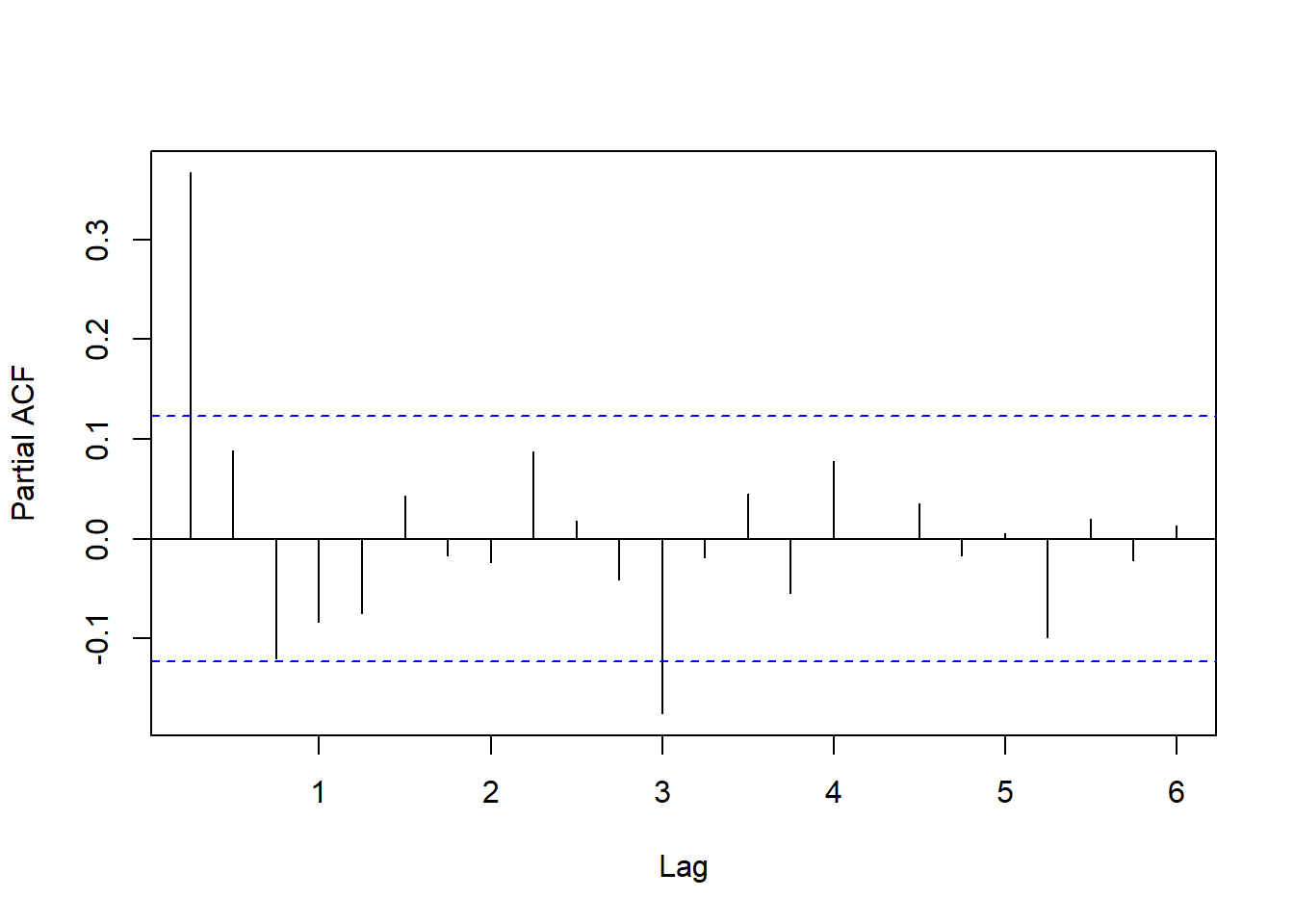
图14.4: GDP对数增长率的PACF
PACF在滞后12处还显著。 低阶可考虑AR(3)。
用AIC对AR模型定阶:
##
## Call:
## ar(x = dgdp, method = "mle")
##
## Coefficients:
## 1 2 3
## 0.3461 0.1299 -0.1224
##
## Order selected 3 sigma^2 estimated as 8.324e-05选择了3阶。
用arima()建模:
##
## Call:
## arima(x = dgdp, order = c(3, 0, 0))
##
## Coefficients:
## ar1 ar2 ar3 intercept
## 0.3462 0.1299 -0.1225 0.0079
## s.e. 0.0623 0.0655 0.0624 0.0009
##
## sigma^2 estimated as 8.323e-05: log likelihood = 829.23, aic = -1648.45因为是季度序列, 考虑模型ARIMA\((3,0,0)(1,0,1)_4\):
##
## Call:
## arima(x = dgdp, order = c(3, 0, 0), seasonal = list(order = c(1, 0, 1), period = 4))
##
## Coefficients:
## ar1 ar2 ar3 sar1 sma1 intercept
## 0.3305 0.1521 -0.1103 0.4966 -0.5865 0.0079
## s.e. 0.0633 0.0668 0.0635 0.2578 0.2357 0.0008
##
## sigma^2 estimated as 8.24e-05: log likelihood = 830.47, aic = -1646.93从AIC来看第一个模型更好。
下面比较其一步预测误差, 先写一个计算回测检验统计量的通用函数, 这时从(Tsay 2013)的伴随网站中提供的函数改进得到的。 具体程序参见14.5。
两个模型的回测检验,从前面的215个开始建模并每次增加一个样本点计算一步预测误差:
cat("==== Model 1\n")
res1 <- backtest(resm1, dgdp, n_min_sample=215, h=1)
print(res1$stats)
cat("==== Model 2\n")
res2 <- backtest(resm2, dgdp, n_min_sample=215, h=1)
print(res2$stats)用样本外一步预测均方误差平方根比较, 模型一为0.006153, 模型二为0.006322, 模型一略好, 考虑到模型一还更简单, 所以不论从样本内还是样本外比较都应选择模型一, 即AR(3)模型。
14.5 附录:backtest函数
改进版本的回测程序:
backtest <- function(
modres, # 全集建模结果
y, # 要建模的时间序列
h=1, # 预测的最大步数
n_min_sample, # 回测时最少的样本量
time_y = NULL, # y对应的时间标签
x_list = NULL, # 外生自变量,列表或数据框,序列长度与y相等
fixed = NULL){
library(tidyverse, quietly = TRUE)
library(purrr, quietly = TRUE)
library(xts, quietly = TRUE)
## 提取模型信息
# (p,d,q):
order0 <- modres$arma[c(1, 6, 2)]
# 季节(Q,D,Q)
orders <- modres$arma[c(3,7,4)]
# 周期
period <- modres$arma[5]
# fixed选项,默认为与模型中输出结果相同
if(is.null(fixed)){
fixed <- rep(NA, length(modres$mask))
fixed[!modres$mask] <- coef(modres)[!modres$mask]
}
## 提取include.mean选项
get_include_mean <- function(){
s <- as.character(as.expression(modres$call))
s1 <- gsub("[ \n]", "", s)
!grepl("include.mean=FALSE", s1, fixed=TRUE)[1]
}
include.mean <- get_include_mean()
## 将时间标签与数据分离,
## 时间标签存入time_y,
## 数据向量存入y0
if(is.ts(y) || is.xts(y)){
y <- as.xts(y)
y0 <- c(coredata(y))
if(is.null(time_y)){
time_y <- index(y)
}
} else if(is.numeric(y)){
y0 <- c(y)
if(is.null(time_y)){
time_y <- seq_along(y)
}
} else {
stop("Type of y should be numeric, or ts, or xts!")
}
stopifnot(length(time_y) == length(y))
stopifnot(is.numeric(h), length(h) == 1, h >= 1)
## 序号时间和真实时间的对应表
dtime <- tibble(
t = seq_along(y0),
time = time_y
)
## 真实数据序号与数值
dtrue <- tibble(
t = seq_along(y0),
y = y0
)
## 序列总长度
T <- length(y0)
## 如果有外生自变量且为时间序列,要求与y等长,且时间标签一致。转换为向量或矩阵。
## 为了适应多步预测,将T+1开始的h-1个值设置为NA
make_xreg <- function(){
xreg <- NULL
if(!is.null(x_list)){
if(is.numeric(x_list)) {
x_list <- list(x = x_list)
}
x_list %>%
# 每个列表元素长度必须等于输入时间序列长度
walk(function(x){
if(length(x) != length(y0))
stop("Length of independent variable should equal length of time series!")
} ) %>%
# 选择ts和xts类型
keep(function(x) is.ts(x) || is.xts(x)) %>%
## 对于时间序列,要求与输入时间序列时间完全匹配
walk(function(x) {
if(!all.equal(index(as.xts(x)), time_y))
stop("Time of independent variable does not conform with time series!")
})
## arima函数和predict.Arima函数要求的xreg和newxreg选项为矩阵
xreg <- as.matrix(as.data.frame(x_list))
if(h>1){
# 在多步预测时,会用到T+1到T+h-1处的外生自变量值,补为NA
xreg <- rbind(
xreg,
matrix(NA, nrow=h-1, ncol=ncol(xreg))
)
}
} # if 非NULL
xreg
} # function
xreg <- make_xreg()
n_ahead <- seq(1, h, by=1)
# 对t=n_min_sample, .+1, ..., T-1作超前一步预测,以h=1为例。
# 先生成结果数据框
dres <- tibble(
t = dtime$t,
pred = vector("list", length=T))
for(n in seq(n_min_sample, T-1)){
ytrain <- y0[1:n] # 本轮建模用的样本
# 分无外生自变量和有外生自变量两种情形
if(is.null(xreg)){
# 没有外生自变量
mod1 <- arima(
ytrain,
order = order0,
seasonal = list(
order = orders,
period = period),
fixed = fixed,
include.mean=include.mean)
pre <- predict(
mod1,
n.ahead=h,
se.fit=TRUE)
} else {
# 有外生自变量
xtrain <- xreg[1:n,,drop=FALSE]
xtest <- xreg[(n+1):(n+h),,drop=FALSE]
mod1 <- arima(
ytrain,
order = order0,
seasonal = list(
order = orders,
period = period),
xreg = xtrain,
fixed = fixed,
include.mean=include.mean)
pre <- predict(
mod1,
newxreg = xtest,
n.ahead = h,
se.fit=TRUE)
}
## 将基于1:n的预测结果作为子数据框存入到
## 结果dres的[n,"pred"]位置作为列表类型列
dres[["pred"]][n] <- list(tibble(
n_ahead = n_ahead,
predict = as.vector(pre$pred),
se = as.vector(pre$se) ) )
} # for t
## 结果仅保留有预测的时间点, 应为T - n_min_sample行
dres <- dres[n_min_sample:(T-1), ]
## 获得1:n_ahead步的预测结果,与真实值按时间对齐后计算预测误差
dtest <- dres %>%
# 将每步预测的子数据框展开
unnest(cols=c(pred)) %>%
ungroup() %>%
# 计算预测值对应的时间
mutate(time_pred = t + n_ahead) %>%
# 去掉time,即所用的训练样本截止时间
select(-t) %>%
# 取预测值对应时间小于等于T
dplyr::filter(time_pred <= T) %>%
# 将预测值对应的时间与真实值对应的时间对齐,
inner_join(dtrue, by = c("time_pred" = "t")) %>%
# 预测值对应的序号时间time_pred改名为t
rename(t = time_pred) %>%
mutate(error = predict - y) %>%
# 增加真实时间列time
inner_join(dtime, by = "t") %>%
select(t, time, n_ahead, y, predict, se, error) %>%
arrange(t, n_ahead)
# RMSE和MAE
stats <- dtest %>%
select(n_ahead, error) %>%
group_by(n_ahead) %>%
summarise(
rmse = sqrt(mean(error^2)),
mae = mean(abs(error)))
list(predict = dtest, stats = stats)
}改进版本的测试程序:
gen_arma42 <- function(n=100){
set.seed(101)
y <- arima.sim(
model=list(
ar=c(-0.9, -1.4, -0.7, -0.6),
ma=c(0.5, -0.4)),
n = n,
sd = sqrt(4))
as.vector(y)
}
## ARMA(4,2)无自变量,超前1步
test11 <- function(){
y <- 100 + gen_arma42(n=100)
mod <- arima(
y, order = c(4, 0, 2),
include.mean=TRUE
)
res <- backtest(
mod, y,
h=1, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
include.mean=TRUE
)
pred1 <- predict(mod1)
pre[t] <- pred1$pred
se[t] <- pred1$se
}
stats <- res$stats
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功。
## 将测试程序中两处inlude.mean=TRUE改为FALSE也成功。
## ARMA(4,2)无自变量,超前2步
test12 <- function(){
y <- 100 + gen_arma42(n=100)
mod <- arima(
y, order = c(4, 0, 2),
include.mean=TRUE
)
res <- backtest(
mod, y,
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
include.mean=TRUE
)
pred1 <- predict(mod1)
pre[t] <- pred1$pred
se[t] <- pred1$se
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
include.mean=TRUE
)
pred1 <- predict(mod1, n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功
## 对ts类型的测试
## ARMA(4,2)无自变量,超前1步
test21 <- function(){
y <- 100 + gen_arma42(n=100)
y <- ts(y, start=c(1900,1), frequency=4)
mod <- arima(
y, order = c(4, 0, 2),
include.mean=TRUE
)
res <- backtest(
mod, y,
h=1, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
include.mean=TRUE
)
pred1 <- predict(mod1)
pre[t] <- pred1$pred
se[t] <- pred1$se
}
stats <- res$stats
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功
## ARMA(4,2)无自变量,超前2步,xts日数据,时间不连贯
test22 <- function(){
y <- 100 + gen_arma42(n=100)
time <- sort(sample(lubridate::ymd("2001-01-03") + 1:130, size=100))
y <- xts(y, time)
mod <- arima(
y, order = c(4, 0, 2),
include.mean=TRUE
)
res <- backtest(
mod, y,
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
include.mean=TRUE
)
pred1 <- predict(mod1)
pre[t] <- pred1$pred
se[t] <- pred1$se
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
include.mean=TRUE
)
pred1 <- predict(mod1, n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功
gen_arima412 <- function(n=100){
set.seed(101)
y <- arima.sim(
model=list(
ar=c(-0.9, -1.4, -0.7, -0.6),
ma=c(0.5, -0.4),
order=c(4,1,2)),
n = n,
sd = sqrt(4))
as.vector(y)[-1]
}
## ARIMA(4,1,2)无自变量,超前2步
test31 <- function(){
y <- 100 + gen_arima412(n=100)
mod <- arima(
y, order = c(4, 1, 2) )
res <- backtest(
mod, y,
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 1, 2) )
pred1 <- predict(mod1)
pre[t] <- pred1$pred[1]
se[t] <- pred1$se[1]
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 1, 2))
pred1 <- predict(mod1, n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功。
## 模拟ARIMA(1,1,1)(1,1,1)_4
## $$(1-0.5B)(1 - 0.3B^4)(1-B)(1-B^4) y_t
## = (1+0.3B)(1+0.1B^4) e_t$$
gen_arimas <- function(n=100){
set.seed(101)
y <- arima.sim(
model=list(
ar=c(0.5, 0, 0, 0.3, -0.15),
ma=c(0.3, 0, 0, 0.1, 0.03),
order=c(5,1,5)),
n = n + 40,
sd = sqrt(4))
nn <- length(y)
y <- y[1:(nn-4)] + y[5:nn]
nn <- length(y)
as.vector(y)[(nn-n+1):nn]
}
## ARIMA(1,1,1)(1,1,1)_4无自变量,超前2步
test41 <- function(){
y <- 100 + gen_arimas(n=100)
mod <- arima(
y, order = c(1, 1, 1),
seasonal = list(order = c(1,1,1), period=4))
res <- backtest(
mod, y,
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(1,1,1),
seasonal = list(order = c(1,1,1), period=4) )
pred1 <- predict(mod1)
pre[t] <- pred1$pred[1]
se[t] <- pred1$se[1]
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(1,1,1),
seasonal = list(order = c(1,1,1), period=4) )
pred1 <- predict(mod1, n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 模拟稀疏系数ARMA(5,5)
## 模拟ARIMA(1,1,1)(1,1,1)_4
## $$(1-0.5B)(1 - 0.3B^4) y_t
## = (1+0.3B)(1+0.1B^4) e_t$$
gen_arma55 <- function(n=100){
set.seed(101)
y <- arima.sim(
model=list(
ar=c(0.5, 0, 0, 0.3, -0.15),
ma=c(0.3, 0, 0, 0.1, 0.03),
order=c(5,0,5)),
n = n + 40,
sd = sqrt(4))
nn <- length(y)
as.vector(y)[(nn-n+1):nn]
}
test51 <- function(){
y <- 100 + gen_arma55(n=100)
fixed <- rep(NA, 11)
fixed[c(2,3,7,8)] <- 0
mod <- arima(
y, order = c(5,0,5),
fixed = fixed, transform.pars = FALSE)
res <- backtest(
mod, y,
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(5,0,5),
fixed = fixed, transform.pars = FALSE )
pred1 <- predict(mod1)
pre[t] <- pred1$pred[1]
se[t] <- pred1$se[1]
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(5,0,5),
fixed = fixed, transform.pars = FALSE)
pred1 <- predict(mod1, n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功
## 带有一个自变量的ARMA(4,2),超前1步
test61 <- function(n=100){
yerr <- gen_arma42(n=n)
x1 <- sample(1:10, size=n, replace=TRUE)
y <- 100 + 2 * x1 + yerr
mod <- arima(
y, order = c(4, 0, 2),
xreg = x1)
res <- backtest(
mod, y,
x_list = list(x1),
h=1, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
print(res)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
xreg = x1[1:(80+t-1)])
pred1 <- predict(mod1, newxreg = x1[80+t])
pre[t] <- pred1$pred[1]
se[t] <- pred1$se[1]
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功
## 带有一个自变量的ARMA(4,2),超前2步
test62 <- function(n=100){
yerr <- gen_arma42(n=n)
x1 <- sample(1:10, size=n, replace=TRUE)
y <- 100 + 2 * x1 + yerr
mod <- arima(
y, order = c(4, 0, 2),
xreg = x1)
res <- backtest(
mod, y,
x_list = list(x1),
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
xreg = x1[1:(80+t-1)])
pred1 <- predict(mod1, newxreg = x1[80+t])
pre[t] <- pred1$pred[1]
se[t] <- pred1$se[1]
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
xreg = x1[1:(80+t-1)])
pred1 <- predict(mod1, newxreg = cbind(x1[80+t+(0:1)]), n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 带有两个个自变量的ARMA(4,2),超前2步
test63 <- function(n=100){
yerr <- gen_arma42(n=n)
x1 <- sample(1:10, size=n, replace=TRUE)
x2 <- sample(11:20, size=n, replace=TRUE)
xx <- cbind(x1, x2)
y <- 100 + 2 * x1 + 0.5*x2 + yerr
mod <- arima(
y, order = c(4, 0, 2),
xreg = xx)
res <- backtest(
mod, y,
x_list = list(x1, x2),
h=2, # 预测的最大步数
n_min_sample = 80 # 回测时最少的样本量
)
# 手工检查预测, 1步
pre <- numeric(20)
se <- numeric(20)
for(t in 1:20){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
xreg = xx[1:(80+t-1),,drop=FALSE])
pred1 <- predict(mod1, newxreg = xx[80+t,,drop=FALSE])
pre[t] <- pred1$pred[1]
se[t] <- pred1$se[1]
}
stats <- res$stats[1,]
rmse <- sqrt(mean((y[81:100] - pre)^2))
mae <- mean(abs(y[81:100] - pre))
cat("1 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
# 手工检查预测, 2步
pre <- numeric(19)
se <- numeric(19)
for(t in 1:19){
mod1 <- arima(
y[1:(80+t-1)], order = c(4, 0, 2),
xreg = xx[1:(80+t-1),,drop=FALSE])
pred1 <- predict(
mod1, newxreg = xx[80+t+(0:1),,drop=FALSE], n.ahead=2)
pre[t] <- pred1$pred[2]
se[t] <- pred1$se[2]
}
stats <- res$stats[2,]
rmse <- sqrt(mean((y[82:100] - pre)^2))
mae <- mean(abs(y[82:100] - pre))
cat("2 step ahead -- RMSE error: ", rmse - stats[["rmse"]],
" MAE error: ", mae - stats[["mae"]], "\n")
}
## 成功
## 运行所有测试
run.all.tests <- function(){
fun.list <- list(
test11, test12,
test21, test22,
test31,
test41,
test51,
test61, test62
)
for(fun in fun.list)
fun()
}蔡瑞胸教授的原始版本:
"backtest" <- function(m1, rt, orig, h, xre=NULL, fixed=NULL, inc.mean=TRUE){
# m1: is a time-series model object
# orig: is the starting forecast origin
# rt: the time series
# xre: the independent variables
# h: forecast horizon
# fixed: parameter constraint
# inc.mean: flag for constant term of the model.
#
regor=c(m1$arma[1],m1$arma[6],m1$arma[2])
seaor=list(order=c(m1$arma[3],m1$arma[7],m1$arma[4]),period=m1$arma[5])
T=length(rt)
if(!is.null(xre) && !is.matrix(xre)) xre=as.matrix(xre)
ncx=ncol(xre)
if(orig > T) orig=T
if(h < 1) h=1
rmse=rep(0,h)
mabso=rep(0,h)
nori=T-orig
err=matrix(0,nori,h)
jlast=T-1
for (n in orig:jlast){
jcnt=n-orig+1
x=rt[1:n]
if (!is.null(xre)){
pretor=xre[1:n,]
mm=arima(x,order=regor,seasonal=seaor,xreg=pretor,fixed=fixed,include.mean=inc.mean)
nx=xre[(n+1):(n+h),]
if(h==1)nx=matrix(nx,1,ncx)
fore=predict(mm,h,newxreg=nx)
}
else {
mm=arima(x,order=regor,seasonal=seaor,xreg=NULL,fixed=fixed,include.mean=inc.mean)
fore=predict(mm,h,newxreg=NULL)
}
kk=min(T,(n+h))
# nof is the effective number of forecats at the forecast origin n.
nof=kk-n
pred=fore$pred[1:nof]
obsd=rt[(n+1):kk]
err[jcnt,1:nof]=obsd-pred
}
#
for (i in 1:h){
iend=nori-i+1
tmp=err[1:iend,i]
mabso[i]=sum(abs(tmp))/iend
rmse[i]=sqrt(sum(tmp^2)/iend)
}
print("RMSE of out-of-sample forecasts")
print(rmse)
print("Mean absolute error of out-of-sample forecasts")
print(mabso)
backtest <- list(origin=orig,error=err,rmse=rmse,mabso=mabso)
}