18 GARCH模型

本章来自(Tsay 2013)§4.6-4.8内容。

ARCH模型用来描述波动率能得到很好的效果， 但实际建模时可能需要较高的阶数， 比如§17.5.3的欧元汇率波动率建模用了11阶的ARCH模型。 考虑类似从AR推广到ARMA的模型变化。

18.1 模型方程

(Bollerslev 1986)提出了ARCH模型的一种重要推广模型， 称为GARCH模型。 对于一个对数收益率序列\(r_t\)， 令\(a_t = r_t - \mu_t = r_t - E(r_t | F_{t-1})\)为其新息序列， 称\(\{ a_t \}\)服从GARCH(\(m,s\))模型， 如果\(a_t\)满足 \[\begin{align} a_t = \sigma_t \varepsilon_t, \quad \sigma_t^2 = \alpha_0 + \sum_{i=1}^m \alpha_i a_{t-i}^2 + \sum_{j=1}^s \beta_j \sigma_{t-j}^2 \tag{18.1} \end{align}\] 其中\(\{ \varepsilon_t \}\)为零均值单位方差的独立同分布白噪声列， \(\alpha_0>0\), \(\alpha_i \geq 0\), \(\beta_j \geq 0\), \(0 < \sum_{i=1}^m \alpha_i + \sum_{j=1}^s \beta_j < 1\)， 这最后一个条件用来保证满足模型的\(a_t\)的无条件方差有限且不变， 而条件方差\(\sigma_t^2\)可以随时间\(t\)而变。

18.2 与ARMA模型比较

模型(18.1)表面上像是如下的\(x_t = \sigma_t^2\)的类似于ARMA(\(s,m\))的模型： \[ X_t^2 - \sum_{j=1}^s \beta_j X_{t-j}^2 = \alpha_0 + \sum_{i=1}^m \alpha_i a_{t-i}^2 , \] 但是这里的\(\sigma_{t-i}^2\)和\(a_{t-i}^2\)是有关系的， \(\sigma_{t-i}^2\)是\(a_{t-i}\)的条件方差， ARMA模型中的\(x_{t-i}\)与模型中的白噪声\(\varepsilon_{t-i}\)并没有这样的关系。

为了利用GARCH模型与ARMA模型的相似性， 令\(\alpha_i=0\), 当\(i>m\)； 令\(\beta_j = 0\), 当\(j>s\)。 令\(\eta_t = a_t^2 - \sigma_t^2\)， 下一小节证明了\(E a_t = 0\)， 而\(\sigma_t^2 = \text{Var}(a_t | F_{t-1}) = E(a_t^2 | F_{t-1})\), 当\(a_t\)为严平稳列时\(\eta_t\)是鞅差序列，这是比宽白噪声严一些， 比零均值独立同分布白噪声宽一些的条件。 将\(\sigma_{t-i}^2 = a_{t-i}^2 - \eta_{t-i}\)代入模型(18.1)得 \[\begin{align} a_t^2 = \alpha_0 + \sum_{i=1}^{\max(m,s)} (\alpha_i + \beta_i) a_{t-i}^2 + \eta_t - \sum_{j=1}^s \beta_j \eta_{t-j} . \tag{18.2} \end{align}\] 这就是关于\(\{a_t^2\}\)的ARMA(\(\max(m,s)\), \(s\))模型， 由ARMA模型的无条件期望的公式得 \[ E a_t^2 = \frac{\alpha_0}{1 - \sum_{i=1}^{\max(m,s)} (\alpha_i + \beta_i)} = \frac{\alpha_0}{1 - \sum_{i=1}^m \alpha_i - \sum_{j=1}^s \beta_j} . \] 这要求分母为正，即要求\(\sum_{i=1}^m \alpha_i + \sum_{j=1}^s \beta_j < 1\)。 这时\(a_t\)的无条件方差\(\text{Var}(a_t)\)也等于上式。

18.3 GARCH模型的性质

下面以最简单的GARCH(1,1)为例研究GARCH模型的性质。 令\(F_{t-1}\)表示截止到\(t-1\)时刻的\(a_{t-i}\)和\(\sigma_{t-j}\)所包含的信息。 模型为 \[\begin{align} a_t =& \sigma_t \varepsilon_t, \quad \varepsilon_t \text{ i.i.d. WN} (0,1) , \\ \sigma_t^2 =& \alpha_0 + \alpha_1 a_{t-1}^2 + \beta_1 \sigma_{t-1}^2 . \tag{18.3} \end{align}\]

为了计算无条件均值\(Ea_t\)，先计算条件期望 \[ E(a_t | F_{t-1}) = E(\sigma_t \varepsilon_t | F_{t-1}) = \sigma_t E(\varepsilon_t | F_{t-1}) = 0 . \] 这里用了\(\sigma_t \in F_{t-1}\)而\(\varepsilon_t\)与\(F_{t-1}\)独立。 于是 \[ E a_t = E[ E(a_t | F_{t-1})] = 0 . \] 即GARCH模型的新息\(a_t\)的无条件期望为零。

来计算\(a_t\)的无条件方差。 设模型(18.1)的\(\{ a_t \}\)序列存在严平稳解，则 \[ \begin{aligned} \text{Var}(a_t) =& E(a_t^2) = E[ E(a_t^2 | F_{t-1})] = E[ E(\sigma_t^2 \varepsilon_t^2 | F_{t-1})]\\ =& E[\sigma_t^2 E(\varepsilon_t^2 | F_{t-1})] = E[\sigma_t^2 E(\varepsilon_t^2)] \\ =& E[\sigma_t^2] = E[\alpha_0 + \alpha_1 a_{t-1}^2 + \beta_1 \sigma_{t-1}^2] \\ =& \alpha_0 + \alpha_1 E(a_{t-1}^2) + \beta_1 E[E(a_{t-1}^2|F_{t-2})]\\ =& \alpha_0 + (\alpha_1 + \beta_1) E(a_{t-1}^2) . \end{aligned} \] 令\(E a_t^2 = E a_{t-1}^2\)， 解得 \[ \text{Var}(a_t) = E a_t^2 = \frac{\alpha_0}{1 - \alpha_1 - \beta_1} . \]

GARCH(1,1)模型的性质：

第一，像ARCH模型一样，\(a_t\)存在波动率聚集， 一个较大的\(a_{t-1}\)或\(\sigma_{t-1}\)使得\(1\)步以后的条件方差变大， 从而倾向于出现较大的对数收益率。

第二，当\(\varepsilon_t\)为标准正态分布时， 在如下条件下\(a_t\)有无条件四阶矩： \[ 1 - 2 \alpha_1^2 - (\alpha_1 + \beta_1)^2 > 0 . \] 这时超额峰度为 \[ \frac{E a_t^4}{(Ea_t^2)^2} - 3 = \frac{2\left[1 - (\alpha_1 + \beta_1)^2 + \alpha_1^2 \right]} {1 - (\alpha_1 + \beta_1)^2 - 2\alpha_1^2} > 0 . \] 即\(a_t\)分布厚尾。 但是， 对实际数据建模时即使使用条件t分布， 对数据的厚尾性的拟合仍可能不足。

第三，GARCH模型给出了一个比较简单的波动率模型。

第四，因为\(\sigma_t^2\)对\(a_{t-i}\)的依赖是通过\(a_{t-i}^2\)， 所以一个取正值的扰动\(a_{t-i}\)和一个取负值的\(a_{t-i}\)， 只要绝对值相等， 对后续波动率的影响就是相等的， 不能体现杠杆效应。

18.4 预测

可以用类似ARMA预测的方法预测波动率。 仍以GARCH(1,1)为例， 由模型(18.3)， 基于截止到\(h\)时刻的观测作超前一步预测： \[ \sigma_{h+1}^2 = \alpha_0 + \alpha_1 a_{h}^2 + \beta_1 \sigma_{h}^2 \in F_{h} . \] 所以 \[\begin{align} \sigma_h^2(1) = E(\sigma_{h+1}^2 | F_{h}) = \sigma_{h+1}^2 = \alpha_0 + \alpha_1 a_{h}^2 + \beta_1 \sigma_{h}^2 . \tag{18.4} \end{align}\] 对\(\sigma_{h+2}^2\)，利用\(a_t^2 = \sigma_t^2 \varepsilon_t^2\)，有 \[ \begin{aligned} \sigma_{h+2}^2 =& \alpha_0 + \alpha_1 a_{h+1}^2 + \beta_1 \sigma_{h+1}^2 \\ =& \alpha_0 + \alpha_1 \sigma_{h+1}^2 \varepsilon_{h+1}^2 + \beta_1 \sigma_{h+1}^2 \\ =& \alpha_0 + (\alpha_1 \varepsilon_{h+1}^2 + \beta_1) \sigma_{h+1}^2 \end{aligned} \] 于是 \[\begin{aligned} \sigma_h^2(2) =& E(\sigma_{h+2}^2 | F_{h}) = \alpha_0 + E(\alpha_1 \varepsilon_{h+1}^2 + \beta_1 | F_h) \sigma_{h+1}^2 \\ =& \alpha_0 + (\alpha_1 + \beta_1) \sigma_h^2(1) . \end{aligned}\] 类似地，对\(\ell \geq 2\)有 \[ \sigma_{h+\ell}^2 = \alpha_0 + \alpha_1 \varepsilon_{h+\ell-1}^2 \sigma_{h+\ell-1}^2 + \beta_1 \sigma_{h+\ell-1}^2 = \alpha_0 + (\alpha_1 \varepsilon_{h+\ell-1}^2 + \beta_1) \sigma_{h+\ell-1}^2 , \] 于是 \[\begin{align} \sigma_h^2(\ell) =& E\left\{ \sigma_{h+\ell}^2 | F_h \right\} = \alpha_0 + E\left\{ (\alpha_1 \varepsilon_{h+\ell-1}^2 + \beta_1) \sigma_{h+\ell-1}^2 | F_h \right\} \\ =& \alpha_0 + E\left\{ E\left[ (\alpha_1 \varepsilon_{h+\ell-1}^2 + \beta_1) \sigma_{h+\ell-1}^2 | F_{h+\ell-2} \right] | F_h \right\} \\ =& \alpha_0 + E\left\{ \sigma_{h+\ell-1}^2 E\left[ \alpha_1 \varepsilon_{h+\ell-1}^2 + \beta_1 | F_{h+\ell-2} \right] | F_h \right\} \quad(\text{注意}\sigma_{h+\ell-1}^2 \in F_{h+\ell-2}) \\ =& \alpha_0 + \left\{ \sigma_{h+\ell-1}^2 (\alpha_1 + \beta_1) | F_h \right\} \\ =& \alpha_0 + (\alpha_1 + \beta_1) \sigma_h^2(\ell-1) . \tag{18.5} \end{align}\]

预测公式与自回归系数为\((\alpha_1 + \beta_1)\)的ARMA(1,1)的超前预测公式相同。

从\(\ell=2\)迭代计算得 \[ \sigma_h^2(\ell) = \frac{\alpha_0[1 - (\alpha_1 + \beta_1)^{\ell-1}]}{1 - (\alpha_1 + \beta_1)} + (\alpha_1 + \beta_1)^{(\ell-1)} \sigma_h^2(1) . \] 只要\(\alpha_1 + \beta_1 < 1\)就有 \[ \sigma_h^2(\ell) \to \frac{\alpha_0}{1 - \alpha_1 - \beta_1} = \text{Var}(a_t) . \] 即超前多步条件方差预测趋于\(a_t\)的无条件方差。

18.5 模型估计

ARCH模型的建模步骤也适用于GARCH模型的建模。 GARCH模型的定阶方法研究不多， 一般用试错法尝试较低阶的GARCH模型， 如GARCH(1,1), GARCH(2,1), GARCH(1,2)等。 许多情况下GARCH(1,1)就能解决问题。

为了估计参数， 可以假定初始的\(\sigma_t^2\)已知， 递推计算后续的\(\sigma_t^2\)并计算条件似然函数， 求条件似然函数的最大值点得到参数估计。 有时用\(a_t\)的样本方差作为初始的\(\sigma_t\)的值。

为了检验模型的充分性， 可以计算标准化残差 \[ \tilde a_t = \frac{a_t}{\sigma_t} , \] 通过对\(\tilde a_t\)和\(\tilde a_t^2\)的白噪声检验确认模型可以接受， 还可以做\(\tilde a_t\)相对于条件分布的QQ图以检验模型假设的条件分布的拟合优度。

18.5.1 Intel公司股票收益率的波动率建模实例

继续使用§17.5.1中的Intel公司股票从1973-1到2009-12的月度对数收益率数据， 有444个观测值。 §17.5.1中的ARCH(1)模型(17.10)在模型检验中有一些不足， 比如关于标准化残差平方的Ljung-Box检验的滞后15和滞后20检验是显著的。 尝试用GARCH(1,1)模型来改进。记\(r_t\)为对数收益率序列。

数据读入：

d.intel <- read_table(
  "m-intcsp7309.txt",
  col_types=cols(
    .default=col_double(),
    date=col_date("%Y%m%d")
  ))
xts.intel <- xts(
  log(1 + d.intel[["intc"]]), d.intel[["date"]]
)
tclass(xts.intel) <- "yearmon"
ts.intel <- ts(c(coredata(xts.intel)), start=c(1973,1), frequency=12)
at <- ts.intel - mean(ts.intel)

对数收益率的时间序列图：

plot(ts.intel, ylab="log return", main="Intel Stock Price Monthly Log Return")

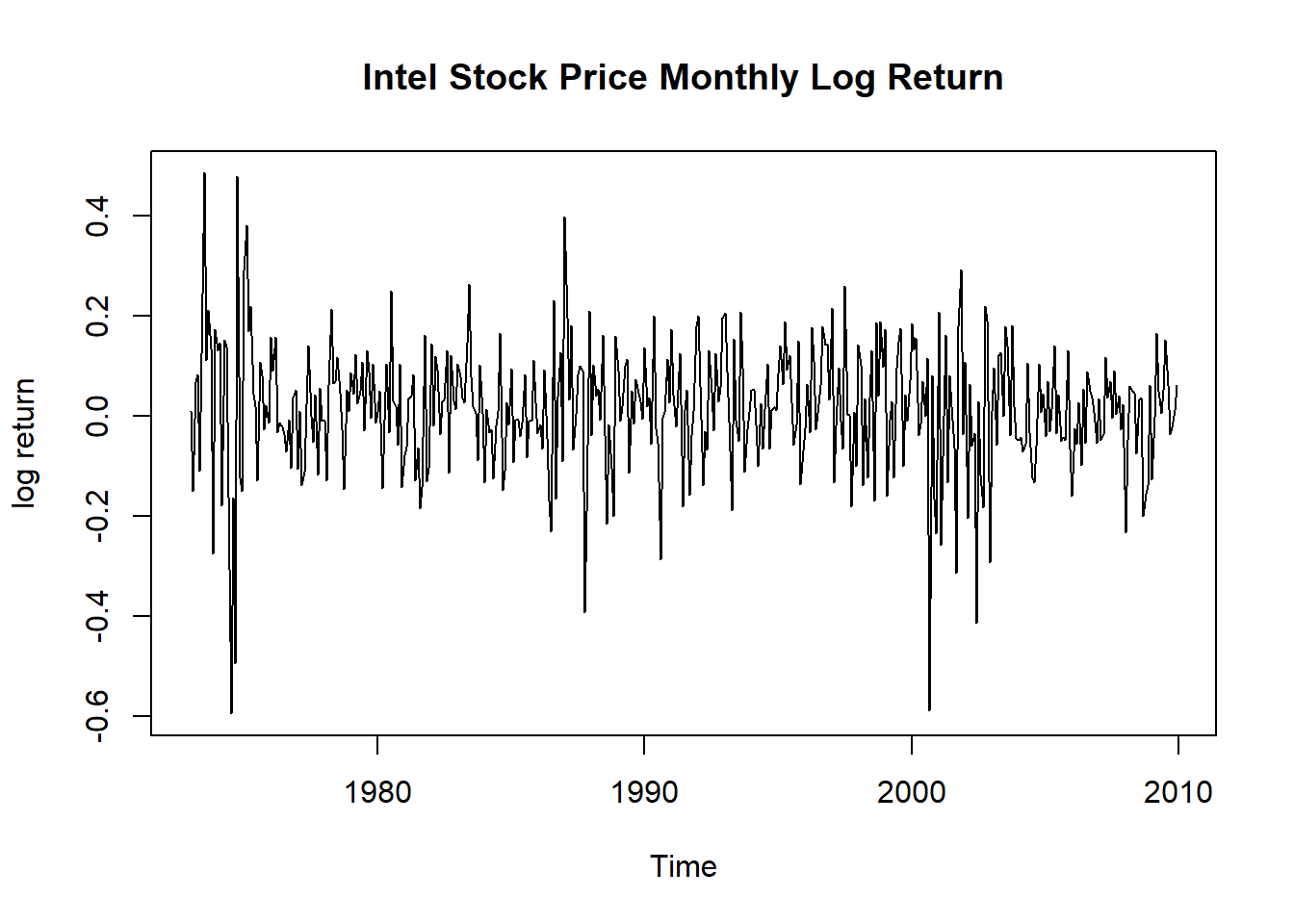
图18.1: Intel月对数收益率时间序列

18.5.2 使用条件正态分布

采用正态条件分布建立GARCH(1,1)模型：

library(fGarch, quietly = TRUE)
mod1 <- garchFit(~ 1 + garch(1,1), data=ts.intel, trace=FALSE)

## Warning: Using formula(x) is deprecated when x is a character vector of length > 1.
##   Consider formula(paste(x, collapse = " ")) instead.

summary(mod1)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = ts.intel, trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000000002e4bf538>
##  [data = ts.intel]
## 
## Conditional Distribution:
##  norm 
## 
## Coefficient(s):
##         mu       omega      alpha1       beta1  
## 0.01126568  0.00091902  0.08643831  0.85258554  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu     0.0112657   0.0053931    2.089  0.03672 *  
## omega  0.0009190   0.0003888    2.364  0.01808 *  
## alpha1 0.0864383   0.0265439    3.256  0.00113 ** 
## beta1  0.8525855   0.0394322   21.622  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  312.3307    normalized:  0.7034475 
## 
## Description:
##  Wed May 11 16:54:53 2022 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  174.904   0           
##  Shapiro-Wilk Test  R    W      0.9709615 1.030282e-07
##  Ljung-Box Test     R    Q(10)  8.016844  0.6271916   
##  Ljung-Box Test     R    Q(15)  15.5006   0.4159946   
##  Ljung-Box Test     R    Q(20)  16.41549  0.6905368   
##  Ljung-Box Test     R^2  Q(10)  0.8746345 0.9999072   
##  Ljung-Box Test     R^2  Q(15)  11.35935  0.7267295   
##  Ljung-Box Test     R^2  Q(20)  12.55994  0.8954573   
##  LM Arch Test       R    TR^2   10.51401  0.5709617   
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -1.388877 -1.351978 -1.389037 -1.374326

对标准化残差及其平方的白噪声检验结果都通过了。 比§17.5.1要好， 而且ACI值\(-1.3889\)比(17.10)的AIC值\(-1.3375\)也更好。 条件分布的正态性检验仍通不过。

模型可以写成： \[\begin{align} r_t =& 0.0113 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \epsilon_t \text{ i.i.d. } \sim \text{N}(0,1) \\ \sigma_t^2 =& 0.00092 + 0.0864 a_{t-1}^2 + 0.8526 \sigma_{t-1}^2 \tag{18.6} \end{align}\] \(\sigma_t^2\)对过去的依赖主要来源于\(\beta_1 = 0.85\)。

拟合的波动率图形：

##plot(mod1, which=2)
vola <- volatility(mod1)
plot(ts(vola, start=start(ts.intel), frequency=frequency(ts.intel)), 
     xlab="年", ylab="波动率")
abline(h=sd(ts.intel), col="green")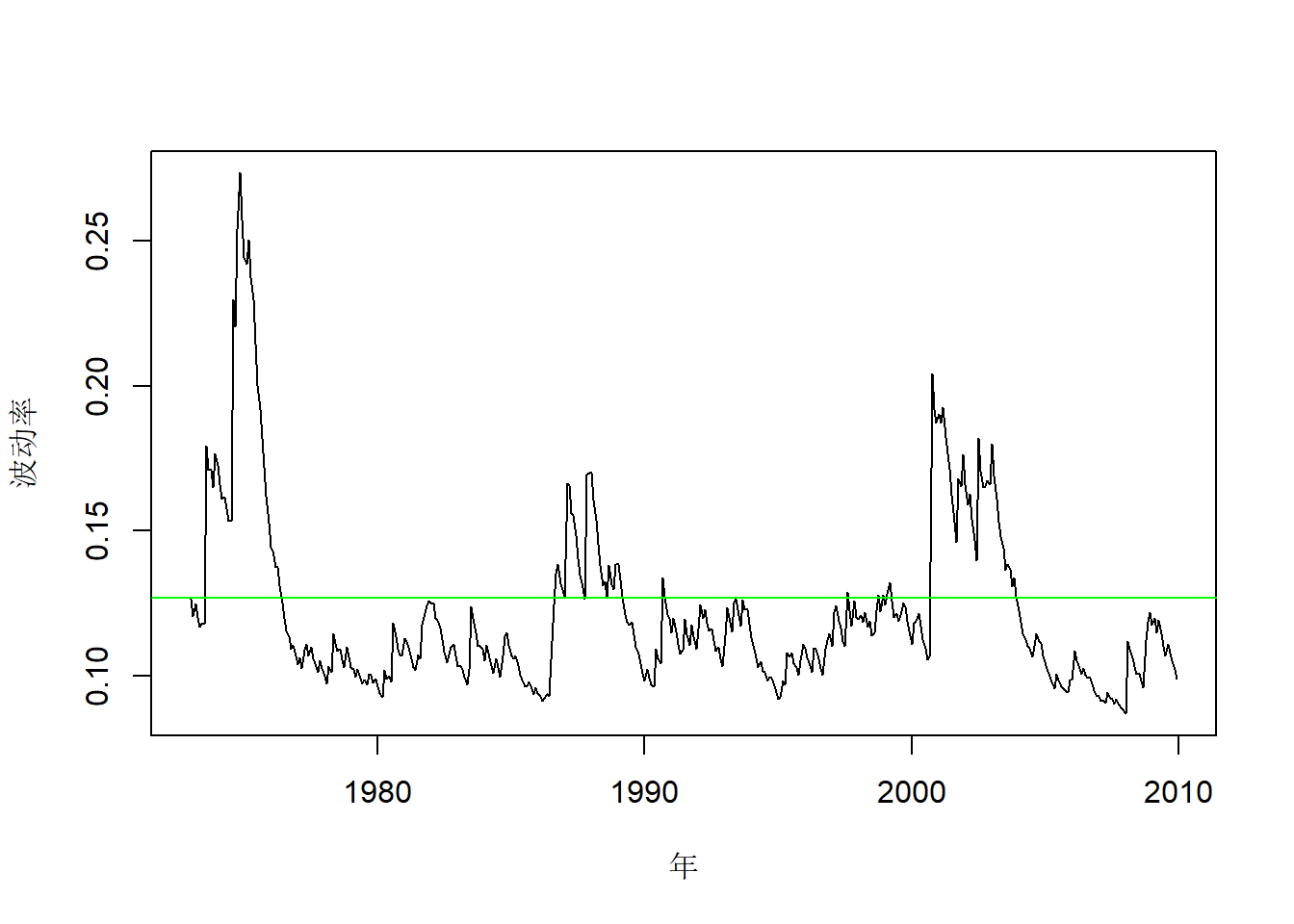

图18.2: Intel股票建模拟合波动率

可以看出波动率在1973-1974石油危机期间和2000年的互联网泡沫期间最高。 波动率图形中绿色横线为样本标准差，值为：

sd(ts.intel)

## [1] 0.1269101

按模型计算的对数收益率无条件标准差为:

tmpx <- coef(mod1)
unname(sqrt(tmpx["omega"]/(1 - tmpx["alpha1"] - tmpx["beta1"])))

## [1] 0.122767

模型计算的无条件标准差与样本标准差很接近。

标准化残差的时间序列图：

##plot(mod1, which=9)
resi <- residuals(mod1, standardize=TRUE)
plot(ts(resi, start=start(ts.intel), frequency=frequency(ts.intel)), 
     xlab="年", ylab="标准化残差")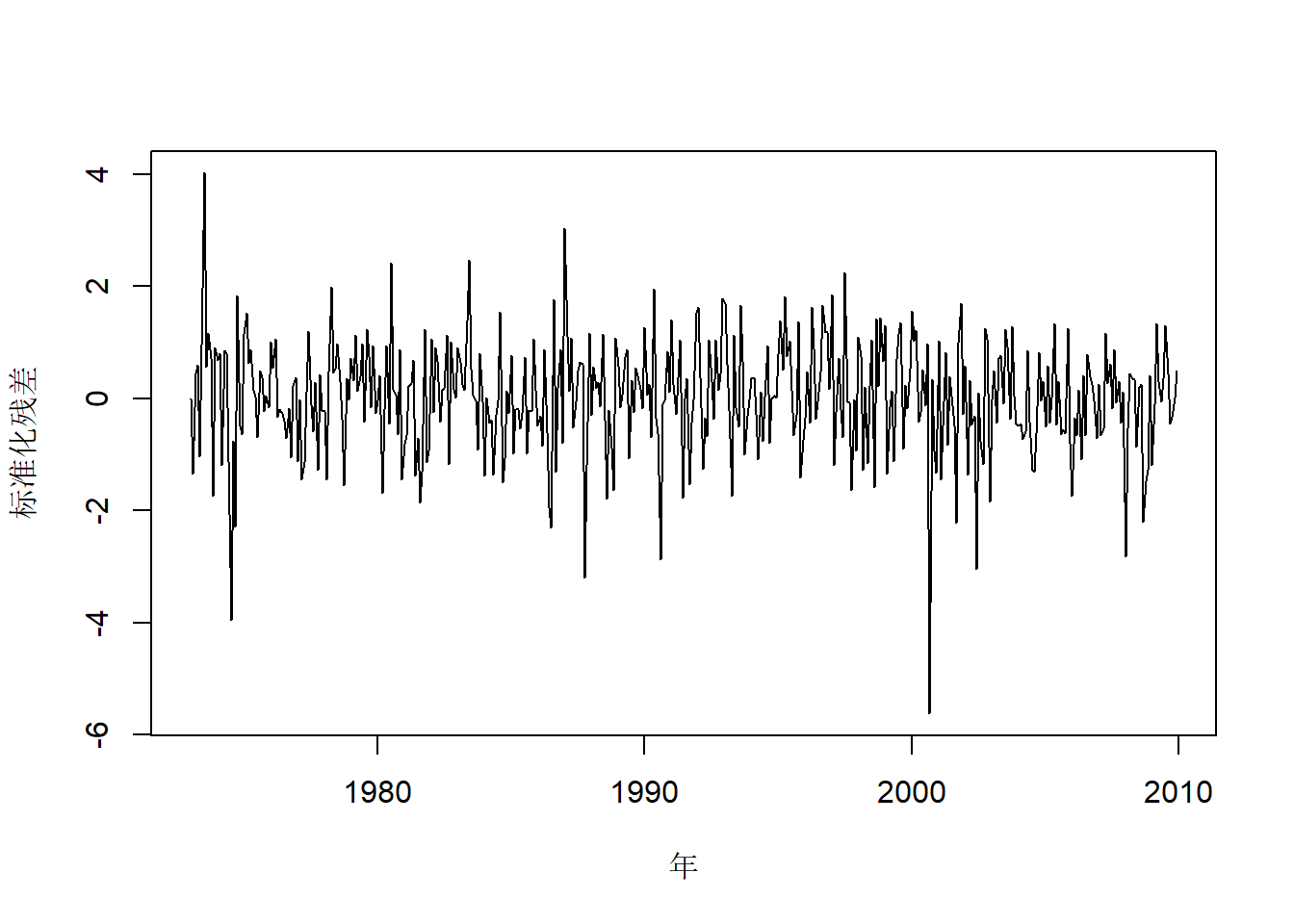

图18.3: Intel股票建模标准化残差

除了个别异常值，标准化残差看不出不符合独立同分布序列的特征。

\(\tilde a_t\)的ACF:

plot(mod1, which=10)

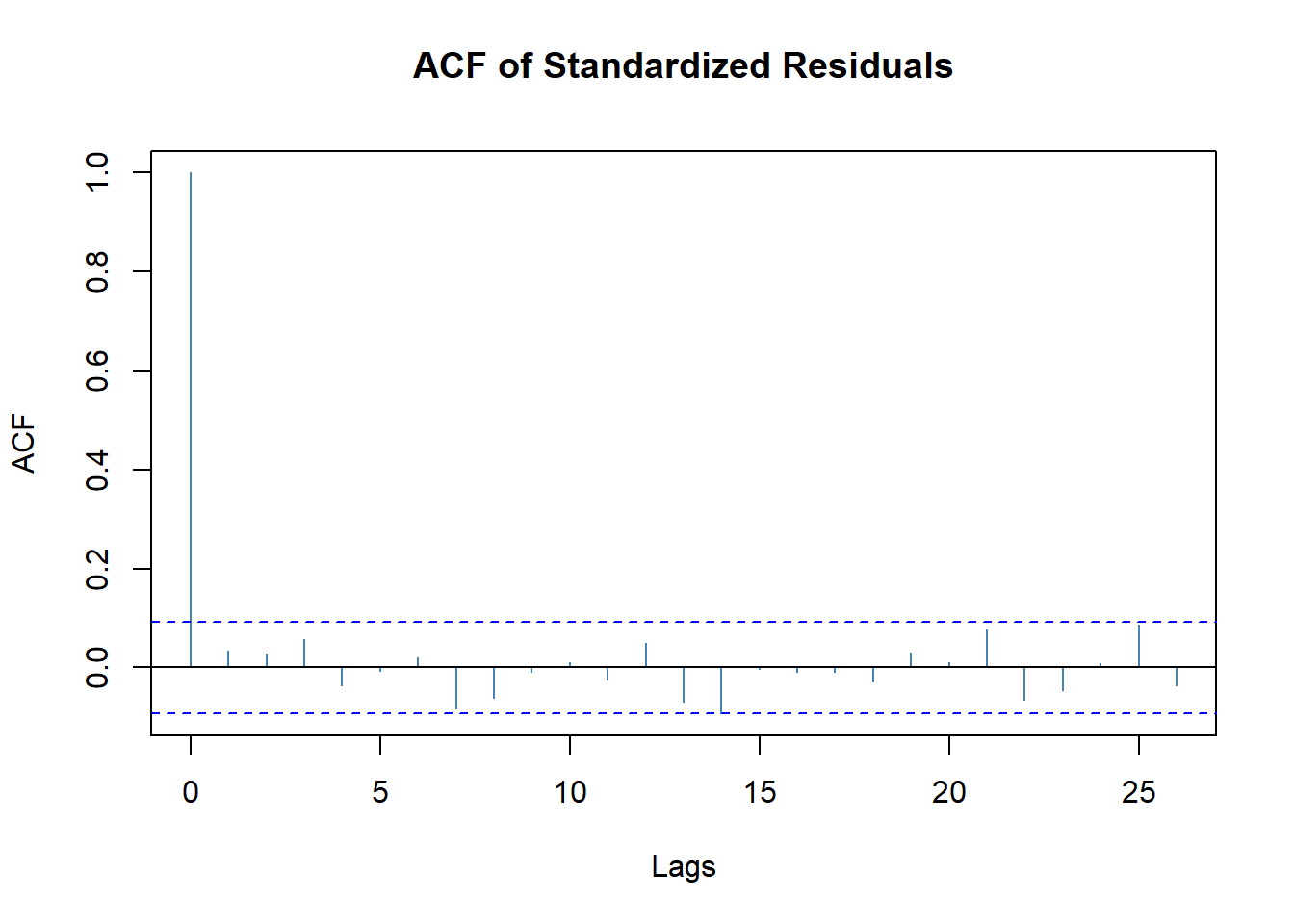
图18.4: Intel股票建模标准化残差的ACF

\(\tilde a_t^2\)的ACF:

plot(mod1, which=11)

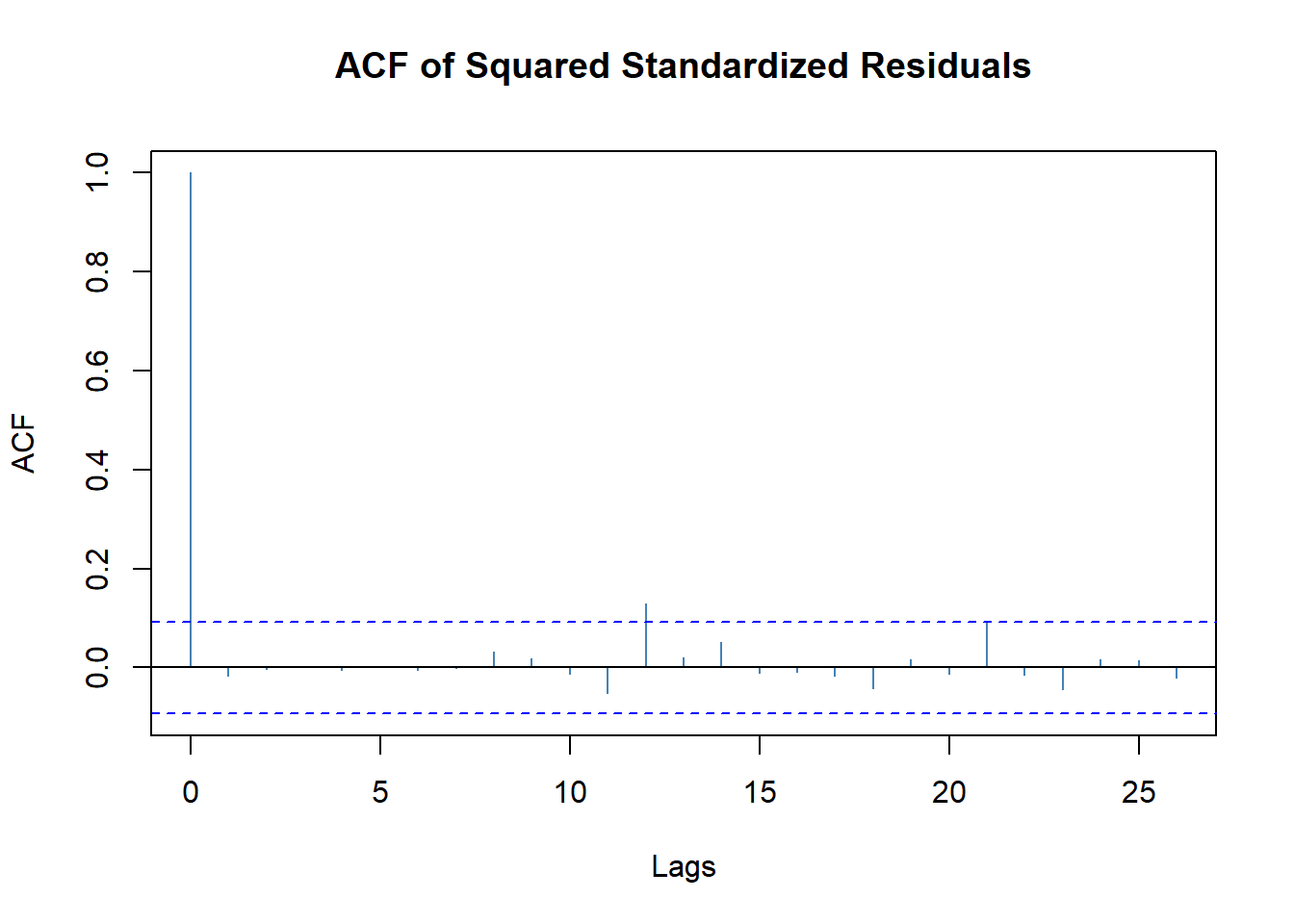
图18.5: Intel股票建模标准化残差平方的ACF

\(\tilde a_t^2\)的ACF在滞后12处略超出。 总的来说模型是满意的。

用\(\hat\mu + 2\hat\sigma_t\)可以作为\(r_t\)的近似95%置信区间， 将置信下限和置信下限分别延\(t\)轴方向连成曲线，得到如下图形：

plot(mod1, which=3)

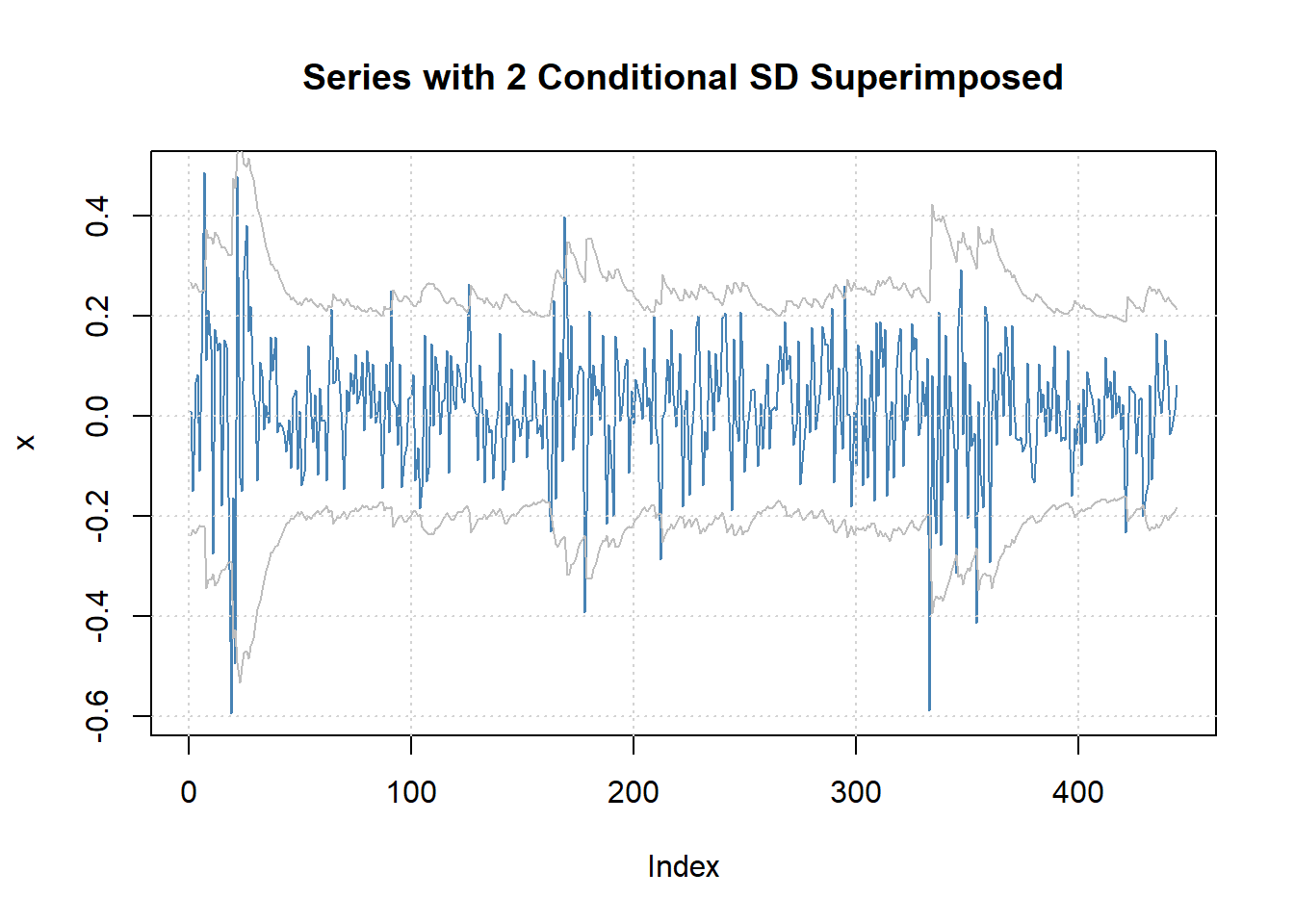
图18.6: Intel股票对数收益率的逐点95%预测界限

可见对数收益率的取值基本都在预测区间之内。 预测是滚动的超前一步预测。

上图直接提取数据也可以编程做出，如：

vola <- volatility(mod1)
hatmu <- coef(mod1)["mu"]
lb.intel <- hatmu - 2*vola
ub.intel <- hatmu + 2*vola
ylim <- range(c(ts.intel, lb.intel, ub.intel))
x.intel <- c(time(ts.intel))
plot(x.intel, c(ts.intel), type="l",
     xlab="年", ylab="对数收益率")
lines(x.intel, c(lb.intel), col="red")
lines(x.intel, c(ub.intel), col="red")

tseries包的garch()函数也可以用来拟合GARCH模型， 只能使用条件正态分布。 函数结果支持一系列的信息提取函数， 如summary()。

18.5.3 使用条件t分布

应用条件t分布的新息，拟合模型：

library(fGarch, quietly = TRUE)
mod2 <- garchFit(~ 1 + garch(1,1), data=ts.intel, 
                 cond.dist="std", trace=FALSE)

## Warning: Using formula(x) is deprecated when x is a character vector of length > 1.
##   Consider formula(paste(x, collapse = " ")) instead.

summary(mod2)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = ts.intel, cond.dist = "std", 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x00000000285cd0b0>
##  [data = ts.intel]
## 
## Conditional Distribution:
##  std 
## 
## Coefficient(s):
##        mu      omega     alpha1      beta1      shape  
## 0.0165075  0.0011576  0.1059030  0.8171313  6.7723503  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu     0.0165075   0.0051031    3.235 0.001217 ** 
## omega  0.0011576   0.0005782    2.002 0.045286 *  
## alpha1 0.1059030   0.0372047    2.846 0.004420 ** 
## beta1  0.8171313   0.0580141   14.085  < 2e-16 ***
## shape  6.7723503   1.8572388    3.646 0.000266 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  326.2264    normalized:  0.734744 
## 
## Description:
##  Wed May 11 16:54:54 2022 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  203.4933  0           
##  Shapiro-Wilk Test  R    W      0.9687607 3.970603e-08
##  Ljung-Box Test     R    Q(10)  7.877778  0.6407741   
##  Ljung-Box Test     R    Q(15)  15.5522   0.4124197   
##  Ljung-Box Test     R    Q(20)  16.50475  0.6848581   
##  Ljung-Box Test     R^2  Q(10)  1.066054  0.9997694   
##  Ljung-Box Test     R^2  Q(15)  11.49875  0.7165045   
##  Ljung-Box Test     R^2  Q(20)  12.61496  0.8932865   
##  LM Arch Test       R    TR^2   10.80739  0.5454935   
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -1.446966 -1.400841 -1.447215 -1.428776

模型的检验也比较满意。 模型可以写成： \[\begin{align} r_t =& 0.0165 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \epsilon_t \text{ i.i.d. } \sim t^*(6.77) \\ \sigma_t^2 =& 0.00116 + 0.1059 a_{t-1}^2 + 0.8171 \sigma_{t-1}^2 \tag{18.7} \end{align}\] 其中\(t^*\)表示标准化t分布。 AIC为\(-1.447\)， 正态分布时的AIC为\(-1.389\)， t分布结果的样本内比较占优。

模型(18.7)隐含的\(a_t\)的无条件标准差为

tmpx <- coef(mod2)
unname(sqrt(tmpx["omega"]/(1 - tmpx["alpha1"] - tmpx["beta1"])))

## [1] 0.1226399

即\(0.1226\)，样本标准差为\(0.1269\)， 正态时模型隐含的无条件标准差为\(0.1228\)， 不同分布隐含的无条件标准差基本相同。

标准化残差相对于标准化t分布的QQ图：

  plot(mod2, which=13)

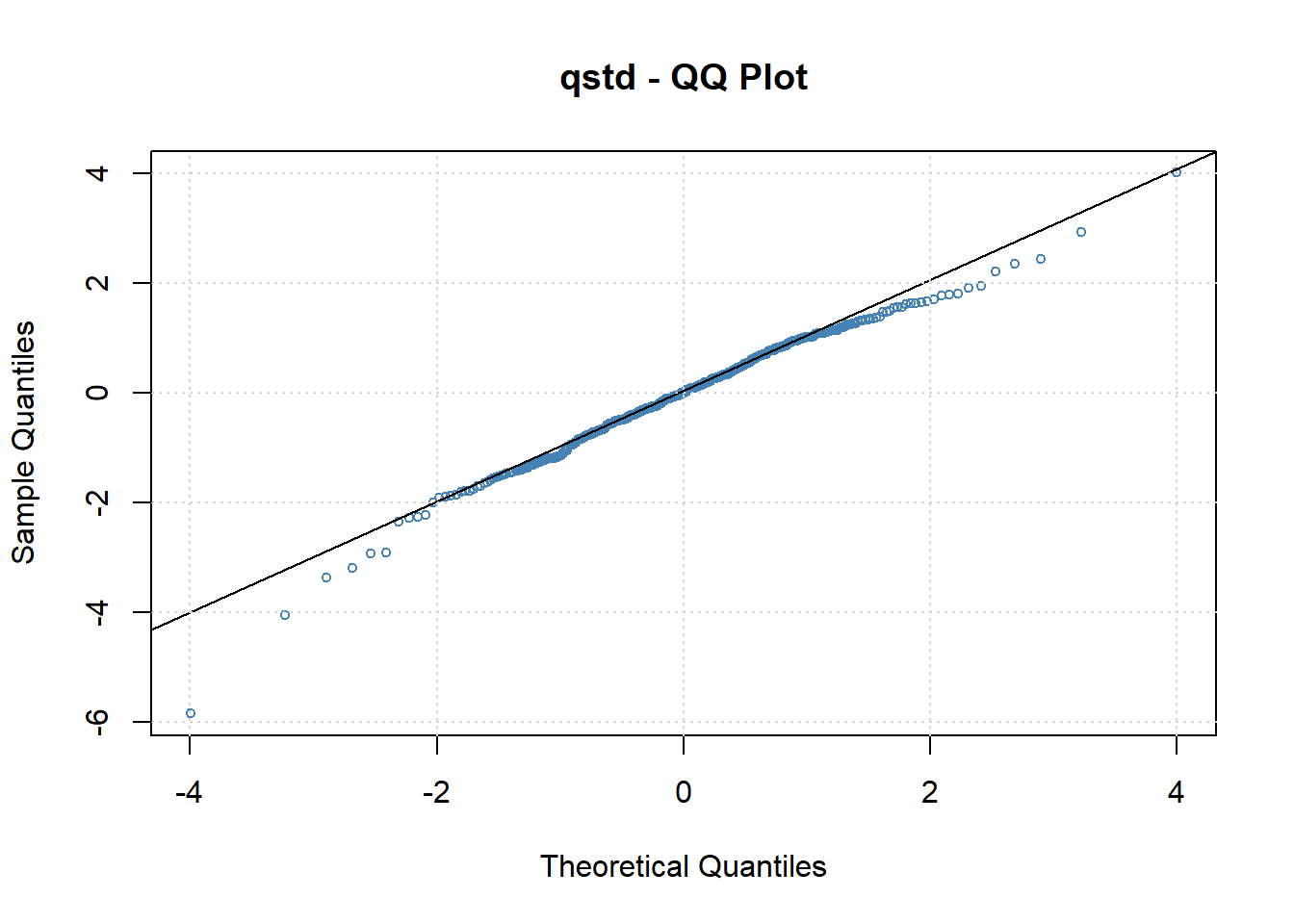
可见分布拟合不够好，仍有重尾和左偏。

18.5.4 使用条件有偏t分布

对数收益率序列\(r_t\)的样本偏度为

skewness.test <- function(x, na.rm=TRUE){
  if(na.rm) x <- x[!is.na(x)]
  z <- (x - mean(x))/sd(x)
  n <- length(x)
  sk <- n/(n-1)/(n-2) * sum(z^3)
  t.sk <- sk / sqrt(6/n)
  p.sk <- 2*(1 - pnorm(abs(t.sk)))
  c(estimate=sk, statistic=t.sk, pvalue=p.sk)
}
skewness.test(as.vector(ts.intel))

##      estimate     statistic        pvalue 
## -5.563719e-01 -4.786092e+00  1.700598e-06

偏度估计为\(-0.56\)， 偏度为零的零假设的检验p值很小， 所以收益率分布是显著左偏（负偏）的。 这样， \(\varepsilon_t\)的分布最好采用左偏的分布。

在fGarch的garchFit()中指定cond.dist="sstd"， 则条件分布为有偏的标准化t分布：

library(fGarch, quietly = TRUE)
mod3 <- garchFit(~ 1 + garch(1,1), data=ts.intel, 
  cond.dist="sstd", trace=FALSE)

## Warning: Using formula(x) is deprecated when x is a character vector of length > 1.
##   Consider formula(paste(x, collapse = " ")) instead.

summary(mod3)

## 
## Title:
##  GARCH Modelling 
## 
## Call:
##  garchFit(formula = ~1 + garch(1, 1), data = ts.intel, cond.dist = "sstd", 
##     trace = FALSE) 
## 
## Mean and Variance Equation:
##  data ~ 1 + garch(1, 1)
## <environment: 0x000000002e8fe108>
##  [data = ts.intel]
## 
## Conditional Distribution:
##  sstd 
## 
## Coefficient(s):
##        mu      omega     alpha1      beta1       skew      shape  
## 0.0133343  0.0011621  0.1049289  0.8177875  0.8717220  7.2344225  
## 
## Std. Errors:
##  based on Hessian 
## 
## Error Analysis:
##         Estimate  Std. Error  t value Pr(>|t|)    
## mu     0.0133343   0.0053430    2.496 0.012572 *  
## omega  0.0011621   0.0005587    2.080 0.037519 *  
## alpha1 0.1049289   0.0358860    2.924 0.003456 ** 
## beta1  0.8177875   0.0559863   14.607  < 2e-16 ***
## skew   0.8717220   0.0629129   13.856  < 2e-16 ***
## shape  7.2344225   2.1018042    3.442 0.000577 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Log Likelihood:
##  328.0995    normalized:  0.7389628 
## 
## Description:
##  Wed May 11 16:54:54 2022 by user: Lenovo 
## 
## 
## Standardised Residuals Tests:
##                                 Statistic p-Value     
##  Jarque-Bera Test   R    Chi^2  195.2178  0           
##  Shapiro-Wilk Test  R    W      0.9692506 4.892686e-08
##  Ljung-Box Test     R    Q(10)  7.882126  0.6403496   
##  Ljung-Box Test     R    Q(15)  15.62496  0.4074054   
##  Ljung-Box Test     R    Q(20)  16.5774   0.6802193   
##  Ljung-Box Test     R^2  Q(10)  1.078429  0.9997569   
##  Ljung-Box Test     R^2  Q(15)  11.95155  0.6826923   
##  Ljung-Box Test     R^2  Q(20)  13.03792  0.8757513   
##  LM Arch Test       R    TR^2   11.18826  0.5128574   
## 
## Information Criterion Statistics:
##       AIC       BIC       SIC      HQIC 
## -1.450899 -1.395550 -1.451257 -1.429071

模型为： \[\begin{align} r_t =& 0.0133 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \epsilon_t \text{ i.i.d. } \sim t^*_{0.87, 7.23} \\ \sigma_t^2 =& 0.00116 + 0.1049 a_{t-1}^2 + 0.8178 \sigma_{t-1}^2 \tag{18.8} \end{align}\] 其中\(t^*_{\xi,d}\)表示标准化的有偏的t分布， 偏度参数为\(\xi\)，自由度为\(d\)。

输出的检验结果表明模型充分。 AIC为\(-1.451\)， 相比对称的标准化t分布的\(-1.447\)， 和正态分布时的AIC为\(-1.389\)， 有偏t分布的AIC较优。

输出中偏度参数\(\xi\)的检验是\(H_0: \xi=0\)的检验， 但是我们需要的是\(H_0: \xi=1\)的检验。 计算\(z\)检验如下：

z <- (0.8717220 - 1) / 0.0629129
pv <- 2*(1 - pnorm(abs(z)))
c(statistic=z, pvalue=pv)

##   statistic      pvalue 
## -2.03897770  0.04145225

可以认为偏度参数\(\xi\)是显著小于1的， 模型中的条件分布是左偏的。 也可以计算估计量加减两倍标准误差作为参数的近似95%置信区间， 如 \[ 0.8717 \pm 2 \times 0.0629 \approx (0.745, 0.9975), \] 区间在1的左侧，说明在0.05水平下参数显著地小于1。

作标准化残差相对于\(t^*(0.87, 7.23)\)分布的QQ图：

plot(mod3, which=13)

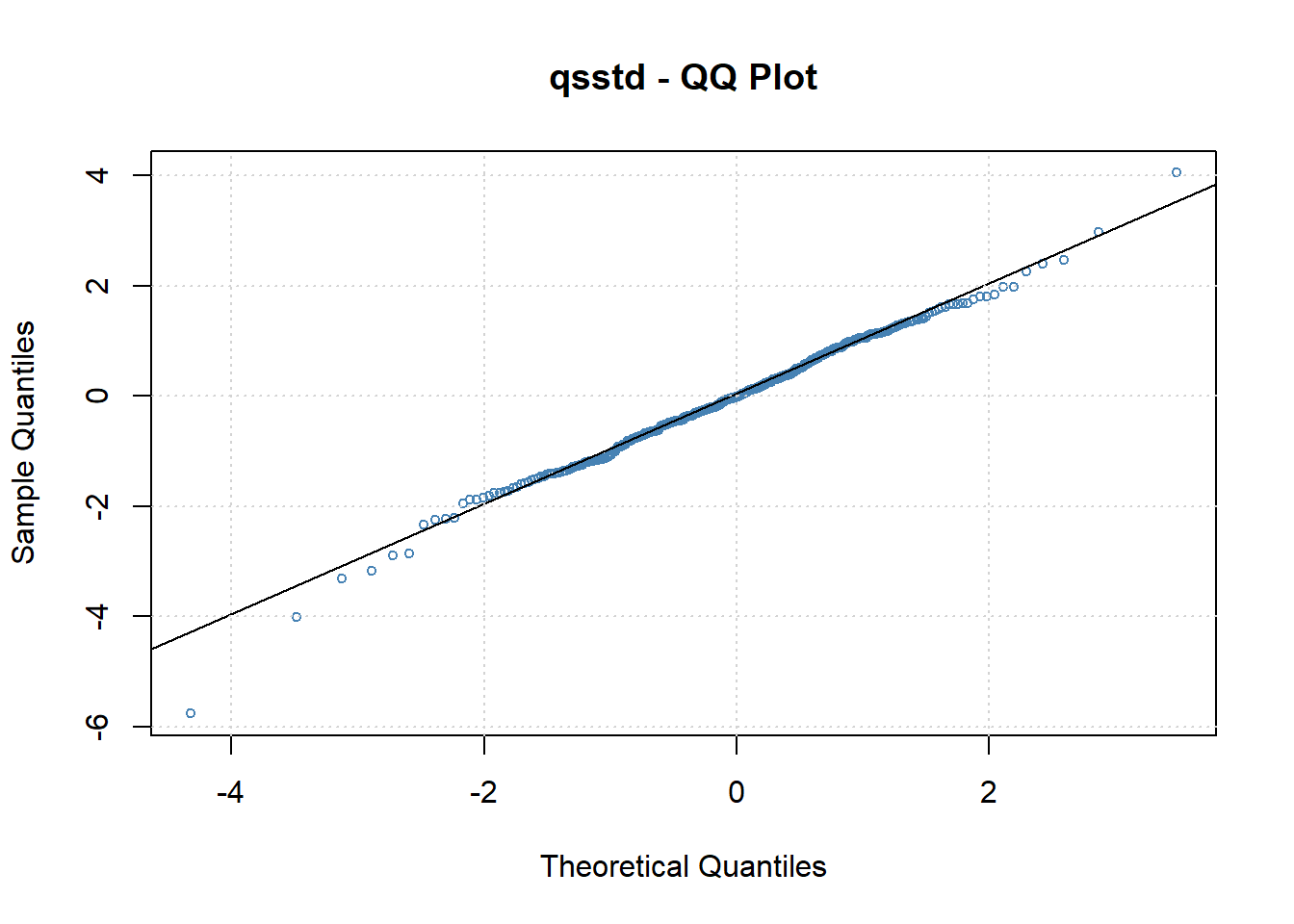
图18.7: 标准化残差在有偏t分布假设时的QQ图

从QQ图来看标准化残差比理论分布略重尾， 但左偏已经不明显， 比正态分布和标准化t分布拟合更好。

18.5.5 讨论和比较

对Intel的月对数收益率建模， 同一采用了常数均值作为均值模型， GARCH(1,1)作为波动率模型， 但采用了三种不同的条件分布：

• 正态分布;
• t分布；
• 有偏t分布。

从对\(\tilde a_t\)和\(\tilde a_t^2\)的白噪声检验来看三个模型都很好地拟合了数据。 如果采用AIC来选择， 那么有偏t分布较优。 如果采用BIC来选择， 则会选择对称t分布， 实际上BIC倾向于参数较少的模型， 而且有偏t分布拟合得到的参数\(\xi\)与1（对称时）差距并不太大。 这也说明不同的比较准则可能会选择不同的模型。

将三个模型估计的波动率绘制在同一坐标系中进行比较， 可以看到三个模型拟合的波动率基本相同：

x.intel <- as.vector(time(ts.intel))
vola1 <- volatility(mod1)
vola2 <- volatility(mod2)
vola3 <- volatility(mod3)
matplot(x.intel, cbind(vola1, vola2, vola3),
        type="l",
        lty=1, col=c("green", "blue", "red"), 
        xlab="年", ylab="波动率")
legend("top", lty=1, col=c("green", "blue", "red"), 
       legend=c("标准正态分布", "对称标准化t分布", "有偏标准化t分布"))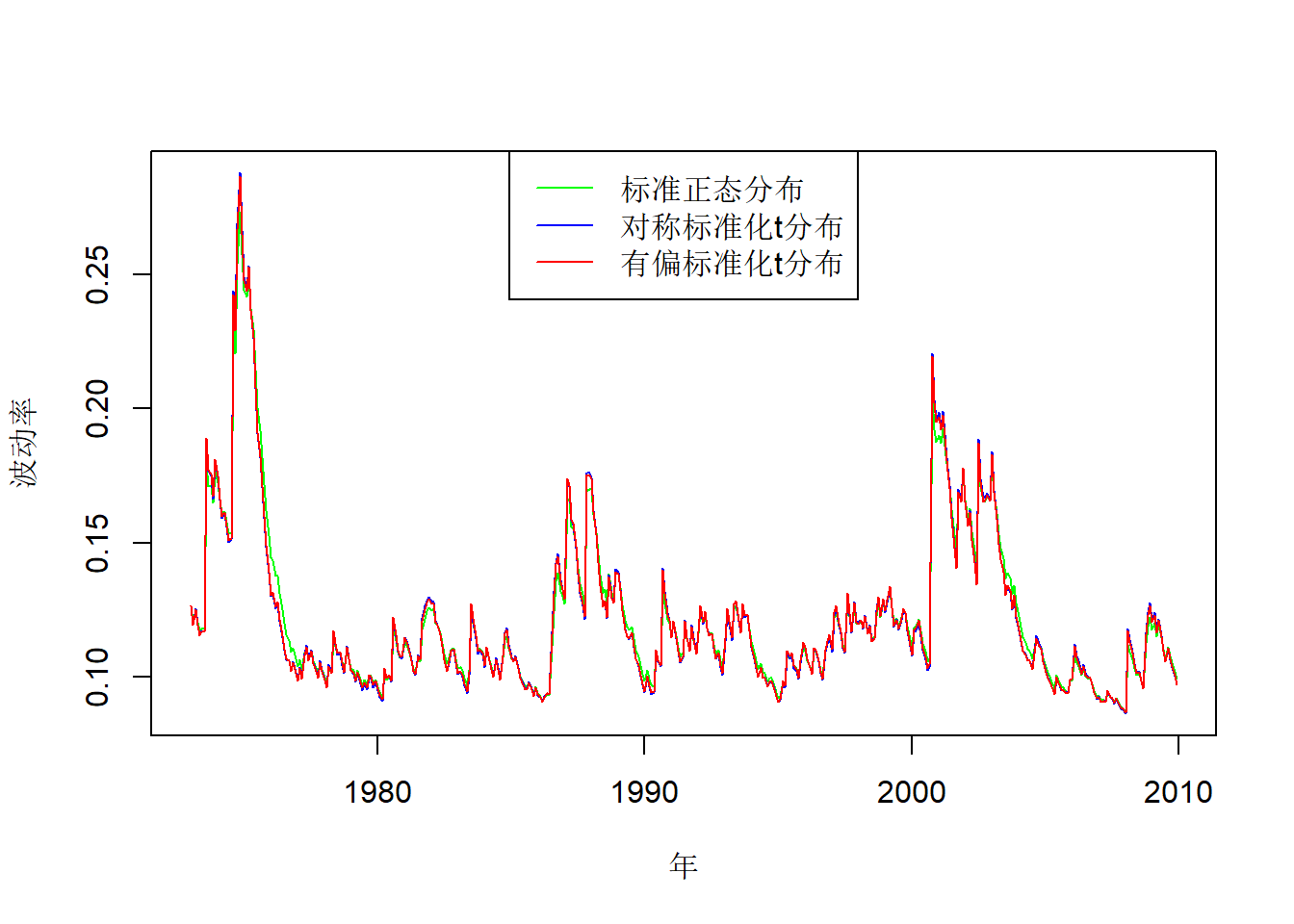

图18.8: Intel股票三种模型估计的波动率比较

下面比较三个模型的波动率超前1到12步的预测结果， 预测基于截止到2009年12月的数据：

p1 <- predict(mod1, n.ahead=12)[["standardDeviation"]]
p2 <- predict(mod2, n.ahead=12)[["standardDeviation"]]
p3 <- predict(mod3, n.ahead=12)[["standardDeviation"]]
pred.tab <- tibble(
  "预测步数"=1:12,
  "正态"=p1,
  "对称t"=p2,
  "有偏t"=p3
)
knitr::kable(pred.tab, digits=4)

预测步数	正态	对称t	有偏t
1	0.0975	0.0951	0.0955
2	0.0993	0.0975	0.0979
3	0.1009	0.0997	0.1000
4	0.1023	0.1016	0.1019
5	0.1037	0.1034	0.1037
6	0.1050	0.1050	0.1053
7	0.1061	0.1065	0.1067
8	0.1072	0.1078	0.1080
9	0.1082	0.1090	0.1092
10	0.1092	0.1101	0.1103
11	0.1100	0.1111	0.1113
12	0.1109	0.1121	0.1122

三个模型的波动率多步预报基本相同。

18.5.6 预测的评估

波动率的三种定义都不是直接可观测的， 基本都来自模型估计。 所以， 比较不同波动率模型的预测结果具有挑战性。 有人用样本外预测进行评估， 比较波动率平方的预测值\(\sigma_h^2(\ell)\)与同期的扰动值\(a^2_{h+\ell}\)， 但计算两者的相关系数一般是数值很小的。 这是因为虽然\(a_t^2\)是\(\sigma_t^2\)的无偏估计， 但仅用单个点作为估计误差太大， 没有实际意义。 有人用已实现波动率作为标准进行评估， 这就需要将已实现波动率作为真实的波动率， 也没有充分的依据。

评估的更多信息参见Anderson和Bollerslev(1998)。

18.5.7 使用rugarch包

rugarch扩展包提供了更多的GARCH变种（改进）模型的估计功能， 我们用rugarch包估计intel股票月度对数收益率的GARCH模型，使用有偏t分布：

library(rugarch)
spec1 <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE  ),
  variance.model = list(
    model = "sGARCH", # standard GARCH model
    garchOrder = c(1,1) ),
  distribution.model="sstd" ) 
mod2ru <- ugarchfit(spec = spec1, data = ts.intel)
show(mod2ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : sGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : sstd 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.013349    0.005344   2.4980 0.012491
## omega   0.001161    0.000559   2.0783 0.037684
## alpha1  0.104594    0.035883   2.9149 0.003558
## beta1   0.817922    0.056054  14.5918 0.000000
## skew    0.871842    0.062835  13.8750 0.000000
## shape   7.249880    2.107754   3.4396 0.000583
## 
## Robust Standard Errors:
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.013349    0.005724   2.3321 0.019694
## omega   0.001161    0.000508   2.2865 0.022227
## alpha1  0.104594    0.030754   3.4010 0.000671
## beta1   0.817922    0.048373  16.9088 0.000000
## skew    0.871842    0.061014  14.2891 0.000000
## shape   7.249880    1.994303   3.6353 0.000278
## 
## LogLikelihood : 328.1036 
## 
## Information Criteria
## ------------------------------------
##                     
## Akaike       -1.4509
## Bayes        -1.3956
## Shibata      -1.4513
## Hannan-Quinn -1.4291
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.5396  0.4626
## Lag[2*(p+q)+(p+q)-1][2]    0.7088  0.6032
## Lag[4*(p+q)+(p+q)-1][5]    1.8503  0.6542
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.2528  0.6151
## Lag[2*(p+q)+(p+q)-1][5]    0.3020  0.9835
## Lag[4*(p+q)+(p+q)-1][9]    0.4598  0.9988
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]  0.005877 0.500 2.000  0.9389
## ARCH Lag[5]  0.038486 1.440 1.667  0.9966
## ARCH Lag[7]  0.068421 2.315 1.543  0.9997
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.337
## Individual Statistics:              
## mu     0.15846
## omega  0.13798
## alpha1 0.10627
## beta1  0.10705
## skew   0.04290
## shape  0.06739
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.49 1.68 2.12
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value   prob sig
## Sign Bias          0.17515 0.8610    
## Negative Sign Bias 0.26118 0.7941    
## Positive Sign Bias 0.07641 0.9391    
## Joint Effect       0.09363 0.9926    
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     16.27       0.6392
## 2    30     29.78       0.4249
## 3    40     35.28       0.6403
## 4    50     52.17       0.3517
## 
## 
## Elapsed time : 0.09191203

结果与18.5.4中用fGARCH包计算的结果基本一致。 distribution.model的默认条件分布是"norm"， 即条件正态分布。

结果中包含参数估计和标准误差估计、检验， 以及稳健标准误差估计结果。 各个信息准则(Akaike, Bayes, Shibata, Hannan-Quinn)的公式为：

\[\begin{aligned} \text{AIC} =& \frac{-2 \ln L}{T} + \frac{2 (m+s)}{T}, \\ \text{BIC} =& \frac{-2 \ln L}{T} + \frac{(m+s) \ln T}{T}, \\ \text{SIC} =& \frac{-2 \ln L}{T} + \ln\frac{T + 2 (m+s)}{T}, \\ \text{HQIC} =& \frac{-2 \ln L}{T} + \frac{2(m+s) \ln\ln T}{T} . \end{aligned}\]

为了检验标准化残差和其平方是否白噪声， 使用了Fisher and Gallagher(2012)提出的加权Ljung-Box检验法， 这种方法考虑到了输入不是原始数据而是建模残差对统计量分布的影响。 结果表明标准化残差和其平方都是白噪声。 加权ARCH LM检验也是这样的对标准化残差进行的修改的ARCH效应检验。

符号偏差检验(Sign Bias Test)来自Engle and Ng(1993)，用于检验有没有杠杆效应。

修正的Pearson拟合优度检验用来检验标准化残差与假设的\(\varepsilon_t\)分布的一致性。 这里的结果是拟合充分。

Nyblom检验用来检验模型参数是否满足平稳性条件。 联合检验的统计量1.337，没有超过5%的临界值1.68， 所以结果不显著， 可以认为模型参数满足平稳性条件。

rugarch也可以用plot()函数对建模拟合结果制作各种诊断图形， 如标准化残差相对于理论分布的QQ图：

plot(mod2ru, which=9)

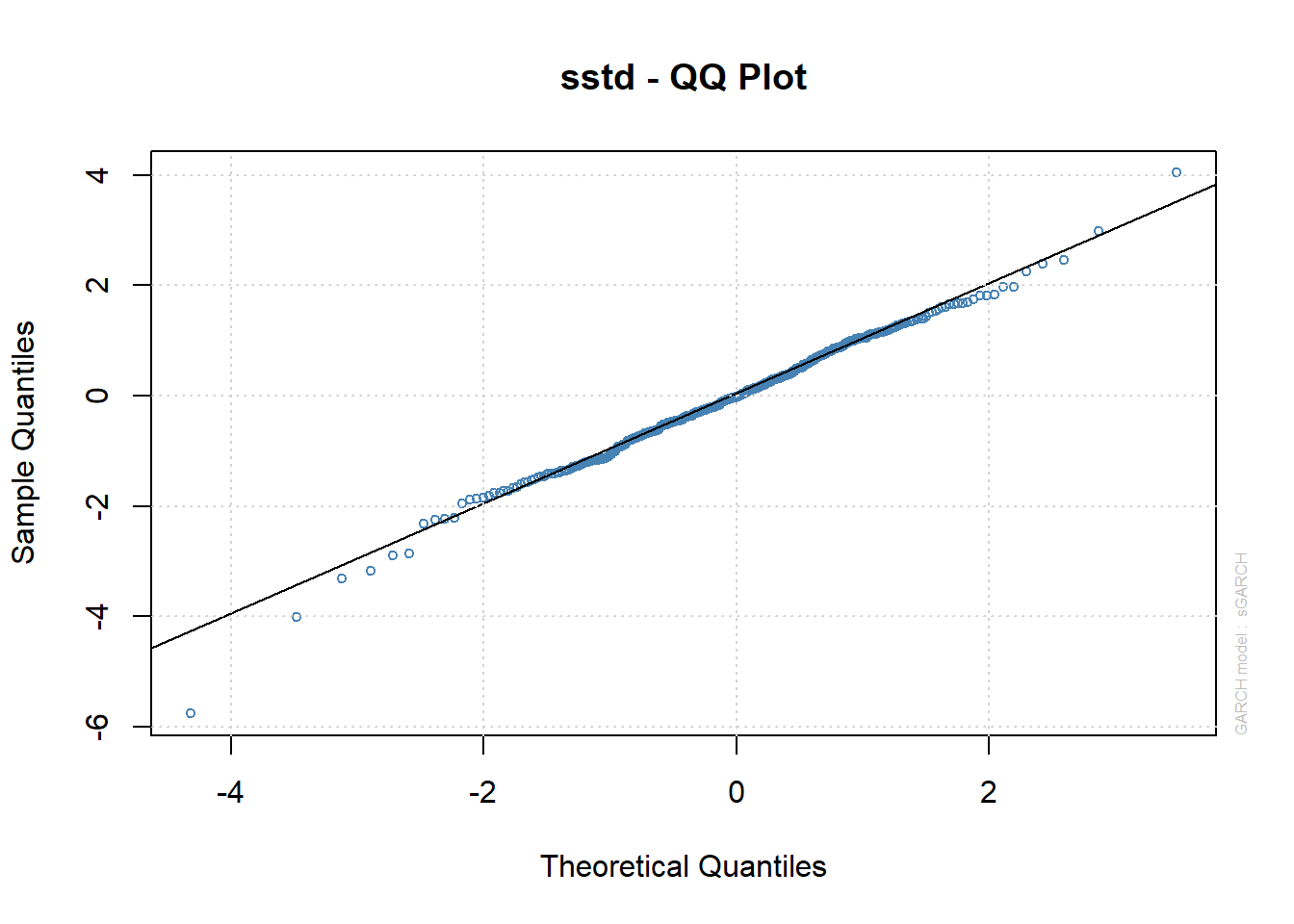
支持的作图类型包括：

1. 输入序列叠加正负两倍波动率；
2. 输入序列叠加1%的VaR限；
3. 波动率与收益率绝对值的叠加图形；
4. 输入序列的ACF图；
5. 输入序列平方的ACF图；
6. 输入序列绝对值的ACF图；
7. 输入序列和平方序列的互相关函数图；
8. 标准化残差的直方图和参数密度估计图；
9. 标准化残差相对于假设的理论分布的QQ图；
10. 标准化残差的ACF图；
11. 标准化残差平方的ACF图；
12. 不同的新息符号对波动率影响的曲线图。

18.6 两步估计法

参考(18.2)对ARMA的模仿： \[ a_t^2 = \alpha_0 + \sum_{i=1}^{\max(m,s)} (\alpha_i + \beta_i) a_{t-i}^2 + \eta_t - \sum_{j=1}^s \beta_j \eta_{t-j}, \] 提出如下的两步估计方法来估计GARCH模型。

第一，忽略ARCH效应， 用线性时间序列建模方法（如最大似然估计）对收益率序列建立均值方程。 残差序列用\(a_t\)表示。

第二， 将\(\{ a_t^2 \}\)作为观测序列， 可以用最大似然估计方法估计式(18.2)中的参数。 用\(\hat\phi_i\)和\(\hat\theta_i\)分别表示AR和MA部分的系数估计值。 则GARCH模型参数估计为 \(\hat\beta_i = -\hat\theta_i\), \(\hat\alpha_i = \hat\phi_i + \hat\theta_i\)。 这种估计方法只是一种近似， 没有理论结果证明其合理性， 但是一些经验显示这样的估计往往能够给出不错的近似结果， 尤其是大中样本情形。

例如，对Intel月对数收益率序列， 先用常数作为均值方程，计算残差\(a_t\):

hatmu <- mean(ts.intel); hatmu

## [1] 0.0143273

at <- ts.intel - hatmu
at2 <- at^2

关于\(a_t^2\)用ARMA(1,1)估计：

mod4 <- arima(at2, order=c(1,0,1)); mod4

## 
## Call:
## arima(x = at2, order = c(1, 0, 1))
## 
## Coefficients:
##          ar1      ma1  intercept
##       0.9119  -0.7915     0.0161
## s.e.  0.0430   0.0635     0.0039
## 
## sigma^2 estimated as 0.001223:  log likelihood = 858.64,  aic = -1709.28

这里\(\hat\phi_1=0.9119\), \(\hat\theta_1 = -0.7915\)， 所以\(\hat\beta_1 = 0.7915\), \(\hat\alpha_1 = 0.1204\)。 \[ \hat\alpha_0 = \hat\mu (1 - \hat\phi_1) = 0.0161(1 - 0.9919) = 0.00013 \] (注意arima()函数输出的intecept是模型均值而不是\(\phi_0\)参数)

这样的两步法得到的模型估计为： \[ r_t = 0.0143 + a_t, \quad a_t = \sigma_t \varepsilon_t, \quad \sigma_t^2 = 0.00013 + 0.1204 a_{t-1}^2 + 0.7915 \sigma_{t-1}^2 \] 与garchFit()得到的估计结果十分接近。

这样得到的误差波动率的估计为：

vola4 <- sqrt(at2 - mod4$residuals)

与有偏t分布的GARCH拟合的波动率计算相关系数：

cor(vola3, vola4)

## [1] 0.9976242

两者十分相似。

18.7 IGARCH模型

GARCH模型可以写成(18.2)这样的关于\(a_t^2\)的ARMA形式， 其中\(\eta_t = a_t^2 - \sigma_t^2\)是模型的扰动， 是鞅差白噪声： \[\begin{align} a_t^2 = \alpha_0 + \sum_{i=1}^{\max(m,s)} (\alpha_i + \beta_i) a_{t-i}^2 + \eta_t - \sum_{j=1}^s \beta_j \eta_{t-j}, \end{align}\] 如果这个模型中的AR部分有单位根（有特征根等于1）， 则对应的模型不再满足GARCH模型条件， 称为IGARCH模型，或单位根GARCH模型。 类似于ARIMA模型， IGARCH模型的扰动\(\eta_t = a_t^2 - \sigma_t^2\)对\(a_t^2\)的影响是持久的、不衰减的。

IGARCH(1,1)模型可以写成 \[ a_t = \sigma_t \varepsilon_t, \quad \sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 + (1 - \alpha_1) \sigma_{t-1}^2 . \]

Intel股票的月对数收益率建立IGARCH(1,1)模型：

library(rugarch)
speci <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE  ),
  variance.model = list(
    model = "iGARCH", # itegrated GARCH model
    garchOrder = c(1,1) ) )
mod5ru <- ugarchfit(spec = speci, data = xts.intel)
show(mod5ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : iGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.009665    0.005340   1.8100 0.070298
## omega   0.000345    0.000182   1.8990 0.057561
## alpha1  0.127533    0.033626   3.7927 0.000149
## beta1   0.872467          NA       NA       NA
## 
## Robust Standard Errors:
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.009665    0.006240   1.5488 0.121425
## omega   0.000345    0.000191   1.8060 0.070925
## alpha1  0.127533    0.031820   4.0079 0.000061
## beta1   0.872467          NA       NA       NA
## 
## LogLikelihood : 308.1861 
## 
## Information Criteria
## ------------------------------------
##                     
## Akaike       -1.3747
## Bayes        -1.3470
## Shibata      -1.3748
## Hannan-Quinn -1.3638
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.6333  0.4261
## Lag[2*(p+q)+(p+q)-1][2]    0.8602  0.5459
## Lag[4*(p+q)+(p+q)-1][5]    1.8181  0.6620
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.2326  0.6296
## Lag[2*(p+q)+(p+q)-1][5]    0.5702  0.9463
## Lag[4*(p+q)+(p+q)-1][9]    0.8666  0.9911
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]    0.1295 0.500 2.000  0.7190
## ARCH Lag[5]    0.2649 1.440 1.667  0.9495
## ARCH Lag[7]    0.3838 2.315 1.543  0.9877
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.1698
## Individual Statistics:              
## mu     0.22485
## omega  0.03416
## alpha1 0.21842
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          0.846 1.01 1.35
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value   prob sig
## Sign Bias          0.24275 0.8083    
## Negative Sign Bias 0.06684 0.9467    
## Positive Sign Bias 0.25664 0.7976    
## Joint Effect       0.10895 0.9907    
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     27.71      0.08914
## 2    30     37.08      0.14416
## 3    40     57.98      0.02571
## 4    50     59.38      0.14717
## 
## 
## Elapsed time : 0.02591205

模型为 \[\begin{aligned} r_t =& 0.009665 + a_t, \ a_t = \sigma_t \varepsilon_t, \\ \sigma_t^2 =& 0.000345 + 0.1275 a_{t-1}^2 + 0.8725 \sigma_{t-1}^2 . \end{aligned}\]

标准化残差及其平方的白噪声检验通过， 残余ARCH效应检验通过。 条件分布的拟合优度检验中有三个通过，有一个没有通过（水平0.05）。

模型的AIC=\(-1.3747\)， 使用有偏t分布的标准GARCH(1,1)的AIC=\(-1.4509\)， 不建议使用IGARCH。

18.8 GARCH-M模型

有些金融资产的收益率的条件均值受到其波动率的影响，称为风险溢价。 GARCH-M模型就是用来描述这样的现象, M表示条件均值依赖于GARCH模型。 一种简单的GARCH-M(1,1)模型为 \[\begin{align} r_t =& \mu + c \sigma_t^2 + a_t, \quad a_t = \sigma_t \varepsilon_t,\\ \sigma_t^2 =& \alpha_0 + \alpha_1 a_{t-1}^2 + \beta_1 \sigma_{t-1}^2 \tag{18.9} \end{align}\] 模型中的收益率条件均值为 \(E(r_t | F_{t-1}) = \mu + c \sigma_t^2\) 需要用条件方差\(\sigma_t^2 = \text{Var}(r_t | F_{t-1})\)描述。 参数\(c\)称为风险溢价参数, 如果\(c\)为正值则收益率与波动率正相关。

文献中还有其他的风险溢价模型形式，如 \[\begin{aligned} r_t =& \mu + c \sigma_t + a_t \\ r_t =& \mu + c \ln\sigma_t^2 + a_t \end{aligned}\]

式(18.9)中的收益率\(r_t\)不再是不相关列， 而是序列相关的， 相关性来自\(\sigma_t^2\)的序列相关性。 风险溢价的存在是股票收益率具有序列相关性的原因之一。

18.8.1 Intel股票月对数收益率的GARCH-M建模

用rugarch包估计GARCH-M模型：

library(rugarch)
specm <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE,
    archm=TRUE, archpow=2),
  variance.model = list(
    model = "sGARCH", # standard GARCH model
    garchOrder = c(1,1) ) )
mod6ru <- ugarchfit(spec = specm, data = xts.intel)
show(mod6ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : sGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error   t value Pr(>|t|)
## mu     -0.000181    0.013692 -0.013241 0.989436
## archm   0.855449    0.949115  0.901312 0.367422
## omega   0.000944    0.000392  2.409028 0.015995
## alpha1  0.087240    0.026657  3.272698 0.001065
## beta1   0.849721    0.039232 21.658619 0.000000
## 
## Robust Standard Errors:
##         Estimate  Std. Error  t value Pr(>|t|)
## mu     -0.000181    0.015260 -0.01188 0.990521
## archm   0.855449    1.097417  0.77951 0.435678
## omega   0.000944    0.000465  2.02972 0.042385
## alpha1  0.087240    0.029543  2.95293 0.003148
## beta1   0.849721    0.041844 20.30706 0.000000
## 
## LogLikelihood : 312.7599 
## 
## Information Criteria
## ------------------------------------
##                     
## Akaike       -1.3863
## Bayes        -1.3402
## Shibata      -1.3866
## Hannan-Quinn -1.3681
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.6479  0.4209
## Lag[2*(p+q)+(p+q)-1][2]    0.8671  0.5434
## Lag[4*(p+q)+(p+q)-1][5]    2.1293  0.5882
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.1373  0.7110
## Lag[2*(p+q)+(p+q)-1][5]    0.1496  0.9958
## Lag[4*(p+q)+(p+q)-1][9]    0.3173  0.9997
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3] 0.0002648 0.500 2.000  0.9870
## ARCH Lag[5] 0.0167638 1.440 1.667  0.9990
## ARCH Lag[7] 0.0530451 2.315 1.543  0.9999
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.5298
## Individual Statistics:              
## mu     0.15304
## archm  0.17085
## omega  0.07592
## alpha1 0.09511
## beta1  0.07486
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.28 1.47 1.88
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value   prob sig
## Sign Bias           0.2498 0.8028    
## Negative Sign Bias  0.4723 0.6370    
## Positive Sign Bias  0.1415 0.8875    
## Joint Effect        0.2692 0.9657    
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     17.35       0.5661
## 2    30     22.76       0.7876
## 3    40     30.77       0.8236
## 4    50     49.47       0.4544
## 
## 
## Elapsed time : 0.113569

注意输入数据没有乘以100。 其中的archm项不显著， 所以没有风险溢价效应。

18.8.2 标普500指数月超额收益率的GARCH-M建模

考虑标普500指数从1926年到1991年的月超额收益率。 共792个观测。

x.sp <- scan("sp500.txt", quiet=TRUE)*100
ts.sp <- ts(x.sp, start=c(1926,1), frequency = 12)

plot(ts.sp, main="标普500的月超额收益率(%)", xlab="年", ylab="超额收益率")

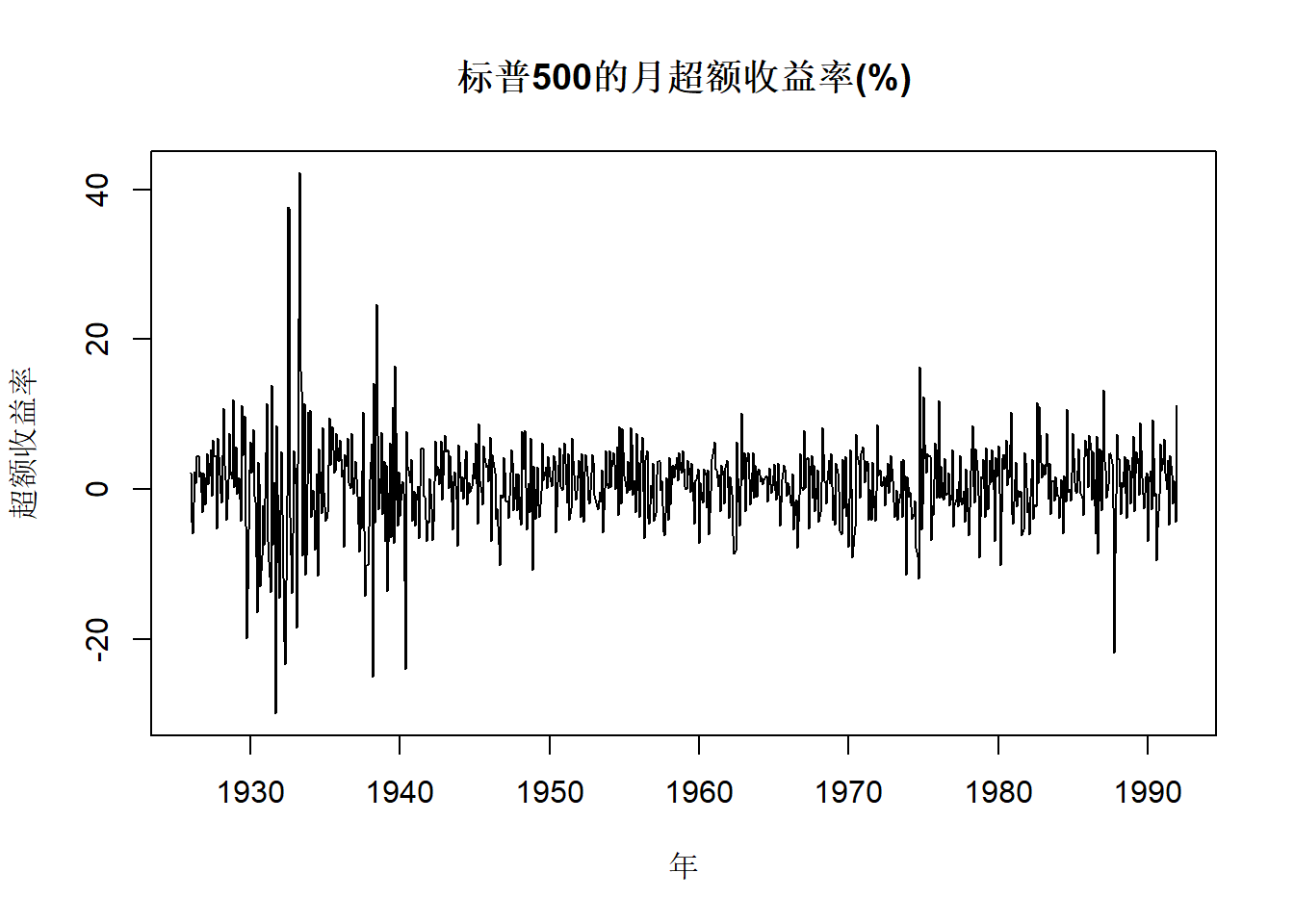
图18.9: 标普500的月超额收益率(%)

用GARCH(1,1)模型：

library(rugarch)
spec.sp1 <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE  ),
  variance.model = list(
    model = "sGARCH", # standard GARCH model
    garchOrder = c(1,1) ) ) 
mod7ru <- ugarchfit(spec = spec.sp1, data = ts.sp)
show(mod7ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : sGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error  t value Pr(>|t|)
## mu       0.74496    0.153760   4.8449 0.000001
## omega    0.80400    0.284208   2.8289 0.004671
## alpha1   0.12226    0.022102   5.5315 0.000000
## beta1    0.85434    0.021813  39.1665 0.000000
## 
## Robust Standard Errors:
##         Estimate  Std. Error  t value Pr(>|t|)
## mu       0.74496    0.171721   4.3382 0.000014
## omega    0.80400    0.336108   2.3921 0.016753
## alpha1   0.12226    0.028162   4.3413 0.000014
## beta1    0.85434    0.026423  32.3330 0.000000
## 
## LogLikelihood : -2377.839 
## 
## Information Criteria
## ------------------------------------
##                    
## Akaike       6.0147
## Bayes        6.0384
## Shibata      6.0147
## Hannan-Quinn 6.0238
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.6270  0.4284
## Lag[2*(p+q)+(p+q)-1][2]    0.6322  0.6347
## Lag[4*(p+q)+(p+q)-1][5]    2.7320  0.4582
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.6221  0.4303
## Lag[2*(p+q)+(p+q)-1][5]    1.8668  0.6502
## Lag[4*(p+q)+(p+q)-1][9]    3.6708  0.6450
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]    0.6535 0.500 2.000  0.4189
## ARCH Lag[5]    1.3390 1.440 1.667  0.6356
## ARCH Lag[7]    1.9550 2.315 1.543  0.7269
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.0291
## Individual Statistics:              
## mu     0.08927
## omega  0.20235
## alpha1 0.27140
## beta1  0.16486
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.07 1.24 1.6
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value      prob sig
## Sign Bias           3.1027 0.0019860 ***
## Negative Sign Bias  0.9191 0.3583459    
## Positive Sign Bias  0.7084 0.4788764    
## Joint Effect       17.6089 0.0005296 ***
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     30.73      0.04324
## 2    30     40.27      0.07958
## 3    40     48.40      0.14373
## 4    50     61.41      0.10989
## 
## 
## Elapsed time : 0.05299807

模型的标准化残差及其平方的白噪声检验通过， 正态性假设中有一个没有通过。 得到的模型为 \[\begin{aligned} 100 r_t =& 0.7450 + a_t, \quad a_t = \sigma_t \varepsilon_t, \\ \sigma_t^2 =& 0.8040 + 0.1223 a_{t-1}^2 + 0.8543 \sigma_{t-1}^2 . \end{aligned}\] 模型很接近IGARCH条件。

尝试对标普500超额收益率拟合GARCH-M(1,1)模型：

library(rugarch)
spec.sp2 <- ugarchspec(
  mean.model = list(
    armaOrder=c(0,0),
    include.mean=TRUE,
    archm=TRUE, archpow=2),
  variance.model = list(
    model = "sGARCH", # standard GARCH model
    garchOrder = c(1,1) ) )
mod8ru <- ugarchfit(spec = spec.sp2, data = ts.sp)
show(mod8ru)

## 
## *---------------------------------*
## *          GARCH Model Fit        *
## *---------------------------------*
## 
## Conditional Variance Dynamics    
## -----------------------------------
## GARCH Model  : sGARCH(1,1)
## Mean Model   : ARFIMA(0,0,0)
## Distribution : norm 
## 
## Optimal Parameters
## ------------------------------------
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.542048    0.236018   2.2966 0.021639
## archm   0.010081    0.008885   1.1346 0.256536
## omega   0.829648    0.293212   2.8295 0.004662
## alpha1  0.123124    0.022286   5.5247 0.000000
## beta1   0.852261    0.022400  38.0479 0.000000
## 
## Robust Standard Errors:
##         Estimate  Std. Error  t value Pr(>|t|)
## mu      0.542048    0.243967   2.2218 0.026296
## archm   0.010081    0.008913   1.1311 0.258024
## omega   0.829648    0.347874   2.3849 0.017083
## alpha1  0.123124    0.027802   4.4286 0.000009
## beta1   0.852261    0.027061  31.4946 0.000000
## 
## LogLikelihood : -2377.192 
## 
## Information Criteria
## ------------------------------------
##                    
## Akaike       6.0156
## Bayes        6.0451
## Shibata      6.0156
## Hannan-Quinn 6.0270
## 
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.7246  0.3946
## Lag[2*(p+q)+(p+q)-1][2]    0.7501  0.5869
## Lag[4*(p+q)+(p+q)-1][5]    3.0243  0.4026
## d.o.f=0
## H0 : No serial correlation
## 
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
##                         statistic p-value
## Lag[1]                     0.7589  0.3837
## Lag[2*(p+q)+(p+q)-1][5]    1.8690  0.6497
## Lag[4*(p+q)+(p+q)-1][9]    3.4842  0.6771
## d.o.f=2
## 
## Weighted ARCH LM Tests
## ------------------------------------
##             Statistic Shape Scale P-Value
## ARCH Lag[3]    0.5048 0.500 2.000  0.4774
## ARCH Lag[5]    1.0892 1.440 1.667  0.7066
## ARCH Lag[7]    1.6862 2.315 1.543  0.7833
## 
## Nyblom stability test
## ------------------------------------
## Joint Statistic:  1.327
## Individual Statistics:              
## mu     0.06463
## archm  0.03109
## omega  0.21419
## alpha1 0.26216
## beta1  0.16482
## 
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic:          1.28 1.47 1.88
## Individual Statistic:     0.35 0.47 0.75
## 
## Sign Bias Test
## ------------------------------------
##                    t-value      prob sig
## Sign Bias           3.5833 3.601e-04 ***
## Negative Sign Bias  1.1596 2.466e-01    
## Positive Sign Bias  0.6211 5.347e-01    
## Joint Effect       22.1805 5.983e-05 ***
## 
## 
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
##   group statistic p-value(g-1)
## 1    20     23.86      0.20163
## 2    30     41.11      0.06741
## 3    40     40.63      0.39861
## 4    50     56.86      0.20554
## 
## 
## Elapsed time : 0.1140001

拟合的模型为： \[\begin{aligned} \mu_t =& 0.54 + 0.010 \sigma_t^2 + a_t, \quad a_t = \sigma_t \varepsilon_t ,\\ \sigma_t^2 =& 0.83 + 0.12 a_{t-1}^2 + 0.85 \sigma_{t-1}^2 . \end{aligned}\] 其中\(c=0.010\)不显著， 说明标普500的月超额收益率不存在GARCH-M现象， 没有风险溢价。 从AIC比较来看， 标准GARCH模型的AIC更低。

B 参考文献

Bollerslev, T. 1986. “Generalized Autoregressive Conditional Heterskedastici.” Journal of Econom. 31: 307–27.

———. 2013. 金融数据分析导论：基于R语言. 机械工业出版社.