8 季节模型
经济和金融中的月度、季度数据一般有明显的周期, 日数据也会有按照周、月、年周期的变化。 这样的性质称为季节性, 含有周期变化的时间序列称为季节时间序列。
如:可口可乐公司1983第1季度到2009第3季度公布的季度盈利数据。 每个季度的盈利数据在季度结束后约一个月以后公布。 共107个观测。 考虑季度盈利的对数值。
da <- read_table(
"q-ko-earns8309.txt",
col_types=cols(pends=col_date("%Y%m%d"),
anntime=col_date("%Y%m%d"),
value = col_double()))
xts.koqtr <- xts(da[["value"]], ymd(da[["pends"]]))
ko <- ts(log(da[["value"]]), start=c(1983,1), frequency=4)注:原始的q-ko-earns8309.txt第一行末尾有一个多余的空格,
会使得read_table()函数认为还有第4列。
已人为删除此空格。
read_table()函数应添加自动删除行首和行尾空格的功能。
季度盈利的对数值序列图:
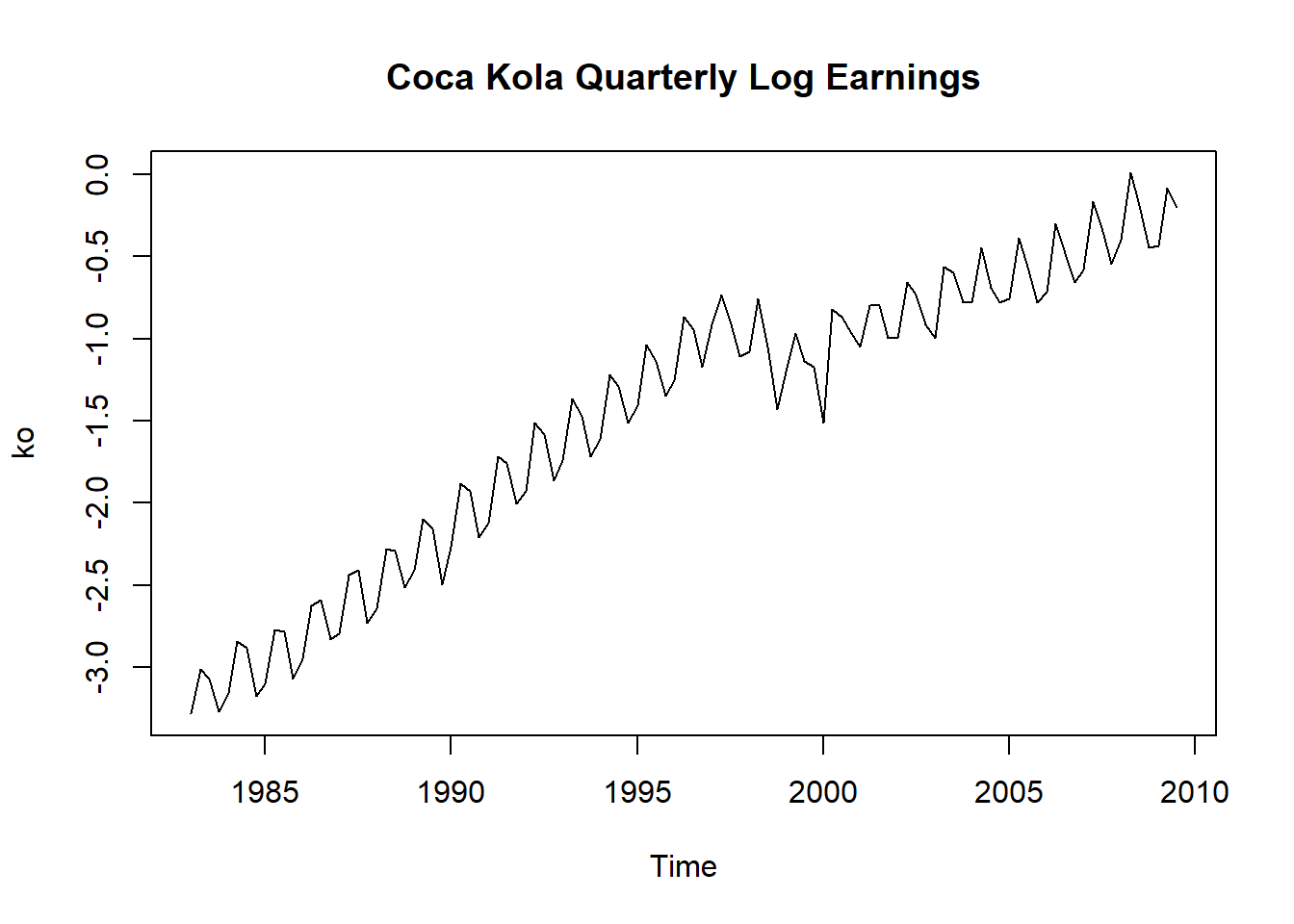
图8.1: 可口可乐公司季度盈利对数值
图8.1序列呈现出明显的周期为4的波动。 如果是月度数据,周期为12。 盈利做了对数变换, 其中一个理由是消除指数增长(倍数增长)现象, 对数变化可以将指数增长变成线性增长。
农产品等与天气有关的衍生产品定价、能源期货定阶等与天气有关的金融产品研究中, 季节性是重要的考虑因素。
经济研究中有时希望排除季节性影响, 用某种方法去掉季节性的序列称为季节调整序列(seasonally adjusted series), 如美国季节调整的GNP序列。 X12-ARIMA是一个成熟的季节调整方法。
季节因素的建模, 也包括动态模型(类似于随机游动)和非随机模型(类似于固定线性趋势模型)。
8.1 季节差分
考虑可口可乐公司每股季度盈利对数值序列, 记为\(\{x_t\}\),见图8.1。 因为图形呈现出线性增长,明显是不平稳的, 所以考虑其一阶差分:
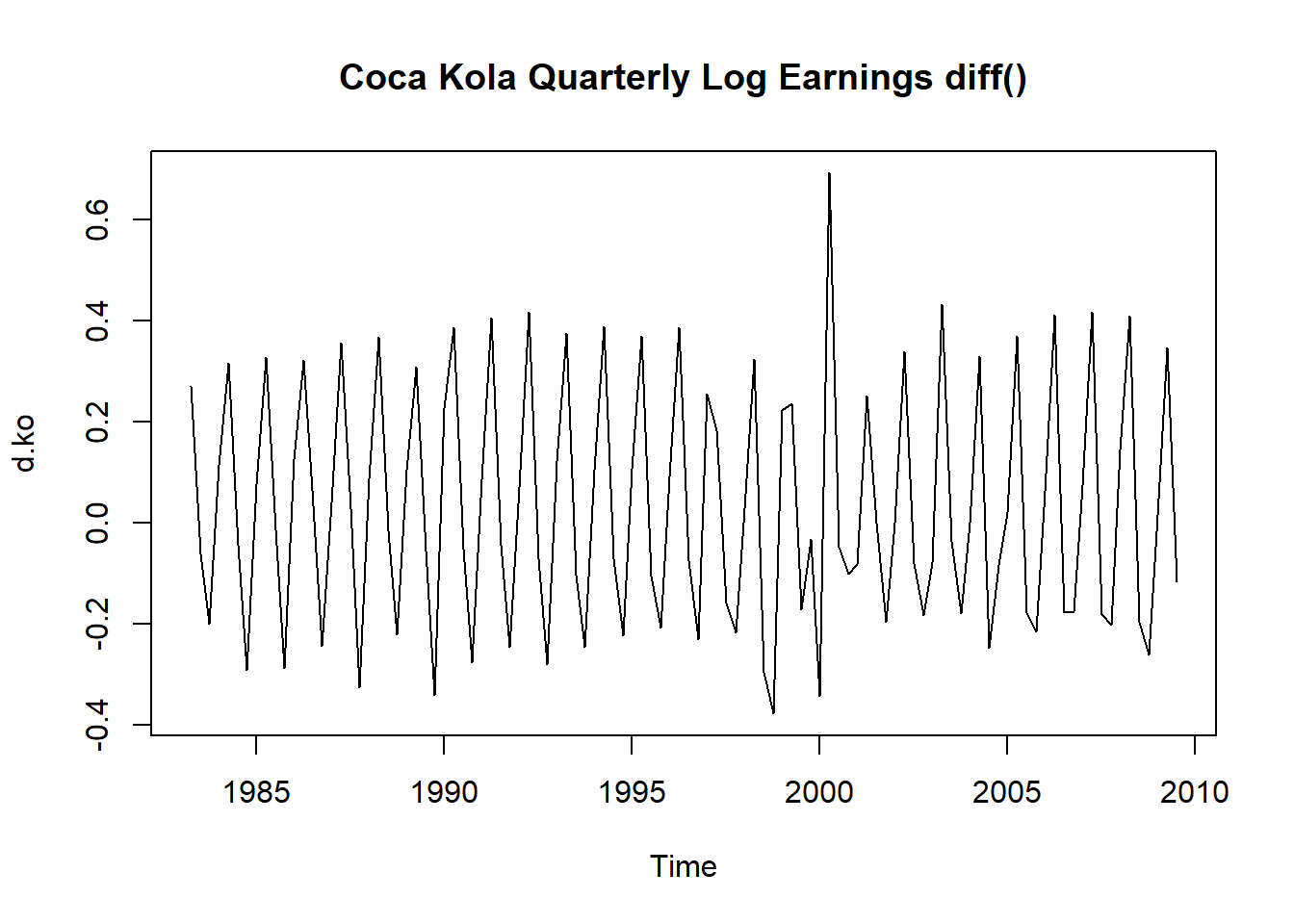
图8.2: 可口可乐公司季度盈利对数值一阶差分
一阶差分后,消除了线性增长趋势, 但是还有明显的季节性, 这往往也是不平稳的表现, 看其ACF:
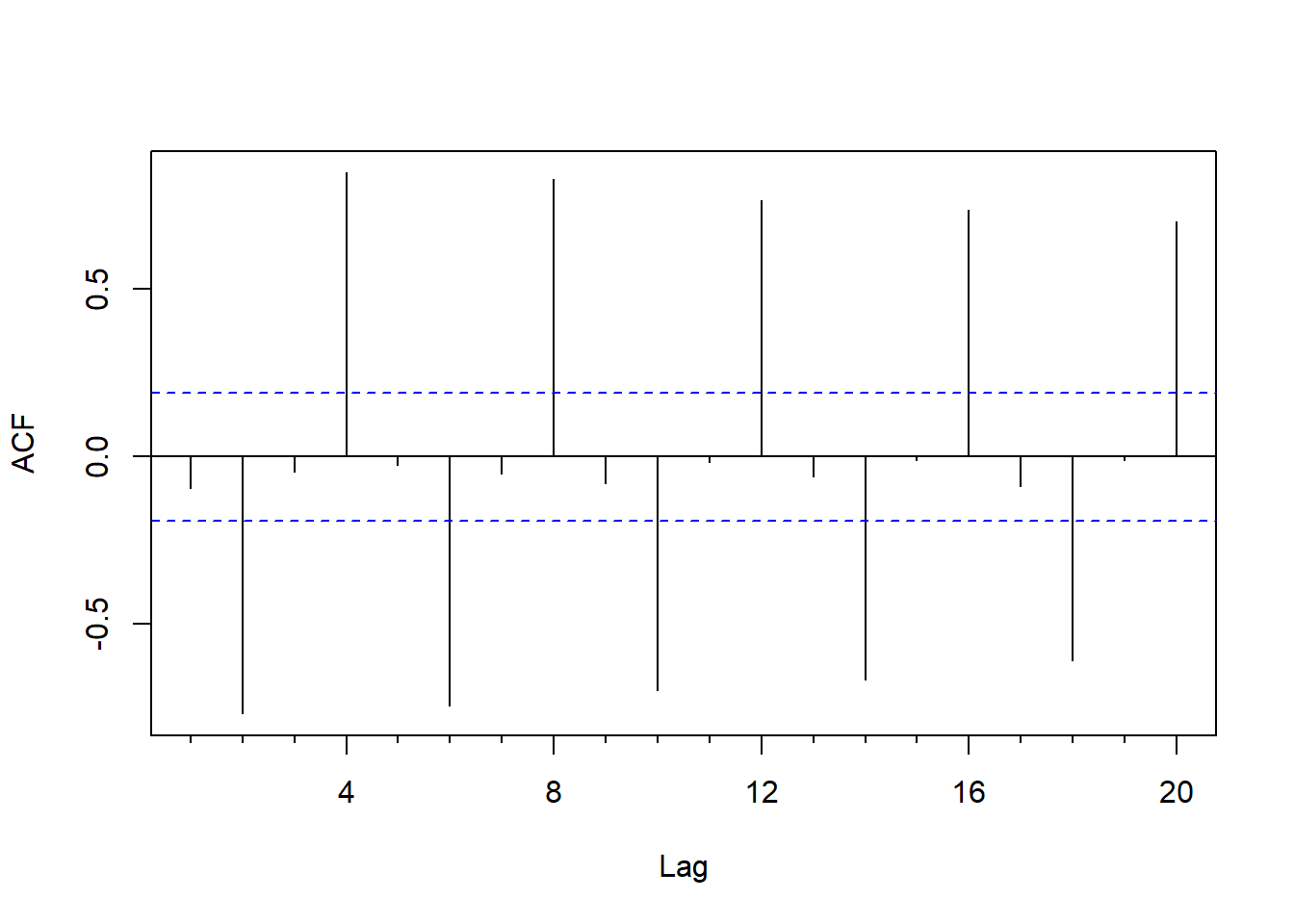
图8.3: 可口可乐公司季度盈利对数值一阶差分的ACF
一阶差分的ACF衰减速度很慢, 不适于用低阶的ARMA建模。 一般ARMA序列应该是ACF衰减速度很快的。
消除季节性影响的方法是,
第二年第一季度值减去第一年第一季度值,
第二年第二季度值减去第一年第二季度值,
第二年第三季度值减去第一年第三季度值,
第二年第四季度值减去第一年第四季度值。
有些类似于经济数据中指标的“同比”的概念。
这称为季节差分,实际是计算\((1 - B^4) x_t = x_t - x_{t-4}\),
R中用diff(x, lag=4)计算这样的季节差分。
例如:
## Qtr1 Qtr2 Qtr3 Qtr4
## 1983 -3.283414 -3.011862 -3.072613 -3.272804
## 1984 -3.158251 -2.842153 -2.885981 -3.177254
## 1985 -3.101093 -2.772589 -2.785471 -3.072613## Qtr1 Qtr2 Qtr3 Qtr4
## 1984 0.12516314 0.16970847 0.18663191 0.09555002
## 1985 0.05715841 0.06956446 0.10051006 0.10464083对数盈利季节差分后的序列:

季节差分序列的ACF:

可以看出仅进行季节差分, 结果序列已经基本平稳, 这是因为季节差分也有消除趋势的功能, 比如设\(x_t = a + b t\), 则\((1 - B^4) x_t = 4b\), 季节差分消除了趋势。 对这个数据, 有可能不需要既进行普通差分又进行季节差分。
我们先试验一下同时进行两种差分的效果。 先做一阶差分\((1-B)x_t\), 然后再做一阶季度差分\((1-B^4)(1-B)x_t=x_t - x_{t-1} - x_{t-4} + x_{t-5}\), 得到新的序列\(\{ y_t \}\):
## Time-Series [1:102] from 1984 to 2010: 0.0445 0.0169 -0.0911 -0.0384 0.0124 ...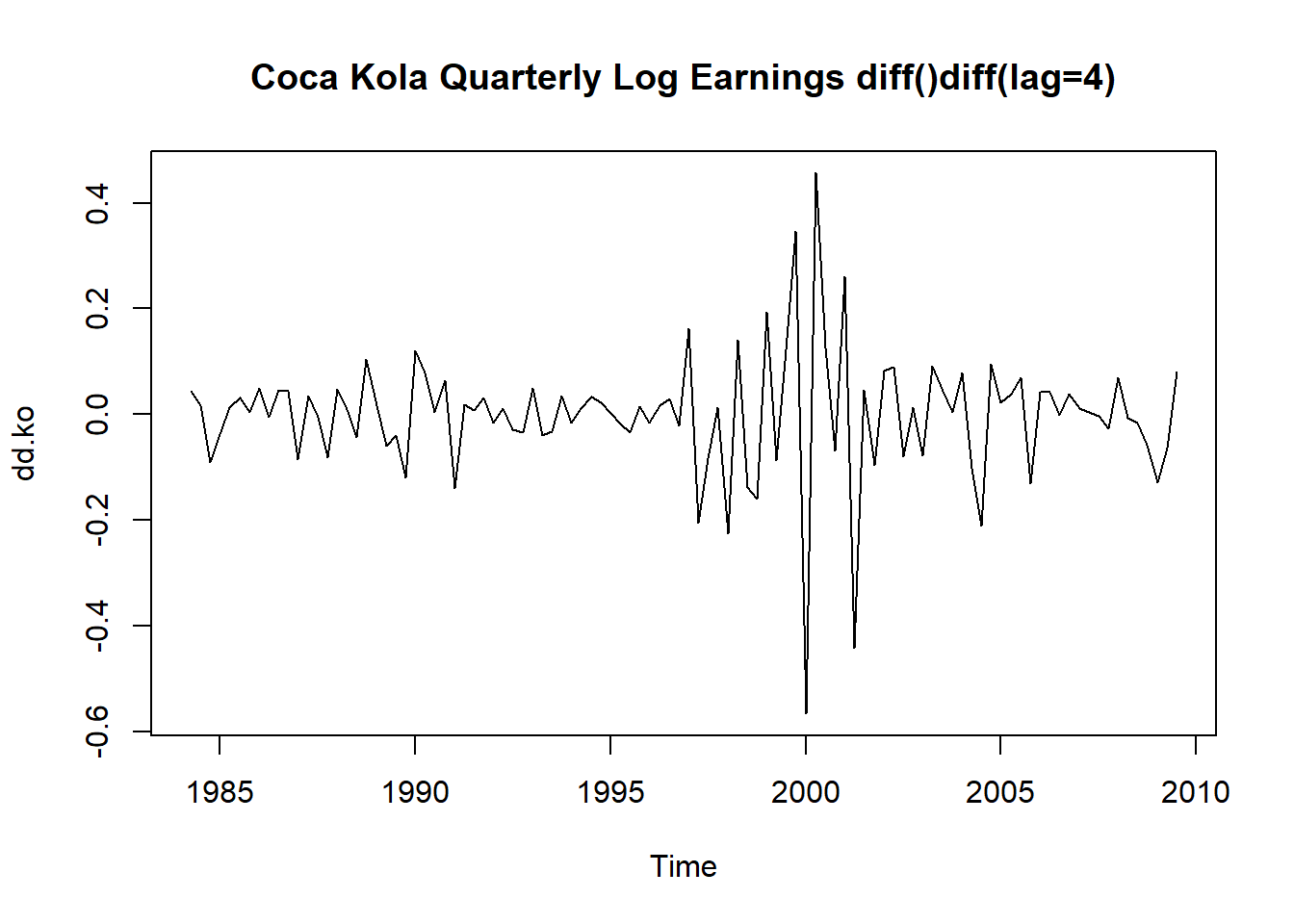
图8.4: 可口可乐公司季度盈利对数值一阶差分和一阶季节差分后的序列
因为需要用到\(x_{t-5}\),所以变换后的序列从原来的第6个观测开始。 从序列图形看已经消除了线性趋势与大部分季节波动。
查看一阶差分与一阶季度差分后的序列的ACF:
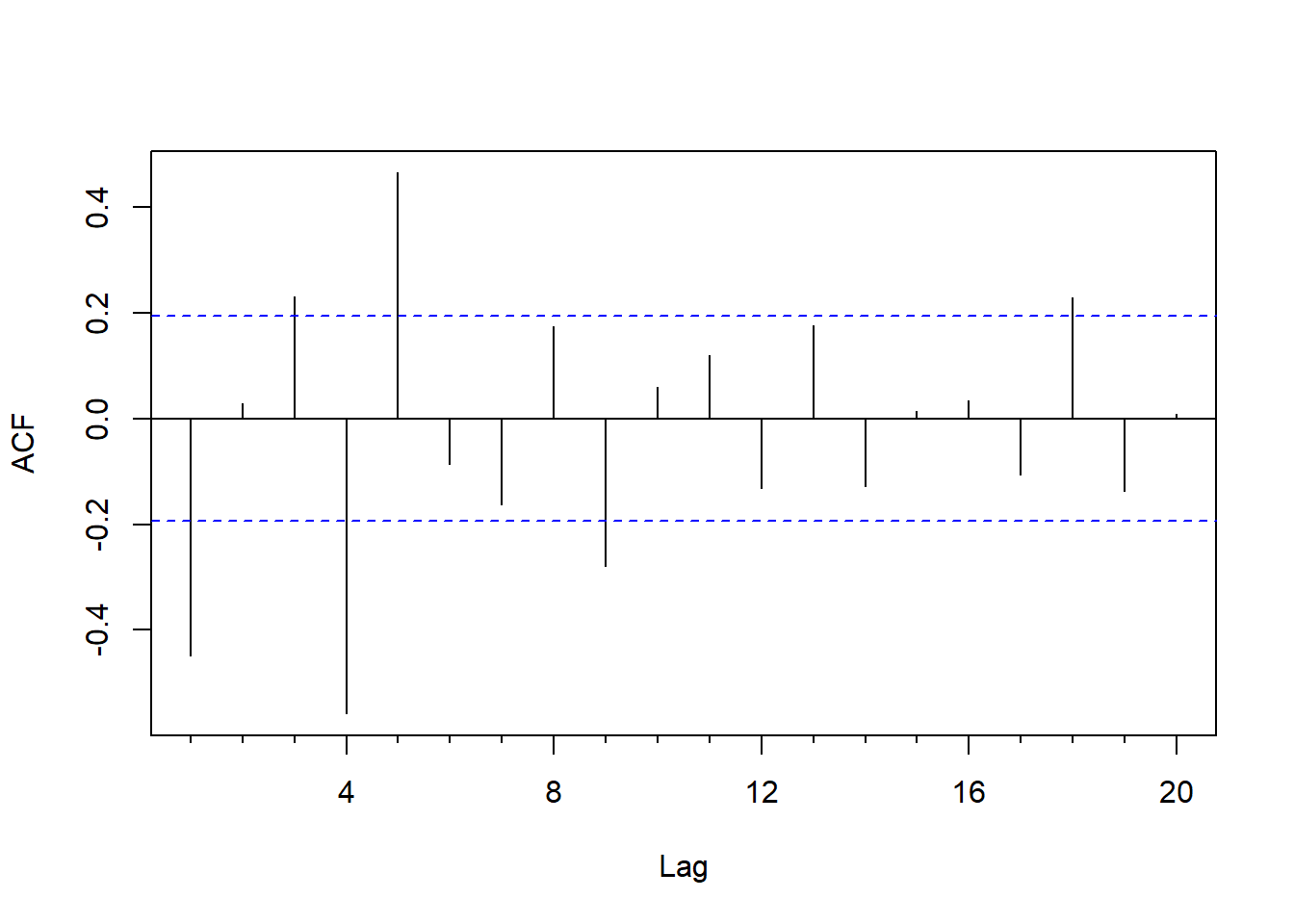
图8.5: 可口可乐公司季度盈利对数值一阶差分和一阶季节差分的ACF
注意ACF则滞后1和滞后4(滞后4对应季节波动)都是显著的负值, 这与一阶差分和季度差分有关, 预示作两种差分有可能是不适当的。 ACF在滞后5也是显著的正值, 部分理由是\((1-B^4)(1-B)\)中包含\(B^5\)项。 这些ACF表现是许多经过一阶差分和季节差分的序列共同的特征。
我们决定仅做季节差分, 不做普通差分。 季节差分序列的PACF图:
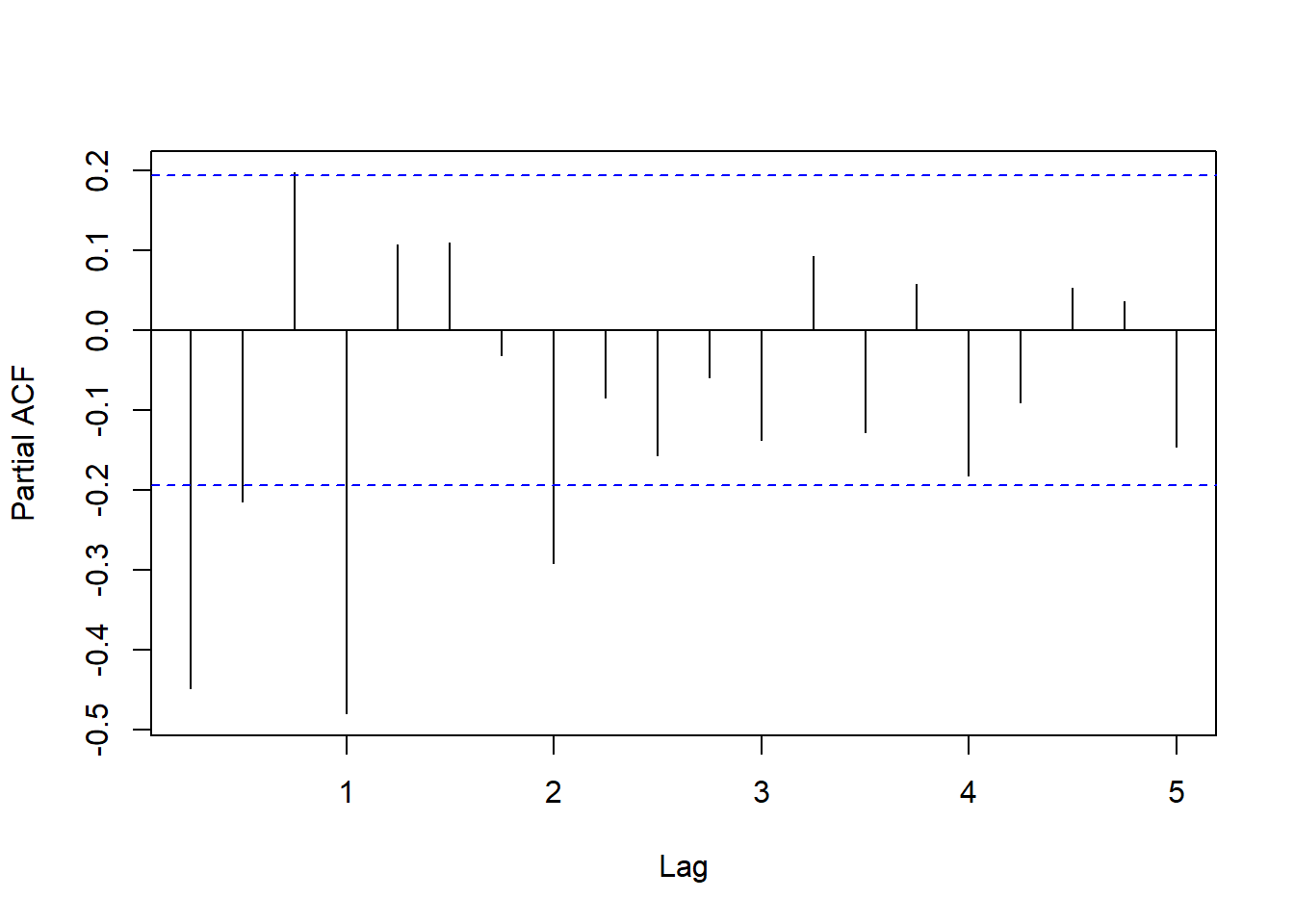
图8.6: 可口可乐公司季度盈利对数值一阶差分和一阶季节差分的PACF
可以考虑5阶的AR, 或者使用乘性季节模型。
8.2 乘性季节模型
季节性的时间序列如果进行了一阶差分和季节差分, 结果序列常常滞后1、4、5这些位置呈现出自相关 (如果是月度数据,则为滞后1、12、13)。 为此,对差分后序列建立MA序列,这样,\(\{x_t \}\)的模型为 \[\begin{equation} (1-B)(1 - B^s) x_t = (1 - \theta B)(1 - \Theta B^s) \varepsilon_t . \tag{8.1} \end{equation}\] 其中\(s\)是周期,对上面的季度数据\(s=4\)。 这个模型称为航空模型, 最早用在分析航空乘客数月度数据当中。 更复杂的数据可以增加一个\(B^{2s}\)项。
如果仅进行季节差分, 其ACF也有可能在滞后4(对季度数据)呈现自相关, PACF在滞后4呈现偏自相关。 所以可以在MA部分使用\(1 - \Theta B^s\)这样的乘性因子, 在AR部分使用\(1 - \Phi B^s\)这样的乘性因子。 如 \[\begin{equation} (1 - B^s) (1 - \Phi B^s) x_t = (1 - \theta B)(1 - \Theta B^s) \varepsilon_t . \tag{8.2} \end{equation}\]
在arima()函数中,
可以用seasonal=指定季节模型,
包括季节AR阶、季节差分阶、季节MA阶以及周期。
如
## Series: ko
## ARIMA(1,0,1)(1,1,1)[4]
##
## Coefficients:
## ar1 ma1 sar1 sma1
## 0.9978 -0.4272 0.1105 -0.8620
## s.e. 0.0039 0.0882 0.1267 0.0806
##
## sigma^2 = 0.007447: log likelihood = 105.44
## AIC=-200.87 AICc=-200.25 BIC=-187.7其中的sar1项不显著,简化模型为:
## Series: ko
## ARIMA(1,0,1)(0,1,1)[4]
##
## Coefficients:
## ar1 ma1 sma1
## 0.9967 -0.4076 -0.8158
## s.e. 0.0052 0.0872 0.0783
##
## sigma^2 = 0.007448: log likelihood = 105.06
## AIC=-202.13 AICc=-201.72 BIC=-191.59考虑航空模型:
## Series: ko
## ARIMA(0,1,1)(0,1,1)[4]
##
## Coefficients:
## ma1 sma1
## -0.4096 -0.8203
## s.e. 0.0866 0.0743
##
## sigma^2 = 0.007386: log likelihood = 104.25
## AIC=-202.5 AICc=-202.26 BIC=-194.63从resm2和resm3的AIC值来看,
两者效果相近,
但resm3略占优,
所以我们选用航空模型的结果。
结果模型为
\[
(1-B)(1-B^4) x_t
= (1 - 0.4096 B)(1 - 0.8203 B^4) \varepsilon_t .
\]
\(\hat\sigma^2 = 0.00724\)。
注意arima()函数给出的MA多项式是\(1 + \theta_1 B + \dots + \theta_q B^q\)形式的。
对模型残差做LB白噪声检验:
##
## Box-Pierce test
##
## data: resm3$residuals
## X-squared = 12.233, df = 10, p-value = 0.2698结果不显著,表示承认模型合适。
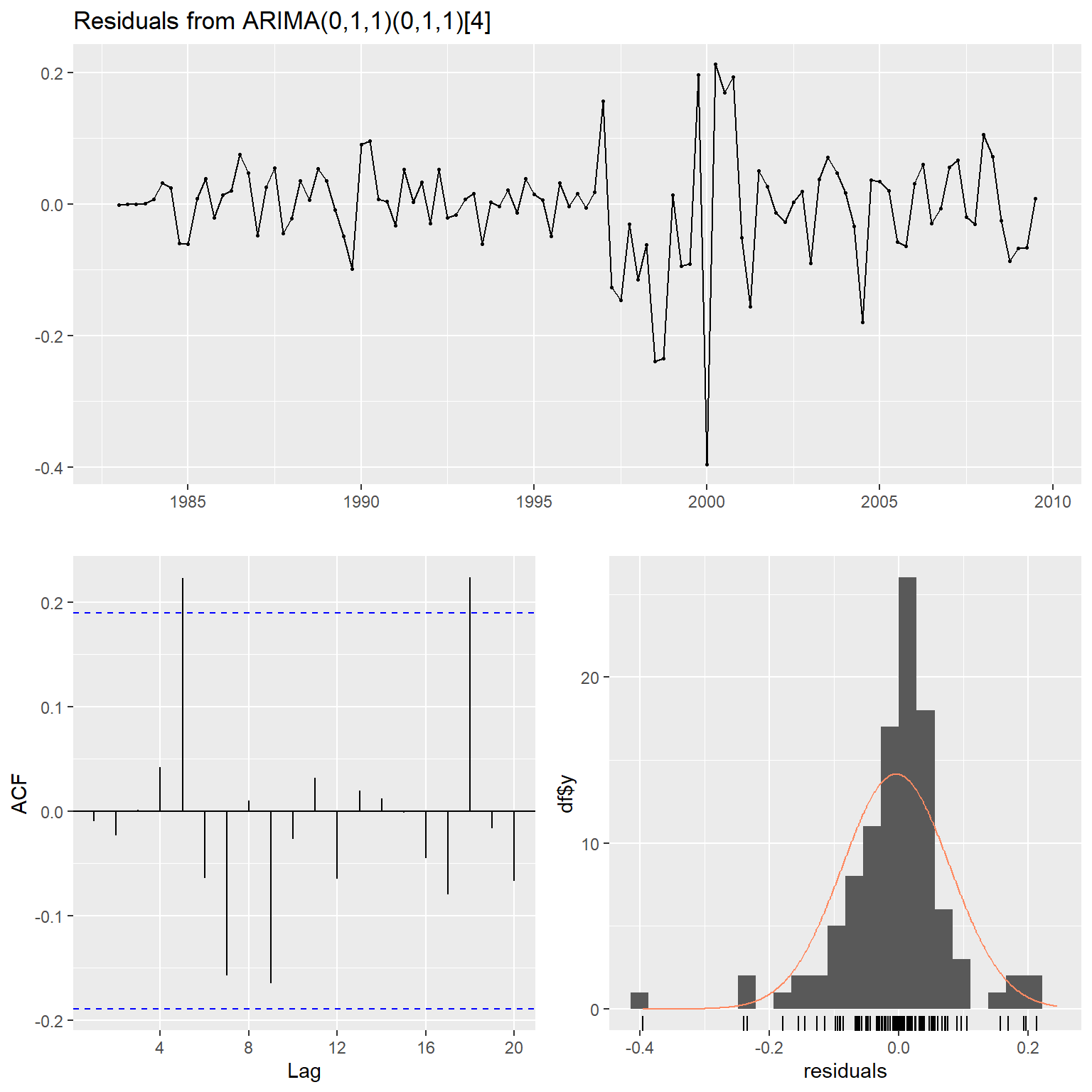
可以用forecast包的checkresiduals()函数对残差进行诊断分析,如:
##
## Ljung-Box test
##
## data: Residuals from ARIMA(0,1,1)(0,1,1)[4]
## Q* = 9.3484, df = 6, p-value = 0.1549
##
## Model df: 2. Total lags used: 8诊断图中的第一个图是残差; 第二个图是残差的ACF,应该落入两条水平线之间; 第三个图是残差直方图叠加正态密度估计。 结果包括残差的LB白噪声检验, 可以用lag指定要检验的自相关系数个数, 用df指定零假设下检验统计量服从的卡方分布的自由度参数。 上面的结果利用了缺省设置, 检验了8个自相关函数值, 模型估计用掉了2个自由度, 残差白噪声检验的卡方统计量取为6个自由度。
下面用航空模型做超前多步预报。 用1983年到2007年这25年的100个观测值建模, 对剩余的7个值作超前多步预报:
tmp.y <- window(ko, start=start(ko), end=c(2007,4))
resm4 <- forecast::Arima(
tmp.y, order=c(0,1,1),
seasonal=list(order=c(0,1,1), period=4))
resm4## Series: tmp.y
## ARIMA(0,1,1)(0,1,1)[4]
##
## Coefficients:
## ma1 sma1
## -0.4209 -0.8099
## s.e. 0.0874 0.0767
##
## sigma^2 = 0.007593: log likelihood = 95.78
## AIC=-185.57 AICc=-185.3 BIC=-177.91## Observed Predicted SE
## 2008 Q1 -0.400477567 -0.5060620 0.08713799
## 2008 Q2 0.009950331 -0.1237792 0.10069359
## 2008 Q3 -0.186329578 -0.2669296 0.11262934
## 2008 Q4 -0.446287103 -0.4501580 0.12341611
## 2009 Q1 -0.430782916 -0.4219704 0.14044044
## 2009 Q2 -0.083381609 -0.0396876 0.15274016
## 2009 Q3 -0.198450939 -0.1828380 0.16412067也可以使用forecast包的forecast函数预测,
输出预测值和\(80\%\)、\(95\%\)预测区间,如:
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 2008 Q1 -0.5060620 -0.6177339 -0.394390208 -0.6768494 -0.33527471
## 2008 Q2 -0.1237792 -0.2528233 0.005264784 -0.3211350 0.07357656
## 2008 Q3 -0.2669296 -0.4112699 -0.122589325 -0.4876791 -0.04618018
## 2008 Q4 -0.4501580 -0.6083221 -0.291993895 -0.6920491 -0.20826687
## 2009 Q1 -0.4219704 -0.6019521 -0.241988726 -0.6972286 -0.14671218
## 2009 Q2 -0.0396876 -0.2354320 0.156056789 -0.3390528 0.25967761
## 2009 Q3 -0.1828380 -0.3931671 0.027491113 -0.5045086 0.13883261这是关于每股盈利对数值的预测。
forecast包的autoplot可以对forecast函数的预测结果作图,
但还是在对数尺度上作图。如:

这是每股季度盈利的对数值的预测。 但是,如何得到每股季度盈利的预测,而非其对数值的预测? 为了得到无偏估计, 需要利用对数正态分布的性质进行期望校正。 如果随机变量\(\ln Y \sim \text{N}(\mu, \sigma^2)\), 则\(E Y = \exp(\mu + \frac12 \sigma^2)\), \(\text{Var}(Y)= \exp(2\mu+\sigma^2)(e^{\sigma^2}-1)\)。
写成R函数:
lognorm_adjust <- function(pred_list){
pred <- pred_list$pred
se <- pred_list$se
xnew <- exp(pred + 0.5*se^2)
senew <- sqrt(exp(2*pred + se^2)*(exp(se^2)-1))
list(pred = xnew, se=senew)
}据此得到关于每股季度盈利的预测:
pred4adj <- lognorm_adjust(pred4)
pred4p <- pred4adj$pred
se4 <- pred4adj$se
cbind(Observed=c(coredata(xts.koqtr))[101:107],
Predicted=round(pred4p, 2), SE=round(se4, 2))## Observed Predicted SE
## 2008 Q1 0.67 0.61 0.05
## 2008 Q2 1.01 0.89 0.09
## 2008 Q3 0.83 0.77 0.09
## 2008 Q4 0.64 0.64 0.08
## 2009 Q1 0.65 0.66 0.09
## 2009 Q2 0.92 0.97 0.15
## 2009 Q3 0.82 0.84 0.14对预报效果作图, 从2003年开始:
tmp.x <- ts(c(coredata(xts.koqtr["2003/"])), start=c(2003,1), frequency = 4)
tmp.p <- ts(c(pred4p), start=c(2008,1), frequency = 4)
tmp.lb <- ts(c(pred4p) - 2*c(se4), start=c(2008,1), frequency = 4)
tmp.ub <- ts(c(pred4p) + 2*c(se4), start=c(2008,1), frequency = 4)
plot(tmp.x, ylim=c(0.3, 1.2), type="l", lwd=2,
xlab="Year", ylab="")
lines(tmp.p, type="b", pch=2, lty=2, col="red")
lines(tmp.lb, lty=3, col="green")
lines(tmp.ub, lty=3, col="green")
legend("topleft", lty=c(1,2,3), lwd=c(2,1,1), pch=c(NA,2,NA),
col=c("black", "red", "green"),
legend=c("Observed", "Predicted", "95% Prediction Limits"))
○○○○○
8.3 季节哑变量
另一种表示季节性的方法是用非随机的回归项表示固定的季节模式。 这样的模式虽然也可以通过季节差分消除, 但是与动态模型和非随机线性趋势模型的关系类似, 固定的季节模型不应该用季节差分处理。
非随机的季节因素用回归哑变量表示。 \(s=4\)时, 用3个哑变量就可以表示4个不同季节的固定水平。 为了判断非随机季节模型是否使用, 可以先拟合动态的季节ARIMA\((1,0,1)(1,0,1)_s\)模型, 当发现其中的季节因素可以忽略时, 就可考虑采用非随机的季节模型。下面举例说明。
例8.1 考虑CRSP最高10分位资产组合的月简单收益率, 从1970年1月到2008年12月共39年,468个观测。
读入数据:
da <- read_table(
"m-deciles08.txt",
col_types=cols(.default = col_double(),
date=col_date("%Y%m%d")))
xts.dec10 <- xts(da[["CAP1RET"]], ymd(da[["date"]]))
dec10 <- ts(da[["CAP1RET"]], start=c(1970, 1), frequency=12)收益率序列图:
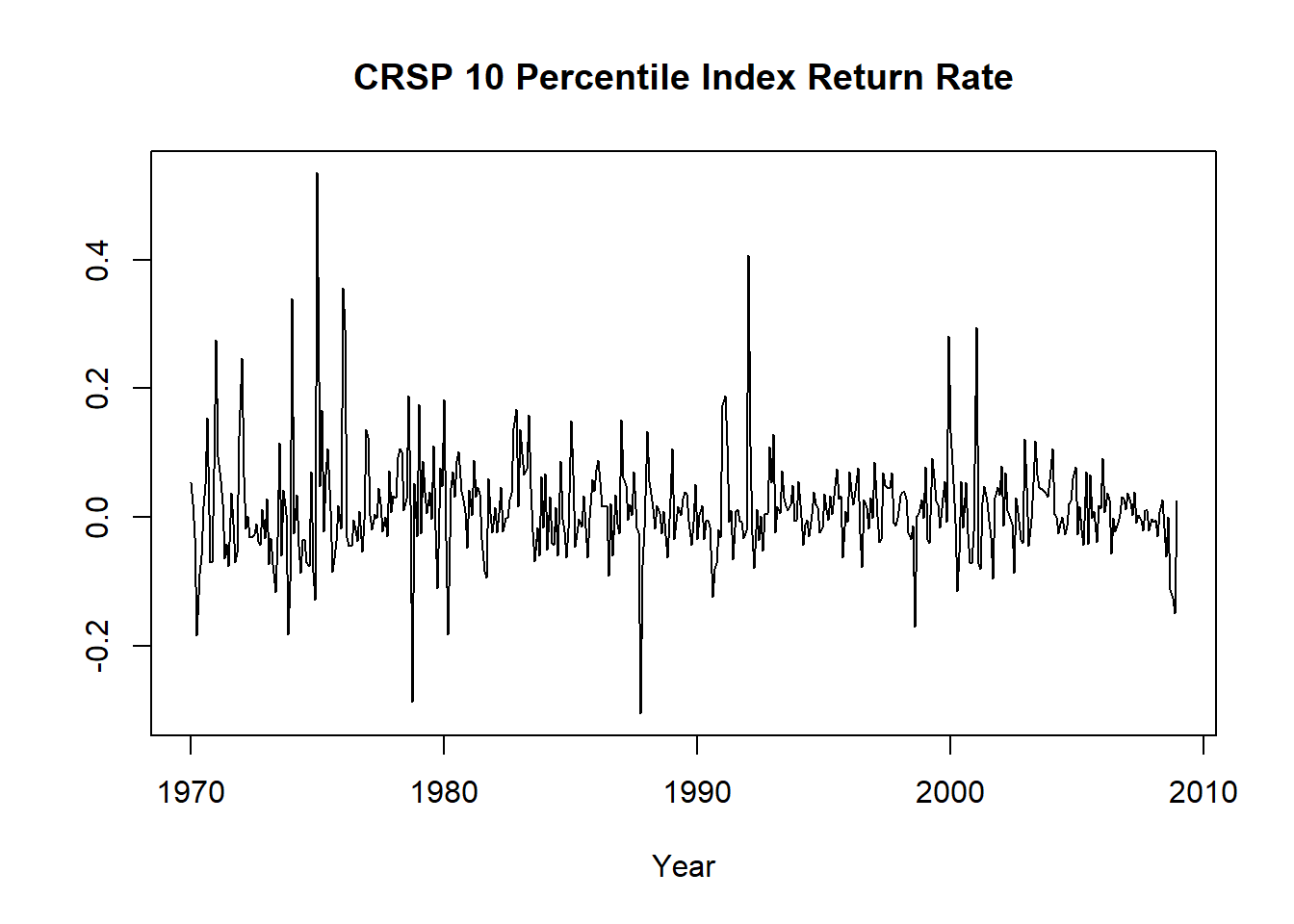
图8.7: CRSP 10分位指数的收益率
序列图本身没有表现出明显的趋势与周期性。取最近3年的数据来看:
plot(window(dec10, start=c(2006,1), end=c(2008,12)),
main="CRSP 10 Percentile Index Return Rate",
xlab="Year", ylab="")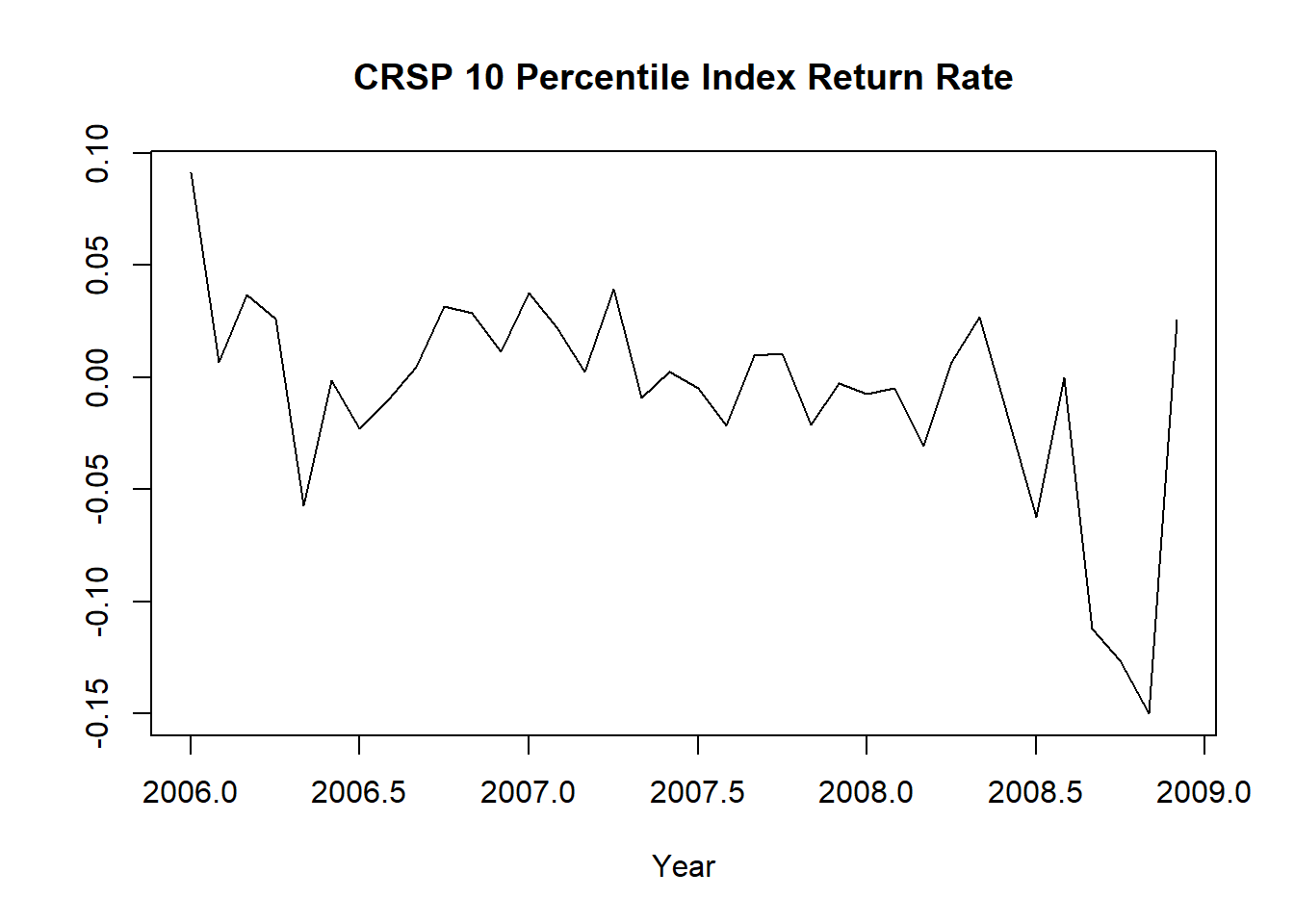
图8.8: CRSP 10分位指数的收益率(近三年)
也看不出周期性。
作ACF图:
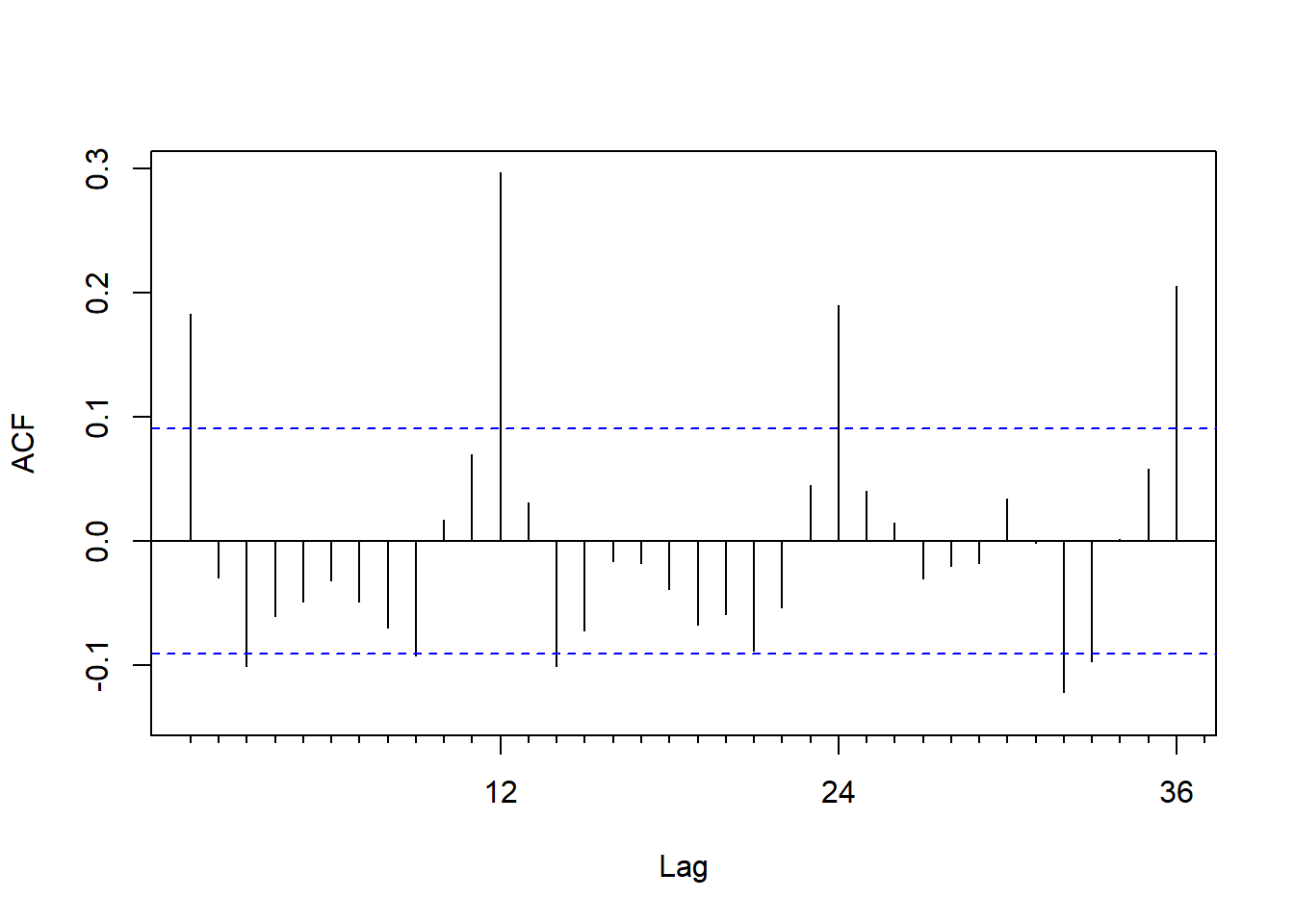
图8.9: CRSP 10分位指数收益率的ACF
ACF函数在12的倍数的滞后上显著不等于零, 这体现出了周期性。 来拟合ARIMA\((1,0,1)(1,0,1)_{12}\):
##
## Call:
## arima(x = dec10, order = c(1, 0, 1), seasonal = list(order = c(1, 0, 1), period = 12))
##
## Coefficients:
## ar1 ma1 sar1 sma1 intercept
## -0.0639 0.2508 0.9882 -0.9142 0.0117
## s.e. 0.2205 0.2130 0.0092 0.0332 0.0125
##
## sigma^2 estimated as 0.004704: log likelihood = 584.69, aic = -1157.39得到的模型可以写成 \[ (1 + 0.0639 B)(1 - 0.9882 B^{12}) (X_t - 0.0117 ) = (1 + 0.2508 B)(1 - 0.9142 B^{12}) \varepsilon_t \]
其中的\(1 - 0.9882 B^{12}\)项与\(1 - 0.9142 B^{12}\)近似可以消去, 所以这个结果提示可能不需要使用动态季节模型。
采用非随机的哑变量模型来建模。 为简单起见, 仅考虑一月份的效应, 因为实证发现一月份的收益率倾向为正值。
##
## Call:
## lm(formula = c(dec10) ~ jan)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.30861 -0.03475 -0.00176 0.03254 0.40671
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.002864 0.003333 0.859 0.391
## jan 0.125251 0.011546 10.848 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.06904 on 466 degrees of freedom
## Multiple R-squared: 0.2016, Adjusted R-squared: 0.1999
## F-statistic: 117.7 on 1 and 466 DF, p-value: < 2.2e-16可以看出在以一月份为哑变量的线性回归中, 自变量是显著的。 拟合的模型为
\[ \hat x_t = 0.002864 + 0.1253 \text{Jan}_t \] 其中\(\text{Jan}_t\)当\(t\)的月份为一月份时等于1, 否则等于0。
但是,这个模型是有缺陷的, 因为线性回归假定随机误差项独立, 而这里的随机误差项显然是有自相关的:

图8.10: 固定季节项回归残差的ACF
其滞后1还显著不等于0。 在滞后为12的倍数的位置已经不再显著。 为此, 可以使用带有外生自变量的时间序列模型, 或者回归模型中误差项有序列自相关的模型, 见13。
○○○○○