12 用arima模型建模预测

前面已经讲过了AR、MA、ARMA模型， 单位根过程， arima模型。 这里讲用fable包建模和预测。 fable包提供了一系列探索性图形、建模、诊断、比较、预测、作图的方便使用的函数。

本章内容来自(R. J. Hyndman and Athanasopoulos 2021)第九章。

12.1 平稳性、差分、季节差分、单位根

回顾平稳（宽平稳）定义， 平稳序列的观测必须围绕一条水平线上下波动， 波动振幅不能随时间变化， 不能有固定的周期变化， 不能有明显趋势。 平稳序列也可以有缓慢波动， 这有时与单位根过程不容易区分。

12.1.1 用ACF图形发现单位根

如果序列有单位根， 则其ACF估计衰减很慢， \(\hat\rho_k\)数值都很接近于1。

可以用基本R的acf()、forecast包的Acf()作ACF图， 也可以用feasts包的ACF()配合autoplot()作图。

例12.1 考虑tsibbledata包的global_economy中的中国GDP数据， 判断其平稳性。

解答：

data(global_economy, package="tsibbledata")
gdp_tsib <- global_economy |>
  filter(Country == "China") |>
  mutate(GDP_per_capita = GDP / Population,
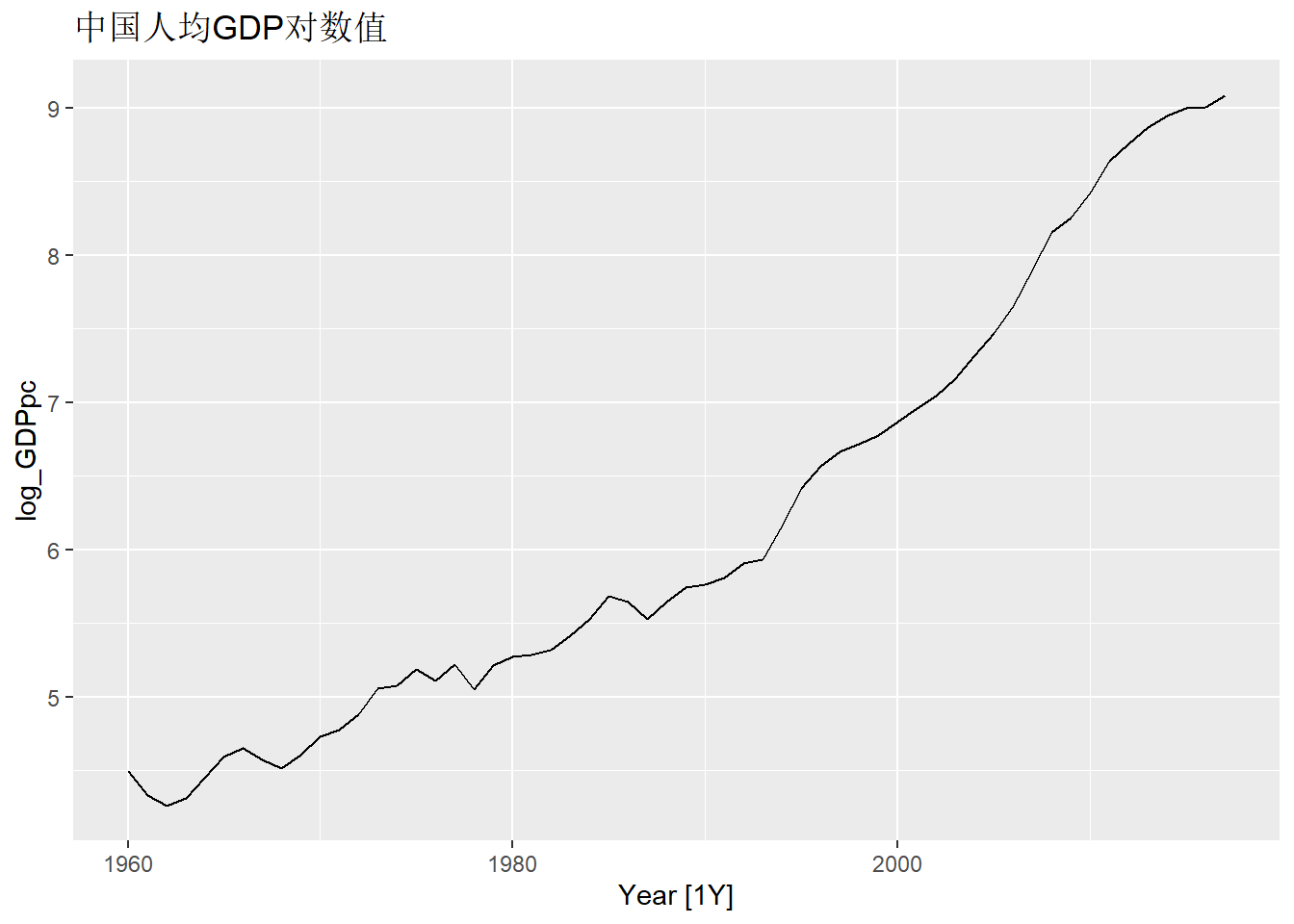
    log_GDPpc = log(GDP_per_capita)) |>
  select(Year, GDP_per_capita, log_GDPpc)
gdp_tsib |>
  autoplot(GDP_per_capita) +
  labs(title="中国人均GDP")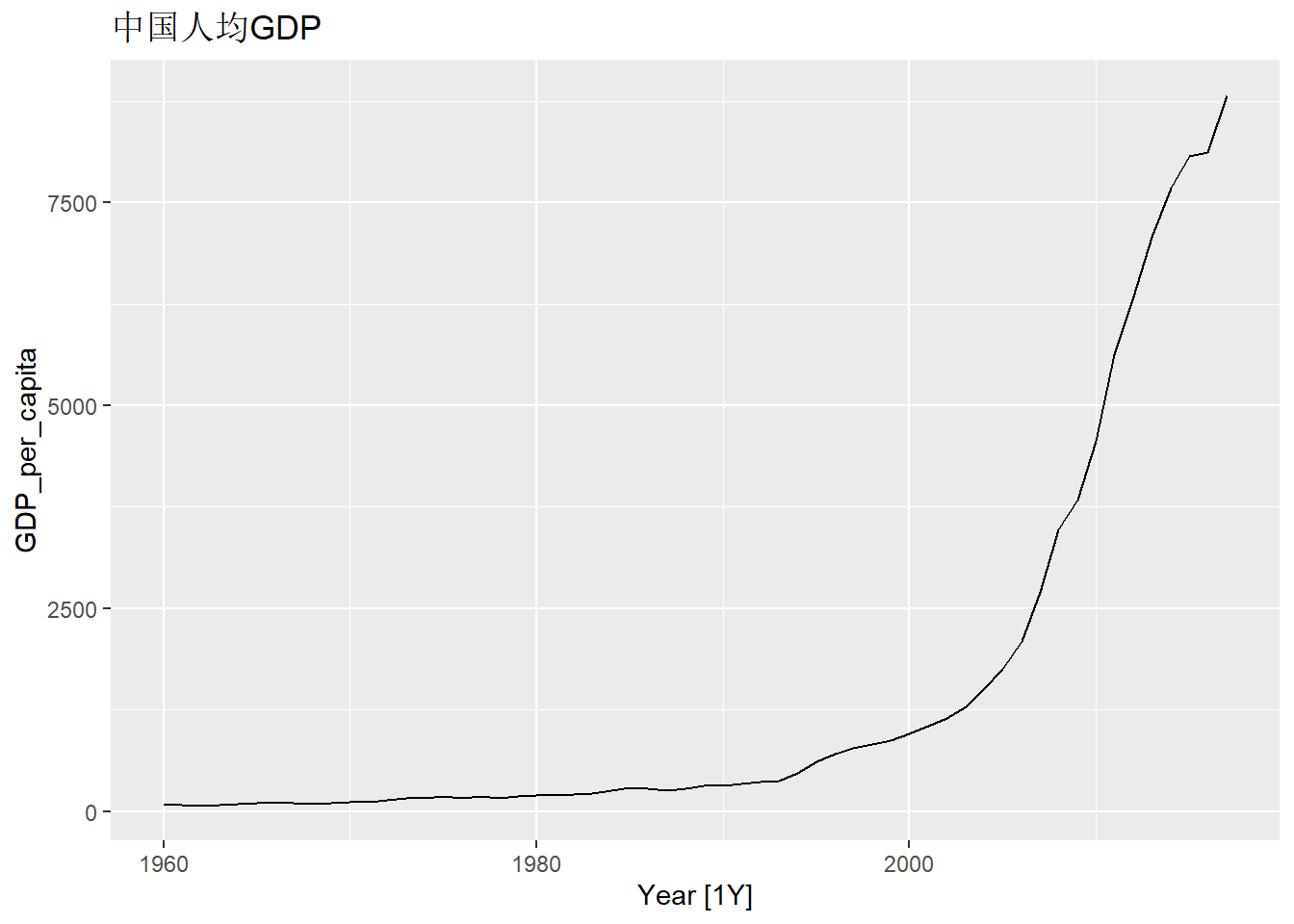

gdp_tsib |>
  autoplot(log_GDPpc) +
  labs(title="中国人均GDP对数值")

作ACF图：

gdp_tsib |>
  ACF(GDP_per_capita) |>
  autoplot() +
  labs(title="GDP的ACF")

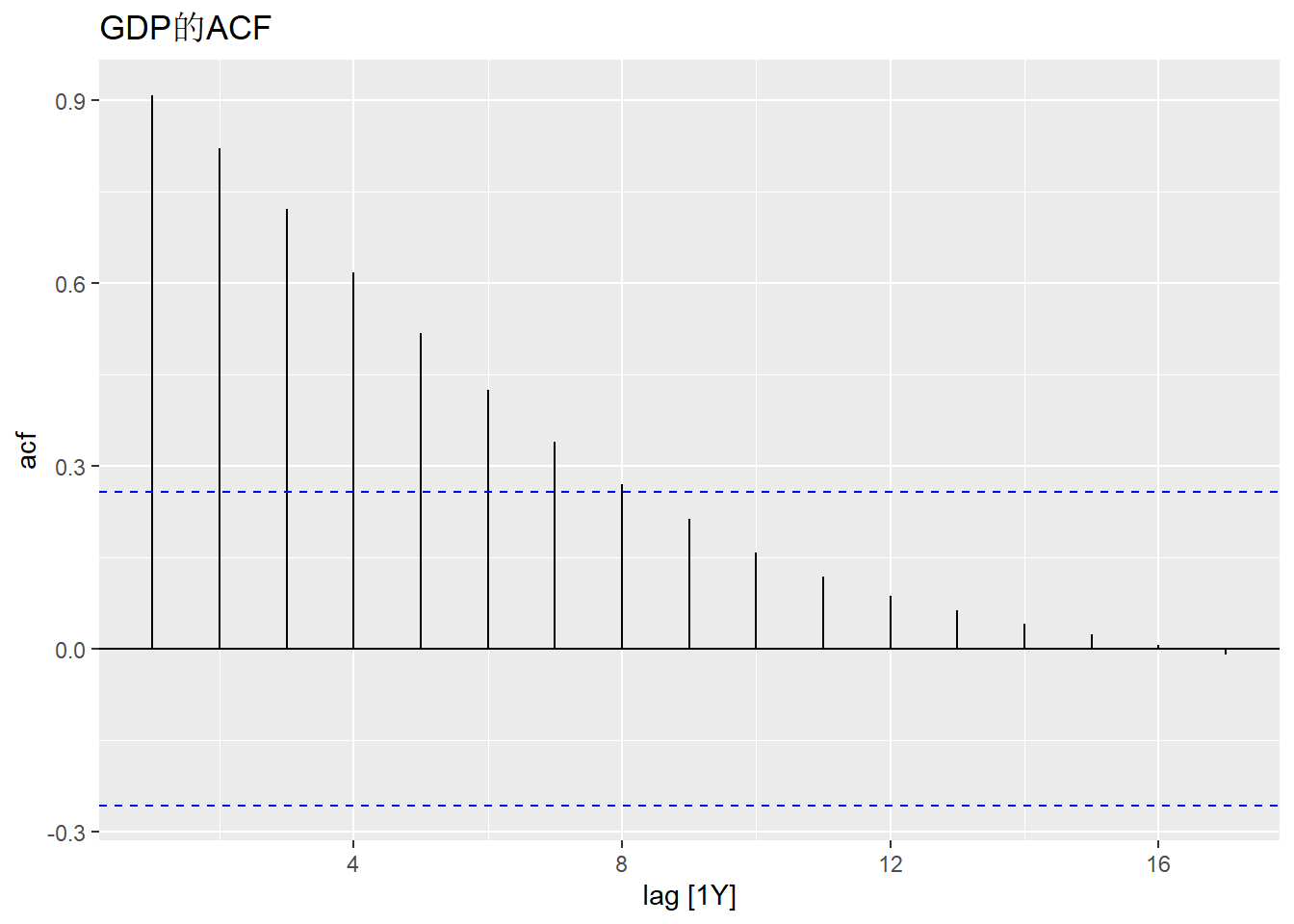
这个ACF不是典型的一阶单位根过程的样子。 后续我们使用单位根检验来判断。

其一阶差分的ACF图：

gdp_tsib |>
  ACF(difference(GDP_per_capita)) |>
  autoplot() +
  labs(title="GDP一阶差分的ACF")

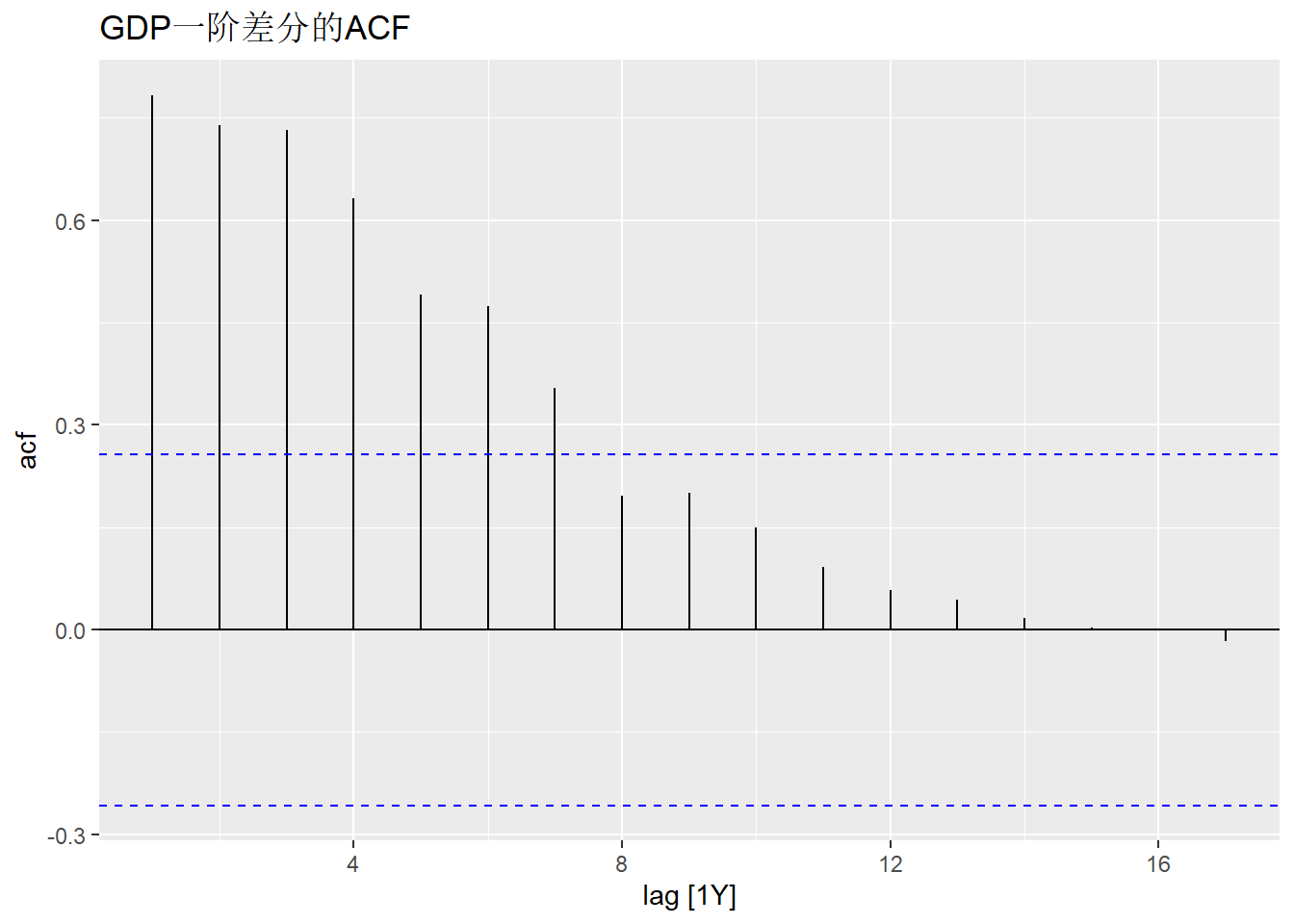
程序中的difference()是tsibble包提供的一个计算差分的函数， 与基本R的diff()类似。

GDP二阶差分的ACF图：

gdp_tsib |>
  ACF(difference(GDP_per_capita, differences = 2)) |>
  autoplot() +
  labs(title="GDP一阶差分的ACF")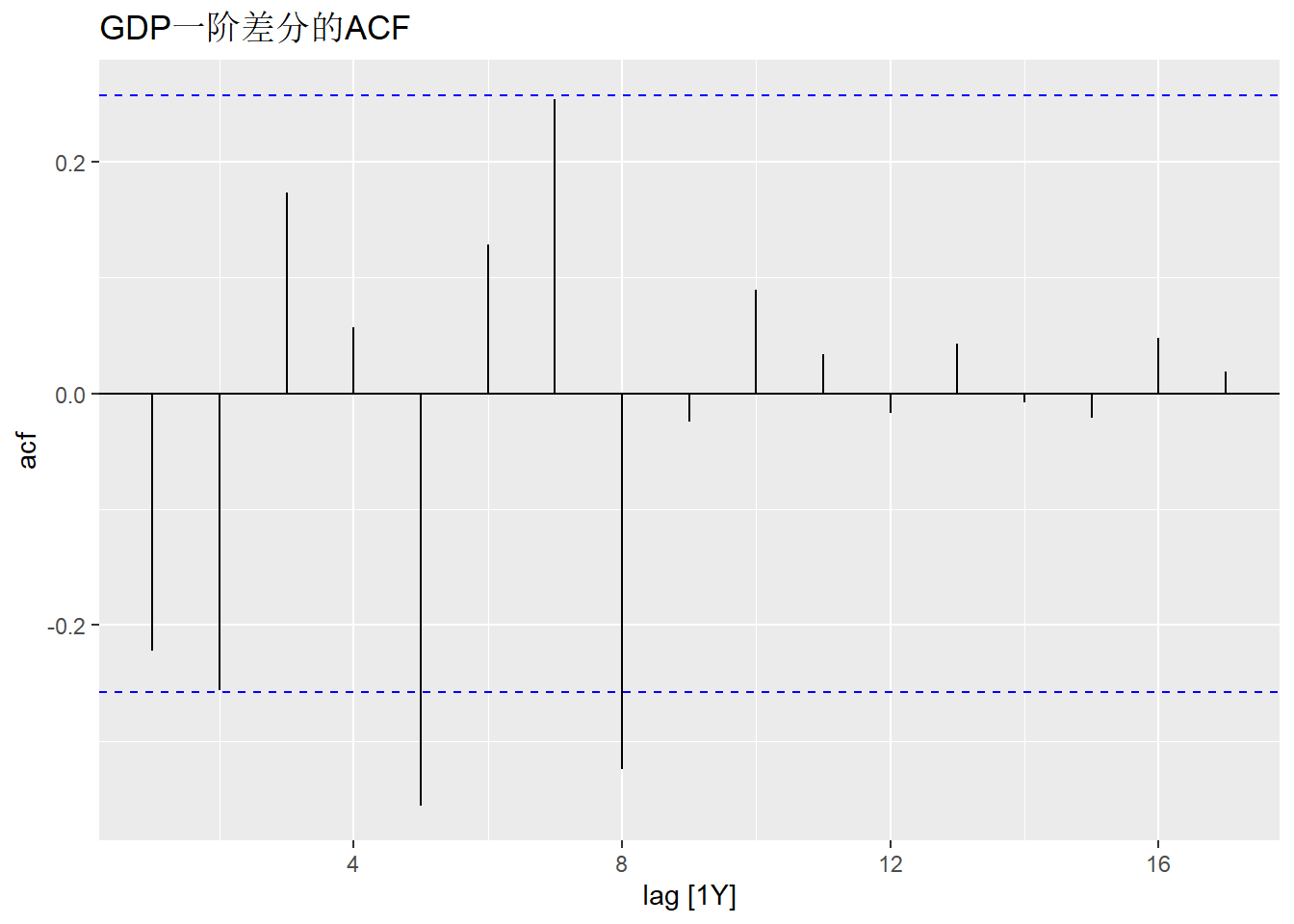

二阶差分才表现得比较平稳。

用Ljung-Box方法建议二阶差分是否白噪声：

gdp_tsib |>
  mutate(diff2 = difference(GDP_per_capita, differences = 2)) |>
  features(diff2, ljung_box, lag = 8)

## # A tibble: 1 × 2
##   lb_stat lb_pvalue
##     <dbl>     <dbl>
## 1    29.4  0.000272

结果显著， 说明二阶差分序列不是白噪声。

○○○○○○

12.1.2 季节差分

如果数据是月度或季度数据， 则序列一般呈现明显季节变化。 最简单的模型为 \[ y_t - y_{t-m} = \varepsilon_t, \] 其中\(\{\varepsilon_t \}\)是零均值白噪声， \(m\)为季节性的频率。

这个模型的预测用同月（季度）的最近一个已知值来计算， 对应于简单预测方法中的季节平移预测。

季节差分\((1 - B^m) y_t\)在去除季节性的同时， 也能够去掉一定的趋势性。 比如， 若\(y_t = a + bt\)， 则\(y_t - y_{t-m} = b m\)不随时间变化。

例12.2 考虑航空乘客数AirPassengers， 这是月度数据。 考虑其季节性。

ap_tsib <- as_tsibble(AirPassengers) |>
  mutate(
    ap = value,
    log_ap = log(value)  ) |>
  select(-value)
ap_tsib |>
  autoplot(ap) +
  labs(title = "航空乘客数")

ap_tsib |>
  autoplot(log_ap) +
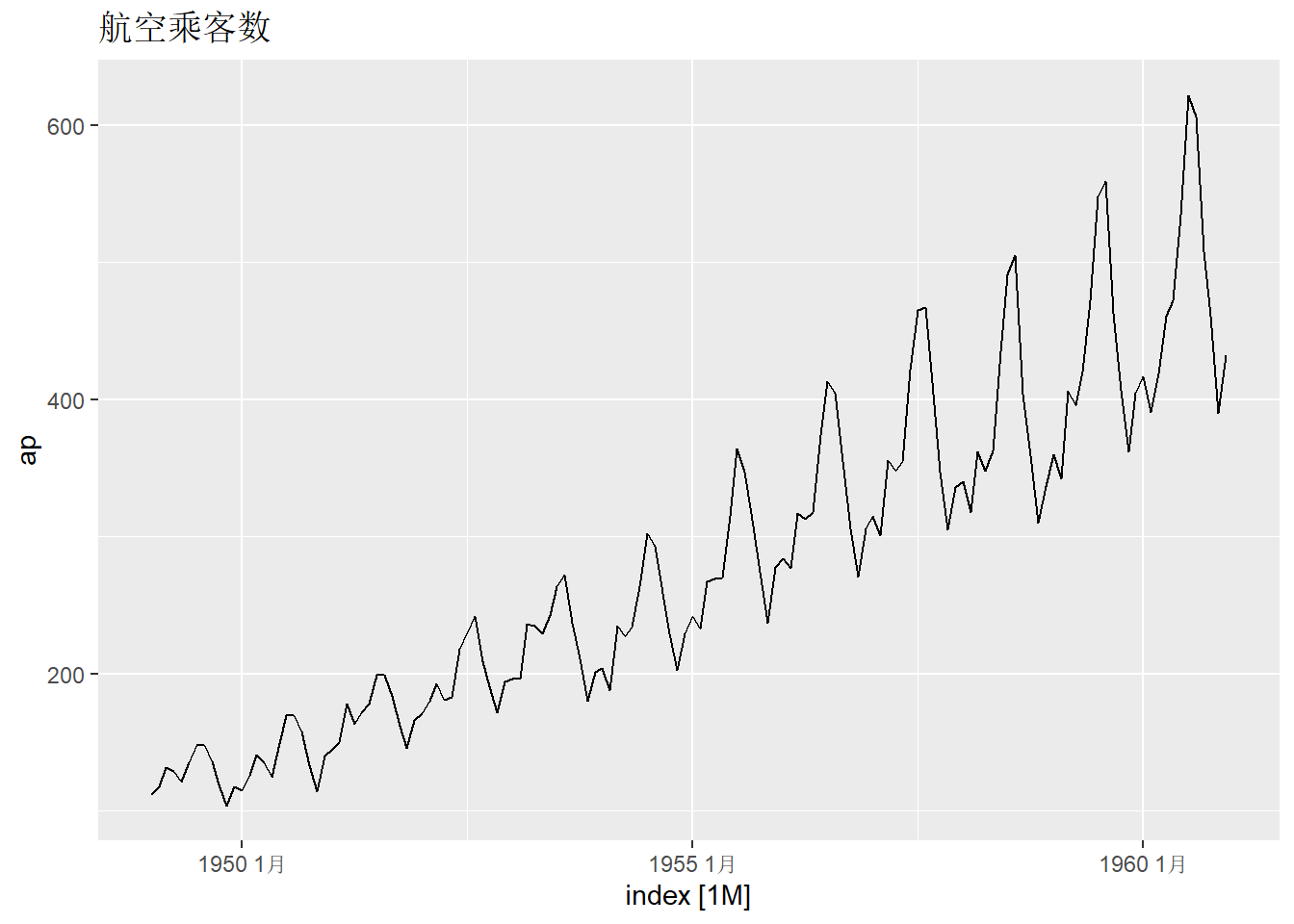
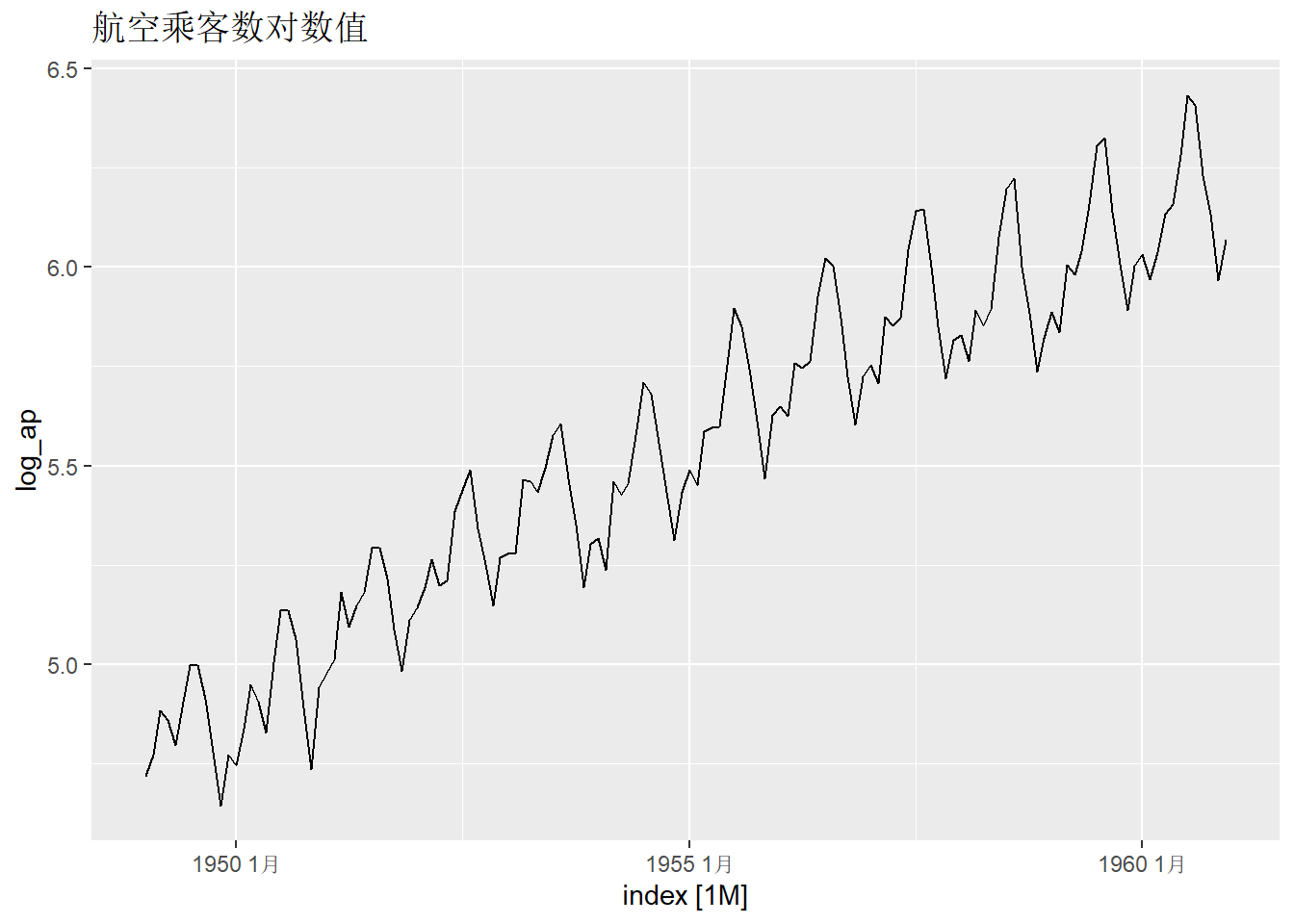
  labs(title = "航空乘客数对数值")

对数序列的ACF:

ap_tsib |>
  ACF(log_ap) |>
  autoplot() +
  labs(title = "对数序列的ACF")

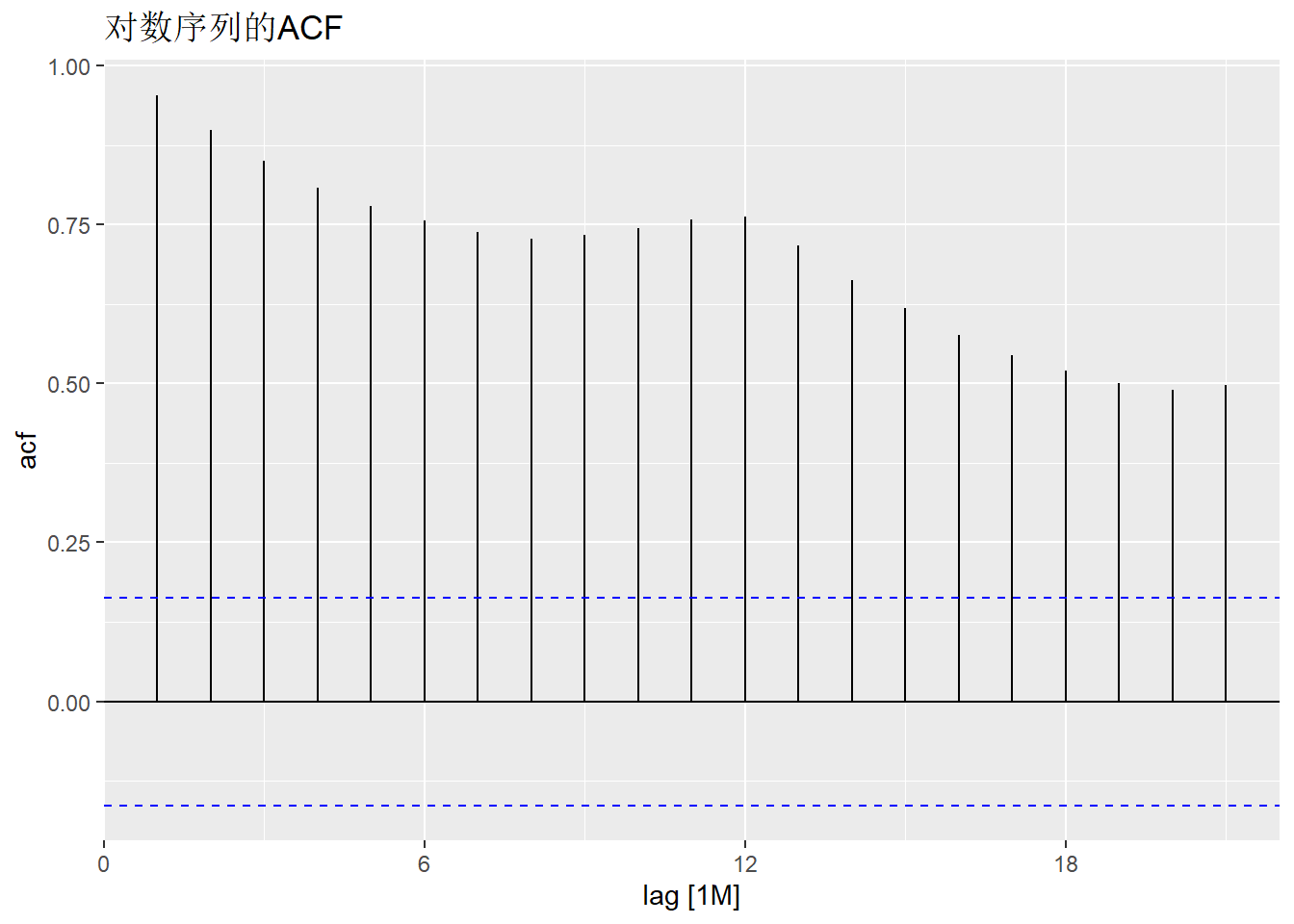
这是明显有单位根的样子。

季节差分的ACF:

ap_tsib |>
  ACF(difference(log_ap, 12)) |>
  autoplot() +
  labs(title = "对数序列季节差分的ACF")

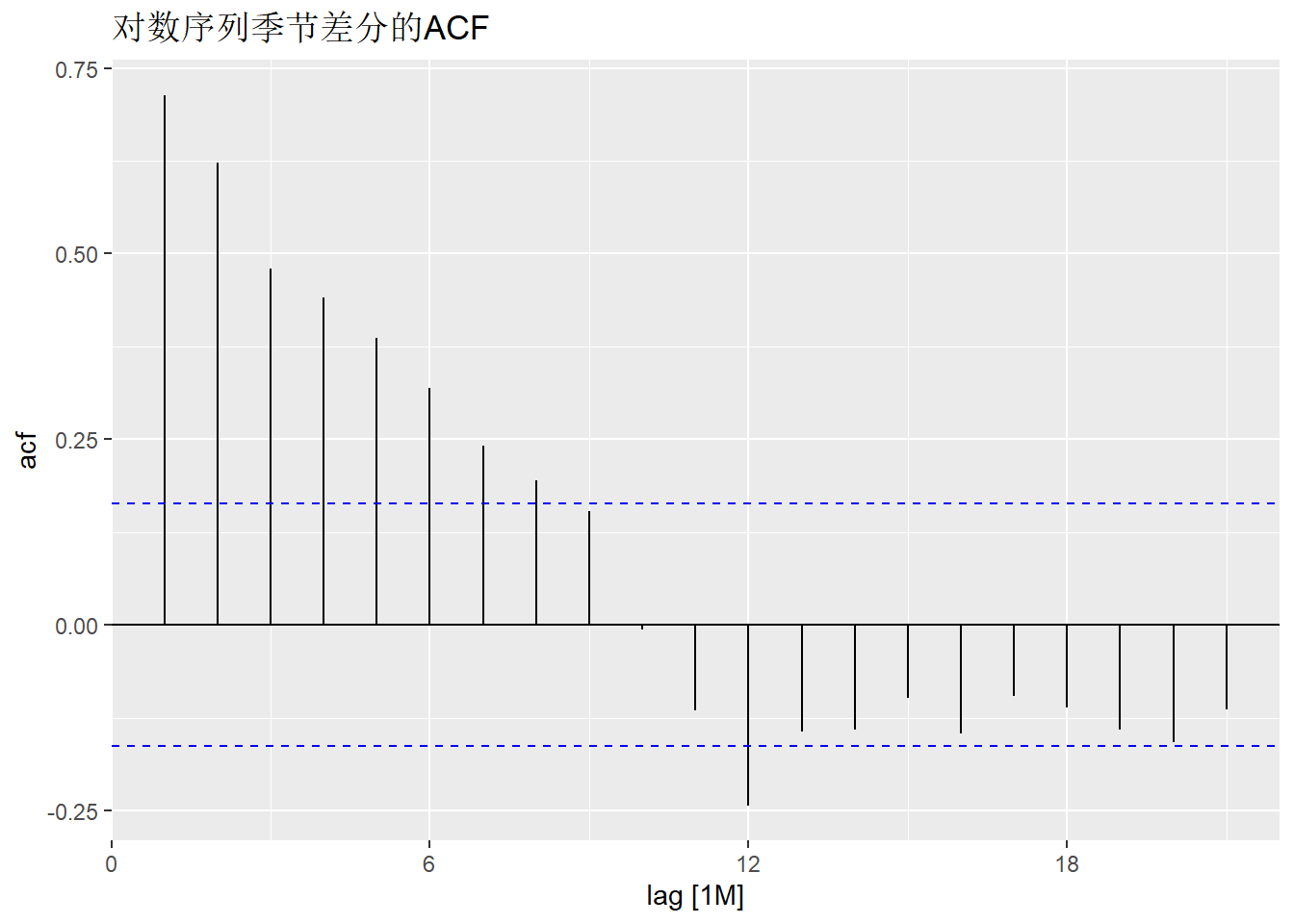
上述ACF已经不是明显有单位根的。 考虑既作季节差分也作普通差分：

ap_tsib |>
  ACF(difference(difference(log_ap, 12))) |>
  autoplot() +
  labs(title = "对数序列两种差分的ACF")

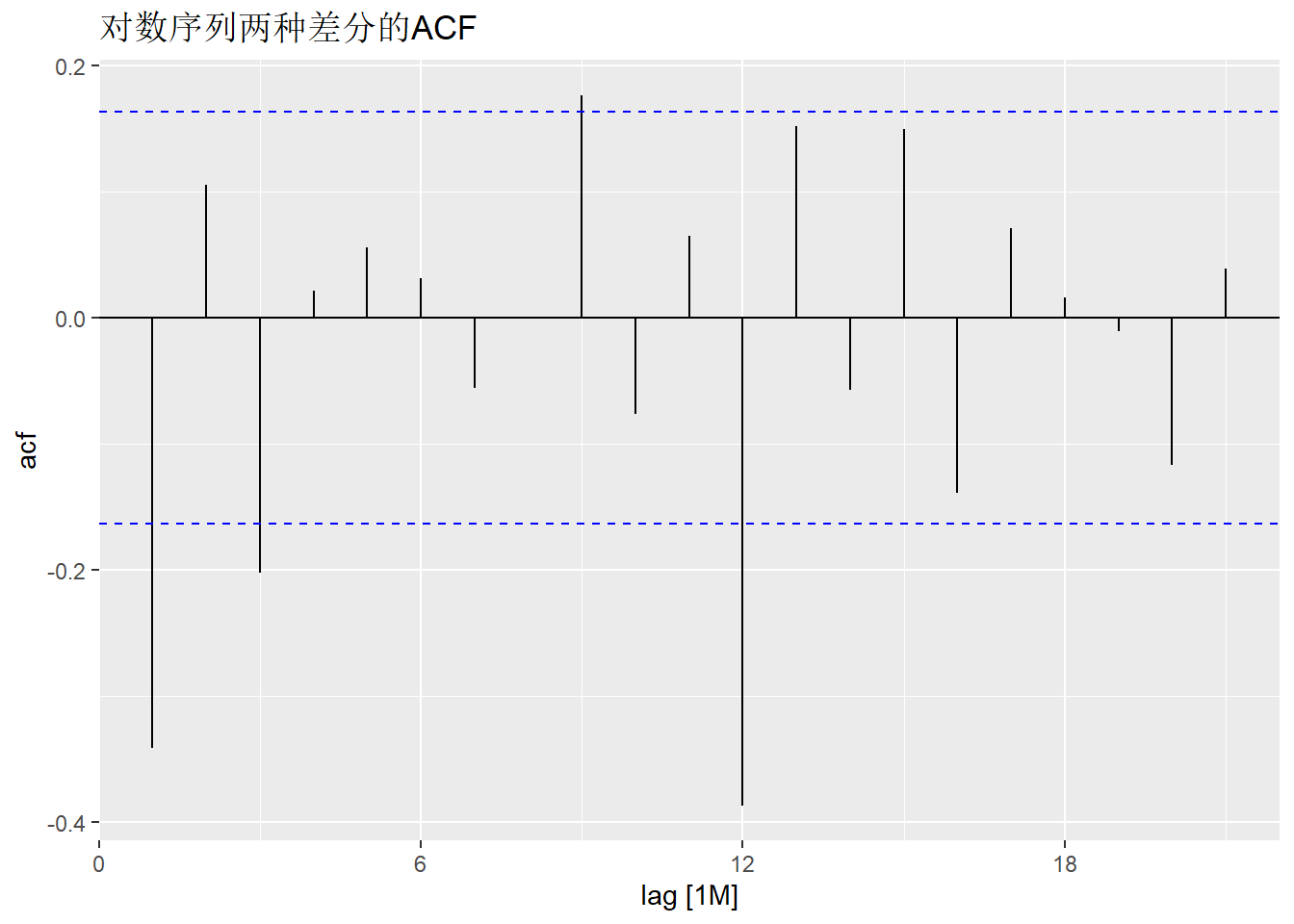
这已经呈现出平稳的样子。

要注意平稳后就不能再继续差分， 否则会使得模型被错误辨识。

○○○○○○

12.1.3 KPSS单位根检验

feasts包提供了一个KPSS单位根检验， 这个检验的零假设是序列平稳（与ADF检验的零假设相反）， 参考文献为(Kwiatkowski et al. 1992)。

例12.3 讨论中国人均GDP序列及其差分的平稳性。

原始序列的KPSS单位根检验：

gdp_tsib |>
  features(GDP_per_capita, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
0.9907344	0.01

因为零假设是序列平稳， 取检验水平\(0.05\)， p值为\(0.01\)， 拒绝零假设， 认为有单位根。

一阶差分的单位根检验：

gdp_tsib |>
  mutate(diff1 = difference(GDP_per_capita)) |>
  features(diff1, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
0.9580079	0.01

这说明一阶差分仍不平稳。

二阶差分的单位根检验：

gdp_tsib |>
  mutate(diff2 = difference(GDP_per_capita, differences = 2)) |>
  features(diff2, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
0.11276	0.1

在\(0.05\)水平下可以认为二阶差分序列平稳。

从人均GDP看人均GDP增长呈现强烈的非线性， 对数变换有可能改善。 对数变换的单位根检验：

gdp_tsib |>
  mutate(diff1 = difference(log_GDPpc)) |>
  features(diff1, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
0.6541984	0.0177092

在\(0.05\)水平下认为人均GDP对数值序列的一阶差分有单位根。

二阶差分结果：

gdp_tsib |>
  mutate(diff2 = difference(log_GDPpc, differences = 2)) |>
  features(diff2, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
0.1025083	0.1

二阶差分后平稳。

可以用feasts包的unitroot_ndiffs()函数自动判断需要的差分阶数， 如：

gdp_tsib |>
  features(log_GDPpc, unitroot_ndiffs) |>
  knitr::kable()

ndiffs
2

结果也说明需要二阶差分才能平稳。

○○○○○○

例12.4 讨论航空乘客数对数序列需要的差分阶数。

解答：

对数序列本身的KPSS检验：

ap_tsib |>
  features(log_ap, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
2.828675	0.01

结果为不平稳。

季节差分的平稳性检验：

ap_tsib |>
  mutate(diffs = difference(log_ap, 12)) |>
  features(diffs, unitroot_kpss) |>
  knitr::kable()

kpss_stat	kpss_pvalue
0.3681637	0.0908777

结果在\(0.05\)水平下可以认为已经是平稳的， 所以可以不再作普通差分。

函数unitroot_nsdiffs()可以用来检验需要进行的季节差分阶数：

ap_tsib |>
  features(log_ap, unitroot_nsdiffs) |>
  knitr::kable()

nsdiffs
1

但如果用unitroot_ndiffs()检验需要的普通差分阶数， 结果也是一阶：

ap_tsib |>
  features(log_ap, unitroot_ndiffs) |>
  knitr::kable()

ndiffs
1

先季节差分后， 再判断需要的普通差分阶数：

ap_tsib |>
  mutate(diffs = difference(log_ap, 12)) |>
  features(diffs, unitroot_ndiffs) |>
  knitr::kable()

ndiffs
0

检验给出的建议是经过季节差分后， 不需要再进行普通差分。

○○○○○○

12.2 ARIMA建模

12.2.1 自动建模例子

fable的ARIMA()函数提供了类似forecast::auto.arima()的功能， 可以对输入时间序列自动选择适当的ARIMA模型。 ARIMA()默认使用AICc准则选择最优模型， 也可以用ic参数指定其它准则如AIC、BIC等。

例12.5 tsibbledata包的global_economy数据包含了不同国家的年度经济时间序列数据。 考虑其中的埃及的出口指标（作为GDP百分比）， 建立ARIMA模型。

解答： 数据

export_tsib <- global_economy |>
  filter(Code == "EGY") |>
  select(Year, Exports)
export_tsib |>
  autoplot(Exports) +
  labs(title = "埃及出口指标")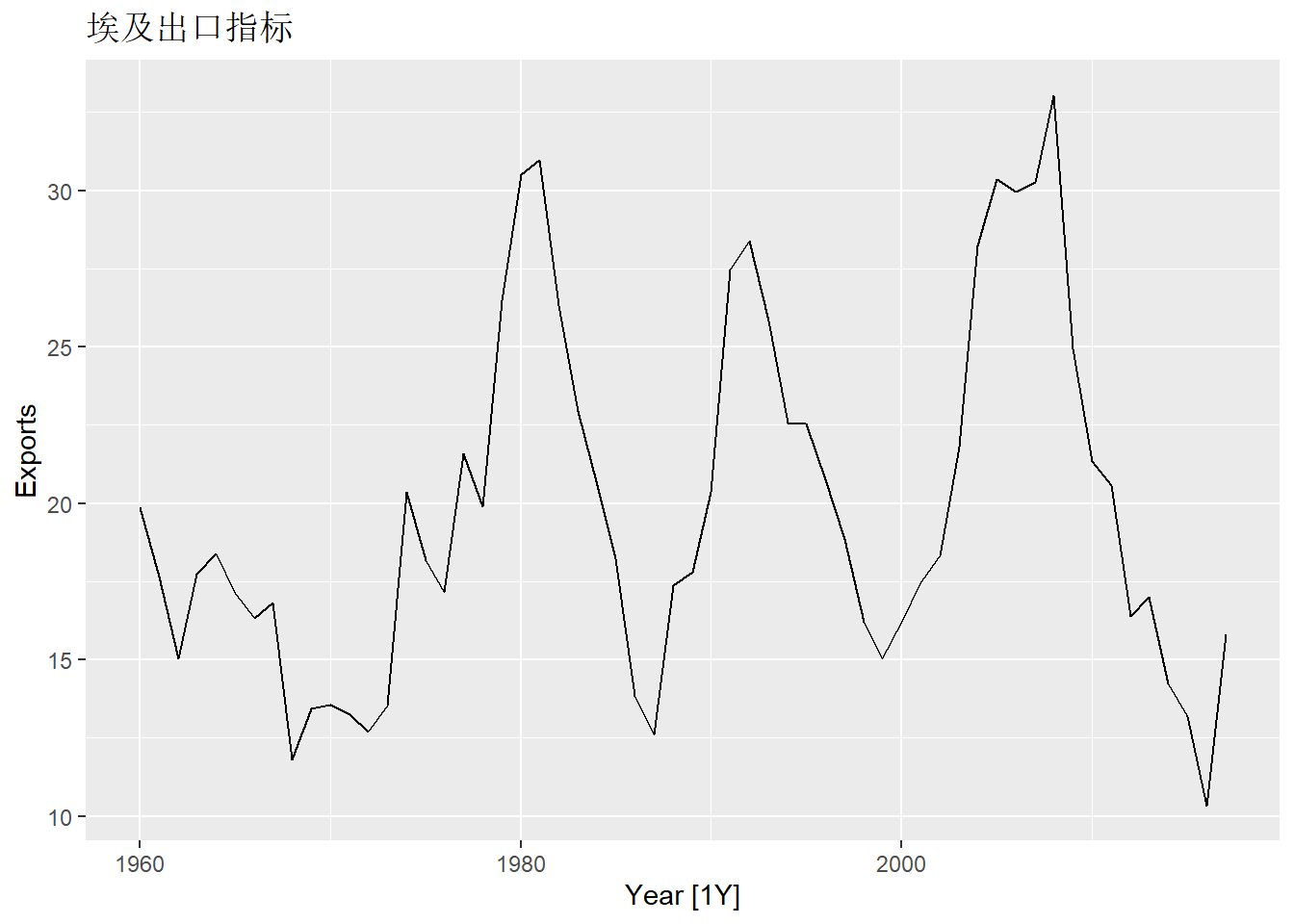

查看ACF与PACF图：

export_tsib |>
  ACF() |>
  autoplot()

## Response variable not specified, automatically selected `var = Exports`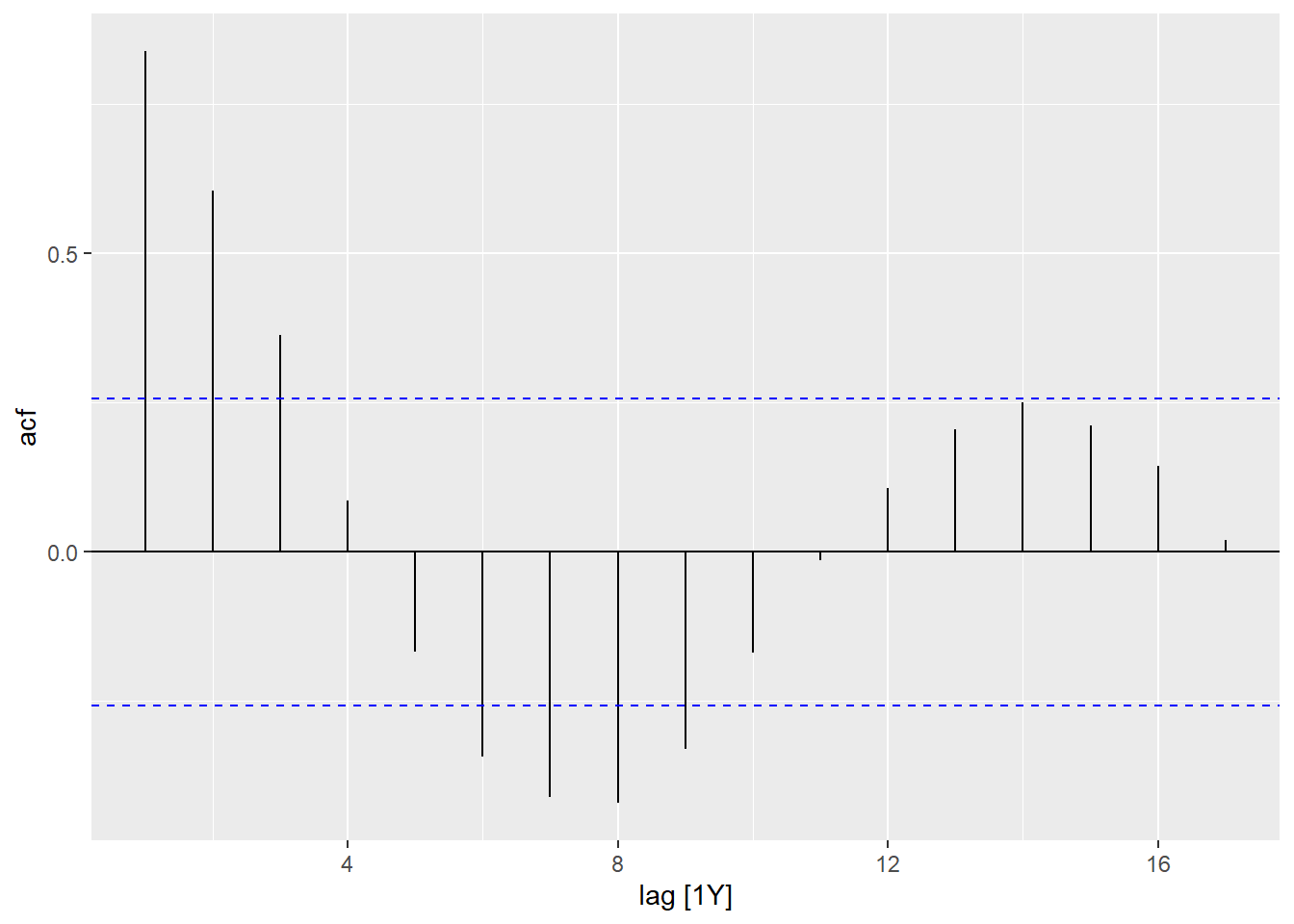

export_tsib |>
  PACF() |>
  autoplot()

## Response variable not specified, automatically selected `var = Exports`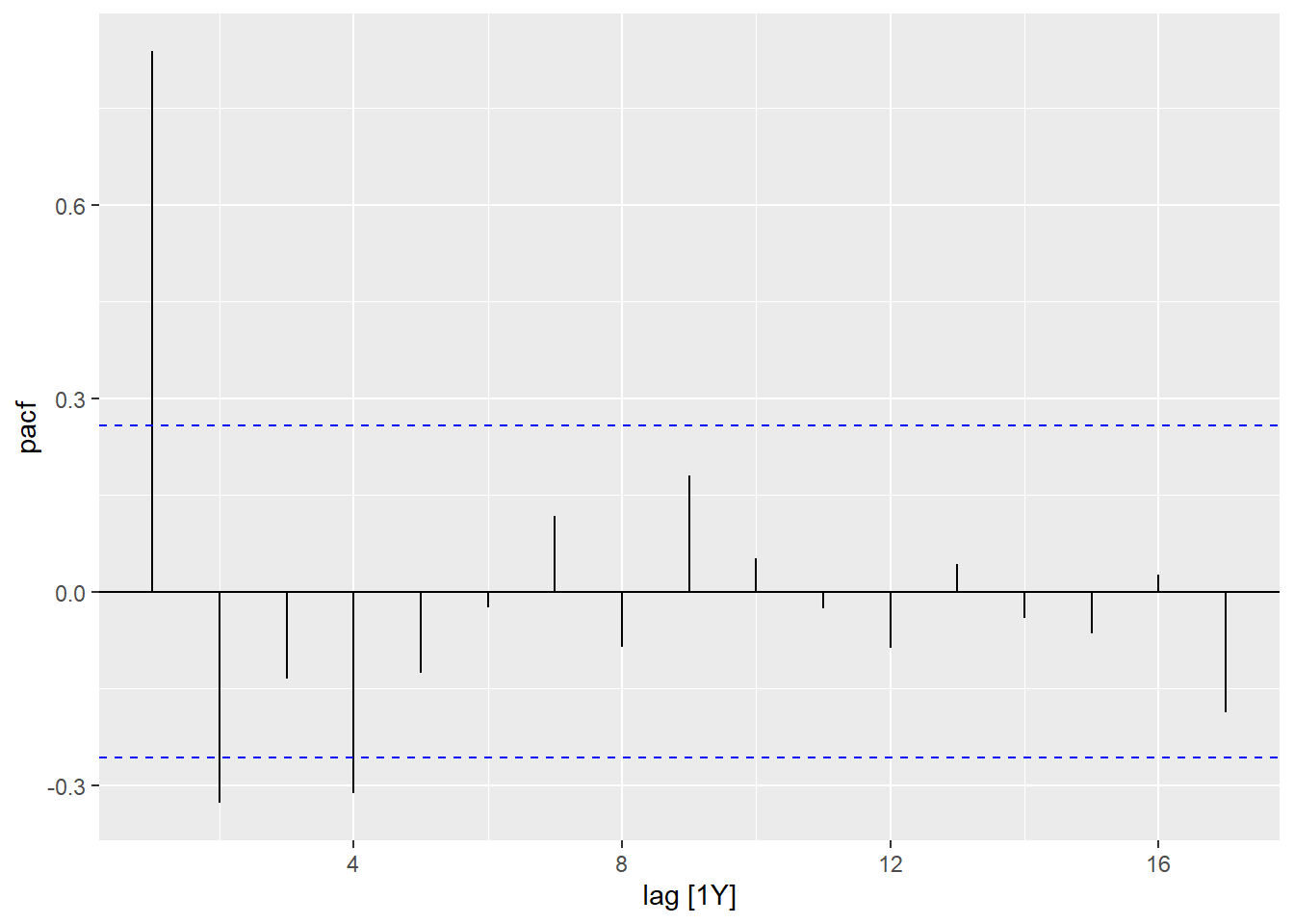

可以用gg_tsdisplay()函数同时显示一个序列的时间序列曲线图、ACF图和PACF图：

export_tsib |>
  gg_tsdisplay(Exports,
    plot_type = "partial")

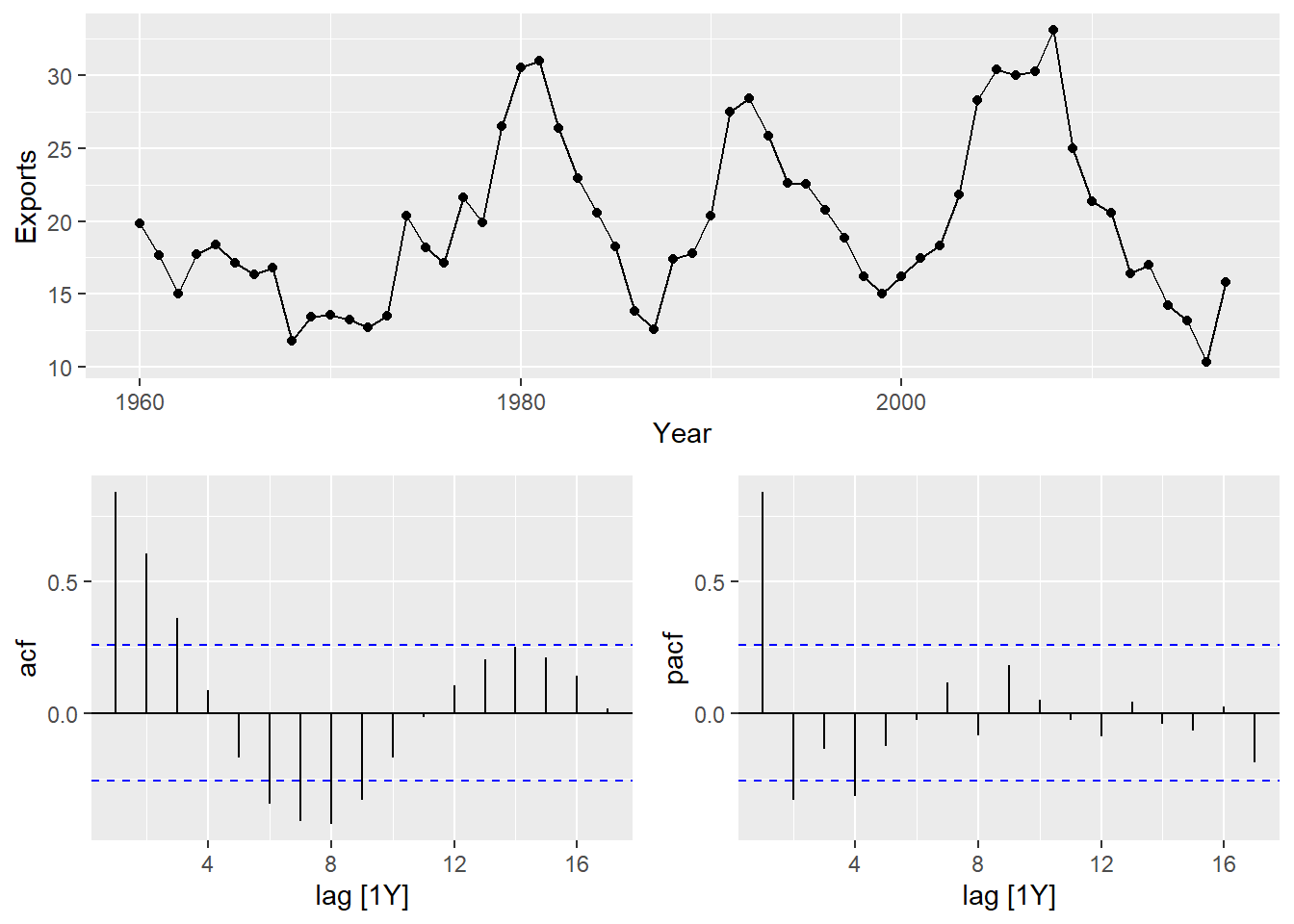
用ARIMA()函数自动建模：

export_fit <- export_tsib |>
  model(ARIMA(Exports))
report(export_fit)

## Series: Exports 
## Model: ARIMA(2,0,1) w/ mean 
## 
## Coefficients:
##          ar1      ar2      ma1  constant
##       1.6764  -0.8034  -0.6896    2.5623
## s.e.  0.1111   0.0928   0.1492    0.1161
## 
## sigma^2 estimated as 8.046:  log likelihood=-141.57
## AIC=293.13   AICc=294.29   BIC=303.43

这建立了一个ARIMA(2,0,1)模型， 有常数项。 模型公式可以写成 \[\begin{aligned} & (1 - 1.6764 B + 0.8034 B^2)y_t \\ =& 2.5623 + (1 - 0.6896 B) \varepsilon_t, \\ \ \varepsilon_t \sim& \text{WN}(0, 8.046) . \end{aligned}\] 注意这里的输出结果中Constant项与arima()和forecast::Arima()结果解释不同， 这里Constant项是模型方程的截距项， 而arima()和forecast::Arima()结果中的intercept在没有差分时实际是样本均值。 均值应该是 \[\begin{aligned} \hat\mu =& (1 - 1.6764 B + 0.8034 B^2)^{-1} 2.5623 \\ =& \frac{2.5623}{1 - 1.6764 + 0.8034} = 20.18 \end{aligned}\]

用得到的模型作向前多步预测并作图：

export_fit |>
  forecast(h = 10) |>
  autoplot(export_tsib) + 
  labs(title = "埃及出口指标用ARIMA(2,0,1)预测")

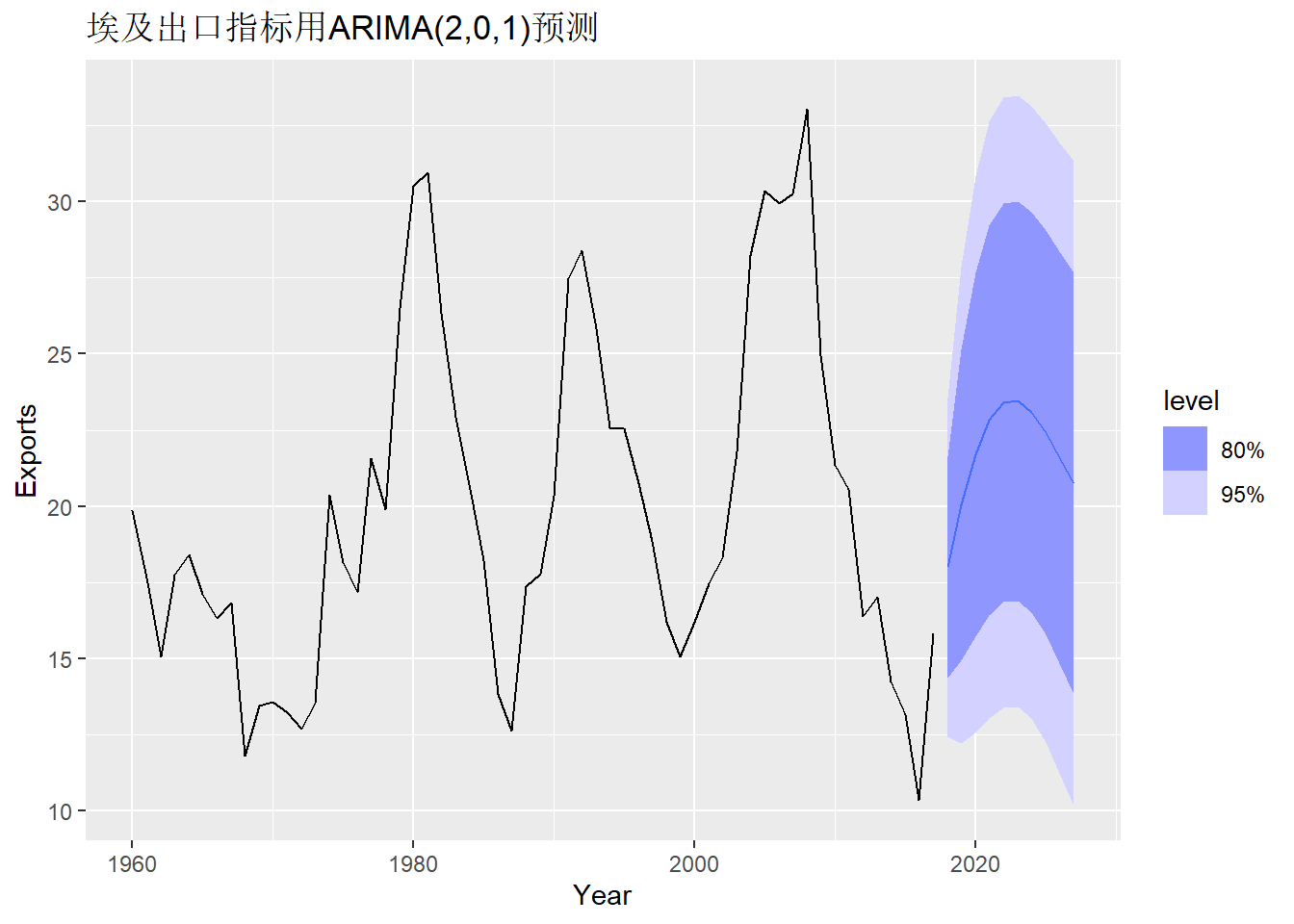
长期预测体现出了埃及出口的商业周期波动。

ARIMA()函数也允许人为指定模型的\(p, d, q\)。 比如， 从ACF和PACF判断序列平稳， PACF基本在4步以后截尾， 所以可以建立一个AR(4):

export_tsib |>
  model(ARIMA(Exports ~ pdq(4,0,0))) |>
  report()

## Series: Exports 
## Model: ARIMA(4,0,0) w/ mean 
## 
## Coefficients:
##          ar1      ar2     ar3      ar4  constant
##       0.9861  -0.1715  0.1807  -0.3283    6.6922
## s.e.  0.1247   0.1865  0.1865   0.1273    0.3562
## 
## sigma^2 estimated as 7.885:  log likelihood=-140.53
## AIC=293.05   AICc=294.7   BIC=305.41

结果AICc为\(294.7\)， 而自动建模的ARIMA(2,0,1)的AICc为\(294.29\)， 自动建模的AICc指标略优于人工选择的模型。

ARIMA()还可以允许指定一系列的\((p,d,q)\)值对多个模型进行比较并选出最优模型， 如ARIMA(y ~ pdq(p = 1:3, d = 0:1, q = 0:2))。

○○○○○○

12.2.2 模型性质

fable包的ARIMA模型在不带有季节成分时可以写成 \[\begin{equation} (1 - \phi_1 B - \dots - \phi_p B^p) (1 - B)^d y_t = c + (1 + \theta_1 B + \dots + \theta_q B^q) \varepsilon_t . \tag{12.1} \end{equation}\]

若\(d=0\)，\(\{y_t \}\)平稳， 则\(c\)决定了\(y_t\)的均值 \[ \mu = E(y_t) = \frac{c}{1 - \phi_1 - \dots - \phi_p} . \] 预测值\(\hat y_{T+h|T}\)当\(h \to \infty\)时趋于常数\(\hat \mu\)。

如果\(d=1\)或\(d=2\)， 则基本R的arima()函数不允许\(c \neq 0\)， forecast::Arima()允许\(d=1\)时\(c \neq 0\)， fable::ARIMA()也是允许\(d=1\)时\(c \neq 0\)。

若\(d=1\)且\(c = 0\)， 则\(\{y_t \}\)服从不带漂移项的ARIMA(\(p,1,q\))模型。 其预测值\(\hat y_{T+h|T}\)当\(h \to \infty\)时趋于常数。

若\(d=1\)但\(c \neq 0\)， 这类似于漂移随机游动， 漂移随机游动等于一个非随机线性函数加上一个随机游动， 所以预测值\(\hat y_{T+h|T}\)当\(h \to \infty\)时趋于一条斜率为\(c\)的斜线。

若\(d=2\)且\(c=0\)， 这样的模型是允许的， 其预测值\(\hat y_{T+h|T}\)当\(h \to \infty\)时趋于一条斜线。

若\(d=2\)且\(c \neq 0\)， fable::ARIMA()也不允许估计这样的模型， 理论上其预测值\(\hat y_{T+h|T}\)当\(h \to \infty\)时趋于一条抛物线。

预测区间宽度会随超前步数\(h\)增大而增大， 差分阶数变大时， 预测区间宽度随\(h\)增大越快。 如果\(d=0\)， 模型平稳， 预测区间宽度趋于常数值， 理论上正比于\(y_t\)的标准差。

AR部分的为特征多项式 \[ \Phi(z) = 1 - \phi_1 z - \dots - \phi_p z^p, \] 其要求特征多项式的根都满足模大于1（特征根都在单位圆外）， 有共轭复根时， 当根离单位圆较近时， \(\{y_t \}\)序列能表现出近似的周期性， 角频率等于该对共轭复根的辐角。

12.2.3 模型参数估计和模型选择

12.2.3.1 模型最大似然估计

fable包用最大似然估计方法估计模型参数。 最大似然估计方法得到的结果与最小二乘估计结果接近。 不同的软件包使用了不同的计算方法、优化算法， 所得的参数估计结果可能会有微小差别。

估计结果中会包含对数似然函数值， 即最大化的似然函数值的对数值。

12.2.3.2 新息准则

ARIMA估计的AIC值定义为 \[ \text{AIC} = -2 \log(L) + 2(p+q+k+1), \] 其中\(L\)是最大化的似然函数值， 当常数项\(c = 0\)时\(k=0\)， \(c \neq 0\)时\(k=1\)。 这是模型中要估计的未知参数个数， 包括一个\(\sigma^2\)参数。

修正(corrected)的AIC定义为 \[ \text{AICc} = \text{AIC} + 2(p+q+k+1)\frac{p+q+k+2}{T - (p+q+k+2)} . \] AICc准则能够减轻中小样本量时AIC容易选择参数更多的模型的缺点。

BIC准则值为 \[ \text{BIC} = \text{AIC} + 2(p+q+k+1)\frac{\log(T) - 2}{2} . \]

fable包默认使用AICc选择最优模型。

注意这些准则值仅用于选择\(p\), \(q\)以及\(c\)是否非零， 但不能用于选择差分阶\(d\)。 不同的差分阶对应的计算似然函数用的数据不同， 对应的模型的似然函数不可比。

12.3 fable包arima建模说明

12.3.1 ARIMA()函数运作机理

ARIMA()函数建模计算使用了(Rob J. Hyndman and Khandakar 2008)一文中的算法的修改版本， 结合了单位根检验， 最大似然估计， AICc定阶。 ARIMA()函数提供了多个选项用来修改算法细节。

下面是ARIMA()的默认做法，使用了(Rob J. Hyndman and Khandakar 2008)中的方法：

1. 用KPSS检验确定需要的差分阶数\(d\)。

2. 针对已经差分变换后的序列， 用AICc准则以及逐步搜索方法确定\(p, q\)的值：

   1. 先估计四个模型：ARIMA(0,\(d\),0)；ARIMA(2,\(d\),2)； ARIMA(1,\(d\),0)；ARIMA(0,\(d\),1)。 当\(d=0,1\)时这四个模型总是有常数项， 并且额外估计一个不带常数项的ARIMA(0,\(d\),0)； 当\(d=2\)时这四个模型都不带常数项。
   2. 将以上的四个或五个模型中按AICc选择最优模型作为当前模型。
   3. 不断考虑当前模型的变化， 变化方式包括\(p\)或者\(q\)加1或者减1， 包括或者不包括常数项。
   4. 不断重复c)步直到AICc值不再下降。

此算法不一定能获得AICc的全局最优解， 可以在ARIMA()函数中指定stepwise = FALSE去搜索全局最优。

12.3.2 用fable包建立arima模型的一般步骤

这里暂不考虑有季节性的情形。 fable包用户要建立arima模型， 一般步骤如下：

1. 整理数据为tsibble格式， 对数据作图，猜测可能需要的变换、差分， 识别异常观测；
2. 需要时对数据作对数变换、Box-Cox变换等处理；
3. 若数据不平稳，作差分使得数据变平稳；
4. 对已经变平稳的序列， 作PACF图和ACF图， 判断AR或者MA模型是否可行；
5. 尝试若干个候选模型， 用AICc比较选出最优模型；
6. 对模型作残差诊断， 看残差的ACF图是否呈现白噪声应有表现， 作Ljung-Box白噪声检验。 如果残差诊断反映模型不合适， 就修改模型。
7. 残差诊断通过后， 模型可用。 可以用模型作预测。

注意ARIMA()函数不能检查异常值， 不能分析是否需要变换， 不能自动作残差诊断。

12.3.3 残差的白噪声检验

残差的Ljung-Box白噪声检验需要进行自由度调整。 设检验统计量用到了\(\ell\)个自相关函数值的平方， 对原始序列， 统计量在\(H_0\)下近似服从\(\chi^2_{\ell}\)分布； 但是对ARIMA建模的残差作检验， 需要将自由度\(\ell\)调整为\(\ell - K\)， \(K\)是模型中的AR和MA部分的系数个数， 即\(p+q\)。 在ljung_box()函数中用dof输入\(K\)的值。

例12.6 考虑例12.5的模型诊断。

解答： 数据图形见例12.5。 数据不需要变换。 从后面自动建模结果看不需要差分。

对建立的有常数项的ARIMA(2,0,1)模型， 用gg_tsresiduals()作残差的时间序列图、ACF图、PACF图：

export_fit |>
  gg_tsresiduals()

从残差ACF看符合白噪声要求。

作残差白噪声检验：

export_fit |>
  augment() |>
  features(.innov, ljung_box, lag = 10, dof = 3)

## # A tibble: 1 × 3
##   .model         lb_stat lb_pvalue
##   <chr>            <dbl>     <dbl>
## 1 ARIMA(Exports)    5.78     0.565

因为模型\(p=2\), \(q=1\)，所以dof取值为\(p+q=3\)。 白噪声检验不显著。

○○○○○○

例12.7 考虑例12.5的人为模型选择。

从PACF图看， 可以考虑AR(4)， 从ACF图看，可以考虑MA(9)。 另外比较用逐步方法搜索以及全局搜索。

export_fits <- export_tsib |>
  model(
    ar4 = ARIMA(Exports ~ 1 + pdq(4,0,0)),
    ma9 = ARIMA(Exports ~ 1 + pdq(0,0,9), 
      order_constraint = TRUE),
    stepwise = ARIMA(Exports),
    global = ARIMA(Exports, stepwise = FALSE)  )

结果中包含了4个模型， 可以用glance()概略比较：

glance(export_fits)

## # A tibble: 4 × 8
##   .model   sigma2 log_lik   AIC  AICc   BIC ar_roots  ma_roots 
##   <chr>     <dbl>   <dbl> <dbl> <dbl> <dbl> <list>    <list>   
## 1 ar4        7.88   -141.  293.  295.  305. <cpl [4]> <cpl [0]>
## 2 ma9        7.64   -139.  301.  306.  323. <cpl [0]> <cpl [9]>
## 3 stepwise   8.05   -142.  293.  294.  303. <cpl [2]> <cpl [1]>
## 4 global     8.05   -142.  293.  294.  303. <cpl [2]> <cpl [1]>

从AICc可以看出MA(9)明显很差， 逐步搜索与全局搜索得到的AICc值相同， AR(4)结果略差一些。

在同时拟合了多个模型时不能直接用report()查看单个模型的估计结果， 可以用tidy()同时查看模型的估计结果中参数估计情况，如：

tidy(export_fits) |>
  knitr::kable()

.model	term	estimate	std.error	statistic	p.value
ar4	ar1	0.9860939	0.1246601	7.9102637	0.0000000
ar4	ar2	-0.1715288	0.1864690	-0.9198783	0.3614465
ar4	ar3	0.1807232	0.1865368	0.9688340	0.3366509
ar4	ar4	-0.3282555	0.1273358	-2.5778732	0.0125037
ar4	constant	6.6921689	0.3562360	18.7857749	0.0000000
ma9	ma1	1.0717305	0.1992002	5.3801670	0.0000014
ma9	ma2	0.7479920	0.2223936	3.3633708	0.0013691
ma9	ma3	0.8601330	0.2700157	3.1854927	0.0023267
ma9	ma4	0.5494279	0.3370153	1.6302758	0.1084626
ma9	ma5	0.4520942	0.4131365	1.0942974	0.2783484
ma9	ma6	-0.0096608	0.3859351	-0.0250322	0.9801152
ma9	ma7	-0.1771601	0.3519570	-0.5033573	0.6166195
ma9	ma8	-0.1224128	0.3152541	-0.3882989	0.6992165
ma9	ma9	-0.3732928	0.1560745	-2.3917602	0.0200306
ma9	constant	20.0044341	1.3051850	15.3268954	0.0000000
stepwise	ar1	1.6764333	0.1110585	15.0950538	0.0000000
stepwise	ar2	-0.8034121	0.0927730	-8.6599741	0.0000000
stepwise	ma1	-0.6896299	0.1491713	-4.6230749	0.0000216
stepwise	constant	2.5623058	0.1160878	22.0721333	0.0000000
global	ar1	1.6764333	0.1110585	15.0950538	0.0000000
global	ar2	-0.8034121	0.0927730	-8.6599741	0.0000000
global	ma1	-0.6896299	0.1491713	-4.6230749	0.0000216
global	constant	2.5623058	0.1160878	22.0721333	0.0000000

为了用report()查看单个模型， 可以将横向存放的4个模型转为纵向存放， 筛选要考察的模型， 然后查看：

export_fits |> 
  select(ar4) |> 
  report()

## Series: Exports 
## Model: ARIMA(4,0,0) w/ mean 
## 
## Coefficients:
##          ar1      ar2     ar3      ar4  constant
##       0.9861  -0.1715  0.1807  -0.3283    6.6922
## s.e.  0.1247   0.1865  0.1865   0.1273    0.3562
## 
## sigma^2 estimated as 7.885:  log likelihood=-140.53
## AIC=293.05   AICc=294.7   BIC=305.41

○○○○○○

12.3.4 关于常数项的进一步说明

fable的arima模型在没有季节项时， 公式为 \[ (1 - \phi_1 B - \dots - \phi_p B^p) (1 - B)^d y_t = c + (1 + \theta_1 B + \dots + \theta_q B^q) \varepsilon_t . \] 估计结果中的constant就是上式中的\(c\)。 当\(d \geq 2\)时fable仅允许\(c=0\)。

对\(d=0\)， 由平稳性易见 \[ \mu = E(y_t) = c / (1 - \phi_1 - \dots - \phi_p) . \]

对\(d=1\)， \((1- B) y_t\)平稳， 所以 \[ \mu := E[(1- B) y_t] = c / (1 - \phi_1 - \dots - \phi_p), \] 有 \[ (1 - \phi_1 B - \dots - \phi_p B^p) [(1 - B) y_t - \mu] = (1 + \theta_1 B + \dots + \theta_q B^q) \varepsilon_t . \] 其中的 \[ (1 - B) y_t - \mu = (1 - B)[y_t - (\beta_0 + \mu t)] , \] \(\beta_0\)在差分时会消失。 所以\(d=1\)时若\(c \neq 0\)， 相当于\(y_t\)与\(c = 0\)的情形相比多了一个\(t\)的一阶多项式。

如果允许\(d \geq 2\)时\(c \neq 0\)， 则 \[ \mu := E[(1-B)^d y_t] = c / (1 - \phi_1 - \dots - \phi_p), \] 模型可以写成 \[ (1 - \phi_1 B - \dots - \phi_p B^p) [(1 - B)^d y_t - \mu] = (1 + \theta_1 B + \dots + \theta_q B^q) \varepsilon_t , \] 其中的 \[ (1 - B)^d y_t - \mu = (1 - B)^d[y_t - (\beta_0 + \beta_1 t + \dots + \beta_{d-1} t^{d-1} + \frac{\mu}{d!} t^d)], \] 其中关于\(t\)的0次到\(d-1\)次项在\(d\)次差分时都会消掉， \(c \neq 0\)的\(y_t\)与\(c=0\)的\(y_t\)相比只是多了一个关于\(t\)的\(d\)次多项式， 其预测值中也会含有一个关于\(t\)的\(d\)次多项式； 如果\(c = 0\)则\(\mu=0\)， 这时\(y_t\)中可以含有一个关于\(t\)的\(d-1\)次多项式（因为\(d\)阶差分会将其消去）， 预测值中也会含有一个关于\(t\)的\(d-1\)次多项式。

fable包在\(d=0,1\)时用AICc判断是否应该包含常数项； 在\(d \geq 2\)时不允许\(c \neq 0\)， 因为\(d = 2\)就意味着预测公式中包含了\(t\)的二次项， 这是很强的模型假定， 一般数据都不满足条件。

ARIMA()函数中可以在~右边用0表示没有常数项， 用1表示有常数项， 如ARIMA(Exports ~ 1 + pdq(4,0,0)。

12.3.5 关于特征根

ARMA模型的AR部分有如下的特征多项式： \[ A(z) = 1 - \phi_1 z - \dots - \phi_p z^p, \ z \in \mathbb Z . \] 其中\(\mathbb Z\)表示复数域。 ARMA模型要求\(A(z)\)的根（称为特征根）都满足复数模大于1的条件， 在复平面上看， 就是要求特征根都在单位圆（以原点为圆心、半径等于1的圆）外。 对ARMA模型， 特征根越接近于单位圆， 模型相关性越强， 与白噪声列差别越大。 如果有一对共轭复根\(\rho e^{\pm i \omega}\)， 且\(\rho\)的值接近于1， 则序列会呈现以\(2\pi/\omega\)为近似周期的波动。

ARMA模型的MA部分也有如下的特征多项式： \[ B(z) = 1 + \theta_1 z + \dots + \theta_q z^q, \ z \in \mathbb Z . \] 当这个多项式的根都在单位圆外时， 称ARMA模型为可逆的。

gg_arma()对AR部分与MA部分的特征根倒数在单位圆内作图， 如：

export_fit |>
  gg_arma()

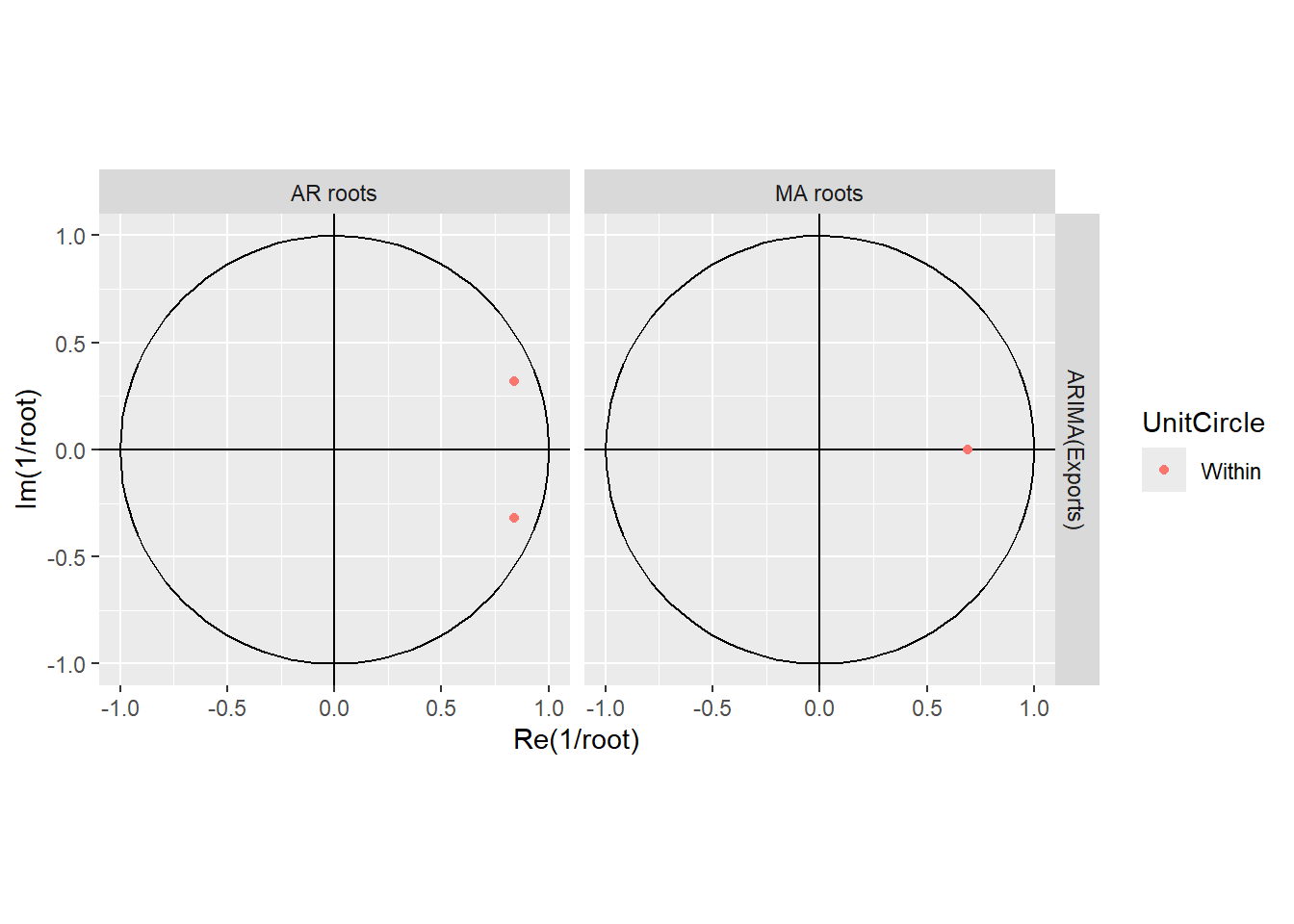
可以看出AR部分有一对特征根且离单位圆较近， 会呈现出一定的随机周期性。

12.4 预测公式

12.4.1 点预测

对ARIMA模型(12.1)， 令 \[ \tilde A(z) = (1 - \phi_1 z - \dots - \phi_p z^p)(1 - z)^d = 1 - \tilde\phi_1 z - \dots - \tilde\phi_{p+d} z^{p+d}, \] 就可以将模型写成 \[\begin{aligned} y_t =& c + \tilde\phi_1 y_{t-1} + \dots + \tilde\phi_{p+d} y_{t-p-d} \\ & + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q}, \end{aligned}\]

以\(t = T+h\)代入有 \[\begin{aligned} y_{T+h} =& c + \tilde\phi_1 y_{T+h-1} + \dots + \tilde\phi_{p+d} y_{T+h-p-d} \\ & + \varepsilon_{T+h} + \theta_1 \varepsilon_{T+h-1} + \dots + \theta_q \varepsilon_{T+h-q}, \end{aligned}\] 预测值为 \[\begin{equation} \begin{aligned} \hat y_{T+h} =& \hat y_{T+h|T} = E(y_{T+h} \,|\, y_1, \dots, y_{T+h}) \\ \approx& c + \tilde\phi_1 \hat y_{T+h-1} + \tilde\phi_{p+d} \hat y_{T+h-p-d} \\ & + e_{T+h} + \theta_1 e_{T+h-1} + \dots + \theta_q e_{T+h-q}, \end{aligned} \tag{12.2} \end{equation}\] 其中 \[ \hat y_{T+h-j} = \begin{cases} \hat y_{T+h-j | T}, & \text{当} T+h-j > T, \\ y_{T+h-j}, & \text{当} T+h-j \leq T . \end{cases} \] 而\(e_t\)用是\(\varepsilon_t\)的估计值， 用模型残差代替， 当\(t > T\)时取\(e_t = 0\)。 对\(j=1,2,\dots, h\)按(12.2)递推计算就可以得到超前1步到超前\(h\)步的点预测值。

12.4.2 预测区间

对超前一步预测， 设\(\hat\sigma^2\)是从拟合残差得到的新息方差估计， 则超前一步\(1 - \alpha\)预测区间可以取为 \[ \hat y_{T+1|T} \pm z_{1 - \alpha/2} \hat\sigma . \] 当参数都取理论真值且\(\hat\sigma\)也取理论真值， 并且\(T \to \infty\)时， 这时上述公式是理论上正确的。 但此公式没有考虑到使用观测样本估计参数并代入预测公式所产生的额外误差。

为了将超前一步预测区间推广到多步预测区间， 可以使用ARMA模型的平稳解（Wold表示）， 参见6.5。

关于\(T\)有限时上述公式的误差， 在假设序列为高斯时间序列时， 可以用递推预测(见本科生金融时间序列分析讲义)或者线性高斯状态空间模型(参见32)获得理论上精确的置信区间（仍没有考虑参数估计误差的影响）。

当随着\(h\)增大， 置信区间会变宽， 对\(d=0\)， 序列是平稳的， 这个置信区间宽度会趋于一个有限值； 当\(d \geq 1\)时， \(h \to \infty\)时置信区间宽度会趋于无穷。

为了考虑参数估计误差的影响， 应该用估计出的参数重新生成多组模拟观测值， 对每组模拟观测值重新估计参数， 生成点预测， 用多组点预测产生区间预测。 fable包没有这样的设置。

fable包提供了bootstrap预测功能， 这个功能没有重新生成多组模拟观测值所以不能修正参数估计误差的影响， 但可以修正时间序列分布非高斯的影响。 参见10.3.5.3。

12.5 季节ARIMA模型

12.5.1 模型

季节ARIMA模型， 设周期为\(m\)， 可以在模型中引入季节差分\((1 - B^m)^D\)， 在模型左侧引入乘性的季节AR部分的因子\(1 - \Phi_1 B^m - \dots - \Phi_P B^{Pm}\)， 在模型右侧引入乘性的季节MA部分的因子\(1 + \Theta_1 B^m + \dots + \Theta_Q B^{Qm}\)， 模型变成 \[\begin{aligned} & (1 - \phi_1 B - \dots - \phi_p B^p) \\ & (1 - \Phi_1 B^m - \dots - \Phi_p B^{Pm}) \\ & (1 - B)^d (1 - B^m)^D \\ =& c + (1 + \theta_1 B + \dots + \theta_q B^q) \\ & (1 + \Theta_1 B^m + \dots + \Theta_Q B^{Qm}) \varepsilon_t . \end{aligned}\] 这样的模型记为ARIMA\((p,d,q)(P,D,Q)_m\)。

12.5.2 ACF和PACF表现

将模型左右两侧的多项式乘在一起，写成 \[ (1 - \tilde\phi_1 B - \dots - \tilde\phi_{\tilde p} B^{\tilde p}) y_t = (1 + \tilde\theta_1 + \dots + \tilde\theta_{\tilde q} B^{\tilde q}) \varepsilon_t, \] 则ACF和PACF的表现可以从两边的多项式反映出来。

如果\(d \geq 1\)， 则ACF会衰减很缓慢； 如果\(D \geq 1\)， 则ACF在\(m\)的倍数处会衰减很缓慢。

如果\(d=D=0\)， 则ACF和PACF受到模型方程中系数的影响。 比如， 一个ARIMA\((0,0,0)(0,0,1)_{12}\)序列的ACF在滞后12处显著不为零。

12.5.3 例子

12.5.3.1 就业人数例子

下面用几个例子说明建模预测过程。 这些例子来自(R. J. Hyndman and Athanasopoulos 2021)节9.9。

例12.8 fpp3包的us_employment数据包含了美国就业有关的月度数据， 用Series_ID编码区分不同行业， 实际解释放在Title变量中。 Month为时间， Employed是以百万计数的就业人数。 对其中的休闲服务业(Leisure and Hospitality)建模预测。

解答： 数据整理

library(fpp3)
leis_tsib <- us_employment |>
  filter(Title == "Leisure and Hospitality",
    year(Month) > 2000) |>
  select(Month, Employed)
leis_tsib |>
  autoplot(Employed) + 
  labs(y = "人数(百万)",
    title = "美国休闲服务业就业人数")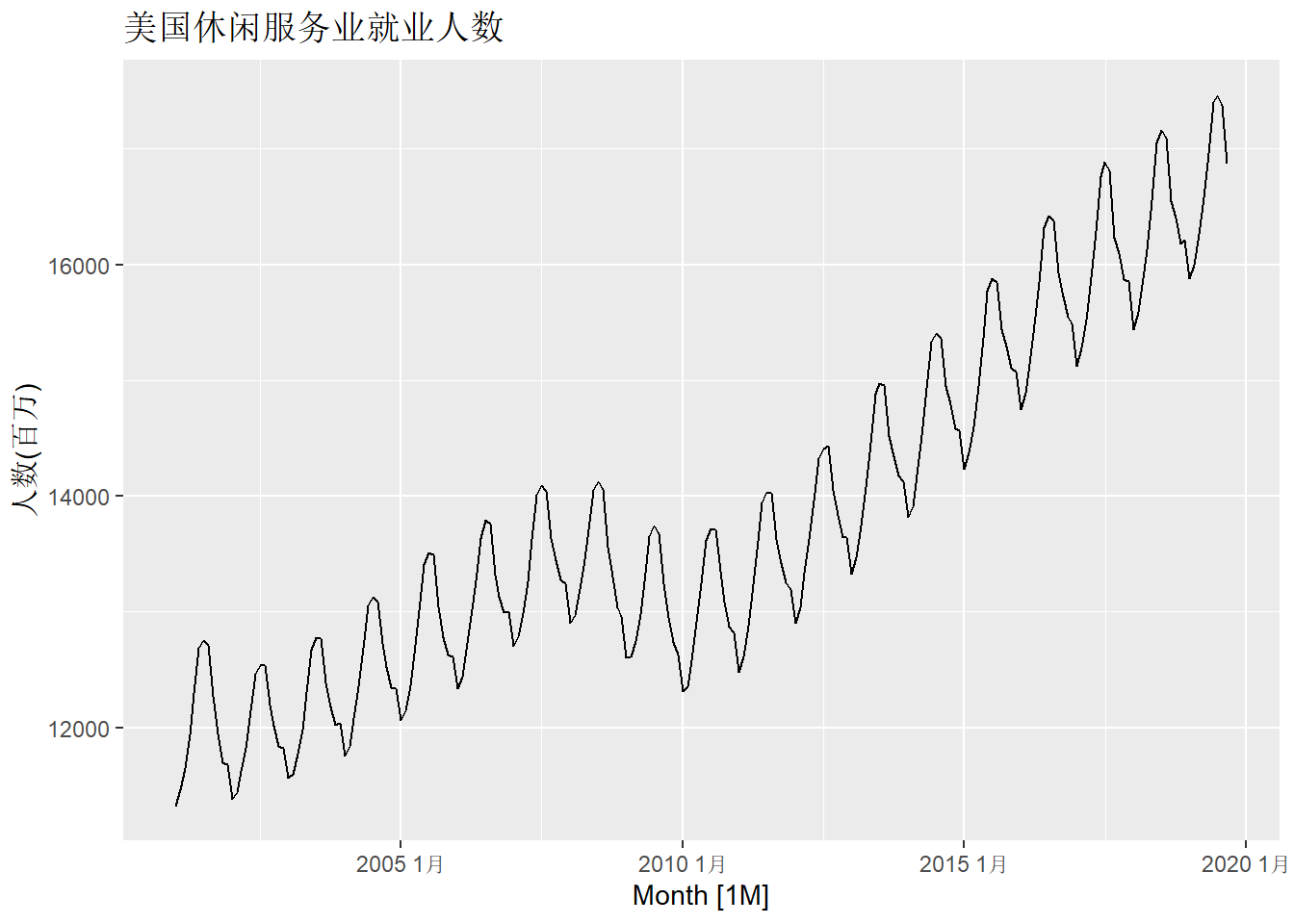

数据在2008年磁带危机期间有明显落差。 数据呈现趋势性、季节性。

自动建模：

leis_fita <- leis_tsib |>
  model(ARIMA(Employed))
report(leis_fita)

## Series: Employed 
## Model: ARIMA(1,1,1)(2,1,1)[12] 
## 
## Coefficients:
##          ar1      ma1    sar1     sar2     sma1
##       0.8502  -0.6934  0.2665  -0.0413  -0.6966
## s.e.  0.1325   0.1869  0.1466   0.0989   0.1246
## 
## sigma^2 estimated as 1427:  log likelihood=-1069.76
## AIC=2151.53   AICc=2151.94   BIC=2171.67

自动搜索程序建立了一个不带常数项的ARIMA\((1,1,1)(2,1,1)_{12}\)模型， AICc为\(2151.94\)。

用该模型向前预测一年：

leis_forea <- leis_fita |>
  forecast(h = "3 years")
leis_forea |> 
  autoplot(leis_tsib) + 
  labs(title = "就业人数自动ARIMA预测")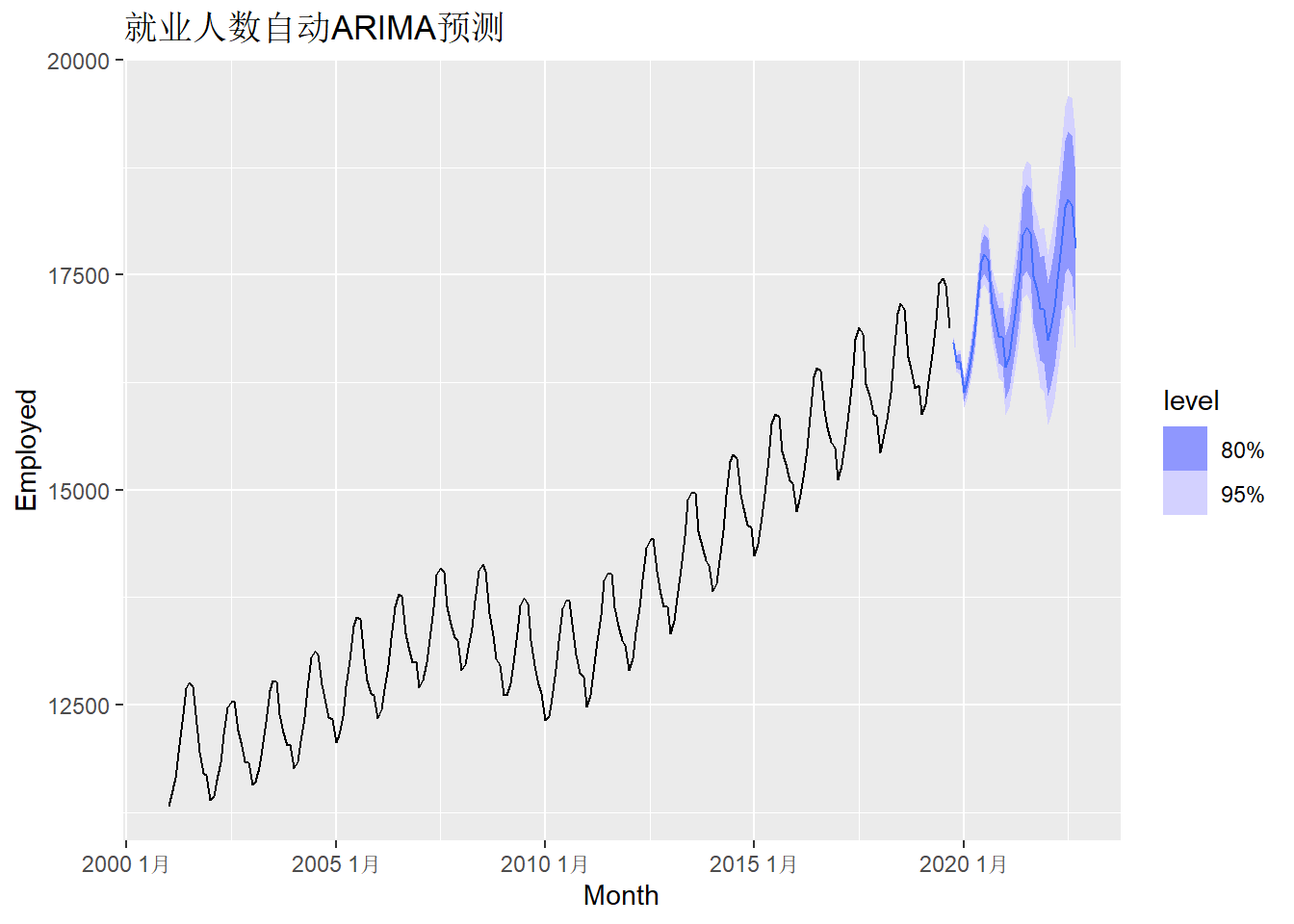

下面人为控制建模过程。 查看季节差分后的序列情况：

leis_tsib |>
  gg_tsdisplay(
    difference(Employed, 12),
    plot_type = "partial",
    lag = 36  ) +
  labs(title = "季节差分序列", y = "")

## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_line()`).

## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_point()`).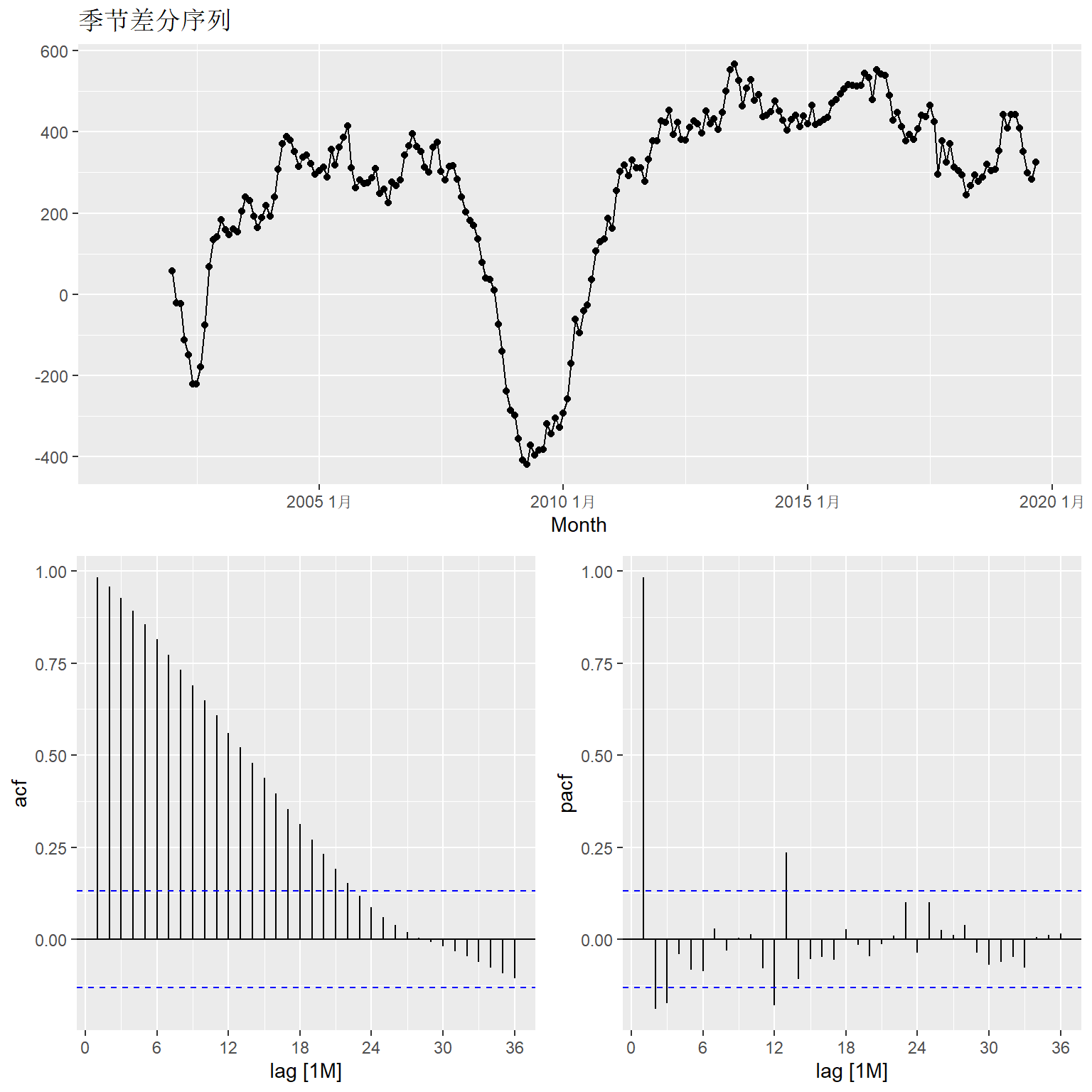

其ACF仍呈现出缓慢的下降， 所以怀疑仍需要进行普通差分。 进行两种差分再查看序列情况：

leis_tsib |>
  gg_tsdisplay(
    difference(Employed, 12) |> difference(),
    plot_type = "partial",
    lag = 36  ) +
  labs(title = "季节差分且普通差分后序列", y = "")

## Warning: Removed 13 rows containing missing values or values outside the scale range
## (`geom_line()`).

## Warning: Removed 13 rows containing missing values or values outside the scale range
## (`geom_point()`).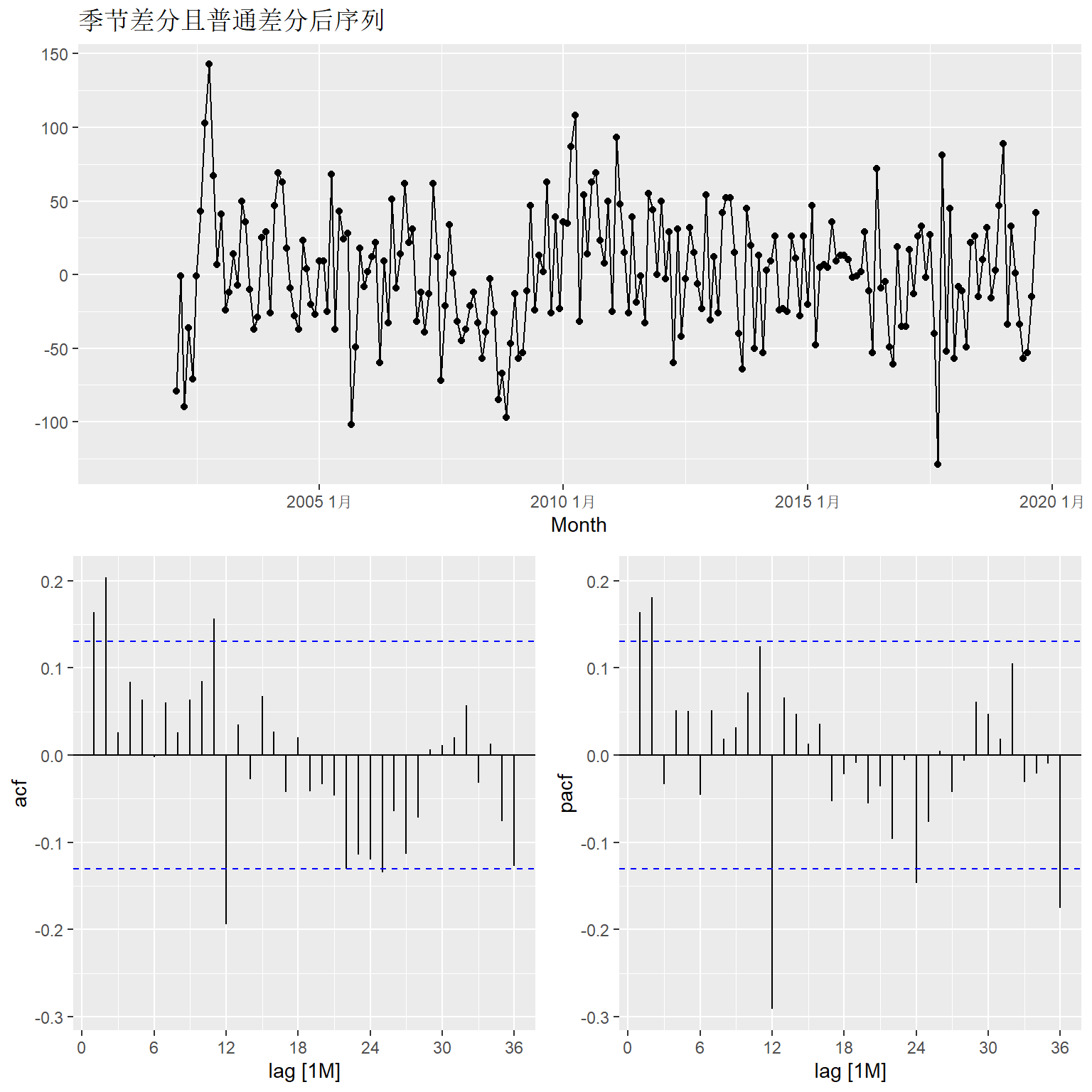

这已经表现得比较平稳， 但在季节滞后12处有较大相关性。 提示需要乘性季节成分。

对差分后序列， 如果从ACF看， 应该拟合一个ARIMA\((0,1,2)(0,1,1)_{12}\)模型。 如果从PACF看， 可以拟合一个ARIMA\((2,1,0)(0,1,1)_{12}\)模型。 全局选择也可以加入。

leis_fits <- leis_tsib |>
  model(
    arima012011 = ARIMA(
      Employed ~ pdq(0,1,2) + PDQ(0,1,1)),
    arima210011 = ARIMA(
      Employed ~ pdq(2,1,0) + PDQ(0,1,1)),
    auto = ARIMA(
      Employed, stepwise = FALSE, approx = FALSE)  )

用glance()查看模型拟合比较：

glance(leis_fits) |>
  select(.model, AICc) |>
  knitr::kable()

.model	AICc
arima012011	2154.182
arima210011	2152.892
auto	2149.256

从AICc看自动全局搜索的结果最优。 看一看各个模型的定阶：

leis_fits |>
  pivot_longer(everything(),
    names_to = "model", 
    values_to = "Orders") |>
  knitr::kable()

model	Orders
arima012011	<ARIMA(0,1,2)(0,1,1)[12]>
arima210011	<ARIMA(2,1,0)(0,1,1)[12]>
auto	<ARIMA(2,1,0)(1,1,1)[12]>

全局搜索与前面逐步搜索得到的模型相同。

提取auto对应的模型， 显示其估计结果：

leis_fits |>
  select(auto) |>
  report()

## Series: Employed 
## Model: ARIMA(2,1,0)(1,1,1)[12] 
## 
## Coefficients:
##          ar1     ar2    sar1     sma1
##       0.1786  0.1855  0.3295  -0.7507
## s.e.  0.0695  0.0679  0.1273   0.0936
## 
## sigma^2 estimated as 1415:  log likelihood=-1069.48
## AIC=2148.96   AICc=2149.26   BIC=2165.75

对全局搜索得到的模型进行残差诊断：

leis_fits |>
  select(auto) |>
  gg_tsresiduals(lag = 36)

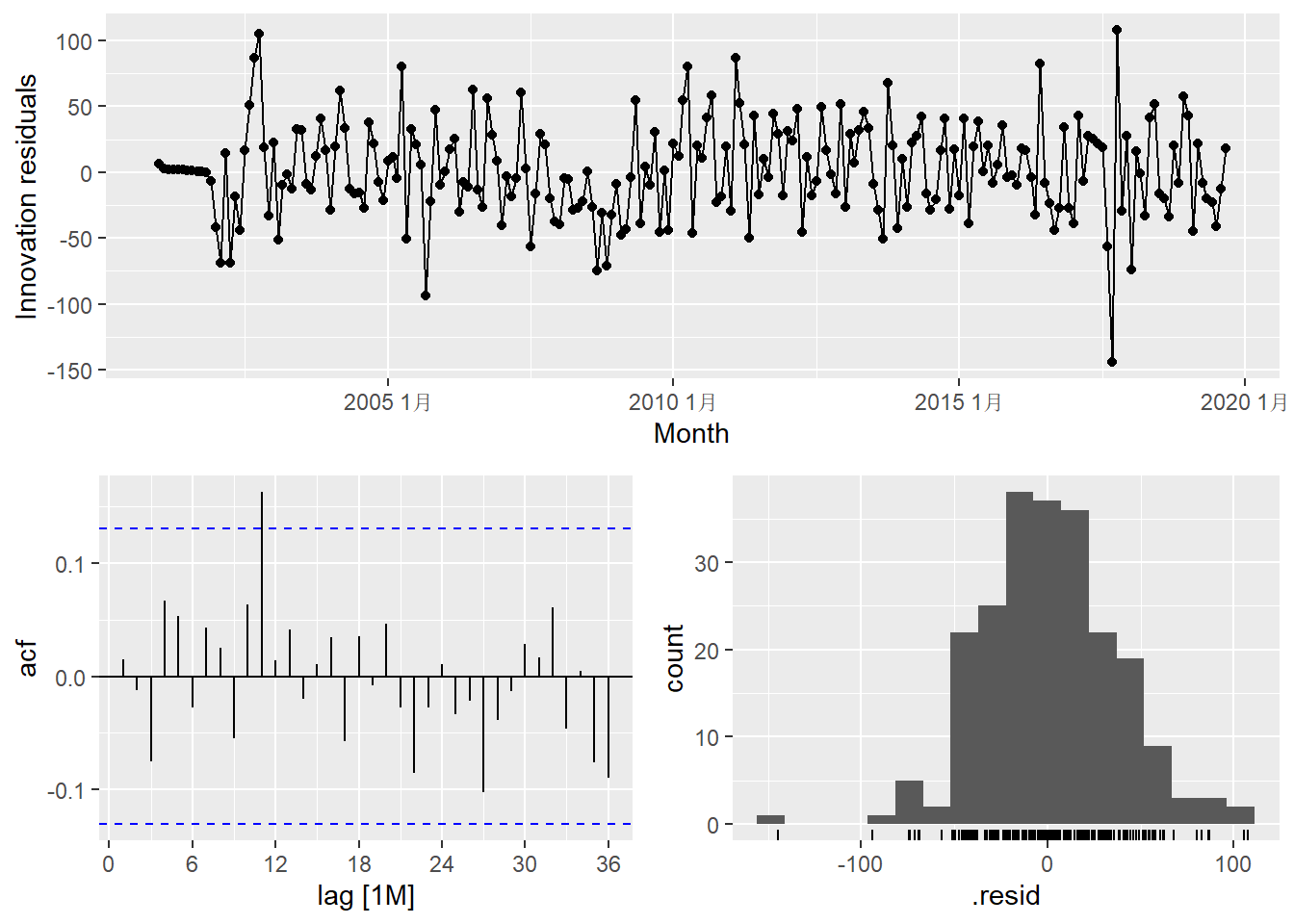
这个模型的残差的ACF在滞后12处仍略有突出。 进行残差白噪声检验：

leis_fits |>
  augment() |>
  filter(.model == "auto") |>
  features(.innov, ljung_box, lag=24, dof=4)

## # A tibble: 1 × 3
##   .model lb_stat lb_pvalue
##   <chr>    <dbl>     <dbl>
## 1 auto      16.6     0.680

其中的dof用了\(p+q+P+Q\)的值。 从残差白噪声检验来看模型可以接受。

12.5.3.2 销售额例子

例12.9 tsibbledata包的PBS数据包含了澳大利亚许多种药品的月度消费数量和金额， 用四个键变量区分类型。 对其中的皮质类固醇药物销售额建模预测。

解答： 数据整理

h02_tsib <- PBS |>
  filter(ATC2 == "H02") |>
  summarise(Cost = sum(Cost)/1e6) |>
  mutate(log_Cost = log(Cost))
h02_tsib |>
  autoplot(Cost) +
  labs(title = "皮质类固醇药物月度销售额")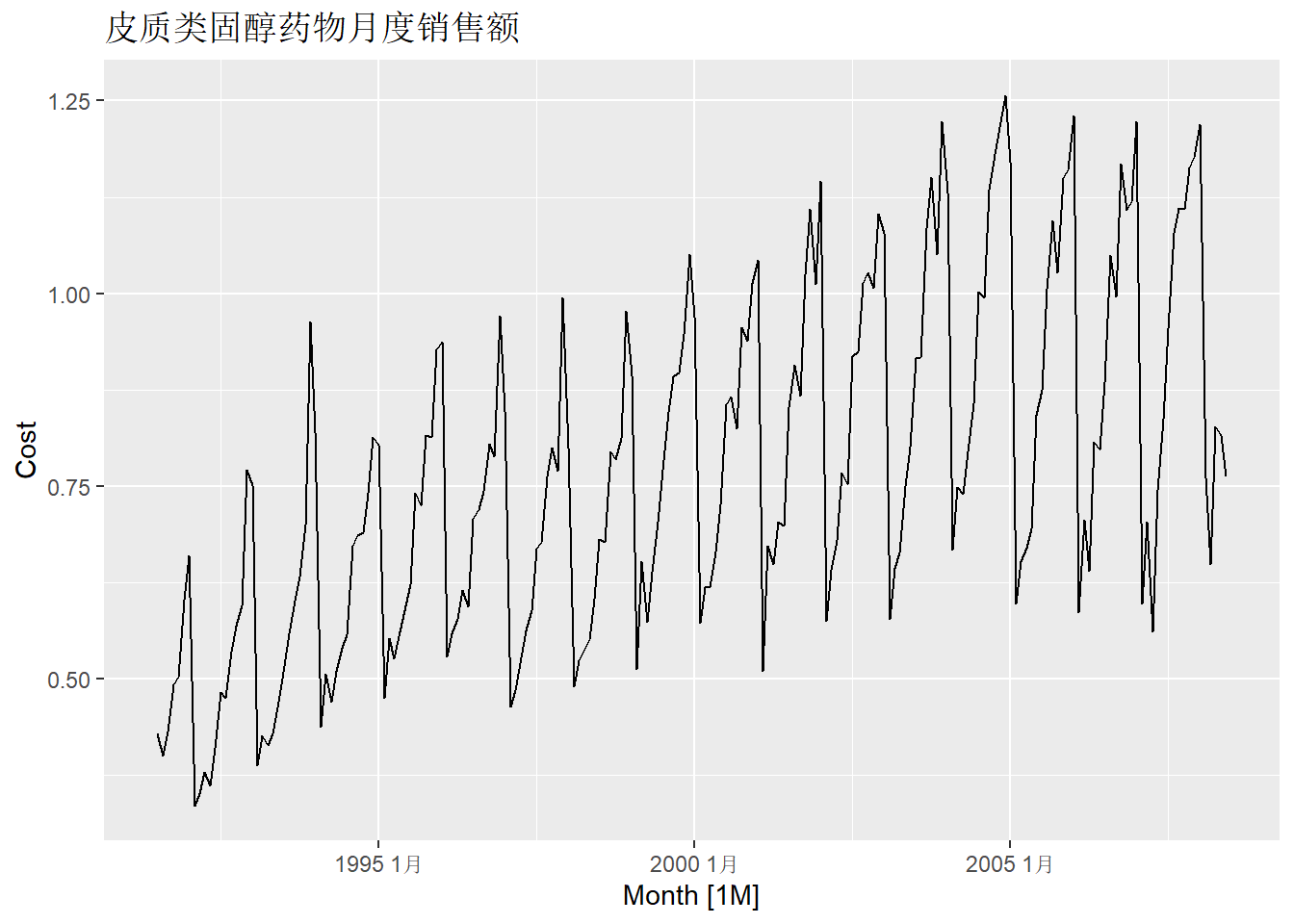

数据呈现明显季节性，有趋势性。 振幅有一定程度的增长。 作对数变换后的序列：

h02_tsib |>
  autoplot(log_Cost) +
  labs(title = "皮质类固醇药物月度销售额对数值")

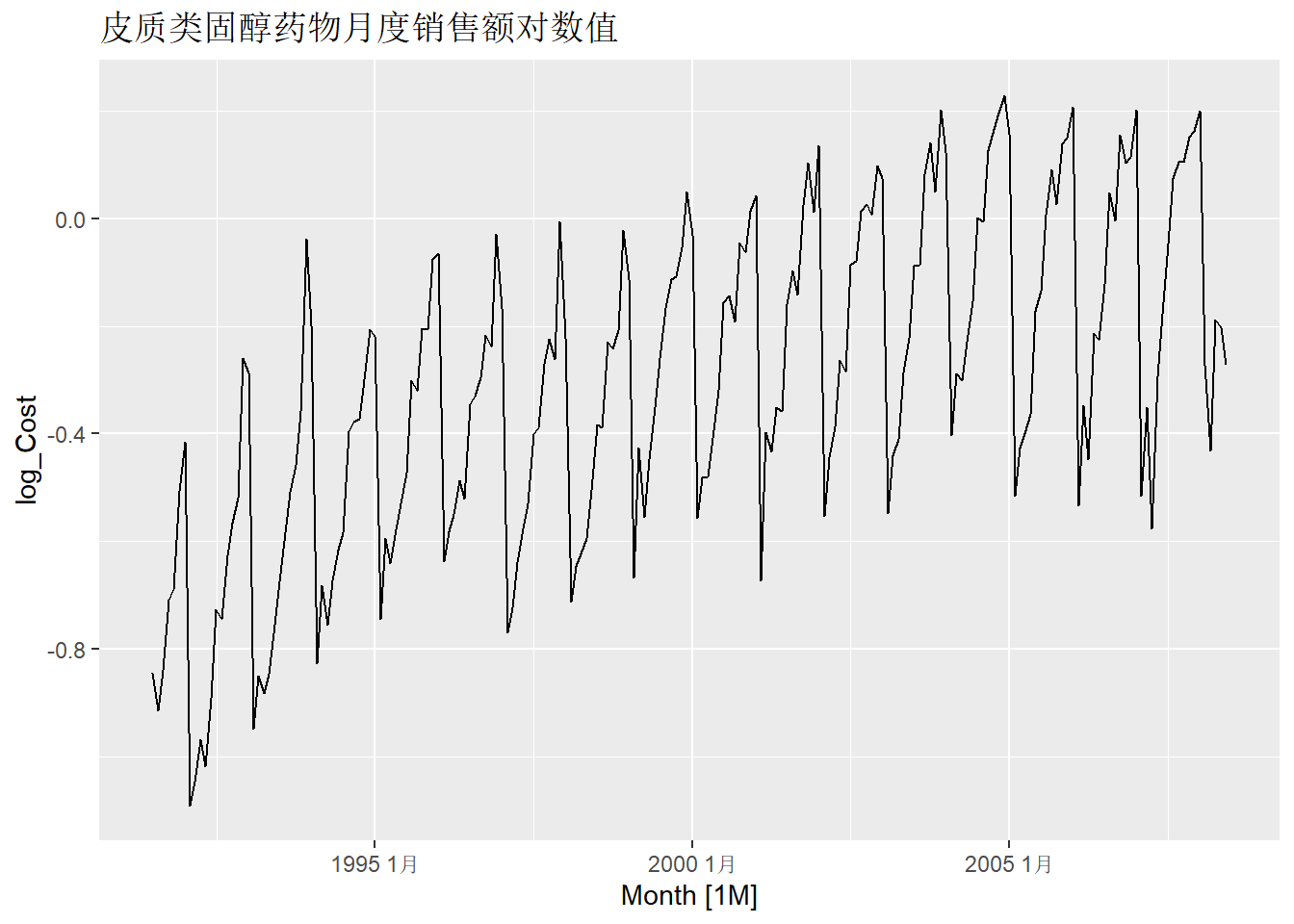
选择使用对数变换。 进行季节差分，查看是否平稳：

h02_tsib |>
  gg_tsdisplay(difference(log_Cost, 12),
    plot_type = "partial", lag = 36)

## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_line()`).

## Warning: Removed 12 rows containing missing values or values outside the scale range
## (`geom_point()`).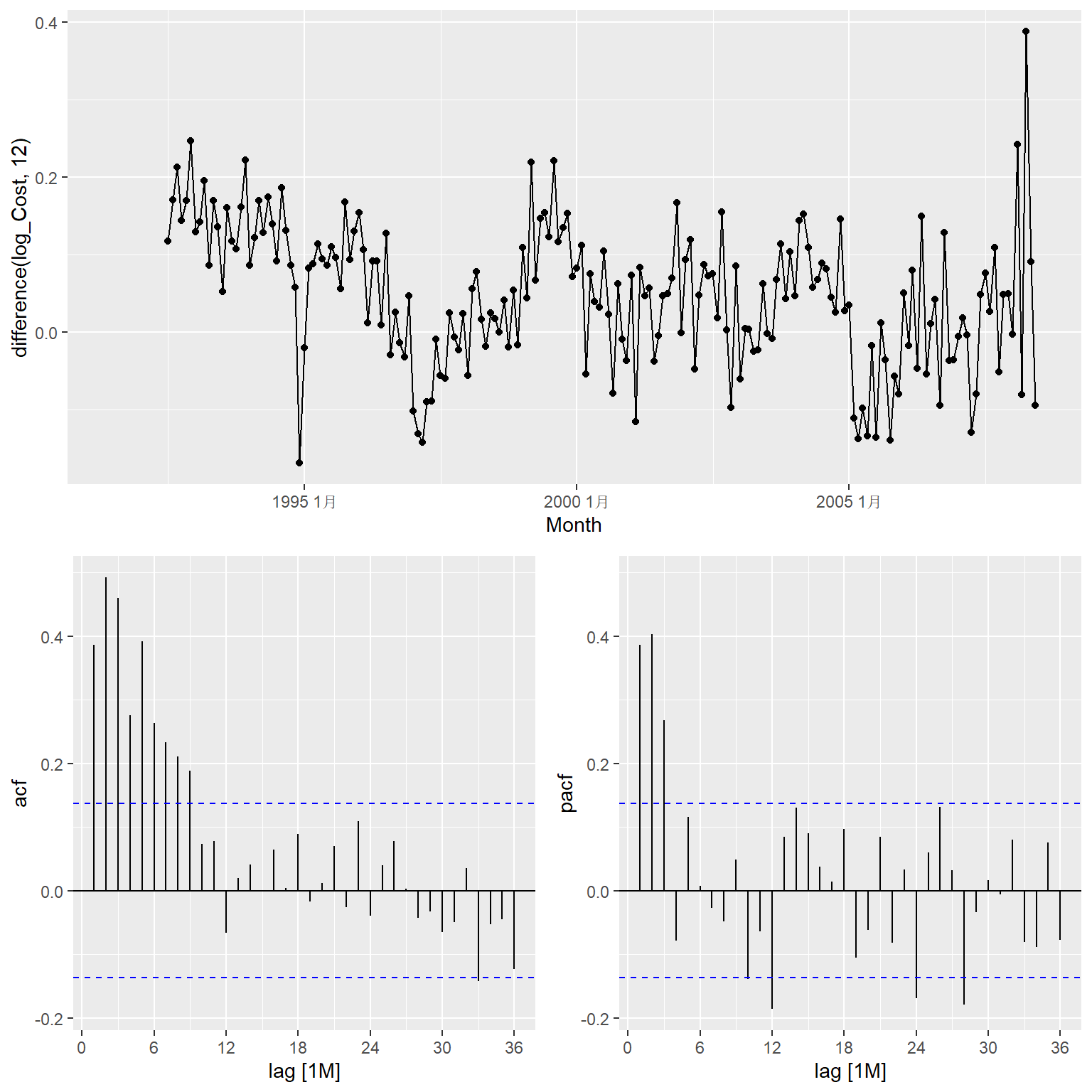

仍有一定的非平稳性。 作FPSS单位根检验：

h02_tsib |>
  mutate(diffs_logc = difference(log_Cost, 12)) |>
  features(diffs_logc, unitroot_kpss)

## # A tibble: 1 × 2
##   kpss_stat kpss_pvalue
##       <dbl>       <dbl>
## 1     0.867        0.01

KPSS检验的零假设是平稳， 所以检验结果季节差分序列表明非平稳。

考察季节差分与普通差分并行的序列：

h02_tsib |>
  gg_tsdisplay(difference(log_Cost, 12) |> difference(),
    plot_type = "partial", lag = 36) +
  labs(title = "季节差分与普通差分并行")

## Warning: Removed 13 rows containing missing values or values outside the scale range
## (`geom_line()`).

## Warning: Removed 13 rows containing missing values or values outside the scale range
## (`geom_point()`).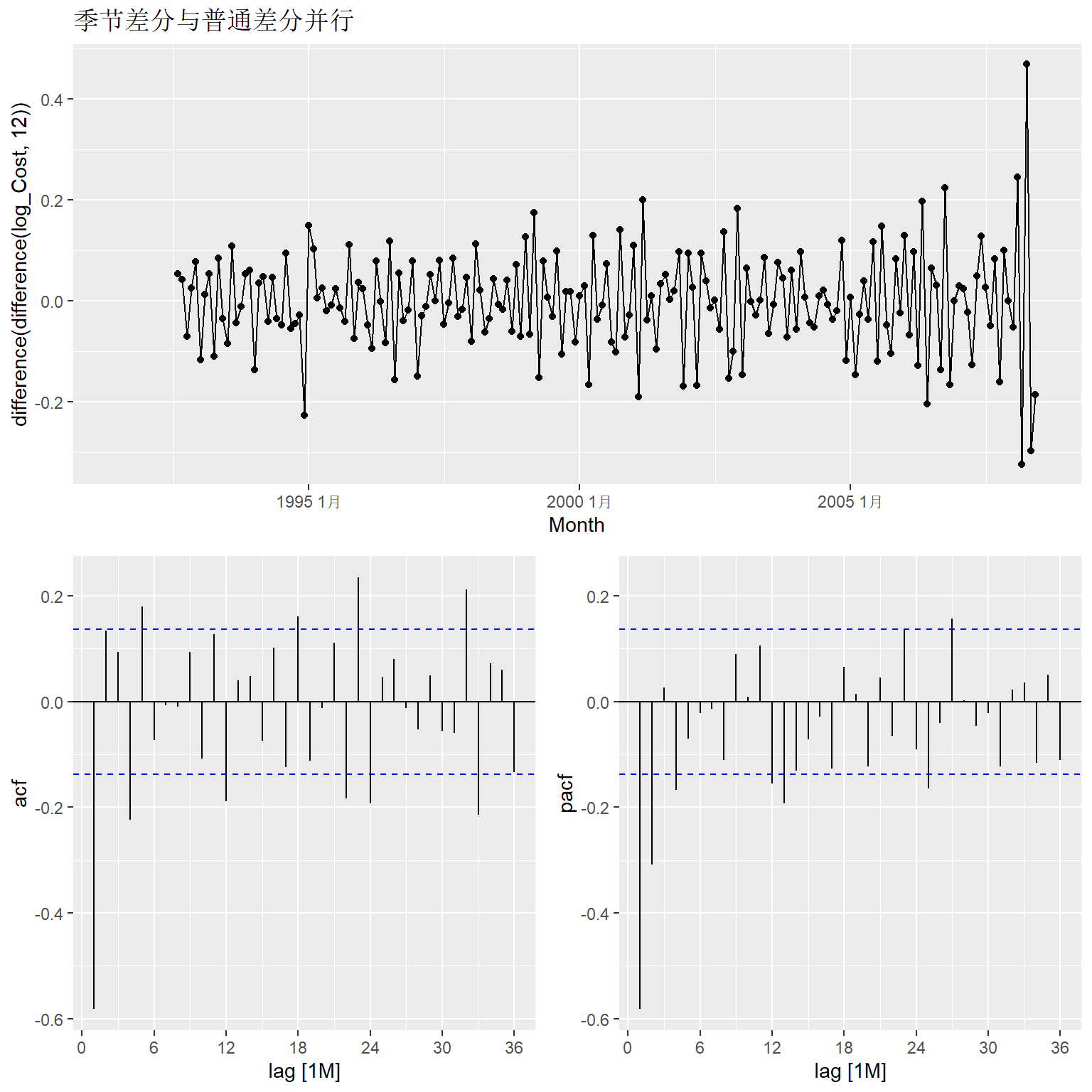

这可以考虑一个ARIMA\((1,1,1)(0,1,0)_{12}\)模型。 同时进行局部搜索。

h02_fits <- h02_tsib |>
  model(
    manual = ARIMA(log(Cost) ~ pdq(1,1,1) + PDQ(0,1,0)),
    auto = ARIMA(log(Cost))  )
glance(h02_fits) |>
  select(.model, AICc) |>
  knitr::kable()

.model	AICc
manual	-439.4665
auto	-482.5602

从AICc看人为选择的模型比自动选择的模型差得多。

h02_fits |>
  select(auto) |>
  report()

## Series: Cost 
## Model: ARIMA(2,1,0)(0,1,1)[12] 
## Transformation: log(Cost) 
## 
## Coefficients:
##           ar1      ar2     sma1
##       -0.8491  -0.4207  -0.6401
## s.e.   0.0712   0.0714   0.0694
## 
## sigma^2 estimated as 0.004387:  log likelihood=245.39
## AIC=-482.78   AICc=-482.56   BIC=-469.77

自动选择的是关于对数变换序列的ARIMA\((2,1,0)(0,1,1)_{12}\)模型。

自动选择的模型的残差诊断：

h02_fits |>
  select(auto) |>
  gg_tsresiduals(lag = 36)

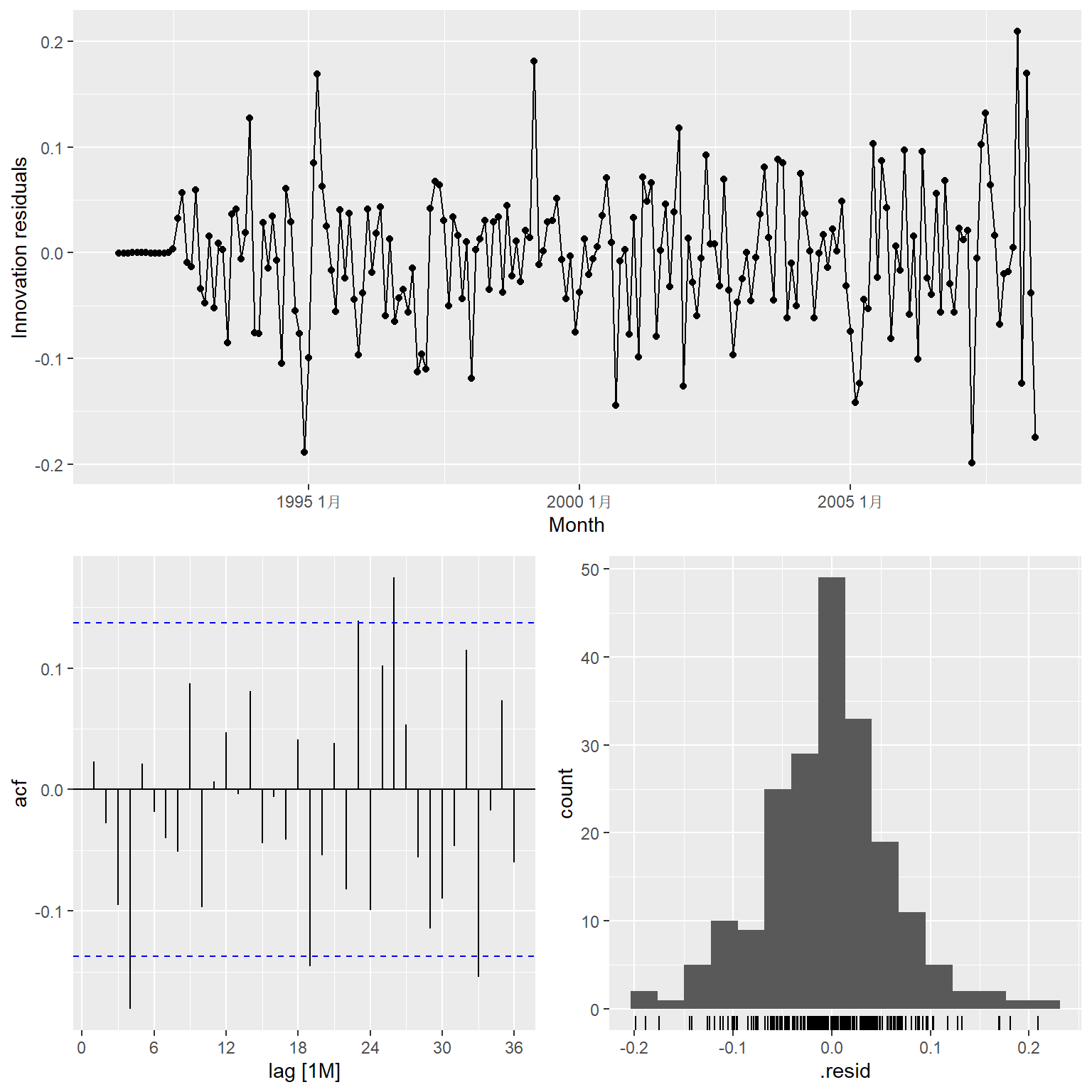
注意其中的Innovation residuals指的是对数变换以后的序列的拟合残差。

拟合残差的白噪声检验：

h02_fits |>
  select(auto) |>
  augment() |>
  features(.innov, ljung_box, lag=12, dof=3)

## # A tibble: 1 × 3
##   .model lb_stat lb_pvalue
##   <chr>    <dbl>     <dbl>
## 1 auto      14.3     0.113

在0.05水平下可以接受自动选择的模型。

向前3年预测：

h02_fits |>
  select(auto) |>
  forecast(h = "3 years") |>
  autoplot(h02_tsib)

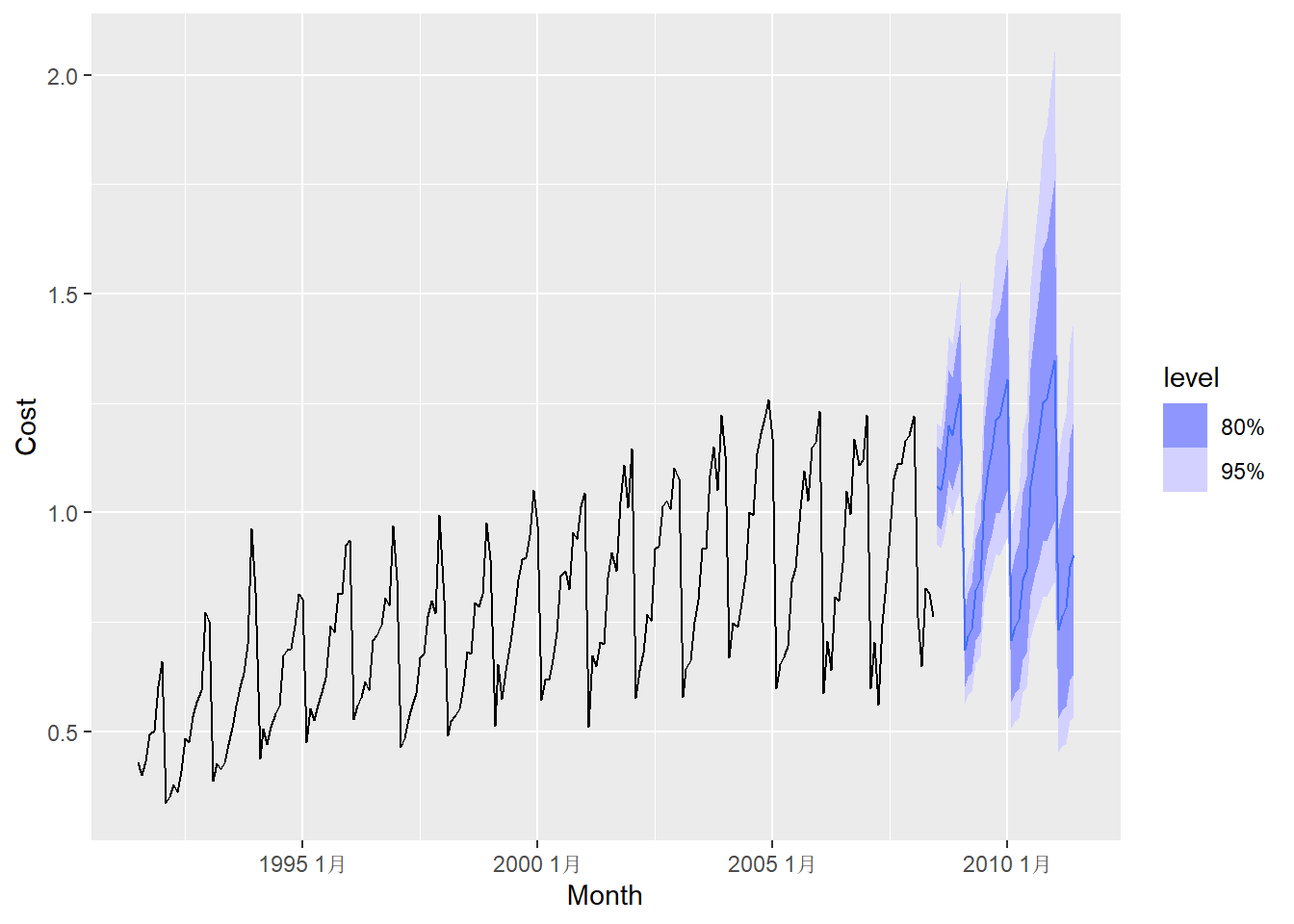
因为对数变换的原因， 点预测值的振幅也越来越大。

12.5.4 样本外比较与模型选择

可以进行滚动向前一步预测， 计算一步预测误差的RMSE等预测精度指标， 用来比较模型的预测能力。

以例12.9的销售额序列为例， 比较建立的两个模型。

我们用最初的114个数据点选择模型， 然后用剩余的90个数据点评估一步预测精度。 先用保留的最小训练集选择模型：

h02_tsib |>
  model(auto = ARIMA(log(Cost))) |>
  report()

## Series: Cost 
## Model: ARIMA(2,1,0)(0,1,1)[12] 
## Transformation: log(Cost) 
## 
## Coefficients:
##           ar1      ar2     sma1
##       -0.8491  -0.4207  -0.6401
## s.e.   0.0712   0.0714   0.0694
## 
## sigma^2 estimated as 0.004387:  log likelihood=245.39
## AIC=-482.78   AICc=-482.56   BIC=-469.77

这仍选择了ARIMA\((2,1,0)(0,1,1)_{12}\)模型。 下面保持前114个数据点不动， 每次向前滚动一步建模， 作向前一步预测， 模型结构保持不变但训练集和模型参数变化：

h02_pred1_cv <- h02_tsib |>
  stretch_tsibble(
    .init = 114, .step = 1 ) |>
  model(
    manual = ARIMA(log(Cost) ~ pdq(1,1,1) + PDQ(0,1,0)),
    auto = ARIMA(log(Cost) ~ pdq(2,1,0) + PDQ(0,1,1)) ) |>
  forecast(h = 1)

计算精度指标：

h02_pred1_cv |>
  accuracy(h02_tsib) |>
  knitr::kable()

## Warning: The future dataset is incomplete, incomplete out-of-sample data will be treated as missing. 
## 1 observation is missing at 2008 7月

.model	.type	ME	RMSE	MAE	MPE	MAPE	MASE	RMSSE	ACF1
auto	Test	-0.0012509	0.0632208	0.0502905	-0.5198711	5.834631	0.8296263	0.8525371	-0.1794585
manual	Test	-0.0006973	0.0762687	0.0585799	-0.4288399	6.705212	0.9663727	1.0284886	-0.2009481

从RMSE和MAE来看都是自动选择的模型更优。

这样的模型比较称为样本外比较， 从预测性能角度来看这是更客观的比较。 用AICc等准则作比较称为样本内比较。

注意AICc等准则在比较不同模型时， 所用的变换、差分必须完全相同， 只能变化\(p,q,P,Q\)和是否有常数项。 而样本外比较没有这样的限制。

有时选择的模型不一定能够在样本内比较、样本外比较、残差诊断都达到合格或最优， 可以综合判断选择适当的模型。

12.6 ARIMA模型与ETS模型的比较

ARIMA模型与ETS模型有一些交集， 也有不同之处。

• 所有线性（可加）的ETS模型都可以表达为ARIMA模型。
• 包含乘性元素的ETS模型不能表达为ARIMA模型。
• ETS都是非平稳的，ARIMA允许平稳。
• ETS考虑成分分解， ARIMA考虑相关性、偏相关性、新息。
• ETS模型参数个数有上限， ARIMA模型可以由许多参数。

可以用AICc在差分阶相同的多个ARIMA模型中选出最优， 也可以在多个ETS模型中选出最优， 但不能用来比较ARIMA模型和ETS模型， 其似然函数计算方法不同。

如果使用滚动向前一步预测作样本外比较， 则ARIMA与ETS是可比的。

B 参考文献

Hyndman, R. J., and G Athanasopoulos. 2021. Forecasting: Principles and Practice. 3rd edition. OTexts: Melbourne, Australia. http://OTexts.com/fpp3.

Hyndman, Rob J., and Yeasmin Khandakar. 2008. “Automatic Time Series Forecasting: TheforecastPackage forR.” Journal of Statistical Software 27 (3). https://doi.org/10.18637/jss.v027.i03.

Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. “Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root.” Journal of Econometrics 54 (1–3): 159–78. https://doi.org/10.1016/0304-4076(92)90104-y.