4 统计图形
图形比描述统计量更能直观、全面地反映变量分布和变量之间的关系。 直方图、密度估计图、盒形图、茎叶图、QQ图可以用来查看单个变量分布情况; 散点图可以用来查看两个变量的变化关系; 三维曲面图、等值线图、数字图像可以反映自变量\(x,y\)与因变量\(z\)的关系。
R软件的统计图形详见http://www.math.pku.edu.cn/teachers/lidf/docs/Rbook/html/_Rbook/index.html的第26——28章, Julia语言的作图详见https://www.math.pku.edu.cn/teachers/lidf/docs/Julia/html/_book/index.html第12、19、20章。
4.1 直方图
用描述统计量可以把连续型分布的最重要的特征概括表示, 但是,为了了解分布密度的形状, 应该对分布密度\(p(y)\)进行估计。 比如,分布密度有两个峰的现象就是上面叙述的描述统计量无法发现的。
直方图(histogram)是最简单的估计分布密度的方法。
设随机变量\(Y \sim f(y)\), 分布密度\(f(y)\)连续, \(y_1, y_2, \dots, y_n\)为\(Y\)的简单随机样本。 取分点\(t_0 < t_1 < \dots < t_{m}\), 把\(Y\)的取值范围分为\(m\)个小区间: \(\cup_{k=1}^m (t_{k-1}, t_k]\); 令 \[\begin{aligned} p_k =& P \{ t_{k-1} < Y \leq t_k \} \\ =& \int_{t_{k-1}}^{t_{k}} f(y) dy = f(\xi_k) (t_k - t_{k-1}) , \ k=1,2,\dots,m, \end{aligned}\] 其中\(\xi_k \in (t_{k-1}, t_k]\)。 设样本值\(y_1, y_2, \dots, y_n\)落入第\(k\)个小区间\((t_{k-1}, t_k]\)的个数为\(u_k\)(称为频数), 用\(u_k / n\)估计\(p_k\), 称\(u_k / n\)为样本落入第\(k\)个小区间的频率或百分比。 当\(n \to \infty\)时, 取分点\(\{t_k\}\)使小区间长度趋于零,即 \[\begin{aligned} d = \max\{t_k - t_{k-1}: k =1, 2, \dots, m \} \to 0, \end{aligned}\] 如果\(Y\)的取值范围没有下界, 则要求\(t_0 \to -\infty\); 如果\(Y\)的取值范围没有上界, 则要求\(t_{m} \to +\infty\)。 这时有\(u_k / n \to p_k\), \(k=1,2,\dots, m\), a.s., 于是 \[\begin{aligned} \left | \frac{u_k}{n (t_k - t_{k-1})} - f(y) \right| \to 0, \ \text{a.s.}, \ y \in (t_{k-1}, t_k], \end{aligned}\] 即\(f(x)\)可以用\(x\)所在的小区间上的频率除以小区间长度来估计。 令 \[\begin{aligned} f_n(y) = \begin{cases} \sum_{k=1}^{m} \frac{u_k / n}{t_k - t_{k-1}} I_{(t_{k-1}, t_k]}(y), & \ \text{当 } \ t_0 < y \leq t_{m} \\ 0, & \text{当 } \ y \leq t_0 \text{ 或 }\ y > t_m, \end{cases} \end{aligned}\] 则\(n\to\infty\)时\(f_n(y) \to f(y)\), a.s.。 另外,\(f_n(y) \geq 0, y \in (-\infty, \infty)\), \(\int_{-\infty}^\infty f_n(y) dy = 1\), 满足密度函数的一般要求。
根据上述讨论,我们可以用如下的等距概率直方图来估计分布密度\(f(y)\)。 确定区间端点\((a, b)\)使得样本值\(y_1, y_2, \dots, y_n\)都落入\((a,b)\)内, 确定分组数\(m\),令组距\(h = \frac{b-a}{m}\), 分点 \[\begin{aligned} t_k = a + k h, \ k=0, 1, \dots, m, \end{aligned}\] 计算样本值落入第\(k\)个小区间的个数\(u_k\)和频率\(u_k/n\)。 以\((t_{k-1}, t_k]\)为底, \((u_k / n) / (t_i - t_{i-1}) = (u_k / n) / h\)为高画长方形, 这\(m\)个长方形的顶部为密度估计值。
另一种等距直方图用小区间对应的频数\(u_k\)作为这些长方形的高度, 这样的等距直方图不是密度函数的估计, 但是与等距概率直方图只差常数倍\(n h\)。
那么,如何确定分组数\(m\)呢? 这个问题没有公认的做法。 样本量\(n\)大时组数应当大, 数据取值范围小时组数应当小, 数据有效位少使得不同值少时组数应当小, 一般应使得每一小区间不为空,观测数达到5以上更好。 实际取\(m\)和分点时,还需要使得分点的小数位数较少。
按照AMISE(平方误差积分渐近期望)最小原则, 可取区间长度\(h\)为 \[\begin{aligned} h = 3.49 \sigma n^{-1/3}, \end{aligned}\] 其中总体标准差\(\sigma\)可用样本标准差代替, 或者用IQR来估计\(\sigma\),得 \[\begin{aligned} h = 2 \cdot \mbox{IQR} \cdot n^{-1/3}. \end{aligned}\]
按绝对误差一致最小准则, 可取 \[\begin{aligned} h = 1.66 S \left( \frac{\ln n}{n} \right)^{1/3} \end{aligned}\] 其中S是样本标准差。
关于直方图分组数\(m\)选取的讨论参见(Gentle 2002)§9.2。
在R软件中,
用hist(x, freq=FALSE)作估计分布密度的等距概率直方图,
分组按默认规则分组(见Sturges(1926));
或者用MASS::truehist()函数。
但是,
ggplot2包的作图功能更灵活、强大、美观,
下面尽可能使用ggplot2包作图。
下面的程序首先生成了100个标准正态分布随机数 (可以理解为来自标准正态分布的样本量为100的一组简单随机样本), 然后作了等距概率直方图:
set.seed(101); x <- rnorm(100)
d <- tibble(x = x)
ggplot(data=d, mapping=aes(x=x)) +
geom_histogram()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
可以用bins指定分组数:
每组条形高度默认使用该组的观测个数,
可以用y=..density..指定使用密度估计:
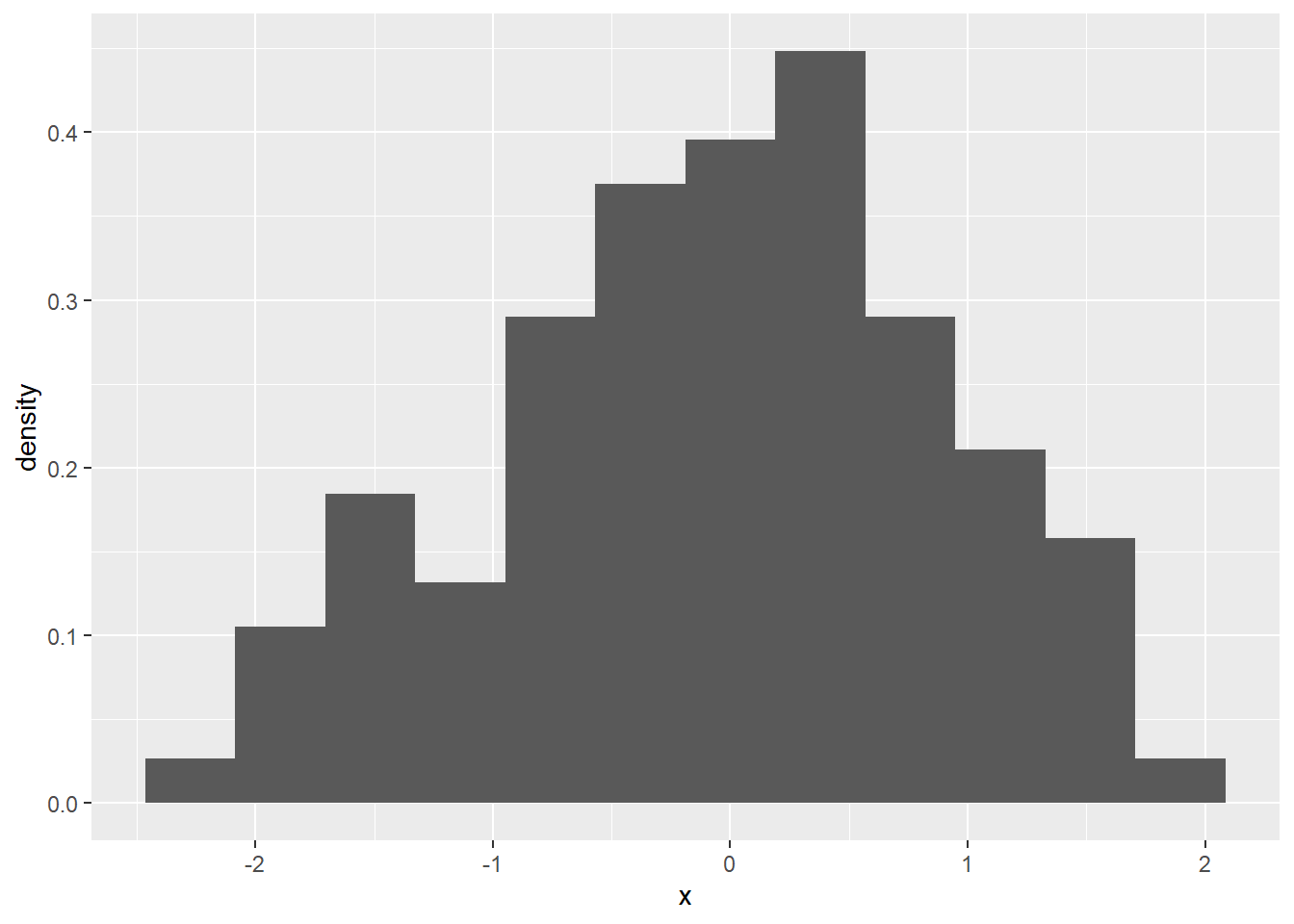
对于正态分布密度这样的非重尾的密度, 等距概率直方图可以比较好地反映分布密度形状。 但是,如果分布在两侧或一侧有重尾, 这时直方图的部分小区间可能只有很少点甚至没有点, 部分小区间则集中了过多的点, 等距概率直方图就不能很好地反映分布密度形状。
如下生成了100个柯西分布随机数, 然后对这组样本做了等距概率直方图, 可以看出效果较差:
set.seed(103); x <- rcauchy(100)
d <- tibble(x = x)
ggplot(data=d, mapping=aes(x=x, y=..density..)) +
geom_histogram(bins=12)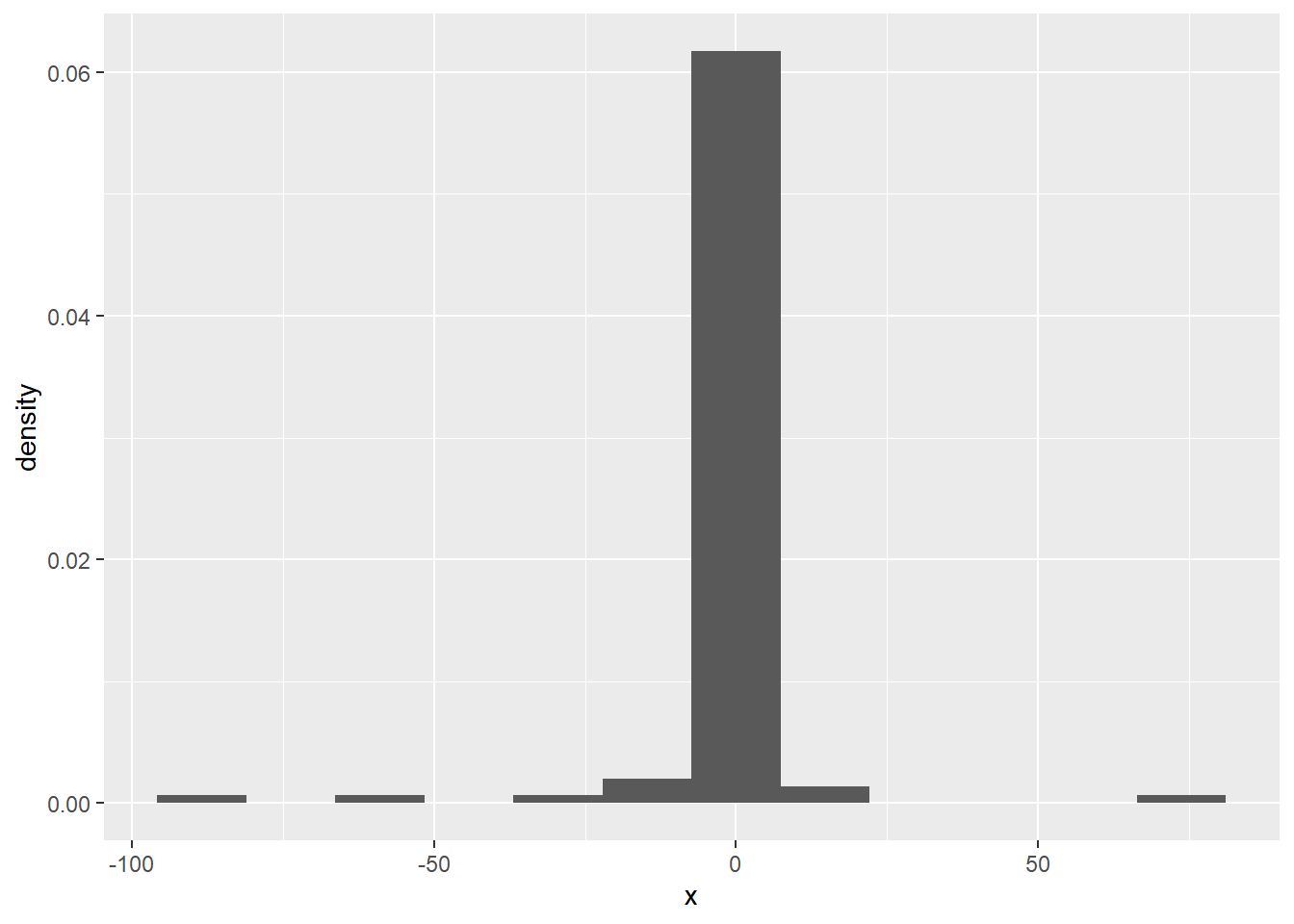
这种情况下可以把频数少的小区间合并, 把频数过大的小区间拆分, 产生不等距的概率直方图。 比如,上面的柯西分布随机数可以用如下程序得到较好的直方图:
ggplot(data=d, mapping=aes(x=x, y=..density..)) +
geom_histogram(breaks=c(
-100, -50, -30, -10, -5, -2, -1, 0,
1, 2, 5, 10, 30, 100))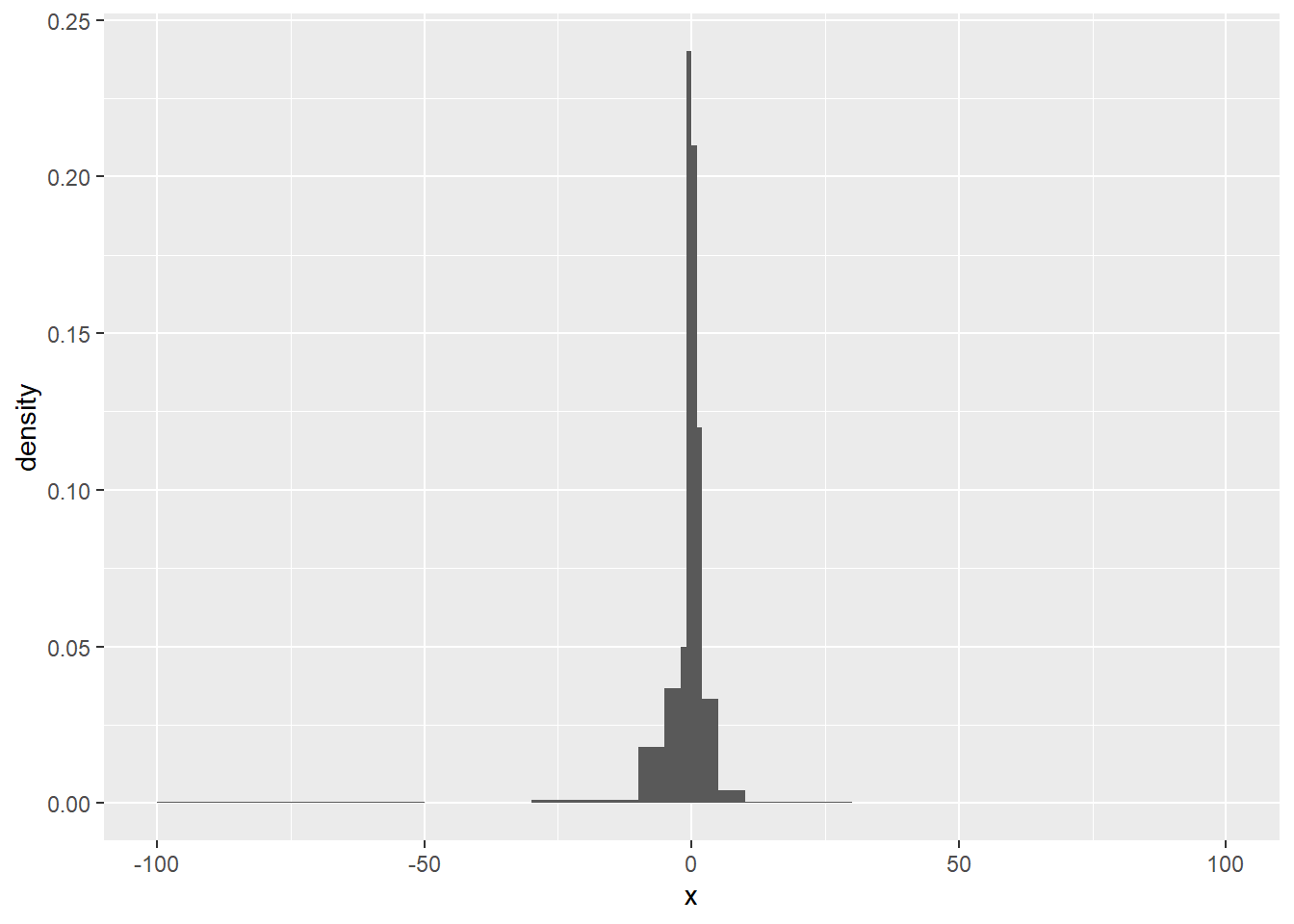
4.2 核密度估计
在等距概率直方图作法中, 估计\(y_0\)处的密度\(p(y_0)\)时其所在区间\((t_{k-1}, t_k]\)的所有\(p(y)\)都估计成同一个值, 这些分点\(\{ t_k \}\)是预先取好的,与要估计\(p(y)\)的自变量\(y\)的位置无关。 我们可以针对每一个\(y\), 以\(y\)为中心、\(\frac{h}{2}\)为半径做小区间 \(\left[y - \frac{h}{2}, y + \frac{h}{2} \right]\), 用 \[\begin{aligned} \tilde p(y) = \frac{\#\left(\left\{y_i: y_i \in \left[ y - \frac{h}{2}, y + \frac{h}{2} \right] \right\} \right) / n}{h} \end{aligned}\] 来估计\(p(y)\), 其中\(\#(A)\)表示集合\(A\)的元素个数。上式可以写成 \[\begin{aligned} \tilde p(y) =& \frac{1}{h} \frac{1}{n} \sum_{i=1}^n I_{\left[ y - \frac{h}{2}, y + \frac{h}{2} \right]}(y_i) \\ =& \frac{1}{n} \sum_{i=1}^n \frac{1}{h} I_{\left[-\frac12, \frac12 \right]}(\frac{y - y_i}{h}), \ y \in (-\infty, \infty). \end{aligned}\]
这个分布密度估计叫做Rosenblatt直方图估计。 如果把上面的区间改为左开右闭区间\(\left( y - \frac{h}{2}, y + \frac{h}{2} \right]\), \(\tilde p(y)\)与经验分布函数\(F_n(y)\)恰好满足如下关系: \[\begin{aligned} \tilde p(y) = \frac{F_n \left( y + \frac{h}{2} \right) - F_n \left( y - \frac{h}{2} \right)} {h}, \ y \in (-\infty, \infty). \end{aligned}\] 即\(\tilde p(y)\)是对经验分布函数用差商近似估计\(F(x)\)导数的结果。
设函数\(K_1(x) = I_{\left[-\frac12, \frac12 \right]}(x)\), Rosenblatt直方图估计可以写成 \[\begin{aligned} \tilde p(y) =& \frac{1}{n} \sum_{i=1}^n \frac{1}{h} K_1\left( \frac{y - y_i}{h} \right), \end{aligned}\] 这样形式的密度估计叫做核密度估计, \(K_1(x)\)叫做核函数。
一般地,核函数应该满足如下要求:
\(K(x) \geq 0\);
\(\int_{-\infty}^\infty K(x) dx = 1\);
\(K(x)\)是偶函数;
\(\int_{-\infty}^\infty x^2 K(x) dx < +\infty\)。
一般核密度估计为 \[\begin{aligned} \hat p(y) =& \frac{1}{n} \sum_{i=1}^n \frac{1}{h} K\left( \frac{y - y_i}{h} \right) \end{aligned}\] \(K(x)\)的条件(1)和(2)使得 \(\hat p(y)\)满足\(\hat p(y) \geq 0, y \in (-\infty, \infty)\), \(\int_{-\infty}^\infty \hat p(y) dy = 1\)。 当\(h\)很小时, 密度估计很不光滑, 在每个\(y_i\)处有一个尖锐的峰而没有观测值的地方密度估计为零, 估计偏差小而方差大。 当\(h\)较大时, 估计比较光滑, 估计偏差大而方差小。 渐近地取\(h = O(n^{-1/5})\), 核密度估计的均方误差为\(O(n^{-4/5})\), 优于直方图估计, 参见(Gentle 2002) §9.3。
注意,核密度估计可以很容易地推广到随机向量联合分布密度的估计。
其它核函数还有: \[\begin{aligned} K_2(x) =& (1 - |x|) I_{[-1,1]}(x) \text{(三角形核)} \\ K_3(x) =& \frac{3}{4}(1 - x^2) I_{[-1,1]}(x) \text{(二次曲线核)} \\ K_4(x) =& \frac{15}{16}(1 - x^2)^2 I_{[-1,1]}(x) \text{(双二次核)} \\ K_5(x) =& \frac{70}{81}(1 - |x|^3)^3 I_{[-1,1]}(x) \text{(双三次核)} \\ K_6(x) =& \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \text{(高斯核)} \end{aligned}\]
R软件中函数density(x)进行核密度估计。
ggplot2包用geom_density()画核密度估计曲线。
上面例子中柯西分布随机数的直方图可以用
如下程序增加核密度估计曲线:
ggplot(data=d, mapping=aes(x=x, y=..density..)) +
geom_histogram(breaks=c(
-100, -50, -30, -10, -5, -2, -1, 0,
1, 2, 5, 10, 30, 100)) +
geom_density(color="red", size=1)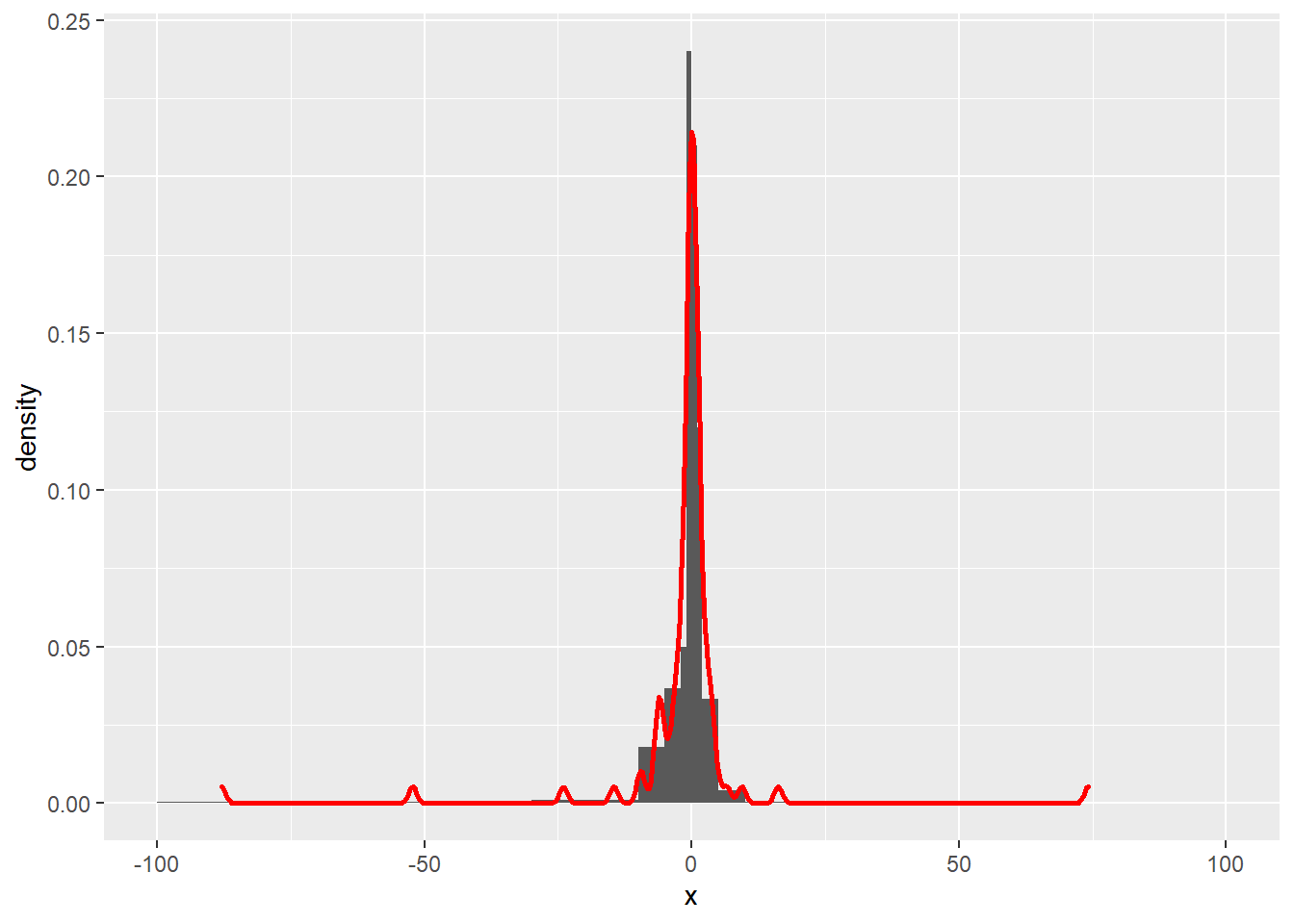
4.3 盒形图
对于单峰的分布密度, 盒形图(boxplot)可以概括地表现其分布情况。
100个对数正态分布随机数的直方图,直方图上叠加了估计的对数正态密度曲线:
set.seed(101)
x <- exp(rnorm(100))
d <- tibble(x=x)
d1 <- tibble(x = seq(0, max(x), length=200)) %>%
mutate(y=dlnorm(x), mean(log(x)), sd(log(x)))
ggplot(data=d, mapping=aes(x=x, y=..density..)) +
geom_histogram(bins=20) +
geom_line(data=d1, mapping=aes(x=x, y=y), col="red", size=1)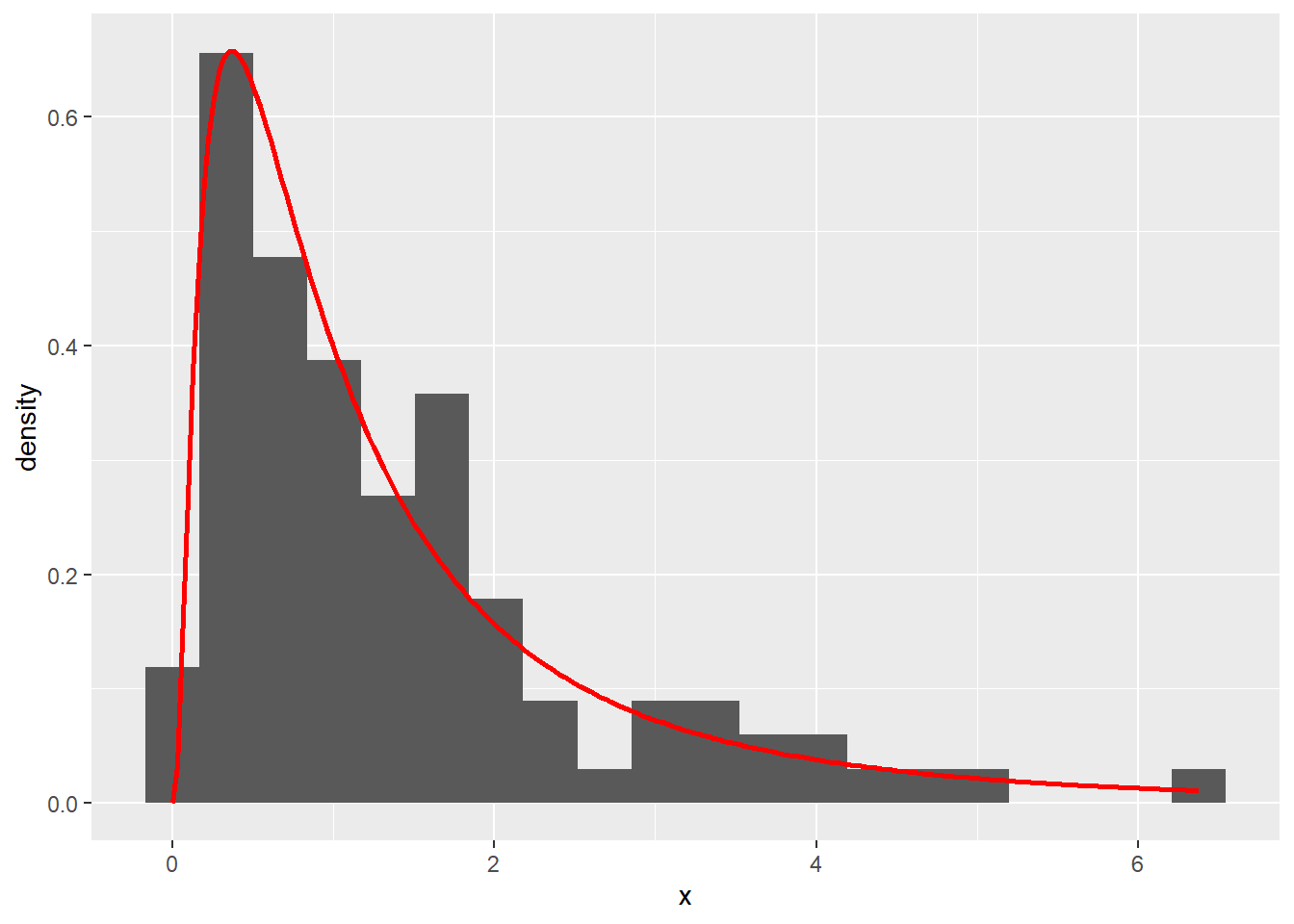
盒形图:
ggplot(data=d, mapping=aes(x=1, y=x)) +
geom_boxplot() +
scale_x_continuous(breaks=NULL) +
labs(x=NULL, y=NULL)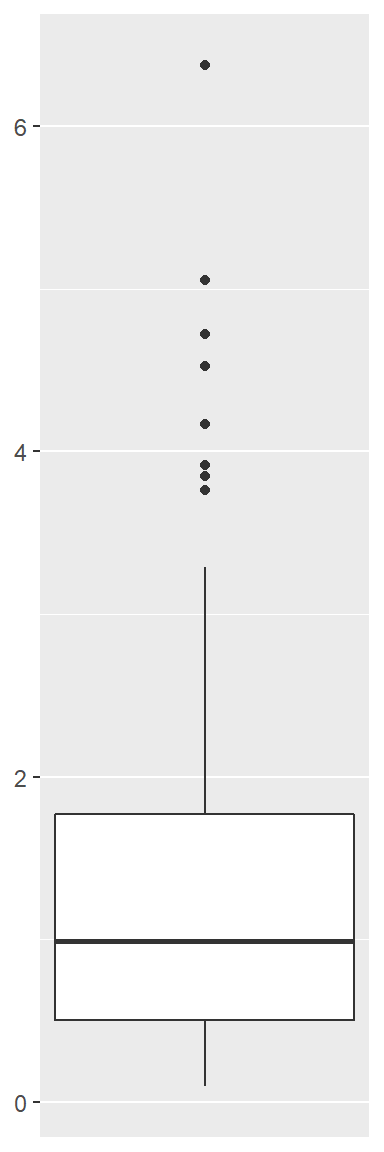
对数正态分布是右偏的单峰分布。 盒形图中间有条粗线, 位于分布的中位数上; 盒子的下边缘和上边缘分别位于分布的\(1/4\)分位数和\(3/4\)分位数处, 所以盒形的范围内包括了样本值分布从小到大排列中间的\(1/2\)的样本值。 在盒子两端的外侧分别向下和向上延伸出两条线, 叫做触须线, 触须线长度小于等于1.5倍IQR(即盒子高度)并最长只能延伸到最小值或最大值的地方。 如果有样本值超出了触须线的范围,就用散点符号画出, 这些样本值距离分布中心较远, 称为离群值(outliers)。 如果有较多、较远的离群值, 这个样本分布就是重尾的。
所以,我们能够从盒形图上看到中位数、\(1/4\)分位数、\(3/4\)分位数、最小值、最大值的位置, 并能发现离群值,判断分布左端和分布右端是否有重尾。 另外,比较中位数上方和中位数下方的长度可以发现分布是对称的、左偏的, 还是右偏的。上图中的盒形图是右偏的。
在R软件中,用boxplot(x)作盒形图。
在ggplot2中用geom_boxplot()作盒形图,
但是需要有x变量,
可以定义x变量为常数,
y变量为要作图的变量。
盒形图更常用于并排作多个,
比较不同类别的观测,
或者比较若干个变量。
4.4 茎叶图
茎叶图是一种低精度的图形, 用来检查数据输入和分布形状。
在R软件中用stem(x)作茎叶图。
如下程序输入了若干个人的身高(单位: 厘米)并作了茎叶图,
结果如下
The decimal point is 1 digit(s) to the right of the |
14 | 5
15 | 0569
16 | 06
17 | 0
18 |
19 | 0图形分为竖线左边的“茎”和右边的“叶”两部分。 茎部分构成了纵坐标轴, 小数点位置在竖线的地方, 但是根据数据范围的不同可能需要调整, 比如上图的说明部分约定了小数点位置是向竖线右方移动一位(即乘以10)。 叶部分的每个数字是一片叶子, 代表了一个样本点, 叶子是样本值最后一个有效数字(或四舍五入后的值)。 比如,茎“15”右边有5片叶子, 分别代表样本值150、155、156、159。
把这个图逆时针旋转90度来看, 可以看成是一个直方图,某个茎右侧的叶子越多, 分布密度在这个值附近越大。
图中的190明显远离了其它值。 由此可见, 从茎叶图可以比较容易地发现离群点。
4.5 正态QQ图和正态概率图
在许多统计模型中都要假设模型中的随机变量服从正态分布。 对随机变量\(Y\), 设\(y_1, y_2, \dots, y_n\)是\(Y\)的简单随机样本, 如何判断\(Y\)是否服从正态分布?
可以使用假设检验的方法, 零假设为\(Y\)服从正态分布, 对立假设为\(Y\)不服从正态分布。 这样的检验有Shapiro-Wilk检验等。
另外,我们也可以从分布图形来直观地判断。 直方图与核密度估计图可以直接查看分布密度形状是否与正态分布相近。
正态分布随机数的正态QQ图:
set.seed(101)
x <- rnorm(100)
d <- tibble(x=x)
ggplot(data=d, mapping=aes(sample=x)) +
stat_qq() +
geom_qq_line(color="red")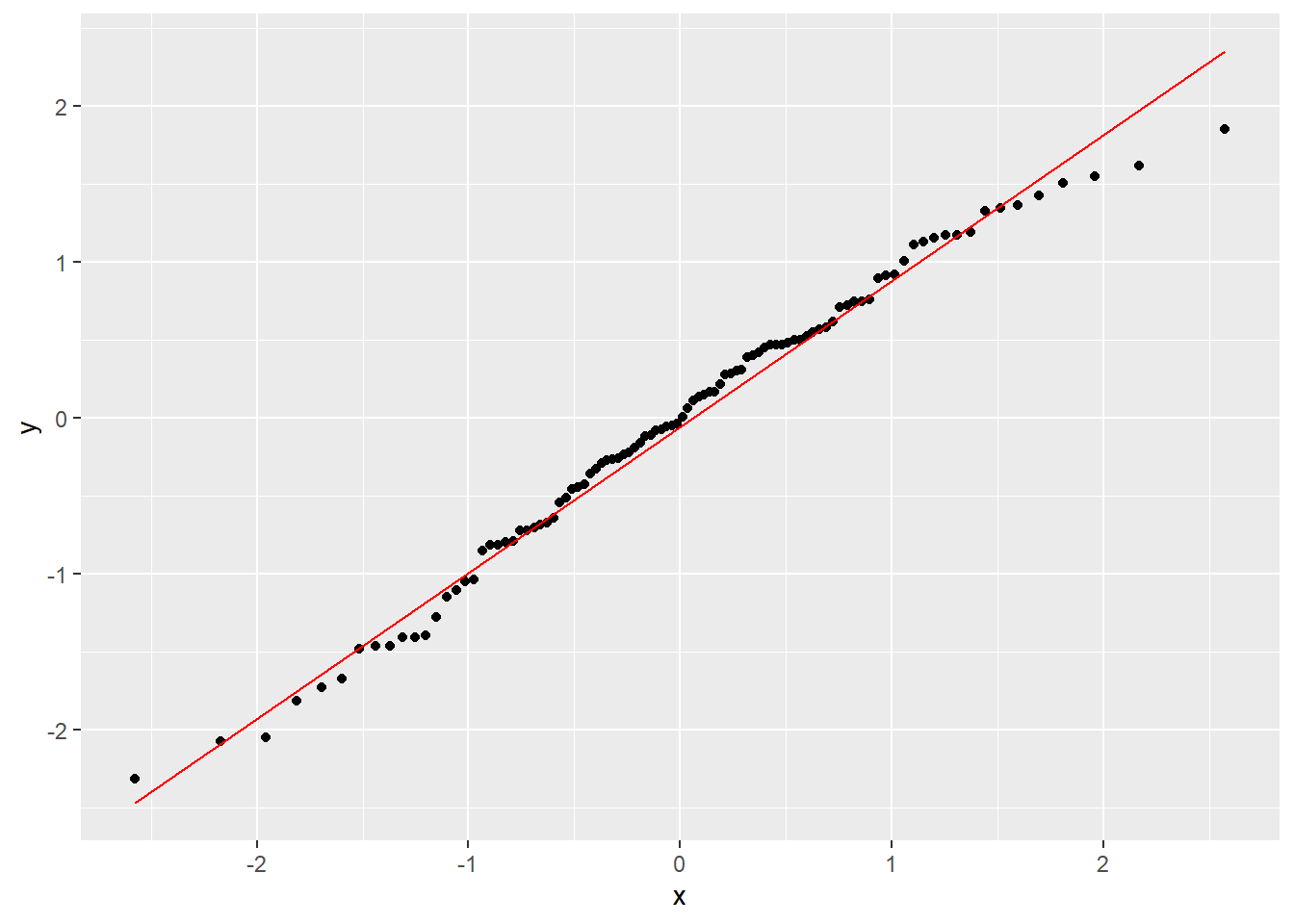
图4.1: 正态样本的正态QQ图
对数正态分布随机数的正态QQ图:
set.seed(101)
x <- rlnorm(100)
d <- tibble(x=x)
ggplot(data=d, mapping=aes(sample=x)) +
stat_qq() +
geom_qq_line(color="red")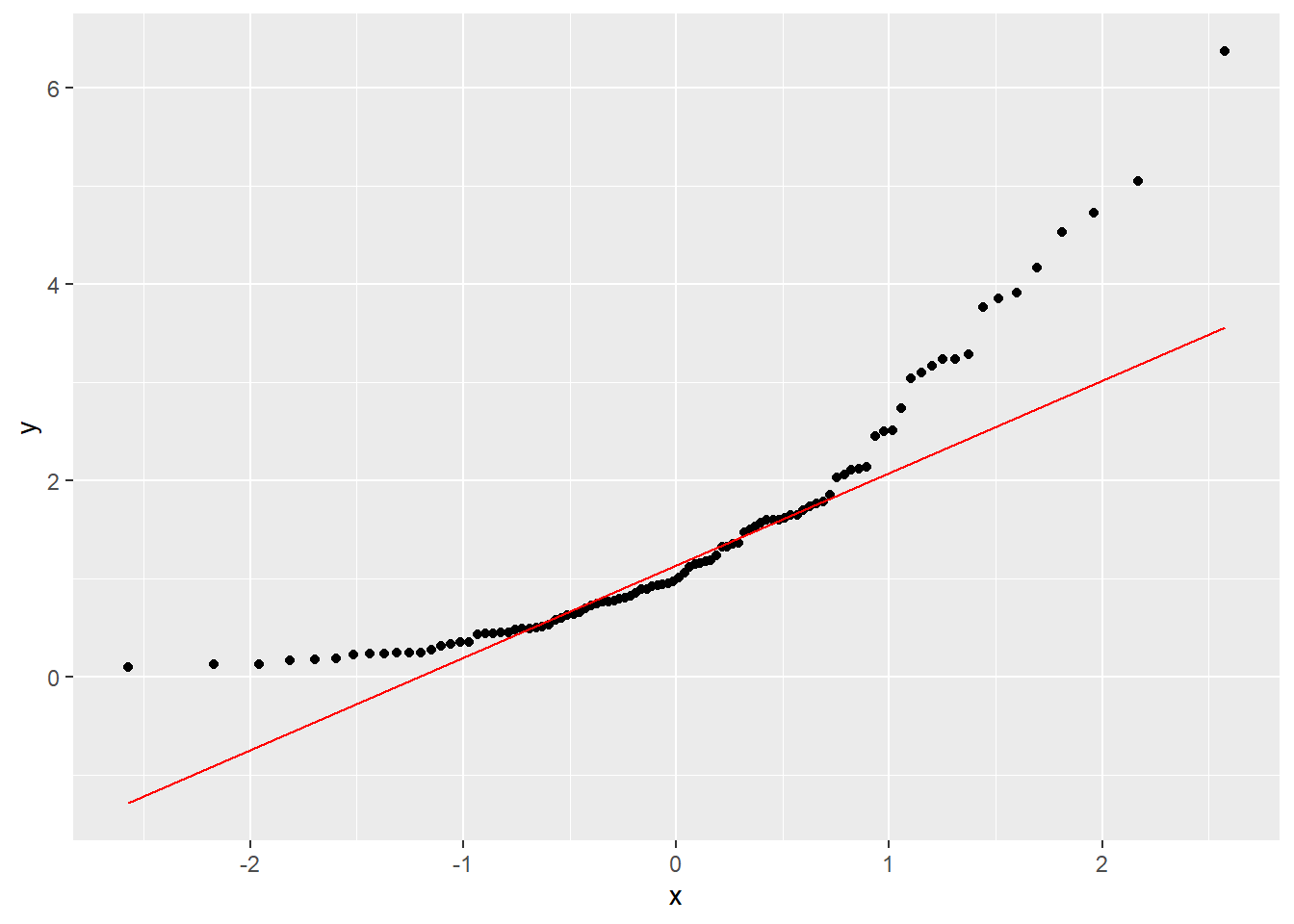
图4.2: 对数正态样本的正态QQ图
这样的形状表示右偏分布。
指数分布随机数相反数的正态QQ图:
set.seed(101)
x <- -rexp(100)
d <- tibble(x=x)
ggplot(data=d, mapping=aes(sample=x)) +
stat_qq() +
geom_qq_line(color="red")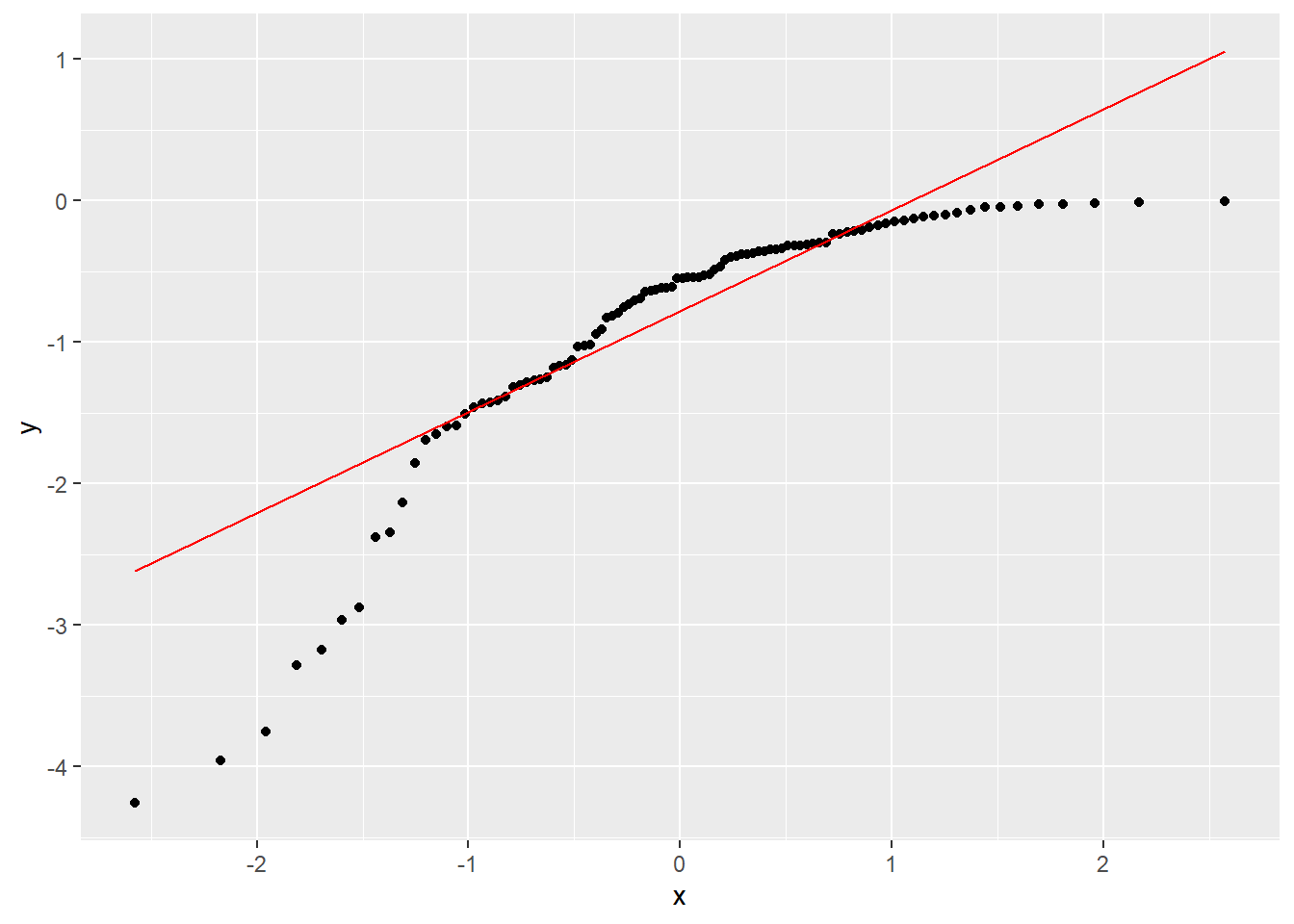
图4.3: 指数分布相反数样本的正态QQ图
这样的形状表示左偏分布。
t(2)分布随机数的正态QQ图:
set.seed(101)
x <- rt(100, 2)
d <- tibble(x=x)
ggplot(data=d, mapping=aes(sample=x)) +
stat_qq() +
geom_qq_line(color="red")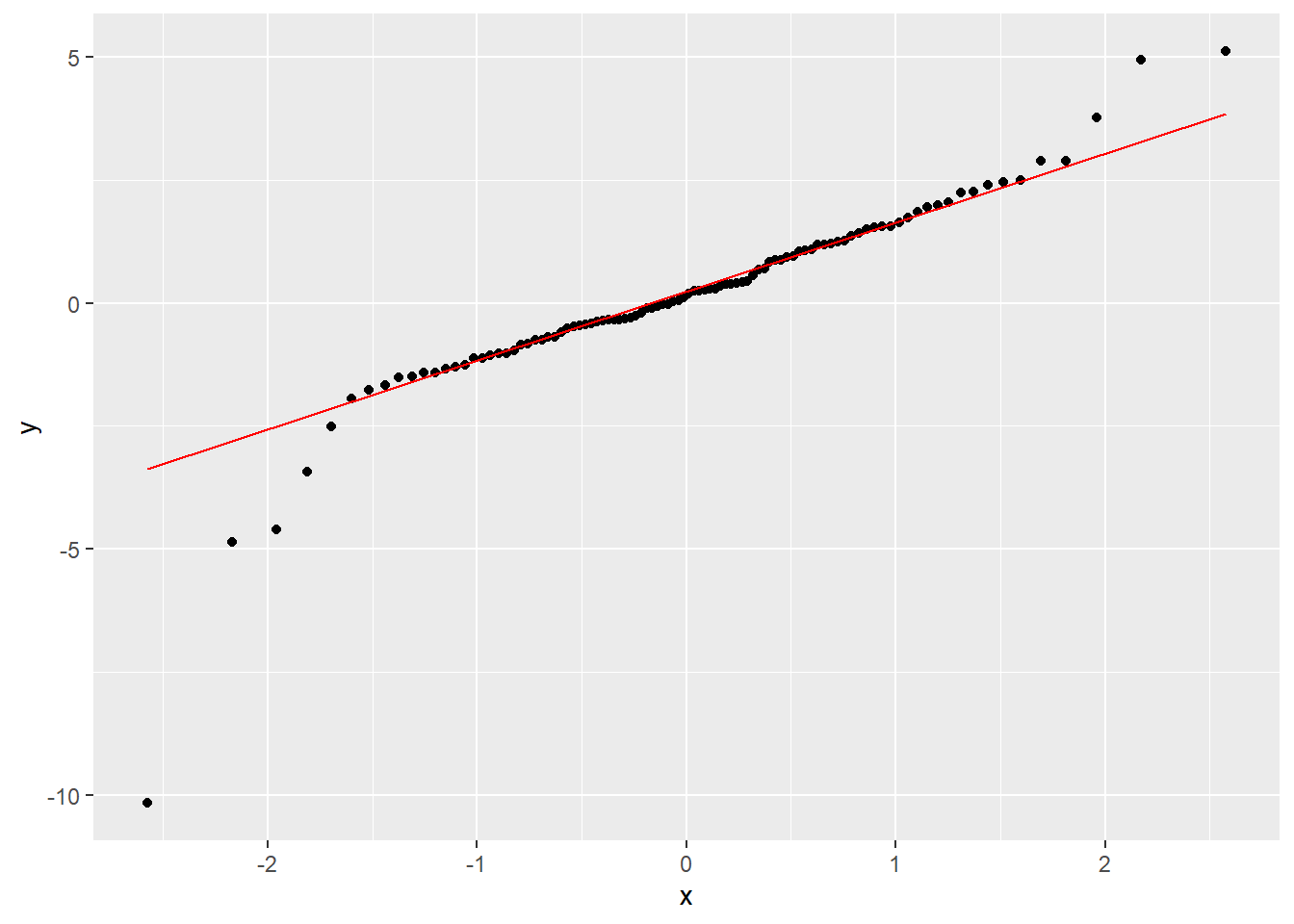
图4.4: t分布样本的正态QQ图
这样的形状表示分布两侧有厚尾现象。
上面四个图形叫做正态QQ图, 对应的样本分别来自为正态分布、对数正态分布、指数分布的相反数、t(2)分布的随机数。
正态QQ图包括一组散点和一条直线。 设样本次序统计量为\(y_{(1)}, y_{(2)}, \dots, y_{(n)}\), 则\(y_{(i)}\) 可以作为是总体的\(i/n\)分位数的估计。 设标准正态分布的分布函数为\(\Phi(\cdot)\), 令\(x_i = \Phi^{-1}(i/n)\), 则\((x_i, y_{(i)})\)分别是标准正态分布\(i/n\)分位数和样本的\(i/n\)分位数, 以\((x_i, y_{(i)}), i=1,2,\dots,n\)为坐标在直角坐标系中作图就得到了正态QQ图中的散点。 通过代表\(1/4\)分位数和\(3/4\)分位数的两个点作直线, 就是正态QQ图中的那些直线。
如果样本来自正态\(N(\mu, \sigma^2)\) , 记N\((\mu, \sigma^2)\) 的分布函数为\(F(x)\), 易见\(F(x) = \Phi\left(\frac{x-\mu}{\sigma} \right)\)。 因为\(y_{(i)}\)是样本的\(i/n\)分位数, 应该近似等于\(F(x)\)的\(i/n\)分位数\(F^{-1}(i/n)\),所以 \[\begin{aligned} y_{(i)} \approx& F^{-1}(i/n) \\ F(y_{(i)}) \approx& \frac{i}{n} \\ \Phi\left(\frac{y_{(i)} - \mu}{\sigma} \right) \approx& \frac{i}{n} \\ \frac{y_{(i)} - \mu}{\sigma} \approx& \Phi^{-1}(i/n) = x_i \\ y_{(i)} \approx& \mu + \sigma x_i \end{aligned}\] 可见这时正态QQ图中的散点应该落在以\(\mu\)为截距、以\(\sigma\)为斜率的直线附近。 图4.1就是这样的情况。
上述讨论中我们取\(y_{(i)}\)作为总体的\(i/n\)分位数的估计, 这样,最小值\(y_{(1)}\)代表\(1/n\)分位数而最大值\(y_{(n)}\)代表100%分位数, 两侧不对称。实际作图时,\(y_{(i)}\)对应的概率\(p\)可能会进行一些修正; 比如,SAS软件中的正态QQ图把 \(y_{(i)}\)作为\((i - \frac{3}{8})/(n + \frac{1}{4})\)分位数的估计。
如果样本来自于右偏的分布, 正态QQ图就会呈现出下凸形状(见图4.2)。 这是因为,图中直线上端代表了正态分布情况下在\(3/4\)分位数之后应有的走势, 图中散点的上端高于代表正态分布的直线, 说明实际数据的分布密度的右端比正态分布密度要长; 此图的左端的散点高于代表正态分布的直线, 说明实际数据的分布密度的左端比正态分布密度要短。 这正是右偏分布的典型特征。
类似地, 图4.3是典型的左偏分布的形状, 而图4.4则是分布基本对称但两端的尾部都比正态分布长, 从而是对称重尾分布的典型形状。
正态QQ图的一个变种是正态概率图, 这时散点坐标和直线都不变, 但是横坐标轴的刻度不是QQ图中\(x_i\)的值, 而是标为\(\Phi(x_i)\)的值, 即\((x_i, y_i)\)所对应的概率值。
还可以针对用其它理论分布的分位数为x轴作QQ图, 例如, 针对t(2)分布的QQ图:
params <- as.list(MASS::fitdistr(d$x, "t")$estimate)
## Warning in log(s): NaNs produced
ggplot(data=d, mapping=aes(sample=x)) +
stat_qq(distribution=qt, dparams=params["df"]) +
geom_qq_line(color="red")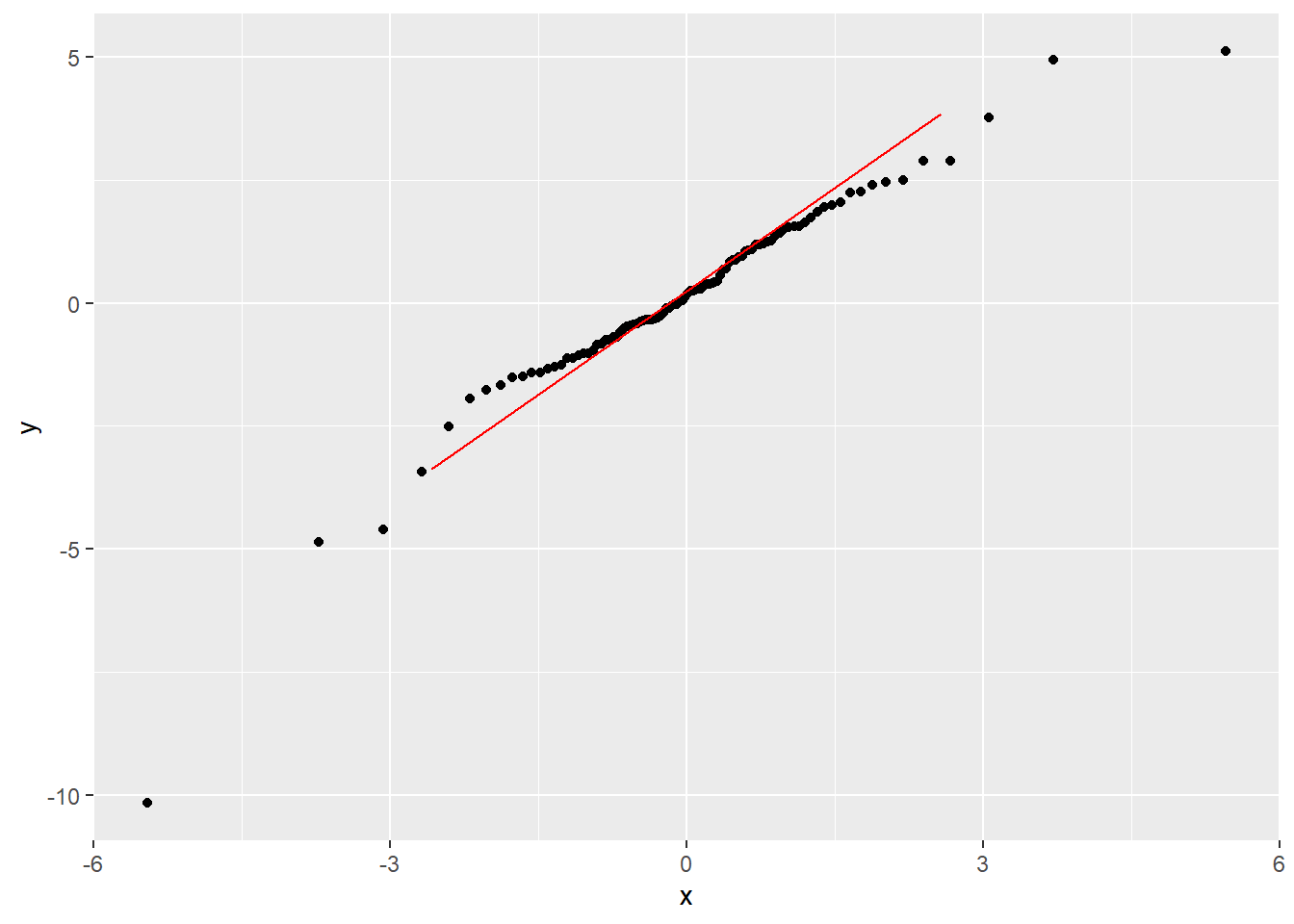
4.6 散点图和曲线图
设有两个变量\(X\)和\(Y\)以及它们的\(n\)组观测值 \((x_i, y_i), i=1,2,\dots,\)。 以\((x_i, y_i)\)为坐标画点, 把这\(n\)组观测值画在平面直角坐标系中, 叫做散点图。
散点图能够比较直观地表现两个变量之间的关系, 两个变量的取值范围, 取值的聚集、分组, 离群点等情况。
set.seed(101); n <- 30
d <- tibble(x = runif(n, 2, 10)) %>%
mutate(y = 10 + 2.5*x + 2*rnorm(n))
ggplot(data=d, mapping=aes(x=x, y=y)) +
geom_point()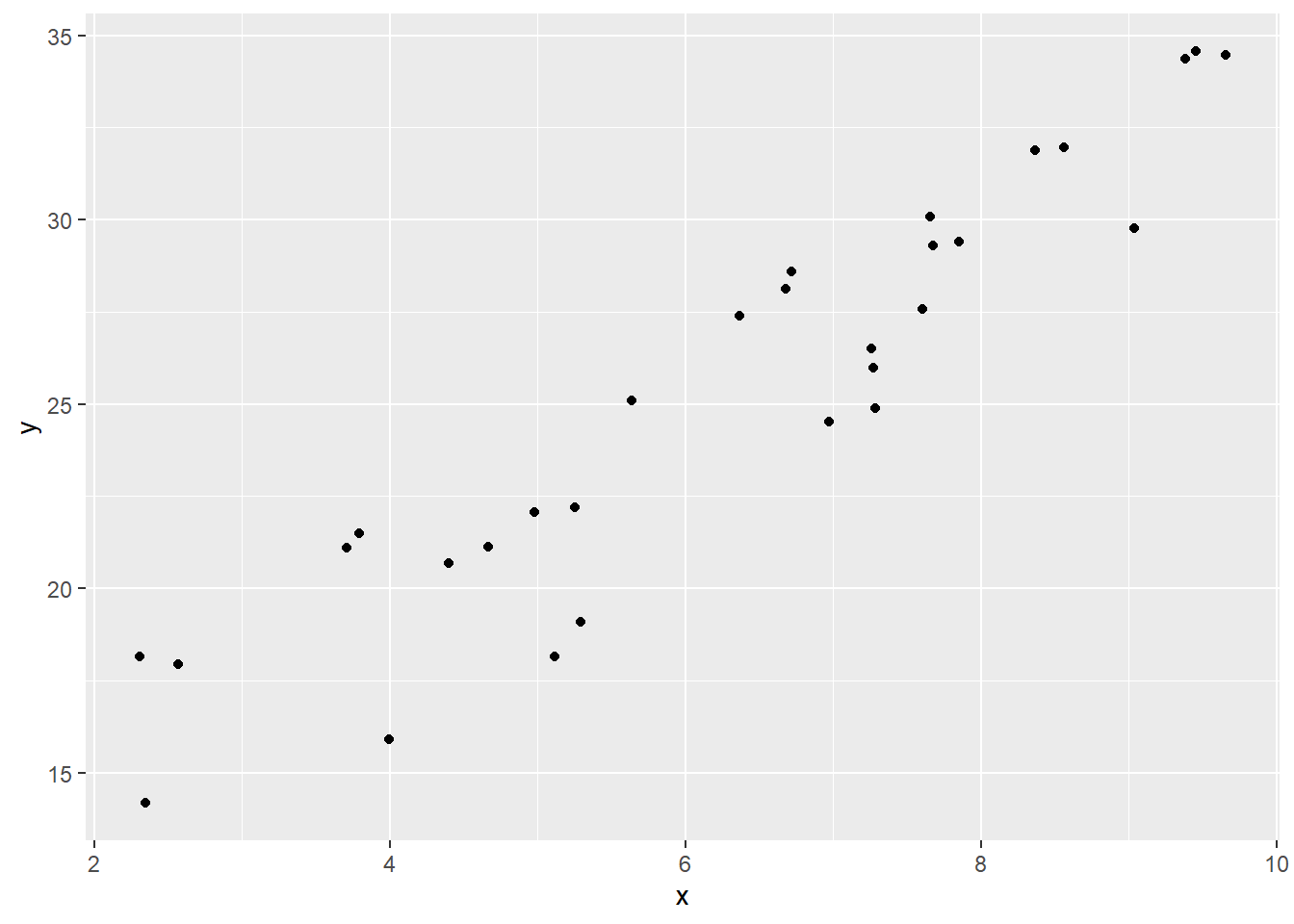
上图中的\(X\)和\(Y\)有线性相关关系, 且\(X\)增加\(Y\)也倾向于增加。
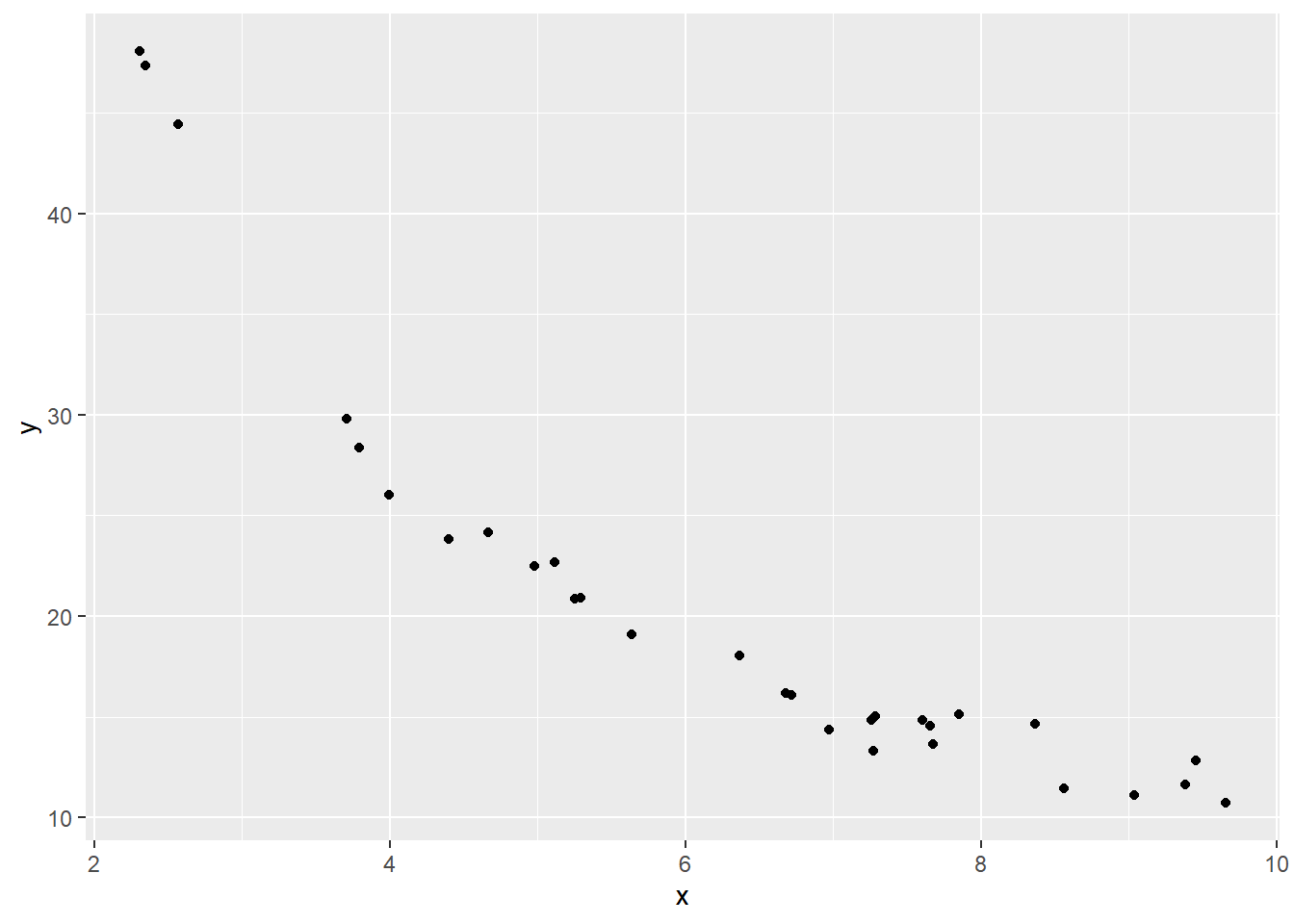
上图中的\(X\)和\(Y\) 有非线性相关关系, \(X\)增加时\(Y\)倾向于减少。
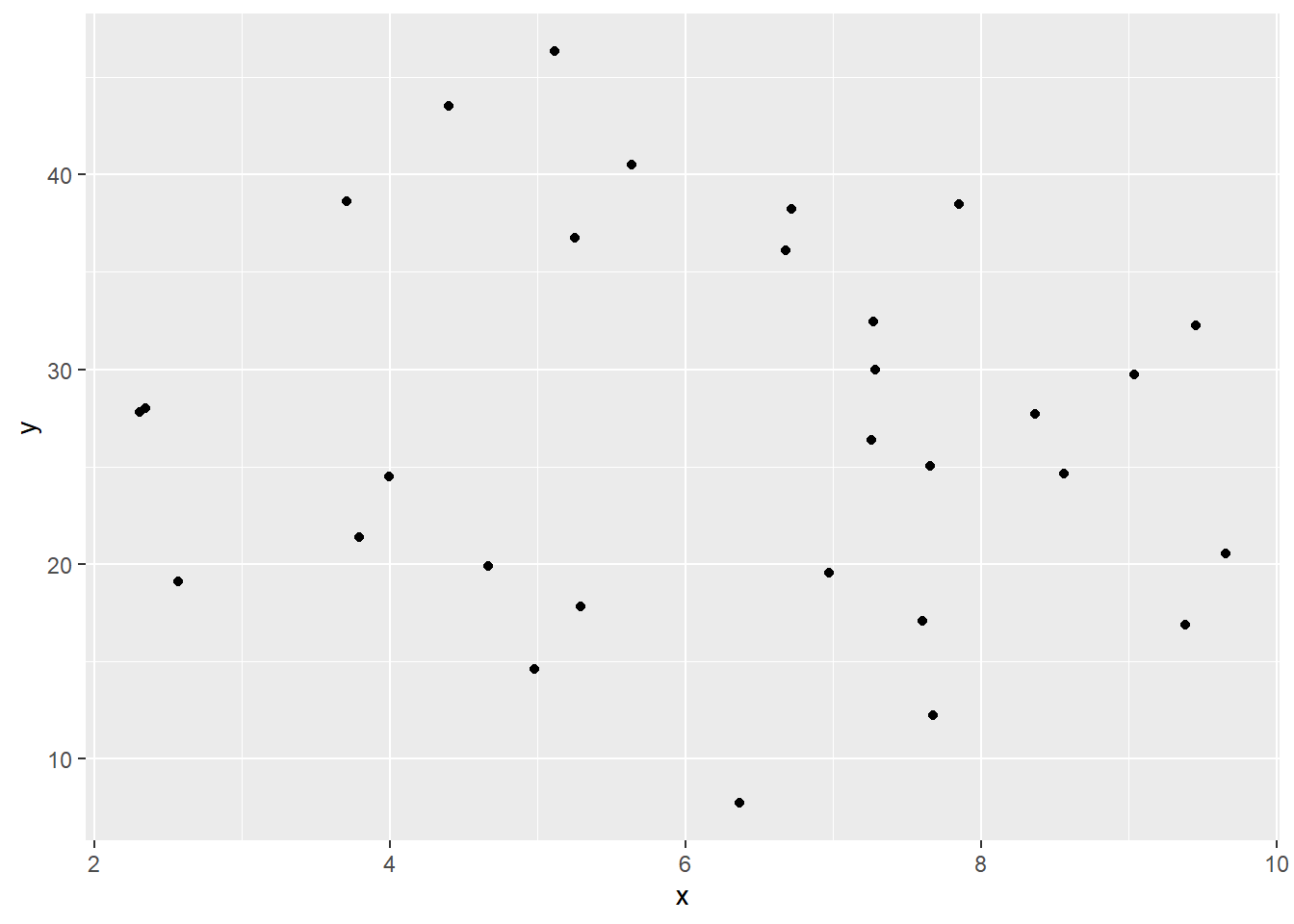
上图中的\(X\)和\(Y\)没有明显的相关, 也没有明显的聚集模式。
set.seed(101); n <- 30
d4a <- tibble(x = runif(n/2, 2, 5)) %>%
mutate(y = 20 - 2*x + 0.3*rnorm(n/2))
d4b <- tibble(x = runif(n/2, 7, 10)) %>%
mutate(y = 53 - 2*x + 0.3*rnorm(n/2))
d4 <- rbind(d4a, d4b)
ggplot(data=d4, mapping=aes(x=x, y=y)) +
geom_point()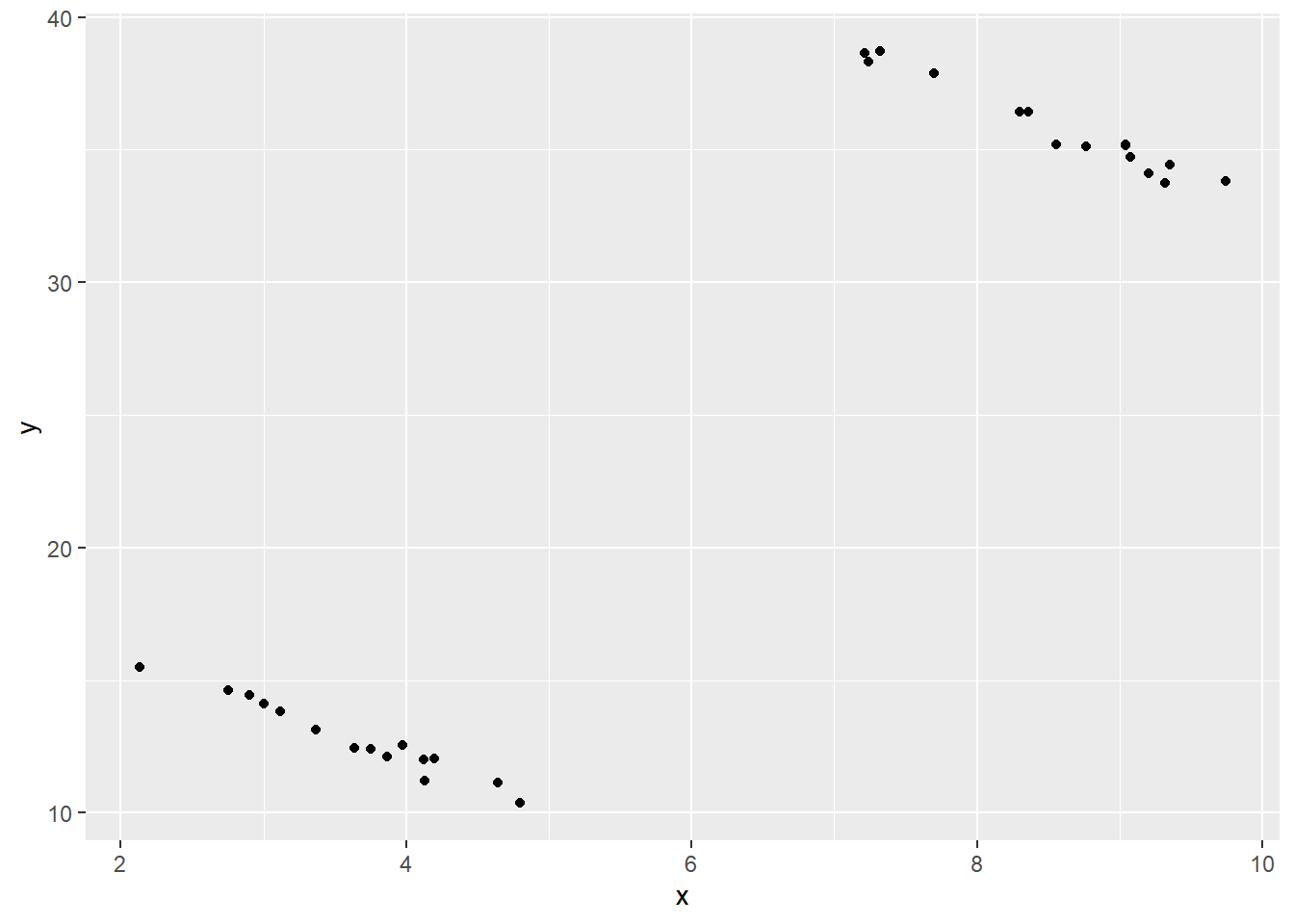
上图中的\(X\)和\(Y\)的观测值明显地分成两组, 且在每一组内部\(X\)和\(Y\)的值是负相关的。 注意,如果对第四组数据不画图而直接作线性回归, 结果也会有显著的线性相关, 但是\(X\)和\(Y\)会被误认为有正相关。
在R软件中用plot(x, y)画散点图。
ggplot2用geom_point()画散点图。
如果x或者y变量取离散值, 则散点图中的点可能有重叠,如:
set.seed(101); n <- 200
d5 <- tibble(x = sample(0:10, size=n, replace=TRUE)) %>%
mutate(y = 50 + 2*x + sample((-2):2, size=n, replace=TRUE))
ggplot(data=d5, mapping=aes(x=x, y=y)) +
geom_point()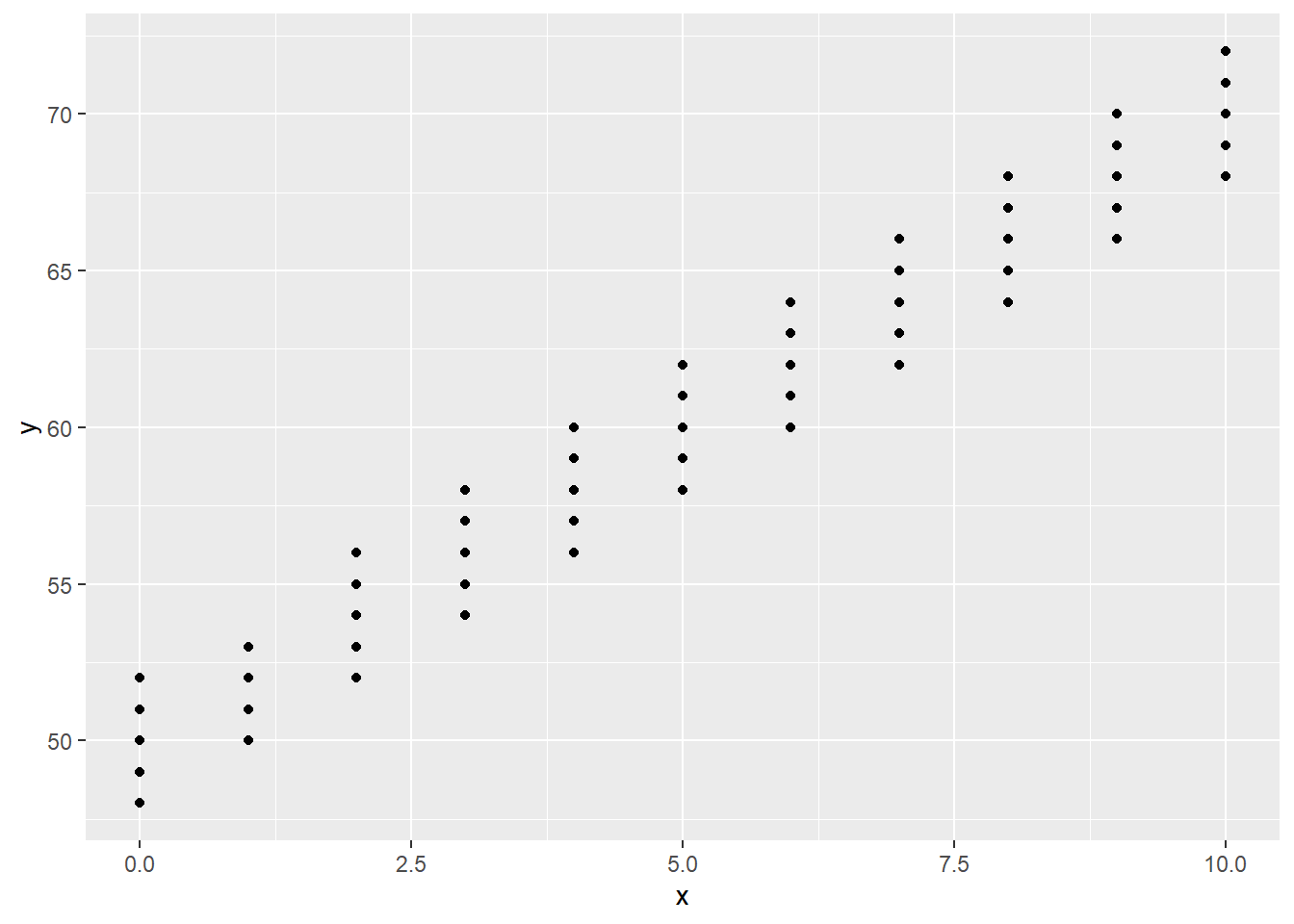
上图是200对观测值的散点图,
但是因为图中的点是在水平方向和竖直方向对齐的,
很多点重合在一起, 使我们不容易发现数据的规律。
R软件的jitter(x, amount)函数可以对输入的x
加一个\(\pm\)amount幅度内的扰动,
对扰动后的x和y作散点图就可以避免过多的点重合。
ggplot2的geom_jitter()可以将每个点进行小的扰动,
避免重叠。
设置一定的透明度也可以表现出局部点的疏密程度。
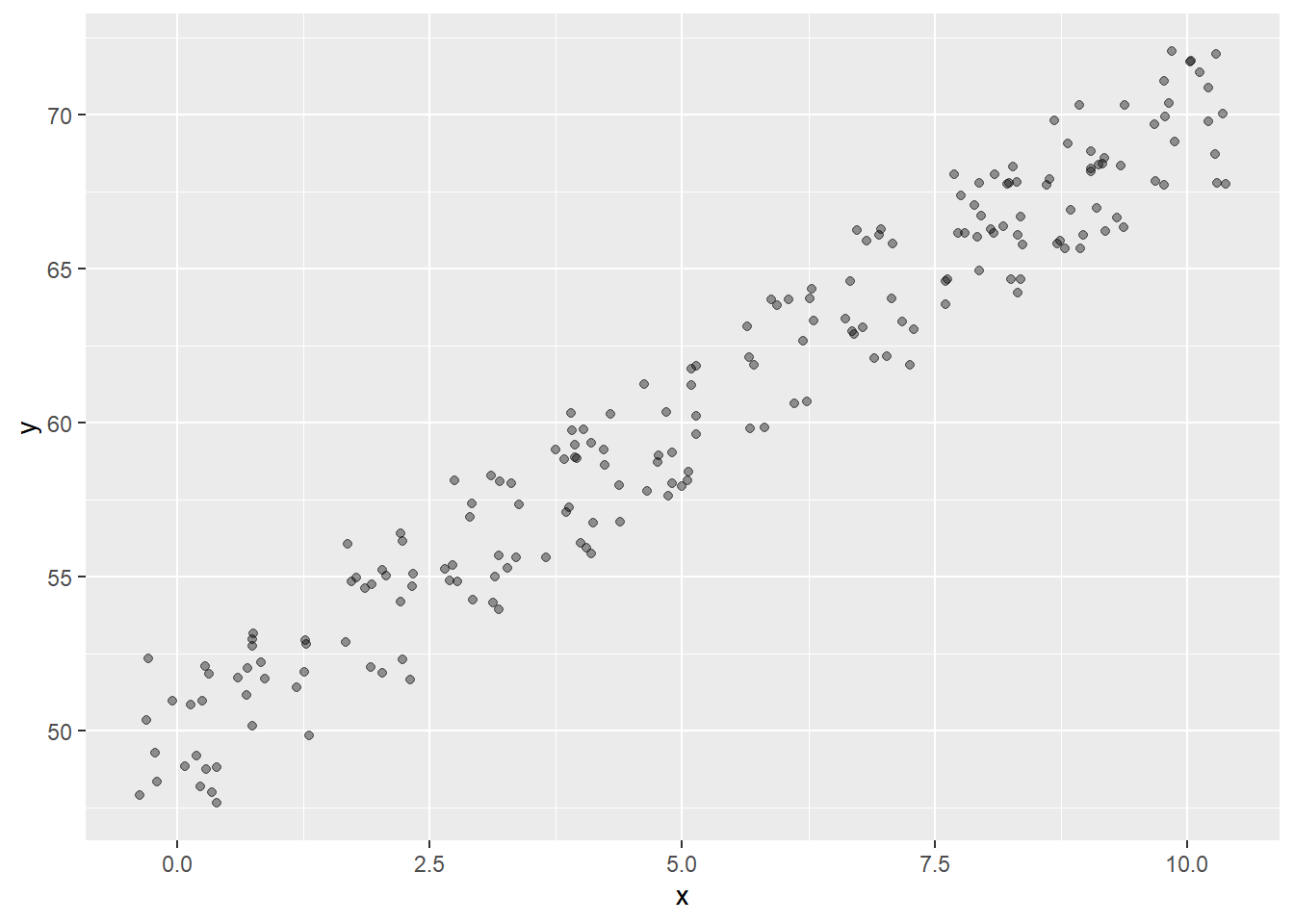
有些数据是随时间变化的, 而数据中有时已经有时间变量, 也可能没有明显的时间变量。 在没有时间变量时,有时输入数据的次序号可以作为时间变量。 为了考察随时间变化的量(称为时间序列), 可以把以此变量为纵坐标、以时间为横坐标的点用线相连, 称这样的图为曲线图或时间序列图, 实际上,这样的图是折线图, 曲线图是一种习惯称呼。
在R中,用plot(x, y, type=l)作曲线图。
用lines(x, y)在已有图形上添加线, 用points(x, y)在已有图形上添加点,
用abline(h=...)在已有图形上添加横线,
用abline(v=...)在已有图形上添加竖线。
用rug函数可以在把点的横坐标值或纵坐标值用短线标在坐标区域边缘。
ggplot2的geom_line()作折线图(曲线图)。
如下R程序作了正弦曲线和余弦曲线图:
d6 <- tibble(x = seq(0, 2*pi, length=100)) %>%
mutate(y1 = sin(x), y2=cos(x))
ggplot(data = d6, mapping=aes(x=x)) +
geom_line(mapping=aes(y=y1), col="red") +
geom_line(mapping=aes(y=y2), col="blue") +
geom_hline(yintercept=0) +
geom_vline(xintercept=0)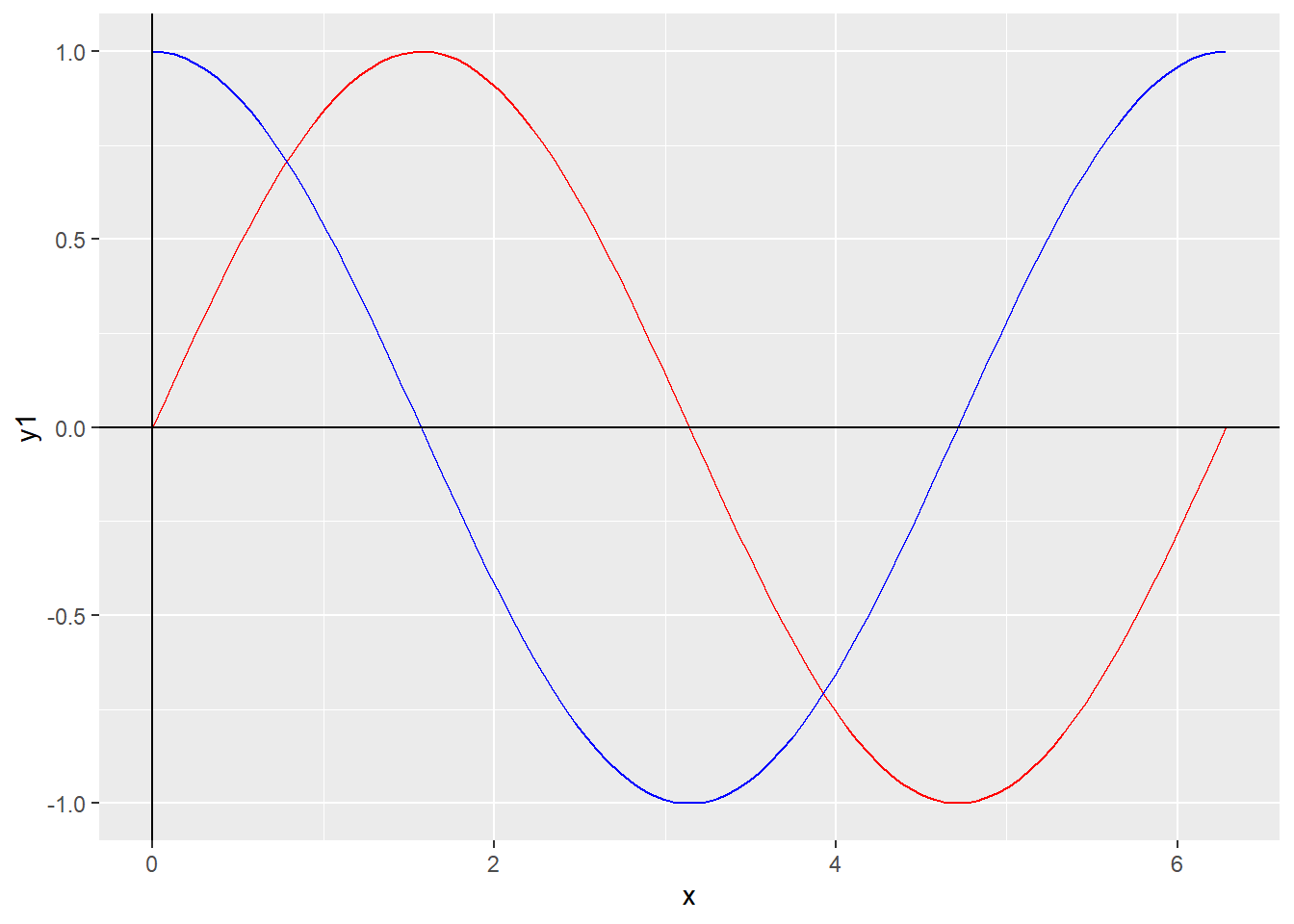
R函数matplot可以在同一坐标系中做多条曲线或多组散点图。
R中有专门的时间序列数据类型, 这种数据类型是向量的变种,
定义了序列的开始时间和采样频率 (比如每月一次的数据的采样频率为12),
所以序列中每个数值都有对应的时间。 用ts函数定义时间序列。
如果y是时间序列, plot(y)可以直接作时间序列曲线图。
下图是美国泛美航空公司1949—1960年每月国际航班订票数的时间序列图:
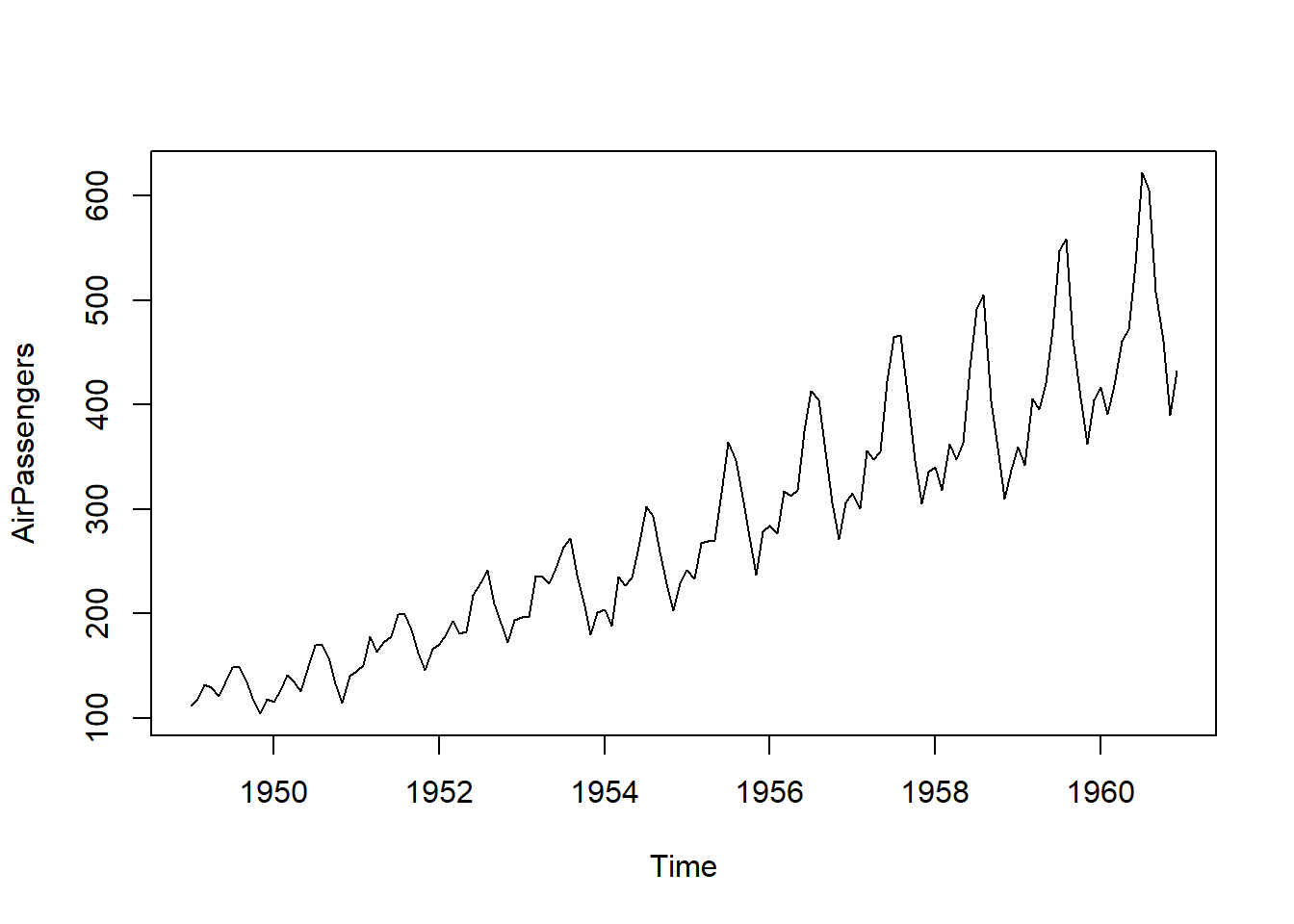
对于时间序列,还可以以\((y_i, y_{i+1}), i=1,2,\dots,n-1\)为坐标画散点图以查看自相关情况。 时间序列还有一些专门的图形, 如自相关函数图、偏相关函数图、谱密度估计图等。
有时随时间变化的是变量间的关系, 这就更困难, 可以做一系列随时间变化的图形。
散点图、曲线图等图形的坐标轴刻度一般是自动确定的, 大致取为该维数据的最小值到最大值的范围。 如果需要比较多幅图, 要注意坐标范围的问题, 必要时可以使多幅图的坐标范围统一化。 ggplot2可以按一个或者几个分类变量将观测分类, 每一类作一幅小图, 小图的坐标范围自动统一化。
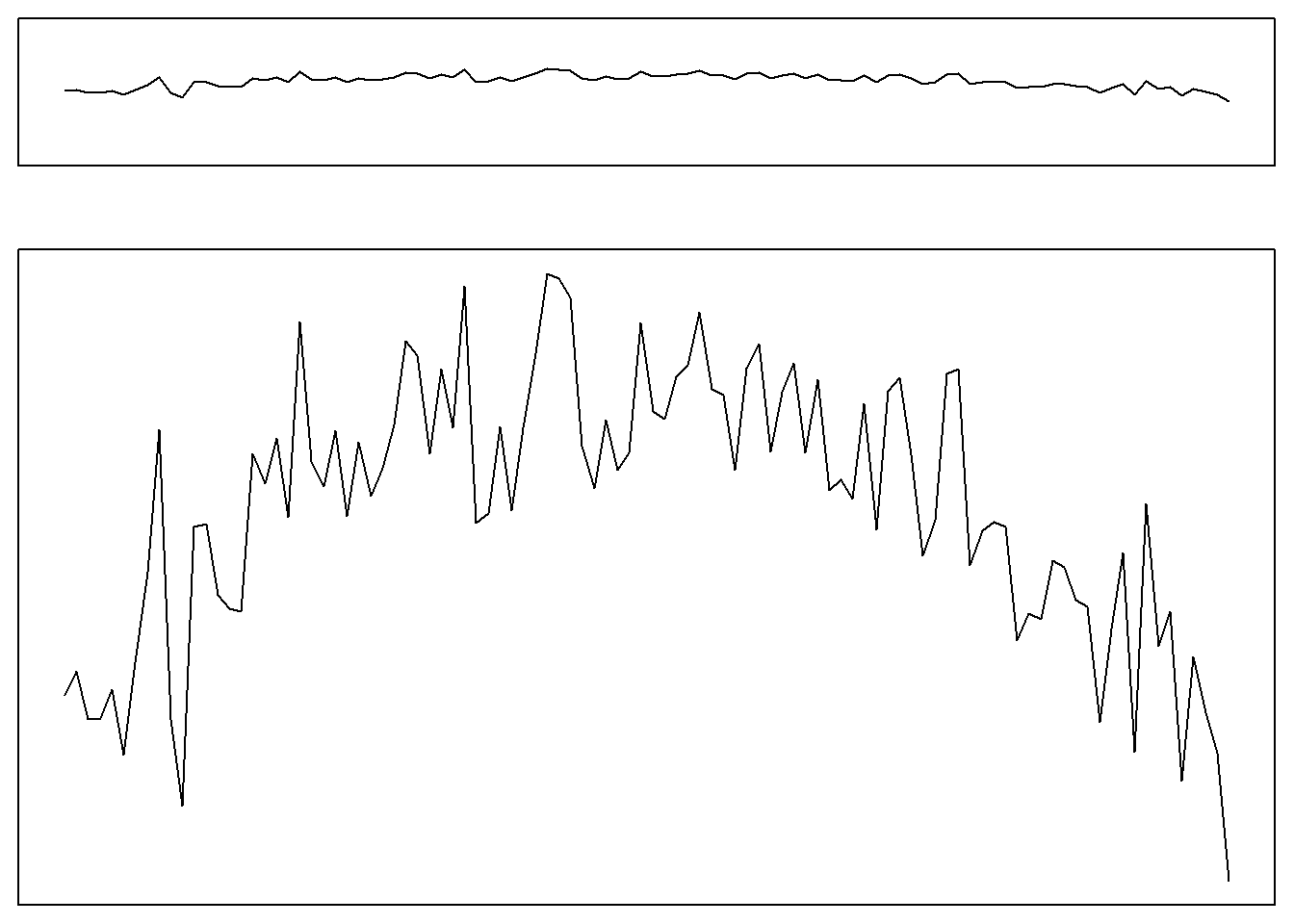
曲线图的宽高比不仅影响视觉效果, 不合适的宽高比可能误导我们对变化规律的认识。 下面有两幅时间序列图, 实际是同一时间序列, 但是下面的图清楚地表现了一个有先升后降趋势的序列, 而上面的图表面上看是一个在某一水平线上下波动的序列:
4.7 三维图
如果有多个数值型变量, 可以两两作散点图, 构成散点图矩阵。
在R中可以用pairs函数作散点图矩阵。
ggplot2和GGally包提供了散点图矩阵功能。
下图是三种不同的鸢尾花的150个样品的花瓣、花萼长、宽的数据的散点图矩阵:
library(GGally, quietly=TRUE, warn.conflicts=FALSE)
## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2
ggscatmat(data=iris, columns=1:4)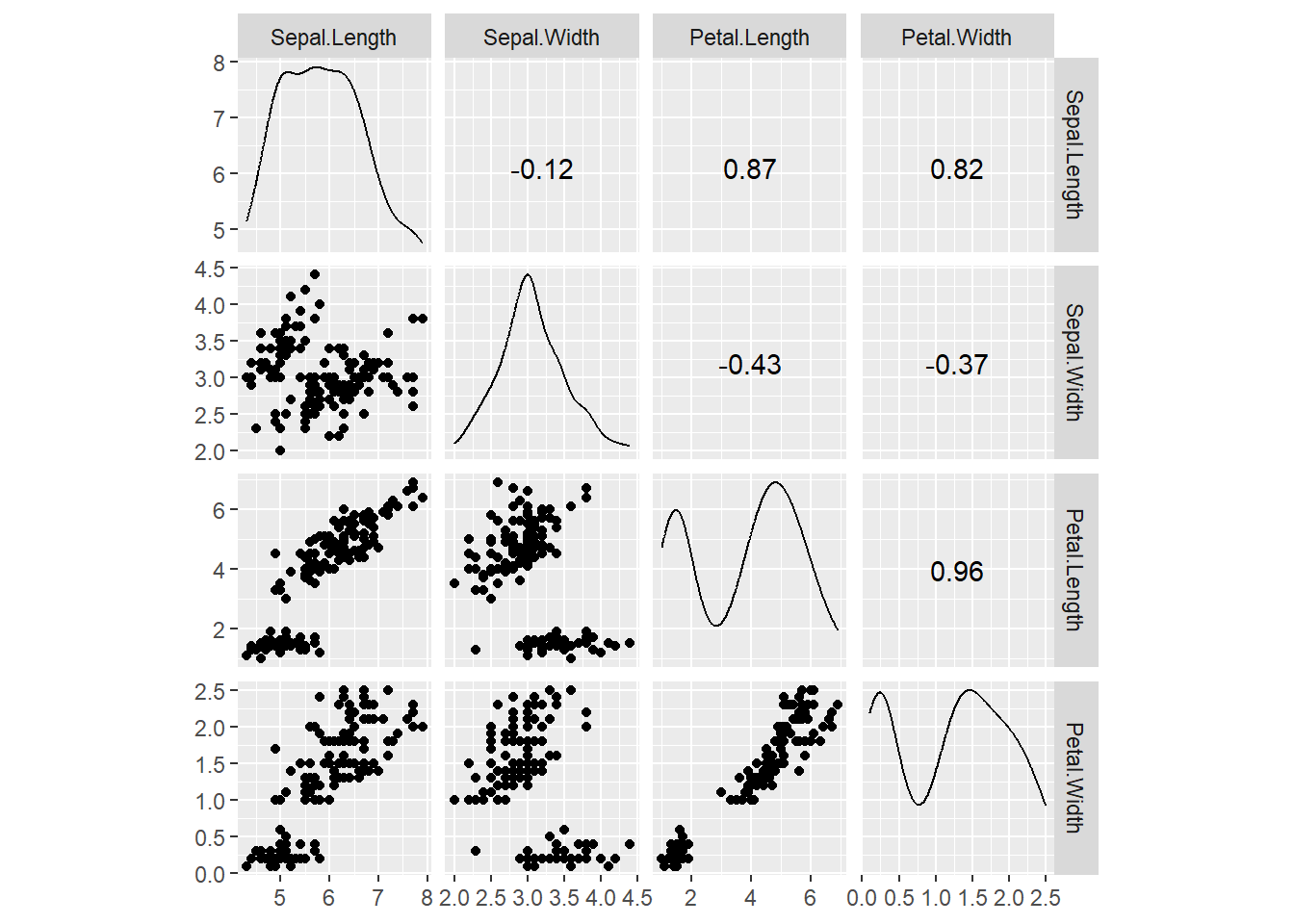
对于三个区间变量\(X, Y, Z\)之间的关系, 可以用各种三维图形直观地查看。
为了查看二元函数\(z = f(x, y)\)的图像, 可以作曲面图、等值线图和栅格图。
R软件的surface(x, y, z)作曲面图,
其中向量x和向量y的值构成Oxy平面上的一张网格,
z为一个矩阵,第\(i\)行第\(j\)列元素为\(f(x_i, y_j)\)的值。
R函数contour(x, y, z)作等值线图, 这也是反映曲面\(f(x,y)\)形状的图形,
想法来自于地图中的等高线。 R函数image(x, y, z)作栅格图,
每个\((x_i, y_j)\)处用不同的颜色或灰度代表不同的\(z=f(x_i, y_j)\)的值。
ggplot2的geom_contour()作等值线图,
geom_raster()作栅格图。
设随机向量\((X, Y)\)服从联合正态分布, \(E X = E Y = 0\), \(\text{Var}(X) = \sigma_1^2\), \(\text{Var}(Y) = \sigma_2^2\), \(\rho(X, Y) = R\)。 则\((X, Y)\)的联合密度为 \[\begin{aligned} f(x,y) = \frac{1}{2\pi \sqrt{\sigma_1^2 \sigma_2^2 (1 - R^2)}} \exp\left\{ -\frac12 \frac{\sigma_2^2 x^2 + \sigma_1^2 y^2 - 2R \sigma_1 \sigma_2 x y} {\sigma_1^2 \sigma_2^2 (1 - R^2)} \right\} \end{aligned} \]
如下的R程序作\(f(x,y)\)的等值线图:
ng <- 30
s1 <- 1; s2 <- 2
R <- 0.5
d <- s1^2 * s2^2 * (1 - R^2)
f <- function(x, y) 1 / (2*pi*sqrt(d)) *
exp(-0.5 * (s2^2 * x^2 + s1^2 * y^2 - 2*R*s1*s2*x*y)/d)
d7 <- expand_grid(
x = seq(-3, 3, length=ng)*s1,
y = seq(-3, 3, length=ng)*s2) %>%
mutate(z = f(x, y))
ggplot(data = d7, mapping = aes(x=x, y=y, z=z, color=..level..)) +
geom_contour()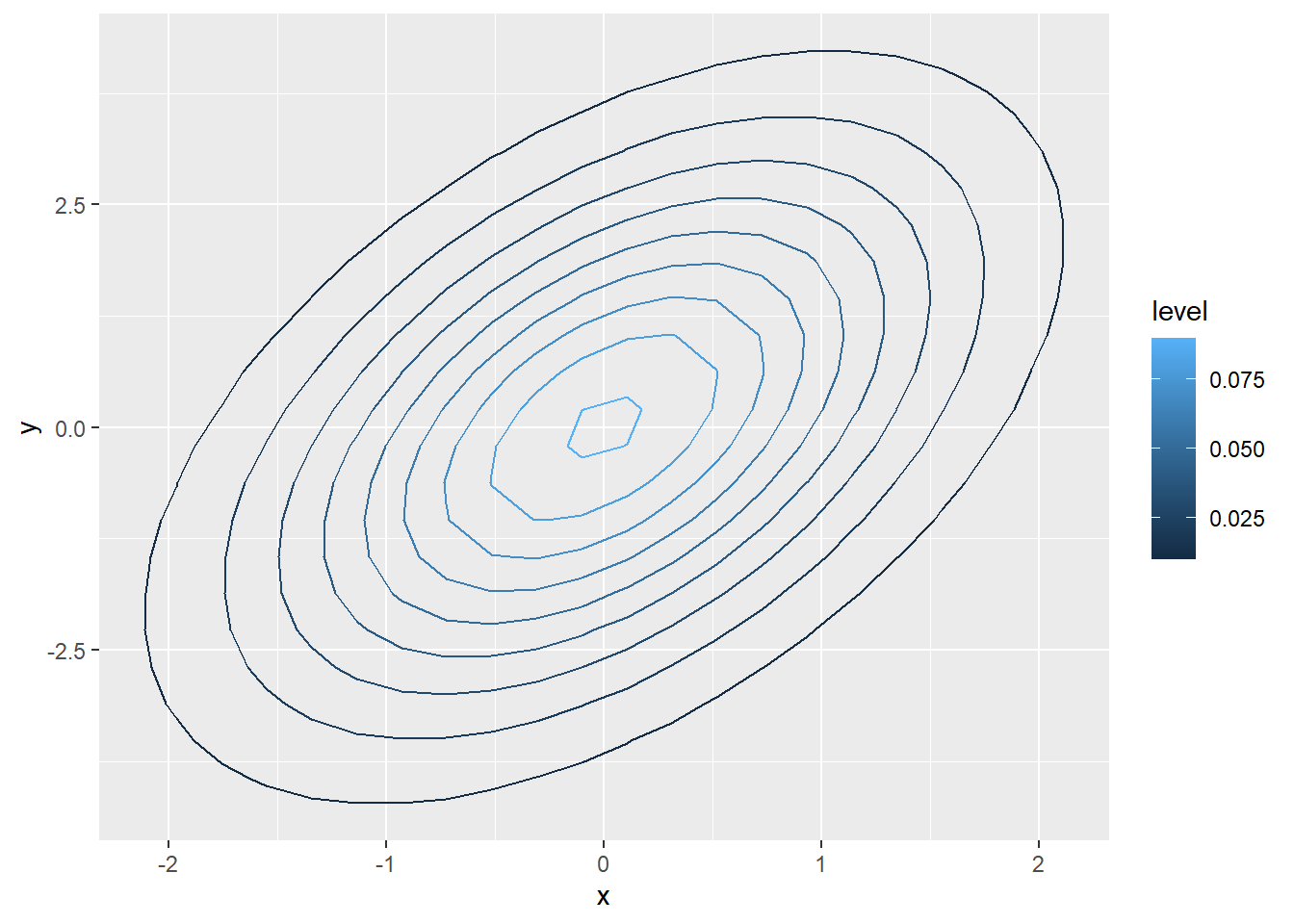
栅格图:
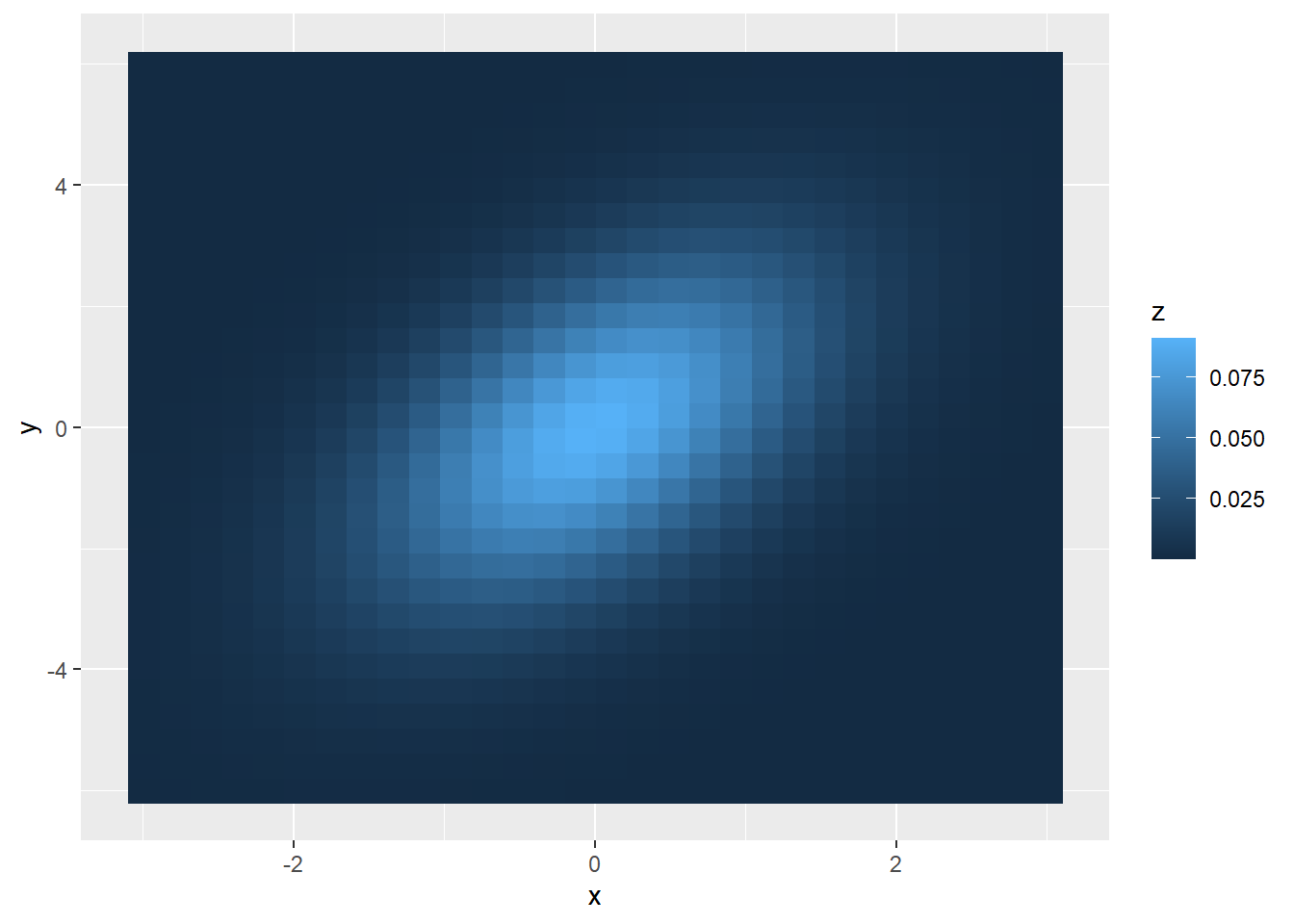
类似于散点图,三维散点图可以反映三个变量之间的关系。
在R中,可以用lattice包的cloud函数作三维散点图。
如果变量\(X\)和\(Y\)是数值型的, 变量\(Z\)是分类的, 则可以画\((X,Y)\)散点图,
但每个点根据\(Z\)的不同值使用不同符号(圈、三角、加号、星号、点等)
或不同颜色, 这样可以用散点图表达出三维信息。 如果变量\(Z\)是数值型的,
可以用散点图中绘点符号的大小来表示\(Z\)的大小。
下图是三种鸢尾花各50朵的花瓣长、宽数据的散点图,
用了不同符号和颜色来代表不同种类。
R函数plot、lines、points的pch参数可以用来规定绘点符号, col参数可以用来规定绘点颜色,
cex参数可以用来规定绘点符号的大小。
ggplot2支持color, fill, shape等维度。
ggplot(data = iris, mapping = aes(
x = Petal.Length, y = Petal.Width,
color = Species, shape = Species)) +
geom_point(size=2, alpha=0.5)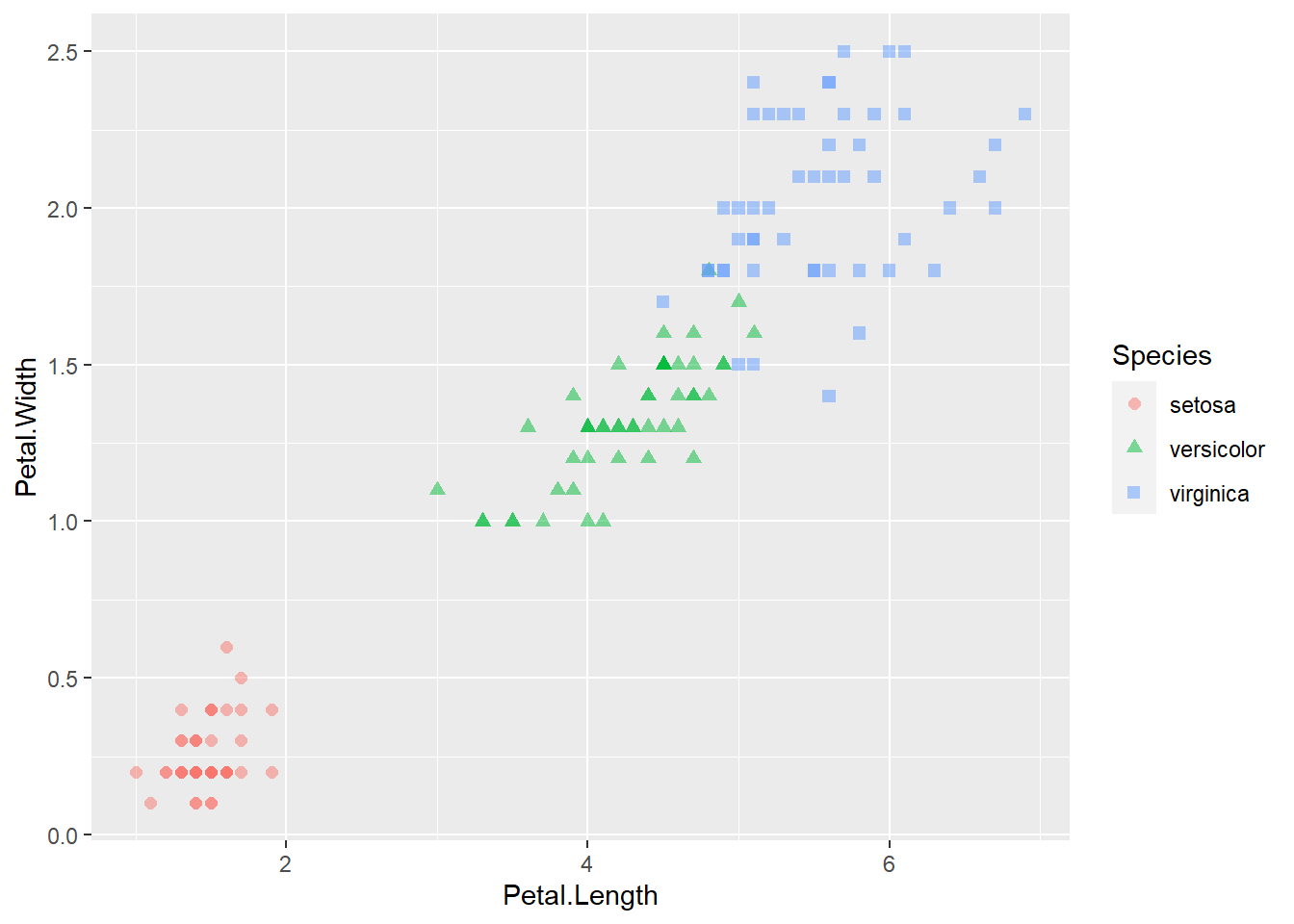
rgl扩展包提供了绘制动态三维散点图的功能。程序如
library(rgl)
with(iris, plot3d(
Sepal.Length, Sepal.Width, Petal.Length,
type='s', col=as.numeric(factor(Species))))rgl可以绘制二元正态分布动态曲面图: