12 重要抽样法
\(I = \int_C h(\boldsymbol x) \,d \boldsymbol x\)中积分区域\(C\)可能是任意形状的, 也可能无界,\(h(\boldsymbol x)\)在\(C\)内各处的取值大小差异可能很大, 使得直接用平均值法估计\(I\)时, 很多样本点处于\(|h(\boldsymbol x)|\)接近于零的地方, 造成浪费,另外使得\(\hat I_2\)的渐近方差(见式(11.23))中的 \(\text{Var}(h(\boldsymbol U))\)很大(\(\boldsymbol U \sim \text{U}(C)\))。 为此,考虑用非均匀抽样: \(|h(\boldsymbol x)|\)大的地方密集投点, \(|h(\boldsymbol x)|\)小的地方稀疏投点。 这样可以有效利用样本。 设\(g(\boldsymbol x), \boldsymbol x \in C\)是一个密度, 其形状与\(|h(\boldsymbol x)|\)相近, 且当\(g(\boldsymbol x)=0\)时\(h(\boldsymbol x)=0\), 当\(\| \boldsymbol x \| \to \infty\)时 \(h(\boldsymbol x) = o(g(\boldsymbol x))\)。 称\(g(\boldsymbol x)\)为试投密度或重要抽样密度。
设\(\boldsymbol X_i\) iid \(\sim g(\boldsymbol x)\), \(i=1,2,\ldots, N\)。 令 \[\begin{aligned} \eta_i = \frac{h(\boldsymbol X_i)}{g(\boldsymbol X_i)}, \ i=1,2,\dots,N, \end{aligned}\] 则 \[\begin{aligned} E \eta_1 = \int_C \frac{h(\boldsymbol x)}{g(\boldsymbol x)} g(\boldsymbol x) \,d \boldsymbol x = \int_C h(\boldsymbol x) \,d \boldsymbol x = I, \end{aligned}\] 因此可以用\(\{ \eta_i, i=1,2,\dots, N \}\)的样本平均值来估计\(I\),即 \[\begin{align} \hat I_3 = \bar\eta = \frac{1}{N} \sum_{i=1}^N \frac{h(\boldsymbol X_i)}{g(\boldsymbol X_i)}. \tag{12.1} \end{align}\] \(\hat I_3\)是\(I\)的无偏估计和强相合估计。 \(\hat I_3\)的渐近方差为 \[\begin{align} \text{Var}(\hat I_3) = \text{Var}\left( \frac{h(\boldsymbol X)}{g(\boldsymbol X)} \right) \frac{1}{N} = O(\frac{1}{N}), \tag{12.2} \end{align}\] 当\(g(\boldsymbol x)\)和\(|h(\boldsymbol x)|\)形状很接近时\(\frac{|h(\boldsymbol x)|}{g(\boldsymbol x)}\)近似为常数, 方差\(\text{Var}(\hat I_3)\)很小, 这时\(\hat I_3\)的随机误差可以很小。 用(12.1)式估计\(I\)与舍选法II有类似的想法, 这种方法叫做重要抽样法(importance sampling), 是随机模拟的重要方法。
为什么当\(g(\boldsymbol x)\)和\(|h(\boldsymbol x)|\)形状很接近时\(\text{Var}(\hat I_3)\)很小? 事实上, \[\begin{align} \text{Var}\left( \frac{h(\boldsymbol X)}{g(\boldsymbol X)} \right) =& E \left( \frac{h^2(\boldsymbol X)}{g^2(\boldsymbol X)} \right) - \left( E \frac{h(\boldsymbol X)}{g(\boldsymbol X)} \right)^2 = E \left( \frac{h^2(\boldsymbol X)}{g^2(\boldsymbol X)} \right) - \left( \int_C h(\boldsymbol x) \,d\boldsymbol x \right)^2 \nonumber \\ \geq& \left( E \frac{|h(\boldsymbol X)|}{g(\boldsymbol X)} \right)^2 - I^2 \quad \text{(Jensen不等式)} \tag{12.3} \\ =& \left( \int_C |h(\boldsymbol x)| \,d\boldsymbol x \right)^2 - I^2 , \end{align}\] 当且仅当\(\frac{|h(\boldsymbol X)|}{g(\boldsymbol X)}\)为常数时(12.3)的不等式中的等号成立, 即\(g(\boldsymbol x) = \frac{1}{\int_C |h(\boldsymbol t)| \,d\boldsymbol t} |h(\boldsymbol x)|, \boldsymbol x \in C\) 时\(\text{Var}(\hat I_3)\)达到最小。
上述求积分的问题也可以表述为求随机变量函数的期望问题。 设\(\boldsymbol Y \sim f(\boldsymbol y)\), 要求\(\boldsymbol Y\)的函数\(h(\boldsymbol Y)\) 的期望值\(E h(\boldsymbol Y) = \int h(\boldsymbol y) f(\boldsymbol y) \,d\boldsymbol y\), 可以抽取\(\boldsymbol Y\)的随机数\(\boldsymbol Y_i, i=1,2,\dots,N\), 然后用平均值法 \(\frac{1}{N} \sum_{i=1}^N h(\boldsymbol Y_i)\)估计\(E h(\boldsymbol Y)\)。 但是,如果很难生成\(\boldsymbol Y\)的随机数, 或者\(\boldsymbol Y\)的分布集中于\(h(\boldsymbol y)\)接近于零的位置以至于积分效率很低, 可以找一个试投密度\(g(\boldsymbol x)\), 从\(g(\boldsymbol x)\)产生随机数\(\boldsymbol X_i, i=1,2,\dots,N\), 用如下重要抽样法 \[\begin{align} \hat I_{3.1} =& \frac{1}{N} \sum_{i=1}^N h(\boldsymbol X_i) \frac{f(\boldsymbol X_i)}{g(\boldsymbol X_i)} \tag{12.4} \end{align}\] 估计\(E h(\boldsymbol Y)\), 易见\(E \hat I_{3.1} = E h(\boldsymbol Y)\)。 称\(W_i = \frac{f(\boldsymbol X_i)}{g(\boldsymbol X_i)}\)为重要性权重, \(E h(\boldsymbol Y)\)可以用重要性权重估计为 \[\begin{align} \hat I_{3.1} =& \frac{1}{N} \sum_{i=1}^N W_i h(\boldsymbol X_i) . \tag{12.5} \end{align}\]
选取试投密度\(g(\boldsymbol x)\)时, 要求当\(h(\boldsymbol x) f(\boldsymbol x) \neq 0\)时\(g(\boldsymbol x) \neq 0\), 当\(\boldsymbol x\)趋于无穷时 \(h(\boldsymbol x) f(\boldsymbol x) = o(g(\boldsymbol x))\)(\(g(\boldsymbol x)\)相对厚尾), 一般还要求\(g(\boldsymbol x)\)的形状与\(|h(\boldsymbol x)| f(\boldsymbol x)\)形状接近。 如果\(g(\boldsymbol x)\)的相对厚尾性难以确定, 可以使用如下保险的试投密度 \[\begin{align} \tilde g(\boldsymbol x) = \rho g(\boldsymbol x) + (1-\rho) r(\boldsymbol x), \tag{12.6} \end{align}\] 其中\(\rho\)接近于1, \(r(\boldsymbol x)\)是柯西分布或Pareto分布这样的重尾分布。 要生成\(N\)个\(\tilde g(\boldsymbol x)\)的随机数, 只要生成\(N \rho\)个\(g(\boldsymbol x)\)的随机数和\(N(1-\rho)\)个\(r(\boldsymbol x)\)的随机数。
选取不适当的试投密度会把绝大多数样本点投到了对计算积分不重要的位置, 使得样本点中只有极少数点是真正有作用的。 在多维问题中合适的试投密度尤其难找, 经常需要反复试验。
例12.1 用MC积分法计算 \(I = \int_0^1 e^x \,dx = e-1 \approx 1.718\)。 对被积函数\(h(x)=e^x\)做泰勒展开得 \[\begin{aligned} e^x = 1 + x + \frac{x^2}{2!} + \cdots \end{aligned}\]
取 \[\begin{aligned} g(x)=c(1+x) = \frac{2}{3}(1+x) \end{aligned}\] 要产生\(g(x)\)的随机数可以用逆变换法, 密度\(g(x)\)的分布函数\(G(x)\)的反函数为 \[\begin{aligned} G^{-1}(y) = \sqrt{1+3y}-1, \ 0<y<1 \end{aligned}\] 因此,取\(U_i\) iid U(0,1), 令\(X_i = \sqrt{1+3U_i}-1\), \(i=1,2,\ldots,N\), 则重要抽样法的积分公式为 \[\begin{aligned} \hat I_3 = \frac{1}{N} \sum_{i=1}^N \frac{e^{X_i}}{\frac{2}{3}(1+X_i)} \end{aligned}\] 渐近方差为 \[\begin{aligned} \text{Var}(\hat I_3) = \frac{1}{N} \left( \frac{3}{2}\int_0^1 \frac{e^{2x}}{1+x} dx - I^2 \right) \approx 0.02691/N. \end{aligned}\]
积分真值:
重要抽样法的程序实现:
set.seed(1)
N <- 10000
Ginv <- function(y) sqrt(1 + 3*y) - 1
X <- Ginv(runif(N))
eta <- exp(X) / (2/3*(1 + X))
I3 <- mean( eta )
var3 <- var(eta)一次模拟的估计值和绝对误差、相对误差:
相对误差很小,说明有效位数在三位以上。
用一次模拟的结果估计平均相对误差为:
说明估计精度大约有三位有效数字。
从一次模拟中对\(N \cdot \text{Var}(\hat I_3)\)进行估计:
理论值是0.02691。
如果用平均值法, 估计公式为 \[\begin{aligned} \hat I_2 = \frac{1}{N} \sum_{i=1}^N e^{U_i}, \end{aligned}\] 渐近方差为 \[\begin{aligned} \text{Var}(\hat I_2) = \frac{1}{N} \left(\int_0^1 e^{2x} \,dx - I^2 \right) \approx 0.2420/N \approx 9.0 \times \text{Var}(\hat I_3) \end{aligned}\] 是重要抽样法方差的9倍。 因为随机模拟误差的方差通常是\(\text{Var}(Y_i)/N\), 其中\(Y_i\)是重复\(N\)次抽样中的一次的估计, 所以方差的倍数可以换算成计算量的倍数。 在这个问题中, 为了达到相同的精度, 重要抽样法只需要平均值法的\(1/9\)的样本量。
平均值法的R程序:
一次模拟的估计值和绝对误差、相对误差:
相对误差很小,说明有效位数约有三位。
用一次模拟的结果估计平均相对误差为:
说明估计精度大约有二位有效数字。
从一次模拟中对\(\text{Var}(\hat I_2)*N\)进行估计:
理论值是0.2420。
如果用随机投点法,\(h(x)=e^x \leq e(0 < x < 1)\), 取上界\(M=e\), 向\([0,1] \times [0,M]\)随机投点,落到\(f(x)\)下方的概率为 \[\begin{aligned} p = I/(M(b-a)) = (e-1)/e, \end{aligned}\] 设投\(N\)点落到\(h(x)\)下方的频率为\(\hat p\), 用随机投点法估计\(I\)的公式为 \[\begin{aligned} \hat I_1 = \hat p \cdot M (b-a) = e \hat p, \end{aligned}\] 渐近方差为 \[\begin{aligned} \text{Var}(\hat I_1) = e^2 p(1-p) / N = (e-1)/N \approx 1.718 / N \approx 7.1 \times \text{Var}(\hat I_2) \approx 64.8 \times \text{Var}(\hat I_3) \end{aligned}\] 即重要抽样法只需要随机投点法的\(1/65\)的样本量。 可见选择合适的抽样算法对减少计算量、提高精度是十分重要的。
随机投点法的R程序:
set.seed(1)
N <- 10000
phat <- mean(runif(N) <= exp(runif(N)-1))
I1 <- phat*exp(1)
var1 <- exp(2)*phat*(1-phat)一次模拟的估计值和绝对误差、相对误差:
相对误差很小,说明有效位数将近三位。
用一次模拟的结果估计平均相对误差为:
说明估计精度大约有二位有效数字。
从一次模拟中对\(N \cdot \text{Var}(\hat I_1)\)进行估计:
理论值是1.718。
※※※※※
例12.2 (一个二元函数定积分(*)) 设二元函数\(f(x,y)\)定义如下 \[\begin{aligned} f(x,y) =& \exp\{ -45(x + 0.4)^2 - 60(y-0.5)^2 \} + 0.5 \exp\{ -90(x-0.5)^2 - 45(y+0.1)^4 \} \end{aligned}\] 求如下二重定积分 \[\begin{aligned} I =& \int_{-1}^1 \int_{-1}^1 f(x,y) \,dx\,dy \end{aligned}\]
\(f(x,y)\)有两个分别以\((-0.4, 0.5)\)和\((0.5, -0.1)\)为中心的峰, 对积分有贡献的区域主要集中在\((-0.4,0.5)\)和\((0.5, -0.1)\)附近, 在其他地方函数值很小,对积分贡献很小。
\(f(x,y)\)写成R函数:
用平均值法, 取点数\(N=10000\)。
N <- 10000
set.seed(1)
X <- runif(N, -1, 1)
Y <- runif(N, -1, 1)
eta <- f(X, Y)
I2 <- 4*mean(eta)
sd2 <- 4*sd(eta)一次模拟的估计值为:
估计的平均相对误差为:
\(\hat I_2\)的一个估计值为\(\hat I_2 = 0.126\), 从这一次模拟估计的平均相对误差为0.03, 仅有一位有效数字精度, 只能保证\(\hat I_2=0.1\)基本可信。
平均值法的缺点是在整个正方形区域\((-1,1) \times (-1,1)\)上均匀布点, 而被积函数\(f(x,y)\)仅在两个峰附近有较大正值, 其它区域基本是零。 用重要抽样法改进。取试投密度为 \[\begin{aligned} g(x,y) \propto& \tilde g(x,y) \\ =& \exp \{ -45(x+0.4)^2 - 60(y-0.5)^2 \} + 0.5 \exp\{ -90(x-0.5)^2 - 10(y+0.1)^2 \}, \\ & -\infty < x < \infty, -\infty < y < \infty, \end{aligned}\] 这样抽取到\([-1,1]\times [-1,1]\)范围外的点对积分没有贡献, 因为构成\(g(x,y)\)的两个密度都很集中,所以效率损失不大。 需要求使得\(\tilde g(x,y)\)化为密度的比例常数。 记N(\(\mu, \sigma^2)\)的分布密度为 \(f(x;\mu, \sigma^2)\),对\(\tilde g(x,y)\)积分得 \[\begin{aligned} \int_{-\infty}^\infty \int_{-\infty}^\infty \tilde g(x,y) =& \sqrt{2\pi/90} \int_{-\infty}^\infty f(x;-0.4, 90^{-1}) dx \cdot \sqrt{2\pi/120} \int_{-\infty}^\infty f(y;0.5,120^{-1}) dy \\ & + 0.5 \sqrt{2\pi/180} \int_{-\infty}^\infty f(x;0.5,180^{-1}) dx \cdot \sqrt{2\pi/20} \int_{-\infty}^\infty f(y;-0.1,20^{-1}) dy \\ =& \sqrt{2\pi/90}\sqrt{2\pi/120} + 0.5 \sqrt{2\pi/180}\sqrt{2\pi/20} \\ \approx& 0.1128199 \end{aligned}\]
c1 <- sqrt(2*pi/90*2*pi/120) + 0.5*sqrt(2*pi/180*2*pi/20); c1
## [1] 0.1128199
pmix <- sqrt(2*pi/90*2*pi/120)/c1; pmix
## [1] 0.5358984
0.5*sqrt(2*pi/180*2*pi/20)/c1
## [1] 0.4641016于是令 \[\begin{aligned} g(x,y) =& \tilde g(x,y) / 0.1128199 \\ =& 0.5358984 f(x;-0.4,90^{-1}) f(y;0.5,120^{-1}) \\ & + 0.4641016 f(x;0.5,180^{-1}) f(y;-0.1,20^{-1}), \\ & -\infty < x < \infty, -\infty < y < \infty, \end{aligned}\] 用复合抽样法对\(g(x,y)\)抽样,然后用重要抽样法得到估计值\(\hat I_3\)。 注意用重要抽样法计算时需要\(X_i\)独立同分布, 但是其次序并不重要, 当\(N\)很大时, 可以固定取混合分布中两个分布的样本个数严格等于混合比例, 而不需要从两个分布中随机抽取。
N <- 10000
g <- function(x, y){
0.5358984*dnorm(x,-0.4,sqrt(1/90))*dnorm(y,0.5,sqrt(1/120)) +
0.4641016*dnorm(x,0.5,sqrt(1/180))*dnorm(y,-0.1,sqrt(1/20))
}
set.seed(1)
N1 <- round(N*pmix)
N2 <- N-N1
X <- c(rnorm(N1, -0.4, sqrt(1/90)), rnorm(N2, 0.5, sqrt(1/180)))
Y <- c(rnorm(N1, 0.5, sqrt(1/120)), rnorm(N2, -0.1, sqrt(1/20)))
eta <- ifelse(-1 < X & X < 1 & -1 < Y & Y < 1, f(X, Y)/g(X,Y), 0)
I3 <- mean(eta)
sd3 <- sd(eta)一次模拟的估计值为:
估计的平均相对误差为:
\(N=10000\)时一次模拟得到的\(\hat I_3 = 0.1253\), 从这一次模拟估计的平均相对误差为0.002, 估计精度有两位有效数字以上, 估计结果可报告为0.13。
重要抽样法与平均值法的方差相比:
两种方法的方差差距有200倍以上, 说明重要抽样法节省了200倍的计算量。
※※※※※
12.1 标准化重要抽样法
有时\(\boldsymbol Y \sim f(\cdot)\)不仅很难直接抽样, 而且\(f(\cdot)\)本身未知, 只能确定到差一个常数倍的\(\tilde f(\boldsymbol x) = c f(\boldsymbol x)\), 常数\(c\)未知,为了求常数\(c\)需要计算\(c = \int \tilde f(\boldsymbol y) \,d\boldsymbol y\), 计算\(c\)一般很困难。 这时,定义重要性权重为\(W_i = \frac{\tilde f(\boldsymbol X_i)}{g(\boldsymbol X_i)}\), 公式(12.5)可以改成 \[\begin{align} \hat I_{4} =& \frac{ \sum_{i=1}^N W_i h(\boldsymbol X_i) } {\sum_{i=1}^N W_i} \tag{12.7} \end{align}\] 这称为标准化重要抽样法。 对(12.7)的分子和分母都除以\(cN\) 后分子a.s.收敛到 \(Eh(\boldsymbol Y)\), 分母a.s.收敛到1, 所以(12.7)是\(E h(\boldsymbol Y)\)的强相合估计, 但不是无偏的。 标准化重要抽样估计往往比无偏估计\(\hat I_{3.1}\)有更小的均方误差。 关于标准化重要抽样法的渐近方差的讨论参见(Liu 2001) §2.5.3。
如果需要对多个不同的函数\(h(\cdot)\)计算\(Eh(\boldsymbol Y)\), 则选取试抽样密度\(g(\boldsymbol x)\)时应使得\(g(\boldsymbol x)\)尽可能与\(\boldsymbol Y\)的密度\(f(\boldsymbol x)\)形状接近, 这样权重\(W_i = \frac{\tilde f(\boldsymbol X_i)}{g(\boldsymbol X_i)}\)的分布不过于偏斜, 不至于出现绝大部分权重集中于少数样本点的情形。 抽样值\(\boldsymbol X_i\)与权重\(W_i\)一起可以看作是分布\(f(\cdot)\)的某种抽样。
定义12.1 (适当加权抽样) 随机变量序列\(\{(\boldsymbol X_i, W_i), \, i=1,2,\dots,N \}\) 称为关于密度\(f(\cdot)\)的适当加权抽样, 如果对于任何平方可积函数\(h(\cdot)\)都有 \[\begin{aligned} E[ h(X_i) W_i ] = c E_f[h(X)] = c \int h(\boldsymbol x) f(\boldsymbol x) \,d\boldsymbol x, \ i=1,2,\dots,N, \end{aligned}\] 其中\(c\)是归一化常数。
设随机变量\((\boldsymbol X, W)\)联合密度为\(g(\boldsymbol x, w)\), 则\((\boldsymbol X, W)\)的样本为密度\(f(\cdot)\)的适当加权抽样的充分必要条件是 \[\begin{aligned} E_g(W|\boldsymbol x) = E_g(W) \frac{f(\boldsymbol x)}{g(\boldsymbol x)}, \ \forall \boldsymbol x, \end{aligned}\] 其中\(E_g(W)\)是关于\(W\)的边缘密度的期望, \(E_g(W|\boldsymbol x)\)是在\((\boldsymbol X, W)\)的联合密度下条件期望\(E(W|\boldsymbol X)\)在\(\boldsymbol X=\boldsymbol x\)处的值。
例12.3 (贝塔—二项分布推断(*)) 标准化的重要抽样法在贝叶斯统计推断中有重要作用。 例如,设独立的观测样本\(Y_j\)服从如下的贝塔—二项分布: \[\begin{align} & f(y_j | K, \eta) = P(Y_j = y_j) \\ =& \binom{n_j}{y_j} \frac{B(K\eta + y_j,\ K(1-\eta) + n_j - y_j)}{B(K\eta,\, K(1-\eta))}, \ y_j=0,1,\dots, n_j, \tag{12.8} \end{align}\] 其中\(B(\cdot, \cdot)\)是贝塔函数, \(n_j\)为已知的正整数,\(K>0\)和\(0<\eta<1\)为未知参数。 贝塔—二项分布用于描述比二项分布更为分散的随机变量分布。 按照贝叶斯统计的做法, 假设参数\((K, \eta)\)也是随机变量, 具有所谓的“先验分布”, 假设\((K, \eta)\)有如下的“无信息”先验分布密度: \[\begin{align} \pi(K, \eta) \propto \frac{1}{(1+K)^2} \frac{1}{\eta(1-\eta)}, \tag{12.9} \end{align}\] 则\((K, \eta)\)有如下的“后验密度”: \[\begin{align} \tilde p(K, \eta | \boldsymbol Y) \propto& \pi(K, \eta) \prod_{j=1}^n f(y_j | K, \eta) \nonumber \\ \propto& \frac{1}{(1+K)^2} \frac{1}{\eta(1-\eta)} \prod_{j=1}^n \frac{B(K\eta + y_j,\ K(1-\eta) + n_j - y_j)}{B(K\eta,\, K(1-\eta))}. \tag{12.10} \end{align}\] 要求 \(E (\log K | \boldsymbol Y) = \int_0^\infty \log K \, \tilde p(K, \eta | \boldsymbol Y) \,dK\)的值。
如果可以从后验密度\(\tilde p(K, \eta | \boldsymbol Y)\)直接抽样, 可以用平均值法估计\(E (\log K | \boldsymbol Y)\), 但从(12.10)来看很难直接抽样。 为此,使用标准化的重要抽样法。 为了解除\((K, \eta)\)的取值限制, 作变换\(\alpha = \log K\), \(\beta = \log \frac{\eta}{1-\eta}\), 则\(\alpha, \beta \in (-\infty, \infty)\), 而(12.10)对应的\((\alpha, \beta)\)的后验密度为: \[\begin{align} p(\alpha, \beta | \boldsymbol Y) \propto \frac{e^\alpha}{(1 + e^\alpha)^2} \prod_{j=1}^n \frac{B(\frac{e^{\alpha}}{1 + e^{-\beta}} + y_j, \ \frac{e^{\alpha}}{1 + e^{\beta}} + n_j - y_j)} {B(\frac{e^{\alpha}}{1 + e^{-\beta}}, \ \frac{e^{\alpha}}{1 + e^{\beta}})}. \tag{12.11} \end{align}\] 取值无限制的随机变量试抽样密度经常使用自由度较小的t分布, 比如t(4)分布,设t(4)分布密度函数为\(g(\cdot)\), 用独立的t(4)分布生成\((\alpha, \beta)\) 的试抽样样本\((\alpha_i, \beta_i), i=1,2,\dots,N\), 可以估计\(E(\log K | \boldsymbol Y)\)为 \[\begin{aligned} \hat \alpha = \frac{\sum_{i=1}^N \alpha_i \frac{p(\alpha_i, \beta_i | \boldsymbol Y)}{g(\alpha_i) g(\beta_i)}} {\sum_{i=1}^N \frac{p(\alpha_i, \beta_i | \boldsymbol Y)}{g(\alpha_i) g(\beta_i)}}. \end{aligned} \] 其中的\(p(\alpha_i, \beta_i | \boldsymbol Y)\)只要用(12.11)的右侧计算, 因为分子和分母的归一化常数可以消掉。
下面用R语言产生一组模拟的观测数据\(\boldsymbol Y\),然后对这组数据估计\(E(\log K | \boldsymbol Y)\)。
先定义贝塔-二项分布的概率质量函数:
dbetabin <- function(y, n, K, eta){
choose(n, y)*beta(K*eta + y, K*(1-eta) + n-y)/beta(K*eta, K*(1-eta))
}其中\(n\)是正整数,\(y\)是非负整数且\(0 \leq y \leq n\),
K和eta是上述分布参数\(K\)和\(\eta\)。
给定\(n\)个独立观测,
设这组观测的\(n_1, \dots, n_n\)保存在向量narr中,
\(y_1, \dots, y_n\)保存在向量yarr中,
于是以\((\alpha, \beta)\)为自变量的后验密度函数(差一个未知的常数倍),
将\(\alpha\)和\(\beta\)记为自变量a, b,R函数为:
p.post <- function(a, b){
K <- exp(a)
eta <- 1/(1 + exp(-b))
val <- K / (1+K)^2
beta0 <- beta(K*eta, K*(1-eta))
for(j in seq(n)){
val <- val * beta(K*eta + yarr[j], K*(1-eta) + narr[j] - yarr[j]) / beta0
}
val[beta0==0] <- 0
val
}注意其中的narr和yarr是还没有赋值的全局变量。
在R的函数定义中,
允许使用尚未定义的变量,
只要调用该函数时变量已经在该函数定义的环境中赋值就可以。
下面用模拟方法生成观测样本,然后认为观测样本已知。
set.seed(1)
K.true <- 10
eta.true <- 0.2
narr <- c(20, 30, 25, 30, 40, 20, 50, 30, 20, 20)
n <- length(narr)
yarr <- numeric(n)
for(j in seq(n)){
parr <- dbetabin(seq(0, narr[j]), narr[j], K.true, eta.true)
yarr[j] <- sample(seq(0, narr[j]), size=1, prob=parr, replace=TRUE)
}
rbind(narr, yarr)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## narr 20 30 25 30 40 20 50 30 20 20
## yarr 3 2 6 12 6 8 22 8 5 2将这些模拟生成的数据固定下来。
下面用标准化的重要抽样法估计\(E(\log K | \boldsymbol Y)=E(\alpha | \boldsymbol Y)\)。 取\(\alpha\)和\(\beta\)的试抽样分布为t(4)。
set.seed(1)
N <- 10000
df.t <- 4
alpha.samp <- rt(N, df.t)
beta.samp <- rt(N, df.t)
wei <- p.post(alpha.samp, beta.samp) / dt(alpha.samp, df.t) / dt(beta.samp, df.t)
est <- sum(alpha.samp*wei) / sum(wei)\(\log(K)\)真值为:
用10000个抽样的重要抽样法给出的\(\log(K)\)的后验估计为:
重要性权重最好取值比较均匀, 否则重要性权重很小的抽样点基本不起作用, 效率较低。 上述模拟的归一化重要性权重的分布情况:
wei <- wei/sum(wei)*N
summary(wei)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00000 0.00000 0.00005 1.00000 0.00470 201.56573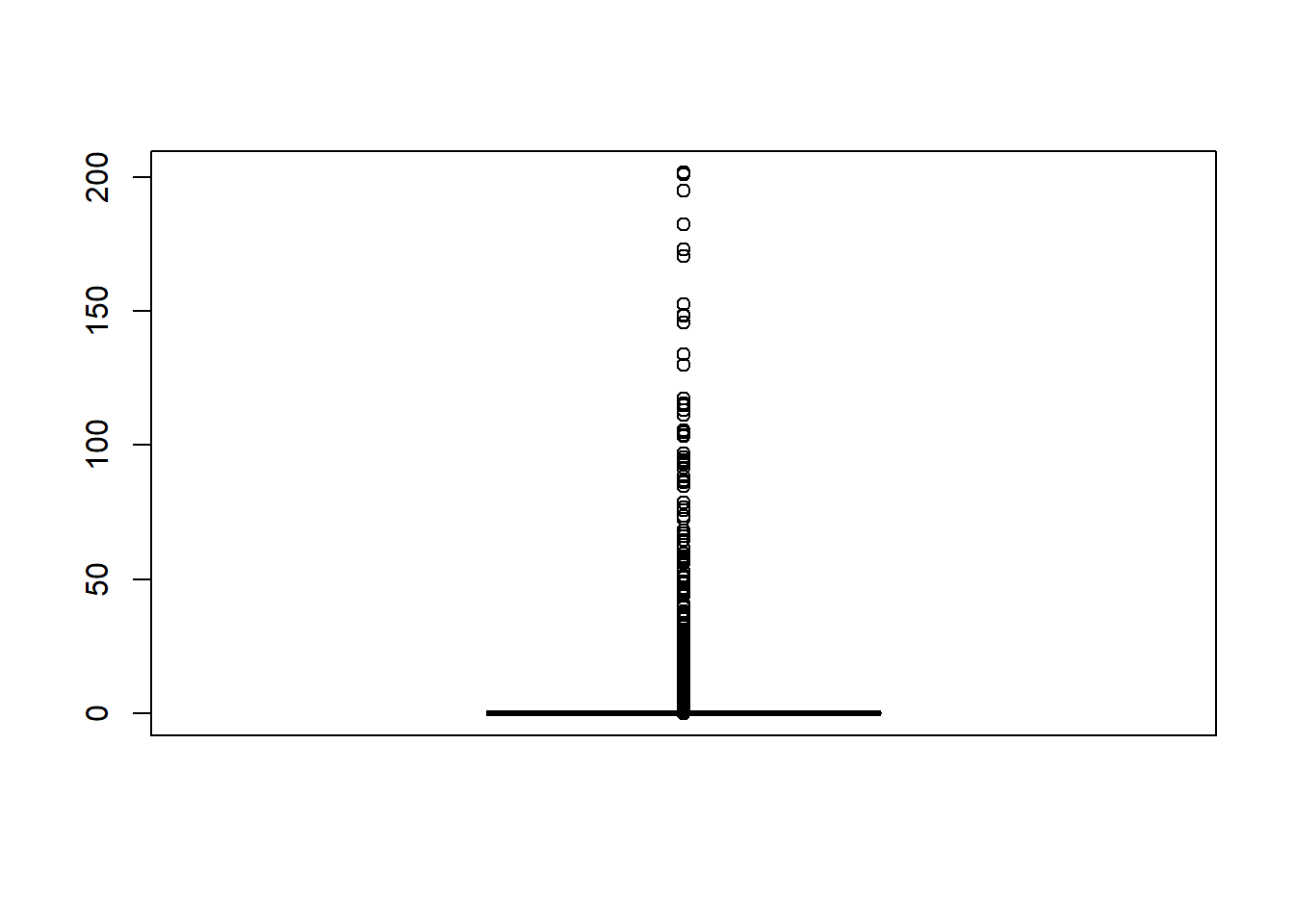
可见绝大多数抽样点都贡献很小。 这也是求解比较复杂的问题时重要抽样法应用的普遍现象。
舍选控制是解决这样问题的一种技术, 下面尝试采用这一技术。先看权重的分为点:
quantile(wei, c(0.5, 0.75, 0.8, 0.85, 0.9, 0.95, 0.99))
## 50% 75% 80% 85% 90% 95%
## 5.187513e-05 4.696631e-03 1.314482e-02 4.262636e-02 1.663021e-01 1.244243e+00
## 99%
## 2.447960e+01取舍选控制阈值\(c\)为90%分位数。
对\(N\)个权重,超过阈值的都保留; 小于阈值的, 以概率\(W_i/c\)保留,\(c\)是阈值, 其它的丢弃,这样减少了样本量。 原来的舍选控制法是预先选好阈值\(c\), 对每个\(i=1,2,\dots, N\)的每个, 从\(g(\boldsymbol x)\)中抽取后\(X_i\)后, 都进行舍选控制;如果第\(i\)个被丢弃,就重新从\(g(\boldsymbol)\)中抽取,直到被接受。 在R的向量化做法中,可以多抽取一些, 然后丢弃的就不再重复抽取。
舍选控制:
sele <- wei < wei.cut; n.sele <- sum(sele)
i.over <- seq(N)[!sele] # 超过阈值的下标,保留
i.under <- seq(N)[sele] # 低于阈值的下标,按概率保留
i.accept <- i.under[runif(n.sele) < wei[sele] / wei.cut] # 选出按概率保留部分
i.keep <- c(i.over, i.accept)
N1 <- length(i.keep); N1
## [1] 1371原来的10000个抽样仅保留了1000多个。 权重修改为:
wei.new <- pmax(wei[i.keep], wei.cut)
summary(wei.new)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.1663 0.1663 0.5231 7.2917 3.2660 201.5657在新的权重下保留的抽样是关于后验密度适当加权的。 新的估计为:
※※※※※
12.2 带有舍选控制的重要抽样法(*)
在重要抽样法和标准化重要抽样法的实际应用中, 好的试抽样分布很难获得, 所以权重\(\{ W_i = f(\boldsymbol X_i)/g(\boldsymbol X_i) \}\)经常会差别很大, 使得抽样样本主要集中在少数几个权重最大的样本点上。 为此,可以舍弃权重太小的样本点, 重新抽样替换这样的样本点, 这种方法称为带有舍选控制的重要抽样法。 需要预先选定权重的一个阈值\(c\),并计算 \[\begin{align*} p_c = \int \min\left\{1, \frac{f(\boldsymbol x)}{c g(\boldsymbol x)} \right\} g(\boldsymbol x) \,d\boldsymbol x = \int \min\left\{g(\boldsymbol x), \frac{f(\boldsymbol x)}{c} \right\} \,d\boldsymbol x . \end{align*}\] 在产生每个抽样点\(\boldsymbol X_i\)时,计算权重\(W_i\), 当权重\(W_i \geq c\)时接受此抽样点,但权重改为\(W_i^* = p_c W_i\); 当\(W_i < c\)时仅以\(W_i/c\)的概率接受此抽样点,并调整权重为\(p_c c\), 如果没有被接受则重新从\(g(\cdot)\)中抽取。
算法如下:
| 带有舍选控制的重要抽样法 |
|---|
| for(\(i\) in \(1:N\)) { |
| \(\quad\) repeat { |
| \(\qquad\) 从\(g(\cdot)\)抽取\(\boldsymbol\xi_i\) |
| \(\qquad\) 计算\(W_i \leftarrow f(\boldsymbol\xi_i)/g(\boldsymbol\xi_i)\) |
| \(\qquad\) if(\(W_i \geq c\)) { |
| \(\qquad\quad\) 令\(\boldsymbol X_i \leftarrow \boldsymbol\xi_i\), \(W_i^* \leftarrow p_c W_i\) |
| \(\qquad\quad\) break |
| \(\qquad\) } else { |
| \(\qquad\quad\) 从U(0,1)抽取\(U\) |
| \(\qquad\quad\) if(\(U < W_i / c\)) { |
| \(\qquad\qquad\) 令\(\boldsymbol X_i \leftarrow \boldsymbol\xi_i\), \(W_i^* \leftarrow p_c c\) |
| \(\qquad\qquad\) break |
| \(\qquad\quad\) } |
| \(\qquad\) } |
| \(\quad\) } # repeat |
| } # for |
| 输出\((\boldsymbol X_i^*, W_i^*)\), \(i=1,2,\dots,N\) |
在实际应用带有舍选控制的重要抽样法时, 一般先选略小的抽样量\(N_0\)进行原始的重要抽样, 分析权重\(W_i\)的分布, 据此选择权重\(c\), 比如可以选\(\{ W_i \}\)的某个分位数。 舍选控制算法中的\(p_c\)是归一化常数, 如果使用标准化重要抽样法, \(p_c\)可以省略, 否则, \(p_c\)可以从原始的重要抽样法结果中估计为 \[\begin{align} \hat p_c = \frac{1}{N_0} \sum_{i=1}^{N_0} \min\left\{1, \; \frac{W_i}{c} \right\}. \end{align}\]
带有舍选控制的重要抽样法得到的\(\{(\boldsymbol X_i, W_i^*), \ i=1,\dots,N \}\)是关于\(f(\cdot)\)适当加权的, 被接受的\(\boldsymbol X_i^*\)的分布密度不再是试投密度\(g(\boldsymbol x)\),而是改成了 \[\begin{align} g^*(\boldsymbol x) = \frac{1}{p_c} \min\left\{g(\boldsymbol x), \frac{f(\boldsymbol x)}{c} \right\}. \tag{12.12} \end{align}\]
习题
习题1
设\(X \sim \text{N}(0,1)\), \(h(x) = \exp(-\frac12 (x-3)^2) + \exp(-\frac12 (x-6)^2)\)。 令\(I = E h(X)\)。
- 推导\(I\)的精确表达式并计算结果。
- 用\(N=1000\)次函数计算的平均值法估计\(I\)并估计误差大小。
- 设计适当的重要抽样方法取\(N=1000\)估计\(I\)并估计误差大小。
习题2
设\(X \sim \text{N}(0,1)\), 则\(\theta = P(X > 4.5) = 3.398 \times 10^{-6}\)。
- 如果直接生成\(N\)个\(X\)的随机数, 用\(X_i > 4.5\)的比例估计\(P(X>4.5)\), 平均多少个样本点中才能有一个样本点满足\(X_i > 4.5\)?
- 取\(V\)为指数分布Exp(1), 令\(W = V + 4.5\), 用\(W\)的样本进行重要抽样估计\(\theta\), 取样本点个数\(N=1000\), 求估计值并估计误差大小。
习题3
在例12.3中, 设\(n=10\), 已知\((n_j, y_j)\)的值为: \[\begin{array}{*9cccc} n_j & 20 & 30 & 25 & 30 & 40 & 20 & 50 & 30 & 20 & 20 \\ y_j & 6 & 1 & 1 & 0 & 5 & 4 & 1 & 8 & 4 & 7 \end{array}\]
编写\(R\)程序估计\(E(\log K | y_1, y_2, \dots, y_n)\)。