25 R中的近似计算函数(*)
25.1 多项式
R用扩展包polynom提供了一元多项式类, 用多项式系数表示一个多项式, 提供了多项式运算、微分、积分等功能。
用polynomial(coef)生成一个多项式,
自变量coef是多项式的0次、1次、2次、……项系数的向量。
例如,\(P(x)= -3 + 2x + x^2\)可表示为:
也可以利用多项式的根定义多项式, 如\((x+1)(x-1)\):
## -1 + x^2用as.character(p)可以将多项式p转换成R的表达式字符串,如:
## [1] "-3 + 2*x + x^2"用coef(p)可以提取多项式的升幂表示的各个系数为一个向量,如
## [1] -3 2 1用as.function(p)可以将多项式转换成一个R函数,
这时它才能对自变量值求函数值,
如
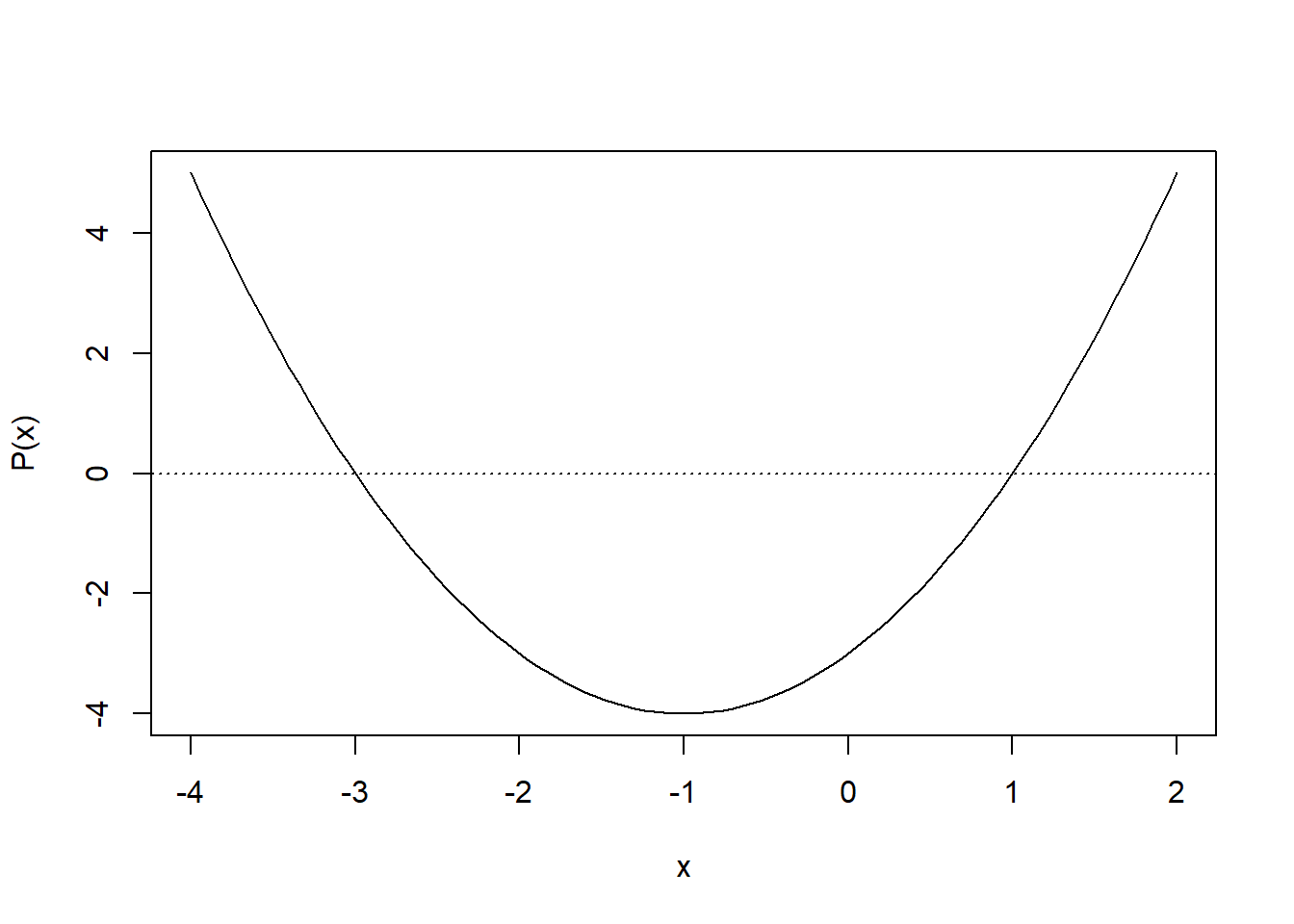
实际上, 可以直接对多项式作图, 如
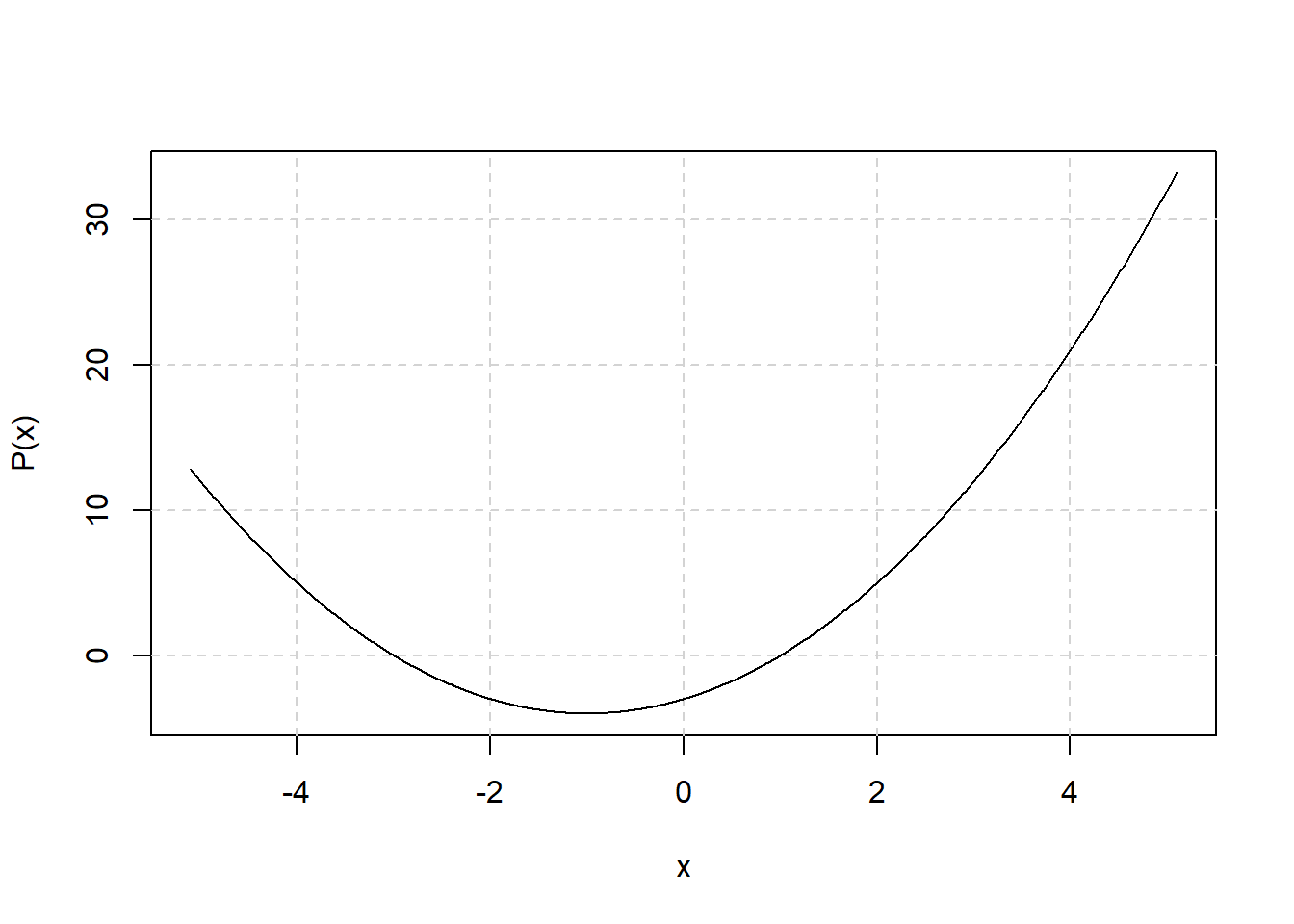
多项式可以进行通常的加、减、乘法,如
## -5 + 3*x + x^2## 6 - 7*x + x^3多项式除法比较特殊。 除尽时:
## -1 + x除不尽时:
## 1 + x## -4这说明 \[ \frac{-3 + 2x + x^2}{1 + x} = 1 + x + \frac{-4}{1+x} \]
可以用函数GCD()求多项式的最大公因式,
用LCM()求多项式的最小公倍式。
用deriv(p)求多项式p的一阶导数,如
## 2 + 2*x用integral(p)求多项式p的不定积分,
看成是\(\int_0^x p(t) \,dt\)。
integral(p, limits)则可求定积分,
其中limits是表示积分上界和下界的两个元素的向量。如
## -3*x + x^2 + 0.3333333*x^3## [1] -10.66667poly.calc(x, y)可以从给定的x值和y值的组合计算相应的Lagrange插值多项式,
阶数由点数决定。
例25.1 对\(h(x)=\sqrt(x)\)在\(x=1/16\), \(1/4\), \(1\)用抛物线插值。
## 0.1555556 + 1.555556*x - 0.7111111*x^2可以用MASS包的fractions()函数得到分数表示:
## [1] 7/45 14/9 -32/45即此插值多项式的理论值是 \[ \frac{1}{45} \left( 7 + 70x - 32 x^2 \right) . \]
用polylist()可以生成若干个多项式的列表,
可以用sum()函数求多项式的和,
用prod()求多项式乘积,
用deriv()对其中每个微分,
用integral()对其中每个积分。
25.2 插值
R函数approx(x, y)对给定的x和y坐标计算线性插值,
输出格子点上的x, y坐标的列表。
可以用n=指定输出的格子点的个数,
可以用xout=指定需要计算的x坐标。
approx.fun(x, y)计算插值函数,
结果是类型为R函数的插值函数。
25.3 样条插值
R函数spline(x, y)对给定的x和y坐标计算样条插值,
输出格子点上的x, y坐标的列表。
可以用n=指定输出的格子点的个数,
可以用xout=指定需要计算的x坐标。
默认使用fmm样条,
这时在两端用各自最边缘处的4格点分别拟合三次多项式。
选method="natural"用自然样条。
splinefun(x, y)计算样条插值函数,
结果是类型为R函数的插值函数,
得到的插值函数可以用来计算x处的插值函数值及导数值,
在调用生成的插值函数时加选项deriv=可以指定导数阶数,
最多3阶。
函数spline.smooth()可以计算样条曲线拟合。
在用lm()模型,
可以用bs()函数计算给定的自变量\(x\)的若干阶的样条基函数值作为非线性项。