7 随机向量和随机过程的随机数
7.1 条件分布法
产生随机向量的一种方法是条件分布法。 设\(\boldsymbol X = (X_1, X_2, \dots, X_r)\)的分布密度或分布概率 \(p(x_1, x_2, \dots, x_r)\)可以分解为 \[\begin{aligned} p(x_1, x_2, \dots, x_r) = p(x_1) p(x_2 | x_1) p(x_3 | x_1, x_2) \cdots p(x_r | x_1, x_2, \dots, x_{r-1}) \end{aligned}\] 则可以先生成\(X_1\), 由已知的\(X_1\)的值从条件分布\(p(x_2 | x_1)\)产生\(X_2\), 再从已知的\(X_1, X_2\)的值从条件分布\(p(x_3 | x_1, x_2)\)产生\(X_3\), 如此重复直到产生\(X_r\)。
7.1.1 多项分布随机数
进行了\(n\)次独立重复试验\(Y_1, Y_2, \dots, Y_n\), 每次的试验结果\(Y_i\)在\(1,2,\dots,r\)中取值, \(P(Y_i = j) = p_j, j=1,2,\dots,r; i=1,2,\dots,n\)。 令\(X_j\)为这\(n\)次试验中结果\(j\)的个数(\(j=1,2,\dots,r\)), 称\(\boldsymbol X = (X_1, X_2, \dots, X_r)\)服从多项分布, 其联合概率函数为 \[\begin{aligned} P(X_j=x_j, j=1,2,\dots,r) = \frac{n!}{x_1! x_2! \dots x_r!} p_1^{x_1} p_2^{x_2} \dots p_r^{x_r}. \end{aligned}\] (其中\(\sum_{j=1}^r x_j = n\))。
要生成\(\boldsymbol X\)的随机数,考虑不同结果数\(r\)与试验次数\(n\)的比较。 当\(r\)和\(n\)相比很大时, 每个结果的出现次数都不多,而且许多结果可能根本不出现, 这样,可以模拟产生\(Y_i, i=1,2,\dots,n\)然后从\(\{ Y_i \}\)中计数得到 \((X_1, X_2, \dots, X_r)\)。 当\(r\)与\(n\)相比较小时, 每个结果出现次数都比较多,可以使用条件分布逐个地产生\(X_1, X_2, \dots, X_r\)。
\(X_1\)表示\(n\)次重复试验中结果1的出现次数, 以结果1作为成功,其它结果作为失败, 显然\(X_1 \sim \text{B}(n, p_1)\)。 产生\(X_1\)的值\(x_1\)后, \(n\)次试验剩余的\(n - x_1\)次试验结果只有\(2,3,\dots,r\)可取, 于是在\(X_1 = x_1\)条件下结果2的出现概率是 \[\begin{aligned} P(Y_i = 2 | Y_i \neq 1) = \frac{P(Y_i=2)}{\sum_{k=2}^r P(Y_i=k)} = \frac{p_2}{1 - p_1} \end{aligned}\] 于是剩下的\(n - x_1\)次试验中结果2的出现次数服从\(\text{B}(n-x_1, \frac{p_2}{1-p_1})\)分布, 从这个条件分布产生\(X_2 = x_2\)。 类似地, 剩下的\(n - x_1 - x_2\)次试验中结果3的出现次数服从 \(\textbf{B}(n-x_1-x_2, \frac{p_3}{1-p_1-p_2})\)分布, 从这个条件分布中抽取\(X_3=x_3\), 如此重复可以产生多项分布\(\boldsymbol X\)的随机数\((x_1, x_2, \dots, x_r)\)。
Julia实现:
## 输入
## - n: 需要输出的随机数个数
## - m: 模型中的独立重复试验次数
## - prob: 每次试验,各个结果出现的概率
## 输出:n行r列矩阵,r是不同结果个数
using Random, Distributions
function randmultnom(n, m, prob)
local r, pc, xmat, m1
r = length(prob)
pc = [0.0; cumsum(prob)]
xmat = zeros(Int, n, r) # 每一行是一个抽样向量
for i=1:n
m1 = m
for k=1:(r-1)
xmat[i, k] = rand(Binomial(m1, prob[k]/(1 - pc[k])))
m1 -= xmat[i, k]
end # for k
xmat[i,r] = m1
end # for i
return xmat
end测试:
using StatsBase
Random.seed!(101)
prob = [0.1, 0.3, 0.6]
x = randmultnom(100_000, 5, prob)
# (1,2,2)的概率:
p122 = 30*prod(prob .^ [1,2,2]); p122
## 0.0972
mean((x[:,1] .== 1) .& (x[:,2] .== 2) .& (x[:,3] .== 2) )
## 0.09767
# (1,1,3)的概率:
p113 = 20*prod(prob .^ [1,1,3]); p113
# 0.1296
mean((x[:,1] .== 1) .& (x[:,2] .== 1) .& (x[:,3] .== 3) )
# 0.129747.2 多元正态分布模拟
设随机向量\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\)服从多元正态分布 \(\text{N}(\boldsymbol \mu, \Sigma)\), 联合密度函数为 \[\begin{aligned} p(\boldsymbol x) = (2\pi)^{-\frac{p}{2}} |\Sigma|^{-\frac12} \exp\left\{ -\frac12 (\boldsymbol x - \boldsymbol \mu)^T \Sigma^{-1} (\boldsymbol x - \boldsymbol \mu) \right\}, \ \boldsymbol x \in R^p \end{aligned}\] 正定矩阵\(\Sigma\)有Cholesky分解\(\Sigma = C C^T\), 其中\(C\)为下三角矩阵。 设\(\boldsymbol Z = (Z_1, Z_2, \dots, Z_p)^T\)服从\(p\)元标准正态分布 \(\text{N}(\boldsymbol 0, I)\)(\(I\)表示单位阵), 则\(\boldsymbol X = \boldsymbol\mu + C \boldsymbol Z\) 服从\(\text{N}(\boldsymbol \mu, \Sigma)\)分布。
随机数发生器的程序:
## 生成多元正态分布随机数,
## n是需要的个数,
## mu是均值向量,
## Sigma是协方差阵,需要是对称正定阵。
rng.mnorm <- function(n, mu, Sigma){
m <- length(mu)
M <- chol(Sigma) # Sigma = M' M
y <- matrix(rnorm(n*m), n, m) %*% M
for(j in seq(along=mu)){
y[,j] <- y[,j] + mu[j]
}
y
}测试:
x <- rng.mnorm(1000, c(3,2), rbind(c(4, 1), c(1, 1)))
plot(x[,1], x[,2], type="p", cex=0.1)
abline(v=3, h=2, col="green")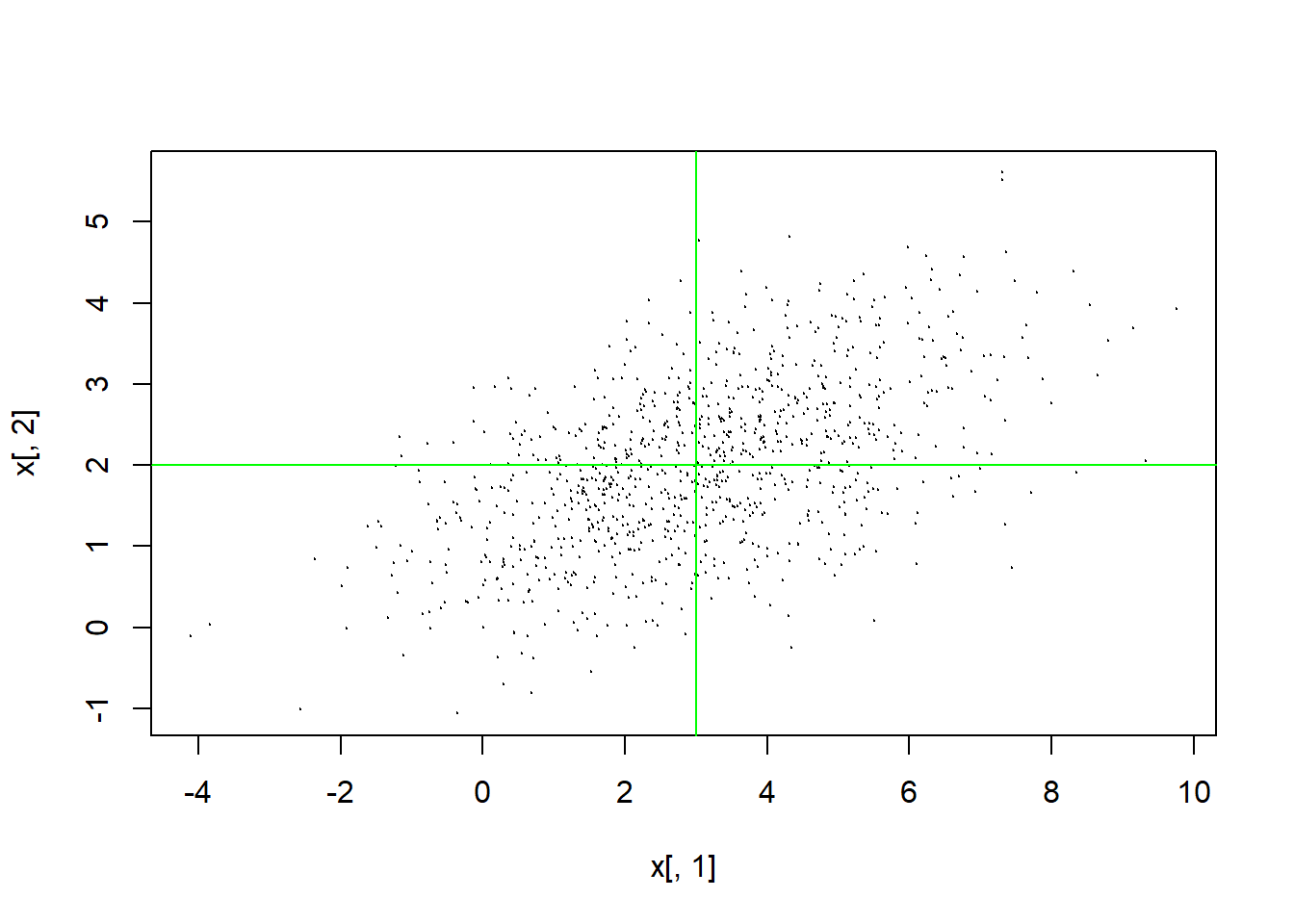
Julia版本:
using LinearAlgebra
function randmnorm(n, μ, Σ)
local m, L, y
m = length(μ)
L = cholesky(Σ).L
y = randn(n, m) * L
y = y .+ μ'
return y
end测试程序:
using Random
using CairoMakie, AlgebraOfGraphics
CairoMakie.activate!()
x = randmnorm(1000, [3, 2], [4 1; 1 1])
plt = data((; x=x[:,1], y=x[:,2])) * mapping(:x, :y) * visual(Scatter)
draw(plt)
cov(x)结果略。
事实上,
Julia的Distributions包的MvNormal(mu, Sigma)函数可以用来表示多元正态分布,
然后可以用rand函数产生此分布的随机向量抽样值。
为了生成\(m\)条轨道,方法如:
其中mu均值向量,
Sigma为协方差阵。
7.3 泊松过程模拟
参数为\(\lambda\)的泊松过程\(N(t), t\geq 0\)是取整数值的随机过程, \(N(t)\)表示到时刻\(t\)为止到来的事件个数, 两次事件到来的时间间隔相互独立, 都服从指数分布Exp(\(\lambda\))。
所以,如果要生成泊松过程前\(n\)个事件到来的时间, 只要生成\(n\)个独立的Exp(\(\lambda\))随机数\(X_1, X_2, \dots, X_n\), 则\(S_k = \sum_{i=1}^k X_i, k=1,2,\dots,n\)为各个事件到来的时间。
如果要生成泊松过程在时刻\(T\)之前的状态, 只要知道发生在\(T\)之前的所有事件到来时间就可以了。
Julia程序:
# 泊松过程模拟
function randpproc(T=100.0, λ=1.0)
local xs, S, nev, X
xs = Float64[]
S = 0.0 # 当前时刻
nev = 0 # 已发生事件个数
while true
X = -log(rand()) / λ
S += X
if S <= T
nev += 1
push!(xs, S)
else
break
end
end # while true
return xs
end测试:
using Random, Distributions
using CairoMakie, AlgebraOfGraphics
CairoMakie.activate!()
Random.seed!(101)
x = randpproc(50, 1)
plt = data((; x=x)) * mapping(:x) * visual(VLines)
draw(plt)
## 估计速率
mean(x[2:end] .- x[begin:end-1])
## 0.8870887289991723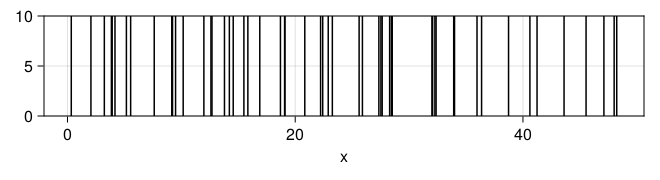
生成泊松过程在时刻\(T\)之前的状态的另外一种方法是先生成\(N(T) \sim \text{Poisson}(\lambda)\), 设\(N(T)\)的值为\(n\), 再生成\(n\)个独立的U(0,1)随机变量\(U_1, U_2, \dots, U_n\), 从小到大排序为\(U_{(1)} \leq U_{(2)} \leq \dots U_{(n)}\), 则\((T U_{(1)} , T U_{(2)} , \dots, T U_{(n)})\)为时刻\(T\)之前的所有事件到来时间。
为了生成强度函数为\(\lambda(t), t\geq 0\)的非齐次泊松过程到时刻\(T\)为止的状态, 如果\(\lambda(t)\)满足 \[\begin{aligned} \lambda(t) \leq M, \ \forall t \geq 0, \end{aligned}\] 则可以按照生成参数为\(M\)的齐次泊松过程的方法去生成各个事件到来时刻, 但是以\(\lambda(t)/M\)的概率实际记录各个时刻。 Julia程序如下:
function randnhpproc(T, λ = x -> 1.0, M=1.0)
local xs
xs = randpproc(T, M)
xs = [t for t in xs if rand() < λ(t) / M]
return xs
end 测试。假设前50分钟速率为0.2, 后50分钟速率为1。
fl(t) = t <= 50 ? 0.2 : 1.0
Random.seed!(101)
x = randnhpproc(100.0, fl, 1.0)
plt = data((; x=x)) * mapping(:x) * visual(VLines)
dr = draw(plt; axis = (; width=600, height=100))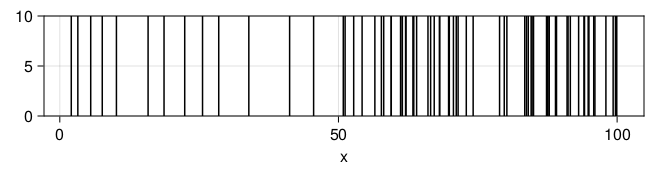
7.4 高斯过程模拟
7.4.1 布朗运动模拟
布朗运动是具有独立增量性的高斯过程, 其模拟比一般高斯过程更简单。
时间区间\([0, T]\)上的一维的标准布朗运动为随机过程\(\{ W(t), 0 \leq t \leq T \}\), 满足:
- \(W(0)=0\);
- 以概率1地,\(W(t)\)作为\(t\)的函数,(每条轨道)在\([0,T]\)连续;
- 独立增量;
- \(W(t) - W(s) \sim \text{N}(0, t-s)\), 对任意\(0 \leq s < t \leq T\)。
\(W(t)\)分布为 \[ W(t) \sim \text{N}(0, t), \ 0 < t \leq T. \]
对标准布朗运动\(W(t)\),令 \[ X(t) = \mu t + \sigma W(t), 0 \leq t \leq T, \] 称\(X(t)\)为有漂移\(\mu\)和扩散系数\(\sigma^2\)的布朗运动, 简记为BM(\(\mu, \sigma^2\))。 其中\(\mu\),\(\sigma\)为常数,\(\sigma>0\)。 \(X(t)\)仍是高斯过程, 从0出发, 有独立增量, 轨道连续, 边缘分布为 \[ X(t) \sim \text{N}(\mu t, \sigma^2 t) . \]
也可以构造\(X(0)=x\)的解, 只要给每个\(X(t)\)加\(x\)即可。
可以定义漂移和扩散系数时变的布朗运动, 存在时变的函数\(\mu(t)\)和\(\sigma(t)\), 使得增量\(X(t) - X(s)\)(\(0 \leq s < t \leq T\))服从正态分布,期望为 \[ E[X(t) - X(s)] = \int_s^t \mu(u) \,du, \] 方差为 \[ \text{Var}[X(t) - X(s)] = \int_s^t \sigma^2(u) \,du . \]
设\(0 < t_1 < t_2 < \dots < t_n \leq T\), 要生成\((W(t_1), \dots, W(t_n))\)或者\((X(t_1), \dots, X(t_n))\)的抽样, 最简单的方法是利用布朗运动的独立增量性和正态性。 设\(Z_1, \dots, Z_n\)是独立同标准正态分布的随机变量(随机数), \(t_0=0\), \(W(0)=0\), \(X(0)=0\)。
令 \[\begin{align} W(t_{i+1}) = W(t_i) + \sqrt{t_{i+1} - t_i} Z_{i+1}, \ i=0,1,\dots, n-1 . \tag{7.1} \end{align}\]
对\(X(t) \sim \text{BM}(\mu, \sigma^2)\),令 \[\begin{align} X(t_{i+1}) = X(t_i) + \mu \cdot (t_{i+1} - t_i) + \sigma \sqrt{t_{i+1} - t_i} Z_{i+1}, \ i=0,1,\dots, n-1 . \tag{7.2} \end{align}\]
对于漂移和扩散系数时变的\(X(t)\),令 \[\begin{align} X(t_{i+1}) = X(t_i) + \int_{t_i}^{t_{i+1}}\mu(u) \,du + \left( \int_{t_i}^{t_{i+1}}\sigma^2(u) \,du \right)^{1/2} Z_{i+1}, \ i=0,1,\dots, n-1 . \tag{7.3} \end{align}\]
只要输入的\(Z_1, \dots, Z_n\)的联合分布正确, 则输出的\((W(t_1), \dots, W(t_n))\)和\((X(t_1), \dots, X(t_n))\)的联合分布也是正确的, 没有离散化误差。
这只输出了\(t_1, t_2, \dots, t_n\)这有限个点上的轨道的值, 中间的值未知, 如果用通常的线性插值等方法近似, 就会产生离散化误差, 分布也不准确。
在漂移和扩散系数时变时, 如果将(7.3)中的积分替换成如下的欧拉(Euler)近似: \[ X(t_{i+1}) = X(t_i) + \mu(t_i) \cdot (t_{i+1} - t_i) + \sigma(t_i) \sqrt{t_{i+1} - t_i} Z_{i+1}, \ i=0,1,\dots, n-1 , \] 则输出的\((X(t_1), \dots, X(t_n))\)的联合分布也是近似的, 带有离散化误差(discretization error), 而且这种误差是累积的, 时间越往后误差越大。
如下的Julia函数输入时间点的数组, 输出模拟的标准布朗运动轨道在这些时间点的值:
function sim_bm(ts::Vector)
xs = zeros(length(ts))
t0 = 0
x0 = 0.0
for i in eachindex(ts)
x1 = x0 + sqrt(ts[i] - t0)*randn()
xs[i] = x1
t0 = ts[i]
x0 = x1
end
return (ts, xs)
end
function sim_bm(T::Real, n::Integer)
ts = collect(1:n) .* (T/n)
return sim_bm(ts)
end测试:
using Random
using CairoMakie
CairoMakie.activate!()
Random.seed!(101)
n = 100
ts, xs = sim_bm(10.0, 100)
lines(ts, xs)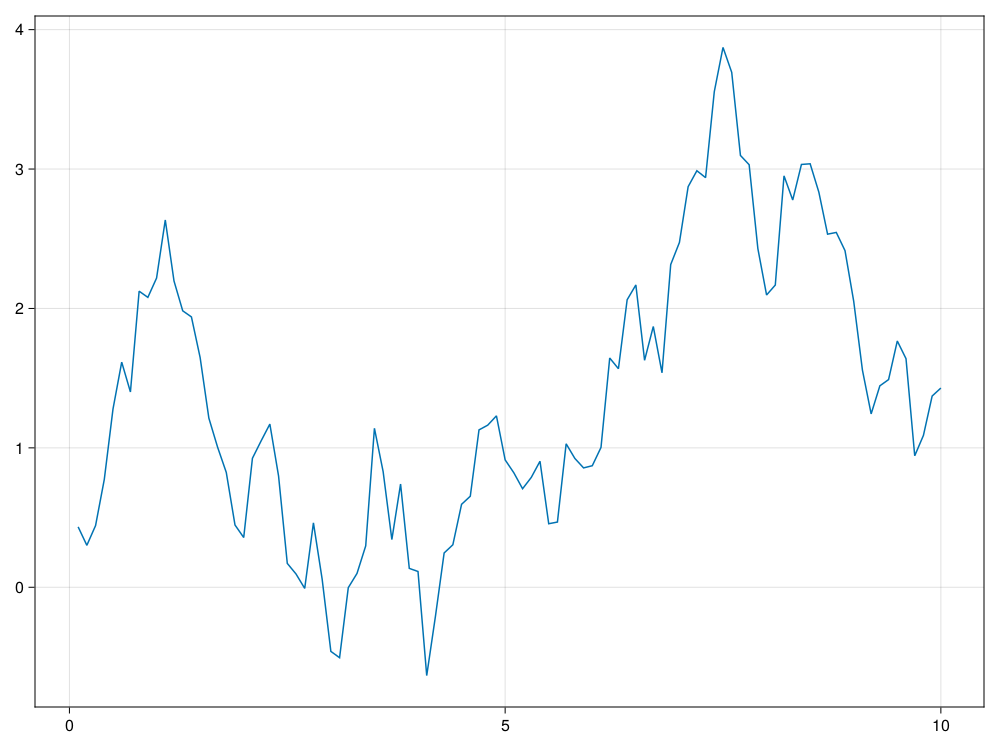
7.4.2 抽样点较少情形
设\(\{X(t), t \geq 0 \}\)为一般的高斯过程, 均值函数为\(\mu(t)\), 协方差函数为\(\sigma(t, s)\), 即\(E[X(t)] = \mu(t)\), \(\text{Cov}[X(t), X(s)] = \sigma(t, s)\)。 为了模拟\(X\)的一条轨道, 先确定\(n\)个要输出\(X\)的观测值的时间点\(t_1, \dots, t_n\), 经常取为 \[ t_i = \frac{i}{n} T , \] 其中\(T\)为一个时间长度。 然后, 可以计算\(\boldsymbol \mu = (\mu(t_1), \dots, \mu(t_n))^T\), \[ \Sigma = (\sigma(t_i, t_j))_{i=1,\dots,n; j=1,\dots,n} . \]
于是,随机向量\(\boldsymbol X = (X(t_1), \dots, X(t_n))\)服从多元正态分布\(\text{N}(\boldsymbol\mu, \Sigma)\), 可以用多元正态分布模拟方法产生\(n\)维随机向量\(\boldsymbol X\)的\(n\)个随机数。
这样做法有一个问题: 虽然在理论上\(\Sigma\)矩阵是正定矩阵, 但是当采样点个数\(n\)较大时, 这个矩阵很可能接近于不满秩, 为了产生多元正态分布随机向量的抽样值而计算\(\Sigma\)的Cholesky分解时数值算法可能会出错。 为此,借鉴(Kochenderfer 2019)中的做法, 将\(\Sigma\)替换成\(\Sigma + \epsilon I\), 其中\(\epsilon\)是较小的正常数,如\(10^{-6}\),这保证了可逆。
这种方法适用于非平稳、采样点不一定等间隔的高斯过程采样, 但因为要计算并保存\(n\times n\)的协方差阵, 算法所需的Cholesky分解计算量大且可能会产生数值不稳定, 所以不适用于采样点数\(n\)过于巨大的情形。
例7.1 高斯核的高斯平稳过程的模拟。
设高斯过程\(X(t), t \geq 0\)满足: \(X(0)=0\), \(E[X(t)]=0\), \[ \sigma(t,s) = \text{Cov}[X(t), X(s)] = \exp\left(-\frac{(t-s)^2}{2 \ell^2}\right) . \] 因为协方差函数\(\sigma(t,s)\)仅依赖于\(t-s\), 均值函数为常数, 所以这是一个高斯平稳过程。 参数\(\ell\)越大, \(X(t)\)和\(X(s)\)当时间距离\(t-s\)增大时相关性的衰减越慢, 结果的轨道越光滑。 等间隔采样的高斯平稳过程有递推计算的模拟算法,见下一小节, 这里使用产生多元正态分布随机向量的方法。
模拟产生这样的高斯平稳过程轨道的Julia函数如下:
using Distributions
# 给定表示时间点的向量ts, 需要的轨道条数npath,
# 高斯核参数decay, 保证Cholesky分解可行的扰动量inflate,
# 输出模拟结果为n*m矩阵,每列为一条轨道.
function sim_Gauss(ts::Vector, npath::Integer,
decay=1.0; inflate = 1e-6)
n = length(ts)
ker(t, s) = exp(-(t-s)^2 / (2*decay^2))
Sig = [ker(ts[i], ts[j]) for i=1:n, j=1:n]
dist = MvNormal(zeros(n), Sig + inflate .* I)
xs = rand(dist, npath)
return ts, xs
end
# 输入要生成的时间长度T,等分时间点点数n的模拟函数
function sim_Gauss(T::Real, n::Integer, npath=1,
decay=1.0; inflate=1e-6)
ts = collect(1:n) .* (T/n)
return sim_Gauss(ts, npath, decay; inflate=inflate)
end测试,模拟100个时间点,取\(\ell=2.0\), 模拟5条轨道:
using CairoMakie
CairoMakie.activate!()
ts, xs = sim_Gauss(10.0, 100, 5, 2.0)
fig = lines(ts, xs[:,1])
for i=2:5 ; lines!(ts, xs[:,i]); end
fig 结果图形:
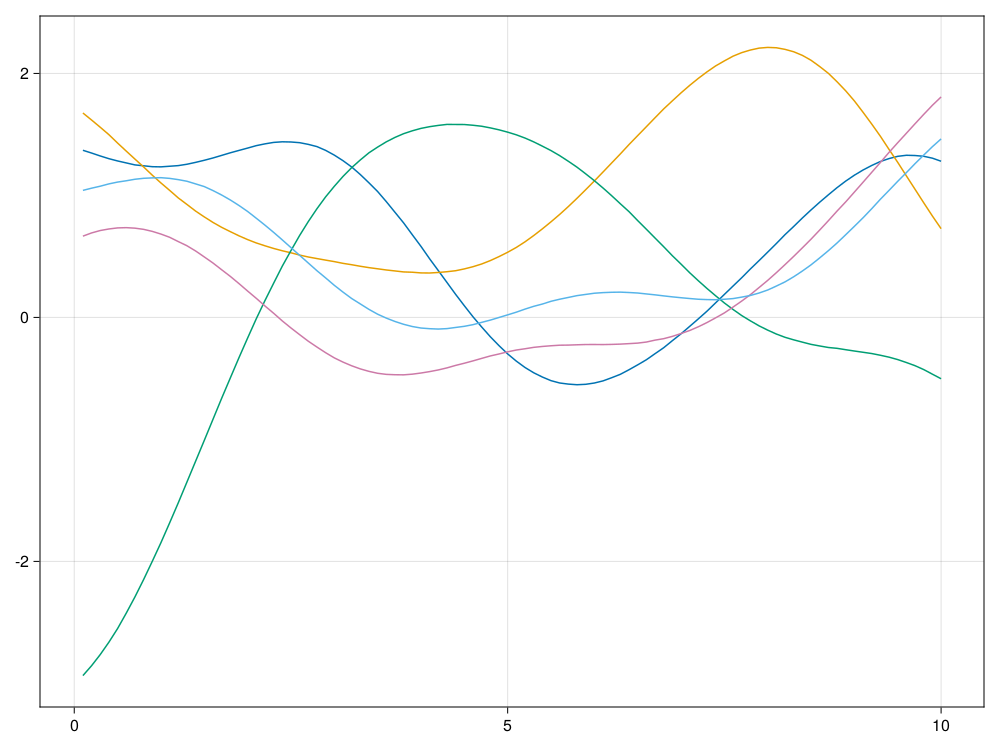
7.4.3 平稳高斯列
若\(X(t)\)为平稳高斯列, 均值为0, 协方差函数为\(\gamma_k, k=0,1,2,\dots\), 则有限维分布完全由\(\{\gamma_k \}\)决定。 为了生成\(X(t)\)的一条长度为\(n\)的轨道, 可以递推地进行抽样。 抽取\(X(1) \sim \text{N}(0, \gamma_0)\), 然后, 对\(X(t+1)\), \(t=1,\dots, n-1\), 因为\(X(t+1) | X(t), \dots, X(1)\)是条件正态分布, 有
\[\begin{aligned} E(X(t+1) | X(t), \dots, X(1)) &= \sum_{j=1}^t a_{t,j} X(t+1-j) \\ =& a_{t,1} X(t) + a_{t,2} X(t-1) + \dots + a_{t,t} X(1), \\ \text{Var}(X(t+1) | X(t), \dots, X(1)) =& \sigma_t^2, \end{aligned}\] 其中\(\sigma_0^2, \sigma_1^2, \dots\)和\(a_{t,j}, j=1,\dots, t\), \(t=1,2,\dots\)可以用如下的Levinson递推公式从\(\{\gamma_k \}\)序列计算得到: \[\begin{align} \sigma_0^2 =& \gamma_0 \\ a_{1,1} =& \gamma_1 / \gamma_0 \\ \sigma_k^2 =& \sigma_{k-1}^2 (1 - a_{k,k}^2) \\ a_{k+1,k+1} =& \frac{\gamma_{k+1} - a_{k,1} \gamma_k - a_{k,2} \gamma_{k-1} - \dots - a_{k,k} \gamma_1}{ \gamma_0 - a_{k,1} \gamma_1 - a_{k,2} \gamma_2 - \dots - a_{k,k} \gamma_k } \\ a_{k+1,j} =& a_{k,j} - a_{k+1,k+1} a_{k,k+1-j}, \quad 1 \leq j \leq k \tag{7.4} \end{align}\]
这样,就可以递推地计算出\(X(t+1) | X(t), \dots, X(1)\)的条件期望和条件方差, 从这个条件分布抽样得到\(X(t+1)\)。
在递推过程中, 如果平稳高斯序列\(\{ X(t) \}\)相关性较强, 有可能出现\(\sigma_k^2 \to 0\)(\(k\to\infty\))的情况。 这时, 可以设置一个阈值\(\epsilon\), 当\(\sigma_p^2 < \epsilon\)时, 对\(t > p\)就不再用所有的\(X(1), \dots, X(t-1)\)计算条件分布, 而是仅使用\(X(t-1), \dots, X(t-p)\)这\(p\)个, 递推预测系数统一使用\(a_{p,j}\), \(j=1,\dots,p\)。
下面的函数gauss_levinson函数输入长度为\(n\)的自协方差函数序列\(\{ \gamma_k, k=0,1,\dots,n-1 \}\),
要求的轨道条数npath,
输出一个结果矩阵,
每行为一条轨道的\(n\)个观测值。
也可以输入一个计算\(\gamma_k\)的函数,
此函数输入非负整数值\(k\),
返回\(\gamma_k\)的值,
用这个函数规定自协方差函数,
进行模拟。
function gauss_levinson(gam_vec::Vector{Float64}, npath=1; eps=1e-6)
n = length(gam_vec)
x = zeros(npath, n)
a1 = zeros(n)
a2 = zeros(n)
S2 = zeros(n)
S2[1+0] = gam_vec[0+1] # 用0个去预报下一个的方差
x[:,1] .= rand_norm(zeros(npath), sqrt(S2[1]), npath)
a1[1] = gam_vec[1+1]/gam_vec[0+1] # a_{1,1},用X_1预报X_2的系数
# 下面是Levinson递推计算条件分布的条件期望的线性组合系数,
# 与条件分布的方差,
# 并从条件分布抽样
p = -1
for k=1:(n-1)
# 从前k个预报第k+1个的方差
S2[1+k] = S2[k] * (1 - a1[k]^2)
#@show S2[1+k]
# 如果基本可完全线性预报,不需要更多预报系数
if S2[1+k] < eps
p = k
break
end
# 从前k个给出条件期望和条件方差,抽取第k+1个
cond_mean = sum(a1[j] .* x[:,k+1-j] for j=1:k)
x[:,1+k] .= rand_norm(cond_mean, sqrt(S2[1+k]), npath)
# 不需要计算用n个预报n+1个的公式
k == n-1 && break
# 继续计算从前k+1个预报第k+2个的系数
a2[1+k] = (gam_vec[1+(k+1)] -
sum(a1[1:k] .* gam_vec[(1+k):-1:(1+1)])) /
S2[1+k]
#println("a[",k+1,", ", k+1, "]=", a2[1+k])
a2[1:k] .= a1[1:k] .- a2[1+k] .* a1[k:-1:1]
# 重复利用a1, a2的空间,用a1表示当前可用的预报系数
a1, a2 = a2, a1
end # for k
if p > 0 # 用p个可完全线性预报
for k=(p+1):n
cond_mean = sum(a1[j] .* x[:,k-j] for j=1:p)
x[:,k] .= rand_norm(cond_mean, sqrt(S2[1+p]), npath)
end
end # if p>0
#show(round.(S2, digits=4))
return x
end
# 输入:自协方差函数gam(k),以函数形式输入
# n是需要输出的长度
function gauss_levinson(gam::Function,
n::Int = 100, npath=1; eps=1e-6)
gam_vec = gam.(0:(n-1))
#@show gam_vec
return gauss_levinson(gam_vec, npath;
eps = eps)
end设某个高斯平稳列的协方差函数\(\{\gamma_k \}\)满足 \[ \gamma_k = \exp(-k^2 / (2 \ell^2)), \] 其中\(\ell>0\)描述了前后相关性持续的时间长度, \(\ell\)越大相关性越强, 结果的轨道越光滑。 测试,生成5条轨道:
using CairoMakie
CairoMakie.activate!()
using Random
n, npath, ell = 200, 5, 5.0
Random.seed!(101)
x = gauss_levinson(k -> exp(-k^2 / (2*ell^2)), n, npath);
fig = series(1:n, x)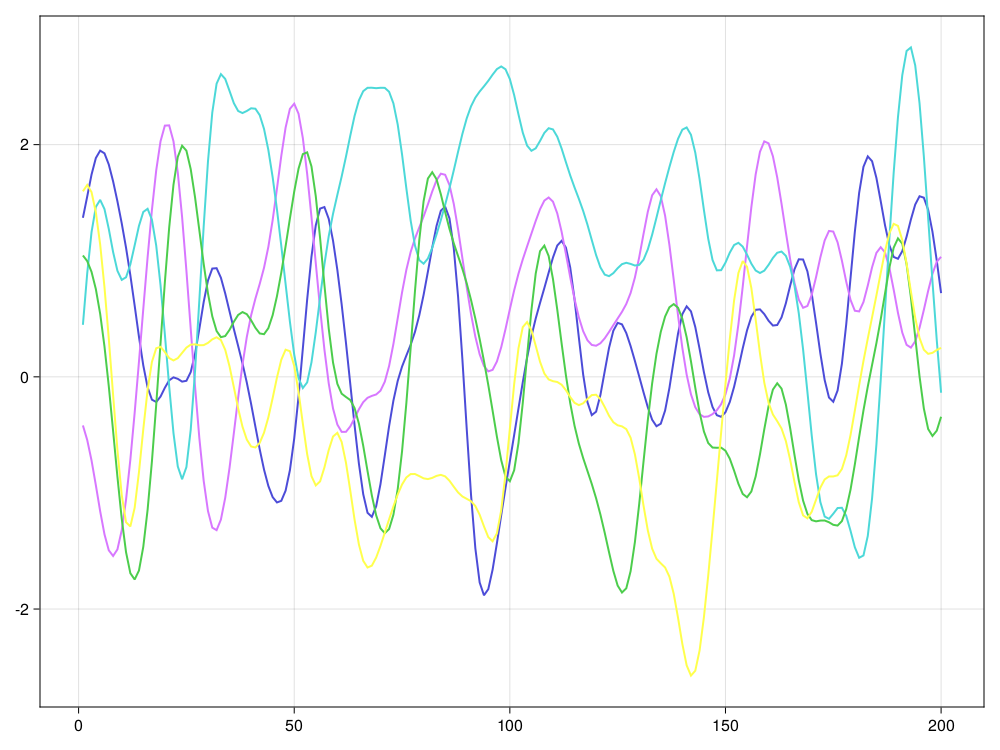
7.5 ARMA模型模拟(*)
平稳时间序列中的ARMA模型可以递推生成。
7.5.1 AR模型
对AR(\(p\))模型 \[\begin{aligned} X_t = a_1 X_{t-1} + a_2 X_{t-2} + \dots + a_p X_{t-p} + \varepsilon_t, \ t \in \mathbb{Z} \end{aligned}\] (\(\mathbb{Z}\)表示所有整数的集合), 其中系数\(a_1, a_2, \dots, a_p\)满足 \[ 1 - a_1 z - a_2 z^2 - \dots - a_p z^p \neq 0, \ \forall z \in \{ z: |z| \leq 1, z \in \mathbb C \} . \] \(\{ \varepsilon_t \}\)为白噪声WN(0,\(\sigma^2\)), 即方差都为\(\sigma^2\)、彼此不相关的随机变量序列, \(\{ \varepsilon_t \}\)可以用N(0,\(\sigma^2\))分布的独立序列来模拟, 也可以用其它有二阶矩的分布。 因为AR(\(p\))模型具有所谓“稳定性”, 所以我们从任意初值出发按照递推\(N_0\)步(\(N_0\)是一个较大正整数)后, 再继续递推\(N\)步后得到的\(N\)个\(X_t\)就可以作为上述AR(\(p\))模型的一次实现。 根据模型稳定性的好坏, \(N_0\)可取为\(50 \sim 1000\)之间。
下面是用直接递推的方法模拟的Julia程序。 Julia程序有即时编译功能, 所以递推循环不降低程序执行效率。
# 输入:
# a_vec为a1, a2, ..., ap系数
# n: 样本点数
# npath: 需要模拟的轨道条数
# sigma: 白噪声标准差
# n0: 为达到平稳需要删除的点数
# 输出:npath行n列矩阵,每行为一条轨道
function ar_gen(a_vec::Vector{Float64}, n::Int=100,
npath::Int=1;
sigma=1.0, n0=1000)
n2 = n0 + n
p = length(a_vec)
x2 = zeros(npath, n2)
eps = sigma .* randn(npath, n2)
for t = p+1:n2
x2[:, t] .= eps[:, t] .+ sum(
a_vec[j] .* x2[:, t-j] for j=1:p )
end
x = copy(x2[:, (n0+1):n2])
return x
endR如果用循环进行递推则效率很低,
R函数stats::filter可以进行递推和卷积计算。
另外,R函数arima.sim可以直接进行ARMA模型和ARIMA模型模拟。
下面用stats::filter()函数进行递推方法的模拟计算:
ar.gen <- function(n, a, sigma=1.0,
n0=1000,
x0=numeric(length(a))){
n2 <- n0 + n
p <- length(a)
eps <- rnorm(n2, 0, sigma)
x2 <- stats::filter(
eps, a, method="recursive", sides=1, init=x0)
x <- x2[(n0+1):n2]
x <- ts(x)
attr(x, "model") <- "AR"
attr(x, "a") <- a
attr(x, "sigma") <- sigma
x
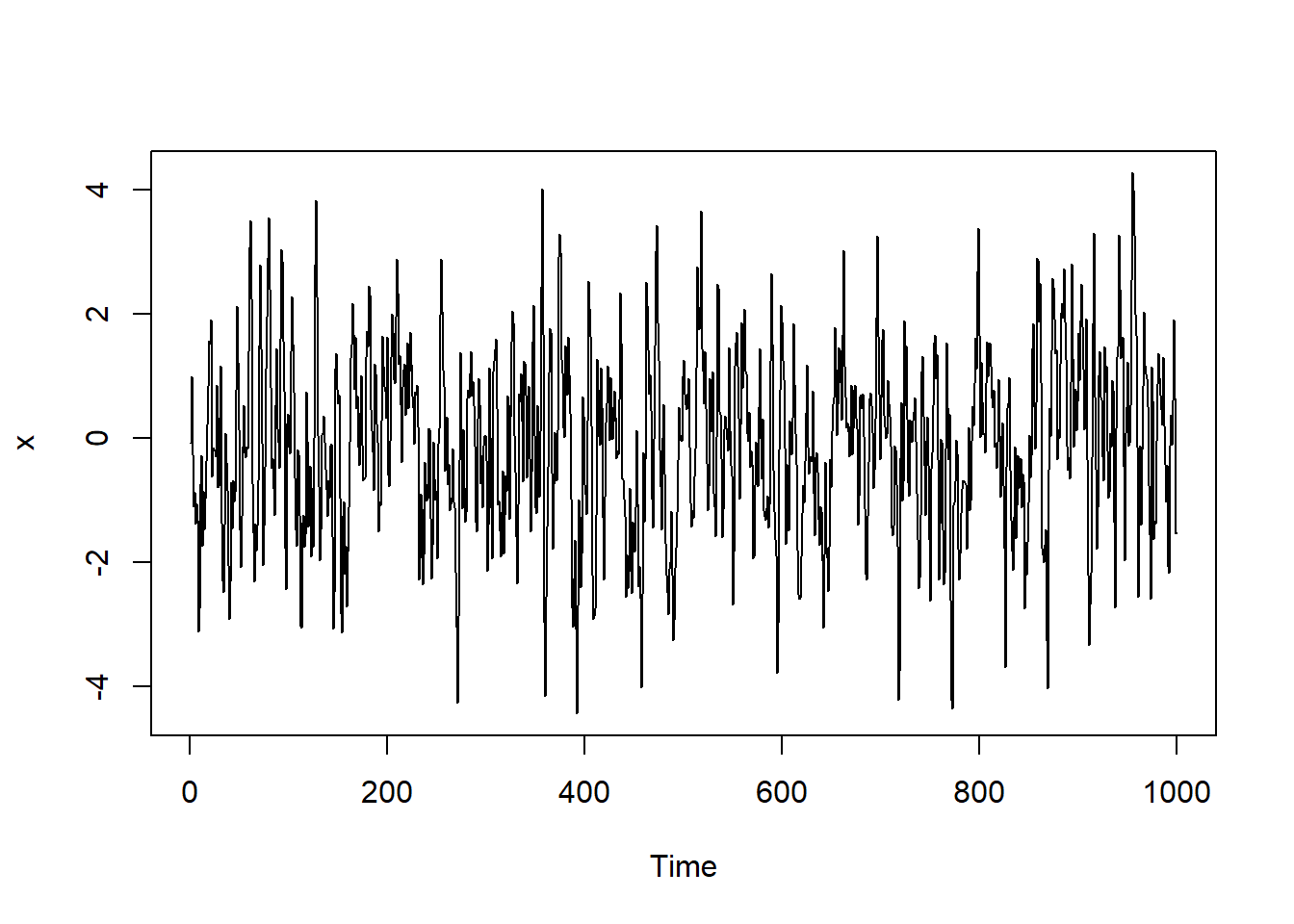
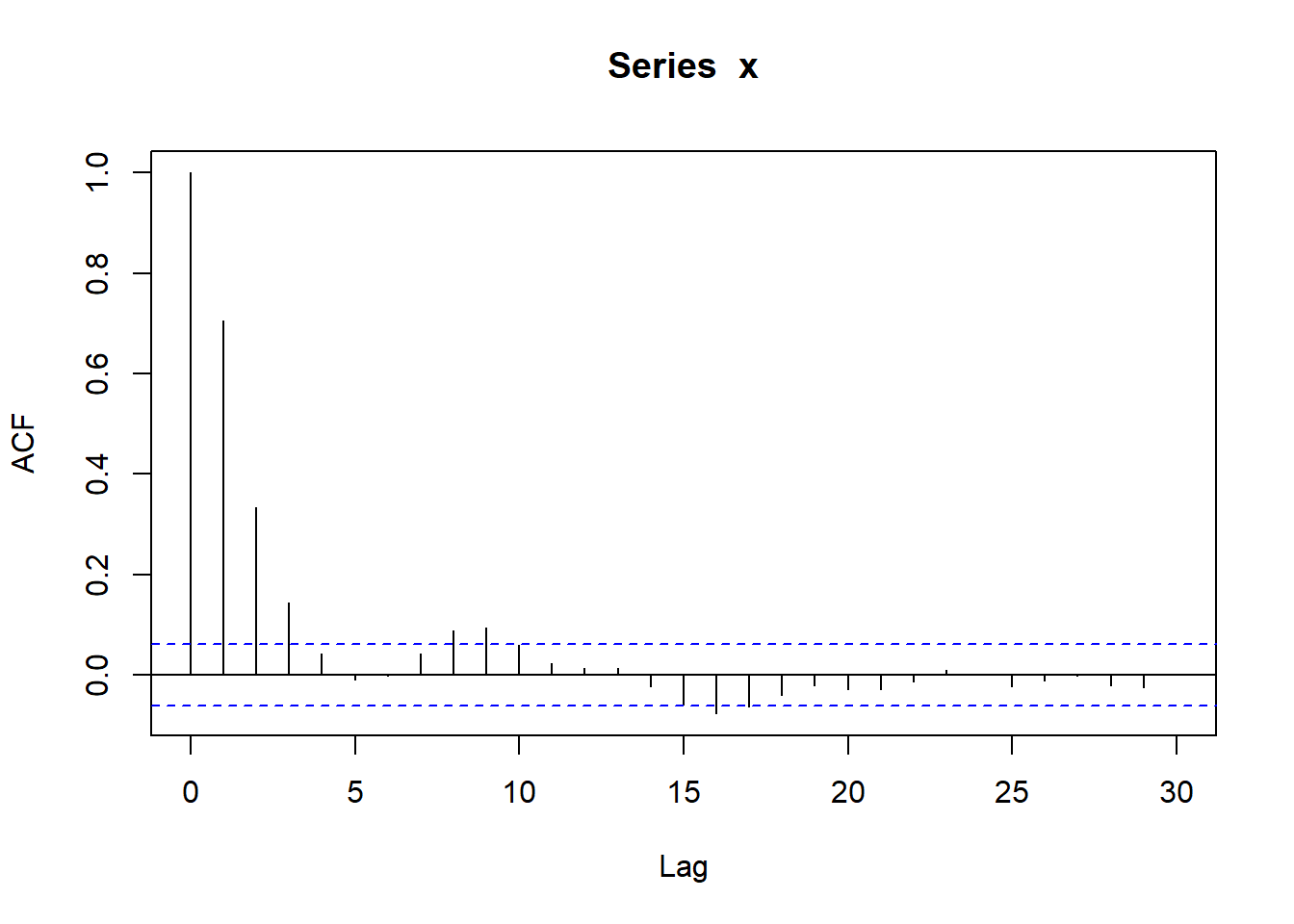
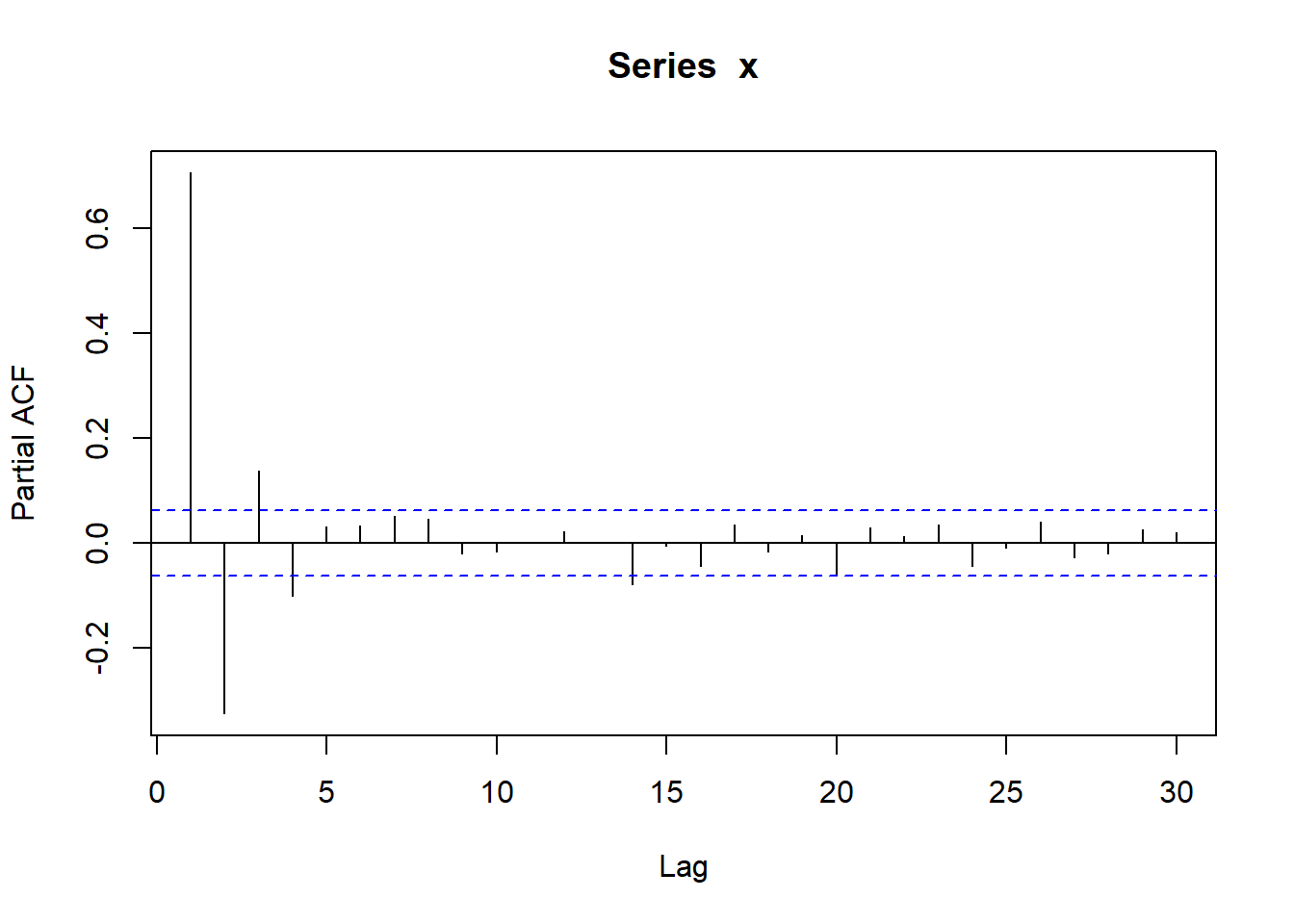
}测试,用如下AR(1)模型: \[ X_t = 0.5*X_{t-1} + \varepsilon_t, \ \varepsilon_t \sim \text{N}(0, 2^2) \]
测试:
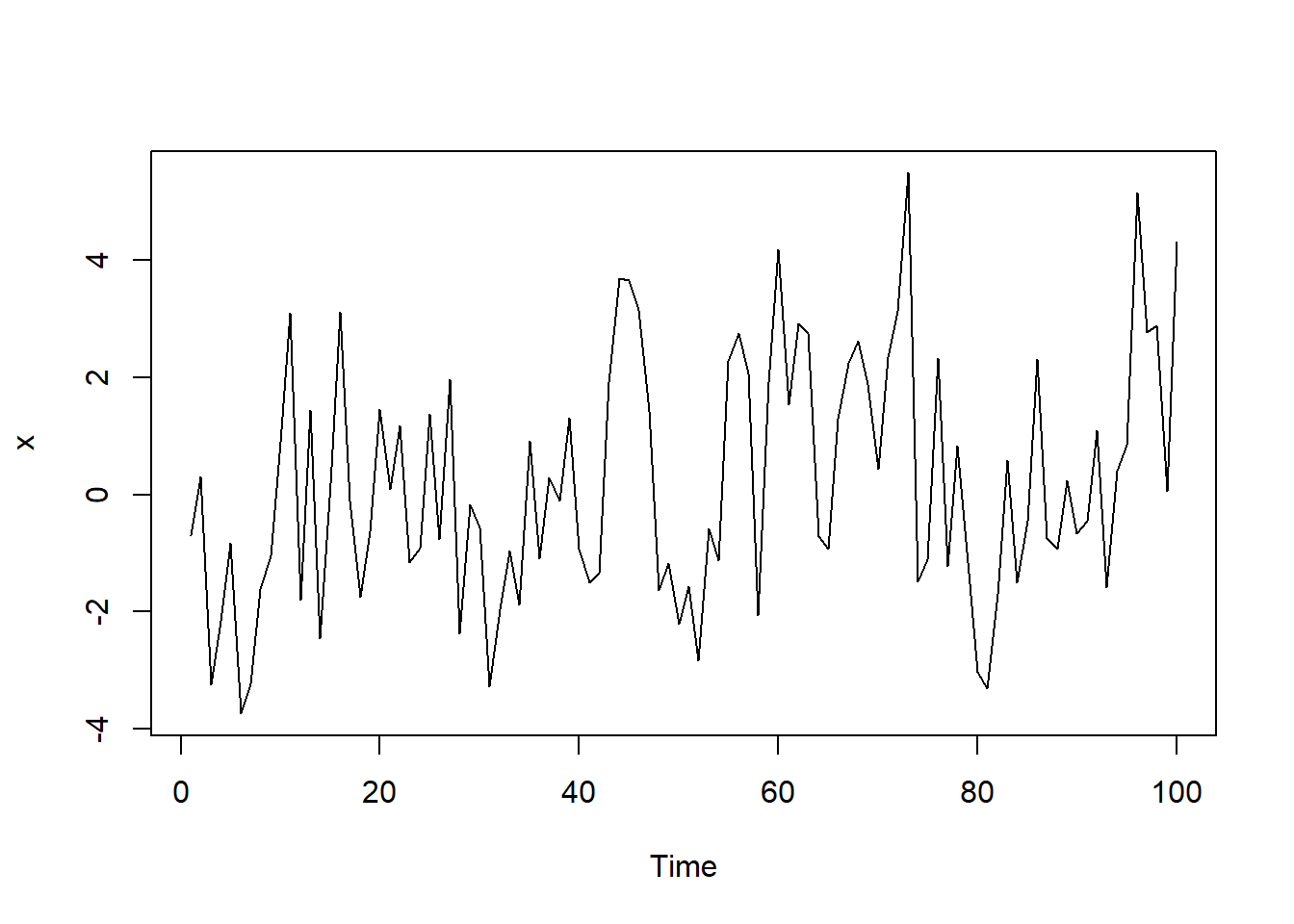
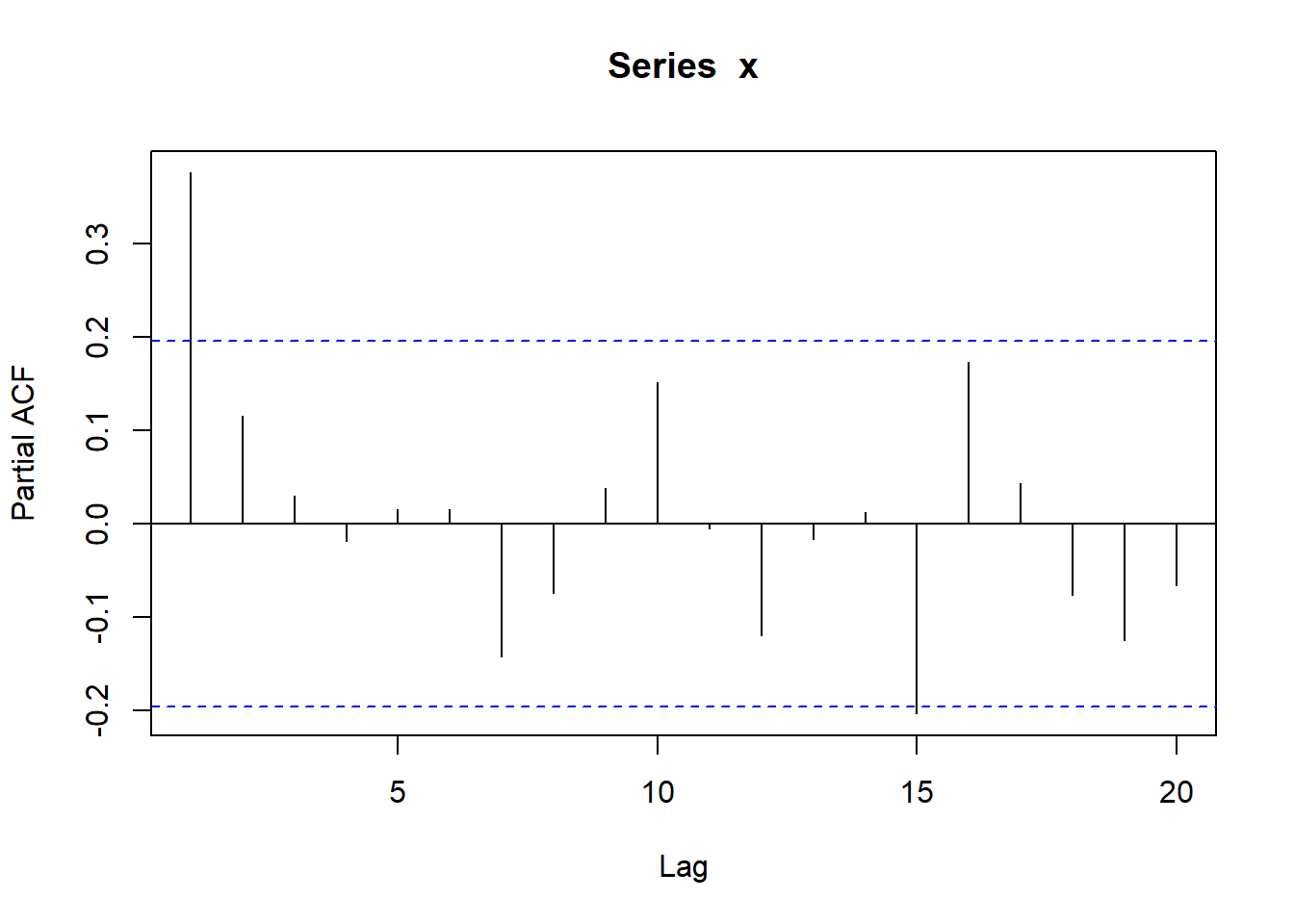
7.5.2 MA模型
对于MA(\(q\))模型 \[\begin{aligned} X_t = \varepsilon_t + b_1 \varepsilon_{t-1} + \dots + b_q \varepsilon_{t-q}, \ t \in \mathbb{Z} \end{aligned}\] 生成\(\varepsilon_{1-q}, \varepsilon_{2-q}, \dots, \varepsilon_0, \varepsilon_1, \dots, \varepsilon_N\)后可以直接对\(t=1,2,\dots,N\)按公式 计算得到\(\{X_t, t=1,2,\dots,N \}\)。
模拟MA(\(q\))的Julia程序:
function ma_gen(b_vec::Vector{Float64},
n::Int=100, npath::Int=1;
sigma=1.0)
q = length(b_vec)
n2 = n + q
bv = [1.0; b_vec]
eps = sigma .* randn(npath, n2)
x2 = zeros(npath, n2)
for t = (q+1):(q+n)
x2[:, t] .= sum(bv[1+j] .* eps[:, t-j] for j=0:q)
end
x = copy(x2[:, (q+1):(q+n)])
return x
end模拟MA(\(q\))的R程序:
ma.gen <- function(n, a, sigma=1.0){
q <- length(a)
n2 <- n+q
eps <- rnorm(n2, 0, sigma)
x2 <- stats::filter(
eps, c(1,a), method="convolution", sides=1)
x <- x2[(q+1):n2]
x <- ts(x)
attr(x, "model") <- "MA"
attr(x, "b") <- a
attr(x, "sigma") <- sigma
x
}测试,模型为
\[ X_t = \varepsilon_t + 0.5 \varepsilon_{t-1}, \ \varepsilon_t \sim \text{N}(0, 2^2) \]
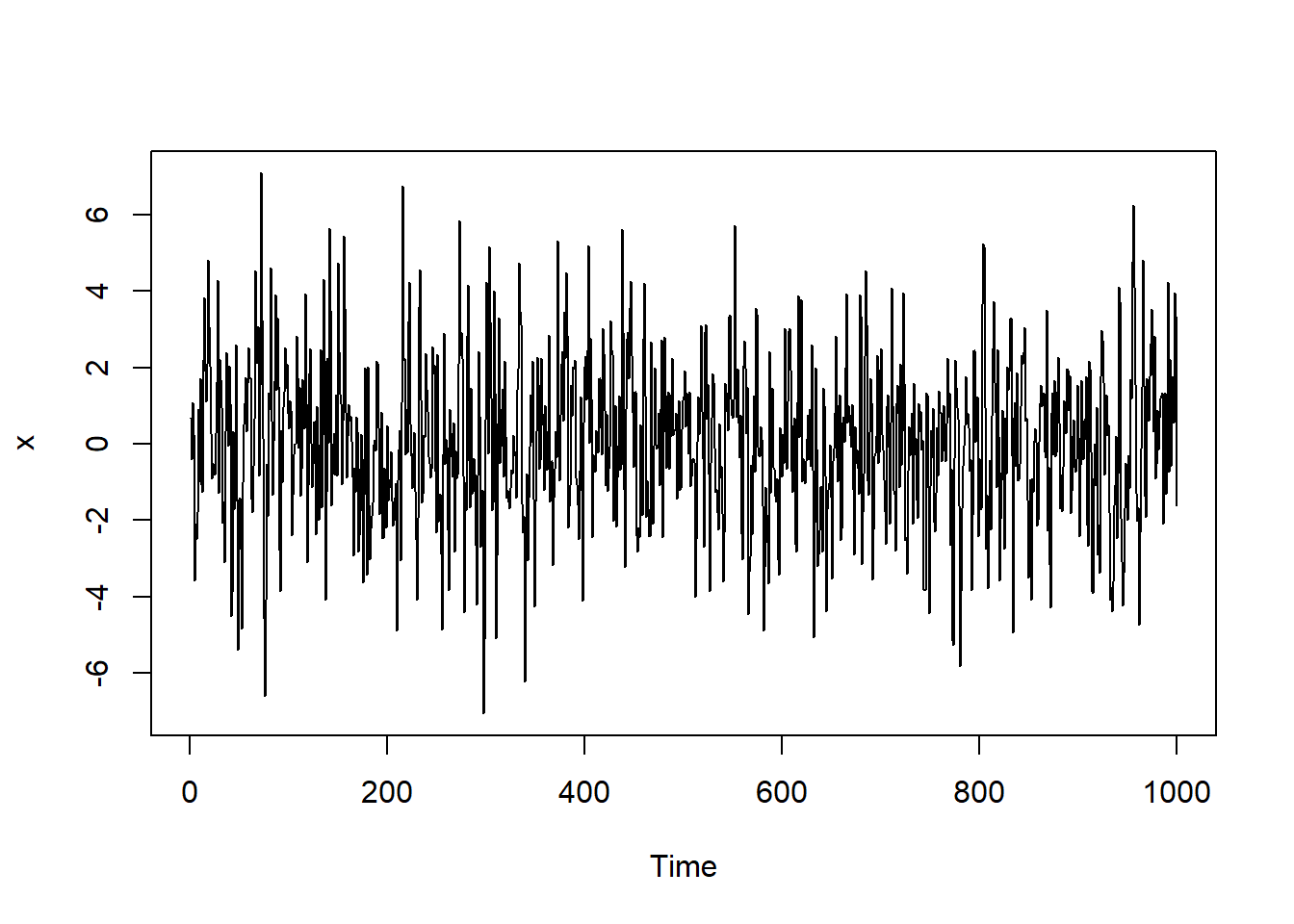
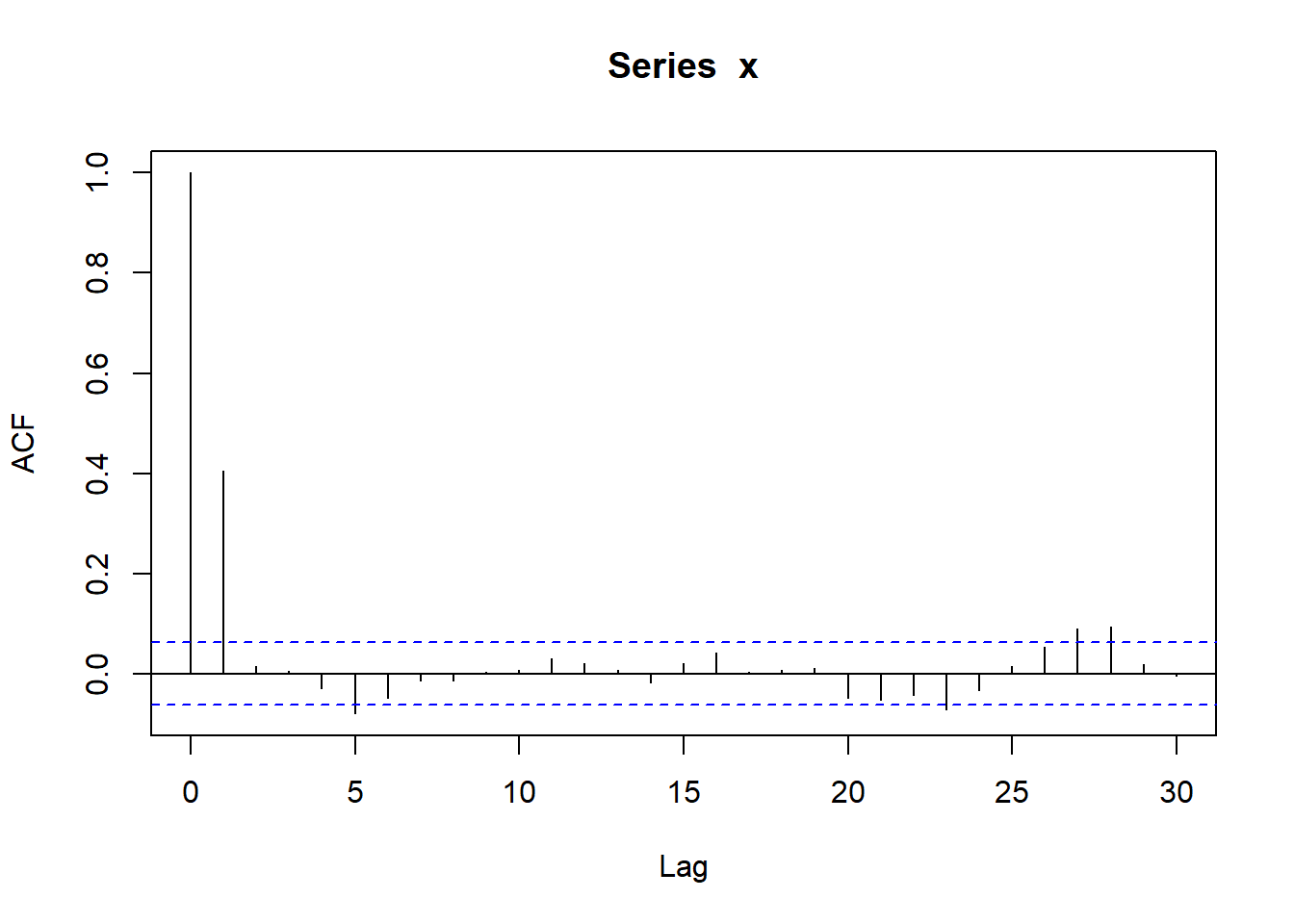
7.5.3 ARMA模型
对于ARMA(\(p,q\))模型 \[\begin{aligned} X_t = a_1 X_{t-1} + a_2 X_{t-2} + \dots + a_p X_{t-p} + \varepsilon_t + b_1 \varepsilon_{t-1} + \dots + b_q \varepsilon_{t-q}, \ t \in \mathbb{Z} \end{aligned}\] 也可以从初值零出发递推生成\(N_0 + N\)个然后只取最后的\(N\)个作为 ARMA(\(p,q\))模型的一次实现。
模拟ARMA模型的Julia程序如下:
function arma_gen(
a_vec::Vector{Float64},
b_vec::Vector{Float64},
n::Int=100,
npath::Int=1;
sigma=1.0, n0=1000)
p = length(a_vec)
q = length(b_vec)
bv = [1.0; b_vec]
mpq = max(p, q)
n0 = max(n0, mpq)
n2 = n0 + n
x2 = zeros(npath, n2)
eps = sigma .* randn(npath, n2)
for t = mpq+1:n2
x2[:, t] .= sum(
a_vec[j] .* x2[:, t-j] for j=1:p ) .+ sum(
bv[1+j] .* eps[:, t-j] for j=0:q )
end
x = copy(x2[:, (n0+1):n2])
return x
end用R的arima.sim模拟,并估计: