36 一维搜索与求根
即使目标函数\(f(x)\)是一元函数, 求最小值点也经常需要使用数值迭代方法。 另外,在多元目标函数优化中, 一般每次迭代从上一步的\(\boldsymbol x^{(t)}\)先确定一个下降方向\(\boldsymbol d^{(t)}\), 然后对派生出的一元函数\(h(\alpha) = f(\boldsymbol x^{(t)} + \alpha \boldsymbol d^{(t)})\), \(\alpha \geq 0\)求最小值点得到下降的步长\(\alpha_t\), 并令\(\boldsymbol x^{(t+1)} = \boldsymbol x^{(t)} + \alpha_t \boldsymbol d^{(t)}\), 求步长的过程称为一维搜索, 搜索可以是求一元函数\(h(\alpha)\)的精确最小值点, 也可以求一个使得目标函数下降足够多的\(\alpha\)作为步长。 对于多元目标函数\(f(\boldsymbol x)\), \(\boldsymbol x \in \mathbb R^d\), 有一种优化方法是先沿\(x_1\)坐标轴方向搜索, 再沿\(x_2\)坐标轴方向搜索, 直到沿\(x_d\)坐标轴方向搜索后再重复地从\(x_1\)坐标轴方向开始, 这种方法叫做坐标循环下降法。
一元函数的求根问题和优化问题使用的算法类似,
下面讨论一元函数的优化和求根问题。
在R语言中,uniroot()函数可以用来进行一元函数求根,
polyroot()可以求多项式的所有复根,
optimize()可以进行一元函数优化。
36.1 二分法求根
优化问题与求根问题密切相关, 很多优化问题会归结为一个求根问题。 对一元目标函数\(f(x)\), 若\(f(x)\)连续可微, 极值点一定是\(f'(x)=0\)的根。 二分法是实际数值计算中一元函数求根使用最多的方法, 这种方法简单而又有比较高的收敛速度。
设函数\(f(x)\)在闭区间\([a,b]\)连续, 且\(f(a) f(b) \leq 0\), 由中间值定理,至少有一个点\(x^* \in [a,b]\)使得\(f(x^*) = 0\)。 如果\(f(x)\)在\([a,b]\)上还是严格单调函数则解\(x^*\)存在唯一。
二分法求根用区间\([a,b]\)中点\(c\)处函数值\(f(c)\)的正负号来判断根在区间中点的左边还是右边, 显然,如果\(f(c)\)与\(f(a)\)异号,则\([a,c]\)中有根; 如果\(f(c)\)与\(f(b)\)异号,则\([c,b]\)中有根。 根据这样的想法,可以迭代地每次用区间的左半部分或右半部分代替原来的含根区间, 逐步缩小含根的区间。 设求根的绝对误差限规定为\(\epsilon\)。算法如下:
| 二分法求根算法 |
|---|
| 令\(f_a = f(a), \ f_b = f(b)\) |
| until (\(b-a < \epsilon\)) { |
| \(\qquad\) 令\(c \leftarrow \frac12 (a+b)\), \(f_c \leftarrow f(c)\) |
| \(\qquad\) if (\(f_a f_c \leq 0\)) { |
| \(\qquad\qquad\) \(b \leftarrow c\), \(f_b \leftarrow f_c\) |
| \(\qquad\) } else { |
| \(\qquad\qquad\) \(a \leftarrow c\), \(f_a \leftarrow f_c\) |
| \(\qquad\) } |
| } |
| 输出\(c\)作为根 |
设真实根为\(x^*\),第\(k\)步的区间中点为\(x^{(k)}\), 则 \[\begin{align*} |x^{(k)} - x^*| \leq (b-a) \left(\frac12 \right)^k , \end{align*}\] 二分法具有线性收敛速度。
如果\(f(x)\)是\([a, \infty)\)区间上的严格单调的连续函数, 且\(\lim_{x\to\infty} f(x)\)与\(f(a)\)反号, 则\(f(x)\)在\([a, \infty)\)上存在唯一的根, 这时需要先找到闭区间\([a,b]\)使得\(f(a)\)与\(f(b)\)反号, 二分法算法需要略作调整:
| 区间右侧无穷的二分法求根算法 |
|---|
| 取步长\(h >0\), 倍数\(\gamma>1\) |
| until (\(f(a) f(b) \leq 0\)) { |
| \(\qquad\) \(b \leftarrow a + h\) |
| \(\qquad\) \(h \leftarrow \gamma h\) |
| } |
| 用闭区间上的二分法在\([a,b]\)内求根 |
其它的情况,比如\(f(x)\)定义在\((-\infty, \infty)\), \((a, b)\)的情况可类似处理, 都需要先找到使得区间端点函数值符号相反的闭区间。
例36.1 设某种建筑钢梁的强度\(X\)服从正态\(\text{N}(\mu, \sigma^2)\)分布, \(\mu, \sigma^2\)未知, 根据设计要求,当\(X>L\)(\(L\)已知)时钢梁的强度才达到要求, 称\(L\)为强度的下规范限, 称强度达到要求的概率\(R = P(X > L)\)为单侧性能可靠度, 在可靠性评估中需要在给了总体\(X\)的一组样本\(X_1, X_2, \dots, X_n\) 以后求可靠度\(R\)的\(1-\alpha\)置信下限(\(0<\alpha<1\))。
记\(K = (\mu-L)/\sigma\),则\(R = \Phi(K)\), 所以\(R\)是\(K\)的严格单调增连续函数, 只要求\(K\)的置信下限。
假设从样本\(X_1, X_2, \dots, X_n\)中计算了样本平均值\(\bar X\)和样本方差\(S^2\), 定义\(\hat K \stackrel{\triangle}{=} (\bar X - L)/S\), \(\hat K\)的分布仅依赖于\(K\), 经过简单推导可以得知\(\sqrt{n} \hat K\)服从非中心 \(\text{t}(n-1, \sqrt{n} K)\)分布, 设其分布函数为\(\text{pt}(\cdot, n-1, \sqrt{n} K)\)。
按照置信下限的统计量法(见 (陈家鼎、孙山泽、李东风、刘力平 2006) §2.3),只要定义 \[\begin{align*} G(u,K) =& P(\hat K \geq u), \ u \in (0,1), \ K \in \mathbb R,\\ g(u) =& \inf_{K \in (-\infty, \infty)} \{ K:\ G(u,K) > \alpha \}, \ u \in (0,1), \end{align*}\] 则\(g(\hat K)\)是\(K\)的\(1-\alpha\)置信下限, 从而\(\Phi(g(\hat K))\)是\(R\)的置信下限。 而 \[\begin{align*} G(u,K) =& 1 - \text{pt}(\sqrt{n} u, n-1, \sqrt{n} K) \end{align*}\] 是\(K\)的严格单调增函数, 且\(\lim_{K\to -\infty} G(u, K)=0\), \(\lim_{K\to +\infty} G(u, K)=1\), 所以在\(G(u,K) > \alpha\)约束下求\(K\)的下确界, 等价于在固定\(u\)的情况下对关于\(K\)严格单调增的连续函数 \(f(K) \stackrel{\triangle}{=} G(u,K) - \alpha\)求根, 易见根存在唯一, 只要用二分法求根即可。 需要先求得包含根的闭区间。
| 求含根区间的算法 |
|---|
| 取初始步长\(h_0 > 0\), 倍数\(\gamma>1\) |
| \(h \leftarrow h_0\), \(a \leftarrow 0\), \(b \leftarrow 0\) |
| while (\(f(a) > 0\)) { # 这时不需要单独找\(b\) |
| \(\qquad\) \(b \leftarrow a\) |
| \(\qquad\) \(a \leftarrow a - h\) |
| \(\qquad\) \(h \leftarrow \gamma h\) |
| } |
| \(h \leftarrow h_0\) |
| while (\(f(b) \leq 0\)) { # 这时不需要单独找\(a\) |
| \(\qquad\) \(a \leftarrow b\) |
| \(\qquad\) \(b \leftarrow b + h\) |
| \(\qquad\) \(h \leftarrow \gamma h\) |
| } |
| 用闭区间上的二分法在\([a,b]\)内求根 |
※※※※※
36.2 牛顿法
设目标函数\(f(x)\)有连续二阶导数, 求最小值点可以通过求解\(f'(x)=0\)的根实现。 记\(g(x) = f'(x)\)。 设\(x^*\)是\(f(x)\)的一个最小值点, 则\(g(x^*) = 0\), 设\(x_0\)是\(x^*\)附近的一个点。 在\(x_0\)附近对\(g(x)\)作一阶泰勒近似得 \[\begin{align*} g(x) \approx g(x_0) + g'(x_0) (x - x_0), \end{align*}\] 令\(g(x)=0\),得\(x\)近似为 \[\begin{align*} x_1 = x_0 - \frac{g(x_0)}{g'(x_0)}, \end{align*}\] 写成迭代公式,即 \[\begin{align} x_{t+1} = x_t - \frac{g(x_t)}{g'(x_t)}, \ t=0,1,2,\dots \tag{36.1} \end{align}\] 或 \[\begin{align} x_{t+1} = x_t - \frac{f'(x_t)}{f''(x_t)}, \ t=0,1,2,\dots \tag{36.2} \end{align}\]
如果\(g'(x)\)在\(x^*\)的一个邻域\([x^*-\delta, x^*+\delta]\)内都为正, 初值\(x_0 \in [x^*-\delta, x^*+\delta]\), 则牛顿法产生的迭代数列\(\{ x_t \}\)收敛到\(x^*\)。 如果初值接近于最小值点并且目标函数满足一定正则性条件, 牛顿法有二阶收敛速度。 但是,如果迭代过程中遇到\(g'(x)\)接近于零的点, 下一个迭代点可能会被抛到远离根\(x^*\)的地方, 造成不收敛。 另外,牛顿法迭代的停止法则, 可以取为\(|x_{t+1}-x_t| < \epsilon_x\)或\(|g(x_t)| < \epsilon_g\), \(\epsilon_x\)和\(\epsilon_g\)是预定的精度值。 在实际数值计算中, 函数\(g(x)\)和\(g'(x)\)只有一定的计算精度, 所以算法中对\(\epsilon_x\)和\(\epsilon_g\)的选取并不是越小越好, 一般够用就可以了, 取\(\epsilon\)太小有可能导致算法在\(x^*\)附近反复跳跃而不能满足收敛法则。 判断算法收敛, 可以使用绝对变化量也可以使用相对变化量。 实际算法经常使用\(U^{1/4}\)作为相对变化量的界限, 其中\(U\)是双精度值的机器单位。 为了保险起见, 还应该设置一个迭代最大次数, 迭代超过最大次数时宣告算法失败。
牛顿法是方程求根方法, 也可以通过求\(f(x)\)的导数\(g(x)\)的根来求最小值点。 这里给出牛顿法的一个几何解释。 设\(x_t\)是根\(x^*\)附近的一个点, 从曲线\(g(x)\)上的点\((x_t, g(x_t))\)作切线(见图36.1), 切线方程为 \[\begin{align*} y = g(x_t) + g'(x_t) (x - x_t), \end{align*}\] 用切线在\(x_t\)附近作为曲线\(g(x)\)的近似, 把求\(g(x)=0\)的根近似地变成求切线与\(x\)轴交点的问题,令 \[\begin{align*} 0 = g(x_t) + g'(x_t) (x - x_t), \end{align*}\] 则交点\(x\)的值就是公式(36.1)的下一个迭代值\(x_{t+1}\)。
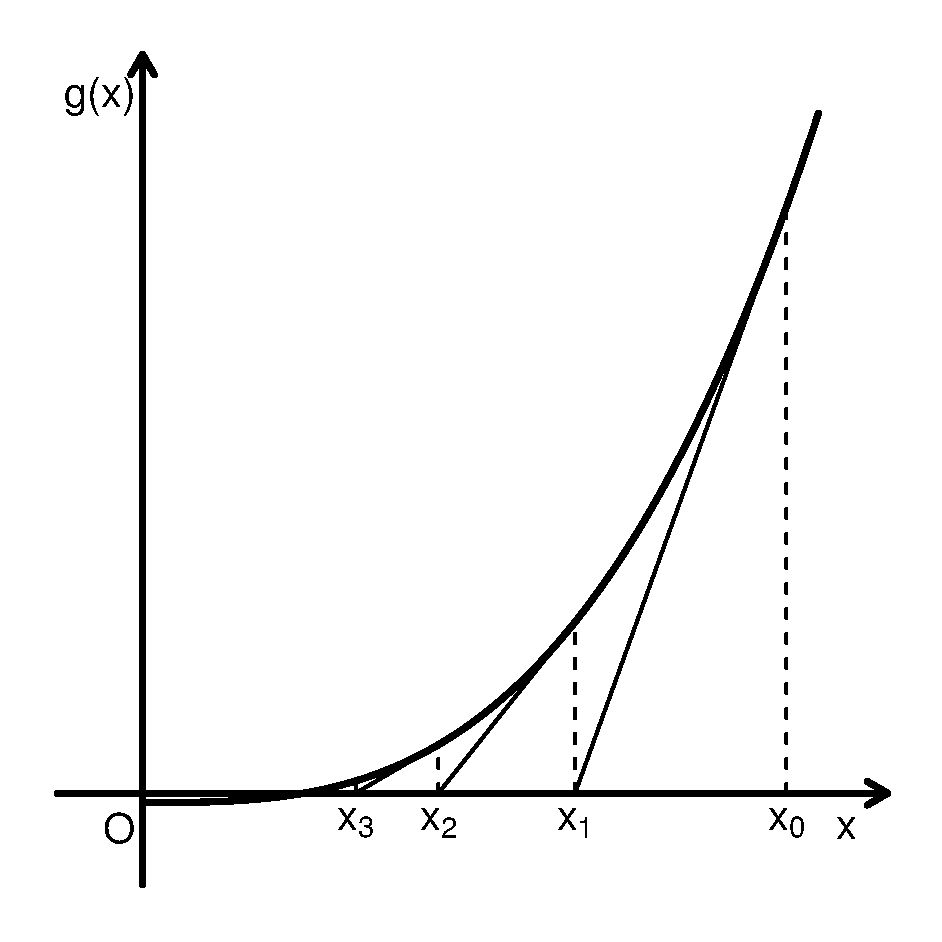
图36.1: 用牛顿法解一元非线性方程
例36.2 对函数\(f(x)=\frac14 x^4 - \frac18 x\),求\(\mathop{\text{argmin}}_{x \geq 0} f(x)\)。
令\(g(x) = f'(x) = x^3 - \frac18\), 显然\(g(x)=0\)在\(x\geq 0\)有唯一的根\(x^*=\frac12\)。 取\(x_0=2\),用(36.1)进行迭代的过程如图36.1。 迭代的前几个近似值为\(x_1=1.3438\), \(x_2=0.9189\), \(x_3=0.6619\)。 从图中可以看出, 牛顿法当\(g(x)\)斜率大且形状接近直线时收敛最快。
用R的uniroot()求解:
结果:
$root
[1] 0.5000279
$f.root
[1] 2.095328e-05
$iter
[1] 13
$init.it
[1] NA
$estim.prec
[1] 6.103516e-05※※※※※
如果待求根的函数\(g(x)\)的导数\(g'(x)\)没有表达式或很难推导, 也可以用数值微分方法计算\(g'(x)\)。 另一种方法是用函数图像上连接两次迭代的两个点\((x_{t-1}, g(x_{t-1}))\)和\((x_{t}, g(x_{t}))\) 的连线斜率代替公式(36.1)中的\(g'(x_t)\), 公式变成 \[\begin{align} x_{t+1} = x_t - \frac{x_t - x_{t-1}}{g(x_t) - g(x_{t-1})} g(x_t), \tag{36.3} \end{align}\] 这种方法称为割线法, 适当正则条件下具有超线性收敛速度但比牛顿法差一些。 割线法简单易行, 但是和牛顿法一样,遇到\(g'(x)\)接近于零的点会使得近似点被抛离真值\(x^*\)。 有一些方法结合割线法与二分法的优点, 具有超线性收敛速度而且保证根总在迭代的区间内, 参见 Monahan (2001) §8.3。
36.3 一维搜索的区间
一维搜索一般需要先确定包含极小值点的区间, 方程求根时可能也需要确定根所在的区间。
对一元连续函数\(f(x)\), 若存在\(A < x^* < B\)使得\(f(x)\)在\((A, x^*]\)单调下降, 在\([x^*, B)\)单调上升, 则称\(f(x)\)在\((A, B)\)是单谷的。 这时, 若存在\(A < a < c < b < B\)使得\(f(c) < f(a)\), \(f(c) < f(b)\), 则\(x^*\)必在\((a, b)\)中。这是因为如果\(x^* \leq a\), 则\(a, c, b\)三个点在单调上升分支, 必有\(f(a) \leq f(c) \leq f(b)\), 如果\(x^* \geq b\)则\(a, c, b\)三个点在单调下降分支, 必有\(f(a) \geq f(c) \geq f(b)\), 都会导致矛盾。
设定义于\((-\infty, \infty)\)或\((0,\infty)\)的连续目标函数\(f(x)\)存在局部极小值点\(x^*\), 且设\(f(x)\)在\(x^*\)的一个邻域内是单谷的, 则只要能找到三个点\(a<c<b\)使得\(f(a)>f(c)\), \(f(c) < f(b)\), 则在\((a,b)\)内必存在\(f(x)\)的一个极小值点。
为了求\(a\), \(b\), 从两个初始点\(x_0, x_1\)出发, 如果\(f(x_0)>f(x_1)\), 则最小值点可能在\(x_1\)右侧, 向右侧搜索找到一个函数值超过\(f(x_1)\)的点\(x_2\), 这时最小值点应该在\((x_0, x_2)\)内部; 如果\(f(x_0) < f(x_1)\), 则最小值点可能在\(x_0\)左侧, 向左侧搜索(参考图36.2)。
| 求含根区间\([a,b]\)的算法 |
|---|
| 取步长\(h>0\),步长倍数\(\gamma>1\), 初始点\(x_0\),\(x_1 \leftarrow x_0 + h\), \(k \leftarrow 0\) |
| if (\(f(x_0) > f(x_1)\)) { # 这时可以向右搜索得到\(a,c,b\) |
| \(\qquad\) until (\(f(x_{k+1}) > f(x_k)\)) { |
| \(\qquad\qquad\) \(k \leftarrow k+1\) |
| \(\qquad\qquad\) \(x_{k+1} \leftarrow x_k + \gamma^k h\) |
| \(\qquad\) } |
| \(\qquad\) \(a \leftarrow x_{k-1}, c \leftarrow x_{k}, b \leftarrow x_{k+1}\) |
| } else { # 这时可以向左搜索 |
| \(\qquad\) 交换\(x_0\)与\(x_1\),这样\(x_1<x_0\), \(f(x_0) > f(x_1)\) |
| \(\qquad\) until (\(f(x_{k+1}) > f(x_k)\)) { |
| \(\qquad\qquad\) \(k \leftarrow k+1\) |
| \(\qquad\qquad\) \(x_{k+1} \leftarrow x_k - \gamma^k h\) |
| \(\qquad\) } |
| \(\qquad\) \(a \leftarrow x_{k+1}, c \leftarrow x_{k}, b \leftarrow x_{k-1}\) |
| } |
| 输出\([a,b]\)作为包含极小值点的区间 |
如果函数\(f(x)\)的定义域为\(x \in (0, \infty)\),以上的算法应取初值\(x_0>0\), 如果出现向左搜索,可取迭代公式为\(x_{k+1} = \frac{1}{\gamma} x_k\)。
如果目标函数\(f(x)\)连续可导, 则求最小值点所在区间也可以通过求\(a<b\)使得\(f'(a)<0\), \(f'(b)>0\)来解决。 可取初值\(x_0\),如果\(f'(x_0)<0\),则类似上面算法那样向右搜索找到\(b\)使得\(f'(b)>0\); 如果\(f'(x_0)>0\),则向左搜索找到\(a<x_0\)使得\(f'(a)<0\)。 用最后得到的两个点作为\(a,b\)。 可以看出,这里描述的搜索方法适用于一元函数求根时寻找包含根的区间的问题。
36.4 0.618法(*)
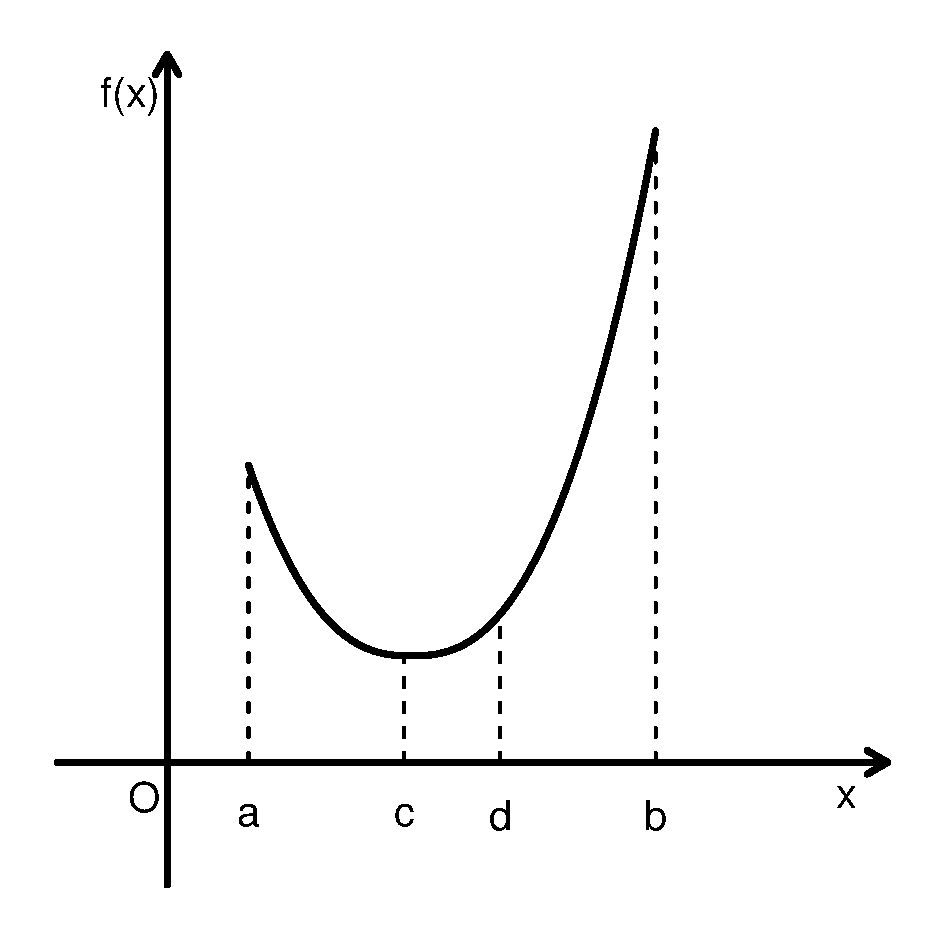
图36.2: 0.618法
0.618法(黄金分割法)是一种常用的不需要导数信息的一维搜索方法。 假设\(f(x)\)在闭区间\([a,b]\)内是单谷的, 存在最小值点\(x^* \in (a,b)\), 这时可以用0.618法求最小值点。
在区间\([a,b]\)内对称地取两个点\(c < d\)在所谓的黄金分割点上(见图36.2), 即 \[\begin{align*} \frac{d - a}{b-a} = \rho \stackrel{\triangle}{=} \frac{\sqrt{5}-1}{2} \approx 0.618, \quad \frac{b - c}{b-a} = \rho, \end{align*}\] 黄金分割比例\(\rho\)满足 \[\begin{align*} \frac{1-\rho}{\rho} = \rho, \end{align*}\] 这样的比例的特点是, 当区间缩小到\([a,d]\)时, \(c\)仍为缩小后的区间的右侧黄金分割点; 当区间缩小到\([c,b]\)时, \(d\)仍为缩小后的区间的左侧黄金分割点。 这样选了\(c, d\)两个点后, 比较\(f(c)\)和\(f(d)\)的值, 如果\(f(c)\)较小, 则因为\(a < c < d\), \(f(a)>f(c)\), \(f(c)<f(d)\), 最小值点\(x^*\)一定在区间\([a, d]\)内, 可以把搜索区间缩小到\([a, d]\), 以\([a,d]\)作为含有最小值点的区间再比较其中两个黄金分割点的函数值, 而且这时\(c\)是\([a,d]\)中右侧的黄金分割点, 只要再添加左侧的黄金分割点就可以了。 如果比较\(f(c)\)和\(f(d)\)时发现\(f(d)\)较小, 则把搜索区间缩小到\([c,b]\), 这时\(d\)是\([c,b]\)内的左侧黄金分割点,只要再添加右侧黄金分割点。 每次迭代使得区间长度缩小到原来的0.618倍, 缩小后的两个黄金分割点中一个的坐标和函数值是已经算过的。
设规定的最小值点绝对误差限为\(\epsilon\),算法如下:
| 0.618法 |
|---|
| 令\(\rho \leftarrow 0.618\), \(t \leftarrow 0\) |
| 令 \(a_0 \leftarrow a\), \(b_0 \leftarrow b\) |
| 令\(c_0 \leftarrow \rho a_0 + (1-\rho) b_0\), \(d_0 \leftarrow (1-\rho) a_0 + \rho b_0\) |
| until (\(b_t - a_t < \epsilon)\)) { |
| \(\qquad\) if (\(f(c_t) < f(d_t)\)) { # 保留左侧 |
| \(\qquad\qquad\) \(a_{t+1} \leftarrow a_t\), \(b_{t+1} \leftarrow d_t\) |
| \(\qquad\qquad\) \(d_{t+1} \leftarrow c_{t+1}\), \(c_{t+1} \leftarrow \rho a_{t+1} + (1-\rho) b_{t+1}\) |
| \(\qquad\) } else { # 保留右侧 |
| \(\qquad\qquad\) \(a_{t+1} \leftarrow c_t\), \(b_{t+1} \leftarrow b_t\) |
| \(\qquad\qquad\) \(c_{t+1} \leftarrow d_t\), \(d_{t+1} \leftarrow (1-\rho) a_{t+1} + \rho b_{t+1}\) |
| \(\qquad\) } |
| \(\qquad\) \(t \leftarrow t+1\) |
| } # end until |
| 令\(x^* \leftarrow \frac12 (a_t + b_t)\) |
| 输出\(x^*\)作为最小值点近似值 |
0.618法具有线性收敛速度。
36.5 抛物线法(*)
牛顿法需要计算导数,在初值合适的情况下收敛快。 牛顿法本质上是利用\(f(x)\)的一、二阶导数对\(f(x)\)用二次多项式进行近似并求近似函数的最小值点作为下一个近似值。 事实上,为了用二次多项式逼近\(f(x)\),只要有\(f(x)\)函数图像上的三个点就可以。 仍假设\(f(x)\)在闭区间\([a,b]\)内是单谷的, 存在最小值点\(x^* \in (a,b)\)。 设\(c \in (a, b)\), 利用\((a, f(a))\), \((c, f(c))\), \((b, f(b))\)三个点求得二次插值多项式\(\varphi(x)\), 用\(\varphi(x)\)的最小值点作为下一个近似值。
设插值多项式为 \[\begin{align*} \varphi(x) = \beta_0 + \beta_1 x + \beta_2 x^2, \end{align*}\] 其中\(\beta_2>0\), 在给定了\(a<c<b\)和相应函数值后,可以解出 \[\begin{align*} \beta_2 =& \frac{1}{b-a} \left[ \frac{f(b) - f(c)}{b-c} - \frac{f(c) - f(a)}{c-a} \right], \\ \beta_1 =& \frac{f(c) - f(a)}{c-a} - \beta_2 (c+a), \end{align*}\] 从而求得\(\varphi(\cdot)\)的最小值点 \[\begin{align*} \tilde x = -\frac{\beta_1}{2\beta_2} \end{align*}\]
如果\(\tilde x < c\), 则以\(a, \tilde x, c\)为新的插值节点继续计算插值多项式并求插值多项式的最小值点; 如果\(\tilde x > c\), 则以\(c, \tilde x, b\)为新的插值节点继续计算插值多项式并求插值多项式的最小值点, 如此迭代直至三个插值点足够接近。
适当条件下抛物线法达到超线性收敛速度。
在R软件中,用optimize函数求一元函数极值点,
函数结合使用了0.618法和抛物线法。
36.6 Brent法求根(*)
二分法求根只有线性收敛速度, 参考上面的抛物线法, 利用二次多项式反向插值方法得到根的下一个近似值。
设已知含根区间为\((a, c)\), 令\(x_1 = a\), \(x_2 = c\), \(x_3 = (x_1 + x_2)/2\)。 设迭代\(k\)步以后, 记\(a = x_{k-2}\), \(b = x_{k}\), \(c = x_{k-1}\), 应有\(a < b < c\)。 不妨设\(f(a) f(b) < 0\)(否则应有\(f(b)f(c)<0\),可类似处理)。 在区间\((a,c)\)内设函数\(y = f(x)\)可逆, 将\(x\)看成\(y\)的函数, 利用Lagrange插值法得到插值公式: \[\begin{aligned} x =\ & a \frac{[y - f(b)] [y - f(c)]}{[f(a) - f(b)] [f(a) - f(c)]} \\ +\, & b \frac{[y - f(a)] [y - f(c)]}{[f(b) - f(a)] [f(b) - f(c)]} \\ +\, & c \frac{[y - f(a)] [y - f(b)]}{[f(c) - f(a)] [f(c) - f(b)]} \end{aligned}\] 上式中令\(y=0\),得 \[\begin{aligned} x_{k+1}^* =\ & a \frac{f(b)f(c)}{[f(a) - f(b)] [f(a) - f(c)]} \\ +\, & b \frac{f(a)f(c)}{[f(b) - f(a)] [f(b) - f(c)]} \\ +\, & c \frac{f(a)f(b)}{[f(c) - f(a)] [f(c) - f(b)]} \end{aligned}\] 如果\(x_{k+1}^* \in (a, b)\)(在含根区间内), 则取\(x_{k+1} = x_{k+1}^*\); 如果\(x_{k+1}^* \notin (a, c)\), 则退回到二分法,取\(x_{k+1} = \frac{a+b}{2}\)。 如此迭代直到区间长度小于指定精度值。
这种方法称为Brent求根法, 它和二分法一样需要找到含根区间并设在区间内函数连续, 在此条件下算法保证收敛且至少有线性收敛速度, 但此方法又能够利用局部二次多项式逼近, 所以收敛速度一般比二分法快。
R的uniroot()函数实现了Brent法。
36.7 沃尔夫准则
在求多元函数优化问题时经常需要进行一维搜索, 一维搜索可以在搜索方向上求精确最小值点, 也可以求一个使得函数值下降足够多的点, 称为不精确一维搜索。
设目标函数\(f(\boldsymbol x)\)有连续二阶偏导数, 当前的最小值点近似值为\(\boldsymbol x^{(t)}\), 当前的搜索方向为\(\boldsymbol d^{(t)}\), 满足\([\nabla f(\boldsymbol x^{(t)})]^T \boldsymbol d^{(t)} < 0\)。 令\(h(\alpha) = f(\boldsymbol x^{(t)} + \alpha \boldsymbol d^{(t)})\), \(\alpha \geq 0\), 则 \[\begin{align*} h'(\alpha) =& [ \nabla f(\boldsymbol x^{(t)} + \alpha \boldsymbol d^{(t)}) ]^T \boldsymbol d^{(t)}, \\ h'(0) =& [ \nabla f(\boldsymbol x^{(t)}) ]^T \boldsymbol d^{(t)} < 0, \\ h(\alpha) =& h(0) + h'(0) \alpha + o(\alpha), \end{align*}\] 由\(h'(\alpha)\)的连续性可知\(h(\alpha)\)在0的一个右侧邻域中严格单调下降。
取\(\mu \in (0, \frac12)\), \(\sigma \in (\mu, 1)\), 不精确一维搜索的沃尔夫准则要求步长\(\alpha\)满足如下两个条件: \[\begin{align} h(0) - h(\alpha) \geq&\; \mu [ -h'(0) ] \alpha, \tag{36.4} \\ -h'(\alpha) \leq&\; \sigma [-h'(0)]. \tag{36.5} \end{align}\] 第一个限制条件要求函数值下降足够多, 第二个限制条件要求\(|h'(\alpha)|\)已经比较接近于零(精确一维搜索要求\(h'(\alpha)=0\))。 有许多个\(\alpha\)可以使这两个条件成立。把这两个条件用目标函数\(f(\cdot)\)表示, 可以写成 \[\begin{align*} f(\boldsymbol x^{(t)}) - f(\boldsymbol x^{(t)} + \alpha \boldsymbol d^{(t)}) \geq &\; \mu \left\{ - [ \nabla f(\boldsymbol x^{(t)}) ]^T \boldsymbol d^{(t)} \right\} \alpha, \\ - [\nabla f(\boldsymbol x^{(t)} + \alpha \boldsymbol d^{(t)})]^T \boldsymbol d^{(t)} \leq&\; \sigma \left\{ - [ \nabla f(\boldsymbol x^{(t)}) ]^T \boldsymbol d^{(t)} \right\} . \end{align*}\]
\(\sigma\)取值越小,一维搜索越精确,花费的时间也越长。 实际中常取\(\mu=0.1\), \(\sigma \in [0.6, 0.8]\)。
下面的算法可以找到满足沃尔夫准则的两个条件的步长\(\alpha\)。 想法是, 如果条件不满足, 就利用现有的\(h(\alpha)\)的函数值和一阶导数值构造\(h(\alpha)\)的二阶插值多项式, 计算插值多项式的最小值点\(\tilde\alpha\) 作为\(\alpha\)的下一个试验值。 算法如下:
| 不精确一维搜索的Wolfe法 |
|---|
| 取定\(\mu \in (0, \frac12)\), \(\sigma \in (\mu, 1)\), 最大步长\(\overline{\alpha}\), 令\(\alpha_0 \leftarrow 0\), \(\alpha_2 \leftarrow \overline{\alpha}\) |
| 计算\(y_0 \leftarrow h(0)\), \(y_0' = h'(0) = [ \nabla f(\boldsymbol x^{(t)}) ]^T \boldsymbol d^{(t)}\) |
| 令\(\alpha_1 \leftarrow \alpha_0\), \(y_1 \leftarrow y_0\), \(y_1' \leftarrow y_0'\) |
| 取\(\alpha \in (0, \alpha_2)\) |
| 令\(\text{finished} \leftarrow \text{FALSE}\) |
| until (finished) { |
| \(\qquad\) 计算\(y \leftarrow h(\alpha)\) |
| \(\qquad\) if(\(y_0 - y \geq -\mu y_0' \alpha\)) { # 满足沃尔夫条件1 |
| \(\qquad\qquad\) 计算\(y' \leftarrow h'(\alpha)\) |
| \(\qquad\qquad\) if(\(-y' \leq -\sigma y_0'\)) { # 满足沃尔夫条件1,2 |
| \(\qquad\qquad\) finished \(\leftarrow\) TRUE; break |
| \(\qquad\qquad\) } else { # 满足条件1但不满足条件2, 延伸搜索 |
| \(\qquad\qquad\qquad\) 由\(\alpha_1, y_1, y_1'\)和\(\alpha, y'\)计算\(\displaystyle \tilde\alpha \leftarrow \alpha_1 - \frac{\alpha - \alpha_1}{y' - y_1'} y_1'\) |
| \(\qquad\qquad\qquad\) 令\(\alpha_1 \leftarrow \alpha\), \(y_1 \leftarrow y\), \(y_1' \leftarrow y'\), \(\alpha \leftarrow \tilde \alpha\) |
| \(\qquad\qquad\) } |
| \(\qquad\) } else { # 不满足沃尔夫条件1, 收缩搜索 |
| \(\qquad\qquad\) 由\(\alpha_1, y_1, y_1'\)和\(\alpha, y\)计算\(\displaystyle \tilde\alpha \leftarrow - \frac{(\alpha^2 - \alpha_1^2) y_1' - 2 \alpha_1(y - y_1)}{2[y - y_1 - (\alpha - \alpha_1) y_1']}\) |
| \(\qquad\qquad\) 令\(\alpha_2 \leftarrow \alpha\), \(\alpha \leftarrow \tilde\alpha\) |
| \(\qquad\) } |
| } # until |
| 输出\(\alpha\)作为步长 |
36.8 附录:二分法求根的程序(*)
输入要求根的函数,
含有根的区间\(a, b\),
根的误差界限ϵ,
输出缩小的含根区间。
参见(Kochenderfer 2019)。
## 二分法求根
function bisection(f, a, b, ϵ)
if a > b
# 确保a < b
a,b = b,a
end
ya, yb = f(a), f(b)
if ya == 0 # 已经是根
b = a
end
if yb == 0 #已经是根
a = b
end
while b - a > ϵ
x = (a+b)/2
y = f(x)
if y == 0
a, b = x, x # 已经是根
elseif sign(y) == sign(ya)
a = x # 根在右半边
else
b = x # 根在左半边
end
end
# 返回缩小的含根区间
return (a,b)
end下面是一个简化的求含根区间的程序,
设f定义在\((-\infty, \infty)\)上:
36.9 附录:求最小值所在区间的程序(*)
输入要求最大值的函数f,
初值x,
设f是凸函数,
求含最小值的区间。
参见(Kochenderfer 2019)。
function bracket_minimum(f, x=0; s=1e-2, k=2.0)
a, ya = x, f(x) # 初始值
# 向右一步,希望下降
b, yb = a + s, f(a + s)
if yb > ya
# 如果非下降,就改为向左
a, b = b, a
ya, yb = yb, ya
s = -s
end
# 此处已经满足ya > yb条件,只要找到yc > yb
while true
c, yc = b + s, f(b + s)
if yc > yb
# 找到c使得ya>yb, yc>yb则满足条件
return a < c ? (a, c) : (c, a)
end
# 没有找到c,则增大步长,继续沿原方向查找
a, ya, b, yb = b, yb, c, yc
s *= k
end # while
end36.10 附录:0.618法的程序(*)
输入单谷函数f,
含最小值的区间\((a, b)\),
迭代次数\(n\),
求迭代\(n\)次后的含最小值区间。
每次迭代区间长度减小到原来的0.618倍。
参见(Kochenderfer 2019)。
# 一元凸函数黄金分割法求最小值。
function golden_section_search(f, a, b, n)
# 0.618黄金分割比
ρ = (sqrt(5)-1)/2
# d: (a,b)中靠近b的黄金分割点
d = ρ * b + (1 - ρ)*a
yd = f(d)
for i = 1 : n-1
# c: (a, b)中靠近a的黄金分割点
c = ρ*a + (1 - ρ)*b
yc = f(c)
# 比较a, b, c, d四个点的函数值
if yc < yd
# 这时(a, d)是含最小值区间
# c是区间(a,d)的靠近d的黄金分割点
# 仍用a, b表示含最小值区间,d表示靠近b的黄金分割点
d, b, yd = c, d, yc
else
# 这时(c, b)是含最小值区间
# d是(c, b)的中靠近c的黄金分割点
# 用b, a表示含最小值区间,
# 则d相对于(b, a)仍是靠近b的黄金分割点
a, b = b, c
end
end
# 返回含最小值的区间。
return a < b ? (a, b) : (b, a)
end36.11 附录:抛物线法的程序(*)
这里的程序比节36.5的做法略有改进,
对一元单谷函数f,
需要输入三个点\(a < b < c\)使得\(f(a)>f(b)\), \(f(c)>f(b)\),
迭代次数\(n\),
输出缩减后的\(a < b < c\)。
在迭代过程中要求每一步产生的新的\(a < b < c\)都满足\(f(a)>f(b)\), \(f(c)>f(b)\),
即最小值一定在\((a, c)\)内。
直接利用Lagrange插值公式写出二次多项式,
并用导数等于零解出多项式的最小值点,
可得从\(a, b, c\)计算下一个点的迭代公式:
\[
x^* = \frac{1}{2}\frac{y_a (b^2 - c^2) + y_b(c^2 - a^2) + y_c(a^2 - b^2)}{
y_a(b-c) + y_b(c-a) + y_c(a-b)}
\]
产生\(x^*\)后,
利用\(a, b, c, x^*\)这四个点中找到含最小值的缩小的区间并仍用\(a, b, c\)三个点表示。
节36.5的算法迭代不保证最小值点在拟合抛物线所用的三个点构成的区间内。
参见(Kochenderfer 2019)。
## 抛物线法的程序。
function quadratic_fit_search(f, a, b, c, n)
ya, yb, yc = f(a), f(b), f(c)
for i in 1:n-3
# x: 逼近序列中的下一个点
x = 0.5*(ya*(b^2-c^2)+yb*(c^2-a^2)+yc*(a^2-b^2)) /
(ya*(b-c) +yb*(c-a) +yc*(a-b))
yx = f(x)
if x > b
if yx > yb
# 用 a < b < x 作为新的起点
c, yc = x, yx
else
# # 用 b < x < c作为新的起点
a, ya, b, yb = b, yb, x, yx
end
elseif x < b
if yx > yb
# 用 x < b < c作为新的起点
a, ya = x, yx
else
# 用 a < x < b作为新的起点
c, yc, b, yb = b, yb, x, yx
end
end
end # for i
# 返回 a < b < c, 使得f(a)>f(b), f(c)>f(b) .
return (a, b, c)
end36.12 附录:Brent法程序(*)
R语言程序:
brent <- function(f, lower, upper){
## 初始化,先生成三个点
x1 <- lower; y1 <- f(x1)
x2 <- upper; y2 <- f(x2)
x3 <- (x1 + x2)/2; y3 <- f(x3)
eps <- .Machine$double.eps^0.25
while(abs(x2 - x1) > eps){
xs <- ( x1*y3*y2/(y1-y3)/(y1-y2) +
x3*y1*y2/(y3-y1)/(y3-y2) +
x2*y1*y3/(y2-y1)/(y2-y3) )
if(y3*y1 < 0){ # 含根区间在(x1, x3)中
if(xs > x1 && xs < x3) { # 近似根在含根区间中
x4 <- xs
} else {
x4 <- (x1 + x3)/2
}
} else { # 含根区间在(x3, x2)中
if(xs > x3 && xs < x2){
x4 <- xs
} else {
x4 <- (x3 + x2)/2
}
}
y4 <- f(x4)
x1 <- x2; y1 <- y2
x2 <- x3; y2 <- y3
x3 <- x4; y3 <- y4
}
x3
}习题
习题1
设一元函数\(f(x) = \frac43 \log(1+x) - x\)定义在\((0,1)\)中, 先求其最大值点的精确值,然后编写R程序, 分别用0.618法和二分法求其最大值点, 比较\(5\)次和\(10\)次迭代后,两种方法的绝对误差大小。
习题2
对例36.1, 编写程序,给定\(n, \bar X, S, U, 1-\alpha\)后计算\(K\)的\(1-\alpha\)置信下限。
习题3
对二次多项式\(\varphi(x) = \beta_0 + \beta_1 x + \beta_2 x^2\), \(\beta_2>0\), \(\beta_0, \beta_1, \beta_2\)都未知, 若已知\(a < c < b\)和\(y_a = \varphi(a)\), \(y_c = \varphi(c)\), \(y_b = \varphi(b)\), 求\(\varphi(\cdot)\)的最小值点。
习题4
对二次多项式函数 \(\varphi(x)=\beta_0 + \beta_1 x + \beta_2 x^2\), 设\(\beta_2 > 0\), \(\beta_0, \beta_1, \beta_2\)未知。 若已知\(x_1 \neq x_2\)和\(y_1=\varphi(x_1)\), \(y_2=\varphi(x_2)\),\(y_1' = \varphi'(x_1)\), 求\(\varphi(x)\)的最小值点。