C Maxima介绍(*)
C.1 Maxima初步认识
C.1.1 介绍
计算机代数软件可以进行多项式化简、分解因式、分式化简、通分、积分、微分等公式推导。 这种运算又称为“符号计算”,与“数值计算”相对。 著名的计算机代数系统有Maple、Mathematica、Maxima。 Maxima是一个免费的计算机代数软件, 可安装在各种不同的操作系统中。 具有计算机代数系统必须的各种功能。 用Lisp语言编制,是一个有悠久历史的软件, 开发历史可追溯至1968年到1982年之间在MIT开发的DOE Macsyma, 后来转由Texas大学William F. Schelter教授维护, 在1998年转为GNU GPL版权协议。
在MS Windows系统中, 可以下载安装wxMaxima软件(http://http://andrejv.github.io/wxmaxima/index.html)。 wxMaxima运行界面是一个窗口形式, 在窗口中逐行输入命令,命令以分号结尾, 用Shift+RETURN键运行每行命令。 命令用$代替分号作为结尾则不显示命令的结果。

图C.1: wsMaxima运行界面示例
在命令行界面,
可以用%访问上一个公式的输出;
用%i1, %o1等访问历史的输入与输出。
用%th(k)访问向上数第\(k\)个结果。
用冒号定义一个变量。
用? 命令查询一个命令,如
? diff
0: diff (Functions and Variables for Differentiation)
1: diff <1> (Functions and Variables for Differentiation)
2: diff <2> (Functions and Variables for itensor)这时可以输入数字后按Shift+RETURN查询某个匹配的项。
C.1.2 四则运算
四则运算符号用+ - * /,
乘方用^表示。
Maxima中不带小数点的四则计算结果保存为有理式,
不作近似。如
12/5 + 6*(2^3 + 1/11);结果为 \[\frac{2802}{55}\]
为了求以上结果的近似值,用numer函数开关,或float()函数,如
12/5 + 6*(2^3 + 1/11), numer;或
float(%);结果为50.94545454545455。 这样,Maxima可以当作一个高级计算器使用。
C.1.3 数值类型
Maxima的数值类型有整数、有理数、普通浮点数、高精度的浮点数。
普通浮点数如1.2, 1.2E-3。
高精度浮点数如1.2B0, 1.2B-3,
有效位数用变量fpprec控制。
函数float(x)把x转为浮点型,
函数bfloat(x)将x转为高精度浮点型。
有高精度浮点数参加运算的算式结果为高精度浮点数;
没有高精度浮点数但有浮点数算式结果为浮点数。
用%e、%pi表示\(e\)和\(\pi\),
用%i表示虚数单位。
inf, minf,分别表示\(+\infty\), \(-\infty\),
infinity表示复数无穷大。
如
cos(%pi/6)结果为 \[ \frac{\sqrt{3}}{2} \]
C.2 多项式
C.2.1 多项式合并
考虑如下的一个推导问题。 甲、乙比赛,每局比赛甲赢的概率\(p \in (0.5, 1)\)。 问:三局两胜还是五局三胜对甲有利? 三局两胜中甲赢的概率为 \[\begin{aligned} & P(\text{三局两胜中甲赢}) = P(\text{甲赢2局}) + P(\text{甲赢3局}) \\ =& C_3^2 p^2 (1-p) + p^3 = 3 p^2 - 2 p^3, \end{aligned}\] 五局三胜中甲赢的概率为 \[\begin{aligned} & P(\text{五局三胜中甲赢}) \\ =& P(\text{甲赢3局}) + P(\text{甲赢4局}) + P(\text{甲赢5局}) \\ =& C_5^3 p^3 (1-p)^2 + C_5^4 p^4(1-p) + p^5 = 10 p^3 - 15 p^4 + 6 p^5, \end{aligned}\]
在wxMaxima中用如下两个命令定义了这两个概率:
P1 : 3*p^2*(1-p) + p^3;
P2 : 10*p^3*(1-p)^2 + 5*p^4*(1-p) + p^5;这里P1和P2是两个以p为变量的符号表达式,
用来表示\(p\)的一元多项式。
用expand()函数可以把多项式合并同类项化简:
expand(P1);
expand(P2);如下命令计算两个多项式的差并合并同类项:
P3 : expand(P2-P1);结果得到两个概率的差为 \[\begin{aligned} 6 p^5 - 15 p^4 + 12 p^3 - 3 p^2 \end{aligned}\]
C.3 分式化简
考虑如下分式:
R1 : (x+1)^2/(x-1) + 1/(x+1);结果为
\[\frac{{\left( x+1\right) }^{2}}{x-1}+\frac{1}{x+1}\]
expand()函数可以分别展开分子分母中的多项式,但不能通分合并:
expand(R1);结果为 \[\frac{1}{x+1}+\frac{{x}^{2}}{x-1}+\frac{2\,x}{x-1}+\frac{1}{x-1}\]
函数ratexpand()可以把分式的分子分母中多项式合并同类项,
然后通分, 结果表示为分子每个不同幂次单独一个分式的加法:
ratexpand(R1);结果为
\[\frac{{x}^{3}}{{x}^{2}-1}+\frac{3\,{x}^{2}}{{x}^{2}-1}+\frac{4\,x}{{x}^{2}-1}\]
函数ratsimp()把分式之和通分合并变成一个分式:
ratsimp(R1);结果为 \[\frac{{x}^{3}+3\,{x}^{2}+4\,x}{{x}^{2}-1}\]
factor()函数可以对分式的分子分母分别进行因式分解,如
factor(%);结果为 \[\frac{x\,\left( {x}^{2}+3\,x+4\right) }{\left( x-1\right) \,\left( x+1\right) }\]
C.4 三角函数化简
Maxima用如下函数进行三角函数化简:
trigexpand和差化积;trigreduce积化和差;trigsimp利用\(\sin^2 x + \cos^2 x = 1\)之类化简;trigrat把三角有理分式化为\(\sin\)和\(\cos\)的线性函数。
C.4.1 和差化积
考虑如下三角函数有理式:
T1 : sin(2*x)/cos(x) + cos(2*x);结果显示为
\[\frac{\mathrm{sin}\left( 2\,x\right) }{\mathrm{cos}\left( x\right) }
+\mathrm{cos}\left( 2\,x\right) \]
trigexpand把\(\sin(2x)\)展开为\(2 \sin x \cos x\),
把\(\cos(2x)\)展开为\(\cos^2 x - \sin^2 x\):
T2 : trigexpand(T1);结果显示为 \[-{\mathrm{sin}\left( x\right) }^{2}+2\,\mathrm{sin}\left( x\right) +{\mathrm{cos}\left( x\right) }^{2} \]
上述结果中同时有\(\cos^2 x\)和\(\sin^2 x\),用trigsimp化简
trigsimp(%);结果为 \[2\,\mathrm{sin}\left( x\right) +2\,{\mathrm{cos}\left( x\right) }^{2}-1\]
C.4.2 积化和差
如下程序中
T3 : trigreduce(T2);\(\sin^2 x\), \(\cos^2x\)被化为一次式, 结果显示为
\[\frac{\mathrm{cos}\left( 2\,x\right) +1}{2}
+\frac{\mathrm{cos}\left( 2\,x\right) }{2}+2\,\mathrm{sin}\left( x\right) -\frac{1}{2}
\]
用expand简单地合并同类项:
expand(%);结果为 \[\mathrm{cos}\left( 2\,x\right) +2\,\mathrm{sin}\left( x\right) \]
用trigsimp()或trigrat()也可以合并同类项。
C.4.3 三角函数有理式化简
对T1
\[\frac{\mathrm{sin}\left( 2\,x\right) }{\mathrm{cos}\left( x\right) }
+\mathrm{cos}\left( 2\,x\right)
\]
这样的三角函数有理分式,
用ratsimp()可以直接化简为三角函数线性式,
或分子、分母都是三角函数线性项的有理式:
trigrat(T1);结果为 \[\mathrm{cos}\left( 2\,x\right) +2\,\mathrm{sin}\left( x\right) \]
ratsimp(T1);结果为 \[ \frac{\sin(2x) + \cos(x)\cos(2x)}{\cos(x)} \]
又如,
T4 : sin(x)^2 / cos(x) + cos(2*x);为
\[\mathrm{cos}\left( 2\,x\right)
+\frac{{\mathrm{sin}\left( x\right) }^{2}}{\mathrm{cos}\left( x\right) }
\]
用trigrat作用:
trigrat(%);结果为 \[\frac{\mathrm{cos}\left( 3\,x\right) -\mathrm{cos}\left( 2\,x\right) +\mathrm{cos}\left( x\right) +1} {2\,\mathrm{cos}\left( x\right) } \]
又可以用trigexpand()和trigsimp()作用:
trigexpand(%);结果为 \[\frac{-3\,\mathrm{cos}\left( x\right) \,{\mathrm{sin}\left( x\right) }^{2} +{\mathrm{sin}\left( x\right) }^{2} +{\mathrm{cos}\left( x\right) }^{3} -{\mathrm{cos}\left( x\right) }^{2} +\mathrm{cos}\left( x\right) +1} {2\,\mathrm{cos}\left( x\right) } \]
trigsimp(%);结果为 \[\frac{2\,{\mathrm{cos}\left( x\right) }^{3} -{\mathrm{cos}\left( x\right) }^{2} -\mathrm{cos}\left( x\right) +1} {\mathrm{cos}\left( x\right) } \]
C.5 函数和微积分
C.5.1 常用初等函数
sqrt(), abs(), max(), min(), sign()
exp(), log()
sin(), cos(), tan(), cot(), sec(), csc()
asin(), acos(), atan(), acot(), asec(), acsc()
sinh(), cosh(), tanh(), coth(), sech(), csch()
asinh(), acosh(), atanh(), acoth(), asech(), acsch()C.5.3 自定义变量和自定义函数
用冒号定义变量,可以是数值,也可以是代数式,如:
g : 9.8;
P1 : 3*p^2*(1-p) + p^3;用:=定义函数,如
f(x,y) := 1/2*g*x^2*y;结果显示为 \[\mathrm{f}\left( x,y\right) :=\frac{1}{2}\,g\,{x}^{2}\,y\] 调用如
f(2,10);结果为196.0。
C.5.4 代换
带有未知数的式子可以用逗号格式把未知数代换为数值或其他代数式,如
P1 : 3*p^2*(1-p) + p^3;
P1, p=0.5;
P1, p=1;后面两式的结果分别为0.5和1。
用\(\frac12 + a\)替换\(p\),如
expand(P1), p=1/2 + a;结果为 \[-2\,{a}^{3}+\frac{3\,a}{2}+\frac{1}{2}\]
C.5.5 级数与连乘
用sum函数表示级数和,如
sum(i^2, i, 1, 10);表示\(\sum_{i=1}^{10} i^2\), 结果为385。 而
sum(i^2, i, 1, n);显示为 \[ \sum_{i=1}^{10} i^2 \]
用simpsum()进行级数化简,如
%, simpsum;结果为 \[\frac{2\,{n}^{3}+3\,{n}^{2}+n}{6}\]
\(\prod_{i=m}^n i^2\)可以表示为product(i^2, i, m, n)。
用simpproduct化简连乘积,如
product(i, i, 1, n), simpproduct;结果为 \[ n! \]
C.5.6 微分
diff(f(x), x, n)求\(\frac{d^n f(x)}{dx^n}\)。
如
diff(sin(x)*exp(2*x), x, 1);结果为 \[2\,{e}^{2\,x}\,\mathrm{sin}\left( x\right) +{e}^{2\,x}\,\mathrm{cos}\left( x\right) \] 又
diff(sin(x)*exp(2*x), x, 2);结果为 \[3\,{e}^{2\,x}\,\mathrm{sin}\left( x\right) +4\,{e}^{2\,x}\,\mathrm{cos}\left( x\right) \]
C.6 方程
C.6.1 一元方程
用solve(eqn, x)求解关于未知数\(x\)的一元方程,如
eq1 : a*x^2 + b*x + c = 0;显示为 \[a\,{x}^{2}+b\,x+c=0\] 求解是符号运算:
solve(eq1, x);结果为 \[[x=-\frac{\sqrt{{b}^{2}-4\,a\,c}+b}{2\,a},x=\frac{\sqrt{{b}^{2}-4\,a\,c}-b}{2\,a}]\]
以上一般解代入具体参数计算,如
%, a=1, b=2, c=1;结果为 \[[x=-1,x=-1]\]
又如,以下的三次方程(注意可以只给出方程左端)
solve(x^3 + 2*x^2 + 3*x + 4, x);结果为 \[\begin{aligned} \Bigg[ x=&-\frac{5\,\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }{9\,{\left( \frac{5\,\sqrt{2}}{{3}^{\frac{3}{2}}}-\frac{35}{27}\right) }^{\frac{1}{3}}}+{\left( \frac{5\,\sqrt{2}}{{3}^{\frac{3}{2}}}-\frac{35}{27}\right) }^{\frac{1}{3}}\,\left( -\frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) -\frac{2}{3}, \\ x=&{\left( \frac{5\,\sqrt{2}}{{3}^{\frac{3}{2}}}-\frac{35}{27}\right) }^{\frac{1}{3}}\,\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) -\frac{5\,\left( -\frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }{9\,{\left( \frac{5\,\sqrt{2}}{{3}^{\frac{3}{2}}}-\frac{35}{27}\right) }^{\frac{1}{3}}}-\frac{2}{3}, \\ x=&{\left( \frac{5\,\sqrt{2}}{{3}^{\frac{3}{2}}}-\frac{35}{27}\right) }^{\frac{1}{3}}-\frac{5}{9\,{\left( \frac{5\,\sqrt{2}}{{3}^{\frac{3}{2}}}-\frac{35}{27}\right) }^{\frac{1}{3}}}-\frac{2}{3} \Bigg] \end{aligned}\]
设函数 \[ f(x) = a x^4 + x + 1 \] 其中\(a>0\), 求\(f(x)\)的最小值点和最小值。 在Maxima中计算:
f: a*x^4 + x + 1;
diff(%, x);\[ 4*a*x^3+1 \]
solve(%, [x]);\[[x=-\frac{\sqrt{3} i-1}{2 {{4}^{\frac{1}{3}}}\, {{a}^{\frac{1}{3}}}},x=\frac{\sqrt{3} i+1}{2 {{4}^{\frac{1}{3}}}\, {{a}^{\frac{1}{3}}}},x=-\frac{1}{{{4}^{\frac{1}{3}}}\, {{a}^{\frac{1}{3}}}}]\]
求解导数等于零的方程得到三个根, 但仅有第三个是实根:
rhs(%[3]);\[-\frac{1}{{{4}^{\frac{1}{3}}}\, {{a}^{\frac{1}{3}}}}\]
这就是最小值点。最小值为:
f, x=%;\[-\frac{1}{{{4}^{\frac{1}{3}}}\, {{a}^{\frac{1}{3}}}}+\frac{1}{{{4}^{\frac{4}{3}}}\, {{a}^{\frac{1}{3}}}}+1\]
即最小值为
\[ 1 - \frac{3}{4^{4/3} a^{1/3}} \]
C.6.2 二元方程组
二元方程求解也使用solve,其中方程和未知数都用方括号表示的列表表示。
如
eq1 : y + 2*c = 0;
eq2 : 2*x*y - c*y = 5;对应于 \[y+2\,c=0\] \[2\,x\,y-c\,y=5\]
求解如
solve([eq1, eq2], [x, y]);结果为 \[[[x=\frac{2\,{c}^{2}-5}{4\,c},y=-2\,c]]\] 结果表示为解的列表, 每个解又是包含\(x, y\)两部分的列表。
一个二元二次方程组的例子:
solve([ (x-1)^2 + y^2 = 4, x*y=1], [x, y]);结果为 \[\begin{aligned} \big[ & [x=0.51535959522949,y=1.94039270687237], \\ & [x=0.3167481152931\,i-0.74342140598106, \\ & \ \ y=-0.48506249405943\,i-1.138462468793731], \\ & [x=-0.3167481152931\,i-0.74342140598106, \\ & \ \ y=0.48506249405943\,i-1.138462468793731], \\ & [x=2.971483220309511,y=0.3365322722219] \big] \end{aligned}\]
一次方程组可以用linsolve()求解,如
linsolve ([3*x + 4*y = 7, 2*x + a*y = 13], [x, y]);\[[x=\frac{7 a-52}{3 a-8},y=\frac{25}{3 a-8}]\]
C.7 图形
C.7.1 曲线图
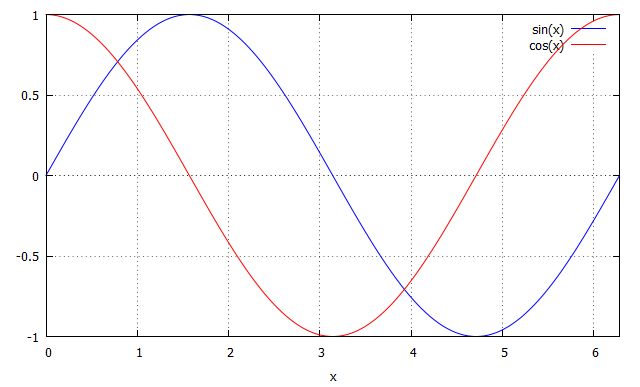
函数的曲线图使用plot2d()函数,用如
plot2d(sin(x), [x, 0, 2*%pi]);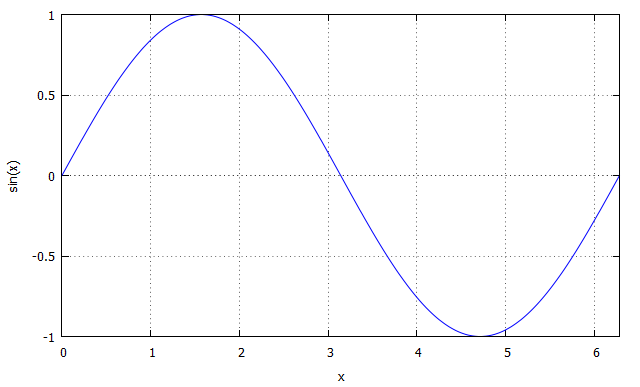
可以指定纵坐标范围,如
plot2d(sin(x), [x, 0, 2*%pi],
[y, -1.2, 1.2]);C.7.2 图形文件
作图结果可以复制到Windows剪贴板, 然后粘贴到Word中, 或粘贴到画图程序中再保存为图形文件。 也可以直接保存为图形文件, 如
plot2d(sin(x), [x, 0, 2*%pi],
[gnuplot_term, png],
[gnuplot_out_file, "test-save.png"]);C.7.4 对数坐标轴
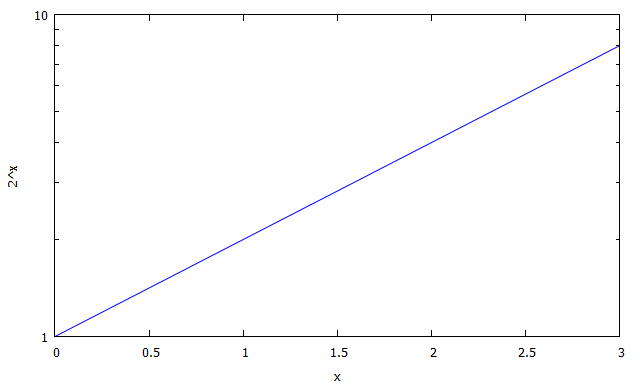
plot2d中加选项[logy]使得\(y\)轴为对数轴,
加选项[logx, logy]使得\(x, y\)轴都为对数轴,如
plot2d(2^x, [x, 0, 3]);
plot2d(2^x, [x, 0, 3], [logy]);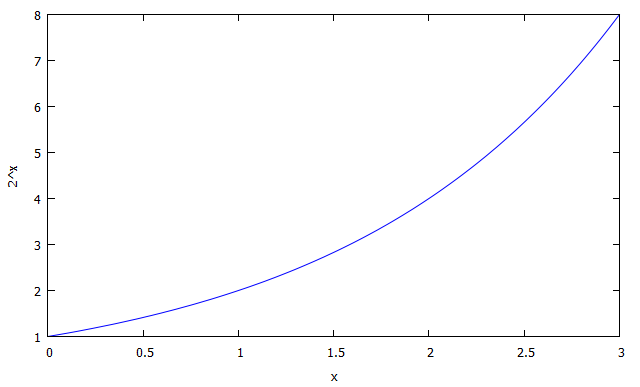
C.7.5 参数方程作图
在plot2d中把要绘图的函数用
[parametrix, y(t), x(t), [t, tmin, tmax]]表示,
可以进行参数方程作图。
例如,如下参数方程表示的曲线
\[\begin{aligned}
\begin{cases}
x(t) = cos(t), \\
y(t) = sin(3t),
\end{cases}
t \in [0, 2\pi]
\end{aligned}\]
可以作图如下:
plot2d([parametric, cos(t), sin(3*t),
[t, 0, 2*%pi]],
[x, -1.2, 1.2], [y, -1.2, 1.2],
[nticks, 200]);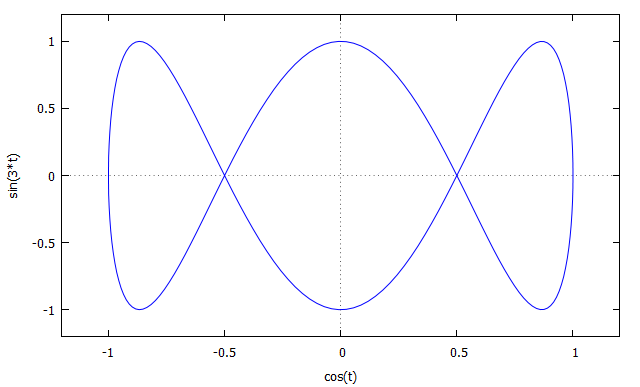
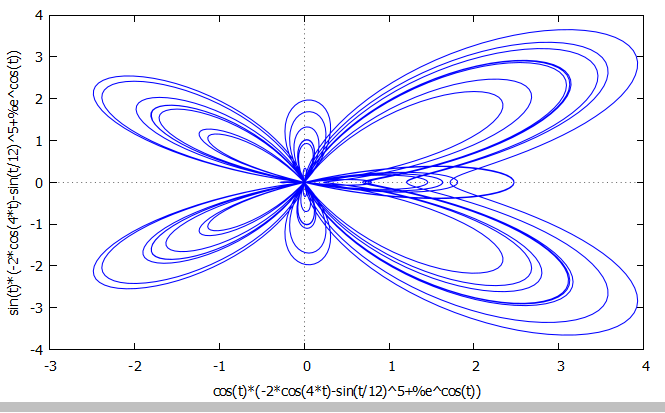
极坐标参数曲线可以化为直角坐标后参数作图,如 \[\begin{aligned} z(t) =& \left[ e^{\cos t} - 2 \cos 4t - \sin^5 \frac{t}{12} \right] e^{it}, \ t \in [-8\pi, 8\pi], \end{aligned}\] 程序如
r : (exp(cos(t)) - 2*cos(4*t) - sin(t/12)^5);
plot2d([parametric, r*sin(t), r*cos(t),
[t, -8*%pi, 8*%pi]],
[nticks, 2000]);