39 统计计算中的优化问题

统计中许多问题的计算最终都归结为一个最优化问题，典型代表是最大似然估计(MLE)、各种拟似然估计方法、非线性回归、惩罚函数方法（如svm、lasso）等。

在统计优化问题中，目标函数往往不象数学函数优化问题那样可以计算到机器精度，目标函数精度一般都是有限的，甚至于是用随机模拟方法计算的。这样，统计问题优化需要稳定性比较高的算法，对于目标函数的小的扰动应该具有良好适应能力，算法迭代收敛条件也不要取得过于严苛，否则可能无法收敛。比如，在最大似然估计问题中，样本值精度受限于测量精度，实际上都存在较大的测量误差，如果优化算法结果对于样本值的微小变化就产生很大变化，这样的算法就是不可取的。

39.1 最大似然估计

最大似然估计经常需要用最优化算法计算，最大似然估计问题有自身的特点，可以直接用一般优化方法进行最大似然估计的计算，但是利用最大似然估计的特点可以得到更有效的算法。

设总体\(\boldsymbol X\)有密度或概率函数\(p(\boldsymbol x |\boldsymbol\theta)\), \(\boldsymbol\theta\)为\(m\)维的分布参数。有了一组样本\(\boldsymbol X_1, \boldsymbol X_2, \dots, \boldsymbol X_n\)后，似然函数为 \[\begin{align} L(\boldsymbol\theta) = \prod_{i=1}^n p(\boldsymbol X_i | \boldsymbol\theta), \end{align}\] 对数似然函数为 \[\begin{align} l(\boldsymbol\theta) = \sum_{i=1}^n \log p(\boldsymbol X_i | \boldsymbol\theta), \end{align}\]

R的stats4包的mle()提供了最大似然估计计算功能，除了参数估计值以外还能给出参数标准误差的估计。

39.1.1 得分法

设对数似然函数\(l(\boldsymbol\theta)\)有二阶连续偏导数, \(\nabla l(\boldsymbol\theta)\)称为得分函数(score function), 求最大似然估计可以通过解方程\(\nabla l(\boldsymbol\theta)=\boldsymbol 0\)实现，这个方程称为估计方程。设参数真值为\(\boldsymbol\theta_*\), \(l(\boldsymbol\theta)\)最大值点为\(\hat{\boldsymbol\theta}\), 在适当正则性条件下 \(\hat{\boldsymbol\theta}\)渐近正态分布: \[\begin{align} \sqrt{n} (\hat{\boldsymbol\theta} - \boldsymbol\theta_*) \stackrel{\text{d}}{\longrightarrow} \text{N}(\boldsymbol 0, I^{-1}(\boldsymbol\theta_*)), \ n \to \infty, \end{align}\] 其中 \[\begin{align} I(\boldsymbol\theta_*) = \text{Var}(\nabla \log p(X | \boldsymbol\theta_*)) = \frac{1}{n} \text{Var}(\nabla l(\boldsymbol\theta_*)) = E \left[ -\nabla^2 \log p(X | \boldsymbol\theta_*) \right] = \frac{1}{n} E \left[ -\nabla^2 l(\boldsymbol\theta_*) \right] \end{align}\] 是\(X\)的信息阵。记\(I_n(\boldsymbol\theta_*) = \text{Var}(\nabla l(\boldsymbol\theta_*))\)，称\(I_n(\boldsymbol\theta_*)\)为\((X_1, X_2, \dots, X_n)\)的信息阵, 当\(X_1, X_2, \dots, X_n\)独立同分布时\(I_n(\boldsymbol\theta_*) = nI(\boldsymbol\theta_*)\)。

注意最大似然估计求最大值点，与前面求最小值点的问题略有差别，有时讨论负对数似然函数更方便。因为多元正态分布的负对数似然函数是正定二次型，所以如果初值取得比较合适，负对数似然函数\(-l(\boldsymbol\theta)\)与多元正态分布的负对数似然函数相近，接近于正定二次型，这时求\(-l(\boldsymbol\theta)\)的最小值点会比较容易。求得最大似然估计\(\hat{\boldsymbol\theta}\)后，可以用\(\big[ I_n(\hat{\boldsymbol\theta}) \big]^{-1}\)估计\(\hat{\boldsymbol\theta}\)的协方差阵。

\(l(\boldsymbol\theta)\)最大值点\(\hat{\boldsymbol\theta}\)的求解可以用通常的牛顿法、BFGS法，用到的对数似然函数偏导数和二阶偏导数可以推导解析表达式来计算，也可以用数值微分代替。用数值微分可以避免偏导数推导和编程时的错误。如果用牛顿法求最大值点， \(\hat{\boldsymbol\theta}\)的协方差阵可以用\([ - \nabla^2 l(\hat{\boldsymbol\theta}) ]^{-1}\)来估计。

注意到当样本量充分大且\(\boldsymbol\theta\)接近于真值\(\boldsymbol\theta_*\)时海色阵\(\nabla^2 l(\boldsymbol\theta) \approx -I_n(\boldsymbol\theta)\)，如果信息阵的公式很容易得到，在牛顿法的迭代中可以用负信息阵代替对数似然函数的海色阵，迭代为 \[\begin{align} \hat{\boldsymbol\theta}^{(t+1)} = \hat{\boldsymbol\theta}^{(t)} - \left[- I_n(\hat{\boldsymbol\theta}^{(t)}) \right]^{-1} \nabla l(\hat{\boldsymbol\theta}^{(t)}). \end{align}\] 这种方法叫做得分法(scoring)。

例39.1 (逻辑斯谛回归参数估计) 设\(Y_i \sim \text{B}(m_i, \pi_i)\), \(i=1,2,\dots,n\), \(Y_1, Y_2, \dots, Y_n\)相互独立，其中\(\pi_i = \exp(\boldsymbol\beta^T \boldsymbol x_i) / [1 + \exp(\boldsymbol\beta^T \boldsymbol x_i)]\), \(\boldsymbol\beta\)为未知参数向量，自变量\(\boldsymbol x_i, i=1,2,\dots,n\)已知。这样的模型称为逻辑斯谛回归模型，函数\(\text{logit}(\pi) \stackrel{\triangle}{=} \log \frac{\pi}{1-\pi}\), \(\pi \in (0,1)\)称为逻辑斯谛函数，其反函数为\(\text{logit}^{-1}(\gamma) = \frac{\exp(\gamma)}{1 + \exp(\gamma)}\)。上面模型中的\(\pi_i\)满足\(\text{logit} (\pi_i) = \boldsymbol\beta^T \boldsymbol x_i\), \(\pi_i = \text{logit}^{-1}(\boldsymbol\beta^T \boldsymbol x_i)\)。

\(Y_i\)的概率函数及其对数为 \[\begin{aligned} P(Y_i = y_i) =& \binom{m_i}{y_i} \pi_i^{y_i} (1 - \pi_i)^{m_i - y_i} = \binom{m_i}{y_i} \left[ 1 + \exp(\boldsymbol\beta^T \boldsymbol x_i) \right]^{-m_i} \left[\exp\left(\boldsymbol\beta^T \boldsymbol x_i \right)\right]^{y_i}, \\ \log P(Y_i = y_i) =& \log\binom{m_i}{y_i} + y_i \cdot \boldsymbol\beta^T \boldsymbol x_i - m_i \log\left[ 1 + \exp(\boldsymbol\beta^T \boldsymbol x_i) \right], \end{aligned}\] 对数似然函数为（省略了不随\(\boldsymbol\beta\)变化的部分） \[\begin{aligned} l(\boldsymbol\beta) =& \sum_{i=1}^n \Big\{ y_i \cdot \boldsymbol\beta^T \boldsymbol x_i - m_i \log\left[ 1 + \exp(\boldsymbol\beta^T \boldsymbol x_i) \right] \Big\} \end{aligned}\] 梯度和海色阵为 \[\begin{aligned} \nabla l(\boldsymbol\beta) =& \sum_{i=1}^n \left( y_i \boldsymbol x_i - \frac{m_i \exp(\boldsymbol\beta^T \boldsymbol x_i)}{1 + \exp(\boldsymbol\beta^T \boldsymbol x_i)} \boldsymbol x_i \right) = \sum_{i=1}^n (y_i - m_i \pi_i) \boldsymbol x_i, \\ \nabla^2 l(\boldsymbol\beta) =& -\sum_{i=1}^n m_i \frac{\exp(\boldsymbol\beta^T \boldsymbol x_i)}{[ 1 + \exp(\boldsymbol\beta^T \boldsymbol x_i)]^2} \cdot \boldsymbol x_i \boldsymbol x_i^T = -\sum_{i=1}^n m_i \pi_i (1 - \pi_i) \boldsymbol x_i \boldsymbol x_i^T. \end{aligned}\] 因为海色阵不包含随机成分，所以\(\boldsymbol Y = (Y_1, \dots, Y_n)\)的信息阵 \[\begin{aligned} I_n(\boldsymbol\beta) = E\left(-\nabla^2 l(\boldsymbol\beta) \right) = -\nabla^2 l(\boldsymbol\beta), \end{aligned}\] 得分法和普通牛顿法是相同的, 迭代公式同为 \[\begin{aligned} \begin{cases} \pi_i^{(t)} = \text{logit}^{-1}\left([\boldsymbol\beta^{(t)}]^T \boldsymbol x_i \right), \ i=1,2,\dots, n, \\ \boldsymbol\beta^{(t+1)} = \boldsymbol\beta^{(t)} - \left[ - \sum_{i=1}^n m_i \pi_i^{(t)} (1 - \pi_i^{(t)}) \boldsymbol x_i \boldsymbol x_i^T \right]^{-1} \left[ \sum_{i=1}^n (y_i - m_i \pi_i^{(t)}) \boldsymbol x_i \right] , \\ \qquad\qquad t=0,1,2,\dots \end{cases} \end{aligned}\]

应该用一个合理的初始估计作为\(\boldsymbol\beta\)的初值\(\boldsymbol\beta^{(0)}\)。记\(\hat \pi_i = y_i / m_i\), 以\((\boldsymbol x_i, \hat\pi_i)\), \(i=1,2,\dots,n\) 为自变量和因变量做普通最小二乘回归得到回归系数估计可以用作\(\boldsymbol\beta^{(0)}\)。这里不用\(\text{logit}(\hat \pi_i)\)作为因变量是因为\(\hat \pi_i=0\)或\(1\) 时\(\text{logit}^{-1}(\hat\pi_i)\)无定义。

※※※※※

39.1.2 精简最大似然估计

在最大似然估计问题中，如果能分步求得最大值，则可以减少问题的维数从而降低难度。设参数\(\boldsymbol\theta\)分为\(\boldsymbol\theta_1\)和\(\boldsymbol\theta_2\)两部分, 如果对任意\(\boldsymbol\theta_1\)，都能比较容易地求得 \[\begin{align*} \mathop{\text{argmax}}_{\boldsymbol\theta_2} l(\boldsymbol\theta_1, \boldsymbol\theta_2) = \hat{\boldsymbol\theta}_2(\boldsymbol\theta_1), \end{align*}\] 则 \[\begin{align*} \max_{\boldsymbol\theta_1, \boldsymbol\theta_2} l(\boldsymbol\theta_1, \boldsymbol\theta_2) = \max_{\boldsymbol\theta_1} \max_{\boldsymbol\theta_2} l(\boldsymbol\theta_1, \boldsymbol\theta_2) = \max_{\boldsymbol\theta_1} l(\boldsymbol\theta_1, \hat{\boldsymbol\theta}_2(\boldsymbol\theta_1)), \end{align*}\] 问题简化为以\(\boldsymbol\theta_1\)为自变量的优化问题。这样的方法称为精简最大似然方法(concentrated MLE)。

如果给定\(\boldsymbol\theta_2\)后也很容易得到关于\(\boldsymbol\theta_1\) 的最大值点\(\hat{\boldsymbol\theta}_1(\boldsymbol\theta_2)\)，那么，可以迭代地求两部分的最大值。首先取\(\boldsymbol\theta_1\)的适当初值\(\boldsymbol\theta_1^{(0)}\)，求得\(\boldsymbol\theta_2^{(0)} \stackrel{\triangle}{=} \hat{\boldsymbol\theta}_2(\boldsymbol\theta_1^{(0)})\), 再令\(\boldsymbol\theta_1^{(1)} \stackrel{\triangle}{=} \hat{\boldsymbol\theta}_1(\boldsymbol\theta_2^{(0)})\), \(\boldsymbol\theta_2^{(1)} \stackrel{\triangle}{=} \hat{\boldsymbol\theta}_2(\boldsymbol\theta_1^{(1)})\), 如此迭代直至收敛，这就构成了一种分块松弛法（见37.1）。这样的方法实现简单，但有可能速度比较慢。

例39.2 设总体\(X\)服从\(\Gamma(\alpha, \lambda)\)分布，密度为 \[\begin{aligned} p(x; \alpha, \lambda) = \begin{cases} \frac{\lambda^\alpha x^{\alpha-1}}{\Gamma(\alpha)} e^{-\lambda x}, & x>0, \alpha>0, \lambda>0, \\ 0, & \text{其它} \end{cases} \end{aligned}\]

设有\(X\)的简单随机样本\(X_1, X_2, \dots, X_n\)，则对数似然函数为 \[\begin{aligned} l(\alpha, \lambda) =& n \alpha \log \lambda - n \log \Gamma(\alpha) + \alpha \sum \log X_i - \lambda \sum X_i - \sum \log X_i, \end{aligned}\] 给定\(\alpha>0\)，先关于\(\lambda\)求最大值。易见 \[\begin{aligned} \frac{\partial l}{\partial \lambda} =& \frac{n\alpha}{\lambda} - \sum X_i, \end{aligned}\] 解得稳定点\(\hat\lambda = \hat\lambda(\alpha) = \alpha/\bar X\), 其中\(\bar X = \frac{1}{n} \sum X_i\)。又\(\frac{\partial^2 l}{\partial \lambda^2} = -\frac{n\alpha}{\lambda^2} < 0\), \(\forall \lambda>0\), 所以\(\hat\lambda(\alpha)\)是给定\(\alpha\)情形下\(l(\alpha,\lambda)\)关于自变量\(\lambda\)的最大值点。令\(\tilde l(\alpha) = l(\alpha, \hat\lambda(\alpha))\), 则 \[\begin{aligned} \tilde l(\alpha) =& n \alpha \log\alpha - n \log \Gamma(\alpha) + \alpha \left[ \sum \log \frac{X_i}{\bar X} - n \right] - \sum \log X_i, \\ \tilde l'(\alpha) =& n \log\alpha - n \psi(\alpha) + \sum\log\frac{X_i}{\bar X}, \end{aligned}\] 其中\(\psi(\alpha) = \frac{d}{d\alpha} \log\Gamma(\alpha)\)称为digamma函数。可以证明\(\tilde l'(\alpha)\)严格单调减，方程\(\tilde l'(\alpha) = 0\)存在唯一解\(\hat\alpha\)，且\(\hat\alpha = \mathop{\text{argmax}}_{\alpha>0} \tilde l(\alpha)\)，从而\((\hat\alpha, \hat\lambda(\hat\alpha))\)为总体参数的最大似然估计。原来二维的优化问题简化为一个一元函数\(\tilde l(\alpha)\)的优化问题，可以用二分法或牛顿法求解方程\(\tilde l'(\alpha) = 0\)。

Julia模拟例子：

using Random, Distributions, SpecialFunctions, Statistics

Random.seed!(101)
α,λ=(2.0, 3.0)
n = 100
dist = Gamma(α, 1/λ)
samp = rand(dist, n)
xbar = mean(samp)

using Roots

c1 = sum(log.(samp ./ xbar))
function g(alpha)
    n * log(alpha) - n*digamma(alpha) + c1
end
alphahat = Roots.find_zero(g, 1.0)
lambdahat = alphahat / xbar
alphahat, lambdahat
## (1.9778484307569368, 2.9858680740265013)

※※※※※

39.2 非线性回归

首先要注意有些非线性回归可以轻易地转换为线性回归。比如， \(y = A e^{- \beta x}\)可以变成\(\log y = a - \beta x\), 其中\(a = \log A\)。又如，\(y = A \cos(2\pi f t + \varphi)\)(\(f\)已知)可以变成 \(y = a \cos(2\pi f t) + b \sin(2\pi f t)\), 其中\(a = A \cos\varphi\), \(b = -A \sin\varphi\)。

考虑如下的非线性回归问题 \[\begin{align*} Y_i = \varphi(\boldsymbol x_i, \boldsymbol\beta) + \varepsilon_i, \ i=1,2,\dots,n, \end{align*}\] 其中\(\varepsilon_i\)独立同N(0,\(\sigma^2\))分布， \(\boldsymbol\beta \in \mathbb R^p\)为未知参数向量， \(Y_i\)为因变量，\(\boldsymbol x_i\)为非随机的自变量， \(\varphi\)为关于\(\boldsymbol \beta\)非线性的函数。

记\(\gamma = \sigma^{-2}\)(这可以使得似然函数偏导数形式更简单), \(\boldsymbol Y = (Y_1, \dots, Y_n)^T\), \(g_i(\boldsymbol\beta) = \varphi(\boldsymbol x_i, \boldsymbol\beta)\), \(\boldsymbol g = \boldsymbol g(\boldsymbol\beta) = (g_1(\boldsymbol\beta), \dots, g_n(\boldsymbol\beta))^T\), \[\begin{aligned} G =& G(\boldsymbol\beta) = \left(\frac{\partial g_i(\boldsymbol\beta)}{\partial \beta_j} \right)_{\substack{i=1,\dots,n\\j=1,\dots,p}} , \\ S(\boldsymbol\beta) =& \sum_{i=1}^n \big[ Y_i - g_i(\boldsymbol\beta) \big]^2 = \| \boldsymbol Y - \boldsymbol g(\boldsymbol\beta) \|^2 . \end{aligned}\] 最小化\(S(\boldsymbol\beta)\)可以得到参数\(\boldsymbol\beta\)的最小二乘估计，容易验证最小二乘估计也是最大似然估计。求非线性最小二乘估计可以用通常的牛顿法、拟牛顿法、Nelder-Mead等方法，下面结合非线性回归模型最大似然估计的特点讨论更为高效的参数估计算法。

上述模型的对数似然函数为(省略常数项) \[\begin{align*} l(\boldsymbol\beta, \gamma) =& \frac{n}{2} \log \gamma - \frac{\gamma}{2} S(\boldsymbol\beta), \end{align*}\] 梯度和海色阵为 \[\begin{align*} \nabla l(\boldsymbol\beta, \gamma) =& \left( \begin{array}{c} \gamma G^T (\boldsymbol Y - \boldsymbol g) \\ \frac{n}{2\gamma} - \frac12 S(\boldsymbol\beta) \end{array}\right), \\ \nabla^2 l(\boldsymbol\beta, \gamma) =& \left( \begin{array}{cc} \gamma \sum_{i=1}^n [Y_i - g_i(\boldsymbol\beta)] \nabla^2 g_i(\boldsymbol\beta) - \gamma G^T G & G^T(\boldsymbol Y - \boldsymbol g) \\ (\boldsymbol Y - \boldsymbol g)^T G & -\frac{n}{2} \gamma^{-2} \end{array}\right), \end{align*}\] 由此得\(\boldsymbol Y\)的信息阵为 \[\begin{align*} I_n(\boldsymbol\beta, \gamma) =& E\big[ -\nabla^2 l(\boldsymbol\beta, \gamma) \big] = \left( \begin{array}{cc} \gamma G^T G & 0 \\ 0 & \frac{n}{2} \gamma^{-2} \end{array}\right), \end{align*}\] 可见信息阵比海色阵简单得多，用得分法迭代估计参数比牛顿法更简单，迭代公式为 \[\begin{align} \boldsymbol\beta^{(t+1)} =& \boldsymbol\beta^{(t)} + \left[ G^T(\boldsymbol\beta^{(t)}) G(\boldsymbol\beta^{(t)}) \right]^{-1} G^T(\boldsymbol\beta^{(t)}) \left[\boldsymbol Y - \boldsymbol g(\boldsymbol\beta^{(t)}) \right] , \tag{39.1} \end{align}\] 这种方法称为高斯–牛顿法。如果拟合误差\(Y_i - g_i(\boldsymbol\beta)\)都比较小，这时\(-I_n(\boldsymbol\beta, \gamma)\)与海色阵\(\nabla^2 l(\boldsymbol\beta, \gamma)\)会很接近，这种情况下高斯–牛顿法具有很好的效果。与牛顿法的缺点类似，高斯–牛顿法有可能步长过大，使得\(S(\boldsymbol\beta)\)变大而不是变小，这时可以在(39.1)中增加一个步长\(\alpha\)，从\(\alpha=1\)开始每次步长减半直到迭代使\(S(\boldsymbol\beta)\)变小。

当拟合误差\(Y_i - g_i(\boldsymbol\beta)\)较大时，高斯–牛顿法效果会变差。把公式(39.1)改为 \[\begin{align} \boldsymbol\beta^{(t+1)} =& \boldsymbol\beta^{(t)} + \left[ G^T(\boldsymbol\beta^{(t)}) G(\boldsymbol\beta^{(t)}) + \lambda_t I_p \right]^{-1} G^T(\boldsymbol\beta^{(t)}) \left[\boldsymbol Y - \boldsymbol g(\boldsymbol\beta^{(t)}) \right] , \tag{39.2} \end{align}\] 其中\(\lambda_t \geq 0\), \(\lambda_t \geq 0\)可以迭代地更新。此算法称为LMF(Levenberg-Marquardt-Fletcher)算法。公式(39.2) 可以看成是取搜索方向为高斯–牛顿法的搜索方向和最速下降法的搜索方向之间的一个方向, 记搜索方向为 \[\begin{align} \boldsymbol d^{(t)} = \left[ G^T(\boldsymbol\beta^{(t)}) G(\boldsymbol\beta^{(t)}) + \lambda_t I_p \right]^{-1} G^T(\boldsymbol\beta^{(t)}) \left[\boldsymbol Y - \boldsymbol g(\boldsymbol\beta^{(t)}) \right] \tag{39.3} \end{align}\] 并记 \[\begin{align*} \Delta S_t =& S(\boldsymbol\beta^{(t)}) - S(\boldsymbol\beta^{(t)} + \boldsymbol d^{(t)}), \\ \Delta q_t =& (\boldsymbol d^{(t)})^T \left[ \lambda_t \boldsymbol d^{(t)} + G^T(\boldsymbol\beta^{(t)}) \left( \boldsymbol Y - \boldsymbol g(\boldsymbol\beta^{(t)}) \right) \right], \end{align*}\]

LMF算法

LMF算法
取初值\(\boldsymbol\beta^{(0)}\), \(\lambda_0>0\), 精度\(\epsilon>0\), \(t\leftarrow 0\)
until (迭代收敛) {
\(\qquad\) 用(39.3)求\(\boldsymbol d^{(t)}\)
\(\qquad\) 计算\(\gamma_t = \Delta S_t / \Delta q_t\)
\(\qquad\) if(\(\gamma_t < 0.25\)) {
\(\qquad\qquad\) \(\lambda_{t+1} \leftarrow 4 \lambda_t\)
\(\qquad\) } else if(\(\lambda_t > 0.75\)) {
\(\qquad\qquad\) \(\lambda_{t+1} \leftarrow \frac12 \lambda_t\)
\(\qquad\) }
\(\qquad\) if(\(\gamma_t \leq 0\)) {
\(\qquad\qquad\) \(\boldsymbol\beta^{(t+1)} \leftarrow \boldsymbol\beta^{(t)}\)
\(\qquad\) } else {
\(\qquad\qquad\) \(\boldsymbol\beta^{(t+1)} \leftarrow \boldsymbol\beta^{(t)} + \boldsymbol d^{(t)}\)
\(\qquad\) }
\(\qquad\) \(t \leftarrow t+1\)
} # until
输出\(\boldsymbol\beta^{(t)}\)作为最小二乘估计

参见高立 (2014) §5.3。

39.3 EM算法

EM算法最初用于缺失数据模型参数估计，现在已经用在许多优化问题中。设模型中包含\(\boldsymbol X_{\text{obs}}\)和\(\boldsymbol X_{\text{mis}}\)两个随机成分，有联合密度函数或概率函数\(f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta)\), \(\boldsymbol\theta\)为未知参数。称\(f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta)\)为完全数据的密度，一般具有简单的形式。实际上我们只有\(\boldsymbol X_{\text{obs}}\)的观测数据\(\boldsymbol X_{\text{obs}}=\boldsymbol x_{\text{obs}}\)， \(\boldsymbol X_{\text{mis}}\)不能观测得到，这一部分可能是缺失观测数据，也可能是潜在影响因素。所以实际的似然函数为 \[\begin{align} L(\boldsymbol\theta) = f(\boldsymbol x_{\text{obs}}|\boldsymbol\theta) = \int f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta) \,d \boldsymbol x_{\text{mis}}, \tag{39.4} \end{align}\] 这个似然函数通常比完全数据的似然函数复杂得多，所以很难直接从\(L(\boldsymbol\theta)\)求最大似然估计。

EM算法的想法是，已经有了参数的近似估计值\(\boldsymbol\theta^{(t)}\)后，假设\((\boldsymbol X_{\text{obs}},\boldsymbol X_{\text{mis}})\) 近似服从完全密度\(f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta^{(t)})\), 这里\(\boldsymbol X_{\text{obs}} = \boldsymbol x_{\text{obs}}\)已知，所以认为\(\boldsymbol X_{\text{mis}}\)近似服从由\(f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta^{(t)})\) 导出的条件分布 \[\begin{aligned} f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) =& \frac{f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta^{(t)})} {f(\boldsymbol x_{\text{obs}}| \boldsymbol\theta^{(t)})}, \end{aligned}\] 其中\(f(\boldsymbol x_{\text{obs}}| \boldsymbol\theta^{(t)})\)是由\(f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta^{(t)})\)决定的边缘密度。据此近似条件分布，在完全数据对数似然函数\(\log f(\boldsymbol X_{\text{obs}}, \boldsymbol X_{\text{mis}} | \boldsymbol\theta)\)中，把\(\boldsymbol X_{\text{obs}}=\boldsymbol x_{\text{obs}}\)看成已知，关于未知部分\(\boldsymbol X_{\text{mis}}\)按密度\(f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)})\)求期望，得到\(\boldsymbol\theta\)的函数\(Q_t(\boldsymbol\theta)\)，再求\(Q_t(\boldsymbol\theta)\)的最大值点作为下一个\(\boldsymbol\theta^{(t+1)}\)。

EM算法每次迭代有如下的E步（期望步）和M步（最大化步）:

E步: 计算完全数据对数似然函数的期望 \(Q_t(\boldsymbol\theta) = E \big\{ \log f(\boldsymbol x_{\text{obs}}, \boldsymbol X_{\text{mis}} | \boldsymbol\theta) \}\), 其中期望针对随机变量\(\boldsymbol X_{\text{mis}}\)，求期望时假定\(\boldsymbol X_{\text{mis}}\) 服从条件密度\(f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)})\)决定的分布。
M步: 求\(Q_t(\boldsymbol\theta)\)的最大值点，记为\(\boldsymbol\theta^{(t+1)}\)，迭代进入下一步。

定理39.1 EM算法得到的估计序列\(\boldsymbol\theta^{(t)}\) 使得(39.4)中的似然函数值\(L(\boldsymbol\theta^{(t)})\)单调不减。

证明: 对任意参数\(\boldsymbol \theta\)，有 \[\begin{aligned} \ln L(\theta) =& \ln f(\boldsymbol x_{\text{obs}} | \theta) \cdot \int f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d \boldsymbol x_{\text{mis}} \\ =& \int \big[ \log f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta) - \log f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta) \big] f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \\ =& \int \log f(\boldsymbol x_{\text{obs}}, \boldsymbol x_{\text{mis}} | \boldsymbol\theta) f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \\ & - \int \log f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta) f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \\ =& Q_t(\boldsymbol\theta) - \int \log f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta) f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \end{aligned}\] 由信息不等式知 \[\begin{aligned} &\int \log f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta) f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \\ \leq& \int \log f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \end{aligned}\] 又EM迭代使得\(Q_t(\boldsymbol\theta^{(t+1)}) \geq Q_t(\boldsymbol\theta^{(t)})\), 所以 \[\begin{aligned} \log L(\boldsymbol\theta^{(t+1)}) \geq & Q_t(\boldsymbol\theta^{(t)}) - \int \log f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) f(\boldsymbol x_{\text{mis}} | \boldsymbol x_{\text{obs}}, \boldsymbol\theta^{(t)}) \,d\boldsymbol x_{\text{mis}} \\ =& \log L(\boldsymbol\theta^{(t)}) . \end{aligned}\] 定理证毕。

※※※※※

在适当正则性条件下， EM算法的迭代序列\(\boldsymbol\theta^{(t)}\)依概率收敛到\(L(\boldsymbol\theta)\) 的最大值点\(\hat{\boldsymbol\theta}\)。但是，定理39.1仅保证EM算法最终能收敛，但不能保证EM算法会收敛到似然函数的全局最大值点，算法也可能收敛到局部极大值点或者鞍点。

在实际问题中，往往E步和M步都比较简单，有时E步和M步都有解析表达式，这时EM算法实现很简单。 EM算法优点是计算稳定，可以保持原有的参数约束，缺点是收敛可能很慢，尤其是接近最大值点时可能收敛更慢。如果(39.4)中的似然函数不是凸函数，算法可能收敛不到全局最大值点，遇到这样的问题可以多取不同初值比较，用矩估计等合适的近似值作为初值。

例39.3 (多项分布) 设\(X\)取值于\(\{1,2,3,4 \}\), 分布概率为\(p(x | \theta) \stackrel{\triangle}{=} \pi_x(\theta)\): \[\begin{aligned} \pi_1(\theta) =& \frac14 (2 + \theta), & \pi_2(\theta) =& \frac14 (1 - \theta), \\ \pi_3(\theta) =& \frac14 (1 - \theta), & \pi_4(\theta) =& \frac14 \theta . \end{aligned}\] 设\(n\)次试验得到的\(X\)值有\(n_j\)个\(j\)(\(j=1,2,3,4\))，求参数\(\theta\)的最大似然估计。

这是 (Dempster, Lairdk, and Rubin 1977) 文章中的例子。观测数据的对数似然函数为(去掉了与参数无关的加性常数) \[\begin{align*} l(\theta) = n_1 \log(2+\theta) + (n_2 + n_3) \log(1-\theta) + n_4 \log\theta . \end{align*}\]

令\(l'(\theta)=0\)得到一个关于\(\theta\)的二次方程，由此写出\(\mathop{\text{argmax}} l(\theta)\)的解析表达式:

\[ l'(\theta) = \frac{n_1}{2+\theta} - \frac{n_2 + n_3}{1-\theta} + \frac{n_4}{\theta} \] 令\(l'(\theta)=0\)，即求解二次方程 \[ n \theta^2 + (-n_1 + 2n_2 + 2n_3 + n_4) \theta - 2 n_4 = 0 . \] 得最大似然估计为 \[ \hat\theta = \frac{-b + \sqrt{b^2 + 8 n n_4}}{2n} \] 其中\(b = -n_1 + 2n_2 + 2n_3 + n_4\)。

例如， \(n=400\), \(n_1=80\), \(n_2=120\), \(n_3=110\), \(n_4=90\)时：

n = 400; n1=80; n2=120; n3=110; n4=90
b = -n1 + 2*n2 + 2*n3 + n4
hattheta = (-b + sqrt(b^2 + 8*n*n4))/(2*n)
hattheta

## [1] 0.3042153

下面用EM算法迭代估计\(\theta\)。将结果1分解为11和12， \(n_1\)分解为\(Z_1 + Z_2\)，其中\(P(X=11)=\frac12\), \(P(X=12)=\frac14\theta\)。这时\(Z_2 + n_4\)代表结果12和结果4的出现次数，这两种结果出现概率为\(\frac12\theta\)，其它结果(11, 2, 3)的出现概率为\(1 - \frac12\theta\)。令\(Y = Z_2 + n_4\)，则\(Y \sim \text{B}(n, \frac12\theta)\)。

数据\((Z_1, Z_2, n_2, n_3, n_4)\)的全似然函数为 \[ L_c(\theta) \propto (\frac12)^{Z_1} (\frac{\theta}{4})^{Z_2} (\frac14 - \frac{\theta}{4})^{n_2 + n_3} (\frac{\theta}{4})^{n_4} \] 对数似然函数（差一个与\(\theta\)无关的常数项）为 \[ l_c(\theta) = \ln L_c(\theta) = (Z_2 + n_4) \ln \theta + (n_2 + n_3) \ln(1 - \theta) \]

在EM迭代中，假设已经得到的参数\(\theta\)近似值为\(\theta^{(t)}\)，设\(\theta=\theta^{(t)}\)，在给定\(n, n_1, n_2, n_3, n_4\)条件下求\(l_c(\theta)\)的条件期望，这时\(Z_2\)的条件分布为 \[ \text{B} \left( n_1, \frac{\theta^{(t)}}{2 + \theta^{(t)}} \right) , \] 于是 \[ Z_2^{(t)} = E(Z_2 | \theta^{(t)}, n, n_1, n_2, n_3, n_4) = n_1 \frac{\theta^{(t)}}{2 + \theta^{(t)}} , \] 从而完全对数似然函数的条件期望为 \[ Q_t(\theta) = E(\ln L_c(\theta) | \theta^{(t)}, n, n_1, n_2, n_3, n_4) = (Z_2^{(t)} + n_4) \ln\theta + (n_2 + n_3) \ln(1 - \theta) . \] 求解\(Q_t(\theta)\)的最大值，令 \[ \frac{d}{d\theta} Q_t(\theta) = \frac{n_4 + Z_2^{(t)}}{\theta} - \frac{n_2 + n_3}{1 - \theta} = 0 , \] 得下一个参数近似值为 \[ \theta^{(t+1)} = \frac{n_4 + Z_2^{(t)}}{n_2 + n_3 + n_4 + Z_2^{(t)}} . \]

于是, EM迭代步骤从某个\(\theta^{(0)}\)出发，比如\(\theta^{(0)} = \frac12\)，在第\(t\)步计算 \[ Z_2^{(t)} = n_1 \frac{\theta^{(t)}}{2 + \theta^{(t)}}, \quad \theta^{(t+1)} = \frac{n_4 + Z_2^{(t)}}{n_2 + n_3 + n_4 + Z_2^{(t)}} \] 迭代到两次的近似参数值变化小于\(\epsilon=10^{-6}\)为止。

程序例：

n = 400; n1=80; n2=120; n3=110; n4=90
logL <- function(th) {
  n1*log(2+th) + (n2+n3)*log(1-th) + n4*log(th)
}
eps <- 1E-6
theta <- 0.5
k <- 0
repeat{
  k <- k+1
  theta0 <- theta # 保存上一个$\theta$值
  z2t <- n1 * theta0 / (2 + theta0)
  theta <- (n4 + z2t) / (n2+n3+n4 + z2t) # 新的$\theta$估计
  cat("log L(theta[", k, "]) = log L(", 
      theta, ") = ", logL(theta), "\n", sep="")
  if(abs(theta - theta0) < eps || k >= 500) break
}

## log L(theta[1]) = log L(0.3154762) = -123.8386
## log L(theta[2]) = log L(0.3049254) = -123.7474
## log L(theta[3]) = log L(0.3042604) = -123.747
## log L(theta[4]) = log L(0.3042182) = -123.747
## log L(theta[5]) = log L(0.3042155) = -123.747
## log L(theta[6]) = log L(0.3042154) = -123.747

cat("迭代次数=", k, " EM参数估计=", theta, "\n")

## 迭代次数= 6  EM参数估计= 0.3042154

仅需要6次迭代就达到了小数点后6位精度。

※※※※※

例39.4 (指数分布右删失(*)) 设某种设备的寿命总体\(Y \sim \text{Exp}(1/\theta)\)， \(EY=\theta\)，对\(n\)个这样的设备进行寿命试验，其中\(n_1\)个观测到失效时间\(t_1, \dots, t_{n_1}\)，另外的\(n_2 = n - n_1\)个没有观测到失效，仅知道失效时间分别超过\(c_j, j=n_1+1, \dots, n\)。求参数的最大似然估计。

观测数据为 \[ \boldsymbol x = (x_1, \dots, x_{n_1}, x_{n_1 + 1}, \dots, x_n) = (t_1, \dots, t_{n_1}, c_{n_1+1}, \dots, c_n) \] 观测数据的似然函数为 \[ L(\theta) = (\frac{1}{\theta})^{n_1} \exp\{ -\frac{1}{\theta} \sum_{1}^{n_1} t_i \} \exp\{ -\frac{1}{\theta} \sum_{n_1+1}^n c_j \} = \theta^{-n_1} \exp\{ -\frac{1}{\theta} \sum_{1}^n x_i \} \] 对数似然函数为 \[ \ln L(\theta) = -n_1 \ln\theta - \frac{1}{\theta} \sum_1^n x_i \] 令\(\frac{d}{d \theta} \ln L(\theta)=0\)得最大似然估计为 \[ \hat\theta = \frac{1}{n_1} \sum_{i=1}^n x_i \]

下面用EM算法估计\(\theta\)。设完全数据为\((t_1, \dots, t_{n_1}, t_{n_1+1}, \dots, t_n)\)都是失效时间，完全数据的似然函数为 \[ L_c(\theta) = \theta^{-n} \exp\{ -\frac{1}{\theta} \sum_1^n t_i \} \] 完全的对数似然函数为 \[ \ln L_c(\theta) = -n \ln\theta - \frac{1}{\theta} \sum_1^{n_1} t_i - \frac{1}{\theta} \sum_{n_1+1}^{n} t_j \]

取适当初值\(\theta^{(0)}\)，如\(\theta^{(0)} = \frac{1}{n} x_i\)。在迭代中设已有\(\theta^{(t)}\)，在已知\(\theta=\theta^{(t)}\), \(t_i, i=1,\dots, n_1\)， \(t_j > c_j, j=n_1+1, \dots, n\)的条件下求\(\ln L_c(\theta)\)的条件期望，先求 \(E(t_j | \theta^{(t)}, t_j > c_j)\)，\(j=n_1+1, \dots, n\)。易见\(t_j - c_j\)的条件分布为\(\text{Exp}(\frac{1}{\theta^{(t)}})\)，所以 \[ E(t_j | \theta^{(t)}, t_j > c_j) = c_j + E(t_j - c_j | \theta^{(t)}, t_j > c_j) = c_j + \theta^{(t)} \] 所以 \[ \begin{aligned} Q_t(\theta) =& E \left[ \ln L_c(\theta) \;|\; \boldsymbol x \right] = -n \ln\theta - \frac{1}{\theta} \sum_{1}^{n_1} t_i - \frac{1}{\theta} \sum_{n_1}^n (c_j + \theta^{(t)}) \\ =& -n \ln\theta - \frac{1}{\theta} \sum_{1}^{n} x_i - n_2 \frac{\theta^{(t)}}{\theta} \end{aligned} \] 令\(\frac{d}{d \theta} Q_t(\theta)=0\)得参数的迭代公式为 \[ \theta^{(t+1)} = \frac{1}{n} \left( \sum_{1}^n x_i + n_2 \theta^{(t)} \right) \]

模拟实例：

set.seed(101)
true.theta <- 2.0
n <- 25
t.comp <- rexp(n, 1/true.theta)
t.cens <- rexp(n, 1/true.theta)
sele <- t.comp <= t.cens
x.comp <- t.comp[sele]
x.cens <- t.cens[!sele]
x <- c(x.comp, x.cens) # 观测数据
n1 <- length(x.comp)
n2 <- n - n1
cat("n=", n, " n1=", n1, " n2=", n2, "\n")

## n= 25  n1= 9  n2= 16

## MLE:
sumx <- sum(x)
hat.theta <- sumx / n1
cat("MLE=", hat.theta, "\n")

## MLE= 2.555051

## EM:
eps <- 1E-6
max.iter <- 500
theta <- mean(x)
k <- 0
repeat{
  k <- k+1
  theta0 <- theta # 上一个$\theta$值
  theta <- 1/n*(sumx + n2*theta0)
  if(abs(theta - theta0) < eps || k >= max.iter) break
}
cat("迭代次数=", k, " EM estimate=", theta, "\n")

## 迭代次数= 31  EM estimate= 2.555049

※※※※※

例39.5 (另一指数分布右删失) 设某种设备的寿命总体\(Y \sim \text{Exp}(1/\theta)\)， \(EY=\theta\)，设对\(n\)个这样的设备进行寿命试验，得到了失效时间\(x_1, \dots, x_n\)，对另外的\(m\)个这样的设备进行寿命试验，仅知道其中\(r\)个在时刻\(s\)之前失效， \(m-r\)个未失效。用EM方法求\(\theta\)的最大似然估计。

观测数据为 \[ \boldsymbol x = (x_1, \dots, x_{n}, r), \] 观测数据的似然函数为 \[ L(\theta) \propto \theta^{-n} \exp\{ -\frac{1}{\theta} \sum_1^n x_i \} (1 - e^{-s/\theta})^r e^{-(m-r)s/\theta} , \] 对数似然函数为 \[ \ln L(\theta) = -n\ln\theta + r \ln(1 - e^{-s/\theta}) - \frac{1}{\theta} \left[\sum_1^n x_i + (m-r)s \right] , \] 直接求MLE有困难。

下面用EM算法估计\(\theta\)。设第二批的\(m\)个试验的具体失效时间为\(u_j, j=1,\dots, m\)。完全数据的似然函数为 \[ L_c(\theta) = \theta^{-n-m} \exp\left\{ -\frac{1}{\theta} \left[ \sum_1^n x_i + \sum_1^m u_j \right] \right\} , \] 完全的对数似然函数为 \[ \ln L_c(\theta) = -(n+m) \ln\theta -\frac{1}{\theta} \left[ \sum_1^n x_i + \sum_1^m u_j \right] . \]

取适当初值\(\theta^{(0)}\)，如\(\theta^{(0)} = \frac{1}{n} x_i\)。在迭代中设已有\(\theta^{(t)}\)，在已知\(\theta=\theta^{(t)}\)和观测数据\(\boldsymbol x\)的条件下求\(\ln L_c(\theta)\)的条件期望。先求 \(E(u_j | \theta^{(t)}, \boldsymbol x)\)，\(j=n_1+1, \dots, n\)。在给定\(\theta=\theta^{(t)}\)，观测数据\(\boldsymbol x\)和\(u_j < s\)条件下， \(u_j\)的条件分布是Exp\((1/\theta^{(t)})\)在\(u_j < s\)下的条件分布， \[ P(u_j > u | u_j < s) = \frac{P(u < u_j < s)}{P(u_j < s)} = \frac{e^{-u/\theta^{(t)}} - e^{-s/\theta^{(t)}}}{1 - e^{-s/\theta^{(t)}}} , \] 这时 \[ E(u_j | \theta^{(t)}, u_j < s) = \int_0^s P(u_j > u | u_j < s) \,du = \theta^{(t)} + s - \frac{s}{1 - e^{-s/\theta^{(t)}}} . \] 在给定\(\theta=\theta^{(t)}\)，观测数据\(\boldsymbol x\)和\(u_j \geq s\)条件下， \(u_j - s\)条件分布是Exp\((1/\theta^{(t)})\)，所以 \[ E(u_j | \theta^{(t)}, u_j \geq s) = s + \theta^{(t)} . \] 于是 \[ \begin{aligned} E(u_j | \theta^{(t)}, \boldsymbol x) =& E(u_j | \theta^{(t)}, u_j < s) P(u_j < s) + E(u_j | \theta^{(t)}, u_j \geq s) P(u_j \geq s) \\ =& \left( \theta^{(t)} + s - \frac{s}{1 - e^{-s/\theta^{(t)}}} \right) \frac{r}{m} + (s + \theta^{(t)}) \frac{m-r}{m} . \end{aligned} \] 所以 \[\begin{aligned} Q_t(\theta) =& E \left[ \ln L_c(\theta) | \theta^{(t)}, \boldsymbol x \right] \\ =& -(n+m) \ln\theta - \frac{1}{\theta}\left[ \sum_1^n x_i \right. \\ & + \left. \left( \theta^{(t)} + s - \frac{s}{1 - e^{-s/\theta^{(t)}}} \right) r + (s + \theta^{(t)}) (m-r) \right] . \end{aligned}\] 求 \[\begin{aligned} & \frac{d}{d\theta} Q_t(\theta) \\ =& - \frac{n+m}{\theta} + \frac{1}{\theta^2} \left[\sum_1^n x_i \right. \\ &+ \left. \left( \theta^{(t)} + s - \frac{s}{1 - e^{-s/\theta^{(t)}}} \right) r + (s + \theta^{(t)}) (m-r) \right] \\ =& 0 , \end{aligned}\] 解得迭代公式为 \[ \theta^{(t+1)} = \frac{1}{n+m} \left[ \sum_1^n x_i + m(\theta^{(t)} + s) - \frac{rs}{1 - e^{-s/\theta^{(t)}}} \right] . \]

模拟实例：

set.seed(101)
true.theta <- 2.0
n <- 10
m <- 8
s <- 1.5*true.theta
x1 <- rexp(n, 1/true.theta)
r <- sum(rexp(m, 1/true.theta) < s)

## EM:
eps <- 1E-6
max.iter <- 500
theta <- mean(x1)
sumx1 <- sum(x1)
k <- 0
repeat{
  k <- k+1
  theta0 <- theta # 上一个$\theta$值
  theta <- 1/(n+m)*(sumx1 + m*(theta0 + s) - r*s/(1 - exp(-s/theta0)))
  if(abs(theta - theta0) < eps || k >= max.iter) break
}
cat("迭代次数=", k, " EM 估计=", theta, "\n")

## 迭代次数= 7  EM 估计= 1.800224

图形验证：

logL <- function(th){
  (-n * log(th) + r*log(1 - exp(-s/th))
   - 1/th*(sumx1 + (m-r)*s) )
}
curve(logL, 1.0, 3.0)
abline(v=theta, col="red")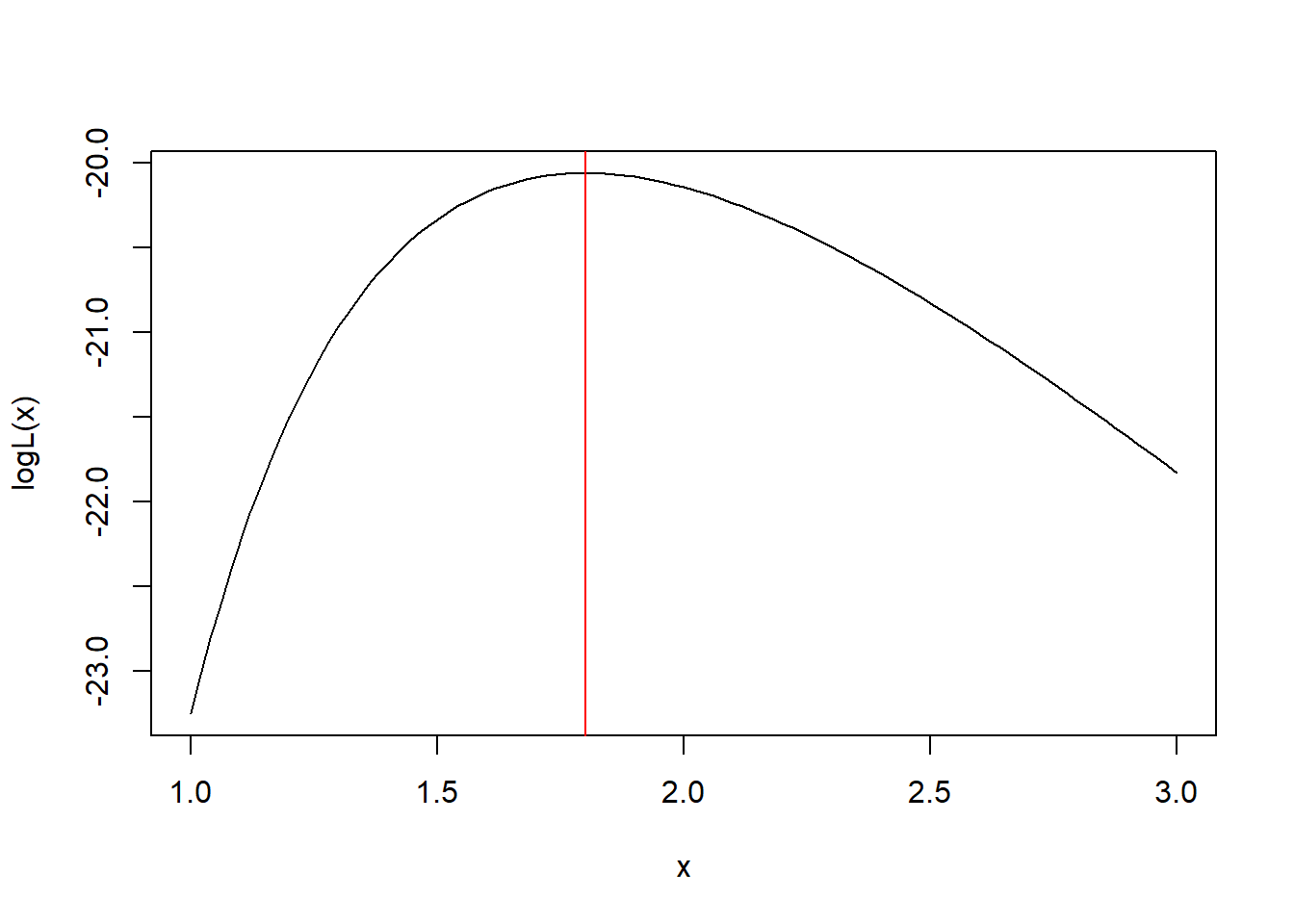

※※※※※

例39.6 (正态分布右删失(*)) 设总体为N(\(\theta\),1)分布，观测样本\(X_1, \dots, X_n\)有观测值\(x_1, \dots, x_n\), 另外有\(Z_1, \dots, Z_m\)仅知道\(Z_j > a\), \(j=1, \dots, m\)，称\(Z_j\)是右删失观测。假设这些观测都相互独立，则实际的似然函数为 \[\begin{align} L(\theta) = f(\boldsymbol x | \theta) = \left[ 1 - \Phi(a - \theta) \right]^m \prod_{i=1}^n \phi(x_i - \theta), \end{align}\] 其中\(\phi(\cdot)\)和\(\Phi(\cdot)\)分别为标准正态分布的分布密度和分布函数。

用EM算法求最大似然估计，以\(\boldsymbol X = (X_1, \dots, X_n)\)为有观测的部分，以\(\boldsymbol Z = (Z_1, \dots, Z_m)\)为没有观测的部分。完全数据的联合密度为 \[\begin{aligned} f(\boldsymbol x, \boldsymbol z | \theta) = \prod_{i=1}^n \phi(x_i - \theta) \prod_{j=1}^m \phi(z_j - \theta) . \end{aligned}\]

在E步，设\(\theta^{(t)}\)为参数的一个估计值，在已知\(\boldsymbol X = \boldsymbol x\)条件下， \(\boldsymbol Z\)的条件密度可以从完全数据联合密度导出: \[\begin{aligned} f(\boldsymbol z | \boldsymbol x, \theta^{(t)}) =& \frac{f(\boldsymbol x, \boldsymbol z | \theta^{(t)})}{f(\boldsymbol x | \theta^{(t)})} = [ 1 - \Phi(a-\theta^{(t)}) ]^{-m} \prod_{j=1}^m \phi(z_j - \theta^{(t)}), \end{aligned}\] 这个条件分布可以看成是与\(\boldsymbol X\)独立，且\(Z_1, \dots, Z_m\)独立，有共同的条件密度\(\phi(z - \theta^{(t)})/[1 - \Phi(a-\theta^{(t)})]\), \(z > a\)。求完全数据对数似然关于\(\boldsymbol Z\)的条件期望, 有 \[\begin{aligned} Q_t(\theta) =& E \log \left[ \prod_{i=1}^n \phi(x_i - \theta) \prod_{j=1}^m \phi(Z_j - \theta) \right] \\ =& \sum_{i=1}^n \log\phi(x_i - \theta) + \sum_{j=1}^m E \log \phi(Z_j - \theta), \end{aligned}\] 其中\(Z_j\)独立，有共同密度\(\phi(z - \theta^{(t)})/[1 - \Phi(a-\theta^{(t)})]\),\(z>a\), 所以 \[\begin{aligned} Q_t(\theta) =& \sum_{i=1}^n \log\phi(x_i - \theta) + m \int_a^\infty \log \phi(z - \theta) \cdot \frac{\phi(z - \theta^{(t)})}{1 - \Phi(a-\theta^{(t)})} \,dz. \end{aligned}\]

在M步，要求\(Q_t(\theta)\)的最大值点。注意\(\frac{d}{dx} \log \phi(x) = \phi'(x)/\phi(x) = -x\), 得 \[\begin{aligned} Q_t'(\theta) =& \sum_{i=1}^n (x_i - \theta) + m \int_a^\infty (z - \theta) \frac{\phi(z - \theta^{(t)})}{1 - \Phi(a-\theta^{(t)})} \,dz \\ =& n \bar X - n \theta + m \int_a^\infty (z - \theta^{(t)}) \frac{\phi(z - \theta^{(t)})}{1 - \Phi(a-\theta^{(t)})} \,dz + m ( \theta^{(t)} - \theta) \\ =& n \bar X - n \theta + m\theta^{(t)} - m \theta + m \frac{1}{1 - \Phi(a - \theta^{(t)})}\int_{a - \theta^{(t)}}^\infty u \phi(u) \,du \\ & \quad(\text{令}u = z - \theta^{(t)}) \\ =& -(n+m)\theta + n \bar X + m\theta^{(t)} + m \frac{\phi(a-\theta^{(t)})}{1 - \Phi(a-\theta^{(t)})} . \end{aligned}\] 令\(Q_t'(\theta)=0\)得 \[\begin{align} \theta^{(t+1)} = \frac{1}{n+m} \left[ n \bar X + m\theta^{(t)} + m \frac{\phi(a-\theta^{(t)})}{1 - \Phi(a-\theta^{(t)})} \right] \tag{39.5} \end{align}\] 为\(Q_t(\theta)\)的最大值点。选取适当初值\(\theta^{(0)}\) 按(39.5)迭代就可以求得带有右删失数据的正态总体参数\(\theta\)的最大似然估计。

※※※※※

例39.7 (混合分布) EM算法可以用来估计混合分布的参数。设随机变量\(Y_1 \sim \text{N}(\mu_1, \delta_1)\), \(Y_2 \sim \text{N}(\mu_2, \delta_2)\), \(Y_1, Y_2\)独立。记\(N(\mu,\delta)\)的密度为\(f(x|\mu, \delta)\)。设随机变量\(W \sim \text{b}(1, \lambda)\), \(0<\lambda<1\), \(W\)与\(Y_1, Y_2\)独立，令 \[\begin{aligned} X = (1-W) Y_1 + W Y_2, \end{aligned}\] 则\(W=0\)条件下\(X \sim \text{N}(\mu_1, \delta_1)\), \(W=1\)条件下\(X \sim \text{N}(\mu_2, \delta_2)\), 但\(X\)的边缘密度为 \[\begin{aligned} f(x|\boldsymbol\theta) = (1-\lambda) f(x|\mu_1, \delta_1) + \lambda f(x|\mu_2, \delta_2) , \end{aligned}\] 其中\(\boldsymbol\theta=(\mu_1, \delta_1, \mu_2, \delta_2, \lambda)\)。

设\(X\)有样本\(\boldsymbol X = (X_1, \dots, X_n)\), 样本值为\(\boldsymbol x\)，实际观测数据的似然函数为 \[\begin{aligned} L(\boldsymbol\theta) = \prod_{i=1}^n f(x_i|\boldsymbol\theta) , \end{aligned}\] 这个函数是光滑函数但是形状很复杂，直接求极值很容易停留在局部极值点。

用EM算法，以\(\boldsymbol W = (W_1, \dots, W_n)\)为没有观测到的部分, 完全数据的似然函数和对数似然函数为 \[\begin{aligned} \tilde L(\boldsymbol\theta | \boldsymbol x, \boldsymbol W) =& \prod_{W_i=0} f(x_i | \mu_1, \delta_1) \ \prod_{W_i=1} f(x_i | \mu_2, \delta_2) \ \lambda^{\sum_{i=1}^n W_i} (1-\lambda)^{n - \sum_{i=1}^n W_i} , \nonumber\\ \tilde l(\boldsymbol\theta | \boldsymbol x, \boldsymbol W) =& \sum_{i=1}^n \Big[ (1-W_i) \log f(x_i | \mu_1, \delta_1) + W_i \log f(x_i | \mu_2, \delta_2) \Big] \nonumber\\ & + \left(\sum_{i=1}^n W_i \right) \log \lambda + \left(n - \sum_{i=1}^n W_i \right) \log(1-\lambda) . \end{aligned}\]

在E步，设已有\(\boldsymbol\theta\) 的近似值\(\boldsymbol\theta^{(t)} = (\mu_1^{(t)}, \delta_1^{(t)}, \mu_2^{(t)}, \delta_2^{(t)}, \lambda^{(t)})\), 以\(\boldsymbol\theta^{(t)}\)为分布参数，在\(\boldsymbol X = \boldsymbol x\)条件下， \(W_i\)的条件分布为 \[\begin{align} \gamma_i^{(t)} \stackrel{\triangle}{=} & P(W_i=1 | \boldsymbol x, \boldsymbol\theta^{(t)}) = P(W_i=1 | X_i=x_i, \boldsymbol\theta^{(t)}) \nonumber\\ =& \frac{\lambda^{(t)} f(x_i | \mu_2^{(t)}, \delta_2^{(t)})} { (1 - \lambda^{(t)}) f(x_i | \mu_1^{(t)}, \delta_1^{(t)}) + \lambda^{(t)} f(x_i | \mu_2^{(t)}, \delta_2^{(t)}) } . \tag{39.6} \end{align}\] 这里的推导类似于逆概率公式。利用\(W_i\)的条件分布求完全数据对数似然的期望，得 \[\begin{aligned} Q_t(\boldsymbol\theta) =& \sum_{i=1}^n \left[ (1 - \gamma_i^{(t)}) \log f(x_i | \mu_1, \delta_1) + \gamma_i^{(t)} \log f(x_i | \mu_2, \delta_2) \right] \nonumber\\ & + \left(\sum_{i=1}^n \gamma_i^{(t)} \right) \log \lambda + \left(n - \sum_{i=1}^n \gamma_i^{(t)} \right) \log(1-\lambda) . \end{aligned}\]

令\(\nabla Q_t(\boldsymbol\theta) = \boldsymbol 0\)，求得\(Q_t(\boldsymbol\theta)\)的最大值点\(\boldsymbol\theta^{(t+1)}\)为 \[\begin{align} \begin{cases} \mu_1^{(t+1)} = \frac{ \sum_{i=1}^n (1 - \gamma_i^{(t)}) x_i } { \sum_{i=1}^n (1 - \gamma_i^{(t)}) } \\ \delta_1^{(t+1)} = \frac{ \sum_{i=1}^n (1 - \gamma_i^{(t)}) (x_i - \mu_1^{(t+1)})^2 } { \sum_{i=1}^n (1 - \gamma_i^{(t)}) } \\ \mu_2^{(t+1)} = \frac{ \sum_{i=1}^n \gamma_i^{(t)} x_i } { \sum_{i=1}^n \gamma_i^{(t)} } \\ \delta_2^{(t+1)} = \frac{ \sum_{i=1}^n \gamma_i^{(t)}(x_i - \mu_2^{(t+1)})^2 } { \sum_{i=1}^n \gamma_i^{(t)} } \\ \lambda^{(t+1)} = \frac{1}{n} \sum_{i=1}^n \gamma_i^{(t)} \\ \end{cases} \tag{39.7} \end{align}\] 适当选取初值\(\boldsymbol\theta^{(0)}\)用(39.6)和(39.7)迭代就可以计算\(\boldsymbol\theta\)的最大似然估计。

※※※※※

习题

习题1

设\(f(\boldsymbol x)\), \(g(\boldsymbol x)\)是定义在集合\(A\)上的两个密度， \(f(\boldsymbol x)\), \(g(\boldsymbol x)\)在\(A\)上都为正值。证明如下信息不等式: \[\begin{align*} \int_A [\log f(\boldsymbol x) ] f(\boldsymbol x) \,d \boldsymbol x \geq \int_A [\log g(\boldsymbol x) ] f(\boldsymbol x) \,d \boldsymbol x . \end{align*}\]

习题2

设总体\(X\)服从如下的logistic分布: \[\begin{align*} f(x | \theta) =& \frac{\exp(-(x-\theta))}{(1 + \exp(-(x-\theta)))^2}, \ -\infty < x < \infty, \ -\infty < \theta < \infty, \end{align*}\] 设\(\boldsymbol X = (X_1, \dots, X_n)\)为\(X\)的简单随机样本。

写出对数似然函数\(l(\theta)\)和导数\(l'(\theta)\)。
证明方程\(l'(\theta)=0\)存在唯一解，解为最大似然估计。
写出用牛顿法求解方程\(l'(\theta)=0\)的迭代公式。
设一个样本为\(-0.63, 0.18, -0.84, 1.6, 0.33, -0.82, 0.49, 0.74, 0.58, -0.31\), 计算\(\hat\theta\)。

习题3

设总体\(X\)取值于正整数集合\(\mathbb Z_+ \stackrel{\triangle}{=} \{ 1, 2, 3, \dots \}\)，有概率函数 \[\begin{align*} p(x; \theta) = \theta^x x^{-1} [-\log(1-\theta)]^{-1}, \ x=1,2,\dots, \end{align*}\] 其中\(\theta \in (0, 1)\)为未知参数。设\(x_1, x_2, \dots, x_n\)为\(X\)的简单随机样本，设\(\sum_{i=1}^n x_n = s\)。

令\(f(\theta)\)为负对数似然函数，写出\(f(\theta)\)和\(g(\theta) = f'(\theta)\)以及\(g'(\theta)\)的表达式。
设\(n=10\), \(s=15\), 编写程序，作\(f(x)\)和\(g(x)\)的图像;
编写程序，分别用二分法、牛顿法和割线法求\(\theta\)的最大似然估计(即\(f(\theta)\)的最小值点)。

习题4

考虑如下最大似然估计计算问题。设\(X\)取值于\(\{1,2,3,4 \}\), 分布概率为\(p(x | \theta_1, \theta_2) \stackrel{\triangle}{=} \pi_x(\theta_1, \theta_2)\): \[\begin{align*} \pi_1(\theta_1, \theta_2) =& 2\theta_1 \theta_2, & \pi_2(\theta_1, \theta_2) =& \theta_1(2 - \theta_1 - 2\theta_2), \\ \pi_3(\theta_1, \theta_2) =& \theta_2(2 - \theta_2 - 2 \theta_1), & \pi_4(\theta_1, \theta_2) =& (1 - \theta_1 - \theta_2)^2. \end{align*}\] 设\(n\)次试验得到的\(X\)值有\(n_j\)个\(j\)(\(j=1,2,3,4\))，则对数似然函数为(去掉了与参数无关的加性常数) \[\begin{align*} l(\theta_1, \theta_2) = \sum_{j=1}^4 n_j \log \pi_j(\theta_1, \theta_2) \end{align*}\] 设\(n=435\), \(n_1=17\), \(n_2=182\), \(n_3=60\), \(n_4=176\)。编写程序，分别用牛顿法、阻尼牛顿法、BFGS方法、得分法和Nelder-Mead方法求最大似然估计，比较这几种方法的收敛速度。

习题5

设\(Y_i \sim \text{B}(m_i, \text{logit}^{-1}(\beta_0 + \beta_1 x_i))\), \(i=1,\dots,n\)相互独立，\(n=4\)， \((m_i, y_i, x_i)\)的4组数据为 \((55, 0, 7)\), \((157, 2, 14)\), \((159, 7, 27)\), \((16, 3, 51)\)。编写程序用牛顿法求\(\boldsymbol\beta=(\beta_0, \beta_1)\)的最大似然估计。写出模型的对数似然函数及其梯度、海色阵，写出最大似然估计的牛顿法迭代公式。

习题6

设随机变量\(Y_i \sim \text{Poisson}( \exp[ \boldsymbol\beta^T \boldsymbol x_i])\), \(i=1,2,\dots, n\), \(Y_1, \dots, Y_n\)相互独立， \(\boldsymbol\beta\)为未知参数向量，自变量\(\boldsymbol x_i, i=1,\dots,n\)已知。写出模型的对数似然函数及其梯度、海色阵，写出最大似然估计的牛顿法迭代公式。

习题7

写出例39.2中的简化似然函数\(\tilde l(\alpha)\)，编写程序，分别用二分法和牛顿法求\(\tilde l(\alpha)\)的最大值点。设有样本 \(0.08, 0.36, 0.35, 0.21, 0.39, 0.25, 0.23, 0.11, 0.07, 0.08\), 求参数最大似然估计。

习题8

设总体\(X\)服从威布尔分布W(\(\alpha, \eta\))，密度函数为 \[\begin{align*} p(x; \alpha,\eta) = \begin{cases} \frac{\alpha}{\eta} \left(\frac{x}{\eta} \right)^{\alpha-1} \exp\left\{ -\left(\frac{x}{\eta} \right)^{\alpha} \right\}, & x>0, \alpha>0, \eta>0, \\ 0, & \text{其它} \end{cases} \end{align*}\] 设\(X_1, X_2, \dots, X_n\)为\(X\)的简单随机样本。

求对数似然函数\(l(\alpha,\eta)\)及其梯度\(\nabla l(\alpha,\eta)\)、海色阵\(\nabla^2 l(\alpha,\eta)\);
编写程序，用牛顿法求最大似然估计；
用分步求最大值的方法，先对固定\(\alpha\)求最大值点\(\hat\eta(\alpha)\)，再关于\(\alpha\)求最大值，编写R程序实现算法；
用随机模拟方法生成多组样本，比较两种算法方法的收敛速度。比较随机模拟得到的最大似然估计的方差与牛顿法结束迭代时用海色阵得到的渐近方差。

习题9

考虑如下非线性回归模型： \[\begin{align*} y_i = A \cos(\omega x_i + \theta) + \varepsilon_i, \ i=1,2,\dots,n, \end{align*}\] 其中\(\varepsilon_i\)独立同\(\text{N}(0, \sigma^2)\)分布， \(A, \omega, \theta, \sigma^2\)为未知参数。设\(n=100\), \(x_i = 2\pi i/n\), \(A=10\), \(\omega=2\), \(\theta=0.5\), \(\sigma^2=2^2\)。编写程序，生成随机模拟样本, 分别用高斯–牛顿法和LMF方法给出参数最小二乘估计。

参考文献

Dempster, A. P., N. M. Lairdk, and D. B. Rubin. 1977. “Maximum Likelihood from Incomplete Data via the EM Algorithm.” Journal of the Royal Statistical Society, Series B 39: 1–38.

高立. 2014. 数值最优化方法. 北京大学出版社.