37 无约束优化方法
37.1 分块松弛法
对多元目标函数\(f(\boldsymbol x), \boldsymbol x \in \mathbb R^d\), 可以反复地分别沿每个坐标轴方向进行一维搜索, 称为坐标循环下降法。 按这种方法进行引申, 可以把\(\boldsymbol x\)的分量分成若干组, 每次固定其它分量不变, 针对某一组分量进行优化, 然后轮换其它组进行优化, 这样的方法叫做分块松弛法。 这种方法常常得到比较简单易行的算法, 只不过其收敛速度不一定是最优的。
例37.1 (k均值聚类) 设在\(\mathbb R^d\)中有\(n\)个点\(\boldsymbol x^{(i)}, i=1,\dots,n\), 要把这\(n\)个点按照距离分为\(k\)个类。 设\(C = \{ C_1, \dots, C_k \}\), \(C_j\)是分到第\(j\)个类中的点的集合, \(\boldsymbol\mu = \{ \boldsymbol\mu_1, \dots, \boldsymbol\mu_k \}\)是各类的中心(该类中的点的均值), 聚类问题就是求\(C\)和\(\boldsymbol\mu\)使得 \[\begin{align} f(\boldsymbol\mu, C) = \sum_{j=1}^k \sum_{\boldsymbol x^{(i)} \in C_j} \| \boldsymbol x^{(i)} - \boldsymbol\mu_j \|^2 \end{align}\] 最小。
如果已知\(\boldsymbol\mu\),则对每个点计算该点到每个\(\boldsymbol\mu_j\)的距离, 把该点归类到距离最近的类中。 如果已知\(C\),则\(\boldsymbol\mu_j\)取第\(j\)类所有点的平均值。
在\(\boldsymbol\mu\)和\(C\)都未知的情况下求\(f(\boldsymbol\mu, \boldsymbol C)\)的最小值点,可以使用分块松弛法。 作为初始中心,可以随机地选\(k\)个不同的\(\boldsymbol x^{(i)}\)点当作初始的\(\boldsymbol\mu_j, j=1,\dots,k\), 但是最好能让这\(k\)个初始中心相互距离远一些。 然后,轮流地,先把所有点按照到类中心的距离分配到\(k\)个类中, 再重新计算类中心\(\{ \boldsymbol\mu_j \}\), 如此重复直到结果不再变动。 这个算法简单有效。
※※※※※
37.2 梯度法
37.2.1 最速下降法
在目标函数\(f(\boldsymbol x)\)一阶可导时, 应利用导数(梯度)的信息, 向负梯度方向搜索前进, 使得每一步的目标函数值都减小。 最速下降法沿负梯度方向搜索找到函数值下降最多的步长, 基本的算法为:
| 最速下降法 |
|---|
| 取初值\(\boldsymbol x^{(0)} \in \mathbb R^d\), 置\(t \leftarrow 0\) |
| until (迭代收敛) { |
| \(\qquad\) 求\(\boldsymbol g^{(t)} \leftarrow -\nabla f(\boldsymbol x^{(t)})\) |
| \(\qquad\) 求最优步长\(\lambda_t > 0\)使得 \(f(\boldsymbol x^{(t)} + \lambda_t \boldsymbol g^{(t)}) = \min\limits_{\lambda>0} f(\boldsymbol x^{(t)} + \lambda \boldsymbol g^{(t)})\) |
| \(\qquad\) \(\boldsymbol x^{(t+1)} \leftarrow \boldsymbol x^{(t)} + \lambda_t \boldsymbol g^{(t)}\) |
| } |
| 输出\(\boldsymbol x^{(t+1)}\)作为极小值点 |
在算法中,“迭代收敛”可以用梯度向量长度小于某个预定值, 或者两次迭代间函数值变化小于某个预定值来判断。 迭代中需要用某种一维搜索方法求步长\(\lambda_t\)。
在适当正则性条件下, 最速下降法可以收敛到局部极小值点并且具有线性收敛速度。 但是, 最速下降法连续两次的下降方向\(-\nabla f(\boldsymbol x^{(t)})\)和 \(-\nabla f(\boldsymbol x^{(t+1)})\)是正交的, 这是因为在第\(t\)步沿\(-\nabla f(\boldsymbol x^{(t)})\) 搜索时找到点\(\boldsymbol x^{(t+1)}\)时已经使得函数值在该方向上不再变化, 下一个搜索方向如果与该方向不正交就不是下降最快的方向。 这样,最速下降法收敛速度比较慢。 所以, 在每次迭代的一维搜索时, 可以不要求找到一维搜索的极小值点, 而是函数值足够降低就结束一维搜索。 见沃尔夫准则。
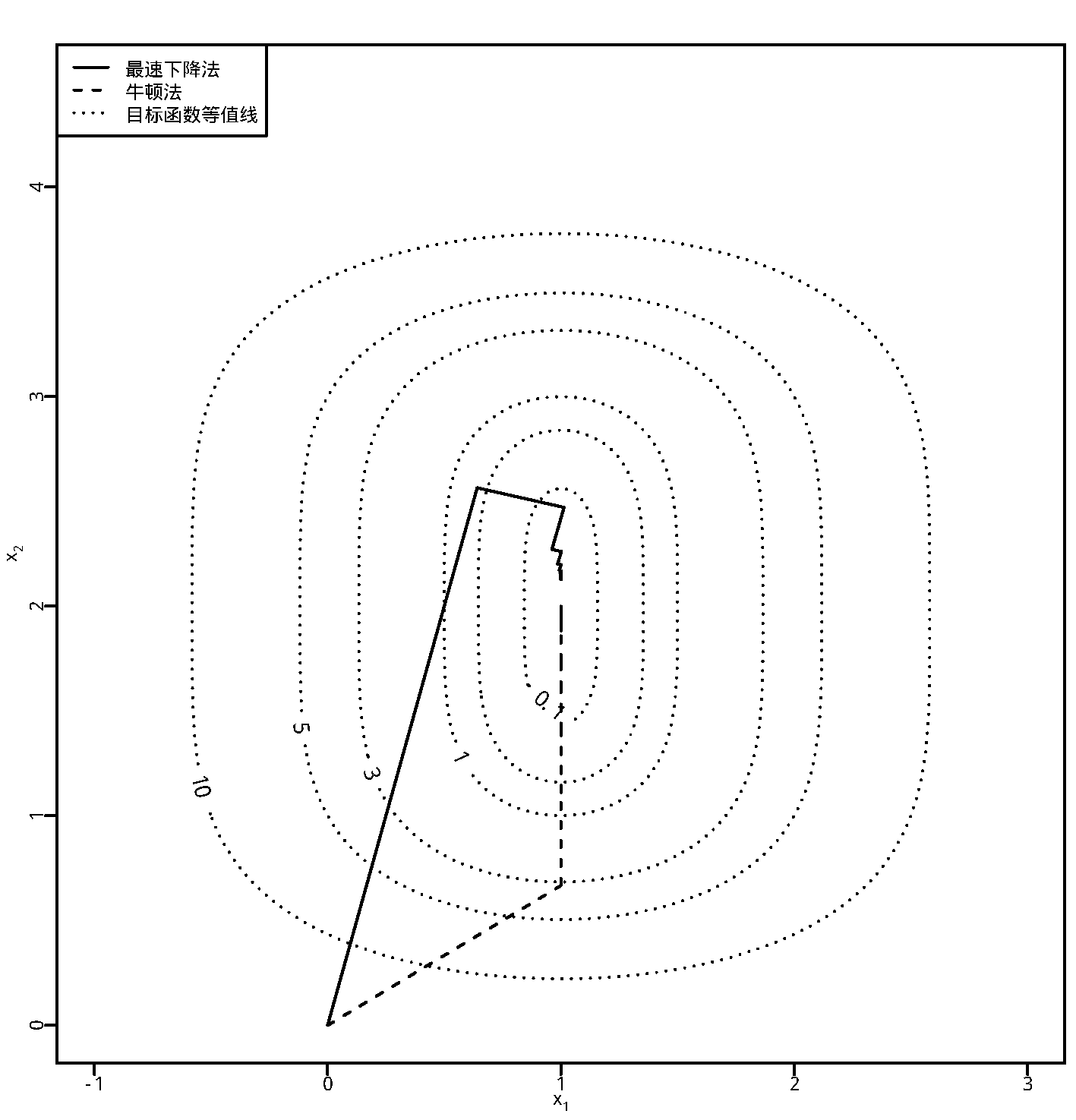
图37.1: 最速下降法和牛顿法
例37.2 求解无约束最优化问题 \[\begin{aligned} \mathop{\text{argmin}}_{(x_1, x_2) \in \mathbb R^2} 4 (x_1 - 1)^2 + (x_2 - 2)^4 . \end{aligned}\]
显然,函数有全局最小值点\(\boldsymbol x^* = (1, 2)\)。
用最速下降法求解。易见 \[\begin{aligned} \nabla f(\boldsymbol x) =& \left( 8(x_1 - 1), \; 4 (x_2 - 2)^3 \right)^T, \end{aligned}\] 假设从点\(\boldsymbol x^{(0)} = (0, 0)\)出发,函数的等值线图以及迭代轨迹见图37.1中的实线, 轨迹中部分点坐标如下: \[\begin{aligned} & \boldsymbol x^{(1)} = (0.641, 2.565), \ \boldsymbol x^{(2)} = (1.014, 2.471), \ \boldsymbol x^{(3)} = (0.962, 2.471), \ \boldsymbol x^{(4)} = (1.002, 2.271), \\ & \boldsymbol x^{(5)} = (0.986, 2.202), \ \boldsymbol x^{(6)} = (1.001, 2.197), \ \ldots, \ \boldsymbol x^{(10)} = (1.001, 2.156), \\ & \boldsymbol x^{(20)} = (1.001, 2.127), \ \boldsymbol x^{(40)} = (1.001, 2.099), \ \boldsymbol x^{(60)} = (1.001, 2.083), \ \boldsymbol x^{(80)} = (1.001, 2.074), \\ & \boldsymbol x^{(100)} = (1.001, 2.067), \ \boldsymbol x^{(150)} = (1.001, 2.055), \ \boldsymbol x^{(200)} = (1.001, 2.048) \end{aligned}\]
使用R函数optim求解(不是最速下降法):
结果:
$par
[1] 1.000000 2.001276
$value
[1] 2.648515e-12
$counts
function gradient
121 98
$convergence
[1] 0
$message
NULL使用Julia的Optim包求解:
using Optim
function f(xvec)
x, y = xvec
4*(x-1)^2 + (y-2)^4
end
# 使用BFGS方法求解,使用自动微分方法
ores = optimize(f, [0.0, 0.0], Newton(); autodiff = :forward)
@show Optim.minimizer(ores);结果:
* Status: success
* Candidate solution
Final objective value: 7.322602e-29
* Found with
Algorithm: Newton's Method
* Convergence measures
|x - x'| = 4.63e-08 ≰ 0.0e+00
|x - x'|/|x'| = 2.31e-08 ≰ 0.0e+00
|f(x) - f(x')| = 2.86e-17 ≰ 0.0e+00
|f(x) - f(x')|/|f(x')| = 3.90e+11 ≰ 0.0e+00
|g(x)| = 3.17e-21 ≤ 1.0e-08
* Work counters
Seconds run: 0 (vs limit Inf)
Iterations: 10
f(x) calls: 31
∇f(x) calls: 31
∇²f(x) calls: 10
Optim.minimizer(ores) = [1.0, 1.9999999074947545]※※※※※
从例子可以看出,最速下降法的相邻两次搜索方向正交, 而且越到最小值点附近接近得越慢。 所以,一维搜索不必找到一维的最小值点, 而是使得函数值足够降低就可以了。
37.2.2 梯度下降法
现代机器学习(统计学习)算法中普遍使用最速下降法的各种变种, 称为梯度下降法,公式为: \[\begin{align} \boldsymbol x^{(t+1)} \leftarrow \boldsymbol x^{(t)} + \lambda_t \boldsymbol g^{(t)}, \tag{37.1} \end{align}\] 其中\(\lambda_t\)不是通过一维搜索得到而是预先设定, 一般取为很小的正数, 称为学习速率。 如果取\(\lambda_t\)为常数, 则较大的\(\lambda_t\)使得收敛较快, 但有可能跨越最小值点; 较小的\(\lambda_t\)收敛比较稳定但速度太慢。 也可以取\(\lambda_t \to 0\), 比如取\(\lambda_t = \lambda_0 \rho^t\)(\(0 < \rho < 1\))。 这避免了两次搜索方向总是正交的问题, 在统计学习中可以减少过度拟合。
37.2.3 随机梯度下降法
许多机器学习算法基于最小化平均损失: \[\begin{align} \min_{\boldsymbol\theta} \frac{1}{N} \sum_{i=1}^N L(\boldsymbol y_i; \boldsymbol \theta), \tag{37.2} \end{align}\] 其中\(\boldsymbol y_i\)是独立同分布样本观测, \(L(\boldsymbol y_i; \boldsymbol \theta)\)是模型参数为\(\boldsymbol \theta\)时第\(i\)个观测对损失函数的贡献, 如残差平方,负对数似然值。 如果对上述目标函数用梯度法求最小值点, 当样本量\(N\)特别巨大时, 计算每一个\(\frac{\partial}{\partial \boldsymbol \theta} L(\boldsymbol y_i; \boldsymbol \theta)\)会占用过多的计算资源使得算法不可行。 这时, 注意到 \[ \frac{1}{N} \sum_{i=1}^N L(\boldsymbol y_i; \theta) \approx E [L(\boldsymbol y; \boldsymbol\theta)], \] 在迭代的第\(t\)步, 可以从\(N\)个样本点中随机抽取\(N' \ll N\)个样本, 记这些抽取的子样本下标集合为\(S_t\), 用 \[ \frac{1}{N'} \sum_{i \in S_t} L(\boldsymbol y_i; \boldsymbol\theta^{(t)}) \] 估计(37.2)目标函数, 取 \[ \boldsymbol g^{(t)} = - \frac{1}{N'} \sum_{i \in S_t} \frac{\partial}{\partial \boldsymbol \theta} L(\boldsymbol y_i; \boldsymbol\theta^{(t)}) , \] 作迭代 \[\begin{align} \boldsymbol\theta^{(t+1)} = \boldsymbol\theta^{(t)} + \lambda_t \boldsymbol g^{(t)} . \tag{37.3} \end{align}\] 每一步重新抽样并利用(37.3)进行优化逼近, 称这种方法为随机梯度法。
当\(N\)特别巨大时, \(N'\)可以不随\(N\)的增大而增大, 使得梯度法能适用于训练样本量过于巨大的训练数据集。
在深度学习中, 取一个固定的较小的\(N'\), 每次顺序地从所有样本点中抽取\(N'\)个, 用(37.3)更新参数值, 称为小批次随机梯度下降法。 这样可以处理样本量很大的问题, 算法也更高效。
37.2.4 共轭梯度法(*)
最速下降法收敛速度较慢, 而且越靠近最小值点步长越短, 速度越慢。 对于一个函数曲面为狭长的山谷形状的目标函数, 为了达到山谷的最低点, 会沿相互正交的梯度方向反复跳跃。
一种解决的方法是前面所说的不使用最优一维搜索而是使用预先确定的步长或步长序列, 还有一种方法是将两步之间的梯度正交, 推广到两步之间为“共轭”关系,即对某个矩阵\(A_t\)使得 \[ \;[\boldsymbol g^{(t)}]^T A_t \boldsymbol g^{(t+1)} = 0 . \]
这种方法的来源是对目标函数\(f(\boldsymbol x)\)用二次多项式近似: \[ f(\boldsymbol x) \approx \frac{1}{2} \boldsymbol x^T A \boldsymbol x + \boldsymbol b^T \boldsymbol x + c, \] 而为了将一个\(d\)元的凸二次多项式达到最小值点, 只要从负梯度方向出发,沿着\(d\)个相互都关于\(A\)共轭的方向进行一维搜索就保证达到最小值点。 连续可微函数在最小值点附近一般都很接近于一个凸二次多项式函数, 所以共轭梯度法能够克服最速下降法在靠近最小值点时收敛变慢的问题。
\(A_t\)矩阵选取最好是海色阵\(\nabla^2 f(\boldsymbol x^{(t)})\), 但海色阵一般比梯度更难获得, 使用海色阵的方法见节37.3和节37.4。 共轭梯度法实际的算法并不去求\(A_t\), 而是从\(\boldsymbol x^{(1)}\)的负梯度出发, 然后每次用当前\(\boldsymbol x^{(t)}\)处的负梯度和上一步的共轭方向的线性组合作为\(t\)到\(t+1\)步的搜索方向。即:
\[\begin{aligned} \boldsymbol d^{(1)} =& -\boldsymbol g^{(1)}; \\ \boldsymbol d^{(t)} =& -\boldsymbol g^{(t)} + \beta^{(t)} \boldsymbol d^{(t-1)}, \ t=2,3,\ldots. \end{aligned}\]
对\(d\)元凸二次多项式,其中的系数\(\beta^{(t)}\)可以用\(A\)解出精确公式, 使得各个\(d^{(t)}\)彼此共轭。 但是对一般目标函数\(f(\boldsymbol x)\), 只能使用一些近似的\(\beta^{(t)}\), 方法如:
\[\begin{aligned} \text{Fletcher-Reeves: } & \beta^{(k)} = \max\left(0, \; \frac{[\boldsymbol g^{(k)}]^T \boldsymbol g^{(k)} }{ [\boldsymbol g^{(k-1)}]^T \boldsymbol g^{(k-1)} } \right) . \\ \text{Polak-Ribière: } & \beta^{(k)} = \frac{[\boldsymbol g^{(k)}]^T [\boldsymbol g^{(k)} - \boldsymbol g^{(k-1)}] }{ [\boldsymbol g^{(k-1)}]^T \boldsymbol g^{(k-1)} } . \end{aligned}\]
Fletcher-Reeves共轭梯度法在极小值点附近可以确保收敛。
参见:(Kochenderfer 2019)。
37.2.5 动量方法(*)
梯度方法在梯度很接近于0的地方也会移动很慢。 “动量”方法可以将前面的梯度方向进行保存, 与当前的梯度方向作线性组合, 从而可以积累朝向一个搜索方向的“动量”, 就好比一个球在比较平坦的曲面滚动, 如果下降方向是相对固定的, 即使开始时滚动比较慢, 积累的朝向正确下降方向的动量也会使得速度变快。 算法迭代公式为:
\[\begin{aligned} \boldsymbol v^{(k+1)} =& \beta \boldsymbol v^{(k)} - \alpha \boldsymbol g^{(k)}, \\ \boldsymbol x^{(k+1)} =& \boldsymbol x^{(k)} + \boldsymbol v^{(k+1)} . \end{aligned}\]
其中\(\boldsymbol v^{(k)}\)起到了将以往的梯度进行累积的作用, 系数\(\beta\)代表这种记忆的衰减因子, \(\alpha\)代表对当前负梯度方向的贡献的衰减。 最速下降法会在相互正交的方向上反复转折, 而动量方法则会积累并放大正确的下降方向的作用, 使得在梯度接近于零的位置的下降方向变快。
动量法的缺点是在靠近最小值点处的前进速度不会下降, 可能会跨过最小值点。 一种改进(称为Nesterov方法)是使用沿上一步相同方向前进一步处梯度, 而不是当前点的梯度, 这样如果前进一步后的梯度与当前搜索方向变得相反, 就可以起到减慢前进速度的作用。迭代公式为:
\[\begin{aligned} \boldsymbol v^{(k+1)} =& \beta \boldsymbol v^{(k)} - \alpha \nabla f(\boldsymbol x^{(k)} + \beta \boldsymbol v^{(k)}), \\ \boldsymbol x^{(k+1)} =& \boldsymbol x^{(k)} + \boldsymbol v^{(k+1)} . \end{aligned}\]
动量法还有许多针对学习速率的改进, 比如, 对于每个自变量分量分别使用不同步长的Adagrad算法, Adagrad的改进RMSProp算法, Adadelta算法,Adam算法。
37.2.6 超梯度下降方法(*)
梯度下降方法(37.1)中的学习速率\(\lambda_t\)是决定梯度下降法性能的关键。 超梯度下降法将学习速度\(\lambda_t\)作为优化任务的自变量之一, 使用如下的学习速度:
\[\begin{align} \lambda_t = \lambda_{t-1} + \mu [\boldsymbol g^{(k)}]^T \boldsymbol g^{(k-1)}, \tag{37.4} \end{align}\] 其中参数\(\mu\)称为超梯度学习速率。
这个公式是将\(\lambda_t\)作为最优化\(f\)的自变量使用梯度下降方法产生的。 令 \[ h(\lambda) = f(\boldsymbol x^{(t-1)} - \lambda \boldsymbol g^{(t-1)}), \] 则 \[ h(\lambda_{t-1}) = f(\boldsymbol x^{(t)}), \] 可计算得 \[ h'(\lambda) = \frac{\partial f(\boldsymbol x^{(t-1)} - \lambda \boldsymbol g^{(t-1)})}{\partial(- \boldsymbol g^{(t-1)})} \] 于是 \[ h'(\lambda_{t-1}) = [\nabla f(\boldsymbol x^{(t)})]^T (- \boldsymbol g^{(t-1)}) = - [\boldsymbol g^{(t)}]^T \boldsymbol g^{(t-1)} . \] 然后对\(h(\lambda)\)使用学习率为\(\mu\)的梯度下降法, 即 \[ \lambda_t = \lambda_{t-1} - \mu h'(\lambda_{t-1}) . \]
此方法的优点是克服了梯度下降方法对学习速率的敏感问题。 公式(37.4)中的\(\boldsymbol g^{(k)}\)也可以取为其它的下降方向如动量法的方向。
参见:(Kochenderfer 2019)第5章。
37.3 牛顿法
牛顿法利用海色阵和梯度向量求下一步, 不需要一维搜索, 对于二次多项式函数可以一步得到最小值点。 许多光滑的目标函数在靠近极小值点的邻域内可以很好地用凸二阶多项式逼近。 对一个存在二阶连续偏导的\(d\)元函数\(f(\boldsymbol x)\), 有如下的泰勒近似 \[\begin{align} f(\boldsymbol x) \approx f(\boldsymbol x^{(0)}) + \nabla f(\boldsymbol x_0)^T (\boldsymbol x - \boldsymbol x^{(0)}) + \frac12 (\boldsymbol x - \boldsymbol x^{(0)})^T \nabla^2 f(\boldsymbol x^{(0)}) (\boldsymbol x - \boldsymbol x^{(0)}), \tag{37.5} \end{align}\] 若\(\nabla^2 f(\boldsymbol x^{(0)})\)为正定矩阵,上式右侧的二次多项式函数的最小值点在 \[\begin{aligned} \boldsymbol x^* = \boldsymbol x^{(0)} - \left[\nabla^2 f(\boldsymbol x^{(0)}) \right]^{-1} \, \nabla f(\boldsymbol x^{(0)}) \end{aligned}\] 处达到。所以牛顿法取初值\(\boldsymbol x^{(0)}\)后,用公式 \[\begin{align} \boldsymbol x^{(t+1)} = \boldsymbol x^{(t)} - \left[\nabla^2 f(\boldsymbol x^{(t)}) \right]^{-1} \, \nabla f(\boldsymbol x^{(t)}), \ t=0,1,2,\dots \tag{37.6} \end{align}\] 进行迭代,直至收敛。 收敛的判断准则可以取为\(\| \nabla \boldsymbol f(x) \|\)足够小, 或者取为\(| f(\boldsymbol x^{(t+1)}) - f(\boldsymbol x^{(t)}) |\)足够小。
(37.6)在算法实现时, 应将逆矩阵表示改为如下的线性方程组求解: \[\begin{align} \nabla^2 f(\boldsymbol x^{(t)}) \boldsymbol d^{(t)} = -\nabla f(\boldsymbol x^{(t)}), \quad \boldsymbol x^{(t+1)} = \boldsymbol x^{(t)} - \boldsymbol d^{(t)} \tag{37.7} \end{align}\]
如果初值接近于最小值点并且目标函数满足一定正则性条件, 牛顿法有二阶收敛速度。
牛顿法的性能对海色阵\(H(\boldsymbol x)\)十分依赖。 如果\(H(\boldsymbol x^{(t)})\)不满秩, 则(37.7)的解不唯一, 算法无法进行; 如果\(H(\boldsymbol x^{(t)})\)很接近于不满秩, 则\(H(\boldsymbol x^{(t)})^{-1} \nabla f(\boldsymbol x^{(t)})\)的计算很不稳定, 而且会将下一个近似点\(\boldsymbol x^{(t+1)}\)远离\(\boldsymbol x^{(t)}\),这很可能会使得逼近失败。 另外,从(37.5)看出, 海色阵也是函数的局部性质的重要特征。 如果\(\boldsymbol x_*\)是一个稳定点, 即\(\nabla f(\boldsymbol x_*)=0\), 海色阵与此处目标函数的曲面形状密切相关。 如果\(H(\boldsymbol x_*)\)是正定的, 则\(\boldsymbol x_*\)是局部极小值点。 如果\(H(\boldsymbol x_*)\)是负定的, 则\(\boldsymbol x_*\)是局部极大值点。 如果\(H(\boldsymbol x_*)\)既有正特征值又有负特征值, 则\(\boldsymbol x_*\)是目标函数的鞍点,不是局部极值点。
使用牛顿法求最小值时, 最好的情况是海色阵始终为正定阵, 这时函数是严格凸函数, 极小值点也是全局最小值点。 在线性最小二乘问题中(见节35.2.1), 目标函数的海色阵是\(X^T X\)矩阵。
如果目标函数非负定但是接近于不满秩, 可以考虑给\(H(\boldsymbol x^{(t)})\)加一个对角的正定阵, 例如,岭回归就是将\(X^T X\)替换成\(X^T X + \lambda I\)。
例37.3 再次考虑例37.2,用牛顿法。
易见\(f(\boldsymbol x)\)的海色阵为 \[\begin{aligned} \nabla^2 f(\boldsymbol x) = \left(\begin{array}{cc} 8 & 0 \\ 0 & 12 (x_2 - 2)^2 \end{array}\right), \end{aligned}\] 用牛顿法,迭代公式为 \[\begin{aligned} \boldsymbol x^{(t)} = \boldsymbol x^{(t-1)} - \left[\nabla^2 f(\boldsymbol x^{(t-1)}) \right]^{-1} \, \nabla f(\boldsymbol x^{(t-1)}) = \boldsymbol x^{(t-1)} - (x_1 - 1, \; \frac13 (x_2 - 2))^T. \end{aligned}\] 迭代过程见图37.1中的虚线。 轨迹中部分点坐标如下: \[\begin{aligned} & \boldsymbol x^{(1)} = (1, 0.667), \ \boldsymbol x^{(2)} = (1, 1.111), \ \boldsymbol x^{(3)} = (1, 1.407), \ \boldsymbol x^{(4)} = (1, 1.605), \\ & \boldsymbol x^{(5)} = (1, 1.737), \ \boldsymbol x^{(6)} = (1, 1.824), \ \ldots, \ \boldsymbol x^{(10)} = (1, 1.965), \\ & \boldsymbol x^{(15)} = (1, 1.995), \ \boldsymbol x^{(20)} = (1, 1.999) \end{aligned}\] 没有发生最速下降法那样反复折向前进的问题, 而且收敛速度相对较快。
※※※※※
37.3.1 阻尼牛顿法
牛顿法在目标函数具有较好光滑性而且海色阵正定时有很好的收敛速度。 但是,牛顿法需要目标函数有二阶导数, 还需要在每步迭代都计算海色阵的逆矩阵, 在海色阵非正定时可能会失败。
在公式(37.6)中, 把其中的海色阵\(\nabla^2 f(\boldsymbol x^{(t)})\) 替换成一个保证正定的矩阵\(H_t\), 则\(-H_t^{-1} \nabla f(\boldsymbol x^{(t)})\)是\(f(\boldsymbol x)\)在\(\boldsymbol x^{(t)}\)处的一个下降方向, 即当\(\lambda>0\)充分小而且\(\nabla f(\boldsymbol x^{(t)}) \neq \boldsymbol 0\)时一定有 \[\begin{aligned} f\left( \boldsymbol x^{(t)} - \lambda H_t^{-1} \nabla f(\boldsymbol x^{(t)}) \right) < f(\boldsymbol x^{(t)}), \end{aligned}\] 于是可以用一维搜索方法求步长\(\lambda_{t+1}\)使得 \[\begin{align} \begin{cases} \lambda_{t+1} =& \mathop{\text{argmin}}_{\lambda > 0} f\left( \boldsymbol x^{(t)} - \lambda H_t^{-1} \nabla f(\boldsymbol x^{(t)}) \right), \\ \boldsymbol x^{(t+1)} =& \boldsymbol x^{(t)} - \lambda_t H_t^{-1} \nabla f(\boldsymbol x^{(t)}). \end{cases} \tag{37.8} \end{align}\] 这样得到了保证函数值每次迭代都下降的算法。
这里正定矩阵\(H_t\)的选取有各种各样的方法, 比如,取\(H_t\)为单位阵,则(37.8)变成最速下降法。
在(37.8)中取\(H_t\)为海色阵\(\nabla^2 f(\boldsymbol x^{(t)})\), 算法就变成增加了一维搜索的牛顿法, 称之为阻尼牛顿法。 其中的步长\(\lambda_{t+1}\)可以用一种一维搜索方法来求, 最简单的做法是, 依次考虑\(\lambda=1, 1/2, 1/4, \dots\), 一旦\(f\left( \boldsymbol x^{(t)} - \lambda H_t^{-1} \nabla f(\boldsymbol x^{(t)}) \right) < f(\boldsymbol x^{(t)})\)就停止搜索。 阻尼牛顿法也需要海色阵正定, 所以实际使用阻尼牛顿法时, 如果某步的海色阵不可逆或者\(\left[ \nabla f(\boldsymbol x^{(t)}) \right]^T \left[\nabla^2 f(\boldsymbol x^{(t)}) \right]^{-1} \nabla f(\boldsymbol x^{(t)}) \leq 0\), 可以在此步以\(-\nabla f(\boldsymbol x^{(t)})\)为搜索方向(最速下降法), 这样修改后可以使得阻尼牛顿法每步都减小目标函数值。
最速下降法、牛顿法、阻尼牛顿法在迭代中遇到不是局部最小值点的稳定点时都不能正常运行。 这时需要一些特殊的方法求得下降方向。 参见 徐成贤, 陈志平, and 李乃成 (2002) §3.2.2。
37.4 拟牛顿法
另外一些构造公式(37.8)中\(H_t\)的方法可以不用计算二阶偏导数而仅需要计算目标函数值和一阶偏导数值, 可以迭代地构造\(H_t\)或\(H_t^{-1}\), 这样的算法有很多,统称为拟牛顿法或变尺度法。 这样的\(H_t\)应该满足如下条件:
- \(H_t\)是对称正定阵,从而\(\boldsymbol d^{(t)} \stackrel{\triangle}{=} - H_t^{-1} \nabla f(\boldsymbol x^{(t)})\)是下降方向(称\(\boldsymbol d^{(t)}\)为拟牛顿方向)。
- \(H_{t+1}\)由\(H_t\)迭代得到: \[\begin{align*} H_{t+1} = H_t + \Delta H_t, \end{align*}\] 称\(\Delta H_t\)是修正矩阵。
- \(H_{t+1}\)必须满足如下拟牛顿条件: \[\begin{align} H_{t+1} \boldsymbol\delta^{(t)} = \boldsymbol\zeta^{(t)} . \tag{37.9} \end{align}\] 其中\(\boldsymbol\delta^{(t)} \stackrel{\triangle}{=} \boldsymbol x^{(t+1)} - \boldsymbol x^{(t)}\), \(\boldsymbol\zeta^{(t)} \stackrel{\triangle}{=} \nabla f(\boldsymbol x^{(t+1)}) - \nabla f(\boldsymbol x^{(t)})\)。
第二条可以替换成\(H_{t+1}^{-1}\)可以用\(H_{t}^{-1}\)递推得到。 前两个条件比较自然,下面解释第三个条件的理由。
设迭代已经得到了\(H_t\)和\(\boldsymbol x^{(t+1)}\), 需要给出下一步的\(H_{t+1}\)。 把\(f(\boldsymbol x)\)在\(\boldsymbol x^{(t+1)}\)处作二阶泰勒展开得 \[\begin{aligned} f(\boldsymbol x) \approx& f(\boldsymbol x^{(t+1)}) + \nabla f(\boldsymbol x^{(t+1)})^T (\boldsymbol x - \boldsymbol x^{(t+1)}) \nonumber\\ & + \frac12 (\boldsymbol x - \boldsymbol x^{(t+1)})^T \nabla^2 f(\boldsymbol x^{(t+1)}) (\boldsymbol x - \boldsymbol x^{(t+1)}), \end{aligned}\] 这意味着 \[\begin{aligned} \nabla f(\boldsymbol x) \approx \nabla f(\boldsymbol x^{(t+1)}) + \nabla^2 f(\boldsymbol x^{(t+1)}) (\boldsymbol x - \boldsymbol x^{(t+1)}), \end{aligned}\] 在上式中取\(\boldsymbol x = \boldsymbol x^{(t)}\)得 \[\begin{aligned} \nabla f(\boldsymbol x^{(t)}) \approx \nabla f(\boldsymbol x^{(t+1)}) + \nabla^2 f(\boldsymbol x^{(t+1)}) (\boldsymbol x^{(t)} - \boldsymbol x^{(t+1)}) , \end{aligned}\] 则有 \[\begin{aligned} \nabla^2 f(\boldsymbol x^{(t+1)}) (\boldsymbol x^{(t+1)} - \boldsymbol x^{(t)}) \approx \nabla f(\boldsymbol x^{(t+1)}) - \nabla f(\boldsymbol x^{(t)}) = \boldsymbol\zeta^{(t)}, \end{aligned}\] 因为\(H_{t+1}\)是用来代替海色阵的,所以根据上式需要\(H_{t+1}\)满足拟牛顿条件(37.9)。
37.4.1 BFGS拟牛顿法
修正矩阵\(\Delta H_t\)有多种取法, 其中一种比较高效而稳定的算法称为BFGS算法 (Broyden-Fletcher-Goldfarb-Shanno), 在多元目标函数无约束优化问题中被广泛应用。 BFGS算法的修正公式为 \[\begin{align} H_{t+1} = H_t + \frac{\boldsymbol\zeta^{(t)} (\boldsymbol\zeta^{(t)})^T} {(\boldsymbol\zeta^{(t)})^T \boldsymbol\delta^{(t)}} - \frac{(H_t \boldsymbol\delta^{(t)}) \; (H_t \boldsymbol\delta^{(t)})^T}{(\boldsymbol\delta^{(t)})^T H_t \boldsymbol\delta^{(t)}}, \tag{37.10} \end{align}\] 一般取初值\(H_0\)为单位阵, 这样按(37.8)和(37.10)迭代, 如果一维搜索采用精确一维搜索或沃尔夫准则, (37.10)中的分母\((\boldsymbol\zeta^{(t)})^T \boldsymbol\delta^{(t)}\)可以保证为正值, 使得\(\{ H_t \}\)总是对称正定矩阵, 搜索方向\(-H_t^{-1} \nabla f(\boldsymbol x^{(t)})\)总是下降方向。 在适当正则性条件下BFGS方法具有超线性收敛速度。 详见 徐成贤, 陈志平, and 李乃成 (2002) §3.3。
在(37.8)中计算\(H_t^{-1} \nabla f(\boldsymbol x^{(t)})\)要解一个线性方程组, 需要\(O(d^3)\)阶的计算量(\(d\)是\(\boldsymbol x\)的维数)。 事实上,在BFGS算法中\(H_t^{-1}\)可以递推计算而不需直接求逆或求解线性方程组。 记\(V_t = H_t^{-1}\), 这些逆矩阵有如下递推公式: \[\begin{aligned} V_{t+1} =& V_t + \left[ 1 + \frac{(\boldsymbol\zeta^{(t)})^T V_t \boldsymbol\zeta^{(t)}} {(\boldsymbol\zeta^{(t)})^T \boldsymbol\delta^{(t)}} \right] \frac{\boldsymbol\delta^{(t)} (\boldsymbol\delta^{(t)})^T} {(\boldsymbol\zeta^{(t)})^T \boldsymbol\delta^{(t)}} - \frac{H_t \boldsymbol\zeta^{(t)} (\boldsymbol\delta^{(t)})^T + \left[ H_t \boldsymbol\zeta^{(t)} (\boldsymbol\delta^{(t)})^T \right]^T} {(\boldsymbol\zeta^{(t)})^T \boldsymbol\delta^{(t)}} . \end{aligned}\]
37.5 Nelder-Mead方法
在导数不存在或很难获得时, 求解多元函数无约束最小值经常使用Nelder-Mead单纯型方法 (Nelder and Mead 1965)。 单纯型(simplex)指在\(\mathbb R^d\)空间中的\(d+1\)个点作为顶点的图形构成的凸集, 比如,在\(\mathbb R^2\)中给定了三个顶点的一个三角形是一个单纯型, 在\(\mathbb R^3\)中给定了四个顶点的一个四面体是一个单纯型。 单纯型是\(\mathbb R^d\)中最简单的多面体。
Nelder-Mead方法是一种直接搜索算法,不使用导数或数值导数。 算法开始时要找到\(d+1\)个点\(\boldsymbol x_0, \boldsymbol x_1, \dots, \boldsymbol x_d\)构成一个单纯型 (要求这\(d+1\)个点不能位于一个超平面内), 计算相应的目标函数值\(y_j = f(\boldsymbol x_j), j=0,1,\dots,d\)。 然后,进行反复迭代, 对当前的单纯型进行变换使得目标函数值变小。 单纯型在开始没有找到最小值点附近时可以沿目标函数值下降的方向扩大, 以包含最小值点所在区域; 可以保持大小不变移动位置, 以接近最小值点; 在靠近最小值点后可以缩小以获得精确搜索结果。 迭代在单纯型变得足够小或者函数值的变化变得足够小时结束, 保险起见,如果迭代次数超过一个预定次数就认为算法失败而结束。
选取初值时,可以任意选取初值\(\boldsymbol x_0\), 然后其他\(d\)个点可以从\(\boldsymbol x_0\)出发分别沿\(d\)个正坐标轴方向前进一段距离得到。 初始的单纯型不要取得太小, 否则很容易停留在附近的局部极小值点。
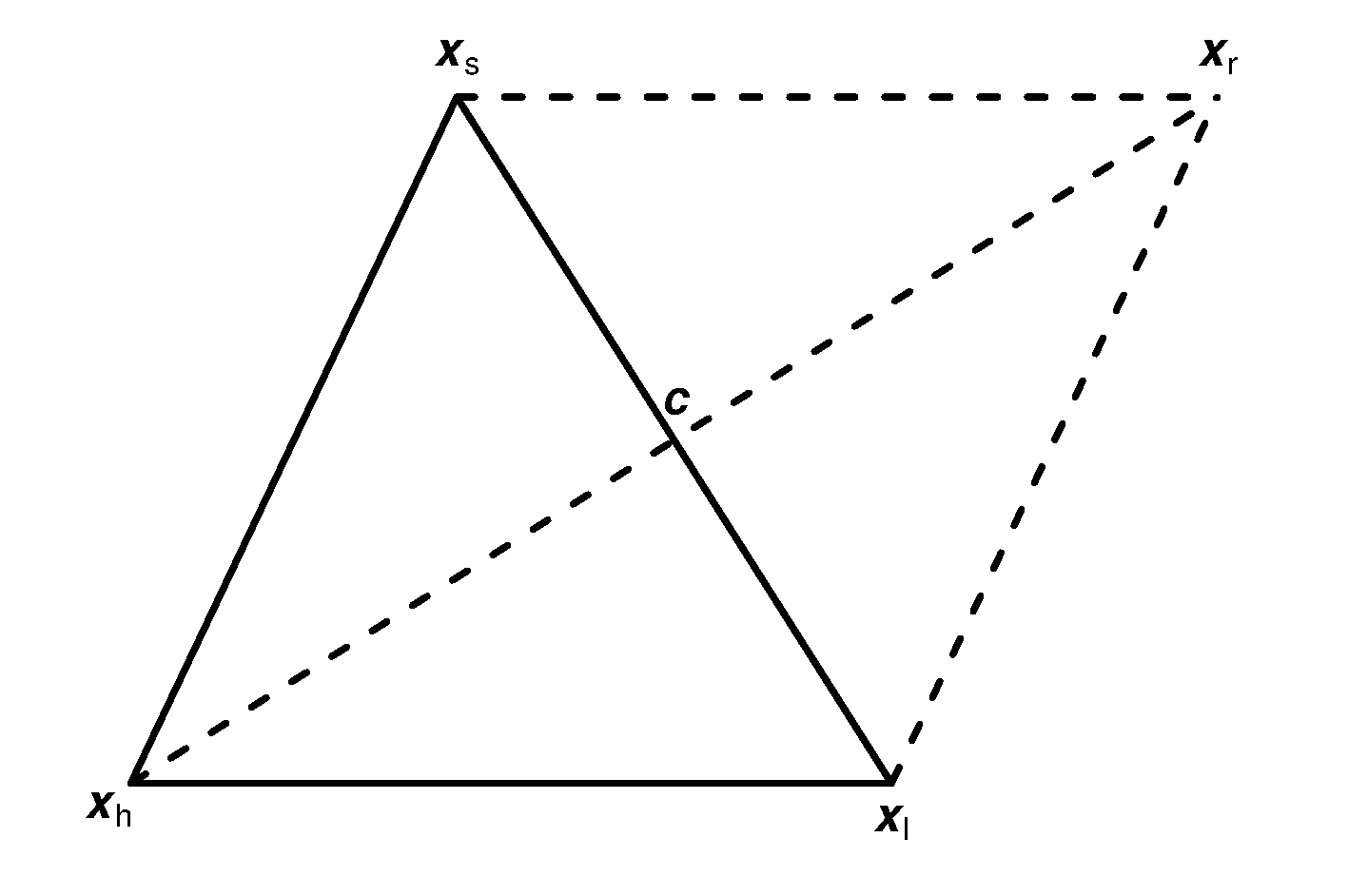
图37.2: Nelder-Mead算法反射变换图示,其它变换类似
在算法迭代的每一步, 假设当前单纯型为\((\boldsymbol x_0, \boldsymbol x_1, \dots, \boldsymbol x_d)\), 相应的函数值为\((y_0, y_1, \dots, y_d)\), 首先从中找到最坏的、次坏的、最好的函数值\(y_h, y_s, y_l\), 如果每次得到新的单纯型都把单纯型\(d+1\)个点次序重排使其函数值由小到大排列, 则\(y_l = y_0, y_s = y_{d-1}, y_h = y_d\)。 然后,计算除最坏点之外的\(d\)个顶点的重心\(\boldsymbol c = \frac{1}{d} \sum_{j \neq h} \boldsymbol x_j\)。 然后对单纯型进行变换以减小函数值。
单纯型的变换有反射、退缩(contraction)、延伸(expansion)和缩小(shrinkage)等四种, 变化量分别由四个参数\(\alpha>0\), \(\beta \in (0, 1)\), \(\gamma>\alpha\), \(\delta \in (0,1)\)控制, 这四个参数一般取为\(\alpha=1\), \(\beta=\frac12\), \(\gamma=2\), \(\delta=\frac12\)。
首先考虑反射是否有效, 计算反射点\(\boldsymbol x_r \stackrel{\triangle}{=} \boldsymbol c + \alpha (\boldsymbol c - \boldsymbol x_h)\), 这实际是把最坏点\(\boldsymbol x_h\)与中心\(\boldsymbol c\)连线后把连线延长得到点\(\boldsymbol x_r\)(见图37.2), 这样点\(\boldsymbol x_h, \boldsymbol c, \boldsymbol x_r\) 在一条直线上但是最坏点\(\boldsymbol x_h\)与反射点\(\boldsymbol x_r\)分别在\(\boldsymbol c\)的两侧。 这样沿最坏点的反方向搜索期望能改善目标函数值。 如果这时\(y_r \stackrel{\triangle}{=} f(\boldsymbol x_r)\)满足\(y_l \leq y_r < y_s\) (反射点比原次坏点好、但不优于原最好点), 则接受\(\boldsymbol x_r\)为本迭代步的新顶点, 替换原来的最坏点\(\boldsymbol x_h\)即可。
如果反射点\(\boldsymbol x_r\)的目标函数值比原最好点还小(\(y_r < y_l\)), 则考虑把生成\(\boldsymbol x_r\)的延长线进一步延伸, 得到延伸点\(\boldsymbol x_e \stackrel{\triangle}{=} \boldsymbol c + \gamma (\boldsymbol x_r - \boldsymbol c)\)。 令\(y_e = f(\boldsymbol x_e)\), 如果比反射点进一步改善(\(y_e < y_r\)), 则接受延伸点\(\boldsymbol x_e\)为本迭代步的新顶点, 在单纯型中替换原来的最坏点\(\boldsymbol x_h\)即可, 本步迭代结束。 如果延伸后\(\boldsymbol x_e\)的函数值不如反射点\(\boldsymbol x_r\)的函数值(\(y_e \geq y_r\)), 则接受反射点\(\boldsymbol x_r\)为本迭代步的新顶点, 在单纯型中替换原来的最坏点\(\boldsymbol x_h\)即可, 本步迭代结束。
在尝试反射\(\boldsymbol x_r\)后如果发现其不优于次坏点\(\boldsymbol x_s\)(\(y_r \geq y_s\)), 则反射点不能使用。 这时, 可以在\(\boldsymbol x_h, \boldsymbol c, \boldsymbol x_r\)构成的线段上另找一个点, 看这个点是否可以接受, 这样的变换称为退缩。 新的点可以在\(\boldsymbol c\)到\(\boldsymbol x_r\)之间(单纯型外部), 也可以在\(\boldsymbol x_h\)和\(\boldsymbol c\)之间(单纯型内部)。 这时, 如果反射点的函数值\(y_r\)介于原次坏点与最坏点之间(\(y_s \leq y_r \leq y_h\)), 那么单纯型外部有希望改善目标函数, 所以取\(\boldsymbol x_c = \boldsymbol c + \beta(\boldsymbol x_r - \boldsymbol c)\)(在单纯型外部); 否则,若\(y_r\)比原最坏点还差(\(y_r > y_h\)), 则只能在单纯型内部考虑, 取\(\boldsymbol x_c = \boldsymbol c - \beta(\boldsymbol c - \boldsymbol x_h)\)(在单纯型内部)。 得到\(\boldsymbol x_c\)后令\(y_c = f(\boldsymbol x_c)\), 如果比反射点有改善(\(y_c < y_r\)), 则接受退缩点\(\boldsymbol x_c\)为本迭代步的新顶点, 在单纯型中替换原来的最坏点\(\boldsymbol x_h\)即可, 本步迭代结束。 否则,就要执行第四种变换:缩小。
当反射、延伸、退缩都失败时, 执行缩小变换。 缩小变换是保持原来的最好点\(\boldsymbol x_l\)不动, 其它点都按比例向\(\boldsymbol x_l\)收缩: \(\boldsymbol x_j \leftarrow \boldsymbol x_l + \delta (\boldsymbol x_j - \boldsymbol x_l)\), \(j \neq l\)。单纯型缩小后希望其它\(d\)个点的目标函数值能有所改善。
算法的停止法则可以取为最后的\(d+1\)个定点处的\(d+1\)个函数值的样本标准差小于某一预先设定的精度阈值, 或迭代次数超过某一界限后宣布算法失败。
Nelder-Mead方法的收敛性很难确定。
在R软件中,用optim函数求解多元函数无约束优化问题,
该函数提供了BFGS、Nelder-Mead、共轭梯度、模拟淬火等算法。
37.6 模拟退火算法(*)
退火是一种机械加工技术, 加热金属零件到一定温度后进行加工, 然后控制温度缓慢地下降到常温。 在高温时, 分子运动速度较快, 在缓慢降温时可以调整机械应力、减少缺陷。
模拟退火算法的名称是利用了“缓慢降温”的做法和“温度”参数, 这种算法利用随机性进行全局优化, 用类似于Metropolis-Hasting的MCMC算法那样的方法在目标函数定义域进行随机游动, 试图找到全局最小值点。 算法从当前位置\(\boldsymbol x^{(t)}\)按照某种抽样分布生成随机数\(\boldsymbol \epsilon^{(t)}\), 令\(\boldsymbol x' = \boldsymbol x^{(t)} + \boldsymbol \epsilon^{(t)}\), 记\(\Delta y = f(\boldsymbol x') - f(\boldsymbol x^{(t)})\), 以如下概率令\(\boldsymbol x^{(t+1)} = \boldsymbol x'\): \[ p^{(t+1)} = \begin{cases} 1, & \text{若} \Delta y \leq 0, \\ \exp(- \Delta y / T^{(t+1)}), & \text{若} \Delta y > 0 . \end{cases} \] 否则令\(\boldsymbol x^{(t+1)} = \boldsymbol x^{(t)}\)。 即随机移动一步, 如果目标函数值变小, 则确认移动; 如果目标函数值变大, 就以一定正概率移动, 否则停留不动,等待下一次随机转移。 这里\(T^{(t+1)}\)是转移概率的参数, 类似于退火时的温度, \(T^{(t+1)}\)越大, 则\(p^{(t+1)}\)越大, 逆向的随机跳转越频繁, 可以用来从局部极小值点跳开; 随着迭代的进行, \(T^{(t+1)}\)应该逐步变小, 使得逆向随机跳转变稀少, 这样迭代能最终收敛。
\(T^{(t+1)}\)应选取为趋于0的数列, 在一定条件下如果取 \[ T^{(t)} = T^{(0)} \frac{\ln 2}{\ln (t+1)}, \] 可以确保迭代收敛到全局最小值点, 但显然这个速度太慢了。 实际应用中往往用 \[ T^{(t+1)} = \gamma T^{(t)}, \] 其中\(0 < \gamma < 1\), 或取\(T^{(t)} = T^{(0)} / t\)。
\(\boldsymbol \epsilon^{(t+1)}\)的分布可取为多元标准正态分布, 或取与各自变量的取值更匹配的一元分布合成多元分布。
参见(Kochenderfer 2019)第8章。
37.7 遗传算法(*)
模拟退火算法是利用随机移动来寻找全局最优点。 遗传算法是另一类算法的典型代表, 它产生多个搜索点, 利用这些搜索点以及搜索点之间的交互去接近全局最优点。
遗传算法利用了生物学中择优配对、交叉遗传、遗传突变的思想使得整个种群(搜索点集合)不断进化(接近全局最优点)。 设要求\(\min_{\boldsymbol x \in \mathbb R^d} f(\boldsymbol x)\), 算法的核心包括:
- 初始化。可以预先获得包含最优点的范围, 比如一个超长方体, 然后在其中均匀产生\(m\)个初始的搜索点\(\boldsymbol x^{(i)}\), \(i=1,2,\ldots,m\)。 也可以用多元正态分布抽样, 方差阵用对角阵。 也可以用重要抽样思想, 使用对于可能包含最优点的区域的先验知识构造初始搜索点的抽样分布。 每个搜索点称为一个“染色体”。
- 每一步先选出\(m\)对父本, 从父本用交叉遗传产生下一代的搜索点。 在选父本时,要体现择优配对的思想, 比如,仅从\(m\)个现有搜索点中的\(k\)个表现最优的点(目标函数值最小)中抽取父本; 或者,令被抽取为父本的概率,与目标函数值反向相关,等等。
- 对选出的\(m\)对父本中的每一对,如\(\boldsymbol x^{(i)}\), \(\boldsymbol x^{(j)}\), 进行染色体交叉, 获得一个子代的搜索点(染色体)。 交叉的方法有多种, 比如\(d\)维的每一分量随机地从两个父本对应分量中任选一个。
- 经过交叉遗传获得下一代染色体后, 如果没有别的步骤, 这个种群(搜索点集合)就会仅在有限个点上活动, 不可能搜索全定义域。 所以,还要有一个“突变”步骤, 使得搜索点能够转移到附近的位置。 一般是选择对每个搜索点加多元标准正态噪声乘以一个小的步长。
详见(Kochenderfer 2019)第9章。 这种利用多个搜索点的方法还有许多, 例如“粒子蜂拥”方法,记录每一个搜索点的位置、速度、历史最优点, 更新速度为倾向于自己的历史最优点和群体的历史最优点。 “萤火虫”方法, 是每个搜索点都逐次被每一个优于自己的点吸引。
这些利用群体随机变化寻找全局最优的方法有利用查找比较广泛的定义域, 但是收敛到最小值点比较慢, 所以可以配合一些局部搜索算法; 可以对每一个搜索点都作局部搜索, 并更新搜索点和目标函数值; 也可以对每一个搜索点都作局部搜索后, 仅更新其搜索得到的局部更优的目标函数值, 但并不更新搜索点本身, 这种做法更能避开局部最小点的吸引。