18 置换检验(*)
18.1 介绍
设有两个独立的总体\(X \sim F(\cdot)\)和\(Y \sim G(\cdot)\), 分别有简单随机样本\(X_1, \dots, X_{n_1}\)和\(Y_1, \dots, Y_{n_2}\), \(n = n_1 + n_2\)。 要检验如下零假设: \[ H_0:\; F = G . \]
两个分布相同的检验有许多, 比如, 在假定两个总体都服从正态分布的情况下, 可以检验其方差和均值都相等的两个假设。 非参数检验方法有适用于连续分布的Kolmogorov-Smirnov检验。 对于更一般的分布, 已有的检验统计量没有零假设的理论分布或者渐近分布, 无法使用已有的方法。
置换检验是基于对称性的一种计算密集型检验方法, 可以利用已有的检验统计量进行检验, 检验p值通过零假设下样本值的对称性进行计算。
18.2 肿瘤大小比较案例
我们用一个案例来讲解置换检验的做法。
例18.1 有22个肺癌病人的肿瘤大小数据, 其中10个为腺癌,12个为鳞癌,数据为: \[ \begin{array}{l*{12}r} X: & 13 & 27 & 33 & 40 & 43 & 61 & 125 & 135 & 161 & 330 & & \\ Y: & 2 & 3 & 6 & 7 & 9 & 12 & 24 & 35 & 35 & 74 & 112 & 122 \end{array} \] 从这组数据比较这两种类型的肿瘤大小有无显著差异。
两个变量的大小比较, 常用独立两样本t检验, 但是该检验要求两个样本都服从正态分布或者样本量充分大, 而这两个样本都有明显的右偏,不服从正态分布,样本量也不够大, 所以如下的t检验给出的p值是不可信的:
dc <- data.frame(
x = c(c(13, 27, 33, 40, 43, 61, 125, 135, 161, 330),
c(2, 3, 6, 7, 9, 12, 24, 35, 35, 74, 112, 122)),
type = factor(rep(c("腺癌", "鳞癌"), c(10, 12)),
levels=c("腺癌", "鳞癌")))
ttc <- t.test(x ~ type, data = dc,
var.equal=TRUE); ttc
##
## Two Sample t-test
##
## data: x by type
## t = 1.9433, df = 20, p-value = 0.06619
## alternative hypothesis: true difference in means between group 腺癌 and group 鳞癌 is not equal to 0
## 95 percent confidence interval:
## -4.409599 124.509599
## sample estimates:
## mean in group 腺癌 mean in group 鳞癌
## 96.80 36.75取零假设\(H_0\)为两种类型的肿瘤大小分布相同。 考虑零假设成立时两样本t统计量的分布, t统计量为: \[ t = \frac{\bar x - \bar y}{\sqrt{\frac{1}{n_1+n_2-2} \left[ \sum_{i=1}^{n_1} (x_i - \bar x)^2 + \sum_{i=1}^{n_2}(y_i - \bar y)^2 \right] \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}} . \]
记 \[ Z_i = \begin{cases} X_i, & i=1,2,\dots, n_1; \\ Y_{i-n_1}, & i=n_1+1, \dots, n . \end{cases} \] 则在\(H_0\)下\(Z_i, i=1,2,\dots,n\)是来自于同一总体的简单随机样本, 这样, \(Z_i, i=1,2,\dots,n\)任意打乱次序, 重新计算t统计量, 新的t统计量的分布应该是不变的。 因为如果仅在\(\{1,\dots,n_1\}\)或者\(\{n_1+1, \dots, n\}\)集合内部打乱次序并不改变t统计量的值, 所以仅需考虑\(\{1, \dots, n \}\)的\(n!\)个排列中, \(K = \binom{n}{n_1}\)种不同的将\(n\)个样本值划分为前\(n_1\)个与后\(n_2\)个的划分方法, 根据对称性, 在\(H_0\)下这\(K\)种划分是概率相等的, 每一种的概率都等于\(\frac{1}{K}\)。 如果我们将这\(K\)种划分穷举出来, 每一种划分可以计算一个t统计量值, 就可以计算\(K\)个t统计量的值\(\{ t_1, \dots, t_K \}\), 可以认为当零假设成立时我们从当前样本得到的t统计量的值是从离散均匀分布\(\{ t_1, \dots, t_K \}\)随机抽取出来的, 称这个分布为置换分布, 利用置换分布可以计算t统计量的双侧或者单侧p值。
用\(T\)表示服从置换分布的随机变量, 定义检验的右侧p值为\(P(T \geq t_0)\)(\(t_0\)表示t统计量的值, 如本例中\(t_0=1.9433\)), 左侧p值为\(P(T \leq t_0)\), 双侧p值为 \[ 2 \min\{ P(T \leq t_0), \; P(T \geq t_0) \} . \] 如果穷举了所有\(K\)个置换分布的取值\(\{t_1, \dots, t_K\}\), 就可以计算p值, 比如,右侧p值可以计算为 \[ \frac{1}{K} \sum_{j=1}^K I_{\{t_j \geq t_0 \}}, \] 其中\(I_A\)表示事件\(A\)的示性函数。
\(\binom{22}{10}\)约为64万种组合,
虽然对本例来说可以罗列(R的combn()函数)并进行计算,
但罗列所有组合一般都计算量太大而无法完成,
所以置换检验的做法一般是从所有\(K\)个组合中随机有放回抽取\(M\)个(\(M<K\)),
然后用这\(M\)个对应的t统计量值组成一个t统计量的置换分布的随机样本,
近似估计p值。
比如,
设抽取的\(M\)个组合对应的t统计量值为\(\{t_j, j=1,2,\dots,M\}\),
则双侧p值可以估计为
\[
2 \min\left( \frac{1}{M+1} \sum_{j=0}^M I_{\{t_j \leq t_0 \}},
\; \frac{1}{M+1} \sum_{j=0}^M I_{\{t_j \geq t_0 \}} \right).
\]
这个公式中用的\(M+1\)是把实际样本计算出的统计量\(t_0\)也作为置换分布的一个随机样本点计算在内了。
R的sample()函数可以从一个集合中随机无放回地抽取指定个数。
如下的R程序重复产生999个服从置换分布的t统计量值,
用置换检验计算了两样本t检验的双侧p值:
set.seed(1)
tsamp <- replicate(999, {
ind <- sample(22, size=10, replace=FALSE)
t.test(dc[["x"]][ind], dc[["x"]][-ind],
var.equal = TRUE)$statistic })
t0 <- ttc$statistic
pvalue.2s <- 2 * min(
mean(c(t0, tsamp) <= t0),
mean(c(t0, tsamp) >= t0))
cat("置换检验双侧p值 =", pvalue.2s, "\n")
## 置换检验双侧p值 = 0.056
hist(tsamp)
abline(v=ttc$statistic, col="red")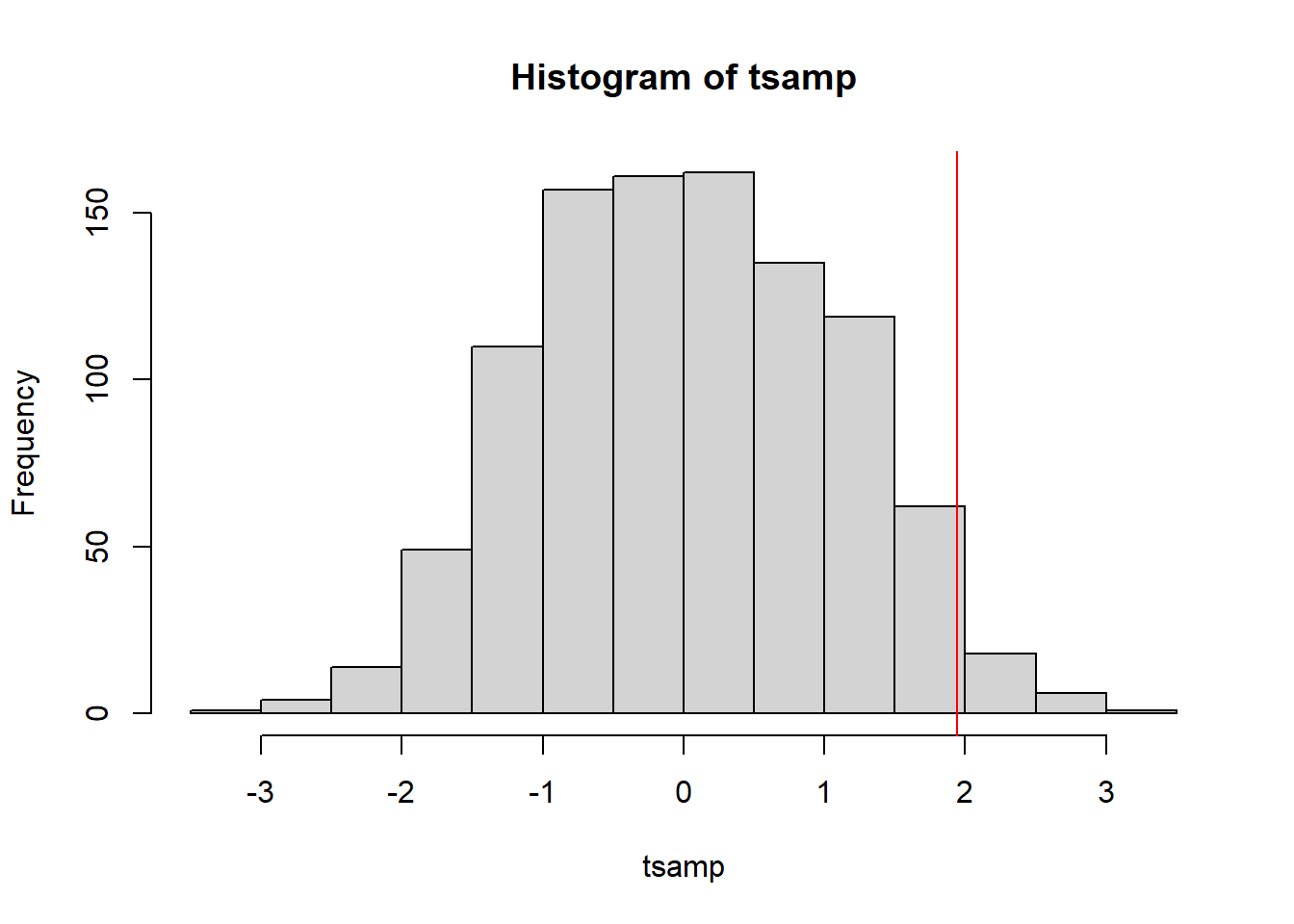
图18.1: 置换分布与t统计量值
结果得到的p值为0.056, 与正态假设下的0.066的p值很接近。
R的boot扩展包的boot()函数也支持对样本进行重排列。
上面的程序改用boot::boot()计算:
set.seed(1)
stat <- function(da, ind){
n1 <- 10
n2 <- 12
n <- n1 + n2
z <- da[["x"]][ind]
t.test(z[1:n1], z[(n1+1):n],
var.equal = TRUE)$statistic
}
bt <- boot::boot(dc, sim = "permutation",
statistic = stat, R=999)
pvalue3 <- 2*min(mean(c(bt$t, bt$t0) <= bt$t0),
mean(c(bt$t, bt$t0) >= bt$t0))
cat("用boot包计算置换检验双侧p值 =", pvalue3, "\n")
## 用boot包计算置换检验双侧p值 = 0.058 boot::boot()函数的结果为一个列表,
其中成员t是多次重复模拟每次得到的统计量值组成的向量,
这是其statistic参数计算的结果;
成员t0是从原始样本计算的统计量结果。
加选项sim = "permutation"后boot::boot()的每次模拟就是生成样本次序的一个随机排列。
因为置换检验的p值是利用随机模拟计算的, 所以存在随机误差。
用Julia程序罗列所有组合, 计算置换检验的p值:
using Combinatorics
# 两样本t统计量计算函数
function tstat(x, y)
n1 = length(x)
n2 = length(y)
mx = mean(x)
my = mean(y)
S2p = 1/(n1+n2-2)*(
sum((x .- mx) .^ 2) +
sum((y .- my) .^ 2))
tstat = (mx - my) / sqrt(S2p * (1/n1 + 1/n2))
return tstat
end
xv = [13, 27, 33, 40, 43, 61, 125, 135, 161, 330]
yv = [2, 3, 6, 7, 9, 12, 24, 35, 35, 74, 112, 122]
n1 = length(xv)
n2 = length(yv)
mixedxy = [xv; yv]
# 真实样本的统计量值
t0 = tstat(xv, yv)
# 所有的从n1+n2个样本点中取出n1个的罗列,
# 其中每一个是1:(n1+n2)的n1个下标的集合
allcomb = Combinatorics.combinations(1:(n1+n2), n1)
# 计算每一个的置换样本的统计量
tstats = map(allcomb) do ix
xv1 = mixedxy[ix]
yv1 = mixedxy[setdiff(1:(n1+n2), ix)]
tstat(xv1, yv1)
end
# 双侧检验
pvalue = 2*min(mean(tstats .> t0),
mean(tstats .< t0))
@show pvalue;
## pvalue = 0.0577472063540175Julia函数randperm(n)生成\(1:n\)的随机排列。
随机抽样方法计算置换检验双侧p值的Julia程序和结果如下:
using Random
Random.seed!(101)
M = 10_000
tstats = map(1:M) do _
rp = Random.randperm(n1+n2)
xv1 = mixedxy[rp[1:n1]]
yv1 = mixedxy[rp[n1+1:end]]
tstat(xv1, yv1)
end
pvalue = 2*min(mean([t0; tstats] .>= t0),
mean([t0; tstats] .<= t0))
@show pvalue;
## pvalue = 0.0613938606139386置换检验也适用于比较两个分布的其它检验统计量的p值计算, 包括两个多元分布的比较问题, 也可以推广到多个分布的比较问题。
18.3 独立性检验
用置换检验比较两个分布是否相同, 是利用了分布相同的零假设下样本次序的对称性。 这种对称性也可以用来检验独立性。
设\((\boldsymbol X, \boldsymbol Y)\)是随机向量, \(\boldsymbol X \sim F(\cdot)\), \(\boldsymbol Y \sim G(\cdot)\), 有样本\((\boldsymbol X_i, \boldsymbol Y_i)\), \(i=1,2,\dots,n\)。 要检验零假设 \[ H_0: \boldsymbol X \text{与} \boldsymbol Y \text{相互独立} . \]
设\(\nu = (i_1, i_2, \dots, i_n)\)是序列\(1,2,\dots,n\)的任意一个排列, 则根据对称性, \((\boldsymbol X_j, \boldsymbol Y_{i_j})\), \(j=1,2,\dots,n\)在\(H_0\)成立时与\((\boldsymbol X_i, \boldsymbol Y_i)\), \(i=1,2,\dots,n\)同分布, 一共有\(n!\)个这样的样本, 每一个和原始样本出现概率相同。 如果检验统计量\(\phi(X_1, \dots, X_n, Y_1, \dots, Y_n)\)可以用来检验\(H_0\), 当统计量较大时代表应拒绝\(H_0\), 则当\(H_0\)成立时\(\phi(X_1, \dots, X_n, Y_1, \dots, Y_n)\)和\(\phi(X_1, \dots, X_n, Y_{i_1}, \dots, Y_{i_n})\)同分布, 一共有\(K=n!\)个这样的统计量值, 且这些统计量值概率相等。 设从样本中计算得到的统计量值为\(t_0\), 记\(\{t_1, \dots, t_K \}\)为\(\phi(X_1, \dots, X_n, Y_{i_1}, \dots, Y_{i_n})\)的集合, 则可以用置换检验法计算检验的p值为 \[ \frac{1}{K} \sum_{j=1}^K I_{\{t_j \geq t_0\}} . \]
为节省计算量, 可以从\((1,2,\dots,n)\)的所有\(K=n!\)个排列中随机有放回地抽取\(M\)个, 设从第\(j\)个随机抽取的排列计算得到的检验统计量值为\(t_j\), 可以估计p值为 \[ \frac{1}{M+1} \sum_{j=0}^{M+1} I_{\{t_j \geq t_0\}} . \]
独立性检验的统计量\(\phi\)可以用相关系数、独立性卡方统计量等。