38 约束优化方法
考虑约束最优化问题。 约束最优化问题比无约束优化问题复杂得多, 也没有很好的通用解决方法, 在这个方面有大量研究。 现有的方法大致上有如下三类:
把约束问题转化为一系列无约束问题, 用这些无约束问题的极小值点去逼近约束极小值点, 称这样的方法为序列无约束优化方法(SUMT), 如惩罚函数法、乘子罚函数法。
在迭代的每一步用一个二次函数逼近目标函数, 用线性约束近似一般约束,构造一系列二次规划来逼近原问题, 称这样的方法为序列二次规划(SQP)法。
每次迭代找到可行下降方向, 保证迭代始终处于可行域内, 这样的方法称为可行方向法。
38.1 约束的化简
最简单的一些约束可以通过参数变换转化成无约束问题。 例如,对\(f(x)\)在\(x \in (0, \infty)\)求最小值, 可令\(x = e^t\), \(h(u) = f(e^u), u \in (-\infty, \infty)\), 若求得\(\mathop{\text{argmin}}_{u \in \mathbb R} h(u) = u^*\), 则\(x^* \stackrel{\triangle}{=} e^{u^*}\)是\(f(x)\)在\((0, \infty)\)的最小值点。
类似地,对\(x\)限制在有限开区间\((a,b)\)的情形,可以作变换 \[\begin{aligned} x = a + \frac{b-a}{1 + e^{-u}}, \ u \in (-\infty, \infty) . \end{aligned}\]
对\(x\)限制在有限闭区间\([a,b]\)的情形, 可以做变换 \[\begin{aligned} x = a + (b-a) \sin^2 u, \ u \in (-\infty, \infty) . \end{aligned}\] 也可以不使用三角函数,而是作变换 \[\begin{aligned} x = \frac{a + b}{2} + \frac{b - a}{2} \frac{2u}{1 + u^2} , \ u \in (-\infty, \infty) . \end{aligned}\]
对\(\boldsymbol x = (x_1, x_2, x_3)\)限制为\(0 \leq x_1 \leq x_2 \leq x_3\)的情形, 可以做变换 \[\begin{aligned} x_1 = u_1^2, \quad x_2 = u_1^2 + u_2^2, \quad x_3 = u_1^2 + u_2^2 + u_3^2, \ (u_1, u_2, u_3) \in \mathbb R^3 . \end{aligned}\]
对于\(\boldsymbol x = (x_1, x_2)\)限制为\(x_1 > 0, x_2 > 0, x_1 + x_2 < 1\)的情形, 可以做变换 \[\begin{aligned} x_1 =& \frac{e^{t_1}}{1 + e^{t_1} + e^{t_2}} , \quad x_2 = \frac{e^{t_2}}{1 + e^{t_1} + e^{t_2}} , \ (t_1, t_2) \in \mathbb R^2. \end{aligned}\] 这些变换可以把原来的约束优化问题转化为无约束优化问题, 或者减少约束个数。
对于等式约束, 如果有显式解, 可以从中解出部分自变量, 简化原来的问题。
38.2 线性规划的单纯形法介绍
对约束最优化问题(35.1), 如果\(f(\boldsymbol x), c_i(\boldsymbol x)\)都是线性函数(可以带有截距项), 称这样的问题为线性规划问题。 等式约束\(\boldsymbol c_i^T \boldsymbol x = b_i\)可以写成两个不等式约束\(\boldsymbol c_i^T \boldsymbol x \geq b_i\)和\((-\boldsymbol c_i)^T \boldsymbol x \geq b_i\), 所以线性规划问题可以写成 \[\begin{equation} \begin{aligned} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } \boldsymbol c^T \boldsymbol x, \quad \text{s.t.} \\ & A \boldsymbol x \geq \boldsymbol b, \end{aligned} \tag{38.1} \end{equation}\] 其中\(\boldsymbol c \in \mathbb R^d\), \(A\)为\(m \times d\)矩阵(\(m < d\)), \(\boldsymbol b \in \mathbb R^m\), \(A \boldsymbol x \geq \boldsymbol b\)中的大于等于号表示对每一行成立。
线性规划问题(38.1)不够通用, 如下的一般形式更容易在实际建模中使用: \[\begin{equation} \begin{aligned} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } \boldsymbol c^T \boldsymbol x, \quad \text{s.t.} \\ & A_{\text{GE}} \boldsymbol x \geq \boldsymbol b_{\text{GE}}, \\ & A_{\text{LE}} \boldsymbol x \leq \boldsymbol b_{\text{LE}}, \\ & A_{\text{EQ}} \boldsymbol x = \boldsymbol b_{\text{EQ}} . \end{aligned} \tag{38.2} \end{equation}\]
在线型规划的文献中还经常使用如下的标准形式: \[\begin{equation} \begin{aligned} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } \boldsymbol c^T \boldsymbol x, \quad \text{s.t.} \\ & A \boldsymbol x \leq \boldsymbol b, \\ & \boldsymbol x \geq \boldsymbol 0 . \end{aligned} \tag{38.3} \end{equation}\] 其中\(A\)为\(m \times d\)行满秩矩阵,\(m < d\)。
在讨论求解时, 对标准形式(38.3), 可以增加松弛变量\(\boldsymbol s = \boldsymbol b - A \boldsymbol x \geq \boldsymbol 0\), 使得问题变成如下等式约束形式: \[\begin{equation} \begin{aligned} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } \boldsymbol c^T \boldsymbol x, \quad \text{s.t.} \\ & A \boldsymbol x = \boldsymbol b, \\ & \boldsymbol x \geq \boldsymbol 0 . \end{aligned} \tag{38.4} \end{equation}\]
这四种形式都可以互相转化,本质上是等价的。
问题(38.4)的可行域是凸多面体, 边界为超平面(当\(d=2\)时为线段或射线), 凸多面体的顶点, 在二维平面和三维空间就是初等几何学中的顶点, 在高维空间,定义为不在可行域的任意两个点之间的点。
约束最小值点如果存在, 可能在可行域的什么位置出现?
可行域的内点一定不是最优点, 因为目标函数\(\boldsymbol c^T \boldsymbol x\)沿负梯度方向\(-\boldsymbol c^T\)下降, 内点可以向负梯度方向移动一个小的步长, 不超出可行域但使得目标函数下降。 所以约束最小值如果存在, 一定出现在可行域的边界。
可行域的边界超平面图形(比如, 三维空间中的四面体, 边界是平面三角形)的内点(比如,三角形内部的点)如果是约束最小值点, 这个超平面的法线方向必须是\(\boldsymbol c\), 因为如果这个超平面的法线方向不是\(\boldsymbol c\), 内点一定可以沿\(-\boldsymbol c\)在这个超平面的投影方向移动一个小的步长, 使得目标函数变小。
同理可行域的边界超平面图形的棱线(比如,四面体的边)的内部的点如果是约束最小值点, 则此棱线必垂直于\(\boldsymbol c\)。
约束最小值如果存在, 还可能存在于形状为\(d\)维凸多面体的可行域的顶点处, 称这些顶点为基本可行点, 基本可行点只有有限个; 如果线性规划问题存在约束最小值点, 则可行域至少有一个基本可行点, 而且基本可行点中至少有一个是最优点(可能存在多个最优点, 甚至于无穷多个最优点)。 根据上面的讨论,如果边界超平面图形内部、棱线内部有最优值, 则相应的各个顶点也都是最优点, 所以只需要在这有限个顶点中寻找最优值。 线性规划的问题是当问题规模很大时, 如何不利用穷举法快速找到目标函数值全局最优的顶点。
问题(38.4)的顶点, 其结构一定满足\(\boldsymbol x = (x_1, \dots, x_d)\)的分量中有\(d-m\)个0, 记这些分量的下标集合为\(V\), 其它分量的下标集合为\(B\), 在给定取0的分量的条件下解方程\(A \boldsymbol x = \boldsymbol b\)可以求出\(B\)中的分量的值, 这些值大于等于零,如此可以求出顶点坐标。 但是,满足这样条件的点不一定都是顶点, 而且不容易判断是否顶点。
单纯形法是线性规划问题的经典求解方法, 算法先初始化, 找到一个基本可行点(顶点), 这可以通过构造一个辅助的初始可行点已知的线性规划求解得到, 用这种方法得到初始可行点, 需要对原始线性规划问题进行适当的变换才能继续迭代。 有了初始可行点后, 单纯形算法在相邻基本可行点之间迭代, 每次在下标集合\(B\)和\(C\)之间交换一个下标并使得这样交换产生的目标函数下降最多, 这样每次迭代都使得目标函数值下降, 一般可以很快收敛。
对于线性规划, 满足KKT条件的点一定是约束全局最小值点, 所以可以用KKT条件检测每一个迭代经过的顶点是否最优点。 只要问题有可行点, 且在可行域内目标函数有下界, 则单纯型法一定能找到约束的全局最小值点。
单纯型算法是针对(38.4)问题求解的, 其它几种形式可以转换成(38.4)的形式, 求解软件一般能自动进行转换。
R的boot包中提供了simplex()函数,
可以用来求解线性规划问题。
例38.1 考虑如下的线性规划问题: \[\begin{aligned} \begin{cases} \mathop{\text{argmin}}\limits_{(x_1, x_2) \in \mathbb R^3} \ x_1 + x_2, \ \text{s.t.}\\ 2x - y \geq 0, \\ -x + 2y \geq 3, \\ 3x - y \leq 13 . \end{cases} \end{aligned}\]
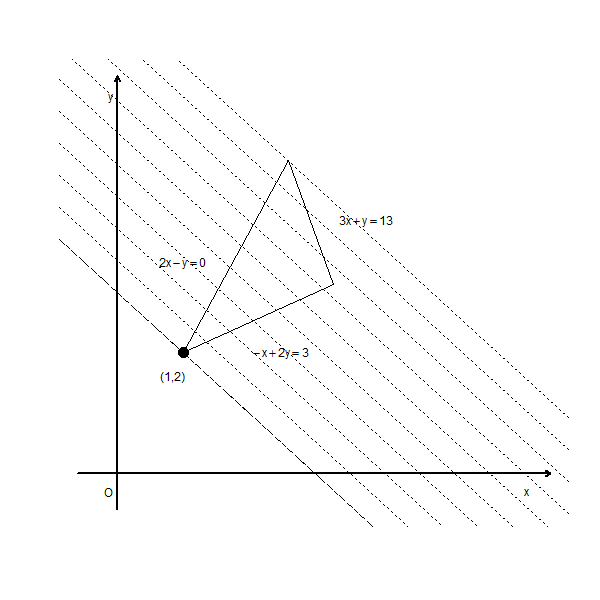
图38.1: 例38.1图形。三角形是可行域,虚线是目标函数的等值线,圆点是最小值点。
用R的boot::simplex()求解:
boot::simplex(
a = c(1, 1), # 目标函数系数
A1 = rbind(c(3, -1)),
b1 = 13, # <=约束
A2 = rbind(c(2, -1),
c(-1, 2)),
b2 = c(0, 3), # >=约束,所有自变量非负约束为默认
A3 = NULL, b3 = NULL) # =约束##
## Linear Programming Results
##
## Call : boot::simplex(a = c(1, 1), A1 = rbind(c(3, -1)), b1 = 13, A2 = rbind(c(2,
## -1), c(-1, 2)), b2 = c(0, 3), A3 = NULL, b3 = NULL)
##
## Minimization Problem with Objective Function Coefficients
## x1 x2
## 1 1
##
##
## Optimal solution has the following values
## x1 x2
## 1 2
## The optimal value of the objective function is 3.最小值点为\((1, 2)\),最小值为\(3\)。
使用Julia的JuMP包求解, 利用GLPK包作为实际求解的后端:
using JuMP, GLPK
# 建立最优化模型框架
om = Model(GLPK.Optimizer)
# 定义优化问题要求解的变量
@variable(om, x)
@variable(om, y)
# 定义优化目标
@objective(om, Min, x + y)
# 定义三个约束
@constraint(om, 2x - y >= 0)
@constraint(om, -x + 2y >= 3)
@constraint(om, 3x - y <= 13)
# 显示定义的优化问题
print(om)
# 进行优化求解
JuMP.optimize!(om)
# 检查是否得到最优解
println(termination_status(om))
## OPTIMAL
println("最优目标函数值:", objective_value(om))
## 最优目标函数值:3.0
println("最优解:x=", value(x), " y=", value(y))
## 最优解:x=1.0 y=2.038.3 仅含线性等式约束的情形(*)
如果约束仅包含线性方程组, 可以把问题(35.1)用矩阵形式写成 \[\begin{align} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ \text{s.t.} \\ & A^T \boldsymbol x = \boldsymbol b, \end{cases} \tag{38.5} \end{align}\] 其中\(A\)为\(d \times p\)矩阵, 各列为\(\boldsymbol a_i, i=1,\dots,p\), \(\boldsymbol b = (b_1, \dots, b_p)^T\), 即问题仅有\(p\)个线性约束\(\boldsymbol a_i^T \boldsymbol x = b_i, i=1,2,\dots,p\)。 设\(p < d\)且\(A\)列满秩, 当\(A\)规模很小时, 可以预先用消元法把\(\boldsymbol x\)的\(p\)个分量用其余的\(d-p\)个线性表出, 把问题转化为\(d-p\)维的无约束优化问题。
下面讨论当\(A\)规模较大时的处理方法。
记\(\mu(A)\)为\(A\)的各列在\(\mathbb R^d\)中张成的线性空间, 即 \[\begin{aligned} \mu(A) \stackrel{\triangle}{=} \{ \boldsymbol x \in \mathbb R^d: \boldsymbol x = A \boldsymbol u, \boldsymbol u \in \mathbb R^p \} = \{ \boldsymbol x \in \mathbb R^d: \boldsymbol x = \sum_{i=1}^p c_i \boldsymbol a_i, \ c_1, \dots, c_p \in \mathbb R \} \end{aligned}\] 则\(\mathbb R^d\)可以分解为\(\mu(A)\)与\(\mu(A)\)的正交补空间 \[\begin{aligned} \mu(A)^\perp \stackrel{\triangle}{=} \{ \boldsymbol x \in \mathbb R^d: A^T \boldsymbol x = 0 \} \end{aligned}\] 的直和: \[\begin{aligned} \mathbb R^d = \mu(A) \oplus \mu(A)^\perp. \end{aligned}\] 设\(A\)有\(QR\)分解 \[\begin{aligned} A = Q \left( \begin{array}{c} R \\ 0 \end{array} \right) = (Q_1, Q_2) \left( \begin{array}{c} R \\ 0 \end{array} \right) = Q_1 R, \end{aligned}\] 其中\(Q\)为\(d\times d\)正交阵, \(R\)为\(p\times p\)上三角阵, \(Q_1\)为\(d \times p\)矩阵, 易见\(Q_1\)各列构成\(\mu(A)\)的标准正交基, \(Q_2\)各列构成\(\mu(A)^\perp\)的标准正交基。 若\(\boldsymbol x\)满足约束\(A \boldsymbol x = b\), 设 \[\begin{aligned} \boldsymbol x = Q_1 \boldsymbol u \oplus Q_2 \boldsymbol v, \ \boldsymbol u \in \mathbb R^p, \ \boldsymbol v \in \mathbb R^{d-p}, \end{aligned}\] 则 \[\begin{aligned} A^T \boldsymbol x = R^T Q_1^T \boldsymbol x = R^T \boldsymbol u = \boldsymbol b \end{aligned}\] 可得\(\boldsymbol u = R^{-T} \boldsymbol b\)(简记\((R^T)^{-1}\)为\(R^{-T}\)), 于是 \[\begin{align} \boldsymbol x = Q_1 R^{-T} \boldsymbol b + Q_2 \boldsymbol v, \ \boldsymbol v \in \mathbb R^{d-p}, \tag{38.6} \end{align}\] 只要对目标函数\(f(Q_1 R^{-T} \boldsymbol b + Q_2 \boldsymbol v)\), \(\boldsymbol v \in \mathbb R^{d-p}\)求解无约束最优化问题即可。
在\(\boldsymbol x\)的分解式(38.6)中, 易见 \[\begin{aligned} P \stackrel{\triangle}{=}& Q_2 Q_2^T = I_n - Q_1 Q_1^T = I_n - A R^{-1} R^{-T} A^T = I_n - A (R^T R)^{-1} A^T \\ =& I_n - A (A^T A)^{-1} A^T, \end{aligned}\] 这是向正交补空间\(\mu(A)^\perp\)投影的投影矩阵, 所以(38.6)中属于正交补空间\(\mu(A)^\perp\)的部分\(Q_2 \boldsymbol v\), 在已知\(\boldsymbol x\)时可以用投影表示为\(P \boldsymbol x\)。 后文中的投影梯度法利用了这样的思想。
如果\(\boldsymbol x^{(t)}\)是一个可行点, 为了使得\(\boldsymbol x^{(t+1)} = \boldsymbol x^{(t)} + \boldsymbol d\)也是可行点, 需要\(A^T \boldsymbol d = 0\)。 注意问题(38.5)是一般约束问题(35.1)仅含等式约束的版本, 这里\(c_i(\boldsymbol x) = \boldsymbol a_i^T \boldsymbol x\), \(\boldsymbol a_i\)是\(A\)的第\(i\)列, 可见\(\nabla c_i(\boldsymbol x) = \boldsymbol a_i\), 上述对\(\boldsymbol d\)的要求\(A^T \boldsymbol d=0\)可以表示为 \[\begin{aligned} \boldsymbol d^T \nabla c_i(\boldsymbol x) = 0, i=1,\dots, p, \end{aligned}\] 这个要求可以推广到非线性等式约束的情形, 即为了\(\boldsymbol x^{(t)} + \boldsymbol d\)继续满足等式约束, 搜索方向\(\boldsymbol d\)必须和等式约束函数的梯度都正交, 否则会使得\(c_i(\boldsymbol x)\)的值改变。
38.4 线性约束最优化方法(*)
在约束最优化问题中, 如果所有约束都是线性函数, 这样的问题相对比较容易处理, 但是也能体现约束优化问题的困难。 如下的约束优化问题称为线性约束优化问题: \[\begin{align} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ \text{s.t.} \\ & \boldsymbol a_i^T \boldsymbol x = b_i, \ i=1,\dots, p, \\ & \boldsymbol a_i^T \boldsymbol x \leq b_i, \ i=p+1, \dots, q, \end{cases} \tag{38.7} \end{align}\] 其中\(\boldsymbol a_i \in \mathbb R^d, i=1, \dots, p+q\), \(b_i \in \mathbb R, i=1,\dots,p+q\)。
前面已经讨论了仅有线性等式约束的情形, 下面讨论含有线性不等式约束的情形。
38.4.1 投影梯度法
从(38.6)看出, 当约束为线性等式约束时, 搜索时应该在和各\(\boldsymbol a_i\)正交的方向上搜索。 这提示我们, 对于包含不等式约束的优化问题(38.7), 如果\(\boldsymbol x^{(t)}\)是一个可行点, 希望找到使得函数值下降的可行方向, 只需考虑所有等式约束和起作用的不等式约束。 假设\(\boldsymbol x^{(t)}\)处起作用的不等式约束下标为\(p+1, \dots, p+r\), 记 \[\begin{align} \mathcal B = \{ \boldsymbol d \in \mathbb R^d:\ \boldsymbol a_i^T \boldsymbol d = 0, \ i=1, \dots, p+r \} \tag{38.8} \end{align}\] 设负梯度\(-\nabla f(\boldsymbol x^{(t)})\) 投影到\(\mathcal B\)中得到\(\boldsymbol d\), 如果\(\boldsymbol d \neq \boldsymbol 0\), \(\boldsymbol d\)就是一个可行下降方向, 沿方向\(\boldsymbol d\)搜索使得函数值下降且保持所有\(p+q\)个约束成立。 有了可行下降方向\(\boldsymbol d\)以后, 从\(\boldsymbol x^{(t)}\)出发沿\(\boldsymbol d\)方向进行一维搜索, 得到下一个近似极小值点\(\boldsymbol x^{(t+1)}\), 如此迭代逼近。
如果投影得到的\(\boldsymbol d = \boldsymbol 0\), 必存在\(\lambda_i^{(t)}, i=1,\dots,p+r\), 满足 \[\begin{aligned} \sum_{i=1}^{p+r} \lambda_i^{(t)} \boldsymbol a_i = -\nabla f(\boldsymbol x^{(t)}) . \end{aligned}\] 解出\(\lambda_i^{(t)}, i=1,\dots,p+r\), 如果\(\lambda_i^{(t)} \geq 0, i=p+1, \dots, p+r\), 只要令\(\lambda_i^{(t)} = 0, i=p+r+1, \dots, p+q\), \(\boldsymbol\lambda^{(t)} = (\lambda_1^{(t)}, \dots, \lambda_{p+q}^{(t)})^T\), 则\((\boldsymbol x^{(t)}, \boldsymbol\lambda^{(t)})\)是问题(38.7)的KKT对, 算法不再继续,只要设法判断\(\boldsymbol x^{(t)}\)是否极小值点。
如果\(\boldsymbol d = \boldsymbol 0\)但是解出的\(\lambda_i^{(t)}, i=p+1,\dots,p+r\)中有负值, 则设\(\lambda_{i_0}^{(t)} = \min\{\lambda_i^{(t)}, i=p+1,\dots,p+r \}\), 令 \[\begin{aligned} \mathcal B' = \{ \boldsymbol d \in \mathbb R^d:\ \boldsymbol a_i^T \boldsymbol d = 0, \ i=1, \dots, p+r, i \neq i_0 \} \end{aligned}\] 令\(\tilde{\boldsymbol d}\)为\(-\nabla f(\boldsymbol x^{(t)})\)向\(\mathcal B'\)的投影, 则\(\tilde{\boldsymbol d}\)一定是可行下降方向。
这种方法称为投影梯度法, 是一种比较早期的可行方向法, 具体算法略。 投影梯度法以及与之类似的简约梯度法优点是比较简单, 缺点是仅利用梯度信息而没有试图采用高阶逼近, 收敛速度慢。
38.4.2 简约梯度法
在一般线性约束优化问题(38.7)中, 一般无约束的分量\(x_i\)可以写成 \(x_j = x_j^+ - x_j^-\), 其中\(x_j^+ = \max(x_j, 0)\), \(x_j^- = -\min(x_j, 0)\), 这样,可以设所有的分量都满足\(x_j \geq 0\)。 对不等式约束\(\boldsymbol a_i^T \boldsymbol x \geq b_i\), 可以引入新自变量\(z_i \geq 0\)使得\(\boldsymbol a_i^T \boldsymbol x - z_i = b_i\), 这样,可以设所有自变量非负, 所有的其它约束都是等式约束, 于是问题(38.7)可以写成 \[\begin{align} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ \text{s.t.} \\ & C \boldsymbol x = \boldsymbol b, \\ & \boldsymbol x \geq \boldsymbol 0 . \end{cases} \tag{38.9} \end{align}\] 设\(C\)为\(p \times d\)矩阵, 并设\(C\)行满秩, 不妨设\(C = (C_B, C_N)\), 其中\(C_B\)为\(p \times p\)满秩方阵, 把\(\boldsymbol x\)拆分为\((\boldsymbol x_B, \boldsymbol x_N)\), 由\(C \boldsymbol x = \boldsymbol b\)可解出 \[\begin{aligned} \boldsymbol x_B = \boldsymbol x_B(\boldsymbol x_N) = C_B^{-1} \boldsymbol b - C_B^{-1} C_N \boldsymbol x_N, \ \boldsymbol x_N \in \mathbb R^{d-p}, \end{aligned}\] 问题可简化为 \[\begin{aligned} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol x_N \in \mathbb R^{d-p} } h(\boldsymbol x_N) = f(\boldsymbol x_B(\boldsymbol x_N), \boldsymbol x_N), \ \text{s.t.} \\ & \boldsymbol x_N \geq \boldsymbol 0 , \boldsymbol x_B(\boldsymbol x_N) \geq \boldsymbol 0. \end{cases} \end{aligned}\] 记\(f(\boldsymbol x)\)的梯度前\(p\)个为\(G_B(\boldsymbol x)\), 后\(d-p\)个为\(G_N(\boldsymbol x)\), 则目标函数\(h(\boldsymbol x_N)\)的梯度为 \[\begin{aligned} \nabla h(\boldsymbol x_N) = G_N(\boldsymbol x) - (C_B^{-1} C_N)^T G_B(\boldsymbol x), \end{aligned}\] 称为\(f(\boldsymbol x)\)的简约梯度, 其中\(\boldsymbol x = (\boldsymbol x_B(\boldsymbol x_N), \boldsymbol x_N)\)。 记\(\tilde {\boldsymbol d}_N = -\nabla h(\boldsymbol x_N)\), 这是目标函数\(h(\boldsymbol x_N)\)的下降方向。 在迭代逼近约束最小值点的过程中, 如果负简约梯度方向\(\tilde {\boldsymbol d}_N\)所有分量都大于零或等于零, 则它指向\(\boldsymbol x_N\)的分量都增加或不变的方向, 关于\(\boldsymbol x_N\)部分是可行下降方向, \(\boldsymbol x_N\)部分只要延\(\tilde {\boldsymbol d}\)方向搜索即可; 如果\(\tilde {\boldsymbol d}_N\)的某个分量(设为第\(j\)个)小于零, 因为则该分量指向\(x_j\)减小的方向, 有可能使得搜索跳出可行域, 所以要把\(\tilde {\boldsymbol d}_N\)的这样的分量修改为\(x_j \tilde d_j\), 这样,当\(x_j>0\)时, 搜索方向是使得\(x_j\)减少的方向, 当\(x_j = 0\)时,搜索方向使得\(x_j\)不变从而不会离开可行域。 设修改后的\(\tilde{\boldsymbol d}_N\)为\(\boldsymbol d_N\), 对于\(\boldsymbol x_B\)部分, 令相应的搜索方向为\(\boldsymbol d_B = - C_B^{-1} C_N \boldsymbol d_N\), 令\(\boldsymbol d = (\boldsymbol d_B^T, \boldsymbol d_N^T)^T\)为搜索方向, 进行一维搜索,搜索要限制在可行域内。 在每次迭代中,都重新把\(\boldsymbol x\)拆分为\(\boldsymbol x_B\)和\(\boldsymbol x_N\), \(\boldsymbol x_B\)部分要求分量都取正值。 利用这样的方法对原目标函数\(f(\boldsymbol x)\)进行迭代搜索, 可以保证每次迭代延可行下降方向搜索, 当满足KKT条件时停止。 这样的方法叫做简约梯度法。 详见 徐成贤, 陈志平, and 李乃成 (2002) §6.1.2。
投影梯度法和简约梯度法优点是比较简单, 缺点是仅利用梯度信息而没有试图采用高阶逼近, 收敛速度慢。
38.4.3 有效集方法
有效集方法可以看成是投影梯度法的推广。 对问题(38.7), 假设已有约束最小值点的近似值\(\boldsymbol x^{(t)}\)是可行点(满足约束条件), 设\(\boldsymbol x^{(t)}\)处不等式约束中\(c_i, i=p+1, \dots, p+r\)是起作用约束, \(c_i, i=p+r+1, \dots, p+q\)不起作用。 如前所述,搜索方向必须与\(\boldsymbol a_i, i=1, \dots, p+r\)正交, 仍按(38.8)定义\(\mathcal B\)为这些方向的集合。 投影梯度法是把负梯度向量投影到线性子空间\(\mathcal B\)上作为搜索方向, 有效集方法推广了这种方法,仍要求搜索方向在\(\mathcal B\)中, 但不限于负梯度投影方向,即在第\(t+1\)步求解如下的仅含线性约束的子问题 \[\begin{align} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol d \in \mathbb R^d } f(\boldsymbol x^{(t)} + \boldsymbol d), \ \text{s.t.} \\ & \boldsymbol a_i^T \boldsymbol d = 0, \ i=1,\dots, p+r \end{cases} \tag{38.10} \end{align}\] 这个子问题可以比较容易地求解。
设解(38.10)得到\(\boldsymbol d^{(t)}\)。 如果\(\boldsymbol d^{(t)} = \boldsymbol 0\), 这说明仅含等式约束的子问题 \[\begin{align} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ \text{s.t.} \\ & \boldsymbol a_i^T \boldsymbol x = b_i, \ i=1,\dots, p+r \end{cases} \tag{38.11} \end{align}\] 以\(\boldsymbol x^{(t)}\)为最小值点, 由定理35.8, 可以解出拉格朗日乘子\(\lambda_i^{(t)}, i=1,\dots,p+r\)使得 \[\begin{aligned} \sum_{i=1}^{p+r} \lambda_i^{(t)} \boldsymbol a_i = -\nabla f(\boldsymbol x) . \end{aligned}\] 如果\(\lambda_i^{(t)} \geq 0, i=p+1,\dots,p+r\), 只要令\(\lambda_i^{(t)} = 0, i=p+r+1, \dots, p+q\), \(\boldsymbol\lambda^{(t)} = (\lambda_1^{(t)}, \dots, \lambda_{p+q}^{(t)})^T\), 则由定理35.9可知\((\boldsymbol x^{(t)}, \boldsymbol\lambda^{(t)})\)是问题(38.7)的KKT对, 只要判断\(\boldsymbol x^{(t)}\)是不是极小值点。
如果\(\boldsymbol d^{(t)} = \boldsymbol 0\)但是解出的\(\lambda_i^{(t)}, i=p+1,\dots,p+r\)中有负值, 设\(\lambda_{i_0}^{(t)} = \min\{\lambda_i^{(t)}, i=p+1,\dots,p+r \}\), 只要从子问题(38.10)的约束中删去第\(i_0\)个重新求解。
如果子问题(38.10)的解\(\boldsymbol d^{(t)} \neq \boldsymbol 0\), 这时如果\(\boldsymbol x^{(t)} + \boldsymbol d^{(t)}\)是可行点, 满足所有的等式约束和不等式约束(包括不起作用的不等式约束), 则令\(\boldsymbol x^{(t+1)} = \boldsymbol x^{(t)} + \boldsymbol d^{(t)}\), 否则就把\(\boldsymbol d\)当作一个可行下降方向做一维搜索, 一维搜索时要注意不起作用约束也要满足。
具体算法从略,详见 徐成贤, 陈志平, and 李乃成 (2002) §6.3.1。
38.5 二次规划问题(*)
在仅含线性约束的非线性规划问题中, 如果\(f(\boldsymbol x)\)是二次多项式函数, 称这样的问题为二次规划问题, 这是最简单的非线性规划问题, 这种问题有很多实际应用, 另外, 非线性约束优化问题的求解也往往需要通过求解一系列二次规划子问题实现。
38.5.1 仅含等式约束的二次规划问题
考虑如下的二次规划问题: \[\begin{align} \begin{cases} \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d} q(\boldsymbol x) \stackrel{\triangle}{=} \frac12 \boldsymbol x^T H \boldsymbol x + \boldsymbol g^T \boldsymbol x, \quad \text{s.t.}\\ A^T \boldsymbol x = \boldsymbol b, \end{cases} \tag{38.12} \end{align}\] 其中\(H\)为\(d\)阶实对称矩阵, \(\boldsymbol g \in \mathbb R^d\), \(A\)为\(n\times p\)列满秩矩阵,各列为\(\boldsymbol a_i, i=1,\dots, p\), \(\boldsymbol b \in \mathbb R^p\)。 此问题可以用§38.3的方法求解。
设\(A\)有如下QR分解 \[\begin{aligned} A = Q \left( \begin{array}{c} R \\ 0 \end{array} \right) = (Q_1, Q_2) \left( \begin{array}{c} R \\ 0 \end{array} \right) = Q_1 R, \end{aligned}\] 其中\(Q\)为\(d\times d\)正交阵, \(R\)为\(p\times p\)满秩上三角阵, \(Q_1\)为\(d \times p\)矩阵, \(Q_1^T Q_1 = I_p\), \(Q_1^T Q_2 = \boldsymbol 0\)。 满足约束的可行点\(\boldsymbol x\)的通解为 \[\begin{align} \boldsymbol x = Q_1 R^{-T} \boldsymbol b + Q_2 \boldsymbol v, \quad \boldsymbol v \in \mathbb R^{d-p}, \tag{38.13} \end{align}\] 令 \[\begin{align} \tilde q(\boldsymbol v) = q(Q_1 R^{-T} \boldsymbol b + Q_2 \boldsymbol v) \stackrel{\triangle}{=} \frac12 \boldsymbol v^T \tilde H \boldsymbol v + \tilde{\boldsymbol g}^T \boldsymbol v + \tilde c, \quad \boldsymbol v \in \mathbb R^{d-p}, \tag{38.14} \end{align}\] 其中 \[\begin{aligned} \tilde H =& Q_2^T H Q_2, \quad \tilde{\boldsymbol g} = Q_2^T \boldsymbol g + Q_2^T H Q_1 R^{-T} \boldsymbol b, \end{aligned}\] \(\tilde c\)为与\(\boldsymbol v\)无关的常数项。 只要求解无约束优化问题\(\mathop{\text{argmin}} \tilde q(\boldsymbol v)\)得到\(\boldsymbol v^*\), 再用(38.13)就可以得到问题(38.12)的最小值点\(\boldsymbol x^*\)。
在(38.14)的目标函数\(\tilde q(\boldsymbol v)\)中, 海色阵\(\tilde H\)如果有负特征值, 则\(\tilde q(\boldsymbol v)\)的最小值是\(-\infty\), 问题无解。 事实上,设有\(\lambda<0\)以及\(\boldsymbol d \neq \boldsymbol 0\)使得\(\tilde H \boldsymbol d = \lambda \boldsymbol d\), 取\(\boldsymbol v^{(k)} = k \boldsymbol d\), 则 \[\begin{aligned} \tilde q(\boldsymbol v^{(k)}) = \frac12 \lambda \| \boldsymbol d \|^2 \cdot k^2 + \tilde{\boldsymbol g}^T \boldsymbol d \cdot k \to -\infty, \quad \text{当}k \to \infty. \end{aligned}\] 所以,不妨设\(\tilde H\)为非负定阵。
如果\(\tilde H\)是正定阵, 则\(\tilde q(\boldsymbol v)\)是严格凸函数, 有全局严格最小值点\(\boldsymbol v^* = - \tilde H^{-1} \tilde{\boldsymbol g}\), 代入(38.13)可得问题(38.12)的最小值点\(\boldsymbol x^*\)。 这时,再考虑拉格朗日函数 \[\begin{aligned} L(\boldsymbol x, \boldsymbol\lambda) = q(\boldsymbol x) - \boldsymbol\lambda^T (A^T \boldsymbol x - \boldsymbol b), \end{aligned}\] 来求拉格朗日函数的稳定点, 其中\(\boldsymbol x^*\)已知, 由定理35.8知拉格朗日乘子\(\boldsymbol\lambda^*\)满足 \[\begin{aligned} \nabla q(\boldsymbol x^*) - A \boldsymbol\lambda^* =& 0, \\ A \boldsymbol\lambda^* =& H \boldsymbol x^* + \boldsymbol g, \end{aligned}\] 由\(A = Q_1 R\)得 \[\begin{aligned} R \boldsymbol\lambda^* = Q_1^T (H \boldsymbol x^* + \boldsymbol g), \end{aligned}\] 用回代法解此方程可得拉格朗日乘子\(\boldsymbol\lambda^*\)。
如果\(\tilde H\)仅为非负定阵而不是正定阵, \(\tilde q(\boldsymbol v)\)仍然是凸函数, 最小值点与稳定点等价, 稳定点存在当且仅当\(\tilde H \boldsymbol v = -\tilde{\boldsymbol g}\)有解, 这等价于\(\tilde{\boldsymbol g}\)属于\(\mu(\tilde H)\) (\(\mu(\tilde H)\)是\(\tilde H\)的各列张成的线性子空间), 又等价于 \[\begin{align} (I - \tilde H \tilde H^+) \tilde{\boldsymbol g} = 0, \tag{38.15} \end{align}\] 其中\(\tilde H^+\)是\(\tilde H\)的加号逆。 由定理32.12, 当(38.15)成立时\(\tilde q(\boldsymbol v)\)有无穷多个最小值点, 可以表达为 \[\begin{aligned} \boldsymbol v^* = - \tilde H^+ \tilde g + (I - \tilde H^+ \tilde H) \boldsymbol u, \quad \forall \boldsymbol u \in \mathbb R^{n-p} , \end{aligned}\] 再代入(38.13)可得问题(38.12)的无穷多个最小值点\(\boldsymbol x^*\)。
在问题(38.12)规模很大的时候, 求解线性方程组计算量很大, 可以用共轭梯度法迭代地求解, 由于二次目标函数\(q(\boldsymbol x)\)的特殊性, 迭代最多只需要\(n-p\)次就可以收敛到最小值点。 参见 徐成贤, 陈志平, and 李乃成 (2002) §6.4.1。
38.5.2 含有不等式约束的二次规划问题
考虑如下的二次规划问题: \[\begin{align} \begin{cases} \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d} q(\boldsymbol x) \stackrel{\triangle}{=} \frac12 \boldsymbol x^T H \boldsymbol x + \boldsymbol g^T \boldsymbol x, \quad \text{s.t.}\\ \boldsymbol a_i^T \boldsymbol x = b_i, \ i=1,\dots,p \\ \boldsymbol a_i^T \boldsymbol x \leq b_i, \ i=p+1,\dots,p+q \\ \end{cases} \tag{38.16} \end{align}\] 其中\(H\)为\(d\)阶实对称矩阵, \(\boldsymbol g \in \mathbb R^d\), \(\boldsymbol a_i \in \mathbb R^d, i=1, \dots, p+q\), \(b_i \in \mathbb R, i=1,\dots,p+q\)。
用前面所述关于一般线性约束的有效集方法可以把含有不等式约束的二次规划问题转化为一系列仅含等式约束的二次规划问题。 假设经过\(t\)步迭代得到问题(38.16)的一个可行点\(\boldsymbol x^{(t)}\), \(\boldsymbol x^{(t)}\)处不等式约束中\(c_i, i=p+1, \dots, p+r\)是起作用约束, \(c_i, i=p+r+1, \dots, p+q\)不起作用。 考虑如下只有等式约束的子问题 \[\begin{align} \begin{cases} \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d} \frac12 \boldsymbol x^T H \boldsymbol x + \boldsymbol g^T \boldsymbol x, \quad \text{s.t.}\\ \boldsymbol a_i^T \boldsymbol x = b_i, \ i=1,\dots,p+r \\ \end{cases} \tag{38.17} \end{align}\] 令\(\boldsymbol x = \boldsymbol x^{(t)} + \boldsymbol d\), 问题(38.17)可以等价地写成 \[\begin{align} \begin{cases} \mathop{\text{argmin}}\limits_{\boldsymbol d \in \mathbb R^d} \frac12 \boldsymbol d^T H \boldsymbol d + (\boldsymbol g + H \boldsymbol x^{(t)})^T \boldsymbol d, \quad \text{s.t.}\\ \boldsymbol a_i^T \boldsymbol d = 0, \ i=1,\dots,p+r \\ \end{cases} \tag{38.18} \end{align}\] 记\(\mathcal B = \{ \boldsymbol d \in \mathbb R^d: \boldsymbol a_i^T \boldsymbol d = 0, i=1,\dots, p+r \}\), 如果以\(\boldsymbol a_i, i=1, \dots, p+r\)为列向量组成矩阵\(A\), 则\(\mathcal B = \mu(A)^\perp\)。
通过前面对仅含等式约束的二次规划问题的讨论可以知道, 如果 \[\begin{align} \boldsymbol d^T H \boldsymbol d >0, \ \forall \boldsymbol d \in \mathcal B \backslash \{\boldsymbol 0 \}, \tag{38.19} \end{align}\] 则子问题(38.18)存在唯一的全局严格最小值点, 设其为\(\boldsymbol d^{(t)}\)。 如果\(\boldsymbol d^{(t)}= \boldsymbol 0\), 就说明\(\boldsymbol x^{(t)}\)已经是子问题(38.17)的约束最小值点, 可以解出相应的拉格朗日乘子\(\lambda_i^{(t)}, i=1,\dots, p+r\)。 如果解出的\(\lambda_i^{(t)} \geq 0, i=p+1,\dots, p+r\), 则令\(\lambda_i^{(t)} = 0, i=p+r+1, \dots, p+q\), \(\boldsymbol\lambda^{(t)} = (\lambda_1^{(t)}, \dots, \lambda_{p+q}^{(t)})^T\), 这时\((\boldsymbol x^{(t)}, \boldsymbol\lambda^{(t)})\)为原始问题(38.16)的KKT对, 由于二次目标函数的特殊性以及(38.19)条件可知\(\boldsymbol x^{(t)}\) 是问题(38.16)的约束全局严格最小值点。
如果\(\boldsymbol d^{(t)} = \boldsymbol 0\)但是\(\lambda_{i_0}^{(t)} = \min \{\lambda_i^{(t)}: i=p+1, \dots, p+r \} < 0\), 把对应于\(i_0\)的约束从子问题(38.18)中删除, 可以证明新的子问题有非零解\(\tilde{\boldsymbol d}^{(t)}\), 且\(\tilde{\boldsymbol d}^{(t)}\)是原问题(38.16)的可行下降方向。
如果\(\boldsymbol d^{(t)} \neq \boldsymbol 0\), 则\(\boldsymbol d^{(t)}\)是原问题(38.16)的可行下降方向。
设\(\boldsymbol d^{(t)}\)是原问题(38.16)的可行下降方向。 若\(\boldsymbol x^{(t)} + \boldsymbol d^{(t)}\)是原问题(38.16)的可行点, 直接取为\(\boldsymbol x^{(t+1)}\)继续迭代即可。 如果\(\boldsymbol x^{(t)} + \boldsymbol d^{(t)}\)超出了(38.16)的可行域, 这一定是不起作用的不等式约束中的某些被突破了, 可以从\(\boldsymbol x^{(t)}\)出发沿\(\boldsymbol d^{(t)}\)方向进行线性搜索, 由二次目标函数的特点知道线性搜索的最小值点在可行域边界处达到, 直接取步长为 \[\begin{align} \alpha_t = \min\left\{ \frac{b_i - \boldsymbol a_i^T \boldsymbol x^{(t)}}{\boldsymbol a_i^T \boldsymbol d^{(t)}} : \ p+r+1 \leq i \leq p+q \text{且} \boldsymbol a_i^T \boldsymbol d^{(t)} > 0 \right\} \tag{38.20} \end{align}\] 注意到\(\boldsymbol d^{(t)}\)已经是子问题(38.18)的约束最小值点, 所以如果得到的\(\alpha_t > 1\)只要取\(\alpha_t = 1\)。 如果\(\alpha_t<1\), 设(38.20)的最小值是在第\(i_1\)个约束处达到的, 则\(\boldsymbol x^{(t+1)} = \boldsymbol x^{(t)} + \alpha_t \boldsymbol d^{(t)}\)比\(\boldsymbol x^{(t)}\)增加了一个起作用的不等式约束\(i_1\), 下一步迭代时子问题(38.18)的约束中需要增加约束\(\boldsymbol a_{i_1}^T \boldsymbol x = b_{i_1}\)。
详细算法从略。
38.6 非线性约束优化问题
当约束中含有非线性函数时, 问题比无约束和线性约束问题都要复杂得多。 这时, 很难求得可行的下降方向, 而且由于数值误差的因素, 对于不等式约束很难判断是否起作用。 所以一般的非线性约束问题没有通用的解决方法, 更没有可靠的软件。 来自于线性约束优化的一些做法仍可以采用, 但是算法会很复杂。 比较容易实现的方法是各类罚函数法, 定义一系列增加了惩罚项的目标函数, 用一系列无约束优化问题的解逼近约束问题的解, 这样的方法又称为序列无约束最小化方法 (Sequential Unconstrained Minimization Teckniques, SUMT), 特点是实现简单, 但是收敛慢而且惩罚很重时问题适定性很差, 所以难以求得比较精确的结果。 另一类方法是在每步迭代时构造一个二次规划子问题作为近似, 通过求解一系列二次规划问题逼近一般非线性约束问题的解, 这种方法称为序列二次规划法(Sequential Quadratic Programming, SQP), 是现在较好的方法。
38.6.1 外点罚函数法
罚函数法引入包括原来的目标函数和对偏离约束的惩罚两部分的新目标函数, 对新目标函数求无约束最小值点。
对一般的约束优化问题(35.1), 等式约束可以用\(| c_i(\boldsymbol x) |\)惩罚, 不等式约束可以用\(\max(0, c_i(\boldsymbol x))\)惩罚, 取惩罚函数为 \[\begin{align} \bar p(\boldsymbol x) = \sum_{i=1}^p c_i^2(\boldsymbol x) + \sum_{i=p+1}^{p+q} \left[ \max(0, c_i(\boldsymbol x)) \right]^2, \tag{38.21} \end{align}\] 当且仅当\(\boldsymbol x\)是可行点时\(\bar p(\boldsymbol x)=0\)。 定义新的目标函数 \[\begin{aligned} \bar f(\boldsymbol x) = f(\boldsymbol x) + \sigma \bar p(\boldsymbol x), \end{aligned}\] 其中\(\sigma>0\)称为罚因子。 若\(\bar{\boldsymbol x}\)是\(\bar f(\boldsymbol x)\) 的一个无约束极值点且\(\bar{\boldsymbol x}\)是(35.1)的可行点, 则对(35.1)的任意可行点\(\tilde{\boldsymbol x}\), 都有 \[\begin{aligned} \bar f(\bar{\boldsymbol x}) =& f(\bar{\boldsymbol x}) + \sigma \bar p(\bar{\boldsymbol x}) = \min \big[ f(\boldsymbol x) + \sigma \bar p(\boldsymbol x) ] \leq f(\tilde{\boldsymbol x}) + \sigma \bar p(\tilde{\boldsymbol x}) = f(\tilde{\boldsymbol x}) \end{aligned}\] 即只要无约束问题\(\mathop{\text{argmin}} \bar f(\boldsymbol x)\)的解是约束问题的可行点就是约束极小值点。 \(\sigma\)越大,对无约束极小值点不在可行域内的惩罚越大, 所以\(\mathop{\text{argmin}} \bar f(\boldsymbol x)\)也越可能落在可行域内。 算法迭代进行,只要找到的无约束解不可行就增大罚因子\(\sigma\)然后继续求解无约束极值点。 算法如下:算法实现时可以取\(\sigma_0=1\), \(c=10\)。 求解无约束问题时迭代停止的条件可以取为梯度向量长度\(\| \nabla \bar f(\boldsymbol x) \|\)小于预定精度值。
运用这样的算法, 可以任意选取初始点, 不需要初始点在可行域内, 每次迭代得到的近似解都在可行域外, 只有最后一个解近似地落入可行域而且是近似约束最小值点, 所以这种方法称为外点罚函数法。 这种方法要求目标函数在\(\mathbb R^d\)上都有定义, 如果目标函数仅在与可行域有关的子集上有定义则无法使用; 最后的解不一定严格满足可行性条件, 如果要求解严格可行此种方法也无法使用。 另外,随着\(\sigma\)的增大, 在新目标函数\(\bar f(\boldsymbol x)\)中目标函数占的比例越来越小, 约束惩罚占的比例越来越大, 使得优化问题的适定性变得越来越差, 求解无约束优化问题会变得很困难, 计算误差变得很大。 所以,罚函数法虽然看起来很简单, 但是不一定能得到好的结果。
38.6.2 内点罚函数法
内点罚函数法要求每次迭代严格地在可行域内进行。 定义新的无约束目标函数, 当近似极小值点接近可行域边界时新目标函数变得很大(通常在可行域边界处趋于无穷大), 相当于在可行域边界处设立了无限高的墙壁不允许搜索越过可行域边界, 所以这种方法又称为障碍罚函数法。 内点罚函数法不能处理含有等式约束的问题, 而且要求可行域含有内点。 对于如下仅含不等式约束的优化问题 \[\begin{align} \begin{cases} & \mathop{\text{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ \text{s.t.} \\ & c_i(\boldsymbol x) \leq 0, \ i=1, \dots, q \end{cases} \tag{38.22} \end{align}\] 定义罚函数为\(\bar p(\boldsymbol x) = -\sum_{i=1}^q \log |c_i(\boldsymbol x)|\) 或\(\bar p(\boldsymbol x) = \sum_{i=1}^q \frac{1}{|c_i(\boldsymbol x)|}\), \(\boldsymbol x\)只能是严格可行点, 即所有\(c_i(\boldsymbol x)<0\), 当某个\(c_i(\boldsymbol x)=0\)时\(\bar p(\boldsymbol x) = +\infty\)。 取新的目标函数 \[\begin{aligned} \bar f(\boldsymbol x) = f(\boldsymbol x) + \sigma \bar p(\boldsymbol x), \end{aligned}\] 因为真正的约束最小值点允许取边界处的值, 需要取\(\{ \sigma_t \}\)使得\(\sigma_t \to 0\), 如此减轻对接近可行域边界的惩罚。 内点罚函数法和外点罚函数法类似, 先取较大的\(\sigma\), 求\(\bar f(\boldsymbol x)\)的无约束最小值点, 每次迭代减小\(\sigma\)的值后求无约束极值点, 直到近似约束最小值点达到足够精度。
由于可行域边界处的高墙的存在, 内点罚函数法在近似点靠近可行域边界时加罚的目标函数\(\bar f(\boldsymbol x)\)也会变得病态, 难以求得最小值点, 并且求\(\bar f(\boldsymbol x)\)的最小值点时要注意搜索不能跳出可行域。 内点罚函数法要求初值在可行域内, 可以设法先找可行点。
求初始的可行点的一种方法是以二次惩罚函数(38.21)为目标函数进行无约束优化, 求得令\(\bar p(\boldsymbol x) = 0\)的点\(\boldsymbol x\), 就是满足约束的可行点。
惩罚函数法的一个变种是把内点罚函数和外点罚函数结合使用, 对等式约束和初始点不满足的不等式约束, 可以采用外点罚函数, 其它不等式约束采用内点罚函数, 这样的方法称为混合罚函数法。
乘子罚函数法针对普通罚函数方法的病态问题做了改进, 参见(高立 2014) §7.3、§7.4。
38.6.3 序列二次规划法(SQP)(*)
序列二次规划法(SQP方法)每一步迭代解决一个二次规划子问题, 这种方法在中小规模的非线性约束规划问题中是比较好的方法。 SQP的思想类似于无约束规划中的牛顿法, 在局部对目标函数用二次函数逼近, 对约束用线性函数逼近, 得到二次规划子问题。
对一般约束优化问题(35.1), 设\(f\)有二阶连续偏导数, 设各\(c_i\)有一阶连续偏导数。 设\(\boldsymbol x^{(t)}\)为迭代\(t\)步后得到的近似约束最小值点, 在\(\boldsymbol x^{(t)}\)处对\(f(\boldsymbol x)\)作如下的二阶泰勒展开近似: \[\begin{aligned} f(\boldsymbol x^{(t)} + \boldsymbol d) \approx& f(\boldsymbol x^{(t)}) + [ \nabla f(\boldsymbol x^{(t)})]^T \boldsymbol d + \frac12 \boldsymbol d^T [ \nabla^2 f(\boldsymbol x^{(t)})]^T \boldsymbol d, \ \boldsymbol d \in \mathbb R^d, \end{aligned}\] 对\(c_i(\boldsymbol x)\)作如下的一阶泰勒展开近似: \[\begin{aligned} c_i(\boldsymbol x^{(t)} + \boldsymbol d) \approx& c_i(\boldsymbol x^{(t)}) + [ \nabla c_i(\boldsymbol x^{(t)})]^T \boldsymbol d, \ \boldsymbol d \in \mathbb R^d. \end{aligned}\] 进行这样的近似后, 考虑如下的二次规划子问题 \[\begin{align} \begin{cases} \mathop{\text{argmin}}\limits_{\boldsymbol d \in \mathbb R^d} \ \frac12 \boldsymbol d^T [ \nabla^2 f(\boldsymbol x^{(t)})]^T \boldsymbol d + [ \nabla f(\boldsymbol x^{(t)})]^T \boldsymbol d, \quad \text{s.t.} \\ c_i(\boldsymbol x^{(t)}) + [ \nabla c_i(\boldsymbol x^{(t)})]^T \boldsymbol d = 0, i=1,\dots, p, \\ c_i(\boldsymbol x^{(t)}) + [ \nabla c_i(\boldsymbol x^{(t)})]^T \boldsymbol d \leq 0, i=p+1,\dots, p+q \\ \end{cases} \tag{38.23} \end{align}\] 通过求解这样的二次规划子问题得到下一个近似点\(\boldsymbol x^{(t+1)}\)。
SQP算法需要考虑的问题比较多, 这里略去详细的讨论, 感兴趣的读者可以参考 高立 (2014) 第九章。
38.7 用Julia的JuMP包进行优化(*)
Julia语言提供了多个进行最优化建模计算的扩展程序包, 其中JuMP是比较优秀的一个, JuMP适用范围广, 使用简单, 支持多种求解后端。
考虑如下的目标函数优化: \[ \min (1 - x)^2 + 100(y - x^2)^2 . \] 显然无约束全局最小值点为\((1, 1)\)。
用JuMP调用Ipopt后端求解无约束优化问题:
# JuMP优化例子
using JuMP
using Ipopt # 一个优化后端,自由软件
om = JuMP.Model(Ipopt.Optimizer)
@variable(om, x, start=0.0)
@variable(om, y, start=0.0)
@NLobjective(om, Min, (1 - x)^2 + 100 * (y - x^2)^2)
optimize!(om)
## .....
## EXIT: Optimal Solution Found.
println("最小化目标函数值 = ", objective_value(om))
## 最小化目标函数值 = 1.3288608467480825e-28
println("最小值点:x = ", value(x), " y = ", value(y))
## 最小值点:x = 0.9999999999999899 y = 0.9999999999999792增加一个线性等式约束\(x + y = 10\)后求解:
@constraint(om, x + y == 10.0)
optimize!(om)
println("最小化目标函数值 = ", objective_value(om))
## 最小化目标函数值 = 2.89460755048946
println("最小值点:x = ", value(x), " y = ", value(y))
## 最小值点:x = 2.701147124098218 y = 7.2988528759017814继续增加两个线性不等式约束\(x \geq 1.25\), \(y \geq -2.1\)后求解:
习题
习题1
用外点罚函数法求解如下约束优化问题: \[\begin{align*} \begin{cases} \mathop{\text{argmin}} x_1^2 + x_2^2, \quad \text{s.t.}\\ x_1 - x_2 + 1 = 0 . \end{cases} \end{align*}\]