16 统计研究与随机模拟
现代统计学期刊发表的论文中一半以上包括随机模拟结果(也叫数值结果)。 随机模拟可以辅助说明新模型或新方法的有效性, 尤其是在很难获得关于有效性的理论结果的情况下让我们也能说明自己的新方法的优点。
比如,为了掌握统计量的抽样分布经常需要依靠随机模拟。 在独立正态样本情况下, 我们已经有样本均值和样本方差的分布, 但是对其它分布\(F(x)\)的样本, 我们一般只能得到统计量\(\hat \theta\)的大样本性质, 在中小样本情况下很难得到\(\hat\theta\)的抽样分布理论结果, 随机模拟可以解决这样的问题。 在抽取\(F(x)\)的很多批样本后, 得到很多个统计量\(\hat\theta\)样本值, 从这些样本值可以估计\(\hat\theta\)的抽样分布, 并研究样本量多大时\(\hat\theta\)的抽样分布与大样本极限分布相符, 计算估计的均方误差,等等。
下面举一个置信区间比较的例子说明统计研究中随机模拟的做法。 实际应用中经常需要计算某个百分比的置信区间, 比如北京市成年人口中希望房价降低的人的百分比的置信区间。
设随机抽取了样本量为\(n\)的样本,其中成功个数为\(X\)个, 则\(X \sim \text{B}(n,p)\), \(p\)为成功概率, 要计算\(p\)的置信度为\(1-\alpha\)的置信区间。 记样本中成功百分比为\(\hat p = X/n\)。 假设样本量\(n \geq 30\)。
当\(n\)较大时由中心极限定理可知 \[\begin{align} W = \frac{\hat p - p}{\sqrt{p(1-p)}/\sqrt{n}} \tag{16.1} \end{align}\] 近似服从标准正态分布。 因为\(\hat p \to p\) a.s. \((n\to\infty)\), 所以把(16.1)式分母中的\(p\)换成\(\hat p\), 仍有 \[\begin{align*} Z = \frac{\hat p - p}{\sqrt{\hat p(1 - \hat p)} / \sqrt{n}} \end{align*}\] 近似服从标准正态分布。 于是可以构造\(p\)的置信度\(1-\alpha\)的置信区间为 \[\begin{align} \hat p \pm \frac{\lambda}{\sqrt{n}} \sqrt{\hat p(1 - \hat p)} \tag{16.2} \end{align}\] 其中\(\lambda = z_{1-\frac{\alpha}{2}}\)是标准正态分布的\(1-\frac{\alpha}{2}\)分位数。 当\(n\)很大时这个置信区间应该是比较精确的, 即\(p\)落入置信区间的实际概率应该很接近于标称的置信度\(1-\alpha\), 但是在\(n\)不是太大的时候, \(p\)落入置信区间的实际概率就可能与标称的置信度\(1-\alpha\)有一定的差距, 我们要用随机模拟考察\(1-\alpha, n, p\)的不同取值下置信区间(16.2)的覆盖率。 称置信区间实际包含真实参数的概率为覆盖率。
参数\(p\)的另一个置信区间, 称为Wilson置信区间, 是直接求解关于\(p\)求解不等式 \[\begin{align} \left| \frac{\hat p - p}{\sqrt{p(1-p)}/\sqrt{n}} \right| \leq \lambda. \tag{16.3} \end{align}\] 记 \[\begin{align*} \tilde p = \frac{\hat p + \frac{\lambda^2}{2n}}{1 + \frac{\lambda^2}{n}}, \quad \delta = \frac{\lambda}{\sqrt{n}} \frac{\sqrt{\hat p (1 - \hat p) + \frac{\lambda^2}{4n}}}{1 + \frac{\lambda^2}{n}}, \end{align*}\] 则求解(16.3)得到的\(p\)的置信区间为 \[\begin{align} \tilde p \pm \delta . \tag{16.4} \end{align}\] 我们用随机模拟来考察(16.2)和(16.4)在不同\(n, p\)下的覆盖率并比较这两种置信区间。
好的置信区间应该满足如下两条要求:
- 覆盖率大于等于置信度, 两者越接近越好;
- 置信区间越短越好。
下面设计这个模拟试验。 首先需要估算抽样次数。 设总共重复试验\(M\)次。 \(M\)越大,对覆盖率和置信区间长度期望估计的随机误差越小。 比如我们希望模拟计算的覆盖率误差控制在\(0.1\%\)以下(在95%置信度下)。 对每组样本,真值是否落入计算得到的置信区间是一个成败型试验, 设真实覆盖率为\(r\), \(M\)次重复试验中置信区间包含真实参数的次数为\(V\), 则\(V \sim \text{B}(M,r)\), 覆盖率的估计值为\(V/M\), 此估计的标准误差为\(\sqrt{r(1-r)} / \sqrt{M}\)。 如果覆盖率\(r\)近似等于置信区间的置信度\(1-\alpha\), 则若\(1-\alpha \geq 0.8\),近似地有 \(r(1-r) \leq 0.8\times 0.2=0.16\), \(M\)次试验的覆盖率估计的标准误差为\(\sqrt{0.16}/\sqrt{M} = 0.4 / \sqrt{M}\), 以2倍标准误差作为覆盖率估计的误差大小界限 (根据中心极限定理可知有95%的概率使得\(|\frac{V}{M} - r|\)小于2倍标准误差), 令\(2 \times 0.4 / \sqrt{M} \leq 0.001\)则有 \(M = 640000\), 这个试验重复量很大, 如果程序耗时过长我们只好降低对随机误差幅度的要求。 对于更复杂的问题, 如果难以得到所需重复次数\(M\)的理论值, 可以逐步增加\(M\), 直到结果在需要的精度上不再变化为止。
其次考虑需要模拟的不同情形,一般是不同的模型参数。 比较(16.2)和(16.4)要考虑多种\((n,p, 1-\alpha)\)组合的影响。 取\(1-\alpha = 0.99, 0.95, 0.90, 0.80\)几种。 \((n,p)\)的值要考虑到各种不同情况, 初步选取如下的一些\((n,p)\)组合: \[\begin{align*} & n=30, p=0.1, 0.3, 0.5, 0.7, 0.9; \\ & n=120, p=0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95 \\ & n=480, p=0.01, 0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95, 0.99 \end{align*}\] 这样,我们设计了\((n,p,1-\alpha)\)的\(4 \times (5 + 7 + 9) = 84\)种不同情况, 对每种情况重复试验\(M\)次, \(M\)次重复模拟中每一次可以得到四个数值:
对\((n,p,1-\alpha)\)的每一种情况的\(M\)次重复模拟进行汇总, 可以得到每种情况下的如下汇总统计量:
- 置信区间(16.2)的覆盖率\(\hat r_1\);
- 置信区间(16.4)的覆盖率\(\hat r_2\);
- 置信区间(16.2)的平均长度\(\bar l_1\)和长度标准差\(s_1\);
- 置信区间(16.4)的平均长度\(\bar l_2\)和长度标准差\(s_2\)。
实际编程时,我们先编写84种不同情况中的一种情况去试验, 并在开始时先试验较少的重复数,比如\(M=100\)。 下面是对一种参数组合进行模拟R程序例子:
confp.sim1 <- function(n=30, p=0.3, gam=0.95, M=100){
lam <- qnorm((1+gam)/2)
hatp <- rbinom(M, n, p) / n
rad1 <- lam * sqrt(hatp*(1-hatp)) / sqrt(n)
tildep <- 0.5*lam^2 / (n + lam^2) + n*hatp / (n + lam^2)
rad2 <- (lam / sqrt(n) *
sqrt( hatp * (1 - hatp) + lam^2/(4*n))/
(1 + lam^2/n))
cov1 <- mean(abs(p - hatp) <= rad1)
ncov1 <- M*cov1
cov2 <- mean(abs(p - tildep) <= rad2)
ncov2 <- M*cov2
len1 <- 2*mean(rad1)
sd1 <- 2*sd(rad1)
len2 <- 2*mean(rad2)
sd2 <- 2*sd(rad2)
c(cover1=cov1, cover2=cov2,
n1=ncov1, n2=ncov2,
len1=len1, len2=len2,
sd1=sd1, sd2=sd2)
}当程序检查无误后,再逐步增大重复次数看计算时间和存储能力是否可以接受。 对此例发现\(M=640000\)可行。
最后,用循环处理所有84种情况, 每种情况重复试验\(M=640000\)次。 试验程序如下:
demo.sim.confp <- function(M=640000){
t0 <- proc.time()[3]
ncomb <- 84
resm <- matrix(0, nrow=ncomb, ncol=10)
colnames(resm) <-
c('i', 'confidence', 'n', 'p',
'cover1', 'cover2',
'len1', 'sd1', 'len2', 'sd2')
resm[,'i'] <- seq(ncomb)
resm[,'confidence'] <- rep(c(0.99, 0.95, 0.90, 0.80), each=21)
resm[, 'n'] <- rep(rep(c(30, 120, 480), c(5, 7, 9)), 4)
resm[, 'p'] <- rep(c(0.1, 0.3, 0.5, 0.7, 0.9,
0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95,
0.01, 0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95, 0.99), 4)
for(ii in seq(ncomb)){
cat('组合号码=', ii, '\n')
gam <- resm[ii, 'confidence']
n <- resm[ii, 'n']
p <- resm[ii, 'p']
res <- confp.sim1(n=n, p=p, gam=gam, M=M)
resm[ii, 'cover1'] <- res['cover1']
resm[ii, 'cover2'] <- res['cover2']
resm[ii, 'len1'] <- res['len1']
resm[ii, 'len2'] <- res['len2']
resm[ii, 'sd1'] <- res['sd1']
resm[ii, 'sd2'] <- res['sd2']
save(res, file="置信区间比较模拟中间结果.RData")
}
t1 <- proc.time()[3]
tt <- t1 - t0
cat("重复次数M=", M, " 花费时间=", tt, "\n")
resm
}实际执行:
最后的结果汇总成表表格。 表中每一行是一种\((1-\alpha, n, p)\)的组合。 注意, \(\bar l_1\)和\(\bar l_2\)的精度可以用其标准误差 \(\mbox{SE}_1 = s_1 / \sqrt{M}\)和\(\mbox{SE}_2 = s_2 / \sqrt{M}\)来估计。
结果如下:
library(tidyverse)
for(j in 5:10) tab.stat[,j] <- round(tab.stat[,j], 3)
knitr::kable(tab.stat, longtable=TRUE)| i | confidence | n | p | cover1 | cover2 | len1 | sd1 | len2 | sd2 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.99 | 30 | 0.10 | 0.957 | 0.992 | 0.265 | 0.083 | 0.287 | 0.045 |
| 2 | 0.99 | 30 | 0.30 | 0.968 | 0.992 | 0.422 | 0.038 | 0.391 | 0.027 |
| 3 | 0.99 | 30 | 0.50 | 0.984 | 0.995 | 0.462 | 0.012 | 0.420 | 0.008 |
| 4 | 0.99 | 30 | 0.70 | 0.967 | 0.991 | 0.422 | 0.038 | 0.390 | 0.027 |
| 5 | 0.99 | 30 | 0.90 | 0.957 | 0.992 | 0.265 | 0.083 | 0.287 | 0.045 |
| 6 | 0.99 | 120 | 0.05 | 0.942 | 0.993 | 0.100 | 0.020 | 0.109 | 0.016 |
| 7 | 0.99 | 120 | 0.10 | 0.983 | 0.991 | 0.139 | 0.018 | 0.142 | 0.015 |
| 8 | 0.99 | 120 | 0.30 | 0.986 | 0.988 | 0.214 | 0.009 | 0.210 | 0.008 |
| 9 | 0.99 | 120 | 0.50 | 0.986 | 0.992 | 0.234 | 0.001 | 0.228 | 0.001 |
| 10 | 0.99 | 120 | 0.70 | 0.987 | 0.988 | 0.214 | 0.009 | 0.210 | 0.008 |
| 11 | 0.99 | 120 | 0.90 | 0.983 | 0.991 | 0.139 | 0.018 | 0.142 | 0.015 |
| 12 | 0.99 | 120 | 0.95 | 0.942 | 0.993 | 0.100 | 0.020 | 0.109 | 0.016 |
| 13 | 0.99 | 480 | 0.01 | 0.952 | 0.990 | 0.023 | 0.006 | 0.026 | 0.005 |
| 14 | 0.99 | 480 | 0.05 | 0.981 | 0.991 | 0.051 | 0.005 | 0.052 | 0.005 |
| 15 | 0.99 | 480 | 0.10 | 0.987 | 0.988 | 0.070 | 0.004 | 0.071 | 0.004 |
| 16 | 0.99 | 480 | 0.30 | 0.990 | 0.989 | 0.108 | 0.002 | 0.107 | 0.002 |
| 17 | 0.99 | 480 | 0.50 | 0.991 | 0.991 | 0.117 | 0.000 | 0.117 | 0.000 |
| 18 | 0.99 | 480 | 0.70 | 0.990 | 0.989 | 0.108 | 0.002 | 0.107 | 0.002 |
| 19 | 0.99 | 480 | 0.90 | 0.987 | 0.988 | 0.070 | 0.004 | 0.071 | 0.004 |
| 20 | 0.99 | 480 | 0.95 | 0.981 | 0.991 | 0.051 | 0.005 | 0.052 | 0.005 |
| 21 | 0.99 | 480 | 0.99 | 0.953 | 0.990 | 0.023 | 0.006 | 0.026 | 0.005 |
| 22 | 0.95 | 30 | 0.10 | 0.809 | 0.974 | 0.201 | 0.063 | 0.215 | 0.041 |
| 23 | 0.95 | 30 | 0.30 | 0.953 | 0.930 | 0.321 | 0.029 | 0.307 | 0.023 |
| 24 | 0.95 | 30 | 0.50 | 0.957 | 0.957 | 0.352 | 0.009 | 0.332 | 0.007 |
| 25 | 0.95 | 30 | 0.70 | 0.953 | 0.930 | 0.321 | 0.029 | 0.307 | 0.023 |
| 26 | 0.95 | 30 | 0.90 | 0.808 | 0.974 | 0.201 | 0.063 | 0.215 | 0.041 |
| 27 | 0.95 | 120 | 0.05 | 0.935 | 0.946 | 0.076 | 0.016 | 0.080 | 0.013 |
| 28 | 0.95 | 120 | 0.10 | 0.954 | 0.954 | 0.106 | 0.013 | 0.107 | 0.012 |
| 29 | 0.95 | 120 | 0.30 | 0.937 | 0.942 | 0.163 | 0.007 | 0.161 | 0.006 |
| 30 | 0.95 | 120 | 0.50 | 0.945 | 0.945 | 0.178 | 0.001 | 0.175 | 0.001 |
| 31 | 0.95 | 120 | 0.70 | 0.937 | 0.942 | 0.163 | 0.007 | 0.161 | 0.006 |
| 32 | 0.95 | 120 | 0.90 | 0.954 | 0.955 | 0.106 | 0.013 | 0.107 | 0.012 |
| 33 | 0.95 | 120 | 0.95 | 0.935 | 0.946 | 0.076 | 0.016 | 0.080 | 0.014 |
| 34 | 0.95 | 480 | 0.01 | 0.855 | 0.967 | 0.017 | 0.004 | 0.019 | 0.004 |
| 35 | 0.95 | 480 | 0.05 | 0.937 | 0.955 | 0.039 | 0.004 | 0.039 | 0.004 |
| 36 | 0.95 | 480 | 0.10 | 0.947 | 0.943 | 0.054 | 0.003 | 0.054 | 0.003 |
| 37 | 0.95 | 480 | 0.30 | 0.947 | 0.948 | 0.082 | 0.002 | 0.082 | 0.002 |
| 38 | 0.95 | 480 | 0.50 | 0.950 | 0.950 | 0.089 | 0.000 | 0.089 | 0.000 |
| 39 | 0.95 | 480 | 0.70 | 0.947 | 0.948 | 0.082 | 0.002 | 0.082 | 0.002 |
| 40 | 0.95 | 480 | 0.90 | 0.947 | 0.943 | 0.054 | 0.003 | 0.054 | 0.003 |
| 41 | 0.95 | 480 | 0.95 | 0.937 | 0.954 | 0.039 | 0.004 | 0.039 | 0.004 |
| 42 | 0.95 | 480 | 0.99 | 0.855 | 0.968 | 0.017 | 0.004 | 0.019 | 0.004 |
| 43 | 0.90 | 30 | 0.10 | 0.790 | 0.884 | 0.169 | 0.053 | 0.178 | 0.038 |
| 44 | 0.90 | 30 | 0.30 | 0.883 | 0.930 | 0.270 | 0.024 | 0.261 | 0.021 |
| 45 | 0.90 | 30 | 0.50 | 0.901 | 0.901 | 0.295 | 0.007 | 0.283 | 0.006 |
| 46 | 0.90 | 30 | 0.70 | 0.883 | 0.930 | 0.269 | 0.024 | 0.261 | 0.021 |
| 47 | 0.90 | 30 | 0.90 | 0.791 | 0.885 | 0.169 | 0.053 | 0.178 | 0.038 |
| 48 | 0.90 | 120 | 0.05 | 0.838 | 0.864 | 0.064 | 0.013 | 0.066 | 0.012 |
| 49 | 0.90 | 120 | 0.10 | 0.892 | 0.909 | 0.089 | 0.011 | 0.090 | 0.011 |
| 50 | 0.90 | 120 | 0.30 | 0.887 | 0.910 | 0.137 | 0.006 | 0.136 | 0.005 |
| 51 | 0.90 | 120 | 0.50 | 0.879 | 0.917 | 0.150 | 0.001 | 0.148 | 0.001 |
| 52 | 0.90 | 120 | 0.70 | 0.888 | 0.910 | 0.137 | 0.006 | 0.136 | 0.005 |
| 53 | 0.90 | 120 | 0.90 | 0.892 | 0.909 | 0.089 | 0.011 | 0.090 | 0.011 |
| 54 | 0.90 | 120 | 0.95 | 0.838 | 0.863 | 0.064 | 0.013 | 0.066 | 0.012 |
| 55 | 0.90 | 480 | 0.01 | 0.834 | 0.898 | 0.014 | 0.004 | 0.016 | 0.003 |
| 56 | 0.90 | 480 | 0.05 | 0.891 | 0.886 | 0.033 | 0.003 | 0.033 | 0.003 |
| 57 | 0.90 | 480 | 0.10 | 0.886 | 0.890 | 0.045 | 0.003 | 0.045 | 0.003 |
| 58 | 0.90 | 480 | 0.30 | 0.899 | 0.901 | 0.069 | 0.001 | 0.069 | 0.001 |
| 59 | 0.90 | 480 | 0.50 | 0.890 | 0.909 | 0.075 | 0.000 | 0.075 | 0.000 |
| 60 | 0.90 | 480 | 0.70 | 0.898 | 0.900 | 0.069 | 0.001 | 0.069 | 0.001 |
| 61 | 0.90 | 480 | 0.90 | 0.886 | 0.891 | 0.045 | 0.003 | 0.045 | 0.003 |
| 62 | 0.90 | 480 | 0.95 | 0.891 | 0.886 | 0.033 | 0.003 | 0.033 | 0.003 |
| 63 | 0.90 | 480 | 0.99 | 0.834 | 0.898 | 0.014 | 0.004 | 0.016 | 0.003 |
| 64 | 0.80 | 30 | 0.10 | 0.743 | 0.884 | 0.132 | 0.041 | 0.137 | 0.032 |
| 65 | 0.80 | 30 | 0.30 | 0.757 | 0.839 | 0.210 | 0.019 | 0.206 | 0.017 |
| 66 | 0.80 | 30 | 0.50 | 0.799 | 0.799 | 0.230 | 0.006 | 0.224 | 0.005 |
| 67 | 0.80 | 30 | 0.70 | 0.756 | 0.839 | 0.210 | 0.019 | 0.206 | 0.017 |
| 68 | 0.80 | 30 | 0.90 | 0.744 | 0.885 | 0.132 | 0.041 | 0.137 | 0.032 |
| 69 | 0.80 | 120 | 0.05 | 0.777 | 0.864 | 0.050 | 0.010 | 0.051 | 0.009 |
| 70 | 0.80 | 120 | 0.10 | 0.769 | 0.831 | 0.069 | 0.009 | 0.070 | 0.008 |
| 71 | 0.80 | 120 | 0.30 | 0.805 | 0.805 | 0.107 | 0.004 | 0.106 | 0.004 |
| 72 | 0.80 | 120 | 0.50 | 0.764 | 0.829 | 0.116 | 0.001 | 0.116 | 0.001 |
| 73 | 0.80 | 120 | 0.70 | 0.805 | 0.805 | 0.107 | 0.004 | 0.106 | 0.004 |
| 74 | 0.80 | 120 | 0.90 | 0.770 | 0.833 | 0.069 | 0.009 | 0.070 | 0.008 |
| 75 | 0.80 | 120 | 0.95 | 0.776 | 0.864 | 0.050 | 0.010 | 0.051 | 0.009 |
| 76 | 0.80 | 480 | 0.01 | 0.805 | 0.747 | 0.011 | 0.003 | 0.012 | 0.003 |
| 77 | 0.80 | 480 | 0.05 | 0.788 | 0.828 | 0.025 | 0.002 | 0.025 | 0.002 |
| 78 | 0.80 | 480 | 0.10 | 0.798 | 0.805 | 0.035 | 0.002 | 0.035 | 0.002 |
| 79 | 0.80 | 480 | 0.30 | 0.805 | 0.788 | 0.054 | 0.001 | 0.053 | 0.001 |
| 80 | 0.80 | 480 | 0.50 | 0.814 | 0.814 | 0.058 | 0.000 | 0.058 | 0.000 |
| 81 | 0.80 | 480 | 0.70 | 0.803 | 0.786 | 0.054 | 0.001 | 0.053 | 0.001 |
| 82 | 0.80 | 480 | 0.90 | 0.797 | 0.805 | 0.035 | 0.002 | 0.035 | 0.002 |
| 83 | 0.80 | 480 | 0.95 | 0.787 | 0.828 | 0.025 | 0.002 | 0.026 | 0.002 |
| 84 | 0.80 | 480 | 0.99 | 0.804 | 0.747 | 0.011 | 0.003 | 0.012 | 0.003 |
结果内容比较多。 R的数据选择功能可以让我们比较不同参数的影响。 例如,取样本量\(n=480\), 比较两种方法在置信度、\(p\)值下的覆盖率:
tab1 <- as_tibble(tab.stat) |>
dplyr::filter(n==480) |>
select(p, confidence, cover1, cover2) |>
arrange(p, confidence)
knitr::kable(tab1)| p | confidence | cover1 | cover2 |
|---|---|---|---|
| 0.01 | 0.80 | 0.805 | 0.747 |
| 0.01 | 0.90 | 0.834 | 0.898 |
| 0.01 | 0.95 | 0.855 | 0.967 |
| 0.01 | 0.99 | 0.952 | 0.990 |
| 0.05 | 0.80 | 0.788 | 0.828 |
| 0.05 | 0.90 | 0.891 | 0.886 |
| 0.05 | 0.95 | 0.937 | 0.955 |
| 0.05 | 0.99 | 0.981 | 0.991 |
| 0.10 | 0.80 | 0.798 | 0.805 |
| 0.10 | 0.90 | 0.886 | 0.890 |
| 0.10 | 0.95 | 0.947 | 0.943 |
| 0.10 | 0.99 | 0.987 | 0.988 |
| 0.30 | 0.80 | 0.805 | 0.788 |
| 0.30 | 0.90 | 0.899 | 0.901 |
| 0.30 | 0.95 | 0.947 | 0.948 |
| 0.30 | 0.99 | 0.990 | 0.989 |
| 0.50 | 0.80 | 0.814 | 0.814 |
| 0.50 | 0.90 | 0.890 | 0.909 |
| 0.50 | 0.95 | 0.950 | 0.950 |
| 0.50 | 0.99 | 0.991 | 0.991 |
| 0.70 | 0.80 | 0.803 | 0.786 |
| 0.70 | 0.90 | 0.898 | 0.900 |
| 0.70 | 0.95 | 0.947 | 0.948 |
| 0.70 | 0.99 | 0.990 | 0.989 |
| 0.90 | 0.80 | 0.797 | 0.805 |
| 0.90 | 0.90 | 0.886 | 0.891 |
| 0.90 | 0.95 | 0.947 | 0.943 |
| 0.90 | 0.99 | 0.987 | 0.988 |
| 0.95 | 0.80 | 0.787 | 0.828 |
| 0.95 | 0.90 | 0.891 | 0.886 |
| 0.95 | 0.95 | 0.937 | 0.954 |
| 0.95 | 0.99 | 0.981 | 0.991 |
| 0.99 | 0.80 | 0.804 | 0.747 |
| 0.99 | 0.90 | 0.834 | 0.898 |
| 0.99 | 0.95 | 0.855 | 0.968 |
| 0.99 | 0.99 | 0.953 | 0.990 |
可以看出\(n=480\)时, 方法1在\(p=0.95\), \(1-\alpha=0.80\)时覆盖率仅有0.787; 方法2在\(p=0.01, 0.99\), \(1-\alpha=0.80\)时覆盖率仅有0.747。 应进一步试验,研究其原因。
另一方面,从置信区间平均长度来看,两种方法差距不大。
下面做更多的模拟来确认公式(16.4)在\(n=480\), \(p=0.01\),\(1-\alpha=0.80\)时的缺陷。 写一个简单的仅模拟计算(16.4)的覆盖率的函数:
confp.sim2 <- function(n=480, p=0.01, gam=0.80, M=640000){
lam <- qnorm((1+gam)/2)
hatp <- rbinom(M, n, p) / n
tildep <- 0.5*lam^2 / (n + lam^2) + n*hatp / (n + lam^2)
rad2 <- (lam / sqrt(n) *
sqrt( hatp * (1 - hatp) + lam^2/(4*n))/
(1 + lam^2/n))
cov2 <- mean(abs(p - tildep) <= rad2)
ncov2 <- M*cov2
cov2
}R的replicate()函数可以用来做简单的重复模拟:
set.seed(1)
tab2 <- replicate(100, confp.sim2())
summary(tab2)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.7449 0.7462 0.7465 0.7465 0.7467 0.7477可见重复了100次, 覆盖率最高也不超过75%, 说明公式(16.4)在\(n=480\), \(p=0.01\),\(1-\alpha=0.80\)时不能达到标称的置信度, 实际低了5个百分点以上。 从结果也可以看出我们取\(M=640000\)可以使得覆盖率估计基本达到0.001精度。
习题
习题1
设\(X \sim \text{b}(1,p)\), \(X_1, X_2, \dots, X_n\)为样本。 令 \(S_0 = \sum_{i=1}^n X_i\), \(\hat p = S_0/n = \frac{1}{n}\sum_{i=1}^n X_i\)。 用模拟方法比较如下五种置信区间:
利用正态近似。当\(n\)很大时 \[\begin{aligned} \frac{\hat p - p}{\sqrt{\frac{1}{n} \hat p (1 - \hat p)}} \end{aligned}\] 近似服从\(\text{N}(0,1)\),于是得置信区间 \[\begin{aligned} \hat p \pm z_{1-\frac{\alpha}{2}} \sqrt{\frac{1}{n} \hat p (1 - \hat p)} . \end{aligned}\]
利用正态近似,令 \[\begin{aligned} S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \hat p)^2 = \frac{n}{n-1} \hat p (1 - \hat p), \end{aligned}\] \(n\)很大时 \[\begin{aligned} \frac{\hat p - p}{\sqrt{\frac{1}{n} S^2}} \end{aligned}\] 近似服从\(\text{N}(0,1)\),于是得置信区间 \[\begin{aligned} \hat p \pm z_{1-\frac{\alpha}{2}} \sqrt{\frac{1}{n} S^2} . \end{aligned}\]
Wilson置信区间。利用正态近似,\(n\)很大时 \[\begin{aligned} \frac{\hat p - p}{\sqrt{\frac{1}{n} p (1 - p)}} \end{aligned}\] 近似服从\(\text{N}(0,1)\),解关于\(p\)的不等式 \[\begin{aligned} \left| \frac{\hat p - p}{\sqrt{\frac{1}{n} p (1-p)}} \right| \leq z_{1-\frac{\alpha}{2}}, \end{aligned}\] 得置信区间(\(\lambda = z_{1-\frac{\alpha}{2}}\)) \[\begin{aligned} \frac{\hat p + \frac{\lambda^2}{2n}}{1 + \frac{\lambda^2}{n}} \pm \frac{\lambda \sqrt{\frac{\lambda^2}{4n} + \hat p (1 - \hat p)}} {\sqrt{n} \left(1 + \frac{\lambda^2}{n} \right)} . \end{aligned}\]
Agresti and Coull(1998)方法。 先计算Wilson区间中心(\(\lambda = z_{1-\frac{\alpha}{2}}\)) \[\begin{aligned} \tilde p = \frac{\hat p + \frac{\lambda^2}{2n}}{1 + \frac{\lambda^2}{n}}, \end{aligned}\] 取置信区间为 \[\begin{aligned} \tilde p \pm \lambda \frac{\sqrt{\tilde p(1 - \tilde p)}}{\sqrt{n} \sqrt{1 + \frac{\lambda^2}{n}}}. \end{aligned}\]
用二项分布导出\(p\)的置信区间。令 \[\begin{aligned} p_1 =& \left\{ 1 + \frac{n-S_0+1}{S_0} F_{1-\frac{\alpha}{2}}(2(n-S_0+1), 2S_0) \right\}^{-1} \\ p_2 =& \left\{ 1 + \frac{n-S_0}{S_0+1} \frac{1}{F_{1-\frac{\alpha}{2}}(2(S_0+1), 2(n-S_0))} \right\}^{-1} \end{aligned}\] 取置信区间为\([p_1, p_2]\), 其中\(F_q(n_1, n_2)\)表示\(\text{F}(n_1,n_2)\)分布的\(q\)分位数。
对不同\(n, p, 1-\alpha\),比较这五种置信区间的优劣。
习题2
不同的检验法有不同的功效, 在难以得到功效函数的显式表达式的时候, 模拟方法可以起到重要补充作用。
对无截距项的回归模型 \[\begin{aligned} y_i =& b x_i + \varepsilon_i, \quad i=1,2,\dots, n \\ & \varepsilon_1, \varepsilon_2, \dots, \varepsilon_n \text{iid} \sim \text{N}(0,\sigma^2) \end{aligned}\] 为检验\(H_0: b = 0\),有如下两种检验方法:
\(b=0\)时\(y_i = \varepsilon_i\), 于是在\(H_0\)下 \[\begin{aligned} t = \frac{\bar y}{\sqrt{\frac{1}{n} \frac{1}{n-1} \sum_{i=1}^n (y_i - \bar y)^2}} \end{aligned}\] 服从t(\(n-1\))分布。 设\(\lambda\)为\(\text{t}(n-1)\)分布的\(1-\frac{\alpha}{2}\)分位数, 取否定域为\(\{ |t| > \lambda \}\)。
令 \[\begin{aligned} \hat b =& \frac{\sum_{i=1}^n x_i y_i}{\sum_{i=1}^n x_i^2}, & U =& \hat b^2 \sum_{i=1}^n x_i^2 \\ Q =& \sum_{i=1}^n y_i^2 - U, & F =& \frac{U}{Q/(n-1)} \end{aligned}\] 设\(\lambda'\)为\(\text{F}(1,n-1)\)的\(1-\alpha\)分位数, 取否定域为\(\{ F > \lambda' \}\)。
对不同的\(b, \sigma^2, n, \alpha\)以及不同的\(\{ x_i \}\)模拟比较这两种检验方法的功效。
习题3
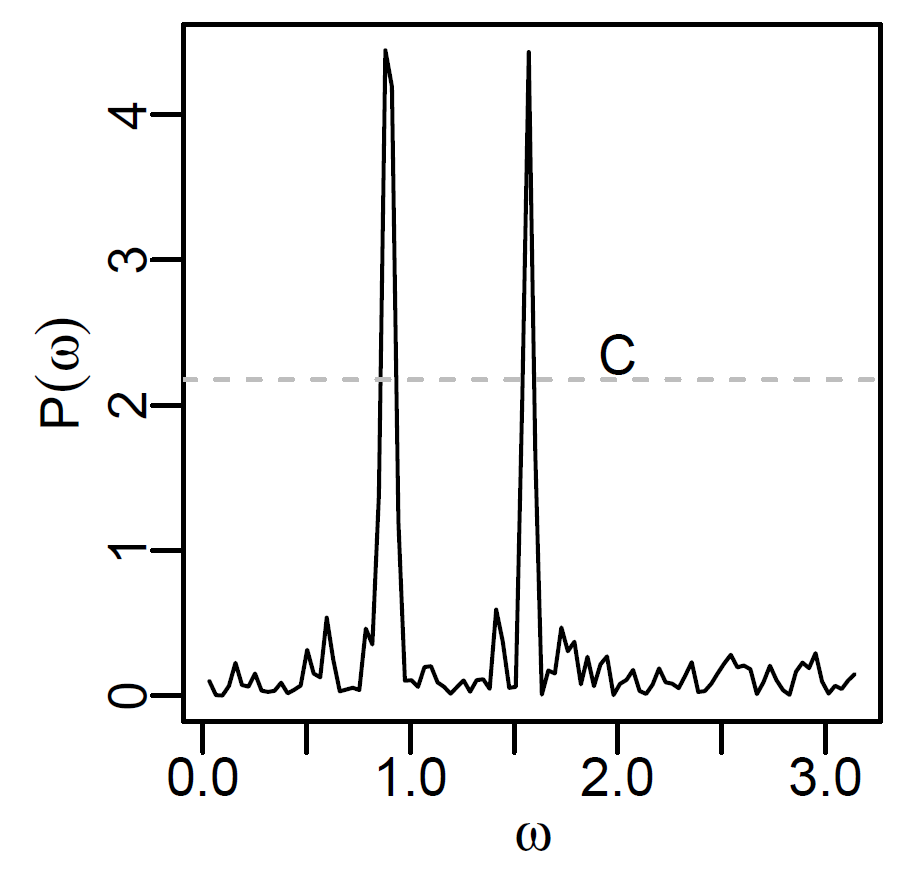
设时间序列\(\{ y_t \}\)有如下模型: \[\begin{aligned} y_t = \sum_{k=1}^m A_k \cos(\lambda_k t + \phi_k) + x_t, \ t=1,2,\dots \end{aligned}\] 其中\(x_t\)为线性平稳时间序列, \(\lambda_k \in (0,\pi)\), \(k=1,2,\dots,m\)。 这样的模型称为潜周期模型。 如果有\(\{ y_t \}\)的一组样本\(y_1, y_2, \dots, y_n\), 可以定义周期图函数(如上图) \[\begin{aligned} P(\omega) = \frac{1}{2\pi n} \left| \sum_{t=1}^n y_t e^{-it\omega} \right|^2, \ \omega \in [0, \pi]. \end{aligned} \] 在\(\lambda_j\)的对应位置\(P(\omega)\)会有尖峰, 而且当\(n\to\infty\)时尖峰高度趋于无穷。
如下算法可以在\(n\)较大时估计\(m\)和\(\{\lambda_k \}\): 首先,对\(\omega_j=\pi j / n\), \(j=1,2,\dots,n\)计算\(h_j = P(\omega_j)\), 求\(\{ h_j, j=1,2,\dots, n \}\)的3/4分位数记为\(q\)。 令\(C = q n^{1/2}\),以\(C\)作为分界线, 设\(\{ h_j \}\)中大于\(C\)的下标\(j\)的集合为\(J\), 当\(J\)非空时,把\(J\)中相邻点分入一组, 但是当两个下标的差大于等于\(n^{3/4}\)时就把后一个点归入新的一组。 在每组中,以该组的\(h_j\)的最大值点对应的角频率\(j \pi / n\)作为潜频率\(\{ \lambda_k \}\)中的一个的估计。
用如下R程序可以模拟生成一组\(\{ y_t \}\)的观测数据:
set.seed(1); n <- 100; tt <- seq(n)
m <- 2; lam <- 2*pi/c(4, 7); A <- c(1, 1.2)
y <- A[1]*cos(lam[1]*tt) + A[2]*cos(lam[2]*tt) + rnorm(n)编写R程序:
- 编写计算\(P(\omega)\)的函数, 输入\(\boldsymbol y = (y_1, y_2, \dots, y_n)^T\)和\(\boldsymbol\omega = (\omega_1, \omega_2, \dots, \omega_n)^T\), 输出\((P(\omega_1), P(\omega_2), \dots, P(\omega_s))\)。
- 用R函数fft计算\(h_j=P(\pi j / n), j=1,2,\dots,n\)。
- 对输入的时间序列样本\(y_1, y_2, \dots, y_n\), 编写函数用以上描述的算法估计\(m\)和\(\{ \lambda_j, j=1,2,\dots,m \}\)。
习题4
设\(p(x, \mu, \sigma)\)表示\(\text{N}(\mu, \sigma^2)\)的分布密度函数, 设总体\(X\)分布密度为 \[ f(x) = \lambda p(x, \mu, \sigma) + (1-\lambda) p(x, \mu, k\sigma) \] 其中\(0<\lambda<1\),\(k>1\)。 这称为混合正态分布。 从总体中抽取简单随机样本\(X_1, X_2, \dots, X_n\), 对参数\(\mu\)进行估计, 有两种估计方法:
- 样本均值\(\bar x\);
- 取\(0 < p < 0.5\),计算删去最小的\(p\)比例和最大的\(p\)比例的样本值之后的样本平均值, 记作\(\bar x_p\),称为Winsorized mean。
这两个估计都是无偏的, 哪一个的方差更小?理论上不容易解决。 用随机模拟方法研究。 需要设定一些不同的\(\mu\), \(\sigma\), \(\lambda\), \(k\), \(p\), \(n\)的值, 估计需要的重复次数\(N\), 比较不同情况下两种方法的估计方差。
习题5
分位数估计。 设总体\(X\)有密度函数\(p(x)\)和分布函数\(F(x)\), 一组简单随机样本为\(X_1, X_2, \dots, X_n\), 次序统计量为\(X_{(1)}, X_{(2)}, \dots, X_{(n)}\)。 为估计\(p\)分位数\(x_p = F^{-1}(p)\), 最简单的方法是\(X_{([np])}\), 其中\([np]\)表示\(np\)向下取整。
更好的做法是用Beta分布作为线性组合系数, 对次序统计量作线性组合估计\(x_p\)。 记\(G(x; p)\)为Beta(\((n+1)p\), \((n+1)(1-p)\))分布的分布函数, 取\(x_p\)估计为 \[ \tilde x_p = \sum_{i=1}^n [G(i/n; p) - G((i-1)/n; p)] X_{(i)} \] 称为Harrell-Davis估计量。
\(p=\frac12\)时\(x_p\)称为中位数。 最简单的样本中位数估计是样本中位数\(\hat m\): 奇数个样本取中间一个, 偶数个样本取中间两个的平均值。 用随机模拟方法比较样本中位数与Harrell-Davis估计, \(F(\cdot)\)取正态分布、柯西分布、伽马分布等多种, 样本量\(n\)取\(25\)和\(100\)两种。 用随机模拟比较两种方法的均方误差、偏差、方差, 取适当的模拟重复次数\(N\)。