3 概括统计量
3.1 总体和样本
统计的主要作用在于分析数据, 发现数据中的规律。 统计学是以概率论为数学基础的。 我们先回顾一些基本概念。
假设一个变量的多个观测值\(x_1, x_2, \dots, x_n\) 可以看成某随机变量\(X\)的\(n\)个独立观测, 称\(X\)为总体, 称\(x_1, x_2, \dots, x_n\)为总体\(X\)的简单随机样本(简称样本), 称不需要未知参数的值、仅从样本计算得到的量为统计量。
对样本\(x_1, x_2, \dots, x_n\)从小到大排序得到 \(x_{(1)} \leq x_{(2)} \leq \cdots x_{(n)}\), 称为样本的次序统计量。
为了估计\(F(x) = P(X \leq x)\), 使用如下统计量 \[\begin{align*} F_n(x) = \frac{ \#(\{ i: \, x_i \leq x \}) }{n} = \frac{1}{n} \sum_{i=1}^n I_{(-\infty, x]}(x_i) \end{align*}\] 其中\(\#(A)\)表示集合\(A\)中元素的个数, \(I_A(x)\)是集合\(A\)的示性函数, 当\(x \in A\)时等于1,当\(x \notin A\)时等于0。 \(F_n(x)\)是样本统计量,也是\(x\)的函数, 称\(F_n(x)\)为经验分布函数。 如果\(x_{(1)} < x_{(2)} < \dots < x_{(n)}\), 易见 \[\begin{align*} F_n(x) = \begin{cases} 0 & \text{当$x < x_{(1)}$} \\ \frac{1}{n} & \text{当$x_{(1)} \leq x < x_{(2)}$} \\ \cdots & \cdots\cdots \\ \frac{i-1}{n} & \text{当$x_{(i-1)} \leq x < x_{(i)}$} \\ \cdots & \cdots\cdots \\ \frac{n-1}{n} & \text{当$x_{(n-1)} \leq x < x_{(n)}$} \\ 1 & \text{当$x \geq x_{(n)}$} \end{cases} \end{align*}\] 可见\(F_n(x)\)是\(x\)的单调递增右连续阶梯函数, 跳跃点为各\(x_{(i)}\)处, 跳跃高度为\(\frac{1}{n}\)。 如果有\(x_{(i)}\)有\(k\)个相等的观测值, 则在\(x_{(i)}\)处跳跃高度为\(\frac{k}{n}\)。 由强大数律易见 \(\lim_{n\to\infty} F_n(x) = F(x), \ \text{a.s. } \forall x \in (-\infty, \infty)\), 即\(F_n(x)\)是\(F(x)\)的强相合估计。 进一步地,\(F_n(x)\)是\(F(x)\)的一致强相合估计。
事实上, \(F_n(x)\)也是一个真正的分布函数。 设随机变量\(W \sim F_n(x)\), 则\(W\)服从离散分布, 在\(\{x_1, x_2, \dots, x_n \}\)内取值, 如果各\(x_i\)互不相同则\(W\)服从\(\{x_1, x_2, \dots, x_n \}\)上的离散均匀分布, \(P(W=x_i) = \frac{1}{n}, \; i=1,2,\dots,n\)。 如果\(\{x_1, x_2, \dots, x_n \}\)中有相同的观测值则其相应的取值概率是\(\frac{1}{n}\)乘以重复次数。
下面给出分位数函数的定义。 设随机变量\(X\)的分布函数\(F(x)\)严格单调上升且连续, 则存在反函数\(F^{-1}(p)\) \((0 < p < 1)\)使得 \[\begin{align*} F( F^{-1}(p) ) = p, \ \forall 0<p<1. \end{align*}\] 称\(F^{-1}(p)\)为\(X\)或\(F(x)\)的分位数函数, 称\(x_p = F^{-1}(p)\)为\(F(x)\)的\(p\)分位数。 如果\(F(x)\)没有反函数(当\(F(x)\)在某个区间等于常数时), 则只要\(x_p\)满足 \[\begin{align*} P(X \leq x_p) \geq p, \quad P(X \geq x_p) \geq 1 - p \end{align*}\] 就称\(x_p\)是\(X\)(或\(F(x)\))的\(p\)分位数。 这样的\(x_p\)可能不唯一, 取其中最小的一个, 可得 \[\begin{align*} x_p = \inf \{ x: F(x) \geq p \}. \end{align*}\]
3.2 样本的描述统计量
在对数据建模分析之前, 我们需要预先排除数据中的错误, 了解数据的特点, 考察数据是否符合模型假定的前提条件。 这些前期准备工作统称为探索性数据分析 (Exploratory Data Analysis, EDA)。
最常见的数据形式是一个变量的多次观测, 或一组变量的多次观测。 对单个变量,我们关心其分布情况; 对多个变量, 我们还关心变量之间的关系。
下面介绍用描述统计量来概括数据的方法。
随机变量主要有两种, 离散型和连续型。 离散型随机变量可以代表某种分类值, 比如性别、行业、省份, 也可以是离散取值的数值变量, 比如\(n\)次独立重复试验的成功次数, 一块电路板上的缺陷个数,等等。
对于取分类值的随机变量, EDA的作用是考察其取值集合, 计算取每个不同值的次数和比例, 并纠正不一致的输入。 比如,变量
保存了5个人的性别, 用
可以求得每个不同值的取值次数, 并且可以发现输入存在不一致性。
Julia版本:
Dict{String,Int64} with 3 entries:
"女" => 2
"男" => 2
"男… => 1对于数值型的变量(包括离散取值和连续取值), 我们主要关心其分布情况。 如果是离散取值的, 我们需要确定其可取值集合; 如果是连续取值, 我们需要了解其可取值的区间或集合。 然后, 我们可以从样本中计算描述分布特征的统计量, 来描述变量分布。称这样的统计量为描述统计量。
作为基础,先给出估计分位数的方法。
设\(x_{(1)} \leq x_{(2)} \leq \dots \leq x_{(n)}\)
为样本的次序统计量,
用
\[\begin{align*}
\hat x_p = x_{([np])}
\end{align*}\]
可以估计\(x_p\)。
其中\([x]\)表示对实数\(x\)向下取整,
即小于等于\(x\)的最大整数。
当\(x_p\)唯一时,\(\hat x_p\)是\(x_p\)的强相合估计。
但是,当\(n\)不太大时,
这样的估计方法有些粗略。
改进\(x_p\)估计的想法是,
因为\(x_p\)是\(F(x)=p\)的解,
可以用适当方法把阶梯函数\(F_n(x)\)变成严格单调上升连续函数,
设改进后\(\tilde F_n(x) \approx F(x)\),
再解\(\tilde F_n(x)=p\)得到\(x_p\)的估计。
例如,令
\[\begin{align*}
\tilde F_n(x_{(i)}) = \frac{i - \frac13}{n + \frac13},
\ i=1,2,\dots,n
\end{align*}\]
(如果有若干个\(x_{(i)}\)取值相等,\(i\)取最小下标)
并把相邻点用线段相连来定义\(\tilde F_n(x)\),
求\(\tilde F_n(x)=p\)得到\(x_p\)的估计。
详见(Hyndman and Fan 1996)。
R语言中函数quantile(x)可以计算样本分位数,
并提供了(Hyndman and Fan 1996)描述的9种不同的计算方法。
Julia语言中Statistics.quantile函数计算样本分位数。
为了概括地描述数值型的随机变量分布, 可以使用以下几类常用的数字特征:
3.2.1 位置特征量
假设\(F(x)\)是一个分布函数, 则\(\{ F(x - \theta), \, \theta \in \mathbb R \}\)构成了一族分布, 其中\(\theta\)是代表分布位置的数字特征。 例如,\(\text{N}(\mu, \sigma^2)\)分布中\(\mu\)是代表分布位置的数字特征。
可以用来描述总体\(X\)的分布位置的数字特征包括 期望值\(EX\),中位数\(m\), 众数\(d\)。
3.2.1.1 均值
期望值\(EX\)是样本取值用取值概率或概率密度作为加权的加权平均。
比如,在总共10000张售价1元的彩票中仅有1张是有5000元奖金的,
则随机抽取一张的获利\(Y\)的期望为如下加权平均:
\[\begin{align*}
E X =& (5000-1) \times P(\text{中奖}) + (-1) \times P(\text{不中奖}) \\
=& (5000-1) \times \frac{1}{10000} + (-1) \times \frac{9999}{10000}
= -0.5 \text{(元)}
\end{align*}\]
对样本\(x_1, x_2, \dots, x_n\),
用样本平均数
\[\begin{align*}
\bar x = \frac{1}{n} \sum_{i=1}^n x_i
\end{align*}\]
估计\(EX\)。
在R语言中用mean(x)求平均值。
在Julia中用Statistics.mean(x)求平均值。
样本平均值受到极端值的影响很大。 比如,某企业有1名经理和100名员工, 经理月薪100000元,其他员工月薪1000元, 则101位雇员的平均工资为 \[\begin{aligned} \bar x = \frac{1}{101}(100000 + 100 \times 1000) \approx 1980.2 \end{aligned}\] 并不能真实反映工资的一般情况。
例3.1 (样本均值递推算法(*)) 用递推方法计算均值, 并用R程序和Julia程序实现。
如果我们需要递推地计算样本平均值, 记\(\bar x_k = \frac{1}{k} \sum_{i=1}^k x_i\), 可以用如下算法:
| 样本平均值递推计算 |
|---|
| \(\bar x_1 \leftarrow x_1\) |
| for (\(k\) in \(2:n\)) { |
| \(\qquad\) \(\bar x_k \leftarrow \frac{k-1}{k} \bar x_{k-1} + \frac{1}{k} x_k\) |
| } |
R程序实现:
测试:
set.seed(1)
x <- round(runif(5), 2); x
## [1] 0.27 0.37 0.57 0.91 0.20
mean(x)
## [1] 0.464
mean.it(x)
## [1] 0.464Julia函数:
function mean_iter(x::Vector)
n = length(x)
xm::Float64 = x[1]
for k = 2:n
xm = (k-1.0)/k*xm + x[k]/k
end
xm
end测试:
using Random, Statistics
Random.seed!(101)
x = round.(rand(5), digits=2);
@show x;
## x = [0.72, 0.18, 0.31, 0.54, 0.93]
@show mean_iter(x);
## mean_iter(x) = 0.536
@show mean(x);
## mean(x) = 0.536※※※※※
3.2.1.2 中位数
总体\(X\)的中位数\(m\)是满足
\[\begin{align*}
P(X \leq m) \geq \frac12, \quad P(X \geq m) \geq \frac12
\end{align*}\]
的数,
即\(X\)的\(\frac12\)分位数。
对一组样本\(X_1, X_2, \dots, X_n\),
当\(n\)为奇数时令\(\hat m = x_{(\frac{n+1}{2})}\),
即从小到大排序后中间一个的值,
当\(n\)为偶数时令\(\hat m = \frac12 ( x_{(\frac{n}{2})} + x_{(\frac{n}{2} + 1)})\),
即从小到大排序后中间两个的平均值。
称这样得到的\(\hat m\)为样本中位数,
用来估计总体中位数\(m\)。
在R语言中用median(x)求样本中位数。
在Julia语言中用Statistics.median(x)。
3.2.1.3 众数
总体\(X\)的众数\(d\)是\(X\)的分布密度的最大值点, 或\(X\)的概率分布中概率值最大的取值点, 可以用样本值中出现最多的一个数来估计。 如果需要更精确的众数估计可以先估计分布密度, 再设法估计密度的最大值点。 对于纯数值型的变量来说,众数作为位置特征量比较粗略, 实际用处不大。
例3.2 (正态样本众数计算(*)) 设\(X \sim \text{N}(\mu, \sigma^2)\), 则总体期望值、中位数和众数都是\(\mu\)。 对模拟样本计算。
编写一个求众数的自定义函数:
sample.mode <- function(x){
tf <- table(x)
maxf <- max(tf)
strmode <- names(tf)[tf == maxf]
if(length(strmode) < length(x)){
sort(as.numeric(strmode))
} else {
numeric(0)
}
}这个自定义函数规定如果每个值都恰好出现一次就没有样本众数, 否则众数可以是一个或者多个。 测试:
set.seed(101)
x <- round(rnorm(100, 10, 2), 2)
mean(x)
## [1] 9.9255
median(x)
## [1] 9.97
sample.mode(x)
## [1] 7.07 7.18 10.56 10.93 12.35有多个众数。
作直方图并显示样本均值、中位数、众数的位置:
demo.location <- function(x, title=""){
d1 <- rbind(
tibble(x=mean(x), stat="均值"),
tibble(x=median(x), stat="中位数"),
tibble(x=sample.mode(x), stat="众数"))
ggplot(data=tibble(x=x), mapping=aes(x=x)) +
geom_histogram(bins=10) +
geom_vline(data=d1, mapping=aes(
xintercept=x, col=stat),
size=1.5, alpha=0.5) +
labs(title=title)
}
demo.location(x, title="100个正态分布N(10,2^2)随机数")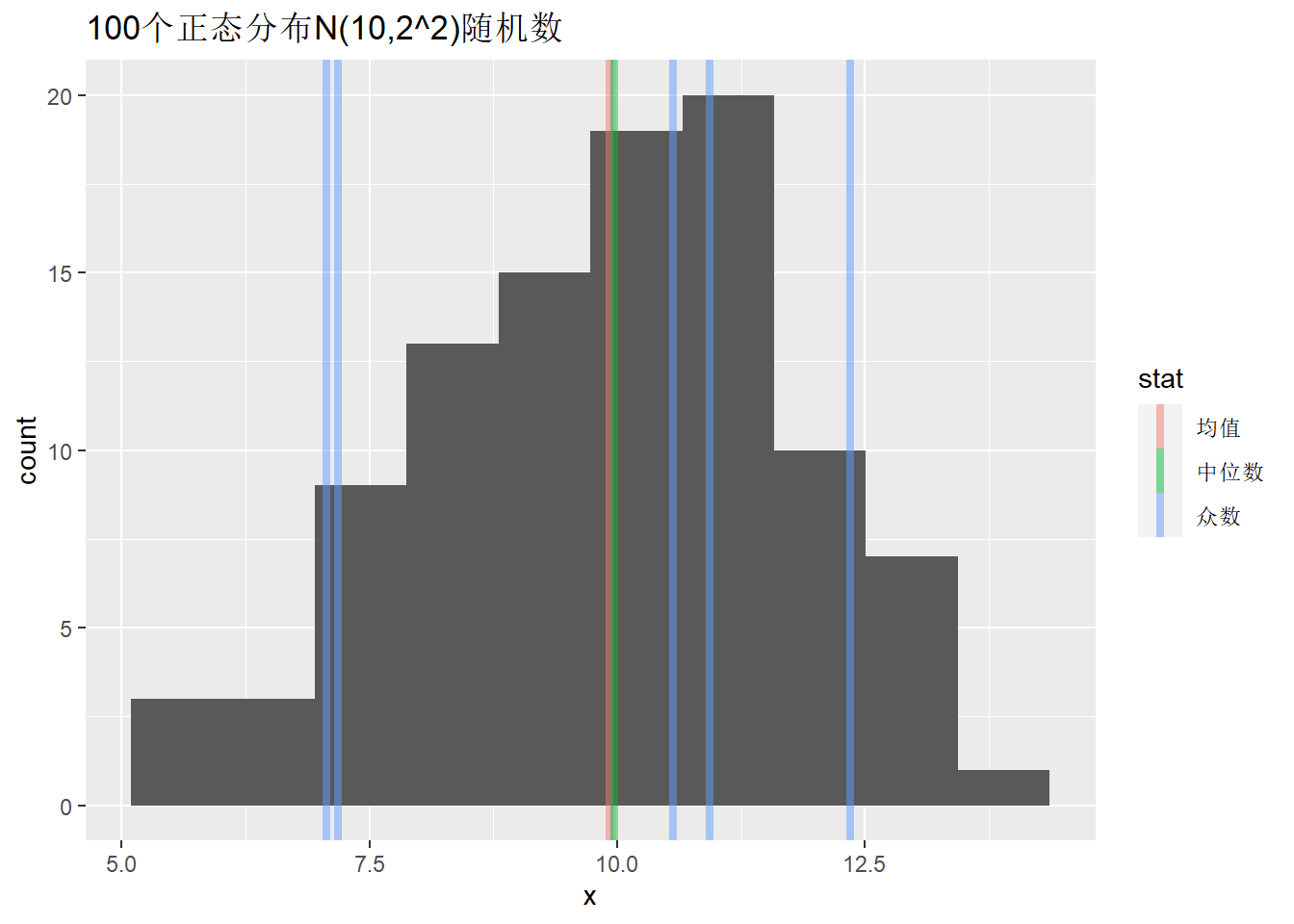
例3.3 (对数正态样本众数计算(*)) 设\(\ln X \sim \text{N}(\mu, \sigma^2)\), 即\(X\)服从对数正态分布。 对模拟样本计算。
取\(\ln X\)为标准正态分布。
set.seed(102)
x <- round(exp(rnorm(100)), 2)
mean(x)
## [1] 2.0901
median(x)
## [1] 0.995
sample.mode(x)
## [1] 0.57 1.05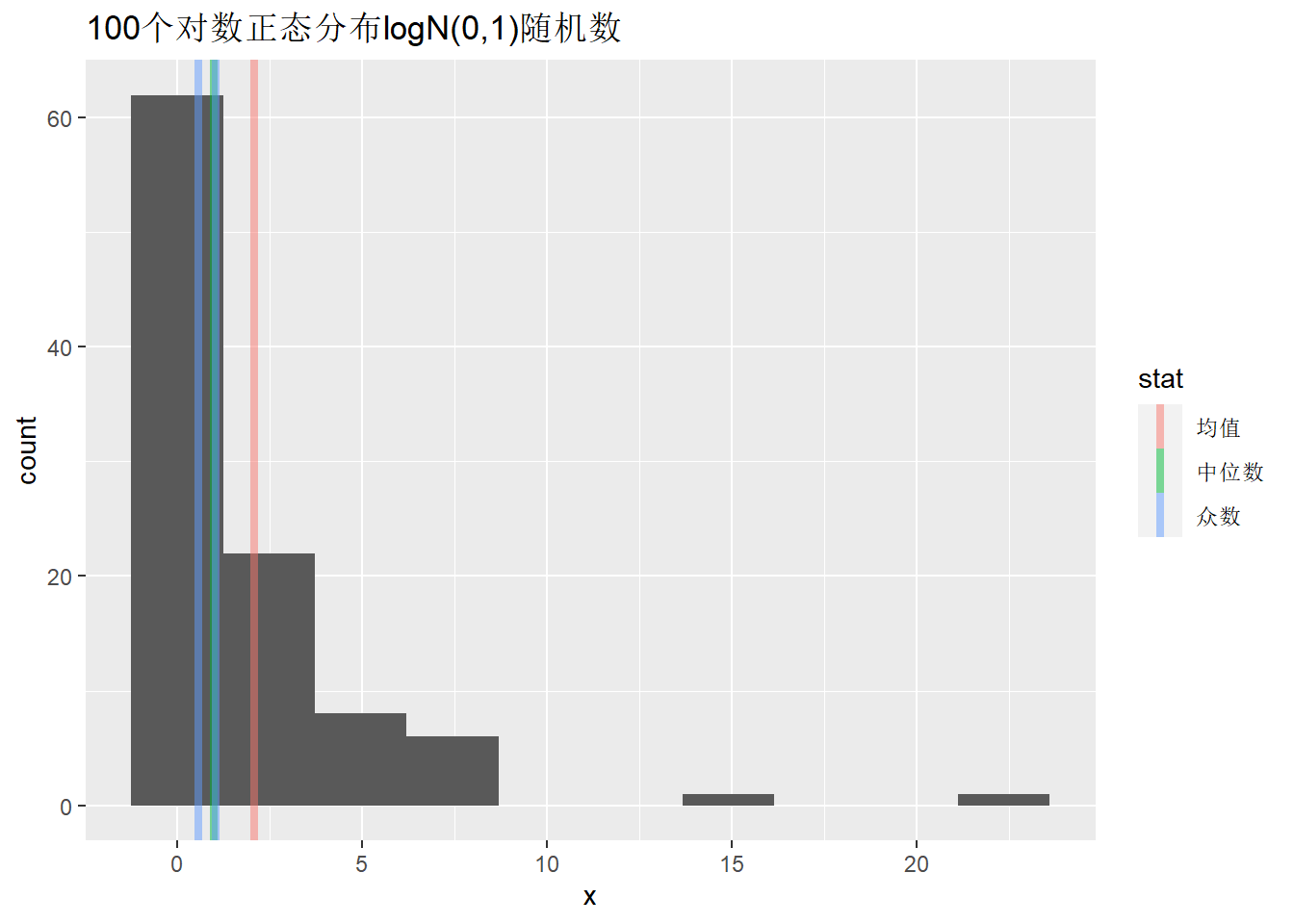
例3.4 (泊松样本众数计算(*)) Poisson模拟样本的计算。
set.seed(103)
x <- rpois(100, lambda=0.8)
mean(x)
## [1] 0.81
median(x)
## [1] 1
sample.mode(x)
## [1] 0
table(x)
## x
## 0 1 2 3 4
## 43 37 17 2 1d1 <- rbind(
tibble(x=mean(x), stat="均值"),
tibble(x=median(x), stat="中位数"),
tibble(x=sample.mode(x), stat="众数"))
d2 <- tibble(x=x) %>%
count(x)
ggplot(data=d2, mapping=aes(
x=x, y=n)) +
geom_col() +
geom_vline(data=d1, mapping=aes(
xintercept=x, col=stat),
size=1.5, alpha=0.5) +
labs(title="100个Poisson(0.8)随机数")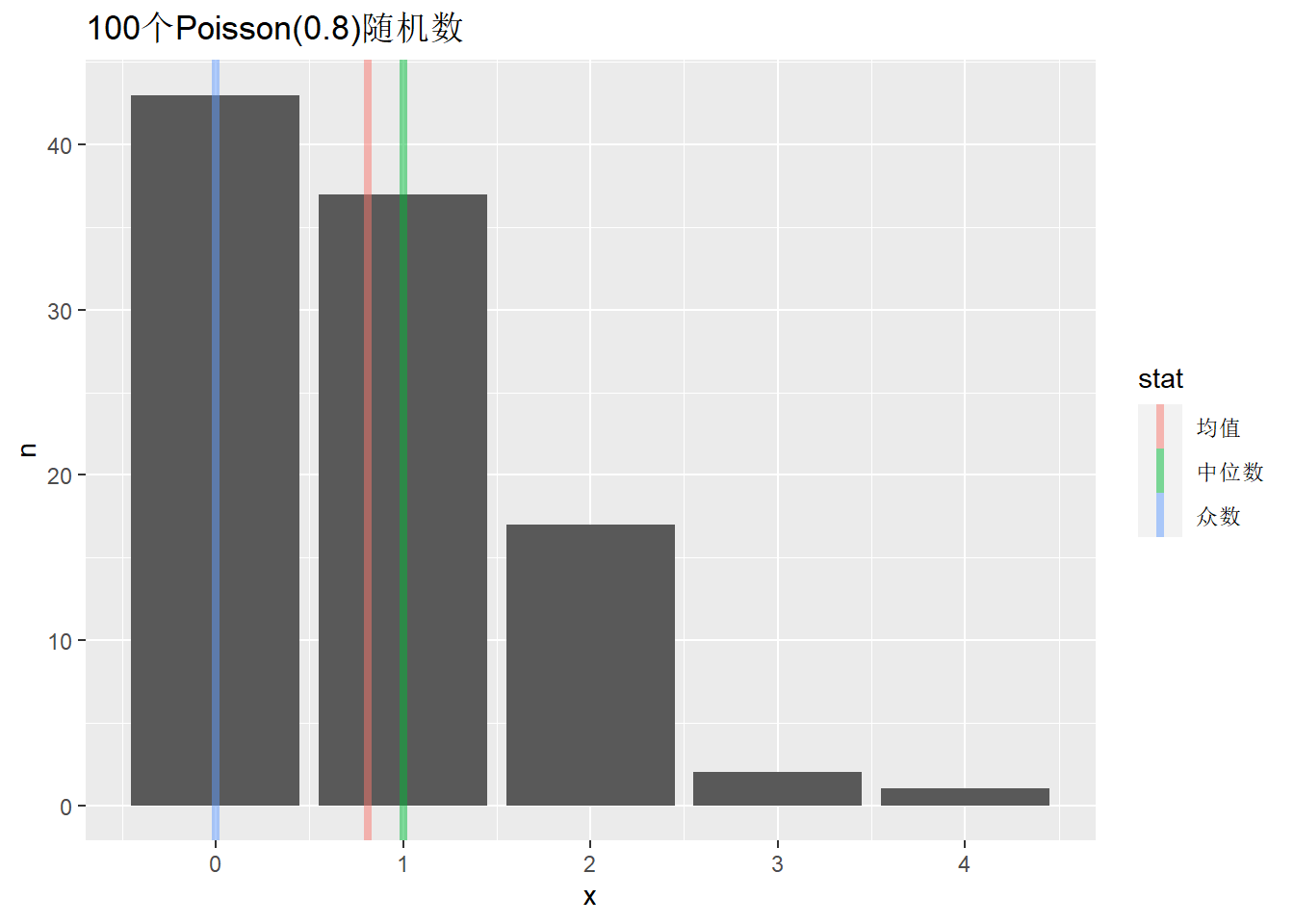
3.2.2 分散程度(变异性)特征量
不同分布之间的差别, 除了大小差别(用位置特征代表), 还包括分散程度的差别。 比如, 两个合唱小组的身高分别为(单位:厘米) \[\begin{matrix} A & 159 & 160 & 162 & 160 & 159 \\ B & 150 & 160 & 180 & 160 & 150 \end{matrix} \] 则两个组的平均身高都是160厘米, 但整齐程度就相差甚远。
可以衡量分散程度的特征量包括标准差、方差、变异系数、极差、四分位间距。
3.2.2.1 方差和标准差
总体\(X\)的方差为\(\text{Var}(X) = E(X - EX)^2\),
标准差为\(\sigma_X = \sqrt{\text{Var}(X)}\)。
样本\(x_1, x_2, \dots, x_n\)的样本方差和样本标准差分别为
\[\begin{align*}
S^2 =& \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2 \\
S =& \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2}
\end{align*}\]
其中分母\(n-1\)在\(x_1, x_2, \dots, x_n\)是\(Y\)的独立重复抽样时
保证了\(S^2\)是\(\text{Var}(X)\)的无偏估计。
在R语言中用var(x)求样本方差,
用sd(x)求样本标准差。
在Julia语言中用Statistics.var(x)求样本方差,
用Statistics.std(x)求样本标准差。
数据分析中主要使用标准差而不使用方差, 这是因为标准差与原来数据具有相同量纲, 而方差的量纲与原来数据量纲不同。 上面的两个合唱小组的身高标准差分别为1.225厘米和12.25厘米。
因为方差和标准差基于数学期望, 它们会受到极端值的影响。 比如,在上面所举的月薪的例子中, 标准差为9851元, 其中经理的月薪值是一个极端值, 去掉这个值之后标准差为零。
例3.5 (方差递推算法(*)) 给出方差递推算法, 并用R和Julia实现。
如果需要递推计算方差, 记\(S_k^2 = \frac{1}{k-1} \sum_{i=1}^k (x_i - \bar x_k)^2\), 可用如下递推算法:
| 样本方差递推算法 |
|---|
| \(\bar x_1 = x_1; \ S_1^2 = 0\) |
| for (\(k\) in \(2:n\)) { |
| \(\qquad\) \(S_k^2 = \frac{k-2}{k-1} S_{k-1}^2 + \frac{1}{k} (x_k - \bar x_{k-1})^2\) |
| \(\qquad\) \(\bar x_k = \frac{k-1}{k} \bar x_{k-1} + \frac{1}{k} x_k\) |
| } |
(其中\(S_1^2\)仅作为初值使用)
R函数:
var.it <- function(x){
n <- length(x)
xm <- x[1]
ss <- 0
for(k in 2:n){
ss <- (k-2)/(k-1)*ss + (x[k] - xm)^2 / k
xm <- (k-1)/k*xm + x[k]/k
}
ss
}测试:
set.seed(1)
x <- round(runif(5), 2); x
## [1] 0.27 0.37 0.57 0.91 0.20
var(x)
## [1] 0.08158
var.it(x)
## [1] 0.08158Julia版本:
function var_iter(x::Vector)
n = length(x)
xm::Float64 = x[1]
ss = 0.0
for k=2:n
ss = (k-2)/(k-1)*ss + (x[k] - xm)^2 / k
xm = (k-1)/k*xm + x[k]/k
end
ss
end测试:
※※※※※
3.2.2.2 变异系数
标准差是有量纲的分散程度特征, 用变异系数 \[\begin{aligned} \text{CV} = \frac{S}{\bar x} \times 100\% \end{aligned}\] 可以表示变量相对于其平均值的变化情况, 是一个无量纲的量。 比如, 100克的标准差, 如果是来自平均500克一袋的奶粉, 变异系数达到20%, 说明此种奶粉的装袋质量很差; 如果同样是100克的标准差但是来自平均50千克一袋的面粉, 则变异系数为0.2%,说明此种面粉的装袋质量很好。
3.2.2.3 极差和四分位间距
样本的极差定义为样本的最大值减去样本的最小值, 也能比较直观地反映样本值分散程度。
设\(\hat x_{1/4}\)和\(\hat x_{3/4}\)是从样本\(x_1, x_2, \dots, x_n\)中估计的分位数\(x_{1/4}\)和\(x_{3/4}\), 称\(\hat x_{3/4} - \hat x_{1/4}\)为四分位间距 (Inter-Quartile Range, IQR,又称为四分位差、内距)。 四分位间距是最靠近分布中心的50%的样本值所占的范围大小, 可以反映样本分散程度, 而且不受到极端值影响。
受前面传统的中位数估计方法的启发, 我们可以用如下方法计算\(1/4\)和\(3/4\)分位数。 把样本从小到大排序后, 如果\(n\)为奇数, 则用\(x_{(1)}, x_{(2)}, \dots, x_{(\frac{n+1}{2})}\)的中位数作为 \(x_{1/4}\)的估计, 用\(x_{(\frac{n+1}{2})}, x_{(\frac{n+1}{2}+1)}, \dots, x_{(n)}\)的中位数作为 \(x_{3/4}\)的估计。 如果\(n\)为偶数, 则用\(x_{(1)}, x_{(2)}, \dots, x_{(\frac{n}{2})}\)的中位数作为 \(x_{1/4}\)的估计, 用\(x_{(\frac{n}{2} + 1)}, x_{(\frac{n}{2} + 2)}, \dots, x_{(n)}\)的中位数作为 \(x_{3/4}\)的估计。
3.2.3 与分布形状有关的特征量
包括偏度\(w\)和峰度\(k\)。 总体\(X\)的偏度和(超额)峰度分别定义为 \[\begin{align*} w =& \frac{E (X - EX)^3}{\left( \text{Var}(X) \right)^{3/2}} , & k =& \frac{E (X - EX)^4}{\left( \text{Var}(X) \right)^{2}} - 3 \end{align*}\] 从样本\(x_1, x_2, \dots, x_n\)计算的偏度和峰度分别定义为 (见(SAS Institute Inc. 2010) 328–329) \[\begin{aligned} \hat w =& \frac{n}{(n - 1)(n - 2)} \sum_{i=1}^n \left( \frac{x_i - \overline x }{S} \right)^3 \\ \hat k =& \frac{n(n + 1)}{(n - 1)(n - 2)(n -3)} \sum_{i=1}^n \left( \frac{ x_i - \overline x}{S} \right)^4 - \frac{3(n - 1)^2 }{(n - 2)(n - 3)} \end{aligned}\] 其中\(\bar x\)和\(S\)分别为样本平均值和样本标准差。
例3.6 (样本偏度和样本峰度的程序(*)) 用R和Julia计算样本偏度和样本峰度。
R函数:
skewness <- function(x){
n <- length(x)
(n /(n-1) * n/(n-2)) *
mean((x - mean(x))^3) / (var(x))^1.5
}
kurtosis <- function(x){
n <- length(x)
((n+1)/(n-1) * n/(n-2) * n/(n-3)) *
mean((x - mean(x))^4) / (var(x))^2 -
3*(n-1)^2/(n-2)/(n-3)
}测试:
set.seed(1)
x <- round(rnorm(10, 10, 2), 2); x
## [1] 8.75 10.37 8.33 13.19 10.66 8.36 10.97 11.48 11.15 9.39
skewness(x)
## [1] 0.3516643
kurtosis(x)
## [1] -0.3150973Julia函数:
function skewness(x)
n = length(x)
s = 0.0
xm = mean(x)
xsd = std(x)
for k=1:n
s += (x[k] - xm)^3
end
n/(n-1)*n/(n-2)/n*s/std(x)^3
end
function kurtosis(x)
n = length(x)
s = 0.0
xm = mean(x)
xsd = std(x)
for k=1:n
s += (x[k] - xm)^4
end
(n+1)/(n-1)*n/(n-2)/(n-3)*s/std(x)^4 - 3*(n-1)/(n-2)*(n-1)/(n-3)
end测试:
x = [8.75, 10.37, 8.33, 13.19, 10.66, 8.36, 10.97, 11.48, 11.15, 9.39]
skewness(x)
## 0.35166432816653354
kurtosis(x)
## -0.3150972802809626※※※※※
偏度\(w\)反映了分布的对称性。 以连续型分布为例, 设\(X\)有分布密度\(p(x)\), 若\(p(x)\)关于\(EX\)对称, 则\(w=0\)。 如果\(p(x)\)左右两个尾部不对称, 右尾长而左尾短, 则\(w > 0\), 称这样的分布为右偏分布。 反之,如果\(p(x)\)的左尾长而右尾短, 则\(w<0\), 称这样的分布为左偏分布。
峰度\(k\)反映了分布的两个尾部的衰减速度情况。 如果\(p(x)\)在\(y \to \pm \infty\)衰减速度较慢 (比如\(p(x) = O(\frac{1}{x^p})\), \(p > 1\)), 则称\(p(x)\)是重尾(厚尾)分布, 这时\(k>0\)。 对于正态分布\(\text{N}(\mu, \sigma^2)\),\(k \equiv 0\)。 重尾分布的样本会有比较多的极端值, 即与分布中心距离很远的值。
3.2.4 相关系数
对于多个随机变量, 可以用相关系数来简单描述两两之间的关系。 随机变量\(X\)和\(Y\)的相关系数定义为 \[\begin{align*} \rho = \rho(X, Y) = \frac{E[(X - EX)(Y - EY)]}{\sqrt{\text{Var}(X) \cdot \text{Var}(Y)}} \end{align*}\] 这是一个取值于\([-1, 1]\)的数, 当\(|\rho|\)接近于1时代表\(X\)和\(Y\)有很强的线性相关关系。 对于\(X\)和\(Y\)的一组样本 \((x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\), 相关系数估计为 \[\begin{align*} R = \frac{\sum_{i=1}^n [(x_i - \bar x) (y_i - \bar y)]} {\sqrt{ \sum_{i=1}^n (x_i - \bar x)^2 \cdot \sum_{i=1}^n(y_i - \bar y)^2 }} \end{align*}\] 也满足\(-1 \leq R \leq 1\)。
注意,相关系数只考虑了两个变量之间的线性相关性。 例如,\(X \sim \text{N}(0,1)\), \(Y = X^2\)是\(X\)的函数,但是\(X\)和\(Y\)的相关系数等于零。 实际数据中, 样本相关系数绝对值很小不表明两个变量相互独立; 样本相关系数绝对值较大, 则两个变量之间很可能是不独立的, 但不能仅靠相关系数确认两个变量之间有线性相关性: 非线性的相关也可能导致相关系数绝对值较大。
如果我们有\(p\)个随机变量\((X_1, X_2, \dots, X_p)^T\)(\(T\)表示矩阵转置), 看成随机向量\(\boldsymbol X\), \(\boldsymbol X\)的期望为\(E \boldsymbol X = (E X_1, E X_2, \dots, E X_p)^T\), 协方差阵为\(\text{Var} (\boldsymbol X) = E[(\boldsymbol X - E \boldsymbol X)(\boldsymbol X - E \boldsymbol X)^T]\), \(\text{Var} (\boldsymbol X)\)的第\(k\)行第\(j\)列元素为 \[\begin{align*} \text{Cov}(X_k, X_j) = E[(X_k - E X_k)(X_j - E X_j)], \ k, j=1,2,\dots,p. \end{align*}\] \(\boldsymbol X\)的相关阵\(R\)是\(\boldsymbol X\)的各分量的相关系数组成的矩阵, 主对角线元素等于1, 第\(k\)行第\(j\)列元素为\(\rho(X_k, X_j)\)。
对\(\boldsymbol X\)进行\(n\)次独立观测得到样本 \((x_{i1}, x_{i2}, \dots, x_{ip}), \, i=1,2,\dots,n\), 用 \[\begin{align*} \bar x_{\cdot j} = \frac{1}{n} \sum_{i=1}^n x_{ij}, \ j=1,2,\dots,p \end{align*}\] 估计\(E \boldsymbol X\), 用 \[\begin{align*} \gamma_{kj} = \frac{1}{n-1} \sum_{i=1}^n (x_{ik} - \bar x_{\cdot k}) (x_{ij} - \bar x_{\cdot j}) \end{align*}\] 估计\(\text{Cov}(X_k, X_j)\), 矩阵\((\gamma_{kj})_{k,j=1,2,\dots,p}\)叫做样本协方差阵, 用来估计\(\boldsymbol X\)的协方差阵。 \(\boldsymbol X\)的样本相关系数组成的矩阵叫做样本相关系数阵。
在R中,如果x是一个\(n\times p\)的矩阵或者数据框,
每行看作\(p\)元随机向量的独立观测,
则var(x)计算其样本协方差阵,
cor(x)计算其样本相关系数阵。
在Julia中用Statistics.cov(X)计算样本协方差阵,
用Statistics.cor(X)计算样本相关系数矩阵,
用Statistics.cor(x, y)计算样本相关系数。
习题
习题1
编写R函数, 输入向量的值后,按如下公式 \[\begin{align*} \phi = \frac{n}{{(n - 1)(n - 2)}}\sum_{i=1}^n {\left( {\frac{{x_i - \bar x }}{s}} \right)^3 } \end{align*}\] 计算样本偏度, 其中\(n\)为的元素个数, \(\bar x\)和\(s\)分别为中元素的样本平均值和样本标准差。