6 非均匀随机数生成
6.1 逆变换法
定理6.1 设\(X\)为连续型随机变量,取值于区间\((a,b)\)(可包括\(\pm \infty\)和端点), \(X\)的密度在\((a,b)\)上取正值, \(X\)的分布函数为\(F(x)\), \(U \sim \text{U}(0,1)\), 则\(Y = F^{-1}(U) \sim F(\cdot)\)。
定理6.2 设\(X\)为离散型随机变量, 取值于集合\(\{a_1, a_2, \dots \}\)(\(a_1 < a_2 < \dots\)), \(F(x)\)为\(X\)的分布函数, \(U \sim \text{U}(0,1)\), 根据\(U\)的值定义随机变量\(Y\)为 \[\begin{aligned} Y =& a_i \ \text{当且仅当}\ F(a_{i-1}) < U \leq F(a_{i}), \ i=1,2,\dots \end{aligned}\] (定义\(F(a_0)=0\)) 则\(Y \sim F(y)\)。
6.2 用逆变换法生成离散型随机数
例6.1 (离散均匀分布) 如果随机变量\(X\)在\(\{1,2,\dots,m \}\)中取值且\(P(X=i)=\frac{1}{m}, i=1,2,\dots,m\), 则称\(X\)服从离散均匀分布。
用均匀分布生成:
其中n是要生成的个数,m是离散均匀分布的取值个数。
尝试用它生成60次骰子点数:
rng.discrete.uni(60, m=6)
## [1] 3 1 5 4 2 2 4 3 4 4 6 5 5 6 3 4 5 2 3 1 5 6 2 4 6 5 1 3 3 4 3 2 2 1 4 6 2 5
## [39] 1 6 3 3 5 2 3 2 1 6 5 1 1 3 5 5 3 5 5 4 5 4实际上, R中已经有这样的函数。
sample.int(m, size=n, replace=TRUE)可以从\(\{1, 2, \dots, m \}\)中随机有放回地抽取\(n\)个。
如
sample.int(6, size=60, replace=TRUE)
## [1] 1 5 1 4 3 2 1 5 3 2 4 2 1 5 4 6 5 6 4 6 1 4 5 4 2 2 1 4 6 6 6 2 1 2 5 6 2 1
## [39] 2 5 3 3 1 2 6 4 1 3 4 2 2 4 4 3 4 2 6 1 1 1例6.2 (一般有限离散分布(*)) 设\(X\)为一个仅在\(\{a_1, a_2, \dots, a_m \}\)中取值的离散随机变量, \(P(X=a_i) = p_i, i=1,2,\dots,m\)。 为了由\(U \sim \text{U}[0,1]\)生成\(X\)的随机数, 可以利用定理2.2.2, 即当且仅当\(F(a_{i-1}) < U \leq F(a_i)\)时取\(X=a_i\)。
第一种算法的Julia程序版本:
function rnddis_v1(x, prob, n)
Fvs = cumsum(prob)
m = length(prob)
y = similar(x, (n,))
for k=1:n
U = rand()
for i=1:m
if U <= Fvs[i]
y[k] = x[i]
break
end
end
end
return y
end以\(P(X=1)=0.1\), \(P(X=2)=0.3\), \(P(X=3)=0.6\)为例。 测试1000个:
using Random, StatsBase
Random.seed!(101)
y = rnddis_v1(1:3, [0.1, 0.3, 0.6], 1000)
counts(y)
## counts(y) = [91, 319, 590]上面的算法依次判断\(U\)是否小于等于\(F(a_1)\), 是否小于等于\(F(a_2)\),\(\ldots\),是否小于等于\(F(a_m)=1\)。 一旦条件成立就不再继续判断, 所以排在前面的判断成立概率越大, 平均需要的判断次数越少。 只要重排\(X\)的取值次序使得取值概率大的排在前面就可以改进效率。 但是要注意重排过程也需要耗费时间。
改进后的Julia程序:
function rnddis_v2(x, prob, n)
m = length(x)
ind = sortperm(prob, rev=true)
xs = copy(x)[ind]
Fvs = cumsum(prob[ind])
y = similar(x, (n,))
for k=1:n
U = rand()
for i=1:m
if U <= Fvs[i]
y[k] = xs[i]
break
end
end
end
return y
end经过测试, 第二个版本一般效率不如第一个版本, 仅在有许多小概率类别时,第二个版本才有轻微的优势, 如:
using BenchmarkTools
prob = [fill(0.01, 50); 0.5]
@btime y = rnddis_v1(1:length(prob), prob, 100_000);
## 2.440 ms (4 allocations: 781.81 KiB)
@btime y = rnddis_v2(1:length(prob), prob, 100_000);
## 1.422 ms (8 allocations: 783.28 KiB)事实上,R函数sample()已经可以对有限离散进行有放回抽样,
做法是
如
set.seed(101)
x <- sample(1:3, size=1000, replace=TRUE,
prob=c(0.1, 0.3, 0.6))
prop.table(table(x))
## x
## 1 2 3
## 0.098 0.299 0.603例6.3 (无放回抽样(*)) 生成\((1,2,\dots,n)\)的一个随机排列。
第一种想法是从\(A=(1,2,\dots,n)\)中随机抽取一个,设为\(i_1\), 令\(B=(i_1)\);然后把\(i_1\)从\(A\)中剔除, 从剩下的\(n-1\)个元素中继续随机抽取一个, 设为\(i_2\),令\(B=(i_1, i_2)\), 如此重复直至\(A\)中的元素都被抽取到\(B\)中。
这种做法需要两个向量\(A\)和\(B\)来存储。 为了减少存储的使用, \(A\)中仅剩\(k\)个元素时, 向量\(A\)的后面\(n-k\)个位置可以用来存放已经抽取出来的元素。 从\(A\)的前\(k\)个中随机抽取一个后, 可以把这个元素放在\(A_k\)的位置并把原来\(A_k\)填在抽取产生的空位。 程序如下:
function randperm(n)
x = collect(1:n)
for k=n:-1:2
i = ceil(Int, k * rand())
if i ≠ k
x[k], x[i] = x[i], x[k]
end
end
return x
end
using Random
Random.seed!(101)
@show randperm(5);
## randperm(5) = [3, 2, 5, 1, 4]如果仅需要从\(\{1, 2, \dots, n \}\)中随机无放回第抽取\(r\)个, 只要修改上面程序中的循环使其只执行\(r\)次即可。 程序为:
function randperm(n, size=n)
x = collect(1:n)
for k=n:-1:(n-size+2)
i = ceil(Int, k * rand())
if i ≠ k
x[k], x[i] = x[i], x[k]
end
end
return x[(n-size+1):n]
end比如,从\(1:10\)中随机无放回地抽取5个:
随机无放回抽取\(r\)个可以假设\(r \leq \frac{n}2\), 否则只要抽取余集就可以了。
R已有进行随机无放回抽取的函数。
sample.int(n)就可以实现对\(\{1, 2, \dots, n \}\)的一个随机排列。
如
用sample.int(n, size)可以从\(\{1, 2, \dots, n \}\)随机无放回地抽取size个,如
例6.4 (几何分布随机数) 设随机变量\(X\)表示在成功概率为\(p\)(\(0<p<1\))的独立重复试验中首次成功所需的试验次数, 则\(X\)的概率分布为 \[\begin{align*} P(X=k) = p q^{k-1}, k=1,2,\dots, \ (q=1-p) \end{align*}\] 称\(X\)服从几何分布, 记为\(X \sim \text{Geom}(p)\)。
设\(U \sim \text{U}(0,1)\), 注意到 \[\begin{aligned} F(k) =& P(X \leq k) = P(\text{在前}k\text{次试验中至少一次成功}) \\ =& 1 - P(\text{前}k\text{次试验都失败}) \\ =& 1 - q^k, \ k=1,2,\dots \end{aligned}\] 利用定理6.2, 生成\(X\)的方法为当且仅当\(1 - q^{k-1} < U \leq 1 - q^k\)时取\(X=k\), \(k=1,2,\dots\)。此条件等价于 \[\begin{aligned} q^k \leq 1 - U < q^{k-1} \end{aligned}\] 取 \[\begin{aligned} X =& \min\{ k: q^k \leq 1 - U \} \\ =& \min\{ k: k\log(q) \leq \log(1 - U) \} \\ =& \min\{ k: k \geq \frac{\log(1 - U)}{\log(q)} \} \\ =& \mbox{ceil}\left( \frac{\log(1 - U)}{\log(q)} \right) \end{aligned}\] 在没有指定底数时,\(\log(\cdot)\)默认使用自然对数。 注意到\(1-U\)也是服从U(0,1)分布的,所以只要取 \[\begin{aligned} X = \mbox{ceil}\left( \frac{\ln(U)}{\ln(q)} \right). \end{aligned}\] 则\(X\)服从几何分布。
## 输入
## - n: 需要输出的个数
## - p: 成功概率
rng.geom <- function(n=1, p=0.5){
ceiling(log(runif(n)) / log(1-p))
}测试:
事实上,rgeom(size, prob)生成size个成功概率为prob的几何分布随机数。
例6.5 (用几何分布生成独立试验序列(*)) 产生\(X_1, X_2, \dots, X_N\) iid b(1,\(p\)), 即 \[\begin{align*} P(X_i=1) = p = 1 - P(X_i=0), \ i=1,2,\dots,N \end{align*}\] 设\((U_1, U_2, \dots, U_n)\) iid U(0,1), 则当\(U_i \leq p\)时取\(X_i=1\), 当\(U_i > p\)时取\(X_i=0\)可以构造独立试验序列\((X_1, X_2, \dots, X_N)\)。
当\(p\)比较小的时候利用几何分布可以更快地构造独立试验序列。
想法是生成首次成功时间, 则在成功之前的试验都是失败, 然后再生成下次成功时间, 两次成功之间的试验为失败, 一直到凑够\(N\)次试验为止。 Julia程序:
function randb(n=1, p=0.5)
x = fill(0, n)
k = 0
while k <= n
# 几何分布随机数:
T = ceil(Int, log(rand())/log(1-p))
if(k+T <= n)
x[k+T] = 1
end
k += T
end
return x
end测试:
例6.6 (二项分布随机数(*)) 设\(X\)为\(n\)次成功概率为\(p\)的独立重复试验的成功次数, 则 \[ p_k = P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}, \ k=0,1,\dots,n\ (0<p<1) \] 称\(X\)服从二项分布,记为\(X \sim \text{B}(n,p)\)。 \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\)是从\(n\)个中取出\(k\)个的不同组合的个数。
为了生成二项分布随机数, 可以生成\(n\)个两点分布随机数(长度为\(n\)的独立试验序列), 其和为一个二项分布随机数, 依次从独立试验序列中每\(n\)个求和就可以得到二项分布随机数序列。 这样的算法效率较差。
设法用定理6.2构造二项分布随机数。 二项分布取值概率有如下递推式: \[ p_{k+1} = \frac{n-k}{k+1} \frac{p}{1-p} \, p_k, \ k=0,1,\dots,n-1 \] 所以在利用定理6.2构造二项分布随机数时, 可以递推计算 \[ F(k+1) = F(k) + p_{k+1} = F(k) + \frac{n-k}{k+1} \frac{p}{1-p} \, p_k, \ k=0,1,\dots,n-1 \]
初步的Julia程序如下:
## 输入:
## - n: 需要输出的个数(注意不是二项分布参数!)
## - size: 二项分布参数中的试验次数
function randbinom_v1(n, size=1, prob=0.5)
x = fill(0, n)
for i = 1:n
U = rand()
k = 0
cc = prob/(1-prob)
a = (1-prob)^size
F = a
while U > F
a *= cc*(size-k)/(k+1)
F += a
k += 1
end
x[i] = k
end
x
end 测试:
上面的程序每生成一个随机数都要计算许多个分布函数值。 如果需要生成的随机数很多, 而二项分布的试验次数参数不大, 应该预先将这些分布函数值存储在一个向量中。 改进版本如:
## 输入:
## - n: 需要输出的个数(注意不是二项分布参数!)
## - size: 二项分布参数中的试验次数
function randbinom_v2(n, size=1, prob=0.5)
x = fill(0, n)
Fvs = zeros(size+1)
k = 0
cc = prob/(1-prob)
a = (1-prob)^size
Fvs[0+1] = a
for k = 0:(size-1)
a *= cc*(size-k)/(k+1)
Fvs[(k+1)+1] = Fvs[k+1] + a
end
Uvs = rand(n)
for i = 1:n
U = Uvs[i]
k = 0
while U > Fvs[k+1]
k += 1
end
x[i] = k
end
return x
end当\(p>\frac12\)时, 可以用上述算法生成\(Y \sim \text{B}(n, 1-p)\), 令\(X = n-Y\)则\(X \sim \text{B}(n,p)\), 可以减少判断次数。
上面的算法先判断\(X\)是否应该取0, 如不是再判断\(X\)是否应该取1,\(\cdots\cdots\), 判断次数为\(X\)的值加1, 所以平均判断次数为\(EX+1 = np+1\)。 当\(np\)较大时, 应该先判断取值概率较大的那些值。 \(P(X=k)\)在\(np\)附近达到最大值。 令\(K = \mbox{floor}(np)\), 应先判断要生成的随机变量\(X\)是小于等于\(K\)还是大于\(K\)。 先计算出\(F(K)\)。 当\(U \leq F(K)\)时,\(X\)取值小于等于\(K\), 这时可依次判断\(X\)是否应取\(K, K-1, \dots, 0\), 在这个过程中可以反向递推计算各个\(F(k)\)的值。 当\(U > F(K)\)时,\(X\)取值大于\(K\), 这时可依次判断\(X\)是否应取\(K+1, K+2, \dots, n\), 在这个过程中可以递推计算各个\(F(k)\)的值。
改进后需要的判断次数约为\(|X - np| + 1\), 因为\(n\)较大时二项分布近似正态分布\(\text{N}(np, np(1-p))\), 所以平均判断次数约为 \[\begin{aligned} & 1 + E|X - np| \\ =& 1 + \sqrt{np(1-p)} E \left| \frac{X - np}{\sqrt{np(1-p)}} \right| \\ \approx& 1 + \sqrt{np(1-p)} E |Z| \quad(\text{其中}Z \sim \text{N}(0,1)) \\ =& 1 + 0.798 \sqrt{p(1-p)} \cdot \sqrt{n} . \end{aligned}\] 当\(n\to\infty\)时判断次数比原来的\(O(n)\)降低到了\(O(\sqrt{n})\)。
例6.7 (泊松分布随机数(*)) 设离散型随机变量\(X\)分布为 \[\begin{aligned} p_k =& P(X = k) = e^{-\lambda} \frac{\lambda^k}{k!}, \ k=0,1,2,\dots (\lambda>0) \end{aligned}\] 称\(X\)服从泊松分布,记为\(X\sim\) Poisson(\(\lambda\))。
易见 \[\begin{aligned} p_{k+1} =& \frac{\lambda}{k+1} p_k, \ k=0,1,2,\dots \end{aligned}\] 所以在利用定理6.2构造泊松随机数时, 可以递推计算 \[\begin{aligned} F(k+1) =& F(k) + p_{k+1} = F(k) + \frac{\lambda}{k+1} p_k, \ k=0,1,2,\dots \label{eq:rng-poi-F} \end{aligned}\]
Julia程序如下:
## 输入:
## - n: 需要输出的个数(注意不是二项分布参数!)
## - lambda: 泊松分布的速率参数
function randpois_v1(n, λ=1)
x = fill(0, n)
for i = 1:n
U = rand()
p = exp(-λ)
F = p
k = 0
while U > F
p *= λ/(k+1)
F += p
k += 1
end
x[i] = k
end
x
end 测试:
这样的算法先判断是否令\(X\)取0, 不成立则再判断是否令\(X\)取1, 如此重复, 判断的次数为\(X\)的值加1, 所以平均判断次数需要\(EX+1=\lambda+1\)次, 当\(\lambda\)较小时这种方法效率不错; 如果\(\lambda\)比较大, 这时\(p(k) = e^{-\lambda} \frac{\lambda^k}{k!}\)在最接近于\(\lambda\)的两个整数之一上最大, 应该先判断这两个整数及其邻近的点。 令\(K = \mbox{floor}(\lambda)\), 先递推计算出\(F(K)\)和\(F(K+1)\), 然后判断\(F(K)<U \leq F(K+1)\)是否成立, 如果成立就令\(X=K+1\); 否则,如果\(U \leq F(K)\)则依次判断是否应取\(X\)为\(K, K-1, \dots, 0\), 在这个过程中可以反向递推计算各\(F(k)\); 如果\(U > F(K+1)\)则依次判断是否应取\(X\)为\(K+2, K+3, \dots\), 这个过程中仍然用递推计算各\(F(k)\)。
这样的改进的算法需要的判断次数约为\(|X - \lambda| + 1\), 所以平均判断次数为\(E|X-\lambda|+1\)。 因为\(\lambda\)较大时泊松分布渐近正态分布\(\text{N}(\lambda, \lambda)\), 所以平均判断次数约为 \[\begin{aligned} 1 + E|X-\lambda| =& 1 + \sqrt{\lambda} E \left| \frac{X-\lambda}{\sqrt{\lambda}} \right| \\ \approx& 1 + \sqrt{\lambda} E |Z| \quad\text{(where $Z \sim \text{N}(0,1)$)} \\ =& 1 + 0.798\sqrt{\lambda} \end{aligned}\] 当\(\lambda\)很大时平均判断次数由\(O(\lambda)\)降低到了\(O(\sqrt{\lambda})\)。
6.3 用逆变换法生成连续型随机数
连续型分布的随机数都可以用逆变换法生成:\(X = F^{-1}(U)\), \(U \sim \text{U}(0,1)\)。 对于反函数\(F^{-1}\)容易计算的情形, 逆变换法是最方便的。
例6.8 (三角形分布) 用逆变换法生成各种三角形分布的随机数。
Beta(2,1)分布的分布密度和分布函数分别为 \[\begin{aligned} p(x)=& 2x, \ x \in [0,1] & F(x) =& x^2, \ x \in [0,1] . \end{aligned}\] 密度函数为三角形。 若\(U \sim \text{U}(0,1)\), 则\(X = \sqrt{U}\)为Beta(2,1)随机数。
Beta(1,2)分布的分布密度和分布函数分别为 \[\begin{aligned} p(x)=& 2(1-x), \ x \in [0,1] & F(x) =& 1 - (1-x)^2, \ x \in [0,1] . \end{aligned}\] 密度函数为三角形。若\(U \sim \text{U}(0,1)\), 则\(X = 1 - \sqrt{1 - U}\)为Beta(1,2)随机数, 因为\(U\)与\(1-U\)同分布所以\(X = 1 - \sqrt{U}\)也是Beta(1,2)随机数。
对于\(0<m<1\),三角形分布Tri(0,1,\(m\))的密度函数为 \[\begin{aligned} p(x) =& \begin{cases} \frac{2}{m} x, & 0<x \leq m \\ \frac{2}{1-m} (1-x), & m < x < 1 . \end{cases} \end{aligned}\] 分布函数为 \[\begin{aligned} F(x) =& \begin{cases} \frac{x^2}{m}, & 0<x \leq m \\ 1 - \frac{(1-x)^2}{1-m}, & m < x < 1 . \end{cases} \end{aligned}\] 反函数为 \[\begin{aligned} F^{-1}(u) = \begin{cases} \sqrt{mu}, & 0< u \leq m \\ 1 - \sqrt{(1-m)(1-u)}, & m < u < 1 . \end{cases} \end{aligned}\] 所以若\(U \sim \text{U}(0,1)\), 则\(X = F^{-1}(U)\)服从三角形分布Tri(0,1,\(m\))。
标准右三角形分布Beta(2,1)的随机数的R程序:
标准左三角形分布Beta(1,2)的随机数的R函数:
标准三角形分布Tri(\(0, 1, m\))的随机数:
用直方图测试:
pdftri <- function(x, m) {
ifelse(x <= m, 2/m*x, 2/(1-m)*(1-x))
}
set.seed(101)
x = rng.tri(10000, 0.6)
hist(x, breaks=15, prob=TRUE, ylim=c(0,2))
curve(pdftri(x, 0.6), 0, 1, add=TRUE, col="red")用Julia编程:
用直方图和密度曲线测试:
function hist_with_pdf(
x, pdf, x1=minimum(x), x2=maximum(x))
xs = range(x1, x2, length=100)
ys = pdf.(xs)
plt = data((; x=x)) * mapping(:x) *
histogram(bins=50, normalization=:pdf)
plt2 = data((; x=xs, y=ys)) * mapping(:x, :y) *
visual(Lines, color=:red)
draw(plt+plt2)
end
using Random, Distributions
using CairoMakie, AlgebraOfGraphics
CairoMakie.activate!()
m = 0.6
x = randtri(10000, m)
f = x -> x <= m ? 2/m*x : 2/(1-m)*(1-x)
dr = hist_with_pdf(x, f, 0.0, 1.0)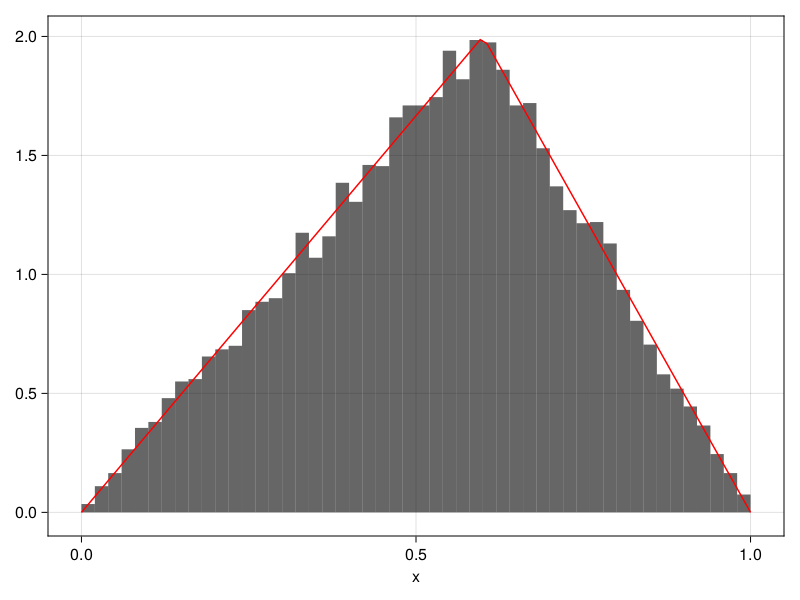
例6.9 (指数分布随机数) 生成指数分布的随机数。
服从指数分布\(\text{Exp}(\lambda)\) (\(\lambda>0\))的随机变量\(X\)的分布密度和分布函数分别为 \[\begin{aligned} p(x) =& \lambda e^{-\lambda x}, \ x>0 \\ F(x) =& 1 - e^{-\lambda x}, \ x>0. \end{aligned}\] 反函数为 \[\begin{aligned} F^{-1}(u) = -\lambda^{-1} \log(1-u) . \end{aligned}\] 所以\(U \sim \text{U}(0,1)\)时\(X = -\lambda^{-1} \log(1-U)\)服从Exp(\(\lambda\))。 因为\(1 - U\)与\(U\)同分布, 所以取\(X = -\lambda^{-1} \log U\)也服从Exp(\(\lambda\))。
当\(\lambda=1\)时Exp(1)叫做标准指数分布, \(-\log U\)服从标准指数分布, 标准指数分布乘以\(\lambda^{-1}\)即为Exp(\(\lambda\))分布。
指数分布随机数发生器R函数:
R已经提供了rexp(n, rate=1)函数。
使用Julia语言编程:
例6.10 (利用指数分布随机数产生泊松随机数(*)) 利用指数分布和泊松过程的关系生成泊松随机数。
\(N(t)\)为到时刻\(t\)为止到来的事件个数(\(t \geq 0\)), 如果两个事件到来之间的间隔都服从独立的Exp(\(\lambda\))分布则 \(N(t)\)为泊松过程, 且\(N=N(1)\)服从参数为\(\lambda\)的泊松分布。 若\(U_1, U_2, \dots\)是独立的U(0,1)随机变量列, \(X_1, X_2, \dots\)是独立的Exp(\(\lambda\))随机变量列, 则 \[\begin{aligned} N = \max\{ n:\ \sum_{i=1}^n X_i \leq 1 \} . \end{aligned}\] \(X_i\)可以用\(-\lambda^{-1} \ln U_i\)生成, 所以 \[\begin{aligned} N =& \max\{ n:\ -\lambda^{-1} \sum_{i=1}^n \ln U_i \leq 1 \} \\ =& \max\{ n:\ U_1 U_2 \dots U_n \geq e^{-\lambda} \} . \end{aligned}\]
可以这样生成泊松随机数:相继生成均匀随机数, 直至其连乘积小于\(e^{-\lambda}\), 取\(n\)为使用的均匀随机数个数减1,即 \[\begin{aligned} N = \min\{n:\ U_1 U_2 \dots U_n < e^{-\lambda} \} - 1. \end{aligned}\] Julia程序:
function randpois_v2(n, λ=1)
x = fill(0, n)
a = exp(-λ)
for i = 1:n
p = 1
k = 0
while true
k += 1
p *= rand()
if p < a
break
end
end
x[i] = k-1
end
x
end 测试:
6.4 利用变换生成随机数
定理6.3 设随机变量\(X\)有密度\(p(x)\), \(Y=g(X)\)是\(X\)的函数, 函数\(g(\cdot)\)有反函数\(x = g^{-1}(y) = h(y)\), \(h(y)\)有一阶连续导数,则\(Y\)有密度 \[\begin{aligned} f(y) = p(h(y)) \cdot | h'(y) |. \end{aligned}\]
定理6.4 设随机向量\((X,Y)\)具有联合密度函数\(p(x,y)\),令 \[\begin{aligned} \begin{cases} u = g_1(x, y), \\ v = g_2(x, y), \end{cases} \end{aligned}\] 设\((u,v) = (g_1(x,y), g_2(x,y))\)的反变换存在唯一, 记为 \[\begin{aligned} \begin{cases} x = h_1(u,v), \\ y = h_2(u,v), \end{cases} \end{aligned}\] 设\(h_1, h_2\)的一阶偏导数存在,反变换的Jacobi行列式 \[\begin{aligned} J = \left|\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array}\right| \neq 0, \end{aligned}\] 则随机向量\((U,V)\)的联合密度为 \[\begin{aligned} f(u,v) = p(h_1(u,v), h_2(u,v)) \cdot |J|. \label{eq:rng-mul-conv} \end{aligned}\]
有些分布之间有已知的关系, 可以利用这样的关系产生随机数。 如:
二项分布B(\(n,p\))是\(n\)个伯努利分布b(1,\(p\))之和, 可以产生\(n\)个伯努利分布b(1,\(p\))随机数求和得到二项分布随机数。
如果\(U\)服从标准均匀分布U(0,1), 则\(X = a + (b-a)U\)服从U(\(a,b\))。
如果\(Z\)服从标准正态分布, 则可以用\(X = \mu + \sigma Z\)服从N(\(\mu, \sigma^2\))分布。
如果\(Z\)服从标准指数分布Exp(1), 则\(X = \lambda^{-1} Z\)服从指数分布Exp(\(\lambda\))。
如果\(Z\)服从标准伽马分布Gamma(\(\alpha\),1), 则\(X = \lambda^{-1} Z\)服从伽马分布Gamma(\(\alpha\), \(\lambda\))。
\(n\)个独立的Exp(\(\lambda\))指数分布随机变量之和服从伽马分布Gamma(\(n, \lambda\))。 设\(U_1, U_2, \dots, U_n\)为独立U(0,1)随机变量,令 \[\begin{aligned} X =& \sum_{i=1}^n (-\lambda^{-1}) \ln U_i \\ =& -\lambda^{-1} \ln(U_1 U_2 \dots U_n) \end{aligned}\] 则\(X\)服从Gamma(\(n,\lambda\))分布。
若\(Z_1, Z_2, \dots, Z_n\)独立同标准正态分布, 则\(X = Z_1^2 + Z_2^2 + \dots + Z_n^2 \sim \chi^2(n)\)分布。
如果\(X \sim \text{Gamma}(\frac{n}{2}, 1)\), 则\(2 X \sim \chi^2(n)\)。
若\(Y \sim \text{N}(0,1)\), \(Z \sim \chi^2(n)\)且\(Y\)与\(Z\)相互独立, 则\(X = Y / \sqrt{Z}\)服从t(\(n\))分布。
若\(Y \sim \chi^2(n_1)\), \(Z \sim \chi^2(n_2)\), \(Y\)与\(Z\)相互独立, 则\(X = \frac{Y/n_1}{Z/n_2} \sim \text{F}(n_1, n_2)\)。
下面的定理给出了一种生成标准正态随机数的算法。
定理6.5 设\(U_1, U_2\)独立且都服从U(0,1), \[\begin{aligned} X =& \sqrt{-2\ln U_1} \cos(2\pi U_2), \\ Y =& \sqrt{-2\ln U_1} \sin(2\pi U_2) . \end{aligned}\] 则\(X, Y\)独立且都服从标准正态分布。 叫做Box-Muller变换。
例6.11 (用Box-Muller变换生成正态随机数) 只要生成两个独立的U(0,1)随机变量\(U_1\)和\(U_2\), 按照上述定理就可以生成两个独立的标准正态分布随机数。
R程序实现:
6.5 舍选法
设随机变量\(Z\)的分布函数很难求反函数\(F^{-1}(u)\)。 如果\(Z\)取值于有限区间\([a,b]\)且\(p(x)\)有上界\(M\): \[\begin{aligned} p(x) \leq M, \ \forall x \in [a,b] \end{aligned}\] 则可以用如下算法生成\(Z\)的随机数:
| 舍选法I |
|---|
| until(\(Y \leq p(X)\)){ |
| \(\qquad\) 从U(0,1)抽取\(U_1\), \(U_2\) |
| \(\qquad\) 取\(X \leftarrow a + (b-a)*U_1, \ Y \leftarrow M*U_2\) |
| } |
| 输出\(Z \leftarrow X\) |
这种方法叫做舍选法I。 每次循环生成的\((X, Y)\)实际上构成了矩形\([a,b] \times [0,M]\)上的二维均匀分布, 循环退出条件为\(Y \leq p(X)\), 循环退出时\((X, Y)\)的值落入了\(p(x)\)曲线下方, 这时\((X, Y)\)服从曲边梯形 \(\{(x,y): a \leq x \leq b, 0 \leq y \leq p(x) \}\)上的二维均匀分布, 所以循环退出时\(Z=X\)在\(x\)附近取值的概率是与\(p(x)\)成正比的。
定理6.6 舍选法I产生的\(Z\)密度为\(p(x)\), 算法所需的迭代次数是均值为\(M(b-a)\)的几何分布随机变量。
舍选法I的优点是只要随机变量在有限区间取值且密度函数有界就可以使用这种方法。 但是,舍选法I有许多缺点: 首先,\(X\)的取值范围必须有界; 其次,\(X\)的密度\(p(x)\)必须有界; 第三, 当算法中\(X\)取到\(p(x)\)值很小的位置时, 被拒绝的概率很大, \(X\)被接受的概率实际是曲线\(p(x)\)下的面积和整个矩形面积之比, 当\(p(x)\)高低变化很大时这个比例很低, 算法效率很差。
为了解决第一个和第二个问题, 我们抽取\(X\)时不再从U\((a,b)\)抽取, 而可以从一个一般密度\(g(x)\)抽取, 称这个密度为“试投密度”, 要求\(g(x)\)的随机数容易生成。 为了解决第三个问题, 我们应该力图使得\(g(x)\)形状与\(p(x)\)相像, 即\(p(x)\)大时相应\(g(x)\)也大, \(p(x)\)小时相应\(g(x)\)也小, 这样目标密度小的地方尝试抽取\(X\)也少。 在很多实际问题中, 目标密度(要生成随机数的密度)\(p(x)\)可能本身是未知的, 只知道\(\tilde p(x) = a p(x)\), 其中\(a\)为未知常数。 要求存在常数\(c\)使得 \[\begin{aligned} \frac{\tilde p(x)}{g(x)} \leq c, \ \forall x \end{aligned}\] 这样,如果\(\tilde p(x)\)在接近\(\pm \infty\)处有定义, 需要满足\(\tilde p(x) = O(g(x))\)(\(x \to \pm \infty\))。 选取试投密度\(g(\cdot)\)时上述常数\(c\)越小越好。
这时算法改为如下的舍选法II:
| 舍选法II |
|---|
| until \(\left(Y \leq \frac{\tilde p(X)}{(c g(X))} \right)\){ |
| \(\qquad\) 从\(g(x)\)抽取\(X\) |
| \(\qquad\) 从U(0,1)抽取\(Y\) |
| } |
| 输出\(Z \leftarrow X\) |
定理6.7 舍选法II产生的\(Z\)密度为\(p(x)\), 算法所需的迭代次数是均值为\(\frac{c}{a}\)的几何分布随机变量。
从定理可以看出, 为了提高舍选法II的效率, 应该取试投密度\(g(x)\)使得\(g(x)\)与\(p(x)\)形状越接近越好, 常数\(c\)越小越好。
例6.12 (用舍选法生成Beta(2,4)随机数) 用舍选法产生Beta(2,4)的随机数,密度为 \[\begin{aligned} p(x) = 20 x (1 - x)^3, \ 0<x<1. \end{aligned}\]
可以用舍选法I, 这时 \[\begin{aligned} M=\max_{0 \leq x \leq 1} p(x) = p(\frac14) = \frac{135}{64}, \end{aligned}\]
平均迭代次数为\(\frac{135}{64} \approx 2.1\)。
程序:
function randbeta24(n)
xs = zeros(n)
local x, y
for i = 1:n
while true
x = rand()
y = 135/64*rand()
y <= 20*x*(1-x)^3 && break
end
xs[i] = x
end
return xs
end事实上R已经提供了rbeta(n, shape1, shape2)函数。
例6.13 (用舍选法生成Gamma(3/2,1)随机数) 生成Gamma(\(\frac{3}{2}, 1\))的随机数\(Z\),密度为 \[\begin{aligned} p(x) =& \frac{1}{\Gamma(\frac32)} x^{\frac12} e^{-x}, \ x>0 . \end{aligned}\] 其中\(\Gamma(\frac32) = \frac{\sqrt{\pi}}{2}\)。
用舍选法II。 \(p(x)\)形状在尾部与指数分布相近, 且\(EZ=\frac{3}{2}\), 所以使用期望为\(\frac32\)的指数分布作为试投密度 \(g(x) = \frac23 e^{-\frac23 x}\), 求常数\(c\)使得\(\sup (p(x)/g(x)) \leq c\)。 用微分法求得\(p(x)/g(x)\)最大值点\(\frac32\), 最大值为 \(c = \frac{3\sqrt{3}}{\sqrt{2\pi e}}\), 这时 \[\begin{aligned} \frac{p(x)}{c g(x)} = \sqrt{\frac{2e}{3}} x^{\frac12} e^{-\frac13 x}, \end{aligned}\]
平均迭代次数为 \(c = \frac{3\sqrt{3}}{\sqrt{2\pi e}} \approx 1.257\).
Julia程序:
function randgamma1(n)
local a, x, y, xs
xs = zeros(n)
a = sqrt(2*exp(1)/3)
for i=1:n
while true
x = -1.5*log(rand())
y = rand()
y <= a * sqrt(x) * exp(-1/3*x) && break
end
xs[i] = x
end
return xs
end 例6.14 (用舍选法生成Gamma随机数(*)) 讨论生成一般的Gamma分布随机数的问题。
设\(Z\)服从伽马分布Gamma(\(\alpha, \lambda\)),密度为 \[\begin{aligned} p(x) = \frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x}, \ x>0\ (\alpha>0, \lambda>0) . \end{aligned}\] \(Z\)的期望值为\(\alpha/\lambda\)。 注意到如果\(W\)服从Gamma(\(\alpha, 1\))分布则\(W/\lambda\)服从Gamma(\(\alpha, \lambda\)), 所以只需要考虑\(\lambda=1\)的情形。 这时密度为 \[\begin{aligned} p(x) = \frac{1}{\Gamma(\alpha)} x^{\alpha-1} e^{- x}, \ x>0\ (\alpha>0) . \end{aligned}\]
为生成Gamma(\(\alpha, 1\))的随机数, 尝试使用指数分布Exp\((t)\)作为试投密度\(g(x)\), 如何取\(t\)呢?
令 \[\begin{aligned} h(x) = \frac{p(x)}{g(x)} = \frac{1}{t \Gamma(\alpha)} x^{\alpha-1} e^{-(1 - t) x}, \end{aligned}\] \(t\)需要使得\(h(x)\)有上界且上界最小。 当\(0<\alpha<1\)时\(\lim_{x\to 0} h(x) = +\infty\) 所以\(0<\alpha<1\)时不能使用指数分布作为试投密度。
当\(\alpha=1\)时伽马分布就是指数分布。
所以首先考虑\(\alpha>1\)时\(t\)的取法。 用微分法求得\(h(x)\)的最大值点。 事实上,当\(t \geq 1\)时\(\lim_{x\to +\infty} h(x) = \infty\), 所以只有\(0 < t < 1\)时\(h(x)\)才有界, 令 \[ u(x) = x^{a-1} e^{-bx}, \ a>1, b>0, x>0 \] 则 \[ u'(x) = x^{a-2} e^{-bx}((a-1) - bx) \] 解\(u'(x)=0\)得\(x_0=(a-1)/b\)且易见\(x_0\)是\(u(x)\)的最大值点。 于是\(h(x)\)的最大值为\(x_0 = \frac{\alpha - 1}{1 - t}\)。 令\(c(t)\)为\(h(x_0)\)随\(t \in (0, 1)\)变化的函数,则 \[\begin{aligned} c(t) = h(x_0) = \frac{1}{\Gamma(\alpha)} (\alpha - 1)^{\alpha - 1} e^{-(\alpha-1)} \frac{1}{t (1 - t)^{\alpha-1}}, \end{aligned} \] 为了求最小的\(c(t)\)只要求\(t (1 - t)^{\alpha-1}\)的最大值点, 用微分法易得\(t = \frac{1}{\alpha} = \frac{1}{EX}\)时\(c(t)\)最小, 所以试投密度的期望与\(p(x)\)期望相同。 \(c(t)\)的最大值为 \[ c_0 = c(\frac{1}{\alpha}) = \frac{\alpha^\alpha e^{-(\alpha-1)}}{\Gamma(\alpha)} . \] 当\(t = \frac{1}{\alpha}\)时 \[ h(x) = \frac{\alpha \lambda^{\alpha-1}}{\Gamma(\alpha)} x^{\alpha-1} \exp\left\{ - \frac{\alpha-1}{\alpha} x \right\}, x > 0, \alpha > 1 . \]
所以\(t = \frac{1}{\alpha}\)时 \[ h_1(x) = \frac{p(x)}{c_0 g(x)} = \frac{e^{\alpha-1}}{\alpha^{\alpha-1}} x^{\alpha-1} e^{- \frac{\alpha-1}{\alpha} x}, x>0, \alpha>1 \] \(h_1(x)\)的最大值为1。
\(\alpha>1\)时Gamma(\(\alpha, \lambda\))分布的随机数发生器Julia程序:
function randgammg(n, α=2.0, λ=1.0)
local xs, x, y, t
function h(x)
exp(α-1) / α^(α-1) *
x^(α-1) * exp(-(α-1)/α *x)
end
xs = zeros(n)
t = 1 / α
for i=1:n
while true
x = -log(rand()) / t
y = rand()
y <= h(x) && break
end
xs[i] = x
end
return xs ./ λ
end当伽马分布的参数\(\alpha \in (0,1)\), \(\lambda=1\)时, 可以找到如下分为\(0 < x \leq 1\)和\(x>1\)两段的控制函数: \[\begin{aligned} M(x) =& \begin{cases} \frac{1}{\Gamma(\alpha)} x^{\alpha-1}, & 0<x \leq 1, \\ \frac{1}{\Gamma(\alpha)} e^{-x}, & x>1 \end{cases} \end{aligned}\] 使得\(p(x) \leq M(x)\), 然后把\(M(x)\)归一化为一个密度就可以作为试投密度。 积分得 \[ c_1 = \int_0^\infty M(x) \,dx = \frac{1}{\Gamma(\alpha)}\left( \frac{1}{\alpha} + e^{-1} \right) \] 令 \[ g(x) = \frac{1}{c_1} M(x) = \frac{1}{\frac{1}{\alpha} + e^{-1}} \cdot \begin{cases} x^{\alpha-1}, & 0<x \leq 1, \\ e^{-x}, & x>1 \end{cases} \] 设\(G(x)\)为对应的分布函数, 则 \[ G(x) = \begin{cases} \frac{1}{1+\alpha e^{-1}} x^\alpha, & 0<x\leq 1, \\ \frac{1}{1+\alpha e^{-1}} + \frac{\alpha}{1+\alpha e^{-1}}(e^{-1} - e^{-x}), & x>1 \end{cases} \] 求反函数\(G^{-1}(p)\)。 \(G(1) = \frac{1}{1+\alpha e^{-1}}\), 反函数也分\(p \leq \frac{1}{1+\alpha e^{-1}}\)和 \(p > \frac{1}{1+\alpha e^{-1}}\)两段。 解得 \[ G^{-1}(p) = \begin{cases} [(1 + \alpha e^{-1}) p]^{\frac{1}{\alpha}}, & 0<p \leq \frac{1}{1+\alpha e^{-1}}, \\ -\ln\left( e^{-1} - \frac{1}{\alpha} \left( p(1 + \alpha e^{-1}) - 1 \right) \right), & \frac{1}{1+\alpha e^{-1}} < p < 1 \end{cases} \]
对\(0<\alpha<1\),令 \[ h_2(x) = \frac{p(x)}{g(x)} =\begin{cases} \frac{\frac{1}{\alpha} + e^{-1}}{\Gamma(\alpha)} e^{- x}, & 0<x\leq 1, \\ \frac{\frac{1}{\alpha} + e^{-1}}{\Gamma(\alpha)} x^{\alpha-1}, & x>1 \end{cases} \] 这个分段函数的两段的最大值都分别在区间的左端点达到, 所以 \[ c_3 = \max_{x>0} h_2(x) = \frac{\frac{1}{\alpha} + e^{-1}}{\Gamma(\alpha)} \] 令 \[ h_3(x) = \frac{p(x)}{c_3 g(x)} = \begin{cases} e^{- x}, & 0<x\leq 1, \\ x^{\alpha-1}, & x>1 \end{cases} \] 则\(h_3(x)\)最大值为1。
\(0<\alpha<1\)时Gamma(\(\alpha, \lambda\))分布的随机数发生器Julia程序:
function randgammas(n, α=0.5, λ=1.0)
local xs, x, y, t
h(x) = x < 1 ? exp(-x) : x^(α-1)
function Ginv(p)
if p < 1/(1+α*exp(-1))
((1 + α*exp(-1))*p)^(1/α)
else
-log(exp(-1) - 1/α*(p*(1 + α*exp(-1)) - 1))
end
end
xs = zeros(n)
t = 1 / α
for i=1:n
while true
x = Ginv(rand())
y = rand()
y <= h(x) && break
end
xs[i] = x
end
return xs ./ λ
end例6.15 (用舍选法生成正态随机数(*)) 如果\(X \sim \text{N}(0,1)\)则\(Y = \mu + \sigma X \sim \text{N}(\mu, \sigma^2)\), 所以只要产生N(0,1)随机数\(Z\)。 用舍选法II, 标准正态分布密度在尾部正比于\(e^{-\frac12 x^2}\), 用标准指数分布密度来作为试投密度(可以像例6.14那样证明在指数分布中 参数为1的指数分布是最优的)。
因为指数分布是非负的, 所以先产生\(|Z|\)的随机数, 易见\(|Z|\)的密度函数为 \[\begin{aligned} p(x) = \sqrt\frac{2}{\pi} e^{-\frac12 x^2}, \ x>0\end{aligned}\] 取\(g(x) = e^{-x}, x>0\), \[\begin{aligned} h(x) = \frac{p(x)}{g(x)} = \sqrt\frac{2}{\pi} e^{x - \frac12 x^2}, \ x>0\end{aligned}\] 为使\(h(x)\)最大只要使\(x - \frac12 x^2\)最大, 所以\(h(x)\)最大值点为\(x_0=1\), 取 \[\begin{aligned} c =& h(1) = \sqrt\frac{2e}{\pi}, \quad \frac{p(x)}{c g(x)} = e^{-\frac12 (x-1)^2},\end{aligned}\] 产生\(|Z|\)随机数后只需要以各自\(\frac12\)的概率加上正负号。 算法迭代次数为\(c = \sqrt\frac{2e}{\pi} \approx 1.32\)。
例6.16 (用舍选法和Box-Muller变换生成正态随机数(*)) 在Box-Muller公式中令\(R = \sqrt{-2\ln U_1}\), \(\theta=2\pi U_2\), 则\(R^2\)与\(\theta\)独立, \(R^2 \sim \text{Exp}(\frac12)\), \(\theta \sim \text{U}(0,2\pi)\), \(R\)是\((X,Y)\)的极径, \(\theta\)是\((X,Y)\)的极角, 是一个均匀随机角度。 我们只要能生成极角服从U(\(0,2\pi\))的随机点的直角坐标就可以获得 \(\cos\theta\)和\(\sin\theta\)的值而不需要计算正弦和余弦。
设随机向量\((V_1, V_2)\)服从单位圆 \(C = \{(x,y): x^2 + y^2 \leq 1 \}\)上的均匀分布U(\(C\)), 则\((V_1, V_2)\)的极角\(\theta\)服从U(\(0,2\pi\))。 \((V_1, V_2)\)可以用舍选法产生。 得到这样的\((V_1, V_2)\)后只要令 \[\begin{aligned} X = \sqrt{-2\ln U_1} \frac{V_1}{\sqrt{V_1^2 + V_2^2}}, \ Y = \sqrt{-2\ln U_1} \frac{V_1}{\sqrt{V_2^2 + V_2^2}} \end{aligned}\] 则\(X,Y\)服从独立的标准正态分布。
另外还可以证明, 若\((V_1, V_2)\)服从单位圆上的均匀分布U(\(C\)), 则\(S = V_1^2 + V_2^2\)服从U(0,1) 且与\((V_1, V_2)\)的极角\(\theta\)独立。 这样,\(U_1\)可以用\(S\)代替。
Julia程序:
function randnormdsbm(n, μ=0.0, σ=1.0)
local n2, nn, xs, v1, v2, s, amp
n2 = ceil(Int, n/2)
nn = 2*n2
xs = zeros(nn)
for i=1:n2
while true
v1 = 2*rand()-1
v2 = 2*rand()-1
s = v1^2 + v2^2
s <= 1 && break
end
amp = sqrt(-2*log(s)/s)
xs[i] = amp*v1
xs[n2+i] = amp*v2
end
if n<nn
pop!(xs)
end
return μ .+ σ .* xs
end 例6.17 (条件伽马分布随机数) 生成取值大于5的Gamma(2,1)的随机数\(Z\)。密度为 \[\begin{aligned} p(x) = \frac{x e^{-x}}{\int_5^\infty u e^{-u} du} = \frac{x e^{-x}}{6 e^{-5}}, \ x > 5 \end{aligned}\]
一个显然的算法为:
这样的算法舍去小于5的试投值比较多, 接受概率只有约0.04, 效率很低。
仍使用舍选法II, 试投密度使用大于5的指数分布。 因为Gamma(2,1)期望为\(2/1=2\), 使用大于5的Exp(1/2), 密度为 \[\begin{aligned} g(x) = \frac{e^{-\frac12 x}}{\int_5^\infty e^{-\frac12 u} du} = \frac{1}{2} e^{\frac52} e^{-\frac12 x}, \ x > 5 \end{aligned}\] 比值 \[\begin{aligned} h(x) = \frac{p(x)}{g(x)} = \frac13 e^{\frac52} x e^{-\frac12 x}, \ x>5 \end{aligned}\] 是单调减函数,所以\(h(x) \leq c = h(5) = \frac53\), \[\begin{aligned} \frac{p(x)}{c g(x)} = \frac15 e^{\frac52} x e^{-\frac12 x}. \end{aligned}\]
如何生成\(g(x)\)的随机数呢? 注意指数分布的随机变量\(\xi\)有如下的无记忆性: \(P(\xi > a+b | \xi > a) = P(\xi > b)\), 所以在\(\xi > a\)条件下的指数分布, 可以看成是从\(a\)出发的一个指数分布, 即在\(\xi > a\)条件下的指数分布与\(\xi + a\)同分布。 所以\(g(x)\)的随机数可以用指数分布随机数加5实现。 Julia程序如下:
6.6 复合法
设离散型随机变量\(I\)的概率分布为 \[\begin{aligned} P(I=i) = \alpha_i, \ i=1,2,\dots,m\end{aligned}\] 若随机变量\(Z_1, Z_2, \dots, Z_m\)都是离散型随机变量, 定义随机变量\(X\)的值为 \[\begin{aligned} X = \begin{cases} Z_1, & \text{当} I=1, \\ Z_2, & \text{当} I=2, \\ \cdots & \cdots\cdots \\ Z_m, & \text{当} I=m . \end{cases} \end{aligned}\] 则\(X\)是离散型随机变量,且 \[\begin{aligned} P(X=x) = \sum_{i=1}^m P(X=x | I=i) P(I=i) = \sum_{i=1}^m \alpha_i P(Z_i=x) . \end{aligned}\] 如果\(X\)的分布可以这样定义,则可以先生成\(I\)的样本, 再根据\(I\)的值生成\(Z_I\)的样本, 结果就是\(X\)的样本。
如果上面的\(Z_1, Z_2, \dots, Z_m\)都是连续型随机变量, 密度函数分别为\(p_1(z), p_2(z), \dots, p_m(z)\), 则\(X\)的分布函数为 \[\begin{aligned} F(x) =& P(X \leq x) = \sum_{i=1}^m P(X \leq x | I=i) P(I=i) \\ =& \sum_{i=1}^m \alpha_i P(Z_i \leq x) . \end{aligned}\] 于是\(X\)有分布密度 \[\begin{aligned} p(x) = F'(x) = \sum_{i=1}^m \alpha_i p_i(x) . \end{aligned}\] 如果\(X\)的分布密度有这样的形式,可以先生成\(I\), 然后根据\(I\)的值生成\(Z_I\)作为\(X\)。
复合法需要比较多的随机数, 在其它方法很难实现或效率较低时复合法有它的优势。
例6.18 设离散型随机变量\(X\)的分布为 \[\begin{aligned} P(X=k) =& \begin{cases} 0.05, & j=1,2,3,4,5 \\ 0.15, & j=6,7,8,9,10 \end{cases} \end{aligned}\]
虽然可以当作普通的取有限个值的离散型随机变量来生成, 但是\(X\)的分布明显可以看成如下的混合分布: 随机变量\(I\)分布为 \[\begin{aligned} P(V=1)=0.25, \ P(V=2)=0.75 \end{aligned}\] 随机变量\(Z_1\)服从\(1,2,3,4,5\)上的离散均匀分布, 随机变量\(Z_2\)服从\(6,7,8,9,10\)上的离散均匀分布, \(X\)的分布为\(I=1\)时取\(Z_1\), \(I=2\)时取\(Z_2\)。 所以,生成\(X\)的随机数的Julia程序如下:
function randmix(n)
local xs, u1, u2
xs = zeros(n)
for i=1:n
u1, u2 = rand(2)
if u1 < 0.75
xs[i] = ceil(Int, 5*u2) + 5
else
xs[i] = ceil(Int, 5*u2)
end
end
return xs
end例6.19 (梯形分布(*)) 对\(0<a<1\),考虑梯形密度 \[ p_1(x) = a + 2(1-a) x,\ 0<x<1, \] 或 \[ p_2(x) = 2-a - 2(1-a)x, \ 0<x<1 \]
因为分布函数为 \[ F_1(x) = ax + (1-a) x^2, \ 0<x<1 \] 或 \[ F_2(x) = (2-a)x - (1-a)x^2, \ 0<x<1 \] 分布函数反函数为 \[ F_1^{-1}(u) = \frac{-a + \sqrt{a^2 + 4(1-a) u}}{2(1-a)}, \ 0<u<1 \] 或 \[ F_2^{-1}(u) = \frac{2-a - \sqrt{(2-a)^2 - 4(1-a)u}}{2(1-a)}, \ 0<u<1 \] 可以用逆变换法获得\(p_1(x)\)和\(p_2(x)\)的随机数。 另外,注意\(X \sim p_1(x)\)当且仅当\(1-X \sim p_2(x)\), 为了生成\(p_2(x)\)的随机数, 也可以生成\(X \sim p_1(x)\)然后用\(1-X\)作为\(p_2(x)\)的随机数。
下面给出复合法生成\(p_1(x)\)随机数的做法。 \(p_1(x)\)下的区域可以分解为一个面积等于\(a\)的矩形和一个面积等于\(1-a\)的三角形, 令 \[\begin{aligned} g_1(x) =& 1, \ 0<x<1, \\ g_2(x) =& 2x, \ 0<x<1, \\ p_1(x) =& a \cdot g_1(x) + (1-a) \cdot g_2(x), \ 0<x<1 \end{aligned}\] 可见\(p_1(x)\)是由一个均匀分布和一个三角形分布复合而成。 于是,生成梯形\(p_1(x)\)的随机数的Julia程序为
习题
习题1
写程序生成\(n\)个如下离散型分布随机数: \(P(X=1)=1/3\), \(P(X=2)=2/3\)。
- 生成\(n=100\)个这样的随机数,计算\(X\)取1的百分比;
- 生成\(n=1000\)个这样的随机数,计算\(X\)取1的百分比;
- 生成\(n=10000\)个这样的随机数,计算\(X\)取1的百分比;
- 用中心极限定理推导\(n\)个这样的随机数取1的百分比\(f_n\)的渐近分布, 并用此渐近分布检验上面的三组样本是否与\(P(X=1)=1/3\)相符。
习题3
洗好一副编号分别为\(1,2,\ldots,54\)的纸牌, 依次抽取出来,若第\(i\)次抽取到编号\(i\)的纸牌则称为成功抽取。 编写程序估计成功抽取个数\(T\)的期望和方差, 推导理论公式并与模拟结果进行比较。
习题5
编写例6.6中原始的和改进的生成二项分布随机数的算法并用R程序实现, 比较两种算法得到的序列是否相同。
习题6
编写例6.7中原始的和改进的生成泊松分布随机数的算法并用R程序实现, 比较两种算法得到的序列是否相同。
习题7
设随机变量\(X\)表示成功概率为\(p\)的独立重复试验中第\(r\)次成功所需要的试验次数, 称\(X\)服从负二项分布。
- 利用负二项分布与几何分布的关系构造\(X\)的随机数。
- 直接利用负二项分布的概率分布构造\(X\)的随机数。
习题8
用变换法生成如下分布的随机数:
- Beta(\(\frac{1}{n}, 1\))分布,密度为 \[\begin{aligned} p(x) = \frac{1}{n} x^{\frac{1}{n} - 1}, x \in [0,1] \end{aligned}\]
- Beta(\(n, 1\))分布,密度为 \[\begin{aligned} p(x) = n x^{n - 1}, x \in [0,1] \end{aligned}\]
- 密度为 \[\begin{aligned} p(x) = \frac{2}{\pi \sqrt{1 - x^2}}, x \in [0,1] \end{aligned} \]
- 柯西分布,密度为 \[\begin{aligned} p(x) = \frac{1}{\pi (1 + x^2)}, x \in (-\infty, \infty) \end{aligned}\]
- 密度为 \[\begin{aligned} p(x) = \cos(x), x \in [0, \frac{\pi}{2}] \end{aligned}\]
- 威布尔分布,密度为 \[\begin{aligned} p(x) = \frac{\alpha}{\eta} x^{\alpha-1} e^{-\frac{x^\alpha}{\eta}}, \ x>0 \ (\alpha>0, \eta>0) \end{aligned}\]
习题9
设\(X\)为标准指数分布Exp(1)随机变量, 模拟在\(X<0.05\)条件下\(X\)的分布, 密度为 \[\begin{aligned} p(x) = \frac{e^{-x}}{1 - e^{-0.05}},\ 0<x<0.05 \end{aligned}\] 生成1000个这样的随机数, 并用它们估计\(E(X | X < 0.05)\), 推导\(E(X | X < 0.05)\)的精确值并与模拟结果比较。
习题10
设随机变量\(X\)分布为 \[\begin{aligned} P(X=k) = \frac{e^{-\lambda}\frac{\lambda^k}{k!}} {\sum_{i=0}^m e^{-\lambda}\frac{\lambda^i}{i!}}, \ k=0,1,\dots,m \end{aligned}\] 给出模拟此分布的两种方法。
习题11
设\(X \sim \text{B}(n,p)\), \(k\)为满足\(0 \leq k \leq n\)的给定的整数, 随机变量\(Y\)的分布函数为\(P(Y \leq y) = P(X \leq y | X \geq k)\)。 记\(\alpha = P(X \geq k)\)。 分别用逆变换法和舍选法生成\(Y\)的随机数。 当\(\alpha\)取值大的时候还是取值小的时候舍选法不可取?
习题13
设随机变量分别以概率0.06, 0.06, 0.06, 0.06, 0.06, 0.15, 0.13, 0.14, 0.15, 0.13 取值\(1,2,\dots,10\), 应用复合方法给出产生此分布随机数的算法。
习题14
设随机变量\(X\)的分布为 \[\begin{aligned} P(X=k) = \frac{1}{2^{k+1}} + \frac{2^{k-1}}{3^k}, \ k=1,2,\dots \end{aligned}\] 给出模拟此随机变量的算法。
习题15
设随机变量\(X\)的分布密度为 \[\begin{aligned} p(x) = \frac12 e^{-|x|}, \ -\infty < x < \infty \end{aligned}\] 称\(X\)服从双指数分布或Laplace分布。 分别用逆变换法和复合法生成\(X\)的随机数。
习题16
给出生成密度函数为 \[\begin{aligned} p(x) = \frac{1}{0.000336} x(1-x)^3, 0.8 < x < 1 \end{aligned}\] 的随机数的有效算法。
习题17
设\(X\)密度为 \[\begin{aligned} p_R(x) = \frac{2(x-a)}{(b-a)^2}, \ x \in (a,b) \end{aligned} \] 此密度单调上升,是以\([a,b]\)为底的三角形,叫做RT(\(a,b\))分布; 若\(X\)的密度为 \[\begin{aligned} p_L(x) = \frac{2(b-x)}{(b-a)^2}, \ x \in (a,b) \end{aligned} \] 此密度单调下降,也是以\([a,b]\)为底的三角形,叫做LT(\(a,b\))分布。 试证明:
- 若\(X \sim \text{RT}(0,1)\),则 \(Y = a + (b-a)X \sim \text{RT}(a,b)\); 若\(X \sim \text{LT}(0,1)\),则 \(Y = a + (b-a)X \sim \text{LT}(a,b)\)。
- \(X \sim \text{RT}(0,1)\)当且仅当\(1-X \sim \text{LT}(0,1)\)。
- 若\(U_1, U_2\)独立且分别服从U(0,1)分布, 则\(X = \max(U_1, U_2) \sim \text{RT}(0,1)\), \(Y = \min(U_1, U_2) \sim \text{LT}(0,1)\)。
习题18
设\(\alpha \sim \text{U}(0, 2\pi)\), \(R \sim \text{Exp}(\frac12)\)与\(\alpha\)独立,令 \[\begin{aligned} \begin{cases} X = \sqrt{R} \cos \alpha \\ Y = \sqrt{R} \sin \alpha \end{cases} \end{aligned}\] 证明\(X, Y\)相互独立且都服从N(0,1)分布。
习题19
设\(U_1, U_2, \dots, U_k, V_1, V_2, \dots, V_{k-1}\)独立同U(0,1)分布。 令\(T = -\log(U_1 U_2 \dots U_k)\), 设\(V_1, V_2, \dots, V_{k-1}\)从小到大排列结果为 \(V_{(1)} \leq V_{(2)} \leq \dots V_{(k-1)}\), 记\(V_{(0)}=0\), \(V_{(k)}=1\), 令 \[\begin{aligned} X_i = T(V_{(i)} - V_{(i-1)}), \ i=1,2,\dots,k, \end{aligned} \] 证明\(X_1, X_2, \dots, X_k\)独立同标准指数分布Exp(1)。
习题20
设随机向量\((X,Y)\)服从单位圆\(C = \{(x,y): x^2 + y^2 \leq 1 \}\)上的均匀分布, \(R^2 = X^2 + Y^2\), \(\theta\)为\((X,Y)\)的极角, 则\(R^2\)与\(\theta\)独立, \(R^2 \sim \text{U(0,1)}\), \(\theta \sim \text{U}(0,2\pi)\)。
习题21
设随机变量\(X\)分布函数为\(G(x)\),密度函数为\(g(x)\)。 对\(a<b\),令 \[\begin{aligned} F(x) = \frac{G(x) - G(a)}{G(b) - G(a)}, a \leq x \leq b \end{aligned}\]
- \(F(x)\)是一个分布函数, 其对应的分布是\(X\)在什么条件下的条件分布?
- 证明可以用如下方法生成\(F(x)\)的随机数: 反复生成\(X \sim G(x)\), 直到\(X \in [a,b]\), 输出\(X\)的值为\(F(x)\)的随机数。
习题22
设随机变量\(X\)的概率分布为\(p_k = P(X=k), k=1,2,\dots\), \(\sum_{k=1}^\infty p_k=1\)。记 \[\begin{aligned} \lambda_n = P(X=n | X > n-1) = \frac{p_n}{1 - \sum_{k=1}^{n-1} p_k}, \ n=1,2,\dots \end{aligned}\]
- 证明\(p_1 = \lambda_1\), \(p_n = (1-\lambda_1)(1-\lambda_2) \cdots (1 - \lambda_{n-1}) \lambda_n\) (\(n=2,3,\dots\))。 如果把\(X\)看成某种产品的寿命, 则\(\lambda_n\)表示此产品在其寿命大于\(n-1\)的条件下, 寿命为\(n\)的概率。 \(\{ \lambda_n, n \geq 1 \}\)叫做离散机会比。 一个生成\(X\)的随机数的方法是连续生成均匀随机数直到第\(n\)个小于\(\lambda_n\), 叫做离散机会比方法,算法如下:
\[ \begin{aligned} & k \leftarrow 0 \\ & \text{until} (U < \lambda_k) \{ \\ & \qquad \text{Generate } U \sim \text{U}(0,1) \\ & \qquad k \leftarrow k+1 \\ & \} \\ & X \leftarrow k \end{aligned} \]
证明上述算法产生的随机数符合\(X\)的分布。
假设\(X\)是一个参数为\(p\)的几何分布随机变量, 求\(\lambda_n, n=1,2,\dots\)。 说明此时上述算法是用来做什么的, 它的有效性为什么是明显的?
习题23
假设\(X\)为取值于\(\{1,2,\dots \}\)的随机变量, \(\lambda_n, n=1,2,\dots\)为其离散机会比,满足 \(0 \leq \lambda_n \leq \lambda, n=1,2,\dots\)。 用如下算法产生\(X\)的随机数:
\[ \begin{aligned} & S \leftarrow 0 \\ & \text{until}(U_2 \leq \lambda_S / \lambda) \{ \\ & \qquad \text{Generate } U_1 \sim \text{U}(0,1), \text{ let } Y \leftarrow \mbox{ceil}\left(\frac{\log(U_1)}{\log(1-\lambda)} \right) \\ & \qquad S \leftarrow S + Y \\ & \qquad \text{Generate } U_2 \sim \text{U}(0,1) \\ & \}\\ & X \leftarrow S \end{aligned} \]
算法中的\(Y\)服从什么分布?
证明这样得到的\(X\)是离散机会比为\(\{ \lambda_n \}\)的离散型随机变量。