22 插值
22.1 多项式插值
例22.1 下表是\(F(1,n)\)分布的\(0.95\)分位数的部分值: \[ \begin{array}{c*9r} n & \cdots & 20 & \cdots & 29 & 30 & 40 & 60 & 120 & \infty \\ \hline h(n) & \cdots & 4.35 & \cdots & 4.18 & 4.17 & 4.08 & 4.00 & 3.92 & 3.84 \end{array} \] 设关于函数\(h(n)\)我们只有上述知识,但是还知道\(h(n)\)具有一定光滑性。 这里\(h(30)=4.17\), \(h(40)=4.08\), 为了计算\(h(32)\),只要把\((30, h(30))\)和\((40, h(40))\)这两个点用线段连接, 在\((30, 40)\)之间用连接的线段作为\(h(x)\)的近似值,就可以计算 \[\begin{aligned} h(32) = h(30) + \frac{h(40) - h(30)}{40-30} (32 - 30) \approx 4.15 \end{aligned}\] 称这样的近似计算为线性插值。
还可以进一步地近似。比如我们还知道\(h(20) = 4.35\), 则存在唯一的二次多项式\(f(x)\)使得\(f(x)\)穿过 \((20,h(20))\), \((30, h(30))\), \((40, h(40))\)这三个点, 用\(f(32)\)来近似\(h(32)\), 这叫做抛物线插值。
一般地, 设已知函数\(h(x)\)在点\(x_1, x_2, \dots, x_n\)上的值 \(z_1, z_2, \dots, z_n\) (\(z_i=h(x_i)\)), 在假定\(h(x)\)具有一定光滑度的条件下可以用函数\(f(x)\) 近似计算\(h(x)\)在自变量\(x\)处的值。 称\(h(x)\)为被插值函数, \(x_1, x_2, \dots, x_n\)叫做节点, \(f(x)\)叫做插值函数, 一般使用多项式或分段多项式作插值函数。 如果我们只能获得\(h(x)\)在有限个点上的值, 可以用插值方法近似计算\(h(x)\)在其它自变量处的值。 如果函数\(h(x)\)每计算一个函数值到所需精度都要花费很长时间, 可以预先在一些自变量处计算函数值并保存好, 然后需要用到\(h(x)\)的值时用插值法近似计算整个定义域上的函数值。 如果\(h(x)\)的计算精度要求不高, 也可以预先计算并保存部分自变量处的函数值, 然后用插值来近似函数值。 插值得到的表达式可以用于积分、微分计算。
例22.1中用连接两点的线段作为插值公式的方法叫做线性插值。 一般地, 设已知\((x_i, z_i), i=1,\ldots,n\), \(z_i = h(x_i)\)。 对\(x \in [x_{i-1}, x_i]\), 令 \[\begin{align} h(x) \approx f(x) = z_{i-1} + \frac{z_i - z_{i-1}}{x_i - x_{i-1}} (x-x_{i-1}) \tag{22.1} \end{align}\] (这就是直线方程的斜截式)。 如果记\(\alpha = \frac{x-x_{i-1}}{x_i - x_{i-1}}\), 即点\(x\)在插值区间\([x_{i-1}, x_i]\)中前后位置比例,则 \[\begin{align} f(x) = (1 - \alpha) z_{i-1} + \alpha z_i . \tag{22.2} \end{align}\] 当\(h(x)\)本身在\([x_{i-1}, x_i]\)就是一次多项式时插值是精确的。
R中用函数approx对给定的\(n\)个点在相邻点之间做线性插值。
当已知三个点的函数值时可以找到穿过这三个点的抛物线, 用对应的二次多项式作为\(h(x)\)的近似值。 设\(x_{-1}, x_0, x_1\)是三个点且距离为\(x_0 - x_{-1} = x_{1} - x_0 = d\), 函数值分别为\(z_{-1}, z_0, z_1\)。 对\(x \in [x_{-1}, x_1]\), 令\(\alpha = \frac{x-x_0}{d}\),则\(\alpha \in [-1,1]\), 令 \[\begin{aligned} f(\alpha) = \frac{z_{-1} -2z_0 + z_1}{2} \alpha^2 + \frac{z_1 - z_{-1}}{2} \alpha + z_0 , \end{aligned}\] 则\(f(\alpha)\)是\(x\)的二次函数, 且经过\((x_{-1}, z_{-1})\), \((x_0, z_0)\), \((x_1, z_1)\)这三个点, 可以用\(f(\alpha)\)近似\(h(x)\)的值。
如果有\(n\)个等距格点及对应函数值\((x_i, z_i), i=1,2,\ldots,n\), \(z_i = h(x_i)\), 为了用抛物线插值方法近似计算\(h(x)\), \(x \in [x_1, x_n]\), 取\(m_i\)为区间\([x_i, x_{i+1}]\)的中点, 对\(x \in [m_i, m_{i+1}]\)用\((x_i, x_{i+1}, x_{i+2})\)三点插值 \((m=2,3,\dots, m_{n-2})\), 在\([x_1, m_1]\)内用\((x_1, x_2, x_3)\)三个点插值, 在\([m_{n-1}, x_n]\)内用\(x_{n-2}, x_{n-1}, x_n\)三个点插值。
下面的定理保证了插值多项式的存在唯一性。
定理22.1 设有\(\{(x_i, z_i), i=1,2,\dots,n \}\), \(\{ x_i, i=1,2,\dots,n \}\)互不相同, 则存在唯一的不超过\(n-1\)阶的多项式\(P_{n-1}(x)\)使得 \[\begin{aligned} P_{n-1}(x_i) = z_i, \ i=1,2,\dots,n. \end{aligned}\]
证明: 设\(P_{n-1}(x) = a_0 + a_1 x + \ldots + a_{n-1}x^{n-1}\)为多项式, 其中\(a_0, a_1, \dots, a_{n-1}\)为待定常数。 为使\(P_{n-1}(x_i)=z_i\), \(i=1,2,\dots,n\),应有 \[\begin{align} \left( {\begin{array}{*{20}c} 1 & {x_1 } & {x_1^2 } & \cdots & {x_1^{n - 1} } \\ 1 & {x_2 } & {x_2^2 } & \cdots & {x_2^{n - 1} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & {x_n } & {x_n^2 } & \cdots & {x_n^{n - 1} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {a_0 } \\ {a_1 } \\ {a_2 } \\ \vdots \\ {a_{n - 1} } \end{array} } \right) = \left( {\begin{array}{*{20}c} {z_1 } \\ {z_2 } \\ \vdots \\ {z_n } \end{array} } \right) \tag{22.3} \end{align}\] 注意到此方程组的系数矩阵行列式为Vandermonde行列式, 行列式值为 \[\begin{aligned} \prod_{1 \leq i < j \leq n} (x_j - x_i) \neq 0, \end{aligned}\] 所以方程组存在唯一解, 即存在唯一的次数不超过\(n-1\)的多项式\(P_{n-1}(x)\)使\(P_{n-1}(x)\)通过 \((x_i, z_i), i=1,2,\dots,n\)这\(n\)个点。
由定理22.1的证明可见 求插值多项式的方法之一是解线性方程组(22.3), 但是这样难以得到用初始值\((x_i, z_i), i=1,2,\dots,n\)表示的函数表达式。
22.2 Lagrange插值法
获得插值多项式表达式的一种方法是Lagrange插值法。 令 \[\begin{aligned} d_i(x) = \frac{\prod\limits_{j \neq i}(x - x_j)} {\prod\limits_{j \neq i}(x_i - x_j)} \end{aligned}\] 则\(d_i(x)\)是\(n-1\)阶多项式, 在各\(\{x_i\}\)上满足: \[\begin{aligned} \begin{cases} d_i(x_i) = 1 \\ d_i(x_k) = 0, k \neq i \end{cases} \end{aligned}\] 令 \[\begin{align} f(x) = \sum_{i=1}^n z_i d_i(x), \tag{22.4} \end{align}\] 则\(f(x)\)是通过指定的\(n\)个点的不超过\(n-1\)阶的多项式, 根据定理22.1可知(22.4)给出的多项式是唯一的插值多项式。
为了用Lagrange方法插值,首先需要确定\(n\)个多项式\(d_i(x), i=1,2,\dots,n\)的系数。 为了便于计算,记 \[\begin{align} g(x) = (x - x_1) (x - x_2) \cdots (x - x_n) = \prod_{i=1}^n (x - x_i), \tag{22.5} \end{align}\] 则有 \[\begin{aligned} g'(x) =& \sum_{k=1}^n \prod_{j \neq k} (x - x_j), \\ g'(x_i) =& \sum_{k=1}^n \prod_{j \neq k} (x_i - x_j) = \prod_{j \neq i} (x_i - x_j) \end{aligned}\] 于是可知 \[\begin{align} d_i(x) = \frac{g(x) / (x - x_i)}{g'(x_i)}. \tag{22.6} \end{align}\] 这样, 只要算出\(g(x)\)的系数和\(g'(x)\)的系数, 然后用多项式除法写出\(g(x) / (x - x_i)\)的系数, 就可以用(22.6)得到\(d_i(x)\)的系数。
| 计算插值多项式\(f(x)\)的系数的算法 |
|---|
| 写出\(g(x)\)的展开式\(g(x) = \sum_{i=0}^{n} a_i x^i\). |
| 写出\(g'(x)\)的展开式\(g'(x) = \sum_{i=0}^{n-1} (i+1) a_{i+1} x^i\). |
| 计算各\(g'(x_i)\). |
| 写出各\(g(x) / (x - x_i)\)的展开式. |
| 用下式给出插值多项式表达式: |
| \(\quad\) \(f(x) = \sum_{i=1}^n \frac{z_i}{g'(x_i)} [g(x) / (x-x_i)]\) |
上述算法中用到了多项式加减法、乘法和除法。
为计算多项式乘法\(\sum_{i=0}^n a_i x^i \sum_{j=0}^m b_j x^j\), 记\(a_i = 0 ( i>n)\), \(b_j=0 ( j>m)\), 有 \[\begin{aligned} & \sum_{i=0}^n a_i x^i \sum_{j=0}^m b_j x^j = \sum_{i=0}^n \sum_{j=0}^m a_i b_j x^{i+j} \text{ (令$k = i+j$)} \\ =& \sum_{i=0}^n \sum_{k=i}^{i+m} a_i b_{k-i} x^k = \sum_{k=0}^{m+n} \left( \sum_{i=0}^{k} a_i b_{k-i} \right) x^k \\ =& \sum_{k=0}^{m+n} \left( \sum_{i=\max(0,k-m)}^{\min(k,n)} a_i b_{k-i} \right) x^k \ \text{ (注意$0 \leq i \leq n$, $0 \leq k-i \leq m$)} \\ =& \sum_{k=0}^{m+n} c_k x^k, \end{aligned}\] 乘积多项式的系数为 \[\begin{align} c_k =& \sum_{i=\max(0,k-m)}^{\min(k,n)} a_i b_{k-i}, \ k=0,1,\dots,m+n. \tag{22.7} \end{align}\] \(\{c_k \}\)是\(\{a_k \}\)和\(\{ b_k \}\)的卷积。 如果\(\{ a_k \}\), \(\{ b_k \}\)是两个数列,称 \[\begin{aligned} c_k =& \sum_{i=-\infty}^\infty a_i b_{k-i}, \ k \in \mathbb Z \end{aligned}\] (\(\mathbb Z\)为所有整数)为\(\{ a_k \}\), \(\{ b_k \}\)的卷积。
注: R函数filter和convolve可以计算两个有限序列的卷积。
关于多项式插值的误差有如下定理。
定理22.2 设\(h(x) \in C^{n-1}[a,b]\),\(h^{(n)}(x)\)在\((a,b)\)内存在, 设\(\{x_i, i=1,2,\ldots,n\}\)互不相同, \(f(x)\)和\(g(x)\)分别由(22.4)、(22.5)定义, \(\{x_i, i=1,2,\ldots,n\}\)的最小值到最大值的区间为\(I\), 则对\(\forall x \in I\), 存在\(\xi \in I\)使 \[\begin{align} R(x) = h(x) - f(x) = \frac{h^{(n)}(\xi)}{n!} g(x) . \tag{22.8} \end{align}\]
证明 不妨设\(x_1,x_2,\ldots,x_n\)从小到大排列。 对\(x \in \{ x_1, x_2, \ldots, x_n \}\), 显然\(R(x) = 0\)。 对给定的\(x \in [a,b] \backslash \{x_1,x_2,\ldots,x_n\}\), 定义辅助函数 \[ H(t) = R(t) - \frac{g(t)}{g(x)} R(x) \] 易见 \(H(x_i) = 0, i=1,2,\ldots,n\),且\(H(x)=0\), 所以\(H(t)\)有\(n+1\)个相异零点。 由Rolle定理,\(H(t)\)的每两个相邻零点中间必有一个点导数等于零, 所以\(H^{(1)}(t)\)至少有\(n\)个相异零点。类似讨论可知 \(H^{(j)}(t)\)至少有\(n+1-j\)个相异零点,\(j=1,2,\ldots,n\)。 因此\(H^{(n)}(t)\)至少有一个零点。 设\(\xi\)是\(H^{(n)}(t)\)的一个零点, 则 \[\begin{aligned} 0 =& H^{(n)}(\xi) = R^{(n)}(\xi) - \frac{g^{(n)}(\xi)}{g(x)} R(x) \\ =& h^{(n)}(\xi) - f^{(n)}(\xi) - \frac{n!}{g(x)} R(x) \\ =& h^{(n)}(\xi) - \frac{n!}{g(x)} R(x) \end{aligned}\] 于是 \[ R(x) = \frac{h^{(n)}(\xi)}{n!} g(x) \] 定理得证。
※※※※※
\(g(x)\)在靠近\(\{ x_i \}\)最小值和最大值的位置绝对值较大, 说明多项式插值在边界处误差较大, 见图22.1的左下图。 所以, 多项式插值并不是多项式的阶数越高越好, 阶数太高的多项式的曲线形状会变得很复杂, 插值误差反而会很大。
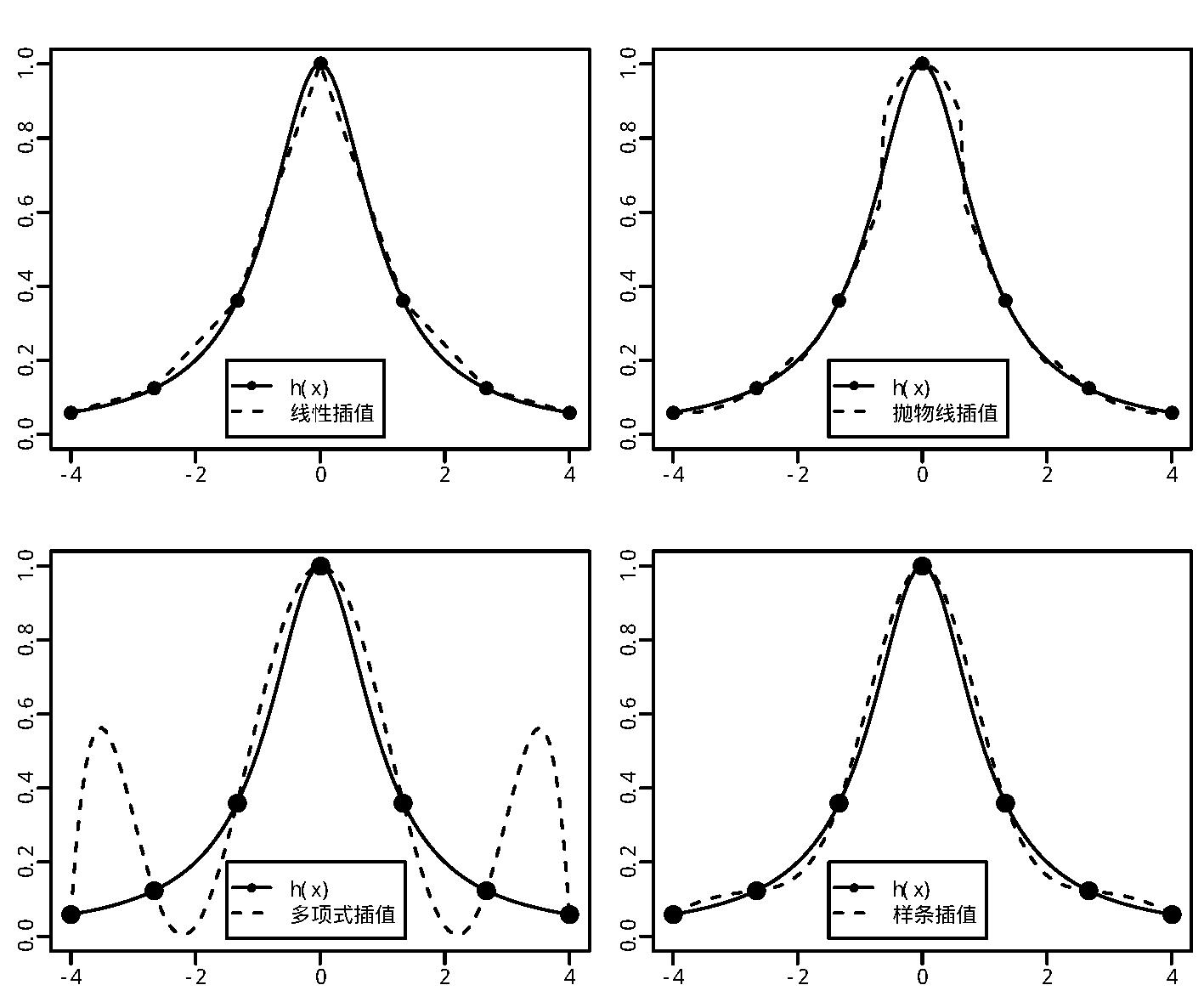
图22.1: 函数\(1/(1+x^2)\)的线性插值、抛物线插值、\(n-1\)阶多项式插值和样条插值
为了使(22.8)中的\(g(x)\)不要太大, 还可以考虑适当选取\(x_i\)的位置。 对\((-1,1)\)区间, 取\(x_i\)为Chebyshev I型多项式\(T_n(x)\)的零点 \(x_i = \cos\left( \frac{2i-1}{2n} \pi \right)\) (\(i=1,2,\dots,n\))可以使\(g(x)\)最小。
例22.2 (用Lagrange法进行二次插值) 设已知\((x_i, z_i), i=1,2,3\)三个点, 求通过这三个点的抛物线方程。 按照Lagrange方法,令 \[\begin{aligned} u_1(x) =& (x-x_2)(x-x_3) = x^2 - (x_2 + x_3)x + x_2 x_3 \\ u_2(x) =& (x-x_1)(x-x_3) = x^2 - (x_1 + x_3)x + x_1 x_3 \\ u_3(x) =& (x-x_1)(x-x_2) = x^2 - (x_1 + x_2)x + x_1 x_2 \end{aligned}\] 则\(d_i(x) = u_i(x) / u_i(x_i)\)。 记\(b_i = z_i / u_i(x_i)\)则\(f(x) = \sum_{i=1}^3 b_i u_i(x)\), 于是抛物线插值公式为 \[\begin{aligned} f(x) =& ( b_1 + b_2 + b_3) x^2 \nonumber\\ & - \left( b_1(x_2 + x_3) + b_2(x_1 + x_3) + b_3(x_1 + x_2) \right) x \nonumber\\ & + \left( b_1 x_2 x_3 + b_2 x_1 x_3 + b_3 x_1 x_2 \right) \end{aligned}\]
例如,对\(h(x) = \sqrt{x}\)在\(x=1/16, 1/4, 1\)用抛物线插值, 有 \[\begin{aligned} b_1 = \frac{1/4}{u_1(\frac{1}{16})} = \frac{64}{45}, \ b_2 = \frac{1/2}{u_2(\frac{1}{4})} = - \frac{32}{9} = -\frac{160}{45}, \ b_3 = \frac{1}{u_3(1)} = \frac{64}{45} \end{aligned}\] 于是插值函数 \[\begin{aligned} h(x) =& \left(\frac{64}{45} -\frac{160}{45} + \frac{64}{45}\right) x^2 \\ & - \left(\frac{64}{45}(\frac14 + 1) -\frac{160}{45}(\frac{1}{16}+1) + \frac{64}{45}(\frac{1}{16} + \frac14) \right) x \\ & + \left(\frac{64}{45} \frac{1}{16} \frac14 -\frac{160}{45} \frac{1}{16} \cdot 1 + \frac{64}{45} \frac14 \cdot 1 \right) \\ =& \frac{1}{45}(7 + 70x - 32 x^2) \end{aligned}\] 在\([0, 1]\)插值的平均绝对误差约为\(0.033\)。
在\((-1,1)\)区间按照Chebyshev I型零点取\(x_i\)为\(-\sqrt{3}/2, 0, \sqrt{3}/2\), 于是在\([0,1]\)区间取\(x_i\)分别为\(\frac{2-\sqrt{3}}{4}, \frac12, \frac{2+\sqrt{3}}{4}\), 这时在\([0,1]\)区间插值的平均绝对误差约为\(0.015\)。
也可以考虑用有理函数插值。设 \[\begin{aligned} f(x) = \frac{a_0 + a_1 x}{1 + b_1 x}, \end{aligned}\] 令\(f(x_i) = z_i\), \(i=1,2,3\),仍取\(x_i\)为\(1/16, 1/4, 1\), 可得方程 \[\begin{aligned} a_0 + \frac{1}{16} a_1 =& \frac{1}{4}\left( 1 + \frac{1}{16} b_1 \right) \\ a_0 + \frac{1}{4} a_1 =& \frac{1}{2} \left( 1 + \frac{1}{4} b_1 \right) \\ a_0 + a_1 =& 1 \cdot(1 + b_1) \end{aligned}\] 解得 \[\begin{aligned} f(x) = \frac{\frac17 + 2x}{1 + \frac87 x}, \end{aligned}\] 这时在\([0,1]\)区间插值的平均绝对误差约为\(0.014\)。
R的polynom包的poly.calc(x,y)用给定的x, y坐标计算插值多项式。
22.3 牛顿差商公式(*)
牛顿差商公式是另外一种给出插值多项式表达式的方法。 对函数\(h(x)\),分点\(x_i, i=1,\ldots,n\),定义各阶差商为: \[\begin{aligned} h[x_i] =& h(x_i) \\ h[x_i, x_j] =& \frac{h(x_j) - h(x_i)}{x_j - x_i} \\ h[x_i, x_j, x_k] =& \frac{h[x_j,x_k] - h[x_i, x_j]}{x_k - x_i} \\ \cdots & \cdots \cdots \\ h[x_1, x_{2}, \ldots, x_{n}] =& \frac{h[x_{2}, x_{3}, \ldots, x_{n}] - h[x_1, x_{2}, \ldots, x_{n-1}]}{x_{n} - x_1} \end{aligned}\] 则\(h[x_1, x_2, \ldots, x_n]\)关于自变量对称, 即以任意自变量次序计算\(h[x_1, x_2, \ldots, x_n]\)结果都相同。 另外,在定理22.2条件下存在\(\xi \in [\min \{x_i\}, \max \{x_i\}]\)使得 \[\begin{aligned} h[x_1, x_2, \ldots, x_n] = \frac{h^{(n-1)}(\xi)}{(n-1)!}. \end{aligned}\]
利用牛顿差商公式也可以得到多项式插值公式 \[\begin{aligned} h(x) =& P_{n-1}(x) + R_{n}(x) \nonumber\\ P_{n-1}(x) =& h(x_1) + (x-x_1)h[x_1, x_2] \nonumber\\ & + (x-x_1)(x-x_2)h[x_1,x_2,x_3] \nonumber\\ & + \cdots \nonumber\\ & + (x-x_1)(x-x_2) \cdots (x-x_{n-1})h[x_1, x_2, \ldots, x_n] \\ R_n(x) =& (x-x_1)(x-x_2) \cdots (x-x_{n-1})(x-x_n) \nonumber\\ & \cdot h[x_1, x_2, \ldots, x_n, x] \end{aligned}\] 其中\(P_{n-1}(x)\)是\(n-1\)次插值多项式, 根据定理22.1可知\(P_{n-1}(x)\)与Lagrange插值多项式相同。 \(R_n(x)\)为余项,关于余项估计有: \[\begin{aligned} h[x_1, x_2, \ldots, x_n, x] = \frac{h^{(n)}(\eta)}{n!}, \end{aligned}\] 其中\(\eta \in [\min(x_1, x_2, \dots, x_n, x), \max(x_1, x_2, \dots, x_n, x)]\)。
22.4 样条插值介绍(*)
如果有\(n\)个点\(\{(x_i, z_i), i=1,2,\dots,n \}\)要插值, 当\(n\)较大时,用\(n-1\)阶插值多项式可以通过这些点, 但是得到的曲线会过于复杂, 与真实值差距很大, 如果用插值函数计算\(\{(x_i, z_i), i=1,2,\dots,n \}\)所在区间外的点则误差更大。 如果仅仅用线段连接或者用抛物线连接, 那么在两段交界的地方又不够光滑。 图22.1用几种方法对函数 \(h(x) = 1/(1+x^2)\)在\(x \in [-4,4]\)进行了插值, 只用到了7个已知点。 从例图可以看出,线性插值可能在连接两段的地方形成尖角转弯, 抛物线插值在两段连接的地方也有明显转折, 用通过给定的7个点的6阶多项式插值, 出现了很大的波折,与真实函数差距较大。 样条插值也是用分段的多项式进行插值, 但样条插值保证连接处是光滑的, 同时构成的曲线又不会太复杂。
设已知\(n\)个点\(\{(x_i, z_i), i=1,\ldots,n \}\), \(x_1 < x_2 < \dots < x_n\), 求有二阶连续导数的\(S(x)\)使得\(S(x)\)通过这\(n\)个点, 即求\(S(x)\)使 \[\begin{aligned} \begin{cases} S(x_i) = z_i, i=1,\ldots,n \nonumber \\ \min\limits_{S} \int | S''(x) |^2 dx \end{cases} \end{aligned}\] 满足条件的函数就是三次样条函数。 三次样条函数是分段函数,以各\(x_i\)为分界点, 称\(\{x_1, x_2, \dots, x_n \}\)为结点(knots), 三次样条函数\(S(x)\)在每一段内为三次多项式, 其一阶导数\(S'(x)\)连续,为分段二次多项式, 其二阶导数\(S''(x)\)连续,为分段线性函数。
样条插值优点是保证了曲线光滑, 可以对比较光滑的各种形状的函数进行插值同时插值曲线不会太复杂, 得到的函数表达式可以用于数值积分和数值微分。
为了求样条函数\(S(x)\)的每一段的表达式, 记\(d_j = x_j - x_{j-1}, j=2,\ldots,n\)。 因为\(S''(x)\)分段线性,可记\(S''(x_j) = M_j\), 用线性插值公式,对\(x \in [x_{j-1}, x_j]\)有 \[\begin{aligned} S''(x) = \frac{M_{j-1}(x_j - x)}{d_j} +\frac{M_j (x - x_{j-1})}{d_j} , \end{aligned}\] 积分得 \[\begin{aligned} S'(x) =& c_1 + (-1) \frac{M_{j-1}(x_j - x)^2}{2d_j} + \frac{M_j(x - x_{j-1})^2}{2d_j} ,\\ S(x) =& c_1 x + c_2 + \frac{M_{j-1}(x_j - x)^3}{6d_j} + \frac{M_j(x - x_{j-1})^3}{6d_j} , \end{aligned}\] 改写为 \[\begin{aligned} S(x) =& \frac{M_{j-1}(x_j - x)^3 + M_j(x - x_{j-1})^3}{6d_j} + c_1' \frac{x_j - x}{d_j} + c_2' \frac{x - x_{j-1}}{d_j} . \end{aligned}\] 根据\(S(x_{j-1})=z_{j-1}\)和\(S(x_j) = z_j\)解出\(c_1', c_2'\),有 \[\begin{aligned} S(x) =& \frac{M_{j-1}(x_j - x)^3 + M_j(x - x_{j-1})^3}{6d_j} \\ & + \left(z_{j-1} - \frac{M_{j-1}d_j^2}{6} \right) \frac{x_j - x}{d_j} + \left(z_j - \frac{M_j d_j^2}{6} \right) \frac{x - x_{j-1}}{d_j} , \\ & x \in [x_{j-1}, x_j]. \end{aligned}\] 只要求出\(M_j, j=1,\ldots,n\),则三次样条插值函数\(S(x)\)在每一段的表达式就完全确定。
用\(S'(x_j-0) = S'(x_j+0), j=2,\ldots,n-1\)可以得到 \(\{M_j \}\)的\(n-2\)个线性方程, 每一方程只涉及\(M_{j-1}, M_j, M_{j+1}\). 再增加两个线性限制条件可以解出\(\{M_j, j=1,\ldots,n\}\)。 比如, 加限制条件\(M_1=0, M_n=0\), 即在边界处函数为线性函数,这样解出的样条插值函数称为自然样条。
R中样条插值函数为
spline(x, y, n, method="natural"),
结果为包含元素x和y的列表,
这是在等间隔的\(x\)点上计算的样条插值结果。
样条函数除了可以用于插值, 还可以用于平滑点\((x_i, z_i), i=1,2,\dots,n\)。 插值函数需要穿过所有已知点, 而平滑则只要与已知点很接近就可以了。 用样条函数在点\((x_i, z_i), i=1,2,\dots,n\)处进行平滑叫做样条回归, 结果是以\(x_1, x_2, \dots, x_n\)为结点的三次样条函数, 但在\(x_i\)处的值不需要等于\(z_i\)。 样条回归是使得 \[\begin{aligned} Q(S) = \sum_{i=1}^n (z_i - S(x_i))^2 + \lambda n \int |S''(x)|^2 dx \end{aligned}\] 最小的函数, 其中\(\lambda>0\)是代表光滑程度的参数, \(\lambda\)越大得到的样条函数越光滑。
R的smooth.spline()函数计算样条平滑。
样条函数用作回归函数时也可以不取已知点\(\{ (x_i, z_i), i=1,2,\dots,n \}\)的横坐标为结点, 而是单独取结点\(k_1, k_2, \dots, k_m\), 一般\(m\)比\(n\)小得多, 结点\(k_j\)作为回归关系改变的分界点。