11 随机模拟积分
某些非随机的问题也可以通过概率模型引入随机变量, 化为求随机模型的未知参数的问题。 例10.1中用随机投点法估计\(\pi\)就是这样的一个例子。
随机模拟解决非随机问题的典型代表是计算定积分。 通过对随机模拟定积分的讨论, 可以展示随机模拟中大部分的问题和技巧。 随机模拟积分也称为蒙特卡洛(Monte Carlo)积分(简称MC积分)。 实际上,统计中最常见的计算问题就是积分和最优化问题。
11.1 随机投点法
设函数\(h(x)\)在有限区间\([a,b]\)上定义且有界, 不妨设\(0 \leq h(x)\leq M\)。 要计算\(I=\int_a^b h(x) dx\), 相当于计算曲线下的区域\(D=\{(x,y): 0 \leq y \leq h(x), x \in C = [a,b]\}\) 的面积。 为此在\(G = [a,b]\times(0,M)\)上均匀抽样\(N\)次, 得随机点\(Z_1, Z_2, \ldots, Z_N\), \(Z_i = (X_i, Y_i), i=1,2,\dots,N\)。 令 \[\begin{aligned} \xi_i = \begin{cases} 1, & Z_i \in D \\ 0, & \mbox{其它}, \end{cases}, \quad i=1,\ldots,N . \end{aligned}\] 则\(\{ \xi_i \}\) 是独立重复试验结果, \(\{ \xi_i \}\) 独立同 b(1,\(p\))分布, \[\begin{align} p = P(Z_i \in D) = V(D)/V(G) = I / [M(b-a)] . \tag{11.1} \end{align}\] 其中\(V(\cdot)\)表示区域面积。
从模拟产生的随机样本\(Z_1, Z_2, \ldots, Z_N\), 可以用这\(N\)个点中落入曲线下方区域\(D\)的百分比\(\hat p\)来估计 (11.1)中的概率\(p\), 然后由\(I = p M (b-a)\)得到定积分\(I\)的近似值 \[\begin{align} \hat I = \hat p M (b-a) . \tag{11.2} \end{align}\] 这种方法叫做随机投点法。 这样计算的定积分有随机性, 误差中包含了随机模拟误差。
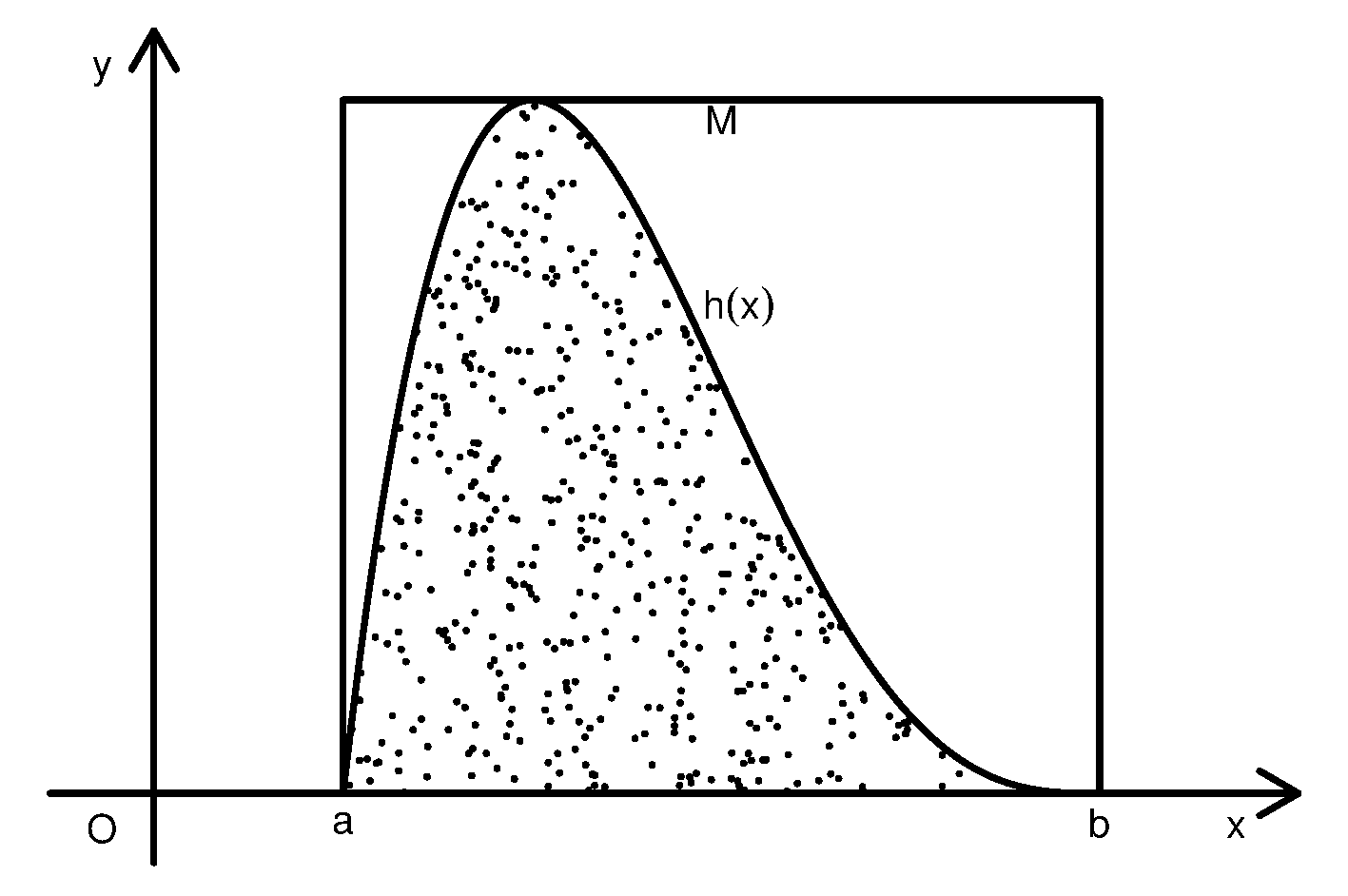
由强大数律可知 \[\begin{aligned} \hat p =& \frac{\sum \xi_i}{N} \to p, \ \text{a.s.}\ (N \to \infty), \\ \hat I =& \hat p M (b-a) \to p M (b-a) = I, \ \text{a.s.}\ (N \to \infty) . \end{aligned} \] 即\(N\to\infty\)时精度可以无限地提高(当然, 在计算机中要受到数值精度的限制)。
那么,提高精度需要多大的代价呢? 由中心极限定理可知 \[\begin{aligned} \sqrt{N}(\hat p - p)/\sqrt{p(1-p)} \stackrel{\mbox{d}}{\longrightarrow} \text{N}(0,1), \ (N\to\infty), \end{aligned}\] 从而 \[\begin{align} \sqrt{N}(\hat I - I) = M(b-a) (\hat p - p) \stackrel{\mbox{d}}{\longrightarrow} \text{N} \big(0, [M(b-a)]^2 p(1-p) \big) \tag{11.3} \end{align}\] 当\(N\)很大时\(\hat I\)近似服从 \(\text{N}(I, [M(b-a)]^2 p(1-p) / N)\)分布, 称此近似分布的方差\([M(b-a)]^2 p(1-p) / N\)为\(\hat I\)的渐近方差。 计算渐近方差可以用\(\hat p\)代替\(p\)估计为 \([M(b-a)]^2 \hat p(1 - \hat p) / N\)。 式(11.3)说明 \(\hat I\)的误差为\(O_p(\frac{1}{\sqrt{N}})\), 这样,计算\(\hat I\)的精度每增加一位小数, 计算量需要增加100倍。随机模拟积分一般都服从这样的规律。
11.2 平均值法
为了计算\(I = \int_a^b h(x) \,dx\), 上面的随机投点法用了类似于舍选法的做法, 在非随机问题中引入随机性时用了二维均匀分布和两点分布, 靠求两点分布概率来估计积分\(I\)。 随机投点法容易理解, 但是效率较低, 另一种效率更高的方法是利用期望值的估计。 取\(U \sim \text{U}(a,b)\), 则 \[\begin{aligned} E [h(U)] =& \int_a^b h(u) \frac{1}{b-a} du = \frac{I}{b-a} , \\ I =& (b-a) \cdot E h(U) . \end{aligned}\] 若取\(\{ U_i, i=1,\ldots,N \}\) 独立同U(\(a,b\))分布, 则\(Y_i = h(U_i), i=1,2,\dots,N\)是iid随机变量列, 由强大数律, \[\begin{aligned} \bar Y = \frac{1}{N} \sum_{i=1}^N h(U_i) \to E h(U) = \frac{I}{b-a}, \quad \text{a.s.} \ (N \to \infty) \end{aligned}\] 于是 \[\begin{align} \tilde I = \frac{b-a}{N} \sum_{i=1}^N h(U_i) \tag{11.4} \end{align}\] 是\(I\)的强相合估计。称这样计算定积分\(I\)的方法为平均值法。
由中心极限定理有 \[\begin{aligned} \sqrt{N}(\tilde I - I) \stackrel{\mbox{d}}{\longrightarrow} \text{N}\big(0, (b-a)^2 \text{Var}(h(U)) \big) . \end{aligned}\] 其中 \[\begin{align} \text{Var}[h(U)] = \int_a^b \big[h(u) - Eh(U) \big]^2 \frac{1}{b-a} du \tag{11.5} \end{align}\] 仅与\(h\)有关, 仍有\(\tilde I - I = O_p(\frac{1}{\sqrt{N}})\), 但是(11.4)的渐近方差小于(11.2)的渐近方差(见11.4)。 \(\text{Var}[h(U)]\)可以用模拟样本\(\{ Y_i = h(U_i) \}\)估计为 \[\begin{align*} \text{Var}(h(U)) \approx \frac{1}{N} \sum_{i=1}^N (Y_i - \bar Y)^2. \end{align*}\]
如果定积分区间是无穷区间, 比如\(\int_0^\infty h(x) \, dx\), 为了使用均匀分布随机数以及平均值法计算积分可以做积分变换, 使积分区间变成有限区间。 例如,作变换\(t = 1/(x+1)\), 则 \[\begin{aligned} \int_0^\infty h(x) \, dx = \int_0^1 h(\frac{1}{t} - 1) \frac{1}{t^2} \,dt. \end{aligned}\]
从平均值法看出, 定积分问题\(\int_a^b h(x) \,dx\)等价于求 \(E h(U)\),其中\(U \sim \text{U}(a,b)\)。 所以这一节讨论的方法也是用来求随机变量函数期望的随机模拟方法。 对一般随机变量\(X\), 其取值范围不必局限于有限区间, 为了求\(X\)的函数\(h(X)\)的期望\(I = E h(X)\), 对\(X\)的随机数\(X_i, i=1,2,\dots,N\), 令\(Y_i = h(X_i)\), 也可以用平均值法 \(\hat I = \frac{1}{N} \sum_{i=1}^N h(X_i)\)来估计\(Eh(X)\), \(\hat I\)是\(E h(X)\)的无偏估计和强相合估计, 若\(\text{Var}(h(X))\)存在, 则\(\hat I\)的方差为\(\frac{1}{N} \text{Var}(h(X))\), \(\hat I\)有渐近正态分布\(\text{N}(Eh(X), \frac{1}{N} \text{Var}(h(X)))\)。 设\(\{ Y_i \}\)的样本方差为\(S_N^2\), 可以用\(S_N^2/N\)估计\(\hat I\)的方差, 用\(\hat I \pm 2 S_N/\sqrt{N}\)作为\(I\)的近似95%置信区间。
例11.1 设\(X \sim \text{N}(0,1)\),求\(I = E |X|^{\frac32}\)。
作变量替换积分可得 \[\begin{aligned} I =& 2 \int_0^{\infty} x^{\frac32} \frac{1}{\sqrt{2\pi}} e^{-\frac12 x^2} \,dx \quad (\text{令} t = \frac12 x^2) \\ =& \frac{2^{\frac34} \Gamma(\frac54)}{\sqrt{\pi}} \approx 0.86004 \end{aligned}\]
如果用平均值法估计\(I\), 取抽样样本量\(N=10000\), 产生标准正态随机数\(X_i, i=1,2,\dots, n\), 令\(Y_i = |X_i|^{\frac32}\), 令 \[\begin{aligned} \hat I =& \bar Y = \frac{1}{N} \sum_{i=1}^N |X_i|^{\frac32}, \\ S_N^2 =& \frac{1}{N} \sum_{i=1}^N (|X_i|^{\frac32} - \hat I)^2 , \end{aligned}\] 一次模拟的结果得到\(\hat I = 0.8514\), \(S_N = 0.0.9138\), 因为\(I\)有精确值所以可以计算误差为\(0.8514 - 0.86004 = -0.0086\)。
模拟的R程序:
set.seed(101)
I.true <- 2^(3/4)*gamma(5/4)/sqrt(pi); I.true
## 0.86004
N <- 10000
yvec <- abs(rnorm(N))^1.5
I.hat <- mean(yvec); I.hat
## [1] 0.8513514
sd.hat <- sd(yvec); sd.hat
## [1] 0.9137678
## 误差:
I.hat - I.true
## -0.008688552
## 估计量的标准误差二倍:
2 * sd.hat / sqrt(N)
## 0.01827536Julia语言的模拟程序:
using Random, Distributions
using SpecialFunctions
Random.seed!(101)
Itrue = 2^(3/4)*gamma(5/4)/sqrt(pi); Itrue
## 0.8600399873245196
N = 10000
yvec = abs.(rand(Normal(), N)) .^ 1.5;
Ihat = mean(yvec); Ihat
## 0.943961419517864
sdhat = std(yvec); sdhat
## 0.943961419517864
## 误差:
Ihat - Itrue
## 0.01718023857011053
## 估计量的标准误差二倍:
2* sdhat / sqrt(N)
## 0.018879228390357283※※※※※
实际上,一维积分用数值方法均匀布点计算一般更有效。 比如,
令\(x_i = a + \frac{b-a}{N} i\), \(i=0,1,\dots,N\),
估计\(I\)为(复合梯形求积公式)
\[\begin{align}
I_0 = \frac{b-a}{N} \left[ \frac12 h(a) + \sum_{i=1}^{N-1} h(x_i) + \frac12 h(b) \right]
\tag{11.6}
\end{align}\]
则当\(h(x)\)在\([a,b]\)上二阶连续可微时误差\(I_0 - I\)仅为\(O(\frac{1}{N^2})\)阶,
比随机模拟方法得到的精度要高得多,
而且当\(h(x)\)有更好的光滑性时还可以用更精确的求积公式得到更高精度。
所以,被积函数比较光滑的一元定积分问题一般不需要用随机模拟来计算。
在R中可以用integrate(f, lower, upper)计算定积分。
如例11.1中求\(E|X|^{3/2}\)涉及到的积分可以用R函数计算为:
I.int <- integrate(function(x) x^1.5*dnorm(x), 0, Inf); I.int
## 0.43002 with absolute error < 1e-06
2*I.int$value
## [1] 0.86004Julia的QuadGK包的quadgk()函数用自适应高斯-康拉德数值积分方法计算一元函数积分,如
import QuadGK
Itrue, err = QuadGK.quadgk(x -> x^1.5/sqrt(2*pi)*exp(-0.5*x^2), 0, Inf)
## (0.43001999365557575, 4.014291709725467e-9)quadgk()返回包括积分值和误差估计界限的二元组。
有表达式的定积分问题, 有时可以利用符号计算软件求得精确结果, 附录C介绍了符号计算软件Maxima。 对例11.1的期望问题, 在wxMaxima中键入
2*integrate(x^(3/2)*1/sqrt(2*%pi)*exp(-1/2*x^2), x, 0, inf);然后按Shift+Enter组合键进行计算, 显示结果为 \[ \frac{\Gamma\left(\frac14 \right)}{2^{5/4} \sqrt{\pi}} \]
※※※※※
11.3 随机模拟估计误差的评估与样本量计算
许多简单的随机模拟问题都可以看成是估计\(\theta=EY\)的问题, 设\(\text{Var}(Y)=\sigma^2\), 生成\(Y\)的独立同分布样本\(Y_i, i=1,2,\dots, N\), 用 \[\begin{align} \hat\theta = \bar Y_N = \frac{1}{N} \sum_{i=1}^N Y_i \tag{11.7} \end{align}\] 估计\(\theta\)。 令 \[\begin{aligned} S_N^2 = \frac{1}{N} \sum_{i=1}^N (Y_i - \bar Y_N)^2 . \end{aligned}\] 当\(N\to\infty\)时\(\hat\theta \to \theta\) a.s., \(S_N^2 \to \sigma^2\) a.s., 且\(\hat\theta\)近似服从如下正态分布: \[\begin{align} \text{N}\left(\theta, \frac{\sigma^2}{N} \right), \tag{11.8} \end{align}\] 其中的\(\sigma^2\)可以用\(S_N^2\)近似,即 \[ \begin{aligned} \frac{\hat\theta - \theta}{S_N / \sqrt{N}} \stackrel{\mbox{d}}{\longrightarrow} \text{N}\left(0, 1 \right), \end{aligned} \] 所以\(N\)充分大时\(\hat\theta\)近似服从正态分布 \[ \text{N}\left(\theta, \frac{S_N^2}{N} \right), \]
因为估计\(\hat\theta\)有随机误差, 这里给出估计误差的一些度量。
定义估计的根均方误差为 \[\begin{align} \text{RMSE} = \sqrt{ E(\hat\theta - \theta)^2 } . \tag{11.9} \end{align}\] 在以上用独立同分布样本均值估计期望值\(\theta=EY\)的做法中, 因为\(E \hat\theta = \theta\),所以 \[\begin{align} \text{RMSE} = \sqrt{ \text{Var}(\hat\theta) } = \sqrt{ \text{Var}(\bar{Y}_n) } = \frac{\sigma}{\sqrt{N}} , \tag{11.10} \end{align}\] 所以根均方误差可以用\(\frac{S_N}{\sqrt{N}}\)估计。
定义估计的平均绝对误差为 \[\begin{align} \text{MAE} = E|\hat\theta - \theta| . \tag{11.11} \end{align}\] 当\(N\)充分大时由\(\hat\theta\)的近似正态分布式(11.8)可知 \[\begin{align} \text{MAE} =& E|\hat\theta - \theta| = \frac{\sigma}{\sqrt{N}} E \left| \frac{\hat\theta - \theta}{\sigma/\sqrt{N}} \right| \nonumber\\ \approx& \sqrt{\frac{2}{\pi}} \frac{\sigma}{\sqrt{N}} \approx 0.7979 \frac{\sigma}{\sqrt{N}} . \tag{11.12} \end{align}\] 所以平均绝对误差可以用\(0.80 \frac{S_N}{\sqrt{N}} = 0.80 \text{RMSE}\)估计。
定义估计的平均相对误差为 \[\begin{align} \text{MRE} = E\left| \frac{\hat\theta - \theta}{\theta} \right | = \text{MAE}/\theta \tag{11.13} \end{align}\] 所以平均相对误差可以用\(0.80 \frac{S_N}{\sqrt{N} \hat\theta} = 0.80 \frac{\text{RMSE}}{\hat\theta}\)估计。 平均相对误差为0.005相当于估计结果有两位有效数字, 平均相对误差为0.0005相当于估计结果有三位有效数字。
由\(\hat\theta\)的近似正态分布式(11.8), 估计\(\hat\theta\)的绝对误差\(| \hat\theta - \theta |\)的近似95%上界为\(2 \frac{S_N}{\sqrt{N}}\): \[\begin{aligned} P\left( | \hat\theta - \theta | \leq 2 \frac{S_N}{\sqrt{N}} \right) \approx 95\% , \end{aligned} \] 所以也可以用\(2 \frac{S_N}{ \sqrt{N}} = 2\text{RMSE}\)作为绝对误差大小的一个度量, 用\(2 \frac{S_N}{ \sqrt{N} \hat\theta}\)作为相对误差大小的一个度量。
为了计算样本量\(N\)需要取多大才能控制估计的根均方误差小于\(\sigma_0\), 可以先取较小的\(N_0\)抽取\(N_0\)个样本值计算出\(S_{N_0}^2\), 用\(S_{N_0}^2\)估计总体方差\(\sigma^2\), 然后求需要的\(N\)的大小: \[\begin{aligned} \frac{S_{N_0}}{\sqrt{N}} < \sigma_0, \quad N > \frac{S_{N_0}^2}{\sigma_0^2}. \end{aligned}\]
用\(\hat\theta=\bar Y_N\)估计\(\theta=EY\)时, 可以利用近似正态分布式(11.8)计算\(\theta\)的近似95%置信区间: \[\begin{align} \hat\theta \pm 2 \frac{S_N}{ \sqrt{N}} . \tag{11.14} \end{align}\]
在更复杂的随机模拟问题中, 参数\(\theta\)不是用独立同分布样本的均值来估计, 设样本量为\(N\)时参数估计为\(\hat\theta\)并设\(\hat\theta\)是\(\theta\)的相合估计。 这时\(\hat\theta\)的方差\(\text{Var}(\hat\theta)\)没有简单的公式, \(\hat\theta\)也没有简单易得的渐近分布。 为了评估\(\hat\theta\)的随机误差大小, 可以独立地执行\(B\)次模拟, 每次得到一个估计量\(\hat\theta^{(j)}\), \(j=1,2,\dots,B\)。 令\(\bar\theta = \frac{1}{B} \sum_{j=1}^B \hat\theta^{(j)}\)。 估计根均方误差RMSE为 \[\begin{align} \widehat{\text{RMSE}} = \sqrt{\frac{1}{B} \sum_{j=1}^B (\hat\theta^{(j)} - \theta)^2}, \tag{11.15} \end{align}\] 但其中的\(\theta\)未知,仅能在已知\(\theta\)真值的验证问题中采用此计算公式。 如果已知\(\hat\theta\)是无偏或渐近无偏估计,则可估计根均方误差为 \[\begin{align} \widehat{\text{RMSE}} = \sqrt{\frac{1}{B} \sum_{j=1}^B (\hat\theta^{(j)} - \bar\theta)^2} . \tag{11.16} \end{align}\]
类似地,若\(\theta\)已知,估计平均绝对误差为 \[\begin{align} \widehat{\text{MAE}} = \frac{1}{B} \sum_{j=1}^B \left| \hat\theta^{(j)} - \theta \right|, \tag{11.17} \end{align}\] 估计平均相对误差为 \[\begin{align} \widehat{\text{MRE}} = \frac{1}{\theta} \frac{1}{B} \sum_{j=1}^B \left| \hat\theta^{(j)} - \theta \right|, \tag{11.18} \end{align}\] 在\(\hat\theta\)无偏或渐近无偏时可以将式(11.17)和(11.18)中的\(\theta\) 用\(\bar\theta\)代替。
重复\(B\)次模拟试验有时需要耗费太多时间, 以至于无法做到。 这时,可以参考后面讲到的bootstrap估计的想法来评估估计误差。
例11.2 对例11.1用平均值法做的估计进行误差分析。
取\(N=10000\)个样本点的一次模拟的结果得到\(\hat I =0.8754\), \(S_N = 0.9409\), 根均方误差的估计为\(\text{RMSE} = \frac{S_N}{\sqrt{N}} = 0.0094\), 平均绝对误差的估计为\(\text{MAE} = 0.80 \text{RMSE} = 0.0075\), 平均相对误差的估计为\(\text{MRE} = \text{MAE}/\hat I = 0.0087\), 说明结果只有约两位有效数字精度。 为了达到四位小数的精度,需要平均相对误差控制在\(0.00005\)左右, 需要解\(0.8 \frac{S_N}{\sqrt{N} \hat I} = 0.00005\), 代入得\(N\)需要约3亿次, 可见随机模拟方法提高精度的困难程度。
以上结果的计算程序:
set.seed(1)
I.true <- 2^(3/4)*gamma(5/4)/sqrt(pi); I.true
## [1] 0.86004
N <- 10000
yvec <- abs(rnorm(N))^1.5
I.hat <- mean(yvec); I.hat
## [1] 0.8753857
sd.hat <- sd(yvec); sd.hat
## [1] 0.9409092
RMSE <- sd.hat/sqrt(N); RMSE
## [1] 0.009409092
MAE <- 0.80*RMSE; MAE
## [1] 0.007527274
MRE <- MAE/I.hat; MRE
## [1] 0.008598809
N.more <- (0.8*sd.hat/I.hat/0.00005)^2; N.more
## [1] 295758038为了得到更可靠的RMSE、MAE和MRE的估计, 重复模拟\(B=100\)次,得到100个\(\hat I\)的值, 从而估计RMSE为0.0082, MAE为0.0070, MRE为0.0081。 从一次模拟得到的误差估计与重复100次得到的误差估计相差不大。
计算程序为:
set.seed(2)
I.true <- 2^(3/4)*gamma(5/4)/sqrt(pi)
N <- 10000
B <- 100
xvec <- numeric(B) # 保存B个估计值
for(j in 1:B){
xvec[j] <- mean(abs(rnorm(N))^1.5)
}
bar.I <- mean(xvec)
RMSE2 <- sqrt( mean( (xvec - bar.I)^2 )); RMSE2
## [1] 0.00823417
MAE2 <- mean( abs(xvec - bar.I) ); MAE2
## [1] 0.006991147
MRE2 <- MAE2 / bar.I; MRE2
## [1] 0.00813205※※※※※
上面的误差评估仅考虑了精度与计算量之间的关系, 在相同精度下, 如果重复模拟次数\(N\)较少的算法每次模拟耗时很多, 最终可能\(N\)较小的算法反而花费更多的时间。 所以我们考虑在总耗时约束(也可以推广到计算资源约束)下不同算法的选择问题。 设模拟计算总的时间限制为\(T\), (11.7)算法计算每个\(Y_i\)需要的时间长度为\(t\), 所以在时间约束下可以采用的重复次数\(N = \mbox{floor}(T/t) \approx T/t\)。 这样,因为 \[ \frac{\hat\theta - \theta}{\sigma / \sqrt{N}} \stackrel{\mbox{d}}{\longrightarrow} \mbox{N}(0, 1), \ (N \to \infty) \] 有 \[ \frac{\hat\theta - \theta}{\sigma / \sqrt{T/t}} \stackrel{\mbox{d}}{\longrightarrow} \mbox{N}(0, 1), \ (T \to \infty) \] 从而 \[ \sqrt{T}(\hat\theta - \theta) \stackrel{\mbox{d}}{\longrightarrow} \mbox{N}\left(0, \sigma^2 t \right), \ (T \to \infty) \] 从而\(\hat\theta\)近似服从 \[ \mbox{N}\left(\theta, \frac{\sigma^2 t}{T} \right) . \] 如果两个算法分别的单次模拟耗时为\(t_1, t_2\), 分别的单次模拟方差为\(\sigma_1^2, \sigma_2^2\), 则为了比较在相同总耗时约束下两个算法的计算精度, 只要比较\(\sigma_1^2 t_1\)和\(\sigma_2^2 t_2\)的值, 此值较小的算法在相同的总耗时下可以获得更高精度, 在相同的精度下可以花费更少的计算时间完成模拟。 参见(Glasserman 2004)。
11.4 高维定积分
上面的两种计算一元函数定积分的方法可以很容易地推广到多元函数定积分, 或称高维定积分。 设\(d\)元函数\(h(x_1, x_2, \dots, x_d)\)定义于超矩形 \[\begin{aligned} C = \{(x_1, x_2, \ldots, x_d): a_i \leq x_i \leq b_i, i=1,2,\ldots,d \} \end{aligned}\] 且 \[\begin{aligned} 0 \leq h(x_1, \ldots, x_d) \leq M, \ \forall x \in C. \end{aligned}\] 令 \[\begin{aligned} D =& \{(x_1, x_2, \ldots, x_d, y): (x_1, x_2, \ldots, x_d) \in C, \ 0 \leq y \leq h(x_1, x_2, \ldots, x_d) \}, \\ G =& \{(x_1, x_2, \ldots, x_d, y): (x_1, x_2, \ldots, x_d) \in C, \ 0 \leq y \leq M \} \end{aligned}\] 为计算\(d\)维定积分 \[\begin{align} I = \int_{a_d}^{b_d} \cdots \int_{a_2}^{b_2} \int_{a_1}^{b_1} h(x_1, x_2, \ldots,x_d) \, dx_1 d x_2 \cdots dx_d, \tag{11.19} \end{align}\] 产生服从\(d+1\)维空间中的超矩形\(G\)内的均匀分布的独立抽样 \(\boldsymbol Z_1, \boldsymbol Z_2, \ldots, \boldsymbol Z_N\), 令 \[\begin{aligned} \xi_i = \begin{cases} 1, & \boldsymbol Z_i \in D \\ 0, & \boldsymbol Z_i \in G-D \end{cases}, \quad i=1,2,\ldots,N \end{aligned}\] 则\(\xi_i\) iid b(1,\(p\)), \[\begin{aligned} p = P(\boldsymbol Z_i \in D) = \frac{V(D)}{V(G)} = \frac{I}{M V(C)} = \frac{I}{M \prod_{j=1}^d (b_j-a_j)} \end{aligned}\] 其中\(V(\cdot)\)表示区域体积。 令\(\hat p\)为\(N\)个随机点中落入\(D\)的百分比,则 \[\begin{aligned} \hat p =& \frac{\sum \xi_i}{N} \to p, \ \text{a.s.} (N \to \infty), \end{aligned}\] 用 \[\begin{align} \hat I_1 = \hat p V(G) = \hat p \cdot M \, V(C) = \hat p \cdot M \prod_{j=1}^d (b_j-a_j) \tag{11.20} \end{align}\] 估计积分\(I\), 则\(\hat I_1\)是\(I\)的无偏估计和强相合估计。 称用式(11.20)计算高维定积分\(I\)的方法为随机投点法。
由中心极限定理知 \[\begin{aligned} \sqrt{N}(\hat p - p)/\sqrt{p(1-p)} \stackrel{d}{\longrightarrow}& \text{N}(0,1), \\ \sqrt{N}(\hat I_1 - I) \stackrel{d}{\longrightarrow}& \text{N}\left(0, \left(M \prod_{j=1}^n (b_j - a_j) \right)^2 p(1-p)\right), \end{aligned} \] \(\hat I_1\)的渐近方差为 \[\begin{align} \frac{\left(M \prod_{j=1}^n (b_j - a_j)\right)^2 p(1-p)}{N} \tag{11.21} \end{align}\] 所以\(\hat I_1\)的随机误差仍为\(O_p\left(\frac{1}{\sqrt{N}}\right)\), \(N\to\infty\)时的误差阶不受维数\(d\)的影响, 这是随机模拟方法与其它数值计算方法相比一个重大优势。
在计算高维积分(11.19)时, 仍可以通过估计\(E h(\boldsymbol U)\)来获得, 其中\(\boldsymbol U\)服从\(R^d\)中的超矩形\(C\)上的均匀分布。 设\(\boldsymbol U_i \sim\) iid U(\(C\)),\(i=1,2,\ldots,N\), 则\(h(\boldsymbol U_i), i=1,2,\ldots,N\)是iid随机变量列, \[\begin{aligned} E h(\boldsymbol U_i) = \int_C h(\boldsymbol u) \frac{1}{\prod_{j=1}^d (b_j - a_j)} d \boldsymbol u = \frac{I}{\prod_{j=1}^d (b_j - a_j)}, \end{aligned}\] 估计\(I\)为 \[\begin{align} \hat I_2 = \prod_{j=1}^d (b_j - a_j) \cdot \frac{1}{N} \sum_{i=1}^N h(U_i), \tag{11.22} \end{align}\] 称用式(11.22)计算高维定积分\(I\)的方法为平均值法。 由强大数律 \[\begin{aligned} \hat I_2 \to \prod_{j=1}^d (b_j - a_j) E h(U) = I, \ \text{a.s.} (N \to \infty), \end{aligned}\] \(\hat I_2\)的渐近方差为 \[\begin{align} \frac{(V(C) )^2 \text{Var}(h(\boldsymbol U))}{N} = \frac{\left(\prod_{j=1}^d (b_j - a_j) \right)^2 \text{Var}(h(\boldsymbol U))}{N}. \tag{11.23} \end{align}\] \(N \to \infty\)时的误差阶也不受维数\(d\)的影响。
我们来比较随机投点法(11.20)与平均值法(11.22)的精度, 只要比较其渐近方差。 对\(I = \int_C h(\boldsymbol x) d \boldsymbol x\), 设\(\hat I_1\)为随机投点法的估计, \(\hat I_2\)为平均值法的估计。 因设\(0 \leq h(\boldsymbol x) \leq M\), 不妨设\(0 \leq h(\boldsymbol x) \leq 1\), 取\(h(\boldsymbol x)\)的上界\(M=1\)。
令\(\boldsymbol X_i \sim\) iid U(\(C\)), \(\eta_i = h(\boldsymbol X_i)\), \(Y_i \sim\) iid U(0,1)与\(\{\boldsymbol X_i\}\)独立, \[\begin{aligned} \xi_i = \begin{cases} 1, & \text{当 } Y_i \leq h(\boldsymbol X_i) \\ 0, & \text{当 } Y_i > h(\boldsymbol X_i) \end{cases} \ i=1,2,\ldots,N, \end{aligned}\] 这时有 \[\begin{aligned} \hat I_1 &= V(C) \frac{1}{N} \sum_{i=1}^N \xi_i, \qquad \hat I_2 = V(C) \frac{1}{N} \sum_{i=1}^N \eta_i \\ \text{Var}(\hat I_1) &= \frac{1}{N} V^2(C) \cdot \frac{I}{V(C)} \left(1 - \frac{I}{V(C)} \right) \\ \text{Var}(\hat I_2) &= \frac{1}{N} V^2(C) \cdot \left( \frac{1}{V(C)} \int_C h^2(\boldsymbol x)d \boldsymbol x - \left( \frac{I}{V(C)} \right)^2 \right) \\ \text{Var}(\hat I_1) - \text{Var}(\hat I_2) &= \frac{V(C)}{N} \int_C \left\{ h(\boldsymbol x) - h^2(\boldsymbol x) \right \} \,d\boldsymbol x \geq 0 \end{aligned}\] 可见平均值法精度更高。 事实上,随机投点法多用了随机数\(Y_i\),必然会增加抽样随机误差。
在计算高维积分(11.19)时, 如果用网格法作数值积分, 把超矩形\(C = [a_1, b_1] \times [a_2, b_2] \times \cdots \times [a_d, b_d]\) 的每个边分成\(n\)个格子,就需要\(N=n^d\)个格子点, 如果用每个小超矩形的中心作为代表点, 可以达到\(O(n^{-2})\)精度, 即\(O(N^{-2/d})\), 当维数增加时为了提高一倍精度需要\(2^{d/2}\)倍的代表点。 比如\(d=8\),精度只有\(O(N^{-1/4})\)。 高维的问题当维数增加时计算量会迅猛增加, 以至于无法计算, 这个问题称为维数诅咒。 如果用Monte Carlo积分,则精度为\(O_p(N^{-1/2})\), 与\(d\)关系不大。 所以Monte Carlo方法在高维积分中有重要应用。 为了提高积分计算精度,需要减小\(O_\text{p}(N^{-1/2})\)中的常数项, 即减小\(\hat I\)的渐近方差。
例11.3 考虑 \[\begin{aligned} & f(x_1, x_2, \ldots, x_d) = x_1^2 x_2^2 \cdots x_d^2, \ 0 \leq x_1 \leq 1, 0 \leq x_2 \leq 1, \dots, 0 \leq x_d \leq 1 \end{aligned}\] 的积分 \[\begin{aligned} I = \int_0^1 \cdots \int_0^1 \int_0^1 x_1^2 x_2^2 \cdots x_d^2 \, dx_1 dx_2 \cdots dx_d \end{aligned}\] 当然,这个积分是有精确解\(I = (1/3)^d\)的, 对估计\(I\)的结果我们可以直接计算误差。 以\(d=8\)为例比较网格点法、随机投点法、平均值法的精度, 这时真值\(I = (1/3)^8 \approx 1.5241587 \times 10^{-4}\)。
用\(n\)网格点法,\(N=n^d\),公式为 \[\begin{aligned} I_0 = \frac{1}{N} \sum_{i_1=1}^n \sum_{i_2=1}^n \cdots \sum_{i_d=1}^n f(\frac{2i_1-1}{2n}, \frac{2i_2-1}{2n}, \ldots, \frac{2i_d-1}{2n}) \end{aligned}\] 误差绝对值为\(e_0 = | I_0 - I |\)。 如果取\(n=5, d=8\),需要计算\(N=390625\)个点的函数值, 计算量相当大。
计算程序:
积分真值:
网格法:
网格法误差和相对误差:
相对误差约8%,误差较大。
用随机投点法求\(I\), 先在\((0,1)^d \times (0,1)\)均匀抽样 \((\xi_i^{(1)}, \xi_i^{(2)}, \ldots, \xi_i^{(d)}, y_i), i=1,\ldots, N\), 令\(\hat I_1\)为\(y_i \leq f(\xi_i^{(1)}, \xi_i^{(2)}, \ldots, \xi_i^{(d)})\)成立的百分比。 一次估计的程序和结果为
set.seed(1)
x <- runif(N*d)
y <- runif(N)
fx <- apply(matrix(x, ncol=d)^2, 1, prod)
I1 <- mean(y <= fx); I1
## [1] 0.0001664
sd1 <- sqrt(I1*(1-I1)); sd1
## 0.01289854估计RMSE、MAE和MRE来度量误差大小:
RMSE1 <- sd1/sqrt(N); RMSE1
## [1] 2.063766e-05
MAE1 <- 0.8*RMSE1; MAE1
## [1] 1.651013e-05
MRE1 <- MAE1/I1; MRE1
## [1] 0.09921953估计的相对误差约为10个百分点, 误差较大。 为了确认这样的误差估计, 将随机投点法重复模拟\(B=100\)次,得到100个\(I\)的估计,程序为:
set.seed(1)
B <- 100
Ihat <- numeric(B)
for(ib in 1:B){
x <- runif(N*d)
y <- runif(N)
fx <- apply(matrix(x, ncol=d)^2, 1, prod)
Ihat[ib] <- mean(y <= fx)
}用\(B=100\)次重复模拟估计平均相对误差:
这确认了从一次模拟给出的平均相对误差估计,两者基本相同。
用平均值方法,公式为 \[\begin{aligned} \hat I_2 = \frac{1}{N} \sum_{i=1}^N f(\xi^{(1)}_i, \xi^{(2)}_i, \cdots, \xi^{(d)}_i) \end{aligned}\] 其中\(\xi^{(j)}_i, i=1, \ldots, N, j=1,\ldots,d\) 独立同U(0,1)分布。 一次计算的程序为:
set.seed(1)
x <- runif(N*d)
fx <- apply(matrix(x, ncol=d)^2, 1, prod)
I2 <- mean(fx); I2
## [1] 0.0001513103
sd2 <- sd(fx); sd2
## [1] 0.001638286平均值法的各种误差度量为:
RMSE2 <- sd2/sqrt(N); RMSE2
## [1] 2.621258e-06
MAE2 <- 0.8*RMSE2; MAE2
## [1] 2.097006e-06
MRE2 <- MAE2/I2; MRE2
## [1] 0.01385898相对误差约为1.3个百分点。
类似地, 重复\(B=100\)次,估计MRE:
set.seed(1)
B <- 100
Ihat2 <- numeric(B)
for(ib in 1:B){
x <- runif(N*d)
y <- runif(N)
fx <- apply(matrix(x, ncol=d)^2, 1, prod)
Ihat2[ib] <- mean(fx)
}用\(B=100\)次重复模拟估计平均相对误差:
相对误差约为1.4个百分点, 与从一次模拟估算的平均相对误差相同。
随机模拟程序是消耗计算资源特别严重的计算任务之一, 设计更高效的算法、程序进行优化、考虑并行计算, 都是随机模拟问题的实现需要考虑的。 对随机模拟问题, 高效的算法主要指估计的方差更小, 这样误差小, 达到一定精度需要的计算量就小。
最后,三种方法计算量相同(都计算\(N=5^8\)次函数值)的情况下, 平均相对误差分别为:
随机投点法的误差与网格法相近; 平均值法的误差只有随机投点法的13%。
※※※※※
习题
习题1
设\(\{ U_i, i=1,2,\dots \}\)为独立同U(0,1)分布的随机变量序列。 令 \[\begin{aligned} K = \min\left\{k \,:\, \sum_{i=1}^k U_i > 1 \right\}. \end{aligned}\]
- 证明\(E K = e\)。
- 生成\(K\)的\(N\)个独立抽样,用平均值\(\bar K\)估计\(e\)。
- 估计\(\bar K\)的标准差,给出\(e\)的近似95%置信区间。
习题2
设\(\{ U_i, i=1,2,\dots \}\)为独立同U(0,1)分布的随机变量序列。 令\(M\)为序列中第一个比前一个值小的元素的序号,即 \[\begin{aligned} M = \min\left\{m \,:\, U_1 \leq U_2 \leq \cdots \leq U_{m-1}, U_{m-1} > U_m, \ m \geq 2 \right\} \end{aligned}\]
- 证明\(P(M > n) = \frac{1}{n!}\), \(n \geq 2\)。
- 用概率论中的恒等式\(E M = \sum_{n=0}^\infty P(M>n)\)证明\(EM=e\)。
- 生成\(M\)的\(N\)个独立抽样,用平均值\(\bar M\)估计\(e\)。
- 估计\(\bar M\)的标准差,给出\(e\)的近似95%置信区间。