23 数值积分
23.1 数值积分的用途
在11给出了用随机模拟积分的方法。 随机模拟积分在高维或者积分区域不规则时有优势, 在低维、积分区域规则且被积函数比较光滑时用数值积分方法可以得到更高精度, 也不会引入随机误差。
积分、最优化、矩阵计算都是在统计问题中最常见的计算问题, 在统计计算中经常需要计算积分。 比如,从密度\(p(x)\)计算分布函数\(F(x)\),如果没有解析表达式和精确的计算公式, 需要用积分来计算: \[\begin{aligned} F(x) = \int_{-\infty}^x p(u) du , \end{aligned}\] 用积分给出部分函数值后可以用插值和函数逼近得到\(F(x)\)的近似公式。
已知联合密度\(p(\boldsymbol x_1, \boldsymbol x_2)\)要求边缘密度\(p(\boldsymbol x_1)\), 要用积分计算 \[\begin{aligned} p(\boldsymbol x_1) = \int p(\boldsymbol x_1, \boldsymbol x_2) d \boldsymbol x_2. \end{aligned}\]
贝叶斯分析的主要问题是已知先验密度\(\pi(\theta)\)和似然函数\(p(\boldsymbol x | \theta)\)后求后验密度\(p(\theta | \boldsymbol x)\): \[\begin{aligned} p(\theta | \boldsymbol x) =& \frac{p(\theta, \boldsymbol x)}{p(\boldsymbol x)} = \dfrac{\pi(\theta) p(\boldsymbol x | \theta)}{\int \pi(u) p(\boldsymbol x | u) d u} , \end{aligned}\] 大多数情况下不能得到后验密度\(p(\theta | \boldsymbol x)\)的解析表达式, 也可能需要计算积分, 用后验密度求期望、平均损失函数也需要计算积分。
R的integrate(f, lower, upper)函数可以计算有限区间或无穷区间定积分,
如果要指定无穷区间,
取lower为-Inf或取upper为Inf。
R的MASS包中的area函数可以计算有限区间上的定积分,
结果比integrate更为可靠。
对于可以积分得到显示表达式的情况, 可以用一些符号计算软件来辅助推导积分, 这样的软件有Mathematica, Maple, Maxima等, 其中Maxima是自由软件。
23.2 一维数值积分
数值积分的最简单方法是直接用达布和计算。 更精确的积分方法是对被积函数进行多项式逼近然后对近似多项式用代数方法求积分。 这些近似多项式可以不依赖于被积函数,只需要用被积函数的若干值。 多项式逼近可以是在全积分区间上进行,也可以把积分区间分为很多小区间在小区间上逼近。 分为小区间的方法适用性更好。
23.2.1 计算达布和的积分方法
为求定积分 \[\begin{aligned} I = \int_a^b f(x) dx, \end{aligned}\] 把区间\([a,b]\)均匀分为\(n\)段, 分点为\(x_0=a, x_1, \ldots, x_{n-1}, x_n=b\), 间隔为\(h = (b-a)/n\), 可以用 \[\begin{align} D_n = \sum_{i=1}^n f(x_i) h \tag{23.1} \end{align}\] 近似计算\(I\)。 把\(D_n\)改写成 \[\begin{aligned} D_n = \sum_{i=0}^{n-1} f(x_{i+1}) h \end{aligned}\] 可以看出相当于把曲边梯形面积 \[\begin{aligned} \int_{x_{i}}^{x_{i+1}} f(x) dx \end{aligned}\] 用以\([x_{i}, x_{i+1}]\)为底、右侧高度\(f(x_{i+1})\)为高的矩形面积近似 (见图23.1)。 (23.1)中的\(f(x_i)\)是小区间右端点的函数值。
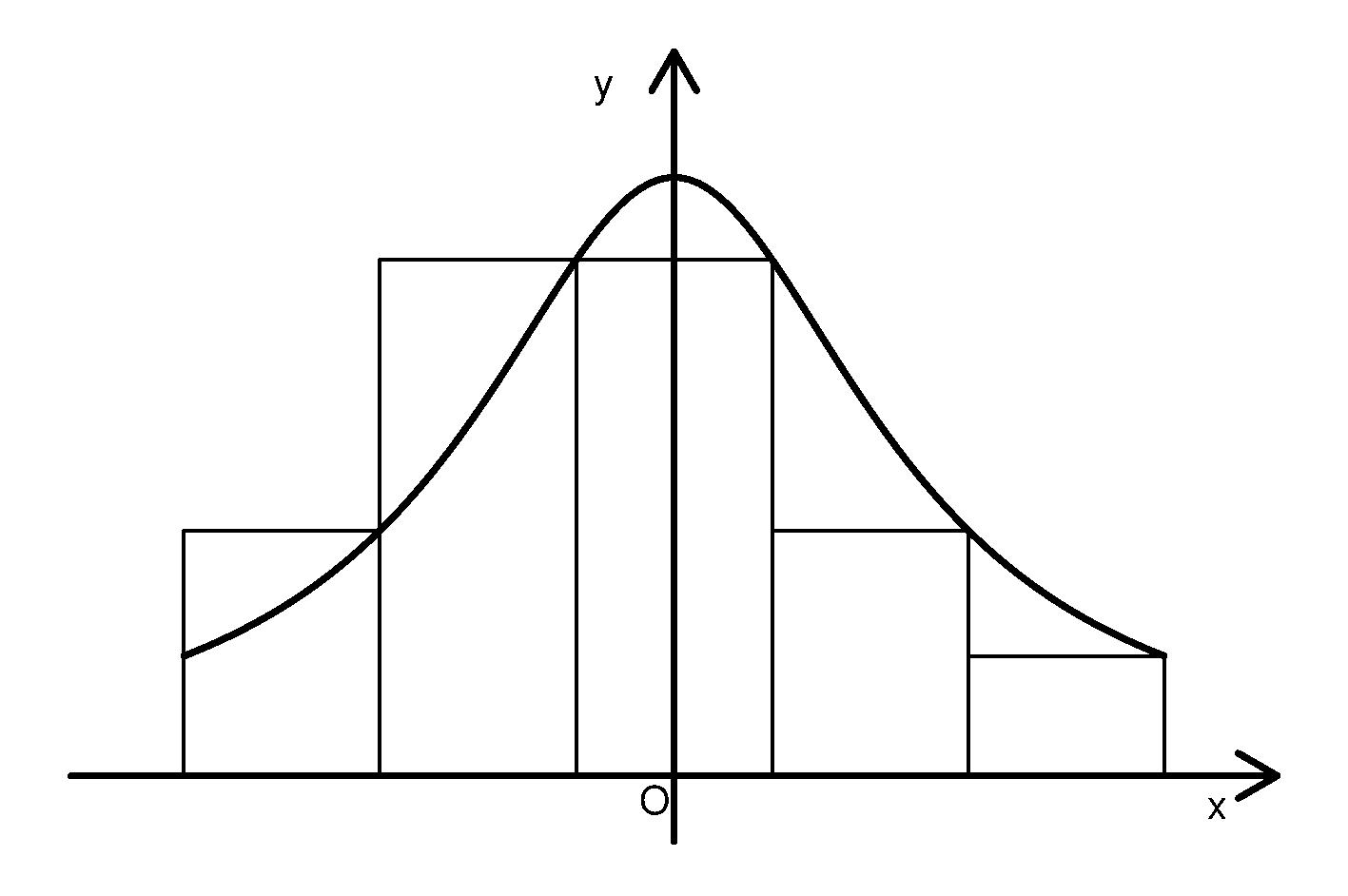
图23.1: 达布和数值积分图示
达布和积分方法容易理解, 但用区间端点近似整个区间的函数值误差较大,精度不好, 基本不使用公式(23.1)计算一元函数积分。 如果使用区间中点作为代表,公式变成 \[\begin{align} M_n = h \sum_{i=0}^{n-1} f\left(a + \left(i+\frac12 \right) h \right) \quad(h = \frac{b-a}{n}) \tag{23.2} \end{align}\] 这个公式称为中点法则,余项为 \[\begin{align} R_n = I - M_n = \frac{(b-a)^3}{24 n^2} f''(\xi), \ \xi \in [a,b], \tag{23.3} \end{align}\] 当\(f''(x)\)有界时中点法则的精度为\(O(n^{-2})\), 精度比(23.1)高得多, 与下面的梯形法则精度相近。
23.2.2 梯形法则
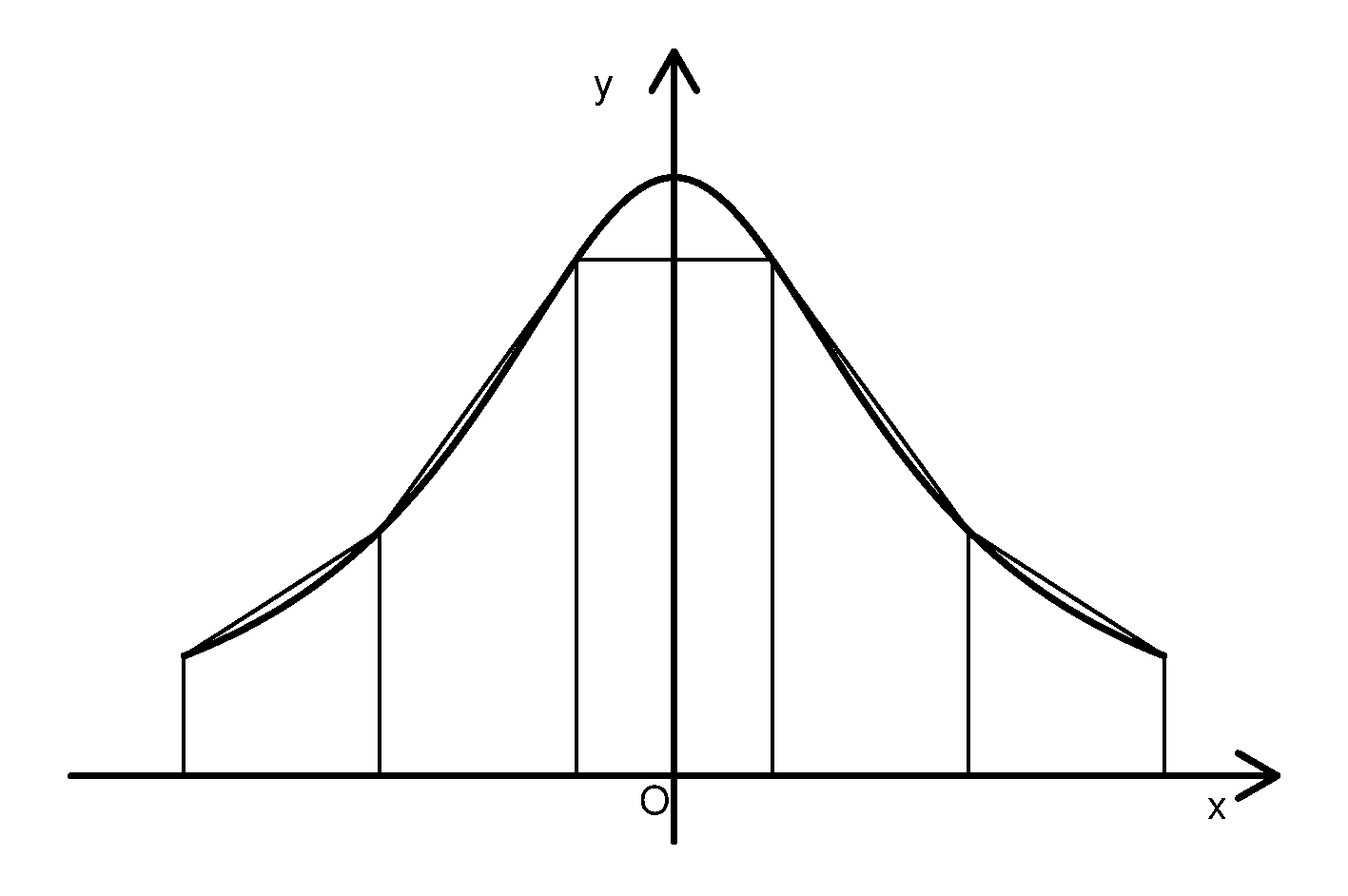
图23.2: 梯形法则数值积分图示
在小区间\([x_i, x_{i+1}]\)内不是用常数而是用线性插值代替\(f(x)\), 即用梯形代替曲边梯形(参见图23.2), 可以得到如下的积分公式 \[\begin{align} f(x) \approx& f(x_i) + \frac{f(x_{i+1}) - f(x_i)}{h} (x - x_i), \ x \in [x_i, x_{i+1}] \nonumber\\ \int_{x_i}^{x_{i+1}} f(x) dx \approx& \frac{f(x_i) + f(x_{i+1})}{2} h \tag{23.4} \\ \int_a^b f(x) \, dx =& \sum_{i=0}^{n-1} \int_{x_{i}}^{x_{i+1}} f(x) \, dx \nonumber\\ \approx& \frac{h}{2} \left\{ f(a) + 2 \sum_{i=1}^{n-1} f(x_i) + f(b) \right\} \stackrel{\triangle}{=} T_n \tag{23.5} \end{align}\] 余项为 \[\begin{aligned} R_n = I - T_n = -\frac{(b-a)^3}{12 n^2} f''(\xi), \xi \in (a,b) . \end{aligned}\] (23.5)叫做复合梯形公式, 在\(f''(x)\)有界时算法精度为\(O(n^{-2})\)。
23.2.3 辛普森(Simpson)法则(*)
在等距的\((x_{-1}, x_0, x_{1})\)的区间中用抛物线插值公式近似\(f(x)\): \[\begin{aligned} f(x) \approx& \frac{1}{2}\left( f(x_{-1}) -2f(x_0) + f(x_{1}) \right) \left(\frac{x-x_0}{h/2} \right)^2 \nonumber\\ & + \frac{1}{2} \left( f(x_{1}) - f(x_{-1}) \right) \left(\frac{x-x_0}{h/2} \right) + f(x_0) \end{aligned}\] 其中\(h = x_{1} - x_{-1} = 2(x_0 - x_{-1})\), 积分得 \[\begin{align} \int_{x_{-1}}^{x_{1}} f(x) \, dx = \frac{h}{6} \left\{ f(x_{-1}) + 4 f(x_0) + f(x_{1}) \right\} , h=x_{1} - x_{-1}. \tag{23.6} \end{align}\]
把区间\([a,b]\)等分为\(n\)份, 记\(h = (b-a)/n\), 记\(x_i = a + ih\), \(i=0,1,2,\dots,n\), 则\(x_0, x_1, \dots, x_n\)把\([a,b]\)等分为\(n\)份, 然后在每个小区间内取中点,记为 \(x_{i+\frac12} = a + (i+\frac12)h\), \(i=0,1,\dots,n-1\), 在\([x_i, x_{i+1}]\)内用公式(23.6)并把\(n\)个小区间的积分相加,得 \[\begin{align} I =& \int_a^b f(x) \, dx \nonumber\\ \approx& \frac{h}{6} \left( f(a) + 4\sum_{i=0}^{n-1} f(x_{i+\frac12}) + 2\sum_{i=1}^{n-1} f(x_{i}) + f(b) \right) \stackrel{\triangle}{=} S_n, \tag{23.7} \end{align}\] 余项为 \[\begin{aligned} R_n = I - S_n = -\frac{(b-a)^5}{2880 n^4} f^{(4)}(\xi), \xi \in (a,b) . \end{aligned}\] (23.7)叫做复合辛普森公式, 在\(f^{(4)}(x)\)有界时复合辛普森公式误差为\(O(n^{-4})\)。
23.2.4 牛顿-柯蒂斯(Newton-Cotes公式)(*)
公式(23.4)和(23.6)分别是在小区间用线性插值和抛物线插值近似被积函数\(f(x)\)得到的积分公式。 一般地,对等距节点\((x_0=a, x_1, \ldots, x_n=b)\)可以进行Lagrange插值, 得到\(n\)阶插值多项式\(P_n(x)\): \[\begin{aligned} P_n(x) = \sum_{j=0}^n f(x_j) \frac{\prod_{k \neq j} (x - x_k)}{\prod_{k \neq j} (x_j - x_k)} \end{aligned}\] 用\(P_n(x)\)在\([a, b]\)上的积分近似\(\int_{a}^{b} f(x) dx\), 有 \[\begin{aligned} \int_{a}^{b} f(x) \, dx \approx& \int_{a}^{b} P_n(x) \, dx \\ =& \sum_{j=0}^n \left\{ \int_a^b \frac{\prod_{k \neq j} (x - x_k)}{\prod_{k \neq j} (x_j - x_k)} dx \right\} f(x_j) \end{aligned}\] 注意到\(x_j = a + j h\), \(h = (b-a)/n\), 做变量替换\(x = a + t h\), 上式变成 \[\begin{align} \int_{a}^{b} f(x) \, dx \approx& \frac{b-a}{n} \sum_{j=0}^n \left\{ \int_0^n \frac{\prod_{k \neq j} (t - k)}{\prod_{k \neq j} (j - k)} dt \right\} f(x_j) \nonumber\\ =& (b-a) \sum_{j=0}^{n} C_j^{(n)} f(x_j) \tag{23.8} \end{align}\] 这是被积函数在节点上函数\(f(x_i)\)值的线性组合, 其中各线性组合系数\(C_j^{(n)}\)不依赖于\(f\)和积分区间: \[\begin{align} C_j^{(n)} = \frac{1}{n} \int_0^n \frac{\prod_{k \neq j} (t - k)}{\prod_{k \neq j} (j - k)} dt = \frac{1}{n} \frac{(-1)^{n-j}}{j!(n-j)!} \int_0^n \prod_{k \neq j} (t - k) dt. \tag{23.9} \end{align}\] 公式(23.8)称为牛顿-柯蒂斯(Newton-Cotes)公式, 公式(23.4)和(23.6)分别是 \(n=1\)和\(n=2\)的特例。 一些\(C_j^{(n)}\)的值见表23.1。 \(n=4\)的牛顿-柯蒂斯公式叫做柯蒂斯法则, 积分公式为 \[\begin{align} I =& \int_a^b f(x) dx \approx \frac{b-a}{90} \left\{ 7 f(x_0) + 32 f(x_1) + 12 f(x_2) + 32 f(x_3) + 7 f(x_4) \right\}, \\ & \ x_i = a + i \cdot \frac{b-a}{4}, \ i=0,1,2,3,4. \tag{23.10} \end{align}\] 复合柯蒂斯公式把\([a,b]\)等分为\(n\)份, 令\(h = (b-a)/n\), \(x_i = a + ih, i=0,1,\dots,n\), 然后把每个小区间\([x_i, x_{i+1}]\)等分为4份, 内部分点为 \(x_{i+\frac14} = x_i + \frac14 h\), \(x_{i+\frac12} = x_i + \frac12 h\), \(x_{i+\frac34} = x_i + \frac34 h\), \(i=0,1,\dots,n-1\), 在每个小区间\([x_i, x_{i+1}]\)内用(23.10)积分然后相加, 得复合柯蒂斯公式 \[\begin{aligned} \int_a^b f(x) dx \approx& \frac{h}{90}\left\{ 7 f(a) + 32 \sum_{i=0}^{n-1} f(x_{i+\frac14}) + 12 \sum_{i=0}^{n-1} f(x_{i+\frac12}) \right. \nonumber\\ & \qquad \left. + 32 \sum_{i=0}^{n-1} f(x_{i+\frac34}) + 14 \sum_{i=1}^{n-1} f(x_i) + 7 f(b) \right\} \end{aligned}\] 余项为 \[\begin{aligned} R = -\frac{(b-a)^7}{1013760 n^6} f^{(6)}(\xi), \ \xi \in (a,b). \end{aligned}\]
| \(n\) | \(C_j^{(n)}\) |
|---|---|
| 1 | \(\frac12, \ \frac12\) |
| 2 | \(\frac16, \ \frac23, \ \frac16\) |
| 3 | \(\frac18, \ \frac38, \ \frac38, \ \frac18\) |
| 4 | \(\frac{7}{90}, \ \frac{32}{90}, \ \frac{12}{90}, \ \frac{32}{90}, \ \frac{7}{90}\) |
| 5 | \(\frac{19}{288},\ \frac{75}{288},\ \frac{50}{288}, \ \frac{50}{288},\ \frac{75}{288},\ \frac{19}{288}\) |
| 6 | \(\frac{41}{840},\ \frac{216}{840},\ \frac{27}{840},\ \frac{272}{840},\ \frac{27}{840},\ \frac{216}{840}, \ \frac{41}{840}\) |
虽然我们可以得到高阶的牛顿-柯蒂斯公式, 但是高阶的插值多项式一般在边界处会有很大误差, 实际中我们一般最多用到4阶, 然后用复合方法把\([a,b]\)划分为小区间, 在小区间内用低阶的牛顿-柯蒂斯公式。
23.2.5 数值积分的代数精度(*)
为计算积分 \[\begin{aligned} I = \int_a^b f(x) d\,x , \end{aligned}\] 可以在\([a,b]\)的\(n\)个节点 \(a \leq x_1 < x_2 < \dots < x_n \leq b\)上对\(f(x)\) 用\(n-1\)阶多项式进行插值, 用插值多项式的积分近似积分\(I\)。 由Lagrange插值公式(22.4)得 \[\begin{align} I \approx& \sum_{j=1}^n \left\{ \int_a^b \frac{\prod_{k \neq j} (x - x_k)}{\prod_{k \neq j} (x_j - x_k)} d\,x \right\} f(x_j) \\ =& \sum_{j=1}^n A_j f(x_j), \tag{23.11} \end{align}\] 其中\(\{ A_j \}\)不依赖于被积函数\(f(x)\)。
在理想情况下(23.11)可以有较高精度。 如果某插值方法对不超过\(n-1\)次的多项式可精确表示而不能精确表示\(n\)次多项式, 则称该插值方法有\(n-1\)次代数精度。 (23.11)若对不超过\(n-1\)次的多项式积分可以得到准确值而\(n\)次则不行, 则称此数值积分方法具有\(n-1\)次代数精度。 (23.11)至少具有\(n-1\)次代数精度, 所以牛顿-柯蒂斯积分公式(23.8) 至少具有\(n\)次代数精度。
23.2.6 高斯-勒让德(Gauss-Legendre)积分公式(*)
公式(23.11)至少有\(n-1\)次代数精度。 在(23.11)中适当选取节点\(\{ x_j \}\)的位置可以得到更高的代数精度, \(n\)个节点可以达到\(2n-1\)次代数精度, 还可以在无穷区间上积分。 这样的数值积分方法叫做高斯型数值积分。
对至多\(2n-1\)次多项式\(f(x)\), 取\(n\)个节点\(\{x_k\}\)为\(n\)次Legendre正交多项式\(P_n(x)\)的\(n\)个零点,即 \[\begin{aligned} P_n(x) = c (x - x_1) \cdots (x - x_n), \end{aligned}\] 则 \[\begin{aligned} f(x) = q(x) P_n(x) + r(x) \end{aligned}\] 其中\(q(x)\)和\(r(x)\)都是至多\(n-1\)次的多项式。 由正交多项式性质, \(P_n(x)\)与任意至多\(n-1\)次多项式都正交, 于是 \[\begin{aligned} \int_{-1}^1 q(x) P_n(x) \, dx = 0. \end{aligned}\] 故 \[\begin{aligned} \int_{-1}^1 f(x) \, dx = \int_{-1}^1 r(x) \, dx, \end{aligned}\] 而\(r(x)\)为至多\(n-1\)阶,其插值方法的积分是精确的,即 \[\begin{aligned} \int_{-1}^1 f(x) \, dx = \int_{-1}^1 r(x) \, dx = \sum_{k=1}^n A_k r(x_k) \end{aligned}\] 等式成立,注意 \[\begin{aligned} P_n(x_k)=0, k=1,2,\ldots,n, \end{aligned}\] 所以\(r(x_k) = f(x_k)\), 于是 \[\begin{aligned} \int_{-1}^1 f(x) \, dx = \sum_{k=1}^n A_k f(x_k) \end{aligned}\] 即当\(f(x)\)为至多\(2n-1\)次多项式时这样选取节点的(23.11)是精确的。 可预先把\(x_k\)和\(A_k\)做表。
对于其他的积分区间及权函数\(w(x)\),要计算 \[\begin{aligned} I = \int_a^b f(x) w(x) \, dx, \end{aligned}\] 也可以可以利用相应的正交多项式及零点解决。 比如Gauss-Laguerre积分 \[\begin{aligned} \int_0^\infty f(x) e^{-x} \, dx \end{aligned}\] 可以利用Laguerre多项式的零点作为节点进行插值, Gauss-Hermite积分 \[\begin{aligned} \int_{-\infty}^\infty f(x) e^{-x^2} dx \end{aligned}\] 可以利用Hermite多项式的零点作为节点进行插值。 这样可以计算无穷区间上的积分。
高斯型积分适用于函数足够光滑, 需要反复计算积分但每次计算被积函数值都耗时很多的情况, 不适用于一般的被积函数。
R的gss包的gauss.quad()函数可以对给定点数和区间端点计算高斯-勒让德积分的节点位置和相应积分权重。
Julia的QuadGK包的quadgk()函数输入被积函数和区间端点,
返回积分值和误差上限估计。
例23.1 编写高斯-勒让德积分的Julia程序。
解:
勒让德多项式:
using Polynomials
function legendre(i)
n = i-1
p = Polynomial([-1,0,1])^n
for i in 1 : n
p = derivative(p)
end
return p / (2^n * factorial(n))
end生成权重\(w_i\)和节点\(x_i\)的函数:
function quadrule_legendre(m)
bs = [legendre(i) for i in 1 : m+1]
xs = roots(bs[end])
A = [bs[k](xs[i]) for k in 1 : m, i in 1 : m]
b = zeros(m)
b[1] = 2
ws = A\b
return (ws, xs)
end输入被积函数和积分权重、节点后计算积分的函数:
function quadint(f, quadrule)
sum(w*f(x) for (w,x) in zip(quadrule[1], quadrule[2]))
end
function quadint(f, quadrule, a, b)
α = (b-a)/2
β = (a+b)/2
g = x -> α*f(α*x+β)
return quadint(g, quadrule)
end测试:
23.2.7 变步长积分(*)
对一般的函数, 提高插值多项式阶数并不能改善积分精度, 复合方法如(23.5)和(23.7)则取点越多精度越高。 因为很难预估需要的点数, 所以我们可以逐步增加取点个数直至达到需要的积分精度。 一种节省取点个数的方法是每次取点仅增加原来小区间的中点, 这样点数每次增加一倍但是仅需要再多计算一半点上的函数值。
比如,使用复合梯形公式(23.5): \[\begin{aligned} T_n =& \frac{d}{2} \left\{ f(a) + 2 \sum_{i=1}^{n-1} f(x_i) + f(b) \right\}, \\ & x_i = a + i d, \ i=0,1,\dots, n,\ d = \frac{b-a}{n}, \end{aligned}\] 变步长为\(d/2\),节点增加到\(2n+1\)个, 原来的一个小区间\([x_i, x_{i+1}]\)中又增加了一个分点 \(x_{i+\frac12} = x_i + \frac{d}{2}\), 原来在\([x_i, x_{i+1}]\)的梯形法则积分结果为 \[\begin{aligned} I_1 = \frac{d}{2} \left\{ f(x_i) + f(x_{i+1}) \right\}, \end{aligned}\] 增加\(x_{i+\frac12}\)节点后在\([x_i, x_{i+1}]\)的积分变成\(x_{i+\frac12}\)前后两半的积分之和,为 \[\begin{aligned} I_2 =& \frac{d}{4} \left\{ f(x_i) + f(x_{i+\frac12}) \right\} + \frac{d}{4} \left\{ f(x_{i+\frac12}) + f(x_{i+1}) \right\} \\ =& \frac{d}{4} \left\{ f(x_i) + 2f(x_{i+\frac12}) + f(x_{i+1}) \right\} \\ =& \frac12 I_1 + \frac{d}{2} f(x_{i+\frac12}) \end{aligned}\] 于是\(n+1\)个节点的梯形公式结果\(T_n\)与\(2n+1\)个节点的\(T_{2n}\)的关系为 \[\begin{align} T_{2n} = \frac12 T_n + \frac{d}{2} \sum_{i=0}^{n-1} f(x_{i+\frac12}). \tag{23.12} \end{align}\] 只需要计算新增的\(n\)个节点上的函数值。 实际计算积分时预先确定一个误差限\(\varepsilon\), 当\(|T_{2n} - T_n| < \varepsilon\)时停止增加节点, 以\(T_{2n}\)为积分近似值。 注意, 如果被积函数在很大范围基本不变, 比如等于零, 这样的停止规则可能给出完全错误的积分计算结果。
23.3 多维数值积分(*)
多元函数\(f(x_1, x_2, \dots, x_d)\)的积分比一元函数积分困难得多, 这时很难再取多元的插值多项式然后对插值函数积分, 计算量也要比一维积分大得多。
对定义在矩形\([a,b]\times [c,d]\)上的二元函数\(f(x,y)\), 为计算二重积分 \[\begin{aligned} I = \int_a^b \int_c^d f(x,y) \,dy \,dx \end{aligned}\] 可以用如下的中点法则近似: \[\begin{aligned} M_{n,m} =& \frac{b-a}{n} \frac{d-c}{m} \sum_{i=0}^{n-1} \sum_{j=0}^{m-1} f\left(a + \left(i+\frac12 \right)h, \ c + \left(j+\frac12 \right) g\right), \\ & \ \left(h = \frac{b-a}{n}, \ g = \frac{d-c}{m} \right). \end{aligned}\] 对于\(R^d\)空间中超立方体上的积分也可以类似计算。
高维空间的积分需要大量的计算, 计算量可能会大到不适用。 比如,如果一维需要\(n\)个节点, 计算\(n\)次被积函数值, 那么\(d\)维积分就需要计算\(N = n^d = e^{d \ln n}\)次被积函数值, 计算量随着\(d\)的增长而指数增长。 随机模拟积分(见11)的精度为\(O_p(N^{-1/2})\), 受维数\(d\)的影响较小, 但高维时也需要计算很多点上的函数值才能相对准确地计算积分。
拟随机积分是另外一种计算积分的方法, 它结合了数值积分和随机模拟积分的优点, 在特殊选取的格子点上计算函数值并计算积分, 这样的布点位置称为拟随机数(quasi-random)。 我国数学家方开泰和王元(Fang and Wang 1994) 开创了基于数论并在试验设计、高维积分有良好应用效果的“均匀设计”学科, 利用他们提出的拟随机数布点可以进行高维积分计算。 均匀设计布点有“均匀分散”和“整齐可比”两个特点, 使布点既具有代表性,又是有规律的。 随机模拟积分的随机误差界为\(O(\sqrt{N^{-1} \log\log N})\), 而拟随机积分的误差可以达到\(O(N^{-1} (\log N)^d)\) (见 Monahan (2001) §10.6, Lemieux (2009))。
习题
习题1
证明复合辛普森积分公式(23.7)。
习题3
把变步长梯形法则积分算法推广到\([0,\infty)\)上的定积分: 设已用\(n\)等分计算\([0, b]\)上的积分, 下一步增加原有\(n\)个区间的中点作为节点, 并在\((b,2b]\)增加\(2n\)个节点, 计算\([0,2b]\)上的定积分, 直到结果变化小于给定的误差限\(\varepsilon\)。 用\(\int_0^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac12 x^2} dx = \frac12\)验证。
习题4
在贝叶斯分析中先验分布为\(\pi(\theta) = 6\theta(1-\theta)\), 似然函数为\(L(\theta) \propto \theta^{15} / (-\log(1-\theta))^{10}\), 后验密度为(差一个比例系数) \[\begin{aligned} p^*(\theta) \propto \theta^{16} (1-\theta) (-\log(1-\theta))^{10}. \end{aligned}\] 分别对\(h_0(\theta)=1\), \(h_1(\theta)=\theta\), \(h_2(\theta)=\theta^2\)计算数值积分\(\int_0^1 h_i(\theta) p^*(\theta) d\theta\), 分别用中点法则、复合梯形法则和复合辛普森法则计算, 比较达到小数点后1位的精度所需要的节点个数。