2 线性平稳序列和线性滤波

2.1 有限运动平均

线性平稳序列是白噪声的线性组合得到的序列。最简单的线性平稳序列是有限运动平均。

设\(\{\varepsilon_t\}=\{\varepsilon_t: \ t \in \mathbb Z\}\) 是\(\text{WN}(0,\sigma^2)\). 对于非负整数\(q\)和常数 \(a_0,a_1,\ldots,a_q\)(\(a_0 \neq 0, a_q \neq 0\)), 我们称 \[ X_t = \sum_{j=0}^q a_j \varepsilon_{t-j} = a_0\varepsilon_t +a_1\varepsilon_{t-1}+\cdots + a_q\varepsilon_{t-q}, \ \ t \in \mathbb Z \] 是白噪声\(\{\varepsilon_t\}\)的(有限)运动平均或滑动平均, 简称为 MA (Moving Average).

MA的平稳性:

\[\begin{aligned} E X_t =& 0 , \\ E (X_{t+k} X_t) =& \begin{cases} \sigma^2 \sum_{j=0}^{q-k} a_j a_{j+k}, & 0 \leq k \leq q, \\ 0, & k > q \end{cases} \end{aligned}\]

可见\(\{X_t\}\)平稳。 \(\gamma_k = 0\), \(\forall k>q\), 称这样的序列为\(q\)相关的。

2.2 线性平稳序列

2.2.1 期望与极限交换次序

随机变量有限平均到随机变量无穷级数的推广需要概率论的极限理论。

定理2.1 (单调收敛定理) 如果非负随机变量序列\(\{\xi_n \}\)单调不减: \(0\leq \xi_1 \leq \xi_2 \leq \cdots\), 则当 \(\xi_n \to \xi\) a.s. 时, 有\(E\xi =\lim_{n\to \infty} E\xi_n\).

这里的随机变量是广义随机变量，允许取\(+\infty\)值。

对于任何时间序列 \(\{Y_t\}\), 利用单调收敛定理得到 \[\begin{aligned} E\left[ \sum_{t=-\infty}^{\infty} |Y_t| \right]=& \lim_{n\to \infty} E \left[ \sum_{t=-n}^{n} |Y_t| \right] \\ =& \lim_{n\to \infty}\sum_{t=-n}^{n} E|Y_t| = \sum_{t=-\infty}^{\infty} E |Y_t|. \end{aligned}\]

定理2.2 (控制收敛定理) 如果随机变量序列\(\{\xi_n\}\)满足\(|\xi_n|\leq \xi_0\) a.s. 和 \(E|\xi_0|< \infty\), 则当\(\xi_n \to \xi\), a.s.时, \(E|\xi|<\infty\) 并且 \(E\xi_n \to E\xi\).

在定理2.1和定理2.2条件下均有， \[\begin{aligned} \lim_{n \to \infty} E \xi_n = E \lim_{n \to \infty} \xi_n. \end{aligned}\] 即期望与极限可以交换次序。

推论2.1 如果随机变量序列\(\{Y_n\}\)满足\(\sum_{i=-\infty}^\infty E|Y_i|\leq \infty\)，则 \(\sum_{i=-\infty}^\infty Y_i\) a.s.收敛, \(E|\sum_{i=-\infty}^\infty Y_i| < \infty\)且 \[\begin{aligned} E \sum_{n=-\infty}^\infty Y_n = \sum_{n=-\infty}^\infty E Y_n \end{aligned}\]

证明令 \[ \eta = \sum_{i=-\infty}^\infty |Y_i| \] 则\(\eta\)是随机变量，由单调收敛定理知\(E\eta < \infty\), \(\eta < \infty\), a.s.。

令 \[ \xi_n = \sum_{i=-n}^n Y_i \] 则 \[ |\xi_n| \leq \eta, \] 记事件\(A = \{ \eta < \infty \}\)，则\(P(A) = 1\)，对\(\omega \in A\), 有\(\sum_{i=-\infty}^\infty |Y_i(\omega)| < \infty\)所以\(\sum_{i=-\infty}^\infty Y_i(\omega)\)收敛， \(\lim_{n\to\infty} \xi_n(\omega)\)收敛，记为\(\xi(\omega)\)；对\(\omega \notin A\), 定义\(\xi(\omega) = 0\)，则\(\xi\)是随机变量，且 \[ \lim_{n\to\infty} \xi_n = \xi, \text{ a.s.} \] 记 \[ \xi = \sum_{i=-\infty}^\infty \xi_i . \] 由控制收敛定理 \[ \lim_{n\to\infty} E \xi_n = E \xi, \] 而 \[ \lim_{n\to\infty} E \xi_n = \lim_{n\to\infty} E \sum_{i=-n}^n Y_i = \lim_{n\to\infty} \sum_{i=-n}^n E Y_i = \sum_{i=-\infty}^\infty E Y_i, \] 于是有 \[ E \sum_{i=-\infty}^\infty \xi_i = \sum_{i=-\infty}^\infty E \xi_i . \] ○○○○○○

如果实数列 \(\{a_j\}\) 满足 \[ \sum_{j=-\infty}^{\infty} |a_j| < \infty, \] 则称\(\{a_j\}\)是绝对可和的. 记\(\{a_j\} \in l_1\).

注意: \(\{a_j\} \in l_1\)则\(\{a_j\} \in l_2\) (即\(\sum_j a_j^2 < \infty\)). 反之不一定成立。

2.2.2 线性序列定义

对于绝对可和的实数列\(\{a_j\}\), 定义零均值白噪声\(\{\varepsilon_t\}\)的无穷滑动和如下 \[ X_t=\sum_{j=-\infty}^{\infty} a_j \varepsilon_{t-j}, \ \ t \in \mathbb Z. \] 则\(\{X_t\}\)是平稳序列。 \(E X_t = 0\), \[\begin{align} \gamma_k = \sigma^2 \sum_{j=-\infty}^\infty a_j a_{j+k}, k \in \mathbb Z . \tag{2.1} \end{align}\]

令\(c_k = \sum_{j=-\infty}^\infty a_j a_{j+k}\), \(k \in \mathbb Z\)。

2.2.3 线性序列的a.s.收敛性

作为无穷和\(\{X_t\}\)有没有定义？由Schwarz不等式， \[ E|\varepsilon_t| = E(|\varepsilon_t| \cdot 1) \leq \sqrt{E \varepsilon_t^2 \cdot 1} = \sigma, \] 所以 \[ \sum_{j=-\infty}^\infty E |a_j \varepsilon_{t-j}| = \sum_{j=-\infty}^\infty |a_j| E|\varepsilon_{t-j}| \leq \sigma \sum_{j=-\infty}^\infty |a_j| < \infty, \] 由推论2.1可知\(\sum_{j=-\infty}^\infty a_j \varepsilon_{t-j}\) a.s.收敛。

2.2.4 线性序列的L1收敛性

级数的余项的\(L_1\)模 \[\begin{aligned} & E \left| \sum_{|j|>N} a_j \varepsilon_{t-j} \right| \leq \sum_{|j|>N} |a_j| E |\varepsilon_{t-j}| \leq \sigma \sum_{|j|>N} |a_j| \to 0 \end{aligned}\] 即线性平稳列在\(L_1\)意义下收敛。

2.2.5 线性序列的平稳性

由推论2.1可知 \[\begin{aligned} E \sum_{j=-\infty}^\infty a_j \varepsilon_{t-j} &= \sum_{j=-\infty}^\infty a_j E \varepsilon_{t-j} = 0 \end{aligned}\]

由Schwarz不等式知\(E|\epsilon_{t-j} \epsilon_{t+k-l}| \leq \sigma^2\), 于是 \[ \sum_{j=-\infty}^\infty \sum_{l=-\infty}^\infty E |a_j a_l \epsilon_{t-j} \epsilon_{t+k-l}| \leq \sigma^2 \sum_{j=-\infty}^\infty \sum_{l=-\infty}^\infty |a_j|\; |a_l| = \sigma^2 \left( \sum_{j=-\infty}^\infty |a_j| \right)^2 < \infty, \] 由推论2.1， \[\begin{aligned} E X_t X_{t+k} &= E \sum_{j=-\infty}^\infty a_j \varepsilon_{t-j} \sum_{l=-\infty}^\infty a_l \varepsilon_{t+k-l} \\ &= \sum_{j=-\infty}^\infty \sum_{l=-\infty}^\infty a_j a_l E(\varepsilon_{t-j} \varepsilon_{t+k-l}) \\ &= \sigma^2 \sum_{j=-\infty}^\infty a_j a_{j+k} \end{aligned}\] 即\(\{X_t\}\)是平稳序列, \(E X_t=0\)， \(\gamma_k = \sigma^2 \sum_{j=-\infty}^\infty a_j a_{j+k}\).

2.2.6 线性序列的L2收敛性

设\(\{a_j\} \in l_2\)，即\(\sum_j a_j^2 < \infty\)，则 \[\begin{aligned} X_t=\sum_{j=-\infty}^{\infty} a_j \varepsilon_{t-j}\ (L^2) \end{aligned}\] 也是平稳序列。期望为零，自协方差函数同上。

\(X_t\)定义的无穷级数是\(L^2\)收敛的。证明需要应用Hilbert空间性质。见5.1.5。

注意\(\{a_j \} \in l_1 \Longrightarrow \{a_j \} \in l_2\)。

2.2.7 线性序列的自协方差函数收敛性

当\(\{a_j\} \in l_1\)时 \[ \sum_{k=-\infty}^{\infty} |\gamma_k| < \infty \] 事实上， \[\begin{aligned} & \sum_{k=-\infty}^{\infty} |\gamma_k| \leq \sigma^2 \sum_{k=-\infty}^{\infty} \sum_{j=-\infty}^{\infty} |a_j a_{j+k}| \\ & = \sigma^2 \sum_{j=-\infty}^{\infty} |a_j| \sum_{k=-\infty}^{\infty} |a_{j+k}| = \sigma^2 (\sum_{j=-\infty}^{\infty}|a_j|)^2 < \infty \end{aligned}\]

定理2.3 当\(\{a_j\} \in l_2\)时, 自协方差函数 \(\lim_{k\to \infty}\gamma_k =0\).

证明: 利用Cauchy不等式 \(|\sum a_j b_j | \leq \left( \sum a_j^2 \sum b_j^2 \right)^{1/2}\) 得到 \[\begin{aligned} |\gamma_k| =& \sigma^2 \left| \sum_{j=-\infty}^{\infty} a_j a_{j+k} \right| \\ \leq& \sigma^2 \sum_{|j| \leq k/2} | a_j a_{j+k} | + \sigma^2 \sum_{|j| > k/2} | a_j a_{j+k} | \\ \leq& \sigma^2 \left[ \sum_{j=-\infty}^{\infty} a_j^2 \sum_{|j| \leq k/2} a_{j+k}^2 \right]^{1/2} + \sigma^2 \left[ \sum_{|j| > k/2} a_j^2 \sum_{j=-\infty}^{\infty} a_j^2 \right]^{1/2} \\ \leq& 2\sigma^2 \left[ \sum_{j=-\infty}^{\infty} a_j^2 \right]^{1/2} \left[ \sum_{|j| \geq k/2} a_j^2 \right]^{1/2} \to 0 \quad (k \to \infty) \end{aligned}\]

○○○○○○

线性序列的应用：

线性序列描述了自协方差函数衰减到零的时间序列。只要样本自协方差函数衰减到零就可以用线性序列来描述。

单边线性序列：

\[ X_t = \sum_{j={\mathbf 0}}^\infty a_j \varepsilon_{t-j}, \ t \in \mathbb Z \] 称为单边运动平均(MA)，或单边无穷滑动和。这样的\(X_t\)有因果性：\(X_t\)只受\(s \leq t\)的\(\varepsilon_s\)影响而不受 \(t\)时刻以后的\(\varepsilon_s\)影响。 \[ \gamma_k = \begin{cases} \sum_{j=0}^\infty a_j a_{j+k},\ & k \geq 0 \\ \gamma_{-k} \ & k < 0 \end{cases} \]

2.3 时间序列的线性滤波

对序列\(\{X_t \}\)进行滑动求和： \[ Y_t = \sum_{j=-\infty}^\infty h_j X_{t-j}, \ \ t\in \mathbb Z \] 称为对\(\{X_t\}\)进行线性滤波。其中绝对可和的\(\{h_j\}\)称为一个保时线性滤波器。如果输入信号\(\{X_t\}\)是平稳列则输出\(\{Y_t\}\)也是平稳列。 \(\{ Y_t \}\)的收敛性可以用推论2.1得出。

关于线性滤波的性质7.1还有进一步讨论。

当\(\{ X_t \}\)平稳时，由推论2.1， \[ \mu_Y = E Y_t = \sum_{j=-\infty}^\infty h_j E X_{t-j} = \mu_X \sum_{j=-\infty}^\infty h_j \]

\[\begin{aligned} \gamma_Y(n) &= \text{Cov}(Y_{n+1}, Y_1) \\ &= \sum_{j, k=-\infty}^\infty h_j h_k E[(X_{n+1-j}-\mu)(X_{1-k}-\mu)] \\ &= \sum_{j, k= -\infty}^\infty h_j h_k \gamma_{n+k-j} \end{aligned}\]

例取 \[ h_j = \begin{cases} \frac{1}{2M+1}, \ & |j| \leq M \\ 0, & |j|>M. \end{cases} \] 则 \[ Y_t = \frac{1}{2M+1} \sum_{j=-M}^M x_{t-j} \] 是\({X_t}\)的滑动平均，这种滤波称为矩形窗滤波器。可以平滑\(\{X_t\}\)，抑制高频信号。高频信号表现是粗糙和复杂的曲线，低频信号表现为缓慢和光滑的变化。

例2.1 (余弦波信号的滤波) 设 \[ X_t = S_t + \varepsilon_t = b\cos(\omega t+U) +\varepsilon_t, \ \ t \in \mathbb Z \] 其中\(U \sim\)U(\(0, 2\pi\)), \(\{\varepsilon_t\}\)零均值平稳, \(U\)与\(\{\varepsilon_t\}\)独立。信号\(\{S_t\}\)方差\(b^2/2\)，噪声\(\{\varepsilon_t\}\)方差\(\sigma^2\), 信号与方差之比称为信噪比，等于\(b^2/(2\sigma^2)\)。

作矩形窗滤波: \[\begin{aligned} Y_t &= \frac{1}{2M+1} \sum_{j=-M}^M X_{t-j} \\ &= \frac{b\sin[\omega (M+0.5)]}{(2M+1)\sin(\omega /2)} \cos(\omega t+U) + \eta_t \\ \eta_t &= \frac{1}{2M+1}\sum_{j=-M}^M \varepsilon_{t-j} \end{aligned}\]

除了\(\eta_t\)项之外，结果与原始信号相比只有幅度有了成比例变化。上式的化简可以用复数的极坐标表示来推导有关三角函数求和的公式。 \(\text{Var}(\eta_t) = \frac{\sigma^2}{2M+1}\).

新的信噪比为 \[ \frac{b^2}{2\sigma^2} \frac{\sin^2[\omega (M+0.5)]}{(2M+1)\sin^2(\omega /2)}. \] 特别当\(\omega(M+0.5) = \pi/2\)时信噪比为 \[ \frac{b^2 \omega}{2\pi \sigma^2 \sin^2(\omega /2)} > \frac{2b^2}{\pi \omega \sigma^2} = \frac{b^2}{2\sigma^2} \cdot \frac{4}{\pi\omega} \] 信噪比至少增大到\(4/(\pi\omega)\)倍， \(\omega\)越小信噪比提高越多。 \(\omega\)越小，\(M\)应越大。

演示：

demo.mafilt <- function(b=3, M=3){
  n <- 100
  ##om <- pi/7
  om <- pi/12
  sigma <- 1.0
  eps <- rnorm(n, 0, sigma)
  sn0 <- b^2 / (2*sigma^2)
  tt <- seq(n)
  u <- runif(1)
  signal <- b * cos(om*tt + 2*pi*u)
  y <- signal + eps
  filt <- rep(1/(2*M+1), 2*M+1)
  yf <- filter(y, filt, method="convolution")
  rg <- range(c(y, yf))
  sn <- round(b^2 / (2*sigma^2), 3)
  plot(tt, y, main=paste("MA filter: SN=", sn, sep=""),
       type="l", xlab='time', ylab='y',
       xlim=c(0,120),
       ylim=c(-b*1.5,b*1.5))
  lines(tt, signal, col="green", lwd=2)
  lines(tt, yf, col="red", lwd=2)
  legend("topright", lty=c(1,1,1), lwd=c(1,2,2),
         col=c("black", "green", "red"),
         legend=c("序列", "信号", "滤波"))
}
demo.mafilt()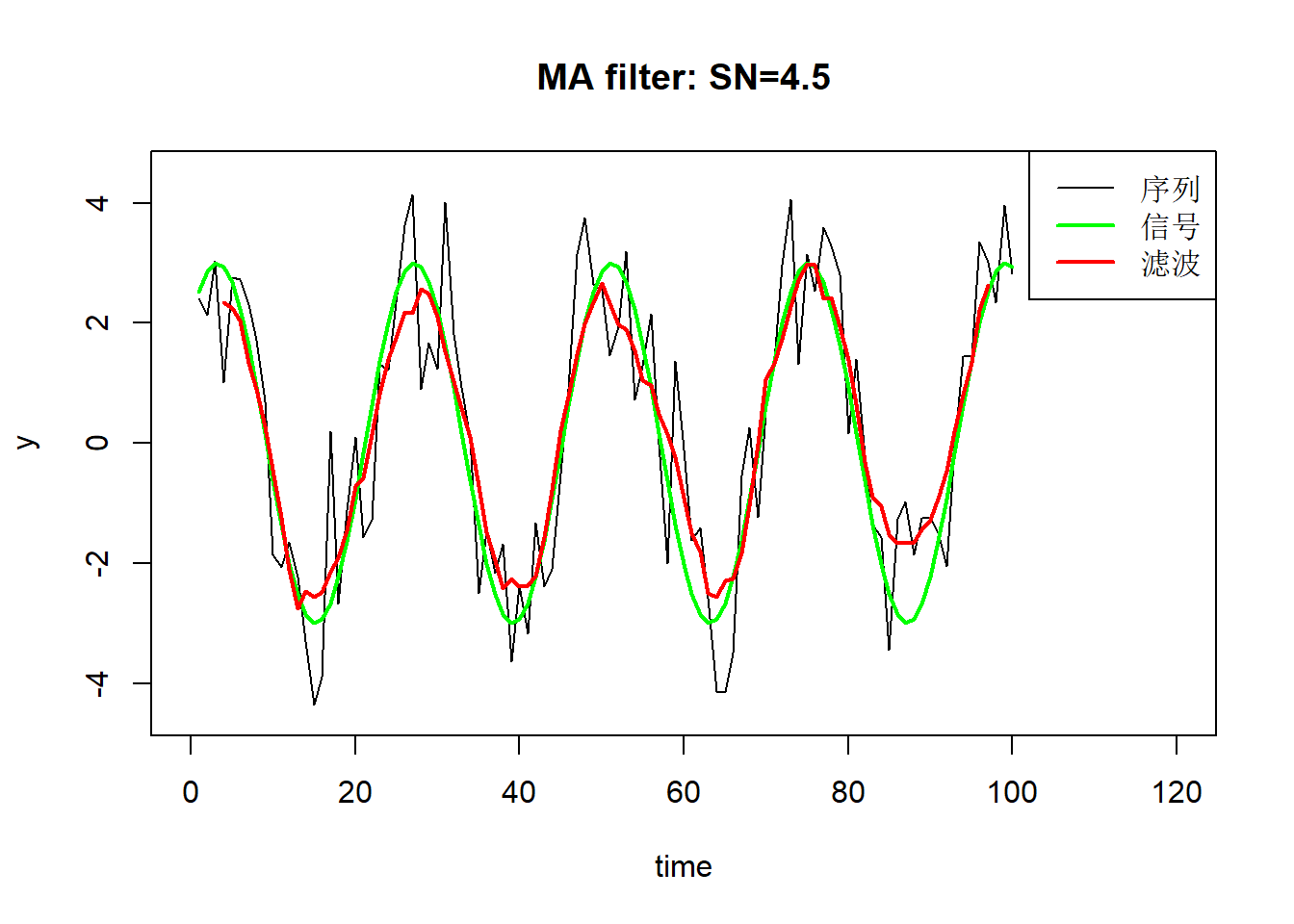

○○○○○○

2.4 附录：补充证明

2.4.1 不独立的白噪声示例

考虑如下的模型。设\(\{ \varepsilon_t \}\)为iid 标准正态分布随机变量列， \(\alpha_0>0\), \(0 < \alpha_1 < 1\)。令 \[ a_t = \sigma_t \varepsilon_t, \quad \sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 \]

令\(\mathscr F_t = \sigma\{ \varepsilon_t, \varepsilon_{t-1}, \dots \}\)，则\(\varepsilon_t \in \mathscr F_t\), \(\varepsilon_t\)与\(\mathscr F_{t-1}\)独立。应可证明\(\sigma_t \in \mathscr F_{t-1}\), \(a_t \in \mathscr F_t\), \(\mathscr F_t = \sigma \{ a_t, a_{t-1}, \dots \}\) (严格证明?)

于是 \[\begin{aligned} E a_t =& E[ E(\sigma_t \varepsilon_t | \mathscr F_{t-1}) ] \\ =& E[ \sigma_t E( \varepsilon_t | \mathscr F_{t-1}) ] \\ =& E[ \sigma_t E(\varepsilon_t )] = 0 \end{aligned}\]

对\(k=1,2,\dots\)， \[\begin{aligned} E (a_t a_{t-k}) =& E[ E(\sigma_t \sigma_{t-k} \varepsilon_t \varepsilon_{t-k} | \mathscr F_{t-1}) ] \\ =& E[ \sigma_t \sigma_{t-k} \varepsilon_{t-k} E( \varepsilon_t | \mathscr F_{t-1}) ] \\ =& E[ \sigma_t \sigma_{t-k} \varepsilon_{t-k} E(\varepsilon_t )] = 0 \end{aligned}\]

所以\(\{ a_t \}\)是不相关列，而 \[\begin{aligned} \text{Var}(a_t | a_{t-1}, a_{t-2}, \dots) =& E(a_t^2 | a_{t-1}, a_{t-2}, \dots) \\ =& E(\sigma_t^2 \varepsilon_t^2 | a_{t-1}, a_{t-2}, \dots) \\ =& \sigma_t^2 E ( \varepsilon_t^2 | a_{t-1}, a_{t-2}, \dots) \\ =& \sigma_t^2 = \alpha_0 + \alpha_1 a_{t-1}^2 \end{aligned}\] 可见\(a_t\)与\(a_{t-1}\)不独立。

如果模型中的\(\{ a_t \}\)平稳，则\(E a_t^2 = E a_{t-1}^2\)，有 \[\begin{aligned} E(a_t^2) =& E[ E(a_t^2 | \mathscr F_{t-1}) ] \\ =& E[ E(\sigma_t^2 \varepsilon_t^2 | \mathscr F_{t-1}) ] \\ =& E[ \sigma_t^2 E(\varepsilon_t^2 | \mathscr F_{t-1}) ] \\ =& E[ \sigma_t^2 E(\varepsilon_t^2) ] \\ =& E[ \sigma_t^2 ] = \alpha_0 + \alpha_1 E a_{t-1}^2 \end{aligned}\] 解得 \[ \text{Var}(a_t) = E(a_t^2) = \frac{\alpha_0}{1 - \alpha_1} \] 但是\(a_t\)平稳的证明不显然。

2.4.2 三角级数求和的简化推导

\[\begin{aligned} & \sum_{j=-M}^M b \cos(\omega (t-j) + U) \\ =& \Re\left\{ \sum_{j=-M}^M b \exp\{ i [\omega(t-j) + U] \} \right\} \\ =& \Re\left\{ b e^{i(\omega t + U)} \sum_{j=-M}^M e^{-i \omega j} \right\} \end{aligned}\] 其中 \[\begin{aligned} & \sum_{j=-M}^M e^{-i \omega j} = \frac{e^{i\omega M} - e^{-i \omega(M+1)}}{1 - e^{-i \omega}} \\ =& \frac{\left( e^{i\omega M} - e^{-i \omega(M+1)} \right) (1 - e^{i \omega})}{ | 1 - e^{-i \omega} |^2 } \\ =& \frac{e^{i\omega M} - e^{-i\omega(M+1)} - e^{i\omega(M+1)} + e^{-i\omega M}} {(1 + \cos\omega)^2 + \sin^2 \omega} \\ =& \frac{2 \cos(M\omega) - 2 \cos[(M+1)\omega]}{2 + 2 \cos\omega} \\ =& \frac{-4 \cos[(2M+1)\omega/2] \sin(-\frac12 \omega)} {e \sin^2 \frac{\omega}{2}} \\ =& \frac{\sin[(M + \frac12)\omega]}{ \sin\frac{\omega}{2}} \end{aligned}\] 所以 \[\begin{aligned} & \sum_{j=-M}^M b \cos(\omega (t-j) + U) = b\cos(\omega t + U) \frac{\sin[(M + \frac12)\omega]}{ \sin\frac{\omega}{2}} \end{aligned}\]