11 AR模型举例

11.1 AR(1)模型

\(|a|<1\), AR(1)模型 \[\begin{align*} X_t =& a X_{t-1} + \varepsilon_t, \quad t \in \mathbb Z \\ \{\varepsilon_t\} \sim& \text{WN}(0,\sigma^2) \end{align*}\] 有平稳解 \[\begin{align*} X_t = \sum_{j=0}^\infty a^j \varepsilon_{t-j} \end{align*}\] 自协方差函数 \[\begin{align*} \gamma_0 =& \sigma^2 \sum_{j=0}^{\infty} a^{2j} = \frac{\sigma^2}{1 - a^2} \\ \gamma_k =& a \gamma_{k-1} = \dots = a^k \gamma_0, \quad k \geq 1 \tag{5.2} \end{align*}\]

自相关系数 \[\begin{align} \rho_k = \frac{\gamma_k}{\gamma_0} = a^k \end{align}\] 谱密度 \[\begin{align} f(\lambda) =& \frac{\sigma^2}{2\pi} \frac{1}{\left| 1 - a e^{i\lambda} \right|^2} \\ =& \frac{\sigma^2}{2\pi} [ 1 + a^2 - 2 a \cos \lambda ]^{-2}, \quad \lambda \in [-\pi, \pi] \end{align}\]

演示: \(a=\pm 0.85\)时序列的演示。

demo.ar1.example <- function(){
  oldpar <- par(mfrow=c(2,2)); on.exit(par(oldpar))
  n <- 100
  a1 <- 0.85

  y1 <- ar.gen(n, a1, sigma=1.0, plot.it=FALSE)
  y2 <- ar.gen(n, -a1, sigma=1.0, plot.it=FALSE)
  plot(y1, main="AR(1): a = 0.85")
  acf1 <- exp(seq(from=0, by=log(a1), length=21))
  plot(0:20, acf1, type="l",
       xlab="k", ylab="ACF",
       main="ACF of AR(1): a = 0.85")
  ar.true.spectrum(attr(y1, "a"))
  #plot(y1, type="n", axes=F, xlab="", ylab="")
  acf(y1, main="Estimated ACF")

  plot(y2, main="AR(1): a = -0.85")
  acf2 <- (-a1)^seq(from=0, length=21)
  plot(0:20, acf2, type="l",
       xlab="k", ylab="ACF",
       main="ACF of AR(1): a = -0.85")
  abline(h=0)
  ar.true.spectrum(attr(y2, "a"))
  #plot(y1, type="n", axes=F, xlab="", ylab="")
  acf(y2, main="Estimated ACF")
  invisible()
}
demo.ar1.example()

比较:

AR(1)正负系数的比较
\(a = 0.85\) \(a = -0.85\)
(1) 数据表现出趋势性, 相邻的数据差别不大; 数据上下摆动，趋势性不明显;
(2) (1)中的现象在\(\{\rho_k\}\)得到体现: 相邻随机变量正相关 (1)中的现象在\(\{\rho_k\}\)得到体现: 相邻随机变量负相关
(3) \(\rho_k\) 单调减少趋于0 (3) \(\rho_k\) 正负交替 趋于0
(4) 谱密度的能量集中在低频, \(f(\lambda)<f(0), \lambda \in (0,\pi]\), 数据无周期现象, 周期 \(T=\frac{2\pi}{0}=\infty\) 谱密度能量集中在高频, \(f(\lambda) <f(\pi), \lambda \in [0,\pi)\), 数据有周期现象, 周期 \(T=\frac{2\pi}{\pi} =2\)
(5) 偏相关系数 \(a_{1,1}= 0.85\), \(a_{k,k}=0\), 当 \(k>1\) 偏相关系数 \(a_{1,1}=- 0.85\), \(a_{k,k}=0\), 当 \(k>1\)
(6) 随 \(a\)接近于0, 以更快的速度收敛到\(0\) 上述性质随 \(a\) 接近\(-1\)变得更明显, 随\(a\) 接近\(0\)变得不明显

11.2 AR(2)模型

11.2.1 稳定域和允许域

AR(2)模型为 \[\begin{aligned} X_t =& a_1 X_{t-1} + a_2 X_{t-2} + \varepsilon_t, \quad \varepsilon_t \sim \text{WN}(0,\sigma^2) \\ A(z) =& 1 - a_1 z - a_2 z^2 \neq 0, |z| \leq 1 \end{aligned}\] 稳定性条件为： \[\begin{aligned} a_2 \pm a_1 < 1, \quad |a_2| < 1 \end{aligned}\]

稳定性条件的证明比较长， 区分复根与实根两种情况； 复根时，求复根的模大于1的条件， 比较容易得到充要条件为 \[ |a_1| < 2, \ -1 < a_2 < 0, \ a_2 < -\frac14 a_1^2 . \] 实根的情况， 可以分\(a_2 > 0\)和\(a_2 < 0\)讨论， 每种情况中继续分\(a_1 \geq 0\)和\(a_1 < 0\)讨论， 即分四种情况讨论。 最终可以得到稳定性条件。

AR(2)稳定性条件(蓝色：实根；红色：复根)

图11.1: AR(2)稳定性条件(蓝色：实根；红色：复根)

设\(A(z)\)的根为 \(z_1 = b_1 e^{i\lambda_1}\), \(z_2 = b_2 e^{i\lambda_2}\)。 由Y-W方程 \[\begin{aligned} \rho_0 =& 1, \quad \\ \rho_1 =& \frac{a_1}{1-a_2} \\ \rho_k =& a_1 \rho_{k-1} + a_2 \rho_{k-2}, \quad k \geq 1 \end{aligned}\] \(a_{11} = \rho_1\), \(a_{2,2}=a_2\), \(a_{k,k}=0(k\geq 3)\)。

\[\begin{aligned} \mathscr{A} = \{(a_1, a_2): a_2 \pm a_1 < 1, |a_2| < 1 \} \end{aligned}\] 称为AR(2)的稳定域。

从Y-W方程可以用\(\rho_1, \rho_2\)表示\(a_1, a_2\): \[\begin{aligned} a_1 = \frac{\rho_1(1-\rho_2)}{1-\rho_1^2},\quad a_2 = \frac{\rho_2 - \rho_1^2}{1-\rho_1^2} \end{aligned}\] 反之有 \[\begin{aligned} \rho_1 = \frac{a_1}{1-a_2}, \quad \rho_2 = a_2 + \frac{a_1^2}{1-a_2} \end{aligned}\] \((a_1, a_2) \in \mathscr{A}\) \(\Longleftrightarrow\) \((\rho_1, \rho_2) \in\) \[\begin{aligned} \mathscr{C} = \{(\rho_1, \rho_2): \rho_1^2 < (1+\rho_2)/2, |\rho_1|<1, |\rho_2|<1 \} \end{aligned}\] \(\mathscr{C}\)称为AR(2)的允许域。

11.2.2 特征根与系数关系

特征根与系数有如下关系 \[\begin{aligned} 1 - a_1 z - a_2 z^2 = (1 - \frac{z}{z_1})(1 - \frac{z}{z_2}) \\ a_1 = \frac{1}{z_1} + \frac{1}{z_2}, \quad a_2 = -\frac{1}{z_1}\frac{1}{z_2} \\ z_1 z_2 = \frac{1}{(-a_2)},\quad z_1 + z_2 = \frac{a_1}{(-a_2)} \end{aligned}\]

谱密度为 \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi} \frac{1}{|a_2| | e^{i\lambda} - b_1 e^{i\lambda_1}|^2 \cdot | e^{i\lambda} - b_2 e^{i\lambda_2}|^2} \end{aligned}\]

11.2.3 AR(2)实特征根时的表现

  • 当\(a_1^2 + 4a_2 \geq 0\)时(蓝色区域)特征方程有两个实根。

  • 当\(a_2>0\)时\(z_1\)和\(z_2\)异号，设\(z_1<-1, z_2>1\)。 \(f(\lambda)\)在\(0\)和\(\pi\)处有峰值。 由\(z_1 + z_2 = \frac{(-a_1)}{a_2}\)知

    • \(a_1>0\)时\(z_1 + z_2<0\), 正根\(z_2\)离单位圆更近，\(f(\lambda)\)在\(0\)点最大。 \(\rho_k\)都为正数，震荡衰减。\(\{X_t\}\)表现出相邻点的正相关。
    • \(a_1<0\)时\(z_1 + z_2>0\)，负根\(z_1\)离单位圆更近，\(f(\lambda)\)在\(\pi\)点最大。 \(\rho_k\)主要呈现正负交替衰减。\(\{X_t\}\)也表现出正负振荡。
    • \(a_1=0\)时\(z_1 = -z_2\)，离单位圆一样近，\(f(\lambda)\)在\(0,\pi\)一样高。 \(\rho_k\)都非负，表现出振荡衰减。\(\{X_t\}\)表现出正负振荡。

  • 当\(a_2<0\)有复根或实根；为实根时\(z_1\)与\(z_2\)同号，与\(a_1\)同号。

  • \(a_1>0\)时有两个正根, \(f(\lambda)\)只在\(0\)点有峰值。 \(\rho_k\)单调衰减。\(\{X_t\}\)表现出相邻点的正相关。

  • \(a_1<0\)时有两个负根, \(f(\lambda)\)只在\(\pi\)点有峰值。 \(\rho_k\)正负交替衰减。\(\{X_t\}\)表现出正负振荡。

11.2.4 AR(2)虚特征根时的表现

\(z_1, z_2\)是虚根\(\Longleftrightarrow\) \(a_1^2 + 4 a_2 < 0\)(红色区域)。 \[\begin{aligned} z_1, z_2 = b e^{\pm i \lambda_0}, \quad b>1, \lambda_0 \neq 0,\pi \end{aligned}\]

由(9.11)得 \[\begin{align} \rho_k = \frac{\cos(k\lambda_0 + \theta_0)}{b^k \cos(\theta_0)}, \quad k \geq 0 \tag{11.1} \end{align}\] 这时\(\{\rho_k\}\)振荡衰减，振荡角频率为\(\lambda_0\)。

\(\{X_t\}\)也呈现出在频率\(\lambda_0\)处的振荡。

用R对AR(2)的各种情形作模拟图如下。

demo.ar2.example <- function(){
  oldpar <- par(mfrow=c(3,1)); on.exit(par(oldpar))
  n <- 100
  acomplex <- cbind(2/1.1*cos(c(pi/6, pi/2, 2*pi/3)),
                    -1/1.1^2)
  alist <- rbind(c(0.1, 0.5),
                 c(-0.1, 0.5),
                 c(0, 0.8),
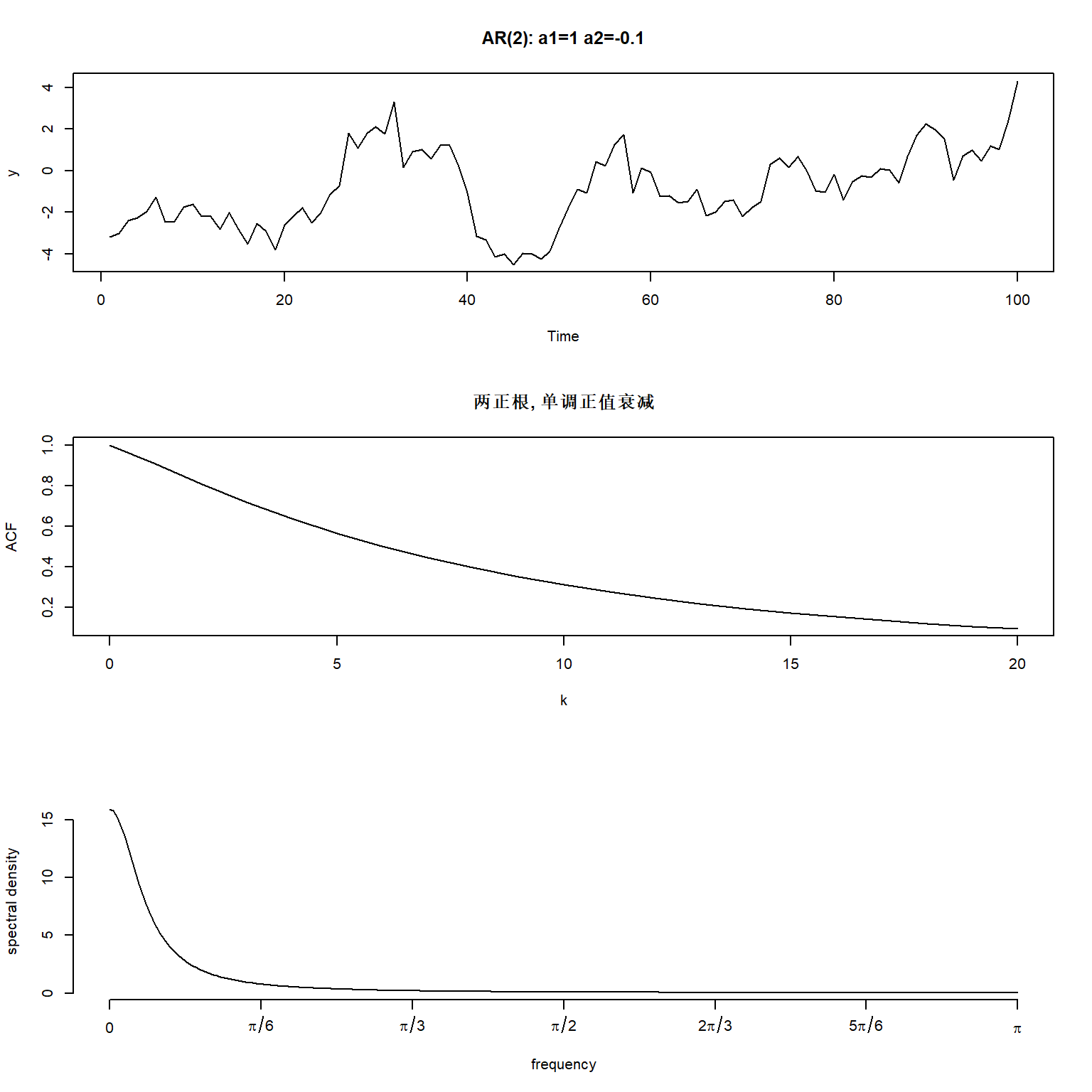
                 c(1, -0.1),
                 c(-1, -0.1),
                 acomplex)
  tlist.y <- paste("AR(2): a1=", round(alist[,1],3),
                   " a2=", round(alist[,2],3), sep="")
  tlist.rho <- c("反号实根, 正根近单位圆, 取震荡的正值衰减",
                 "反号实根, 负根近单位圆, 正负交替衰减",
                 "根为相反数, 非负震荡衰减",
                 "两正根, 单调正值衰减",
                 "两负根, 正负交替衰减",
                 "共轭复根, 以周期12震荡衰减",
                 "共轭复根, 以周期4震荡衰减",
                 "共轭复根, 以周期3震荡衰减")

  m <- 20
  acfv <- numeric(m+1)
  acfv[1] <- 1
  for(ii in seq(nrow(alist))){
    y <- ar.gen(n, alist[ii,], sigma=1.0, plot.it=FALSE)
    a1 <- alist[ii,1];
    a2 <- alist[ii,2];
    acfv[2] <- a1 / (1 - a2)
    for(jj in seq(3, m+1)){
      acfv[jj] <- a1*acfv[jj-1] + a2*acfv[jj-2]
    }
    plot(y, main=tlist.y[ii], type="l")
    plot(0:m, acfv, type="l",
         xlab="k", ylab="ACF",
         main=tlist.rho[ii])
    abline(h=0)
    ar.true.spectrum(attr(y, "a"), title="")
  }
  invisible()
}
demo.ar2.example()

11.3 附录：AR模型有关的一些R函数

11.3.1 模拟和基本统计

arima.sim()可以用来模拟生成来自AR(\(p\))模型的数据。 例如， 对如下AR(2)： \[ X_t = X_{t-1} - 0.1 X_{t-2} + \varepsilon_t, \ \varepsilon_t \sim \text{WN}(0, 0.2^2) \] 可以用如下程序生成模拟数据， 长度500：

set.seed(2)
y = arima.sim(model=list(ar=c(1, -0.1)), n=500, sd=0.2)
head(y)
## [1]  0.23049850  0.02289326 -0.39333224 -0.46021578 -0.23371005  0.04015748

对时间序列数据用plot()作时间序列图：

plot(y)

用acf()作时间序列的自相关函数图：

acf(y)

用pacf()作时间序列的偏相关函数图：

pacf(y)

下面是自定义的一个AR(\(p\))模拟程序， 允许自己指定特征多项式的根作为模型参数， 可以指定模拟初值， 并且不要求模型必须平稳：

## simulate AR(p) model.
## a is vector a_1, \dots, a_p
## Model is X_t = a_1 X_{t-1} + \dots + a_p X_{t-p} + \epsilon_t
## \Var(\epsilon_t) = sigma^2
## This version use the ``filter'' function.
ar.gen <- function(n, a, sigma=1.0, by.roots=FALSE,
                   plot.it=FALSE, n0=1000,
                   x0=numeric(length(a))){
  if(by.roots){
    require(polynom)
    cf <- Re(coef(poly.calc(a)))
    cf <- cf / cf[1]
    a <- -cf[-1]
  }
  n2 <- n0 + n
  p <- length(a)
  eps <- rnorm(n2, 0, sigma)
  x2 <- filter(eps, a, method="recursive", side=1, init=x0)
  x <- x2[(n0+1):n2]
  x <- ts(x)
  attr(x, "model") <- "AR"
  attr(x, "a") <- a
  attr(x, "sigma") <- sigma
  if(plot.it) plot(x)
  x
}

11.3.2 特征多项式的根

对多项式\(A(z) = a_0 + a_1 z + \dots + a_p z^p\)， 函数polyroot(c(a0, a1, ..., ap))求多项式的所有复根。 所以特征多项式为\(A(z) = 1 - a_1 z - \dots - a_p z^p\)的AR(\(p\))模型的所有特征根可以用polyroot得到。 比如，上面的AR(2)模型的所有特征根：

polyroot(c(1, -c(1, -0.1)))
## [1] 1.127017-0i 8.872983+0i

求特征根的模，平稳的AR模型的特征多项式的模大于1：

abs(polyroot(c(1, -c(1, -0.1))))
## [1] 1.127017 8.872983

11.3.3 模型的理论谱密度图

下面的程序输入AR的系数，绘制理论谱密度图形：

## AR theoretical spectral density plot given AR coefficients
ar.true.spectrum <- function(a, ngrid=256, sigma=1, plot.it=TRUE, 
                             title="AR True Spectral Density"){
  p <- length(a)
  freqs <- seq(from=0, to=pi, length=ngrid)
  spec <- numeric(ngrid)
  for(ii in seq(ngrid)){
    spec[ii] <- sigma^2 / (2*pi) / 
      abs(1 - sum(complex(mod=a, arg=freqs[ii]*seq(p))))^2
  }
  if(plot.it){
    plot(freqs, spec, type='l',
         main=title,
         xlab="frequency", ylab="spectral density",
         axes=FALSE)
    axis(2)
    axis(1, at=(0:6)/6*pi,
         labels=c(0, expression(pi/6),
           expression(pi/3), expression(pi/2),
           expression(2*pi/3), expression(5*pi/6), expression(pi)))
  }
  invisible(list(frequencies=freqs, spectrum=spec,
            ar.coefficients=a, sigma=sigma))
}

例如，对上面的AR(2)模型做理论谱密度图：

ar.true.spectrum(c(1, -0.1))

11.3.4 AR模型估计

R中ar()可以从数据估计AR模型， 还可以自动确定阶\(p\)。

arima()函数指定模型阶后估计模型。 一般的时间序列不一定是零均值的， 所以估计函数同时估计模型的均值。

如：

set.seed(2)
y = 100 + arima.sim(model=list(ar=c(1, -0.1)), n=500, sd=0.2)
arm01 <- arima(y, order=c(2, 0, 0))
print(arm01)
## 
## Call:
## arima(x = y, order = c(2, 0, 0))
## 
## Coefficients:
##          ar1      ar2  intercept
##       0.9998  -0.0901   100.1638
## s.e.  0.0445   0.0445     0.0989
## 
## sigma^2 estimated as 0.04126:  log likelihood = 86.59,  aic = -165.18

其中order=c(2,0,0)表示拟合AR(2)模型。 结果中intercept是模型期望值\(EX_t\)的估计。