8 自回归模型及其平稳性
8.1 特例: AR(1)
\[\begin{align} X_t = a X_{t-1} + \varepsilon_t, \quad t \in \mathbb Z, \quad \{\varepsilon_t\} \sim \text{WN}(0,\sigma^2) \tag{8.1} \end{align}\]
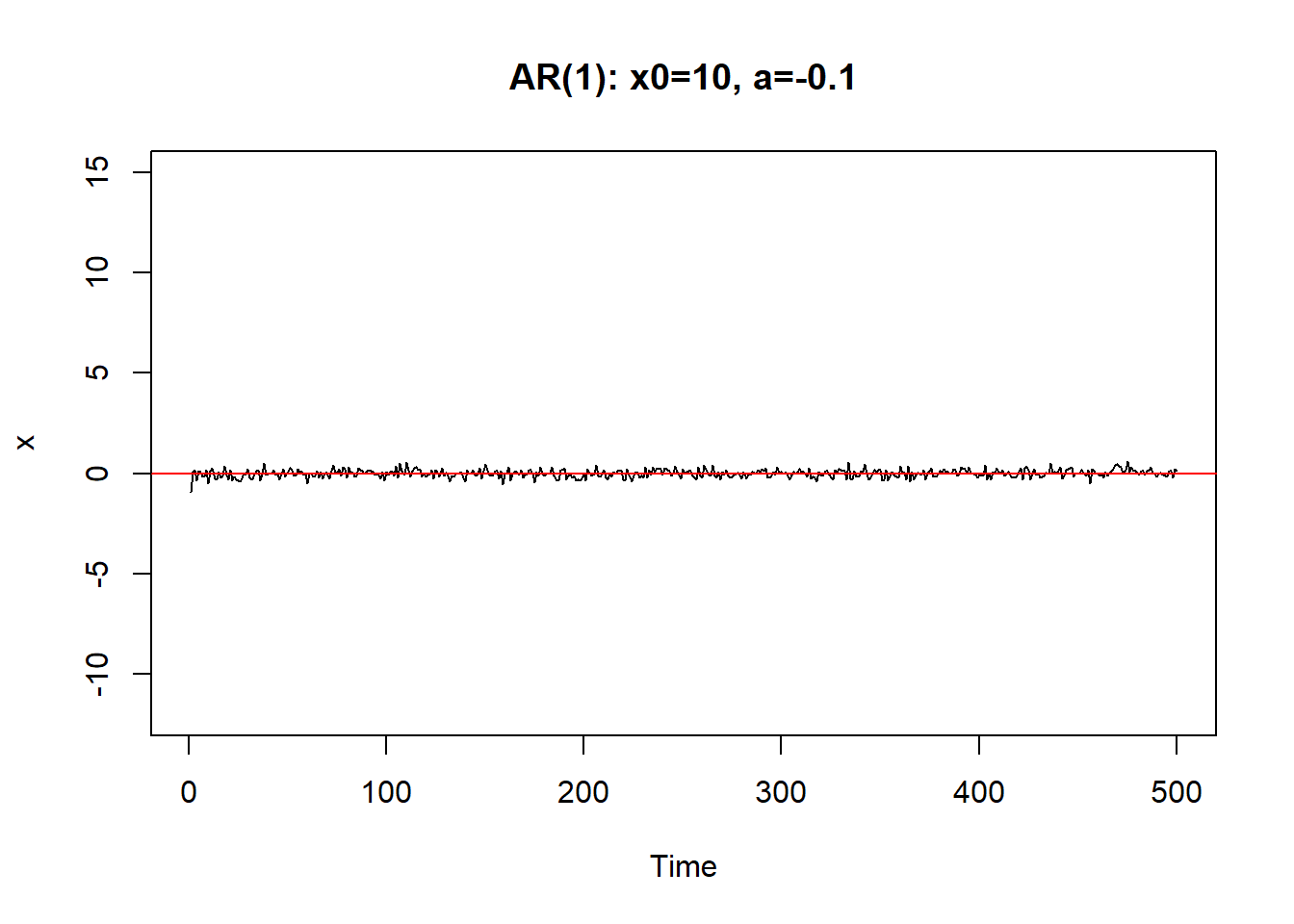
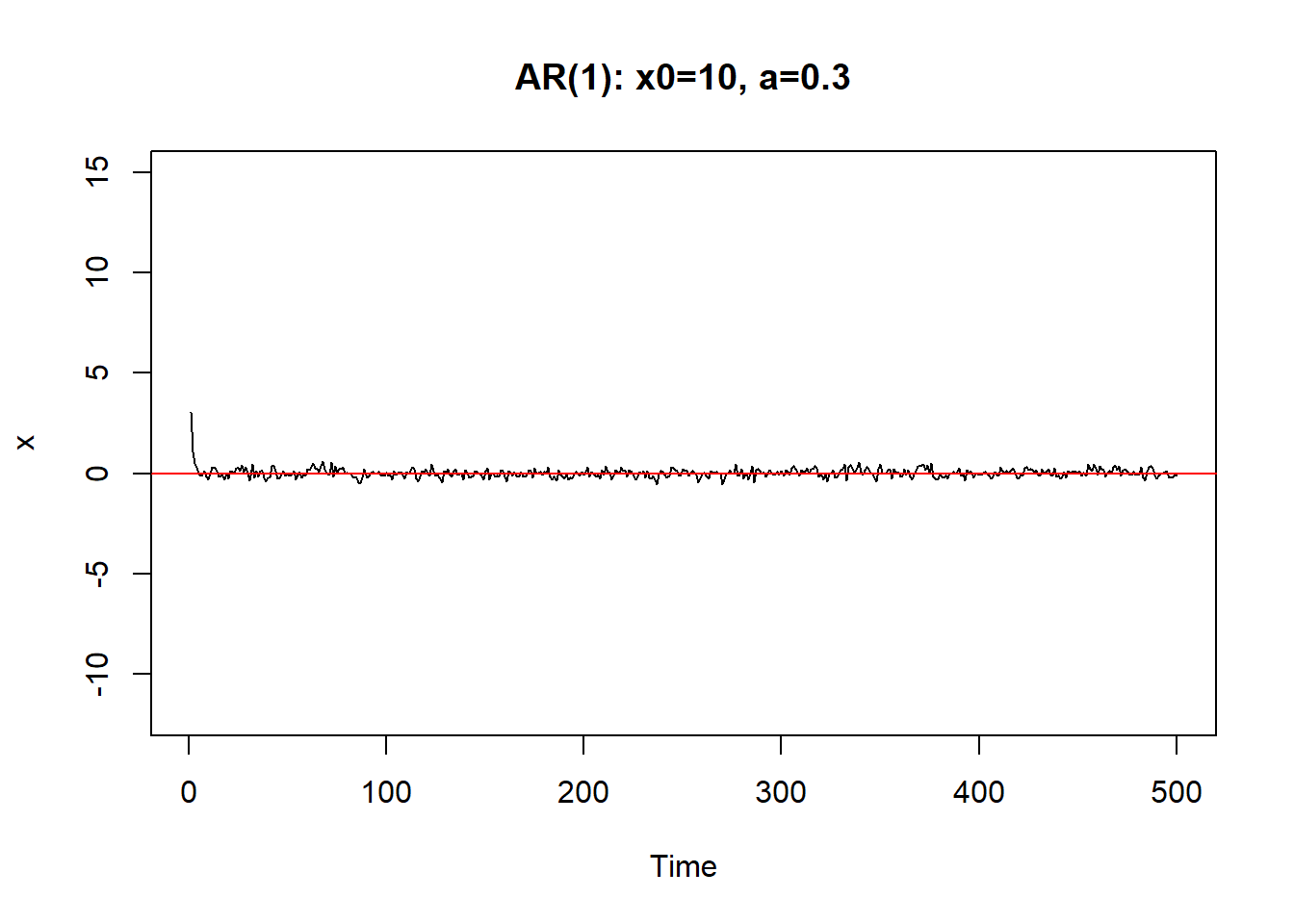
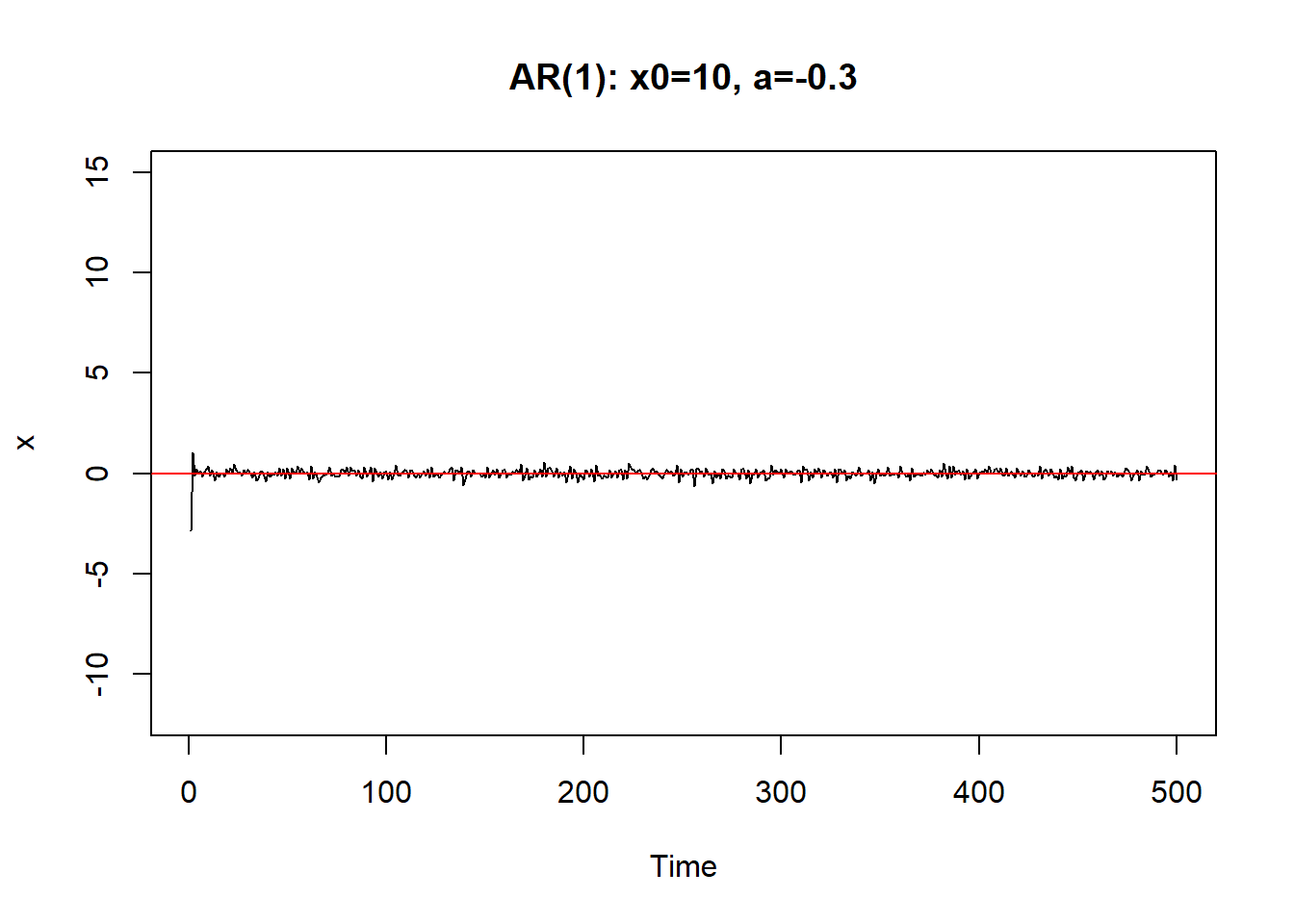
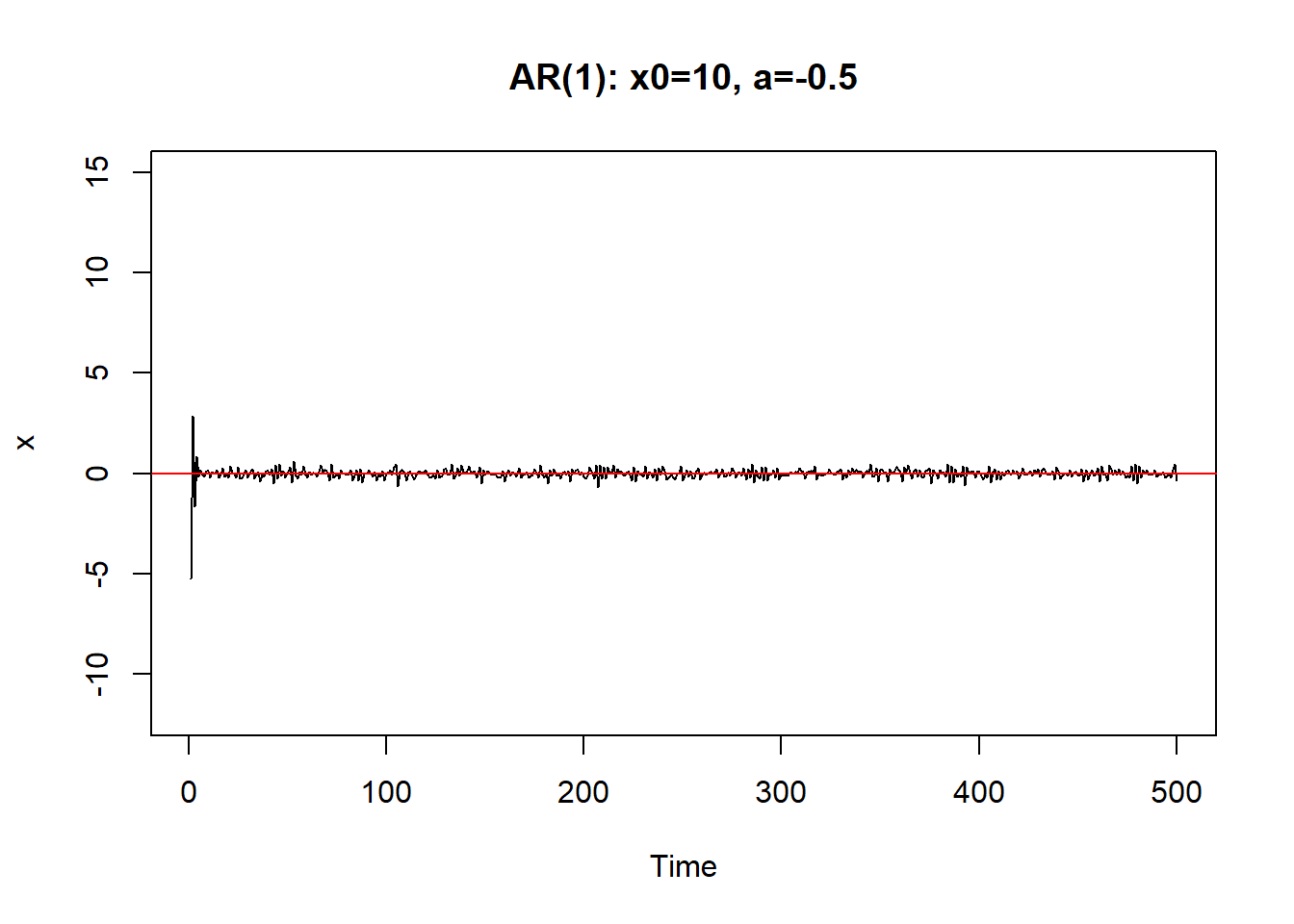
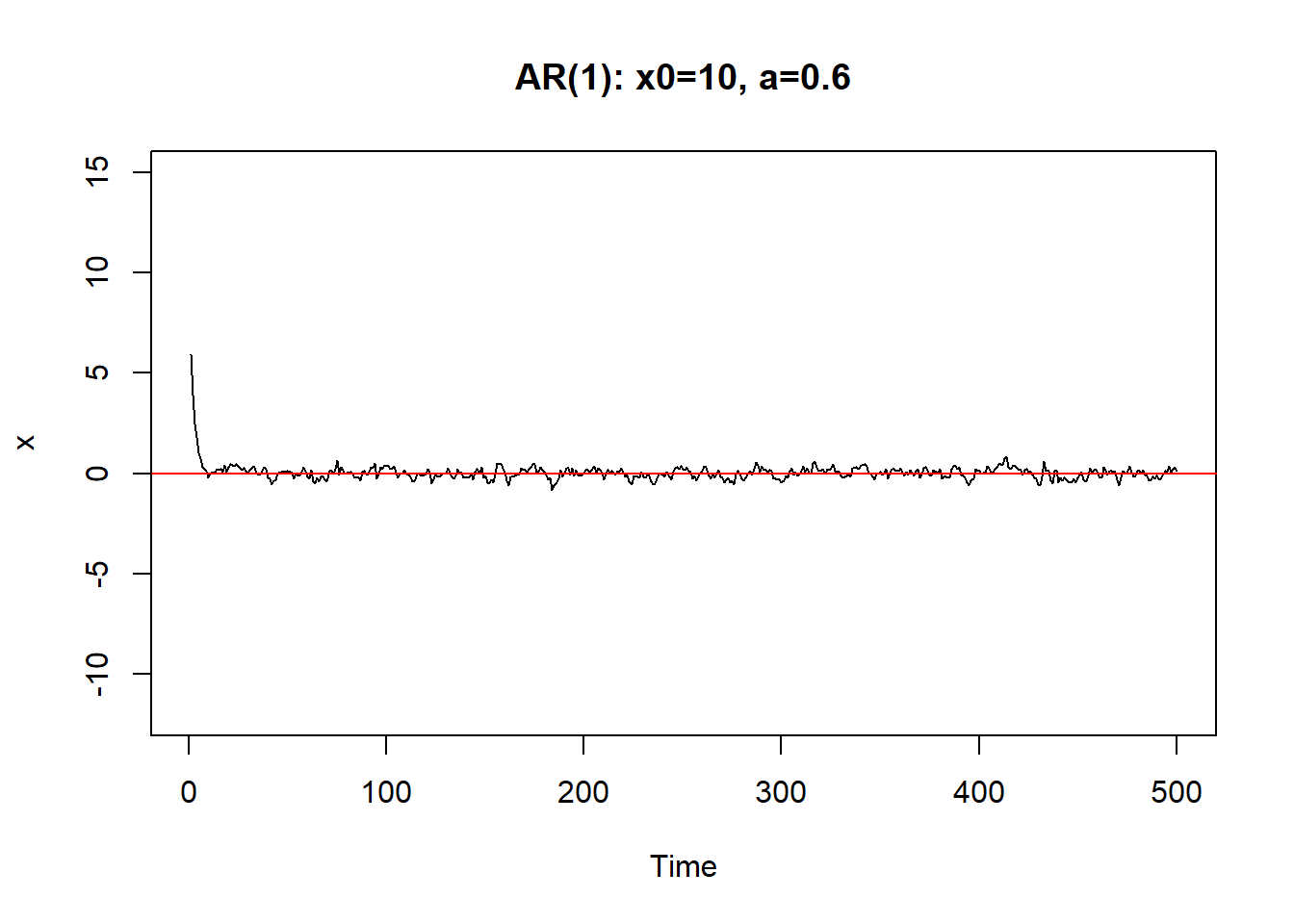
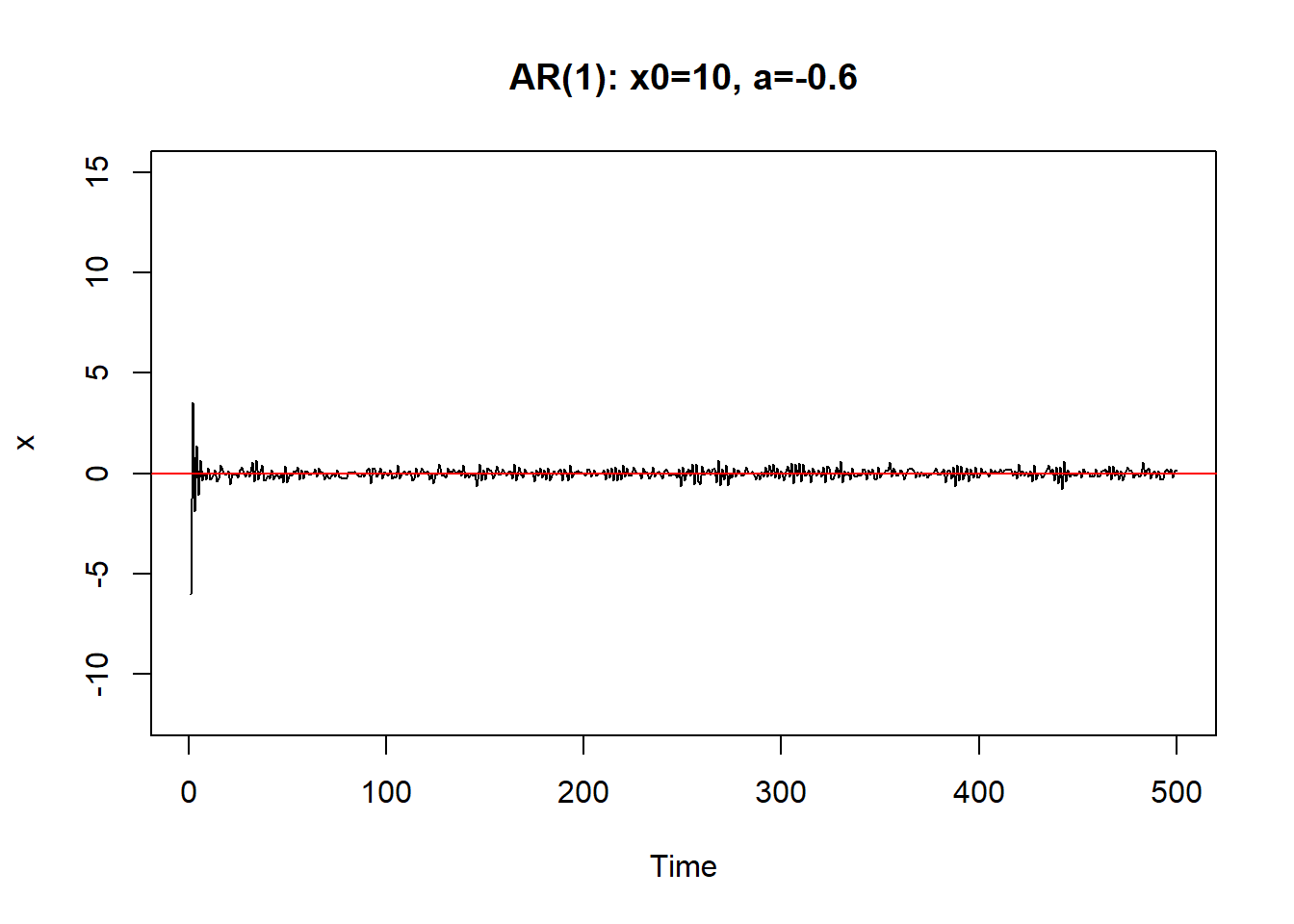
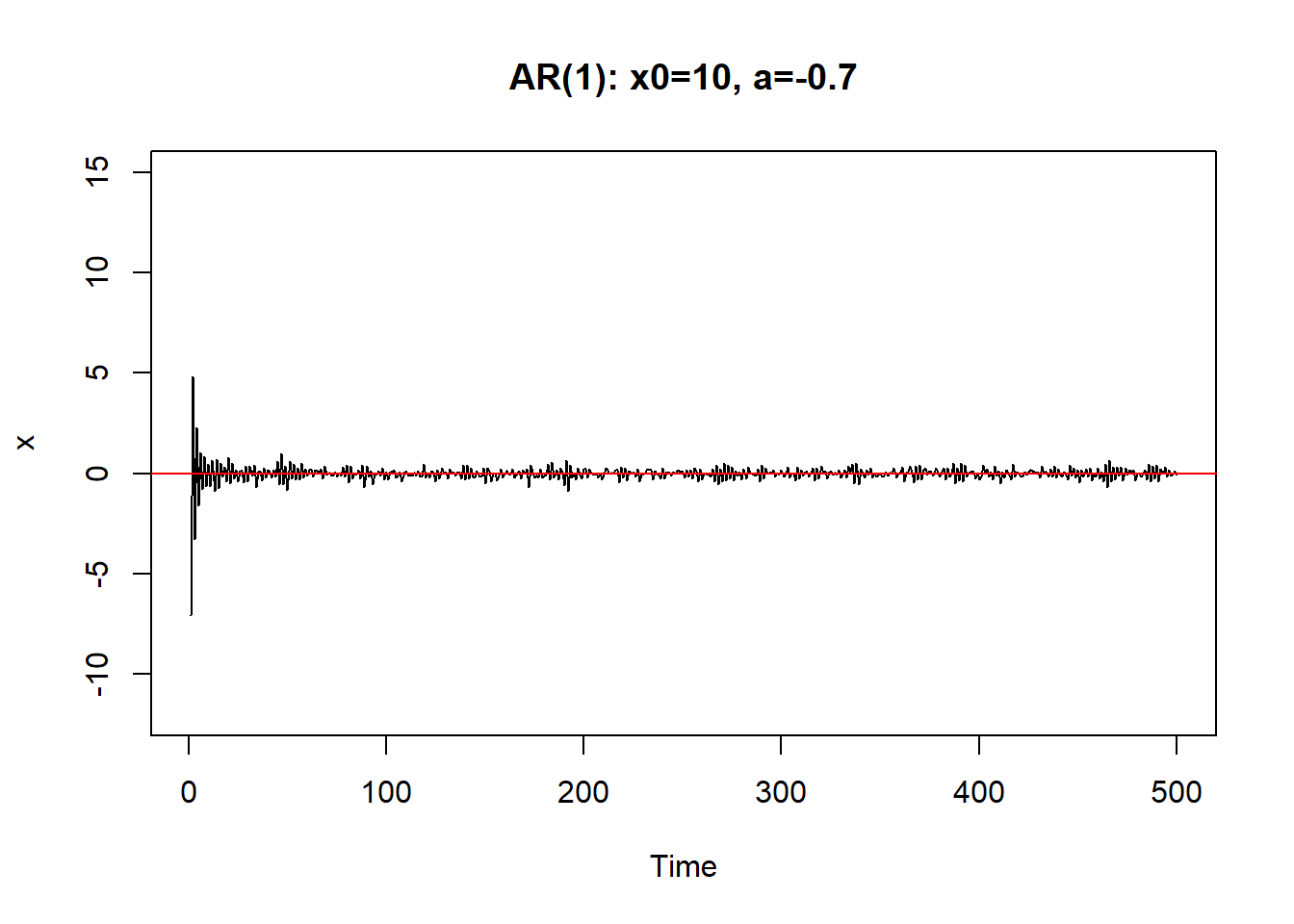
从初值\(X_0\)出发。\(a\)越小，初值影响减小越快。 \(|a|\)接近于1时，初值和前面的\(\varepsilon_{t-j}\)影响减小越慢， 序列振荡。
只要\(|a|<1\)，序列最终可以稳定下来。称系统(8.1)是稳定的。
如果\(a=\pm 1\)则序列振荡越来越大，呈爆炸型。
\(|a|>1\)时序列也不能稳定。 \(|a| \geq 1\)时称(8.1)是非稳定的.
ar1.gen <- function(n, a, sigma=1.0,
plot.it=FALSE, n0=1000,
x0=numeric(length(a))){
n2 <- n0 + n
eps <- rnorm(n2, 0, sigma)
x2 <- filter(eps, a, method="recursive", side=1, init=x0)
x <- x2[(n0+1):n2]
x <- ts(x)
attr(x, "model") <- "AR(1)"
attr(x, "a") <- a
attr(x, "sigma") <- sigma
if(plot.it) plot(x)
x
}
demo.ar1 <- function(){
as <- c(0.1, 0.3, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 0.99, 1.0, 1.001)
x0 <- 10
n <- 500
for(a in as){
for(a1 in c(a, -a)){
x <- ar1.gen(n=n, a=a1, sigma=0.2,
n0=0, x0=x0)
plot(x, main=paste("AR(1): x0=10, a=", a1, sep=""),
ylim=c(-12, 15))
abline(h=0, col="red")
}
}
}
set.seed(106)
demo.ar1()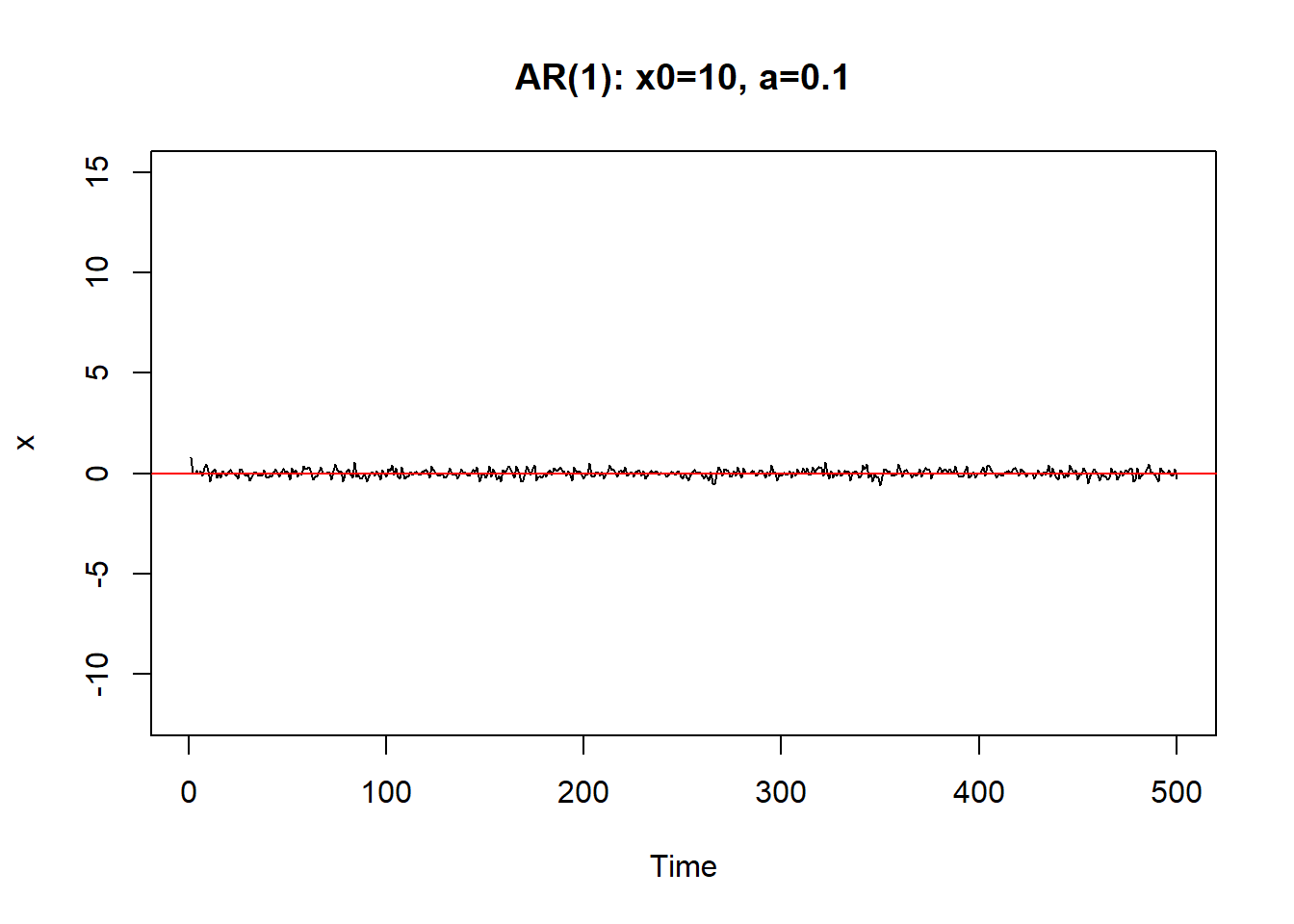
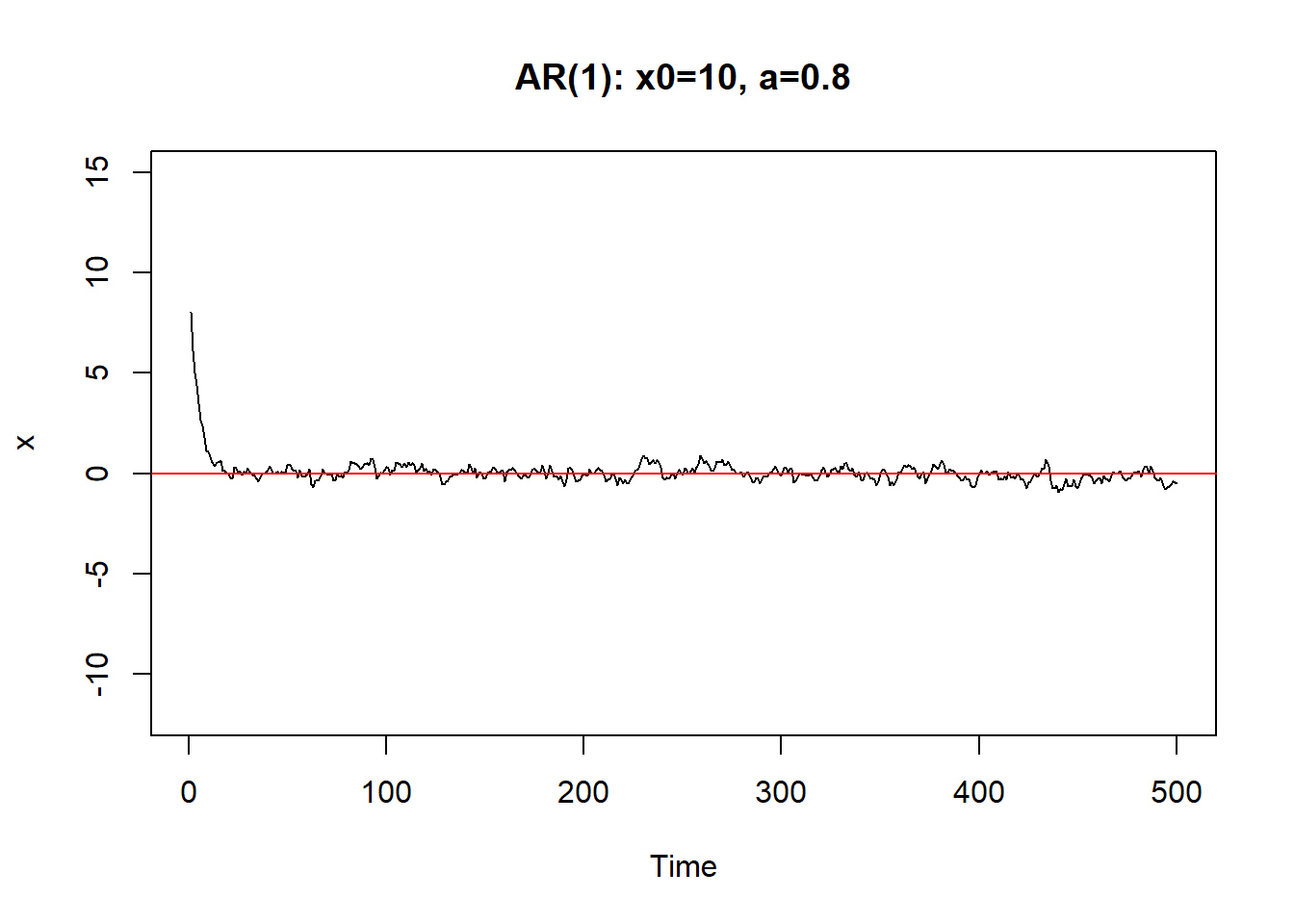
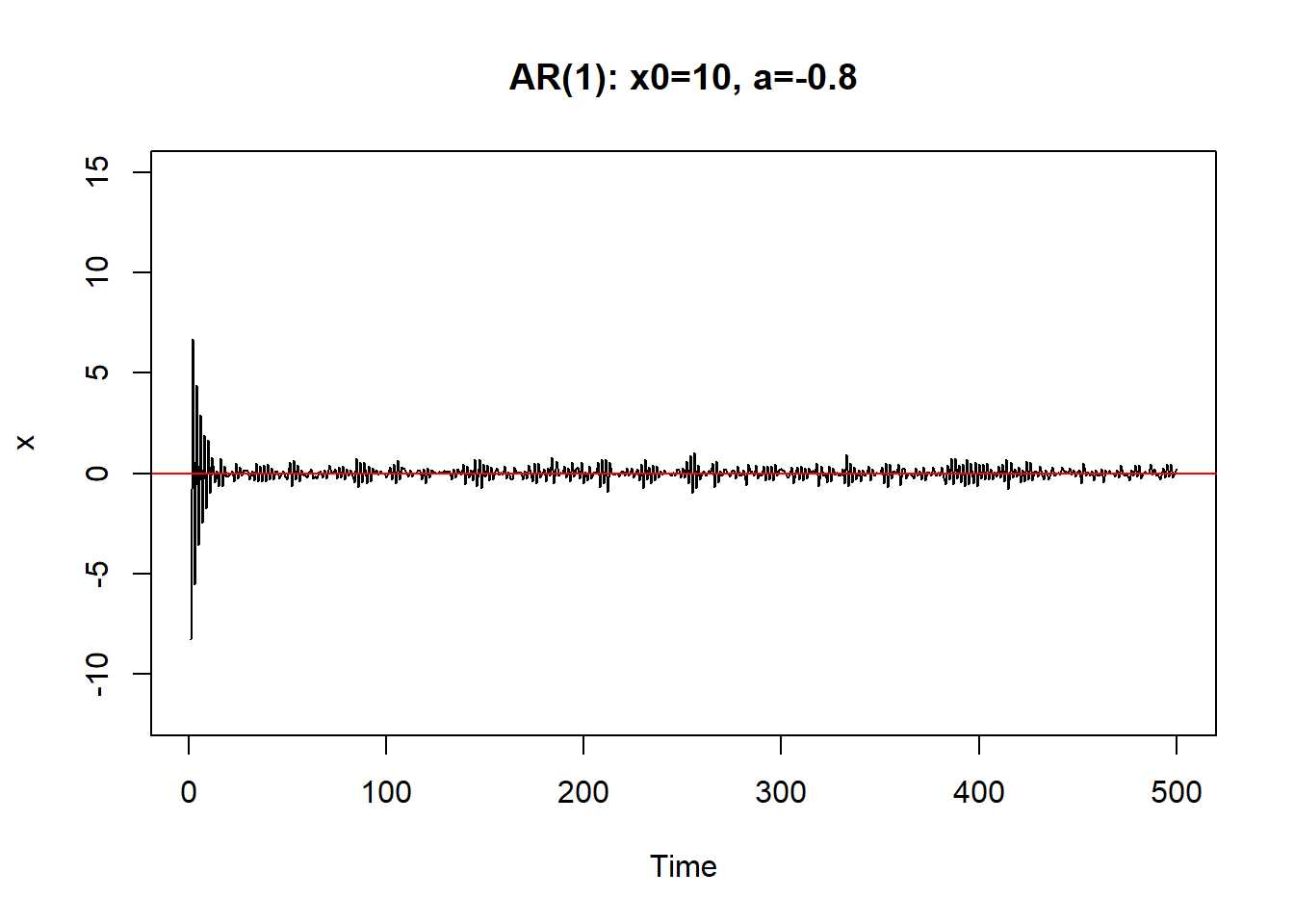
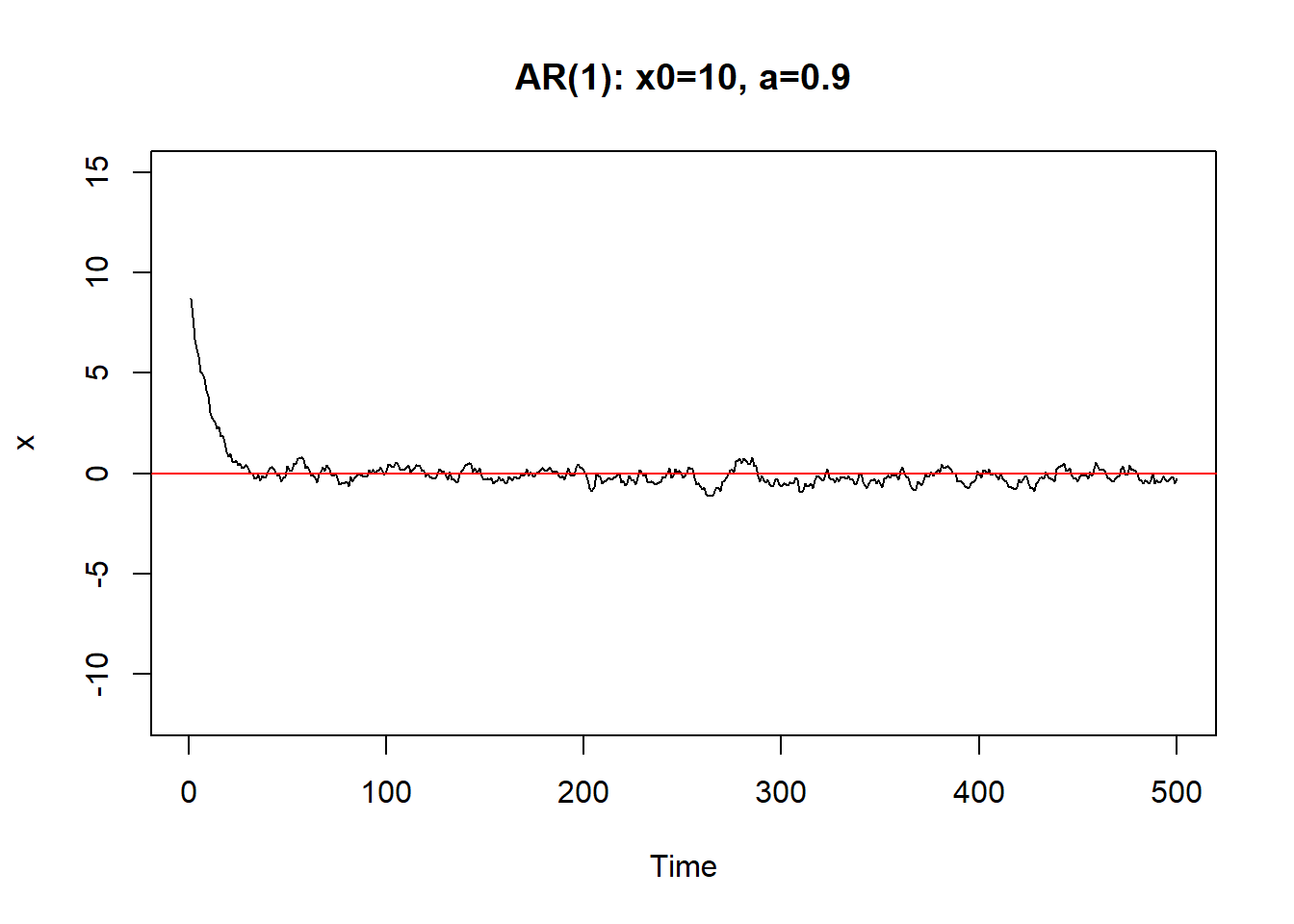
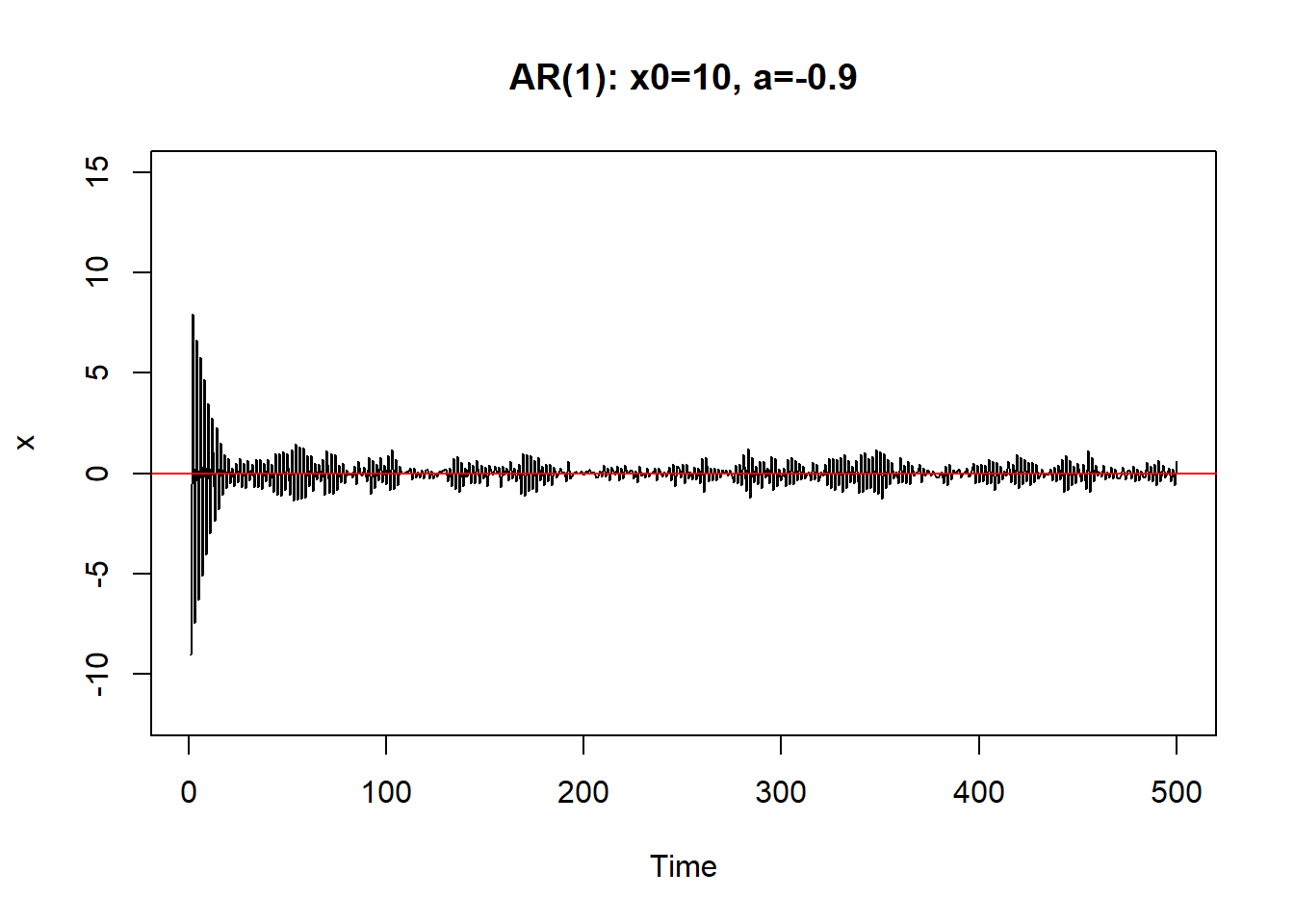
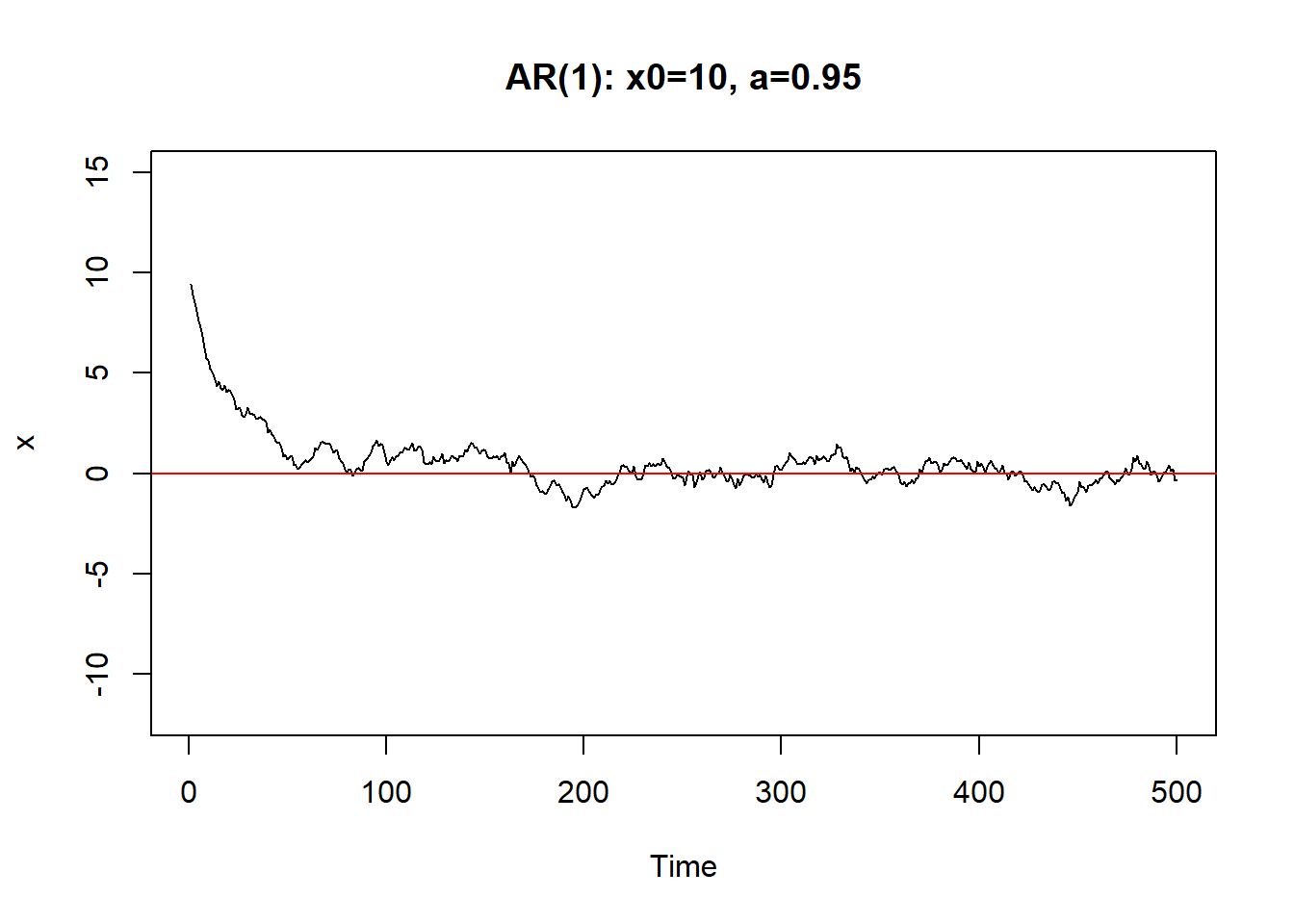
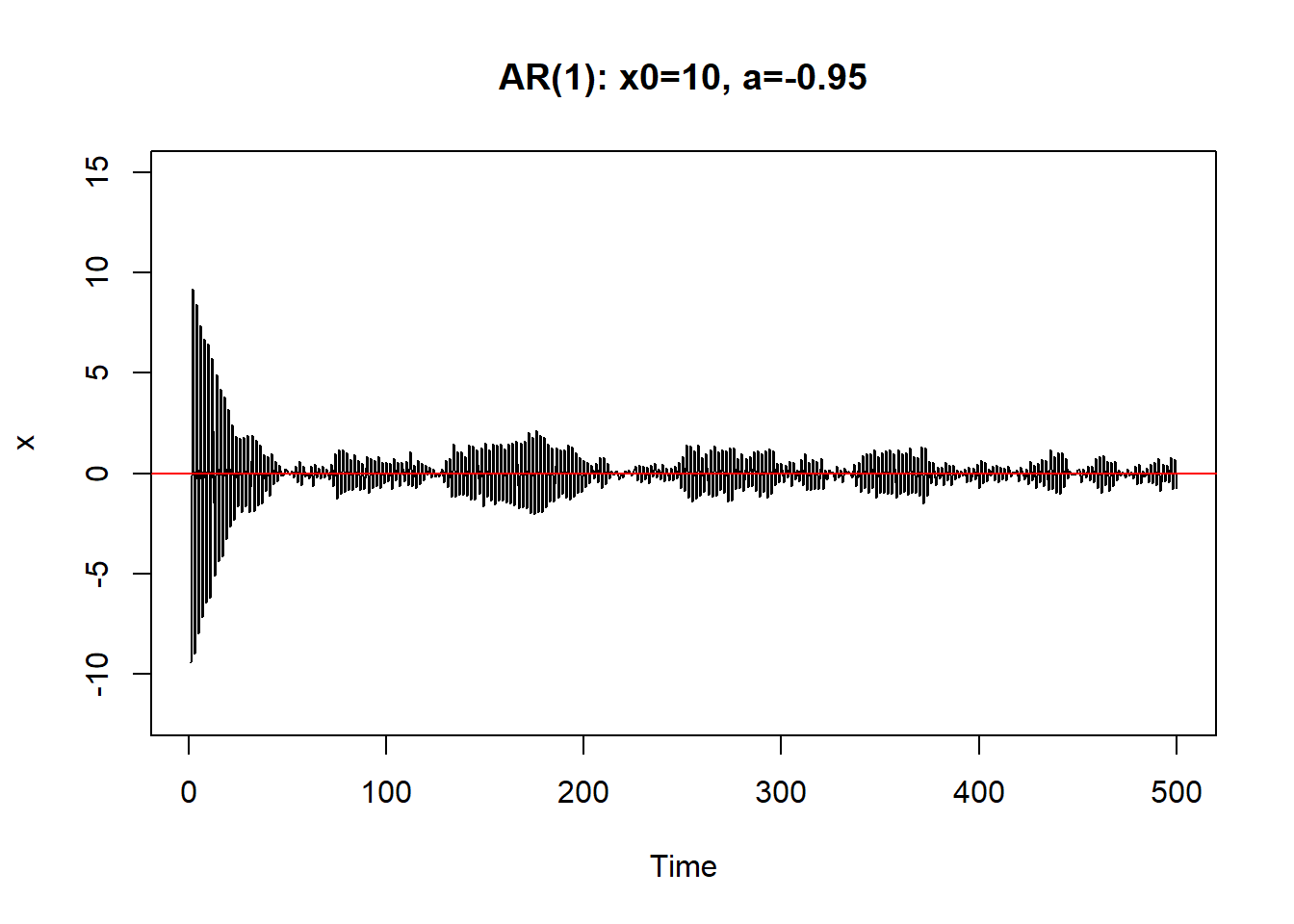
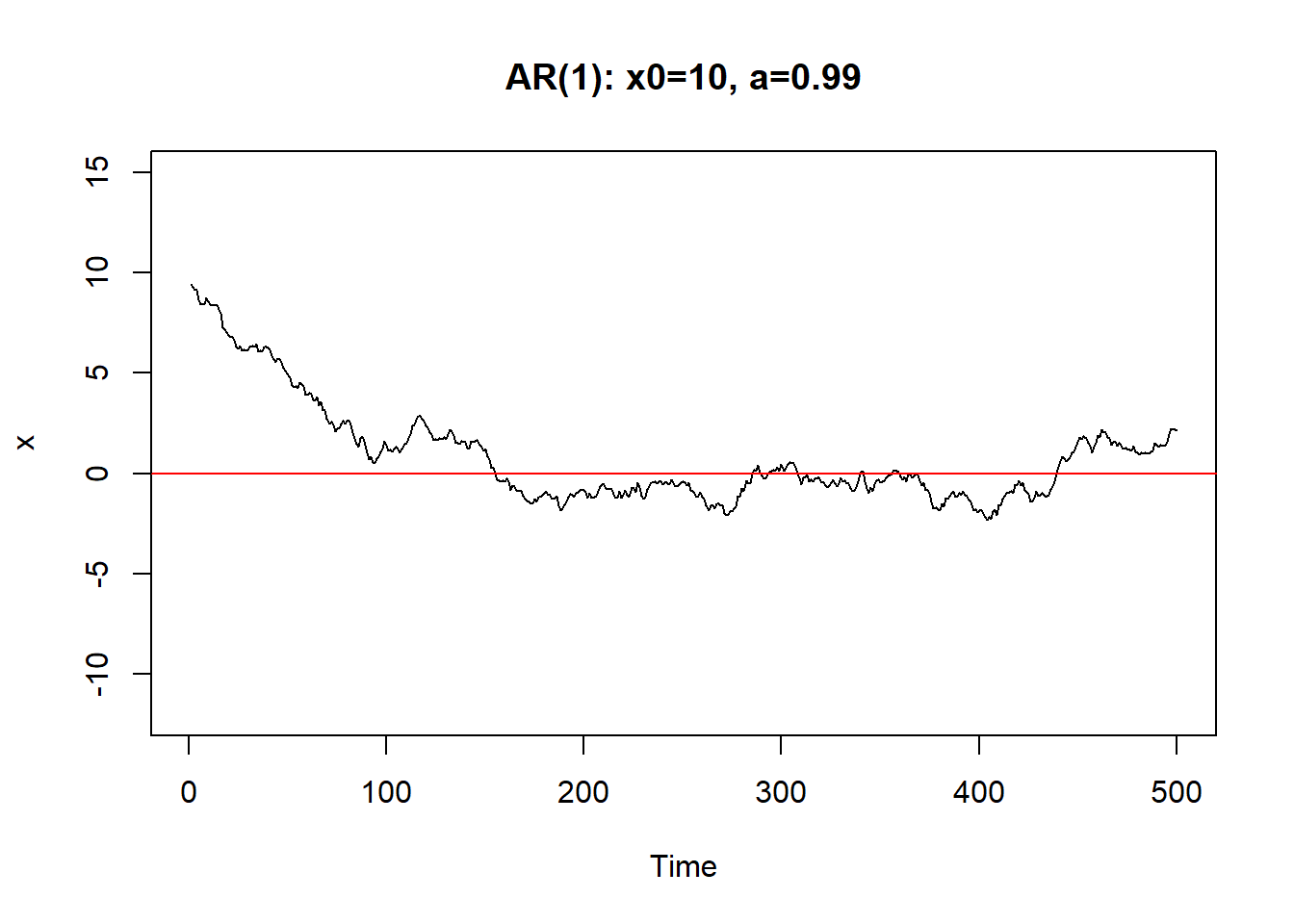
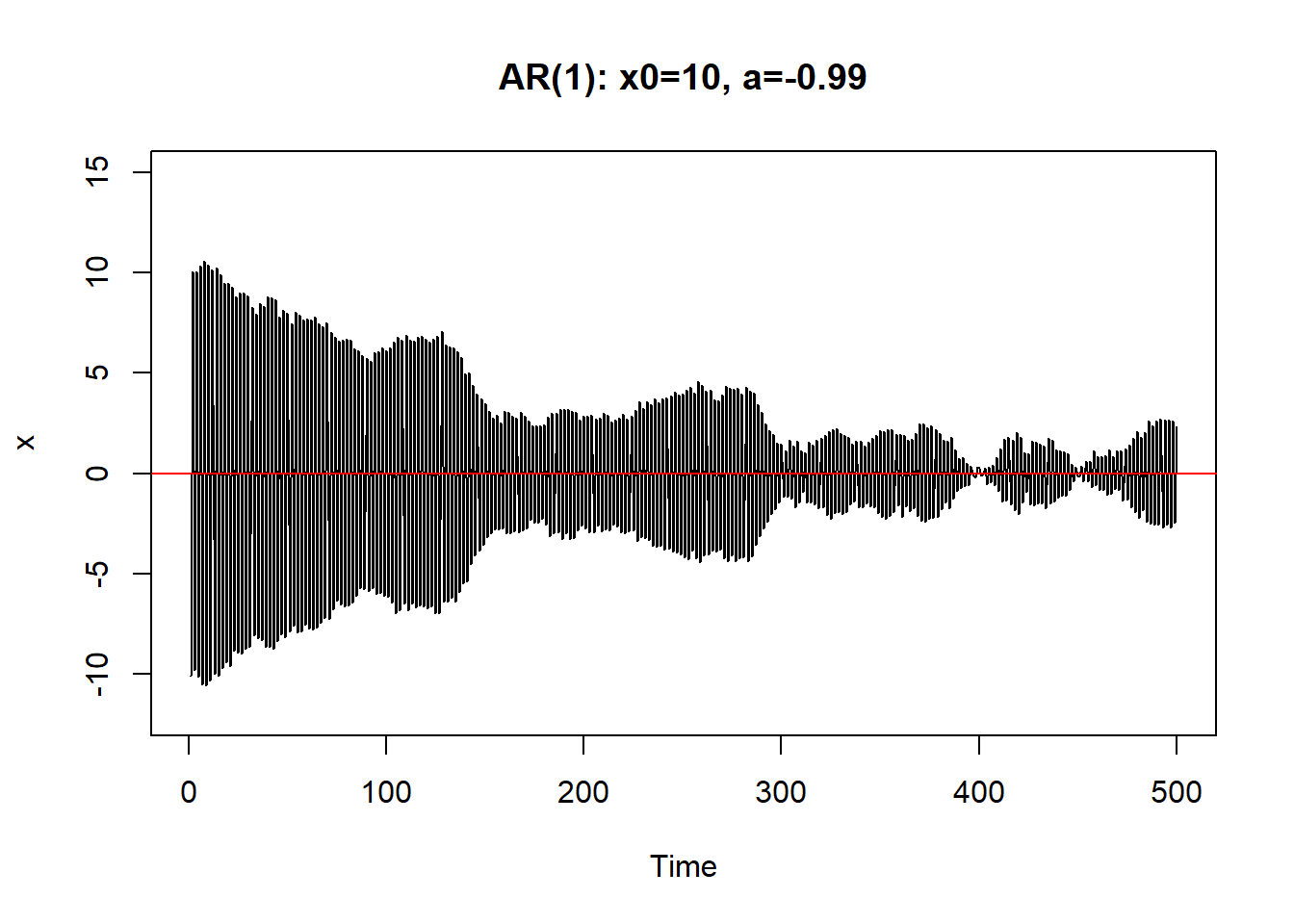
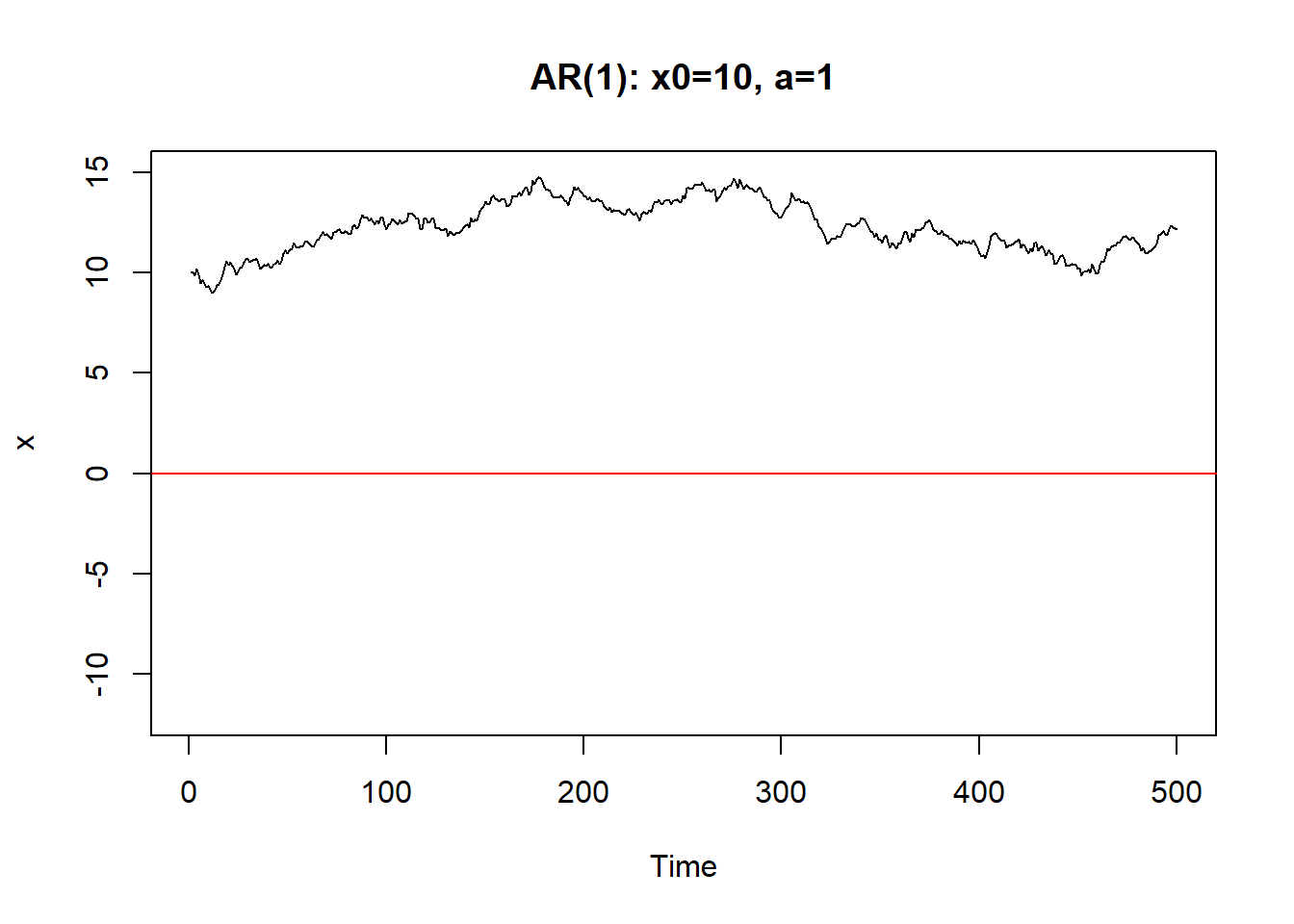
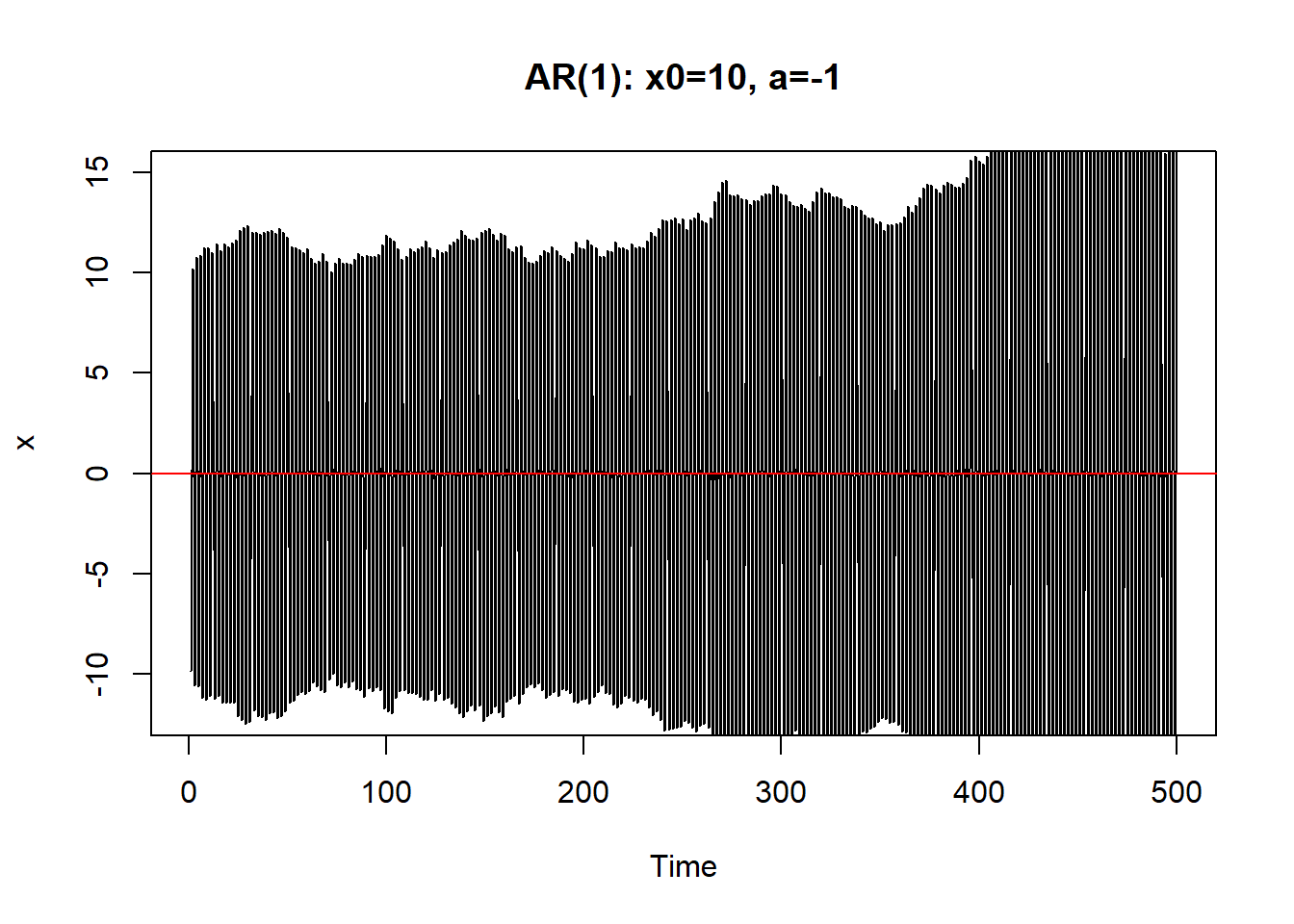
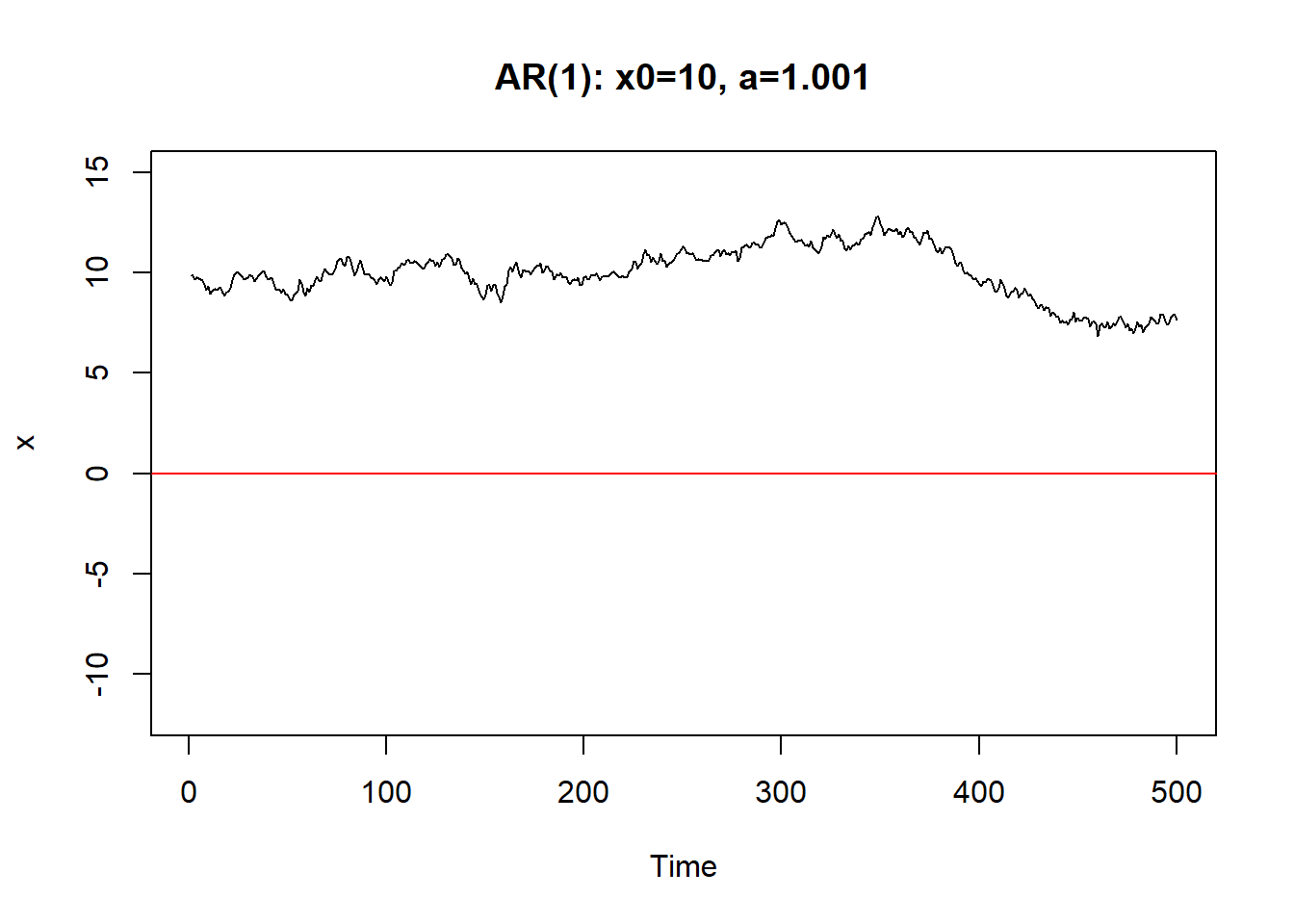
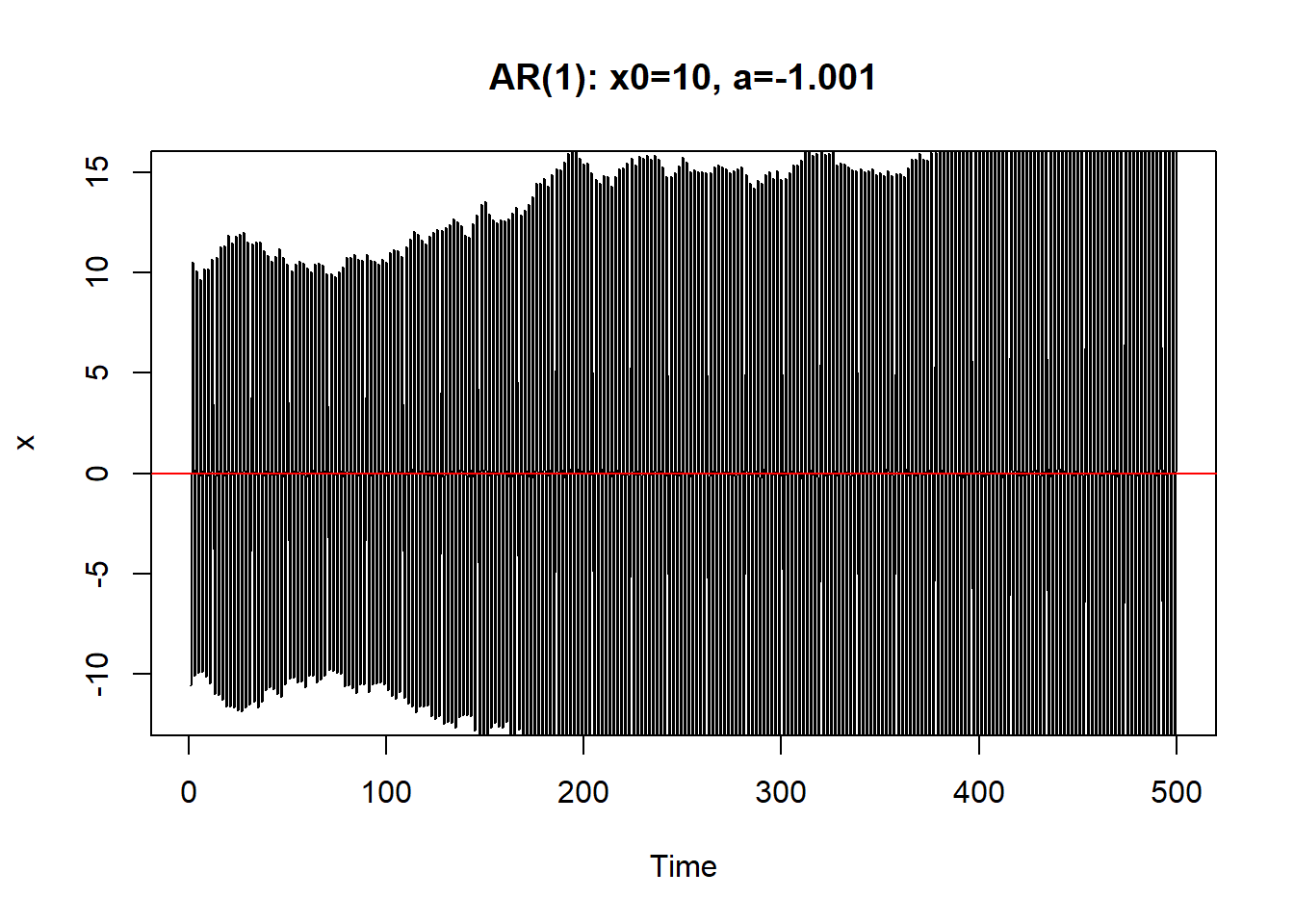
8.1.1 AR(1)的差分方程及平稳解
\(A(z) = 1 - a z\)是差分方程(8.1)的特征多项式。 \(z_1 = \frac{1}{a}\)是特征根。 稳定的充分必要条件是\(|a|<1\)，或\(|z_1|>1\)， 即特征根都在单位圆外。
当\(|a|<1\)时下面的线性序列有定义: \[\begin{align} X_t = \sum_{j=0}^\infty a^j \varepsilon_{t-j}, \quad t \in \mathbb Z \tag{8.2} \end{align}\]
\[\begin{aligned} a X_{t-1} + \varepsilon_t =& a \sum_{j=0}^\infty a^j \varepsilon_{t-1-j} + \varepsilon_t \\ =& \sum_{i=1}^\infty a^i \varepsilon_{t-i} + \varepsilon_t \quad (i = j+1) \\ =& X_t \end{aligned}\] 于是平稳序列(8.2)是非齐次差分方程(8.1)的解， 称为平稳解。
(8.1)的通解为 \[\begin{align} X_t = \sum_{j=0}^\infty a^j \varepsilon_{t-j}, + \xi a^t, \quad t \in \mathbb Z \tag{8.3} \end{align}\] 当\(t \to \infty\)时(8.1)的所有解a.s.收敛到平稳解(8.2)。 收敛速度是负指数速度\(|a|^t\)。 平稳解可以看成系统(8.1)处于稳定状态的情况。 特征根\(\frac{1}{a}\)离单位圆越远，稳定性越好。
8.2 一般AR(\(p\))
定义8.1 如果\(\{\varepsilon_t\}\)是白噪声\(\text{WN}(0,\sigma^2)\), 实数\(a_1,a_2,\dots,a_p\) \((a_p\neq 0)\) 使得多项式\(A(z)\)的零点都在单位圆外: \[\begin{align} A(z)=1-\sum_{j=1}^p a_j z^j \neq 0, \ |z|\leq 1, \tag{8.4} \end{align}\] 则称\(p\)阶差分方程 \[\begin{align} X_t=\sum_{j=1}^p a_j X_{t-j} +\varepsilon_t, \ \ t\in \mathbb Z, \tag{8.5} \end{align}\] 是一个\(p\)阶自回归模型, 简称为AR(\(p\))模型.
满足 AR\((p)\)模型(8.5)的平稳时间序列\(\{X_t\}\)
称为(8.5)的平稳解,
也称作AR(\(p\))序列.
称\(\boldsymbol a = (a_1,a_2,\cdots,a_p)^T\) 是AR\((p)\)模型的自回归系数.
称条件(8.4)是稳定性条件或最小相位条件.
\(A(z)\)称为模型(8.5)的特征多项式。
模型可用推移算子写成
\[\begin{align}
A(\mathscr B) X_t = \varepsilon_t, \quad t \in \mathbb Z
\tag{8.6}
\end{align}\]
8.3 平稳解和通解
8.3.1 AR(\(p\))的平稳解
设多项式\(A(z)\)的互异根是\(z_1,z_2,..,z_k\). 取\(1< \rho < \min\{|z_j|\}\). \(A^{-1}(z)=1/A(z)\) 是\(\{z: |z|\leq \rho \}\)内的解析函数. 从而有Taylor级数 \[\begin{align} A^{-1}(z) = \sum_{j=0}^\infty \psi_j z^j, \ |z| \leq \rho. \tag{8.7} \end{align}\] 由级数(8.7)在\(z=\rho\) 的收敛性得到 \(|\psi_j \rho^j|\to 0\), 当\(j\to \infty\). 于是由 \[\begin{align} \psi_j= o(\rho^{-j}), \ \hbox{ 当} \ j\to \infty \tag{8.8} \end{align}\] 知道\(\{\psi_j\}\)绝对可和. 而且, \(\min\{|z_j|\}\)越大, \(\psi_j\)趋于零越快.
令 \[\begin{aligned} A^{-1}(\mathscr B)=\sum_{j=0}^\infty \psi_j \mathscr B^j. \end{aligned}\] 如果\(\{X_t\}\)是(8.6)的平稳解， 则由定理7.2知 \[\begin{align} X_t = A^{-1}(\mathscr B) A(\mathscr B) X_t = A^{-1}(\mathscr B)\varepsilon_t, \ \ t\in \mathbb Z. \tag{8.9} \end{align}\] 可见平稳解如果存在必然为 \[\begin{align} X_t=A^{-1}(\mathscr B)\varepsilon_t =\sum_{j=0}^\infty \psi_j \varepsilon_{t-j}, \quad t\in \mathbb Z, \tag{8.10} \end{align}\] \(\{\psi_j\}\)称为平稳序列\(\{X_t\}\)的Wold系数。 显然(8.10)是线性平稳列， 将其代入模型(8.6)可以验证其满足模型， 所以\(X_t = A^{-1}(\mathscr B) \varepsilon_t\)是模型(8.6)的唯一的平稳解 （唯一是a.s.意义下）。
8.3.2 Wold系数的递推公式
记\(a_0=-1\)则\(A(z)=-\sum_{j=0}^p a_j z^j\)， \[\begin{aligned} 1 = A(z) A^{-1}(z) = -\sum_{m=0}^\infty \left(\sum_{j=0}^p a_j \psi_{m-j}\right) z^m \end{aligned}\] 故\(\psi_0=1\), \(\sum_{j=0}^p a_j \psi_{m-j} = 0\), \(m>0\)。 于是 \[\begin{aligned} \begin{cases} \psi_0 = 1, \\ \psi_m = \sum_{j=1}^p a_j \psi_{m-j}, & m=1, 2, \dots \\ \psi_m =0, & m<0 \end{cases} \end{aligned}\] 用推移算子表示为 \[ \psi_m =0, m<0; \quad \psi_0 = 1; \quad A(\mathscr B) \psi_m = 0, m \geq 1 . \]