26 潜周期模型
26.1 介绍
实际问题中有很多的数据表现出明显的周期特性. 例如考虑北京地区的气温变化, 以每个小时的平均气温为一个记录数据, 则观测数据\(x_1,x_2,\cdots,x_N\)以每年的\(365\times 24\)小时为一个大周期, 以每天的24小时为一个小周期. 对于这种具有明显周期的数据可以考虑用潜周期模型(26.1)描述.
在信号处理领域, 余弦波信号是一种常见信号. 在随机干扰背景下能否成功地检测出 各信号的角频率成分及其振幅是一个有实际意义的问题. 通常的余弦波信号也是用潜周期模型(26.1)描述的.
\[\begin{align} x_t = \sum_{j=1}^k A_j\cos(\omega_j t + \phi_j) + \xi_t, \ \ t \in \mathbb N_+, \tag{26.1} \end{align}\] 其中 \(0< \omega_1<\omega_2<\cdots<\omega_k\leq \pi\). 正数\(A_j\)是相应于第\(j\)个角频率\(\omega_j\)的振幅. 对\(\omega_j >0\), 从 \[ \cos(\omega_j (t + 2\pi/\omega_j) + \phi_j) = \cos(\omega_j t + \phi_j), \ \ t\in \mathbb Z, \] 知道相应于角频率\(\omega_j\)的周期是\(T_j = 2\pi/ \omega_j\). \(\phi_j \in [0, 2\pi)\)是相应于角频率\(\lambda_j\)的初始相位. \(\{\xi_t\}\)是一个零均值的线性平稳序列, 被称为有色噪声. 它是对周期叠加项 \[\begin{align} y_t = \sum_{j=1}^k A_j \cos(\omega_j t + \phi_j) \tag{26.2} \end{align}\] 的随机干扰. 当\(k=0\)定义\(\sum_{j=1}^0 \equiv 0\). 这时\(\{x_t\}=\{\xi_t\}\)是平稳序列.
满足模型(26.1)的时间序列被称为潜频率或潜周期序列. 在模型(26.1)中, 可以不要求\(\omega_1>0\). 但是\(\omega_1=0\)就相当于(26.1)的右边有一个常数项. 由于在实际问题的计算中, 需要先对原始数据进行零均值化, 所以常数项实际上是不起作用的. 模型(26.1)中还可以要求振幅\(\boldsymbol A =(A_1, A_2,\cdots,A_q)\)和初相位\(\boldsymbol\phi = (\phi_1, \phi_2,\cdots, \phi_q)\)是随机的. 但是由于在时间序列分析中, 我们只能得到时间序列的一次实现, 因而在数据中\(\boldsymbol A\) 和 \(\boldsymbol\phi\)的取值都是常数. 这样就没有必要把\(\boldsymbol A\)和\(\boldsymbol\phi\)当作随机向量来考虑了. 所以, 我们认为\(A_j\), \(\phi_j\)是常数.
在模型(26.1)中, 用\(\sigma = \sqrt{\text{Var}(\xi_t)}\)表示噪声项的标准差. 称 \[\begin{align} \eta_j = A_j/\sigma \tag{26.3} \end{align}\] 为相应于角频率\(\lambda_j\)的信噪比(信号和噪声的比率). 明显, 信噪比\(\eta_j\) 越大, 说明频率项\(A_j\cos( \omega_jt + \phi_j)\)的作用越大, 在给定的数据中越容易发现或估计出相应的角频率\(\omega_j\)和振幅\(A_j\). 以下的分析说明, 无论是怎样的信噪比, 只要有较大的数据量都可以十分准确地估计出每个角频率、振幅和初始相位.
模型(26.1)是三角函数项的叠加, 所以又被称为调和模型. 它在气象, 天文, 机械振动, 共振研究和调和信号处理方面有广泛的应用.
如果用三角公式把模型(26.1)进行展开, 可以得到等价的模型 \[\begin{align} x_t = \sum_{j=1}^k [a_j \cos(\omega_j t) + b_j \sin(\omega_j t) ] + \xi_t , \ \ t\in \mathbb N_+, \tag{26.4} \end{align}\] 其中 \[ a_j = A_j \cos(\phi_j), \ \ b_j = -A_j\sin(\phi_j). \] 如果\(\{\omega_j \}\)已知, 就变成了一个线性回归问题。
模型(26.1)还可以写成复的形式.
在模型(26.1)中, 定义
\[\begin{align}
& q =2k \\ \\
& \lambda_j = \begin{cases}
\omega_j, \ \ & j =1,2,\cdots,k \\
-\omega_{j-k}, & j= k+1, k+2,\cdots,q.
\end{cases} \\ \\
& \alpha_j= \begin{cases}
\frac12 A_j \exp(i\phi_j), \ \ & j=1,2,\cdots,k \\
\frac12 A_{j-k} \exp( -i \phi_{j-k}), \ \ & j=k+1,k+2,\cdots, q.
\end{cases}
\tag{26.5}
\end{align}\]
就得到
\[\begin{align}
x_t = \sum_{j=1}^q
\alpha_j \exp(it \lambda_j)+ \xi_t,
\ \ t \in \mathbb N_+.
\tag{26.6}
\end{align}\]
模型(26.6)是复值潜周期模型.
这个模型更方便进行理论推导。
为了说话的方便, 对潜周期模型(26.6)通常还要求如下的条件:
(1) \(\{\xi_t\}\)是一个零均值线性平稳序列,
它是对周期叠加项
\[\begin{align}
y_t = \sum_{j=1}^q \alpha_j \exp(it \lambda_j)
\tag{26.7}
\end{align}\]
的随机干扰.
(2) 实向量\(\boldsymbol\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_q)^T\)满足
\[\begin{align}
-\pi < \lambda_1 < \lambda_2 < \cdots
< \lambda_q \leq \pi.
\tag{26.8}
\end{align}\]
(3) 复值向量\(\boldsymbol\alpha=(\alpha_1,\alpha_2,\cdots,\alpha_q)^\tau\)中的每一个分量不等于零:
\[
\prod_{j=1}^q \alpha_j \neq 0 .
\]
当\(q \geq 1\), \(\boldsymbol \lambda\)是潜频率序列\(\{x_t\}\)的角频率, \(\boldsymbol\alpha\) 是\(\{x_t\}\)的振幅. 对于\(\lambda_j \neq 0\), 由于 \[ \exp \left( i \lambda_j (t+ 2\pi/\lambda_j) \right) = \exp(i\lambda_j t ), \ \ t \in \mathbb Z, \] 所以相应于角频率\(\lambda_j\)的周期是\(T_j = 2\pi / \lambda_j\), 振幅是\(\alpha_j\).
满足模型(26.6)的时间序列也被称为潜频率序列. 在模型(26.6)中, 只有潜频率序列\(\{x_t\}\)是可以观测的. 如果观测序列\(\{x_t\}\)和随机干扰项 \(\{\xi_t\}\)都是实值的, 由(26.7)定义的\(\{y_t\}\)就是实值的. 这时如果设实数\(a_j\), \(b_j\)使得\(\alpha_j = a_j +i b_j\), 利用三角公式就可以得到 \[\begin{align} y_t = & \sum_{j=1}^q \alpha_j \exp( i\lambda_jt) = \sum_{j=1}^q (a_j+ ib_j) [\cos(\lambda_j t) +i \sin(\lambda_j t) ] \\ = & \sum_{j=1}^q [a_j \cos(\lambda_j t) - b_j \sin(\lambda_j t) ] + i \sum_{j=1}^q [a_j \sin(\lambda_j t) + b_j \cos(\lambda_j t) ]\\ =& \sum_{j=1}^q [a_j \cos(\lambda_j t) - b_j \sin(\lambda_j t) ]. \tag{26.9} \end{align}\] 于是, 利用 \[\begin{align} \sum_{j=1}^q [a_j \sin(\lambda_j t) + b_j \cos(\lambda_j t) ] = 0, \ \ t \in \mathbb N_+, \tag{26.10} \end{align}\] 对(26.9)进行适当的整理合并, 就得到(26.2). 参数之间的关系仍然由(26.5)式决定.
对实值的潜周期模型(26.1)进行统计分析不如对复值潜周期模型(26.6)的统计分析来的方便. 如果对复值模型 (26.6)给出了参数\(q\), \(\boldsymbol \lambda\) 和\(\boldsymbol \alpha\)的估计, 通过参数之间的变换(26.5)就可以得到模型(26.1)的参数估计.
26.2 潜周期模型的参数估计
为了分析潜周期模型中有色噪声项对周期信号\(\{y_t\}\)影响的大小, 我们需要了解噪声\(\{\xi_t\}\)的加权部分和的收敛性质.
定理26.1 设\(\{\varepsilon_t\}\)是独立同分布的\(\text{WN}(0,\sigma^2)\), 线性滤波器\(\{c_j\}\)满足 \[\begin{align} \sum_{j=0}^\infty j |c_j|< \infty. \tag{26.11} \end{align}\] 平稳噪声\(\{\xi_t\}\)由 \[\begin{align} \xi_t = \sum_{j=0}^\infty c_j \varepsilon_{t-j} \tag{26.12} \end{align}\] 定义, 则有如下的结果 \[ \limsup_{N \to \infty} \frac{1}{\sqrt{N\ln N}} \sup_{\lambda} \left| \sum_{t=1}^N \xi_t e^{-i\lambda t} \right| \leq \sqrt{2\pi \sup_{\lambda} f(\lambda)}, \ \text{a.s.} , \] 其中 \[ f(\lambda) = \frac{\sigma^2}{2\pi} \left|\sum_{j=0}^\infty c_j e^{i j \lambda} \right|^2 \] 是\(\{\xi_t\}\)的谱密度.
定理26.1是对模型(26.6)进行统计分析的基本定理. 除了它, 我们还需要了解Dirichlet 核 \[ D_N(\lambda) = \frac{\sin(N\lambda/2)}{\sin(\lambda/2) } , \ \lambda \in (-\pi,\pi] \] 的基本性质. \(D_N(\lambda)\)是偶函数, 在\(\lambda = 0\)取得最大值\(D_N(0)=N\), 在区间\([0,\pi / 2N]\)上单调减少, 利用不等式 \(x \geq \sin x > 2x/\pi\), \(x \in (0,\pi/2)\), 得到 \[\begin{align} D_N(x) \geq D_N(\pi/2N) = \frac{\sin(\pi/4)}{\sin(\pi/4N)} \geq \frac{2\sqrt{2}N}{\pi}, \ x \in [0, \frac{\pi}{2N}]. \tag{26.13} \end{align}\] 另一方面, 对于\(\lambda \geq 1/ (2\sqrt{N})\), \[\begin{align} |D_N(\lambda) | \leq \left( \sin(\frac{1}{4\sqrt{N}})\right)^{-1} \leq \frac{4\pi \sqrt{N}}{2} = 2\pi \sqrt{N}. \tag{26.14} \end{align}\]
26.2.1 复值潜周期模型的初估计
在利用数据进行参数估计前应当先对数据进行零均值化处理, 以下设数据已经零均值化. 对于来自复值潜周期模型(26.6)的观测数据\(x_1,x_2,\cdots,x_N\), 引入函数 \[\begin{align} S_N(\lambda) = \sum_{t=1}^N x_t e^{-i\lambda t}, \tag{26.15} \end{align}\] 这称为\(\{x_t, t=1,2,\dots,N \}\)序列的离散傅里叶变换。 类似地定义 \[ C_N(\xi, \lambda) = \sum_{t=1}^N \xi_t e^{-i\lambda t}, \ \ C_N(\lambda) = \sum_{t=1}^N e^{-i\lambda t}. \] 利用求和公式 \[ C_N(-\lambda) = D_N(\lambda) \exp(i \lambda (N+1)/2), \] 得到 \[\begin{align} |C_N(\lambda)| = |D_N(\lambda)|. \tag{26.16} \end{align}\] 于是有 \[\begin{align} S_N(\lambda) =& \sum_{t=1}^N y_t e^{-i\lambda t} + \sum_{t=1}^N \xi_t e^{-i\lambda t} \\ =& \sum_{j=1}^q \alpha_j \sum_{t=1}^N \exp(i(\lambda_j -\lambda)t) + C_N(\xi, \lambda) \\ =& \sum_{j=1}^q \alpha_j C_N(\lambda - \lambda_j) + C_N(\xi, \lambda). \tag{26.17} \end{align}\] 由于\(S_N(\lambda)\), \(C_N(\lambda)\)和\(C_N(\xi,\lambda)\)都是\(\lambda\)的周期为\(2\pi\)的函数, 为说话方便引入 \[\begin{align} \lambda_{q+1} = \lambda_{1} + 2\pi, \ \ \lambda_0 = \lambda_q - 2 \pi. \tag{26.18} \end{align}\]
对于角频率\(\lambda_j\), \((1\leq j \leq q)\), 定义 \[\begin{align} \delta = \min_{1 \leq j \leq q} ( \delta_j ), \ \text{ 其中 } \ \ \delta_j = \min\{|\lambda_j - \lambda_{j+1}|, |\lambda_j - \lambda_{j-1}| \}. \tag{26.19} \end{align}\]
如果样本量\(N\)充分大, 且使得 \[ \delta_j \leq \frac{1}{\sqrt{N}}, \] 我们就可以检测出\(\lambda_j\). 实际上, 在\(\lambda_j\)的\(\pi/2N\)邻域内, 利用(26.13)和(26.14)得到 \[\begin{align} |S_N(\lambda)| &\geq |\alpha_j C_N(\lambda -\lambda_j)| - \sum_{l \neq j} |\alpha_l C_N(\lambda - \lambda_l)| - |C_N(\xi, \lambda)| \\ &\geq |\alpha_j D_N(\lambda - \lambda_j)| - \sum_{l \neq j} |\alpha_l| 2\pi \sqrt{N} - |C_N(\xi, \lambda)| \\ &\geq |\alpha_j| 2 \sqrt{2}N/\pi - O(\sqrt{N \ln N}). \\ &\geq 0.9 |\alpha_j| N, \ \ \text{a.s.}, \tag{26.20} \end{align}\] 而在所有的\(\lambda_j\), \(0 \leq j \leq q+1\) 的\(1/(2\sqrt{N})\)邻域外, 也就是在集合 \[\begin{align} {\mathcal A} = \{\lambda \in [-\pi, \pi] : \ |\lambda - \lambda_j| \geq 1/(2\sqrt{N}), \ j = 0,1,2,\cdots,q+1 \} \tag{26.21} \end{align}\] 上, 利用(26.14)和定理26.1 得到 \[\begin{align} |S_N(\lambda)| \leq& \sum_{l =1}^q |\alpha_l C_N(\lambda_l - \lambda)| + |C_N(\xi, \lambda)| \\ &\leq \sum_{l =1} |\alpha_l| 2 \pi \sqrt{N} + |C_N(\xi, \lambda)| \\ &= O(\sqrt{N\ln N}). \tag{26.22} \end{align}\] 于是看出当\(N\)充分大后, 实值连续函数\(|S_N(\lambda)|\)在区间\([-\pi, \pi]\)上的图形具有如下的形状:
\(|S_N(\lambda)|\)在每个\(\lambda_j\)的\(1/(2\sqrt{N})\)邻域内有一峰群, 其最高峰的高度大于 \(0.9|\alpha_j| N\). 最高峰的下面隐藏着角频率\(\lambda_j\).
在所有的\(\lambda_j\)的\(1/(2\sqrt{N})\)邻域外, 也就是在集合\({\mathcal A}\)上, \(|S_N(\lambda)| = O(\sqrt{N\ln N}).\)
峰群的个数就是潜周期模型中的周期(或角频率)个数的估计.
根据\(|S_N(\lambda)|\) 的图形形状, 可以给出潜周期模型(26.6)中的角频率个数\(q\), 角频率向量 \(\boldsymbol \lambda\)和振幅向量 \(\boldsymbol \alpha\)的估计方法如下.
由于很难把\(|S_N(\lambda)|\)的所有取值计算出来, 为了节约计算时间, 同时也能够大致的保持\(|S_N(\lambda)|\)的图形, 可以采用如下的离散化计算方法.
26.2.1.1 方法一
当潜周期模型中的各振幅\(\alpha_j\)的绝对值差别不大, 并且平稳噪声\(\{\xi_t\}\) 的谱密度\(f(\lambda)\)没有明显的峰值时可以采用本方法.
取\(A_N > 0\)满足: 当\(N \to \infty\)时, \(A_N=O(N^{0.75})\).
第一步: 定义\(\mu(j)={j\pi}/(2N)-\pi\), 计算 \[\begin{align} d(\mu(j))=|S_N(\mu(j))|, \ \ j=1,2,\cdots,4N. \tag{26.23} \end{align}\] 在下面计算中, 如果最大值不惟一, 可任取其中一个.
第二步:
计算\(d(\mu(j))\)的最大值\(d(\mu(j_1))\).
当\(d(\mu(j_1)) \leq A_N\),
定义\(\hat q=0\), 停止计算.
否则, 定义
\[
{\mathcal A}(1)
= \left\{
\lambda \in (-\pi,\pi]:
\ 1/\sqrt{N} \leq |\lambda - \mu(j_1)|
\leq 2\pi - 1/\sqrt{N}\right\}.
\]
在\({\mathcal A}(1)\)中,
计算\(d(\mu(j))\)的最大值\(d(\mu(j_2))\).
当\(d(\mu(j_2)) \leq A_N\),
定义\(\hat q=1\),
\(\hat \lambda_1 = \mu(j_1)\), 停止计算.
依次类推.
当\(d(\mu(j_l))\)在
\[\begin{aligned}
& {\mathcal A}(p-1) \\
=& \left \{\lambda \in (-\pi,\pi] :
\ 1/\sqrt{N}\leq
|\lambda - \mu(j_l)|
\leq 2\pi - 1/ \sqrt{N},
l =1,2,\cdots,p-1 \right \}
\end{aligned}\]
中的个最大值\(d(\mu(j_p))>A_N\), 在
\[\begin{aligned}
& {\mathcal A}(p) \\
=& \left\{
\lambda \in (-\pi,\pi]:
\ 1/\sqrt{N}
\leq |\lambda - \mu(j_l)|
\leq 2\pi - 1/\sqrt{N},
l =1,2,\cdots,p \right \}
\end{aligned}\]
中的最大值\(d(\mu(j_{p+1})) \leq A_N\)时,
定义\(q\)的估计为 \(\hat q = p\).
并将最大值点\(\mu(j_1), \mu(j_2),\cdots,\mu(j_{\hat q})\) 从小到大重排后得到角频率\(\boldsymbol \lambda\)的初估计
\[\begin{align}
{\hat \lambda}
= ({\hat \lambda}_1,
{\hat \lambda}_2,\cdots,
{\hat \lambda}_{{\hat q}(N)}).
\tag{26.24}
\end{align}\]
26.2.1.2 方法二
当潜周期模型中的各振幅\(\alpha_j\)的绝对值有较大的差别, 但是平稳噪声\(\{\xi_t\}\)的谱密度\(f(\lambda)\)没有明显的峰值时可以采用本方法.
取正整数 \(A_N >0\)满足: 当\(N \to \infty\), \(A_N=o(N)\)和\(\sqrt{N\ln N}=o(A_N)\).
第一步: 定义\(\mu(j) = {j\pi}/(2N) - \pi\). 计算 \[\begin{align} d(\mu(j)) = |S_N(\mu(j)) - S_N(\mu(j-6))|, \ \ j=1,2,\cdots,4N. \tag{26.25} \end{align}\]
第二步和方法一中的第二步相同. 最后得到角频率向量\(\boldsymbol\lambda\)的初估计(26.24).
26.2.1.3 方法三
当 潜周期模型中的各振幅\(\alpha_j\)的绝对值差别较大, 并且平稳噪声\(\{\xi_t\}\)的谱密度\(f(\lambda)\)有陡峭的峰值时可以采用本方法.
第一步: 取正数\(B_0 \in (1,3\sqrt{2})\), 定义\(\mu(j) = j\pi/(2N) - \pi\). 计算 \[\begin{align} d(\mu(j)) = \frac{S_N(\mu(j)) + \sqrt{N} \ln N}{S_N(\mu(j-6)) + \sqrt{N} \ln N}, \ j=1,2,\cdots,4N \tag{26.26} \end{align}\]
第二步和方法一中的第二步相同. 最后得到角频率向量\(\boldsymbol\lambda\)的初估计(26.24).
应当说明, 上面的三种计算方法只是为了计算机编写程序的方便. 实际问题中根据\(|S_N(\lambda)|\)的具体形状确定潜周期的个数是最行之有效的. 按上面的方法得到的估计量实际上已经是很准确的估计了. 它的估计精度可以由以下的定理进行描述.
定理26.2 设模型(26.6)中的平稳噪声\(\{\xi_t\}\)满足定理26.1中的条件, 则几乎必然地当\(N\)充分大后, 由上面的三种方法定义的\(\hat q\)和初估计\(\hat \lambda_1, \hat \lambda_2,\cdots, \hat \lambda_q\)满足 \[ \hat q = q, \ \ | \hat \lambda_j -\lambda_j| \leq \pi/N. \]
有了角频率的估计量(26.24), 就可以定义振幅\(\alpha_j\)的估计如下: \[\begin{align} \hat \alpha_j = \frac{1}{N} \sum_{t=1}^N x_t e^{-i \hat \lambda_j t} , \ 1 \leq j \leq \hat q. \tag{26.27} \end{align}\]
由角频率的初估计\(\hat \lambda_j\)定义的\(\hat \alpha_j\)在理论上还不能保证有很好的估计精度. 也就是说, 当\(N\to \infty\)时, \(\hat \alpha_j\)收敛到\(\alpha_j\)速度还不够好. 为了得到精度更高的估计量, 还需要对角频率的初估计\(\hat \lambda_j\)进行改造. 得到更精确的估计, 称为精估计.
26.2.2 角频率的精估计
得到了角频率的初估计(26.24)后, 可以用以下的方法改进估计的精度, 得到精度更高的估计量.
26.2.2.1 方法一
对每一个初估计\(\hat \lambda_j\), 在它的\(8/N\)邻域\([\hat \lambda_j-4/N, \hat \lambda_j+4/N]\)中 加密计算函数\(|S_N(\lambda)|\), 得到加密计算后\(|S_N(\lambda)|\)的最大值点\(\tilde \lambda_j\). 如果计算的密度可以到达 \(o(N^{-1.6})\), 则称\(\tilde \lambda_j\)为\(\lambda_j\)的周期图最大估计. 用周期图最大估计\(\tilde \lambda_j\)代替(26.27)中的初估计\(\hat \lambda_j\) 得到振幅\(\alpha_j\)的精估计: \[\begin{align} \tilde \alpha_j = \frac{1}{N} \sum_{t=1}^N x_t e^{-i \tilde \lambda_j t} , \ 1 \leq j\leq \hat q. \tag{26.28} \end{align}\]
对于潜周期模型(26.6)的精估计, 有以下的强相合性结果.
定理26.3 设模型(26.6)中的平稳噪声\(\{\xi_t\}\)满足定理26.1中的条件, 则有如下的结果: \[\begin{aligned} &\limsup_{N \to \infty}\sqrt{\frac{N^3}{\ln N}}|{\tilde \lambda}_j-\lambda_j|= 0, \ \text{a.s.}, \\ &\limsup_{N \to \infty}\sqrt{\frac{N}{\ln N}}|{\tilde \alpha}_j-\alpha_j| =0 , \ \text{a.s.} \end{aligned}\]
在参数估计问题中, 估计量的a.s.收敛速度一般只达到\(O(( N/\ln \ln N)^{-1/2})\), 这里角频率\(\lambda_j\)的周期图最大估计\(\tilde \lambda\)的 a.s.收敛速度可以达到\(o((N^3/\ln N)^{-1/2})\).
26.2.2.2 方法二
改进角频率的初估计\(\hat \lambda_j\)还可以采用二次分析法以减少计算量. 传统的二次分析方法在Fourier分析和时间序列分析中有很多的应用. 利用角频率的初估计和二次分析方法可以给出改进角频率的初估计的方法如下.
用\(\arg(c)\)表示复数\(c\)的辐角. 取正整数\(M>1\), 则存在正整数\(m\)满足 \[\begin{align} N = m M + M', 0 \leq M' < M. \tag{26.29} \end{align}\] 对于\(s=1,2,\cdots,M\), 定义 \[\begin{aligned} & T_j(s) = \sum_{t=(s-1)m+1}^{s m} x_t \exp(-it{\hat \lambda}_j), \\ & {\theta}_j = \arg{\Big[\sum_{s=1}^M T_j(s)/|T_j(s)| \Big]}, \\ & z_j(s) = \arg[T_j(s) \exp(-i{\theta}_j)], \\ & \beta_j = \sum_{s=1}^M z_j(s) \Big(s - \frac{M+1}{2} \Big) / \sum_{s=1}^M \Big(s - \frac{M+1}{2} \Big)^2. \end{aligned}\] 最后, 改进的初估计由 \[\begin{align} {\tilde \lambda}_j={\hat \lambda}_j +\beta_j/m \tag{26.30} \end{align}\] 定义. 将改进的初估计\(\tilde \lambda_j\)代入(26.28), 就得到\(\alpha_j\)的估计\(\tilde \alpha_j\). 对于用二次分析法改进的估计量, 也可以证明定理26.3中的收敛速度.
26.2.3 实值模型的参数估计
最后回到实值潜周期模型(26.1)的参数估计问题. 由于观测数据是实值的, 所以\(|S_N(\lambda)|\)是偶函数, 因而只要按照前述的方法在\([0, \pi]\)上找出峰群的个数\(\hat k\)作为角频率个数\(k\)的估计. 每个峰群中的最高峰下对应于一个角频率的估计\(\hat \lambda_j\). 设\(\hat \alpha_j\)由(26.27)或(26.28)定义. 定义\(A_k\)的估计\(\hat A_k\)如下:
如果\(\hat \lambda_k=\pi\), 取\(\hat A_k=\hat \alpha_k\), \(\hat \phi_1=0\), \(\hat \omega_1=\pi\);
如果\(\hat \lambda_j \in (0,\pi)\), 取\(\hat \omega_j = \hat \lambda_j\), \(\hat A_j = 2 |\hat \alpha_j|\), 初始相位\(\phi_j\)的估计取作\(\hat \phi_j = \arg(\hat \alpha_j)\).
不难看出, 这样定义的估计量都有很好的强相合性质.
26.2.4 模型的检测
对于实值模型(26.1)得到周期个数的估计\(\hat k\), 角频率的估计\(\hat \omega_j\), \(1 \leq j \leq \hat k\), 振幅的估计\(\hat A_j\), \(1 \leq j \leq \hat k\)和初相位的估计\(\hat \phi_j\), \(1 \leq j \leq \hat k\)后, 为了检测拟合的模型 \[ x_t = \sum_{j=1}^{\hat k} \hat A_j \cos(\hat\omega_j t + \hat \phi_j) + \xi_t, \ \ t \in \mathcal N_+ \] 是否合理, 需要计算残差 \[\begin{align} \hat \xi_t = x_t - \sum_{j=1}^{\hat k} \hat A_j \cos(\hat\omega_j t + \hat\phi_j), \ t=1,2,\cdots,N \tag{26.31} \end{align}\] 和它的样本自协方差函数 \[ \hat\gamma_k = \frac{1}{N} \sum_{j=1}^{N-k} (\hat \xi_j - \hat \mu) (\hat \xi_{j+k} -\hat \mu), \ k=1,2,\cdots, [\sqrt{N}], \] 这里\(\hat \mu\)是\(\hat \xi_t\)的样本均值.
如果\(\hat \gamma_k\)有收敛到零的性质, 就可以认为模型合适. 需要的话, 对于实值的潜周期模型(26.1), 还可以进一步为残差(26.31)建立AR或ARMA模型. 如果建立的AR或ARMA模型可以通过模型检测, 就应当肯定拟合模型的合理性.
例26.1 观测序列\(\{x_t\}\)来自潜周期模型(26.1),
其中\(k=5\),
\[\begin{aligned}
&\boldsymbol{\omega}=(0.23, 0.98, 1.54, 1.98, 2.67)^T, \\
&\boldsymbol A=(1.44, 2.89, 1.98, 4.98, 1.78)^T,\\
&\boldsymbol\phi=(0.2, 2.9, 0.8, 2.3, 1.6)^T.
\end{aligned}\]
有色噪声\(\{\xi_t\}\)是由
\[\begin{equation}
\xi_t
= 1.16\xi_{t-1} - 0.37\xi_{t-2}
-0.11\xi_{t-3} + 0.18\xi_{t-4}
+ \varepsilon_t
\tag{26.32}
\end{equation}\]
产生的\(AR(4)\)序列.
这里\(\{\varepsilon_t\}\)是正态\(\text{WN}(0,1)\),
\(\text{Var}(\xi_t)=4.422\).
信噪比
\[\begin{equation}
\boldsymbol A/ \sqrt{\text{Var}(\xi_t)}
= ( 0.6847 \ \ 1.3741 \ \ 0.9414 \ \ 2.3678 \ \ 0.8463 )^T. \tag{26.33}
\end{equation}\]
观测数据的80个样本由图26.1给出.
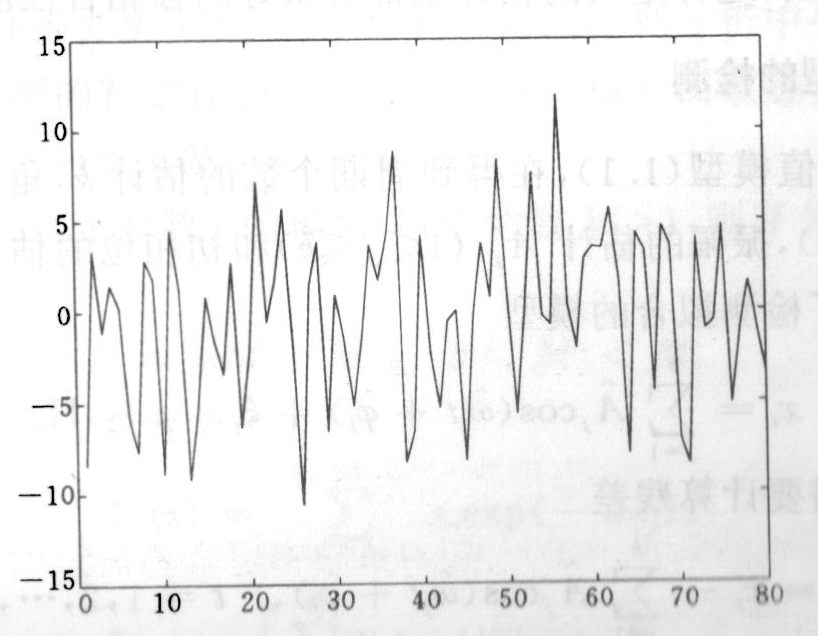
图26.1: 原始数据
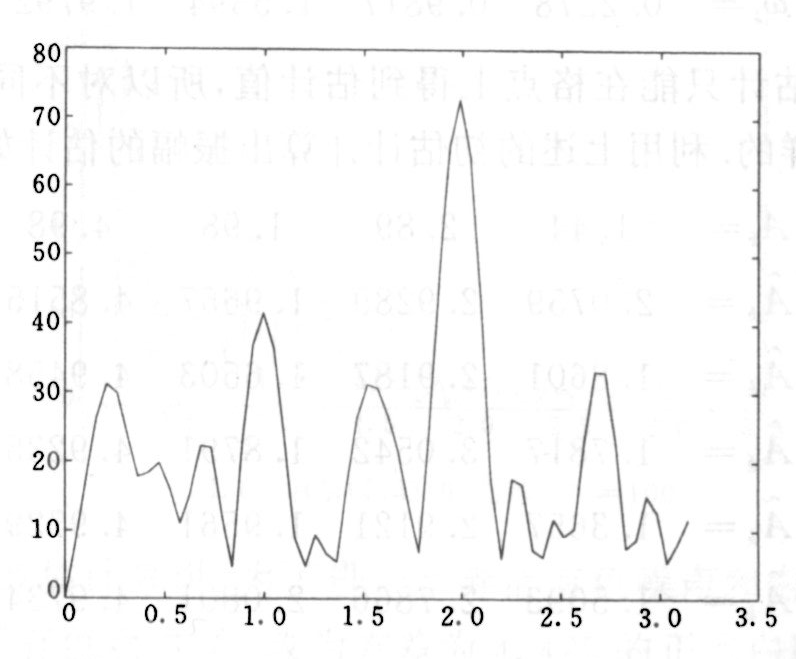
图26.2: \(|S_{30}(\lambda)|\)
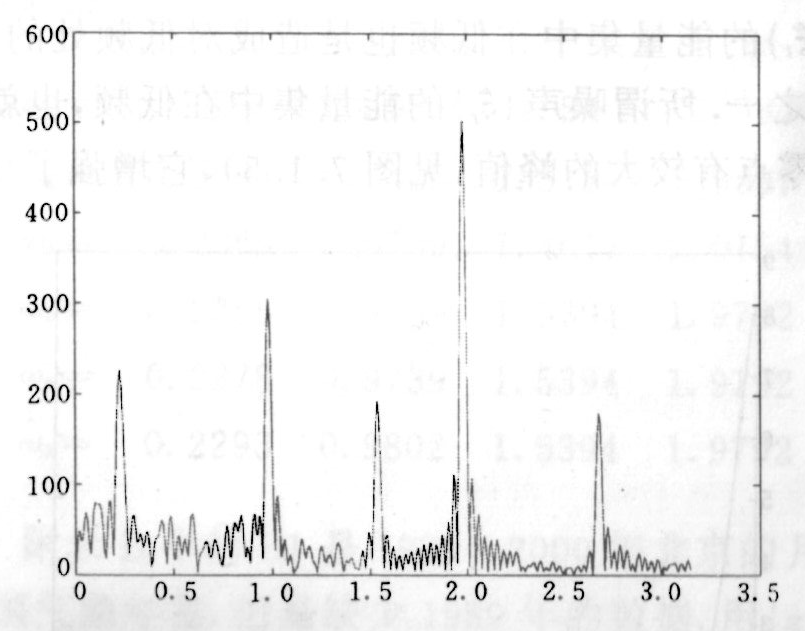
图26.3: \(|S_{200}(\lambda)|\)
解答:
仅从数据图很难判断数据的潜周期个数.
图26.2和图26.3 分别是\(N=30,200\)时函数\(|S_N(\lambda)|\)的图形.
由于观测数据是实值的,
只需绘出\([0,\pi]\)部分.
计算密度是\(\pi/(2N)\).
实际计算\(S_N(\lambda)\)时,
先对数据进行了零均值化处理.
从上述图形看出, 信噪比高的角频率更容易被识别出来. 从方法一可以得到角频率的估计如下.
\[
\begin{array}{lrrrrrrr}
\hbox{真值} & \omega_k = & 0.23 & 0.98 & 1.54&1.98&2.67 \\
N=30 &\hat \omega_k= & 0.2094 &\ 0.9948 &\ 1.5708 &\ 1.9897 &\ 2.6704\\
N=50 &\hat \omega_k = & 0.2513 &\ 0.9739 &\ 1.5394 &\ 1.9792&\ 2.6704\\
N=100 &\hat \omega_k = &0.2513 &\ 0.9739 &\ 1.5394 &\ 1.9792 &\ 2.6861\\
N=200 &\hat \omega_k= &0.2356 &\ 0.9739 &\ 1.5394 &\ 1.9792 &\ 2.6861\\
N=500 &\hat \omega_k= &0.2278 &\ 0.9817 &\ 1.5394 &\ 1.9792&\ 2.6704
\end{array}
\]
由于初估计只能在格点上得到估计值, 所以对不同的\(N\), 估计值有时是一样的. 利用上述的初估计计算出振幅的估计如下:
\[
\begin{array}{lrrrrrrr}
\hbox{真值}& A_k=& 1.44 &\ 2.89 &\ 1.98 &\ 4.98 &\ 1.78\\
N=30 &\hat A_k =& 2.0759& 2.9289 & 1.9657 & 4.8515 & 2.2403\\
N=50 &\hat A_k =& 1.8601 &\ 2.9187 &\ 1.6503 &\ 4.9458 &\ 2.1115\\
N=100 &\hat A_k =& 1.7817 &\ 3.0542 &\ 1.8791 &\ 4.9235 &\ 1.8209\\
N=200 &\hat A_k= & 1.3657 &\ 2.9121 &\ 1.9561 &\ 4.9729 &\ 1.8273\\
N=500 &\hat A_k= & 1.5093 &\ 2.7866 &\ 2.0801 &\ 4.9734 &\ 1.8009
\end{array}
\]
可以看出, 当\(N\leq 100\),
对角频率\(\omega_1=0.23\)和振幅\(A_1=1.44\)的估计精度较差.
这是因为角频率\(\omega_1\)的信噪比最小的原因.
另外, 在本例中, 噪声\(\{\xi_t\}\)的能量集中在低频也是造成对低频处的角频率估计不准的原因之一.
所谓噪声\(\{\xi_t\}\)的能量集中在低频也就是说\(\{\xi_t\}\)的谱密度在零点有较大的峰值(见图7.1.5),
它增强了\(|C_N(\xi, \lambda)|\)在零点的振荡,
以致影响到对潜频率\(\lambda_1\) 和振幅\(A_1\)的估计精度.
参见图7.1.6.
本例中, \(|C_N(\xi,\lambda)|\)在低频比其他地方振荡要大很多.
对于参数估计来讲, 为了进一步弄清有色噪声和白噪声的不同影响, 我们把有色噪声\(\{\xi_t\}\)改为
方差为\(4.422\)的正态白噪声,
以保证信噪比(26.33)不变. 经过计算, 得到的角频率估计在低频确是有所改进.
计算的结果如下.
\[
\begin{array}{lrrrrrrrr}
\hbox{真值} & \omega_k = & 0.23 & 0.98 & 1.54&1.98&2.67 \\
N=30 &\hat \omega_k= & 0.2094 &\ 0.9425 &\ 1.5184 &\ 1.9897 &\ 2.6704\\
N=50 &\hat \omega_k = & 0.2369 & 0.9739 & 1.4017 & 2.0154 & 2.8636 \\
N=100 &\hat \omega_k = & 0.2356 &\ 0.9739 &\ 1.5394 &\ 1.9792 &\ 2.6861 \\
N=200 &\hat \omega_k= & 0.2278 &\ 0.9739 &\ 1.5394 &\ 1.9792 &\ 2.6704\\
N=500 &\hat \omega_k= & 0.2293 &\ 0.9802 &\ 1.5394 &\ 1.9792 &\ 2.6672
\end{array}
\]