6 时间序列的谱

遍历的时间序列可以从一次实现的时间分布进行统计分析，称为时域分析。平稳时间序列的二阶性质也可以从其频率分解来研究，称为频域分析。频谱的典型代表是声音。

6.1 声音频谱演示

利用Audacity软件演示声音波形和频谱。

在Audacity中显示并播放笛子曲片段music-demo1.wav。界面见图6.1。
其中有一个C5音主频率为523Hz，相应的片段存入了music-demo1b.wav, 在Audacity中打开此片段并聆听，见图6.2。放大局部见图6.3。谱密度图见图6.4。其中最大值点就是乐器当前振动的频率，音阶为C5(523Hz左右)。还有一些其他的峰，在基础频率的倍数的位置。谱估计的纵轴用了对数尺度。
我们人为用正弦波生成了频率为523Hz的声音文件，存入了music-demo1c.wav。在Audacity中聆听、看波形、频谱图。放大的波形图见图6.5，这是一个严格的正弦波。频谱图见6.6。一个频率为$f_0$的正弦波声音，其振动波形的方程为 \[ y_t = \sin(2\pi f_0 t), t>0 \] $t$为以秒为单位的连续时间。

连续波形必须按一定的采样频率变成离散时间的时间序列，比如每秒8000点，称为采样频率8kHz, 这只要按每秒钟按上述方程生成8000个$y_t$值即可。常用的采样频率如CD音质，为44.1kHz。可以记录单声道或者双声道，每个采样点的值一般用若干二进制位表示，比如CD音质使用16bit记录一个采样点的值，波形取值在$\pm 2^{15}$之间。

保存声音的数据文件可以进行压缩，比如MP3格式就是一种压缩的有失真的压缩声音文件格式。用比特率表示保存每秒所需要的二进制位数，比如MP3常用的标准音质为128kbps，即每秒钟16K字节，或每分钟0.9M字节。
在R中读入music-demo2.wav，这是笛子演奏片段，有三个音阶C5--D#5--C5。在R中画C5(523Hz)0.05秒片段时间序列图、谱密度估计图、动态谱峰图。见§6.4.4。
在R中人为生成523Hz正弦波，画时间序列图、谱密度估计和动态谱峰图。见§6.4.4。保存为music-demo2b.wav。可在Audacity中查看和聆听。
在R中直接生成的两个单音C4和C5叠加的复音的序列图和谱密度估计、动态谱峰图。保存为music-demo2c.wav。可在Audacity中查看和聆听。

音调和频率的对照表：

音调	低音(3)	中音(4)	高音(5)
C	131	262	523
D	147	294	587
E	165	330	659
F	175	349	698
G	196	392	784
A	220	440	880
B	247	494	988

频率262是中音C或C4，是钢琴键盘的最中间8度音的C音，这一组是小字1组；频率440是中音A或A440，频率440是国际标准音高。

在十二音阶中，相差八度音的两个音调（比如C4, 262Hz与C5, 523Hz）的频率相差一倍；每个半音的频率为上一个半音频率的$\sqrt[12]{2}$倍。

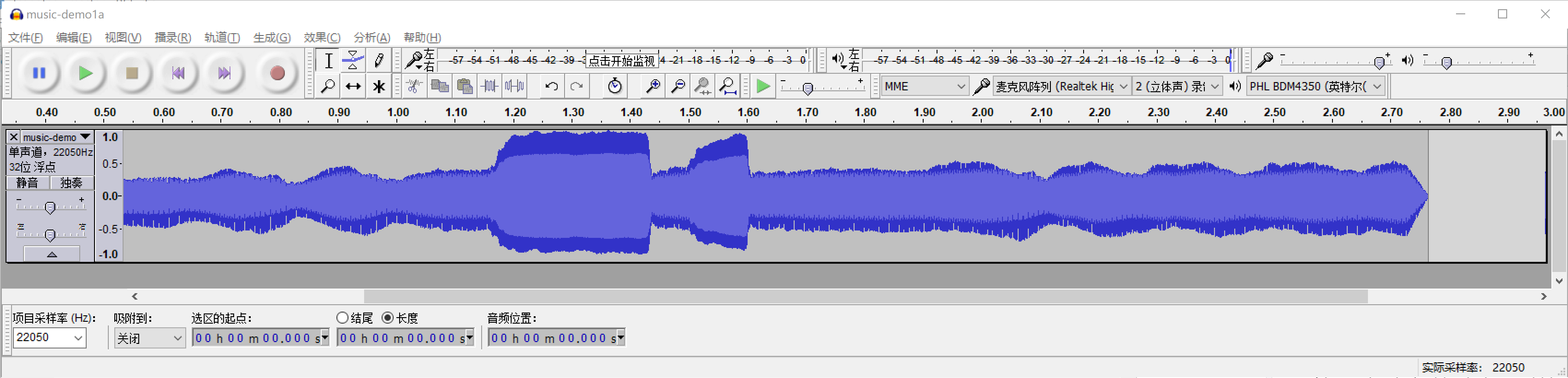
图6.1: Audacity运行界面

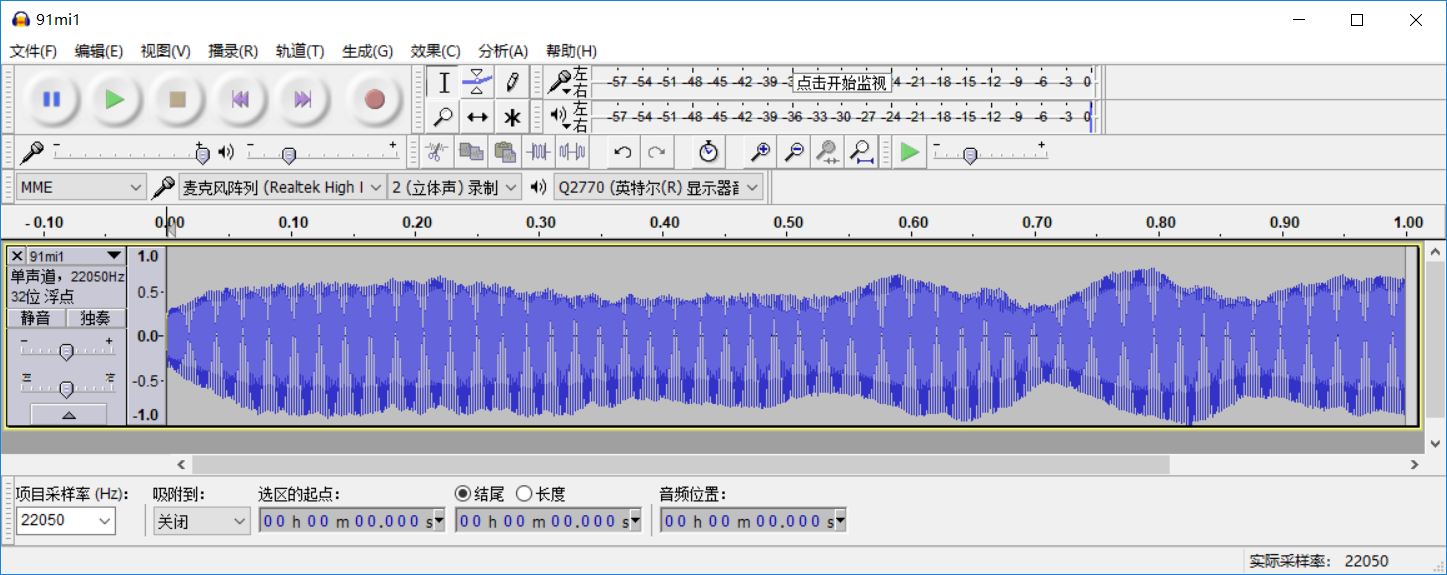
图6.2: Audacity中笛子音C5

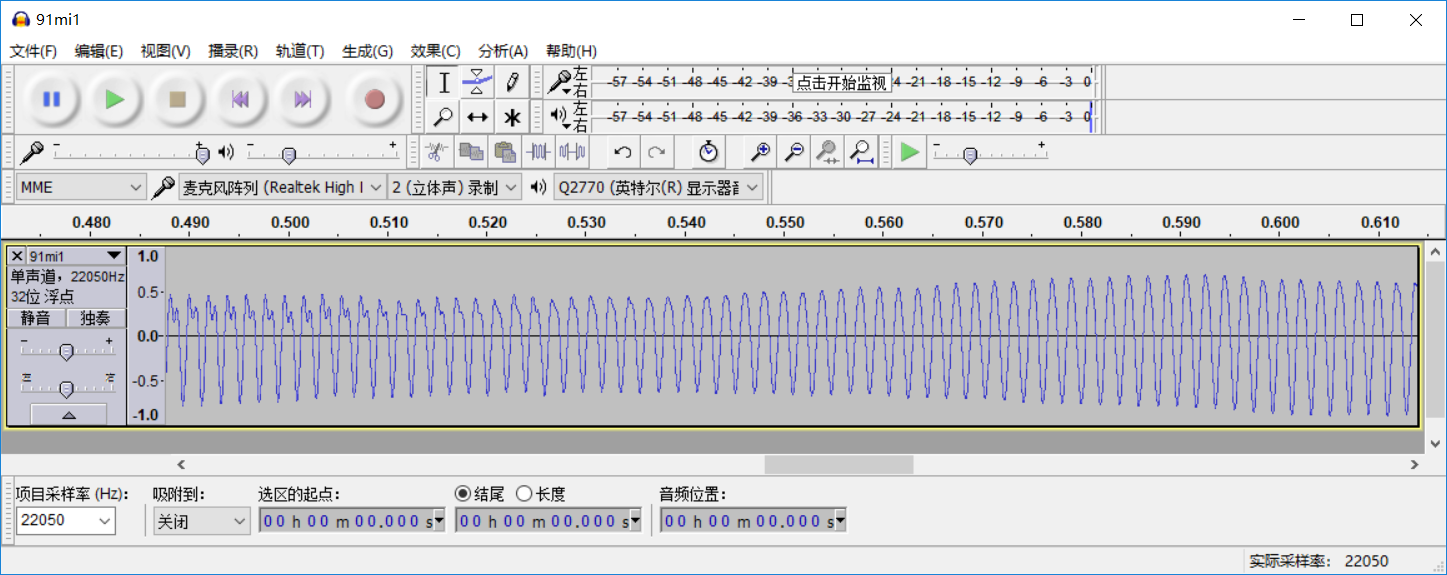
图6.3: Audacity中笛子音C5画面放大

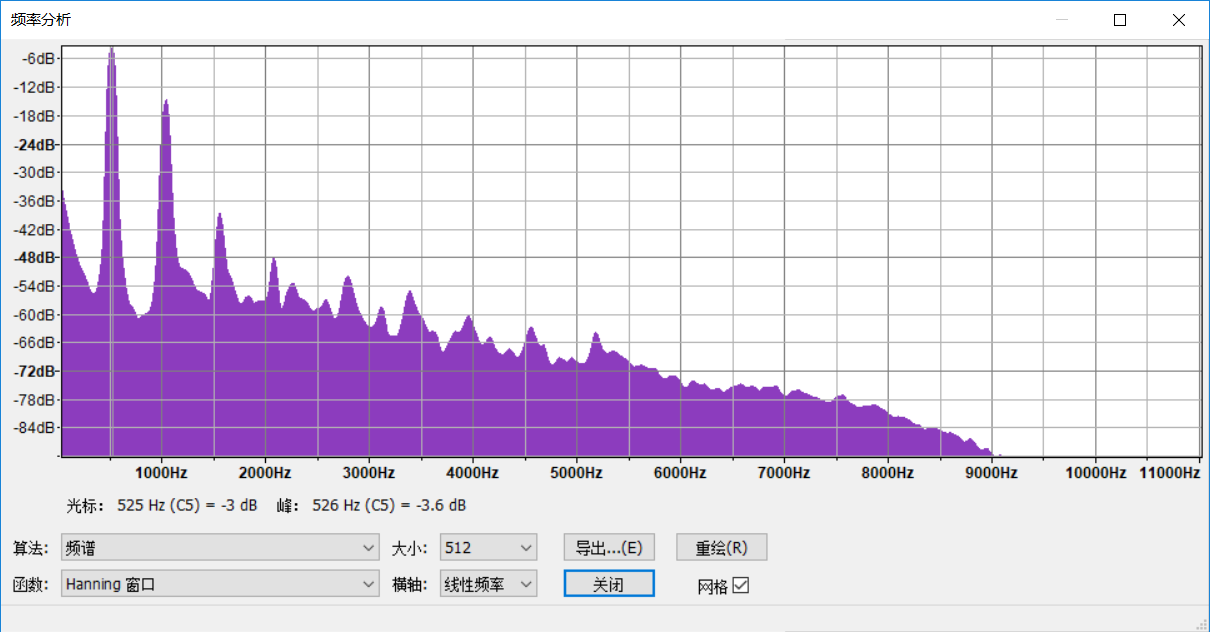
图6.4: Audacity中笛子音C5片段的谱密度

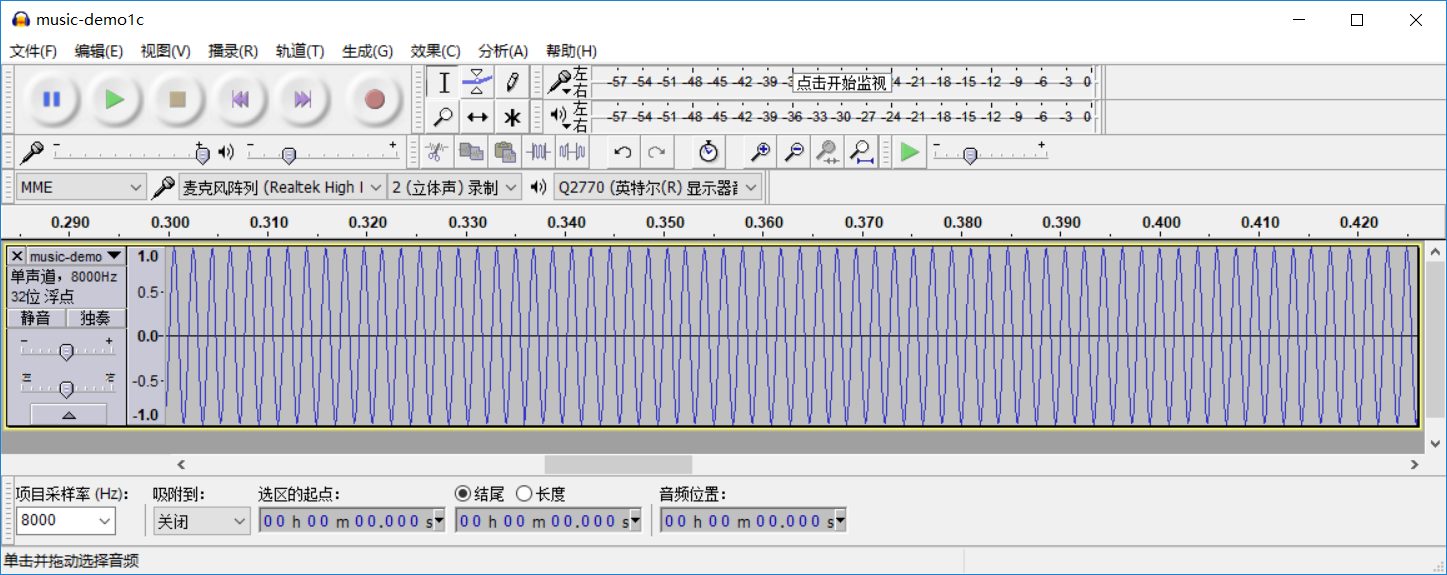
图6.5: Audacity中单音C5片段放大

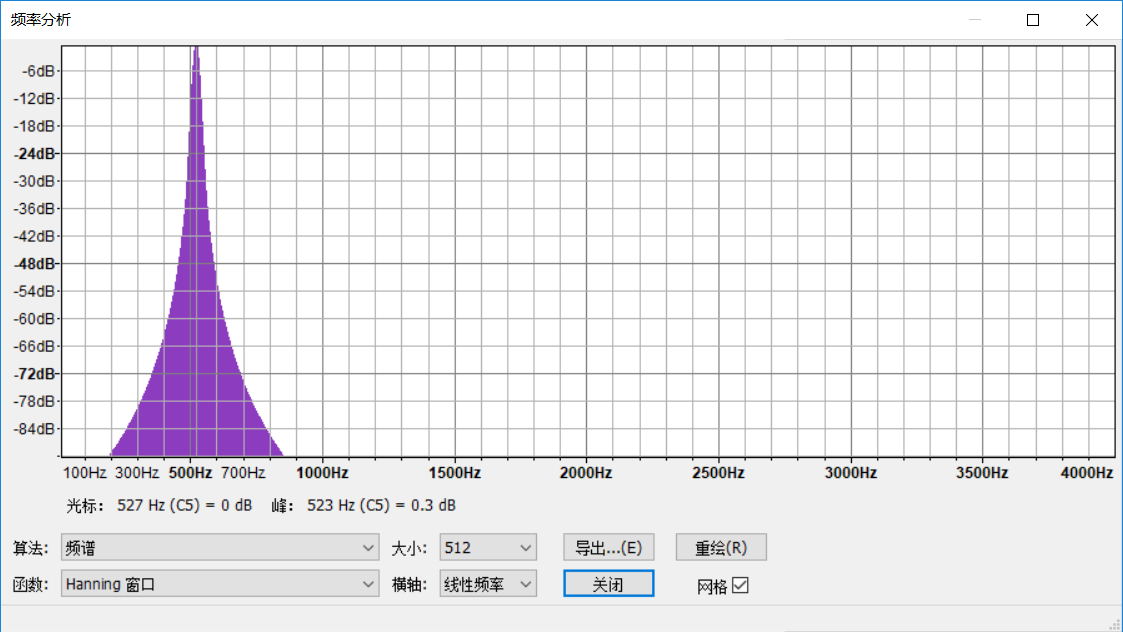
图6.6: Audacity中单音C5谱密度

6.2 平稳序列的谱

6.2.1 平稳序列的谱函数

设平稳序列$\{X_t\}$ 有自协方差函数 $\{\gamma_k\}$. 如果有$[-\pi,\pi]$上的单调不减右连续的函数$F(\lambda)$使得 \[\begin{equation} \gamma_k \ = \int_{-\pi}^{\pi} e^{ik\lambda}\ dF(\lambda), \ \ F(-\pi)=0, \ \ k\in \mathbb Z, \tag{6.1} \end{equation}\] 则称 $F(\lambda)$是$\{X_t\}$ 或 $\{\gamma_k\}$的谱分布函数, 简称为谱函数; 如果有$[-\pi,\pi]$上的非负函数$f(\lambda)$使得 \[\begin{equation} \gamma_k \ = \int_{-\pi}^{\pi} f(\lambda) e^{ik\lambda}\ d\lambda, \quad k\in \mathbb Z, \tag{6.2} \end{equation}\] 则称$f(\lambda)$是$\{X_t\}$ 或 $\{\gamma_k\}$的谱密度函数或功率谱密度, 简称为谱密度或功率谱.

谱反映了平稳序列的相关结构。谱密度是将原始序列看成许多个不同频率的余弦波的叠加时，不同频率的振幅平方大小，谱密度越高的地方，对应的频率成分的振幅越大。

例6.1 演示：高频时间序列和低频时间序列的序列图和密度.

演示：低频时间序列图形

set.seed(1)
m <- 10
n <- 100+m+1
fil <- rep(1/(m+1), m+1)
eps <- rnorm(n)
x <- filter(eps, fil, method="convolution", sides=1)
eps <- eps[-seq(m+1)]
x <- x[-seq(m+1)]
ts.plot(x, col="black", main="Low frequency t.s.",
        xlab="time", ylab="y")

低频时间序列的谱密度样例（横坐标为$[0,\pi]$内的角频率）：

fr <- seq(0, pi, length=100)
sp <- numeric(length(fr))
for(j in seq(along=fr)){
  sp[j] <- abs(sum(complex(mod=1, arg=-(0:m)*fr[j])))^2
}
sp <- sp/(2*pi*(m+1)^2)
plot(fr, sp, type='l', main="Spectral density of LOW frequency t.s.",
     xlab="Frequency", ylab="Density")

高频时间序列的模拟数据：

r0 <- complex(mod=1.1, arg=4/5*pi)
poly1 <- c(1, -2*Re(r0), Mod(r0)^2)
poly2 <- poly1 / poly1[3]
poly2 <- rev(poly2)
eps <- rnorm(n+100)
y <- numeric(length(eps))
for(j in 3:length(y)){
  y[j] = -poly2[2]*y[j-1] - poly2[3]*y[j-2] + eps[j]
}
y <- y[-seq(100)]
ts.plot(y, main="High frequency t.s.",
        xlab="time", ylab="y")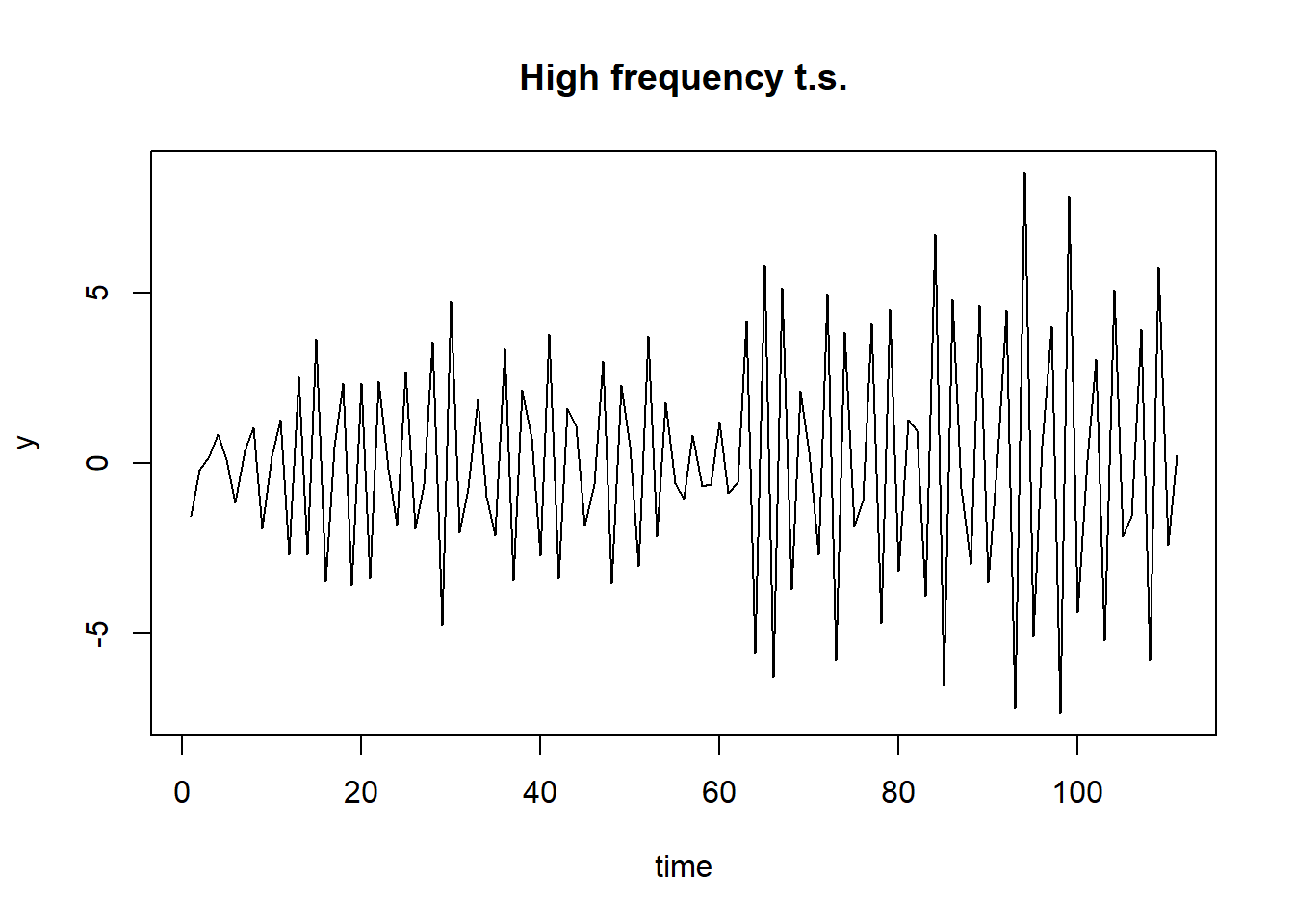

高频时间序列的谱密度样例：

sp2 <- numeric(length(fr))
for(j in seq(along=fr)){
  sp2[j] <- abs(sum(poly2 * complex(mod=1, arg=(0:2)*fr[j])))^2
}
sp2 <- 1/(2*pi) / sp2
plot(fr, sp2, type='l', main="Spectral density of HIGH frequency t.s.",
     xlab="Frequency", ylab="Density")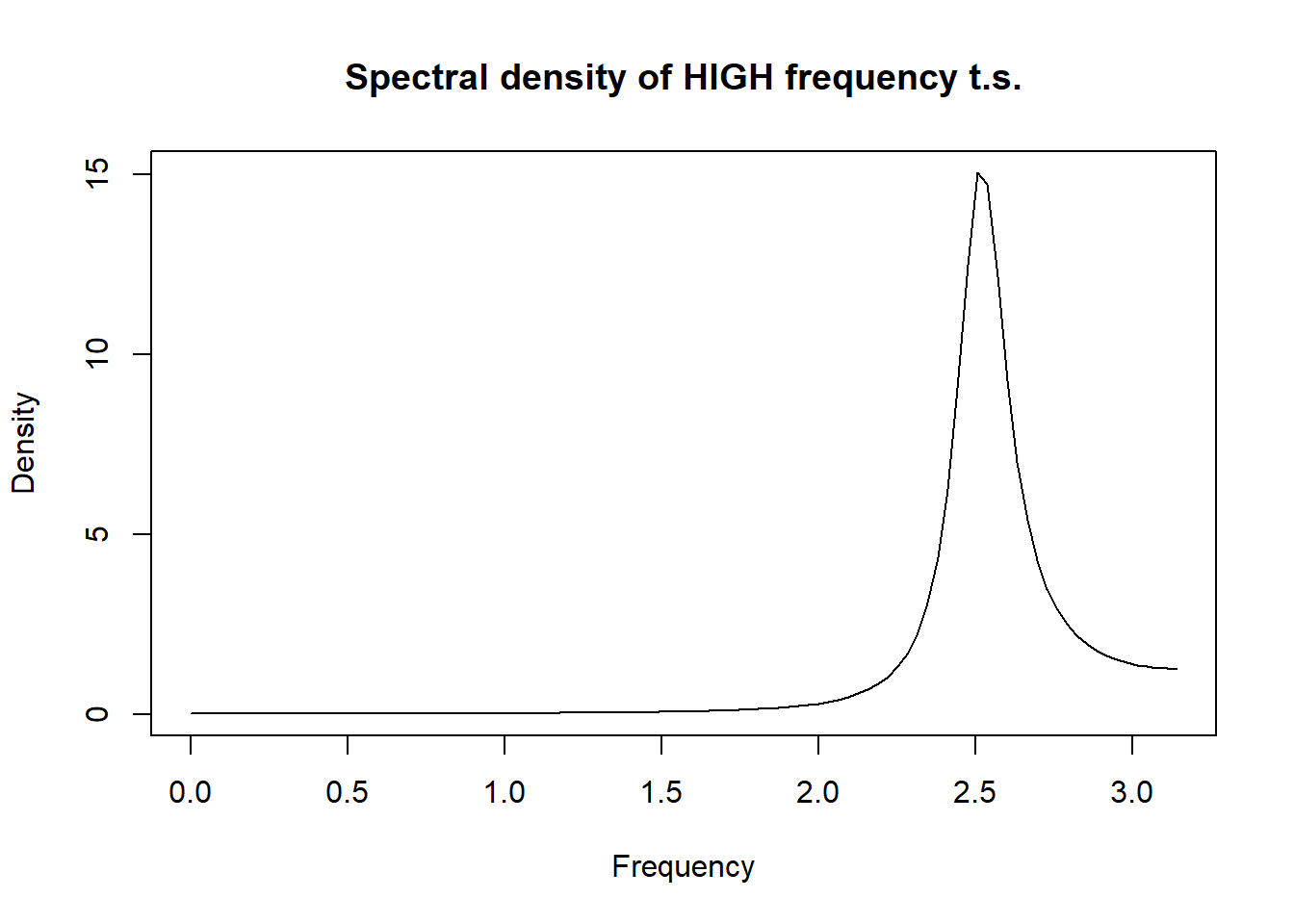

○○○○○○

定理6.1 (Herglotz定理) 平稳序列的谱函数是惟一存在的.

(参见(谢衷洁 1990)P21定理1.6)

若$F(\lambda)$和$f(\lambda)$同时存在则 \[\begin{align} F(\lambda) = \int_{-\pi}^\lambda f(s) \,ds \tag{6.3} \end{align}\]

若$F(\lambda)$绝对连续则其几乎处处导数$F'(\lambda)$为谱密度。若$F(\lambda)$是连续函数，除去有限点外导函数存在且连续则 \[\begin{aligned} f(\lambda) = \begin{cases} F'(\lambda) & \ \text{当$F'(\lambda)$存在}\\ 0 & \ \text{当$F'(\lambda)$不存在} \end{cases} \end{aligned}\] 是谱密度。

6.2.2 白噪声列的谱密度

设$\{\varepsilon_t \}$为白噪声列WN($\mu$, $\sigma^2$)。自协方差函数为 \[\begin{aligned} \gamma_k = \sigma^2 \delta_k, \quad k \in \mathbb Z \end{aligned}\] 显然，令 \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi}, \quad \lambda \in [-\pi, \pi] \end{aligned}\] 有 \[\begin{aligned} \gamma_k = \int_{-\pi}^{\pi} f(\lambda) e^{ik\lambda} d\lambda, \quad k \in \mathbb Z \end{aligned}\] 即白噪声列有常数谱密度。

反之，有常数谱密度的平稳列一定是白噪声列。

6.2.3 线性平稳列的谱密度

定理6.2 如果 $\{\varepsilon_t\}$ 是 $\text{WN}(0,\sigma^2)$, 实数列 $\{a_j\}$平方可和, 则线性平稳序列 \[ X_t = \sum_{j=-\infty}^{\infty} a_j \varepsilon_{t-j}, \ \ t\in \mathbb Z, \] 有谱密度 \[\begin{align} f(\lambda) = \frac{\sigma^2}{2\pi } \left|\sum_{j=-\infty}^{\infty} a_j e^{ij\lambda}\right|^2. \tag{6.4} \end{align}\]

证明:

§5.1.5已经证明$\{X_t\}$的自协方差函数为 \[\begin{aligned} \gamma_k = \sigma^2 \sum_{j=-\infty}^\infty a_j a_{j+k} \end{aligned}\] 由§5.2的式(5.1)，可得到 \[\begin{aligned} \sigma^2 \sum_{j=-\infty}^\infty a_j a_{j+k} = \int_{-\pi}^{\pi} f(y) e^{iky} dy, \quad k \in \mathbb Z \end{aligned}\] 其中 \[\begin{aligned} f(\lambda) =& \frac{\sigma^2}{2\pi} \left| \sum_{j=-\infty}^{\infty} a_j e^{ij\lambda} \right|^2 \end{aligned}\] 于是 \[\begin{aligned} \gamma_k = \int_{-\pi}^{\pi} f(y) e^{iky} dy, \quad k \in \mathbb Z \end{aligned}\] 即$f(\lambda)$是$\{X_t \}$的谱密度。

○○○○○○

实际上，存在谱密度也是线性序列的充分条件：

定理6.3 若平稳列$\{ X_t \}$有谱密度，则存在白噪声列$\{ \varepsilon_t \}$和平方可和的数列$\{ a_j \}$使得 \[ x_t = \sum_{j=-\infty}^{\infty} a_j \varepsilon_{t-j}, \ t \in \mathbb Z . \]

参见(谢衷洁 1990) P.49定理1.14。

6.2.4 两正交序列的谱

定理6.4 设$\{X_t\}$ 和$\{Y_t\}$是相互正交的零均值平稳序列, $c$是常数, 定义 \[ Z_t=X_t+Y_t +c, \ \ t\in \mathbb Z. \]

如果$\{X_t\}$ 和$\{Y_t\}$分别有谱函数 $F_X(\lambda)$ 和 $F_Y(\lambda)$, 则平稳序列 $\{Z_t\}$ 有谱函数 $F_Z(\lambda)=F_X(\lambda)+F_Y(\lambda)$.
如果$\{X_t\}$ 和$\{Y_t\}$分别有谱密度 $f_X(\lambda)$ 和 $f_Y(\lambda)$, 则$\{Z_t\}$ 有谱密度 $f_Z(\lambda)=f_X(\lambda)+f_Y(\lambda)$.

证明: 主要由 \[ \gamma_Z(k) = \gamma_X(k) + \gamma_Y(k) \] 及谱函数和谱密度定义可得。

○○○○○○

6.2.5 线性滤波与谱

设平稳序列$\{X_t\}$有谱函数$F_X(\lambda)$和自协方差函数$\{\gamma_k\}$. $H=\{h_j\}$是一个绝对可和的保时线性滤波器(参见§2.3). 当输入过程是$\{X_t\}$时, 输出过程是 \[\begin{align} Y_t=\sum_{j=-\infty}^\infty h_j X_{t-j}, \ \ t\in \mathbb Z. a.s. \tag{6.5} \end{align}\] 输出的自协方差为 \[\begin{align} \gamma_Y(k)=\sum_{l, j=-\infty}^\infty h_l h_j \gamma(k+l-j). \tag{6.6} \end{align}\] 求和意义为实数级数绝对收敛。

由控制收敛定理 \[\begin{align} \gamma_Y(k)=& \sum_{l,j=-\infty}^\infty h_l h_j \int_{-\pi}^\pi \exp(i(k+l-j)\lambda)\ dF_X(\lambda) \nonumber\\ =& \int_{-\pi}^\pi \sum_{l,j=-\infty}^\infty h_l h_j \exp(i(l-j)\lambda) e^{ik\lambda}\ dF_X(\lambda) \nonumber\\ =& \int_{-\pi}^\pi \left| \sum_{j=-\infty}^\infty h_j \exp(-ij\lambda) \right |^2 e^{ik\lambda}\ dF_X(\lambda) \nonumber\\ =& \int_{-\pi}^\pi |H(e^{-i\lambda})|^2 e^{ik\lambda} \;dF_X(\lambda), \tag{6.7} \end{align}\] 其中 \[\begin{align} H(z)=\sum_{j=-\infty}^\infty h_j z^j, \ |z|\leq 1. \tag{6.8} \end{align}\]

线性滤波输出$\{Y_t\}$的谱函数为 \[\begin{align} F_Y(\lambda) = \int_{-\pi}^\lambda |H(e^{-is})|^2 \ dF_X(s). \tag{6.9} \end{align}\] 当$\{X_t\}$有谱密度$f_X(\lambda)$时 \[\begin{align} F_Y(\lambda) = \int_{-\pi}^\lambda |H(e^{-is})|^2 f_X(s)\ ds. \tag{6.10} \end{align}\] 即$\{Y_t\}$谱密度为 \[\begin{align} f_Y(\lambda) = |H(e^{-i\lambda})|^2 f_X(\lambda) \tag{6.11} \end{align}\]

结论归纳成如下定理.

定理6.5 设$\{X_t\}$是平稳序列，$H=\{h_j\}$是绝对可和的保时线性滤波器， $\{Y_t\}$为滤波输出 \[\begin{align} Y_t=\sum_{j=-\infty}^\infty h_j X_{t-j}, \ \ t\in \mathbb Z. a.s. \tag{6.12} \end{align}\] $H(z)$是滤波器$H$的特征多项式 \[\begin{align} H(z)=\sum_{j=-\infty}^\infty h_j z^j, \ |z|\leq 1. \tag{6.13} \end{align}\]

如果$\{X_t\}$有谱函数$F_X(\lambda)$, 则$\{Y_t\}$有谱函数 \[\begin{align} F_Y(\lambda) = \int_{-\pi}^\lambda |H(e^{-is})|^2 \ dF_X(s). \tag{6.14} \end{align}\]
如果$\{X_t\}$有谱密度$f_X(\lambda)$, 则$\{Y_t\}$有谱密度 \[\begin{align} f_Y(\lambda) = |H(e^{-i\lambda})|^2 f_X(\lambda) \tag{6.15} \end{align}\]

由于(6.12)，序列$\{ h_j \}$看成$j \in \mathbb Z$的函数，称为保时线性滤波器的脉冲响应函数。由于(6.15), $H(e^{-i\lambda})|^2$称为频率响应函数。

脉冲响应的含义是，如果输入$\{ X_t \}$中仅$X_0=1$，其它都等于0，则$Y_j = h_j$，即输入在$t=0$时的一个单位的扰动，由于线性滤波的影响，输出在$t=j$时受到的影响是$h_j$。

频率响应的含义是，原来在$\lambda_0$频率附近的震荡能量，经过滤波后被放大到了原来的$|H(e^{-i\lambda_0})|^2$倍。

6.2.6 采样定理

设$\{X(t), t\in \mathbb R\}$是连续时的实值随机过程，若 \[\begin{aligned} & E X(t) \equiv \mu, \quad \forall t \in \mathbb R \\ & \text{Cov}(X(t), X(s)) = \gamma(t-s), \quad t,s \in \mathbb R \end{aligned}\] 则称$\{X(t)\}$为连续时平稳过程。 $\{\gamma(\tau), \tau \in \mathbb R \}$称为$\{X(t)\}$的自协方差函数。

对连续时平稳过程$\{X(t), t\in \mathbb R\}$，设自协方差函数为$\{\gamma(\tau) \}$，若有$(-\infty,\infty)$上的单调不减右连续的函数$F(\lambda)$使得 \[\begin{aligned} \gamma(\tau) \ = \int_{-\infty}^{\infty} e^{i\tau\lambda}\ dF(\lambda), \ \ F(-\infty)=0, \ \ \tau\in \mathbb R, \end{aligned}\] 则称 $F(\lambda)$是$\{X_t\}$ 或 $\{\gamma(\tau)\}$的谱函数, 在一定理论条件下也有类似于Herglotz定理的结论。

如果有$(-\infty,\infty)$上的非负函数$f(\lambda)$使得 \[\begin{aligned} \gamma(\tau) \ = \int_{-\infty}^{\infty} f(\lambda) e^{i\tau\lambda}\ d\lambda, \ \ \tau\in \mathbb R, \end{aligned}\] 则称 $f(\lambda)$是$\{X_t\}$ 或 $\{\gamma(\tau)\}$的谱密度函数或功率谱密度, 简称为谱密度或功率谱.

连续时的平稳过程只能以一定的时间间隔记录，称为采样。如何保证不损失信息？

定理6.6 (采样定理) 设$\{X(t), t \in \mathbb R \}$为连续时平稳过程，有谱函数$F(\lambda)$且谱函数满足 \[\begin{aligned} \int_{|\lambda| \geq 2\pi f_0} dF(\lambda) = 0 \end{aligned}\] 则 \[\begin{aligned} X_t = \sum_{n=-\infty}^\infty X\left(\frac{n}{2 f_0} \right) \dfrac{\sin(2\pi f_0 t - n\pi)} {2\pi f_0 t - n\pi} \quad (L^2), \quad t \in \mathbb R \end{aligned}\] 这时记$Y_n = X\left(\frac{n}{2 f_0} \right), n \in \mathbb Z$, 则平稳时间序列$\{Y_n\}$是$X(t)$以$\Delta = \frac{1}{2 f_0}$ 等间隔取样的结果。从采样$\{Y_n, n \in \mathbb Z \}$可以恢复原信号$\{X(t), t \in \mathbb R\}$。

参见：(谢衷洁 1990) P50定理1.15。

$f_0$称为上界频率，采样间隔不大于$\Delta = \frac{1}{2 f_0}$ 采样恢复原始信号。

如果采样间隔大于$\Delta$，信号的高频部分有丢失和混杂入低频的问题。

6.2.6.1 声音信号采样

数字音频信号以一定频率采样，并把信号强度数字化为8位、16位等。采样频率越高、数字化位数越多则信号保真度越高。 CD音质采样频率为44.1kHz(即采样间隔为$\Delta = 1 / 44100$秒, 上界频率为22.05kHz), 信号强度用每声道16位记录。这样，立体声音频每秒钟记录的数据比特数为 $44100\times 16 \times 2 = 1411200$ (称为码率1411.2kbps)。每分钟约80MB数据。

MP3编码使用比较低的采样速率和数字化位数，并利用听觉心理学进行了压缩，码率一般在$32\sim 320$kbps。

6.3 离散谱序列及其周期性

6.3.1 简单的离散谱序列

设随机变量$\xi,\eta$。$E\xi=0, E\eta=0$; $E(\xi \eta)=0$, $E \xi^2 = E\eta^2 = \sigma^2$。常数$\lambda_0 \in (0,\pi]$。令 \[\begin{align} Z_t = \xi \cos(\lambda_0 t) + \eta \sin(\lambda_0 t), t \in \mathbb N_+ \tag{6.16} \end{align}\] 写成极坐标表示: \[\begin{align} A =& \sqrt{\xi^2 + \eta^2}, \quad \cos\theta = \frac{\xi}A, \ \sin\theta = \frac{\eta}A \tag{6.17} \\ Z_t =& A \cos(t\lambda_0 - \theta) \tag{6.18} \end{align}\] 其实现是一个相位为$-\theta$的角频率为$\lambda_0$的余弦函数的离散采样，表现并不随机，随机性表现在多个实现样本。

如果$\xi$, $\eta$服从独立的标准正态分布， $A$服从Rayleigh分布， $\theta$服从U($-\pi, \pi$)， $A$和$\theta$独立。

易见$E Z_t=0$。自协方差函数为 \[\begin{aligned} \gamma_{t-s} =& E(Z_t Z_s) \\ =& \Big[E(\xi^2) \cos(t\lambda_0)\cos(s\lambda_0) + E(\eta^2) \sin(t\lambda_0)\sin(s\lambda_0) \\ & + E(\xi\eta) \cos(t\lambda_0)\sin(s\lambda_0) + E(\xi\eta) \cos(s\lambda_0)\sin(t\lambda_0) \Big] \\ =& \sigma^2\left[\cos(t\lambda_0)\cos(s\lambda_0) + \sin(t\lambda_0)\sin(s\lambda_0) \right] + 0 + 0 \\ &\quad(\text{注意}\xi,\eta\text{正交}) \\ =& \sigma^2 \cos((t-s)\lambda_0) \end{aligned}\] 所以(6.18)定义的$\{Z_t \}$平稳，有自协方差函数$\{\gamma_k\}$。

现 \[\begin{aligned} \gamma_k =& \sigma^2 \cos(k\lambda_0),\ k \in \mathbb Z \end{aligned}\] 若$\lambda_0 \neq \pi$, 谱函数为 \[\begin{aligned} F(\lambda) = \sigma^2 [ 0.5 I_{[-\lambda_0,\pi]}(\lambda) + 0.5 I_{[\lambda_0,\pi]}(\lambda)] \end{aligned}\]

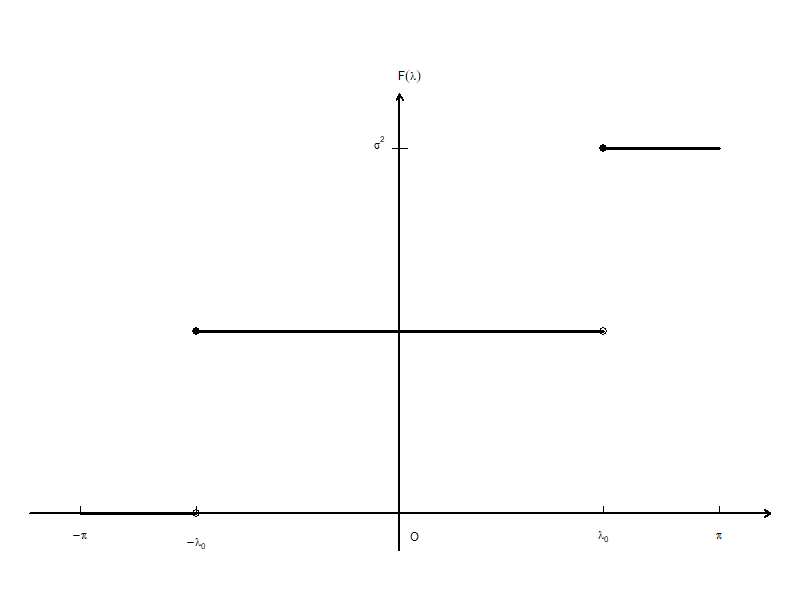
图6.7: 简单离散谱序列的谱函数

这样的阶梯函数形式的谱函数表示在$[-\pi,\pi]$上的一个测度，此测度仅在$-\lambda_0$和 $\lambda_0$两个点上有质量$\sigma^2/2$。由积分与测度的关系可知 \[\begin{aligned} \int_{-\pi}^\pi e^{ik\lambda} dF(\lambda) = \frac{\sigma^2}{2} [ e^{-ik\lambda_0} + e^{ik\lambda_0} ] = \gamma_k \end{aligned}\]

若$\lambda_0 = \pi$, 则$\gamma_k = \sigma^2 \cos(k\pi)$, \[\begin{aligned} F(\lambda) = \sigma^2 I_{\{\pi\}}(\lambda), \ \lambda \in [-\pi,\pi] \end{aligned}\]

如果将$\gamma_k$看成是$k \in [0, \infty)$的函数，这是以$\frac{2\pi}{\lambda_0}$为周期的一个余弦函数，当$k$等于周期的倍数时达到最大值，也就是说， $\rho(X_t, X_{t+k})$当$k$为轨道的周期的倍数时最大，而轨道的周期恰好是谱函数的跳跃点或者谱密度的峰值点。注意谱函数和谱密度是序列中不同频率振动的强度的度量，这个例子告诉我们，如果从谱函数和谱密度中看出某个频率占优，则相应的周期上的相关性也最强。 $\gamma_k$与$f(\lambda)$是傅立叶系数与傅立叶级数函数之间的关系，从时间序列来看， $\gamma_k$与$\rho_k$反映了相关性大小，谱密度反映不同频率的振动能量大小，相关性强的滞后值$k$会对应于谱密度$\frac{2\pi}{k}$附近的峰值。

6.3.2 离散谱

阶梯函数的谱函数称为离散谱函数，相应的平稳序列称为离散谱序列。离散谱函数对应$[-\pi,\pi]$上的一个只在离散点上取值的测度。

离散谱函数没有对应的谱密度，但是可以逼近。令 \[\begin{aligned} f_n(\lambda) =& n \sigma^2 I_{[-\lambda_0, -\lambda_0 + 1/(2n)] \cup [\lambda_0 - 1/(2n), \lambda_0]}(\lambda) \\ F_n(\lambda) =& \int_{-\pi}^\lambda f_n(u) du \end{aligned}\] 则$f_n$是一个仅在两个长度为$\frac{1}{2n}$的小区间上非零的分段函数。 $F_n(\lambda)$为连续的折线函数，仅在上述两个小区间上为线性增函数，在其它位置为水平线。有极限 \[\begin{aligned} F_n(\lambda) \to F(\lambda), \ \lambda \neq \pm \lambda_0, \ n \to \infty. \end{aligned}\]

$f_n(\lambda)$是某平稳列的谱密度。当$n\to\infty$时 \[\begin{aligned} g_k(n) \stackrel{\triangle}{=}& \int_{-\pi}^\pi e^{ik\lambda} f_n(\lambda) d\lambda \\ =& n\sigma^2 \left(\int_{-\lambda_0}^{-\lambda_0 + \frac{1}{2n}} e^{ik\lambda} d\lambda + \int_{\lambda_0 - \frac{1}{2n}}^{\lambda_0} e^{ik\lambda} d\lambda \right) \\ =& 2 n \sigma^2 \int_{\lambda_0 - \frac{1}{2n}}^{\lambda_0} \cos(k\lambda) d\lambda \\ & \quad (\sin\text{在关于原点对称的区间积分为零})\\ =& 2 n \sigma^2 \cos(k(\lambda_0 + \alpha_n)) \cdot \frac{1}{2n} \quad\text{(积分中值定理)} \\ =& \sigma^2 \cos(k\lambda_0 + k\alpha_n) \\ \to& \sigma^2 \cos(k\lambda_0) = \gamma_k, \ n \to \infty \end{aligned}\] 其中数列$\{\alpha_n \}$满足$\alpha_n \in (-\frac{1}{2n}, 0), n\in \mathbb N_+$。

当$n$很大时， $f_n(\lambda)$对应的平稳列和$\{Z_t\}$的表现已经很接近，其轨道表现为近似周期函数形式。

推广来看，如果某平稳列的谱密度在某处有很高的峰，则此序列的轨道在峰对应的频率(角频率)处应该表现出周期性。比如，月度数据的谱密度在角频率$\frac{2\pi}{12}$处表现出高的峰值。设$\omega$为角频率，$f$为频率，$T$为周期，则 \[\begin{aligned} \omega = 2\pi f, \quad T = \frac{1}{f} \end{aligned}\]

例6.2 国际航空订票数据的随机项的谱密度在周期12处有显著峰值。考察数据的周期性变化是谱密度估计的重要应用之一。

plot(AirPassengers)

spec.pgram(AirPassengers)

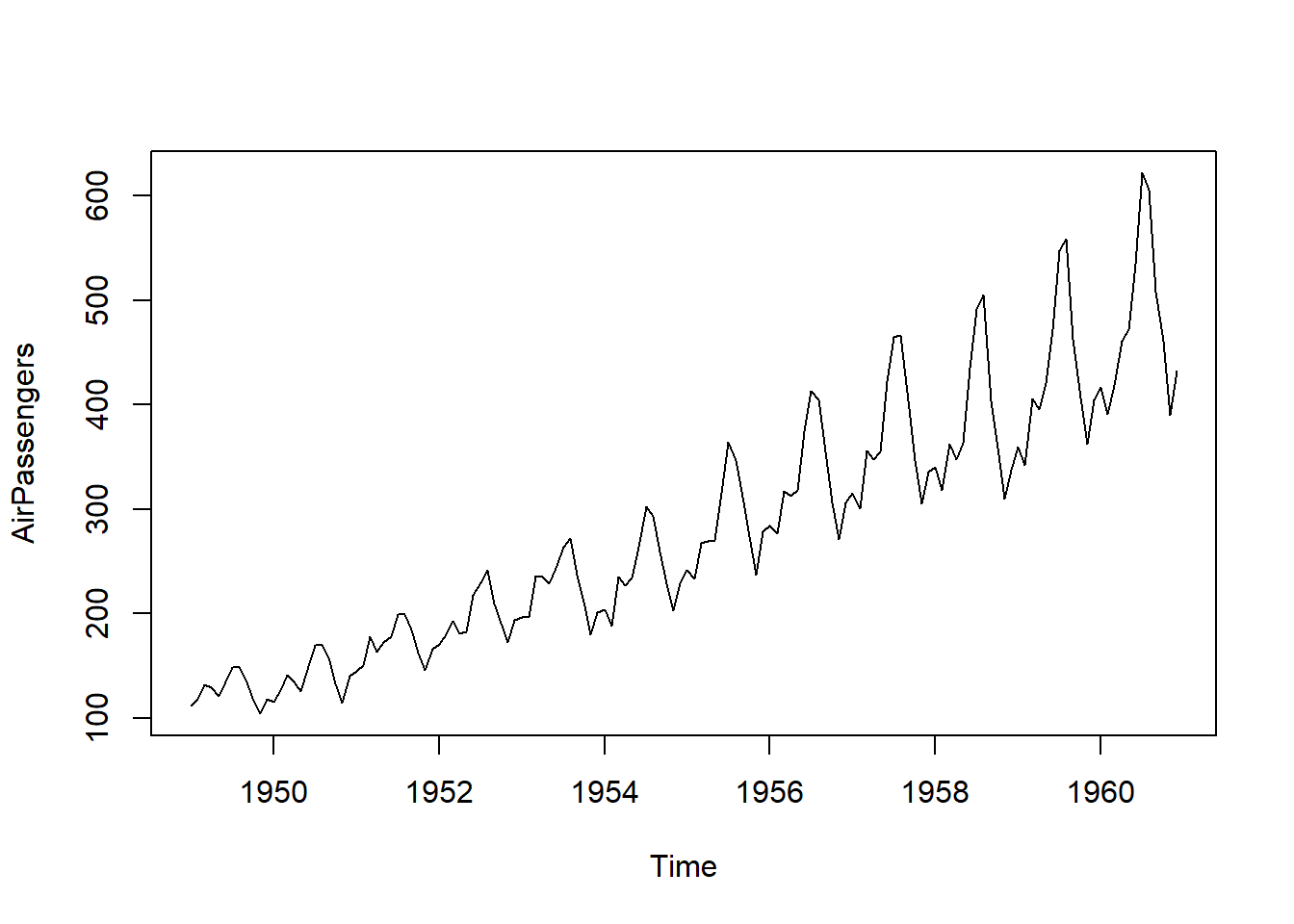
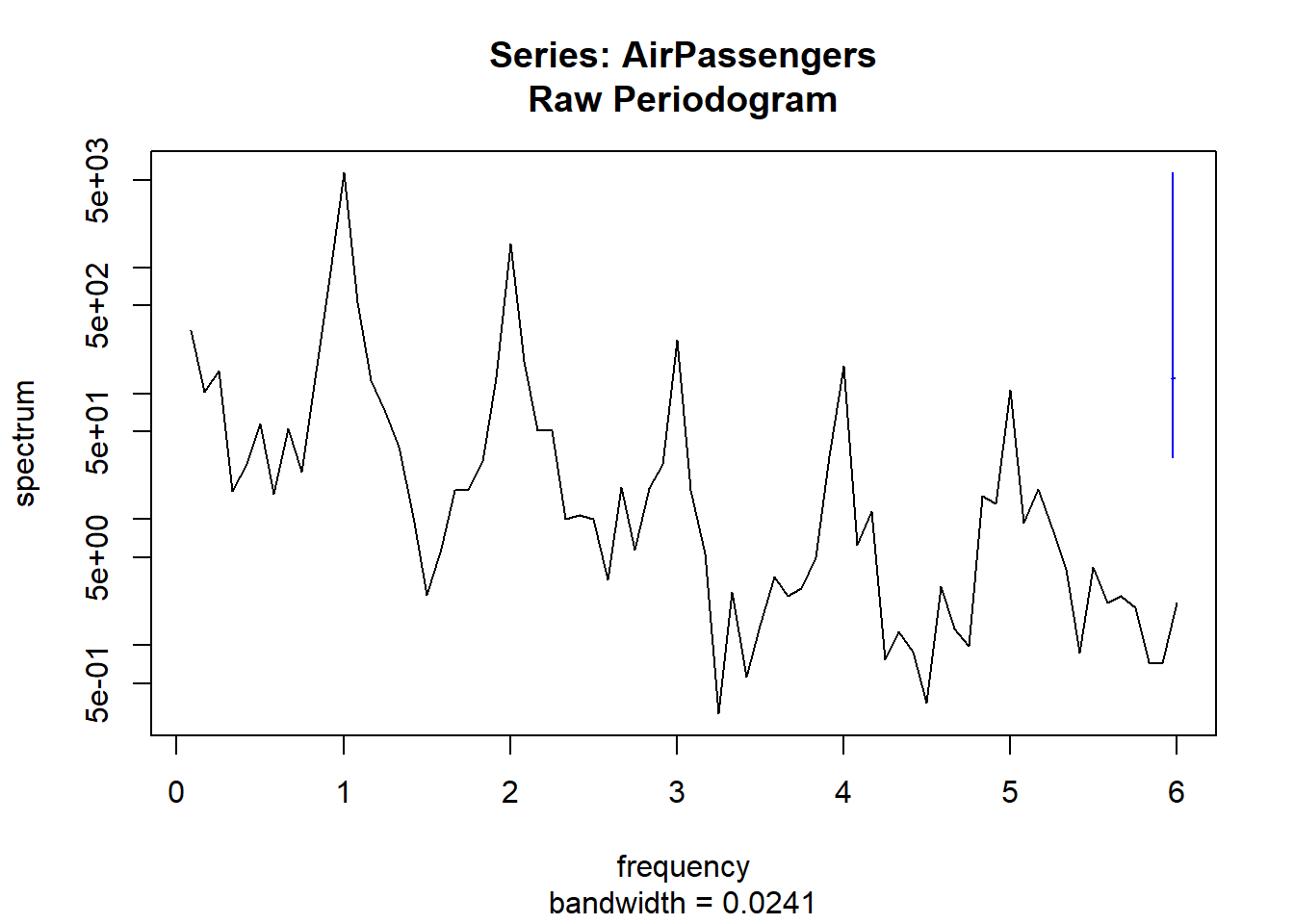
这里的横坐标频率单位是以$1/T$为单位，这里$T=12$。

○○○○○○

6.3.3 离散谱序列

实际中的离散谱序列经常会有多个频率成分。设有$2p$个随机变量$\xi_k, \eta_k, k=1,\dots,p$, 所有$2p$个两两正交，满足 \[\begin{align} E\xi_j = E\eta_j = 0, \quad E\xi_j^2 = E\eta_j^2 = \sigma_j^2 \tag{6.19} \end{align}\] 设$\lambda_j \in (0,\pi], j=1,\dots,p$，定义 \[\begin{align} Z_t =& \sum_{j=1}^p [\xi_j \cos(\lambda_j t) + \eta_j \sin(\lambda_j t) ] \nonumber \\ =& \sum_{j=1}^p A_j \cos(\lambda_j t - \theta_j), \quad t \in \mathbb N_+ \tag{6.20} \end{align}\] 其轨道表现为有$p$个频率成分的非随机函数。

$\{Z_t\}$为零均值平稳列, \[\begin{align} \gamma_k = \sum_{j=1}^p \sigma_j^2 \cos(k\lambda_j), \quad k \in \mathbb Z. \tag{6.21} \end{align}\]

设所有$\lambda_j \neq \pi$, 这时谱函数为 \[\begin{aligned} F(\lambda) = \sum_{j=1}^p \frac{\sigma_j^2}{2} \left[ I_{[-\lambda_j, \pi]}(\lambda) + I_{[\lambda_j, \pi]}(\lambda) \right], \ \lambda \in [-\pi,\pi] \end{aligned}\] 此谱函数表现为在$\pm \lambda_j$处有跳跃$\frac{\sigma_j^2}{2}$ 的阶梯函数，表明谱的能量集中在这$2p$个频率上。

§6.1讲谱时的单音例子就是离散谱的例子。

离散谱序列可以由可列个简单的离散谱序列叠加而成。设$\xi_j, \eta_k, (j,k=1,2,\dots)$两两正交，满足 \[\begin{align} E\xi_j = E\eta_j = 0, \quad E\xi_j^2 = E\eta_j^2 = \sigma_j^2 \tag{6.22} \end{align}\] 且 \[\begin{align} \sum_{j=1}^\infty \sigma_j^2 < \infty \tag{6.23} \end{align}\] 设$\lambda_j \in (0,\pi], j=1,2,\dots$。

定义 \[\begin{align} Z_t =& \sum_{j=1}^\infty [\xi_j \cos(\lambda_j t) + \eta_j \sin(\lambda_j t) ] \quad t \in \mathbb N_+ \tag{6.24} \end{align}\] 改写为 \[\begin{align} Z_t = \sum_{j=1}^\infty \left[ \sigma_j \cos(t\lambda_j) (\xi_j / \sigma_j) + \sigma_j \sin(t\lambda_j) (\eta_j / \sigma_j) \right], \tag{6.25} \end{align}\] 其中$\{\xi_j/\sigma_j\}$和$\{\eta_j/\sigma_j\}$可以合并为一个WN(0,1)，级数中组合系数平方可和： \[\begin{aligned} \sum_{j=1}^\infty \left[ (\sigma_j \cos(t\lambda_j))^2 + (\sigma_j \sin(t\lambda_j))^2 \right] = \sum_{j=1}^\infty \sigma_j^2 < \infty \end{aligned}\] 所以级数(6.24)的右端均方收敛。

由$L^2$中内积的连续性, 对$\forall t, s \in \mathbb Z$有 \[\begin{aligned} E(Z_t) =& E(Z_t \cdot 1) \\ =& \sum_{j=1}^\infty E [\xi_j \cos(\lambda_j t) + \eta_j \sin(\lambda_j t) ] \\ =& 0 \\ E(Z_t Z_s) =& \lim_{n\to\infty} \Big\{ \sum_{j=1}^n [\xi_j \cos(\lambda_j t) + \eta_j \sin(\lambda_j t) ] \\ & \cdot \sum_{j=1}^n [\xi_j \cos(\lambda_j s) + \eta_j \sin(\lambda_j s) ] \Big\} \\ =& \lim_{n\to\infty} \sum_{j=1}^n \sigma_j^2 \cos[(t-s)\lambda_j] \\ =& \sum_{j=1}^\infty \sigma_j^2 \cos[(t-s)\lambda_j] \end{aligned}\]

所以，由可列个简单离散谱序列叠加得到的序列(6.24)是零均值平稳列。它由可列个正弦波和余弦波叠加构成。有自协方差函数 \[\begin{align} \gamma_k = \sum_{j=1}^\infty \sigma_j^2 \cos(k\lambda_j), \ k \in \mathbb Z \tag{6.26} \end{align}\] 谱函数为 \[\begin{align} F(\lambda) = \sum_{j=1}^\infty \frac{\sigma_j^2}{2} \left[ I_{[-\lambda_j, \pi]}(\lambda) + I_{[\lambda_j, \pi]}(\lambda) \right], \ \lambda \in [-\pi,\pi] \tag{6.27} \end{align}\] 是一个有可列个跳跃点的阶梯函数，在$\pm \lambda_j$有跳跃$\sigma_j^2/2$，对应于$[-\pi,\pi]$的一个离散测度。如果某个$\lambda_j=\pi$，它对$F(\lambda)$的贡献应该写成, $\sigma_j I_{\{\pi\}}(\lambda)$。

尽管离散谱序列是随机的，但它的每一次观测是确定的三角函数相加在整数点上的取值。实际工作中也经常把这样的模型看作非随机的，这时 \[\begin{aligned} Z_t = \sum_{j=1}^p A_j \cos(\lambda_j t + \theta_j), \ t \in \mathbb Z \end{aligned}\] 其中$A_j, \theta_j$非随机。称这样的模型为调和模型(harmonic model)。

6.4 附录：用R程序处理声音

6.4.1 tuneR包

tuneR包可以读写WAV格式的声音文件，并作一些简单操作。还可以读入MP3格式，读入Midi格式，分辨音符并输出为lilipond格式。

读入一个WAV文件，用如

library(tuneR)
mus <- readWave("data/music-demo2.wav")

还可以指定from, to, units="seconds"来读取WAV文件的一个片段。读入的左声道数据为mus@left, 采样率为mus@samp.rate。读入的声音数据没有自动标准化，取值可能是在$\pm 2^{\text{bit}-1}$范围而不是$[-1,1]$范围。

readMP3()函数可以读取MP3文件。

用writeWave将声音保存为WAV文件，如

y2 <- tuneR::sine(freq=523, samp.rate=8000, duration=1, xunit="time")
writeWave(y2, filename="data/music-demo2b.wav")

可以用stereo()函数将两个单声道组合成立体声，可以用mono()函数从立体声取出其中一个声道。

6.4.2 sound包

R软件的sound包可以读写WAV格式的声音文件并进行简单的操作。可以在WAV格式与矩阵格式之间进行转换。

读入一个WAV文件，用如

library(sound)
mus <- loadSample("data/music-demo2.wav")

这样读入一个声音对象。用rate(mus)求采样频率。

用saveSample把声音片段保存为WAV格式，如

saveSample(mus, filename="tmp.wav")

6.4.3 seewave包

seewave包可以分析、合成声音，进行时间、振幅、频率分析，估计声音之间的数量差别，生成新的声音用于回放。

读入的声音，可以是向量、矩阵、时间序列(ts, mts)，或者tuneR包的Wave类型， audio包的audioSample类型。

对于普通向量，矩阵，只要指定采样频率，就可以看成是声音。

对于ts或者mts类型的时间序列，其frequency对应于声音的采样频率。多元时间序列在seewave中只使用其中第一列。

oscillo()绘制声音波形图。 spec()作谱密度估计图。 spectro()作动态谱峰图。

6.4.4 演示程序

如下的程序读入music-demo2.wav音乐文件，此文件包含了笛子演奏片段，有三个音符：

library(seewave)
library(tuneR)
mus <- readWave("data/music-demo2.wav")

## Warning in readChar(con, 4): 在non-UTF-8 MBCS语言环境里只能读取字节

## Warning in readChar(con, 4): 在non-UTF-8 MBCS语言环境里只能读取字节

## Warning in readChar(con, 4): 在non-UTF-8 MBCS语言环境里只能读取字节

## Warning in readChar(con, 4): 在non-UTF-8 MBCS语言环境里只能读取字节

f <- mus@samp.rate
cat("采样频率=", f, "\n")

## 采样频率= 22050

用seewave::cutw()函数截取从0.125秒到1.125秒的音高为C5的片段，以及其中0.05秒的片段：

## mi1: 1秒长的一段C5音阶。
mi1 <- cutw(mus, from=0.125, to=1.125,
            output="Wave")
## mi1a: 0.05秒长的一段C5音阶。
mi1a <- cutw(mus, from=0.500, to=0.550,
             output="Wave")

显示0.05秒的序列图，标题中的f=22050是采样频率，音阶是C5(523Hz)：

oscillo(mi1a, 
        title='0.05秒的声音时间序列图')

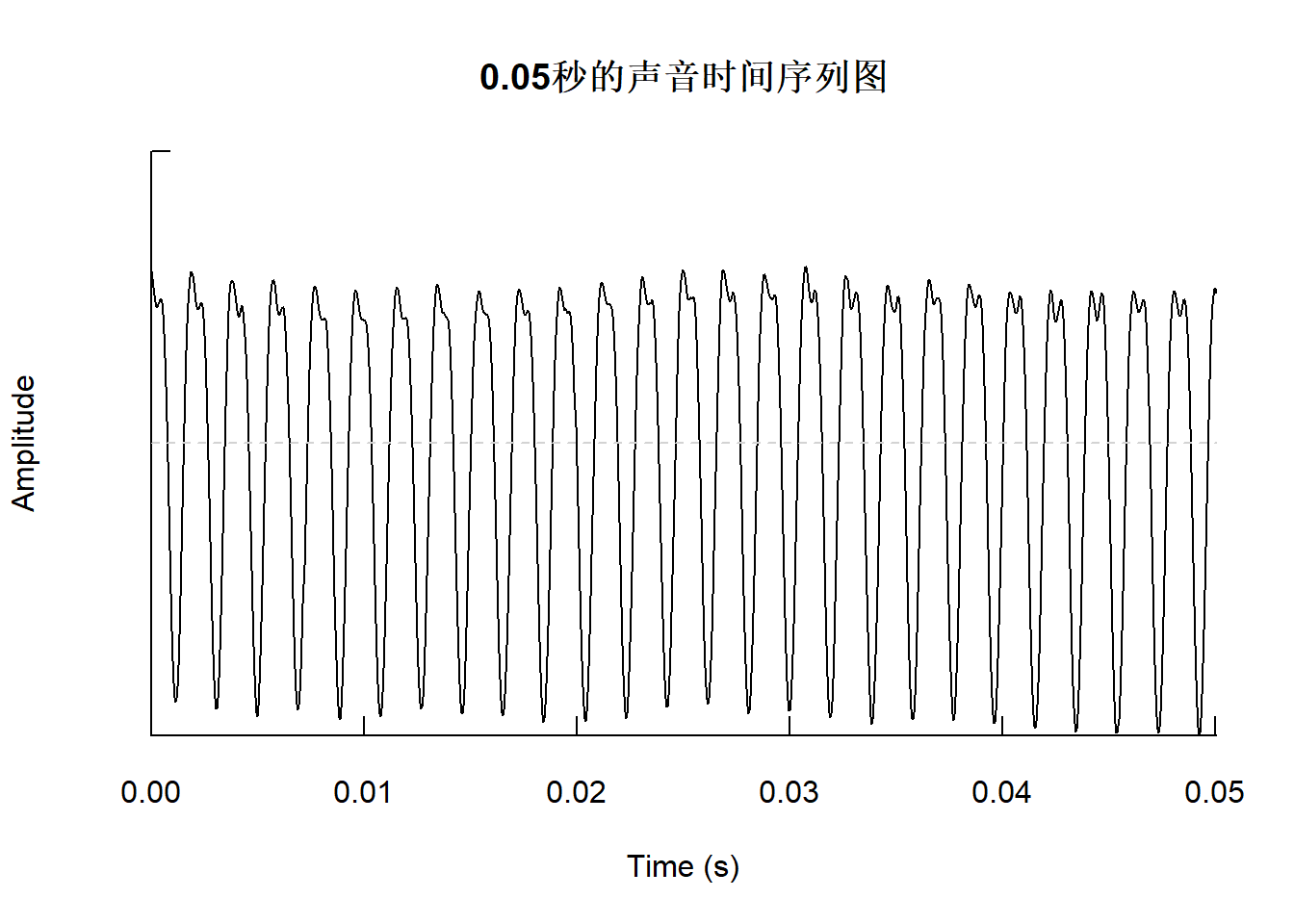
对0.05秒的C5音阶录音用时间序列分析的spec.pgram()函数做加窗谱估计，注意纵轴用了对数刻度:

spec.pgram(ts(mi1a@left, frequency=mi1a@samp.rate), spans=c(5,7),
           xlim=c(0,10000), main="用spec.pgram进行谱估计",
           xlab="")

用seewave包的spec()函数显示0.05秒的C5音阶的频谱，纵轴没有用对数刻度：

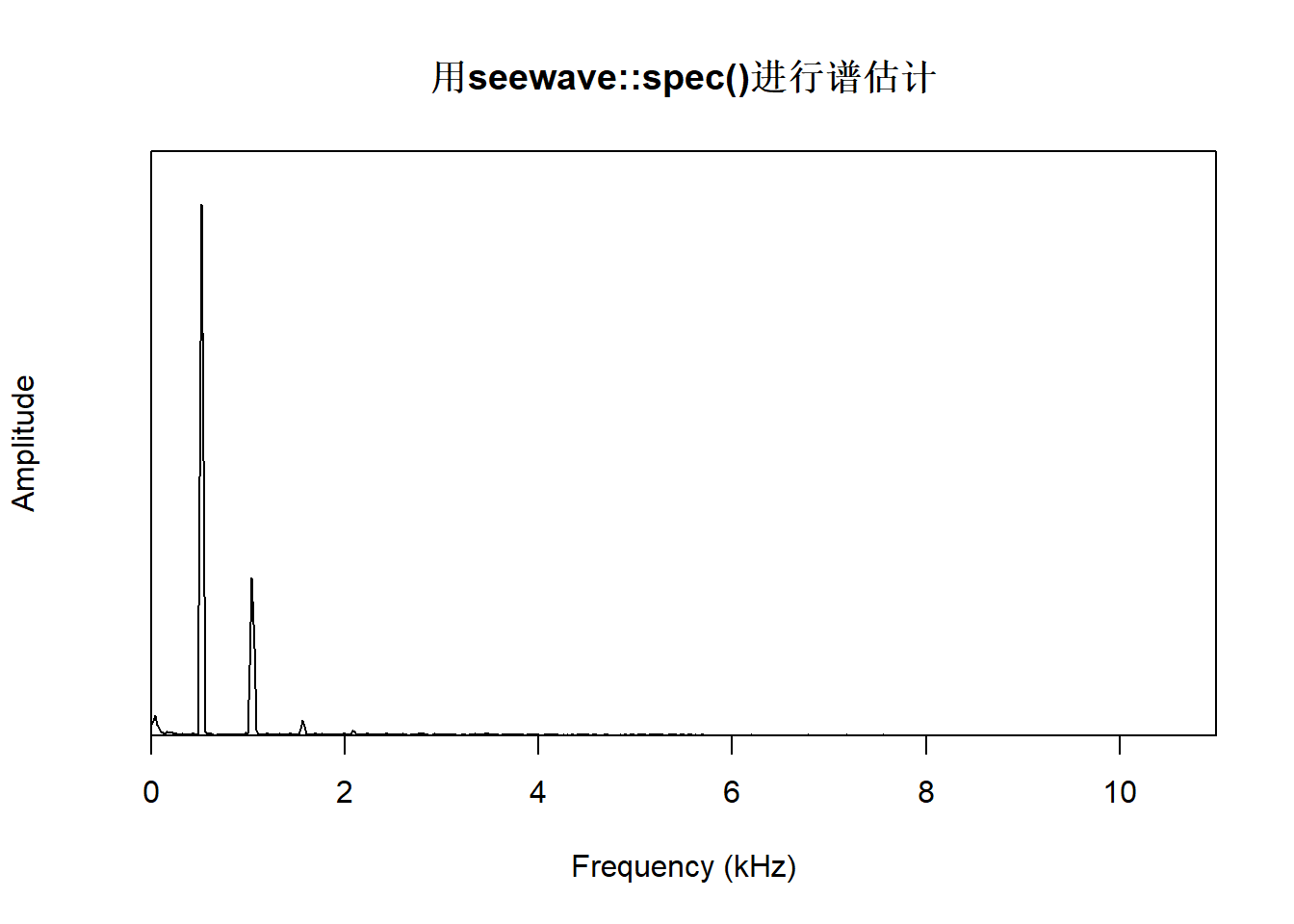
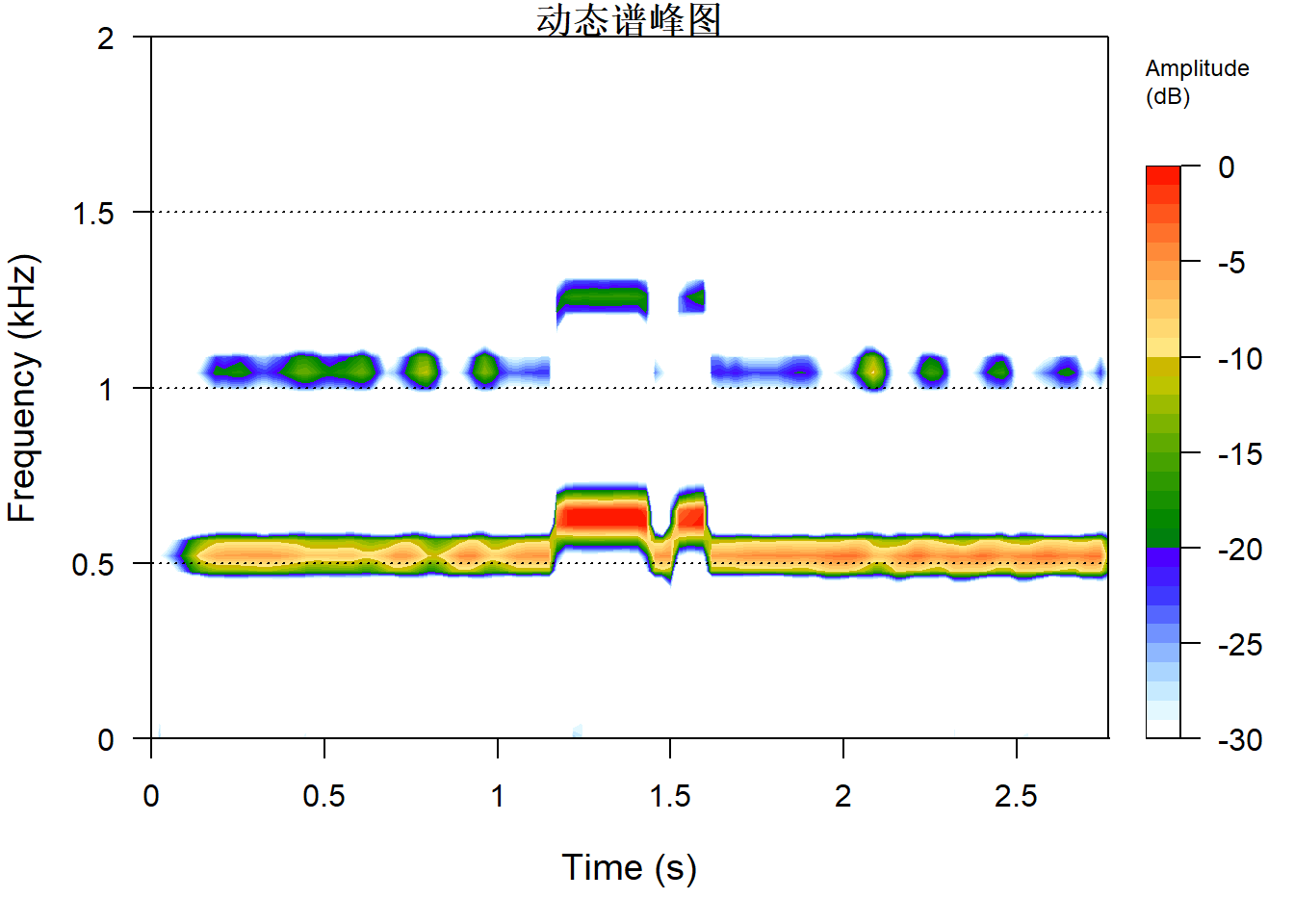
seewave::spec(mi1a, main="用seewave::spec()进行谱估计")

下面用seewave包的spectro()函数对包含三个音阶的笛子演奏片段做动态谱峰图, 动态显示随时间变化的主要谱峰位置。横坐标是时间，纵坐标是声音频率，颜色为在该时间、该频率上的振幅（注意同一时刻只有一个主要频率有振幅）能看出C5--D#5--C5的频率主峰变化。

seewave::spectro(mus, flim=c(0,2), main="动态谱峰图")

如下的程序用R的基本函数生成一个523Hz声音(音调C5)的1秒的波形，作为一个R向量，并显示前0.05秒的波形图：

f8000 <- 8000 ## 采样频率8kHz。
## timey: 为[0,1]中等间隔8000个点的时间。采样频率8000Hz。
timey <- seq(0,1, length.out=f8000*1)
## y: 直接用sin函数生成的523Hz单音，向量长度为8000个点，组成1秒钟。
y <- sin(2*pi*523*timey)
## 用oscillo函数作波形图，仅取前0.05秒：
seewave::oscillo(
  cutw(y, f=f8000, from=0, to=0.05),
  f=f8000,
  title='直接用sin函数生成523Hz单音')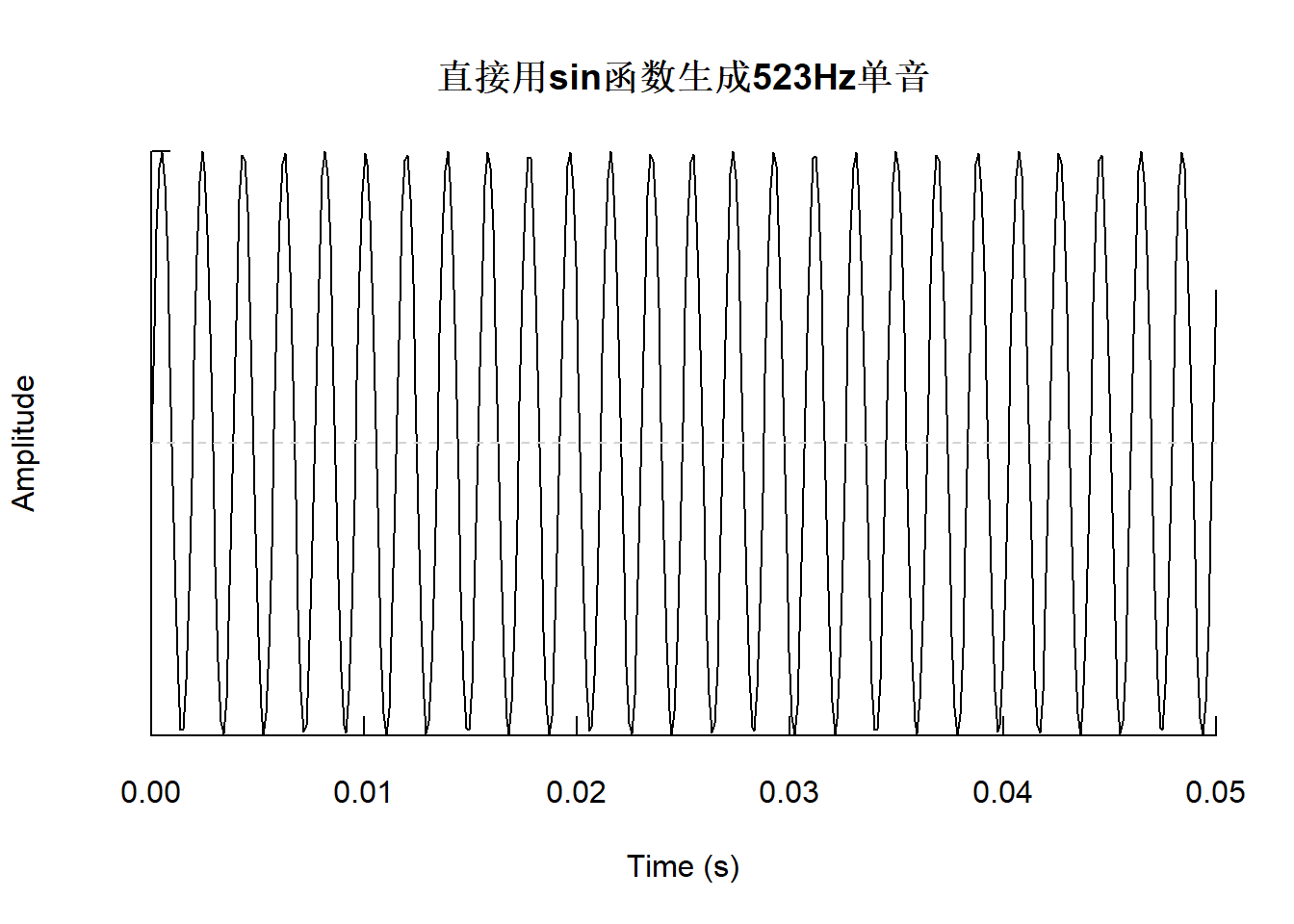

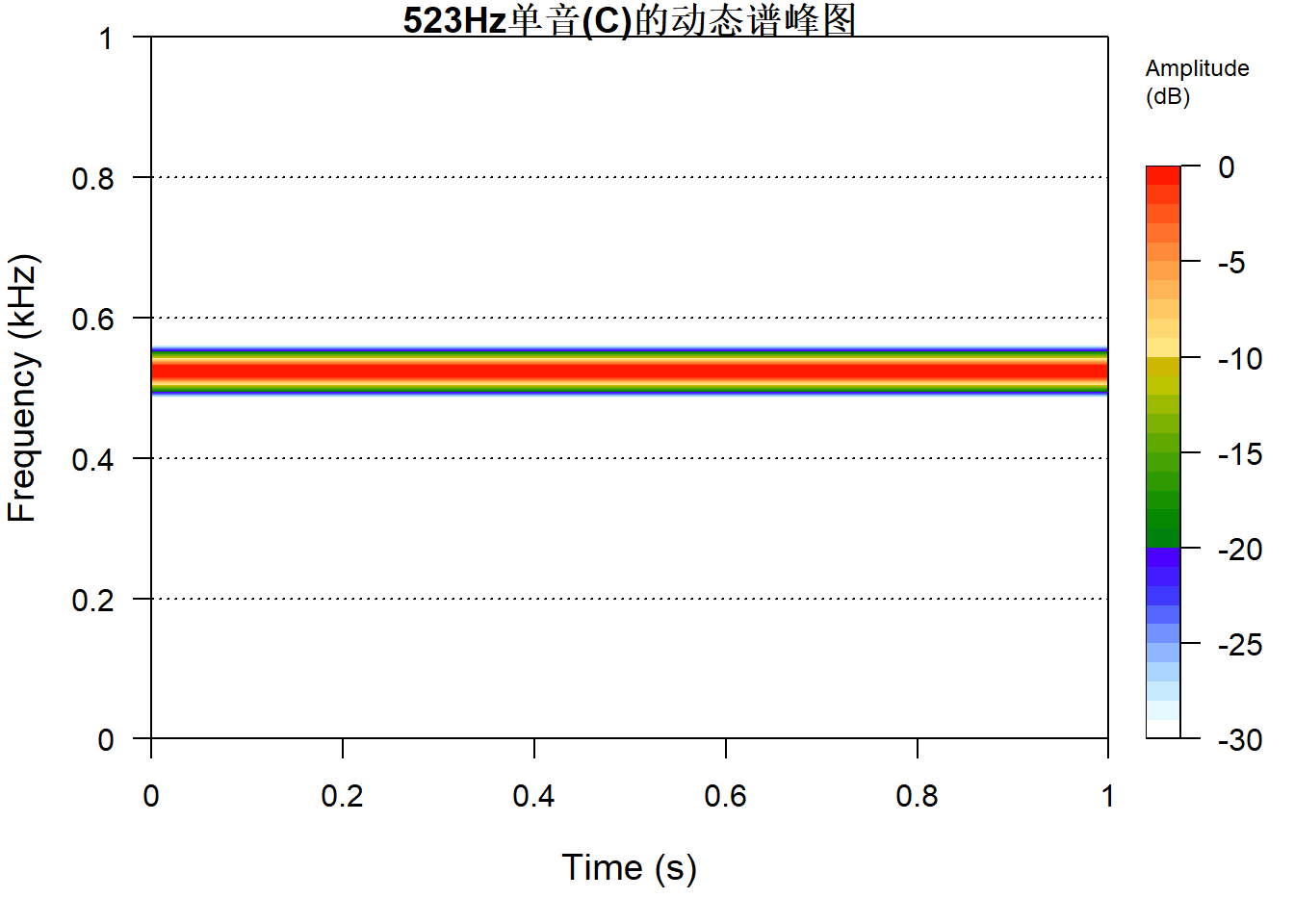
事实上， tuneR包的sine()函数可以更容易地生成这种单音的文件，如

y2 <- tuneR::sine(freq=523, samp.rate=8000, duration=1, xunit="time")

人造单音的动态频谱图:

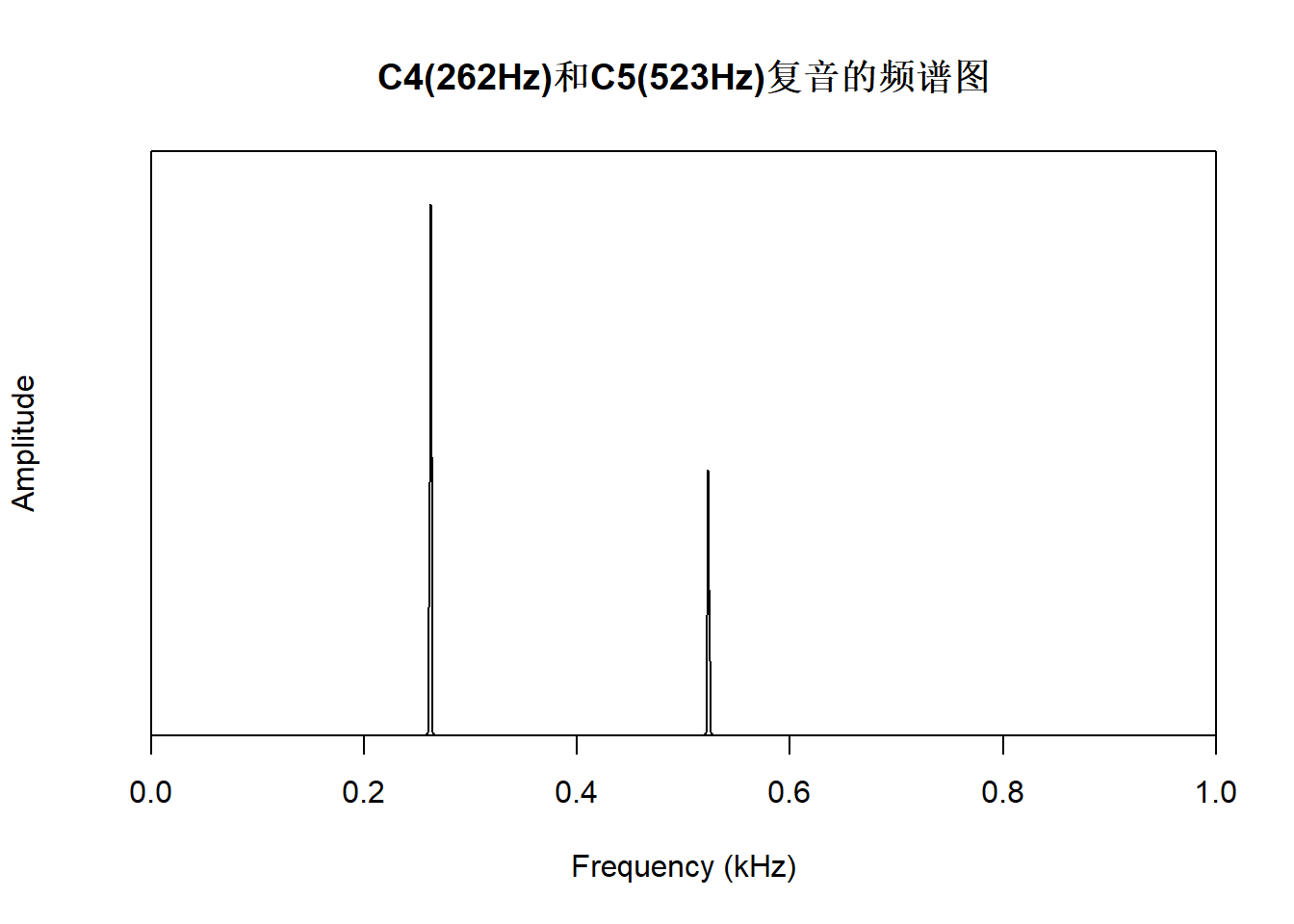
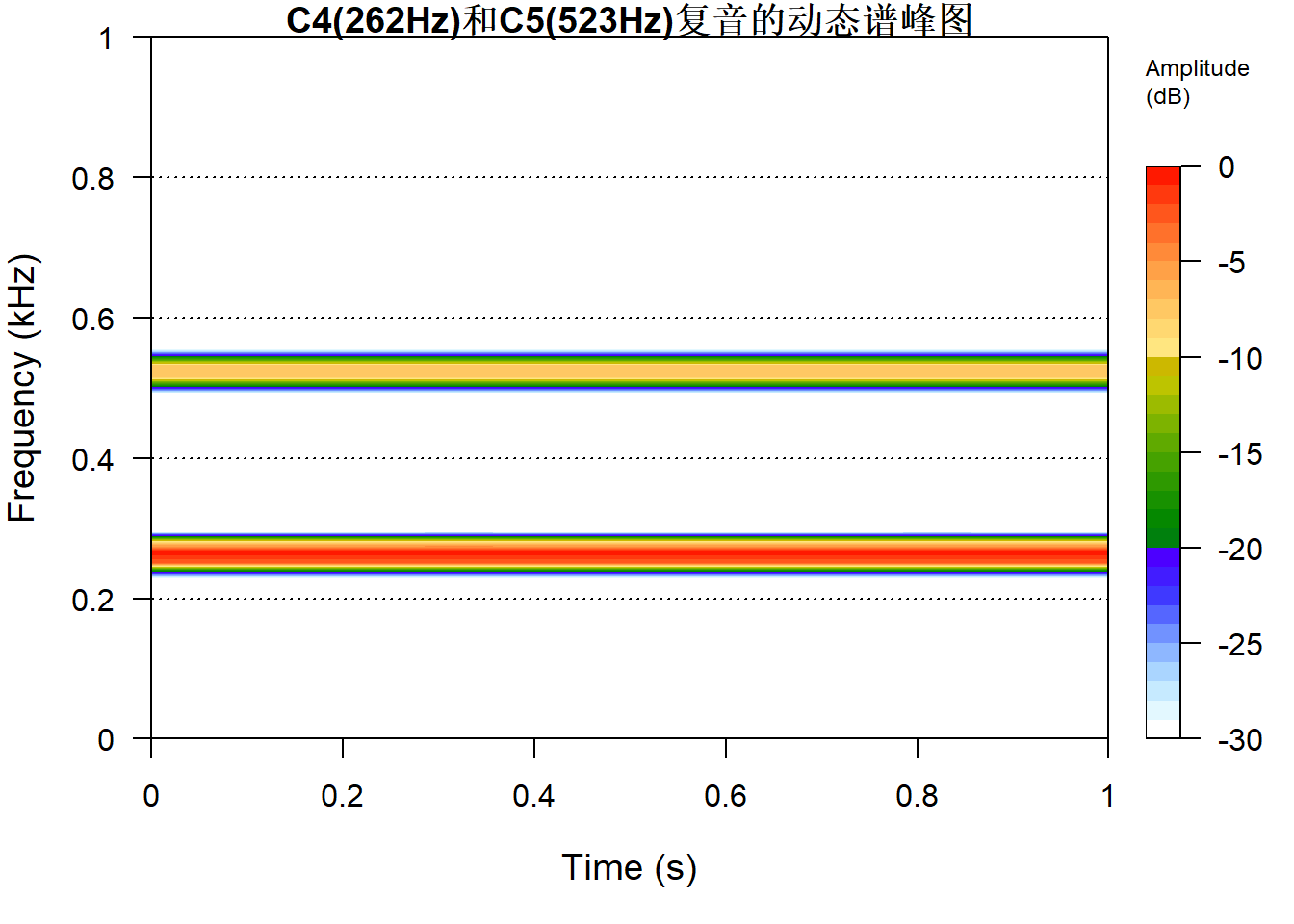
seewave::spectro(y, f=f8000, flim=c(0,1.0), main="523Hz单音(C)的动态谱峰图")

下面用基本R函数生成C4+C5复音，以C4为主（振幅比值为2）。作前0.05秒的波形图：

f8000 <- 8000
y3 <- 0.5*sin(2*pi*262*seq(0,1, length.out=f8000*1)) + # C4音阶
  0.25 * sin(2*pi*523*seq(0,1, length.out=f8000*1))
##writeWave(Wave(y3*2^15, samp.rate=f8000, bit=16), 
##          filename="data/music-demo2c.wav")
oscillo(cutw(y3, f=f8000, from=0, to=0.05), f=f8000,
          title='低音C和中音C的复音')

人造复音的频谱图:

seewave::spec(y3, f=f8000, main="C4(262Hz)和C5(523Hz)复音的频谱图", flim=c(0, 1))

人造复音的动态频谱图:

seewave::spectro(y3, f=f8000, flim=c(0,1.0), main="C4(262Hz)和C5(523Hz)复音的动态谱峰图")

6.5 谱函数和谱密度补充

当平稳时间序列的自协方差函数绝对可和时，谱密度存在且与自协方差函数是傅立叶级数和傅立叶系数的关系。对于连续时平稳过程的自协方差函数绝对可积时，也有谱密度，且自协方差函数与谱密度为傅立叶变换关系。

设复值平稳列$\{ \xi_t, t\in \mathbb Z \}$的谱函数为$F(\lambda)$， $\{\xi_t \}$张成的Hilbert空间$H_\xi$与 \[\begin{aligned} L^2(dF) = \{\varphi(\lambda): \int_{-\pi}^\pi |\varphi(\lambda)|^2 d F(\lambda) \} \end{aligned}\] 存在等距对应映射$\mathcal K$把$L^2(dF)$映射到$H_\xi$使得两空间同构， $\mathcal K$把$e^{it\lambda}$映射为$\xi_t$。

定理6.7 (平稳序列谱表示) 对复值平稳时间序列$\{\xi_t, t\in \mathbb Z\}$，存在$[-\pi,\pi]$上的零均值连续时正交增量左$L^2$连续复值随机过程 $\{Z(\lambda), \lambda \in [-\pi,\pi]\}$，使得$Z(-\pi)=0$, \[\begin{aligned} E| Z(\lambda_2) - Z(\lambda_1) |^2 = F_\xi(\lambda_2) - F_\xi(\lambda_1), \ -\pi \leq \lambda_1 < \lambda_2 \leq \pi. \end{aligned}\] 对任意$\varphi \in L^2(dF_\xi)$，可以定义随机积分 \[\begin{aligned} \int_{-\pi}^\pi \varphi(\lambda) dZ(\lambda) \end{aligned}\] 这时 \[\begin{aligned} \xi_t = \int_{-\pi}^{\pi} e^{it\lambda} dZ(\lambda) \end{aligned}\] 称为平稳时间序列的谱表示，含义是如下极限 \[\begin{aligned} \xi_t = \lim_{\max |\Delta \lambda_k| \to 0} \sum_{k} e^{it\lambda_k} Z^{(b)}(\Delta\lambda_k) \end{aligned}\]

见(谢衷洁 1990)PP30–40。

定理6.8 有谱密度的平稳列必为系数平方可和的线性序列。

见(谢衷洁 1990)P49。

6.6 给定谱密度后的时间序列模拟生成

设某平稳列$\{ X_t \}$谱密度为$f(\lambda)$，希望生成$\{ X_t \}$的模拟数据$X_1, X_2, \dots, X_n$。

因为$f(\lambda)$决定了自协方差函数$\{\gamma_k\}$，可以先计算$\gamma_0, \gamma_1, \dots, \gamma_{n-1}$，具体可以使用数值积分方法计算 \[ \gamma_k = 2\int_0^\pi f(\lambda) \cos(k\lambda) \,d\lambda, \ k=0,1,\dots, n-1 \] 得到随机向量$\boldsymbol X = (X_1, X_2, \dots, X_n)$的协方差阵$\Gamma_n$。

当$n$不太大时，可以计算$\Gamma_n$的Cholesky分解$\Gamma_n = B B^T$， $B$为下三角阵且对角线元素为正值。生成独立同标准正态分布的$Z_1, Z_2, \dots, Z_n$，令$\boldsymbol Z = (Z_1, Z_2, \dots, Z_n)^T$，令$\boldsymbol X = B Z$，则$X_1, X_2, \dots, X_n$为自协方差函数为$\{ \gamma_k \}$，谱密度为$f(\lambda)$的零均值正态平稳列的样本。

当$n$很大时，计算很多个$\{\gamma_k \}$计算量很大也不必要，因为$\gamma_k \to 0$；存储和计算Cholesky分解也可能需要许多存储空间与计算时间，而且由于计算误差可能导致$\Gamma_n$不正定。这时可以用条件分布法，设定一个界限$p$，认为条件分布$X_k | X_{k-1}, \dots, X_1$近似等于条件分布$X_k | X_{k-1}, \dots, X_{k-p}$，然后仅利用$\Gamma_p$产生条件期望和条件方差，逐步向前推进模拟。可以从$\gamma_0, \dots, \gamma_p$求解出一个AR($p$)模型，模拟这个AR($p$)代替要模拟的序列。

作为例子，我们来模拟6.3.2中用阶梯函数谱密度逼近离散谱序列的问题。只有一个频率的离散谱序列为 \[ X_t = \xi \cos(\lambda_0 t) + \eta \sin(\lambda_0 t) \] 其中$\xi, \eta$不相关，零均值，方差都等于$\sigma^2$。自协方差函数为 \[ \gamma_k = \sigma^2 \cos(k \lambda_0) \] $\{X_t \}$的谱函数为 \[\begin{aligned} F(\lambda) = \sigma^2 [ 0.5 I_{[-\lambda_0,\pi]}(\lambda) + 0.5 I_{[\lambda_0,\pi]}(\lambda)] \end{aligned}\] 是仅在$-\lambda_0$和$\lambda_0$处有跳跃的阶梯函数，见图6.7。

取谱密度 \[\begin{aligned} f_n(\lambda) =& n \sigma^2 I_{[-\lambda_0, -\lambda_0 + 1/(2n)] \cup [\lambda_0 - 1/(2n), \lambda_0]}(\lambda) \\ F_n(\lambda) =& \int_{-\pi}^\lambda f_n(u) du \end{aligned}\] 则$f_n$是一个仅在两个长度为$\frac{1}{2n}$的小区间上非零的分段函数。 $F_n(\lambda)$为连续的折线函数，仅在上述两个小区间上为线性增函数，在其它位置为水平线。有极限 \[\begin{aligned} F_n(\lambda) \to F(\lambda), \ \lambda \neq \pm \lambda_0, \ n \to \infty. \end{aligned}\]

来模拟生成谱密度为$f_n(\lambda)$的平稳列。对应的协方差函数为 \[\begin{aligned} g_k(n) =& \int_{-\pi}^\pi f(\lambda) \cos k\lambda \\ =& \frac{2 n \sigma^2}{k} \left[ \sin(k \lambda_0) - \sin(k (\lambda_0 - \frac{1}{2n}) ) \right], k=1,2,\dots, \\ g_0(n) =& \sigma^2 \end{aligned}\]

取$\lambda_0 = \frac{2\pi}{4}$，对应于周期4，取$n = 10$。下面的函数中, T是要模拟的序列长度， T0是离散谱的周期，对应于$\frac{2\pi}{\lambda_0}$， $n$是用来近似的谱密度$f_n(\lambda)$的逼近程度， $n$越大，模拟的谱函数越接近于离散谱函数。

## 一般的给定自协方差函数的模拟程序
sim.fromgam <- function(gamfun){
  n <- length(gamfun)
  Gmat <- outer(1:n, 1:n, function(i, j) gamfun[abs(i-j) + 1])
  B <- chol(Gmat) # 结果是n*n上三角矩阵
  c(rnorm(n) %*% B)
}
sim.disc2dens <- function(T = 64, T0 = 4, n = 10, sigma = 1){
  ## 先计算\gamma_0, \dots, \gamma_{T-1}
  lam0 <- 2*pi / T0
  lam1 <- lam0 - 1/(2*n)
  kk <- 1:(T-1)
  gamfun <- (2*n*sigma^2) * c(1/(2*n), 1/kk * (
    sin(kk*lam0) - sin(kk*lam1) ) )
  sim.fromgam(gamfun)
}

模拟一次：

xdd <- sim.disc2dens(T = 64, T0 = 4, n = 10)
## Error in chol.default(Gmat) : the leading minor of order 11 is not positive definite

经过试验发现，由于数值误差以及近似为离散谱的原因，即使对比较小的$n$， $\Gamma_T$矩阵也很快变得不满秩。由于计算误差的影响，上面结果中的$\Gamma_T$矩阵计算出的特征值从第28个开始就为负值了。所以，我们取一个较低阶的AR($p$)作为近似。取$p = 6$。

sim.disc2dens <- function(T = 128, T0 = 4, n = 10, p = 6, sigma = 1){
  ## 先计算\gamma_0, \dots, \gamma_{p}
  lam0 <- 2*pi / T0
  lam1 <- lam0 - 1/(2*n)
  kk <- 1:p
  gamfun <- (2*n*sigma^2) * c(1/(2*n), 1/kk * (
    sin(kk*lam0) - sin(kk*lam1) ) )
  ## 求解Y-W方程得到a_1, \dots, a_p和AR模型的白噪声方差
  Gmat <- outer(1:p, 1:p, function(i, j) gamfun[abs(i-j) + 1])
  avec <- solve(Gmat, gamfun[-1])
  s2ar <- gamfun[1] - sum(gamfun[-1] * avec)
  arima.sim(model = list(ar = avec), n = T) * sqrt(s2ar)
}
xdd <- sim.disc2dens(T = 128, T0 = 4, n = 10, p = 6)
ts.plot(xdd)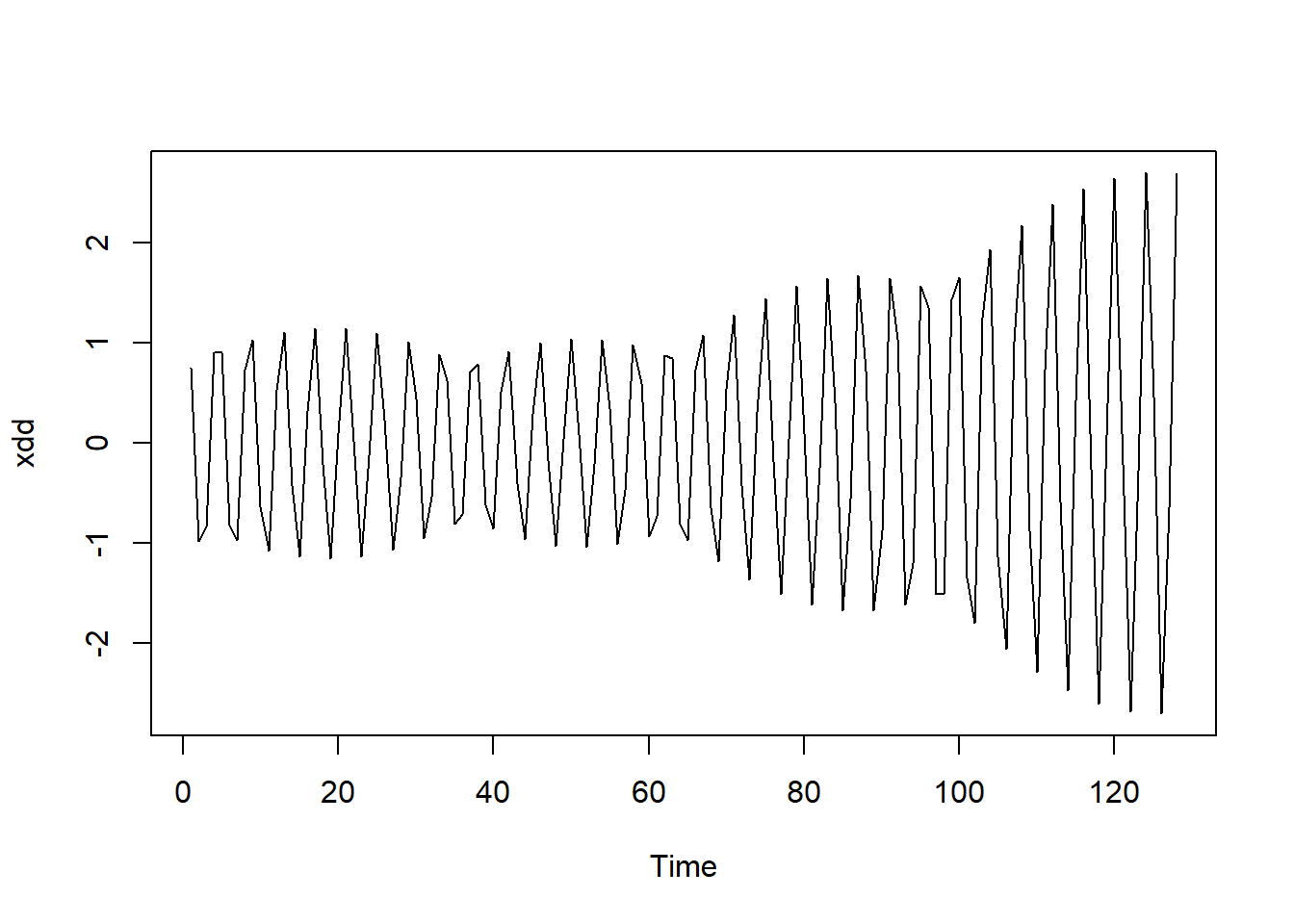

结果中可以看出明显的周期性，但是又和离散谱序列轨道哪种严格的周期函数不同。估计其谱密度：

spectrum(xdd, method = "ar")

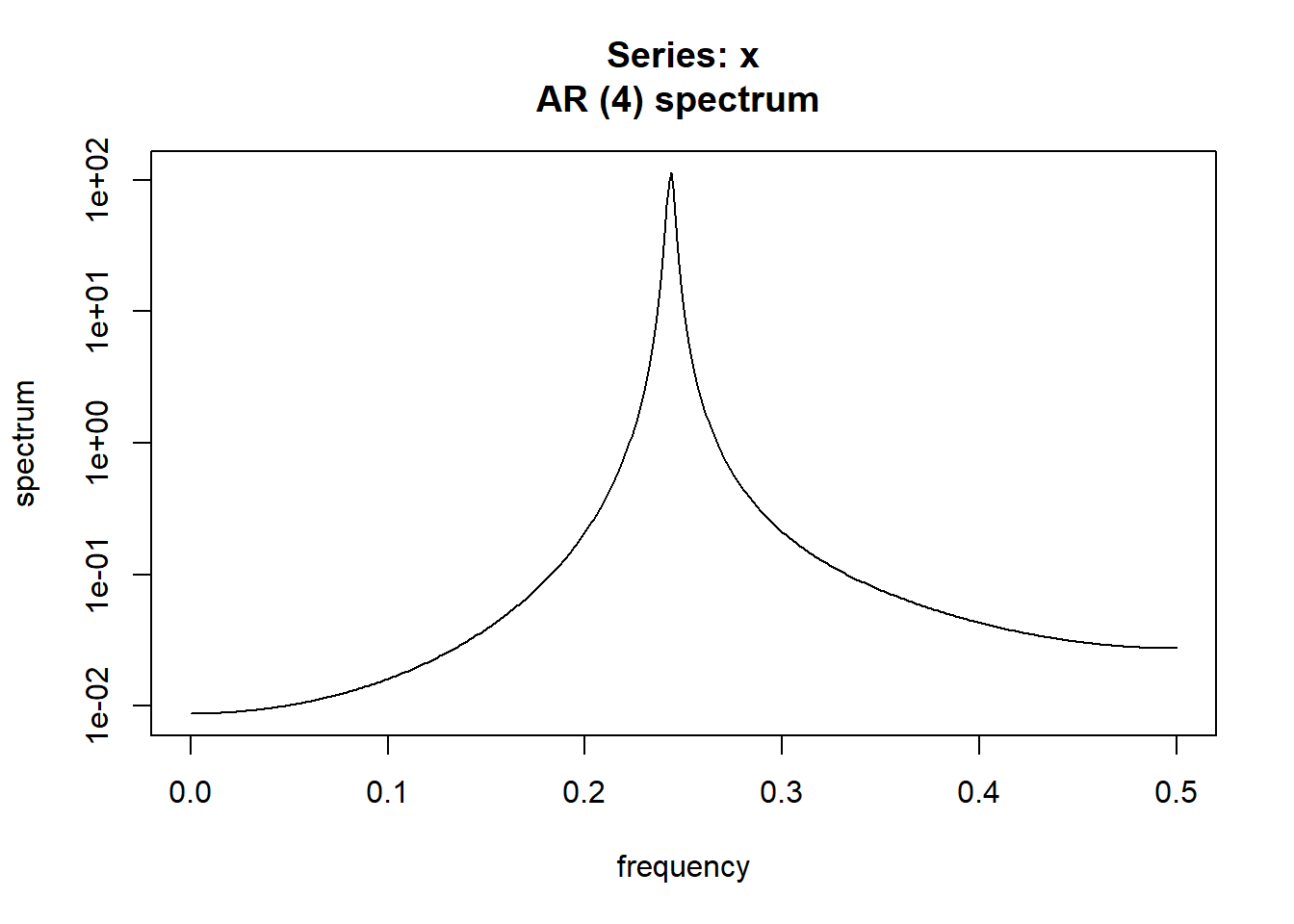
估计的谱密度在$\lambda_0 = \frac{2\pi}{4} = 0.25$处有唯一一个高峰。

References

谢衷洁. 1990. 时间序列分析. 北京大学出版社.

音调	低音(3)	中音(4)	高音(5)
C	131	262	523
D	147	294	587
E	165	330	659
F	175	349	698
G	196	392	784
A	220	440	880
B	247	494	988

音调	低音(3)	中音(4)	高音(5)
C	131	262	523
D	147	294	587
E	165	330	659
F	175	349	698
G	196	392	784
A	220	440	880
B	247	494	988

音调	低音(3)	中音(4)	高音(5)
C	131	262	523
D	147	294	587
E	165	330	659
F	175	349	698
G	196	392	784
A	220	440	880
B	247	494	988