16 自协方差函数的估计
16.1 自协方差估计公式及正定性
\[\begin{align} \hat\gamma_k =& \frac{1}{N} \sum_{j=1}^{N-k} (x_j - \bar x_N) (x_{j+k} - \bar x_N), \quad 0 \leq k \leq N-1 , \tag{16.1} \\ \hat\gamma_{-k} =& \hat\gamma_k \nonumber \end{align}\]
样本自相关系数(ACF)估计为 \[\begin{align} \hat\rho_k = \frac{\hat\gamma_k}{\hat\gamma_0}, \quad |k| \leq N-1 \tag{16.2} \end{align}\] \(k\)较大时参与平均的项减少所以\(\hat\gamma_k\)估计误差会随\(k\)增大而变大。
估计\(\gamma_k\)一般不使用除以\(N-k\)的估计形式: \[\begin{align} \hat\gamma_k =& \frac{1}{N-k} \sum_{j=1}^{N-k} (x_j - \bar x_N) (x_{j+k} - \bar x_N) \tag{16.3} \end{align}\] 因为:
- 我们不对大的\(k\)计算\(\hat\gamma_k\);
- 更重要的是只有除以\(N\)的估计式才是正定的。
只要观测\(x_1,x_2,\dots,x_N\)不全相同则 \[\begin{aligned} \hat\Gamma_N = (\hat\gamma_{k-j})_{k,j=1,2,\dots,N} \end{aligned}\] 正定。
令\(y_j = x_j - \bar x_N\),记 \[\begin{align} A=\left ( \begin{array}{*{10}c} &0 \ &\cdots\ & 0\ &y_1 \ &y_2 \ &\cdots&\ y_{N-1} \ &y_N \\ &0 \ &\cdots\ &y_1 &y_2 \ &y_3\ &\cdots&\ y_{N} \ & 0 \\ &\vdots \ &\cdots\ &\vdots & \vdots &\vdots & \cdots& \vdots &\vdots\\ &y_1 &\cdots& y_{N-1} & y_N &0 &\cdots &0 &0 \end{array} \right) \tag{16.4} \end{align}\] 则 \[\begin{aligned} \hat\Gamma_N = \frac{1}{N} A A^T \end{aligned}\] 只要\(y_j\)不全是零则\(A\)满秩。
事实上,设\(y_1=\dots=y_{k-1}=0\), \(y_k \neq 0\),则\(A\)矩阵左面会出现一个以\(y_k\)值开始非零的斜面, 显然是满秩的。 故\(x_1,\dots,x_N\)不全相同时\(\hat\Gamma_N\)正定。 \(\hat\Gamma_n\)(\(1\leq n \leq N\))作为\(\hat\Gamma_N\)的主子式也是正定的。
16.2 \(\hat\gamma_k\)的相合性
定理16.1 设平稳序列的样本自协方差函数\(\hat \gamma_k\) 由(16.3)或(16.3)定义.
(1) 如果当\(k\to \infty\) 时 \(\gamma_k \to 0\), 则对每个确定的\(k\), \(\hat \gamma_k\) 是 \(\gamma_k\)的渐近无偏估计: \[ \lim_{N\to \infty} E\hat \gamma_k = \gamma_k. \]
(2) 如果\(\{X_t\}\)是严平稳遍历序列, 则对每个确定的\(k\), \(\hat \gamma_k\) 和 \(\hat \rho_k\) 分别是 \(\gamma_k\) 和\(\rho_k\) 的强相合估计: \[ \lim_{N\to \infty} \hat \gamma_k =\gamma_k \ , \text{a.s.}, \quad \lim_{N\to \infty} \hat \rho_k =\rho_k \ , \text{a.s.} \]
证明
下面只对由(16.3)定义的样本自协方差函数证明, 对由(16.3)定义的\(\hat \gamma_k\)的证明是一样的.
设\(\mu=EX_1\), 则 \(\{Y_t\}=\{X_t-\mu\}\) 是零均值的平稳序列. 利用 \[ \bar Y_N= \frac1N\sum_{j=1}^N Y_j = \bar X_N - \mu \] 得到 \[\begin{align} \hat \gamma_k =& \frac1N \sum_{j=1}^{N-k} (Y_j- \bar Y_N)(Y_{j+k}- \bar Y_N) \\ =& \frac1N\sum_{j=1}^{N-k} [ Y_j Y_{j+k} - \bar Y_N( Y_{j+k} +Y_j) + \bar Y_N ^2 ]. \tag{16.5} \end{align}\]
利用(15.2)得到 \(E\bar Y_N^2=E(\bar X_N - \mu)^2 \to 0\). 利用Schwarz不等式得到 \[\begin{aligned} E|\bar Y_N( Y_{j+k} +Y_j)| \leq [E\bar Y_N^2 E(Y_{j+k} +Y_j)^2]^{1/2} \leq [E\bar Y_N^2 \cdot 4 \gamma_0]^{1/2} \to 0. \end{aligned}\] 所以当\(N\to \infty\), \[ E\hat \gamma_k = \frac1N\sum_{j=1}^{N-k}E(Y_j Y_{j+k}) +o(1) = \frac{N-k}N \gamma_k +o(1) \to \gamma_k. \]
强相合性的证明: 用遍历定理得到 \[\begin{aligned} &\bar Y_N \to E Y_1=0, \text{a.s.}, \\ &\frac1N\sum_{j=1}^{N-k} (Y_{j+k}+Y_j) =\frac1N \left(\sum_{j=1}^{N} Y_j - \sum_{j=1}^{k} Y_j + \sum_{j=1}^{N-k} Y_j \right) \\ =& \bar Y_N - \frac{1}{N}\sum_{j=1}^k Y_j + \frac{N-k}{N} \bar Y_{N-k} \to 0, \text{a.s.}, \end{aligned}\] 于是, 从(16.5)式可知 \[ \hat \gamma_k = \frac1N\sum_{j=1}^{N-k} Y_j Y_{j+k} + o(1) \to E(Y_1 Y_{1+k}) = \gamma_k, \ \text{a.s.} \]
○○○○○○
16.3 \(\hat\gamma_k\)的渐近分布
只考虑线性序列。
设\(\{\varepsilon_t\}\)是4阶矩有限的独立同分布的
\(\text{WN}(0, \sigma^2)\)(\(\sigma^2>0\)),
实数列\(\{\psi_k\}\)平方可和.
线性平稳序列
\[\begin{align}
X_t = \sum_{j=-\infty}^{\infty}
\psi_j\varepsilon_{t-j},
\quad t\in \mathbb Z,
\tag{16.6}
\end{align}\]
\(\{X_t\}\)有自协方差函数
\[\begin{align}
\gamma_k = \sigma^2 \sum_{j=-\infty}^{\infty}
\psi_j\psi_{j+k}
\tag{16.7}
\end{align}\]
\(\{X_t\}\)有谱密度
\[\begin{align}
f(\lambda) = \frac{\sigma^2}{2\pi}
\left|\sum_{j=-\infty}^{\infty}\psi_j e^{ij\lambda}\right|^2.
\tag{16.8}
\end{align}\]
设自协方差函数列\(\{\gamma_k\}\)平方可和。 设\(\{W_t\}\)为独立同分布N(0,1)。 令 \[\begin{aligned} \mu_4 = E \varepsilon_1^4, \quad M_0 = \frac{1}{\sigma^2}(\mu_4 - \sigma^4)^{1/2} > 0 \end{aligned}\] 定义正态时间序列 \[\begin{align} \xi_j =& (M_0 \gamma_j)W_0 + \sum_{t=1}^\infty (\gamma_{t+j} + \gamma_{t-j}) W_t, \quad j\geq 0 \tag{2.11} \\ R_j =& \sum_{t=1}^\infty (\rho_{t+j} + \rho_{t-j} - 2\rho_t\rho_j) W_t, \quad j \geq 1, \tag{16.9} \end{align}\]
定理16.2 设\(\{\varepsilon_t\}\)是独立同分布的\(\text{WN}(0,\sigma^2)\), 满足 \(\mu_4=E\varepsilon_1^4<\infty\). 如果线性平稳序列(16.6)的谱密度(16.8)平方可积: \[ \int_{-\pi}^\pi [f(\lambda)]^2 \ d \lambda < \infty, \] 则对任何正整数 \(h\), 当\(N\to \infty\)时, 有以下结果
(1) \(\sqrt{N}(\hat \gamma_0 -\gamma_0, \hat \gamma_1 -\gamma_1,\dots,\hat \gamma_h -\gamma_h)\) 依分布收敛到\((\xi_0,\xi_1,\dots,\xi_h)\).
(2) \(\sqrt{N}(\hat \rho_1 -\rho_1, \hat \rho_2 -\rho_2, \dots, \hat \rho_h -\rho_h)\) 依分布收敛到\((R_1,R_2,\dots,R_h)\)
可以据此构造\(\gamma_k\)和\(\rho_k\)的近似的区间估计和近似的假设检验。
16.3.1 MA(\(q\))序列的自相关截尾的检验
对MA\((q)\)序列\(\{X_t\}\), 利用定理16.2可知, 只要\(m>q\): \(\sqrt{N} \hat \rho_m\)依分布收敛到\(R_m\)的分布。 \[\begin{aligned} R_m =& \sum_{t=1}^\infty(\rho_{t+m} + \rho_{t-m} - 2\rho_t\rho_m) W_t, \quad m \geq q+1 \end{aligned}\] 注意\(m \geq q+1\)时\(\rho_m=0, \rho_{t+m}=0\), \(\rho_{t-m}\)中的\(t-m\)应属于\([-q,q]\),所以令 \(l=t-m\)有 \[\begin{aligned} R_m =& \sum_{l=-q}^q \rho_l W_{l+m} \end{aligned}\] \(R_m\)为期望为0, 方差为 \(1+2\rho_1^2 + 2\rho_2^2+\dots+ 2\rho_q^2\)的正态分布.
在假设\(H_0\): \(\{X_t\}\)是MA\((q)\)下, 对\(m> q\)有 \[ \Pr\left (\frac{ \sqrt{N}|\hat \rho_m| } {\sqrt{1+2 \rho_1^2 + 2 \rho_2^2+\dots+ 2\rho_q^2}} \geq 1.96\right )\approx 0.05. \] 令 \[ T_q(m) = \frac{ \sqrt{N}\hat \rho_{m+q}} {\sqrt{1+2\hat \rho_1^2 + 2\hat \rho_2^2+\dots+ 2\hat \rho_q^2}}, \ m > q \] 则在\(H_0\)下\(T_q(m)\)近似服从标准正态分布, 可以用\(\{ |T_q(m)| > 1.96 \}\)作为\(H_0\)的水平为0.05的近似检验否定域。
例16.1 现在用\(\{X_t\}\)表示第12章例12.1中差分后的化学浓度数据, 在\(H_0\): \(\{X_t\}\)是MA\((q)\)下, 分别对\(q=0,1\)计算出\(T_q(m)\), \(m=1,2,\dots,6\)。
\[ \begin{array}{lrrrrrrr} m = &1&2&3&4&5&6\\ q=0 &-5.778 & 0.281 & -0.951 & -0.121 & -1.071& -0.116 \\ q=1 & 0.243 & -0.821 & -0.104 & -0.925 & -0.100& 1.631 \end{array} \] 在\(q=0\)的假设下,\(|T_0(1)|=5.778>1.96\), 所以应当否定\(q=0\).
也可以计算检验的近似p值,如\(q=0\), \(m=1\)时 \[ p=P(|Z| \geq |-5.778|), \] 其中\(Z\)表示标准正态分布随机变量 \(p\)值越小,数据提供的否定原假设的依据越充分. 这里的p值基本为0,所以应该拒绝\(q=0\)的假设。
取\(q=1\)时 \(|T_1(m)|<1.96(1 \leq m\leq 6)\), 所以不能拒绝\(\{X_t\}\)是MA\((1)\)的假设.
16.3.2 谱密度平方可积的充要条件
对于实际工作者来讲谱密度平方可积的条件通常很难验证, 于是希望能把定理16.2中谱密度平方可积的条件改加在自协方差函数\(\{\gamma_k\}\)的收敛速度上.
定理16.3 对任一平稳序列\(\{X_t\}\), 它的自协方差函数平方可和的充分必要条件是它的谱密度平方可积.
这个结论主要是利用实变函数论中Fourier级数的理论, 只有证明\(f(\lambda)\geq 0\)时用了周期图(如定理9.1的证明, 那里\(\{\gamma_k\}\)绝对可和)。证明略。
16.3.3 \(\psi_k\)快速收敛条件下的中心极限定理
定理 16.2 要求白噪声的方差有4阶矩. 下面关于线性平稳序列的样本自相关系数的中心极限定理不要求噪声项的4阶矩有限.
定理16.4 设\(\{\varepsilon_t\}\)是独立同分布的\(\text{WN}(0,\sigma^2)\), 线性平稳序列\(\{X_t\}\)由(16.6)定义. 如果自协方差函数\(\{\gamma_k\}\)平方可和, 并且对某个常数\(\alpha> 0.5\), \[\begin{align} m^{\alpha} \sum_{|k| \geq m} \psi_k^2 \ \to \ 0 , \ \ m\to \infty, \tag{16.10} \end{align}\] 则对任何正整数 \(h\), 当\(N\to \infty\)时 \[ \sqrt{N}(\hat \rho_1 -\rho_1,\hat \rho_2 -\rho_2,\dots, \hat \rho_h -\rho_h) \] 依分布收敛到 \[ (R_1,R_2,\cdots,R_h). \]
ARMA序列的\(\{\psi_j\}\)满足(16.10)所以ARMA序列的白噪声列是独立同分布序列时定理16.4结论成立。
16.3.4 关于独立同分布列的中心极限定理
推论16.2 如果\(\{X_t\}\)是独立同分布的白噪声, \[ \hat \rho_k = \frac{\sum_{t=1}^{N-k}(x_t-\bar x_N)(x_{t+k}-\bar x_N)} {\sum_{t=1}^N (x_t-\bar x_N)^2} \] 是样本自相关系数, 则对任何正整数\(h\)
(1) \[ \sqrt{N}(\hat \rho_1, \hat \rho_2 , \cdots, \hat \rho_h ) \] 依分布收敛到多元标准正态分布\(N(0, I_h)\). 这里, \(I_h\)是 \(h\times h\)的单位矩阵.
(2) 如果 \(\mu_4=EX_t^4 <\infty\), 则 \[ \sqrt{N}( \hat \gamma_0 -\sigma^2 ,\hat \gamma_1 , \dots, \hat \gamma_h ) \] 依分布收敛到 \[ \sigma^2 (M_0 W_0, W_1,\dots,W_h). \]
证明:
对白噪声,\(\gamma_0 = \sigma^2\), \[\begin{aligned} R_j =& \sum_{t=1}^\infty(\rho_{t+j} + \rho_{t-j} - 2\rho_t \rho_j) W_t = W_j, j \geq 1 \\ \xi_j =& (M_0 \gamma_j) W_0 + \sum_{t=1}^\infty(\gamma_{t+j} + \gamma_{t-j}) W_t \\ =& \gamma_0 W_j = \sigma^2 W_j \\ \xi_0 =& (M_0 \gamma_0) W_0 + \sum_{t=1}^\infty(\gamma_{t+0} + \gamma_{t-0}) W_t \\ =& M_0 \gamma_0 W_0 = \sigma^2 M_0 W_0 \end{aligned}\] 定理16.4的条件满足。 第二条满足推论16.1的条件。
16.4 模拟计算
首先用图形表示\(N\)不同时\(\hat\gamma_k\)的误差。 然后重复\(M=400\)次计算400个\(\hat\gamma_k\)的标准差(称为标准误差)。 发现\(N\)增大时标准误差减小。 误差随\(N\)减小的速度为\(N^{-1/2}\)。 根离单位圆近的模型其估计标准误差大。
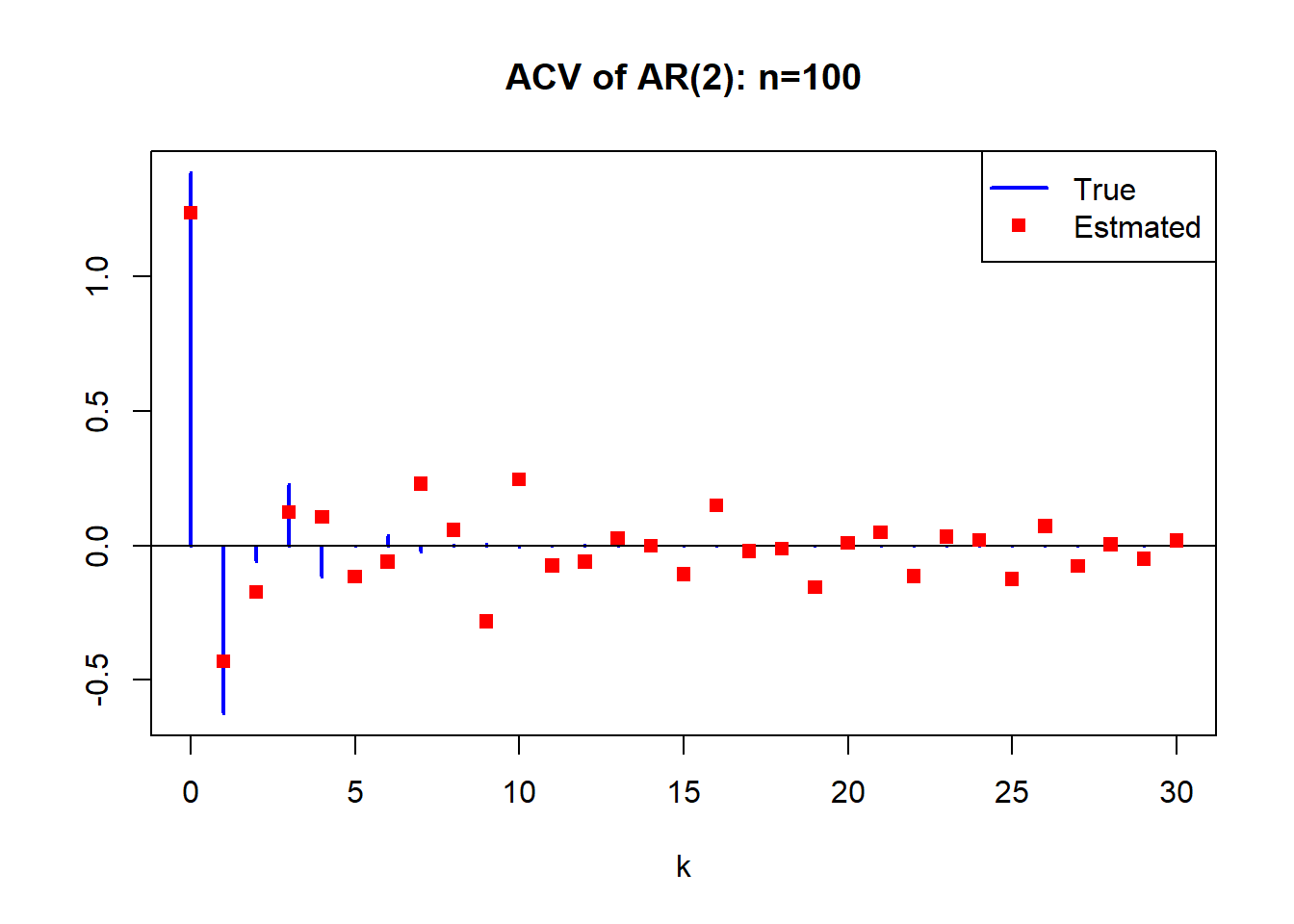
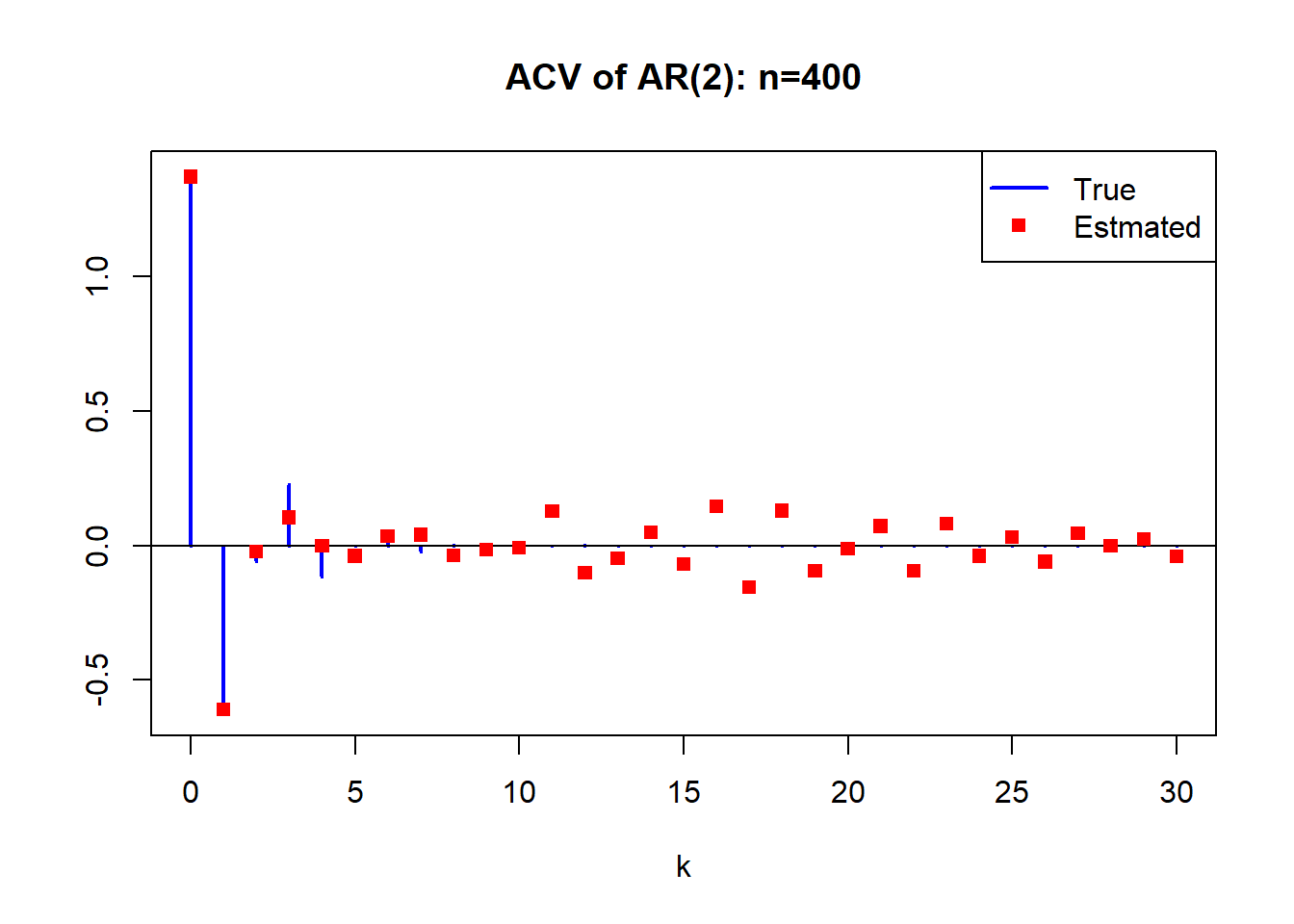
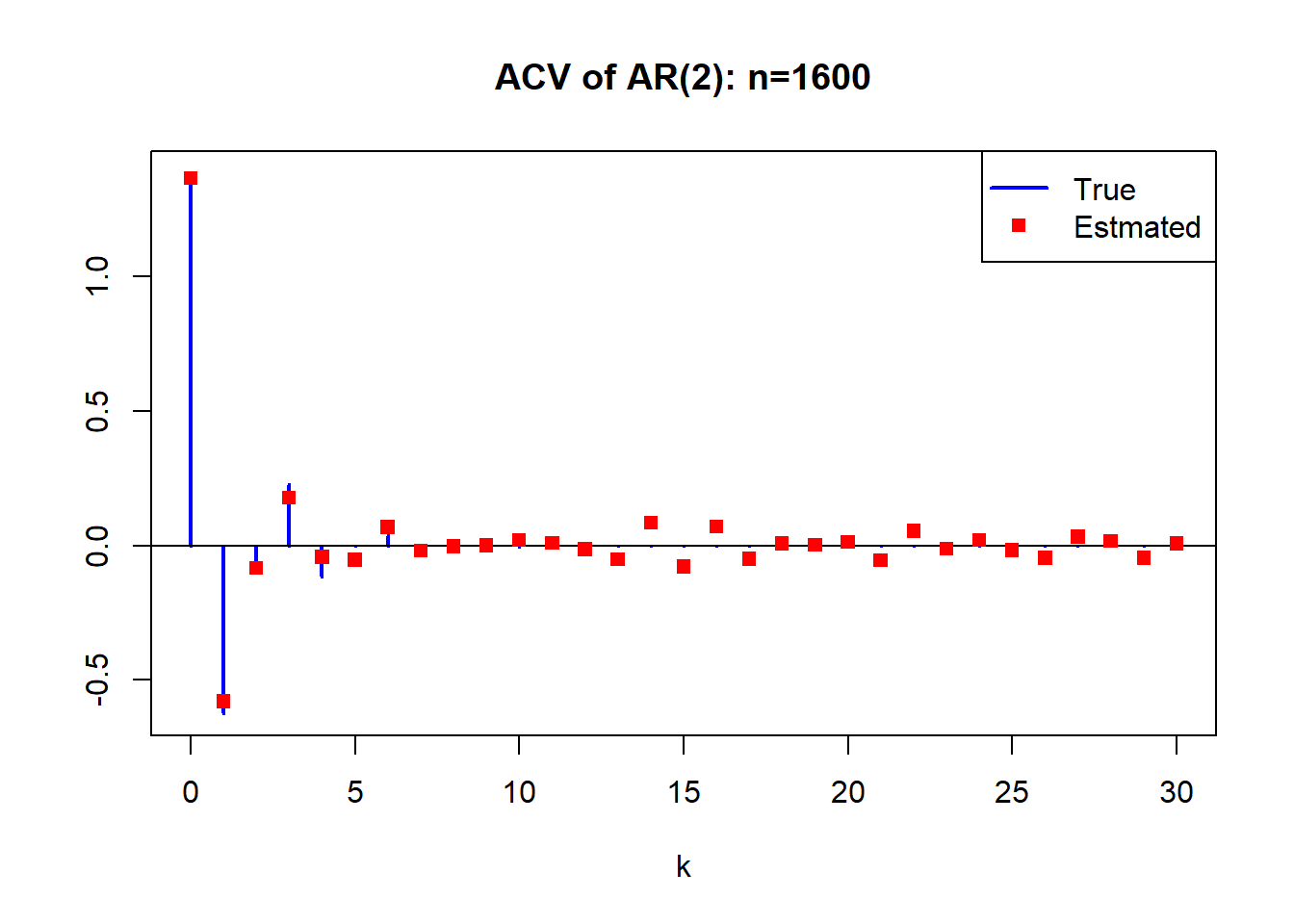
利用AR(2)模型进行模拟, 选择两个不同的AR(2)模型, 特征根分别为: \[ 1.8 e^{\pm i 2.13}, \ 1.1 e^{\pm i 2.13} \] 首先考察样本量的变化对\(\hat\gamma_k\)估计的影响。 计算\(\hat\gamma_k, k=0,1,\dots,30\)。 这里仅使用第一个模型,即特征根离单位圆较远的那个模型。
ar.gen <- function(n, a, sigma=1.0, by.roots=FALSE,
plot.it=FALSE, n0=1000,
x0=numeric(length(a))){
if(by.roots){
cf <- Re(coef(poly.calc(a)))
cf <- cf / cf[1]
a <- -cf[-1]
}
n2 <- n0 + n
p <- length(a)
eps <- rnorm(n2, 0, sigma)
x2 <- filter(eps, a, method="recursive", side=1, init=x0)
x <- x2[(n0+1):n2]
x <- ts(x)
attr(x, "model") <- "AR"
attr(x, "a") <- a
attr(x, "sigma") <- sigma
if(plot.it) plot(x)
x
}
arma.Wold <- function(n, a, b=numeric(0)){
p <- length(a)
q <- length(b)
arev <- rev(a)
psi <- numeric(n)
psi[1] <- 1
for(j in seq(n-1)){
if(j <= q) bj=b[j]
else bj=0
psis <- psi[max(1, j+1-p):j]
np <- length(psis)
if(np < p) psis <- c(rep(0,p-np), psis)
psi[j+1] <- bj + sum(arev * psis)
}
psi
}
arma.gamma.by.Wold <- function(n, a, b=numeric(0), sigma=1){
nn <- n + 100
psi <- arma.Wold(nn, a, b)
gam <- numeric(n)
for(ii in seq(0, n-1)){
gam[ii+1] <- sum(psi[1:(nn-ii)] * psi[(ii+1):nn])
}
gam <- (sigma^2) * gam
gam
}
arma.gamma <- arma.gamma.by.Woldroots <- complex(mod=c(1/1.8, 1/1.1),
arg=c(2.13, 2.13))
coefs <- cbind(2*Re(roots), -Mod(roots)^2)
sigma <- 1
ngam <- 31
L <- 1600
x <- ar.gen(L, a=coefs[1,])
true.gam <- arma.gamma.by.Wold(ngam, a=coefs[1,],
sigma=sigma)
for(nn in c(100, 400, 1600)){
est.gam <- acf(x[1:nn], lag.max=ngam-1, type="covariance",
plot=F)$acf
plot(0:(ngam-1), true.gam,
type="h", col='blue', lwd=2,
main=paste("ACV of AR(2): n=", nn, sep=""),
ylim=range(c(true.gam, est.gam)),
xlab="k", ylab="")
abline(h=0)
points(0:(ngam-1), est.gam, pch=15, col='red')
legend("topright", pch=c(NA, 15), lty=c(1, 0),
lwd=c(2,1), col=c("blue", "red"),
legend=c("True", "Estmated"))
}
下面对两个AR(2)模型模拟产生多条(\(M=400\))轨道, 针对不同的样本量\(n\)估计\(\hat\gamma_k\)。 模拟函数:
demo.estacv.se <- function(a){
M <- 400
ns <- c(1600, 400, 100, 25)
L <- max(ns)
ngam <- 6
stderrs <- matrix(0, nrow=length(ns), ncol=ngam)
colnames(stderrs) <- 0:(ngam-1)
rownames(stderrs) <- ns
gams <- as.list(ns)
for(ii in seq(along=gams)){
gams[[ii]] <- matrix(0, nrow=M, ncol=ngam)
}
true.gam <- arma.gamma.by.Wold(ngam, a=a,
sigma=sigma)
for(mm in seq(M)){
x <- ar.gen(L, a=a)
for(ig in seq(along=ns)){
n <- ns[ig]
est.gam <- acf(x[1:n], lag.max=ngam-1,
type="covariance",
plot=F)$acf
gams[[ig]][mm,] <- est.gam
}
}
rats <- numeric(length(ns))
rats[length(rats)] <- NA
for(ig in seq(along=ns)){
stderrs[ig,] <- apply(gams[[ig]], 2, sd)
}
for(ig in seq(along=ns)){
if(ig<length(ns))
rats[ig] <- mean(stderrs[ig+1]/stderrs[ig])
}
cat("Roots of characteristic polynomial: ",
abs(1/roots[1]), "*Exp(", Arg(1/roots[1]), " i)\n", sep="")
cat("True gamma's\n")
print(round(true.gam[0:(ngam-1)],2))
cat("Standard deviation of \\hat\\gamma_k ===\n")
print(round(cbind(stderrs, "ratio"=rats),2))
}首先对特征根离单位圆比较远的那个AR(2)模型进行模拟:
## Roots of characteristic polynomial: 1.8*Exp(-2.13 i)
## True gamma's
## [1] 1.39 -0.62 -0.06 0.23 -0.12
## Standard deviation of \hat\gamma_k ===
## 0 1 2 3 4 5 ratio
## 1600 0.06 0.04 0.04 0.04 0.04 0.04 1.97
## 400 0.12 0.09 0.08 0.09 0.08 0.08 2.01
## 100 0.24 0.17 0.15 0.16 0.16 0.16 1.99
## 25 0.47 0.32 0.29 0.32 0.32 0.30 NA其次对特征根离单位圆比较近的那个AR(2)模型进行模拟:
## Roots of characteristic polynomial: 1.8*Exp(-2.13 i)
## True gamma's
## [1] 4.37 -2.31 -1.39 3.25 -1.99
## Standard deviation of \hat\gamma_k ===
## 0 1 2 3 4 5 ratio
## 1600 0.37 0.20 0.17 0.36 0.23 0.18 1.99
## 400 0.73 0.40 0.33 0.70 0.47 0.32 1.86
## 100 1.36 0.74 0.61 1.28 0.84 0.61 1.82
## 25 2.49 1.32 1.07 2.17 1.43 1.03 NA16.5 附录:均值和自协方差估计的强大数律
当平稳列\(X_t\)的自协方差函数绝对可和或以幂率收敛时, 对\(\forall \lambda \in [-\pi,\pi]\), 有 \[\begin{aligned} \lim_{n\to\infty} \frac{1}{n} \sum_{j=1}^n X_j e^{-ij\lambda} = 0, \ \text{a.s.} \end{aligned}\] 其中\(\lambda=0\)时即样本均值服从强大数律。 详见谢衷洁《时间序列分析》PP53–57定理1.16及推论。 何书元教材中定理4.1.1是均方收敛的结论。
当零均值正态实值平稳列\(X_t\)的自协方差函数以幂率收敛时, 有 \[\begin{aligned} \lim_{n\to\infty} \frac{1}{n} \sum_{j=1}^n X_{k+j} X_j = \gamma_k, \ \text{a.s.} \end{aligned}\] 详见谢衷洁《时间序列分析》PP58–60定理1.17,1.18及推论。 关于自协方差的条件还可以减弱到谱函数连续, 从而自协方差绝对可和或有谱密度时也可以。 何书元教材的条件为严平稳遍历。