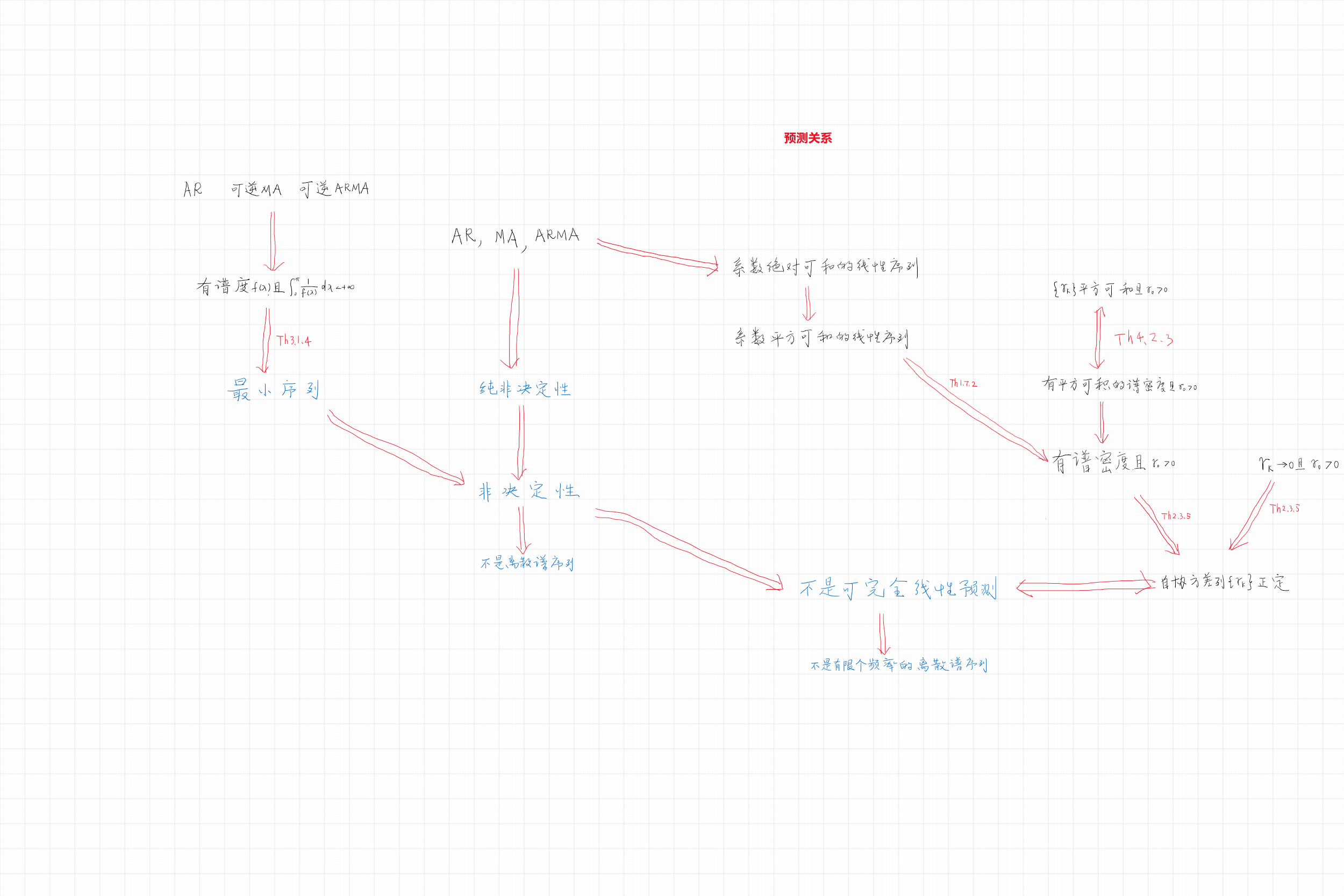
23 非决定性平稳序列及其Wold表示
23.1 非决定性平稳序列
对平稳序列, 考虑用所有的历史\(\{X_t, \ t\leq n\}\)对\(X_{n+1}\)进行最佳线性预测. 当预测误差是零时, \(X_{n+1}\)的信息完全含在历史资料中. 这样的平稳序列被称为决定性的. §9.5中\(\Gamma_{n+1}\)不满秩造成\(X_t\) 可以被\(X_{t-1}, \dots, X_{t-n}\)完全线性预测, 是决定性平稳列的特例。
最小序列: 用\(\{X_s: s \neq t \}\)预报\(X_t\)误差不为零。 决定性序列不是最小序列。
实际问题中, 决定性平稳序列描述事物的发展没有新的信息出现.
如果用\(\{X_t, \ t\leq n\}\)对\(X_{n+1}\)做线性预测的误差不是零, 说明\(X_{n+1}\)的信息不能由历史资料的线性组合及其极限完全确定, 我们称这种时间序列是非决定性的.
非决定性平稳序列描述事物的发展总伴随新的信息出现.
最小序列一定是非决定性的。
平稳序列的Wold定理表示告诉我们, 非决定性平稳序列总是可以分解成白噪声的单边滑动和加上一个决定性平稳序列.
从应用的角度讲, 非决定性平稳序列总是白噪声的单边滑动和加上一个离散谱序列.
23.1.1 最佳线性预测均方误差的极限
设\(\{X_n:n\in \mathbb Z \}\)是零均值平稳序列. 记 \[\boldsymbol{X}_{n, m}=(X_{n},X_{n-1},\cdots,X_{n-m+1})^{T},\] 这里 \(n\)表示向量的第一个脚标, \(m\)表示向量的维数.
定义 \[ \hat{X}_{n+1,m}=L(X_{n+1} |\boldsymbol{X}_{n,m}). \] 从最佳线性预测的性质8知道 \(\sigma^2_{1,m}=E(X_{n+1}-\hat{X}_{n+1,m})^2\)是\(m\)的单调减函数, 于是定义 \[ \sigma^2_1 \stackrel{\triangle}{=} \lim_{m\rightarrow \infty}\sigma^2_{1,m}< \infty. \]
定理23.1 \(\sigma^2_1 \stackrel{\triangle}{=} \lim_{m\rightarrow \infty}\sigma^2_{1,m}\)与\(n\)无关.
证明: 设\(\boldsymbol{a}=(a_1,a_2,\dots,a_m)^{T}\) 是预测方程(22.3)的解, 则\(\boldsymbol a\)和\(n\)无关. 由于 \[\begin{align} Y_n \stackrel{\triangle}{=} X_{n+1}-\sum_{j=1}^ma_jX_{n+1-j} =X_{n+1}- \hat{X}_{n+1,m} , \quad n\in \mathbb Z, \tag{23.1} \end{align}\] 是平稳序列, 所以\(\sigma_{1,m}^2=E Y_n^2=E Y_0^2\)与\(n\)无关. 最后\(\sigma^2_1=\lim_{m\to \infty} \sigma^2_{1,m}\)与\(n\)无关.
○○○○○○
23.1.2 决定性与非决定性的严格定义
对充分大的\(m\), \(L(X_{n+1}|\boldsymbol X_{n,m})\)表示用充分多的历史对未来\(X_{n+1}\)进行预测. \(\sigma_{1,m}^2\)表示的是预测的均方误差. 当\(m \to \infty\)时, \(\sigma_{1,m}^2 \to 0\) 说明\(X_{n+1}\) 可以由所有历史\(X_{n}, X_{n-1},\dots\)进行完全预测. 当\(\sigma_1^2 > 0\) 说明\(X_{n+1}\)不可以由所有历史\(X_{n}, X_{n-1},\dots\)的线性组合以及极限进行完全预测.
定义23.1 设\(\{X_t\}\)是零均值平稳序列.
- 如果\(\sigma^2_1=0\), 称\(\{X_t\}\)是决定性平稳序列;
- 如果\(\sigma^2_1>0\), 称\(\{X_t\}\)是非决定性平稳序列, 并且称\(\sigma^2_1=\lim_{m\rightarrow\infty}\sigma^2_{1,m}\) 为\(\{X_t\}\)的一步(线性)预测的均方误差。
对于平稳序列\(\{X_t\}\), 如果\(EX_t=\mu\), 引入\(\{Z_t\}=\{X_t-\mu\}\) 和\(m\)维向量 \(\boldsymbol{\mu}_m=(\mu,\dots,\mu)^T\).
按照最佳线性预测的定义22.2, \[\begin{aligned} \hat{X}_{n+1,m} =& \mu+ L(X_{n+1}-\mu |\boldsymbol{X}_{n,m} - \boldsymbol{\mu}_m) \\ =& \mu+ L(Z_{n+1} |\boldsymbol{Z}_{n,m}) =\mu+ \hat Z_{n+1,m}. \end{aligned}\] 于是 \[ E(Z_{n+1} - \hat Z_{n+1,m} )^2 = E(X_{n+1} -\hat X_{n+1,m})^2. \] 即对\(X\)预报的均方误差等于对中心化得到的\(Z\)预报的均方误差。 因而, 当且仅当\(\{X_t - \mu\}\)是决定性平稳序列时, 称\(\{X_t\}\)是决定性平稳序列. 于是以后只需要讨论零均值的平稳序列.
23.1.3 可完全线性预测
设平稳列\(\{X_t\}\)的\(n+1\)阶自协方差阵\(\Gamma_{n+1}\)退化, \(|\Gamma_n|>0\)。 则\(X_1,X_2,\cdots,X_{n+1}\)线性相关, 所以\(X_{n+1}\)可以由\(X_{n}, X_{n-1},\dots,X_1\)线性表示. 于是, \(L(X_{n+1}|X_n,\dots,X_1)=X_{n+1}\). 当\(m \geq n\)时, \[\begin{aligned} L(X_{n+1}|X_n,\dots,X_{n-m+1})=X_{n+1}, \end{aligned}\] 即有\(\sigma^2_{1, m}=0\), \(\{X_t\}\)是决定性平稳列。
最简单的决定性平稳列是\(X_t \equiv \xi\), \(\xi\)为随机变量。
23.1.4 离散谱序列
设零均值随机变量\(\xi_j, \eta_k (j,k=1,2,\dots,p)\) 两两正交, 满足 \[\begin{align} E(\xi_j^2)=E(\eta_j^2)=\sigma^2_j, \ j=1,2,\dots \tag{23.2} \end{align}\] 对确定的\(j\), 定义简单离散谱序列 \[\begin{align} Z_j(t) = \xi_j \cos(t\lambda_j) + \eta_j\sin(t\lambda_j), \quad t\in \mathbb Z. \tag{23.3} \end{align}\] 可以证明\(\{Z_j(t)\}\)是平稳序列。 事实上,易见\(E Z_j(t) \equiv 0\)。 而 \[\begin{aligned} E[Z_j(t) Z_j(s)] =& E\xi_j^2 \cos(\lambda_j t) \cos(\lambda_j s) + E\eta_j^2 \sin(\lambda_j t) \sin(\lambda_j s) \\ =& \sigma_j^2 \cos((t-s)\lambda_j) \end{aligned}\] 只依赖于\(t-s\)。
\(\{Z_j(t)\}\)的每一次实现是周期函数, 由§2.3的定理3.7 知道\(\{Z_j(t)\}\)的3阶自协方差矩阵是退化的, 因此(23.3)是可完全线性预测的, \(Z_j(n)\)可以被\(Z_j(n-1), Z_j(n-2)\)完全线性预测,是决定性序列。
事实上容易证明 \[\begin{aligned} & Z_j(t) = (2\cos\lambda_j) Z_j(t-1) - Z_j(t-2) \end{aligned}\] 定义离散谱序列 \[\begin{align} Z_t=\sum_{j=1}^p Z_j(t), \quad t \in \mathbb Z. \tag{23.4} \end{align}\] 这是\(p\)个简单离散谱序列的叠加. 由§9.4的定理9.4知道由(23.4)定义的离散谱序列也是决定性的. \(Z_{n}\)可以被\(Z_{n-1}, Z_{n-2}, \dots, Z_{n-2p}\)完全线性预测。
23.1.5 纯非决定性
决定性与非决定性取决于一步线性预报误差是否为零。
对非决定性序列, 用\(\{X_s, s \leq n \}\)预报\(X_{n+k}\)的误差会随\(k\)增大而增大。 记 \[\begin{aligned} \sigma_{k,m}^2 =& E [ X_{n+k} - L(X_{n+k} | X_n, X_{n-1}, \dots, X_{n-m+1})]^2 \end{aligned}\] 则\(\sigma_{k,m}\)也是\(m\)的单调递减函数,与\(n\)无关。可定义 \[\begin{aligned} \sigma_k^2 =& \lim_{m\to\infty} \sigma_{k,m}^2 \end{aligned}\] 在极限意义下可以证明\(\sigma_k^2 \geq \sigma_{k-1}^2\): \[\begin{align} \sigma_k^2 =& \lim_{m \to \infty} E(X_{n+k} - L(X_{n+k}|X_{n},X_{n-1},\dots,X_{n-m}))^2\\ =& \lim_{m \to \infty} E[X_{n+k-1}-L(X_{n+k-1}|X_{n-1},X_{n-2},\dots,X_{n-1-m})]^2 \\ \geq& \lim_{m \to \infty} E[X_{n+k-1}-L(X_{n+k-1}|X_{n},X_{n-1},\dots,X_{n-m-1})]^2\\ =& \lim_{m \to \infty} \sigma_{k-1,m+1}^2 =\sigma^2_{k-1}. \tag{23.5} \end{align}\]
注意上面证明中没有说明\(\sigma_{k,m}^2\)是\(k\)的增函数。 反例:AR(2)序列 \[\begin{aligned} X_t = \frac12 X_{t-2} + \varepsilon_t, \quad \varepsilon_t \sim \text{WN}(0,\sigma^2) \end{aligned}\] 平稳解为 \[\begin{aligned} X_t = \sum_{j=0}^\infty \left(\frac12 \right)^j \varepsilon_{t-2j} \end{aligned}\] \[\begin{aligned} \gamma_0 =& \frac43 \sigma^2 \quad \gamma_1 = 0 \\ \gamma_2 =& \frac23 \sigma^2 \end{aligned}\] \[\begin{aligned} L(X_t | X_{t-1}) =& 0 \quad \sigma_{1,1}^2 = \frac43 \sigma^2 \\ L(X_t | X_{t-2}) =& \frac12 X_{t-2} \quad \sigma_{2,1}^2 = \sigma^2 < \sigma_{1,1}^2 \end{aligned}\]
由最佳线性预测定义知 \[\begin{aligned} \sigma_{k,m}^2 =& E[X_{n+k} - L(X_{n+k} | X_{n}, X_{n-1}, \dots, X_{n-m+1})]^2\\ \leq& E[X_{n+k}-0]^2 = \gamma_0 \end{aligned}\] 所以\(\sigma_k^2 \leq \gamma_0\)。 \(k\to\infty\)时如果\(\sigma_k^2\to\gamma_0\) 则最佳线性预测与用平均值0预测效果相同,没有作用。
定义23.2 设\(\{X_t\}\)是非决定性的平稳序列. 如果\(\lim_{k\to\infty}\sigma^2_k=\gamma_0\), 则称\(\{X_t\}\)是纯非决定性的.
纯非决定性的平稳列不能作长期预报。 非决定性但不是纯非决定性的平稳列作长期预报是有意义的; 当然,决定性序列可以精确地长期预报。
对纯非决定性的平稳序列, 有如下的结果: \[\begin{align} \lim_{k\rightarrow\infty} \lim_{m\rightarrow\infty} E[L(X_{n+k}|X_{n},X_{n-1},\dots,X_{n-m+1})]^2=0. \tag{23.6} \end{align}\]
实际上, 记\(\hat{X}_{n+k,m}=L(X_{n+k}|X_{n},X_{n-1},\dots,X_{n-m+1})\). 由投影的正交性得 \[ \sigma_{k,m}^2 = E(X_{n+k} - \hat{X}_{n+k,m} )^2 = E X_{n+k}^2 -E\hat{X}_{n+k,m}^2. \] 于是得到 \[\begin{align} \lim_{k\rightarrow\infty}\lim_{m\rightarrow\infty} E\hat{X}_{n+k,m}^2 =\lim_{k\rightarrow\infty}\lim_{m\rightarrow\infty} ( \gamma_0 -\sigma^2_{k,m}) = \gamma_0- \gamma_0 =0. \tag{23.7} \end{align}\]
从(23.6)也可看出, 对于纯非决定性的平稳序列做长期或超长期预测是不合适的.
23.2 Wold表示定理
23.2.1 线性闭包
设\(A\)为Hilbert空间\(H\)的子集, 记\(\mbox{sp}(A)\)或\(L_A\)为\(A\)的所有有限线性组合构成的集合, 记\(\overline{\mbox{sp}}(A)\)或\(\bar L_A\)为\(\mbox{sp}(A)\)的元素及其元素极限组成的集合, 记\(H_A\)为包含\(A\)的最小的闭子空间。
引理23.1 设\(A\)为Hilbert空间\(H\)的子集 则 \[ H_A = \overline{\mbox{sp}}(A) \] 于是\(\forall \xi \in H_A\), 必存在\(\xi_n \in \mbox{sp}(A), n=1,2,\dots\) 使得 \[\begin{aligned} \| \xi_n - \xi \| \to 0, \quad n\to\infty. \end{aligned}\]
称\(\overline{\mbox{sp}}(A)\)为\(A\)的线性闭包, 或由\(A\)生成的子希尔伯特空间, 或由\(A\)张成的子希尔伯特空间。
证明: 易见\(\mbox{sp}(A) \subset \overline{\mbox{sp}}(A) \subset H\)。
首先,\(H_A\)存在而且是\(H\)的闭子空间。 事实上,令 \[ H_A = \bigcap_{B\text{是}H \text{的闭子空间且} B \supset A} B \] 因为\(H \supset A\)所以\(H_A\)非空。 易见\(H_A\)也是线性空间,且也是闭集, 所以\(H_A\)是包含\(A\)的最小闭子空间。
易见\(\mbox{sp}(A)\)为\(H\)的子线性空间, 且由\(A \subset H_A\)和\(H_A\)是线性空间知\(\mbox{sp}(A) \subset H_A\)。 因为\(H_A\)是闭集所以 \(\overline{\mbox{sp}}(A) \subset H_A\)。
另一方面,可以证明\(\overline{\mbox{sp}}(A)\)是闭子空间, 由\(H_A\)的定义及\(A \subset \overline{\mbox{sp}}(A)\)得 \(H_A \subset \overline{\mbox{sp}}(A)\)。
易见\(\overline{\mbox{sp}}(A)\)是\(H\)的线性子空间。 下面证明\(\overline{\mbox{sp}}(A)\)是闭集。
设\(\xi_n \in \overline{\mbox{sp}}(A)\), \(\xi \in H\)使得\(\lim_{n\to\infty} \| \xi_n - \xi \| = 0\), 只要证明\(\xi \in \overline{\mbox{sp}}(A)\)。 对\(\xi_n\),存在\(\eta_n \in \mbox{sp}(A)\)使得 \[ \| \xi_n - \eta_n \| < \frac{1}{n} \] 所以 \[\begin{aligned} \| \eta_n - \xi \| \leq& \| \xi_n - \eta_n \| + \| \xi_n - \xi \| \\ \leq& \frac{1}{n} + \| \xi_n - \xi \| \\ \to& 0, \ (n\to\infty) \end{aligned}\] 即\(\xi \in \overline{\mbox{sp}}(A)\), 所以\(\overline{\mbox{sp}}(A)\)是闭子空间, 于是\(\overline{\mbox{sp}}(A) \supset H_A\), 从而\(H_A = \overline{\mbox{sp}}(A)\)。证毕。
○○○○○○
23.2.2 无穷历史的线性预测
记\(H_n\)为\(X_n, X_{n-1}, \dots\)生成的闭子空间(线性闭包)。 \(L(X_{n+k} | X_n, X_{n-1}, \dots, X_{n-m+1})\)当 \(m\to\infty\)时为\(L(X_{n+k}|H_n)\)(见后面的定理23.3)。
定理23.2 设\(Y \in L^2\), \(\xi \in H_n\), 则\(\xi=L(Y|H_n)\)的充分必要条件是 \[\begin{align} Y-\xi \perp X_j, \quad j=n,n-1,n-2,\dots \tag{23.8} \end{align}\]
证明:
必要性: 由定理22.1得到\(Y - \xi \perp H_n\)所以有(23.8)。
充分性: 记\(A = \{X_n, X_{n-1}, \dots \}\), 则由(23.8)可知\(Y - \xi \perp L_A\)。 由引理23.1, 对\(\eta \in H_n\)有\(\eta_m \in L_A\)使\(\eta_m \to \eta\), 由内积的连续性可得 \[\begin{aligned} E((Y-\xi)\eta) = \lim_{m\to\infty} E((Y-\xi) \eta_m) = 0 \end{aligned}\] 即\(Y-\xi \perp H_n\), 由定理22.1即得\(\xi=L(X_{n+k}|H_n)\)。
○○○○○○
\(H_n\)为\(\{X_s, s \leq n\}\)所张成的子Hilbert空间, \(L(X_{n+k}|H_n)\)是一个投影。 下面的定理说明这个投影是有穷维最佳线性预测的极限。
定理23.3 设\(\boldsymbol{X}_{n,m} = (X_n, X_{n-1}, \dots, X_{n-m+1})^T\), 当\(m \to\infty\)时 \[\begin{align} L(Y|\boldsymbol{X}_{n,m}) \stackrel{\text{m.s.}}{\longrightarrow} \hat Y \stackrel{\triangle}{=} L(Y|H_n) \tag{23.9} \end{align}\]
证明: 记\(\hat Y_m = L(Y|\boldsymbol{X}_{n,m})\)。 先证明\(\{\hat Y_m\}\)是\(H_n\)中基本列。 显然\(\hat Y_m \in H_n\),设当\(m \to\infty\)时 \[\begin{aligned} \eta_m^2 \stackrel{\triangle}{=} E(Y - \hat Y_m)^2 \to \eta^2 \qquad\text{(注意单调性)} \end{aligned}\]
对\(m,k\to\infty\), 注意\(\hat Y_m, \hat Y_{m+k}\)都和\(Y - \hat Y_{m+k}\)正交,得 \[\begin{aligned} & \|\hat Y_m - \hat Y_{m+k} \|^2 = \| \hat Y_m - Y + Y - \hat Y_{m+k} \|^2 \\ =& \| \hat Y_m - Y \|^2 + \| Y - \hat Y_{m+k} \|^2 + 2 \langle \hat Y_m - Y, Y - \hat Y_{m+k} \rangle \\ =& \eta_m^2 + \eta_{m+k}^2 - 2 \langle Y, Y - \hat Y_{m+k} \rangle \\ =& \eta_m^2 + \eta_{m+k}^2 - 2 \langle Y - \hat Y_{m+k}, Y - \hat Y_{m+k} \rangle \\ =& \eta_m^2 + \eta_{m+k}^2 - 2 \eta_{m+k}^2 \to 0 \end{aligned}\] 因此\(\{\hat Y_m\}\)是\(H_n\)的基本列, 在\(H_n\)中存在唯一极限\(\xi\)。
由内积的连续性, 对任何\(X_s, s \leq n\)有 \[\begin{aligned} \langle X_s, Y - \xi \rangle = \lim_{m \to \infty} \langle X_s, Y - L(Y|\boldsymbol{X}_{n,m}) \rangle = 0 \end{aligned}\] 由定理23.2得到\(\xi = L(Y|H_n)\)。
○○○○○○
23.2.3 无穷历史最优线性预测方差
由内积连续性, \[\begin{aligned} \sigma_1^2 \stackrel{\triangle}{=}& \lim_{m\to\infty} \| X_{n+1} - L(X_{n+1} | \boldsymbol{X}_{n,m}) \|^2 \\ =& \| X_{n+1} - L(X_{n+1} | H_n) \|^2 = \| X_1 - L(X_1|H_0) \|^2 \end{aligned}\] 最后一个等号是因为等号右边也可以写成有限自变量预报均方误差极限。
\(\sigma_1^2 = 0 \Leftrightarrow X_1 = L(X_1 | H_0)\), 所以\(\sigma_1^2 = 0 \Rightarrow X_1 \in H_0\)。 反之,如果\(X_1 \in H_0\), 则\(E(X_1 - X_1)^2 = 0\)最小所以\(X_1=L(X_1|H_0)\)。 即\(\sigma_1^2 = 0 \Leftrightarrow X_1 \in H_0\)。 这时\(\{X_t \}\)是决定性序列。 类似地, \[\begin{aligned} \sigma_k^2 \stackrel{\triangle}{=}& \lim_{m\to\infty} \| X_{n+k} - L(X_{n+k} | \boldsymbol{X}_{n,m}) \|^2 \\ =& \| X_{n+k} - L(X_{n+k} | H_n) \|^2 = \| X_k - L(X_k|H_0) \|^2 \end{aligned}\]
定理23.4 设 \(\{X_t\}\)是零均值平稳列,
(1) \(\{X_t\}\)是决定性序列当且仅当对某个\(n\)有 \[\begin{align} X_{n+1} \in H_n; \tag{23.10} \end{align}\] 并且如果(23.10)对某个\(n\)成立则对所有\(n\)成立, 这时\(H_n = H_{n-1}, \forall n \in \mathbb Z\)。
(2) \(\{X_t\}\)是纯非决定性的当且仅当对某个\(n\),有 \[\begin{align} \sigma_k^2 = \|X_{n+k} - L(X_{n+k}|H_n) \|^2 \to \gamma_0, \quad k \to \infty \tag{23.11} \end{align}\] 并且如果(23.11)对某个\(n\)成立则对所有\(n\)成立。
23.2.4 Wold表示定理
定理23.5 (Wold表示定理) 任一非决定性的零均值平稳列可以表示成 \[\begin{align} X_t = \sum_{j=0}^\infty a_j \varepsilon_{t-j} + V_t, \quad t \in \mathbb Z \tag{23.12} \end{align}\] 其中
(1) \(\varepsilon_t = X_t - L(X_t | X_{t-1}, X_{t-2}, \dots)\) 是零均值白噪声,满足 \[\begin{aligned} & E \varepsilon_t^2 = \sigma^2 > 0, \quad a_0 = 1 \\ & a_j = E(X_t \varepsilon_{t-j}) / \sigma^2,\\ & \sum_{j=0}^\infty a_j^2 < \infty \end{aligned}\]
(2) \(\{U_t = \sum_{j=0}^\infty a_j \varepsilon_{t-j}, \ t \in \mathbb Z\}\) 和\(\{V_t\}\)都是平稳列且两者互相正交;
(3) 定义\(H_\varepsilon(t) = \bar{\text{sp}}\{\varepsilon_s: s \leq t\}\), \(H_U(t) = \bar{\text{sp}}\{U_s: s \leq t\}\), 则\(\forall t\) \[\begin{aligned} H_U(t) = H_\varepsilon(t) \end{aligned}\]
(4) \(\{U_t\}\)是纯非决定性的平稳序列, 有谱密度 \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi} \left| \sum_{j=0}^\infty a_j e^{ij\lambda} \right|^2 \end{aligned}\]
(5) \(\{V_t\}\)是决定性的平稳序列。 对任何\(t, k \in \mathbb Z\), \(V_t \in H_{t-k}\)。
定义23.3 在Wold表示定理中
- (1) 称(23.12)是\(\{X_t\}\)的Wold表示;
- (2) 称\(\{U_t\}\)是\(\{X_t\}\)的纯非决定性部分, 称\(\{V_t\}\)是\(\{X_t\}\)的决定性部分;
- (3) 称\(\{a_j\}\)是\(\{X_t\}\)的Wold系数;
- (4) 称一步预测误差 \(\varepsilon_t = X_t - L(X_t | X_{t-1}, X_{t-2}, \dots)\) 为\(\{X_t\}\)的新息序列;
- (5) 称\(\sigma^2 = E \varepsilon_t^2\)为 一步(线性)预测的均方误差。
这里新息的意思是不能被历史线性预测的部分。 由Wold定理可知任何纯非决定性平稳序列可以表达为新息的单边滑动和。 事实上,任何白噪声的单边滑动和(系数平方可和)一定是纯非决定性的, 但其中的白噪声不一定恰好是新息。
23.2.4.1 ARMA序列的Wold表示
设\(\{X_t\}\)是ARMA(\(p,q\))序列,模型方程为 \[\begin{aligned} A(\mathscr B) X_t = B(\mathscr B) \varepsilon_t,\quad t\in\mathbb Z, \end{aligned}\] 设\(A^{-1}(z) B(z)\)有Taylor展开式 \[\begin{aligned} \Psi(z) = A^{-1}(z) B(z) = \sum_{j=0}^\infty \psi_j z^j, \quad |z| \leq 1 \end{aligned}\] 则 \[\begin{align} X_t = \sum_{j=0}^\infty \psi_j \varepsilon_{t-j}, \quad t \in \mathbb Z. \tag{23.13} \end{align}\] 下面证明\(\{X_t\}\)是纯非决定性的平稳序列, (23.13)是\(\{X_t\}\)的Wold表示, \(\{\varepsilon_t\}\)是\(\{X_t\}\)的新息序列, \(\{\psi_j\}\)是\(\{X_t\}\)的Wold系数。
我们只对比较容易的可逆ARMA的情况证明。 由(23.13)看出\(X_t \in H_\varepsilon(t)\), 利用可逆性, \(\varepsilon_t = B^{-1}(\mathscr B) A(\mathscr B) X_t \in H_t\), 所以\(H_t = H_\varepsilon(t)\). 于是 \[\begin{aligned} X_t - \varepsilon_t = \sum_{j=1}^\infty \psi_j \varepsilon_{t-j} \in H_\varepsilon(t-1) = H_{t-1} \end{aligned}\] 来证\(X_t - \varepsilon_t = L(X_t | H_{t-1})\)。 只要证明\(X_t - (X_t - \varepsilon_t) \perp H_{t-1}\).
事实上, 由于\(\varepsilon_t\)与\(\varepsilon_{t-j}, j\geq 1\)正交可知 \(\varepsilon_t \perp H_\varepsilon(t-1) = H_{t-1}\)。故 \[\begin{aligned} X_t - \varepsilon_t =& L(X_t | H_{t-1}) \\ \varepsilon_t =& X_t - L(X_t | H_{t-1}) \end{aligned}\] 即\(\{\varepsilon_t\}\)是\(\{X_t\}\)的新息列, \(\sigma^2 = E\varepsilon_t^2\)是一步预测均方误差, 在(23.13)两边同乘以\(\varepsilon_{t-j}\)后取期望, 利用内积的连续性可得 \[\begin{aligned} \psi_j = \langle X_t, \varepsilon_{t-j} \rangle /\sigma^2 \end{aligned}\] 即\(\{\psi_j\}\)是\(\{X_t\}\)的Wold系数列。
○○○○○○
23.2.4.2 Wold表示定理证明
取\(\varepsilon_t = X_t - L(X_t|H_{t-1})\), \(H_\varepsilon(t) = \overline{\mbox{sp}}\{\varepsilon_s:\; s \leq t \}\), 易见\(\varepsilon_t \in H_t\), 由\(H_t\)的单调性可知 \(\varepsilon_t \in H_s, \forall t < s\),因此 \(H_\varepsilon(t) \subset H_t\)。
来证明\(\{\varepsilon_t\}\)是白噪声。
由定理23.3 \[\begin{aligned} L(X_t|H_{t-1}) =& \lim_{m\to\infty} L(X_t | X_{t-1}, \dots, X_{t-m}) \quad(L^2)\\ =& \lim_{m\to\infty} \boldsymbol{a}_m^T \boldsymbol{X}_{t-1,m} \end{aligned}\] 其中\(\boldsymbol{a}_m\)是\(m\)阶Y-W系数(预测方程的解), 不依赖于\(t\), 由内积的连续性 \[\begin{aligned} E \varepsilon_t^2 =& \lim_{m\to\infty} \| X_t - L(X_t | X_{t-1}, \dots, X_{t-m}) \|^2 \\ =& \lim_{m\to\infty} ( \gamma_0 - \boldsymbol{a}_m^T \Gamma_m \boldsymbol{a}_m) \quad\text{(与}t\text{无关)}\\ =& \lim_{m\to\infty} \sigma_{1,m}^2 = \sigma^2 > 0 \quad\text{(由非决定性定义)} \end{aligned}\] 对\(s>t\),\(\varepsilon_s \perp H_{s-1} \supset H_t\)所以 \(\varepsilon_s \perp \varepsilon_t\), (\(s>t\)时)。即 \[\begin{aligned} \{\varepsilon_t\} \sim \text{WN}(0,\sigma^2), \quad \sigma^2>0 \end{aligned}\]
○○○
定义\(V_t = X_t - L(X_t|H_\varepsilon(t))\), 则\(V_t \in H_t\)。 来证明\(\{\varepsilon_t\}\)和\(\{V_t\}\)正交。
由投影性质,\(V_t \perp H_\varepsilon(t)\),即 \(V_t \perp \varepsilon_s\), \(\forall s \leq t\)。 当\(s>t\)时, 注意\(\varepsilon_s \perp H_{s-1} \supset H_t\), 而\(V_t \in H_t\)所以\(\varepsilon_s \perp V_t\), \(\forall s>t\)。 于是\(\{\varepsilon_t\}\)和\(\{V_t\}\)正交。
○○○
来证明\(\{\varepsilon_t\}\)和\(\{X_t\}\)平稳相关。
当\(s>t\)时\(\varepsilon_s \perp H_t\)所以 \(\langle \varepsilon_s, X_t \rangle=0\), \(\forall s>t\)。
当\(s \leq t\)时,由定理23.3, \[\begin{aligned} L(X_t|H_{t-1}) =& \lim_{m\to\infty} L(X_t | \boldsymbol{X}_{t-1,m}) \quad (L^2) \\ =& \lim_{m\to\infty} \boldsymbol{a}_m^T \boldsymbol{X}_{t-1,m} \end{aligned}\] 由内积的连续性, \(s \leq t\)时 \[\begin{aligned} \langle X_t, \varepsilon_s \rangle =& \lim_{m\to\infty} \langle X_t, X_s - \boldsymbol{a}_m^T \boldsymbol{X}_{s-1,m} \rangle \\ =& \gamma_{t-s} - \lim_{m\to\infty}(a_{m1}\gamma_{t-s+1} + \dots + a_{mm}\gamma_{t-s+m}) \end{aligned}\] 只依赖于\(t-s\)。 所以\(\{\varepsilon_t\}\)和\(\{X_t\}\)平稳相关。
○○○
由\(\{\varepsilon_t\}\)和\(\{X_t\}\)平稳相关, 若定义 \[\begin{aligned} a_j =& \langle X_t, \varepsilon_{t-j} \rangle / \sigma^2 \quad (j \geq 0) \end{aligned}\] 则\(a_j\)与\(t\)无关。且 \[\begin{aligned} a_0 =& \langle X_t, \varepsilon_{t} \rangle / \sigma^2 \\ =& \langle \varepsilon_t + L(X_t|H_{t-1}), \varepsilon_{t} \rangle / \sigma^2 \\ =& \langle \varepsilon_t, \varepsilon_t \rangle / \sigma^2 = 1 \end{aligned}\]
○○○
令\(U_t = L(X_t|H_\varepsilon(t))\), 则\(V_t = X_t - L(X_t|H_\varepsilon(t)) = X_t - U_t\), \(X_t = U_t + V_t\)。 来证明 \[\begin{align} U_t = \sum_{j=0}^\infty a_j \varepsilon_{t-j} \tag{23.14} \end{align}\]
定义\(U_{t,n} = L(X_t | \varepsilon_t, \varepsilon_{t-1}, \dots, \varepsilon_{t-n})\). 设\(U_{t,n}=\sum_{j=0}^n b_j \varepsilon_{t-j}\), 由\(\{\varepsilon_t\}\)与\(\{ X_t \}\)平稳相关可知\(\{ b_j \}\)与\(t\)无关。 对\(j=0,1,\dots,n\) \[\begin{aligned} \sigma^2 a_j =& \langle X_t, \varepsilon_{t-j} \rangle = \langle U_{t,n} + (X_t - U_{t,n}), \varepsilon_{t-j} \rangle \\ =& \langle U_{t,n}, \varepsilon_{t-j} \rangle = \sigma^2 b_j \end{aligned}\] 即\(b_j=a_j\), \[\begin{aligned} U_{t,n} = L(X_t | \varepsilon_t, \varepsilon_{t-1}, \dots, \varepsilon_{t-n}) = \sum_{j=0}^n a_j \varepsilon_{t-j} \end{aligned}\]
注意\(U_{t,n}\)是\(X_t\)的投影所以 \(\|U_{t,n}\|^2 \leq \|X_t \|^2 = \gamma_0\), 所以 \[\begin{aligned} \|U_{t,n} \|^2 = \sigma^2 \sum_{j=0}^n a_j^2 \leq \gamma_0 < \infty \end{aligned}\] 故\(\sum_{j=0}^\infty a_j^2 < \infty\), \(\sum_{j=0}^n a_j \varepsilon_{t-j}\)均方收敛到 \(\sum_{j=0}^\infty a_j \varepsilon_{t-j}\)。 由定理23.3知\(U_{t,n}\)均方收敛到\(U_t=L(X_t | H_\varepsilon(t))\), 所以(23.14)成立。
\(\{U_t\}\)是线性平稳列, 其谱密度立即可得(结论(4)的第二部分)。
○○○
由于\(\{\varepsilon_t\}\)与\(\{V_t\}\)正交所以 \(V_s \perp H_\varepsilon(t), \forall s,t \in \mathbb Z\), 而\(U_t \in H_\varepsilon(t)\)所以\(V_s \perp U_t\), \(\{V_t\}\)与\(\{U_t\}\)正交。 由\(\{U_t \}\)和\(\{V_t \}\)正交, \(X_t = U_t + V_t\), \(\{ X_t \}\)和\(\{ U_t \}\)平稳可知 \(V_t = X_t - U_t\)也是平稳列。
至此定理的(1)(2)已证明。
○○○
来证明第(3)条结论。 定义\(H_U(t) = \bar{\text{sp}}\{U_s:\; s\leq t\}\), 来证明\(H_U(t) = H_\varepsilon(t)\)。
显然\(U_t \in H_\varepsilon(t)\)所以\(H_U(t) \subset H_\varepsilon(t)\)。 只要证明\(H_\varepsilon(t) \subset H_U(t)\)。
注意\(\varepsilon_t \in H_t \subset \bar{\text{sp}}\{U_s, V_s:\; s\leq t\}\), 由引理23.1, 存在\(\xi_m \in L{\{V_t, V_{t-1}, \dots, V_{t-m}\}}\), \(\eta_m \in L{\{U_t, U_{t-1}, \dots, U_{t-m}\}}\), 使 \[\begin{aligned} \| \xi_m + \eta_m - \varepsilon_t \|^2 \to 0 \ (m\to\infty) \end{aligned}\] 但前面已证明\(\{V_t\}\)与\(\{\varepsilon_t\}\)正交,也与\(\{U_t\}\)正交, 所以 \[\begin{aligned} & \| \xi_m + \eta_m - \varepsilon_t \|^2 \\ =& \| \xi_m \|^2 + \| \eta_m - \varepsilon_t \|^2 \\ \geq& \| \eta_m - \varepsilon_t \|^2 \end{aligned}\] 令\(m\to\infty\)得 \(\| \eta_m - \varepsilon_t \|^2 \to 0\), 由引理23.1知\(\varepsilon_t \in H_U(t)\)。 所以\(H_\varepsilon(t) \subset H_U(t)\), \(H_\varepsilon(t) = H_U(t)\)。 结论(3)证毕。
○○○
来证明\(\{U_t\}\)是纯非决定性的(结论(4))。 利用定理22.2(4)(5) \[\begin{aligned} & L(U_{t+k}|H_U(t)) = L(U_{t+k} | H_\varepsilon(t)) \\ =& L \left[ \sum_{j=0}^{k-1} a_j \varepsilon_{t+k-j} + \sum_{j=k}^\infty a_j \varepsilon_{t+k-j} | H_\varepsilon(t) \right] \\ =& \sum_{j=k}^\infty a_j \varepsilon_{t+k-j} \end{aligned}\] 于是 \[\begin{aligned} & \| U_{t+k} - L(U_{t+k}|H_U(t)) \|^2 = \| \sum_{j=0}^{k-1} a_j \varepsilon_{t+k-j} \|^2 \\ = & \sigma^2 \sum_{j=0}^{k-1} a_j^2 \to \sigma^2 \sum_{j=0}^\infty a_j^2 = E U_t^2 \end{aligned}\] 按定义可知\(\{U_t\}\)为纯非决定性的。
注意:这个证明对一般单边线性序列不适用。
○○○
已证明\(\{V_t\}\)平稳,来证明\(\{V_t\}\)是决定性的。 用定理23.4。 注意\(\varepsilon_{t-j} \in H_{t-j}\), \[\begin{aligned} V_t =& X_t - U_t = X_t - \varepsilon_t - \sum_{j=1}^\infty a_j \varepsilon_{t-j} \\ =& L(X_t | H_{t-1}) - \sum_{j=1}^\infty a_j \varepsilon_{t-j} \end{aligned}\] 其中\(L(X_t | H_{t-1}) \in H_{t-1}\), \(\sum_{j=1}^\infty a_j \varepsilon_{t-j} \in H_\varepsilon(t-1) \subset H_{t-1}\), 所以\(V_t \in H_{t-1}\)。
注意\(H_{t-1} \subset \bar{\text{sp}}\{U_s, V_s:\; s \leq t-1\}\), 由引理23.1, 存在\(\xi_m \in L_{\{V_{t-1}, \dots, V_{t-m}\}}\), \(\eta_m \in L_{\{U_{t-1}, \dots, U_{t-m}\}}\), 使 \[\begin{aligned} \| \xi_m + \eta_m - V_t \|^2 \to 0 \end{aligned}\] 已证明\(\{V_t\}\)与\(\{U_t\}\)正交所以\(\eta_m\)与\(\xi_m - V_t\)正交, 于是 \[\begin{aligned} & \| \xi_m + \eta_m - V_t \|^2 = \| \xi_m - V_t \|^2 + \| \eta_m \|^2 \\ \geq& \| \xi_m - V_t \|^2 \end{aligned}\] 故\(\| \xi_m - V_t \|^2 \to 0(m \to \infty)\), 由引理23.1知\(V_t \in H_V(t-1)=\bar{\text{sp}}\{V_s:\; s\leq t-1\}\)。 由定理23.4知\(\{V_t\}\)为决定性的, 且\(H_V(t) = H_V(t-j), j\in \mathbb Z\), 所以\(V_t \in H_V(t-j), \; t,j \in \mathbb Z\)。
○○○○○○
23.2.4.3 关于新息的讨论
\(\varepsilon_t = X_t - L(X_t | H_{t-1})\)是 \(X_t\)提供的比\(X_{t-1}, X_{t-2}, \dots\)多的信息(线性意义下)。
可以证明 \[\begin{align} H_t = \text{sp}(\varepsilon_t) \oplus H_{t-1} \tag{23.15} \end{align}\] 这样 \[\begin{aligned} H_t = \mathop\oplus\limits_{j=0}^\infty \text{sp}(\varepsilon_{t-j}) \oplus H_{-\infty} , \end{aligned}\] 其中\(H_{-\infty} = \mathop\cap\limits_{t} H_t\)。 \(V_t \in H_{-\infty}\)。
事实上,(23.15)右侧两项正交, 都是闭子空间,且都包含于\(H_t\), 则(参见23.5.2) \[ \text{sp}(\varepsilon_t) \oplus H_{t-1} = \{ \alpha \varepsilon_t + \xi: \alpha \in \mathbb R, \xi \in H_{t-1} \} \] 是\(H_t\)内的闭子空间, \(\text{sp}(\varepsilon_t) \oplus H_{t-1} \subset H_t\)。
来证\(H_t \subset \text{sp}(\varepsilon_t) \oplus H_{t-1}\)。 由引理23.1只要证明\(X_s \in \text{sp}(\varepsilon_t) \oplus H_{t-1}, s \leq t\)。
当\(s < t\)时显然,对\(X_t\),因为 \[\begin{aligned} X_t = \varepsilon_t + L(X_t|H_{t-1}) \end{aligned}\] 所以\(X_t \in \text{sp}(\varepsilon_t) \oplus H_{t-1}\), 于是有 \[\begin{aligned} H_t = \text{sp}(\varepsilon_t) \oplus H_{t-1} . \end{aligned}\]
○○○○○○
23.3 Kolmogorov公式
考虑多步预报的均方误差。 设\(\{X_t\}\)是非决定性的平稳列, 由Wold表示定理(5),\(V_{t+n} \in H_t\), 所以用无穷长历史进行的最佳线性预测为 \[\begin{align} L(X_{t+n}|H_t) =& L(U_{t+n}|H_t) + L(V_{t+n}|H_t) \\ =& L(\sum_{j=0}^\infty a_j \varepsilon_{t+n-j} | H_t) + V_{t+n} \\ =& \sum_{j=n}^\infty a_j \varepsilon_{t+n-j} + V_{t+n} \tag{23.16} \end{align}\] 称\(L(X_{t+n}|H_t)\)是\(X_{t+n}\)的\(n\)步预报, 由Wold分解公式知预报误差为 \[\begin{align} X_{t+n} - L(X_{t+n}|H_t) = \sum_{j=0}^{n-1} a_j \varepsilon_{t+n-j} \tag{23.17} \end{align}\] 预报的均方误差为 \[\begin{align} \sigma^2(n) = \sigma^2 \sum_{j=0}^{n-1} a_j^2 \tag{23.18} \end{align}\] \(n\to\infty\)时\(\sigma^2(n) \to E U_t^2\).
定理23.6 (Kolmogorov公式) 设\(\{U_t\}\)是非决定性平稳序列\(\{X_t\}\)的 纯非决定性部分, \(f(\lambda)\)是\(\{U_t\}\)的谱密度. 则有 \[\begin{align} \sigma^2 = E[X_t-L(X_t|H_{t-1})]^2 = 2\pi \exp\left(\frac{1}{2\pi} \int^{\pi}_{-\pi} \ln f(\lambda)d\lambda \right). \tag{23.19} \end{align}\]
公式(23.19)的证明需要较多解析函数的知识. 当\(\{U_t\}\)是白噪声时, 公式(23.19)明显是成立的.
从Kolmogorov公式(23.19)看到, 如果\(\{X_t\}\)是非决定性的, 则它的纯非决定性部分的谱密度\(f(\lambda)\)必是\(\ln\)可积的, 即 \[\begin{align} \int^{\pi}_{-\pi} \ln f(\lambda)d\lambda > -\infty. \tag{23.20} \end{align}\]
23.4 最佳预测和最佳线性预测相等的条件
设\(\{X_t\}\)是平稳序列, 用 \(\mathscr F_t=\sigma\{X_t,X_{t-1},\dots\}\) 表示由\(X_t, X_{t-1},\dots\)生成的\(\sigma\)-代数. 称条件数学期望 \[ E(X_{t+k}| \mathscr F_t) \] 是用全体历史\(\{X_j: j \leq t\}\)对\(X_{t+k}\)进行预测时的最佳预测.
最佳预测是均方误差最小的, 这是因为条件数学期望\(E(X_{t+k}| \mathscr F_t)\)是\(X_{t-1}, X_{t-2},\dots\)的函数, 二阶矩有限: \[ E[E(X_{t+k}| \mathscr F_t)]^2 \leq E [E(X_{t+k}^2| \mathscr F_t)] = EX_{t+k}^2 < \infty. \] 由概率论中数学期望性质可以证明对任意二阶矩有限的\(X_t, X_{t-1},\dots\)的函数\(\xi\)有 \[\begin{align} E(X_{t+k} - \xi)^2 \geq E[X_{t+k} - E(X_{t+k}|\mathscr F_t)]^2 \tag{23.21} \end{align}\]
事实上,对\(\xi \in \mathscr F_t\), \[\begin{aligned} & E\left[ (X_{t+k} - \xi)^2 \right] \\ =& E \left\{ \left[ ( X_{t+k} - E(X_{t+k}|\mathscr F_t) ) + ( E(X_{t+k}|\mathscr F_t) - \xi ) \right]^2 \right\} \\ =& E \left\{ [ X_{t+k} - E(X_{t+k}|\mathscr F_t) ]^2 \right\} + E \left\{ [ E(X_{t+k}|\mathscr F_t) - \xi ) ]^2 \right\} \\ & + 2 E \left\{ ( X_{t+k} - E(X_{t+k}|\mathscr F_t) ) ( E(X_{t+k}|\mathscr F_t) - \xi ) \right\} \end{aligned}\] 而交叉项 \[\begin{aligned} & E \left\{ ( X_{t+k} - E(X_{t+k}|\mathscr F_t) ) ( E(X_{t+k}|\mathscr F_t) - \xi ) \right\} \\ =& E \left\{ E \left[ ( X_{t+k} - E(X_{t+k}|\mathscr F_t) ) ( E(X_{t+k}|\mathscr F_t) - \xi ) \,|\, \mathscr F_t \right] \right\} \\ =& E \left\{ ( E(X_{t+k}|\mathscr F_t) - \xi ) \; E \left[ X_{t+k} - E(X_{t+k}|\mathscr F_t) \,|\, \mathscr F_t \right] \right\} \\ = 0 \end{aligned}\] 所以 \[\begin{aligned} & E\left[ (X_{t+k} - \xi)^2 \right] \\ =& E \left\{ [ X_{t+k} - E(X_{t+k}|\mathscr F_t) ]^2 \right\} + E \left\{ [ E(X_{t+k}|\mathscr F_t) - \xi ) ]^2 \right\} \\ \geq& E \left\{ [ X_{t+k} - E(X_{t+k}|\mathscr F_t) ]^2 \right\} \end{aligned}\]
最佳预测一般比最佳线性预测好,但是对纯非决定性序列如果其新息是独立序列则二者等价。
定理23.7 设平稳序列\(\{X_t\}\)有Wold表示 \[\begin{align} X_{t}=\sum_{j=0}^{\infty} a_j \varepsilon_{t-j}, \ \ t \in \mathbb Z. \tag{23.22} \end{align}\] 则 \[\begin{align} L(X_{t+n}|H_t)=E(X_{t+n}|\mathscr F_t), \ n \geq 1, \ \ t\in \mathbb Z, \tag{23.23} \end{align}\] 成立的充分必要条件是 \[\begin{align} E(\varepsilon_{t+1}|\varepsilon_{t},\varepsilon_{t-1},\dots) =0, \ \ t\in \mathbb Z. \tag{23.24} \end{align}\]
(23.24)的条件称为鞅差。 零均值独立白噪声列是鞅差的特例。
推论23.1 设ARMA(\(p,q\))序列\(\{X_t\}\)中的新息\(\{\varepsilon_t\}\)是独立白噪声, 则用全体历史\(\{X_t,X_{t-1},\dots\}\)对\(X_{t+n}\)进行预测时, 最佳预测和最佳线性预测相等.
23.5 附录:补充
非决定性也称为非奇异,决定性序列称为奇异序列。 见谢衷洁《时间序列分析》P.82。 纯非决定性序列叫做正则序列, 见谢衷洁《时间序列分析》P.118第13题。
23.5.2 正交直和分解
定理:设\(H\)为Hilbert空间, \(H_1\)和\(H_2\)是\(H\)的闭子空间, \(H_1\)与\(H_2\)正交, \(M = H_1 \oplus H_2 = \{ x + y: x \in H_1, y \in H_2 \}\), 则\(M\)是\(H\)的闭子空间, 且\(\forall \xi \in H\), \[ L(\xi | M) = L(\xi | H_1) \oplus L(\xi | H_2), \] 其中\(\oplus\)表示求和, 且求和的两项正交。
证明: 对\(\xi, \eta \in M\), 应有\(\xi_1, \eta_1 \in H_1\), \(\xi_2, \eta_2 \in H_2\)使得\(\xi = \xi_1 + \xi_2\), \(\eta = \eta_1 + \eta_2\), 于是\(\xi + \eta = (\xi_1 + \eta_1) + (\xi_2 + \eta_2) \in M\); 对\(\alpha \in \mathbb R\), \(\alpha \xi = (\alpha \xi_1) + (\alpha \xi_2) \in M\), 所以\(M\)是\(H\)的子线性空间。
对\(M\)中的基本列\(\{ \xi_n \}\), 有分解\(\xi_n = \xi_{1,n} + \xi_{2,n}\), \(\xi_{1,n} \in H_1\), \(\xi_{2,n} \in H_2\), \[\begin{aligned} 0 =& \lim_{n,m \to \infty} \| \xi_n - \xi_m \|^2 = \lim_{n,m \to \infty} \left( \| \xi_{1,n} - \xi_{1,m} \|^2 + \| \xi_{2,n} - \xi_{2,m} \|^2 \right) \end{aligned}\] 从而\(\{ \xi_{1,n} \}\)是\(H_1\)的基本列, \(\{ \xi_{2,n} \}\)是\(H_2\)的基本列, 存在\(\xi_1 \in H_1\), \(\xi_2 \in H_2\), 使得\(\lim \| \xi_{1,n} - \xi_1 \| = 0\), \(\lim \| \xi_{2,n} - \xi_2 \| = 0\), 于是 \[ \lim_{n\to\infty} \| \xi_n - (\xi_1 + \xi_2) \|^2 = \lim_{n\to\infty} \left( \| \xi_{1,n} - \xi_1 \|^2 + \| \xi_{2,n} - \xi_2 \|^2 \right) = 0 \] 因\(\xi_1 + \xi_2 \in M\), 所以\(M\)是\(H\)的闭子空间。
\(\forall \xi \in H\), 令\(\xi_1 = L(\xi | H_1)\), \(\xi_2 = L(\xi | H_2)\), 则\(\xi_1 + \xi_2 \in M\), 且 \[\begin{aligned} \xi - (\xi_1 + \xi_2) =& (\xi - \xi_1) + (-\xi_2) \perp H_1, \\ \xi - (\xi_1 + \xi_2) =& - \xi_1 + (\xi - \xi_2) \perp H_2, \\ \end{aligned}\] 因此\(\xi - (\xi_1 + \xi_2)\)与\(M = H_1 + H_2\)正交, 从而\(\xi_1 + \xi_2 = L(\xi | M)\), 且\(\xi_1 \perp \xi_2\)。 结论得证。
23.5.3 单边线性序列与Wold表示
单边线性序列一定是纯非决定性的, 但其中的白噪声不一定是新息, 所以表达式本身不一定是Wold表示。
如 \[\begin{aligned} X_t = \varepsilon_t + 2 \varepsilon_{t-1} \end{aligned}\] 是纯非决定性序列, 其谱密度 \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi} | 1 + 2 e^{i\lambda} |^2 = \frac{4\sigma^2}{2\pi} | 1 + \frac12 e^{i\lambda} |^2 \end{aligned}\] 但\(\varepsilon_t \neq X_t - L(X_t | H_{t-1})\)。
令 \[ \eta_t = (1 - \frac12 \mathscr B)^{-1} X_t \] 则\(\{ \eta_t \}\)是\(\{ X_t \}\)的系数绝对可和的线性滤波, 故平稳, 且\(\{ \eta_t \}\)的谱密度为 \[ f_\eta(\lambda) = | 1 - \frac12 e^{-i\lambda} |^{-2} f(\lambda) = \frac{4\sigma^2}{2\pi} \] 所以\(\{ \eta_t \}\)是WN(0, \(4\sigma^2\)), \[ X_t = \eta_t + \frac12 \eta_{t-1} \] 是可逆MA(1)模型。 由上面关于可逆ARMA模型的一般结论可知\(\eta_t\)是\(\{ X_t \}\)的新息, 而\(\varepsilon_t\)与\(\eta_t\)方差不同, 不会a.s.相等, 由新息的唯一性可知\(\{ \varepsilon_t \}\)不是\(\{ X_t \}\)的新息。 所以单边线性序列中的白噪声列不一定是新息。
23.5.4 离散谱序列可完全线性预测的直接证明
对 \[\begin{aligned} Z_j(t) =& \xi_j \cos(t\lambda_j) + \eta_j \sin(t \lambda_j), \ t \in \mathbb Z, \end{aligned}\] 有 \[\begin{aligned} & 2 \cos\lambda_j Z_j(t-1) - Z_j(t-2) \\ =& \xi_j \{ 2\cos\lambda_j \cos[(t-1)\lambda_j] - \cos[(t-2)\lambda_j] \} \\ & + \eta_j \{ 2\cos\lambda_j \sin[(t-1)\lambda_j] - \sin[(t-2)\lambda_j] \} \\ =& \xi_j \{ \cos(t\lambda_j) + \cos[(t-2)\lambda_j] - \cos[(t-2)\lambda_j] \} \\ & + \eta_j \{ \sin(t\lambda_j) + \sin[(t-2)\lambda_j] - \sin[(t-2)\lambda_j] \} \\ =& Z_j(t) \end{aligned}\] 所以 \[\begin{aligned} L(Z_j(t) | Z_j(t-1), Z_j(t-2)) = 2\cos\lambda_j Z_j(t-1) - Z_j(t-2). \end{aligned}\] 但是混合多个频率的离散谱序列的预测公式就没有这么容易。