27 平稳序列谱表示
本章内容:
- 随机积分;
- 平稳序列谱表示;
- 线性平稳列的谱表示;
- 离散谱序列的特征及其谱表示;
- 平稳序列的频率性质;
- 平稳序列的分解。
内容待补充。
借助于\(L^2\)空间中的随机积分, 可以将平稳序列表示成随机积分形势, 能够帮助我们理解平稳时间序列的时域和谱域的关系。
复值随机变量:如果\(\xi, \eta\)是随机变量, \(Z = \xi + i\eta\)称为复值随机变量。
复值时间序列:如果\(\{ \xi_t \}\), \(\{ \eta_t \}\)是时间序列, \(Z_t = \xi_t + \eta_t\)称为复值时间序列。
学习本章需要学生学过实变函数论中的勒贝格测度和勒贝格积分概念。
27.1 随机积分定义
27.1.1 随机测度
定义27.1 (正交增量过程) 称复值随机过程\(\{ Z(\lambda), \lambda \in [-\pi, \pi]\)是正交增量过程,如果
(1) 对一切\(\lambda \in [-\pi, \pi]\), \(E Z(\lambda) = 0\), \(E|Z(\lambda)|^2 < \infty\);
(2) 对任何\(-\pi \leq \lambda_1 < \lambda_2 \leq \lambda_3 < \lambda_4 \leq \pi\),有 \[ E\left\{ [Z(\lambda_2) - Z(\lambda_1)] \overline{[Z(\lambda_4) - Z(\lambda_3)]} \right\} = 0, \] 其中\(\overline{\xi}\)表示\(\xi\)的复共轭。
定义27.2 (右连续的正交增量过程) 称正交增量过程\(\{ Z(\lambda) \}\)是右连续的,如果当\(\delta \downarrow 0\)时, 对任何\(\lambda \in [-\pi, \pi]\)都有 \[ E|Z(\lambda + \delta) - Z(\lambda)|^2 \to 0 . \]
本章中无特殊声明情况下,正交增量过程总假定是右连续的,并且满足\(Z(-\pi)=0\)。
称\([-\pi, \pi]\)上任何单调不减、右连续的非负有界函数为分布函数。 这是取值于\([-\pi,\pi]\)的随机变量的分布函数的推广,不要求在\(\pi\)处等于1。
任何正交增量过程都唯一地对应一个在\(-\pi\)处等于零的分布函数。
定理27.1 设\(\{Z(\lambda) \}\)是正交增量过程,右连续,且\(Z(-\pi)=0\), 则存在唯一的分布函数\(F(\lambda)\),满足对任何\(-\pi \leq \lambda < \mu \leq \pi\),有 \[\begin{align} F(\mu) - F(\lambda) = E| Z(\mu) - Z(\lambda)|^2, \ F(-\pi) = 0 . \tag{27.1} \end{align}\]
实际上,\(F(\cdot)\)在\([-\pi, \pi]\)定义了一个有限测度, 定理说明\(Z(\cdot)\)像是一个测度,但结果是随机变量。 称\(Z(\cdot)\)为一个随机测度。
称(27.1)确定的分布函数\(F(\cdot)\)为正交增量过程\(\{ Z(\lambda) \}\)的分布分数。
证明: 取\(F(\lambda) = E|Z(\lambda)|^2\)。 则 \[ F(-\pi) = E|0|^2 = 0 . \]
对\(\lambda < \mu\),利用正交增量性得 \[\begin{aligned} F(\mu)=& E | Z(\mu) - Z(\lambda) + Z(\lambda) - Z(-\pi) |^2 \\ =& E | Z(\mu) - Z(\lambda) |^2 + E | Z(\lambda) - Z(-\pi) |^2 \\ =& E | Z(\mu) - Z(\lambda) |^2 + E | Z(\lambda) |^2 \\ =& E | Z(\mu) - Z(\lambda) |^2 - F(\lambda) \end{aligned}\]
所以(27.1)成立,且\(F(\cdot)\)单调不减, 由(27.1)和\(Z(\cdot)\)的右连续性可知\(\mu \downarrow \lambda\) 时\(F(\mu) \to F(\lambda)\),即\(F(\cdot)\)右连续。
对任何满足(27.1)条件的分布函数\(F\), 在(27.1)中令\(\lambda = -\pi\)就有\(F(\mu) = E|Z(\mu)|^2\), 是唯一确定的。
○○○○○○
例27.1 (布朗运动) 设\(\{B(t), t \in [-\pi, \pi] \}\)为独立增量过程, 对\(\lambda < \mu\),满足\(B(-\pi) = 0\), \[ B(\mu) - B(\lambda) \sim \text{N}(0, \sigma^2 (\mu - \lambda)) . \] 则\(\{ B(t) \}\)是\([-\pi, \pi]\)上的布朗运动。
\[ E|B(\mu) - B(\lambda)|^2 = \sigma^2 (\mu - \lambda) \] 所以是右连续过程。 按定理27.1的构造方法,令 \[ F(\lambda) = E|B(\lambda)|^2 = \sigma^2 (\lambda + \pi), \ \lambda \in [-\pi, \pi], \] 则\(F(-\pi) = 0\), \(F(\cdot)\)是\([-\pi, \pi]\)上的分布函数, 是\(\{ B(t) \}\)对应的分布函数。
○○○○○○
27.1.2 平方可积函数空间
设\(\Omega = [-\pi, \pi]\), \(\mathscr B\)是\(\Omega\)上的Borel \(\sigma\)代数, 则分布函数\(F\)是可测空间\((\Omega, \mathscr B)\)上的有限测度, \((\Omega, \mathscr B, F)\)是一个测度空间。
用\(L^2(F)\)表示\((\Omega, \mathscr B, F)\)上复值平方可积函数的全体: \[\begin{align} L^2(F) = \left\{ g(x):\; \int_{-\pi}^\pi |g(x)|^2 dF(x) < \infty \right\} \tag{27.2} \end{align}\] 在内积 \[ \langle f, g \rangle = \int_{-\pi}^\pi f(s) \overline{g(s)} \,d F(s) \] 下, \(L^2(F)\)是复数域上的Hilbert空间。 参见(何书元 2003)第八章习题1.2。
27.1.3 随机积分定义的步骤
设\(\{ Z(\lambda) \}\)是正交增量过程,\(F\)是其分布函数, 要定义随机积分: \[ I(g) = \int_{-\pi}^\pi g(s) d Z(s) \] 结果\(I(g)\)是一个复值随机变量。定义类似于勒贝格积分定义步骤:
- 先对阶梯函数\(g\)定义;
- 讨论这样的随机积分的性质;
- 将阶梯函数的随机积分推广到一般平方可积函数。
27.1.4 对阶梯函数定义随机积分
设\(g\)是\(L^2(F)\)中的阶梯函数, 表示为 \[\begin{align} g(s) = \sum_{j=0}^n a_j I_{(\lambda_j, \lambda_{j+1}]}(s), \ -\pi = \lambda_0 < \lambda_1 < \dots < \lambda_{n+1} = \pi, \tag{27.3} \end{align}\] 其中\(a_j\)是复常数,\(I_A(s)\)是集合\(A\)的示性函数。
定义 \[\begin{align} I(g) = \sum_{j=0}^n a_j [Z(\lambda_{j+1}) - Z(\lambda_j)] \tag{27.4} \end{align}\] 则 \[ E I(g) = 0 . \] 阶梯函数\(g\)的表达式不必唯一,但是结果\(I(g)\)是唯一的。
用\(\mathscr D\)表示形如(27.3)的阶梯函数全体。 对于复常数\(a, b\)和\(f, g \in \mathscr D\), \(a f + b g\)仍是阶梯函数, 且有\(n\), \(\{ \lambda_j \}\), \(\{ a_j \}\), \(\{ b_j \}\)使得 \[ f(s) = \sum_{j=0}^n a_j I_{(\lambda_j, \lambda_{j+1}]}(s), \ g(s) = \sum_{j=0}^n b_j I_{(\lambda_j, \lambda_{j+1}]}(s), \] 于是 \[\begin{align} a f(s) + b g(s) = \sum_{j=0}^n [a a_j + b b_j] I_{(\lambda_j, \lambda_{j+1}]}(s) \in \mathscr{D}, \tag{27.5} \end{align}\]
阶梯函数的随机积分\(I(g)\)满足如下性质: \[\begin{align} I(a f + b g) =& a I(f) + b I(g), \tag{27.6} \\ E[ I(f) \overline{I(g)} ] =& \int_{-\pi}^\pi f(s) \overline{g(s)} \, dF(\lambda), \tag{27.7} \\ E| I(f) - I(g) |^2 =& \int_{-\pi}^\pi | f(s) - g(s) |^2 \,dF(s) . \tag{27.8} \end{align}\]
性质(27.6)证明:
由(27.5)和阶梯函数的随机积分定义有 \[\begin{aligned} I(a f + b g) =& \sum_{j=0}^n [a a_j + b b_j] [Z(\lambda_{j+1}) - Z(\lambda_j)] \\ =& a \sum_{j=0}^n a_j [Z(\lambda_{j+1}) - Z(\lambda_j)] + b \sum_{j=0}^n b_j [Z(\lambda_{j+1}) - Z(\lambda_j)] \\ =& a I(f) + b I(g) . \end{aligned}\]
性质(27.7)证明:
利用正交增量性可得 \[\begin{aligned} & E[ I(f) \overline{I(g)} ] \\ =& \sum_{j=0}^n \sum_{k=0}^n a_j \bar b_k E \left\{ [Z(\lambda_{j+1}) - Z(\lambda_j)] [ \overline{Z(\lambda_{k+1})} - \overline{Z(\lambda_k)} ]\right\} \\ =& \sum_{j=0}^n a_j \bar b_j E | Z(\lambda_{j+1}) - Z(\lambda_j) |^2 = \sum_{j=0}^n a_j \bar b_j [ F(\lambda_{j+1} - F(\lambda_j) ] \\ =& \sum_{j=0}^n \int_{-\pi}^\pi a_j \bar b_j I_{(\lambda_j, \lambda_{j+1}]}(s) \,dF(s) = \int_{-\pi}^\pi \sum_{j=0}^n a_j \bar b_j I_{(\lambda_j, \lambda_{j+1}]}(s) \,dF(s) \\ =& \int_{-\pi}^\pi f(s) \overline{g(s)} \,dF(s) . \end{aligned}\]
性质(27.8)证明:
在(27.7)中将\(f, g\)都替换成\(f - g\), 利用(27.6)式可得 \[\begin{aligned} E | I(f) - I(g) |^2 =& E | I(f-g) |^2 \\ =& E \left\{ I(f-g) \overline{I(f-g)} \right\} \\ =& \int_{-\pi}^\pi [f(s) - g(s)] \overline{[f(s) - g(s)]} \,dF(s) \\ =& \int_{-\pi}^\pi | f(s) - g(s) |^2 \,dF(s) . \end{aligned}\]
27.1.5 随机积分定义推广到一般函数
用\(L^2\)表示方差有限的复值随机变量的全体,\(L^2\)在内积 \[ \langle X, Y \rangle = E(X \bar Y) \] 下是复数域上的Hilbert空间。 对\(g \in \mathscr D\),\(I(g) \in L^2\)。考虑\(g\)为一般\(L^2(F)\)函数的随机积分。
由实变函数论,对\(g \in L^2(F)\),存在函数序列\(g_n \in \mathscr D\)使得 \[ \lim_{n\to\infty} \int_{-\pi}^\pi |g_n(s) - g(s)|^2 \,dF(s) = 0 . \] 来证明\(I(g_n)\)是\(L^2\)中的基本列。
利用(27.8)和不等式 \[ |a + b|^2 \leq 2 |a|^2 + 2 |b|^2 \] 可得 \[\begin{aligned} & E|I(g_n) - I(g_m)|^2 = \int_{-\pi}^\pi | g_n(s) - g_m(s) |^2 \,dF(s) \\ =& \int_{-\pi}^\pi \left| [g_n(s) - g(s)] - [g_m(s) - g(s)] \right|^2 \,dF(s) \\ \leq& 2 \int_{-\pi}^\pi |g_n(s) - g(s)|^2 \,dF(s) + 2 \int_{-\pi}^\pi |g_m(s) - g(s)|^2 \,dF(s) \\ \to& 0, \quad n, m \to \infty . \end{aligned}\] 由\(L^2\)的完备性可知\(I(g_n)\)在\(L^2\)中有极限,记为\(I(g)\),使得 \[\begin{align} E | I(g_n) - I(g) |^2 \to 0, \quad n \to \infty. \tag{27.9} \end{align}\]
还要说明\(I(g)\)的值不依赖于\(g_n\)的选取。 假设又有\(f_n \in \mathscr D\)使得 \[ \int_{-\pi}^\pi | f_n(s) - g(s) |^2 \,dF(s) \to 0, \quad n \to \infty. \] 则有 \[\begin{aligned} & E| I(f_n) - I(g) |^2 = E\left| [I(f_n) - I(g_n)] + [I(g_n) - I(g)] \right|^2 \\ \leq& 2 E| I(f_n) - I(g_n) |^2 + 2 E| I(g_n) - I(g) |^2 \\ =& 2 \int_{-\pi}^\pi | f_n(s) - g_n(s) |^2 \,dF(s) + 2 E| I(g_n) - I(g) |^2 \\ =& 2 \int_{-\pi}^\pi \left| [f_n(s) - g(s)] - [g_n(s) - g(s)] \right|^2 \,dF(s) + 2 E| I(g_n) - I(g) |^2 \\ \leq& 4 \int_{-\pi}^\pi | f_n(s) - g(s) |^2 \,dF(s) + 4 \int_{-\pi}^\pi | g_n(s) - g(s) |^2 \,dF(s) + 2 E| I(g_n) - I(g) |^2 \\ \to& 0, \quad n \to \infty . \end{aligned}\] 即必有相同的\(L^2\)极限,两个极限a.s.相等。
将上述方法定义的\(I(g)\)称为函数\(g \in L^2(F)\)关于随机测度\(\{ Z(\lambda) \}\)的随机积分,记作 \[\begin{align} I(g) = \int_{-\pi}^\pi g(\lambda) \,dZ(\lambda) . \tag{27.10} \end{align}\]
右连续正交增量过程\(\{ Z(\lambda), \lambda \in [-\pi, \pi] \}\)且\(Z(-\pi) = 0\)则称为一个随机测度。
随机积分还有其它的不同的定义,比如,按每条轨道的积分,用类似达布和极限定义的积分,等等。
27.2 随机积分的性质
定理27.2 设\(\{ Z(\lambda), \lambda \in [-\pi, \pi] \}\)是右连续正交增量过程,\(Z(-\pi)=0\), 有分布函数\(F(\lambda) = E|Z(\lambda)|^2\),对于\(f, g \in L^2(F)\), 随机积分\(I(\cdot)\)有如下性质:
- (1) \(E I(f) = 0\) .
- (2) \(E(af + bg) = a I(f) + b I(g)\), 其中\(a, b\)为复常数。
- (3) \[ E[I(f) \overline{I(g)}] = \int_{-\pi}^\pi f(s) \overline{g(s)} \,dF(s) . \]
- (4) \[ E | I(f) - I(g) |^2 = \int_{-\pi}^\pi | f(s) - g(s) |^2 \,dF(s) . \]
证明: 设阶梯函数\(f_n, g_n \in \mathscr D\)使得\(n\to\infty\)时 \[ E| I(f_n) - I(f) |^2 \to 0, \quad E| I(g_n) - I(g) |^2 \to 0 . \]
(1) 利用内积的连续性, \[ E I(f) = \lim_{n\to\infty} E[I(f_n) \cdot 1] = 0 . \]
(2) 阶梯函数\(a f_n + b g_n\)在\(L^2(F)\)中收敛到\(a f + b g\), 由(27.6), \[ I(a f_n + b g_n) = a I(f_n) + b I(g_n) \] 易见\(a I(f_n) + b I(g_n)\)在\(L^2\)中收敛到\(a I(f) + b I(g)\), 由随机积分定义可知 \[ I(a f + b g) = a I(f) + b I(g) . \]
(3) 利用内积的连续性和(27.7)得到 \[\begin{aligned} E[ I(f) \overline{I(g)} ] =& \lim_{n\to\infty} E[ I(f_n) \overline{I(g_n)} ] \\ =& \lim_{n\to\infty} \int_{-\pi}^\pi f_n(s) \overline{g_n(s)} \,dF(s) \\ =& \int_{-\pi}^\pi f(s) \overline{g(s)} \,dF(s), \end{aligned}\] 最后一个等式利用了\(L^2(F)\)内积连续性。
(4) 在性质(3)中将\(f, g\)都替换成\(f-g\),再利用性质(2)可得 \[\begin{aligned} E | I(f) - I(g) |^2 =& E| I(f-g) |^2 = E[I(f-g) \overline{I(f-g)}] \\ =& \int_{-\pi}^\pi (f(s) - g(s)) \overline{(f(s) - g(s))} \,dF(s) \\ =& \int_{-\pi}^\pi |f(s) - g(s)|^2 \,dF(s) . \end{aligned}\]
○○○○○○
27.3 平稳序列的谱表示
设\(\{Z(\lambda)\}\)为随机测度, 有相应的分布函数\(F(\lambda)\), 由于\(e^{it\lambda} \in L^2(F)\), 所以用随机积分定义时间序列 \[\begin{align} X_t = \int_{-\pi}^\pi e^{it\lambda} \,dZ(\lambda) . \tag{27.11} \end{align}\] 由定理27.2, \[\begin{aligned} E X_t =& 0, \\ E(X_{t+k} \overline{X_t}) =& \int_{-\pi}^\pi e^{i(t+k)\lambda} e^{it\lambda} \,dF(\lambda) = \int_{-\pi}^\pi e^{ik\lambda} \,dF(\lambda) \end{aligned}\] 所以\(\{ X_t \}\)是复值零均值平稳列,自协方差函数 \[ \gamma_k = \int_{-\pi}^\pi e^{ik\lambda} \,dF(\lambda), \] \(F\)是\(\{ X_t \}\)的谱函数。
从随机测度可以定义对应的复值零均值平稳列; 反之,每一个复值零均值平稳列,都有一个对应的随机测度,使其表示成随机积分。
定理27.3 (谱表示定理) 对复值零均值平稳列\(\{ X_t \}\),有\([-\pi, \pi]\)上的随机测度\(\{ Z_X(\lambda) \}\)使得 \[\begin{align} X_t = \int_{-\pi}^\pi e^{it\lambda} \,dZ_X(\lambda) , \tag{27.12} \end{align}\] 并且\(\{ Z_X(\lambda) \}\)对应的分布函数\(F\)为\(\{ X_t \}\)的谱函数。 如果另有随机测度\(\{ \xi(\lambda) \}\)也满足上述条件, 则 \[ P( \xi(\lambda) = Z_X(\lambda)) = 1, \quad \forall \lambda \in [-\pi, \pi] . \]
称\(\{ Z_X(\lambda) \}\)为\(\{ X_t \}\)的随机测度。 定理证明见(Brockwell and Davis 1987) P.138节4.8。
例27.2 (布朗运动与白噪声) 对例27.1中的布朗运动\(\{ B(t), t \in [-\pi, \pi] \}\), 因为\(\{ B(t) \}\)是随机测度, 定义 \[ \varepsilon_t = \int_{-\pi}^\pi e^{it\lambda} dB(\lambda), \quad t \in \mathbb{Z}, \]
\(\{ \varepsilon_t \}\)有谱函数 \[ F(\lambda) = \sigma^2(\lambda + \pi) \] 和谱密度 \[ f(\lambda) = \sigma^2 . \] 所以\(\{ \varepsilon_t \}\)是WN(0, \(2\pi \sigma^2\))。 由联合正态分布性质和随机积分定义可以证明\(\{ \varepsilon_t \}\)是正态时间序列, 所以是独立同分布零均值白噪声列。
○○○○○○
27.4 线性平稳列的谱表示
设\(\{ \varepsilon_t \}\)为WN(0, \(\sigma^2\)), 则其谱密度为\(f_\varepsilon(\lambda) = \frac{\sigma^2}{2\pi}\), 谱函数为 \[ F_\varepsilon(\lambda) = \int_{-\pi}^\lambda f(s) \,ds = \frac{\sigma^2}{2\pi}(\lambda + \pi) . \] 由谱表示定理,存在随机测度\(\{ Z_\varepsilon(\lambda)\}\),使得 \[\begin{aligned} \varepsilon_t =& \int_{-\pi}^\pi e^{it\lambda} \,dZ_\varepsilon(\lambda), \\ F_\varepsilon(\lambda) =& E |Z_\varepsilon(\lambda)|^2 . \end{aligned}\] 设实数列\(\{ a_j \}\)平方可和,考虑线性平稳列 \[ X_t = \sum_{j=-\infty}^\infty a_j \varepsilon_{t-j}, \quad t \in \mathbb{Z} . \]
由线性平稳列性质,\(\{ X_t \}\)有谱密度和谱函数如下: \[\begin{align} f(\lambda) =& \frac{\sigma^2}{2\pi} \left| \sum_{j=-\infty}^\infty a_j e^{-ij\lambda} \right|^2, \quad F(\lambda) = \int_{-\pi}^\lambda f(s) \,ds . \tag{27.13} \end{align}\]
级数\(\sum_{j=-\infty}^\infty a_j e^{-ij\lambda}\)在\(L^2[-\pi,\pi]\)中均方收敛, 所以在\(L^2\)中 \[\begin{aligned} X_t =& \sum_{j=-\infty}^\infty a_j \int_{-\pi}^\pi e^{i(t-j)\lambda} \,dZ_\varepsilon(\lambda) \\ =& \int_{-\pi}^\pi e^{it\lambda} \sum_{j=-\infty}^\infty a_j e^{-ij\lambda} \,dZ_\varepsilon(\lambda) \\ =& \int_{-\pi}^\pi e^{it\lambda} \,dZ_X(\lambda), \end{aligned}\] 其中\(\{ Z_X(\lambda) \}\)是\(\{ X_t \}\)的随机测度。
\(\{ Z_X(\lambda) \}\)与\(\{ Z_\varepsilon(\lambda) \}\)之间的关系是 \[ Z_X(\lambda) = \int_{-\pi}^\lambda \sum_{j=-\infty}^\infty a_j e^{-ij\lambda} \,dZ_\varepsilon(\lambda) . \]
事实上,如果用上式定义一个随机过程\(Z(\lambda)\), 可以证明其为右连续独立增量过程,\(Z(-\pi)=0\), 且对任意\(L^2[-\pi, \pi]\)中的函数\(g\)都有 \[ \int_{-\pi}^\pi g(s) d Z(s) = \int_{-\pi}^\pi g(s) \sum_{j=-\infty}^\infty a_j e^{-ij\lambda} \,dZ_\varepsilon(\lambda), \] 因此\(Z(\lambda)\)也是\(\{ X_t \}\)的随机测度。
27.5 离散谱序列的特征
设平稳序列\(\{ X_t \}\)的谱函数\(F(\lambda)\)是阶梯函数, 来证明\(\{ X_t \}\)是离散谱序列
设\(\{ X_t \}\)有谱表示 \[\begin{align} X_t = \int_{-\pi}^\pi e^{it\lambda} \,dZ_X(\lambda), \quad t \in \mathbb Z . \tag{27.14} \end{align}\] 则 \[ F(\lambda) = E |Z_X(\lambda)|^2 . \] 不妨设\(F(\lambda)\)仅在\(\lambda_j, j=1,2,\dots\)处有跳跃且\(-\pi < \lambda_1 < \lambda_2 < \dots \leq \pi\)。 设\(F(\cdot)\)在\(\lambda_j\)处跳跃高度为\(\sigma_j^2>0\)。这时 \[ F(\lambda) = \sum_{j=1}^\infty \sigma_j^2 I_{[\lambda_j, \pi]}(\lambda) = \sum_{j=1}^\infty F_j(\lambda), \] 其中 \[ F_j(\lambda) = \sigma_j^2 I_{[\lambda_j, \pi]}(\lambda), \quad j=1,2,\dots \] \(F(\pi) = \sum_{j=1}^\infty \sigma_j^2 < \infty\)。
自协方差函数用谱函数表示为 \[\begin{aligned} E(X_{t+k} \bar X_t) =& \int_{-\pi}^\pi e^{ik\lambda} \,dF(\lambda) \\ =& \sum_{j=1}^\infty \sigma_j^2 e^{ik\lambda_j} \\ =& \sum_{j=1}^\infty \int_{-\pi}^\pi e^{ik\lambda} \,dF_j(\lambda) . \end{aligned}\]
定义 \[ g_j(s) = \begin{cases} 1, & s = \lambda_j, \\ 0, & s \neq \lambda_j, \end{cases} \] 则\(g_j \in L^2(F)\),于是可以定义随机积分 \[ \xi_j = \int_{-\pi}^\pi g_j(\lambda) \,dZ_X(\lambda), \quad j=1,2,\dots \]
利用定理27.2的(3)可得 \[\begin{align} E(\xi_j \bar \xi_k) = \int_{-\pi}^\pi g_j(s) \overline{g_k(s)} \,dF(s) = \delta_{j-k} \sigma_j^2 . \tag{27.15} \end{align}\]
定义 \[ Y_t = \int_{-\pi}^\pi \left[ 1 - \sum_{j=1}^\infty g_j(\lambda) \right] e^{it\lambda} \,dZ_X(\lambda), \] 则\(E Y_t = 0\), \[\begin{aligned} E |Y_t|^2 =& \int_{-\pi}^\pi \left| 1 - \sum_{j=1}^\infty g_j(\lambda) \right|^2 \,dF(\lambda) = 0 \end{aligned}\] (被积函数在每个跳跃点都等于零,) 所以\(Y_t = 0\), a.s.。
所以a.s.意义下 \[\begin{aligned} X_t =& \int_{-\pi}^\pi e^{it\lambda} \,dZ_X(\lambda) \\ =& \int_{-\pi}^\pi e^{it\lambda} \sum_{j=1}^\infty g_j(\lambda) \,dZ_X(\lambda) + Y_t \\ =& \sum_{j=1}^\infty \int_{-\pi}^\pi e^{it\lambda_j} g_j(\lambda) \,dZ_X(\lambda) \\ =& \sum_{j=1}^\infty \xi_j e^{it\lambda_j} . \end{aligned}\] 这就是复值离散谱序列的表达式。
定理27.4 如果平稳序列\(\{ X_t \}\)的谱函数\(F(\lambda)\)是阶梯函数,且只在\(\lambda_j\)有跳跃高度\(\sigma_j^2\) (\(j=1,2,\dots\)), 则当\(-\pi < \lambda_1 < \lambda_2 < \dots \leq \pi\)时, 存在复值零均值随机变量序列,使得\(E(\xi_j \bar \xi_k) = \delta_{j-k} \sigma_j^2\),且 \[ X_t = \sum_{j=1}^\infty \xi_j e^{it \lambda_j}, \quad\text{a.s.}, \quad t \in \mathbb Z. \]
特别地,当\(F(\lambda)\)只有\(p\)个跳跃点时, \[ X_t = \sum_{j=1}^p \xi_j e^{it \lambda_j}, \quad\text{a.s.}, \quad t \in \mathbb Z. \]
27.6 离散谱序列的随机测度
设\(-\pi < \lambda_1 < \lambda_2 < \dots \leq \pi\), \[ F(\lambda) = \sum_{j=1}^\infty \sigma_j^2 I_{[\lambda_j, \pi]}(\lambda), \ \lambda \in [-\pi, \pi], \] \(F(\pi) = \sum \sigma_j^2 < \infty\), 复值随机变量序列\(\{ \xi_j \}\)满足\(E(\xi_j \bar \xi_k) = \sigma_j^2 \delta_{j-k}\)。 \[ X_t = \sum_{j=1}^\infty \xi_j e^{it \lambda_j}, \ t \in \mathbb Z . \] 令 \[\begin{align} Z(\lambda) = \sum_{j=1}^\infty \xi_j I_{[\lambda_j, \pi]}(\lambda), \tag{27.16} \end{align}\] 来证明\(\{ Z(\lambda) \}\)是\(\{ X_t \}\)的随机测度。
定义 \[ Z_j(\lambda) = \xi_j I{[\lambda_j, \pi]}(\lambda), \ j=1,2,\dots \] 则\(j \neq k\)时\(\{ Z_j(\lambda) \}\)与\(\{ Z_k(\lambda) \}\)为相互正交的随机过程。
对每个给定的\(j\),对任意\(-\pi \leq s_1 < s_2 \leq s_3 < s_4 \leq \pi\),都有 \[ [Z(s_2) - Z(s_1)]\overline{[Z(s_4) - Z(s_3)]} = |\xi_j|^2 I_{(s_1, s_2]}(\lambda_j) I_{(s_3, s_4]}(\lambda_j) \equiv 0, \] 所以\(\{ Z_j(\lambda) \}\)是正交增量过程,由定义\(Z_j(-\pi) = 0\)。 对\(\lambda < \pi\),总可以取\(\epsilon>0\), \(\lambda + \epsilon < \pi\), 使得\(Z(\lambda + \epsilon) = Z(\lambda)\),于是右连续。在\(\lambda=\pi\)处不用讨论是否右连续。 于是\(\{ Z_j(\lambda) \}\)是随机测度,相互之间正交。
由随机积分的定义可以证明关于\(Z_j(\lambda)\)的随机积分\(\int_{-\pi}^\pi g(s) dZ_j(s) = g(\lambda_j) \xi_j\)。
相应于\(\{ Z_j(\lambda) \}\)的分布函数是 \[ F_j(\lambda) = E | Z_j(\lambda) |^2 = \sigma_j^2 I_{[\lambda_j, \pi]}(\lambda) . \] 且 \[ \int_{-\pi}^\pi e^{i t \lambda} \,dZ_j(\lambda) = \xi_j e^{i t \lambda_j} . \]
定义 \[ Z(\lambda) = \sum_{j=1}^\infty Z_j(\lambda), \] 则\(\{ Z(\lambda) \}\)也是随机测度, 对应的分布函数为 \[\begin{aligned} F(\lambda) =& E |Z(\lambda)|^2 = \sum_{j=1}^\infty \sum_{k=1}^\infty E[Z_j(\lambda) \overline{Z_k(\lambda)}] \\ =& \sum_{j=1}^\infty E |Z_j(\lambda)|^2 = \sum_{j=1}^\infty \sigma_j^2 I_{[\lambda_j, \pi]}(\lambda) . \end{aligned}\]
定义平稳序列 \[ Y_t = \int_{-\pi}^\pi e^{it\lambda} \,dZ(\lambda) , \] 利用内积的连续型和随机积分定义,得 \[\begin{aligned} Y_t =& \int_{-\pi}^\pi \sum_{j=1}^\infty e^{it\lambda} \,dZ_j(\lambda) \\ =& \sum_{j=1}^\infty \int_{-\pi}^\pi e^{it\lambda} \,dZ_j(\lambda) \\ =& \sum_{j=1}^\infty \xi_j e^{i t \lambda_j}, \ t \in \mathbb Z . \end{aligned}\] 可见\(\{ Z(\lambda) \}\)是\(\{ X_t \}\)的随机测度。
在离散谱序列的这两节中可以不要求\(\lambda_1\)最小。
27.7 谱密度的频率特征
设平稳序列\(\{ X_t \}\)有谱表示 \[\begin{aligned} X_t = \int_{-\pi}^\pi e^{it\lambda} \,dZ_X(\lambda) . \end{aligned}\] 谱函数与随机测度之间满足\(F(\lambda) = E |Z_X(\lambda)|^2\)。 当谱函数绝对连续时,\(\{ X_t \}\)有谱密度\(f(\lambda) = F'(\lambda)\)。
如果\(f(\lambda)\)在\(\lambda_0\)处有一个峰值,则\(F(\lambda)\)在\(\lambda_0\)左右的增量为 \[\begin{aligned} & F(\lambda_0 + \delta) - F(\lambda_0 - \delta) \\ =& E | Z(\lambda_0 + \delta) - Z(\lambda_0 - \delta) |^2 \\ =& \int_{\lambda_0 - \delta}^{\lambda_0 + \delta} f(\lambda) \,d\lambda , \end{aligned}\] 可以看成是随机测度在\(\lambda_0\)附近集中的能量。
例27.3 考虑AR(2)模型 \[ X_t = -0.276 X_{t-1} - 0.756 X_{t-2} + \varepsilon_t, \ \varepsilon_t \sim \text{WN}(0, 4) \] 谱密度\(f(\lambda)\)在\(\lambda_0 = 1.73\)处有唯一的峰, 见图27.1。
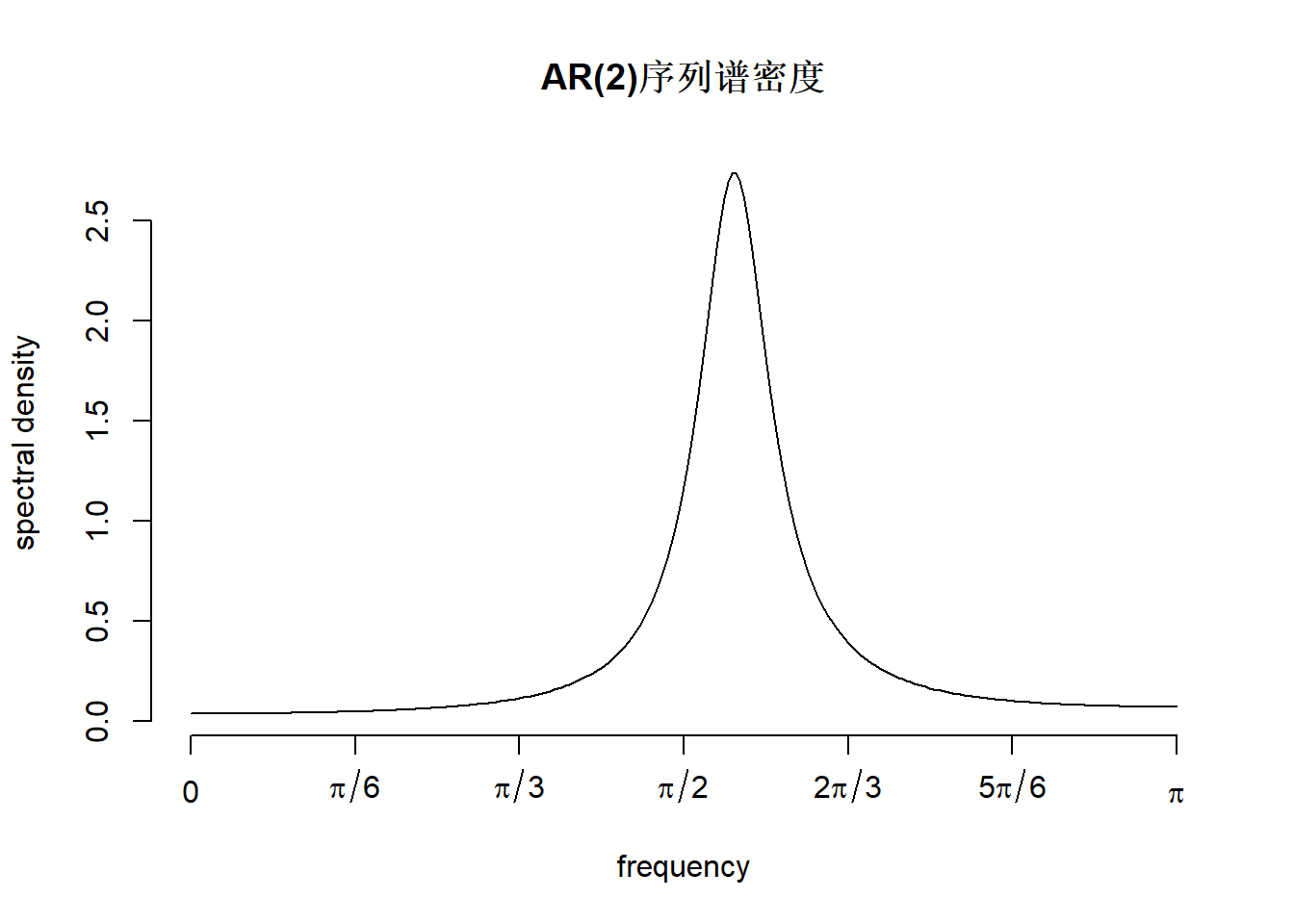
图27.1: AR(2)谱密度
用\(g(s)\)表示集合\((\lambda_0 - \delta, \lambda_0 + \delta]\)的示性函数。 \(\delta\)的取值与\(\lambda_0\)处\(f(\lambda)\)的峰的宽度有关。 将\(X_t\)分解为 \[\begin{align} X_t =& \int_{-\pi}^\pi g(\lambda) e^{it\lambda} \,dZ_X(\lambda) + \int_{-\pi}^\pi [1 - g(\lambda)] e^{it\lambda} \,dZ_X(\lambda) \nonumber \\ =& \xi_t + \eta_t . \tag{27.17} \end{align}\] 其中\(\{ \xi(t) \}\)是平稳序列,有自协方差函数 \[ \gamma_\xi(k) = \int_{-\pi}^\pi e^{ik\lambda} g(\lambda) f(\lambda) \,d\lambda, \] 和谱密度\(g(\lambda) f(\lambda)\)。 \(\{ \eta_t \}\)也是平稳序列,有自协方差函数 \[ \gamma_\eta(k) = \int_{-\pi}^\pi e^{ik\lambda} [1 - g(\lambda)] f(\lambda) \,d\lambda, \] 和谱密度\([1 - g(\lambda)] f(\lambda)\)。
\(\{ \xi_t \}\)的随机测度为\(\int_{-\pi}^\lambda g(s) dZ_X(s)\), \(\{ \eta_t \}\)的随机测度为\(\int_{-\pi}^\lambda [1 - g(s)] dZ_X(s)\), 因为\(g(s) [1 - g(s)] \equiv 0\)所以两个随机测度正交, 故\(\{ \xi_t \}\)与\(\{ \eta_t \}\)也相互正交。
所以\(\{ X_t \}\)的自协方差函数\(\gamma_k\)可分解为 \[\begin{aligned} \gamma_k =& \gamma_\xi(k) + \gamma_\eta(k) \\ =& \int_{\lambda_0 - \delta}^{\lambda_0 + \delta} e^{ik\lambda} f(\lambda) \,d\lambda + \int_{-\pi}^\pi [1 - g(\lambda)] e^{ik\lambda} f(\lambda) \,d\lambda . \end{aligned}\] 在角频率\(\lambda_0\)附近,谱密度\(f(\lambda)\)为自协方差函数\(\{ \gamma_k \}\)提供的能量是 \[ \int_{\lambda_0 - \delta}^{\lambda_0 + \delta} e^{ik\lambda} f(\lambda) \,d\lambda \approx e^{ik\lambda_0} \int_{\lambda_0 - \delta}^{\lambda_0 + \delta} f(\lambda) \,d\lambda \]
又有 \[ \xi_t \approx e^{it\lambda_0} [ Z_X(\lambda_0 + \delta) - Z_X(\lambda_0 - \delta)] \] 是\(\{ X_t \}\)受到角频率\(\lambda_0\)影响的波动, 周期对应于\(\frac{2\pi}{\lambda_0}\), \([ Z_X(\lambda_0 + \delta) - Z_X(\lambda_0 - \delta)]\)为随机振幅, 平方期望和方差约为\(\int_{\lambda_0 - \delta}^{\lambda_0 + \delta} f(\lambda) \,d\lambda\)。
当谱密度\(f(\lambda)\)在\(\lambda_0\)处有尖锐的峰时, \(\{ \gamma_k \}\)的变化集中在\(e^{ik\lambda_0}\)附近, \(\{ X_t \}\)的变化集中在\(e^{it\lambda_0}\)周期波动附近, \(\gamma_k\)和\(\{ X_t \}\)都明显表现出周期为\(\frac{2\pi}{\lambda_0}\)的波动。
同理,当\(\{X_t\}\)的谱密度在\(\lambda_1, \dots, \lambda_p\)处有峰值时, \(\{ \gamma_k \}\)和\(\{X_t \}\)的轨道会体现出角频率\(\lambda_1, \dots, \lambda_p\)的波动。 \(\lambda_j\)处谱密度峰值越大、形状越陡峭,\(\lambda_j\)的影响越明显。
对实平稳列\(\{ X_t \}\),谱密度存在时必为偶函数。 这时谱密度在\(\lambda_0\)处为\(\gamma_k\)提供的贡献约为\(e^{ik\lambda_0} \int_{\lambda_0 - \delta}^{\lambda_0 + \delta}f(\lambda) \,d\lambda\), 在\(-\lambda_0\)处为\(\gamma_k\)提供的贡献约为\(e^{-ik\lambda_0} \int_{\lambda_0 - \delta}^{\lambda_0 + \delta}f(\lambda) \,d\lambda\), 在\(\pm \lambda_0\)处为\(\gamma_k\)提供的总能量约为 \[ 2 \cos(k \lambda_0) \int_{\lambda_0 - \delta}^{\lambda_0 + \delta}f(\lambda) \,d\lambda . \]
27.8 平稳序列的分解
实变函数论给出了如下结论:每个分布函数\(F(\lambda)\)都可以唯一分解成如下三个部分: \[\begin{align} F(\lambda) = F_1(\lambda) + F_2(\lambda) + F_3(\lambda) \tag{27.18} \end{align}\] 其中\(F_1\)绝对连续,\(F_2\)为跳跃函数, \(F_3\)是奇异部分,\(F_3\)相对于勒贝格测度都为0。 分解称为勒贝格分解。
对平稳列从谱域也有类似分解。
定理27.5 设零均值复值平稳列\(\{ X_t \}\)有谱函数\(F(\lambda)\), 相应于\(F(\lambda)\)的勒贝格分解(1.20), \(\{ X_t \}\)可以唯一分解成三个相互正交的零均值平稳序列的和: \[\begin{align} X_t = X_1(t) + X_2(t) + X_3(t), \ t \in \mathbb Z, \tag{27.19} \end{align}\] 其中\(\{ X_i(t) \}\)有谱函数\(F_i(\lambda)\)。
27.5说明\(X_2(t)\)是离散谱序列。 可以证明,\(X_1(t)\)是线性平稳列。 \(\{ X_3(t) \}\)是奇异部分。 如果不考虑奇异部分, 平稳列都可以分解成线性平稳列与离散谱序列的叠加。