19 AR模型的参数估计

对时间序列观测数据建立模型可以更深入了解数据的内在规律，也有利于预报。估计模型的一般指导原则是其他条件相同时较简单的模型更有利。建立模型，要兼顾对观测到的数据的拟合情况和模型的可推广性。下面讨论相合性时，由第4章定理4.2可知， ARMA模型中白噪声项如果是独立同分布的则该平稳列为严平稳遍历。

19.1 依概率有界

定义19.1 (依概率有界) 设\(\{\xi_n\}\)是时间序列，\(\{c_n\}\)是非零常数列，如果对任意\(\varepsilon>0\)，存在正数\(M\)，使得 \[\begin{aligned} \sup_n P(|\xi_n|>M) \leq \varepsilon \end{aligned}\] 就称时间序列\(\{\xi_n\}\)是依概率有界的，记做\(\xi_n = O_p(1)\)。如果\(\{\xi_n / c_n \} = O_p(1)\)，就称\(\xi_n = O_p(c_n)\)。

依概率有界就是除去一个概率任意小的集合后序列有界。若\(\{\xi_n / c_n\} \stackrel{\text{Pr}}{\to} 0\)则称 \(\xi_n = o_p(c_n)\)。

依概率有界的等价定义为：称\(\{ \xi_n \}\)依概率有界，若\(\forall \varepsilon>0\), \(\exists M>0\)和\(N\)使得当\(n \geq N\)时 \[\begin{aligned} P(|\xi_n| \leq M) \geq 1 - \varepsilon. \end{aligned}\] 事实上，当原定义条件成立时显然此等价定义的条件也成立。

若此等价定义条件成立，则对\(n \geq N\)有 \[\begin{aligned} P(|\xi_n| \leq M) \geq 1 - \varepsilon, \quad P(|\xi_n| > M) < \varepsilon. \end{aligned}\] 对\(j=1,2,\dots,N\)，存在\(M_j>0\)使得 \[\begin{aligned} P(|\xi_j| > M_j) < \varepsilon \end{aligned}\] 令\(M' = \max(M, M_1, M_2, \dots, M_N)\)，则 \[\begin{aligned} P(|\xi_n| > M') <& \varepsilon, \ \forall n \in \mathbb N_+, \\ \sup_{n \in \mathbb N_+} P(|\xi_n| > M') \leq& \varepsilon, \end{aligned}\] 满足原定义。

引理19.1 若\(\xi_n = o_p(c_n)\)则\(\xi_n = O_p(c_n)\)。

事实上，按依概率收敛定义， \(\forall \delta>0\), \(\forall \varepsilon>0\)，存在\(N\)使\(n>N\)时 \[\begin{aligned} \mbox{P}( |\xi_n / c_n| > \delta) < \varepsilon \end{aligned}\] 取\(M \geq \delta\)使得 \[\begin{aligned} \mbox{P}(|\xi_n / c_n| > M) \leq \varepsilon, \quad n=1,2,\dots, N \end{aligned}\] 于是 \[\begin{aligned} \mbox{P}(|\xi_n / c_n| > M) \leq \varepsilon, \quad n=1,2,\dots \end{aligned}\] 即\(\xi_n/c_n = O_p(1)\).

引理19.2 如果\(\xi_n = O_p(1)\)而\(c_n \to \infty\)则 \(\xi_n / c_n = o_p(1)\)。

证明略。

对随机变量\(\xi\)，\(\xi=O_p(1)\).

引理19.3 若\(\{\xi_n\}\)同分布，则\(\xi_n=O_p(1)\)。

事实上，\(\forall \varepsilon>0\), \(\exists M>0\)使 \(\mbox{P}(|\xi_1|>M)<\varepsilon\)。由同分布性知 \(\mbox{P}(|\xi_t|>M)=\mbox{P}(|\xi_1|>M)<\varepsilon\)。

引理19.4 \[\begin{aligned} O_p(1) \pm O_p(1) =& O_p(1) \\ O_p(1) \cdot O_p(1) =& O_p(1) \\ O_p(1) \pm o_p(1) =& O_p(1) \\ O_p(1) \cdot o_p(1) =& o_p(1). \end{aligned}\]

引理19.5 若\(\xi_n\)依概率收敛到\(\xi\)则\(\{\xi_n\} = O_p(1)\)。

事实上\(\xi_n = \xi + (\xi_n - \xi) = O_p(1) + o_p(1)\)。另外，若\(\xi_n\)依分布收敛到\(\xi\)则\(\{\xi_n\} = O_p(1)\)。

引理19.6 若存在非负随机变量\(\xi\)使得\(|\xi_n| \leq \xi\) a.s.则\(\xi_n=O_p(1)\)。

由\(P(|\xi_n| \leq \xi)=1\)， \(\forall \varepsilon>0\), \(\exists M>0\)使\(P(\xi > M)<\varepsilon\)，于是\(P(|\xi_n|>M) \leq P(\xi > M) < \varepsilon\), \(\forall n \in \mathbb N\)。

更多的讨论见第18章。

19.2 Yule-Walker估计

对AR(\(p\))模型: \[\begin{align} X_t = a_1 X_{t-1} + \dots + a_p X_{t-p} + \varepsilon_t \tag{19.1} \end{align}\] 需要估计系数\(a_1, a_2, \dots, a_p\)和白噪声方差\(\sigma^2\)。先假定\(p\)已知。

如果AR(\(p\))序列的理论自协方差函数\(\{\gamma_k\}\) 已知则由Yule-Walker方程可以解出\(a_1, \dots, a_p\)和\(\sigma^2\), 见§9.2定理9.2.

设\(x_1, x_2, \dots, x_N\)为观测数据，建模前一般先中心化: \[\begin{aligned} y_t = x_t - \bar x_N, \quad t=1,2,\dots,N \end{aligned}\] 中心化以后，可以据此估计样本自协方差函数： \[\begin{align} \hat\gamma_k = \frac{1}{N} \sum_{j=1}^{N-k} y_j y_{j+k}, k=0,1,\dots,N-1 \tag{19.2} \end{align}\]

在Y-W方程中用\(\hat\gamma_k\)代替\(\gamma_k\)可以解出\(\hat a_1, \dots, \hat a_p, \hat\sigma^2\): \[\begin{align} & \hat\Gamma_p \hat{\boldsymbol a} = \hat{\boldsymbol\gamma}_p \tag{19.3} \\ & \hat\sigma^2 = \hat\gamma_0 - \hat{\boldsymbol a}^T \hat{\boldsymbol\gamma}_p \tag{19.4} \end{align}\]

由§16.1的讨论，如果\(x_1,\dots,x_N\)不全相同则\(\hat\Gamma_{p+1}\)正定， Y-W方程的解存在唯一。由§10.2定理10.1可知这样解出的\(\hat a_1, \dots, \hat a_p\)满足最小相位条件。

为了避免计算\(\hat\Gamma_p\)的逆可以用Levinson递推公式解Y-W方程得到\(\hat a_1, \dots, \hat a_p\)和\(\hat \sigma^2\)。这样得到的AR(\(p\))参数估计叫做Y-W估计或Levinson估计。优点是保证最小相位性，计算简单。

由§9.4定理9.3知AR(\(p\))的\(\Gamma_{p}\)正定，根据线性代数中求解线性方程组的Cramer法则可知\(a_1, \dots, a_p, \sigma^2\)是\(\gamma_0, \gamma_1, \dots, \gamma_p\)的连续函数。如果\(\hat\gamma_k\)是\(\gamma_k\)的强相合估计，则\(\hat a_1, \dots, \hat a_p, \hat\sigma^2\)也是相应参数的强相合估计。要使\(\hat\gamma_k\)强相合，由§16.2定理16.1, 一个充分条件是白噪声\(\{\varepsilon_t\}\)独立同分布。这时ARMA序列严平稳遍历。

定理19.1 如果AR(\(p\))模型(19.1)中的\(\{\varepsilon_t\}\)是独立同分布的WN(0,\(\sigma^2\))， \(E \varepsilon_t^4 < \infty\), 则当\(N \to \infty\)时

(1) \(\hat\sigma^2 \to \sigma^2\), \(\hat a_j \to a_j\), a.s., \(1 \leq j \leq p\).
(2) \(\sqrt{N}(\hat a_1 - a_1, \dots, \hat a_p - a_p)^T\) 依分布收敛到\(p\)维正态分布\(N(0, \sigma^2 \Gamma_p^{-1})\)。
(3) \(\sqrt{N}\sup\limits_{1\leq j \leq p} |\hat a_j - a_j| = O(\sqrt{\ln\ln N})\), a.s., \(\sqrt{N} |\hat \sigma^2 - \sigma^2| = O(\sqrt{\ln\ln N})\), a.s.

证明: (1) 由§16.2定理16.1知\(\hat\gamma_k\)强相合，再根据\(a_k, \sigma^2\)为\(\{\gamma_k\}\)的连续函数知\(\hat a_k, \hat\sigma^2\)强相合。

(2) 证明略(详见(Brockwell and Davis 1987))。

(3) 证明略。

○○○○○○

当定理成立时参数估计有近似正态分布，可以用来作置信区间和假设检验。设\(\sigma_{jj}\)为\(\sigma^2 \Gamma_p^{-1}\)的第\(j\times j\)元素，则\(\hat a_j\)近似服从N(\(a_j, \sigma_{jj}/N\))，于是\(a_j\)的近似\(95\%\)置信区间为 \[ [\hat a_j - 1.96 \sqrt{\sigma_{jj}}/\sqrt{N}, \ \hat a_j + 1.96 \sqrt{\sigma_{jj}}/\sqrt{N}] \] 其中\(\sigma_{jj}\)可以用\(\hat\sigma^2 \hat\Gamma_p^{-1}\)的元素\(\hat\sigma_{jj}\)代替。

19.3 最小二乘估计

19.3.1 估计方程

最小二乘估计计算简单，不需要计算自协方差。最小二乘估计使残差平方和最小: \[\begin{aligned} \min S(a_1, \dots, a_p) \stackrel{\triangle}{=} \sum_{t=p+1}^N [ y_t - (a_1 y_{t-1} + \dots + a_p y_{t-p}) ]^2 \end{aligned}\] 最小值点\(\hat a_1, \dots, \hat a_p\)称为参数的最小二乘估计。

用线性模型理论，写出最小二乘对应的正规方程为 \[\begin{align} & \boldsymbol{Y} = \left(\begin{array}{c} y_{p+1} \\ y_{p+2} \\ \dots\\ y_N \end{array} \right),\\ & \boldsymbol{X} = \left(\begin{array}{cccc} y_p & y_{p-1} & \cdots & y_1 \\ y_{p+1} & y_p & \cdots & y_2 \\ \vdots & \vdots & & \vdots \\ y_{N-1} & y_{N-2} & \cdots & y_{N-p} \end{array} \right) = \left( y_{p+t-j} \right)_{\begin{subarray}{l} t=1,\dots,N-p;\\ j=1,\dots,p \end{subarray}}\\ & \boldsymbol{a} = \left(\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_p \end{array} \right), \quad (\boldsymbol{X}'\boldsymbol{X}) \boldsymbol{a} = \boldsymbol{X}' \boldsymbol{Y} \tag{19.5} \end{align}\] 最小二乘估计\(\tilde a_1, \dots, \tilde a_p\)是正规方程(19.5)的解。当\(p\times p\)矩阵\(\boldsymbol{X}^T \boldsymbol{X}\)正定时方程有唯一解 \[\begin{aligned} \tilde{\boldsymbol{a}} = (\boldsymbol{X}^T \boldsymbol{X})^{-1} \boldsymbol{X}^T \boldsymbol{Y} \end{aligned}\]

19.3.2 LS估计与YW估计的比较

样本自协方差函数估计为 \[ \hat\gamma_k = \sum_{j=1}^{N-k} y_j y_{j+k} = \sum_{j=1}^{N-k} (x_j - \bar x_N)(x_{j+k} - \bar x_N) \] 注意对于\(1\leq k\leq j \leq p\),
矩阵 \((1/N)\boldsymbol{X}^T\boldsymbol{X}\)的第\((j,k)\)元素是 \[\begin{align} \tilde \gamma_{jk} =& \frac1N \sum_{t=1}^{N-p} y_{t+p-j} y_{t+p-k} = \frac1N \sum_{t=p-j+1}^{N-j} y_{t}y_{t+j-k} \nonumber\\ =& \frac1N \sum_{t=1}^{N-(j-k)}y_{t}y_{t+j-k} - \frac1N \sum_{t=1}^{p-j}y_{t}y_{t+j-k} -\frac1N\sum_{t=N-j+1}^{N-(j-k)} y_{t}y_{t+j-k} \nonumber\\ =& \hat\gamma_{j-k} - \frac1N \sum_{t=1}^{p-j}y_{t}y_{t+j-k} -\frac1N\sum_{t=N-j+1}^{N-(j-k)} y_{t}y_{t+j-k}. \tag{19.6} \end{align}\]

完全类似地得到 \((1/N)\boldsymbol{X}^T \boldsymbol{Y}\)的第\(j\)个元素 \[\begin{align} \tilde \gamma_j =& \frac1N \sum_{t=1}^{N-p} y_{t+p-j}y_{t+p} = \frac1N \sum_{t=p-j+1}^{N-j} y_{t}y_{t+j} \nonumber\\ =& \frac1N \sum_{t=1}^{N-j}y_{t}y_{t+j} - \frac1N \sum_{t=1}^{p-j}y_{t}y_{t+j} \nonumber\\ =& \hat\gamma_{j} - \frac1N \sum_{t=1}^{p-j}y_{t}y_{t+j}. \tag{19.7} \end{align}\]

由\(\{\varepsilon_t\}\)独立同分布知AR(\(p\))序列\(\{X_t\}\)严平稳遍历，所以\(\tilde\gamma_{jk}\)的分解式(19.6)中第二项 \[\begin{align} & \frac{1}{N} \sum_{t=1}^{p-j} y_t y_{t+j-k} \nonumber\\ =& \frac{1}{N} \sum_{t=1}^{p-j} (x_t - \bar x_N)(x_{t+j-k} - \bar x_N) \nonumber\\ =& \frac{1}{N} \sum_{t=1}^{p-j} x_t x_{t+j-k} - \bar x_N \frac{1}{N} \sum_{t=1}^{p-j} x_t - \bar x_N \frac{1}{N} \sum_{t=1}^{p-j} x_{t+j-k} + \bar x_N^2 \frac{p-j}{N} \tag{19.8} \end{align}\] 因为\(\sum_{t=1}^{p-j} x_t x_{t+j-k}\)是一个不随\(N\)而变的随机变量所以第一项a.s.趋于0，同理\(\frac{1}{N} \sum_{t=1}^{p-j} x_t\)和\(\frac{1}{N} \sum_{t=1}^{p-j} x_{t+j-k}\)也a.s.趋于0，由严平稳遍历性知\(\bar x_N\) a.s.趋于\(\mu=EX_t\)，所以\(\tilde \gamma_{jk}\)的分解中的第二项a.s.趋于0。

类似可知\(\tilde \gamma_j\)的分解(19.7)中第二项\(\frac1N \sum_{t=1}^{p-j}y_{t}y_{t+j}\)a.s.趋于0。

考虑\(\tilde \gamma_{jk}\)的分解(19.6)中的第三项。记\(Z_t = X_t - \mu\)，则\(\{ Z_t \}\)为零均值严平稳遍历序列。作分解 \[\begin{align} & \frac1N \sum_{t=N-j+1}^{N-(j-k)} y_t y_{t+j-k} \nonumber\\ =& \frac1N \sum_{t=N-j+1}^{N-(j-k)} (z_t - \bar z_N)(z_{t+j-k} - \bar z_N) \nonumber\\ =& \frac1N \sum_{t=N-j+1}^{N-(j-k)} z_t z_{t+j-k} - \bar z_N \frac1N \sum_{t=N-j+1}^{N-(j-k)} z_t - \bar z_N \frac1N \sum_{t=N-j+1}^{N-(j-k)} z_{t+j-k} + \bar z_N^2 \frac{k}{N} \tag{19.9} \end{align}\] 由\(X_t\)严平稳遍历可知\(\xi_t = Z_t Z_{t+j-k}\)也是严平稳遍历序列，且\(E\xi_t = \gamma_{j-k}\)。有 \[\begin{aligned} & \frac{1}{N} \sum_{t=N-j+1}^{N-(j-k)} z_t z_{t+j-k} \\ =& \frac{1}{N} \sum_{t=N-j+1}^{N-(j-k)} \xi_t \\ =& \frac{1}{N} \sum_{t=1}^{N-(j-k)} \xi_t - \frac{1}{N} \sum_1^{t=N-j} \xi_t \\ =& \frac{N-(j-k)}{N} \frac{1}{N-(j-k)} \sum_{t=1}^{N-(j-k)} \xi_t - \frac{N-j}{N} \frac{1}{N-j} \sum_1^{t=N-j} \xi_t \\ \to& 1 \cdot E \xi_t - 1 \cdot E\xi_t = 0, \quad \text{a.s.} \ (N\to\infty) \end{aligned}\]

类似有 \[\begin{aligned} & \frac{1}{N} \sum_{t=N-j+1}^{N-(j-k)} z_t \to 0 \quad \text{a.s.} \\ & \frac{1}{N} \sum_{t=N-j+1}^{N-(j-k)} z_{t+j-k} \to 0 \quad \text{a.s.} \\ & \bar z_n \to E Z_t = 0 \quad \text{a.s.} \end{aligned}\] 所以\(\tilde \gamma_{jk}\)的分解(19.6)中的第三项a.s.趋于0。

于是, 对\(1 \leq k \leq j\leq p\)有 \[ \tilde \gamma_{jk} - \hat\gamma_{j-k} \to 0, \ \tilde \gamma_j - \hat\gamma_j \to 0, \ \text{a.s.}, \] 由\(\hat\gamma_j\)的强相合性知 \(\tilde \gamma_{jk}\to \gamma_{j-k}\), \(\tilde \gamma_j \to \gamma_j\), a.s.

这样,当\(N\to \infty\) \[\begin{aligned} (\boldsymbol{X}^T \boldsymbol{X})^{-1} \boldsymbol{X}^T \boldsymbol{Y} =& \left( \frac1N \boldsymbol{X}^T \boldsymbol{X} \right)^{-1} \left( \frac1N \boldsymbol{X}^T \boldsymbol{Y} \right) \\ \to& \Gamma_p^{-1} \boldsymbol{\gamma}_p = \boldsymbol{a}, \quad\text{a.s.} \end{aligned}\] 即最小二乘估计也是强相合的。

来计算\(\tilde \gamma_{jk} - \hat\gamma_{k-j}\)和\(\tilde\gamma_j - \hat\gamma_j\)的依概率上界。

\[\begin{align} \tilde \gamma_{jk} - \hat\gamma_{k-j} =& -\frac{1}{N} \sum_{t=1}^{p-j} y_t y_{t+j-k} - \frac{1}{N} \sum_{t=N-j+1}^{N-(j-k)} y_t y_{t+j-k} \tag{19.10} \\ \tilde\gamma_j - \hat\gamma_j =& \frac{1}{N} \sum_{t=1}^{p-j} y_t y_{t+j} \tag{19.11} \end{align}\]

考虑 \[\begin{aligned} E \left| \sum_{t=N-j+1}^{N-(j-k)} y_t y_{t+j-k} \right| \leq& \sum_{t=N-j+1}^{N-(j-k)} E | y_t y_{t+j-k} | \\ \leq& \sum_{t=N-j+1}^{N-(j-k)} \sqrt{E y_t^2 \; E y_{t+j-k}^2} \end{aligned}\] 对任意\(t\)， \[\begin{aligned} E y_t^2 =& E (Z_t - \bar Z_N)^2 \\ \leq& E(2 Z_t^2 + 2 \bar Z_N^2) \\ =& 2 \gamma_0 + 2 E \bar Z_N^2 \end{aligned}\] 而 \[\begin{aligned} E \bar Z_N^2 =& E (\frac{1}{N} \sum_{t=1}^N Z_t)^2 \\ =& \frac{1}{N^2} E \left( \sum_{t=1}^N \sum_{s=1}^N Z_t Z_s \right) \\ =& \frac{1}{N^2} \sum_{t=1}^N \sum_{s=1}^N \gamma_{s-t} \\ \leq& \gamma_0 \end{aligned}\] 所以 \[ E y_t^2 \leq 4\gamma_0, \ \forall t \]

所以 \[\begin{aligned} E \left| \sum_{t=N-j+1}^{N-(j-k)} y_t y_{t+j-k} \right| \leq 4 \gamma_0 k, \ \forall N \end{aligned}\]

引理：对随机变量序列\(\{ \xi_n \}\)，如果\(E|\xi_n|\)有界，则\(\xi_n = O_p(1)\)。可以用马尔可夫不等式证明。

于是(19.10)中的\(\sum_{t=N-j+1}^{N-(j-k)} y_t y_{t+j-k} = O_p(1)\)，其它几项类似，所以有 \[\begin{aligned} \tilde\gamma_{kj} - \hat\gamma_{k-j} = O_p(\frac{1}{N}), \quad \tilde\gamma_{j} - \hat\gamma_{j} = O_p(\frac{1}{N}) . \end{aligned}\]

用\(\hat a=(\hat a_1,\hat a_2,\cdots,\hat a_p)^T\)和\(\tilde a =(\tilde a_1,\tilde a_2,\dots,\tilde a_p)^T\) 分别表示 Yule-Walker估计和最小二乘估计. 记 \(\boldsymbol{\hat\gamma}_p = (\hat \gamma_1, \hat \gamma_2,\dots,\hat \gamma_p)^T\), 就有 \[\begin{align} \tilde a - \hat a =& (\boldsymbol{X}^T \boldsymbol{X})^{-1} \boldsymbol{X}^T \boldsymbol{Y} - \hat\Gamma_p^{-1} \hat\gamma_p \\ =& (\frac1N \boldsymbol{X}^T \boldsymbol{X})^{-1} \Big(\frac1N \boldsymbol{X}^T \boldsymbol{Y} - \hat \gamma_p \Big) + \Big[(\frac1N \boldsymbol{X}^T \boldsymbol{X})^{-1} - \hat \Gamma_p^{-1} \Big]\hat \gamma_p \\ =& (\frac1N \boldsymbol{X}^T \boldsymbol{X})^{-1} O_p(1/N) + (\frac1N \boldsymbol{X}^T \boldsymbol{X})^{-1} \Big[\hat \Gamma_p - \frac1N \boldsymbol{X}^T \boldsymbol{X} \Big] {\hat \Gamma_p}^{-1} {\hat \gamma_p} \\ =& O_p(1/N), \ \hbox{ 当} \ N\to \infty. \tag{19.12} \end{align}\] 上式说明对 \(1\leq j \leq p\), \(\hat a_j -\tilde a_j = O_p(1/N)\). 由于\(1/N\)收敛到零的速度是很快的, 所以也可以说对较大的\(N\), 最小二乘估计和Yule-Walker 估计的差别不大.

定理19.2 设AR(\(p\))模型(19.1)中的白噪声\(\{\varepsilon_t\}\)是独立同分布的, \(E\varepsilon_t^4<\infty\), \((\tilde a_1, \tilde a_2, \dots, \tilde a_p)\)是自回归系数 \((a_1, a_2, \dots, a_p)\)的最小二乘估计. 则当\(N\to \infty\)时 \[ \sqrt{N} (\tilde a_1 - a_1, \tilde a_2- a_2, \dots, \tilde a_p-a_p) \] 依分布收敛到\(p\)-维正态分布\(N(0,\sigma^2 \Gamma_p^{-1})\).

即最小二乘估计和Y-W估计有相同的渐近分布。定理19.2的证明由定理19.1和(19.12)直接得到.

例19.1 Y-W估计和LS估计的模拟比较。

取\(\{\varepsilon_t\}\)为标准正态白噪声，模拟产生AR(4)序列 \[\begin{aligned} X_t =& 1.16 X_{t-1} - 0.37 X_{t-2} - 0.11 X_{t-3} \\ & + 0.18 X_{t-4} + \varepsilon_t, t=1,2,\dots, N \end{aligned}\] 分别取\(N=25, 100, 400, 1600\)，重复\(M=10000\)次产生模拟数据并分别用Y-W方法和最小二乘方法估计参数。

结果发现在样本量较小时，系数估计Y-W方法较好，预测方差\(\sigma^2\)估计最小二乘方法较好。样本量大时二者没有明显差别。

demo.ar.estb <- function(n=50, m=400){
  a <- c(1.16, -0.37, -0.11, 0.18)
  sig <- 1.0
  ests.yw <- matrix(0, nrow=m, ncol=5)
  ests.ls <- matrix(0, nrow=m, ncol=5)
  for(ii in seq(m)){
    x <- arima.sim(
      model=list(ar=a), n=n,
      rand.gen=function(n, ...) rnorm(n, 0, sig))
    ## do Levinson estimation and LS estimation
    fit.yw <- ar(x, aic=FALSE, order.max=4,
                 method="yule-walker")
    ests.yw[ii,] <- c(fit.yw$ar, fit.yw$var.pred)
    fit.ls <- ar(x, aic=F, order.max=4,
                 method="ols")
    ests.ls[ii,] <- c(fit.ls$ar, fit.ls$var.pred)
  }
  res <- matrix(0, nrow=7, ncol=5)
  rownames(res) <- c("真实参数", "Y-W估计均值", "LS估计均值",
                     "Y-W估计标准差", "LS估计标准差",
                     "Y-W估计根均方误差", "LS估计根均方误差"
                     )
  colnames(res) <- c("a1", "a2", "a3", "a4", "s2")
  res[1,] <- c(a, sig^2)
  res[2,] <- apply(ests.yw, 2, mean)
  res[3,] <- apply(ests.ls, 2, mean)
  res[4,] <- apply(ests.yw, 2, sd)
  res[5,] <- apply(ests.ls, 2, sd)
  res[6,] <- sqrt(1/m*( (m-1)*res[4,]^2 + m*(res[2,]-res[1,])^2))
  res[7,] <- sqrt(1/m*( (m-1)*res[5,]^2 + m*(res[3,]-res[1,])^2))
  cat("\n\n==== AR模型模拟: 样本量=", n, " 重复", m, "次估计比较\n")
  print(round(res, 4))

  invisible(res)
}

demo.ar.est <- function(n=c(25,50,100,400,1600), m=400){
  for(ni in n){
    demo.ar.estb(ni, m)
  }
}
set.seed(1)
demo.ar.est(m=10000)

## 
## 
## ==== AR模型模拟: 样本量= 25  重复 10000 次估计比较
##                       a1      a2      a3     a4     s2
## 真实参数          1.1600 -0.3700 -0.1100 0.1800 1.0000
## Y-W估计均值       0.9216 -0.3005 -0.0567 0.0196 1.3005
## LS估计均值        1.0049 -0.3760 -0.0610 0.0519 0.7489
## Y-W估计标准差     0.2094  0.2465  0.2254 0.1585 0.5076
## LS估计标准差      0.2540  0.3307  0.3170 0.2269 0.2649
## Y-W估计根均方误差 0.3173  0.2561  0.2316 0.2255 0.5899
## LS估计根均方误差  0.2976  0.3307  0.3208 0.2605 0.3650
## 
## 
## ==== AR模型模拟: 样本量= 50  重复 10000 次估计比较
##                       a1      a2      a3     a4     s2
## 真实参数          1.1600 -0.3700 -0.1100 0.1800 1.0000
## Y-W估计均值       1.0366 -0.3202 -0.0718 0.0906 1.1649
## LS估计均值        1.0951 -0.3718 -0.0783 0.1140 0.8915
## Y-W估计标准差     0.1454  0.1901  0.1833 0.1251 0.2911
## LS估计标准差      0.1575  0.2214  0.2201 0.1466 0.1958
## Y-W估计根均方误差 0.1907  0.1965  0.1872 0.1538 0.3345
## LS估计根均方误差  0.1704  0.2214  0.2223 0.1607 0.2238
## 
## 
## ==== AR模型模拟: 样本量= 100  重复 10000 次估计比较
##                       a1      a2      a3     a4     s2
## 真实参数          1.1600 -0.3700 -0.1100 0.1800 1.0000
## Y-W估计均值       1.1019 -0.3464 -0.0872 0.1336 1.0824
## LS估计均值        1.1354 -0.3765 -0.0922 0.1474 0.9468
## Y-W估计标准差     0.1006  0.1443  0.1393 0.0935 0.1760
## LS估计标准差      0.1038  0.1566  0.1544 0.1007 0.1402
## Y-W估计根均方误差 0.1162  0.1462  0.1412 0.1043 0.1943
## LS估计根均方误差  0.1067  0.1568  0.1554 0.1059 0.1499
## 
## 
## ==== AR模型模拟: 样本量= 400  重复 10000 次估计比较
##                       a1      a2      a3     a4     s2
## 真实参数          1.1600 -0.3700 -0.1100 0.1800 1.0000
## Y-W估计均值       1.1448 -0.3626 -0.1039 0.1682 1.0215
## LS估计均值        1.1539 -0.3710 -0.1055 0.1720 0.9877
## Y-W估计标准差     0.0496  0.0747  0.0744 0.0490 0.0757
## LS估计标准差      0.0498  0.0763  0.0762 0.0497 0.0706
## Y-W估计根均方误差 0.0518  0.0750  0.0746 0.0503 0.0787
## LS估计根均方误差  0.0502  0.0763  0.0763 0.0503 0.0716
## 
## 
## ==== AR模型模拟: 样本量= 1600  重复 10000 次估计比较
##                       a1      a2      a3     a4     s2
## 真实参数          1.1600 -0.3700 -0.1100 0.1800 1.0000
## Y-W估计均值       1.1561 -0.3680 -0.1084 0.1769 1.0051
## LS估计均值        1.1584 -0.3701 -0.1088 0.1779 0.9967
## Y-W估计标准差     0.0246  0.0376  0.0380 0.0247 0.0364
## LS估计标准差      0.0246  0.0378  0.0383 0.0248 0.0357
## Y-W估计根均方误差 0.0249  0.0376  0.0380 0.0249 0.0367
## LS估计根均方误差  0.0246  0.0378  0.0383 0.0249 0.0359

19.4 最大似然估计

Y-W估计是矩估计，最小二乘估计与Y-W估计渐近相同。矩估计容易计算但可能精度不高。最大似然估计一般精度较高。

设AR(\(p\))模型(19.1)的白噪声\(\{\varepsilon_t \}\)是正态白噪声，则\(\{ X_t \}\)是正态平稳列，给定观测\(x_1, x_2, \dots, x_N\)，似然函数是联合正态分布密度函数。

记参数\(\boldsymbol{\theta} = (a_1, a_2, \dots, a_p, \sigma^2)\)，则似然函数为 \[\begin{aligned} L(\boldsymbol{\theta}) =& p(x_1, \dots, x_N|\boldsymbol{\theta}) \\ =& p(x_1, \dots, x_p | \boldsymbol{\theta}) \prod_{t=p+1}^N p(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta}) \end{aligned}\] 其中\(p(x_1, \dots, x_p | \boldsymbol{\theta})\)是\((X_1, \dots, X_p)\)的联合密度，是一个联合正态密度； \(p(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta})\)是\(x_t\)的条件密度，是一个一元正态条件密度。

一元正态条件密度完全由其条件期望和条件方差确定，而\(t > p\)时 \[\begin{aligned} E(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta}) =& E(\varepsilon_t + a_1 x_{t-1} + \dots + a_p x_{t-p} | x_{t-1}, \dots, x_1, \boldsymbol{\theta}) \\ =& 0 + a_1 x_{t-1} + \dots + a_p x_{t-p} \\ \text{Var}(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta}) =& E\left( [x_t - E(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta})]^2 | x_{t-1}, \dots, x_1, \boldsymbol{\theta}\right) \\ =& E\left( \varepsilon_t^2 | x_{t-1}, \dots, x_1, \boldsymbol{\theta}\right) \\ =& \sigma^2 \end{aligned}\] 所以\(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta}\) 服从\(\text{N}(a_1 x_{t-1} + \dots + a_p x_{t-p}, \sigma^2)\)。 \[ p(x_t | x_{t-1}, \dots, x_1, \boldsymbol{\theta}) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left\{ \frac{1}{2\sigma^2} (x_t - a_1 x_{t-1} - \dots - a_p x_{t-p})^2 \right\}, \ t=p+1, \dots, n . \]

但是，联合密度分解式中的\(p(x_1, \dots, x_p | \boldsymbol{\theta})\)部分比较难以表示成\(a_1, \dots, a_p, \sigma^2\)的简单函数。故此，当\(N\)较大时，仅考虑似然函数中的主要部分，忽略\(p(x_1, \dots, x_p | \boldsymbol{\theta})\)这一部分，得到一个简化的似然函数(profile likelihood) \[\begin{aligned} & \tilde L(a_1, \dots, a_p, \sigma^2) \\ =& \prod_{t=p+1}^N \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left\{ \frac{1}{2\sigma^2} (x_t - a_1 x_{t-1} - \dots - a_p x_{t-p})^2 \right\} \\ =& (2\pi\sigma^2)^{-(N-p)/2} \exp\left\{ -\frac{1}{2\sigma^2} \sum_{t=p+1}^N (x_t - a_1 x_{t-1} - \dots - a_p x_{t-p})^2 \right\} \end{aligned}\] 这实际是给定\((x_1, \dots, x_p)\)条件下\((x_{p+1}, \dots, x_N)\)的条件密度。

实际中的数据不一定是零均值的，令\(y_t = x_t - \bar X_N\)，将\(\{ y_t \}\)作为零均值的AR(\(p\))序列的观测值。记\(\boldsymbol{a} = (a_1, \dots, a_p)\)， \[ S(\boldsymbol{a}) = \sum_{t=p+1}^N (x_t - a_1 x_{t-1} - \dots - a_p x_{t-p})^2 \] 则\(\tilde L\)对应的对数似然函数为 \[\begin{aligned} & \ell(\boldsymbol{a}, \sigma^2) \\ =& -\frac{N-p}{2} \ln (2\pi) - \frac{N-p}{2}\ln(\sigma^2) -\frac{1}{2\sigma^2} S(\boldsymbol{a}) . \end{aligned}\]

\(\ell(\boldsymbol{a}, \sigma^2)\)关于\(\sigma^2\)求偏导并令偏导等于零，得 \[\begin{align} \sigma^2 = \frac{1}{N-p} S(\boldsymbol{a}) \tag{19.13} \end{align}\] 于是最大值点是\(S(\boldsymbol{a})\)的最小值点，最大似然估计等于最小二乘估计。

19.5 AR模型定阶

对于时间序列观测样本，假设它来自某个AR(\(p\))模型，但是\(p\)一般是未知的。要想办法估计\(p\)。

估计\(p\)可以用AR(\(p\))的偏相关\(p\)步截尾性质，计算样本偏相关系数\(\{\hat a_{kk}\}\)，看\(\{\hat a_{kk}\}\)在何处截尾。估计\(p\)也可以在拟合优度和模型简单之间进行权衡， AIC和BIC准则就是这样的办法。

19.5.1 样本偏相关系数

只要观测样本\(x_1, \dots, x_N\)不完全相同则样本自协方差阵\(\hat\Gamma_k\)正定(\(k<N\))。样本偏相关系数\(\{\hat a_{k,k}\}\)可以由样本自协方差唯一决定 \[\begin{aligned} \left(\begin{array}{cccc} \hat\gamma_0 & \hat\gamma_1 & \cdots & \hat\gamma_{k-1} \\ \hat\gamma_1 & \hat\gamma_0 & \cdots & \hat\gamma_{k-2} \\ \vdots & \vdots & & \vdots \\ \hat\gamma_{k-1} & \hat\gamma_{k-2} & \cdots & \hat\gamma_0 \end{array}\right) \left(\begin{array}{c} \hat a_{k,1} \\ \hat a_{k,2} \\ \vdots \\ \hat a_{k,k} \end{array}\right) = \left(\begin{array}{c} \hat \gamma_1 \\ \hat \gamma_2 \\ \vdots \\ \hat \gamma_k \end{array}\right) \end{aligned}\] 可以用Levinson递推公式计算样本偏相关系数。

定理19.3 如果AR(\(p\))模型(19.1)中的白噪声时独立同分布的，则对任何\(k \geq p\)，有 \[\begin{align} \lim_{N\to\infty} \hat a_{k,j} = \begin{cases} a_j, & \text{当}j\leq p,\\ 0, & \text{当}j> p.\\ \end{cases} \text{ a.s.} \tag{19.14} \end{align}\]

证明:

对\(k>p\)证明，\(k=p\)情况类似。

由§16.2的定理16.1知道样本自协方差函数\(\hat \gamma_k\)是\(\gamma_k\)的强相合估计. 对任何矩阵 \((c_{j,k}(N))\)定义极限符号 \[ \lim_{N\to \infty} \big(c_{j,k}(N) \big) \stackrel{\triangle}{=} \big(\lim_{N\to\infty}c_{j,k}(N) \big). \] 对任何 \(k>p\), 利用\(\Gamma_k\)的正定性得到: \[\begin{aligned} & \lim_{N\to \infty} \left(\begin{array}{c} \hat a_{k,1} \\ \hat a_{k,2} \\ {\vdots} \\ \hat a_{k,k} \end{array} \right ) \\ =& \lim_{N\to \infty} \left ( \begin{array}{llll} \hat \gamma_0 \ &\hat \gamma_1 \ & \cdots& \hat \gamma_{k-1}\\ \hat \gamma_{1}\ & \hat \gamma_{0} \ &\cdots&\hat \gamma_{k-2}\\ {..}& {..}& \cdots &{..} \\ \hat \gamma_{k-1}\ &\hat \gamma_{k-2} \ &\cdots&\hat \gamma_{0} \end{array} \right )^{-1} \times \lim_{N\to \infty} \left ( \begin{array}{l} \hat \gamma_1\\ \hat \gamma_2\\ \vdots \\ \hat \gamma_k \end{array} \right ) \\ =& \left ( \begin{array}{llll} \gamma_0 \ & \gamma_1 \ &\cdots& \gamma_{k-1}\\ \gamma_{1}\ & \gamma_{0} \ &\cdots& \gamma_{k-2}\\ {\vdots}& {\vdots}& &{\vdots} \\ \gamma_{k-1}\ & \gamma_{k-2} \ &\cdots& \gamma_{0} \end{array} \right )^{-1} \times \left ( \begin{array}{l} \gamma_1\\ \gamma_2\\ {\vdots} \\ \gamma_k \end{array} \right ) \\ = & \left ( \begin{array}{l} a_{k,1}\\ a_{k,2}\\ {..} \\ a_{k,k} \end{array} \right ). \end{aligned}\]

从§9.2的定理9.2知道 \[\begin{align} (a_{k,1}, a_{k,2}, \dots ,a_{k,k}) =(a_1,a_2,..,a_p,0,\cdots,0). \tag{19.15} \end{align}\] 所以(19.14)成立.

19.5.2 偏相关系数的检验

为检验\(H_0:\ a_{k,k}=0\)，需要知道\(\hat a_{k,k}\)的分布。但我们只能得到\(\hat a_{k,k}\)的极限分布。

定理19.4 设\((a_{k,1}, a_{k,2}, \dots ,a_{k,k})\)由(19.15)定义, 如果AR(\(p\))模型(19.1)中的白噪声是独立同分布的, \(E\varepsilon_t^4<\infty\), 则对确定的\(k > p\), 当\(N\to \infty\)时, \[ \sqrt{N}(\hat a_{k,1}- a_{k,1}, \ \hat a_{k,2} - a_{k,2}, \ \cdots, \ \hat a_{k,k} - a_{k,k}) \] 依分布收敛到 \(k\)-维正态分布 \(N(0, \sigma^2 \Gamma_k^{-1})\).

详见(Brockwell and Davis 1987)。

引理19.7 在定理19.4的条件下, 对\(k>p\), \(\sqrt{N} \hat a_{k,k}\)依分布收敛到标准正态分布 \(N(0,1)\).

推论的证明：从定理19.4知道只需对\(k>p\)证明\(\sigma^2\Gamma_k^{-1}\)的第\((k,k)\)元素是\(1\). 用\(A_{(j,j)}\)表示矩阵\(A\)的第\((j,j)\)元素. 利用\(\Gamma_k^{-1}\)的伴随矩阵表示得到 \[ \Gamma_k^{-1} =\frac{1}{\det(\Gamma_k)} \left( \begin{array}{llll} \det(\Gamma_{k-1}) & & * \\ & \ddots & \\ * && \det(\Gamma_{k-1}) \end{array} \right). \] 于是 \[ (\Gamma_{k}^{-1})_{(k,k)} =(\Gamma_{k}^{-1})_{(1,1)} =\frac{\det(\Gamma_{k-1})}{\det(\Gamma_{k})}, \ \forall k \geq 1. \] 对\(k\geq p\), 利用 Yule-Walker 方程得到 \[ \Gamma_{k+1} \left( \begin{array}{llll} 1\\ -\boldsymbol{a}_k \end{array} \right) =\left( \begin{array}{llll} \sigma^2\\ 0 \\ \vdots \\0 \end{array} \right) \ \ \ \hbox{从而有} \ \ \ \left( \begin{array}{llll} 1 \\ -\boldsymbol{a}_k \end{array} \right) = \Gamma_{k+1}^{-1} \left( \begin{array}{llll} \sigma^2\\ 0\\ \vdots\\ 0 \end{array} \right) \] 于是得到 \[ \left( \sigma^2 \Gamma_{k+1}^{-1} \right)_{(k+1,k+1)} =\left( \sigma^2 \Gamma_{k+1}^{-1} \right)_{(1,1)} = 1, \ k \geq p. \] 推论证毕。

○○○○○○

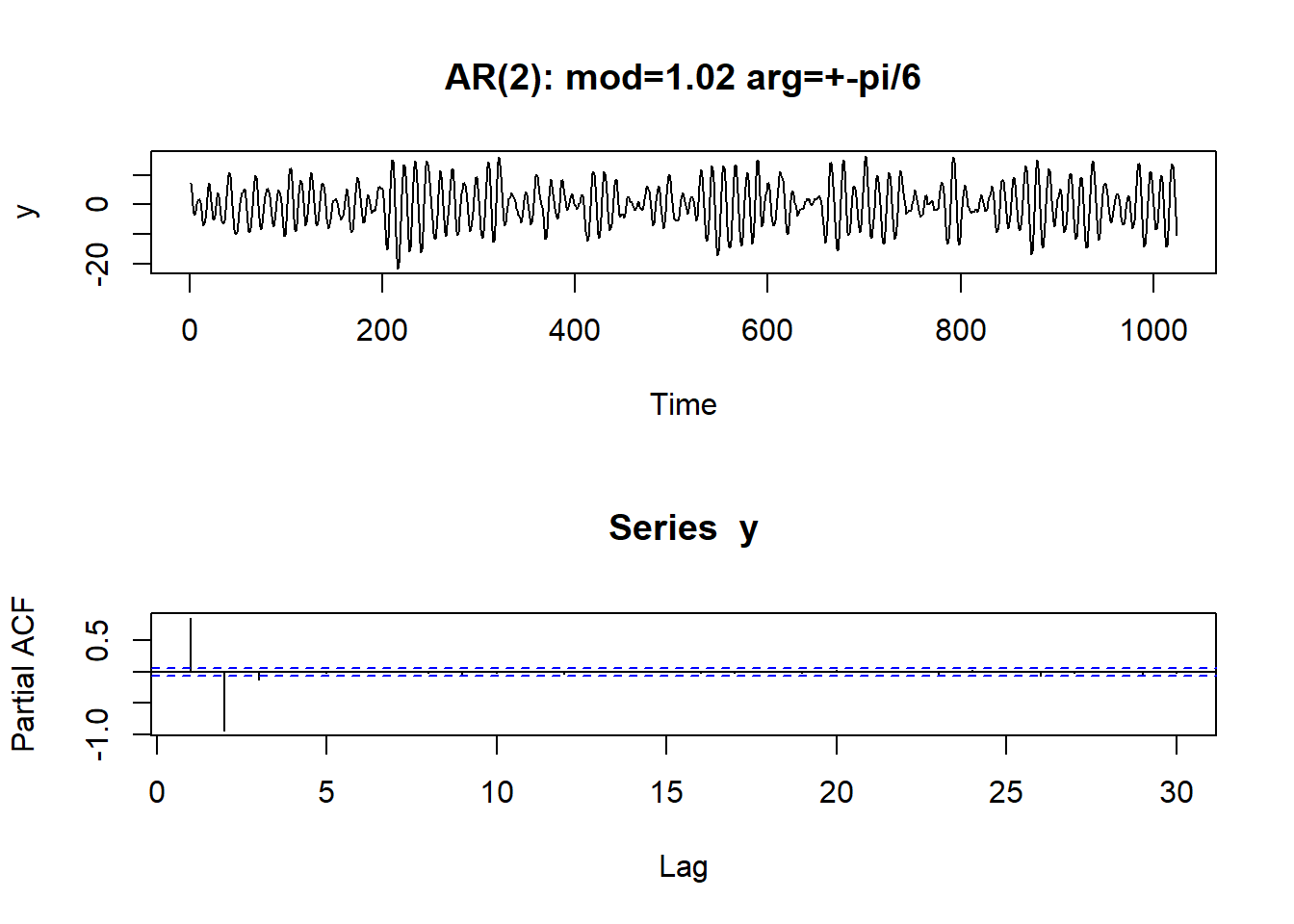
用样本偏相关系数可以为AR模型定阶。 \(N\)较大时若\(k>p\)则\(\sqrt{N}\hat a_{k,k}\)近似服从N(0,1)， \(\hat a_{k,k}\)约以\(95\%\)概率落入区间 \[\begin{aligned} (-1.96/\sqrt{N}, \ 1.96/\sqrt{N}). \end{aligned}\] 对某固定的\(K\)，以 \[\begin{aligned} \hat p = \max\{j: |\hat a_{j,j}| > 1.96/\sqrt{N}, 1\leq j\leq K\} \end{aligned}\] 作为\(p\)的估计是合理的。实际问题中可以取\(K\)为允许的阶数的一个上界。

这种办法只要画出样本偏相关系数图就可以定阶。 (R中用pacf(x)作样本偏相关系数图)。

演示： AR order selection by PACF.

demo.pacf <- function(n=1024){
  rtlis <- list(c(complex(mod=1.09, arg=pi/3*c(1,-1)),
                  complex(mod=1.098, arg=pi*2/3*c(1,-1))),
                c(complex(mod=1.264, arg=pi/3*c(1,-1)),
                  complex(mod=1.273, arg=pi*2/3*c(1,-1))),
                c(complex(mod=1.635, arg=pi/3*c(1,-1)),
                  complex(mod=1.647, arg=pi*2/3*c(1,-1))),
                complex(mod=1.02, arg=pi/6*c(1,-1)),
                complex(mod=1.02, arg=pi/2*c(1,-1)),
                c(complex(mod=1.05, arg=pi/6*c(1,-1)),
                  complex(mod=1.05, arg=pi/2*c(1,-1))))
  tits <- c("AR(4): 1.09exp(+-i pi/3), 1.098exp(+-i 2pi/3)",
            "AR(4): 1.264exp(+-i pi/3), 1.273exp(+-i 2pi/3)",
            "AR(4): 1.635exp(+-i pi/3), 1.647exp(+-i 2pi/3)",
            "AR(2): mod=1.02 arg=+-pi/6",
            "AR(2): mod=1.02 arg=+-pi/2",
            "AR(4): mod=1.05 arg=+-pi/6,+-pi/2")
  oldpar <- par(mfrow=c(2,1)); on.exit(par(oldpar))
  for(ii in seq(along=rtlis)){
    rt = rtlis[[ii]]
    y <- ar.gen(n, rt, sigma=1.0, by.roots=TRUE,
                plot.it=FALSE)
    plot(y, main=tits[ii])
    pacf(y)
  }
}
set.seed(1)
demo.pacf(n=1024)

## Warning in polynomial(p): 强制改变时丢弃了虚数部分

## Warning in polynomial(p): 强制改变时丢弃了虚数部分

## Warning in polynomial(p): 强制改变时丢弃了虚数部分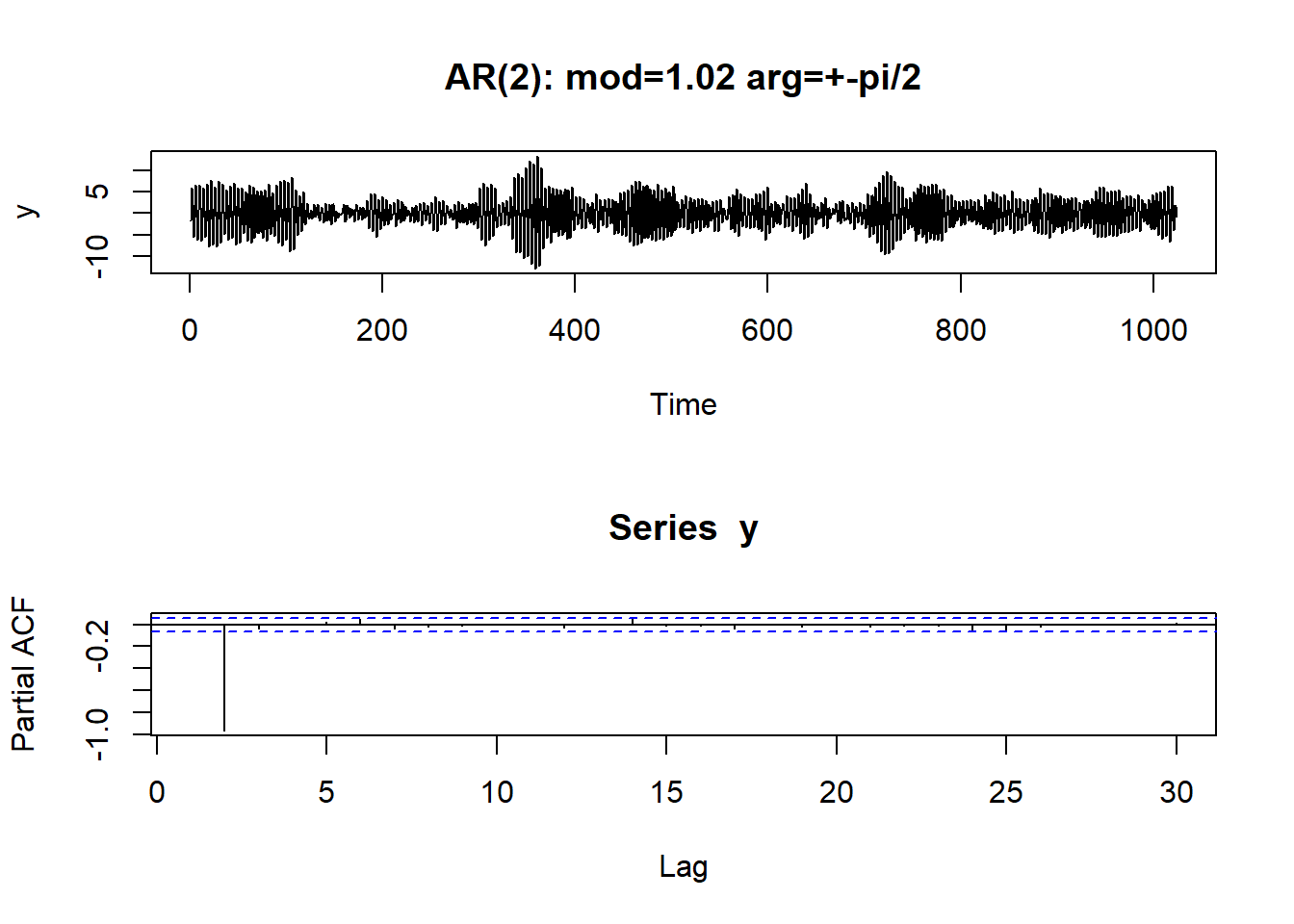

19.5.3 AIC和BIC定阶

可以通过对拟合优度的要求加上对参数个数的惩罚指定一个准则来定阶。 AIC准则: \[\begin{aligned} \text{AIC}(k) = \ln\hat\sigma_k^2 + \frac{2k}{N}, \quad k=0, 1, \dots, P_0 \end{aligned}\] (\(P_0\)是可取的阶的上限)

BIC定阶: \[\begin{aligned} \text{BIC}(k) = \ln\hat\sigma_k^2 + \frac{k\ln N}{N}, \quad k=0, 1, \dots, P_0 \end{aligned}\] 取AIC或BIC的最小值点作为\(p\)的估计。

AIC定阶不相合, 倾向于高估； BIC定阶在\(N\to\infty\)时是强相合的，但对较小的\(N\)倾向于低估。

参考：

HIROTUGU AKAIKE, Fitting Autoregressive Models for Prediction, Annals of the Institute of Statistical Mathematics AC-19 (1974), pp. 364 – 385
GIDEON SCHWARZ, Estimating the Dimensions of a Model, Annals of Statistics 6(1978), pp. 461 – 464

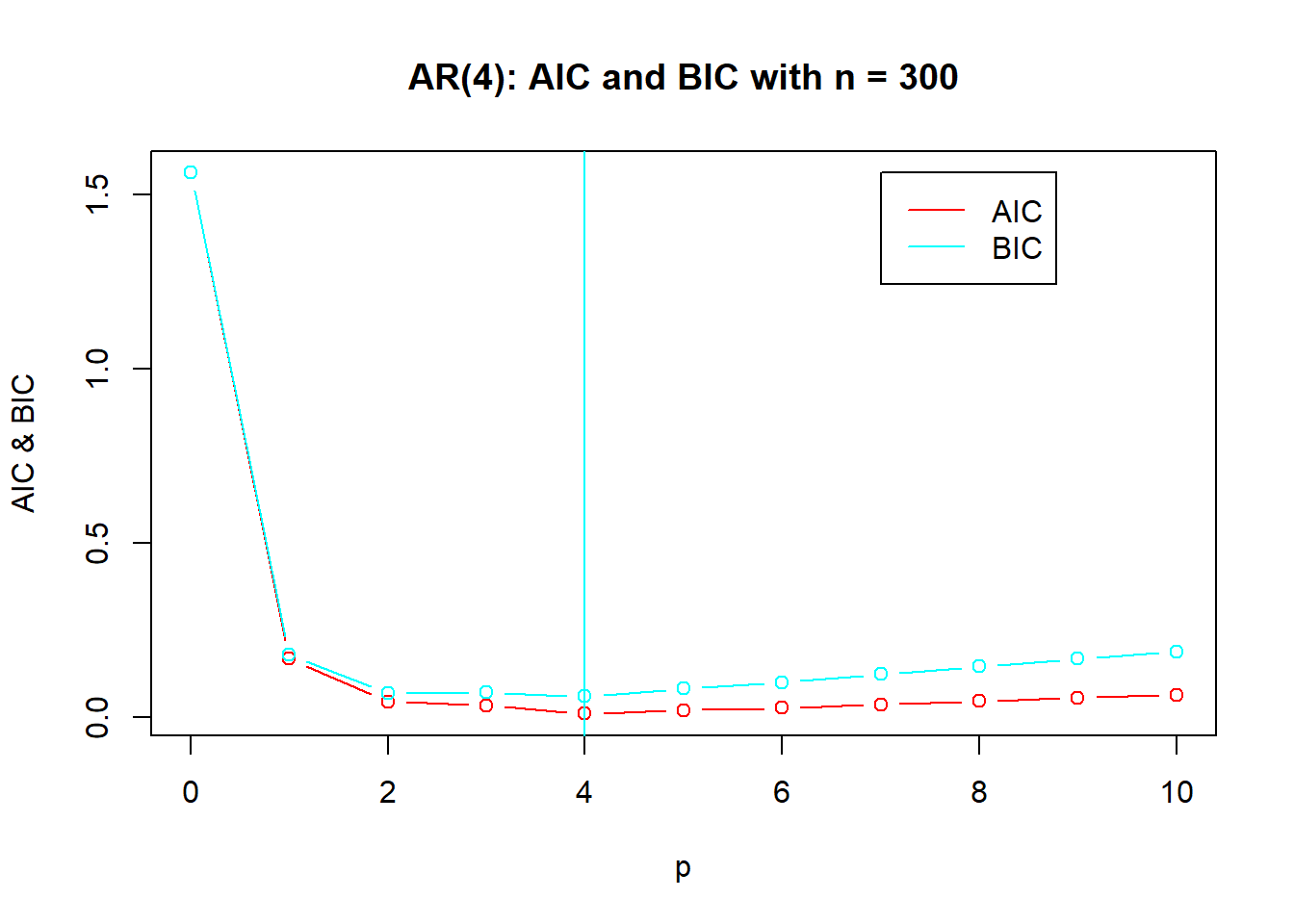
演示：AR order selection by AIC and BIC. 模拟AR(4)模型： \[ X_t = 1.16 X_{t-1} - 0.37 X_{t-2} - 0.11 X_{t-3} + 0.18 X_{t-4} + \varepsilon_t, \ \varepsilon_t \sim \text{N}(0,1) \] 生成400组样本，用AIC或者BIC定阶，对前5组做了定阶选择图形。统计了选择的不同阶数的出现频次。

ar.bic <- function(x, order.max=10){
  aics <- numeric(order.max+1)
  bics <- numeric(order.max+1)
  aics[1] <- log(var(x))
  bics[1] <- log(var(x))
  n <- length(x)
  for(ii in 1:order.max){
    s2 <- ar(x, aic=F, order.max=ii,
             method="yule-walker")$var.pred
    aics[ii+1] <- log(s2) + ii*2/n
    bics[ii+1] <- log(s2) + ii*log(n)/n
  }
  p <- which.min(bics) - 1
  list(p=p, bics=bics, aics=aics)
}
demo.ar.order <- function(n=300, m=100){
  a <- c(1.16, -0.37, -0.11, 0.18)
  sig <- 1.0
  orders.aic <- numeric(m)
  orders.bic <- numeric(m)
  for(ii in seq(m)){
    x <- ar.gen(n, a, sigma=sig)
    ## do Levinson estimation and LS estimation
    fit.yw <- ar(x, aic=T, order.max=10,
                 method="yule-walker")
    p.aic <- fit.yw$order
    fit.bic <- ar.bic(x, order.max=10)
    aics <- fit.bic$aics
    bics <- fit.bic$bics
    p.bic <- fit.bic$p
    orders.aic[ii] <- p.aic
    orders.bic[ii] <- p.bic
    if(ii<=5){
      yr <- range(c(aics, bics))
      plot(0:10, aics, type="b", col="red",
           main=paste("AR(4): AIC and BIC with n =", n),
           xlab="p", ylab="AIC & BIC")
      lines(0:10, bics, type="b", col="cyan")
      abline(v=p.aic, col="red")
      abline(v=p.bic, col="cyan")
      legend(7,yr[2], lty=1,
             col=c("red", "cyan"),
             legend=c("AIC", "BIC"))
    }
  }
  cat("\nAR模型AIC和BIC定阶，样本量=", n, " 重复", m, "次的结果:\n")
  cat("AIC order:\n")
  print(table(orders.aic))
  cat("BIC order:\n")
  print(table(orders.bic))
}
set.seed(1)
demo.ar.order(m=400)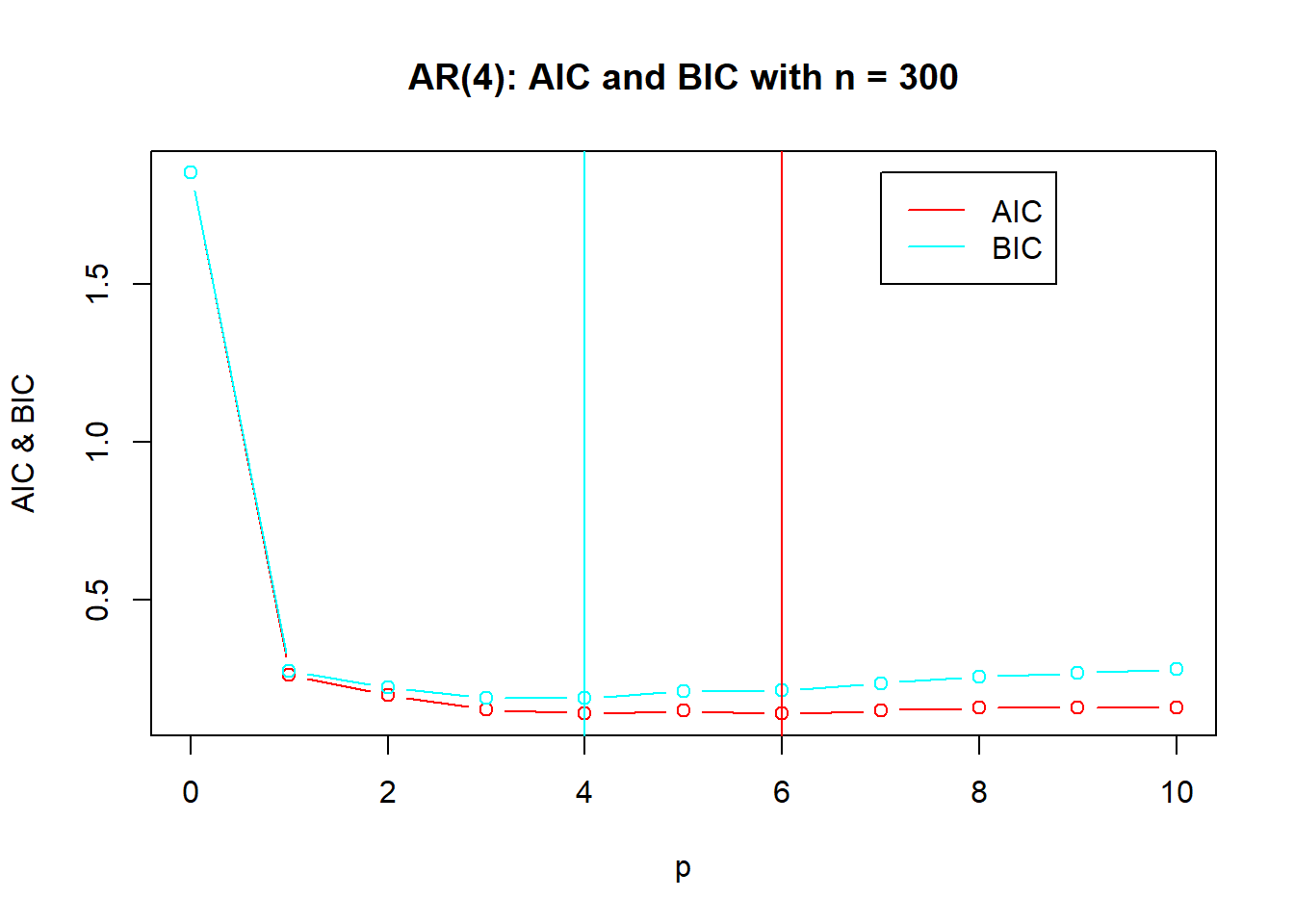

## 
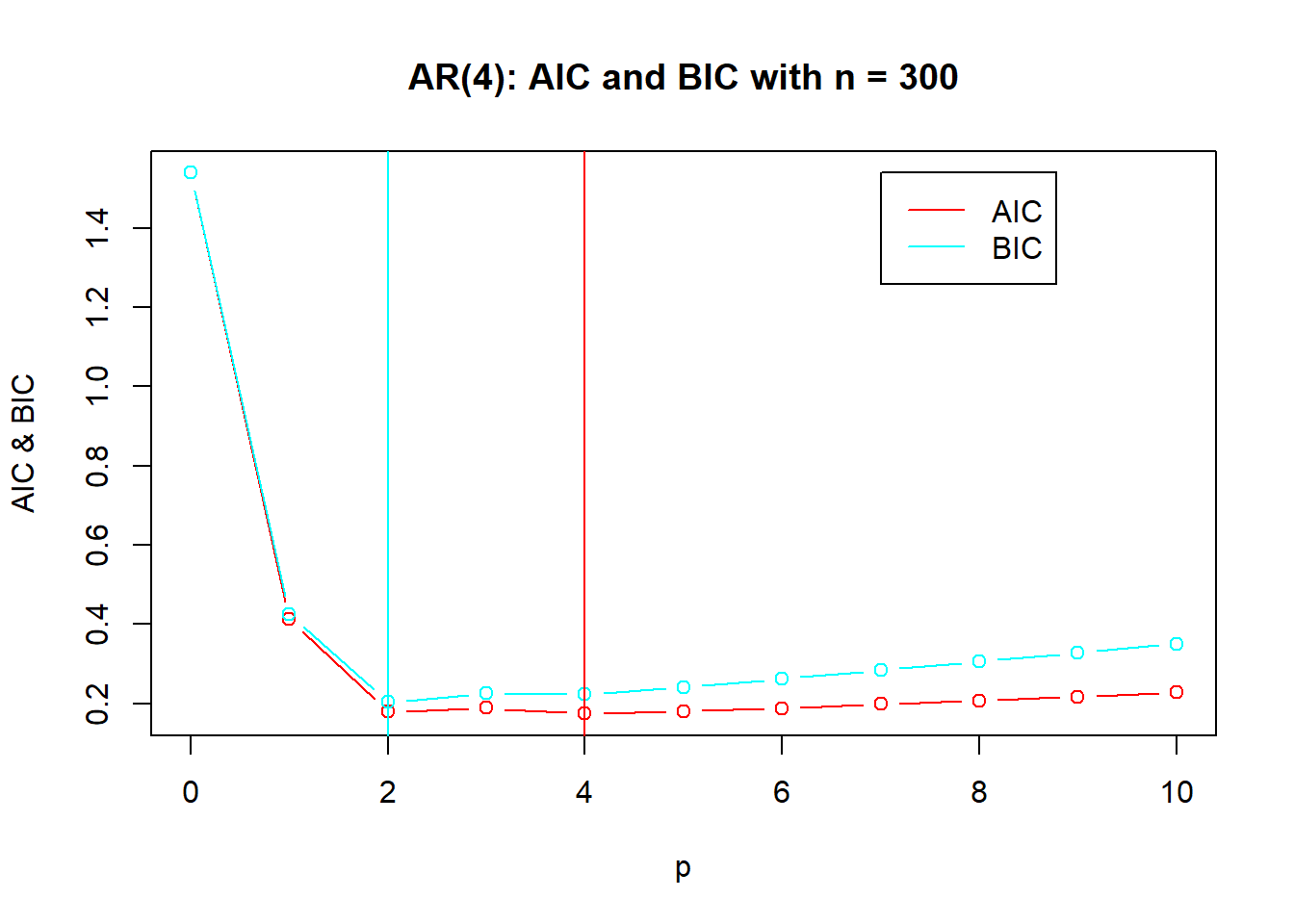
## AR模型AIC和BIC定阶，样本量= 300  重复 400 次的结果:
## AIC order:
## orders.aic
##   2   3   4   5   6   7   8   9  10 
##  19  12 276  42  18  10  10   9   4 
## BIC order:
## orders.bic
##   2   3   4   5 
## 222  19 158   1

19.6 模型拟合检验

对观测数据\(x_1,x_2,\cdots,x_N\), 如果得到了AR\((p)\)的阶\(p\)和自回归系数\((a_1,a_2,\cdots,a_p)\)的估计量 \(\hat p\) 和, \((\hat a_1, \hat a_2,\cdots,\hat a_{\hat p})\), 定义残差 \[\begin{align} \hat \varepsilon_t = y_t - \sum _{j=1}^{\hat p} \hat a_j y_{t-j}, \quad t=\hat p+1, \hat p+2,\dots,N. \tag{19.16} \end{align}\] 这里的\(y_t=x_t-\bar x_N\)是\(x_t\)零均值化.

对上述的残差序列进行白噪声的检验. 如果能够判定(19.16)是白噪声, 就认为建立的模型是合理的. 否则可以改动\(\hat p\) 的值后重新计算, 或改用MA(\(q\)) 或 ARMA(\(p,q\)) 模型 .

19.7 AR谱密度估计

满足AR\((p)\)模型(19.1)的AR\((p)\)序列有谱密度函数 \[\begin{align} f(\lambda) = \frac{\sigma^2}{2\pi} \left|1-\sum_{j=1}^p a_je^{ij\lambda}\right |^{-2}. \tag{19.17} \end{align}\] 把\(\sigma^2\), \(p\)和\((a_1,a_2,\dots,a_p)\)的估计量 \(\hat \sigma^2\), \(\hat p\)和\((\hat a_1, \hat a_2,\dots,\hat a_p)\)代入(19.17)后, 得到\(f(\lambda)\)的估计 \[\begin{align} \hat f(\lambda) =\frac{\hat \sigma^2}{2\pi} \left|1-\sum_{j=1}^{\hat p} \hat a_j e^{ij \lambda}\right |^{-2}. \tag{19.18} \end{align}\] 通常称\(\hat f(\lambda)\)为AR谱估计或极大熵谱估计.

对于AIC或BIC定阶\(\hat p\), 如果\(\{\varepsilon_t\}\)是独立同分布的WN(0,\(\sigma^2\)), 可以证明\(\hat f(\lambda)\)一致收敛到\(f(\lambda)\).

19.8 附录：问题

问： AIC和BIC是否受到\(\{X_t \}\)的量纲的影响？

答不受影响。比如令\(Y_t = K X_t\), 则从\(\{ Y_t \}\)估计的新息方差\(\hat\sigma_{Y,p}^2\)是从\(\{ X_t \}\)估计的新息方差\(\hat\sigma_{X,p}^2\)的\(K^2\)倍，取\(\ln\)后变成了AIC一致地增加\(\ln K^2\)，最小值点不变。

用随机模拟方法验证：

demo.aic.sc <- function(fac=100, shift=20, n=300){
  a <- c(1.16, -0.37, -0.11, 0.18)
  sig <- 1
  x1 <- ar.gen(n, a, sigma=sig)
  x2 <- x1 * fac + shift
  ## do Levinson estimation and LS estimation
  fit1 <- ar(x1, aic=T, order.max=10,
             method="yule-walker")
  print(fit1$aic)
  fit2 <- ar(x2, aic=T, order.max=10,
             method="yule-walker")
  print(fit2$aic)
}
demo.aic.sc()

##           0           1           2           3           4           5 
## 409.4603465  31.1461075   6.4023019   6.4645791   0.0000000   0.7616954 
##           6           7           8           9          10 
##   2.7610739   4.1566591   4.3684998   6.3193517   8.1556399 
##           0           1           2           3           4           5 
## 409.4603465  31.1461075   6.4023019   6.4645791   0.0000000   0.7616954 
##           6           7           8           9          10 
##   2.7610739   4.1566591   4.3684998   6.3193517   8.1556399

可见经过平移与伸缩的序列观测值给出的AIC值是完全相等的。

References

Brockwell, P. J., and R. A. Davis. 1987. Time Series: Theory and Methods. Springer-Verlag.