12 滑动平均模型
12.1 模型引入
平稳序列\(\{X_t\}\)的自协方差函数若满足\(\gamma_q \neq 0\), \(\gamma_k=0, k>q\),则称\(\{X_t\}\)是\(q\)步相关的。 有限项的线性平稳列具有\(q\)步相关性,称为滑动平均模型。
例12.1 考虑每隔2小时记录的化学反应数据时间序列\(\{x_t, t=1,\dots,197\}\)的模型。
读入数据并作序列图(见图12.1):
x <- scan(textConnection("
17.0 16.6 16.3 16.1 17.1 16.9 16.8 17.4 17.1 17.0 16.7 17.4 17.2
17.4 17.4 17.0 17.3 17.2 17.4 16.8 17.1 17.4 17.4 17.5 17.4 17.6
17.4 17.3 17.0 17.8 17.5 18.1 17.5 17.4 17.4 17.1 17.5 17.7 17.4
17.8 17.6 17.5 16.5 17.8 17.3 17.3 17.1 17.4 16.9 17.3 17.6 16.9
16.7 16.8 16.8 17.2 16.8 17.6 17.2 16.6 17.1 16.9 16.6 18.0 17.2
17.3 17.0 16.9 17.3 16.8 17.3 17.4 17.7 16.8 16.9 17.0 16.9 17.0
16.6 16.7 16.8 16.7 16.4 16.5 16.4 16.6 16.5 16.7 16.4 16.4 16.2
16.4 16.3 16.4 17.0 16.9 17.1 17.1 16.7 16.9 16.5 17.2 16.4 17.0
17.0 16.7 16.2 16.6 16.9 16.5 16.6 16.6 17.0 17.1 17.1 16.7 16.8
16.3 16.6 16.8 16.9 17.1 16.8 17.0 17.2 17.3 17.2 17.3 17.2 17.2
17.5 16.9 16.9 16.9 17.0 16.5 16.7 16.8 16.7 16.7 16.6 16.5 17.0
16.7 16.7 16.9 17.4 17.1 17.0 16.8 17.2 17.2 17.4 17.2 16.9 16.8
17.0 17.4 17.2 17.2 17.1 17.1 17.1 17.4 17.2 16.9 16.9 17.0 16.7
16.9 17.3 17.8 17.8 17.6 17.5 17.0 16.9 17.1 17.2 17.4 17.5 17.9
17.0 17.0 17.0 17.2 17.3 17.4 17.4 17.0 18.0 18.2 17.6 17.8 17.7
17.2 17.4
"), quiet=TRUE)
x <- ts(x)
plot(x, main="Chemical reaction time series")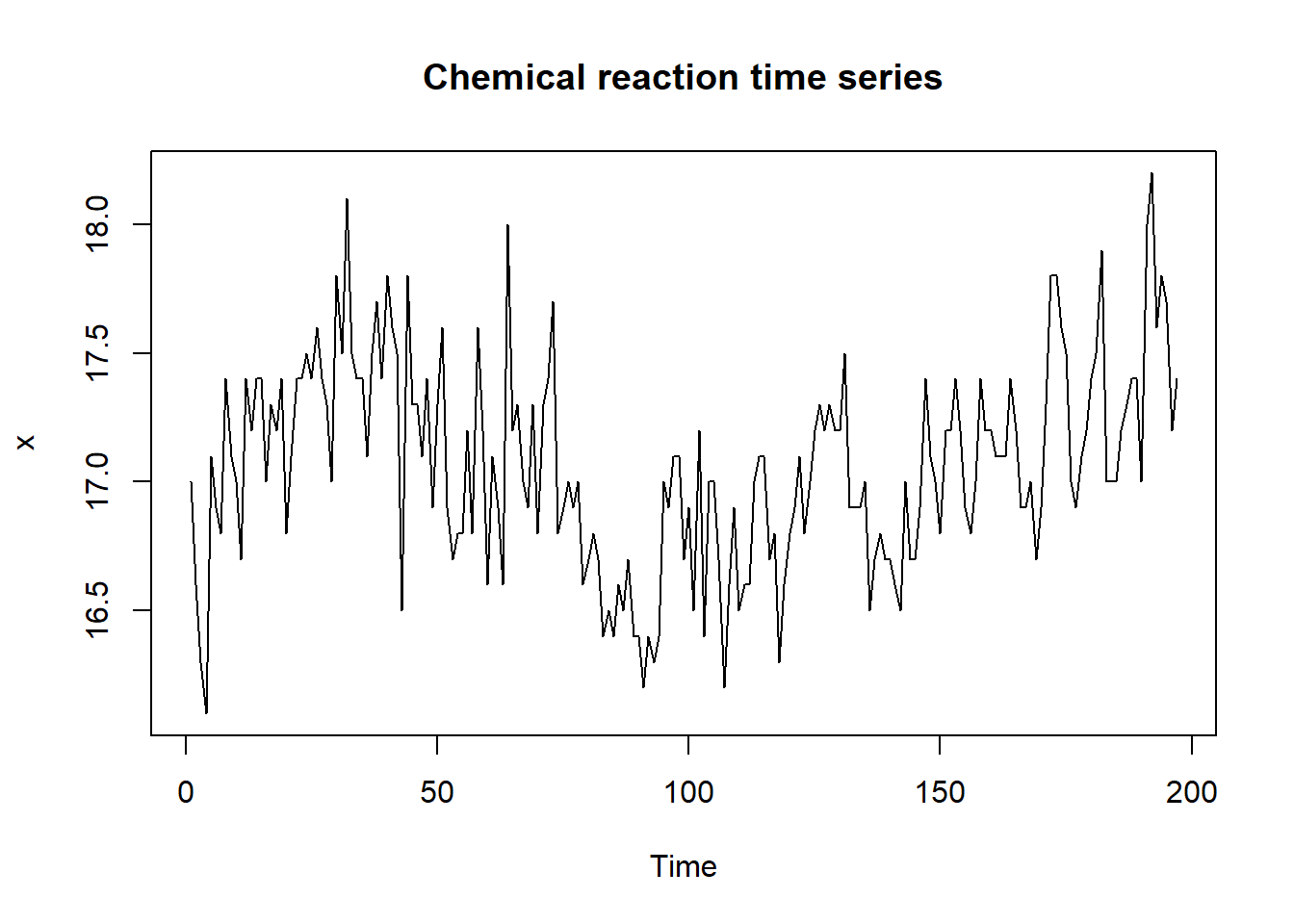
图12.1: 某化学试验溶液浓度的时间序列
序列看起来不像是均值恒定的。 一阶差分得 \[\begin{aligned} y_t = x_t - x_{t-1}, t=2, \dots, 197 \end{aligned}\] 差分后的序列看起来像是平稳的。 见图12.2。
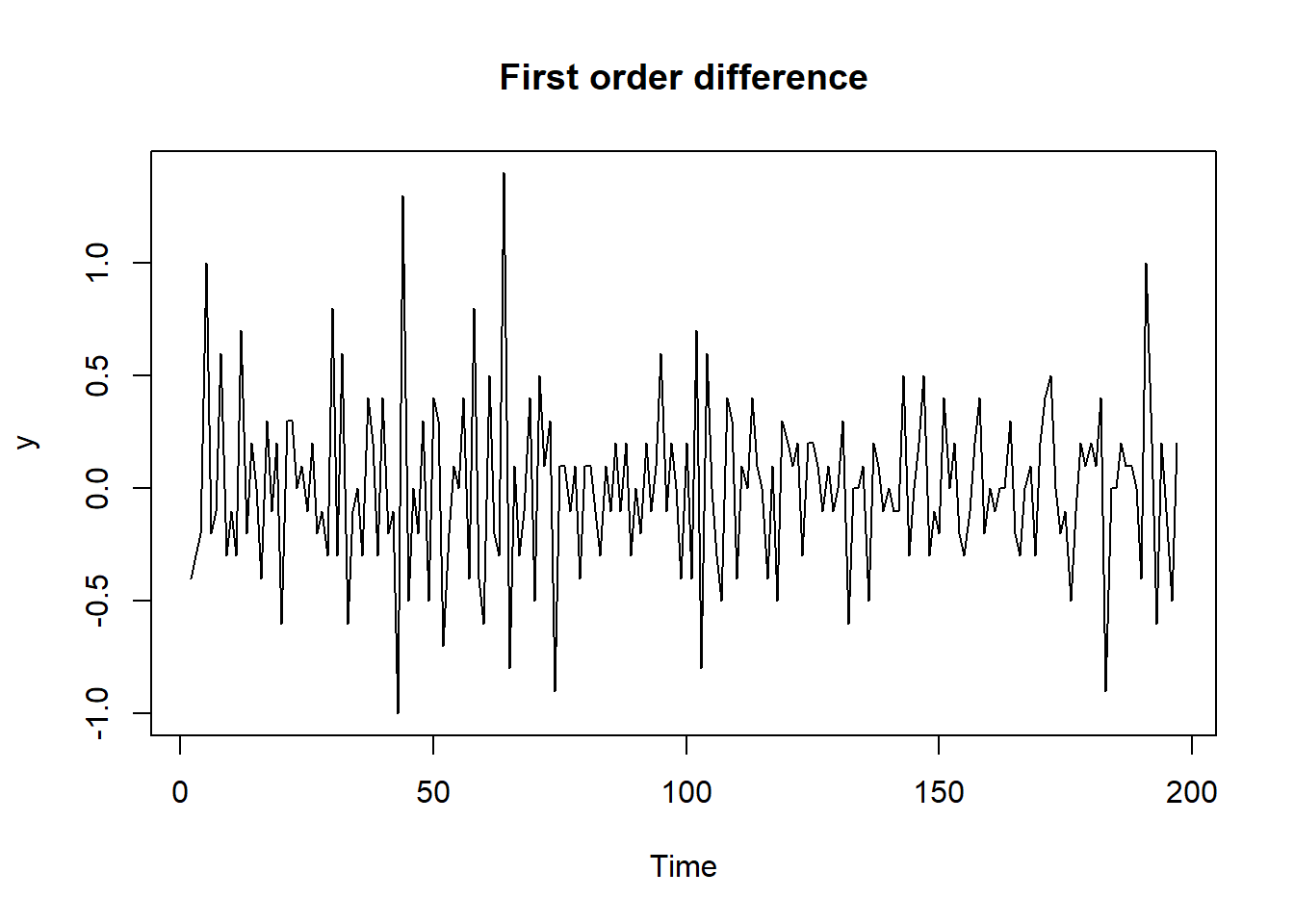
图12.2: 浓度差分序列
\(\{y_t\}\)的样本自相关系数列呈现截尾性, ACF在滞后1处比较显著,\(k>1\)时都很小, 见图12.3。
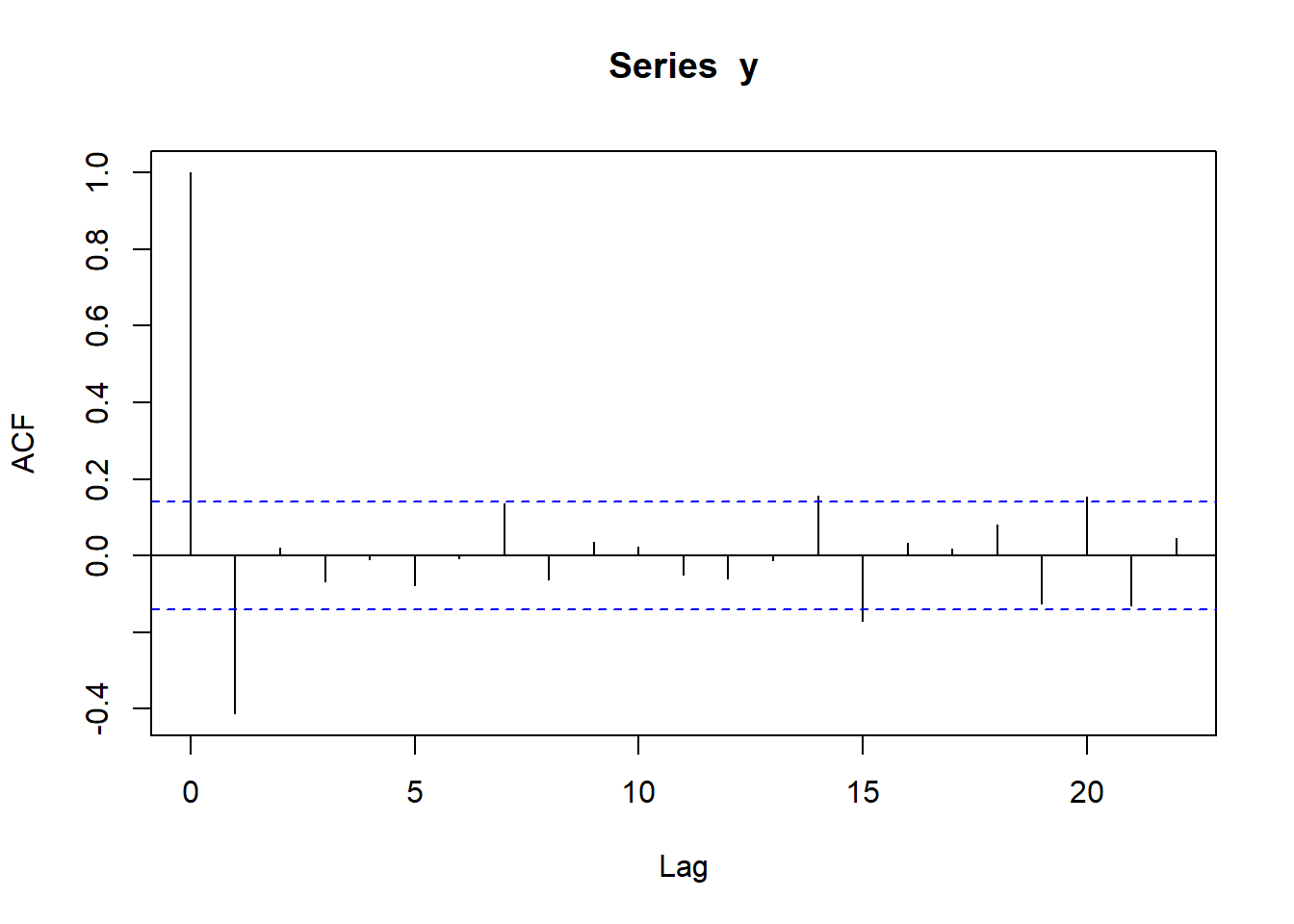
图12.3: 浓度差分序列ACF
对差分序列,可以拟合如下模型 \[\begin{align} Y_t = \varepsilon_t + \hat b \varepsilon_{t-1}, t \in \mathbb Z \tag{12.1} \end{align}\] 模型特点是\(\{\gamma_k\}\) 1步截尾。
○○○○○○
12.2 MA(\(q\))模型和MA(\(q\))序列
定义12.1 (滑动平均模型) 设\(\{\varepsilon_t\}\) 是WN\((0,\sigma^2)\), 如果实数\(b_1,b_2,\dots,b_q\) \((b_q\neq 0 )\)使得 \[ B(z)=1+\sum^{q}_{j=1}{b_j z^j}\neq 0,\ |z|<1 , \] 则称 \[\begin{align} X_t=\varepsilon_t + \sum^{q}_{j=1}{b_j\varepsilon_{t-j}}, \quad t\in \mathbb Z , \tag{12.2} \end{align}\] 是\(q\)阶滑动平均模型, 简称为MA\((q)\)模型。
模型(12.2)中的\(\{X_t \}\)显然是平稳列。 称由(12.2)决定的平稳序列\(\{X_t\}\)是滑动平均序列, 简称为MA\((q)\)序列.
如果进一步要求多项式\(B(z)\)在单位圆上也没有零点: \(B(z)\neq 0\) 当 \(|z|\leq 1\), 则称(12.2)是可逆的MA\((q)\)模型, 称相应的平稳序列是可逆的MA\((q)\)序列.
12.3 MA的特征
低阶的MA与AR相比较光滑(滑动平均),振荡较轻。 稳定性较好。 高阶的MA可以模拟AR的特征。
用推移算子把模型写为 \[\begin{align} X_t = B(\mathscr B) \varepsilon_t, \quad t \in \mathbb Z \tag{12.3} \end{align}\]
对于可逆MA,\(B^{-1}(z)\)有Taylor展式 \[\begin{aligned} B^{-1}(z) = \sum_{j=0}^\infty \phi_j z^j, \quad |z| \leq 1 + \delta \ (\delta>0) \end{aligned}\] 所以 \[\begin{align} \varepsilon_t = B^{-1}(\mathscr B) X_t = \sum_{j=0}^\infty \phi_j X_{t-j} \tag{12.4} \end{align}\]
12.4 MA序列的自协方差函数
记\(b_0=1\),则对MA(\(q\))序列有\(E X_t=0\), \[\begin{align} \gamma_k =& E(X_t X_{t+k}) \\ =& \begin{cases} \sigma^2 \sum_{j=0}^{q-k} b_j b_{j+k}, \quad & 0 \leq k \leq q \\ 0, & k > q \end{cases} \tag{12.5} \end{align}\]
12.5 MA序列的谱密度
定理12.1 MA(\(q\))序列\(\{X_t\}\)的自协方差函数是\(q\)步截尾的: \[\begin{align} \gamma_q = \sigma^2 b_q \neq 0, \quad \gamma_k =0 , \; |k|>q. \tag{12.6} \end{align}\] 并且有谱密度 \[\begin{align} f(\lambda) =& \frac{\sigma^2}{2\pi} |B(e^{i\lambda})|^2 \\ =& \frac{1}{2\pi} \sum^{q}_{k=-q} \gamma_k e^{-ik\lambda}, \quad \lambda \in [-\pi,\pi]. \tag{12.7} \end{align}\]
(12.7)的第一条可以用线性平稳列的定理6.2或用谱密度定义直接证明。 第二条用自协方差绝对可和时谱密度公式(定理9.1)得到也可以用谱密度定义得到。
12.6 MA(\(q\))序列的充要条件
MA(\(q\))序列是自协方差函数\(q\)步截尾的, 反之若平稳列\(\{X_t\}\)自协方差函数\(q\)步截尾 则其必为MA(\(q\))序列。
定理12.2 (自协方差截尾的充要性) 设零均值平稳序列\(\{X_t\}\)有自协方差函数\(\{\gamma_k\}\), 则\(\{X_t\}\)是MA(\(q\))序列的充分必要条件是 \[ \gamma_q \neq 0,\ \gamma_k=0, \ |k|>q. \]
只需要证明充分性。 证明需要一个复变函数引理。
引理12.1 设实常数\(\{ c_j \}\)使得\(c_q\neq 0\) 和 \[ g(\lambda)=\frac{1}{2\pi} \sum^{q}_{j=-q} c_j e^{-ij\lambda}\geq 0, \lambda \in [-\pi,\pi], \] 则有惟一的实系数多项式: \[\begin{align} B(z)=1+\sum^{q}_{j=1}{b_j z^j}\neq 0, \ |z|<1, \ b_q\neq 0. \tag{12.8} \end{align}\] 使得 \[\begin{aligned} g(\lambda)=\frac{\sigma^2}{2\pi} |B(e^{i\lambda})|^2. \end{aligned}\] 这里\(\sigma^2\)为某个正常数.
证明时,令\(G(z) = \sum_{j=-q}^q c_j z^{j+q}\)则\(G(z)\)的\(2q\) 个根中\(z_1\)是根必有\(z_1^{-1}\)也是根。\(z_1 \neq \pm 1\)时\(z_1^{-1}\neq z_1\)。 把这样成对的根只取其中一个且要求不在单位圆内即可组成\(B(.)\)。 详见谢衷洁《时间序列分析》(谢衷洁 1990) P89–P92。
定理12.2证明:
由自协方差绝对可和时谱密度公式得 \[\begin{aligned} f(\lambda) = \frac{1}{2\pi} \sum_{k=-q}^q \gamma_k e^{-ik\lambda} \end{aligned}\] 由引理12.1, \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi} |B(e^{-i\lambda})|^2, \quad \text{$B(z)$单位园内没有根.} \end{aligned}\]
如果\(B(z)\)在单位圆内和单位圆上都没有根, 即\(f(\lambda)\)在\([0, \pi]\)上恒正, 则可定义 \[ \varepsilon_t = B^{-1}(\mathscr B) X_t = \sum_{j=0}^\infty h_j X_{t-j} \] 其中\(B^{-1}(z) = \sum_{j=0}^\infty h_j z^j\)是\(B^{-1}(z)\)在\(|z| < 1+\delta\)的泰勒展开式, \(B(z)\)的根的模都大于\(1 + \delta\)。 泰勒展开系数\(\{ h_j \}\)绝对可和, 所以\(\{ \varepsilon_t \}\)是平稳列, 且\(E \varepsilon_t = 0\), 用线性滤波的谱密度公式(见定理6.5)可得\(\{\varepsilon_t\}\)的谱密度为 \[\begin{aligned} f_{\varepsilon}(\lambda) =& \left| \sum_{j=0}^\infty h_j e^{ij\lambda} \right|^2 f(\lambda) \\ =& \left| B(e^{i\lambda}) \right|^{-2} \frac{\sigma^2}{2\pi} |B(e^{-i\lambda})|^2 \\ =& \frac{\sigma^2}{2\pi} \end{aligned}\] 这是白噪声的谱密度, 由谱密度与自协方差函数的关系可知\(\{ \varepsilon_t \}\)是WN(0, \(\sigma^2\)), 所以\(f(\lambda)\)在\([0, \pi]\)上恒正时定理的充分性得证。
对于\(B(z)\)单位园上可能有根的一般情况可以用Hilbert空间预测的方法证明。 (见(Brockwell and Davis 1987) §3.2.1, P.89, 但那里的MA没有根的条件; 或参考(谢衷洁 1990) P92.)。
○○○○○○
12.7 最小序列
定义12.2 (最小序列) 设\(\{X_t: \ t\in \mathbb Z\}\)是平稳序列. 用\(H_x\)表示\(\{X_t\}\)产生的Hilbert空间, 用\(H_x(s)\)表示由 \(\{X_t: t\neq s\}\)产生的Hilbert空间. 如果 \[ H_x \neq H_x(s)\] 对某个\(s \in \mathbb Z\)成立 , 则称\(\{X_t\}\)是最小序列.
对平稳序列,可以证明对某个\(s\)成立\(H_x(s)\neq H_x\)则对所有 的\(s\)成立\(H_x(s)\neq H_x\)。 说明最小序列的每个\(X_t\)都含有其他\(X_s\)中没有的信息。 可完全线性预测的平稳序列(某\(\Gamma_n\)不满秩)非最小序列。
定理12.3 (最小序列的谱密度条件) 设平稳序列\(\{X_t\}\)有谱密度\(f(\lambda)\), 则 \(\{X_t\}\)是最小序列的充分必要条件是 \[\begin{align} \int_{-\pi}^\pi \frac{d\lambda}{f(\lambda)} <\infty. \tag{12.9} \end{align}\]
证明参见Kolgomorov著, 郑绍濂、陶宗英等译等译的“希尔伯脱空间中的平稳序列”, 上海科学技术出版社1963。
○○○○○○
由以上定理可见谱密度连续恒正的平稳列是最小序列。 于是,AR(\(p\))序列是最小序列。 可逆的MA(\(q\))序列的谱密度连续有正下界所以是最小序列。
单位圆上有根的MA(\(q\))序列其谱密度\(f(\lambda)\)中有 \[\begin{aligned} |1 - e^{i(\lambda-\lambda_j)}|^2 = O(|\lambda - \lambda_j|^2) \end{aligned}\] 成分所以其倒数不可积, 因此不可逆的MA(\(q\))序列不是最小序列。
平稳的最小序列一定不能\(n\)步完全线性预测,所以其自协方差列正定。
12.8 MA(\(q\))系数的递推计算
MA(\(q\))序列的系数 \((b_1, b_2, \dots, b_q)\)及\(\sigma^2\) 可以被\(\gamma_0, \gamma_1, \dots, \gamma_q\) 唯一确定。 可以用如下文献方法计算模型参数: 李雷(1991), 平稳过程的状态空间模型及随机实现算法时多元情况的解决, 北京大学硕士论文。
记 \[\begin{align} \begin{array}{llr} A=\left( \begin{array}{llllll} 0 & 1 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 1 & \cdots & 0 & 0 \\ \cdots & \cdots & & \cdots & \cdots & \\ 0 & 0 & 0 & \cdots & 0 & 1 \\ 0 & 0 & 0 & \cdots & 0 & 0 \end{array} \right )_{q\times q}, & C=\left( \begin{array}{c} 1 \\ 0 \\ \vdots \\0 \end{array} \right)_{q \times 1} \\ \\ \Omega_k=\left( \begin{array}{llll} \gamma_1 & \gamma_2 & \cdots & \gamma_k \\ \gamma_2 & \gamma_3 & \cdots & \gamma_{k+1} \\ \cdots & \cdots & \cdots & \cdots \\ \gamma_q & \gamma_{q+1} & \cdots & \gamma_{q+k-1} \end{array} \right), & \boldsymbol{\gamma}_q=\left( \begin{array}{c} \gamma_1 \\ \gamma_2 \\ \vdots \\ \gamma_q \end{array} \right) & \end{array} \tag{12.10} \end{align}\] 则有: \[\begin{align} \boldsymbol{b}_q = \frac{1}{\sigma^2}(\boldsymbol{\gamma}_q -A\Pi C), \ \sigma^2=\gamma_0-C{^\tau}\Pi C, \tag{12.11} \end{align}\] 其中 \[\begin{align} \Pi=\lim_{k\to \infty} \Omega_k\Gamma_k^{-1}\Omega_k^T. \tag{12.12} \end{align}\] 公式(12.11), (12.12)为以后用观测样本估计MA\((q)\)模型的参数打下了基础.
12.9 MA(\(q\))模型举例
12.9.1 MA(1)
可逆MA(1)模型为 \[\begin{aligned} X_t = \varepsilon_t + b \varepsilon_{t-1}, \quad \varepsilon_t \sim \text{WN}(0,\sigma^2), \quad |b|<1 \end{aligned}\]
自协方差和自相关 \[\begin{aligned} &\begin{cases} \gamma_0 =& \sigma^2 (1 + b^2) \\ \gamma_1 =& \sigma^2 b \\ \gamma_k =& 0, \quad k\geq 2 \end{cases} \\ &\begin{cases} \rho_1 =& \frac{b}{1+b^2} \\ \rho_k =& 0, \quad k \geq 2 \end{cases} \end{aligned}\]
谱密度 \[\begin{aligned} f(\lambda) =& \frac{\sigma^2}{2\pi} | 1+b e^{i\lambda} |^2 \\ =& \frac{\sigma^2}{2\pi} (1 + b^2 + 2b\cos\lambda), \quad \lambda \in [-\pi,\pi] \end{aligned}\]
偏相关系数不截尾: \[\begin{aligned} a_{k,k} = -\frac{(-b)^k (1-b^2)}{(1 - b^{2k+2})}, \quad k \geq 1 \end{aligned}\]
逆表示 \[\begin{aligned} \varepsilon_t = \sum_{j=0}^\infty (-b)^j X_{t-j} \end{aligned}\]
12.9.2 MA(1)实例
先提供几个自定义R函数。
绘制MA理论谱密度曲线的函数,模拟MA序列的函数, 从自协方差函数利用递推方法估计模型参数的函数:
## MA theoretical spectrum given MA coefficients
ma.true.spectrum <- function(a, ngrid=256, sigma=1,
tit="True MA Spectral Density",
plot.it=TRUE){
p <- length(a)
freqs <- seq(from=0, to=pi, length=ngrid)
spec <- numeric(ngrid)
for(ii in seq(ngrid)){
spec[ii] <- 1 + sum(complex(mod=a, arg=freqs[ii]*seq(p)))
}
spec = sigma^2 / (2*pi) * abs(spec)^2
if(plot.it){
plot(freqs, spec, type='l',
main=tit,
xlab="frequency", ylab="spectrum",
axes=FALSE)
axis(2)
axis(1, at=(0:6)/6*pi,
labels=c(0, expression(pi/6),
expression(pi/3), expression(pi/2),
expression(2*pi/3), expression(5*pi/6), expression(pi)))
box()
}
invisible(list(frequencies=freqs, spectrum=spec,
ma.coefficients=a, sigma=sigma))
}
## simulate MA(q) model.
## a is vector a_1, \dots, a_q
## Model is X_t = eps_t + a_1 eps_{t-1} + \dots + a_q eps_{t-q}
## \Var(\epsilon_t) = sigma^2
## This version uses the filter function.
ma.gen <- function(n, a, sigma=1.0, by.roots=FALSE,
plot.it=FALSE){
if(by.roots){
require(polynom)
cf <- Re(c(poly.calc(a)))
cf <- cf / cf[1]
a <- cf
}
q <- length(a)
n2 <- n+q
eps <- rnorm(n2, 0, sigma)
x2 <- filter(eps, c(1,a), method="convolution", side=1)
x <- x2[(q+1):n2]
x <- ts(x)
attr(x, "model") <- "MA"
attr(x, "b") <- a
attr(x, "sigma") <- sigma
if(plot.it) plot(x)
x
}
## Given \gamma_0, \gamma_1, \dots, \gamma_q,
## Solve MA(q) coefficients b_1, \dots, b_q, \sigma^2
## Using Li Lei's algorithm.
## Input: gms -- \gamma_0, \gamma_1, \dots, \gamma_q
ma.solve <- function(gms, k=100){
q <- length(gms)-1
if(q==1){
rho1 <- gms[2] / gms[1]
b <- (1 - sqrt(1 - 4*rho1^2))/(2*rho1)
s2 <- gms[1] / (1 + b^2)
return(list(b=b, s2=s2))
}
A <- matrix(0, nrow=q, ncol=q)
for(j in seq(2,q)){
A[j-1,j] <- 1
}
cc <- numeric(q); cc[1] <- 1
gamma0 <- gms[1]
gammas <- numeric(q+k)
gammas[1:(q+1)] <- gms
gamq <- gms[-1]
Gammak <- matrix(0, nrow=k, ncol=k)
for(ii in seq(k)){
for(jj in seq(k)){
Gammak[ii,jj] <- gammas[abs(ii-jj)+1]
}
}
Omk <- matrix(0, nrow=q, ncol=k)
for(ii in seq(q)){
for(jj in seq(k)){
Omk[ii,jj] <- gammas[ii+jj-1+1]
}
}
PI <- Omk %*% solve(Gammak, t(Omk))
s2 <- gamma0 - c(t(cc) %*% PI %*% cc)
b <- 1/s2 * c(gamq - A %*% PI %*% cc)
return(list(b=b, s2=s2))
}一个系数\(b_1 > 0\)的MA(1)模型为: \[ X_t = \varepsilon_t + 0.6 \varepsilon_{t-1}, \ \{\varepsilon_t \} \sim \text{i.i.d N}(0,1) \]
下面产生了长度\(n=100\)的模拟数据, 时间序列图见图12.4, 理论谱密度见图12.5。
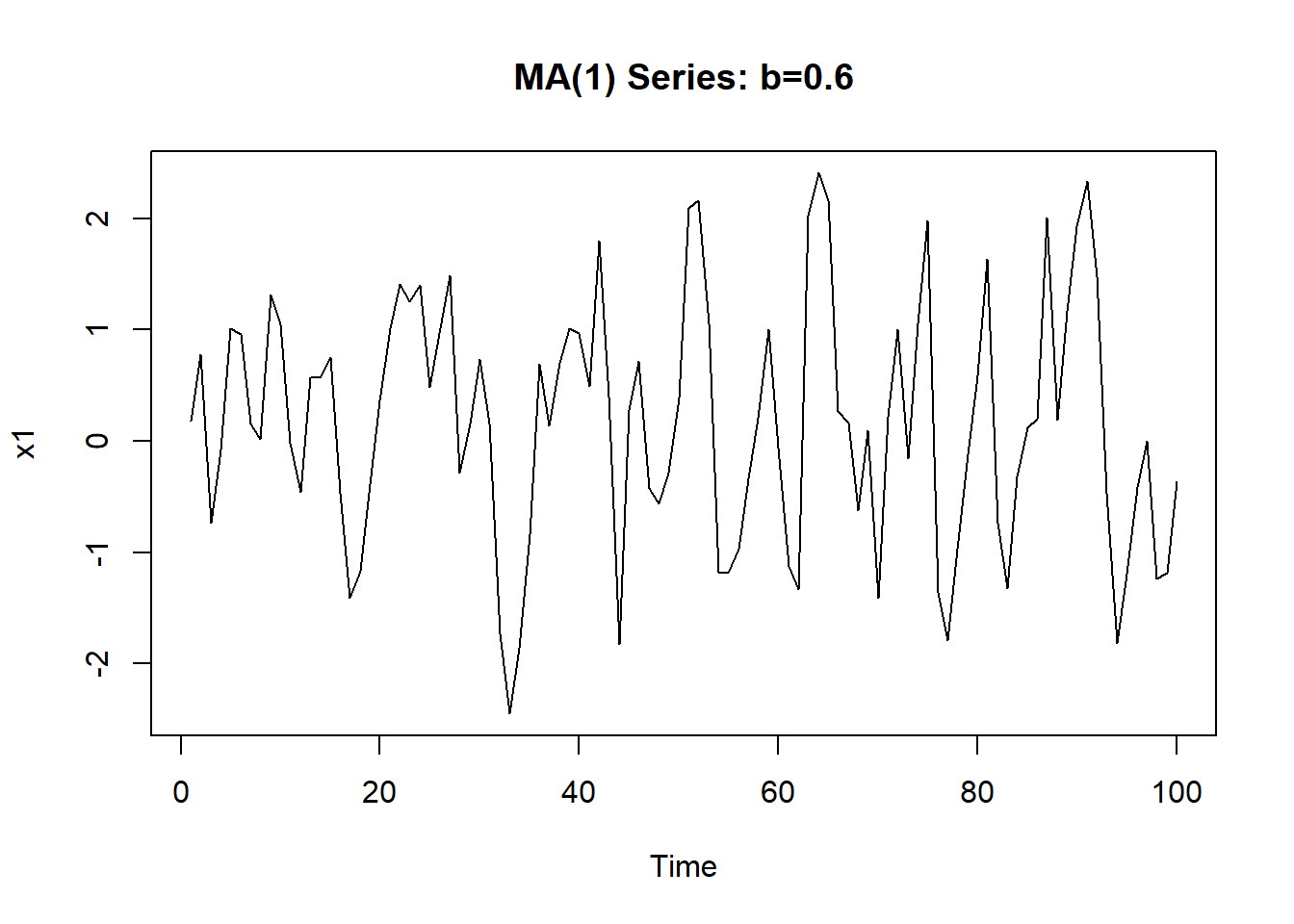
图12.4: 正系数MA(1)模型模拟序列
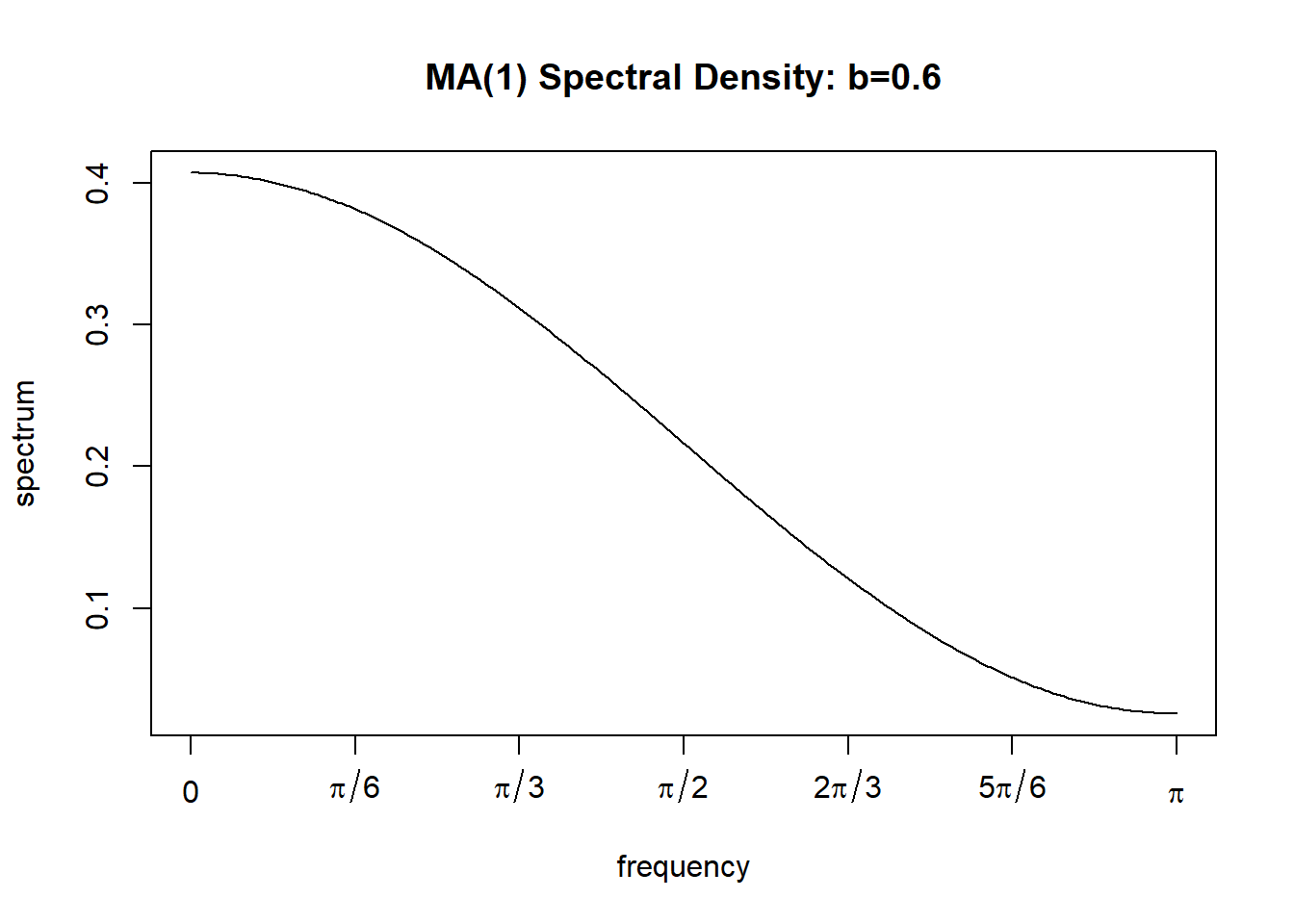
图12.5: 正系数MA(1)模型的理论谱密度
一个系数\(b_1 < 0\)的MA(1)模型为: \[ X_t = \varepsilon_t - 0.6 \varepsilon_{t-1}, \ \{\varepsilon_t \} \sim \text{i.i.d N}(0,1) \]
下面产生了长度\(n=100\)的模拟数据, 时间序列图见图12.6, 理论谱密度见图12.7。
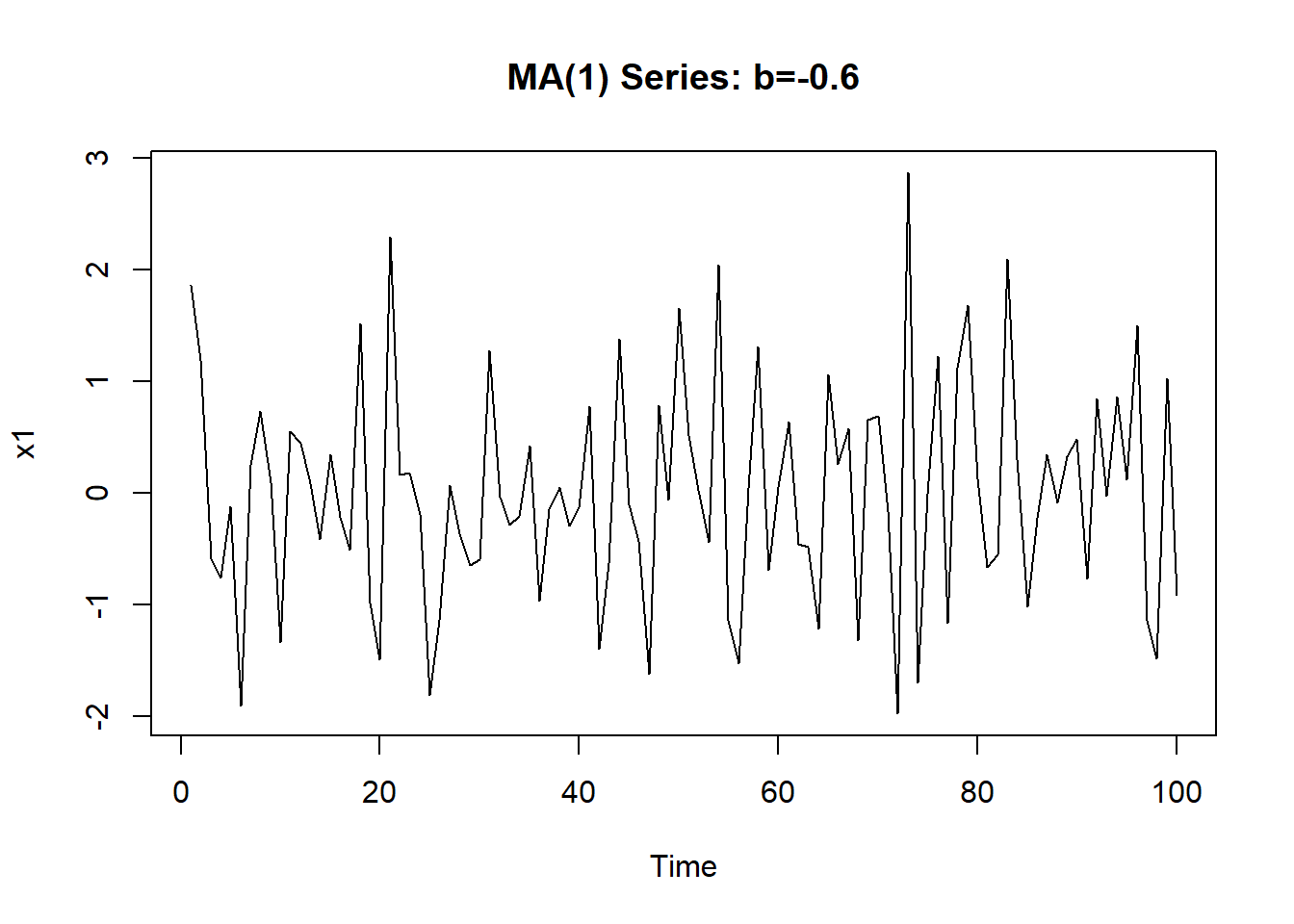
图12.6: 负系数MA(1)模型模拟序列
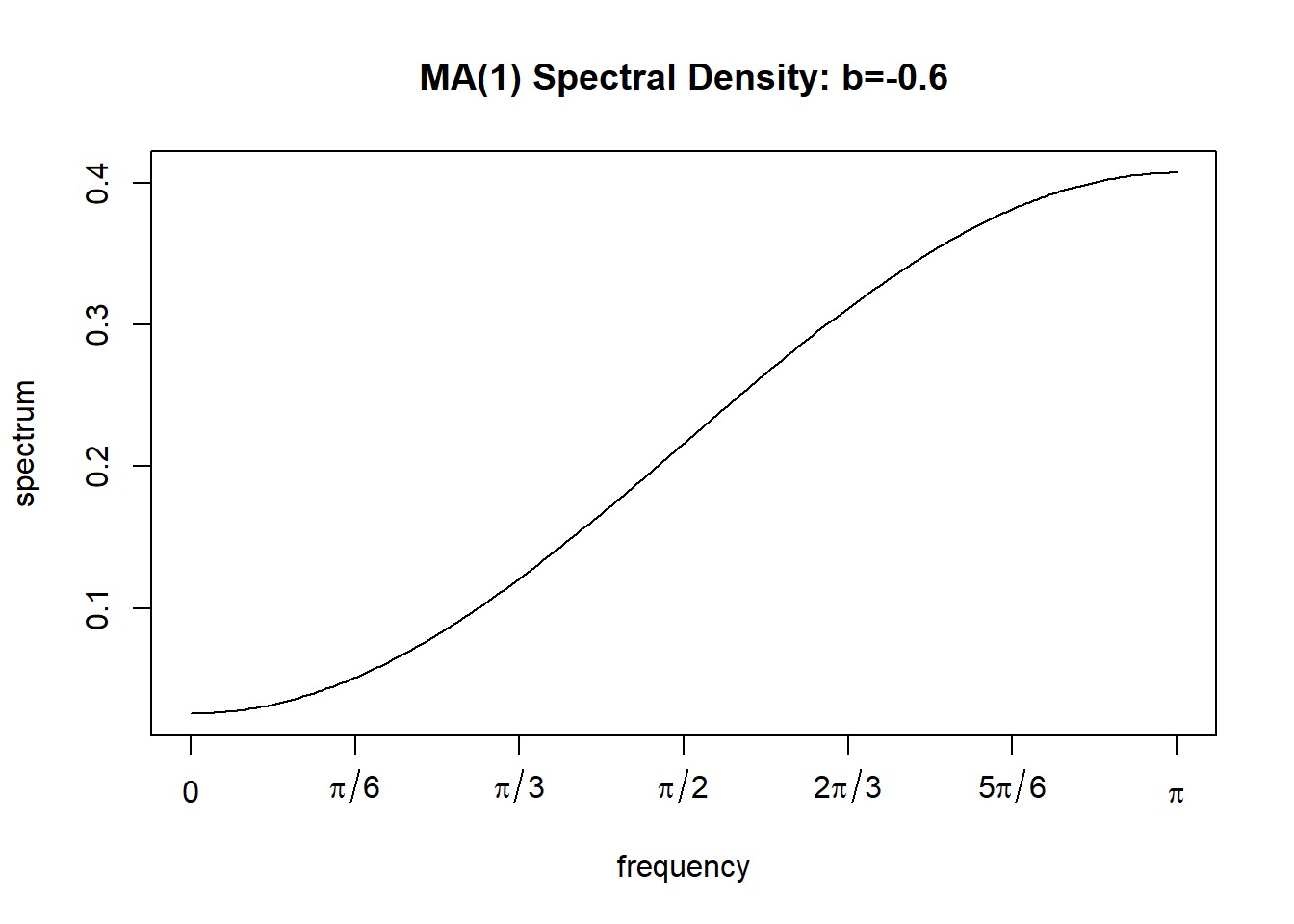
图12.7: 负系数MA(1)模型的理论谱密度
与AR模型相比, 低阶MA模型的谱都很平缓。 \(b_1 > 0\)时谱密度峰出现在低频, \(b_1 < 0\)是谱密度峰出现在高频。
12.9.3 MA(2)
可逆MA(2) \[\begin{aligned} X_t = \varepsilon_t + b_1 \varepsilon_{t-1} + b_2 \varepsilon_{t-2},\ t \in \mathbb Z \end{aligned}\]
\[ B(z) = 1 + b_1 z + b_2 z^2 \neq 0, \ |z|\leq 1 \]
可逆域: \[\begin{aligned} & \{(b_1, b_2): B(z)\neq 0, |z|\leq 1\} \\ =& \{(b_1, b_2): b_2 \pm b_1 > -1, |b_2|<1 \} \end{aligned}\]
自协方差 \[\begin{aligned} \gamma_0 =& \sigma^2 ( 1 + b_1^2 + b_2^2) \\ \gamma_1 =& \sigma^2 (b_1 + b_1 b_2) \\ \gamma_2 =& \sigma^2 b_2 \\ \gamma_k =& 0, \quad k>2 \end{aligned}\]
自相关系数 \[\begin{aligned} \rho_1 =& \frac{b_1 + b_1 b_2}{1 + b_1^2 + b_2^2}, \quad \rho_2 = \frac{b_2}{1 + b_1^2 + b_2^2} \\ \rho_k =& 0, \quad k>2 \end{aligned}\]
谱密度 \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi} \left| 1 + b_1 e^{i\lambda} + b_2 e^{i\,2\lambda} \right|^2 \end{aligned}\]
12.9.4 MA(2)实例
MA(2)的一个实际例子: \[\begin{aligned} X_t = \varepsilon_t - 0.36 \varepsilon_{t-1} + 0.85 \varepsilon_{t-2} \end{aligned}\] 特征根为\(1.084652 e^{\pm i 1.374297}\)。
如下程序求特征根、特征根的模和辐角:
## [1] 1.084652 1.084652## [1] 1.374297 -1.374297自协方差函数: \[\begin{aligned} \gamma_0 &= \sigma^2(1 + b_1^2 + b_2^2)& &= 7.4084 \\ \gamma_1 &= \sigma^2(b_1 + b_1 b_2)& &= -2.664 \\ \gamma_2 &= \sigma^2 b_2 & &= 3.4 \\ \gamma_k & & &= 0, \quad k>2 \end{aligned}\]
自相关函数: \[ (\rho_1, \rho_2) = (-0.3596, 0,4589)) \]
下面产生了长度\(n=120\)的模拟数据, 时间序列图见图12.8, 理论谱密度见图12.9。
n <- 120
sigma <- 2
b <- c(-0.36, 0.85)
x <- ma.gen(n, sigma=2, a=b)
plot(x, main="MA(2) Series: b=(-0.36,0.85)")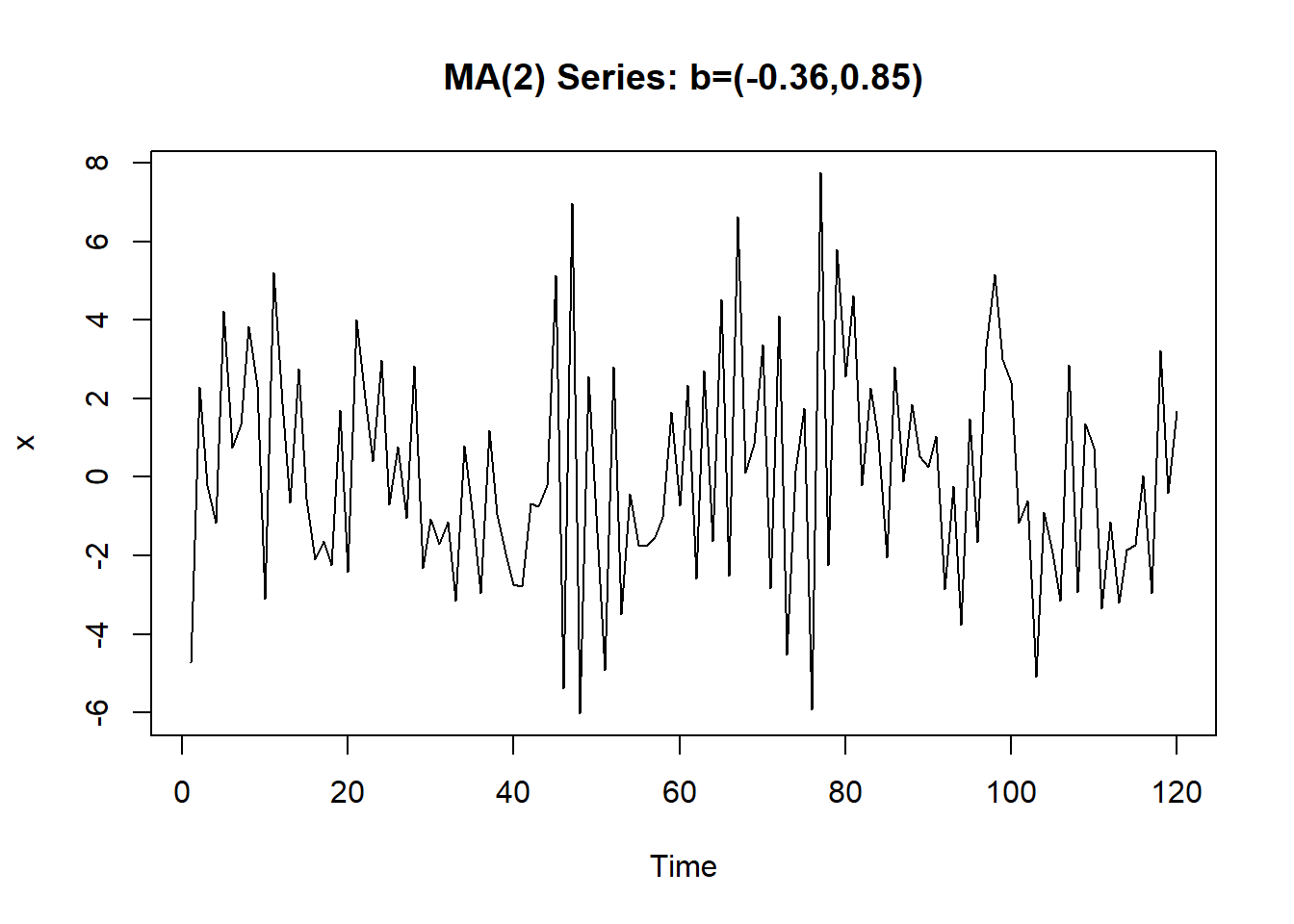
图12.8: MA(2)模型模拟数据
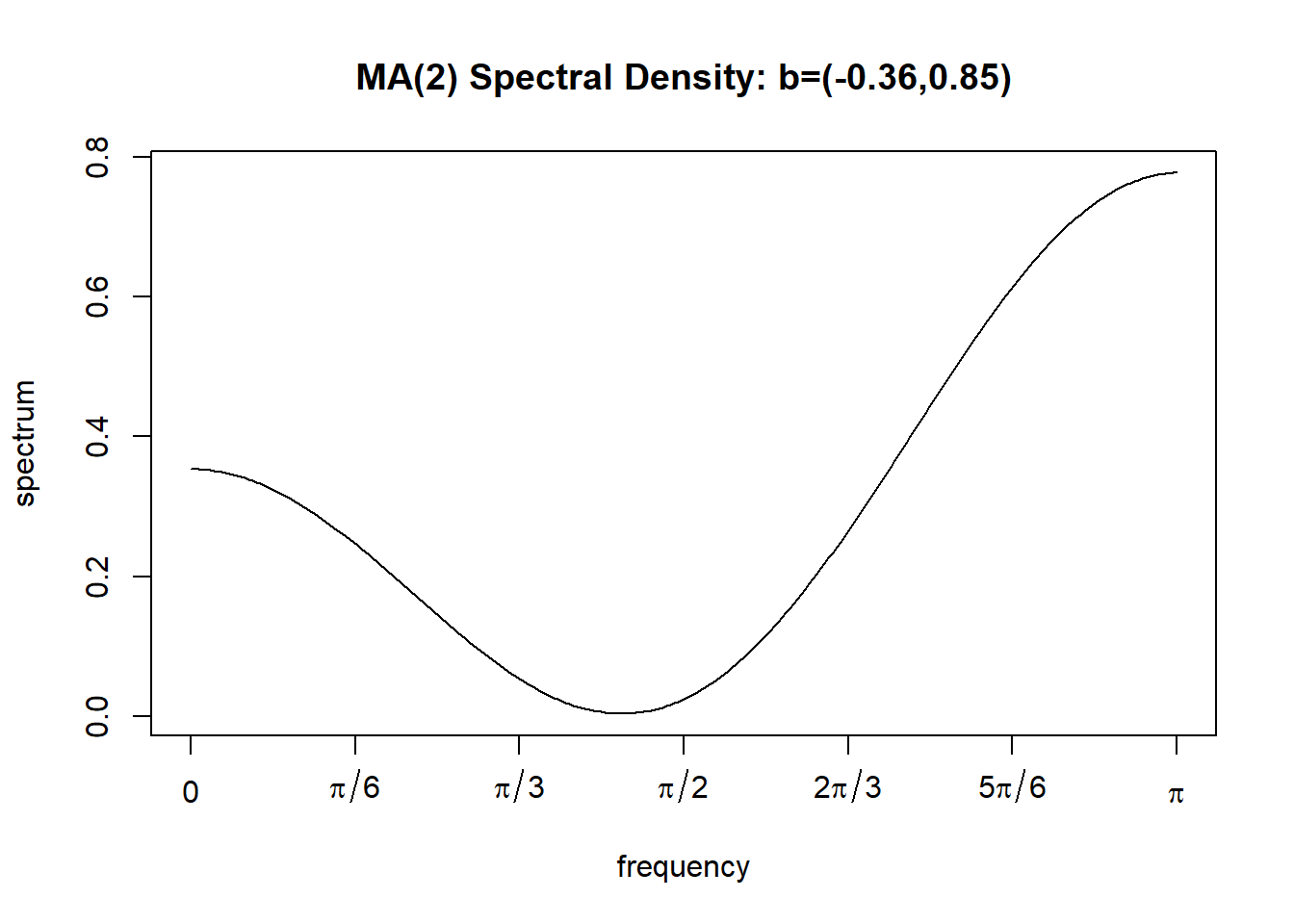
图12.9: MA(2)模型理论谱密度
下面的程序尝试利用前面的矩阵递推计算方法,首先计算理论自协方差函数值:
sigma <- 2
b <- c(-0.36, 0.85)
gms <- numeric(3)
gms[1] <- sigma^2 * (1 + b[1]^2 + b[2]^2)
gms[2] <- sigma^2 * (b[1] + b[1]*b[2])
gms[3] <- sigma^2 * b[2]
names(gms) <- 0:2
cat("======== Autocovariances ==========\n")## ======== Autocovariances ==========## 0 1 2
## 7.4084 -2.6640 3.4000下面利用递推极限估计模型参数, 极限\(k\)值分别取6, 12, ……,100。
ks <- c(6, 12, 20, 30, 40, 50, 60, 100)
nks <- length(ks)
results <- matrix(0, nrow=nks, ncol=3)
rownames(results) <- ks
for(ii in seq(along=ks)){
k <- ks[ii]
res <- ma.solve(gms, k=k)
results[ii,] <- c(res$b[1], res$b[2], res$s2)
}
cat("======== Solving MA coefficients ========\n")## ======== Solving MA coefficients ========## True coefficients: -0.36 0.85## True white noise variance = 4## Coefficients estimates using true autocovariance and k=6,12,...:## [,1] [,2] [,3]
## 6 -0.3367354 0.7514921 4.524332
## 12 -0.3527358 0.8233976 4.129233
## 20 -0.3587046 0.8421336 4.037364
## 30 -0.3597471 0.8486942 4.006155
## 40 -0.3599178 0.8497082 4.001374
## 50 -0.3599929 0.8499442 4.000262
## 60 -0.3599973 0.8499899 4.000047
## 100 -0.3600000 0.8500000 4.000000可见极限\(k\)值取到100时逼近精度已经基本在小数点后第8位。 当然,如果自协方差函数时估计值, 估计误差会主要来自数据的随机性。
12.10 附录:充要条件
设平稳列\(\{X_t \}\)有恒正谱密度, 则\(\{X_t \}\)是可逆MA \(\Longleftrightarrow\) \(\{X_t \}\)自协方差\(q\)后截尾 \(\Longleftrightarrow\) 谱密度可以写成 \[\begin{aligned} f(\lambda) = \frac{\sigma^2}{2\pi} |B(e^{-i\lambda})|^2 \end{aligned}\] (其中\(B(\cdot)\)根都在单位圆外)。 见谢衷洁《时间序列分析》(谢衷洁 1990) P89定理2.10。 当自协方差\(q\)后截尾时必为MA序列(不一定可逆), 见(谢衷洁 1990) P92定理2.11, 这一点不需要假设有谱密度(自协方差截尾推出有谱密度)。 单位圆上有复根的话必为共轭出现且有偶数重。
自协方差\(q\)后截尾必为广义MA\((q)\)(无根条件), 证明见(Brockwell and Davis 1987) §3.2 Proposition 3.2.1. 用了新息分解,正交分解来证明。 \(b_1, b_2, \dots, b_q\)是关于新息张成的空间上的投影系数。