17 白噪声检验
17.1 白噪声的\(\chi^2\)检验
若\(\{X_t\}\)是独立同分布的白噪声, 根据推论16.2, \(N\)足够大时 \[\begin{aligned} \sqrt{N}(\hat\rho_1, \hat\rho_2,\dots,\hat\rho_m) \end{aligned}\] 服从iid标准正态分布。于是 \[\begin{aligned} \hat\chi^2(m) \stackrel{\triangle}{=} N(\hat\rho_1^2 + \hat\rho_2^2 + \dots + \hat\rho_m^2) \end{aligned}\] 近似服从\(\chi^2(m)\)分布。
要检验\(H_0: \{X_t\}\)为独立同分布白噪声,可以用否定域 \[\begin{aligned} \{\hat\chi^2(m) > \lambda_\alpha(m) \} \end{aligned}\] 其中\(\lambda_\alpha(m)\)为\(\chi^2(m)\)的右侧\(\alpha\)分位数。 检验的\(p\)值为 \[\begin{aligned} \Pr(\chi^2(m) > \hat\chi^2(m)) = 1 - F_m(\hat\chi^2(m)) \end{aligned}\] 其中\(F_m(.)\)为\(\chi^2(m)\)分布函数。 虽然\(H_0\)要求\(\{X_t\}\)独立同分布, 此方法可以用作一般性的白噪声检验。
上述检验叫做Box-Pierce检验。
类似可以使用统计量 \[\begin{align*} \hat\chi_\text{LB}^2(m) \stackrel{\triangle}{=} N(N-1) \sum_{k=1}^m \frac{\hat\rho_k^2}{N-k} \end{align*}\] 在\(H_0\)下也近似服从\(\chi_m^2\)分布。 相应的检验称为Ljung-Box检验。
17.1.1 白噪声检验的模拟比较
R的Box.test()函数提供了Box-Pierce检验和Ljung-Box检验功能。
R的portes包提供了多种一元和多元白噪声检验功能。
下面用一些非白噪声的序列数据来考察LB检验的功效。 首先选用AR(2)序列, 对AR(2)序列, 特征根离单位圆越远, 序列越表现得像是白噪声, 检验功效越差; 特征根离单位圆较近时则白噪声检验功效较高。 特征根的模分别取为\(1000, 10, 6, 4, 3, 2, 1.5\), 辐角为\(1.13\)。 样本量\(N=400\), 卡方检验的平方和项数\(m=5\)和\(m=20\)。 使用Ljung-Box检验。 输出结果是不同的特征根模\(\rho\)对应的检验功效, 分别取\(m=5\)和\(m=20\)。
mods <- c("1000", "10", "6", "4", "3", "2", "1.5")
revroots <- complex(mod=1/c(1000, 10, 6, 4, 3, 2, 1.5),
arg=1.13)
coefs <- cbind(2*Re(revroots), -Mod(revroots)^2)
nmodels <- length(revroots)
sigma <- 1
N <- 400 ## sample size
nrep <- 1000 ## number repetitions
alpha <- 0.05 ## test level
power <- numeric(nmodels)
res <- data.frame(rho=mods, pv5=0, pv20=0)
set.seed(1)
for(jj in seq(nmodels)){
p5 <- 0
p20 <- 0
for(ii in seq(nrep)){
#x <- ar.gen(n=N, a=coefs[jj,], sigma=sigma)
x <- arima.sim(model=list(ar=coefs[jj,]), n=N, rand.gen=function(n, ...) rnorm(n, 0, sigma))
p5 <- p5 + (Box.test(x, lag=5, type="Ljung")$p.value < alpha)
p20 <- p20 + (Box.test(x, lag=20, type="Ljung")$p.value < alpha)
}
## correct rate
res[jj, "pv5"] <- 100 * p5 / nrep
res[jj, "pv20"] <- 100 * p20 / nrep
}
##print(res, quote=F)
knitr::kable(res)| rho | pv5 | pv20 |
|---|---|---|
| 1000 | 5.0 | 4.0 |
| 10 | 18.3 | 12.4 |
| 6 | 52.0 | 31.6 |
| 4 | 92.0 | 68.6 |
| 3 | 99.9 | 94.4 |
| 2 | 100.0 | 100.0 |
| 1.5 | 100.0 | 100.0 |
对于MA模型, 不能使用特征根来选择与白噪声的差别大小。 考虑MA(1)模型, \(b_1\)越接近于0, 序列越接近于白噪声。
bs <- c(0.001, 0.1, 0.15, 0.2, 0.3, 0.5, 0.8, 0.9)
nmodels <- length(bs)
sigma <- 1
N <- 400 ## sample size
nrep <- 1000 ## number repetitions
alpha <- 0.05 ## test level
power <- numeric(nmodels)
res <- data.frame(b=bs, pv5=0, pv20=0)
set.seed(1)
for(jj in seq(nmodels)){
p5 <- 0
p20 <- 0
for(ii in seq(nrep)){
x <- arima.sim(model=list(ma=bs[jj]), n=N, rand.gen=function(n, ...) rnorm(n, 0, sigma))
p5 <- p5 + (Box.test(x, lag=5, type="Ljung")$p.value < alpha)
p20 <- p20 + (Box.test(x, lag=20, type="Ljung")$p.value < alpha)
}
## correct rate
res[jj, "pv5"] <- 100 * p5 / nrep
res[jj, "pv20"] <- 100 * p20 / nrep
}
##print(res, quote=F)
knitr::kable(res)| b | pv5 | pv20 |
|---|---|---|
| 0.001 | 4.8 | 5.3 |
| 0.100 | 25.8 | 15.8 |
| 0.150 | 57.5 | 35.2 |
| 0.200 | 87.5 | 61.9 |
| 0.300 | 100.0 | 96.8 |
| 0.500 | 100.0 | 100.0 |
| 0.800 | 100.0 | 100.0 |
| 0.900 | 100.0 | 100.0 |
关于\(\hat\chi^2(m)\)中项数\(m\)的选取: \(m=5\)比\(m=20\)有效。 注意以ARMA模型为例,当\(k\)较大时\(\rho_k\)已经很小, 所以\(\hat\rho_k^2\)贡献不大, 取太大的\(m\)容易使检验不敏感。
17.2 样本自相关置信区间检验法
当\(\{X_t\}\)为独立同分布白噪声时 \(\sqrt{N}(\hat\rho_1, \hat\rho_2, \dots, \hat\rho_m)\) 近似\(m\)维标准正态分布。 \[\Pr(\sqrt{N}|\hat\rho_k| > 1.96) \approx 0.05 \] 如果超过\(5\%\)的\(|\hat\rho_j| \geq 1.96/\sqrt{n}\) 可否定\(H_0: \{X_t\}\)为独立同分布白噪声。 与\(\chi^2\)检验理由类似,\(m\)不应取太大。
对WN(0,1)的检验通常不显著,检验成功。 对MA(1)的检验如果取\(m=20\)则很可能不显著, 使检验失败, 因为一般只有\(\hat\rho_1\)超过界限。 对AR的检验一般是显著的,检验成功,因为其相关系数不截尾。
下面模拟演示。
白噪声的ACF:
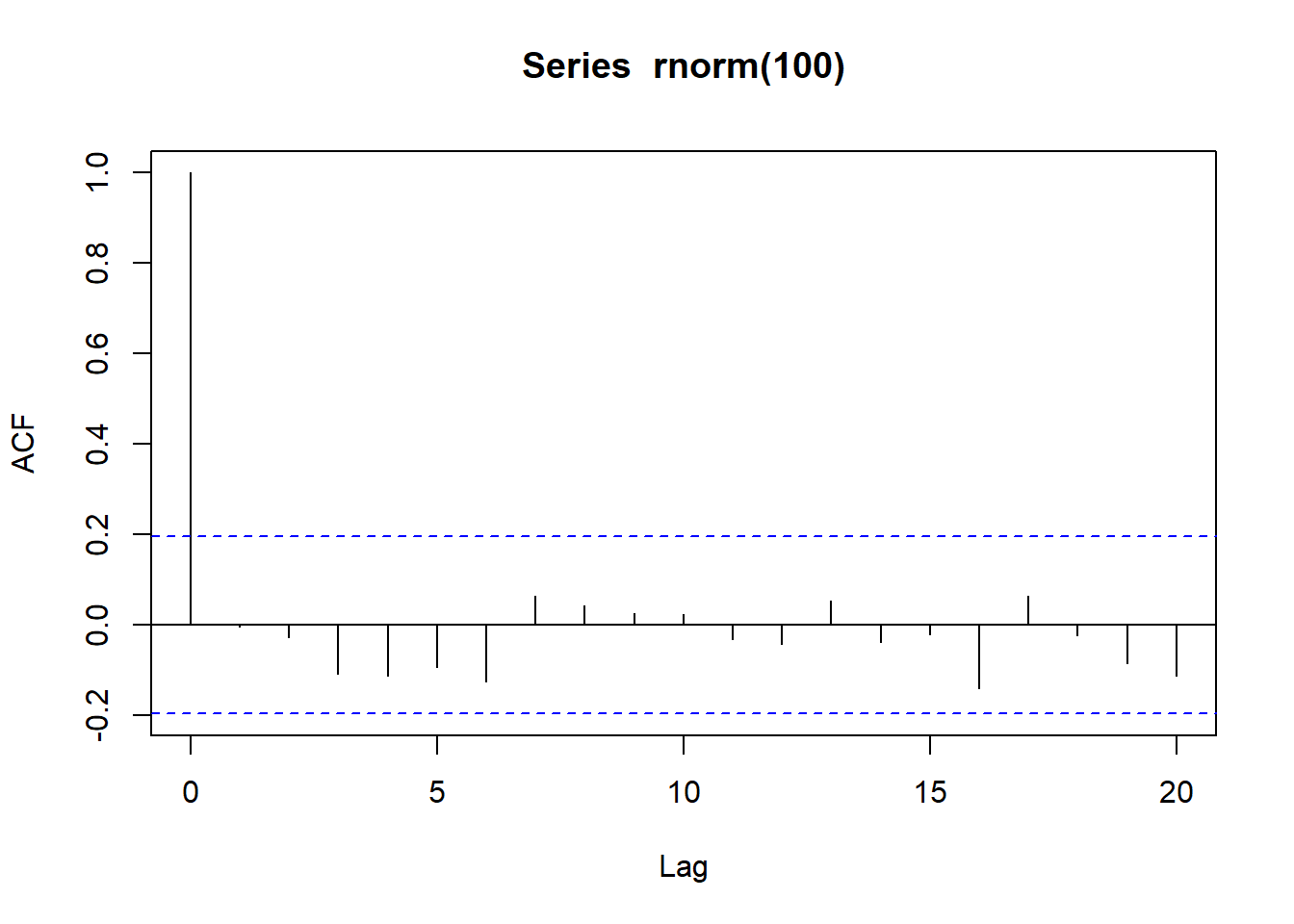
MA(1)当\(b=0.5\)时的ACF:
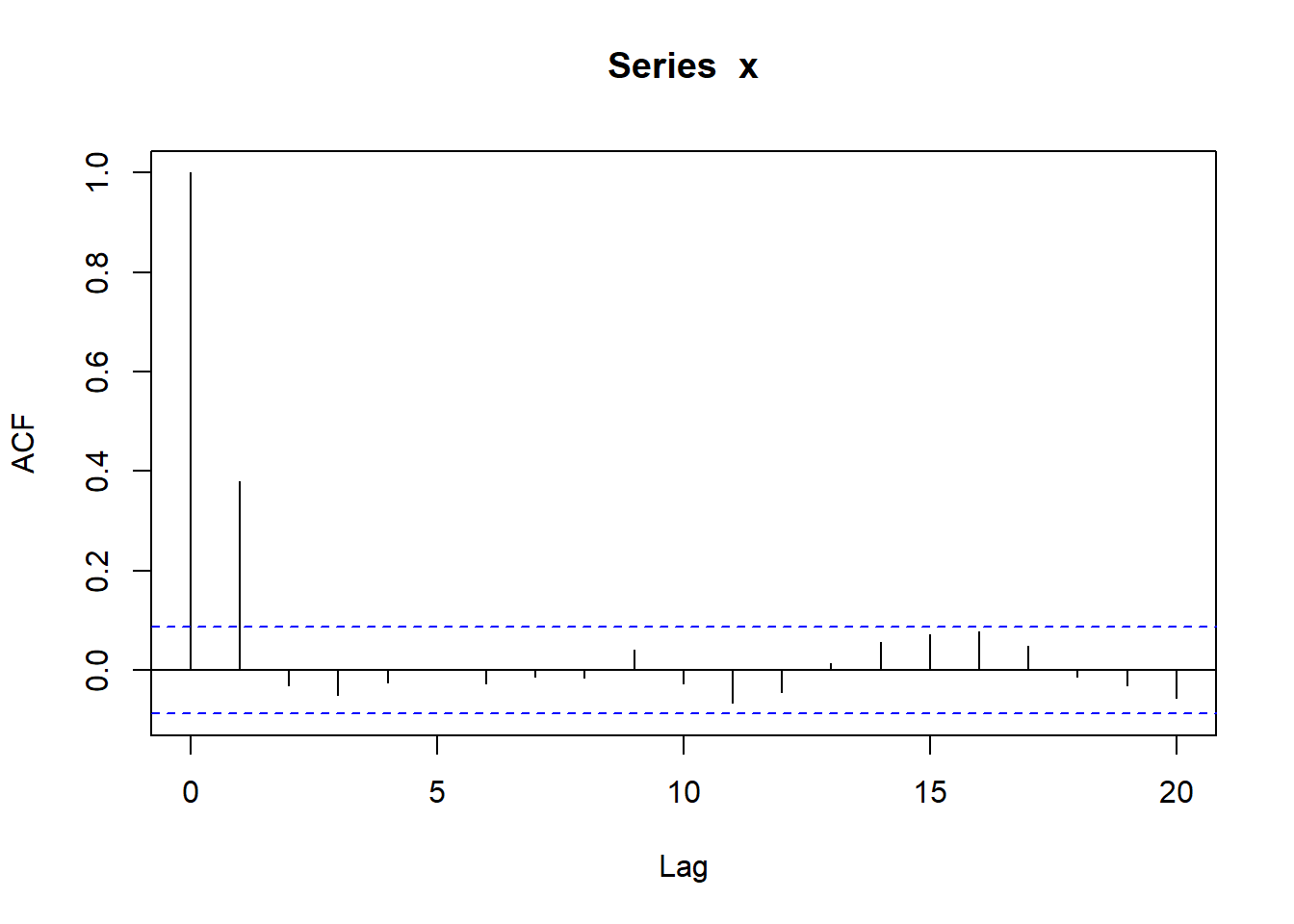
\(\hat\rho_1\)到\(\hat\rho_{20}\)中只有\(\hat\rho_1\)超界。 不能拒绝白噪声假设。
AR(1)当\(a = 0.5\)时的ACF:
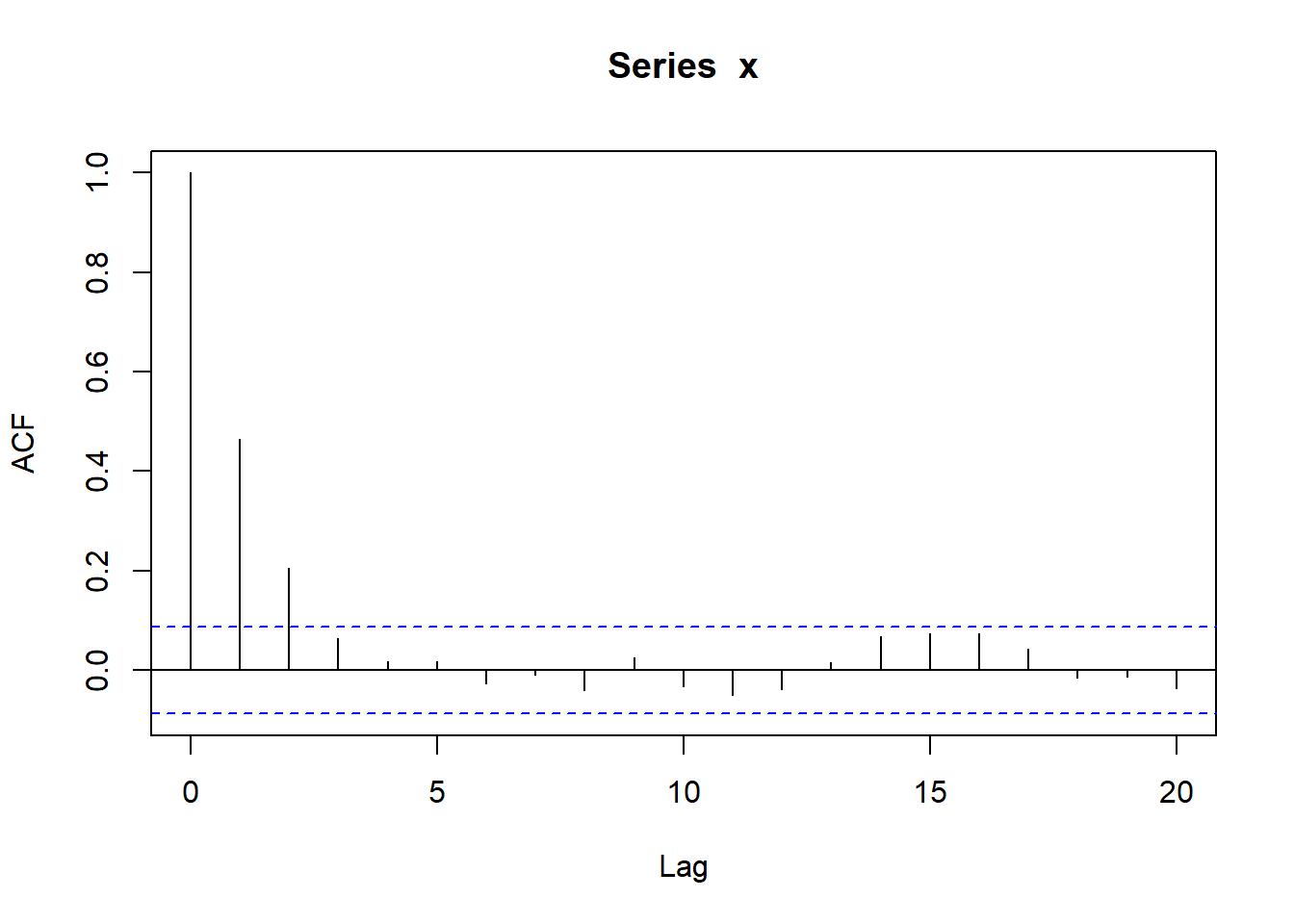
\(\hat\rho_1\)和\(\hat\rho_2\)都明显超界。
利用\(\sqrt{N}(\hat\rho_1, \hat\rho_2,\dots,\hat\rho_m)\)近似独立标准正态做白噪声检验不如卡方检验, 因为利用标准正态检验仅看超界的个数, 而卡方检验还查看超界的量。 在查看ACF时,如果某个\(\hat\rho_k\)超界较多, 也应怀疑非白噪声。
17.3 白噪声卡方检验的自由度调整
如果输入的序列\(\{X_t \}\)是原始序列, 计算Box-Pierce统计量或者Ljung-Box统计量, 在白噪声零假设下统计量近似服从\(\chi^2(m)\)分布。
自定义的Ljung-Box统计量计算函数:
LB_stat <- function(x, m = round(log(lenth(x)))){
if(m < 1) m <- 1
x <- as.vector(x)
n <- length(x)
rhos <- acf(x, lag.max = m, plot = FALSE)$acf[-1]
stat <- n*(n-1)*sum(rhos^2 / (n - (1:m)))
stat
}下面是做一组模拟:
上面是模拟一次并计算LB统计量的函数。
n是样本量,m是卡方统计量中使用的自相关系数的个数,
mean和sd是白噪声的均值和标准差。
写一个重复模拟多次, 计算许多个LB卡方统计量, 并估计卡方统计量自由度的函数:
sim <- function(nrep = 1E4, fun = simwn1, n=1024, m=10){
resm <- replicate(
nrep, fun(n=n, m=m) )
est.df <- mean(resm)
cat("平方和中的项数 = ", m, " 模拟估计自由度 = ", est.df, "\n")
}上述程序中nrep是重复模拟次数,fun是一次模拟的函数。
模拟一万次,估计自由度:
## 平方和中的项数 = 10 模拟估计自由度 = 9.976223如果要检验的数据不是原始数据, 而是ARIMA建模的残差, 则自由度需要减去估计的系数个数(不包括截距项), 而且自由度的误差较大。
下面模拟一个\(\phi_1 = 0.9\)的AR(1)模型, 并重复一万次, 估计LB卡方统计量的实际自由度。 AR(1)的系数\(\phi_1\)可以用\(\rho_1\)估计。
set.seed(101)
simar1 <- function(n = 1024, m = 10, mean = 100, sd = 10){
x <- mean + sd*arima.sim(model = list(ar = c(0.9)), n = n)
phi1 <- acf(x, lag.max=1, plot = FALSE)$acf[2]
resi <- filter(x, c(1, -phi1), method = "convolution", sides = 1)[-1]
LB_stat(resi, m)
}
sim(1E4, fun = simar1)## 平方和中的项数 = 10 模拟估计自由度 = 9.151771可见模拟得到的自由度估计近似等于平方和中项数减去模型系数个数, 但误差较大, 而且系数个数中不计入截距项或者序列均值。
下面模拟一个ARMA(2,1)的残差白噪声检验。 自由度应该减去3。
set.seed(101)
simarma21 <- function(
n = 1024, m = 10,
mean = 100, sd = 10){
x <- mean + sd*arima.sim(
model = list(ar = c(1.6, -0.64), ma=c(0.4)),
n = n)
mod <- arima(x, order=c(2,0,1), include.mean=TRUE)
resi <- residuals(mod)
LB_stat(resi, m)
}
sim(1E4, fun = simarma21)
## 平方和中的项数 = 10 模拟估计自由度 = 7.272344 在讨论条件异方差问题时, 可以对ARMA模型的残差的平方进行白噪声检验。 这时,检验统计量的自由度也需要调整吗? 略修改上面的ARMA(2,1)模拟检验程序进行探索:
set.seed(101)
simarma21B <- function(
n = 1024, m = 10,
mean = 100, sd = 10){
x <- mean + sd*arima.sim(
model = list(ar = c(1.6, -0.64), ma=c(0.4)),
n = n)
mod <- arima(x, order=c(2,0,1), include.mean=TRUE)
resi2 <- as.vector(residuals(mod))^2
LB_stat(resi2, m)
}
sim(1E4, fun = simarma21B)
## 平方和中的项数 = 10 模拟估计自由度 = 9.862679从这个模拟看出, 一旦对ARMA的残差计算了平方, 再计算LB检验就不需要调整自由度了。