28 谱估计
28.1 平稳序列的周期图
周期图是估计谱密度的基础。 对零均值平稳序列的观测\(x_1, x_2, \dots, x_N\),记 \[\begin{aligned} \bar x =& \frac1N \sum x_k, \\ \hat\gamma_k =& \frac1N \sum_{t=1}^{N-k} (x_t - \bar x)(x_{t+k} - \bar x), \\ \hat\gamma_{-k} =& \hat\gamma_k, k=0,1,\dots, N-1, \\ \tilde f(\lambda) =& \frac{1}{2\pi}\sum_{k=-N+1}^{N-1} \hat\gamma_k e^{-ik\lambda}. \end{aligned}\] 记 \[\begin{aligned} J_N(\lambda) = \frac{1}{2\pi N} \left| \sum_{k=1}^N (x_k - \bar x) e^{-ik\lambda} \right|^2, \quad \lambda \in [-\pi, \pi] \end{aligned}\]
引理28.1 \[\begin{aligned} \tilde f(\lambda) = J_N(\lambda). \end{aligned}\]
证明: 记\(y_t = (x_t - \bar x) e^{-i t \lambda}\), \(t=1,2,\dots,N\), 用\(\boldsymbol 1\)表示元素都是1的\(N\)维向量。 则 \[\begin{aligned} J_N(\lambda) =& \frac{1}{2\pi N} \sum_{j=1}^N \sum_{k=1}^N (x_k - \bar x)(x_j - \bar x) e^{-i (k-j) \lambda} \\ =& \frac{1}{2\pi N} \sum_{j=1}^N \sum_{k=1}^N y_k \bar y_j \\ =& \frac{1}{2\pi N} \boldsymbol 1^T \left(\begin{array}{cccc} y_1 \bar y_1 & y_1 \bar y_2 & \cdots & y_1 \bar y_N \\ y_2 \bar y_1 & y_2 \bar y_2 & \cdots & y_2 \bar y_N \\ \vdots & \vdots & & \vdots \\ y_N \bar y_1 & y_N \bar y_2 & \cdots & y_N \bar y_N \end{array}\right) \boldsymbol 1 \\ =& \frac{1}{2\pi}( \hat\gamma_0 + \hat\gamma_1 e^{i\lambda} + \dots + \hat\gamma_{N-1} e^{i(N-1)\lambda} \\ & + \hat\gamma_1 e^{-i\lambda} + \dots + \hat\gamma_{N-1} e^{-i(N-1)\lambda}) \\ =& \tilde f(\lambda) \end{aligned}\]
定义Fourier频率点为 \[\begin{aligned} \lambda_j = \frac{2\pi j}{N}, j=1,2,\dots,N-1. \end{aligned}\] 记 \[\begin{aligned} I_N(\lambda) = \frac{1}{2\pi N} \left| \sum_{k=1}^N x_k e^{-ik\lambda} \right|^2, \end{aligned}\] 由于 \[\begin{aligned} \sum_{k=1}^N e^{-ik\lambda} = \frac{1 - e^{-iN\lambda}}{1 - e^{-i\lambda}} e^{-i\lambda} \end{aligned}\] 和\(e^{-iN\lambda_j} = e^{-i2\pi j} = 1\)得\(\sum_{k=1}^N e^{-ik\lambda_j} = 0\)。 所以在Fourier频率点上 \[\begin{aligned} I_N(\lambda_j) = J_N(\lambda_j), j=1,2,\dots, N-1. \end{aligned}\]
定义28.1 (周期图) \(I_N(\lambda)\)称为观测数据的周期图。
定理28.1 对于零均值时间序列的观测值\(x_1, x_2, \dots, x_N\), 若定义 \[\begin{align} \hat\gamma_{\pm k} = \frac{1}{N} \sum_{t=1}^{N-k} x_t x_{t+k}, \quad k=0,1,\dots, N-1 \tag{28.1} \end{align}\] 则 \[\begin{align} I_N(\lambda) = \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \hat\gamma_k e^{-ik\lambda}, \quad \lambda \in [-\pi,\pi]. \tag{28.2} \end{align}\]
定理28.2 (周期图的渐近无偏性) 如果零均值平稳序列\(\{X_t\}\)的自协方差函数绝对可和: \[ \sum_{k=1}^{\infty} |\gamma_k| < \infty \] 则\(I_N(\lambda)\)是谱密度\(f(\lambda)\)的渐近无偏估计: \[\begin{aligned} E I_N(\lambda) \to f(\lambda), \quad N \to \infty. \end{aligned}\]
证明: \[\begin{aligned} E I_N(\lambda) =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} E \hat\gamma_k e^{-ik\lambda} \quad(\text{这里}\hat\gamma_k\text{按不减去均值的公式定义}) \\ =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \frac{N-|k|}{N} \gamma_k e^{-ik\lambda} \\ =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \gamma_k e^{-ik\lambda} - \frac{1}{2\pi N} \sum_{k=-N+1}^{N-1} |k| \gamma_k e^{-ik\lambda} \\ \to& \frac{1}{2\pi} \sum_{k=-\infty}^{\infty} \gamma_k e^{-ik\lambda} \\ & \quad(\text{由Kronecker引理及}\{\gamma_k \}\text{绝对可和知后一项趋于零}) \\ =& f(\lambda) \end{aligned}\] 最后一个等式用到了定理9.1。
○○○○○○
下面的定理说明, \(I_N(\lambda)\)不是\(f(\lambda)\)的相合估计。
定理28.3 设\(\{\varepsilon_t\}\)是独立同分布的WN(\(0,\sigma^2\)), 实数列\(\{c_j\}\)满足 \[ \sum_{j=0}^\infty j |c_j| < \infty \] 线性平稳列 \[\begin{align} X_t = \sum_{j=0}^\infty c_j \varepsilon_{t-j} \tag{28.3} \end{align}\] \(I_N(\lambda)\)为\(X_1,X_2,\dots,X_N\)的周期图, \(f(\lambda)\)为\(\{X_t\}\)的谱密度, 则 \[\begin{align} \limsup_{N\to\infty} \frac{1}{\ln\ln N} I_N(\lambda) = \begin{cases} f(\lambda), & \lambda \neq 0,\pi \\ 2f(\lambda), & \lambda=0,\pi, \end{cases} \text{a.s.} \tag{28.4} \end{align}\]
定理说明\(|I_N(\lambda) - f(\lambda)|\)不趋于零。
例28.1 设\(\{X_t\}\)为标准正态白噪声。 其谱密度\(f(\lambda) = \frac{1}{2\pi}\)。 \(\frac{1}{\sqrt{N}} \sum_{j=1}^N X_j \sim \text{N}(0,1)\). \[ I_N(0) = \frac{1}{2\pi}\left(\frac{1}{\sqrt{N}} \sum_{j=1}^N X_j \right)^2 \] 为\(\chi^2_1\)分布的\(\frac{1}{2\pi}\)倍, 与\(N\)无关。
周期图一般不是谱密度的相合估计, 因为使用了所有的\(\hat\gamma_k\), 其中\(k\)接近于\(N-1\)时\(\hat\gamma_k\) 估计偏差很大: \[\begin{aligned} E\hat\gamma_k - \gamma_k = \frac{N-k}N \gamma_k - \gamma_k = -\frac{k}N \gamma_k. \end{aligned}\] 减少使用的\(\hat\gamma_k\)可以改善估计, 称为截断周期图: \[\begin{align} \hat f(\lambda) = \frac{1}{2\pi} \sum_{k=-N_1}^{N_1} \hat\gamma_k e^{-ik\lambda} \tag{28.5} \end{align}\] (\(N_1 < N-1\))
例28.2 AR(2)序列的周期图和截断周期图。 \[ X_t = 0.1132 X_{t-1} - 0.64 X_{t-2} + \varepsilon_t, \ \varepsilon_t \sim \text{WN}(0,4) \] 理论谱密度为 \[ f(\lambda) = \frac{4}{2\pi} \frac{1}{\left| 1 - 0.1132 e^{-i\lambda} + 0.64 e^{-i2\lambda} \right|^2} \] 产生模拟数据(长度\(N=123\)), 将理论谱密度、周期图、截断周期图与极大熵谱估计对比作图。 取\(N_1=\sqrt{N}\)。
direct.periodogram <- function(y, freqs=seq(0,pi,length=101),
demean=FALSE){
N <- length(y)
if(demean) y <- y - mean(y)
II <- numeric(length(freqs))
for(j in seq(along=freqs)){
II[j] <- 1/(2*pi*N)*Mod(sum(y * complex(mod=1, arg=freqs[j]*seq(1,N))))^2
}
list(frequencies=freqs, spectrum=II)
}
## AR theoretical spectrum given AR coefficients
ar.true.spectrum <- function(a, ngrid=256, sigma=1, plot.it=TRUE){
p <- length(a)
freqs <- seq(from=0, to=pi, length=ngrid)
spec <- numeric(ngrid)
for(ii in seq(ngrid)){
spec[ii] <- 1 - sum(complex(mod=a, arg=freqs[ii]*seq(p)))
}
spec = sigma^2 / (2*pi) / abs(spec)^2
if(plot.it){
plot(freqs, spec, type='l',
main="AR True Spectral Density",
xlab="frequency", ylab="spectrum",
axes=FALSE)
axis(2)
axis(1, at=(0:6)/6*pi,
labels=c(0, expression(pi/6),
expression(pi/3), expression(pi/2),
expression(2*pi/3), expression(5*pi/6), expression(pi)))
}
list(frequencies=freqs, spectrum=spec,
ar.coefficients=a, sigma=sigma)
}
demo.ar.pdg <- function(seed=7){
set.seed(seed)
N <- 120
a <- c(0.1132, -0.64)
y <- arima.sim(list(ar=a), n=N)*2
## 理论谱密度
ft <- function(lambda){
4 / (2*pi) / Mod(1 - complex(mod=0.113, arg=-lambda)
+ complex(mod=0.64, arg=-2*lambda))^2
}
lams <- seq(0, pi, length=201)
spec0 <- ft(lams)
## 周期图
spec1 <- direct.periodogram(y, freqs=lams, demean=FALSE)$spectrum
## 截断周期图
N1 <- round(sqrt(N))
gams <- c(acf(y, lag.max=N1,
type="covariance", plot=FALSE)$acf)
spec2 <- numeric(length(lams))
for(j in seq(along=lams))
spec2[j] <- 1/(2*pi)*(gams[1] +
2*sum(gams[2:(N1+1)] *
cos(-seq(N1)*lams[j])))
## AR模型
arr <- ar(y)
spec3 <- ar.true.spectrum(arr$ar, ngrid=length(lams),
sigma=sqrt(arr$var.pred),
plot.it=FALSE)$spectrum
plot(lams, spec0, lwd=3, type="l",
ylim=c(0,10),
main="Periodogram of an AR(2) series",
xlab="frequency", ylab="")
lines(lams, spec1, col="red", lwd=2, lty=3)
lines(lams, spec2, col="cyan", lwd=2, lty=2)
lines(lams, spec3, col="green", lwd=2, lty=4)
legend("topright", lwd=c(3,2,2,2), lty=c(1,3,2,4),
col=c("black", "red", "cyan", "green"),
legend=c("True", "Periodogram", "Truncated-pdg", "AR Model"))
}
demo.ar.pdg()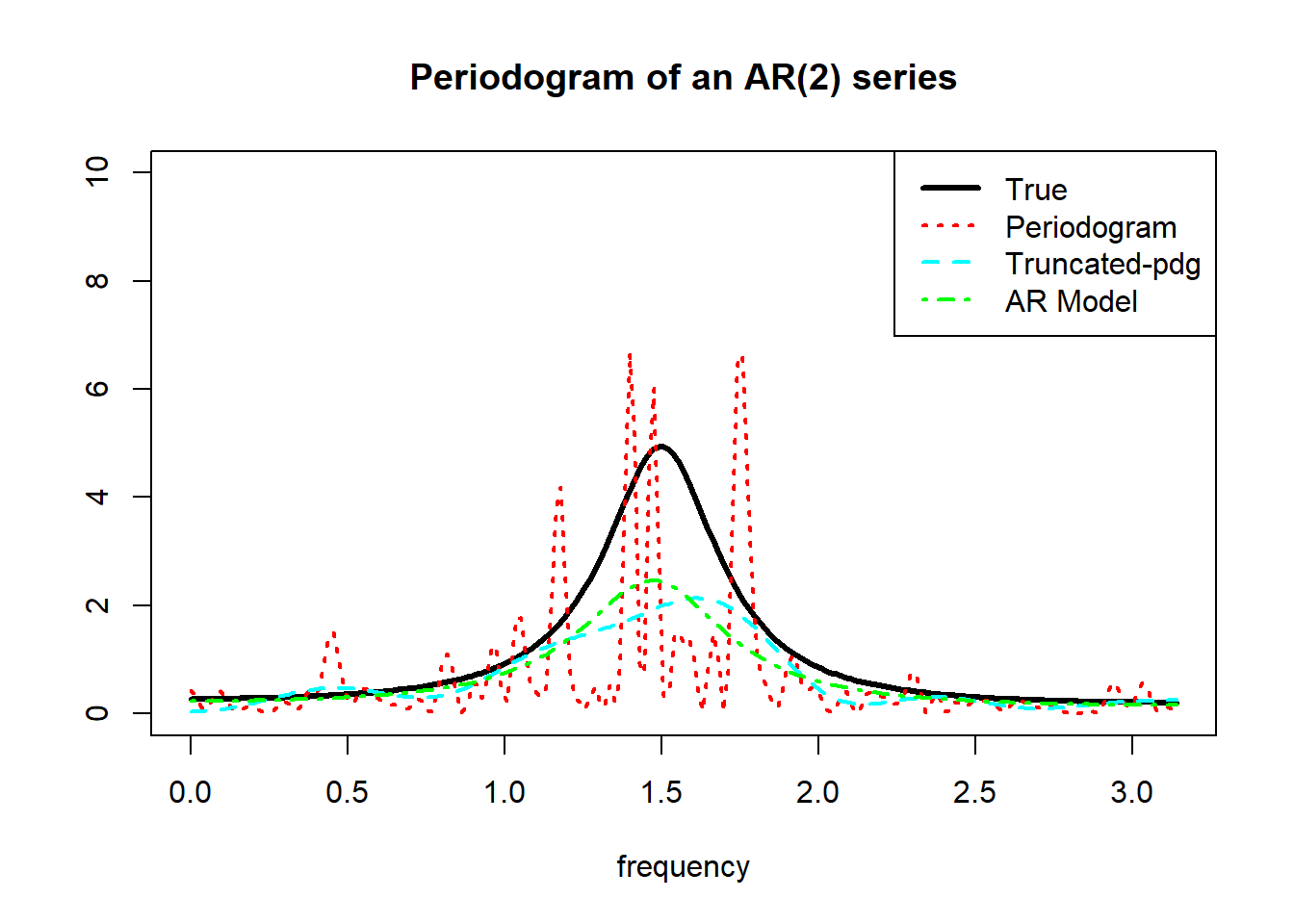
28.2 加窗谱估计
28.2.1 加时窗的谱估计
克服周期图不相合性的经典方法是加窗谱估计。 令 \[\begin{align} \hat f(\lambda) = \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \lambda_N(k) \hat \gamma_k e^{-ik\lambda} \tag{28.6} \end{align}\] 其中\(\lambda_N(k)\)是\(|k|\)的减函数, 称为时窗, 称\(\hat f(\lambda)\)为加时窗窗谱估计, 简称加窗谱估计。
例28.3 取时窗为 \[\begin{aligned} \lambda_N(k) = \begin{cases} 1, & |k| \leq \sqrt{N} \\ 0, & |k| > \sqrt{N} \end{cases} \end{aligned}\] 即为截断周期图估计。
例28.4 MA(\(q\))序列。则谱密度为 \[\begin{aligned} f(\lambda) = \frac{1}{2\pi} \sum_{k=-q}^q \gamma_k e^{-ik\lambda}. \end{aligned}\]
取\(M\geq q\),时窗 \[\begin{aligned} \lambda_N(k) = \begin{cases} 1, & |k| \leq M \\ 0, & |k| > M \end{cases} \end{aligned}\] 加窗谱估计为 \[\begin{aligned} \hat f(\lambda) = \frac{1}{2\pi} \sum_{k=-M}^M \hat\gamma_k e^{-ik\lambda}. \end{aligned}\] 如果\(\{\varepsilon_t\}\)是独立白噪声, 则\(N\to \infty\)时\(\hat\gamma_k \to \gamma_k\), a.s., 有 \[\begin{aligned} \lim_{N\to\infty} \hat f(\lambda) =& \frac{1}{2\pi} \sum_{k=-M}^M \gamma_k e^{-ik\lambda} \\ =& \frac{1}{2\pi} \sum_{k=-q}^q \gamma_k e^{-ik\lambda} = f(\lambda), \quad \text{a.s.} \end{aligned}\] 加窗后\(\hat f(\lambda)\)为\(f(\lambda)\)的强相合估计。
见演示:例3.2(MA(2)截断窗谱估计)。
## MA theoretical spectrum given MA coefficients
ma.true.spectrum <- function(a, ngrid=256, sigma=1,
tit="True MA Spectral Density",
plot.it=TRUE){
p <- length(a)
freqs <- seq(from=0, to=pi, length=ngrid)
spec <- numeric(ngrid)
for(ii in seq(ngrid)){
spec[ii] <- 1 + sum(complex(mod=a, arg=freqs[ii]*seq(p)))
}
spec = sigma^2 / (2*pi) * abs(spec)^2
if(plot.it){
plot(freqs, spec, type='l',
main=tit,
xlab="frequency", ylab="spectrum",
axes=FALSE)
axis(2)
axis(1, at=(0:6)/6*pi,
labels=c(0, expression(pi/6),
expression(pi/3), expression(pi/2),
expression(2*pi/3), expression(5*pi/6), expression(pi)))
box()
}
list(frequencies=freqs, spectrum=spec,
ma.coefficients=a, sigma=sigma)
}
### 截断时窗谱估计
spec.rect <- function(y, freqs=seq(0,pi,length=101),
M = round(2*sqrt(length(y))),
demean=FALSE){
N <- length(y)
if(demean) y <- y - mean(y)
spec <- numeric(length(freqs))
gams <- c(acf(y, lag.max=M,
type="covariance", plot=FALSE)$acf)
for(j in seq(along=freqs))
spec[j] <- 1/(2*pi)*(gams[1] +
2*sum(gams[2:(M+1)] *
cos(seq(M)*freqs[j])))
list(frequencies=freqs, spectrum=spec)
}
demo.ma.spec <- function(seed=1,
window=c('truncation', 'Bartlett',
'Daniell', 'Turkey-Hamming',
'Turkey-Hanning',
'Parzen',
'Bartlett-Priestley')){
set.seed(seed)
N <- 100
b <- c(0.0943, -0.4444)
sigma <- 1
y <- arima.sim(list(ma=b), n=N)*sigma
## 理论谱密度
lams <- seq(0, pi, length=201)
res1 <- ma.true.spectrum(b, sigma=sigma, plot.it=FALSE)
lams <- res1$frequencies
spec0 <- res1$spectrum
## 周期图
spec1 <- direct.periodogram(y, freqs=lams, demean=FALSE)$spectrum
## 加窗谱估计
if(window[1]=='truncation'){
spec2 <- spec.rect(y, freqs=lams, M=3, demean=FALSE)$spectrum
} else if(window[1]=='Bartlett'){
spec2 <- spec.Bartlett(y, freqs=lams, M=10, demean=FALSE)$spectrum
} else if(window[1]=='Daniell'){
spec2 <- spec.Daniell(y, freqs=lams, M=6, demean=FALSE)$spectrum
} else if(window[1]=='Turkey-Hamming'){
spec2 <- spec.Turkey(y, freqs=lams, demean=FALSE, M=8, a=0.23)$spectrum
} else if(window[1]=='Turkey-Hanning'){
spec2 <- spec.Turkey(y, freqs=lams, demean=FALSE, M=8, a=0.25)$spectrum
} else if(window[1]=='Parzen'){
spec2 <- spec.Parzen(y, freqs=lams, demean=FALSE, M=10)$spectrum
} else if(window[1]=='Bartlett-Priestley'){
spec2 <- spec.Priestley(y, freqs=lams, demean=FALSE, M=10)$spectrum
}
ylim <- c(0,1.0)
plot(lams, spec0, lwd=3, type="l",
ylim=ylim,
main="MA(2)序列窗谱估计",
xlab="frequency", ylab="")
lines(lams, spec1, col="red", lwd=2, lty=3)
lines(lams, spec2, col="blue", lwd=2, lty=2)
legend("topright", lwd=c(3,2,2), lty=c(1,3,2),
col=c("black", "red", "blue"),
legend=c("True", "Periodogram", paste(window,'window')))
}
demo.ma.spec(window="truncation")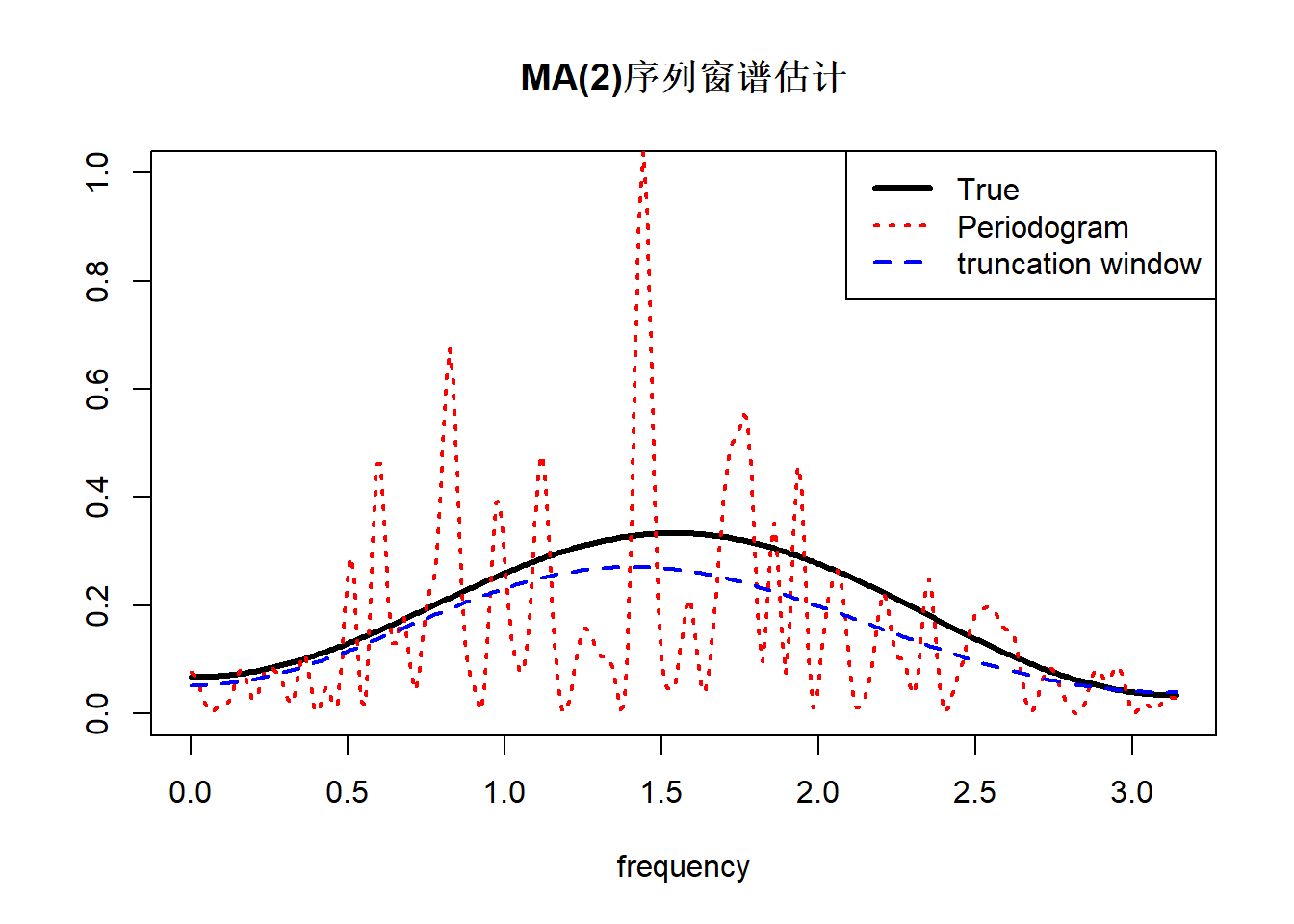
○○○○○○
28.2.2 加谱窗的谱估计
\[\begin{aligned} I_N(\lambda) =& \frac{1}{2\pi N} \left| \sum_{k=1}^N x_k e^{-ik\lambda} \right|^2 \\ =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \hat\gamma_k e^{-ik\lambda} \end{aligned}\] 所以 \[\begin{align} \hat\gamma_k =& \int_{-\pi}^\pi I_N(s) e^{iks} ds, \quad |k| \leq N-1. \tag{28.7} \end{align}\] (其中\(\hat\gamma_k\)使用不减去均值的计算公式)
于是 \[\begin{aligned} \hat f(\lambda) =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \lambda_N(k) \hat\gamma_k e^{-ik\lambda} \\ =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \lambda_N(k) e^{-ik\lambda} \int_{-\pi}^\pi I_N(s) e^{iks} ds \\ =& \int_{-\pi}^\pi I_N(s) \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \lambda_N(k) e^{-ik(\lambda-s)} ds \\ \stackrel{\triangle}{=} & \int_{-\pi}^\pi I_N(s) W_N(\lambda-s) ds, \\ \end{aligned}\] 其中 \[\begin{aligned} W_N(\lambda) \stackrel{\triangle}{=} & \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \lambda_N(k) e^{-ik\lambda} \end{aligned}\]
定义28.2 设\(W_N(\lambda)\)为满足一定要求的权函数, \[\begin{align} \hat f(\lambda) = \int_{-\pi}^\pi I_N(s) W_N(\lambda-s) ds \tag{28.8} \end{align}\] 称为\(f(\lambda)\)的加谱窗谱估计, 简称为加窗谱估计。 权函数\(W_N(\lambda)\)称为谱窗。
加谱窗的谱估计是对周期图用一个权函数做卷积, 取\(W_N(\cdot)\)为偶函数, 在0点最高的钟形曲线, 则加谱窗谱估计是对周期图的局部光滑, 可以克服周期图的不相合性。 直观想法是取小的\(\delta>0\)令 \(W_N(\lambda) = \frac{1}{2\delta}I_{[\lambda-\delta, \lambda+\delta]}\), \(\hat f(\lambda) = \frac{1}{2\delta} \int_{\lambda-\delta}^{\lambda+\delta} I_N(s)ds\)。 更一般的\(W_N(\lambda)\)是其它的局部加权平均方法。
时窗\(\lambda_N(k)\)和谱窗\(W_N(\lambda)\)的关系为 \[\begin{aligned} W_N(\lambda) =& \frac{1}{2\pi} \sum_{k=-N+1}^{N-1} \lambda_N(k) e^{-ik\lambda} \\ \lambda_N(k) =& \int_{-\pi}^\pi W_N(s) e^{iks}ds. \end{aligned}\]
谱窗应有的性质:
- \(\int_{-\pi}^\pi W_N(\lambda) d\lambda = 1\) (等价于\(\lambda_N(0)=1\))。
- \(\int_{-\pi}^\pi W_N^2(\lambda) d\lambda < \infty\);
- \(\forall \varepsilon>0\), \(N\to \infty\)时 \(\sup_{|\lambda|>\varepsilon} W_N(\lambda) \to 0\); (即\(N\to\infty\)时谱窗向着\(\lambda=0\)处集中)
- 对称性: \(W_N(-\lambda) = W_N(\lambda)\);
- 对任何正数\(A\),当\(N \to \infty\)时, \[\begin{aligned} \max_{|\mu| \leq A/N} \left| \frac{ \int_{-\pi}^\pi W_N(\lambda) W_N(\mu + \lambda) d\lambda} {\int_{-\pi}^\pi W_N^2(\lambda) d\lambda} - 1 \right| \to 0. \end{aligned}\] (要求谱窗随\(N \to \infty\)不要变窄太快)
28.2.3 常用谱窗和时窗
28.2.3.1 截断窗
取\(M_N = o(N)\), \(M_N \to \infty\), 比如 \(M_N = A[\sqrt{N}]\), \(A\)取值1到3之间。 截断窗函数: \[\begin{aligned} \lambda_N(k) = \begin{cases} 1, & |k| \leq M_N \\ 0, & |k| > M_N. \end{cases} \end{aligned}\] 谱估计: \[\begin{aligned} \hat f(\lambda) = \frac{1}{2\pi} \sum_{|k| \leq M_N} \hat\gamma_k e^{-ik\lambda} \end{aligned}\] 对应谱窗 \[\begin{aligned} W_N(\lambda) =& \frac{1}{2\pi} \sum_{|k| \leq M_N} e^{-ik\lambda} \\ =& \frac{1}{2\pi} \frac{\sin[(2M_n+1)\lambda/2]}{\sin(\lambda/2)} \stackrel{\triangle}{=} \frac{1}{2\pi} D_{2M_N+1}(\lambda) \end{aligned}\] \(D_{K}(\lambda)\)称为Dirichlet核。 它有正有负。
demo.rect <- function(){
N <- 100
M <- 10
x <- seq(-N, N)
y <- numeric(length(x))
y[abs(x) <= M] <- 1
plot(x, y, type="l", lwd=2,
main=paste("截断窗(N=100,M=10)", sep=""))
abline(h=0)
abline(v=0)
}
demo.rect()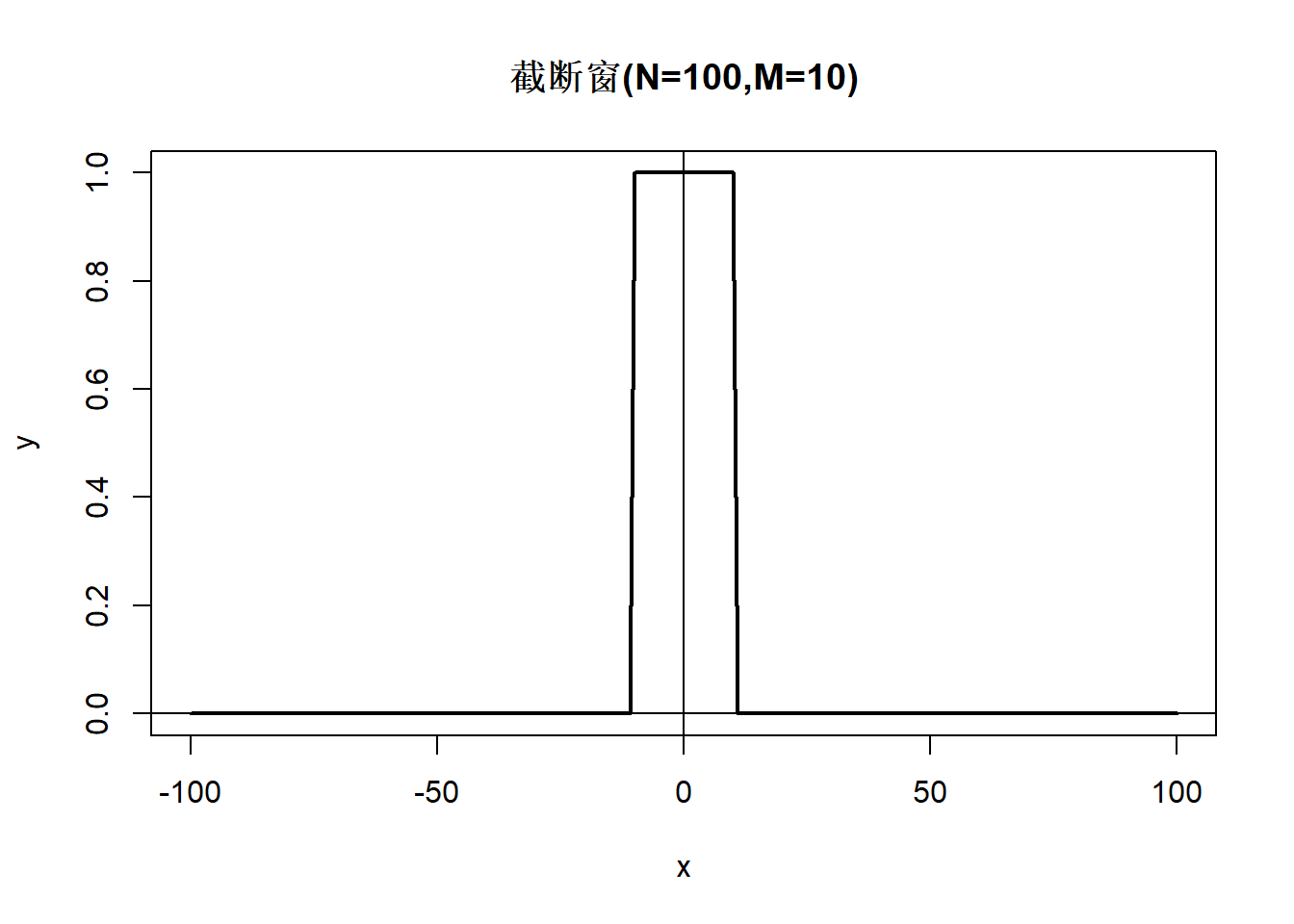
demo.dirichlet <- function(K=11){
x <- seq(-pi, pi, length=300)
y <- 1/(2*pi) * sin(K*x/2) / sin(x/2)
plot(x, y, type="l", lwd=2,
main=paste("Dirichlet_{", K, "} Kernel", sep=""))
abline(h=0)
abline(v=0)
}
demo.dirichlet(21)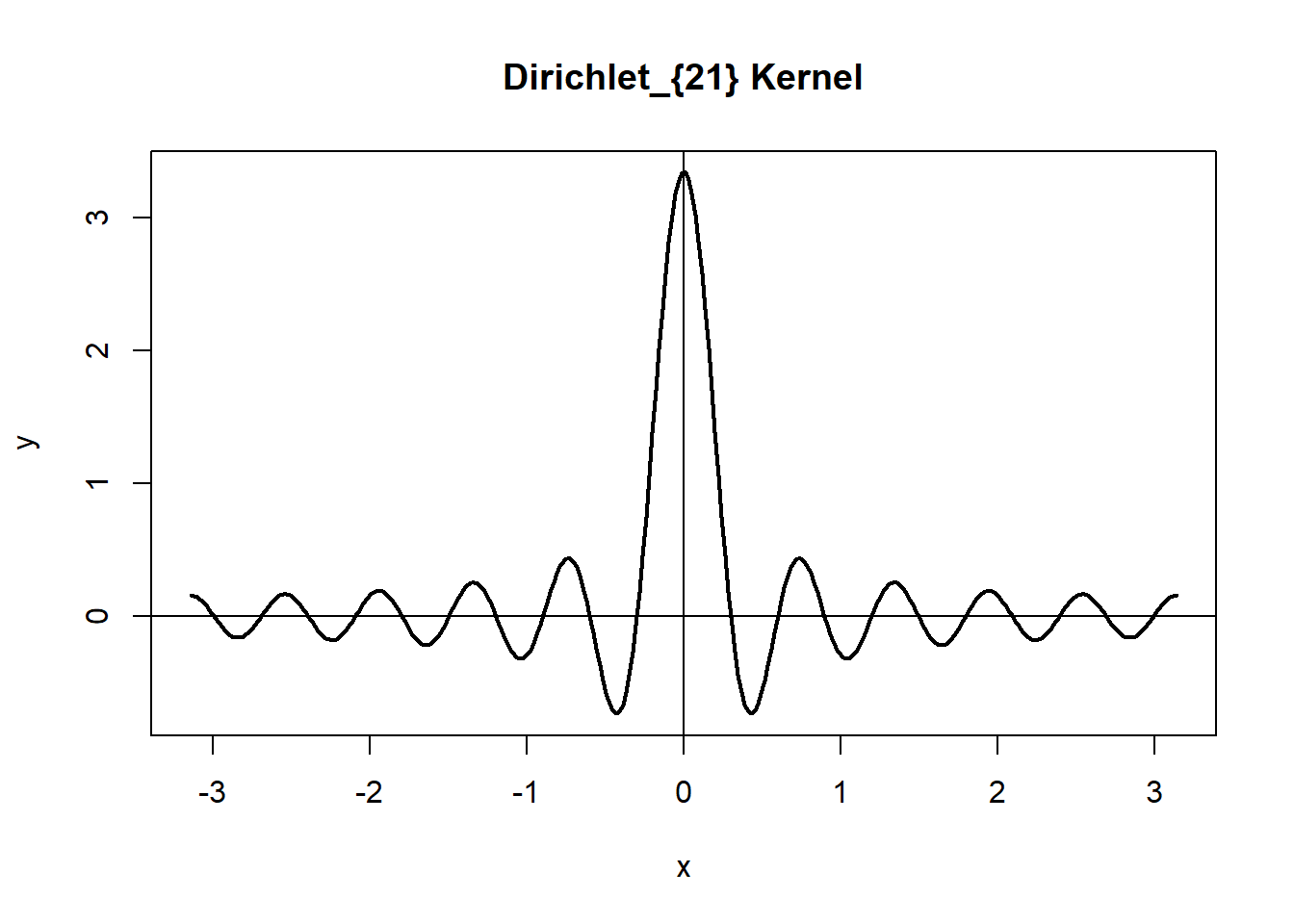
28.2.3.2 Bartlett窗
时窗函数 \[\begin{aligned} \lambda_N(k) = \begin{cases} 1 - \frac{|k|}{M_N}, & |k| \leq M_N \\ 0, & |k| > M_N \end{cases} \end{aligned}\] 谱窗函数 \[\begin{aligned} W_N(\lambda) =& \frac{1}{2\pi} \sum_{|k| \leq M_N} \left( 1 - \frac{|k|}{M_N} \right) e^{-ik\lambda} \\ =& \frac{1}{2\pi M_N} \left( \frac{\sin(M_N \lambda/2)}{\sin(\lambda/2)} \right)^2 \stackrel{\triangle}{=} F_{M_N}(\lambda) \end{aligned}\] \(F_{M_N}(\lambda)\)称为Fejer核。是全非负的。
demo.tri <- function(){
N <- 100
M <- 10
x <- seq(-N, N)
y <- numeric(length(x))
y[abs(x) <= M] <- 1 - abs(x[abs(x) <= M])/M
plot(x, y, type="l", lwd=2,
main=paste("Bartlett窗(N=100,M=10)", sep=""))
abline(h=0)
abline(v=0)
}
demo.tri()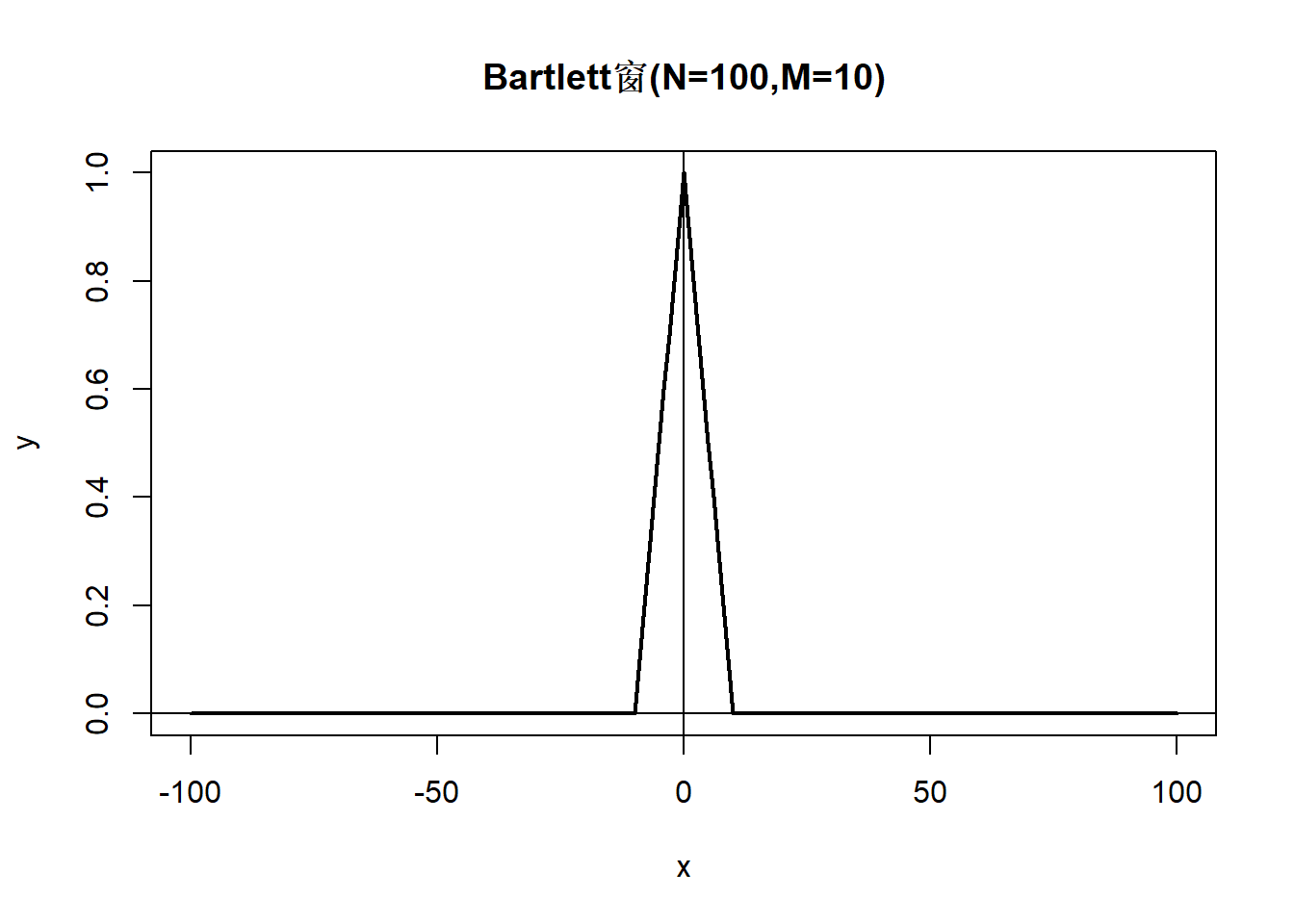
demo.fejer <- function(K=10){
x <- seq(-pi, pi, length=300)
y <- 1/(2*pi *K) * (sin(K*x/2) / sin(x/2))^2
plot(x, y, type="l", lwd=2,
main=paste("Fejer_{", K, "} Kernel", sep=""))
abline(h=0)
abline(v=0)
}
demo.fejer()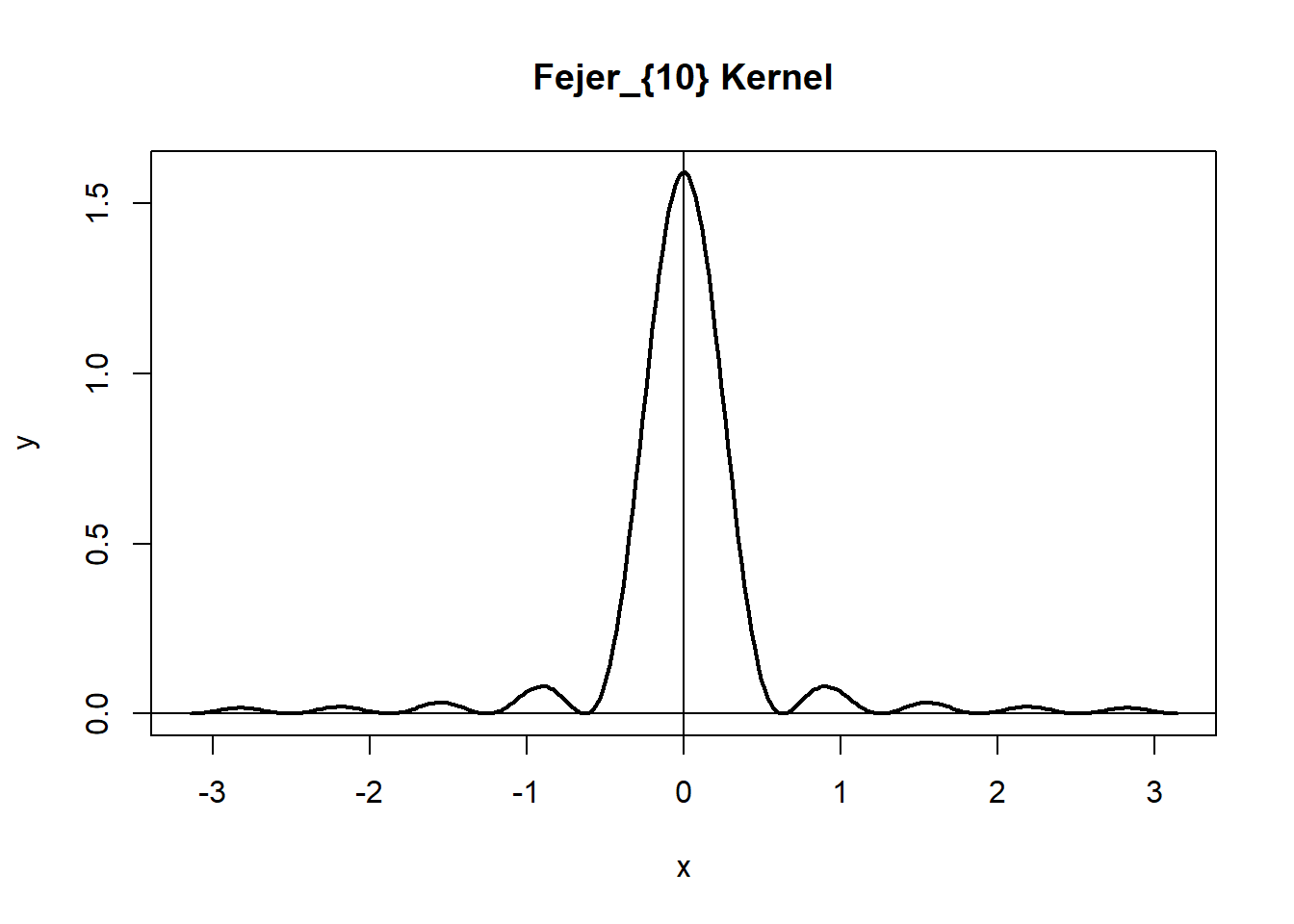
28.2.3.3 Daniell窗
谱窗函数: \[\begin{aligned} W_N(\lambda) = \begin{cases} \frac{M_N}{2\pi}, & |\lambda| \leq \frac{\pi}{M_N}, \\ 0, & |\lambda| > \frac{\pi}{M_N}. \end{cases} \end{aligned}\] 谱估计 \[\begin{aligned} \hat f(\lambda) = \frac{M_N}{2\pi} \int_{\lambda - \frac{\pi}{M_N}}^{\lambda + \frac{\pi}{M_N}} I_N(s) ds \end{aligned}\] 是\(I_N(s)\)在\([\lambda - \frac{\pi}{M_N}, \lambda + \frac{\pi}{M_N}]\) 的平均。 对应的时窗函数为 \[\begin{aligned} \lambda_N(k) = \sin\frac{k\pi}{M_N} / \frac{k\pi}{M_N}. \end{aligned}\]
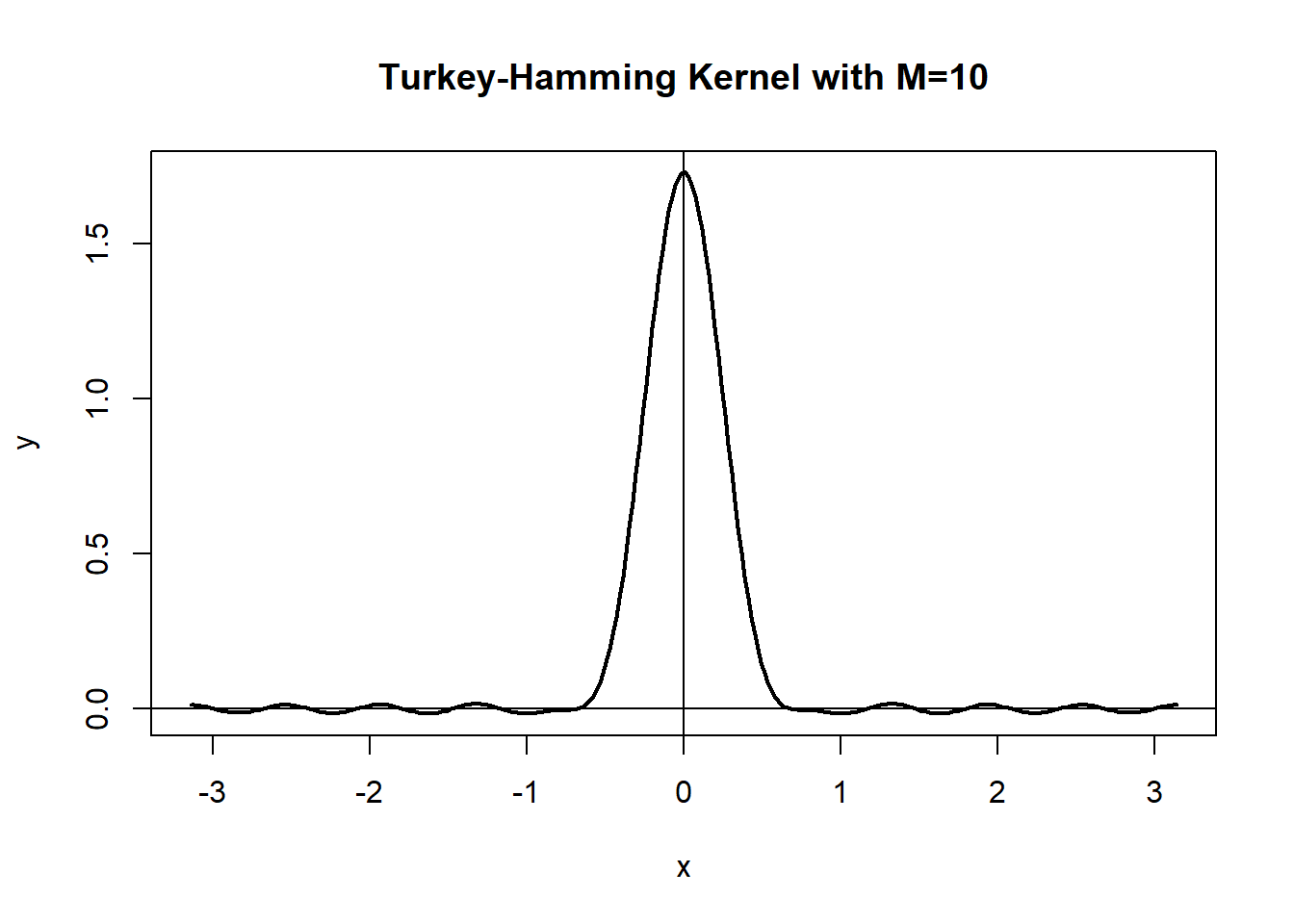
28.2.3.4 Turkey窗
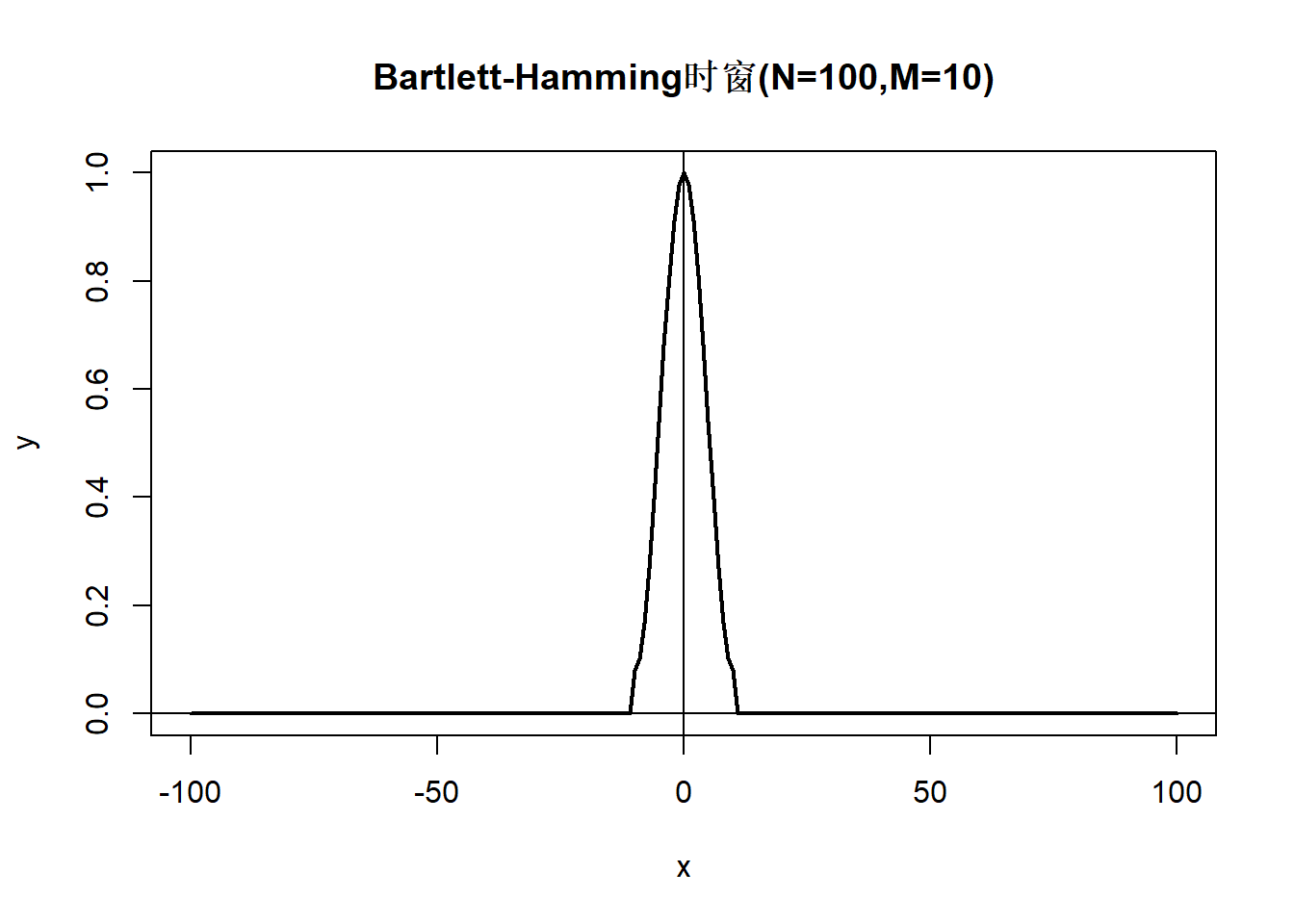
时窗函数为 \[\begin{aligned} \lambda_N(k) = \begin{cases} 1 - 2a + 2a \cos\frac{k\pi}{M_N}, & |k| \leq M_N, \\ 0, & |k| > M_N. \end{cases} \end{aligned}\] \(a \in (0, 0.25]\). \(a=0.25\)称为Turkey-Hanning窗, \(a=0.23\)称为Turkey-Hamming窗。 对应谱窗函数为 \[\begin{aligned} W_N(\lambda) =& a D(\lambda - \frac{\pi}{M_N}) + (1 - 2a)D(\lambda) + a D(\lambda + \frac{\pi}{M_N}), \\ D(\lambda) \stackrel{\triangle}{=} & \frac{\sin[ (2M_N+1)\lambda/2]}{2\pi \sin(\lambda/2)} \end{aligned}\] 谱窗有负值。
demo.turkey.t <- function(){
N <- 100
M <- 10
x <- seq(-N, N)
y <- numeric(length(x))
a <- 0.25 # Hanning
y[abs(x) <= M] <- 1 - 2*a + 2*a*cos(x[abs(x) <= M]*pi/M)
plot(x, y, type="l", lwd=2,
main=paste("Bartlett-Hanning时窗(N=100,M=10)", sep=""))
abline(h=0)
abline(v=0)
a <- 0.23 # Hamming
y[abs(x) <= M] <- 1 - 2*a + 2*a*cos(x[abs(x) <= M]*pi/M)
plot(x, y, type="l", lwd=2,
main=paste("Bartlett-Hamming时窗(N=100,M=10)", sep=""))
abline(h=0)
abline(v=0)
}
demo.turkey.t()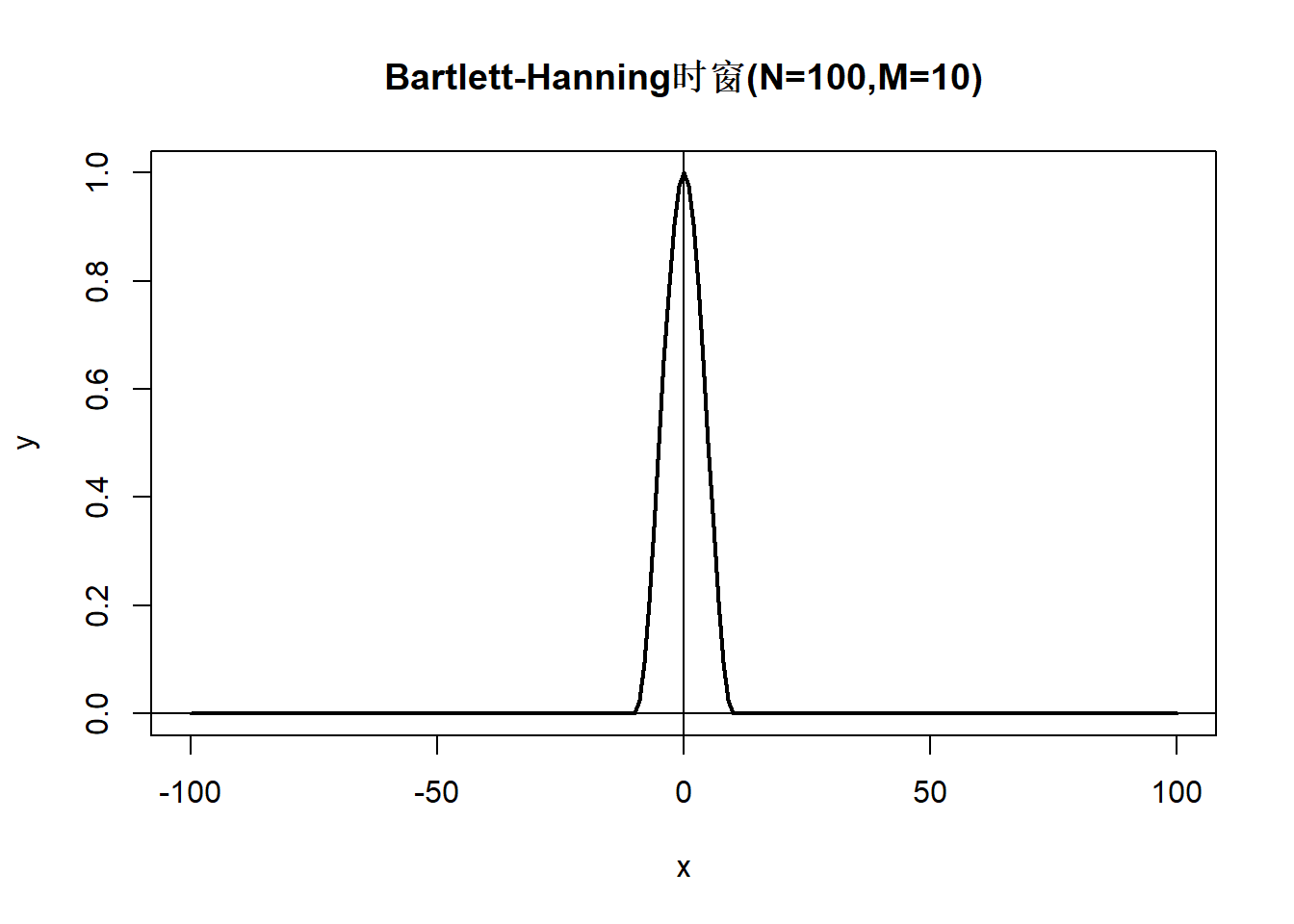
demo.turkey <- function(a = 0.25, M=10){
x <- seq(-pi, pi, length=300)
D <- function(x) 1/(2*pi) * sin((2*M+1)*x/2) / sin(x/2)
y = a*D(x - pi/M) + (1-2*a)*D(x) + a*D(x + pi/M)
if(a==0.25){
tit <- paste("Turkey-Hanning Kernel with M=", M, sep="")
} else if(a==0.23){
tit <- paste("Turkey-Hamming Kernel with M=", M, sep="")
} else {
tit <- paste("Turkey Kernel with M=", M, " a=", a, sep="")
}
plot(x, y, type="l", lwd=2, main=tit)
abline(h=0)
abline(v=0)
}
demo.turkey(a=0.25)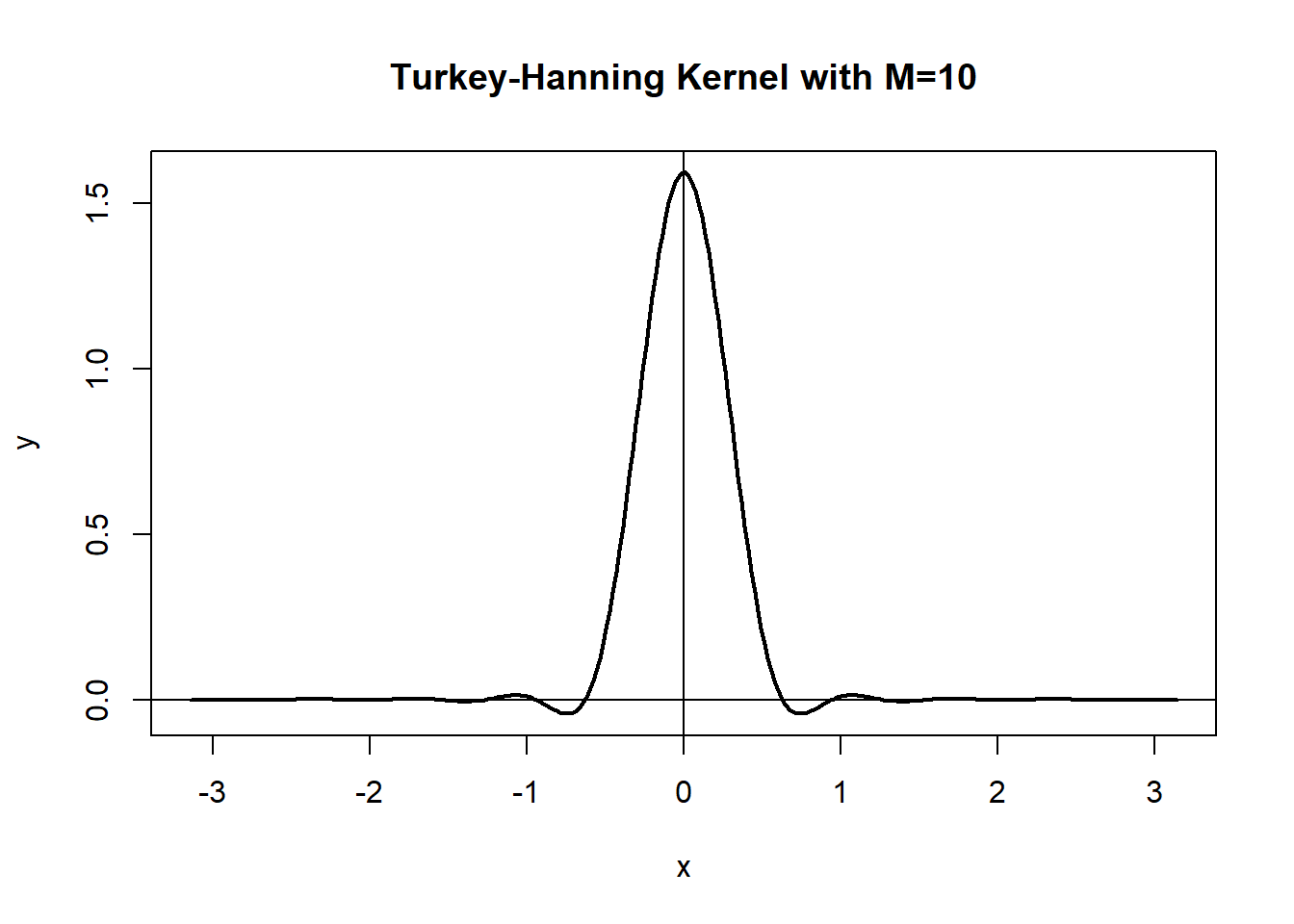
28.2.3.5 Parzen窗
时窗函数为 \[\begin{aligned} \lambda_N(k) = \begin{cases} 1 - 6(k/M_N)^2 + 6(|k|/M_N)^3, & |k| \leq M_N/2, \\ 2(1 - |k|/M_N)^3, & M_N/2<k \leq M_N, \\ 0, & |k| > M_N. \end{cases} \end{aligned}\] 对应谱窗函数为 \[\begin{aligned} W_N(\lambda) = \frac{3}{8\pi M_N^3} \left( \frac{\sin(M_N \lambda / 4)}{\sin(\lambda/2)/2} \right)^4 \left(1 - \frac{2}{3} \sin^2 \frac{\lambda}{2} \right). \end{aligned}\] 谱窗非负。 Parzen窗在这几个加窗谱估计中估计方差最小。
demo.parzen.t <- function(){
N <- 100
M <- 10
M1 <- M/2
x <- seq(-N, N)
y <- numeric(length(x))
a <- 0.25 # Hanning
sele <- abs(x)<=M1
y[sele] <- 1 - 6*(x[sele]/M)^2 + 6*(abs(x[sele]/M)^3)
sele <- abs(x)>M1 & abs(x) <= M
y[sele] <- 2*(1 - abs(x[sele])/M)^3
plot(x, y, type="l", lwd=2,
main=paste("Parzen时窗(N=100,M=10)", sep=""))
abline(h=0)
abline(v=0)
}
demo.parzen.t()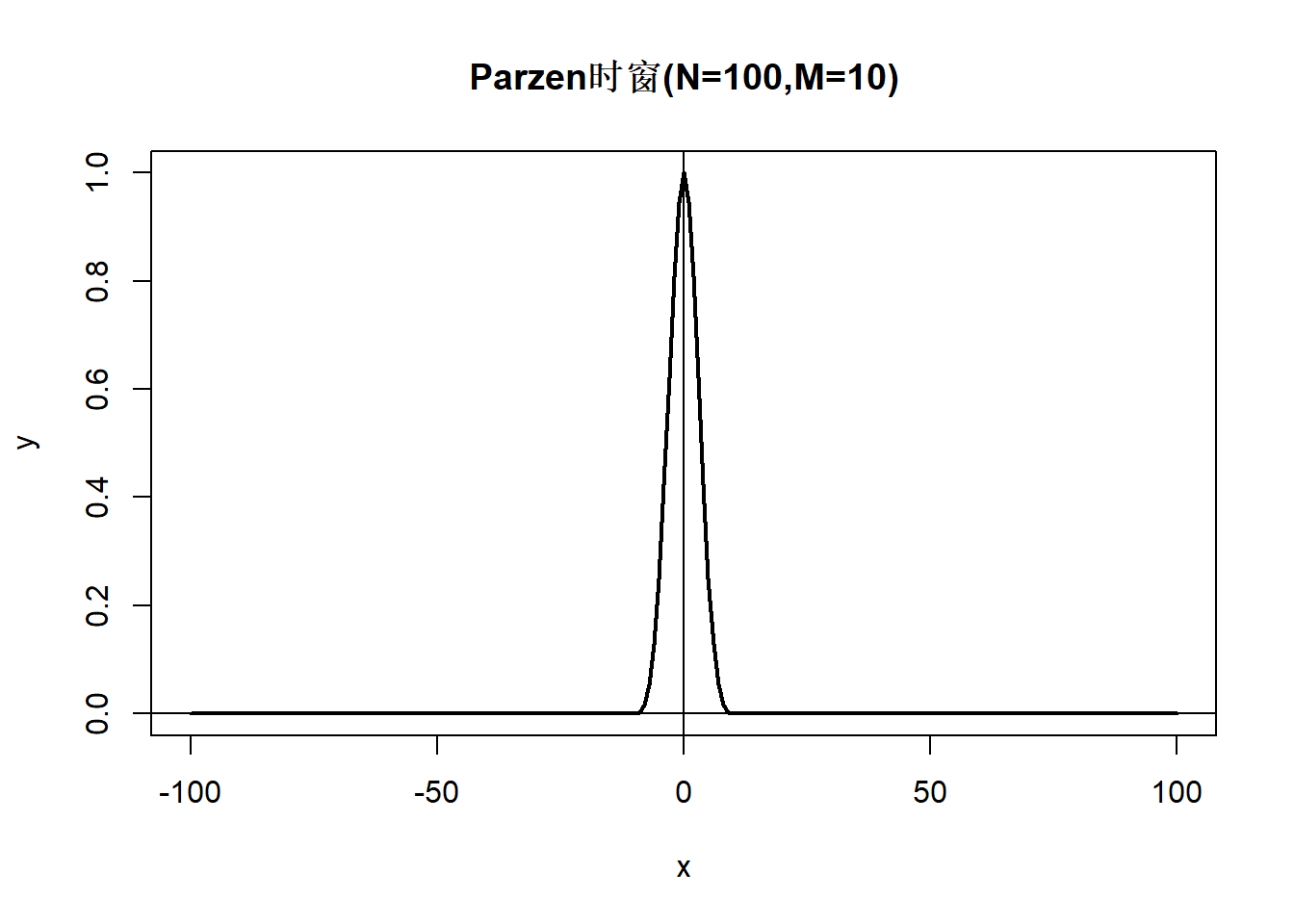
demo.parzen <- function(M=10){
x <- seq(-pi, pi, length=300)
y <- ((3/(8*pi*M^3)) * (sin(M*x/4) / (sin(x/2)/2))^4 *
(1 - 2/3*sin(x/2)^2))
plot(x, y, type="l", lwd=2,
main=paste("Parzen Kernel(M=", M, ")", sep=""))
abline(h=0)
abline(v=0)
}
demo.parzen()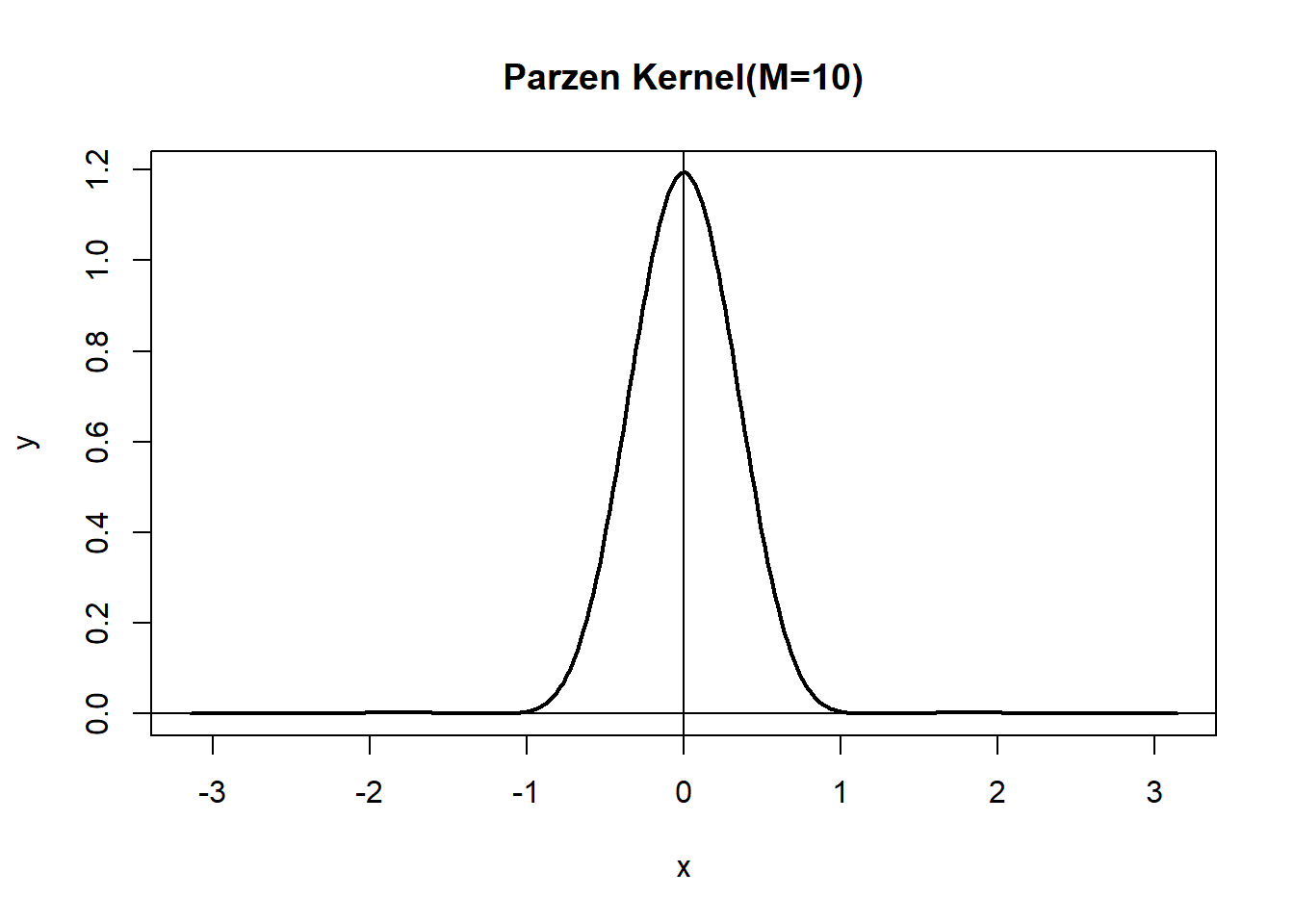
28.2.3.6 Bartlett-Priestley窗
谱窗函数为 \[\begin{aligned} W_N(\lambda) = \begin{cases} \frac{3 M_N}{4\pi} [ 1 - (M_N \lambda / \pi)^2 ], & |\lambda| \leq \pi / M_N \\ 0, & |\lambda| > \pi / M_N \end{cases} \end{aligned}\] 是二次函数。 对应的时窗函数为 \[\begin{aligned} \lambda_N(k) = \begin{cases} \frac{3 M_N^2}{(\pi k)^2} \left[ \frac{\sin(\pi k / M_N)}{\pi k / M_N} - \cos(\pi k / M_N) \right], & 0 < |k| \leq M_N ,\\ 1, & k=0, \\ 0, & |k| > M_N \end{cases} \end{aligned}\]
demo.priestly.t <- function(){
N <- 100
M <- 10
x <- seq(-N, N)
y <- numeric(length(x))
sele <- abs(x)<=M & x != 0
y[sele] <- (3*M^2/(pi*x[sele])^2 *
(sin(pi*x[sele]/M)/(pi*x[sele]/M) - cos(pi*x[sele]/M)))
y[abs(x)<0.5] <- 1
plot(x, y, type="l", lwd=2,
main=paste("Priestly时窗(N=100,M=10)", sep=""))
abline(h=0)
abline(v=0)
}
demo.priestly.t()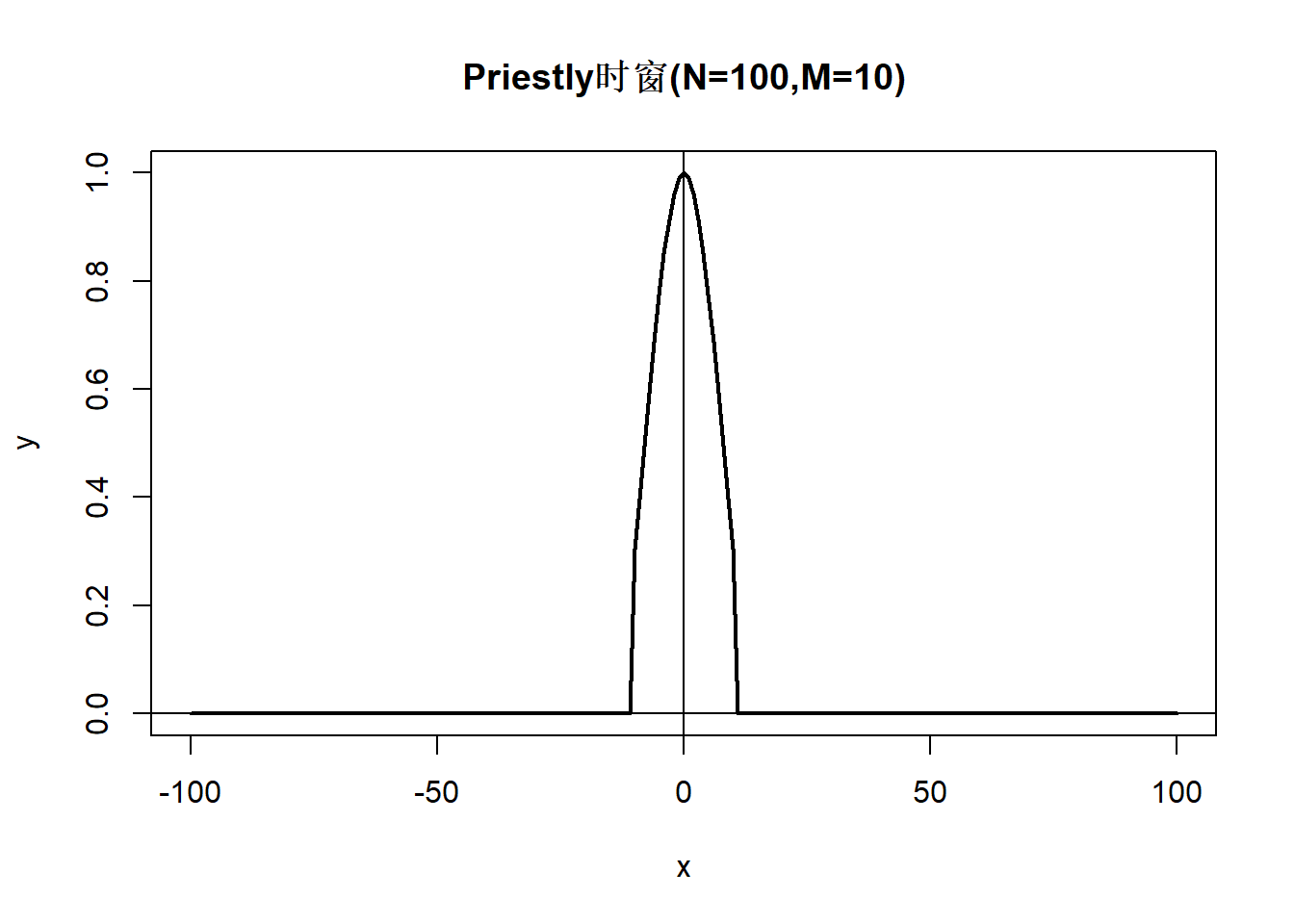
demo.priestly <- function(M=10){
x <- seq(-pi, pi, length=300)
y <- numeric(length(x))
sele <- abs(x) <= pi/M
y[sele] <- 3*M/4/pi*(1 - (M*x[sele]/pi)^2)
plot(x, y, type="l", lwd=2,
main=paste("Priestly Kernel(M=", M, ")", sep=""))
abline(h=0)
abline(v=0)
}
demo.priestly()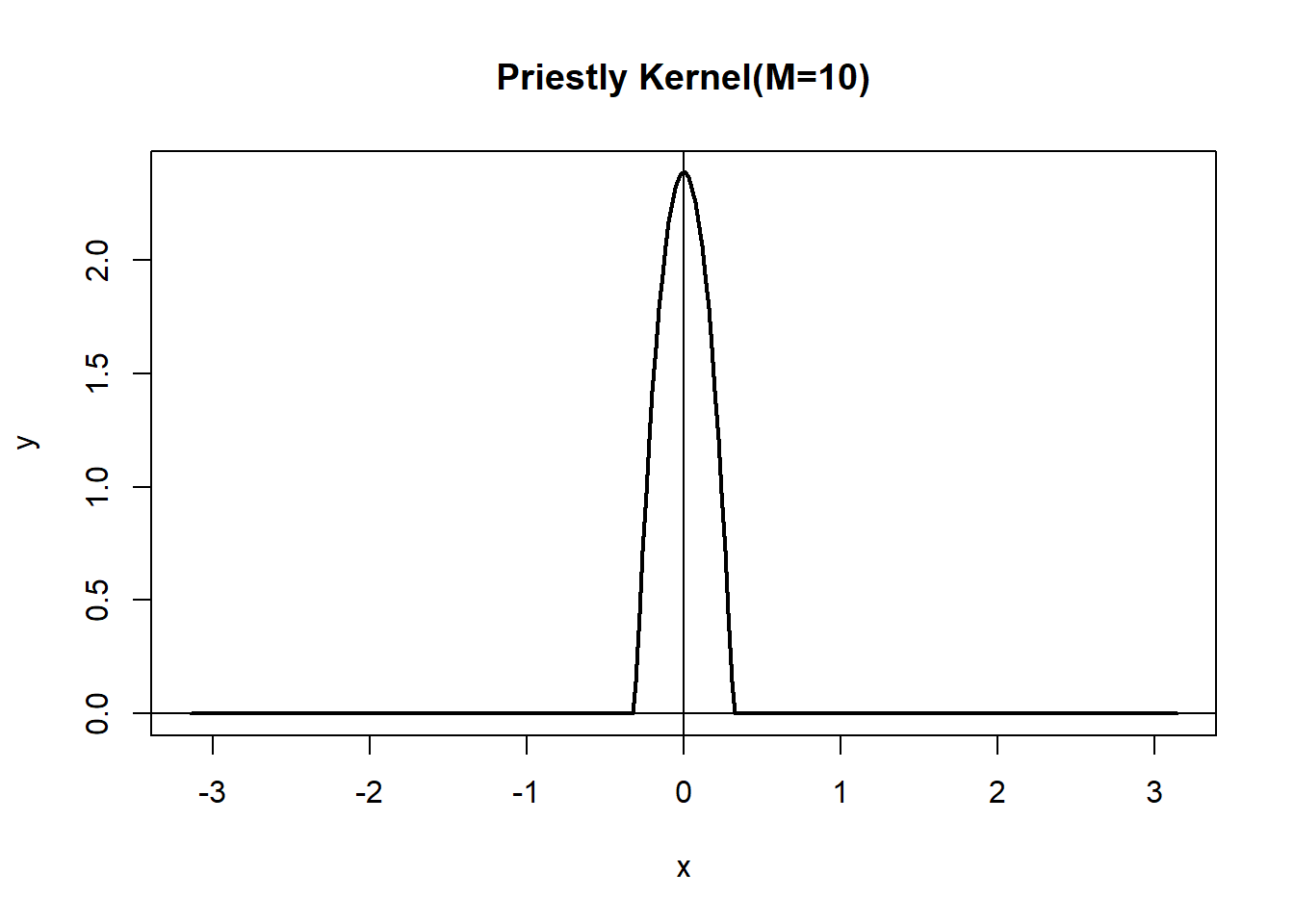
28.3 加窗谱估计的比较
28.3.1 方差的比较
定理28.4 设\(\{X_t\}\)是平稳正态序列, 有连续可微的谱密度\(f(\lambda)\), 谱窗函数\(W_N(\lambda)\)满足§28.2.2中的五个条件。 加窗谱估计\(\hat f(\lambda)\)由(28.8)定义。 则有如下结果:
(1) \(\hat f(\lambda)\)是\(f(\lambda)\)的渐近无偏估计。
(2) \(\hat f(\lambda)\)是\(f(\lambda)\)的均方相合估计。
(3) 当\(N\)充分大后,有 \[\begin{aligned} \text{Var}(\hat f(\lambda)) \approx& \begin{cases} \frac{M_N}{N} f(\lambda)^2 K^2, & \lambda \neq 0, \pm \pi, \\ 2 \frac{M_N}{N} f(\lambda)^2 K^2, & \lambda = 0, \pm \pi, \end{cases} \\ K^2 =& \frac{2\pi}{M_N} \int_{-\pi}^\pi W_N^2(\lambda) d\lambda. \end{aligned}\]
虽然减小\(M_N\)会减小方差,但是可能因为减小\(M_N\)使得谱窗变宽, 增加估计的光滑程度,所以可能会增加偏差,降低分辨率。
各谱窗方差比较:
\[ \begin{array}{ll} \text{窗名} & K^2 \\ \hline \text{截断窗} & 2.0000 \\ \text{Bartlett} & 0.6667 \\ \text{Daniell} & 1.0000 \\ \text{Turkey-Hamming} & 0.7948 \\ \text{Parzen} & \mathbf{0.5392} \\ \text{Bartlett-Priestley} & 1.2000 \end{array} \]
28.3.2 分辨率的比较
谱估计对峰的个数、位置很感兴趣。 两个相邻的峰需要能分开,不被混在一起。 只有谱窗宽度比两个峰距离更短时才有可能分开。
例28.5 考虑AR(4)模型 \[\begin{aligned} X_t =& a_1 X_{t-1} + a_2 X_{t-2} + a_3 X_{t-3} + a_4 X_{t-4} + \varepsilon, \ t \in \mathbb Z \\ \end{aligned}\] 其中 \[\begin{aligned} \{ \varepsilon_t \} \sim& \text{WN}(0,4), \\ \boldsymbol a =& (-0.9337, -1.4599, -0.7528, -0.6355)^T \end{aligned}\] 特征多项式有两对共轭复根 \[\begin{aligned} 1.115e^{\pm 1.5i},\ 1.125e^{\pm 2.2i} \end{aligned}\] 谱密度\(f(\lambda)\)在\(\lambda=1.5, 2.2\)处有明显峰值, 距离为\(2.2-1.5=0.7\)。
考虑用Daniell谱窗做谱估计: \[\begin{aligned} W_N(\lambda) =& \begin{cases} M_N / (2\pi) & |\lambda| \leq \pi/M_N \\ 0 & |\lambda| > \pi/M_N \end{cases} \end{aligned}\] \(M_N\)越大,谱窗越窄。 加窗谱估计为 \[\begin{aligned} \hat f(\lambda) =& \frac{M_N}{2\pi} \int_{\lambda - \pi/M_N}^{\lambda + \pi/M_N} I_N(s) ds \end{aligned}\] 由周期图的渐近无偏性 \[\begin{aligned} E\hat f(\lambda) \approx& \frac{M_N}{2\pi} \int_{\lambda - \pi/M_N}^{\lambda + \pi/M_N} f(s) ds \end{aligned}\] 所以\(E \hat f(\lambda)\)是\(f(s)\)在\(\lambda\)的小邻域 \([\lambda - \pi/M_N, \ \lambda + \pi/M_N]\)上的近似平均。 如果这个小邻域太宽(\(M_N\)太小),就会把两个峰混在一起。
### Daniel谱窗谱估计
spec.Daniell <- function(y, freqs=seq(0,pi,length=101),
M = round(2*sqrt(length(y))),
demean=FALSE){
N <- length(y)
if(demean) y <- y - mean(y)
spec <- numeric(length(freqs))
gams <- c(acf(y, lag.max=N-1,
type="covariance", plot=FALSE)$acf)
jjs <- seq(N-1)
for(j in seq(along=freqs))
spec[j] <- 1/(2*pi)*(gams[1] +
2*sum(gams[jjs+1] *
( sin(jjs*pi/M) / (jjs*pi/M) ) *
cos(jjs*freqs[j])))
list(frequencies=freqs, spectrum=spec)
}
demo.resolution <- function(seed=1){
set.seed(seed)
N <- 120
a <- c(-0.9337, -1.4599, -0.7528, -0.6355)
sigma <- 1
y <- arima.sim(list(ar=a), n=N)*sigma
## 理论谱密度
lams <- seq(0, pi, length=201)
res1 <- ar.true.spectrum(a, sigma=sigma, plot.it=FALSE)
lams <- res1$frequencies
spec0 <- res1$spectrum
spec1 <- spec.Daniell(y, freqs=lams, demean=FALSE, M=25)$spectrum
spec2 <- spec.Daniell(y, freqs=lams, demean=FALSE, M=15)$spectrum
spec3 <- spec.Daniell(y, freqs=lams, demean=FALSE, M=10)$spectrum
ylim <- c(0, max(c(spec0, spec1, spec2, spec3)*1.2))
plot(lams, spec0, lwd=3, type="l",
ylim=ylim,
main="Daniell窗谱估计不同窗宽分辨率",
xlab="frequency", ylab="")
lines(lams, spec1, col="green", lwd=2, lty=2)
lines(lams, spec2, col="blue", lwd=2, lty=2)
lines(lams, spec3, col="red", lwd=2, lty=3)
abline(v=c(1.508,2.199), lty=3, col="gray")
legend("topleft", lwd=c(3,2,2,2), lty=c(1,2,2,3),
col=c("black", "green", "blue", "red"),
legend=c("True", "M=25", "M=15", "M=10"))
}
demo.resolution()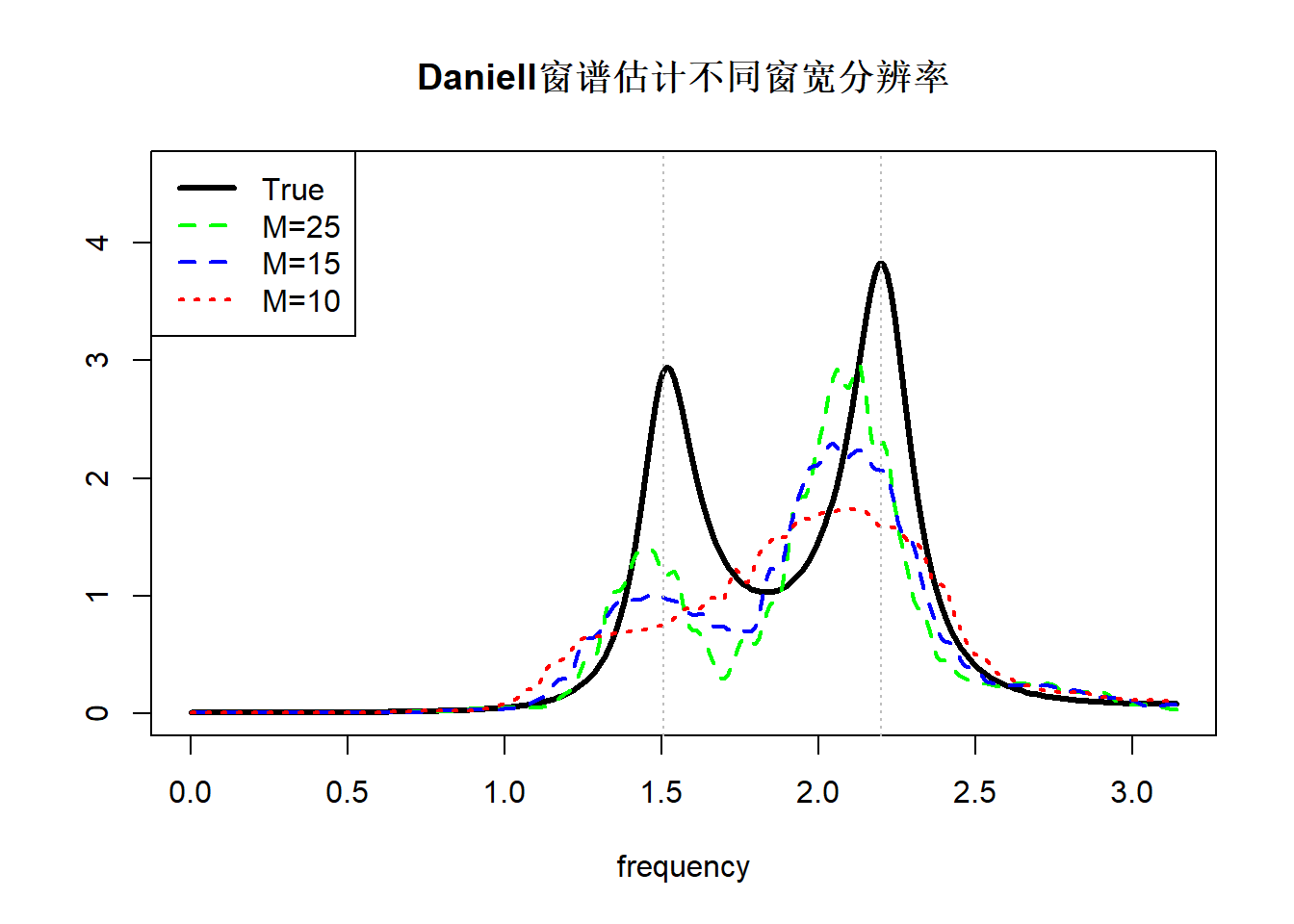
○○○○○○
谱窗宽度的选择:
只有谱窗宽度比两个峰距离小很多时才有可能分开。 但是,谱窗太窄(\(M_N\)太大),估计方差会变大, 估计的结果变得很不光滑,出现许多虚假的峰。 谱密度和谱窗的宽度用带宽来描述。
设谱密度\(f(\lambda)\)连续, 在\(\lambda_0\)处有一个明显的峰值, 如果有\(\omega_1 < \lambda_0 < \omega_2\) 使得 \[\begin{align} f(\omega_1) =& f(\omega_2) = \frac{1}{2} f(\lambda_0), \tag{28.9} \\ f(\lambda) >& \frac{1}{2} f(\lambda_0),\quad \text{当} \lambda \in (\omega_1, \omega_2), \end{align}\] 则称\(\omega_2 - \omega_1\)为\(f(\lambda)\)在\(\lambda_0\)处的带宽。
若\(f(\lambda)\)在\(\lambda_0\)处有一个明显的低谷, 如果有\(\omega_1 < \lambda_0 < \omega_2\) 使得 \[\begin{aligned} f(\omega_1) =& f(\omega_2) = 2 f(\lambda_0), \\ f(\lambda) <& 2 f(\lambda_0),\quad \text{当} \lambda \in (\omega_1, \omega_2), \end{aligned}\] 则称\(\omega_2 - \omega_1\)为\(f(\lambda)\)在\(\lambda_0\)处的带宽。
加窗谱估计要求谱窗的带宽比谱密度的带宽小很多, 才能分辨出谱密度的峰值情况。
半功率带宽: \(B_{\text{HP}} = 2\theta_1\), \(\theta_1\)由 \[\begin{aligned} W_N(\theta_1) = \frac{1}{2} W_N(0). \end{aligned}\] 这种谱窗带宽定义与(28.9)的谱密度带宽定义是一致的。
Parzen带宽: \(B_\text{P} = 1 / W_N(0)\).
Jenkin带宽: \[\begin{aligned} B_\text{J} = \frac{2\pi}{\sum_{|k| \leq N-1} \lambda_N^2(k)}. \end{aligned}\]
增加\(M_N\)可以减小谱窗的窗宽从而提高分辨率, 但是会增大方差。 不同\(M_N\)取值对分辨率的影响参见例28.5。