1 时间序列概念
时间序列定义: 按时间顺序排列的随机变量序列。
观测样本: 时间序列各随机变量的观测样本。一定是有限多个。
一次实现(一条轨道): 时间序列的一组实际观测。
时间序列分析的任务: 数据建模,解释、控制或预报。
记号: \(\{X_t\}\), \(\{x_t\}\), \(X(t)\), \(x(t)\).
例:北京地区洪涝灾害数据
北京地区从1949年到1964年的受灾面积与成灾面积(单位:万亩)数据。
flood.data <- matrix(c(
1949 , 1 , 331.12 , 243.96 ,
1950 , 2 , 380.44 , 293.90 ,
1951 , 3 , 59.63 , 59.63,
1952 , 4 , 37.89 , 18.09,
1953 , 5 , 103.66 ,72.92,
1954 , 6 , 316.67 , 244.57,
1955 , 7 , 208.72 , 155.77,
1956 , 8 , 288.79 , 255.22,
1957 , 9 , 25.00 , 0.50,
1958 , 10 , 84.72 , 48.59,
1959 , 11 , 260.89 ,202.96,
1960, 12 , 27.18 ,15.02,
1961, 13 , 20.74 ,17.09,
1962 , 14 , 52.99 ,14.66,
1963 , 15 , 99.25 , 45.61,
1964 , 16 , 55.36 ,41.90),
byrow=T, ncol=4,
dimnames=list(1949:1964,
c("year", "t", "area1", "area2")))
flood <- ts(flood.data, start=1949, frequency=1)## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
## ✔ ggplot2 3.3.6 ✔ purrr 0.3.4
## ✔ tibble 3.1.8 ✔ dplyr 1.0.9
## ✔ tidyr 1.2.0 ✔ stringr 1.4.0
## ✔ readr 2.1.2 ✔ forcats 0.5.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()ggplot(data = as_tibble(flood.data)) +
geom_line(mapping = aes(
x = year, y = area1, color = "受灾面积")) +
geom_line(mapping = aes(
x = year, y = area2, color = "成灾面积")) +
scale_color_manual(
name = NULL,
breaks = c("受灾面积", "成灾面积"),
values = c(
"受灾面积" = "orangered2",
"成灾面积" = "turquoise")) +
labs(y = NULL) +
theme(
legend.position = c(0.98, 0.98),
legend.justification = c(1,1) )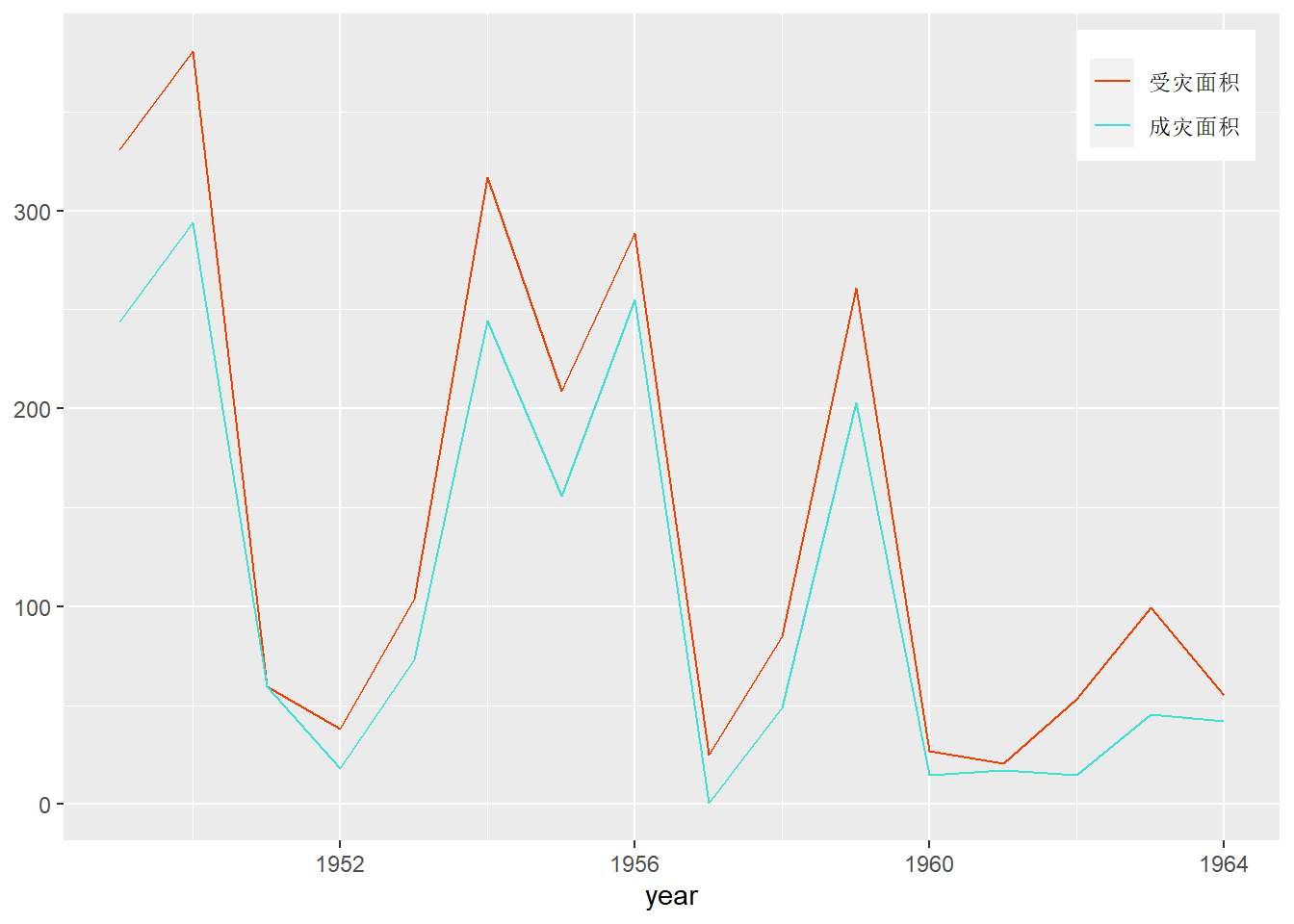
图1.1: 北京地区洪灾数据
1.1 时间序列分解
\[ X_t = T_t + S_t + R_t, \ t=1,2,\ldots \]
- 趋势项
- 季节项
- 随机项
- 有时还有随机周期项(Cycle)
季节项模型有: * 固定的周期季节项: \(S(t+s) = S(t), \forall t\). 只需要\(S_1, \ldots, S_s\)且可设 \(\sum_{j=1}^s S_j = 0\)
关于随机项,可设\(E R_t = 0, \forall t\)。
1.1.1 例子: 居民用煤消耗季度值
coal.consumption <-
ts(c(
6878.4 , 5343.7 , 4847.9 , 6421.9 ,
6815.4 , 5532.6 , 4745.6 , 6406.2 ,
6634.4 , 5658.5 , 4674.8 , 6445.5 ,
7130.2 , 5532.6 , 4989.6 , 6642.3 ,
7413.5 , 5863.1 , 4997.4 , 6776.1 ,
7476.5 , 5965.5 , 5202.1 , 6894.1 ),
frequency=4, start=c(1991,1))demo.coal.data <- function(){
opar <- par(mar=c(3,3,3,1), mgp=c(1.5,0.5,0))
on.exit(par(opar))
plot(coal.consumption, lty=1, type='b',
main='居民季度用煤消耗量',
xlab='年', ylab='消耗量(吨)')
abline(v=1991:1996, lty=3)
}
demo.coal.data()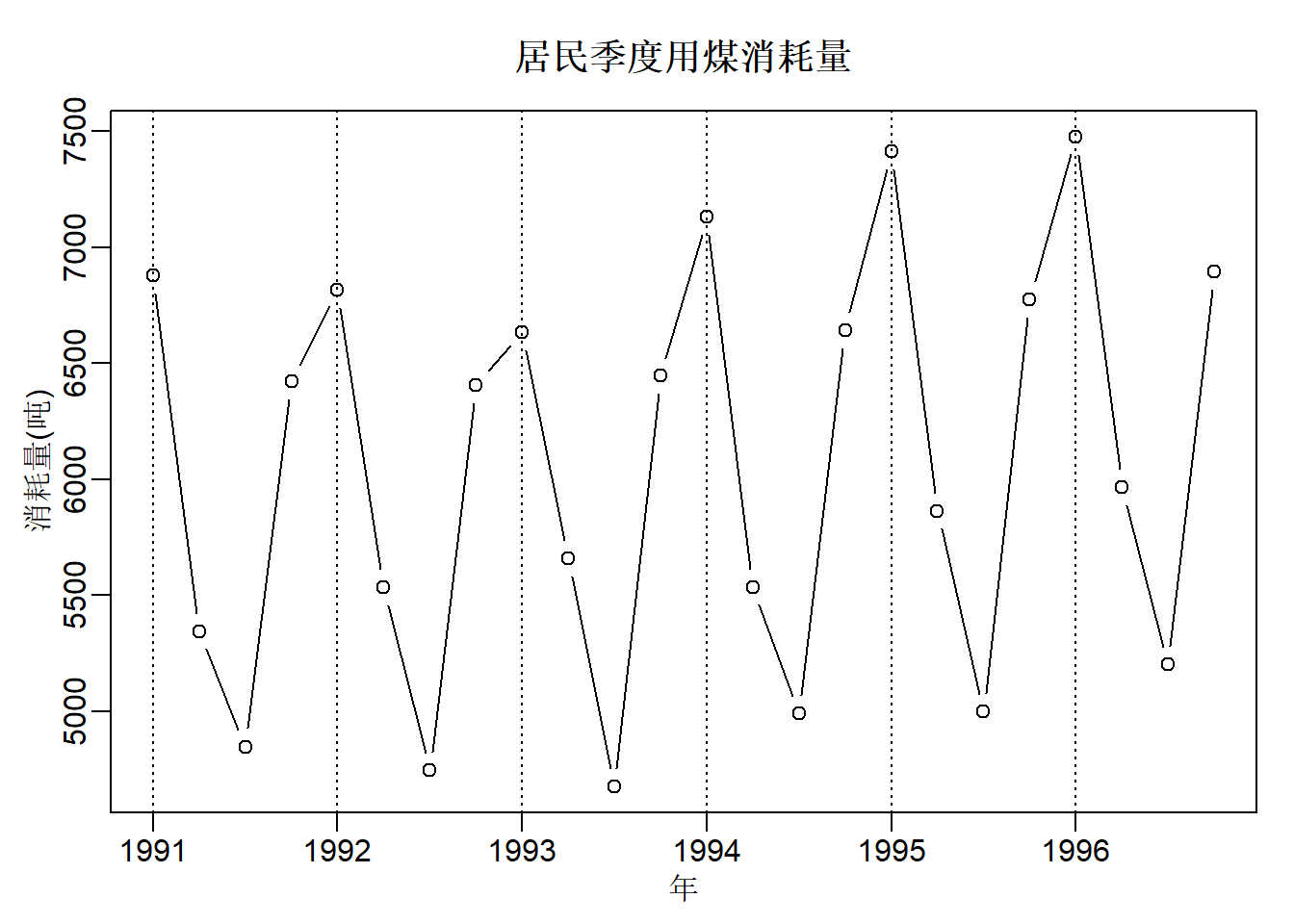
1.1.1.1 分解方法
估计趋势\(\{\hat T_t\}\)后, \(X_t - \hat T_t\)主要由季节项和 随机项组成,季节项可以用\(X_t - \hat T_t\) 每个季节平均得到;
趋势估计可用:
每年平均;
线性回归拟合直线;
二次曲线回归;
滑动平均估计;
得到\(\hat T_t\)和\(\hat S_t\)后可以再从\(X_t - \hat S_t\) 估计新的\(\hat{\hat{T_t}}\)。
季节项估计还可以直接列入模型用哑变量表示(注意共线问题)。
用\(\hat{T_t} + \hat{S_t}\)拟合或预报\(y_t\)。
还可以建立趋势、季节项、随机项的状态空间模型。
1.1.1.2 用每年的平均值作为趋势项估计, 季度平均作为季节项
这样的趋势是阶梯函数, 每年的4个季度的趋势相等。 去趋势后同季度平均作为季节项。
y <- coal.consumption
ymore <- ts(c(y, rep(NA,4)), start=start(y), frequency=4)
ymat <- matrix(c(y), byrow=TRUE, nrow=6, ncol=4)
cols <- rainbow(20)
ic <- 1
## 用同季度的值平均得到四个季节项
get.season <- function(yd){ # input: Detrended series
ymat <- matrix(c(yd), byrow=TRUE, ncol=4)
cy <- as.vector(cycle(yd))
## season
seas0 <- tapply(yd, cy, mean, na.rm=TRUE)
seas0
}
## 画去除趋势后的序列、季节项和随机项
plot.season <- function(yd, seas0){ # input: Detrended series
## season
seas <- rep(seas0, 6)
seas <- ts(seas, start=c(1991,1), frequency=4)
## Error
r <- as.vector(yd) - seas
r <- ts(r, frequency=4, start=c(1991,1))
plot(yd, type='b', lwd=2,
main="Detrended Series(black), Seasonal(red) and Random(cyan)",
xlim=c(1991,1998), ylab="")
abline(v=1991:1996, col="gray")
abline(h=0, col="gray")
lines(seas, type="l", col="red")
lines(r, type="l", col="cyan")
}下图为原始序列、趋势、拟合(包括趋势与季节项):
tr0 <- rowMeans(ymat, na.rm=TRUE)
tr <- rep(tr0, each=4)
tr <- ts(tr, frequency=4, start=c(1991,1))
y.detrended <- y - tr
seas0 <- get.season(y.detrended)
tr.more <- ts(c(tr, rep(tr[length(tr)],4)),
start=start(y), frequency=4)
seas.more <- ts(rep(seas0, 7),
start=start(y), frequency=4)
y.pred <- tr.more + seas.more
plot(ymore,
main="Series(black), Year average trend(red), Fit(green)",
lwd=2,
type="b", col="black",
ylab="")
abline(v=1991:1997, col="gray")
lines(tr.more, col="red", type="l")
lines(y.pred, col="green", type="l")
下图为去掉了趋势后的序列、季节项、取掉了趋势与季节项后的随机项:
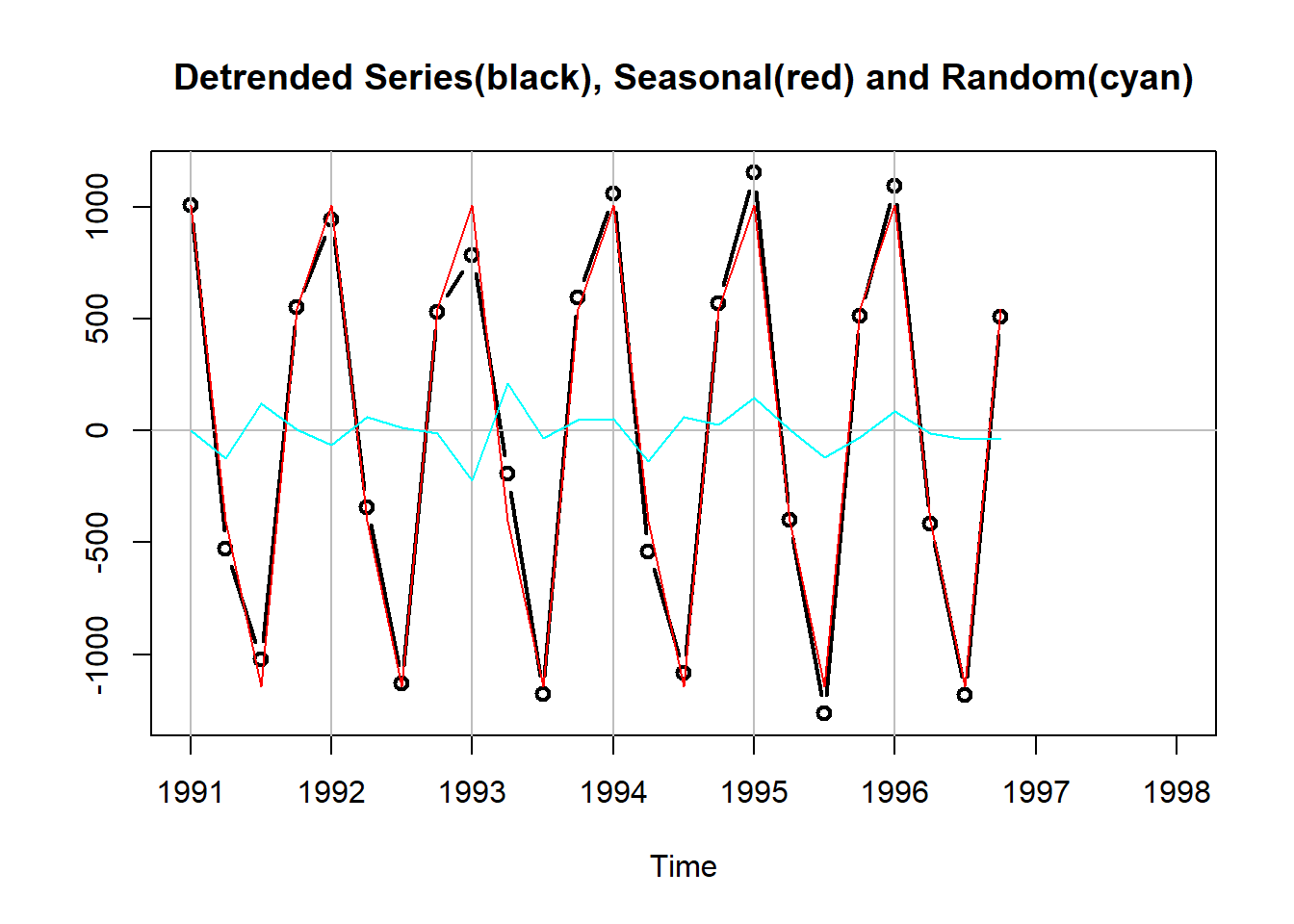
1.1.1.3 用时间的线性回归作为趋势项估计, 季度平均作为季节项
可以设趋势为\(T_t = a + bt\), 用一元线性回归程序估计趋势并预测。 下图绘制了原始数据、估计的趋势、拟合值(包括趋势与季节项):
yy <- as.vector(y)
tt <- seq(along=y)
lmr <- lm(yy ~ tt)
tr.more <- ts(predict(lmr, newdata=list(tt=seq(length(y)+4))),
frequency=4, start=c(1991,1))
## season
y.detrended <- y - tr.more[1:length(y)]
seas0 <- get.season(y.detrended)
seas.more <- ts(rep(seas0, 7),
start=start(y), frequency=4)
y.pred <- tr.more + seas.more
plot(ymore, main="Series(black), Linear trend(red) and Fit(green)",
lwd=2,
type="b", col="black")
lines(tr.more, col="red", type="l")
lines(y.pred, col="green", type="l")
下图为去掉了趋势后的序列、季节项、取掉了趋势与季节项后的随机项:

1.1.1.4 二次曲线趋势
可以用\(T_t = a + b t + c t^2\)作为趋势模型, 用多元线性回归程序估计模型并预测。
下图绘制了原始数据、估计的趋势、拟合值(包括趋势与季节项):
yy <- as.vector(y)
tt <- seq(along = y)
lmr <- lm(yy ~ tt + I(tt^2))
tr.more <- ts(predict(lmr, new.data=list(tt=seq(length(y)+4))),
frequency=4, start=c(1991,1))
## season
y.detrended <- y - tr.more[1:length(y)]
seas0 <- get.season(y.detrended)
seas.more <- ts(rep(seas0, 7),
start=start(y), frequency=4)
y.pred <- tr.more + seas.more
plot(ymore, main="Series(black), Quadratic trend(red) and Fit(cyan)",
lwd=2,
type="b", col="black")
lines(tr.more, col="red", type="l")
lines(y.pred, col="green", type="l")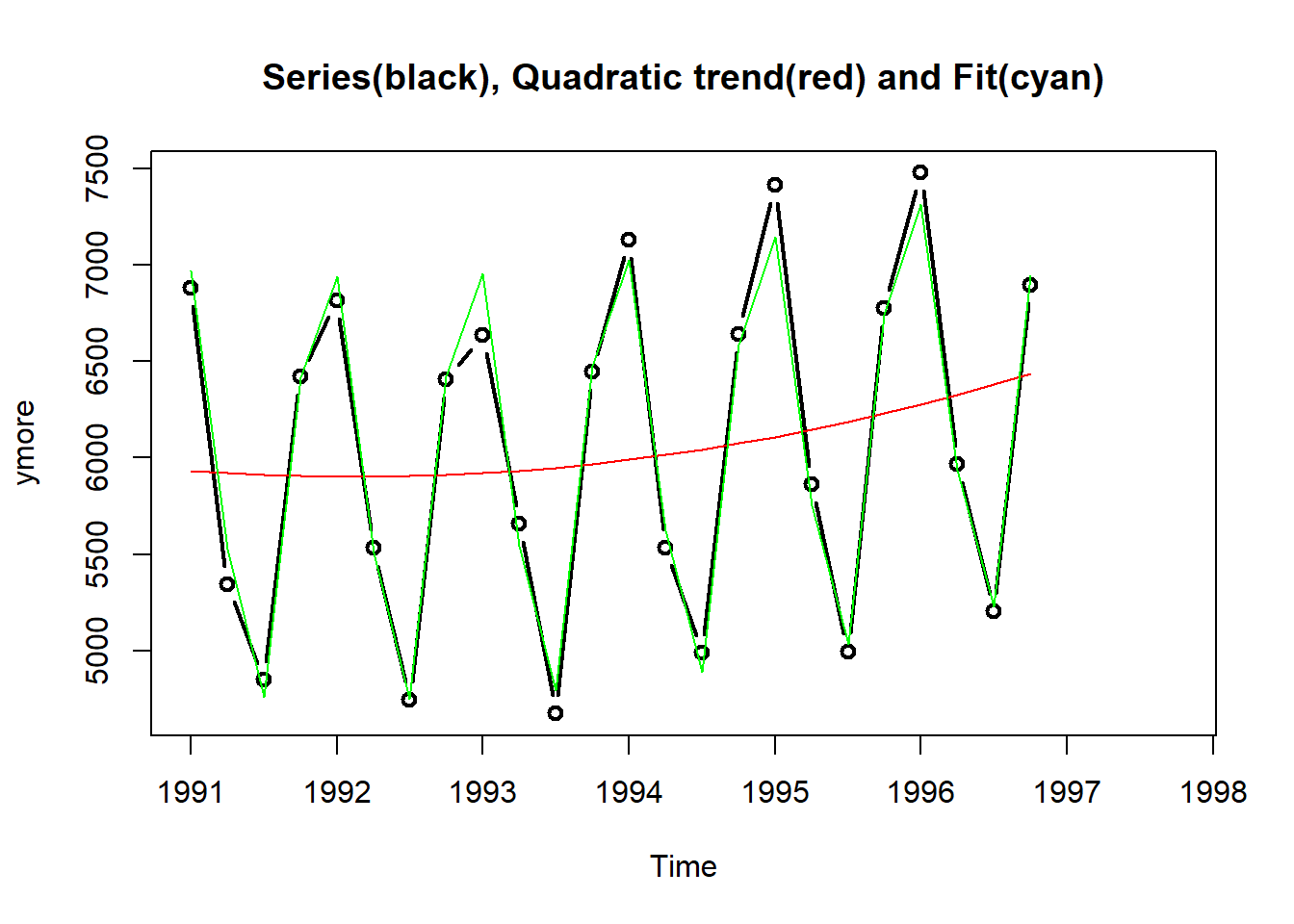
下图为去掉了趋势后的序列、季节项、取掉了趋势与季节项后的随机项:
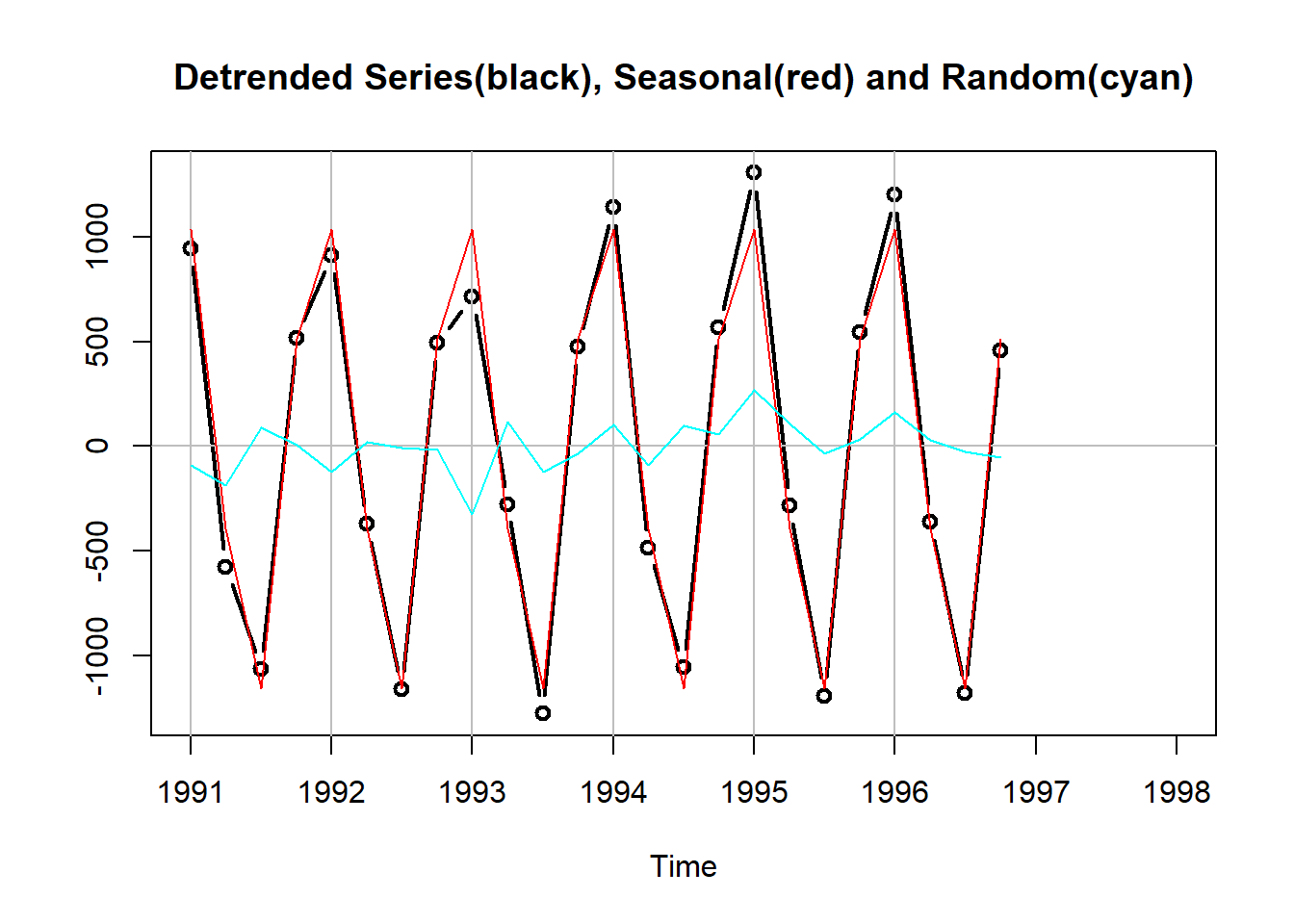
1.1.1.5 用线性回归同时估计趋势与季节项
可以设趋势加季节项为 \(T_t + S_t = bt + c_1 I_1 + c_2 I_2 + c_3 I_3 + c_4 I_4\), 其中\(I_1, I_2, I_3, I_4\)是各个季度的示性函数。 用线性回归程序估计趋势和季节项并预测。 下图绘制了原始数据、估计的趋势、拟合值(包括趋势与季节项):
yy <- as.vector(y)
tt <- seq(along = y)
ss <- factor(as.vector(cycle(y)), levels=1:4)
lmr <- lm(yy ~ -1 + tt + ss)
y.pred <- ts(
predict(lmr,
newdata=data.frame(
tt=seq(length(y)+4),
ss=factor(rep(1:4, 7), levels=1:4))),
frequency=4, start=c(1991,1))
plot(ymore, main="Series(black) and Fit(green)",
lwd=2,
type="b", col="black")
lines(y.pred, col="green", type="l")
1.1.1.6 加权移动平均趋势
均线法是常用的估计趋势的方法。 这里用非等权的5点滑动平均方法估计趋势, 权重为\(1/8, 1/4, 1/4, 1/4, 1/8\)。
下图绘制了原始数据、估计的趋势、拟合值(包括趋势与季节项):
yy <- c(y)
tr <- ts(stats::filter(yy, c(1/8, 1/4, 1/4, 1/4, 1/8),
method="convolution"),
frequency=4, start=c(1991,1))
ind2 <- max(which(!is.na(tr)))
tr.more <- ts(c(tr, rep(NA,4)),
start=start(y), frequency=4)
tr.more[(ind2+1):length(tr.more)] <- tr.more[ind2]
y.detrended <- y - tr.more[1:length(y)]
seas0 <- get.season(y.detrended)
seas.more <- ts(rep(seas0, 7),
start=start(y), frequency=4)
y.pred <- tr.more + seas.more
plot(ymore, main="Series(black), MA trend(red), Fit(green)",
lwd=2,
type="b", col="black")
abline(v=1991:1997, col="gray")
lines(tr.more, col="red", type="l")
lines(y.pred, col="green", type="l")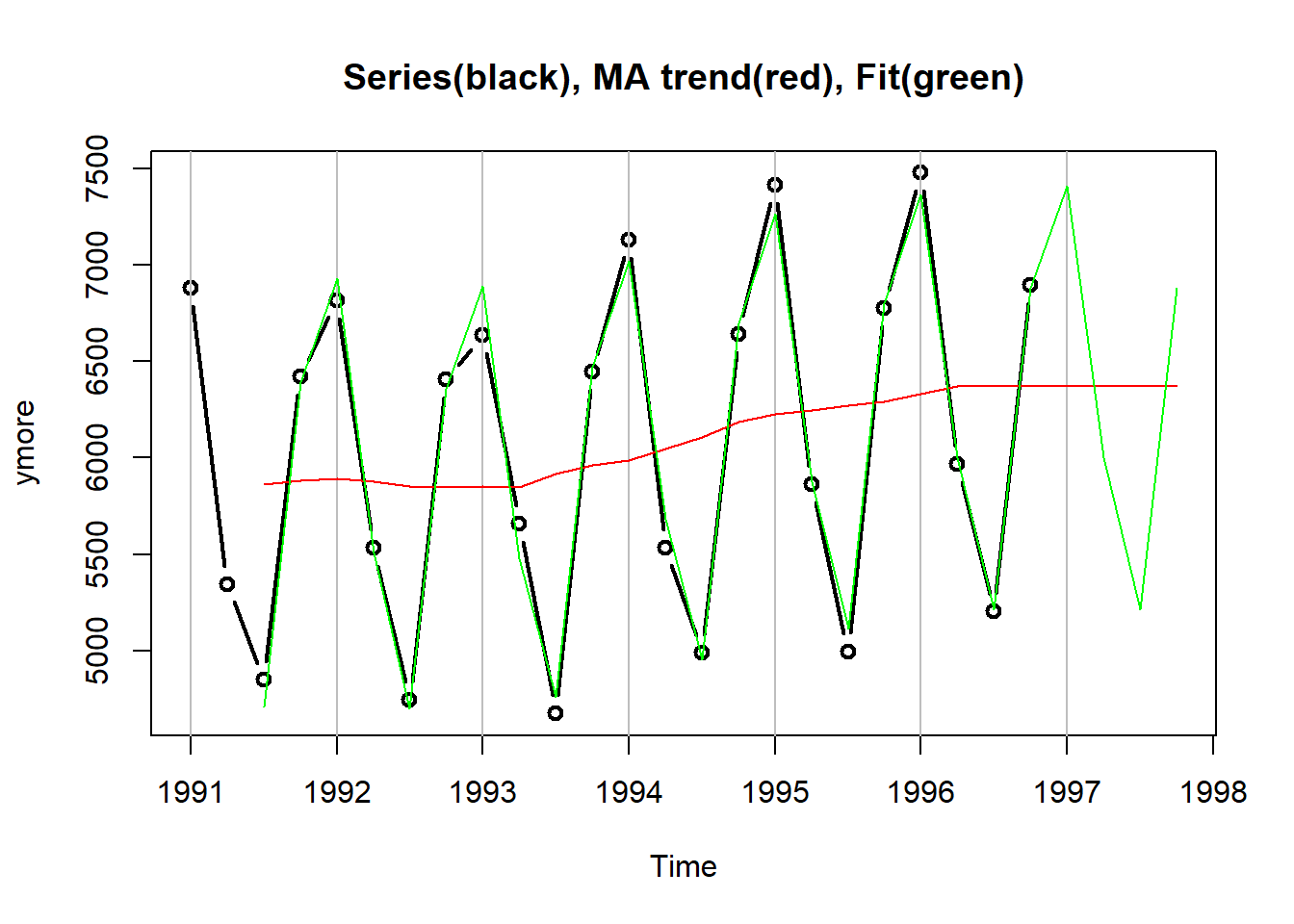
下图为去掉了趋势后的序列、季节项、取掉了趋势与季节项后的随机项:
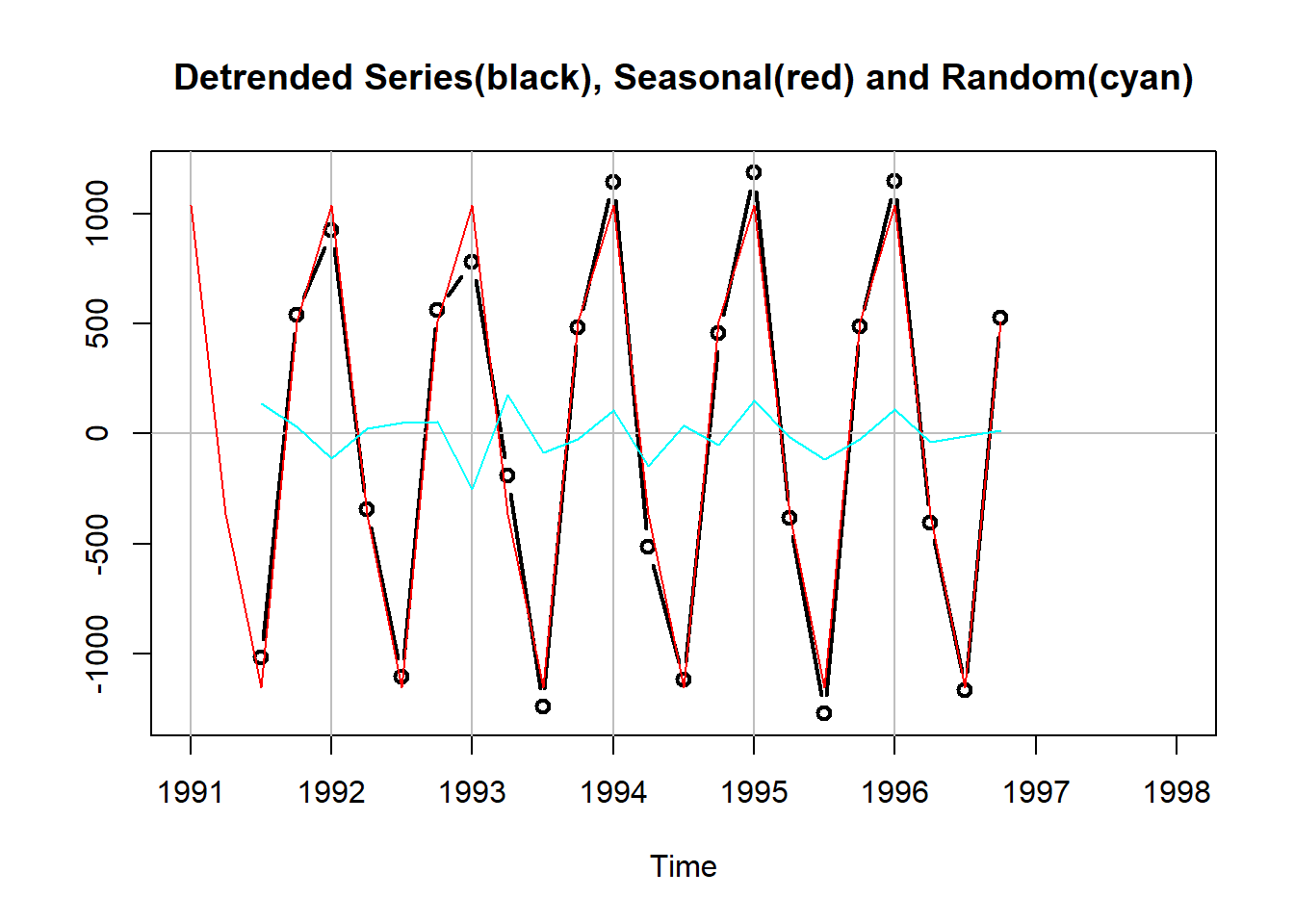
1.1.2 decompose()函数
R的stats包的decompose()函数输入一个时间序列,
将其分解为趋势项、季节项和随机项。
去趋势的方法是中心对称滑动平均。
可以用type="additive"或type="multiplicative"
指定各项之间是相加还是相乘。
比如, 城市季度用煤量序列的分解:

分别是原始序列、趋势估计、季节项估计和随机项估计。
函数输出结果为一个列表,
各项为x, seasonal, trend, random等。
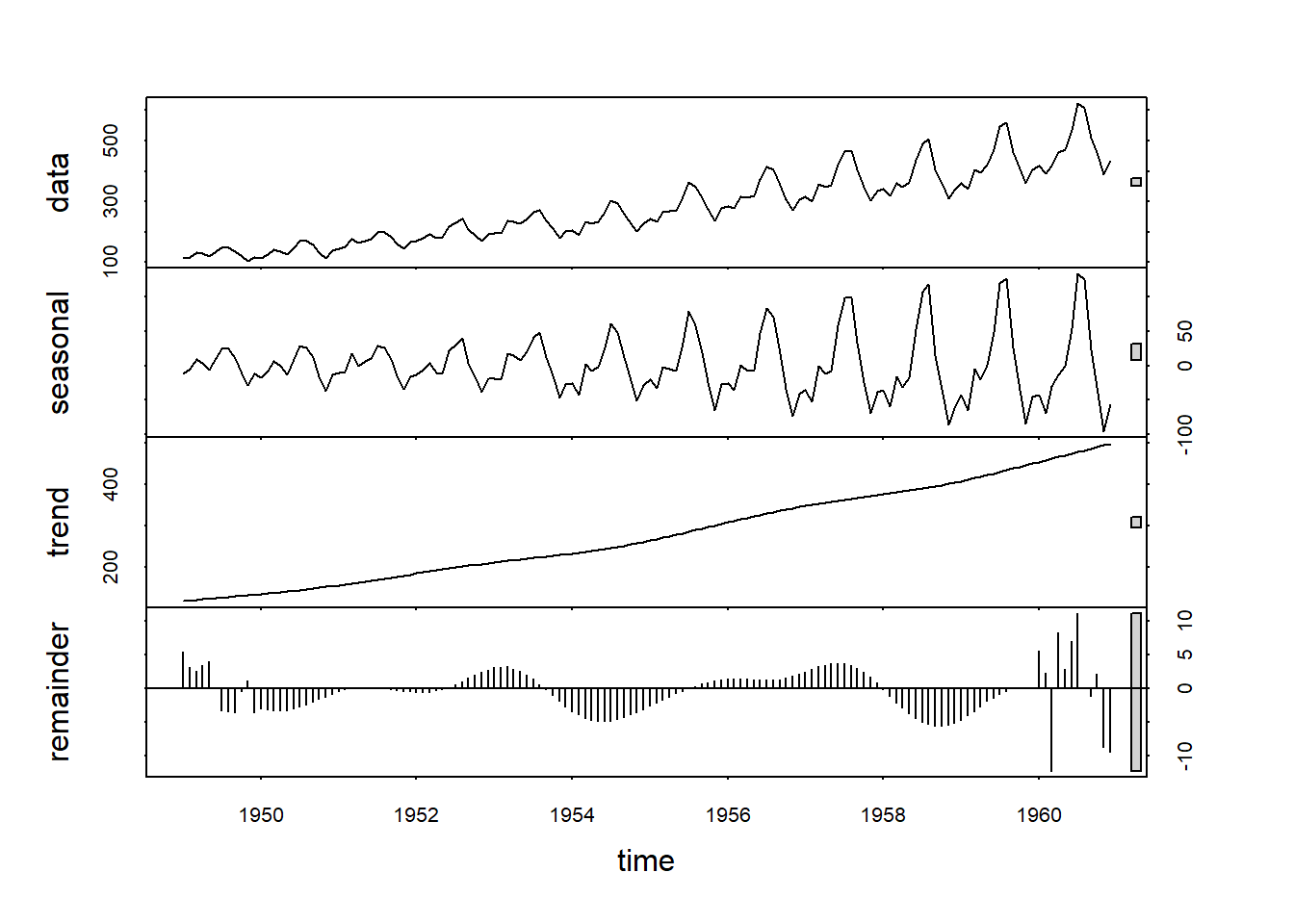
又比如,考虑著名的美国泛美航空公司1949-1960 的国际航班订票数的月度数据(单位:千人),12年144个月的数据。 序列图:

分解:

1.1.3 stl()函数
滑动平均是平滑(smoothing)的一种,
中心对称的滑动平均会丢失序列开始和结束部分的若干点。
R的stats包提供了函数stl(),
该函数基于loess局部加权回归估计季节项,
可以减少异常点的影响,
属于稳健回归。
用同月份(季度)的数值估计平滑的季节变动,
减去季节项后再用平滑方法估计趋势。
参见[R.B.Cleveland1990]。
滑动平均和loess局部加权回归都不能表示成公式模型。 平滑的另一说法是“滤波”。
如
1.1.4 StructTS()函数
R的stats包的StructTS()函数用状态空间模型表示时间序列分解,
用最大似然方法估计各个成分。
结果列表中的fitted有三列level, slope, sea。
如:
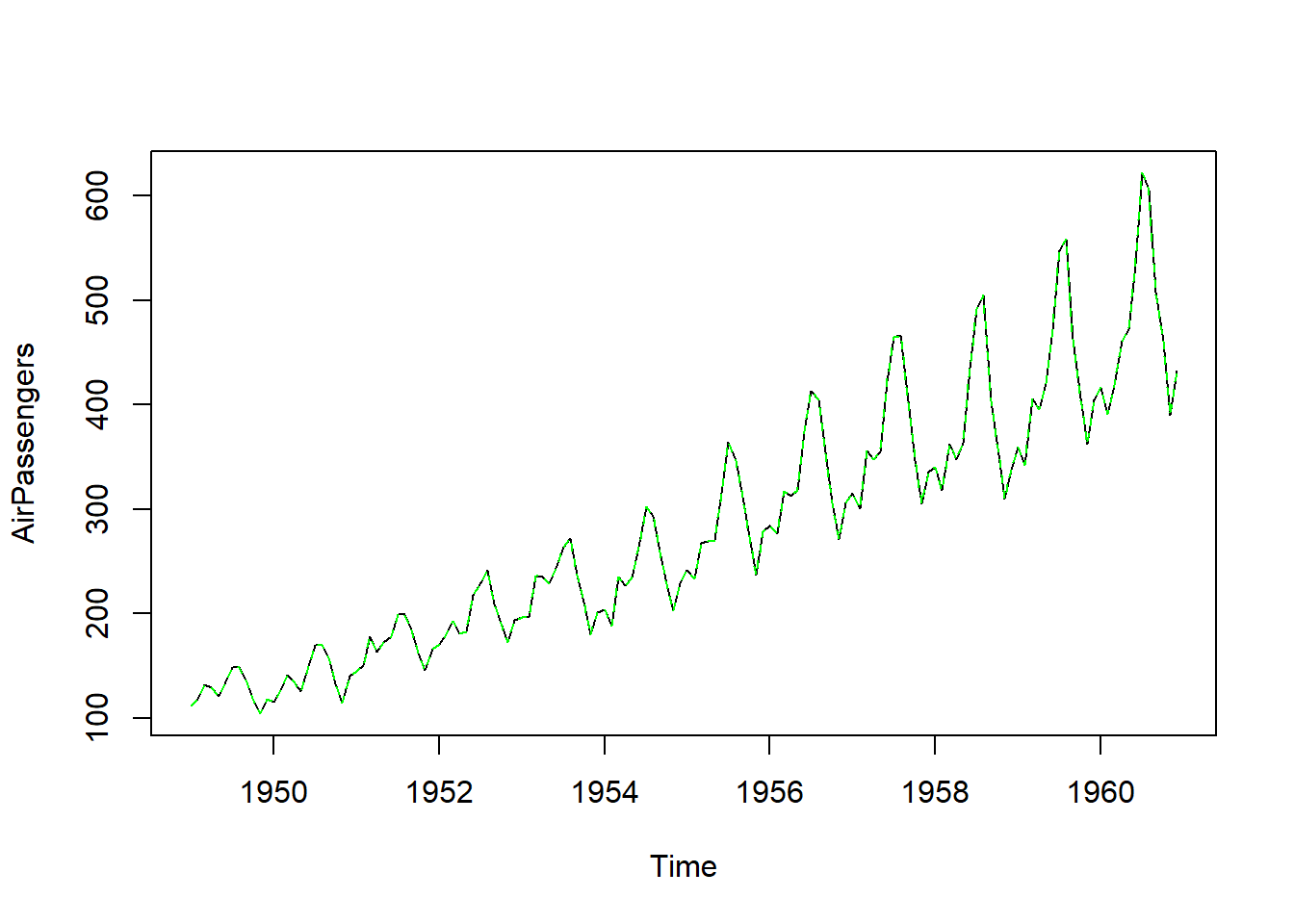
res2 <- StructTS(log(AirPassengers), type="BSM")
res2b <- cbind(log(AirPassengers), fitted(res2), resid(res2))
colnames(res2b) <- c(
"Series", "level", "slope", "seasonal", "residual"
)
plot(res2b)
序列(实线)与拟合值(绿色虚线):
1.2 平稳序列
随机过程的概念: 指标集\(\mathcal{T}\)。 \(\{X_t: t \in \mathcal{T} \}\)称为随机过程。
时间序列: \(\mathcal{T}\)为全体整数或正整数时,随机过程称为随机序列; 把整数下标看成时间则称随机序列为时间序列。
连续时随机过程、连续时时间序列: \(\mathcal{T}\)为全体实数或全体非负实数时称随机过程为连续时随机过程。 下标看成时间时称为连续时的时间序列。
离散采样: 连续时的时间序列记录下来就变成了离散时间。
平稳性: 去除趋势项和季节项后的随机部分经常具有平稳性。
序列分解中趋势和季节部分可以用非随机函数描述,但也可以用随机模型。 随机项通常是平稳的。 表现:水平没有明显变化;方差没有明显变化;相关性结构不随时间变化。
独立序列不能预报;平稳序列可以用历史值预报。
记号:
- \(\mathbb Z\)—所有整数的集合;。
- \(\mathbb N_+\)—所有正整数的集合;。
- \(\mathbb N\)—表示\(\mathbb Z\)或\(\mathbb N_+\)。
1.2.1 平稳序列及其自协方差函数
定义1.1 (平稳序列) 如果时间序列 \(\{X_t\} =\{X_t: t\in \mathbb N \}\) 满足
- 对任何 \(t\in \mathbb N\), \(EX_t^2<\infty\);
- 对任何 \(t\in \mathbb N\), \(EX_t=\mu\);
- 对任何 \(t,s \in \mathbb N\), \(E[(X_t-\mu)(X_s-\mu)]=\gamma_{t-s}\), 则称 \(\{X_t\}\) 是平稳时间序列, 简称为平稳序列或平稳列. 称实数列 \(\{\gamma_t\}\)为 \(\{X_t\}\)的自协方差函数.
性质:
- 期望、方差与\(t\)无关。
- 时间平移不影响两时刻的相关系数。
- 又称平稳序列为二阶矩平稳序列, 还称为宽平稳列或弱平稳列。
自协方差函数性质:
(1) 对称性: \(\gamma_k = \gamma_{-k}, \forall k \in \mathbb Z\).
(2) 非负定性: \[ \Gamma_n = (\gamma_{k-j})_{k,j=1}^n = \left( \begin{array}{llll} \gamma_{0}\ &\gamma_1 \ &\cdots&\gamma_{n-1}\\ \gamma_{1}\ &\gamma_{0} \ &\cdots&\gamma_{n-2}\\ ..& ..& \cdots &.. \\ \gamma_{n-1}\ &\gamma_{n-2} \ &\cdots&\gamma_{0}\\ \end{array} \right) \text{非负定}(\forall n \in \mathbb N_+) \] (3) 有界性: \(|\gamma_k| \leq \gamma_0\), \(\forall k \in \mathbb Z\)。
任何满足上述三个性质的实数列都被称为非负定序列. 所以平稳序列的自协方差函数是非负定序列. 可以证明, 每个非负定序列都可以是一个平稳序列的自协方差函数.
\(\Gamma_n\)的元素通项: \[\begin{aligned} \Gamma_n = \left( \gamma_{|i-j|} \right)_{\substack{i=1,2,\dots,n}{j=1,2,\dots,n}} \end{aligned}\] 记 \[\begin{aligned} \boldsymbol X = \left( \begin{array}{c} X_1 \\ X_2 \\ \vdots \\ X_n \end{array} \right) \end{aligned}\] 则\(\Gamma_n = \text{Var}(\boldsymbol X)\)。
关于随机向量\({\boldsymbol X}\)与矩阵\(A\), \(B\),有 \[\begin{aligned} E(A + B {\boldsymbol X}) =& A + B E(\boldsymbol X ) \\ \text{Var}(A + B {\boldsymbol X}) =& B \text{Var}(\boldsymbol X) B^T \end{aligned}\] 且\(\boldsymbol X\)的协方差阵\(\text{Var}(\boldsymbol X)\)总是非负定的。
非负定性及随机变量的线性相关:
因为\(\Gamma_n\)是协方差阵,所以非负定。 事实上, 设\(\boldsymbol\alpha = (a_1, \ldots, a_n)^T\), 则 \[\begin{aligned} & \text{Var}(\boldsymbol\alpha^T \boldsymbol X) \\ =& \boldsymbol\alpha^T \Gamma_n \boldsymbol\alpha \\ =& \text{Var}\left( \sum_{i=1}^n a_i X_i \right) \geq 0 . \end{aligned}\]
\(\Gamma_n\)退化(不满秩)当且仅当存在\(\boldsymbol\alpha \neq 0\)使得 \[ \text{Var}\left( \sum_{i=1}^n a_i X_i \right) = 0 \] 这时称随机变量\(X_1, \ldots, X_n\)是线性相关的。 即\(X_1, \ldots, X_n\)的非零线性组合是退化随机变量。 如果\(X_1, \ldots, X_n\)线性相关, 则\(m \geq n\)时\(X_1, \ldots, X_m\) 线性相关。
Schwarz不等式:
\[ | E(XY) | \leq \sqrt{E X^2 E Y^2} \]
\[ | \text{Cov}(X,Y) | \leq \sqrt{\text{Var}(X) \text{Var}(Y)} \]
推论: \[ E |X| \leq \sqrt{E |X|^2} \]
\[ |\gamma_t| = |\text{Cov}(X_1, X_{t+1})| \leq \gamma_0 \]
例1.1 (平稳序列的线性变换) 设\(\{X_t\}\)为平稳序列,期望\(\mu\),自协方差函数\(\gamma(t)\)。
令\(Y_t = a + bX_t, t \in \mathbb Z\)。 则\(E Y_t = a + b \mu\), \(\text{Cov}(Y_s, Y_{s+t}) = b^2 \text{Cov}(X_t, X_{t+s}) = b^2 \gamma(t)\). 可见\(\{Y_t\}\)平稳。
若取 \[ Y_t = \frac{X_t - \mu}{\sqrt{\gamma_0}} \] 则\(E Y_t = 0\), \(\text{Var}(Y_t) = 1\), 称\(\{Y_t\}\)为\(\{X_t\}\)的标准化序列。
定义1.2 (自相关系数) 设平稳序列\(\{X_t\}\)的标准化序列是\(\{Y_t\}\). \(\{Y_t\}\)的自协方差函数 \[ \rho_k = \gamma_k/\gamma_0, \ \ k\in \mathbb Z, \] 称为平稳序列\(\{X_t\}\)的自相关系数(ACF, auto-correlation function), 或自相关函数.
事实上, \(\rho_k = \text{corr}(X_t, X_{t+k})\), 其中\(\text{corr}(\cdot, \cdot)\)表示两个随机变量的相关系数。 自相关系数 \(\{\rho_t\}\)是满足\(\rho_0=1\)的自协方差函数, 从而也是非负定序列.
例1.2 (调和平稳序列) 设 \(a, b\)是常数,随机变量\(U\) 在 \((-\pi,\pi)\)内均匀分布, 则 \[ X_t=b\cos(at+U), \ \ t\in \mathbb Z \] 是平稳序列,称为调和平稳列.
\[\begin{aligned} E X_t &= \frac{1}{2\pi}\int_{-\pi}^{\pi }b \cos(at+u) \ du =0, \\ E(X_t X_s) &= \frac{1}{2\pi}\int_{-\pi}^{\pi }b^2 \cos(at+u) \cos(as+u) \ du \\ &= \frac12 b^2\cos((t-s)a), \end{aligned}\] 这个平稳序列的观测样本和自协方差函数 \(\gamma_k=0.5b^2 \cos(ak)\) 都是以 \(a\)为角频率, 以 \(2\pi/a\)为周期的函数.
这个例子告诉我们,平稳序列也可以有很强的周期性. \(\{X_t\}\)的一次实现是一个周期函数,不表现出随机性。
sim_harm <- function(a=2*pi*0.05, b=1, n=100){
tt = seq(n)
us <- runif(10, -pi, pi)
ys = outer(tt, us, function(t, u) b*cos(a*t + u))
matplot(ys, type="l")
}
set.seed(102)
sim_harm()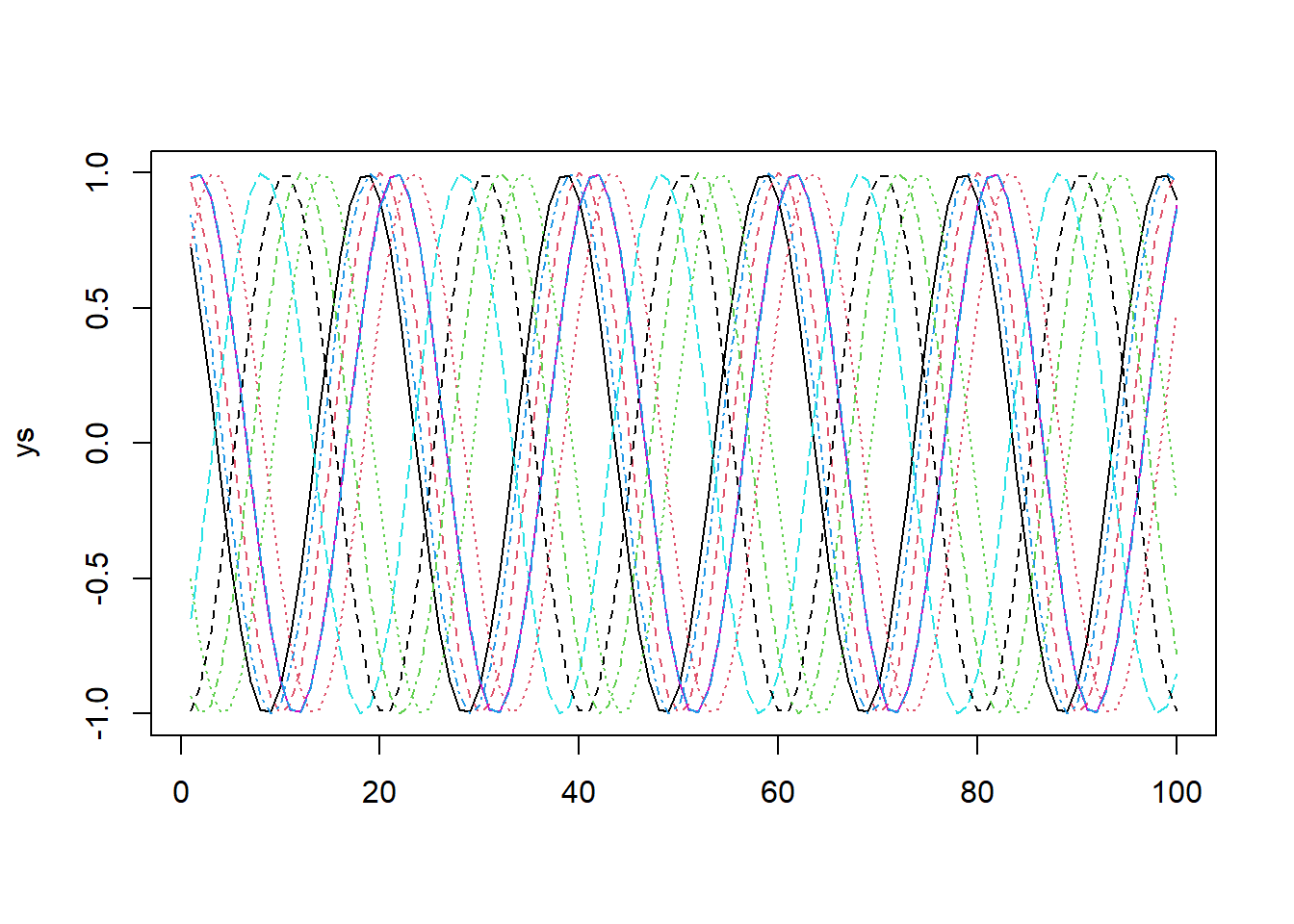
○○○○○○
1.2.2 白噪声
定义1.3 (白噪声) 设\(\{\varepsilon_t\}\) 是一个平稳序列. 如果对任何 \(s,t\in \mathbb N\), \[\begin{aligned} E \varepsilon_t =& \mu, \\ \text{Cov}(\varepsilon_t, \varepsilon_s) =& \sigma^2 \delta_{t-s} = \begin{cases} \sigma^2, \ &t=s, \\ 0, & t\neq s, \end{cases} \end{aligned}\] 则称 \(\{\varepsilon_t\}\)是一个白噪声, 记做 \(\text{WN}(\mu,\sigma^2)\).
设 \(\{\varepsilon_t\}\)是白噪声, 当 \(\{\varepsilon_t\}\) 是独立序列时, 称 \(\{\varepsilon_t\}\) 是独立白噪声。
当 \(\mu=0\) 时, 称 \(\{\varepsilon_t\}\) 为零均值白噪声。 白噪声的另一种定义要求零均值, 本书中用到的白噪声一般都是零均值的。
当 \(\mu=0, \sigma^2=1\) 时, 称 \(\{\varepsilon_t\}\) 为标准白噪声。
当 \(\varepsilon_t\)服从正态分布时, 称\(\{\varepsilon_t\}\)是正态白噪声或高斯白噪声。 正态白噪声总是独立白噪声。
利用Kronecker函数\(\delta_t\), 白噪声满足条件 \(\text{Cov}(\varepsilon_t, \varepsilon_s) = \sigma^2 \delta_{t-s}\).
例1.3 (Poisson白噪声) 这是服从Poisson独立白噪声的例子。
如果连续时的随机过程\(\{N(t): t\in [0,\infty)\}\)满足 (1) \(N(0)=0\), 且对任何\(s \geq 0, t>0\) 和非负整数\(k\), \[ P(N(t+s)-N(s)=k)=\frac{(\lambda t)^k}{k!}\exp[-\lambda t], (\lambda > 0,) \] (2) \(\{N(t)\}\) 有独立增量性: 对任何 \(n> 1\) 和 \(0 \leq t_0<t_1<\cdots<t_n\), 随机变量 \(N(t_j)-N(t_{j-1}), \ \ j=1,2,\cdots,n\) 相互独立,
则称 \(\{N(t)\}\) 是一个强度\(\lambda\)的Poisson 过程. \(E N(t) = \lambda t\), \(\text{Var}(N(t)) = \lambda t\).
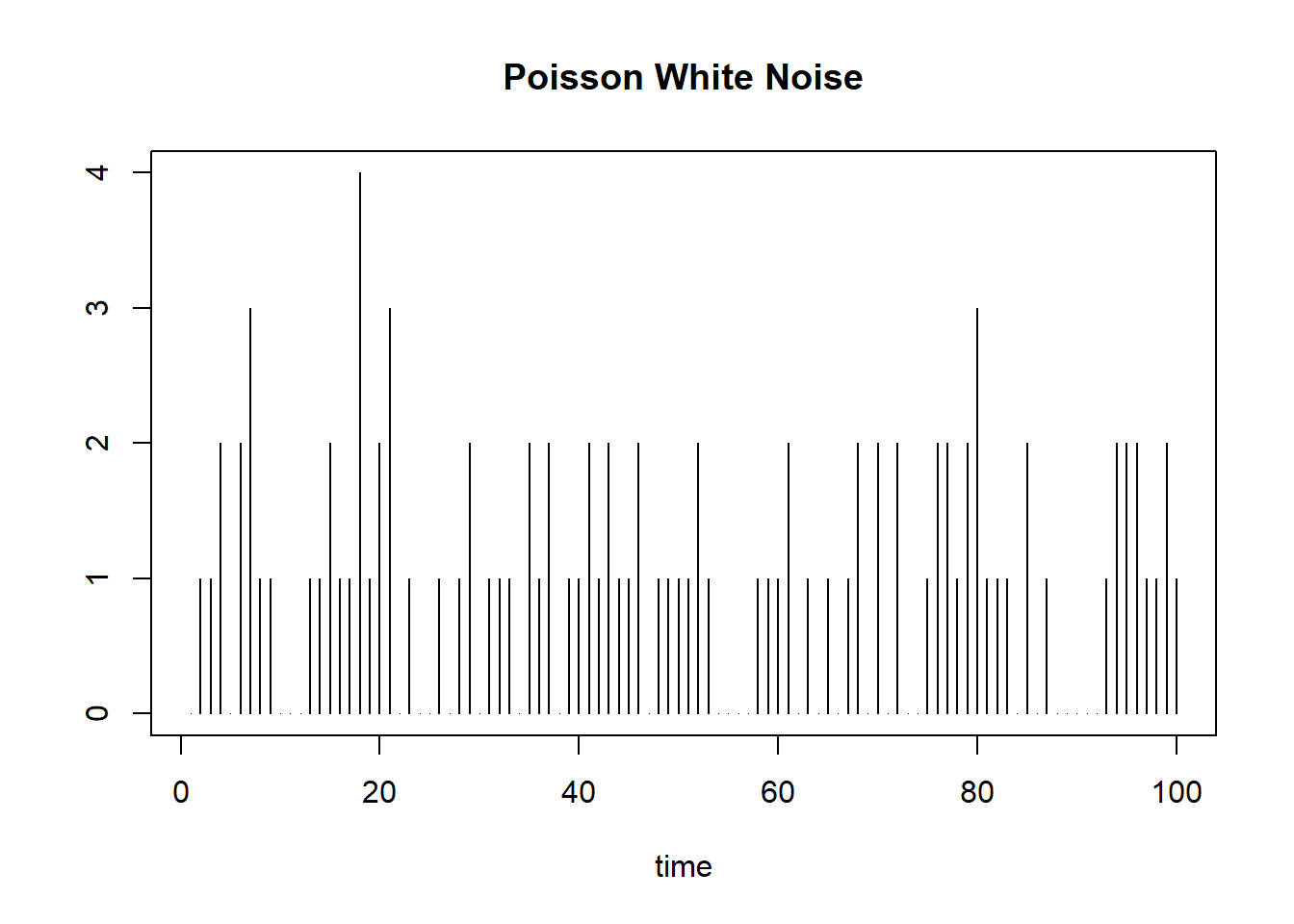
令 \[ \varepsilon_n= N(n+1)-N(n)-\lambda, \ \ n=1,2,\ldots, \] 则\(E\varepsilon_n=0\), \(\text{Var}(\varepsilon_n)=\lambda\), \(\{\varepsilon_n\}\)是独立白噪声, 称为Poisson白噪声.
模拟的Poisson白噪声:
○○○○○○
例1.4 (布朗运动) 这是一种典型的随机过程。
如果连续时的随机过程\(\{B(t): t\in [0,\infty)\}\)满足
- \(B(0)=0\), 且对任何 \(s\geq 0, t>0\), \(B(t+s)-B(s)\)服从正态分布 \(N(0,t)\);
- \(\{B(t)\}\) 有独立增量性,
则称\(\{B(t)\}\)是一个标准布朗运动.
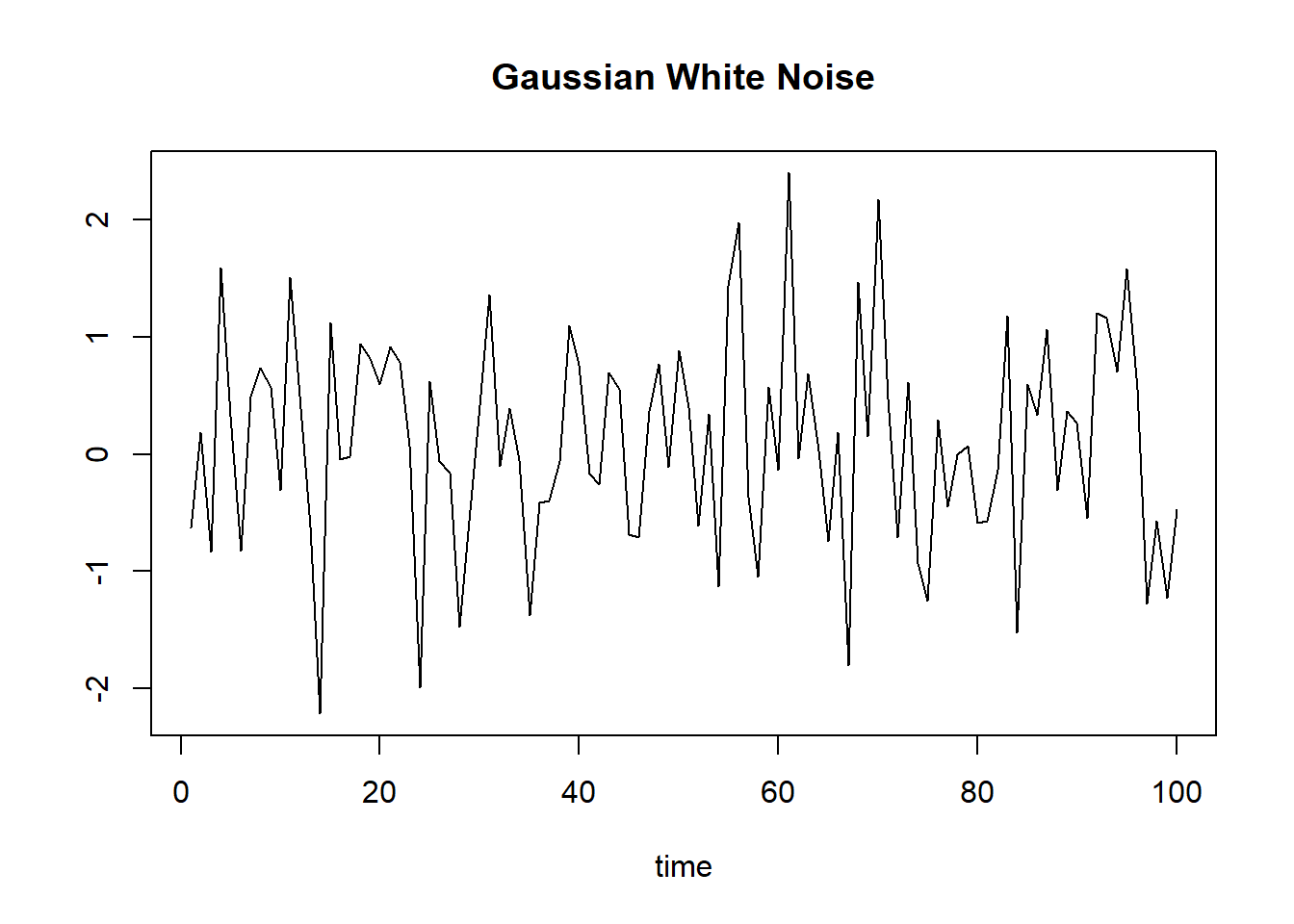
定义 \[ \varepsilon_n= B(n+1)-B(n), \ \ n=1,2,\ldots, \] 则\(\{\varepsilon_n\}\) 是一个标准正态白噪声.
模拟的标准正态白噪声:
○○○○○○
例1.5 (随机相位) 设\(U_1,U_2,\cdots\) iid U(\(0, 2\pi\)). 令 \[ X_t=b\cos(at+U_t), \ \ t\in \mathbb Z, \] 其中\(a, b\)为常数。 则\(X_t\) 为独立序列; \(E X_t = 0\), \(\text{Var}( X_t) = 0.5 b^2\), 即\(X_t\)是独立白噪声。
模拟的随机相位白噪声:
set.seed(1)
x <- cos(2*pi/12*(1:100) + runif(100, 0, 2*pi))
plot(x, type="l", xlab="time", ylab="",
main="Random Phase White Noise")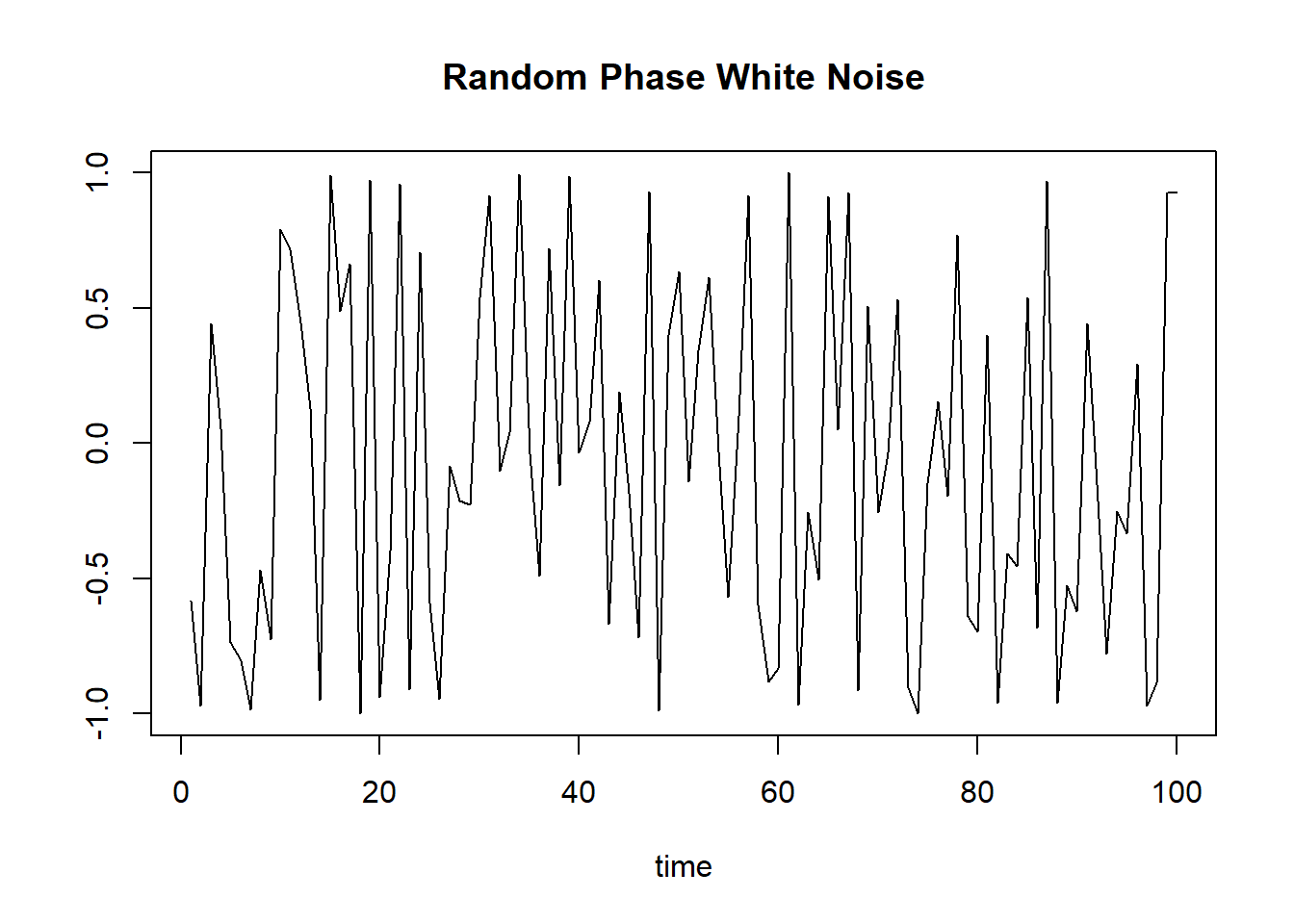
○○○○○○
1.2.3 正交平稳序列
两个平稳列\(\{X_t\}\)和\(\{Y_t \}\)称为平稳相关, 如果\(\text{Cov}(X_t, Y_s)\)仅依赖于\(t-s\)。 正交和不相关的平稳列是平稳相关的平稳列的最简单情况。
随机变量\(X,Y\)不相关:\(\text{Cov}(X,Y) = 0\); 正交:\(E (X Y) = 0\).
对零均值随机变量正交与不相关等价。 对平稳列\(\{X_t\}\)和\(\{Y_t\}\),
- 两个序列不相关: \(\text{Cov}(X_t, Y_s) = 0\), \(\forall t,s\).
- 两个序列正交:\(E(X_t Y_s) = 0\), \(\forall t,s\).
定理1.1 对平稳列\(\{X_t\}\), \(\{Y_t\}\), 设自协方差函数分别为\(\gamma_X(t)\), \(\gamma_Y(t)\), 期望分别为\(\mu_X\), \(\mu_Y\)。 令 \[ Z_t = X_t + Y_t, t \in \mathbb Z \]
如果\(\{X_t\}\) 和\(\{Y_t\}\)正交, 则\(\{Z_t\}\)是平稳序列, 有自协方差函数 \[\gamma_Z(k)=\gamma_X(k) + \gamma_Y(k) - 2\mu_X\mu_Y, \ \ k=0,1,2,\ldots \]
如果\(\{X_t\}\) 和\(\{Y_t\}\)不相关, 则 \(\{Z_t\}\)是平稳序列, 有自协方差函数 \[ \gamma_Z(k)=\gamma_X(k) +\gamma_Y(k), \ k=0,1,2,\ldots. \]
当\(\mu_X=\mu_Y=0\)且两序列正交时第2条的结论成立。
1.3 附录:补充知识
定理1.2 设\(\{ \gamma_k, k \in \mathbb Z\}\)是非负定列, 必存在平稳列\(\{ X_t \}\)使得\(\{ X_t \}\)的自协方差函数为\(\{ \gamma_k \}\)。
证明
由§4.3定理4.4可得此结论。 也可参见(Brockwell and Davis 1987)§1.5定理1.5.1。
○○○○○○
注
为了验证某个实数列\(\{\gamma_k \}\)是否非负定列, 直接按照定义检查有时比较困难, 这时, 如果能找到某个平稳列以\(\{\gamma_k \}\)为自协方差函数, 就证明了它是非负定列。 或者, 根据§6.2.1的谱函数、谱密度与自协方差函数的关系, 如果存在\([-\pi, \pi]\)上单调不减右连续函数\(G(\lambda)\)使得 \(\gamma_k = \int_{-\pi}^{\pi} e^{ik\lambda} dG(\lambda)\), 或者存在非负可积函数\(f(\lambda)\)使得 \(\gamma_k = \int_{-\pi}^{\pi} e^{ik\lambda} f(\lambda) \,d\lambda\), 则可证明\(\{ \gamma_k \}\)是非负定列。